Prerpints.org logo
Preprint
Article

A Study on Possibility of Detrimental Effects of Soil-Structure Interaction in Seismic Design Due to a Shift of System Frequency

This version is not peer-reviewed.

Submitted:

04 June 2024

Posted:

05 June 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Soil-structure interaction (SSI) leads to a modification of dynamic properties of a structure, but due to the complexity on analysis, it is traditionally assumed in seismic designs that the structure is fixed-supported at the ground, which unavoidably gives potential dangers to seismic performances of the structure. This study focuses on the possibility of the detrimental effects of SSI by comparing the dynamic responses of SSI system to fixed-base structure. The SSI model consists of an oscillator, a three-dimensional foundation and a multilayered half-space. In indirect boundary element method is employed, combined with non-singular Green’s functions of distributed loads to calculate the foundation impedances for substructure method. Although the SSI mechanism dampens peak amplitude of structure response in frequency domain, case studies on four buildings to 42 earthquakes in time history show a possibility of 15%-20% that SSI amplifies the dynamic responses, depending on the frequency component of incident waves. Also, a neural network algorithm is proposed to provide a new idea of involving SSI analysis into the traditional seismic designs, to eliminate potential hazards of SSI.
Keywords: 
Soil-structure interaction
;  
Indirect boundary element method
;  
Foundation impedances
;  
System frequency
;  
System responses
;  
Detrimental effects
;  
Beneficial effects
;  
Seismic design
Subject: 
Engineering  -   Civil Engineering

1. Introduction

It is assumed in traditional seismic designs that structures are fixed-supported on the foundation. Actually, the soil performs obvious flexibility for dynamic excitations, such as earthquakes, which gives the mechanism of soil-structure interaction (SSI). Although the soil performs as a cushion under the structure foundation, scholars have come to realize that this mechanism has detrimental effects sometimes to seismic performances of structures, and ignoring this mechanism results potential risks to seismic designs [1-6]. Nevertheless, due to the complexity and the cost, seismic designs involving the SSI analysis up to now are applicable only to few important infrastructures, such as nuclear power stations and huge bridges [7-11], or to few civil structures for some special reasons [12]. Most civil structures, however, receive little attention on the seismic designs involving SSI and the fixed-base assumption is adopted for convenience.
The foundation of a structure, usually with various shapes, is a group of multi-scatters in infinite half-space, so it leads to complex scattering field under seismic excitations. Currently, the numerical simulations are still computation-consuming and technique-demanding. Actually, in the past decades, this problem has been improved much, such as raising the incident wave to a more shallow layer to reduce the range of near-field [13], setting incident waves inside the artificial boundary to reduce the data storage on free-field motion and seismic loads [14], or carrying large-scale calculation from earthquake source to structure site through multi-scale simulation [15], and so on. Nevertheless, for most civil structures, it is only possible to determine the potentially detrimental effects of SSI very roughly by the shear wave velocity, or the period, of site. The method, although widely used among civil engineers, is not accurate and cannot be parametrically quantified. For example, many studies by numerical simulations [16, 17] and earthquake damage investigations [1, 18] reveal that, structures with some same features in a certain area, exhibit much more serious damage than other structures without the features.
Certainly, there is still much work trying to integrate the SSI analysis into the framework of traditional seismic designs, for wide applications in engineering practice. In ASCE/SCI-7 [19] and NEHRP (FEMA P-1050-1/2015) [20], there are coded provisions in recommended chapters in all versions after 1990’s (v1997, v2000, v2003, v2009, v2015) to involve the SSI analysis, which is based on substructure method and foundation impedance functions. In CSCE 160 (General Rules for performance-based seismic design of buildings) [21], it is also recommended similar provisions and improved the formulas on evaluation of structure modes. A research report of the National Institute of Standards and Technology (NIST) provides modified coefficient curves considering SSI based on the concept of traditional coefficient curves in seismic designs [22]. Nevertheless, these methods are rarely adopted in practice for the following two reasons. The analysis involves the calculation of foundation impedance functions, which are too complex for engineering designs. Also, the analysis considers only the beneficial effects of SSI and reduces base shear force at most 30%, which is unsafe or lack of safety reverse.
Under earthquake excitations, it is coupled between kinematic interaction and inertial interaction for SSI, so some studies focus on the former by a half-space with a foundation [23, 24], or on the latter by a structure in uniform half-space [25]. At present, there is a lack of researches considering meanwhile the two types of interactions, and the target parameters in the researches are limited [26], which is difficult to support seismic analysis in engineering. This paper investigates the possibility of detrimental effects of SSI quantitively by comparing the dynamic responses of an SSI system to a fixed-base structure. The SSI model consists of an oscillator, a 3D rectangular foundation, and a multi-layered half-space, which considers the two interactions. Also, a feasible idea based on neural network algorithm is proposed at last, taking into account the complexity of site conditions, diversity of structure formats, and uncertainty of seismic effects, to shed some light on SSI analysis in engineering seismic designs.

2. Model and Results

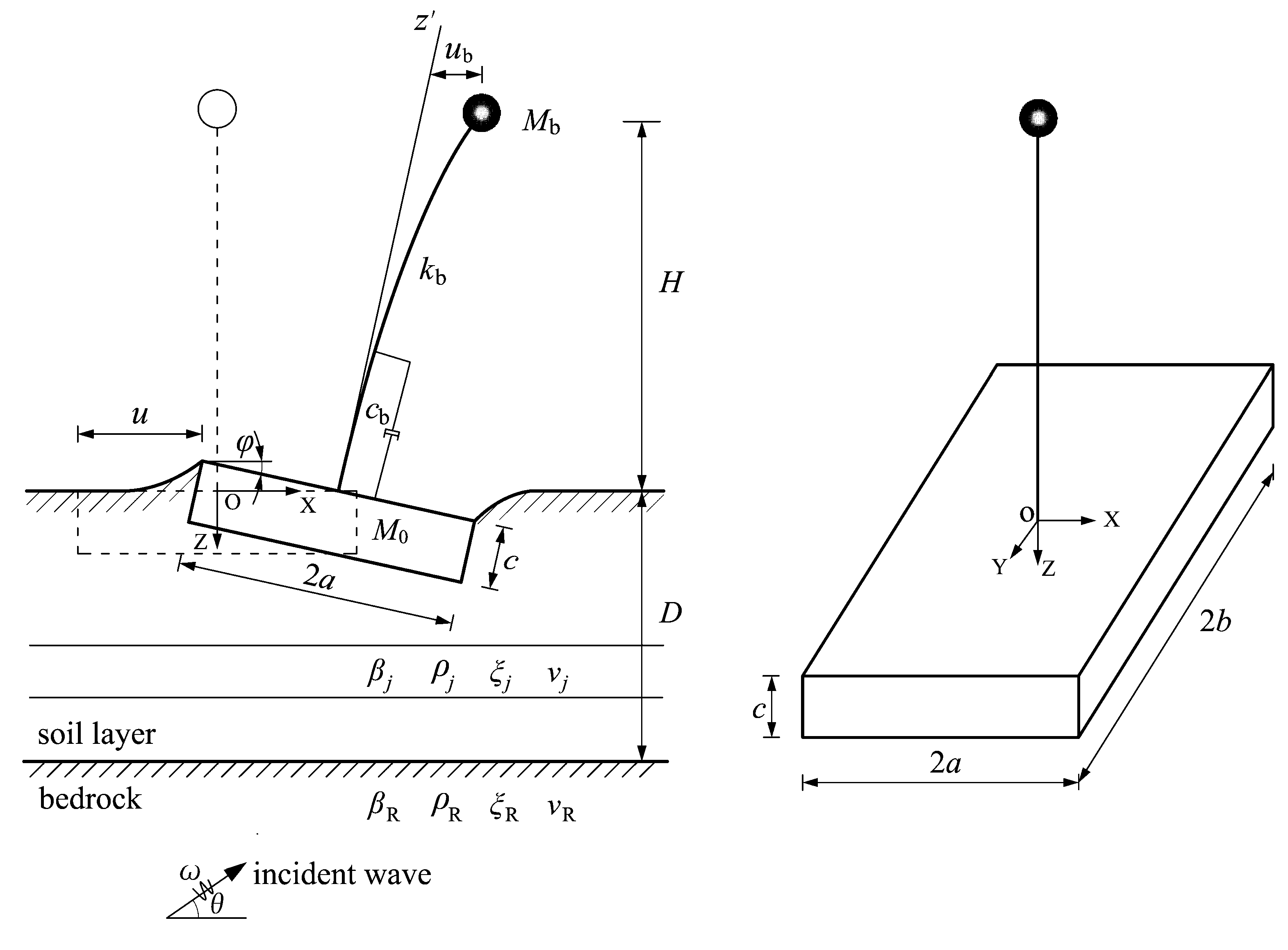
The model of Soil-Structure Interaction system (SSI) consists of a superstructure, a three-dimensional rectangular foundation, and a horizontally multi-layered half-space, as shown in Figure 1. The superstructure is simplified to a single-degree-of-freedom (SDOF) oscillator, and its dynamic properties are characterized by mass Mb, spring coefficient kb, damping coefficient cb and height H, so the fixed-base frequency is ω b = k b / M b and the damping ratio is ξ b = c b / 2 M b ω b . The foundation is represented by a rigid rectangular foundation of mass M0, width a, length b and embedment c. The half-space consists of a soil layer of thickness D on a bedrock, and each sub-layer, as well as the bedrock, are assumed to be elastic and isotropic. The material properties of jth sub-layer are characterized by shear-wave velocity βj, Poisson’s ratio νj, mass density ρj and damping ratio ξj, and those of the bedrock are characterized by shear-wave velocity βR, Poisson’s ratio νR, mass density ρR and damping ratio ξR. The SSI system is excited by a train of harmonic SV wave coming from the bedrock, with motion in the XOZ-plane. The circular frequency of the excitation is ω, and the incident angle is θ measured horizontally.
The deformation of the structure is represented by the relative horizontal translation ub with respect to z’-axis which is fixed on the foundation, and the foundation motion is represented by the generalized vector U = { u , φ } T e i ω t , with u of the horizontal translation and φ of the clockwise rotation about the reference point (0, 0, c), and eiωt is the harmonic time factor, omitted hereafter. The vertical displacement, as well as the torsional motion, of the SSI system are not considered in our problem. The dimensionless parameters necessary in the following analysis are:
(1) The dimensionless mass of the foundation and the structure are M0/Ms and Mb/M0, respectively, where Ms is the mass of soil replaced by the foundation.
(2) The dimensionless frequency is defined as η = λ 1 / 2 a = ω a / π β 1 , where λ 1 is the shear wavelength of the first sublayer. Correspondingly, the dimensionless fixed-base frequency is η b = ω b a / π β L , and a general range of ηb in engineering practice is 0-0.4, and the dimensionless system frequency is η ˜ b = ω ˜ b a / π β L .
(3) The dimensionless size of the foundation and the dimensionless thickness of the soil layer are a/a, b/a, c/a and D/a, respectively.
(4) The dimensionless mass density and the shear wave velocity of the soil layer are ρR/ρj and βR/βj, respectively.

2.1. Dynamic Equilibrium

The dynamic equilibrium equations of the SSI are [27-29]
M V ¨ + C V ˙ + K V = − M ′ U ¨ *
where
M = [ M b M b M b M b M 0 + M b S 0 + M b M b S 0 + M b I 0 + I b ] ,   C = [ c b 0 0 0 c hh c hm 0 c mh c mm ] ,   K = [ k b 0 0 0 k hh k hm 0 k mh k mm ] ,   M ′ = [ M b M b M 0 + M b S 0 + M b S 0 + M b I 0 + M b ] ,   V = { u b u 0 φ 0 H ′ / a }
Symbol S0 is the area moment of the foundation with respect to the axis z=c, I0 and Ib are the inertia moments of the foundation and the superstructure, respectively, and we have Ib =MbH’ for simplicity here. That H’=H+c is the structure height from the structure top to the foundation bottom. Vector U * = { u * , φ * } T is the foundation input motion (response of the excavation where the foundation is placed) [30, 31]. Foundation impedances are complex-valued and are shown by
K 0 ( ω ) = [ K hh ( ω ) K hm ( ω ) K mh ( ω ) K mm ( ω ) ] = [ k hh ( ω ) k hm ( ω ) k mh ( ω ) k mm ( ω ) ] + i ω [ c hh ( ω ) c hm ( ω ) c mh ( ω ) c mm ( ω ) ]
The real and the imaginary parts perform as spring and dashpot coefficients of the site, with the elements Khh of horizontal impedance, Khm=Kmh of coupled horizontal-rocking impedance and Kmm of rocking impedance. Foundation impedances are obtained by an Indirect boundary Element method (IBEM), combined with non-singular Green’s functions of distributed loads presented in [31]. The foundation impedances in Equation (5) are already normalized by H’/a, to be unified to the same units.

2.2. Dynamic Properties of SSI

A simplest layered half-space, a single soil layer on bedrock, is taken for analysis on dynamic properties of SSI system. The following parameters of the site are used ρR/ρj=1, νR=νj=1/3, ξR=ξj=0.02, βR/βj=2, D/a=2, (j=1, 2, 3, …). The foundation embedment is c/a=0.5, and the foundation mass is M0/Ms=0.2. While for the structure, we have the damping ratio ξb=0.02, the height H/a=2, and the mass Mb/M0=10 following the recommended relationship Mb/M0=4.9H/a in [32]. The length-to-width ratio of the foundation varies as b/a=1/4, 1/2, 1, 2 and 4.
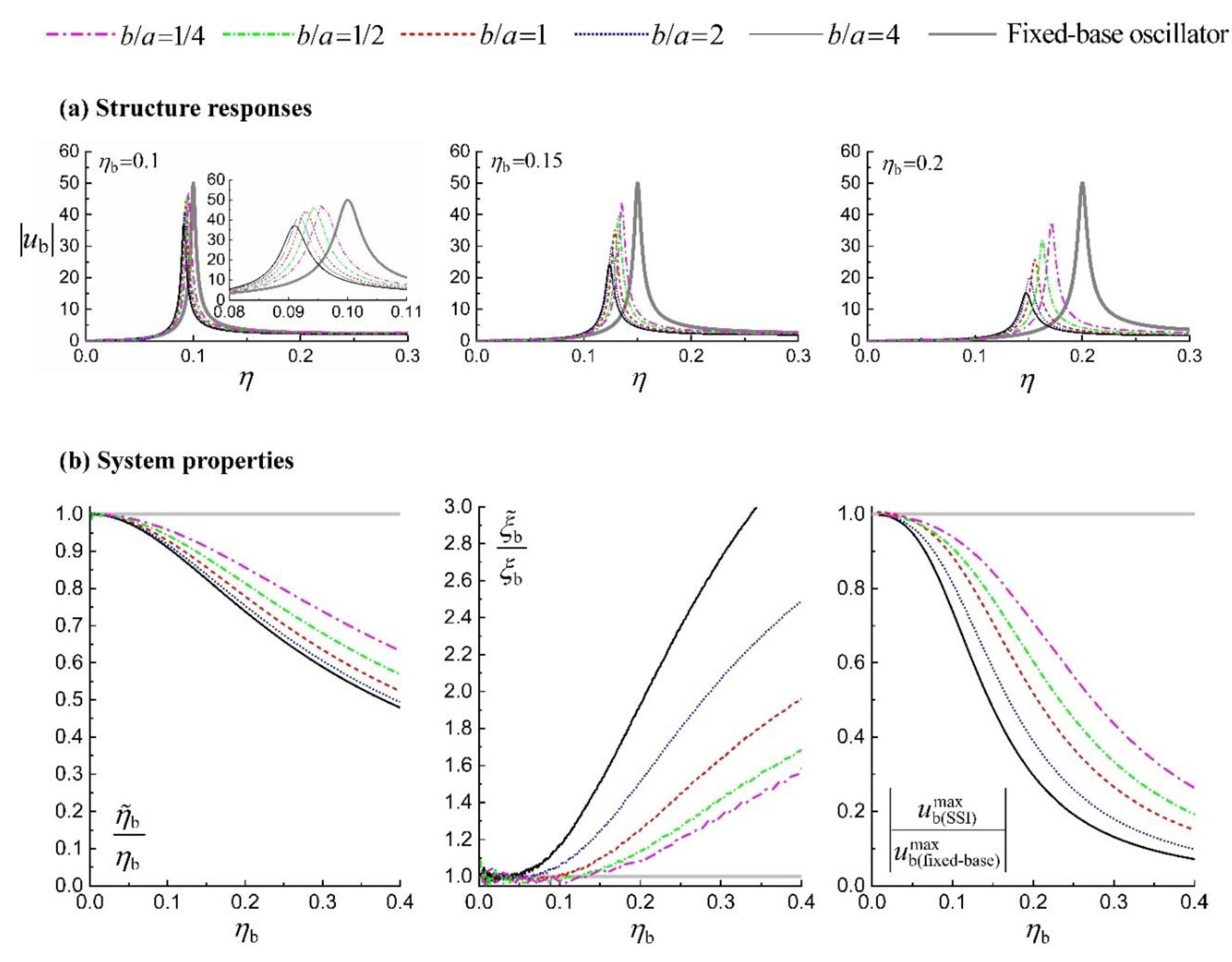
Figure 2(a) shows the spectrum amplitude of structure response | u b | for a fixed-base oscillator and SSI systems with varying b/a ratio. The x-axis is the dimensionless incident frequency η=0-0.3, which covers the predominant frequency domain of energy in earthquakes. Three structure frequency is concerned ηb=0.1, 0.15, 0.2. For a fixed-base oscillator, a rigid connection between the structure and the ground is assumed without any energy dissipation through the soil, while for an SSI system, the soil behaves like a cushion under the structure and adds additional flexibility to the system, so the system frequency of SSI is obviously lower than the resonant frequency of the corresponding fixed-base oscillator. Further, as the length-to-width ratio b/a decreasing, the peak has higher frequency and higher amplitude, approaching the fixed-base case.
Figure 2(b) shows the system frequency, system damping and peak amplitude with varying b/a ratios [29, 33], but the x-axis is the dimensionless structure frequency ηb=0-3. Although the spectrum shape is similar between the fixed-base oscillator and the SSI system with various length-to-width ratio, the system frequency of the latter shifts up to 50% from the resonant frequency of the former. Actually, a shift of peak frequency leads to a different correspondence with respect to the frequency of excitations.
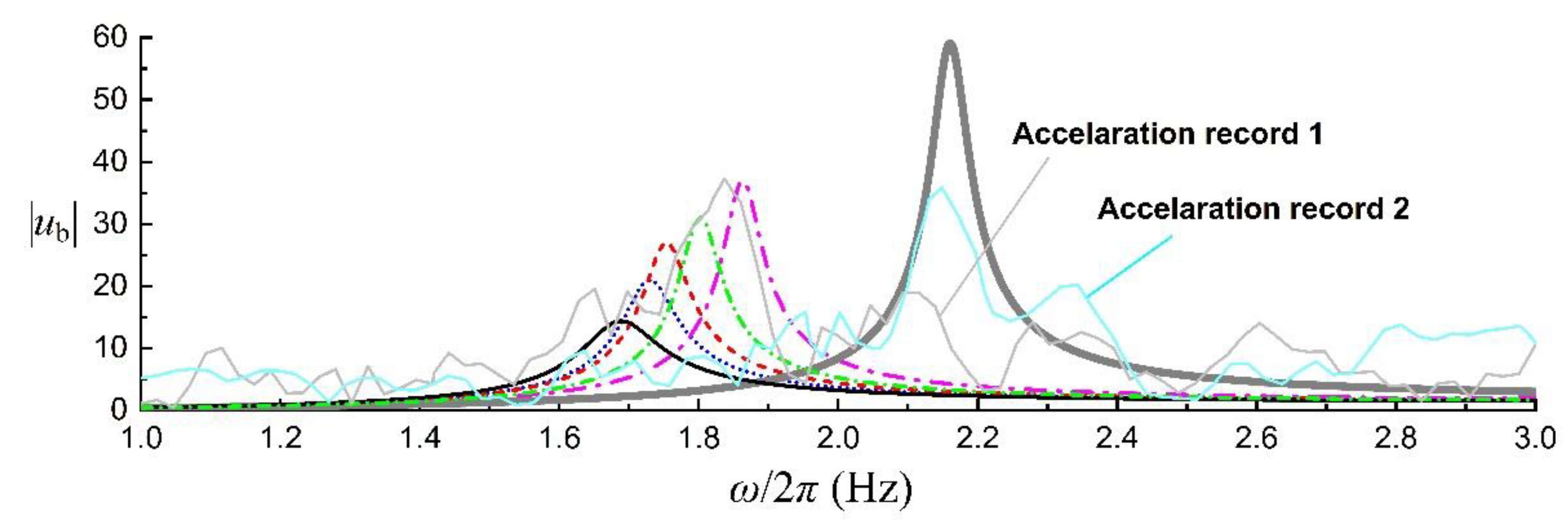
Due to the shift of peak frequency, the SSI system displays different seismic performances from the fixed-base oscillator. For a case that the predominant frequency of incident wave matches the peak frequency of SSI system (Acceleration record 1 in Figure 3), the dynamic responses of SSI system are probably larger than the fixed-base oscillator, which probably gives a detrimental effects of SSI effects on seismic performances of a structure, so the seismic designs on the assumption of fixed-base oscillator are probably unsafe. While for a case that the predominant frequency matches that of the fixed-base oscillator (Acceleration record 2 in Figure 3), the responses of the former are probably smaller than the latter, which probably gives a beneficial effects of SSI effects, so the seismic designs on the assumption is probably too conservative. Certainly, for a case that the predominant frequency of incident wave is not obvious, it also probably results in beneficial effects of SSI effects, since the peak amplitude of SSI system is always smaller than that of the corresponding fixed-base oscillator. In summary, it is avoidable that SSI effects are sometimes detrimental to the seismic performances of structures, depending on the dynamic properties of both the structure itself and the soil.

3. Case Studies

3.1. Data on Structures and Sites

A further study in time domain is performed on four buildings in California, USA, to investigate the possibility of detrimental effects of SSI. The parameters are selected from the published literature ---- Hollywood Storage Building (California Strong Motion Instrumentation Program (CSMIP) station No. 24236) [34], Millikan Library (National Strong Motion Project (NSMP) No. 5407) [35], a building in Sherman Oaks (CSMIP station No. 24322) and a building in Walnut Creek (CSMIP station No. 58364) [22]. These buildings have been instrumented for strong-motion observations for decades, and their structural and site data are available. The details of the four buildings and the stratifications of the site can be found in our previous paper [36], and we listed key information of the buildings in Table 1. The fixed-base frequency ωb/2π for the four buildings is from 0.83Hz to 2.16Hz, and the shear-wave velocity of the soil at the top of the site is from 184.7m/s to 336m/s, which gives relatively soft sites with respect to the structures. It is anticipated that soft sites lead to obvious soil-structure interaction and consequently introduce much influence to structure responses.
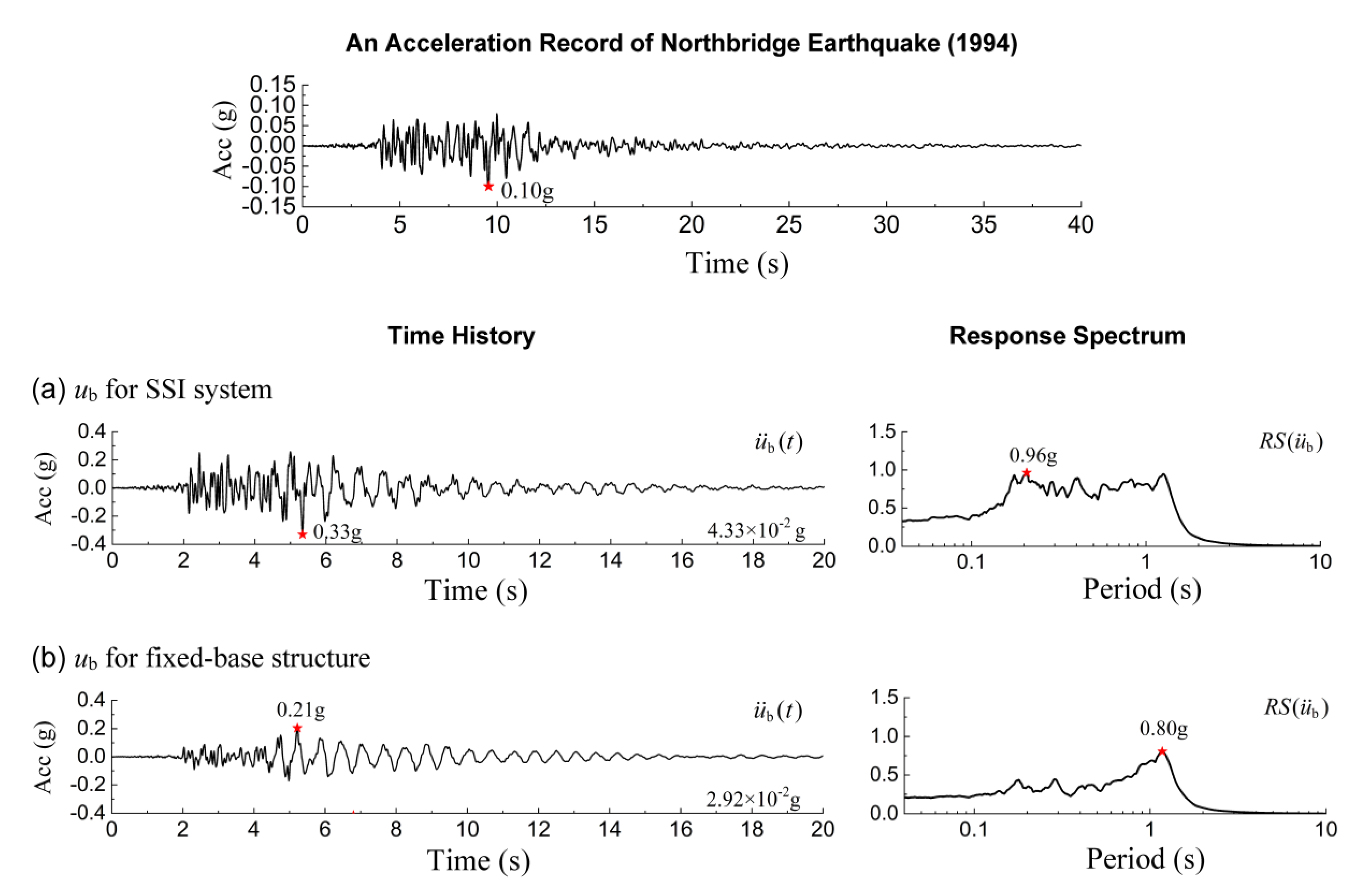
Figure 4(a) and 4(b) are the dynamic responses of Hollywood Storage Building for an assumed SSI system and an assumed fixed-base structure, respectively. The excitation, as shown at the top, is an earthquake record obtained at the ground floor in the NS direction in Northbridge Earthquake in Year 1994, and it is normalized to an acceleration of peak value 0.1 g. The record can be found from a USGS website https://strongmotioncenter.org/. It is also assumed that the excitation is a train of SV wave coming from the bedrock with incident angle θ = 90°. The acceleration responses of both the SSI system and the fixed-base structure are shown in time history u ¨ b ( t ) (left column) and response spectrum of the time history R S ( u ¨ b ) (right column).

3.2. Implementation

The responses in time history in Figure 4 are conducted in the following steps. First, the time history of an earthquake acceleration was converted into the frequency domain at 4096+1 equally spaced points from 0 to 50 Hz using Fourier transformation to acquire the spectrum of earthquake acceleration. The corresponding values on the spectrum of the structure response ub were calculated at these frequency points as well. Thereafter, the spectrum of the structure response is multiplied by the spectrum of the earthquake acceleration at the corresponding frequency points to acquire the amplified spectrum of the structure. Finally, the response in the frequency domain is converted to the time domain using inverse Fast Fourier Transformation.
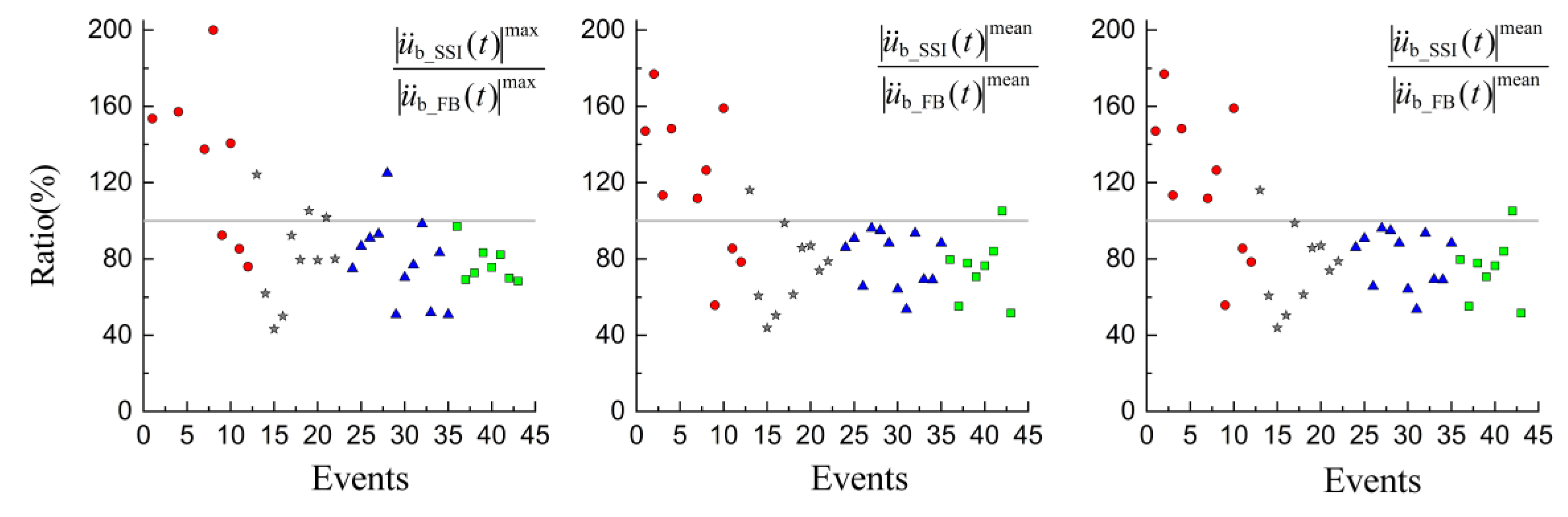
In the time history graph (left column), for the time window of 0–40s, the value denoted by an asterisk “*” is the maximum value, and the value presented in the bottom right corner is the mean value. While in the response spectrum graph, the value denoted by an asterisk shows the same. It is noticed that, the maximum value and the mean value in time history of SSI system is 57% and 48%, respectively, larger than that of the fixed-base oscillator, while the maximum value in response spectrum of the former is 25% larger than that of the latter. These three values for both the SSI system and the fixed-base oscillator of the four buildings to 42 earthquake events, are listed in Table 2 (XOZ-plane) and Table 3 (YOZ-plane), respectively. The excitations are the acceleration records on the ground floor of each building for each earthquake event (https://strongmotioncenter.org/).
Figure 5 illustrates the ratio of the three responses (maximum response in the time history, mean response in time history, and maximum response spectrum) of the SSI system to these of the fixed-base oscillator. The x-axis corresponds to each event in Table 1 and Table 2, and y-axis is the percentage value. Symbol “FB” represents “fixed-base oscillator”. The value larger than 100% in y-axis indicates a detrimental effect of SSI in the seismic design of structures. As shown in the figure, about 15%-20% of the 42 earthquake events gives the detrimental effects, and SSI mechanism amplifies the structure responses even up to 1.5 times for few cases. It justifies that a shift on the spectrum may lead to considerably different responses in the time domain, depending on the frequency component of the incident waves, the parameters of the structure as well as the soil.

4. Conclusions and Discussions

Up to now, it is assumed in most seismic design works that the structures are fixed-supported on the foundation, or the underlying soil is completely rigid. Actually, the mechanism of soil-structure interaction introduces considerable differences to the seismic performances of a structure. This study investigated the possibility of the detrimental effects of SSI on the seismic performances, by comparing the dynamic responses of SSI system and fixed-base structure. The SSI model consists of an oscillator, a 3D rectangular foundation, and a multilayered half-space, and the foundation impedance functions were obtained using a high precision Indirect Boundary Element Method. Although the amplitude spectrum of SSI system is smaller than that of a fixed-base oscillator, by case studies on four buildings to 42 earthquakes, it still shows 15%-20% in possibility that SSI gives detrimental effects on seismic performances of a structure.
Seismic hazard assessment on SSI, however, is computation-demanding and time-consuming even for linear problems. For an engineering seismic analysis, efficient methods are necessary which are applicable to be involved in the standard procedures of seismic codes. Since the structure period is the most important parameter in the seismic designs, we describe a possible method at the end of the paper to evaluate the system frequency of SSI promptly. The dynamic properties of SSI depend on the properties of the structure itself as well as the underlying soil, which are determined by a few dozens of parameters, such as the data we used in Section 2 and Section 3. So a neural network function mapping the parameters of the two substructures (structure and soil) to SSI system is feasible. First, the soil that determines the dynamic characteristics of SSI is the surface layer of dozens or hundreds of meters, the constructions and the parameters of which are statistically consistent in adjacent areas of the same geological environment. Second, the structure parameters follow general principles in structural designs and engineering practices.
Actually, SSI system is multi-parametric. By traditional studies on Dynamics, it needs orthogonal comparisons on dozens of target parameters, which gives considerably large workloads, and it is difficult to obtain the global function mapping parameters of subdomains to the dynamic properties of SSI system. Neural network function is an algorithm that fits complex mapping process of multiple inputs and outputs, for which, it is difficult to obtain explicit functions. Through appropriate settings on network structure and machine learning, neural network algorithm can converge to any function theoretically. The method is applicable to cities whose geological stratum data is plentifully accumulated in the past decades, to obtain a numerical model on seismic hazard assessment involving SSI effects. This method is our future work. It should be noted that both the soil and structure are likely to experience some degree of nonlinearity during strong earthquake events, and the neural network method under nonlinear conditions are also our future work.

Acknowledgments

This study was supported by the Provincial Natural Science Foundation of Shaanxi (2022JM-226, 2022JQ-513), National Natural Science Foundation of China (52278218), Fundamental Research Funds for Central Universities (G2021KY05103). The computations of impedance functions were carried out at TianHe-1 (A) of the National Supercomputer Center in Tianjin, China. Their support is gratefully acknowledged.

References

  1. Mylonakis G, Gazetas C. Seismic soil-structure interaction: Beneficial or detrimental? Journal of Earthquake Engineering 2000, 4, 277–301. [Google Scholar] [CrossRef]
  2. Khosravikia F, Mahsuli M, Ghannad MA. The effect of soil–structure interaction on the seismic risk to buildings. Bulletin of Earthquake Engineering 2018, 16, 3653–3673. [Google Scholar] [CrossRef]
  3. Zhang X, Far H. Seismic behaviour of high-rise frame-core tube structures considering dynamic soil–structure interaction. Bulletin of Earthquake Engineering 2022, 20, 5073–5105. [Google Scholar] [CrossRef]
  4. Forcellini, D. Seismic fragility of tall buildings considering soil structure interaction (SSI) effects. Structures 2022, 45, 999–1011. [Google Scholar] [CrossRef]
  5. Tomeo R, Pitilakis D, Bilotta A, Nigro E. SSI effects on seismic demand of reinforced concrete moment resisting frames. Engineering Structures 2018, 173, 559–572. [Google Scholar] [CrossRef]
  6. de Silva F, Ceroni F, Sica S, Silvestri F. Non-linear analysis of the Carmine bell tower under seismic actions accounting for soil-foundation-structure interaction. Bulletin of Earthquake Engineering 2018, 16, 2775–2808. [Google Scholar] [CrossRef]
  7. Zhang N, Wang L, Zhang Y, et al. Effect of a V-shaped canyon on the seismic response of a bridge under oblique incident SH waves. Earthquake Engineering and Structural Dynamics 2023, 53, 496–514. [Google Scholar]
  8. Dezi F, Carbonari S, Tombari A, et al. Soil-structure interaction in the seismic response of an isolated three span motorway overcrossing founded on piles. Soil Dynamics and Earthquake Engineering 2012, 41, 151–163. [Google Scholar] [CrossRef]
  9. Cui C, Zhang S, Chapman D, et al. Dynamic impedance of a floating pile embedded in poro-visco-elastic soils subjected to vertical harmonic loads. Geomechanics and Engineering 2018, 15, 793–803. [Google Scholar]
  10. Cui C, Meng K, Wu Y, et al. Dynamic response of pipe pile embedded in layered visco-elastic media with radial inhomogeneity under vertical excitation. Geomechanics and Engineering 2018, 16, 609–618. [Google Scholar]
  11. Zheng S, Shi X, Jia H, etal. Seismic response analysis of long-span and asymmetrical suspension bridges subjected to near-fault ground motion. Engineering Failure Analysis 2020, 115, 104615. [Google Scholar] [CrossRef]
  12. Oztoprak S, Cinicioglu SF, Oztorun NK, etal. Impact of neighbouring deep excavation on high-rise sun plaza building and its surrounding. Engineering Failure Analysis 2020, 111, 104495. [Google Scholar] [CrossRef]
  13. Zhao M, Liu P, Zhang J, etal. A direct time-domain FEM-SBFEM-SBPML method for soil-structure interaction analysis using quadtree mesh. Computers and Geotechnics 2023, 161, 105597. [Google Scholar] [CrossRef]
  14. Liu Jingbo, Bao Xin, Wang Dongyang, Tan Hui, Li Shutao. The internal substructue method for seismic wave input in 3D dynamic soil-structure interaction analysis. Soil Dynamics and Earthquake Engineering 2019, 127, 105847. [Google Scholar] [CrossRef]
  15. Zhang Lei, Wang Jinting, Xu Yanjie, He Chunhui, Zhang Chuhan. A Procedure for 3D Seismic Simulation from Rupture to Structures by Coupling SEM and FEM. Bulletin of the Seismological Society of America, 2020, 110, 1134–1148.
  16. Renzi S, Madiai C, Vannucchi. G. A simplified empirical method for assessing seismic soil-structure interaction effects on ordinary shear-type buildings. Soil Dynamics and Earthquake Engineering 2013, 55, 100–107. [Google Scholar] [CrossRef]
  17. Fu J, Todorovska MI, Liang J. Correction factors for SSI effects predicted by simplified models: 2D versus 3D rectangular embedded foundations. Earthquake Engineering and Structural Dynamics 2018, 47, 1963–1983. [Google Scholar] [CrossRef]
  18. Cinna, L. Mexico, San Francisco, Los Angeles and Kobe: What next? . Natural Hazards 1997, 16, 287–296. [Google Scholar]
  19. American Society of Civil Engineers. Minimum Design Loads for Buildings and Other structures: ASCE/SEI 7-16. Virginia, 2016.
  20. Building Seismic Safety Council (BSSC). National Earthquake Hazard Reduction Program (NEHRP) recommended seismic provisions for new buildings and other structures, Part 2 Commentary: FEMA P-1050-1/2015. Washington, 2015.
  21. 21. Standard of China Engineering Construction Standardization Association. General Rules for performance-based seismic design of buildings (Trial version). CECS 160: 2004.
  22. National Institute of Standards and Technology. Soil-structure interaction for building structures. Report No. NIST GCR 12-917-21, 2012.
  23. Luis AP, Suarez A, Aznarez JJ, Maeso O. Kinematic internal forces in deep foundations with inclined piles. Earthquake Engineering and Structural Dynamics 2015, 44, 2129–2135. [Google Scholar] [CrossRef]
  24. Chen Shishuenn, Liao Kehung, Shi Junyang. A dimensionless parametric study for forced vibrations of foundation-soil systems. Computers and Geotechnics 2016, 76, 184–193. [Google Scholar] [CrossRef]
  25. Ghannad MA, Jahankhah H. Site-dependent strength reduction factors for soil-structure systems. Soil Dynamics and Earthquake Engineering 2007, 27, 99–110. [Google Scholar] [CrossRef]
  26. Romero A, Galvin P. A BEM-FEM using layered half-space Green’s funciton in time domain for SSI analyses. Engineering Analysis with Boundary Elements 2015, 55, 93–103. [Google Scholar] [CrossRef]
  27. Luco JE, Lanzi A. Approximate soil-structure interaction analysis by a perturbation approach: The case of stiff soils. Soil Dynamics and Earthquake Engineering 2013, 51, 97–110. [Google Scholar] [CrossRef]
  28. Lanzi A, Luco JE. Approximate soil-structure interaction analysis by a perturbation approach: The case of soft soils. Soil Dynamics and Earthquake Engineering 2014, 66, 415–428. [Google Scholar] [CrossRef]
  29. Fu J, Liang J, Todorovska MI, Trifunac MD. Soil-structure system frequency and damping by an eigenvalue approach. Soil-structure system frequency and damping: estimation from eigenvalues and results for a 2D model in layered half-space. Earthquake Engineering and Structural Dynamics 2018, 47, 2055–2075.
  30. Luco JE, On the relation between radiataion and scattering problems for foundations embedded in an elastic half-space, Soil Dynamics and Earthquake Engineering 1986, 5, 97–101. 5.
  31. Fu J, Liang J, Ba Z. Non-singular boundary element method on impedances of three-dimensional rectangular foundations. Engineering Analysis with Boundary Elements 2019, 99, 100–110. [Google Scholar] [CrossRef]
  32. Luco, JE. Soil-structure interaction and identification of structural models. Proceedings of 2nd ASCE Conference on Civil Rngineering and Nuclear Power. (Knoxville, Tennessee, Sept. 15-17, 1980). Vol. II, Geotechnical Topics, ASCE, New York, New York, 10.1 -10.30.
  33. Todorovska MI, Trifunac MD. The system damping, the system frequency and the system response peak amplitudes during in-plane building-soil interaction. Earthquake Engineering and Structrual Dynamics 1992, 21, 127–144. [Google Scholar] [CrossRef]
  34. Trifunac MD, Hao TY, Todorovska MI. Response of a 14-story reinforced concrete structure to nine earthquakes: 61 years of observation in the Hollywood Storage Building. Report CE 01-02, Department of Civil Engineer-ing, University of Southern California, Los Angeles, 2001.
  35. Luco JE, Wong HL, Trifunac MD. Soil-structure interaction effects on forced vibration tests. Report 86-05. University of Southern California, Department of Civil Engineering. Los Angeles, California. 1986.
  36. Fu J, Liang J. Performance degradation of tuned-mass-dampers arising from ignoring soil-structure interaction effects. Soil Dynamics and Earthquake Engineering 2019, 125, 105701. [Google Scholar] [CrossRef]
Preprints 108310 g001
Figure 1. SSI model consisting of a superstructure, a three-dimensional rectangular foundation, and a horizontally multi-layered half-space.
Figure 1. SSI model consisting of a superstructure, a three-dimensional rectangular foundation, and a horizontally multi-layered half-space.
Preprints 108310 g001
Preprints 108310 g002
Figure 2. Dynamic responses (a) and dynamic properties (b) of SSI system (βR/βj=2, D/a=2, c/a=0.5, Mb/M0=10, H/a=2).
Figure 2. Dynamic responses (a) and dynamic properties (b) of SSI system (βR/βj=2, D/a=2, c/a=0.5, Mb/M0=10, H/a=2).
Preprints 108310 g002
Preprints 108310 g003
Figure 3. Peak frequency of structure response and Predominant frequency of excitations.
Figure 3. Peak frequency of structure response and Predominant frequency of excitations.
Preprints 108310 g003
Preprints 108310 g004
Figure 4. (Top) An acceleration record obtained at the ground floor of Hollywood Storage Building in NS direction in Northbridge Earthquake in 1994; (a) Structural response of SSI system for time history (left) and for response spectrum (right); (b) Structural response of fixed-base oscillator for time history (left) and for response spectrum (right).
Figure 4. (Top) An acceleration record obtained at the ground floor of Hollywood Storage Building in NS direction in Northbridge Earthquake in 1994; (a) Structural response of SSI system for time history (left) and for response spectrum (right); (b) Structural response of fixed-base oscillator for time history (left) and for response spectrum (right).
Preprints 108310 g004
Preprints 108310 g005
Figure 5. Ratio of dynamic responses between SSI system and Fixed-base oscillator (shown by “FB”) (Red circle: Hollywood Storage building, gray star: Millikan library, blue triangle: Sherman Oaks building, and green rectangle: Walnuts Creek building).
Figure 5. Ratio of dynamic responses between SSI system and Fixed-base oscillator (shown by “FB”) (Red circle: Hollywood Storage building, gray star: Millikan library, blue triangle: Sherman Oaks building, and green rectangle: Walnuts Creek building).
Preprints 108310 g005
Table 1. Buildings for case studies.
Table 1. Buildings for case studies.
Parameters Hollywood Storage Building Millikan Library Sherman Oaks Building Walnut Creek Building
a (short side) 7.77 m 11.65 m 18.15 m 15.9 m
b (long side) 33.15 m 12.55 m 28.8 m 22.6 m
c 2.74 m + 6 m 4.3 m 6.2 m + 9.9 m 4.2 m
H ˜ 45.6 m 43.9 m 50 m 39.2 m
M0 (kg) 1.38×107 (total) 1.43×106 kg 4.57×107 (total) 1.43×106 kg
Mb 1.17×107 kg 1.07×107 kg 1.66×107 kg 1.07×107 kg
ξ ˜ b 2 % 2 % 2 % 2 %
XOZ b/a 4.27 0.93 1.59 1.42
c/a 1.12 0.34 0.89 0.26
H/a 3.39 0.88 1.59 1.42
ω b / 2 π 0.83 Hz 2.16 Hz 1.54 Hz 1.52 Hz
YOZ a/b 0.23 1.08 0.63 0.70
c/b 0.26 0.37 0.56 0.186
H/b 0.79 2.18 1.00 1.00
ω b / 2 π 2.0 Hz 1.26 Hz 1.69 Hz 2.1 Hz
Table 2. Dynamic responses in the time domain of target buildings in the XOZ-plane.
Table 2. Dynamic responses in the time domain of target buildings in the XOZ-plane.
Earthquake Year Time History u ¨ b ( t ) R S ( u ¨ b )
Maximum (g) Mean (g)×10−2 Maximum (g)
SSI system Fixed-base SSI system Fixed-base SSI system Fixed-base
Hollywood Storage Building (NS)
Kern County 1952 0.43 0.28 7.72 5.25 1.67 1.40
San Fernando 1971 0.37 0.15 5.52 3.12 1.17 0.85
Whittier Narrow 1987 0.32 0.15 4.92 4.34 0.97 0.90
Northridge 1994 0.33 0.21 4.33 2.92 0.96 0.80
Chinohills 2008 0.41 0.18 7.24 2.75 1.73 0.68
Encino 2014 0.27 0.11 1.49 0.61 0.57 0.23
Millikan Library (NS)
Lytle Creek 1970 0.41 0.33 11.40 9.83 3.44 2.56
San Fernando 1971 0.13 0.21 3.41 5.61 0.57 1.10
Whittier Narrow 1987 0.16 0.37 3.12 7.10 0.90 2.66
Yorba Linda 2002 0.13 0.26 2.91 5.76 0.69 1.96
San Simeon 2003 0.12 0.13 3.45 3.49 0.87 1.03
Sherman Oaks Building (NS)
Lander 1992 0.21 0.28 5.64 6.55 1.30 1.66
Whittier Narrow 1987 0.13 0.15 1.38 1.52 0.34 0.33
Northridge 1994 0.20 0.22 2.43 3.70 0.78 1.51
Chatsworth 2007 0.095 0.102 1.00 1.04 0.33 0.47
Chinohills 2008 0.20 0.16 2.44 2.57 0.73 1.01
Encino 2014 0.061 0.12 0.053 0.06 0.18 0.33
Walnut Creek Building (EW)
Livermore 1980 0.33 0.34 4.94 6.20 1.32 1.48
Livermore Aftershock 1980 0.27 0.39 4.33 7.84 1.50 2.37
LomaPrieta 1989 0.24 0.33 4.54 5.83 1.19 1.68
Alamo 2008 0.10 0.12 1.25 1.77 0.30 0.45
Table 3. Dynamic responses in the time domain of target buildings in the YOZ-plane.
Table 3. Dynamic responses in the time domain of target buildings in the YOZ-plane.
Earthquake Year Time History u ¨ b ( t ) R S ( u ¨ b )
Maximum (g) Mean (g)×10−2 Maximum (g)
SSI system Fixed-base SSI system Fixed-base SSI system Fixed-base
Hollywood Storage Building (EW)
Kern County 1952 0.44 0.32 7.84 7.02 2.39 2.50
San Fernando 1971 0.38 0.19 4.01 3.17 1.45 1.36
Whittier Narrow 1987 0.49 0.53 8.60 15.42 2.09 4.69
Northridge 1994 0.45 0.32 6.60 4.15 3.11 1.95
Chinohills 2008 0.35 0.41 5.52 6.45 1.94 3.14
Encino 2014 0.19 0.25 2.88 3.67 0.88 1.48
Millikan Library (EW)
Lytle Creek 1970 0.39 0.49 9.47 15.44 2.37 3.77
San Fernando 1971 0.20 0.19 6.65 7.74 1.35 1.53
Whittier Narrow 1987 0.27 0.34 5.53 6.36 1.30 1.80
Yorba Linda 2002 0.107 0.105 2.62 3.54 0.56 0.70
San Simeon 2003 0.44 0.55 11.74 14.90 3.13 4.19
Sherman Oaks Building (EW)
Lander 1992 0.19 0.27 5.20 8.10 1.20 1.99
Whittier Narrow 1987 0.20 0.26 2.95 5.50 0.87 1.64
Northridge 1994 0.187 0.190 2.91 3.11 1.13 1.15
Chatsworth 2007 0.055 0.106 0.05999 0.0866 0.19 0.43
Chinohills 2008 0.20 0.24 3.58 5.18 1.46 1.63
Encino 2014 0.061 0.12 0.053 0.06 0.18 0.33
Walnut Creek Building (NS)
Livermore 1980 0.28 0.37 6.25 8.17 2.07 2.42
Livermore Aftershock 1980 0.14 0.17 2.75 3.27 0.85 1.01
LomaPrieta 1989 0.14 0.20 3.09 2.94 0.96 1.33
Alamo 2008 0.13 0.19 1.11 2.15 0.36 0.59
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

114

Views

35

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated