A Verifiable Multi-Secret Sharing Scheme for Hierarchical Access Structure

1. Introduction

Information such as encryption keys, missile launch codes, and numbered bank accounts must be highly confidential. Exposure to such sensitive information could be dangerous. Secret sharing schemes provide an efficient way of storing such sensitive and vital information and prevent unauthorized access. Apart from core cryptography, Researchers have been using secret sharing concepts in various applications such as the cloud and IoT. Recently, Gutte and Paraser [15] have used secret sharing for visual cryptography and suggested a weed optimization algorithm for image sharing. Similarly, Wang et al. [44] , and Ren et al. [35] have worked on low latency cloud-based indoor localization system and secure, anonymous data aggregation schemes, respectively. Considerable work has been done on this topic during the last few years (cf.; [9,12,19,24,26,32,34,36,42] where further references can be found).

Initially, some core concepts of algebra were used by authors to design secret sharing schemes. Shamir [39] used polynomials, Blakley [6] used hyperplane geometry and Simmons [40] as well as Asmuth and Bloom [1] used Chinese remainder theorem. In secret sharing schemes, secret S is distributed among n shareholders $P_1,P_1,\cdots ,P_n$ in such a way that t shareholders or more than t shareholders can reconstruct the secret but less than t shareholders know nothing about the secret. Such a scheme is known as the $(t,n)$-threshold scheme. Schemes given by [1,6,39] have several common drawbacks as follows:

• These are single secret sharing schemes.
• For every new secret, a new share has to be generated for every participant after the reconstruction of the previous secret
• Private channels are essential for the communication between dealers and participants and among the participants.
• These schemes are not capable of identifying the cheater.

To solve the first and the second problem, "multi secret sharing schemes" have been introduced [20,21,25]. Instead of having a single secret, multiple secrets are shared among the participants in a multi-secret sharing scheme. To include verification and cheater detection, a "Verifiable secret sharing scheme" was proposed in [13,43]. In [17,18], Harn et al. proposed the protected secret sharing scheme to avoid a separate communication channel while exchanging shares among different shareholders. The application of Shamir’s scheme is an ideal for the condition where all participants(shareholders) play the same role and there is no distribution of share-based on priority or any unique properties. However, employees are categorized based on their work responsibilities in organizations such as multinational companies and educational institutions. Among several structures, the Hierarchical structure is trendy in which every participant has some weight according to his/her role. Shares are distributed or assigned according to their weight. Hierarchical secret sharing schemes are proposed in the literature, [2,30,40,48,49] .

In hierarchical secret sharing schemes, all the participants are divided into m disjoint sets called levels say $l_1,l_2,...l_m$. The $i^{th}$ level consists of $n_i$ participants with $t_i$ threshold. In reconstruction of the secret there may be two situations: In the first situation particular level $l_i$ has $t_i$ or more participants on the same level while in the other situation the number of participants in level $l_i$ is less than $t_i$. In the second situation involvement of the higher level participant is needed.

Let us assume that in a particular level $l_i$ participants are less in number say $r_i$, than the $t_i$. So $t_i-r_i$ remaining participants are needed from the upper level to reconstruct the secret. In this paper the level $l_i$ is higher than the level $l_{i+1},1\le i<m$.

In 2004, Yang et al. [46] proposed a unique multi-secret sharing scheme using a single polynomial, known as the YCH scheme. Low computation and less number public values are required in the YCH scheme. In the YCH scheme, a single polynomial is used for multiple secrets instead of using separate polynomials for individual secrets. We have included a YCH scheme for each level in our work, making the scheme efficient. We have used two variable one-way functions for verifiability, which verify the dealer and other participants. Here we summarize the contribution of this paper:

• Proposed scheme is efficient due to the use of YCH scheme.
• The proposed scheme can quickly identify the cheater, whether the dealer or the other participants.
• Participant’s share can be used for both the reconstruction and verification.

The rest of the paper is organized as follows. In Section 2, related literature is explained. In Section 3, we present preliminaries related to our proposed scheme. Section 4 deals with the identification of problems and motivation. Our proposed scheme is discussed in Section 5. In Section 6, the security and performance analysis of the scheme is discussed. In Section 7, a comparison with exiting schemes is explained. Finally, we conclude the paper with future work in Section 8.

2. Related Work

The Shamir [39] and Blakley [6] threshold secret sharing schemes are two particular examples of hierarchical secret sharing (HSS) in which all participants have the same privileges. In order to improve the applicability of hierarchical secret sharing, many researchers have focused on specific families of access structures. Blundo et al. [7] have focused on graph-based access structure, Pardo et al. [33] explained bipartite access structure and Tentu et al. [41] includes multipartite access structure, compartmented access structure, and hierarchical access structure.

In 1979, the weighted thresold secret sharing mechanism was suggested by Shamir [39]. However, this approach is inefficient since it assigns multiple shares to each participant equal to its integral weight. Simmons [40] then proposed a multipartite access structure in 1988, defining the compartmented access structure and the hierarchical access structure. Following Simmons, Brickell [8] proposed a strategy for constructing an optimal secret sharing scheme that takes into account multilevel and compartmented access arrangements. However, the approach is inefficient since nonsingular matrices require exponential operations. The multipartite access structure is defined as the split of all members of a group into subsets, with members of the same subset having the same rights. The compartmented access structure and the hierarchical access structure are two types of multipartite access structures. The conjunctive hierarchical access structure and the disjunctive hierarchical access structure belong to the hierarchical access structure family. In 2009, Lin et al. [28] had incorporated some modifications to Shamir’s scheme [39] and explained hierarchical secret sharing(HTSS) scheme with two types of variations." Multilevel threshold secret sharing (MTSS), and compartmented threshold secret sharing (CTSS)".

Verification of shares is also one of the major concerns in secret sharing schemes. In [13,43] authors have specifically explained the verification of shares in a secret sharing scheme. In 2015, Chanu et al. [10] used Two variable one-way functions to verify the correctness of the received share. Further, in 2017, Basit et al. [4] used Shamir’s scheme with the successive application of one-way function and shifted and key technique to propose Multi-stage, Multi-secret sharing for hierarchical Access Structure.

Apart from the above papers, the Hierarchical secret sharing (HSSS) scheme are discussed in [3,4,10,17,28,29,47], but his scheme lacks fairness. In 2018, Banerjee et al.[3] proposed Cheating detection and cheater Identification for hierarchical structure but lacks correctness. In 2021 Bisht and Deshmukh [5] proposed work on multi-level secret sharing but lacks fairness and perfectness. Similarly, Yuan et al. [47] used homogenous recurrence relation to propose a new efficient scheme that deals with the multi-secret hierarchical scheme.

This scheme has been proposed to overcome the shortcomings of the above-discussed schemes and incorporate the features in the following ways:

• It supports the hierarchical access structures as discussed in the first paragraph of the current section. It improves and enhances the applicability of the hierarchical access structure.
• It supports weighted threshold secret sharing as discussed in the second paragraph without any exponential operation and extra burden.
• It supports secret sharing with multi-stage, multi-level properties with verification of shares lacking in schemes discussed in the third and fourth paragraphs.
• In the last paragraph of this section, novel schemes is discussed. These schemes do not explain security features such as correctness and forward/backward secrecy.
  Proposed schemes provide essential security features such as fairness and correctness. At the same time, the proposed scheme’s computational cost and storage cost is much less.

3. Preliminaries/Foundations

This section describes some of the preliminaries required to design our scheme.

3.1. Shamir’s ($t,n$) Secret Sharing Scheme

In secret sharing principle objective is to partition the secret S into n pieces $s_1,s_2,\dots ,s_n$ such that:

• Learning of t or more $s_i$ pieces makes S to be uniquely determined.
• Learning of any $t-1$ or less $s_i$ pieces leaves S totally unpredictable.

This scheme depends on polynomial interpolation.The fundamental idea of Adi Shamir’s threshold scheme can be understand by a simple example:

• At least 2 points are necessary to draw a line. (i.e, one point is not sufficient)
• At least 3 points are necessary to draw a parabola (i.e, less than 3 points are not sufficient )
• Similarly, it takes at least ’t’ points to draw a polynomial of degree ’$t-1$’ (i.e, less than t points are not sufficient).

Following are the main phases of $(t,n)$ threshold scheme, where n is total number of shareholders and t is minimum number of shareholders necessary to reconstruct the secret S. Distribution phase::

• Select a prime number Q
• Randomly select a function $g\left(x\right)=b_0+b_{1}x+b_2{x}^2+\cdots +b_{t-1}{x}^{t-1}$
• Compute (i, g(i)) corresponding to the $i^{th}$ shareholder, $i=1,2,\dots ,n.$
• These points (i, g(i)) are distributed securely to n share holder/participants

Reconstruction phase:

• Compute Lagrange’s interpolating polynomial using t shares

  $$g\left(x\right)=\sum _{i=1}^{t}g\left(i\right)\prod _{j=1,j\ne i}^t\frac{x-x_j}{x_i-x_j}modQ$$
• In this way, we get the polynomial in the form

  $$g\left(x\right)=b_0+b_{1}x+b_2{x}^2+\cdots +b_{t-1}{x}^{t-1},$$

  where $b_0$ = S, is the secret.

3.2. Hierarchical Access Structure

Access Structure($\Gamma$) Recovery of secret is authorized for some group of people and it is unauthorized for another group of people. Those sets which are authorized is known as access structure. Adversary Structure($\overline{\Gamma }$) The set of all non authorized sets that do not have any information related to the secret, is said to be an adversary structure.

In $(t,n)$ threshold access structure any set of t or more participants out of n is said to be an authorized set and any set less than t in number is said to be non-authorized set. Let $\lambda$ be the set of n participants. In Set builder form a $(t,n)$ threshold access structure and the corresponding adversary structures are::

$$\Gamma =\{X\in 2^{\lambda }:|X|\ge t\}$$

and

$$\overline{\Gamma }=\{X\in 2^{\lambda }:\left|X\right|<t\}$$

respectively.

In 2006, Herranz et al. [22] explained importance of multipartite structure. According to Herranz “In multipartite structure the set of players is divided into K disjoint classes, and all players in each class play exactly the same role within the access structure. These access structures can make a lot of sense in real life applications, where persons or machines are divided into different groups according to their position in a company, their responsibilities, their computational resources or their probability of being corrupted by an attacker ”.

A multipartite access structure splits the set of participants in $\lambda$ into m disjoint sets$l_1,l_2\cdots ,l_m$ called levels and all participants in each level play exactly the same role inside the particular access structure.

3.3. Overview of YCH Scheme

Initialization phase

• In this scheme following notations are used :

• $(t,n)$- scheme. where t is for threshold and n is for number of participants.
• $B_1,B_2,\dots ,B_k,$ denotes the k secrets to be shared.
• n secret shadows $s_0,s_1,s_2,\dots ,s_n$ are randomly chosen by the dealer and distributed to the participants through a secure channel.
• A random value `r’ is chosen.
• A 2-variable 1-way function h(r,$s_i$) , $i=1,2,\dots ,n$. is chosen.

Construction phase

• $k\le t$ ( Number of secrets are less than the threshold)

  (a)

  A prime number ’Q’ is chosen by the dealer.

  (b)

  The dealer choose a polynomial $f\left(x\right)$mod Q. Degree of polynomial is $(t-1)$ where,

  (c)

  $B_1,B_2,\cdots ,B_k$ are the secrets to be shared and $b_1,b_2,b_3,\cdots b_{t-k}$ are random numbers.

  (d)

  $$f\left(x\right)=B_1+B_{2}x+,\cdots ,+B_k{x}^{k-1}+b_1{x}^k+b_2{x}^{k+1}+\cdots +b_{t-k}{x}^{t-1}modQ$$

  (e)

  For every $i^{th}$ participant the dealer computes $g_i=f\left(h(r,s_i)\right)$ mod Q

  (f)

  Publish $(r,g_1,g_2,\cdots ,g_n)$ .

• $k>t$ (Number of secrets is greater than the threshold)

  (a)

  A prime number Q and a polynomial $f\left(x\right)modQ$ is chosen by dealer. Degree of polynomial is $(k-1)$. where $B_1,B_2,\cdots ,B_k$ are the secrets.

  $$f\left(x\right)=B_1+B_{2}x+\cdots +B_k{x}^{k-1}modQ$$

  (b)

  For i=1 to n. $g_i=f\left(h(r,s_i)\right)modQ$ is computed.

  (c)

  For $i=1ton$. $f\left(i\right)modQ$ is computed

  (d)

  calculated values like $r,g_1,g_2,\dots ,g_n$ are publicly published.

  (e)

  $f\left(1\right),f\left(2\right),\cdots ,f(k-t)$ are also published in public.

Recovery phase

In order to recover the secrets $B_1,B_2,\cdots ,B_k,$

• Each participant uses his/her share to compute $h(r,s_i)$ (for i=1 to t)
• The polynomial $f\left(x\right)$ is determined as follows:
• $k\le t$ ( Number of secrets are less than the threshold )

  $$\begin{array}{cc}\hfill f\left(x\right)& =\sum _{i=1}^t{g}_i\prod _{j=1,j\ne i}^t\frac{x-h(r,s_j)}{h(r,s_i)-h(r,s_j)}modQ\hfill \\ \hfill & =B_1+B_{2}x+\cdots +B_k{x}^{k-1}+a_1{x}^k+a_2{x}^{k+1}+\cdots +a_{t-k}{x}^{t-1}modQ.\hfill \end{array}$$
• for $k>t$(Number of secrets is greater than the threshold)

  $$\begin{array}{cc}\hfill f\left(x\right)& =\sum _{i=1}^k{g}_i\prod _{j=1,j\ne i}^k\frac{x-h(r,s_j)}{h(r,s_i)-h(r,s_j)}+\sum _{i=1}^{k-t}f\left(i\right)\prod _{j=1,j\ne i}^{k-t}\frac{x-j}{i-j}modQ\hfill \\ \hfill & =B_1+B_{2}x+\cdots +B_k{x}^{k-1}modQ.\hfill \end{array}$$
• from the above equations, we get the secrets

  $$B_1,B_2,\cdots ,B_k$$

3.4. 2- Variable 1- Way Function

Definition A 2-Variable,1-way function $h(r,s)$ is a function that maps a random value r and a share s onto a bit string of fixed length.

Properties: 

It contains following properties:

• when r and s, are given $h(r,s)$ is easily computable. But for a givens and $h(r,s)$, it is very difficult to compute r.
• It is hard to compute $h(r,s)$ when there is no knowledge of s.
• For the given s, it is hard to find two different values $r_1$ and $r_2$ that satisfy the situation $h(r_1,s)=h(r_2,s)$.
• It is tough to compute s, for the given r and $h(r,s)$.
• If we have pairs of r and $h(r,s)$, it is difficult to find $h(r^{\prime },s)=h(r,s)$ for which $r^{\prime }\ne r$ .

4. Identification of Problem and Motivation

In all the existing scheme, a separate polynomial is taken corresponding to each secret which results in overhead of public values and calculations. Verification in hierarchical system is included in papers like [3] with some limitations. In the present work, we try to reduce the limitations in the verification phase.

4.1. Contribution

In our work, we have proposed “multi-secret sharing scheme for hierarchical access structure ”using the YCH scheme. By using YCH scheme we get following advantages:

• It permits parallel reconstruction of secrets.
• Number of the secrets to be distributed can be dynamically determined.
• This scheme is of multi-use. Furthermore, fewer public values, less storage, as well as computing time, are needed in our scheme.

By using 2-variables 1-way function we get the following advantages:

• Any participant can identify the cheater whether he/she is the dealer or the participant.
• There is no need of secure channel between the Dealer and the participant.
• This scheme can also detect the invalid shares.

5. Proposed Scheme

5.1. Overview

All participants are classified into m levels. Each level has fixed ($t,n$) pair where t is the threshold out of n participants. Dealer chooses pseudo share $s_i^l$ for the $i^{th}$ participant at level l. Pseudo share is distributed through secure channel. $B_1,B_2,\cdots ,B_k$ are the secrets. Using YCH scheme dealer computes actual share ($d_i^l$) for each participant. public share ($Z_i^l$) is calculated on addition of actual share in the 1-way function.

In the Reconstruction phase, the actual share of the participants is calculated by subtracting 1-way function from the public share. This actual share is used in the Lagrange interpolation polynomial and generates the polynomial having coefficients as secrets. If share’s number in a particular level is less than its threshold value then upper-level shareholder provides his share to reconstruct the secret.

5.2. Initialization

• Number of participants is n.
• Number of level is m.They are $l_1,l_2,\dots ,l_m$.
• Each level is associated with a $(t_j,n_j)$, $j\in [1,m]$ access structure.
• Dealer chooses n shares $s_i^j$, $i\in [1,n_j]$, $j\in [1,m]$.

5.3. Distribution

At each level l there may be two situations:

• Number of secrets k is less than the threshold
• Number of secrets k is more than the threshold.

• $k\le t_j$ ( number of secret is less than or equal to $t_j$)

  (a)

  A prime number Q is chosen by the dealer.

  (b)

  The dealer construct polynomial $f\left(x\right)$mod Q. The degree of polynomial is ($t_j-1$). Let ,

  $$f\left(x\right)=B_1+\cdots +B_k{x}^{k-1}+b_1{x}^k+\cdots +b_{t-k}{x}^{t-1}modQ,$$

  where $B_1,B_2,\cdots ,B_k,$ are the secrets,

  (c)

  $b_1,b_2,b_3,\cdots ,b_{t_j-k}$ ,$j\in [1,m]$ are randomly chosen numbers.

  (d)

  For the $i^{th}$ participant the dealer computes $g_i=f\left(h(r,s_i)\right)modQ$, $i\in [1,n]$.

  (e)

  Publish $(r,g_1,g_2,\cdots ,g_n)$ .

• $k>t_j$( Number of secrets is greater than $t_j$.)

  (a)

  A prime number Q is chosen.

  (b)

  Dealer construct a polynomial $f\left(x\right)modQ$ of degree $(t_j-1)$. Let

  $$f\left(x\right)=B_1+B_{2}x+\cdots +B_k{x}^{k-1}modQ,$$

  where $B_1,B_2,\cdots ,B_k$ are the secrets.

  (c)

  For $i=1,2,3,\dots ,n$. $g_i=f\left(h(r,s_i)\right)modQ$ is Computed.

  (d)

  For $i=1ton$. $f\left(i\right)modQ$ is Computed

  (e)

  calculated values like $r,g_1,g_2,\cdots ,g_n$ are made public

  (f)

  $f\left(1\right),f\left(2\right),\cdots ,f(k-t)$ are published in public.

For both the cases, dealer perform the following calculations:

1.

Calculate actual share ($d_i^l$) and pseudo share($Z_i^l$) for the $i^{th}$ participant of level l using following formulas:

$$d_i^l=f\left(I{D}_i^l\right)and{Z}_i^l=d_i^l+g\left(s_i^l\right)$$

where g is one-way function in which $s_i^l$ denotes the share of $i^{th}$ participant of level l

2.

Calculate actual share ( $d_i^{l_u}$) and pseudo share ( $Z_i^{l_u}$) of the $i^{th}$ participant of upper level u using formula::

$$d_i^{l_u}=f\left(I{D}_i^{l_u}\right)and{Z}_i^{l_u}=d_i^{l_u}+g\left(s_i^{l_u}\right)$$

where $I{D}_i^{l_u}$ is the identifier for $i^{th}$ element of $u^{th}$ level.

3.

$s_i^l$ and $s_i^{l_u}$(if needed) is distributed to each participant using a secure channel.

4.

All $Z_i^{l_r}$ ,r values are published.

5.4. Reconstruction

Each participant compute actual share of other participants involved in the reconstruction by using formula

$$d_i^l=Z_i^l-g\left(s_i^l\right)$$

and then following two cases are considered

• Case 1

Particular level have sufficient number of participant i.e greater or equal to threshold,then participant of same level exchange their pseudo share and use the following formula:

• for $k\le t$

  $$\begin{array}{cc}\hfill h\left(x\right)& =\sum _{i=1}^n{d}_i\prod _{j=1,j\ne i}^n\frac{x-I{D}_j}{I{D}_i-I{D}_j}modQ\hfill \\ \hfill & =B_1+B_{2}x+\cdots +B_k{x}^{k-1}+a_1{x}^k+a_2{x}^{k+1}+\cdots +a_{t-k}{x}^{t-1}modQ.\hfill \end{array}$$
• for $k>t$

  $$\begin{array}{cc}\hfill h\left(x\right)& =\sum _{i=1}^n{d}_i\prod _{j=1,j\ne i}^n\frac{x-I{D}_j}{I{D}_i-I{D}_j}+\sum _{i=1}^{k-t}f\left(i\right)\prod _{j=1,j\ne i}^{k-t}\frac{x-j}{i-j}modQ\hfill \\ \hfill & =B_1+B_{2}x+....+B_k{x}^{k-1}modZ\hfill \end{array}$$

• Case 2

Particular level have insufficient number of threshold, then the share of the upper level participant for this level is used in the above formula. Thus we get the secret $B_1,B_2,B_3,\dots ,B_K$.

5.5. Verification

Following steps are involved in verification phase:

• Pseudo share $s_i^l$ is distributed to participants securely by dealer.
• Each $i^{th}$ participant uses his actual share ($d_i^l$) in two variable one way function with random variable r. Let that two way variable function is $q_i(r,d_i^l)$.
• Calculated $q_i$ values made public.
• Public share $Z_i^l$ is also published.
  Now at the time of exchange of shares:
• Each participant compute actual share of each participants

  $$d_i^l=Z_i^l-g\left(s_i^l\right).$$
• Using that actual share , $q_i(r,d_i^l)$ is calculated for $i_{th}$ participant.
• If $q_i(r,d_i^l)$ is equal to already public value of $q_i$ then participant share is valid otherwise the actual share of participant is not valid.
• In a similar way, an individual participant will be able to check the legitimacy of his/her share given by the dealer.

5.6. Example

We can understand proposed scheme more clearly by following example with small parameters.Let us consider the hierarchical system with two levels $l_1$ and $l_2$. Upper level is $l_1$ and lower is $l_2$. Dealer has two secrets, i.e., $B_1=2$ and $B_2=3$. Identifiers $I{D}_1^{l_1}=1$, $I{D}_2^{l_1}=2$, $I{D}_3^{l_1}=3$ for the level $l_1$ and $I{D}_1^{l_2}=4$, $I{D}_2^{l_2}=5$, $I{D}_3^{l_2}=6$ for the level $l_2$.

Dealer chooses shares $s_1^1=10$, $s_2^1=11$, $s_3^1=12$ for the level-1 and $s_1^2=13$, $s_2^2=14$, $s_3^2=15$ for the level-2.

5.6.1. Distribution

For the sake of easiness in calculation, we perform calculations on 2nd level.

$$h\left(x\right)=2+3x+4x^{2}mod23$$

calculate actual share for the $i^{th}$ participants for the level-2 by using formula: $d_i^{l_r}$ = h($I{D}_i^{l_r}$) are

$$d_1^{l_2}=9,d_2^{l_1}=2,d_3^{l_1}=3$$

Actual share of $i^{th}$ participants of upper level for the level-2

$$d_1^{l_{2,1}}=h\left(I{D}_1^{l_1}\right)=9.$$

Similarly, we obtain $d_2^{l_{2,1}}$ = 1 and $d_3^{l_{2,1}}$ = 1

Choose one-way function $g=2^{s_i^{l_r}}$ mod 23.

Compute pseudo share of the $i^{th}$ participants of the level R.

$$Z_i^{l_r}=d_i^{l_r}+g\left(s_i^{l_r}\right).$$

Therefore, we get $Z_1^{l_2}$ = 13, $Z_2^{l_2}$ = 10, $Z_3^{l_2}$ = 19.

Similarly, pseudo share of the participants of upper level for the level-2 are

$$Z_1^{l_{2,1}}=21,Z_2^{l_{2,1}}=2,Z_3^{l_{2,1}}=3$$

()

Publish all pseudo share and distribute $S_i^{l_r}$ to every participants through secure channel.

Table 1. Comparison in tabular form.

Table 1. Comparison in tabular form.

5.6.2. Reconstruction

In reconstruction phase each participant has pseuodoshare and the share $s_i^{l_r}$ for the particular level actual share is computed by using

$$d_i^{l_r}=Z_i^{l_r}-g\left(s_i^{l_r}\right).$$

Hence, we have

$$d_1^{l_2}=9,d_2^{l_2}=2,d_3^{l_2}=16$$

Similarly, actual share of the upper level participants for level-2 is as follows:

$$d_1^{l_2}=9,d_2^{l_2}=1,d_3^{l_2}=1$$

Now, there is possibility of two case:

• Particular level (here level-2) has sufficient number of participants
• Particular level has less no of participants then upper level participant takes part in reconstruction of secret.

Case-1

$$\begin{array}{cc}\hfill h\left(x\right)& =\sum _{i=1}^t{d}_i^l\prod _{j=1,j\ne i}^t\frac{x-I{D}_j}{I{D}_i-I{D}_j}modQ\hfill \\ & =B_1+B_{2}x+..+B_k{x}^{k-1}+a_1^i{x}^k+a_2^i{x}^{k+1}+a_{t-k}^i{x}^{t-1}modQ\hfill \\ \hfill & =9*\frac{(x-5)(x-6)}{(4-5)(4-6)}+2*\frac{(x-4)(x-6)}{(5-4)(5-6)}+3*\frac{(x-4)(x-5)}{(6-4)(6-5)}.\hfill \end{array}$$

That is,

$$h\left(x\right)=2+3X+4X^2. \mathrm{So} \mathrm{the} \mathrm{secrets} \mathrm{are} 2, \mathrm{and} 3$$

()

Case-2 No. of participants in level-2 is one less than the threshold. Therefore, one of upper level participants takes part in reconstruction. Hence, the pair of (ID,actual share) are::(4,9)(5,2)(1,9) applying same formula as in the Case-1.

$$h\left(x\right)=9*\frac{(x-5)(x-1)}{(4-5)(4-1)}+2*\frac{(x-4)(x-1)}{(5-4)(5-1)}+3*\frac{(x-4)(x-5)}{(1-4)(1-5)}$$

$h\left(x\right)=2+3x+4x^2$. Thus, the secrets are 2 and 3.

6. Security and Performance Analysis

While choosing a scheme, we must be clear about the capabilities of adversary along with the explanation of security properties it supports. There must be an strong analysis about computational and communication cost. In this section, we have explained all these concepts in details.

6.1. Adversary Model

There must be an adversary model against which the scheme is safe. The most common adversarial model for analyzing security protocols was presented by Dolev and Yao [14] in 1983. Apart from this, we have considered two types of adversaries:

• Insider Adversary, These are legitimate shareholders who acquired shares from the dealer.
• Outsider Adversary, The external adversary is an attacker who does not own any of the dealer’s shares but may try to gain unauthorized access.
  In general, a dealer is considered as trustworthy as in [3], but here we have considered the worst situation that the dealer is committing fraud by providing fake shares to the participants.

6.2. Security analysis

Any scheme must pass through formal and Informal analysis to verify its applicability in current scenario. In proposed scheme, We have used Random Oracle Modal (RoM) for formal analysis. In informal analysis we have proved our scheme safe from several attacks.

6.2.1. Formal Security Analysis (Random Oracle Model)

A cryptographic hash function H is treated as a really random function by the random-oracle model. The random-oracle model more particularly hypothesises the existence of a public, random function H that can only be evaluated by "querying" an oracle, which can be thought of as a "black box," that returns $H\left(x\right)$ when given input x. A formal approach that can be used to create and verify cryptographic methods is provided by the random-oracle model. In 2014, Herranz et al. [23] provided the formal definition of security for MSS in the random oracle model. Moreover, they proposed an MSS formally proved its computational security in ROM. As far as we know, that is an MSS’s first formal security analysis. Security analysis of multi secret sharing scheme has been performed by [31]. In this section, we prove the computational security of the proposed scheme $\Omega$ assuming that the hash function H behaves as a random oracle.

Before we proceed with the proof, the following are the assumptions:

• We assume the proposed scheme as the set of tuples, $\Omega =\left(Int,dist,Rec\right)$ where Int stands for Intilization/setup phase, dist stands for distribution and Rec is for recovery phase.
• PP(Public parameters)= $(\left(p,H,\rho ,t\right)$
  • p : prime number p > n such that p is at least $\lambda$ bits long
  • H : a hash function, $H:{\mathbb{Z}}_p^{*}\to \mathbb{Z}$
  • $\rho$: Set of participants
  • t: threshold
• There is an adversary $A_1$ contains set of participants $\rho$ and threshold value t.

Theorem For an adversary $\lambda$, we have

$$\left|pr\left[GM{S}_{A_1}^{SA}\left(\lambda \right)=1\right]-\frac{1}{2}\right|\le \left|\frac{q_H^n}{{\lambda }^{\lambda +2}}+0\left(\frac{q_H^n}{2^{2\lambda +1}}\right)\right|$$

here adversary makes at most $qH$ queries to the random oracle for H against the GMS and $\Omega$.

Proof For proof we follow the following steps:

Step1 We act as the challenger of the security game $G1$ described in [31].

Step2 We pass public parameters to the initialization algorithm and send the result to the adversary.

Step3$A1$ broadcast $Bϵ\rho$, we choose $s{h}_iϵZ_p$, $\forall p_iϵ\rho$

Step4 after masking hash query x to the random oracle H, if $xϵ\left\{s{h}_i\right\}{p}_iϵB$ then abort the game, otherwise proceed for the next step.

Step4 a random value is $kϵZ_p$ is chosen and send to adversary. At the same time, $(x,k)$ is saved in the table.

Step4 Two global secrets

$$S^0=(s_1^0,s_2^0,\cdots ,s_l^0)$$

$$\ne (s_1^1,s_1^2,\cdots ,s_l^1)=S^1$$

are broadcasted by adversary $A_1$.

Step5 We choose a random value $rϵZ_p^{*}$ such that $r\ne s{h}_i$ for $P_iϵ\rho$ and adversary doesn’t query $r,2r,\dots ,lr$ to the random oracle H.

Step6 a random polynomial $f\left(x\right)$ is chosen where, $f\left(0\right)=r$ and compute $h_i=H\left(s{h}_i\right)$ and $r_i=f\left(i\right)-h_{i}modp$ and again store $(s{h}_i,h_i)$ in the hash table. Similarly choose l no. of random values $(k_1,\dots ,k_l)ϵZ_p$ and store $(r,k_1),(2r,k_2),\dots ,(lr,k_l)$ in the hash table.

Step7 Choose a random bit $bϵ\left\{0,1\right\}$ and compute $y_j=k_j-s_b^{j}modp\forall 1\le j\le l$ and give shares of corrupted players ${(i,s{h}_i)}_{p_iϵB}$ . along with this public output $Ou{t}_{pub}=\left\{r_1,r_2,\dots ,r_n,y_1,\dots ,y_l\right\}$ are also shared.

Step8 after continuous query to $H(.)$, adversary $A_1$, outputs a bit $b^{\prime }$ which is defined in the following equation

$$o/p=\left\{\begin{array}{c}1,\mathrm{if}b=b^{\prime }\hfill \\ 0,\mathrm{if}b\ne b^{\prime }\hfill \end{array}\right.$$

(1)

from above steps, we conclude that $A_1$ is not allowed to query $s{h}_i$ such that $p_iϵB$ and $1\ge j\le l$ .

6.2.2. Informal Security Analysis

Any proposed protocol must be passed through the following goals:

• Correctness : In verification phase Each participant compute actual share of other participants $d_i^l=Z_i^l-g\left(s_i^l\right)$ using that actual share , $q_i(r,d_i^l)$ is calculated for $i_{th}$ participant. If $q_i(r,d_i^l)$ is equal to already public value of $q_i$ then participant share is valid otherwise the actual share of participant is not valid.
• Forward secrecy: keys like $q_i(r,d_i^l)$ can only be computed or stored by members of the closed communication group; if a member leaves the group, the departing member will be unable to access the content of future conversations.
• perfectness: We use Shamir’s (t, n) secret sharing scheme for share distribution at each level in the proposed scheme. It is well known that fewer than t participants in Shamir’s (t, n) secret sharing scheme cannot reconstruct the secret. Hence, our scheme is also perfect.
• Fairness of secret sharing One desirable quality in secret sharing is Fairness, which indicates that if one member obtains the secret, the other participants are not harmed. Halpern and Teague [16] were the first to offer rational cryptographic protocols in 2004. They pointed out that any method for reassembling secrets with a well-known upper constraint on the running duration is unstable and that parties will not submit anything in the final round since they have no reason to do so because the other participant does. Regrettably, earlier secret-sharing systems necessitated numerous rounds with high overheads. Zhang et al. [48,49] explain the scheme’s. Fairness but leave out the access mechanism. To summarise, existing fairness schemes necessitate a trusted third party or many rounds of communication. The proposed scheme provides Fairness without the dependency on a third party and extra overheads in communication.
• Freshness of keys: In the proposed scheme, all the exchangeable values depend upon the random bi-variate polynomial. It makes pseudo share, and shares are always fresh. Hence, it is impossible to impersonate a member by recording a previously used key.
• Eavesdropping attack In proposed scheme, each $i^{th}$ participant uses his actual share ($d_i^l$) in two variable one way function with random variable r which makes it independent of public parameters. Therefore, an adversary will not be able to know any secret information from communication parameters. So, the proposed scheme is safe from eavesdropping activities.
• Cheating identification In the proposed scheme, an individual participant can check the legitimacy of his/her share given by the dealer. Thus, the proposed scheme provides cheating identification.
• Verifiability In the reconstruction phase, participants can verify shares received from other participants and dealers. On the other hand, a dealer can also verify the participant’s shares. Thus, the proposed scheme provides verifiability.
• Unconditional security While exploring the security analysis, both types of adversaries are considered with their capacity to the full extent. It implies that no assumptions are made about an adversary’s computing power and resources.

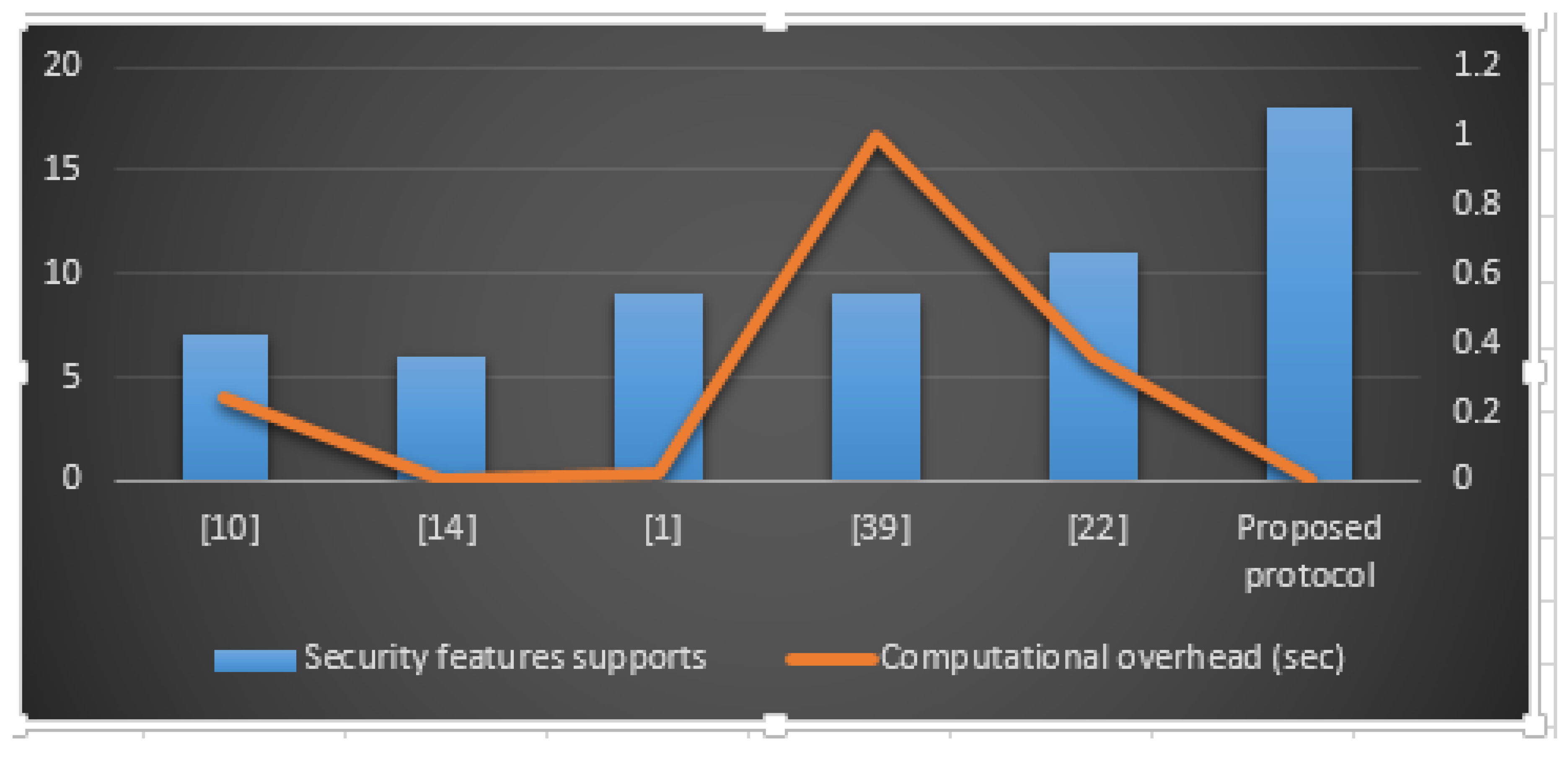
6.3. Performance analysis

6.3.1. Computational cost

In the proposed scheme, each member must compute pairwise shared keys with others in the verification phase. According to Horner’s rule [27], t and h computations are required for each univariate polynomial of $t-1$ and $h-1$ degree. In the proposed protocol, calculation reduces to Shamir’s secret sharing scheme. According to [38] computational time for 8 person is 0.0039 second. There is a slight change in computation time as we increase the number of persons, Basit et al. [4] uses extra polynomial, and Tentu et al.[41] uses modular exponentiation, which increases computational cost. The computational cost for the same no. of persons are 0.2439 second and 80.003 second of [4] and [41] respectively. Similarly, computational cost for 8 persons in [49] is 0.23 second. So we conclude that the computation cost is meager compared to the other existing schemes. For more clarity, we have presented a graphical comparison of schemes in terms of computational time and security features it supports in Figure 1.

6.3.2. Storage Cost

Each member has to store only uni-variate polynomial of modulus $\mathbb{P}$. So the storage requirement for each member is $tlog\mathbb{P}$ bits. This polynomial-based modulus is far less than the public-key-based modulus [45]. Here threshold is t. To get collusion-free authentication, each member must simultaneously deal with $t+1$ univariate polynomial. So overall storage cost is significantly less compared to symmetric key-based schemes.

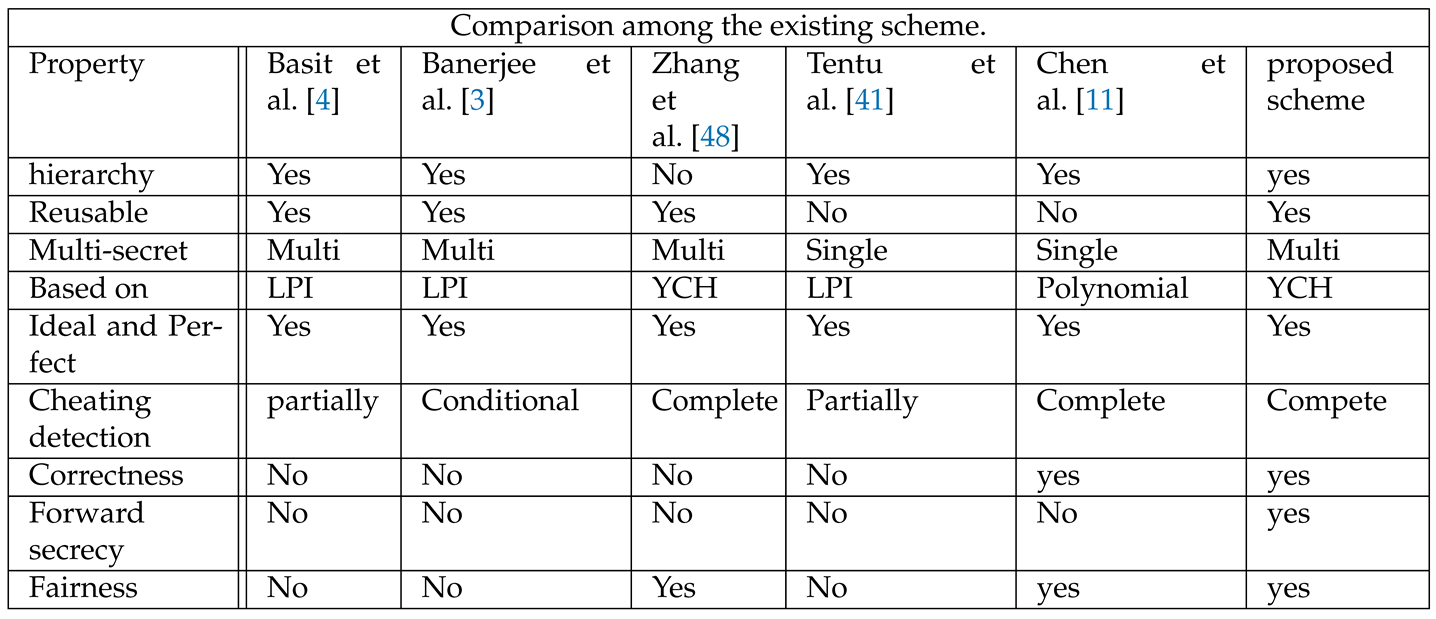
7. Comparison with Existing Scheme

The proposed scheme uses the YCH scheme, while all other schemes for hierarchical access structures use simply shamir’s scheme. In the proposed scheme “Multiple-secrets ”are shared among a group of people for different levels. Our scheme provides a mechanism for verifying the shares, which is also new for hierarchical access structures. This is more efficient than other schemes. Basit et al. [4] used Shamir’s scheme with the successive application of one-way function and shift key technique to propose Multi-stage, Multi-secret sharing for hierarchical Access Structure. Apart from the above papers, the Hierarchical secret sharing (HSSS)scheme is discussed in [3,5,28] but his scheme lacks fairness. Banerjee et al. [3] proposed Cheating detection and cheater Identification for hierarchical structure but lacks correctness. Bisht et al. [5] proposed work on multi-level secret sharing but lacks fairness and perfectness. Similarly, Yuan et al. [46] used homogenous recurrence relation to propose a new efficient scheme that deals with a multi-secret hierarchical scheme. It is a novel work but lacks explanation about correctness and forward/backward secrecy Our scheme also avoids the problem of Chen et al. scheme’s [11] which requires checking the non-singularity of multiple matrices. Furthermore, during the entire scheme, each participant keeps only one share, which is as long as the secret, indicating that our method is optimum. Furthermore, despite requiring more public values, our scheme can simultaneously disclose many secrets. In Table 1, we can see the importance of the present scheme in comparison with other schemes.

In our proposed scheme, we have used a one-way function, which restricts the outsider Adversary from stealing or breaching information about the secret. To deal with the situation of Case-1 and Case-2,Two variable one-way functions are used. Using a two-variable one-way function, every participant can verify the share received from the dealer and other participants. Our scheme also satisfies the security goals like correctness and secrecy. In Table I, we have compared the recent scheme for multi-secret sharing. From there, we conclude that our scheme can provide many security properties in the case of IoT authentication. Furthermore, in Figure 1, we can see that computational is significantly less than others and security features are more in numbers supported by proposed scheme.

8. Conclusions

In the present work, we categorized participants into different levels with varying thresholds, aligning with a hierarchical structure. Subsequently, we proposed a hierarchical multi-secret sharing scheme based on the YCH scheme. The YCH scheme is highly efficient, and the inclusion of a one-way function enhances its security, making it unconditionally secure. The reusability of shares eliminates the need for frequent refreshment of shares for future communication. In addition to being reusable, multi-secret, and hierarchical, our scheme includes a valuable feature: the verification of shares. Specific participants can verify the shares they receive from other participants or the dealer. This verification feature makes our proposed scheme particularly useful for robust security solutions. Comparisons with existing schemes demonstrate its superiority in preserving security. Our scheme not only improves operational efficiency but also provides a scalable solution adaptable to various access structures. Future work could explore further optimizations and applications in complex, multi-stage security environments.