Introduction
A palindrome number is an integer that has the same value after the digits in it are reversed. For example, 121 and 1221 are both palindrome numbers. Formally, let be the digits of a k-digit decimal number denoted as a concatenation of digits as . Then, the number is a palindrome number if and only if for all i. To eliminate the case of constructing new palindrome numbers simply by padding 0’s at the two ends of an existing one, it is required that throughout this paper.
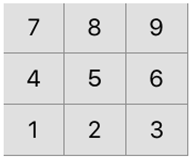
Shown in the figure below is an ordinary calculator keypad. A total of 16 6-digit palindrome numbers can be constructed using the rows, columns and diagonals of this keypad, e.g., .
An interesting fact about all these 16 palindrome numbers is that they are all divisible by 37 [
1]. Inspired by this observation, this paper studies the existence and construction of palindrome numbers of arbitrary length that are divisible by 37, which is the 12
th prime with many interesting properties [
2,
3]. An easy observation to make is that none in the set of 2-digit palindrome numbers,
, is divisible by 37. Thus, only palindrome numbers with 3 or more digits are considered here.
This paper is organized as follows. A lemma on the periodicity in taking powers of 10 modulo 37 is first proven in the next section. This lemma is critical in proving the results on palindrome numbers divisible by 37. Before applying this lemma on the general problem of palindrome numbers of arbitrary length divisible by 37, short palindrome numbers with 3, 4, and 5 digits divisible by 37 are shown to exist and constructed. Then, it is shown that this is also true for palindrome numbers of arbitrary longer length. Finally, conclusions are made on the existence and construction of palindrome numbers divisible by 37.
1. Powers of 10 Modulo 37
A k-digit palindrome number may have an even or odd number of digits. When for some , the palindrome number can be expressed as . The decimal value of this palindrome number is therefore , where the sums of pairs of powers of 10 in the parentheses are called coefficients. Similarly, when for some , the palindrome number can be expressed as , where stands for the digit in the middle. The decimal value of this palindrome number is therefore . It is not hard to see that the coefficients decide if the palindrome is divisible by 37 or not. This implies that it is worthwhile to look into how the set of different powers of 10 behave modulo 37. The following lemma shows an important property of powers of 10 modulo 37.
Lemma 1.1.
for all nonnegative integer i.
Proof. Note that . Since , . □
As a consequence of this lemma, a power of 10 is congruent to only three possible distinct values modulo 37, namely 1, 10, and 26. In other words, the set of powers of 10, , is congruent to the set modulo 37.
2. Existence and Construction of Palindrome Numbers Divisible by 37
The problem of wether palindrome numbers divisible by 37 of arbitrary length greater than 2 exist and how to construct them if they do will be studied in this section. The case when k, the number of digits in the palindrome number, is small is discussed first.
2.1. or 5
When , the palindrome number can be expressed as . According to the following lemma, 3-digit palindrome numbers divisible by 37 exist and can be easily constructed.
Lemma 2.1. A 3-digit palindrome number is divisible by 37 if and only if .
Proof. Note that the decimal vale of the palindrome number
can be found as
Suppose that
. Then,
, or, equivalently,
. This implies
.
The other direction can be easily shown simply by reversing the above steps. □
As a consequence of this lemma, all digits must be equal for a 3-digit palindrome number to be divisible by 37. Thus, there are nine nonzero palindrome numbers that are divisible by 37. Namely, they are 111, 222, 333, 444, 555, 666, 777, 888, 999. Notice that they are also divisible by 3 and 111.
Similarly, the following lemmas concern the cases when and .
Lemma 2.2. A 4-digit palindrome number is divisible by 37 if and only if .
Proof. Note that
Suppose that
. Then,
. This implies
.
The other direction can be easily shown simply by reversing the above steps. □
As a consequence of this lemma, there are only four 4-digit palindrome numbers that are divisible by 37. Namely, they are 1221, 2442, 3663, 4884. Notice that they are also divisible by 3 and 111.
Lemma 2.3. A 5-digit palindrome number is divisible by 37 if and only if .
Proof. Note that
Suppose that
. Then,
. This implies
.
The other direction can be easily shown simply by reversing the above steps. □
Notice that, since , the sum of all digits in the palindrome number is . Thus, the palindrome number is also divisible by 3, and consequently, by 111.
The problem when can be divided into two cases: even or odd number of digits in the palindrome number.
2.2. Even Number of Digits
Suppose that there are digits in the palindrome numbers for some integer . The palindrome can then be expressed as . The decimal value of this palindrome number can be found as . Note that all coefficients are sums of two powers of 10. Using lemma 1.1, these coefficients are congruent to one of the following three sets of values:
for ,
for , and
for .
The following observations can be made to all three sets: there are only two distinct values in each set, the two distinct values have opposite signs, and the absolute value of one of the two distinct values is twice the other. All these guarantee the existence of -digit palindrome numbers divisible by 37 for all . The following theorem, which is already proven, summarizes this result.
Theorem 2.4. There always exist -digit palindrome numbers, denoted as , that are divisible by 37 for all . To construct such a number, there are following three cases:
Case 1: When for , the -digit palindrome number is divisible by 37 if and only if the digits satisfy the identity .
Case 2: When for , the -digit palindrome number is divisible by 37 if and only if the digits satisfy the identity .
Case 3: When for , the -digit palindrome number is divisible by 37 if and only if the digits satisfy the identity .
Example: Consider 6-digit palindrome numbers.
Since , using case 1 in the theorem, the 3 digits, , in the palindrome number must satisfy the identity such that it is divisible by 37. This implies that must be an average of and . This explains why all 16 palindrome numbers constructed from the calculator keypad are divisible by 37.
Example: Construct a 16-digit palindrome number divisible by 37.
Since , the palindrome number looks like . Using case 3 in the theorem, must satisfy the identity . Let and . Then, .
2.3. Odd Number of Digits
Suppose that there are digits in the palindrome numbers for some integer . The palindrome can then be expressed as , where is the digit in the middle. The decimal value of this palindrome number is therefore .
Again, the coefficients decide if the palindrome number is divisible by 37 or not. Using lemma 1.1, this set of coefficients is congruent to one of the following three sets of values:
for ,
for , and
for .
Ignoring the first coefficient for m in each set, these sets show exactly the same structures, and thus, have the same properties as those in the previous section. Adding the coefficient of m to the sets does add a new distinct value to them. However, it does not add any new distinct absolute value to the sets. This guarantees the existence of -digit palindrome numbers that are divisible by 37. The following theorem, which is already proven, summarizes this result:
Theorem 2.5. There always exist -digit palindrome numbers, denoted as , that are divisible by 37 for all . To construct such a palindrome number, there are following three cases:
Case 1: When , the -digit palindrome number is divisible by 37 if and only if m and digits satisfy the identity .
Case 2: When , the -digit palindrome number is divisible by 37 if and only if m and digits satisfy the identity .
Case 3: When , the -digit palindrome number is divisible by 37 if and only if m and digits satisfy the identity .
Example: Construct a 15-digit palindrome number divisible by 37.
Since , the palindrome number looks like . Using case 2 in the theorem, m and must satisfy the identity . Let and . Then, .