Prerpints.org logo
Preprint
Essay

The Unexpected Similarities Between Strong and Electromagnetic Interactions

This version is not peer-reviewed.

Submitted:

18 May 2024

Posted:

20 May 2024

You are already at the latest version

Abstract
In this article, many experimental similarities between electromagnetic fields (which are applied in systems of electrons, atoms, and liquids) and strong interaction fields (which are applied in systems of quarks, nucleons, and nuclei) are reviewed. The currently accepted theories describing electromagnetic fields differ fundamentally from those describing strong fields. Therefore, the many similarities are quite surprising, and some are not adequately explained even today. Several such unexplained similarities are listed among the top open problems in particle physics, such as the “EMC effect,” the “proton spin crisis,” and the “strong CP problem.” This paper highlights, for the first time, the underlying common characteristics of these problems, potentially offering valuable contribution to future explanations.
Keywords: 
EMC effect
;  
proton spin crisis
;  
strong CP problem
;  
liquid drop model
;  
quark photon interaction
;  
neutron charge radius
Subject: 
Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

A drop of noble atoms comprises atoms that attract one another and form a liquid. Atoms comprise a nucleus and electron shells. Electrons carry an electric charge that interacts electromagnetically with other atomic components.
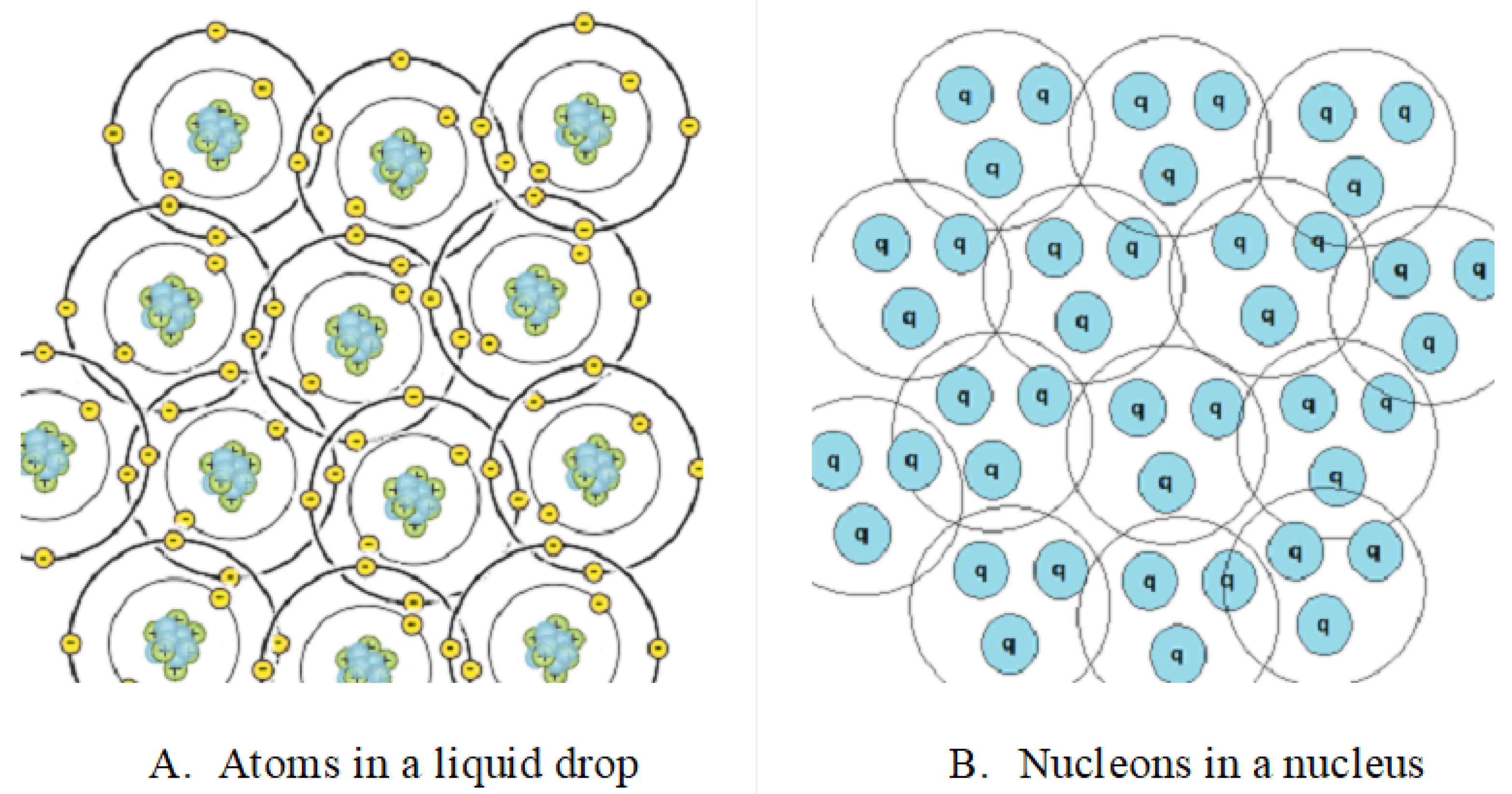
The scenario within the atomic nucleus exhibits a dualistic nature. The nucleus contains nucleons (protons and neutrons) that attract one another and form a nucleus. Nucleons contain quarks. Phenomenologically, quarks carry a kind of strong charge that exerts strong forces on a nucleon’s components (see Figure 1).
We will show below many examples presenting that nucleons resemble noble atoms with several electronic shells. In other cases, nucleons resemble atoms with closed shells of electrons and three valence electrons. This article describes numerous different pairs of phenomena, and each pair encompasses a phenomenon in the electromagnetic domain and a similar phenomenon in the strong interaction domain. We describe the similar properties between drops of liquid and atomic nuclei, the similarities between atoms with several electronic shells and nucleons, the similarities between electrons and quarks, and the similarities between electromagnetic fields and strong interaction fields. These pairs of similar features pertain to physical objects’ fundamental attributes (see Table 1).
This work provides a new point of view on well-documented phenomena. Although each topic discussed here was published earlier in textbooks or scientific journals, this is probably the first time that all these pairs of similar effects have been compiled into one article. In some cases, I provide a textbook explanation of the electromagnetic domain phenomenon.
Based on the prevailing knowledge, the system of electrons, atoms, and atomic nuclei (cores) is described by electromagnetic theory and the corresponding quantum mechanics, while the system of quarks and nucleons (or baryons) is described by quantum chromodynamics (QCD). According to these theories, the two systems are very different. The fundamental differences between the theories describing the atom and those describing the nucleon (see Table 2), make one expect that systems of atoms and systems of nucleons will behave differently in many aspects. Indeed, my personal experience shows that many of the similarities pointed out in this article have surprised particle physicists, and some of them are not yet understood.

2. A Liquid Drop and A Nucleus: The Nuclear Liquid Drop Model

The similarity between a liquid drop and a nucleus was observed by the Russian-born American physicist George Gamow, who applied the model in 1928 to explain alpha radiation [1]. This similarity is called “the nuclear liquid drop model” in the literature. Gamow assumed that the nucleus had a surface tension comparable to that in a liquid drop. In alpha radiation, an alpha particle exits the nucleus like a liquid drop that splits into two smaller drops. The alpha disintegration of a heavy nucleus is a quantum effect called “tunneling.”
This nuclear liquid drop model was used to formulate the Bethe–Weizsäcker mass formula (1935), which calculates the mass of a nucleus. The nuclear liquid drop model also explains phenomena such as the radius of nuclei (except a few very light nuclei), nuclear fission (1939), and others [2]. Let us see the underlying similarities that make this model so successful.
When atoms are far from one another, there is no force that attracts them. This is because the positive electric charge of the atomic nucleus is screened by the negative electric charge of the electrons. Similarly, when two nucleons (e.g., a proton and a neutron) are far from each other, there is no force between them.
The van der Waals force attracts noble atoms in a liquid drop when they approach each other. One atom’s electrons share some space with a nearby atom’s electrons; therefore, the screening is incomplete, and quantum effects arise. Similarly, an attractive force between two nucleons occurs when they are close to each other. It is called “nuclear force.”
Since a liquid drop cannot be compressed, its volume is proportional to the number of molecules (or atoms) in the liquid. This concept is explained by the Pauli exclusion principle, which states that the single-particle wave function of several electrons is antisymmetric. Therefore, one atom’s electronic state must be orthogonal to a neighboring atom’s quantum state. Similarly, the volume of a nucleus—which is not very light—is proportional to the number of nucleons.
Two atoms do not merge into one atom in chemical processes. Similarly, two nucleons do not merge into one strongly bound particle. For example, the deuteron is a particle that comprises two distinct particles: a proton and a neutron. These particles are bound by nuclear force, not strong force. Experiments indicate the difference between these forces. The nuclear force between nucleons is measured in several MeV, and the strong force is measured in several hundreds of MeV.
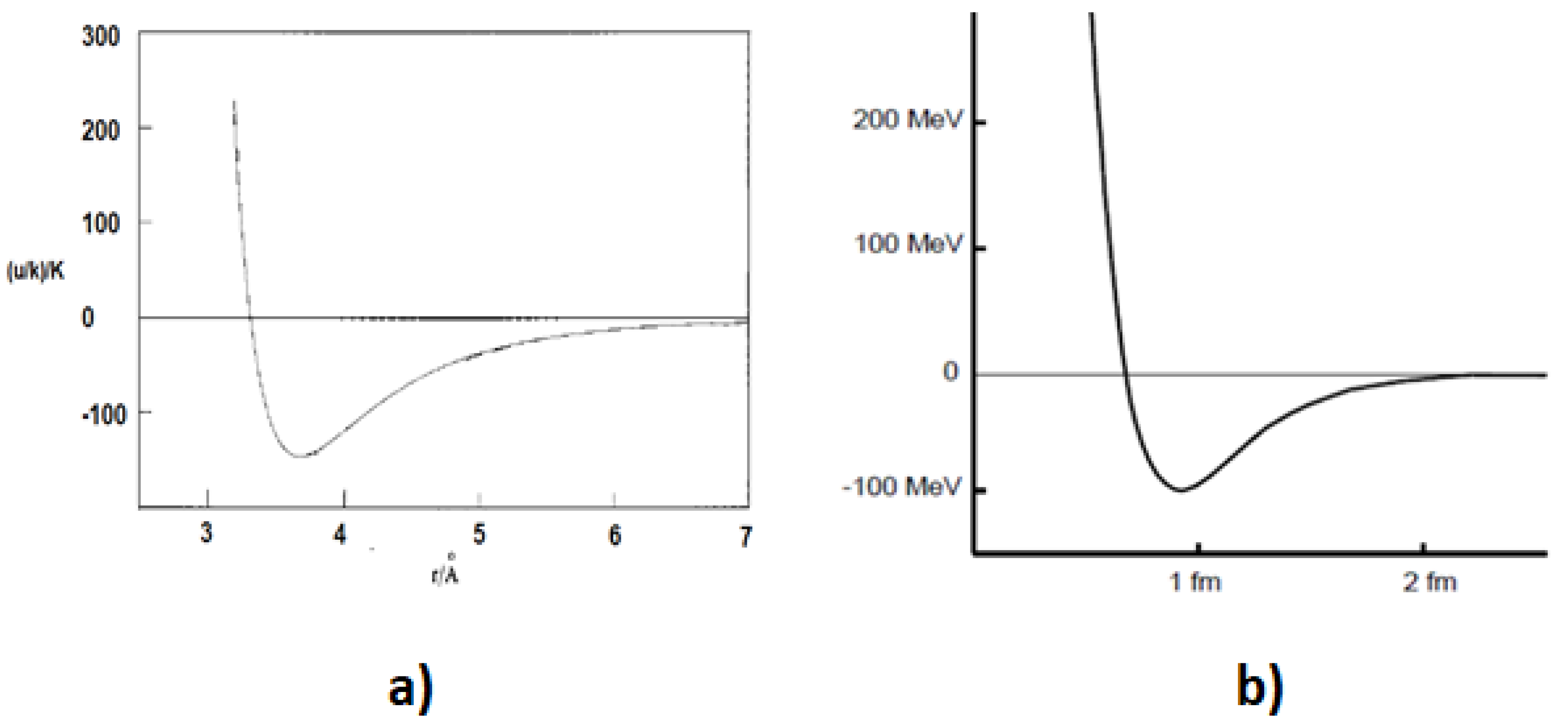
One of the most striking examples of the analogy between electromagnetic and strong interactions is the similarity between the graph of the potential versus the distance between two atoms of a noble gas and the corresponding graph for two nucleons (see Figure 2 A [3] and B [4]).
The well-known European Muon Collaboration (EMC) effect demonstrates another interesting similarity. The electronic radius of an atom inside a liquid drop, which is sometimes called “the van der Waals volume,” is larger than the electronic radius of a free atom [5,6]. Similarly, in 1983, the EMC team of CERN found that nucleonic quarks inside a nucleus have a larger volume than the quarks of free nucleons [7].

3. Properties of Electrons, Quarks, and Photons

Electrons are Dirac particles that obey the Dirac equation. Therefore, they are point-like, spin-½ particles. Electrons are attracted to their antiparticles. They may form positronium, which is a bound particle of the electron and the positron. The spin and parity J π = 0 − of the positronium’s ground state decays into two photons [8].
Quarks are also point-like, spin- 1 / 2 . Particles. They are attracted to their antiparticles. They may form mesons, such as π 0 , which is the bound particle of u and d light quarks with their antiparticles. This particle’s spin and parity are J π = 0 − . Like the positronium’s corresponding state, the π 0 , decays mostly into two photons [9].
Photons interact with electric charges, and Maxwell equations show this effect. The equation of the photon stems from Maxwellian electrodynamics, in which similar charges repel each other and different charges attract each other. This force declines proportionally to the square of the distance between two charged particles [10,11].
Photons also interact strongly. This property has been known for more than half a century, and it has been noted in the literature as “the hadronic properties of the photon” [12].
The electromagnetic collision of charges emits radiation (photons). The photons’ spin and parity are J π = 1 − . Bremsstrahlung radiation is one type of this effect [13].
An analog of bremsstrahlung radiation also appears in strong interactions. In 1978, high-energy electron–positron collisions produced a “three-jet event.” Generally, a jet is associated with an initial energetic quark produced by the primary colliding particles. In a three-jet event, the collision produces a third jet that interacts with hadrons. The spin of the third particle that created the jet is calculated, and like the photon, it has a spin of 1 [14,15].

4. Conservation Laws

Several quantities are conserved in all interactions, such as energy, momentum, angular momentum, and charge. In Table 3, we present the conservation laws that are not satisfied by all kinds of interactions. For example, electromagnetic interactions and strong interactions conserve parity and charge conjugation. This strong interaction’s conservation is surprising, and it is called the “strong CP problem” in the literature [16]. (In this description, C denotes the charge conjugation symmetry and P denotes parity conservation.)
Experiments indicate another kind of similarity between a process whose results are determined by electromagnetic interactions and a corresponding strong interaction process. In chemical processes, the number of atoms is conserved since each atom has a nucleus that does not participate in these processes. Electromagnetic interactions explain a chemical process. Similarly, in all interactions, the number of baryons is conserved [17]. Physicists have attempted to explore violations of baryon conservation [18]. According to some unconfirmed theories, only the B − L number (i.e., the number of baryons minus the number of leptons) is conserved [19], but the baryon number conservation law has not been violated in any experiment [17,18].

5. Mass of Atoms, Electrons, Baryons, and Quarks

The intensity of strong interactions is much greater than that of electromagnetic interactions. Strong interactions are of the same order of magnitude as the particles’ mass. For example, the mass of the π mesons is about 140 MeV, and the mass of the ρ mesons—which contain the same quarks as the π mesons—exceeds 750 MeV. Another example is the nucleonic mass, which is about 940 MeV, and the Δ baryons (which, like nucleons, contain u and d quarks), whose mass exceeds 1,230 MeV.
In contrast, electromagnetic interactions’ intensity is much less. The mass of the positronium, the bound state of an electron and a positron, is greater than one MeV, while its interaction energy is just a few eV. In this section, we examine several pairs of systems and show that, despite the great difference between their scales, strong interactions and electromagnetic interactions have analogous properties.
In atoms, the valence electrons do not carry the entire atomic mass. This quality is obvious because an atom contains a massive nucleus, and most atoms have internal closed shells of electrons. An analogous effect was found in nucleons. In the 1970s, a team at the Stanford Linear Accelerator Center (SLAC) found that the quarks of the proton carry about one-half of the proton’s mass [8]. This outcome stems from the analysis of data on deep, inelastic electron–proton scattering.
The positronium’s mass is much less than the mass of any atom. Similarly, the mass of a pion, the bound state of the quark–antiquark of the u-and-d flavor, is much less than the nucleon mass.
Let us examine another kind of experimental property. Atoms contain massive elements aside from valence electrons, such as the nucleus and internal electronic closed shells. An examination of the data on nucleons reveals a similar situation. It is explained below that the analysis of proton–proton scattering experiments shows an analogous feature: the proton comprises a massive object beside the valence quarks.
Recent high-energy CERN Large Hadron Collider (LHC) measurements of the elastic proton–proton cross-section have shown that the number of elastic collisions divided by the total number of collisions increases when the collision energy increases (see Figure 3 a–c). In very energetic collisions, nearly 30% of events are elastic [20]. This effect is not observed in the electron–proton collision, which is an electromagnetic process. In this case, the total cross-section of the Rutherford, Mott, and Rosenbluth formulas shows that this cross-section decreases monotonically with an increase in the collision energy; and at high energy, the relative portion of the elastic events is negligible. The increase in the elastic and total cross-sections of high-energy proton–proton scattering indicates that, aside from quarks and gluons, the proton contains another massive object. This object must be electrically neutral because it is not seen in electron–proton scattering. According to the Heisenberg uncertainty law the results of a higher-energy process are determined at a smaller spatial volume. Here, the increase in the cross-sections at higher energy and the projectile’s shorter wavelength indicate that the volume of this massive object is much less than the proton’s volume. These effects are attributed to the existence of pomerons [21]. In any case, these data point out another kind of similarity between atoms and nucleons: in atoms, valence electrons account for chemical processes’ primary features, and the nucleus—together with the inner closed shells—occupies a smaller inner volume. Similarly, in the proton and the neutron, the valence quarks do not account for the particle’s entire mass. Furthermore, the proton comprises an inner object that affects the results of energetic proton–proton scattering. This example also depicts the analogy between a proton and an atom.
A comparison between the binding energy of electrons and quarks exhibits another similarity. The binding energy of an electron in the lowest state of the positronium is greater than the first ionization energy of a valence electron in atoms containing several electronic shells. Several features produce this effect. Consider the orthogonality between the valence electron’s single-particle quantum function and quantum state of the closed shells’ electrons. In this context, the electronic states in the higher shells have greater kinetic energy, and the higher shells are farther away from the nucleus and the inner shells. The first effect increases the electron’s positive kinetic energy and the second effect reduces the negative binding energy between the electron and the nucleus together with the inner closed shells.
A similar phenomenon occurs in the quarks of a pion and of a nucleon. The energy of a single quark in a pion is about 70 MeV, which is significantly smaller than the energy of a valence quark in a proton. This outcome stems from the fact that nearly half of the proton mass is carried by valence quarks. Therefore, the binding energy of a quark in a pion exceeds that of a quark in a proton.

6. Spin and Orbital Angular Momentum

Angular momentum is conserved in physical processes, and the mathematics of the quantum mechanical description of an atom’s angular momentum is well understood. Each electron has a spin- 1 / 2 , and if the electron is not in its ground state, it may have orbital angular momentum, which takes an integral number. The total vectorial sum of the spin and orbital angular momentum of all electrons is the atom’s angular momentum. (This discussion ignores the angular momentum of nuclei.)
The electrons in an atom with more than one electron are arranged in a linear combination of several “configurations” [22]. Unfortunately, this well-documented issue is not generally known. In each configuration, the electrons are arranged in different angular states. In all the configurations of a given atomic state, the total angular momentum of the electrons and the parity are the same. Each specific configuration has a probability of finding the atom in that specific configuration.
The mathematics that computes the probability of each configuration was developed during the 1930s and 1940s. The calculations’ outcomes show that the configurations are significant. In the case of an atom with many electrons, the configuration state of a given atomic state is significant, and the probability that the electrons are arranged in higher configurations should not be ignored. Even in the helium atom, which has only two electrons, the probability of electrons in higher configurations is not negligible [23].
As we described above, the spin of a valence electron is coupled with the orbital angular momentum. As a result, the spins of individual valence electrons are not necessarily parallel. Therefore, the vectorial sum of the valence electrons’ spins in an atom is much less than the atom’s total angular momentum because the electrons also carry orbital angular momentum. Hence, the electrons’ spins are not parallel. This effect is even more meaningful in atoms with several electronic shells.
Considering the proton, the European Muon Collaboration obtained an analogous result in 1988. Their experiment proved that the sum of the quark spins was much less than that of the proton spin [24]. This well-known effect is called the “proton spin crisis.”
Isospin symmetry indicates that an analogous effect should hold for the neutron. Indeed, in 2004, a group at Jefferson Lab published an article about its experiments on the neutron angular momentum structure, concluding that the neutron’s quarks carry significant orbital angular momentum [25]. This effect indicates that the quarks’ spins do not point in the same direction. In turn, these effects present another example of the analogy between electrons’ electromagnetic systems and strong interactions’ systems of quarks.
Another well-known result in atoms is called “the Hund law,” which states that valence electrons in atoms with several electronic shells prefer quantum states with parallel spins [26]. This effect does not appear when three electrons are in the ground state, but it is common in atoms with several shells. The textbook explanation says that parallel spins of several electrons mean the spin component of their wave functions is symmetric. Hence, the Pauli law entails that the spatial part of the total wave function is antisymmetric. Therefore, the effective distance between the electrons increases, and the repulsive energy decreases [26]. This effect is due to the general law stating that a physical state prefers lower energy.
In baryons, a similar situation was found. Due to the intensity of strong interactions, we can measure the change in the particle mass. For example, the four-isospin quartet Δ (1232) baryons are the particles with parallel spin and total angular momentum of 3 / 2 + . They have less energy than the corresponding excited unparallel-spin baryons with a total angular momentum of N(1440) 1 / 2 + [9]. A similar phenomenon occurs in the case of the Ω- baryon with three strange quarks.

7. Electron and Quark Distribution

According to quantum mechanics equations, the electron density decreases with the distance from the atomic center. The hydrogen atom’s electronic functions decrease by a factor exp(- α r), where α is a positive quantity [13]. In nucleons’ case, measurements of the quarks’ electromagnetic form factors also show an exponential decrease [8]. As quarks carry the nucleon’s electric charge like atomic electrons, the nucleon quark density decreases exponentially with respect to the proton’s center.
Let us examine another kind of data. According to quantum field theory (QFT), an electronic state may have an additional electron–positron pair. In nucleons, the probability of finding extra quark–antiquark pairs is significant. Experiments detected a non-negligible number of antiquarks of the u, d, and s flavor in the proton [27].
In the case of an extra electron–positron pair in an atom, we expect that the positron tends to be located farther away from the atomic center because it has a positive electric charge; therefore, it is repelled from the nucleus, which also holds a positive charge.
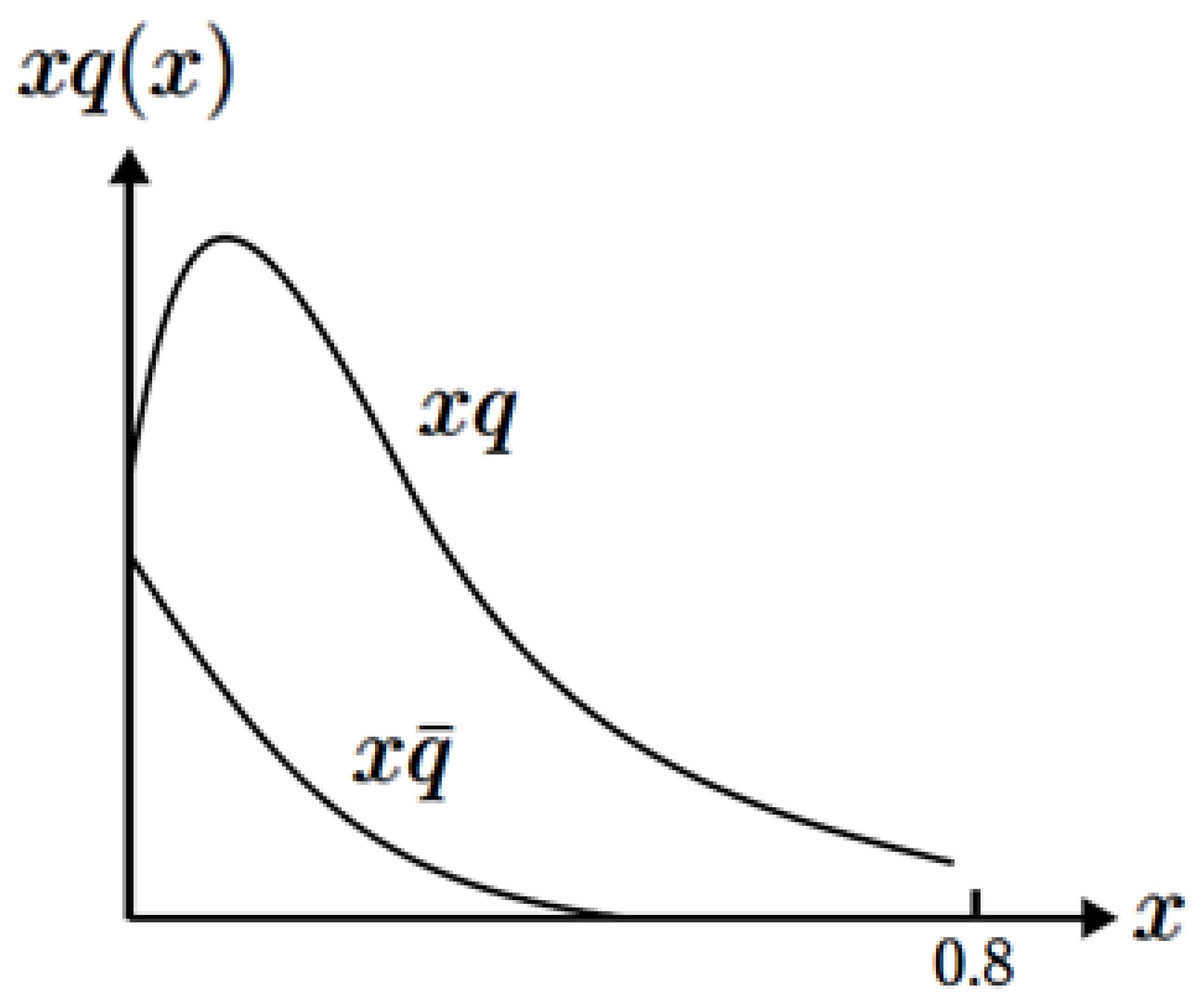
The same phenomenon was found in the antiquark within the nucleon. Measurements showed the momentum distribution of the nucleon’s quark and its antiquarks as a function of Bjorken x [8,28]. Figure 4 shows the main features of these data. The quark’s graph is wider than that of the antiquarks. The fundamental principles of physics explain the two graphs’ meanings in this figure. The nucleon’s quarks are confined inside its volume, and the Heisenberg position–momentum uncertainty principle proves that they acquire a Fermi motion. This motion is the underlying reason for the graphs’ width in Figure 4 (see [8], pp. 266–271). In other words, the stronger the Fermi motion of a given nucleon component, the wider its graph would become in Figure 4. Furthermore, the Heisenberg uncertainty principle states that the quarks’ stronger Fermi motion proves they are enclosed inside a smaller volume of the proton. Conversely, the antiquarks’ smaller Fermi motions prove that they are spread over a wider space, and they are located in the proton’s peripheral region.
The data presented in Figure 4 were obtained in the 1970s and published in textbooks during the 1980s (see [8], p. 281). This figure proves that the quarks’ widths are much larger than the antiquarks’ widths. Therefore, the quarks’ region is smaller than the antiquarks’. Unfortunately, this property of the antiquark is not commonly known, and its self-evident meaning has not been adequately discussed in the literature. Fundamental electromagnetic properties suggest that a positron of an electron–positron pair in quantum field theory should be pushed toward the atom’s outer part. Figure 4 demonstrates a corresponding feature of the proton’s quarks.
Another kind of information supports this conclusion. The data in Figure 4 also explain the neutron’s negative charge radius. This neutron property has been well documented [9]. The neutron’s antiquark flavor comprises a u-bar more than a d-bar, and the u-bar holds an electric charge of − 2 / 3 , whereas the d-bar has a charge of + 1 / 3 . This issue explains the neutron’s negative charge radius because, as explained above, antiquarks are located farther away from the neutron’s center.
The analogous isospin phenomenon was also found in the proton. In the proton, the dominant antiquark flavor is a d-bar, which holds an electric charge of + 1 / 3 . Indeed, in 2001, the periphery of the proton was found to tend to have a more positive charge than expected [29]. For example, Kees de Jager of the Jefferson Lab said, “Charge may actually increase with distance from the center at certain radiuses” [30].

8. Radius and Mass of Electron States and Quark Systems

Let us compare the qualitative properties of the mass–energy dependence on the radius of electrons’ bound states with the corresponding data for quarks’ states (see Table 4). Several particles are examined.
Table 4 shows the mass and radius of two-body systems. The last row shows heavier particles. It indicates that the particle’s radius decreases with an increase in mass. The electromagnetic data of the positronium and the hydrogen atom are derived from the well-established quantum theory (see, e.g., [31]). In the first row, the π + is analogous to the positronium because both are particle–antiparticle-bound states of electron–positron and u-and-d-quark–antiquark pairs. The mass of each particle’s components is practically the same. In the last row, the hydrogen atom is analogous to K + because one component of the bound pair is significantly more massive than that of the other. In conclusion, a comparison of the table’s rows proves that the radius of heavier particle decreases with an increase in the components’ mass. This aspect represents another similarity between electromagnetic and strong interactions.

9. Summary

This article has discussed more than two dozen pairs of analogous phenomena in the electromagnetic and strong interaction domains. Each pair’s electromagnetic phenomenon is well explained by electrodynamics of quantum systems, but the literature indicates that the theoretical explanation of its strong-interaction companion is unclear in many cases. Many of these similarities have surprised physicists. Some are regarded as open problems even today, while others are still “under the radar” and not discussed, though all the phenomena introduced in this paper have been known for many years. Table 5 summarizes this work and presents pairs of corresponding electromagnetic and strong-interaction effects.
Physicists’ comments about these issues are interesting to read.
  • When Wilczek wondered why the proton and the neutron of the deuteron do not merge into one particle, he stated, “Ironically, from the perspective of QCD, the foundations of nuclear physics appear distinctly unsound” [33].;
  • Londergan recalled the mid-1970s findings that quarks did not carry all of the proton’s momentum: “A major surprise occurred with the quantitative understanding of the distribution of the proton’s momentum” [34].;
  • Some physicists consider the strong CP problem “the most underrated puzzle in all of physics” [35] or “one of the three greatest problems plaguing the general realm of particle physics” [36].;
  • The EMC effect has also surprised physicists: “The results are in complete disagreement with the calculations... We are not aware of any published detailed prediction presently available which can explain the behaviour of these data” [7]. This effect remains puzzling today [37].;
  • Physicists were stunned by the proton spin crisis: “In 1988, however, physicists were shocked to find experimental evidence suggesting that very little—perhaps none—of the proton’s spin comes from the spin of the quarks” [38].;
  • Physicists were also surprised by the proton charge distribution: “The new findings come as a shock to nuclear and particle physicists who have considered this aspect of the proton to be well understood for more than a half century” [30].;
Other phenomena have been mentioned in the past, but they have not received the attention they deserve. Examples of these phenomena are the hard photons’ interactions with quarks, the location of the antiquark in the proton’s peripheral region, and the significance of the elastic proton–proton cross section in very high energy.
This paper shows an outstanding similarity between electromagnetic and strong interaction effects, many of them are considered as open problems. I believe that this analogy sheds new light on these problems and calls for new ideas to solve them.

Funding

This research received no external funding

Data Availability Statement

The datasets generated during and/or analyzed in the present study are available upon request from the corresponding author.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Gamow, G. Zur Quantentheorie des Atomkernes. Zeitschrift für Physik 1928, 51, 204–212. [Google Scholar] [CrossRef]
  2. Krane, K.S. Introductory Nuclear Physics. Wiley, New York 1988.
  3. Aziz, R.A.; Slaman, M.J. The argon and krypton interatomic potentials revisited. Mol Phys. 1986, 58, 679–697. [Google Scholar] [CrossRef]
  4. Wong, S.S.M. Introductory Nuclear Physics. Wiley, New York 1998.
  5. Pendry, J.B. The electronic structure of liquids. J. Phys. C 1980, 13, 3357–3368. [Google Scholar] [CrossRef]
  6. Zhang, Y.; Xu, Z. Atomic radii of noble gas elements in condensed phases. American Mineralogist 1995, 80, 670–675. [Google Scholar] [CrossRef]
  7. Aubert, J.J. The ratio of the nucleon structure functions F2N for iron and deuterium. Phys. Lett. 1983, 123B, 275–278. [Google Scholar] [CrossRef]
  8. Perkins, D.H. Introduction to High Energy Physics. Addison, Menlo Park CA 1987.
  9. Zyla, P.A. The Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 083C01. [Google Scholar]
  10. Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields. Amsterdam, Elsevier 2005.
  11. Jackson, J.D. Classical Electrodynamics. John Wiley, New York 1975.
  12. Bauer, T.H.; Spital, R.D.; Yennie, D.R.; and Pipkin, F. M. The hadronic properties of the photon in high-energy interactions. Rev. Mod. Phys. 1978, 50, 261–438. [Google Scholar] [CrossRef]
  13. Bjorken, J.D.; Drell, S.D. Relativistic Quantum Mechanics. McGraw-Hill, New York 1964.
  14. Ellis, J.R.; Karliner, I. Measuring the Spin of the Gluon in e+e- Annihilation. Nucl. Phys. B 1979, 148, 141–147. [Google Scholar] [CrossRef]
  15. Brandelik, R. Evidence for a spin-1 gluon in three-jet events. Phys. Lett. B 1980, 97, 453–458. [Google Scholar] [CrossRef]
  16. Cheng, H.Y. The strong CP problem revisited. Phys. Rep. 1988, 158, 1–89. [Google Scholar] [CrossRef]
  17. Primakoff, H.; Rosen, S.P. Baryon number and lepton number conservation laws. Ann. Rev. Nucl. Part. Sci. 1981, 31, 145–192. [Google Scholar] [CrossRef]
  18. Goldhaber, M. Search for Nucleon Instability (Origin and History). Proceedings of International Workshop, Oak Ridge, US 1996.
  19. Kamyshkov, Y. Nucleon Instability and (B-L) non-conservation. Proceedings of the International Workshop on Next Generation Nucleon Decay and Neutrino Detector, Stony Brook 1999.
  20. Antchev, G. First measurement of elastic, inelastic and total crosssection, at s=13 TeV by TOTEM and overview of cross-section data at LHC energies. Eur. Phys. J. C 2019, 79, 1–10. [Google Scholar] [CrossRef]
  21. Broilo, M.; Fagundes, D.A.; Luna, E.G.S.; Peláez, M. Soft Pomeron in light of the LHC correlated data. Phys. Rev. D 2021, 103, 014019. [Google Scholar] [CrossRef]
  22. Condon, E.U.; Shortley, G.H. The Theory of Atomic Spectra. Cambridge University Press, Cambridge 1964.
  23. Weiss, A.W. Configuration Interaction in Simple Atomic Systems. Phys. Rev. 1961, 122, 1826–1836. [Google Scholar] [CrossRef]
  24. Ashman, J. A Measurement of the Spin Asymmetry and Determination of the Structure Function g1 in Deep Inelastic Muon-Proton Scattering. Phys. Lett. B 1988, 206, 364–370. [Google Scholar] [CrossRef]
  25. Zheng, X. Precision Measurement of the Neutron Spin Asymmetry A1n and Spin-Flavor Decomposition in the Valence Quark Region. Phys. Rev. Lett. 2004, 92, 012004. [Google Scholar] [CrossRef]
  26. Landau, L.D.; Lifshitz, E.M. Quantum Mechanics. Pergamon, London 1959.
  27. Aad, G. Determination of the parton distribution functions of the proton using diverse ATLAS data from pp collisions at s = 7, 8 and 13 TeV. Eur. Phys. J. C 2022, 82, 1–70. [Google Scholar]
  28. Thomson, M. Modern Particle Physics. Cambridge University Press, Cambridge 2013.
  29. Gayou, O. Measurements of the elastic electromagnetic form factor ratio μpGEp/GMp via polarization transfer. Phys. Rev. C 2001, 64, 038202. [Google Scholar] [CrossRef]
  30. Weiss, P. New probe reveals unfamiliar inner proton. Science News 2001, 159. [Google Scholar] [CrossRef]
  31. Griffiths, D. Introduction to elementary particles. Wiley-VCH, Weinheim 2008.
  32. https://en.wikipedia.org/wiki/Atomic_radius#Empirically_measured_atomic_radius.
  33. Wilczek, F. Hard-core revelations. Nature 2007, 445, 156–157. [Google Scholar] [CrossRef] [PubMed]
  34. Londergan, J.T. Nucleon resonances and quark structure. Int. J. Mod. Phys. 2009, 18, 1135–1165. [Google Scholar] [CrossRef]
  35. Siegel, E. The Strong CP Problem is the Most Underrated Puzzle in All of Physics. https://www.forbes.com/sites/startswithabang/2019/11/19/the-strong-cp-problem-is-the-most-underrated-puzzle-in-all-of-physics/?sh=389b95771ea7.
  36. Strassler, M. C, P, T (And Their Combinations). https://profmattstrassler.com/articles-and-posts/particle-physics-basics/c-p-t-and-their-combinations/.
  37. Higinbotham, D.; Miller, G.A.; Hen, O.; Rith, K. The EMC effect still puzzles after 30 years, CERN courier. https://cerncourier.com/a/the-emc-effect-still-puzzles-after-30-years/.
  38. Peterson, I. Proton-Go-Round, Whence does the proton get its spin? Science News 1997, 152, 158–159. [Google Scholar] [CrossRef]
Preprints 106896 g001
Figure 1. Systems of noble atoms in a liquid and nucleons in a nucleus.
Figure 1. Systems of noble atoms in a liquid and nucleons in a nucleus.
Preprints 106896 g001
Preprints 106896 g002
Figure 2. (a) Potential vs. distance between two argon atoms. (b) Potential vs. distance between two nucleons.
Figure 2. (a) Potential vs. distance between two argon atoms. (b) Potential vs. distance between two nucleons.
Preprints 106896 g002
Preprints 106896 g003
Figure 3. (a) Proton−proton total and elastic cross−section vs. energy (the old data). (b) Total and elastic cross−section vs. energy (new data). (c) Ratio between elastic and total cross−section vs. energy (new data).
Figure 3. (a) Proton−proton total and elastic cross−section vs. energy (the old data). (b) Total and elastic cross−section vs. energy (new data). (c) Ratio between elastic and total cross−section vs. energy (new data).
Preprints 106896 g003
Preprints 106896 g004
Figure 4. Bjorken-x dependence of momentum distribution of the nucleon’s quarks and antiquarks .
Figure 4. Bjorken-x dependence of momentum distribution of the nucleon’s quarks and antiquarks .
Preprints 106896 g004
Table 1. Analogous physical objects.
Table 1. Analogous physical objects.
Electromagnetic domain Strong Interaction domain
Liquid drop Nucleus
Atoms (in particular, noble atoms with several electronic shells) Nucleons (proton, neutron)
Electrons Quarks
Electromagnetic fields Strong fields
Table 2. Fundamental differences between the theories describing electromagnetic systems and strong interaction systems.
Table 2. Fundamental differences between the theories describing electromagnetic systems and strong interaction systems.
Electromagnetic domain: Electromagnetic theory and quantum mechanics Strong interaction domain: Quantum Chromodynamics
Group U(1) (commutative) Group SU(3) (non-commutative)
An electric charge can take a negative or positive value A strong charge has three positive or three negative colors
Charges of the same sign repel each other; charges of opposite signs attract each other In nucleons, quarks of the same color attract each other
The force between the two electrically charged particles declines with an increase in the distance between them The coefficient of the strong force increases with an increase in distance (this feature is called “asymptotic freedom”).
Atoms contain a massive core beside the valence electrons. The core comprises the nucleus and closed shells of electrons. Nucleons do not contain massive elements besides the three valence quarks and quark–antiquark pairs
Table 3. The three interactions’ fundamental properties.
Table 3. The three interactions’ fundamental properties.
Process Electromagnetic interactions Strong interactions Weak interactions
P (parity transformation) Conserved Conserved Not Conserved
C (charge conjugation) Conserved Conserved Not Conserved
CP Conserved Conserved Not Conserved
Flavor Conserved Conserved Not Conserved
Interaction with photons* Exists Exists Does not exist
* The interaction with photons was mentioned in the previous section. It is included here for clarity.
Table 4. Data of electronic systems [31,32] and quark systems [9].
Table 4. Data of electronic systems [31,32] and quark systems [9].
Electrically bound particles Strongly bound particles
Particle Mass (MeV) Radius (pm) Particle Mass (MeV) Charge radius (fm)
Positronium 1.022 106 Pion ( π + ) 140 0.66
Hydrogen atom 938.783 53 K + 494 0.56
Table 5. Summary of corresponding electromagnetic and strong-interaction effects.
Table 5. Summary of corresponding electromagnetic and strong-interaction effects.
No. Electromagnetic effect Strong interaction effect See section
1 If atoms are far from each other, then there is no force between them If nucleons are far from each other, then there is no force between them 2
2 If noble atoms in a liquid drop come closer to each other, then there is an attractive force between them (the van der Waals force) If two nucleons are close to each other, then there is an attractive force between them (the strong nuclear force) 2
3 The volume of a liquid drop is proportional to the number of molecules in the liquid The volume of a nucleus that is not too light is proportional to the number of nucleons 2
4 Atoms do not merge into a larger atom in chemical processes In nuclear processes, nucleons do not merge into a larger, strongly bound particle 2
When depicting the force between two noble gas
5 atoms, the graph of potential vs. distance is 2
similar to the corresponding graph between
nucleons (see Figure 2 a and b)
6 The electronic radius of an atom inside a liquid drop exceeds the electronic radius of a free atom of the same kind Nucleonic quarks inside a nucleus have a larger volume than free nucleons (the EMC effect) 2
7 An electron is a point-like particle A quark is a point-like particle 3
8 An electron has a spin of 1 / 2 A quark has a spin of 1 / 2 3
9 Electrons are attracted to their antiparticles Quarks are attracted to their antiparticles 3
10 Positronium is a bound particle of an electron and a positron π 0 is the lightest neutral bound particle of u-and-d quarks with their antiparticle 3
11 The spin and parity J π = 0 − state of the positronium decays into two photons The spin and parity J π = 0 − state of π 0 decays into two photons 3
13 The electromagnetic collision of charges emits radiation—namely, photons (bremsstrahlung High-energy electron–positron collisions produced a third particle (the three-jet event) 3
14 The photon’s spin and parity are J π = 1 − In the three-jet event, the spin of the third particle is also 1 3
15 Electromagnetic interactions conserve parity Strong interactions conserve parity 4
16 Electromagnetic interactions obey charge conjugation Strong interactions obey charge conjugation (the strong CP problem) 4
17 Electromagnetic interactions conserve flavor Strong interactions conserve flavor 4
18 In chemical processes, the number of atoms is conserved In all interactions, the number of baryons is conserved 4
19 In atoms, valence electrons do not carry the entire atomic mass In nucleons, quarks do not carry the entire nucleonic mass 5
20 The mass of the positronium is much less than the mass of any atom The mass of a pion is much less than the nucleon’s mass 5
21 Atoms contain massive elements, aside from valence electrons Nucleons contain massive elements, aside from quarks (the pomeron idea pertains to this effect) 5
22 The binding energy of an electron in the positronium’s lowest state exceeds that of a valence electron in atoms that contain several electronic shells The binding energy of a quark in a pion is greater than that of a quark in a proton 5
23 The vectorial sum of the valence electrons’ spins in a many-electron atom is much less than the atom’s total angular momentum The vectorial sum of the quark spins is much less than that of the proton spins (the proton spin crisis) 6
24 In atoms, electrons carry orbital angular momentum In nucleons, quarks carry orbital angular momentum 6
25 Valence electrons in atoms with several electronic shells prefer configurations with parallel spins (the Hund law) Quarks in baryons, such as Δ (1232) and Ω − , prefer configurations with parallel spins 6
26 The electron tends to be found closer to the atomic center Quarks tend to be found closer to the proton center (the exponential decrease in the proton’s electromagnetic form factors) 7
27 The positron (of a QFT additional electron–positron pair) tends to be farther away from the atomic center Antiquarks tend to be farther away from the nucleonic center 7
28 The radius of positronium is larger than that of a hydrogen atom, which has a greater mass The radius of pion π + is larger than that of K + , which has a larger mass 8
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

93

Views

33

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated