Submitted:
15 May 2024
Posted:
15 May 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
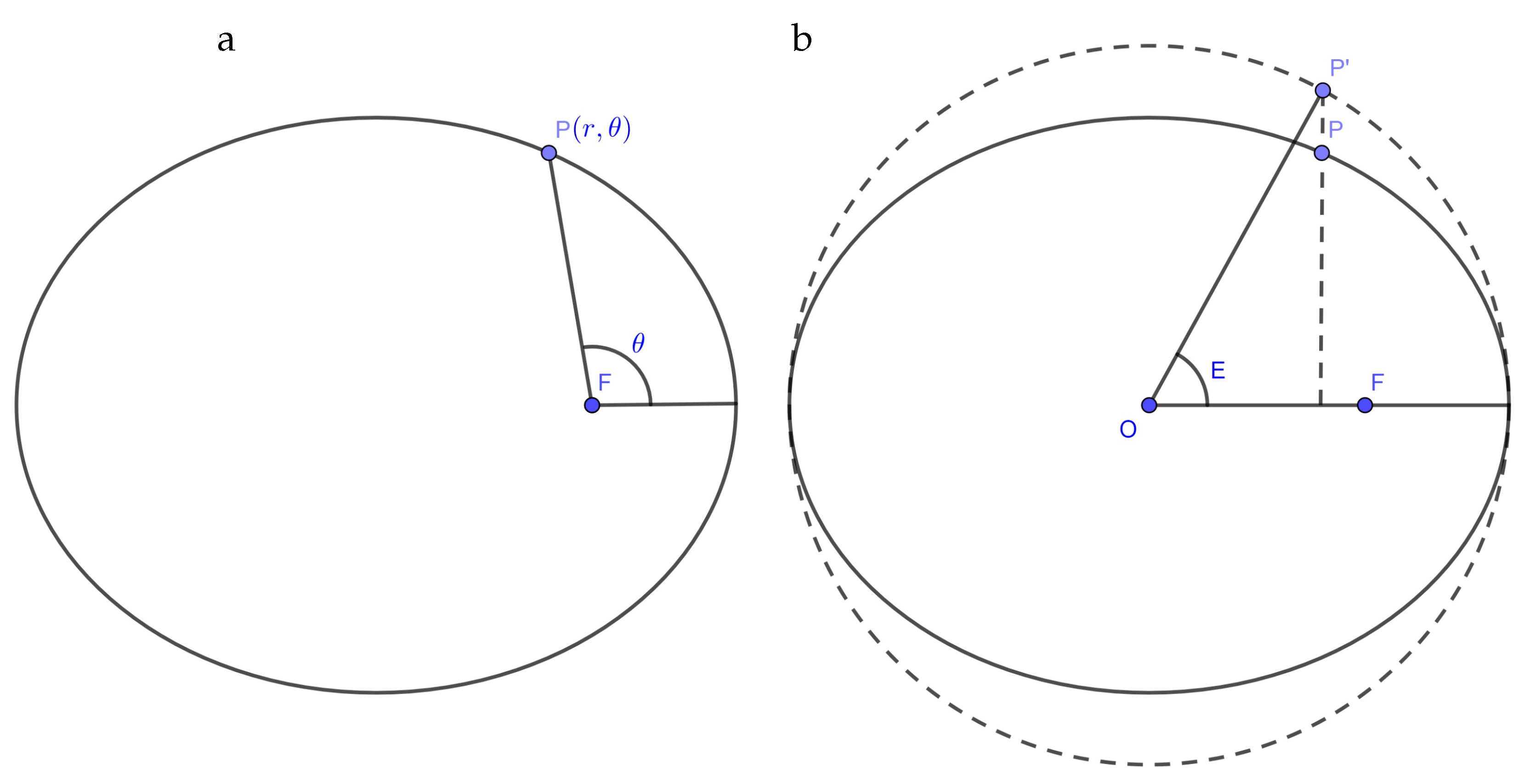
1.1. The Orbit Equation
2. Methodology
2.1. Step 0
2.2. Step 1
2.3. Step 2
2.4. Step 3
2.4.1. Method A
2.4.2. Method B
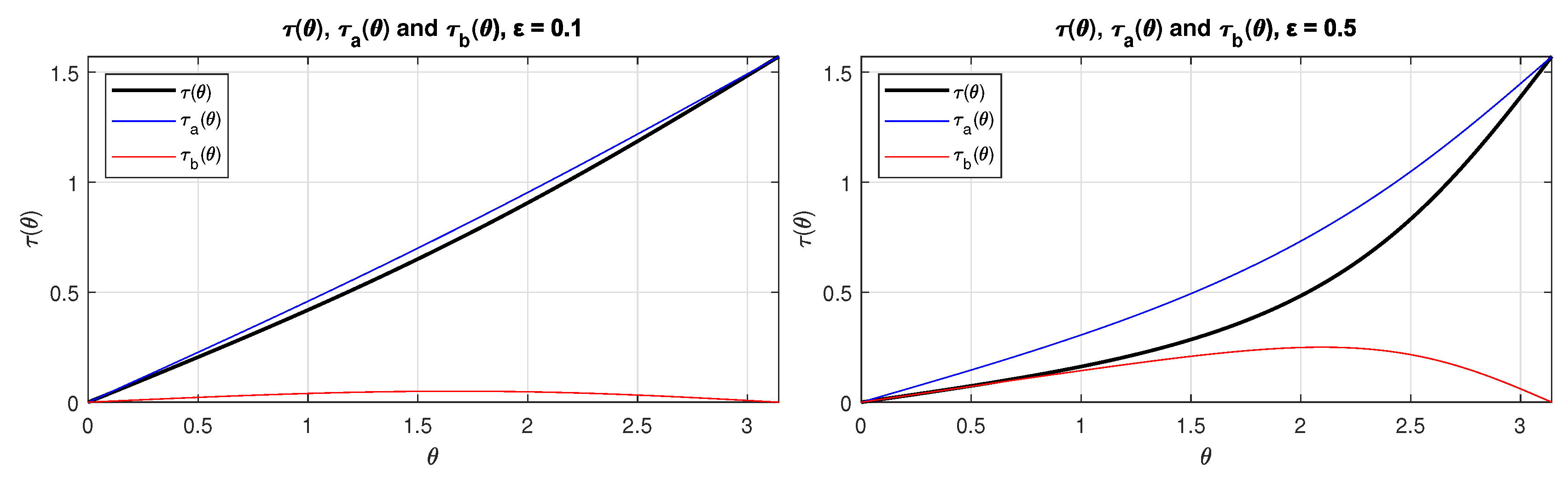
3. Results
3.1. Method A
3.2. Method B
3.3. Equations of Motion for the Planets
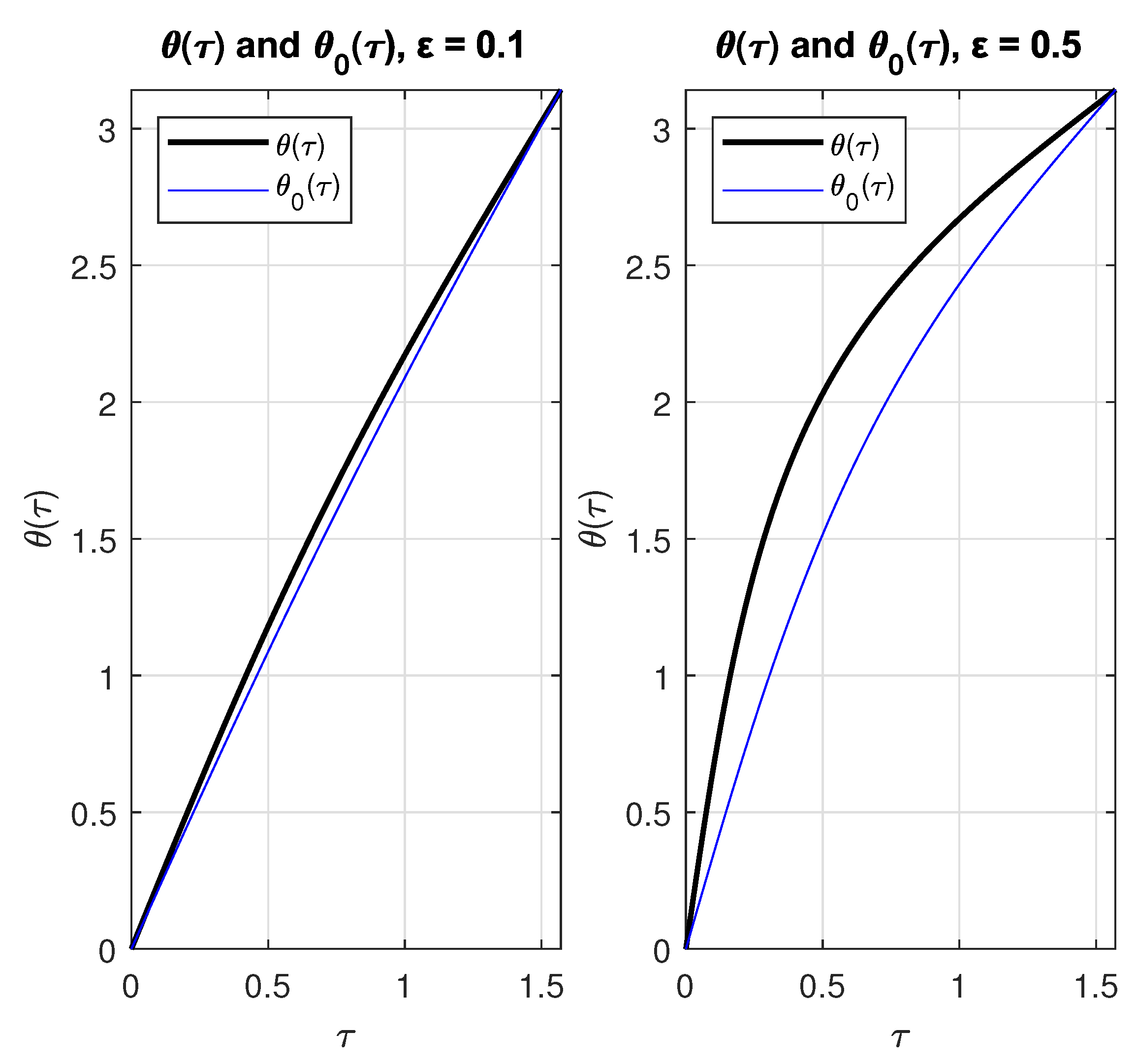
4. Solution to Kepler’s Equation
5. Remarks and Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Appendix A. Integration of Eq. (1)
Appendix B. Proofs of limits Eq. (18) and Eq. (19)
References
- K. Krisciunas, Demonstrating the elliptical orbit of Mars using naked eye data, Am. J. Phys. (2019). [CrossRef]
- H. Goldstein, Classical Mechanics, 2nd ed. Addison-Wesley, Reading. (2020).
- W. Baisheng, Y. Zhou, C. Lim and H. Zhong, A new solution approach via analytical approximation of the elliptic kepler equation, Acta Astronautica (2023). [CrossRef]
- P. Colwell, Solving Kepler’s Equation over Three Centuries, Willman-Bell, Inc., Richmond (1993).
- L. D. Landau and E. M. Lifshitz, Mechanics, 3rd ed. Elsevier Butterworth-Heinemann, Burlington (1976).
- A. W. Odell and R. H. Gooding, Procedures for solving Kepler’s equation, Cel. Mech. (1986).
- O. González-Gaxiola and S. Hernández-Linares, An Efficient Iterative Method for Solving the Elliptical Kepler’s Equation, Int. J. Appl. Comput. Math (2021). [CrossRef]
- G. G. Elenin and T. G. Elenina, Parametrization of the Solution of the Kepler Problem and New Adaptive Numerical Methods Based on This Parametrization, Diff Equat (2018). [CrossRef]
- F. L. Markley, Kepler Equation solver, Celestial Mech Dyn Astr (1995). [CrossRef]
- A. Simha, An algebra and trigonometry-based proof of Kepler’s first law, Am. J. Phys. (2021). [CrossRef]
- M. Zheng, J. Luo and Z. Dang, Machine learning-based solution of Kepler’s equation, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series (2022). [CrossRef]
- R. W. Easton, R. L. Anderson and M. W. Lo, Conic transfer arcs for Kepler’s problem, Am. J. Phys. (2022). [CrossRef]
- M. Calvo, A. Elipe and L. Rández, On the integral solution of elliptic Kepler?s equation, Celest. Mech. Dyn. Astron. (2023). [CrossRef]
- F. Orlando, C. Farina de Souza, C. Zarro and P. Terra, Kepler’s equation and some of its pearls, Am. J. of Phys. (2018). [CrossRef]
- J. B. Marion, Kepler’s equation and some of its pearls, Academic Press Inc. 1st Edition (1965).
- S. A. Mikkola, A cubic approximation for Kepler’s equation, Cel. Mech. (2018). [CrossRef]
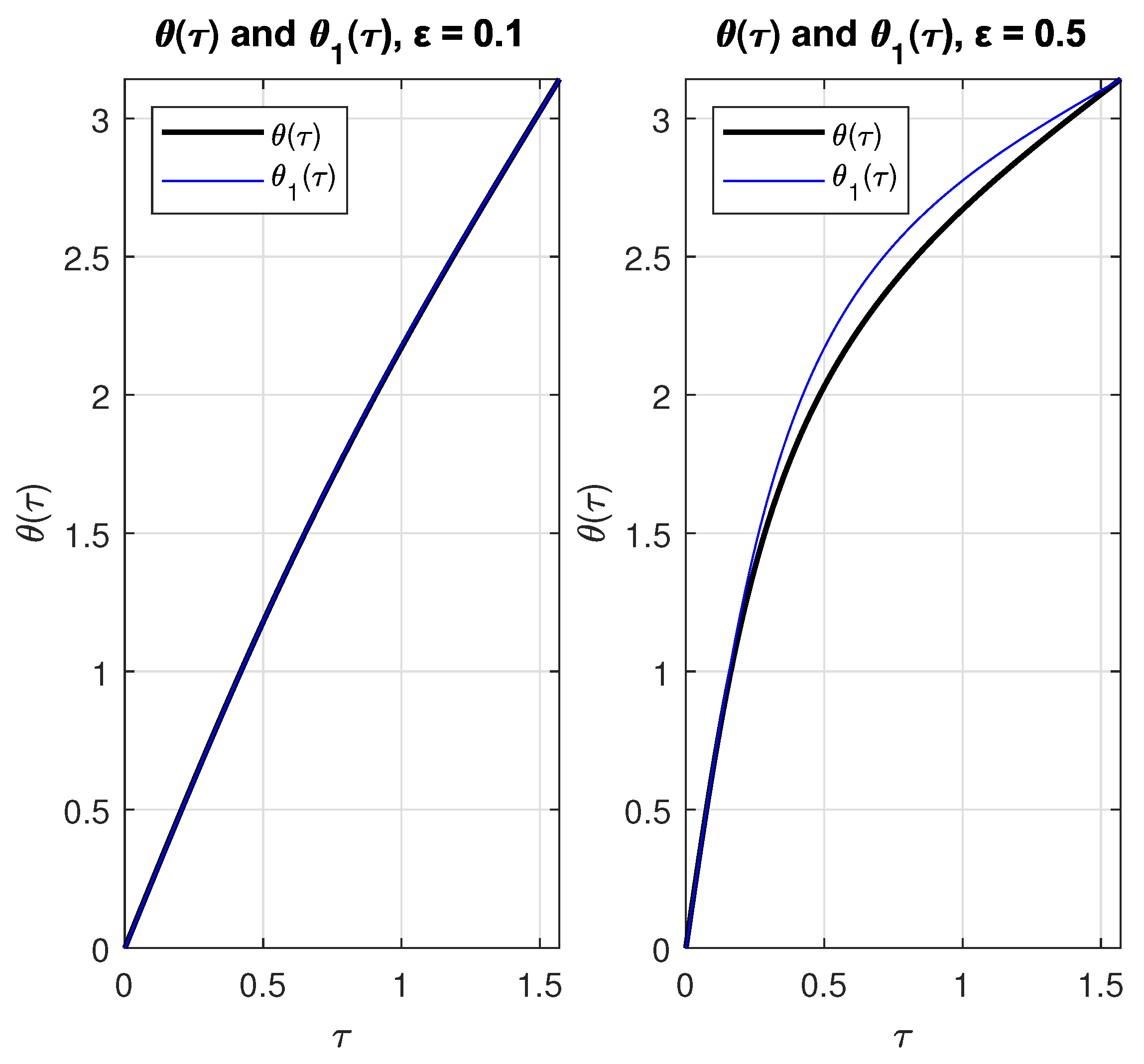
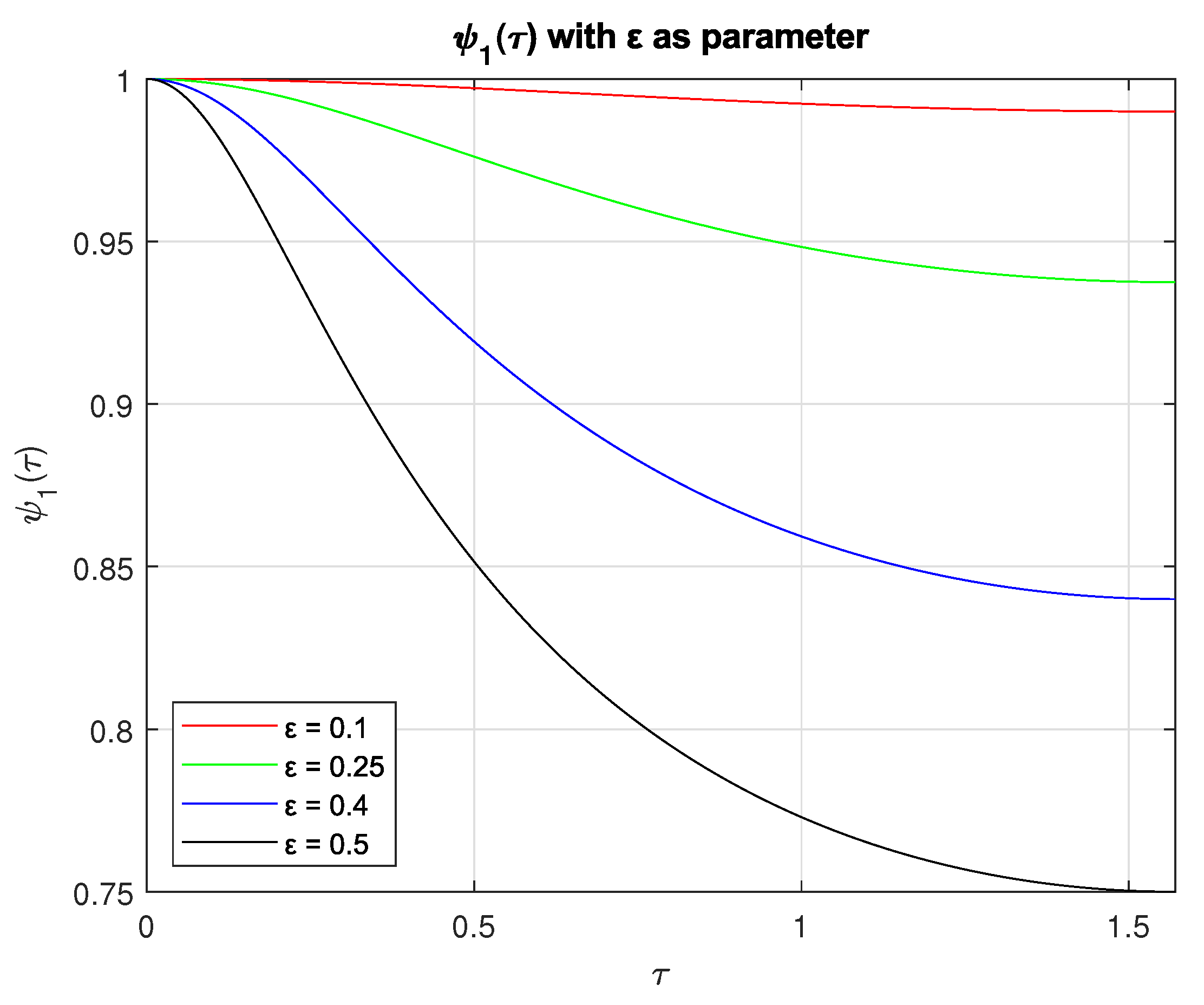
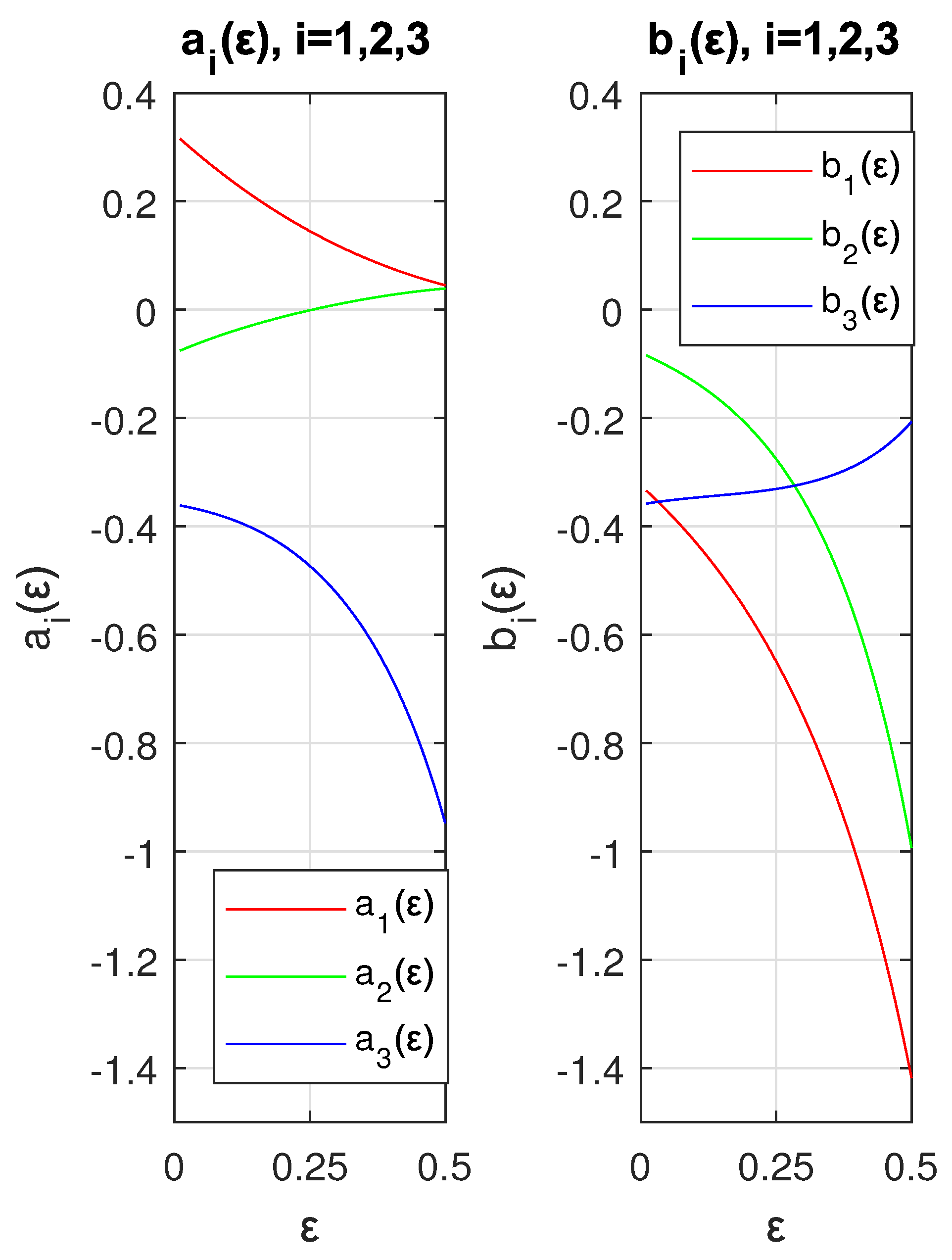
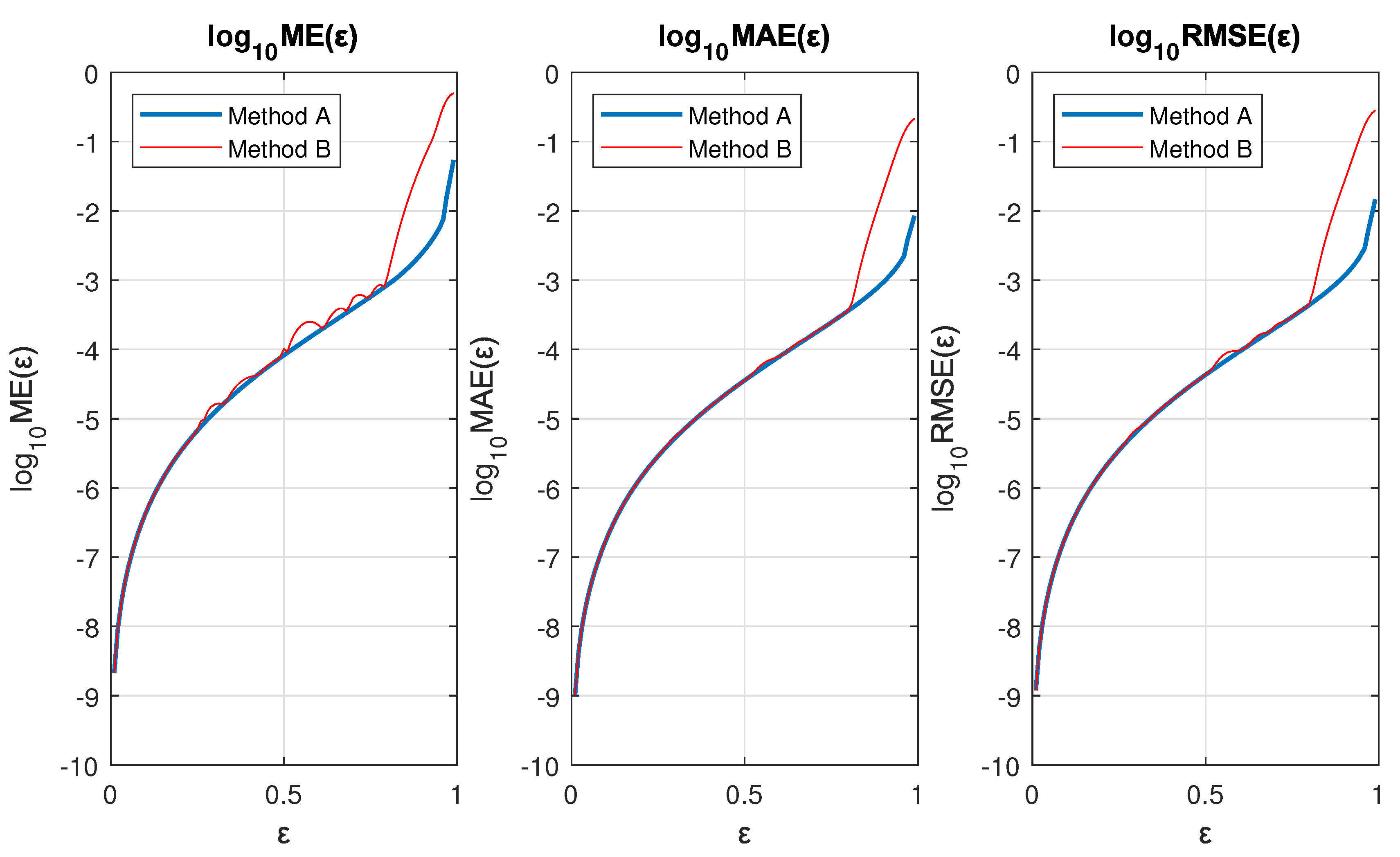
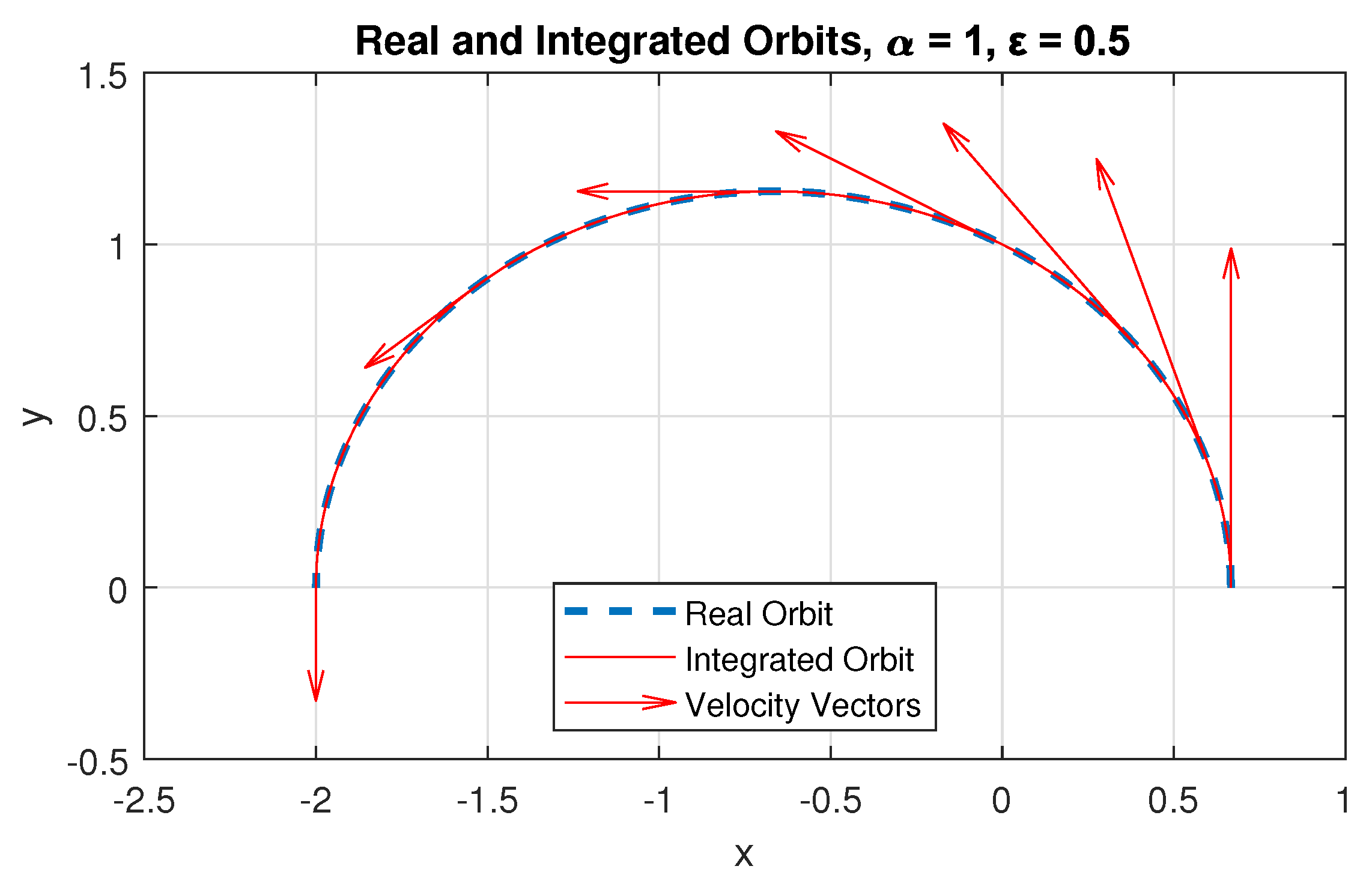
| Planet | ME | MAE | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Earth | 0.0167 | 0.310 | -0.073 | -0.363 | -0.340 | -0.087 | -0.357 | |||
| Pluto | 0.2488 | 0.146 | -0.001 | -0.472 | -0.647 | -0.274 | -0.331 |
| Mercury | Venus | Earth | Mars | Jupiter | Saturn | Uranus | Neptune | Pluto | |
|---|---|---|---|---|---|---|---|---|---|
| 0.2056 | 0.0067 | 0.0167 | 0.0935 | 0.0489 | 0.0565 | 0.0457 | 0.0113 | 0.2488 | |
| 0.17053517 | 0.31862395 | 0.30977503 | 0.24694331 | 0.28234256 | 0.27609996 | 0.28499728 | 0.31453377 | 0.14561949 | |
| -0.01166110 | -0.07705003 | -0.0728542 | -0.04432541 | -0.06014655 | -0.05731287 | -0.06135776 | -0.07510434 | -0.0012376 | |
| -0.43861374 | -0.36086494 | -0.36274460 | -0.38289299 | -0.36985666 | -0.37179675 | -0.36907139 | -0.36171170 | -0.47217706 | |
| -0.57282655 | -0.33074668 | -0.34005421 | -0.42023391 | -0.37170483 | -0.37957121 | -0.36843946 | -0.33499871 | -0.64694223 | |
| -0.22240872 | -0.08288098 | -0.08742593 | -0.12920751 | -0.10334339 | -0.10741403 | -0.10166725 | -0.08494978 | -0.27396065 | |
| -0.33681377 | -0.35855961 | -0.35697508 | -0.34764211 | -0.35253989 | -0.35161930 | -0.35294044 | -0.35781706 | -0.33108759 | |
| ME | |||||||||
| MAE | |||||||||
| RMSE | |||||||||
| 208 | 0.11 | 0.92 | 80 | 52 | 131 | 163 | 12 | 39,000 |
| Range of | (0,0.1] | (0.1,0.25] | (0.25,0.5] | (0.5,0.7] | (0.7,1.0) |
|---|---|---|---|---|---|
| 0.32464090 | 0.32455984 | 0.32493519 | 0.33117795 | 0.34799892 | |
| -0.90342437 | -0.90136299 | -0.90443788 | -0.94434644 | -1.02378174 | |
| 0.79798292 | 0.77956682 | 0.78688870 | 0.87179816 | 0.99672027 | |
| -0.24897861 | -0.19074605 | -0.19470806 | -0.25486105 | -0.32027157 | |
| -0.07992819 | -0.07920359 | -0.07197522 | -0.06646582 | -0.11098658 | |
| 0.43404410 | 0.41648507 | 0.33665965 | 0.29615322 | 0.50088661 | |
| -0.64017363 | -0.49188569 | -0.19208276 | -0.09396227 | -0.40748236 | |
| 0.75341116 | 0.31132787 | -0.07256170 | -0.15093252 | 0.00894242 | |
| -0.35968044 | -0.35742442 | -0.15675162 | 6.29837377 | 154.50791377 | |
| -0.17220655 | -0.22278632 | -2.20357719 | -41.92862343 | -715.24316797 | |
| -0.64666864 | -0.26055305 | 6.28024901 | 87.40520959 | 1105.82612363 | |
| -1.78408496 | -2.80408480 | -10.06884121 | -65.08749455 | -577.96129585 | |
| -0.32463507 | -0.32142203 | -0.09294215 | 6.21933680 | 138.39317241 | |
| -0.90434048 | -0.97722350 | -3.24616805 | -42.18802414 | -643.15766068 | |
| -1.11071449 | -0.54525397 | 7.00356134 | 86.74796714 | 996.53861794 | |
| -1.63153199 | -3.15712303 | -11.61829996 | -65.86504267 | -524.44755555 | |
| -0.07992299 | -0.07527391 | 0.29080466 | 11.97863173 | 287.23614950 | |
| -0.43571269 | -0.54094614 | -4.16198706 | -76.07319110 | -1326.12648115 | |
| -0.78063318 | 0.03353877 | 12.02291626 | 158.84151291 | 2048.91985911 | |
| -2.10660888 | -4.29567159 | -17.65734989 | -117.20310761 | -1068.68369232 | |
| -0.35968350 | -0.36025835 | -0.44346730 | -3.54853992 | -81.17535211 | |
| 0.17171182 | 0.18402819 | 0.99888552 | 20.06864682 | 372.42195877 | |
| -0.59524043 | -0.68312683 | -3.34688052 | -42.20159066 | -574.67488149 | |
| 1.45594036 | 1.66666199 | 4.58818969 | 30.87266047 | 298.77577747 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





