Prerpints.org logo
Preprint
Article

Revolutionizing Quantum Computing: Essence-Units and Energy States as Fundamental Programming Units

This version is not peer-reviewed.

Submitted:

08 May 2024

Posted:

10 May 2024

Read the latest preprint version here

Abstract
Harnessing Quantum Energy States for Unprecedented Computing Capabilities In this proposal, we advocate for the use of energy states as fundamental units of quantum computer programming. Each unit of programming is conceptualized as an energy state, manifested as an essence-unit. An essence-unit, defined as the minimal form encapsulating complete uniqueness or specificity, serves as the cornerstone of this paradigm. This approach enables the recording of various forms of matter on quantum computers in essence-units, portraying their energy states. The recording of energy states is achieved through the creation of four distinct coherent potentials, facilitated by quantum dots or crystals. Crucially, these energy states embodied in essence-units resist subdivision. The study explores the intricate relationship among similarity, fractals, and uniqueness in quantum dot operations, revealing their profound implications for information transfer efficiency. Normalized entropy characterizes charge localized in quantum dot impurities in systems that have distortions. Through the utilization of N-level recording and entropy-fractal dimension equivalence, the paper elucidates the potential of quantum dots in reducing transmission time and modeling complex systems. The proposed methodology signifies a paradigm shift in quantum computing, presenting unparalleled possibilities for tackling hitherto insurmountable challenges.
Keywords: 
quantum dot
;  
Tsalllis entropy
;  
Renyi entropy
;  
quantum computer
;  
fractal dimension
;  
distortion model
;  
information processing unit
;  
energy state
Subject: 
Computer Science and Mathematics  -   Other

Introduction

Quantum computing's unparalleled speed promises a transformative leap in computational capabilities [1,2]. The current representation of qubit programming showcases both the potential and limitations of quantum computers [3,4]. The potential of quantum computing is underscored by the ability to record qubit states, despite the challenges of spin superposition and scaling uncertainties [5]. The development of quantum computers, with a limited number of qubits, necessitates precision and scalability, highlighting the need for a large number of qubits working cohesively [6]. The coherent manipulation of superconducting spin qubits and the potential for quantum supremacy with superconducting qubits further underscore the potential of these technologies [7,8]. The challenges of scaling quantum computers, such as qubit connectivity and gate expressivity, are also highlighted [9]. Despite this, the effectiveness of programming with qubits for specific problems has been demonstrated [6]. Navigating the complexities of quantum computing development requires addressing key challenges, including materials limitations, network design constraints, and the need for a paradigm shift in computing foundations [10,11,12]. Addressing quantum decoherence and qubit inter-connectivity presents additional challenges [13].
This paper focuses on programming solutions utilizing quantum dots, exploiting their properties to enable n! (n factorial) possible operations [14,15,16]. The ensuing exploration delves into the potential opportunities unlocked by quantum dots, offering a promising avenue for advancing quantum computing beyond existing constraints [17]. Our approach taps into the energy interaction, simplifying the understanding of quantum entities' manifestation through their influence on each other. This article proposes a distinctive solution expressed through the energy states of quantum dots, marking a shift in programming paradigms [18].

Operation on Quantum Dots

Currently, the development of quantum computers is focused on composite quantum dots, which offer a promising path for future advancements [19]. Quantum dots possess unique properties, such as the ability to generate single photons on demand [20] and their potential use in quantum dot-based devices [21].
A compositional structure, especially one capable of transferring, trapping, or releasing electrons across inertial or N-dimensional states, offers an intriguing solution [22,23]. Imagine volumetric holographic elements where information content remains constant with increasing unit size—an N-dimensional programming unit expressed in the energy states of programming units ([24,25,26]). Leveraging properties such as dipole moment, tunnel effect, and recombination effect, each quantum dot can be represented as a dual system—one for information reception and another as a photo-luminescence emitter, forming data for the first quantum dot [24,27]. This system is one possible solution for effectively implementing our idea.

Recording Method

In our case to record data, we propose the creation of four charged centers situated on the second and third inner layers of quantum dots. These centers, characterized by polarized, coherent, or controlled (one-direction) and disordered spin states, generate electric fields that reflect the energy states of matter. The performance of essence-units is unveiled during their interaction with these electric fields.
Our novel approach involves programming energy states where the essence is a result of the superposition of electromagnetic fields created by four potentials. The unit of such recording is termed the Field of Active Recording of Nature (FARNA), representing the energy state of matter. FARNA, in essence, captures and defines this energy state. We suggest utilizing Aristotle's four causes – depth of charge profiling – as indicators of wavelength for recording. The four causes serve as a guide, allowing us to pinpoint four wavelengths that represent the energy states of essence-units. Precision in defining these values contributes to the accurate formation of energy states through charge profiling of essence units.
Central to our model is the concept of programming using essence-units as energy states recorded through four or more potentials. These potentials, represented by four points, intricately determine the unique characteristics of energy states in (at least) a three-dimensional space. The relations between these potentials define the distinctiveness of essence-units through FARNA, offering a sophisticated approach to quantum computing data encoding.

Methodology of FARNA determination

The methodology employed for FARNA determination revolves around the representation of the minimal energy state characterizing essence-units. FARNA serves as a pivotal concept, embodying the essence-unit's fundamental energy state, and its selection is integral to our approach.
In the realm of programming using essence-units, our methodology focuses on minimizing the number of permitted combinations, thereby streamlining the programming process and drastically enhancing execution speed. The resulting array with significantly restricted values compared to their initial counterparts encompassed all possible combinations of subject values. The efficiency gained through this minimization is paramount for computational efficacy.
Our proposed methodology enables the recording of energy states for any essence-unit. These energy states are elucidated through four bound potentials, each creating specific electromagnetic fields that represent the essence-unit's energy states. To capture these potentials, we employ wavelengths ranging from 390 to 730 nanometers, encompassing (390-410nm), (415-435nm), (440-480nm), (495-515nm), (515-545nm), (550-575nm), 580-605nm), (610-635nm), (640-680nm), (690-730nm). This wavelength range is strategically chosen to align with the properties of essence-units and optimize the recording process.

Recording a Cat's Energy State using FARNA

A child effortlessly recognizes a cat in a book or on the street without needing intricate details about its breed or habits. This simplicity arises from the cat itself forming a unique essence-unit characteristic in the visible range when observed. Unlike breaking down the cat into numerous small squares, our volumetric sensing and recording approach save substantial energy by treating each new cat as a distinct object identification.
In this discussion, we adhere to general principles, focusing on the recording of the energy state of Aristotle's conventional cat, not Schrödinger's cat in a box. Aligning with Aristotle's four causes – Material, Formal, Efficient, and Final – we aim to link these causes to four potentials, graded on a scale from 1 to 10 to determine the accuracy of our definition.

Potentials Grading and Programming FARNA

We grade the potentials associated with 10-(390-410nm), 9-(415-435nm), 8-(440-480nm), 7-(495-515nm), 6-(515-545nm), 5-(550-575nm), 4-(580-605nm), 3-(610-635nm), 2-(640-680nm), 1-(690-730nm) on a scale of 1 to 10, representing the causes (Material, Formal, Efficient, Final). The programming of FARNA, expressed as (2 4 5 7), generates four waves corresponding to the potentials.

Quantum Dots and Charge Localization:

Quantum dots play a crucial role in this process, containing electron traps where charge localization occurs, forming the potentials. To determine the charge's value, we calculate the time of exposure to the irradiation of an electron beam. The resulting time values are then scaled from 0.1 to 0.9, with FARNA values correlating to the time of exposure: 2 corresponds to 0.8, 4 to 0.6, 5 to 0.5, and 7 to 0.3.

Properties of Similarity, Fractals, and Uniqueness in Quantum Dot Operations

The interplay of three fundamental properties – similarity, fractals, and uniqueness – offers a realm of possibilities for quantum dot operation and control. The structural similarities inherent in quantum dots grant them identical properties. Leveraging N-level recording at a singular point facilitates instantaneous transference of these properties to all other similar points or selectively to designated ones. This remarkable capability results in a significant reduction in time for information transfer, surpassing traditional methods that involve transmitting entire arrays.
In [28] it was demonstrated that the ratio of actual entropy to the maximum entropy is equal to the ratio of actual fractal dimension to the maximum fractal dimension.
Characteristic value of the corresponding spatial entropy defines fractal dimension. Relation between entropy and generalized fractal dimension can be derived through Renyi entropy. It was shown that normalized entropy equals the normalized fractal dimension (the fractal dimension is based on box-counting method, i.e. the probability of discovering fractal elements within defined radius from the box). Entropy theory can be used to explain fractal evolution of complex systems. In particular, it can be used to determine the influence of distortion in double-cone quantum dots to model resulting quantum systems.
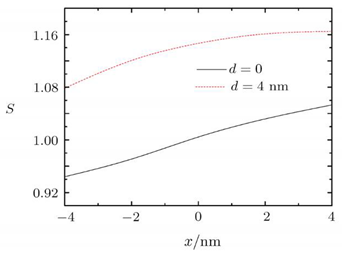
It was shown in [29] that greater impurity leads to growth of disorder in the system. To measure such a disorder Tsallis formalism was employed. Tsallis entropy is calculated as E = k 1 − ∑ i = 1 w p i q q − 1 where q is parameter connecting the Boltzmann and Gibbs entropies, ∑ i = 1 w p i = 1 , k is a constant, and pi are the probabilities of microscopic configurations, and w is total number such configurations. The results demonstrate that if distance between double-cone quantum dots increases then entropy rises. On the other side, disorder in electron movement diminishes if electrons move in direction opposite of direction of electric field. The diagram below (in [29]) shows entropy as a function of the impurity position for different values of d
Thus, entropy can be used to determine changes in electric fields under influence of impurities.
Preprints 106010 i001

Quantum Dot-Enabled Language Learning: Harnessing Structured Dynamics for Rapid Proficiency Acquisition

Consider language learning as an illustrative application. By structuring the language-learning framework at one quantum dot, the acquired form can be seamlessly transferred to another point. This novel approach allows for rapid assimilation of multiple languages, where each language is acquired or known in the shortest possible time. The efficacy of this process is contingent upon the clarity and correctness of the quantum dot's internal structure. The more precise and well-defined the energy levels, representing constraints from the minimum starting base to the maximum limit, the more robust the knowledge.
The representation of language proficiency through sub-levels within the energy structure elucidates the dynamics of language retention. A well-fixed language, with numerous sub-levels between extrema, shows a stronger and more enduring comprehension of the language. This explains why individuals tend to forget languages not used for an extended period, retaining only a minimal understanding. Conversely, a language with a meticulously constructed structure – comprising numerous near-level sub-levels – enables seamless navigation through linguistic nuances. In essence, such a highly organized system can engage in dialogue instantly, processing information without the burden of energy consumption or the need for prolonged reflection on individual words.
The stability of a highly organized and fixed quantum dot system defines the level of language proficiency, allowing for swift comprehension and response to linguistic stimuli. This innovative approach, underpinned by quantum dot properties, introduces a paradigm shift in language learning and retention.

Possibility: The Irrational Formation of the Information Processing Center – Analogous to Riding a Bike

The acquisition of certain skills, like riding a bike, often defies theoretical explanations until one engages in practical experience. Unlike language knowledge, the ability to ride a bike persists even after years of disuse. The seemingly irrational act of maintaining balance on two wheels along a straight line becomes natural through movement. The stability of two-wheeled vehicles is enhanced during motion, enabling effective maneuvering and control. In our quantum dot system, a parallel analogy can be drawn: the logical and conceivable creation of energy structures on a quantum dot is subject to the reliability determined by the persistence of energy levels.
Similar to the fading levels in language knowledge without practice, maintaining a baseline level of knowledge in our system requires the continuous creation of new "defects" in the structure, such as connections between quantum dots. These newly formed centers act as chemical hubs, facilitating communication between clusters. If these changes are not temporary but, for instance, physically integrated aggregates or pits forming permanent defects, the alterations become ingrained in the system. Once established, these changes endure indefinitely, preserving any information recorded at the minimal knowledge level for as long as the chemical properties of the system permit.
The system thus exhibits the potential for rapid and ultra-efficient learning and information processing, whether executed rationally or irrationally. The introduction of an alteration, akin to the persistent ability to ride a bike, remains a lasting change in the system—something irremovable. The stored information, maintained at a minimum level, persists as long as the chemical properties of the entire system endure. At this stage, we confine our considerations to the limitations imposed by the speed of light.
The paper introduces the concept of irrational formation in quantum computing, drawing parallels to riding a bike. By continually creating new defects in the system, akin to chemical hubs between quantum dots, the system ensures the persistent storage of information at a minimum knowledge level. This not only enhances the learning process but also opens avenues for ultra-fast information processing.

Discussion: Revolutionizing Quantum Computing Through Quantum Dot-Based Programming

In the pursuit of advancing quantum computing, this paper explores a groundbreaking paradigm by leveraging the unique properties of quantum dots. These confined semiconductor systems, operating at the nano-scale, offer an unparalleled platform for constructing an innovative microchip structure. Quantum dots, distributed either evenly or chaotically, or even within lattice sites of crystals, present a myriad of possibilities for developing a new generation of computers.
The internal structure of quantum dots, characterized by intricate levels of covalent and valence bonds, allows for diverse energy excitations. Viewing quantum dots as homogeneous hetero-structures, comprising multiple quantum elements, introduces a multi-functional aspect to their nature. This property forms the basis for building qubits, and with each added shell, the potential number of qubits grows exponentially.

Conclusion

In conclusion, this paper presents a revolutionary approach to quantum computing, capitalizing on the distinctive properties of quantum dots. The proposed paradigm promises to redefine the landscape of computing, offering unprecedented speed, efficiency, and versatility. Essential to our model is the paradigm of programming, wherein essence-units represent energy states of any matter, recorded through four or more potentials. These potentials, represented at least by four charged points, intricately determine the unique characteristics of energy states in a three or more-dimensional space. The relations between these potentials define the distinctiveness of essence-units through FARNA, offering a sophisticated approach to quantum computing data encoding. The proposed methodology for determining the minimal energy state, FARNA (Field of Active Recording of Nature), facilitates the recording of energy states of essence-units. This method utilizes four bound potentials, representing unique characteristics of energy states in a multi-dimensional space. The methodology records these energy states through wavelengths across the electromagnetic spectrum, from deep ultraviolet to infrared.
In summary, this investigation underscores the pivotal role of similarity, fractals, and uniqueness in enhancing quantum dot operations. By leveraging insights from entropy-fractal dimension relationships and the Tsallis formalism, the study unveils new avenues for controlling disorder and optimizing information transfer in quantum systems. These findings not only contribute to advancing our understanding of quantum dot dynamics but also pave the way for innovative applications in various technological domains. The potential applications are vast, ranging from language processing to rapid learning, making this paradigm a promising avenue for the future of quantum computing. Rigorous experimentation and further research are essential to validate and refine the proposed concepts, paving the way for a quantum leap in computational capabilities.

References

  1. Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2018, 2, 79. [Google Scholar] [CrossRef]
  2. Nielsen, M.A.; Chuang, I.; Grover, L.K. Quantum Computation and Quantum Information. Cambridge University Press 2002, 70, 558–559. [Google Scholar] [CrossRef]
  3. DiVincenzo D., P. (2000). The physical implementation of quantum computation. Fortschritte der Physik, 48(9-11), 771-783.
  4. Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
  5. Brassard G., I. Chuang, S. Lloyd, C. Monroe (1998). Quantum computing, Proceedings of the National Academy of Sciences of the United States of America vol. 95 (19) 11032-11033.
  6. Bravyi, S.; Dial, O.; Gambetta, J.M.; Gil, D.; Nazario, Z. The future of quantum computing with superconducting qubits. J. Appl. Phys. 2022, 132, 160902. [Google Scholar] [CrossRef]
  7. Hays, M.; Fatemi, V.; Bouman, D.; Cerrillo, J.; Diamond, S.; Serniak, K.; Connolly, T.; Krogstrup, P.; Nygård, J.; Yeyati, A.L.; et al. Coherent manipulation of an Andreev spin qubit. Science 2021, 373, 430–433. [Google Scholar] [CrossRef] [PubMed]
  8. Neill, C.; Roushan, P.; Kechedzhi, K.; Boixo, S.; Isakov, S.V.; Smelyanskiy, V.; Megrant, A.; Chiaro, B.; Dunsworth, A.; Arya, K.; et al. A blueprint for demonstrating quantum supremacy with superconducting qubits. Science 2018, 360, 195–198. [Google Scholar] [CrossRef] [PubMed]
  9. Linke, N.M.; Maslov, D.; Roetteler, M.; Debnath, S.; Figgatt, C.; Landsman, K.A.; Wright, K.; Monroe, C. Experimental comparison of two quantum computing architectures. Proc. Natl. Acad. Sci. 2017, 114, 3305–3310. [Google Scholar] [CrossRef] [PubMed]
  10. de Leon, N.P.; Itoh, K.M.; Kim, D.; Mehta, K.K.; Northup, T.E.; Paik, H.; Palmer, B.S.; Samarth, N.; Sangtawesin, S.; Steuerman, D.W. Materials challenges and opportunities for quantum computing hardware. Science 2021, 372, 253. [Google Scholar] [CrossRef] [PubMed]
  11. Cacciapuoti, A.S.; Caleffi, M.; Tafuri, F.; Cataliotti, F.S.; Gherardini, S.; Bianchi, G. Quantum Internet: Networking Challenges in Distributed Quantum Computing. IEEE Netw. 2020, 34, 137–143. [Google Scholar] [CrossRef]
  12. Gruska, J. , (2001). Computer Science, Quantum Computing Challenges. Physics, Mathematics.
  13. Gill S., S. , Kumar Adarsh, Harvinder Singh, Manmeet Singh, K. Kaur, Muhammad Usman, R. Buyya, (2020). Quantum computing: A taxonomy, systematic review and future directions. Journal of Software: Practice & Experience Volume 52, Issue 1, pp. 66-114.
  14. Adamowski, J. , Kwasniowski A., Szafran B. (2005), LO-phonon-induced screening of electron–electron interaction in D- centres and quantum dots, Journal of Physics: Condensed Matter, Volume 17, Number 28.
  15. Troiani, F.; Hohenester, U.; Molinari, E. Exploiting exciton-exciton interactions in semiconductor quantum dots for quantum-information processing. Phys. Rev. B 2000, 62, R2263–R2266. [Google Scholar] [CrossRef]
  16. Troiani, F.; Hohenester, U.; Molinari, E. Quantum-Information Processing in Semiconductor Quantum Dots. Physica Status Solidi B-basic Solid State Physics 2001, 224, 849–853. [Google Scholar] [CrossRef]
  17. DiVincenzo D., P. (2000). The physical implementation of quantum computation. Fortschritte der Physik, 48(9-11), 771-783.
  18. Loss, D.; DiVincenzo, D.P. Quantum computation with quantum dots. Phys. Rev. A 1998, 57, 120–126. [Google Scholar] [CrossRef]
  19. Smith Marcus, J. , Lin, Shengtao Yu C., Tsukruk V. (2018). Composite Structures with Emissive Quantum Dots for Light Enhancement. Advanced Optical Materials, Volume 7, Issue 4 1801072.
  20. Heindel, T.; Kim, J.-H.; Gregersen, N.; Rastelli, A.; Reitzenstein, S. Quantum dots for photonic quantum information technology. Adv. Opt. Photon- 2023, 15, 613–738. [Google Scholar] [CrossRef]
  21. Arakawa, Y. (2007). Prospects of Quantum Dots for Advanced Nanophotonic Devices. Conference on Lasers and Electro-Optics. [CrossRef]
  22. Waissman, J.; Honig, M.; Pecker, S.; Benyamini, A.; Hamo, A.; Ilani, S. Realization of pristine and locally tunable one-dimensional electron systems in carbon nanotubes. Nat. Nanotechnol. 2013, 8, 569–574. [Google Scholar] [CrossRef]
  23. Pettaa J., R. C. Johnsonj. M. Taylore. A. Lairda. Yacobym. D. Lukinc. M. Marcusm. P. Hansona. C. Gossard (2005). Coherent Manipulation of Coupled Electron Spins in Semiconductor Quantum Dots, Science 309 (5744), 2180-2184.
  24. Nielsen, M.A.; Chuang, I. Quantum Computation and Quantum Information. Cambridge University Press 2002, 70, 558–559. [Google Scholar] [CrossRef]
  25. Vasilyev, D. Sokolov I.,. Polzik E. (2010). Quantum volume hologram, Phys. Rev. A 81, 020302®.
  26. Kim I., H. (2017). Holographic quantum simulation, arXiv:1702.02093.
  27. Maslov, D. Dueck G. (2003). Improved quantum cost for n-bit Toffoli gates, Electronics Letters Vol. 39, Issue 25, pp. 1790-1791.
  28. Chen, Y. Equivalent relation between normalized spatial entropy and fractal dimension. Phys. A: Stat. Mech. its Appl. 2020, 553, 124627. [Google Scholar] [CrossRef]
  29. Khordad, R.; Sedehi, H.R.R.; Bahramiyan, H. Simultaneous Effects of Impurity and Electric Field on Entropy Behavior in Double Cone-Like Quantum Dot. Commun. Theor. Phys. 2018, 69, 95–100. [Google Scholar] [CrossRef]
  30. Alivisatos, A. P. (1996). Semiconductor quantum dots. Science, 271(5251), 933-937.
  31. Bertaina, S.; Gambarelli, S.; Tkachuk, A.; Kurkin, I.N.; Malkin, B.; Stepanov, A.; Barbara, B. Rare-earth solid-state qubits. Nat. Nanotechnol. 2007, 2, 39–42. [Google Scholar] [CrossRef]
  32. Bimberg Dieter, Grundmann Marius, Ledentsov Nikolai N, Quantum Dot Heterostructures, John Wiley & Sons, 1999.
  33. Chen Yanguang, Equivalent Relation between Normalized Spatial Entropy and Fractal Dimension (2020), Physica A: Statistical Mechanics and its Applications, Vol. 553, 124627.
  34. Efros, A.L.; Rosen, M. The Electronic Structure of Semiconductor Nanocrystals. Annu. Rev. Mater. Sci. 2000, 30, 475–521. [Google Scholar] [CrossRef]
  35. Hirayama, R.; Naruse, M.; Nakayama, H.; Tate, N.; Shiraki, A.; Kakue, T.; Shimobaba, T.; Ohtsu, M.; Ito, T. Design, Implementation and Characterization of a Quantum-Dot-Based Volumetric Display. Sci. Rep. 2015, 5, 8472–8472. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

215

Views

60

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated