On the Spanwise Periodicity within the Gap between Two Different-Sized Tandem Circular Cylinders at Re=3900

1. Introduction

Despite the simplicity of the geometry, the flow around cylindrical structures is of fundamental significance and involves complex flow mechanisms, including vortex shedding/impingement/interaction, shear layer separation/reattachment, transition from steady to unsteady state, transition from two-dimensional (2D) to three-dimensional (3D) state, fluid-structure interaction and flow-induced noise/vibration [1,2,3,4,5]. Abundant studies have been conducted to elucidate the flow around circular or square cylinders, due to their extensive engineering applications [6,7,8,9,10]. Especially, two tandem circular cylinders have attracted considerable attention in recent decades [11,12,13,14,15].

The flow around two tandem circular cylinders is influenced by the Reynolds number (Re), the spacing ratio (L/D, where L is the center-to-center distance between two cylinders and D is the cylinder diameter), the turbulence intensity of the approaching flow, the boundary condition, the blockage ratio and the cylinder aspect ratio [16,17,18]. No consensus has been reached about the classification of flow patterns, being ascribed to diverse influencing factors and different classification standards. On one hand, experimental studies categorized flow pattern with the aid of various flow visualization techniques, such as surface oil-flow visualization, soap film visualization, laser-induced fluorescence and smoke-wire flow visualization [19,20]. On the other hand, numerical studies defined diverse flow regimes by various physical quantities, such as vorticity/velocity field, Q-criterion, λ₂-criterion, pressure/force coefficient, Strouhal number and streamlines [21,22,23].

The flow around two tandem circular cylinders with equal diameters is classified into Single Body Flow (i.e., proximity flow, extended-body flow or overshoot flow), Reattachment Flow, Bi-stable Flow and Co-shedding Flow (i.e., binary-vortex flow) [24,25]. Particularly, Zdravkovich [26] found that, when 1.2 ≤ L/D ≤ 4.0, the shear layers might reattach on the downstream cylinder in three different manners, namely alternate reattachment, quasi-steady reattachment and intermittent reattachment. Alam et al. [27] and Alam [28] provided four types of reattachment flow, namely the reverse-flow reattachment, the front-side reattachment, the front reattachment and the rear-side reattachment. Zhou and Alam [12] pointed out that about 50% of previous investigations were conducted at Re = 1×10⁴~ 3.5×10⁵, but approximate 20% at Re = 1×10³~1×10⁴ and only 3% at Re > 3.5×10⁵. Rastan and Alam [29] indicated that Single Body Flow (SB) was absent for Re ≥ 2×10⁴, a hysteresis zone (HS) was observed within Re = 50~500, and Bi-Stable Flow (BS) was acquired at Re ≥ 1000, being distinguished by spontaneous intermittent switches between the alternate reattachment flow (AR) and the co-shedding flow (CS) at a fixed Re and L/D.

Only few investigations were devoted to clarifying the flow around two different-sized tandem circular cylinders. Alam and Zhou [30] analyzed the wake of two tandem circular cylinders with d/D = 0.24~1.0 and L’/d = 5.5 at Re = 2.72×10⁴, where d was the upstream-cylinder (UC) diameter, D was the downstream-cylinder (DC) diameter, and L’ was the distance from the UC center to the forward stagnation point of the DC. Co-shedding Flow was subdivided into Intermittent Lock-in (d/D ≥ 0.4) and No Lock-in (d/D = 0.24). Zafar and Alam [31] found that, when 0.3 ≤ d/D ≤ 1.0 (Co-shedding Flow), the DC wake featured a primary vortex street followed by a secondary vortex street, having a frequency 1.73 times smaller than the primary frequency. Shan [32] classified Co-shedding Flow into prime vortex shedding (PVS) mode, two-layer vortex shedding (TVS) mode and secondary vortex shedding (SVS) mode. Wang et al. [33] categorized Co-shedding Flow into Lock-in (L’/d ≥ 3.0 at d/D = 1.0; L’/d ≥ 3.5 at d/D = 0.8), Subharmonic Lock-in (L’/d ≥ 3.5 at d/D = 0.6) and No Lock-in (L’/d ≥ 4.5 at d/D = 0.4; L’/d ≥ 7.0 at d/D = 0.2). Alam et al. [34] investigated two tandem cylinders with d/D = 0.25~1.0 and L’/d = 5.5~20 at Re = 0.8×10⁴~2.42×10⁴. Five flow regimes were identified, namely Reattachment Flow, Lock-in, Intermittent Lock-in, Subharmonic Lock-in and No Lock-in. Mahir and Altaç [35] observed four flow patterns, including over-shoot, symmetric-reattachment, front-side reattachment and co-shedding, for d/D = 0.3~2.0 and G/D = 0.5~4.0 at Re = 100~200, where G was the gap distance. Gao et al. [36] displayed that, for d/D = 2/3 and L/D = 1.8~3.8 at Re = 200, the flow was characterized by a bi-stability phenomenon, and co-shedding might occur depending on the initial perturbation.

Special attention should be paid to the spanwise periodicity of the flow field between two tandem circular cylinders. Papaioannou et al. [37] disclosed that the case of d/D = 1.0 and L/D = 2.0 at Re = 500 belonged to Reattachment Flow, and obvious spanwise periodicity was observed for both the gap region and the DC downstream in terms of the instantaneous vorticity field. Hu et al. [38] showed that, for d/D = 1 and L/D = 1.5~2.5 at Re = 2.8×10⁵~7.0×10⁵, whether for Reattachment Flow (L/D = 1.5) or for Co-shedding Flow (L/D = 2.5), both the instantaneous velocity contours at different Z planes and the instantaneous vorticity contours in the Y = 0 plane demonstrated the evident spanwise periodicity. Deng et al. [39] examined the spatial evolution of vortices in the wake of two tandem circular cylinders with d/D = 1 and L/D = 1.5~8.0 at Re = 220, and verified the existence of the spanwise periodicity in terms of both instantaneous streamlines and instantaneous vorticity contours.

This study is dedicated to systematically analyzing the spanwise periodicity of time-averaged flow structures within the gap, and further defining different flow regimes for the flow around two tandem circular cylinders with a diameter ratio of d/D = 0.6 at Re = 3900. Seventeen spacing ratios (i.e., L/D = 1.00, 1.10, 1.15, 1.20, 1.25, 1.50, 2.00, 2.25, 2.50, 3.00, 3.15, 3.24, 3.30, 3.50, 4.00, 5.00 and 6.00) are considered in an effort to adequately capture various flow regimes and detailedly illustrate the transition process among them. Flow properties and statistical parameters are presented for each flow regime, such as velocity contours, vorticity contours, force coefficient, reattachment/separation angle, Strouhal number, wavelet scalogram, Q-criterion iso-surface and the spanwise periodicity length.

2. Materials and Methods

2.1. Governing Equation

This study solves the turbulence by using the large eddy simulation (LES) technique. The filtered incompressible continuity and momentum equations can be written as [40]:

$$\frac{\partial {\overline{u}}_i}{\partial x_i}=0$$

(1)

$$\frac{\partial {\overline{u}}_i}{\partial t}+\nabla \cdot ({\overline{u}}_i{\overline{u}}_j)=-\frac{1}{\rho }\nabla \overline{p}+\frac{\partial }{\partial x_j}\left(\nu \frac{\partial {\overline{u}}_i}{\partial x_j}-{\tau }_{ij}\right)$$

(2)

where ${\overline{u}}_i$ (i = 1, 2 and 3) are the filtered velocity components in the streamwise (X axis), transverse (Y axis) and spanwise directions (Z axis) respectively, $\overline{p}$ represents the filtered pressure field, ρ is the density, ν signifies the kinematic viscosity, t symbolizes the time, and τ_ij denotes the subgrid scale stress tensor to be modeled.

$${\tau }_{ij}-\frac{1}{3}{\tau }_{kk}{\delta }_{ij}=-2{\nu }_{SGS}{\overline{S}}_{ij}$$

(3)

$${\overline{S}}_{ij}=\frac{1}{2}\left(\frac{\partial {\overline{u}}_i}{\partial x_j}+\frac{\partial {\overline{u}}_j}{\partial x_i}\right)$$

(4)

where ${\overline{S}}_{ij}$ is the resolved strain rate tensor and ${\nu }_{SGS}$ is the subgrid-scale (SGS) eddy viscosity, which is calculated through the dynamic one equation eddy-viscosity model.

$${\nu }_{SGS}=C_k\sqrt{k_{SGS}}\overline{\Delta },\overline{\Delta }=\sqrt[3]{\Delta x\cdot \Delta y\cdot \Delta z}$$

(5)

$$\frac{\partial k_{SGS}}{\partial t}+\frac{\partial ({\overline{u}}_j{k}_{SGS})}{\partial x_j}-\frac{\partial }{\partial x_j}\left[\nu \frac{\partial k_{SGS}}{\partial x_j}\right]=2{\nu }_{SGS}{\overline{S}}_{ij}\frac{\partial {\overline{u}}_i}{\partial x_j}-C_{\epsilon }\frac{k_{SGS}^{3/2}}{\overline{\Delta }}$$

(6)

where $\overline{\Delta }$ is the grid filter size, and the SGS kinetic energy $k_{SGS}$ is obtained by solving its transport equation. The simple filtering method is employed here, and the maxDeltaRatio coefficient is set as 1.1. For the two model constants, the officially recommended values of C_k = 0.094 and C_ε = 1.048 are utilized in this study [41].

2.2. Boundary Condition

Four kinds of boundary conditions are involved in this study:

(1) Inlet: A fixed uniform velocity is prescribed ($\overline{u}$ = 1 m/s, $\overline{v}$ = $\overline{w}$ = 0 m/s), and the zero-gradient condition is applied for the pressure field ($\partial \overline{p}/\partial n$ = 0). The turbulent intensity is set as I = 0.5%, and therefore the turbulent kinetic energy is fixed as k = 3.75×10^-5 m²/s².

(2) Outlet: For the velocity field, the convective outflow boundary condition is adopted [42,43]: $\frac{\partial \varphi }{\partial t}+u_c\cdot \frac{\partial \varphi }{\partial n}=0$, where $\varphi$ denotes all the three velocity components, and u_c is the convective velocity at the outlet. For the pressure field, the homogeneous Dirichlet condition ($\overline{p}$ = 0 Pa) is exerted at the outlet. For the turbulent kinetic energy, the zero-gradient condition ($\partial k/\partial n$ = 0) is used.

(3) Cylinder surfaces: No-slip impermeable boundary condition is prescribed for the velocity field ($\overline{u}$ = $\overline{v}$ = $\overline{w}$ = 0 m/s), the zero-gradient condition is employed for the pressure field ($\partial \overline{p}/\partial n$ = 0), and the kLowReWallFunction is adopted for the turbulent kinetic energy.

(4) Top, bottom, front and back boundaries: The symmetric boundary condition is utilized, which means that the normal gradient of all variables is equal to zero (i.e., $\partial \overline{u}/\partial n$ = $\partial \overline{v}/\partial n$ = $\partial \overline{w}/\partial n$ = $\partial \overline{p}/\partial n$ = $\partial k/\partial n$ = 0).

2.3. Numerical Scheme

The Pressure Implicit with Splitting of Operators (PISO) algorithm is employed to deal with the pressure-velocity decoupling, the MUSCL scheme is chosen to discretize the convection term, the Gauss linear scheme is employed to discretize both the diffusion term and the pressure gradient term, and the Euler implicit scheme is adopted for the temporal discretization. For details of these numerical algorithms, readers can refer to the references [44,45]. The preconditioned conjugate gradient (PCG) method, combined with the diagonal incomplete Cholesky (DIC) preconditioner, is applied to solve the pressure matrix up to an accuracy of 10^-6 at each time step. The preconditioned biconjugate gradient (PBCG) method, combined with the diagonal incomplete LU (DILU) preconditioner, is used to solve the velocity/scalar matrix up to an accuracy of 10^-7 at each time step.

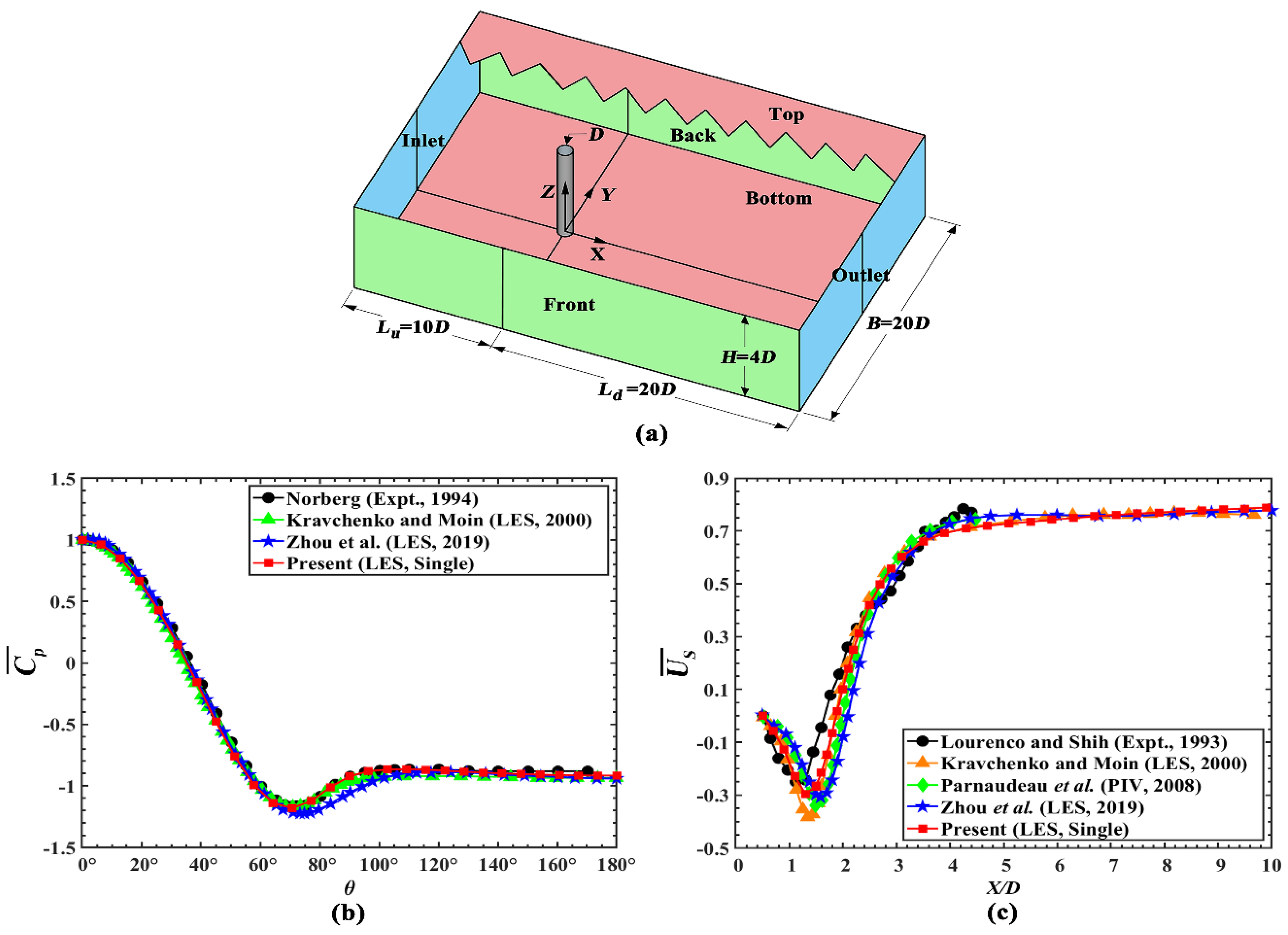
2.4. Validation Case

In order to validate the accuracy of the present numerical model, the flow field around a single cylinder at Re = 3900 is simulated and compared with the results reported in the literature. The circular cylinder, with a diameter of D = 1m and a height of H = 4D, is vertically mounted between the top and bottom planes (Figure 1(a)). The (streamwise) length, (transverse) width and (spanwise) height of the computational domain are L = 30D, B = 20D and H = 4D, respectively. The junction section between the cylinder and the bottom plane is centered at the origin of the Cartesian coordinate system, the inlet plane is located at 10D upstream of the cylinder, and the outlet plane is situated at 20D downstream of the cylinder. Table 1 manifests that the validation case consists of 5.74 million grid points, being clustered near the cylinder surface. The node number along the cylinder circumference (N_C) is set as 280, and the near-wall grid size δ (i.e., the distance between the first-cell centroid and the cylinder surface) is equal to 0.002D, ensuring that the non-dimensional wall distance ($y^{+}$) is less than 1.0. Besides, N_Lu is the node number along L_u (the distance between the inlet plane and the UC center), N_Ld is the node number along L_d (the distance between the DC center and the outlet plane), and N_Z denotes the node number along H (the spanwise height). A grid independence study was performed to guarantee sufficient grid resolution, however only the details of the employed medium mesh are presented here for brevity. In addition, the time step value (∆t) is fixed at 0.002 s, which can guarantee that the maximum Courant-Friedrichs-Lewy (CFL) number is around 0.5.

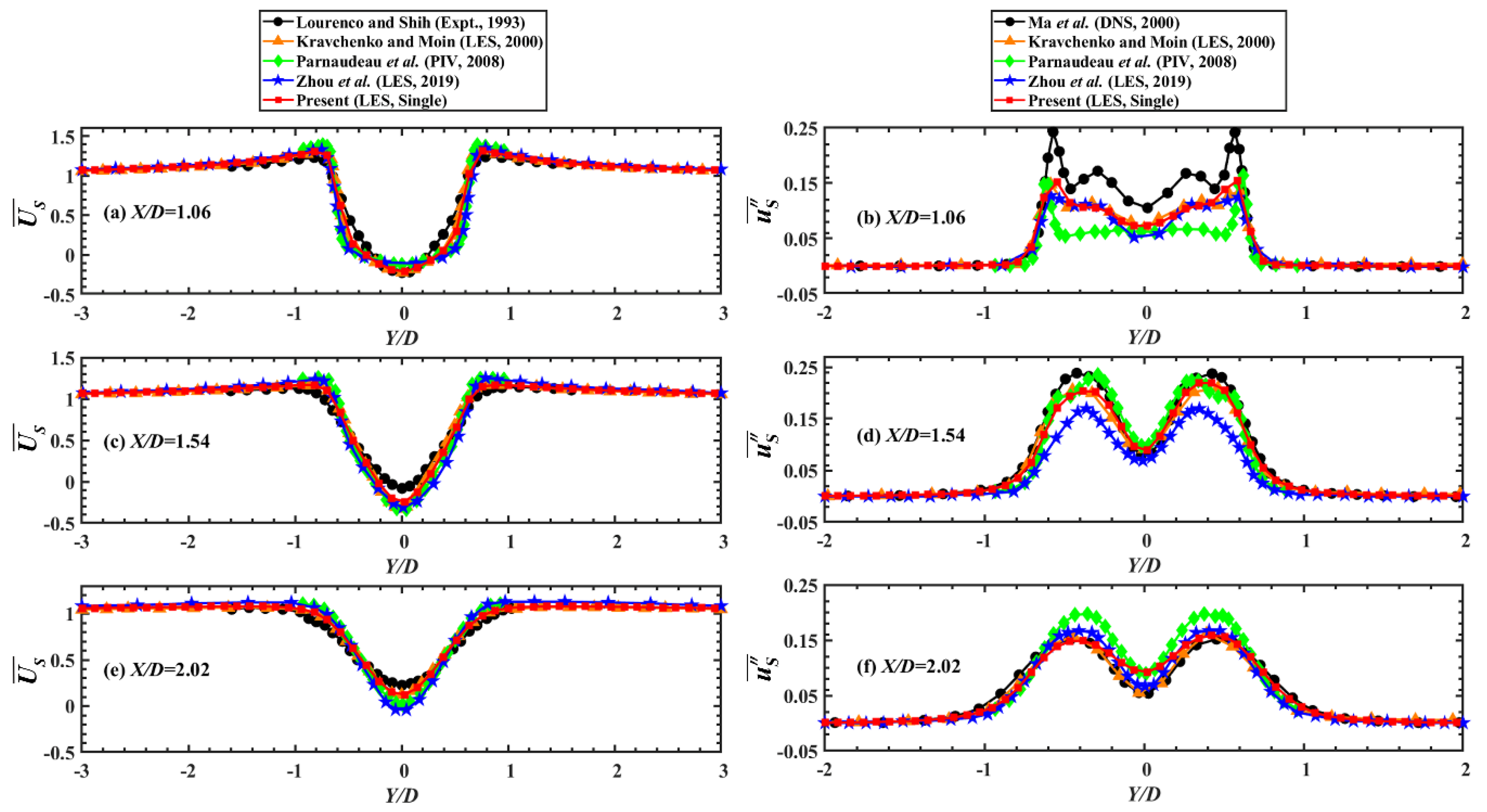
When it comes to the spanwise-averaged time-averaged pressure coefficient ($\overline{C_p}$) along the cylinder surface, the normalized spanwise-averaged time-averaged streamwise velocity (${\overline{U}}_S$) along the Y = 0 line in the wake, and the values of ${\overline{U}}_S$ and $\overline{{u^{″}}_S}$ (the normalized spanwise-averaged fluctuating streamwise velocity) at three cross-sections (i.e., X/D = 1.06, 1.54 and 2.02), Figure 1(b, c) and Figure 2 demonstrate that the present numerical results overall agree well with the results reported by Zhou et al. [40], Lourenco and Shih [46], Norberg [47], Ma et al. [48], Kravchenko and Moin [49] and Parnaudeau et al. [50]. Furthermore, Table 2 proves that the present numerical results are also consistent with the previous experimental or numerical data, in terms of several important statistical parameters (including St, $\overline{C_D}$, ${C^{\prime }}_l$, −$\overline{C_{pb}}$, ${\theta }_s$, L_r/D and $\overline{U_{min}}/U_{\infty }$).

Table 1. Computational grid characteristics of both the validation case and the seventeen research cases.

Case	Computational domain	Time step ∆t (s)	δ/D	NC	NLu	NL	NLd	NZ	Total node number (✕106)
Single Cylinder	30.00D × 20D × 4D	0.0020	0.002	280	113	/	230	61	5.74
L/D = 1.00	31.00D × 20D × 8D	0.0015	0.002	280	134	98	230	121	15.45
L/D = 1.10	31.10D × 20D × 8D	0.0015	0.002	280	134	106	230	121	17.16
L/D = 1.15	31.15D × 20D × 8D	0.0015	0.002	280	134	106	230	121	17.16
L/D = 1.20	31.20D × 20D × 8D	0.0015	0.002	280	134	112	230	121	17.45
L/D = 1.25	31.25D × 20D × 8D	0.0015	0.002	280	134	112	230	121	17.45
L/D = 1.50	31.50D × 20D × 8D	0.0015	0.002	280	136	131	230	121	17.49
L/D = 2.00	32.00D × 20D × 8D	0.0015	0.002	280	113	186	230	121	16.03
L/D = 2.25	32.25D × 20D × 8D	0.0015	0.002	280	113	208	230	121	16.69
L/D = 2.50	32.50D × 20D × 8D	0.0015	0.002	280	113	217	230	121	16.93
L/D = 3.00	33.00D × 20D × 4D	0.0015	0.002	280	113	237	230	61	8.81
L/D = 3.15	33.15D × 20D × 4D	0.0015	0.002	280	113	244	230	61	8.90
L/D = 3.24	33.24D × 20D × 4D	0.0015	0.002	280	113	248	230	61	8.96
L/D = 3.30	33.30D × 20D × 4D	0.0015	0.002	280	113	249	230	61	8.97
L/D = 3.50	33.50D × 20D × 4D	0.0015	0.002	280	113	255	230	61	9.05
L/D = 4.00	34.00D × 20D × 4D	0.0015	0.002	280	113	272	230	61	9.28
L/D = 5.00	35.00D × 20D × 4D	0.0015	0.002	280	113	307	230	61	9.75
L/D = 6.00	36.00D × 20D × 4D	0.0015	0.002	280	113	342	230	61	10.23

Table 1. Computational grid characteristics of both the validation case and the seventeen research cases.

Case	Computational domain	Time step ∆t (s)	δ/D	NC	NLu	NL	NLd	NZ	Total node number (✕106)
Single Cylinder	30.00D × 20D × 4D	0.0020	0.002	280	113	/	230	61	5.74
L/D = 1.00	31.00D × 20D × 8D	0.0015	0.002	280	134	98	230	121	15.45
L/D = 1.10	31.10D × 20D × 8D	0.0015	0.002	280	134	106	230	121	17.16
L/D = 1.15	31.15D × 20D × 8D	0.0015	0.002	280	134	106	230	121	17.16
L/D = 1.20	31.20D × 20D × 8D	0.0015	0.002	280	134	112	230	121	17.45
L/D = 1.25	31.25D × 20D × 8D	0.0015	0.002	280	134	112	230	121	17.45
L/D = 1.50	31.50D × 20D × 8D	0.0015	0.002	280	136	131	230	121	17.49
L/D = 2.00	32.00D × 20D × 8D	0.0015	0.002	280	113	186	230	121	16.03
L/D = 2.25	32.25D × 20D × 8D	0.0015	0.002	280	113	208	230	121	16.69
L/D = 2.50	32.50D × 20D × 8D	0.0015	0.002	280	113	217	230	121	16.93
L/D = 3.00	33.00D × 20D × 4D	0.0015	0.002	280	113	237	230	61	8.81
L/D = 3.15	33.15D × 20D × 4D	0.0015	0.002	280	113	244	230	61	8.90
L/D = 3.24	33.24D × 20D × 4D	0.0015	0.002	280	113	248	230	61	8.96
L/D = 3.30	33.30D × 20D × 4D	0.0015	0.002	280	113	249	230	61	8.97
L/D = 3.50	33.50D × 20D × 4D	0.0015	0.002	280	113	255	230	61	9.05
L/D = 4.00	34.00D × 20D × 4D	0.0015	0.002	280	113	272	230	61	9.28
L/D = 5.00	35.00D × 20D × 4D	0.0015	0.002	280	113	307	230	61	9.75
L/D = 6.00	36.00D × 20D × 4D	0.0015	0.002	280	113	342	230	61	10.23

Table 2. Comparison of the Strouhal number based on the instantaneous lift coefficient (St), the spanwise-averaged time-averaged drag coefficient ($\overline{C_D}$), the spanwise-averaged fluctuating lift coefficient ($C_l^{\prime }$), the spanwise-averaged time-averaged base pressure coefficient (−$\overline{C_{pb}}$), the normalized spanwise-averaged time-averaged recirculation length (L_r/D), the spanwise-averaged time-averaged separation angle (${\theta }_s$) and the normalized spanwise-averaged time-averaged minimum streamwise velocity along the Y = 0 line ($\overline{U_{min}}/U_{\infty }$) for the validation case.

Case	Re	St	$\overline{C_D}$	$C_l^{\prime }$	$-\overline{C_{pb}}$	Lr/D	${\theta }_s$	$\overline{U_{min}}/U_{\infty }$
Present (LES)	3900	0.210	1.030	0.170	0.917	1.374	87.25°	-0.299
Zhou et al. [40] (LES)	3900	0.217	1.000	/	0.890	1.550	/	/
Tian and Xiao [41] (LES)	3900	/	1.040	0.170	0.890	1.400	87.0°	/
Kravchenko and Moin [49] (LES)	3900	0.210	1.040	/	0.940	1.350	88.0°	-0.370
Parnaudeau et al. [50] (Expt.)	3900	0.208	/	/	/	1.510	/	-0.340
Meyer et al. [51] (LES)	3900	0.210	1.050	/	0.920	1.380	88.0°	/
Young and Ooi [52] (LES)	3900	0.212	1.030	0.177	0.908	/	/	/
Dong et al. [53] (Expt.)	4000	/	/	/	/	1.470	/	-0.252
Dong et al. [53] (DNS)	3900	0.208	/	/	0.930	1.360	/	-0.291
Rajani et al. [54] (LES, SSM)	3900	0.214	1.050	/	0.928	1.211	87.5°	-0.270
Rajani et al. [54] (LES, DSM)	3900	0.210	1.010	/	0.900	1.198	87.5°	-0.280
Jiang and Cheng [55] (LES)	3900	0.212	0.994	0.161	0.893	1.444	/	/
Lysenko et al. [56] (LES, SMAG)	3900	0.190	1.180	0.440	0.800	0.900	89.0°	-0.260
Lysenko et al. [56] (LES, TKE)	3900	0.209	0.970	0.090	0.910	1.670	88.0°	-0.270
Wornom et al. [57] (LES)	3900	0.210	0.990	0.108	0.880	1.450	89.0°	/
Franke and Frank [58] (LES)	3900	0.209	0.978	/	0.850	1.640	88.2°	/

Table 2. Comparison of the Strouhal number based on the instantaneous lift coefficient (St), the spanwise-averaged time-averaged drag coefficient ($\overline{C_D}$), the spanwise-averaged fluctuating lift coefficient ($C_l^{\prime }$), the spanwise-averaged time-averaged base pressure coefficient (−$\overline{C_{pb}}$), the normalized spanwise-averaged time-averaged recirculation length (L_r/D), the spanwise-averaged time-averaged separation angle (${\theta }_s$) and the normalized spanwise-averaged time-averaged minimum streamwise velocity along the Y = 0 line ($\overline{U_{min}}/U_{\infty }$) for the validation case.

Case	Re	St	$\overline{C_D}$	$C_l^{\prime }$	$-\overline{C_{pb}}$	Lr/D	${\theta }_s$	$\overline{U_{min}}/U_{\infty }$
Present (LES)	3900	0.210	1.030	0.170	0.917	1.374	87.25°	-0.299
Zhou et al. [40] (LES)	3900	0.217	1.000	/	0.890	1.550	/	/
Tian and Xiao [41] (LES)	3900	/	1.040	0.170	0.890	1.400	87.0°	/
Kravchenko and Moin [49] (LES)	3900	0.210	1.040	/	0.940	1.350	88.0°	-0.370
Parnaudeau et al. [50] (Expt.)	3900	0.208	/	/	/	1.510	/	-0.340
Meyer et al. [51] (LES)	3900	0.210	1.050	/	0.920	1.380	88.0°	/
Young and Ooi [52] (LES)	3900	0.212	1.030	0.177	0.908	/	/	/
Dong et al. [53] (Expt.)	4000	/	/	/	/	1.470	/	-0.252
Dong et al. [53] (DNS)	3900	0.208	/	/	0.930	1.360	/	-0.291
Rajani et al. [54] (LES, SSM)	3900	0.214	1.050	/	0.928	1.211	87.5°	-0.270
Rajani et al. [54] (LES, DSM)	3900	0.210	1.010	/	0.900	1.198	87.5°	-0.280
Jiang and Cheng [55] (LES)	3900	0.212	0.994	0.161	0.893	1.444	/	/
Lysenko et al. [56] (LES, SMAG)	3900	0.190	1.180	0.440	0.800	0.900	89.0°	-0.260
Lysenko et al. [56] (LES, TKE)	3900	0.209	0.970	0.090	0.910	1.670	88.0°	-0.270
Wornom et al. [57] (LES)	3900	0.210	0.990	0.108	0.880	1.450	89.0°	/
Franke and Frank [58] (LES)	3900	0.209	0.978	/	0.850	1.640	88.2°	/

Figure 1. (a) Configuration of the validation case, (b) Comparison of the spanwise-averaged time-averaged pressure coefficient along the cylinder surface, and (c) Comparison of the normalized spanwise-averaged time-averaged streamwise velocity along the Y = 0 line.

Figure 1. (a) Configuration of the validation case, (b) Comparison of the spanwise-averaged time-averaged pressure coefficient along the cylinder surface, and (c) Comparison of the normalized spanwise-averaged time-averaged streamwise velocity along the Y = 0 line.

Figure 2. (a, c, e) Comparison of the normalized spanwise-averaged time-averaged streamwise velocity, and (b, d, f) Comparison of the normalized spanwise-averaged fluctuating streamwise velocity at three cross-sections.

Figure 2. (a, c, e) Comparison of the normalized spanwise-averaged time-averaged streamwise velocity, and (b, d, f) Comparison of the normalized spanwise-averaged fluctuating streamwise velocity at three cross-sections.

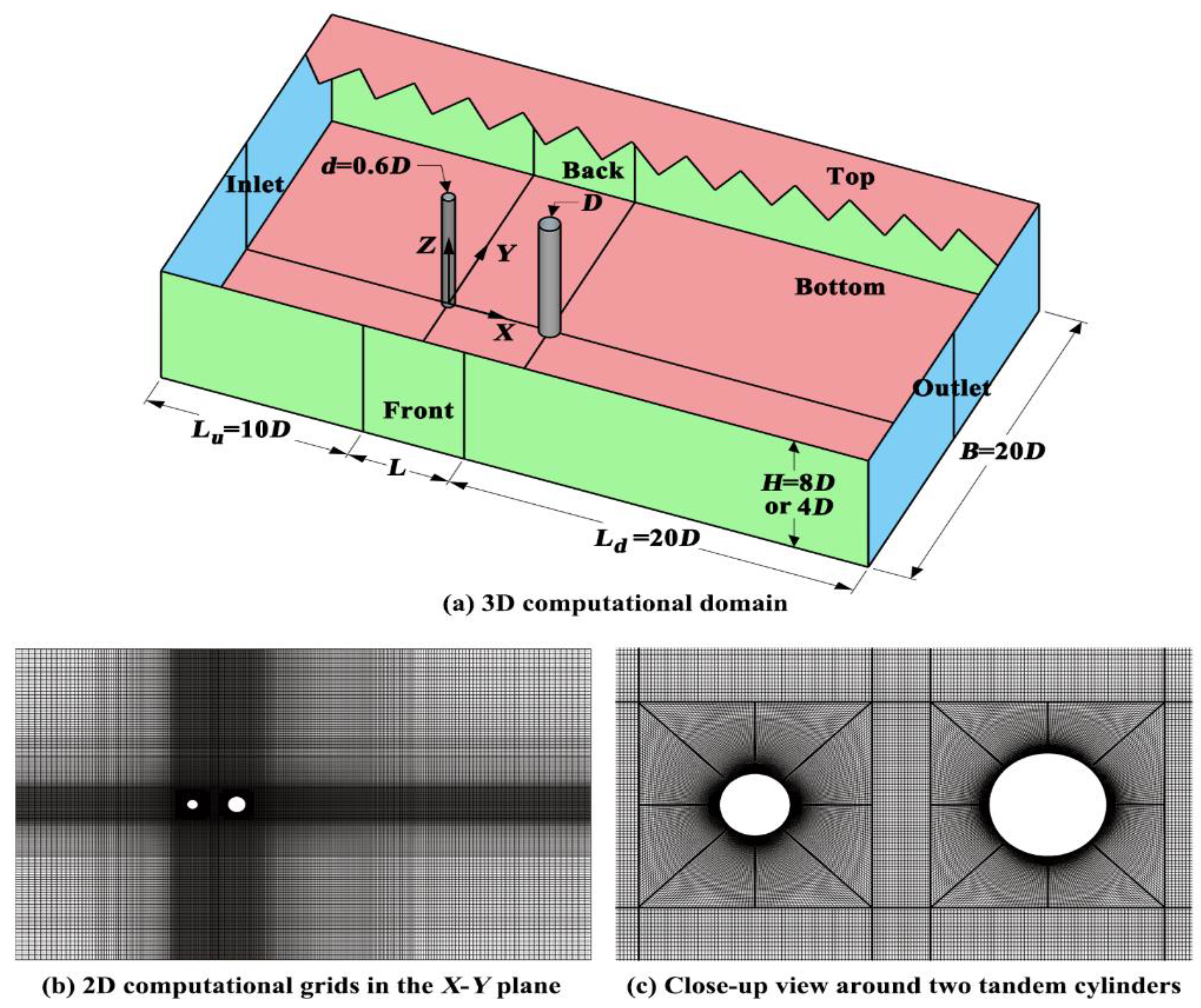
2.5. Research Scope

In order to systematically analyze the spanwise periodicity of the time-averaged flow structure within the gap, seventeen research cases are simulated for two tandem circular cylinders with d/D = 0.6 at Re = 3900, namely L/D = 1.00, 1.10, 1.15, 1.20, 1.25, 1.50, 2.00, 2.25, 2.50, 3.00, 3.15, 3.24, 3.30, 3.50, 4.00, 5.00 and 6.00. As shown by Table 1 and Figure 3, the spanwise height is selected as H = 8D for L/D = 1.00~2.50, because the spanwise periodicity length (P_z) lies in the range of (1.06~5.73)D for these spacing ratios. However, H = 4D is adopted for L/D = 3.00~6.00 due to the fact that the possible spanwise periodicity length is only about (2.14~2.32)D under this condition. The total grid points of each case fall within the scope of 8.81×10⁶~17.49×10⁶, and the grid points are clustered within the gap and near the cylinder surface. With respect to δ/D, N_Lu, N_Ld and the boundary conditions, all the seventeen research cases have the similar characteristics as the validation test. Moreover, N_L (the node number along the distance between two cylinder centers), the time step ∆t and the computational domain are also provided in Table 1. All the simulations are first run over 500s (i.e., approximate 100 vortex-shedding cycles) to reach the fully-developed wake, and then the flow fields are averaged for another 1000s (i.e., about 200 vortex-shedding cycles) to yield statistically independent time-averaged results.

3. Results and Discussion

3.1. Flow Pattern and Statistical Parameter

Different flow regimes are identified by examining the instantaneous spanwise vorticity (${\omega }_z$) contours in the mid-height plane (Z = H/2), the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours in the transverse plane, the time-averaged Q-criterion iso-surfaces within the gap, and the Strouhal number of the UC (St_d) and the DC (St_D). Table 3 proves that six flow patterns can be defined in this study, namely Small-scale Periodic Reattachment Flow (L/D = 1.00~1.50), Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25), Non-periodic Reattachment Flow (L/D = 2.50~3.15), Bi-stable Flow (L/D = 3.24), Intermittent Lock-in Co-shedding Flow (L/D = 3.30~3.50) and Subharmonic Lock-in Co-shedding Flow (L/D = 4.00~6.00).

Table 3 reveals that, in terms of St_d, St_D, $\overline{C_d}$, $\overline{C_D}$, ${\theta }_r^D$, ${\theta }_s^d$ and ${\theta }_s^D$, an abrupt increase or decrease can be always observed in the vicinity of Bi-stable Flow (L/D = 3.24), being consistent with the previous observations [25,27,32,35,37]. With regard to Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25) and Non-periodic Reattachment Flow (L/D = 2.50~3.15), no dominant Strouhal number is recognized for the UC, the reason of which will be given out in the following sub-sections. When it comes to L/D = 3.30~6.00 (Co-shedding Flow), there are two dominant Strouhal numbers for the DC (i.e., the relatively larger $S{t}_D$ = 0.300~0.334 and the relatively smaller $S{t}_{D-2}$ = 0.167~0.169). In this study, the separation or reattachment angle is defined as the turning point between the positive and negative values of the normalized spanwise-averaged time-averaged wall shear stress along the cylinder surface, being similar to Hu et al. [7] and Zhou et al. [40]. Table 3 manifests that ${\theta }_r^D$ only exists at L/D = 1.00~3.24, lying in the range of 51.45°~60.46°. In the vicinity of Bi-stable Flow (L/D = 3.24), a sharp increase from 86.03° to 91.00° can be detected for ${\theta }_s^d$, but, on the contrary, a sudden decline from 107.54° to 97.97° is captured for ${\theta }_s^D$.

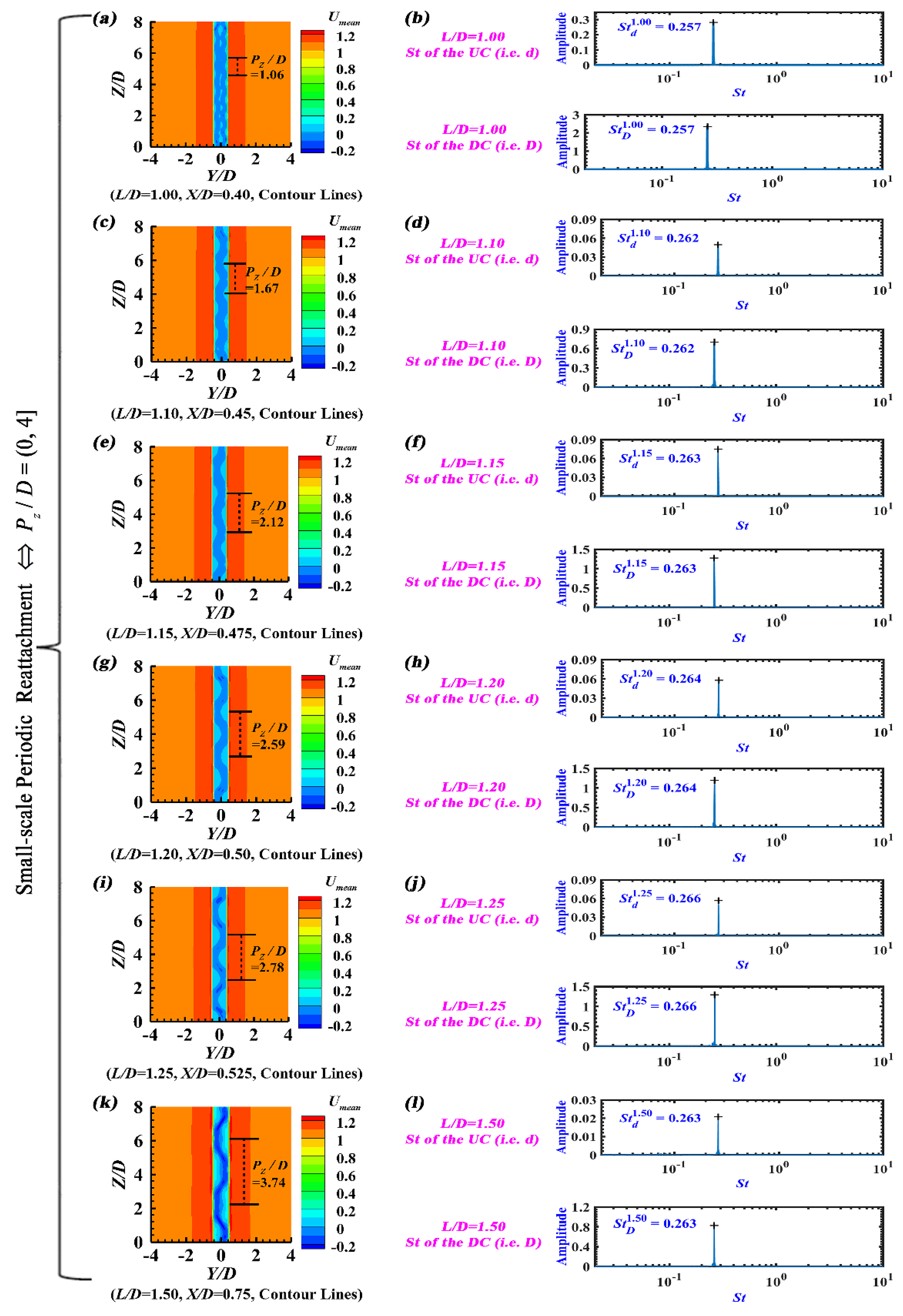
3.2. Small-Scale Periodic Reattachment Flow (L/D = 1.00~1.50)

With the aid of the instantaneous spanwise vorticity (${\omega }_z$) contours in the mid-height plane (Z = H/2), Figure 4(a, d, g, j, m, p) indicates that, when L/D = 1.00~1.50, the UC shear layers continuously reattach on two sides of the DC, and meanwhile a recirculating flow prevails within the gap region. Obviously, this flow pattern belongs to Reattachment Flow in the literature. Furthermore, concerning the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours and the time-averaged streamwise velocity (U_mean) contours in the transverse plane within the gap, small-scale spanwise-periodic time-averaged flow structures (P_z/D = 1.06~3.74) can be observed (Figure 4(b, e, h, k, n, q) and Figure 5(a, c, e, g, i, k)). This is the reason why this flow pattern is named as Small-scale Periodic Reattachment Flow. It should be noted that Single Body Flow can not be identified here for two tandem circular cylinders with d/D = 0.6 at Re = 3900, in accordance with Wang et al. [33].

The 3D time-averaged vortical structures within the gap are displayed by means of the time-averaged Q-criterion iso-surfaces (Q_mean). As expected, Figure 4(c, f, i, l, o, r) manifests that distinct spanwise-periodic 3D time-averaged vortical structures can be recognized for L/D = 1.00~1.50. The strength of 3D time-averaged vortical structures continuously enhances with the increase of L/D, and hence Q_mean = 0.01, 0.05 and 0.10 are selected for L/D = 1.00~1.20, 1.25 and 1.50, respectively. Besides, Figure 5(b, d, f, h, j, l) proves that, with regard to Small-scale Periodic Reattachment Flow (L/D = 1.00~1.50), the two cylinders have the same dominant Strouhal number when implementing the Fast Fourier Transform of the instantaneous lift coefficient (i.e., $S{t}_d^{1.00}$ = $S{t}_D^{1.00}$ = 0.257, $S{t}_d^{1.10}$ = $S{t}_D^{1.10}$ = 0.262, $S{t}_d^{1.15}$ = $S{t}_D^{1.15}$ = 0.263, $S{t}_d^{1.20}$ = $S{t}_D^{1.20}$ = 0.264, $S{t}_d^{1.25}$ = $S{t}_D^{1.25}$ = 0.266 and $S{t}_d^{1.50}$ = $S{t}_D^{1.50}$ = 0.263), being consistent with Liu [18] and Gao et al. [36]. Table 3 and Figure 4(a, d, g, j, m, p) reveal that, under the circumstance of L/D = 1.00~1.50, the spanwise-averaged time-averaged reattachment angle of the DC is relatively large (${\theta }_r^D$ = 57.86°~60.46°), and therefore only a small part of shear-layer vortices, shedding from two sides of the UC, are drawn into the gap region after impinging onto two sides of the DC. Due to the combined effect of both the limited amount of vortices within the gap region and the stabilization action caused by small L/D values, small-scale spanwise-periodic time-averaged flow structures (P_z/D = (0, 4]) are generated between two cylinders, which is actually the formation mechanism of Small-scale Periodic Reattachment Flow (L/D = 1.00~1.50).

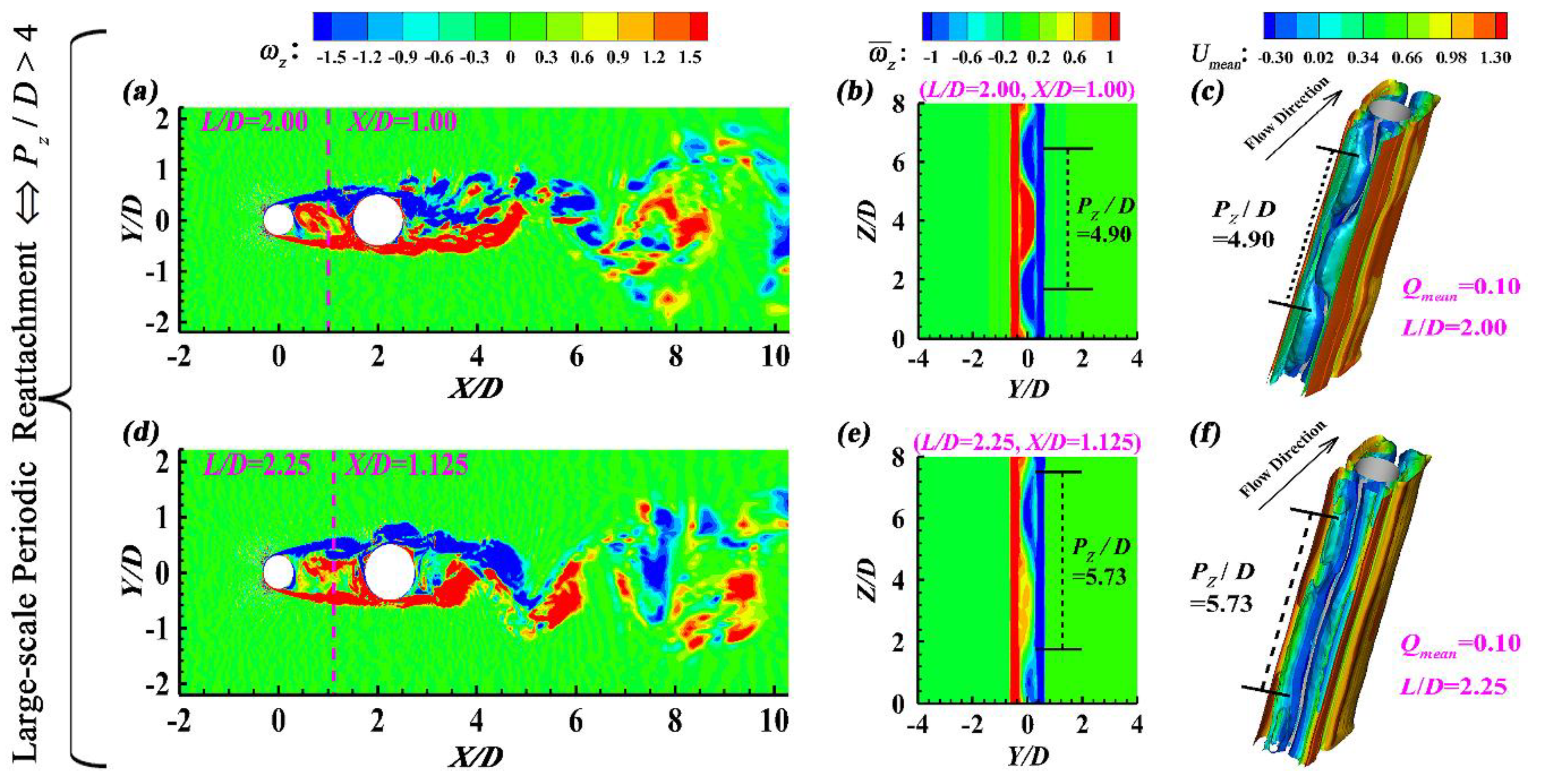
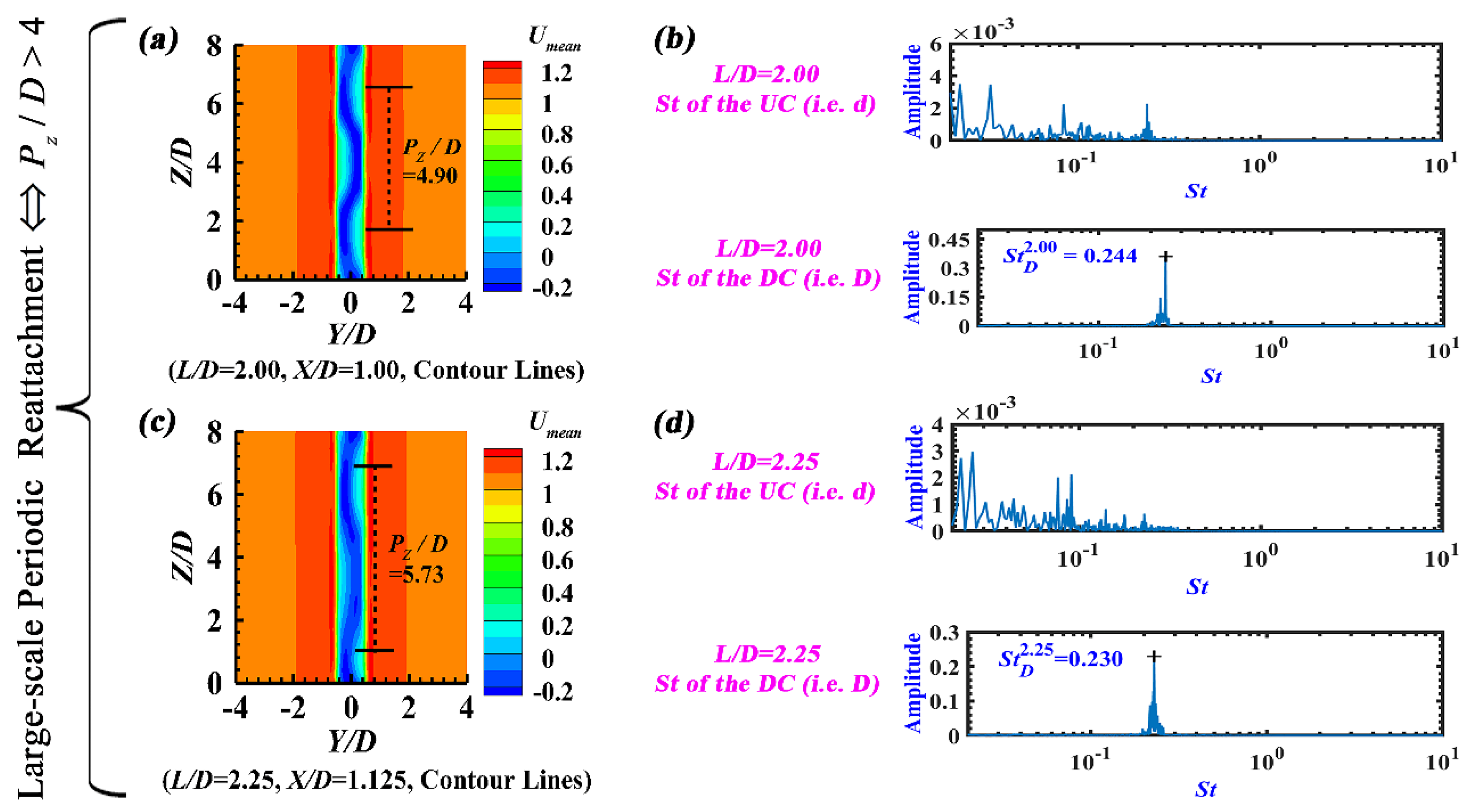
3.3. Large-Scale Periodic Reattachment Flow (L/D = 2.00~2.25)

Figure 6(a, d) shows that, when L/D = 2.00 and 2.25, the UC shear layers still constantly reattach on the DC, and an unsteady recirculating flow occurs within the gap. Moreover, Figure 6(b, e), Figure 6(c, f) and Figure 7(a, c) confirm that large-scale spanwise-periodic time-averaged flow structures (P_z/D = 4.90~5.73) can be captured from the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours and the time-averaged streamwise velocity (U_mean) contours in the transverse plane, as well as the time-averaged Q-criterion iso-surfaces (Q_mean = 0.10) within the gap. Therefore, this flow pattern is called as Large-scale Periodic Reattachment Flow in this study. Figure 7(b, d) reveals that, when L/D = 2.00 and 2.25, the DC possesses one dominant Strouhal number (i.e., $S{t}_D^{2.00}$ = 0.244 and $S{t}_D^{2.25}$ = 0.230), which results from its alternately shedding Karman vortex street in the wake, but the UC has no dominant Strouhal number. One reason is that no vortex shedding occurs from the UC (Figure 6(a, d)), and the other reason is that the feedback effect of the DC vortex shedding on the UC is negligible due to relatively larger L/D values. In fact, both Small-scale Periodic Reattachment Flow (L/D = 1.00~1.50) and Large-scale Periodic Reattachment Flow (L/D = 2.00~ 2.25) share some similarity with Reverse-Flow Reattachment proposed by Alam [28] and Zhou et al. [40], considering that for these flow regimes a part of the reattached shear layers is towards upstream after impinging onto the DC and the reverse flow can extend up to the backside of the UC. Nevertheless, in this study (unequal diameter case), the two shear layers simultaneously reattach on the two sides of the DC (Figure 4(a, d, g, j, m, p) and Figure 6(a, d)), but, in Alam [28] and Zhou et al. [40] (equal diameter case), the two shear layers alternately reattach on the two sides of the DC.

Table 3 and Figure 6(a, d) disclose that, when L/D = 2.00~2.25, the spanwise-averaged time-averaged reattachment angle of the DC is ${\theta }_r^D$ = 53.97°~55.04°, being smaller than ${\theta }_r^D$ = 57.86°~60.46° of Small-scale Periodic Reattachment Flow. Consequently, relative to L/D = 1.00~1.50, more shear-layer vortices, shedding from the two sides of the UC, are drawn into the gap at L/D = 2.00~2.25. Meanwhile, the spacing ratio of L/D = 2.00~2.25 is still small enough to provide the stabilization action necessary for the embroiled shear-layer vortices within the gap to produce the large-scale spanwise-periodic time-averaged flow structures (P_z/D > 4), which is the formation mechanism of Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25). In terms of the time-averaged streamlines, the time-averaged streamwise/vertical velocity contours and the time-averaged spanwise vorticity contours, a pronounced asymmetry was detected in horizontal X-Y planes by Khorrami et al. [59] for Reattachment Flow (d/D = 1.0 and L/D = 1.435), but no clear explanation for its occurrence was given out. From Figure 4~Figure 7, it can be deduced that, in terms of the time-averaged spanwise vorticity contours, the time-averaged streamwise velocity contours and the time-averaged Q-criterion iso-surfaces, a remarkable asymmetry along the transverse direction (Y axis) exists in horizontal X-Y planes within the gap for L/D = 1.00~2.25, which means that both Small-scale Periodic Reattachment Flow and Large-scale Periodic Reattachment Flow are responsible for the aforementioned asymmetry. 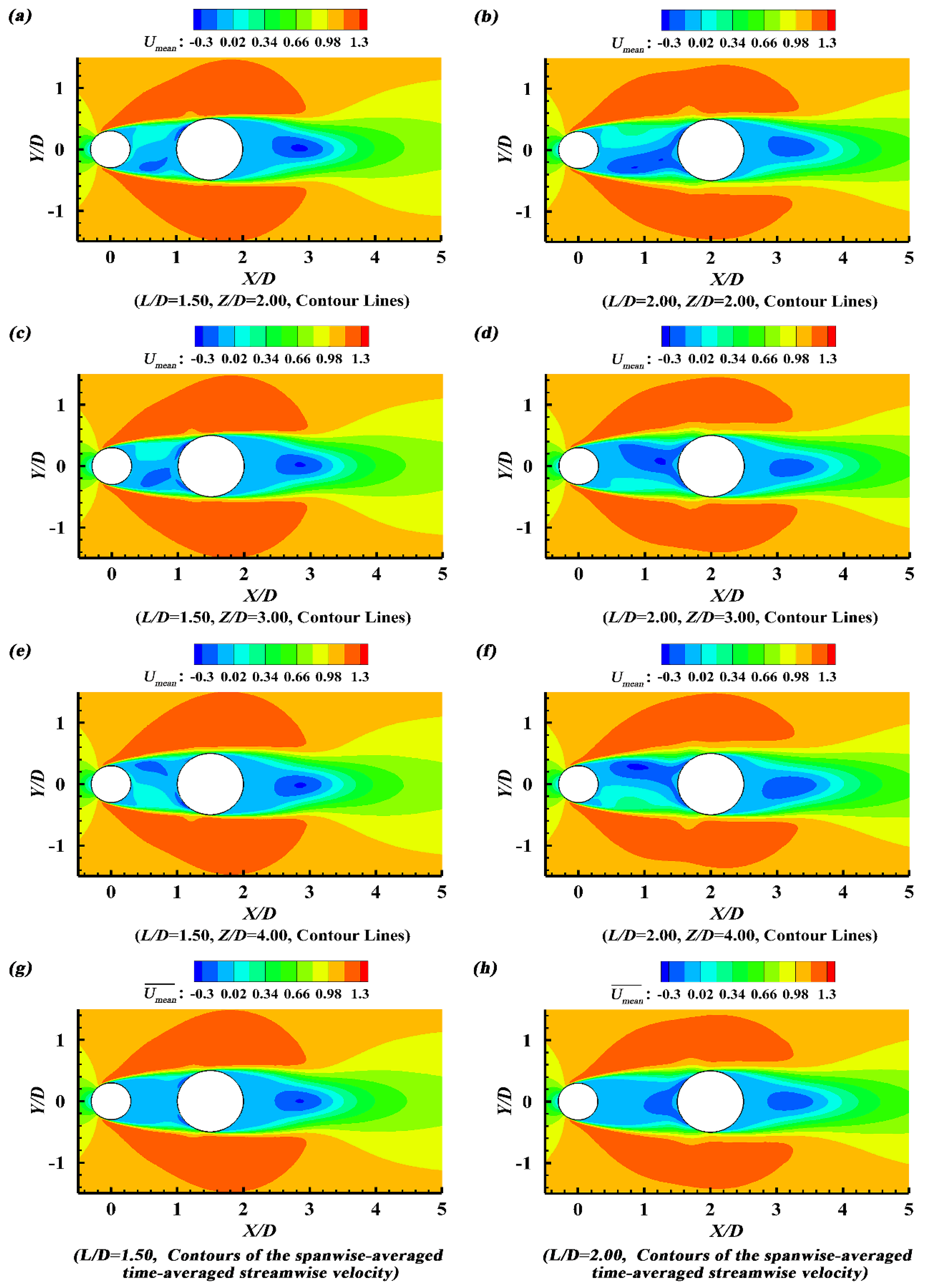For example, Figure 8(a, b, c, d, e, f) illustrates that the time-averaged streamwise velocity (U_mean) contours are asymmetric at different heights for L/D = 1.50 and 2.00, despite that the spanwise-averaged time-averaged streamwise velocity ($\overline{U_{mean}}$) contours are symmetric (Figure 8(g, h)).

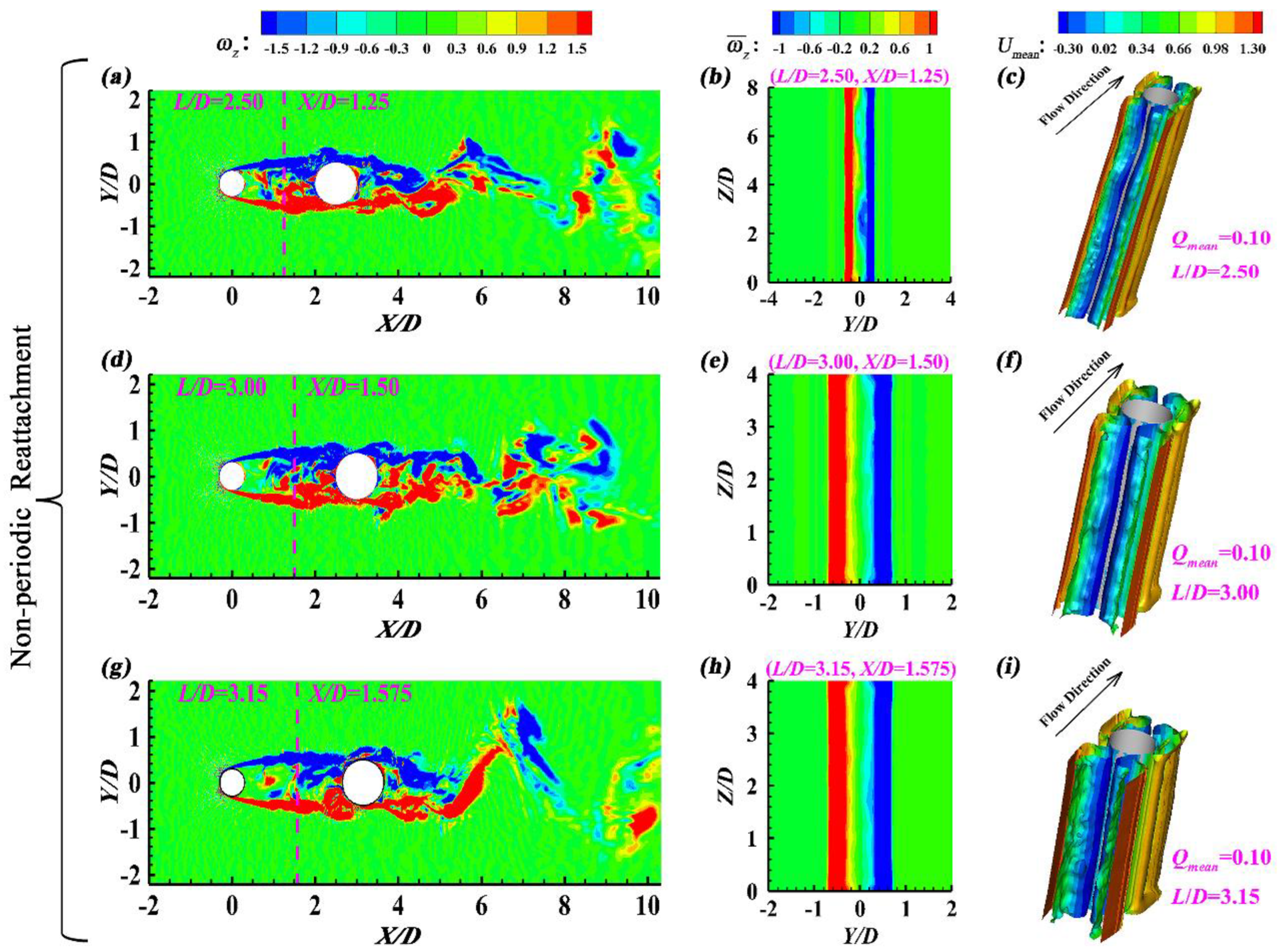
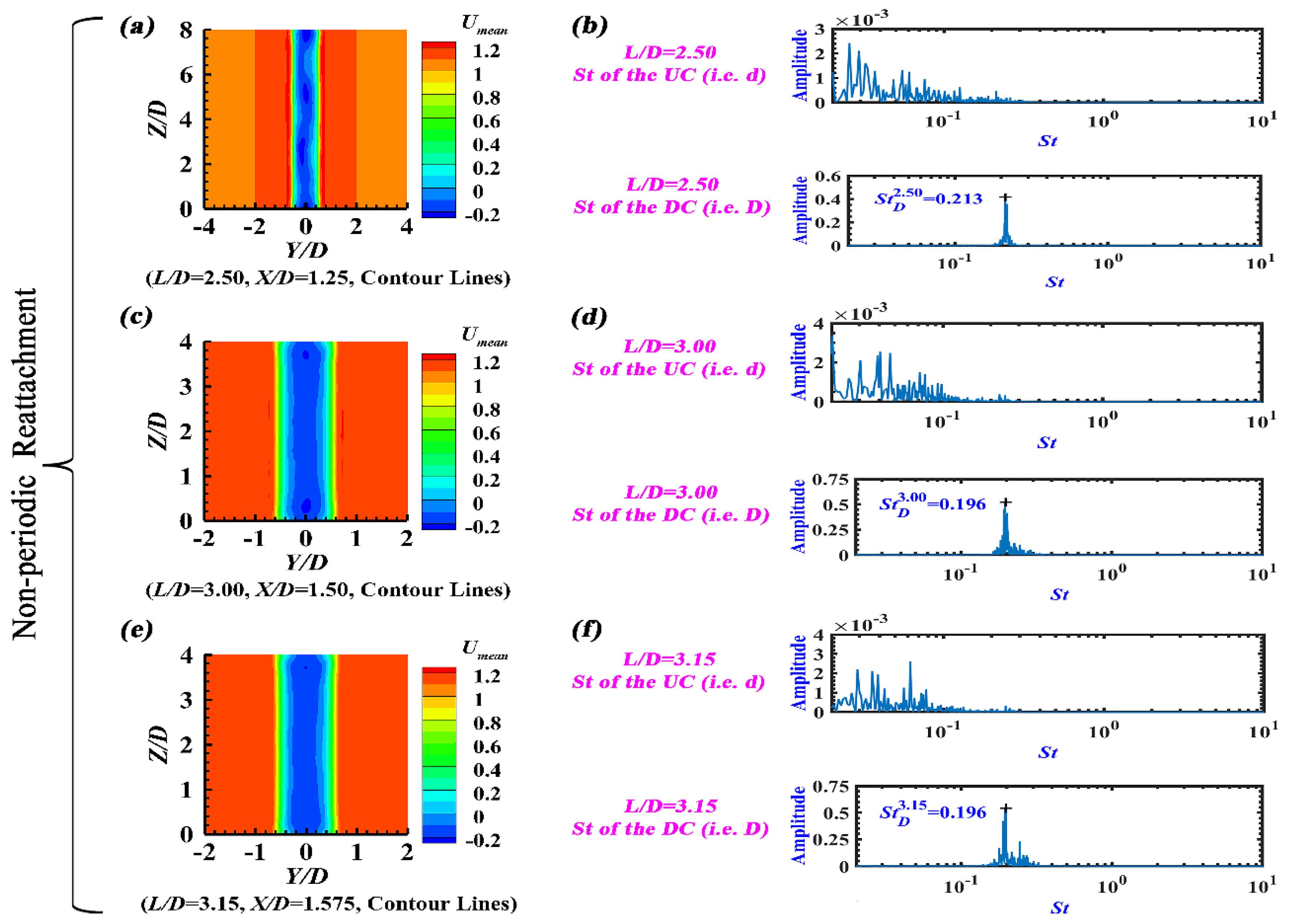
3.4. Non-Periodic Reattachment Flow (L/D = 2.50~3.15)

Figure 9(a, d, g) proves that, when L/D = 2.50~3.15, the UC shear layers also simultaneously reattach on the two sides of the DC. Under this condition, the reverse flow within the gap fails to reach the backside of the UC, behaving like the Reverse-Flow No Reattachment observed by Zhou et al. [40]. Figure 9(b, e, h), Figure 9(c, f, i) and Figure 10(a, c, e) demonstrate that no obvious spanwise-periodic time-averaged flow structures can be recognized for L/D = 2.50~3.15, in terms of the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours, the time-averaged streamwise velocity (U_mean) contours and the time-averaged Q-criterion iso-surfaces of (Q_mean = 0.10) within the gap. Therefore, this flow pattern is defined as Non-periodic Reattachment Flow in this study. Furthermore, Figure 10(b, d, f) makes it clear that, only one dominant Strouhal number is observed for the DC ($S{t}_D^{2.50}$ = 0.213, $S{t}_D^{3.00}$ = 0.196 and $S{t}_D^{3.15}$ = 0.196), but no dominant Strouhal number is discerned for the UC, being identical to both Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25) in this study and the steady reattachment regime reported by Alam et al. [27]. Table 3 and Figure 9(a, d, g) manifest that, when L/D = 2.50~3.15, the spanwise-averaged time-averaged reattachment angle of the DC is ${\theta }_r^D$ = 52.54°~53.74°, being smaller than ${\theta }_r^D$ = 53.97°~55.04° of Large-scale Periodic Reattachment Flow and ${\theta }_r^D$ = 57.86°~60.46° of Small-scale Periodic Reattachment Flow. Consequently, relative to L/D = 1.00~2.25, more shear-layer vortices, shedding from the two sides of the UC, are drawn into the gap at L/D = 2.50~3.15. Meanwhile, the spacing ratio of L/D = 2.50~3.15 is too large to provide the stabilization action necessary for the embroiled shear-layer vortices to generate the spanwise-periodic time-averaged flow structures within the gap, which is the formation mechanism of Non-periodic Reattachment Flow.

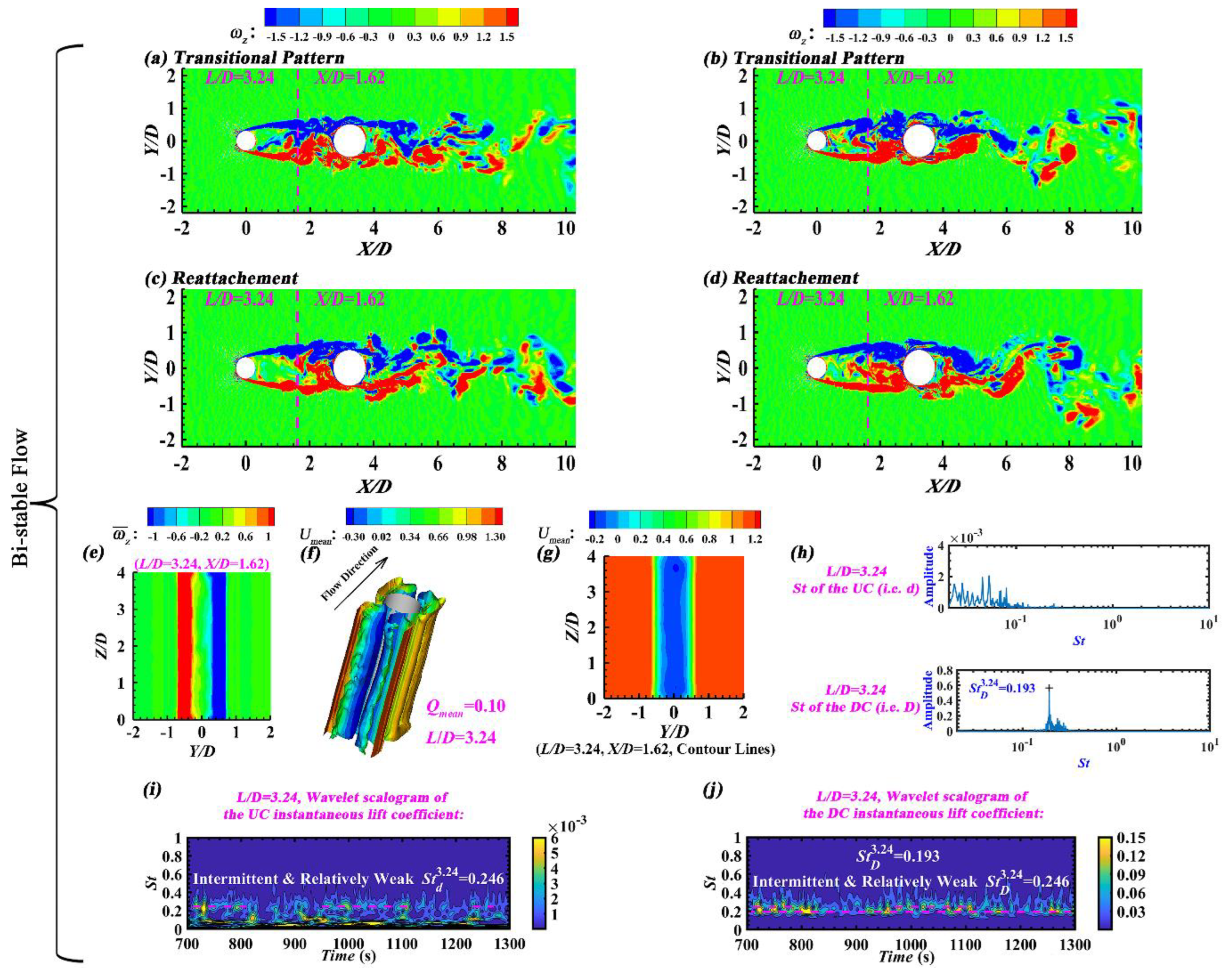
3.5. Bi-Stable Flow (L/D = 3.24)

This study reconfirms the occurrence of the well-known Bi-stable Flow at the transition from Reattachment Flow to Co-shedding Flow [25,60]. Figure 11 verifies the co-existence of two flow states at a given configuration, namely the reattachment pattern (Figure 11(c, d)) and the transitional pattern (Figure 11(a, b)), switching intermittently from one to another. Bi-stable Flow defined in this study is different from that reported by Gao et al. [36] and Carmo et al. [61]. As stated by Rastan and Alam [29], the latter is actually the hysteresis (HS) phenomenon in the literature [19,62,63]. Figure 11(e, f, g) shows that, being identical to Non-periodic Reattachment Flow (L/D = 2.50~3.15), no obvious spanwise-periodic time-averaged flow structures are detected for Bi-stable Flow (L/D = 3.24), in terms of the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours, the time-averaged streamwise velocity (U_mean) contours, and the time-averaged Q-criterion iso-surfaces (Q_mean = 0.10) within the gap. Besides, no dominant Strouhal number is perceived for the UC and only one dominant Strouhal number is recognized for the DC ($S{t}_D^{3.24}$ = 0.193, Figure 11(h)) for L/D = 3.24 when implementing the Fast Fourier Transform of the instantaneous lift coefficient, having similar characteristic as Non-periodic Reattachment Flow (L/D = 2.50~3.15, Figure 10(b, d, f)) and Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25, Figure 7(b, d)). For Bi-stable Flow, the reattachment pattern is predominant, but the transitional pattern is intermittent and relatively weak, being consistent with the results of Kitagawa and Ohta [6] and Alam et al. [64]. Figure 11(i, j) presents that, when performing the continuous wavelet analysis of the instantaneous lift coefficient, an intermittent and relatively weak Strouhal number ($S{t}_d^{3.24}$ = $S{t}_D^{3.24}$ = 0.246) is clearly visible for both cylinders, which corresponds to the transitional pattern of Bi-stable Flow. In addition, the present critical spacing ratio (L/D)_c is equal to 3.24, being close to the value in the literature [6,7,21,23,25,27,33,37,60,65].

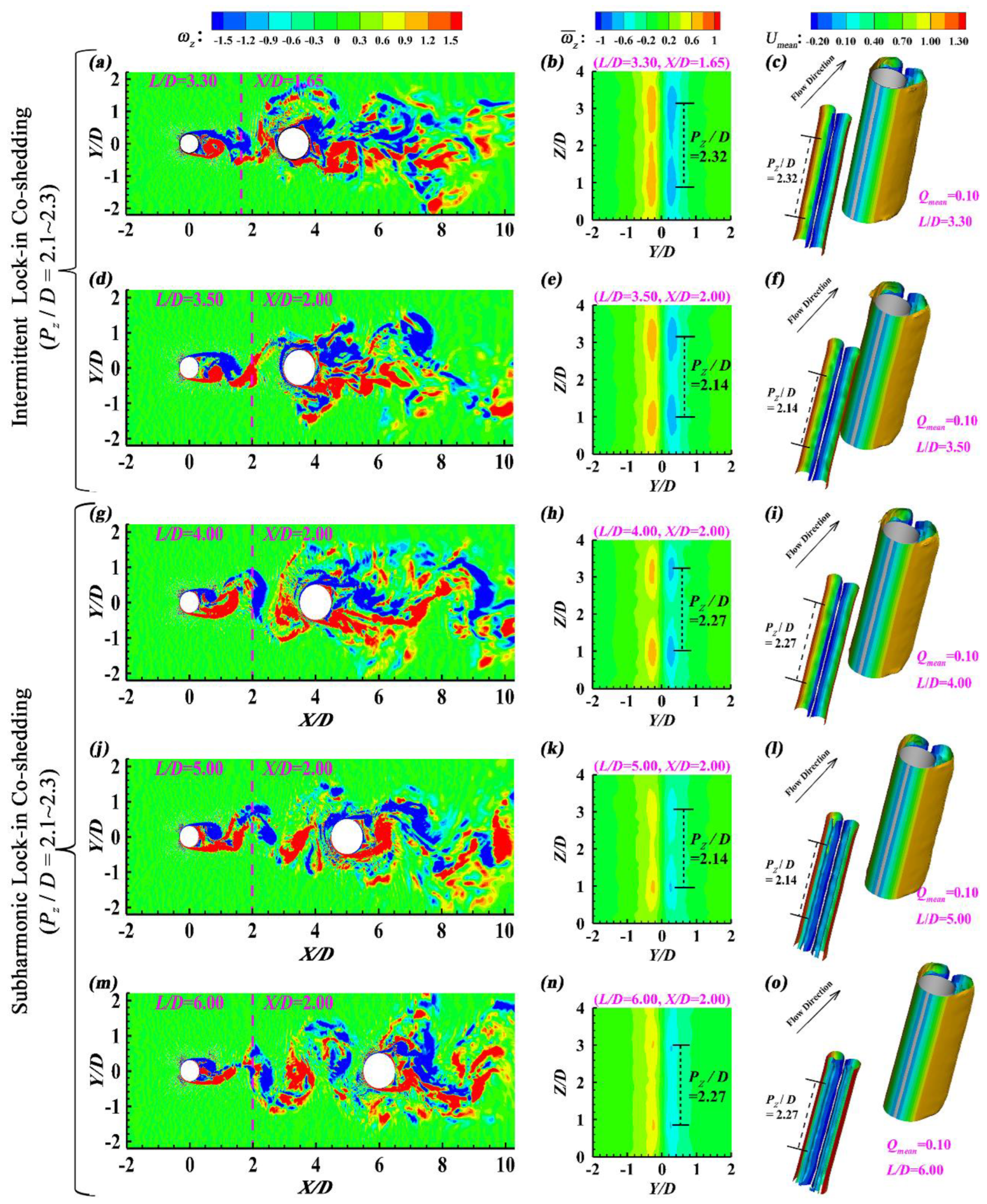
3.6. Co-Shedding Flow (L/D = 3.30~6.00)

Figure 12(a, d, g, j, m) illustrates that antisymmetric Karman vortex shedding mode is captured both within the gap region and behind the DC for L/D = 3.30~6.00, which means the occurrence of Co-shedding Flow. Moreover, Figure 12(b, e, h, k, n), Figure 12(c, f, i, l, o) and Figure 13(a, c, e, g, i) indicate that the spanwise-periodic time-averaged flow structures (P_z/D = 2.14~2.32) can be observed with the aid of the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours, the time-averaged streamwise velocity (U_mean) contours and the time-averaged Q-criterion iso-surfaces (Q_mean = 0.10) within the gap. Alam and Zhou [30], Wang et al. [33] and Alam et al. [34] subdivided Co-shedding Flow into lock-in, intermittent lock-in, subharmonic lock-in and no lock-in, depending on the values of Re, d/D and L/D. 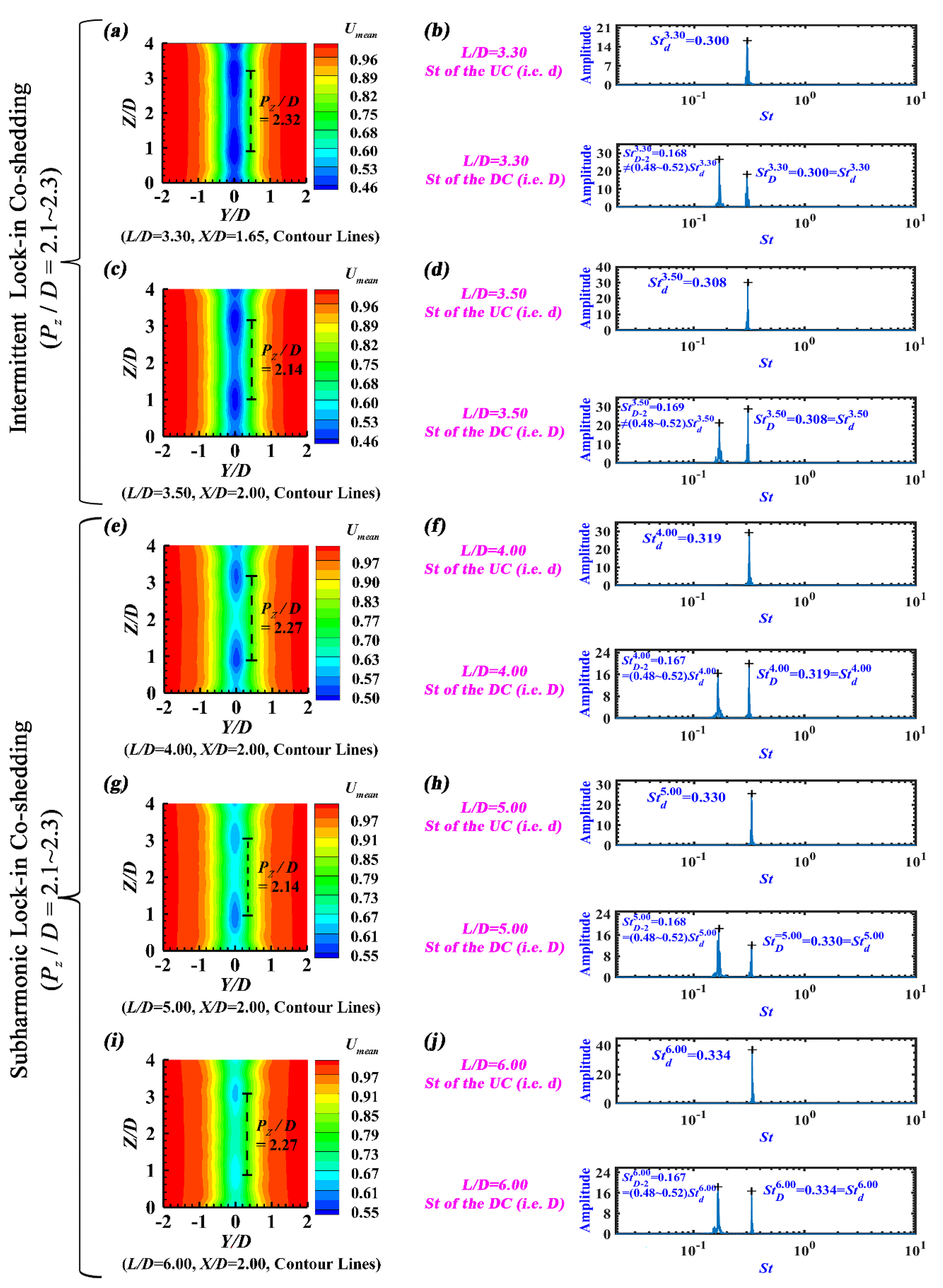Figure 13(b, d) manifests that, for L/D = 3.30 and 3.50, there is only one dominant Strouhal number for the UC (i.e., $S{t}_d^{3.30}$ = 0.300 and $S{t}_d^{3.50}$ = 0.308, respectively), being attributed to the UC vortex-shedding. However, two dominant Strouhal numbers are visible for the DC (i.e., $S{t}_D^{3.30}$ = $S{t}_d^{3.30}$ = 0.300 & $S{t}_{D-2}^{3.30}$ = 0.168 at L/D = 3.30; $S{t}_D^{3.50}$ = $S{t}_d^{3.50}$ = 0.308 & $S{t}_{D-2}^{3.50}$ = 0.169 at L/D = 3.50). Obviously, $S{t}_D^{3.30}$ and $S{t}_D^{3.50}$ are generated by the influence of the UC vortex-shedding, but $S{t}_{D-2}^{3.30}$ and $S{t}_{D-2}^{3.50}$ are caused by the DC vortex-shedding. Considering that $S{t}_D^{3.30}$ = $S{t}_d^{3.30}$, $S{t}_{D-2}^{3.30}$ ≠ (0.48~0.52)$S{t}_d^{3.30}$, $S{t}_D^{3.50}$ = $S{t}_d^{3.50}$ and $S{t}_{D-2}^{3.50}$ ≠ (0.48~0.52)$S{t}_d^{3.50}$, this flow regime belongs to Intermittent Lock-in Co-shedding, which was also observed by Alam et al. [34] (please see the first row of Figure 6(a, d) in their article).

Figure 13(f, h, j) demonstrates that, for L/D = 4.00, 5.00 and 6.00, one dominant Strouhal number of the DC is equal to that of the UC (i.e., $S{t}_D^{4.00}$ = $S{t}_d^{4.00}$ = 0.319, $S{t}_D^{5.00}$ = $S{t}_d^{5.00}$ = 0.330 and $S{t}_D^{6.00}$ = $S{t}_d^{6.00}$ = 0.334, respectively), and the other dominant Strouhal number of the DC is nearly half that of the UC (i.e., $S{t}_{D-2}^{4.00}$ = (0.48~0.52)$S{t}_d^{4.00}$ = 0.167, $S{t}_{D-2}^{5.00}$ = (0.48~0.52) $S{t}_d^{5.00}$ = 0.168 and $S{t}_{D-2}^{6.00}$ = (0.48~0.52)$S{t}_d^{6.00}$ = 0.167, respectively, lying within the uncertainty due to the frequency resolution in power spectral density). Therefore, this flow regime belongs to Subharmonic Lock-in Co-shedding, being in accordance with the results of Alam et al. [34]. In fact, Figure 12(b, e, h, k, n), Figure 12(c, f, i, l, o) and Figure 13(a, c, e, g, i) prove that both Intermittent Lock-in Co-shedding (L/D = 3.30~3.50) and Subharmonic Lock-in Co-shedding (L/D = 4.00~6.00) have the similar spanwise-periodic length (P_z/D = 2.14~2.32) for the time-averaged flow structures within the gap, and the strength of the spanwise periodicity continuously decreases with the increase of L/D.

Figure 12. Co-shedding Flow (L/D = 3.30~6.00): (a, d, g, j, m) The instantaneous spanwise vorticity (${\omega }_z$) contours in the mid-height plane, (b, e, h, k, n) The time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours in the transverse plane, and (c, f, i, l, o) The time-averaged Q-criterion iso-surfaces within the gap.

Figure 12. Co-shedding Flow (L/D = 3.30~6.00): (a, d, g, j, m) The instantaneous spanwise vorticity (${\omega }_z$) contours in the mid-height plane, (b, e, h, k, n) The time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours in the transverse plane, and (c, f, i, l, o) The time-averaged Q-criterion iso-surfaces within the gap.

Figure 13. Co-shedding Flow (L/D = 3.30~6.00): (a, c, e, g, i) The time-averaged streamwise velocity (U_mean) contours in the transverse plane, and (b, d, f, h, j) The Strouhal number based on the instantaneous lift coefficient.

Figure 13. Co-shedding Flow (L/D = 3.30~6.00): (a, c, e, g, i) The time-averaged streamwise velocity (U_mean) contours in the transverse plane, and (b, d, f, h, j) The Strouhal number based on the instantaneous lift coefficient.

4. Conclusions

Flows around two different-sized tandem circular cylinders with d/D = 0.6 are systematically studied at seventeen spacing ratios (L/D = 1.00, 1.10, 1.15, 1.20, 1.25, 1.50, 2.00, 2.25, 2.50, 3.00, 3.15, 3.24, 3.30, 3.50, 4.00, 5.00 and 6.00) at Re = 3900. The analysis focuses on the flow regimes and the spanwise periodicity of the time-averaged flow structures within the gap. The main findings include the following:

By examining the instantaneous spanwise vorticity (${\omega }_z$) contours, the time-averaged spanwise vorticity (${\overline{\omega }}_z$) contours, the time-averaged streamwise velocity (U_mean) contours, the time-averaged Q-criterion iso-surfaces and the Strouhal number based on the instantaneous lift coefficient, the flow is divided into six regimes, namely Small-scale Periodic Reattachment Flow (L/D = 1.00~1.50, P_z/D = (0, 4] within the gap), Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25, P_z/D > 4 within the gap), Non-periodic Reattachment Flow (L/D = 2.50~3.15, no spanwise periodicity within the gap), Bi-stable Flow (L/D = 3.24, no spanwise periodicity within the gap), Intermittent Lock-in Co-shedding (L/D = 3.30~3.50, $S{t}_{D-2}^{}$ ≠ (0.48~0.52)$S{t}_d^{}$, P_z/D = 2.14~2.32 within the gap) and Subharmonic Lock-in Co-shedding (L/D = 4.00~6.00, $S{t}_{D-2}^{}$ = (0.48~0.52)$S{t}_d^{}$, P_z/D = 2.14~2.32 within the gap). Moreover, it is concluded that, the formation mechanisms of the aforementioned three reattachment sub-flow regimes are related to both the L/D value (determining the strength of the stabilization action necessary for the generation of the spanwise-periodic time-averaged flow structures within the gap) and the spanwise-averaged time-averaged reattachment angle of the DC (${\theta }_r^D$, deciding the amount of the UC shear-layer vortices drawn into the gap).

For Bi-stable Flow (L/D = 3.24), the reattachment pattern is predominant, while the transitional pattern is secondary. Although no dominant Strouhal number is detected for the UC and only one dominant Strouhal number is recognized for the DC ($S{t}_D^{3.24}$ = 0.193) when implementing the Fast Fourier Transform, an intermittent and relatively weak Strouhal number ($S{t}_d^{3.24}$ = $S{t}_D^{3.24}$ = 0.246) is clearly visible for both cylinders when performing the continuous wavelet analysis, which corresponds to the frequency of the transitional pattern in Bi-stable Flow. Additionally, with regard to Reattachment Flow, a pronounced asymmetry along the transverse direction was observed within the gap by some researchers, but no clear explanation for its occurrence has ever been given. This study displays that both Small-scale Periodic Reattachment Flow (L/D = 1.00~1.50) and Large-scale Periodic Reattachment Flow (L/D = 2.00~2.25) are essentially responsible for the aforementioned asymmetry.