Submitted:
23 April 2024
Posted:
25 April 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Study on the Working Principle of On-Line Vibrating Tube Liquid Densitometer
2.1. Working Principle of On-Line Vibrating Tube Liquid Densitometer
2.2. Effect of Temperature Variation on Measurement Results
2.3. Pressure Effects on Measurement Results
3. Research and Development of the Experimental Setup
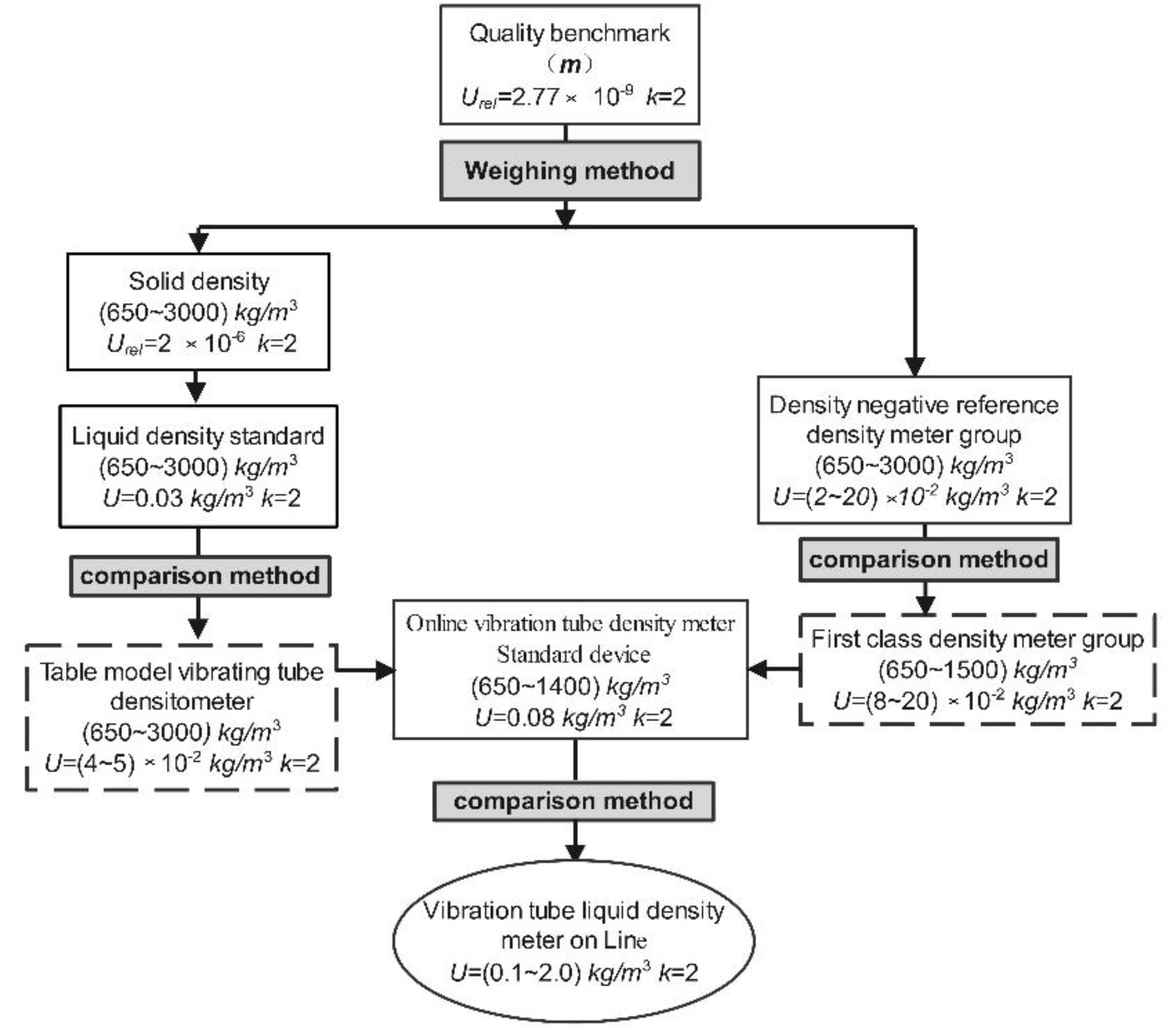
3.1. Establishing the Traceability Chain
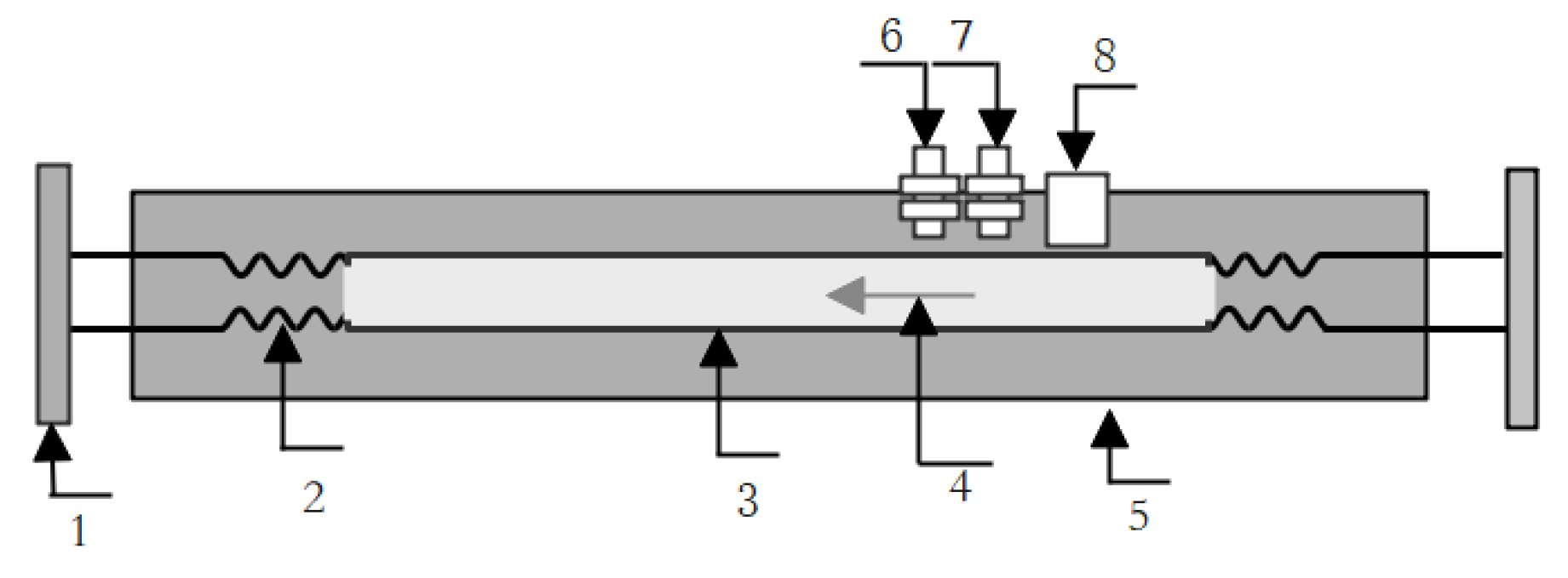
3.2. Device Composition and Structure
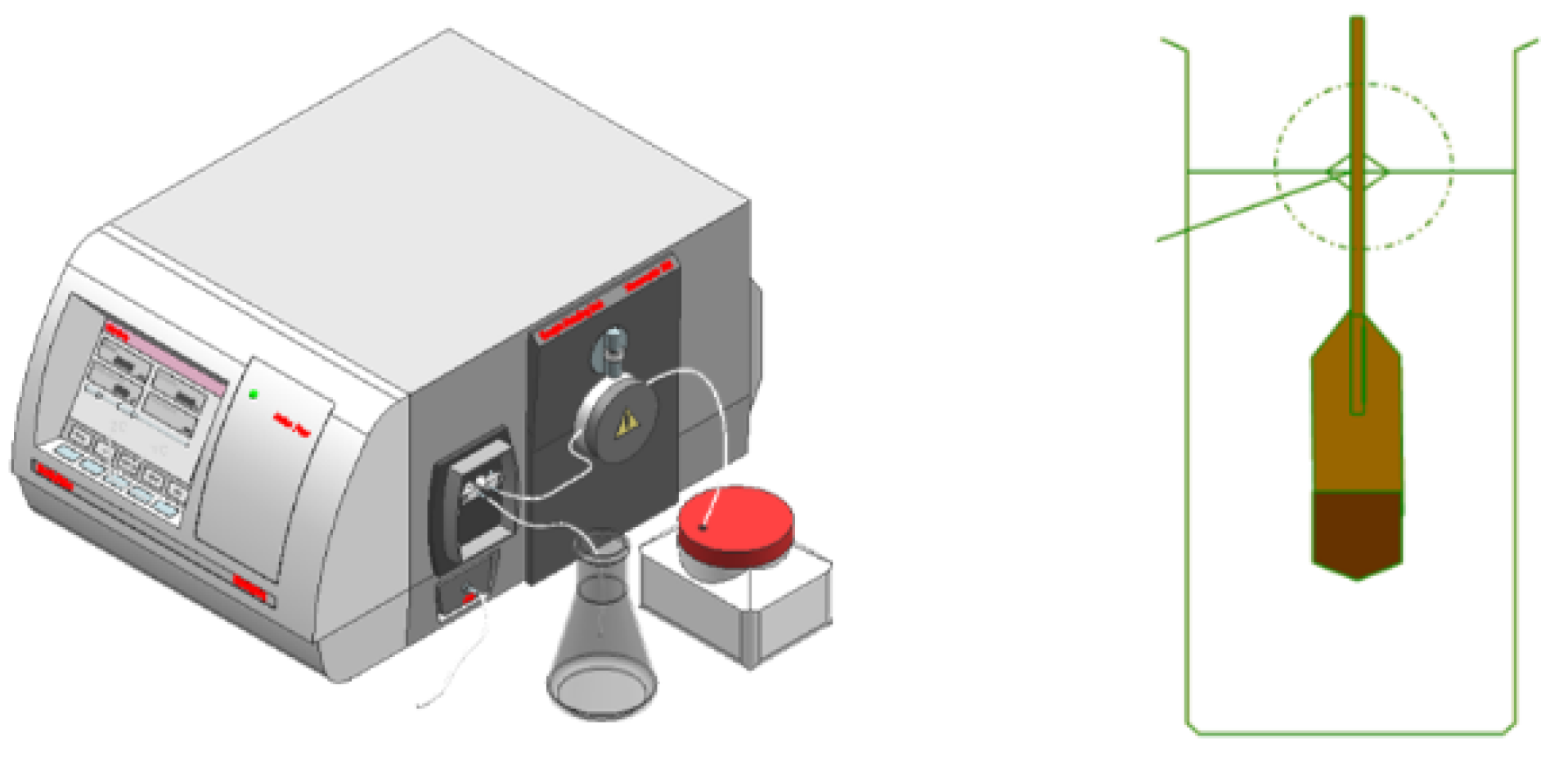
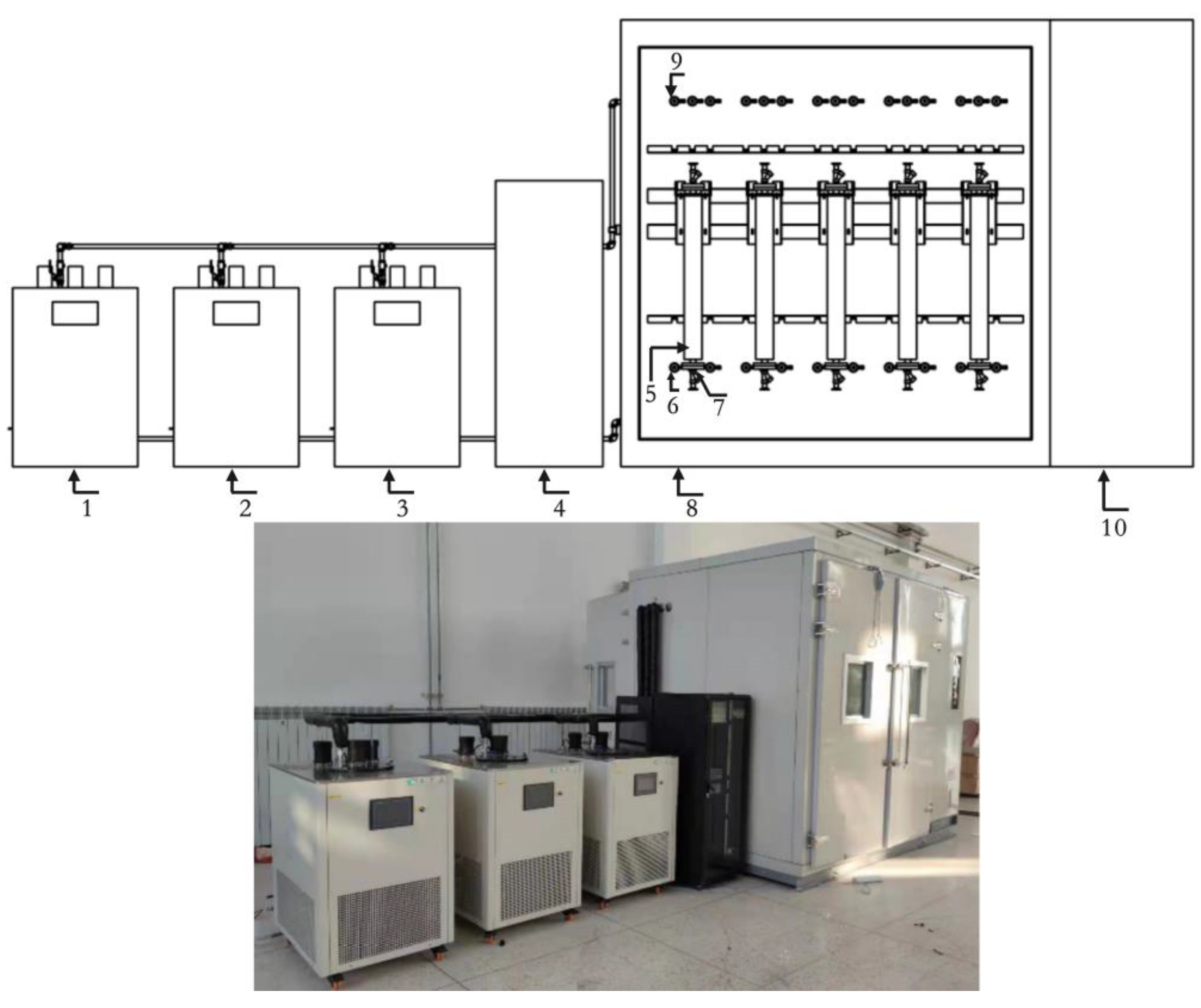
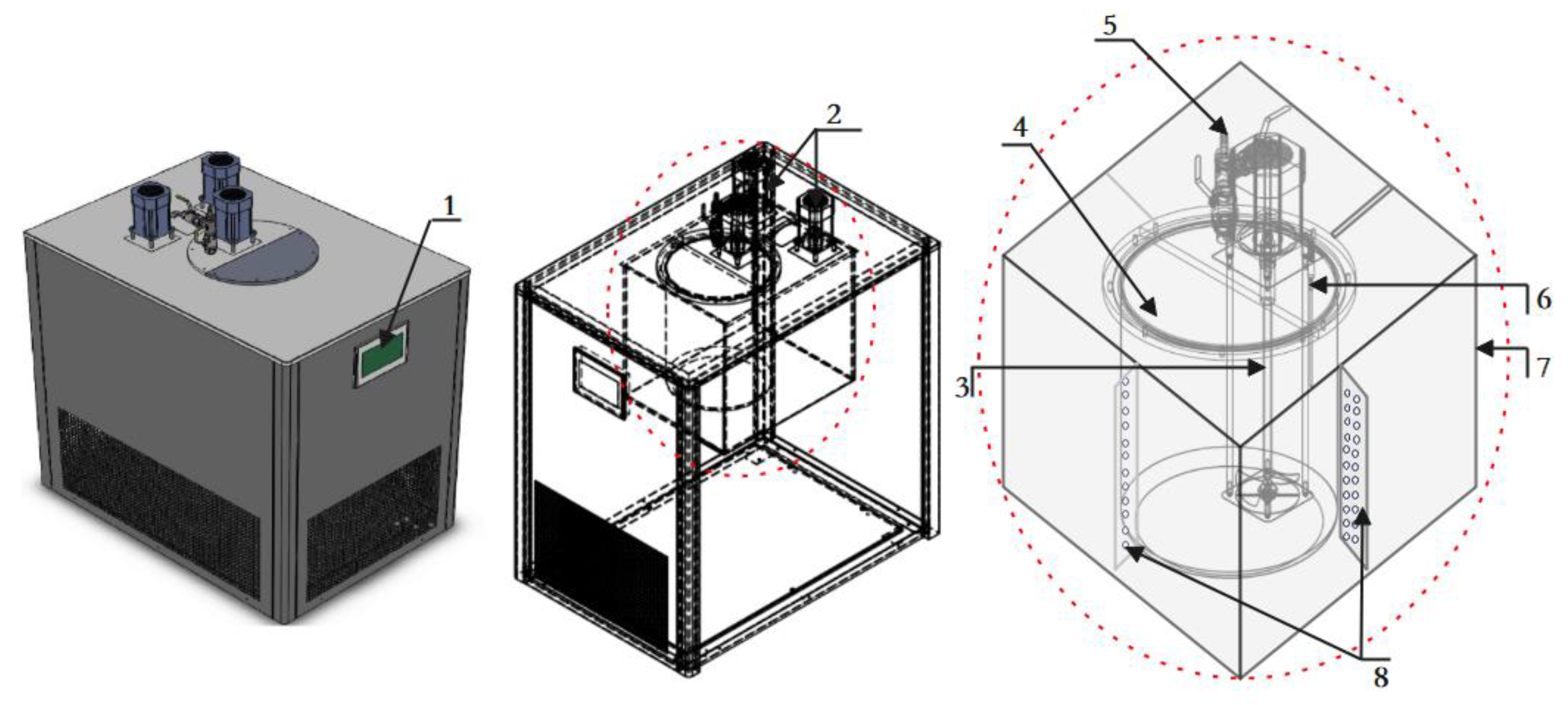
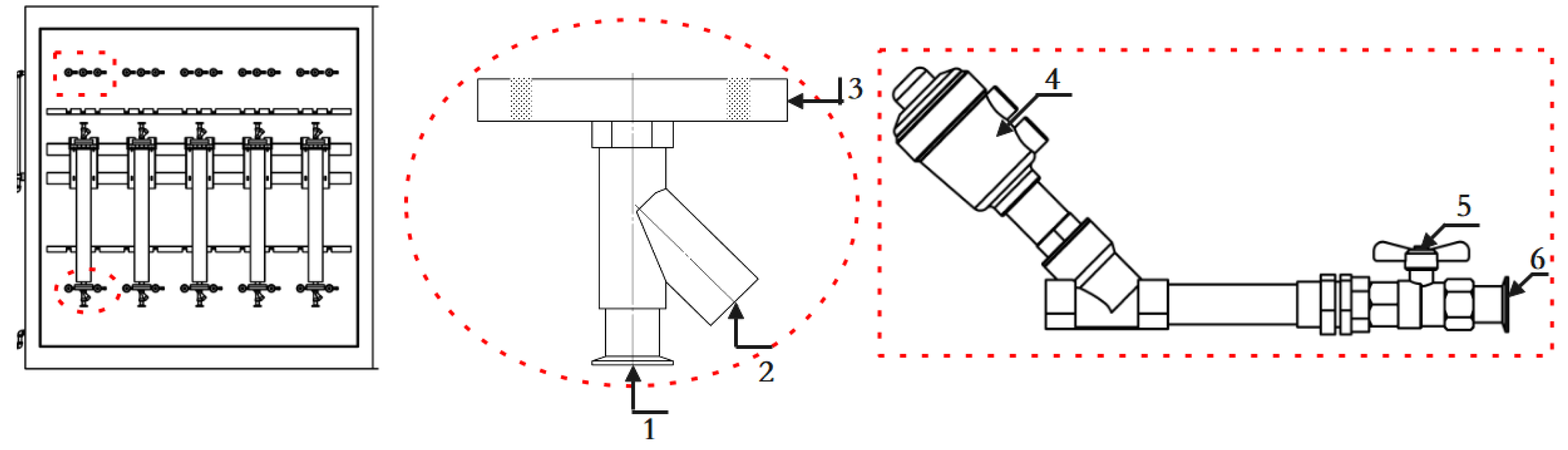

3.3. Device Uncertainty Assessment
| NO. | Source | Type |
u(xi) (kg/m³) |
Combined expanded uncertainty | Combined expanded uncertainty |
|---|---|---|---|---|---|
| 1 | Desktop density meter | B | 0.0225 | 0.039 kg/m3 |
U=0.08 kg/m3 k=2 |
| 2 | densitometer measurement | A | 5.592×10-5 | ||
| 3 | frequency meter measurement | B | 0.00092 | ||
| 4 | temperature measurement | B | 0.007 | ||
| 5 | Fit process | A | 0.031 |
3.4. Workflow of the Experimental Setup
4. Online Vibrating Tube Densitometer Measurement Performance Experiment
4.1. Temperature Vibration Frequency Test
| Liquid name | Measuring temperature(℃) | Vibration period(us) | Standard density(kg/m3) | Fit density(kg/m3) | Fit error(kg/m3) |
| N-Tridecane | 20.001 | 1378.541607 | 756.226 | 756.226 | 0.00 |
| Anhydrous ethanol | 20.000 | 1401.152815 | 823.136 | 823.136 | 0.00 |
| Mixture 1 | 19.995 | 1415.154277 | 865.123 | 865.123 | 0.00 |
| Industrial white oil | 20.001 | 1403.815470 | 831.088 | 831.088 | 0.00 |
| Mixing solution 2 | 19.996 | 1423.031064 | 888.930 | 888.930 | 0.00 |
| Pure water | 20.001 | 1458.638571 | 998.226 | 998.226 | 0.00 |
| Tungstate solution | 20.010 | 1584.048720 | 1405.012 | 1405.013 | 0.01 |
| Liquid name | Measuring temperature(℃) | Vibration period(us) | Standard density(kg/m3) | Fit density(kg/m3) | Fit error(kg/m3) |
| Tridecane | 15.497 | 1379.68479 | 759.442 | 759.526 | -0.08 |
| 20.000 | 1378.53900 | 756.226 | 756.218 | 0.01 | |
| 29.412 | 1376.25237 | 749.509 | 749.630 | -0.12 | |
| 40.231 | 1374.62239 | 745.123 | 744.991 | 0.13 | |
| 45.213 | 1372.95320 | 740.369 | 740.170 | 0.20 | |
| Anhydrous ethanol | 14.253 | 1404.62236 | 833.236 | 833.425 | -0.19 |
| 20.000 | 1403.81547 | 831.088 | 831.088 | 0.00 | |
| 30.123 | 1402.83650 | 828.369 | 828.295 | 0.07 | |
| 40.224 | 1402.19565 | 826.326 | 826.512 | -0.19 | |
| 45.237 | 1400.63691 | 822.136 | 821.925 | 0.21 | |
| Anhydrous ethano2 | 14.953 | 1424.40283 | 892.909 | 893.021 | -0.11 |
| 20.000 | 1423.03450 | 888.930 | 888.940 | -0.01 | |
| 29.096 | 1420.48395 | 881.237 | 881.340 | -0.10 | |
| 36.415 | 1419.56231 | 878.639 | 878.651 | -0.01 | |
| 44.215 | 1418.32352 | 875.236 | 875.011 | 0.22 | |
| Water | 14.362 | 1459.03692 | 999.191 | 999.382 | -0.19 |
| 15.564 | 1458.90888 | 999.009 | 999.002 | 0.01 | |
| 20.002 | 1458.63911 | 998.221 | 998.228 | -0.01 | |
| 29.259 | 1457.84188 | 995.898 | 995.885 | 0.01 | |
| 43.894 | 1456.12524 | 990.651 | 990.767 | -0.12 | |
| Tungstate solution | 14.653 | 1585.58569 | 1410.236 | 1410.112 | 0.12 |
| 20.000 | 1584.04872 | 1405.012 | 1405.012 | 0.00 | |
| 29.251 | 1582.86922 | 1401.236 | 1401.194 | 0.04 | |
| 40.123 | 1582.01231 | 1398.369 | 1398.496 | -0.13 | |
| 45.369 | 1580.97900 | 1395.237 | 1395.104 | 0.13 |
| Liquid name | Measuring temperature(℃) | Vibration period(us) | Standard density(kg/m3) | Fit density(kg/m3) | Fit error(kg/m3) |
| Tridecane | 20.001 | 3659.93511 | 998.226 | 998.208 | -0.02 |
| Anhydrous ethanol | 20.000 | 3607.10110 | 865.123 | 865.198 | 0.08 |
| Mixture 1 | 20.000 | 3590.20928 | 823.136 | 823.080 | -0.06 |
| Industrial white oil | 20.001 | 3563.23146 | 756.226 | 756.225 | -0.00 |
| Mixing solution 2 | 19.996 | 3593.46230 | 831.088 | 831.176 | 0.09 |
| Pure water | 20.001 | 3616.59763 | 888.930 | 888.963 | 0.03 |
| Tungstate solution | 20.010 | 3816.98624 | 1405.012 | 1405.004 | -0.01 |
| Liquid name | Measuring temperature(℃) | Vibration period(us) | Standard density(kg/m3) | Fit density(kg/m3) | Fit error(kg/m3) |
| Tridecane | 15.551 | 3564.05124 | 759.442 | 759.510 | 0.07 |
| 20.000 | 3563.23146 | 756.226 | 756.225 | 0.00 | |
| 29.312 | 3561.62569 | 749.509 | 749.616 | 0.11 | |
| 40.189 | 3561.10569 | 745.123 | 745.239 | 0.12 | |
| 45.112 | 3559.74569 | 740.369 | 740.472 | 0.10 | |
| Anhydrous ethano l | 14.331 | 3593.69892 | 833.236 | 833.312 | 0.08 |
| 20.000 | 3593.46230 | 831.088 | 831.176 | 0.09 | |
| 30.002 | 3593.40000 | 828.369 | 828.291 | -0.08 | |
| 40.224 | 3593.69000 | 826.326 | 826.225 | -0.10 | |
| 45.247 | 3592.55426 | 822.136 | 822.016 | -0.12 | |
| Anhydrous ethano 2 | 14.536 | 3617.61236 | 892.909 | 892.950 | 0.04 |
| 20.000 | 3616.55763 | 888.93 | 888.862 | -0.07 | |
| 29.026 | 3614.44563 | 881.237 | 881.175 | -0.06 | |
| 36.435 | 3614.21369 | 878.639 | 878.626 | -0.01 | |
| 44.215 | 3613.68000 | 875.236 | 875.219 | -0.02 | |
| Water | 14.211 | 3659.75236 | 999.191 | 999.188 | 0.00 |
| 15.113 | 3659.73000 | 999.009 | 998.906 | -0.10 | |
| 20.002 | 3659.95351 | 998.221 | 998.254 | 0.03 | |
| 29.152 | 3659.93123 | 995.898 | 995.917 | 0.02 | |
| 43.544 | 3659.29000 | 990.651 | 990.698 | 0.05 | |
| Tungstate solution | 14.653 | 3818.55000 | 1410.236 | 1410.162 | -0.07 |
| 20.000 | 3816.98624 | 1405.012 | 1405.004 | -0.01 | |
| 29.331 | 3816.26000 | 1401.236 | 1401.294 | 0.06 | |
| 40.023 | 3815.92360 | 1398.369 | 1398.496 | -0.13 | |
| 45.441 | 3815.13123 | 1395.237 | 1395.104 | 0.13 |
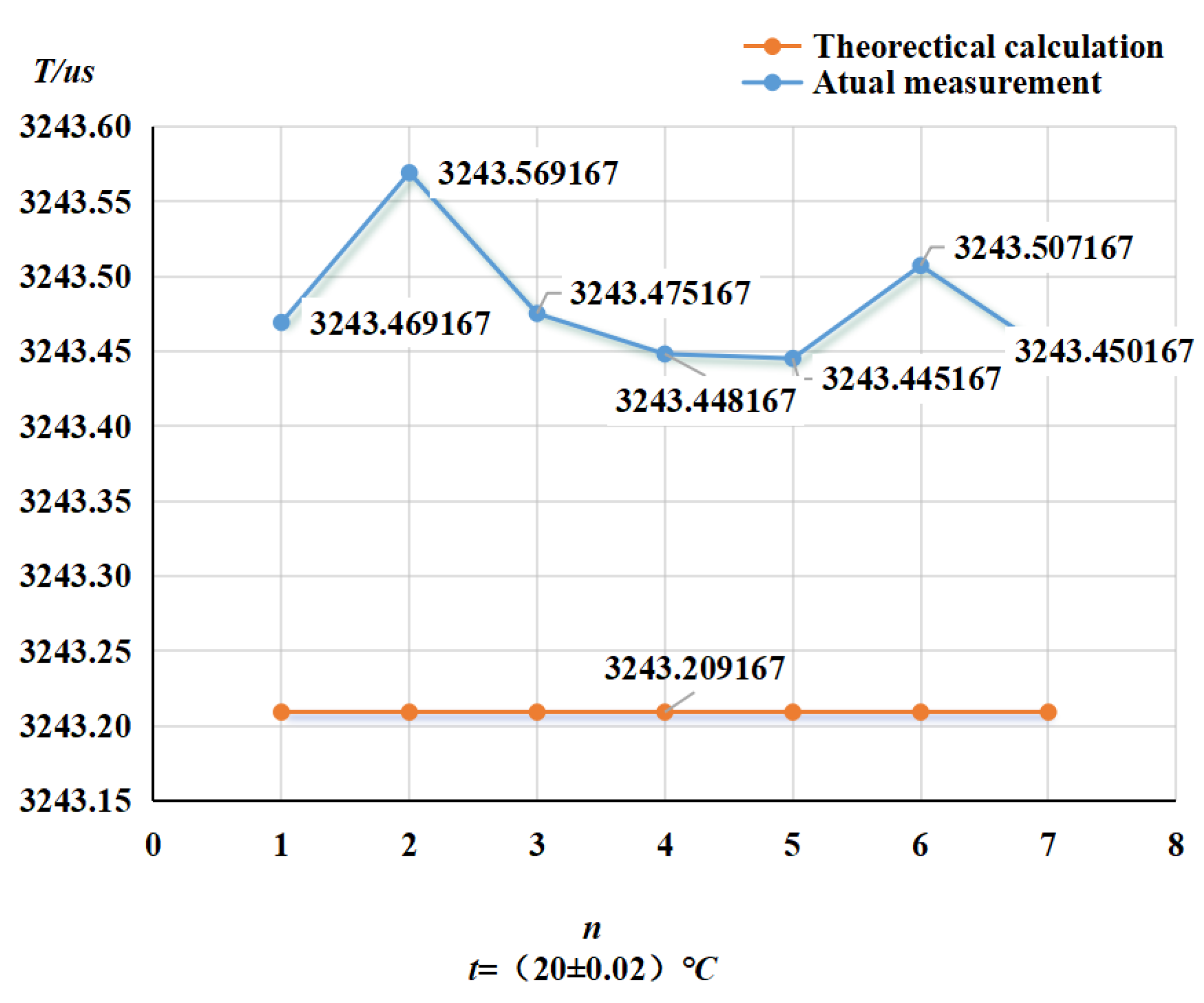
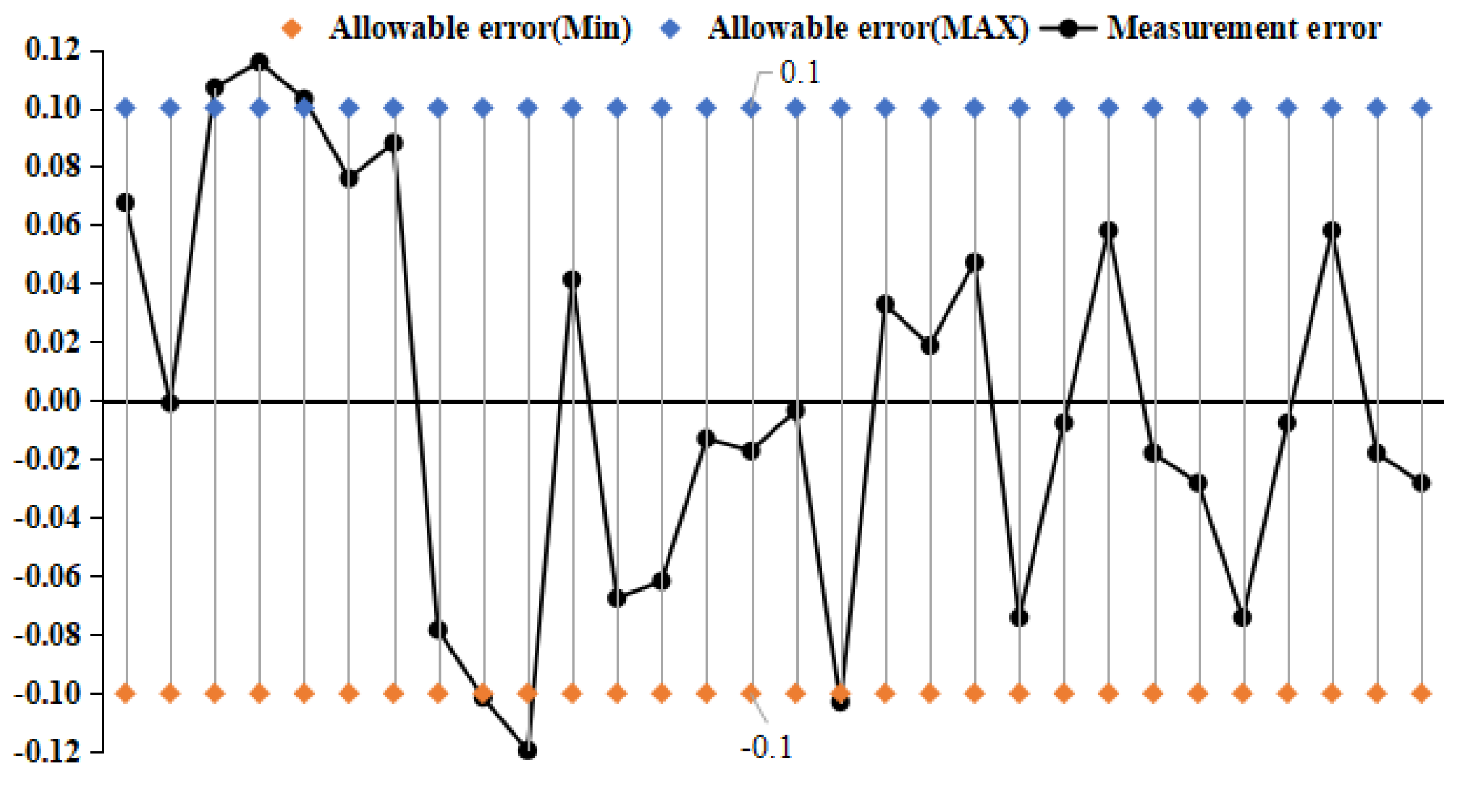
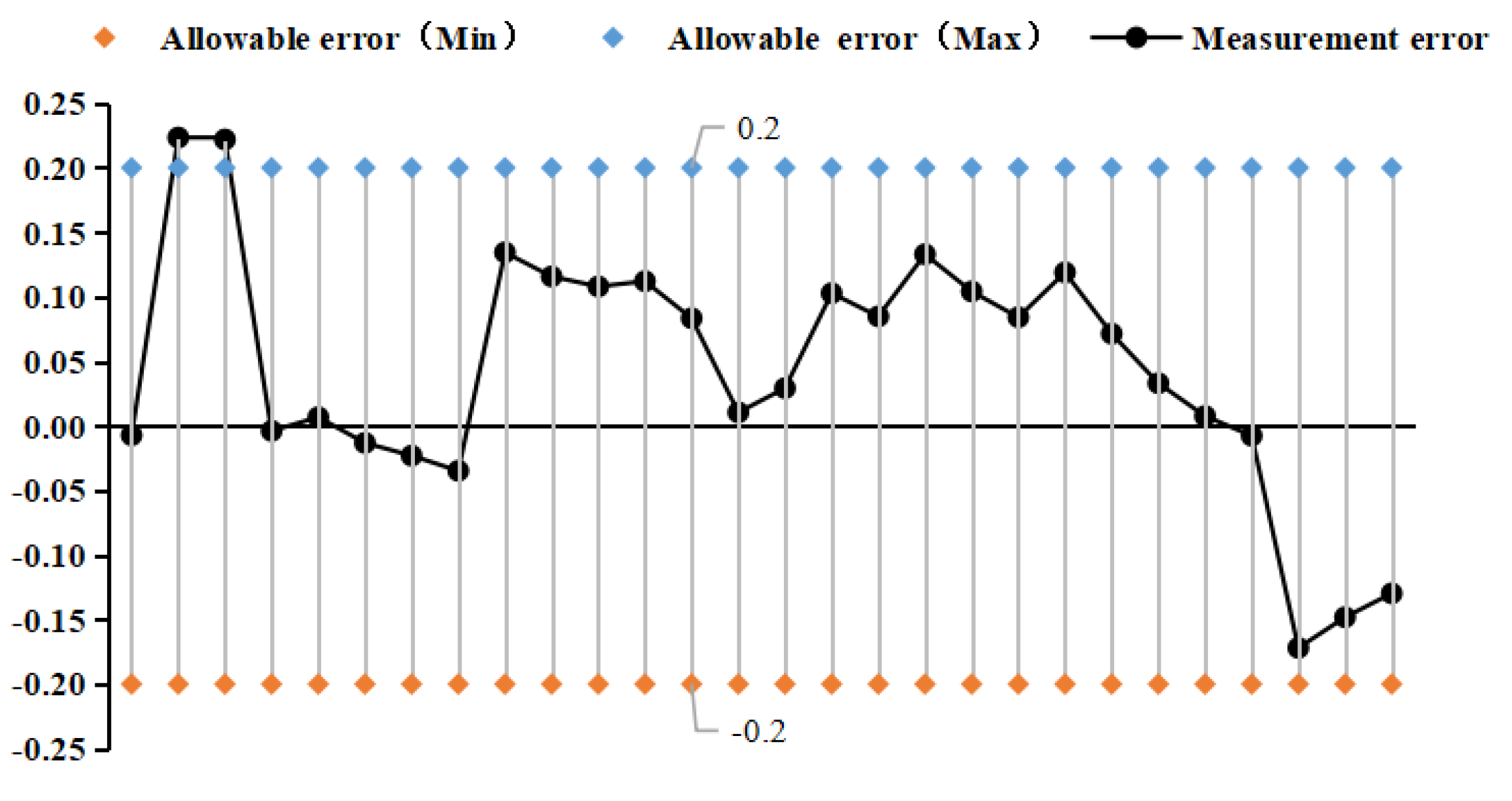
4.2. Pressure Frequency Experiment

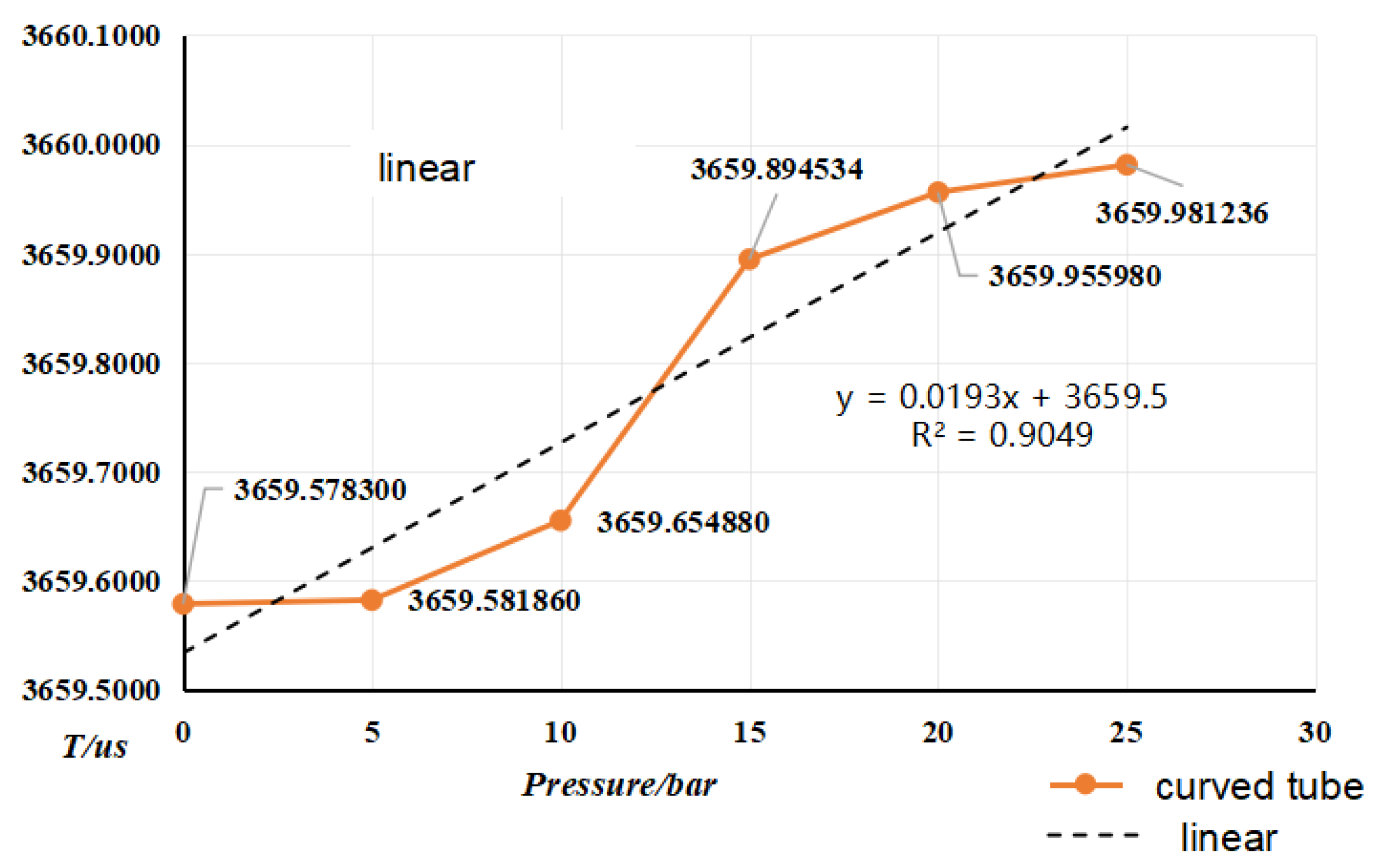
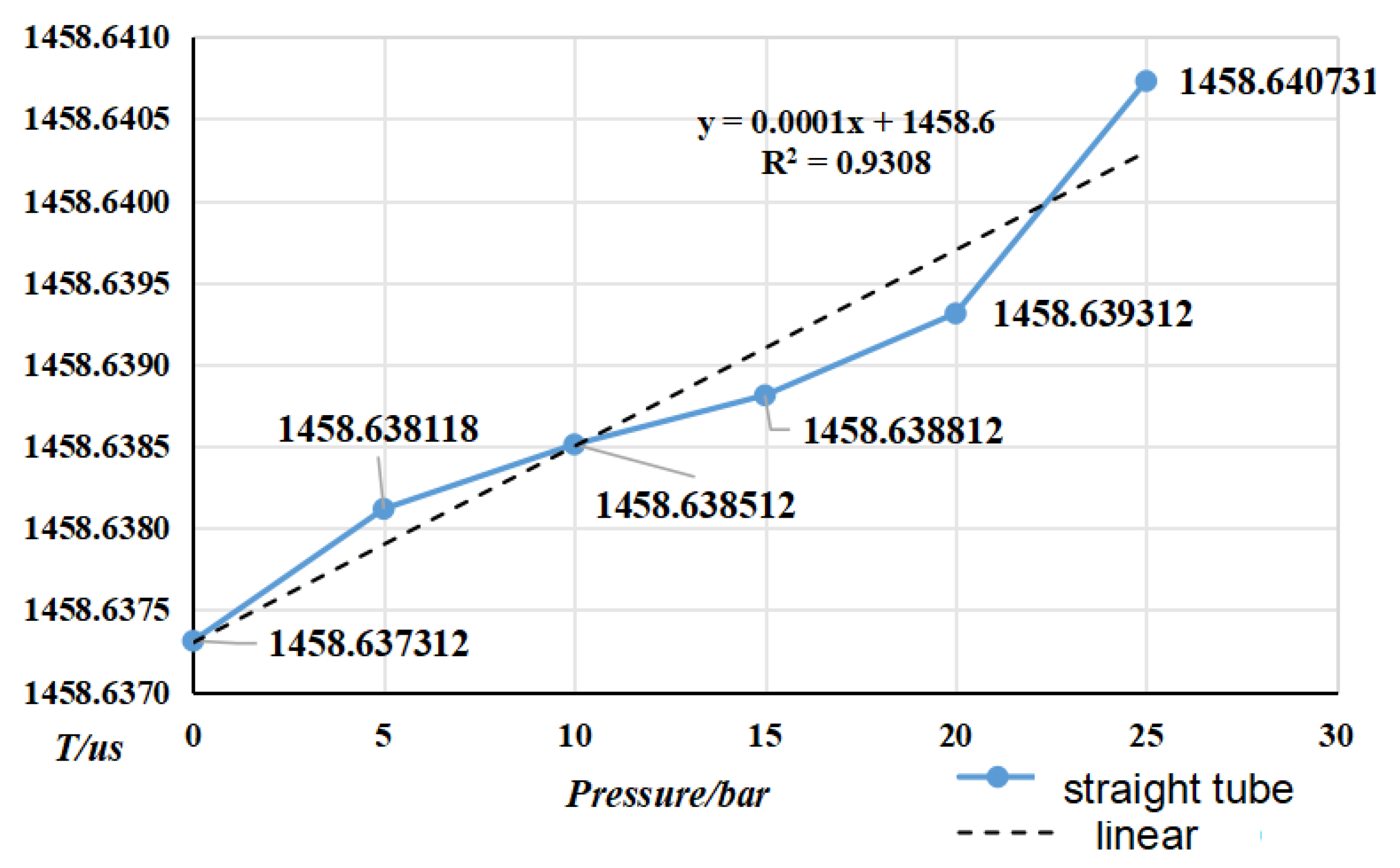
| fit factor | k20a | k20b | k21a | k21b |
| straight tube | -1.4209×10-4 | -2.74958E×10-7 | 1.88777×10-1 | 2.47360×10-4 |
| curved tube | 1.49944×10-2 | 0.00 | 0.00 | 0.00 |
6. Conclusions
-
- A set of on-line vibrating tube liquid densitometer experimental device has been built based on the quantity and value transfer system, the whole device consists of desktop densitometer, multi-temperature thermostatic stirring system, walk-in thermostat, blowing system, frequency acquisition system, etc. The experimental research on 5 densitometers can be carried out at the same time under different temperatures and densities, and the device evaluates the accuracy of U=0.08kg/m3, k=2;
-
- Selected straight tube type and elbow type two kinds of densitometers, in (15~45)℃, selected five kinds of liquids to carry out on-line vibrating tube densitometer metrological performance of the experiment, concluded that different density vibration tube frequency with the increase in density and decrease with the increase in temperature; using the frequency and density values obtained from the experiments, calculated the K coefficient of the theoretical equations, and came up with the fitted density difference, the two kinds of densitometers fitted the error is basically in the nominal The fitting error of the two densitometers is basically within the nominal error, which indicates that the device has a good degree of differentiation and reasonableness; in (0~25) bar carried out on-line vibrating tube densitometer pressure-frequency experiments, it is concluded that the vibration frequency increases with the increase of pressure in the vibrating tube, the pressure in the pipe and the interaction of the Coefficients of the vibrating tube at both ends of the equivalent elasticity coefficient of the corrugated pipe K deviates from the pressure and the elasticity coefficient of the K change rule. Still need to further study, from the trend of change in the bend type density meter by the pressure is more obvious.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lagourette, B, C Boned, H Saint-Guirons, P Xans, and H Zhou. 1992. “Densimeter Calibration Method versus Temperature and Pressure.” Measurement Science and Technology, August, 699–703. [CrossRef]
- Wang, D.l.; Yang, T.T.;Mao, S.; et al.2019. “Analysis of liquid density measurement methods”. Measurement and Testing Technology, November,55-60. [CrossRef]
- Xu, C. “Research on online monitoring system of pipeline liquid density”. Harbin Institute of Technology, Harbin, China 2021. [CrossRef]
- Puttmer, A., P. Hauptmann, and B. Henning. 2000. “Ultrasonic Density Sensor for Liquids.” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, January, 85–92. [CrossRef]
- L, F; Zhang, X.Z.; 2012 “Experimental study on the performance of single straight tube vibrating fluid densitometer”. Nuclear Power Engineering, December,19-22. https://kns.cnki.net/kcms2/article/abstract?v.
- Higuti, Ricardo Tokio, Flávio Buiochi, Júlio Cezar Adamowski, and Francisco Montero de Espinosa. 2006. “Ultrasonic Density Measurement Cell Design and Simulation of Non-Ideal Effects.” Ultrasonics ,302–309. [CrossRef]
- Zheng, D.Z.; Ji, Y. S.; Shang.S. F. 2012. “Design and Theoretical Analysis of a Resonant Sensor for Liquid Density Measurement.” Sensors, June, 320–324. [CrossRef]
- Yin, J.G.; Jiang. W.; Xian,Y. M.; and Ilmutdin Abdulagatov. 2011. “Compressed Liquid Density Measurements of Dimethyl Ether with a Vibrating Tube Densimeter.” The Journal of Chemical Thermodynamics, September,1371-1374. [CrossRef]
- Majer, Vladimir, Lü Hui, Rosa Crovetto, and Robert H. Wood. 1991. “Volumetric Properties of Aqueous 1-1 Electrolyte Solutions near and above the Critical Temperature of Water I. Densities and Apparent Molar Volumes of NaCl (Aq) from 0.0025 Mol·kg−1 to 3.1 Mol·kg−1, 604.4 K to 725.5 K, and 18.5 MPa to 38.0 MPa.” The Journal of Chemical Thermodynamics 23 (3): 213–229. [CrossRef]
- Aida, Tsutomu, Ai Yamazaki, Makoto Akutsu, Takumi Ono, Akihiro Kanno, Taka-aki Hoshina, Masaki Ota, et al. 2007. “Laser-Doppler Vibrating Tube Densimeter for Measurements at High Temperatures and Pressures.” Review of Scientific Instruments 78 (11). [CrossRef]
- JJF 1059-1999 “Measurement Uncertainty Assessment and Representation”.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





