Submitted:
23 April 2024
Posted:
25 April 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Theory
- (1)
- is a well-founded partial ordering on T.
- (2)
- , the set is linearly ordered by .
- (3)
- , there exists such that and . Here, essentially means or .
3. Lemma and Theorem
3.1. Proof of Uniqueness of the Converge Tree
- (1)
- (2)
- →
- (3)
- →
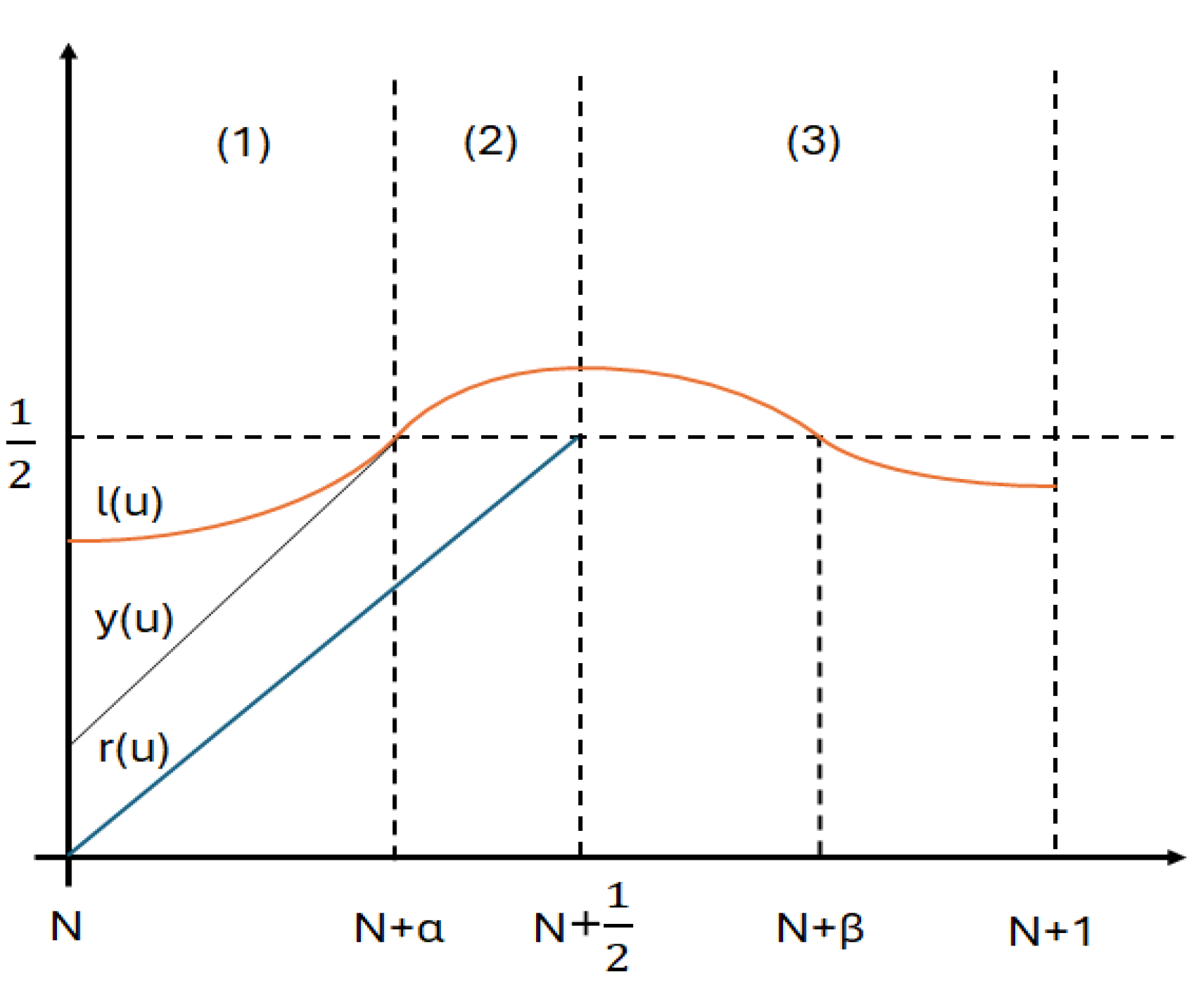
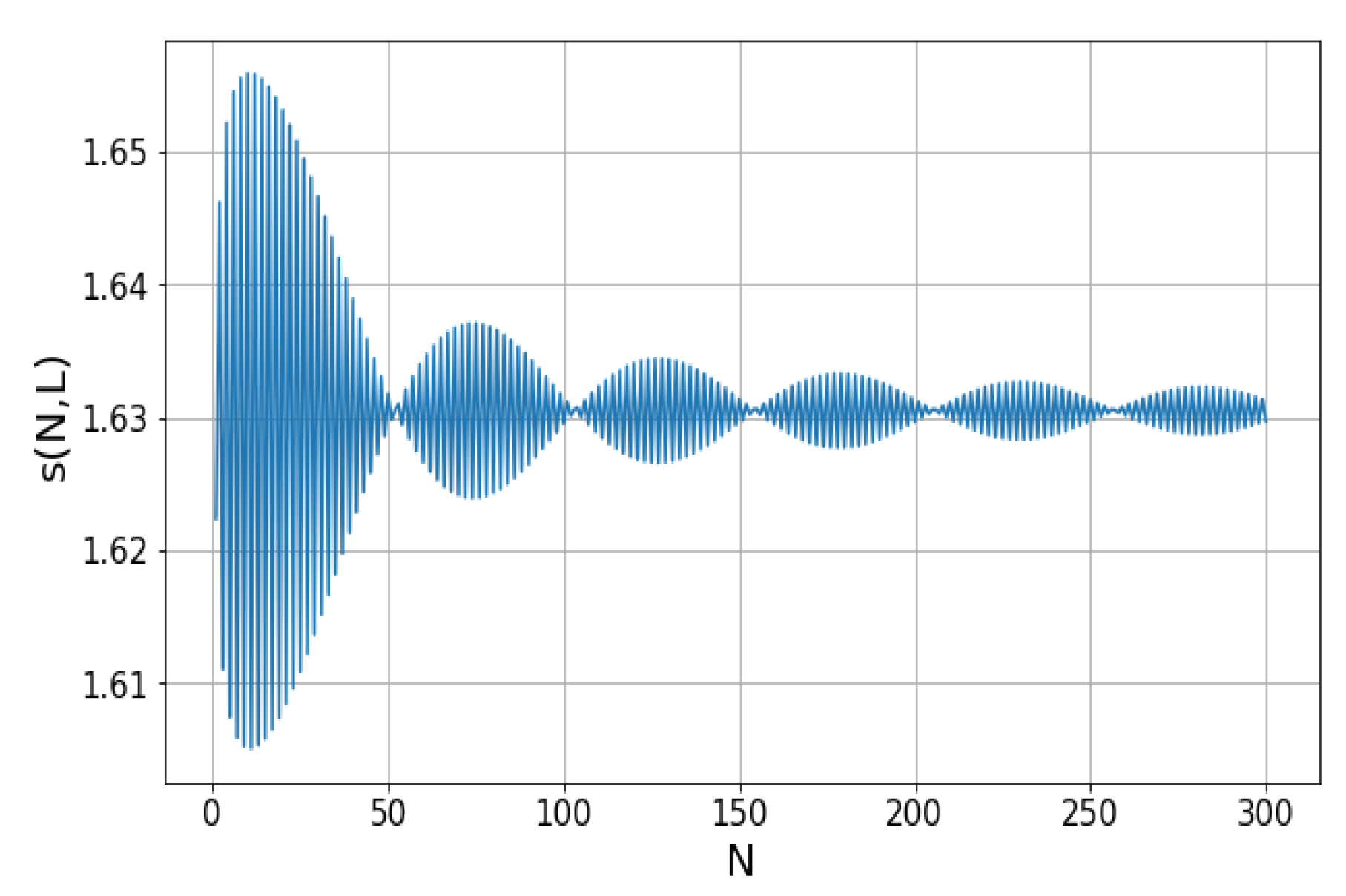
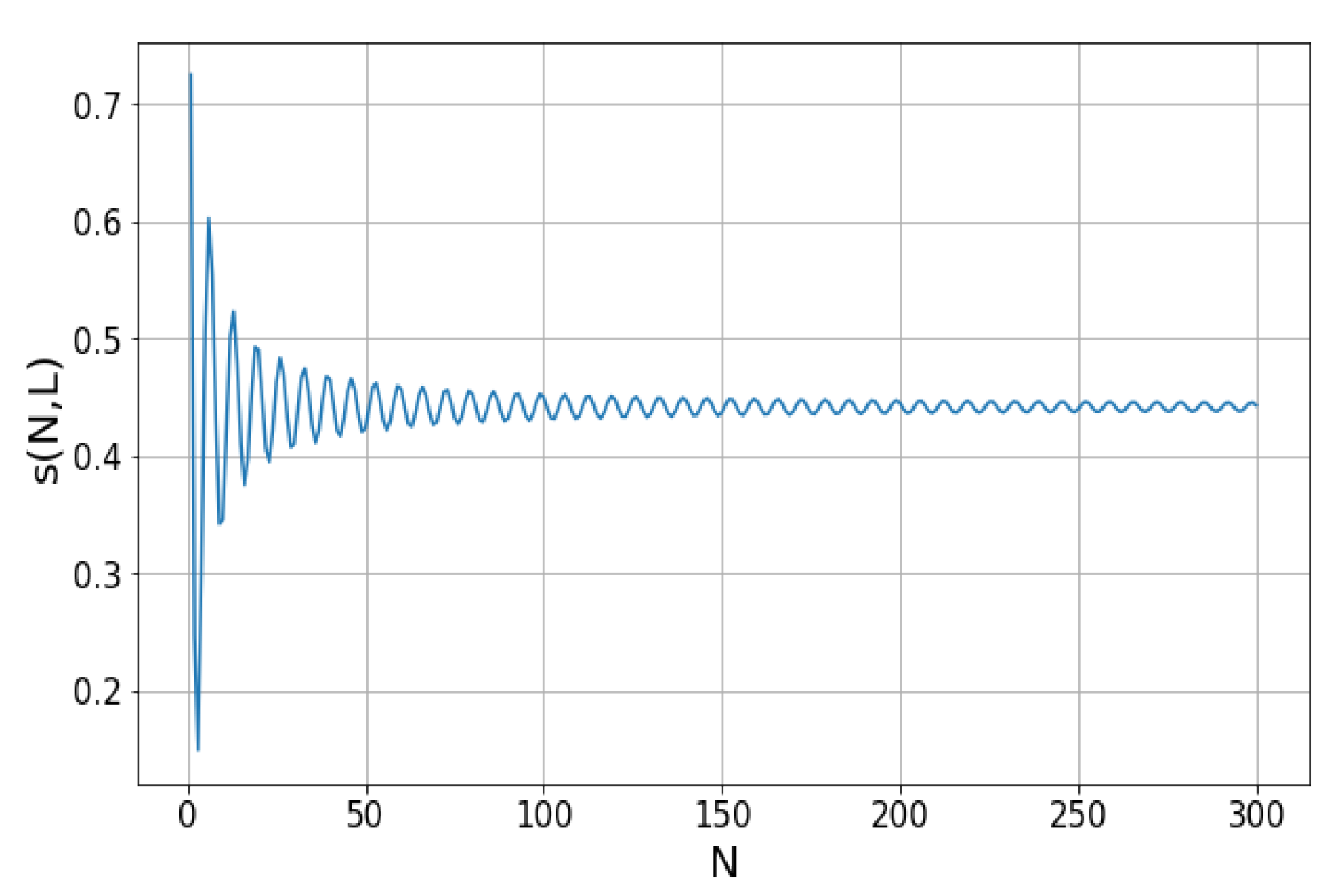
3.2. Disproving the Existence of a Diverge Tree
- (1)
- When , N also has the same stop time as b.
- (2)
- When , . If we apply the Collatz process, . If , . When , which also converges to 1.
- (3)
- When , applying the Collatz process results in convergence to 1, which is 1.
4. Conclusion and Outlook
References
- Riho Terras, “A stopping time problem on the positive integers", ACTA ARITIMETICA (1976). http://matwbn.icm.edu.pl/ksiazki/aa/aa30/aa3034.pdf.
- Eric Roosendaal, “The Terras Theorem", http://www.ericr.nl/wondrous/terras.html.
- Jeffrey C. Lagarias, “The 3x + 1 problem and its generalizations". The American Mathematical Monthly. 92 (1): 3–23, (1985). [CrossRef]
- Jeffrey C. Lagarias, “The 3x+1 Problem: An Overview", 2021, https://arxiv.org/abs/2111.02635.
- Spencer Unger, “Trees in set Theory", https://www.math.toronto.edu/sunger/cmu/TreesTalk.pdf.
- R. L. Graham, D. E. Knuth, O. Patashnik, “Concrete Mathematics", Addison-Wesley (1994), p. 70.
- E. C. Titchmarsh, D. R. Heath-Brown, “The Theory of the Riemann Zeta-function" (2nd ed.), Oxford U. P. (1986), p. 15, Eq. 2.1.7.
- OEIS, “Decimal expansion of log_2(3)", https://oeis.org/A020857.
- Simon Plouffe, “log(3)/log(2) to 10000 digits", https://www.plouffe.fr/simon/constants/log3log2.txt.
- Shalom Eliahou, “Le problème 3n+1: y a-t-il des cycles non triviaux? (III)", Images des Maths, CNRS (2011).
- Terence Tao, “Almost all orbits of the Collatz map attain almost bounded values.", Forum of Mathematics (2022). [CrossRef]
- Ilia Krasikov, Jeffrey C. Lagarias “Bounds for the 3x+1 problem using difference inequalities". Acta Arith., 109, 237–258. (2003). [CrossRef]
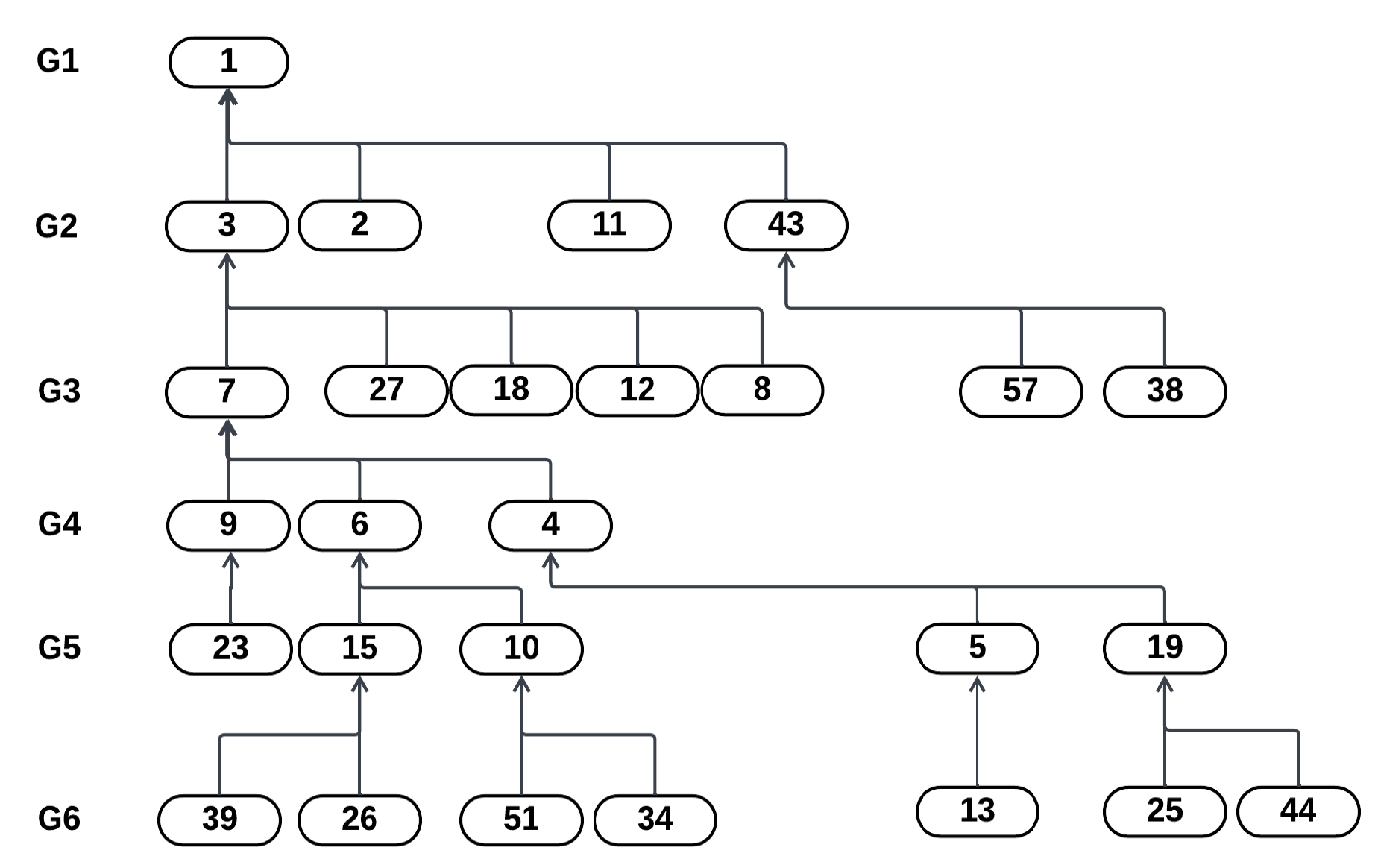
| 1 | |
|---|---|
| 3, 5, 21, 85, 151, 227, 341... | |
| 13, 15, 23, 35, 53, 75, 113... | |
| 7, 11, 17, 61, 69, 93, 141... | |
| 9, 19, 29, 37, 45, 81, 117... | |
| 25, 49, 51, 67, 77, 87, 101... | |
| 33, 39, 43, 59, 65, 79, 89... | |
| 57, 105, 115, 157, 173, 177, 211... | |
| 127, 135, 139, 153, 159, 187, 191... | |
| 123, 169, 185, 247, 249, 283, 339... | |
| 111, 167, 219, 223, 225, 251, 295, 329... | |
| 297, 351, 393, 445, 527, 585, 595... | |
| 175, 263, 395, 519, 593, 615, 699... | |
| 103, 155, 207, 233, 311, 467, 701... | |
| 91, 137, 183, 275, 413, 549, 621... | |
| 63, 95, 121, 143, 215, 243, 323... | |
| 31, 47, 71, 107, 161, 253, 381... | |
| 27, 41, 55, 83, 125, 165, 189... | |
| 73, 109, 147, 195, 199, 221, 291... | |
| 97, 145, 259, 265, 387, 389, 471... | |
| 129, 193, 235, 240, 343, 345, 353... | |
| 171, 240, 257, 313, 415, 427, 457... | |
| 379, 417, 427, 543, 553, 569, 609... |
| 1 | |
|---|---|
| 2, 3, 11, 43, 76, 114, 171... | |
| 7, 8, 12, 18, 27, 38, 57... | |
| 4, 6, 9, 31, 35, 47, 72... | |
| 5, 10, 15, 19, 23, 41, 59... | |
| 13, 25, 26, 34, 39, 44, 51... | |
| 17, 20, 22, 30, 33, 40, 45... | |
| 29, 53, 58, 79, 87, 89, 106... | |
| 64, 68, 70, 77, 80, 94, 96... | |
| 62, 85, 93, 124, 125, 142, 170... |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





