Prerpints.org logo
Preprint
Article

An Improved Approach to Estimate Stocking Rate and Carrying Capacity Based on Remotely Sensed Phenology Timings

This version is not peer-reviewed.

Submitted:

20 April 2024

Posted:

22 April 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Accurate estimation of livestock carrying capacity (LCC) and implementing an appropriate actual stocking rate (ASR) is key to sustainable management of grazing adapted alpine grassland ecosystems. Reliable determination of aboveground biomass is fundamental to these determinations. Peak aboveground biomass (AGBP) captured from satellite data at the peak of the growing season (POS) is widely used as a proxy for annual aboveground biomass (AGBA) to estimate LCC of grasslands. Here we demonstrate limitations of this approach and highlight the ability of POS in the estimation of ASR. We develop and trail new approaches that incorporate remote sensing phenology timings of grassland response to grazing activity, considering relations between biomass growth and consumption dynamics, in efforts to support more accurate and reliable estimation of LCC and ASR. Results show that based on averaged values from large-scale studies of alpine grassland on the Qinghai-Tibet Plateau (QTP), differences between AGBP and AGBA underestimate LCC by about 31%. Findings from a smaller-scale study that incorporate phenology timings into estimation of annual aboveground biomass reveal that Haibei alpine meadows were overgrazed by 11.5% during the study period from 2000-2005. The methods proposed can be extended to map grassland grazing pressure by predicting LCC and tracking ASR, thereby improving sustainable resource use in alpine grasslands.
Keywords: 
alpine grassland
;  
livestock carrying capacity
;  
stocking rate
;  
peak aboveground biomass
;  
remote sensing phenology
Subject: 
Environmental and Earth Sciences  -   Environmental Science

supplementary.docx (29.75KB )

1. Introduction

Appropriate adaptation of actual stocking rate (ASR) and livestock carrying capacity (LCC) is key to sustainable management and environmental protection of alpine grasslands (Bardgett et al. 2021; Yuan et al. 2021). Reliable estimation of aboveground biomass (AGB), based on understandings of interactions between climate, plant growth and land-use intensity, is key to these determinations (Luo et al. 2002; Harris 2010). Given the vast and remote landscapes of the alpine grasslands on earth, automated modelling procedures use remotely sensed data to estimate peak aboveground biomass (AGBP) at the peak of the growing season (POS) as a proxy for annual aboveground biomass (AGBA) to appraise and predict spatial and temporal variability in livestock carrying capacity (LCC) (Piipponen et al. 2022; Yang et al. 2022). Here we demonstrate how AGBP may underestimate LCC as it fails to incorporate understandings of adaptive grazing practices and consumption dynamics in a given setting. Building on research which shows POS as an indicator of grazing activities (Duparc et al. 2013; Wang et al. 2021), we develop and trial a novel approach based on phenology timings that uses as a measure of grazing intensity or ASR to provide a more reliable information base to guide sustainable determinations of ASR and LCC.
The concept of LCC is widely used to determine the appropriate stocking rate that an area of grassland can sustainably support (Oesterheld et al. 1992; Zhang et al. 2014a). This approach considers various factors, such as the quality and quantity of available forage, and the type and size of the livestock being considered. By determining the LCC, it is possible to develop a grazing strategy that ensures the grassland's long-term environmental health and productivity while meeting the needs of the livestock (Cao et al. 2019). LCC is usually estimated based on livestock forage consumption and grassland forage production (Retzer & Reudenbach 2005). Theoretically, forage production is estimated from annual AGB (AGBA), defined as the total amount of AGB over a year (Zhang et al. 2019). However, because estimating AGBA in grazing adapted grasslands is challenging, the peak AGB (AGBP), the maximum amount of AGB in a given area at a certain point in time (POS), is frequently used to estimate LCC (Zhang et al. 2014a; Piipponen et al. 2022; Yang et al. 2022; Zhang et al. 2022b). Various processing methods accurately capture AGBP based on the rich spectral information available via remote sensing imagery (Yang et al. 2018; Zhang et al. 2022a). Although AGBP is often considered as a good proxy for AGBA (Scurlock et al. 2002), the accuracy and uncertainty of using AGBP rather than AGBA to estimate LCC are largely unknown. Furthermore, the variability in estimates of these parameters may result in propagation of errors (Table 1). For example, Zhang et al. (2022b) and Mo et al. (2021) estimated AGB on the Qinghai-Tibet Plateau (QTP) over the period 2000-2018. However, these two studies produced a two-fold difference in estimates of annual biomass (peak AGB), with Zhang et al. reporting 104.2 g/m2 while Mo et al. reported 47.18 g/m2. The difference arises from the ground truthing data used in these studies; the former was collected in non-grazed grassland, but the latter was in grazed grassland.
Limitations and challenges in the use of AGBP to estimate LCC affect its predictive accuracy. Ground truth data of AGBP for the grasslands on the QTP are generally derived from August or September (Liu et al. 2018). In reality, however, AGBP occurs at a specific time in each year, as it marks the AGB peak of the growing season (POS). The AGBp is heterogeneous in space and time as a function of different environmental conditions and grazing regimes in different grasslands. In some cases, AGBP (or modelled NPP back-transformed to AGB) is a useful predictor of livestock carrying capacity (Zhang et al. 2022b); for example, where AGBP was measured in the non-grazed grassland and it actually reflects AGBA, and POS occurs on the same day as the end of the growing season (EOS). In these instances, the amount of vegetation available for grazing supports reliable estimates of the number of animals that can be sustained. However, when the ground-truth data for validating AGBP were collected in grazed grassland (Qin et al. 2021), AGBP was less than the AGBA, because livestock continue consume AGB. Peak AGB observed on grazed grassland is widely used for the estimation of LCC (Table S1), which technically leads to under-estimation of LCC. Moreover, grazing practices vary at different times and locations over a year. Tibetan herders generally graze their stock in summer from May to September in areas above 3,700 m, but in winter months grazing takes place at elevations below 3,700 m (Ping et al. 2010). Moving livestock from winter pasture to summer pasture before mid-June, then returning the livestock to the winter pasture in late September to October (Wei et al. 2020) helps to avoid intensive degradation caused by intensive grazing in early spring and winter season (Wang et al. 2020b; Wang et al. 2022). These rotational grazing regimes cause difficulties in AGBA and AGBP estimation by the dynamics of grazing activities. Furthermore, although ground-truth data can be collected in ungrazed grassland, as most areas are grazed, errors in the estimation of AGBA and LCC are inevitable. Unfortunately, the relationship between AGBP and AGBA is simply not reported in many situations, especially in the seasonal rotational grazing regimes.
POS is one of the most important remote sensing phenology timings (including start of growing season (SOS), and end of growing season (EOS)), it is highly related to livestock grazing activities, but there is little known about the relationship of POS and ASR in the alpine grassland. Previous research has predominantly focused on the impact of climate change on phenology and plant growth (Wu et al. 2021; Möhl et al. 2022; Song et al. 2023). Less attention has been given to the effects of grazing activities on phenology, particularly with respect to POS, and plant growth. Detection of the exact day at which the peak growing season occurs is feasible using remote sensing, even if the underlying mechanisms that govern POS remain largely unknown. The complex interplay between plant growth and consumption by grazing animals (ASR) is a key determinant of the timing of the POS (Richardson et al. 2021; Shen et al. 2022). A recently developed empirical plant growth model for monitoring vegetation growth in alpine meadows on the QTP shows high predictive accuracy with coefficients of determination (r2) ranging from 0.94 to 1.00 (Wang et al. 2021). This plant growth model can be used to evaluate the relationship between POS and grazing activities, such as actual stocking rate (ASR).
Here, we evaluate the use of phenological parameters (here we explicitly mean those derived using remote sensing techniques) to estimate ASR and LCC for alpine grassland. Specifically, we asked the following questions: (1) How reliably does peak biomass (AGBP) represent the annual biomass (AGBA) to calculate LCC? (2) What grazing effects determine the occurrence of POS in alpine grasslands? (3) How can remote sensing phenology timings (RPT) improve estimations of the actual stocking rate (ASR) and carrying capacity (LCC)?

2. Study Area

The research area encompasses the diverse alpine grasslands of northern China, including the Qinghai-Tibet Plateau (QTP), Inner Mongolia Plateau, and Hulun Buir Plateau. Temperate continental and plateau climate support five distinct vegetation types: desert steppe, typical steppe, meadow steppe, alpine meadow, and alpine steppe (Mao et al. 2014; Zhang et al. 2014b). Annual precipitation across the region varies from 500 mm in the northeast to as little as 50 mm in the northwest, with approximately 70% occurring between July and September (Chai et al. 2015). Annual evaporation rates range from 1,500 to 2,600 mm (Deng et al. 2006). Livestock grazing is the primary land use activity, serving as the cornerstone of local livelihoods.

3. Methodology

3.1. Modelling theory

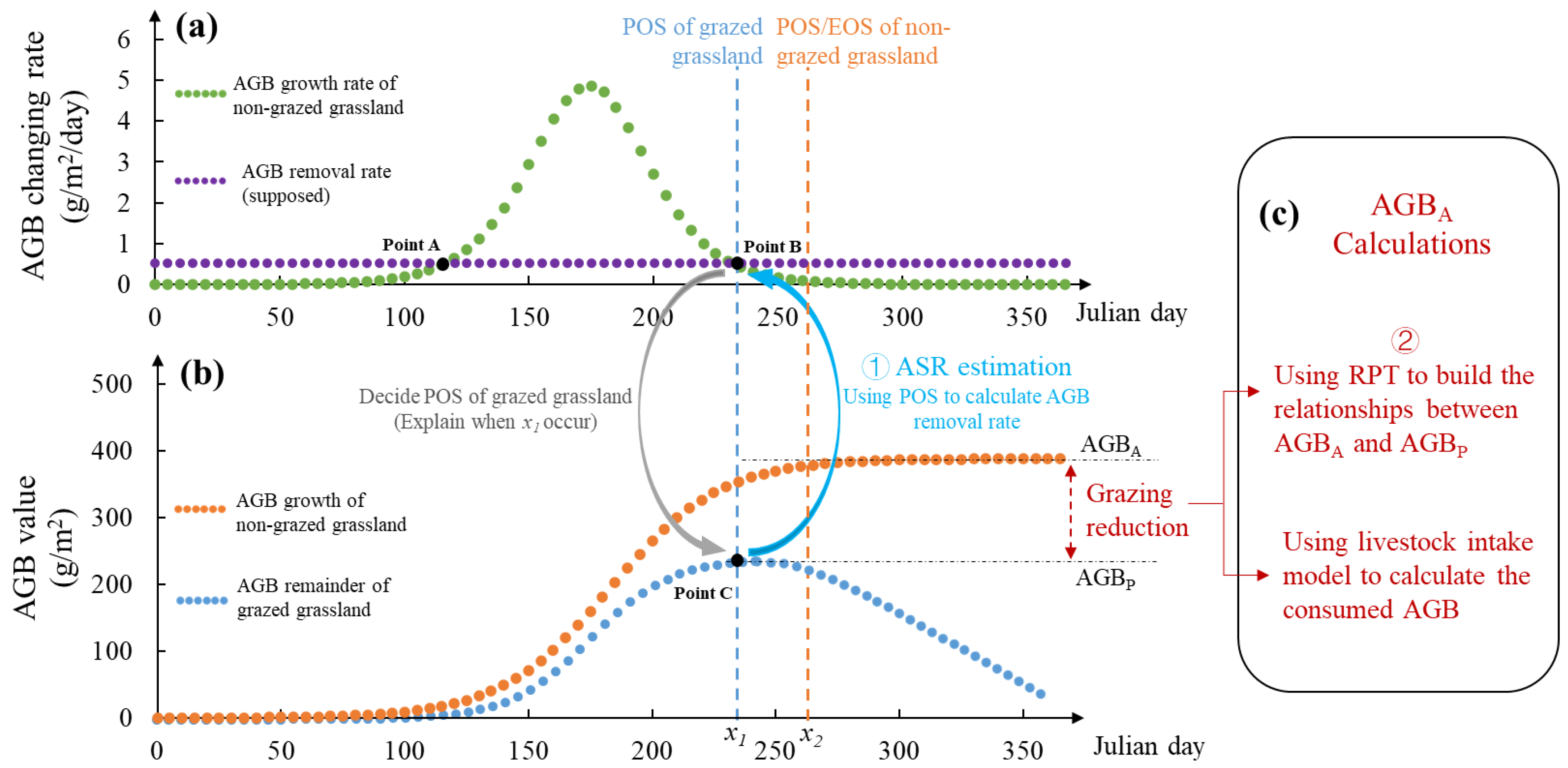
The theoretical models for estimating AGBA and ASR are delineated in Figure 1. Figure 1a illustrates the respective trendlines for the growth rate of AGB in non-grazed grassland (green) and the AGB removal rate (purple) due to livestock grazing. Figure 1b presents a comparative analysis of two trendlines, AGB growth of non-grazed grassland (orange) and AGB remainder of grazed grassland (blue), illustrating the commonly ignored consumed AGB caused by livestock (explanations displayed in Figure 1).
The key connection between Figure 1a and Figure 1b is POS (x1 and x2), which links Point B and Point C. In scenarios where grassland undergoes grazing in Figure 1a, Point B, one of the point of intersections between these two trendlines, signifies an equilibrium where the AGB growth rate is equivalent to the AGB removal rate. Beyond this intersection, the growth rate subsequently falls behind the removal rate. Consequently, in Figure 1b, the peak of AGB for the grazed grassland is attained at the juncture marked by Point C, which correlates to the POS (x1) for the grazed grassland (Figure 1b). The path from Point B to Point C in Figure 1 explicates the methodology for deciding the POS (x1) in a grazed grassland context. This process explains the underlying mechanisms to determine when x1 occurs. Inversely, the POS of grazed grassland can be employed to calculate the AGB removal rate by the path from Point C to Point B (① in Figure 1b), thereby serving as an indirect measure of the stocking rate.
Figure 1c shows two methods used to improve AGBA and LCC estimation. The first one uses RPT derived from remote sensing images to build the relationships between AGBA and AGBP (② in Figure 1b). The second one employs a livestock intake model to calculate the consumed AGB if the livestock stocking rate is applicable. Our primary focus in this paper is on the first method, exploring the potential of RPT to enhance AGBA estimation.
As seasonal grazing is generally used in alpine grasslands, we evaluate the effectiveness of the modelling methods with and without the consideration of rotational grazing regimes. While the above modelling process is based on an assumption of pastures without seasonal rotational grazing regimes, it still works in a seasonal rotational grazed pastures for the growing season.

3.2. Overall workflow

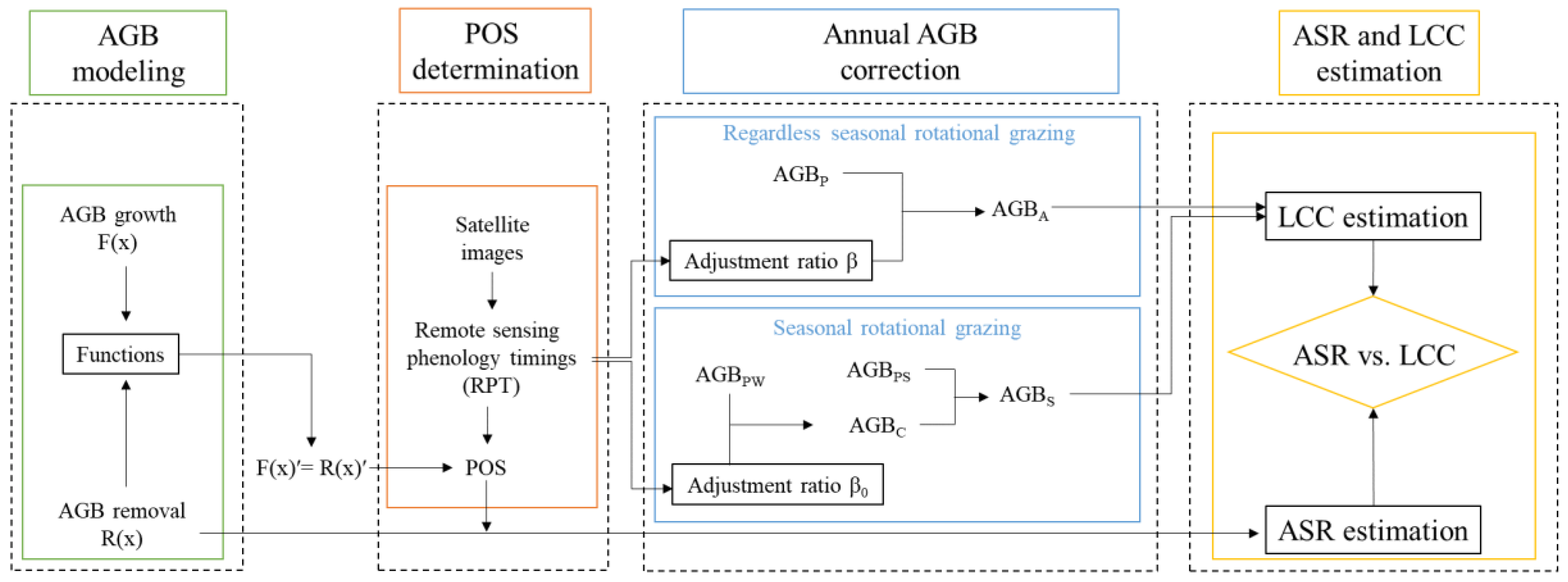
The workflow for estimating AGBP, LCC and ASR based on remote sensing phenology timings has four main steps (Figure 2): (1) AGB modelling (including AGB growth and consumption models), (2) POS determination, (3) the correction of annual AGB estimation, and (4) LCC and ASR estimation and comparison. All the abbreviations in this study are listed in Table S2 in the supplementary files.
First, we introduce models of AGB growth F(x) (in the condition of grazing exclusion) and AGB removal R(x) (consumption by livestock) to explain the underlying mechanisms between AGB accumulation and consumption. Second, the determination of POS is a priority to accurately estimate the AGBP. On one hand, phenological parameters including SOS, POS, EOS, and the length of the growing season can be determined using a smoothed VI time series (Xie et al. 2020). On the other hand, POS can be calculated through functions representing AGB growth rate and AGB removal rate (Figure 1). This study focuses solely on the latter, as the former has been extensively researched and is widely documented in the existing literature (Wang et al. 2018; Song et al. 2023). Third, we propose two adjustment ratios, β0 and β, to characterise relations between peak and annual above ground biomass for situations with and without rotational grazing, respectively. The basis for these adjustment ratios is derived from the theory of AGB growth and consumption, as AGBP is not necessarily representative of AGBA in the context of grazed grasslands. Fourth, a comparative analysis between ASR and LCC is used to evaluate the grazing pressure on grassland ecosystems.

3.2.1. AGB modelling

In alpine grassland, changes in AGB can be represented by a logistic function with three parameters (Huang et al. 2018; Wang et al. 2020a), expressed as:
F ( x ) = A G B m a x 1 + e − k × ( x − X )  
( x ) ′ = A G B m a x × e − k × ( x − X ) 20 × ( 1 + e − k × ( x − X ) ) 2
where: F(x) is the AGB growth representing the remaining AGB on the ground in the non-grazed grassland, F(x)ʹ is the derivative of F(x) and is the AGB growth rate. x is the Julian date. AGBmax is the maximum AGB by the day of EOS, which is the peak AGB in non-grazed grassland. X is the day (FOS) having the fastest growth rate, k is the standardized AGB growth rate (dividing the fastest AGB growth rate by AGBmax).
The AGB removal function refers to the daily consumption of AGB by livestock, and can be expressed as a linear function:
R ( x ) = x × A G B A 365
R ( x ) ′ = A G B A 365
where R(x)ʹ is the AGB removal rate, which is a constant; 365 represents 365 days.

3.2.2. The determination of POS

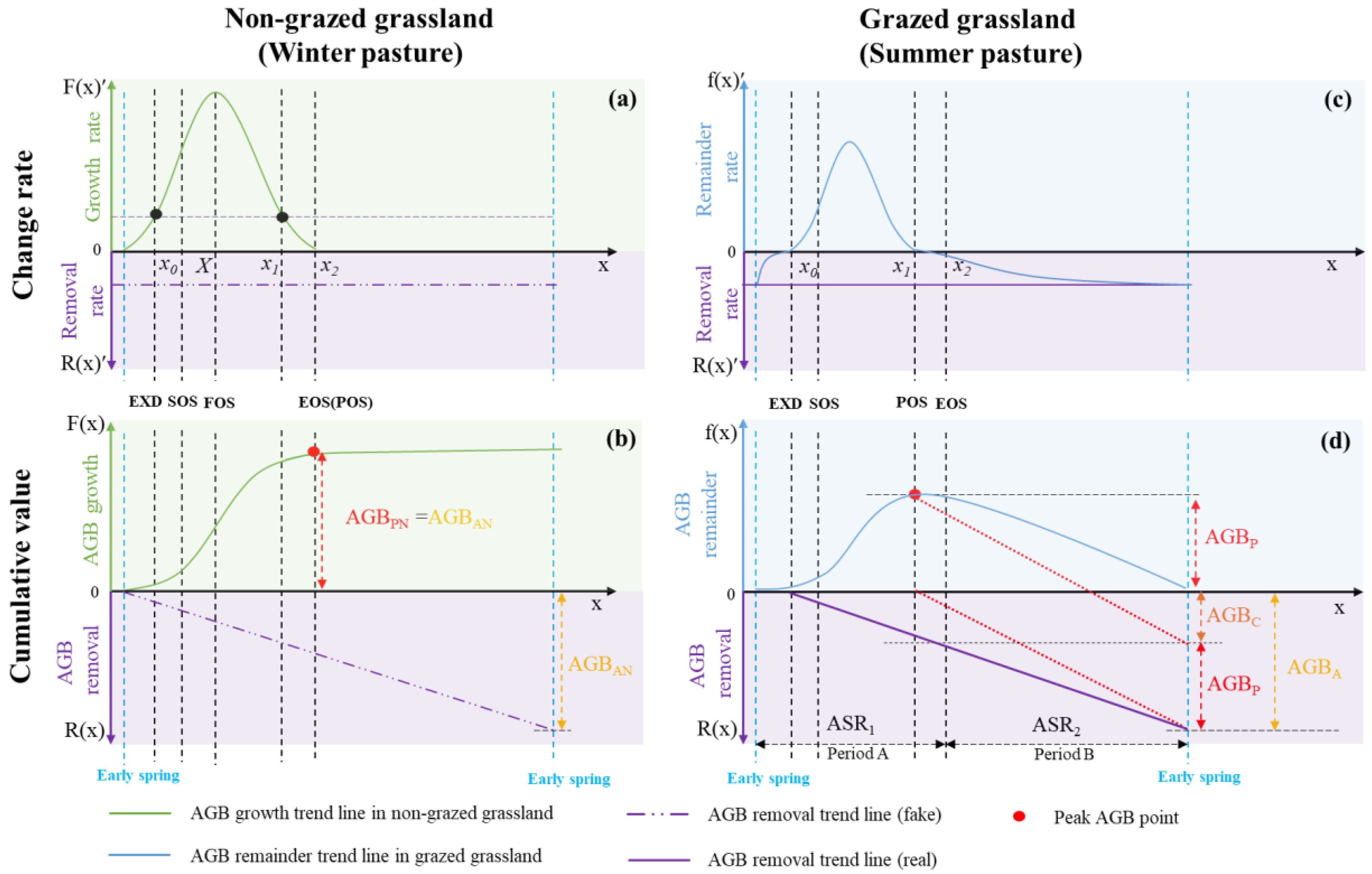
Figure 3 presents a schematic illustration of AGB cumulative value and its change rate in grazed and non-grazed grasslands, showing relationships between AGB and RPT. It is worth noting that the remote sensing detected phonology timings may slightly earlier than the ground observations, it should be considered in the algorithms.
In non-grazed grassland, AGBP occurs at the end of the grazing season, so in those settings POS is the same as EOS in Julian day (Figure 3b). The AGB growth rate, F(x)ʹ, for non-grazed grassland is simply the plant growth rate, but the AGB accumulation rate f(x)ʹ for grazed grassland is the joint effect of plant growth and livestock consumption (Figure 3d). Obviously, POS occurs before EOS in the grazed grassland, and it occurs when the AGB growth rate of non-grazed grassland (F(x)ʹ) is equal to the AGB removal rate (R(x)ʹ), just before the end of the growing season; this time point is displayed as x1 in Figure 3a. Thus, POS (x1) and EXD (x0) can be derived by the cross point of F(x)ʹ and R(x)ʹ as:
F ( x ) ′ = R ( x ) ′
x 1 = P O S = { x ,       F ( x ) ′ = R ( x ) ′ F ( x ) ″ < 0 }
x 0 = E X D = { x ,       F ( x ) ′ = R ( x ) ′ F ( x ) ″ > 0 }
where F(x)ʹʹ < 0 secures the second point of the intersections of F(x)ʹ and R(x)ʹ. It is noteworthy that at the juncture denoted by x0, the AGB growth rate F(x)ʹ surpasses the AGB removal rate R(x)ʹ, whereas at x1, the AGB growth rate F(x)ʹ lags behind the AGB removal rate R(x)ʹ. In another word, f(x0)ʹ and f(x1)ʹ are zero as shown in Figure 3d.

3.2.3. Annual AGB correction

In ungrazed grassland (Figure 3c,d), AGB growth rate peaks at the end of the growing season:
A G B A N = A G B P N
A G B A N = A G B P N = { F ( x ) ,         F ( x ) ′ = 0 F ( x ) ″ < 0 }
where F(x)ʹ=0 secures the extreme and F(x)ʹʹ<0 ensures the POS (EOS).
Similarly, the peak biomass for the grazed grassland can be derived as (Figure 3c,d):
A G B A > A G B P = { f ( x ) ,         f ( x ) ′ = 0 f ( x ) ″ < 0 }
where f(x)ʹ=0 secures the extremes and f(x)ʹʹ<0 ensures the POS (x1).
The situation in the grazed grassland is more complex, due to the effects of livestock on the biomass dynamics of the system. AGBP is generally estimated through remotely sensed images obtained around POS, it can be regarded as the forage storage used to feed livestock in dormant season (period B), which is the period after POS until growing re-commences, as shown in Figure 3d. Thus, AGBA includes AGBP and AGBC:
A G B A = A G B C + A G B P
where: AGBC is the plant biomass consumed by livestock in growing season (period A), during which biomass is accumulating. It is worth noting that if AGB is in shortage or plenty by the end of winter season, the forage supplementary and the remanent biomass should be added and deducted in equation 11, respectively.
Based on the concept outlined in Figure 3d, AGBC and AGBP can be used to calculate livestock carrying capacity for the period A and B, respectively (Figure 3):
A S R 1 = A G B C × R s L × ( E O S − S O S )
A S R 2 = A G B P × R s L × ( 365 − E O S )
where ASR1 and ASR2 stand for the actual stocking rate of periods A and B, respectively. Rs is a ratio including biomass use efficiency, availability, and edibility; it is assigned a value of 0.456 according to previous studies (Yu et al. 2010; He et al. 2020). L is the daily intake for a standard sheep unit (SU), it is 1.8 kg/SU (NY/T635-2015) (Cao et al. 2020).
Theoretically, some livestock would be slaughtered after the growing season (regardless of the birth and death rates throughout the year). The actual stocking rate for the two periods (period A and B) can be described as equation 14. Thus, the relationship between AGBA and AGBP can be derived from equations 11-14:
A S R 1 × ( 1 − S r a t e ) = A S R 2
A G B A = { ( 1 + E O S − S O S ( 1 − S r a t e ) × ( 365 − E O S ) ) × A G B P ,       A S R 1 × S r a t e = A S R 2 }
  β = ( 1 + E O S − S O S ( 1 − S r a t e ) × ( 365 − E O S ) ) = A G B A A G B P
where Srate is slaughter rate, β is the adjustment ratio needed to convert AGBP to AGBA for the grazed grassland assuming that grasslands were grazed in the same place across the year.

3.2.4. LCC and ASR estimation

According to the definition and equation 15, the annual LCC can be expressed as:
L C C = A G B A × R s L × 365 = β × A G B P × R s L × 365
According to equations 5-6, POS is determined by F(x) (AGB growth of non-grazed grassland) and R(x) (the AGB removal function). With converse thinking, POS can also reflect important information of plant growth (F(x)) and livestock grazing (R(x)). ASR can be calculated by two steps. First, deriving POS from VI time series data of the grazed grassland, and then assign this POS(x1) to F(x)ʹ (AGB growth rate of non-grazed grassland) to calculate R(x)ʹ (the AGB removal rate). So, ASR can be expressed as:
R ( x ) ′ = { F ( x 1 ) ′ ,       x 1 = P O S P O S = f ( V I ) }
A S R = R ( x ) ′ × R S L
where ASR is the actual stocking rate by the time of POS.

3.3. Model application in seasonal rotational grazing regimes

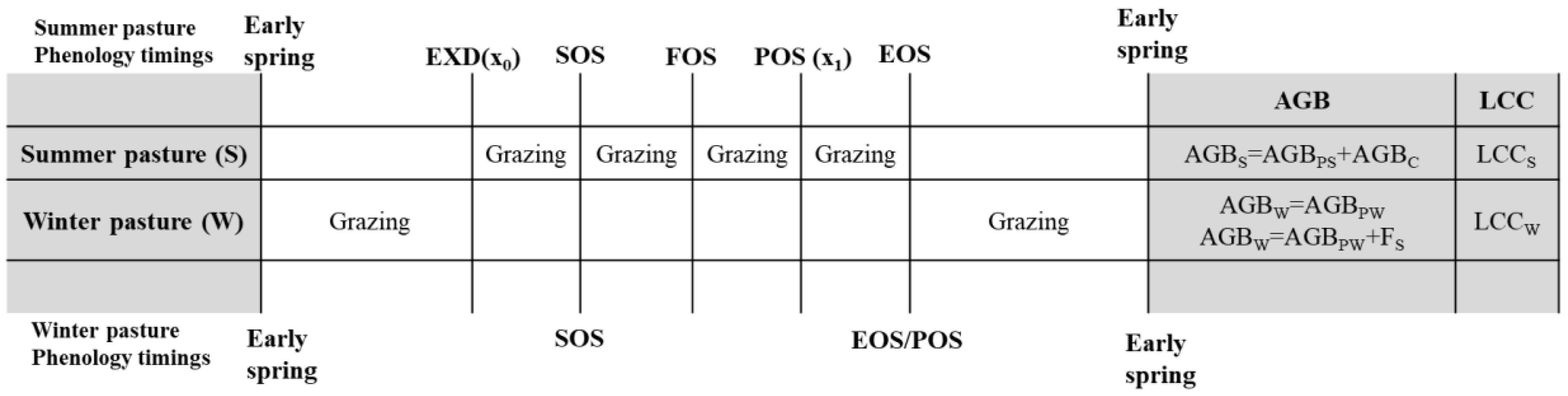
In theoretical terms, EXD and EOS on Figure 3a denote the optimal timing for the translocation of livestock between winter and summer pastures (see Figure 4). The temporal interval spanning from EXD to EOS signifies a state of abundance in AGB, whereas the days falling outside this temporal range are characterized by a scarcity of AGB. Grazing of summer pastures extends from EXD to EOS while livestock stay at winter pasture at other times of a year.
Thus, the calculation of AGBS should include AGBPS (the peak biomass of summer pasture) and AGBC (livestock consumed biomass). So, AGBS can be described as:
A G B S = A G B P S +   A G B C
In winter pastures, AGBPW is produced in the summer season, and it is consumed in the winter season. The incorporation of FS (Forage Supplement) becomes imperative due to the diminished quality of AGB throughout the winter season. So, AGBW can be expressed as:
A G B W = { A G B P W ,   w i t h o u t   f o r a g e   s u p p l e m e n t A G B P W + F S ,   w i t h   f o r a g e   s u p p l e m e n t   }
Based on the grazing status for a year displayed in Figure 4, the stocking rate in two pastures can be expressed as:
A S R S = A G B C × R s L × ( E O S − E X D )
A S R W = A G B W × R s L × ( 365 − E O S + E X D )
A S R S × ( 1 − S r a t e ) = A S R W
ASRS is the actual stocking rate for summer pasture, ASRW is the actual stocking rate for winter pasture, Srate is slaughter rate.
During the winter season, there is an observed decline in the crude protein content of the grasses from the summer season, decreasing notably from 10.43% to 5.56% (Cai et al. 2022). So, the forage quality declined to 53.3% (Q) of the original (calculated by 5.56%/10.43%) based on the protein content. According to equations 22-24, AGBC can be expressed as:
A G B C = A G B W × Q × E O S − E X D ( 1 − S r a t e ) × ( 365 − E O S + E X D )
β 0 = Q × ( E O S − E X D ) ( 1 − S r a t e ) × ( 365 − E O S + E X D )
where β0 is the adjustment factor for calculating AGBC by the time of POS in summer pasture based on AGBW. So, AGBS can be expressed as:
A G B S = A G B P S + A G B W × E O S − E X D ( 1 − S r a t e ) × ( 365 − E O S + E X D )
So, the livestock carrying capacity for two kinds of pastures can be expressed as:
L C C S = A G B S × R s L × ( E O S − E X D )
L C C W = A G B W × R s L × ( 365 − E O S + E X D )
where LCCS and LCCW represent LCC for summer pasture and winter pasture, respectively. The determination of grassland carrying capacity is contingent upon the manner of utilization. For a grassland household with one summer pasture and one winter pasture, the best stocking rate during the summer season should be LCCS, and is should be reduced to LCCW during the winter season.
The expression of ASR at the time of POS within the summer pasture can be derived in a similar manner to use of equations 18 and 19.

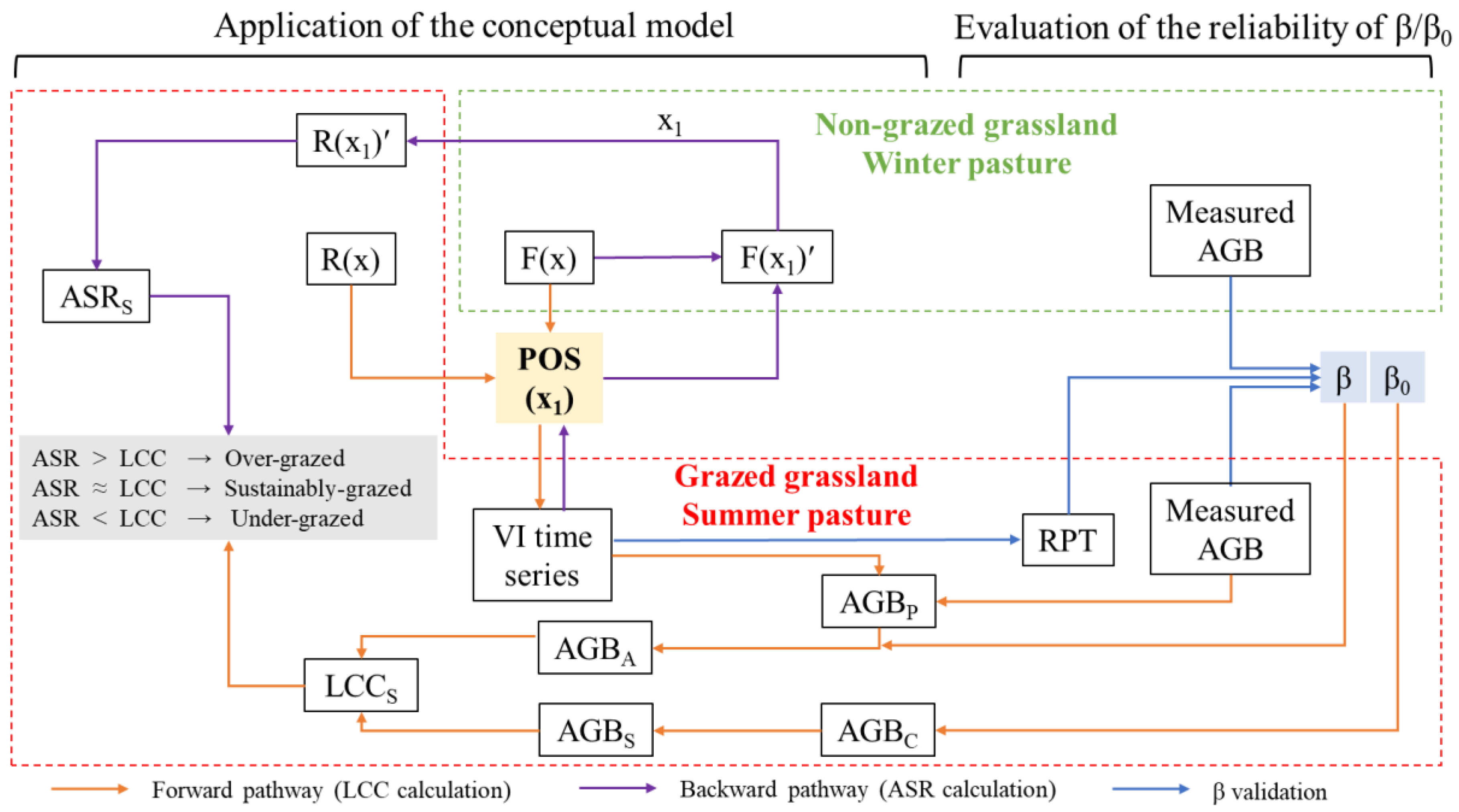
3.4. Case study

Figure 5 shows the workflow of the case study to test and validate the proposed models based on data derived from previously published papers (see Tables 1-5). The flow chart includes two parts, one is ‘Evaluation of the reliability of β/β0’, the other one is ‘Application of the conceptual model’. The reliability of  was evaluated and validation of β draws on field-measured biomass and estimated RPT based on Equation 16-17 (blue arrows in Figure 5). Unfortunately, we are unable to evaluate  in this study due to the lack of data (controlled experiments).
The conceptual models start with POS and then via backward and forward pathways we estimate ASRS and LCCS, respectively. Comparison of ASRS and LCCS indicates grassland grazing pressure: ASR > LCC means grassland is over-grazed, ASR ≈ LCC means grassland is grazed at a sustainable level, and ASR < LCC means grassland is grazed at a level lower than it could be. This conceptual model was applied to pastures with seasonal rotational grazing regimes to evaluate the grassland grazing pressure.

4. Results

4.1. The reliability of β

Based on Equation 16, the value of β was estimated in two ways. The first approach is based on a meta-analysis of prior studies (Table 3), which is involved estimating β through the use of phenological timings derived from VI time series images classified by vegetation type, covering alpine grasslands in QTP and Inner Mongolia from 1982-2016. Across these studies, the average value of β was derived as 1.47 ± 0.10 (mean ± SD).
The second approach calculated β using biomass data collected from non-grazed and grazed plot experiments (Table 4). In these studies, the non-grazed grassland areas were those where fencing had been established to exclude livestock and the grazed grassland is open to free grazing animals (at an unknown grazing intensity). The average value of β obtained through this approach was 1.45 ± 0.11 (mean ± SD). That both approaches yielded remarkably similar values of β confirms the accuracy of Equations 11-15 and highlights the strong coupling between AGBA and AGBP and phenological timing, regardless of the grazing intensity. Thus, on average AGBA is about 1.45-1.47 larger than AGBP. Similarly, estimates of LCC based on AGBP are underestimated by about 31% (0.45/1.45 to 0.47/1.47).

4.2. The estimation of LCC and ASR

The estimation of LCCS and ASRS is based on the mechanisms displayed in Figure 3. POS was determined by the joint effects of plant growth and grazing activity (Hu et al. 2021; Shen et al. 2022). Conversely, POS can be used to reflect the grazing severity through plant growth function as shown in equations 18-19. The data used to estimate LCCS and ASRS were taken from the same place to ensure a similar plant growth function under similar ecological and environmental conditions. These studies were carried out in the alpine grasslands in Haibei alpine meadow, Qinghai, China (Table 5). The value of the variables is averaged corresponding to their observation periods. RPT variables were observed from the study of Zhu et al. (2019). Moreover, the peak AGB estimated by remote sensing for summer pastures is varied, so the mean value was used in the model (Table 5).
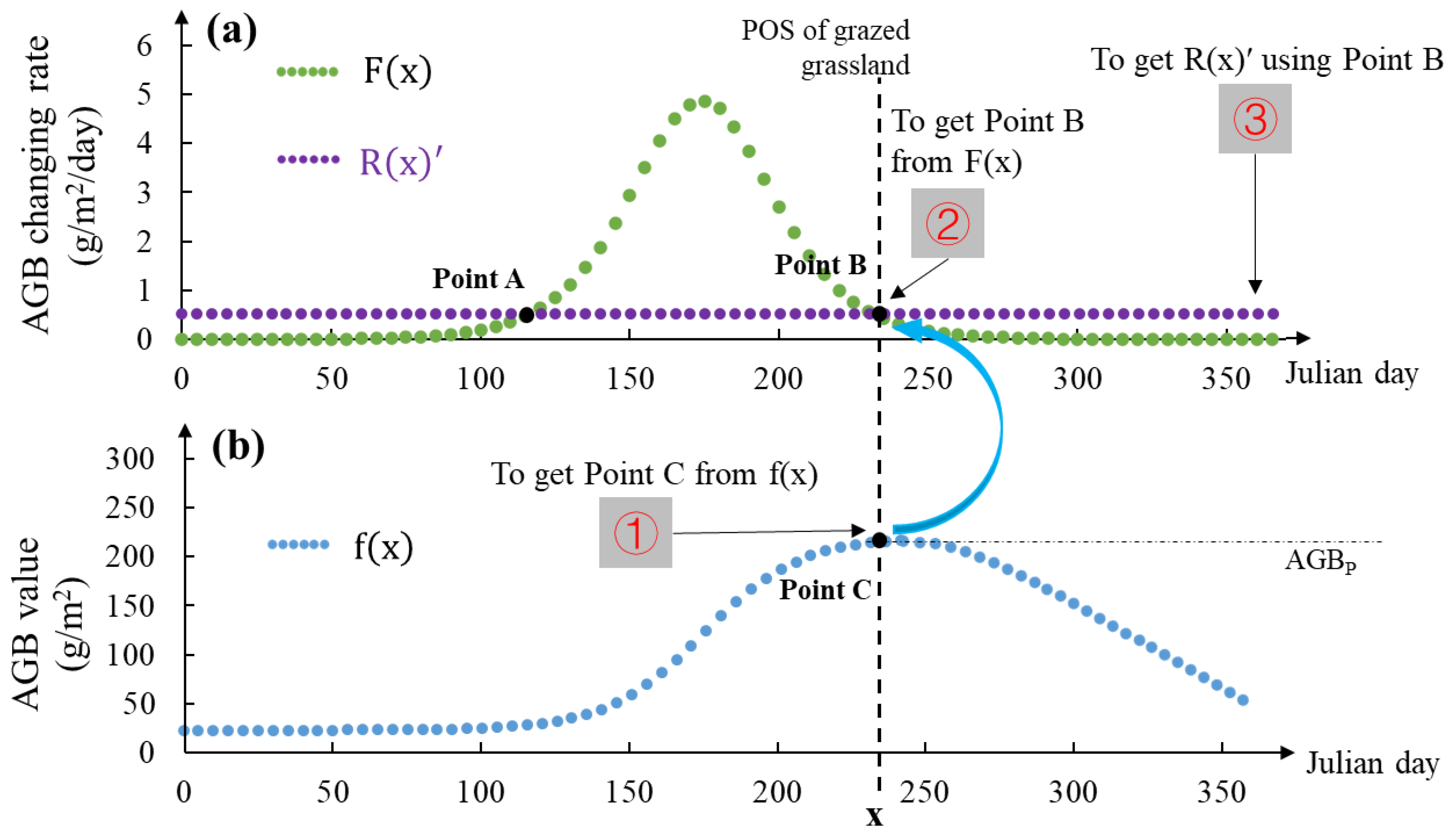
The plant growth rate model (Equation 30 is from Equation 2) was implemented based on the study of Wang et al. (2020a). Figure 6 shows a simplified workflow using POS to calculate AGB removal rate based on Figure 1. After the POS (x1, in grazed grassland) was derived from remote sensing images (step ①), it was used to calculate the AGB removal rate (R(x)ʹ) via Point B (step ② and ③).
F ( x ) ' = 390 × e − 0.062 × ( x − 174 ) 20 × ( 1 + e − 0.062 × ( x − 174 ) ) 2
The results displayed in Table 6, which calculate EXD(x0) and β0 from observations in Table 5, were 131 Julian day and 0.434, respectively. Based on these two important factors, ASR and LCC can be derived. ASRS was 2.91 SU/ha and LCCS was 2.61 SU/ha. Thus, it appears that the summer pastures in Haibei alpine grassland were averagely over-stocked by 11.5% in the period from 2000-2005. Prospectively, methods outlined here to evaluate grazing pressure using phenology timings based on remote sensing imagery using a plant growth model could provide a solution to map the dynamics of grazing activities for large scale studies.

5. Discussion

Accurate prediction of ASR and LCC is key to determinations of grazing pressure that underpin interpretations of successful livestock management (Piipponen et al. 2022). Prospects for sustainable grazing reflect the balance between land-use practices (especially stocking rates and rotational grazing practices) and grassland productivity (Huang et al. 2016). Estimation of ASR and LCC via remote sensing requires an understanding of biomass growth and consumption mechanisms (Piipponen et al. 2022; Shen et al. 2022; Song et al. 2023). Findings from this study show the reliability and effectiveness of two ratios, β and β0, which link AGBP and AGBC to AGBA. These results enhance the utility of the models presented in Figure 1, highlighting the importance of phenological timings in the estimation of ASR and LCC.
Traditional models that do not incorporate spatial and temporal variability in forage production (Wang et al. 2022) or knowledge of seasonal grazing patterns (Briske et al. 2020) are likely to overestimate AGBA and LCC. Conversely, utilizing AGBP instead of AGBA likely underestimates LCC. For averaged values in the large-scale studies of alpine grassland on QTP, our results indicate that LCC estimated based on AGBP is underestimated by about 31% due to the difference between AGBP and AGBA (β). This explains why previous studies that use AGBP as a proxy for AGBA have yielded inconsistent results for the same area over the same period (Table S1). Although ground truth data can be measured in non-grazed grassland, as most areas on the QTP are grazed, using only non-grazed information causes errors in spatial analyses of biomass and productivity. Furthermore, while most studies have collected ground truth data in grazed grassland (Table S1), what is stated to be annual AGB is actually the peak biomass. In any case, the proposed adjustment ratio β can be used to avoid underestimation of LCC for the pastures with and without the consideration of rotational grazing regimes. This exemplifies the critical importance of underlying assumptions and analytical procedures in using automated procedures (O'Neil 2017).
Determining and implementing an appropriate grazing intensity and ASR is key to the sustainable management of grassland resources (Zhang et al. 2018). An excessively high stocking rate may cause land degradation and desertification (Li et al. 2018), whereas appropriately managed grazing (e.g. rotational grazing regimes) can contribute to the provision of ecosystem services (Bengtsson et al. 2019). In this study grazing pressure was evaluated by using phenology timings derived from remote sensing images with the assistance of a plant growth model. The results indicate that the summer pastures in Haibei alpine grassland were averagely over-stocked by 11.5% in the period of 2000-2005. The ability of remote sensing phenological timings to estimate ASR provides a solution to map the spatial dynamic of grazing activities, such as stocking rate and grazing intensity. However, multiple plant growth models are required to conduct such large scale mapping studies.
Livestock grazing and plant growth alter biomass dynamics and determine POS in tandem. In some instances, more productive plant communities in free-grazing alpine grasslands reach their POS later than less-productive plant communities (Duparc et al. 2013). Hence, parameterisation (and structure) of plant community growth models will likely need to vary from place-to-place to reflect local conditions in plant composition and the environment (Huang et al. 2018; Sanaei et al. 2019). For example, it has been argued that stocking rate should be estimated for different topographic positions, as topography (e.g. aspect) controls biomass and its availability to livestock (Sanaei et al. 2019; Hua et al. 2022). Given the sharply changing rate of F(x)ʹ (plant growth rate) displayed in Figure 5, R(x)ʹ (relevant to ASR and x0), it is critical to accurately estimate POS. Observations and analyses of specific plant community growth models and remote sensing phenology are required to support reliable transfer of LCC predictions in space and across scales. Accurate determination of POS can help to predict appropriate grazing intensity or stocking rate, thereby supporting livestock producers and land managers alike. Multiple plant growth models, reflecting different community or vegetation type, may be required to estimate ASR across large spatial extents. The availability of high-resolution and high-frequency satellite imageries, such as Sentinel 2 and Planet Scope satellites now provides strong foundations to support applications of procedures outlined in this study.

6. Conclusions

This study evaluated, for the first time, the underlying mechanisms between remote sensing phenology and grazing activity. Evidence provided highlights the importance of relationships between AGBP, AGBC and AGBA, and associated implications for determination of ASR and LCC. We present a new approach based upon phenological timings of plant growth models to support such tasks. A statistical method based on relationships between AGBP, AGBC and AGBA is used to derive adjustment ratios based on remote sensing phenology timings. The reliability of these ratios and the feasibility of the proposed models were corroborated and tested by observations from previous studies. Our novel method uses remote sensing phenology timings to estimate ASR based on plant growth models in a backward pathway. Estimates of LCC based on remote-sensed biomass are adjusted by β and β0 for different scale studies. Our method efficiently tracks stocking rate and predicts carrying capacity, thereby supporting sustainable grazing strategies in alpine grasslands.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Yan Shi conceived the ideas and designed methodology; Gary Brierley contributed to the conception and the original draft. Yan Shi led the writing of the manuscript with contributions from George L W Perry, Jay Gao, Xilai Li, and Alexander V. Prishchepov, Meiqin Han and Jiexia Li. All authors contributed critically to the drafts and gave final approval for publication.

Data Availability Statement

Data are already published and publicly available, with those items properly cited in this submission. Data (Wang et al. 2020a) are available from Figshare: https://doi.org/10.6084/m9.figshare.11663997, while other data is presented in the tables within this manuscript.

Acknowledgments

This study was supported by the China Postdoctoral Science Foundation (GZC20230998), the National Natural Science Foundation of China (U23A20159), the Opening Foundation of Key Laboratory of the Alpine Grassland Ecology in the Three River Region, Ministry of Education (2023-SJY-KF-05) and Discipline Innovation and Introducing Talents Program of Higher Education Institutions (D18013).

Conflicts of Interest

The authors have no conflicts of interest.

References

  1. Bardgett, R.D., Bullock, J.M., Lavorel, S., Manning, P., Schaffner, U., Ostle, N., Chomel, M., Durigan, G., L. Fry, E., Johnson, D., Lavallee, J.M., Le Provost, G., Luo, S., Png, K., Sankaran, M., Hou, X., Zhou, H., Ma, L., Ren, W., Li, X., Ding, Y., Li, Y. & Shi, H. (2021) Combatting global grassland degradation. Nature Reviews Earth & Environment, 2, 720-735. [CrossRef]
  2. Bengtsson, J., Bullock, J.M., Egoh, B., Everson, C., Everson, T., O'Connor, T., O'Farrell, P.J., Smith, H.G. & Lindborg, R. (2019) Grasslands—more important for ecosystem services than you might think. Ecosphere, 10. [CrossRef]
  3. Briske, D.D., Coppock, D.L., Illius, A.W. & Fuhlendorf, S.D. (2020) Strategies for global rangeland stewardship: Assessment through the lens of the equilibrium–non-equilibrium debate. Journal of Applied Ecology, 57, 1056– 1067. [CrossRef]
  4. Cai, Z., Song, P., Wang, J., Jiang, F., Liang, C., Zhang, J., Gao, H. & Zhang, T. (2022) Grazing pressure index considering both wildlife and livestock in Three-River Headwaters, Qinghai-Tibetan Plateau. Ecological Indicators, 143. [CrossRef]
  5. Cao, Y., Wu, J., Zhang, X., Niu, B. & He, Y. (2020) Comparison of Methods for Evaluating the Forage-Livestock Balance of Alpine Grasslands on the Northern Tibetan Plateau. Journal of Resources and Ecology, 11, 272-282. [CrossRef]
  6. Cao, Y., Wu, J., Zhang, X., Niu, B., Li, M., Zhang, Y., Wang, X. & Wang, Z. (2019) Dynamic forage-livestock balance analysis in alpine grasslands on the Northern Tibetan Plateau. Journal of Environmental Management, 238, 352-359. [CrossRef]
  7. Chai, Q., Gan, Y., Zhao, C., Xu, H.-L., Waskom, R.M., Niu, Y. & Siddique, K.H.M. (2015) Regulated deficit irrigation for crop production under drought stress. A review. Agronomy for Sustainable Development, 36, 3. [CrossRef]
  8. Deng, X.-P., Shan, L., Zhang, H. & Turner, N.C. (2006) Improving agricultural water use efficiency in arid and semiarid areas of China. Agricultural Water Management, 80, 23-40. [CrossRef]
  9. Ding, M.J., Zhang, Y.L., Sun, X.M., Liu, L.S., Wang, Z.F. & Bai, W.Q. (2013) Spatiotemporal variation in alpine grassland phenology in the Qinghai-Tibetan Plateau from 1999 to 2009. Chinese Science Bulletin, 58, 396-405. [CrossRef]
  10. Duparc, A., Redjadj, C., Viard-Crétat, F., Lavorel, S., Austrheim, G. & Loison, A. (2013) Co-variation between plant above-ground biomass and phenology in sub-alpine grasslands. Applied Vegetation Science, 16, 305-316. [CrossRef]
  11. Gao, X.X., Dong, S.K., Li, S., Xu, Y.D., Liu, S.L., Zhao, H.D., Yeomans, J., Li, Y., Shen, H., Wu, S.N. & Zhi, Y.L. (2020) Using the random forest model and validated MODIS with the field spectrometer measurement promote the accuracy of estimating aboveground biomass and coverage of alpine grasslands on the Qinghai-Tibetan Plateau. Ecological Indicators, 112, 106114. [CrossRef]
  12. Harris, R.B. (2010) Rangeland degradation on the Qinghai-Tibetan plateau: A review of the evidence of its magnitude and causes. Journal of Arid Environments, 74, 1-12. [CrossRef]
  13. He, F., Chen, D., Li, Q., Chen, X., Huo, L., Zhao, L. & Zhao, X. (2020) Temporal and spatial distribution of herbage nutrition in alpine grassland of Sanjiangyuan. Acta Ecologica Sinica, 40, 6304-6313. [CrossRef]
  14. Hu, G., Gao, Q., Ganjurjav, H., Wang, Z., Luo, W., Wu, H., Li, Y., Yan, Y., Gornish, E.S., Schwartz, M.W., Wan, Y. & Li, Y. (2021) The divergent impact of phenology change on the productivity of alpine grassland due to different timing of drought on the Tibetan Plateau. Land Degradation and Development, 32, 4033-4041. [CrossRef]
  15. Hua, X., Ohlemüller, R. & Sirguey, P. (2022) Differential effects of topography on the timing of the growing season in mountainous grassland ecosystems. Environmental Advances, 8, 100234. [CrossRef]
  16. Huang, L., Koubek, T., Weiser, M. & Herben, T. (2018) Environmental drivers and phylogenetic constraints of growth phenologies across a large set of herbaceous species. Journal of Ecology, 106, 1621-1633. [CrossRef]
  17. Huang, W., Bruemmer, B. & Huntsinger, L. (2016) Incorporating measures of grassland productivity into efficiency estimates for livestock grazing on the Qinghai-Tibetan Plateau in China. Ecological Economics, 122, 1-11. [CrossRef]
  18. Jia, W.X., Liu, M., Yang, Y.H., He, H.L., Zhu, X.D., Yang, F., Yin, C. & Xiang, W.N. (2016) Estimation and uncertainty analyses of grassland biomass in Northern China: Comparison of multiple remote sensing data sources and modeling approaches. Ecological Indicators, 60, 1031-1040. [CrossRef]
  19. Li, W., Ma, X. & Chen, Q. (2009) Research on grassland resources yield and balance between forage resources and livestock numbers in Haidong and Haibei prefecture of Qinghai. Acta Prataculturae Sinica, 18, 270-275.
  20. Li, X., Perry, G.L.W. & Brierley, G.J. (2018) A spatial simulation model to assess controls upon grassland degradation on the Qinghai-Tibet Plateau, China. Applied Geography, 98, 166-176. [CrossRef]
  21. Liu, H., Mi, Z., Lin, L., Wang, Y., Zhang, Z., Zhang, F., Wang, H., Liu, L., Zhu, B., Cao, G., Zhao, X., Sanders, N.J., Classen, A.T., Reich, P.B. & He, J.-S. (2018) Shifting plant species composition in response to climate change stabilizes grassland primary production. Proceedings of the National Academy of Sciences, 115, 4051-4056. [CrossRef]
  22. Luo, T., Li, W. & Zhu, H. (2002) ESTIMATED BIOMASS AND PRODUCTIVITY OF NATURAL VEGETATION ON THE TIBETAN PLATEAU. Ecological Applications, 12, 980-997. [CrossRef]
  23. Mao, D., Wang, Z., Li, L. & Ma, W. (2014) Spatiotemporal dynamics of grassland aboveground net primary productivity and its association with climatic pattern and changes in Northern China. Ecological Indicators, 41, 40-48. [CrossRef]
  24. Mo, X.G., Liu, W., Meng, C.C., Hu, S., Liu, S.X. & Lin, Z.H. (2021) Variations of forage yield and forage-livestock balance in grasslands over the Tibetan Plateau, China. Chinese Journal of Applied Ecology, 32, 2415-2425. [CrossRef]
  25. Möhl, P., von Büren, R.S. & Hiltbrunner, E. (2022) Growth of alpine grassland will start and stop earlier under climate warming. Nature Communications, 13, 7398. [CrossRef]
  26. O'Neil, C. (2017) Weapons of math destruction: How big data increases inequality and threatens democracy. Crown.
  27. Oesterheld, M., Sala, O.E. & McNaughton, S.J. (1992) Effect of animal husbandry on herbivore-carrying capacity at a regional scale. Nature, 356, 234-236. [CrossRef]
  28. Piipponen, J., Jalava, M., de Leeuw, J., Rizayeva, A., Godde, C., Cramer, G., Herrero, M. & Kummu, M. (2022) Global trends in grassland carrying capacity and relative stocking density of livestock. Global Change Biology, 28, 3902-3919. [CrossRef]
  29. Ping, W., Zhiwei, W., Xuetong, Z., Qisheng, F., Cili, J. & Quangong, C. (2010) GIS-based classification of seasonal pasture in Qinghai province. Pratacultural Science, 27, 119-128.
  30. Qin, P., Sun, B., Li, Z., Gao, Z., Li, Y., Yan, Z. & Gao, T. (2021) Estimation of grassland carrying capacity by applying high spatiotemporal remote sensing techniques in Zhenglan Banner, Inner Mongolia, China. Sustainability (Switzerland), 13. [CrossRef]
  31. Retzer, V. & Reudenbach, C. (2005) Modelling the carrying capacity and coexistence of pika and livestock in the mountain steppe of the South Gobi, Mongolia. Ecological Modelling, 189, 89-104. [CrossRef]
  32. Richardson, W., Stringham, T.K., Lieurance, W. & Snyder, K.A. (2021) Changes in Meadow Phenology in Response to Grazing Management at Multiple Scales of Measurement. Remote Sensing, 13, 4028. [CrossRef]
  33. Sanaei, A., Li, M. & Ali, A. (2019) Topography, grazing, and soil textures control over rangelands' vegetation quantity and quality. Science of the Total Environment, 697, 134153. [CrossRef]
  34. Scurlock, J.M., Johnson, K. & Olson, R.J. (2002) Estimating net primary productivity from grassland biomass dynamics measurements. Global Change Biology, 8, 736-753. [CrossRef]
  35. Shen, M., Wang, S., Jiang, N., Sun, J., Cao, R., Ling, X., Fang, B., Zhang, L., Zhang, L., Xu, X., Lv, W., Li, B., Sun, Q., Meng, F., Jiang, Y., Dorji, T., Fu, Y., Iler, A., Vitasse, Y., Steltzer, H., Ji, Z., Zhao, W., Piao, S. & Fu, B. (2022) Plant phenology changes and drivers on the Qinghai–Tibetan Plateau. Nature Reviews Earth & Environment, 3, 633-651. [CrossRef]
  36. Song, Y., Munch, S.B. & Zhu, K. (2023) Prediction-based approach for quantifying phenological mismatch across landscapes under climate change. Landscape Ecology. [CrossRef]
  37. Wang, H., Liu, H., Cao, G., Ma, Z., Li, Y., Zhang, F., Zhao, X., Zhao, X., Jiang, L., Sanders, N.J., Classen, A.T. & He, J.S. (2020a) Alpine grassland plants grow earlier and faster but biomass remains unchanged over 35 years of climate change. Ecology Letters, 23, 701-710. [CrossRef]
  38. Wang, H., Liu, H., Huang, N., Bi, J., Ma, X., Ma, Z., Shangguan, Z., Zhao, H., Feng, Q., Liang, T., Cao, G., Schmid, B. & He, J.-S. (2021) Satellite-derived NDVI underestimates the advancement of alpine vegetation growth over the past three decades. Ecology, 102, e03518. [CrossRef]
  39. Wang, J., Zhou, T. & Peng, P. (2018) Phenology Response to Climatic Dynamic across China’s Grasslands from 1985 to 2010. ISPRS International Journal of Geo-Information, 7, 290. [CrossRef]
  40. Wang, X., Li, F.Y., Tang, K., Wang, Y., Suri, G., Bai, Z. & Baoyin, T. (2020b) Land use alters relationships of grassland productivity with plant and arthropod diversity in Inner Mongolian grassland. Ecological Applications, 30, e02052. [CrossRef]
  41. Wang, Y., Lv, W., Xue, K., Wang, S., Zhang, L., Hu, R., Zeng, H., Xu, X., Li, Y., Jiang, L., Hao, Y., Du, J., Sun, J., Dorji, T., Piao, S., Wang, C., Luo, C., Zhang, Z., Chang, X., Zhang, M., Hu, Y., Wu, T., Wang, J., Li, B., Liu, P., Zhou, Y., Wang, A., Dong, S., Zhang, X., Gao, Q., Zhou, H., Shen, M., Wilkes, A., Miehe, G., Zhao, X. & Niu, H. (2022) Grassland changes and adaptive management on the Qinghai–Tibetan Plateau. Nature Reviews Earth & Environment, 3, 668-683. [CrossRef]
  42. Wei, D., Zhao, H., Zhang, J., Qi, Y. & Wang, X. (2020) Human activities alter response of alpine grasslands on Tibetan Plateau to climate change. J Environ Manage, 262, 110335. [CrossRef]
  43. Wu, J., Zhang, X., Shen, Z., Shi, P., Xu, X. & Li, X. (2013) Grazing-Exclusion Effects on Aboveground Biomass and Water-Use Efficiency of Alpine Grasslands on the Northern Tibetan Plateau. Rangeland Ecology & Management, 66, 454-461. [CrossRef]
  44. Wu, M., Vico, G., Manzoni, S., Cai, Z., Bassiouni, M., Tian, F., Zhang, J., Ye, K. & Messori, G. (2021) Early Growing Season Anomalies in Vegetation Activity Determine the Large-Scale Climate-Vegetation Coupling in Europe. Journal of Geophysical Research: Biogeosciences, 126, e2020JG006167. [CrossRef]
  45. Xie, J., Jonas, T., Rixen, C., de Jong, R., Garonna, I., Notarnicola, C., Asam, S., Schaepman, M. & Kneubühler, M. (2020) Land surface phenology and greenness in Alpine grasslands driven by seasonal snow and meteorological factors. Science of the Total Environment. [CrossRef]
  46. Yang, J., Dong, J., Xiao, X., Dai, J., Wu, C., Xia, J., Zhao, G., Zhao, M., Li, Z., Zhang, Y. & Ge, Q. (2019) Divergent shifts in peak photosynthesis timing of temperate and alpine grasslands in China. Remote Sensing of Environment, 233. [CrossRef]
  47. Yang, S.X., Feng, Q.S., Liang, T.G., Liu, B.K., Zhang, W.J. & Xie, H.J. (2018) Modeling grassland above-ground biomass based on artificial neural network and remote sensing in the Three-River Headwaters Region. Remote Sensing of Environment, 204, 448-455. [CrossRef]
  48. Yang, Y., Fang, J., Pan, Y. & Ji, C. (2009) Aboveground biomass in Tibetan grasslands. Journal of Arid Environments, 73, 91-95. [CrossRef]
  49. Yang, Y., Zhao, D. & Chen, H. (2022) Full Title: Quantifying the ecological carrying capacity of alpine grasslands on the Qinghai-Tibet Plateau. Ecological Indicators, 136, 108634. [CrossRef]
  50. Yu, H., Wu, Y., Niu, L., Chai, Y., Feng, Q., Wang, W. & Liang, T. (2021) A method to avoid spatial overfitting in estimation of grassland above-ground biomass on the Tibetan Plateau. Ecological Indicators, 125, 107450. [CrossRef]
  51. Yu, L., Zhou, L., Liu, W. & Zhou, H.-K. (2010) Using Remote Sensing and GIS Technologies to Estimate Grass Yield and Livestock Carrying Capacity of Alpine Grasslands in Golog Prefecture, China. Pedosphere, 20, 342-351. [CrossRef]
  52. Yuan, Q., Yuan, Q. & Ren, P. (2021) Coupled effect of climate change and human activities on the restoration/degradation of the Qinghai-Tibet Plateau grassland. Journal of Geographical Sciences, 31, 1299-1327. [CrossRef]
  53. Zhang, C., Dong, Q., Chu, H., Shi, J., Li, S., Wang, Y. & Yang, X. (2018) Grassland Community Composition Response to Grazing Intensity Under Different Grazing Regimes. Rangeland Ecology & Management, 71, 196-204. [CrossRef]
  54. Zhang, C., Zhang, Y., Wang, Z., Li, J. & Odeh, I. (2020) Monitoring Phenology in the Temperate Grasslands of China from 1982 to 2015 and Its Relation to Net Primary Productivity. Sustainability, 12, 12. [CrossRef]
  55. Zhang, J., Fang, S. & Liu, H. (2022a) Estimation of alpine grassland above-ground biomass and its response to climate on the Qinghai-Tibet Plateau during 2001 to 2019. Global Ecology and Conservation, 35, e02065. [CrossRef]
  56. Zhang, J., Zhang, L., Liu, W., Qi, Y. & Wo, X. (2014a) Livestock-carrying capacity and overgrazing status of alpine grassland in the Three-River Headwaters region, China. Journal of Geographical Sciences, 24, 303-312. [CrossRef]
  57. Zhang, J., Zhang, L., Liu, X. & Qiao, Q. (2019) Research on sustainable development in an alpine pastoral area based on equilibrium analysis between the grassland yield, livestock carrying capacity, and animal husbandry population. Sustainability (Switzerland), 11. [CrossRef]
  58. Zhang, L., Guo, H., Jia, G., Wylie, B., Gilmanov, T., Howard, D., Ji, L., Xiao, J., Li, J., Yuan, W., Zhao, T., Chen, S., Zhou, G. & Kato, T. (2014b) Net ecosystem productivity of temperate grasslands in northern China: An upscaling study. Agricultural and Forest Meteorology, 184, 71-81. [CrossRef]
  59. Zhang, X., Li, M., Wu, J., He, Y. & Niu, B. (2022b) Alpine Grassland Aboveground Biomass and Theoretical Livestock Carrying Capacity on the Tibetan Plateau. Journal of Resources and Ecology, 13, 129-141. [CrossRef]
  60. Zhao, J., Sun, F. & Tian, L. (2019) Altitudinal pattern of grazing exclusion effects on vegetation characteristics and soil properties in alpine grasslands on the central Tibetan Plateau. Journal of Soils and Sediments, 19, 750-761. [CrossRef]
  61. Zhu, Y., Zhang, Y., Zu, J., Wang, Z., Huang, K., Cong, N. & Tang, Z. (2019) Effects of data temporal resolution on phenology extractions from the alpine grasslands of the Tibetan Plateau. Ecological Indicators, 104, 365-377. [CrossRef]
Preprints 104426 g001
Figure 1. Modelling theory of AGBA correction and ASR estimation.
Figure 1. Modelling theory of AGBA correction and ASR estimation.
Preprints 104426 g001
Preprints 104426 g002
Figure 2. A framework for LCC and ASR estimation. F(x) is the AGB growth function, F(x)ʹ refers to AGB growth rate. R(x) and R(x)ʹ are functions of AGB removal and removal rate, AGBPW is the peak above ground biomass of winter pasture, AGBPS the peak above ground biomass of summer pasture, AGBC is the plant biomass consumed by livestock in growing season, LCC is livestock carrying capacity, ASR is the actual stocking rate.
Figure 2. A framework for LCC and ASR estimation. F(x) is the AGB growth function, F(x)ʹ refers to AGB growth rate. R(x) and R(x)ʹ are functions of AGB removal and removal rate, AGBPW is the peak above ground biomass of winter pasture, AGBPS the peak above ground biomass of summer pasture, AGBC is the plant biomass consumed by livestock in growing season, LCC is livestock carrying capacity, ASR is the actual stocking rate.
Preprints 104426 g002
Preprints 104426 g003
Figure 3. Schematic illustration of AGB production and consumption (AGBAN and AGBPN are for non-grazed grassland (or winter pasture), AGBA and AGBP are for grazed grassland (or summer pasture). F(x) is the AGB growth representing the remaining AGB in the non-grazed grassland, F(x)ʹ refers to AGB growth rate. f(x) represents the remainder AGB in the grazed grassland, f(x)ʹ refers to AGB remainder rate. R(x) and R(x)ʹ are AGB removal and removal rate. X is the day having the fastest growth rate (FOS) in the grazed grassland, x0 (EXD) is the day of when F(x)ʹ exceed R(x)ʹ, x1 is the day of when F(x)ʹ lags behind R(x)ʹ).
Figure 3. Schematic illustration of AGB production and consumption (AGBAN and AGBPN are for non-grazed grassland (or winter pasture), AGBA and AGBP are for grazed grassland (or summer pasture). F(x) is the AGB growth representing the remaining AGB in the non-grazed grassland, F(x)ʹ refers to AGB growth rate. f(x) represents the remainder AGB in the grazed grassland, f(x)ʹ refers to AGB remainder rate. R(x) and R(x)ʹ are AGB removal and removal rate. X is the day having the fastest growth rate (FOS) in the grazed grassland, x0 (EXD) is the day of when F(x)ʹ exceed R(x)ʹ, x1 is the day of when F(x)ʹ lags behind R(x)ʹ).
Preprints 104426 g003
Preprints 104426 g004
Figure 4. Grazing status for summer and winter pastures at different phenology timings (AGBS is the total produced AGB on summer pasture, AGBW is the total demanded AGB for livestock on winter pasture; AGBPS and AGBPW represent AGBP for summer pasture and winter pasture, respectively. LCCS and LCCW represent LCC for summer pasture and winter pasture, respectively).
Figure 4. Grazing status for summer and winter pastures at different phenology timings (AGBS is the total produced AGB on summer pasture, AGBW is the total demanded AGB for livestock on winter pasture; AGBPS and AGBPW represent AGBP for summer pasture and winter pasture, respectively. LCCS and LCCW represent LCC for summer pasture and winter pasture, respectively).
Preprints 104426 g004
Preprints 104426 g005
Figure 5. Flow chart of the case study. F(x) is AGB growth function, F(x)ʹ is AGB growth rate function, R(x) is AGB removal function, R(x)ʹ is AGB removal rate function, x1 is the day of POS in the grazed grassland.
Figure 5. Flow chart of the case study. F(x) is AGB growth function, F(x)ʹ is AGB growth rate function, R(x) is AGB removal function, R(x)ʹ is AGB removal rate function, x1 is the day of POS in the grazed grassland.
Preprints 104426 g005
Preprints 104426 g006
Figure 6. Illustration of using POS to calculate AGB removal rate (a simplified workflow of Figure 1, ①-③ are three steps).
Figure 6. Illustration of using POS to calculate AGB removal rate (a simplified workflow of Figure 1, ①-③ are three steps).
Preprints 104426 g006
Table 3. Statistical summary of the phenological timings information used to calculate β.
Table 3. Statistical summary of the phenological timings information used to calculate β.
Site Period Vegetation SOS POS β References
QTP 2000-2005 Alpine meadow 154 221 1.47 Zhu et al. (2019)
Alpine steppe 160 226 1.47
1999-2009 All grasslands 145 211 1.43 Ding et al. (2013)
North-west China 1985-2010 Alpine meadow 129 204 1.47 Wang et al. (2018)
Alpine steppe 129 204 1.47
Desert steppe 121 198 1.46
Meadow steppe 123 198 1.45
Temperate meadow 126 197 1.42
Typical steppe 122 198 1.46
2000-2016 Alpine grassland 150 212 1.41 Yang et al. (2019)
Temperate grassland 152 211 1.38
Inner Mongolia 1982-2015 Temperate grassland 110 220 1.76 Zhang et al. (2020)
Mean 135.08 208.33 1.47
SD 16.20 10.10 0.10
Note: SD is the standard deviation. The units of SOS, POS and EOS are Julian days.
Table 4. Statistical summary of the field measurements of AGB in plot experiments used to calculate β.
Table 4. Statistical summary of the field measurements of AGB in plot experiments used to calculate β.
Study region Period Vegetation/location AGB (g m-2) β References
Non-grazed (AGBA) Grazed
(AGBP)
Northern Tibetan Plateau 2006-2010 Alpine meadow 55.6 47.2 1.27 Wu et al. (2013)
Alpine steppe 27.9 20.7 1.34
Alpine desert steppe 8.7 6.0 1.45
2000–2014 Alpine grassland 52.5 34.0 1.54 Cao et al. (2019)
Central Tibetan Plateau 2006 Elevation 4650 95.00 145.00 1.53 Zhao et al. (2019)
Elevation 4950 180.00 280.00 1.56
Elevation 5100 145.00 210.00 1.45
Mean 80.67 106.13 1.45
SD 62.71 106.87 0.11
Note: SD is standard deviation.
Table 5. Description of variables used in the model application.
Table 5. Description of variables used in the model application.
Description Variable Value Period Reference
Non-grazed Plot experiment used for monitoring plant growth over growing season AGBmax(g/m2) 390 2002-2014 Wang et al. (2021)
k 0.062
X 174
Peak AGB of winter pasture AGBPW (g/m2) 353.7 2007 Li et al. (2009)
Grazed VI time series images used for estimating remote sensing phenology parameters POS(x1) 218 2000-2005 Zhu et al. (2019)
EOS 264
Forage quality decreasing rate Q 0.53 Cai et al. (2022)
Peak AGB of summer pasture AGBPS (g/m2) 230.0 2001-2005 Jia et al. (2016)
220.0 2000-2005 Gao et al. (2020)
200.0 2001-2005 Yu et al. (2021)
210.5 2001-2004 Yang et al. (2009)
Mean 215.1
SD 12.8
Note: AGBmax is the maximum AGB over the growing season in the non-grazed grassland, k is the standardized fastest AGB growth rate, X is the day having the fastest growth rate. Forage supplement (FS) is not available in this case study.
Table 6. Comparison of modelling results.
Table 6. Comparison of modelling results.
Description Variable Results
The day of AGB growth rate F(x)ʹ exceed AGB removal rate R(x)ʹ EXD(x0) 131
The adjustment factor for calculating AGBC (by the time of POS in summer pasture) based on AGBW , Equation 25-26 β0 0.434
AGB removal rate is estimated by the reverse verification process, Equation 18 R(x)ʹ (g/m2/day) 1.152
ASRS as calculated by Equation 24 ASRS (SU/ha) 2.91
LCCS as calculated by Equation 28-29, AGBP was adjusted by β0 LCCS (SU/ha) 2.61
Comparison between ASRS and LCCS according to Figure 4 Grazing severity Over-grazed
Over-stock rate 11.5%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

69

Views

36

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated