Prerpints.org logo
Preprint
Article

Penrose Scattering in Quantum Vacuum

This version is not peer-reviewed.

Submitted:

16 April 2024

Posted:

16 April 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Scattering of a probe laser pulse by an intense light spring in QED vacuum is considered. This new scattering configuration can be seen as the vacuum equivalent to the process originally associated with scattering of light by a rotating black hole, usually called Penrose superradiance. Here the rotating object is an intense laser beam containing two different components of orbital angular momentum. Due to these two components with slightly different frequencies, the energy profile of the intense laser beam rotates with a frequency that depends on the frequency difference. The nonlinear properties of quantum vacuum are described by first order Euler-Heisenberg Lagrangian. It is shown that, in such a configuration, nonlinear photon-photon coupling leads to scattered radiation, with frequency shift and angular dispersion. These two distinct properties, of frequency and propagation direction, could eventually be favourable for possible experimental observations. In principle, this new scattering configuration can also be reproduced in a nonlinear optical medium.
Keywords: 
Laser QED
;  
scattering
;  
nonlinear quantum vacuum
Subject: 
Physical Sciences  -   Optics and Photonics

1. Introduction

The recent development of intense laser systems at the Peta-Watt level [1] opens the opportunity for a possible exploration of quantum vacuum and its nonlinear optical properties. This has been discussed in several recent review papers (see for instance [2,3,4]). Many different physical geometries have been proposed for possible experiments with intense lasers in vacuum, specially those associated with photon-photon scattering, vacuum birefringence, four-wave mixing, photon reflection and acceleration, among others [5,6,7,8,9].
Most of these processes take place with moderately high electromagnetic radiation, not involving the creation of real electron-positron pairs, but simply the excitation of virtual pairs which can be seen as the components of a virtual plasma state. This state can be excited using field amplitudes that are very large when compared with common laser beams, but stay well below the critical field [10], known as the Schwinger field. Vacuum optical processes in this moderately high regime can be described with the lowest order Heisenberg-Euler Lagrangian theory [11].
Due to the smallness of such vacuum quantum effects, several strategies have been proposed to increase these effects. Recent proposals include photon-photon scattering of high-harmonic laser pulses and vacuum superradiance [12,13]. Here we propose another possible configuration, which is directly inspired by traditional optical experiments using rotating mirrors, and that more recently was recreated in a gravitational context. This new context was first explored by Penrose [14], Zeldovich [15] and others, as a way to extract energy from a rotating black hole, and is sometimes called Penrose superradiance [16,17]. Recent observations of similar phenomena were claimed in nonlinear optics [18], in acoustics [19] and in hydrodynamics [20].
In previous papers, it was shown that vortex structures containing two or more internal modes with different frequency and helicity, called light springs, can be used for particle acceleration in plasmas [21,22]. Although somewhat surprising, the name of light spring becomes obvious near a plasma cutoff, when these optical structures behave like a mechanical spring [23]. Here, we consider the possible use of similar structures in pure vacuum. The energy density of such structures rotates around the propagation direction with an angular velocity that depends on the frequency difference of their internal modes. At high intensities, they can be used as a nonlinear scattering object for a probe beam propagating in the perpendicular direction. Here we study the corresponding scattering process.
We describe the vacuum properties using the Euler-Heisenberg Lagrangian. The optical nonlinearity associated with an intense light spring is described in Section II. The nonlinear quantum currents resulting from the interaction of this structure with a probe beam are described in Sections III, and the properties of the scattered radiation resulting from this interaction are detailed in Section IV. The field amplitude, frequency and wavevector spectrum of the scattered radiation are given, and simple order of magnitude estimates are established. Finally, in Section VI, we state some conclusions.

2. Light Spring in Vacuum

We consider an intense laser pulse propagating in vacuum with orbital angular momentum (OAM). We assume that the pulse propagates along some arbitrary z-direction, and is made of a superposition of two OAM modes, with different frequencies ω 1 and ω 2 , and different helicity characterised by the topological charges, or poloidal quantum numbers, ℓ 1 and ℓ 2 . This pulse configuration is sometimes called a light spring [22,24]. Using cylindrical coordinates, r ≡ ( r , θ , z ) , we can write the total electric field of the pulse as
E 0 ( r , t ) = ∑ ν = 1 , 2 E ν F ν ( r , θ ) exp i k ν z − i ω ν t + c . c . ,
where ν = 1 , 2 represent the two different helicity components. The transverse beam profile of each component is described by a Laguerre-Gauss function F ν ( r , θ ) , and each value of ν represent two quantum numbers ( p , ℓ ) , where p characterizes the number of zeros in the radial direction, and ℓ defines the poloidal mode structure, as given by
F ν ( r , θ ) = C p ℓ X | ℓ | / 2 L p | ℓ | ( X ) exp i ℓ ν θ − X 2 + i φ G .
Here, L p ℓ are the Laguerre-Gauss functions of the dimensionless variable X = r 2 / w 2 , where the laser beam waist w slowly varies in the z direction. Due to propagation in vacuum, we necessarily have k ν = ω ν / c . In this expression, we have included the Guoy phase, defined as
φ G = 1 + 2 p + | ℓ | arctan ( z / L R ) ,
where L R is the Rayleigh length, defining the size of the focal region. This phase only plays a minor role in the present problem and can be ignored. The light spring intensity is determined by the following expression
E 0 2 = ∑ ν = 1 , 2 | E ν | 2 F ν ( r ) 2 + 2 E 1 · E 2 F 1 ( r ) F 2 ( r ) exp Δ k z + Δ ℓ θ − Δ ω t ,
where we have used the notation F ν ( r ) = F ν ( r , θ ) exp ( − i ℓ θ ) , and defined the differences
Δ ℓ = ℓ 1 − ℓ 2 , Δ ω = ω 1 − ω 2 , Δ k = Δ ω / c ,
between the two internal modes of the light spring. This expression is very interesting because it shows that the maximum intensity of the light spring follows a helical curve defined by [22]
θ ( z , t ) = ( z − c t ) Δ k Δ ℓ ≡ ( z − c t ) ( ω 1 − ω 2 ) c ( ℓ 1 − ℓ 2 ) ,
For a given scattering position, z = constant, it therefore defines the angular rotation of a purely electromagnetic object moving in vacuum. Of particular interest for experimental purposes is the case where Δ ℓ ≃ 1 ≪ ℓ ν and Δ ω ≪ ω ν . An intense light spring can then locally excite electron-positron (e-p) virtual states, thus leading to scattering of a probe pulse propagating in a perpendicular direction. The geometry of our problem is represented in Figure 1.
We describe quantum vacuum using the lowest order Euler-Heisenberg Lagrangian [11]. This is valid for field amplitudes well below the Schwinger limit, when real e-p pairs are absent, and QED vacuum effects are dominated by virtual pairs. This is the appropriate regime for possible experiments with the existing high intensity laser systems. In this approach, the electromagnetic vacuum response is determined by the polarization and magnetization vectors, P and M , given by the two symmetric expressions
P = 2 ζ 4 F E + 7 c G B , M = − 2 ζ c 2 4 F B + 7 c G E / c .
Here, E are B is the magnetic field amplitudes, and F and G are the two invariant quantities
F = 1 2 c 2 B 2 − E 2 , G = c E · B .
We have also used the nonlinear quantum parameter ζ , which determines the strength of the quantum vacuum nonlinearity, defined as
ζ = 2 α 2 ϵ 0 2 ℏ 3 45 m 4 c 5 , α = e 2 2 ϵ 0 h c ,
where ϵ 0 = 1 / c 2 μ 0 is the vacuum permittivity, ℏ = h / 2 π is Planck’s constant divided by 2 π , m is the electron mass, and α ≃ 1 / 137 is fine structure constant. As already mentioned, such a description is valid for weak fields, E ≪ E S , where the Schwinger field is E S = m 2 c 3 / e ℏ ≃ 1.32 × 10 18 V / m . In order to describe the properties of the scattered signal, we use the wave equation valid for a disturbed quantum, of the form
∇ 2 − 1 c 2 ∂ 2 ∂ t 2 E = μ 0 ∂ J ∂ t + c 2 ∇ ∇ · P ,
where the nonlinear current J is
J = ∂ P ∂ t + ∇ × M ,
In the next section we calculate the currents responsible for the emission of scattered radiation.
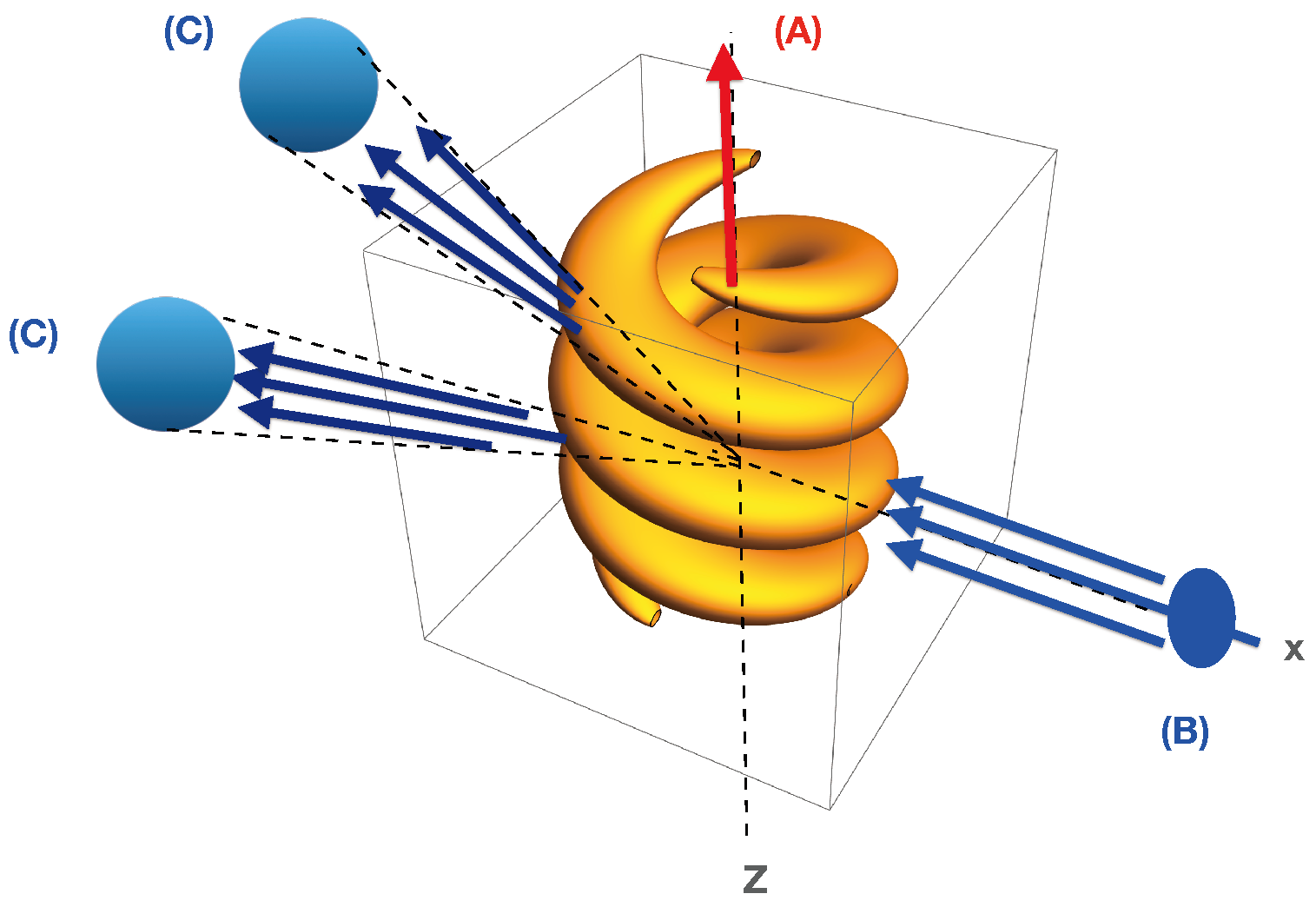
Preprints 104055 g001
Figure 1. Geometry of Penrose scattering in vacuum: ( A ) —an intense light spring propagates in the z direction, with frequencies ω 1 and ω 2 , its intensity rotates around the z axis; ( B ) a probe pulse with frequency ω i propagates along the (negative) x direction and collides perpendicularly with the light spring; ( C ) scattered signals are emitted with frequencies ω ± , and an angular spread dictated by the light spring structure.
Figure 1. Geometry of Penrose scattering in vacuum: ( A ) —an intense light spring propagates in the z direction, with frequencies ω 1 and ω 2 , its intensity rotates around the z axis; ( B ) a probe pulse with frequency ω i propagates along the (negative) x direction and collides perpendicularly with the light spring; ( C ) scattered signals are emitted with frequencies ω ± , and an angular spread dictated by the light spring structure.
Preprints 104055 g001

3. Quantum Currents

Let us then assume an incident probe field propagating in the perpendicular direction, as described by
E i ( r , t ) = E i exp ( i k i · r − i ω i t ) ,
where k i = − k i e x (See Figure 1). If we ignore nonlinear dispersion corrections due to the light spring, we can write k i = ω i / c . Our aim is to calculate the field scattered by the rotating nonlinear structure described by the field E 0 , defined in eq. (1). The total field of our problem can therefore be written as
E = E 0 + E i + E s , B = B 0 + B i + B s ,
where E i and B i are the probe fields, and E s and B s are the second order scattered fields. Notice that the magnetic field associated with the light spring is given by
B 0 ( r , t ) = ∑ ν = 1 , 2 B ν F ν ( r , θ ) exp i k ν · z − i ω ν t + c . c . ,
where
B ν = E ν c k ν c ω ν × e ν + i ℓ ν r e r + 1 F ν ∂ F ν ∂ r e θ .
In the particular case of k ν = k ν e z mentioned earlier, and assuming that the two light spring components are linearly polarized at an angle θ ν relative the the x axis, we get
k ν c ω ν × e ν = − e θ .
According to equations (10) and (13), the wave equation for the scattered radiation is given by
∇ 2 − 1 c 2 ∂ 2 ∂ t 2 E s = μ 0 ∂ J s ∂ t + c 2 ∇ ∇ · P s ,
where the source terms are independent of the second order fields, and therefore J s ≡ J s ( E ν , E i ) and P s ≡ P s ( E ν , E i ) . In order to calculate these terms, we start with the invariantes (8). They can be approximately written as
F s = 1 2 ∑ ν c 2 B ν * · B i − E ν * · E i F ν ( r ) exp ( i φ ν ) + c . c . ,
and
G s = c ∑ ν E ν * · B i + E i · B ν * F ν ( r ) exp ( i φ ν ) + c . c . ,
with the phase
φ ν = − ℓ ν θ + ( k i − k ν ) · r − ( ω i − ω ν ) t .
In these expressions we have used the equality ( c 2 B i 2 − E i 2 ) = 0 . We also assumed that ( c 2 B ν 2 − E ν 2 ) ≃ 0 , which corresponds to neglecting the second term in eq. (15). This term would lead to corrections of order 1 / k ν w , assumed much smaller than one, where w is the beam waist. Notice that, in the above expressions, the other neglected contributions are second order corrections to the dispersion relation of the scattered field. These simplifying assumptions don’t significantly contribute to the final result.
The above invariants can be used to calculate the quantities J s an P s , where only terms of the form ( E ν * E ν E i ) contribute to the scattered radiation, for frequencies determined by ω ± = ( ω i ± Δ ω ) , as shown next. We first write the nonlinear polarization P s , and magnetization M s as
P s = − 2 ζ 4 F s E 0 − 7 c G s B 0 , M s = − 2 c ζ 4 c F s B 0 + 7 G s E 0 .
After a straightforward calculation, we obtain
P s = − 2 ζ ∑ ν , ν ′ p s E ν * E ν ′ E i F ν F ν ′ exp ( i φ s ′ ) .
and
M s = − 2 c ζ ∑ ν , ν ′ m s E ν * E ν ′ B i F ν F ν ′ exp ( i φ ν ν ′ ) .
where we have used the auxiliary phase functions
φ ν ν ′ = ℓ ν − ℓ ν ′ θ + k i − k ν + k ν ′ · r − ω i − ω ν + ω ν ′ t ,
and the auxiliary polarization and magnetization vectors
p s = 2 b ν * · b i − e ν · e i e ν ′ − 7 e ν * · e i + b ν * · e i b ν ′ ,
and
m s = 2 b ν * · b i − e ν · e i b ν ′ + 7 e ν * · e i + b ν * · e i e ν ′ ,
The unit vectors e = E / | E | and b = B / | B | , with appropriate subscripts, were also used. Of particular interest is the case considered here, where the two components of the light spring propagate along the z-axis, with k ν = k ν e z , and the probe propagates along the x-axis, in the negative direction, with k i = − k i e x . To simplify, we also use e ν = e x . In this case, we can write the auxiliary polarization vectors in a much simpler form, as
p s = 2 b ν * · b i e ν ′ − 7 b ν * · e i b ν ′ ,
This allows us to write the nonlinear current as J s = J 0 + J ± , where the first term corresponds to ν = ν . It only contributes to elastic scattering, because it evolves in space and time according to the phase φ i , and will be ignored in the subsequent discussion. As for the other term, we have
J ± = 2 i R 12 ( r ) ζ | E 1 E 2 | E i ∑ ± ω ± j ± exp ( i φ ± ) ,
where R 12 ( r ) = F 1 ( r ) F 2 ( r ) determines the radial structure, ω ± = ω i ± Δ ω are the emitted frequencies, and the phase functions become
φ ± = ± Δ θ + k ± · r − ω ± t ,
with k ± = k i ± Δ k . Finally, we have used the auxiliary current vector
j ± = p s + k ± c ω ± × m ±
where m ± is defined below, p + = p s ( ν = 1 , ν ′ = 2 ) and p − = p s ( ν = 2 , ν ′ = 1 ) . Similarly, for the nonlinear magnetization we have M s = M 0 + M ± , where the terms contributing to inelastic scattering are
M ± = 2 c R 12 ( r ) ζ | E 1 E 2 | B i ∑ ± m ± exp ( i φ ± ) ,
with
m + = 2 b 1 * · b i b 2 + 7 b 1 * · e i e 2 ,
and m − is obtained by interchanging the subscripts 1 and 2. Notice that the quantities J 0 and M 0 only give negligible nonlinear corrections to the refractive index of the incident wave at frequency ω i . Although they are not explicitly written, because not relevant to scattering, they are of the same order of magnitude as J ± and M ± .

4. Scattered Radiation

Let us now go back to the wave equation for the scattered field, eq. (17), and search for a solution of the form
E s ( r , t ) = E s ( r , ω ) exp ( − i ω t ) .
The quantity E s ( r , ω ± ) is a solution of
∇ 2 + ω 2 c 2 E s ( r ; ω ) = − i μ 0 ∫ d t ω J s ( r ; ω ) exp ( i ω t ) ,
Here we only retain the dominant term (see a detailed discussion in [25]). Using eq. (28), we can write
∇ 2 + ω 2 c 2 E s ( r ; ω ) = 2 ω μ 0 R 12 ( r ) ζ | E 1 E 2 | E i I ω ,
with the integral
I ω = ∫ ω ± j ± exp ( i φ ± ) d t ,
From here, we can easily get
I ω = 2 π ω ± j ± δ ( ω − ω ± ) e i ± Δ ℓ θ e i k ± · r ,
Noting that the scattered field in eq. (35) has to satisfy the vacuum dispersion relation k = ω / c , we can write for the field amplitude
E s ( r , ω ) = 2 ω 2 k μ 0 ζ | E 1 E 2 | E i ( e s * · j ± ) I ( r ) e i k · r ,
with the new integral
I ( r ) = ∫ r R 12 ( r ′ ) e ± i Δ ℓ θ e i ( k ± − k ) · r ′ d r ′ ,
where e s is the unit polarization vector of the scattered field. At this point, it is important to note that the wavevector k is not identical to k ± , because it has to satisfy the vacuum dispersion relation k = ω / c . In contrast, the frequency of the scattering radiation is exactly defined by ω = ω ± ≡ ω i ± Δ ω . This leads to the relation k 2 = ( k i ± Δ k ) 2 . On the other hand, given that k i and Δ k are ortogonal, we immediately have k ± 2 = k i 2 ± Δ k 2 and we conclude that k ≠ k ± .
Therefore, due to momentum conservation, the scattered radiation receives an additional amount of momentum, coming from the light spring structure described by R 12 ( r ) . This is an important aspect of the present scattering mechanism. To understand it properly, we define: k = − k i e x ± Δ k e z + q , and assume that the additional amount of momentum is in the x direction: q = − q x e x . Replacing this in eq. (39), and integrating in z, we obtain
I ( r ) = 2 π ∫ r ⊥ R 12 ( r ′ ) e ± i Δ ℓ θ + i q x x ′ d r ′ ⊥ ,
where d r ⊥ = r d r d θ . From here, we can easily get
I ( r ) = ( 2 π ) 2 ∑ ℓ ′ w ′ J ℓ ′ ( q x w ′ ) δ ( ℓ ′ ± Δ ℓ ) ,
where J ℓ ′ are Bessel functions of the first kind. The quantity w ′ in this expression is nearly equal to the light spring spot-size w, and is more exactly defined by the equality
w ′ J ℓ ′ ( q x w ′ ) = ∫ 0 ∞ R 12 ( r ) J ℓ ′ ( q x r ) r d r .
We see that this quantity is of order one, as illustrated in Figure 2. As a final step of our calculation, we arrive at an expression for the scattered field amplitude, of the form
E s ( r , ω ) = 2 3 π a 0 2 E i R ( e s * · j ± ) ∑ ℓ ′ ( k w ′ ) J ℓ ′ ( q x w ′ ) δ ( ℓ ′ ± Δ ℓ ) ,
where a 0 = e E 0 / m c ω 0 is the dimensionless field amplitude of the intense light spring, and E 1 = E 2 = E 0 is assumed, and the quantity R is the fundamental nonlinear parameter of vacuum introduced in [25]. Here it takes a slightly different form, as
R = α 45 ℏ ω 1 m c 2 2 ω 2 ω 1 ,
where α is the fine structure constant. Similarly, we can consider the case of the scattered radiation with a small y component. For this purpose we now use q x = 0 , and assume that q = q y e y . This leads to a similar expression for the scattered field, where the quantity J ℓ ′ ( q x w ′ ) δ ( ℓ ′ ± Δ ℓ ) is replaced by J ℓ ′ ( q y w ′ ) ( i ) ℓ ′ δ ( ℓ ′ ∓ Δ ℓ ) .
We arrive at the conclusion that the scattered radiation, with frequency ω = ω ± , spreads with nearly equal amplitude over a spot-size of order w ′ around the direction defined by the wavevector k ± , in both the x and the y-directions. This is due to the additional amount of momentum imparted by the light spring structure. This additional amount of momentum q is always of order Δ k . The resulting scattered field amplitude can then be written, in order of magnitude, as
| E s | E i ≃ 2 3 ( k w ) α 45 a 0 2 ℏ ω 1 m c 2 2 ω 2 ω 1 .
We notice the numerical factor 2 π ( α / 45 ) ∼ 10 − 2 . This amplitude is essentially determined by the intensity of the light spring a 0 2 , and by the initial photon frequencies ω 1 , 2 . It is actually of the same order of magnitude as other wave-mixing phenomena resulting from photon-photon scattering in vacuum, which is no surprise. The main advantage of the present configuration is that the frequency of the scattered field can be very different from the incident frequency, ω ≠ ω i . In the same way, the direction of propagation, k ≠ k i , could provide a good experimental geometry. But the more interesting property of the present scattering configuration is that the scattering direction is not only determined by the wave vectors of the interacting waves, but also the helical nature of the nonlinear object. Therefore, it provides a new and somewhat unexpected vacuum configuration for what can be considered an analogue of the Penrose scattering process.
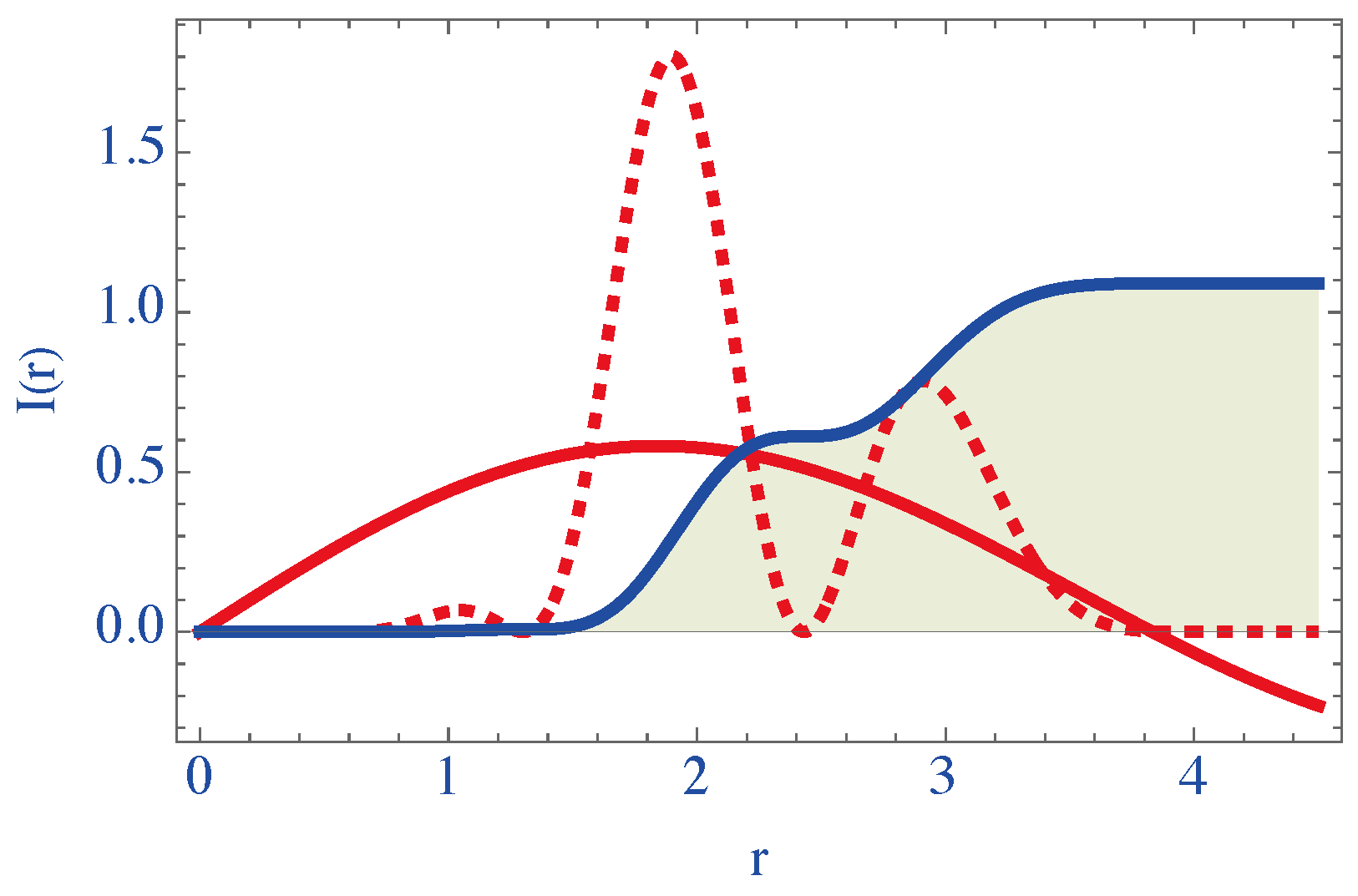
Preprints 104055 g002
Figure 2. Representation of the radial integral I ( r ) , for Δ ℓ = 1 , with J 1 ( r ) in red, R 12 ( r ) in dashed red. We have used ℓ 1 = 14 and k = 1 .
Figure 2. Representation of the radial integral I ( r ) , for Δ ℓ = 1 , with J 1 ( r ) in red, R 12 ( r ) in dashed red. We have used ℓ 1 = 14 and k = 1 .
Preprints 104055 g002

5. Conclusions

In this work, we have considered a new mechanism of photon-photon scattering in quantum vacuum, which is inspired in the Penrose scattering process. In our model, the scatterer is not a black hole but a rotating object made of purely electromagnetic radiation with orbital angular momentum (OAM), that propagates in vacuum as a light spring. This electromagnetic object is made of two twisted modes with different frequencies ω 1 and ω 2 and different helicity states, ℓ 1 and ℓ 2 . In recent years, intense laser beams have been produced experimentally at the PetaWatt intensity level, and the use of light springs at these intensities is therefore conceivable [26,27].
An incident probe pulse, with frequency ω i is scattered in two different directions, determined by the light spring structure. As expected, the photon-photon coupling efficiency associated with this new scattering process is not different from that of the already known configurations [7,25]. However, it could represent some experimental interest, because the scattered frequencies and directions of propagation are clearly distinct from that of the initial laser pulses. This is important, because it could improve the signal-to-noise ratio, which imposes severe constraints in this kind of experiments.
It should be added that the present model, although directly inspired by the Penrose process of light scattering by a rotating black hole, is only partly related to this process. In particular, we were not able to demonstrate the amplification of the incident signal, which is a characteristic feature of the original model. Here, we observe total energy conservation, typical of a nonlinear wave mixing process.

Funding

This research received no external funding.

Acknowledgments

The author would like to thank Prof. Gert Brodin for stimulating discussions on laser QED problems, during a short visit to Umeå University.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Yoon, J.W.; Kim, Y.G.; Choi, I.W.; Sung, J.H.; Lee, H.W.; S.K. Lee, S.K.; C.H. Nam, C.H. Realization of Laser Intensity over 1023W/cm2. Optica 2021, 8, 630. [Google Scholar] [CrossRef]
  2. Di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely High-Intensity Laser Interactions with Fundamental Quantum Systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef]
  3. Gonoskov, A.; Blackburn, T.G.; Marklund, M.; S.S. Bulanov, S.S. Charged Particle Motion and Radiation in Strong Electromagnetic Fields. Rev. Mod. Phys. 2022, 94, 045001. [Google Scholar] [CrossRef]
  4. Fedotov, A.; Ilderton, A.; Karbstein, F.; King, B.; Seipt, D.; Taya, T.; G. Torgrimsson, G. Advances in QED with Intense Background Fields. Phys. Rep. 2023, 1010, 1. [Google Scholar] [CrossRef]
  5. Brodin, G.; Marklund, M.; Stenflo, L. Proposal for Detection of QED Vacuum Nonlinearities in Maxwell’s Equations by the Use of Waveguides. Phys. Rev. Lett. 2001, 87, 171801. [Google Scholar] [CrossRef] [PubMed]
  6. Bialynicka-Birula, Z.; Bialynicki-Birula, I. Nonlinear Effects in Quantum Electrodynamics. Photon Propagation and Photon Splitting in an External Field. Phys. Rev. D 1970, 2, 2341. [Google Scholar] [CrossRef]
  7. Lundstrom, E.; Brodin, G.; Lundin, J.; Marklund, M.; Bingham, R.; Collier, J.; Mendonça, J.T.; Norreys, P. Using High-Power Lasers for Detection of Elastic Photon-Photon Scattering. Phys. Rev. Lett. 2006, 96, 083602. [Google Scholar] [CrossRef] [PubMed]
  8. Gies, H.; Karbstein, F.; Seegert, N. Quantum Reflection of Photons off Spatio-temporal Electromagnetic Field Inhomogeneities. New J. Phys. 2015, 17, 043060. [Google Scholar] [CrossRef]
  9. Mendonça, J.T.; Marklund, M.; Shukla, P.K.; Brodin, G. Photon Acceleration in Vacuum. Phys. Lett. A 2006, 359, 700. [Google Scholar] [CrossRef]
  10. Schwinger, J. On Gauge Invariance and Vacuum Polarization. Phys. Rev. 1951, 82, 664. [Google Scholar] [CrossRef]
  11. Heisenberg, W.; Euler, H. Consequences of Dirac’s Theory of Positrons. Z. Phys. 1936, 98, 714. [Google Scholar] [CrossRef]
  12. Mendonça, J.T. Superradiance in Quantum Vacuum. Quantum Rep. 2021, 3, 42. [Google Scholar] [CrossRef]
  13. Mendonça, J.T. Particle-Pair Creation by High-Harmonic Laser Fields. Phys. Scr. 2023, 98, 125606. [Google Scholar] [CrossRef]
  14. Penrose, R. Gravitational Collapse: The Role of General Relativity. 1969, 252–276. [Google Scholar]
  15. Zel’dovich, Y.B. Amplification of Cylindrical Electromagnetic Waves Reflected from a Rotating Body. Sov. Phys. JETP 1972, 35, 1085. [Google Scholar]
  16. Brito, R.; Cardoso, V.; Pani, P. Superradiance. Lecture Notes in Physics 2015, 906, 1–237. [Google Scholar]
  17. Zhang, H.; Zhang, B. Shielding of Penrose Superradiance in Optical Black Holes. Eur. Phys. J. C 2023, 83, 233. [Google Scholar] [CrossRef]
  18. Braidotti, M.C.; Prizia, R.; Maitland, C.; Marino, F.; Prain, A.; Starshynov, I.; Westerberg, N.; Wright, E.M.; Faccio, D. Measurement of Penrose Superradiance in a Photon Superfluid. Phys. Rev. Lett. 2022, 128, 013901. [Google Scholar] [CrossRef]
  19. Cromb, M.; Gibson, G.M.; Toninelli, E.; Padgett, M.J.; Wright, E.M.; Faccio, D. Amplification of Waves from a Rotating Body. Nat. Phys. 2020, 16, 1069. [Google Scholar] [CrossRef]
  20. Torres, T.; Patrick, S.; Coutant, A.; Richartz, M.; Tedford, E.W.; Weinfurtner, S. Rotational Superradiant Scattering in a Vortex Flow. Nat. Phys. 2017, 13, 833. [Google Scholar] [CrossRef]
  21. Mendonça, J.T.; Vieira, J.; Willim, C.; Fedele, R. Particle Acceleration by Twisted Laser Beams. Front. Phys. 2022, 10, 995379. [Google Scholar] [CrossRef]
  22. Vieira, J.; Mendonça, J.T.; Quéré, F. Optical Control of the Topology of Laser-Plasma Accelerators. Phys. Rev. Lett. 2018, 121, 054801. [Google Scholar] [CrossRef]
  23. Mendonça, J.T.; Willim, C.; Vieira, J. Twisted Waves near a Plasma Cutoff. Symmetry 2022, 14, 146. [Google Scholar] [CrossRef]
  24. Pariente, G.; Quéré, F. Spatio-Temporal Light Springs: Extended Encoding of Orbital Angular Momentum in Ultrashort Pulses. Opt. Lett. 2015, 40, 2037. [Google Scholar] [CrossRef] [PubMed]
  25. Mendonça, J.T. Emission of Twisted Photons from Quantum Vacuum. EuroPhys. Lett. 2017, 120, 61001. [Google Scholar] [CrossRef]
  26. Li, S.; Li, G.; Ain, Q.; Hur, M.S.; Ting, A.C.; Kulagin, V.V.; Kamperidis, C.; Hafz, N.A.M. A laser-plasma accelerator driven by two-color relativistic femtosecond laser pulses. Sci. Adv. 2019, 5, eaav7940. [Google Scholar] [CrossRef]
  27. Wang, J.W.; Zepf, M.; Rykovanov, S.G. Intense Attosecond Pulses Carrying Orbital Angular Momentum using Laser Plasma Interactions. Nat. Commun. 2019, 10, 5554. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

99

Views

31

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated