Drag Reduction by Dried Malted Rice Solutions in Pipe Flow

1. Introduction

Some high-molecular-weight polymers reduce the drag [1] in turbulent flows in pipes. Consequently, considerable research has been conducted on pipe flow to elucidate the mechanism of the drag reduction phenomenon [2], as well as on the application of polymeric drag-reducing additives to save energy in crude oil pipeline systems [3]. Although polymer additives reduce the drag, discarded artificial high-molecular-weight polymers do not decompose naturally. Thus, this drag reduction method is not environmentally friendly for application in open-pipeline systems. Therefore, biopolymers [4], particularly biodegradable ones, have been extensively investigated.

Hoyt [5] clarified that phytoplankton exudates in culture media and extracts from littoral algae contain significant quantities of extracellular materials with molecular weights of over 50,000 and conducted turbulent flow measurements using a special rheometer. Based on the results of phytoplankton cultures, algae are a source of extremely high-molecular-weight substances in the sea. It was shown that the red alga Porphyridium cruentum typically produced friction reductions as high as 60%, and Seaweed samples in the Chlorophyta, Phaeophyta, and Rhodophyta exhibited major changes in the corresponding turbulent friction coefficients; in some cases, the friction was less than 1/2 that of pure seawater. From the result, it was concluded that algal exudates can be a prominent source of high molecular weight compounds in the sea. Therefore, Polysaccharides, constitutive components of biopolymers, have been of research interest.

Wyatt et al. [6] showed that dilute solutions of many polysaccharides have lower frictional resistances in turbulent flows in pipes than in pure water. Furthermore, the drag reduction of xanthan gum solutions [7] and the flow characteristics of guar gum solutions [8] have been investigated, considering the application of polysaccharide solutions based on natural biodegradable polymers.

Peterson et al. [9] used yeast to produce polysaccharides as a promising new drag-reducing additive. They studied the relationships among the primary, secondary, and tertiary structures of polysaccharides that exhibit the rheological properties of drag reduction in turbulent flows. They found an exopolysaccharide from the yeast Cryptococcus laurentii. The exopolysaccharide possessed a high molecular weight but exhibited a lower drag reduction than expected. Earlier correlations by Hoyt showed that beta 1 3, beta 2 4, and alpha 1 3 linkages in polysaccharides favored drag reduction; these were expanded to include correlations with secondary structure. The results showed that drag reduction can be achieved using a substance that can produce polysaccharides. Petersen et al. [10] investigated yeast strains that can be cultured on methanol, ethanol, or glucose to produce exopolysaccharides that reduce friction in turbulent liquid flows.

These studies clarified that an aqueous solution of polysaccharide leachate and its products causes drag reduction in turbulent flow regions. However, there is limited experimental data over an extensive Reynolds number (Re) range, including laminar flows. In addition, the friction factors and velocity profiles in these regions have not been extensively investigated.

Therefore, in this study, we experimentally investigated the pipe friction characteristics under laminar and turbulent flows using dried malted rice as a drag-reducing additive. The dried malted rice produces polysaccharides in water, similar to yeast. The malt is a type of mold and has two main types: dried malt and raw malt. However, as raw malt is susceptible to bacteria and tends to deteriorate in quality to self-fermentation, it is difficult to preserve. Therefore, the dried malt was used to compensate for the shortcomings and is included in production of soy sauce, miso, and other fermented foods in Japan, besides other Asian countries.

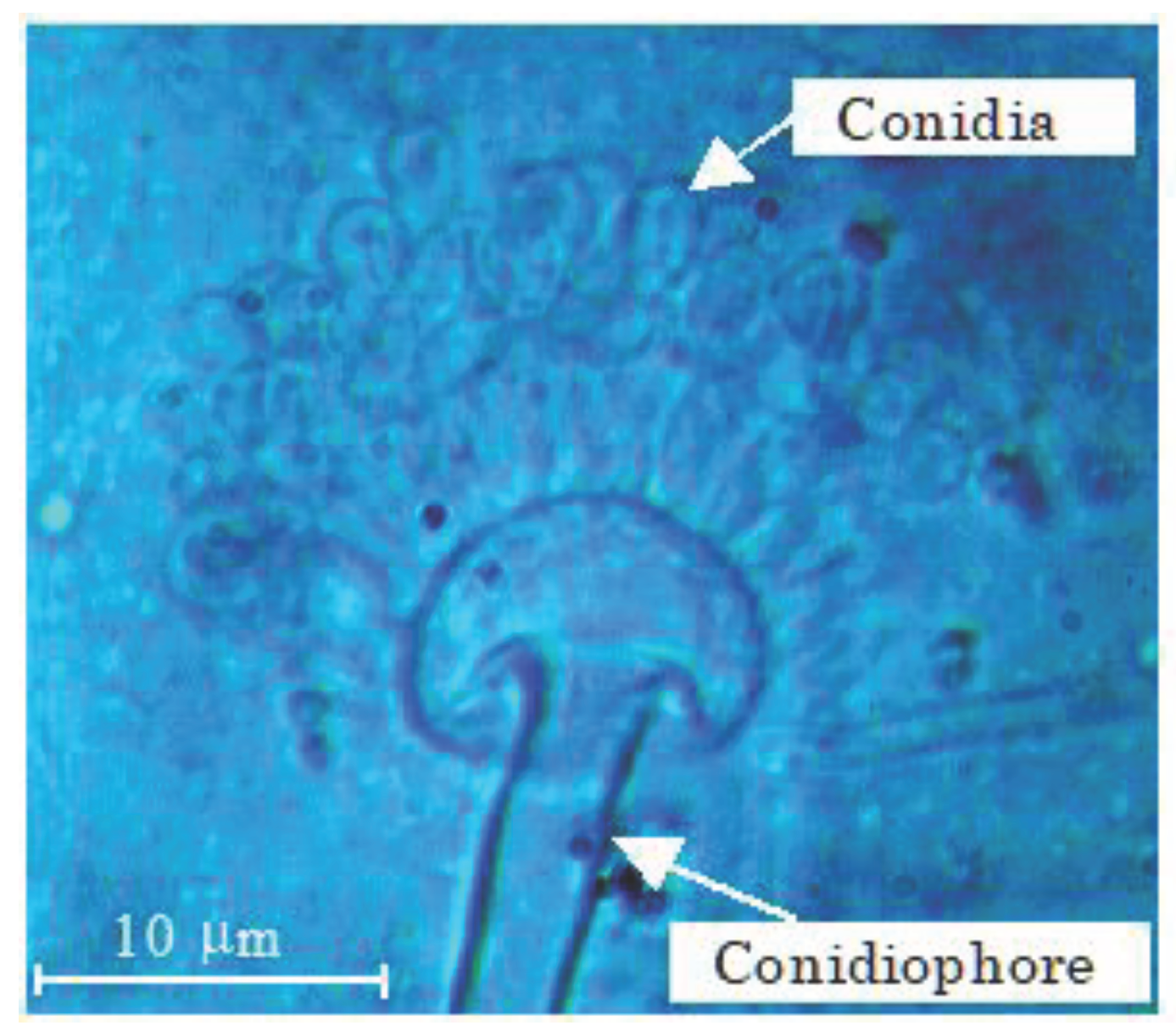
Figure 1 presents Aspergillus oryzae extracted from the dried malted rice used in this study. Aspergillus oryzae is a type of fungus that produces and releases the starch and proteins from the tips of its hyphae.

Turbulent drag reduction using dried malted rice has not been reported previously. The flow behavior of the biopolymer was described, and the velocity profile was predicted using a semi-theoretical equation in the turbulent flow region in which drag reduction occurs.

2. Experimental Methods

The drag reduction was measured using the pressure loss in the circular pipe: the corresponding experimental equipment included a piston, syringe, and test pipe. The syringe is hard heat-resistant glass, with the volume of 200 ml. The tip of the syringe is an aluminum locking tip that can be installed with one touch for the measurement pipe. The syringe is 2,000 mm in length with a smooth inner wall, and a square cutoff pipe with the outer diameter of approximately 4 mm and inner diameter of 2.01 mm. The inner diameter was measured using an enlarged photograph of the cross section. The fully developed flow was obtained in the measurement section. For the pressure measurement, holes with the diameter of 0.3mm were drilled at intervals of 100 mm. The pressure loss was determined using a variable pressure transducer with measurement accuracy of $\pm 0.25$%. The reported value was the best estimated of the result, and with a 95% confidence limit, the value was believed to lie within $\pm 0.89\%$ of the estimated value in the laminar flow range.

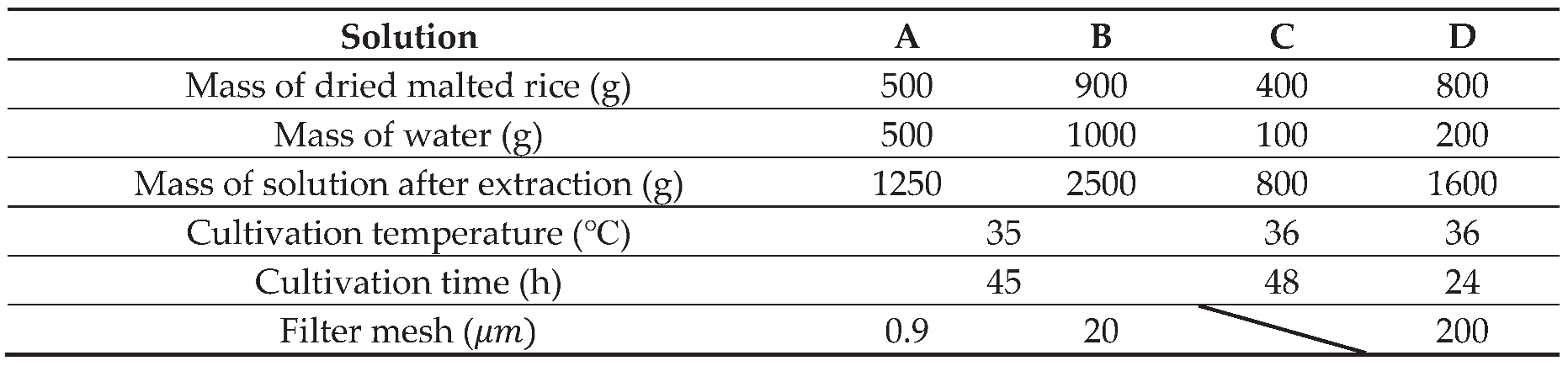
The aqueous test solutions were prepared using dried malted rice according to the following procedure.

i. Dried brown rice with Aspergillus was added to water and a constant temperature was maintained during the cultivation.

ii. The resulting hard cake in the liquid was removed, and the Aspergillus in the liquid was cultured for a period at 35 °C.

iii. Tap water was added to the culture and these liquid solutions were used as test solutions.

The test solutions are listed in Table 1. The disaccharide contents in the aqueous test solutions were measured using a sugar content meter with a Brix accuracy of ±0.2%. Four solutions (A–D in Table 1) were tested under different preparation conditions. For solution C, only the precipitated solids were removed from the cultivation liquid without using a filter. Fungi were cultured in water containing malt and photographed under a microscope. Fungal cells were collected from areas where conidia were formed. The size of the fungus, including conidia and conidiophore, was 5‒10 μm.

3. Results and Discussion

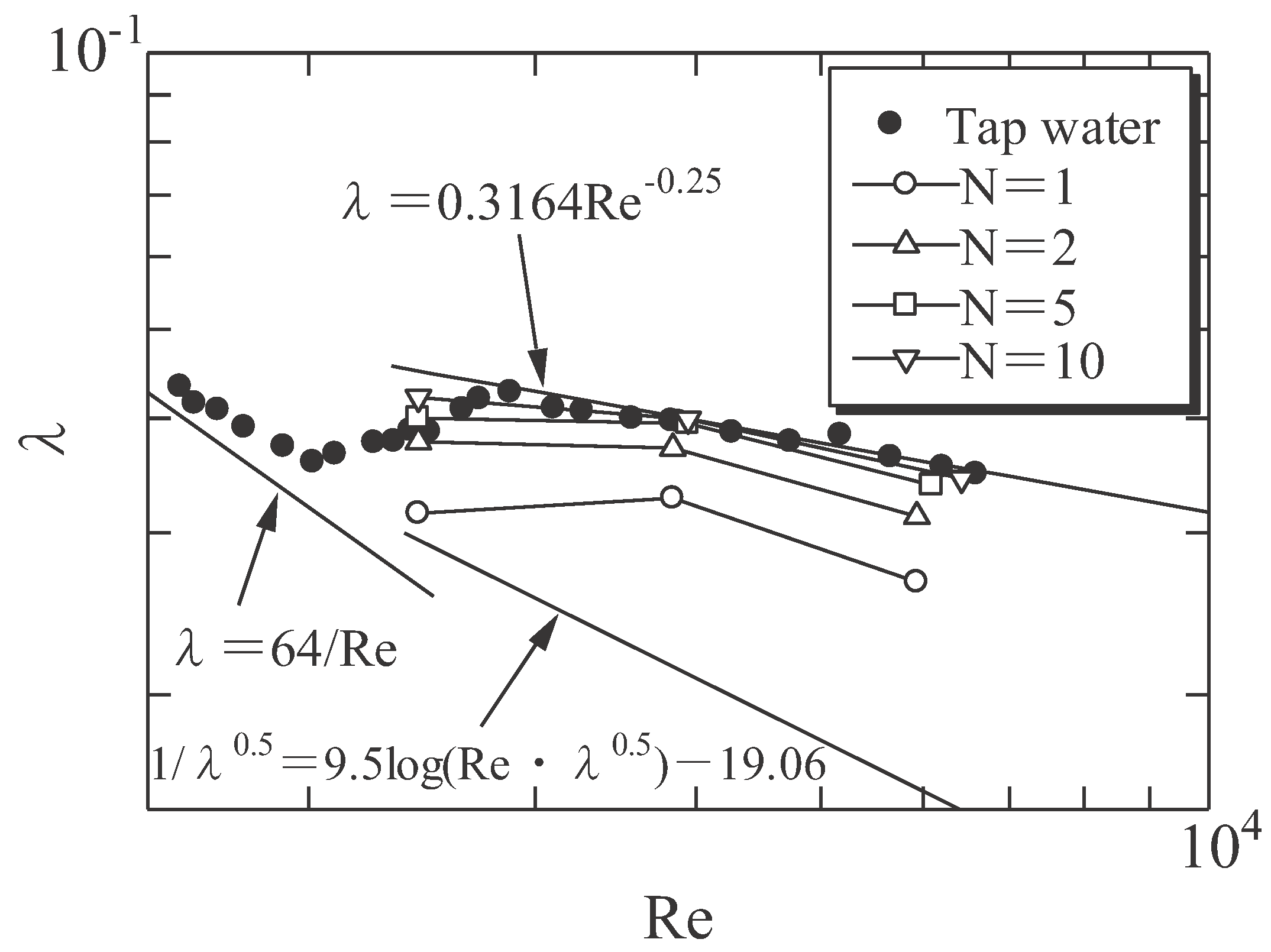
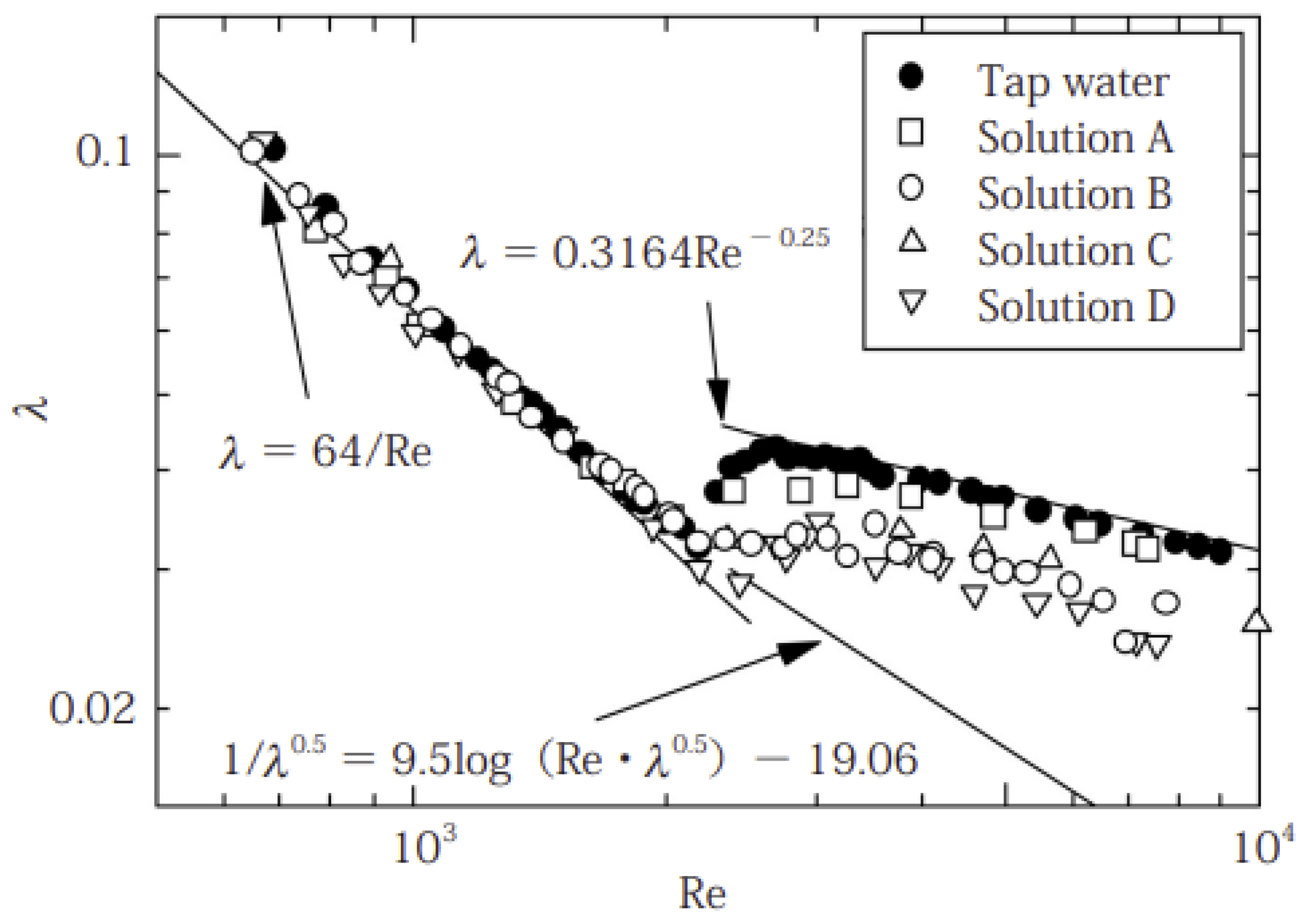
The flow curve confirmed that the dried malted rice test solutions were Newtonian fluids. The measured range is 10³ $\le \dot{\dot{\gamma }\le 5\times {10}^3}$ in the shear rate. The experimental results for the friction factor λ󠅍 based on the pressure loss data are shown in Figure 2. It is defined as $\lambda =\mathsf{\Delta }p/\frac{l}{d}\frac{\rho U^2}{2}$. Where, $\mathsf{\Delta }p,d,\rho andU$ are the pressure loss, the pipe diameter, the density, and mean velocity, respectively. Reynolds number is defined as $Re=Ud/\nu$ using the kinematic viscosity ν. The friction factor of tap water matches well with that of Newtonian fluids in the laminar and turbulent flow ranges. Drag reduction occurred for all the test solutions. 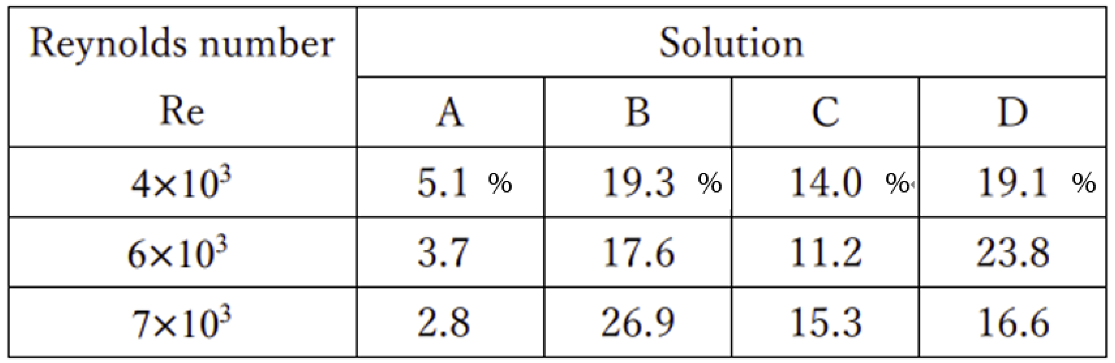Table 2 lists the drag reductions (%). The maximum drag reduction was approximately 27%. In the friction factor vs. Re plots in Figure 2, the friction factors of these biopolymer solutions are parallel to and below those of water, which indicates type-B drag reduction [11,12]. This phenomenon occurs in partially hydrolyzed polyacrylamide with linear random-coil-structured macromolecules in solution. Because the reduced friction factors of the test solutions were aligned parallel to those of Newtonian fluids, the drag reduction of the malt-rice solutions was type B.

For solution D, the transition Re increased compared with that of tap water. Drag reduction in solution B was greater than that in solution A, although the culture temperature and time remained the same (Table 1). The initial masses of dry malt were 500 and 500g for solutions A. The most divergent solution preparation conditions involved the removal of the solid components after culturing using a filter mesh. The sizes of these meshes were 0.9 and 20$\mu$m for solutions A and B, respectively. The Aspergillus (5–10$\mu$m) was removed with an extremely fine 0.9-μm filter. Solutions C and D contained reduced amounts of dried malted rice and water compared to solutions A and B, respectively. The aqueous test solution with the largest drag reduction was Solution D, which required a shorter culture time than the other solutions. However, the current experimental data cannot be used to determine the culture conditions for a specific drag reduction %.

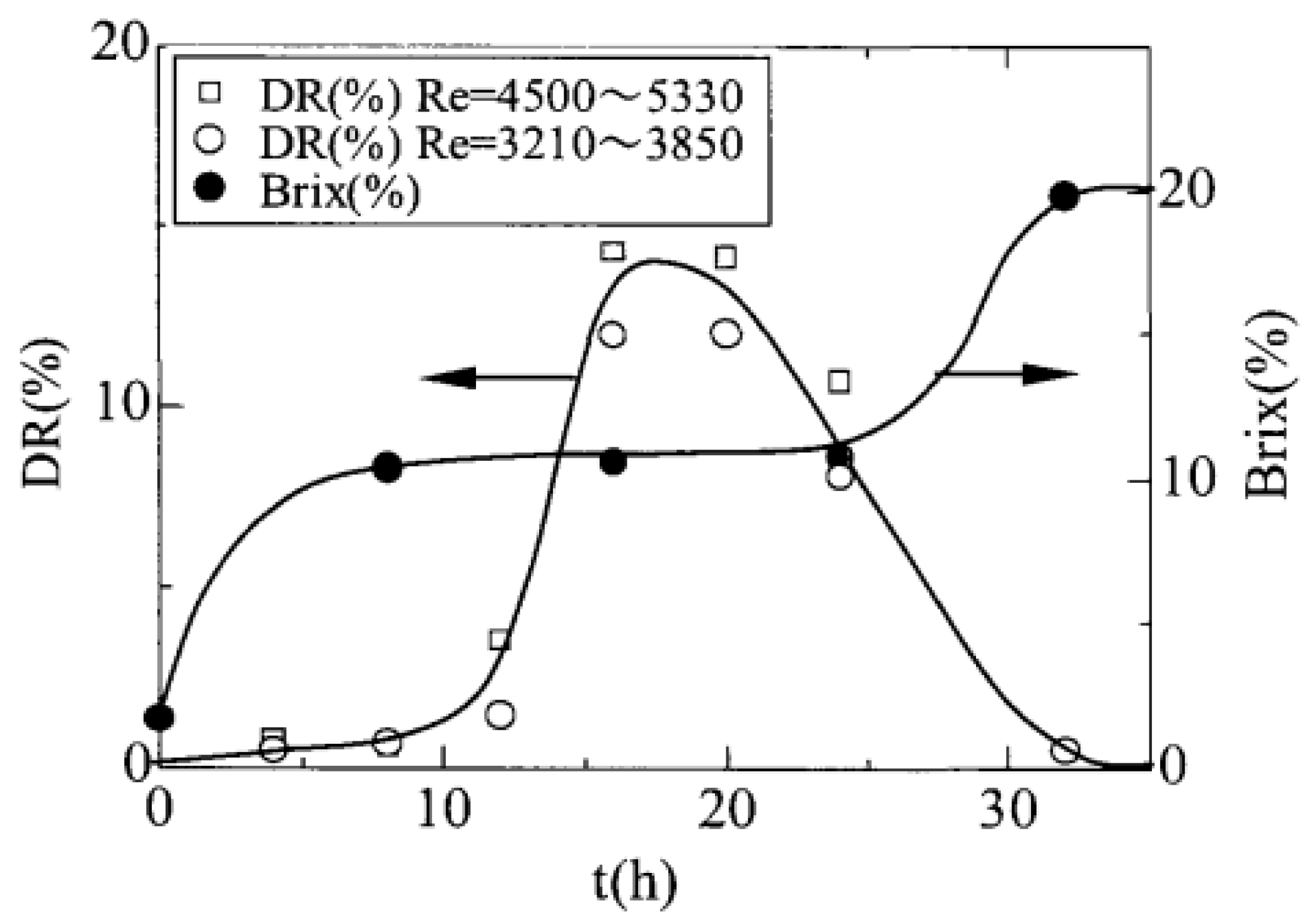
We determined the relationship between the sugar content (degrees Brix) resulting from the culture process and the culture time. Figure 3 shows the variations in drag reduction and sugar content with culture time for solutions with other preparation conditions, similar to those of solution D. As shown in Figure 3, the number of disaccharides produced initially increased with cultivation time, plateaued with a further increase in cultivation time, and then increased again with the cultivation time.

The drag reduction % was maximized in the region where the sugar content remained constant over time during cultivation. Thus, it can be inferred that polysaccharides were produced by the cultivation of Aspergillus oryzae. However, the quantitative relationship between disaccharide content and drag reduction is unknown. The malt-to-water ratios were identical for solutions C and D. However, the drag reduction in solution D is significantly higher than that in solution C. It can be considered that, in solution C, the cultivation of the Aspergillus was in a state of saturation owing to the increased cultivation time.

The friction factor λ󠅍, based on the pipe pressure difference (Figure 2), can be used to conveniently calculate the pressure of pipeline systems. However, it is not sufficient to analyze the flow behavior of a circular pipe. The friction factor f based on the shear stress τ_w acting on the pipe wall was used to obtain the relationship between the friction factor and velocity profile. This relationship is necessary for explaining the onset and mechanism of the drag reduction phenomenon.

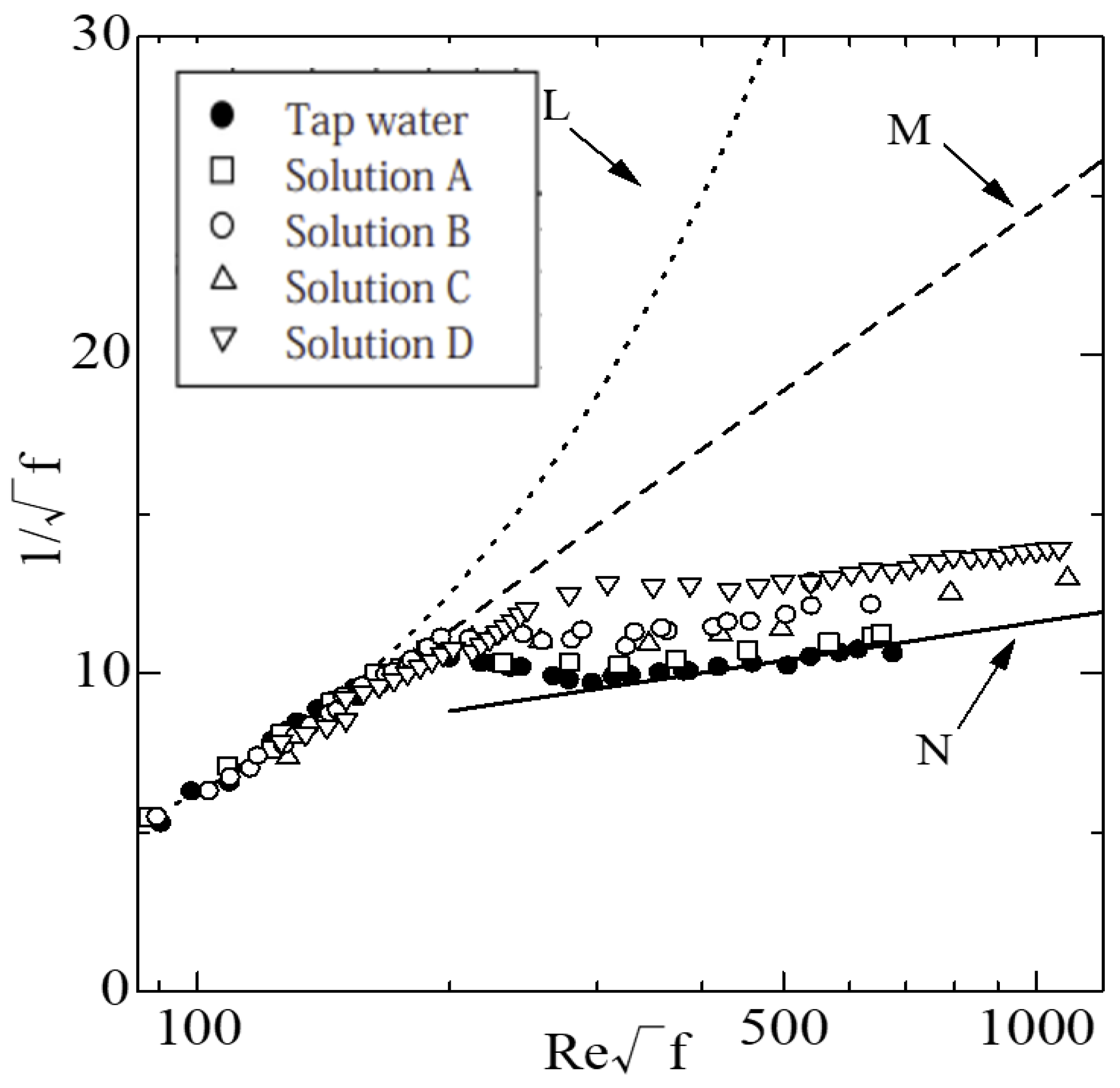
Figure 4 shows the friction factor based on the wall shear stress. As mentioned above, the friction factor f is defined as $f={\tau }_w/\frac{\rho U^2}{2}$. In Figure 4, L (dotted line) and N (solid line) represent the results for the laminar and turbulent flows of Newtonian fluids, respectively, and M (dashed line) is the MDRA obtained by Virk [13,14]. The experimental data points diverge from the MDRA at Re√f ≅200~250 and align above and nearly parallel to N. According to the results, Re√f ≅ 200 marks the onset of the drag reduction phenomenon.

In the turbulent flow range, the experimental data points were aligned parallel to those of Newtonian fluids, which indicated type-B drag reduction. To understand flow behavior, it is necessary to analyze the velocity profile. Because the velocity profile in the pipe was not measured in this study, we predicted it using analytical results considering type-B drag reduction.

Virk [12] defined the flow enhancement during type-B drag reduction as 　

$$S\text{＝}\frac{1}{\sqrt{f}}-\frac{1}{\sqrt{f_n}},$$

(1)

where f and f_n are the friction factors of the aqueous test solutions and the Newtonian fluid, respectively. The second term on the right side of Eq. (1) represents the Prandtl–Karman equation:

$$\frac{\mathrm{１}}{\sqrt{f_n}}=4.0{\log }_{10}Re\sqrt{f_n}-0.4.$$

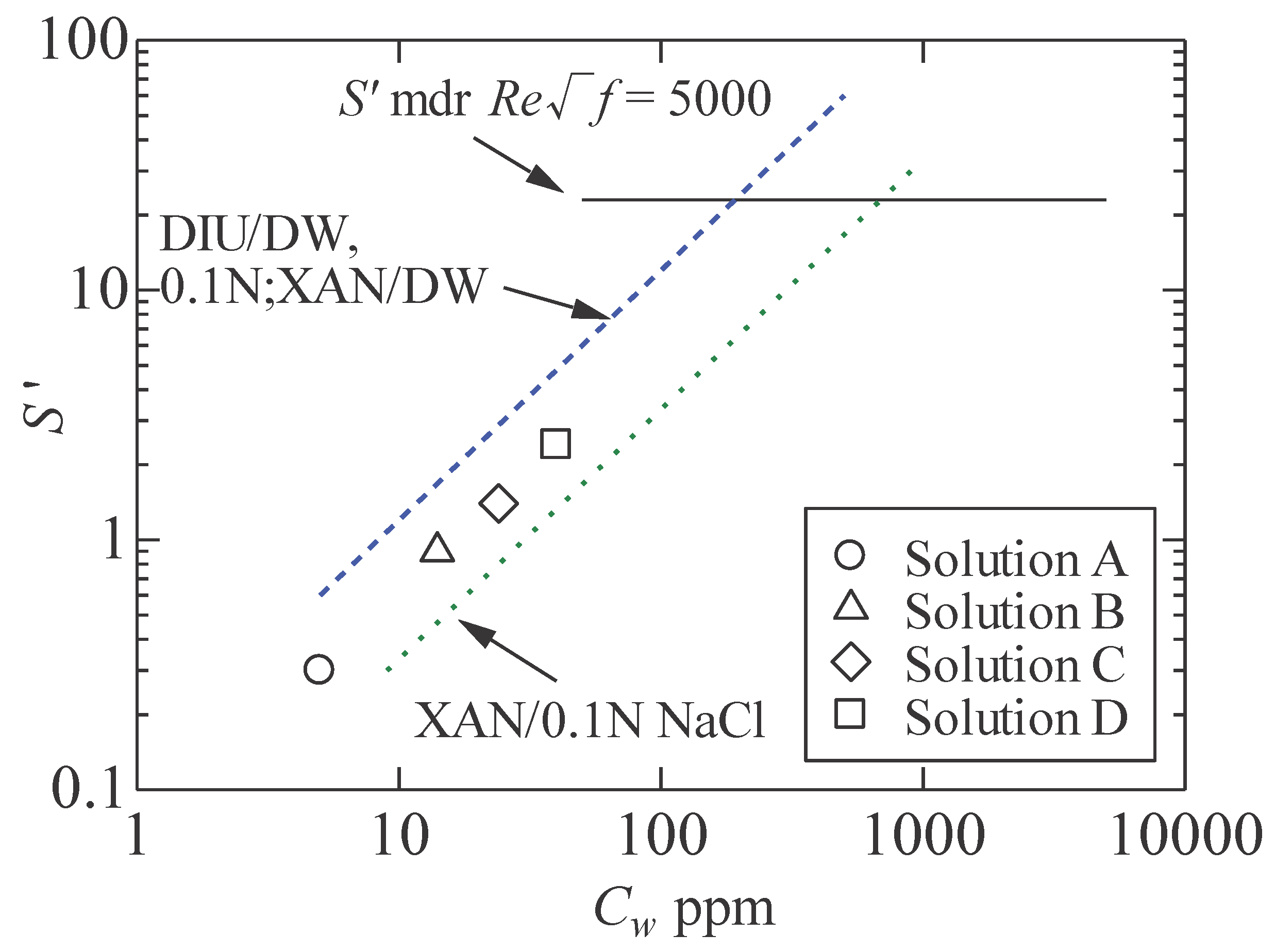
Because the concentrations of the aqueous test solutions could not be measured in this study, we estimated the concentration of the test solution by comparing it with that of the xanthan gum solution. The results of the test solutions were extrapolated from Virk’s data using S' obtained from Eq. (1), as shown in Figure 5. Solutions D and C_w=50-ppm xanthan-gum solutions exhibited equivalent drag reduction characteristics.

The mean velocity in the pipe flow must be determined to determine the drag-reduction mechanism. Watanabe and Ogata [15] derived an equation to predict the mean velocity by S'.

The mean velocity profile for a fully developed turbulent flow through a smooth pipe is

$$u^{+}=\frac{1}{\kappa }\ln y^{+}+C,$$

(2)

where $u^{+}=\frac{ū}{u_{*}}$ and$y^{+}=\frac{u_{*}}{\nu }y$. ū is the mean velocity over time and $u_{*}$ is the friction velocity ($u_{*}=\sqrt{{\tau }_w/\rho }$), where τ_ｗ and ρ are the shear stress and density, respectively. The parameter y is the distance measured from the wall, y = (ɑ – r), where ɑ is inner pipe radius.

Using an example from the experimental results for the friction factor of aqueous dried malted-rice solutions in regions of turbulent flow, we assumed that the velocity profile is expressed by Eq. (2).

The friction factor is calculated by

$$\frac{\mathrm{１}}{\sqrt{f}}=\frac{\mathrm{１}}{\kappa \sqrt{2}}\ln \mathrm{R}\mathrm{e}\sqrt{f}-\frac{\mathrm{１}}{\kappa \sqrt{2}}\ln 2\sqrt{2}+\frac{\mathrm{１}}{\sqrt{2}}\left(C-\frac{3}{2\kappa }\right).$$

(3)

For Newtonian fluids, we set κ and C equal to 0.4 and 5.5, respectively. Thus, Eq. (3) becomes

$$\frac{\mathrm{１}}{\sqrt{f_n}}=4.0{\log }_{10}Re\sqrt{f_n}-0.6.$$

(4)

The constant 0.6 in Eq. (4) must be modified so that the flow characteristics agree with the experimental data. Hence, we modified Eq. (3) to

$$\frac{\mathrm{１}}{\sqrt{f}}=\frac{\mathrm{１}}{\kappa \sqrt{2}}\ln Re\sqrt{f}-\mathsf{\zeta }\left[\frac{\mathrm{１}}{\kappa \sqrt{2}}\ln 2\sqrt{2}-\frac{\mathrm{１}}{\sqrt{2}}\left(C-\frac{3}{2\kappa }\right)\right].$$

(5)

If ζ = 2/3, κ = 0.4, and C = 5.5 are substituted into Eq. (5), we obtain the Prandtl–Karman formula:

Because the friction factor of the suspensions decreased parallel to those obtained using the Prandtl–Karman formula, as shown in Figure 3, it is reasonable to fix κ as a constant of 0.4. The substitution of Eq. (5) into Eq. (1) and modifying the constant value to fit that of Newtonian fluids when S' = 0 yields

$$C=5.5+\frac{3}{\sqrt{2}}{S}^{\mathit{\text{'}}}.$$

(6)

Equation (6) enables prediction of the friction factors of Newtonian fluids. Finally, we estimated the mean velocity profile of the pipe flows of aqueous dried malted-rice solutions using C from Eq. (6), if the value of S' is obtained from experimental data using the friction factor.

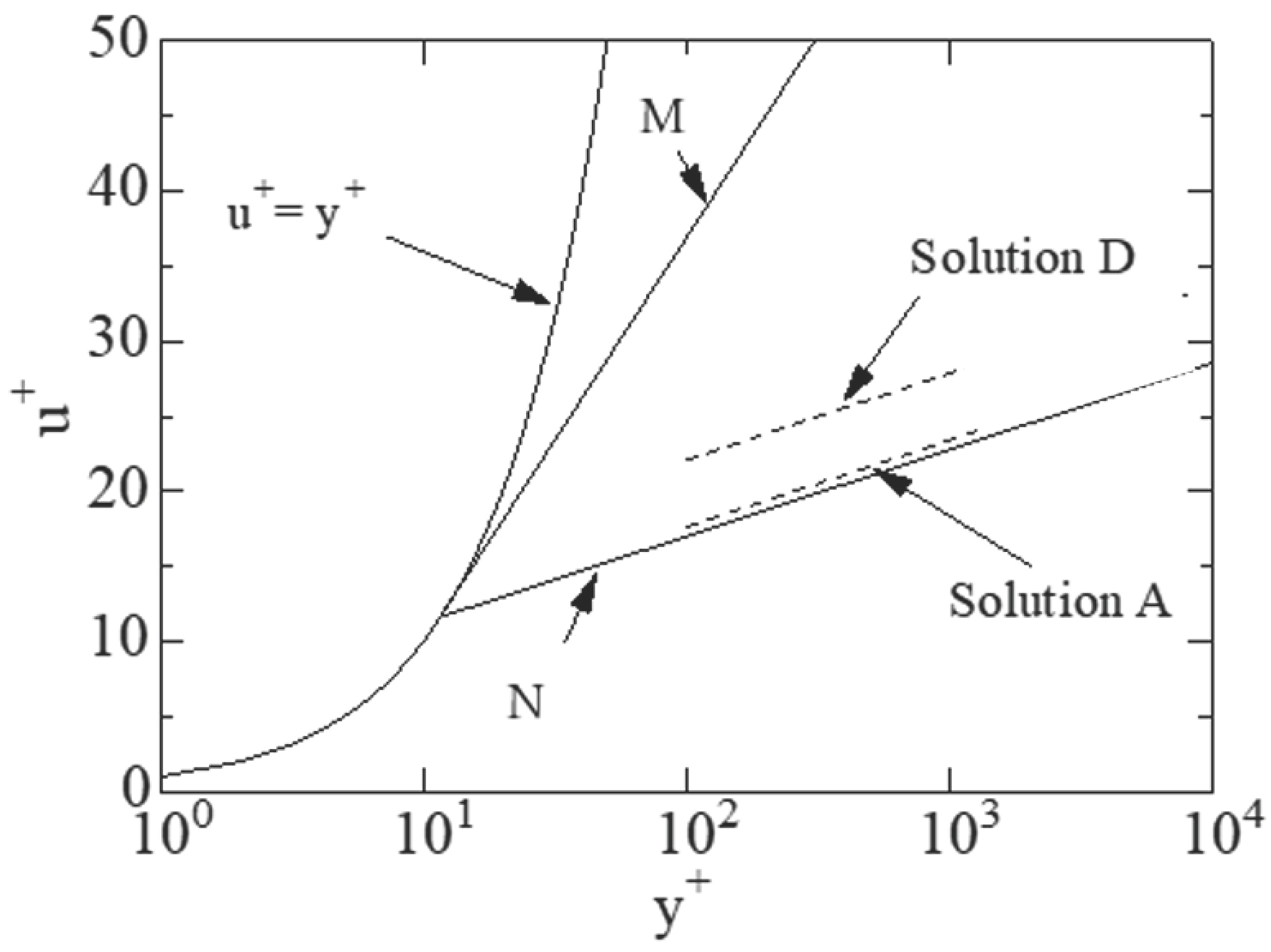
For example, using the experimental values of S' = 0.3 and S' = 2.4, for solutions A and D from Figure 3, the velocity profile was estimated as

$$\begin{gathered} u^{+}=2.5\ln y^{+}+6.1, \mathrm{for} \mathrm{solution} \mathrm{A}, \mathrm{and} \\ {u}^{+}=2.5\ln y^{+}+10.6, \mathrm{for} \mathrm{solution} \mathrm{D} \end{gathered}$$

Figure 6 shows the predicted velocity profiles. The viscous layer thickens in the region where the drag reduction occurs. Because the predicted velocity distribution shifts upward with increasing drag reduction rate, the thickness of the viscous layer increases.

Japper-Jaafar et al. [15] experimentally investigated the drag reduction in a fully developed turbulent pipe flow of an aqueous solution of a rigid “rod-like” polymer, scleroglucan, at concentrations of 0.005% and 0.01% (similar to type-B drag reduction). Mean velocity profiles and turbulent fluctuation levels were measured using a laser Doppler anemometer. The experimental friction factor curves were parallel to those of Newtonian fluids, and the experimental friction factors were lower than those of Newtonian fluids. This finding is qualitatively consistent with the results of this study.

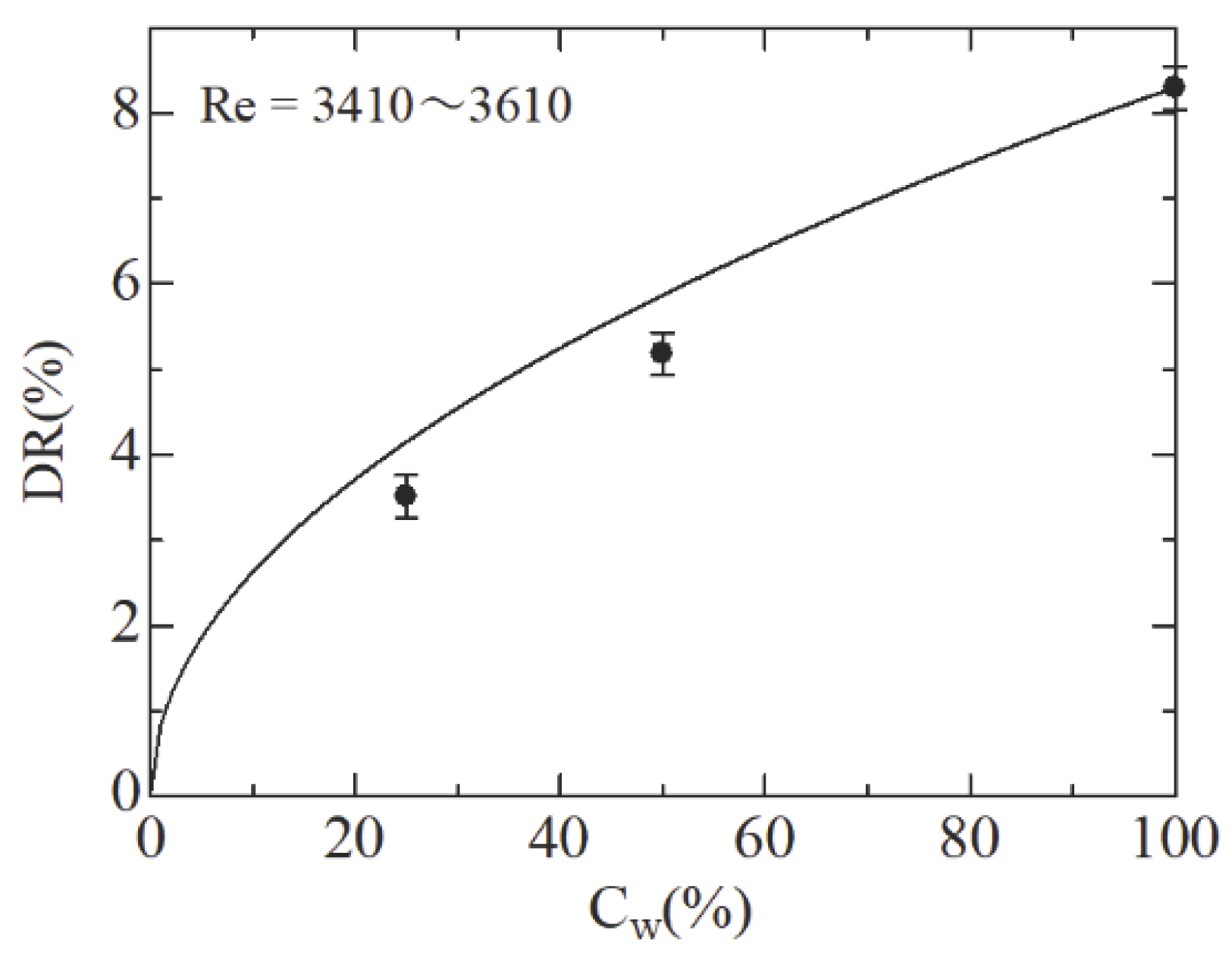
Meanwhile, prediction of the drag reduction ratio of diluted solutions will be convenient for the actual application of this biopolymer solution. Figure 7 depicts the effect of the drag reduction of the diluted solution. The test solution was cultured under the same conditions as Solution D in Table 1. In the experiment, the stock solution was diluted twice and four times with water and the drag reduction ratio was measured at Re = 3410~3610. As a result, the maximum drag reduction ratio was 8.3% at Re = 6x10³. The solid line in the figure is given by $DR=0.083\sqrt{C_w}$, here $C_w$ is a concentration regarding 100% as 1. The results are in agreement with the experimental data, with the errors of 11% and 15% at $C_w$=50% and 25%, respectively. Therefore, if the drag reduction ratio of the stock solution is known, the drag reduction ratio of the diluted solution can be predicted from $DR=k\sqrt{C_w}$ within a 15% error range.

The physical properties of polymer solutions degrade depending on external changes. Mechanical shear degradation is particularly problematic, and can hamper the practical application of polymer solutions for turbulent drag reduction phenomena. Mechanical degradation refers to the chemical process in which the activation energy of polymer chain scission is exceeded by the mechanical action on the polymer chain, and bond rupture occurs. Many corresponding experiments have been performed under turbulent flow conditions using various experimental apparatus. We examined the mechanical degradation of test solutions experimentally. 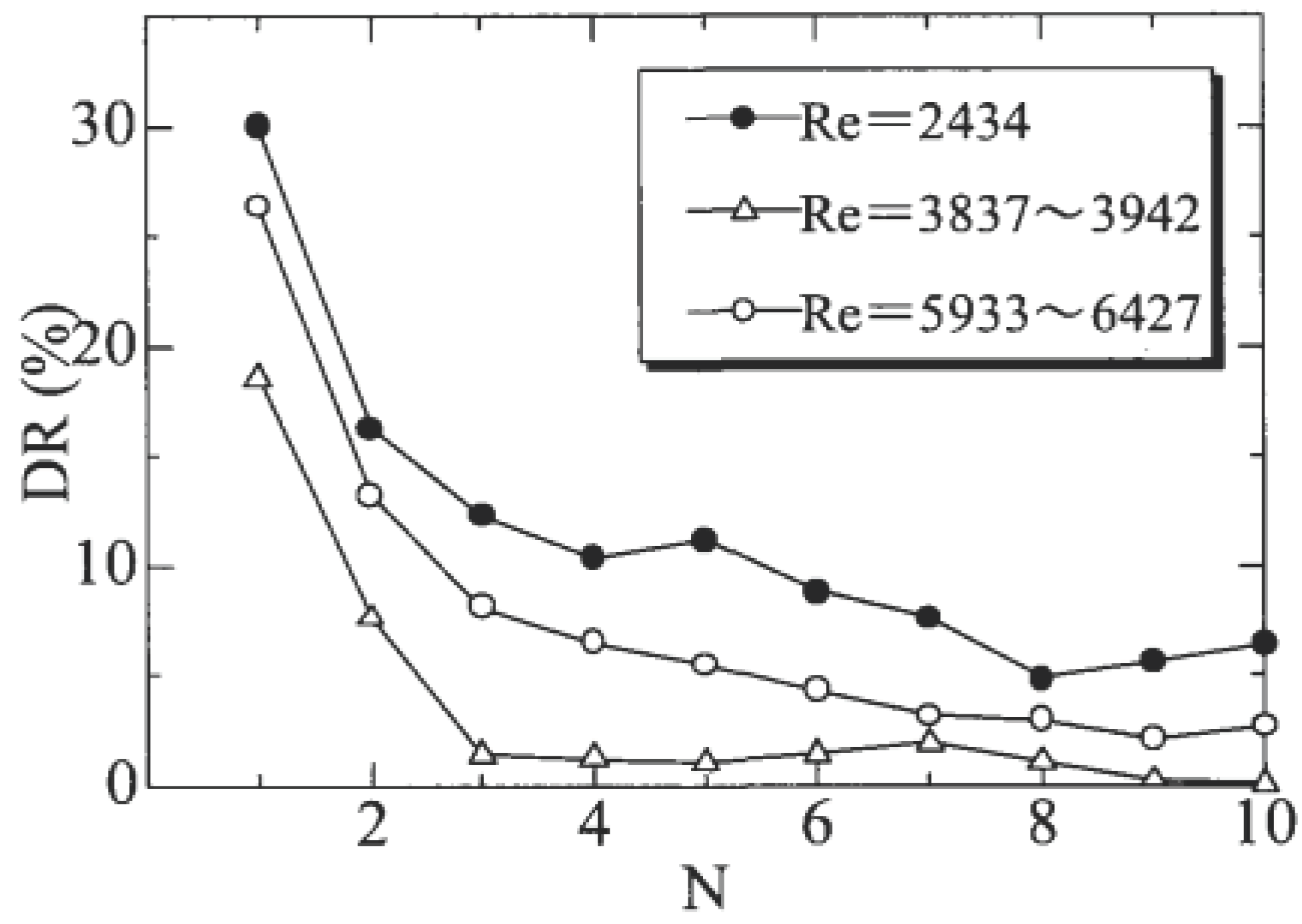In this study, a discharge pipeline system [14] was employed to measure the pressure loss relative to the mechanical degradation. The system comprises a syringe-type pump and a syringe directed into a test pipe. The test solution is fed into the syringe and the pressure loss is measured repeatedly. The results are presented in Figure 8. From Figure 7, the drag reduction ratio clearly decreases after two to three repetitions and then asymptotically approached a constant value. However, the drag reduction phenomenon disappears in the high-Re range. This is replotted in Figure 9 for clarity incorporating the experimental data of the friction factor.

Observation of microscopic photographs of the solution in which the drag reduction phenomenon has disappeared, reveal that the size of the conidial spore itself had decreased, and had been cut by the mechanical shearing. From these observation results, it is not possible to clearly determine changes in the molecular bonding state of polysaccharides. It will be necessary to clarify the mechanical degradation of biopolymer, including the effects on the growth of conidia and its modification according to turbulent flow in the future.

4. Conclusions

In this study, we conducted experiments investigating the effect of turbulence on drag reduction in a circular pipe flow using dried malted rice, a product in fermented foods in Japan, among other Asian countries. As a result, the liquid extracted from the rice was confirmed as an effective drag-reducing agent. $Re\sqrt{f}\cong 200~250$ was achieved for the onset of the drag reduction phenomena, where Re and $f$ are the Reynolds number and friction factor, respectively.

The drag reduction effectiveness increased with the solution concentration, and the change in the friction factor for Re coincided with that of the Type B drag reduction phenomenon. The maximum drag reduction was approximately 27%, corresponding to the drag reduction resulting from the 5–50 ppm xanthan-gum solutions reported by Virk et al.

Not only the friction factor, but also the turbulent velocity profile in the pipe flow should be determined to consider the drag reduction mechanism. In this study, the turbulent velocity profile was estimated using a semi theoretical equation, including the difference between the experimental results of the friction factor for the tested solutions and those of Newtonian fluids. The result was quantitatively displayed along with that of Newtonian fluids. In conclusion, the mechanism of the drag reduction phenomena is predominantly the thickening of the viscous layer. Further investigation is necessary on the velocity profile near the pipe wall.