Secure Key Exchange in Tropical Cryptography: Leveraging Efficiency with Advanced Block Matrix Protocols

Preprint

Article

Secure Key Exchange in Tropical Cryptography: Leveraging Efficiency with Advanced Block Matrix Protocols

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 April 2024

Posted:

02 April 2024

You are already at the latest version

Alerts

Abstract

In the quest for robust and efficient digital communication, this paper introduces cutting-edge key exchange protocols leveraging tropical semirings’ computational prowess and block matrices’ structural resilience. Moving away from the conventional use of finite fields, these protocols deliver markedly faster processing speeds and heightened security. We present two implementations of our concept, each utilizing a different platform for the set of commuting matrices: one employing tropical polynomials of matrices and the other employing Linde-de la Puente matrices. The inherent simplicity of tropical semirings leads to a decrease in operational complexity, and using block matrices enhances our protocols’ security profile. The security of these protocols relies on the Matrix Decomposition Problem. We also provide a comparative analysis of our protocols against existing matrix block-based protocols in finite fields. This research marks a significant shift in cryptographic protocol design, specifically tailored for demanding engineering applications, and sets a new standard in secure and efficient digital communication.

Keywords:

Subject: Computer Science and Mathematics - Security Systems

1. Introduction and Motivation

In an era where digital communication underpins the fabric of global connectivity, the role of cryptography is more critical than ever. Ensuring the security and integrity of data in transit has led to the evolution of sophisticated cryptographic protocols. Traditional approaches often rely on the well-established mathematical frameworks of finite fields, but with the advent of advanced computational capabilities and emerging cyber threats, the need for innovative and more efficient cryptographic methods is evident. This paper contributes to this ongoing evolution by introducing a groundbreaking approach to key exchange protocols utilizing the untapped potential of tropical semirings and block matrices.

This research transcends the conventional boundaries of cryptographic solutions, delving into the realms of tropical mathematics to harness the simplicity and computational efficiency offered by tropical semirings. Coupled with this, the use of block matrices introduces a structural robustness that enhances security measures. This combination not only serves as a novel approach but also sets a new benchmark in operational efficiency, steering away from the computational complexities inherent in finite fields

F_{q}

Historically, matrices have been instrumental in various cryptographic mechanisms. The lineage of matrix-based cryptosystems, stretching back to foundational works such as [1], has been marked by continual advancements. Diverse matrix forms were incorporated, ranging from singular [2,3] and non-singular matrices [4] to matrices over bit strings [5]; Tribonacci matrices [6]; Hadamar matrices [7]; non-negative [8] and lattice matrices [9]. Tropical matrices are also of interest ([10,11,12,13,14,15]). Yet, despite these developments, vulnerabilities have persisted, as evidenced by different documented attacks (see, for example, [16,17,18,19]).

In recent years, a variety of block matrix cryptosystems have emerged: [20] introduced a method employing the Hilbert matrix for authentication and confidentiality, emphasizing shared key encryption; [21] constructed an invertible block matrix using Fibonacci sequences and devised an asymmetric cryptosystem utilizing the skewed affine cipher over elliptic curves; [22] proposed a novel block-cipher mechanism for ensuring information security in cloud systems, prioritizing high defense, low complexity, and random operations. Together, these studies showcase the potential of block matrix cryptosystems in enhancing data security.

Our protocols are designed to counteract the vulnerabilities of the schemes based on tropical matrices by employing commutative properties of block matrices, resulting in a more streamlined and secure key exchange process.

The contributions of this study are multifaceted and significant:

1.: We introduce two key exchange protocols that exploit the commutative properties of tropical block matrices, thereby simplifying the key exchange process while enhancing security.
2.: A thorough analysis is presented, demonstrating the reduced operational overhead compared to existing block matrix schemes. This includes comparative evaluations showing lower computational complexity while maintaining equivalent key sizes.
3.: We anchor our security claims in the inherent difficulty of matrix decomposition within tropical semirings, a challenge that poses significant barriers to conventional attack methodologies.
4.: The paper also includes illustrative examples and comparative analyses to underscore the tangible efficiency gains our protocols offer.

This paper is structured to guide the reader through the critical aspects of our research. Section 2 sets the mathematical foundation by introducing block matrices, tropical semirings, and commutative matrices. Section 3 provides a detailed exposition of our proposed key exchange protocols. Section 4 delves into the security analysis, benchmarking our approach against current cryptographic standards. Finally, we conclude in Section 5 with reflections on the broader implications of our work and its potential to inspire future research in cryptography.

2. Preliminaries

Definition 1

(Block Matrix). A block matrix is a matrix partitioned into submatrices, referred to as blocks. For instance, a block matrix M comprising four blocks can be denoted as:

M = [\begin{matrix} A & B \\ C & D \end{matrix}],

where

A, B, C,

and D are such blocks. These blocks may vary in size, and the total number of blocks and their configuration is dependent on how the original matrix is partitioned.

Definition 2

(Semiring). A semiring is an algebraic structure represented by

(S, \oplus, \otimes, 0, 1)

, where S is a set, and the operations ⊕ (addition) and ⊗ (multiplication) satisfy the following conditions:

$(S, \oplus, 0)$ forms a commutative monoid with identity element 0.
$(S, \otimes, 1)$ forms a monoid with identity element 1.
⊗ distributes over ⊕.
For all $a \in S$ , $0 \otimes a = 0 = a \otimes 0$ .

The semiring is commutative if

a \otimes b = b \otimes a

for all

a, b \in S

Definition 3

(Matrix Operations over Semirings). Given matrices A and B over a semiring

(S, \oplus, \otimes)

, the operations are defined as follows:

Addition $(A \oplus B)$ is the element-wise operation $c_{i j} = a_{i j} \oplus b_{i j}$ .
Multiplication $(A \otimes B)$ is performed using the standard matrix multiplication rules applied with ⊗.
Scalar multiplication $(x \otimes A)$ scales each matrix element $a_{i j}$ by x to obtain $b_{i j} = x \otimes a_{i j}$ .

These operations follow the distributive, associative, and commutative laws pertaining to the semiring.

2.1. Exponentiation of Block Matrices

We examine block matrices formed as:

B l (A, B, C) = (\begin{matrix} A & B \\ O & C \end{matrix}),

where

A, B,

and C are square matrices of the same order over a considered semiring, and O is the corresponding zero matrix.

Theorem 1.

[23] Let

B l (A, B, C) = (\begin{matrix} A & B \\ O & C \end{matrix})

be a block matrix. Then for any natural number k, it holds that

B l {(A, B, C)}^{k} = (\begin{matrix} A^{k} & B_{k} \\ O & C^{k} \end{matrix}),

with

\begin{matrix} B_{k} & = \sum_{n = 0}^{k - 1} A^{k - 1 - n} B C^{n}, \end{matrix}

(1)

and furthermore,

{(B l {(A, B, C)}^{k})}^{l} = {(B l {(A, B, C)}^{l})}^{k} = (\begin{matrix} A^{k l} & B_{k, l} \\ O & C^{k l} \end{matrix}),

with

B_{k, l} = B_{l, k}

for all

k, l \in N

Theorem 2.

[23] Let

A, B, C, D,

and E be square matrices of the same order such that

A D = D A

C E = E C

, and consider the block matrices

B l (A, B, C)

and

B l (D, B, E)

. Then

B_{k, l} = B_{l, k}

for all

k, l \in N

2.2. Tropical Semirings

A tropical semiring, such as

R_{\max, +}

( or

R_{\min, +}

) is a set equipped with two operations that mimic conventional addition and multiplication, but instead are defined using the maximum and addition (or maximum and addition), respectively. This semiring and its operations enable the definition of tropical matrix operations and polynomials.

Definition 4

(Tropical Polynomial). A tropical polynomial of a variable x with coefficients in a tropical semiring is an expression of the form

P (x) = ⨁_{i = 0}^{n} a_{i} \otimes x^{\otimes i},

where n indicates the degree of the polynomial.

Proposition 1.

For tropical polynomials

p (x)

and

q (x)

, and a matrix M over a tropical semiring, it holds that

p (M) \otimes q (M) = q (M) \otimes p (M) .

Proof.

The commutativity follows from the properties of matrix multiplication in tropical semirings. □

2.3. Commutative Matrices in Tropical Semirings

Commutative matrices in tropical semirings have the property that their product, irrespective of the order, yields the same result. This property is crucial for the development of cryptographic protocols that rely on the difficulty of matrix decomposition in tropical semirings.

Definition 5

(Linde-de la Puente Matrix). A matrix L in the semiring

R_{\max, +}

is called a Linde-de la Puente matrix if it satisfies certain criteria based on specified non-negative real number c for its diagonal entries and its off-diagonal entries are from the range

[2 r, r]

, where r is a non-positive real number. Such a matrix is denoted as:

L_{c}^{r}

Theorem 3.

[15] Given a tropical semiring

R_{\max, +}

. All Linde-de la Puente matrices A and B commute under the multiplication in this semiring.

Corollary 1.

Given a tropical semiring

R_{\max, +}

. For Linde-de la Puente matrices A and B, and natural numbers m and n, the matrices

A^{m}

and

B^{n}

commute.

Proof.

This result is a direct consequence of the commutative property of Linde-de la Puente matrices. □

3. Block Matrix Key Exchange Protocols

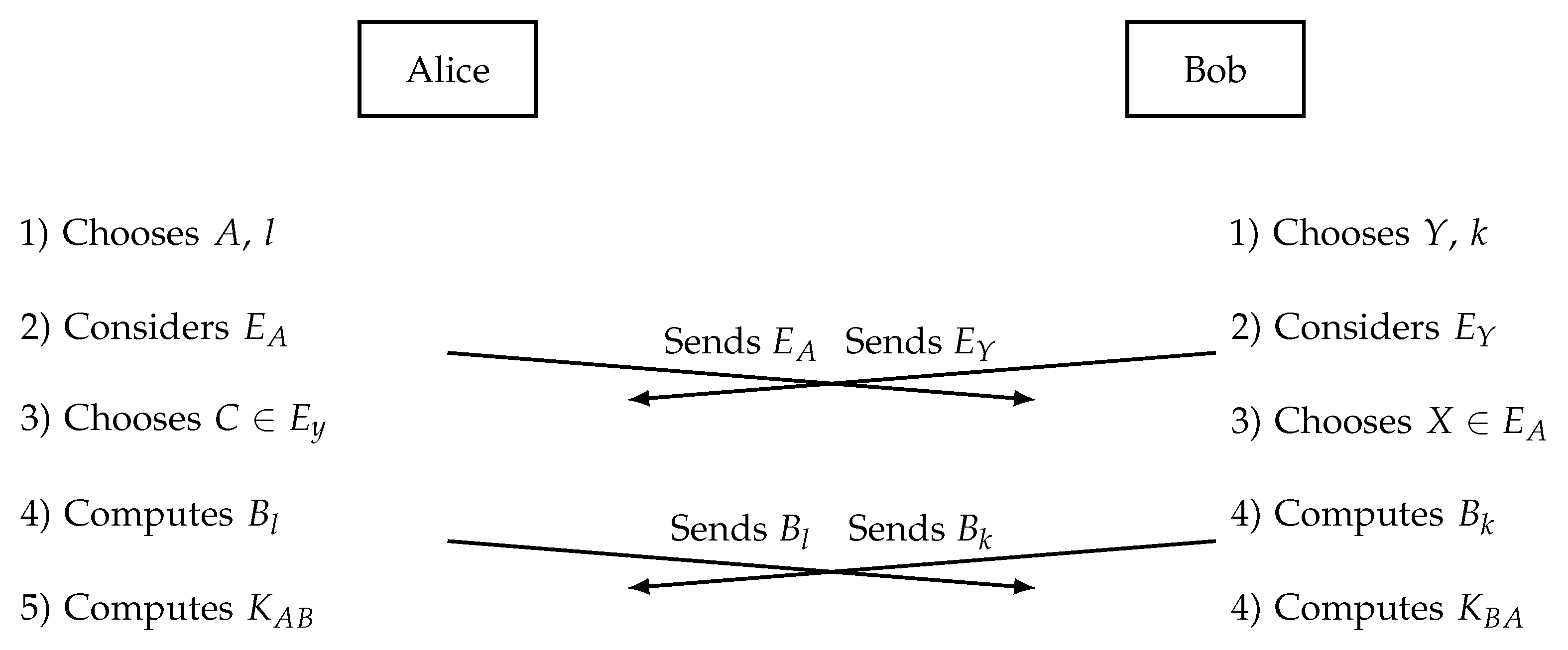
In this section, we propose an improvement on a well-known Block Matrix Key Exchange Protocol (BMKEP) proposed by [23].

3.1. The original protocol

We first recall the BMKEP suggested in [23]. The domain parameters of this protocol are prime number p and a square matrix B with entries from the finite field

F_{q}

(where q is a power of p).

1.: Alice chooses as her private keys: one positive integer l and a matrix $A \in M (F_{q})$ . She transmits the set $E_{A}$ of matrices commuting with A.
2.: Bob chooses as his private keys: one positive integer k and a matrix $Y \in M (F_{q})$ . He transmits the set $E_{Y}$ of matrices commuting with Y.
3.: Alice chooses her second private key: a matrix $C \in E_{Y}$ . She calculates:

$B l {(A, B, C)}^{l} = (\begin{matrix} A^{l} & B_{l} \\ O & C^{l} \end{matrix})$

and sends $B_{l}$ to Bob.
4.: Bob chooses his second private key: a matrix $X \in E_{A}$ . He calculates:

$B l {(X, B, Y)}^{k} = (\begin{matrix} X^{k} & B_{k} \\ O & Y^{k} \end{matrix})$

and sends $B_{k}$ to Alice.
5.: Alice computes the common private key:

$K_{A B} = {(B l {(X, B, Y)}^{k})}^{l} .$
6.: Bob computes the common private key:

$K_{B A} = {(B l {(A, B, C)}^{l})}^{k} .$

At the end of the protocol, the users get the same key, due to the fact that

A X = X A

C Y = Y C

, and the properties of the block matrices (Theorem 2).

This protocol requires the exchange of sets of matrices

E_{A}

and

E_{Y}

commuting with A and Y, respectively. This means more time and space. To overcome this problem, we suggest avoiding these steps by using properly selected commutative matrices. In general, our idea for improving this protocol is as follows:

1.: Alice selects matrices A and B, and Bob selects matrices C and D with the property that A and C commute; B and D also commute. This means that A and C belong to the same set of commuting matrices, B and D belong to the same set of commuting matrices. Alice and Bob agree on a matrix T. The secret keys of the users are positive integers a and b, respectively,
2.: Alice computes

$B l (A, T, B) = (\begin{matrix} A & T \\ O & B \end{matrix}),$

$B l {(A, T, B)}^{a} = (\begin{matrix} A^{a} & T_{a} \\ O & B^{a} \end{matrix}),$

where

$T_{a} = \sum_{n = 0}^{a - 1} A^{(a - 1 - n)} \cdot T \cdot B^{n} .$

She sends her public key $K_{A} = T_{a}$ to Bob.
3.: Bob computes:

$B l (C, T, D) = (\begin{matrix} C & T \\ O & D \end{matrix}),$

$B l {(C, T, D)}^{b} = (\begin{matrix} C^{b} & T_{b} \\ O & D^{b} \end{matrix}),$

where

$T_{b} = \sum_{m = 0}^{b - 1} C^{(b - 1 - m)} \cdot T \cdot D^{m} .$

He sends his public key $K_{B} = T_{b}$ to Alice.
4.: Alice computes the common key:

$K_{A B} = \sum_{n = 0}^{a - 1} A^{(a - 1 - n)} \cdot K_{B} \cdot B^{n} .$
5.: Bob computes the common key:

$K_{B A} = \sum_{m = 0}^{b - 1} C^{\cdot (b - 1 - m)} \cdot K_{A} \cdot D^{m} .$

The implementation of the protocol is shown in Figure 1.

3.2. Proposed Solution

The main idea behind our protocols is to utilize block matrices with commutative matrix blocks to simplify the key exchange process. By selecting matrix blocks that commute, we eliminate the need to transmit sets of commuting matrices publicly.

We construct block matrices of the form:

(\begin{matrix} A & T \\ O & B \end{matrix}), (\begin{matrix} C & T \\ O & D \end{matrix})

Here

A, B, C, D

and T are square matrices of the same order, and O is the zero matrix of this order. Alice and Bob each select their own their own pair of matrices (

A, B

) and (

C, D

) such that A commutes with C, and B commutes with D. This allows them to compute a common key.

3.3. Protocol Steps

The refined protocol unfolds in the following sequence:

1.: Both parties agree on a common matrix T.
2.: Alice opts for matrices A and B, while Bob picks matrices C and D. They ensure that A commutes with C and B with D.
3.: Alice calculates ${[B l (A, T, B)]}^{a}$ . Her public key is set as $K_{A} = T_{a}$ .
4.: Bob, in a parallel manner, computes ${[B l (C, T, D)]}^{b}$ . He sets his public key as $K_{B} = T_{b}$ .
5.: They then exchange their public keys.
6.: Using Bob’s public key and her private matrices, Alice computes the shared key, $K_{A B}$ .
7.: Similarly, using Alice’s public key and his private matrices, Bob computes the shared key, $K_{B A}$ .
8.: Due to the inherent commutative properties, both parties find that $K_{A B} = K_{B A}$ .

Here we give two examples for implementation of the above presented protocol, based on a tropical semiring.

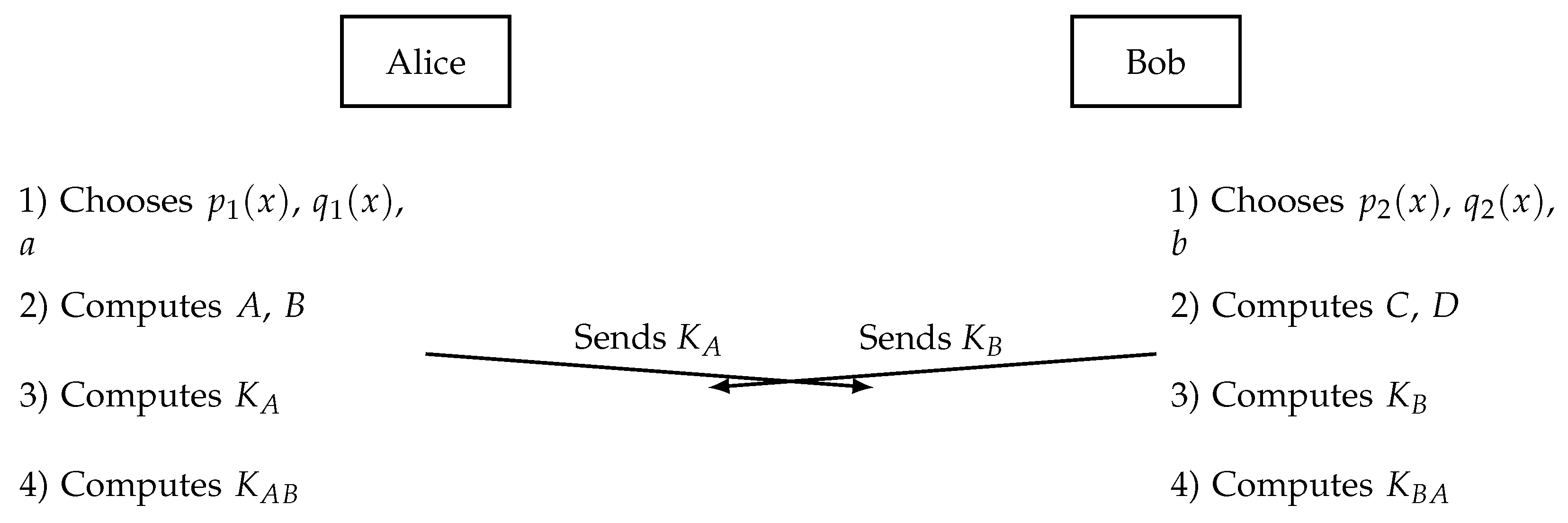
3.4. Implementation one - Tropical Block Matrix KEP using Polynomials of Matrices

The domain parameters of this protocol are: tropical semiring

R_{\max, +} = 〈 R \cup {- \infty}, \max, + 〉

R_{\min, +} = 〈 R \cup {+ \infty}, \min, + 〉

, and three arbitrary square tropical matrices M, N, and T of order n over this semiring.

1.: Alice selects as her secret key two tropical polynomials $p_{1} (x)$ and $q_{1} (x)$ , and a positive integer a. She computes:

$A = p_{1} (M), B = q_{1} (N)$

For Alice,

$B l (A, T, B) = (\begin{matrix} A & T \\ O & B \end{matrix}),$

$B l {(A, T, B)}^{\otimes a} = (\begin{matrix} A^{\otimes a} & T_{a} \\ O & B^{\otimes a} \end{matrix}),$

where

$T_{a} = ⨁_{n = 0}^{a - 1} A^{\otimes (a - 1 - n)} \otimes T \otimes B^{n} .$

She sends her public key $K_{A} = T_{a}$ to Bob.
2.: Bob selects as his secret key two tropical polynomials $p_{2} (x)$ and $q_{2} (x)$ , and a positive integer b. He computes:

$C = p_{2} (M), D = q_{2} (N)$

For Bob,

$B l (C, T, D) = (\begin{matrix} C & T \\ O & D \end{matrix}),$

$B l {(C, T, D)}^{\otimes b} = (\begin{matrix} C^{\otimes b} & T_{b} \\ O & D^{\otimes b} \end{matrix}),$

where

$T_{b} = ⨁_{m = 0}^{b - 1} C^{\otimes (b - 1 - m)} \otimes T \otimes D^{m} .$

He sends his public key $K_{B} = T_{b}$ to Alice.
3.: Alice computes the common key:

$K_{A B} = ⨁_{n = 0}^{a - 1} A^{\otimes (a - 1 - n)} \otimes K_{B} \otimes B^{n} .$
4.: Bob computes the common key:

$K_{B A} = ⨁_{m = 0}^{b - 1} C^{\otimes (b - 1 - m)} \otimes K_{A} \otimes D^{m} .$

At the end of the protocol, the users obtain the same secret key due to the following:

Theorem 4.

K_{A B} = ⨁_{n = 0}^{a - 1} A^{\otimes (a - 1 - n)} \otimes K_{B} \otimes B^{n} = ⨁_{m = 0}^{b - 1} C^{\otimes (b - 1 - m)} \otimes K_{A} \otimes D^{m} = K_{B A} .

Proof.

In accordance with the choice of the matrices A, B, C, D, it follows that

A \otimes C = C \otimes A, B \otimes D = D \otimes B

(the multiplication of tropical polynomials of matrices is commutative). Additionally, conforming to Theorem 2:

K_{A B} = ⨁_{n = 0}^{a - 1} ⨁_{m = 0}^{b - 1} A^{\otimes (a - 1 - n)} \otimes C^{\otimes (b - 1 - m)} \otimes T \otimes D^{\otimes (m)} \otimes B^{\otimes (n)}

= ⨁_{m = 0}^{b - 1} ⨁_{n = 0}^{a - 1} C^{\otimes (b - 1 - m)} \otimes A^{\otimes (a - 1 - n)} \otimes T \otimes B^{\otimes (n)} \otimes D^{\otimes (m)} = K_{B A} .

□

The execution of this protocol is illustrated in Figure 2.

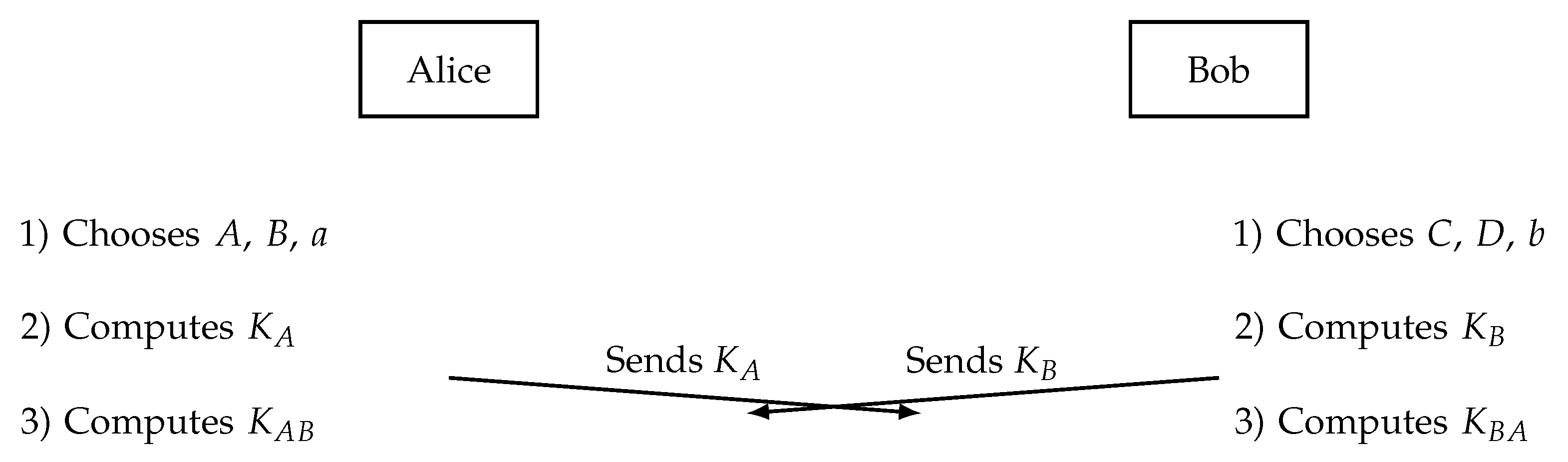
3.5. Implementation two - Tropical Block Matrix KEP using Linde-de la Puente Matrices

The domain parameters of this protocol are: tropical semiring

R_{\max, +} = 〈 R \cup {- \infty}, \max, + 〉

, one negative real number r, one positive real number c, and an arbitrary square tropical matrix T of order n over this semiring.

1.: Alice selects as her secret key two Linde-de la Puente matrices $A = L_{r_{1}}^{c_{1}}$ and $B = L_{r_{2}}^{c_{2}}$ , and a positive integer a. She computes:

$B l (A, T, B) = (\begin{matrix} A & T \\ O & B \end{matrix}),$

$B l {(A, T, B)}^{\otimes a} = (\begin{matrix} A^{\otimes a} & T_{a} \\ O & B^{\otimes a} \end{matrix})$

where

$T_{a} = ⨁_{n = 0}^{a - 1} A^{\otimes (a - 1 - n)} \otimes T \otimes B^{n} .$

She sends her public key $K_{A} = T_{a}$ to Bob.
2.: Bob selects as his secret key two Linde-de la Puente matrices $C = L_{r_{3}}^{c_{3}}$ and $D = L_{r_{4}}^{c_{4}}$ , and a positive integer b. He computes:

$B l (C, T, D) = (\begin{matrix} C & T \\ O & D \end{matrix}),$

$B l {(C, T, D)}^{\otimes b} = (\begin{matrix} C^{\otimes b} & T_{b} \\ O & D^{\otimes b} \end{matrix}),$

where

$T_{b} = ⨁_{m = 0}^{b - 1} C^{\otimes (b - 1 - m)} \otimes T \otimes D^{m} .$

He sends his public key $K_{B} = T_{b}$ to Alice.
3.: Alice computes the common key:

$K_{A B} = ⨁_{n = 0}^{a - 1} A^{\otimes (a - 1 - n)} \otimes K_{B} \otimes B^{n} .$
4.: Bob computes the common key:

$K_{B A} = ⨁_{m = 0}^{b - 1} C^{\otimes (b - 1 - m)} \otimes K_{A} \otimes D^{m} .$

At the end of the protocol, the users obtain the same secret key due to Theorem 3 and Corollary 3.1.

The execution of the protocol is shown in Figure 3.

3.6. Advantages of our Protocols

Here we outline some of the advantages of our protocols:

In the protocol suggested in [23], 4 messages are exchanged between users via a public (unsecured) channel. In our protocols, only two messages are exchanged. This results in Improved security and Saving time and resources.
Our protocols operate in tropical semirings, where the operations are only max/min and +. This means that operations in our protocols are significantly faster than operations in the finite field $F_{q}$ .
Our protocols do not use linear expressions for the general term, thus rendering traditional linear algebra tools ineffective.

4. Security Analysis

The security framework of our proposed tropical block matrix key exchange protocols is anchored in the computational hardness of the Matrix Decomposition Problem within tropical semirings. This problem is known for its formidable complexity, making it an ideal basis for cryptographic security. Crucially, our protocols are designed such that, even with knowledge of the communication transcript and public parameters, an adversary cannot feasibly distinguish the session key derived from the protocol from a random bitstring. This aligns with the contemporary standards for cryptographic protocol security [24].

4.1. Matrix Decomposition Problem

The core challenge underpinning our protocols is the Matrix Decomposition Problem, defined as follows: Given matrices

K, T \in R_{max, +}^{n \times n}

, the problem is to find matrices

A, B \in R_{max, +}^{n \times n}

and an integer a satisfying the equation:

K = ⨁_{i = 0}^{a - 1} A^{\otimes (a - 1 - i)} \otimes T \otimes B^{i} .

Essentially, this entails decomposing the matrix K into a series of operations involving its constituent block matrices. The complexity of this problem is a crucial aspect of our security argument. Notably, the best-known algorithms for such a decomposition, including Gauss-Jordan elimination and LU decomposition, exhibit exponential runtime complexity (

O (2^{n})

) for a matrix of dimension n. This level of computational demand renders the problem intractable for practical purposes, especially when considering the suggested parameter sizes [1].

4.2. Parameters for Enhanced Security

To strengthen the resistance against brute-force attacks and to align with the cryptographic principle that the session key should be indistinguishable from a random bitstring by an adversary, we recommend the following parameter settings for our protocols:

Employ tropical matrices of at least order 60, ensuring a substantial level of complexity in the matrix operations.
Select matrix entries randomly within the range $[- 10^{5}, 10^{5}]$ , which expands the solution space significantly.
The secret integers a and b should be chosen to be no less than $10^{5}$ , further increasing the computational challenge for any potential attacker.

With these parameters, our protocols not only meet but exceed the contemporary requirements for cryptographic security, effectively mitigating the risk of key exposure and unauthorized decryption.

4.3. Comparison with Existing Protocols

Compared to conventional commutative matrix-based key exchange protocols, the proposed tropical matrix protocols exhibit several advantages:

Reduced key sizes are a feature since commuting matrix sets are not exchanged. For an $n \times n$ matrix, only $n^{2}$ values are transmitted instead of $2 n^{4}$ .
The protocols leverage the computational efficiency of tropical semirings, where matrix multiplication is performed in $O (n^{3})$ time rather than $O (n^{3} log n)$ time as in finite fields.
A decrease in the number of message exchanges is also observed, with the proposed protocols requiring only two exchanges compared to four in traditional approaches, thus reducing communication overhead.

The performance and resource usage metrics are detailed in Table 1, which illustrates the duration (in seconds) and memory sizes (in MB) for each protocol variation across different matrix sizes. As matrix size increases, the resource demands also tend to increase, which is a crucial factor in evaluating the scalability of the protocols.

Table 2 depicts the private and public key sizes (in KB) for each protocol variation. It shows the growth of key sizes with an increase in matrix dimension, highlighting the trade-off between security and resource requirements. The disproportionality between private and public key sizes is also noteworthy, indicating the asymmetry in the computational load between key generation and verification processes.

5. Conclusion

In the dynamic realm of cryptographic research, innovations are imperative to address the ever-evolving challenges of digital security. Our study has ventured into the unique domain of tropical semirings and block matrices, presenting protocols that are poised to redefine the efficiency and security paradigms of key exchange mechanisms.

Central to our contribution is the operational efficiency that tropical semirings introduce. Moreover, our protocols do not employ linear expressions for the general term, which makes traditional linear algebra tools ineffective. By circumventing the computational intricacies typical of finite fields

F_{q}

, our approach manifests both swiftness and an enhanced layer of security. This duality is paramount in today’s digital age, where secure communications underpin a plethora of applications, from financial transactions to personal messaging.

Furthermore, our research does not just stand as an endpoint but rather as a launchpad for future explorations. The mathematical properties of tropical semirings, juxtaposed with the versatility of block matrices, hint at vast cryptographic landscapes yet to be charted. There’s also the tantalizing opportunity of amalgamating our protocols with existing cryptographic frameworks, giving rise to hybrid systems that could potentially be more resilient than their individual counterparts.

In closing, our exploration underscores the profound impact that novel mathematical structures can impart to the field of cryptography. As we harness the capabilities of tropical semirings and block matrices, we’re not only charting a new course for key exchange protocols but also kindling a beacon for future endeavors in the realm of secure communications. The cryptographic community now has a fertile ground for further research, and it will be intriguing to witness the subsequent innovations that build upon our foundational work.

References

Varadharajan, V.; Odoni, R. Extension of rsa cryptosystems to matrix rings. Cryptologia 1985, 9, 140–153. [Google Scholar] [CrossRef]
Maxrizal. Public Key Cryptosystem Based on Singular Matrix. Trends in Sciences 2022, 19. [Google Scholar] [CrossRef]
Maxrizal; Prayanti, B.; Sujono. Generalization of Public Key Cryptosystem Based on Singular Matrix Using Ring of Integer Modulo 2022. pp. 1–4. [CrossRef]
Maxrizal; Irawadi, S. Nonsingular matrix as private key on ElGamal cryptosystem 2021. 1821. [CrossRef]
Rahman, N.; Shpilrain, V. MOBS: Matrices Over Bit Strings public key exchange. IACR Cryptology ePrint Archive 2021, pp. 1–7. Also available at: https://ia.cr/2021/560.
Gupta, S.; Sanghi, M. A New Digital Signature Scheme Using Tribonacci Matrices. International Journal of Computer and Information Technology(2279-0764) 2020, 9, 64–71. [Google Scholar] [CrossRef]
Koukouvinos, C.; Simos, D. Encryption Schemes based on Hadamard Matrices with Circulant Cores Design of Cryptographic Algorithms. Unknown Journal 2013, 3, 17–41. [Google Scholar]
Zhang, L., T. C.S.Y.H.H.T.H.; Lei, Z. Optical single-channel cryptosystem based on the non-negative matrix factorization and face biometric in cyan-magenta-yellow-black color space. Journal of the Optical Society of America. A, Optics, image science, and vision 2023, 40, 2146–2155. [Google Scholar] [CrossRef] [PubMed]
Gudepu, R.; Rao, D. A public key cryptosystem based on lattice matrices. Journal of Mathematical and Computational Science 2020, 10, 2408–2421. [Google Scholar] [CrossRef]
Durcheva, M. Semirings as building blocks in cryptography; Cambridge Scholars Publishing, 2020.
Durcheva, M. TrES: Tropical Encryption Scheme Based on Double Key Exchange. European Journal of Information Technologies and Computer Science 2022, 2, 11–17. [Google Scholar] [CrossRef]
Huang, H.; Li, C.; Deng, L. Public-Key Cryptography Based on Tropical Circular Matrices. Applied Sciences 2022, 12, 1–12. [Google Scholar] [CrossRef]
Huang, H. Cryptosystems Based on Tropical Congruent Transformation of Symmetric Matrices. Symmetry 2022, 14. [Google Scholar] [CrossRef]
Huang, H.; Li, C. Tropical Cryptography Based on Multiple Exponentiation Problem of Matrices. Security and Communication Networks 2022. [Google Scholar] [CrossRef]
Muanalifah, A.; Sergeev, S. Modifying the Tropical Version of Stickel’s Key Exchange Protocol. Applications of Mathematics 2020, 65, 727–753. [Google Scholar] [CrossRef]
Battarbee, C.; Kahrobaei, D.; Shahandashti, S. Cryptanalysis of Semidirect Product Key Exchange Using Matrices Over Non-Commutative Rings 2021. pp. 1–11.
Battarbee, C.; others. On the efficiency of a general attack against the MOBS cryptosystem. Journal of Mathematical Cryptology 2022, 16, 289–297. [Google Scholar] [CrossRef]
Jiang, X.; Huang, H.; Pan, G. Cryptanalysis of Tropical Encryption Scheme Based on Double Key Exchange. Journal of Cyber Security and Mobility 2023, 12, 205–220. [Google Scholar] [CrossRef]
Brown, D.; Koblitz, N.; Legrow, J. Cryptanalysis of “ MAKE ”. Journal of Mathematical Cryptology 2022, 16, 98–102. [Google Scholar] [CrossRef]
Raja, K. N..A.P. A Cryptosystem Based on Hilbert Matrix using Cipher Block Chaining Mode. ArXiv, abs/1110.1498, 2011. [Google Scholar]
Jayanti, S., C. K..A.C. Cryptosystem of Skewed Affine Cipher Over Elliptic Curves with Block Matrix. ECS Transactions 2022, 07(1), 15071–15080. [Google Scholar] [CrossRef]
Ramesh, M.; Kumar, B.H.; Srinagesh, A. A Novel Block-Cipher Mechanism for Information Security in Cloud System. 2016 IEEE 6th International Conference on Advanced Computing (IACC) 2016, pp. 524–528. [CrossRef]
Zeriouh, M.; Chillali, A.; Boua, A. Cryptography based on the matrices. Boletim da Sociedade Paranaense de Matematica 2019, 37, 75–83. [Google Scholar] [CrossRef]
An, J.H. Authenticated encryption in the public-key setting: Security notions and analyses. 169.

Figure 1. Block Matrix KEP.

Figure 2. Tropical Block Matrix KEP using Polynomials of Matrices between Alice and Bob.

Figure 3. Tropical Block Matrix KEP using Linde-de la Puente matrices.

Table 1. Duration (in seconds) and Memory Sizes (in MB) for each protocol.

Matrix Size	Duration 1	Duration 2	Duration 3	Memory 1	Memory 2	Memory 3
60	0.03	0.01	0.02	0.05	0.05	0.05
65	0.04	0.02	0.03	0.06	0.06	0.06
70	0.06	0.03	0.04	0.07	0.07	0.07
75	0.08	0.04	0.06	0.08	0.08	0.08
80	0.12	0.06	0.09	0.09	0.09	0.09
85	0.18	0.09	0.13	0.10	0.10	0.10
90	0.24	0.13	0.18	0.12	0.12	0.12

Table 2. Private and Public Key Sizes (in MB) for each protocol.

Matrix Size	Private 1	Public 1	Private 2	Public 2	Private 3	Public 3
60	27.3	2191.2	27.3	27.3	27.3	27.3
65	32.3	2592.5	32.3	32.3	32.3	32.3
70	37.5	3008.7	37.5	37.5	37.5	37.5
75	43.0	3439.9	43.0	43.0	43.0	43.0
80	48.8	3885.9	48.8	48.8	48.8	48.8
85	54.8	4346.9	54.8	54.8	54.8	54.8
90	61.0	4822.7	61.0	61.0	61.0	61.0

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Secure Key Exchange in Tropical Cryptography: Leveraging Efficiency with Advanced Block Matrix Protocols

Abstract

1. Introduction and Motivation

2. Preliminaries

2.1. Exponentiation of Block Matrices

2.2. Tropical Semirings

2.3. Commutative Matrices in Tropical Semirings

3. Block Matrix Key Exchange Protocols

3.1. The original protocol

3.2. Proposed Solution

3.3. Protocol Steps

3.4. Implementation one - Tropical Block Matrix KEP using Polynomials of Matrices

3.5. Implementation two - Tropical Block Matrix KEP using Linde-de la Puente Matrices

3.6. Advantages of our Protocols

4. Security Analysis

4.1. Matrix Decomposition Problem

4.2. Parameters for Enhanced Security

4.3. Comparison with Existing Protocols

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe