Submitted:
07 March 2024
Posted:
28 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Preliminaries
3. Main Results
4. Applications
4.1. Improvements of Theorems 2, 3, 4 and 5
4.2. Approximations of the Function
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MTP | Mixed Trigonometric Polynomial |
References
- Qi, F.; Guo, B.-N. On generalizations of Jordan’s inequality (in Chinese). Coal Higher Education, supplement, 1993; 32–33. [Google Scholar]
- Qi, F. Extensions and sharpenings of Jordan’s and Kober’s inequality (in Chinese). Journal of Mathematics for Technology, 1996; 12, 98–101. [Google Scholar]
- Deng, K. The noted Jordan’s inequality and its extensions (in Chinese). Journal of Xiangtan Mining Institute, 1995; 10, 60–63. [Google Scholar]
- Jiang, W. D.; Yun, H. Sharpening of Jordan’s inequality and its applications. Journal of Inequalities in Pure and Applied Mathematics, 2006; 7, 1–4. [Google Scholar]
- Li, J.-L.; Li, Y.-L. On the Strengthened Jordan’s Inequality. Journal of Inequalities and Applications 2008, 2007, 1–8. [Google Scholar] [CrossRef]
- Malešević, B.; Mihailović, B. A minimax approximant in the theory of analytic inequalities. Applicable Analysis and Discrete Mathematics, 2021; 15, 486–509. [Google Scholar]
- Mitrinović, D. Analytic Inequalities; Publisher: Springler-Verlag Berlin, Germany, 1970. [Google Scholar]
- Qi, F.; Niu, D.-W. Refinements, Generalizations, and Applications of Jordan’s Inequality and Related Problems. Journal of Inequalities and Applications 2009, 2009, 1–52. [Google Scholar] [CrossRef]
- Özban, A. Y. A new refined form of Jordan’s inequality and its applications. Applied Mathematics Letters 2006, 19, 155–160. [Google Scholar] [CrossRef]
- Li, J.-L. An identity related to Jordan’s inequality. International Journal of Mathematics and Mathematical Sciences 2006, 2006, 1–6. [Google Scholar] [CrossRef]
- Zhu, L. Sharpening Jordan’s inequality and the Yang Le inequality. Applied Mathematics Letters 2006, 19, 240–243. [Google Scholar] [CrossRef]
- Zhu, L. Sharpening Jordan’s inequality and the Yang Le inequality, II. Applied Mathematics Letters 2006, 19, 990–994. [Google Scholar] [CrossRef]
- Zhu, L. A general refinement of Jordan-type inequality. Computers & Mathematics with Applications 2008, 55, 2498–2505. [Google Scholar]
- Niu, D.-W.; Huo, Z.-H.; Cao, J.; Qi, F. A general refinement of Jordan’s inequality and a refinement of L. Yang’s inequality. Integral Transforms and Special Functions, 2008; 19, 157–164. [Google Scholar]
- Chen, C.-P.; Debnath, L. Sharpness and generalization of Jordan’s inequality and its application. Applied Mathematics Letters 2012, 25, 594–599. [Google Scholar] [CrossRef]
- Barbu, C.; Pişcoran, L.-I. Jordan type inequalities using monotony of functions. Journal of Mathematical Inequalities, 2014; 8, 83–89. [Google Scholar]
- Aharonov, D.; Elias, U. More Jordan type inequalities. Mathematical Inequalities & Applications; 2014; Volume 17, pp. 1563–1577. [Google Scholar]
- Alzer, H.; Kwong, M. K. On Jordan’s inequality. Periodica Mathematica Hungarica 2018, 77, 191–200. [Google Scholar] [CrossRef]
- Zhang, L.; Ma, X. New Refinements and Improvements of Jordan’s Inequality. Mathematics, 2018; 2018, 1–8. [Google Scholar]
- Zhang, L.; Ma, X. New Polynomial Bounds for Jordan’s and Kober’s Inequalities Based on the Interpolation and Approximation Method. Mathematics, 2019; 7, 1–9. [Google Scholar]
- Zhang, B.; Chen, C.-P. Sharpness and generalization of Jordan, Becker-Stark and Papenfuss inequalities with an application. Journal of Mathematical Inequalities, 2019; 13, 1209–1234. [Google Scholar]
- Haque, N. A Short Calculus Proof of Jordan’s Inequality. Cambridge Open Engage (Preprint) 2020, 1–1. [Google Scholar]
- Popa, E. C. A note on Jordan’s inequality. General Mathematics, 2020; 28, 97–102. [Google Scholar]
- Malešević, B.; Mićović, M. Exponential Polynomials and Stratification in the Theory of Analytic Inequalities. Journal of Science and Arts, 2023; 23, 659–670. [Google Scholar]
- Malešević, B.; Jovanović, D. Frame’s Types of Inequalities and Stratification. CUBO, A Mathematical Journal, 2024; 26, 1–15. [Google Scholar]
- Chen, S.; Ge, X. A solution to an open problem for Wilker-type inequalities. Journal of Mathematical Inequalities, 2021; 15, 59–65. [Google Scholar]
- Malešević, B.; Mihailović, B.; Nenezić Jović, M.; Milinković, L. Some minimax approximants of D’Aurizio trigonometric inequalities. HAL (Preprint) 2022, 1–9. [Google Scholar]
- Chen, C.-P.; Mortici, C. The relationship between Huygens’ and Wilker’s inequalities and further remarks. Applicable Analysis and Discrete Mathematics, 2023; 17, 92–100. [Google Scholar]
- Sándor, J. On D’Aurizio’s trigonometric inequality. Journal of Mathematical Inequalities, 2016; 10, 885–888. [Google Scholar]
- Sándor, J. Extensions of D’Aurizio’s trigonometric inequality. Notes on Number Theory and Discrete Mathematics, 2017; 23, 81–83. [Google Scholar]
- Hung, L.-C.; Li, P.-Y. On generalization of D’Aurizio-Sándor inequalities involving a parameter. Journal of Mathematical Inequalities, 2018; 12, 853–860. [Google Scholar]
- Malešević, B.; Makragić, M. A method for proving some inequalities on mixed trigonometric polynomial functions. Journal of Mathematical Inequalities, 2016; 10, 849–876. [Google Scholar]
- Pinelis, I. L’Hospital type rules for monotonicity, with applications. Journal of Inequalities in Pure and Applied Mathematics, 2002; 3, 1–5. [Google Scholar]
- Estrada, R.; Pavlović, M. L’Hôpital’s monotone rule, Gromov’s theorem, and operations that preserve the monotonicity of quotients. Publications de l’Institut Mathematique, 2017; 101, 11–24. [Google Scholar]
- Cutland, N. Computalibity: an introduction to recursive funtion theory; Publisher: Cambridge University Press, Great Britain, 1980. [Google Scholar]
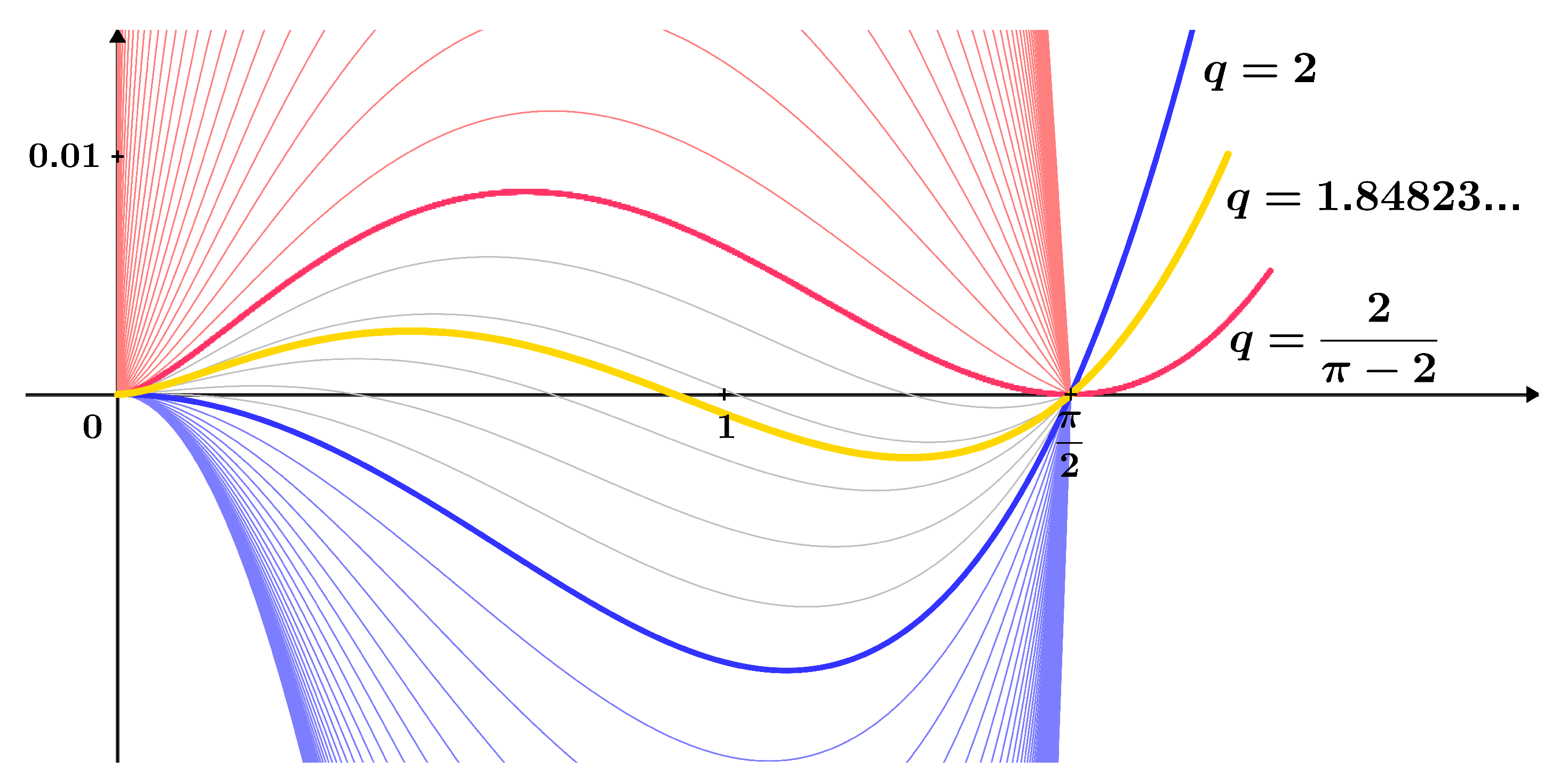

| Maximum deviation | |
|---|---|
| Upper bound of the function | from the function |
| over the interval | |
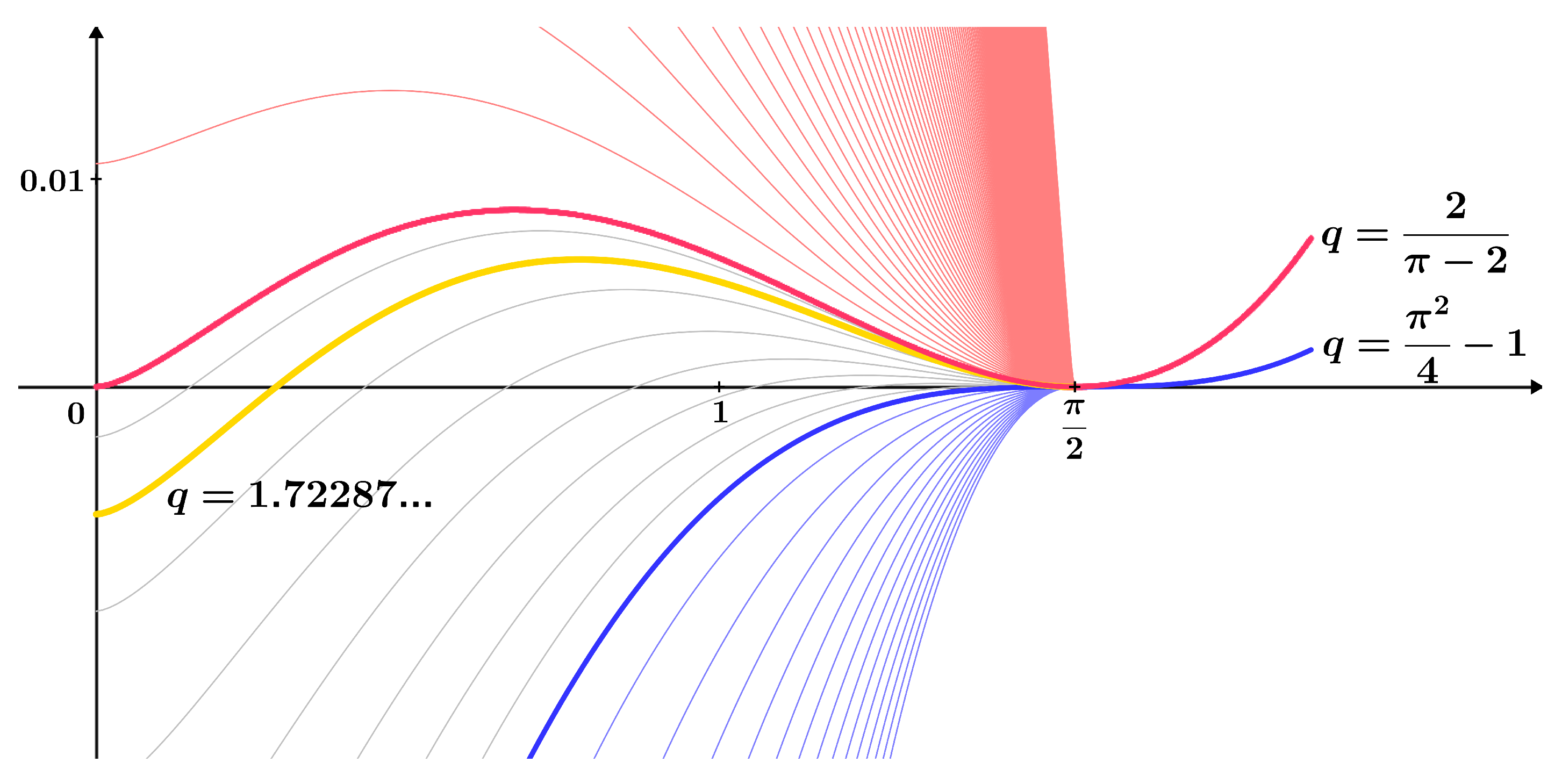
| Maximum deviation | |
|---|---|
| Lower bound of the function | from the function |
| over the interval | |
| Maximum deviation | |
|---|---|
| Minimax approximation of the function | from the function |
| over the interval | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




