A Nonlinear ODE Model for a Consumeristic Society

Preprint

Article

A Nonlinear ODE Model for a Consumeristic Society

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 March 2024

Posted:

22 March 2024

You are already at the latest version

Alerts

Abstract

In this paper we introduce an ODE system to model the interaction between nature resources and human exploitation in a rich consumeristic society. In this model the rate of change of population depends on wealth per capita, and the rate of consumption has a quadratic growth with respect to population and wealth. As in our previous work \cite{BaCra_1}, we distinguish between renewable and non renewable resources, and we introduce a replenishment term for non renewable resources. We first get some information on the asymptotic behaviour of wealth and population, then we compute all the equilibria of the system and we study their stability when the parameter of exploitation of resources is small. Some numerical simulations confirm the theoretical results, and give suggestions for future research.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

In this paper we study a model of interactions between society and nature, inspired by the HANDY model introduced in [7] (see also [8]). The original HANDY model is a set of four differential equations whose variables are natural resources, wealth produced by human work, and the population, splitted in the two classes of Commoner and Elite. Using computer simulations, the paper [7] shows different possibilities for the evolution of society, including collapse. It is a simple model that seems to allow a rich panel of behaviour, so it attracted attention, and several papers have been devoted to its exploration, see [1,2,4,9,10,11]. In [2] various developments of the original model are introduced, among others the division of natural resources between renewable and non renewable. This idea has been developped in the paper [10], where some general results are obtained and again numerical simulations show different possibilities for the evolution of society. In [10] the dynamics of nonrenewable resources is given by the following equation

\frac{d y_{n}}{d t} = - δ_{n} x_{c} y_{n},

where

y_{n}

are the nonrenewable resources,

x_{c}

is the Commoner population and

δ_{n} > 0

a parameter. Clearly, this equation translates the idea of a given amount and an irreversible depletion of

y_{n}

. In our previous work [3] we have pursued this idea but we have introduced a replenishment term for nonrenewable resources. This is due to the optimistic argument, that is often used in public debate on these subjects, that human ingenuity and scientific progress can substitute depleted resources with new ones. The term of replenishment that we have added is given by

k \frac{x w}{x w + 1} z

depending on

x w

, where x is population and w is wealth, while z is the level of non renewables and k a constant. Hence, the dynamics of non renewable resources z in [3] is given by

z^{'} = k \frac{x w}{x w + 1} z - δ z x,

The replenishment term is obtained from a function

\frac{t}{t + 1}

which, in population dynamics, is a Holling II type function (see [6], page 25 and passim), used to model saturation effects. The equation above states that the replenishment is possible but cannot be above a level k, and we can call this an hypothesis of “moderate optimism”. Another characteristic of [3] is that we dropped the distinction between Commoner and Elite, so we obtained a four variable model, which is as follows

\{\begin{matrix} x^{'} (t) & = (β - α_{m}) x - \frac{1}{ρ} (α_{M} - α_{m}) {(ρ x - w)}^{+} \\ y^{'} (t) & = γ y (λ - y) - δ_{1} x y \\ z^{'} (t) & = - δ_{2} x z + k_{1} \frac{δ_{3} x w}{δ_{3} x w + k_{2}} z \\ w^{'} (t) & = δ_{1} x y + δ_{2} x z - δ_{3} x w - s [x - \frac{1}{ρ} {(ρ x - w)}^{+}] . \end{matrix}

(1)

Here, as we said above, x is the population,

y, z

indicate respectively renewable and nonrenewable resources, w is the wealth. An interesting result in [3] is that it cannot happen that

x, w

go to infinity as t goes to infinity. This means that, even assuming “moderate optimism”, there cannot be an indefinite growth in population and wealth. In [3] we also obtained all the critical points of the system, and we studied their stability. In the final section of [3] numerical simulations support the theoretical results and also suggest the possibility, not yet treated in a rigorous way, of periodic orbits and chaotic dynamics.

The present paper originated from the attempt to adapt the HANDY model to contemporary, rich, consumeristic societies (like contemporary western countries). Indeed, the HANDY model seems to be a very nice and simple way to treat the interaction of nature and society for a large class of historical societies, but, in our opinion, it has some serious flaws when dealing with contemporary, rich, consumeristic societies. The main one is probably the fact that in the original model the birth rate is constant and the death rate decays when wealth increases, leading to the conclusion that a wealthy society should show sustained population growth. This is definitely not true in contemporary western societies, and the reason is due to the fact that birth rate is not constant, and indeed, in most of contemporary rich societies, it is falling. Hence, in the present paper we introduce an equation for population dynamics which is different from that of HANDY model, and it is as follows

x^{'} = - c x + d \frac{μ x w}{w^{2} + μ^{2} x^{2}} x .

Here we have a negative term

- c x

which is contrasted by the term

d \frac{μ x w}{w^{2} + μ^{2} x^{2}} x = d \frac{\frac{w}{μ x}}{{(\frac{w}{μ x})}^{2} + 1} x

depending on the wealth per capita

w / x

via a constant

μ

. When

w / μ x

is very small or very large, the positive term is small and the population falls. In an intermediate region, the population grows. This seems fitting better with the recent history of rich countries.

Another difference compared to the HANDY model (and to [3]) is that there the depletion of natural resources depend on the population, while it seems reasonable that in a consumeristic society it should depend more on wealth than on population. Hence, a first idea should be to substitute populations with wealth (x with w) in the depletion terms, giving rise to quadratic terms

w^{2}

. We will pursue this idea in a forthcoming paper. In the present paper, however, we are interested to preserve some influence of population on consumption of natural resources, so we introduce the function

m = m (x, w) = max {x, w}

and we substitute x with m in the depletion terms. We notice also that the consumption term in the equation for

w^{'}

in [3], which is given by by

s [x - \frac{1}{ρ} {(ρ x - w)}^{+}],

has a linear growth, while here, to model a consumeristic society, we use a quadratic term

m (x, w) w

, where the consumption is led mostly by wealth. In this way, we can put together the negative terms in the equation for

w^{'}

in (1). Summing up all this ideas, we introduce the model that we are going to study. We apply some standard rescaling setting

k_{2} = 1

, and we assume

δ_{1} = δ_{2}

, that is, we assume that the rate of depletion is the same for renewable and nonrenewable resources. This is a simplifying assumption, that we hope to drop in future research. In our previous paper [3], some simulations seemed to suggest that the dynamics do not change too much taking different values for

δ_{1}

and

δ_{2}

. In section 7 of the present paper, some simulations show a different dependence of the dynamics on

δ_{1}

and

δ_{2}

, and this seems an interesting topic for future research. In conclusion our model is as follows.

\{\begin{matrix} x^{'} & = - c x + d \frac{μ x w}{w^{2} + μ^{2} x^{2}} x, \\ y^{'} & = γ y (λ - y) - δ y m (x, w), \\ z^{'} & = k \frac{m (x, w) w}{m (x, w) w + 1} z - δ z m (x, w), \\ w^{'} & = δ y m (x, w) + δ z m (x, w) - σ m (x, w) w . \end{matrix}

(2)

where, as we said above,

m (x, w) = max {x, w} = \frac{1}{2} (x + w + | x - w |)

. . We assume

d > 2 c

, which is necessary to have a positive growth of x for some range of

\frac{w}{μ x}

. We also assume

μ ⩾ 1

, which means that the negative effect on the population growth of the increasing wealth becomes relevant only for large values of wealth per capita. We also assume

μ \neq \frac{d + \sqrt{d^{2} - 4 c^{2}}}{2 c}

, which is just a technical assumption that we hope to drop in future work.

The paper is organized as follows: after the introduction, in section 2 we obtain general results of existence and positivity of the solutions, and also some results on their asymptotic behavior. In particular, we prove that it can’t happen

x \to + \infty

w \to + \infty

z \to + \infty

t \to + \infty

In sections 3, 4, 5, 6 we compute all the equilibrium points of system (2), and we study their stability properties. We distinguish the cases

x < w

x > w

x = w = 0

, while the case

x = w > 0

is excluded by our hypotheses. There is a rich variety of such equilibria. We are able to give a complete description of the stability properties for some of them, but it seems very difficult to do the same for all of them. So we decided to study the stability in the limit of

δ \to 0^{+}

, which is reasonable, in our opinion, because

δ

is a parameter depending on human choices. Using standard linearization techniques and asymptotic developments, we are able to describe the stability properties of all the equilibria when

δ \to 0^{+}

(and the other parameters are fixed).

In sections 7 we give some numerical simulations, both for corroborate the theoretical results of the preceding sections and to try to get some hint on the cases for which we don’t have such results. It is interesting to see that in some simulations the conditions stated by our results for small

δ

’s (stability or instability) are preserved for larger

δ

’s, while they are not in other cases: so this seems to be an interesting subject of future research.

We end this introduction by indicating, for the reader’s sake, some of the results obtained in the present paper.

In section 2 we obtain that it cannot be $x (t) \to + \infty$ or $w (t) \to + \infty$ or $z (t) \to + \infty$ as $t \to + \infty$ . We got a similar result in [3] and, as in that case, the result does not necessarily mean that $x, w, z$ are bounded, but that, if they grow above a critical level, then they will start to oscillate.
The critical points with $x = w = 0$ are all unstable.
Most of the equilibria are unstable as $δ \to 0^{+}$ , but for some ranges of the parameters, there are asymptotically stable equilibrium points, and also someone with positive values for populations and wealth: see below cases ii8) and iii3). See also Figure 13 in section 7.

2. General Results on the Solutions

We set

X = (x, y, z, w) \in R^{4}

and

F (X) = (f_{1} (X), f_{2} (X), f_{3} (X), f_{4} (X))

where

\{\begin{matrix} f_{1} (X) = - c x + d \frac{μ x w}{w^{2} + μ^{2} x^{2}} x \\ f_{2} (X) = γ y (λ - y) - δ y m (x, w) \\ f_{3} (X) = k \frac{m (x, w) w}{m (x, w) w + 1} z - δ z m (x, w) \\ f_{4} (X) = δ y m (x, w) + δ z m (x, w) - σ m (x, w) w \end{matrix}

We are interested in non negative solutions, so we work the cone

C = \{(x, y, z, w) \in R^{4} | x > 0, y > 0, z > 0, w > 0\}

or possibly in its closure

\bar{C} = \{(x, y, z, w) \in R^{4} | x \geq 0, y \geq 0, z \geq 0, w \geq 0\} .

It is obvious that F is locally Lipschitz at any point of

\bar{C}

, so the standard theory of ODE gives the following result:

Proposition 1.

For any

(t_{0}, X_{0}) \in R \times \bar{C}

, there exists a unique maximal solution

X (t)

to the Cauchy problem

\{\begin{matrix} X^{'} = F (X) \\ X (t_{0}) = X_{0} \end{matrix}

(3)

defined in

J = (a, b)

, with

a < t_{0} < b

In the following, we will set

t_{0} = 0

and

X_{0} = (x_{0}, y_{0}, z_{0}, w_{0}) with x_{0}, y_{0}, z_{0} > 0 and w_{0} ⩾ 0 .

As first thing we prove that, if

X_{0}

is as above, the solution stays in

C

for any

t > 0

Proposition 2.

Let

X (t) = (x (t), y (t), z (t), w (t))

be a solution to (3) with

t_{0} = 0

and

x_{0}, y_{0}, z_{0} > 0, w_{0} ⩾ 0

. Then

X (t) \in C

for every

t \in (0, b)

Proof.

It’s straightforward to derive that

x (t), y (t), z (t) > 0

for any

t \in J = (a, b)

, because the zero constant is a solution in the three equations for

x^{'} (t), y^{'} (t), z^{'} (t)

, so it can’t be crossed, and

x_{0}, y_{0}, z_{0} > 0

. As for w, we first observe that there exists a

ε > 0

such that

w (t) > 0, \forall t \in (0, ε)

: this is obvious if

w_{0} > 0

, due to continuity, whereas if

w_{0} = 0

we have

w^{'} (0) = δ x_{0} y_{0} + δ x_{0} z_{0} > 0

, and the thesis follows. Now let us then define

t_{1} = sup {t > 0 ∣ w (s) > 0 for every s \in (0, t)} .

t_{1} = b

, we easily conclude that

w (t) > 0

(0, b)

. If

t_{1} < b

, it’s easy to see that

w (t_{1}) = 0

and

w (t) > 0

for any

t \in (0, t_{1})

, so

w^{'} (t_{1}) \leq 0

. But from the equation we get

w^{'} (t_{1}) = δ x (t_{1}) y (t_{1}) + δ x (t_{1}) z (t_{1}) > 0,

and the contradiction proves that

t_{1} = b

and thus

w (t) > 0, \forall t \in (0, b)

. □

Proposition 3.

Under the same assumptions as in Proposition 2 it holds

b = + \infty

Proof.

We argue by contradiction, so we assume

b < + \infty

. From the first equation we easily get

x^{'} \leq c_{1} x

for some

c_{1} > 0

, hence

\begin{matrix} x (t) \leq x_{0} e^{c_{1} t} \leq x_{0} e^{c_{1} b} : = c_{2} . \end{matrix}

As for

y (t)

, using the same argument as in [3], we get that y is bounded in

[0, b)

and, more precisely, we have

0 \leq y (t) \leq max {λ, y_{0}}, \forall t \in [0, b)

. Notice that this holds also when

b = + \infty

From the equation for

z (t)

we get

z^{'} \leq k z

, hence

\begin{matrix} z (t) \leq z_{0} e^{k t} \leq z_{0} e^{k b} : = c_{3}, \end{matrix}

and thus,

\begin{matrix} w^{'} & \leq m (x, w) (δ y + δ z) \leq c_{4} (w + c_{2}) \\ = c_{4} w + c_{5} . \end{matrix}

From this it follows that

w (t) \leq c_{6}

b < + \infty

. Therefore, if

b < + \infty

we get that

X (t)

is bounded in

[0, b)

, which is impossible due to known theorems. Hence,

b = + \infty

□

We now prove some asymptotic results on x and w.

Proposition 4.

It cannot be

{lim}_{t \to + \infty} x (t) = + \infty

Proof.

We argue by contradiction, so we assume

{lim}_{t \to + \infty} x (t) = + \infty

. For the sake of simplicity, let us set

m (t) = m (x (t), w (t))

. As

x (t) \to + \infty

, of course we have also

m (t) \to + \infty

. To get the result, we have to study the asymptotic behavior of

y, z, w

, in the hypothesis

x (t) \to + \infty

Claim 1:

{lim}_{t \to + \infty} y (t) = 0

. We have

y^{'} \leq y (γ λ - γ y - m) .

Given that

y (t)

is bounded and

m (t) \to + \infty

y (t)

is decreasing as

t \to + \infty

. Hence, there exists a limit

l_{+} = {lim}_{t \to + \infty} y (t) \geq 0

. If

l_{+} > 0

, then

y^{'} (t) \to - \infty

, which is a contradiction with known theorems. Therefore

l_{+} = 0

Claim 2:

{lim}_{t \to + \infty} z (t) = 0

. We have

z^{'} \leq k z - δ z m = z (k - δ m) < 0

t \to + \infty

. Thus, there exists a limit

l_{+} = lim_{t \to + \infty} z (t) \geq 0 .

l_{+} > 0

, then

{lim}_{t \to + \infty} z^{'} (t) = - \infty

, which is, as above, a contradiction.

Claim 3:

w (t)

is bounded on

[0, + \infty)

Let

T > 0

be such that for all

t \geq T

\frac{δ y (t) + δ z (t)}{σ} < 1

. We distinguish two cases:

Suppose $w (t) \geq \frac{δ y (t) + δ z (t)}{σ}$ for all $t \geq T$ . In this case, we have

$w^{'} = m (x, w) (δ y + δ z - σ w) \leq 0,$

which means that $w (t)$ is decreasing on $(T, + \infty)$ and thus it is bounded in $[0, + \infty)$ .
Suppose now that there exists $t_{1} \geq T$ such that $w (t_{1}) < \frac{δ y (t_{1}) + δ z (t_{1})}{σ}$ . Let $t > t_{1}$ . If $w (t) \leq \frac{δ y (t) + δ z (t)}{σ}$ , then $w (t) < 1$ . Otherwise, if $w (t) > \frac{δ y (t) + δ z (t)}{σ}$ , define

$t_{2} = inf \{τ \in (t_{1}, t) | w (s) > \frac{δ y (s) + δ z (s)}{σ}, \forall s \in (τ, t)\} .$

We have that $t_{2} > t_{1}$ . Because of continuity we also have $w (s) > \frac{δ y (s) + δ z (s)}{σ} \forall s \in (t_{2}, t)$ and $w (t_{2}) = \frac{δ y (t_{2}) + δ z (t_{2})}{σ} < 1$ . Hence we have $w^{'} (s) < 0$ in $(t_{2}, t)$ implying that $w (s)$ is decreasing in $(t_{2}, t)$ and thus $w (t) \leq w (t_{2}) < 1$ . In conclusion, $w (t) < 1$ for every $t \geq t_{1}$ , and therefore w is bounded on $[0, + \infty)$ .

End of the proof: from the previous claims, we obtain, as w is bounded and

x (t) \to + \infty

, that

\frac{w}{μ x} \to 0

t \to + \infty

, and thus

\frac{μ x w}{w^{2} + μ^{2} x^{2}} \to 0

. This implies

x^{'} < 0

on a half-line

[t_{3}, + \infty)

, and therefore we get a contradiction with the hypothesis that

{lim}_{t \to + \infty} x (t) = + \infty

□

Proposition 5.

It cannot be

{lim}_{t \to + \infty} w (t) = + \infty

Proof.

Since

m = m (x, w) \geq w

we can repeat the previous arguments and obtain

{lim}_{t \to + \infty} y (t) = {lim}_{t \to + \infty} z (t) = 0

. From this we deduce, again as above, that

w (t)

is bounded, and this is a contradiction. □

Proposition 6.

It cannot be

{lim}_{t \to + \infty} z (t) = + \infty

Proof.

Also in this case we argue by contradiction. We will show that, if

{lim}_{t \to + \infty} z (t) = + \infty

, then it holds also

{lim}_{t \to + \infty} w (t) = + \infty

, and this impossible by Proposition 5. So, let us assume

{lim}_{t \to + \infty} z (t) = + \infty

. As a consequence, for any

γ > 0

we can fix

T_{γ} > 0

such that for all

t \geq T_{γ}

z (t) \geq γ (1 + \frac{σ}{δ})

Claim: it cannot be

w (t) \leq \frac{δ}{σ} (y + z) (t)

for all

t \geq T_{γ}

. Indeed, in this case it would be

w^{'} (t) \geq 0

for all

t \geq T_{γ}

, implying w is increasing on

[T_{γ}, + \infty)

. Thus, there would be a limit

l_{+} = {lim}_{t \to + \infty} w (t) > 0

. By Proposition 5 it cannot be

l_{+} = + \infty

, so it must be

l_{+} < + \infty

, hence

δ y + δ z - σ w

would go to

+ \infty

, leading to

w^{'} \geq a w

for some

a > 0

in a half-line

(α, + \infty)

. This of course implies

{lim}_{t \to + \infty} w (t) = + \infty

contradicting the assumption

l_{+} < + \infty

. The contradiction proves the claim.

Thanks to the previous claim, we can state that there exists

t_{γ} \geq T_{γ}

such that

w (t_{γ}) > \frac{δ}{σ} (y (t_{γ}) + z (t_{γ})) .

Let us now prove that

w (t) > γ

for all

t \geq t_{γ}

. Fix

t > t_{γ}

. If

w (t) \geq \frac{δ}{σ} (y (t) + z (t))

, then

w (t) \geq \frac{δ}{σ} z (t) > γ

(since

t > t_{γ} \geq T_{γ}

). Otherwise, if

w (t) < \frac{δ}{σ} (y (t) + z (t))

, define

τ_{1} = inf \{τ \in (t_{γ}, t) | w (s) < \frac{δ}{σ} (y (s) + z (s)), \forall s \in (τ, t)\} .

By continuity,

w (s) < \frac{δ}{σ} (y (s) + z (s))

for all s in

(τ_{1}, t)

. Hence w is increasing in

(τ_{1}, t)

, implying

w (t) \geq w (τ_{1})

. Furthermore, by standard continuity arguments,

w (τ_{1}) = \frac{δ}{σ} (y (τ_{1}) + z (τ_{1})) \geq γ

. Thus,

w (t) \geq γ

for all

t \geq t_{γ}

. Since this holds for any

γ > 0

, we conclude that

{lim}_{t \to + \infty} w (t) = + \infty

. However, Proposition 5 states that this is not possible, and the contradiction proves that

z (t)

cannot tend to

+ \infty

as t tends to

+ \infty

□

3. Steady States if $x \leq w$

We are now going to compute all the steady states of the system (2) in

\bar{C}

, and to study their stability. As we said in the introduction, in most cases we will be able to get an answer about the stability only for

δ \to 0^{+}

. In this section we deal with the case

x \leq w

. In this subset the equilibrium points are the solutions of the following system

\begin{matrix} x [- c + d \frac{μ x w}{w^{2} + μ^{2} x^{2}}] = 0 \end{matrix}

(4a)

\begin{matrix} y (γ λ - γ y - δ w) = 0 \end{matrix}

(4b)

\begin{matrix} z w [k \frac{w}{w^{2} + 1} - δ] = 0 \end{matrix}

(4c)

\begin{matrix} w [δ y + δ z - σ w] = 0 \end{matrix}

(4d)

We can consider the following cases:

i)

w = 0

. In this case we get

x = 0

, and from (4b) we have two possibilities: either

y = 0

y = λ

. There are no conditions on z, so we have two families of critical points:

\begin{matrix} \{(0, 0, Z, 0), Z \geq 0\} \end{matrix}

(5a)

\begin{matrix} \{(0, λ, Z, 0), Z \geq 0\} \end{matrix}

(5b)

We notice that the points (5a) correspond to what is called "desert state" in [11], while the points (5b) correspond to what is called "nature state" in the same paper.

ii)

w \neq 0

. In this situation we have

\begin{matrix} (4 a) \Rightarrow x = 0, & or c = d \frac{μ x w}{w^{2} + μ^{2} x^{2}} \\ (4 b) \Rightarrow y = 0, & or γ λ - γ y - δ w = 0 \\ (4 c) \Rightarrow z = 0, & or δ w^{2} - k w + δ = 0 \end{matrix}

and we can count 8 different cases.

We note that, if

x \neq 0

from (4a) we have

d \frac{μ x w}{w^{2} + μ^{2} x^{2}} = c \Rightarrow d \frac{\frac{w}{μ x}}{{(\frac{w}{μ x})}^{2} + 1} = c \Rightarrow d \frac{t}{t^{2} + 1} = c \Rightarrow c t^{2} - d t + c = 0

with

t = \frac{w}{μ x}

and so

\begin{matrix} t_{1} & = \frac{d - \sqrt{d^{2} - 4 c^{2}}}{2 c} \in (0, 1) \\ t_{2} & = \frac{d + \sqrt{d^{2} - 4 c^{2}}}{2 c} > 1 . \end{matrix}

(6)

Notice that the hypothesis

d > 2 c

rules out the case

t_{1} = t_{2} = 1

We then obtain two possible values for x given by

x_{1} = \frac{w}{μ t_{1}}, x_{2} = \frac{w}{μ t_{2}},

(7)

with

t_{1}, t_{2}

as in (6).

y \neq 0

then, from (4b),

γ λ - γ y - δ w = 0

, i.e.

y = λ - \frac{δ}{γ} w .

(8)

Finally, if

z \neq 0

then

w_{1} = \frac{k - \sqrt{k^{2} - 4 δ^{2}}}{2 δ}, w_{2} = \frac{k + \sqrt{k^{2} - 4 δ^{2}}}{2 δ}, with k \geq 2 δ .

(9)

We can now write down a complete list of equilibrium points, in the half-space

x \leq w

, when

w > 0

ii.1): First, we observe that if $x = y = z = 0$ , then from (4d) we get $w = 0$ , and thus we exclude this possibility, because we have already dealt with it (see above the case $w = 0$ ).
ii.2): If $x = y = 0$ and $z \neq 0$ from (4c) we have $w = w_{1, 2}$ and from (4d) $z_{1, 2} = \frac{σ}{δ} w_{1, 2}$ . Therefore, we have the two equilibrium points

$P_{i} = (0, 0, \frac{σ}{δ} w_{i}, w_{i}), i = 1, 2, k \geq 2 δ,$

(10)

where $w_{1}, w_{2}$ are given by (9).
ii.3): If $x = z = 0, y = λ - \frac{δ}{γ} w$ , then from (4d) we have $w = \frac{δ}{σ} y$ so that

$w = \frac{γ λ δ}{γ σ + δ^{2}}, y = \frac{γ λ σ}{γ σ + δ^{2}},$

(11)

and we obtain the equilibrium point

$P = (0, \frac{γ λ σ}{γ σ + δ^{2}}, 0, \frac{γ λ δ}{γ σ + δ^{2}}) .$

(12)
ii.4): If $x = 0, y = λ - \frac{δ}{γ} w$ , $z \neq 0$ , we obtain $w = w_{1, 2}$ , hence from (4d) we deduce

$z = - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w .$

We then get two equilibrium points

$P_{i} = (0, λ - \frac{δ}{γ} w_{i}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{i}, w_{i}), i = 1, 2, k \geq 2 δ .$

(13)
ii.5): If $x > 0$ and $y = z = 0$ , from (4d) we obtain $w = 0$ and we exclude this case because we are assuming $x \leq w$ .
ii.6): If $x > 0$ , $y = 0$ and $z > 0$ , from (4c) we get $w = w_{1, 2}$ , with $k \geq 2 δ$ . For x we get (7) with $d \geq 2 c$ , and from (4d) $z = \frac{σ w}{δ}$ . We have then 4 equilibrium points

$P_{i, j} = (\frac{w_{j}}{μ t_{i}}, 0, \frac{σ w_{j}}{δ}, w_{j}), i, j = 1, 2, k \geq 2 δ, d \geq 2 c .$

(14)

with $w_{j}$ as in (9) and $t_{i}$ as in (6).
ii.7): If $x > 0$ , $y > 0$ , $z = 0$ , from (4d) we deduce for y and w the same values as in (11). Also, x is as in (7), and we obtain the two equilibrium points

$P_{i} = (\frac{δ γ λ}{μ t_{i} (γ σ + δ^{2})}, \frac{γ λ σ}{γ σ + δ^{2}}, 0, \frac{δ γ λ}{γ σ + δ^{2}}), i = 1, 2, d \geq 2 c .$

(15)
ii.8): If $x > 0, y > 0, z > 0$ , then $λ - \frac{δ}{γ} w$ and arguing as in [ii.7] wee obtain 4 equilibrium points

$P_{i, j} = (\frac{w_{j}}{μ t_{i}}, λ - \frac{δ}{γ} w_{j}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{j}, w_{j}), i, j = 1, 2, k \geq 2 δ, d \geq 2 c .$

(16)

with $w_{j}$ as in (9) and $t_{i}$ as in (6).

In the two next sections we are going to discuss the stability of these equilibrium points. In the case

w = 0

we will obtain a complete result. For all the other equilibria above, we will study the stability as

δ \to 0^{+}

4. Instability of Equilibria in the Case $w = 0$

In this section we study the stability of the two families of equilibria (5a), (5b). We will obtain that they all are unstable.

Proposition 7.

Let

Z \geq 0

and

P = (0, 0, Z, 0)

. Then P is an unstable equilibrium point.

Proof.

Let

ϵ = min \{\frac{γ λ}{3 δ}, \frac{λ}{3}\}

and let

B_{ϵ} (P)

be the ball with center P and radius

ϵ

. Let

Q = (x_{q}, y_{q}, z_{q}, w_{q})

be in

B_{ϵ} (P) \cap C

, where

C

is the positive cone defined above. Let

u (t, Q) = (x (t), y (t), z (t), w (t))

be the trajectory starting from Q, so that

u (0, Q) = Q

. We want to prove that there exists

t > 0

such that

u (t, Q) \notin B_{ϵ} (P)

. By contradiction, assume

u (t, Q) \in B_{ϵ} (P)

for every

t \geq 0

. Then

0 < y (t) < \frac{λ}{3}

and

m (x (t), w (t)) < \frac{γ λ}{3 δ}

for every

t \geq 0

, thus

γ y < \frac{γ λ}{3}

and

δ m (x, w) < \frac{γ λ}{3}

, hence

γ λ - γ y - δ m (x, w) > γ λ - \frac{γ λ}{3} - \frac{γ λ}{3} = \frac{γ λ}{3}

[0, + \infty)

. From this, we obtain

y^{'} = y (λ γ - γ y - δ m (x, w)) > y \frac{γ λ}{3}

and it easily follows that

y (t) \geq y_{0} e^{\frac{γ λ}{3} t} \to + \infty for t \to + \infty .

This contradicts the assumption

u (t, Q) \in B_{ϵ} (P)

and the contradiction proves our thesis, which in turn implies the instability of P.

□

Proposition 8.

Let

Z \geq 0

and

P = (0, λ, Z, 0)

. Then P is an unstable equilibrium point.

Proof.

Let

ϵ > 0

be such that

ϵ < \frac{λ δ}{2 (δ + σ)}

. This implies

δ (λ - ϵ) - σ ϵ > \frac{δ λ}{2} .

Let

B_{ϵ} (P)

be the ball centered at P with radius

ϵ

and let

Q = (x_{q}, y_{q}, z_{q}, w_{q}) \in B_{ϵ} (P) \cap C

. As in the previous proposition, we argue by contradiction. Let

u (t, Q)

be the trajectory starting from Q. If it were

u (t, Q) \in B_{ϵ} (P)

for any

t \geq 0

we would have

y (t) > λ - ϵ

and

w (t) < ϵ

for every

t \geq 0

, hence

δ y + δ z - σ w \geq δ (λ - ϵ) - σ ϵ > \frac{δ λ}{2}

thus

w^{'} = m (x, w) (δ y + δ z - σ w) \geq m (x, w) \frac{δ λ}{2} \geq w \frac{δ λ}{2} .

Therefore, we obtain

w (t) \geq w_{0} e^{\frac{δ λ}{2} t}

for every

t \geq 0

and thus

w \to + \infty

, contradicting the hypothesis

u (t, Q) \in B_{ϵ} (P)

for every

t \geq 0

. The contradiction proves that there exists

t > 0

such that

u (t, Q) \notin B_{ϵ} (P)

and since this holds for every

Q \in B_{ϵ} (P) \cap C

, it follows that P is unstable.

□

5. Stability of Equilibria in the Case $w \neq 0$

In this section we study the stability of equilibrium points with

x \leq w

and

w \neq 0

. These are the equilibria listed above from ii2) to ii8), recalling that we have ruled out the cases ii1) and ii5). We will limit our study to what happens as

δ \to 0^{+}

, assuming that the other parameters remain fixed. We will analyze the Jacobian matrix at equilibria, and this is not possible if an equilibrium lies on the hyperplane

x = w

, because there the vector field F is not differentiable. So let us prove, as first thing, the following proposition.

Proposition 9.

P = (x_{0}, y_{0}, z_{0}, w_{0})

is an equilibrium point and

w_{0} > 0

, then

x_{0} \neq w_{0}

Proof.

We argue by contradiction. If P is an equilibrium point and

x_{0} = w_{0} > 0

, then by (4a) we obtain

- c + \frac{d μ}{1 + μ^{2}} = 0,

that is,

μ = \frac{d + \sqrt{d^{2} - 4 c^{2}}}{2 c}

μ = \frac{d - \sqrt{d^{2} - 4 c^{2}}}{2 c} \leq 1

. Our hypotheses on

μ

rule out both these possibilities.

□

To study the stability of the problem, we introduce the Jacobian matrix of the differential model (2). Recall that we are studying the case

x \leq w

w > 0

, and by the previous proposition we can assume

x < w

. We obtain

J (X) = (\begin{matrix} - c + 2 d μ \frac{x w^{3}}{{(w^{2} + μ^{2} x^{2})}^{2}} & 0 & 0 & \frac{d μ x^{2} (μ^{2} x^{2} - w^{2})}{{(w^{2} + μ^{2} x^{2})}^{2}} \\ 0 & γ λ - 2 γ y - δ w & 0 & - δ y \\ 0 & 0 & \frac{k w^{2}}{w^{2} + 1} - δ w & \frac{2 k w z}{{(w^{2} + 1)}^{2}} - δ z \\ 0 & δ w & δ w & δ y + δ z - 2 σ w \end{matrix}) .

As we can see,

ρ_{1} = - c + 2 d μ \frac{x w^{3}}{{(w^{2} + μ^{2} x^{2})}^{2}}

is always an eigenvalue of the Jacobian calculated at the critical points. In cases from ii.2) to ii.4), as

x = 0

, we get

ρ_{1} = - c < 0

. In cases ii.6) to ii.8) we note that

\frac{μ x w^{3}}{{(w^{2} + μ^{2} x^{2})}^{2}} = {(\frac{w}{μ x})}^{3} \frac{1}{{(1 + {(\frac{w}{μ x})}^{2})}^{2}} = \frac{t^{3}}{{(1 + t^{2})}^{2}}

where

t = w / μ x

, so

ρ_{1} (t) = - c + 2 d μ \frac{x w^{3}}{{(w^{2} + μ^{2} x^{2})}^{2}} = - c + 2 d \frac{t^{3}}{{(1 + t^{2})}^{2}} = \frac{c}{d} (2 t c - d)

since we are in the case in which

d \frac{t}{1 + t^{2}} = c

. When

t = t_{2} = \frac{d + \sqrt{d^{2} - 4 c^{2}}}{2 c}

we have

ρ_{1} (t_{2}) = \frac{c}{d} \sqrt{d^{2} - 4 c^{2}} > 0

(17)

and when

t = t_{1} = \frac{d - \sqrt{d^{2} - 4 c^{2}}}{2 c}

we have

ρ_{1} (t_{1}) = - \frac{c}{d} \sqrt{d^{2} - 4 c^{2}} < 0 .

(18)

Thus, in cases from ii.6) to ii.8), the points corresponding to

t_{2}

are always unstable, for any value of the parameters, while for equilibrium points corresponding to

t = t_{1}

a more detailed analysis will be carried on.

Let’s now study the various cases previously determined.

ii.2): As we just said an eigenvalue of the Jacobian matrix $J (P_{i})$ is given by $ρ_{1} = - c < 0$ . So we have to study the eigenvalues of the submatrix

$(\begin{matrix} γ λ - δ w & 0 & 0 \\ 0 & \frac{k w^{2}}{w^{2} + 1} - δ w & \frac{2 k w z}{{(w^{2} + 1)}^{2}} - δ z \\ δ w & δ w & δ z - 2 σ w \end{matrix}) .$

(19)

We note that we have the eigenvalue $ρ_{2} = γ λ - δ w$ and, for $w_{1}, w_{2}$ as in (9), with $k \geq 2 δ$ , $δ \to 0^{+}$ , we obtain the following expansions

$\begin{matrix} w_{1} & = \frac{δ}{k} + O (δ^{3}), \end{matrix}$

(20)

$\begin{matrix} w_{2} & = \frac{k}{δ} - \frac{δ}{k} + O (δ^{3}) . \end{matrix}$

(21)

We need to distinguish the two cases $P_{1} = (0, 0, \frac{σ}{δ} w_{1}, w_{1})$ and $P_{2} = (0, 0, \frac{σ}{δ} w_{2}, w_{2})$ . Due to the continuous dependence of the eigenvalues on the coefficients of the matrix, we can conclude that the point $P_{1}$ is unstable as $δ \to 0^{+}$ because $J (P_{1})$ has the eigenvalue $ρ_{2} = γ λ - δ w_{1} > 0$ , given that $δ w_{1} \to 0^{+}$ . We have then proved the following proposition.

Proposition 10.
The point $P_{1} = (0, 0, \frac{σ}{δ} w_{1}, w_{1})$ , with $w_{1}$ as in (9), is an unstable equilibrium point as $δ \to 0^{+}$ .

As to $P_{2}$ we notice that $δ w_{2} \to k$ for $δ \to 0^{+}$ , and therefore we must take in account the sign of $γ λ - k$ . If $γ λ - k > 0$ we have that the matrix $J (P_{2})$ has an eigenvalue $ρ_{2} = ρ_{2} (δ)$ which, by continuous dependance of the eigenvalues of a matrix on the entries, tends to the value $γ λ - k > 0$ as $δ \to 0^{+}$ . We then obtain, in this case, the instability for the point $P_{2}$ as $δ \to 0^{+}$ . Let us now assume $γ λ - k < 0$ . We consider the submatrix $\hat{J} (P_{2})$ defined as follows

$\hat{J} (P_{2}) = (\begin{matrix} \frac{k w_{2}^{2}}{w_{2}^{2} + 1} - δ w_{2} & \frac{2 k w_{2} z}{{(w_{2}^{2} + 1)}^{2}} - δ z \\ δ w_{2} & δ z - 2 σ w_{2} \end{matrix}) = (\begin{matrix} O (δ^{2}) & - \frac{k σ}{δ} + O (δ) \\ k + O (δ^{2}) & - \frac{k σ}{δ} + O (δ) \end{matrix}) .$

(22)

We easily get that, as $δ \to 0^{+}$ , the trace of the matrix $\hat{J} (P_{2})$ becomes negative and its determinant positive. This implies that the eigenvalues of $\hat{J} (P_{2})$ have strictly negative real parts. Now, the eigenvalues of the matrix $J (P_{2})$ are given by $ρ_{1} = - c < 0, ρ_{2} = γ λ - k$ and by the two eigenvalues of $\hat{J} (P_{2})$ . Hence, we have proved the following proposition.

Proposition 11.
As $δ \to 0^{+}$ , the point $P_{2} = (0, 0, \frac{σ}{δ} w_{2}, w_{2})$ , with $w_{2}$ as in (9), is an unstable equilibrium point if $γ λ - k > 0$ , and it is an asymptotically stable equilibrium point if $γ λ - k < 0$ .
ii.3): We refer to P as (12). We consider $J (P)$ for $δ \to 0^{+}$ and we obtain

$J (P) = (\begin{matrix} - c & 0 & 0 & 0 \\ 0 & - γ λ + O (δ^{2}) & 0 & - λ δ + O (δ^{3}) \\ 0 & 0 & \frac{k λ - σ}{σ^{2}} λ δ^{2} + O (δ^{4}) & 0 \\ 0 & \frac{λ}{σ} δ^{2} + O (δ^{4}) & \frac{λ}{σ} δ^{2} + O (δ^{4}) & - λ δ + O (δ^{3}) \end{matrix})$

With some lengthy but standard computations we obtain the following eigenvalues

$\begin{matrix} ρ_{1} = - c < 0, & ρ_{2} = - λ δ + O (δ^{2}) < 0, \\ ρ_{3} = - γ λ + O (δ) < 0, & ρ_{4} = \frac{λ (k λ - σ)}{σ^{2}} δ^{2} + O (δ^{4}) . \end{matrix}$

As a consequence, we have the following result.

Proposition 12.
The point $P = (0, \frac{γ λ σ}{γ σ + δ^{2}}, 0, \frac{γ λ δ}{γ σ + δ^{2}})$ is an unstable equilibrium point if $k λ - σ > 0$ and is an asymptotically stable equilibrium point if $k λ - σ < 0$ as $δ \to 0^{+}$ .
ii.4): The Jacobian matrix calculated at the points $P_{i}, i = 1, 2$ is as follows

$J (P_{i}) = (\begin{matrix} - c & 0 & 0 & 0 \\ 0 & - γ λ + δ w & 0 & - δ y \\ 0 & 0 & 0 & δ z (\frac{2 δ}{k w} - 1) \\ 0 & δ w & δ w & - σ w \end{matrix}), i = 1, 2 .$

We use the Routh-Hurwitz criterion (see [5]) . As $ρ_{1} = - c$ is an eigenvalue, we can write the characteristic polynomial of $J (P_{i}), i = 1, 2$ , in the following form

$p_{4} (ρ) = (ρ + c) p_{3} (ρ) .$

(23)

with $p_{3} (ρ) = ρ^{3} + a_{1} ρ^{2} + a_{2} ρ + a_{3}$ . According to the Routh-Hurwitz criterion. the necessary and sufficient conditions for all roots of $p_{3} (ρ)$ to have a strictly negative real part are the following

$\begin{matrix} a_{1} > 0 \\ a_{1} a_{2} > a_{3} > 0 . \end{matrix}$

(24)

Let’s study the stability of the point $P_{1}$ obtained by setting $w = w_{1}$ as in (9). After some lengthy but standard computations we get

$\begin{matrix} a_{1} = γ λ + O (δ) > 0 \\ a_{2} = \frac{γ λ σ}{k} δ + O (δ^{3}) > 0 \\ a_{3} = \frac{γ λ (k λ - σ)}{k^{2}} δ^{3} + O (δ^{5}) \\ a_{1} a_{2} - a_{3} = \frac{γ^{2} λ^{2} σ}{k} δ + O (δ^{2}) > 0 . \end{matrix}$

Hence, we get instability when $k λ - σ < 0$ , stability when $k λ - σ > 0$ . However, the asymptotic development of the z component of $P_{1}$ gives

$z = - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{1} = - \frac{1}{k} (k λ - σ) + O (δ^{3}),$

hence, in the case of stability, the equilibrium $P_{1}$ is not in $\bar{C}$ , as $δ \to 0$ . We conclude that the following proposition holds true.

Proposition 13.
The point $P_{1} = (0, λ - \frac{δ}{γ} w_{1}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{1}, w_{1}), k \geq 2 δ$ , with $w_{1}$ as in (9), is an unstable equilibrium as $δ \to 0^{+}$ if $k λ - σ < 0$ . If $k λ - σ > 0$ the point $P_{1}$ is an asymptotically stable equilibrium of the ODE system (2), but it is not in $\bar{C}$ , as $δ \to 0^{+}$ .

We now study the point $P_{2}$ with $w = w_{2}$ as in (9). After some computations, we obtain the following results for the coefficients of $p_{3}$ :

$\begin{matrix} a_{1} = \frac{k σ}{δ} + O (1) > 0 \\ a_{2} = \frac{k γ λ σ}{δ} + O (δ) > 0 \\ a_{3} = \frac{k^{2} σ (γ λ - k)}{δ} + O (δ) \\ a_{1} a_{2} - a_{3} = \frac{γ λ σ^{2} k^{2}}{δ^{2}} + O (δ^{- 1}) > 0 . \end{matrix}$

Hence, by applying the Routh-Hurwitz criterion again, we get that, as $δ \to 0^{+}$ , the critical point $P_{2}$ is stable when $γ λ - k > 0$ , unstable when $γ λ - k < 0$ . But in $P_{2}$ we have

$y = λ - \frac{δ}{γ} w_{2} = λ - \frac{k}{γ} + O (δ^{2}) .$

Hence, in the instability case $γ λ - k < 0$ , we have $y < 0$ as $δ \to 0^{+}$ , and $P_{2}$ is not in $\bar{C}$ . We have then proved the following proposition.

Proposition 14.
The point $P_{2} = (0, λ - \frac{δ}{γ} w_{2}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{2}, w_{2}), k \geq 2 δ$ , with $w_{2}$ as in (9), is an asymptotically stable equilibrium point if $γ λ - k > 0$ as $δ \to 0^{+}$ . When $γ λ - k < 0$ $P_{2}$ is an unstable equilibrium point of the ODE system (2), but it is not in $\bar{C}$ , as $δ \to 0^{+}$ .
ii.6): In this case we have 4 critical point $P_{i, j} = P (t_{i}, w_{j}), i, j = 1, 2$ as in (14) with $t_{i}, w_{j}$ given in (6), (9) respectively. For sake of simplicity, we report the expression of the Jacobian matrix calculated at these points.

$J (P_{i, j}) = (\begin{matrix} - c + 2 d μ \frac{x w^{3}}{{(w^{2} + μ^{2} x^{2})}^{2}} & 0 & 0 & \frac{d μ x^{2} (μ^{2} x^{2} - w^{2})}{{(w^{2} + μ^{2} x^{2})}^{2}} \\ 0 & γ λ - δ w & 0 & 0 \\ 0 & 0 & 0 & \frac{2 k w z}{{(w^{2} + 1)}^{2}} - δ z \\ 0 & δ w & δ w & - σ w \end{matrix})$

Based on what is established in (17), the following proposition holds.

Proposition 15.
The points $P_{2, j} = (\frac{w_{j}}{μ t_{2}}, 0, \frac{σ w_{j}}{δ}, w_{j}), j = 1, 2, k \geq 2 δ, d \geq 2 c$ , with $t_{2}$ as in (6) and $w_{j}$ as in (9), are unstable equilibrium points.

Let’s now begin the study in the case $t = t_{1} = \frac{d - \sqrt{d^{2} - 4 c^{2}}}{2 c}$ where $ρ_{1} (t_{1}) < 0$ as seen in (18).

Let’s then analyze the eigenvalue $ρ_{2} = γ λ - δ w$ . We have

$\begin{matrix} ρ_{2} & = γ λ - k + O (δ^{2}) if w = w_{2} \\ ρ_{2} & = γ λ + O (δ^{2}) if w = w_{1} . \end{matrix}$

Therefore, the Jacobian calculated at point $P_{1, 1}$ has a positive eigenvalue for $δ \to 0^{+}$ and thus the equilibrium $P_{1, 1}$ is unstable. As for point $P_{1, 2}$ , we must distinguish between two cases. If $γ λ - k > 0$ then this equilibrium will also be unstable, so let us see what happens if $γ λ - k < 0 .$ . In this case the eigenvalues of $J (P_{1, 2})$ are as follows. A first one is given by $ρ_{1} (t_{1})$ as in (18), a second one is $ρ_{2} = γ λ - k + O (δ^{2}) < 0$ . The last two are the eigenvalues of the following matrix $\hat{J} (P_{1, 2})$ :

$\hat{J} (P_{1, 2}) = (\begin{matrix} 0 & \frac{2 k w_{2} z}{{(w_{2}^{2} + 1)}^{2}} - δ z \\ δ w_{2} & - σ w_{2} \end{matrix}) = (\begin{matrix} 0 & - \frac{k σ}{δ} + O (δ) \\ k + O (δ^{2}) & - \frac{k σ}{δ} + O (δ) \end{matrix}) .$

As $δ \to 0^{+}$ this matrix has strictly negative trace and strictly positive determinant, so its eigenvalues have strictly negative real parts. Thus we have proved that, in this case, the point $P_{1, 2}$ is a stable equilibrium. Let’s summarize everything in the following proposition.

Proposition 16.
The point $P_{1, 1} = (\frac{w_{1}}{μ t_{1}}, 0, \frac{σ w_{1}}{δ}, w_{1}), k \geq 2 δ, d \geq 2 c$ , with $t_{1}$ as in (6) and $w_{1}$ as in (9), is an unstable equilibrium. The point $P_{1, 2} = (\frac{w_{2}}{μ t_{1}}, 0, \frac{σ w_{2}}{δ}, w_{2}), k \geq 2 δ, d \geq 2 c$ , with $t_{1}$ as in (6) and $w_{2}$ as in (9), is an unstable equilibrium if $γ λ - k > 0$ and is an asymptotically stable equilibrium if $γ λ - k < 0$ .
ii.7): Based on what is established in (17), the following proposition holds.

Proposition 17.
The point $P_{2} = (\frac{δ γ λ}{μ t_{2} (γ σ + δ^{2})}, \frac{γ λ σ}{γ σ + δ^{2}}, 0, \frac{γ λ δ}{γ σ + δ^{2}})$ is an unstable equilibrium point.

Let’s then analyze the behavior of the Jacobian matrix calculated at point $P_{1} = (\frac{δ γ λ}{μ t_{1} (γ σ + δ^{2})}, \frac{γ λ σ}{γ σ + δ^{2}}, 0, \frac{δ γ λ}{γ σ + δ^{2}}) .$ In this case, the Jacobian matrix is almost the same one computed at point P in case ii.3). Indeed, the two points differ only for their first entry, and the two Jacobian matrices only for the entries $j_{1, 1}$ (first row, first column). Hence, the two matrices have different $ρ_{1}$ eigenvalues ( $ρ_{1} = - c$ in case ii.3), $ρ_{1} = - \frac{c}{d} \sqrt{d^{2} - 4 c^{2}}$ in the present case), but both are negative, while the other three eigenvalues are the same as in the case ii.3). Using the results we have obtained in that case, we get the following proposition

Proposition 18.
The point $P_{1} = (\frac{δ γ λ}{μ t_{1} (γ σ + δ^{2})}, \frac{γ λ σ}{γ σ + δ^{2}}, 0, \frac{γ λ δ}{γ σ + δ^{2}})$ is an unstable equilibrium if $k λ - σ > 0$ and is an asymptotically stable equilibrium if $k λ - σ < 0$ as $δ \to 0^{+}$ .
ii.8): In this case we have 4 critical point $P_{i, j} = P (t_{i}, w_{j}), i, j = 1, 2$ as in (16) with $t_{i}, w_{j}$ given in (6), (9) respectively. Based on what is established in (17), the following proposition holds.

Proposition 19.
The points $P_{2, j} = (\frac{w_{j}}{μ t_{2}}, λ - \frac{δ}{γ} w_{j}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{j}, w_{j}),$ $j = 1, 2, k \geq 2 δ, d \geq 2 c$ with $t_{2}$ as in (6) and $w_{j}$ as in (9), are unstable equilibria.

Regarding the points $P_{1, j}$ ( $j = 1, 2$ ) we argue as we have just done for the previous case ii.7). Indeed, in this case, the Jacobian matrix is almost the same one computed at point $P_{2}$ in case ii.4): the two points differ only for their first entry, and the two Jacobian matrices only for the entries $j_{1, 1}$ , hence the two matrices have different $ρ_{1}$ eigenvalues, which are both negative, while the other three eigenvalues are the same in the two cases. Using the arguments and the results of case ii.4), we get the following proposition

Proposition 20.
The point $P_{1, 1} = (\frac{w_{1}}{μ t_{1}}, λ - \frac{δ}{γ} w_{1}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{1}, w_{1})$ , with $w_{1}$ as in (9), is an unstable equilibrium as $δ \to 0^{+}$ if $k λ - σ < 0$ . If $k λ - σ > 0$ the point $P_{1, 1}$ is an asymptotically stable equilibrium of the ODE system (2), but it is not in $\bar{C}$ , as $δ \to 0^{+}$ . The point

$P_{1, 2} = (\frac{w_{2}}{μ t_{1}}, λ - \frac{δ}{γ} w_{2}, - λ + (\frac{δ}{γ} + \frac{σ}{δ}) w_{2}, w_{2}), k \geq 2 δ$ ,

with $w_{2}$ as in (9) is an asymptotically stable equilibrium if $γ λ - k > 0$ as $δ \to 0^{+}$ . When $γ λ - k < 0$ $P_{1, 2}$ is an unstable equilibrium of ODE system (2), but it is not in $\bar{C}$ , as $δ \to 0^{+}$ .

6. Fixed points and stability if $x > w$

We are now going to look for the equilibria, and their stability, in the case

x > w

. To compute the equilibria we need to consider the system

\begin{matrix} x [- c + d \frac{μ x w}{w^{2} + μ^{2} x^{2}}] = 0 \end{matrix}

(25a)

\begin{matrix} y (γ λ - γ y - δ x) = 0 \end{matrix}

(25b)

\begin{matrix} x z [k \frac{w}{x w + 1} - δ] = 0 \end{matrix}

(25c)

\begin{matrix} x [δ y + δ z - σ w] = 0 \end{matrix}

(25d)

We note that x cannot be zero since

x > w \geq 0

. Therefore, as equation (4a) coincides with (25a), we will always have the relation

w = t_{i} μ x, i = 1, 2

(26)

with

t_{i}

given by (6). Moreover, it cannot be

y = z = 0

because this would lead, from (25d), to

w = 0

and, as just stated,

x = 0

We distinguish the following cases:

iii.1): $y = 0$ and $z \neq 0$ . From (25d) we obtain $z = \frac{σ}{δ} w$ . From (25c), we obtain

$\begin{matrix} w_{1} (t) & = \frac{k μ t - \sqrt{k^{2} μ^{2} t^{2} - 4 δ^{2} t μ}}{2 δ}, \\ w_{2} (t) & = \frac{k μ t + \sqrt{k^{2} μ^{2} t^{2} - 4 δ^{2} t μ}}{2 δ}, k^{2} μ t - 4 δ^{2} \geq 0 . \end{matrix}$

(27)

Let us set $w_{i, j} = w_{j} (t_{i}),$ with $i, j = 1, 2,$ and $t_{i}$ as in (6). We have the expression for x from (26). Hence, we obtain the following equilibria

$P_{i, j} = (\frac{w_{i, j}}{μ t_{i}}, 0, \frac{σ}{δ} w_{i, j}, w_{i, j}) i, j = 1, 2 .$

(28)
iii.2): $z = 0$ and $y \neq 0$ . From (25d) and (26), we have $y = \frac{σ}{δ} w = σ t_{i} μ x / δ$ that substituite in (25b) give us the expression for x

$x = \frac{δ γ λ}{δ^{2} + γ μ σ t_{i}}, i = 1, 2 .$

(29)

Then we have two equilibrium points

$P_{i} = (\frac{δ γ λ}{δ^{2} + γ μ σ t_{i}}, \frac{γ λ μ σ t_{i}}{δ^{2} + γ μ σ t_{i}}, 0, \frac{δ γ λ μ t_{i}}{δ^{2} + γ μ σ t_{i}}) i = 1, 2 .$

(30)
iii.3): $y \neq 0, z \neq 0$ . From (25c) we obtain the expression (27) for w and from (26) the expression for x. Then (25b) gives us the expression for y and finally the (25d) the value of z. So we have four equilibrium points

$P_{i, j} = (\frac{w_{i, j}}{μ t_{i}}, λ - \frac{δ}{γ μ t_{i}} w_{i, j}, - λ + (\frac{δ}{γ μ t_{i}} + \frac{σ}{δ}) w_{i, j}, w_{i, j}) i, j = 1, 2 .$

(31)

with $k^{2} μ t_{i} - 4 δ^{2} \geq 0$ .

Let us now study the stability of these equilibria. For this, we compute the Jacobian matrix of the differential model (2) with

x > w

. Recalling that

c = d \frac{t}{t^{2} + 1}

and considering (26) we obtain

J (X) = (\begin{matrix} \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} & 0 & 0 & - \frac{d (t^{2} - 1)}{μ {(t^{2} + 1)}^{2}} \\ - δ y & γ λ - 2 γ y - δ x & 0 & 0 \\ \frac{k w z}{{(x w + 1)}^{2}} - δ z & 0 & \frac{k x w}{x w + 1} - δ x & \frac{k x z}{{(x w + 1)}^{2}} \\ δ y + δ z - σ w & δ x & δ x & - σ x \end{matrix}),

so that

j_{1, 4} = - \frac{j_{1, 1}}{μ t}

. Since

t_{1} \in (0, 1)

and

t_{2} > 1

we have that if

t = t_{2}

then

j_{1, 1} > 0

j_{1, 4} < 0

and vice versa for

t = t_{1}

iii.1): As $y = 0$ , in this case the entry $j_{2, 2} = γ λ - δ x$ is an eigenvalue (with $x = x_{i, j} = w_{i, j} / μ t_{i}$ ). Let us call $ρ_{1}$ this eigenvalue. Considering the asymptotic for $δ \to 0^{+}$ we obtain

$\begin{matrix} w_{1} (t) & = \frac{1}{k} δ + O (δ^{3}) \\ w_{2} (t) & = \frac{k μ t}{δ} + O (δ) \end{matrix}$

(32)

and we can state

$\begin{matrix} ρ_{1} & = γ λ + O (δ^{2}) & if w = w_{i, 1}, i = 1, 2, \\ ρ_{1} & = γ λ - k + O (δ^{2}) & if w = w_{i, 2}, i = 1, 2 . \end{matrix}$

(33)

Therefore, the Jacobian matrix calculated at the points $P_{i, 1}$ for $δ \to 0^{+}$ has at least one positive eigenvalue, and therefore the equilibria $P_{i, 1}$ are unstable. We thus state the following proposition.

Proposition 21.
The critical points $P_{i, 1} = (\frac{w_{i, 1}}{μ t_{i}}, 0, \frac{σ}{δ} w_{i, 1}, w_{i, 1}), i = 1, 2$ with $w_{i, 1}$ given in (27) and $t_{i}$ given in (6), are unstable equilibria for $δ \to 0^{+}$ .

The behavior of the points $P_{i, 2}$ depends instead on the sign of $γ λ - k$ . If $γ λ - k > 0$ these equilibria are unstable. We then study the behavior of such points under the assumption $γ λ - k < 0 .$ We examine the asymptotic behavior for $δ \to 0^{+}$ . The asymptotic of the Jacobian matrix $J (P_{i, 2})$ becomes

$J (P_{i, 2}) = (\begin{matrix} \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} & 0 & 0 & - \frac{d (t^{2} - 1)}{μ {(t^{2} + 1)}^{2}} \\ 0 & γ λ - k + O (δ^{2}) & 0 & 0 \\ - \frac{k μ σ t}{δ} + O (δ) & 0 & 0 & \frac{σ}{k μ t} δ + O (δ^{3}) \\ 0 & k + O (δ^{2}) & k + O (δ^{2}) & - \frac{k σ}{δ} + O (δ) \end{matrix}) .$

We use the Routh-Hurwitz criterion. We introduce the characteristic polynomial of $J (P_{i, 2})$

$p_{4} (ρ) = (ρ - γ λ + k + O (δ^{2})) (ρ^{3} + a_{1} ρ^{2} + a_{2} ρ + a_{3}) .$

(34)

Through some lengthy but standard computations we get

$\begin{matrix} a_{1} & = \frac{k σ}{δ} + O (1) \\ a_{2} & = \frac{k σ d t (1 - t^{2})}{{(t^{2} + 1)}^{2} δ} + O (δ) \\ a_{3} & = \frac{(1 - t^{2}) d k^{2} σ t}{{(t^{2} + 1)}^{2} δ} + O (δ) . \end{matrix}$

Let us recall that the necessary and sufficient condition for the roots of the polynomial $p_{3} (ρ) = ρ^{3} + a_{1} ρ^{2} + a_{2} ρ + a_{3}$ to have strictly negative real parts is that $a_{1}, a_{3} > 0$ e $a_{1} a_{2} - a_{3} > 0$ . We recall that $t_{1} \in (0, 1)$ and $t_{2} > 1$ as given in (6). Therefore, $a_{2} < 0$ and $a_{3} < 0$ if $t = t_{2}$ making $P_{2, 2}$ unstable. Conversely, $a_{2} > 0$ and $a_{3} > 0$ if $t = t_{1}$ with

$a_{1} a_{2} - a_{3} = \frac{k^{2} σ^{2} d t (1 - t^{2})}{{(t^{2} + 1)}^{2} δ^{2}} + O (δ^{- 1}) > 0 .$

We can therefore summarize in the following proposition.

Proposition 22.
The equilibrium point $P_{2, 2} = (\frac{w_{2, 2}}{μ t_{2}}, 0, \frac{σ}{δ} w_{2, 2}, w_{2, 2}),$ with $w_{2, 2}$ given in (27) and $t_{2}$ given in (6), is unstable for $δ \to 0^{+}$ . The equilibrium point $P_{1, 2} = (\frac{w_{1, 2}}{μ t_{1}}, 0, \frac{σ}{δ} w_{1, 2}, w_{1, 2}),$ with $w_{1, 2}$ given in (27) and $t_{1}$ given in (6), is unstable for $δ \to 0^{+}$ if $γ λ - k > 0$ . The equilibrium $P_{1, 2}$ is asymptotically stable for $δ \to 0^{+}$ if $γ λ - k < 0$ .
iii.2): In this case, we have two critical points $P_{i}, i = 1, 2$ as in (30). By doing the asymptotic expansion of the variables, for $δ \to 0^{+}$ , we obtain

$\begin{matrix} x_{i} & = \frac{δ γ λ}{δ^{2} + γ μ σ t_{i}} = \frac{λ}{μ σ t_{i}} δ + O (δ^{3}) \\ y_{i} & = \frac{γ λ μ σ t_{i}}{δ^{2} + γ μ σ t_{i}} = λ + O (δ^{2}) \\ z_{i} & = 0 \\ w_{i} & = \frac{δ γ λ μ t_{i}}{δ^{2} + γ μ σ t_{i}} = \frac{λ}{σ} δ + O (δ^{3}) \end{matrix}$

(35)

and the asymptotic Jacobian matrix calculated at these points becomes

$J (P_{i}) = (\begin{matrix} \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} & 0 & 0 & - \frac{d (t^{2} - 1)}{μ {(t^{2} + 1)}^{2}} \\ - λ δ + O (δ^{3}) & - γ λ + O (δ^{2}) & 0 & 0 \\ 0 & 0 & \frac{λ (k λ - σ)}{μ σ^{2} t} δ^{2} + O (δ^{4}) & 0 \\ 0 & \frac{λ}{μ σ t} δ^{2} + O (δ^{4}) & \frac{λ}{μ σ t} δ^{2} + O (δ^{4}) & - \frac{λ}{μ t} δ + O (δ^{3}) \end{matrix}),$

with $t = t_{1}, t_{2}$ . For $δ = 0$ , this matrix reduces to a diagonal matrix with an eigenvalue given by

$ρ_{1} = \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} .$

We have repeatedly noted that $ρ_{1} > 0$ if $t = t_{2}$ and $ρ_{1} < 0$ if $t = t_{1}$ . Due to the continuity of eigenvalues with respect to the elements of the matrix, in the case $t = t_{2}$ for $δ \to 0^{+}$ there is an eigenvalue of the Jacobian matrix that tends to a positive value, and therefore the critical point $P_{2}$ is unstable. If $t = t_{1}$ , we obtain instead $ρ_{1} < 0$ , hence we must apply the Routh-Hurwitz criterion to the characteristic polynomial $p_{4} (ρ)$ . The criterion states, in this case, that the necessary and sufficient conditions for all roots of characteristic polynomial $p_{4} (ρ) = ρ^{4} + a_{1} ρ^{3} + a_{2} ρ^{2} + a_{3} ρ + a_{4}$ to have a strictly negative real part are the following

$\{\begin{matrix} a_{i} > 0 i = 0, \dots, 4 \\ a_{1} a_{2} - a_{3} > 0 \\ a_{1} a_{2} a_{3} - a_{1}^{2} a_{4} - a_{3}^{2} > 0 . \end{matrix}$

(36)

After lengthy computations we obtain the following asymptotic developments of the coefficients of the polynomial $p_{4} (ρ)$ as $δ \to 0^{+}$

$\begin{matrix} a_{4} = - \frac{(k λ - σ) γ λ^{3} (1 - t^{2}) d}{μ^{2} σ^{2} t {(t^{2} + 1)}^{2}} δ^{3} + O (δ^{5}) \\ a_{3} = \frac{γ λ^{2} d (1 - t^{2})}{μ {(t^{2} + 1)}^{2}} δ + O (δ^{2}) \\ a_{2} = \frac{γ λ (1 - t^{2}) d t}{{(t^{2} + 1)}^{2}} + O (δ) \\ a_{1} = γ λ + \frac{d t (1 - t^{2})}{{(t^{2} + 1)}^{2}} + O (δ) \\ a_{1} a_{2} - a_{3} = a_{1} a_{2} + O (δ) \\ a_{1} a_{2} a_{3} - a_{1}^{2} a_{4} - a_{3}^{2} = a_{1} a_{2} a_{3} + O (δ^{2}) . \end{matrix}$

(37)

Recalling that $1 - t_{1}^{2} > 0$ , we have that $a_{1}, a_{2}, a_{3} > 0$ for $t = t_{1}$ . Also, we have $a_{4} > 0$ if $k λ - σ < 0$ . Analyzing the orders of magnitude of the coefficients, the last two conditions are definitely met when the leading terms of the coefficients of the characteristic polynomial are positive. On the other hand $p_{4} (ρ)$ obviously has a positive root if $a_{4} < 0$ . We can therefore conclude with the following proposition

Proposition 23.
The point $P_{2} = (\frac{δ γ λ}{δ^{2} + γ μ σ t_{2}}, \frac{γ λ μ σ t_{2}}{δ^{2} + γ μ σ t_{2}}, 0, \frac{δ γ λ μ t_{2}}{δ^{2} + γ μ σ t_{2}})$ , for $t_{2}$ defined in (6), is an unstable equilibrium point. The point $P_{1} = (\frac{δ γ λ}{δ^{2} + γ μ σ t_{1}}, \frac{γ λ μ σ t_{1}}{δ^{2} + γ μ σ t_{1}}, 0, \frac{δ γ λ μ t_{1}}{δ^{2} + γ μ σ t_{1}})$ , for $t_{1}$ defined in (6), is an asymptotically stable equilibrium point if $k λ - σ < 0$ and is unstable if $k λ - σ > 0$ .
iii.3): In this case, we have four equilibrium points varying with the values of $w_{i, j}$ see (27) and $t_{i}$ , see (6). We start with $w_{i, 1}$ for $i = 1, 2$ . Considering the asymptotic expansions of the variables for $δ \to 0^{+}$ , we obtain

$\begin{matrix} x_{i, 1} & = \frac{w_{i, 1}}{μ t_{i}} = \frac{δ}{k μ t_{i}} + O (δ^{3}) \\ y_{i, 1} & = λ - \frac{δ}{γ} x_{i, 1} = λ + O (δ^{2}) \\ z_{i, 1} & = - y_{i, 1} + \frac{σ}{δ} w_{i, 1} = \frac{σ}{k} - λ + O (δ^{2}) \\ w_{i, 1} & = \frac{k μ t_{i} - \sqrt{k^{2} μ^{2} t_{i}^{2} - 4 δ^{2} t_{i} μ}}{2 δ} = \frac{δ}{k} + O (δ^{3}) . \end{matrix}$

(38)

Notice that, when $λ k - σ > 0$ , we obtain $z_{i, 1} < 0$ as $δ \to 0^{+}$ , hence in this case the points $P_{i, 1}$ are not in the cone $C$ .

The developments above, when substituted into the Jacobian matrix, lead to

$J (P_{i, 1}) = (\begin{matrix} \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} & 0 & 0 & - \frac{d (t^{2} - 1)}{μ {(t^{2} + 1)}^{2}} \\ - λ δ + O (δ^{3}) & - γ λ + O (δ^{2}) & 0 & 0 \\ O (δ^{3}) & 0 & 0 & \frac{σ - k λ}{k μ t} δ + O (δ^{3}) \\ 0 & \frac{δ^{2}}{k t μ} + O (δ^{4}) & \frac{δ^{2}}{k t μ} + O (δ^{4}) & - \frac{σ}{k t μ} δ + O (δ^{3}) \end{matrix}) .$

We now argue as in the previous case, noticing that, when $δ = 0$ , this matrix reduces to a diagonal matrix with an eigenvalue

$ρ_{1} = \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} .$

As we know, this value satisfies $ρ_{1} > 0$ if $t = t_{2} > 1$ and $ρ_{1} < 0$ if $t = t_{1} \in (0, 1) .$ Therefore, when $t = t_{2}$ , due to the continuity of eigenvalues with respect to the elements of the matrix, there exists at least one positive eigenvalue as $δ \to 0^{+}$ , and thus the equilibrium point $P_{2, 1}$ is unstable.

We now proceed by studying the stability of the point $P_{1, 1}$ . We apply again Routh-Hurwitz criterion, and we study the characteristic polynomial $p_{4} (ρ)$ of the matrix and its coefficients $a_{i}$ , $i = 1, . ., 4$ . We want to study what happens for $δ \to 0^{+}$ , so we look at the asymptotic behavior of the $a_{i}$ ’s. We start noticing that

$\begin{matrix} a_{4} = \frac{(k λ - σ) γ λ (1 - t^{2}) d}{k^{2} μ^{2} t {(t^{2} + 1)}^{2}} δ^{3} + O (δ^{5}) \\ a_{3} = \frac{γ λ σ (1 - t^{2}) d t}{k μ t {(t^{2} + 1)}^{2}} δ + O (δ^{3}) \\ a_{2} = \frac{γ λ (1 - t^{2}) d t}{{(t^{2} + 1)}^{2}} + O (δ) \\ a_{1} = \frac{γ λ {(1 + t^{2})}^{2} + d t (1 - t^{2})}{{(t^{2} + 1)}^{2}} + O (δ) \\ a_{1} a_{2} - a_{3} = a_{1} a_{2} + O (δ) \\ a_{1} a_{2} a_{3} - a_{1}^{2} a_{4} - a_{3}^{2} = a_{1} a_{2} a_{3} + O (δ^{2}) \end{matrix}$

(39)

We have that $a_{1}, a_{2}, a_{3} > 0$ for $t = t_{1}$ and $a_{4} > 0$ for $t = t_{1}$ and $k λ - σ > 0 .$ Under these conditions, the $a_{1} a_{2} - a_{3}$ and $a_{1} a_{2} a_{3} - a_{1}^{2} a_{4} - a_{3}^{2}$ are also positive, as $δ \to 0^{+}$ .

We recall that the equilibria $P_{i, 1}$ are not in $C$ when $k λ - σ > 0$ . We collect our results in the following proposition:

Proposition 24.
$P_{2, 1}$ is an unstable equilibrium. If $k λ - σ > 0$ the equilibrium $P_{1, 1}$ is asymptotically stable but is not in $\bar{C}$ , together with $P_{2, 1}$ , as $δ \to 0^{+}$ . If $k λ - σ < 0$ the two equilibria are in $C$ and are unstable, as $δ \to 0^{+}$ .

We now proceed with the study of the stability of the points $P_{i, 2} .$ The asymptotic developments in this case are

$\begin{matrix} x_{i, 2} & = \frac{w_{i, 2}}{μ t_{i}} = \frac{k}{δ} + O (δ) \\ y_{i, 2} & = λ - \frac{δ}{γ} x_{i, 2} = λ - \frac{k}{γ} + O (δ^{2}) \\ z_{i, 2} & = - y_{i, 2} + \frac{σ}{δ} w_{i, 2} = \frac{σ k μ t_{i}}{δ^{2}} + O (1) \\ w_{i, 2} & = \frac{k μ t_{i} + \sqrt{k^{2} μ^{2} t_{i}^{2} - 4 δ^{2} t_{i} μ}}{2 δ} = \frac{k μ t_{i}}{δ} + O (δ) \end{matrix}$

(40)

which lead to the Jacobian matrix calculated at $P_{i, 2}$

$J (P_{i, 2}) = (\begin{matrix} \frac{d t (t^{2} - 1)}{{(t^{2} + 1)}^{2}} & 0 & 0 & - \frac{d (t^{2} - 1)}{μ {(t^{2} + 1)}^{2}} \\ (- λ + \frac{k}{γ}) δ + O (δ^{3}) & - γ λ + k + O (δ^{2}) & 0 & 0 \\ - \frac{σ k μ t}{δ} + O (δ) & 0 & O (δ^{6}) & \frac{σ δ}{k μ t} + O (δ^{3}) \\ 0 & k + O (δ^{2}) & k + O (δ^{2}) & - \frac{σ k}{δ} + O (δ) \end{matrix}) .$

We now apply the Routh-Hurwitz criterion to the characteristic polynomial $p_{4} (ρ) = ρ^{4} + a_{1} ρ^{3} + a_{2} ρ^{2} + a_{3} ρ + a_{1}$ with

$\begin{matrix} a_{4} = \frac{(γ λ - k) (1 - t^{2}) d k^{2} σ t}{{(t^{2} + 1)}^{2} δ} + O (δ) \\ a_{3} = \frac{γ λ σ k (1 - t^{2}) d t}{{(t^{2} + 1)}^{2} δ} + O (δ) \\ a_{2} = k σ [(γ λ - k) + \frac{d t (1 - t^{2})}{{(t^{2} + 1)}^{2}}] \frac{1}{δ} + O (1) \\ a_{1} = \frac{σ k}{δ} + O (1) \end{matrix}$

(41)

If we assume $γ λ - k < 0$ and $t = t_{1} \in (0, 1)$ we have $a_{4} < 0$ , while if $t = t_{2} > 1$ it holds $a_{2}, a_{3} < 0$ , and in both cases we obtain that there is an eigenvalue with strictly positive real part. Hence, in this case, the two equilibrium points we are dealing with are unstable. Notice also that from $γ λ - k < 0$ we derive $y_{i, 2} < 0$ as $δ \to 0^{+}$ , so in this case the two points are not in the positive cone.

Let us now assume $γ λ - k > 0$ . If $t = t_{2} > 1$ we obtain $a_{4} < 0$ and the equilibrium is unstable. If $t = t_{1} \in (0, 1)$ all the coefficients $a_{i}$ are positive. For the stability we have then to verify that, at least for $δ \to 0^{+}$ , it holds

$a_{1} a_{2} > a_{3}, a_{1} a_{2} a_{3} > {a_{1}}^{2} a_{4} + {a_{3}}^{2} .$

We have that $a_{1} a_{2}$ is led by a term of the type $c / δ^{2}$ , with $c > 0$ , while $a_{3} = O (δ^{- 1})$ , so the first inequality above is verified for small $δ$ ’s. Regarding the last condition, that is $a_{1} a_{2} a_{3} - a_{1}^{2} a_{4} - a_{3}^{2} > 0$ , we notice that $a_{3}^{2} = O (δ^{- 2})$ while $a_{1} a_{2} a_{3} = O (δ^{- 3})$ and $a_{1}^{2} a_{4} = O (δ^{- 3}) .$ Therefore, the last condition is simplified by requiring $a_{2} a_{3} - a_{1} a_{4} > 0 .$ With simple calculations, we obtain

$a_{2} a_{3} - a_{1} a_{4} = \frac{σ^{2} k^{2} d t (1 - t^{2})}{{(t^{2} + 1)}^{2}} [{(γ λ - k)}^{2} + γ λ \frac{d t (1 - t^{2})}{{(t^{2} + 1)}^{2}}] \frac{1}{δ^{2}} + O (δ^{- 1}),$

so the second condition is verified for $t = t_{1}$ and $δ \to 0^{+}$ . We summarize in the following proposition

Proposition 25.
If $γ λ - k < 0$ the two points $P_{i, 2}$ are both unstable equilibria of the system (2), but are not in $\bar{C}$ , as $δ \to 0^{+}$ . If $γ λ - k > 0$ and $δ \to 0^{+}$ , the point $P_{2, 2}$ is an unstable equilibrium, while the point $P_{1, 2}$ is an asymptotically stable equilibrium (and both are in $C$ ).

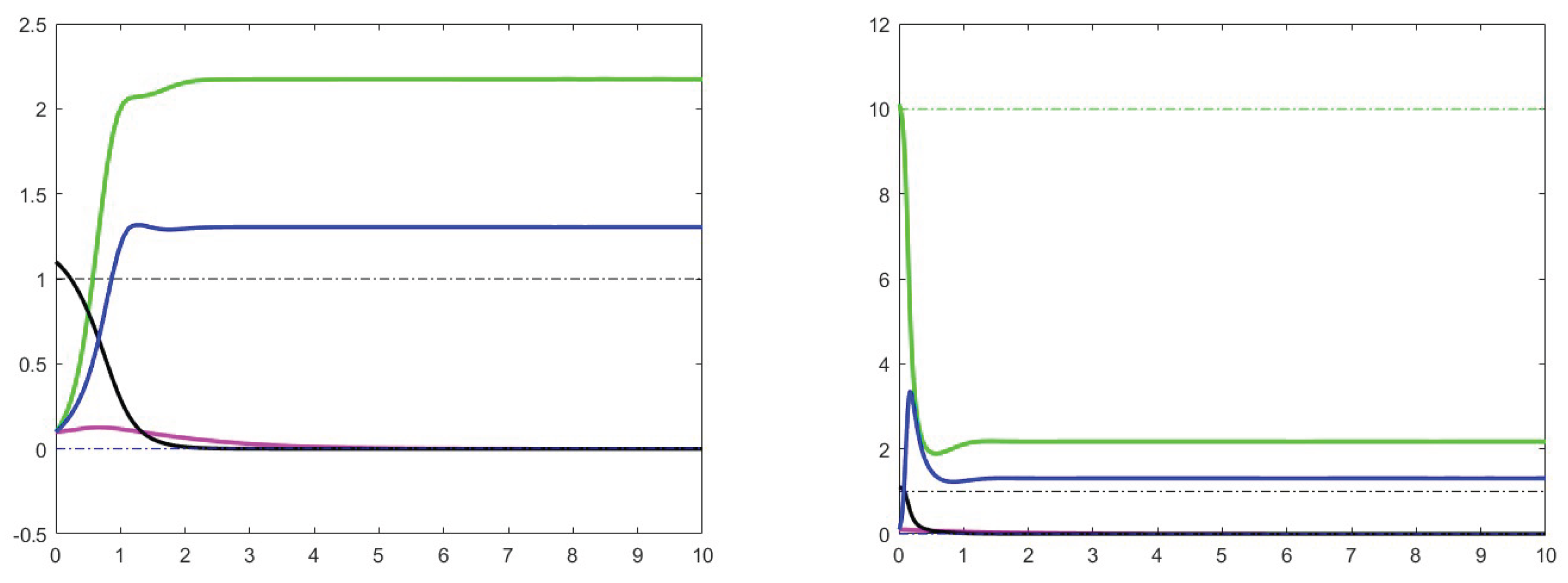
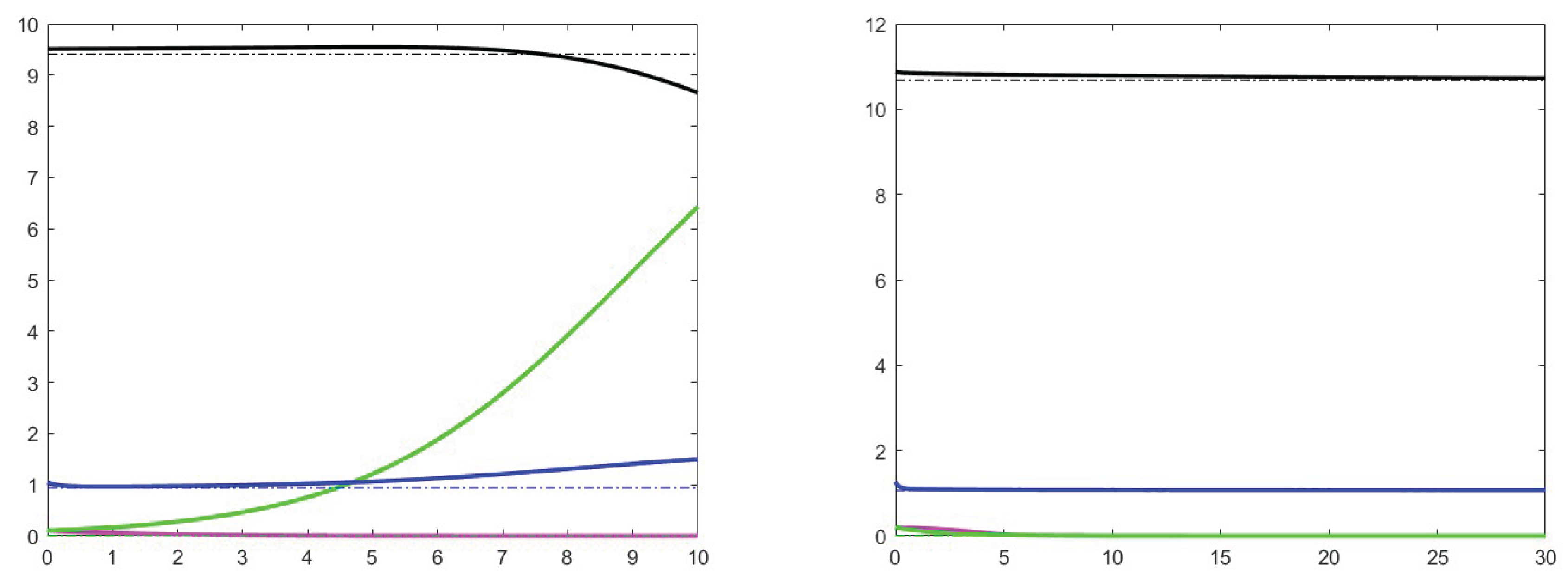
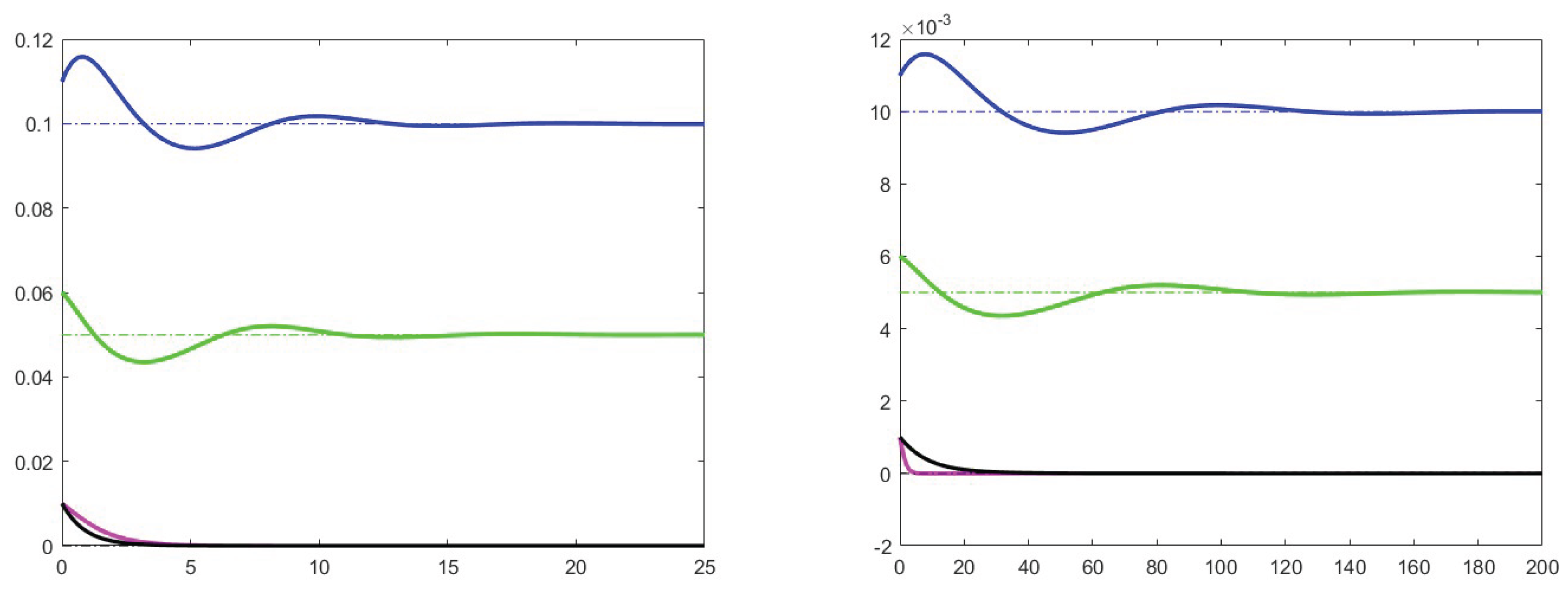
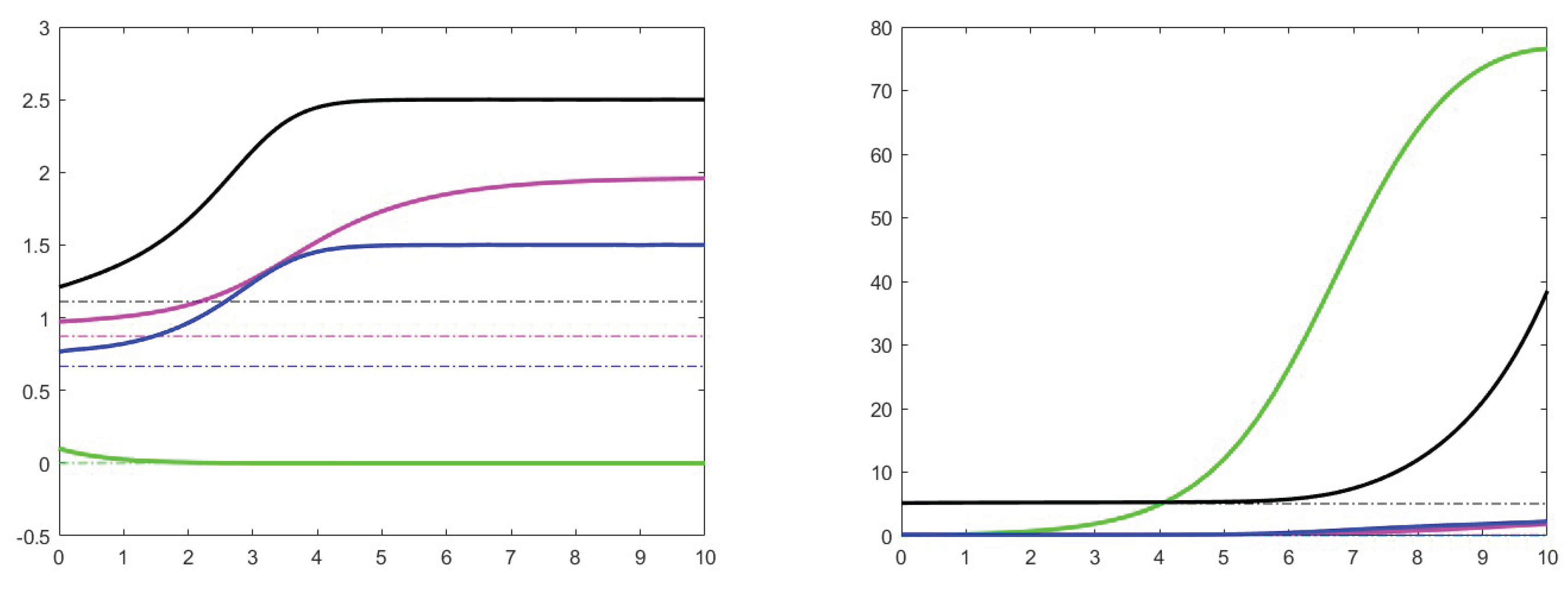
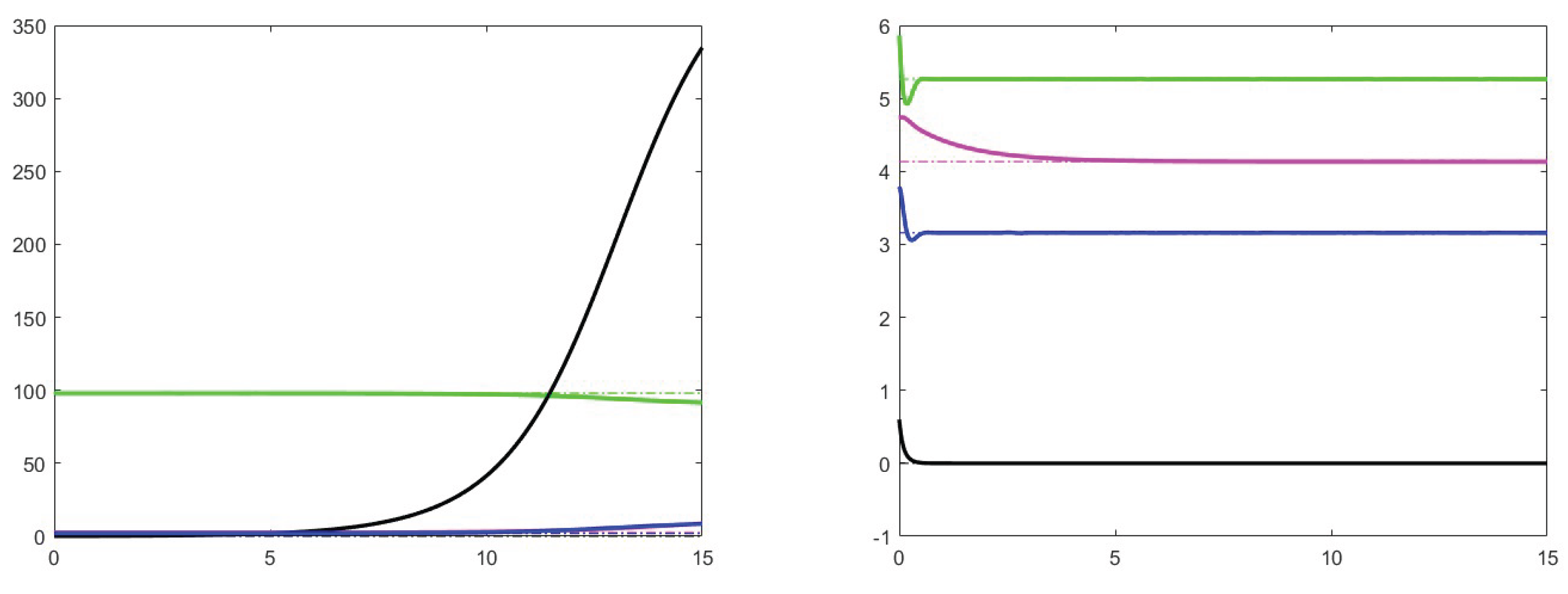
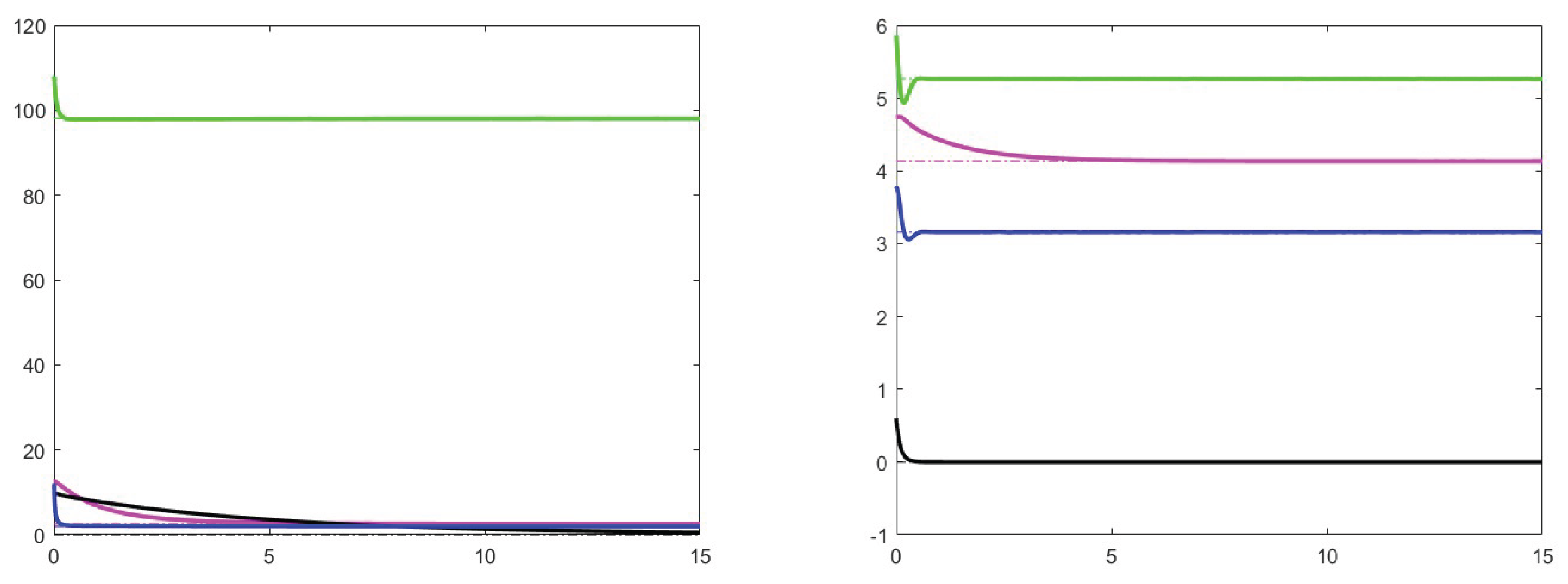
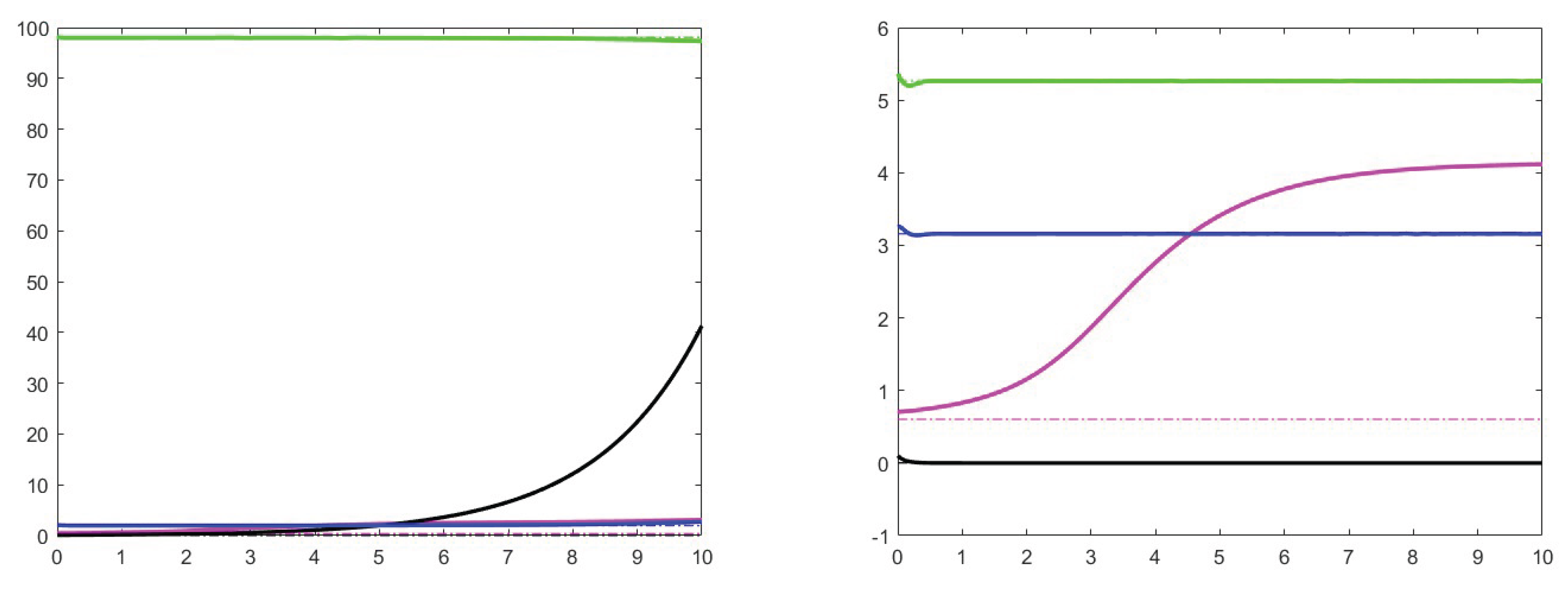
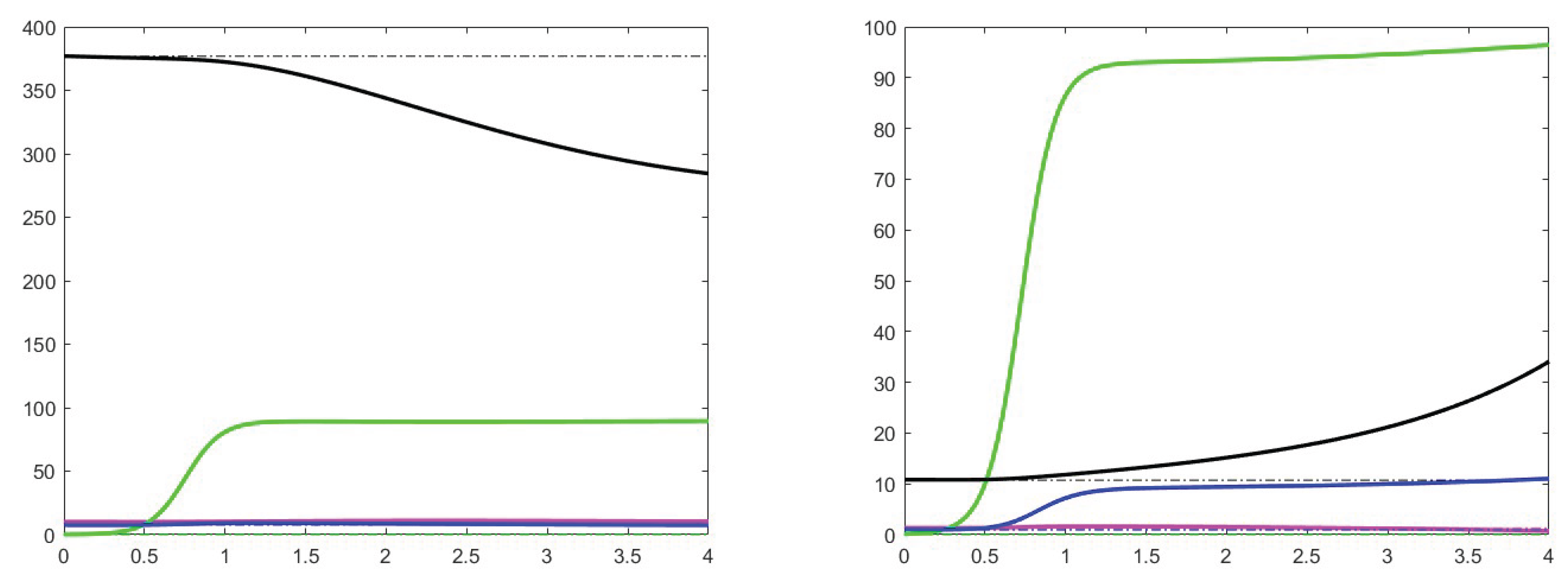
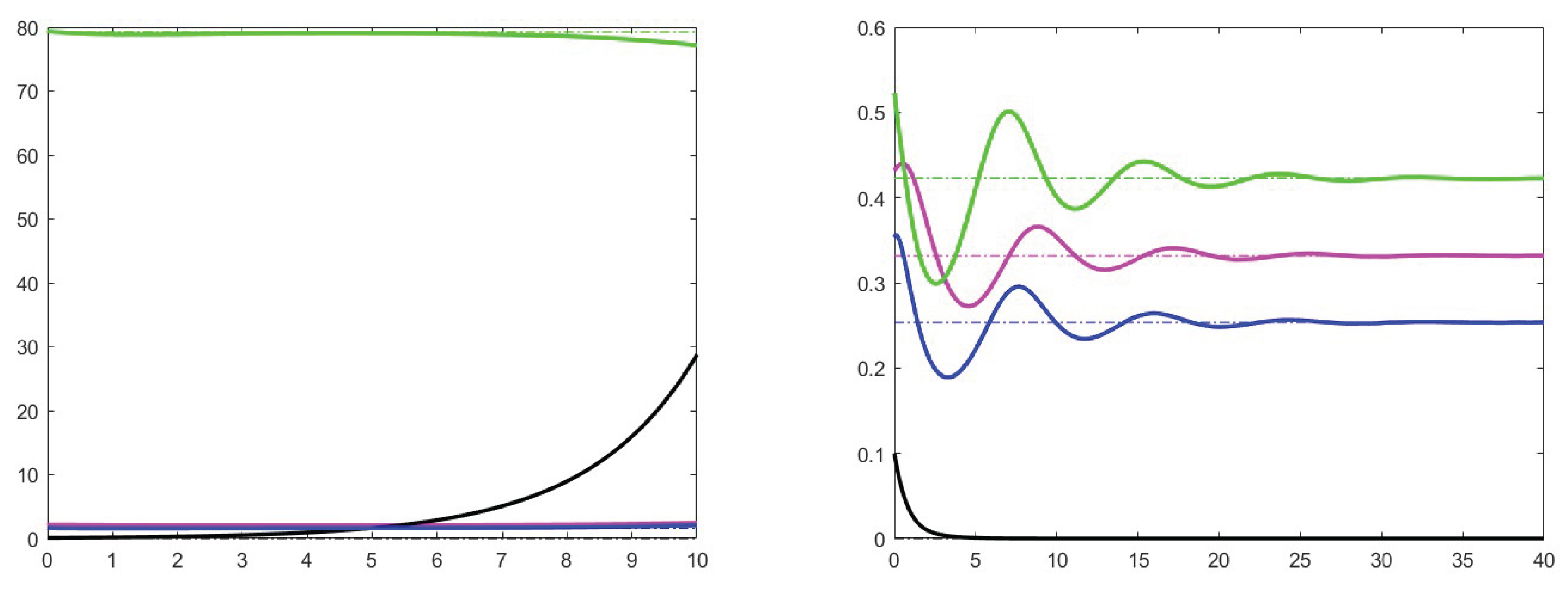
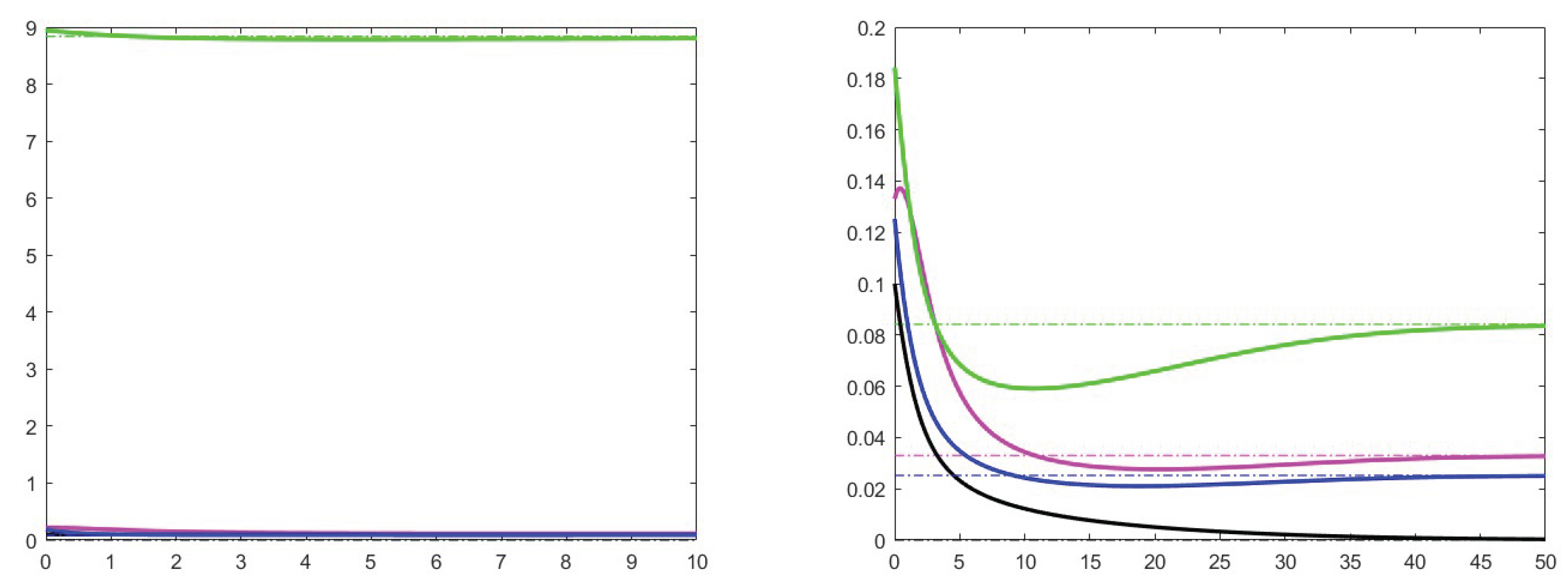
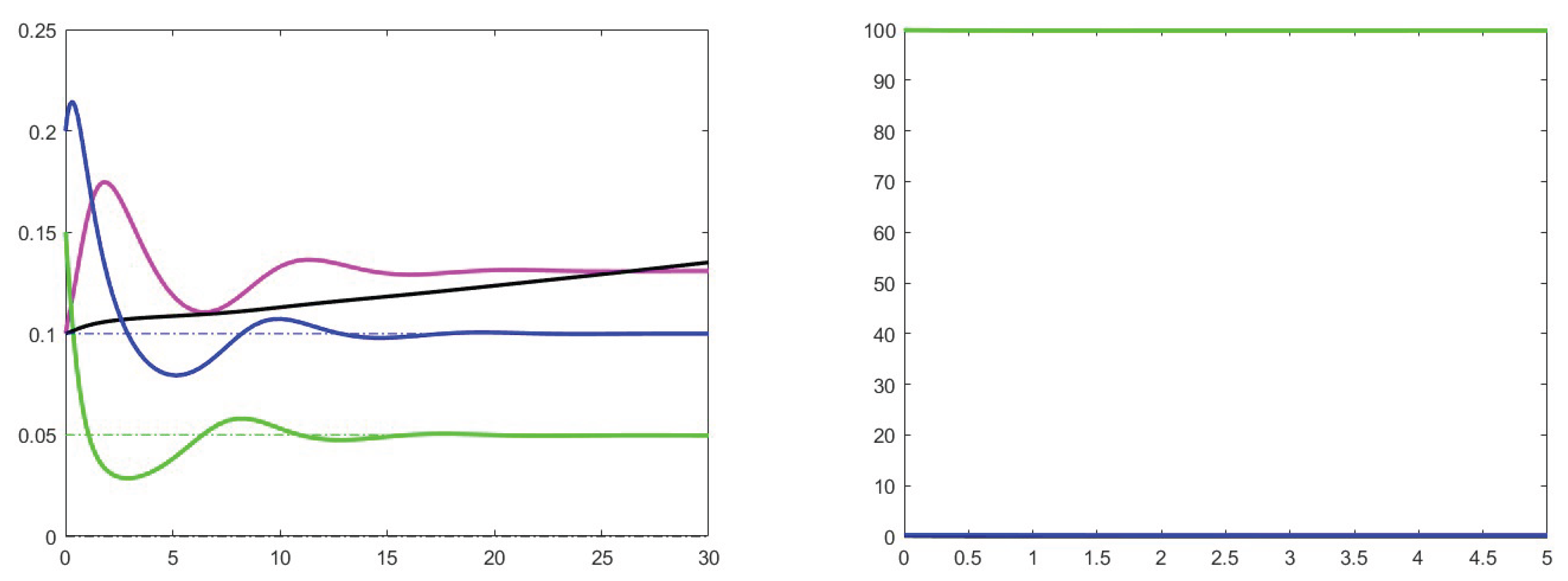
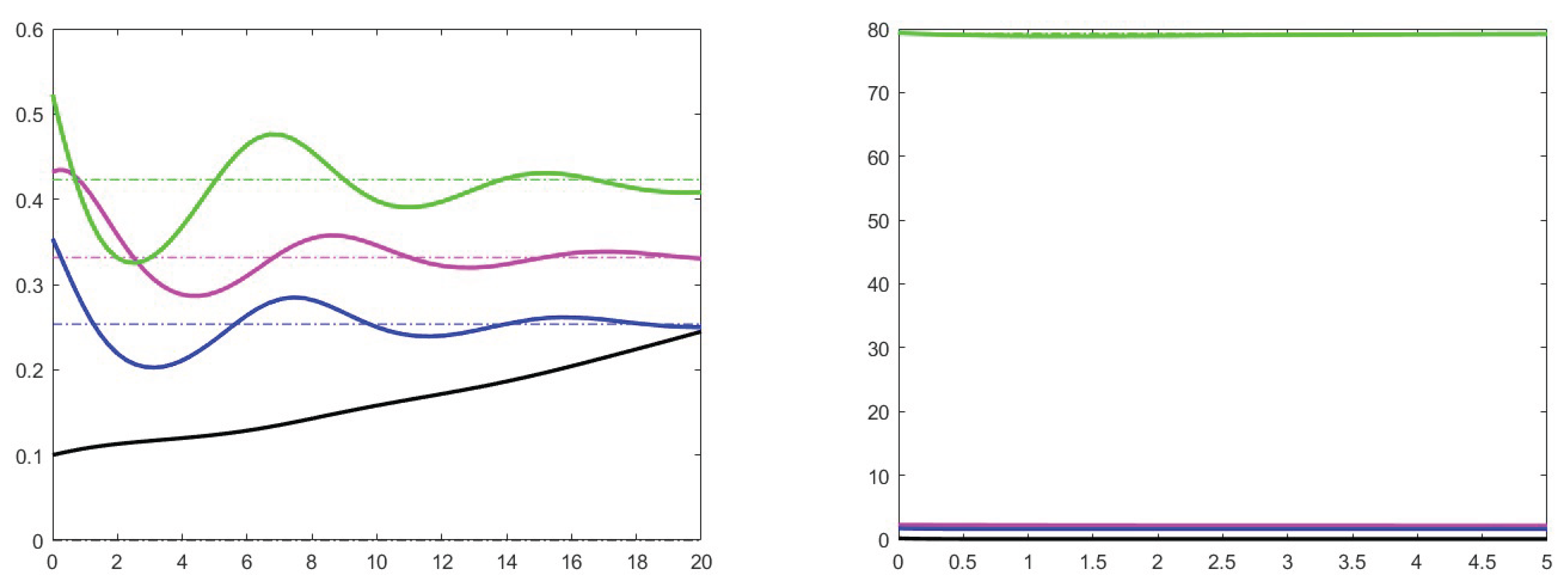
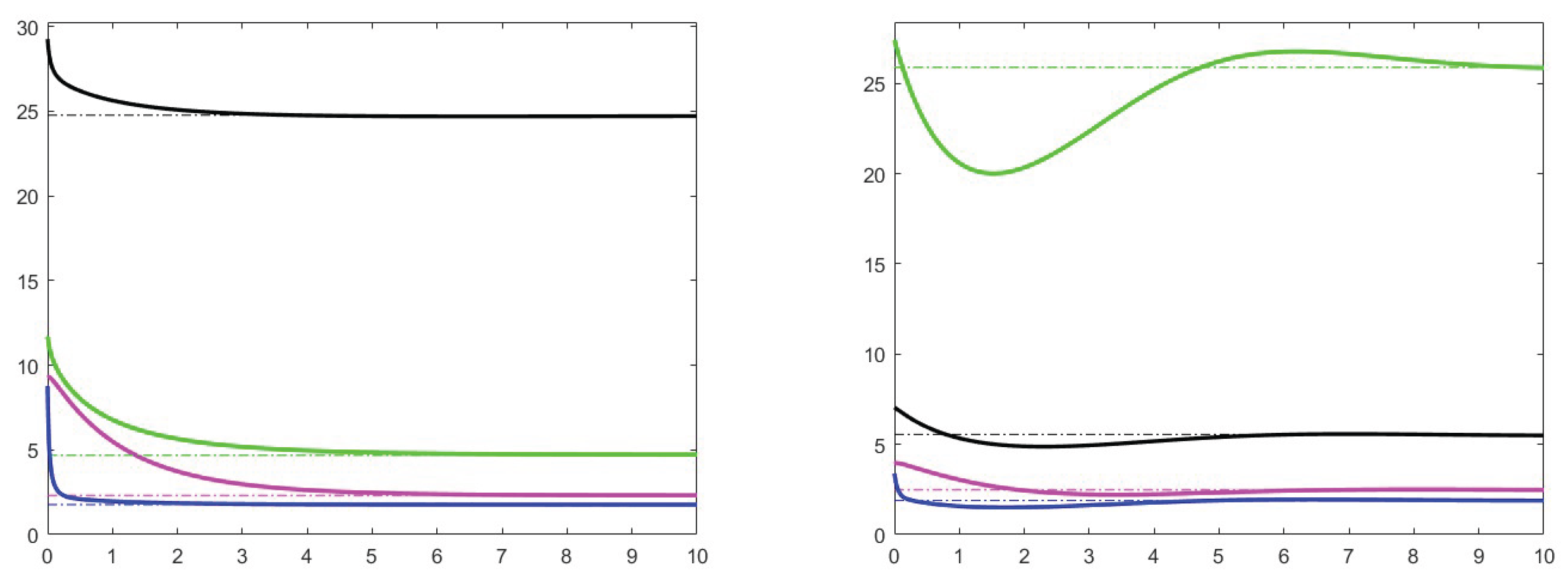
7. Simulation results

We now introduce the results derived from simulations conducted with Matlab’s ode45 solver, which applies an explicit adaptive Runge-Kutta method. In all depicted graphs, the evolution of variables is illustrated using distinct colors: the population in magenta, renewable resources in green, non-renewable resources in black, and accumulated wealth in blue. Dashed lines indicate the coordinates of the equilibrium point under consideration, with matching colors for corresponding components (i.e., magenta for the population, and so forth).

In these simulations, we first wanted to test our theoretical analyses, and therefore we have depicted in each chart the dashed line that represents the equilibrium point and the curve obtained by uniformly perturbing the the initial value with respect to the equilibrium point. Alongside these verifications, we analyzed the behavior of the solution curves as the depletion coefficient

δ

of both renewable and non-renewable resources increases, sometimes obtaining results different from those achieved for a small

δ

(in the literature small

δ

’s are usually considered). We also analyzed the behavior of the solutions obtained by considering different depletion factors between renewable and non-renewable resources. Finally, we tested the stability of some equilibrium points supporting positive values for all the variables. On the x-axis, we consider a generic unit for time which does not necessarily translate into days, months, or years. It’s a generic unit that doesn’t necessarily span too long intervals. Indeed, we suspend our simulation when the behavior appears to be identified. In the captions, we have included the data related to the equilibrium point examined and, in particular, the value assumed and the eigenvalues of the Jacobian matrix calculated at that point. In these experiments, we kept certain parameter values constant, setting them to the values generally found in the literature (see [10,11]). However, we deliberately altered other parameters to study their behavior. In particular, if not stated otherwise in the comment of the individual figure, we consider the natures carrying capacity

λ = 100

, the natures regeneration factor

γ = 0.01

, the wealth consumption

σ = 5

, the factor that regulates the possible increase of non-renewable resources

k = 1

and finally, the factors that govern the dynamics of populations

c = 1, d = 3, μ = 2

. Our simulations, on the other hand, were conducted by varying the parameter

δ

7.1. Analysis of theoretical results and $δ$ increase effects

In analyzing the correctness of our theoretical studies, we started from the case

x \leq w

, that is when wealth is greater than the current population. When

w = 0

the critical points are given by two families of points that we have denoted by Q and R, representing the desert state and the nature state, respectively. These are two families of unstable points that in Figure 1 we have represented in the case of

δ = 3, Z = 1

. For better readability of the chart, achieved with variable values of the same order of magnitude, we have set

λ = 10, γ = 0.5

We then analyzed the situation near the critical points of case ii.2) both to verify the correctness of our analyses and to see the possible scenario near such points. The behavior was confirmed in both the case of a small

δ

and the case of a possible large value. We have illustrated in Figure 2 the case with

δ = 0.49 < k / 2

. In case ii.2), we also analyzed the behavior of

P_{2}

with a large delta value, specifically

δ = 5

, by setting

k = 2 δ + 1

. We obtained results aligned with what was predicted by our analyses for small

δ

, both in the case of

γ λ - k < 0

and in the case of

γ λ - k > 0

We recall that, as for case ii.3), we have a single stable critical point for

k λ - σ < 0

and unstable in the opposite case. These results were confirmed by numerous simulations with small

δ

. It should be noted that, in the case of stability, we had to reduce the perturbation applied to P to achieve convergence to this equilibrium point. With the usual perturbation

ϵ = 10^{- 1}

, convergence occurs towards point

P_{1}

of case ii.7), which differs from P only in the value assumed by the population. In Figure 3, we report the results obtained about the analysis of point P in case ii.3) for large

δ

. This point is stable regardless of the value assumed by

k λ - σ

. However, we note that the basin of attraction of this point is extremely small. As in the case mentioned above for small

δ

, we had to reduce the usual perturbation to a value equal to

10^{- 3}

to achieve convergence to point P and not to point

P_{1}

of case ii.7). In the case of Figure 3, however, the point P is close to zero in each of its components, therefore, a perturbation of the order of

10^{- 3}

seems to us to be quite reasonable; a situation different is, for example, if

k λ - σ = - 2

, obtained with

k = 0.3, λ = 10

and

δ = 0.1

for which

P = (0, 8.3333, 0, 0.1667)

and the perturbation must be equally small.

In Figure 4, we report the analysis of point

P_{11}

of ii.6), as

δ

varies, always unstable according to the theory.

In Figure 5, Figure 6, and Figure 7, we have reported some of our experiments regarding the critical points indicated in case ii.7). Specifically, in Figure 5 and Figure 6, we analyzed point

P_{1}

, as

δ

varies, unstable if

k λ - σ > 0

, stable otherwise. For the sake of greater readability of the graphs, these figures refer to

γ = 0.1

. While stability can occur as

δ

varies, see Figure 6, the instability of the point is not obtained for large values of

δ

, differently from what our theoretical results state for

δ \to 0^{+}

, see Figure 5. Finally, in Figure 7, we report the analysis of point

P_{2}

, always unstable as

δ

varies.

We now report some experiments conducted in the case

x > w

Specifically, in Figure 8, we analyze, as

δ

varies, the behavior of solutions starting nearby the equilibrium point, predicted to be unstable if

γ λ - k > 0

and indicated as

P_{12}

in the situation iii.1). In the case of

γ λ - k < 0

, for which we have stability for small values of

δ

, we obtained a situation of instability by pushing

δ

to the maximum value allowed while keeping

k = 1

fixed. Finally, in Figure 9 and Figure 10, we have reported some of our studies on point

P_{1}

of case iii.2). Here too, we are in a situation in which we have instability for small

δ

’s, while the simulations suggest a change to stability for larger

δ

’s.

7.2. Analysis of the $δ_{1} \neq δ_{2}$ case

We wanted to explore situations similar to those seen in Figure 3 and Figure 9, but considering

δ_{1} \neq δ_{2}

. We have presented some results of these analyses in the Figure 11 and Figure 12.

For the case ii.3), we examine the point P for

δ_{1} \neq δ_{2}

, in the case

k λ - σ > 0

unstable for small

δ

’s, from theoretical results. The simulations suggest a change to stability for large values of

δ

. The critical point depends only on

δ_{1}

but it seems that the behavior is dictated by

δ_{2}

as can be seen in Figure 11.

In case iii.2), the analysis of point

P_{1}

with

δ_{1} \neq δ_{2}

when

k λ - σ > 0

, gives a situation of stability for

δ \to 0^{+}

. Referring to Figure 9, we had seen that instability was verified for small

δ

, while the simulations suggested stability for large

δ

. The equilibrium points do not depend on

δ_{2}

, and indeed we obtain the same equilibrium points as in Figure 9 for cases

δ_{1} = δ

. Even in this case, it would seem that

δ_{2}

controls the behavior of the equilibrium point, whose coordinates depend only on

δ_{1}

We would have liked to further analyze the scenario presented in ii.4), because the critical point depends on both

δ_{1}

and

δ_{2}

, but studies for significantly different values of the two parameters are not possible because, as they increase, the point exits the cone.

7.3. Stability for $x > 0$

A situation of stability with a positive population is represented in Figure 13. We analyzed the scenario indicated in cases ii.8) and iii.3) in the predicted cases of stability as

δ \to 0^{+}

References

Akhavan, N.; Yorke, A. Population collapse in Elite-dominated societies: a differential model without differential equations. SIAM J. Appl. Dyn. Syst. 2020, 19, 1736–1757. [Google Scholar] [CrossRef]
T. A. K. A. Al-Khawaja, Mathematical Models, Analysis and Simulations of the HANDY Model with Middle Class, Doctoral dissertation, Oakland University, 2021. https://our.oakland.edu/handle/10323/11946.
Badiale, M.; Cravero, I. A HANDY type model with non renewable resources. Nonlinear Anal. RWA 2024, 77. [Google Scholar] [CrossRef]
B. Grammaticos, R. Willox, J. Satsuma: Revisiting the Human and Nature Dynamics Model. Regular and Chaotic Dynamics, 2020, Vol. 25, No. 2, pp.178-198.
F. R: Gantmacher: The theory of matrices 2, AMS Chelsea Publishing, 2000.
M. Iannelli, A. Pugliese, An Introduction to Mathematical Population Dynamics, Springer, 2014.
Motesharrei, S.; Rivas, J.; Kalnay, E. Human and nature dynamics (HANDY): Modeling inequality and use of resource in the collapse or sustainability of societies. Ecological Economics 2014, 101, 90–102. [Google Scholar] [CrossRef]
Motesharrei, S.; Rivas, J.; Kalnay, E.; et al. Modeling sustainability: population, inequality, consumption, and bidirectional coupling of the Earth and Human Systems. National Science Review 2016, 3(4), 470–494. [Google Scholar] [CrossRef] [PubMed]
Sendera, M. Data adaptation in handy economy-ideology model. arXiv 2019, arXiv:1904.04309. [Google Scholar]
Shillor, M.; Ali Kadhim, T. Analysis and simulation of tha HANDY model with social mobility, renewables and nonrenewables. Electronic JDE URL: https://ejde.math.txstate.edu, https://ejde.math.unt.edu. 2023, 59, 1–22. [Google Scholar] [CrossRef]
Tonnelier, A. Sustainability or societal collapse, dynamics and bifurcations of the handy model. SIAM J. Appl. Dyn. Syst. 2023, 22(3). [Google Scholar] [CrossRef]

Figure 1. Case i) with

δ = 3

. Scenario around the unstable critical points. On the left:

Q = (0, 0, 1, 0)

. On the right:

R = (0, 10, 1, 0)

Figure 1. Case i) with

δ = 3

. Scenario around the unstable critical points. On the left:

Q = (0, 0, 1, 0)

. On the right:

R = (0, 10, 1, 0)

Figure 2. Case ii.2), analysis of the points

P_{1}

and

P_{2}

, with small

δ = 0.4990 < \frac{k}{2}

. On the left:

P_{1} = (0, 0, 9.4054, 0.9387)

, with

λ = 100

. The eigenvalues of

J (P_{1})

are

ρ_{k} = 0.0294, - 4.7227, - 1.0, 0.5316

, unstable according to the theory. On the right:

P_{2} = (0, 0, 10.6748, 1.0653)

with

λ = 10

so that

γ λ - k = - 0.9

. The eigenvalues of

J (P_{2})

are

ρ_{k} = - 0.0338, - 5.2929, - 1.0000, - 0.4316

, stable according to the theory.

Figure 2. Case ii.2), analysis of the points

P_{1}

and

P_{2}

, with small

δ = 0.4990 < \frac{k}{2}

. On the left:

P_{1} = (0, 0, 9.4054, 0.9387)

, with

λ = 100

. The eigenvalues of

J (P_{1})

are

ρ_{k} = 0.0294, - 4.7227, - 1.0, 0.5316

, unstable according to the theory. On the right:

P_{2} = (0, 0, 10.6748, 1.0653)

with

λ = 10

so that

γ λ - k = - 0.9

. The eigenvalues of

J (P_{2})

are

ρ_{k} = - 0.0338, - 5.2929, - 1.0000, - 0.4316

, stable according to the theory.

Figure 3. Case ii.3), analysis of the point P with

δ = 10

. On the left:

P = (0, 0.0500, 0, 0.1000)

when

k λ - σ = 95

, stable, contrary the theory for

δ \to 0^{+}

. The eigenvalues of

J (P)

are

ρ_{k} = - 0.2501 \pm 0.6612 i, - 1.0000, - 0.9896

. With a perturbation

ϵ \geq 10^{- 1}

the point converges to

P_{1} = (0.1308, 0.00500, 0, 0.01000)

of case ii.7) with the same convergence conditions for

δ \to 0

. On the right:

P = (0, 0.00500, 0, 0.01000)

k = 0.3, λ = 10

, so that

k λ - σ = - 2

. The eigenvalues of

J (P)

are

- 0.0250 \pm 0.0661 i, - 1.0000, - 0.0999

. Stability is observed over very long intervals. With a perturbation

ϵ \geq 10^{- 2}

, we have convergence to

P_{1} = (0.0131, 0.00500, 0, 0.01000)

of case ii.7).

Figure 3. Case ii.3), analysis of the point P with

δ = 10

. On the left:

P = (0, 0.0500, 0, 0.1000)

when

k λ - σ = 95

, stable, contrary the theory for

δ \to 0^{+}

. The eigenvalues of

J (P)

are

ρ_{k} = - 0.2501 \pm 0.6612 i, - 1.0000, - 0.9896

. With a perturbation

ϵ \geq 10^{- 1}

the point converges to

P_{1} = (0.1308, 0.00500, 0, 0.01000)

of case ii.7) with the same convergence conditions for

δ \to 0

. On the right:

P = (0, 0.00500, 0, 0.01000)

k = 0.3, λ = 10

, so that

k λ - σ = - 2

. The eigenvalues of

J (P)

are

- 0.0250 \pm 0.0661 i, - 1.0000, - 0.0999

. Stability is observed over very long intervals. With a perturbation

ϵ \geq 10^{- 2}

, we have convergence to

P_{1} = (0.0131, 0.00500, 0, 0.01000)

of case ii.7).

Figure 4. Case ii.6), analysis of the point

P_{11}

δ

varies, always unstable as

δ \to 0

. On the left:

P_{11} = (0.8727, 0, 1.1111, 0.6667)

with

δ = 3, k = 2 δ + 0.5

. Eigenvalues of

J (P_{11})

ρ_{k} = - 0.7454, - 3.9779, 0.6446, - 1.0000

. On the right:

P_{11} = (0.1322, 0, 5.0510, 0.1010)

with

δ = 0.1, k = 1

. Eigenvalues of

J (P_{11})

ρ_{k} = - 0.7454, - 0.5148, 0.0097, 0.9899

Figure 4. Case ii.6), analysis of the point

P_{11}

δ

varies, always unstable as

δ \to 0

. On the left:

P_{11} = (0.8727, 0, 1.1111, 0.6667)

with

δ = 3, k = 2 δ + 0.5

. Eigenvalues of

J (P_{11})

ρ_{k} = - 0.7454, - 3.9779, 0.6446, - 1.0000

. On the right:

P_{11} = (0.1322, 0, 5.0510, 0.1010)

with

δ = 0.1, k = 1

. Eigenvalues of

J (P_{11})

ρ_{k} = - 0.7454, - 0.5148, 0.0097, 0.9899

Figure 5. Case ii.7), analysis of the point

P_{1}

δ

varies with

k λ - σ = 95

, unstable case. On the left:

P_{1} = (2.5667, 98.0392, 0, 1.9608)

with

δ = 0.1

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 9.8039 \pm 1.3865 i, 0.5975

. On the right:

P_{1} = (4.1337, 5.2632, 0, 3.1579)

stable point with

δ = 3

, differently from the case of small

δ

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 8.1579 \pm 9.5574 i, - 8.5648

Figure 5. Case ii.7), analysis of the point

P_{1}

δ

varies with

k λ - σ = 95

, unstable case. On the left:

P_{1} = (2.5667, 98.0392, 0, 1.9608)

with

δ = 0.1

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 9.8039 \pm 1.3865 i, 0.5975

. On the right:

P_{1} = (4.1337, 5.2632, 0, 3.1579)

stable point with

δ = 3

, differently from the case of small

δ

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 8.1579 \pm 9.5574 i, - 8.5648

Figure 6. Case ii.7), analysis of the point

P_{1}

with

k λ - σ = - 4

, stable case, obtained by changing

k = 10^{- 2}

. The simulations are in accordance with the theory as

δ

varies. On the left:

P_{1} = (2.5667, 98.0392, 0, 1.9608)

with

δ = 0.1

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 9.8039 \pm 1.3865 i, - 0.1881

. On the right:

P_{1} = (4.1337, 5.2632, 0, 3.1579)

with

δ = 3

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 8.1579 \pm 9.5574 i, - 9.4646

Figure 6. Case ii.7), analysis of the point

P_{1}

with

k λ - σ = - 4

, stable case, obtained by changing

k = 10^{- 2}

. The simulations are in accordance with the theory as

δ

varies. On the left:

P_{1} = (2.5667, 98.0392, 0, 1.9608)

with

δ = 0.1

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 9.8039 \pm 1.3865 i, - 0.1881

. On the right:

P_{1} = (4.1337, 5.2632, 0, 3.1579)

with

δ = 3

. Eigenvalues of

J (P_{1})

ρ_{k} = - 0.7454, - 8.1579 \pm 9.5574 i, - 9.4646

Figure 7. Case ii.7), analysis of the point

P_{2}

always unstable as

δ

varies. On the left:

P_{2} = (0.3745, 98.0392, 0, 1.9608)

with

δ = 0.1

. Eigenvalues of

J (P_{2})

ρ_{k} = 0.7454, - 9.8039 \pm 1.3865 i, 0.5975

. On the right:

P_{2} = (0.6031, 5.2632, 0, 3.1579)

with

δ = 3

. Eigenvalues of

J (P_{2})

ρ_{k} = 0.7454, - 8.1579 \pm 9.5574 i, - 8.5648

Figure 7. Case ii.7), analysis of the point

P_{2}

always unstable as

δ

varies. On the left:

P_{2} = (0.3745, 98.0392, 0, 1.9608)

with

δ = 0.1

. Eigenvalues of

J (P_{2})

ρ_{k} = 0.7454, - 9.8039 \pm 1.3865 i, 0.5975

. On the right:

P_{2} = (0.6031, 5.2632, 0, 3.1579)

with

δ = 3

. Eigenvalues of

J (P_{2})

ρ_{k} = 0.7454, - 8.1579 \pm 9.5574 i, - 8.5648

Figure 8. Case iii.1) analysis of the point

P_{12}

unstable if

γ λ - k = 9 > 0

, with

γ = 0.1

. On the left: case

δ = 0.1

P_{12} = (9.8673, 0, 376.8988, 7.5380)

. Eigenvalues of

J (P_{12})

ρ_{k} = - 0.3587 \pm 0.7661 i, - 49.3647, 9.0133

. On the right:

δ = k \sqrt{μ t_{1}} / 2 - 0.001 = 0.4360

P_{12} = (1.2243, 0, 10.7251, 0.9353)

. Eigenvalues of

J (P_{12})

ρ_{k} = - 0.0631, - 0.4081, - 6.3956, 9.4662

Figure 8. Case iii.1) analysis of the point

P_{12}

unstable if

γ λ - k = 9 > 0

, with

γ = 0.1

. On the left: case

δ = 0.1

P_{12} = (9.8673, 0, 376.8988, 7.5380)

. Eigenvalues of

J (P_{12})

ρ_{k} = - 0.3587 \pm 0.7661 i, - 49.3647, 9.0133

. On the right:

δ = k \sqrt{μ t_{1}} / 2 - 0.001 = 0.4360

P_{12} = (1.2243, 0, 10.7251, 0.9353)

. Eigenvalues of

J (P_{12})

ρ_{k} = - 0.0631, - 0.4081, - 6.3956, 9.4662

Figure 9. Case iii.2), analysis of the point

P_{1}

, unstable if

k λ - σ = 95 > 0

for

δ \to 0^{+}

. On the left:

δ = 0.1

P_{1} = (2.0748, 79.2516, 0, 1.5850)

, eigenvalues

ρ_{k} = - 0.7603 \pm 0.4076 i, - 10.3915, 0.5593

. On the right:

δ = 3

P_{1} = (0.3319, 0.4226, 0, 0.2536)

, eigenvalues

ρ_{k} = - 0.1567 \pm 0.7521 i, - 2.0957, - 0.9181

then a stability situation,differently from the case of small

δ

Figure 9. Case iii.2), analysis of the point

P_{1}

, unstable if

k λ - σ = 95 > 0

for

δ \to 0^{+}

. On the left:

δ = 0.1

P_{1} = (2.0748, 79.2516, 0, 1.5850)

, eigenvalues

ρ_{k} = - 0.7603 \pm 0.4076 i, - 10.3915, 0.5593

. On the right:

δ = 3

P_{1} = (0.3319, 0.4226, 0, 0.2536)

, eigenvalues

ρ_{k} = - 0.1567 \pm 0.7521 i, - 2.0957, - 0.9181

then a stability situation,differently from the case of small

δ

Figure 10. Case iii.2), analysis of the point

P_{1}

when

k λ - σ = - 3 < 0

obtained with

k = 0.7, σ = 10, λ = 10

, stability situation for

δ \to 0^{+}

, confirmed also for large

δ

. On the left:

δ = 0.1

P_{1} = (0.1157, 8.8425, 0, 0.0884)

, eigenvalues

ρ_{k} = - 0.1032, - 0.7095, - 1.1786, - 0.0045

. On the right:

δ = 3

P_{1} = (0.0331, 0.0842, 0, 0.0253)

, eigenvalues

ρ_{k} = - 0.8086, - 0.1341 \pm 0.1118 i, - 0.0986

Figure 10. Case iii.2), analysis of the point

P_{1}

when

k λ - σ = - 3 < 0

obtained with

k = 0.7, σ = 10, λ = 10

, stability situation for

δ \to 0^{+}

, confirmed also for large

δ

. On the left:

δ = 0.1

P_{1} = (0.1157, 8.8425, 0, 0.0884)

, eigenvalues

ρ_{k} = - 0.1032, - 0.7095, - 1.1786, - 0.0045

. On the right:

δ = 3

P_{1} = (0.0331, 0.0842, 0, 0.0253)

, eigenvalues

ρ_{k} = - 0.8086, - 0.1341 \pm 0.1118 i, - 0.0986

Figure 11. Case ii.3). Analysis of point P for

δ_{1} \neq δ_{2}

, in the case

k λ - σ = 95

unstable from theoretical results. The critical point depends only on

δ_{1}

. On the left:

P = (0, 0.0500, 0, 0.1000)

with

δ_{1} = 10, δ_{2} = 0.01

unstable, according to the theory. Eigenvalues:

ρ_{k} = - 0.2501 \pm 0.6612 i, - 1.0000, 0.0089

. On the right:

P = (0, 99.8004, 0, 0.1996)

and

δ_{1} = 0.01, δ_{2} = 10

. Eigenvalues:

- 0.9980 \pm 0.0446 i, - 1.0000, - 1.9577

. The point is stable according to the behavior observed for large

δ

Figure 11. Case ii.3). Analysis of point P for

δ_{1} \neq δ_{2}

, in the case

k λ - σ = 95

unstable from theoretical results. The critical point depends only on

δ_{1}

. On the left:

P = (0, 0.0500, 0, 0.1000)

with

δ_{1} = 10, δ_{2} = 0.01

unstable, according to the theory. Eigenvalues:

ρ_{k} = - 0.2501 \pm 0.6612 i, - 1.0000, 0.0089

. On the right:

P = (0, 99.8004, 0, 0.1996)

and

δ_{1} = 0.01, δ_{2} = 10

. Eigenvalues:

- 0.9980 \pm 0.0446 i, - 1.0000, - 1.9577

. The point is stable according to the behavior observed for large

δ

Figure 12. Case iii.2), analysis of point

P_{1}

with

δ_{1} \neq δ_{2}

in the case

k λ - σ = 95

, instability situation as

δ \to 0

. On the left:

P_{1} = (0.3319, 0.4226, 0, 0.2536)

with

δ_{1} = 3, δ_{2} = 0.1

, eigenvalues

ρ_{k} = - 0.1567 \pm 0.7521 i, - 2.0957, 0.0444

, unstable. On the right:

P_{1} = (2.0748, 79.2516, 0, 1.5850)

with

δ_{1} = 0.1, δ_{2} = 3

, eigenvalues

ρ_{k} = - 0.7603 \pm 0.4076 i, - 10.3915, - 5.4577

, stable.

Figure 12. Case iii.2), analysis of point

P_{1}

with

δ_{1} \neq δ_{2}

in the case

k λ - σ = 95

, instability situation as

δ \to 0

. On the left:

P_{1} = (0.3319, 0.4226, 0, 0.2536)

with

δ_{1} = 3, δ_{2} = 0.1

, eigenvalues

ρ_{k} = - 0.1567 \pm 0.7521 i, - 2.0957, 0.0444

, unstable. On the right:

P_{1} = (2.0748, 79.2516, 0, 1.5850)

with

δ_{1} = 0.1, δ_{2} = 3

, eigenvalues

ρ_{k} = - 0.7603 \pm 0.4076 i, - 10.3915, - 5.4577

, stable.

Figure 13. Stable critical points with positive population,

δ = 0.3

. On the left: case ii.8) with

P_{12} = (2.3138, 4.6972, 24.7626, 1.7676)

stable and within the cone for

γ λ - k = 0.3 > 0

obtained with

k = 0.7, λ = 10, γ = 0.1

, eigenvalues:

ρ_{k} = - 0.7454, - 8.5064, - 0.6207, - 0.1805

. On the right: case iii.3) with

P_{12} = (2.4700, 25.8987, 5.5504, 1.8869)

, stable and within the cone for

γ λ - k = 0.1 > 0

obtained with

k = 0.9

. Eigenvalues:

ρ_{k} = - 12.4196, - 0.4555 \pm 0.6858 i, - 0.0239

Figure 13. Stable critical points with positive population,

δ = 0.3

. On the left: case ii.8) with

P_{12} = (2.3138, 4.6972, 24.7626, 1.7676)

stable and within the cone for

γ λ - k = 0.3 > 0

obtained with

k = 0.7, λ = 10, γ = 0.1

, eigenvalues:

ρ_{k} = - 0.7454, - 8.5064, - 0.6207, - 0.1805

. On the right: case iii.3) with

P_{12} = (2.4700, 25.8987, 5.5504, 1.8869)

, stable and within the cone for

γ λ - k = 0.1 > 0

obtained with

k = 0.9

. Eigenvalues:

ρ_{k} = - 12.4196, - 0.4555 \pm 0.6858 i, - 0.0239

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Nonlinear ODE Model for a Consumeristic Society

Abstract

1. Introduction

2. General Results on the Solutions

3. Steady States if x ≤ w

4. Instability of Equilibria in the Case w = 0

5. Stability of Equilibria in the Case w ≠ 0

6. Fixed points and stability if x > w

7. Simulation results

7.1. Analysis of theoretical results and δ increase effects

7.2. Analysis of the δ 1 ≠ δ 2 case

7.3. Stability for x > 0

References

MDPI Initiatives

Important Links

Subscribe

3. Steady States if $x \leq w$

4. Instability of Equilibria in the Case $w = 0$

5. Stability of Equilibria in the Case $w \neq 0$

6. Fixed points and stability if $x > w$

7.1. Analysis of theoretical results and $δ$ increase effects

7.2. Analysis of the $δ_{1} \neq δ_{2}$ case

7.3. Stability for $x > 0$