Submitted:
20 March 2024
Posted:
22 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
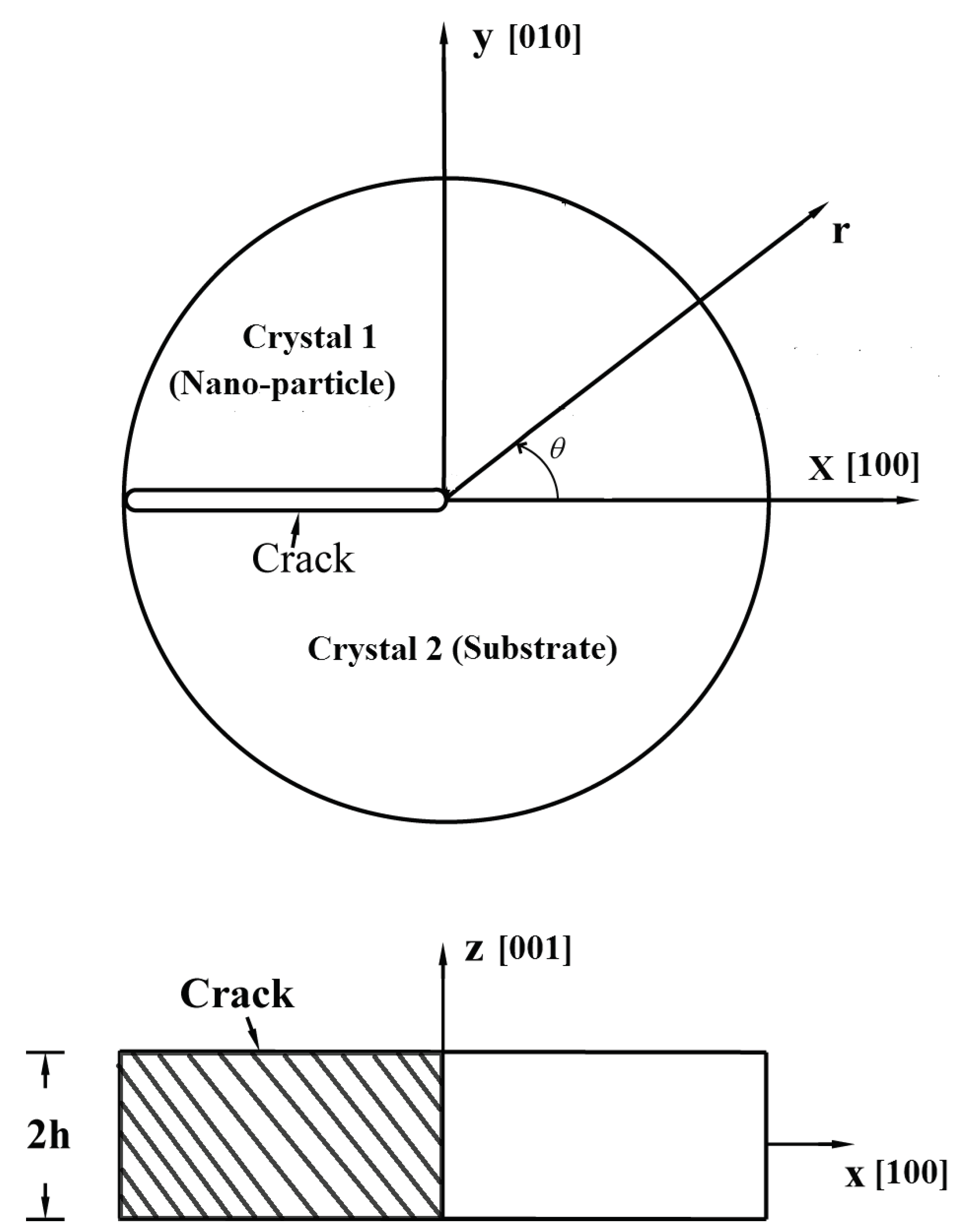
2. Statement of the Problem


3. Singular Stress Fields in the Vicinity of a Crack Front Weakening a Bicrystalline Superlattice with Orthorhombic Phases under General Loading
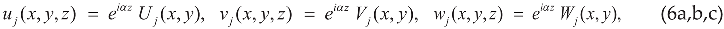
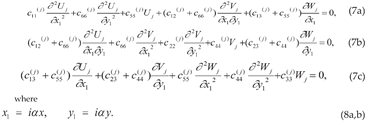

4. Singular Stress Fields in the Vicinity of a (010)[001] Through-Thickness Crack Front Propagating under Mode I (Extension/Bending) and Mode II (Sliding Shear/Twisting) in [100] Direction



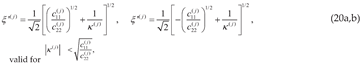
5. Satisfaction of Crack Face Boundary and Interfacial Contact Conditions
5.1. Both Crystal Layers with Complex Roots

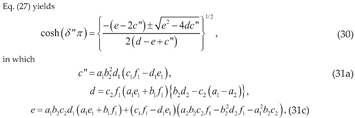
5.2. Both Crystal Layers with Imaginary Roots
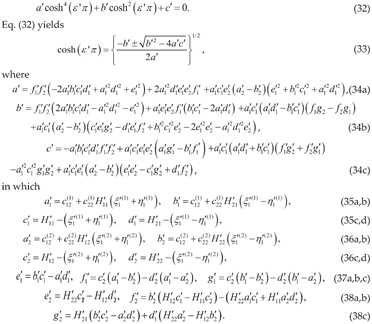
5.3. Top Crystal (Layer 1) with Complex Roots and Bottom Crystal (Layer 2) with Imaginary Roots

6. Boundary Conditions on the Bicrystalline Superlattice Plate Surfaces and Through-Thickness Distribution of Singular Stress Fields
6.1. General Distributed Far-Field Loading
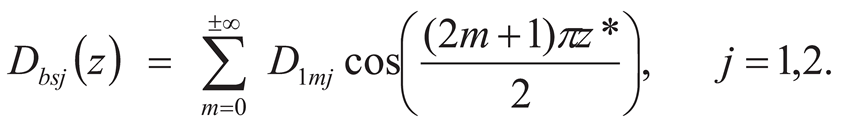
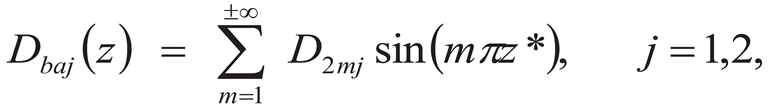
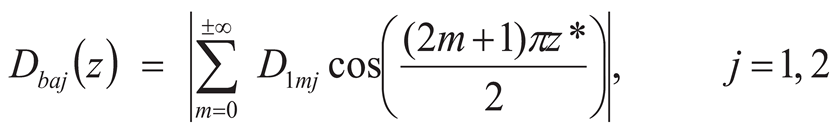
6.2. Hyperbolic Sine Distributed Far-Field Loading

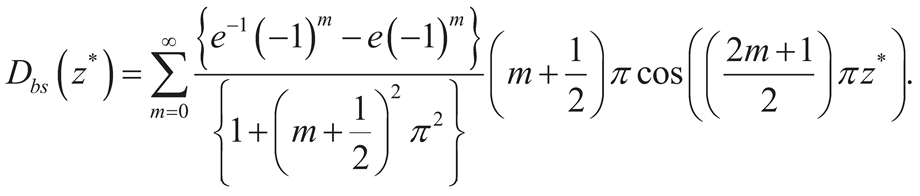
7. Singular Stress Fields in the Vicinity of a Through-Crack Front Propagating under Mode III (Anti-plane Shear) in [100] Direction
8. Crack Path Stability/Instability Criteria
8.1. Necessary Condition −− Griffith-Irwin theory-based crack deflection criterion
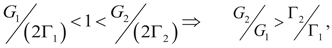
8.2. Sufficient Condition
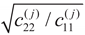 , j = 1, 2, respectively, signifies transitioning from self-similar crack growth or propagation to crack deflection or turning from a difficult cleavage system onto a nearby easy one. This is a significant qualitative as well as quantitative improvement over two-parameters based models, suggested by earlier researchers e.g. [13], in the context of two-dimensional anisotropic fracture mechanics.
, j = 1, 2, respectively, signifies transitioning from self-similar crack growth or propagation to crack deflection or turning from a difficult cleavage system onto a nearby easy one. This is a significant qualitative as well as quantitative improvement over two-parameters based models, suggested by earlier researchers e.g. [13], in the context of two-dimensional anisotropic fracture mechanics.9. Numerical Results and Discussions
9.1. Structure-Fracture Property Relations for Certain Model Bicrystalline Superlattices
 0} (a prism plane) is parallel to the crack face. It may be noted that the rotated crystal displays tetragonal type symmetry.
0} (a prism plane) is parallel to the crack face. It may be noted that the rotated crystal displays tetragonal type symmetry.| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
010)[001] x[100] |
231.0 | 268.0 | 186.0 | 66.0 | 71.0 | 95.0 | 49.0 | 37.0 | 82.0 |
| 2 | SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 348.17 | 348.17 | 348.17 | 100.64 | 100.64 | 100.64 | 454.55 | 454.55 | 454.55 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
(010)[001] x[100] |
231.0 | 268.0 | 186.0 | 66.0 | 71.0 | 95.0 | 49.0 | 37.0 | 82.0 |
| 2 | SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
678.96 | 678.96 | 348.17 | -230.15 | 100.64 | 100.64 | 454.55 | 454.55 | 123.77 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
( 00)[001] 00)[001]x[010] |
268.0 | 231.0 | 186.0 | 66.0 | 95.0 | 71.0 | 37.0 | 49.0 | 82.0 |
| 2 | SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 348.17 | 348.17 | 348.17 | 100.64 | 100.64 | 100.64 | 454.55 | 454.55 | 454.55 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
( 00)[001] 00)[001]x[010] |
268.0 | 231.0 | 186.0 | 66.0 | 95.0 | 71.0 | 37.0 | 49.0 | 82.0 |
| 2 | SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
678.96 | 678.96 | 348.17 | -230.15 | 100.64 | 100.64 | 454.55 | 454.55 | 123.77 |
 10}<001>x<110> through-crack [49], as can be seen from Tables 26, 27, 30 and 31. It can then be inferred that {
10}<001>x<110> through-crack [49], as can be seen from Tables 26, 27, 30 and 31. It can then be inferred that { 10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult.
10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult. 10)[001]x[110] through-crack. This is in contrast to A = 1.5354 and k = 1.8329 being both larger than unity (A > 1, k > = 1), giving rise to complex roots for the (010)[001]x[100] through-crack, as shown in Tables 28, 30 and 38. It can then be inferred that {
10)[001]x[110] through-crack. This is in contrast to A = 1.5354 and k = 1.8329 being both larger than unity (A > 1, k > = 1), giving rise to complex roots for the (010)[001]x[100] through-crack, as shown in Tables 28, 30 and 38. It can then be inferred that { 10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult.
10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult. 10)[001]x[110] through-crack. This is in contrast to A = 3.6727 and k = 16.1473 being both larger than unity (A > 1, k > = 1), giving rise to complex roots for the (010)[001]x[100] through-crack, as shown in Tables 33, 35 and 40. It can then be inferred that {
10)[001]x[110] through-crack. This is in contrast to A = 3.6727 and k = 16.1473 being both larger than unity (A > 1, k > = 1), giving rise to complex roots for the (010)[001]x[100] through-crack, as shown in Tables 33, 35 and 40. It can then be inferred that { 10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult.
10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult. 00)[0
00)[0 0]x[001] through-crack, as shown in Tables 25, 27 and 37. It can then be inferred that {001}<0
0]x[001] through-crack, as shown in Tables 25, 27 and 37. It can then be inferred that {001}<0 0>x<
0>x< 00> and {
00> and { 00}<0
00}<0 0>x<001> would both constitute easy cleavage systems.
0>x<001> would both constitute easy cleavage systems. 10)[001]x[110] through-crack. as shown in Table 35 and Table 36. It can then be inferred that {
10)[001]x[110] through-crack. as shown in Table 35 and Table 36. It can then be inferred that { 10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult.
10}<001>x<110> would constitute an easy cleavage system, while {010}<001>x<100> would be deemed difficult. 00)[001]x[010] through-crack, as shown in Table 44 and Table 45; see also Table 4 of Chaudhuri [59]. It can then be inferred that {001}<100>x<010> would constitute an easy cleavage system.
00)[001]x[010] through-crack, as shown in Table 44 and Table 45; see also Table 4 of Chaudhuri [59]. It can then be inferred that {001}<100>x<010> would constitute an easy cleavage system.9.2. Superlattice Trapping and Superlattice Crack Deflection (SCD)
 10}<001> x<110]>.
10}<001> x<110]>. 10}<001>x<110]> is considered to be the preferred one for crack propagation. This is illustrated in Figure 26(a) of Chaudhuri [49]. Nonvanishing lattice crack deflection (LCD) energy barrier implies that a {010}〈001〉x<100]> through-crack in such single crystals would not deflect right at the appropriate Griffith/Irwin critical stress intensity factor (Kc) for mixed mode propagation because of the lattice effect, but would require additional bond shear strains for Au (Table 48). In the case of nonvanishing lattice crack deflection (LCD) barrier, e.g., in Au with moderately high anisotropic ratio, A = 2.8481 > 1, the difficult {010}〈001〉x<100]> crack may initially get lattice trapped and/or propagate in a “difficult” manner till an applied load somewhat higher than its Griffith mixed mode counterpart is reached, and then only deflect into the easy cleavage system, {
10}<001>x<110]> is considered to be the preferred one for crack propagation. This is illustrated in Figure 26(a) of Chaudhuri [49]. Nonvanishing lattice crack deflection (LCD) energy barrier implies that a {010}〈001〉x<100]> through-crack in such single crystals would not deflect right at the appropriate Griffith/Irwin critical stress intensity factor (Kc) for mixed mode propagation because of the lattice effect, but would require additional bond shear strains for Au (Table 48). In the case of nonvanishing lattice crack deflection (LCD) barrier, e.g., in Au with moderately high anisotropic ratio, A = 2.8481 > 1, the difficult {010}〈001〉x<100]> crack may initially get lattice trapped and/or propagate in a “difficult” manner till an applied load somewhat higher than its Griffith mixed mode counterpart is reached, and then only deflect into the easy cleavage system, { 10}lt;001>x<110]>. In addition, the bond breaking would not be continuous but abrupt. In contrast, for the same crystal with the very low modified anisotropic ratio, A‣ = 0.3494 < 1, lattice crack deflection (LCD) barrier vanishes and the easy {
10}lt;001>x<110]>. In addition, the bond breaking would not be continuous but abrupt. In contrast, for the same crystal with the very low modified anisotropic ratio, A‣ = 0.3494 < 1, lattice crack deflection (LCD) barrier vanishes and the easy { 10}<001>x<110]> crack would begin to propagate right at the Griffith/Irwin critical stress intensity factor. There would be no crack turning.
10}<001>x<110]> crack would begin to propagate right at the Griffith/Irwin critical stress intensity factor. There would be no crack turning.  10}<001>x<110]>, of the component phase with the lower LCD barrier, ∆K* = 0.6414 for MgO (resp. 0.5114 for SrTiO3). In addition, the bond breaking would not be continuous but abrupt. In contrast, for the same bicrystalline superlattice, Au/MgO, with both easy (
10}<001>x<110]>, of the component phase with the lower LCD barrier, ∆K* = 0.6414 for MgO (resp. 0.5114 for SrTiO3). In addition, the bond breaking would not be continuous but abrupt. In contrast, for the same bicrystalline superlattice, Au/MgO, with both easy ( 10)[001]x[110]/(
10)[001]x[110]/( 10)[001]x[110] cleavage systems serving as the interface, the SCD barrier, ∆KS*, vanishes, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous. Interestingly, for the Au/MgO or YBa2C3O7/SrTiO3 superlattice, with one easy and the second one difficult, either (010)[001]x[100]/(
10)[001]x[110] cleavage systems serving as the interface, the SCD barrier, ∆KS*, vanishes, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous. Interestingly, for the Au/MgO or YBa2C3O7/SrTiO3 superlattice, with one easy and the second one difficult, either (010)[001]x[100]/( 10)[001]x[110] or (
10)[001]x[110] or ( 10)[001]x[110]/(010)[001]x[100] cleavage systems serving as the interface, the SCD barrier, ∆KS*, also vanishes, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.
10)[001]x[110]/(010)[001]x[100] cleavage systems serving as the interface, the SCD barrier, ∆KS*, also vanishes, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface. 10)[001]x[110]/(001)[0
10)[001]x[110]/(001)[0 0]x[
0]x[ 00] or (
00] or ( 10)[001]x[110]/(
10)[001]x[110]/( 00)[0
00)[0 0]x[001], serving as the interface, the SCD barrier, ∆KS*, again vanishes, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous. As before, the same superlattice, with one easy and the second one difficult, either (010)[001]x[100]/(001)[0
0]x[001], serving as the interface, the SCD barrier, ∆KS*, again vanishes, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous. As before, the same superlattice, with one easy and the second one difficult, either (010)[001]x[100]/(001)[0 0]x[
0]x[ 00] or (010)[001]x[100]/(
00] or (010)[001]x[100]/( 00)[0
00)[0 0]x[001] cleavage systems serving as the interface, ∆KS* also vanishes, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.
0]x[001] cleavage systems serving as the interface, ∆KS* also vanishes, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface. 00)[0
00)[0 0]x[001], serving as the interface.
0]x[001], serving as the interface. 0]x[
0]x[ 00] cleavage systems serving as the interface, the SCD barrier, ∆KS*, again vanishes, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. Similar results follow for the orthorhombic perovskite/FCC rock salt YBa2C3O7-d/MgO superlattice, with both easy (001)[100]x[010]/(
00] cleavage systems serving as the interface, the SCD barrier, ∆KS*, again vanishes, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. Similar results follow for the orthorhombic perovskite/FCC rock salt YBa2C3O7-d/MgO superlattice, with both easy (001)[100]x[010]/( 10)[001]x[110] cleavage systems serving as the interface.
10)[001]x[110] cleavage systems serving as the interface.  10)[001]x[110] cleavage systems serving as the interface, ∆KS* would again vanish, and the resulting easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous. As before ∆KS* for the same superlattice, with one easy and the second one difficult, (001)[100]x[010]/(010)[001]x[100] would also vanish, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.
10)[001]x[110] cleavage systems serving as the interface, ∆KS* would again vanish, and the resulting easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous. As before ∆KS* for the same superlattice, with one easy and the second one difficult, (001)[100]x[010]/(010)[001]x[100] would also vanish, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface. 10)[001]x[110] (resp., (
10)[001]x[110] (resp., ( 10)[001]x[110]/(
10)[001]x[110]/( 10)[001]x[110]) cleavage systems serving as the interface, ∆KS* would again vanish, and the resulting easy interfacial crack would experience a mixed mode propagation/growth right at the Griffith/Irwin critical complex stress intensity factor. Rice [9] has discussed the computation and interpretation of the resulting complex stress intensity factor (S.I.F.) for an isotropic bimaterial interface crack; see Sec. 9.3 below. The bond breaking is expected to be smooth and continuous. The reason for this exceptional behavior of SrTiO3 lies, as has been explained above, in its unusually high shear stiffness, c66, which is substantially greater than its longitudinal stiffness, c11. However, ∆KS* for the same superlattices, with one easy and the second one difficult, (001)[100]x[010]/(010)[001]x[100] for YBa2C3O7-d/SrTiO3, or ((
10)[001]x[110]) cleavage systems serving as the interface, ∆KS* would again vanish, and the resulting easy interfacial crack would experience a mixed mode propagation/growth right at the Griffith/Irwin critical complex stress intensity factor. Rice [9] has discussed the computation and interpretation of the resulting complex stress intensity factor (S.I.F.) for an isotropic bimaterial interface crack; see Sec. 9.3 below. The bond breaking is expected to be smooth and continuous. The reason for this exceptional behavior of SrTiO3 lies, as has been explained above, in its unusually high shear stiffness, c66, which is substantially greater than its longitudinal stiffness, c11. However, ∆KS* for the same superlattices, with one easy and the second one difficult, (001)[100]x[010]/(010)[001]x[100] for YBa2C3O7-d/SrTiO3, or (( 10)[001]x[110]/(010)[001]x[100] and (010)[001]x[100]/((
10)[001]x[110]/(010)[001]x[100] and (010)[001]x[100]/(( 10)[001]x[110] for YBa2C3O7/SrTiO3 also vanish, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.
10)[001]x[110] for YBa2C3O7/SrTiO3 also vanish, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.9.3. Complex Stress Intensity Factor (S.I.F.) and Raman Spectroscopic Surface Measurement
9.3.1. Complex Stress Intensity Factor (S.I.F.)
9.3.2. Raman Spectroscopic Surface Measurement of Carbon/Graphite Fiber-Epoxy Interfacial Bond
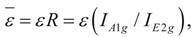
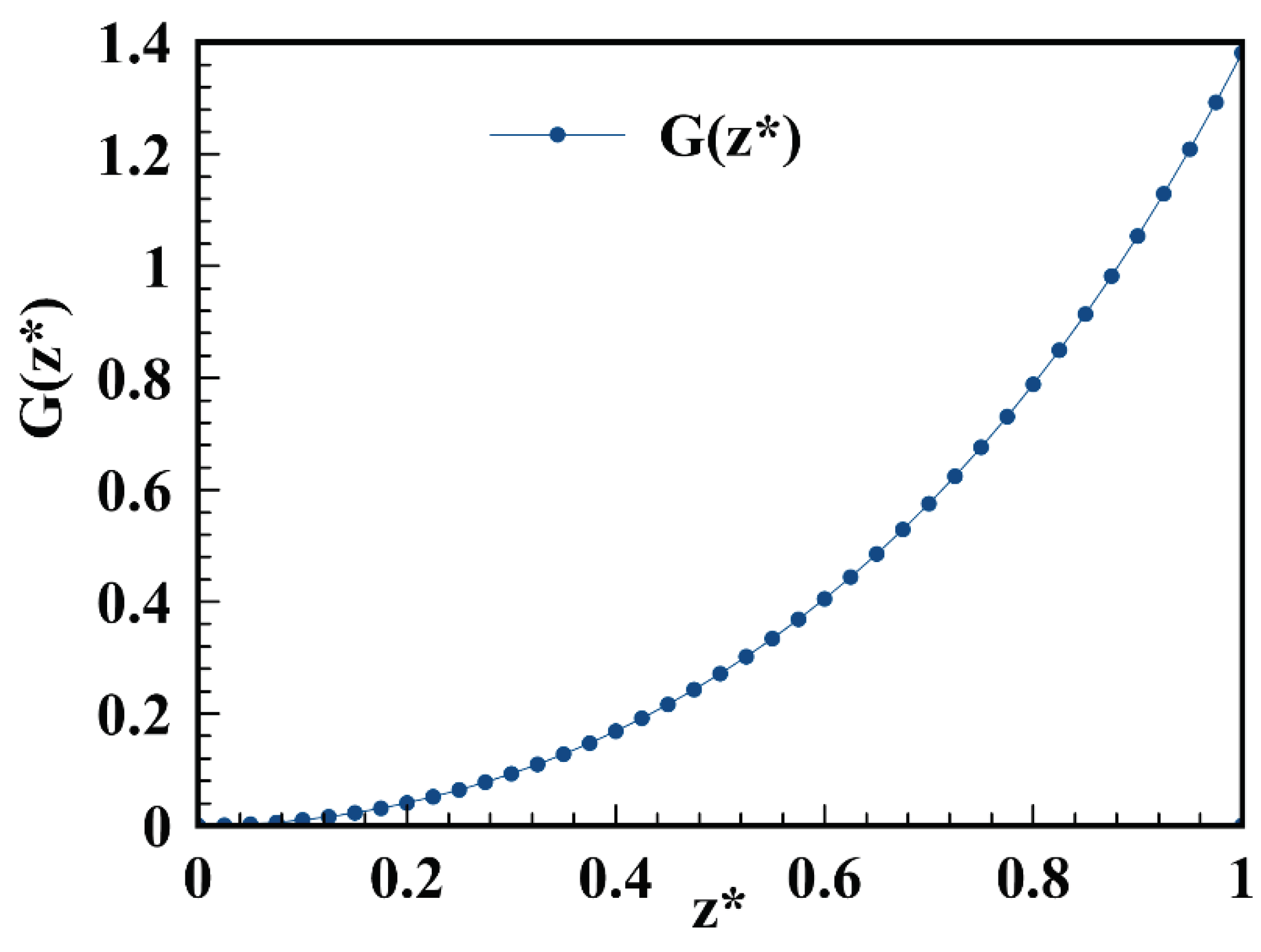
9.4. Through-thickness Distribution of Stress Intensity Factors (Fracture Toughness) and Energy Release Rates (Fracture Energy)
10. Summary and Conclusions
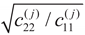 , j = 1, 2, respectively, signifies transitioning from self-similar crack growth or propagation to crack deflection or turning from a difficult cleavage system onto a nearby easy one. This is a significant qualitative as well as quantitative improvement over two-parameters based models, suggested by earlier researchers e.g. [13], in the context of two-dimensional anisotropic fracture mechanics.
, j = 1, 2, respectively, signifies transitioning from self-similar crack growth or propagation to crack deflection or turning from a difficult cleavage system onto a nearby easy one. This is a significant qualitative as well as quantitative improvement over two-parameters based models, suggested by earlier researchers e.g. [13], in the context of two-dimensional anisotropic fracture mechanics. 10)[001]x[110] (resp. (
10)[001]x[110] (resp. ( 10)[001]x[110]/(10)[001]x[110]) cleavage systems serving as the interface, the computed eigenvalues are also complex, resulting in a mixed (I/II) mode interfacial crack growth.
10)[001]x[110]/(10)[001]x[110]) cleavage systems serving as the interface, the computed eigenvalues are also complex, resulting in a mixed (I/II) mode interfacial crack growth. 10}<001>x<110]>, of the component phase with the lower LCD barrier, ΔK* = 0.6414 for MgO (resp. 0.5114 for SrTiO3). In addition, the bond breaking would not be continuous but abrupt.
10}<001>x<110]>, of the component phase with the lower LCD barrier, ΔK* = 0.6414 for MgO (resp. 0.5114 for SrTiO3). In addition, the bond breaking would not be continuous but abrupt. 10)[001]x[110]/(
10)[001]x[110]/( 10)[001]x[110]) cleavage systems serving as the interface, both bond shear strain at superlattice crack deflection, ybdS, and superlattice crack deflection (SCD) barrier, ΔKS*, vanish, and the resulting easy interfacial crack would experience a mixed mode propagation/growth right at the Griffith/Irwin-based critical complex stress intensity factor (S.I.F.), the computation and interpretation of which is expounded by Rice’s [9] extension from a two-dimensional isotropic bimaterial interface crack to its to anisotropic counterpart. The bond breaking is expected to be smooth and continuous.
10)[001]x[110]) cleavage systems serving as the interface, both bond shear strain at superlattice crack deflection, ybdS, and superlattice crack deflection (SCD) barrier, ΔKS*, vanish, and the resulting easy interfacial crack would experience a mixed mode propagation/growth right at the Griffith/Irwin-based critical complex stress intensity factor (S.I.F.), the computation and interpretation of which is expounded by Rice’s [9] extension from a two-dimensional isotropic bimaterial interface crack to its to anisotropic counterpart. The bond breaking is expected to be smooth and continuous. 10)[001]x[110]/(001)[0
10)[001]x[110]/(001)[0 0]x[00] or (
0]x[00] or ( 10)[001]x[110]/(
10)[001]x[110]/( 00)[0
00)[0 0]x[001], serving as the interface, both bond shear strain at superlattice crack deflection, ybdS, and superlattice crack deflection (SCD) barrier, ΔKS*, vanish, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. Likewise, a YBa2C3O7-d/Si3N4 superlattice, with both easy cleavage systems, either {001}<100>x<010>/(001)[0
0]x[001], serving as the interface, both bond shear strain at superlattice crack deflection, ybdS, and superlattice crack deflection (SCD) barrier, ΔKS*, vanish, and the easy interfacial crack would begin to propagate (in the absence of mode mixity) in a self-similar manner right at the Griffith/Irwin critical stress intensity factor. Likewise, a YBa2C3O7-d/Si3N4 superlattice, with both easy cleavage systems, either {001}<100>x<010>/(001)[0 0]x[
0]x[ 00] or {001}<100>x<010>/(
00] or {001}<100>x<010>/( 00)[0
00)[0 0]x[001], serving as the interface, would elicit a similar behavior. Other examples include Au/MgO (resp. YBa2C3O7-d/MgO) bicrystalline superlattice with (
0]x[001], serving as the interface, would elicit a similar behavior. Other examples include Au/MgO (resp. YBa2C3O7-d/MgO) bicrystalline superlattice with ( 10)[001]x[110/(
10)[001]x[110/( 10)[001]x[110] (resp. {001}<100>x<010>/(
10)[001]x[110] (resp. {001}<100>x<010>/( 10)[001]x[110] cleavage systems serving as the interface. Similar response also ensues for the YBa2C3O7-d/SrTiO3 bicrystalline superlattice with (010)[001]x[100]/(
10)[001]x[110] cleavage systems serving as the interface. Similar response also ensues for the YBa2C3O7-d/SrTiO3 bicrystalline superlattice with (010)[001]x[100]/( 10)[001]x[110] or (
10)[001]x[110] or ( 00)[001]x[010]/(
00)[001]x[010]/( 10)[001]x[110] cleavage systems serving as the interface. The bond breaking would be smooth and continuous.
10)[001]x[110] cleavage systems serving as the interface. The bond breaking would be smooth and continuous. 10)[001]x[110] or (
10)[001]x[110] or ( 10)[001]x[110]/(010)[001]x[100] cleavage systems serving as the interface, the SCD barrier, ΔKS*, also vanishes, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. Similar response ensues for the YBa2C3O7-d/SrTiO3 bicrystalline superlattice with {001}<100>x<010>/(010)[001]x[100] cleavage systems serving as the interface. Likewise, the Au/Si3N4 or YBa2C3O7/Si3N4 superlattice with one easy and the second one difficult, either (010)[001]x[100]/(001)[0
10)[001]x[110]/(010)[001]x[100] cleavage systems serving as the interface, the SCD barrier, ΔKS*, also vanishes, and the interfacial crack would begin to propagate (in the absence of mode mixity) on the easier side of and parallel to the interface at the Griffith/Irwin critical stress intensity factor. Similar response ensues for the YBa2C3O7-d/SrTiO3 bicrystalline superlattice with {001}<100>x<010>/(010)[001]x[100] cleavage systems serving as the interface. Likewise, the Au/Si3N4 or YBa2C3O7/Si3N4 superlattice with one easy and the second one difficult, either (010)[001]x[100]/(001)[0 0]x[
0]x[ 00] or (010)[001]x[100]/(
00] or (010)[001]x[100]/( 00)[0
00)[0 0]x[001] cleavage systems serving as the interface, produces the same outcome. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.
0]x[001] cleavage systems serving as the interface, produces the same outcome. The bond breaking would be smooth and continuous on the easier side, but discontinuous and abrupt on the tougher side of the interface.Appendix-A. Details of the Derivation of the Solution Involving Complex Roots for a (010)[001]×[100] Crack (Mode I/II Loading)
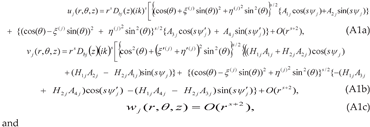

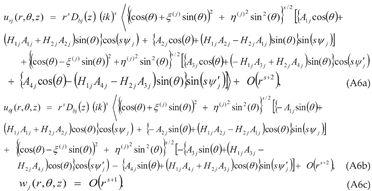
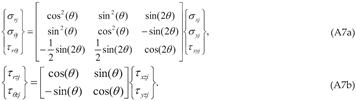
Appendix-B: Details of the Derivation of the Solution Involving Imaginary Roots for a (010)[001]×[100] Crack (Mode I/II Loading)
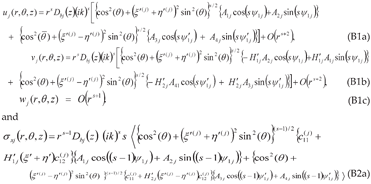

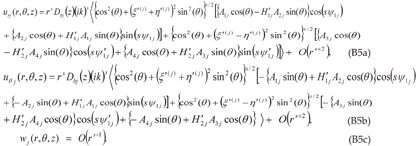
References
- Chaudhuri, RA. Three-dimensional singular stress fields near the circumferential junction corner line of an island/substrate system either free-standing or fully/partially bonded to a rigid block. Eng. Fracture Mech. 2013, 107, 80–97. [Google Scholar] [CrossRef]
- Lin XM, Jaeger HM, Sorensen CM, Klabunde KJ. Formation of long-range-ordered nanocrystal superlattices on silicon nitride substrates. J. Phys. Chem. B, 2001, 105, 3353–3357.
- Ovsyannikov GA, Borisenko IV, Constantinian KY, Kislinski YV, Hakhoumian A, Pogosyan NG, Zakaryan TV. Josephson bicrystal junctions on sapphire substrates for THz frequency application. J. Superconductivity and Novel Magnetism 2006, 19, 669–673. [Google Scholar]
- Pashley DW, Stowell MJ, Jacobs MH, Law TJ. The growth and structure of gold and silver deposits formed by evaporation inside an electron microscope. Philosoph. Magazine 1964, 10, 127–158. [Google Scholar] [CrossRef]
- Yin, E., Rubin MD, Dixon MA. Sputtered YBCO Films on Metal Substrates. J. Mater. Res. 1992, 7, 1636–1640. [CrossRef]
- Lekhnitskii, SG. Anisotropic Plates. Gordon and Breach, New York (1968).
- Stroh, AN. Dislocations and cracks in anisotropic elasticity. Phil. Magazine 1958, 7, 625–646. [Google Scholar] [CrossRef]
- Nazarov, SA. Stress intensity factors and crack deviation conditions in a brittle anisotropic solid. J. Appl. Mech. Techn. Phys. 2005, 36, 386–394. [Google Scholar] [CrossRef]
- Rice, JR. Elastic fracture mechanics concepts for interfacial cracks. ASME J. Appl. Mech. 1988, 55, 98–103. [Google Scholar] [CrossRef]
- Wu K-C. Stress intensity factors and energy release rate for interfacial cracks between dissimilar anisotropic materials. ASME J. Appl. Mech. 1990, 57, 882–886. [Google Scholar] [CrossRef]
- Chaudhuri RA, Xie M, Garala HJ. Stress singularity due to kink band weakening a unidirectional composite under compression. J. Compos. Materials 1996, 30, 672–691. [Google Scholar] [CrossRef]
- Qu J, Bassani JL. Cracks on bimaterial and bicrystal interfaces. J. Mech. Phys. Solids. 1989, 37, 417–433. [Google Scholar] [CrossRef]
- Wang, T.-C. W. , Shih, C. F., Suo, Z. Crack extension and kinking in laminates and bicrystals. International Journal of Solids and Structures 1992, 29, 327–344. [Google Scholar]
- Suo Z, Bao G, Fan B, Wang TC. Orthotropy rescaling and implications for fracture in composites. Int. J. Solids Struct. 1991, 28, 235–248. [Google Scholar] [CrossRef]
- Lin YY, Sung JC. Stress singularities at the apex of a dissimilar anisotropic wedge. ASME J. Appl. Mech. 1998, 65, 454–463. [Google Scholar] [CrossRef]
- Stenger F, Chaudhuri R, Chiu J. Sinc solution of boundary integral form for two-dimensional bi-material elasticity problems. Compos. Sci. Tech. 2000, 60, 2197–2211. [Google Scholar] [CrossRef]
- Dal Corso F, Bigoni D. The interactions between shear bands and rigid lamellar inclusions in a ductile metal matrix. Proc. Royal Soc. A, 2009, 465, 143–163.
- Chaudhuri RA, Xie M. A novel eigenfunction expansion solution for three-dimensional crack problems. Compos. Sci. Tech. 2000, 60, 2565–2580. [Google Scholar] [CrossRef]
- Chaudhuri, RA. On through-thickness distribution of stress intensity factors and energy release rates in the vicinity of crack fronts. Eng. Fracture Mech. 2019, 216, 106478. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Eigenfunction expansion solutions for three-dimensional rigid planar inclusion problem. Int. J. Fracture 2003, 121, 95–110. [Google Scholar] [CrossRef]
- Xie M, Chaudhuri RA. Three-dimensional stress singularity at a bimaterial interface crack front. Compos. Struct. 1997, 40, 137–147. [Google Scholar] [CrossRef]
- Yoon J, Chaudhuri RA. Three-dimensional asymptotic antiplanet shear stress fields at the front of interfacial crack/anticrack type discontinuities in trimaterial bonded plates. Compos. Struct. 2011, 93, 1505–1515. [Google Scholar] [CrossRef]
- Chaudhuri RA, Yoon, J. Three-dimensional asymptotic mode I/II stress fields at the front of interfacial crack/anticrack discontinuities in trimaterial bonded plates. Compos. Struct. 2012, 94, 351–362. [Google Scholar] [CrossRef]
- Chaudhuri RA, Xie M. On three-dimensional asymptotic solution, and applicability of Saint–Venant’s principle to pie-shaped wedge and end face (of a semi-infinite plate) boundary value problems. Eng. Fracture Mech. 2015; 142, 93-107; see also Corrigendum Eng. Fracture Mech. 2019, 217, 106506. [Google Scholar] [CrossRef]
- Chaudhuri, RA. On applicability and uniqueness of the correspondence principle to pie-shaped wedge (“wedge paradox”) with various boundary conditions. Eng. Fracture Mech. 2020, 231, 106991. [Google Scholar] [CrossRef]
- Chaudhuri RA, Xie M. A tale of two saints: St. Venant and “St. Nick” — Does St. Venant's principle apply to bimaterial straight edge and wedge singularity problems? Compos. Sci. Tech. 2000, 60, 2503–2515. [Google Scholar] [CrossRef]
- Xie M, Chaudhuri RA. Three-dimensional asymptotic stress field at the front of a bimaterial wedge of symmetric geometry under antiplane shear loading. Compos. Struct. 2001, 54, 509–514. [Google Scholar] [CrossRef]
- Chiu JSH, Chaudhuri RA. Three-dimensional asymptotic stress field at the front of an unsymmetric bimaterial pie-shaped wedge under antiplane shear loading. Compos. Struct. 2002, 58, 129–137. [Google Scholar] [CrossRef]
- Chaudhuri RA, Xie M. Free-edge stress singularity in a bimaterial laminate. Compos. Struct. 1997, 40, 129–136. [Google Scholar] [CrossRef]
- Chaudhuri RA, Chiu SHJ. Three-Dimensional Asymptotic Stress Field in the Vicinity of an Adhesively Bonded Scarf Joint Interface. Compos. Struct. 2009, 89, 475–483. [Google Scholar] [CrossRef]
- Chiu SHJ, Chaudhuri RA. A three-dimensional eigenfunction expansion approach for singular stress field near an adhesively-bonded scarf joint interface in a rigidly-encased plate. Eng. Fracture Mech. 2011, 78, 2220–2234. [Google Scholar] [CrossRef]
- Yoon J, Chaudhuri RA. Three-dimensional asymptotic stress fields at the front of a trimaterial junction. Compos. Struct. 2012, 94, 337–350. [Google Scholar] [CrossRef]
- Chaudhuri RA, Chiu SHJ. Three-dimensional singular stress field near the interfacial bond line of a tapered jointed plate either free-standing (notch) or (fully/partially) attached to a super-rigid inclusion (antinotch). Eng. Fracture Mech. 2012, 91, 87–102. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional asymptotic stress field in the vicinity of the circumferential tip of a fiber-matrix interfacial debond. Int. J. Eng. Sci. 2004, 42, 1707–1727. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional singular stress field near a partially debonded cylindrical rigid fiber. Compos. Struct. 2006, 72, 141–150. [Google Scholar] [CrossRef]
- Chaudhuri SN, Chaudhuri RA, Benner RE, Penugonda M. Raman spectroscopy for characterization of interfacial debonds between carbon fibers and polymer matrices. Compos. Struct. 2006, 76, 375–387. [Google Scholar] [CrossRef]
- Chaudhuri RA, Chiu SHJ. Three-dimensional asymptotic stress field at the front of an unsymmetric bimaterial wedge associated with matrix cracking or fiber break. Compos. Struct. 2007, 78, 254–263. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional asymptotic stress field in the vicinity of the circumference of a penny shaped discontinuity. Int. J. Solids Struct. 2003, 40, 3787–3805. [Google Scholar] [CrossRef]
- Kaczynski, A. and Kozlowski, W. Thermal stresses in an elastic space with a perfectly rigid flat inclusion under perpendicular heat flow. Int. J. Solids Struct. 2009, 46, 1772–1777. [Google Scholar] [CrossRef]
- Willis, JR. The penny shaped crack on an interface. Quart. J. Mech. Appl. Math. 1972, 25, 367–385. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional asymptotic stress field in the vicinity of the circumference of a bimaterial penny shaped interface discontinuity. Int. J. Fracture 2006, 141, 207–221. [Google Scholar] [CrossRef]
- Folias, ES. The 3D stress field at the intersection of a hole and a free surface. Int. J. Fracture 1987, 35, 187–194. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional asymptotic stress field in the vicinity of the line of intersection of a circular cylindrical through/part-through open/rigidly plugged hole and a plate. Int. J. Fracture 2003, 122, 65–88. [Google Scholar] [CrossRef]
- Folias, ES. On interlaminar stresses of a composite plate around the neighborhood of a hole. Int. J. Solids Struct. 1989, 25, 1193–1200. [Google Scholar] [CrossRef]
- Chaudhuri, RA. An eigenfunction expansion solution for three-dimensional stress field in the vicinity of the circumferential line of intersection of a bimaterial interface and a hole. Int. J. Fracture 2004, 129, 361–384. [Google Scholar] [CrossRef]
- Folias, ES. On the stress singularities at the intersection of a cylindrical inclusion with the free surface of a plate. Int. J. Fracture 1989, 39, 25–34. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional asymptotic stress field in the vicinity of the line of intersection of an inclusion and plate surface. Int. J. Fracture 2002, 117, 207–233. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional singular stress field at the front of a crack weakening a unidirectional fiber reinforced composite plate. Compos. Struct. 2011, 93, 513–527. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional singular stress field at the front of a crack and lattice crack deviation (LCD) in a cubic single crystal plate. Philosophical Magazine 2010, 90, 2049–2113. [Google Scholar] [CrossRef]
- Chaudhuri, RA. On three-dimensional singular stress field at the front of a planar rigid inclusion (anticrack) in an orthorhombic mono-crystalline plate. Int. J. Fracture 2012, 174, 103–126. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional mixed mode I+II+III singular stress field at the front of a (111)[2]×[10] crack weakening a diamond cubic mono-crystalline plate with crack turning and step/ridge formation. Int. J. Fracture 2014, 187, 15–49. [Google Scholar] [CrossRef]
- Chaudhuri, RA. On three-dimensional singular stress/residual stress fields at the front of a crack/anticrack in an orthotropic/orthorhombic plate under anti-plane shear loading. Compos. Struct. 2010, 92, 1977–1984. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Three-dimensional stress/residual stress fields at crack/anticrack fronts in monoclinic plates under antiplane shear loading. Eng. Fracture Mech. 2012, 87, 16–35. [Google Scholar] [CrossRef]
- Yoon J, Chaudhuri RA. Three-dimensional singular antiplane shear stress fields at the fronts of interfacial crack/anticrack/contact type discontinuities in tricrystal anisotropic plates. Eng. Fracture Mech. 2013, 102, 15–31. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Comparison of stress singularities of kinked carbon and glass fibers weakening compressed unidirectional composites: a three-dimensional trimaterial junction stress singularity analysis. Phil. Magazine 2014, 94, 625–667. [Google Scholar] [CrossRef]
- Eshelby JD, Read WT, Shockley W. Anisotropic elasticity with application to dislocation theory. Acta Metall. 1953, 1, 251–259. [Google Scholar] [CrossRef]
- Carslaw, HS. Introduction to the Theory of Fourier Series and Integrals. 3rd edn., Dover, New York (1930).
- Wilcox, CH. Uniqueness theorems for displacement fields with locally finite energy in linear elastostatics. J. Elasticity 1979, 9, 221–243. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Employment of fracture mechanics criteria for accurate assessment of the full set of elastic constants of orthorhombic/tetragonal mono-crystalline YBCO,” Applied Mechanics 2023, 4, 585–643. [CrossRef]
- Riddle J, Gumbsch P, Fischmeister HF. Cleavage Anisotropy in Tungsten Single Crystals. Phys. Rev. Lett. 1996, 76, 3594–3597. [Google Scholar] [CrossRef] [PubMed]
- Hull D, Beardmore P. Velocity of propagation of cleavage cracks in tungsten. Int. J. Fract. Mech. 1966, 2, 468–487. [Google Scholar] [CrossRef]
- Perez R, Gumbsch P. Directional anisotropy in the cleavage fracture of silicon. Phys. Rev. Lett. 2000, 84, 5347–5350. [Google Scholar] [CrossRef]
- Kermode JR, Albaret T, Sherman D, Bernstein N, Gumbsch P, Payne MC, Csányi G, De Vita A. Low-speed fracture instabilities in a brittle crystal. Nature 2008, 455, 1224–1227. [Google Scholar] [CrossRef]
- Newnham, RE. Structure-Property Relations. Springer-Verlag, New York (1975).
- Pauling, L. The Chemical Bond. Cornell Univ. Press, Ithaca, New York (1967).
- Cotton FA, Wilkinson G. Advanced Inorganic Chemistry. 4th edn., John Wiley & Sons, New York (1980).
- Alexandrov IV, Goncharov AF, Stishov SM. State equation and compressibility of YBa2Cu3Ox high temperature superconductor monocrystals under pressure to 20 GPa. Pis’ma Zh. Eksp. Teor. Fiz. 1988, 47, 357–360. [Google Scholar]
- Golding B, Haemmerle WH, Schneemeyer LF, Waszczak JV. Gigahertz ultrasound in single crystal superconducting YBa2Cu3O7. IEEE 1988 Ultrasonics Symp. Proc. Chicago, IL, 1988; vol.2: 1079-1083. [CrossRef]
- Saint-Paul M, Tholence JL, Noel H, Levet JC, Potel M, Gougeon P. Ultrasound study on YBa2Cu3O7−δ and GdBa2Cu3O7−δ single crystals. Solid State Comm. 1989, 69, 1161–1163. [Google Scholar] [CrossRef]
- Saint-Paul M, Henry JY. Elastic anomalies in YBa2Cu3O7−δ single crystals. Solid State Communications 1989, 72, 685–687. [Google Scholar] [CrossRef]
- 71. Jorgensen, JD, Pei S, Lightfoot P, Hinks DG, Veal BW, Dabrowski B, Paulikas AP, Kleb R, Brown ID. Physica C.
- Reichardt W, Pintschovius L, Hennion B, Collin F. Inelastic neutron scattering study of YBa2Cu3O7-x. Supercond. Sci. Tech. 1988, 1, 173–176. [Google Scholar] [CrossRef]
- Baumgart P, Blumenröder S, Erle A, Hillebrands B, Güntherodt G, Schmidt H. Sound velocities of YBa2Cu3O7−δ single crystals measured by Brillouin spectroscopy. Solid State Comm. 1989, 69, 1135–1137. [Google Scholar] [CrossRef]
- Baumgart P, Blumenröder S, Erle A, Hillebrands B, Splittgerber P, Güntherodt G, Schmidt H. Sound velocities of YBa2Cu3O7−δ and Bi2Sr2CaCu2Ox single crystals measured by Brillouin spectroscopy. Physica C: Supercond. Its Applic. 1989, 162–164, 1073–1074. [Google Scholar] [CrossRef]
- Zouboulis E, Kumar S, Chen CH, Chan SK, Grimsditch M, Downey J, McNeil L, Surface waves on the a, b and c faces of untwinned single crystals of YBa2C3O7−δ. Physica C: Superconductivity 1992, 190, 329–332. [CrossRef]
- Lei M, Sarrao JL, Visscher WM, Bell TM, Thompson JD, Migliori A, Welp UW, Veal BM. Elastic constants of a monocrystal of superconducting YBa2Cu3O7-. Phys. Rev. B 1993, 10, 6154–6156. [Google Scholar] [CrossRef]
- Migliori A, et al. Elastic constants and specific-heat measurements on single crystals of La2CuO4. Phys. Rev. B 1990, 41, 2098–2102. [Google Scholar] [CrossRef]
- Nye, JF. Physical Properties of Crystals. Oxford University Press, Oxford (1979).
- D. J. Weidner and G. Simmons. J. Geophys. Res. 1972, 77, 826–847.
- Cook RF, Dinger TR, Clarke DR. Fracture toughness measurements of YBa2Cu3Ox single crystals. Appl. Phys. Lett. 1987, 61, 454–456. [Google Scholar] [CrossRef]
- Raynes AS, Freiman SW, Gayle FW, Kaiser DL. Fracture toughness of YBa2Cu3O6+δ single crystals: Anisotropy and twinning effects. J. Appl. Phys. 1991, 70, 5254–5257. [Google Scholar] [CrossRef]
- Goyal A, Funkenbusch PD, Kroeger DM, Burns SJ. Anisotropic hardness and fracture toughness of highly aligned YBa2Cu3O7−δ. J. Appl. Phys. 1992, 71, 2363–2366. [Google Scholar] [CrossRef]
- Granozio FM, di Uccio US. Gibbs energy and growth habits of YBCO. J. Alloys and Compounds. [CrossRef]
- Streiffer SK, Lairson BM. , Eom CB, Clemens BM, Bravman JC, Geballe TH. Microstructure of ultrathin films of YBa2Cu3O7− δ on MgO. Phys. Rev. B 1991, 43, 13007. [Google Scholar] [CrossRef]
- Fowler DE, Brundle C. R., Lerczac J, Holtzberg FJ. Core and valence XPS spectra of clean, cleaved single crystals of YBa2Cu3O7. Electron Spectroscopy and Related Phenomena 1990, 52, 323–339. [CrossRef]
- Tanaka S, Nakamura T, Tokuda H, Iiyama M. All in situ deposition and characterization of YBa2Cu3O7−x thin films by low-energy electron diffraction and low-energy ion scattering spectroscopy. Appl. Phys. Lett. 1993, 62, 3040. [Google Scholar] [CrossRef]
- Lin CT, Liang WY. Etch defects in YBa2Cu3O7− δ single crystals grown from flux. Physic C 1994, 225, 275–286. [Google Scholar] [CrossRef]
- Chaudhuri, RA. Interfacial Crack Turning in Bi-Crystals of Cubic Symmetry: A Three-Dimensional Stress Singularity Analysis. In Fracture Mechanics: Advances in Research and Applications, ed., R. D. S. G. Campilho, K. Madani, and M. Belhouari, Nova Science Publishers, Inc., 2024.
- Chaudhuri RA, El-Gerwi LA. Estimation of residual stresses in a pressurized thin cylindrical vessel weakened by a finite line crack. In Fracture Mechanics: Advances in Research and Applications, 2024.
- Comninou, M. The interface crack. ASME J. Appl. Mech. 1977, 44, 631–636. [Google Scholar] [CrossRef]
- Hull D, Clyne TW. An Introduction to Composite Materials. 2nd edn., Cambridge, UK; Cambridge University Press, 1996.
- Tuinstra F, Koenig JL. Characterization of graphite fiber surfaces with Raman spectroscopy. Journal of Composite Materials 1970, 4, 492–499. [Google Scholar] [CrossRef]
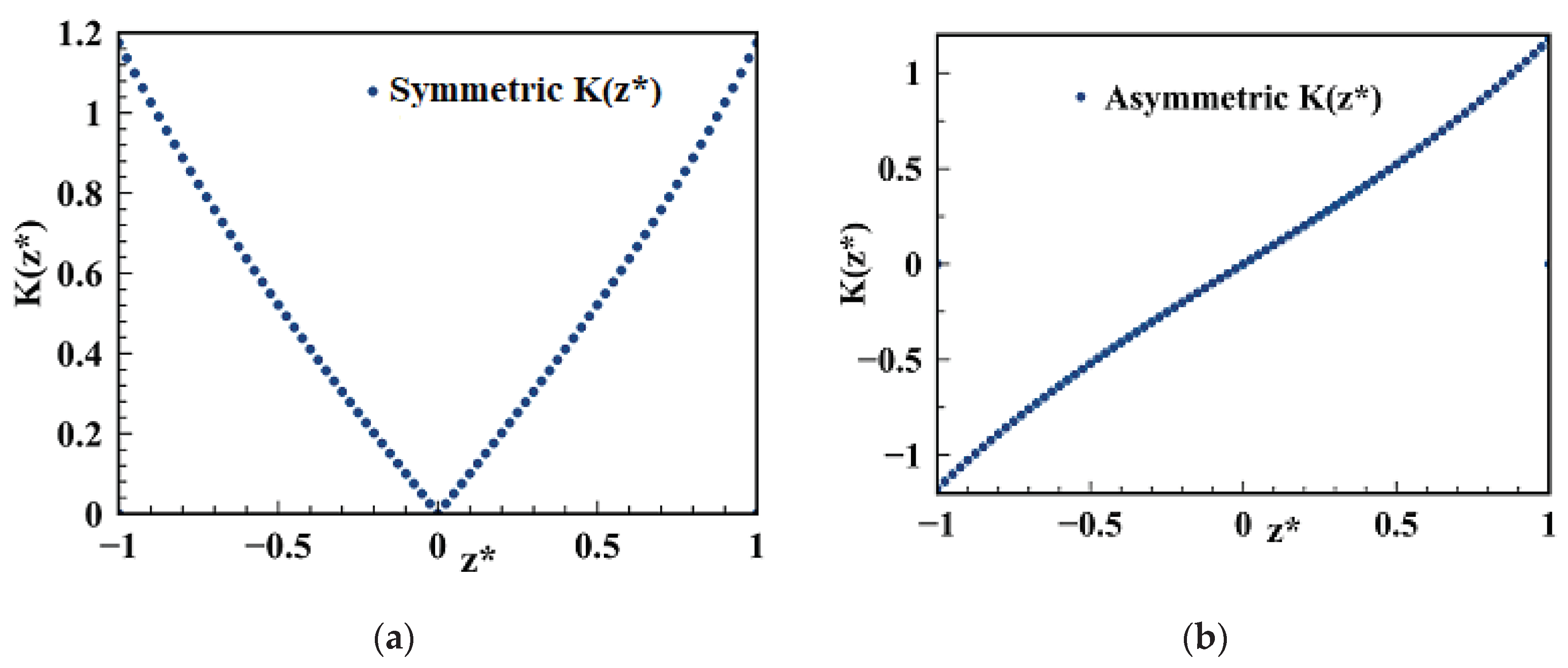
| Single Crystal |
Bravais Lattice | Structure |
C11 (GPa) |
C22 (GPa) |
C33 (GPa) |
C12 (GPa) |
C13 (GPa) |
C23 (GPa) |
C44 (GPa) |
C55 (GPa) |
C66 (GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Au [78] | FCC | FCC | 192.9 | 192.9 | 192.9 | 163.8 | 163.8 | 163.8 | 41.5 | 41.5 | 41.5 |
| MgO [78] | FCC | Rock Salt | 289.3 | 289.3 | 289.3 | 87.70 | 87.70 | 87.70 | 154.77 | 154.77 | 154.77 |
| SrTiO3 [78] |
Simple Cubic | Perovskite | 348.17 | 348.17 | 348.17 | 100.64 | 100.64 | 100.64 | 454.55 | 454.55 | 454.55 |
| Si3N4 | HCP | HCP | 343.0 | 343.0 | 600.0 | 136.0 | 120.0 | 120.0 | 124.0 | 124.0 | 103.5 |
| YBa2C3O7 [72]* |
Tetra-gonal | Perovskite | 230.0 | 230.0 | 150.0 | 100.0 | 100.0 | 100.0 | 50.0 | 50.0 | 85.0 |
| YBa2C3O7-d [59,70,76]† |
Ortho-rhombic | Perovskite | 231.0 | 268.0 | 186.0 | 66.0 | 71.0 | 95.0 | 49.0 | 37.0 | 82.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
(010)[001] x[100] |
192.9 | 192.9 | 192.9 | 163.8 | 163.8 | 163.8 | 41.5 | 41.5 | 41.5 |
| 2* | Si3N4 (HCP) |
(001)[0 0] x[ 0] x[ 00] 00] |
343.0 | 600.0 | 343.0 | 120.0 | 136.0 | 120.0 | 124.0 | 103.5 | 124.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
(010)[001] x[100] |
192.9 | 192.9 | 192.9 | 163.8 | 163.8 | 163.8 | 41.5 | 41.5 | 41.5 |
| 2* | Si3N4 (HCP) |
( 00)[0 00)[0 0] x[001] 0] x[001] |
600.0 | 343.0 | 343.0 | 120.0 | 120.0 | 136.0 | 103.5 | 124.0 | 124.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
219.85 | 219.85 | 192.9 | 136.85 | 163.8 | 163.8 | 41.5 | 41.5 | 14.5 |
| 2* | Si3N4 (HCP) |
(001)[0 0] x[ 0] x[ 00] 00] |
343.0 | 600.0 | 343.0 | 120.0 | 136.0 | 120.0 | 124.0 | 103.5 | 124.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
219.85 | 219.85 | 192.9 | 136.85 | 163.8 | 163.8 | 41.5 | 41.5 | 14.5 |
| 2* | Si3N4 (HCP) |
( 00)[0 00)[0 0] 0]x[001] |
600.0 | 343.0 | 343.0 | 120.0 | 120.0 | 136.0 | 103.5 | 124.0 | 124.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
(010)[001]x[100] | 192.9 | 192.9 | 192.9 | 163.8 | 163.8 | 163.8 | 41.5 | 41.5 | 41.5 |
| 2 | MgO (FCC) |
(010)[001]x[100] | 289.3 | 289.3 | 289.3 | 87.7 | 87.7 | 87.7 | 154.77 | 154.77 | 154.77 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
(010)[001] x[100] |
192.9 | 192.9 | 192.9 | 163.8 | 163.8 | 163.8 | 41.5 | 41.5 | 41.5 |
| 2 | MgO (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
343.27 | 343.27 | 289.3 | 33.73 | 87.7 | 87.7 | 154.77 | 154.77 | 100.8 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
219.85 | 219.85 | 192.9 | 136.85 | 163.8 | 163.8 | 41.5 | 41.5 | 14.5 |
| 2 | MgO (FCC) |
(010)[001]x[100] | 289.3 | 289.3 | 289.3 | 87.7 | 87.7 | 87.7 | 154.77 | 154.77 | 154.77 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
219.85 | 219.85 | 192.9 | 136.85 | 163.8 | 163.8 | 41.5 | 41.5 | 14.5 |
| 2 | MgO (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
343.27 | 343.27 | 289.3 | 33.73 | 87.7 | 87.7 | 154.77 | 154.77 | 100.8 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7 (Tetra-gonal) |
(010)[001] x[100] |
230.0 | 230.0 | 150.0 | 100.0 | 100.0 | 100.0 | 50.0 | 50.0 | 85.0 |
| 2* | Si3N4 (HCP) |
( 00)[0 00)[0 0] x[001] 0] x[001] |
600.0 | 343.0 | 343.0 | 120.0 | 120.0 | 136.0 | 103.5 | 124.0 | 124.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7 (Tetra-gonal) |
(010)[001]x[100] | 230.0 | 230.0 | 150.0 | 100.0 | 100.0 | 100.0 | 50.0 | 50.0 | 85.0 |
| 2 | SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 348.17 | 348.17 | 348.17 | 100.64 | 100.64 | 100.64 | 454.55 | 454.55 | 454.55 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7 (Tetra-gonal) |
(010)[001] x[100] |
230.0 | 230.0 | 150.0 | 100.0 | 100.0 | 100.0 | 50.0 | 50.0 | 85.0 |
| 2 | SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
678.96 | 678.96 | 348.17 | -230.15 | 100.64 | 100.64 | 454.55 | 454.55 | 123.77 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7 (Tetra-gonal) |
( 10)[001] x[110] 10)[001] x[110] |
250.0 | 250.0 | 150.0 | 80.0 | 100.0 | 100.0 | 50.0 | 50.0 | 65.0 |
| 2 | SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
678.96 | 678.96 | 348.17 | -230.15 | 100.64 | 100.64 | 454.55 | 454.55 | 123.77 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7 (Tetra-gonal) |
( 10)[001] x[110] 10)[001] x[110] |
250.0 | 250.0 | 150.0 | 80.0 | 100.0 | 100.0 | 50.0 | 50.0 | 65.0 |
| 2 | SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 348.17 | 348.17 | 348.17 | 100.64 | 100.64 | 100.64 | 454.55 | 454.55 | 454.55 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
(001)[100] x[010] |
268.0 | 186.0 | 231.0 | 95.0 | 66.0 | 71.0 | 37.0 | 82.0 | 49.0 |
| 2* | Si3N4 (HCP) |
(001)[0 0] x[ 0] x[ 00] 00] |
343.0 | 600.0 | 343.0 | 120.0 | 136.0 | 120.0 | 124.0 | 103.5 | 124.0 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
(001)[100] x[010] |
268.0 | 186.0 | 231.0 | 95.0 | 66.0 | 71.0 | 37.0 | 82.0 | 49.0 |
| 2 | MgO (FCC) |
(010)[001]x[100] | 289.3 | 289.3 | 289.3 | 87.7 | 87.7 | 87.7 | 154.77 | 154.77 | 154.77 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
(001)[100] x[010] |
268.0 | 186.0 | 231.0 | 95.0 | 66.0 | 71.0 | 37.0 | 82.0 | 49.0 |
| 2 | MgO (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
343.27 | 343.27 | 289.3 | 33.73 | 87.7 | 87.7 | 154.77 | 154.77 | 100.8 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
(001)[100]x[010] | 268.0 | 186.0 | 231.0 | 95.0 | 66.0 | 71.0 | 37.0 | 82.0 | 49.0 |
| 2 | SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 348.17 | 348.17 | 348.17 | 100.64 | 100.64 | 100.64 | 454.55 | 454.55 | 454.55 |
| Material (j) # | Single Crystal Phase |
Cleavage System |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
(GPa) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | YBa2C3O7-d (Ortho-rhombic) |
(001)[100]x[010] | 268.0 | 186.0 | 231.0 | 95.0 | 66.0 | 71.0 | 37.0 | 82.0 | 49.0 |
| 2 | SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
678.96 | 678.96 | 348.17 | -230.15 | 100.64 | 100.64 | 454.55 | 454.55 | 123.77 |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
(010)[001]x[100] | 2.8522 | 1.0 | 4.9777 | Complex | Difficult |
| Si3N4 (HCP) |
(001)[0 0] x[ 0] x[ 00] 00] |
0.7433 | 1.3226 | 0.9206 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
(010)[001] x[100] |
2.8522 | 1.0 | 4.9777 | Complex | Difficult |
| Si3N4 (HCP) |
( 00)[0 00)[0 0] x[001] 0] x[001] |
0.7433 | 0.5717 | 0.5263 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.3494 | 1.0 | 0.2487 | Imaginary | Easy |
| Si3N4 (HCP) |
(001)[0 0] x[ 0] x[ 00] 00] |
0.7433 | 1.3226 | 0.9206 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.3494 | 1.0 | 0.2487 | Imaginary | Easy |
| Si3N4 (HCP) |
( 00)[0 00)[0 0] x[001] 0] x[001] |
0.7433 | 0.5717 | 0.5263 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
(010)[001]x[100] | 2.8522 | 1.0 | 4.9777 | Complex | Difficult |
| MgO (FCC) |
(010)[001]x[100] | 1.5354 | 1.0 | 1.8329 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
(010)[001]x[100] | 2.8522 | 1.0 | 4.9777 | Complex | Difficult |
| MgO (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.6513 | 1.0 | 0.6297 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.3494 | 1.0 | 0.2487 | Imaginary | Easy |
| MgO (FCC) |
(010)[001] x[100] |
1.5354 | 1.0 | 1.8329 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| Au (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.3494 | 1.0 | 0.2487 | Imaginary | Easy |
| MgO (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.6513 | 1.0 | 0.6297 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7 (Tetra-gonal) |
(010)[001] x[100] |
1.9077 | 1.0 | 3.1514 | Complex | Difficult |
| Si3N4 (HCP) |
( 00)[0 00)[0 0] x[001] 0] x[001] |
0.7433 | 0.5717 | 0.9206 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7 (Tetra-gonal) |
(010)[001]x[100] | 1.9077 | 1.0 | 3.1514 | Complex | Difficult |
| SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 3.6727 | 1.0 | 16.1473 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7 (Tetra-gonal) |
(010)[001]x[100] | 1.9077 | 1.0 | 3.1514 | Complex | Difficult |
| SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
0.2723 | 1.0 | 0.3614 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7 (Tetra-gonal) |
( 10)[001] x[110] 10)[001] x[110] |
0.7647 | 1.0 | 0.7112 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 3.6727 | 1.0 | 16.1473 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7 (Tetra-gonal) |
( 10)[001] x[110] 10)[001] x[110] |
0.7647 | 1.0 | 0.7112 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
0.2723 | 1.0 | 0.3614 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(001)[100] x[010] |
0.764 | 0.8331 | 0.5784 | Imaginary | Easy |
| Si3N4 (HCP) |
(001)[0 0] x[ 0] x[ 00] 00] |
0.7433 | 1.3226 | 0.9206 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(001)[100]x[010] | 0.764 | 0.8331 | 0.5784 | Imaginary | Easy |
| MgO (FCC) |
(010)[001]x[100] | 1.5354 | 1.0 | 1.8329 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(001)[100]x[010] | 0.764 | 0.8331 | 0.5784 | Imaginary | Easy |
| MgO (FCC) |
( 10)[001] x[110] 10)[001] x[110] |
0.6513 | 1.0 | 0.6297 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(001)[100]x[010] | 0.764 | 0.8331 | 0.5784 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 3.6727 | 1.0 | 16.1473 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(001)[100]x[010] | 0.764 | 0.8331 | 0.5784 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
0.2723 | 1.0 | 0.3614 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(010)[001]x[100] | 0.8971 | 1.0771 | 0.9406 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 3.6727 | 1.0 | 16.1473 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
(010)[001]x[100] | 0.8971 | 1.0771 | 0.9406 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
( 10)[001] x[110] 10)[001] x[110] |
0.2723 | 1.0 | 0.3614 | Imaginary | Easy |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
( 00)[001]x[010] 00)[001]x[010] |
0.8971 | 0.9284 | 0.817 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
(010)[001]x[100] | 3.6727 | 1.0 | 16.1473 | Complex | Difficult |
| Material (j) # |
Cleavage System | A′ | K′ | Roots | Cleavage System: Easy or Difficult |
|
|---|---|---|---|---|---|---|
| YBa2C3O7-d (Ortho-rhombic) |
( 00)[001]x[010] 00)[001]x[010] |
0.8971 | 0.9284 | 0.817 | Imaginary | Easy |
| SrTiO3 (Simple Cubic) |
( 10)[0 10)[0 01] x[110] 01] x[110] |
0.2723 | 1.0 | 0.3614 | Imaginary | Easy |
| Bicrystal System # | Nano-film/ Substrate |
Cleavage Systems | Roots | Cleavage System: Easy or Difficult |
s = 0.5 or s = 0.5±ie |
|---|---|---|---|---|---|
| 1 | Au/Si3N4 | (010)[001]x[100]/ (001)[0  0]x[ 0]x[ 00] 00] |
Complex/Imaginary | Difficult/Easy | 0.5 |
| 2 | Au/Si3N4 | (010)[001]x[100]/ (  00)[0 00)[0 0]x[001] 0]x[001] |
Complex/Imaginary | Difficult/Easy | 0.5 |
| 3 | Au/Si3N4 | ( 10)[001]x[110]/ 10)[001]x[110]/(001)[00]x[  00] 00] |
Imaginary/Imaginary | Easy/Easy | 0.5 |
| 4 | Au/Si3N4 | ( 10)[001]x[110]/ 10)[001]x[110]/(  00)[0 00)[0 0]x[001] 0]x[001] |
Imaginary/Imaginary | Easy/Easy | 0.5 |
| 5 | Au/MgO | (010)[001]x[100]/ (010)[001]x[100] | Complex/Complex | Difficult/Difficult | 0.5±0.3814i 0.5±0.2108i |
| 6 | Au/MgO | (010)[001]x[100]/ (10)[001]x[110] |
Complex/Imaginary | Difficult/Easy | 0.5 |
| 7 | Au/MgO | ( 10)[001]x[110]/ 10)[001]x[110]/(010)[001]x[100] |
Imaginary/Complex | Easy/Easy | 0.5 |
| 8 | Au/MgO | ( 10)[001]x[110]/ 10)[001]x[110]/(  10)[001]x[110] 10)[001]x[110] |
Imaginary/Imaginary | Easy/Easy | 0.5 |
| 9 | YBa2C3O7 /Si3N4 |
(010)[001]x[100]/ (  00)[0 00)[0 0]x[001] 0]x[001] |
Complex/Imaginary | Difficult/Easy | 0.5 |
| 10 | YBa2C3O7 /SrTiO3 |
(010)[001]x[100]/ (010)[001]x[100] |
Complex/Complex | Difficult/Difficult | 0.5±0.7636i |
| 11 | YBa2C3O7 /SrTiO3 |
(010)[001]x[100]/ (  10)[001]x[110] 10)[001]x[110] |
Complex/Imaginary | Difficult/Easy | 0.5 |
| 12 | YBa2C3O7 /SrTiO3 |
( 10)[001]x[110]/ 10)[001]x[110]/(010)[001]x[100] |
Imaginary/Complex | Easy/Difficult | 0.5 |
| 13 | YBa2C3O7 /SrTiO3 |
( 10)[001]x[110]/ 10)[001]x[110]/(  10)[001]x[110] 10)[001]x[110] |
Imaginary/Imaginary | Easy/Easy | 0.5±0.0580i |
| 14 | YBa2C3O7-d /Si3N4 | (001)[100]x[010]/ (001)[0  0]x[ 0]x[ 00] 00] |
Imaginary/Imaginary | Easy/Easy | 0.5 |
| 15 | YBa2C3O7-d /MgO | (001)[100]x[010]/ (010)[001]x[100] |
Imaginary/Complex | Easy/Difficult | 0.5 |
| 16 | YBa2C3O7-d /MgO | (001)[100]x[010]/ (  10)[001]x[110] 10)[001]x[110] |
Imaginary/Imaginary | Easy/Easy | 0.5 |
| 17 | YBa2C3O7-d /SrTiO3 | (001)[100]x[010]/ (010)[001]x[100] |
Imaginary/Complex | Easy/Difficult | 0.5 |
| 18 | YBa2C3O7-d /SrTiO3 | (001)[100]x[010]/ (10)[001]x[110] |
Imaginary/Imaginary | Easy/Easy | 0.5±0.1757i |
| 19 | YBa2C3O7-d /SrTiO3 | (010)[001]x[100]/ (010)[001]x[100] |
Imaginary/Imaginary | Easy/Easy | 0 |
| 20 | YBa2C3O7-d /SrTiO3 | (010)[001]x[100]/ (  10)[001]x[110] 10)[001]x[110] |
Imaginary/Imaginary | Easy/Easy | 0 |
| 21 | YBa2C3O7-d /SrTiO3 | ( 00)[001]x[010]/ 00)[001]x[010]/(010)[001]x[100] |
Imaginary/Imaginary | Easy/Easy | 0 |
| 22 | YBa2C3O7-d /SrTiO3 | ( 00)[001]x[010]/ 00)[001]x[010]/(  10)[001]x[110] 10)[001]x[110] |
Imaginary/Imaginary | Easy/Easy | 0 |
| Single Crystal |
Bravais Lattice | Structure |
S11 (10-2 GPa-1) |
S22 (10-2 GPa-1) |
S33 (10-2 GPa-1) |
S12 (10-2 GPa-1) |
S13 (10-2 GPa-1) |
S23 (10-2 GPa-1) |
S44 (10-2 GPa-1) |
S55 (10-2 GPa-1) |
S66 (10-2 GPa-1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Au [78,88] |
FCC | FCC | 2.355 | 2.355 | 2.355 | -1.081 | -1.081 | -1.081 | 2.4096 | 2.4096 | 2.4096 |
| MgO [78] |
FCC | Rock Salt | 0.4024 | 0.4024 | 0.4024 | -0.0936 | -0.0936 | -0.0936 | 0.6461 | 0.6461 | 0.6461 |
| SrTiO3 [78] |
Simple Cubic | Perovskite | 0.33 | 0.33 | 0.33 | -0.074 | -0.074 | -0.074 | 0.22 | 0.22 | 0.22 |
| Si3N4 | HCP | HCP | 0.3576 | 0.3576 | 0.1852 | -0.1255 | -0.0464 | -0.0464 | 0.8065 | 0.8065 | 0.9662 |
| YBa2C3O7 |
Tetra-gonal | Perovskite | 0.6389 | 0.6389 | 1.1186 | -0.1304 | -0.339 | -0.339 | 2.0 | 2.0 | 1.1765 |
| Y Ba2C3O7-d |
Ortho-rhombic | Perovskite | 0.5003 | 0.4648 | 0.7054 | -0.0678 | -0.1564 | -0.2115 | 2.0408 | 2.7027 | 1.2195 |
| Crystal |
Easy Cleavage System (ECS) |
Difficult Cleavage System (DCS) |
Aniso. Ratio, A, at DCS | Bond Shear Strain at Lattice Crack Deflection (ybd) | Lattice Crack Deviation (LCD) Parameter in DCS (ΔK*) |
|---|---|---|---|---|---|
| Au [88] | { 10}<001> 10}<001>x<110]> |
{010}〈001〉 x<110]> |
2.8522 | 0.6438 | 0.8364 |
| MgO |
{ 10}<001> 10}<001>x<110]> |
{010}〈001〉 x<100]> |
1.5354 | 0.5353 | 0.6414 |
| SrTiO3 |
{ 10}<001> 10}<001>x<110]> |
{010}〈001〉 x<100]> |
3.6727 | 0.6075 | 0.5114 |
| Si3N4 | ( 00)[0 00)[0 0] x[001]* 0] x[001]* |
------- | |||
| YBa2C3O7 | { 10}<001> 10}<001>x<110]> |
{010}〈001〉 x<100]> |
1.9077 | 0.5055 | 0.6071 |
| YBa2C3O7-d | {001}<100> x<010> |
------- |
| Bicrystal System # | Nano-film/ Substrate |
Cleavage Systems | Cleavage System: Easy or Difficult |
Bond Shear Strain at Superlattice Crack Deflection (ybdS) |
Superlattice Crack Deviation (SCD) Parameter in DCS (ΔKS*) |
|---|---|---|---|---|---|
| 1 | Au/Si3N4 | (010)[001]x[100]/ (001)[0  0]x[ 0]x[ 00] 00] |
Difficult/Easy | 0 | 0 |
| 2 | Au/Si3N4 | (010)[001]x[100]/ (  00)[0 00)[0 0]x[001] 0]x[001] |
Difficult/Easy | 0 | 0 |
| 3 | Au/Si3N4 | ( 10)[001]x[110]/ 10)[001]x[110]/(001)[0  0]x[ 0]x[ 00] 00] |
Easy/Easy | 0 | 0 |
| 4 | Au/Si3N4 | ( 10)[001]x[110]/ 10)[001]x[110]/(  00)[0 00)[0 0]x[001] 0]x[001] |
Easy/Easy | 0 | 0 |
| 5 | Au/MgO | (010)[001]x[100]/ (010)[001]x[100] | Difficult/Difficult | 0.4710 | 0.7324 |
| 6 | Au/MgO | (010)[001]x[100]/ (  10)[001]x[110] 10)[001]x[110] |
Difficult/Easy | 0 | 0 |
| 7 | Au/MgO | ( 10)[001]x[110]/ 10)[001]x[110]/(010)[001]x[100] |
Easy/Difficult | 0 | 0 |
| 8 | Au/MgO | ( 10)[001]x[110]/ 10)[001]x[110]/(  10)[001]x[110] 10)[001]x[110] |
Easy/Easy | 0 | 0 |
| 9 | YBa2C3O7 /Si3N4 |
(010)[001]x[100]/ (  00)[0 00)[0 0]x[001] 0]x[001] |
Difficult/Easy | 0 | 0 |
| 10 | YBa2C3O7 /SrTiO3 |
(010)[001]x[100]/ (010)[001]x[100] |
Difficult/Difficult | 0.5202 | 0.6240 |
| 11 | YBa2C3O7 /SrTiO3 |
(010)[001]x[100]/ (  10)[001]x[110] 10)[001]x[110] |
Difficult/Easy | 0 | 0 |
| 12 | YBa2C3O7 /SrTiO3 |
( 10)[001]x[110]/ 10)[001]x[110]/(010)[001]x[100] |
Easy/Difficult | 0 | 0 |
| 13 | YBa2C3O7 /SrTiO3 |
( 10)[001]x[110]/ 10)[001]x[110]/(  10)[001]x[110] 10)[001]x[110] |
Easy/Easy | 0 | 0 |
| 14 | YBa2C3O7-d /Si3N4 | (001)[100]x[010]/ (001)[0  0]x[ 0]x[ 00] 00] |
Easy/Easy | 0 | 0 |
| 15 | YBa2C3O7-d /MgO | (001)[100]x[010]/ (010)[001]x[100] |
Easy/Difficult | 0 | 0 |
| 16 | YBa2C3O7-d /MgO | (001)[100]x[010]/ (  10)[001]x[110] 10)[001]x[110] |
Easy/Easy | 0 | 0 |
| 17 | YBa2C3O7-d /SrTiO3 | (001)[100]x[010]/ (010)[001]x[100] |
Easy/Difficult | 0 | 0 |
| 18 | YBa2C3O7-d /SrTiO3 | (001)[100]x[010]/ (  10)[001]x[110] 10)[001]x[110] |
Easy/Easy | 0 | 0 |
| 19 | YBa2C3O7-d /SrTiO3 | (010)[001]x[100]/ (010)[001]x[100] |
Easy/Difficult | 0 | 0 |
| 20 | YBa2C3O7-d /SrTiO3 | (010)[001]x[100]/ (  10)[001]x[110] 10)[001]x[110] |
Easy/Easy | 0 | 0 |
| 21 | YBa2C3O7-d /SrTiO3 | ( 00)[001]x[010]/ 00)[001]x[010]/(010)[001]x[100] |
Easy/Difficult | 0 | 0 |
| 22 | YBa2C3O7-d /SrTiO3 | ( 00)[001]x[010]/ 00)[001]x[010]/(  10)[001]x[110] 10)[001]x[110] |
Easy/Easy | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




