1. Introduction
The increasing prevalence of IoT in our daily lives opens a wealth of opportunities to create new services; many of them personalized and customized for individuals, provided that privacy of individual and sensible data is granted in the process of constructing digests that can be used for public benefit, such as planning, policy making [
1], smart agriculture [
2], and health care [
3], among others.
However, in conjunction with the use of IoT in daily life, the question of data privacy acquires increasing importance, as IoT devices and their data are known to be exposed to significant vulnerabilities from the point of view of modern information security[
4]. In fact, the transmission of raw data without adequate privacy protection measures can lead, for example, to unauthorized virtual profiling, which poses a potential threat to fundamental privacy requirements and public trust [
5]. However, ensuring the privacy of data collected from IoT devices, while leveraging them for social profit and the common good, can be effectively achieved through a combination of secure multiparty computation (SMPC), secret sharing protocols, and masking via one-time pads.
Secure multiparty computation is a process in which multiple parties can jointly compute a function over their own private inputs without revealing them to each other. The only thing that is shared among the participants is the result of the calculation. This ensures that the private inputs remain hidden. SMPC can be used in distributed scenarios together with secret sharing and oblivious transfer techniques in order to ensure data privacy, hence enabling joint computation without compromising individual data privacy. Secret-sharing protocols distribute a secret amongst a group of participants, where the secret can only be reconstructed when a sufficient number of shares are combined. They have been shown to be essential for cryptographic applications, beginning with the groundbreaking work of Diffie-Hellman in 1976 [
6].
An example of a protocol in which secure multiparty computation using secret sharing in a distributed environment is used to preserve user privacy while reducing communication and computation costs can be found in [
7].
Oblivious transfer (OT), on the other hand, allows a party to send one of many pieces of information to another party without revealing which piece was sent; see, for example, [
8].
Additionally, masking through one-time pads, where data are encrypted by XORing with a key known only by the communicating parties, ensures a high level of security, provided the key is used once. This method, when combined with MPC and secret sharing, forms a robust framework to preserve the privacy of sensitive information. This synergy is particularly valuable in applications such as smart agriculture, policy making, and healthcare care, where sensitive personal data must be protected while used for analysis and decision making. The combination of these techniques ensures that even if part of the system is compromised, it should be difficult for third parties to deduce confidential information, as it would require considerable computational resources or processing times for full disclosure of protected data, thus supporting the ethical and secure use of IoT data for public benefit.
In this study, we introduce a straightforward protocol for establishing a communication key in the form of a one-time pad (OTP). The key is generated using true randomness, and the communication between two parties is encrypted via XORing with the key. We achieve this by incorporating a dummy third-party and modifying a classical three-party computation protocol. This modified protocol can be applied in real time to mask communications. The use of true randomness ensures that the generated key is used only once, thus maintaining confidentiality. The details of the protocol are explained in
Section 2, and we implement it in a hybrid environment using ZeroC-Ice, Slice, and Python as described in
Section 3 and
Section 4. Furthermore, an analysis of the security properties is presented in
Section 5 and our findings are discussed in
Section 6.
2. A One Time Pad with True Randomness
In this section, we consider the first building block for the secure multiparty computation (SMPC) among two parties using a third dummy party, in a procedure inspired by [
9]. Although the procedure generally applies to any set of numbers, we consider in particular the numbers in
or
in which
p is an appropriate prime. This is because any message has to be converted into a number (or a block of numbers) for encryption, regardless of the message, whether it is data or not. Once the technique has been illustrated, we concentrate our calculations on
, in which
N is a suitable message length.
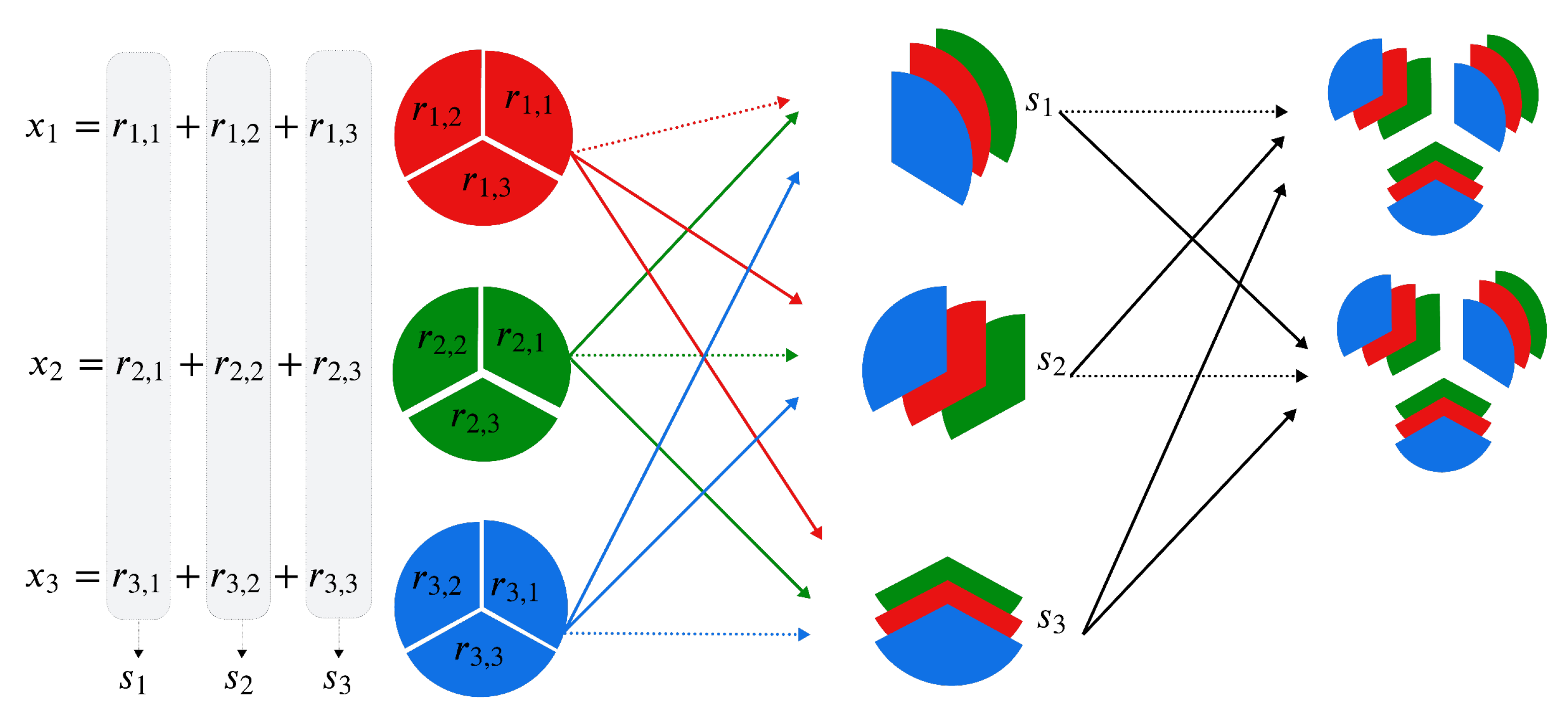
Think of two parties, and , who wish to agree on a common key using a multiparty computation that involves the sum of their individual private inputs , in , but without disclosing them to one another. The procedure needs, of course, a third party, which will be , that is used as an auxiliary server, that only receives inputs and broadcasts the resulting sum of the inputs:
-
Share generation: Each party
,
generates two random shares
and
in
, and computes a third share
as the difference between their private input
and the sum of the two random shares, modulo
p. This is described by the equations:
The party generates three random numbers , .
Standard share distribution (as in [
9]): Each party
sends two of its three shares to the other parties according to a specific rule to ensure that no one party receives all shares from another party. Quote:
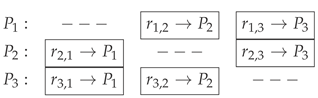
Each sends privately , to , , to , and , to . Hence, the distribution pattern is:
Modified share distribution: Each
sends privately
, to
,
,
. Hence, the distribution pattern is as follows:
-
Partial Sum Determination: In the standard procedure, each party
adds the corresponding shares as:
,
,
. In the modified share distribution, each party
computes the (single) sum of the shares received according to:
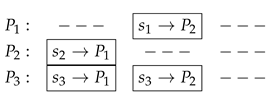
For instance, is aware of his own generated shares, , , and . Additionally, he has obtained from and from . Therefore, can calculate which is expressed as: .
Partial sum distribution: In the standard procedure, each party computes and announces (broadcasts) two values. In our proposed modification,
sends
to
,
sends
to
and
broadcast
to
and
:
Final sum calculation: In the standard procedure, all parties compute the result . In our modified procedure, and calculate both the sum , while learns nothing. Therefore, K will be known only for and , while all private inputs remain private and cannot be deduced from the outputs.
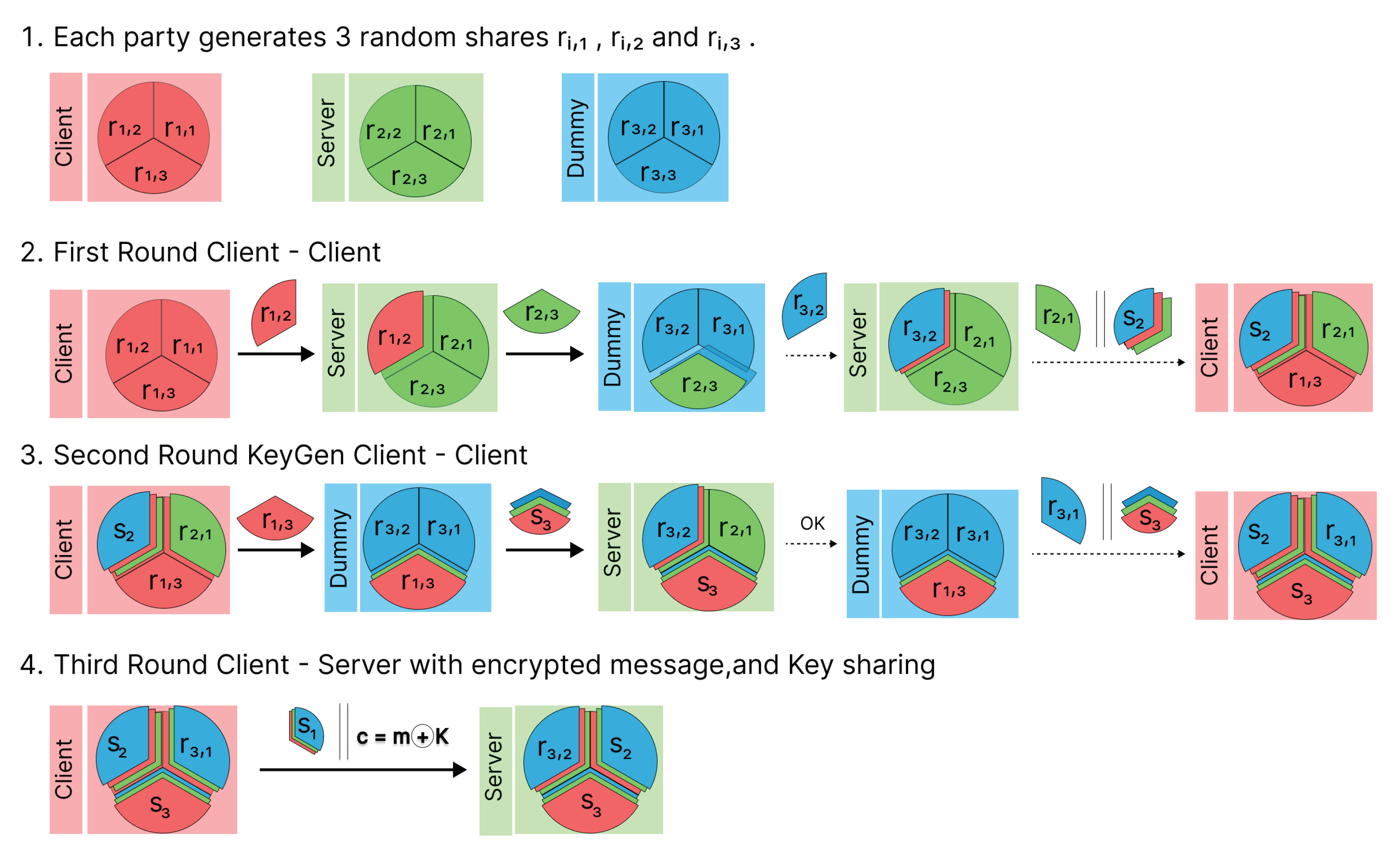
Figure 1 graphically shows our proposal that highlights communication between parties.
Observe that for , the role of randomness guarantees that is never disclosed during communication between parties. In fact, for the first part, only and travel to and , respectively. The third component travels masked in the sum when transmitted. Therefore, even in the case where a malicious eavesdropper was following the interchange between and towards , it is not possible that the output can be correlated with the secure multiparty sum protocol, nor with the random component . Therefore, since the final computation of the key K takes place privately for and , the conclusion is that and have effectively shared a common key K, which can now be used to mask communication between them.
In a usual SMPC summation for three parties, as in [
9], the transmission of the shares is different (10 rounds compared to 12), and allows cross-checking of the partial sums to detect a potential dishonest 1 out of 2 parties. In addition, the key is shared between the three intervening parties. In our procedure, instead, communication can be sequentially arranged so that the total number of rounds can be reduced to 8, which is a reduction of the order of 30% from the standard multiparty summation protocol; see next section.
Now, it should be clear that at this point the space in which the sums are taken can be some for a suitable N, which means that there is no restriction a priori about whether the sums are binary sums or not. This means that the procedure between parties can be performed bit by bit or by blocks of bits of size N. As a classical implementation of the One-Time-Pad protocol, the summation can be executed using the well-known XOR operator.
It is worth noting that it is not necessary to limit the quality of the random shares; they can be pseudo-but also true random bits. These true random bits can be obtained from any source, such as physical true random numbers, which are commonly found in IoT devices (by capturing states from sensors, accelerometers, channel noise, etc.).
3. On the Fly KeyGen and Encryption
It is important to note that while the protocol depicted in
Figure 1 respects the logic behind a three-party sum, as described in [
9], with the exception that the dummy third party does not get knowledge of the final (secure) sum, the actual protocol to be implemented can be significantly improved if the order in which transactions are invoked is taken into account.
Indeed, since any consideration about the messages to be exchanged includes parsimony and duplication avoidance, the protocol can be modified as follows:
|
ProtocolSMP-OTF4IOT: On the Fly KeyGen and Encryption |
 |
We implement the protocol SMP-OTF4IOT described above to establish a common key K between any two IoT devices that can be used as OTP to secure communication between two parties and that requires a third (dummy) server , whose job is to receive inputs and broadcast the sum of the inputs.
The procedure described above can be visualized in the following figure:
Figure 2.
Diagram depicting On the fly Key-agreement and encryption between and using (in blue) as an auxiliary unit in the SMPC protocol.
Figure 2.
Diagram depicting On the fly Key-agreement and encryption between and using (in blue) as an auxiliary unit in the SMPC protocol.
4. Methodology and Implementation
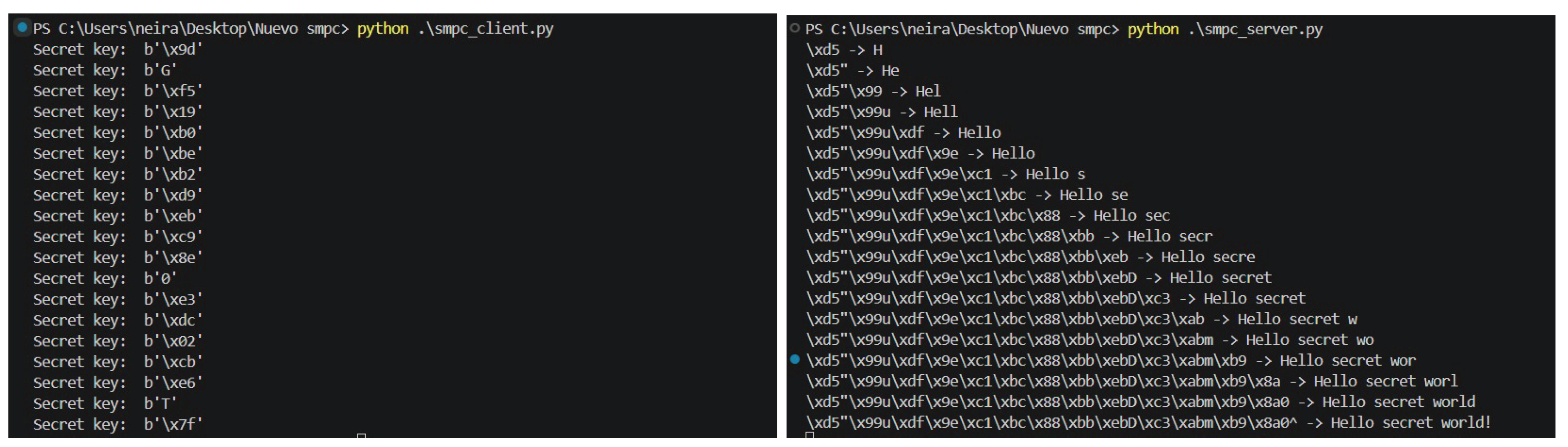
In the
Figure 3, it is shown how a "client" program sends the encrypted message "Hello secret world!" character by character and then the message is decoded as it reaches the "server", which interprets each of the sent characters and reconstructs the original string. All of this is through the SMP-OTF4IOT protocol implemented in Python.
The realization of this process requires the simultaneous functioning of three programs: (1) smpc_dummy.py, which acts as an intermediary for generating random numbers, (2) smpc_server.py, responsible for establishing communication with the "dummy" service where synchronization begins, and finally (3) smpc_client.py, which initializes communication coordination and initiates the sending of encrypted data to the server, synchronously generating keys in real-time to transmit each character. Each of these programs utilizes ZeroC-Ice for network data transfer.
4.1. ZeroC-Ice Implementation on SMP-OTF4IOT
We implement the protocol in ZeroC-Ice, an Internet Communication Engine developed by ZeroC, as described in [
10] using Python [
11] and Slice, a specification language for Ice, see
https://doc.zeroc.com/ice/3.6/the-slice-language. The advantage of using this approach lies in the possibility of connecting three devices from three different platforms with independent architectures, as a raspberry-pi device, a portable device, and the cloud, for example, each running its own script: client, server, and dummy, as well as a masking middleware.
|
Listing 1: ZeroC-Ice SMPC Implementation. |
module SMPC{
interface Server {
void deliverFromClient(int share,
out int shareServer,
out int sumServer
);
void deliverFromDummy(int sum);
void terminate(int sum, byte payload);
}
interface Dummy {
void deliverFromClient(int share,
out int shareDummy,
out int sumDummy
);
void deliverFromServer(int share,
out int shareDummy
);
}
} |
One benefit of utilizing function calls is the ability to include multiple parameters within the call. For instance, in the scenario where the Client’s last message consists of both their partial sum and the encrypted (XORed) message, the Server can retrieve both the key and the message in a single call. Similarly, when making a remote call, it is possible for the call to return multiple values. For example, the Server can return their share and partial sum as a tuple of integers.
By adopting this method, the number of messaging instances for communication is reduced from 11 to 8, including the transmission of the encrypted message (approximately 30% reduction in bandwidth). Notice that the roles described above (Client, Server, Dummy) are used ’as a whole’ for the purposes of secretly communicating between two parties by using (true) random number acquisition and a dummy third party that does not get access to the shared encrypted message, but these roles can be continuously and dynamically changed, so that, in principle, the protocol extends naturally for peer-to-peer secure communication between any number of IoT agents in a real-life application. Note also that if a message
m of size
must be transmitted encrypted according to our algorithm, then the total communication cost for key generation and transmission of an encrypted message would be approximately twice the size of the message; simply because in our setting, the communication time between parties
and
is bounded above by
5. Security Analysis
The security aspects of the SMP-OTP4IOT protocol can be rigorously examined and verified using formal analysis using, say, Tamarin Prover [
12] or Proverif [
13] (see [
14] for an extended review of formal modeling and security analysis of security protocols). However, an accurate description of the formalism required for our protocol lies beyond the scope of this investigation. Instead, we focus on the inherent security properties of the protocol as implemented in ZeroC-Ice.
Under the Dolev-Yao threat model [
15,
16,
17], we assume a semi-honest adversary that has access to all messages exchanged between parties
,
and
and tries to gain some knowledge of the messages being transmitted, without tampering with the transmitted data, or a dishonest adversary, which also actively modifies the messages in transaction.
In the context of the semi-honest participant scenario, all the information being transmitted consists of random numbers and additions. Observing the communication between and , as well as between and in the first round, it is possible to deduce the partial sums and . Subsequently, by monitoring communication between and during encryption and decryption, it is possible to deduce , and consequently the adversary could potentially compute , as well as . We argue that since and differ by , the eavesdropper should need to know exactly the computations that are being performed privately by each of the involved parties, which is conveniently masked by the use of ZeroC-Ice, in order to achieve decryption with the OTP. On the other hand, in the case of a dishonest attacker, any alteration or substitution of the random numbers being transferred can potentially result in a different key for and , rendering the encrypted message useless and may serve as a warning for an eventual unauthorized interception.
We examine our protocol along the lines of [
7] (Section IV) and [
18] (Definition 1.) :
5.1. Privacy, Computation and Communication Costs
As stated by Patel et al. [
7], the protocol must demonstrate the following characteristics: privacy, costs related to communication, and computation. As for privacy, we already noted that the transmitted data consists of random numbers and some partial sums of them. Nothing different from that that flows sequentially during the protocol. Therefore, it is necessary for any attacker, regardless of their level of honesty, to have prior knowledge of the protocol being used. This knowledge, even if it is concealed by the middleware, would still require the attacker to fully impersonate the parties involved in the connection. A side-channel type of attack could in principle be avoided by adequate formatting for the transmitted data. For computational aspects, only sums are required, so that we neglect this overload. A technique known as RJID (Random Code Injection to Mask Power Analysis based Side Channel Attacks) can be used to protect parties from the exposure of simple and differential power analysis, see [
19]. Finally, as stated above, communication costs are approximately equal to 70% of a typical three-party sum, as in [
9].
5.2. Error Correction and Privacy Amplification
It is known that IoT devices are known to be able to calculate hash functions that can be used to improve security by integrating them into the KeyGen protocol. However, the specific functions they can compute depend on the device’s processing power, memory, and energy constraints. They typically have limited resources compared to more powerful devices, such as computers and servers. For this reason, one of the commonly used approaches to improve security in the IoT setting is the use of hash functions. Among them, BLAKE2 appears to be a good choice, since it has versions optimized for 64-bit architectures (BLAKE2b) and optimized for 8 to 32-bit platforms (BLAKE2s) [
20]. With this at hand, one possible procedure for error correction and privacy amplification that can be applied to ensure that the OTP key obtained by the SMP-OTP4IOT procedure is as follows.
|
Protocol KeyGen-security check: Error correction and privacy amplification |
 |
This process enables the user
to verify that
has the same OTP key, which can be utilized by
in the same way. It should be noted that this concept is not novel and has been applied in a different context, such as IoT with a quantum security layer, as illustrated in [
21]. Observe also that the final steps in the KeyGen-security validation might seem unnecessary, since comparing the hash of the entire key should suffice, which is indeed the case. However, the selection of a random subset based on position
b introduces a variable workload on the processor each time the procedure is executed, making it easier to prevent a side-channel attack by monitoring processor energy consumption, as in [
22].
5.3. Abstract Requirements for SMPC
We examine the properties of validity, agreement, termination, and privacy to postulate the security of our protocol, as depicted in [
18], Definition 1.0. Since the key is produced by means of (true) random numbers obtained individually by each party
,
, and the individual contributions to the key are never transmitted,
the individual inputs remain secret to other processes (apart from the shares that are given away), and malicious processes cannot prevent the computation from taking place or influence the computation in favorable ways (quote adapted from [
18]). Therefore, validity is ensured, in the sense that the final result is obtained with at least all the correct inputs in the chain of computation, as the party currently working will utilize its own data and the value received from the previous party to perform the computation, which can only be achieved if the accurate values are supplied. In contrast, agreement is achieved directly during the first half of the protocol, even in the presence of a dishonest attacker, since replacing randoms by other numbers indistinguishable from random will produce the same key agreement. So, only in the second half of the procedure, it is possible that the distribution of
and
to
and
, respectively, if intercepted by a dishonest party, will produce a discrepancy in the OTP key
K calculated by
and derived by
, see
Figure 2, with the result that in this case the message will not be recovered. This can be avoided by using the KeyGen security check, as depicted above.
Finally, it is obvious that termination and privacy are inherent in the process. Termination means that every correct process eventually computes the result intended by the protocol, and privacy means that the specific inputs of the individual parties are never transmitted, computed, or potentially revealed.
6. Discussion
The SMP-OTF4IOT protocol is introduced and implemented using ZeroC-Ice. The proposed procedure establishes a common key between IoT devices for secure communication, where two primary parties ( and ) and a dummy server (), sequentially agree on a key K, using true random numbers, and a modified (but standard) multiparty security sum procedure, which is applied for encrypted communication with a single pad.
The role of the dummy party is to facilitate the establishment of the key, but does not access the shared encrypted message. The implementation in ZeroC-Ice offers the advantage of connecting devices across different platforms and architectures, and the protocol is shown to exhibit a reduction in communication by a factor of approximately 30%.
A notable benefit of this approach is the efficiency in message transmission, where multiple parameters can be included in a single function call, reducing bandwidth requirements. The protocol uses true random number acquisition and dynamic role changes, making it adaptable for peer-to-peer communication between multiple IoT agents.
Although a formal security analysis of the protocol is not extensively covered here, which we leave for a forthcoming article, we focus instead on its inherent security properties as implemented in ZeroC-Ice and suitable generic metrics for assessing security of SMPC protocols.
Under the Dolev-Yao threat model, our protocol assumes the presence of either a semi-honest or a dishonest adversary. In the semi-honest scenario, with no tampering of data, the transmitted information consists of random numbers and their sums, which makes deducing the key challenging unless the adversary knows the exact computations performed by each party. In the case of a dishonest attacker, any alteration in the transmitted random numbers could result in a different key, potentially flagging an interception attempt.
We argue that privacy for parties is maintained since only random numbers and partial sums are transmitted sequentially. In an actual implementation for the IoT setting, a side-channel attack could be mitigated by appropriate data formatting and techniques, such as random code injection techniques. The communication cost is estimated at 70% of the usual three-party sum, which significantly reduces the overhead.
In terms of future work, we plan to propose a formal analysis of the protocol using tools such as Tamarin Prover or Proverif. Additionally, our objective is to explore the scalability of the protocol to federated n-party key agreement and encryption. This analysis and investigation could offer a more comprehensive understanding of the security properties of the protocol and highlight potential advantages or disadvantages, particularly in the IoT domain. It should be noted that our protocol already appears suitable for the IoT, which can be implemented among peers in a one-to-one manner.
Author Contributions
Conceptualization, J.F. and P.G.; software, R.N.; formal analysis, J.F. and P.G.; investigation, J.F., P.G. and F.E.; writing—original draft preparation, J.F.; writing—review and editing, J.F., F.E. and P.G.; visualization, P.G. and R.N.; supervision, J.F. and F.E.; project administration, J.F.; funding acquisition, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Project grant number DI21-0079, Universidad de La Frontera.
Data Availability Statement
Conflicts of Interest
The authors declare no conflict of interest. Sponsors had no role in the design of the study, in the collection, analysis or interpretation of the data, nor in the writing of the manuscript or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| IoT |
Internet of Things |
| OTP |
One Time Pad |
| SMP-OTP4IO |
Secure multiparty One-time pad protocol for IoT |
| XOR |
Exclusive OR |
References
- Vorakulpipat, C.; Rattanalerdnusorn, E.; Thaenkaew, P.; Hai, H.D. Recent challenges, trends, and concerns related to IoT security: An evolutionary study. In Proceedings of the 2018 20th International Conference on Advanced Communication Technology (ICACT). IEEE, 2018, pp. 405–410.
- Cravero, A.; Bustamante, A.; Negrier, M.; Galeas, P. Agricultural Big Data Architectures in the Context of Climate Change: A Systematic Literature Review. Sustentability 2022, 22, 7855. [CrossRef]
- Mohammadi, M.; Al-Fuqaha, A.; Sorour, S.; Guizani, M. Deep learning for IoT big data and streaming analytics: A survey. IEEE Communications Surveys & Tutorials 2018, 20, 2923–2960. [CrossRef]
- Lopez-Fenner, J.; Sepulveda, S.; Bittencourt, L.F.; Costa, F.M.; Georgantas, N. Privacy Preserving Multi Party Computation for Data-Analytics in the IoT-Fog-Cloud Ecosystem. In Proceedings of the CICCSI 2020 : IV International Congress of Computer Sciences and Information Systems, Mendoza / Virtual, Argentina, 2020; CICCSI 2020 Proceedings.
- Hossain, E.; Khan, I.; Un-Noor, F.; Sikander, S.S.; Sunny, M.S.H. Application of big data and machine learning in smart grid, and associated security concerns: A review. Ieee Access 2019, 7, 13960–13988. [CrossRef]
- Diffie, W.; Hellman, M. New directions in cryptography. IEEE Transactions on Information Theory 1976, 22, 644–654. [CrossRef]
- Patel, K. Secure multiparty computation using secret sharing. In Proceedings of the 2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES). IEEE, 2016, pp. 863–866. [CrossRef]
- Niu, Z.; Wang, H.; Li, Z.; Song, X. Privacy-preserving statistical computing protocols for private set intersection. International Journal of Intelligent Systems 2022, 37, 10118–10139. [CrossRef]
- Cramer, R.; Damgård, I.B.; et al. Secure multiparty computation; Cambridge University Press, 2015.
- ZeroC. Ice - The Internet Communications Engine. https://doc.zeroc.com/ice/3.6/introduction, 2022. [Accessed 22 Jan. 2024].
- Van Rossum, G.; Drake Jr, F.L. Python tutorial; Centrum voor Wiskunde en Informatica Amsterdam, The Netherlands, 1995.
- Cremers, C. Symbolic security analysis using the tamarin prover. In Proceedings of the 2017 Formal Methods in Computer Aided Design (FMCAD). IEEE, 2017, pp. 5–5.
- Blanchet, B.; et al. Modeling and verifying security protocols with the applied pi calculus and ProVerif. Foundations and Trends® in Privacy and Security 2016, 1, 1–135.
- Modesti, P.; Garcia, R. Formal Modeling and Security Analysis of Security Protocols. In Handbook of Formal Analysis and Verification in Cryptography; CRC Press, 2023; pp. 213–274.
- Yao, A.C. Protocols for secure computations. In Proceedings of the 23rd annual symposium on foundations of computer science (sfcs 1982). IEEE, 1982, pp. 160–164.
- Yao, A.C.C. How to generate and exchange secrets. In Proceedings of the 27th annual symposium on foundations of computer science (Sfcs 1986). IEEE, 1986, pp. 162–167.
- Dolev, D.; Yao, A. On the security of public key protocols. IEEE Transactions on information theory 1983, 29, 198–208. [CrossRef]
- Fort, M.; Freiling, F.; Penso, L.D.; Benenson, Z.; Kesdogan, D. TrustedPals: Secure multiparty computation implemented with smart cards. In Proceedings of the Computer Security–ESORICS 2006: 11th European Symposium on Research in Computer Security, Hamburg, Germany, September 18-20, 2006. Proceedings 11. Springer, 2006, pp. 34–48.
- Ambrose, J.A.; Ragel, R.G.; Parameswaran, S. RIJID: Random code injection to mask power analysis based side channel attacks. In Proceedings of the Proceedings of the 44th annual Design Automation Conference, 2007, pp. 489–492.
- Aumasson, J.P.; Meier, W.; Phan, R.C.W.; Henzen, L.; Aumasson, J.P.; Meier, W.; Phan, R.C.W.; Henzen, L. Blake2. The Hash Function BLAKE 2014, pp. 165–183.
- Shamshad, S.; Riaz, F.; Riaz, R.; Rizvi, S.S.; Abdulla, S. An enhanced architecture to resolve public-key cryptographic issues in the internet of things (IoT), Employing quantum computing supremacy. Sensors 2022, 22, 8151.
- McCann, D.; Eder, K.; Oswald, E. Characterising and comparing the energy consumption of side channel attack countermeasures and lightweight cryptography on embedded devices. In Proceedings of the 2015 International Workshop on Secure Internet of Things (SIoT). IEEE, 2015, pp. 65–71.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).