Using Physics-Informed Neural Networks (PINNs) for Tumor Cells Growth Modeling

Preprint

Article

Using Physics-Informed Neural Networks (PINNs) for Tumor Cells Growth Modeling

Altmetrics

Downloads

123

Views

Comments

A peer-reviewed article of this preprint also exists.

José A. Rodrigues^*

This version is not peer-reviewed

Submitted:

15 March 2024

Posted:

18 March 2024

You are already at the latest version

Alerts

Abstract

This paper presents a comprehensive investigation into the applicability and performance of two prominent growth models, namely the Verhulst model and the Montroll model, in the context of modeling tumor cell growth dynamics. Leveraging the power of Physics-Informed Neural Networks (PINNs), we aim to assess and compare the predictive capabilities of these models against experimental data obtained from the growth patterns of tumor cells. We employ a dataset comprising detailed measurements of tumor cell growth to train and evaluate the Verhulst and Montroll models. By integrating PINNs, we not only account for experimental noise but also embed physical insights into the learning process, enabling the models to capture the underlying mechanisms governing tumor cell growth. Our findings reveal the strengths and limitations of each growth model in accurately representing tumor cell proliferation dynamics. Furthermore, the study sheds light on the impact of incorporating physics-informed constraints on the model predictions. The insights gained from this comparative analysis contribute to advancing our understanding of growth models and their applications in predicting complex biological phenomena, particularly in the realm of tumor cell proliferation.

Keywords:

Subject: Computer Science and Mathematics - Mathematical and Computational Biology

MSC: 92-08; 92-10

1. Introduction

Physics-informed Neural Networks (PINNs) represent a powerful and innovative approach at the intersection of physics-based modeling and machine learning. These networks seamlessly integrate physical laws or governing equations into the neural network architecture, enabling the incorporation of prior knowledge about a system’s behavior. PINNs have gained prominence in various scientific and engineering domains where traditional numerical simulations may be computationally expensive or challenging.

The key idea behind Physics-informed Neural Networks is to train neural networks to not only learn from observed data but also to adhere to the underlying physics that govern the system. This is achieved by incorporating differential equations or other relevant physical constraints as additional terms in the loss function during training. This unique combination allows PINNs to generalize well beyond the available data and offers a data-driven framework for solving complex physical problems.

PINNs have demonstrated success in a diverse range of applications, including fluid dynamics, heat transfer, structural mechanics, and quantum mechanics. By leveraging the expressive power of neural networks and the interpretability of physics-based constraints, PINNs provide an efficient means to model and simulate complex physical systems.[1,2]

Cell growth is a fundamental process in biology, pivotal for understanding development, tissue regeneration, and disease progression. Over the years, mathematical models have played a crucial role in unraveling the complexities of cell growth dynamics. One such model that has gained prominence is the Verhulst model [3], which originates from the field of population dynamics but finds compelling applications in describing the growth patterns of individual cells.

Another important proposal was developed by Montroll [4] which consists of a general model, that translates the asymptotic growth of a variable taking into account the position of the inflexion point of the curve.

Understanding the growth dynamics of tumor cells is critical for advancing the knowledge of cancer progression and developing effective treatment strategies. Mathematical models play a pivotal role in this endeavor by providing a quantitative framework to describe and predict the complex behavior of tumor cell populations. However, the accurate adjustment of these models to observed data poses significant challenges, particularly in the context of tumor cell growth.

2. Materials and Methods

The objective of this study was to investigate and compare the applicability of two prominent growth models: the Verhulst logistic growth model and the Montroll power-law growth model. The study aimed to understand how these models capture population growth dynamics and to identify scenarios in which one model may be more suitable than the other. The study utilized a combination of numerical simulations and empirical data analysis to evaluate the performance of the Verhulst and Montroll growth models. Numerical simulations allowed for controlled exploration of model behavior, while empirical data analysis provided insights into the models’ capabilities to describe real-world growth patterns.

PINNs are a class of machine learning models that leverage neural networks to approximate solutions to partial differential equations (PDEs) while incorporating physical principles. In this study, we apply PINNs to model growth phenomena, specifically utilizing them for the Verhulst and Montroll growth models.

2.1. Verhulst Growth Model

The Verhulst growth model, representing logistic growth, is described by the differential equation:

\frac{d p}{d t} (t) = k p (t) (1 - \frac{p (t)}{C})

(1)

where p is the population size, t is time, k is the growth rate, and C is the carrying capacity. [3]

2.2. Montroll Growth Model

The Montroll growth model, capturing power-law growth, is expressed as:

\frac{d p}{d t} (t) = k p (t) (1 - {(\frac{p (t)}{C})}^{θ})

(2)

Where the parameter

θ

indicates the position for the inflection point of the growth curve. If

θ = 1

we got the Verhulst growth model.[4]

2.3. Network Architecture

A feedforward neural network was designed to approximate the solutions of the Verhulst and Montroll growth models. The network architecture included an input layer, multiple hidden layers, and an output layer corresponding to the predicted population size.

2.4. Loss Function

The PINN was trained by minimizing a physics-informed loss function, which combines the mean squared error between predicted and observed data with terms enforcing the satisfaction of the underlying growth model equations. The loss function was formulated as:

L_{P I N N} = L_{d a t a} + λ L_{p h y s i c s}

(3)

where

L_{d a t a}

is the data fidelity term and

L_{p h y s i c s}

enforces adherence to the growth model equations, and

λ

is a regularization parameter.[2]

For a set of data points

{(x_{i}, y_{i})}_{i = 1, \dots, N}

, where

x_{i}

are input points and

y_{i}

are corresponding target values, the data-driven loss might look like:

L_{d a t a} = \frac{1}{N} \sum_{i = 1}^{N} {(p (x_{i}) - y_{i})}^{2}

(4)

Here,

p (x_{i})

represents the output of the neural network for the model under study for input

x_{i}

and N is the number of data points.

While the other term is defined by

L_{p h y s i c s} = \frac{1}{N_{R}} \sum_{j = 1}^{N_{R}} R^{2} (x_{j})

(5)

Here,

N_{R}

is the number of points where the model’s restrictions needs to be satisfied and

R (x_{j})

is the residual of the model at point

x_{j}

This component ensures that the solution satisfies the underlying physical laws or constraints. It is formulated based on the governing equations or other physics-related constraints.

3. Results

In this section, we present the results obtained from the application of PINNs, for Verhulst and Montroll growth models, to the dataset of tabulated data in Table 1. For this study we used the previously published data from the Chinese hamster V79 fibroblast tumor cell [5]. It consists of 45 measurements of volumes (

10^{9} ν m^{3}

) during the time period of 60 days.

The main objective of our study was to leverage the combination of supervised learning and physics-based constraints to accurately predict the underlying system behavior and compare the two growth models.

For each method under study, we define the respective loss function depending on the parameters to be determined. Namely, for the Verhulst model

L_{V e r h u l s t d a t a} = L (k, C)

(6)

and for the Montroll model

L_{M o n t r o l l d a t a} = L (k, C, θ)

(7)

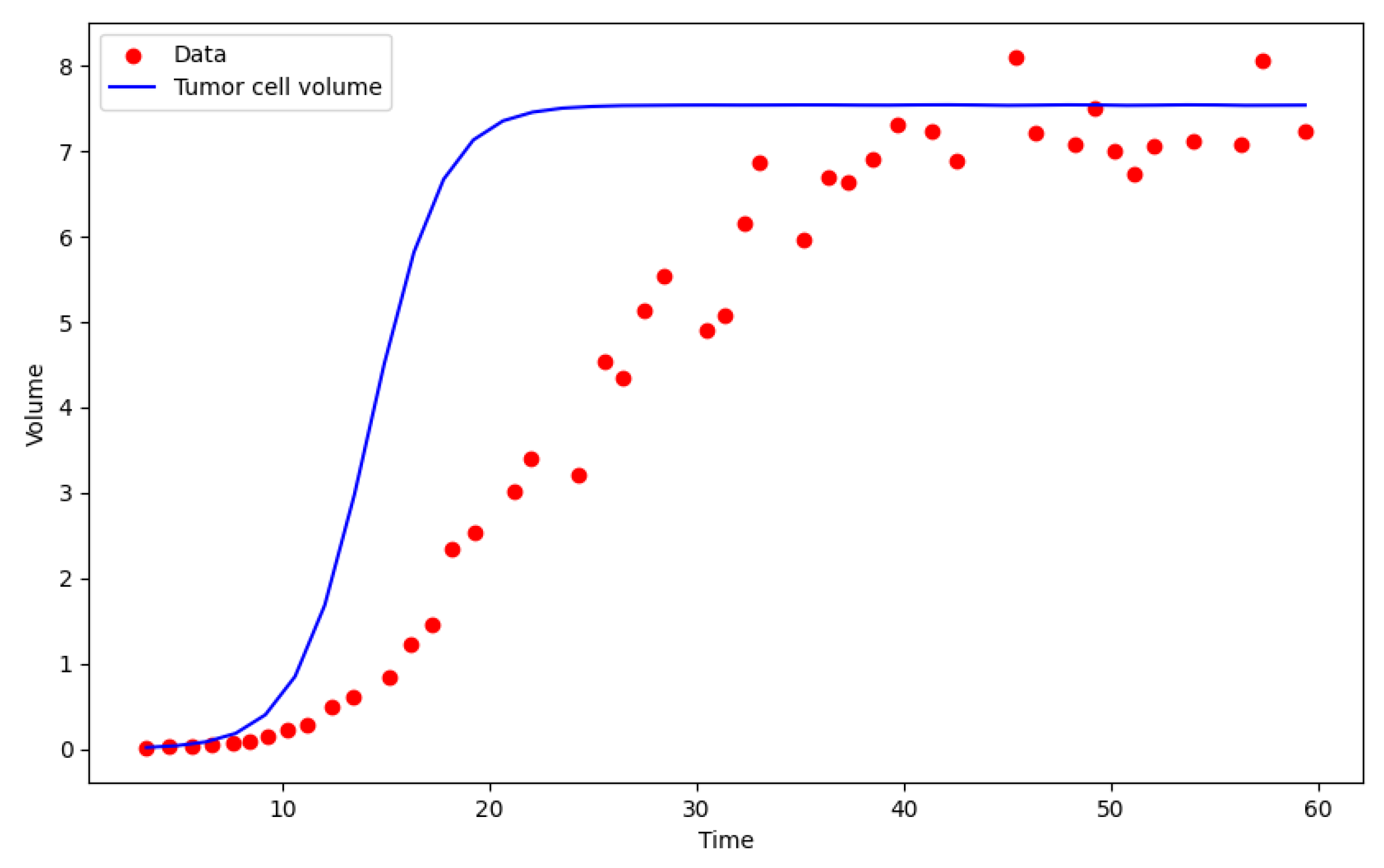
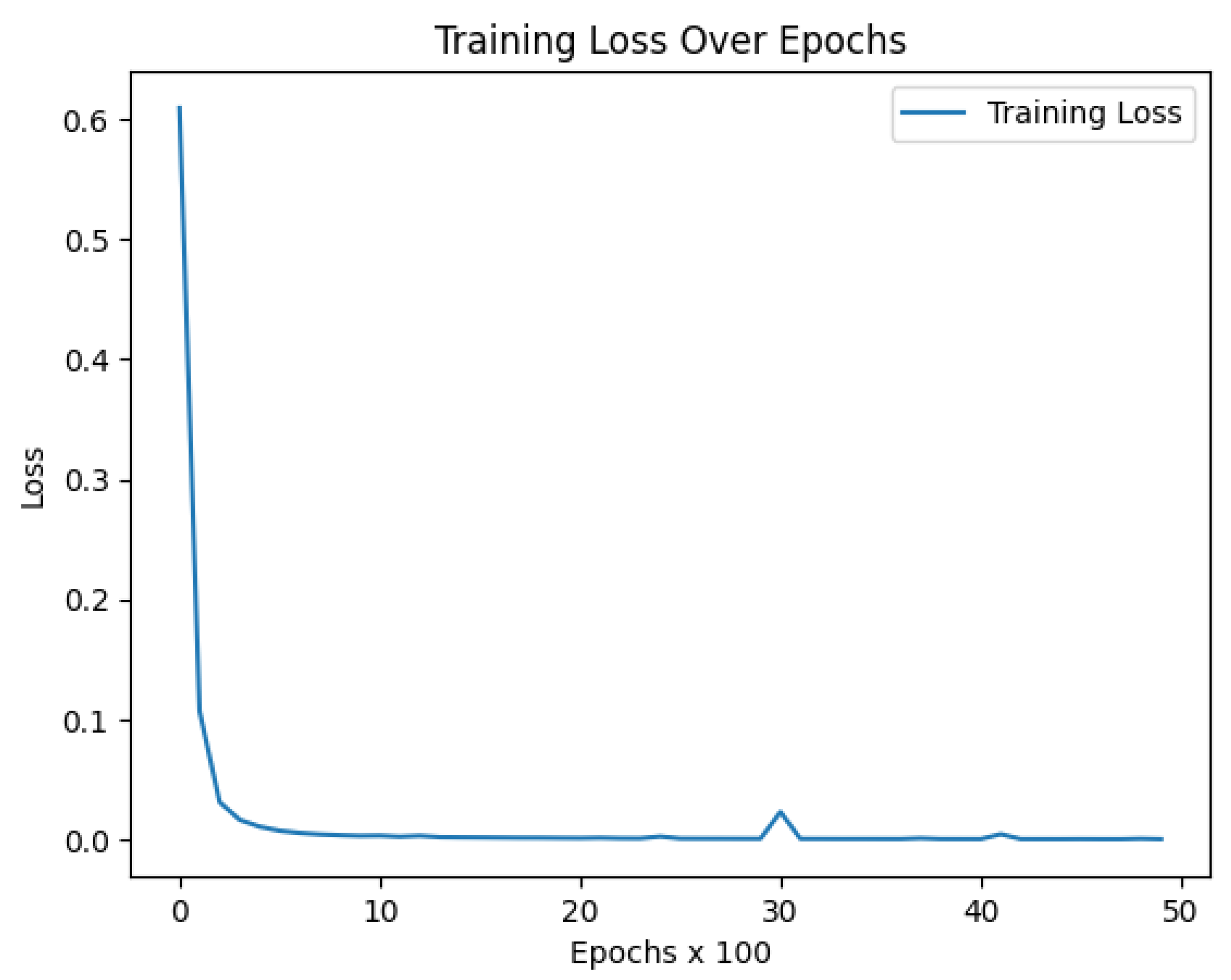
In Figure 1 we see the graph of the solution predicted by the Verhulst model for the data obtained at the end of a process of 5000 Epochs. The evolution of the model’s performance can be seen in Figure 2.

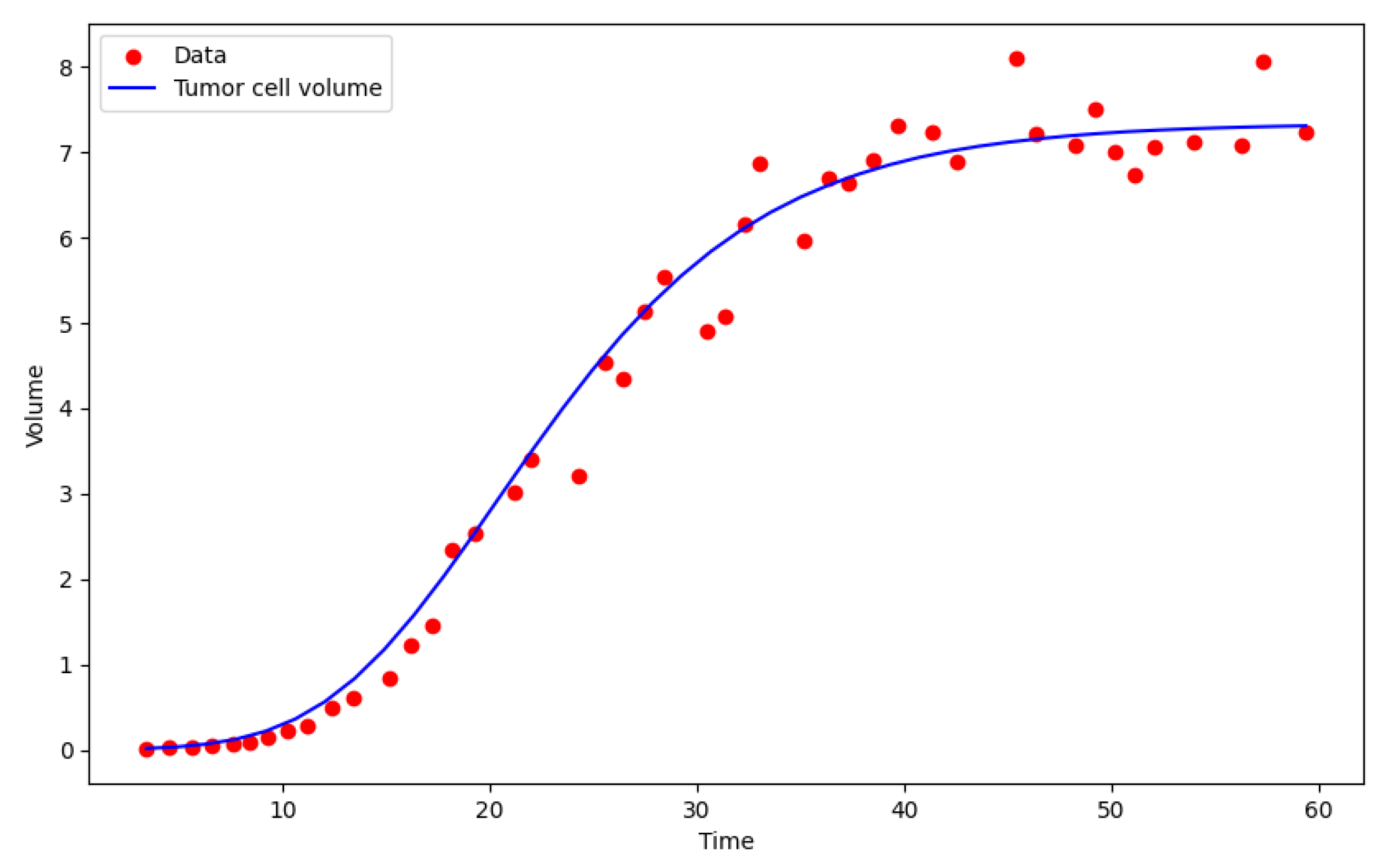
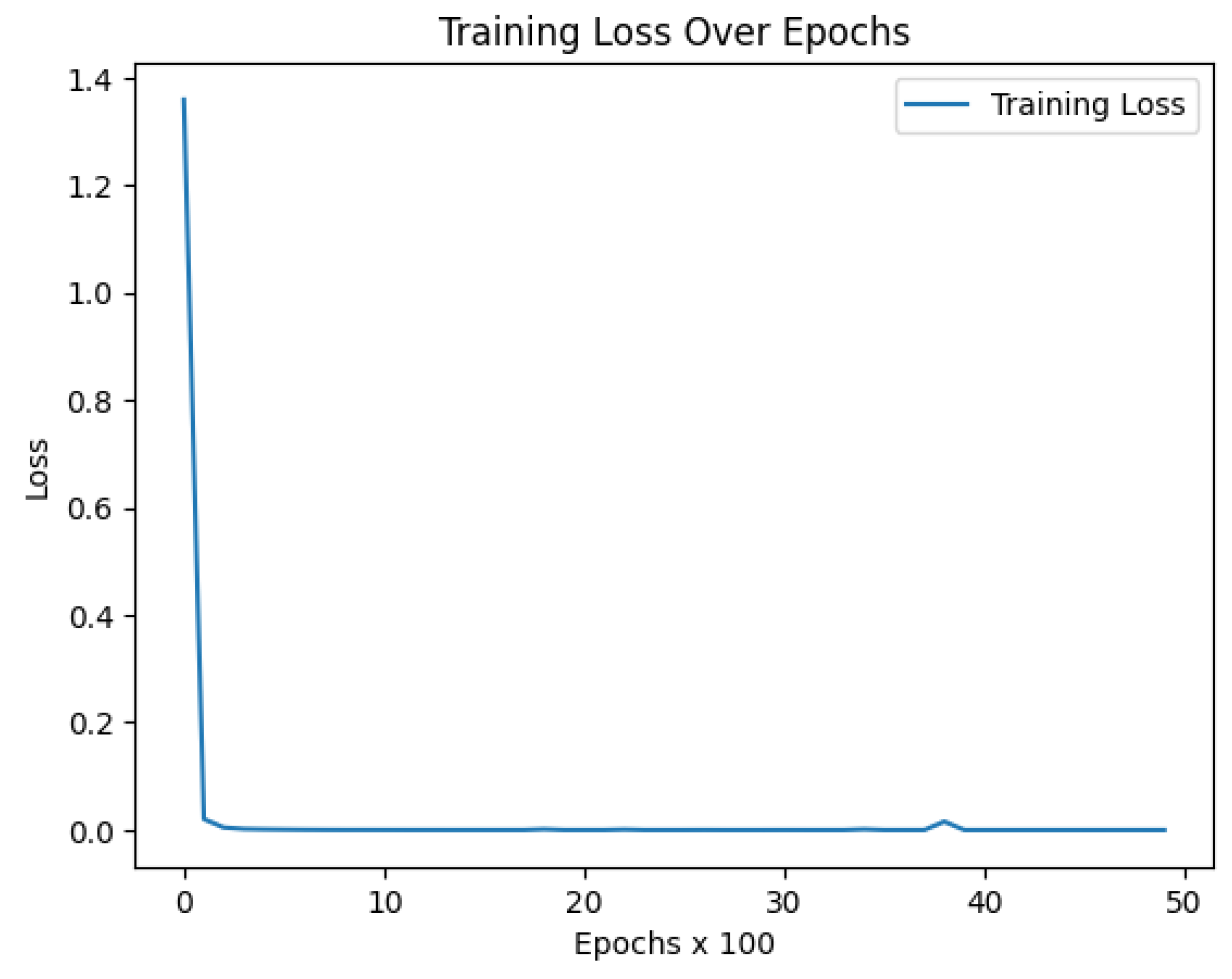
Similarly, in Figure 3 we see the graph of the solution predicted by the Montroll model for the data obtained at the end of the same process of 5000 epochs, while the evolution of the model’s performance can be seen in Figure 4.

The models are well defined when the associated parameters are determined, Table 2 and Table 3 contain the predicted parameters for Verhulst and Montroll models, respectively.

4. Discussion

For both models, we found that the PINN methodology can predict the asymptotic behavior of saturation of tumor cell volume growth. However, the existence of the

θ

parameter of the Montroll model allows a better fit to the data and a better prediction of the location of the inflection point of the growth function graph.

5. Conclusions

This study intended to use physics informed neural networks to choose the method that best fits the data, as in a reverse engineering procedure, determining the parameters intrinsic to each method.

The methodology presented for adjusting the growth model can be adopted for any other phenomenon that is intended to be mathematically modeled based on experimental data.

PINNs provide a means of learning robust and accurate models of systems providing an existing domain knowledge about the models that govern the data, even in situations where the equations don’t exactly match the data.

Funding

This research was partially sponsored with national funds through the Fundação Nacional para a Ciência e Tecnologia, Portugal-FCT, under projects UIDB/04674/2020 (CIMA). https://doi.org/10.54499/UIDB/04674/2020

Conflicts of Interest

The authors declare no conflict of interest.

References

Raissi, M.; Perdikaris, P.; Karniadakis, G. E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. Journal of Computational Physics 2017, 335, 66–97. [CrossRef]
Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. Journal of Computational Physics 2018, 375, 1339–1364. [CrossRef]
Bacaër, N. Verhulst and the logistic Equation (1838). In A Short History of Mathematical Population Dynamics, Springer London, 2011; pp. 35–39.
Goel, Narendra S.; Maitra, Samaresh C.; Montroll, Elliott W. On the Volterra and Other Nonlinear Models of Interacting Populations. Rev. Mod. Phys. 1971, 43, 231–276. [CrossRef]
Marusić M, Bajzer Z.; Freyer J.P.; Vuk-Pavlović S. Analysis of growth of multicellular tumour spheroids by mathematical models. Cell Prolif. 1994, 27(2), 73–94. [CrossRef]

Figure 1. PINN solution for the Verhulst model.

Figure 2. Histories of the total loss function for Verhulst model.

Figure 3. PINN solution for the Montroll model.

Figure 4. Histories of the total loss function for Montroll model.

Table 1. Chinese hamster V79 fibroblast tumor cell.

t	V	t	V	t	V	t	V	t	V
3.46	0.0158	12.39	0.4977	24.33	3.2046	35.2	5.9668	48.29	7.0694
4.58	0.0264	13.42	0.6033	25.58	4.5241	36.34	6.6945	49.24	7.4971
5.67	0.0326	15.19	0.8441	26.43	4.3459	37.29	6.6395	50.19	6.9974
6.64	0.0445	16.24	1.2163	27.44	5.1374	38.5	6.8971	51.14	6.7219
7.63	0.0646	17.23	1.447	28.43	5.5376	39.67	7.2966	52.10	7.0523
8.41	0.0933	18.18	2.3298	30.49	4.8946	41.37	7.2268	54.0	7.1095
9.32	0.1454	19.29	2.5342	31.34	5.0660	42.58	6.8815	56.33	7.0694
10.27	0.2183	21.23	3.0064	32.34	6.1494	45.39	8.0993	57.33	8.0562
11.19	0.2842	21.99	3.4044	33.0	6.8548	46.38	7.2112	59.38	7.2268

Table 2. Predicted final parameters for the Verhulst model.

0.57168955

7.533739

Table 3. Predicted final parameters for the Montroll model.

0.8311218

7.3327312

θ

0.16937177

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Using Physics-Informed Neural Networks (PINNs) for Tumor Cells Growth Modeling

Abstract

1. Introduction

2. Materials and Methods

2.1. Verhulst Growth Model

2.2. Montroll Growth Model

2.3. Network Architecture

2.4. Loss Function

3. Results

4. Discussion

5. Conclusions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe