Prerpints.org logo
Preprint
Communication

Environmental Surveillance through Machine Learning-Empowered Utilization of Optical Networks

This version is not peer-reviewed.

Submitted:

12 March 2024

Posted:

15 March 2024

Read the latest preprint version here

A peer-reviewed article of this preprint also exists.

Abstract
Exploiting the existing optical fiber network’s terrestrial infrastructure offers unexpected solutions to global challenges. We aim to expand the current network by incorporating a streaming telemetry system to integrate earthquake early detection. The purpose is to analyze and interpret alteration of light’s polarization induced by seismic events, particularly Primary earthquake waves that precede destructive Surface waves. This analysis facilitates the development of an early warning system and implementation of earthquakes countermeasures to mitigate humanitarian and economic impact. Consequently, we have developed a Python-based Waveplate Model designed to monitor light’s polarization changes within optical fibers buried underground. The model incorporates real ground displacement data from a 4.9 magnitude earthquake that struck in Marradi region, central Italy. We propose a novel approach of a smart sensing grid of optical network empowered by machine learning, trained on a large number of polarization evolution extracted from two distinct sensing fibers to identify the pattern of polarization change occurring during Marradi earthquake. Test Results demonstrate that this method can detect Primary waves within one second time-frame, achieving an accuracy rate of 99.5%. This system therefore affords nearby regions 52 seconds to take emergency response, and an extended margin of 62 seconds in more distant areas.
Keywords: 
Earthquakes
;  
Polarization
;  
Machine-learning
;  
Early-warnings
;  
Optical-Networks
;  
Sensing
;  
Waveplate-model
Subject: 
Environmental and Earth Sciences  -   Environmental Science

1. Introduction

Earthquakes represent one of the greatest natural disaster risks facing humanity. According to plate tectonics theory, the earth’s lithosphere is divided into plates by seismic zones that move relative to each other. The majority of earthquakes occur along these plates’ boundaries, with seismogenic faults being the geological origins of destructive earthquakes [1]. However, predicting earthquakes is a common scientific challenge for researchers globally. Much of this difficulty stems from the lack of reliable precursory indicators that meet the sufficient and necessary conditions of their occurrence, which is often considered the primary cause of failure in earthquake prediction efforts in earth science research. Monitoring these seismic events is an essential part in trying to predict them, and that employs range of different methods. For instance, absolute measurement of geostress to assess the stress characteristics of significant faults [2], as seen in SAFOD project [3]. Li Siguang, a pioneer of earthquake prediction in China, pointed out that an earthquake is a process of accumulation of stress on seismogenic faults. Real time monitoring of geostress using tools like stress gauges can be leveraged to track changes in fault lines, providing insights into the release of seismic energy [4]. Crustal strain monitoring through strain gauges and GPS technology have been developed for seismic research and prediction as well [5,6]. Additionally, Infrared monitoring method, as the infra-sound signal in the far field is found to be strong within two to eleven days before an earthquake with a magnitude of M7.0 or higher struck, and its spectral characteristics are apparently different from other natural events [7]. Unfortunately, in 1988, seismologists in United States deployed a dense network of monitoring stations focused mainly on "Surface Strain Monitoring", in addition to tracking geo-magnetic, geo-electric, ground-water level, and hydro-chemistry data, to predict an M6 earthquake occurring in the Park-field near the San Andreas fault. Yet, the anticipated earthquake didn’t occur until 2004, 16 years later than expected, and the monitoring equipment failed to pick up any anomalies or precursors [8]. Similarly, in 1995, an M7 earthquake struck in Hanshin, Japan, killing more than 6500 people, where the high density GPS network in place did not capture warning signals. Consequently, the scientific community become increasingly skeptical about earthquake prediction. In March 1997, Robert J. Geller published a paper titled, "Earthquakes cannot be predicted" in Science magazine, which reflected the prevailing opinion on earthquake prediction in the work [9]. Therefore, it is crucial to address this challenge differently by adopting novel methods for widely distributed early detection systems capable of rapidly identifying the event to activate different mitigation strategies and minimize humanitarian and economic impact. According to the International Association of Seismology and Physics of the Earth’s Interior (IASPEI), one of the main potential earthquake precursors is changes in strain rates which are the rates at which the Earth’s crust stretches or compresses [10]. This is because such changes are indicative of stress accumulation in the Earth’s crust, potentially pointing towards upcoming seismic event. Consequently, as optical fiber cables are buried underground, they too experience stretching or compression in response to the strain rate change caused by seismic waves. The mechanical and optical properties of an optical fiber, as well as the physical properties of the light wave propagating inside it, change due to applied mechanical stresses and external disturbances. This trend opens the perspective of using the optical networks as a wide distributed network of sensors for environmental sensing, such as earthquake detection or anthropic activities monitoring [11,12]. Essentially, there are two types of seismic waves, body waves (Primary, P waves and Secondary, S waves) that propagate through the earth’s interior, and Surface waves that propagate along the earth’s surface. Surface waves carry the greatest amount of energy and are usually the primary cause of destruction [13]. Detecting P waves that precede earthquake’s destructive waves allows swift initiation of emergency plans. Therefore, we have witnessed recently the rise of distributed fiber optic sensors that offer the possibility of measuring a slow varying environmental variable at any location along the fiber length within a given sharp spatial resolution. This approach has been developed in last decade to monitor dynamic strain variations induced by external perturbations using optical fibers. Distributed optical fiber sensors utilize the natural scattering processes arising in optical fibers, including Brillouin, Raman, and Rayleigh scattering. Rayleigh scattering combined with Optical Time-Domain Reflectometry (OTDR) or Optical Frequency Domain Reflectometry (OFDR) has allowed the development of Distributed Acoustic Sensing (DAS) [14,15]. DAS employs optoelectronic interrogator, which send short light pulses into the fiber cable and then measure the optical perturbations in the light that scatters back, thereby deriving strain-rate signals proportional to the amount of physical stress impacting the fiber. These systems require dedicated "dark" fibers (i.e., optical fibers used solely for sensing without any communication channels) to operate [16,17,18]. Thus, limiting the overall data carrying capacity in the network. Moreover, these sensing techniques are incompatible with inline optical amplifiers that are commonly found along optical fibers’ path, and this is because the optical isolators inside the amplifiers block the backscattered DAS signals. Although these amplifications could be removed along dark fibers, which would lead to rampant signal attenuation. It is worth mentioning as well, that the usable range of this technology is less than 100 km and requires powerful computational, storage, and processing capabilities that are generally only available in high-cost systems [19,20]. Frequency metrology interferometric techniques came to overcome DAS usable range limitations. These techniques can measure femtoseconds delay experienced by the light of an ultrastable low phase Fabry-Pérot laser cavities traveling in the fiber at micrometer scale over several thousands of kilometers for fiber length [21], but still interferometric techniques considered to be using dedicated and expensive hardware. In this manuscript, we present a novel technique that employs light polarization sensing. Unlike DAS and interferometric systems, State-of-Polarization (SOP) sensing based on machine learning, analyze the integrated polarization alterations of the modulated light traveling through traffic-carrying optical fibers [22]. This approach aimed to leverage the existing terrestrial optical network as a whole smart sensing grid to produce early anomaly warnings by identifying the arrival of earthquake’s P waves without adding expensive equipment to the network, ensuring long-range measurements, and without requiring dedicated dark fibers. Thanks to the centralized design of our smart sensing grid optical network approach, which we detail in this work.
Due to applied mechanical stress, the local refractive index of the fiber core changes and give rise to birefringence. Birefringence leads to different propagation speeds of the optical wave along the x and y axes of the fiber core [23] that results in light polarization change. Hence, SOP variations are dependent on disturbances applied to the fiber and can advantageously be used for sensing purposes, particularly because optical fiber communication networks have become pervasive infrastructure and widely deployed around the globe. In this paper, we examine the effect of a real earthquake that occur southwest of Marradi city in central Italy to early detect the arrival of Surface waves by leveraging our SOP sensing technique empowered by machine learning model analysis. This earthquake, striking in September 2023, had a magnitude of 4.9 and an epicenter depth of 8.4 kilometers. In Section II, we introduce the Waveplate model that is going to be driven by a neural network algorithm to monitor and analyze SOP changes due to birefringence induced by the aforementioned seismic event, Section III covers the experimental and in field point of view for the fiber optic network smart sensing grid approach. This paper demonstrates in Section IV, the case scenario demonstrating the results and discussion of the neural network model analysis over SOP evolution sets of data extracted from the Waveplate Model after integrating the real Marradi earthquake ground motion data, and a conclusion in Section V.

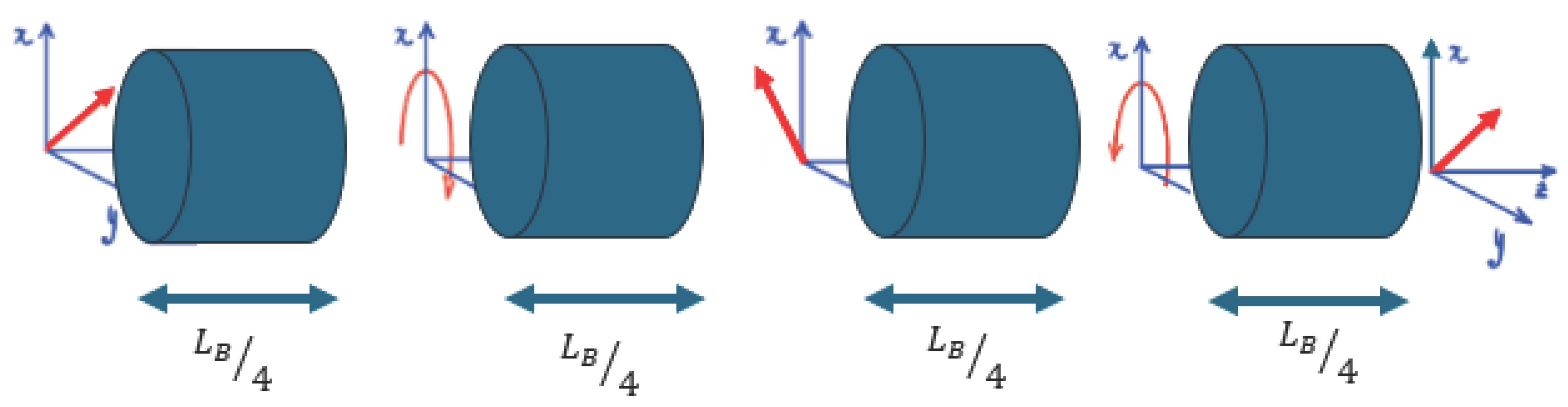
2. Waveplate Model

In an ideal optical fiber, which is typically circular in shape, the silica glass of which it is made is isotropic. In the weakly guiding approximation, such an optical fiber supports the propagation of two degenerate orthogonal polarization modes. In general, the theoretical polarization characteristic of an optical pulse is represented by these two distinct modes. However, in reality, optical fibers are often birefringent due to construction imperfections that disrupt the fiber’s cylindrical symmetry, thus affecting the polarization. This means that, in a fiber section small enough, the perturbation or the internal birefringence from construction imperfections can be assumed spatially uniform [24,25]. Seismic waves are another form of disturbances that cause external birefringence on the fiber and can also affect the polarization. To isolate and study the external disturbances on the light’s polarization within the fiber, it is crucial to understand the influence of internal birefringence. Here, adopting the Waveplate Model is essential to well define the effect of internal birefringence by dividing the fiber into numerous small segments, referred to as ’plates’ to ensure a uniform internal perturbed medium across each section [26]. Hence, the effect on light’s polarization is well defined and can be quantitatively described by 2 π divided by the polarization beat length L B , which is the amount of internal birefringence defined as the propagation length over which the optical path length of the two polarization eigenmodes differs by exactly one wavelength [24,25]. Consequently, any deviations from this established internal behaviour can be attributed to external perturbations, as they would introduce unexpected changes in the state of polarization of light. Without considering any external effect, when linearly polarized light is injected at 45-degree angle with respect to the linear polarization eigenmodes, the light acquires after one quarter of L B a phase shift of π 2 transforming the linear input polarization into a circular one, and after one half of L B a phase shift of π , as depicted in Figure 1. The Waveplate model theory is described in Appendix A.
However, by nature, these plates have random orientations, which can not be controlled, adding complexity to the analysis of external effects. Basically, each plate is assigned with two random angles, Ellipse of polarization or the major axis angle, and the Eccentricity of the ellipse. For simplicity purposes, in this paper we consider only the major axis angle which we present in Appendix A. In [26], the author presented the complete theory. Despite the random orientation of the plates causing varying polarization evolution, the data should contain invariant information linked to a specific earthquake. To overcome this complexity, a large amount of polarization evolution for a given seismic event is collected, where each SOP evolution corresponds to a different set of random plates’ angles as in Figure 2, carrying out a Montecarlo simulation over these different random birefringence orientations’ realizations. The goal is to train a machine learning model that leverage this dataset to identify and understand the patterns of polarization changes that occur with the arrival of Primary earthquake waves in order to early detect the arrival of Surface waves.
This is where the neural network learning model becomes valuable, or the post processing agent we present in the next section. Instead of analysing the changes in the three stokes presented for each SOP evolution (S1, S2, S3) and to reduce computational time, we propose to calculate for each SOP evolution from their stokes representations, the State of Polarization Angular Speed (SOPAS) [27], which we detail in Appendix B. Thus, analyzing one variable instead of three. Moreover, one of the main functions of the python based Waveplate Model we have developed, is to convert earthquake ground displacement values into nanostrain values coupled to the fiber according to the conventional iDAS conversion presented in [28], where each 116 nm of ground displacement corresponds to 11.6 nanostrain of fiber’s deformation.

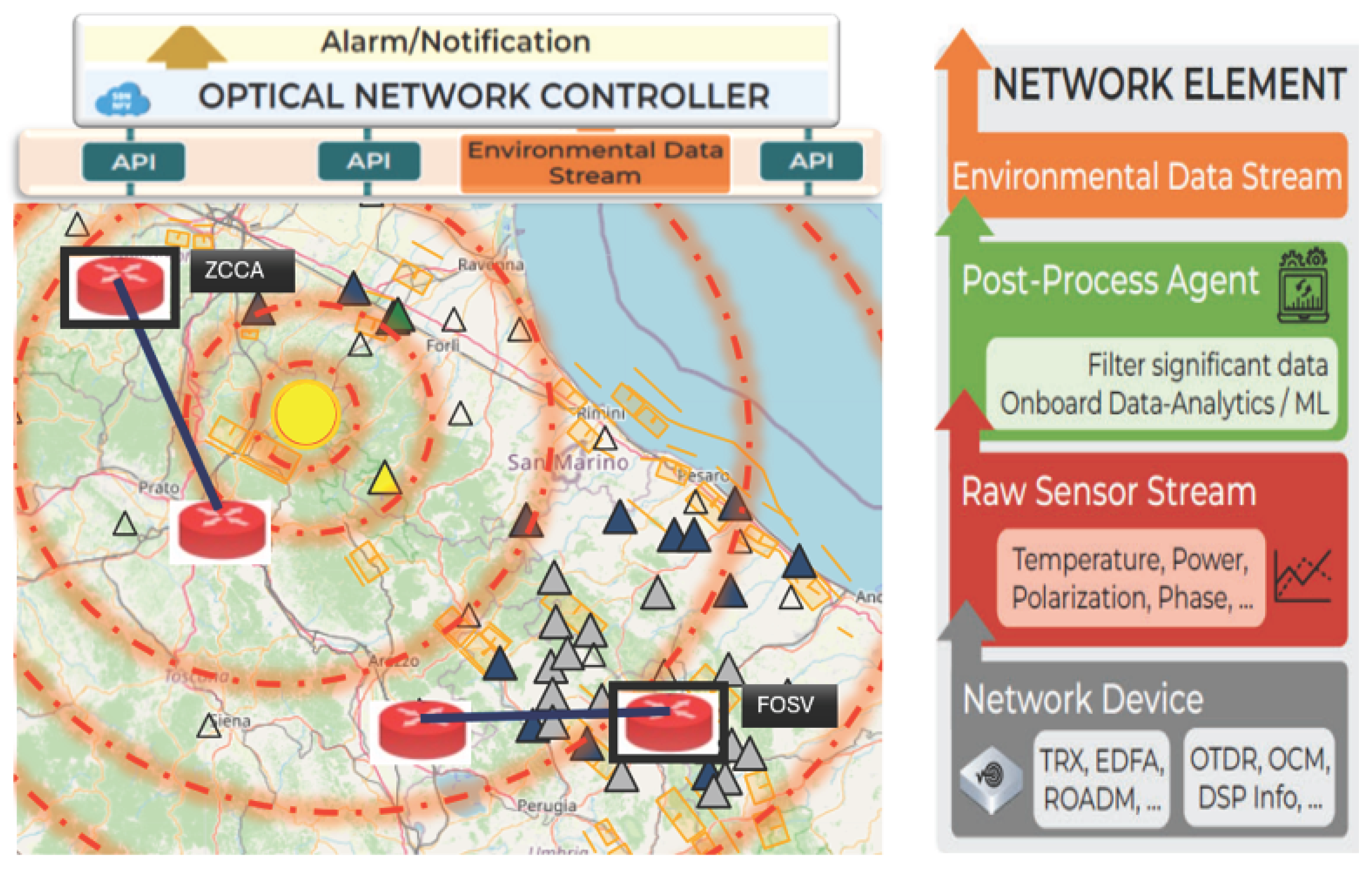
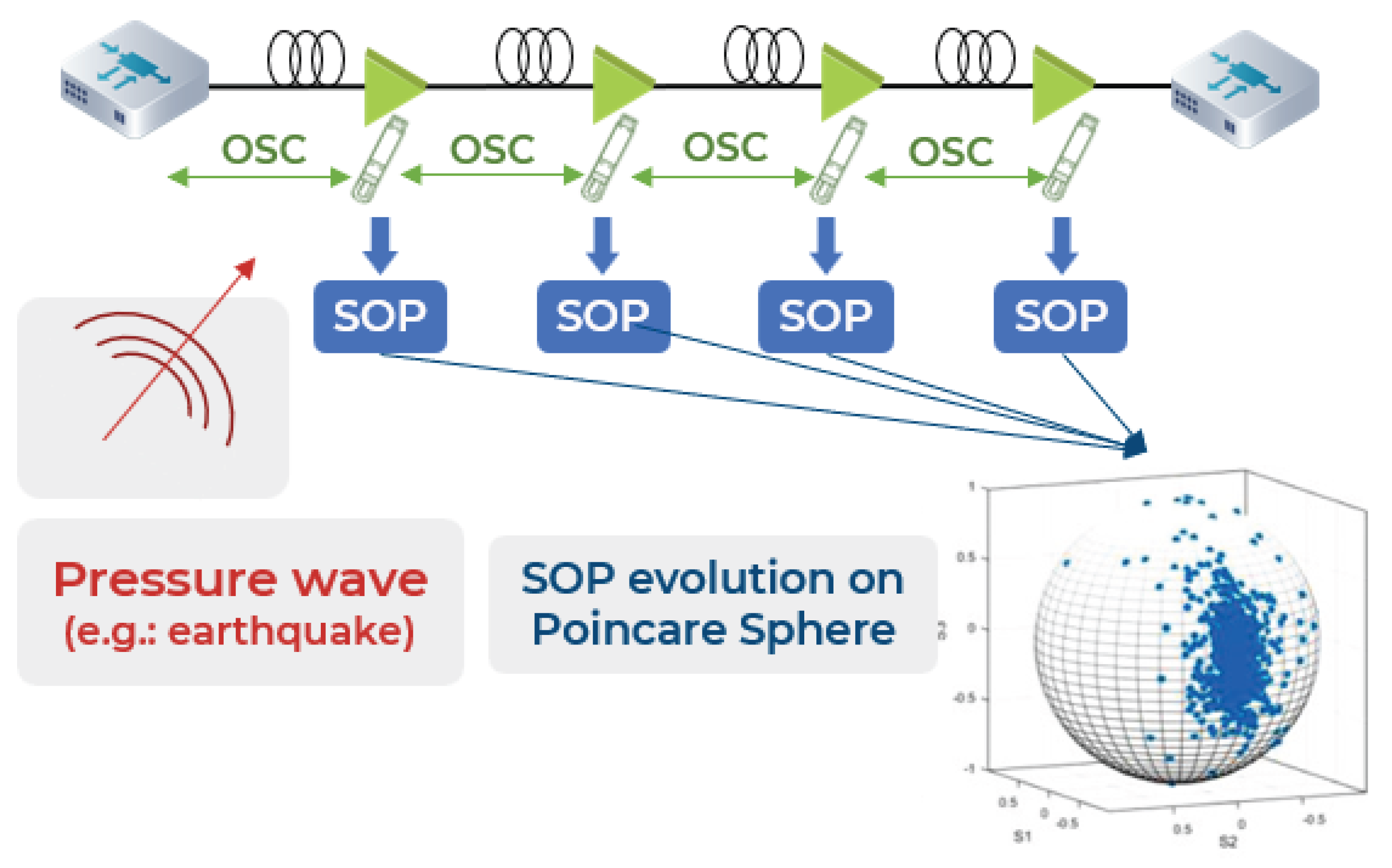
3. Smart Sensing Grid Approach: In-Field Point-of-View

On the 18th of September 2023, an M4.9 earthquake struck in the region of Marradi in Central Italy. The Italian National Institute of Geophysics and Volcanology (INGV) pinpointed the quake’s location [29], noting a seismic wave velocity of 7.10 km/s. This measurement is inline with the Central Italian Appennines (CIA) velocity model, which calculates the speed based on the characteristics of the Earth’s interior in the specific region [30].
To manage the challenges of swiftly evolving traffic patterns, optical networks are evolving towards dynamically re-configurable, autonomous systems. These systems are managed by a centralized Optical Network Controller (ONC), which interacts with Network Elements (NEs) by means of Application Programming Interfaces (API). The ONC leverages various metrics tracked by each NE, constituting the streaming telemetry paradigm for network management purposes. This setup facilitates the provision of varied services to the higher network layers. We propose to expand the streaming telemetry paradigm to integrate earthquake early detection service into the existing network. As shown in Figure 3, the streaming telemetry paradigm entails continuous data transmission from NEs to the ONC to assist network management and control. Devices like Re-Configurable Add/Drop Multiplexers (ROADM) and amplifiers include crucial information like power levels and variations in temperature, whereas devices like coherent transceivers (TRX) capture alterations in phase and SOP of optical signals. External stress affects the phase and SOP of the transmitted signal, thereby, SOP changes carry environmental data that can be leveraged for sensing applications [31,32].
Furthermore, a post-processing agent within the NEs filters only the crucial information to the ONC, and analyze the data by leveraging machine learning algorithms. Coherent transceivers are inaccessible due to vendor lock, yet Intensity Modulated-Direct Detected (IM-DD) TRXs are still popular in metro and access segments with lower data rates or functioning as slower as Optical Supervisory Channels (OSCs) that terminate at every amplification site [33]. Thanks to the polarized nature of OSCs, that facilitates the identification of OSC SOP alterations induced by external stress. This could be achieved by extracting a minor portion of power to supply a polarimeter or a simple Polarization Beam Splitter (PBS) as depicted in Figure 4. The objective here is to leverage the existing terrestrial optical network in the Marradi region as a smart sensing grid, where we extracted the real ground motion data induced by the earthquake with epicenter highlighted in yellow in Figure 3 from the INGV datasets, integrate these sets in the aforementioned Waveplate Model, considering two sensing fibers placed instead of two seismic stations ZCCA and FOSV. The main idea of choosing two sensing points is to firstly train and test a deep learning algorithm exploiting data applied on two distinct points, and secondly to asses the time needed for each municipality to implement earthquake countermeasures and to take emergency response due to the fact of varying distances of the two cities (Zocca city where ZCCA is located and Fassato di Vico city where FOSV is located) from the epicenter. Details are present in the next section. It is worth mentioning that in [34], we have experimentally tested this SOP sensing approach on a deployed fiber ring in the city of Turin, Italy, using IM-DD TRXs and polarimeters as sensing devices to detect and localize car passage by monitoring SOP alterations’ footprint. The experiment showed less than 100 meters of accuracy.
While in [35], the author showed the feasibility of implementing machine learning algorithms for car passage count by means of fiber optics sensing.

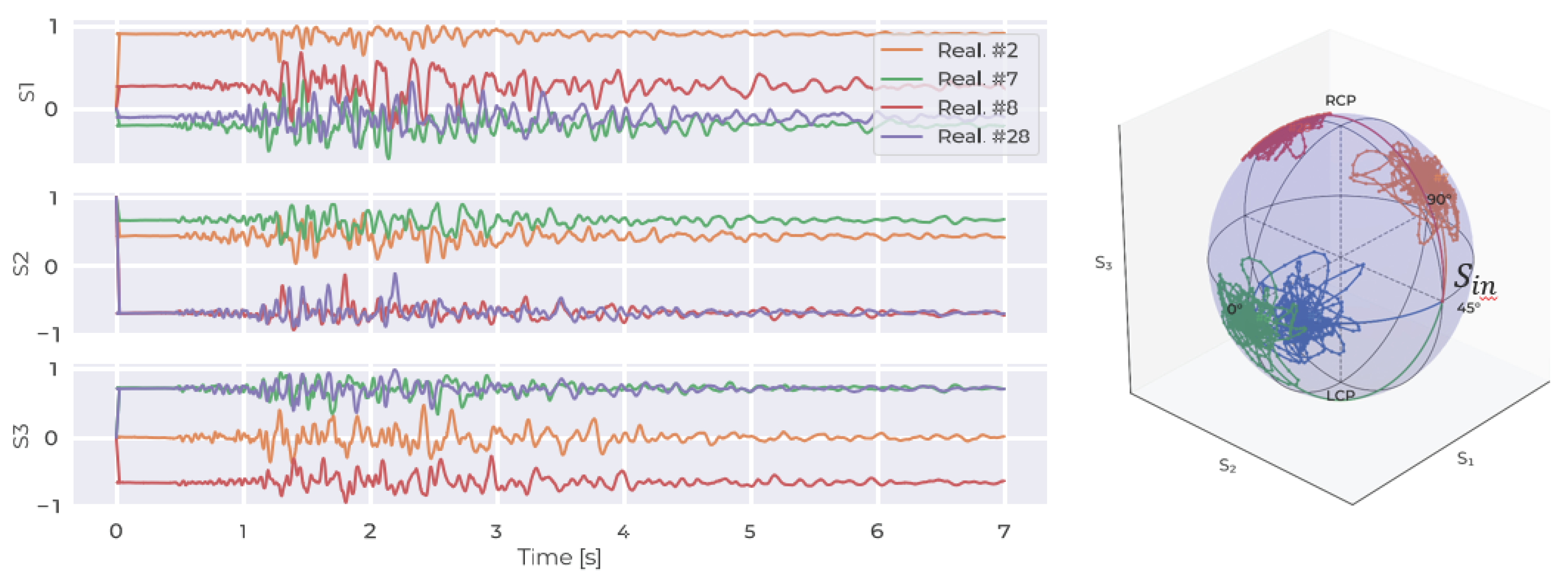
4. Neural Network Algorithm and Related Results

4.1. Case Scenario

Zocca municipality (ZCCA) is located 58.5 km far from the epicenter and Fassato di Vico (FOSV) is 126.9 km far. In place of the two seismic stations (ZCCA and FOSV), we utilize two sections of fiber cable, each extending 10 kilometers, positioned precisely at the same geographical coordinates as the stations. By exploiting the Waveplate Model and after incorporating the real ground displacement motion, we were able to generate the average strain plots along the fiber sections substituting ZCCA and FOSV as shown in Figure 5, demonstrating the arrival of P waves and Surface waves on both fibers. Given the close proximity of ZCCA fiber to the epicenter, it is expected to see the arrival of P wave prior the one of FOSV fiber, and the signal exhibits more oscillations. The data was collected over 300 seconds sampled at 200 Hz. We recommended scaling the time axis by dividing over the sample rate to concentrate more on the central part of the dataset.
Each fiber was divided into 2500 waveplates with 4 meters spatial resolution. P wave reached ZCCA fiber at 0.17 seconds and FOSV fiber at 0.28 seconds. The Surface wave was detected at 0.42 seconds on ZCCA fiber and at 0.50 seconds on FOSV fiber. When multiplied by 200, the time difference between Surface and P waves on ZCCA fiber is 50 seconds, whereas on the FOSV fiber, the difference is 44 seconds. However, the time difference between observations should be consistent, given that the seismic event and velocity model are identical. Several factors can contribute to the 6 seconds discrepancy observed, including inaccuracies in peak detection between the two plots, as the discrepancy corresponds to a 0.03 seconds difference on the plot itself. For simplicity purposes, we have assumed a 45 seconds time difference between the arrival times of the P wave and Surface wave. After coupling the strain into the fiber and injecting 45 degree polarized light, we demonstrate in Figure 6, one simulation out of 100 for a SOP/SOPAS evolution observed.
The SOP/SOPAS showed an expected similar behaviour as the strain with almost the same time difference between earthquake waves. Our main focus is to train the machine learning model on SOPAS data instead of SOP data to reduce computational time.

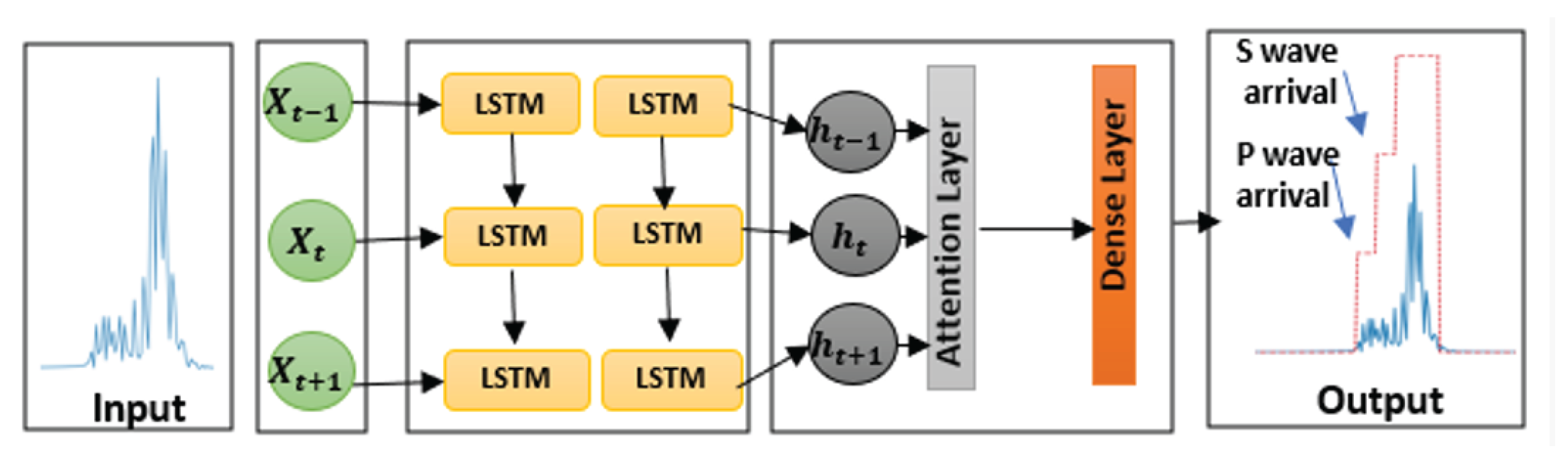
4.2. Neural Network Model

We employ a neural network model using Long Short-Term Memory (LSTM) layers with an attention mechanism for early detection for forthcoming earthquakes. The model is detailed in Figure 7. We use single feature time series of SOPAS for all SOPs as input data. The first LSTM contains 64 units that returns sequences, while the second one build another stacked LSTM with 128 units followed by additional LSTM layers, with 64 units. The attention mechanism calculation apply time distributed dense layer with a single neuron to each time step output of the last LSTM layer. As for the attention mechanism integration, it performs element-wise multiplication between the attention weights and the LSTM outputs to prioritize important features. The output layer is a full connected dense layer with 4 units (assuming it’s a multi class classification problem, detecting No Earthquake, P Waves, S Waves, and Surface Waves) and Softmax activation, generating class probability [36]. The output visible on the right of Figure 7 is just a demonstration for the expected results but not the actual SOPAS result even not the right SOPAS plot.

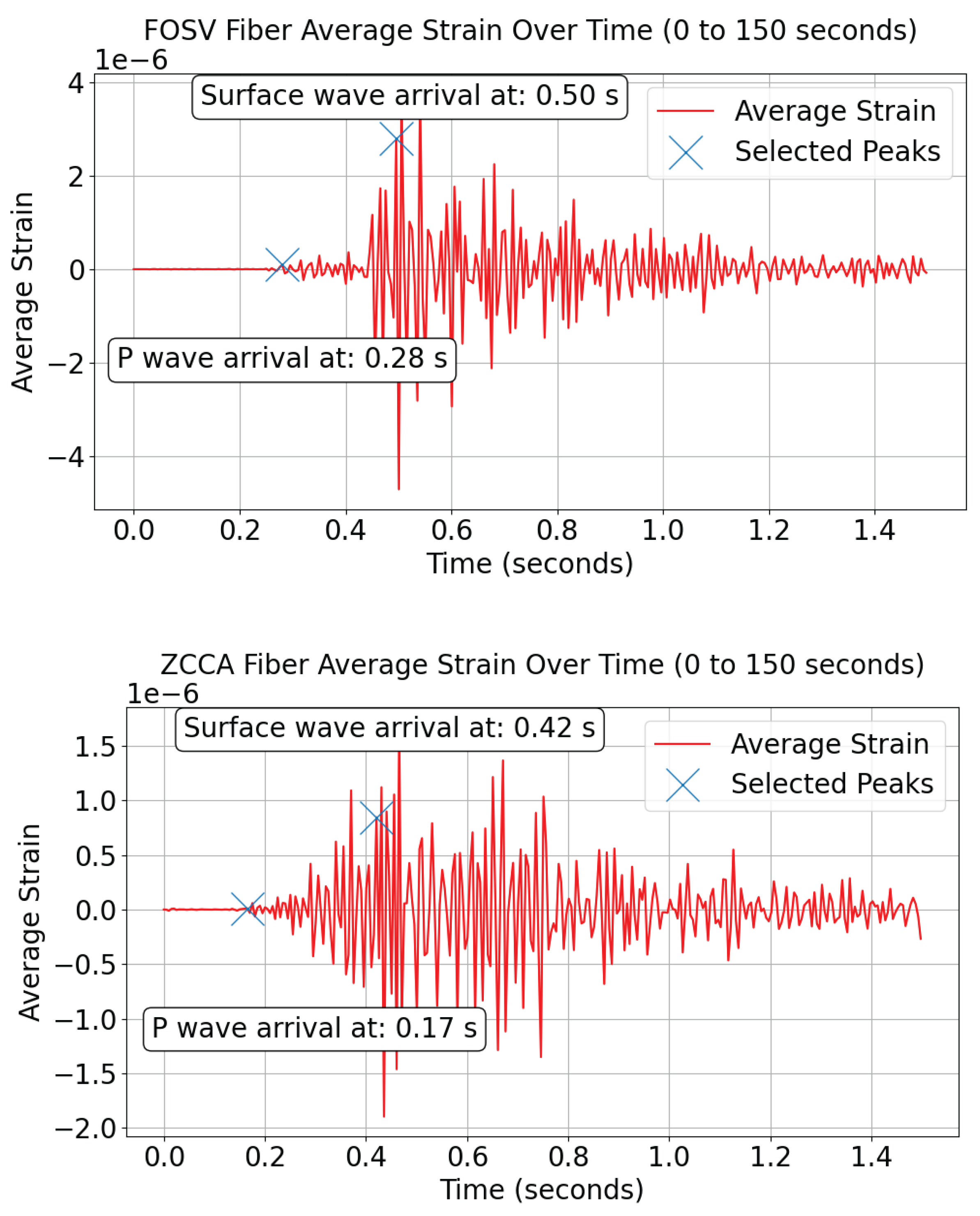
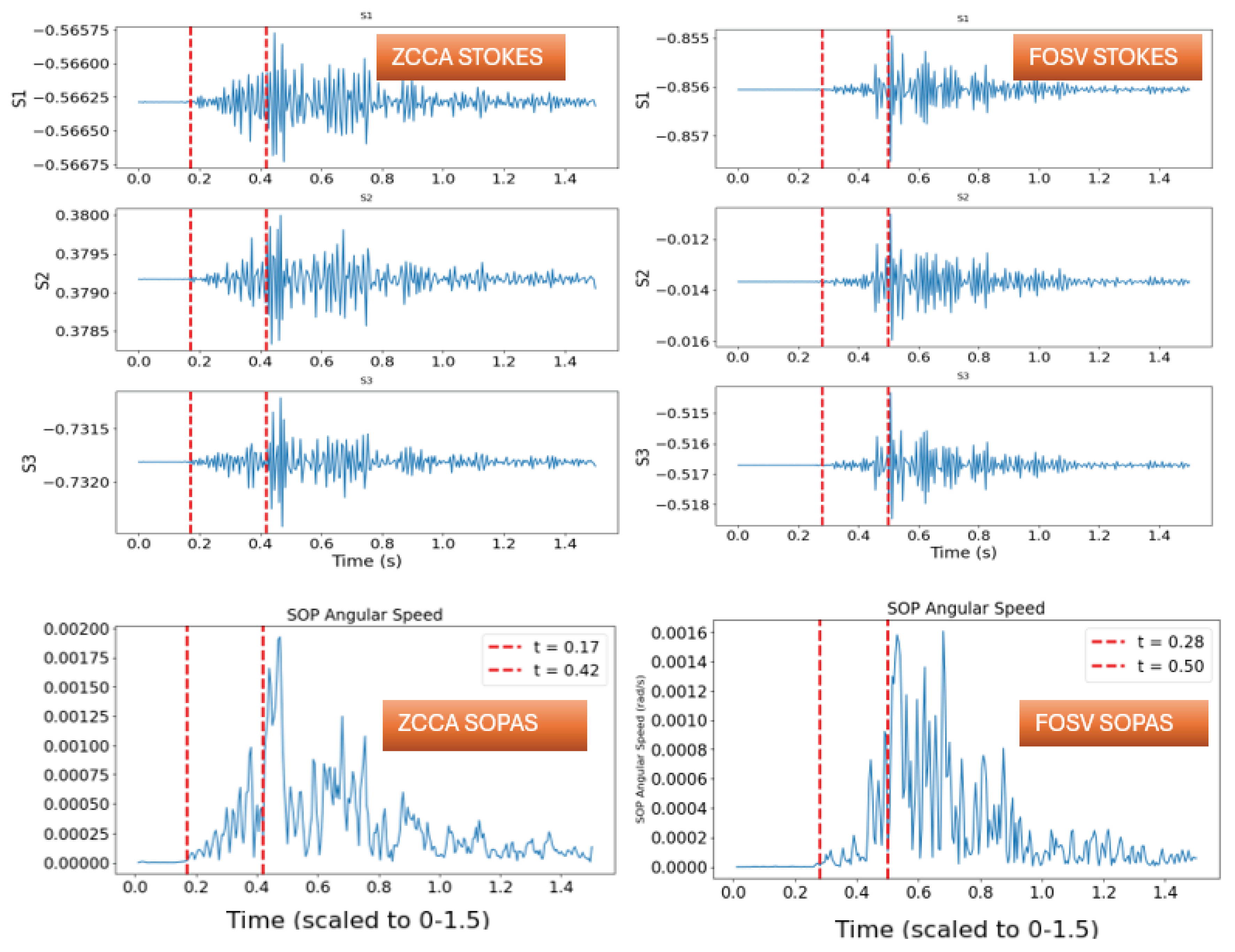
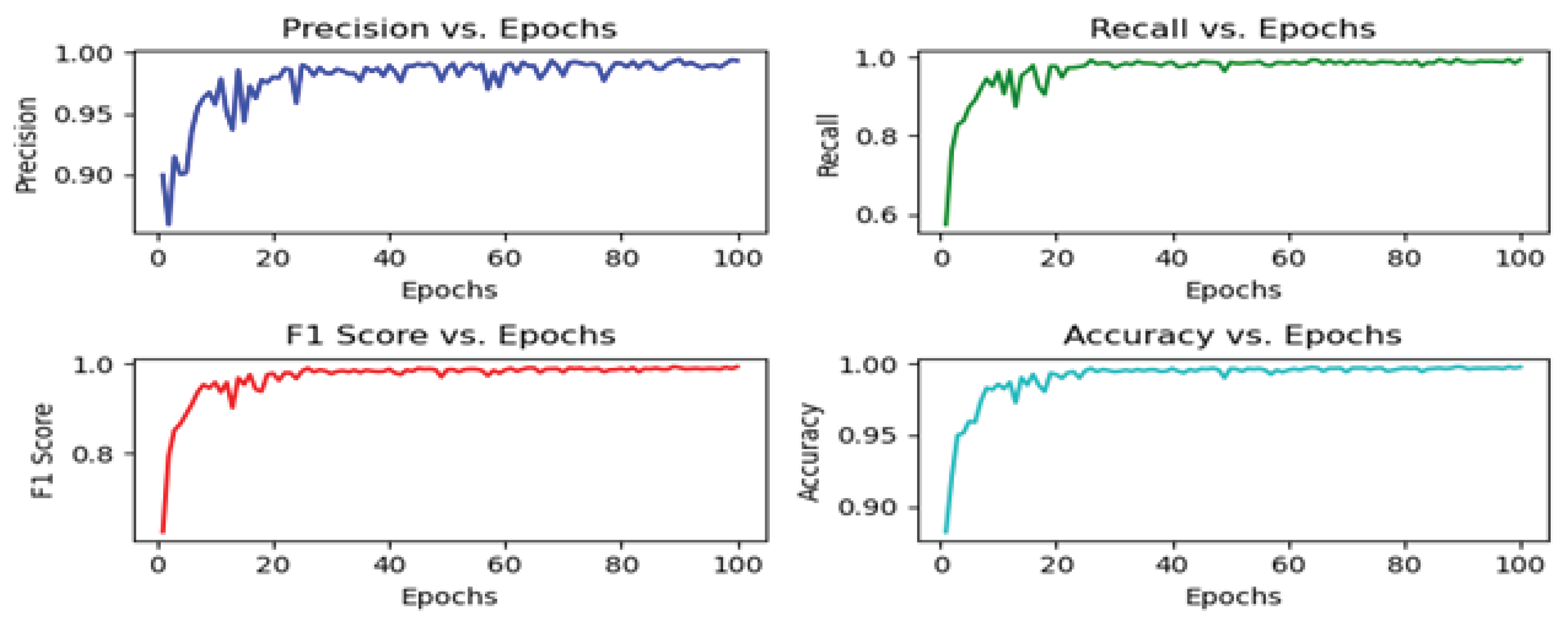
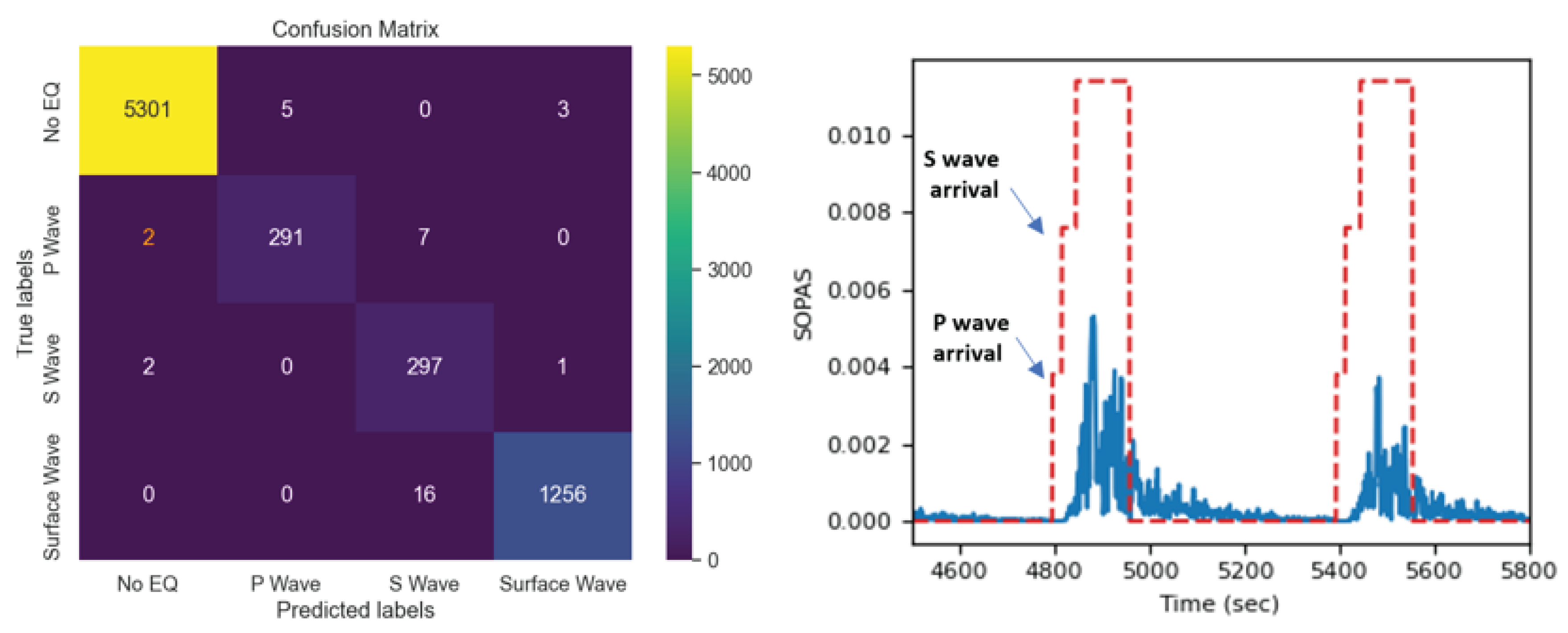
4.3. Results and Discussion

The model is trained on 60% of all the previous data, 20% used for validation, and the rest 20% for testing. In the validation process, Precision (accuracy of positive predictions), Recall (ability of the model to identify all relevant samples), Accuracy (the overall correctness of the model) and F1 score (the balance between precision and recall that implies better model performance for higher values) metrics are used to evaluate the performance of the model, especially in classification tasks. These metrics were evaluated on the validation dataset by varying the number of epochs from 1 to 100. These metrics results are presented in the Figure 8 below.
Our proposed model achieves these metrics reaching 1 within 100 epochs, which indicates excellent performance across these evaluation measures. An accuracy of 1 implies the model making no mistakes, and correctly predicting all samples. Perfect Precision and Recall (both reaching 1) indicate that the model is making no false positive or false negative predictions, respectively. F1 score of 1 indicates a perfect balance between Precision and Recall. Achieving such high scores within 100 epochs is impressive, suggesting that our model quickly learned and generalized well to the data. This is a sign of strong training and validation. This model was able to predict P waves with 99.5% of accuracy on validation dataset.
For testing purposes, we used two SOPAS to better visualize the model, showing P wave detection in one second as depicted in the in the right of Figure 9.
Consequently, with a 45 seconds interval between the P wave and the Surface waves, and accounting to the propagation time of the seismic wave from the epicenter to both locations at 7.10 km/h speed as per the CIA model, the municipality of Zocca has almost 52 seconds (45+[8.23]-1) to implement its emergency plan and countermeasures. In contrast, Fassato di Vico has 62 seconds (45+[17.8]-1) to execute similar actions. [ v = d t ]. The confusion matrix shown at the left of Figure 9, is a table to visualize the performance of a classification model. It shows the correct and incorrect detection made by the model for each class. For instance, for "No Earthquake" class, the model showed 5301 correct detection, 5 wrong detected as P waves and 3 as Surface waves. So on and so forth, for the rest. Therefore, the assessment of model performance based on the confusion matrix showed 99.50% accuracy rate. The model showcased promising performance in detecting P waves, a critical aspect in earthquake early detection.

5. Conclusions

In conclusion, this manuscript demonstrated the innovative use of a centralized smart grid optical network, empowered by a deep learning algorithm, for early earthquake detection. The study utilized a Waveplate Model to analyze state of polarization (SOP) changes in optical fibers due to seismic events. The neural network model successfully identified P-wave arrivals, enabling timely initiation of emergency response measures. This approach offers a promising, cost-effective method for leveraging existing optical fiber networks for environmental sensing and earthquake prediction, enhancing public safety and preparedness.

Author Contributions

Conceptualization, Hasan Awad and Emanuele Virgillito; methodology, Hasan Awad and Vittorio Curri; software, Hasan Awad and Fehmida Usmani; validation, Vittorio Curri, Rudi Bratovich and Stefano Straullu; formal analysis, Hasan Awad; investigation, Hasan Awad; resources, Rudi Bratovich and Rosanna Pastorelli; data curation, Hasan Awad; writing—original draft preparation, Hasan Awad; writing—review and editing, Emanuele Virgillito, Roberto Proietti and Rudi Bratovich; visualization, Vittorio Curri; supervision, Vittorio Curri and Rosanna Pastorelli; project administration, Vittorio Curri; funding acquisition, Rosanna Pastorelli. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by SM-Optics and the Ministry of University and Research (MUR), grant number E12B22000540006.

Data Availability Statement

The data presented in this study can be found at http://ismd.mi.ingv.it/evento.php?var1=36163811&path=230918031014&rev=auto.

Acknowledgments

The presented work has been supported by the Italian National Recovery and Resilience Plan (NRRP) of NextGenerationEU, partnership on “Telecommunications of the Future” (PE00000001 - program “RESTART”).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SAFOD San Andreas Fault Observatory at Depth
GPS Global Positioning System
IASPEI International Association of Seismology and Physics of the Earth’s Interior
P waves Primary waves
S waves Secondary waves
OTDR Optical Time Domain Reflectometer
OFDR Optical Frequency Domain Reflectometry
DAS Distributed Acoustic Sensing
SOP State of Polarization
SOPAS State of Polarization Angular Speed
INGV National Institute of Geophysics and Volcanology
CIA Central Italian Apennines
ONC Optical Network Controller
API Application Programming Interface
NE Network Element
ROADM Re-configurable Optical Add-Drop Multiplexer
TRX Transceiver
OSC Optical Supervisory Channel
IM-DD Intensity Modulated-Direct Detected
PBS Polarization Beam Splitter
LSTM Long Short - Term Memory

Appendix A. Waveplate Model Theory

A long telecommunication fiber is to a good approximation, equivalent to a concatenation of polarization waveplates with random orientation and random external birefringence. In a frequency interval in which the first order approximation for the state of polarization is valid, any fiber section or waveplate is characterized by jones matrix.
M ( ω ) = e j β ( ω ) U ( ω ) = e j β ( ω ) u 1 u 2 − u 2 * u 1 * = e j β ( ω ) R out − 1 M d R in
where β is a quantity not essential for the calculation of the SOPs.
M d = DIAG e j ω Δ τ / 2 , e − j ω Δ τ / 2
Where ω represents the difference between the generic frequency of the optical signal and the central frequency ω 0 , and Δ τ is the Differential Group Delay (DGD) of the fiber and could be described as:
Δ τ = 2 π L b 1 + Δ L i d z d z
where 2 π L b is the internal birefringence presented earlier, and Δ L i is the external birefringence corresponding to the nanostrain value induced by an earthquake.
M d represents a rotation around a fixed axis through an angle equal to ω Δ τ . R in and R out are matrices depending on the state of polarization and described as:
R in = cos θ − sin θ sin θ cos θ
R out = cos θ − sin θ sin θ cos θ
The angle θ , is the major axis angle that we consider in our model and the eccentricity of the ellipse is neglected. In [b26], the full matrices representation was mentioned.
The matrix U ( ω ) of the cascade of two waveplates, described by U 1 and U 2 , is
U = ( U 2 , U 1 ) = ( R out 2 − 1 ( M d 2 ) ( R in 2 ) ) ( R out 1 − 1 ( M d 1 ) ( R in 1 ) ) .
As more segment the fiber into waveplates as better, to ensure small sections and consider uniform internal birefringence at each section. Consequently, the polarization at the output of the fiber is calculated as
S out = U × S in

Appendix B. State of Polarization Angular Speed (SOPAS) Theorem

The state of polarization is the rise of the stokes parameters samples taken at discrete time instants, represented by the vector k with components ( S 1 [ k ] , S 2 [ k ] , S 3 [ k ] ) . The discrete State of Polarization Angular Speed (SOPAS), denoted by ω [ k ] , and the sampling period T s are given by the following relationship where ( S k , S k − 1 ) is the dot product between the Stokes vectors at time k and at time k − 1 . This computation is analogous to the discrete-time derivative of an angle, and the SOPAS is denoted by ω [ k ] , where ω [ k ] is:
ω [ k ] = arccos ( S k · S k − 1 ) ∥ S k ∥ ∥ S k − 1 ∥ · 1 T s

References

  1. He, M.; Ren, S.; Tao, Z. Cross-fault Newton force measurement for Earthquake prediction. Rock Mechanics Bulletin 2022, 1, 1–20. [Google Scholar] [CrossRef]
  2. Lin, W.; Conin, M.; Moore, J.; Chester, F; Nakamura, Y.; Mori, J; Anderson, L; Brodsky, E. Stress State in the Largest Displacement Area of the 2011 Tohoku-Oki Earthquake. Science 2013, 339, 687–690. [Google Scholar] [CrossRef] [PubMed]
  3. Hickman, S; Zoback, M. Stress orientations and Magnitudes in the SAFOD Pilot Hole. Advanced Earth and Space Sciences 2004, 31, 1–4. [Google Scholar] [CrossRef]
  4. Ishii, H.; Asai, Y. Development of a Borehole Stress Meter for Studying Earthquake Predictions and Rock Mechanics, and Stress Seismograms of the 2011 Tohoku Earthquake (M 9.0). SpringerOpen 2015, 67, 1–15. [Google Scholar] [CrossRef]
  5. Gladwin, M. High-Precision Multicomponent Borehole Deformation Monitoring. American Institute of Physics 1984, 55, 2011–2016. [Google Scholar] [CrossRef]
  6. Wu, M; Zhang, C; Fan, T. Stress State of the Baoxing Segment of the Southwestern Longmenshan Fault Zone before and after the Ms 7.0 Lushan Earthquake. Asian Earth Sciences 2016, 121, 9–19. [Google Scholar] [CrossRef]
  7. Jinlai, X; Zhaohua, X. Infrasound waves caused by earthquake on 12 July 1993 in Japan. Acta Acustica 1996, 12, 55–61. [Google Scholar]
  8. Allen, R; Kanamori, H. The Potential for Earthquake Early Warning in Southern California. Science 2003, 300, 786–789. [Google Scholar] [CrossRef]
  9. Geller, R; Jackson, D; Kagan, Y; Mulargia, F. Earthquakes Cannot Be Predicted. Science 1997, 275, 1616. [Google Scholar] [CrossRef]
  10. Jordan, T.; Chen, Y.; Gasparini, P.; Madariaga, R.; Main, I.G.; Marzocchi, W.; Papadopoulos, G.A.; Sobolev, G.A.; Yamaoka, K.; Zschau, J. Operational Earthquake Forecasting: State of Knowledge and Guidelines for Utilization. Annals of Geophysics 2011, 54, 316–391. [Google Scholar]
  11. Mecozzi, A; Antonelli, C; Mazur, M; Fontaine, N; Chen, H; Dallachiesa, L; Ryf, R. Use of Optical Coherent Detection for Environmental Sensing. Journal of Lightwave Technology 2023, 41, 3350–3357. [Google Scholar] [CrossRef]
  12. Mazur, M; Parkin, N; Ryf, R; Iqbal, A; Wright, P; Farrow, K; Fontaine, N; Börjeson, E; Kim, K; Dallachiesa, L; Chen, H; Larsson-Edefors, P; Lord, A; Neilson, D. Continuous Fiber Sensing over Field-Deployed Metro Link using Real-Time Coherent Transceiver and DAS. In Proceedings of the European Conference on Optical Communication (ECOC), Basel, Switzerland, (18 September 2022);
  13. Kulhánek, O. Seismic Waves. In Anatomy of Seismograms, 1st ed; Elsevier Science: Amsterdam, Netherlands, 1990. [Google Scholar]
  14. Fernández-Ruiz, M; Soto, M; Williams, E; Martin-Lopez, S; Zhan, Z; Gonzalez-Herraez, M; Martins, H. Distributed Acoustic Sensing for Seismic Activity Monitoring. APL Photonics 2020, 5, 1–16. [Google Scholar] [CrossRef]
  15. Boffi, P. Sensing Applications in Deployed Telecommunication Fiber Infrastructures. In Proceedings of the European Conference on Optical Communication (ECOC), Basel, Switzerland, (18 September 2022). [Google Scholar]
  16. Eiselt, M.; Azendorf, F.; Sandmann, A. Optical Fiber for Remote Sensing with High Spatial Resolution. In Proceedings of the EASS 2022; 11th GMM-Symposium, Erfurt, Germany, (05 July 2022). [Google Scholar]
  17. Fichtner, A.; Bogris, A.; Nikas, T.; Bowden, D.; Lentas, K.; Melis, N.S.; Simos, C.; Simos, I.; Smolinski, K. Theory of Phase Transmission Fibre-Optic Deformation Sensing. Geophysical Journal International 2022, 231, 1031–1039. [Google Scholar] [CrossRef]
  18. Guerrier, S. High Bandwidth Detection of Mechanical Stress in Optical Fibre Using Coherent Detection of Rayleigh Scattering. PhD Thesis, Institut polytechnique de Paris, Paris, France, 03 February 2022. [Google Scholar]
  19. Dong, B; Popescu, A; Tribaldos, V; Byna, S; Ajo-Franklin, J; Wu, K. Real-Time and Post-Hoc Compression for Data from Distributed Acoustic Sensing. Computers & Geosciences 2022, 166, 1–22. [Google Scholar]
  20. Lellouch, A; Yuan, S; Ellsworth, W; Biondi, B. Velocity-based Earthquake Detection using Downhole Distributed Acoustic Sensing—Examples from the San Andreas Fault Observatory at Depthvelocity-based Earthquake Detection using Downhole Distributed Acoustic Sensing. Bulletin of the Seismological Society of America 2019, 109, 2491–2500. [Google Scholar] [CrossRef]
  21. Marra, G; Clivati, C; Luckett, R; Tampellini, A; Kronjäger, J; Wright, L; Mura, A; Levi, F; Robinson, S; Xuereb, A; Bapite, B; Calonico, D. Ultrastable Laser Interferometry for Earthquake Detection with Terrestrial and Submarine Cables. Science 2018, 361, 486–490. [Google Scholar] [CrossRef] [PubMed]
  22. Cantono, M; Castellanos, J; Batthacharya, S; Yin, S; Zhan, Z; Mecozzi, A; Kamalov; V. Optical Network Sensing: Opportunities and Challenges. In Proceedings of the Optical Fiber Communication Conference (OFC) 2022; San Diego, California, United States, (06 March 2022).
  23. Barcik, P; Munster, P. Measurement of Slow and Fast Polarization Transients on a Fiber-Optic Testbed. OPTICA 2020, 10, 15250–15257. [Google Scholar] [CrossRef]
  24. Zhan, Z; Cantono, M; Kamalov, V; Mecozzi, A; Müller, R; Yin, S; Castellanos, J. Supplementary Materials for Optical Polarization–Based Seismic and Water Wave Sensing on Transoceanic Cables. Science 2021, 371, 931–936. [Google Scholar] [CrossRef]
  25. Zhan, Z; Cantono, M; Kamalov, V; Mecozzi, A; Müller, R; Yin, S; Castellanos, J. Optical Polarization–Based Seismic and Water Wave Sensing on Transoceanic Cables. Science 2021, 371, 931–936. [Google Scholar] [CrossRef]
  26. Curti, F; Daino, B; De Marchis, G; Matera, F. Statistical Treatment of the Evolution of the Principal States of Polarization in Single-Mode Fibers. Journal of Lightwave Technology 1990, 8, 1162–1166. [Google Scholar] [CrossRef]
  27. Pellegrini, S; Rizzelli, G; Barla, M; Gaudino, R. Algorithm Optimization for Rockfalls Alarm System Based on Fiber Polarization Sensing. IEEE Photonics Journal 2023, 15, 1–9. [Google Scholar] [CrossRef]
  28. Feigl, K. Overview and Preliminary Results from the PoroTomo Project at Brady Hot Springs, Nevada: Poroelastic Tomography by Adjoint Inverse Modeling of Data from Seismology, Geodesy, and Hydrology. In Proceedings of the 42nd Workshop on Geothermal Reservoir Engineering 2017; Stanford, California, United States, (13 February 2022). [Google Scholar]
  29. Italian National Institute of Geophysics and Volcanology (INGV). Available online: https://terremoti.ingv.it/en/event/36163811 (accessed on 20 February 2023).
  30. Herrman, R; Malagnini, L; Munafò, I. Regional Moment Tensors of the 2009 L’Aquila Earthquake Sequence. Bulletin of the Seismological Society of America 2009, 101, 975–993. [Google Scholar] [CrossRef]
  31. Bratovich, R; Martinez, F; Straullu, S; Virgillito, E; Castoldi, A; D’Amico, A; Aquilino, F; Pastorelli, R; Curri, V. Surveillance of Metropolitan Anthropic Activities by WDM 10G Optical Data Channels. In Proceedings of the European Conference on Optical Communication (ECOC) 2022; Basel, Switzerland, (18 September 2022).
  32. Virgillito, E; Straullu, S; Aquilino, F; Bratovich, R; Awad, H; Proietti, R; D’Amico, A; Pastorelli, R; Curri, V. Detection, Localization and Emulation of Environmental Activities Using SOP Monitoring of IMDD Optical Data Channels. In Proceedings of the 23rd International Conference on Transparent Optical Networks (ICTON) 2023; Bucharest, Romania, (02 July 2023).
  33. Straullu, S; Aquilino, F; Bratovich, R; Rodriguez, F; D’Amico, A; Virgillito, E; Pastorelli, R; Curri, V. Real-time Detection of Anthropic Events by 10G Channels in Metro Network Segments. In Proceedings of the IEEE Photonics Conference (IPC) 2022; Vancouver, Canada, (13 November 2022).
  34. Awad, H; Virgillito, E; Straullu, S; Bratovich, R; Rodriguez, F; Proietti, R; D’Amico, A; Aquilino, F; Pastorelli, R; Curri, V. Environmental Sensing and Localization via SOP Monitoring of IM-DD Optical Data Channels. In Proceedings of the Optica Sensing Congress 2023 (AIS, FTS, HISE, Sensors, ES) 2023; Munich, Germany, (30 July 2023).
  35. Jousset, P; Reinsch, T; Ryberg, T; Blanck, H; Clarke, A; Aghayev, R; Hersir, G; Henninges, J; Weber, M; Krawczyk, C. Dynamic Strain Determination using Fibre-Optic Cables Allows Imaging of Seismological and Structural Features. Nature Communications 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
  36. Hochreiter, S; Schmidhuber, J. Seismic Waves. In Long Short-Term Memory, Neural Computation, MIT Press: Cambridge, Massachusetts, 1997; 9, pp.:1735–1780.
Preprints 101215 g001
Figure 1. Schematic Representation of Fiber Sections, each of Uniform Internal Birefringence.
Figure 1. Schematic Representation of Fiber Sections, each of Uniform Internal Birefringence.
Preprints 101215 g001
Preprints 101215 g002
Figure 2. Four SOP Evolution for the same Seismic Event with different set of Plates’ Angles.
Figure 2. Four SOP Evolution for the same Seismic Event with different set of Plates’ Angles.
Preprints 101215 g002
Preprints 101215 g003
Figure 3. Sensing Network Architecture.
Figure 3. Sensing Network Architecture.
Preprints 101215 g003
Preprints 101215 g004
Figure 4. In-field SOP Sensing Demonstration.
Figure 4. In-field SOP Sensing Demonstration.
Preprints 101215 g004
Preprints 101215 g005
Figure 5. Average Strain for both Fibers Substitutes.
Figure 5. Average Strain for both Fibers Substitutes.
Preprints 101215 g005
Preprints 101215 g006
Figure 6. ZCCA - FOSV SOP and SOPAS examples.
Figure 6. ZCCA - FOSV SOP and SOPAS examples.
Preprints 101215 g006
Preprints 101215 g007
Figure 7. Neural Network Architecture based LSTM layers.
Figure 7. Neural Network Architecture based LSTM layers.
Preprints 101215 g007
Preprints 101215 g008
Figure 8. Validation Metrics.
Figure 8. Validation Metrics.
Preprints 101215 g008
Preprints 101215 g009
Figure 9. Neural Network Model Final Result
Figure 9. Neural Network Model Final Result
Preprints 101215 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

172

Views

105

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated