Extending Group Dynamics Models: Incorporating Heterogeneous Networks to Analyze Cooperative Behaviors and Collective Intelligence in Biological Groups

1. Introduction

Coordinated consistency in biological groups, a universal phenomenon in nature, highlights the importance of interaction patterns between individuals alongside their inherent characteristics [1,2]. This phenomenon is evident in the high degree of synchrony and coordination of individual actions within groups, allowing organisms to adapt effectively to environmental changes, optimize foraging efficiency, and maintain social structure stability. For instance, fish schools evade predators through coordinated swimming [3,4], and migratory bird communities utilize synchronized flights for long-distance migration [5]. Similarly, bee and ant societies maintain their complex social structures through coordinated behaviors [6]. Studying coordinated consistency in biological groups has significant implications, enhancing our understanding of biology, ecology [7], and contributing to advancements in engineering [8], physics [9], biology [10,11], and social sciences [12].

A key question in studying coordinated consistency in biological groups is understanding the group’s decision-making mechanisms, such as choosing destinations, paths, and departure times. Current insights into group decision-making stem from two primary perspectives. The first suggests that decision-making is distributed among all group members who adhere to established rules [13]. Typically, individuals modify their decisions based on interactions with neighbors, leading to a collective compromise on routes. Research indicates [14] that this compromise strategy suits animal groups with limited information-processing capabilities. However, it can result in inefficiencies, ambiguous responsibilities, and reduced adaptability. The second perspective posits that decision-making in certain advanced animal groups is concentrated among a few leaders with critical information [13]. For instance, a distinct hierarchy is evident in pigeon colony flights [15,16]. Once established, these leadership structures are resilient to change unless leaders receive misleading external information [17,18]. Therefore, the efficiency and effectiveness of group decision-making are influenced by factors such as information availability, group structure, and inter-individual interactions, offering significant insights into biological group behaviors and decision-making processes.

Leadership power within groups can be classified into two main categories [19]: structured leaders and informed leaders. Informed leaders occurs when a subset of the group possesses crucial information and acts upon it [20,21]. For instance, during caribou migration, experienced individuals lead the way, while others react to local food availability and predation threats. Similarly, in elephant herds, typically the older, more experienced female elephants guide the group to essential resources like water, food, and safe habitats, vital for the group’s survival and reproduction. Defining informed leaders in mathematical models and applying network science to uncover their underlying principles remains a challenging and active area of research.

Research on modeling group systems in biology dates to the 1980s. Biologist Reynolds [22] proposed three fundamental behaviors for natural biological groups: separation, alignment, and cohesion. Subsequent advancements include Vicsek’s renowned multi-particle model, which illustrates the synchronized motion of an autonomous system comprising multiple particles [23]. This model demonstrated, through simulations, that particle synchronization is achievable with minimal external interference. Jadbabaie [24] provided a theoretically rigorous proof of the conditions necessary for velocity synchronization in the Vicsek model. Cucker [25] explored particle swarms with Newtonian interactions, quantifying the influence between individuals by their distances and adjusting velocities based on a weighted average of velocity differences. This led to the development of the influential Cucker-Smale (CS) population model. Recent studies have delved into more intricate and realistic dynamics, such as molecular physics [26], local interaction [27], predator-prey [28], and metric distance models [29,30]. Despite discussions of hierarchical relationships in literature, most simulations assume equal status among individuals. Research from the perspective of informed leadership in group behaviors remains relatively unexplored.

This study enhances the understanding of biological groups with informed leaders by refining the Cucker-Smale model with coupling forces, enabling a more precise differentiation of dynamic behaviors within the group. Real biological behaviors were analyzed to develop comprehensive convergence conditions, capturing the nuances of group dynamics. Additionally, we introduced the FLH interactive mode generation algorithm, inspired by the topology of pigeon flocks. The degree distribution of the FLH interactive mode closely aligns with a power-law distribution, as evidenced by statistical tests. Incorporating the FLH and other common interaction patterns, we utilized rolling time windows and time slices to segment group behavior into distinct phases, evaluating them based on group volatility and convergence time. Comparative experiments revealed that models using FLH interactions as inputs exhibited superior metric performance, shedding light on the evolutionary intelligence of biological groups. This paper’s contributions include (1) a refined group model that more accurately reflects biological group movement; (2) the development of the FLH interactive mode generation algorithm, demonstrating biological evolution’s wisdom through quantitative indices; and (3) theoretical and practical insights for studying intelligent behaviors in biological groups and biomimetic robotic systems. The article’s framework is illustrated in Figure 1.

2. Materials and Methods

2.1. Group Dynamics Models

2.1.1. Group Dynamics Model with Coupling Forces

The limited capability of a single individual necessitates that multiple individuals collaborate effectively to adapt to their environment, guided by local perceptions of dynamic conditions. In simulating natural group dynamics, developing artificial intelligence systems, and analyzing social behavior dynamics, the CS group model [31] plays a pivotal role. The traditional CS model is based on the following assumptions:

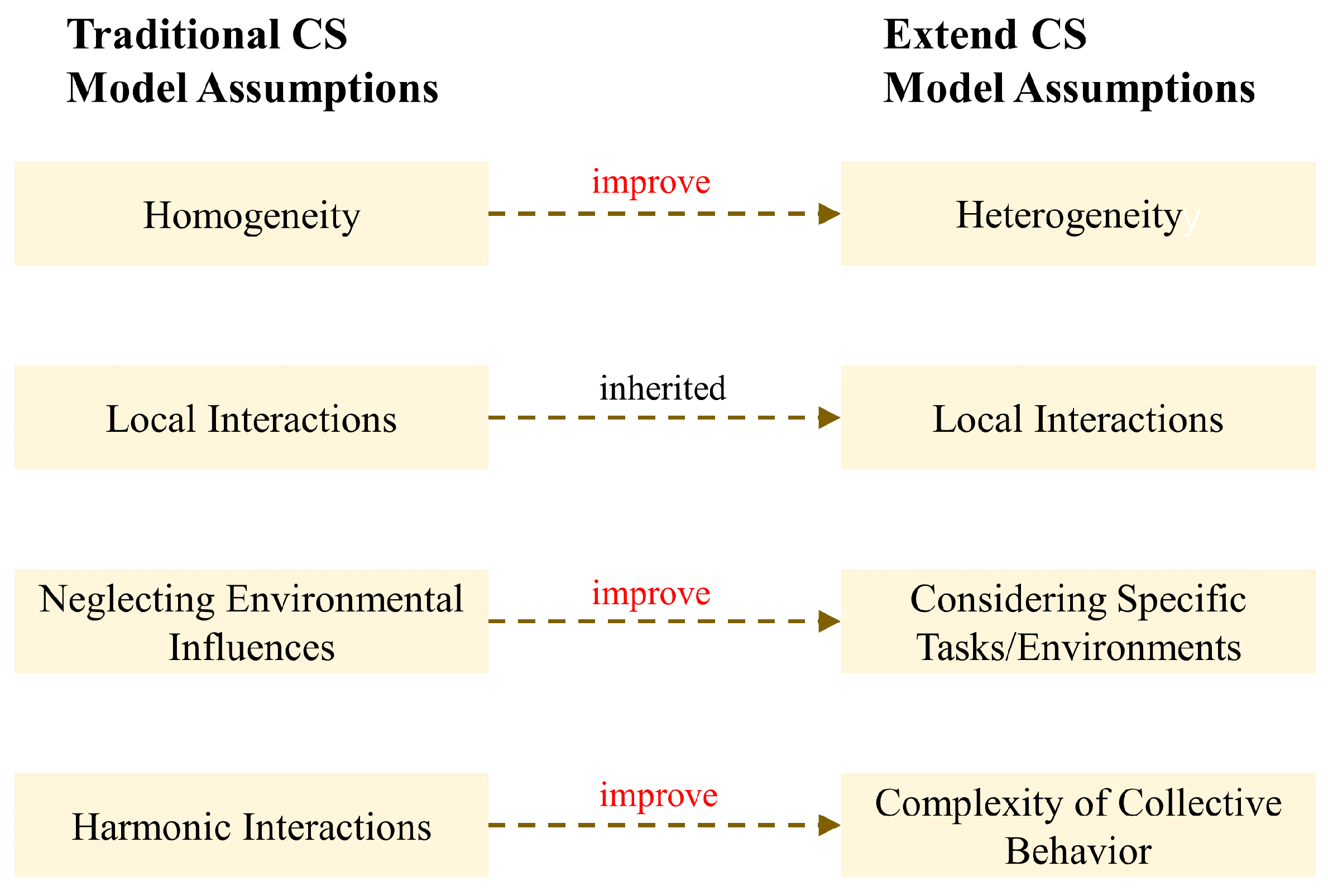
• (1)Homogeneity: The model presupposes that all individuals within the system exhibit uniform behavior, adhering to a common set of rules for updating their states. Specifically, each individual adjusts its velocity by calculating the weighted average of velocity differences with other individuals.
• (2)Local Interactions: The update of an individual’s motion state is contingent upon the states of its immediate neighbors. This mechanism is consistent with the phenomenon of information transmission through visual, auditory, or other sensory means among natural groups such as flocks of birds and schools of fish.
• (3)Neglecting Environmental Influences: The model does not directly incorporate the impact of environmental factors on the motion states of individuals.
• (4)Harmonic Interactions: The interaction force between individuals diminishes with increasing distance, with this force designed to facilitate cohesive and coordinated behavior within the group.

This model is characterized by its strong applicability, realistic interaction depiction, and rigorous mathematical analysis, making it a crucial tool for studying complex group behaviors. The specifics of the model are described as follows:

$$\begin{array}{cc}\hfill & \psi \left(r_{ij}\right)\triangleq 1/{\left(1+r_{ij}^2\right)}^{\beta },\hfill \\ \hfill & \frac{d{\mathbf{x}}_i\left(t\right)}{dt}={\mathbf{v}}_i\left(t\right),t>0,i=1,\cdots \cdots ,N,\hfill \\ \hfill & \frac{d{\mathbf{v}}_i\left(t\right)}{dt}=\frac{\lambda }{N}\sum _{j=1}^N\psi \left(r_{ij}\right)\left(∥{\mathbf{x}}_j\left(t\right)-{\mathbf{x}}_i\left(t\right)∥\right)\left({\mathbf{v}}_j\left(t\right)-{\mathbf{v}}_i\left(t\right)\right),i\ne j.\hfill \end{array}$$

(1)

where $i,j$ respectively represent the individuals i and j. $\psi \left(·\right)$ is the communication rate between individuals, which depends on the square of the Euclidean distance between two individuals i and j, denoted as $r_{ij}^2$ (see Figure 2a). $\beta \ge 0$ signifies the coordination parameter, which determines if the communication rate is long-ranged or short-ranged. An increase in $\beta$ results in a more rapid diminution of the influence between individuals as the distance between them increases. The first differential equation in Equation 1 employs a fundamental form of Newton’s laws of motion, delineating that the rate of change in position of individual i, ${\mathbf{x}}_i\left(t\right)\in {\mathbb{R}}^n$, with respect to time t equals its velocity, ${\mathbf{v}}_i\left(t\right)\in {\mathbb{R}}^n$. The second differential equation in Equation 1 reveals how the velocity vector ${\mathbf{v}}_i\left(t\right)$ evolves over time t. This evolution is determined by the weighted average influence of all other individuals in the group on individual i. When the velocity of another individual j exceeds that of individual i, individual i will attempt to accelerate to match the average velocity of the group, and vice versa. Here, $\lambda$ is a positive constant representing the strength of the coupling effect between individuals, while N denotes the total number of individuals in the group. This interaction mechanism is weighted by the interaction function $\psi \left(r_{ij}\right)$, ensuring that individuals in closer proximity exert a more significant influence on individual i.

We first recall the definition of asymptotic flocking, as described in Definition 1.

Definition 1.

 [32]

For the biological group system ${\left\{({\mathbf{x}}_i,{\mathbf{v}}_i)\right\}}_{i=1}^N$, certain conditions must be simultaneously met to guarantee asymptotic flocking.Considering all individuals $1\le i,j\le N,i\ne j$:

(1) Velocity Alignment. The system’s velocity should achieve asymptotic consistency over time.

$$\underset{t\to \infty }{lim}∥{\mathbf{v}}_i\left(t\right)-{\mathbf{v}}_j\left(t\right)∥=0.$$

(2)

(2) Group Formation. At any given moment t, the distances between individuals in the system remain finite.

$$\underset{0\le t<\infty }{sup}∥{\mathbf{x}}_i\left(t\right)-{\mathbf{x}}_j\left(t\right)∥<\infty .$$

(3)

Additionally, the literature [31] imposes the following constraints on $\beta$ and $\lambda$. The biological group system (Equation 1) attains asymptotic flocking under any of the following conditions:

$$\begin{array}{cc}\hfill & \left(1\right)\beta <\frac{1}{2},\hfill \\ \hfill & \left(2\right)\beta =\frac{1}{2}\mathrm{and}\frac{1}{2}\sum _{1\le i,j\le N}{∥{\mathbf{v}}_i-{\mathbf{v}}_j∥}^2<\left(\frac{{\lambda }^2}{2}\right),\hfill \\ \hfill & \left(3\right)\beta >\frac{1}{2}\mathrm{and}\hfill \\ \hfill & {\left(\frac{{\lambda }_2}{2\left(\frac{1}{2}{\sum _{1\le i,j\le N}∥{\mathbf{v}}_i-{\mathbf{v}}_j∥}^2\right)}\right)}^{\frac{1}{2\beta -1}}\left\{{\left(\frac{1}{2\beta }\right)}^{\frac{1}{2\beta -1}}-{\left(\frac{1}{2\beta }\right)}^{\frac{2\beta }{2\beta -1}}\right\}\hfill \\ \hfill & >2\left(\frac{1}{2}\sum _{1\le i,j\le N}{∥{\mathbf{x}}_i-{\mathbf{x}}_j∥}^2+1\right).\hfill \end{array}$$

(4)

Park [33] introduced the concept of inter-particle coupling forces to the CS model, ensuring collision avoidance while facilitating the system to achieve a more stringent equilibrium configuration, thereby resulting in a tighter arrangement among individuals. The system incorporating coupling forces is described as:

$$\begin{array}{cc}\hfill \frac{d{\mathbf{x}}_i}{dt}& ={\mathbf{v}}_i,t>0,i=1,\cdots \cdots ,N,\hfill \\ \hfill \frac{d{\mathbf{v}}_i}{dt}& =\frac{\lambda }{N}\sum _{j=1}^N\psi \left(r_{ij}\right)\left({\mathbf{v}}_j-{\mathbf{v}}_i\right)\hfill \\ \hfill & +\frac{\sigma }{N}\sum _{j=1}^N\frac{K}{2r_{ij}}\left(r_{ij}-2R\right)\left({\mathbf{x}}_j-{\mathbf{x}}_i\right),i\ne j.\hfill \\ \hfill \end{array}$$

(5)

the system has been improved upon the foundation of Equation 1. Herein, the positive constant $\sigma$ represents the coupling strength of the cohesive force among individuals, and K is a designated positive gain. R is defined as the maximum communication radius between individuals (see Figure 2b. This extended Cucker-Smale model provides a framework capable of describing more complex group dynamics, making it more suitable for studying and understanding collective behaviors in biological groups, such as the flight formations of birds and swimming patterns of fish.

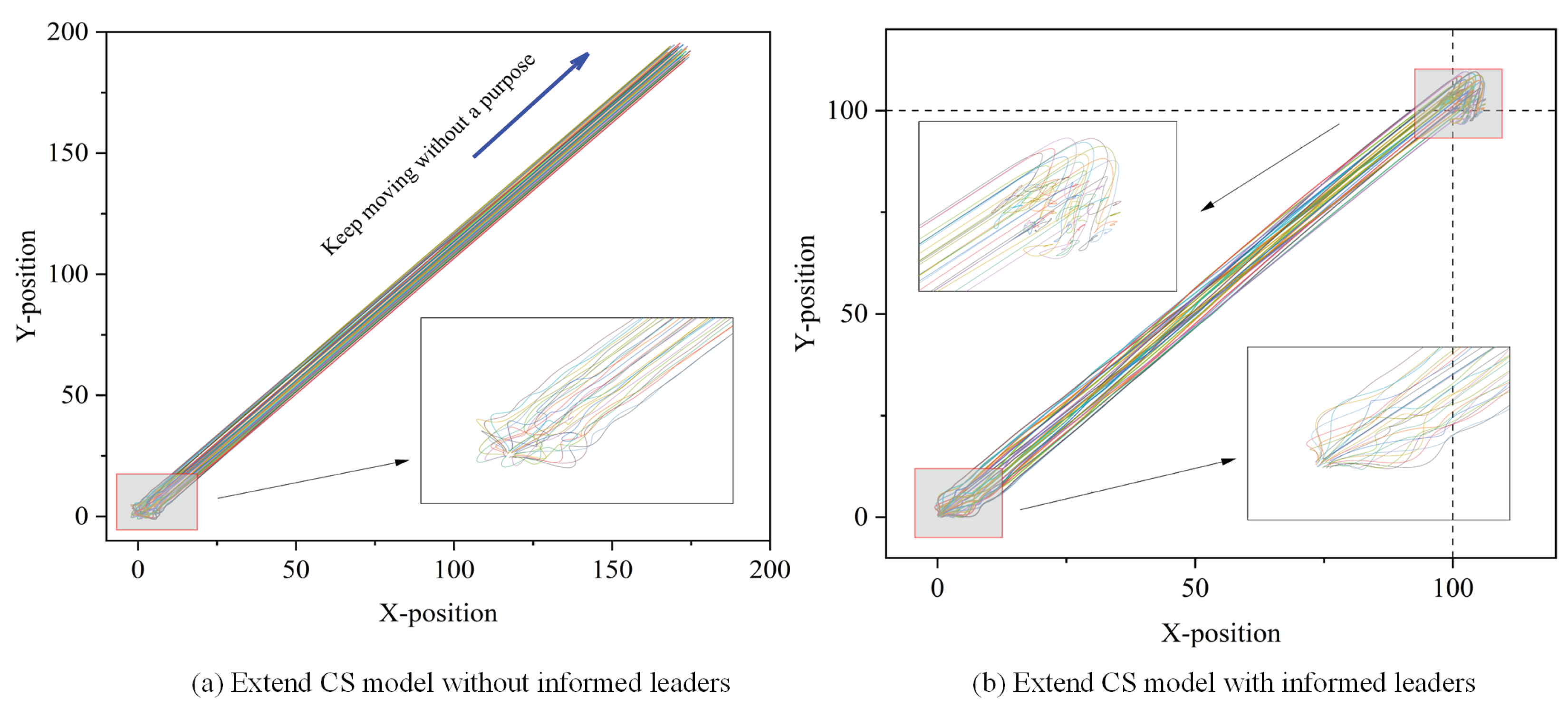
2.1.2. Biological Group Model with Informed Leaders

In real biological group systems, the foundational assumptions of the traditional CS model are overly idealized, primarily manifested in three aspects: First, although treating individuals within a group as homogeneous simplifies the analysis, the reality of internal differences within biological groups (such as age, gender, health status, etc.) significantly impacts their behavior. Secondly, under specific environmental conditions, the influence of environmental factors (e.g., food distribution, predator threats, etc.) on the movement of biological groups cannot be overlooked. Lastly, while the original model can portray some basic group behavior patterns, such as alignment and cohesion, biological groups often exhibit more complex patterns involving leadership-following mechanisms and decision-making processes. Therefore, this section extends the foundational assumptions by introducing informed leaders commonly present in biological group behavior (see Figure 3).

Acknowledging the impracticality of individuals s being infinitely distant and still interacting in realistic biological motion, we refine Section 2.1.1 in Definition 1. An anti-collision upper limit, denoted as ${\Delta }_{max}$, is introduced.

Definition 2.

(Group Formation). For interaction and subsequent asymptotic flocking to occur, the distance between individuals in the system must be less than ${\Delta }_{max}$ at any given moment t.

$$\underset{0\le t<\infty }{sup}∥{\mathbf{x}}_i\left(t\right)-{\mathbf{x}}_j\left(t\right)∥<{\Delta }_{max}.$$

(6)

Equation 5 is set to represent the dynamics of followers within a biological group, upon which we introduce the dynamics of informed leaders as seen in Equation 7.

$$\begin{array}{cc}\hfill \frac{d{\mathbf{x}}_i}{dt}& ={\mathbf{v}}_i,t>0,i=1,\cdots \cdots ,N,\hfill \\ \hfill \frac{d{\mathbf{v}}_i}{dt}& =\frac{\lambda }{N}\sum _{j=1}^N\psi \left(r_{ij}\right)\left({\mathbf{v}}_j-{\mathbf{v}}_i\right)\hfill \\ \hfill & +\frac{\sigma }{N}\sum _{j=1}^N\frac{K}{2r_{ij}}\left(r_{ij}-2R\right)\left({\mathbf{x}}_j-{\mathbf{x}}_i\right)\hfill \\ \hfill & +(e^{∥D-{\mathbf{x}}_i∥}-1)\frac{D-{\mathbf{x}}_i}{∥D-{\mathbf{x}}_i∥}.\hfill \\ \hfill \end{array}$$

(7)

in this model, we have added a unique volitional term for the informed leaders, indicating that the informed leaders are aware of the target point D location and will formulate corresponding action routes, implying an attraction to D. This attraction is modulated by an exponential function, enhancing the attraction as the distance between the individual and the target point increases. This design aims to simulate the natural response of individuals attracted by distant targets and how they adjust their movement direction and speed towards the target.This enhancement allows for more effective information flow control within the group, enhances overall system performance, and facilitates more accurate simulations of intelligent group behavior.

To prevent individuals from breaking away from the flocking system due to excessive velocity or acceleration, Equation 8 establishes upper limits for the velocity and acceleration of each individual in Equation 5 and 7, denoted as ${\mathbf{v}}_{max}$ and ${\mathbf{a}}_{max}$, respectively.Such constraints better reflect the behavior of a realistic biological population, where individual speed and acceleration are not infinite. Additionally, an anti-collision range $\left[{\Delta }_{min},{\Delta }_{max}\right]$ is set to minimize collisions between individuals.

$${\mathbf{v}}_i<{\mathbf{v}}_{max},\frac{d{\mathbf{v}}_i}{dt}<{\mathbf{a}}_{max},r_{ij}\in \left[{\Delta }_{min},{\Delta }_{max}\right].$$

(8)

To distinctly compare the CS model without informed leader (Equation 5) and the CS model with informed leader (Equation 5 and Equation 7), Figure 4 illustrates the positional changes in the group model before and after improvement.

Figure 4 demonstrates the effects of introducing an informed leader into the group dynamics. This addition not only directs the group towards a specific objective but also enables the group to halt upon reaching the target location. The enhanced model offers significant insights into the dynamics of group behavior, highlighting the influential role of an informed leader.

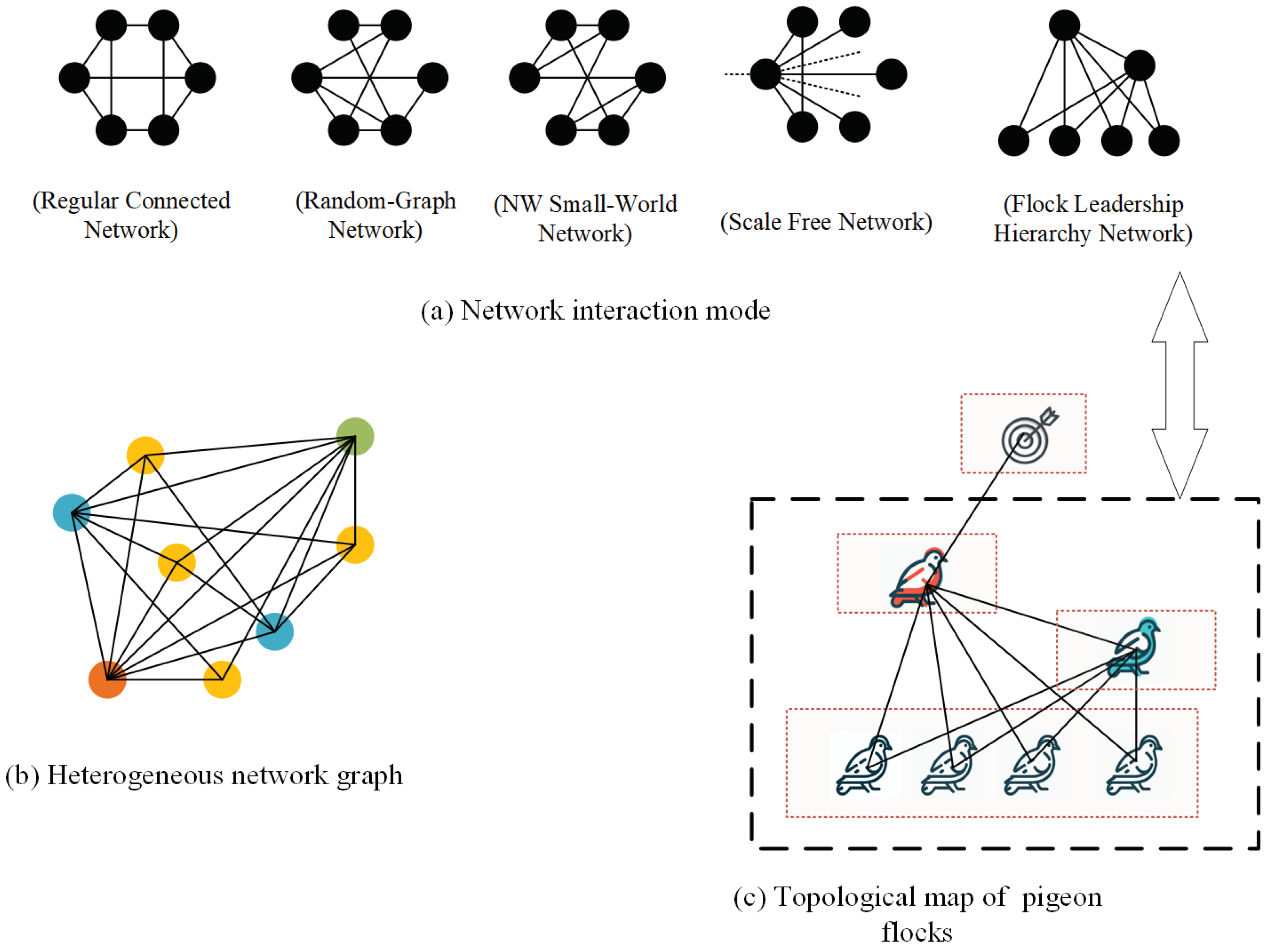
2.2. Individual Interaction Mode

Individual interaction modes are pivotal in shaping group behavior. Within interaction networks, individuals are typically represented as nodes, and the relational roles between them are depicted through connecting edges. Currently, modeling the interaction relationships within biological groups commonly employs several models, including Regularly Connected Networks, Random-Graph Networks, Small-World Networks, and Scale-Free Networks [34].This section introduces four widely recognized interactive mode generation models  [35]. Concurrently, the Flock Leadership Hierarchy Network, inspired by pigeon flocking interaction patterns, aims to model and analyze group behaviors in biology. This approach is particularly relevant to scenarios involving bird groups or other animals led by a hierarchically structured leader. Figure 5 presents a schematic representation of the topology based on five interactive mode generation rules.

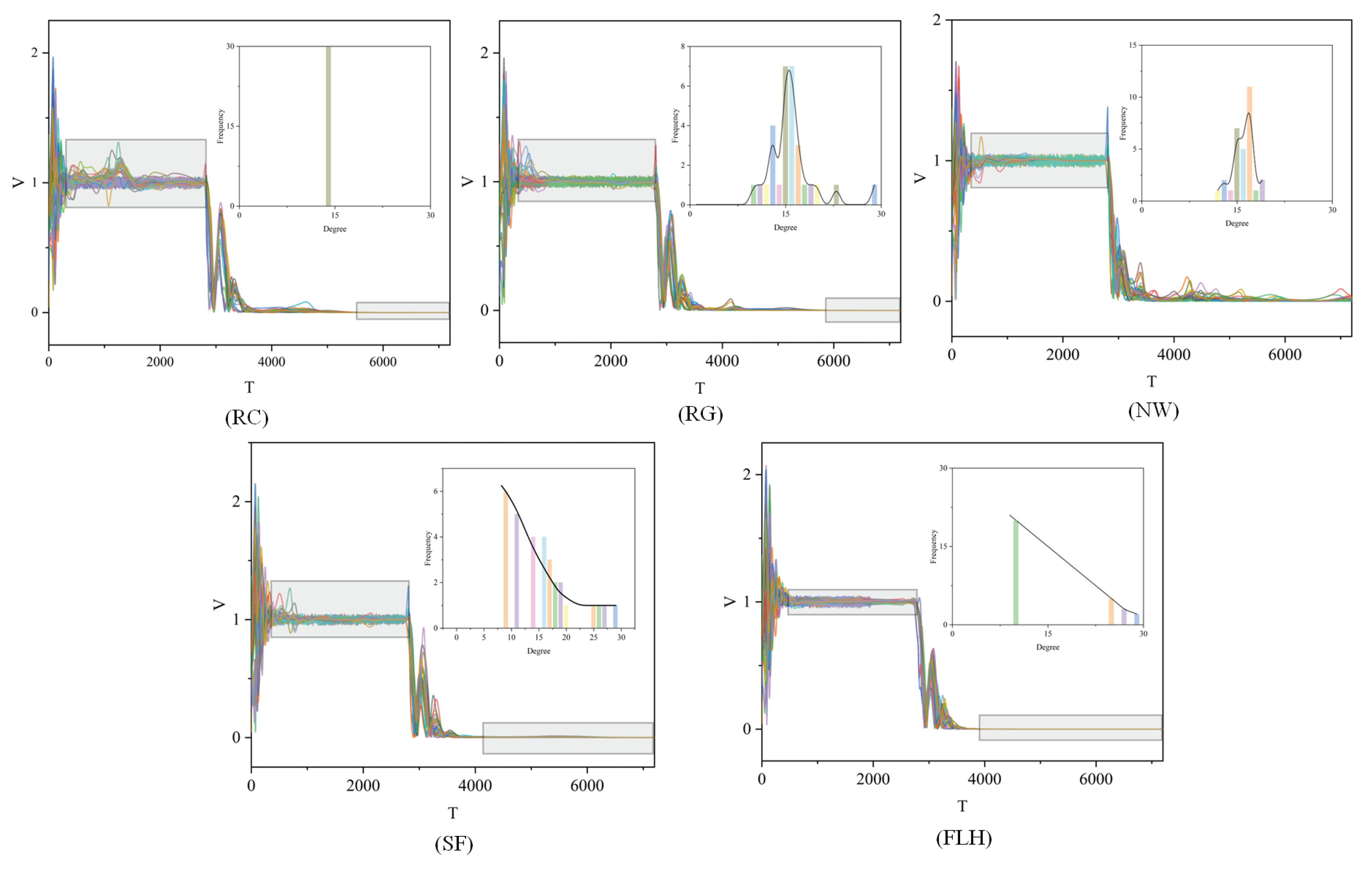
2.2.1. Regular Connected Network(RC)

RC networks are widely observed and easily identifiable both in society and the natural world. For instance, in the field of physics, various crystal structures serve as exemplary cases of regular networks [36], where atoms or molecules are arranged in a highly ordered manner within three-dimensional space. Similarly, in biological structures, such as the hexagonal arrangement of honeycombs [37], can be considered as two-dimensional regular networks. Such arrangements not only maximize the efficiency of space utilization but also enhance structural stability. Hence, despite their highly ordered structure, RC networks are crucial in aiding our understanding of the inherent properties and behavioral patterns of specific systems.

Nodes in regular networks exhibit specific patterns, with a common example being networks where each node has an identical degree, signifying an equal number of outward connections for every node. The generation of RC network involves the following steps:

(1)Initialization: Begin with N isolated nodes.

(2)Connection Process: For each node i (where $i=1,2,\cdots ,N$), establish sequential connections to a set j of E target nodes. To maintain the network’s regularity and ensure that connections loop back as they reach the end of the j list, the target nodes are determined using the modulo operation $j=mod\left(i+k-1,N\right)+1$ (where $k=1,2,\cdots ,E$). The resulting network contains a total of $N\times E$ edges.

2.2.2. Random-Graph Network(RG)

RG networks find extensive application in both social and natural realms. For instance, in social networks, the relationships and interactions among individuals often exhibit characteristics of random connections, appearing to be randomly established [38]. Similarly, in ecosystems, the interaction networks among species demonstrate randomness [39]. RG networks, due to their capacity to capture the randomness and complexity within systems, have become an indispensable tool in researching issues within social and natural sciences. By analyzing the structure and dynamics of random networks, scientists are better equipped to understand the behaviors and patterns of complex systems, thus providing a solid scientific foundation for predicting and managing these systems.

In a RG network, edges are established randomly, without adherence to any specific rule or pattern. Such networks are commonly employed as benchmarks in real-world network analyses, serving as an exemplar of an idealized network structure. The generation of RG network proceeds as follows:

(1) Initialization: Initiate with N isolated nodes.

(2)Connection Process: Consider all distinct node pairs, denoted by i and $j(i\ne j)$, exactly once from the given N nodes. Connect each node pair with an edge at a probability $p_{RG}\in \left[0,1\right]$. The expected number of edges in the RG network is statistically calculated as: $E\left(M\right)=\left(p_{RG}·N\left(N-1\right)\right)/2$.

2.2.3. Newman-Watts-Strogatz Small-World Network (NW)

Small-world properties are commonly observed in social and ecological networks, characterized by rapid information transfer and significant performance shifts due to minor modifications in a few connections. In ecosystems, food webs exhibit characteristics of small-world networks, where species can influence each other through a few intermediary species [40]. This aspect is crucial for the stability of ecosystems and their resistance to external disturbances. Similarly, in gene regulatory networks, the regulatory relationships between genes within cells also form networks with small-world properties [41]. Such networks facilitate cells’ rapid response to environmental changes and the regulation of biological processes.

The generation of NW small-world network proceeds as follows:

(1) Initial Structure: The process begins with a regular graph of N nodes. This graph forms a one-dimensional cyclic lattice, where each node connects to its nearest k neighbors, with $k/2$ on each side.

(2) Edge Addition: For each node pair i and j in the graph, a new edge is added between them at a fixed reconnection probability p. The process prohibits the creation of multiple edges between two nodes (heavy edges) and self-loops. The resulting NW network is distinguished by short characteristic path lengths between nodes and a high clustering coefficient.

2.2.4. Scale Free Network(SF)

SF networks are prevalent in various domains, including physics, biology, sociology, and economics. In the domain of social networks, social media platforms such as Twitter and Facebook exhibit the characteristics of scale-free networks, where a subset of users has a vast number of followers, while the vast majority possess relatively few followers [42]. Regarding neural networks, the connections between neurons within the brain also demonstrate scale-free network traits, with a minority of neurons possessing an exceptionally high number of connections, playing a crucial role in the transmission of neural signals and the brain’s information processing capabilities [43]. The attributes of SF networks not only facilitate our understanding of complex interactions and phenomena within social and natural systems but also provide a significant theoretical foundation and practical value in designing systems resistant to interference, formulating propagation strategies, and controlling diseases.

In these networks, the number of connections per node often adheres to a power-law distribution, where most nodes have few connections, but a few nodes have a significantly higher number. The process for generating SF network is as follows:

(1)Initialization: Begin with N isolated nodes.

(2)Weight Assignment: Assign a weight $w_i={\left(i+\theta \right)}^{-\sigma }$ to each node i, where $\sigma \in \left[0,1\right)$ and $\theta <<N$.

(3)Edge Formation: Randomly select two distinct nodes i and $j\left(i\ne j,i,j=1,2,\dots ,N\right)$ based on probabilities proportional to their respective weights $w_i$ and $w_j$. Add an edge $A_{ij}$ from i to j (if they are not already connected).

(4)Iteration: Continue Step (3) until M edges have been established. The resulting network exhibits a power-law degree distribution $k^{-\gamma }$, where k is the degree variable, and $\gamma =1+\frac{1}{\sigma }$, independent of $\theta$.

2.2.5. Flock Leadership Hierarchy Network(FLH)

Watts [44] conducted extensive experiments that uncovered hierarchical structures and informed leaders in pigeon group behavior. Motivated by these findings, we introduce the Flock Leadership Hierarchy Network (FLH), a model based on the topology of biological groups in nature. The FLH primarily explores hierarchical and leadership dynamics in group decision-making, with a focus on studying complex flight formations during migration and coordinated responses to feeding and predator evasion. This network offers a novel lens for examining biological group dynamics, facilitating insights into information transfer, role allocation, and inter-individual interactions within group behaviors. The subsequent sections will detail the FLH implementation process and the network generation algorithm, with the complete pseudo-code presented in Algorithm 1.

(1)Initialization: Begin with the number of isolated nodes and the number of individuals per layer $lc$ are determined based on the number of pigeons N observed in real pigeon flock experiments [44].

(2)Node Determination: For each node j in level i, where j spans from the start index of the current level to the total number of nodes within that level, establish connections. If i is less than the total number of layers, connect node j to all nodes in higher levels $\left(i+1,i+2,\cdots \right)$.

(3)Iterative Connection: Continue Step (2) until all nodes across the layers are interconnected.

This hierarchical network has applications beyond biology, extending to engineering and robotics. By leveraging insights from leadership and hierarchical structures in animal populations, it facilitates the development of more efficient and adaptable artificial systems. For instance, it can inform the design of autonomous drone swarms or robotic systems that emulate flocking behavior.

Algorithm 1 FLH network generation algorithm

Input:  number of individuals N, number of individuals per layer $lc$ Output:  FLH network interaction matrix  //Check if the sum of individuals in layers equals N if sum($lc$) is not equal to N then end if Error: Sum of individuals in layers must equal total number of individuals  //Create an adjacency matrix Initialize zeros matrix $(N\times N)$  // Populate the FLH adjacency matrix Set Current index $c=1$ fori from 1 to length$\left(lc\right)$ do     for j from Current index to $\left(c+lc\left(i\right)-1\right)$ do  //Create connections from individuals in higher layers to those in lower layers         if i is less than length$\left(lc\right)$ then            for k from $\left(c+lc\left(i\right)\right)$ to N do                Set adjmatrix$(i,j)=1$                Set adjmatrix$(k,j)=1$            end for         end if     end for     Increment c by $lc$ end for

In this study, the strategy for selecting informed leaders involves designating nodes with higher degree counts as leaders and those with lower degree counts as followers. This approach is underpinned by the degree distribution characteristics of the network’s nodes, influencing efficiency in information dissemination. This methodology, as noted in [45], is prevalent in real-world networks. For instance, on social media platforms, users with numerous followers (high-degree nodes(hd)) often serve as opinion leaders or influencers. Their posts rapidly reach a vast audience (low-degree nodes(ld)), potentially impacting public opinion or market trends. Similarly, in biological networks like bird flocks or fish schools, certain individuals assume leadership roles (hd) due to their location or behavioral traits, guiding others as followers (ld). This dynamic is vital for the group’s migratory or predatory activities.

The increasing recognition of the intricacies within biological group systems has led a growing number of scholars to employ complex networks for modeling and analyzing these systems. While most current research simplifies group systems into networks of homogeneous nodes [46,47], treating all nodes as having identical functions and attributes, this approach often overlooks the varied interactions and unique dynamic behaviors of different individual types within biological groups. To address this gap, upon establishing a selection strategy for informed leaders in groups, we introduce a heterogeneous graph [48], denoted as $G=\left(V,E\right)$, comprising a set of objects V and a set of links E. This graph is further characterized by a node-type mapping function $\varphi :V\to V_{type}$ and a link-type mapping function $\psi :E\to E_{type}$, where $V_{type}$ and $E_{type}$ represent the sets of predefined object and link types, respectively, with $\left|V_{type}\right|+\left|E_{type}\right|>2$. We categorize individuals in biological groups into distinct types based on their dynamic behavior and model the group systems using heterogeneous networks as illustrated in Figure 5. This approach more effectively captures the heterogeneity of nodes and the diversity of connections, thereby offering a more comprehensive and precise framework for understanding and analyzing complex population systems.

3. Model Building

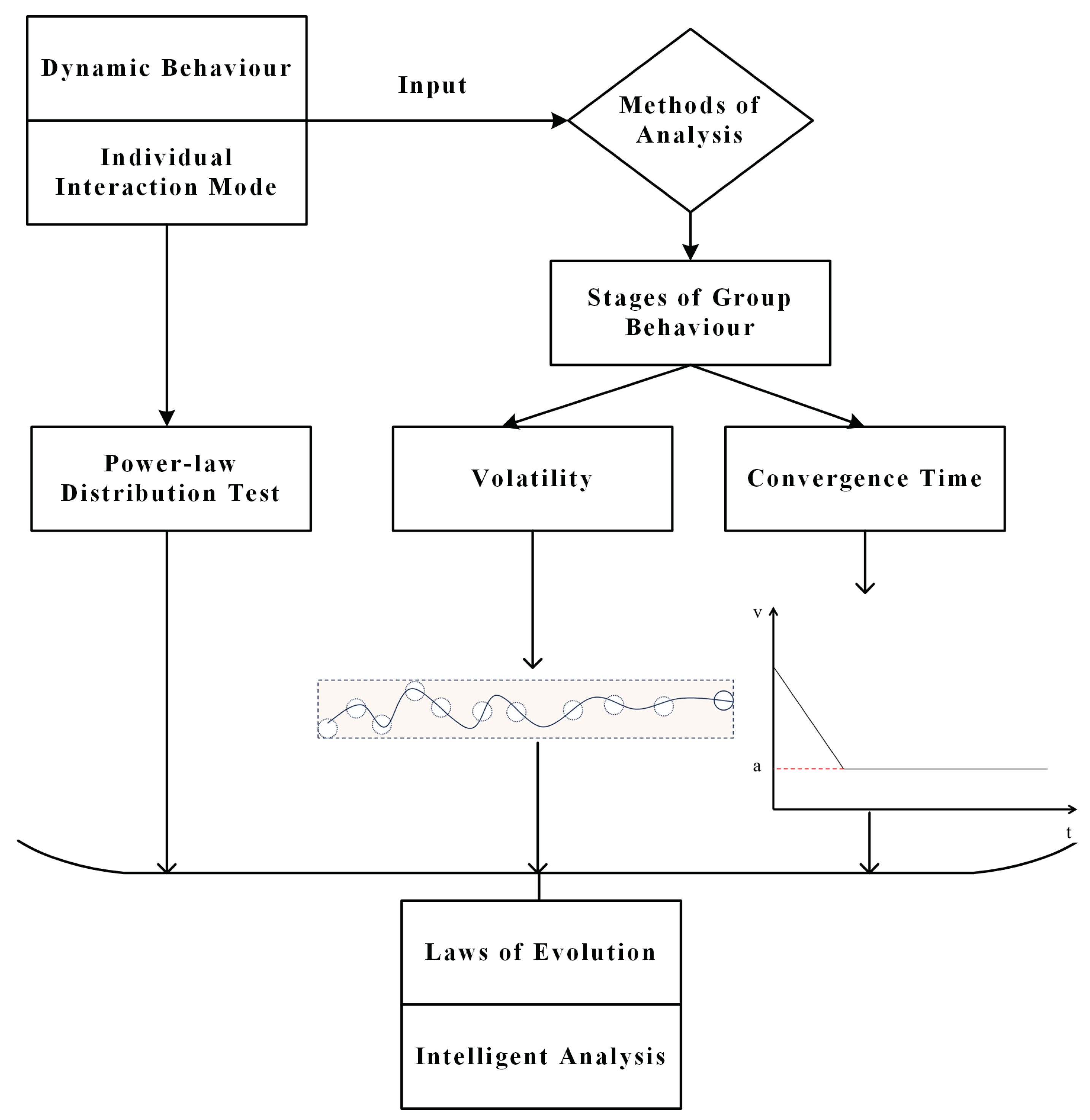
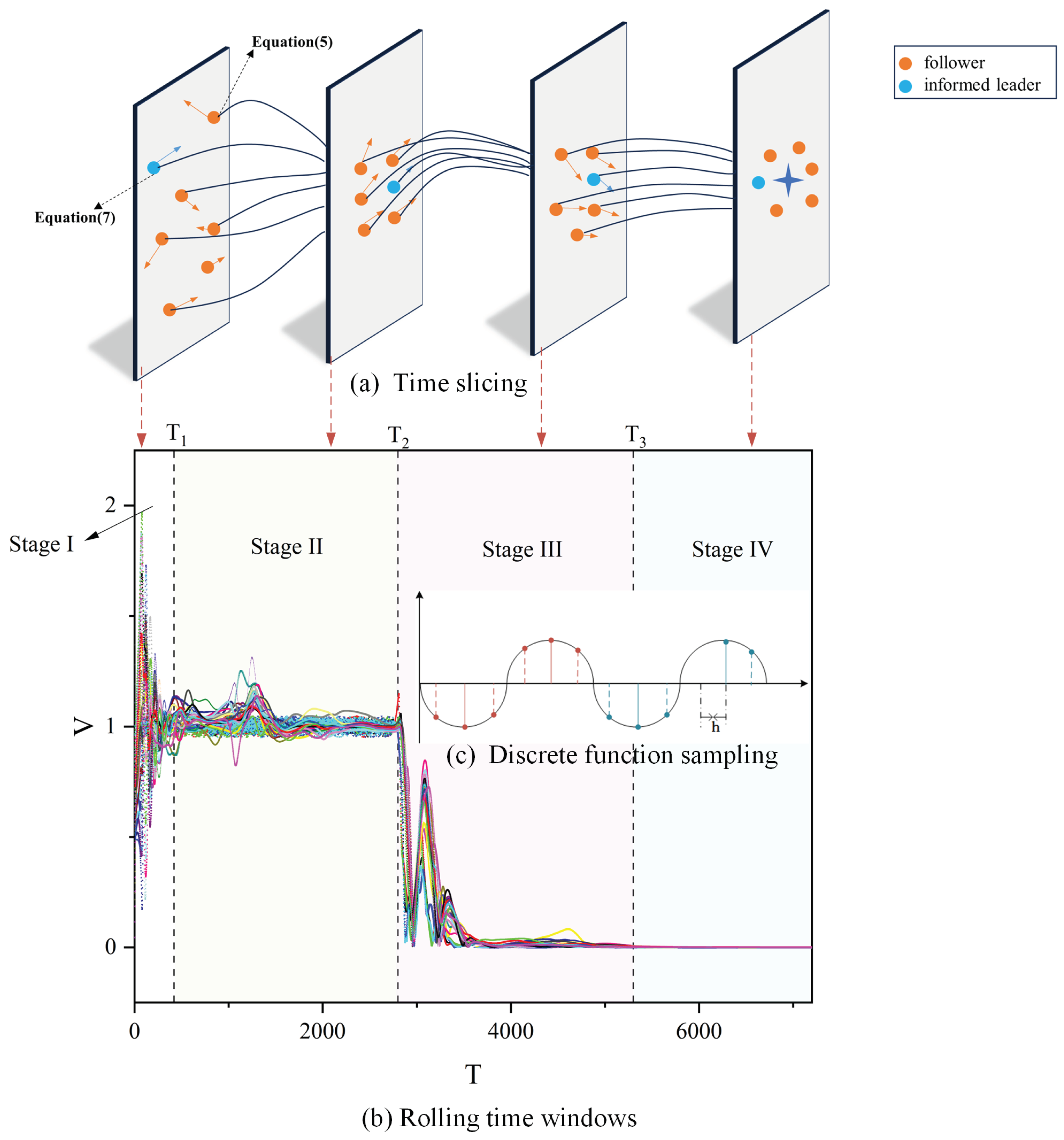
3.1. Stages of Group Behaviour and Demonstration

A comprehensive understanding of the various stages of group behavior is crucial for comprehending the complexities of biological systems. In the realm of biological group behaviors, such as bird flocking, fish schooling, or insect collective actions, it is generally feasible to categorize these behaviors into four distinct phases [49]. Investigating each phase in detail significantly enhances our understanding of the dynamic characteristics of group behavior and its adaptive mechanisms. To facilitate a more precise quantitative analysis of these stages, we have implemented a uniform sampling method with a step size of $h=0.05$ for discretizing the continuous function in Equation 6, as illustrated in part(c) of Figure 6.

In Figure 6b, the interval $0-T_2$ corresponds to the initial formation stage of biological group behavior (Stage I). This phase is marked by groups beginning their movement towards a destination, exhibiting considerable variations in speed and direction, along with notable overall fluctuations. Typically, organisms start to aggregate during this phase for reasons like foraging, defense against predators, migration, etc. Analyzing Stage I is crucial for understanding the conditions initiating group behavior. The period $T_1-T_2$ represents the stabilization phase of group behavior (Stage II), also referred to as the first convergence phase. Here, group motion generally fluctuates around $v=1$, indicating a state of consistency akin to the uninformed leader group model. This stage, characterized by stable structures and patterns, is key to understanding social structures and information transfer within the group. The interval $T_2-T_3$ denotes the decision-making phase (Stage III), where the group, led by an informed leader, heads towards its destination. As the destination nears, individual velocities decrease, and the state of motion undergoes significant changes compared to Stage II. This phase’s analysis is pivotal in uncovering group information processing and decision-making dynamics. Finally, $T_3-\infty$ marks the dissolution phase of group behavior (Stage IV), or the second convergence stage. In this stage, as the group, guided by an informed leader, reaches the vicinity of its destination (illustrated by a blue four-pointed star in Figure 6a), its position stabilizes, and velocity gradually converges to zero. Dissolution in this stage may occur due to various factors, such as reaching the destination, depletion of food sources, or environmental changes. Understanding Stage IV sheds light on the ecological and social dynamics underlying group maintenance and dissolution. To visually depict each stage, we selected specific time points from Figure 6a for each stage and utilized a time-slicing approach for demonstration.

3.2. Metric Performance

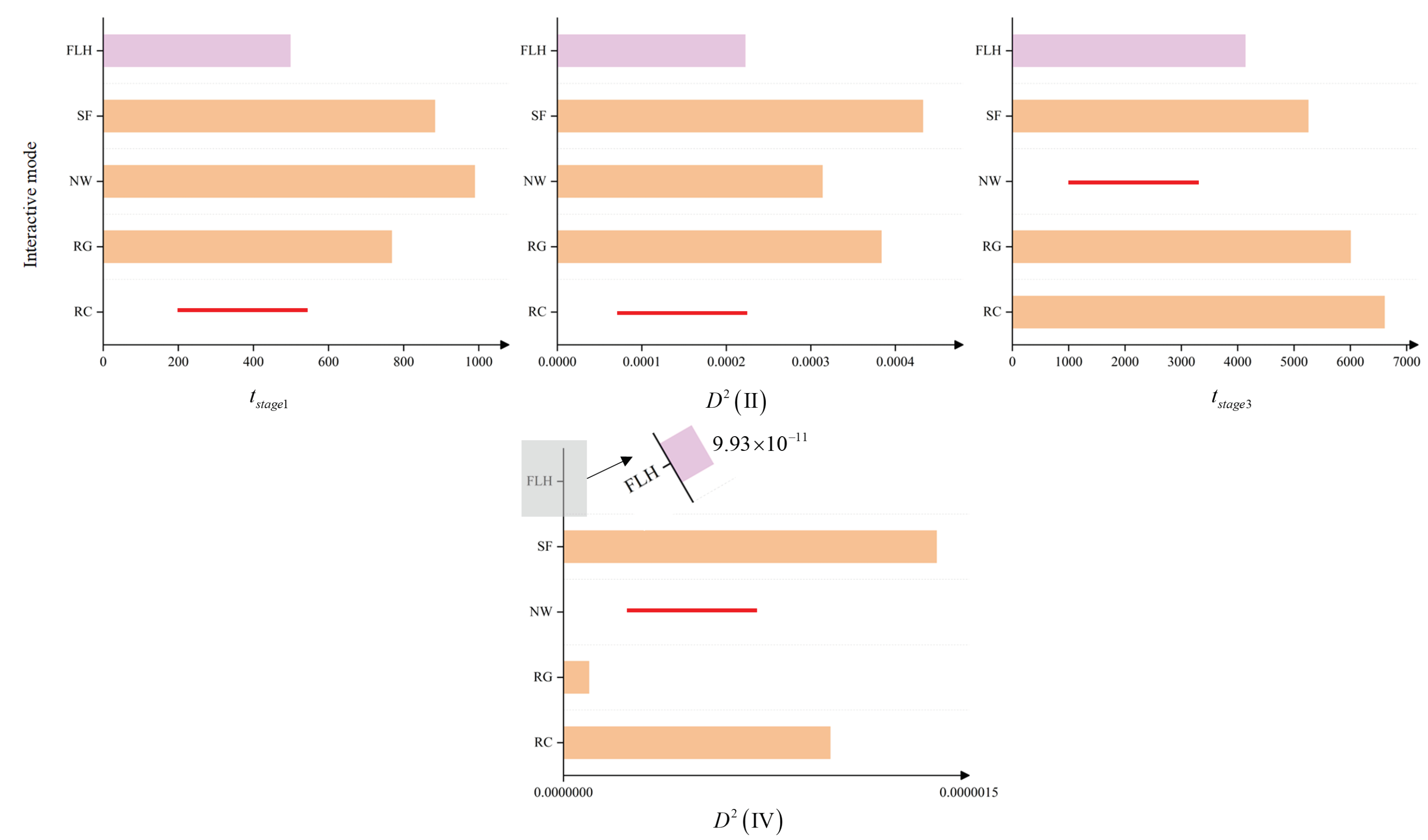
3.2.1. Volatility

Volatility serves as a critical metric in analyzing biological group behavior, quantifying the extent of instability or variability in group movements [50]. Generally, lower volatility indicates a more stable and predictable group behavior, a trait often beneficial for biological populations. In Section 3.1, we categorize stages I and III as phases of group self-adaptation, predominantly marked by groups modulating their state via fluctuations. Consequently, analyzing the volatility in these stages is not substantially relevant. Accordingly, this paper introduces the volatility indicators $D^2\left(II\right)$ and $D^2\left(IV\right)$ to analyze stages II and IV, respectively. Due to the minimal directional variance among individuals in Stage II and IV, the dependent variable of speed in the volatility metric is represented in scalar form.

$$D^2=\frac{{\displaystyle \sum _{j=1}^N}{\displaystyle \sum _{i=1}^M}\left|v_i-v_j\right|}{N\times \frac{T_{tumbling}}{h}}.$$

(9)

where $v_i$ denotes all velocity sampling points of individual i within a specified time window. The variable j represents the total number of individuals in the population. The symbol $\overline{v}$ indicates the average of the sampled velocities for all individuals within this time window. Additionally, $T_{tumbling}$ refers to the duration of the time window under analysis.

3.2.2. Convergence Time

Convergence time is a crucial metric for assessing the efficiency with which a group achieves coherence and is paramount for understanding and evaluating group systems. In natural biological groups, a reduced convergence time is advantageous, enabling groups to more effectively escape predators or adapt to environmental changes. In light of this, this paper introduces the convergence time metrics $t_{stage1}$ and $t_{stage3}$ to denote the termination of Stages I and III, respectively. These metrics indicate the onset of convergence in Stages II and IV.

$$\begin{array}{cc}\hfill & Z^2\left(t_{stage},t_{stage*}\right)=\frac{{\displaystyle \sum _{i=1}^M}\left|v_i-v_j\right|}{\frac{T_{tumbling}}{h}}\le Z_{thre},\hfill \\ \hfill & v_i\left(t_{stage},t_{stage*}\right)=V_{thre}\pm c.\hfill \end{array}$$

(10)

where $Z^2$ represents the volatility of each individual within a designated time window. The term $t_{stage*}$ signifies the end time of this time window. The volatility threshold for each individual during the specified period is denoted by $Z_{thre}$. Furthermore, $V_{thre}$ and c respectively indicate the velocity threshold and the acceptable range of volatility within the same time window.

3.3. Power-Law Distribution Test

The degree distribution of FLH network, as proposed in this paper, exhibits a trend similar to that observed in SF networks. Consequently, we investigate whether the FLH network’s degree distribution also adheres to a power-law distribution. This distribution is defined by $P\left(k\right)=C{k}^{-\alpha }$, where $P\left(k\right)$ represents the probability of nodes with degree k appearing in the network. The exponent $\alpha$, characterizing the power-law distribution, is typically greater than 1. C is a normalization constant ensuring the sum of all probabilities equals 1. The exponential distribution, in contrast, is defined as $f\left(x;\lambda \right)=\lambda e^{-\lambda x}$, with $\lambda$ being the rate parameter. To determine the power-law distribution index $\alpha$, we employ maximum likelihood estimation as detailed in Equation 11.

$$\widehat{\alpha }=1+n{\left[{\sum }_{i=1}^{n}ln\frac{k_i}{k_{min}}\right]}^{-1}.$$

(11)

where $\widehat{\alpha }$ represents the estimated power-law index. The variable n denotes the number of nodes with a degree greater than or equal to $k_{min}$. Each node’s degree is represented by $k_i$, and $k_{min}$ signifies the minimum degree value to which the power-law distribution is applicable.

Subsequently, we compare the logarithmic values of the likelihood function R for the two distributions:

$$R=log{\mathcal{L}}_{model1}-log{\mathcal{L}}_{model2}.$$

(12)

where the likelihood functions for the two distributions are denoted as ${\mathcal{L}}_{model1}$ and ${\mathcal{L}}_{model2}$, respectively. A value of $R>0$ indicates that the power-law distribution is more appropriate than the exponential distribution, whereas $R<0$ suggests that the exponential distribution is a better fit. The fit’s accuracy was evaluated using the Kolmogorov-Smirnov test, which compares the cumulative distribution function of the data with the expected power-law distribution.

$$\begin{array}{cc}\hfill & \widehat{\alpha }=argmin{D}_{\alpha };\hfill \\ \hfill & D_{\alpha }=max\left|P_{emp}\left(x\right)-P_{\alpha }\left(x\right)\right|.\hfill \end{array}$$

(13)

where $P_{emp}\left(x\right)$ and $P_{\alpha }\left(x\right)$ represent the empirical and theoretical values of the cumulative distribution function, respectively. In this study, the determination of $\widehat{\alpha }$ is achieved by minimizing the discrepancy $D_{\alpha }$, where $D_{\alpha }$ represents the maximum difference between the empirical probability distribution $P_{emp}\left(x\right)$ and the assumed power-law distribution probability $P_{\alpha }\left(x\right)$. To facilitate effective comparison, we ensure that both $P_{emp}\left(x\right)$ and $P_{\alpha }\left(x\right)$ are normalized, thus meeting the standards of probability density functions. These functions are utilized to calculate a statistic for evaluating the disparity between the two distributions.

A statistical test is applied to ascertain the significance of this ratio, with the p-value indicating the strength of evidence against the null hypothesis, which posits that the two distributions are identical. A p-value less than 0.05 typically signifies a significant difference between the distributions, lending credibility to R; conversely, a p-value greater than 0.05 suggests that the difference is not significant, thereby questioning the reliability of R.

4. Numerical Simulation

4.1. Experimental Design

The purpose of this experiment is to evaluate the efficacy of the HLF interaction model in modeling group motion. Subsequently, the parameters within Equation 5 and 7 were configured. At time $t=0$, the position ${\mathbf{x}}_i\left(0\right)$ of individual i is randomly generated near the point $\left(0,0\right)$, the magnitude of the velocity ${\mathbf{v}}_i\left(0\right)$ is randomly generated between $0-1$, and their initial directions are also random. Additionally, to mitigate the potential influence of network cost (namely, the number of connected edges) on the experimental outcomes, we maintained a consistent total of approximately 240 edges across the five interaction modes described in Section 2.2. The precise values of these parameters and their corresponding meanings are listed in Table 1.

4.2. Discussion

In this study, we performed a range of simulation experiments using the enhanced group model outlined in Section 2.1 along with the five interaction modes. To guarantee the reliability and precision of our experimental findings, we compiled the average results from multiple experiments. Moreover, we executed several group experiments under various convergence conditions as specified in Equation 4. Pertaining specifically to convergence condition(3) in Equation 4, the experimental outcomes are displayed in Figure 7 and Table 2.

The experimental findings indicate that in the first stage, the biological group employing the FLH interaction mode achieves the shortest convergence time, recorded at $t_{stage1}=467$. This is followed by the NW, SF, RG, and RC modes, in that order. Notably, the FLH structure demonstrates a substantial advantage in the initial convergence time, being nearly three times shorter than that of the RC mode. Regarding the convergence time $t_{stage3}$ in Stage III, the FLH mode continues to outperform, clocking in at $t_{stage3}=3,672$, with the SF, RC, and RG modes trailing behind. The NW mode shows the least effective performance, as evidenced in Figure 7 (NW) at $T=7,200$, where the population system still fails to meet the consistency condition of Stage IV. The individual speeds and their variances remain substantial, suggesting that the population system has not yet reached convergence. Furthermore, the experimental findings reveal that solely the SF and FLH modes conform to the power-law distribution. In conclusion, the FLH model emerges as the most advantageous.

For the volatility metric $D^2\left(II\right)$, the FLH network, with $D^2\left(II\right)=2.3574\times {10}^{-4}$, exhibits the lowest volatility among the five interaction modes. In contrast, the RC network records the highest volatility in Stage II, with $D^2\left(II\right)=3.5\times {10}^{-3}$, markedly differing from the other networks by several orders of magnitude, as highlighted in the grey-shaded area of Figure 5 (referenced). In the case of $D^2\left(IV\right)$, the FLH network maintains its superior performance in Stage IV, registering a value of $D^2\left(IV\right)=3.5375\times {10}^{-7}$. Since the NW network does not reach Stage IV within $T=7,200$, its $D^2\left(IV\right)$ value remains uncalculated. The degree distribution curves of the SF and FLH networks display similar patterns, and hypothesis testing confirms that the FLH model also adheres to a power-law distribution. These two networks rank as the top performers in the group system, thereby underscoring the efficacy of power-law distributions in group behavior from both mathematical and modeling perspectives. Power-law distributions are not only prevalent in biological populations [51] but also in artificial systems such as social and Internet networks, urban systems, and natural phenomena like earthquake intensity, river lengths, and watershed areas.

The experimental outcomes for convergence conditions (2) and (1), as specified in Equation 4, are presented in Table 3 and Table 4. The data unequivocally demonstrate that the FLH interaction mode holds significant advantages over the other four interaction modes, irrespective of the settings incorporating diverse convergence parameters.

In the aforementioned experiments, based on the three convergence conditions proposed in Equation 4, different values of $\lambda$ and $\beta$ were selected for experimentation. These experiments confirmed that the FLH interaction mode has a significant advantage in the CS model with informed leaders. Since the FLH model is derived from real biological group interaction experiments, it further illustrates the collective intelligence exhibited by biological groups during the evolutionary process. Subsequently, to further validate the effectiveness of the model across a wide parameter range and enhance its applicability and generalizability, we fixed the parameters ($\beta =1$, $\lambda =10$) as specified in Table 1 as convergence conditions and conducted multiple controlled variable experiments on the collision coefficient $\sigma$, the maximum radius of communication R, and the number of individuals N.

For the controlled variable experiment regarding $\sigma$, the collision coefficient $\tilde{\sigma }$ was randomly set to $\tilde{\sigma }=\sigma \pm 50\%$ in each experiment. The experimental results for the $\sigma$ parameter are shown in Figure 8, with specific data provided in Table 5 . From Figure 8 , it is evident that in experiments with multiple random settings of $\tilde{\sigma }$, the FLH network interaction mode exhibits significant advantages over the other four networks in terms of the four metrics measuring group behavior capabilities, demonstrated by shorter convergence times and reduced velocity fluctuations among individuals during stable stages. Therefore, the experiment indicates that within a certain range of fluctuations, any value of the collision coefficient $\sigma$ does not affect the superior position of the FLH network interaction mode in the biological group model. This confirms the universal role of this structure in reflecting the collective intelligence of biological groups.

Similarly, for the randomly varying maximum radius of communication R, we set $R=R\pm 50\%$, with the experimental results presented in Table 6. According to the performance in $D^2\left(II\right)$ within Table 6, the NW network performed best, followed by the FLH network. However, considering all four metrics, the FLH network still demonstrates a clear advantage.

Given the correspondence between the number of individuals and informed leaders in real biological groups, with other parameters held constant, we defined the range of the randomly varying number of individuals variable $\tilde{N}$ as $\tilde{N}=N\pm 20\%,\tilde{N}\in {\mathbf{N}}^{+}$, and conducted experiments under five types of interactions, with the results shown in Table 7.

5. Conclusions

In this study, we enhance the CS model with coupling forces to better capture the behavior of biological groups with informed leaders, leading to a more comprehensive portrayal of group dynamics. Additionally, we introduce FLH network generation algorithm, inspired by the interaction patterns observed in pigeon flocks. The group dynamics are then segmented into four distinct phases: formation, stabilization, decision-making, and dissolution. This paper also employs heterogeneous networks to model and analyze biological groups, acknowledging the diversity in nodes and their connections. We utilize two key metrics, volatility and convergence time, to assess population performance. Comparative analyses between the FLH network and four common network models reveal that the FLH-based group model excels in performance metrics and adheres to the power-law distribution, underscoring the strategic evolution of biological populations.

6. Future Research

Looking forward, the enhanced population model and network interaction patterns proposed here hold significant implications not only in biological research but also in the realms of engineering and computer science. For instance, the theoretical framework presented in this paper is highly applicable to the design of autonomous robotic behaviors and the exploration of artificial intelligence algorithms. Finally, the comprehensive description of biological group behavior stages presented in this study has substantial relevance and potential applications in developing biologically inspired algorithms and techniques. It deepens our understanding of complex biological group interactions and may foster novel approaches to modeling group behavior in natural settings. Meanwhile, as our understanding and application of this model continue to deepen, future research will focus on integrating the model with real biological group data to further validate its accuracy and practicality. By analyzing and applying a vast array of real-world data, we aim to significantly enhance the model’s predictive and generalization capabilities, making it more adaptable to real-life scenarios.