5th Order Multivariate Edgeworth Expansions for Parametric Estimates

Preprint

Article

5th Order Multivariate Edgeworth Expansions for Parametric Estimates

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Christopher Withers^*

This version is not peer-reviewed

This preprints belongs to the Topic

Interfacing Statistics, Machine Learning and Data Science from a Probabilistic Modelling Viewpoint

Submitted:

02 March 2024

Posted:

05 March 2024

You are already at the latest version

Alerts

Abstract

The only cases where exact distributions of estimates are known is for samples from exponential families, and then only for special functions of the parameters. So statistical inference was traditionally based on the asymptotic normality of estimates. To improve on this we need the {\it Edgeworth expansion} for the distribution of the standardized estimate. This is an expansion in $n^{-1/2}$ about the normal distribution, where $n$ is typically the sample size. The 1st few terms of this expansion were originally given for the special case of a sample mean. In earlier work we derived it for {\it any } standard estimate, hugely expanding its application. We call an estimate $\hat{w}$ of an unknown vector $w\in R^p$, a {\it standard estimate}, if $E\ \hat{w}\rightarrow w$ as $n\rightarrow \infty$, and for $r\geq 1$ the $r$th order cumulants of $\hat{w}$ have magnitude $n^{1-r}$ and can be expanded in $n^{-1}.$ Here we give another huge extension. We give the expansion of the distribution of {\it any smooth function} of $\hat{w}$, say $t(\hat{w})\in R^q,$ giving its distribution to $n^{-5/2}$. We do this by showing that $t(\hat{w})$, is a standard estimate of $t(w)$. This provides far more accurate approximations for the distribution of $t(\hat{w})$ than its asymptotic normality. %NOT USED: The building blocks of the Edgeworth expansions are the {\it cumulant coefficients } of the estimate. These cumulant coefficients are also needed for bias reduction, Bayes estimates and confidence regions. We give {\it chain rules} for the cumulant coefficients of $t(\hat{w})$ in terms of those of $\hat{w}$ and the derivatives of $t(w)$, up to those needed for 5th order Edgeworth expansions for $t(\hat{w})$ and its {\it tilted expansion}, useful for the tail of the distribution.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction and summary

Suppose that

\hat{w}

is a standard or Type A estimate of an unknown

w \in R^{p}

with respect to a given parameter n. That is,

E \hat{w} \to w

n \to \infty

and for

r \geq 1,

its rth order cumulants have magnitude

n^{1 - r}

and can be expanded as

\begin{matrix} {\bar{k}}^{1 - r} = κ ({\hat{w}}^{i_{1}}, \dots, {\hat{w}}^{i_{r}}) = \sum_{e = r - 1}^{\infty} n^{- e} {\bar{k}}_{e}^{1 - r} f o r 1 \leq i_{1}, \dots, i_{r} \leq p, \end{matrix}

(1)

where the cumulant coefficients

{\bar{k}}_{e}^{1 - r} = k_{e}^{j_{1} - j_{r}}

do not depend on n, or at least are bounded as

n \to \infty

. So

{\bar{k}}_{0}^{1} = w^{i_{1}} .

For example (1) holds for

\hat{w}

a function of a sample mean. We show that if

t (\hat{w})

is a smooth function of a standard estimate

\hat{w}

, then it is a standard estimate of

t (w)

. This is done for

\hat{w}

unbiased in Theorem 3.1, and for

\hat{w}

biased in Theorem 4.1. More generally we call

\hat{w}

a Type B estimate if

E \hat{w} \to w

n \to \infty,

and for

r \geq 1

\begin{matrix} {\bar{k}}^{1 - r} = \sum_{d = 2 r - 2}^{\infty} n^{- d / 2} {\bar{b}}_{d}^{1 - r} f o r 1 \leq i_{1}, \dots, i_{r} \leq p, {\bar{b}}_{d}^{1 - r} = b_{d}^{i_{1} \dots i_{r}} . \end{matrix}

For example this type arises when considering 1-sided confidence regions. If

t (\hat{w})

is a smooth function of a Type B estimate, then it is a Type B estimate of

t (w)

. So for a Type A estimate,

{\bar{b}}_{d}^{1 - r}

{\bar{k}}_{e}^{1 - r}

for

d = 2 e

and 0 for d odd. n is typically the sample size or the minimum sample size if there is more than one sample.

§3 and §4 show that a smooth function of

\hat{w}

, say

t (\hat{w})

, is a standard estimate of

t = t (w)

. They give the cumulant coefficients of

t (\hat{w})

in terms of those of

\hat{w}

and the derivatives of

t (w)

. §3 does this for

\hat{w}

unbiased and §4 for

\hat{w}

biased. So they can be thought of as chain rules for obtaining the cumulant coefficients for

t (\hat{w})

from those of

\hat{w}

. We give the cumulant coefficients needed for Edgeworth expansions of

\hat{t}

O (n^{- 5 / 2})

. Those to

O (n^{- 1})

were given in Withers and Nadarajah (2022). Those to

O (n^{- r / 2})

use the rth derivatives of

t (w)

. §5 specialises to univariate

t (w)

with examples. Theorem 4.1 and Corollary 5.4 correct

{\bar{a}}_{2}^{12} = K_{2}^{j_{1} j_{2}}

and

a_{22}

on p67 and p59 of Withers (1982). §2 extends the shorthand bar notation above and gives the foundation theorem.

We now summarise the expressions for Edgeworth expansions of

\hat{w}

for standard and Type B estimates in terms of the cumulant coefficients

{\bar{k}}_{e}^{1 - r}

and

{\bar{b}}_{d}^{1 - r}

given in Withers and Nadarajah (2010b, 2012a, 2014a):

\begin{matrix} P r o b . (Y_{n w} \leq x) = \sum_{r = 0}^{\infty} n^{- r / 2} P_{r} (x), p_{Y_{n w}} (x) = \sum_{r = 0}^{\infty} n^{- r / 2} p_{r} (x), \end{matrix}

(2)

\begin{matrix} where Y_{n w} = n^{1 / 2} (\hat{w} - w - b_{1} n^{- 1 / 2}), {(b_{1})}_{i} = b_{1}^{i}, P_{0} (x) = Φ_{V} (x), \end{matrix}

(3)

\begin{matrix} P_{r} (x) = {\tilde{B}}_{r} (e (- \partial / \partial x)) Φ_{V} (x) for r \geq 1, \end{matrix}

(4)

\begin{matrix} e_{j} (t) = \sum_{r = 1}^{j + 2} {\bar{b}}_{r + j}^{1 \dots r} t_{i_{1}} \dots t_{i_{r}} / r!, {\bar{b}}_{r + j}^{1 \dots r} = b_{r + j}^{i_{1} \dots i_{r}}, \end{matrix}

(5)

Φ_{V} (x)

is the multivariate normal distribution with zero mean and covariance

V = ({\bar{b}}_{2}^{12})

{\tilde{B}}_{r} (e)

is the complete ordinary Bell polynomial of Comtet (1974):

\begin{matrix} {\tilde{B}}_{1} (e) = e_{1}, {\tilde{B}}_{2} (e) = e_{2} + e_{1}^{2}, {\tilde{B}}_{3} (e) = e_{3} + 2 e_{1} e_{2} + e_{1}^{3}, \\ {\tilde{B}}_{4} (e) = e_{4} + 2 e_{1} e_{3} + e_{2}^{2} + 3 e_{1}^{2} e_{2} + e_{1}^{4} . \end{matrix}

This gives the 5th order Edgeworth expansion for the distribution of

Y_{n w}

, that is, it gives (2) to

O (n^{- 5 / 2})

. Note that (5) uses the tensor summation convention of implicitly summing

i_{1}, \dots, i_{r}

over their range

1, \dots, p

. For example

\begin{matrix} for \partial_{i} = \partial / \partial x_{i} and {\bar{\partial}}_{k} = \partial_{i_{k}}, \\ P_{1} (x) = e_{1} (- \partial / \partial x)) Φ_{V} (x) = \sum_{r = 1}^{3} {\bar{b}}_{r + 1}^{1 \dots r} (- {\bar{\partial}}_{1}) \dots (- {\bar{\partial}}_{r}) Φ_{V} (x) \\ = {\bar{k}}_{1}^{1} (- {\bar{\partial}}_{1}) Φ_{V} (x) + {\bar{k}}_{2}^{1 - 3} (- {\bar{\partial}}_{1}) (- {\bar{\partial}}_{2}) (- {\bar{\partial}}_{3}) Φ_{V} (x) \end{matrix}

for a standard estimate. For a standard estimate,

b_{1} = 0

in (3) and the cumulant coefficients needed for

P_{r} (x), p_{r} (x)

of (2) are

{\bar{k}}_{0}^{1} = w^{i_{1}}

\begin{matrix} for r = 0 : {\bar{k}}_{1}^{12}; for r = 1 : {\bar{k}}_{1}^{1}, {\bar{k}}_{2}^{1 - 3}; for r = 2 : {\bar{k}}_{2}^{12}, {\bar{k}}_{3}^{1 - 4}; \end{matrix}

(6)

(7)

So to obtain the 5th order Edgeworth expansion for the distribution of

n^{1 / 2} (t (\hat{w}) - t (w))

for

\hat{w}

a standard estimate, we just need to replace the coefficients in (6) and (7) where they appear in

P_{r} (x), r \leq 4

, by those of

t (\hat{w})

given in §3-§5.

(9) of Withers and Nadarajah (2010b) gives

P_{r} (x)

for the more general case where

P_{0} (x)

is the distribution function of

Y \in R^{p}

which depends on n but is asymptotic to

Φ_{V} (x)

and has a Type B expansion. One can choose

P_{0} (x)

so that the number of terms in each

P_{r} (x)

greatly reduces: see Withers and Nadarajah (2012d, 2014c, 2015). When

\hat{w}

is lattice, further terms need to be added: see for example Chapter 5 of Bhattacharya and Rao (1976), Cai (2005), and for the density of

Y_{n w}

, p211 of Barndoff-Nielsen and Cox (1989), §5 of Daniels (1983), and §6 of Daniels (1987). Corollary 1 of Withers and Nadarajah (2010b) gives the tilted Edgeworth expansion for

t (\hat{w})

, sometimes called the saddlepoint approximation, or the small sample expansion as it is a series in

n^{- 1}

not just

n^{- 1 / 2}

. It is very useful for the tails of the distribution where Edgeworth expansions perform poorly. Cumulant coefficients are also needed for bias reduction, Bayesian inference, confidence regions and power. See Withers (1984) and Withers and Nadarajah (2008, 2010a, 2011b, 2011c, 2012b, 2012f, 2014b, 2014c, 2015) for examples. For a history of Edgeworth expansions, see §7.

In summary, this paper gives high order expansions for the distribution of a vast range of estimates, by obtaining the cumulant coefficients needed for any smooth function of a standard estimate. This provides unprecedented accuracy for these distributions and avoids the need for simulation methods.

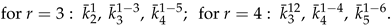
2. Foundations

Given

w = (w^{1}, \dots, w^{p}) \in R^{p}

and an estimate

\hat{w},

suppose that

E \hat{w} \to w

n \to \infty

and that for

r \geq 1,

its rth order cumulants have magnitude

n^{1 - r}

. Given

i_{1}, \dots, i_{r}

1, 2, \dots, p

, we write these cumulants in shorthand as

\begin{matrix} {\bar{k}}^{1 - r} = k^{i_{1} \dots i_{r}} = κ ({\hat{w}}^{i_{1}}, \dots, {\hat{w}}^{i_{r}}) = O (n^{1 - r}) as n \to \infty . \end{matrix}

(1)

For example if

\hat{w} = \bar{X}

is the mean of a random sample of size n, then (1) holds since

{\bar{k}}^{1 - r} = n^{1 - r} κ (X^{i_{1}}, \dots, X^{i_{r}})

where

X^{i}

is the ith component of X. By Theorem 2.1, (1) holds if

\hat{w}

is a smooth function of one or more sample means. Let

t : R^{p} \to R^{q}

be a smooth function in a neighbourhood of w with jth component

t^{j} = t^{j} (w), j = 1, \dots, q

and finite partial derivatives

{\bar{t}}_{s r \dots}^{k} = t_{\cdot i_{s} i_{r} \dots}^{j_{k}} = \partial_{i_{s}} \partial_{i_{r}} \dots t^{j_{k}} (w), {\bar{t}}_{s - r}^{k} = t_{\cdot i_{s} \dots i_{r}}^{j_{k}} f o r s \leq r

where

\partial_{i} = \partial / \partial w^{i} .

We reserve i’s as superscripts for the cumulants of

\hat{w}

and subscripts for partial derivatives of

t (w)

. We reserve j’s as superscripts for the components of

t (w)

and for the joint cumulants of

\hat{t} = t (\hat{w})

. This bar shorthand allows us to shorten expressions by suppressing the i’s and j’s. We write the cumulants of

\hat{t} = t (\hat{w})

\begin{matrix} {\bar{K}}^{1 - r} = K^{j_{1} \dots j_{r}} = κ ({\hat{t}}^{j_{1}}, \dots, {\hat{t}}^{j_{r}}) where \hat{t} = t (\hat{w}), {\hat{t}}^{j} = t^{j} (\hat{w}) . \end{matrix}

(2)

For example

\begin{matrix} {\bar{k}}^{12} = k^{i_{1} i_{2}}, {\bar{K}}^{12} = K^{j_{1} j_{2}} \Rightarrow c o v a r (\hat{w}) = ({\bar{k}}^{12}), and c o v a r (\hat{t}) = ({\bar{K}}^{12}) . \end{matrix}

are

O (n^{- 1})

. We now show that

\begin{matrix} {\bar{K}}^{12} =_{1} {\bar{K}}^{12} + O (n^{- 2}) {w h e r e}_{1} {\bar{K}}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}^{12}, {t h a t i s,}_{1} K^{j_{1} j_{2}} = t_{\cdot i_{1}}^{j_{1}} t_{\cdot i_{2}}^{j_{2}} k^{i_{1} i_{2}}, \end{matrix}

using the tensor sum convention. The rest of this section and all proofs can be skipped on a 1st reading. Theorem 2.1 gives the cumulants of

\hat{t} = t (\hat{w})

when

\hat{w}

is unbiased.

We shall use the notation

\sum^{N} f^{j_{1} j_{2} \dots}

to mean summing over all N permutations of

j_{1}, j_{2}, \dots

giving distinct terms.

Theorem 1.

Suppose that

E \hat{w} = w

and that (1) holds. Then for

r \geq 1

and

1 \leq j_{1}, \dots, j_{r} \leq q, {\bar{K}}^{1 - r}

of (2) satisfies

\begin{matrix} {\bar{K}}^{1 - r} = \sum_{e = r - 1}^{\infty}_{e} {\bar{K}}^{1 - r} w h e r e_{e} {\bar{K}}^{1 - r} =_{e} K^{j_{1} \dots j_{r}} = O (n^{- e}) a s n \to \infty, \end{matrix}

(3)

and the leading

_{e} {\bar{K}}^{1 - r}

are as follows.

\begin{matrix} _{0} {\bar{K}}^{1} = {\bar{t}}^{1}, {t h a t i s,}_{0} K^{j_{1}} = t^{j_{1}}, \\ _{1} {\bar{K}}^{1} = {\bar{t}}_{12}^{1} {\bar{k}}^{12} / 2, t h a t i s,_{1} K^{j_{1}} = t_{\cdot i_{1} i_{2}}^{j_{1}} k^{i_{1} i_{2}} / 2 = \sum_{i_{1}, i_{2} = 1}^{p} t_{\cdot i_{1} i_{2}}^{j_{1}} k^{i_{1} i_{2}} / 2, \\ _{2} {\bar{K}}^{1} = {\bar{t}}_{1 - 3}^{1} {\bar{k}}^{1 - 3} / 6 + {\bar{t}}_{1 - 4}^{1} {\bar{k}}^{12} {\bar{k}}^{34} / 8, \\ {t h a t i s,}_{2} K^{j_{1}} = t_{\cdot i_{1} i_{2} i_{3}}^{j_{1}} k^{i_{1} i_{2} i_{3}} / 6 + t_{\cdot i_{1} - i_{4}}^{j_{1}} {\bar{k}}^{i_{1} i_{2}} {\bar{k}}^{i_{3} i_{4}} / 8, \\ _{3} {\bar{K}}^{1} = {\bar{t}}_{1 - 4}^{1} {\bar{k}}^{1 - 4} / 24 + {\bar{t}}_{1 - 5}^{1} {\bar{k}}^{1 - 3} {\bar{k}}^{45} / 12 + {\bar{t}}_{1 - 6}^{1} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} / 48, \\ _{4} {\bar{K}}^{1} = {\bar{t}}_{1 - 5}^{1} {\bar{k}}^{1 - 5} / 120 + {\bar{t}}_{1 - 6}^{1} ({\bar{k}}^{1 - 4} {\bar{k}}^{56} / 48 + {\bar{k}}^{1 - 3} {\bar{k}}^{4 - 6} / 72) + {\bar{t}}_{1 - 7}^{1} {\bar{k}}^{1 - 3} {\bar{k}}^{45} {\bar{k}}^{67} / 48 \\ + {\bar{t}}_{1 - 8}^{1} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} {\bar{k}}^{78} / 384, \end{matrix}

\begin{matrix} _{1} {\bar{K}}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}^{12},_{2} {\bar{K}}^{12} = T_{1 - 3}^{12} {\bar{k}}^{1 - 3} / 2 + T_{1 - 4}^{12} {\bar{k}}^{12} {\bar{k}}^{34} / 2 w h e r e \\ T_{1 - 3}^{12} = \sum^{2} {\bar{t}}_{12}^{1} {\bar{t}}_{3}^{2}, T_{1 - 4}^{12} = \sum^{2} {\bar{t}}_{1 - 3}^{1} {\bar{t}}_{4}^{2} + {\bar{t}}_{13}^{1} {\bar{t}}_{24}^{2}, \sum^{2} {\bar{t}}_{a - b}^{1} {\bar{t}}_{c - d}^{2} = {\bar{t}}_{a - b}^{1} {\bar{t}}_{c - d}^{2} + {\bar{t}}_{a - b}^{2} {\bar{t}}_{c - d}^{1}, \\ _{3} {\bar{K}}^{12} = U_{1 - 4}^{12} {\bar{k}}^{1 - 4} + T_{1 - 5}^{12} {\bar{k}}^{1 - 3} {\bar{k}}^{45} + T_{1 - 6}^{12} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} / 4 w h e r e \\ U_{1 - 4}^{12} = \sum^{2} {\bar{t}}_{1 - 3}^{1} {\bar{t}}_{4}^{2} / 6 + {\bar{t}}_{12}^{1} {\bar{t}}_{34}^{2} / 4, \\ T_{1 - 5}^{12} = \sum^{2} ({\bar{t}}_{1 - 4}^{1} {\bar{t}}_{5}^{2} / 6 + {\bar{t}}_{1245}^{1} {\bar{t}}_{3}^{2} / 4 + {\bar{t}}_{124}^{1} {\bar{t}}_{35}^{2} / 2 + {\bar{t}}_{1455}^{1} {\bar{t}}_{23}^{2} / 4), \\ T_{1 - 6}^{12} = \sum^{2} {\bar{t}}_{1 - 5}^{1} {\bar{t}}_{6}^{2} / 2 + \sum^{2} {\bar{t}}_{1235}^{1} {\bar{t}}_{46}^{2} + {\bar{t}}_{1 - 3}^{1} {\bar{t}}_{4 - 6}^{2} + 2 {\bar{t}}_{1355}^{1} {\bar{t}}_{246}^{1} / 3, \\ _{2} {\bar{K}}^{1 - 3} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}^{1 - 3} + T_{1 - 4}^{1 - 3} {\bar{k}}^{12} {\bar{k}}^{34} w h e r e T_{1 - 4}^{1 - 3} = \sum^{3} {\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3}, \\ _{3} {\bar{K}}^{1 - 3} = T_{1 - 4}^{1 - 3} {\bar{k}}^{1 - 4} / 2 + T_{1 - 5}^{1 - 3} {\bar{k}}^{1 - 3} {\bar{k}}^{45} + T_{1 - 6}^{1 - 3} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} w h e r e \\ T_{1 - 5}^{1 - 3} = \sum^{6} {\bar{t}}_{124}^{1} {\bar{t}}_{3}^{2} {\bar{t}}_{5}^{3} / 2 + \sum^{3} {\bar{t}}_{145}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} / 2 + \sum^{6} {\bar{t}}_{12}^{1} {\bar{t}}_{34}^{2} {\bar{t}}_{5}^{3} / 2 + \sum^{3} {\bar{t}}_{14}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{3}^{3}, \\ T_{1 - 6}^{1 - 3} = \sum^{3} {\bar{t}}_{1235}^{1} {\bar{t}}_{4}^{2} {\bar{t}}_{6}^{3} / 2 + \sum^{6} {\bar{t}}_{1 - 3}^{1} {\bar{t}}_{45}^{2} {\bar{t}}_{6}^{3} + \sum^{6} {\bar{t}}_{135}^{1} {\bar{t}}_{24}^{2} {\bar{t}}_{6}^{3} / 2 + {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{46}^{3}, \\ _{3} {\bar{K}}^{1 - 4} = {\bar{t}}_{1}^{1} \dots {\bar{t}}_{4}^{4} {\bar{k}}^{1 - 4} + T_{1 - 5}^{1 - 4} {\bar{k}}^{1 - 3} {\bar{k}}^{45} + T_{1 - 6}^{1 - 4} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} w h e r e \\ T_{1 - 5}^{1 - 4} = \sum^{12} {\bar{t}}_{14}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4}, T_{1 - 6}^{1 - 4} = \sum^{4} {\bar{t}}_{135}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} + \sum^{12} {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4}, \\ _{4} {\bar{K}}^{1 - 4} = U_{1 - 5}^{1 - 4} {\bar{k}}^{1 - 5} / 2 + U_{1 - 6}^{1 - 4} {\bar{k}}^{1 - 4} {\bar{k}}^{56} + V_{1 - 6}^{1 - 4} {\bar{k}}^{1 - 3} {\bar{k}}^{4 - 6} + T_{1 - 7}^{1 - 4} {\bar{k}}^{1 - 3} {\bar{k}}^{45} {\bar{k}}^{67} \\ + T_{1 - 8}^{1 - 4} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} {\bar{k}}^{78} w h e r e U_{1 - 5}^{1 - 4} = \sum^{4} {\bar{t}}_{12}^{1} {\bar{t}}_{3}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{5}^{4}, \\ U_{1 - 6}^{1 - 4} = \sum^{12} {\bar{t}}_{125}^{1} {\bar{t}}_{3}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} / 2 + \sum^{4} {\bar{t}}_{156}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4} / 2 + \sum^{24} {\bar{t}}_{12}^{1} {\bar{t}}_{35}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} / 2 + \sum^{6} {\bar{t}}_{15}^{1} {\bar{t}}_{26}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4}), \\ V_{1 - 6}^{1 - 4} = \sum^{12} {\bar{t}}_{124}^{1} {\bar{t}}_{3}^{2} {\bar{t}}_{5}^{3} {\bar{t}}_{6}^{4} / 2 + \sum^{12} {\bar{t}}_{12}^{1} {\bar{t}}_{34}^{2} {\bar{t}}_{5}^{3} {\bar{t}}_{6}^{4} / 2 + \sum^{6} {\bar{t}}_{14}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{6}^{4}, \\ T_{1 - 7}^{1 - 4} = \sum^{12} {\bar{t}}_{1246}^{1} {\bar{t}}_{3}^{2} {\bar{t}}_{5}^{3} {\bar{t}}_{7}^{4} / 2 + \sum^{12} {\bar{t}}_{1456}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{7}^{4} / 2 + \sum^{24} {\bar{t}}_{124}^{1} {\bar{t}}_{36}^{2} {\bar{t}}_{5}^{3} {\bar{t}}_{7}^{4} / 2 + \sum^{24} {\bar{t}}_{124}^{1} {\bar{t}}_{56}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{7}^{4} / 2 \\ + \sum^{24} {\bar{t}}_{145}^{1} {\bar{t}}_{26}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{7}^{4} / 2 + \sum^{12} {\bar{t}}_{146}^{1} {\bar{t}}_{23}^{2} {\bar{t}}_{5}^{3} {\bar{t}}_{7}^{4} + \sum^{24} {\bar{t}}_{146}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{7}^{4} + \sum^{12} {\bar{t}}_{146}^{1} {\bar{t}}_{57}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} / 2 \\ + \sum^{12} {\bar{t}}_{456}^{1} {\bar{t}}_{17}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} + \sum^{24} {\bar{t}}_{12}^{1} {\bar{t}}_{34}^{2} {\bar{t}}_{56}^{3} {\bar{t}}_{7}^{4} / 2 + \sum^{12} {\bar{t}}_{14}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{36}^{3} {\bar{t}}_{7}^{4} + \sum^{12} {\bar{t}}_{14}^{1} {\bar{t}}_{26}^{2} {\bar{t}}_{57}^{3} {\bar{t}}_{3}^{4}),, \\ T_{1 - 8}^{1 - 4} = \sum^{4} {\bar{t}}_{12357}^{1} {\bar{t}}_{4}^{2} {\bar{t}}_{6}^{3} {\bar{t}}_{8}^{4} / 2 + \sum^{24} {\bar{t}}_{1235}^{1} {\bar{t}}_{47}^{2} {\bar{t}}_{6}^{3} {\bar{t}}_{8}^{4} / 2 + \sum^{12} {\bar{t}}_{1357}^{1} {\bar{t}}_{24}^{2} {\bar{t}}_{6}^{3} {\bar{t}}_{8}^{4} / 2 \\ + \sum^{12} {\bar{t}}_{123}^{1} {\bar{t}}_{457}^{2} {\bar{t}}_{6}^{3} {\bar{t}}_{8}^{4} / 2 + \sum^{12} {\bar{t}}_{135}^{1} {\bar{t}}_{247}^{2} {\bar{t}}_{6}^{3} {\bar{t}}_{8}^{4} / 2 + \sum^{24} {\bar{t}}_{123}^{1} {\bar{t}}_{45}^{2} {\bar{t}}_{67}^{3} {\bar{t}}_{8}^{4} / 2 + \sum^{24} {\bar{t}}_{135}^{1} {\bar{t}}_{24}^{2} {\bar{t}}_{67}^{3} {\bar{t}}_{8}^{4} \end{matrix}

\begin{matrix} + \sum^{12} {\bar{t}}_{135}^{1} {\bar{t}}_{27}^{2} {\bar{t}}_{48}^{3} {\bar{t}}_{6}^{4} / 2 + \sum^{3} {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{47}^{3} {\bar{t}}_{68}^{4}, \\ _{4} {\bar{K}}^{1 - 5} = {\bar{t}}_{1}^{1} \dots {\bar{t}}_{5}^{5} {\bar{k}}^{1 - 5} + T_{1 - 6}^{1 - 5} {\bar{k}}^{1 - 4} {\bar{k}}^{56} + U_{1 - 6}^{1 - 5} {\bar{k}}^{1 - 3} {\bar{k}}^{4 - 6} + T_{1 - 7}^{1 - 5} {\bar{k}}^{1 - 3} {\bar{k}}^{45} {\bar{k}}^{67} \\ + T_{1 - 8}^{1 - 5} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} {\bar{k}}^{78} w h e r e \\ T_{1 - 6}^{1 - 5} = \sum^{20} {\bar{t}}_{15}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4} {\bar{t}}_{6}^{5}, U_{1 - 6}^{1 - 5} = \sum^{15} {\bar{t}}_{14}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{6}^{5}, \\ T_{1 - 7}^{1 - 5} = \sum^{30} {\bar{t}}_{146}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{7}^{5} + \sum^{60} {\bar{t}}_{14}^{1} {\bar{t}}_{26}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{7}^{5} + \sum^{60} {\bar{t}}_{14}^{1} {\bar{t}}_{56}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} {\bar{t}}_{7}^{5}, \\ T_{1 - 8}^{1 - 5} = \sum^{5} {\bar{t}}_{1357}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5} / 5 + \sum^{60} {\bar{t}}_{135}^{1} {\bar{t}}_{27}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5} + \sum^{60} {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{47}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5}, \\ _{5} {\bar{K}}^{1 - 6} = {\bar{t}}_{1}^{1} \dots {\bar{t}}_{6}^{5} {\bar{k}}^{1 - 6} + T_{1 - 7}^{1 - 6} {\bar{k}}^{1 - 5} {\bar{k}}^{67} + U_{1 - 7}^{1 - 6} {\bar{k}}^{1 - 4} {\bar{k}}^{5 - 7} + T_{1 - 8}^{1 - 6} {\bar{k}}^{1 - 4} {\bar{k}}^{56} {\bar{k}}^{78} \\ + U_{1 - 8}^{1 - 6} {\bar{k}}^{1 - 3} {\bar{k}}^{4 - 6} {\bar{k}}^{78} + T_{1 - 9}^{1 - 6} {\bar{k}}^{1 - 3} {\bar{k}}^{45} {\bar{k}}^{67} {\bar{k}}^{89} + T_{1 - 10}^{1 - 6} {\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56} {\bar{k}}^{78} {\bar{k}}^{9, 10} w h e r e \\ T_{1 - 7}^{1 - 6} = \sum^{30} {\bar{t}}_{16}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4} {\bar{t}}_{5}^{5} {\bar{t}}_{7}^{6}, U_{1 - 7}^{1 - 6} = \sum^{60} {\bar{t}}_{15}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4} {\bar{t}}_{6}^{5} {\bar{t}}_{7}^{6}, \\ T_{1 - 8}^{1 - 6} = \sum^{60} {\bar{t}}_{157}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4} {\bar{t}}_{6}^{5} {\bar{t}}_{8}^{6} + \sum^{180} {\bar{t}}_{15}^{1} {\bar{t}}_{27}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{4}^{4} {\bar{t}}_{6}^{5} {\bar{t}}_{8}^{6} + \sum^{120} {\bar{t}}_{15}^{1} {\bar{t}}_{67}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} {\bar{t}}_{4}^{5} {\bar{t}}_{8}^{6}, \\ U_{1 - 8}^{1 - 6} = \sum^{90} {\bar{t}}_{147}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{6}^{5} {\bar{t}}_{8}^{6} + \sum^{360} {\bar{t}}_{14}^{1} {\bar{t}}_{27}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{6}^{5} {\bar{t}}_{8}^{6} + \sum^{90} {\bar{t}}_{17}^{1} {\bar{t}}_{48}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} {\bar{t}}_{5}^{5} {\bar{t}}_{6}^{6}, \\ T_{1 - 9}^{1 - 6} = \sum^{60} {\bar{t}}_{1468}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{7}^{5} {\bar{t}}_{9}^{6} + \sum^{360} {\bar{t}}_{146}^{1} {\bar{t}}_{28}^{2} {\bar{t}}_{3}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{7}^{5} {\bar{t}}_{9}^{6} + \sum^{360} {\bar{t}}_{146}^{1} {\bar{t}}_{58}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} {\bar{t}}_{7}^{5} {\bar{t}}_{9}^{6} \\ + \sum^{180} {\bar{t}}_{468}^{1} {\bar{t}}_{15}^{2} {\bar{t}}_{2}^{3} {\bar{t}}_{3}^{4} {\bar{t}}_{7}^{5} {\bar{t}}_{9}^{6} + \sum^{120} {\bar{t}}_{14}^{1} {\bar{t}}_{26}^{2} {\bar{t}}_{38}^{3} {\bar{t}}_{5}^{4} {\bar{t}}_{7}^{5} {\bar{t}}_{9}^{6} + \sum^{720} {\bar{t}}_{14}^{1} {\bar{t}}_{26}^{2} {\bar{t}}_{58}^{3} {\bar{t}}_{3}^{4} {\bar{t}}_{7}^{5} {\bar{t}}_{9}^{6} \\ + \sum^{360} {\bar{t}}_{14}^{1} {\bar{t}}_{56}^{2} {\bar{t}}_{78}^{3} {\bar{t}}_{2}^{4} {\bar{t}}_{3}^{5} {\bar{t}}_{9}^{6}, \\ T_{1 - 10}^{1 - 6} = \sum^{6} {\bar{t}}_{13579}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5} {\bar{t}}_{10}^{6} + \sum^{120} {\bar{t}}_{1357}^{1} {\bar{t}}_{29}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5} {\bar{t}}_{10}^{6} + \sum^{90} {\bar{t}}_{135}^{1} {\bar{t}}_{279}^{2} {\bar{t}}_{4}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5} {\bar{t}}_{10}^{6} \\ + \sum^{360} {\bar{t}}_{135}^{1} {\bar{t}}_{27}^{2} {\bar{t}}_{49}^{3} {\bar{t}}_{6}^{4} {\bar{t}}_{8}^{5} {\bar{t}}_{10}^{6} + \sum^{360} {\bar{t}}_{135}^{1} {\bar{t}}_{27}^{2} {\bar{t}}_{89}^{3} {\bar{t}}_{4}^{4} {\bar{t}}_{6}^{5} {\bar{t}}_{10}^{6} + \sum^{360} {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{47}^{3} {\bar{t}}_{69}^{4} {\bar{t}}_{8}^{5} {\bar{t}}_{10}^{6} . \end{matrix}

NOTE 2.1.

For N in

\sum^{N}

, see p48 of James and Mayne (1962). The understanding here is that

\sum^{N}

in terms like

T_{1 - s}^{1 - r}

only make sense for

N < r!

in the context where they occur. For example, writing

(a b c) = {\bar{t}}_{13}^{a} {\bar{t}}_{2}^{b} {\bar{t}}_{4}^{c}

and recalling that

\sum^{N}

only permutes superscripts but leaves subscripts alone, we have

\begin{matrix} T_{1 - 4}^{1 - 3} = \sum^{N} (123) = (123) + (213) + (321) \end{matrix}

(4)

with

N = 3

not

3!

since

\sum^{3!} (123) = (123) + (132) + (213) + (231) + (321) + (312) = \sum_{k = 1}^{6} S_{k}

say, when multiplied by

{\bar{k}}^{12} {\bar{k}}^{34}

, as in

_{2} {\bar{K}}^{1 - 3}

, gives

\sum_{k = 1}^{6} S_{k}^{'}

say, where for

k = 1, 2, 3, S_{2 k}^{'} = S_{2 k - 1}^{'}

. For example

T_{1 - 4}^{1 - 3} {\bar{k}}^{12} {\bar{k}}^{34}

_{2} {\bar{K}}^{1 - 3}

above is shorthand for

\sum^{3} {\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3} {\bar{k}}^{12} {\bar{k}}^{34}

. For,

S_{2}^{'} = {\bar{t}}_{4}^{2} {\bar{k}}^{43} {\bar{t}}_{31}^{1} {\bar{k}}^{12} {\bar{t}}_{2}^{3} = {\bar{t}}_{1}^{2} {\bar{k}}^{12} {\bar{t}}_{13}^{1} {\bar{k}}^{34} {\bar{t}}_{4}^{3} = S_{1}^{'} \Rightarrow T_{1 - 4}^{1 - 3} {\bar{k}}^{12} {\bar{k}}^{34} = S_{1}^{'} + S_{3}^{'} + S_{5}^{'} .

PROOF This follows by replacing

{\bar{A}}_{1 - r}^{j} = A_{i_{1} \dots i_{r}}^{j}

{\bar{t}}_{1 - r}^{1} / r! = t_{. i_{1} \dots i_{r}}^{j_{1}} / r!

in James and Mayne (1962). □

Similarly one may easily obtain

_{4} {\bar{K}}^{12},_{4} {\bar{K}}^{1 - 3}

from p51–53 of James and Mayne (1962). The tensor form

2 {\bar{K}}_{1}^{1} = {\bar{t}}_{12}^{1} {\bar{k}}_{1}^{12}

can be viewed as a molecule or molecular form of 2 atoms,

{\bar{t}}_{12}^{1}

and

{\bar{k}}_{1}^{12}

, linked by the double bond 1,2, that is,

i_{1}, i_{2}

_{2} {\bar{K}}^{1}

is a linear combination of

{\bar{t}}_{1 - 3}^{1} {\bar{k}}^{1 - 3}

, 2 atoms linked by the triple bond 1,2,3, and secondly

{\bar{k}}^{12} {\bar{t}}_{1 - 4}^{1} {\bar{k}}^{34}

. The last expression has the structure of

C O_{2}

, with 2 identical atoms each linked by a double bond to a central atom. Just as such bonds are depicted in chemistry to illustrate the structure of a molecule, they can be very useful here to illustrate the difference in structure of similar mathematical expressions.

S_{1}^{'}

of Note 2.1 is a linear molecular form with the 4 single bonds 1,2,3,4 and 4 distinct atoms,

{\bar{t}}_{1}^{2}, {\bar{t}}_{1}^{1}, {\bar{t}}_{12}^{1},

and

{\bar{k}}^{12} .

Other expressions have more complex structures. Twice the last term in

_{2} {\bar{K}}^{12}

T_{1 - 4}^{12} {\bar{k}}^{12} {\bar{k}}^{34} = S^{12} + S^{21} + S

where

S^{12} = {\bar{k}}^{12} {\bar{t}}_{1 - 3}^{1} {\bar{k}}^{34} {\bar{t}}_{4}^{2}

is linear with a double bond, 1 and 2, then 2 single bonds, 3 and 4;

S = {\bar{t}}_{31}^{1} {\bar{k}}^{12} {\bar{t}}_{24}^{2} {\bar{k}}^{43}

forms a square or rectangle with 4 single bonds 1,2,4,3 on successive edges of the square. These pictorial forms are a very useful way to distinguish similar expressions in

\sum^{N} f^{j_{1} j_{2} \dots}

§6 provides the ’more complicated’ terms referred to (but not given) on p49 of James and Mayne (1962) when

\hat{w}

is biased. It can be used for an alternative proof of Theorem 4.1 below. From Theorem 2.1, Edgeworth expansions can be obtained for the distribution and density of the standardized form of

t (\hat{w})

\begin{matrix} Y_{n t} = n^{1 / 2} (\hat{t} - t) = n^{1 / 2} (t (\hat{w}) - t (w)), \end{matrix}

(5)

of the form

\begin{matrix} P r o b . (Y_{n t} \leq x) = \sum_{r = 0}^{\infty} P_{r n} (x), p_{Y_{n t}} (x) = \sum_{r = 0}^{\infty} p_{r n} (x), \end{matrix}

(6)

where

P_{r n} (x), p_{r n} (x)

are

O (n^{- r / 2}) .

The

_{e} {\bar{K}}^{1 - r}

of Theorem 2.1 needed for

P_{r n} (x), p_{r n} (x)

are as follows.

\begin{matrix} For P_{0 n} (x), p_{0 n} (x) :_{0} {\bar{K}}^{1} = {\bar{t}}^{1},_{1} {\bar{K}}^{12} . For P_{1 n} (x), p_{1 n} (x) :_{1} {\bar{K}}^{1},_{2} {\bar{K}}^{1 - 3} . \\ For P_{2 n} (x), p_{2 n} (x) :_{2} {\bar{K}}^{12},_{3} {\bar{K}}^{1 - 4} . For P_{3 n} (x), p_{3 n} (x) :_{2} {\bar{K}}^{1},_{3} {\bar{K}}^{1 - 3},_{4} {\bar{K}}^{1 - 5} . \\ For P_{4 n} (x), p_{4 n} (x) :_{3} {\bar{K}}^{1 - 2},_{4} {\bar{K}}^{1 - 4},_{5} {\bar{K}}^{1 - 6} . \end{matrix}

3. Cumulant Coefficients for $t (\hat{w})$ when $E \hat{w} = w$

We now show that for

r \geq 1, 1 \leq j_{1}, \dots, j_{r} \leq q

{\bar{K}}^{1 - r}

of (3) can be expanded as

\begin{matrix} {\bar{K}}^{1 - r} = K^{j_{1} - j_{r}} = κ ({\hat{t}}^{j_{1}}, \dots, {\hat{t}}^{j_{r}}) = \sum_{e = r - 1}^{\infty} n^{- e} {\bar{K}}_{e}^{1 - r} \end{matrix}

(1)

Replacing

{{\bar{k}}^{1 - r}}

{{\bar{K}}^{1 - r}}

in the righthand side of (4), written RHS(4), gives the Edgeworth expansion for

Y_{n t}

of (5). For

π

a product of cumulants of type (1), let

{(π)}_{e}

be the coefficient of

n^{- e}

in the expansion of

π

. For example

{({\bar{k}}^{1 - r})}_{e} = {\bar{k}}_{e}^{1 - r},

(2)

We now give the elements of the expansion (1) when

E \hat{w} = w

Theorem 2.

Suppose that

\hat{w}

is anunbiasedestimate of w satisfying (1) and that

t (w)

has finite derivatives. Then (1) holds with bounded cumulant coefficients

\begin{matrix} {\bar{K}}_{e}^{1 - r} = K_{e}^{j_{1} - j_{r}} = \sum_{k = r - 1}^{e}_{k} {\bar{K}}_{e}^{1 - r} : \\ {\bar{K}}_{r - 1}^{1 - r} =_{r - 1} {\bar{K}}_{r - 1}^{1 - r}, {\bar{K}}_{r}^{1 - r} =_{r - 1} {\bar{K}}_{r}^{1 - r} +_{r} {\bar{K}}_{r}^{1 - r}, \dots \end{matrix}

(3)

The leading coefficients needed for

P_{r} (x), p_{r} (x)

of () for the distribution of

Y_{n t}

of (5) are given in the

T, U, V

notation of Theorem 2.1 as follows.

\begin{matrix} {\bar{K}}_{0}^{1} = {\bar{t}}^{1}, t h a t i s, K_{0}^{j_{1}} = t^{j_{1}} = t^{j_{1}} (w) ._{0} {\bar{K}}_{e}^{1} = 0 f o r e \geq 1 . \\ F o r P_{0} (x) : {\bar{K}}_{1}^{12} =_{1} {\bar{K}}_{1}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1}^{12}, t h a t i s, K_{1}^{j_{1} j_{2}} = t_{\cdot i_{1}}^{j_{1}} t_{\cdot i_{2}}^{j_{2}} k_{1}^{i_{1} i_{2}} . \\ F o r P_{1} (x) : {\bar{K}}_{1}^{1} =_{1} {\bar{K}}_{1}^{1} = {\bar{t}}_{12}^{1} {\bar{k}}_{1}^{12} / 2, t h a t i s, K_{1}^{j_{1}} = t_{\cdot i_{1} i_{2}}^{j_{1}} k_{1}^{i_{1} i_{2}} / 2, \\ {\bar{K}}_{2}^{1 - 3} =_{2} {\bar{K}}_{2}^{1 - 3} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}_{2}^{1 - 3} + T_{1 - 4}^{1 - 3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} . \\ F o r P_{2} (x) : {\bar{K}}_{2}^{12} =_{1} {\bar{K}}_{2}^{12} +_{2} {\bar{K}}_{2}^{12} f o r_{1} {\bar{K}}_{2}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{2}^{12}, \\ _{2} {\bar{K}}_{2}^{12} = T_{1 - 3}^{12} {\bar{k}}_{2}^{1 - 3} / 2 + T_{1 - 4}^{12} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} / 2, \\ {\bar{K}}_{3}^{1 - 4} =_{3} {\bar{K}}_{3}^{1 - 4} = ({\bar{t}}_{1}^{1} \dots {\bar{t}}_{4}^{4}) {\bar{k}}_{3}^{1 - 4} + T_{1 - 5}^{1 - 4} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} + T_{1 - 6}^{1 - 4} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} . \\ F o r P_{3} (x) : {\bar{K}}_{2}^{1} =_{1} {\bar{K}}_{2}^{1} +_{2} {\bar{K}}_{2}^{1} f o r_{1} {\bar{K}}_{2}^{1} = {\bar{t}}_{12}^{1} {\bar{k}}_{2}^{12} / 2,_{2} {\bar{K}}_{2}^{1} = {\bar{t}}_{1 - 3}^{1} {\bar{k}}_{2}^{1 - 3} / 6 \\ + {\bar{t}}_{1 - 4}^{1} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} / 8, t h a t i s, K_{2}^{j_{1}} = t_{\cdot i_{1} i_{2}}^{j_{1}} k_{2}^{i_{1} i_{2}} / 2 + t_{\cdot i_{1} i_{2} i_{3}}^{j_{1}} k_{2}^{i_{1} i_{2} i_{3}} / 6 + t_{\cdot i_{1} - i_{4}}^{j_{1}} k_{1}^{i_{1} i_{2}} k_{1}^{i_{3} i_{4}} / 8, \\ {\bar{K}}_{3}^{1 - 3} = \sum_{k = 2}^{3}_{k} {\bar{K}}_{3}^{1 - 3} f o r_{2} {\bar{K}}_{3}^{1 - 3} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}_{3}^{1 - 3} + T_{1 - 4}^{1 - 3} {({\bar{k}}^{12} {\bar{k}}^{34})}_{3}, \\ _{3} {\bar{K}}_{3}^{1 - 3} = T_{1 - 4}^{1 - 3} {\bar{k}}_{3}^{1 - 4} / 2 + T_{1 - 5}^{1 - 3} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} + T_{1 - 6}^{1 - 3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}, \\ {\bar{K}}_{4}^{1 - 5} =_{4} {\bar{K}}_{4}^{1 - 5} = {\bar{t}}_{1}^{1} \dots {\bar{t}}_{5}^{5} {\bar{k}}_{4}^{1 - 5} + T_{1 - 6}^{1 - 5} {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56} + U_{1 - 6}^{1 - 5} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} \\ + T_{1 - 7}^{1 - 5} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67} + T_{1 - 8}^{1 - 5} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} . \\ F o r P_{4} (x) : {\bar{K}}_{3}^{12} = \sum_{k = 1}^{3}_{k} {\bar{K}}_{3}^{12} f o r_{1} {\bar{K}}_{3}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{3}^{12}, \\ _{2} {\bar{K}}_{3}^{12} = T_{1 - 3}^{12} {\bar{k}}_{3}^{1 - 3} / 2 + T_{1 - 4}^{12} {({\bar{k}}^{12} {\bar{k}}^{34})}_{3} / 2, \\ _{3} {\bar{K}}_{3}^{12} = U_{1 - 4}^{12} {\bar{k}}_{3}^{1 - 4} + T_{1 - 5}^{12} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} + T_{1 - 6}^{12} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} / 4, \\ {\bar{K}}_{4}^{1 - 4} = \sum_{k = 3}^{4}_{k} {\bar{K}}_{4}^{1 - 4} f o r_{3} {\bar{K}}_{4}^{1 - 4} = ({\bar{t}}_{1}^{1} \dots {\bar{t}}_{4}^{4}) {\bar{k}}_{4}^{1 - 4} + T_{1 - 5}^{1 - 4} {({\bar{k}}^{1 - 3} {\bar{k}}^{45})}_{4} \\ + T_{1 - 6}^{1 - 4} {({\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56})}_{4},_{4} {\bar{K}}_{4}^{1 - 4} = U_{1 - 5}^{1 - 4} {\bar{k}}_{4}^{1 - 5} / 2 + U_{1 - 6}^{1 - 4} {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56} \\ + V_{1 - 6}^{1 - 4} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} + T_{1 - 7}^{1 - 4} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67} + T_{1 - 8}^{1 - 4} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78}, \\ {\bar{K}}_{5}^{1 - 6} =_{5} {\bar{K}}_{5}^{1 - 6} = {\bar{t}}_{1}^{1} \dots {\bar{t}}_{6}^{5} {\bar{k}}_{5}^{1 - 6} + T_{1 - 7}^{1 - 6} {\bar{k}}_{4}^{1 - 5} {\bar{k}}_{1}^{67} + U_{1 - 7}^{1 - 6} {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{2}^{5 - 7} + T_{1 - 8}^{1 - 6} {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} \\ + U_{1 - 8}^{1 - 6} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} {\bar{k}}_{2}^{78} + T_{1 - 9}^{1 - 6} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67} {\bar{k}}_{1}^{89} + T_{1 - 10}^{1 - 6} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} {\bar{k}}_{1}^{9, 10} . \\ A l s o, f o r {\bar{K}}_{0}^{1}, {\bar{K}}_{1}^{1}, {\bar{K}}_{2}^{1} a b o v e, E t^{j_{1}} (\hat{w}) = \sum_{e = 0}^{4} n^{- e} {\bar{K}}_{e}^{1} + O (n^{- 5}) w h e r e \end{matrix}

\begin{matrix} {\bar{K}}_{3}^{1} = \sum_{k = 1}^{3}_{k} {\bar{K}}_{3}^{1} f o r_{1} {\bar{K}}_{3}^{1} = {\bar{t}}_{12}^{1} {\bar{k}}_{3}^{12} / 2,_{2} {\bar{K}}_{3}^{1} = {\bar{t}}_{1 - 3}^{1} {\bar{k}}_{3}^{1 - 3} / 6 + {\bar{t}}_{1 - 4}^{1} {\bar{k}}_{1}^{12} {\bar{k}}_{2}^{34} / 4, \\ _{3} {\bar{K}}_{3}^{1} = {\bar{t}}_{1 - 4}^{1} {\bar{k}}_{3}^{1 - 4} / 24 + {\bar{t}}_{1 - 5}^{1} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} / 12 + {\bar{t}}_{1 - 6}^{1} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} / 48, \\ {\bar{K}}_{4}^{1} = \sum_{k = 1}^{4}_{k} {\bar{K}}_{4}^{1} f o r_{1} {\bar{K}}_{4}^{1} = {\bar{t}}_{12}^{1} {\bar{k}}_{4}^{12} / 2, \\ _{2} {\bar{K}}_{4}^{1} = {\bar{t}}_{1 - 3}^{1} {\bar{k}}_{4}^{1 - 3} / 6 + {\bar{t}}_{1 - 4}^{1} (2 {\bar{k}}_{1}^{12} {\bar{k}}_{3}^{34} + {\bar{k}}_{2}^{12} {\bar{k}}_{2}^{34}) / 8, \\ _{3} {\bar{K}}_{4}^{1} = {\bar{t}}_{1 - 4}^{1} {\bar{k}}_{4}^{1 - 4} / 24 + {\bar{t}}_{1 - 5}^{1} ({\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{45} + {\bar{k}}_{3}^{1 - 3} {\bar{k}}_{1}^{45}) / 12 + {\bar{t}}_{1 - 6}^{1} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{2}^{56} / 16, \\ _{4} {\bar{K}}_{4}^{1} = {\bar{t}}_{1 - 5}^{1} {\bar{k}}_{4}^{1 - 5} / 120 + {\bar{t}}_{1 - 6}^{1} ({\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56} / 48 + {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} / 72) + {\bar{t}}_{1 - 7}^{1} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67} / 48 \\ + {\bar{t}}_{1 - 8}^{1} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} / 384 . \end{matrix}

PROOF Substituting (1) into

_{k} {\bar{K}}^{1 - r}

of Theorem 2.1 gives

_{k} {\bar{K}}^{1 - r} = \sum_{e = k}^{\infty}_{k} {\bar{K}}_{e}^{1 - r} n^{- e}

say. So by (3), (1) and (3) hold. □

_{k} {\bar{K}}_{e}^{1 - r} =_{k} K_{e}^{j_{1} \dots j_{r}}

_{k} {\tilde{V}}_{e}^{j_{1} \dots j_{r}}

of Withers (1982).

NOTE 3.1.(4) made explicit the 3 terms needed in

T_{1 - 4}^{1 - 3}

needed for

P_{1} (x)

of Theorem 3.1. Similarly

P_{2} (x)

needs the 12 terms

\begin{matrix} T_{1 - 5}^{1 - 4} = \sum^{12} (1234) = (1234) + (1243) + (2413) + (2431) + (3124) + (3142) \\ + (3241) + (3412) + (4123) + (4132) + (4231) + (4321) \end{matrix}

where

(a b c d) = {\bar{t}}_{14}^{a} {\bar{t}}_{2}^{b} {\bar{t}}_{3}^{c} {\bar{t}}_{5}^{d} .

It also needs the

4 + 12

terms

T_{1 - 6}^{1 - 4} = A + B

where

\begin{matrix} A = \sum^{4} (1234) = (1234) + (2134) + (3124) + (4123) f o r (a b c d) = {\bar{t}}_{135}^{a} {\bar{t}}_{2}^{b} {\bar{t}}_{4}^{c} {\bar{t}}_{6}^{d}, \\ B = \sum^{12} (1234) = (1234) + (1423) + (1432) + (1324) + (2134) + (2314) + (2413) \\ + (3124) + (3214) + (3412) + (4213) + (4312) f o r (a b c d) = {\bar{t}}_{13}^{a} {\bar{t}}_{25}^{b} {\bar{t}}_{4}^{c} {\bar{t}}_{6}^{d} . \end{matrix}

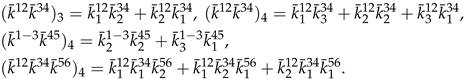
4. Cumulant Coefficients for $t (\hat{w})$ when $E \hat{w} \neq w$

We now remove the assumption that

\hat{w}

is unbiased. We use

{\bar{K}}_{e}^{1 - r}

of Theorem 3.1, and the shorthand

{\bar{f}}_{\cdot m} = \partial_{i_{m}} f

where again

\partial_{i} = \partial / \partial w^{i} .

There is a key difference with Theorem 3.1: there

{\bar{k}}_{e}^{1 - r}

was treated as an algebraic expression. But now we must view each of them as a function of w. So we assume that the distribution of

\hat{w}

is determined by w. This is needed to obtain higher order confidence intervals for

t (w)

when

q = 1

: see Withers (1989). We show that for

Y_{n t}

of (5),

P_{2} (x), p_{2} (x)

need the 1st derivatives

{\bar{k}}_{1 \cdot i}^{12} = \partial_{i} {\bar{k}}_{1}^{12}

for

\partial_{i} = \partial / \partial w^{i}

P_{3} (x), p_{3} (x)

need the 1st derivatives

{\bar{k}}_{2 \cdot 4}^{1 - 3}

, and so on. The derivatives of

{\bar{K}}_{e}^{1 - r}

are given by Leibniz’s rule for the derivatives of a product. For example

\begin{matrix} {\bar{K}}_{1 \cdot 3}^{12} = {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1}^{12})}_{\cdot 3} = (\sum_{12}^{2} {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2}) {\bar{k}}_{1}^{12} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1 \cdot 3}^{12} f o r \sum_{12}^{2} {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2} = {\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} + {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2}, \\ {\bar{K}}_{1 \cdot 3}^{1} = {({\bar{t}}_{12}^{1} {\bar{k}}_{1}^{12})}_{\cdot 3} / 2 = {\bar{t}}_{1 - 3}^{1} {\bar{k}}_{1}^{12} / 2 + {\bar{t}}_{12}^{1} {\bar{k}}_{1 \cdot 3}^{12} / 2, \\ {\bar{K}}_{1 \cdot 34}^{12} = \sum_{12}^{2} [({\bar{t}}_{14}^{1} {\bar{t}}_{23}^{2} + {\bar{t}}_{1}^{1} {\bar{t}}_{2 - 4}^{2}) {\bar{k}}_{1}^{12} + {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2} {\bar{k}}_{1 \cdot 4}^{12} + {\bar{t}}_{14}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1 \cdot 3}^{12}] + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1 \cdot 34}^{12}, \\ {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}_{2}^{1 - 3})}_{\cdot 4} = {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3})}_{\cdot 4} {\bar{k}}_{2}^{1 - 3} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}_{2 \cdot 4}^{1 - 3}, {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3})}_{\cdot 4} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{34}^{3} + {\bar{t}}_{1}^{1} {\bar{t}}_{24}^{2} {\bar{t}}_{3}^{3} + {\bar{t}}_{14}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3}, \\ {(T_{1 - 4}^{1 - 3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34})}_{\cdot 5} = T_{1 - 4 \cdot 5}^{1 - 3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} + T_{1 - 4}^{1 - 3} {({\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34})}_{\cdot 5}, \\ T_{1 - 4 \cdot 5}^{1 - 3} = \sum^{3} ({\bar{t}}_{135}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3} + {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{4}^{3} + {\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{45}^{3}), {({\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34})}_{\cdot 5} = {\bar{k}}_{1 \cdot 5}^{12} {\bar{k}}_{1}^{34} + {\bar{k}}_{1}^{12} {\bar{k}}_{1 \cdot 5}^{34} . \end{matrix}

Theorem 3.

Let

\hat{w} \in R^{p}

be abiasedstandard estimate of w satisfying (1) where

{\bar{k}}_{e}^{1 - r}

depend on w. Then

\hat{t} = t (\hat{w}) \in R^{q}

is a standard estimate of

t (w)

\begin{matrix} κ ({\hat{t}}^{j_{1}}, \dots, {\hat{t}}^{j_{r}}) = \sum_{e = r - 1}^{\infty} n^{- e} {\bar{a}}_{e}^{1 - r} f o r r \geq 1, 1 \leq j_{1}, \dots, j_{r} \leq q, \end{matrix}

(1)

(2)

for

{\bar{K}}_{e}^{1 - r}

of Theorem 3.1, and the other

{\bar{D}}_{e}^{1 - r} = D_{e}^{j_{1} \dots j_{r}}

needed for

P_{r} (x), p_{r} (x)

of (4) for

Y_{n t}

of (5) are as follows.

\begin{matrix} F o r P_{0} (x) : {\bar{D}}_{1}^{12} = 0 \Rightarrow {\bar{a}}_{1}^{12} = {\bar{K}}_{1}^{12} = K_{1}^{j_{1} j_{2}} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1}^{12}, \\ F o r P_{1} (x) : {\bar{D}}_{1}^{1} = {\bar{t}}_{1}^{1} {\bar{k}}_{1}^{1} \Rightarrow {\bar{a}}_{1}^{1} = {\bar{K}}_{1}^{1} + {\bar{D}}_{1}^{1} = {\bar{t}}_{1}^{1} {\bar{k}}_{1}^{1} + {\bar{t}}_{12}^{1} {\bar{k}}_{1}^{12} / 2, \\ F o r P_{2} (x) : {\bar{D}}_{2}^{12} = {\bar{K}}_{1 \cdot 3}^{12} {\bar{k}}_{1}^{3} = [({\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} + {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2}) {\bar{k}}_{1}^{12} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1 \cdot 3}^{12}] {\bar{k}}_{1}^{3} \\ \Rightarrow {\bar{a}}_{2}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{2}^{12} + T_{1 - 3}^{12} {\bar{k}}_{2}^{1 - 3} / 2 + T_{1 - 4}^{12} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} / 2 \\ + [({\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} + {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2}) {\bar{k}}_{1}^{12} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{1 \cdot 3}^{12}] {\bar{k}}_{1}^{3} . \\ F o r P_{3} (x) : {\bar{D}}_{2}^{1} = {\bar{K}}_{1, 1}^{1} + {\bar{K}}_{0, 2}^{1}, {\bar{K}}_{1, 1}^{1} = {\bar{K}}_{1 \cdot 3}^{1} {\bar{k}}_{1}^{3}, {\bar{K}}_{0, 2}^{1} = {\bar{t}}_{1}^{1} {\bar{k}}_{2}^{1} + {\bar{t}}_{12}^{1} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} / 2 \Rightarrow \\ {\bar{a}}_{2}^{1} = {\bar{t}}_{1}^{1} {\bar{k}}_{2}^{1} + {\bar{t}}_{12}^{1} ({\bar{k}}_{2}^{12} + {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} + {\bar{k}}_{1 \cdot 3}^{12} {\bar{k}}_{1}^{3}) / 2 + {\bar{t}}_{1 - 3}^{1} ({\bar{k}}_{2}^{1 - 3} / 6 + {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{23} / 2) + {\bar{t}}_{1 - 4}^{1} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} / 8, \\ {\bar{D}}_{3}^{1 - 3} = {\bar{K}}_{2 \cdot 4}^{1 - 3} {\bar{k}}_{1}^{4} = {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}_{2}^{1 - 3})}_{\cdot 4} {\bar{k}}_{1}^{4} + {(T_{1 - 4}^{1 - 3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34})}_{\cdot 5} {\bar{k}}_{1}^{5} . \end{matrix}

\begin{matrix} F o r P_{4} (x) : {\bar{D}}_{3}^{12} = {\bar{K}}_{2, 1}^{12} + {\bar{K}}_{1, 2}^{12}, {\bar{K}}_{2, 1}^{12} = {\bar{K}}_{2 \cdot 3}^{12} {\bar{k}}_{1}^{3}, {\bar{K}}_{1, 2}^{12} = {\bar{K}}_{1 \cdot 3}^{12} {\bar{k}}_{2}^{3} / 2 + {\bar{K}}_{1 \cdot 34}^{12} {\bar{k}}_{1}^{3} {\bar{k}}_{1}^{4}, \\ {\bar{D}}_{4}^{1 - 4} = {\bar{K}}_{3 \cdot 5}^{1 - 4} {\bar{k}}_{1}^{5}, {\bar{D}}_{5}^{1 - 6} = 0 . \end{matrix}

For

E t^{j_{1}} (\hat{w})

O (n^{- 5})

we also need

{\bar{D}}_{j} = {\bar{D}}_{j}^{1}, j = 3, 4,

given by

\begin{matrix} {\bar{D}}_{3} = {\bar{K}}_{2, 1} + {\bar{K}}_{1, 2} + {\bar{K}}_{0, 3}, {\bar{K}}_{2, 1} = {\bar{K}}_{2 \cdot 1} {\bar{k}}_{1}^{1}, \\ {\bar{K}}_{2 \cdot 1} = ({\bar{t}}_{1 - 3} {\bar{k}}_{2}^{23} + {\bar{t}}_{23} {\bar{k}}_{2 \cdot 1}^{23}) / 2 + ({\bar{t}}_{1 - 4} {\bar{k}}_{2}^{2 - 4} + {\bar{t}}_{2 - 4} {\bar{k}}_{2 \cdot 1}^{2 - 4}) / 6 + {\bar{t}}_{1 - 5} {\bar{k}}_{1}^{23} {\bar{k}}_{1}^{45} / 8 + {\bar{t}}_{2 - 5} {\bar{k}}_{1}^{23} {\bar{k}}_{1 \cdot 1}^{45} / 4, \\ {\bar{K}}_{1, 2} = {\bar{K}}_{1 \cdot 1} {\bar{k}}_{2}^{1} + {\bar{K}}_{1 \cdot 12} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} / 2, \\ 2 {\bar{K}}_{1 \cdot 1} = {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{23} + {\bar{t}}_{23} {\bar{k}}_{1 \cdot 1}^{23}, 2 {\bar{K}}_{1 \cdot 12} = {\bar{t}}_{1 - 4} {\bar{k}}_{1}^{34} + \sum_{12}^{2} {\bar{t}}_{2 - 4} {\bar{k}}_{1 \cdot 1}^{34} + {\bar{t}}_{34} {\bar{k}}_{1 \cdot 12}^{34}, \\ {\bar{K}}_{0, 3} = {\bar{t}}_{1} {\bar{k}}_{3}^{1} + {\bar{t}}_{12} {\bar{k}}_{1}^{1} {\bar{k}}_{2}^{2} + {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} {\bar{k}}_{1}^{3} / 6, \\ {\bar{D}}_{4} = {\bar{K}}_{3, 1} + {\bar{K}}_{2, 2} + {\bar{K}}_{1, 3} + {\bar{K}}_{0, 4}, {\bar{K}}_{3, 1} = {\bar{K}}_{3 \cdot 1} {\bar{k}}_{1}^{1}, \\ {\bar{K}}_{3 \cdot 1} = {\bar{t}}_{1 - 3} {\bar{k}}_{3}^{23} / 2 + {\bar{t}}_{23} {\bar{k}}_{3 \cdot 1}^{23} / 2 + {\bar{t}}_{1 - 4} {\bar{k}}_{3}^{2 - 4} / 6 + {\bar{t}}_{2 - 4} {\bar{k}}_{3 \cdot 1}^{2 - 4} / 6 + {\bar{t}}_{1 - 5} {\bar{k}}_{1}^{23} {\bar{k}}_{2}^{45} / 4 \\ + {\bar{t}}_{2 - 5} {\bar{k}}_{1}^{23} {\bar{k}}_{2 \cdot 1}^{45} / 2 + ({\bar{t}}_{1 - 5} {\bar{k}}_{3}^{2 - 5} + {\bar{t}}_{2 - 5} {\bar{k}}_{3 \cdot 1}^{2 - 5}) / 24 + ({\bar{t}}_{1 - 6} {\bar{k}}_{2}^{2 - 4} {\bar{k}}_{1}^{56} + {\bar{t}}_{2 - 6} {\bar{k}}_{2 \cdot 1}^{2 - 4} {\bar{k}}_{1}^{56} \\ + {\bar{t}}_{2 - 6} {\bar{k}}_{2}^{2 - 4} {\bar{k}}_{1 \cdot 1}^{56}) / 12 + {\bar{k}}_{1}^{23} {\bar{k}}_{1}^{45} ({\bar{t}}_{1 - 7} {\bar{k}}_{1}^{67} / 48 + {\bar{t}}_{2 - 7} {\bar{k}}_{1 \cdot 1}^{67} / 16), \\ {\bar{K}}_{2, 2} = {\bar{K}}_{2 \cdot 1} {\bar{k}}_{2}^{1} + {\bar{K}}_{2 \cdot 12} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} / 2, \\ {\bar{K}}_{2 \cdot 1} = {\bar{t}}_{1 - 3} {\bar{k}}_{2}^{23} / 2 + {\bar{t}}_{23} {\bar{k}}_{2 \cdot 1}^{23} / 2 + {\bar{t}}_{1 - 4} {\bar{k}}_{2}^{2 - 4} / 6 + {\bar{t}}_{2 - 4} {\bar{k}}_{2 \cdot 1}^{2 - 4} / 6 + {\bar{t}}_{1 - 5} {\bar{k}}_{1}^{23} {\bar{k}}_{1}^{45} / 8 + {\bar{t}}_{2 - 5} {\bar{k}}_{1}^{23} {\bar{k}}_{1 \cdot 1}^{45} / 4, \\ 2 {\bar{K}}_{2 \cdot 12} = {\bar{t}}_{1 - 4} {\bar{k}}_{2}^{34} + \sum_{12}^{2} {\bar{t}}_{2 - 4} {\bar{k}}_{2 \cdot 1}^{34} + {\bar{t}}_{34} {\bar{k}}_{2 \cdot 12}^{34} + ({\bar{t}}_{1 - 5} {\bar{k}}_{2}^{3 - 5} + \sum_{12}^{2} {\bar{t}}_{13 - 5} {\bar{k}}_{2 \cdot 2}^{3 - 5} + {\bar{t}}_{3 - 5} {\bar{k}}_{2 \cdot 12}^{3 - 5}) / 3 \\ + {\bar{t}}_{1 - 6} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} / 4 + \sum_{12}^{2} {\bar{t}}_{13 - 6} {\bar{k}}_{1}^{34} {\bar{k}}_{1 \cdot 2}^{56} / 2 + {\bar{t}}_{3 - 6} ({\bar{k}}_{1 \cdot 2}^{34} {\bar{k}}_{1 \cdot 1}^{56} + {\bar{k}}_{1}^{34} {\bar{k}}_{1 \cdot 12}^{56}) / 2, \\ {\bar{K}}_{1, 3} = {\bar{K}}_{1 \cdot 1} {\bar{k}}_{3}^{1} + {\bar{K}}_{1 \cdot 12} {\bar{k}}_{1}^{1} {\bar{k}}_{2}^{2} + {\bar{K}}_{1 \cdot 123} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} {\bar{k}}_{1}^{3} / 6, \\ 2 {\bar{K}}_{1 \cdot 1} = {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{23} + {\bar{t}}_{23} {\bar{k}}_{1 \cdot 1}^{23}, 2 {\bar{K}}_{1 \cdot 12} = {\bar{t}}_{1 - 4} {\bar{k}}_{1}^{34} + \sum_{12}^{2} {\bar{t}}_{134} {\bar{k}}_{1 \cdot 2}^{34} + {\bar{t}}_{34} {\bar{k}}_{1 \cdot 12}^{34}, \\ 2 {\bar{K}}_{1 \cdot 123} = {\bar{t}}_{1 - 5} {\bar{k}}_{1}^{45} + \sum_{1 - 3}^{3} ({\bar{t}}_{1345} {\bar{k}}_{1 \cdot 2}^{45} + {\bar{t}}_{3 - 5} {\bar{k}}_{1 \cdot 12}^{45}) + {\bar{t}}_{45} {\bar{k}}_{1 \cdot 1 - 3}^{45}, \\ {\bar{K}}_{0, 4} = {\bar{t}}_{1} {\bar{k}}_{4}^{1} + {\bar{t}}_{12} ({\bar{k}}_{1}^{1} {\bar{k}}_{3}^{2} + {\bar{k}}_{2}^{1} {\bar{k}}_{2}^{2} / 2) + {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} {\bar{k}}_{2}^{3} / 2 + {\bar{t}}_{1 - 4} {\bar{k}}_{1}^{1} {\bar{k}}_{1}^{2} {\bar{k}}_{1}^{3} {\bar{k}}_{1}^{4} / 24 . \end{matrix}

PROOF

{\bar{K}}^{1 - r} (w) = {\bar{K}}^{1 - r}

and

{\bar{K}}_{e}^{1 - r} (w) = {\bar{K}}_{e}^{1 - r}

are functions of w. By (1)

\begin{matrix} {\bar{K}}^{1 - r} (w_{n}) = \sum_{e = r - 1}^{\infty} n^{- e} {\bar{K}}_{e}^{1 - r} (w_{n}) f o r w_{n} = E \hat{w} = w + d_{n}, \end{matrix}

where by (1),

d_{n}

has

i_{1}

th component

{\bar{d}}_{n}^{1} = d_{n}^{i_{1}} = \sum_{e = 1}^{\infty} n^{- e} {\bar{k}}_{e}^{1} .

Consider the Taylor series expansion

\begin{matrix} {\bar{K}}_{k}^{1 - r} (w + d_{n}) = {\bar{K}}_{k}^{1 - r} + {\bar{K}}_{k \cdot 1}^{1 - r} {\bar{d}}_{n}^{1} + {\bar{K}}_{k \cdot 12}^{1 - r} {\bar{d}}_{n}^{1} {\bar{d}}_{n}^{2} / 2! + \dots = \sum_{e = 0}^{\infty} {\bar{K}}_{k, e}^{1 - r} n^{- e} \end{matrix}

say. Substituting into (1) gives (1) with

\begin{matrix} {\bar{a}}_{c}^{1 - r} = \sum_{k + e = c} {\bar{K}}_{k, e}^{1 - r} = \sum_{e = 0}^{c - r + 1} {\bar{K}}_{c - e, e}^{1 - r} . \end{matrix}

(3)

Also

{\bar{K}}_{k, 0}^{1 - r} = {\bar{K}}_{k}^{1 - r}

so that (2) holds with

\begin{matrix} {\bar{D}}_{c}^{1 - r} & = \sum_{e = 1}^{c - r + 1} {\bar{K}}_{c - e, e}^{1 - r} : \\ {\bar{D}}_{r}^{1 - r} & = {\bar{K}}_{r - 1, 1}^{1 - r}, {\bar{D}}_{r + 1}^{1 - r} = \sum_{e = 1}^{2} {\bar{K}}_{r + 1 - e, e}^{1 - r}, \dots □ \end{matrix}

(4)

An alternative proof can be obtained using §6. This corrects

C_{e} = {\bar{a}}_{e}^{1}

given in Appendix B of Withers (1987). Withers (1982) uses

K_{k}^{j_{1} \dots j_{r}} = {\bar{K}}_{k}^{1 - r}

for

{\bar{a}}_{k}^{1 - r}

but the expression for

K_{2}^{a b}

on p67, lines 2-3 omitted the term

A_{i}^{a} A_{j}^{b} k_{1, k}^{i j} k_{1}^{k}

. That is, the last term in

{\bar{a}}_{2}^{12}

of Theorem 4.1 was omitted. Similarly the results on p67 for

r = 3, 4

are only true when the

\hat{w}

is unbiased or the cumulant coefficients of

\hat{w}

do not depend on w, as they omit the derivatives of

{\bar{k}}_{e}^{1 - r}

. The examples given there are not affected as

\hat{w}

is unbiased. Nor are the nonparametric examples of Withers (1983, 1988) affected, as the empirical distribution is an unbiased estimate of a distribution. Likewise

\hat{w}

is unbiased for the examples of Withers (1989). M-estimates are biased but the results of Withers and Nadarajah (2010a) are not affected as only

K_{1}^{j_{1} j_{2}}, K_{1}^{j_{1}}, K_{2}^{j_{1} j_{2} j_{3}}

are given. No changes are needed for Withers and Nadarajah (2010b, 2011a, 2011b, 2012a, 2012b, 2014b). Applications to non-parametric and parametric confidence intervals were given in Withers (1983, 1988, 1989) and to ellipsoidal confidence regions and power in Withers and Nadarajah (2012a) and Kakizawa (2015). For nonparametric problems,

F (x)

and its empirical distribution

F_{n} (x)

play the role of w and

\hat{w}

; since it is unbiased, no corrections are needed. For

q = 1, a_{r i} = {\bar{a}}_{i}^{1 - r}

were given for parametric and non-parametric problems in Withers (1982, 1983, 1988), and expressions for the classic Edgeworth expansion of

Y_{n w}

in terms of

a_{r i}

were given in Withers (1984). For

q \geq 1

{\bar{a}}_{i}^{1 - r}

for parametric problems were given in Withers (1982), and can be obtained easily from

a_{r i}

given when

q = 1

for 1 sample and multi sample non-parametric problems in Withers (1983, 1988), and for semi-parametric problems in Withers and Nadarajah (2010a, 2011a, 2014b). All these results can be extended to samples with independent non-identically distributed residuals, as done in Withers and Nadarajah (2010 §6, 2011b, 2012b). The extension to matrix

\hat{w}

just needs a slight change in notation. For example in Withers and Nadarajah (2011b, 2011c, 2012b),

\hat{w}

can be viewed as a function of the mean of n independent complex random matrices, although n is actually the number of transmitters or receivers. Extensions to dependent random variables are also possible: see Withers and Nadarajah (2012c).

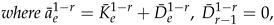
5. Cumulant Coefficients for Univariate $t (\hat{w})$

Now suppose that $q = 1$ . Let

_{k} K_{r e}

be the coefficient of

n^{- e}

_{k} K^{1 - r}

. We write

{\bar{K}}_{e}^{1 - r}

K_{r e}

. For

E \hat{w} = w

, (1), (3) and (4) become

\begin{matrix} K^{r} = κ_{r} (\hat{t}) = \sum_{e = r - 1}^{\infty} n^{- e} K_{r e}, r \geq 1; K_{r e} = \sum_{k = r - 1}^{e}_{k} K_{r e} : \\ K_{r, r - 1} =_{r - 1} K_{r, r - 1}, K_{r r} = \sum_{k = r - 1}^{r}_{k} K_{r r}, K_{r, r + 1} = \sum_{k = r - 1}^{r + 1}_{k} K_{r, r + 1}, \dots \end{matrix}

(1)

For

E \hat{w} \neq w

, (1), (2) and (3) become

\begin{matrix} K^{r} = κ_{r} (\hat{t}) = \sum_{e = r - 1}^{\infty} n^{- e} a_{r e}, r \geq 1; a_{r e} = K_{r e} + D_{r e}, D_{r c} = \sum_{e = 1}^{c - r + 1} K_{r, c - e, e} : \\ D_{r, r - 1} = 0, D_{r r} = K_{r, r - 1, 1}, D_{r, r + 1} = \sum_{e = 1}^{2} K_{r, r + 1 - e, e}, \dots \end{matrix}

Here we give the cumulant coefficients

K_{r e}

needed for the Edgeworth expansion of

Y_{n t}

of (5) for

P_{r} (x), r \leq 4

. We do this when

E \hat{w} = w

in Corollary 5.1 and when

E \hat{w} \neq w

in Corollaries 5.3 and 5.4. To show more clearly the expressions we need in molecular form, we introduce the following ions, (expressions with unpaired suffixes),

(2)

Where a suffix does not have a match then summation does not occur. For example the RHS of

{\bar{s}}^{1} = {\bar{k}}_{1}^{12} {\bar{t}}_{2}

sums over

i_{2}

but not

i_{1}

. Let

v, c_{01}, c_{02}, c_{21}, c_{22}, c_{23},

c_{11}, \dots, c_{1, 10}, c_{31}, \dots, c_{3, 11}

be the 27 functions of

ω

given on p4234–4235 of Withers (1989), labelled there as

I_{2} (\binom{2}{0}), I_{1} (\binom{1}{0}), \dots, I_{301} (\binom{222}{000})

. By Corollaries 5.1, 5.3 below, those needed for

P_{r} (x), r \leq 2

, of (4), that is, for the Edgeworth expansion of

Y_{n t}

of (5) to

O (n^{- 3 / 2})

, are the following molecules.

\begin{matrix} For P_{0} (x) : v = K_{21} = {\bar{t}}_{1} {\bar{k}}_{1}^{12} {\bar{t}}_{2} . \\ For P_{1} (x), K_{11} : c_{02} = {\bar{t}}_{12} {\bar{k}}_{1}^{12}; D_{11} : c_{01} = {\bar{t}}_{1} {\bar{k}}_{1}^{1}; \\ f o r K_{32} : c_{21} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{2}^{1 - 3} = {\bar{t}}_{1} {\bar{y}}^{1}, c_{23} = {\bar{s}}^{1} {\bar{t}}_{12} {\bar{s}}^{2} = {\bar{s}}^{1} {\bar{u}}_{1} . \\ For P_{2} (x), K_{22} : c_{11} = {\bar{t}}_{1} {\bar{k}}_{2}^{12} {\bar{t}}_{2} = {\bar{t}}_{1} {\bar{S}}^{1}, c_{15} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{23}, c_{19} = {\bar{t}}_{12} {\bar{X}}^{12}, \\ c_{1, 10} = {\bar{s}}^{1} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{23} = {\bar{z}}_{23} {\bar{k}}_{1}^{23}; \\ f o r D_{22} : c_{12} = {\bar{k}}_{1}^{1} {\bar{k}}_{1 \cdot 1}^{23} {\bar{t}}_{2} {\bar{t}}_{3}, c_{16} = {\bar{k}}_{1}^{1} {\bar{u}}_{1} = {\bar{k}}_{1}^{1} {\bar{t}}_{. 12} {\bar{k}}_{1}^{23} {\bar{t}}_{3}, \\ f o r K_{43} : c_{31} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{k}}_{3}^{1 - 4}, c_{36} = {\bar{y}}^{3} {\bar{u}}_{3}, c_{3, 10} = {\bar{u}}_{1} {\bar{k}}_{1}^{12} {\bar{u}}_{2}, c_{3, 11} = {\bar{s}}^{1} {\bar{s}}^{2} {\bar{s}}^{3} {\bar{t}}_{1 - 3} . \end{matrix}

Each molecule can be written as a shape. For example

c_{19}

is a rectangle. We now give the molecules

L_{j}, L_{i j}

needed for the Edgeworth expansion to

O (n^{- 5 / 2})

, that is, for

P_{r} (x)

for

r = 3, 4

. Note that

P_{r} (x)

needs the derivatives of

t (w)

up to order

r + 1

\begin{matrix} For P_{3} (x), K_{12} : L_{1} = {\bar{t}}_{12} {\bar{k}}_{2}^{12}, L_{2} = {\bar{t}}_{1 - 3} {\bar{k}}_{2}^{1 - 3}, L_{3} = {\bar{t}}_{1 - 4} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34}; \\ f o r K_{33} : L_{4} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{3}^{1 - 3}, L_{5} = {\bar{u}}_{1} {\bar{S}}^{1}, L_{6} = {\bar{t}}_{13} {\bar{t}}_{2} {\bar{t}}_{4} {\bar{k}}_{3}^{1 - 4}, L_{71} = {\bar{z}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{3}, \\ L_{72} = {\bar{y}}^{1} {\bar{t}}_{145} {\bar{k}}_{1}^{45}, L_{73} = {\bar{t}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{u}}_{3}, L_{74} = {\bar{t}}_{14} {\bar{k}}_{1}^{45} {\bar{t}}_{52} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{3}, \\ L_{81} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 4} {\bar{s}}^{3} {\bar{s}}^{4}, L_{82} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 3} {\bar{v}}^{3}, L_{83} = {\bar{X}}^{34} {\bar{z}}_{34}, \\ L_{84} = {\bar{X}}^{14} {\bar{t}}_{45} {\bar{k}}_{1}^{56} {\bar{t}}_{61}, a s e x a g o n, \\ f o r K_{54} : L_{9} = {\bar{t}}_{1} \dots {\bar{t}}_{5} {\bar{k}}_{4}^{1 - 5}, L_{10} = {\bar{u}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{k}}_{3}^{1 - 4}, L_{11} = {\bar{y}}^{1} {\bar{Y}}_{1} = {\bar{y}}^{1} {\bar{t}}_{12} {\bar{y}}^{2}, \\ L_{121} = {\bar{y}}^{1} {\bar{t}}_{1 - 3} {\bar{s}}^{2} {\bar{s}}^{3}, L_{122} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{u}}_{2} {\bar{u}}_{3}, L_{123} = {\bar{Y}}_{2} {\bar{v}}^{2}, \\ L_{131} = {\bar{s}}^{1} \dots {\bar{s}}^{4} {\bar{t}}_{1 - 4}, L_{132} = {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{v}}^{3}, L_{133} = {\bar{v}}^{1} {\bar{t}}_{12} {\bar{v}}^{2} = {\bar{v}}^{1} {\bar{x}}_{1} . \\ For P_{4} (x), K_{23} : L_{14} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{3}^{12}, L_{15} = {\bar{t}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{3}, L_{161} = {\bar{S}}^{1} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{23}, \\ L_{162} = {\bar{z}}_{12} {\bar{k}}_{2}^{12}, L_{171} = {\bar{X}}^{24} {\bar{t}}_{24} . L_{181} = {\bar{t}}_{1 - 3} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{4}, L_{182} = {\bar{t}}_{12} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{34}, L_{191} = {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{1 - 4} {\bar{s}}^{4}, \end{matrix}

\begin{matrix} L_{192} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 4} {\bar{k}}_{2}^{3 - 5} {\bar{t}}_{5}, L_{193} = {\bar{t}}_{1 - 3} {\bar{k}}_{2}^{2 - 4} {\bar{t}}_{45} {\bar{k}}_{1}^{51}, L_{194} = {\bar{t}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{3 - 5} {\bar{k}}_{1}^{45}, \\ L_{201} = {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{t}}_{1 - 5} {\bar{s}}^{5}, L_{202} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 4} {\bar{X}}^{34}, L_{203} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{34} {\bar{t}}_{4 - 6} {\bar{k}}_{1}^{56}, \\ L_{204} = {\bar{t}}_{135} ({\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}) {\bar{t}}_{246}; \\ f o r K_{44} : L_{21} = \bar{t} \dots {\bar{t}}_{4} {\bar{k}}_{4}^{1 - 4}, L_{221} = {\bar{Y}}_{2} {\bar{k}}_{2}^{23} {\bar{t}}_{3}, L_{222} = {\bar{u}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{3}^{1 - 3}, \\ L_{231} = {\bar{s}}^{1} {\bar{z}}_{12} {\bar{S}}^{2} . L_{241} = {\bar{x}}_{2} {\bar{S}}^{2}, L_{242} = {\bar{u}}_{1} {\bar{k}}_{2}^{12} {\bar{u}}_{2} . \\ L_{25} = {\bar{t}}_{12} {\bar{k}}_{4}^{1 - 5} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{5}, L_{261} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{3 - 5} {\bar{s}}^{5}, L_{262} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{4 - 6} {\bar{k}}_{1}^{56}, \\ L_{263} = {\bar{t}}_{12} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{3} {\bar{u}}_{4}, L_{264} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{3}^{1 - 4} ({\bar{t}}_{35} {\bar{t}}_{46}) {\bar{k}}_{1}^{56}, \\ L_{271} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{2 - 4} {\bar{y}}^{4}, L_{272} = {\bar{t}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{Y}}_{3}, L_{273} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} ({\bar{t}}_{24} {\bar{t}}_{35}) {\bar{k}}_{3}^{4 - 6} {\bar{t}}_{6}, \\ L_{281} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{2 - 5} {\bar{s}}^{4} {\bar{s}}^{5}, L_{282} = {\bar{s}}^{1} {\bar{k}}_{1}^{23} {\bar{t}}_{1 - 4} {\bar{y}}^{4}, L_{283} = {\bar{u}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{z}}_{23}, \\ L_{284} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{2 - 4} {\bar{v}}^{4}, L_{285} = {\bar{Y}}_{2} {\bar{k}}_{1}^{23} {\bar{t}}_{3 - 5} {\bar{k}}_{1}^{45}, L_{286} = {\bar{t}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{z}}_{34} {\bar{s}}^{4}, \\ L_{287} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{24} {\bar{k}}_{1}^{45} {\bar{z}}_{53}, L_{288} = {\bar{y}}^{1} {\bar{t}}_{1 - 3} {\bar{X}}^{23}, \\ L_{289} = {\bar{t}}_{12} {\bar{k}}_{2}^{1 - 3} {\bar{x}}_{3}, L_{2810} = {\bar{u}}_{1} {\bar{k}}_{2}^{1 - 3} ({\bar{t}}_{24} {\bar{t}}_{35}) {\bar{k}}_{1}^{45}, \\ L_{2811} = {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} ({\bar{t}}_{24} {\bar{k}}_{1}^{45} {\bar{t}}_{36} {\bar{k}}_{1}^{67}) {\bar{t}}_{57}, L_{291} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 5} {\bar{s}}^{3} {\bar{s}}^{4} {\bar{s}}^{5}, L_{292} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 4} {\bar{v}}^{3} {\bar{s}}^{4}, \\ L_{293} = {\bar{X}}^{34} {\bar{t}}_{3 - 6} {\bar{s}}^{5} {\bar{s}}^{6}, L_{294} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{34} {\bar{t}}_{4 - 6} {\bar{s}}^{5} {\bar{s}}^{6}, L_{295} = {\bar{k}}_{1}^{12} ({\bar{z}}_{13} {\bar{z}}_{24}) {\bar{k}}_{1}^{34}, \\ L_{296} = {\bar{k}}_{1}^{12} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{34} {\bar{x}}_{4}, L_{297} = {\bar{k}}_{1}^{12} {\bar{t}}_{135} {\bar{v}}^{5} {\bar{t}}_{24} {\bar{k}}_{1}^{34}, \\ L_{298} = {\bar{X}}^{14} {\bar{t}}_{45} {\bar{k}}_{1}^{56} {\bar{z}}_{61}, L_{299} = {\bar{X}}^{14} {\bar{t}}_{45} {\bar{X}}^{58}; \\ f o r K_{65} : L_{30} = {\bar{t}}_{1} \dots {\bar{t}}_{6} k_{5}^{1 - 6}, L_{31} = {\bar{u}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{5} {\bar{k}}_{4}^{1 - 5}, L_{32} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{4}^{1 - 5} {\bar{t}}_{45}, \\ L_{331} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{3}^{1 - 4} {\bar{z}}_{45} {\bar{s}}^{5}, L_{332} = {\bar{u}}_{1} {\bar{u}}_{2} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{3} {\bar{t}}_{4}, L_{333} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{3}^{1 - 4} {\bar{x}}_{4}, \\ L_{341} = {\bar{t}}_{1 - 3} {\bar{y}}^{1} {\bar{s}}^{2} {\bar{y}}^{3}, L_{342} = {\bar{Y}}_{2} {\bar{k}}_{2}^{2 - 4} {\bar{t}}_{3} {\bar{u}}_{4}, L_{343} = {\bar{Y}}_{1} {\bar{k}}_{1}^{12} {\bar{Y}}_{2}, \\ L_{351} = {\bar{y}}^{3} {\bar{t}}_{3 - 6} {\bar{s}}^{4} {\bar{s}}^{5} {\bar{s}}^{6}, L_{352} = {\bar{t}}_{1} {\bar{u}}_{2} {\bar{k}}_{2}^{1 - 3} {\bar{z}}_{34} {\bar{s}}^{4}, \\ L_{353} = {\bar{y}}^{1} {\bar{t}}_{12} {\bar{v}}^{2}, L_{354} = {\bar{Y}}_{4} {\bar{k}}_{1}^{45} {\bar{t}}_{5 - 7} {\bar{s}}^{6} {\bar{s}}^{7}, L_{355} = {\bar{u}}_{1} {\bar{u}}_{2} {\bar{u}}_{3} {\bar{k}}_{2}^{1 - 3}, \\ L_{356} = {\bar{t}}_{1} {\bar{u}}_{2} {\bar{k}}_{2}^{1 - 3} {\bar{x}}_{3}, L_{357} = {\bar{t}}_{3 - 5} {\bar{y}}^{3} {\bar{v}}^{4} {\bar{s}}^{5} . L_{361} = {\bar{s}}^{1} \dots {\bar{s}}^{5} {\bar{t}}_{1 - 5}, \\ L_{362} = {\bar{s}}^{1} {\bar{s}}^{2} {\bar{s}}^{3} {\bar{t}}_{1 - 4} {\bar{v}}^{4}, L_{363} = {\bar{s}}^{1} {\bar{z}}_{13} {\bar{k}}_{1}^{34} {\bar{t}}_{4 - 6} {\bar{s}}^{5} {\bar{s}}^{6}, L_{364} = {\bar{v}}^{1} {\bar{z}}_{12} {\bar{v}}^{2}, \\ L_{365} = {\bar{s}}^{1} {\bar{z}}_{13} {\bar{k}}_{1}^{34} {\bar{x}}_{4}, L_{366} = {\bar{x}}_{1} {\bar{k}}_{1}^{12} {\bar{x}}_{2} . \end{matrix}

These

c_{r s}

and

L_{j}

don’t use derivatives of

{\bar{k}}_{e}^{1 - r}

, the cumulant coefficients of

\hat{w}

Corollary 1.

Suppose that

\hat{w}

is anunbiasedstandard estimate of

w \in R^{p}

with respect to n, and that

q = 1

. Then the cumulants of

\hat{t} = t (\hat{w})

can be expanded as (1) with bounded cumulant coefficients

K_{r e}

. The leading coefficients needed for

P_{r} (x)

of (4) for the distribution of

Y_{n t}

of (5) are as follows.

\begin{matrix} K_{10} = \bar{t} = t (w) . F o r P_{0} (x) : K_{21} = v = {\bar{t}}_{1} {\bar{k}}_{1}^{12} {\bar{t}}_{2} . \\ F o r P_{1} (x) : K_{11} = c_{02} / 2, K_{32} = c_{21} + 3 c_{23} . \\ F o r P_{2} (x) : K_{22} = \sum_{k = 1}^{2}_{k} K_{22},_{1} K_{22} = c_{11},_{2} K_{22} = c_{15} + c_{19} / 2 + c_{1, 10}, \\ K_{43} = c_{31} + 12 c_{36} + 12 c_{3, 10} + 4 c_{3, 11} . \\ F o r P_{3} (x) : K_{12} = \sum_{k = 1}^{2}_{k} K_{12},_{1} K_{12} = L_{1} / 2,_{2} K_{12} = L_{2} / 6 + L_{3} / 8; \end{matrix}

(3)

(4)

(5)

\begin{matrix} L_{35} = \sum_{k = 1}^{7} d_{k} L_{35 k}, d_{1} = 1, d_{2} = d_{3} = d_{7} = 6, d_{4} = 3, d_{5} = 2, d_{6} = 12, \\ L_{36} = \sum_{k = 1}^{6} e_{k} L_{36 k}, e_{1} = 1, e_{2} = 20, e_{3} = 15, e_{7} = 6, e_{4} = e_{5} = e_{6} = 60 . \\ A l s o, K_{13} = {\bar{t}}_{12} {\bar{k}}_{3}^{12} / 2 + {\bar{t}}_{1 - 3} {\bar{k}}_{3}^{1 - 3} / 6 + {\bar{t}}_{1 - 4} {({\bar{k}}^{12} {\bar{k}}^{34})}_{3} / 8 + {\bar{t}}_{1 - 4} {\bar{k}}_{3}^{1 - 4} / 24 \\ + {\bar{t}}_{1 - 5} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} / 12 + {\bar{t}}_{1 - 6} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} / 48, \\ K_{14} = {\bar{t}}_{12} {\bar{k}}_{4}^{12} / 2 + {\bar{t}}_{1 - 3} {\bar{k}}_{4}^{1 - 3} / 6 + {\bar{t}}_{1 - 4} [{({\bar{k}}^{12} {\bar{k}}^{34})}_{4} / 8 + {\bar{k}}_{4}^{1 - 4} / 24] + {\bar{t}}_{1 - 5} [{\bar{k}}_{4}^{1 - 5} / 120 \\ + {({\bar{k}}^{1 - 3} {\bar{k}}^{45})}_{4} / 12] + {\bar{t}}_{1 - 6} [{({\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56})}_{4} / 48 + {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56} / 48 + {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} / 72] \\ + {\bar{t}}_{1 - 7} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67} / 48 + {\bar{t}}_{1 - 8} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} / 384 . \end{matrix}

PROOF Since

q = 1, \sum^{N}

becomes N. We write

T_{1 - s}^{1 - r}, U_{1 - s}^{1 - r}, V_{1 - s}^{1 - r}

T_{1 - s}^{r}, U_{1 - s}^{r}, V_{1 - s}^{r}

. By Theorem 3.1 we need the following.

\begin{matrix} T_{1 - 4}^{3} / 3 = {\bar{t}}_{13} {\bar{t}}_{2} {\bar{t}}_{4}, T_{1 - 3}^{2} / 2 = {\bar{t}}_{12} {\bar{t}}_{3}, T_{1 - 4}^{2} / 2 = {\bar{t}}_{1 - 3} {\bar{t}}_{4} + {\bar{t}}_{13} {\bar{t}}_{24}, \\ T_{1 - 5}^{4} / 12 = {\bar{t}}_{14} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5}, T_{1 - 6}^{4} / 4 = {\bar{t}}_{135} {\bar{t}}_{2} {\bar{t}}_{4} {\bar{t}}_{6} + 3 {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{4} {\bar{t}}_{6}, \\ T_{1 - 5}^{3} / 3 = {\bar{t}}_{124} {\bar{t}}_{3} {\bar{t}}_{5} + 3 {\bar{t}}_{145} {\bar{t}}_{2} {\bar{t}}_{3} / 2 + 3 {\bar{t}}_{12} {\bar{t}}_{34} {\bar{t}}_{5} + 3 {\bar{t}}_{14} {\bar{t}}_{25} {\bar{t}}_{3}, \\ T_{1 - 6}^{3} = 3 {\bar{t}}_{1235} {\bar{t}}_{4} {\bar{t}}_{6} / 2 + 6 {\bar{t}}_{1 - 3} {\bar{t}}_{45} {\bar{t}}_{6} + 3 {\bar{t}}_{135} {\bar{t}}_{24} {\bar{t}}_{6} + {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{46}, \\ T_{1 - 6}^{5} / 20 = {\bar{t}}_{15} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{6}, U_{1 - 6}^{5} / 15 = {\bar{t}}_{14} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{6}, \\ T_{1 - 7}^{5} / 30 = {\bar{t}}_{146} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{7} + 2 {\bar{t}}_{14} {\bar{t}}_{26} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{7} + 2 {\bar{t}}_{14} {\bar{t}}_{56} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{7}, \\ T_{1 - 8}^{5} = {\bar{t}}_{1357} {\bar{t}}_{2} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} + 60 {\bar{t}}_{135} {\bar{t}}_{27} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} + 60 {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{47} {\bar{t}}_{6} {\bar{t}}_{8} . U_{1 - 4}^{2} = {\bar{t}}_{1 - 3} {\bar{t}}_{4} / 3 + {\bar{t}}_{12} {\bar{t}}_{34} / 4, \\ T_{1 - 5}^{2} = {\bar{t}}_{1 - 4} {\bar{t}}_{5} / 3 + {\bar{t}}_{1245} {\bar{t}}_{3} / 2 + {\bar{t}}_{124} {\bar{t}}_{35} + {\bar{t}}_{145} {\bar{t}}_{23} / 2, \\ T_{1 - 6}^{2} = {\bar{t}}_{1 - 5} {\bar{t}}_{6} + 2 {\bar{t}}_{1235} {\bar{t}}_{46} + {\bar{t}}_{1 - 3} {\bar{t}}_{4 - 6} + 2 {\bar{t}}_{135} {\bar{t}}_{246} / 3, \\ T_{1 - 5}^{4} / 12 = {\bar{t}}_{14} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5}, U_{1 - 5}^{4} / 4 = {\bar{t}}_{12} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{5}, \\ U_{1 - 6}^{4} / 2 = 3 {\bar{t}}_{125} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{6} + 2 {\bar{t}}_{156} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} + 6 {\bar{t}}_{12} {\bar{t}}_{35} {\bar{t}}_{4} {\bar{t}}_{6} + 3 {\bar{t}}_{15} {\bar{t}}_{26} {\bar{t}}_{3} {\bar{t}}_{4}, \\ V_{1 - 6}^{4} / 6 = {\bar{t}}_{124} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{6} + {\bar{t}}_{12} {\bar{t}}_{34} {\bar{t}}_{5} {\bar{t}}_{6} + {\bar{t}}_{14} {\bar{t}}_{25} {\bar{t}}_{3} {\bar{t}}_{6}, \\ T_{1 - 7}^{4} = 6 {\bar{t}}_{1246} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{7} + 3 {\bar{t}}_{1456} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{7} + 24 {\bar{t}}_{124} {\bar{t}}_{36} {\bar{t}}_{5} {\bar{t}}_{7} + 12 {\bar{t}}_{124} {\bar{t}}_{56} {\bar{t}}_{3} {\bar{t}}_{7} \\ + 12 {\bar{t}}_{145} {\bar{t}}_{26} {\bar{t}}_{3} {\bar{t}}_{7} + 12 {\bar{t}}_{146} {\bar{t}}_{23} {\bar{t}}_{5} {\bar{t}}_{7} + 24 {\bar{t}}_{146} {\bar{t}}_{25} {\bar{t}}_{3} {\bar{t}}_{7} + 4 {\bar{t}}_{146} {\bar{t}}_{57} {\bar{t}}_{2} {\bar{t}}_{3} \\ + 12 {\bar{t}}_{456} {\bar{t}}_{17} {\bar{t}}_{2} {\bar{t}}_{3} + 12 {\bar{t}}_{12} {\bar{t}}_{34} {\bar{t}}_{56} {\bar{t}}_{7} + 12 {\bar{t}}_{14} {\bar{t}}_{25} {\bar{t}}_{36} {\bar{t}}_{7} + 12 {\bar{t}}_{14} {\bar{t}}_{26} {\bar{t}}_{57} {\bar{t}}_{3}, \\ T_{1 - 8}^{4} = 2 {\bar{t}}_{12357} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} + 12 {\bar{t}}_{1235} {\bar{t}}_{47} {\bar{t}}_{6} {\bar{t}}_{8} + 6 {\bar{t}}_{1357} {\bar{t}}_{24} {\bar{t}}_{6} {\bar{t}}_{8} \\ + 6 {\bar{t}}_{123} {\bar{t}}_{457} {\bar{t}}_{6} {\bar{t}}_{8} + 6 {\bar{t}}_{135} {\bar{t}}_{247} {\bar{t}}_{6} {\bar{t}}_{8} + 12 {\bar{t}}_{123} {\bar{t}}_{45} {\bar{t}}_{67} {\bar{t}}_{8} + 24 {\bar{t}}_{135} {\bar{t}}_{24} {\bar{t}}_{67} {\bar{t}}_{8} \\ + 6 {\bar{t}}_{135} {\bar{t}}_{27} {\bar{t}}_{48} {\bar{t}}_{6} + 3 {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{47} {\bar{t}}_{68}, T_{1 - 7}^{6} / 30 = {\bar{t}}_{16} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{5} {\bar{t}}_{7}, U_{1 - 7}^{6} / 60 = {\bar{t}}_{15} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{7}, \end{matrix}

\begin{matrix} T_{1 - 8}^{6} / 60 = {\bar{t}}_{157} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} + 3 {\bar{t}}_{15} {\bar{t}}_{27} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} + 2 {\bar{t}}_{15} {\bar{t}}_{67} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} {\bar{t}}_{8}, \\ U_{1 - 8}^{6} / 90 = {\bar{t}}_{147} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{6} {\bar{t}}_{8} + 4 {\bar{t}}_{14} {\bar{t}}_{27} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{6} {\bar{t}}_{8} + {\bar{t}}_{17} {\bar{t}}_{48} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{6}, \\ T_{1 - 9}^{6} / 60 = {\bar{t}}_{1468} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{7} {\bar{t}}_{9} + 6 {\bar{t}}_{146} {\bar{t}}_{28} {\bar{t}}_{3} {\bar{t}}_{5} {\bar{t}}_{7} {\bar{t}}_{9} + 6 {\bar{t}}_{146} {\bar{t}}_{58} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{7} {\bar{t}}_{9} \\ + 3 {\bar{t}}_{468} {\bar{t}}_{15} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{7} {\bar{t}}_{9} + 2 {\bar{t}}_{14} {\bar{t}}_{26} {\bar{t}}_{38} {\bar{t}}_{5} {\bar{t}}_{7} {\bar{t}}_{9} + 12 {\bar{t}}_{14} {\bar{t}}_{26} {\bar{t}}_{58} {\bar{t}}_{3} {\bar{t}}_{7} {\bar{t}}_{9} + 6 {\bar{t}}_{14} {\bar{t}}_{56} {\bar{t}}_{78} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{9}, \\ T_{1 - 10}^{6} / 6 = {\bar{t}}_{13579} {\bar{t}}_{2} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} {\bar{t}}_{10} + 20 {\bar{t}}_{1357} {\bar{t}}_{29} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} {\bar{t}}_{10} \\ + 15 {\bar{t}}_{135} {\bar{t}}_{279} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{8} {\bar{t}}_{10} + 60 {\bar{t}}_{135} {\bar{t}}_{27} {\bar{t}}_{49} {\bar{t}}_{6} {\bar{t}}_{8} {\bar{t}}_{10} + 60 {\bar{t}}_{135} {\bar{t}}_{27} {\bar{t}}_{89} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{t}}_{10} + 60 {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{47} {\bar{t}}_{69} {\bar{t}}_{8} {\bar{t}}_{10} . \\ F o r P_{1} (x) : T_{1 - 4}^{3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} = 3 c_{23} . \\ F o r P_{2} (x) : T_{1 - 3}^{2} {\bar{k}}_{2}^{1 - 3} / 2 = c_{15}, T_{1 - 4}^{2} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} / 2 = c_{19} / 2 + c_{1, 10}; \\ K_{43} = c_{31} + g_{1} + g_{2} f o r g_{1} = T_{1 - 5}^{4} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} = 12 c_{36}, \\ g_{2} = T_{1 - 6}^{4} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} = 4 c_{3, 11} + 12 c_{3, 10} . \\ F o r P_{3} (x) :_{2} K_{33} = L_{4} + 3 L_{5}^{'}, L_{5}^{'} = T_{1 - 4}^{3} / 3 {({\bar{k}}^{12} {\bar{k}}^{34})}_{3} = {\bar{t}}_{13} {\bar{t}}_{2} {\bar{t}}_{4} {({\bar{k}}^{12} {\bar{k}}^{34})}_{3} = 2 L_{5}, \\ L_{6} = T_{1 - 4}^{3} / 3 {\bar{k}}_{3}^{1 - 4}, L_{7} = T_{1 - 5}^{3} / 3 {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45}, \\ L_{71} = {\bar{s}}^{4} {\bar{t}}_{412} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{3}, L_{8} = T_{1 - 6}^{3} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}, \\ L_{81} = {\bar{t}}_{1235} {\bar{t}}_{4} {\bar{t}}_{6} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}, L_{82} = {\bar{t}}_{1 - 3} {\bar{t}}_{45} {\bar{t}}_{6} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}, L_{83} = {\bar{t}}_{135} {\bar{t}}_{24} {\bar{t}}_{6} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}, \\ L_{84} = {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{46} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} . \\ K_{54} i s g i v e n b y () w i t h L_{10} = T_{1 - 6}^{5} / 20 {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56}, L_{11} = U_{1 - 6}^{5} / 15 {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6}, \\ L_{12} = T_{1 - 7}^{5} / 30 {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67}, L_{121} = {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{146} {\bar{s}}^{4} {\bar{s}}^{6}, L_{13} = T_{1 - 8}^{5} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} . \\ F o r P_{4} (x) :_{2} K_{23} = L_{15} + L_{16} + L_{17} / 2, L_{15} = T_{1 - 3}^{2} / 2 {\bar{k}}_{3}^{1 - 3}, L_{16} = \sum_{k = 1}^{2} L_{16 k}, \\ L_{162} = {\bar{s}}^{2} {\bar{t}}_{2 - 4} {\bar{k}}_{2}^{34}, L_{17} = T_{1 - 4}^{2} / 2 {({\bar{k}}^{12} {\bar{k}}^{34})}_{3} = \sum_{k = 1}^{2} L_{17 k}, L_{172} = L_{171}; \\ _{3} K_{23} = \sum_{k = 18}^{20} L_{k} : L_{18} = U_{1 - 4}^{2} {\bar{k}}_{3}^{1 - 4} = L_{181} / 3 + L_{182} / 4, \\ L_{19} = T_{1 - 5}^{2} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} = \sum_{k = 1}^{4} L_{19 k} / g_{k} f o r g_{1} = 3, g_{2} = g_{3} = g_{4} = 1, \\ L_{192} = {\bar{t}}_{3} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{1245} {\bar{k}}_{1}^{45}, L_{193} = {\bar{t}}_{412} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{35} {\bar{k}}_{1}^{54}, L_{194} = {\bar{k}}_{1}^{45} {\bar{t}}_{451} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{23}, \\ L_{20} = T_{1 - 6}^{2} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} / 4 = L_{201} / 4 + L_{202} / 2 + L_{203} / 4 + L_{204} / 6, \\ L_{202} = {\bar{k}}_{1}^{12} {\bar{t}}_{1235} ({\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56}) {\bar{t}}_{46} . \\ _{3} K_{44} = L_{21} + 12 L_{22} + 4 L, L = T_{1 - 6}^{4} / 4 {({\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56})}_{4} = L_{23} + 3 L_{24}, \\ L_{22} = T_{1 - 5}^{4} / 12 {({\bar{k}}^{1 - 3} {\bar{k}}^{45})}_{4} = (L_{221} + L_{222}) b y (), \end{matrix}

\begin{matrix} L_{23} = {\bar{t}}_{135} {\bar{t}}_{2} {\bar{t}}_{4} {\bar{t}}_{6} {({\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56})}_{4} = \sum_{k = 1}^{3} L_{23 k} b y (), L_{23 k} \equiv L_{231} . B y (), \\ L_{24} = {\bar{t}}_{13} {\bar{t}}_{25} {\bar{t}}_{4} {\bar{t}}_{6} {({\bar{k}}^{12} {\bar{k}}^{34} {\bar{k}}^{56})}_{4} = 2 L_{241} + L_{242}; \\ _{4} K_{44} = 2 L_{25} + 2 L_{26} + 6 L_{27} + L_{28} + L_{29}, L_{25} = {\bar{k}}_{4}^{1 - 5} U_{1 - 5}^{4} / 4, \\ L_{26} = U_{1 - 6}^{4} / 2 {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56}, L_{27} = V_{1 - 6}^{4} / 6 {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} = \sum_{k = 1}^{3} L_{27 k}, \\ L_{28} = T_{1 - 7}^{4} {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67}, L_{29} = T_{1 - 8}^{4} {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78}; \\ f o r K_{65} : L_{31} = T_{1 - 7}^{6} / 30 k_{4}^{1 - 5} k_{1}^{67}, \\ L_{32} = U_{1 - 7}^{6} / 60 k_{4}^{1 - 5} k_{1}^{67} / v, L_{33} = T_{1 - 8}^{6} / 60 {\bar{k}}_{3}^{1 - 4} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78}, L_{34} = U_{1 - 8}^{6} / 90 {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{2}^{4 - 6} {\bar{k}}_{2}^{78}, \\ L_{35} = T_{1 - 9}^{6} / 60 {\bar{k}}_{2}^{1 - 3} {\bar{k}}_{1}^{45} {\bar{k}}_{1}^{67} {\bar{k}}_{1}^{89}, L_{36} = T_{1 - 10}^{6} / 6 {\bar{k}}_{1}^{12} {\bar{k}}_{1}^{34} {\bar{k}}_{1}^{56} {\bar{k}}_{1}^{78} {\bar{k}}_{1}^{9, 10} . □ \end{matrix}

Example 1.

Suppose that

E \hat{w} = w

and

t (w)

is linear in w. Then

K_{1 e} = 0

for

e \geq 1

. For

r \leq 4

, the

K_{i j}

needed for

P_{r} (x)

of () for the distribution of

Y_{n t}

of (5) are as follows.

\begin{matrix} K_{10} = \bar{t} = t (w) . F o r P_{0} (x) : K_{21} = v . F o r P_{1} (x) : K_{32} = c_{21} . \\ F o r P_{2} (x) : K_{22} =_{1} K_{22} = c_{11}, K_{43} = c_{31} . \\ F o r P_{3} (x) : K_{33} =_{2} K_{33} = L_{4}, K_{54} = L_{9} . \\ F o r P_{4} (x) : K_{23} =_{1} K_{23} = L_{14}, K_{44} =_{3} K_{44} = L_{21}, K_{65} = L_{30} . \end{matrix}

For,

{\bar{u}}_{1}, {\bar{v}}^{1}, {\bar{x}}_{1}, {\bar{z}}_{12}

are 0, as are most

c_{i j}, L_{k}

and

_{2} K_{22},_{3} K_{33},_{2} K_{23},_{3} K_{23},_{4} K_{44} .

So for

r = 0, \dots, 4

, for

P_{r} (x)

we only need to calculate these 3

c_{i j}

and 5

L_{j}

Let

G_{γ}

be a gamma random variable with known mean

γ .

Its rth cumulant is

(r - 1)! γ .

Example 2.

Linear combinations of scale parameters.Suppose that

E \hat{w} = w

and

t (w)

is linear, the components of

\hat{w}

are independent, and for

1 \leq i \leq p, {\hat{w}}^{i} / w^{i}

has a distribution with known rth cumulant

n^{1 - r} κ_{r i}

. Then

K_{r e} = 0

for

e \neq r - 1

and

K_{r, r - 1} = \sum_{i = 1}^{p} t_{\cdot i}^{r} κ_{r i} {(w^{i})}^{r} .

For example if

{\hat{w}}_{i} / w_{i}

is a standard exponential variable then

κ_{r i} = (r - 1)!

For

s \leq r

and any function

f^{i_{s} \dots i_{r}}

, set

\sum_{s - r} {\bar{f}}^{s - r} = \sum_{i_{s}, \dots, i_{r}} f^{i_{s} \dots i_{r}}

summed over their range. In Example 5.3 their range is

1, 2

; for example in

L_{123},

\sum_{1} t_{\cdot 2 i_{1}} {\bar{v}}^{1} = \sum_{i_{1} = 1}^{k} t_{\cdot 2 i_{1}} {\bar{v}}^{1} .

In Example 5.4 their range is

1, \dots, k

; for example

{\bar{u}}_{1} = \sum_{2} {\bar{t}}_{12} {\bar{s}}^{2} = \sum_{i_{2} = 1}^{k} {\bar{t}}_{12} {\bar{s}}^{2} .

Example 3.

Suppose that

\hat{μ} \sim N_{1} (μ, V / n)

and

\hat{V} / V = χ_{f}^{2} / f = G_{γ} / γ

are independent, where

γ = f / 2

has magnitude n. Set

ν = γ / n

. Then

κ_{r} (\hat{μ}) = μ δ_{r 1} + V n^{- 1} δ_{r 2}, κ_{r} (\hat{V}) = k_{r} n^{1 - r}

for

k_{r} = (r - 1)! ν^{1 - r} V^{r}

, and cross-cumulants of

\hat{w}

are zero. Take

p = 2, w_{1} = μ, w_{2} = V

. Then by Corollary 5.1,

K_{r e}

are given in terms of

\begin{matrix} s^{1} & = t_{\cdot 1} V, s^{2} = t_{\cdot 2} k_{2}, u_{1} = t_{\cdot 11} t_{\cdot 1} V + t_{\cdot 12} t_{\cdot 2} k_{2}, u_{2} = t_{\cdot 12} t_{\cdot 1} V + t_{\cdot 22} t_{\cdot 2} k_{2}, \\ v^{1} & = V u_{1}, v^{2} = k_{2} u_{2}, \end{matrix}

as follows.

\begin{matrix} F o r P_{0} (x) : K_{21} = v = t_{\cdot 1}^{2} V + t_{\cdot 2}^{2} k_{2} / 2 . \\ F o r P_{1} (x) : c_{02} = t_{\cdot 11} + t_{\cdot 22} k_{2}, c_{21} = t_{\cdot 2}^{3} k_{3}, c_{23} = \sum_{i = 1}^{2} t_{\cdot i i} {(s^{i})}^{2} . \\ F o r P_{2} (x) : c_{11} = 0, c_{15} = t_{\cdot 22} t_{\cdot 2} k_{3}, c_{19} = {(t_{\cdot 11} V)}^{1} + {(t_{\cdot 22} k_{2})}^{2} + 2 t_{\cdot 12} V k_{2}, \\ c_{31} = t_{\cdot 2}^{4} k_{4}, c_{36} = t_{\cdot 2}^{2} k_{3} u_{2}, c_{3, 10} = u_{1}^{2} V + u_{2}^{2} k_{2}, \\ c_{3, 11} = \sum_{i = 1}^{2} {(s^{i})}^{3} t_{\cdot i i i} + 3 \sum_{12}^{2} {(s^{1})}^{2} s^{2} t_{\cdot 112} w h e r e \sum_{12}^{2} f_{12} = f_{12} + f_{21} . \\ F o r P_{3} (x) : L_{1} = L_{4} = L_{5} = 0, L_{2} = t_{\cdot 222} k_{3}, \\ L_{3} = t_{\cdot 1111} V^{2} + 2 t_{\cdot 1122} V k_{2} + t_{\cdot 2222} k_{2}^{2}, \\ L_{6} = t_{\cdot 22} t_{\cdot 2}^{2} k_{4}, L_{71} = z_{22} k_{3} t_{2}, L_{72} = y^{2} (t_{\cdot 211} V + t_{\cdot 222} k_{3}), L_{73} = t_{\cdot 22} k_{3} u_{2}, \\ L_{74} = (V t_{\cdot 12}^{2} + k_{2} t_{\cdot 22}^{2}) k_{3} t_{\cdot 2}, L_{81} = (V t_{\cdot 1 i_{2} i_{3} i_{4}} + k_{2} t_{\cdot 2 i_{2} i_{3} i_{4}}) {\bar{s}}^{3} {\bar{s}}^{4}, \end{matrix}

\begin{matrix} L_{82} = \sum_{1} (V t_{\cdot 11 i_{1}} + k_{2} t_{\cdot 22 i_{1}}) v^{i_{1}}, L_{83} = V^{2} t_{\cdot 11} z_{11} + 2 V k_{2} t_{\cdot 12} z_{12} + k_{2}^{2} t_{\cdot 22} z_{22}, \\ L_{84} = \sum_{1 - 3} {\bar{k}}_{1}^{11} {\bar{k}}_{1}^{22} {\bar{k}}_{1}^{33} {\bar{t}}_{12} {\bar{t}}_{23} {\bar{t}}_{31}, \\ L_{9} = t_{\cdot 2}^{5} k_{5}, L_{10} = u_{2} t_{\cdot 2}^{3} k_{4}, L_{11} = {(y^{2})}^{2} t_{\cdot 22}, L_{121} = y^{2} \sum_{12} t_{\cdot 2 i_{1} i_{2}} {\bar{s}}^{1} {\bar{s}}^{2}, \\ L_{122} = t_{\cdot 2} k_{3} u_{2}^{2}, L_{123} = y^{2} \sum_{1} t_{\cdot 2 i_{1}} {\bar{v}}^{1}, L_{13} = \sum_{1 - 3} {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{33} {\bar{u}}_{3} . \end{matrix}

Similarly one can write down the Ls needed for

P_{4} (x)

Example 4.

Suppose that we have the summary statistics from k samples of size

n_{i}

from normal populations with means and variances

μ_{i}, V_{i}, 1 \leq i \leq k

. Take

p = 2 k, w_{i} = μ_{i}, w_{i + k} = V_{i}, 1 \leq i \leq k

. So we have p independent statistics,

{\hat{μ}}_{i} \sim N (μ_{i}, V_{i} / n_{i})

and

{\hat{V}}_{i} \sim V_{i} χ_{f_{i}}^{2} / f_{i} = V_{i} G_{γ_{i}} / γ_{i}, 1 \leq i \leq k

where

γ_{i} = f_{i} / 2

has magnitude n, the total sample size. Set

ν_{i} = γ_{i} / n, λ_{i} = n_{i} / n, τ_{i} = V_{i} / λ_{i} .

Then

κ_{r} ({\hat{μ}}_{i}) = μ_{i} δ_{r 1} + V_{i} {(λ_{i} n)}^{- 1} δ_{r 2}, κ_{r} ({\hat{V}}_{i}) = k_{r i} {(λ_{i} n)}^{1 - r}

for

k_{r i} = (r - 1)! ν_{i}^{1 - r}

, and cross-cumulants of

\hat{w}

are zero. Suppose that

t (w)

only depends on

μ_{1}, \dots, μ_{k}

, as in Example 3.3 of Withers (1982). (The notation there is slightly different.) Then

{\bar{s}}^{1} = {\bar{t}}_{1} {\bar{τ}}_{1}, {\bar{u}}_{1} = \sum_{2} {\bar{t}}_{12} {\bar{s}}^{2}, {\bar{v}}^{1} = {\bar{τ}}_{1} {\bar{u}}_{1}, {\bar{z}}_{12} = \sum_{3} {\bar{t}}_{1 - 3} {\bar{s}}^{3},

and by Corollary 5.1, the coefficients needed are as follows.

\begin{matrix} F o r P_{0} (x) : K_{21} = v = {\bar{t}}_{1} {\bar{s}}^{1} = \sum_{1} {\bar{t}}_{1}^{2} {\bar{τ}}_{1}, \\ F o r P_{1} (x) : c_{02} = \sum_{1} {\bar{t}}_{11} {\bar{τ}}_{1}, c_{21} = 0, c_{23} = {\bar{s}}^{1} {\bar{t}}_{12} {\bar{s}}^{2} = \sum_{12} {\bar{t}}_{1} {\bar{τ}}_{1} {\bar{t}}_{12} {\bar{t}}_{2} {\bar{τ}}_{2}, \\ F o r P_{2} (x), K_{22} : c_{11} = c_{15} = 0, c_{19} = \sum_{12} {\bar{t}}_{12}^{2} {\bar{τ}}_{1} {\bar{τ}}_{2}, c_{1, 10} = \sum_{12} {\bar{t}}_{1} {\bar{τ}}_{1} {\bar{t}}_{122} {\bar{τ}}_{2}; \\ F o r K_{43} : c_{31} = c_{36} = 0, c_{3, 10} = \sum_{1} {\bar{u}}_{1}^{2} {\bar{τ}}_{1}, c_{3, 11} = \sum_{1 - 3} {\bar{s}}^{1} {\bar{s}}^{2} {\bar{s}}^{3} {\bar{t}}_{1 - 3} . \\ F o r P_{3} (x), K_{12} = L_{3} / 6 = \sum_{12} {\bar{t}}_{1122} {\bar{τ}}_{1} {\bar{τ}}_{2} / 6 a s L_{1} = L_{2} = 0; \\ f o r K_{33} : L_{4} = L_{5} = L_{6} = L_{7} = 0, L_{81} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{t}}_{1123} {\bar{s}}^{2} {\bar{s}}^{3}, L_{82} = \sum_{12} {\bar{τ}}_{1} {\bar{t}}_{122} {\bar{v}}^{2}, \\ L_{83} = \sum_{12} {\bar{t}}_{12} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{z}}_{12} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{12} {\bar{t}}_{123} {\bar{t}}_{3}, L_{83} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{12} {\bar{t}}_{23} {\bar{t}}_{31}; \\ f o r K_{54} : L_{k} = 0 f o r 10 \leq k \leq 14 . \\ F o r P_{4} (x), K_{23} : L_{i, k} = 0 f o r i = 15, 16, 18, 19, L_{171} = \sum_{12} {\bar{t}}_{12}^{2} {\bar{τ}}_{1} {\bar{τ}}_{2}, \\ L_{201} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{t}}_{11223} {\bar{s}}^{5}, L_{202} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{1123} {\bar{t}}_{23}, L_{203} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{112} {\bar{t}}_{233}, \\ L_{204} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{123}^{2}; \end{matrix}

\begin{matrix} K_{44} = L_{29} a s L_{k} = 0 f o r k = 21, (22, k), (23, 1), (24, k), 25, (26, k), (27, k), (28, k), \\ L_{291} = \sum_{1 - 4} {\bar{τ}}_{1} {\bar{s}}^{2} {\bar{s}}^{3} {\bar{s}}^{4} {\bar{t}}_{11234}, L_{292} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{t}}_{1123} {\bar{v}}^{2} {\bar{s}}^{3}, L_{293} = \sum_{1 - 4} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{s}}^{3} {\bar{s}}^{4} {\bar{t}}_{1234}, \\ L_{294} = \sum_{1 - 4} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{t}}_{112} {\bar{t}}_{234} {\bar{s}}^{3} {\bar{s}}^{4}, L_{295} = \sum_{12} {\bar{τ}}_{1} {\bar{z}}_{12}^{2} {\bar{τ}}_{2}, L_{296} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{112} {\bar{t}}_{23}, \\ L_{297} = \sum_{12} {\bar{τ}}_{1} {\bar{x}}_{12} {\bar{t}}_{12} f o r {\bar{x}}_{12} = \sum_{3} {\bar{t}}_{123} {\bar{v}}^{3}, L_{298} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{12} {\bar{t}}_{23} {\bar{z}}_{31}, \\ L_{299} = \sum_{1 - 4} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{τ}}_{4} {\bar{t}}_{12} {\bar{t}}_{23} {\bar{t}}_{34} {\bar{t}}_{41}; \\ K_{65} = 6 L_{36}, a s t h e o t h e r c o m p o n e n t s o f K_{65} a r e 0 . A l s o, \\ K_{13} = \sum_{1 - 3} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{t}}_{112233} / 48, K_{14} = \sum_{1 - 4} {\bar{τ}}_{1} {\bar{τ}}_{2} {\bar{τ}}_{3} {\bar{τ}}_{4} {\bar{t}}_{11223344} / 384 . \end{matrix}

Corollary 2.

Set

Y_{n} = v^{- 1 / 2} Y_{n t} = {(n / v)}^{1 / 2} (t (\hat{w}) - t (w)) .

Then

\begin{matrix} P r o b . (Y_{n} \leq x) = \sum_{r = 0}^{\infty} n^{- r / 2} P_{r v} (x) \end{matrix}

where

P_{r v} (x)

P_{r} (x)

of Corollary 5.1 with

K_{r e}

replaced by

K_{r e} / v^{r / 2} .

PROOF This is straightforward. □

Looking at

K_{r e}, c_{a b}, v, {\bar{s}}^{2}, {\bar{u}}_{3}

as functions of w, we denote their partial derivatives with respect to

{\bar{w}}_{3} = w_{i_{3}}

, say. by

{\bar{K}}_{r e \cdot 3}, {\bar{c}}_{a b \cdot 3}, {\bar{v}}_{\cdot 3}, {\bar{s}}_{\cdot 3}^{2}, {\bar{u}}_{3 \cdot 3}

and similarly for higher derivatives. We shall give the ones we need in Lemma 5.1. When constructing confidence regions, one needs to assume that the distribution of

\hat{w}

is determined by w. So far we’ve not assumed this. For

\hat{w}

biased, we need

Corollary 3.

Let

\hat{w} \in R^{p}

be abiasedstandard estimate of w satisfying (1) where

{\bar{k}}_{e}^{1 - r}

may depend on w. Then for

q = 1

\hat{t} = t (\hat{w})

is a standard estimate of

t = t (w) \in R

\begin{matrix} κ_{r} (\hat{t}) = \sum_{e = r - 1}^{\infty} n^{- e} a_{r e} f o r r \geq 1, w h e r e a_{r e} = K_{r e} + D_{r e}, D_{r, r - 1} = 0, \end{matrix}

(6)

and the other

D_{r e}

needed for

P_{j} (x)

of () for the distribution of

Y_{n t}

of (5) are as follows.

\begin{matrix} F o r P_{0} (x) : D_{21} = 0 \Rightarrow a_{21} = K_{21} = v = {\bar{t}}_{1} {\bar{k}}_{1}^{12} {\bar{t}}_{2} . \\ F o r P_{1} (x) : D_{11} = c_{01} \Rightarrow a_{11} = c_{01} + c_{02} / 2, a_{32} = K_{32} = c_{21} + 3 c_{23}, \end{matrix}

\begin{matrix} F o r P_{2} (x) : D_{22} = {\bar{v}}_{\cdot 3} {\bar{k}}_{1}^{3} = c_{12} + 2 c_{16}, a_{43} = K_{43} . \\ F o r P_{3} (x) : D_{12} = K_{11, 1} + K_{10, 2}, K_{11, 1} = {\bar{K}}_{11 \cdot 3} {\bar{k}}_{1}^{3}, K_{10, 2} = {\bar{t}}_{1} {\bar{k}}_{2}^{1} + {\bar{k}}_{1}^{1} {\bar{t}}_{12} {\bar{k}}_{1}^{2} / 2, \\ D_{33} = {\bar{K}}_{32 \cdot 4} {\bar{k}}_{1}^{4}, a_{54} = K_{54} . \\ F o r P_{4} (x) : D_{23} = K_{22, 1} + K_{21, 2}, K_{22, 1} = {\bar{K}}_{22 \cdot 3} {\bar{k}}_{1}^{3}, K_{21, 2} = {\bar{v}}_{\cdot 3} {\bar{k}}_{2}^{3} / 2 + {\bar{v}}_{\cdot 34} {\bar{k}}_{1}^{3} {\bar{k}}_{1}^{4}, \\ D_{44} = {\bar{K}}_{43 \cdot 5} {\bar{k}}_{1}^{5}, a_{65} = K_{65} . \end{matrix}

PROOF This follows from Theorem 4.1.

D_{r c} = \sum_{c = 1}^{c - r + 1} K_{r, c - r, e}

where

K_{r k e}

is the coefficient of

n^{- e}

in the expansion of

K_{r k} (E \hat{w})

about

K_{r k}

. □

For

r \leq s

, and any

{\bar{X}}_{r - s}

, let

\sum_{r - s}^{N} {\bar{X}}_{r - s}

sums over all N permutations of

i_{r}, \dots, i_{s}

giving distinct terms. For example

\sum_{3 - 5}^{3} {\bar{t}}_{13} {\bar{t}}_{245} = {\bar{t}}_{13} {\bar{t}}_{245} + {\bar{t}}_{14} {\bar{t}}_{235} + {\bar{t}}_{15} {\bar{t}}_{234} .

The derivatives of

v = K_{21}

and

K_{r e}

needed for Corollary 5.3 are given by by

Lemma 1.

\begin{matrix} {\bar{v}}_{\cdot 3} = 2 {\bar{u}}_{3} + {\bar{T}}_{3}, {\bar{v}}_{\cdot 34} = \sum_{k = 0}^{2} {\bar{v}}_{34 k}, w h e r e {\bar{T}}_{3} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{1 \cdot 3}^{12}, \\ {\bar{v}}_{340} = 2 {\bar{z}}_{34} + 2 {\bar{t}}_{31} {\bar{k}}_{1}^{12} {\bar{t}}_{24}, {\bar{v}}_{341} = 2 {\bar{t}}_{1} ({\bar{k}}_{1 \cdot 3}^{12} {\bar{t}}_{24} + {\bar{k}}_{1 \cdot 4}^{12} {\bar{t}}_{23}), {\bar{v}}_{342} = {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{1 \cdot 34}^{12} . \end{matrix}

(7)

(8)

\begin{matrix} {\bar{K}}_{43 \cdot 5} = c_{31 \cdot 5} + 12 c_{36 \cdot 5} + 12 c_{3, 10 \cdot 5} + 4 c_{3, 11 \cdot 5} f o r c_{31 \cdot 5} = 4 {\bar{t}}_{51} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} \\ + {\bar{t}}_{1} \dots {\bar{t}}_{4} {\bar{k}}_{3 \cdot 5}^{1 - 4}, c_{36 \cdot 5} = 2 {\bar{t}}_{51} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{2} {\bar{u}}_{3} + {\bar{t}}_{1} {\bar{t}}_{2} {\bar{u}}_{3} {\bar{k}}_{2 \cdot 5}^{1 - 3} + {\bar{y}}^{3} {\bar{t}}_{3 - 5} {\bar{s}}^{4} + {\bar{Y}}_{4} ({\bar{k}}_{1 \cdot 5}^{41} {\bar{t}}_{1} + {\bar{k}}_{1}^{41} {\bar{t}}_{15}) . \\ c_{3, 10 \cdot 3} = {\bar{u}}_{1} {\bar{k}}_{1 \cdot 3}^{12} {\bar{u}}_{2} + 2 {\bar{v}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} + 2 {\bar{t}}_{1} {\bar{x}}_{2} {\bar{k}}_{1 \cdot 3}^{12} + 2 {\bar{x}}_{1} {\bar{k}}_{1}^{12} {\bar{t}}_{23}, \\ c_{3, 11 \cdot 5} = 3 {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{s}}_{\cdot 5}^{3} = 3 {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{t}}_{4} {\bar{k}}_{1 \cdot 5}^{34} + 3 {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{34} {\bar{t}}_{45} . \end{matrix}

(9)

PROOF For example substitute

{\bar{u}}_{3 \cdot 5} = {\bar{t}}_{3 - 5} {\bar{s}}^{4} + {\bar{t}}_{34} {\bar{k}}_{1 \cdot 5}^{41} {\bar{t}}_{1} + {\bar{t}}_{34} {\bar{k}}_{1}^{41} {\bar{t}}_{15}

into

c_{36 \cdot 5} = 2 {\bar{t}}_{1} {\bar{t}}_{25} {\bar{k}}_{2}^{1 - 3} {\bar{u}}_{3} + {\bar{t}}_{1} {\bar{t}}_{2} ({\bar{k}}_{2 \cdot 5}^{1 - 3} {\bar{u}}_{3} + {\bar{k}}_{2}^{1 - 3} {\bar{u}}_{3 \cdot 5}) .

□

So now we can write

D_{r e}

needed for Corollary 5.3 in molecular form:

Corollary 4.

Assume that the conditions of Corollary 5.3 hold. Then

D_{r e}

and

K_{r e, j}

given there satisfy

\begin{matrix} D_{22} = c_{12} + 2 c_{16} \Rightarrow a_{22} = c_{11} + c_{15} + c_{19} / 2 + c_{1, 10} + c_{12} + 2 c_{16} . \\ F o r D_{12}, K_{11, 1} = ({\bar{t}}_{1 - 3} {\bar{k}}_{1}^{12} + {\bar{t}}_{12} {\bar{k}}_{1 \cdot 3}^{12}) {\bar{k}}_{1}^{3} / 2 . \\ D_{33} = (3 {\bar{y}}^{3} {\bar{t}}_{34} + {\bar{t}}_{1} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{k}}_{2 \cdot 4}^{1 - 3} + 3 {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{124} + 6 {\bar{v}}^{1} {\bar{t}}_{14} + 6 {\bar{u}}_{1} {\bar{k}}_{1 \cdot 4}^{12} {\bar{t}}_{2}) {\bar{k}}_{1}^{4} . \\ F o r D_{23}, K_{22, 1} = (2 {\bar{t}}_{31} {\bar{S}}^{1} + {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{2 \cdot 3}^{12}) {\bar{k}}_{1}^{3} + ({\bar{t}}_{14} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{23} + {\bar{t}}_{1} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{2 - 4} + {\bar{t}}_{1} {\bar{k}}_{2 \cdot 4}^{1 - 3} {\bar{t}}_{23}) {\bar{k}}_{1}^{4} \\ + ({\bar{t}}_{125} {\bar{X}}^{12} + {\bar{k}}_{1 \cdot 5}^{23} {\bar{t}}_{34} {\bar{k}}_{1}^{41} {\bar{t}}_{12}) {\bar{k}}_{1}^{5} + [{\bar{k}}_{1}^{23} {\bar{t}}_{1 - 3} ({\bar{k}}_{1}^{15} {\bar{t}}_{54} + {\bar{t}}_{5} {\bar{k}}_{1 \cdot 4}^{15}) + {\bar{s}}^{1} {\bar{k}}_{1}^{23} {\bar{t}}_{1 - 4} + {\bar{s}}^{1} {\bar{t}}_{1 - 3} {\bar{k}}_{1 \cdot 4}^{23}] {\bar{k}}_{1}^{4}; \\ K_{21, 2} = (2 {\bar{u}}_{3} + {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{1 \cdot 3}^{12}) {\bar{k}}_{2}^{3} / 2 + [4 {\bar{t}}_{1} {\bar{k}}_{1 \cdot 3}^{12} {\bar{t}}_{24} + {\bar{s}}^{1} {\bar{t}}_{134} + {\bar{t}}_{31} {\bar{k}}_{1}^{12} {\bar{t}}_{24} \\ + {\bar{t}}_{1} {\bar{t}}_{2} {\bar{k}}_{1 \cdot 34}^{12}] {\bar{k}}_{1}^{3} {\bar{k}}_{1}^{4} . \\ D_{44} = [4 {\bar{t}}_{51} {\bar{k}}_{3}^{1 - 4} {\bar{t}}_{2} {\bar{t}}_{3} {\bar{t}}_{4} + {\bar{t}}_{1} \dots {\bar{t}}_{4} {\bar{k}}_{3 \cdot 5}^{1 - 4} + 24 {\bar{t}}_{51} {\bar{k}}_{2}^{1 - 3} {\bar{t}}_{2} {\bar{u}}_{3} + 12 {\bar{t}}_{1} {\bar{t}}_{2} {\bar{u}}_{3} {\bar{k}}_{2 \cdot 5}^{1 - 3} \\ + 12 {\bar{y}}^{3} ({\bar{t}}_{3 - 5} {\bar{s}}^{4} + {\bar{t}}_{34} {\bar{k}}_{1 \cdot 5}^{41} {\bar{t}}_{1} + {\bar{t}}_{34} {\bar{k}}_{1}^{41} {\bar{t}}_{15})] {\bar{k}}_{1}^{5} + 12 [2 {\bar{v}}^{2} {\bar{t}}_{2 - 4} {\bar{s}}^{4} + 2 {\bar{t}}_{1} {\bar{x}}_{2} {\bar{k}}_{1 \cdot 3}^{12} \\ + 2 {\bar{x}}_{1} {\bar{k}}_{1}^{12} {\bar{t}}_{23} + 12 {\bar{u}}_{1} {\bar{k}}_{1 \cdot 3}^{12} {\bar{u}}_{2}] {\bar{k}}_{1}^{3} + 12 ({\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{t}}_{4} {\bar{k}}_{1 \cdot 5}^{34} + {\bar{s}}^{1} {\bar{s}}^{2} {\bar{t}}_{1 - 3} {\bar{k}}_{1}^{34} {\bar{t}}_{45}) {\bar{k}}_{1}^{5} . \end{matrix}

PROOF

a_{1 e}

were given for

i \leq 4

by Theorem 4.1. Corollaries 5.3, 5.4 agree with

a_{11}, a_{32}, a_{22}, a_{43}

given for

P_{r} (x), r \leq 2

on p59 of Withers (1982) except that

D_{22}

a_{22}

was overlooked. □

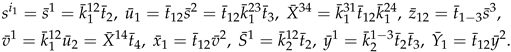
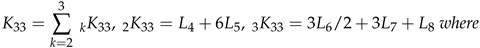
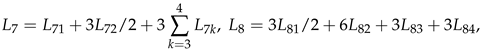
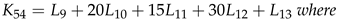
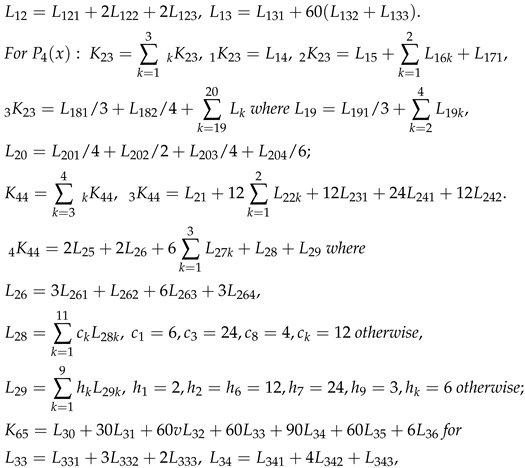
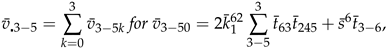
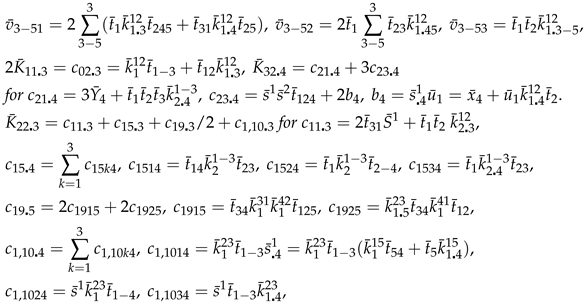
6. An Extension to Theorem 2.1

Here we remove the condition in Theorem 2.1 that

E \hat{w} = w

and give the extra terms referred to but not given on p49 of James and Mayne (1962). We use

_{e} {\bar{K}}^{1 - r}

of Theorem 2.1, and the shorthand

{\bar{f}}_{\cdot m} = \partial_{i_{m}} \bar{f}

where

\partial_{i} = \partial / \partial w_{i} .

Suppose that for

r \geq 1

, the rth order cumulants of (1) can be expanded as

\begin{matrix} {\bar{k}}^{1 - r} = κ ({\hat{w}}^{i_{1}}, \dots, {\hat{w}}^{i_{r}}) = \sum_{e = r - 1}^{\infty}_{e} {\bar{k}}^{1 - r} f o r 1 \leq i_{1}, \dots, i_{r} \leq p, \\ w h e r e_{e} {\bar{k}}^{1 - r} = O (n^{- e}), a n d t h a t \hat{w} \to w a s n \to \infty, s o t h a t_{0} {\bar{k}}^{1} = {\bar{w}}^{1} . \end{matrix}

(1)

There is a key difference with Theorem 2.1: there,

_{e} {\bar{k}}^{1 - r}

was treated as an algebraic expression. But now we must view each of them as a function of w. So we assume that the distribution of

\hat{w}

is determined by w.

The derivatives of

_{e} {\bar{K}}^{1 - r}

of Theorem 2.1 are given by Leibniz’s rule for the derivatives of a product:

\begin{matrix} _{1} {\bar{K}}_{\cdot 3}^{12} = {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}^{12})}_{\cdot 3} = ({\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} + {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2}) {\bar{k}}^{12} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{k}}_{\cdot 3}^{12}, \\ _{1} {\bar{K}}_{\cdot 3}^{1} = {({\bar{t}}_{12}^{1} {\bar{k}}^{12})}_{\cdot 3} / 2 = {\bar{t}}_{1 - 3}^{1} {\bar{k}}^{12} / 2 + {\bar{t}}_{12}^{1} {\bar{k}}_{\cdot 3}^{12} / 2, \\ {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}^{1 - 3})}_{\cdot 4} = {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3})}_{\cdot 4} {\bar{k}}^{1 - 3} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3} {\bar{k}}_{\cdot 4}^{1 - 3}, {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3})}_{\cdot 4} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{34}^{3} + {\bar{t}}_{1}^{1} {\bar{t}}_{24}^{2} {\bar{t}}_{3}^{3} + {\bar{t}}_{14}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3}, \\ {(T_{1 - 4}^{1 - 3} {\bar{k}}^{12} {\bar{k}}^{34})}_{\cdot 5} = {(T_{1 - 4}^{1 - 3})}_{\cdot 5} {\bar{k}}^{12} {\bar{k}}_{1}^{34} + T_{1 - 4}^{1 - 3} {({\bar{k}}^{12} {\bar{k}}^{34})}_{\cdot 5}, \\ {(T_{1 - 4}^{1 - 3})}_{\cdot 5} = \sum^{3} ({\bar{t}}_{135}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{4}^{3} + {\bar{t}}_{13}^{1} {\bar{t}}_{25}^{2} {\bar{t}}_{4}^{3} + {\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{45}^{3}), {({\bar{k}}^{12} {\bar{k}}^{34})}_{\cdot 5} = {\bar{k}}_{\cdot 5}^{12} {\bar{k}}^{34} + {\bar{k}}^{12} {\bar{k}}_{\cdot 5}^{34} . \end{matrix}

Theorem 4.

Let

\hat{w} \in R^{p}

be a biased standard estimate of w satisfying (1). Then

\hat{t} = t (\hat{w}) \in R^{p}

is a standard estimate of

t = t (w)

\begin{matrix} κ ({\hat{t}}^{j_{1}}, \dots, {\hat{t}}^{j_{r}}) = \sum_{e = r - 1}^{\infty}_{e} {\bar{a}}^{1 - r} f o r r \geq 1, 1 \leq j_{1}, \dots, j_{r} \leq q, \end{matrix}

(2)

(3)

and the other

_{e} {\bar{D}}^{1 - r} =_{e} D^{j_{1} \dots j_{r}}

needed for

P_{r n} (x)

of (6) for the distribution of

Y_{n t}

of (5) are as follows.

\begin{matrix} F o r P_{0} (x) :_{1} {\bar{D}}^{12} = 0 \Rightarrow_{1} {\bar{a}}^{12} =_{1} {\bar{K}}^{12} =_{1} K^{j_{1} j_{2}} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2}_{1} {\bar{k}}^{12}], \\ F o r P_{1} (x) :_{1} {\bar{D}}^{1} =_{1} {\bar{t}}^{1} {\bar{k}}^{1} \Rightarrow_{1} {\bar{a}}^{1} = {\bar{t}}_{1}^{1}_{1} {\bar{k}}^{1} + {\bar{t}}_{12}^{1}_{1} {\bar{k}}^{12} / 2, \\ F o r P_{2} (x) :_{2} {\bar{D}}^{12} =_{1} {\bar{K}}_{\cdot 3}^{12}_{1} {\bar{k}}^{3} \Rightarrow {\bar{a}}_{2}^{12} = {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2}_{2} {\bar{k}}^{12} + T_{1 - 3}^{12}_{2} {\bar{k}}^{1 - 3} / 2 \\ + T_{1 - 4}^{12}_{1} {\bar{k}}^{12}_{1} {\bar{k}}^{34} / 2 + ({\bar{t}}_{13}^{1} {\bar{t}}_{2}^{2} + {\bar{t}}_{1}^{1} {\bar{t}}_{23}^{2})_{1} {\bar{k}}^{12} + {\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2}_{1} {\bar{k}}_{\cdot 3}^{12}_{1} {\bar{k}}^{3} . \\ F o r P_{3} (x) :_{2} {\bar{D}}^{1} =_{1} {\bar{K}}_{1}^{1} +_{0} {\bar{K}}_{2}^{1},_{1} {\bar{K}}_{1}^{1} = {(_{1} {\bar{K}}^{1})}_{\cdot 3}_{1} {\bar{k}}^{3}, \\ _{0} {\bar{K}}_{2}^{1} = {\bar{t}}_{1}^{1}_{2} {\bar{k}}^{1} + {\bar{t}}_{12}^{1}_{1} {\bar{k}}^{1}_{1} {\bar{k}}^{2} / 2 \Rightarrow \\ _{2} {\bar{a}}^{1} = {\bar{t}}_{1}^{1}_{2} {\bar{k}}^{1} + {\bar{t}}_{12}^{1} (_{2} {\bar{k}}^{12} +_{1} {\bar{k}}^{1}_{1} {\bar{k}}^{2} +_{1} {\bar{K}}_{\cdot 3}^{12}_{1} {\bar{k}}^{3}) / 2 \\ + {\bar{t}}_{1 - 3}^{1} (_{2} {\bar{k}}^{1 - 3} / 6 +_{1} {\bar{k}}^{1}_{1} {\bar{k}}^{23} / 2) + {\bar{t}}_{1 - 4}^{1}_{1} {\bar{k}}^{12}_{1} {\bar{k}}^{34} / 8, \end{matrix}

\begin{matrix} _{3} {\bar{D}}^{1 - 3} =_{2} {\bar{K}}_{\cdot 4}^{1 - 3} {\bar{k}}_{1}^{4} = {({\bar{t}}_{1}^{1} {\bar{t}}_{2}^{2} {\bar{t}}_{3}^{3}_{2} {\bar{k}}^{1 - 3})}_{\cdot 4}_{1} {\bar{k}}^{4} + {(T_{1 - 4}^{1 - 3}_{1} {\bar{k}}^{12}_{1} {\bar{k}}^{34})}_{\cdot 5}_{1} {\bar{k}}^{5} . \\ F o r P_{4} (x) :_{3} {\bar{D}}^{12} =_{2} {\bar{K}}_{1}^{12} +_{1} {\bar{K}}_{2}^{12},_{2} {\bar{K}}_{1}^{12} =_{2} {\bar{K}}_{\cdot 3}^{12}_{1} {\bar{k}}^{3}, \\ _{1} {\bar{K}}_{2}^{12} =_{1} {\bar{K}}_{\cdot 3}^{12}_{2} {\bar{k}}^{3} / 2 +_{1} {\bar{K}}_{\cdot 34}^{12}_{1} {\bar{k}}^{3}_{1} {\bar{k}}^{4},_{4} {\bar{D}}^{1 - 4} =_{3} {\bar{K}}_{\cdot 5}^{1 - 4}_{1} {\bar{k}}^{5},_{5} {\bar{D}}^{1 - 5} = 0 . \end{matrix}

PROOF

{\bar{K}}^{1 - r} (w) = {\bar{K}}^{1 - r}

and

_{e} {\bar{K}}^{1 - r} (w) =_{e} {\bar{K}}^{1 - r}

are functions of w. By (3)

\begin{matrix} {\bar{K}}^{1 - r} (w_{n}) = \sum_{e = r - 1}^{\infty}_{k} {\bar{K}}^{1 - r} (w_{n}) f o r w_{n} = E \hat{w} = w + d_{n}, \end{matrix}

(4)

where by (1),

d_{n}

has

i_{1}

th component

{\bar{d}}_{n}^{1} = d_{n}^{i_{1}} = \sum_{e = 1}^{\infty}_{e} {\bar{k}}^{1} .

Consider the Taylor series expansion

\begin{matrix} _{k} {\bar{K}}^{1 - r} (w + d_{n}) =_{k} {\bar{K}}^{1 - r} +_{k} {\bar{K}}_{\cdot 1}^{1 - r} {\bar{d}}_{n}^{1} +_{k} {\bar{K}}_{\cdot 12}^{1 - r} {\bar{d}}_{n}^{1} {\bar{d}}_{n}^{2} / 2! + \dots = \sum_{e = 0}^{\infty}_{k} {\bar{K}}_{e}^{1 - r} \end{matrix}

say. Substituting into (3) gives (2) with

_{c} {\bar{a}}^{1 - r} = \sum_{k + e = c}_{k} {\bar{K}}_{e}^{1 - r} = \sum_{e = 0}^{c - r + 1}_{c - e} {\bar{K}}_{e}^{1 - r} .

Also

_{k} {\bar{K}}_{0}^{1 - r} =_{k} {\bar{K}}^{1 - r}

so that (4) holds with

_{c} {\bar{D}}^{1 - r} = \sum_{e = 1}^{c - r + 1}_{c - e} {\bar{K}}_{e}^{1 - r} :_{r} {\bar{D}}^{1 - r} =_{r - 1} {\bar{K}}_{1}^{1 - r},_{r + 1} {\bar{D}}^{1 - r} = \sum_{e = 1}^{2}_{r + 1 - e} {\bar{K}}_{e}^{1 - r}, \dots □

The Edgeworth expansion (6) holds if

{_{e} {\bar{K}}^{1 - r}}

are replaced by

{_{e} {\bar{a}}^{1 - r}}

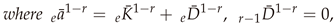
7. Discussion

Approximations to the distributions of estimates is of vital importance in statistical inference. Asymptotic normality uses just the 1st term of the Edgeworth expansion. That approximation can be greatly improved with further terms. When the estimate is a sample mean, basic results were given by Chebyshev, Charlier and Edgeworth in the 19th century with major advances in the 20th century by Cramer, Rao and many others. See Stuart and Ord (1987) for some historical references. For a derivation of the Edgeworth expansion for a sample mean from the Gram-Charlier expansion, see Withers and Nadarajah (2009, 2014a) for the univariate and vector cases. These showed for the 1st time that the coefficients in these expansions were Bell polynomials in the cumulants.

The first extension from a sample mean for univariate estimates was by Cornish and Fisher (1937) and Fisher and Cornish (1960). They assumed that the rth cumulant of the estimate was

κ_{r} (\hat{w}) = n^{1 - r} k_{r}

where

k_{r}

is a constant. However in applications they assumed that

\hat{w}

was a Type A estimate, and collected terms. It was not until Withers (1984) that explicit results were given a univariate Type A estimate. Major advances were made in Withers and Nadarajah (2010b). This gave explicit results for the terms in the Edgeworth expansion of a Type A or B estimate using Bell polynomials, as outlined in §1. It also allowed for expansions about asymptotically normal random variables. The advantage of this approach in greatly reducing the number of terms in each

P_{r} (x)

was illustrated in Withers and Nadarajah (2012d, 2014c).

For univariate estimates, Cornish and Fisher (1937) also showed how to invert the Edgeworth expansion to obtain an expansion for the distribution quantiles. This was extended to Type A estimates in Withers (1984). For extensions to transformations of multivariate estimates, like

t (\hat{w}) = (\hat{w} - w))^{'} V^{- 1} (\hat{w} - w))

, see Hill and Davis (1968) and Withers and Nadarajah (2012a, 2012e). An application to the amplitude and phase of the mean of a complex sample is given in Withers and Nadarajah (2013b).

Turning now to smooth functions of a Type A estimate, the 1st univariate results were given by Withers (1982, 1983). These built on a deep result of James and Mayne (1962). This is why if

\hat{w}

is a Type A (or B) estimate of w, then a smooth function of

\hat{w}

, say

t (\hat{w})

, is a Type A (or B) estimate of

t (w)

The extension from a vector to a matrix estimate is just a matter of relabelling: a single sum becomes a double sum. The first examples of this we know of are in Withers and Nadarajah (2011a, 2011b, 2011c, 2012b, 2020). The extension to a complex scalar or vector or matrix w was given in these same papers. The 1st of these 3 papers applied it to the multi-tone problem in electrical engineering, and the other 4 papers to channel capacity problems where

\hat{w}

is a weighted mean of complex matrix random variables, and n is no longer a sample size, but the number of transmitters or receivers.

A different type of extension can be obtained by identifying a sample mean

\hat{w} = \bar{X}

from a distribution

F (x)

with its empirical distribution

F_{n} (x)

, and

t (w)

with

T (F)

, a smooth functional of

F (x)

, such as the bivariate correlation.

T (F_{n})

is a Type A estimate of

T (F)

, and its cumulant coefficient can be read off those of

t (\hat{w})

. In this way one obtains the Edgeworth expansion for

n^{1 / 2} (T (F_{n}) - T (F)) .

See Withers (1983) Withers and Nadarajah (2008, 2010c, 2012c, 2013a)

A caveat on the use of an Edgeworth expansion is that including more terms makes it more inaccurate in the tails. This is where the tilted expansions, also known as saddlepoint, or small sample expansions, become essential. Results for the density of

Y_{n w}

for a sample mean, were given in §5 of Daniels (1983) and §6 of Daniels (1987). Withers and Nadarajah (2010b) shows how the cumulant coefficients given in this paper can be used to obtain the tilted expansion for the distribution and density of any Type A estimate.

8. Conclusion

Let

\hat{w}

be a Type A estimate of an unknown parameter

w \in R^{p}

. Its cumulant coefficients are defined by (1). They are the building blocks of the Edgeworth expansion (2) in powers of

n^{- 1 / 2}

for its distribution of

\hat{w}

. n is typically the sample size. Those coefficients needed for the rth term,

P_{r} (x)

, are given in (6) and (7). Let

t (\hat{w}) \in R^{q}

be a smooth function of

\hat{w}

. Then it is a Type A estimate of

t (w) \in R^{q}

. This paper gives its cumulant coefficients in terms of those of

\hat{w}

and the derivatives of

\hat{w}

. Replacing the coefficients in (2) by these coefficients provides the Edgeworth expansion of

n^{1 / 2} (t (\hat{w}) - t (w))

n^{- 5 / 2}

The tilted Edgeworth expansion for

\hat{w}

needed for accuracy in the tails, was given in Withers and Nadarajah (2010b) in terms of its cumulant coefficients. Replacing these by those of

t (\hat{w})

given here gives the tilted Edgeworth expansion for

t (\hat{w})

In many practical statistical estimation problems, simulations are a popular way to approximate distributions. However these generally have the severe limitation that the parameters chosen cannot represent the whole parametric landscape.

We have given a number of applications to electrical engineering. For example numerical comparisons of the 1st 3 approximations to channel capacity for multiple arrays were given in Withers and Nadarajah (2020). In that case

p = 1

, so that an expansion for the percentile was possible. Thre are a host of other practical applications possible to electrical engineering and other fields.

Finally we mention some possible future research directions. Chain rules for

t (\hat{w})

can be applied to obtain the cumulant coefficients of its Studentized form. This can be followed up with expansions for the coverage probability of confidence regions, and corrections making them more accurate. Cumulant coefficients can be applied to bias reduction, Bayesian inference, confidence regions and power. The Edgeworth expansion can give a negative value in the tails of a distribution. Tilted expansions avoid this. Another way to get around this, is to choose

y \in R^{p}

such that

\nabla_{n x} = P r o b . (Y_{n w} \leq x + n^{- 1 / 2} y) - Φ_{V} (x)

O (n^{- 1})

. For

p > 1

such y can be chosen in an infinite number of ways, so that it may be possible to choose it so that

\nabla_{n x} = O (n^{- 3 / 2})

or smaller. One could also replace

n^{- 1 / 2} y

y_{(} n) = n^{- 1 / 2} y_{0} + n^{- 1} y_{1}

say, giving more choices.

Abbreviations

The following abbreviations are used in this manuscript:

MDPI	Multidisciplinary Digital Publishing Institute
DOAJ	Directory of open access journals
TLA	Three letter acronym
LD	linear dichroism

Appendix A: Some comments on the references

Here we give some comments and corrections to some of our papers.

Withers (1982): To the expression for

a_{22}

on p.59 add

c_{12} + 2 c_{16}

where

\begin{matrix} c_{12} = I_{2} (\binom{12}{01}) = t_{i} t_{j} k_{1, k}^{i j} k_{1}^{k}, c_{16} = I_{11} (\binom{12}{00}) = t_{i} k_{1}^{i j} t_{j k} k_{1}^{k} . \end{matrix}

This correction does not effect applications in which

\hat{ω}

is unbiased, as in Withers (1982, 1988).

In the expression on p.60 for

{(a_{22})}_{2}

I_{31} (\binom{23}{22})

should be

c_{36} = I_{31} (\binom{23}{00})

On p61, 4 lines before Table 1, replace

{n / 2)}^{r - 1}

{n / 2)}^{1 - r}

On p67 add to

K_{2}^{a b}, t_{i}^{a} t_{j^{b}} k_{1, k}^{i j} k_{1}^{k} .

For

r = 3, 4

see §4.

On p68 in (A3) replace

(\binom{r + 2}{r})

(\binom{r + 2}{2})

. Changing to the simpler notation of Withers and Nadarajah (2008), denote the expressions for

I_{2} (\binom{2}{0}), . . ., I_{301} (\binom{222}{000})

and

I_{3} (\binom{22}{01}), . . ., I_{31} (\binom{222}{001})

given on p.58–59 by

σ^{2} = V = V (w) = t_{i} k_{1}^{i j} t_{j}, c_{01}, c_{02}, c_{21}

, and

c_{23}, c_{11}, c_{15}, c_{19}, c_{1, 10}, c_{31}, c_{36}, c_{3, 10}, c_{3, 11}, c_{22}, c_{12}, c_{14}, c_{17}, c_{32}, c_{34}, c_{35}, c_{38}, c_{39} .

So the expressions on pp59-60 become

\begin{matrix} a_{11} = c_{01} + c_{02} / 2, a_{32} = c_{21} + 3 c_{23}, \\ a_{22} = c_{11} + c_{15} + c_{19} / 2 + c_{1, 10} + c_{12} + 2 c_{16} b y C o r o l l a r y 5.3, \\ a_{43} = c_{31} + 12 c_{36} + 12 c_{3, 10} + 4 c_{3, 11}, \\ {(a_{11})}_{1} = σ^{- 1} (c_{01} + c_{02} / 2) - σ^{- 3} (c_{22} / 2 + c_{23}), {(a_{32})}_{2} = σ^{- 3} (c_{21} - 3 c_{22} - 3 c_{23}), \\ {(a_{22})}_{2} = \sum_{i = 1}^{3} V^{- i} A_{i}, {(a_{43})}_{4} = \sum_{i = 2}^{3} V^{- i} B_{i} f o r \\ A_{1} = c_{11} - c_{14} / 2 + c_{15} - 2 c_{17} - c_{19} / 2, A_{2} = - (c_{01} + c_{02} / 2) (c_{22} + 2 c_{23}) \\ - c_{32} - c_{34} + c_{35} - 2 c_{36} - 4 c_{38} + 2 c_{39} - 2 c_{3, 10} - 2 c_{3, 11}, \\ A_{3} = 7 {(c_{22} + 2 c_{23})}^{2} / 4, B_{2} = c_{31} - 6 c_{32} - 6 c_{34} + 3 c_{35} - 24 c_{38} - 12 c_{3, 10} - 8 c_{3, 11}, \\ B_{3} = 6 (c_{22} + 2 c_{23}) (- c_{21} + 3 c_{22} + 3 c_{23}) . \end{matrix}

We now illustrate how the results on p.60 were obtained. Let

c_{r s}^{'}

denote

c_{r s}

when

t (\hat{w})

is replaced by its Studentized form

t_{(0)} (\hat{w}) .

Then

\begin{matrix} {(a_{22})}_{2} = c_{11}^{'} + c_{15}^{'} + c_{19}^{'} / 2 + c_{1, 10}^{'} + c_{12}^{'} + 2 c_{16}^{'}, \end{matrix}

(A1)

The first few derivatives of

t_{(0)} (\hat{ω})

at w, and of

V (w)

, are

\begin{matrix} t_{0 . i} & = V^{- 1 / 2} t_{i}, t_{0 . i j} = V^{- 1 / 2} t_{i j} - V^{- 3 / 2} (t_{i} V_{j} + t_{j} V_{i}) / 2, \\ t_{0 . i j k} & = V^{- 1 / 2} t_{i j k} - V^{- 3 / 2} \sum_{i j k}^{3} (t_{i j} V_{k} + V_{i j} t_{k}) / 2 + 3 V^{- 5 / 2} \sum_{i j k}^{3} t_{i} V_{j} V_{k} / 4, \\ V_{i} & = 2 t_{i a} k_{1}^{a b} t_{b} + k_{1, i}^{a b} t_{a} t_{b}, a n d \\ V_{i j} & = 2 t_{i j a} k_{1}^{a b} t_{b} + 2 t_{i a} k_{1}^{a b} t_{j b} + 2 \sum_{i j}^{2} t_{i a} k_{1, j}^{a b} t_{b} + k_{1, i j}^{a b} t_{a} t_{b}, w h e r e \\ \sum_{i j}^{2} a_{i} b_{j} & = a_{i} b_{j} + a_{j} b_{i}, \sum_{i j k}^{3} a_{i j} b_{k} = a_{i j} b_{k} + a_{i k} b_{j} + a_{j k} b_{i} f o r a_{i j} = a_{j i} . \\ S o c_{11}^{'} & = V^{- 1} c_{11}, c_{15}^{'} = V^{- 1} c_{15} - V^{- 2} M_{1}, \\ c_{19}^{'} & = V^{- 1} c_{19} - 2 V^{- 2} M_{4} + V^{- 3} (V M_{2} + M_{3}^{2}) / 2, \\ c_{1, 10}^{'} & = V^{- 1} c_{1, 10} - V^{- 2} (M_{3} c_{02} + 2 M_{4} + V M_{5} + 2 M_{6}) / 2 + 3 V^{- 3} (V M_{2} + 2 M_{3}^{2}) / 4, \\ c_{12}^{'} & = V^{- 1} c_{12}, c_{16}^{'} = V^{- 1} c_{16} - V^{- 2} (V M_{7} + c_{01} M_{3}) / 2, w h e r e \end{matrix}

\begin{matrix} M_{1} & = t_{i} t_{j} k_{2}^{i j k} V_{k} = c_{32} + 2 c_{36}, M_{2} = V_{i} k_{1}^{i j} V_{j} = c_{35} + 4 c_{39} + 4 c_{3, 10}, \\ M_{3} & = t_{i} k_{1}^{i j} V_{j} = c_{22} + 2 c_{23} = {\tilde{c}}_{22} s a y, M_{4} = t_{i} k_{1}^{i j} t_{j k} k^{k l} V_{l} = c_{39} + 2 c_{3, 10}, \\ M_{5} & = k_{1}^{i j} V_{i j} = 2 c_{1, 10} + 2 c_{19} + c_{14} + 4 c_{17}, \\ M_{6} & = t_{i} k_{1}^{i j} V_{j k} k_{1}^{k l} t_{l} = 2 c_{3, 10} + 2 c_{3, 11} + c_{34} + 4 c_{38}, \\ M_{7} & = k_{1}^{i} V_{i} = c_{12} + 2 c_{16} \Rightarrow \\ c_{19}^{'} & = V^{- 1} c_{19} + 2 V^{- 2} (4 c_{35} - c_{3, 10}) + V^{- 3} {\tilde{c}}_{22}^{2} / 2, \\ c_{1, 10}^{'} & = \sum_{i = 1}^{3} V^{- i} b_{i} f o r b_{1} = - c_{14} / 2 - 2 c_{17} - c_{19}, b_{3} = 3 {\tilde{c}}_{22}^{2} / 2, \\ b_{2} & = - {\tilde{c}}_{22} c_{02} / 2 - c_{34} + 3 c_{35} / 4 - 4 c_{38} + 2 c_{39} - c_{3, 10} - 2 c_{3, 11} . \end{matrix}

Substitution into (A1) yields

{(a_{22})}_{2}

. The other

a_{r i}^{'} = {(a_{r i})}_{r}

given on p.60 are obtained similarly.

Withers (1984):

p393 In the 5 line expression for

f_{4} (x, L)

, replace

(x^{3} - x) / 30

(x^{3} - 3 x) / 30

, and

+ 2473) / 7776

+ 2473 x) / 7776

p394 In (3.4) replace

(x^{2} - 1) / 2,

(x^{2} - 1) / 6,

p394 In line 2 of Section 4, ’of Section 2’ should be ’of Section 3’.

The following corrigendum for a printer’s error appeared in

Withers, C.S. (1986) Jnl. Royal Statist. Soc. B, 48 p258:

The expression

- l_{3}^{4} (252 x^{5} - 1688 x^{3} + 1511 x) / 7776

should be added to the last line on p393.

That also gives

g_{5} (y)

and

g_{6} (y)

for the last line on p393.

Withers (1987):

p2371 (2.4):

\sum_{i = 1}^{\infty} n^{- i} C_{i}

need not converge. We only require an asymptotic expansion. The same is true for (3.2) p2375.

p2371, 3rd to last paragraph. Replace ’Appendix C, which also’ by ’Appendix D. Appendix C’

p2372, Example 2.2, line 2. Replace

t^{2 j} (θ)

t^{(2 j)} (θ)

, the

2 j

derivative of

t (θ)

. In line 3 and in Example 3.1,

{(y)}_{j} = y (y - 1) \dots (y - j + 1) .

p2377 line 2: replace (1.2) by (2.4)

p2377 line 3: replace

/ N |

/ N

p2377 line 9: replace ’Section 2’ by ’Section 3’ Since

E_{1} = 0, C_{1}

of Example 3.2 p2376 is unaffected.

p2378: these expression for

C_{j}

are correct if

\hat{θ}

is unbiased. In that case the terms on p2378 with a 1 in the top line are zero so that

C_{j}

has only

m_{j}

terms where

m_{1} = 1, m_{2} = 3, m_{3} = 6, m_{4} = 12 .

However if

\hat{θ}

is biased, then these expression for

C_{j}

did not allow for contributions from replacing

θ

E \hat{θ}

in the cumulant coefficients

k_{j}^{a_{1} \dots a_{r}}

of (3.2). These are corrected in Withers, C.S. and Nadarajah, S. (Submitted), Bias-reduced estimates for parametric problems.

p2379 Appendix D. Add at start: For

p = 1

see (3.4) of

Withers, C.S. and Nadarajah, S. (2013), Delta and jackknife estimates of low bias for functions of binomial and multinomial parameters. Journal of Multivariate Analysis, 118, 138–147. DOI: 10.1016/j.jmva.2013.02.006

Withers (1988):

p729: in the 10th line from the bottom, replace “their range

1 \dots p

” by “their range

1 \dots k

”

p732 line 9:

T_{x_{i} x_{j} . . .}^{a_{i} a_{j} . . .}

should be

T_{x_{1} x_{2} . . .}^{a_{1} a_{2} . . .}

p734: in the expression for

h_{1}

in the 5th to last line, replace

H e_{2}

H e_{2} / 6 .

p737: in line 11, “Section 1 and 2 of Withers (1983a)” should read “Section 1 and 2 of Withers (1983b)”.

p741: in the 4th equation from the bottom, at the end of the line, replace

[1^{j}] T_{2}^{j},

{[1^{j}]}_{1} T_{2}^{j},

Withers and Nadarajah (2008):

p743 para 2, line 4. Replace ’about zero.’ by ’about zero when G puts mass 1 at x.’

p754, 756. Replace

w_{i n_{a}}

w_{i n a}

. Different samples can have different weights.

p754 2nd to last line. The first term on RHS,

c_{11} / 2

, should be

c_{11}

p755, line 6. There is a typesetting error in the first of the 2 lines for

a_{220}

. Replace the first line with

a_{220} = σ^{- 2} (c_{11} - c_{12} - c_{14} / 2 + c_{15} - 2 c_{17} - c_{19} / 2) - σ^{- 4} [(c_{01} + c_{02} / 2) (c_{22} + 2 c_{23}) + c_{32}

p756. The 3rd and 4th lines after (8), should be

\begin{matrix} {[1^{r}]}_{a} & = \int T_{F} {(_{x}^{a})}^{r} d F_{a} (x), \\ {[1, 12, 2^{r}]}_{a_{1} a_{2}} & = \int \int T_{F} (_{x_{1}}^{a_{1}}) T_{F} (_{x_{1} x_{2}}^{a_{1} a_{2}}) T_{F} {(_{x_{2}}^{a_{2}})}^{r} d F_{a_{1}} (x_{1}) d F_{a_{2}} (x_{2}), \end{matrix}

Withers and Nadarajah (2009):

p 272. Line 3: Convergence of

S (t)

is not needed, since

B_{r k}

is a finite sum.

κ_{r}

on LHS(1.1) should be

k_{r}

p 273 last paragraph: also

f (x) / ϕ (x)

is only meaningful if X is dimension-free.

p 275. (2.8) is correct but since

B_{1} = B_{2} = 0

, (2.8) can also be written

\int f^{2} / ϕ = 1 + \sum_{k = 3}^{\infty} B_{k}^{2} / k! .

In the 5th line of Section 3 insert after

B_{r k} (α)

, `at

α_{1} = α_{2} = 0

’.

The first line of (3.1) should read

B_{r} = \sum (B_{r k} ϵ^{r - 2 k} : 1 \leq k \leq r / 3)

(3.2) can be written

K_{s} = s - 2 [s / 3]

where

[x]

is the integral part of x.

p276. In the expression for

B_{10}, B_{10, 18}

should be

B_{10, 1}

p 277. In the 2nd to last line,

b_{64}

should be

B_{61}

p 278. In the expession for

b_{4}

, the first term should be doubled. In the expession for

b_{5}

b_{82}

should be

B_{82}

Withers and Nadarajah (2010a):

p3. In 5th and 6th to last lines, replace

= n^{- 2} K_{a b} + O (n^{- 2})

= n^{- 1} K_{a b} + O (n^{- 2})

p5. 2 lines above Theorem 2.2, replace “third moments” by “third central moments”

p7, lines 2-3: delete “and its Studentised version”

p7, lines 3-4: delete “or

n^{- 1 / 2} (β_{a} - β_{a}) {\hat{J}}_{a a}^{- 1 / 2}

”

p7, line 7-10: delete from “So, a one-sided” to “by

O (n^{- 1 / 2});

p9. Move “Set

ϕ^{'} = \dots m = p + 1 .

on the last 2 lines of p9 and 1st line of p 10 to just before “Set” on p9 line 9.

p10, lines 14-15: replace “

g_{i j}

where” by “

g_{i j}

.” and move the rest of the sentence, “

g_{i j} = \dots g_{N . i j \dots}

” to the line after (6.1) p9, preceded by the word “Set”

Withers and Nadarajah (2010b):

p1129 line 7: replace

b_{k}^{i_{1} . . . i_{r}} (Y_{n})

b_{k}^{i_{1} . . . i_{r}} (Y)

To the 9th to last line we can add

{\tilde{P}}_{3} (t, B) = e_{3} (t) + e_{1} (t) e_{2} (t) + e_{1} {(t)}^{3} / 6,

From p1130 line 6 to the end of §5: replace s by p, the dimension of

θ

p1130 line 7 is clearer we replace line 8 by

f o r p_{(n)}^{(k)} (y) = \partial_{k_{1}} \dots \partial_{k_{p}} p_{(n)} (y), \partial_{k} = \partial / \partial y_{k},

p1130 line 9. replace

H_{ν + k} (y)

H_{ν + k} (y, V)

p1130 The 5th and 6th to last lines:

for example

K_{j}^{i_{1} . . . i_{r}} = k_{j}^{(i_{1} . . . i_{r})} (t) = \partial_{i_{1}} \dots \partial_{i_{r}} k_{j} (t)

where

\partial_{i} = \partial / \partial t_{i} .

p1132. A note on Corollary 3.2. For the duality of

I (x)

and

k_{0} (t)

see p176 of McCullagh, P., (1987) Tensor methods in statistics. Chapman and Hall, London.

p1133. In line 14 replace

H_{ν + λ} (θ, V_{t})

H_{ν + λ} (0, V_{t})

Withers and Nadarajah (2014a):

p81. In (2.14), replace

J_{r} (x)

and

J_{r}^{'} (x)

J_{r} (x) / r!

and

J_{r}^{'} (x) / r!

p81. The 2nd line after (2.15) should read

J_{r}^{'} (x) = \int_{V \bar{y} \leq V \bar{x}} {\bar{H}}_{r} (\bar{y}, \bar{V}) ϕ_{\bar{V}} (\bar{y}) d \bar{y}

The next line is correct:

J_{r}^{'} (x) = \int_{V \bar{y} \leq V \bar{x}} {(- \partial_{\bar{y}})}^{r} ϕ_{\bar{V}} (\bar{y}) d \bar{y} .

p82. In (2.20), replace

J_{r} (y_{1}, y_{2})

J_{r} (y_{1}, y_{2}) / r!

p 85. In Withers, C.S. and Nadarajah, S. (2009), replace ’via’ by ’in terms of’.

Withers and Nadarajah (2014c):

p 676. Multiply RHS of (1.13) by

n^{1 / 2}

. That is, replace it by

\begin{matrix} Y_{J K θ} & = {(n / s_{2 K θ})}^{1 / 2} (\hat{θ} - s_{1 J θ}), J \geq 0, K \geq 1 . \end{matrix}

p 699. In the editing of the original paper of 64 pages down to 21 pages, some details had to be removed. Here are some more details for Theorem 1.2 after (1.24).

\begin{matrix} \nabla_{1} & = 0 i f J \geq 1, \nabla_{2} = {\bar{A}}_{43} H_{2} i f K \geq 2, \\ \nabla_{3} & = {\bar{A}}_{33} H_{2} + {\bar{A}}_{54} H_{4} i f J \geq 2, \nabla_{4} = {\bar{A}}_{44} H_{3} + {\bar{A}}_{65} H_{5} i f K \geq 3, \\ \nabla_{5} & = {\bar{A}}_{34} H_{2} + {\bar{A}}_{55} H_{4} + {\bar{A}}_{76} H_{6} i f J \geq 3, \\ \nabla_{6} & = {\bar{A}}_{45} H_{3} + {\bar{A}}_{66} H_{5} + {\bar{A}}_{87} H_{7} i f K \geq 4 . \\ \nabla_{r e} & = 0 i f r \leq 3 f o r e = h, f, g, \nabla_{4 e} = {[4^{2}]}_{0} e (4^{2}), \\ \nabla_{5 e} & = {[45]}_{0} e (45) + {[34]}_{1} e (34), \\ \nabla_{6 e} & = \sum {{[π]}_{0} e (π) : π = 5^{2}, 46, 4^{3}} + \sum {{[π]}_{1} e (π) : π = 4^{2}, 35} + {[3^{2}]}_{2} e (3^{2}), \end{matrix}

where the

e (π), {[π]}_{i}

needed for

e_{r} (x), 1 \leq r \leq 6,

are as follows.

\begin{matrix} h (i j \dots) & = H_{i + j + \dots - 1} s o t h a t h (1^{i_{1}} 2^{i_{2}} \dots) = H_{1 i_{1} + 2 i_{2} + \dots - 1} . \\ F o r r & = 4 : {[4^{2}]}_{0} = {\bar{A}}_{43}^{2} / 2!, h (4^{2}) = H_{7}, \\ f (4^{2}) & = H_{7} - H_{1} H_{3}^{2}, g (4^{2}) = H_{7} - 2 H_{3} H_{4} + H_{1} H_{3}^{2} . \end{matrix}

\begin{matrix} F o r r & = 5 : {[45]}_{0} = {\bar{A}}_{43} {\bar{A}}_{54}, h (45) = H_{8}, \\ f (45) & = H_{8} - H_{1} H_{3} H_{4}, g (45) = H_{8} - H_{3} H_{5} - H_{4}^{2} + H_{1} H_{3} H_{4}, \\ _{1} & = {\bar{A}}_{33} {\bar{A}}_{43}, h (34) = H_{6}, f (34) = H_{6} - H_{1} H_{2} H_{3}, \\ g (34) & = H_{6} - H_{2} H_{4} - H_{3}^{2} + H_{1} H_{2} H_{3} . \\ F o r r & = 6 : {[5^{2}]}_{0} = {\bar{A}}_{54}^{2} / 2!, h (5^{2}) = H_{9}, \\ f (5^{2}) & = H_{9} - H_{1} H_{4}^{2}, g (5^{2}) = H_{9} - 2 H_{4} H_{5} + H_{1} H_{4}^{2}, \\ {[46]}_{0} & = {\bar{A}}_{43} {\bar{A}}_{65}, h (46) = H_{9}, \\ f (46) & = H_{9} - H_{1} H_{3} H_{5}, g (46) = H_{9} - H_{3} H_{6} - H_{4} H_{5} + H_{1} H_{3} H_{5}, \\ {[4^{3}]}_{0} & = {\bar{A}}_{43}^{3} / 3!, h (4^{3}) = H_{11}, f (4^{3}) = H_{11} - 3 H_{1} H_{3} H_{7} - H_{2} H_{3}^{3} + 3 H_{1}^{2} H_{3}^{3}, \\ g (4^{3}) & = H_{11} - 3 H_{3} H_{8} - 3 H_{4} H_{7} + 3 H_{1} H_{3} H_{7} + 3 H_{3}^{2} H_{5} + 6 H_{3} H_{4}^{2} \\ - 9 H_{1} H_{3}^{2} H_{4} - H_{2} H_{3}^{3} + 3 H_{1}^{2} H_{3}^{3}, \\ {[4^{2}]}_{1} & = {\bar{A}}_{43} {\bar{A}}_{44}, \\ {[35]}_{1} & = {\bar{A}}_{33} {\bar{A}}_{54}, f (35) = H_{7} - H_{1} H_{2} H_{4}, g (35) = H_{7} - H_{3} H_{4} - H_{2} H_{5}, \\ {[3^{2}]}_{2} & = {\bar{A}}_{33}^{2} / 2!, f (3^{2}) = H_{5} - H_{1} H_{2}^{2}, g (3^{2}) = H_{5} - 2 H_{2} H_{3} + H_{1} H_{2}^{2} . \end{matrix}

p 702 §2. In the 3rd equation of Theorem 2.1,

ln Γ (μ)

should be

ln Γ (m)

. p 704. Disregard Table 3.

Withers and Nadarajah (2015):

In (22) and the formulas for

d_{2}, \dots, d_{6}

that follow, replace

d_{r}

{\bar{d}}_{r} = r d_{r} = c_{r} (x) / (r - 1)! .

As stated this gives

c_{r} = c_{r} (x) = r! d_{r} .

For example

\begin{matrix} c_{2} & = a_{1}, c_{3} = 2 a_{1}^{2} + a_{2}, c_{4} = 3! a_{1}^{3} + 7 a_{1} a_{2} + a_{3}, \\ c_{5} & = 4! a_{1}^{4} + 46 a_{1}^{2} a_{2} + 11 a_{1} a_{3} + 7 a_{2}^{2} + a_{4}, \\ c_{6} & = 5! a_{1}^{5} + 326 a_{1}^{3} a_{2} + 101 a_{1}^{2} a_{3} + 127 a_{1} a_{2}^{2} + 16 a_{1} a_{4} + 25 a_{2} a_{3} + a_{5} . \end{matrix}

In the first reference, [1], replace J. J. Alfredo by J. A. Jimenez.

References

Barndoff-Nielsen, O.E. and Cox, D.R. (1989). Asymptotic techniques for use in statistics. Chapman & Hall, London.
Bhattacharya, R.N. and Rao, Ranga R. (1976). Normal approximation and asymptotic expansions, Wiley, New York.
Cai, T. (2005) One-sided confidence intervals in discrete distributions. Journal of Stat. Planning and Inference, 131, 63–88.
Comtet,L. (1974) Advanced combinatorics. Reidel, Dordrecht.
Cornish, E.A. and Fisher, R. A. (1937) Moments and cumulants in the specification of distributions. Rev. de l’Inst. Int. de Statist., 5, 307–322. Reproduced in The collected papers of R.A. Fisher, 4.
Daniels, H.E. (1983) Saddlepoint approximations for estimating equations. Biometrika 70, 89–96.
Daniels, H.E. (1987) Tail probability expansions. Intern. Statist. Review 55, 37–48.
Fisher, R. A. and Cornish, E.A. (1960) The percentile points of distributions having known cumulants. Technometrics, 2, 209–225.
Hill, G.W. and Davis, A.W. (1968) Generalised asymptotic expansions of Cornish-Fisher type. Ann. Math. Statist., 39, 1264–1273.
James, G.S. and Mayne, A.J. (1962). Cumulants of functions of random variables. Sankhya A 24, 47–54.
Stuart, A. and Ord, K. (1987). Kendall’s advanced theory of statistics, 1. 5th edition. Griffin, London.
Withers, C.S. (1982) The distribution and quantiles of a function of parameter estimates. Annals of the Institute of Statistical Mathematics, Series A, 34 (1), 55–68. Corrigendum: http://freepages.misc.rootsweb.com/~kitwithers/research/1982a.pdf.
Withers, CS (1983) Expansions for the distribution and quantiles of a regular functional of the empirical distribution with applications to nonparametric confidence intervals. Annals Statist., 11 (2), 577–587.
Withers, C.S. (1984) Asymptotic expansions for distributions and quantiles with power series cumulants. J. Roy. Statist. Soc. B, 46, 389–396.
Withers, C.S. (1987) Bias reduction by Taylor series. Commun. Statist. - Theor. Meth., 16, 2369–2383.
Withers, CS (1988) Nonparametric confidence intervals for functions of several distributions. Annals of the Institute of Statistical Mathematics, Part A, 40 (4), 727–746.
Withers, C.S. (1989) Accurate confidence intervals when nuisance parameters are present. Comm. Statist. - Theory and Methods, 18, 4229–4259.
Withers, C.S. and Nadarajah, S. (2008) Edgeworth expansions for functions of weighted empirical distributions with applications to nonparametric confidence intervals, Journal of Nonparametric Statistics, 20, 751–768. http://www.informaworld.com/smpp/1162981568-85928283/content~db=all~content=a905308777.
Withers, C.S. and Nadarajah, S. (2009) Charlier and Edgeworth expansions for distributions and densities in terms of Bell polynomials. Probab. Math. Statist. 29, 271–280.
Withers, C.S. and Nadarajah, S. (2010a) The bias and skewness of M-estimators in regression, Electronic Journal of Statistics, 4, 1–14. http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdfview_1&handle=euclid.ejs/1262876992.
Withers, C.S. and Nadarajah, S. (2010b) Tilted Edgeworth expansions for asymptotically normal vectors. Annals of the Institute of Statistical Mathematics, 62 (6), 1113–1142. [CrossRef]
Withers, C.S. and Nadarajah, S. (2010c) The distribution and quantiles of functionals of weighted empirical distributions when observations have different distributions. Statistics and Probability Letters, 80 (13-14), 1093–1102. [CrossRef]
Withers, C.S. and Nadarajah, S. (2011a) Expansions for the distribution of M-estimates with applications to the multi-tone problem. ESIAM - Probability and Statistics, 15, 139–167. [CrossRef]
Withers, C.S. and Nadarajah, S. (2011b) Channel capacity for MIMO systems with multiple frequencies and delay spread. Applied Mathematics and Information Sciences, 5 (3), 480–483.
Withers, C.S. and Nadarajah, S. (2011c) Reciprocity for MIMO systems. European Transations on Telecommunications, 22 (6), 276–281. [CrossRef]
Withers, CS and Nadarajah, S (2012a) Improved confidence regions based on Edgeworth expansions. Computational Statistics and Data Analysis, 56 (12), 4366–4380.
Withers, C.S. and Nadarajah, S. (2012b) The distribution of Foschini’s lower bound for channel capacity. Advances in Applied Probability, 44 (1), 260–269. [CrossRef]
Withers, C.S. and Nadarajah, S. (2012c) Cornish-Fisher expansions for sample autocovariances and other functions of sample moments of linear processes. Brazilian Journal of Probability and Statistics, 26 (2), 149–166. [CrossRef]
Withers, C.S. and Nadarajah, S. (2012d) Cornish-Fisher expansions about the F-distribution. Applied Mathematics and Computation, 218 (15), 7947–7957. [CrossRef]
Withers, C.S. and Nadarajah, S. (2012e) Transformations of multivariate Edgeworth-type expansions Statistical Methodology, 9 (3), 423–439. [CrossRef]
Withers, CS and Nadarajah, S (2012f) Nonparametric estimates of low bias. Revstat Statistical Journal, 10 (2), 229–283.
Withers, C. S. and Nadarajah, S. (2013a) Cornish-Fisher expansions for functionals of the partial sum empirical distribution. Statistical Methodology, 12, 1–15. [CrossRef]
Withers, C.S. and Nadarajah, S. (2013b) The distribution of the amplitude and phase of the mean of a sample of complex random variables. Journal of Multivariate Analysis, 113, 128–152. [CrossRef]
Withers, C.S. and Nadarajah, S. (2014a) The dual multivariate Charlier and Edgeworth expansions. Statistics and Probability Letters, 87 (1), 76–85. [CrossRef]
Withers, C.S. and Nadarajah, S. (2014b) Asymptotic properties of M-estimators in linear and nonlinear multivariate regression models, Metrika, 77, 647–673. [CrossRef]
Withers, C.S. and Nadarajah, S. (2014c) Expansions about the gamma for the distribution and quantiles of a standard estimate. Methodol. Comput. Appl. Probab., 16 (3), 693–713. [CrossRef]
Withers, C.S. and Nadarajah, S. (2015) Edgeworth-Cornish-Fisher-Hill-Davis expansions for normal and non-normal limits via Bell polynomials, Stochastics An International Journal of Probability and Stochastic Processes,87 (5), 794–805. [CrossRef]
Withers, C.S. and Nadarajah, S. (2020) The distribution and percentiles of channel capacity for multiple arrays. Sadhana, Indian Academy of Science, 45 (1), 1–25. 2020. https://www.ias.ac.in/article/fulltext/sadh/045/0155.
Withers, C.S. and Nadarajah, S. (2022) Chain rules for multivariate cumulant coefficients. Stat. 11 (1). 2022:11:e451. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

5th Order Multivariate Edgeworth Expansions for Parametric Estimates

Abstract

1. Introduction and summary

2. Foundations

3. Cumulant Coefficients for t ( w ^ ) when E w ^ = w

4. Cumulant Coefficients for t ( w ^ ) when E w ^ ≠ w

5. Cumulant Coefficients for Univariate t ( w ^ )

6. An Extension to Theorem 2.1

7. Discussion

8. Conclusion

Abbreviations

Appendix A: Some comments on the references

References

MDPI Initiatives

Important Links

Subscribe

3. Cumulant Coefficients for $t (\hat{w})$ when $E \hat{w} = w$

4. Cumulant Coefficients for $t (\hat{w})$ when $E \hat{w} \neq w$

5. Cumulant Coefficients for Univariate $t (\hat{w})$