Experimental and Numerical Investigation of Prepreg-RTM Co-Curing Molding Composite Bolted T-joint under Bending Load

A set of polymer composite bolted T-joints with novel configuration consisting of internal skeleton and external skin was fabricated using a prepreg-RTM co-curing molding process. Experiments were conducted to study their mechanical properties under bending load. A finite element model with a polymer resin area between the skin and skeleton was established and verified by the experimental results. Then, the damage propagation process and failure mechanism of the joint and the influence of three factors related to the layer characteristics of the skin and skeleton were investigated by the validated models. The results show that the bending stiffness and the yield limit load of the novel composite T-joint are 0.81 times and 1.65 times that of the 2A12 aluminum T-joint respectively, while at only 55.4% of its weight. The damage of the joint initiates within the resin area and leads to a degradation of the joint bending performances. The preferred stacking sequence of the skeleton is [0/+45/90/-45]ns when primarily subjected to bending loads. The decrease in bending performances is within 5% with the inclining angle of the skeleton less than 12 degrees. The more layers of 90° in the skin, the better bending performances of the joints, while the more layer of 0°, the poorer bending performances.

Keywords:

polymer composites

;

T-joint

;

prepreg-RTM co-curing molding

;

bending performance

;

finite element analysis

;

failure analysis

Subject:

Engineering - Aerospace Engineering

1. Introduction

In modern aerospace industry, polymer composites are gradually taking the place of metals in primary aircraft structure due to their high specific strength and high specific modulus [1,2], e.g., a variety of metal joints are replaced by composite joints. Among these joints, T-joints are widely used for connecting components at the vertical position in wings and tails and have become a hot research topic in the field of composite joint design [3,4].

In recent years, many scholars have investigated the bending performances of composite T-joints of various types and manufacturing processes [5,6,7,8,9,10,11,12,13]. A comparison of these studies reveals that the predominant form of connection for T-joints is adhesive bonding. Adhesive bonding can significantly reduce the number of components and simplify assembly process, but the bending performances of the joint mainly depends on the bonding quality and the material properties of the adhesive. In contrast, bolted connections can provide higher reliability and bending performances and remain a preferred option for primary load-bearing structures [3]. For instance, wings and tails can be connected to the fuselage via bolted T-joints. In these cases, T-joints with bolted connections need to withstand concentrated bending loads derived from the wing surface. Therefore, further research is needed on the bending performances of bolted composite T-joints.

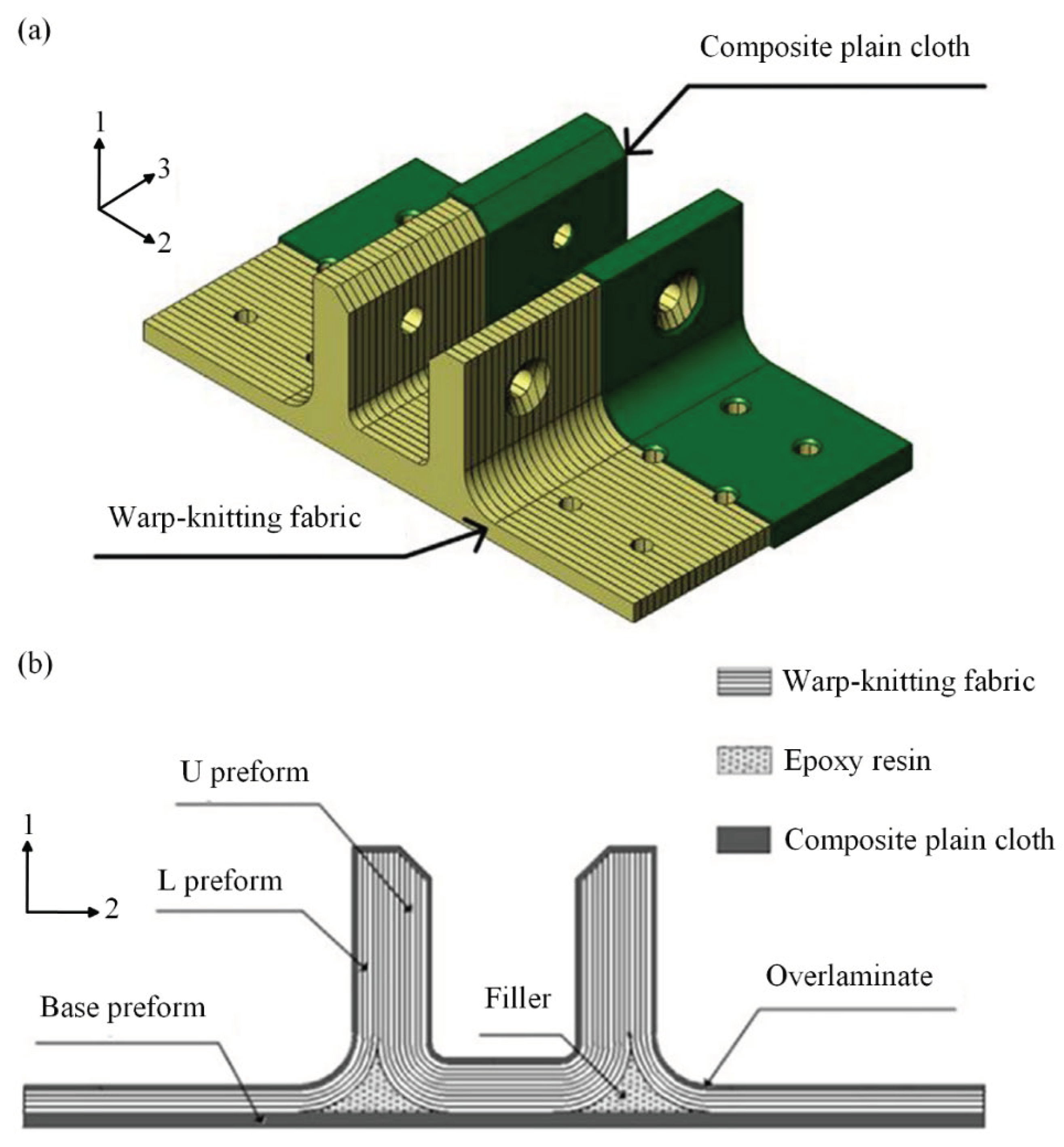
Some studies have found that under bending loads, the primary failure mode of composite T-joints is interlaminar delamination at the R-corner area [10,11,12,13]. Cheng et al. [14,15] investigated the bending performances of a novel configuration composite π-joint. As shown in Figure 1, compared to conventional π-joint [16], this novel configuration lays the warp-knitting fabric along the direction 3, which converts the interlaminar load of the plies at the R-corner area into in-plane load. Experimental results indicate that compared to conventional joint of the same size, the bending ultimate load of the novel configuration joint increases by nearly twice. It can be seen that converting interlaminar load into in-plane load can significantly enhance the load-bearing capacity of composite joints.

Additionally, the manufacturing process also has a significant impact on the mechanical performances of the joints. Some studies have shown that compared to polymer composites based on prepreg molding, products produced by RTM processes have higher fiber volume fractions and higher manufacturing precision. However, RTM preforms are prone to fiber bending deformation and the presence of more voids in the molded products [17,18,19,20]. Li et al. [18] prepared composite laminates respectively fabricated by prepreg-RTM co-curing molding process and prepreg compression molding process. The experimental results indicate that the prepreg-RTM co-curing molding process can effectively reduce the probability of defects such as voids. The interlaminar shear performances and post-impact compression performances of composite laminates fabricated by prepreg-RTM process are superior to those fabricated by prepreg compression molding process. It can be seen that if prepregs with high fiber alignment are used in RTM process, the mechanical performances of RTM products can be effectively improved.

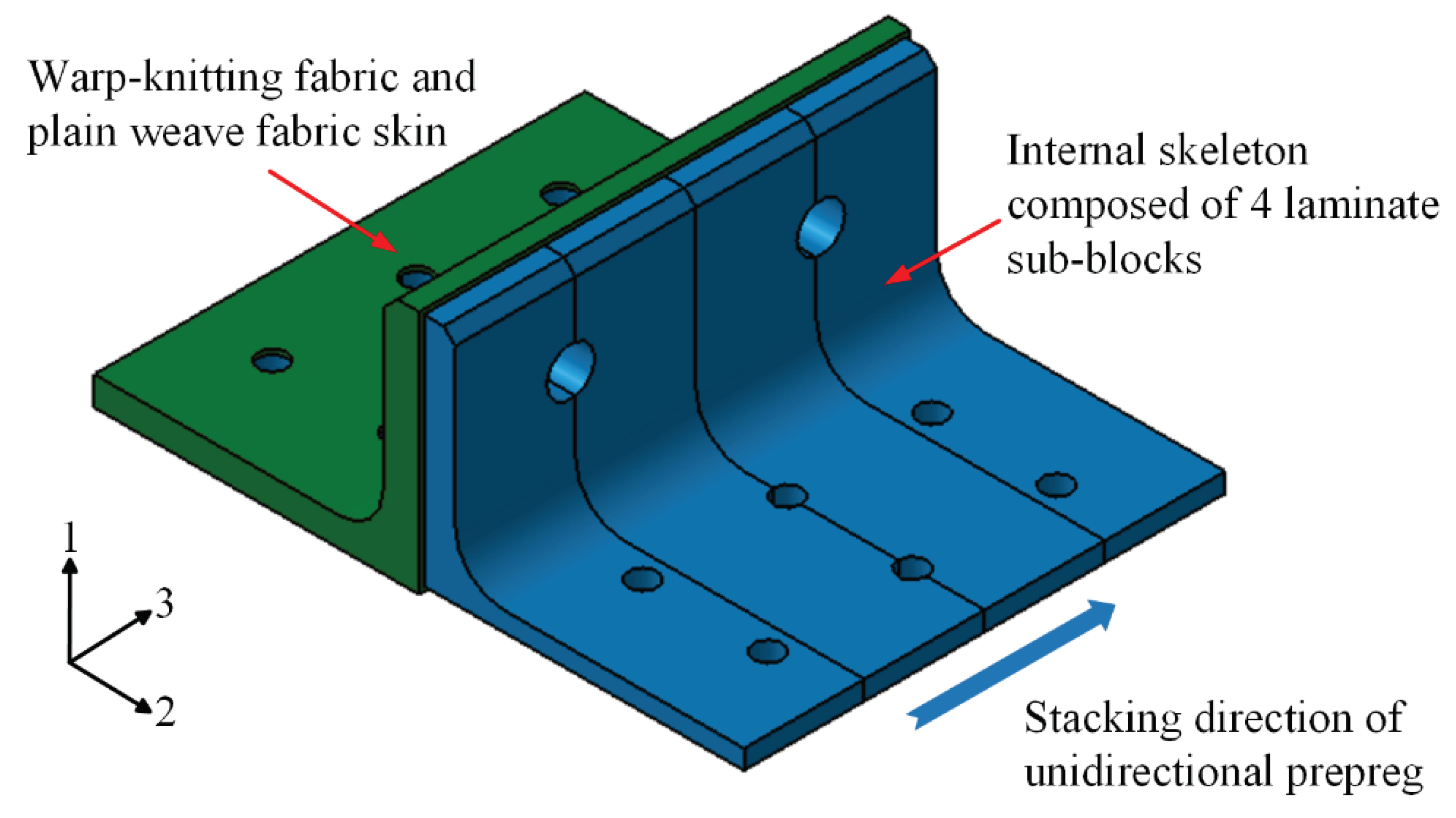
In this present investigation, a set of polymer composite bolted T-joint with novel configuration consisting of internal skeleton, in which plies were laid along the direction 3, and external skin was fabricated based on the stacking method of the novel configuration π-joint, as shown in Figure 2. Also, the prepreg-RTM co-curing molding process was employed to manufacture the novel T-joint. Then, experimental and numerical investigations were conducted to investigate the mechanical properties and failure mechanism of these joints under bending load. Finally, based on validated FE model, numerical investigations were performed to examine the effects of stacking sequence and layer inclining of the internal laminate skeleton, as well as the stacking sequence of the skin, on the bending performances of the novel composite bolted T-joint.

2. Experiment

2.1. Specimen Design

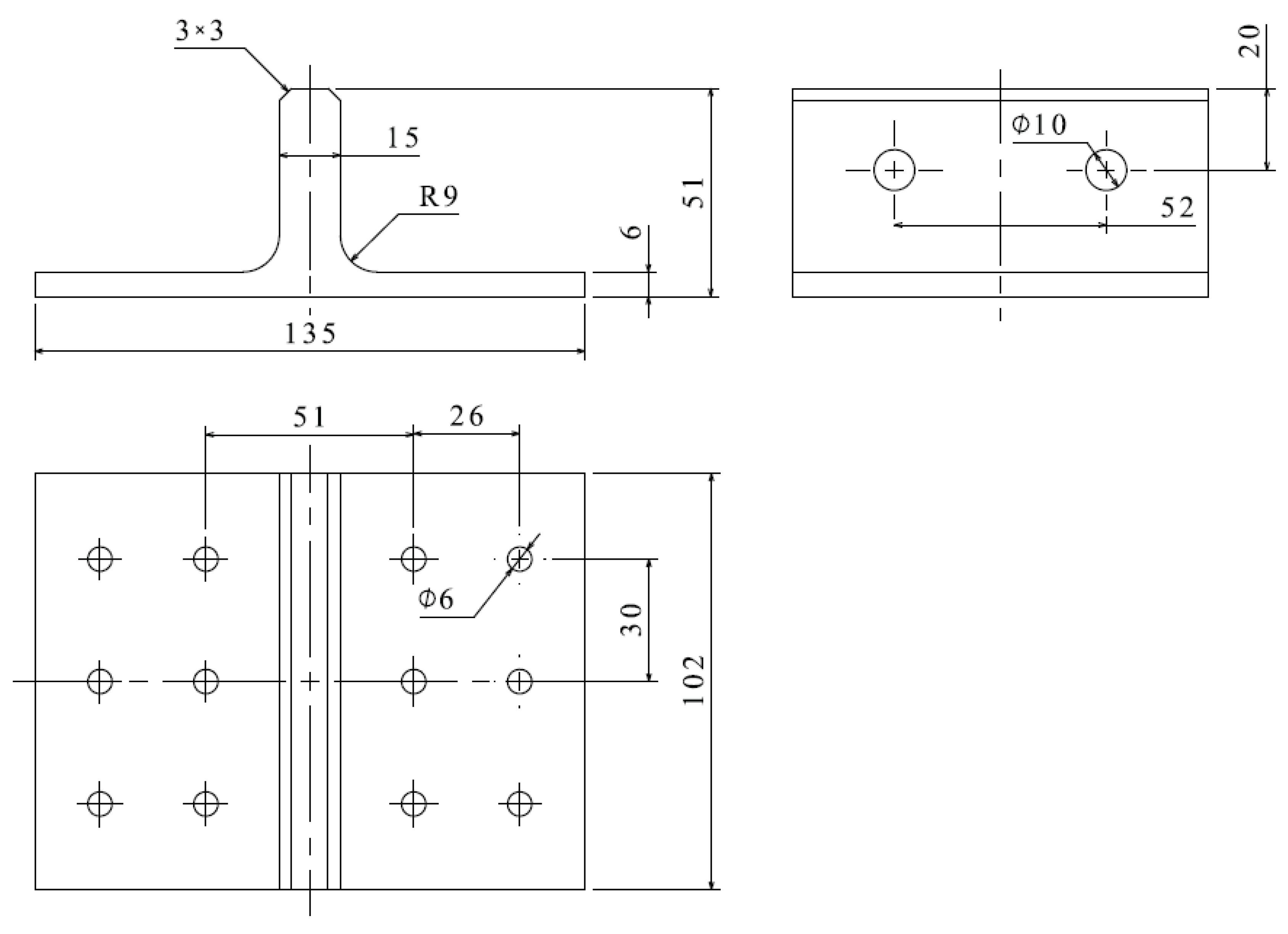
The geometric dimensions of the novel polymer composite bolted T-joint are depicted in Figure 3. The joint was fabricated using a novel prepreg-RTM co-curing molding process, with its configuration design shown in Figure 2. The internal load-bearing skeleton consists of 4 laminate sub-blocks, each 25mm wide, all constructed using ZT7G/9368 unidirectional prepreg stacked along the direction 3 as depicted in Figure 2. 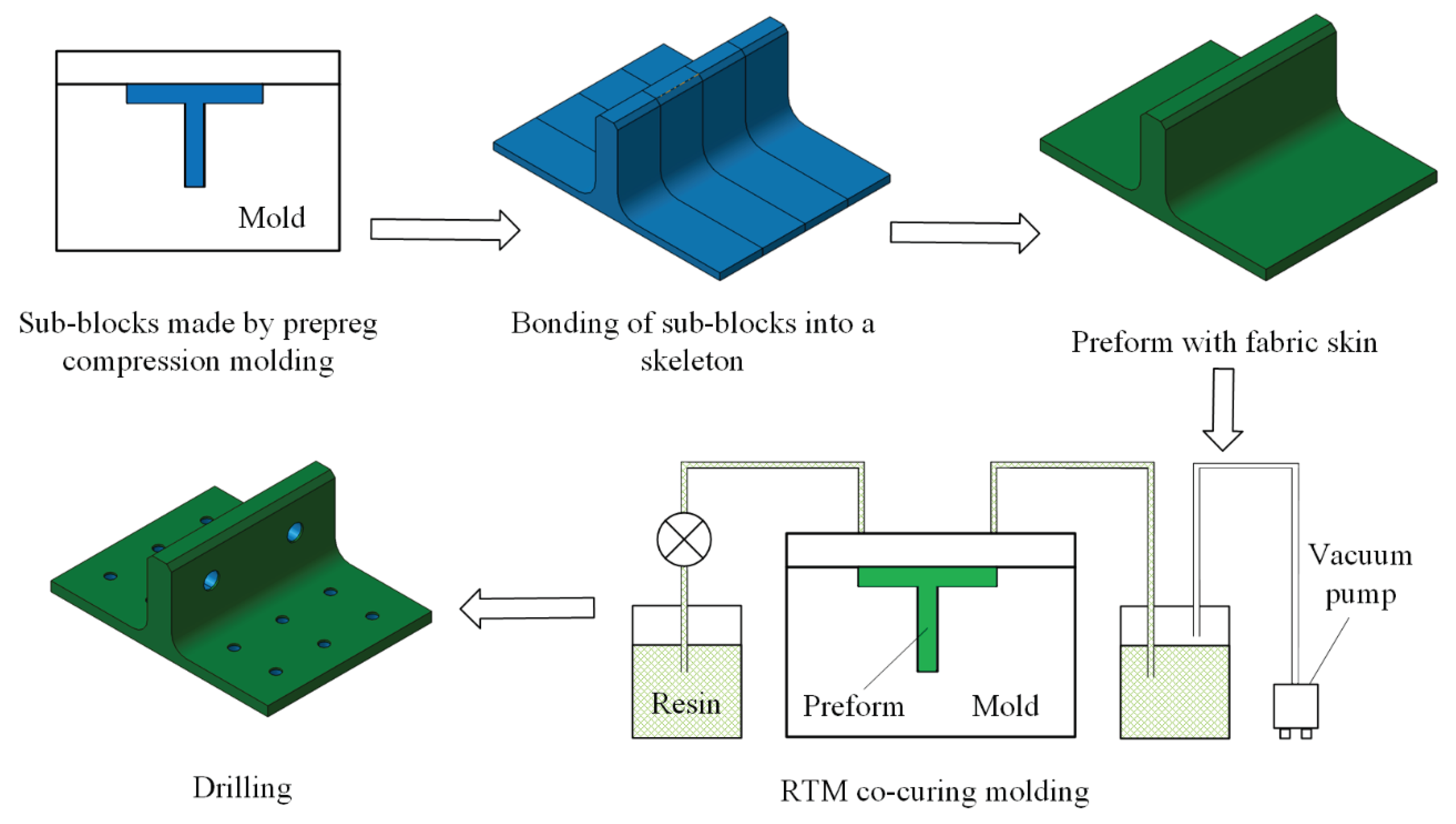The stacking sequence for each sub-block is [0/+45/90/-45]_25s, where the 0° direction corresponds to the direction 1 in Figure 2, and the 90° direction corresponds to the direction 2 in Figure 2. The external skin comprises a total of 5 layers, with 4 internal layers made of ZT7G warp-knitting fabric and the outermost ply made of ZT7G plain weave fabric. The thickness of each warp-knitting fabric layer is 0.125mm, and the thickness of plain weave fabric layer is 0.2mm. The manufacturing process, as illustrated in Figure 4, involves 5 steps. Firstly, prepare 4 laminate sub-blocks using prepreg compression molding and then bond them to form the internal skeleton. Subsequently, dry warp-knitting fabric and plain weave fabric are wrapped around the skeleton to form the preform of the T-joint. Then, the preform is placed into a mold, and 6808 epoxy resin is injected for RTM co-curing molding. Finally, drill holes in the prepared T-joint. Therefore, the matrix material for the internal skeleton is primarily 9368 epoxy resin, while the matrix material for the external skin is mainly 6808 epoxy resin. The material properties of various types of fiber-reinforced polymer composite materials are presented in Table 1, while the material properties of 6068 epoxy resin are provided in Table 2.

2.2. Test Procedure

As shown in Table 3, following the specimen design, three composite specimens with different stacking sequence of the skin were prepared, along with one specimen made of 2A12 aluminum alloy (which has significant potential applications in the aerospace industry [21,22]) of the same size, thus comparing the bending performances between the novel composite T-joint and the aluminum one. Here, the 0° direction corresponds to the direction 3 in Figure 2, while the 90° direction is perpendicular to the 0° direction and normal to the outer surface of the T-joint.

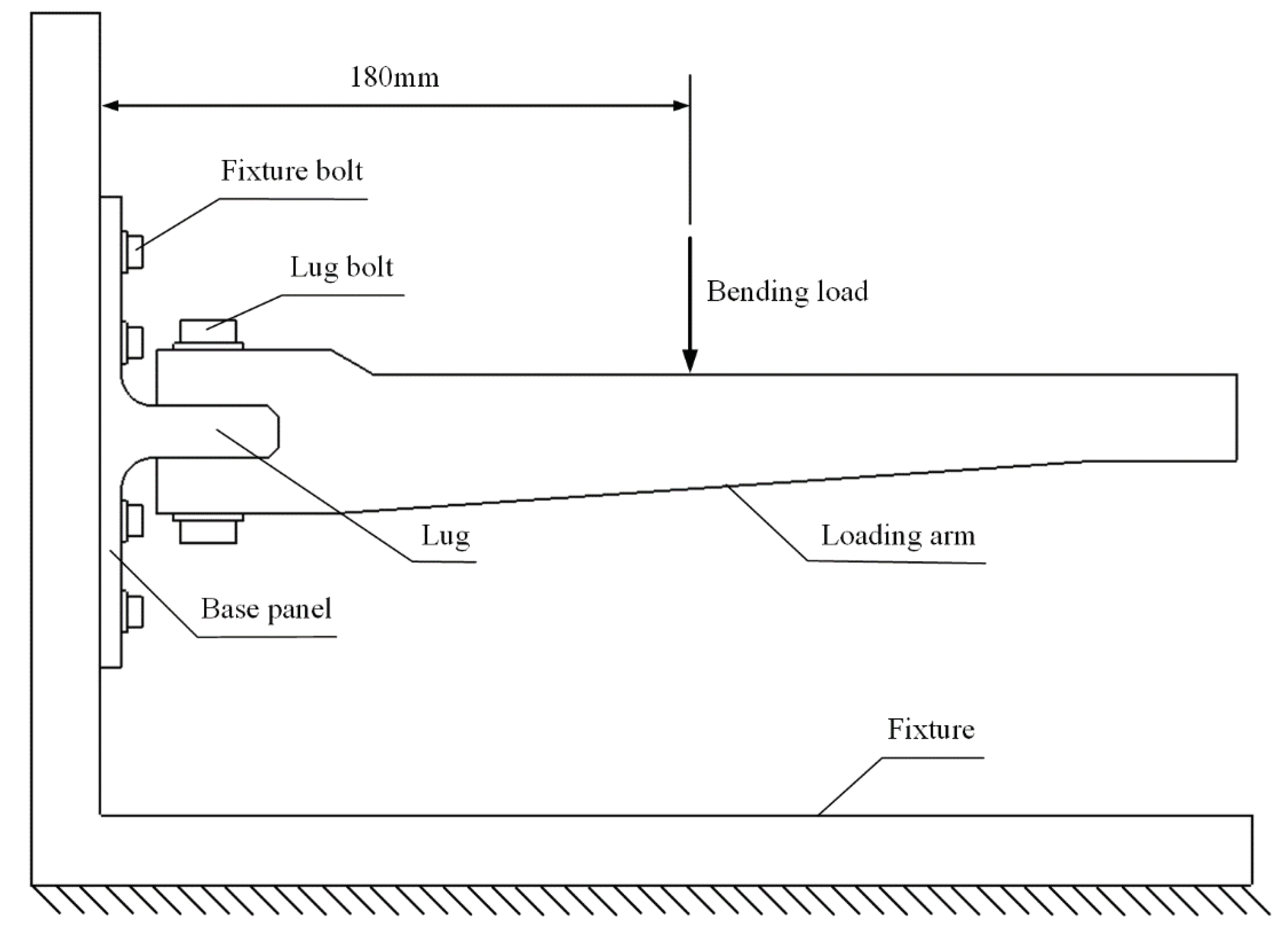
The loading scheme is depicted in Figure 5. The base panel is secured to the L-shaped fixture using twelve steel bolts with a diameter of 6mm. The loading arm is connected to the lug using two steel bolts with a diameter of 10mm. The distance between the loading point and the bottom surface of the joint is 180mm. The experimental setup is illustrated in Figure 6. The L-shaped fixture is fixed on the test platform and reinforced with rib plates welded on both sides to provide sufficient bending stiffness. The load is applied downward by the indenter connected to the loading head of test machine INSTRON 8801 with speed of 0.5 mm/min, exerting bending load on the joint. The load and displacement of the indenter are recorded in real time by the sensors of the testing machine. The materials for the L-shaped fixture, loading arm, and indenter are all 45# steel. The properties of 45# steel are listed in Table 3.

2.3. Results and Discussion

The post-test damage morphologies are depicted in Figure 7. Visible damages of the composite bolted T-joint include cracks around the holes on the base panel, separation of the skin and skeleton, and cracks along the thickness direction of the skeleton at the R-corner area. As shown in Figure 8, the cross-sectional view of the R-corner area after the test reveals the presence of a polymer resin area with non-negligible thickness between the skin and skeleton, with noticeable cracks within this resin area, while no significant delamination is observed in the skin. It can be inferred that the failure of the resin area between the skin and skeleton lead to their separation. Additionally, defects such as voids, layer bending or inclining, and uneven ply lengths are present within the skeleton.

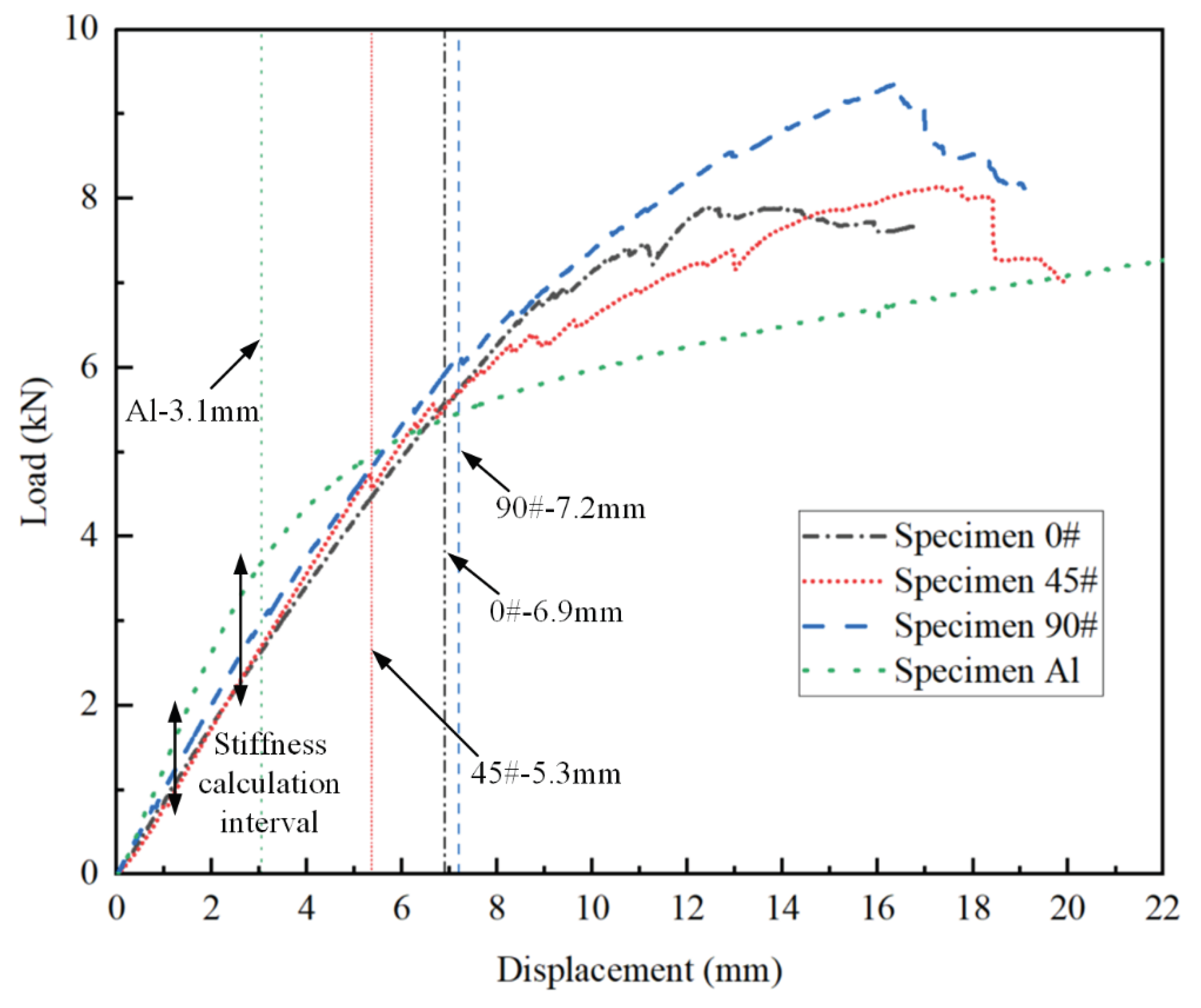
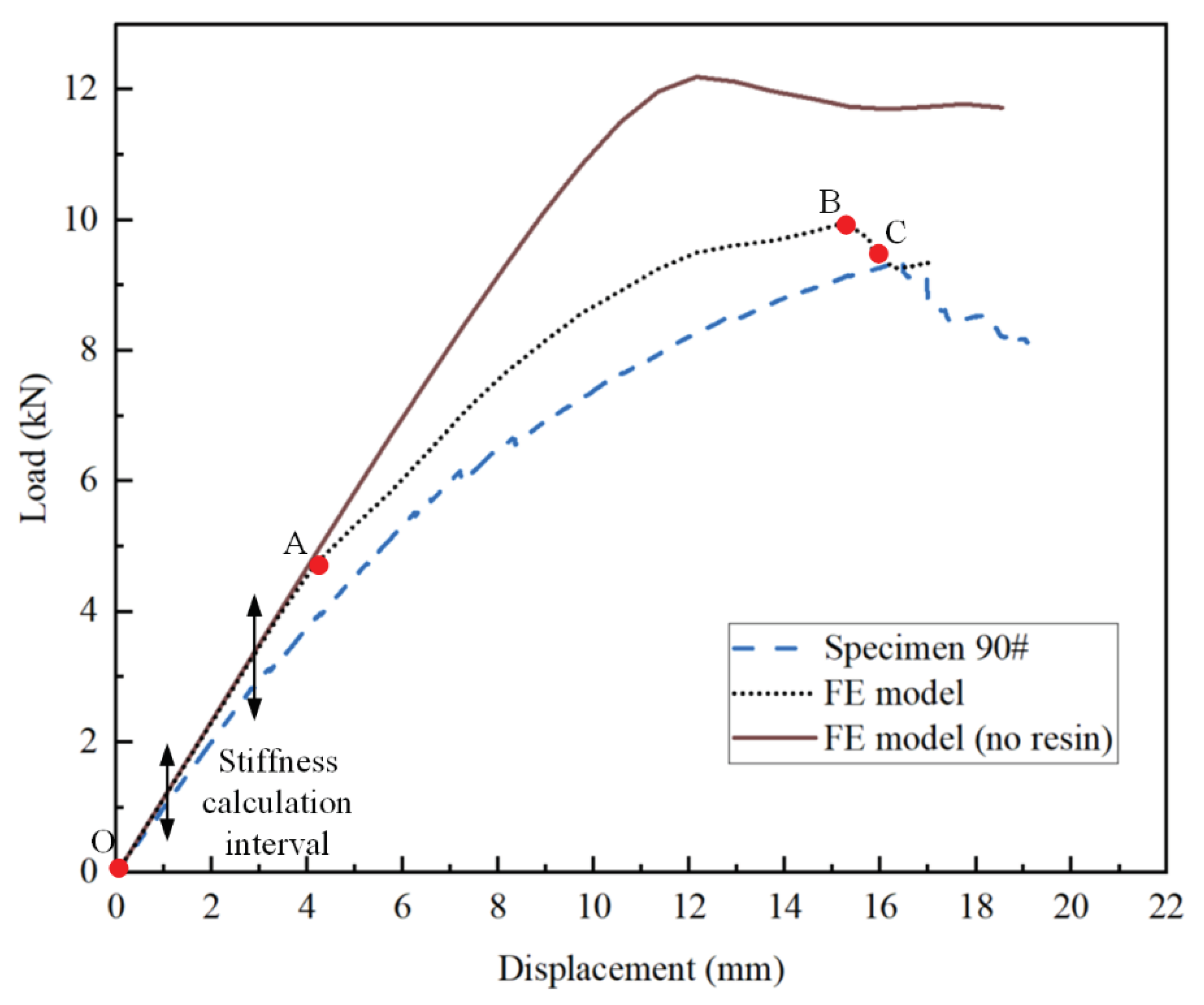
The load-displacement curves obtained from the tests are presented in Figure 9, with the maximum displacement corresponding to significant load changes annotated on the curves. The bending stiffness of each joint is calculated using the linear segments of the data, and the load at which significant load changes occur is taken as the yield limit load for each joint. For composite T-joints, the maximum load from the load-displacement curve is considered as the ultimate load. The test results are summarized in Table 4. It is observed that before plastic deformation occurs in the aluminum T-joint, the bending stiffness of the composite T-joint is lower than that of the aluminum one, but the yield limit load of the composite T-joint is significantly higher than that of the aluminum one. Comparing the test results of specimen Al and Specimen 90#, the bending stiffness of the composite T-joint is 0.81 times that of the aluminum one, while the yield limit load is 1.65 times higher, with the weight being only 55.4% of the aluminum one. Obviously, the novel polymer composite bolted T-joint exhibits excellent bending performances.

Comparing the test results of three composite T-joints, an increasing trend is observed in the bending stiffness and ultimate load of the composite T-joint as the number of 90° layers in the skin increases and the number of 0° layers decreases. Furthermore, Specimen 90# exhibits the highest ultimate load and a smoother change in the load-displacement curve, mainly due to the relatively smaller influence of internal defects in this specimen. Thus, to obtain a finite element model with higher accuracy, it is advisable to establish the finite element model based on the parameters of Specimen 90#.

3. Numerical Study

3.1. Finite Element Model

Finite element models were established by using ABAQUS 2021 commercial software to analyze the stress distribution and corresponding failure mechanisms of the novel polymer composite bolted T-joint under bending load. As mentioned earlier, there exists a layer of 6068 epoxy resin area between the skin and skeleton of the composite T-joint, with a nominal thickness of 0.3mm. Therefore, a layer of resin element was established between the skin and skeleton to represent this resin area. Due to the large number of ply layers in the internal skeleton laminate, precise modeling of each ply layer would significantly increase computational costs and may lead to convergence issues. Composite Layup function in ABAQUS was utilized to simplify the modeling of multi-ply laminate by establishing multiple section points within a single element to represent the [0/+45/90/-45] periodic ply sequence. This method can balance computational costs and accuracy, as demonstrated by Tserpes et al. [23]. Additionally, to optimize computational efficiency, all components of the T-joint and test fixtures were modeled using C3D8R elements, an 8-node linear brick element with reduced integration, known for its efficiency in large models.

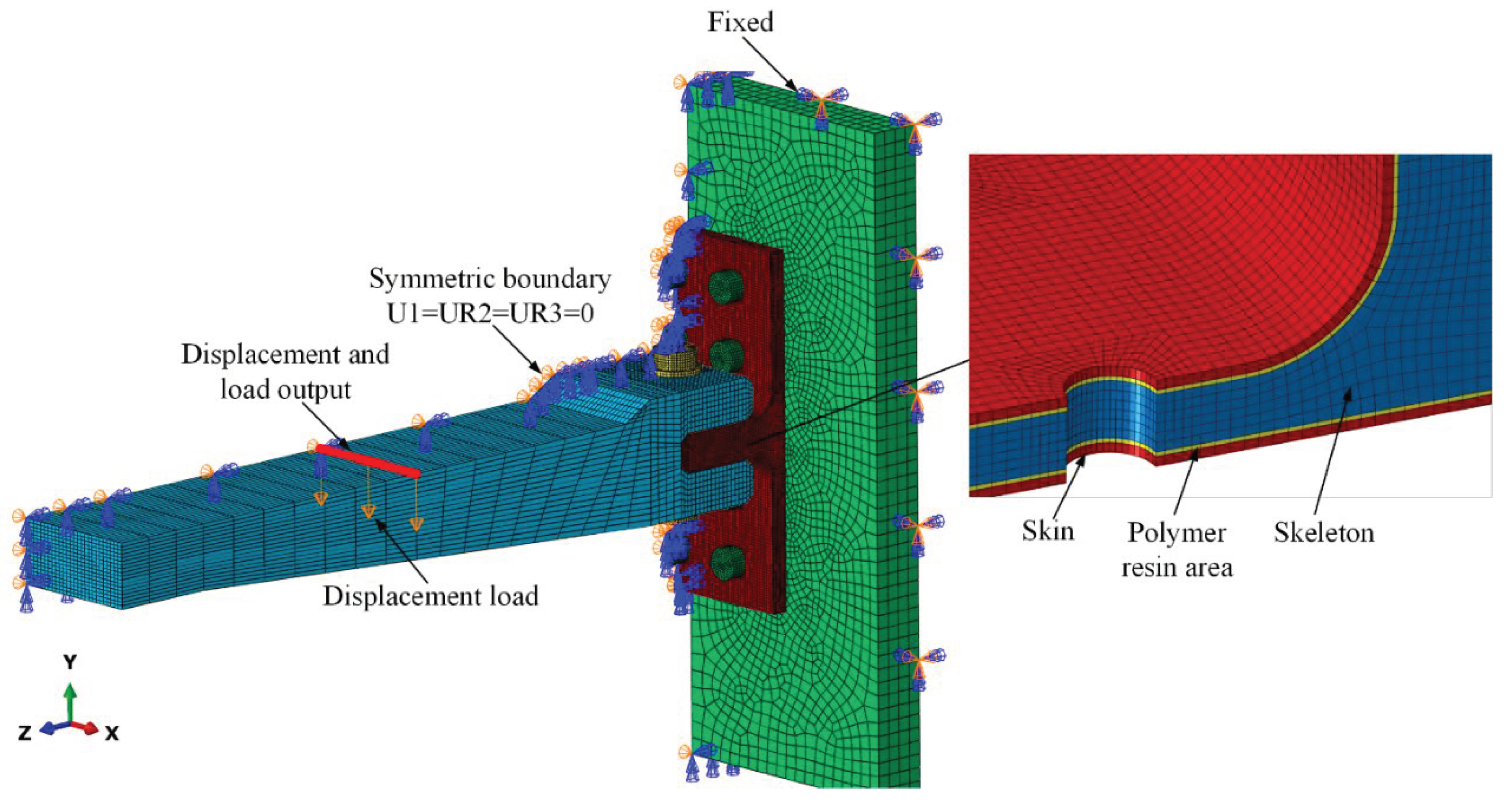
Figure 10 depicts the finite element model, labeled as FE model, of the T-joint under bending load with boundary conditions applied. The mesh near the bolt holes of the T-joint was optimized to better capture the concentrated stresses at the contact interfaces. Solid models of the loading arm, bolts, and fixture were established to accurately represent the loading conditions of the T-joint. Contact interactions between the solid entities were defined as surface-to-surface contacts with a friction coefficient of 0.2. Exploiting the geometric symmetry of the structure, only half of the model was constructed to reduce computational costs, with necessary symmetry constraints applied to the symmetric plane to restrict out-of-plane displacements. Geometric nonlinear analysis was employed to account for relatively significant deformations, especially at the lug region of the T-joint.

Furthermore, a finite element model, labeled as FE model (no resin), was created to validate the significance of the presence of the polymer resin area between the skin and skeleton. FE model (no resin) maintained the same geometry as FE model but removed the resin area by proportionally increasing the thickness of the skin ply layers from 0.7mm to 1mm. The number and stacking sequence of the skin ply layers remained unchanged. All other settings in the FE model (no resin) remained consistent with the original model.

3.2. Material Damage Models

Accurate prediction of failure modes is a critical requirement for validating the accuracy of finite element model. Appropriate failure criteria are crucial for predicting failure modes and damage propagation process. To date, due to the occurrence of various failure behaviors in composite materials, numerous failure criteria tailored to different failure behaviors have been proposed. For unidirectional laminated composite plates, the 3D Hashin criteria can predict fiber and matrix failure behaviors [24,25,26], while the Ye-delamination criteria can effectively predict interlaminar failure behavior [27,28,29], and the Chang fiber-shear failure criteria can predict fiber matrix shear failure behavior [30]. Therefore, for the internal skeleton of composite T-joints, a hybrid failure criterion based on the 3D Hashin criteria, Ye-delamination criteria, and Chang fiber-shear failure criteria was adopted.

According to the experimental results, significant separation occurred in the R-corner region between the skin and skeleton, but the separation interface mainly occurred in the polymer resin area between the skin and skeleton, with almost no delamination within the skin ply layers. Therefore, it is necessary to assess the failure behavior in the resin area while delamination failure within the skin ply layers can be ignored. Since the plain weave fabric of composite materials has the same fiber content in the warp and weft directions, the effect of matrix damage on the in-plane mechanical behavior can be almost neglected. Based on the analysis above, the Von Mises stress failure criterion is adopted to predict the failure behavior of the resin, which is suitable for analyzing the failure behavior of isotropic plastic materials. Simultaneously, only the fiber failure behavior of plain weave fabric and the in-plane fiber and matrix failure behaviors of the warp-knitting fabric are considered, with the 3D Hashin criteria used as their failure criteria. Various failure modes and their failure criteria are listed as shown in Equations (1)-(8).

Fiber tensile failure (σ₁₁>0):

{(\frac{σ_{11}}{X_{T}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} \geq 1

(1)

Fiber compression failure (σ₁₁<0):

{(\frac{σ_{11}}{X_{C}})}^{2} \geq 1

(2)

Matrix tensile failure (σ₂₂>0):

{(\frac{σ_{22}}{Y_{T}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1

(3)

Matrix compression failure (σ₂₂<0):

{(\frac{σ_{22}}{Y_{C}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1

(4)

Fiber matrix shear failure (σ₁₁<0):

{(\frac{σ_{11}}{X_{C}})}^{2} + {(\frac{τ_{12}}{S_{12}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} \geq 1

(5)

Delamination in tension (σ₃₃≥0):

{(\frac{σ_{33}}{Z_{T}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1

(6)

Delamination in compression (σ₃₃<0):

{(\frac{σ_{33}}{Z_{C}})}^{2} + {(\frac{τ_{13}}{S_{13}})}^{2} + {(\frac{τ_{23}}{S_{23}})}^{2} \geq 1

(7)

Polymer resin failure:

\frac{σ_{mises}}{σ_{T}} \geq 1

(8)

where σ₁₁, σ₂₂, σ₃₃ are the normal stress components along the X, Y, and Z directions respectively, as shown in Figure 10. τ₁₂, τ₁₃, τ₂₃ are the shear stress components. σ_mises is the Mises stress. X_T, X_C are tensile and compressive strengths along longitudinal direction. Y_T, Y_C are tensile and compressive strength along transverse direction. Z_T, Z_C are tensile and compressive strength along thickness direction. S_12, S₁₃, S₂₃ are shear strengths.

In finite element models, as soon as the failure is reached, the material properties of the failed elements need to be degraded based on the material property degradation rules [31]. To ensure convergence of the model, the value of material property after degradation should not be too small. In this investigation, the material property degradation rules for composite bolted T-joint are shown in Table 5. Cheng et al. 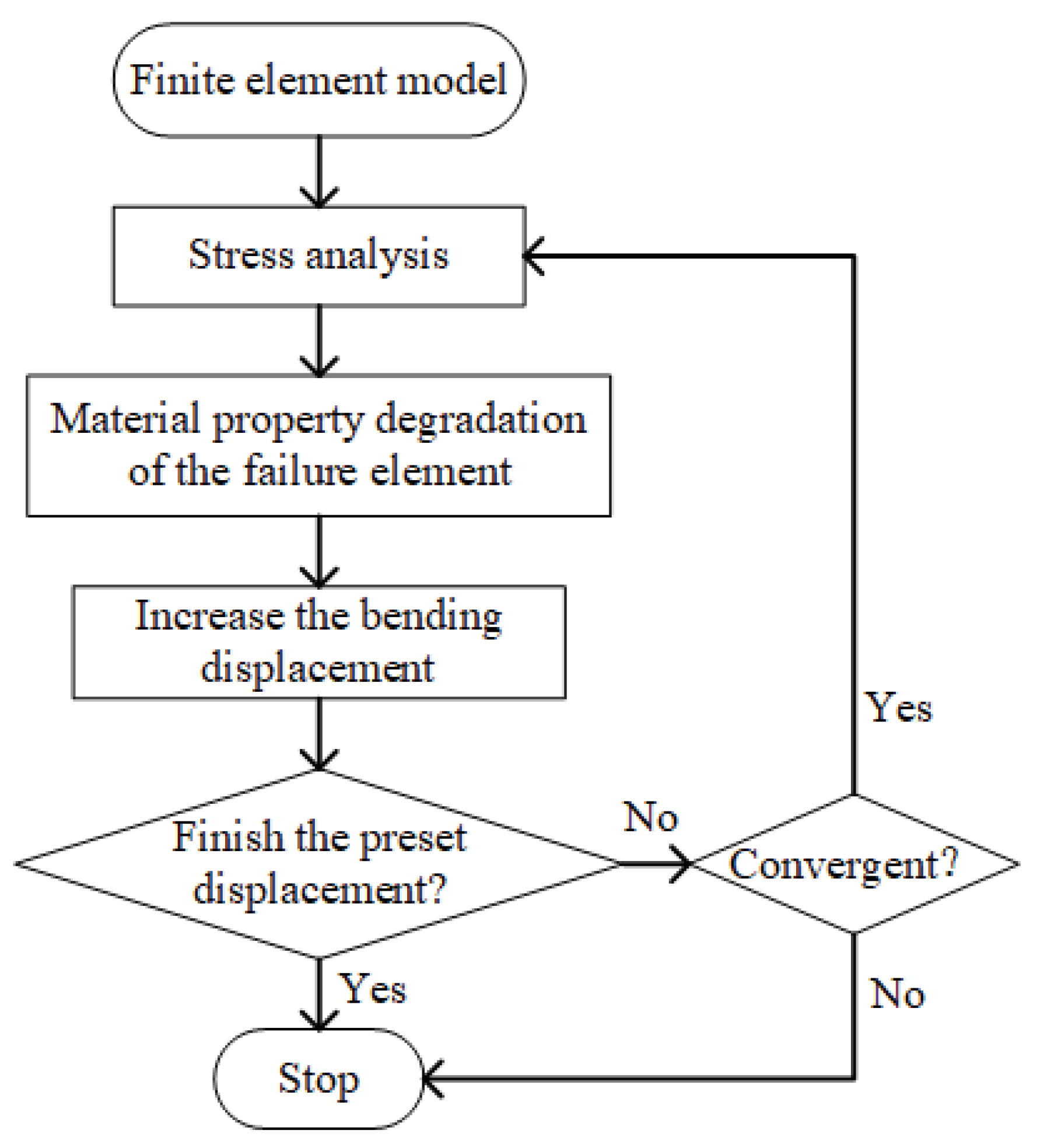[14,15] utilized these material property degradation rules to numerically study the bending performances of composite bolted π-joint and obtained highly accurate simulation results. The corresponding user subroutine USDFLD was developed to implement the determination of element failure and material property degradation. The computational process of the finite element model is illustrated in Figure 11.

3.3. Verification of the Model

As illustrated in Figure 7 and Figure 12, the damage morphology obtained from experiments and finite element models is depicted. It is observed that FE model successfully simulates the damage in the polymer resin area between the skin and skeleton, damage near the holes on the surface, as well as damage along the thickness direction at the R-corner area of the skeleton, which indicates a high level of consistency between the finite element and the experimental results. As shown in Figure 13 and Table 6, a comparison between the computational results of FE model and experimental results is provided. It is noted that the variation trend of the load-displacement curve and the ultimate load obtained from FE model closely align with the experimental results. The overestimation of bending stiffness obtained from FE model is primarily due to the neglect of various significant defects present in the composite T-joint, which lead to a decrease in its performances and subsequently reduce the bending stiffness of the joint.

Comparing the load-displacement curves obtained from FE model and FE model (no resin), within the stiffness calculation interval, the two curves largely coincide, indicating that proportionally increasing the thickness of skin layers in FE model (no resin) has minimal effect on the bending performances of the joint. However, as displacement increases, the load-displacement curve of FE model (no resin) exhibits significantly higher load, deviating notably from the experimental results. This indicates the substantial impact of the polymer resin area between the skin and skeleton on the bending performances of the composite T-joint, necessitating the incorporation of a layer of resin element in the finite element model.

In conclusion, the finite element model considering the polymer resin area between the skin and skeleton provides a good reflection of the bending loading process of novel polymer composite bolted T-joints with decent simulation accuracy.

3.4. Failure Mechanism

As depicted by the load-displacement curve obtained from FE model in Figure 13, the damage propagation process of polymer composite bolted T-joint can be divided into three stages. Base on the validated finite element model, the following findings are obtained.

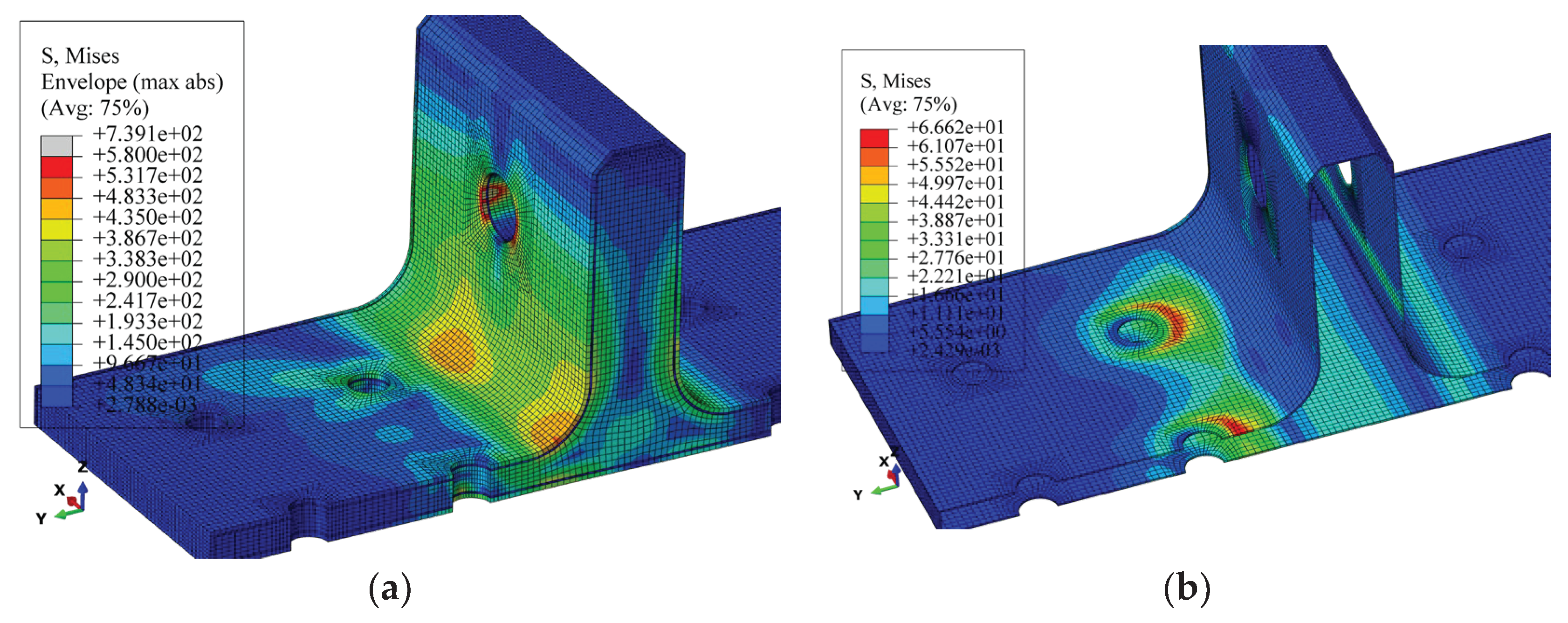
During the OA stage, there is no internal damage within the T-joint, and the load increases linearly with displacement. Upon reaching point A, the distribution of Mises stress in the whole T-joint and polymer resin area is illustrated in Figure 14. Apart from the area near the holes on the lug, the T-joint experiences the maximum load at the R-corner area, while the resin area exhibits significant Mises stress near the holes on the base panel, thus damage initially occurs within the resin near the holes before spreading to the skin and skeleton. 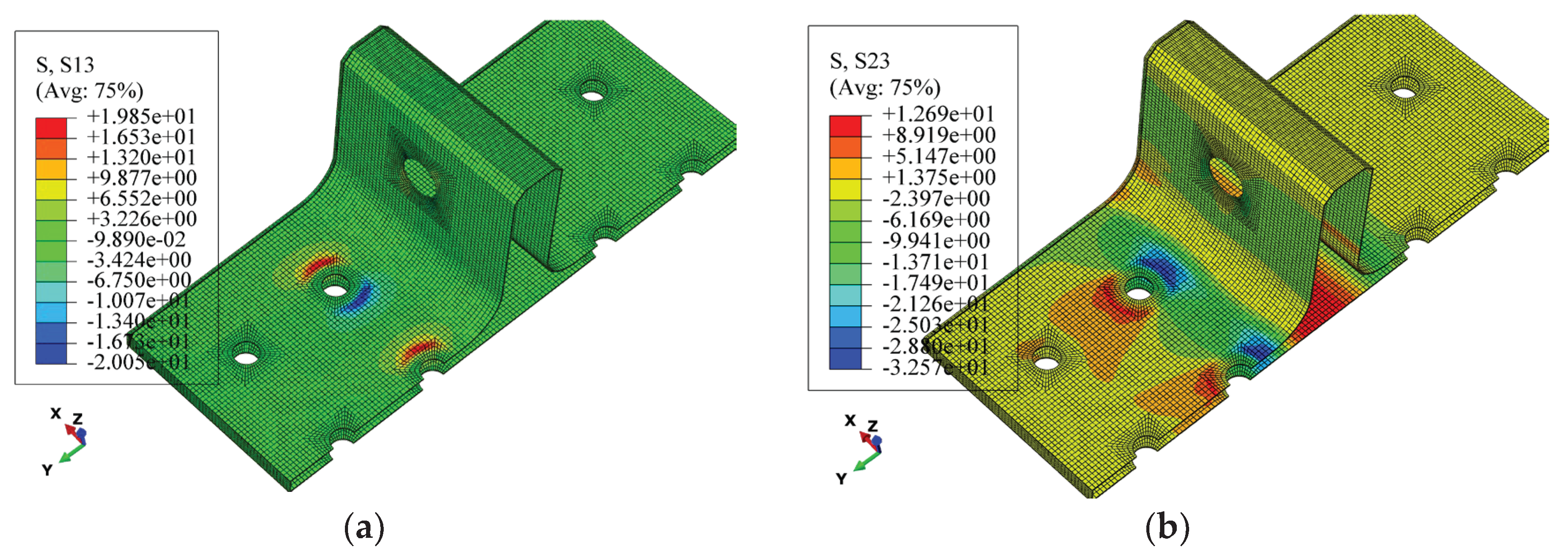Figure 15 shows the out-of-plane shear stress distribution in the polymer resin area at point A, indicating that significant out-of-plane shear stress is concentrated near the holes before the occurrence of damage, and this concentration leads to the initiation of damage. This also indicates that the primary cause of resin area failure is the shear force between the skin, skeleton, and resin area.

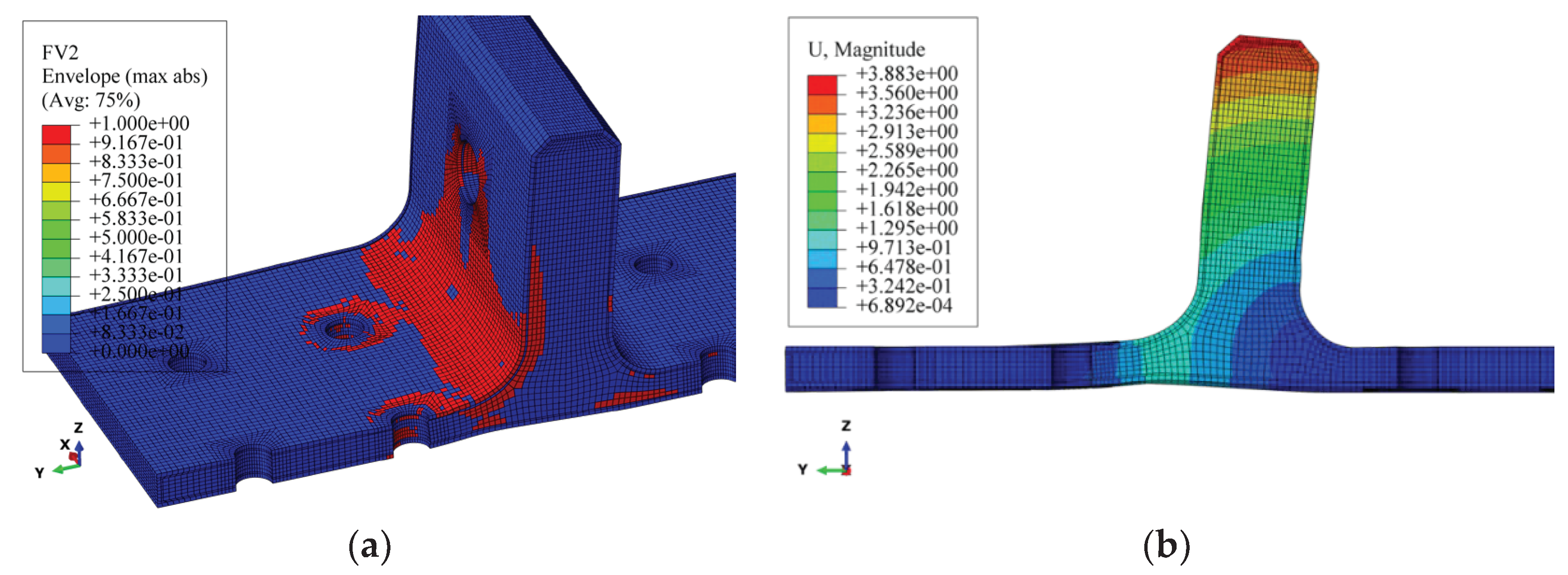
During the AB stage, the damage within the skin, skeleton, and resin area continuously expands from the areas near the holes towards the edges. Upon reaching point B, the damage and deformation of the composite bolted T-joint are illustrated in Figure 16, where damage on the skin has extended to the edges, damage within the skeleton laminate has penetrated the entire base panel, which leads to the final failure of the joint. Simultaneously, noticeable deformation has occurred at the R-corner area of the T-joint. After point B, the R-corner area of the composite bolted T-joint loses its load-bearing capacity, and the bending load begins to decrease.

Further comparison between the curves obtained from FE model and FE model (no resin) in Figure 13 reveals that when there is no polymer resin area between the skin and skeleton, the load at the occurrence of damage is higher, and the ultimate load of the joint is also higher. This demonstrates that the presence of the resin area leads to a decrease in the bending performances of novel polymer composite bolted T-joints.

4. Influence Factors Analysis

As previously discussed, since the novel composite bolted T-joint primarily relies on the skeleton laminate for load-bearing, variations in the stacking sequence of the skeleton may have an impact on the bending performances of the joint. Additionally, experimental results indicate the presence of defects such as layer inclining within the skeleton, which can affect the bending performances of the joint. Furthermore, experimental results also suggest that the stacking sequence of the skin influences the bending performances of the joint. Therefore, based on the validated finite element model, numerical investigations can be conducted to study the effects of variations in the stacking sequence and layer inclining within the skeleton, as well as the stacking sequence of the skin, on the bending performances of composite bolted T-joint.

4.1. Effect of the Stacking Sequence of the Skeleton

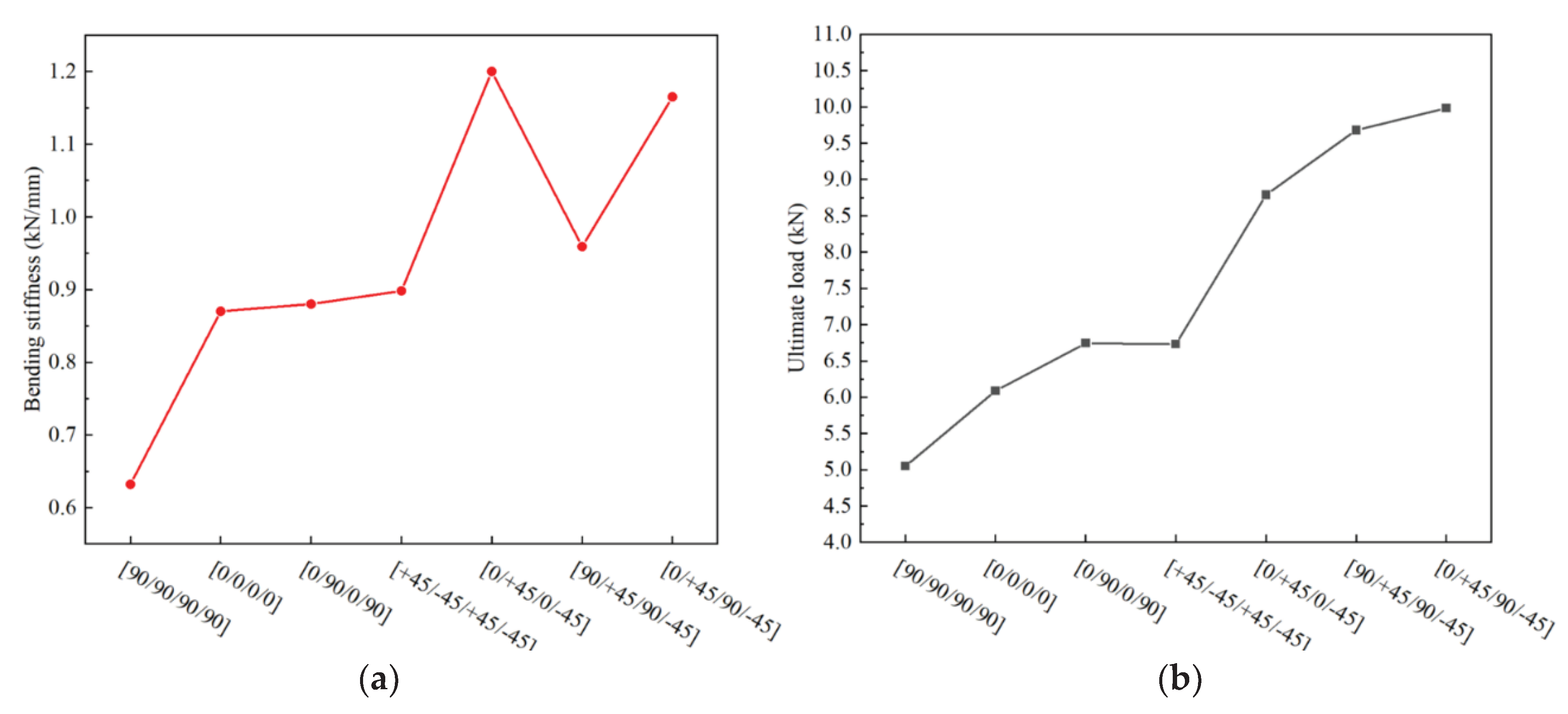
Compared to conventional configuration composite T-joint, the novel composite bolted T-joint can convert interlaminar loads of the skeleton into in-plane loads, thereby enhancing the overall load-bearing capacity of the joint. With the increase in load-bearing capacity, the novel configuration T-joint also introduces the parameter of stacking sequence of the skeleton as a performance influencing factor. Investigating the effect of stacking sequence on the bending performances of the novel configuration T-joint can guide designers in selecting a more rational stacking sequence for the skeleton. Finite element models were established with stacking sequences of [0/0/0/0], [0/+45/0/-45], [0/90/0/90], [+45/-45/+45/-45], [90/+45/90/-45], and [90/90/90/90], in addition to the [0/+45/90/-45] stacking sequence. The computational results are depicted in Figure 17.

The computational results indicate that when the skeleton lacks ±45° layers, the bending performances of the T-joint significantly decreases, primarily because ±45° layers can enhance the shear strength of the joint near the bolt holes. Moreover, when the skeleton contains ±45° layers but lacks 0° or 90° layers, the bending performances of the T-joint also declines to some extent, especially when only ±45° layers are present in the skeleton, leading to a significant decrease in bending performances. Hence, when the T-joint primarily experiences bending loads, the optimal stacking sequence for the skeleton is [0/+45/90/-45]_ns.

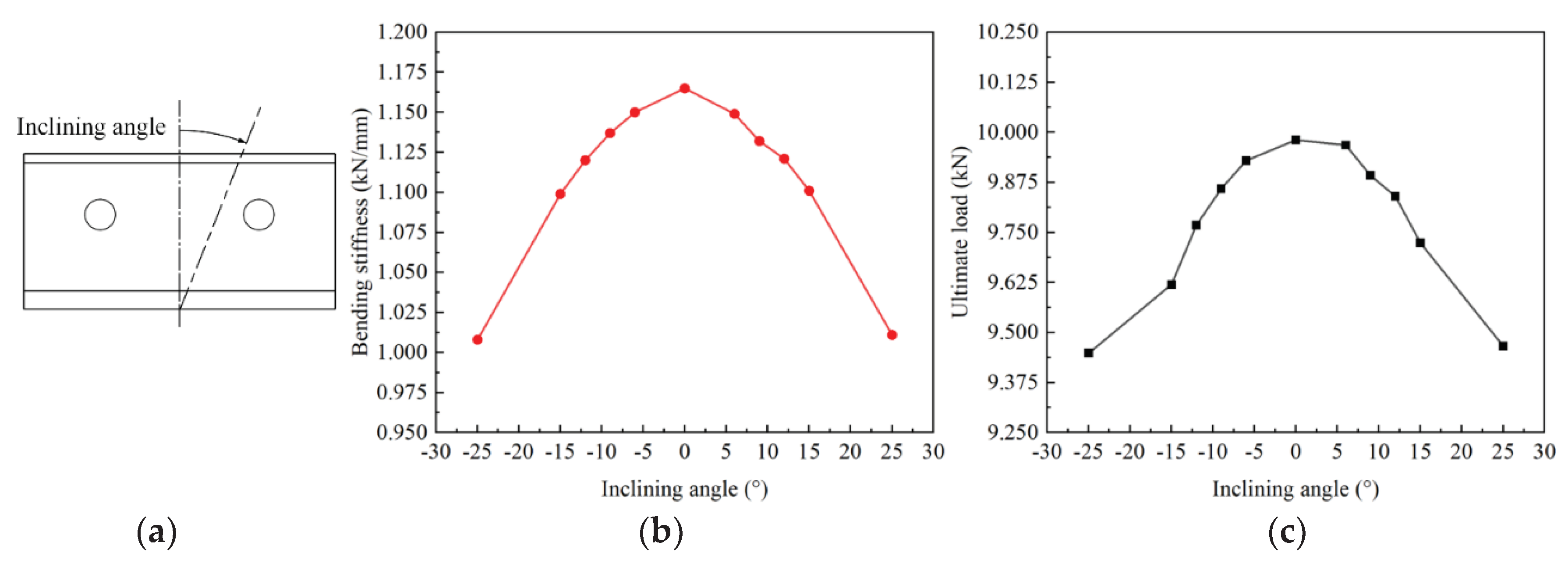
4.2. Effect of the Layer Inclining of the Skeleton

The skeleton is a critical component responsible for bearing loads in the novel composite bolted T-joint. Investigating the effect of layer inclining within the skeleton on bending performances can provide an acceptable range for layer inclining defects when manufacturing the novel T-joints. Considering the symmetry of the finite element model, the case where layers are symmetrically inclined about the T-joint’s symmetry plane can be studied. As seen in Figure 8, the angle of layer inclining is approximately around 10°. Therefore, while keeping other parameters constant, only changing the angle of layer inclining and arranging angles of 6°, 9°, 12°, 15°, and 25°, numerical calculation results are obtained as shown in Figure 18.

It can be observed that when layers are symmetrically inclined about the symmetry plane, both the bending stiffness and ultimate load decrease nonlinearly with increasing inclining angle. Additionally, the bending stiffness and ultimate load under the same absolute value of negative and positive inclining angle are essentially the same. Comparing the bending stiffness and ultimate load under layer inclining with the case without layer inclining, when the absolute value of the inclining angle is less than 12°, the decrease in bending stiffness is no more than 2%, and the decrease in ultimate load is no more than 5%. Therefore, if the criterion is set that the decrease in bending stiffness and ultimate load should not exceed 5%, it can be considered that symmetric layer inclining within the novel T-joint has minimal impact on its bending performances when the absolute value of the inclining angle is less than 12°.

4.3. Effect of the Stacking Sequence of the Skin

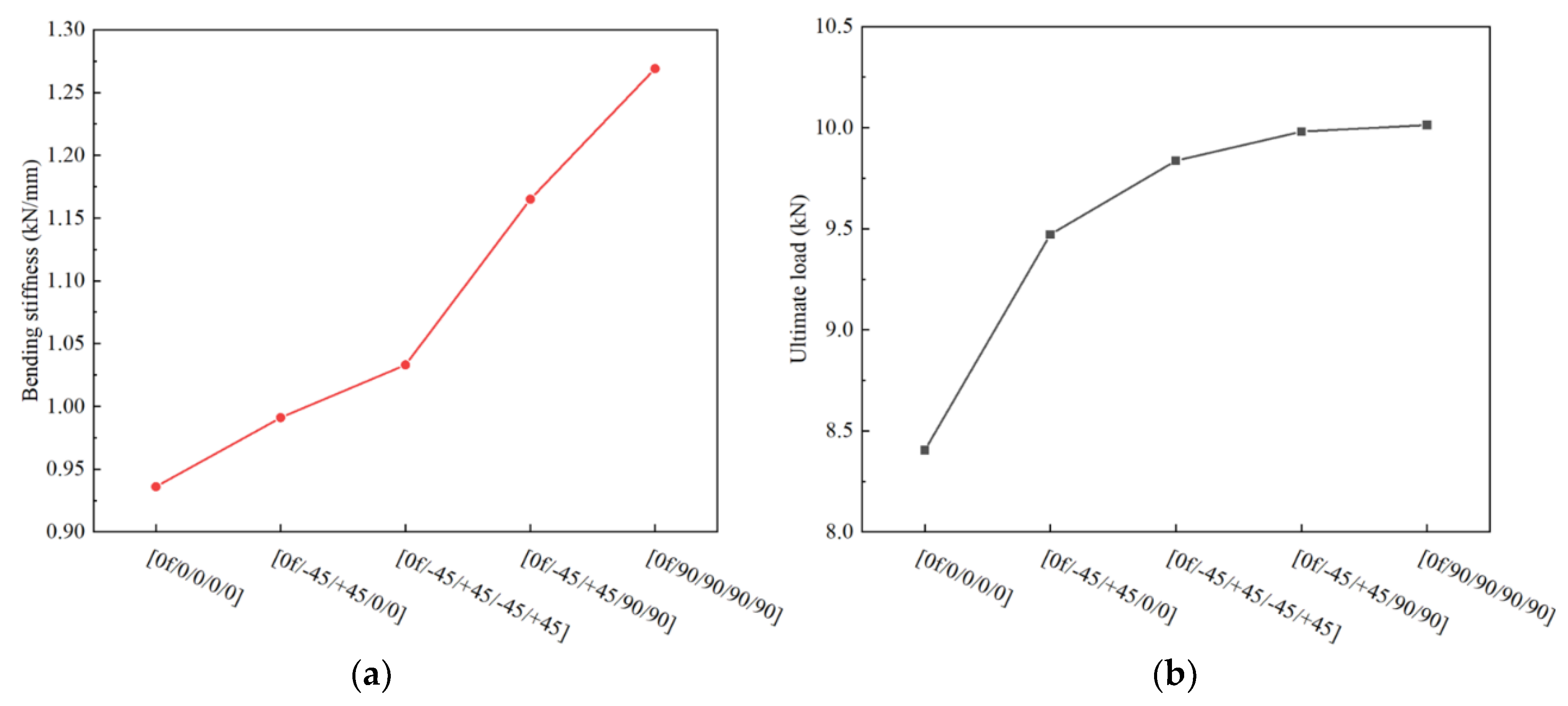
According to the experimental results shown in Figure 9, it is evident that the stacking sequence of the skin affects the bending stiffness and ultimate load of the novel T-joint. However, due to various defects within the test specimens, significant fluctuations in bending load occur before reaching the ultimate load, which significantly impacts the determination of the ultimate load. More accurate comparative data of the influence of the skin stacking sequence on the bending performances of the T-joint can be obtained using the validated finite element model. In addition to the stacking sequence used in the specimens, two additional stacking sequences, namely [0_f/0/0/0/0] and [0_f/90/90/90/90], were included in the finite element models. All models maintain consistent settings except for the stacking sequence. The numerical calculation results are shown in Figure 19.

It is observed that as the proportion of 90° layers increases, both the bending stiffness and ultimate load of the T-joint increase. Conversely, an increase in the proportion of 0° layers leads to a decrease in bending stiffness and ultimate load. The effect of 45° layers lies between that of 90° layers and 0° layers. Furthermore, increasing the proportion of 90° layers has a more significant impact on the increase in bending stiffness compared to the increase in ultimate load. While the influence of 45° layers and 90° layers on the ultimate load is nearly similar, the effect of 90° layers on bending stiffness is more pronounced. Therefore, when designing the stacking sequence of the skin for the novel composite bolted T-joint, in addition to considering factors such as wear resistance, increasing the proportion of 90° layers can enhance the bending stiffness and ultimate load of the joint.

5. Conclusions

(1) The bending stiffness and the yield limit load of the novel composite T-joint are 0.81 times and 1.65 times that of the 2A12 aluminum T-joint respectively, while at only 55.4% of its weight.

(2) There exists a layer of polymer resin area between the skin and skeleton of the novel T-joint, and the presence of this area can lead to a significant decrease in the bending performances of the novel T-joint.

(3) The finite element model with a layer of resin area between the skin and skeleton exhibits excellent accuracy, and the damage of the novel T-joint initiates in the resin area near the bolt holes on the base panel. Subsequently, the damage within the skin, skeleton, and resin area expands from the areas near the holes towards the edges. Finally, damage within the skeleton penetrates the entire base panel, which results in the final failure of the novel T-joint.

(4) When primarily subjected to bending loads, the optimal stacking sequence for the skeleton is [0/+45/90/-45]_ns. Furthermore, when the layer symmetrically inclining angle of the skeleton is less than 12°, the decrease in bending stiffness and in ultimate load are no more than 2% and 5% respectively.

(5) For the stacking sequence of the skin, the more 90° layers there are, the better bending performances, whereas the more 0° layers there are, the poorer bending performances. The influence of 45° layers lies between that of 90° layers and 0° layers.

Author Contributions

Conceptualization, Tao Zhang, Zhitao Luo and Xiaoquan Cheng; Data curation, Kenan Li; Investigation, Tao Zhang and Zhitao Luo; Methodology, Tao Zhang and Zhitao Luo; Project administration, Xiaoquan Cheng; Resources, Tao Zhang; Supervision, Xiaoquan Cheng; Writing – original draft, Zhitao Luo; Writing – review & editing, Xiaoquan Cheng.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflict of interest.

References

Mrázová, M. Advanced Composite Materials of the Future in Aerospace Industry. Incas Bulletin 2013, 5, 139–150. [Google Scholar] [CrossRef]
Rana, S.; Fangueiro, R. 1 - Advanced Composites in Aerospace Engineering. In Advanced Composite Materials for Aerospace Engineering; Rana, S., Fangueiro, R., Eds.; Woodhead Publishing, 2016; pp. 1–15. [CrossRef]
McCarthy, M.; Stanley, W.; Lawlor, V. Bolt-Hole Clearance Test Results, Part 1: Static Tests. 2001, 1-86. [CrossRef]
Peng, Y.Z. Research on Mechanical Properties of Composite T-Joints. Nanjing University of Aeronautics and Astronautics 2020. https://d.wanfangdata.com. 0230. [Google Scholar]
Li, L.; Xu, F.; Zhang, S.W. Research and Analysis on the Mechanical Properties and Optimization for Composite T-Joint. Composites Science and Engineering 2015, 41–46. [Google Scholar] [CrossRef]
Zhou, X.S.; Mei, Z.Y. Research on Damage Mechanism and Lateral Bending Strength Characteristic of Sandwich T-Joint. Journal of Naval University of Engineering 2016, 28, 29–34. [Google Scholar] [CrossRef]
Liu, Y.; Li, M.X.; Lu, X.F.; Zhu, X.L. Failure Mechanism and Strength Prediction Model of T-Joint of Composite Sandwich Structure. Metals 2021, 11, 1197. [Google Scholar] [CrossRef]
Wu, H.; Xiao, J.Y.; Xing, S.L.; Wen, S.W.; Yang, F.B.; Yang, J.S. The Failure Experiment of Composite T-Joints with Induced Defects under Bending Load. Journal of National University of Defense Technology 2015, 128–136. [Google Scholar] [CrossRef]
Koricho, E.G.; Belingardi, G. An Experimental and Finite Element Study of the Transverse Bending Behaviour of CFRP Composite T-Joints in Vehicle Structures. Composites Part B: Engineering 2015, 79, 430–443. [Google Scholar] [CrossRef]
Barzegar, M.; Moallem, M.D.; Mokhtari, M. Progressive Damage Analysis of an Adhesively Bonded Composite T-Joint under Bending, Considering Micro-Scale Effects of Fiber Volume Fraction of Adherends. Composite Structures 2021, 258, 113374. [Google Scholar] [CrossRef]
Hélénon, F.; Wisnom, M.R.; Hallett, S.R.; Trask, R.S. Investigation into Failure of Laminated Composite T-Piece Specimens under Bending Loading. Composites Part A: Applied Science and Manufacturing 2013, 54, 182–189. [Google Scholar] [CrossRef]
Luo, G.; Chai, C.P.; Liu, J.Z.; Xiao, Y.Z.; Chen, Y.S.; Xu, F.X. Investigations on the Mechanical Properties of Composite T-Joints with Defects under Bending Loading. Sustainability 2022, 14, 16609. [Google Scholar] [CrossRef]
Burns, L.; Mouritz, A.P.; Pook, D.; Feih, S. Strengthening of Composite T-Joints Using Novel Ply Design Approaches. Composites Part B: Engineering 2016, 88, 73–84. [Google Scholar] [CrossRef]
Cheng, X.Q.; Fan, J.F.; Liu, S.F.; Guo, X.; Xu, Y.H.; Zhang, T. Design and Investigation of Composite Bolted π-Joints with an Unconventional Configuration under Bending Load. Composites Part B: Engineering 2016, 85, 59–67. [Google Scholar] [CrossRef]
Du, X.Y.; Cheng, X.Q.; Cheng, Y.J.; Huang, W.J.; Chen, G. Analysis and Design Improvement of Composite Bolted π-Joints under Bending Load. J Braz. Soc. Mech. Sci. Eng. 2020, 42, 384. [Google Scholar] [CrossRef]
Fan, J.F.; Cheng, X.Q.; Wang, S.W.; Guo, X.; Zhang, T. Experimental and Numerical Investigation of Composite Bolted π-Joint Subjected to Bending Load. Composites Part B: Engineering 2015, 78, 324–330. [Google Scholar] [CrossRef]
Zhao, A.A.; Yang, W.K.; Yu, F.; Liu, W.H.; Lu, S.H. RTM Process for Large-Scale and High-Performances Composite Components. Journal of Nanjing University of Aeronautics & Astronautics 2020, 52, 39–47. [Google Scholar] [CrossRef]
Li, W.D.; Liu, G.; Bao, J.W.; Hu, X.L.; Yi, X. su Research of Processing Characteristics and Mechanical Properties of Semi-Prepreg RTM Composites. Journal of Aeronautical Materials 2014, 34, 57–62. [Google Scholar] [CrossRef]
Fu, Y.T.; Yao, X.F. A Review on Manufacturing Defects and Their Detection of Fiber Reinforced Resin Matrix Composites. Composites Part C: Open Access 2022, 8, 100276. [Google Scholar] [CrossRef]
Cheng, X.; Xiong, J.J.; Peng, B.; Cheng, Z.L.; Li, H.Y. Mechanical Properties of RTM-Made Composite Cross-Joints. Chinese Journal of Aeronautics 2009, 22, 211–217. [Google Scholar] [CrossRef]
Starke, E.; Staley, J. Application of Modern Aluminum Alloys to Aircraft. Prog Aerospace Sci 1996, 32, 131–172. [Google Scholar] [CrossRef]
Yu, M.; Liu, Y.; Liu, J.; Li, S.; Xue, B.; Zhang, Y.; Yin, X. Effects of Cerium Salts on Corrosion Behaviors of Si–Zr Hybrid Sol–Gel Coatings. Chinese Journal of Aeronautics 2015, 28, 600–608. [Google Scholar] [CrossRef]
Tserpes, K.I.; Pantelakis, Sp.; Kappatos, V. The Effect of Imperfect Bonding on the Pull-out Behavior of Non-Crimp Fabric Pi-Shaped Joints. Computational Materials Science 2011, 50, 1372–1380. [Google Scholar] [CrossRef]
Hashin, Z. Failure Criteria for Unidirectional Fiber Composites. Journal of Applied Mechanics 1980, 47, 329–334. [Google Scholar] [CrossRef]
Shokrieh, M.M.; Lessard, L.B. Progressive Fatigue Damage Modeling of Composite Materials, Part I: Modeling. Journal of Composite Materials 2000, 34, 1056–1080. [Google Scholar] [CrossRef]
Shokrieh, M.M.; Lessard, L.B. Progressive Fatigue Damage Modeling of Composite Materials, Part II: Material Characterization and Model Verification. Journal of Composite Materials 2000, 34, 1081–1116. [Google Scholar] [CrossRef]
Ye, L. Role of Matrix Resin in Delamination Onset and Growth in Composite Laminates. Composites Science and Technology 1988, 33, 257–277. [Google Scholar] [CrossRef]
Oh, J.H.; Kim, Y.G.; Lee, D.G. Optimum Bolted Joints for Hybrid Composite Materials. Composite Structures 1997, 38, 329–341. [Google Scholar] [CrossRef]
Chen, W.H.; Lee, S.S.; Yeh, J.T. Three-Dimensional Contact Stress Analysis of a Composite Laminate with Bolted Joint. Composite Structures 1995, 30, 287–297. [Google Scholar] [CrossRef]
Chang, F.K.; Chang, K.Y. A Progressive Damage Model for Laminated Composites Containing Stress Concentrations. Journal of Composite Materials 1987, 21, 834–855. [Google Scholar] [CrossRef]
Tan, S.C. A Progressive Failure Model for Composite Laminates Containing Openings. Journal of Composite Materials 1991, 25, 556–577. [Google Scholar] [CrossRef]

Figure 1. Configuration of bolted π-joint, novel configuration (a) and conventional configuration (b).

Figure 2. Novel configuration of polymer composite bolted T-joint.

Figure 3. The dimensions of specimen.

Figure 4. Manufacturing process of polymer composite bolted T-joint with novel configuration.

Figure 5. The diagram of loading scheme.

Figure 6. The experimental setup.

Figure 7. Damage morphologies of the specimen.

Figure 8. Profile of the R-corner area after the test.

Figure 9. Load-displacement curves obtained from the tests.

Figure 10. Boundary conditions, loading condition and nodes for result output in FE model.

Figure 11. Flow chart of finite element model.

Figure 12. Comparison of numerical and experimental damage morphologies, polymer resin damage between skin and skeleton (a), skin damage area around the hole (b) and skeleton damage area along the thickness (c).

Figure 13. Load-displacement curves for specimen 90# by experimental and numerical analysis.

Figure 14. Mises stress distribution at point A, the whole T-joint (a) and polymer resin aera (b).

Figure 15. Shear stress distribution of the polymer resin area at point A, shear stress S13 (a) and shear stress S23(b).

Figure 16. Damage distribution at point B (a). Deformation of T-joint at point B (b).

Figure 17. Variation of mechanical properties with the stacking sequence of the skeleton, bending stiffness (a) and ultimate load (b).

Figure 18. Diagram of inclining angle (a). Variation of mechanical properties with the layer inclining angle of the skeleton, bending stiffness (b) and ultimate load (c).

Figure 19. Variation of mechanical properties with the stacking sequence of the skin, bending stiffness (a) and ultimate load (b).

Table 1. Material properties of polymer composite bolted T-joint.

Item	ZT7G/9368	ZT7G warp-knitting fabric/6808	ZT7G plain weave fabric/6808
Longitudinal elastic modulus, E₁₁(GPa)	132	132	61.5
Transverse elastic modulus, E₂₂(GPa)	8.55	9	61.5
Through-thickness elastic modulus, E₃₃(GPa)	8.55	9	8
In-plane shear modulus, G₁₂(GPa)	4.32	5.9	4.89
Out-plane shear modulus, G₁₃(GPa)	4.32	5.9	4.89
Out-plane shear modulus, G₂₃(GPa)	3.35	3.3	4.89
Poisson’s ratio, μ₁₂	0.33	0.3	0.06
Poisson’s ratio, μ₁₃	0.33	0.3	0.3
Poisson’s ratio, μ₂₃	0.33	0.3	0.3
Longitudinal tensile strength, X_T(MPa)	2200	2170	842
Longitudinal compressive strength, X_C(MPa)	1200	938	628
Transverse tensile strength, Y_T(MPa)	38	36.2	842
Transverse compressive strength, Y_C(MPa)	196	192	628
Through-thickness tensile strength, Z_T(MPa)	38	36.2	-
Through-thickness compressive strength, Z_C(MPa)	196	192	-
In-plane shear strength, S₁₂(MPa)	90	88.3	92.2
Out-plane shear strength, S₁₃(MPa)	90	88.3	-
Out-plane shear strength, S₂₃(MPa)	86	68.3	-

Table 2. Material properties of epoxy 6808 and 45# steel.

Material	Modulus, E(GPa)	Poisson’s ratio, μ	Strength, σ_T(MPa)
Epoxy resin 6808	3.3	0.3	65.6
45# steel	210	0.33	-

Table 3. Arrangement of test specimens.

Specimen	Number of specimens	Stacking sequence of the skin	Weight(g)
Specimen 0#	1	[0_f/-45/+45/0/0]	226.22
Specimen 45#	1	[0_f/-45/+45/-45/+45]	226.14
Specimen 90#	1	[0_f/-45/+45/90/90]	227.35
Specimen Al	1	-	410.51

Table 4. Test results.

Specimen	Bending stiffness (kN/mm)	Yield limit load (kN)	Ultimate load (kN)
Specimen 0#	0.873	5.584	7.882
Specimen 45#	0.953	4.702	8.118
Specimen 90#	0.992	6.093	9.360
Specimen Al	1.221	3.694	-

Table 5. Material property degradation rule.

Material	Failure mode	Degradation rule
ZT7G/9368	Fiber breakage	E₁₁=0.1E₁₁
	Matrix cracks	E₂₂=0.2E₂₂, G₁₂=0.2G₁₂, G₂₃=0.2G₂₃
	Delamination	E₃₃=0.01E₃₃, G₁₃=0.01G₁₃, G₂₃=0.01G₂₃, μ₁₃=0.01μ₁₃, μ₂₃=0.01μ₂₃
	Fiber-matrix shear failure	G₁₂=0.2G₁₂, μ₁₂=0.2μ₁₂
ZT7G warp-knitting fabric/6808	Fiber breakage	E₁₁=0.1 E₁₁
ZT7G warp-knitting fabric/6808	Matrix cracks	E₂₂=0.2E₂₂, G₁₂=0.2G₁₂, G₂₃=0.2G₂₃
ZT7G plain weave fabric/6808	Warp fiber breakage	E₁₁=0.1E₁₁, G₁₂=0.2G₁₂, G₁₃=0.01G₁₃, μ₁₂=0.01μ₁₂, μ₁₃=0.01μ₁₃
ZT7G plain weave fabric/6808	Weft fiber breakage	E₂₂=0.1E₂₂, G₁₂=0.2G₁₂, G₂₃=0.01G₂₃, μ₁₂=0.01μ₁₂, μ₂₃=0.01μ₂₃
Epoxy resin 6808	Polymer resin failure	E=0.03E, μ=0.03μ

Table 6. Comparison of experimental and numerical results.

	Bending stiffness (kN/mm)	Ultimate load (kN)
Specimen 90#	0.992	9.360
FE model	1.165	9.981
Difference (%)	17.4	6.63

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

Views

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer