Prerpints.org logo
Preprint
Article

Estimation of Ground Reaction Forces during Sports Movements by Sensor Fusion from Inertial Measurement Units with 3D Forward Dynamics Model

Altmetrics

Downloads

120

Views

50

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

29 February 2024

Posted:

29 February 2024

You are already at the latest version

Alerts
Abstract
Rotational jumps are crucial techniques in sports competitions. Estimating ground reaction forces (GRFs), one of the components constituting jumps, through a biomechanical model-based approach enables analysis even in environments where force plates or machine learning training data cannot be utilized. In this study, rotational jump movements involving twists on land were measured using inertial measurement units (IMUs) and estimated GRFs and body loads using a 3D forward dynamics model. Our estimation method, based on forward dynamics and optimization calculations, generated and optimized body movements using cost functions defined by motion measurements and internal body loads. To reduce the influence of the dynamic acceleration in the optimization calculation, the 3D orientation using sensor fusion composed of acceleration and angular velocity data obtained from IMUs and an extended Kalman filter was estimated. As a result, by generating movements based on the cost function, it was possible to calculate biomechanically valid GRFs while following the measured movements even if not all joints are covered by IMUs. This estimation method allows for 3D motion analysis independent of measurement conditions or training data.
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

In sports such as figure skating, gymnastics, and ballet, where artistic expression plays a significant role, rotational jumps involving twists are indispensable for achieving success and obtaining high scores. One crucial element in these jumping maneuvers is the force generated during takeoff. This takeoff force determines factors such as the jump distance [1], jump height [2], and mid-air posture [3]. The analysis of this takeoff force involves using ground reaction force (GRF) and its moment (ground reaction moment, GRM). Particularly in rotational jumps involving twists, conducting a 3D analysis along with joint torques and muscle forces derived from body movements enable the evaluation of control strategies for optimizing sports movements [4] and injury risks in sports [5], among other aspects. The measurement of these kinematic indicators often involves the use of a force plate fixed to the ground. While force plates can accurately measure GRFs during movements, they require specialized measurement facilities. To ensure successful measurements, participants need to perform movements with their entire foot on the force plate, which may introduce unnatural movements. Consequently, there is a possibility that the measurements may not accurately reflect the same movements as those performed during actual athletic competition. Additionally, in facilities where it is not possible to install multiple expensive force plates, continuous tracking of movements becomes challenging. Moreover, in places like surfaces covered with ice, snow, or spring-based floors where it is necessary to install equipment underneath, introducing measurement facilities can be challenging. The cost of measuring GRFs in sports performed in such environments is substantial, making practical measurements difficult. As a solution, various lightweight and compact measurement devices have been developed. However, these may not be sufficient for sports motion analysis due to concerns about durability, constraints from wearing, and other factors. Wearable force plates, while avoiding facility installation costs, add weight and height to the shoes, limiting their applicability for high-difficulty movements. Insole-type force sensors address some of these challenges but may raise concerns about durability and reproducibility, affecting the credibility of their accuracy [6].
To address these challenges, methods have been studied to measure kinematic elements using only motion capture systems or inertial measurement units (IMUs) and to estimate kinetic elements such as GRF and GRM [7]. In this study, we focused on using IMUs to estimate GRFs. In sports motion measurements, it is advisable to use small, lightweight, and self-contained measurement methods to avoid restricting movement [8]. IMUs meet these conditions, allowing measurements with minimal location constraints and in vast areas, such as outdoors or on a skating rink. Previous studies have explored methods such as the use of inertial sensors and machine learning to estimate the GRFs of gait motion in three dimensions [9], as well as research estimating GRFs during sagittal-plane double limb jumping [10]. While this method demonstrates high prediction accuracy, its application to sports with a limited participant pool, making it difficult to obtain sufficient machine learning training data, poses challenges. Another method involves calculating the posture relative to the absolute coordinate system of each body segment from the measurements of IMUs, and estimating GRFs through inverse dynamics calculations using these values as inputs [11]. However, this method requires the use of 17 IMUs, which may potentially hinder movement in sports motion analysis due to the high number of IMUs. The estimation method that can reduce the number of sensors attached to the body may contribute to advancing sports motion analysis, where the effects of sensor interference on motion should be minimized.
This study focuses on a method for estimating GRFs based on forward dynamics calculations using joint torque [12]. This method generates and optimizes body movements through a 3D human model and cost functions defined by motion measurements and internal load. By utilizing a 3D biomechanical model, this approach can target sports movements that are asymmetrical and non-periodic. Moreover, by generating movements based on the cost function, it is possible to calculate biomechanically valid GRFs while following the measured movements even if not all joints are covered by IMUs, thus enabling the estimation of biomechanically valid GRFs with a small number of IMUs. Haraguchi and Hase [12] directly used acceleration and angular velocity data obtained from IMUs in this cost function. However, in the case of sports movements, there is a possibility of significant noise in the IMU data due to the intensity of the movement. Therefore, in this study, the 3D orientation using sensor fusion composed of acceleration and angular velocity data obtained from IMUs and an extended Kalman filter was estimated, aiming to reduce the influence of this noise by using the estimated values in the optimization calculation.
This study aims to estimate GRFs and body loads using a 3D forward dynamics approach incorporating sensor fusion with an extended Kalman filter, based on measurements of rotational jump movements on land using IMUs.

2. Ground Reaction Force Estimation Methods

This study conducted a biomechanical simulation system that combines forward dynamics simulation using a human model with motion measurement using IMUs. From the generated body movements obtained through forward dynamics simulation, the system estimates GRF, GRM, joint angle and joint torque. The simulation consists of a forward dynamics model and optimization calculations, aiming to minimize the cost function composed of errors between the model and IMUs measurements and evaluations of internal biomechanical loads of the model. This allows the model to reproduce biomechanically plausible body movements while following the measurements from the IMUs. Based on the optimized body movements, GRFs are estimated using a contact model between the human and the ground.
The overall flow of the GRF estimation method is as follows:
  • The height and weight are input into the system, and a human model is constructed based on the inertia parameters calculated from them.
  • Based on the reference joint angles formed by the node points, the forward dynamics model generates body movements.
  • The body movement is evaluated by a cost function comprising errors between the generated body movement and measurements from IMUs, as well as internal biomechanical loads.
  • Steps 2 and 3 are repeated while adjusting the node points of the reference joint angles to minimize the value of the cost function.
  • Estimate GRFs, GRMs, and joint motion using the optimized node points in the forward dynamics model.

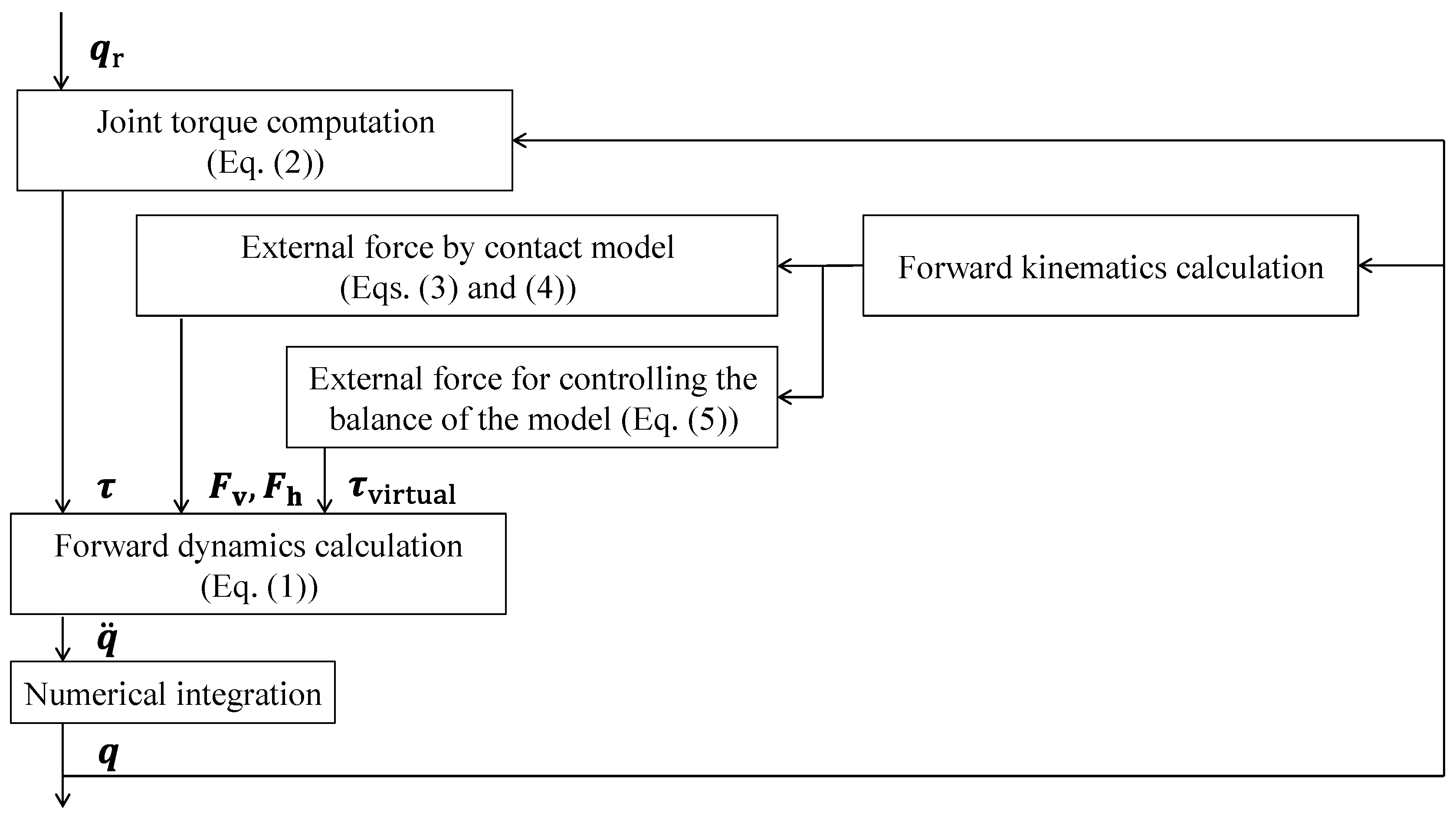
2.1. Forward Dynamics Model

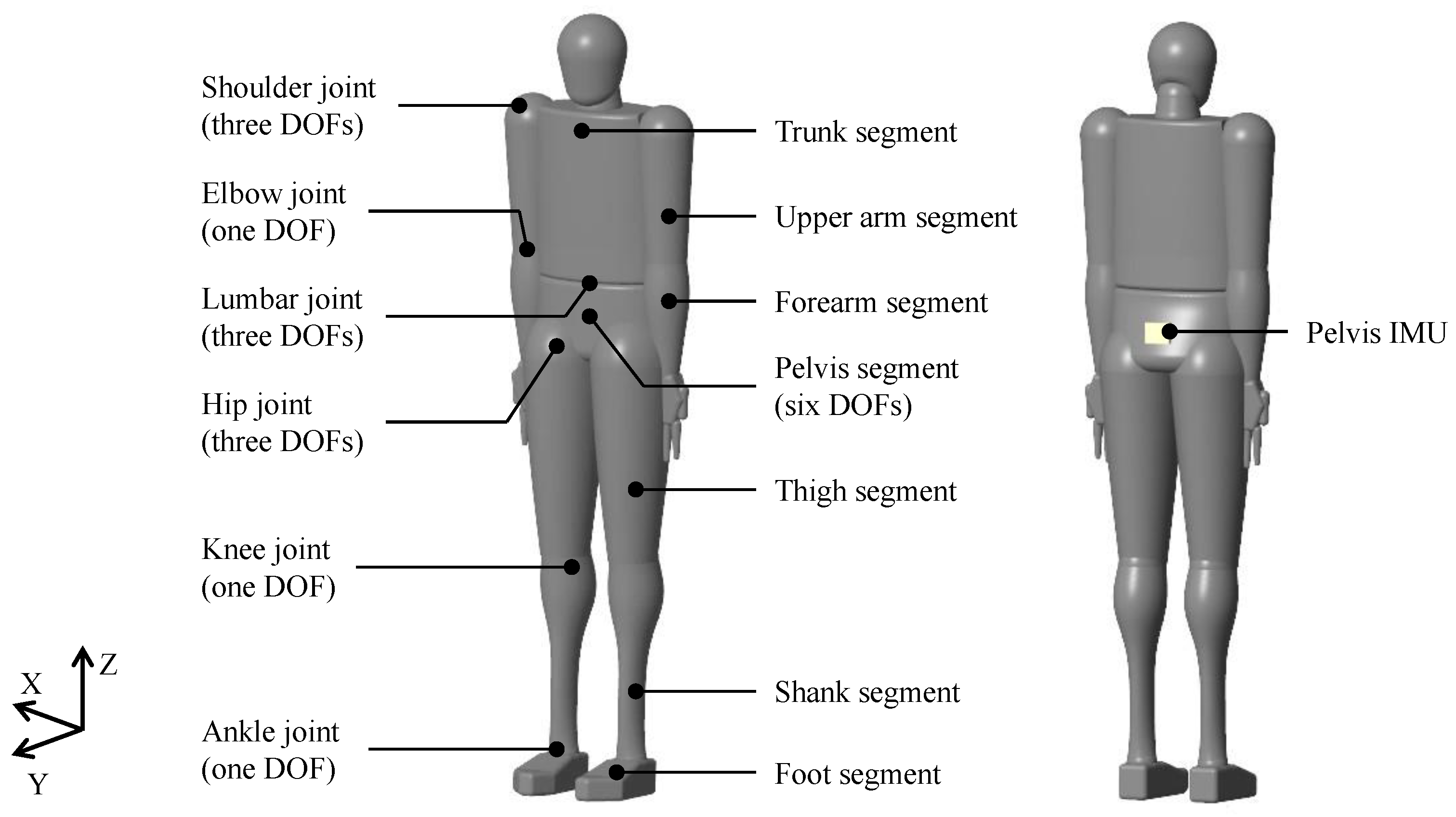
2.1.1. Human Model

The human model is illustrated in Figure 1. The model comprises rigid links representing each segment of the body, with rotational degrees of freedom (DOFs) defined at the junctions to represent joints. The segments include the trunk, pelvis, upper arms, forearms, thighs, shanks, and feet, totaling 12 links. The joints have rotational DOFs: three DOFs for hip, one DOF for knee, one DOF for ankle, three DOFs for lumbar, three DOFs for shoulder, and one DOF for elbow joints, totaling 21 DOFs. Additionally, there are six virtual DOFs accounting for rotational and translational motion between the pelvis segment and the global coordinate system, bringing the total to 27 DOFs. The knee and elbow joints exhibit flexion-extension, while the ankle joint demonstrates plantarflexion-dorsiflexion. The hip, lumbar, shoulder joints and pelvis segment are represented by Euler angles in the X (flexion-extension), Y (adduction-abduction), and Z (rotation) sequence. The lengths, moments of inertia, and center of mass are determined using estimation equations based on height and weight in Japanese [13,14]. The neutral position for each joint was set as shown in Figure 1 and determined by the posture estimation system described in Section 2.2.1
In addition, sensor coordinate systems were defined on the pelvis segment of the human model. This allows the output of relative accelerations to the global coordinate system, enabling a comparison between the motion generated by forward dynamics simulation and the motion obtained from IMU.
In this simulation, the motion is generated by calculating the joint motion when torque is applied to the joints defined in Figure 1 using forward dynamics calculations. At each time step of the forward dynamics calculation, the calculation flow is shown in Figure 2. Additionally, the motion equations of the forward dynamics model are shown in Equation (1).
M q ¨ + Γ q , q ˙ , F v ,   F h ,   τ v i r t u a l = τ ,
where M is the inertia matrix, Γ is the vector consisting of Coriolis forces, centrifugal forces, gravity, and external forces, τ is the joint torque. q is the state variable vector, including joint angles and the six DOFs between the pelvis and the global coordinate system. F v   and   F h are the GRF vectors in the vertical and horizontal directions, respectively, and τ v i r t u a l is an external torque vector preventing the model from falling. By inputting joint torque τ into Equation (1), the state variable vector is calculated, generating the body movement of the model. The human model was developed using MATLAB/Simulink (MathWorks, Inc., USA) and employed the ode45 variable-step solver, which implements a Runge-Kutta method.

2.1.2. Joint Torque Model

The joint torque τ is composed of the active torque τ a generated by muscle forces and the passive torque τ p acting prominently near the joint's range of motion limits (Equation (2)).
τ = τ a q , q ˙ , q r , q r ˙ + τ p q , q ˙ .
The passive torque is represented by a double exponential function to increase the torque near the anatomical joint limits, which are defined by related research [15,16,17,18]. The active torque τ a j for the joint j , a component of τ a , is calculated using proportional-derivative (PD) control torque based on the joint angle q j for the joint j , a component of q , and reference joint angle q r j for the joint j , as given by Equation (3).
τ a j = K P D q r j − q j + D PD q ˙ r j − q ˙ j ,
where K PD and D PD are gains in the PD control, and they were empirically set to K PD = 1000   N · m / r a d and D PD = 10   N · m / r a d / s . The reference joint angle q r j is determined through the optimization calculation described in Section 2.2.

2.1.3. External Force Model

Regarding the forces F v and F h in Equation (1), they are defined as external forces acting on the foot of the human model and modeled by the contact model. In the human model, there are challenges in the dynamic calculations when both feet are in contact and form a closed-loop structure. In gait analysis, statistical models such as transition functions and distribution functions for GRF and GRM during both-foot support, based on past experiments and data, are often used [9,19]. However, in sports movements, there is limited existing data, and statistical models like those used in gait analysis cannot be defined. Therefore, in this study, a contact model was employed to calculate vertical reaction forces by solving the contact problem between the ground and the foot. The horizontal forces were determined by the frictional forces calculated based on the vertical reaction forces. The contact points are set at 22 points for each foot segment, same as the model by Haraguchi and Hase [12], including distances from the ankle to the heel, metatarsophalangeal joint, and the tip of the second proximal phalanx, as well as heel width, metatarsophalangeal joint width, width between the first and second proximal phalanx, and heights from the ground to the ankle and the first proximal phalanx. The vertical GRF F v i at contact point i , a component of F v , and the horizontal GRF F h i at contact point i , a component of F h , were calculated using Equations (4) and (5).
F v i = − K G r z i − r z 0 − D G r ˙ z i ,
F h i = − μ r ˙ x i ,   r ˙ y i , μ s ,   μ d F v i ,
where r x i ,   r y i ,   and r z i represent the position of the contact point, and r z 0 is set as the height of the ground ( r z 0 = 0 ). Additionally, K G and D G are the elastic and viscous coefficients of the ground, respectively. The friction coefficient μ is defined as a function of the penetration velocities r ˙ x i and   r ˙ y i at each contact point, along with the static friction coefficient μ s and dynamic friction coefficient μ d . The values for K G , D G , μ s , and   μ d were determined through trial and error and set to K G = 1.0 × 10 3   N / m ,   D G = 1.0 × 10 4   N / m / s ,   μ s = 0.7 ,   μ d = 0.5 .
Furthermore, to prevent the model from tipping over during the simulation, a virtual torque τ v i r t u a l was defined to constrain the rotation of the model. In forward dynamics analysis, to maintain the balance of the model is essential. When the model attempted to rotate forward, backward, or sideways to the point of tipping over, the virtual torques are applied to a virtual joint. The virtual joint was set between the mass center position of the pelvis segment and the global coordinate system.
τ v i r t u a l = − K v i r t u a l   q v i r t u a l − D v i r t u a l   q ˙ v i r t u a l ,
where q v i r t u a l = q x q y q z T   is the virtual joint angle represented by Euler angles of the pelvis relative to the global coordinates. K v i r t u a l and D v i r t u a l are gains, determined through trial and error and set as K v i r t u a l = 400 400 0 T   N · m / r a d and D v i r t u a l = 40 40 0 T   N · m / r a d / s .

2.2. Optimization Calculation

The body movement of the forward dynamics model is generated based on the reference joint angle q r j used in the joint torque model. Typically, optimization calculations for the reference joint angle are performed at each time step of the simulation. By performing optimization calculations at high frequencies over time steps, the generated motion becomes closer to the measured motion. However, this approach has drawbacks, such as requiring a significant computation time or being susceptible to measurement errors due to large noise of IMUs during certain time steps, like impacts. In this study, to generate motion closer to the measured motion while reducing the frequency of optimization calculations, a method was employed where the reference joint angles were optimized not at each time step but over the entire measurement period. Multiple nodes were used as inputs to the simulation, and their values were determined through optimization calculations to create waveforms of reference joint angles by cubic spline interpolation. The reference joint angles q r j were determined as follow:
q r j ( t ) = s p l i n e ( N 1 j , … , N m j , t ) ,
where, s p l i n e is a spline function defined by multiple nodes N 1 j , … , N m j and the sampling time t . The number of nodes m was determined through trial and error: each upper body joint (shoulder, elbow, lumber) had two nodes at the start and end of the motion, and each joint of the leg involved in the jump (hip, knee, ankle) had five nodes evenly spaced from the start to the end of the motion. Other joints had three nodes set from the start to the end of the motion. The gait motion model proposed by Haraguchi and Hase [12] set node points periodically and symmetrically. However, for the generation of asymmetric and non-periodic movements, node points were set as variable number for all joints with DOFs.
Cost function was established to assess the body movements generated by the forward dynamics simulation, and optimization calculations were performed to minimize this value. Genetic algorithm optimization methods were employed in this study. Cost functions defined by Equation (8).
I all = ξ 1 I Q + ξ 2 I a ,   pelvis + ξ 3 I muscle .
I Q and I a ,   pelvis represent the cost functions for evaluating errors in the 3D orientations of each segment and acceleration of the pelvis segment, respectively, between the simulation model and the experimental record by IMUs, as follow:
I Q = ∑ s = 1 12 ∫ ϕ model s − ϕ exp s 2 + θ model s − θ exp s 2 + ψ model s − ψ exp s 2 d t ,
I a , pelvis = ∫ a model , x pelvis − a exp , x pelvis 2 + a model , y pelvis − a exp , y pelvis 2 + a model , z pelvis − a exp , z pelvis 2 d t ,
where ϕ model s , θ model s , and ψ model s are the simulated orientations of sth segment with respect to the global coordinates, represented by Euler angles in the X, Y, and Z sequence, determined by the Q m o d e l s . ϕ exp s , θ e x p s , and ψ e x p s are the measured orientations of sth segment with respect to the global coordinates, represented by Euler angles in the X, Y, and Z sequence. These Euler angles are determined by the measured 3D orientations Q exp s expressed by quaternions in the global coordinate system recorded by IMUs, which is calculated by the extended Kalman filter, as described in Section 2.2.1. a m o d e l , x p e l v i s , a m o d e l , y p e l v i s , and a m o d e l , z p e l v i s   are the simulated acceleration of the pelvis segment. a e x p , x p e l v i s , a m o d e l , y p e l v i s , and a e x p , z p e l v i s are the measured acceleration of the pelvis by the IMUs. Q model s , a m o d e l , x p e l v i s , a m o d e l , y p e l v i s , and a m o d e l , z p e l v i s are calculated after computing the q , q ˙ , and q ¨ based on the forward dynamics calculation. I Q aims for alignment with the measurements from IMUs regarding joint motion, I a ,   pelvis aims to match the acceleration from the impact at the moment the foot makes contact with the ground and translational motion of the body. I muscle is the cost function for the overall muscle load, as follows:
I muscle = ∑ j = 1 21 ∫ σ + j 3 + σ − j 3 d t ,
σ + j = 0                                 : τ a j < 0 τ a j τ + , max j               : 0 ≤ τ a j ,
σ − j = τ a j τ − , max j                 : τ a j < 0 0                                   : 0 ≤ τ a j ,
where σ + j and σ − j are the active torques normalized by the maximum positive joint torque τ + , m a x j and maximum negative joint torque τ − , m a x j , respectively, for joint j . For instance, the maximum flexion torque at the hip joint is τ + , m a x and the maximum extension torque at the hip joint is τ − , m a x , which were determined from previous studies across whole joints at neck [20], lumbar [21,22,23], shoulder [24,25,26], elbow [27], hip [28,29,30], knee [24], and ankle [31]. I muscle contributes to generating biomechanically valid movements while reducing overall physical load. Additionally, ξ represents the weight factors for each term of the cost function, and they were determined through trial and error as follows: ξ 1 = 10 3   ,   ξ 2 = 10 3   ( r a d 2 ) ,   ξ 3 = 10   ( m / s 2 2 )   .

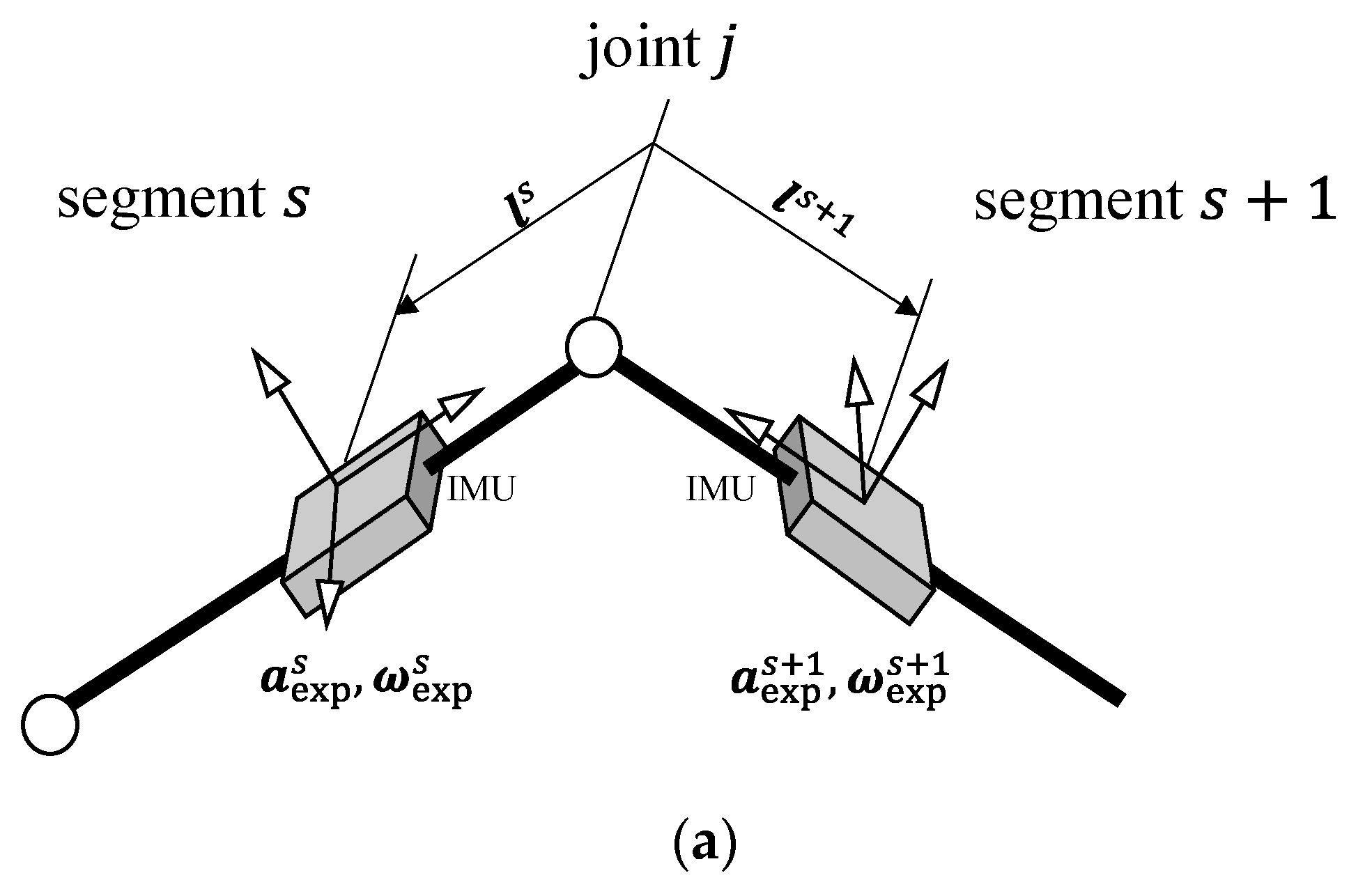
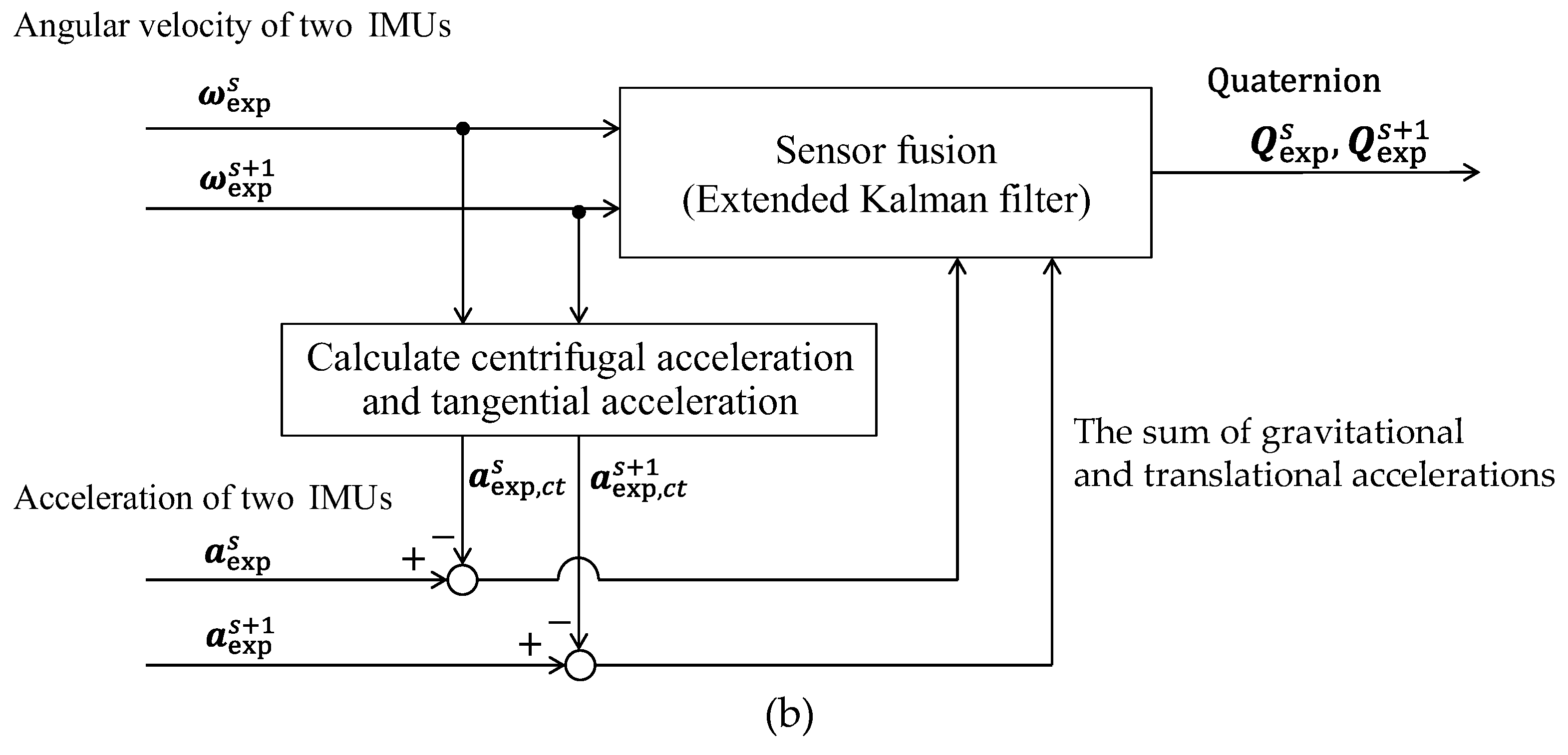
2.2.1. Orientation Estimation

The algorithm for orientation estimation during motion is shown in Figure 3. IMU orientation estimation algorithms are developed, such as utilizing data from 3-axis accelerometers, 3-axis gyroscopes, and 3-axis magnetometers to estimate orientation [32]. However, these methods often struggle to achieve sufficient accuracy when dealing with large dynamic accelerations in sports movements due to compensating for dynamic acceleration as white noise. Additionally, they rely on the magnetic field information obtained from magnetometers, making them challenging to use in indoor sports settings prone to magnetic disturbances. Therefore, in this proposed method, 3D orientations were estimated using sensor fusion of the 3-axis accelerometer and 3-axis gyroscope data from the IMUs [33,34]. It thereby enables estimation of 3D orientation without the effects of drift errors due to integration of angular velocities, dynamic accelerations, and geomagnetic disturbances. This sensor fusion approach is constructed using an extended Kalman filter to address the nonlinearity inherent in the relationship between 3D orientations and acceleration.
The output of acceleration in an IMU a exp s attached to the segment is represented as the sum of translational, centripetal, tangential, and gravitational, and Coriolis accelerations. In this study, the Coriolis acceleration can be neglected due to the constant distance from the joint to the IMU. Additionally, the gravitational and translational accelerations can be obtained by subtracting the centrifugal and tangential accelerations from the sensor output. Considering the entire system, IMU sensors provide the same gravitational and translational accelerations. Therefore, expressing centrifugal and tangential accelerations vector of sth segment at the sampling time t as a exp , ct s , this relationship was expressed as in the observation equation of the extended Kalman filter (Equation (15)). Furthermore, the state values x s = Q e x p s Q e x p s + 1 T were calculated by integrating angular velocity at the sampling time t to calculate the 3D orientations at the next sampling time [35] (Equation (14)). In this study, the 3D orientations ware described using quaternions that are not affected by gimbal lock. The quaternion represents the real part as the first element and the vector of imaginary parts as the subsequent elements.
x s ( t + 1 ) = I + d t 2 Ω s O O Ω s + 1 x s ( t ) + w s ,
a exp s − a exp , ct s a exp s + 1 − a exp , ct s + 1 = R s + 1 s x s ( t ) a exp s + 1 − a exp , ct s + 1 R s s + 1 x s ( t ) a exp s − a exp , ct s + v s ,
a exp , ct s = ω exp s × ω exp s × l s + ω ˙ exp s × l s ,
where R s + 1 s is the rotation matrix from segment s to s + 1 . ω exp s is the angular velocity vector of sth segment at the sampling time t , expressed as ω exp s = ω exp , x s ω exp , y s ω exp , z s T , and l s represents the position vector indicating the location of the IMU attached sth segment from the proximal joint j . Ω s is expressed in terms of angular velocities, as follows:
Ω s = 0 − ω exp , x s − ω exp , y s − ω exp , z s ω exp , x s 0 ω exp , z s − ω exp , y s ω exp , y s − ω exp , z s 0 ω exp , x s ω exp , z s ω exp , y s − ω exp , x s 0 .
In this study, these orientation estimation systems were adapted to the adjacent IMUs across each joint. Additionally, the process noise in the extended Kalman filter was set to w s = 10 − 3     10 − 3     10 − 3     10 − 3     10 − 3     10 − 3     10 − 3     10 − 3 T , and the observation noise to v s = 10 − 1     10 − 1     10 − 1     10 − 1     10 − 1     10 − 1 T ( m / s 2 ) . The initial value of the posterior error covariance matrix P t was set to P t 0 = d i a g { 10 2 ,   10 2 ,   10 2 ,   10 2 ,   10 2 ,   10 2 ,   10 2 ,   10 2 } . These values were determined through trial and error, taking into account the magnitude of noise from the accelerometers and gyroscope sensors.
The initial state values of Equation (14) and the neutral position of the model were determined using IMUs data from the calibration posture and this posture estimation system.

3. Experiment

3.1. Participants

The participants for measurement included seven healthy adult males and three healthy adult females (average body height: 1.69 ± 0.10   m , average body weight: 63.3 ± 12.7   k g , average age: 23.5 ± 2.5 years). This study has been approved by the Ethics Committee of Tokyo Metropolitan University. Participants were provided with written and verbal explanations of the measurement details before the measurements, and their consent was obtained through signed agreement documents before conducting the measurements.

3.2. Conditions

The jumping movement involved a run-up followed by a jump with a takeoff using the left leg. The run-up motion began in the direction of the jump, and on the second step of the run-up, a takeoff motion was performed, followed by a counterclockwise half-turn jump. The distance of the run-up was adjusted so that the participants could jump naturally. The jumping distance was determined with consideration for safety and the participant's athletic ability, with an average ± standard division (SD) value of 0.52 ± 0.19   m . Participants familiarized themselves with the movement before the experiment.

3.3. Measurements

The IMUs (TSND151, ATR-Promotions Inc., Japan) was used to measure 3-axis acceleration and 3-axis angular velocity (sampling frequency: 1,000 Hz, accelerator measurement range: ±16 G (resolution: 0.48 mG), gyroscope measurement range: ±2,000 dps (resolution: 0.061 dps)). 12 IMUs were attached to the participant’s trunk, pelvis, upper arms, forearms, thighs, shanks, and feet. The attachment points were as follows: sensors on the trunk were positioned on the upper thoracic vertebrae, those on the pelvis were at the midpoint of the bilateral posterior superior iliac spines, those on the upper arms were at a quarter of the distance from the elbow joint along the line connecting the shoulder and elbow joints, those on the forearms were at the midpoint along the line connecting the elbow joint and the styloid process of the ulna, those on the thighs were at a quarter of the distance from the lateral condyle of the femur along the line connecting the greater trochanter and the lateral condyle of the femur, those on the shanks were at the midpoint along the line connecting the lateral malleolus and the medial malleolus of the tibia, and those on the feet were at the midpoint along the line connecting the calcaneus and the base of the first metatarsal bone. Two cylindrical rods were attached to the IMUs on the forearms, and they were worn to sandwich the radius and ulna. All IMUs were secured to each segment using elastic belts.
To validate the simulation, GRFs were measured using a force plate (TF-4060-D, Tech Giken Co., Ltd., Japan) at a sampling frequency of 100 Hz. Additionally, the 3D coordinates of markers attached to the entire body were measured at a sampling frequency of 100 Hz using an optical motion capture system (OptiTrack Flex 3, Natural Point Inc., USA). Marker positions and calibration poses were aligned with a full-body musculoskeletal model [36] used for calculating joint angles and joint torques. All measurements underwent processing with a low-pass filter (Butterworth fourth-order type, -3 dB at 18 Hz).

3.4. Data Analysis

The measurements from the IMUs were input into the forward dynamics model. To validate the model, GRF, GRM, joint angle and joint torque were calculated using force plates and an optical motion capture system as the reference values. GRF and GRM were computed from the force plate measurements. The point projected onto the ground as the origin was the ankle joint center, and the calculations were performed in a coordinate system aligned with the foot's horizontal direction. The ankle joint center was determined as the midpoint between markers on the medial and lateral sides of the heel, obtained from the motion capture system. Additionally, these values were normalized by body weight (BW) and the product of BW and body height (BH). Furthermore, using the motion capture system and the open-source musculoskeletal modeling software OpenSim 4.4 [37,38], along with the full-body musculoskeletal model [36], inverse kinematics and inverse dynamics calculations were performed to compute joint angles and joint torques, including virtual joints. The joint torques were normalized by the product of BW and BH. These results are normalized from the moment the stepping foot makes contact with the ground until it leaves the ground.
The concordance between the estimated and true values is assessed using the Pearson correlation coefficient ( ρ ), categorized as weak correlation for ρ ≤ 0.35 , moderate correlation for 0.35 < ρ ≤ 0.67 , strong correlation for 0.67 < ρ ≤ 0.9 , and excellent correlation for 0.9 < ρ [39]. Additionally, the root mean square error (RMSE) and relative RMSE (rRMSE) were calculated. rRMSE normalizes RMSE by the average values of the two data ranges.

4. Results

Figure 4 shows the time-series data of GRFs ((a) the medial direction, (b) the anterior direction, and (c) the vertical direction) and GRM ((d) the sagittal plane, (e) the frontal plane, and (f) the transverse plane). Strong correlations were observed in the vertical GRF ( ρ = 0.749 ,   R M S E = 63.5   % B W , r R M S E = 27.4   % ), moderate correlations in the sagittal GRM ( ρ = 0.520 ,   R M S E = 5.67   % B W ･ B H , r R M S E = 61.6   % ), weak correlations in the medial GRF ( ρ = − 0.0326 , R M S E = 32.1 % B W , r R M S E = 72.9   % ), anterior GRF ( ρ = − 0.206 ,   R M S E = 44.5   % B W , r R M S E = 158   % ), frontal GRM ( ρ = − 0.481 ,   R M S E = 9.38   % B W ･ B H , r R M S E = 84.0   % ), and transverse GRM ( ρ = 0.157 ,   R M S E = 168   % B W ･ B H , r R M S E = 73.7   % ).
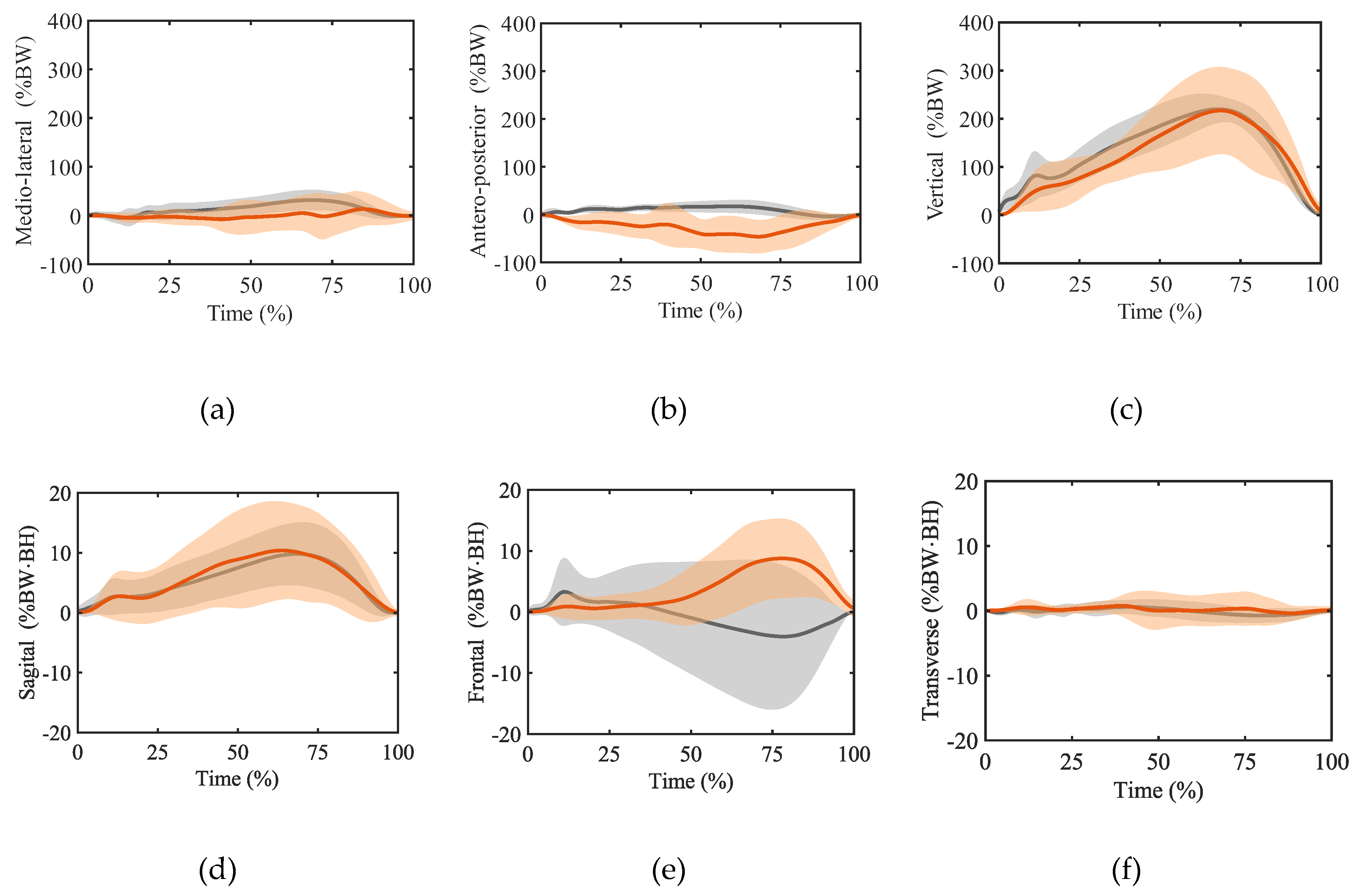
Table 1 shows the estimation accuracy for joint angles and joint torque. Strong correlations were observed in the flexion angles of the hip, knee, and ankle joints. Weak correlations were observed in the abduction and external rotation angles of the hip, and all joint torques.

5. Discussion

5.1. Advantages of the Proposed Approach

In this estimation method, accurate estimation was achieved for joint angles (hip, knee, and ankle flexion angles) with relatively large displacement. This was accomplished by optimizing biomechanically plausible flexion angles using forward dynamics calculations and the cost function defined by motion measurements and internal biomechanical loads. The correct generation of vertical foot movement resulted in high precision in vertical GRF estimation and slightly improved accuracy in sagittal GRM estimation.
In prior research conducted on estimating GRF in jump movements using IMUs and biomechanical models, 17 IMUs were utilized [40]. Additionally, methodologies employing machine learning require a substantial amount of experimental data for training purposes [10]. However, employing a hybrid cost function including internal biomechanical loads and less noise data estimated from sensor fusion with extended Kalman filter, our system requires fewer IMUs and eliminates the need for extensive training data. It enabled cost-effective estimation of GRF, GRM, and joint movements in sports movement. By reducing the hindrance caused by sensor attachment, our proposed estimation approach contributes to sports movement analysis. Moreover, employing a hybrid cost function including internal biomechanical loads necessitates accuracy validation, but also offers the potential to further reduce the number of required IMUs.

5.2. Accuracy

Although this study achieved high accuracy in estimating GRFs and joint movements during rotational jump actions, the precision attained was not sufficient for practical application in sports competitions.
This study employed IMUs to measure motion. IMUs are susceptible to noise in measurement and require robust attachment and careful calibration to avoid inhibiting movement. In this study, 12 IMUs were manually attached according to predefined positions, which may have introduced errors in the estimated GRFs due to positional inaccuracies. Furthermore, movement of segments during jumping and noise from soft tissues could have adversely affected the estimation of GRFs. IMUs measure acceleration and angular velocity of soft tissues relative to bones [41]. During measurement, attachment positions were chosen to minimize the influence of soft tissues and were secured with elastic straps. However, in vigorous activities such as sports movements, IMUs within soft tissues or within the belt might experience significant vibrations, potentially leading to considerable errors in measurements.
When compared to the gait analysis by Haraguchi and Hase [12], the accuracy of anterior and medial GRFs and frontal and transverse GRMs decreased. This is likely due to the lack of consideration for the attenuation of impact acceleration by joints and the virtual torque for fall prevention. The 3D orientation of measured body movement used in the cost function was estimated by sensor fusion of acceleration and angular velocity information obtained from IMUs. The extended Kalman filter for sensor fusion was constructed using the relationship between the two IMUs attached to the two-link system, enabling it to track high-speed movements such as jumping. However, the lack of consideration for the attenuation of impact acceleration by joints may lead to errors in the sum of translational acceleration and gravitational acceleration for each link, particularly during instances of high impact such as ground contact or takeoff in sports movements, resulting in potential errors in the estimated 3D orientation and adversely affecting the optimization of body movements in the model. In joints with a small range of motion, errors due to impact acceleration can have a significant effect on the displacement of the 3D orientation. Consequently, errors may occur in the estimation of non-flexion joint angles, leading to inaccurate foot contact and potentially reducing the accuracy of medial GRF and transverse GRM. Furthermore, while Haraguchi and Hase added virtual forces for fall prevention to the lateral direction based on the relationship between the overall center of gravity position and the support base, this study introduced virtual torques corresponding to the rotation angles of virtual joints to enable the generation of unstable movements such as jumping with a single foot while preventing falls. The addition of virtual torques in the sagittal and frontal plane rotations of the body might have limited movements. The decrease in accuracy of anterior GRF and frontal GRM may be attributed to the application of forces akin to brakes in those directions through virtual torques. The system cannot eliminate the virtual torques for fall prevention of the model. Therefore, reconsidering the reduction of the impact of virtual torques is necessary to improve the accuracy of body movements and joint torques.

5.3. Limitations

This study utilized healthy non-athlete participants. When adapting the system to athletes, there is a potential for errors in the estimated GRFs. Currently, the model is based on inertial parameters determined using estimation formulas based on height and weight and internal values such as joint torques and muscle forces. They were obtained from a population that does not represent athletes. However, when targeting sports movements with athletes as participant, it may be necessary to use parameters specific to the participants or the average values of athlete populations in that sport [42].
In this study, focusing on rotational jump movements, a total of 55 node points were set as parameters for the optimization calculation. These node points are used to calculate the reference joint angle q r j , which serve as inputs to the simulation. Increasing the number of node points may enable the generation of more complex body movements and enhance the accuracy of ground reaction force estimation. However, increasing the variables, represented by node points, in the optimization calculation may negatively impact convergence speed and precision. To reduce measurement and computation costs while improving measurement accuracy and optimization calculation precision, kinematic synergy can be considered. Humans smoothly control the redundant multi-degree-of-freedom musculoskeletal system through a mechanism known as kinematic synergy, reducing the controlled DOFs [43]. This control mechanism flexibly manages joint motion through groups with synergies, allowing for the generation of diverse body movements. By introducing kinematic synergy into this system and controlling reference joint angle q r j for groups with synergies, it may be possible to achieve the generation of body movements and estimate GRFs even with fewer IMUs.
While the accuracy of vertical GRF was high in this system, the precision of anterior GRF and frontal GRM was lower. Although it may not predict the dynamics of all sports, it could use in sports involving sliding, such as those on ice or snow. For example on ice, anterior GRF tends to be small, and the frontal GRM is also diminished due to the narrow width of the blade [44]. Moreover, considering the possibility that virtual torque may have contributed to these low estimation accuracies, this method could be applicable to figure skating rotation jump movements, where these values are small. If this estimation method can be applied to figure skating, it would enable the estimation of forces exerted on the ice surface and physical loads with simple measurements, facilitating their application in movement analysis.
This system requires approximately 24 hours for a single trial (CPU: Intel® Core i9-13900KF, with 24 cores, 32 logical processors, and an average speed of 3.0GHz; memory: 128GB; software: MATLAB R2023a (9.14); operating system: Windows 11 Pro). Therefore, real-time analysis of sports movements is not feasible.

6. Conclusions

We estimated GRFs and body loads using a 3D forward dynamics approach incorporating sensor fusion with an extended Kalman filter, based on measurements of rotational jump movements on land using IMUs. By generating movements based on the cost function, it was possible to calculate biomechanically valid GRFs while following the measured movements even if not all joints are covered by IMUs, thus enabling the estimation of biomechanically valid GRFs with a small number of IMUs. To reduce the influence of the significant noise of IMUs due to sports movements in the optimization calculation, the 3D orientation using sensor fusion composed of acceleration and angular velocity data obtained from IMUs and an extended Kalman filter was estimated. This estimation method enables 3D motion analysis independent of measurement environment and machine learning training data.

Author Contributions

Conceptualization, K.H. and T.T.; methodology, T.K. and N.H.; software, T.K. and N.H.; validation, K.H., T.T., and N.H.; formal analysis, T.K.; investigation, T.K. and Y.H.; resources, K.H.; data curation, T.K.; writing—original draft preparation, T.K.; writing—review and editing, K.H., T.T., and N.H.; visualization, T.K.; supervision, K.H. and T.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of Tokyo Metropolitan University (protocol code H5-52 and approved on March 28, 2023).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study. Written informed consent was also obtained from the participants to publish this paper.

Acknowledgments

We would like to express our sincere gratitude to Mr. Yousuke Takeuchi and Ms. Shoko Ishikawa from the Japan Skating Federation for their advice on our research from an athlete's perspective.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Luhtanen, P.; Komi, P.V. Mechanical power and segmental contribution to force impulses in long jump take-off. European Journal of Applied Physiology and Occupational Physiology 1979, 41, 267–274. [Google Scholar] [CrossRef]
  2. Barker, L.A.; Harry, J.R.; Mercer, J.A. Relationships between countermovement jump ground reaction forces and jump height, reactive strength index, and jump time. Journal of Strength and Conditioning Research 2018, 32, 248–254. [Google Scholar] [CrossRef]
  3. Le, P.A.; Maton, B. Initiation of a vertical jump: the human body's upward propulsion depends on control of forward equilibrium. Neuroscience Letters 2002, 323, 183–186. [Google Scholar] [CrossRef]
  4. Glazier, P.S. Beyond animated skeletons: How can biomechanical feedback be used to enhance sports performance? Journal of Biomechanics 2021, 129, 110686. [Google Scholar] [CrossRef] [PubMed]
  5. Bulat, M.; Korkmaz, C.N.; Arslan, Y.Z.; Herzog, W. Musculoskeletal simulation tools for understanding mechanisms of lower-limb sports injuries. Current Sports Medicine Reports 2019, 18, 210–216. [Google Scholar] [CrossRef]
  6. Low, D.C.; Dixon, S.J. Footscan pressure insoles: accuracy and reliability of force and pressure measurements in running. Gait Posture 2010, 32, 664–666. [Google Scholar] [CrossRef]
  7. Ancillao, A.; Tedesco, S.; Barton, J.; O’ Flynn, B. Indirect measurement of ground reaction forces and moments by means of wearable inertial measurement units: A systematic review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef] [PubMed]
  8. Allen, T.; Shepherd, J.; Wood, J.; Tyler, D.; Duncan, O. Chapter 16 - Wearables for disabled and extreme sports. In Digital Health; Academic Press, 2021; pp. 253–273. [Google Scholar] [CrossRef]
  9. Karatsidis, A.; Bellusci, G.; Schepers, H.M.; de Zee, M.; Andersen, M.S.; Veltink, P.H. Estimation of ground reaction forces and moments during gait using only inertial motion capture. Sensors 2016, 17, 75. [Google Scholar] [CrossRef] [PubMed]
  10. Chaaban, C.R.; Berry, N.T.; Armitano-Lago, C.; Kiefer, A.W; Mazzoleni, M.J.; Padua, D.A. Combining inertial sensors and machine learning to predict vGRF and knee biomechanics during a double limb jump landing task. Sensors 2021, 21, 4383. [Google Scholar] [CrossRef]
  11. Karatsidis, A.; Jung, M.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Veltink, P.H. Michael Skipper Andersen, Musculoskeletal model-based inverse dynamic analysis under ambulatory conditions using inertial motion capture. Medical Engineering & Physics 2019, 65, 68–77. [Google Scholar] [CrossRef]
  12. Haraguchi, N.; Hase, K. Prediction of ground reaction forces and moments and joint kinematics and kinetics by inertial measurement units using 3D forward dynamics model. Journal of Biomechanical Science and Engineering 2024, 19, 23–00130. [Google Scholar] [CrossRef]
  13. Drillis, R.; Contini, R.; Bluestein, M. Body segment parameter: A survey of measurement techniques. Artificial Limbs 1964, 8, 329–351. [Google Scholar]
  14. Ae, M.; Tang, H.; Yokoi, T. Estimation of inertia properties of the body segments in Japanese athletes. Society of Biomechanism Japan (in Japanease). 1992, 11, 23–33. [Google Scholar] [CrossRef]
  15. Davy, D. T.; Audu, M. L. A dynamic optimization technique for predicting muscle forces in the swing phase of gait. Journal of Biomechanics 1987, 20, 187–201. [Google Scholar] [CrossRef] [PubMed]
  16. Engin, A.E. On the biomechanics of the shoulder complex. Journal of Biomechanics 1980, 13, 575–581. [Google Scholar] [CrossRef]
  17. Engin, A.E.; Chen, S.M. Kinematics and passive resistive properties of human elbow complex. Journal of Biomechanical Engineering 1987, 109, 318–323. [Google Scholar] [CrossRef] [PubMed]
  18. Pope, M.H.; Wilder, D.G.; Matteri, R.E.; Frymoyer, J.W. Experimental measurements of vertebral motion underload. Orthopedic Clinics of North America 1977, 8, 155–167. [Google Scholar] [CrossRef] [PubMed]
  19. Ren, L.; Jones, R.K.; Howard, D. Whole body inverse dynamics over a complete gait cycle based only on measured kinematics. Journal of Biomechanics 2008, 41, 2750–2759. [Google Scholar] [CrossRef]
  20. 20. Seng, K-Y.; Peter, V-S.L.; Lam, P-M. Neck muscle strength across the sagittal and coronal planes: an isometric study. Clinical Biomechanics 2002, 17, 545–547. [CrossRef]
  21. Grabiner, M.D.; Jeziorowski, J.J.; Divekar, A.D. Isokinetic measurements of trunk extension and flexion performance collected with the biodex clinical data station. Journal of Orthopaedic & Sports Physical Therapy 1990, 11, 590–598. [Google Scholar] [CrossRef]
  22. Ng, J.K.; Richardson, C.A.; Parnianpour, M.; Kippers, V. EMG activity of trunk muscles and torque output during isometric axial rotation exertion: a comparison between back pain patients and matched controls. Journal of Orthopaedic Research 2002, 20, 112–121. [Google Scholar] [CrossRef]
  23. Lindsay, D.M.; Horton, J.F. Trunk rotation strength and endurance in healthy normal and elite male golfers with and without low back pain. North American journal of sports physical therapy 2006, 1, 80–89, PMC2953310. [Google Scholar]
  24. Smith, J.C.; Darden, G.F. Peak torque comparison between isam 9000 and biodex isokinetic devices. Int J Health Sci 20176, 4, 7–13. [Google Scholar]
  25. Meeteren, J.v.; Roebroeck, M.E.; Stam, H.J. Test-retest reliability in isokinetic muscle strength measurements of the shoulder. Journal of rehabilitation medicine 2002, 34. 91–95. [CrossRef]
  26. Jenp, Y.N.; Malanga, G.A.; Growney, E.S.; An, K.N. Activation of the rotator cuff in generating isometric shoulder rotation torque. The American Journal of Sports Medicine 1996, 24, 477–485. [Google Scholar] [CrossRef] [PubMed]
  27. Lund, H.; Søndergaard, K.; Zachariassen, T.; Christensen, R.; Bülow, P.; Henriksen, M.; Bartels, E.M.; Danneskiold-Samsøe, B.; Bliddal, H. Learning effect of isokinetic measurements in healthy subjects, and reliability and comparability of biodex and lido dynamometers. Clinical physiology and functional imaging 2005, 25, 75–82. [Google Scholar] [CrossRef] [PubMed]
  28. Dean, J.C.; Kuo, A.D.; Alexander, N.B. Age-related changes in maximal hip strength and movement speed. The Journals of Gerontology Series A: Biological Sciences and Medical Sciences 2004, 59, 286–292. [CrossRef]
  29. Sugimoto, D.; Mattacola, C.G.; Mullineaux, D.R.; Palmer, T.G.; Hewett, T.E. Comparison of isokinetic hip abduction and adduction peak torques and ratio between sexes. Clinical journal of sport medicine: official journal of the Canadian Academy of Sport Medicine 2014, 24, 422-428. [CrossRef]
  30. Lindsay, D.M.; Maitland, M.E.; Lowe, R.C.; Kane, T.J. Comparison of isokinetic internal and external hip rotation torques using different testing positions. Journal of Orthopaedic & Sports Physical Therapy 1992, 16, 43–50. [CrossRef]
  31. Fugl-Meyer, A.R. Maximum isokinetic ankle plantar and dorsal flexion torques in trained subjects. European journal of applied physiology and occupational physiology 1981, 47, 393–404. [Google Scholar] [CrossRef] [PubMed]
  32. Jurman, D.; Jankovec, M.; Kamnik, R.; Topic, M. Calibration and data fusion solution for the miniature attitude and heading reference system. Sensors and Actuators A 2007, 138, 411–420. [Google Scholar] [CrossRef]
  33. Kondo, A.; Doki, H.; Hirose, K. A Study on the estimation method of 3D posture in body motion measurement using inertial sensors. Transactions of the Japan Society of Mechanical Engineers (Series C) (in Japanese) 2013, 79, 112-122. [CrossRef]
  34. Simone, S.; Francesco, S.; Luca, F.; Alessandro, R. A sensor fusion algorithm for an integrated angular position estimation with inertial measurement units, 2011 Design. Automation & Test in Europe Conference & Exhibition 2011, 1-4. [CrossRef]
  35. Xu, X.; Sun, Y.; Tian, X.; Zhou, L.; Li, Y. A Double-EKF Orientation Estimator Decoupling Magnetometer Effects on Pitch and Roll Angles. IEEE Transactions on Industrial Electronics 2022, 69, 2055–2066. [Google Scholar] [CrossRef]
  36. Rajagopal, A.; Dembia, C.L.; DeMers, M.S.; Delp, D.D.; Hicks, J.L.; Delp, S.L. Full body musculoskeletal model for muscledriven simulation of human gait. IEEE Transactions on Biomedical Engineering 2016, 63, 2068–2079. [Google Scholar] [CrossRef]
  37. Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans-actions on Biomedical Engineering 2007, 54, 1940-1950. [CrossRef]
  38. Seth, A.; Hicks, J.L.; Uchida, T.K.; Habib, A.; Dembia, C.L.; Dunne, J.J.; Ong, C.F.; DeMers, M.S.; Rajagopal, A.; Millard, M.; Hamner, S.R.; Arnold, E.M.; Yong, J.R.; Lakshmikanth, S.K.; Sherman, M.A.; Ku, J.P.; Delp, S.L. OpenSim: Simulating musculoskeletal dy-namics and neuromuscular control to study human and animal movement. PLoS Computational Biology 2018, 14, e1006223. [Google Scholar] [CrossRef]
  39. Taylor, R. Interpretation of the correlation coefficient: A basic review. Journal of Diagnostic Medical Sonography 1990, 6, 35- 39. [CrossRef]
  40. Recinos, E.; Abella, J.; Riyaz, S.; Demircan, E. Real-Time Vertical Ground Reaction Force Estimation in a Unified Simulation Framework Using Inertial Measurement Unit Sensors. Robotics 2020, 9. [Google Scholar] [CrossRef]
  41. Roetenberg, D.; Luinge, H.; Slycke, P. Xsens MVN: Full 6DOF human motion tracking using miniature inertial sensors. Xsens Motion Technologies BV Technical Report 2009, 3. [Google Scholar]
  42. Infantolino, B.W.; Forrester, S.E.; Pain, M.T.G.; Challis, J.H. The influence of model parameters on model validation. Computer Methods in Biomechanics and Biomedical Engineering 2019, 22, 997–1008. [Google Scholar] [CrossRef] [PubMed]
  43. Esmaeili, S.; Karami, H.; Baniasad, M.; Shojaeefard, M.; Farahmand, F. The association between motor modules and movement primitives of gait: A muscle and kinematic synergy study. Journal of Biomechanics 2022, 134, 110997. [Google Scholar] [CrossRef]
  44. Hara, Y.; Hase, K.; Haraguchi, N.; Koshio, T.; Takahashi, T. A validation method for estimating the reaction force from the ice surface during figure skating jump movements. The 12th Asian-Pacific Conference on Biomechanics, 2023.
Preprints 100204 g001
Figure 1. Human body model. Each segment of the body is composed of rigid body links, with a total of 12 links. Joints are represented by defining rotational degrees of freedom (DOFs) at the joints of each link, with a total of 27 DOFs for the entire body, including a virtual joint with 6 DOFs between the pelvis segment and the global coordinate system.
Figure 1. Human body model. Each segment of the body is composed of rigid body links, with a total of 12 links. Joints are represented by defining rotational degrees of freedom (DOFs) at the joints of each link, with a total of 27 DOFs for the entire body, including a virtual joint with 6 DOFs between the pelvis segment and the global coordinate system.
Preprints 100204 g001
Preprints 100204 g002
Figure 2. Calculation flow of the forward dynamics model at each time step. Body movements are generated by forward dynamics simulation using the reference joint angles q r as the simulation input. Joint angles q are calculated from joint torques τ consisting of active torques τ a and passive torques τ p . Ground reaction forces F v   a n d   F h and external force to balance the model τ virtual are obtained from the external force model.
Figure 2. Calculation flow of the forward dynamics model at each time step. Body movements are generated by forward dynamics simulation using the reference joint angles q r as the simulation input. Joint angles q are calculated from joint torques τ consisting of active torques τ a and passive torques τ p . Ground reaction forces F v   a n d   F h and external force to balance the model τ virtual are obtained from the external force model.
Preprints 100204 g002
Preprints 100204 g003aPreprints 100204 g003b
Figure 3. (a) Two-link model for constructing sensor fusion. (b) Algorithm for 3D attitude estimation. The outputs of the IMUs attached to the two links have the same translational and gravitational acceleration components. Therefore, the sum of the gravitational acceleration and translational acceleration obtained by excluding the centrifugal and tangential acceleration components from IMUs, and the angle obtained by integrating the angular velocity in three dimensions and sensor fusion using an extended Kalman filter are used to estimate the 3D orientation with noise such as drift errors removed. The 3D orientation described using quaternions was estimated.
Figure 3. (a) Two-link model for constructing sensor fusion. (b) Algorithm for 3D attitude estimation. The outputs of the IMUs attached to the two links have the same translational and gravitational acceleration components. Therefore, the sum of the gravitational acceleration and translational acceleration obtained by excluding the centrifugal and tangential acceleration components from IMUs, and the angle obtained by integrating the angular velocity in three dimensions and sensor fusion using an extended Kalman filter are used to estimate the 3D orientation with noise such as drift errors removed. The 3D orientation described using quaternions was estimated.
Preprints 100204 g003aPreprints 100204 g003b
Preprints 100204 g004
Figure 4. Ground reaction forces (GRFs) (a)-(c) and Ground reaction moments (GRMs) (d)-(f) when I a l l , Q u a t e r n i o n were used in the cost function. (a) medio-lateral with the medial direction as positive, (b) antero-posterior with the anterior direction as positive, (c) vertical with the upward direction as positive, (d) sagittal plane around the medial axis, (e) frontal plane around the anterior axis, and (f) transverse plane around the vertically upward axis. These axes have their origin at the point projected onto the ground from the ankle joint center, and the horizontal direction coincides with the coordinate system of the foot. The timing at heel strike of the stepping foot was defined as 0 % phase, and the timing at toe-off of the stepping time was defined as 100 % phase. GRF is normalized by body weight (BW) and GRM is normalized by BW × body height (BH). The red area shows the mean ± standard deviation (SD) of the estimated values, the red solid line shows the mean of the estimated values, the gray area shows the mean ± SD of the measurement values, and the gray solid line shows the mean of the measurement values.
Figure 4. Ground reaction forces (GRFs) (a)-(c) and Ground reaction moments (GRMs) (d)-(f) when I a l l , Q u a t e r n i o n were used in the cost function. (a) medio-lateral with the medial direction as positive, (b) antero-posterior with the anterior direction as positive, (c) vertical with the upward direction as positive, (d) sagittal plane around the medial axis, (e) frontal plane around the anterior axis, and (f) transverse plane around the vertically upward axis. These axes have their origin at the point projected onto the ground from the ankle joint center, and the horizontal direction coincides with the coordinate system of the foot. The timing at heel strike of the stepping foot was defined as 0 % phase, and the timing at toe-off of the stepping time was defined as 100 % phase. GRF is normalized by body weight (BW) and GRM is normalized by BW × body height (BH). The red area shows the mean ± standard deviation (SD) of the estimated values, the red solid line shows the mean of the estimated values, the gray area shows the mean ± SD of the measurement values, and the gray solid line shows the mean of the measurement values.
Preprints 100204 g004
Table 1. Pearson's correlation coefficient ( ρ ), RMSE and rRMSE in joint angle and joint torque.
Table 1. Pearson's correlation coefficient ( ρ ), RMSE and rRMSE in joint angle and joint torque.
Hip Knee Ankle
Flexion Abduction External
Rotation		 Flexion Flexion
ρ
Joint angle 0.682 -0.291 -0.818 0.781 0.723
Joint torque 0.203 -0.510 0.285 0.376 0.313
RMSE
Joint angle ( d e g ) 20.1 15.9 15.9 15.6 12.3
Joint torque B W ･ B H 13.7 10.1 3.39 12.2 4.67
rRMSE
Joint angle ( % ) 56.4 73.7 67.5 43.3 38.6
Joint torque ( % ) 55.0 55.1 66.0 42.1 59.5
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated