Prerpints.org logo
Preprint
Article

Efficient Solutions for Large-Scale Max-Cut Problems: A Hybrid Local Search Heuristic Approach and Comparative Analysis with Quantum Annealing

This version is not peer-reviewed.

Submitted:

28 February 2024

Posted:

29 February 2024

Read the latest preprint version here

Abstract
In this study, we address the formidable challenge of solving large-scale Max-Cut problems (MCP). We introduce a rapid computational procedure utilizing a hybrid 1-flip/r-flip local search heuristic. This innovative strategy significantly reduces the computational time required for MCP problems while consistently generating solutions of exceptional quality. The paper presents substantial computational insights, showcasing the effectiveness of our approach on very-large-scale Max-Cut instances with varying densities. Our proposed heuristic is rigorously evaluated by comparing its performance against a quantum annealing solver, leveraging a multi-start Tabu Search framework. The results underscore the potency of this unique combination as an efficient and effective solution for large-scale QUBO problems. Notably, our hybrid heuristic consistently delivers high-quality solutions within the stringent CPU time limits of 600 seconds, demonstrating its efficacy across Max-Cut instances ranging from 10,000 to 40,000 variables. This research contributes to advancing the state-of-the-art in large-scale QUBO problem-solving, offering a powerful and time-efficient approach with broad applicability.
Keywords: 
hybrid heuristics
;  
quantum annealing solver
;  
max-cut
Subject: 
Business, Economics and Management  -   Other

1. Introduction

The Quadratic Unconstrained Binary Optimization (QUBO) problem holds significant relevance across various applications, particularly as a unifying approach for many combinatorial optimization challenges [1]. The emergence of quantum computing, particularly quantum annealing solvers, has brought QUBO into the spotlight [2]. However, the complexities of modelling and analyzing very large-scale problems on conventional computing platforms often hinder effective solutions through mathematical programming methods.
While quantum computing platforms offer the potential to overcome hardware limitations, transforming real-world problems into the suitable qubit architecture remains challenging. This study addresses the gap between quantum and traditional computing platforms, focusing on the very large-scale Max-Cut problem (MCP)—a critical research area with applications spanning statistical physics [3], communication infrastructure [3], machine learning [4], and computer chip design [5].
The computational landscape of the Max-Cut problem has sparked diverse solution strategies, ranging from approximation algorithms leveraging semidefinite programming to metaheuristic methods and exact approaches. While approximation algorithms like the seminal work of Goemans and Williamson [6] and subsequent contributions by Karish et al. offer theoretical performance guarantees [7], empirical evaluations often reveal their inferiority to other methodologies.
Exact methods, exemplified by Krishnan and Mitchell’s cut and price approach [8] and Rendl et al.’s branch and bound method [9], have emerged as viable alternatives, particularly for smaller problem instances. However, their applicability remains constrained to scenarios with relatively few nodes, typically in the hundreds.
For more substantial Max-Cut instances, characterized by thousands of nodes, metaheuristic methods become imperative. Recent advancements in this domain include the rank-2 relaxation method, dubbed CirCut, by Burer et al. [10], Festa et al.’s hybrid randomized method [11], and Marti et al.’s scatter search method [12]. Computational evaluations consistently demonstrate the superiority of these techniques, with the scatter search method notably achieving outstanding performance across test problems featuring up to 3000 nodes. Additionally, Alidaee et al. proposed a diversification strategy based on sequential local improvement, demonstrating substantial enhancements in solutions for a significant portion of benchmark Max-Cut problems within reasonable CPU time constraints [13].
Further breakthroughs have been made to tackle even larger problem sizes. Kochenberger et al. introduced the DDT approach, delivering state-of-the-art solutions for test problems boasting up to 10,000 nodes [14].
Max-Cut problem is a popular testbed for Quantum Computing platforms and algorithms due to its natural formulations. Recent developments in quantum computing, especially quantum annealing solvers, put Max-Cut in the spotlight [15,16,17,18,19,20,21,22,23,24]. Alam et al. used the graph Max-Cut problem as a prototype while using the quantum approximate optimization algorithm (QAOA) where a quantum circuit and a classical optimizer operate in a closed loop solving hard combinatorial optimization problems [15]. Basso et al. also applied QAOA to Max-Cut on large-girth regular graphs [16]. Galda et al. showed that the transferability of the parameters among QAOA instances and convergence of the optimal parameters around specific values can be predicted based on local graph properties [17]. Bianchi et al. proposed a pooling operator for graph neural networks to generate coarser graphs while maintaining the overall topology of the graph and used a spectral algorithm approximating the Max-Cut solution [18]. Shaydulin et al. utilized a multi-start optimization technique in a QAOA framework to improve the performance of quantum machines on various graph clustering problems [19] and introduced QAOA Kit for the combination and standardization of previously known parameters for Max-Cut problems [20]. Shaydulin and Wild proposed a new method to accelerate the assessment of QAOA energy by using the problem symmetry and implemented the proposed method on the Max-Cut problem using a graph auto-morphism solver and tensor network simulator [21]. Umasankar et al. used a Time-Multiplexed Opto-Electronic Oscillator-based Coherent Ising Machine on Max-Cut Problems [22]. Wurtz and Love defined the Spanning Tree QAOA for Max-Cut and utilizes an “ansatz” whose structure results from an approximate classical solution and reaches the same performance level as the classical algorithm to outperform QAOA at low depth [23].
In this research, we introduce a local search strategy based on the r-flip strategy for QUBO [24]. The dynamic adjustment of the r value in the r-flip strategy strikes a balance between computational cost and solution quality. This approach effectively reduces computational time while reaching superior solutions [25]. Our proposed heuristic achieves results within a strict CPU time limit of 600 seconds, addressing Max-Cut instances ranging from 10,000 to 40,000 variables. Comparative evaluations against a quantum annealing solver based on multi-start Tabu Search [26] provide insights into the efficiency and effectiveness of our proposed approach.
By bridging the gap between quantum and conventional computing, our study contributes to the exploration of quantum computing’s potential in solving complex optimization problems, showcasing a novel local search strategy tailored for QUBO with promising results in the context of the challenging Max-Cut problem.

2. QUBO and MCP Solution

Before we present the r-flip strategy to solve QUBO and MCP in this study, the notations used are given as follows:
n The number of variables
x An initial feasible solution
x* The best solution found by the algorithm
K The largest value of k for r-flip, k ≤ r
π(i) The i-th element of x in the order π(1)⋯π(n)
S {i:xi is tentatively chosen to receive a new value to produce a new solution xi’} restricting consideration to |S| = r
D The set of candidates for an improving move
E ( x i ) Derivative of f(x) with respect to x i
E ( x ) = ( E ( x 1 ) , … , E ( x n ) ) The vector of derivatives
x(.) A vector representing the solution of x
E(.) A vector representing the value of derivative E ( x i )
The general form of QUBO can be given as [27],
M a x   f x = ∑ i = 1 n q i x i + 1 2 ∑ i = 1 n ∑ j ≠ i n q i , j x i x j ,       s . t .     x i ∈ 0,1 ,   i = 1 , ⋯ , n
In (1), 1 2 q i , j is the i,j-th entry of a given n by n symmetric matrix Q and the linear term q i can be the entry in the diagonal of the matrix. Since x i 2 = x i , and Q may be written as an upper triangular matrix by doubling each entry of the upper triangle part of the matrix and letting q i , i = q i , then we can write (1) as (2).
M a x   f x = ∑ i = 1 n ∑ j ≥ i n q i , j x i x j = x T Q x ,   s . t .   x _ i ∈ { 0,1 } , i = 1 , ⋯ , n  
Numerous combinatorial optimization problems lend themselves to reformulation as QUBO by employing a quadratic infeasibility penalty. However, determining the optimal penalty values poses a considerable challenge. In light of this, we focus our investigation on the very large-scale MCP as a prime candidate application, given its inherent and natural formulation within the QUBO framework.

2.1. Max-Cut problems

Max-Cut problem with many real-world implementations is an NP-hard problem which means that exact solution algorithms are not sufficient for large-scale problems, since obtaining a solution is very time-consuming [28]. Following the advances in quantum computers, max-cut problems have received much interest recently [29]. Two formulations, linear and nonlinear, exist for the MCP [27]. Initially, we present the natural QUBO model for MCP.
M a x   ∑ i = 1 n ∑ j = 1 , i < j n q i j x i + x j − 2 ∗ x i x j
s . t .   x i   ∈ 0,1 ∀ i = 1 , … , n
The QUBO model (3) can be transformed to a linear model using classical linearization techniques [30].
M a x   ∑ i = 1 n ∑ j = 1 , i < j n q i j x i + x j − 2 ∗ y i j
  s . t .   y i j ≤ x i ,   ∀ i , j = 1 , … , n   a n d   i < j
y i j ≤ x j ,   ∀ i , j = 1 , … , n   a n d   i < j
y i j ≥ x i + x j − 1 ,   ∀ i , j = 1 , … , n   a n d   i < j
x i   ∈ 0,1 ,   ∀ i = 1 , … , n
y i j ∈ [ 0 , 1 ] ,   ∀ j = 1 , … , n   a n d   i < j
The linear model for the MCP undergoes a substantial increase in size on very large-scale instances, both in terms of the number of variables and constraints. In this research, we specifically present solutions for the QUBO model, solely for the purpose of conducting a comparative analysis with a quantum annealing solver.

2.2. Solution Representation

Here Q is a symmetric matrix. Given a solution x = ( x 1 , … , x n ) define
Δ i ( x ) = q ( i , i ) + ∑ k ≠ i 2 x k q i k ,   i ∈ N
With respect to 1-flip neighborhood, x is locally optimal if and only if it satisfies
Δ i ( x ) ≤ 0 ,     ∀ x i = 0 ,       a n d       Δ i ( x ) > 0 ,     ∀ x i = 1
Then the objective function will satisfy
∆ f = ∑ i ∈ S ( x ' i − x i ) E ( x i ) + ∑ i , j ∈ S , i < j ( x ' i − x i ) ( x ' j − x j ) q i , j
and
∀ j ∈ S ,   E x j ← E x j + ∑ i ∈ S \ { j } x i ' − x i q i , j
The rationale behind the r-flip move is rooted in the notion that a larger value of moves (here, a larger value of r) offers the opportunity to explore a more extensive and diverse solution space. Moreover, when improvement within a specific neighborhood (e.g., a 1-flip move) is exhausted, and a solution x attains local optimality with respect to the 1-flip move, employing another neighborhood move (such as a 2-flip move) becomes viable for further exploration of the solution space. This strategic approach forms the basis for various meta-heuristics. Upon obtaining a locally optimal solution x concerning a 1-flip move, the elements of x are ordered based on the ascending absolute value of derivatives, as follows:
| E ( x π ( 1 ) ) | ≤ ⋯ ≤ | E ( x π ( n ) ) |
Here, π ( i ) means the i-th element of x in the order ( π ( 1 ) , ⋯ , π ( n ) ) . Now, one at a time in the given order, check the summation in (13) for k=1,2,…,n. For m<n, define (m, n) to be the number of combinations of m elements out of n, and let φ = Max i , j ∈ N ⁡ q i , j , and for the r-flip move let M = φ ∗ ( 2 , r ) . Let K be the largest value of k where the inequality (13) holds, and define the set D(n) (14).
∑ i = 1 k | E ( x π ( i ) ) | < M ,   for   k = 1,2 , 3 , ⋯ , n
D ( n ) = { x π ( 1 ) , ⋯ , x π ( K ) }
To implement an r-flip local search, the main decision is to choose a set S with |S|=r at each step and change x i to 1 − x i for all i ∈ S if it improves the objective function. This search process is inherently computationally demanding. The strategies mentioned above, including Lin and Kernighan's approach and very large-scale neighborhood search, are inherently tailored to specific problem domains. For instance, these strategies have predominantly found application in graph theoretic problems. However, in this paper, we introduce a novel implementation of the r-flip strategy, coupled with a sequential diversification technique. This approach enables the exploration of diverse sets S, each comprising r elements, while strategically avoiding non-improving sets. The incorporation of sequential diversification fundamentally reduces the computational time required for QUBO.

2.3. Implementation Details

The solution implementation is detailed in Section 2.2 through Algorithm 1 and Algorithm 2, with a comprehensive comparison of very large-scale MCP instances presented in the subsequent section. For additional insights and theoretical underpinnings, we draw upon the work and proofs by Alidaee and Wang [31], particularly for the novel r-flip results in general QUBO problems. It’s worth noting that in Algorithm 2, the sets S and M dynamically evolve as the search progresses.
Algorithm 1. 1-flip Local Search.
Preprints 100051 i001
Note that, the algorithm is similar to the greedy algorithm for a KP. Here, the value that each time is added to the knapsack is equal to. We used a random sequence to greedily choose items, however, another alternative that many researchers have used is, each time choosingse the item with the maximum contribution to F(x). Furthermore, due to the dynamicsm nature of the problem, when an is changed to it is possible the algorithm will come back to the same variable and change its value to what it was before (this might happen several times during the search possible). Also, note that, reaching a locally optimal solution by the greedy Algorithm 1, is NP-hard, (…).
In a 1-flip search, we only look at one variable at a time to possibly change its value. However, in r-flip search the process is similar to 1-flip search except that up to r variables may be considered for a change of values. The idea behind the r-flip search is that, the larger value of moves (here larger value of r) may provide an opportunity to explore a larger and thus more diverse solution space. In this process when a neighborhood search, for example, k-flip ( ) search, is exhausted, i.e., x is locally optimal with respect to k-flip move, another neighborhood move, for example (k+1)-flip search, may be implemented to explore the solution space. Such a strategy is the basis for several meta-heuristics.
Algorithm 2. r-flip Local Search.
Preprints 100051 i002
An alternative way to implement this algorithm is that k=r throughout the process. The Algorithm 2 is simple but inefficient; it requires some mechanism to choose the set S, and a process mechanism to implement elements of the k-flip move. Below, we give several results that allow an efficient implementation of the r-flip search process.
Lemma 1.
Given a locally optimal solution x with respect to a 1-flip search, we have
( x ' i − x i ) E i ( x ) ≤ 0 , for   i = 1 , … , n
Proof. 
Directly follows from the local optimality condition (6), which states
E i ( x ) ≥ 0 , i f f x i = 1   and   E i ( x ) ≤ 0 , i f f x i = 0 , for   i = 1 , … , n
Lemma 2.
Let S ⊆ N , and |S|=r, given any solution x, and M as defined earlier, we have
∑ i , j ∈ S ( x ' i − x i ) ( x ' j − x j ) q i j ≤ M
Proof. 
For each pair of elements, i,j in S, the left-hand-side (LHS) in (17) is either q i j or − q i j .Using definition of M, the summation in LHS is at most equal to M.
Theorem 3.
Given a locally optimal solution x of f(x) with respect to 1-flip search, a subset S ⊆ N , with |S|=r, is an improving r-flip move if and only if we have
∑ i ∈ S | E i ( x ) | < ∑ i , j ∈ S ( x ' i − x i ) ( x ' j − x j ) q i j
Proof. 
Using (10), a subset S with r elements is an improving r-flop move if and only if we have (19)
∑ i , j ∈ S ( x ' i − x i ) ( x ' j − x j ) q i j > − ∑ i ∈ S ( x ' i − x i ) E i ( x ) = ∑ i ∈ S E i ( x )
Since x is a locally optimal solution with respect to a 1-flip search, it follows from Lemma 1 that
inequality (19) is equivalent to (20); which completes the proof.
∑ i , j ∈ S ( x ' i − x i ) ( x ' j − x j ) q i j > − ∑ i ∈ S ( x ' i − x i ) E i ( x ) = ∑ i ∈ S E i ( x )
Proposition 2.
Let x be any locally optimal solution of f(x) with respect to a 1-flip search. If a subset S ⊆ N , with |S|=r, is an improving r-flip move, then we must have ∑ i ∈ S E i ( x ) < M .
Proof. 
The result follows from Theorem 3 and Lemma 2.
A consequence of Theorem 3 is as follows. Given a locally optimal solution x with respect to a 1-flip search, if there is no subset of S with |S|=r that satisfies (18), then x is also locally optimal solution with respect to an r-flip search. In fact, if there is no subset S of any size that (18) is satisfied, then x is also a locally optimal solution with respect to an r-flip search for all r ≤ n . Similar statements are true also regarding Proposition 2. The result of Proposition 2 is significant in the implementation of an r-flip search. It illustrates that, after having a 1-flip search implemented, if an r-flip search is next served as a locally optimal solution, only those elements with the sum of absolute value of derivatives less than M are eligible for consideration. Furthermore, when deciding about the elements of an r-flip search, we can easily check to see if any element x i by itself or with a combination of other elements is eligible to be a member of an improving r-flip move.
We adopted the following notation for computational results in next section:
BFS Best found solution among 10 runs within the CPU time limit.
APD Average percentage difference: the measurement for the performance of individual algorithm across runs on the same instance.
RPD Relative percentage deviation: the measurement for the relative performance across algorithms/methods on the same instance

3. Computational Experiments

In this investigation, we conducted extensive computational experiments to assess the efficacy of the proposed r-flip strategy across varying problem sizes, densities, and r values. The implementation of Algorithm 2 is executed using the GNU C++ compiler and undergoes 10 runs on the AMD Ryzen 5 3500U processor equipped with 16GB RAM. Simultaneously, the Quantum Annealing Solver (QAS), employing a multi-start tabu search, is implemented via a Python client on the same processor.
For the hybrid 1-flip/r-flip strategy in Algorithm 2 applied to very-large-scale MCP instances, we set a CPU time limit of 600 seconds. To comprehensively evaluate the r-flip strategy’s performance on very large-scale instances, we generate a diverse set of planar graph instances tailored for the MCP. This dataset comprises 120 instances, ranging from Q matrices sized 10,000 by 10,000 to 40,000 by 40,000. Among these instances, three distinct weight types with discrete values are introduced: Type ‘a’ with values of 1 and -1, Type ‘b’ with random discrete values between -10 and 10, and Type ‘c’ with random discrete values between -1,000 and 1,000. The instance data, ranging in size from 10,000 to 40,000, is conveniently accessible in the supplementary materials provided.

4. Numerical Results

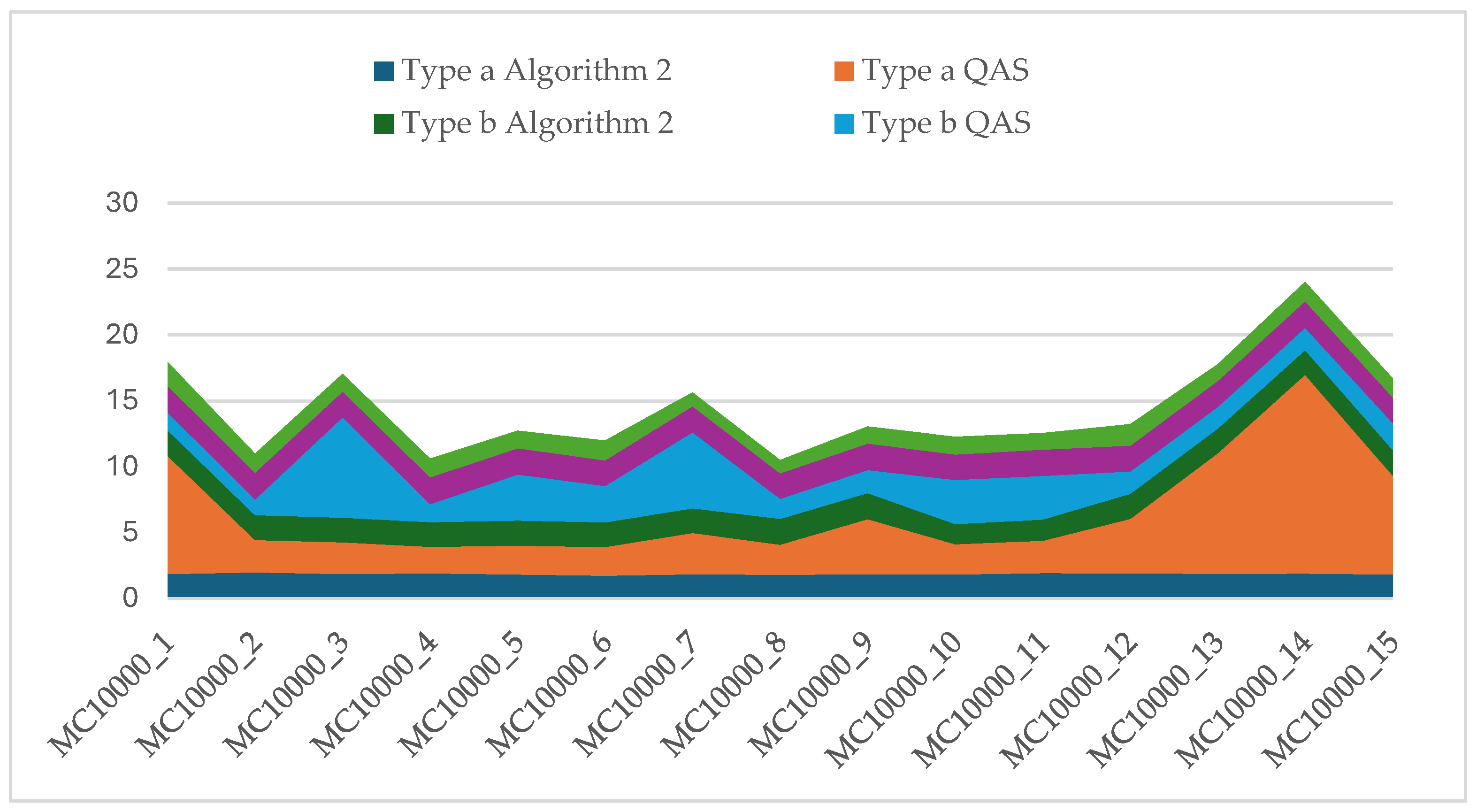
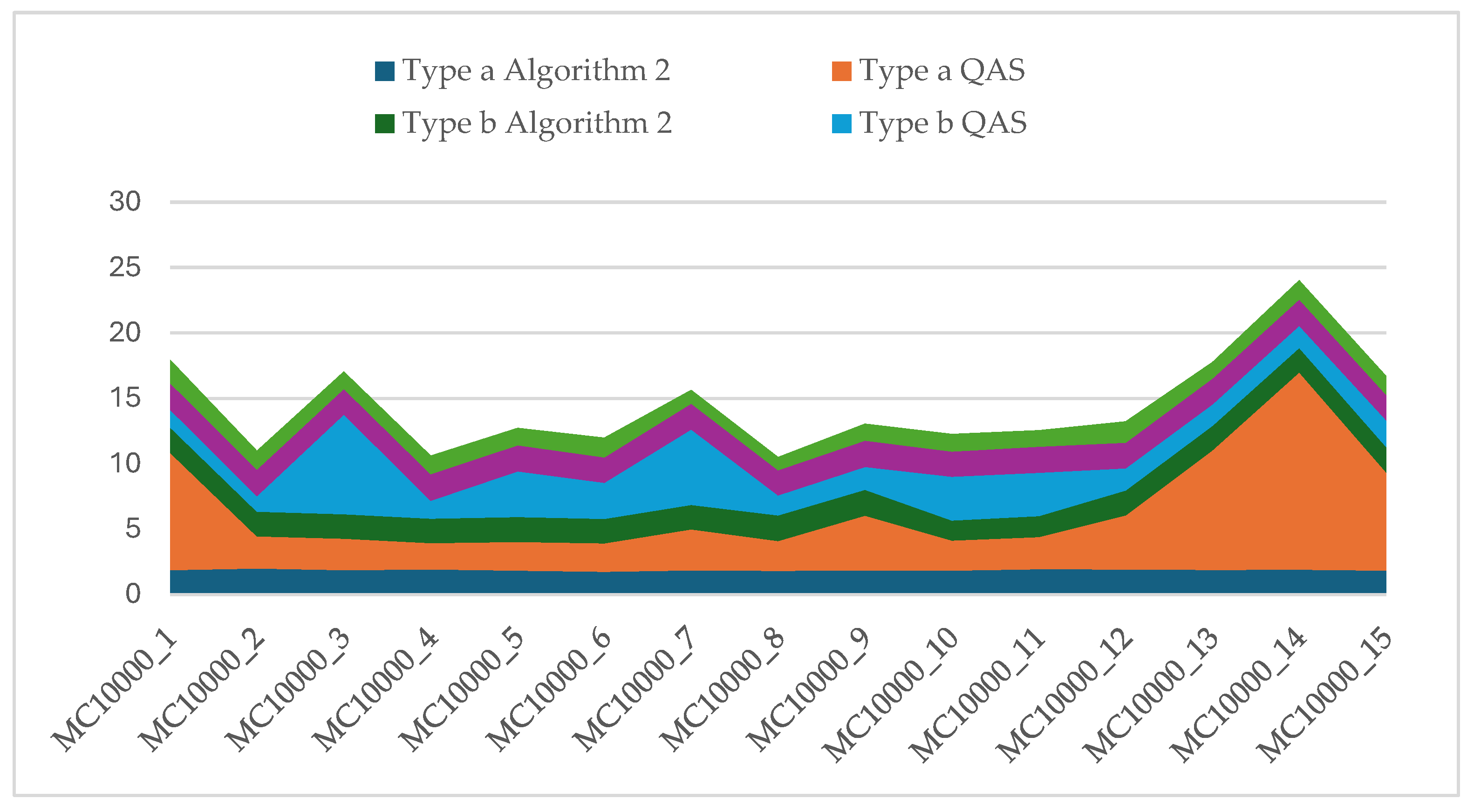
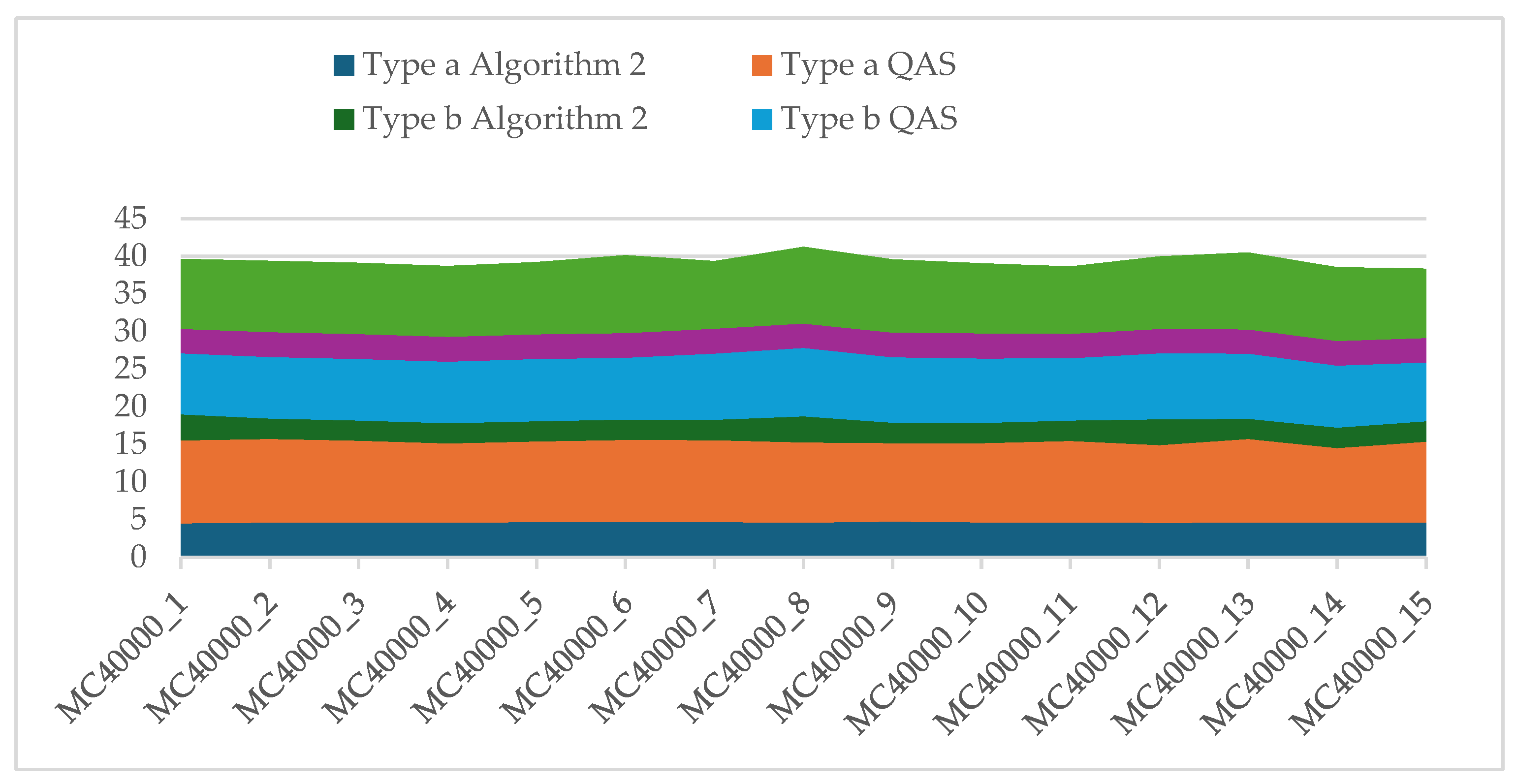
Table 1, Table 2 and Table 3 present the outcomes obtained from both the hybrid 1-flip/r-flip Algorithm 2 and QAS across the 120 instances. It’s crucial to note that the results from the QAS are derived using the sampler approach (sampler=10). In reporting the QAS results, we focus on Relative Percentage Deviation (RPD) as the quality of solutions hinges on the parameter of sufficient reads (num_reads) and the collection of samples for potential solutions.
Concurrently, for Algorithm 2, we provide the Average Percentage Deviation (APD) value to illustrate the consistent performance over 10 runs. This dual reporting approach allows for a comprehensive evaluation of the comparative performance between the hybrid 1-flip/r-flip Algorithm 2 and the Quantum Annealing Solver across the diverse set of instances.
The r-flip strategy holds the potential for integration into various other local search heuristics as an enhancement procedure. A judicious implementation of the hybrid 1-flip/r-flip strategy not only diminishes computing time but also enhances solution quality. The outcomes reported here represent the best solutions obtained from 10 independent runs for each instance using the hybrid 1-flip/r-flip strategy. Given the constraints on computing resources in this study, the solution deviation across these 10 runs is calculated within the specified short CPU time limits. Figure 1, Figure 2 and Figure 3 illustrate the performance of Algorithm 2 vs. QAS for 10, 20, and 40 thousand variables.

5. Conclusions

In this paper, we explore the application of r-flip search within the context of a very large-scale Max-Cut problem, treating it as a case of QUBO. Specifically, our investigation centers on assessing the local optimality of the r-flip search when a 1-flip search has already reached its local optimum. Our computational findings demonstrate a significant reduction in the pool of candidates for potential r-flip implementation, showcasing the efficiency of this novel strategy in solving very large-scale Max-Cut instances within a strict 600-second timeframe.
In our approach, we employed a 1-flip strategy to achieve local optimality. Yet, it’s well recognized that numerous problems, particularly those in constrained optimization, can reap substantial benefits from r-flip strategies as local procedures. Comparisons with alternative methodologies documented in the literature underscore the remarkable performance of our approach, surpassing leading competitors by a significant margin. Notably, our method consistently discovered previously undiscovered optimal solutions for the majority of the problem instances tackled. What distinguishes our achievement is that our solution framework isn’t tailored specifically for the Max-Cut problem but rather accommodates a broader class of problems. Our findings strongly indicate the potential for significant advancements in r-flip solution techniques, hinting at their capacity to tackle even larger-scale Max-Cut challenges with further refinement.
These results present notable advantages, particularly in scenarios where variable neighborhood strategies are being employed for very large-scale problems or sparse matrices. Furthermore, we benchmark our outcomes against those obtained from a quantum annealing solver based on multi-start tabu search. Notably, the quantum annealing solver has also proven effective in addressing the challenges posed by very large-scale MCP. This comparative analysis provides insights into the strengths and applicability of both the r-flip strategy and quantum annealing solver in tackling complex optimization problems.

Author Contributions

Conceptualization, B.A. and H.W.; methodology, B.A.; validation, B.A., H.W. and L.S.S.; formal analysis, H.W.; investigation, H.W.; data curation, H.W.; writing—original draft preparation, B.A.; writing—review and editing, H.W. and L.S.S.; visualization, B.A and L.S.S.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The instance data and solutions will be made available upon request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kochenberger, G.A.; Glover, F.; Alidaee, B.; Rego, C. A unified modeling and solution framework for combinatorial optimization problems. OR Spectr. 2004, 26, 237–250. [Google Scholar] [CrossRef]
  2. Rosenberg, G.; Vazifeh, M.; Woods, B.; Haber, E. Building an iterative heuristic solver for a quantum annealer. Comput. Optim. Appl. 2016, 65, 845–869. [Google Scholar] [CrossRef]
  3. Barahona, F.; Grötschel, M.; Jünger, M.; Reinelt, G. An Application of Combinatorial Optimization to Statistical Physics and Circuit Layout Design. Oper. Res. 1988, 36, 493–513. [Google Scholar] [CrossRef]
  4. Kel’manov, A.V.; Pyatkin, A.V. On complexity of some problems of cluster analysis of vector sequences. J. Appl. Ind. Math. 2013, 7, 363–369. [Google Scholar] [CrossRef]
  5. Liers, F.; Nieberg, T.; Pardella, G. Via Minimization in VLSI Chip Design - Application of a Planar Max-Cut Algorithm. Working Paper. 2011.
  6. Goemans, M.; Williamson, D. Improved approximation algorithms for Max-Cut and satisfiability prob- lems using Semidefinite programming. J. ACM 1995, 42, 1115–1145. [Google Scholar] [CrossRef]
  7. Karish, S.; Rendl, F.; Clausen, J. Solving graph bisection problems with semidefinite programming. SIAM J. Comput. 2000, 12, 177–191. [Google Scholar] [CrossRef]
  8. Krishnan, K.; Mitchell, J. A semidefinite programming based polyhedral cut and price approach for the Max-Cut problem. Comput. Optim. Appl. 2006, 33, 51–71. [Google Scholar] [CrossRef]
  9. Rendl, F.; Rinaldi, G.; Wiegele, A. Solving Max-Cut to optimality by intersecting semidefinite and poly- hedral relaxations. Math. Program. 2008, 121, 307–335. [Google Scholar] [CrossRef]
  10. Burer, S.; Monteiro, D.; Zang, Y. Rank-two relaxation heuristic for Max-Cut and other binary quadratic programs. SIAM J. Optim. 2001, 12, 503–521. [Google Scholar] [CrossRef]
  11. Festa, P.; Pardalos, P.; Resende, M.; Ribeiro, C. Randomized heuristics for the Max-Cut problem. Optim. Methods Softw. 2002, 7, 1033–1058. [Google Scholar] [CrossRef]
  12. Marti, R.; Duarte, A.; Laguna, M. Advanced scatter search for the Max-Cut problem. INFORMS J. Com- Put. 2009, 21, 26–38. [Google Scholar] [CrossRef]
  13. Alidaee, Bahram, Hugh Sloan, and Haibo Wang. Simple and fast novel diversification approach for the UBQP based on sequential improvement local search. Computers & Industrial Engineering. 2017, 111, 164–175. [CrossRef]
  14. Kochenberger, Gary A, Jin-Kao Hao, Zhipeng Lü, Haibo Wang, and Fred Glover. Solving large scale max cut problems via tabu search. Journal of Heuristics. 2013, 19, 565–571. [CrossRef]
  15. Alam M, Ash-Saki A, Ghosh S, editors. Accelerating Quantum Approximate Optimization Algorithm using Machine Learning. 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE); 2020 9-13 March 2020.
  16. Basso J, Farhi E, Marwaha K, et al. The Quantum Approximate Optimization Algorithm at High Depth for MaxCut on Large-Girth Regular Graphs and the Sherrington-Kirkpatrick Model. 2022. p. 7:1-7:21. [CrossRef]
  17. Galda A, Liu X, Lykov D, et al., editors. Transferability of optimal QAOA parameters between random graphs. 2021 IEEE International Conference on Quantum Computing and Engineering (QCE); 2021 17-22 Oct. 2021.
  18. Bianchi FM, Grattarola D, Livi L, et al. Hierarchical Representation Learning in Graph Neural Networks With Node Decimation Pooling. IEEE Transactions on Neural Networks and Learning Systems 2022, 33, 2195–2207. [CrossRef] [PubMed]
  19. Shaydulin R, Safro I, Larson J, editors. Multistart Methods for Quantum Approximate optimization. 2019 IEEE High Performance Extreme Computing Conference (HPEC); 2019 24-26 Sept. 2019.
  20. Shaydulin R, Marwaha K, Wurtz J, et al., editors. QAOAKit: A Toolkit for Reproducible Study, Application, and Verification of the QAOA. 2021 IEEE/ACM Second International Workshop on Quantum Computing Software (QCS); 2021 15-15 Nov. 2021.
  21. Shaydulin, R.; Wild, S.M. Exploiting Symmetry Reduces the Cost of Training QAOA. IEEE Transactions on Quantum Engineering 2021, 2, 1–9. [Google Scholar] [CrossRef]
  22. Umasankar G, Shah PS, Chandrachoodan N, et al., editors. Benchmarking the Poor Man’s Ising Machine. 2021 IEEE Photonics Society Summer Topicals Meeting Series (SUM); 2021 19-21 July 2021.
  23. Wurtz, J.; Love, P.J. Classically Optimal Variational Quantum Algorithms. IEEE Trans. Quantum Engineering. 2021, 2, 1–7. [Google Scholar] [CrossRef]
  24. Alidaee, B.; Kochenberger, G.; Wang, H. Theorems Supporting r-flip Search for Pseudo-Boolean Optimization. Int. J. Appl. Metaheuristic Comput. 2010, 1, 93–109. [Google Scholar] [CrossRef]
  25. Alidaee, B.; Wang, H.; Sua, L.S. An Efficient Closed-Form Formula for Evaluating r-Flip Moves in Quadratic Unconstrained Binary Optimization. Algorithms 2023, 16, 557. [Google Scholar] [CrossRef]
  26. Palubeckis, G. Multistart Tabu Search Strategies for the Unconstrained Binary Quadratic Optimization Problem. Ann. Oper. Res. 2004, 131, 259–282. [Google Scholar] [CrossRef]
  27. Garey, M.R.; Johnson, D.S. Computers and Intractability; A Guide to the Theory of NP-Completeness’ (W. H. Freeman & Co., 1990. 1990).
  28. Gu, S.; Yang, Y. A Deep Learning Algorithm for the Max-Cut Problem Based on Pointer Network Structure with Supervised Learning and Reinforcement Learning Strategies. Mathematics 2020, 8, 298. [Google Scholar] [CrossRef]
  29. Rehfeldt, D.; Koch, T.; Shinano, Y. Faster exact solution of sparse MaxCut and QUBO problems. Math. Prog. Comp. 2023, 15, 445–470. [Google Scholar] [CrossRef]
  30. Glover, F.; Woolsey, E. Converting the 0-1 Polynomial Programming Problem to a 0-1 Linear Program. Oper. Res. 1974, 22, 180–182. [Google Scholar] [CrossRef]
  31. Alidaee, B.; Wang, H. A note on heuristic approach based on UBQP formulation of the maximum diversity problem. J. Oper. Res. Soc. 2017, 68, 102–110. [Google Scholar] [CrossRef]
Preprints 100051 g001
Figure 1. MCP with 10,000 variables.
Figure 1. MCP with 10,000 variables.
Preprints 100051 g001
Preprints 100051 g002
Figure 2. MCP with 20,000 variables.
Figure 2. MCP with 20,000 variables.
Preprints 100051 g002
Preprints 100051 g003
Figure 3. MCP with 40,000 variables.
Figure 3. MCP with 40,000 variables.
Preprints 100051 g003
Table 1. Computational Results of MCP with 10,000 variables.
Table 1. Computational Results of MCP with 10,000 variables.
Instance ID Type a Type b Type c
Algorithm2 QAS Algorithm2 QAS Algorithm2 QAS
BFS APD RPD BFS APD RPD BFS APD RPD
MC10000_1 8156 1.87 8.96 50228 1.94 1.35 4672506 2.03 1.79
MC10000_2 8067 2.00 2.45 50884 1.89 1.2 4572770 2.02 1.43
MC10000_3 8129 1.87 2.4 51390 1.87 7.62 4675380 1.96 1.33
MC10000_4 8253 1.93 2 51680 1.88 1.37 4574974 2.03 1.4
MC10000_5 8218 1.84 2.19 51078 1.9 3.5 4664286 1.98 1.32
MC10000_6 8369 1.75 2.17 50710 1.87 2.76 4622312 1.94 1.5
MC10000_7 8142 1.86 3.13 50322 1.87 5.76 4639744 1.99 1.02
MC10000_8 8218 1.81 2.29 50334 1.96 1.53 4728400 1.92 1
MC10000_9 8190 1.85 4.19 50588 1.98 1.74 4699270 2.02 1.27
MC10000_10 8074 1.84 2.29 50790 1.55 3.34 4749898 1.92 1.33
MC10000_11 8292 1.94 2.45 51800 1.61 3.32 4638566 1.99 1.25
MC10000_12 8011 1.93 4.12 50338 1.91 1.7 4698042 1.95 1.62
MC10000_13 8233 1.89 9.15 50718 1.87 1.64 4585190 1.97 1.25
MC10000_14 8276 1.91 15.08 51338 1.87 1.69 4681668 2.01 1.48
MC10000_15 8224 1.83 7.5 50604 1.94 2.06 4680394 1.93 1.43
Table 2. Computational Result of MCP with 20,000 variables.
Table 2. Computational Result of MCP with 20,000 variables.
Instance ID Type a Type b Type c
Algorithm2 QAS Algorithm2 QAS Algorithm2 QAS
BFS APD RPD BFS APD RPD BFS APD RPD
MC20000_1 16476 1.60 7.03 102580 2.46 3.4 9392660 0.40 2.21
MC20000_2 16368 2.12 6.77 100878 2.52 8.11 9407570 0.53 2.29
MC20000_3 16384 1.65 8.57 102006 2.55 4.99 9217500 2.45 6.18
MC20000_4 16547 2.07 8.22 101174 2.49 7.68 9359374 2.43 4.24
MC20000_5 16365 2.11 6.37 100236 2.59 9.84 9261876 2.45 4.43
MC20000_6 16253 1.69 10.66 101064 2.57 8.51 9268934 2.44 4.46
MC20000_7 16177 2.15 7.08 102820 2.55 8.95 9228882 2.45 4.43
MC20000_8 16492 2.14 7.43 101914 2.47 8.49 9236988 2.50 4.81
MC20000_9 16597 1.62 6.98 103390 2.51 14.7 9345570 2.42 5.02
MC20000_10 16586 1.38 7.65 102896 2.43 4.33 9126342 2.48 4.53
MC20000_11 16307 1.40 6.89 101566 2.49 3.93 9313278 2.48 5.33
MC20000_12 16433 2.10 6.66 102376 2.47 3.83 9439436 2.42 4.23
MC20000_13 16621 1.37 8.36 100238 2.50 4.11 9304690 2.50 4.76
MC20000_14 16407 2.10 8.26 100524 2.57 4.58 9390564 2.41 4.09
MC20000_15 16254 2.13 7.57 102768 2.52 4.03 9215550 2.47 6.36
Table 3. Computational Result of MCP with 40,000 variables.
Table 3. Computational Result of MCP with 40,000 variables.
Instance ID Type a Type b Type c
Algorithm2 QAS Algorithm2 QAS Algorithm2 QAS
BFS APD RPD BFS APD RPD BFS APD RPD
MC40000_1 33036 4.52 11.02 201520 3.46 8.13 18412388 3.23 9.29
MC40000_2 32780 4.60 11.14 202278 2.71 8.19 18533702 3.28 9.47
MC40000_3 32971 4.62 10.87 204676 2.70 8.16 18443578 3.33 9.43
MC40000_4 32797 4.63 10.52 203482 2.69 8.18 18478330 3.28 9.41
MC40000_5 32676 4.68 10.73 204004 2.69 8.27 18351592 3.25 9.59
MC40000_6 32770 4.67 10.94 204288 2.71 8.22 18645472 3.25 10.33
MC40000_7 32833 4.67 10.89 202726 2.74 8.79 18511826 3.29 8.98
MC40000_8 32805 4.62 10.67 201954 3.45 9.1 18520832 3.23 10.18
MC40000_9 32374 4.75 10.43 201384 2.73 8.67 18574756 3.29 9.72
MC40000_10 32922 4.64 10.55 203348 2.68 8.57 18478474 3.31 9.31
MC40000_11 32733 4.64 10.83 201328 2.73 8.25 18516990 3.24 8.94
MC40000_12 33111 4.58 10.34 202800 3.42 8.78 18557510 3.24 9.6
MC40000_13 32863 4.62 11.1 201674 2.71 8.66 18613850 3.21 10.18
MC40000_14 32917 4.63 9.91 204160 2.70 8.27 18448596 3.25 9.76
MC40000_15 33079 4.63 10.75 204466 2.70 7.82 18510938 3.26 9.17
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

282

Views

97

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated