Mathematics of Epidemics: On the General Solution of SIRVD, SIRV, SIRD and SIR Compartment Models

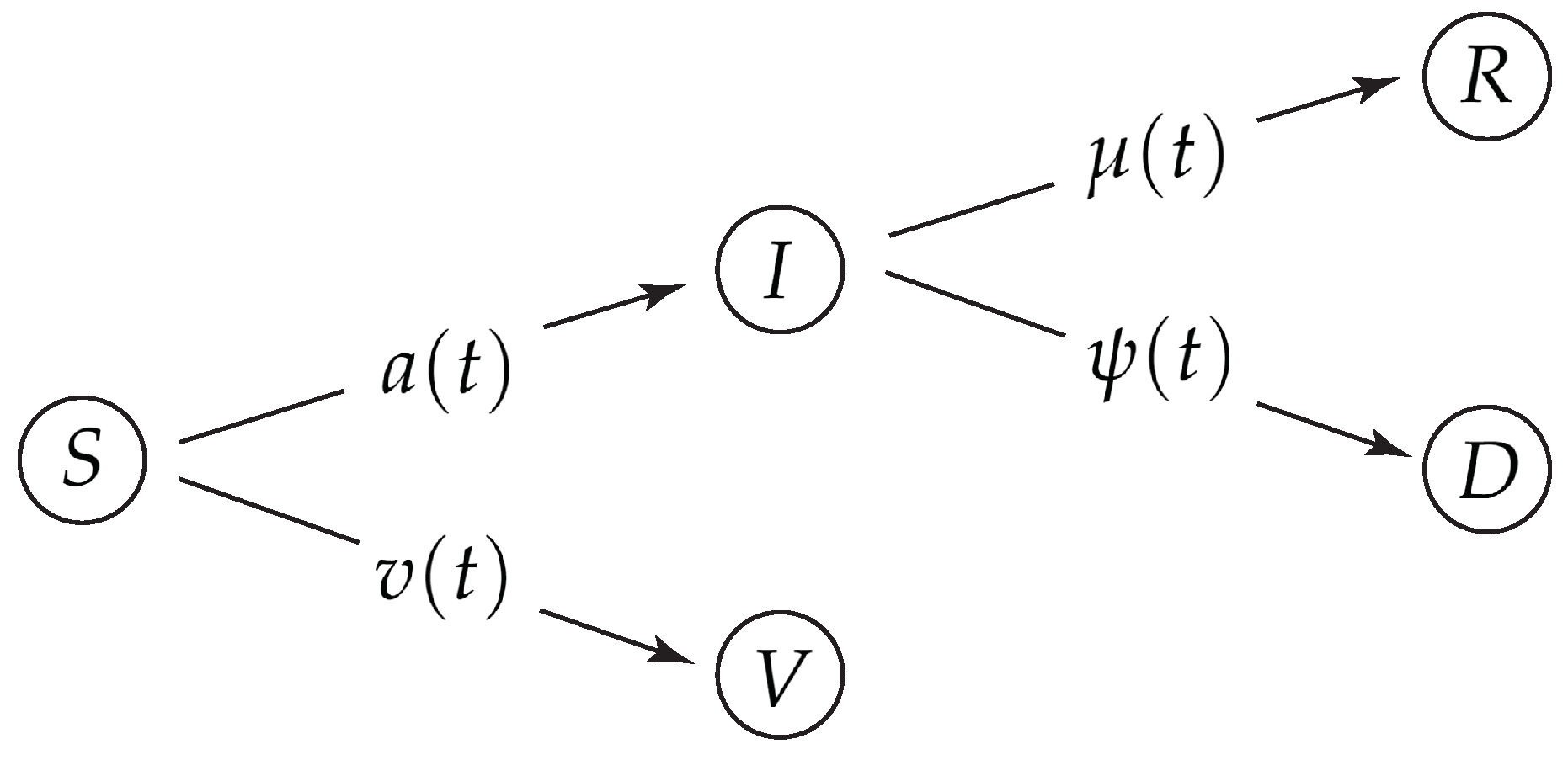
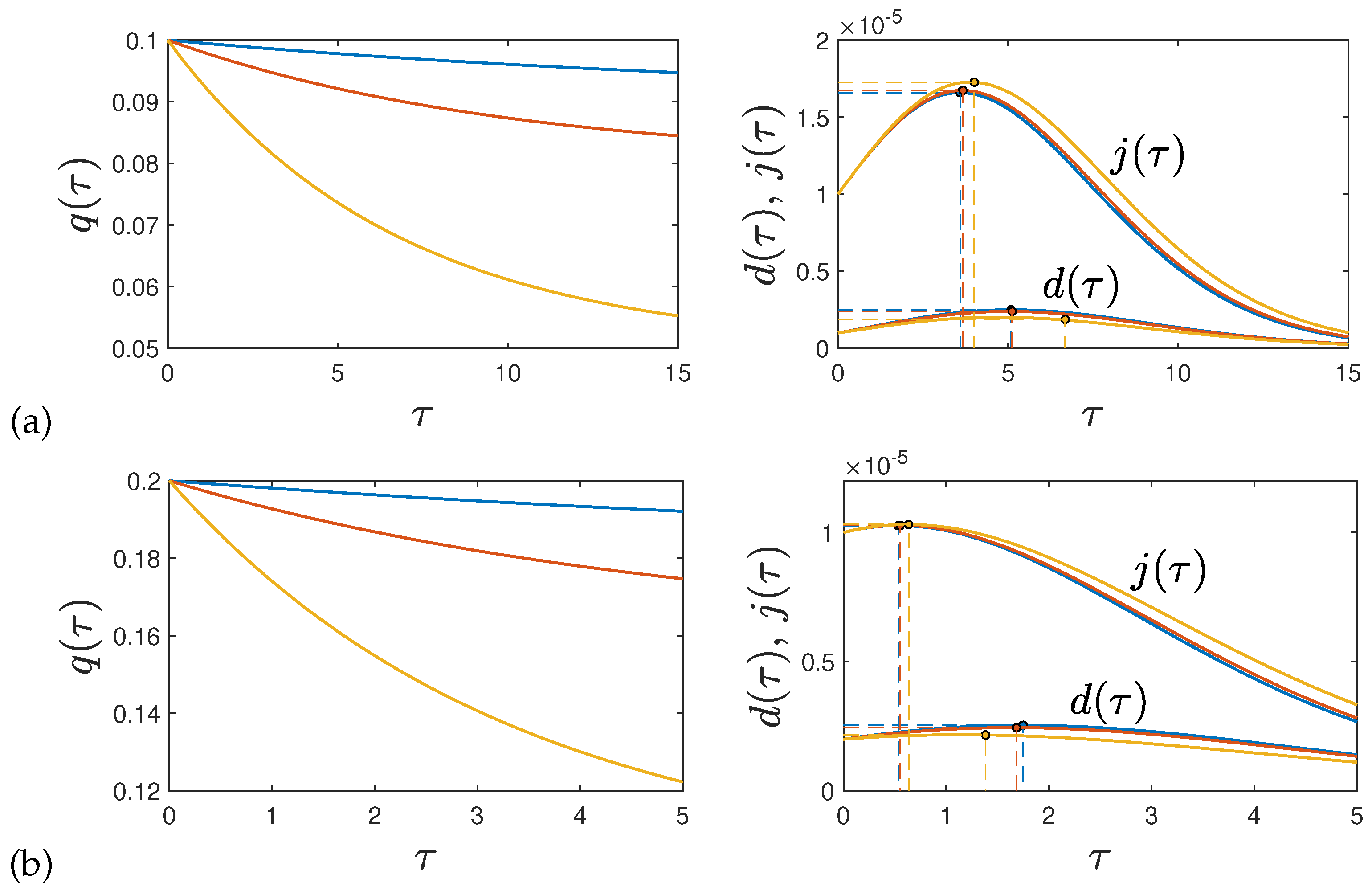1. Introduction

Compartmental mathematical models are very popular and successful to describe the temporal evolution of pandemic and epidemic outbursts in populations of large size (for reviews see ref. [1,2,3]). Their forecasts on hospitalization and death rates help policy makers to install non-pharmaceutical interventions and/or vaccination campaigns at optimized times. As suitable compartments one introduces the fractions of susceptible persons (S), infected persons (I), recovered persons (R), deceased persons (D), and vaccinated persons (V) that no longer can be infected. Individual time-dependent rates regulate the transition between the different compartments. The temporal evolution of the epidemic is then determined by the ratios $k\left(t\right)=\mu \left(t\right)/a\left(t\right)$, $b\left(t\right)=v\left(t\right)/a\left(t\right)$ and $q\left(t\right)=\psi \left(t\right)/a\left(t\right)$ between the recovery ($\mu \left(t\right)$), vaccination ($v\left(t\right)$) and fatality ($\psi \left(t\right)$) rates to the infection ($a\left(t\right)$) rate, respectively. By discriminating e.g. between different age classes in each compartment these models can be generalized to a much larger number of compartments in order to investigate the effects of pandemic and epidemic outbursts on persons of certain age groups. However, from the health care point of view to provide sufficiently enough intensive care beds and facilities is independent from the age of the infected persons.

Historically, the first reasonable compartment model was the susceptible–infected–recovered/removed (SIR) epidemic model [4,5,6,7]. This has been refined to include the effect of vaccination campaigns leading to the susceptible–infected–recovered/removed–vaccinated (SIRV) epidemic model [8,9,10,11,12,13,14,15,16,17,18,19]. The purpose of this manuscript is two-fold. First we will investigate new classes of exact solutions to the SIRVD and SIRD equations. Secondly we will apply the recently developed analytical approximation [20,21] for the SIR and SIRV models also to the more general SIRVD model. These accurate analytical approximations have been derived for all epidemic quantities of interest such as the rate of new infections $\mathring{J}\left(t\right)$ and the corresponding cumulative fraction of infections $J\left(t\right)$. The main difference between the SIRVD and the SIRV model is the discrimination between recovered and deceased persons by introducing two different compartments. This is necessary as the omicron mutant the COVID-19 has a much smaller (about an order of magnitude) fatality rate than earlier mutants [22]. This gradually changing fatality rate is not accompanied by a corresponding change in the time dependence of the recovery rate. Therefore a mathematical description with one combined recovery/removed compartment is not sufficiently accurate anymore.

The organization of the manuscript is as follows. In Section 2, we introduce the starting dynamical equations for all considered compartment models both in terms of the real time t and the reduced time $\tau ={\int }_{t_0}^{t}d\xi a\left(\xi \right)$. It is beneficial for the analysis to express the equations in a form directly involving the observable quantities, such as the cumulative fraction of new infections $J\left(\tau \right)$ and the cumulative fraction of vaccinated persons $V\left(\tau \right)$. It is shown that for given reduced time variations of the ratios $k\left(\tau \right)$, $q\left(\tau \right)$ and $b\left(\tau \right)$ the SIRVD and SIRD equations represent complicated integro-differential equations for the rate of new infections $j\left(\tau \right)$ as well as the cumulative fraction of infections $J\left(\tau \right)$, or $S\left(\tau \right)$ and $I\left(\tau \right)$. However, the integro-differential equations can also be regarded as simpler determining equations for the sum of ratios $k\left(\tau \right)+q\left(\tau \right)=\kappa \left(\tau \right)$ for given variations of the ratio $b\left(\tau \right)$ and the fraction $S\left(\tau \right)$. This new approach is used in Section 3 to derive fully exact analytical solutions for the SIRVD and SIRD models. Especially for the SIRD model it is an effective new method to construct a special class of exact solutions depending on two parameters which are chosen as the values of the ratio $\kappa \left(\tau \right)$ at the start ($\kappa (\tau =0)$) and the end ($\kappa (\tau =\infty$) of the epidemic outburst. The new method for the SIRD case is illustrated in Section 4 for three different choices of the two parameters including a detailed investigation of the properties of the constructed solutions.

Section 5 and Section 6 are concerned with the second main purpose of this manuscript, namely the application of the approximate analytical solution in the limit of small cumulative fractions $J\ll 1$ to the SIRVD model. For general reduced time dependencies of the ratios $k\left(\tau \right)$, $q\left(\tau \right)$ and $b\left(\tau \right)$ the time dependence of all quantities of interest is derived in Section 5, whereas in Section 6 two applications are investigated which were inaccessible to analytical treatment before. Of special interest is the calculation of the death rate $d\left(\tau \right)$ and the corresponding cumulative fraction of deceased persons $D\left(\tau \right)$. Main differences occur between the considered compartment models which reflect two alternative points of view.

In the SIRVD and SIRD case with a predescribed fatality rate $\psi \left(t\right)$, corresponding to the ratio $q\left(\tau \right)$, the death rate is proportional to the fraction $I\left(t\right)$. Moreover, any different reduced time dependencies of the ratios $k\left(\tau \right)$ and $q\left(\tau \right)$ correctly enter the dynamical equations. In contrast, in the SIR models no compartment of deceased persons has been considered. Instead the total fraction of recovered and removed (by death) populations $R_{\mathrm{tot}}\left(t\right)$ and the summed recovery/removed rate ${\mu }_{\mathrm{tot}}\left(t\right)$ are used. Then the solution for the rate of new infections ${\mathring{J}}_{\mathrm{SIR}}\left(t\right)$ is employed to calculate an a posteriori death rate as [6]$d_{\mathrm{a}-\mathrm{pos}}=\psi \left(t\right){\mathring{J}}_{\mathrm{SIR}}\left(t\right)$ from a specified fatality rate $\psi \left(t\right)$. Of course, this fatality rate can be regarded as part of the summed recovery/removed rate, so that it also enters the dynamical SIR model equations. However, the main difference remains for the calculation of the death rate: in the SIRVD/SIRD cases it is proportional to $I\left(t\right)$, whereas in many SIR models it is proportional to $\mathring{J}\left(t\right)$. And the temporal dependence of $I\left(t\right)$ and $\mathring{J}\left(t\right)$ can be different. As we will show the disparity is most pronounced when the effect of vaccinations is included and/or when the real time dependence of the fatality rate $\psi \left(t\right)$ and the recovery rate $\mu \left(t\right)$ are different from each other. The a-posteriori approach not necessarily is incorrect but has his own justification. It assumes that the probability to die from the virus infection is only determined by being or having been infected with it, and thus is proportional to the rate of new infections $\mathring{J}\left(t\right)$. In contrast in the SIRD and SIRVD models the probability to die is the same on every day being infected and thus depends on the duration of the infection. A summary and conclusion (Section 7) completes the manuscript.

2. Compartment Models

2.1. SIRVD Model

We start with the SIRVD epidemics model described by four transition rates regulating the transitions between the five compartments: the fractions of susceptible persons (S), infected persons (I), recovered persons (R), removed by death persons (D), and vaccinated persons (V) that no longer can be infected. The transition rates in general are time-dependent and different from each other. The infection rate $a\left(t\right)$ regulates the transition from $S\to I$, the vaccination rate $v\left(t\right)$ the transition $S\to V$, the fatality rate $\psi \left(t\right)$ the transition $I\to D$, and the recovery rate $\mu \left(t\right)$ the transition $I\to R$, respectively (Figure 1). The SIRVD equations read:

$$\begin{array}{ccc}\hfill \dot{S}& =& -a\left(t\right)SI-v\left(t\right)S,\hfill \end{array}$$

(1a)

$$\begin{array}{ccc}\hfill \dot{I}& =& a\left(t\right)SI-\mu \left(t\right)I-\psi \left(t\right)I,\hfill \end{array}$$

(1b)

$$\begin{array}{ccc}\hfill \dot{R}& =& \mu \left(t\right)I,\hfill \end{array}$$

(1c)

$$\begin{array}{ccc}\hfill \dot{D}& =& \psi \left(t\right)I,\hfill \end{array}$$

(1d)

$$\begin{array}{ccc}\hfill \dot{V}& =& v\left(t\right)S,\hfill \end{array}$$

(1e)

where the dot stands for a derivative with respect to time t. The five fractions obey the sum constraint

$$S\left(t\right)+I\left(t\right)+R\left(t\right)+D\left(t\right)+V\left(t\right)=1$$

(2)

at all times $t\ge t_0$ after the start of the wave at time $t_0$ with the initial conditions of the so-called semi-time case

$$I\left(t_0\right)=\eta ,S\left(t_0\right)=1-\eta ,R\left(t_0\right)=0,D\left(t_0\right)=0,V\left(t_0\right)=0,$$

(3)

where $\eta$ is positive and usually very small, $\eta \ll 1$.

2.2. SIRV, SIRD, SIR and SI Models

The SIRVD model includes as special cases the SIRV, SIRD and SIR epidemics models. For these three simpler models one introduces the total fraction of recovered and removed (by death) populations

$$R_{\mathrm{tot}}\left(t\right)=R\left(t\right)+D\left(t\right),$$

(4)

and the summed recovery/removed rate

$${\mu }_{\mathrm{tot}}\left(t\right)=\mu \left(t\right)+\psi \left(t\right).$$

(5)

By this modification the five individual compartments of the SIRVD models are reduced to four compartments in the SIRV-description and to three compartments in the SIR-description, respectively. Consequently, the SIRVD Equations (1a)–(2) become

$$\begin{array}{ccc}\hfill \dot{S}& =& -a\left(t\right)SI-v\left(t\right)S,\hfill \end{array}$$

(6a)

$$\begin{array}{ccc}\hfill \dot{I}& =& a\left(t\right)SI-{\mu }_{\mathrm{tot}}\left(t\right)I,\hfill \end{array}$$

(6b)

$$\begin{array}{ccc}\hfill {\dot{R}}_{\mathrm{tot}}& =& {\mu }_{\mathrm{tot}}\left(t\right)I,\hfill \end{array}$$

(6c)

$$\begin{array}{ccc}\hfill \dot{V}& =& v\left(t\right)S,\hfill \end{array}$$

(6d)

$$\begin{array}{ccc}\hfill S\left(t\right)+I\left(t\right)& +& R_{\mathrm{tot}}\left(t\right)+V\left(t\right)=1,\hfill \end{array}$$

(6e)

which apart from a slight change in notation ($R_{\mathrm{tot}}$ and ${\mu }_{\mathrm{tot}}$ instead of R and $\mu$ before) agree exactly with the earlier considered Equations (13) - (17) in [21].

The SIRD and SIR models ignore the effect of vaccinations so that $v\left(t\right)=V\left(t\right)=0$. The time evolution in the SIRD model is then given by taking the limit $v\left(t\right)=V\left(t\right)=0$ of the Equations (1)–(2) yielding

$$\begin{array}{ccc}\hfill \dot{S}& =& -a\left(t\right)SI,\hfill \end{array}$$

(7a)

$$\begin{array}{ccc}\hfill \dot{I}& =& a\left(t\right)SI-\mu \left(t\right)I-\psi \left(t\right)I,\hfill \end{array}$$

(7b)

$$\begin{array}{ccc}\hfill \dot{R}& =& \mu \left(t\right)I,\hfill \end{array}$$

(7c)

$$\begin{array}{ccc}\hfill \dot{D}& =& \psi \left(t\right)I,\hfill \end{array}$$

(7d)

$$\begin{array}{ccc}\hfill S\left(t\right)+I\left(t\right)& +& R\left(t\right)+D\left(t\right)+V\left(t\right)=1.\hfill \end{array}$$

(7e)

Likewise, the limit $v\left(t\right)=V\left(t\right)=0$ of the Equations (6) provide the SIR equations for the three remaining compartments:

$$\begin{array}{ccc}\hfill \dot{S}& =& -a\left(t\right)SI-v\left(t\right)S,\hfill \end{array}$$

(8a)

$$\begin{array}{ccc}\hfill \dot{I}& =& a\left(t\right)SI-{\mu }_{\mathrm{tot}}\left(t\right)I,\hfill \end{array}$$

(8b)

$$\begin{array}{ccc}\hfill {\dot{R}}_{\mathrm{tot}}& =& {\mu }_{\mathrm{tot}}\left(t\right)I,\hfill \end{array}$$

(8c)

$$\begin{array}{ccc}\hfill S\left(t\right)+I\left(t\right)& +& R_{\mathrm{tot}}\left(t\right)=1\hfill \end{array}$$

(8d)

For completeness we discuss the SI model where additionally $\mu \left(t\right)=0$ in Appendix A.

2.3. SIRVD Equations in Terms of the Reduced Time Variable

It is convenient to introduce the reduced time [6]

$$\tau ={\int }_{t_0}^{t}d\xi a\left(\xi \right),$$

(9)

and the dimensionless ratios

$$k\left(\tau \right)=\frac{\mu \left(\tau \right(t\left)\right)}{a\left(\tau \right(t\left)\right)},b\left(\tau \right)=\frac{v\left(\tau \right(t\left)\right)}{a\left(\tau \right(t\left)\right)},q\left(\tau \right)=\frac{\psi \left(\tau \right(t\left)\right)}{a\left(\tau \right(t\left)\right)}.$$

(10)

Then the SIRVD Equations (1a)–(2) can be written as

$$\begin{array}{ccc}\hfill \frac{dS}{d\tau }& =& -SI-b\left(\tau \right)S,\hfill \end{array}$$

(11a)

$$\begin{array}{ccc}\hfill \frac{dI}{d\tau }& =& SI-\left[k\right(\tau )+q(\tau \left)\right]I,\hfill \end{array}$$

(11b)

$$\begin{array}{ccc}\hfill \frac{dR}{d\tau }& =& k\left(\tau \right)I,\hfill \end{array}$$

(11c)

$$\begin{array}{ccc}\hfill \frac{dD}{d\tau }& =& q\left(\tau \right)I,\hfill \end{array}$$

(11d)

$$\begin{array}{ccc}\hfill \frac{dV}{d\tau }& =& b\left(\tau \right)S,\hfill \end{array}$$

(11e)

$$\begin{array}{ccc}\hfill S\left(\tau \right)+I\left(\tau \right)& +& R\left(\tau \right)+D\left(\tau \right)+V\left(\tau \right)=1.\hfill \end{array}$$

(11f)

subject to initial conditions $I\left(0\right)=\eta =1-S\left(0\right)$ and $R\left(0\right)=D\left(0\right)=V\left(0\right)=0$.

By solving Equations (11) numerically for the case of stationary ratios $k\left(\tau \right)=0.5$, $b\left(\tau \right)=0.01$, $q\left(\tau \right)=0.1$, one establishes quantitatively different temporal dependencies for the various fractions of the four different models SIR, SIRD, SIRV and SIRVD (see Figure 2). Numerical schemes have been developed especially for the SIR model, see the recent works [14,23,24]. We used a variable-step, variable-order (VSVO) Adams-Bashforth-Moulton PECE solver of orders 1 to 13 to produce Figure 2. The highest order used appears to be 12, however, a formula of order 13 is used to form the error estimate and the function does local extrapolation to advance the integration at order 13 [25]. This Figure is meant as a motivation for the following analysis which has the aim to understand the different behaviors of the four models on the basis of analytical calculations. Our analytical study also will be concerned with in general time dependent ratios $k\left(\tau \right)$, $q\left(\tau \right)$ and $b\left(\tau \right)$. Moreover, it will derive new methods to construct special classes of exact analytical solutions.

To this end it turns out important to introduce the rate of new infections, $\mathring{J}\left(t\right)=a\left(t\right)S\left(t\right)I\left(t\right)$, that determines in the absence of vaccination the reduction of the susceptible compartment according to Equation (1a). Its dimensionless counterpart, appearing in Equation (11a), is

$$j\left(\tau \right)=S\left(\tau \right)I\left(\tau \right)=\frac{dJ\left(\tau \right)}{d\tau },$$

(12)

so that $\mathring{J}\left(t\right)=a\left(t\right)j\left(\tau \right)$ and $j(\tau =0)=\eta (1-\eta )$. In terms of the rate of new infections $j\left(\tau \right)$, and the corresponding cumulative fraction of new infections

$$J\left(t\right)=J\left(\tau \right)=\eta +{\int }_0^{\tau }dxj\left(x\right),$$

(13)

Equations (11a) and (11e)–(11f) readily provide at all times

$$J\left(\tau \right)=1-S\left(\tau \right)-V\left(\tau \right)=R\left(\tau \right)+D\left(\tau \right)+I\left(\tau \right).$$

(14)

Moreover, Equation (11a) yields

$$\begin{array}{ccc}\hfill I\left(\tau \right)& =& -b\left(\tau \right)-\frac{dlnS\left(\tau \right)}{d\tau }=-\frac{dV\left(\tau \right)/d\tau }{1-J\left(\tau \right)-V\left(\tau \right)}\hfill \\ & & +\frac{d}{d\tau }ln(1-J\left(\tau \right)-V\left(\tau \right))=\frac{j\left(\tau \right)}{1-J\left(\tau \right)-V\left(\tau \right)},\hfill \end{array}$$

(15)

where we used Equations (11e), (14) and the first Equation (12). Equation (14) also provides

$$R\left(\tau \right)+D\left(\tau \right)=J\left(\tau \right)-I\left(\tau \right)=J\left(\tau \right)-\frac{j\left(\tau \right)}{1-J\left(\tau \right)-V\left(\tau \right)}.$$

(16)

With Equation (15) we obtain for Equations (11c)–(11d)

$$R\left(\tau \right)={\int }_0^{\tau }dxk\left(x\right)I\left(x\right)={\int }_0^{\tau }dx\frac{k\left(x\right)j\left(x\right)}{1-J\left(x\right)-V\left(x\right)},$$

(17)

and

$$D\left(\tau \right)={\int }_0^{\tau }dxq\left(x\right)I\left(x\right)={\int }_0^{\tau }dx\frac{q\left(x\right)j\left(x\right)}{1-J\left(x\right)-V\left(x\right)},$$

(18)

implying for the rate of new fatalities

$$d\left(\tau \right)=\frac{dD\left(\tau \right)}{d\tau }=q\left(\tau \right)I\left(\tau \right)=\frac{q\left(\tau \right)j\left(\tau \right)}{1-J\left(\tau \right)-V\left(\tau \right)}.$$

(19)

2.4. Solution of the SIRVD Equations

With the first Equation (14) one finds

$$S\left(\tau \right)=1-J\left(\tau \right)-V\left(\tau \right),$$

(20)

so that Equation (11e) can be written in the form

$$b\left(\tau \right)=\frac{dV/d\tau }{1-J\left(\tau \right)-V\left(\tau \right)},$$

(21)

yielding

$$b\left(\tau \right)[1-J\left(\tau \right)]=\frac{dV\left(\tau \right)}{d\tau }+b\left(\tau \right)V\left(\tau \right)=e^{-{\int }_0^{\tau }dxb\left(x\right)}\frac{d}{d\tau }\left[V\left(\tau \right)e^{{\int }_0^{\tau }dxb\left(x\right)}\right].$$

(22)

With the initial condition $V(\tau =0)=0$ Equation (22) integrates to

$$V\left(\tau \right)=1-J\left(\tau \right)+e^{-{\int }_0^{\tau }dxb\left(x\right)}[{\int }_0^{\tau }dxj\left(x\right)e^{{\int }_0^{x}dyb\left(y\right)}-(1-\eta )],$$

(23)

providing

$$S\left(\tau \right)=1-J\left(\tau \right)-V\left(\tau \right)=e^{-{\int }_0^{\tau }dxb\left(x\right)}[1-\eta -{\int }_0^{\tau }dxj\left(x\right)e^{{\int }_0^{x}dyb\left(y\right)}].$$

(24)

Likewise Equation (11b) can be written as

$$\begin{array}{ccc}\hfill k\left(\tau \right)+q\left(\tau \right)& =& S\left(\tau \right)-\frac{dlnI\left(\tau \right)}{d\tau }=1-V\left(\tau \right)-J\left(\tau \right)-\frac{d}{d\tau }ln\left[\frac{j\left(\tau \right)}{1-V\left(\tau \right)-J\left(\tau \right)}\right],\hfill \end{array}$$

(25)

where we used Equations (15) and (24). With the initial conditions Equation (25) integrates to

$$j\left(\tau \right)=\frac{dJ\left(\tau \right)}{d\tau }=\eta [1-V\left(\tau \right)-J\left(\tau \right)]exp{\int }_0^{\tau }dz\left(1-V\left(z\right)-J\left(z\right)-k\left(z\right)-q\left(z\right)\right).$$

(26)

A further integration with the initial condition $J(\tau =0)=\eta$ leads to

$$J\left(\tau \right)=\eta \left[1+{\int }_0^{\tau }dxS\left(x\right)e^{{\int }_0^{x}dz[S\left(z\right)-k\left(z\right)-q\left(z\right)]}\right]$$

(27)

in terms of $S\left(\tau \right)$. Furthermore, Equation (25) is equivalent to

$$\begin{array}{ccc}\hfill k\left(\tau \right)+q\left(\tau \right)& =& S\left(\tau \right)-\frac{d}{d\tau }[lnj\left(\tau \right)-lnS\left(\tau \right)],\hfill \end{array}$$

(28)

and also with Equation (11b) integrated to

$$\begin{array}{ccc}\hfill b\left(\tau \right)& =& -\frac{dlnS\left(\tau \right)}{d\tau }-\eta exp\left({\int }_0^{\tau }dz[S\left(z\right)-k\left(z\right)-q\left(z\right)]\right).\hfill \end{array}$$

(29)

With $S\left(\tau \right)=(1-\eta )exp(-{\int }_0^{\tau }dz[I\left(z\right)+b\left(z\right)])$ obtained from Equation (11a), the first Equation (25) is equivalent to

$$\frac{dlnI\left(\tau \right)}{d\tau }=(1-\eta )e^{-{\int }_0^{\tau }dz[I\left(z\right)+b\left(z\right)]}-k\left(\tau \right)-q\left(\tau \right).$$

(30)

The derived Equations (26)–(30) are nonlinear integro-differential equations for the cumulative fraction of new infections $J\left(\tau \right)$, and $S\left(\tau \right)$, respectively. The great advantage of the SIRVD equation written in the form (26) is the direct involvement of observable and monitored quantities, such the cumulative fractions of new infections $J\left(t\right)=J\left(\tau \right)$, and of vaccinated persons $V\left(t\right)=V\left(\tau \right)$. We emphasize that Equations (26)–(29) are exact, and hold for all, the SIR, SIRV, SIRD, and SIRVD models. The only difference is that in the SIRDcase $J_{\mathrm{SIRD}}\left(\tau \right)=1-S_{\mathrm{SIRD}}\left(\tau \right)$, because here $b\left(\tau \right)=V\left(\tau \right)=0$, whereas in the SIRVD case $J_{\mathrm{SIRVD}}\left(\tau \right)=1-S_{\mathrm{SIRVD}}\left(\tau \right)-V_{\mathrm{SIRVD}}\left(\tau \right)$. If we succeed in either solving the nonlinear integro-differential Equations (26)–(29), or deriving an accurate approximation for their solution, we arrive at a completely analytical solution of all dynamical variables of the SIRVD model and its special cases in dependence on the reduced time $\tau$.

For completeness we note that inserting the exact solution (23) for $V\left(\tau \right)$ in Equation (26) leads to the equivalent nonlinear integro-differential Equations for the rate of new infections

$$\begin{array}{ccc}\hfill j\left(\tau \right)& =& \eta \left[1-\eta -{\int }_0^{\tau }dxj\left(x\right)e^{{\int }_0^{x}dyb\left(y\right)}\right]\times \hfill \\ & & exp{\int }_0^{\tau }dz\left([1-\eta -{\int }_0^{z}dxj\left(x\right)e^{{\int }_0^{x}dyb\left(y\right)}]e^{-{\int }_0^{z}dyb\left(y\right)}-k\left(z\right)-q\left(z\right)-b\left(z\right)\right).\hfill \end{array}$$

(31)

Before proceeding to the approximation we note that in terms of the real time, the Eqs. (21)–(26) read, with the help of Equations (9), (10), (12), (14), (15), (17), (18), and (31),

$$\begin{array}{ccc}\hfill v\left(t\right)& =& \frac{dV/dt}{1-J\left(t\right)-V\left(t\right)},\hfill \end{array}$$

(32a)

$$\begin{array}{ccc}\hfill V\left(t\right)& =& 1-J\left(t\right)+e^{-{\int }_0^{t}dxv\left(x\right)}[{\int }_0^{t}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}-(1-\eta )],\hfill \end{array}$$

(32b)

$$\begin{array}{ccc}\hfill I\left(t\right)& =& \frac{\mathring{J}\left(t\right)}{a\left(t\right)[1-J(t)-V(t\left)\right]}=\frac{\mathring{J}\left(t\right)e^{{\int }_0^{t}dxv\left(x\right)}}{a\left(t\right)[1-\eta -{\int }_0^{t}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}]},\hfill \end{array}$$

(32c)

$$\begin{array}{ccc}\hfill R\left(t\right)& =& {\int }_0^{t}d{t}^{\prime }\frac{\mu \left(t^{\prime }\right)\mathring{J}\left(t^{\prime }\right)}{a\left(t^{\prime }\right)[1-J\left(t^{\prime }\right)-V\left(t^{\prime }\right)]}={\int }_0^{t}d{t}^{\prime }\frac{\mu \left(t^{\prime }\right)\mathring{J}\left(t^{\prime }\right)e^{{\int }_0^{t^{\prime }}dxv\left(x\right)}}{a\left(t^{\prime }\right)[1-\eta -{\int }_0^{t^{\prime }}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}]},\hfill \end{array}$$

(32d)

$$\begin{array}{ccc}\hfill D\left(t\right)& =& {\int }_0^{t}d{t}^{\prime }\frac{\psi \left(t^{\prime }\right)\mathring{J}\left(t^{\prime }\right)}{a\left(t^{\prime }\right)[1-J\left(t^{\prime }\right)-V\left(t^{\prime }\right)]}={\int }_0^{t}d{t}^{\prime }\frac{\psi \left(t^{\prime }\right)\mathring{J}\left(t^{\prime }\right)e^{{\int }_0^{t^{\prime }}dxv\left(x\right)}}{a\left(t^{\prime }\right)[1-\eta -{\int }_0^{t^{\prime }}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}]},\hfill \end{array}$$

(32e)

$$\begin{array}{ccc}\hfill d\left(t\right)& =& \frac{\psi \left(t\right)\mathring{J}\left(t\right)}{a\left(t\right)[1-J(t)-V(t\left)\right]}=\frac{\psi \left(t\right)\mathring{J}\left(t\right)e^{{\int }_0^{t}dxv\left(x\right)}}{a\left(t\right)[1-\eta -{\int }_0^{t}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}]},\hfill \end{array}$$

(32f)

$$\begin{array}{ccc}\hfill \mathring{J}\left(t\right)& =& a\left(t\right)[1-J\left(t\right)-V\left(t\right)]exp{\int }_0^{t}dx\left(a\left(x\right)[1-V(x)-J(x\left)\right]-\mu \left(x\right)-\psi \left(x\right)\right)\hfill \\ & =& a\left(t\right)[1-\eta -{\int }_0^{t}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}]exp{\int }_0^{t}d{t}^{\prime }(a\left(t^{\prime }\right)e^{-{\int }_0^{t^{\prime }}dyv\left(y\right)}[1-\eta \hfill \\ & & -{\int }_0^{t^{\prime }}dx\mathring{J}\left(x\right)e^{{\int }_0^{x}dyv\left(y\right)}]-\mu \left(t^{\prime }\right)-\psi \left(t^{\prime }\right)-v\left(t^{\prime }\right)).\hfill \end{array}$$

(32g)

In some aspects for negligible vaccinations the resulting SIRD-model is simpler than the SIRVD-model, e.g. here the simpler relation $J\left(\tau \right)=1-S\left(\tau \right)$ holds. As a consequence the general integro-differential equations (26)–(30) derived before are eased. In Appendix B we explicitly list the corresponding equations for the SIRD model.

In the following sections we will derive a class of special exact solutions (Section 3 and Section 4) and derive approximate analytical solutions of Equations (21) and (25) in the limit of small $J\left(\tau \right)\ll 1$ (Sect. 5) following our earlier approach [21]. This approximation then leads to analytical approximations of all fractions of the SIRVD epidemics model as a function of time for given time dependencies of the three ratios (10). We will prove its accuracy of this approach by comparing with the exact numerical solutions of these equations for two illustrative examples (Sect. 6.1–6.2) of the reduced time dependence of these ratios. The proposed analytical approximation is self-regulating as the final analytical expression for the cumulative fraction $J_{\infty }={lim}_{t\to \infty }J\left(t\right)$ after infinite time allows us to check the validity of the original assumption $J\left(t\right)=J\left(\tau \right)\le J_{\infty }\ll 1$.

Before proceeding we discuss the differences in calculating the fractions of recovered and deceased persons in the different models.

2.5. Fraction of Deceased Persons

The main difference between the considered compartment models occurs for the determination of the fraction of deceased persons $D\left(\tau \right)=D\left(t\right)$ and the corresponding death rate $d\left(\tau \right)=dD\left(\tau \right)/d\tau$ and $d\left(t\right)=\left(dD\right(t)/dt)/a\left(t\right)$ as a function of the reduced and real time. The disparity is most pronounced if the real time dependence of the fatality rate $\psi \left(t\right)$ and the recovery rate $\mu \left(t\right)$ are different from each other. In the SIRVD and SIRD cases with a predescribed fatality rate $\psi \left(t\right)$, corresponding to the ratio $q\left(\tau \right)$, the death rate is proportional to $I\left(t\right)$ as given correctly by Equations (18)–(19) and Equations (32e)–(32f). Moreover, the different reduced time dependences of the ratios $k\left(\tau \right)$ and $q\left(\tau \right)$ correctly enter the dynamical Equations (26)–(29).

However, in the SIR models no compartment of deceased persons is considered. As mentioned before, see Equations (4)–(5), here the total fraction of recovered and removed (by death) populations $R_{\mathrm{tot}}\left(t\right)$ and the summed recovery/removed rate ${\mu }_{\mathrm{tot}}\left(t\right)$ are introduced. With the solution for ${\mathring{J}}_{\mathrm{SIR}}\left(t\right)$ and $J_{\mathrm{SIR}}\left(t\right)$ the rate of new fatalities and the fraction of deceased persons are then calculated a posteriori as [6]

$$d_{\mathrm{SIR}}\left(t\right)=\alpha {\mathring{J}}_{\mathrm{SIR}}\left(t\right),D_{\mathrm{SIR}}\left(t\right)=\alpha J_{\mathrm{SIR}}\left(t\right),$$

(33)

with $\alpha =D_{\infty }/J_{\infty }$. The difference to Equations (32e)–(32f), which involve $I\left(t\right)=\mathring{J}\left(t\right)/[1-J\left(t\right)]$ and not directly $\mathring{J}\left(t\right)$, is obvious. Only if the temporal dependence of $I\left(t\right)$ is not drastically different from the temporal dependence of $\mathring{J}\left(t\right)$, the a-posteriori approach is justified. As has been emphasized before [21], for COVID-19 outbursts in many countries the monitored cumulative fraction of infected persons $J\left(t\right)\ll 1$ has been much smaller than unity at all times, so that then in the SIR model indeed $I\left(t\right)\simeq j\left(t\right)$.

While Equation (33) refers to past work, we will in the following allow for time-dependent fatality rates $\psi \left(t\right)$ so that the a-posteriori death rate is given by $d_{\mathrm{a}-\mathrm{pos}}\left(t\right)=\psi \left(t\right)\mathring{J}\left(t\right)$ corresponding to

$$d_{\mathrm{a}-\mathrm{pos}}\left(\tau \right)=q\left(\tau \right)j\left(\tau \right)$$

(34)

as a function of reduced time. This way, as opposed to the setting (33), the cumulative $D_{\mathrm{a}-\mathrm{pos}}$ at infinite time must not coincide with $D_{\infty }$. Moreover, in the a-posteriori approach the influence of the later introduced fatality rate $\psi \left(t\right)$ on the dynamical SIR equations is ignored. This is particularly pronounced if the real time dependence of $\psi \left(t\right)$ differs from the real time dependence of the recovery rate $\mu \left(t\right)$. We will elaborate on this below with an illustrative example in Section 6.2.

3. Special Exact Solutions

Equations (28)–(31) are complicated integro-differential equations in the SIRVD and SIRD case, respectively, for given reduced time variations of the ratios $k\left(\tau \right)$, $q\left(\tau \right)$ and $b\left(\tau \right)$. Hovever, they can also be regarded as simpler determining Equations for the ratios $k\left(\tau \right)+q\left(\tau \right)=\kappa \left(\tau \right)$ for given variations of the ratio $b\left(\tau \right)$ and the fraction $S\left(\tau \right)$. This can be used to derive fully exact analytical solutions for the SIRVD and SIRD models.

We know that $S\left(\tau \right)$ starts from the initial values $S(\tau =0)=1-\eta$ and monotonically decreases to its final nonnegative value $S(\tau =\infty )\ge 0$ after finite or infinite time. We also require, in accord with Equation (12) and the initial conditions specified in Section 2.3, that

$$j(\tau =0)=\eta (1-\eta ).$$

(35)

Therefore we adopt the reduced time variation

$$S\left(\tau \right)=\frac{1-\eta +S_{\infty }tanh\frac{{\tau }_{\max }}{{\tau }_0}-(1-\eta -S_{\infty })tanh\frac{\tau -{\tau }_{\max }}{{\tau }_0}}{1+tanh\frac{{\tau }_{\max }}{{\tau }_0}}.$$

(36)

parameterized by $S_{\infty }$, ${\tau }_{\max }$, and ${\tau }_0$. While ${lim}_{\tau \to \infty }S\left(\tau \right)=S_{\infty }$ is formally correct, $S\left(\tau \right)$ may reach zero after finite time ${\tau }_{\mathrm{fin}}$. In that case ${lim}_{\tau \to \infty }S\left(\tau \right)=S\left({\tau }_{\mathrm{fin}}\right)=0$, irrespective of the value of the parameter $S_{\infty }$, that may therefore take positive or negative values in the expression (36). One has1

$${\tau }_{\mathrm{fin}}={\tau }_{\max }+{\tau }_0{tanh}^{-1}\left[\frac{1-\eta +S_{\infty }tanh({\tau }_{\max }/{\tau }_0)}{1-\eta -S_{\infty }}\right]$$

(37)

from Equation (36). Only if the argument of the ${tanh}^{-1}$ resides in the interval $[-1,1]$, a finite ${\tau }_{\mathrm{fin}}$ exists. We are going to see that the special choice of $S_{\infty }=0$ has to be treated with care; it will allow us to absorb with Equation (36), along with a particular choice for ${\tau }_0$, the analytic solution of the SI model, for which $S\left(\tau \right)$ reaches $S_{\infty }$ at ${\tau }_{\mathrm{fin}}=\infty$. Moreover, the initial condition $j\left(0\right)=\eta (1-\eta )$ will be used to establish a relationship between $S_{\infty }$, ${\tau }_{\max }$, and ${\tau }_0$.

We adopt without loss of generality positive values of ${\tau }_0>0$. The choice (36) implies

$$\begin{array}{ccc}\hfill \frac{dS\left(\tau \right)}{d\tau }& =& -\frac{1-\eta -S_{\infty }}{{\tau }_0[1+tanh\frac{{\tau }_{\max }}{{\tau }_0}]{cosh}^2\frac{\tau -{\tau }_{\max }}{{\tau }_0}},\hfill \end{array}$$

(38a)

$$\begin{array}{ccc}\hfill \frac{dlnS\left(\tau \right)}{d\tau }& =& -\frac{1-\eta -S_{\infty }}{{\tau }_0{cosh}^2\frac{\tau -{\tau }_{\max }}{{\tau }_0}(1-\eta +S_{\infty }tanh\frac{{\tau }_{\max }}{{\tau }_0}-[1-\eta -S_{\infty }]tanh\frac{\tau -{\tau }_{\max }}{{\tau }_0})},\hfill \end{array}$$

(38b)

$$\begin{array}{ccc}\hfill \frac{dln\frac{dS\left(\tau \right)}{d\tau }}{d\tau }& =& -\frac{2tanh\left(\frac{\tau -{\tau }_{\max }}{{\tau }_0}\right)}{{\tau }_0}.\hfill \end{array}$$

(38c)

With the first Equation (15) we obtain for the dynamical SIRVD equation (28)

$$\begin{array}{ccc}\hfill k\left(\tau \right)+q\left(\tau \right)& =& \kappa \left(\tau \right)=S\left(\tau \right)-\frac{d}{d\tau }ln\left(-[b\left(\tau \right)+\frac{dlnS\left(\tau \right)}{d\tau }]\right).\hfill \end{array}$$

(39)

After inserting Equations (36) and (38b) this Equation becomes

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& =& \frac{1-\eta +S_{\infty }tanh\frac{{\tau }_{\max }}{{\tau }_0}-(1-\eta -S_{\infty })tanh\frac{\tau -{\tau }_{\max }}{{\tau }_0}}{1+tanh\frac{{\tau }_{\max }}{{\tau }_0}}-\frac{d}{d\tau }ln(-b\left(\tau \right)\hfill \\ & & +\frac{1-\eta -S_{\infty }}{{\tau }_0{cosh}^2\frac{\tau -{\tau }_{\max }}{{\tau }_0}(1-\eta +S_{\infty }tanh\frac{{\tau }_{\max }}{{\tau }_0}-[1-\eta -S_{\infty }]tanh\frac{\tau -{\tau }_{\max }}{{\tau }_0})}).\hfill \end{array}$$

(40)

For given reduced time variations $b\left(\tau \right)$ the combined rate (40) corresponding to the fraction $S\left(\tau \right)$ in Equation (36) can be inferred. In the following we simplify our analysis to the SIRD model.

3.1. SIRD Model

The choice (36) implies for the SIRD model $J\left(\tau \right)=1-S\left(\tau \right)$, $J_{\infty }=1-S_{\infty }$ and

$$\begin{array}{ccc}\hfill j\left(\tau \right)& =& -\frac{dS\left(\tau \right)}{d\tau }=\frac{1-\eta -S_{\infty }}{{\tau }_0[1+tanh\frac{{\tau }_{\max }}{{\tau }_0}]{cosh}^2\frac{\tau -{\tau }_{\max }}{{\tau }_0}},\hfill \end{array}$$

(41a)

$$\begin{array}{ccc}\hfill j(\tau =0)& =& \frac{(1-\eta -S_{\infty })(1-tanh\frac{{\tau }_{\max }}{{\tau }_0})}{{\tau }_0}.\hfill \end{array}$$

(41b)

The rate (41a) is of generalized SI-type (see Equation (A5)) with a width ${\tau }_0$ different from 2 and a general ${\tau }_{\max }$ different from $ln(1-\eta )/\eta$. We thus investigate for which conditions generalized SI-type rates exactly solve the SIRDequations.

The requirement (35) demands

$$\begin{array}{ccc}\hfill S_{\infty }& =& (1-\eta )[1-\frac{\eta {\tau }_0}{1-tanh\frac{{\tau }_{\max }}{{\tau }_0}}],\hfill \end{array}$$

(42)

$$\begin{array}{ccc}\hfill J_{\infty }& =& \eta +\frac{\eta (1-\eta ){\tau }_0}{1-tanh\frac{{\tau }_{\max }}{{\tau }_0}}=\eta +\frac{j(\tau =0){\tau }_0}{1-tanh\frac{{\tau }_{\max }}{{\tau }_0}}.\hfill \end{array}$$

(43)

We emphasize that the ansatz (41a) includes the SI model as special case. Inserting the SI-values $S_{\infty }=0$, $\kappa \left(0\right)=0$, ${\tau }_0=2$ and ${\tau }_{\max }=2{tanh}^{-1}(1-2\eta )$, which follows from Equation (42) for $S_{\infty }=0$, it is straightforward to show that Equation (41a) correctly reproduces the SI-distribution (A5).

The first Equation (41a) then can be written as

$$j\left(\tau \right)=\frac{\eta (1-\eta ){cosh}^2\frac{{\tau }_{\max }}{{\tau }_0}}{{cosh}^2\frac{\tau -{\tau }_{\max }}{{\tau }_0}}=j(\tau =0)\frac{{cosh}^2\frac{{\tau }_{\max }}{{\tau }_0}}{{cosh}^2\frac{\tau -{\tau }_{\max }}{{\tau }_0}}.$$

(44)

Only for ${\tau }_{\max }\gg {\tau }_0$ the maximum rate of new infections at $\tau ={\tau }_{\max }$ is much larger than the initial value $j(\tau =0)$. In this limit

$$J_{\infty }\simeq \frac{\eta (1-\eta ){\tau }_0{e}^{\frac{2{\tau }_{\max }}{{\tau }_0}}}{2},$$

(45)

while Equation (39) for $b\left(\tau \right)=0$ simplifies to

$$\kappa \left(\tau \right)=S\left(\tau \right)-\frac{d}{d\tau }ln\left(-\frac{dlnS\left(\tau \right)}{d\tau }\right).$$

(46)

Within the remainder of this subsection, we use the simplifying abbreviations

$$T=\frac{\tau }{{\tau }_0},\rho =\frac{{\tau }_{\max }}{{\tau }_0},Y\left(\tau \right)=T-\rho$$

(47)

to derive expressions for $\kappa \left(0\right)$ and $\kappa (\infty )$ for the two qualitatively different cases of $S_{\infty }=0$ and $S_{\infty }\ne 0$. With the help of Equation (47) the SIRDequation (36) receives the form

$$S\left(\tau \right)=\frac{1-\eta +S_{\infty }tanh\rho -(1-\eta -S_{\infty })tanhY}{1+tanh\rho },$$

(48)

or equivalently, upon replacing $S_{\infty }$ using Equation (42),

$$\begin{array}{ccc}\hfill S\left(\tau \right)& =& (1-\eta )\left[1-\eta {\tau }_0{cosh}^2\rho \left(tanh(T-\rho )+tanh\rho \right)\right]\hfill \\ & =& (1-\eta )[1-\frac{\eta {\tau }_0}{cothT-tanh\rho }].\hfill \end{array}$$

(49)

Similarly, using Equation (38c) in Equation (46), $\kappa \left(\tau \right)$ becomes

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& =& \frac{2tanh\left(Y\right)}{{\tau }_0}+\frac{1-\eta +S_{\infty }tanh\rho -(1-\eta -S_{\infty })tanh\left(Y\right)}{1+tanh\rho }\hfill \\ & & -\frac{1-\eta -S_{\infty }}{{\tau }_0{cosh}^2\left(Y\right)(1-\eta +S_{\infty }tanh\rho -[1-\eta -S_{\infty }]tanh\left(Y\right))}.\hfill \end{array}$$

(50)

Using $Y\left(0\right)=-\rho$, the initial value $\kappa \left(0\right)$ can be read off from Equation (50). This yields

$$\begin{array}{ccc}\hfill \kappa \left(0\right)& =& 1-\eta +\frac{S_{\infty }(1-tanh\rho )-(1-\eta )(1+tanh\rho )}{(1-\eta ){\tau }_0},\hfill \\ & =& 1-2\eta -\frac{2tanh\rho }{{\tau }_0}=1-2\eta -\frac{2tanh\left(\frac{{\tau }_{\max }}{{\tau }_0}\right)}{{\tau }_0},\hfill \end{array}$$

(51)

where we inserted $S_{\infty }$ from (42) to arrive at the 2nd line in Equation (51). Expression (51) is valid for any $S_{\infty }$.

As long as $S_{\infty }\ne 0$, the final value ${\kappa }_{\infty }={lim}_{Y\to \infty }\kappa \left(\tau \right)$ can be also read off immediately from Equation (50). While the last term in Equation (50) diminishes with increasing Y due to the leading ${cosh}^2\left(Y\right)$, the first terms readily evaluate upon replacing $tanh\left(Y\right)$ by unity, so that

$$\begin{array}{ccc}\hfill {\kappa }_{\infty }& =& \frac{2}{{\tau }_0}+S_{\infty }(S_{\infty }\ne 0)\hfill \\ & =& \frac{2}{{\tau }_0}+(1-\eta )\left[1-\frac{\eta {\tau }_0}{1-tanh\frac{{\tau }_{\max }}{{\tau }_0}}\right],\hfill \end{array}$$

(52)

where we made use again of $S_{\infty }$ from (42). Calculating ${\kappa }_{\infty }$ for the remaining case of $S_{\infty }=0$ requires more care, as the denominator in the last line of Equation (50) does not anymore increase with increasing Y. For $S_{\infty }=0$, one instead finds

$$\begin{array}{ccc}\hfill {\kappa }_{\infty }& =& \frac{2}{{\tau }_0}-\frac{1}{{\tau }_0}\underset{Y\to \infty }{lim}\frac{1}{{cosh}^2\left(Y\right)(1-tanh\left(Y\right))}\hfill \\ & =& \frac{2}{{\tau }_0}-\frac{1}{{\tau }_0}\underset{Y\to \infty }{lim}(1+tanhY)=\frac{2}{{\tau }_0}-\frac{2}{{\tau }_0}=0\hfill \end{array}$$

(53)

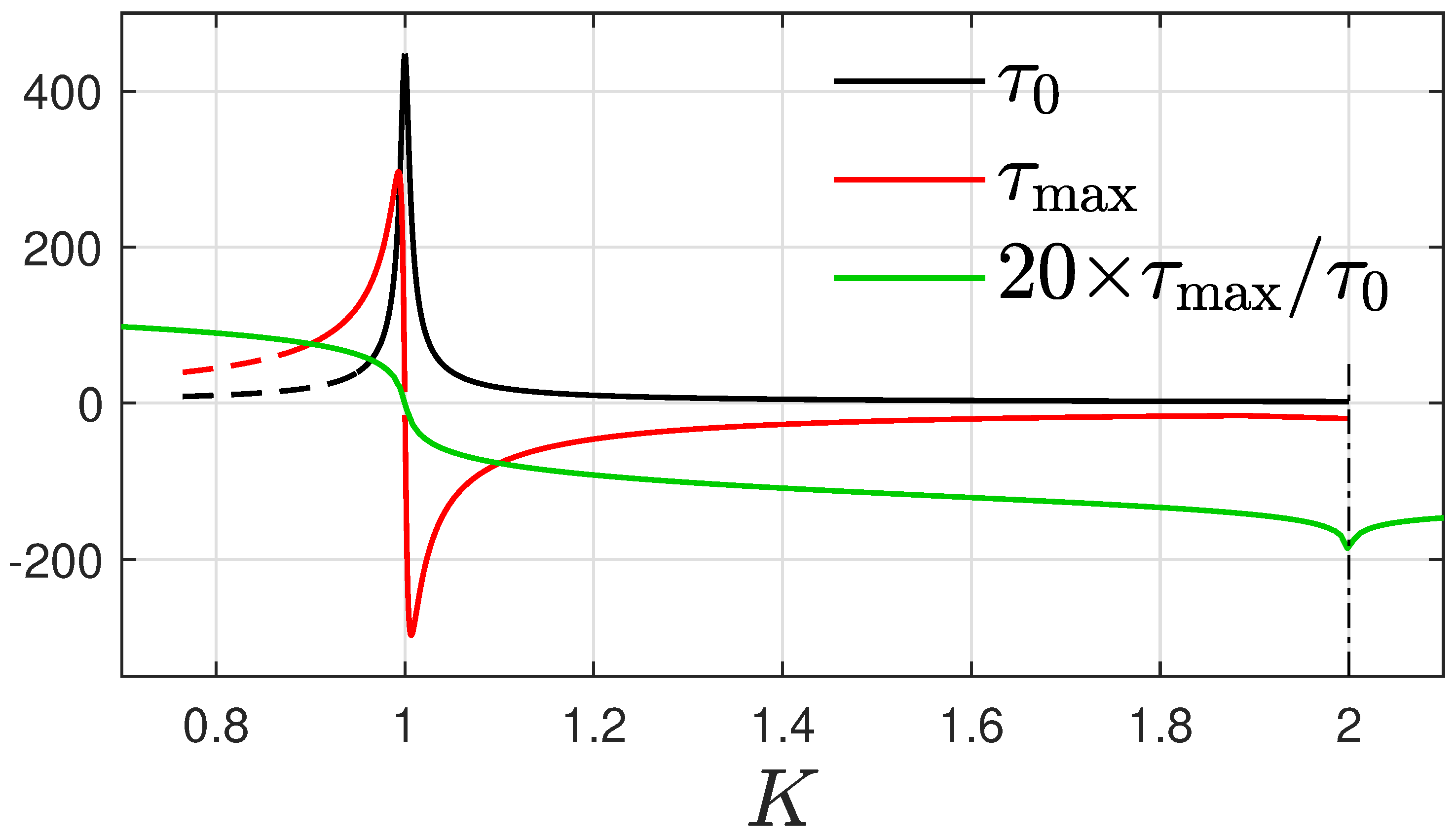
Note the apparent qualitative difference between the two cases. While ${\kappa }_{\infty }=S_{\infty }$ for $S_{\infty }=0$, one has ${\kappa }_{\infty }=S_{\infty }+2/{\tau }_0$ for $S_{\infty }\ne 0$.

3.2. Constraints on the Function $\kappa \left(\tau \right)$

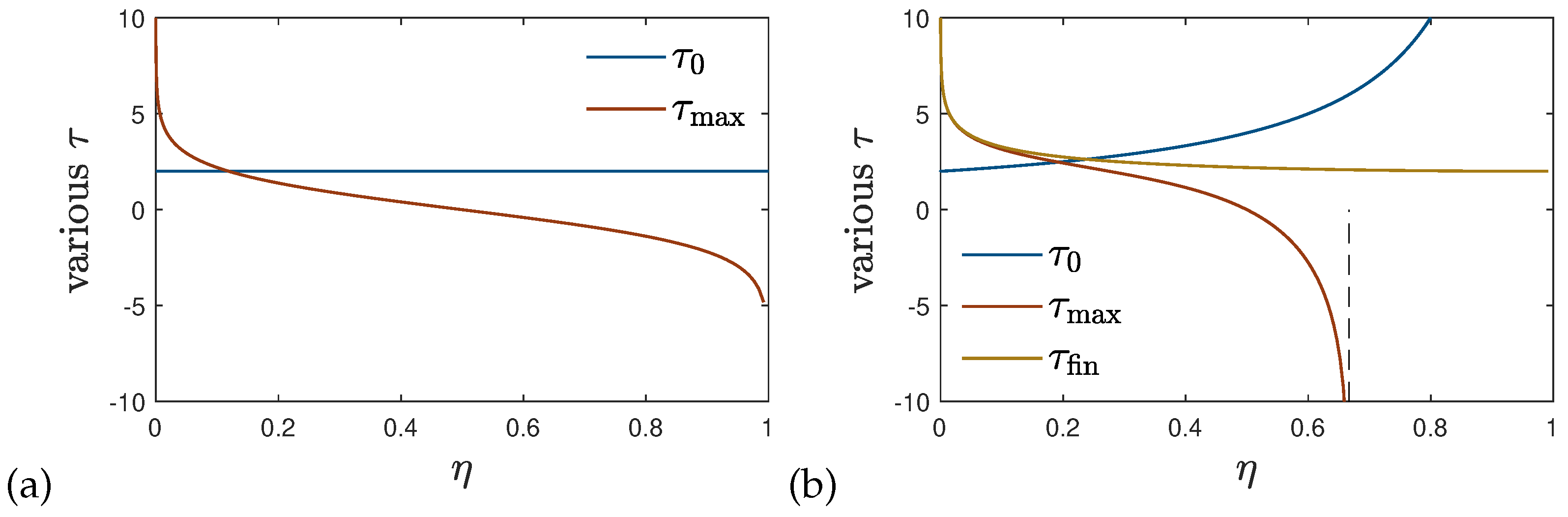
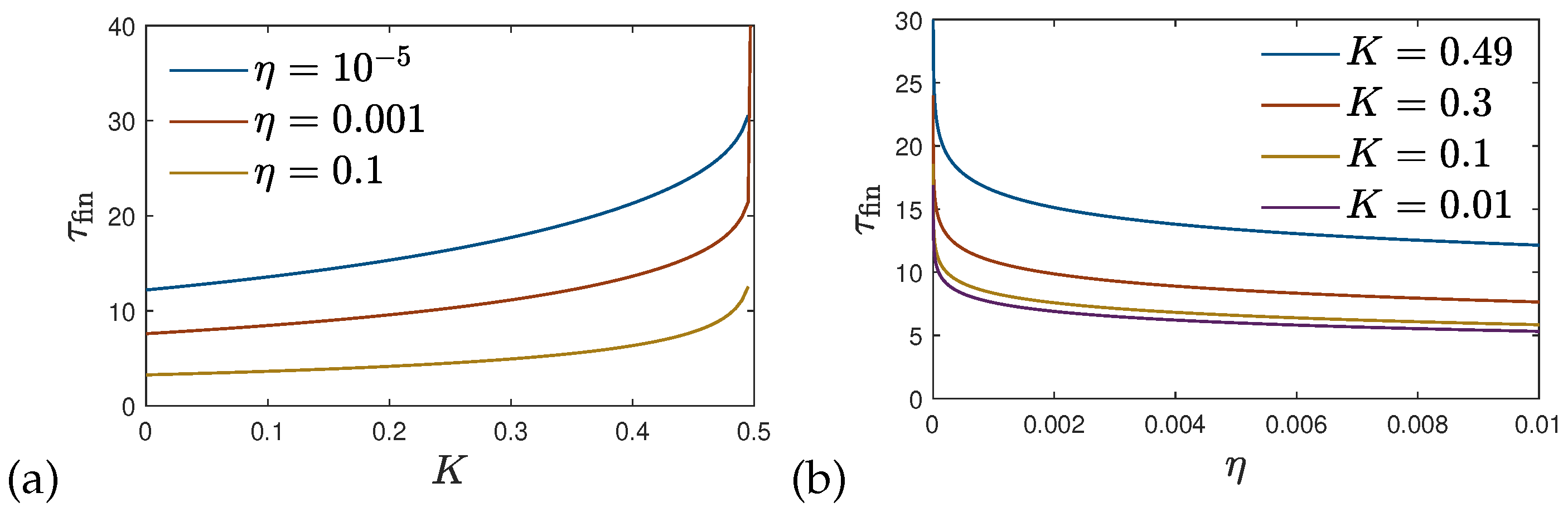
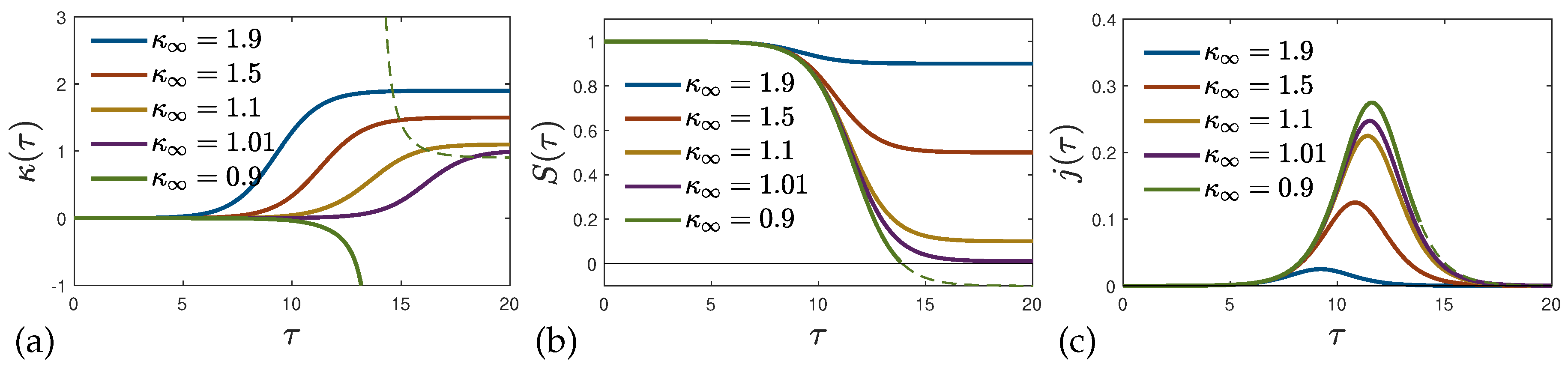
We recall that values of the function $\kappa \left(\tau \right)$ smaller than unity describe the epidemic phase where the infection rate $a\left(t\right)$ is larger than the sum of the recovery and death rate. Hence if still enough susceptible persons are available one expects a rising rate of new infections $\mathring{J}\left(t\right)$. In the opposite case of values of the function $\kappa \left(\tau \right)$ greater than unity the sum of recovery and death rates outnumbers the infection rate so that the rate of new infections will decrease in such a phase. Therefore it is appropriate to start with values of the function $\kappa \left(\tau \right)$ smaller than unity at small reduced times. Subsequently, the function $\kappa \left(\tau \right)$ approaches the value ${\kappa }_{\infty }$ at infinitely large reduced times which can be either smaller or greater than unity depending on the chosen values of ${\tau }_{\max }$ and ${\tau }_0$. However, not all values for ${\tau }_0$ and ${\tau }_{\max }$ are allowed.

The requirement of having a positive $\kappa \left(0\right)\ge 0$ leads to

$$\frac{1-2\eta }{2}{\tau }_0\ge tanh\frac{{\tau }_{\max }}{{\tau }_0}$$

(54)

This is automatically fulfilled for values of

$${\tau }_0>\frac{2}{1-2\eta },$$

(55)

as the right-hand-side of Equation (55) is always smaller or equal than unity. For values of ${\tau }_0\le 2/(1-2\eta )$ it is required that

$${\tau }_{\max }<{\tau }_0{tanh}^{-1}\left[\frac{1-2\eta }{2}{\tau }_0\right].$$

(56)

The inequality $S_{\infty }\ge 0$, corresponding to $J_{\infty }\le 1$, is met as long as the following inequalities hold,

$$\begin{array}{ccc}\hfill tanh\frac{{\tau }_{\max }}{{\tau }_0}& \le & 1-\eta {\tau }_0,\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill {\tau }_{\max }& \le & {\tau }_0{tanh}^{-1}(1-\eta {\tau }_0)\simeq \frac{{\tau }_0}{2}ln\frac{2}{\eta {\tau }_0}=\sqrt{ln\frac{2}{\eta {\tau }_0}}{\tau }_0,\hfill \end{array}$$

(58)

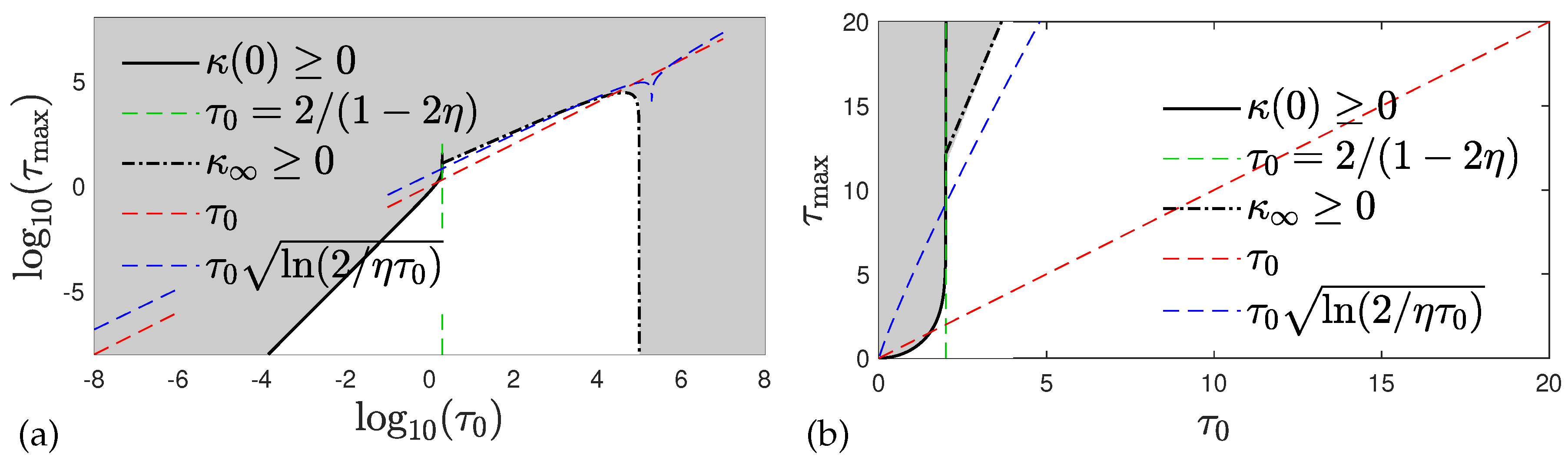
that follow from Equation (42). This condition (58), the regime between red and blue dashed lines in Figure 3, is not compatible with condition (56) but holds for certain values of ${\tau }_0>2/(1-2\eta )$. The condition (57) further guarantees that also $S\left(\tau \right)$, and not only $S_{\infty }$, is non-negative at all times because $S\ge 0$ requires, according to Equation (49),

$$tanh\rho +tanh(T-\rho )\le \frac{1}{\eta {\tau }_0{cosh}^2\rho }=\frac{1-{tanh}^2\rho }{\eta {\tau }_0},$$

(59)

or

$$\frac{tanh\rho +tanh(T-\rho )}{1+tanh\rho }\le \frac{1-tanh\rho }{\eta {\tau }_0},$$

(60)

which is fulfilled for all times $\tau$ because the left-hand side is always smaller than unity while the right-hand side is larger than unity due to condition (57). In cases $S_{\infty }<0$, where the condition (57) is not fulfilled, $S\left({\tau }_{\mathrm{fin}}\right)=0$ vanishes at the finite time ${\tau }_{\mathrm{fin}}$ already stated in Equation (37). In this case the chosen solution (36) or (49) can only be used in the finite time interval $0\le \tau \le {\tau }_{\mathrm{fin}}$.

Equation (50) can also be written as

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& =& \frac{2}{{\tau }_0}tanh(T-\rho )+(1-\eta )[1-\eta {\tau }_0{cosh}^2\rho (tanh\left(T_{\rho }\right)+tanh\rho )]\hfill \\ & & -\frac{\eta {cosh}^2\rho }{{cosh}^2(T-\rho )[1-\eta {\tau }_0{cosh}^2\rho (tanh\left(T_{\rho }\right)+tanh\rho )]}\hfill \\ & =& \frac{2}{{\tau }_0}tanh(T-\rho )+(1-\eta )[1-\frac{\eta {\tau }_0}{cothT-tanh\rho }]-\frac{\eta {cosh}^2\rho }{{cosh}^2(T-\rho )[1-\frac{\eta {\tau }_0}{cothT-tanh\rho }]},\hfill \end{array}$$

(61)

where we used the identity

$${cosh}^2\rho [tanh\left(T_{\rho }\right)+tanh\rho ]=\frac{1}{cothT-tanh\rho }.$$

(62)

The function (61) is positive for $S_{\infty }\ge 0$ and non-negative for all times in the admissible interval $0\le \tau \le {\tau }_{\mathrm{fin}}$. The ratio $\kappa \left(\tau \right)$ is negative and contains singularities if it is used in the regime $\tau >{\tau }_{\mathrm{fin}}$.

4. Details of the Construction of the SIRD Solution

From Equation (51) we obtain, for every $S_{\infty }$,

$$tanh\left(\frac{{\tau }_{\max }}{{\tau }_0}\right)=\frac{1-2\eta -\kappa \left(0\right)}{2}{\tau }_0,$$

(63)

with positive ${\tau }_0>0$. We note that this Equation has a solution provided

$$1-2\eta -\frac{2}{{\tau }_0}\le \kappa \left(0\right)\le 1-2\eta +\frac{2}{{\tau }_0},$$

(64)

because then the right-hand side of Equation (63) lies within the interval $[-1,1]$. While ${\kappa }_{\infty }=0$ for $S_{\infty }=0$, inserting Equation (63) provides for Equation (52),

$${\kappa }_{\infty }=\frac{2}{{\tau }_0}+\frac{(1-\eta )[\frac{2}{{\tau }_0}+\kappa \left(0\right)-1]}{\frac{2}{{\tau }_0}+\kappa \left(0\right)-1+2\eta }(S_{\infty }\ne 0).$$

(65)

Setting $y=2/{\tau }_0$, Equation (65) leads to the quadratic equation

$$y^2+(\kappa \left(0\right)-{\kappa }_{\infty }+\eta )y={\kappa }_{\infty }(\kappa \left(0\right)-1+2\eta )-(1-\eta )(\kappa \left(0\right)-1).$$

(66)

For general and different values of $\kappa \left(0\right)$ und ${\kappa }_{\infty }$ one can use Equation (66) to determine the implied value of ${\tau }_0=2/y$ and with Equation (63) the resulting value of ${\tau }_{\max }$. The knowledge of ${\tau }_0$ and ${\tau }_{\max }$ then determines for the SIRD model the time variation of the ratio $\kappa \left(\tau \right)$ for any value of $S_{\infty }$ and also of the rate of new infections $j\left(\tau \right)$ in Equation (44). We thus have found an effective new method to construct a special class of exact solutions for the SIRD model which also applies to the SIR model for $\psi \left(t\right)=0$. We illustrate this new method for several cases of the ratios $\kappa \left(0\right)$ and ${\kappa }_{\infty }$ in the next subsections.

4.1. SIRD Solution for ${\kappa }_{\infty }=0$

As discussed there are two cases for which ${\kappa }_{\infty }=0$ is realized. If $S_{\infty }=0$, then ${\tau }_{\inf }=\infty$ due to Equation (37), and

$$tanh\left(\rho \right)=1-\eta {\tau }_0=\frac{1-2\eta -\kappa \left(0\right)}{2}{\tau }_0,$$

(67)

according to Equations (42) and (63). This Equation (67) determines ${\tau }_0$ in terms of $\kappa \left(0\right)$, i.e.,

$${\tau }_0=\frac{2}{1-\kappa \left(0\right)}.(S_{\infty }={\kappa }_{\infty }=0)$$

(68)

With ${\tau }_0$ at hand, ${\tau }_{\max }$ is then also determined by Equation (67). To be specific,

$${\tau }_{\max }=\frac{2{tanh}^{-1}[1-2\eta /(1-\kappa \left(0\right))]}{1-\kappa \left(0\right)}.$$

(69)

For the special choice of $\kappa \left(0\right)={\kappa }_{\infty }=S_{\infty }=0$, one therefore recovers with ${\tau }_0=2$ and ${\tau }_{\max }=ln((1-\eta )/\eta )$ the above-mentioned solution of the SI model detailed in Appendix A.

If, on the other hand, $S_{\infty }=-2/{\tau }_0$ is negative, Equation (63), valid for all $S_{\infty }$, yields

$${\tau }_{\max }={\tau }_0{tanh}^{-1}\frac{1-2\eta -\kappa \left(0\right)}{2}{\tau }_0,$$

(70)

so that ${\tau }_{\inf }$ from Equation (37) is finite and given by

$$\begin{array}{ccc}\hfill {\tau }_{\mathrm{fin}}& =& {\tau }_{\max }+{\tau }_0{tanh}^{-1}\left(\frac{(\eta +\kappa \left(0\right)){\tau }_0}{2+(1-\eta ){\tau }_0}\right)\hfill \\ & =& {\tau }_0{tanh}^{-1}\left(\frac{1-2\eta -\kappa \left(0\right)}{2}{\tau }_0\right)+{\tau }_0{tanh}^{-1}\left(\frac{(\eta +\kappa \left(0\right)){\tau }_0}{2+(1-\eta ){\tau }_0}\right).\hfill \end{array}$$

(71)

${\tau }_0$ is also determined by $\kappa \left(0\right)$, as it solves Equation (66) for ${\kappa }_{\infty }=0$, which then simplifies to

$$y^2+(\kappa \left(0\right)+\eta )y=(1-\eta )(1-\kappa \left(0\right)).$$

(72)

The quadratic equation (72) can be solved for $y=2/{\tau }_0$ and thus provides

$${\tau }_0=\frac{4}{\sqrt{{\kappa }^2\left(0\right)-2(2-3\eta )\kappa \left(0\right)+{(2-\eta )}^2}-[\kappa \left(0\right)+\eta ]},$$

(73)

because the 2nd solution leads to negative ${\tau }_0$. The ${\tau }_{\max }$ is then also determined by $\kappa \left(0\right)$, c.f., Equation (71). For the special choice of $\kappa \left(0\right)={\kappa }_{\infty }=0$, the above simplifies to

$$\begin{array}{ccc}\hfill {\tau }_0& =& \frac{2}{1-\eta },S_{\infty }=-(1-\eta ),\hfill \end{array}$$

(74a)

$$\begin{array}{ccc}\hfill {\tau }_{\max }& =& \frac{2}{1-\eta }{tanh}^1\left[1-\frac{\eta }{1-\eta }\right]=\frac{ln\frac{2-3\eta }{\eta }}{1-\eta }\simeq \frac{ln(2/\eta )}{1-\eta },\hfill \\ \hfill {\tau }_{\mathrm{fin}}& =& \frac{2}{1-\eta }\left[{tanh}^{-1}\frac{1-2\eta }{1-\eta }+{tanh}^{-1}\frac{\eta }{2(1-\eta )}\right]\hfill \end{array}$$

(74b)

$$\begin{array}{ccc}& =& \frac{1}{1-\eta }\left[ln\frac{2-3\eta }{\eta }+ln\frac{2-\eta }{\eta }\right]\simeq \frac{2[ln\frac{2}{\eta }-\eta ]}{1-\eta }.\hfill \end{array}$$

(74c)

The results of the present section for the extremal case of $\kappa \left(0\right)=0$ are visualized in Figure 5.

We have thus presented the analytic solutions of the SIRD model for the case of ${\kappa }_{\infty }=0$ and arbitrary $\kappa \left(0\right)$. There is one solution for which S approaches zero at infinite time, and there is another solution for which S reaches zero at finite time ${\tau }_{\mathrm{fin}}$ (71). In both cases the characteristic times ${\tau }_0$ and ${\tau }_{\max }$, as well as $S_{\infty }$ appearing in the analytic expression (36) for $S\left(\tau \right)$ are determined by the initial dimensionless rate $\kappa \left(0\right)$ and $\eta =1-S\left(0\right)$.

4.2. SIRD Solution for Equal $\kappa \left(0\right)={\kappa }_{\infty }\equiv K\ne 0$

For equal values of $\kappa \left(0\right)={\kappa }_{\infty }\equiv K\ne 0$ Equation (66) reduces to

$$y^2+\eta y=K^2-(2-3\eta )K+(1-\eta ),$$

(75)

with the two solutions

$$y_{1,2}=-\frac{\eta }{2}\pm \sqrt{f\left(K\right)},f\left(K\right)=K^2-(2-3\eta )K+{\left(1-\frac{\eta }{2}\right)}^2.$$

(76)

The functions $f\left(K\right)>0$ is positive for all values of $K>0$ and has the slope

$$\frac{df\left(K\right)}{dK}=2[K-(1-\frac{3}{2}\eta )].$$

(77)

It therefore decreases for $0<K\le K_0$ with $K_0=1-(3\eta /2)$, where it attains its minimum $f_{min}=2\eta (1-\eta )$. For values $K\ge K_0$ the function $f\left(K\right)$ is monotonically increasing. For all values of K one obtains $\sqrt{f\left(K\right)}\ge \sqrt{f_{\min }}>(\eta /2)$ because $\eta \ll (8/9)$. Hence only the solution

$$y_1\left(K\right)=\sqrt{f\left(K\right)}-\frac{\eta }{2}=\sqrt{K^2-(2-3\eta )K+{(1-\frac{\eta }{2})}^2}-\frac{\eta }{2}$$

(78)

is useful as it provides positive values of

$${\tau }_0\left(K\right)=\frac{2}{y_1\left(K\right)}=\frac{2}{\sqrt{K^2-(2-3\eta )K+{(1-\frac{\eta }{2})}^2}-\frac{\eta }{2}}.$$

(79)

We first check the requirement (64) reading

$$-y_1\left(K\right)\le K-1+2\eta \le y_1\left(K\right),$$

(80)

or

$$-[\sqrt{f\left(K\right)}-\frac{\eta }{2}]\le K-1+2\eta \le \sqrt{f\left(K\right)}-\frac{\eta }{2}.$$

(81)

The left-hand-side of the inequality (81) can be written as

$$-\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}\le K-K_0,$$

(82)

and is fulfilled for all values of $K\ge 0$. This is obvious for $K\ge K_0$ when the right-hand side of Equation (82) is nonnegative, whereas its left-hand side is negative. For values $0\le K<K_0$ Equation (82) reads

$$K_0-K\le \sqrt{{(K_0-K)}^2+2\eta (1-\eta )},$$

(83)

which is fulfilled. Likewise, the right-hand-side of the inequality (81) can be written as

$$K-(K_0-\eta )\le \sqrt{{(K-K_0)}^2+2\eta (1-\eta )},$$

(84)

which is fulfilled for values of $K\in (0,K_0-\eta ]$, when the left-hand side of Equation (84) is negative while its right-hand side is positive. Recall that the case $K=0$ had been treated in Section 4.1. For large values $K>K_0-\eta$ squaring the inequality (84) yields

$$2(K-K_0)\le 2-3\eta =2K_0,$$

(85)

or

$$K\le 2K_0.$$

(86)

We conclude that the constraint (81) can be fulfilled for all values of $K\in (0,2K_0]$. In this interval the solution (79) is given by

$${\tau }_0(0<K\le 2K_0)=\frac{2}{\sqrt{K^2-(2-3\eta )K+{(1-\frac{\eta }{2})}^2}-\frac{\eta }{2}}=\frac{2}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}},$$

(87)

and shown in Figure 6. The first derivative of Equation (87) is

$$\frac{d{\tau }_0\left(K\right)}{dK}=-\frac{df/dK}{\sqrt{f\left(k\right)}{(\sqrt{f\left(K\right)}-\frac{\eta }{2})}^2}=\frac{2(K_0-K)}{\sqrt{f\left(k\right)}{(\sqrt{f\left(K\right)}-\frac{\eta }{2})}^2},$$

(88)

so that ${\tau }_0\left(K\right)$ attains its maximum value

$${\tau }_{0,E}=\frac{\sqrt{\frac{2}{\eta }}}{\sqrt{1-\eta }-\sqrt{\frac{\eta }{8}}}=\frac{4}{\sqrt{8\eta (1-\eta )}-\eta }=\frac{4}{8-9\eta }[1+\sqrt{\frac{8(1-\eta )}{\eta }}]\simeq \sqrt{\frac{2}{\eta }},$$

(89)

at $K=K_0$. Inserting the solution (87) one obtains for Equation (63)

$$tanh\frac{{\tau }_{\max }}{{\tau }_0\left(K\right)}=\frac{1-2\eta -K}{2}{\tau }_0\left(K\right)=\frac{1-2\eta -K}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}},$$

(90)

yielding

$${\tau }_{\max }(0<K\le 2K_0)=\frac{2{tanh}^{-1}\left[\frac{1-2\eta -K}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}}\right]}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}}.$$

(91)

The solution (91), also shown in Figure 6, is positive for values of $0<K\le 1-2\eta$ and negative for values of $1-2\eta <K\le 2K_0$ due to the property ${tanh}^{-1}(-x)=-{tanh}^{-1}\left(x\right)$. Obviously ${\tau }_{\max }=0$ for $K=1-2\eta$. In order to have positive values of $K_0$ and the zero $1-2\eta$ we should consider only values of $\eta <0.5$.

For completeness we note an alternative ${\tau }_{\max }\left({\tau }_0\right)$. Equating the right hand sides of Equations (51) and (52) leads with $\mathcal{R}\equiv tanh\left(\rho \right)=tanh({\tau }_{\max }/{\tau }_0)$ to

$$1-2\eta -\frac{2\mathcal{R}}{{\tau }_0}=\frac{2}{{\tau }_0}+(1-\eta )\left[1-\frac{\eta {\tau }_0}{1-\mathcal{R}}\right].$$

(92)

Upon multiplying with $(1-\mathcal{R}){\tau }_0$ one obtains

$$(1-\mathcal{R})[(1-2\eta ){\tau }_0-2\mathcal{R}]=2(1-\mathcal{R})+(1-\eta )(1-\eta {\tau }_0-\mathcal{R}){\tau }_0,$$

(93)

or the quadratic equation

$${\mathcal{R}}^2+\frac{\eta {\tau }_0}{2}\mathcal{R}=1+\frac{\eta {\tau }_0}{2}[1-(1-\eta ){\tau }_0],$$

(94)

which is solved by

$$\mathcal{R}=\frac{\pm \sqrt{16+\eta {\tau }_0[8-(8-9\eta ){\tau }_0]}-\eta {\tau }_0}{4},$$

(95)

so that

$${\tau }_{\max }={\tau }_0{tanh}^{-1}\left[\frac{\pm \sqrt{16+\eta {\tau }_0[8-(8-9\eta ){\tau }_0]}-\eta {\tau }_0}{4}\right].$$

(96)

The requirement $\left|\mathcal{R}\right|\le 1$ is fulfilled for all values of $\eta <1$ if the argument of the square root in Equation (95) is nonnegative. The last condition leads to

$${\tau }_0\le \frac{4}{8-9\eta }\left[1+\sqrt{\frac{8(1-\eta )}{\eta }}\right]={\tau }_{0,E},$$

(97)

which is identical to the maximum value (89) derived before. Proof:

$${\tau }_{0,E}=\frac{\sqrt{\frac{2}{\eta }}}{\sqrt{1-\eta }-\sqrt{\frac{\eta }{8}}}=\frac{4}{\sqrt{\eta }[\sqrt{8(1-\eta )}-\sqrt{\eta }]}=\frac{4[\sqrt{8(1-\eta )}+\sqrt{\eta }]}{\sqrt{\eta }[8(1-\eta )-\eta ]}$$

$$=\frac{4}{8-9\eta }\frac{\sqrt{\eta }+\sqrt{8(1-\eta )}}{\sqrt{\eta }}=\frac{4}{8-9\eta }\left(1+\sqrt{\frac{8(1-\eta )}{\eta }}\right)={\tau }_{0,E}.$$

(98)

4.3. Reduced time dependence of $\kappa \left(\tau \right)$, terminal time ${\tau }_{\mathrm{fin}}\left(K\right)$ for $K=\kappa \left(0\right)={\kappa }_{\infty }\ne 0$.

With ${\tau }_0\left(K\right)$ given by Equation (87) we obtain for Equations (47)

$$T=\frac{\tau }{{\tau }_0\left(K\right)},\rho \left(K\right)=\frac{{\tau }_{\max }}{{\tau }_0\left(K\right)}={tanh}^{-1}\frac{1-2\eta -K}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}},$$

(99)

so that Equations (49) and (61) become

$$S\left(\tau \right)=(1-\eta )\left[1-\frac{\eta {\tau }_0\left(K\right)}{cothT-tanh\rho \left(K\right)}\right],$$

(100)

and

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& \simeq & \frac{2}{{\tau }_0\left(K\right)}tanh\left[T-\rho \left(K\right)\right]+(1-\eta )\left[1-\frac{\eta {\tau }_0\left(K\right)}{cothT\left(K\right)-tanh\rho \left(K\right)}\right]\hfill \\ & & -\frac{\eta {cosh}^2\rho \left(K\right)}{{cosh}^2(T-\rho \left(K\right))\left[1-\frac{\eta {\tau }_0\left(K\right)}{cothT\left(K\right)-tanh\rho \left(K\right)}\right]},\hfill \end{array}$$

(101)

which are both shown in Figure 7 for different values of K entering $\rho \left(K\right)$ and ${\tau }_0\left(K\right)$. As $K\ne 0$ the requirement $S\left({\tau }_{\mathrm{fin}}\right)=0$ then provides from Equation (100)

$$\begin{array}{ccc}\hfill {\tau }_{\mathrm{fin}}\left(K\right)& =& {\tau }_0\left(K\right){coth}^{-1}[\eta {\tau }_0\left(K\right)+tanh\rho \left(K\right)]={\tau }_0\left(K\right){coth}^{-1}\left[\frac{1-K}{2}{\tau }_0\left(K\right)\right]\hfill \\ & =& \frac{2}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}}{tanh}^{-1}\frac{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}}{1-K},\hfill \\ \hfill \end{array}$$

(102)

where we used Equation (67) for $\kappa \left(0\right)=K$ and inserted solution (57) for $0<K\le 2K_0$. Obviously, positive values of ${\tau }_{\mathrm{fin}}\left(K\right)$ are only possible for values of $K<1$ smaller then unity, as otherwise the argument of the ${tanh}^{-1}$-function is negative. In order for the argument of the ${tanh}^{-1}$-function to be less or equal unity the condition

$$\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}\le (1+\frac{\eta }{2})-K$$

(103)

is required, which is equivalent to

$$K\le \frac{1}{2}.$$

(104)

Hence, finite values of ${\tau }_{\mathrm{fin}}\left(K\right)$ only occur for values of $K\in (0,0.5]$. In Figure 8 we show the final time (102) for different values of K below 0.5. The final time is monotonically decreasing from its infinitely large value above $K=0.5$ with decreasing values of K.

Particular interesting in Figure 7 are the cases where the combined ratio $\kappa \left(\tau \right)$ at the start and the end of the epidemic outburst have values below $K\le 0.5$ which corresponds to infection rates being twice as large as the sum of the recovery and fatality rate. In this case the epidemic outburst, described by the SI-type ${cosh}^{-2}[(\tau -{\tau }_{\max })/{\tau }_0]$-distribution for the rate of new infections shown in panel 7-d, is so dominated by the rapid infections that at the finite reduced time ${\tau }_{\mathrm{fin}}$ the outburst suddenly terminates as with $S\left({\tau }_{\mathrm{fin}}\right)=0$ (as seen in panel 7-c) no more persons are available to be infected. The situation is comparable to a smooth running car where suddenly the car engine stops as no more fuel is available. For values greater than $K>0.5$ the epidemic outburst lasts infinitely long.

Next, we consider the limits of Equations (101) and (102) for small values of $\eta \ll 1$.

4.4. Limit for Very Small Values of $I\left(0\right)=\eta \ll 1$

We use

$$\begin{array}{ccc}\hfill tanh\rho \left(K\right)& =& \frac{K_0-K-\frac{\eta }{2}}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}},\hfill \end{array}$$

(105a)

$$\begin{array}{ccc}\hfill {\tau }_0\left(K\right)& =& \frac{2}{\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}},\hfill \end{array}$$

(105b)

and Equation (102). For small values of $\eta \ll 1$ we have to distinguish between the cases (i) where $|K-|K_0|\le \sqrt{2\eta }$ and (ii) where $|K-K_0|>\sqrt{2\eta }$. We consider both cases in turn.

4.4.1. Case $|K-K_0|\le \sqrt{2\eta }$

Here we approximate for small values of $\eta \ll 1$

$$\begin{array}{ccc}\hfill \sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}& \simeq & \sqrt{2\eta (1-\eta )}\left[1+\frac{{(K-K_0)}^2}{2\eta (1-\eta )}\right]-\frac{\eta }{2}\hfill \\ & \simeq & \sqrt{2\eta }\left[1+\frac{{(K-K_0)}^2}{2\eta }-\sqrt{\frac{\eta }{8}}\right].\hfill \end{array}$$

(106)

Consequently, we obtain

$$\begin{array}{ccc}\hfill tanh\rho \left(K\right)& \simeq & \frac{[1-2\eta -K][1-\frac{{(K-K_0)}^2}{2\eta }]}{\sqrt{2\eta }},\hfill \end{array}$$

(107a)

$$\begin{array}{ccc}\hfill {\tau }_0\left(K\right)& \simeq & \sqrt{\frac{2}{\eta }}\left[1-\frac{{(K-K_0)}^2}{2\eta }\right],\hfill \\ \hfill {\tau }_{\max }\left(K\right)& \simeq & \sqrt{\frac{2}{\eta }}\left[1-\frac{{(K-K_0)}^2}{2\eta }\right]{tanh}^{-1}\frac{1-2\eta -K}{\sqrt{2\eta }}\hfill \end{array}$$

(107b)

$$\begin{array}{cccc}& & =& \frac{1-\frac{{(K-K_0)}^2}{2\eta }}{\sqrt{2\eta }}ln\frac{\sqrt{2\eta }+(1-2\eta -K)}{\sqrt{2\eta }-(1-2\eta -K)},\hfill \end{array}$$

(107c)

whereas ${\tau }_{\mathrm{fin}}=0$ as all K-values in this interval are greater than $0.5$.

4.4.2. Case $|K-K_0|>\sqrt{2\eta }$

Here we approximate

$$\sqrt{{(K-K_0)}^2+2\eta (1-\eta )}-\frac{\eta }{2}\simeq |K_0-K|-\frac{\eta }{2}+\frac{\eta (1-\eta )}{|K_0-K|},$$

(108)

to obtain for Equations (105) and (102)

$$\begin{array}{ccc}\hfill tanh\rho \left(K\right)& \simeq & \frac{K_0-K-\frac{\eta }{2}}{|K-K_0|-\frac{\eta }{2}+\frac{\eta (1-\eta )}{|K_0-K|}},\hfill \end{array}$$

(109a)

$$\begin{array}{ccc}\hfill {\tau }_0\left(K\right)& \simeq & \frac{2}{|K_0-K|-\frac{\eta }{2}+\frac{\eta (1-\eta )}{|K_0-K|}},\hfill \end{array}$$

(109b)

$$\begin{array}{ccc}\hfill {\tau }_{\mathrm{fin}}\left(K\right)& \simeq & \frac{2}{|K_0-K|-\frac{\eta }{2}+\frac{\eta (1-\eta )}{|K_0-K|}}{tanh}^{-1}\left[\frac{|K-K_0|-\frac{\eta }{2}+\frac{\eta (1-\eta )}{|K_0-K|}}{1-K}\right].\hfill \end{array}$$

(109c)

4.4.3. Finite Time ${\tau }_{\mathrm{fin}}\left(K\right)$

As shown before, c.f. Equation (104), finite values of the finite time only occur for values of $K\le 0.5<K_0$. Consequently for small $\eta \ll 1$ we approximate with $K_0=1-(3/2)\eta$

$$\begin{array}{ccc}\hfill {\tau }_{\mathrm{fin}}\left(K\right)& \simeq & \frac{2}{K_0-K-\frac{\eta }{2}+\frac{\eta (1-\eta )}{K_0-K}}{tanh}^{-1}\left[\frac{K_0-K-\frac{\eta }{2}+\frac{\eta (1-\eta )}{K_0-K}}{1-K}\right]\hfill \\ & =& \frac{2}{1-K-2\eta +\frac{\eta (1-\eta )}{K_0-K}}{tanh}^{-1}\left[\frac{1-K-2\eta +\frac{\eta (1-\eta )}{K_0-K}}{1-K}\right]\hfill \\ & \simeq & \frac{2}{1-K-\frac{\eta [2(K_0-K)-1]}{K_0-K}}{tanh}^{-1}[1-\frac{\eta [2(K_0-K)-1]}{(K_0-K)(1-K)}]\hfill \\ & =& \frac{1}{1-K-\frac{\eta [2(K_0-K)-1]}{K_0-K}}ln\left[\frac{2(K_0-K)(1-K)-\eta [2(K_0-K)-1]}{\eta [2(K_0-K)-1]}\right]\hfill \\ & \simeq & \frac{1}{1-K}ln\frac{2(K_0-K)(1-K)}{\eta [2(K_0-K)-1]}.\hfill \end{array}$$

(110)

Equation (110) only provides real values if the denominator of the ln-function is positive, leading to the requirement

$$K<K_0-\frac{1}{2}=\frac{1-3\eta }{2},$$

(111)

which is consistent with the earlier limit (104) and the time (111) can be further approximated as

$${\tau }_{\mathrm{fin}}\left(K\right)\simeq \frac{1}{1-K}ln\frac{2{(1-K)}^2}{\eta (1-2K)}.$$

(112)

The function (112) monotonically decreases from its infinite large values above $(1-\eta )/2$ with decreasing values of K in agreement with Figure 8.

4.4.4. Values $K<K_0-\sqrt{2\eta }$

For values of $K<K_0-\sqrt{2\eta }$ one obtains

$$\begin{array}{ccc}\hfill tanh\rho \left(K\right)& =& \frac{1}{1+\frac{\eta (1-\eta )}{(K_0-K)(K_0-K-\frac{\eta }{2})}}\simeq 1-\frac{\eta (1-\eta )}{{(K_0-K)}^2},\hfill \end{array}$$

(113a)

$$\begin{array}{ccc}\hfill {\tau }_0\left(K\right)& \simeq & \frac{2}{K_0-K}[1-\frac{\eta (2+K-K_0}{2{(K_0-K)}^2}],\hfill \end{array}$$

(113b)

$$\begin{array}{ccc}\hfill {\tau }_{\max }\left(K\right)& \simeq & \frac{1}{K_0-K}ln\frac{2{(K_0-K)}^2}{\eta }.\hfill \end{array}$$

(113c)

With

$${cosh}^2\rho =\frac{1}{1-{tanh}^2\rho }=\frac{1}{1-{[1-\frac{\eta (1-\eta )}{{(K_0-K)}^2}]}^2}\simeq \frac{{(K_0-K)}^2}{2\eta (1-\eta )}$$

(114)

Equation (101) becomes

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& \simeq & 1-\eta +(K_0-K)tanh(T-\rho )-\frac{2\eta (1-\eta )}{K_0-K}(cothT-tanh\rho )\hfill \\ & & -\frac{{(K_0-K)}^2}{2(1-\eta ){cosh}^2(T-\rho )[1-\frac{2\eta (1-\eta )}{K_0-K}(cothT-tanh\rho )]},\hfill \end{array}$$

(115)

which correctly approaches

$$\kappa (\tau =0)=1-\eta -(K_0-K)tanh\rho -\frac{{(K_0-K)}^2}{2(1-\eta ){cosh}^2\rho }\simeq 1-(K_0-K)=K.$$

(116)

For values of $(1-3\eta )/2<K<K_0-\sqrt{2\eta }$ we find

$$\begin{array}{ccc}\hfill \kappa (\tau =\infty )& =& 1-\eta +(K-K_0)tanh\rho -\frac{2\eta (1-\eta )}{(K_0-K)[1-tanh\rho ]}\hfill \\ & \simeq & 1+K-K_0-2(K_0-K)=1-K_0+K=K,\hfill \end{array}$$

(117)

because for small $\eta \ll 1$ one has $K_0\simeq 1$. The solution (117) holds for all times $\tau$ in the range $(1-3\eta )/2\le K\le K_0=1-(3/2)\eta -\sqrt{2\eta }$. For smaller values of $K<(1-3\eta )/2$ the solution (117) holds only at finite times $\tau <{\tau }_{\mathrm{fin}}\left(K\right)$ given in Equation (112).

4.4.5. Values $K_0+\sqrt{2\eta }<K\le 2K_0$

For values of $K_0+\sqrt{2\eta }<K\le 2K_0$ we obtain

$$\begin{array}{ccc}\hfill {\tau }_0\left(K\right)& \simeq & \frac{2}{K-K_0},\hfill \end{array}$$

(118a)

$$\begin{array}{ccc}\hfill tanh\rho \left(K\right)& \simeq & -\frac{1}{1+\frac{\eta }{K-K_0+\frac{\eta }{2}}\frac{1+K_0-K-\eta }{K-K_0}}\simeq -\left[1-\frac{\eta (1+K_0-K)}{{(K-K_0)}^2}\right],\hfill \end{array}$$

(118b)

$$\begin{array}{ccc}\hfill {\tau }_{\max }\left(K\right)& \simeq & -\frac{1}{K-K_0}ln\frac{2{(K-K_0)}^2}{\eta (1+K_0-K)}\hfill \end{array}$$

(118c)

where the last step in Equation (118b) holds for values of $K<2-(5\eta /2)$, which is justified for all values of $K>K_0$ as the maximum value $2K_0=2-3\eta$ is smaller than $2-(5\eta /2)$. Consequently, one obtains in this case for

$${cosh}^2\rho =\frac{1}{1-{tanh}^2\rho }\simeq \frac{{(K_0-K)}^2}{2\eta (1+K_0-K-\eta )},$$

(119)

so that

$$\eta (1-\eta ){\tau }_0{cosh}^2\rho \simeq \frac{(1-\eta )(K-K_0)}{1+K_0-K}.$$

(120)

We also note that for $K>1-2\eta$ the function $\rho \left(K\right)=-r\left(K\right)$ is negative with

$$r\left(K\right)={tanh}^{-1}\frac{1}{1+\frac{\eta }{K-K_0+\frac{\eta }{2}}\frac{1+K_0-K-\eta }{K-K_0}}\simeq {tanh}^{-1}\left[1-\frac{\eta (1+K_0-K)}{{(K-K_0)}^2}\right],$$

(121)

so that Equation (101) becomes

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& \simeq & \frac{2}{{\tau }_0}tanh(T+r)+(1-\eta )\left[1-\eta {\tau }_0{cosh}^{2}r(tanh(T+r)-tanhr)\right]\hfill \\ & & -\frac{\eta {cosh}^{2}r}{{cosh}^2(T+r)[1-\eta {\tau }_0{cosh}^{2}r(tanh(T+r)-tanhr)]}\hfill \\ & \simeq & (K-K_0)tanh(T+r)+(1-\eta )\left[1-\frac{K-K_0}{1+K_0-K}(tanh(T+r)-tanhr)\right]\hfill \\ & & -\frac{{(K-K_0)}^2}{2{cosh}^2(T+r)[1+K_0-K-(K-K_0)(tanh(T-r)-tanhr)]}\hfill \end{array}$$

(122)

One notices from Figure 6 that $r\left(K\right)\gg 1$ is very large compared to unity, so that Equation (122) with $tanh(T+r)\simeq tanhr\simeq 1$ and ${cosh}^{-2}(T+r)\simeq 0$ simplifies to the constant

$$\kappa \left(\tau \right)\simeq K-K_0+1=K.$$

(123)

4.5. SIRD Solution for $\kappa \left(0\right)=0$

For $\kappa \left(0\right)=0$ Equation (66) for $y=2/{\tau }_0$ reduces to

$$y^2-({\kappa }_{\infty }-\eta )y=1-\eta -(1-2\eta ){\kappa }_{\infty },$$

(124)

with the two solutions

$$\begin{array}{ccc}\hfill y_1& =& \frac{1}{2}[{\kappa }_{\infty }-\eta +\sqrt{{({\kappa }_{\infty }-2+3\eta )}^2+8\eta (1-\eta )}],\hfill \end{array}$$

(125a)

$$\begin{array}{ccc}\hfill y_2& =& \frac{1}{2}[{\kappa }_{\infty }-\eta -\sqrt{{({\kappa }_{\infty }-2+3\eta )}^2+8\eta (1-\eta )}].\hfill \end{array}$$

(125b)

We restrict our analysis to the interesting range of values of $0<{\kappa }_{\infty }<2-3\eta$ (${\kappa }_{\infty }=0$ was treated in Section 4.1 already) and investigate the limit of small $\eta \ll 1$. We then approximate

$$\sqrt{{(2-3\eta -{\kappa }_{\infty })}^2+8\eta (1-\eta )}\simeq 2-3\eta -{\kappa }_{\infty }+\frac{4\eta (1-\eta )}{2-{\kappa }_{\infty }-3\eta },$$

(126)

implying

$$\begin{array}{ccc}\hfill y_1& \simeq & 1-2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }},\hfill \end{array}$$

(127a)

$$\begin{array}{ccc}\hfill y_2& =& {\kappa }_{\infty }-1-\frac{\eta {\kappa }_{\infty }}{2-{\kappa }_{\infty }},\hfill \end{array}$$

(127b)

Accordingly,

$$\begin{array}{ccc}\hfill {\tau }_{0,1}& \simeq & \frac{2}{1-2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}}\simeq 2[1+2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}],\hfill \end{array}$$

(128a)

$$\begin{array}{ccc}\hfill {\tau }_{0,2}& \simeq & \frac{2}{{\kappa }_{\infty }-1}[1+\frac{\eta {\kappa }_{\infty }}{(2-{\kappa }_{\infty })({\kappa }_{\infty }-1)}].\hfill \end{array}$$

(128b)

As ${\tau }_0$ has to be positive the solution (128b) can only be used for values of $1<{\kappa }_{\infty }<2-3\eta$.

For $\kappa \left(0\right)=0$ Equation (63) reads ${\tau }_{\max }={\tau }_0{tanh}^{-1}[(1-2\eta ){\tau }_0/2]$.

The two solutions (128) then provide

$$\begin{array}{ccc}\hfill {\tau }_{\max ,1}& \simeq & 2[1+2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}]{tanh}^{-1}[1-\frac{2\eta }{2-{\kappa }_{\infty }}]\hfill \\ & \simeq & [1+2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}]ln\frac{2-{\kappa }_{\infty }-\eta }{\eta }\simeq ln\frac{2-{\kappa }_{\infty }}{\eta },\hfill \end{array}$$

(129a)

$$\begin{array}{ccc}\hfill {\tau }_{\max ,2}& =& \frac{2}{{\kappa }_{\infty }-1}[1+\frac{\eta {\kappa }_{\infty }}{(2-{\kappa }_{\infty })({\kappa }_{\infty }-1)}]{tanh}^{-1}\left[\frac{1-2\eta }{{\kappa }_{\infty }-1}(1+\frac{\eta {\kappa }_{\infty }}{(2-{\kappa }_{\infty })({\kappa }_{\infty }-1)})\right]\hfill \\ & \simeq & \frac{2}{{\kappa }_{\infty }-1}{tanh}^{-1}\frac{1}{{\kappa }_{\infty }-1}.\hfill \end{array}$$

(129b)

The argument of the ${tanh}^{-1}$ has to be in the interval $(-1,1)$. The requirement ${({\kappa }_{\infty }-1)}^{-1}>-1$ is fulfilled for every positive ${\kappa }_{\infty }>1$. However, the requirement ${({\kappa }_{\infty }-1)}^{-1}<1$ is only possible for values of ${\kappa }_{\infty }>2$ in contradiction to the earlier assumption ${\kappa }_{\infty }\le 2-3\eta$. Therefore the second solution ${\tau }_{\max ,2}$ and ${\tau }_{0,2}$ cannot be used. The only possible solution is this range of $0<{\kappa }_{\infty }\le 2-3\eta$ is

$$\begin{array}{ccc}\hfill {\tau }_0\left({\kappa }_{\infty }\right)& =& {\tau }_{0,1}\left({\kappa }_{\infty }\right)\simeq 2[1+2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}],\hfill \end{array}$$

(130a)

$$\begin{array}{ccc}\hfill {\tau }_{\max }\left({\kappa }_{\infty }\right)& =& {\tau }_{\max ,1}={\tau }_0\left({\kappa }_{\infty }\right){tanh}^{-1}\left[\frac{1-2\eta }{2}{\tau }_0\left({\kappa }_{\infty }\right)\right]\simeq 2\left[1+2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}\right],\hfill \end{array}$$

(130b)

$$\begin{array}{ccc}\hfill \rho \left({\kappa }_{\infty }\right)& =& {tanh}^{-1}\left[\frac{1-2\eta }{2}{\tau }_0\left({\kappa }_{\infty }\right)\right]={tanh}^{-1}\left[(1-2\eta )\left(1+2\eta \frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}\right)\right].\hfill \end{array}$$

(130c)

Consequently we obtain

$$\begin{array}{ccc}\hfill tanh\rho \left({\kappa }_{\infty }\right)& =& 1-\frac{2\eta }{2-{\kappa }_{\infty }}-4{\eta }^2\frac{1-{\kappa }_{\infty }}{2-{\kappa }_{\infty }}\simeq 1-\frac{2\eta }{2-{\kappa }_{\infty }},\hfill \end{array}$$

(131)

$$\begin{array}{ccc}\hfill 1-tanh\rho \left({\kappa }_{\infty }\right)& \simeq & \frac{2\eta }{2-{\kappa }_{\infty }},\hfill \end{array}$$

(132)

$$\begin{array}{ccc}\hfill {cosh}^2\rho \left({\kappa }_{\infty }\right)& \simeq & \frac{1}{1-{[1-\frac{2\eta }{2-{\kappa }_{\infty }}]}^2}\simeq \frac{2-{\kappa }_{\infty }}{4\eta }.\hfill \end{array}$$

(133)

One then obtains for Equation (65) in this case

$$\begin{array}{ccc}\hfill \kappa \left(\tau \right)& \simeq & \frac{2tanh(T-\rho \left({\kappa }_{\infty }\right))}{{\tau }_0\left({\kappa }_{\infty }\right)}\hfill \\ & & +(1-\eta )[1-\eta {\tau }_0\left({\kappa }_{\infty }\right){cosh}^2\rho \left({\kappa }_{\infty }\right)[tanh(T-\rho \left({\kappa }_{\infty }\right))+tanh\rho \left({\kappa }_{\infty }\right)]]\hfill \\ & & -\frac{\eta {cosh}^2\rho \left({\kappa }_{\infty }\right)}{{cosh}^2(T-\rho \left({\kappa }_{\infty }\right))[1-\eta {\tau }_0\left({\kappa }_{\infty }\right)(tanh(T-\rho \left({\kappa }_{\infty }\right))+tanh\rho \left({\kappa }_{\infty }\right))]}.\hfill \end{array}$$

(134)

Here, and in the following two equations, T and $\rho$ stand for $\tau /{\tau }_0\left({\kappa }_{\infty }\right)$ and $\rho \left({\kappa }_{\infty }\right)={\tau }_{\max }\left({\kappa }_{\infty }\right)/{\tau }_0\left({\kappa }_{\infty }\right)$ with ${\tau }_0\left({\kappa }_{\infty }\right)$, ${\tau }_{\max }\left({\kappa }_{\infty }\right)$, and $\rho \left({\kappa }_{\infty }\right)$ given by Equations (130). The temporal evolution of $\kappa \left(\tau \right)$ is shown in Figure 8 for various values of ${\kappa }_{\infty }\in [0,2]$. Equation (134) correctly reproduces

$$\begin{array}{ccc}\hfill \kappa (\tau =0)& =& 1-2\eta -\frac{2tanh\rho }{{\tau }_0}=1-2\eta -2\frac{1-2\eta }{2}=0,\hfill \end{array}$$

(135)

$$\begin{array}{ccc}\hfill \kappa (\tau =\infty )& =& \frac{2}{{\tau }_0\left({\kappa }_{\infty }\right)}+(1-\eta )\left[1-\frac{\eta {\tau }_0}{1-tanh\rho \left({\kappa }_{\infty }\right)})\right]\hfill \\ & \simeq & \frac{2}{{\tau }_0\left({\kappa }_{\infty }\right)}+(1-\eta )[1-\frac{2-{\kappa }_{\infty }}{2}{\tau }_0\left({\kappa }_{\infty }\right)]\simeq {\kappa }_{\infty }\hfill \end{array}$$

(136)

with ${\tau }_0\left({\kappa }_{\infty }\right)\simeq 2$.

5. Approximate Analytical Solutions of the SIRVD Model

Recently, it has been demonstrated that an accurate analytical approximation to the SIR and SIRV equations[21,26] exists if the cumulative fraction of new infections $J\left(t\right)=J\left(\tau \right)$ at all times is much smaller than unity. For the COVID-19 outbreaks in many countries this assumption is well fulfilled.

According to Equation (19) in ref. [21] the approximation $1-J\left(\tau \right)\simeq 1-J_{\infty }$ in Equation (21) provides the solution

$$V\left(\tau \right)\simeq (1-J_{\infty })[1-e^{-{\int }_0^{\tau }dxb\left(x\right)}],$$

(137)

which approaches $V_{\infty }=V(\infty )=1-J_{\infty }$ after infinite time. With this result in the same limit $J\le J_{\infty }\ll 1$ Equation (25) with the initial condition $j\left(0\right)=\eta (1-\eta )$ integrates

$$\begin{array}{ccc}\hfill j\left(\tau \right)& \simeq & \eta (1-\eta )exp{\int }_0^{\tau }dx\left[(1-J_{\infty })e^{-{\int }_0^{x}dyb\left(y\right)}-\kappa \left(x\right)-q\left(x\right)-b\left(x\right)\right]\hfill \\ & \simeq & \eta (1-\eta )exp{\int }_0^{\tau }dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-q\left(x\right)-b\left(x\right)\right],\hfill \end{array}$$

(138)

where the last approximation holds due to the adopted smallness $J_{\infty }\ll 1$. But we keep the $J_{\infty }$ in the solution (137) in order not to violate the restriction $J\left(\tau \right)+V\left(\tau \right)\le J_{\infty }+V_{\infty }\le 1$. By integrating Equation (138) the corresponding cumulative fraction is given by

$$J\left(\tau \right)\simeq \eta +\eta (1-\eta ){\int }_0^{\tau }dzexp\left[{\int }_0^{z}dx(e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-q\left(x\right)-b\left(x\right))\right].$$

(139)

Likewise Equations (15) and (17)–(19) provide the approximations

$$I\left(\tau \right)\simeq \frac{j\left(\tau \right)}{1-J_{\infty }-V\left(\tau \right)}=\frac{\eta (1-\eta )}{1-J_{\infty }}exp{\int }_0^{\tau }dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-q\left(x\right)\right]=j\left(\tau \right)e^{{\int }_0^{\tau }dxb\left(x\right)},$$

(140)

$$R\left(\tau \right)\simeq {\int }_0^{\tau }dx\frac{k\left(x\right)j\left(x\right)}{1-J_{\infty }-V\left(x\right)}=\frac{\eta (1-\eta )}{1-J_{\infty }}{\int }_0^{\tau }dzk\left(z\right)exp{\int }_0^{z}dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-q\left(x\right)\right],$$

(141)

$$D\left(\tau \right)\simeq {\int }_0^{\tau }dx\frac{q\left(x\right)j\left(x\right)}{1-J_{\infty }-V\left(x\right)}=\frac{\eta (1-\eta )}{1-J_{\infty }}{\int }_0^{\tau }dzq\left(z\right)exp{\int }_0^{z}dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-q\left(x\right)\right],$$

(142)

and

$$\begin{array}{ccc}\hfill d\left(\tau \right)& =& \frac{dD\left(\tau \right)}{d\tau }=q\left(\tau \right)I\left(\tau \right)=\frac{q\left(\tau \right)j\left(\tau \right)}{1-J_{\infty }-V\left(\tau \right)}\hfill \\ & \simeq & \frac{\eta (1-\eta )}{1-J_{\infty }}q\left(\tau \right)exp{\int }_0^{\tau }dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-q\left(x\right)\right].\hfill \end{array}$$

(143)

5.1. Difference between the SIRVD Death Rate and the A-Posteriori Death Rate

As it marks the difference of the death rate (143) in the SIRVD model to the a-posteriori death rate $d_{\mathrm{a}-\mathrm{pos}}\left(\tau \right)=q\left(t\right)j\left(\tau \right)$ (34) we consider first the ratio

$$\frac{d_{\mathrm{a}-\mathrm{pos}}\left(\tau \right)}{d\left(\tau \right)}=\frac{j\left(\tau \right)}{I\left(\tau \right)}=S\left(\tau \right)\simeq 1-J_{\infty }-V\left(\tau \right)=(1-J_{\infty })e^{-{\int }_0^{\tau }dxb\left(x\right)}.$$

(144)

For the SIRD model with negligible vaccinations ($b\left(\tau \right)=0$), the ratio (144) is independent of reduced time and practically equals unity as $J_{\infty }\ll 1$. However, for the SIRVD model including vaccinations the ratio (144) depends on time. The SIRVD death rate has a flatter $\tau$-dependence than the a-posteriori death rate.

5.2. Conditions for Extrema

As before [21] it is straightforward to calculate the first and second time derivatives of the approximative solution (138) as

$$\begin{array}{ccc}\hfill \frac{dj}{d\tau }& =& \eta (1-\eta )\left[e^{-{\int }_0^{\tau }dyb\left(y\right)}-k\left(\tau \right)-b\left(\tau \right)-q\left(\tau \right)\right]\times \hfill \\ & & exp{\int }_0^{\tau }dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-b\left(x\right)-q\left(x\right)\right],\hfill \end{array}$$

(145a)

$$\begin{array}{ccc}\hfill \frac{d^{2}j}{d{\tau }^2}& =& \eta (1-\eta )\left({[e^{-{\int }_0^{\tau }dyb\left(y\right)}-k\left(\tau \right)-b\left(\tau \right)-q\left(\tau \right)]}^2-\frac{dk}{d\tau }-\frac{db}{d\tau }-\frac{dq}{d\tau }-b\left(\tau \right)e^{-{\int }_0^{\tau }dyb\left(y\right)}\right)\times \hfill \\ & & exp{\int }_0^{\tau }dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-b\left(x\right)-q\left(x\right)\right].\hfill \end{array}$$

(145b)

Consequently, extrema of the rate of new infections occur at reduced times ${\tau }_E$ determined by

$$k\left({\tau }_E\right)+b\left({\tau }_E\right)+q\left({\tau }_E\right)=e^{-{\int }_0^{{\tau }_E}dyb\left(y\right)}\le 1,$$

(146)

where we indicate that the right-hand-side of this Equation is smaller than or equal to unity. Hence no extrema of infections occur for a sum of variations

$$k\left(\tau \right)+b\left(\tau \right)+q\left({\tau }_E\right)>1.$$

(147)

In the alternative case of reduced time intervals, where

$$k\left(\tau \right)+b\left(\tau \right)+q\left({\tau }_E\right)<1,$$

(148)

extrema are possible. From Equation (145b) one obtains

$$\begin{array}{ccc}\hfill {\left[\frac{d^{2}j}{d{\tau }^2}\right]}_{{\tau }_E}& =& -\eta (1-\eta )\left({\left[\frac{dk}{d\tau }\right]}_{{\tau }_E}+{\left[\frac{db}{d\tau }\right]}_{{\tau }_E}+\frac{dq}{d\tau }{]}_{{\tau }_E}+b^2\left({\tau }_E\right)+b\left({\tau }_E\right)k\left({\tau }_E\right)+b\left({\tau }_E\right)q\left({\tau }_E\right)\right)\times \hfill \\ & & exp\left[{\int }_0^{{\tau }_E}dx\left(e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-b\left(x\right)-q\left(x\right)\right)\right],\hfill \end{array}$$

(149)

Hence, the extrema are maxima if

$${\left[\frac{dk}{d\tau }\right]}_{{\tau }_E}+{\left[\frac{db}{d\tau }\right]}_{{\tau }_E}+\frac{dq}{d\tau }{]}_{{\tau }_E}+b^2\left({\tau }_E\right)+b\left({\tau }_E\right)k\left({\tau }_E\right)+b\left({\tau }_E\right)q\left({\tau }_E\right)>0$$

(150)

is positive. They are minima if

$${\left[\frac{dk}{d\tau }\right]}_{{\tau }_E}+{\left[\frac{db}{d\tau }\right]}_{{\tau }_E}+\frac{dq}{d\tau }{]}_{{\tau }_E}+b^2\left({\tau }_E\right)+b\left({\tau }_E\right)k\left({\tau }_E\right)+b\left({\tau }_E\right)q\left({\tau }_E\right)<0$$

(151)

is negative. There can be multiple minima and maxima depending on the reduced time variation of the ratios $k\left(\tau \right)$ and $b\left(\tau \right)$. The extreme values of the rate of new infections are given by

$$j_E\left({\tau }_E\right)=\eta (1-\eta )e^{{\int }_0^{{\tau }_E}dx\left[e^{-{\int }_0^{x}dyb\left(y\right)}-k\left(x\right)-b\left(x\right)-q\left(x\right)\right]}.$$

(152)

All results given in this Section for the SIRVD model include as special cases the corresponding quantities in the SIRD model for $b\left(\tau \right)=0$ and the SIR model for $b\left(\tau \right)=q\left(\tau \right)=0$, respectively. The excellent agreement with the respective numerical solutions of the SIR and SIRV models [21,26] has proven the validity of the analytical approximation using the smallness of $J\left(\tau \right)\ll 1$.

6. SIRVD Model Applications

Next we illustrate our results from the preceding section with two examples. While Section 6.1 is concerned with the case of stationary ratios, in Section 6.2 we work out the case of a gradually decreasing fatality rate.

6.1. Special Case: Stationary Ratios

We first consider the approximative solutions (137) and (138) in the special case of stationary ratios

$$\begin{array}{ccc}\hfill k\left(\tau \right)& =& k_0,\hfill \\ \hfill b\left(\tau \right)& =& b_0,\hfill \\ \hfill q\left(\tau \right)& =& q_0\hfill \end{array}$$

(153)

This case corresponds to the numerical solutions of the SIRVD model shown before in Figure 2.

If we introduce ${\kappa }_0=k_0+b_0$ we may use the earlier results of ref. [21] to obtain

$$V\left(\tau \right)=(1-J_{\infty })[1-e^{-b_0\tau }],$$

(154)

and

$$j\left(\tau \right)=\eta (1-\eta )exp\left[\frac{1-e^{-b_0\tau }}{b_0}-({\kappa }_0+b_0)\tau \right].$$

(155)

Provided ${\kappa }_0+b_0=k_0+q_0+b_0<1$, the rate of new infections (155) attains its maximum value

$$\begin{array}{ccc}\hfill j_{\max }& =& j\left({\tau }_m\right)=\eta (1-\eta ){({\kappa }_0+b_0)}^{\frac{{\kappa }_0+b_0}{b_0}}{e}^{\frac{1-({\kappa }_0+b_0)}{b_0}}\hfill \\ & =& \eta (1-\eta ){(k_0+q_0+b_0)}^{\frac{k_0+q_0+b_0}{b_0}}{e}^{\frac{1-(k_0+q_0+b_0)}{b_0}}.\hfill \end{array}$$

(156)

at the reduced time

$${\tau }_m=-\frac{ln(k_0+q_0+b_0)}{b_0}.$$

(157)

For the cumulative fraction one finds

$$\begin{array}{ccc}\hfill J\left(\tau \right)& =& \eta +\eta (1-\eta )b_0^{\frac{{\kappa }_0}{b_0}}{e}^{\frac{1}{b_0}}\left[\gamma \left(1+\frac{{\kappa }_0}{b_0},\frac{1}{b_0}\right)-\gamma \left(1+\frac{{\kappa }_0}{b_0},\frac{e^{-b_0\tau }}{b_0}\right)\right]\hfill \\ & =& \eta +\eta (1-\eta )b_0^{\frac{k_0+q_0}{b_0}}{e}^{\frac{1}{b_0}}\left[\gamma \left(1+\frac{k_0+q_0}{b_0},\frac{1}{b_0}\right)-\gamma \left(1+\frac{k_0+q_0}{b_0},\frac{e^{-b_0\tau }}{b_0}\right)\right]\hfill \end{array}$$

(158)

in terms of the lower incomplete gamma function $\gamma$. For infinitely large times, the fraction (158) approaches the final value

$$J_{\infty }=J(\tau =\infty )=\eta +\eta (1-\eta )b_0^{\frac{k_0+q_0}{b_0}}{e}^{\frac{1}{b_0}}\gamma \left(1+\frac{k_0+q_0}{b_0},\frac{1}{b_0}\right).$$

(159)

Likewise, the SIRVD death rate (143) in this case becomes

$$d\left(\tau \right)=\frac{dD\left(\tau \right)}{d\tau }\simeq \eta (1-\eta )q_{0}exp\left[\frac{1-e^{-b_0\tau }}{b_0}-(k_0+q_0)\tau \right]=q_0{e}^{b_0\tau }j\left(\tau \right)=e^{b_0\tau }{d}_{\mathrm{a}-\mathrm{pos}}\left(\tau \right).$$

(160)

It differs from the a-posteriori death rate by the factor $e^{b_0\tau }$ reflecting the ratio between $I\left(\tau \right)$ and $j\left(\tau \right)$. The rate (160) peaks at the time

$${\tau }_d=-\frac{ln(k_0+q_0)}{b_0},$$

(161)

which is greater than the peak time ${\tau }_m$ of the rate of new infections. The maximum SIRVD death rate

$$d_{\max }=q_0\eta (1-\eta ){(k_0+q_0)}^{\frac{k_0+q_0}{b_0}}{e}^{\frac{1-k_0-q_0}{b_0}}=\frac{e^1}{k_0+q_0}{[1+\frac{b_0}{k_0+q_0}]}^{-[1+\frac{k_0+q_0}{b_0}]}{d}_{\max }^{\mathrm{a}-\mathrm{pos}}$$

(162)

is smaller than the maximum a-posteriori death rate.

The corresponding cumulative fraction of fatalities is given by

$$D\left(\tau \right)=q_0\eta (1-\eta )b_0^{\frac{k_0+q_0-b_0}{b_0}}{e}^{\frac{1}{b_0}}\left[\gamma \left(\frac{k_0+q_0}{b_0},\frac{1}{b_0}\right)-\gamma \left(\frac{k_0+q_0}{b_0},\frac{e^{-b_0\tau }}{b_0}\right)\right],$$

(163)

with the final value

$$D_{\infty }=D(\tau =\infty )=q_0\eta (1-\eta )b_0^{\frac{k_0+q_0-b_0}{b_0}}{e}^{\frac{1}{b_0}}\gamma \left(\frac{k_0+q_0}{b_0},\frac{1}{b_0}\right)$$

$$=\frac{q_0\eta (1-\eta )}{k_0+q_0}\left[b_0^{\frac{k_0+q_0}{b_0}}{e}^{\frac{1}{b_0}}\gamma \left(1+\frac{k_0+q_0}{b_0},\frac{1}{b_0}\right)+1\right].$$

(164)

It has been shown before in Equation (57) of ref. [21] that for small values of $b_0\ll 1$ and $b_0<{\kappa }_0=k_0+q_0<1$ the cumulative fractions as well as their final values have to be calculated with the leading order approximation for large values of $z\gg 1$

$$z^{-{\kappa }_{0}z}\gamma (1+{\kappa }_{0}z,z)\simeq \sqrt{2\pi {\kappa }_{0}z}{\kappa }_0^{{\kappa }_{0}z-1}{e}^{-{\kappa }_{0}z}-1.$$

(165)

Applying this approximation to Equations (159) and (164) with $z=b_0^{-1}$ provides

$$\begin{array}{ccc}\hfill J_{\infty }& \simeq & \eta (1-\eta )\left[\sqrt{\frac{2\pi (k_0+q_0)}{b_0}}{e}^{\frac{1-(k_0+q_0)}{b_0}}{(k_0+q_0)}^{\frac{k_0+q_0}{b_0}-1}-1\right],\hfill \end{array}$$

(166a)

$$\begin{array}{ccc}\hfill D_{\infty }& \simeq & \frac{q_0\eta (1-\eta )}{k_0+q_0}\sqrt{\frac{2\pi (k_0+q_0)}{b_0}}{e}^{\frac{1-(k_0+q_0)}{b_0}}{(k_0+q_0)}^{\frac{k_0+q_0}{b_0}-1}\simeq \frac{1}{k_0+q_0}{D}_{\infty }^{\mathrm{a}-\mathrm{pos}}.\hfill \end{array}$$

(166b)

We note that the ratio $D_{\infty }/D_{\infty }^{\mathrm{a}-\mathrm{pos}}$ does not depend on the value of $b_0$.

These differences are clearly seen in the panels of Figure 10. The SIR, SIRV and SIRD curves, representing a-posteriori death rates, have a significant different reduced time dependence compared to the SIRVD curve. For the values of $k_0=0.5$, $b_0=0.1$ and $q_0=0.1$ shown in Figure 10a,b, the maximum death rate is a factor $1.54$ smaller than the maximum a-posteriori death rate, the final cumulative fraction of fatalities is a factor $1.67$ larger than its a-posteriori value, and the death rate peaks at the earlier time ${\tau }_d=5.1$ as compared to ${\tau }_m=3.6$. The performance of the analytical solution $j\left(\tau \right)$ (155) of the SIRVD model over a wide range of its determining parameters ${\kappa }_0$ and $b_0$ is analyzed in Figure 11.

6.2. Gradually Decreasing Fatality Rate

Here we the approximative solutions (137) and (138) in the special case of stationary ratios $K\left(\tau \right)=k_0$, $b\left(\tau \right)=b_0$ but the gradually decreasing fatality rate

$$q\left(\tau \right)=q_0-q_1(1-e^{-G\tau })$$

(167)

with constants $q_0$, $q_1$ and G. The fatality rate (168) starts from the constant value $q_0$ and decreases with the typical time scale $G^{-1}$ to its final constant value $q_1$. Such a behavior accounts well for the COVID-19 omicron which had a much smaller (about an order of magnitude) fatality rate than the earlier mutants [22] occurring about a year earlier. Such a slow gradual decrease is well captured by the adopted fatality rate (168) in the case $G\ll b_0<1$, allowing us the linear approximation

$$q(\tau \le G^{-1})\simeq q_0-q_{1}G\tau ,$$

(168)

if necessary.

The vaccination rate (154) is independent from the fatality rate $q\left(\tau \right)$ and also also here, whereas with the rate (167) the rate of new infections (138) becomes

$$j\left(\tau \right)\simeq \eta (1-\eta )exp\left[\frac{1-e^{-b_0\tau }}{b_0}-(k_0+b_0+q_0-q_1)\tau -q_1\frac{1-e^{-G\tau }}{G}\right].$$

(169)

Consequently, one finds for Equations (140)–(143)

$$\begin{array}{ccc}\hfill I\left(\tau \right)& =& j\left(\tau \right)e^{b_0\tau }\simeq \eta (1-\eta )exp\left[\frac{1-e^{-b_0\tau }}{b_0}-(k_0+q_0-q_1)\tau -q_1\frac{1-e^{-G\tau }}{G}\right],\hfill \end{array}$$

(170a)

$$\begin{array}{ccc}\hfill R\left(\tau \right)& \simeq & k_{0}I\left(\tau \right)=\eta (1-\eta )k_{0}exp\left[\frac{1-e^{-b_0\tau }}{b_0}-(k_0+q_0-q_1)\tau -q_1\frac{1-e^{-G\tau }}{G}\right],\hfill \end{array}$$

(170b)

$$\begin{array}{ccc}\hfill d\left(\tau \right)& =& [q_0-q_1(1-e^{-G\tau })]\eta (1-\eta )exp\left[\frac{1-e^{-b_0\tau }}{b_0}-(k_0+q_0-q_1)\tau -q_1\frac{1-e^{-G\tau }}{G}\right]\hfill \end{array}$$

(170c)

and

$$D\left(\tau \right)\simeq \eta (1-\eta ){\int }_0^{\tau }dz[q_0-q_1(1-e^{-Gz})]exp\left[\frac{1-e^{-b_{0}z}}{b_0}-(k_0+q_0-q_1)z-q_1\frac{1-e^{-Gz}}{G}\right],$$

(171)

respectively, whereas the cumulative fraction of infections is given by

$$J\left(\tau \right)\simeq \eta +\eta (1-\eta ){\int }_0^{\tau }dzexp\left[\frac{1-e^{-b_{0}z}}{b_0}-(k_0+b_0+q_0-q_1)z-q_1\frac{1-e^{-Gz}}{G}\right].$$

(172)

The analytical expressions are in excellent agreement with the numerical solutions of the SIRVD model in the presence of time-dependent $q\left(\tau \right)$. In Figure 13 we show selected results for $j\left(\tau \right)$ and $d\left(\tau \right)$, while all other quantities are equally well captured.

6.2.1. Peak Times

For values of $k_0+b_0+q_0<1$ the rate of new infections (169) peaks at the time given by

$$e^{-b_0{\tau }_m}-q_1{e}^{-G{\tau }_m}=k_0+b_0+q_0-q_1,$$

(173)

whereas the death rate (170c) attains its maximum at ${\tau }_d$ determined by

$$[q_0-q_1(1-e^{-G{\tau }_d})][e^{-b_0{\tau }_d}-k_0]-q_1(G+2q_0-2q_1)e^{-G{\tau }_d}-{(q_0-q_1)}^2-q_1^2{e}^{-2G{\tau }_d}=0$$

(174)

Both Equations (173)–(174) are nonlinear and cannot be solved in closed form2. However, if we use, as in Equation (168), the approximation $e^{-G{\tau }_{m.d}}\simeq 1-G{\tau }_{m,d}$ Equations (173)–(174) can be approximated as

$$e^{-b_0{\tau }_m}\simeq -q_{1}G{\tau }_m+C_0,C_0=k_0+b_0+q_0,$$

(175)

and

$$(q_0-q_{1}G{\tau }_d)e^{-b_0{\tau }_d}=q_0(k_0+q_0)+q_{1}G-q_{1}G(k_0+2q_0+G){\tau }_d.$$

(176)

This latter equation (176), treated below, is of the form of Wright’s transcendental equation. It is easy to see that Equations (169)–(176) in the limit $q_1=0$ correctly reduce to the earlier results in Section 6.1. The applicability of Equations (175) and (176) requires $G\ll b_0$. Introducing the positive $z_m=b_0{\tau }_m$ and the positive combination $a_m=b_0{C}_0/q_{1}G$ of parameters, the first Equation (175) reads $e^{-z_m}=C_0(1-z_m/a_m)$ and thus determines $z_m$ in terms of $a_m$ and $C_0$. This latter equation is solved in terms of the non-principal Lambert function $W_{-1}$ (see Appendix G in ref. [28]) as

$$z_m=a_m+W_0\left(-\frac{e^{-1/a_m}}{a_m{C}_0}\right),{\tau }_m=\frac{C_0}{q_{1}G}+\frac{1}{b_0}{W}_{-1}\left(-\frac{b_0{e}^{-b_0{C}_0/q_{1}G}}{q_{1}G}\right),$$

(177)

where we have just re-inserted $z_m$ and $a_m$ in the second part of Equation (177).

As detailed in Appendix C the solution of Equation (176) is more involved. As for the calculation of ${\tau }_m$, it is helpful to introduce a dimensionless time $z_d=b_0{\tau }_d$, and to simplify Equation (176) using an appropriate combination of the five semipositive parameters $k_0$, $b_0$, $q_0$, $q_1$, G, and $z_d$. As shown in Appendix C it is possible to write Equation (176) in the form of Wright’s transcendental equation,

$$e^{-X}=1-\frac{2b}{b-a-X},$$

(178)

or equivalently

$$a=-X-bcoth(X/2)$$

(179)

upon introducing X, a, and b via

$$\begin{array}{ccc}\hfill X& =& z_d+ln{C}_1,C_1=k_0+2q_0+G,\hfill \\ \hfill a& =& b-\frac{b_0{q}_0}{q_{1}G}-ln{C}_1,\hfill \\ \hfill b& =& \frac{q_0+(1-q_1/q_0)G}{2C_1}\frac{b_0{q}_0}{q_{1}G},\hfill \end{array}$$

(180)

Since $q_1<q_0$ to ensure positive $q\left(\tau \right)$, one has $b>0$. Further, $a<0$ since $G\ll b_0$. For positive values of b and negative values of a, no solutions to Equation (179) with negative X are possible. This is most easily seen by rewriting this equation as $a+X=bcoth(X/2)$. For negative X, the right hand side is negative, while left hand side is positive. Equation (179) hence implies $X>0$, and $z_d>0$ implies $X>ln{C}_1$. The equation (178) is equivalent to Wright’s transcendental equation and known [29] to exhibit real-valued solutions X only for a limited range of a and b values. Using the x-parametric form of the envelope $a=-x-sinh\left(x\right)$ and $b=-1+cosh\left(x\right)$ [29] we derive the condition

$$a\le -\sqrt{b}\sqrt{2+b}-{cosh}^{-1}(1+b)\equiv a_{\max }\le 0$$

(181)

for the existence of a ${\tau }_d$ value. The $a_{\max }$ monotonically decreases with increasing b, starting from $a_{\max }=0$ and $b=0$.

In Appendix C we obtain the following approximations for the exact solution of Equation (179):

$$\begin{array}{ccc}\hfill X_0& \simeq & \frac{b-a}{2}\left[1-\sqrt{1-\frac{8b}{{(b-a)}^2}}\right]\simeq \frac{2b}{b-a},(X\in [0,1])\hfill \end{array}$$

(182a)

$$\begin{array}{ccc}\hfill X_1& \simeq & -\frac{3a+\sqrt{9a^2-12b(6+b)}}{6+b}(X\in [0,2],a<-\frac{2\sqrt{b(6+b)}}{\sqrt{3}},\hfill \end{array}$$

(182b)

$$\begin{array}{ccc}\hfill X_2& \simeq & \frac{a^2-b^2}{2b}+W_{-1}\left(-\frac{{(a-b)}^2{e}^{-(a^2-b^2)/2b}}{2b}\right),(X<b-a)\hfill \end{array}$$

(182c)

Note that $X_0$ approaches unity for $a=a_{\max }$ and $b\to \infty$, while $X_2\to \infty$ behaves correctly in this limit. As detailed in Appendix C, $X_0$ ist most precise for sufficiently small a well below $a_{\max }$, $X_1$ performs extremely well (Figure 12) over the whole a-b range except very close to $a=a_{\max }$ and large b, while $X_2$ has advantages only in the regime where $X_1$ fails. To summarize, ${\tau }_d$ exists as long as $a<a_{\max }$, and is then well approximated by

$${\tau }_d\simeq \frac{X_1-ln(k_0+2q_0+G)}{b_0}$$

(183)

with a and b expressed in terms of $k_0$, $b_0$, $q_0$, $q_1$, and G via Equation (180). In Figure 13 we mark the analytical ${\tau }_m$ and ${\tau }_d$ for a few cases. As visible, they capture the peak times of the analytical solutions for $j\left(\tau \right)$ (169) and $d\left(\tau \right)$ (170c), that moreover are indistinguishable from the numerical solution. Since it is impossible to visualize the performance of the numerical versus analytical results for the case of time-dependent $q\left(\tau \right)$, characterized by 6 parameters $k_0$, $b_0$, $q_0$, $q_1$, G, and $\eta$, we have randomly chosen sets of parameters with $k_0$, $q_0$, $b_0\in [0,1]$, $q_0\in [0,q_1]$, $G\in [0,b_0]$, and $\eta \in [{10}^{-7},{10}^{-3}$]. The comparison is undertaken in Figure 14.

Figure 12. (a)The exact solution X to Equation (178) or (179) versus $a_{\max }/a$ and $b/(b+1)$ with the negative $a_{\max }$ defined by Equation (181). (b) Approximant $X_1$ given by Equation (182b). It is undefined in the small white region in the top right corner, characterized by $a<-2\sqrt{b(6+b)/3}$. Two contourlines are highlighted in each panel: $X=1$ (dashed black) and $X=2$ (solid black). For the remaining approximants $X_0$ and $X_2$ see Figure A1 in Appendix C.

Figure 12. (a)The exact solution X to Equation (178) or (179) versus $a_{\max }/a$ and $b/(b+1)$ with the negative $a_{\max }$ defined by Equation (181). (b) Approximant $X_1$ given by Equation (182b). It is undefined in the small white region in the top right corner, characterized by $a<-2\sqrt{b(6+b)/3}$. Two contourlines are highlighted in each panel: $X=1$ (dashed black) and $X=2$ (solid black). For the remaining approximants $X_0$ and $X_2$ see Figure A1 in Appendix C.

Figure 13. SIRVD model at time-dependent $q\left(\tau \right)=q_0-q_1(1-e^{-G\tau })$. Analytic $d\left(\tau \right)$ and $j\left(\tau \right)$ coincide basically exactly with the numerical solution. Highlighted are the analytic position and height of the maxima, $({\tau }_m,j_{\max })$, Equations (177), (184) and $({\tau }_d,d_{\max })$, Equations (183), (185). Parameters: (a) $k_0=0.5$, $q_0=0.1$, $b_0=0.1$, $\eta ={10}^{-5}$ and (b) $k_0=0.5$, $q_0=0.2$, $b_0=0.2$, $\eta ={10}^{-5}$. In (a,b) the three colors represent $G=0.5b_0$, $q_1=0.1q_0$ (blue), $G=b_0$, $q_1=0.2q_0$ (red), $G=1.5b_0$, $q_1=0.5q_0$ (yellow).

Figure 13. SIRVD model at time-dependent $q\left(\tau \right)=q_0-q_1(1-e^{-G\tau })$. Analytic $d\left(\tau \right)$ and $j\left(\tau \right)$ coincide basically exactly with the numerical solution. Highlighted are the analytic position and height of the maxima, $({\tau }_m,j_{\max })$, Equations (177), (184) and $({\tau }_d,d_{\max })$, Equations (183), (185). Parameters: (a) $k_0=0.5$, $q_0=0.1$, $b_0=0.1$, $\eta ={10}^{-5}$ and (b) $k_0=0.5$, $q_0=0.2$, $b_0=0.2$, $\eta ={10}^{-5}$. In (a,b) the three colors represent $G=0.5b_0$, $q_1=0.1q_0$ (blue), $G=b_0$, $q_1=0.2q_0$ (red), $G=1.5b_0$, $q_1=0.5q_0$ (yellow).

Figure 14. Since it is impossible to visualize the performance of the numerical versus analytical results for the case of time-dependent $q\left(\tau \right)$, characterized by 6 parameters $k_0$, $b_0$, $q_0$, $q_1$, G, and $\eta$, we have randomly chosen sets of parameters with $k_0$, $q_0$, $b_0\in [0,1]$, $q_0\in [0,q_1]$, $G\in [0,b_0]$, and $\eta \in [{10}^{-7},{10}^{-3}$]. The number of sets is (a) 100 and (b) 5000. In (a) we visualize the performance of analytical versus numerical results for ${\tau }_m$ (177) and ${\tau }_d$ (183), while (b) shows ${\tau }_d$ versus ${\tau }_m$, both numerical valus (red circles) and analytical expressions (black squares). The numerical results suggest ${\tau }_d\ge {\tau }_m$, while this is not reflected by 1.5% of the analytical results.

Figure 14. Since it is impossible to visualize the performance of the numerical versus analytical results for the case of time-dependent $q\left(\tau \right)$, characterized by 6 parameters $k_0$, $b_0$, $q_0$, $q_1$, G, and $\eta$, we have randomly chosen sets of parameters with $k_0$, $q_0$, $b_0\in [0,1]$, $q_0\in [0,q_1]$, $G\in [0,b_0]$, and $\eta \in [{10}^{-7},{10}^{-3}$]. The number of sets is (a) 100 and (b) 5000. In (a) we visualize the performance of analytical versus numerical results for ${\tau }_m$ (177) and ${\tau }_d$ (183), while (b) shows ${\tau }_d$ versus ${\tau }_m$, both numerical valus (red circles) and analytical expressions (black squares). The numerical results suggest ${\tau }_d\ge {\tau }_m$, while this is not reflected by 1.5% of the analytical results.

6.2.2. Maximum Rate of New Infections and Death Rate

With the peak times (177) and (183) inserted in Equations (169) and (170c), respectively, the maximum rates of the new infections and the maximum death rates are given by

$$\begin{array}{ccc}\hfill j_{\max }& =& \eta (1-\eta )e^{\frac{1-k_0-b_0-q_0+q_1}{b_0}-\frac{q_1}{G}}exp\left[\frac{q_1(b_0-G)}{b_{0}G}{e}^{-G{\tau }_m}-(k_0+b_0+q_0-q_1){\tau }_m\right]\hfill \\ & \simeq & \eta (1-\eta )e^{\frac{1-k_0-b_0-q_0+q_1}{b_0}-\frac{q_1}{G}}exp[\frac{q_1(b_0-G)}{b_{0}G}{e}^{-\frac{k_0+b_0+q_0}{q_1}-\frac{G}{b_0}{W}_{-1}(-\frac{b_0{e}^{-b_0(k_0+b_0+q_0)/q_{1}G}}{q_{1}G}})\hfill \\ & & -(k_0+b_0+q_0-q_1)[\frac{k_0+b_0+q_0}{q_1}+\frac{1}{b_0}{W}_{-1}(-\frac{b_0{e}^{-b_0(k_0+b_0+q_0)/q_{1}G}}{q_{1}G})]],\hfill \end{array}$$

(184)

where we made use of the determining Equation (173), and

$$\begin{array}{ccc}\hfill d_{\max }& =& [q_0-q_1(1-e^{-G{\tau }_d})]\eta (1-\eta )e^{\frac{1}{b_0}-\frac{q_1}{G}}exp\left[-\frac{e^{-b_0{\tau }_d}}{b_0}-(k_0+q_0-q_1){\tau }_d+\frac{q_1{e}^{-G{\tau }_d}}{G}\right]\hfill \\ & =& [q_0-q_1(1-{(k_0+2q_0+G)}^{\frac{G}{b_0}}{e}^{-\frac{G{X}_1}{b_0}})]\eta (1-\eta )e^{\frac{1}{b_0}-\frac{q_1}{G}}exp[-\frac{(k_0+2q_0+G)e^{-X_1}}{b_0}\hfill \\ & & -\frac{k_0+q_0-q_1}{b_0}(X_1-ln(k_0+2q_0+G)+\frac{q_1}{G}{(k_0+2q_0+G)}^{\frac{G}{b_0}}{e}^{-\frac{G{X}_1}{b_0}}].\hfill \end{array}$$

(185)

6.2.3. Death Rates

In Figure 15 we compare the death rate (170c) and the a-posteriori death rate (34)

$$d_{\mathrm{a}-\mathrm{pos}}\left(\tau \right)=[q_0-q_1(1-e^{-G\tau })]j\left(\tau \right)$$

(186)

with $j\left(\tau \right)$ from Equation (169) for six different choices of parameters. In each case the analytical death rates agree very well with the corresponding numerical solutions of the SIRVD model proving the accuracy of the analytical approximation.

We observe earlier peak-times for the a-posteriori death rates, following the rate $j\left(\tau \right)$ of newly infected individuals, compared with the SIRVD death rate $d\left(\tau \right)$, following $I\left(\tau \right)$. Additionally, the SIRVD death rates are significantly larger compared with those obtained through the a-posteriori treatment, with direct implications for the corresponding $D_{\infty }$ values. Our predictions for these differences are suitable for being corroborated with past monitored pandemic data on the rate of new infections and the death rates of sufficient quality with negligible underestimation i.e. negligible dark numbers.

7. Summary and Conclusions

We have investigated a special class of exact solutions as well as accurate analytical approximations of the SIRVD and SIRD compartment models. For nonlinear models with a high-dimensional parameter space analytical solutions, exact or accurately approximative, are of high importance and interest: not only as suitable benchmarks for numerical codes, but especially as they allow us to understand the critical behavior of epidemic outbursts as well as the decisive role of certain parameters [30]. For given reduced time variations of the ratios $k\left(\tau \right)$, $q\left(\tau \right)$ and $b\left(\tau \right)$ the SIRVD and SIRD equations represent complicated integro-differential equations for the rate of new infections $j\left(\tau \right)$ as well as the cumulative fraction of infections $J\left(\tau \right)$, or $S\left(\tau \right)$ and $I\left(\tau \right)$. However, the integro-differential equations can also be regarded as simpler determining equations for the sum of ratios $k\left(\tau \right)+q\left(\tau \right)=\kappa \left(\tau \right)$ for given variations of the ratio $b\left(\tau \right)$ and the fraction $S\left(\tau \right)$. This new approach has been used to derive fully exact analytical solutions for the SIRVD and SIRD models. Especially for the SIRD model it is an effective new method to construct a special class of exact solutions depending on two parameters which are chosen as the values of the ratio $\kappa \left(\tau \right)$ at the start ($\kappa (\tau =0)$) and the end ($\kappa (\tau =\infty$) of the epidemic outburst. The new method for the SIRDcase is illustrated in Section 4 for three different choices of the two parameters including a detailed investigation of the properties of the constructed solutions. 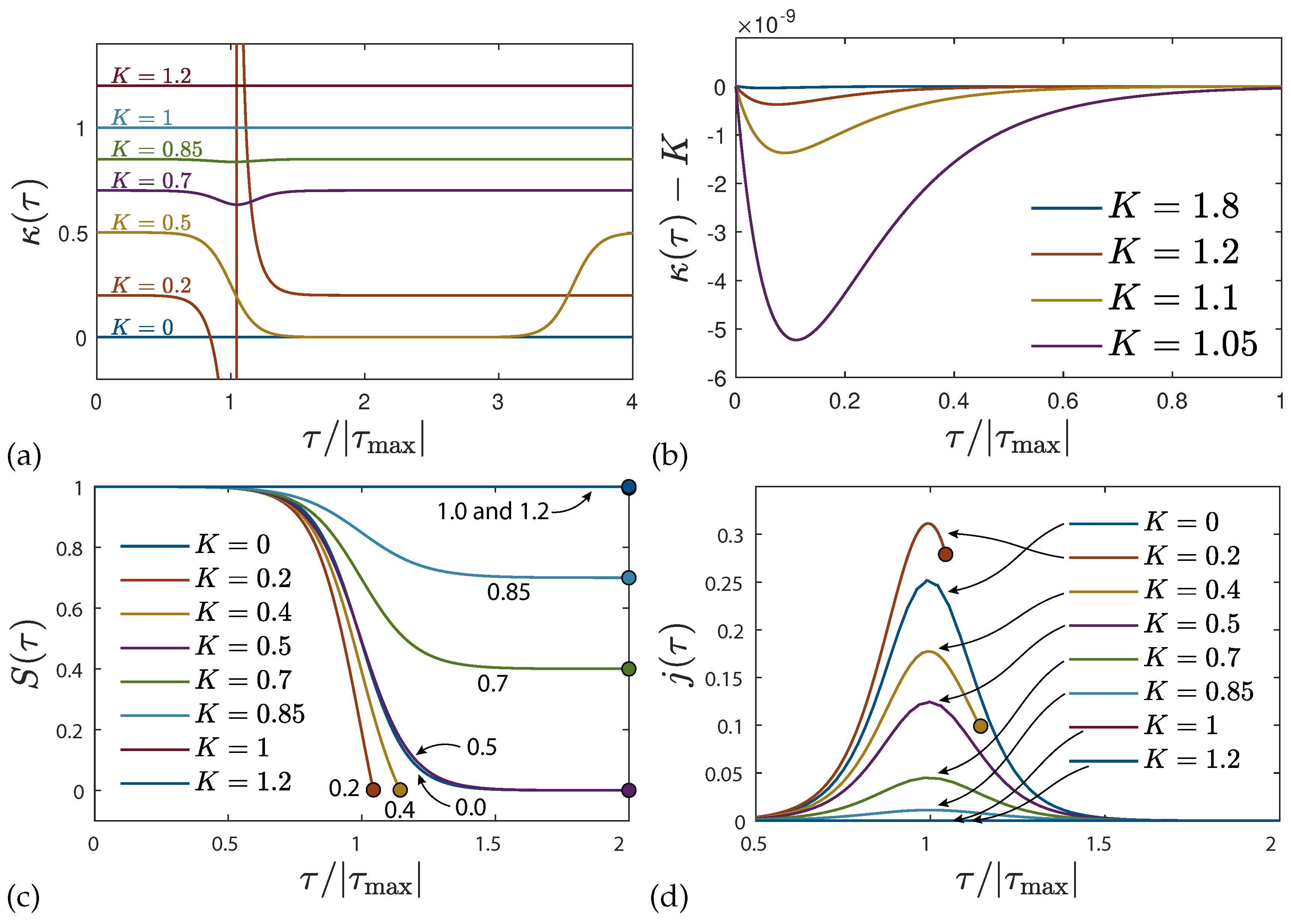Particular interesting are the cases where the combined ratio $\kappa \left(\tau \right)$ at the start and the end of the epidemic outburst have values below $K\le 0.5$ which corresponds to infection rates being twice as large as the sum of the recovery and fatality rate. In this case the epidemic outburst, described by the SI-type ${cosh}^{-2}[(\tau -{\tau }_{\max })/{\tau }_0]$-distribution for the rate of new infections, is so dominated by the rapid infections that at the finite reduced time ${\tau }_{\mathrm{fin}}$ the outburst suddenly terminates as with $S\left({\tau }_{\mathrm{fin}}\right)=0$ no more persons are available to be infected. The situation is comparable to a smooth running car where suddenly the car engine stops as no more fuel is available. For values greater than $K>0.5$ the epidemic outburst lasts until infinitely large times.

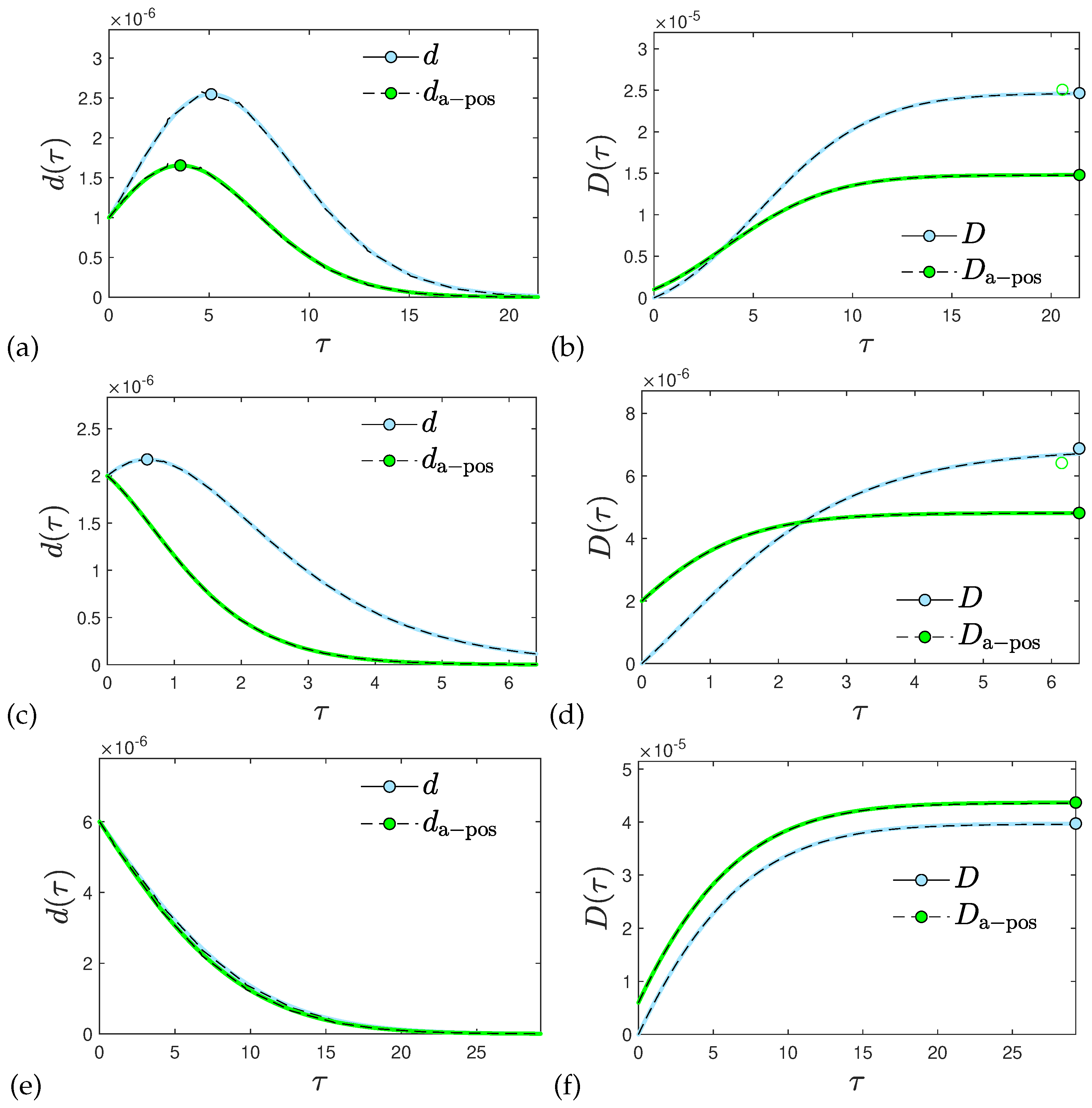
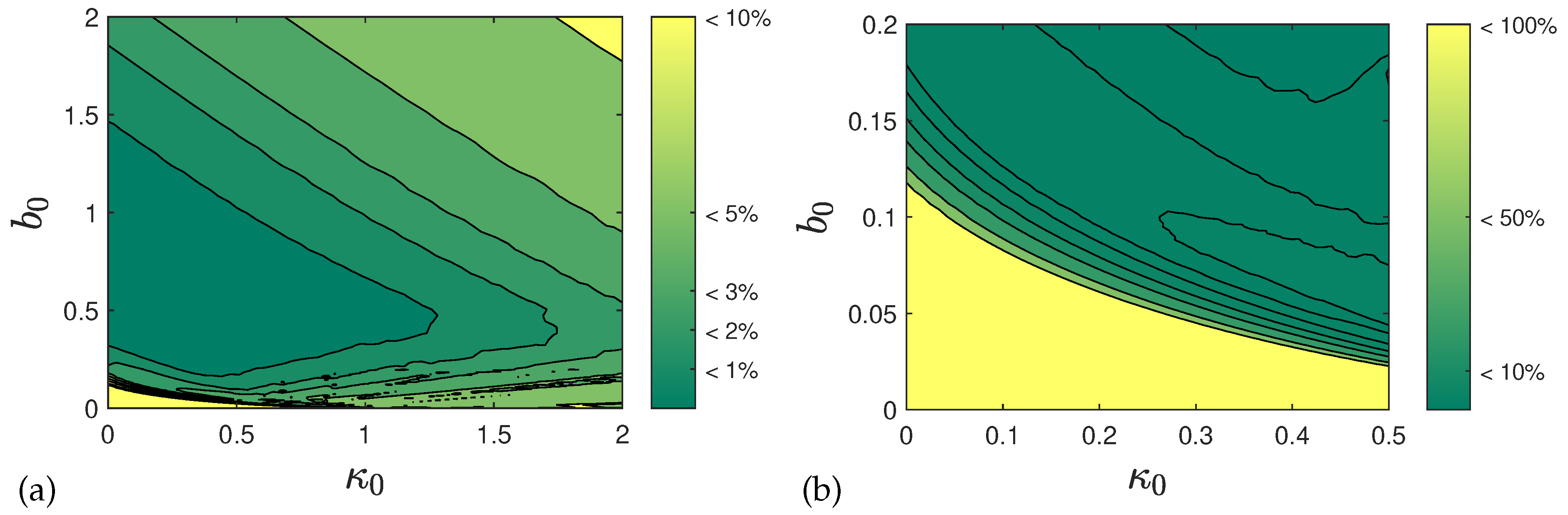
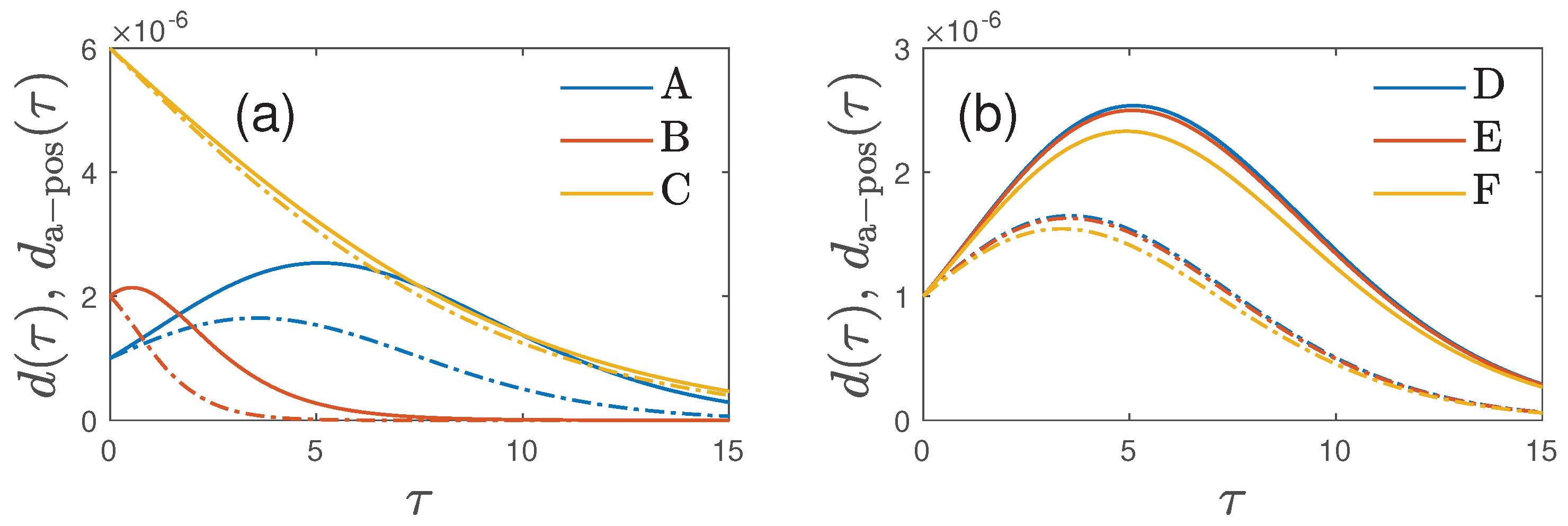
In the second part of the manuscript the recently developed analytical approximation [20,21] for the SIR and SIRV models are applied to the more general SIRVD model. In the limit of small cumulative fractions $J\ll 1$, which very often is fulfilled, this approximation provides accurate analytical expressions for all epidemic quantities of interest such as the rate of new infections $\mathring{J}\left(t\right)$ and the fraction $I\left(t\right)$ of infected persons. As an aside, when determining ${\tau }_d$ in Appendix C we provided accurate approximative solutions to Wright’s transcendental equation (A16), or equivalently, Equation (178). The main difference of the SIRVD to the SIRV model is the discrimination between recovered and deceased persons by introducing two different compartments which affects the calculation of the death rate. In the SIRVD/SIRD cases it is proportional to $I\left(t\right)$, whereas in many SIR models in an a-posteriori approach it is proportional to $\mathring{J}\left(t\right)$. It is shown that the temporal dependence of $I\left(t\right)$ and $\mathring{J}\left(t\right)$ are different when the effect of vaccinations is included and/or when the real time dependence of the fatality rate $\psi \left(t\right)$ and the recovery rate $\mu \left(t\right)$ are different from each other. We illustrate these pronounced differences with two applications: one for stationary ratios $k_0$, $b_0$ and $q_0$, and one for stationray ratios $k_0,b_0$ but a gradually decreasing fatality rate. In our analysis, we observe earlier peak-times for the rate of newly infected individuals compared with death rates. Additionally, our findings indicate significantly smaller death rates compared with those obtained through the a-posteriori treatment. We are hopeful that these differences can be corroborated with past monitored pandemic data on the rate of new infections and the death rates of sufficient quality, with negligible underestimation. We didn’t account for the widely acknowledged 7-day delay between the onset of infection and the resulting death. This delay impacts both the death rate in our SIRVD model and the subsequent a-posteriori death rate analysis in a consistent manner. As a result, the derived difference in peak times remains unchanged.

Appendix C.1. Derivation of X 0

Expanding $e^{-Ay}\simeq 1-Ay$, which requires $y\le A^{-1}$ (or $X\le 1$) we obtain from Equation (A24)

$$y(y-1)\simeq -\frac{2b}{A^2},$$

(A25)

with the two solutions

$$\begin{array}{ccc}\hfill y_1& =& \frac{1-\sqrt{1-8b/A^2}}{2}\simeq \frac{2b}{A^2},\hfill \end{array}$$

(A26a)

$$\begin{array}{ccc}\hfill y_2& =& \frac{1+\sqrt{1-8b/A^2}}{2}\simeq 1-\frac{2b}{A^2}.\hfill \end{array}$$

(A26b)

Because $2b/A^2\ll 1$, since

$$\frac{2b}{A^2}\le \frac{2b}{{(b-a_{\max })}^2}\le \underset{b\to 0}{lim}\frac{2b}{{(b-a_{\max })}^2}=\underset{b\to 0}{lim}\left(\frac{1}{4}-\frac{\sqrt{b}}{4\sqrt{2}}\right)=\frac{1}{4},$$

(A27)

only the solution $y_1$ fulfils the requirement $y_1\le A^{-1}$, corresponding to $(2b/A)\le 1$ which is a valid inequality, as

$$\frac{2b}{A}=\frac{2b}{b-a}\le \frac{2b}{b-a_{\max }}=\frac{2b}{b+\sqrt{b(2+b)+{cosh}^{-1}(1+b)}}\le 1.$$

(A28)

The inequality (A27) therefore also implies that the argument under the square root is positive, $1-8b/A^2>0$. With $X_0=A{y}_1<1$ and $A=b-a$ this completes the derivation of $X_0$ in Equation (182a).

Appendix C.2. Derivation of X 2

Because $y<1$, here we assume $y\ll 1$ and use the approximation ${(1-y)}^{-1}\simeq 1+y$ in Equation (A24) to obtain

$$e^{-Ay}\simeq -\frac{2b}{A}\left(y+1-\frac{A}{2b}\right),$$

(A29)

with the solution

$$y=\frac{A}{2b}-1+\frac{1}{A}{W}_{-1}\left(-\frac{A^2}{2b{e}^{A(\frac{A}{2b}-1)}}\right),$$

(A30)

where $W_{-1}$ is the non-principal branch of Lambert’s W function. For $a<a_{\max }$ stated in Equation (181), the argument of the Lambert function is negative, decreases with increasing b, and resides within the interval $[-1/e,0]$ so that $W_{-1}$ is real-valued and $W_{-1}<-1$ holds. The principal branch $W_0$ of Lambert’s function solves Equation (A29) as well, but can be ruled out by considering the limit $b\to 0$ and $a\to a_{\max }$. In this limit the argument of Lambert’s function evaluates, with $A=b-a$, to

$$\underset{b\to 0}{lim}-\frac{{(b-a_{\max })}^2}{2b{e}^{(b-a_{\max })(\frac{(b-a_{\max })}{2b}-1)}}=-\frac{4}{e^4}.$$

(A31)

On the other hand

$$\underset{b\to 0}{lim}\frac{{(b-a_{\max })}^2}{2b}-b+a_{\max }=4.$$

(A32)

For the argument stated in Equation (A31), Lambert’s functions evaluate to $W_0(-4/e^4)\approx -0.079$ and $W_{-1}(-4/e^4)=-4$, respectively. Since we know that $X=Ay=0$ solves Equation (A23) in the same limit, the principal branch $W_0$ can be ruled out. With $X_2=Ay\ll A$ this completes the derivation of $X_2$ in Equation (182c).

Appendix C.3. Derivation of X 1

Equation (A18), technically divided by $e^Z-1$, can also be written as

$$a=Z+bcoth\left(\frac{Z}{2}\right).$$

(A33)

Here we depart from Wright’s arguments and solve Equation (A33) with asymptotic expansions of the coth-function. For values of $\left|Z\right|\le 2$ we approximate $coth(Z/2)\simeq 2/Z[1+(Z^2/12)]$, so that in this range Equation (A33) reduces to the quadratic

$$\left(1+\frac{b}{6}\right)Z^2-aZ+2b=0,$$

(A34)

with the two solutions

$$Z_{\pm }=\frac{3a\pm \sqrt{9a^2-12b(6+b)}}{6+b}.$$

(A35)

The term under the square root is not strictly semipositive for any $a<a_{\max }$, but $Z_{\pm }$ is real-valued for $a<-2\sqrt{b(6+b)/3}$, which is only slightly below $a_{\max }$; for $b<10$ it is only 3% below $a_{\max }$, giving rise to the tiny white region in top right corner of Figure A1. For this reason the question about the suitable sign in Equation (A35) cannot be answered by considering the limit $b\to 0$ and $a\to a_{\max }$, as before. Instead, consider the following: Inserting $a=Z+\chi sinh\left(Z\right)$ and $b=\chi [cosh(Z)-1]$ solves Equation (A33) for any choice of $\chi$ , i.e., one can write

$$a=Z-\sqrt{b(b+2\chi )},Z=-{cosh}^{-1}\left(\frac{b+\chi }{\chi }\right),$$

(A36)

for positive $\chi$. Using $\chi =1$ we had derived $a_{\max }$. Using $\chi =0$ in Equation (A36) yields $b=0$ and $a=Z$, while the 2nd relation in Equation (A36) in this limit is just the identity $Z=Z$. Inserting this special case of $a=Z$ and $b=0$ into Equation (A35) yields $Z_{\pm }=(Z\pm Z)/2$. As we expect to find $Z_{\pm }=Z$, the suitable solution is $Z_{+}$. With $X_1=-Z_{+}<2$ this completes the derivation of $X_1$ in Equation (182b).

Figure A1. Top row from left to right: The exact solution X to Equation (178) or (179) versus $a_{\max }/a$ and $b/(b+1)$ with the negative $a_{\max }$ defined by Equation (181), approximants $X_{0,a}$, $X_{0,b}$, $X_1$, and $X_2$ given by Equation (182). For any X and b, the exact solution corresponds to $a=-X-bcoth(X/2)$ according to Equation (179). Two contourlines are highlighted in each panel, if they exist: $X=1$ (dashed black) and $X=2$ (solid black). In the $X_1$ panel, the $X_1$ is undefined in the small white region in the top right corner, defined by $a<-2\sqrt{b(6+b)/3}$. In the $X_2$ panel, the $X_2$ cannot be evaluated numerically in the yellow region which is characterized by $X>1$ and $a>a_{\max }/2$. Bottom row from left to right: The relative deviation $\Delta X$ between approximants $X_{0,a}$, $X_{0,b}$, $X_1$ and $X_2$ and the exact numerical solution X, again versus $a_{\max }/a$ and $b/(b+1)$. The color scale ranges from blue (relative deviation below 1%, to yellow (relative deviation above 10%). Approximant $X_1$ performs very well except in the tiny top right corner (large b, a close to $a_{\max }$), where $X_2$ has some advantage.

Figure A1. Top row from left to right: The exact solution X to Equation (178) or (179) versus $a_{\max }/a$ and $b/(b+1)$ with the negative $a_{\max }$ defined by Equation (181), approximants $X_{0,a}$, $X_{0,b}$, $X_1$, and $X_2$ given by Equation (182). For any X and b, the exact solution corresponds to $a=-X-bcoth(X/2)$ according to Equation (179). Two contourlines are highlighted in each panel, if they exist: $X=1$ (dashed black) and $X=2$ (solid black). In the $X_1$ panel, the $X_1$ is undefined in the small white region in the top right corner, defined by $a<-2\sqrt{b(6+b)/3}$. In the $X_2$ panel, the $X_2$ cannot be evaluated numerically in the yellow region which is characterized by $X>1$ and $a>a_{\max }/2$. Bottom row from left to right: The relative deviation $\Delta X$ between approximants $X_{0,a}$, $X_{0,b}$, $X_1$ and $X_2$ and the exact numerical solution X, again versus $a_{\max }/a$ and $b/(b+1)$. The color scale ranges from blue (relative deviation below 1%, to yellow (relative deviation above 10%). Approximant $X_1$ performs very well except in the tiny top right corner (large b, a close to $a_{\max }$), where $X_2$ has some advantage.