Submitted:
22 February 2024
Posted:
23 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Preliminaries
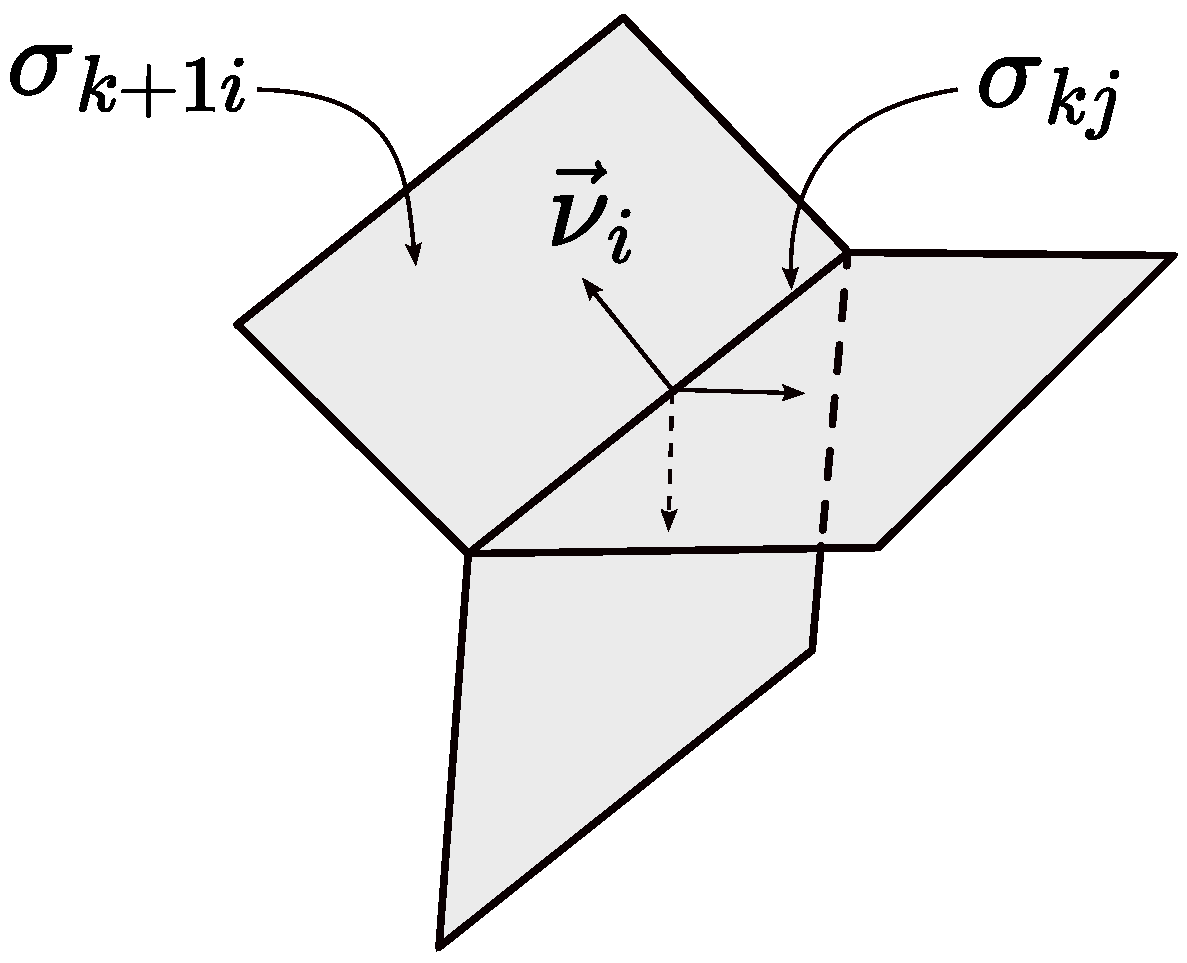
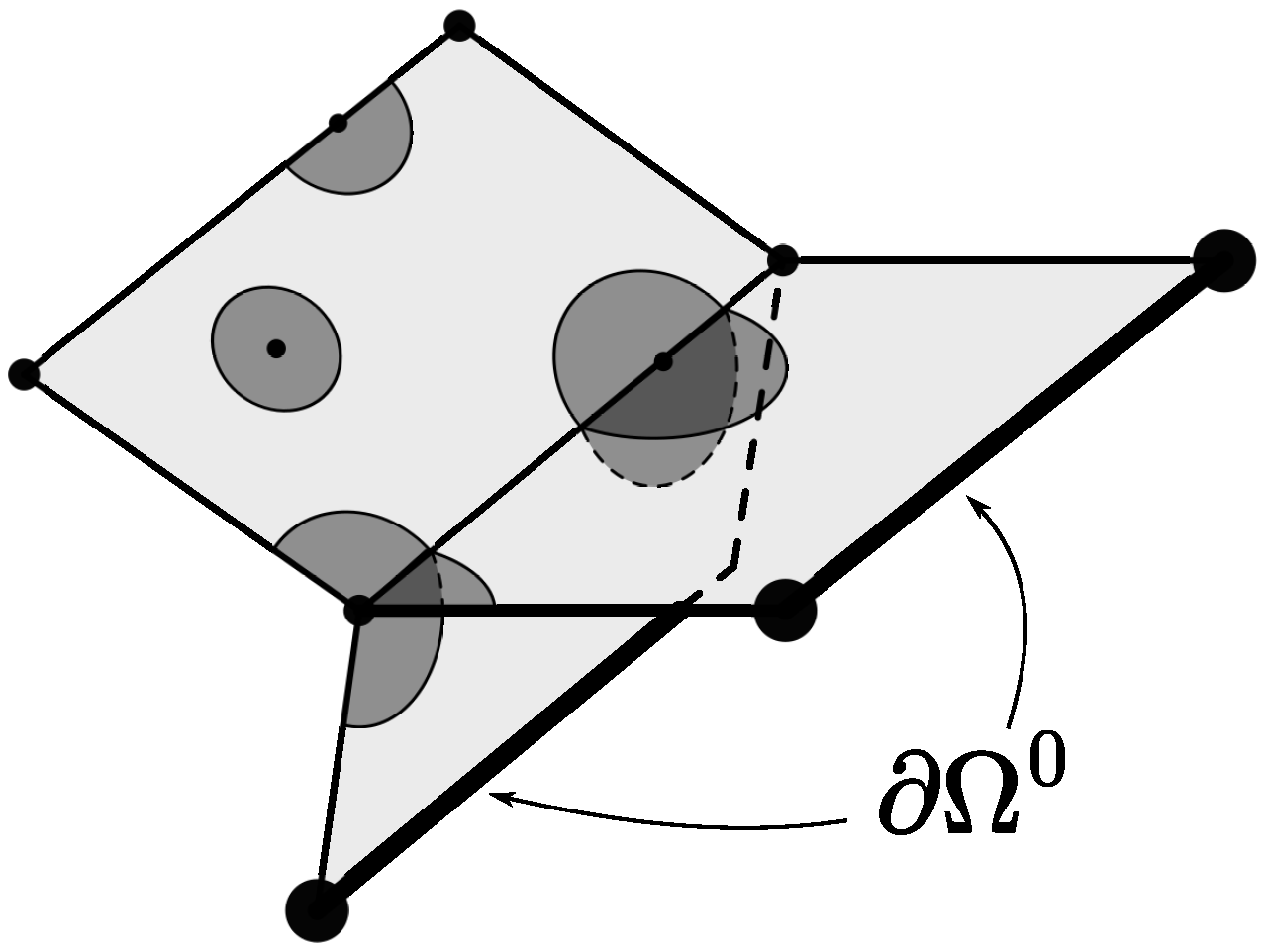
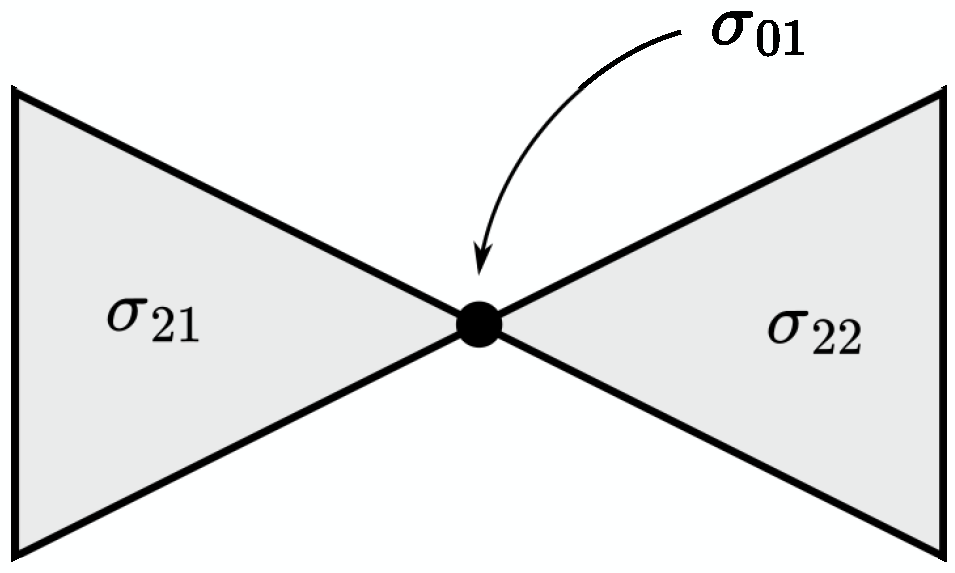
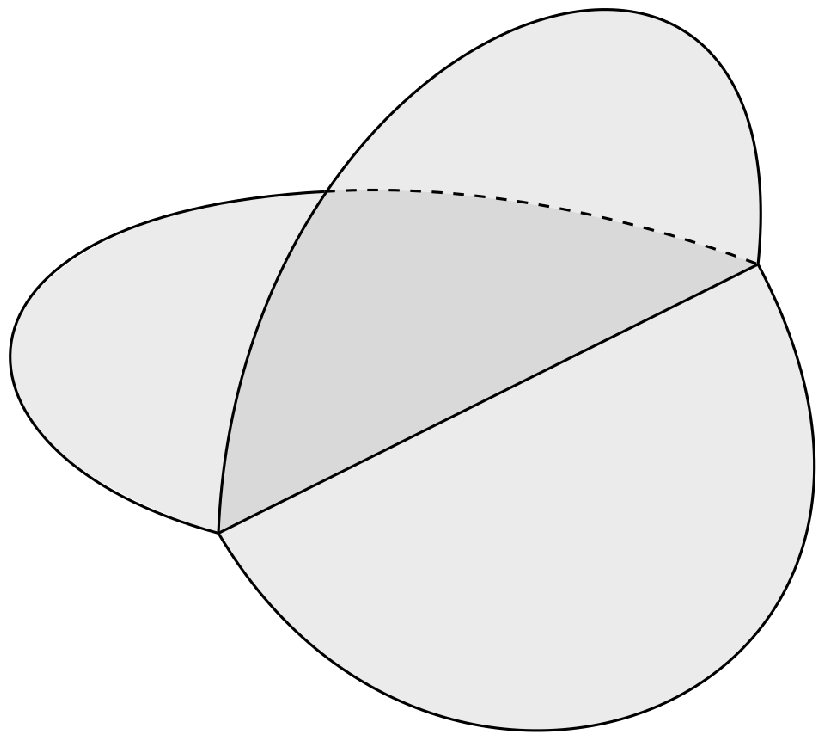
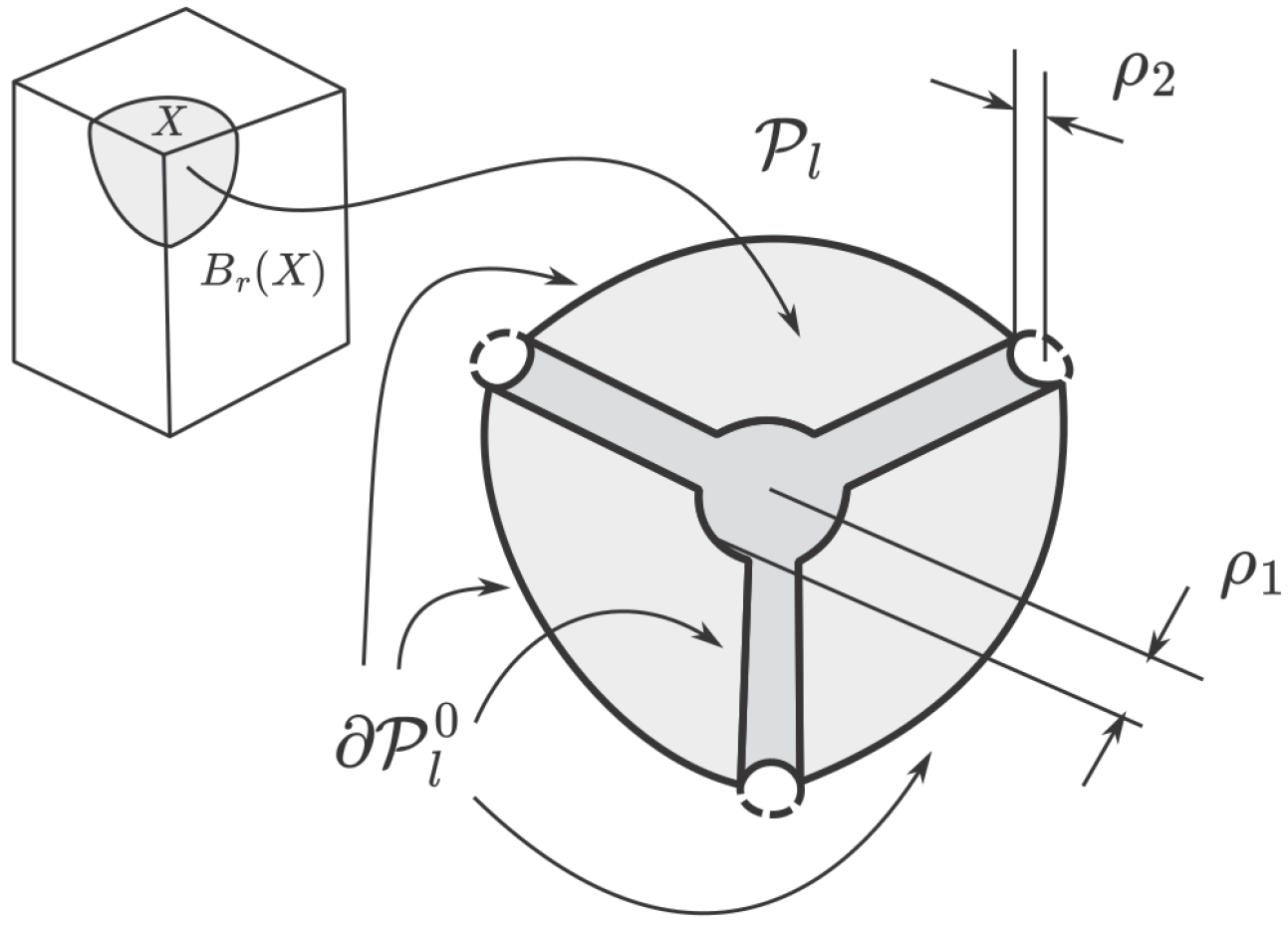
2.1. Stratified Sets
- the closure of every stratum is compact and the boundary is the union of some strata in ;
- for any two strata the intersection of their closures either is empty or consists of some strata in .
2.2. Stratified Measure
2.3. Divergence and Laplacian
- u is continuous on U;
- for every free stratum the restriction is twice continuously differentiable and the gradient of the restriction has a continuous extension to each point of any interior stratum contiguous to .
2.4. Mean Value Theorem and Harnack’s Inequality
3. Removable Singularity Theorem
3.1. Statement
4. Proof of Lemma 3
4.1. Gradient Estimate
4.2. Gradient Flux
4.3. Proof of Lemma 3
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nicaise, S.; Penkin, O. Poincaré–Perron’s method for the Dirichlet problem on stratified sets. J. of Math. An. and Appl. 2004, 296, 504–520. [Google Scholar] [CrossRef]
- Dairbekov, N.S.; Penkin, O.M.; Sarybekova, L.O. An analog of the Sobolev inequality on a stratified set. St. Petersburg Math. J. 2019, 30(5), 869–875. [Google Scholar] [CrossRef]
- Dairbekov, N.S.; Penkin, O.M.; Sarybekova, L.O. The Poincaré inequality and p-connectedness of a stratified Set. Sib. Math. J. 2018, 59, 1024–1033. [Google Scholar] [CrossRef]
- Pham, F. Introduction a l’étude topologique des singularités de Landau; Gauthier-Villars Éditeur: Paris, France, 1967. [Google Scholar]
- Penkin, O.M. About a geometrical approach to multistructures and some qualitative properties of solutions. In Partial Differential Equations on Multistructures; Lecture Notes in Pure and Applied Mathematics, 219; Marcel Dekker Inc: NY, United States, 2001; pp. 183–191. [Google Scholar]
- Penkin, O.M.; Pokorny, Y.V. On incompatible inequalities for elliptic equations on stratified sets. Differ. Equ. 1998, 34, 1111–1117. [Google Scholar]
- Oshchepkova, S.N.; Penkin, O.M. The mean-value theorem for elliptic operators on stratified sets. Math. Notes 2007, 81, 365–372. [Google Scholar] [CrossRef]
- Dairbekov, N.S.; Penkin, O.M.; Savasteev, D.V. Harnack’s inequality for harmonic functions on stratified sets. Sib. Math. J. 2023, 64, 1137–1144. [Google Scholar] [CrossRef]
- Gilbarg, D.; Trudinger, N.S. Elliptic Partial Differential Equations of Second Order; Springer: Berlin, Heidelberg, New York, 2001. [Google Scholar] [CrossRef]
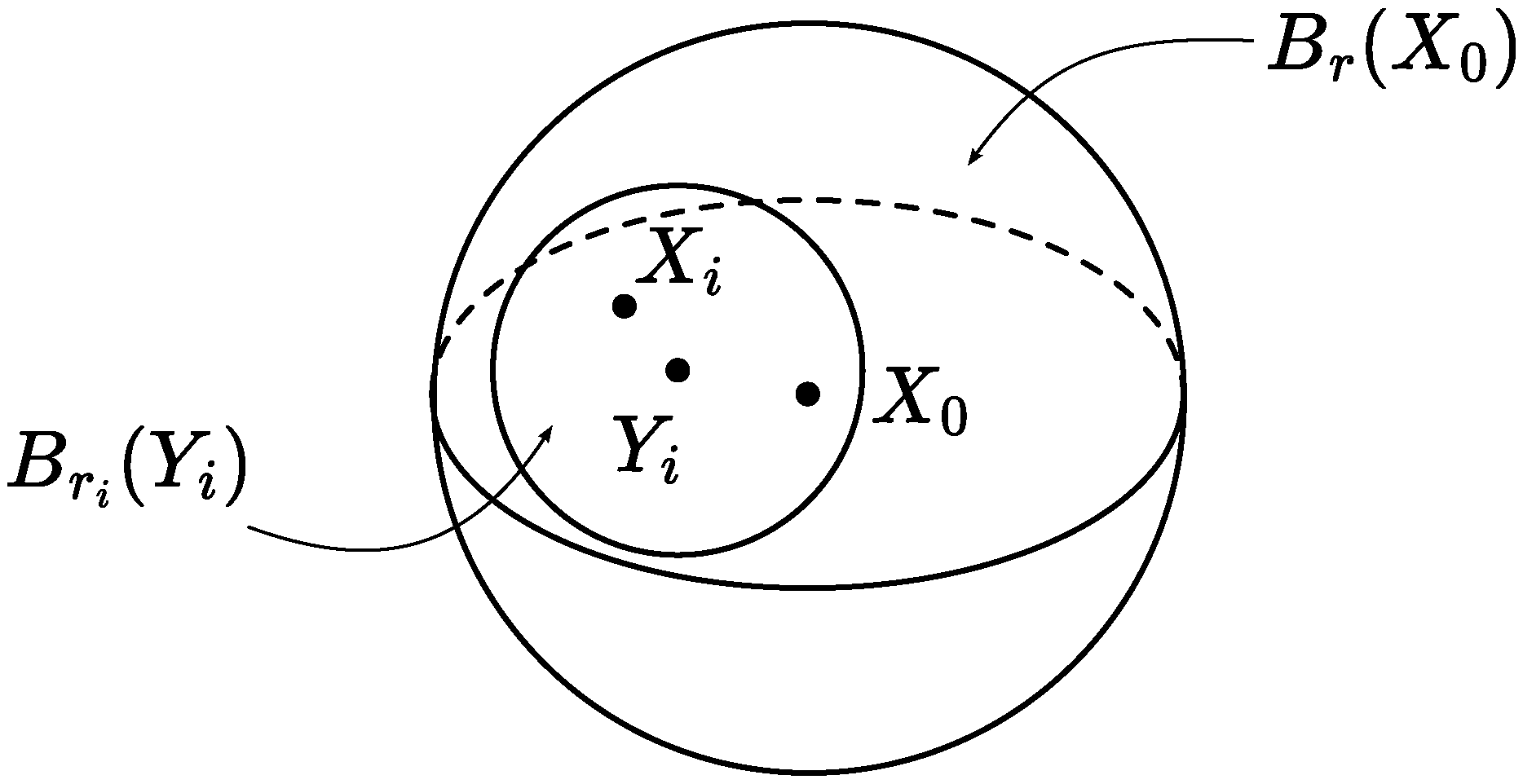
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



