Initial Coefficients Bounds for Bi-univalent Functions Related to Gregory Coefficients

1. Definitions and preliminaries

Let $\mathcal{A}$ denote the class of all analytic functions f defined in the open unit disk $\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$ and normalized by the conditions $f\left(0\right)=0$ and $f^{\prime }\left(0\right)=1$. Thus, each $f\in \mathcal{A}$ has a Taylor–Maclaurin series expansion of the form

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n,z\in \mathbb{D}.$$

(1)

Further, let $\mathcal{S}$ denote the class of all functions $f\in \mathcal{A}$ which are univalent in $\mathbb{D}$.

Let the functions f and g be analytic in $\mathbb{D}$. We say that the function f is subordinate to g, written as $f\left(z\right)\prec g\left(z\right)$, if there exists a function $\varpi$, which is analytic in $\mathbb{D}$ with

$$\varpi \left(0\right)=0\mathrm{and}\left|\varpi \right(z\left)\right|<1,z\in \mathbb{D},$$

such that

$$f\left(z\right)=g\left(\varpi \right(z\left)\right),z\in \mathbb{D}.$$

Besides, if the function g is univalent in $\mathbb{D}$, then the following equivalence holds:

$$f\left(z\right)\prec g\left(z\right)\iff f\left(0\right)=g\left(0\right)\mathrm{and}f\left(\mathbb{D}\right)\subset g\left(\mathbb{D}\right).$$

It is well known that every function $f\in \mathcal{S}$ has an inverse $f^{-1}$, defined by

$$f^{-1}\left(f\left(z\right)\right)=z,z\in \mathbb{D},$$

and

$$f\left(f^{-1}\left(w\right)\right)=w,\left|w\right|<r_0\left(f\right),r_0\left(f\right)\ge \frac{1}{4}.$$

Suppose that $f^{-1}$ has an analytic continuation to $\mathbb{D}$. Then, the function f is said to be bi-univalent in $\mathbb{D}$ if both f and $f^{-1}$ are univalent in $\mathbb{D}$. In this case let

$$g\left(w\right):=f^{-1}\left(w\right)=w-a_2{w}^2+\left(2a_2^2-a_3\right)w^3-\left(5a_2^3-5a_2{a}_3+a_4\right)w^4+\cdots ,$$

(2)

and let $\Sigma$ denote the class of bi-univalent functions in $\mathbb{D}$ given by (1). Examples of functions in the class $\Sigma$ are, for example

$$\frac{z}{1-z},log\frac{1}{1-z},log\sqrt{\frac{1+z}{1-z}.}$$

However, the familiar Koebe function is not a member of $\Sigma$, while other common examples of analytic functions in $\mathbb{D}$ such

$$\frac{2z-z^2}{2}\mathrm{and}\frac{z}{1-z^2}$$

are also not members of $\Sigma$. Lewin [1] investigated the bi-univalent function class $\Sigma$ and showed that $|a_2|<1.51$. Subsequently, Brannan and Clunie [2] conjectured that $|a_2|<\sqrt{2}$. Netanyahu [3], on the other hand, showed that $\underset{f\in \Sigma }{max}\left|a_2\right|=4/3$. The coefficient estimate problem for each of the Taylor–Maclaurin coefficients $|a_n|$ for $n\in \mathbb{N}$, $n\ge 3$, is presumably still an open problem.

Similar to the familiar subclasses ${\mathcal{S}}^{*}\left(\rho \right)$ and $\mathcal{K}\left(\rho \right)$ of starlike and convex function of order $\rho$, $0\le \rho <1$, respectively, Brannan and Taha [4] (see also [5]) introduced certain subclasses of the bi-univalent function class $\Sigma$, namely the subclasses ${\mathcal{S}}_{\Sigma }^{*}\left(\rho \right)$ and ${\mathcal{K}}_{\Sigma }\left(\rho \right)$ of bi-starlike functions and of bi-convex functions of order $\rho$, $0\le \rho <1$, respectively. For each of the function classes ${\mathcal{S}}_{\Sigma }^{*}\left(\rho \right)$ and ${\mathcal{K}}_{\Sigma }\left(\rho \right)$ they found non-sharp estimates of the first two Taylor–Maclaurin coefficients $|a_2|$ and $|a_3|$. In fact, Srivastava et al. [6] have actually revived the study of analytic and bi-univalent functions in recent years for some intriguing examples of functions and characterization of the class $\Sigma$ (see [6,7,8,9,10,11,12,13,14]).

The Fekete-Szegő functional $\left|a_3-\mu a_2^2\right|$ for $f\in \mathcal{S}$ is well known for its rich history in the field of Geometric Function Theory. Its origin was in the disproof by Fekete and Szegő [15] conjecture of Littlewood and Paley, that the coefficients of odd univalent functions are bounded by unity. This functional has since received great attention, particularly for many subclasses of the family of univalent functions. The problem of finding the sharp bounds for this functional of any compact family of functions $f\in \mathcal{S}$ for any complex $\mu$ is commonly known as the classical Fekete-Szegő problem (or inequality).

Gregory coefficients ${\Lambda }_n$. Gregory coefficients also known as reciprocal logarithmic numbers, Bernoulli numbers of the second kind, or Cauchy numbers of the first kind, are the decrease rational numbers ${\displaystyle \frac{1}{2}},-{\displaystyle \frac{1}{12}},{\displaystyle \frac{1}{24}},-{\displaystyle \frac{19}{720}},\cdots$. They occur in the Maclaurin series expansion of the reciprocal logarithm

$$\frac{z}{log(1+z)}=1+\frac{1}{2}z-\frac{1}{12}{z}^2+\frac{1}{24}{z}^3-\frac{19}{720}{z}^4+\cdots ,z\in \mathbb{D}.$$

These numbers are named after James Gregory who introduced them in 1670 in the numerical integration context. They were subsequently rediscovered by many mathematicians and often appear in works of modern authors, Laplace, Mascheroni, Fontana, Bessel, Clausen, Hermit, Pearson and Fisher.

In this paper we considered the generating function of the Gregory coefficients ${\Lambda }_n$ (see [16,17]) to be given by

$$\begin{array}{cc}\hfill \mathfrak{G}\left(z\right)& =\frac{z}{log(1+z)}=\sum _{n=0}^{\infty }{\Lambda }_n{z}^n\hfill \\ \hfill & =1+\frac{1}{2}z-\frac{1}{12}{z}^2+\frac{1}{24}{z}^3-\frac{19}{720}{z}^4+\frac{3}{160}{z}^5-\frac{863}{60480}{z}^6+\cdots ,z\in \mathbb{D}.\hfill \end{array}$$

where the function log is considered at the main branch, that is $log1=0$. Clearly, ${\Lambda }_n$ for some values of $n\in \mathbb{N}$ are

$${\Lambda }_0=1,{\Lambda }_1=\frac{1}{2},{\Lambda }_2=-\frac{1}{12};{\Lambda }_3=\frac{1}{24},{\Lambda }_4=-\frac{19}{720},{\Lambda }_5=\frac{3}{160},\mathrm{and}{\Lambda }_6=-\frac{863}{60480},$$

Finding the upper bound for the Taylor coefficients have been one of the vital topic of research in Geometric function theory as it offers numerous properties for many subclasses of As. Therefore, we will be inquisitive about the subsequent hassle in this segment: find $sup|a_n|$ if $n=2,3,\cdots$ for subclasses of univalent functions. In particular, bound for the second one coefficient offers growth and distortion theorems for features of those subclasses. Further, the use of the Hankel determinants (which also deals with the bounds of the coefficients), and we mention that Cantor [18] proved that “if ratio of two bounded analytic features in $\mathbb{D}$, then the function is rational”.

2. Coefficient bounds of the class ${\mathfrak{HG}}_{\Sigma }$

In 2010 Srivastava et al. [6] have actually revived the study of analytic and bi-univalent functions. Inspired by that, in this section we consider the class of analytic bi-univalent function relating with generating function of the Gregory coefficients to obtain initial coefficients $|a_2|$ and $|a_3|$.

Definition 1.

A function $f\in \Sigma$ given by (1) is said to be in the class ${\mathfrak{HG}}_{\Sigma }$ if the following subordinations

$$\begin{array}{ccc}& & f^{\prime }\left(z\right)\prec \mathfrak{G}\left(z\right),\hfill \end{array}$$

(3)

$$\begin{array}{ccc}& & g^{\prime }\left(w\right)\prec \mathfrak{G}\left(w\right)\hfill \end{array}$$

(4)

are satisfied, and the function $g\left(w\right)=f^{-1}\left(w\right)$ is defined by (2).

Remark 1.

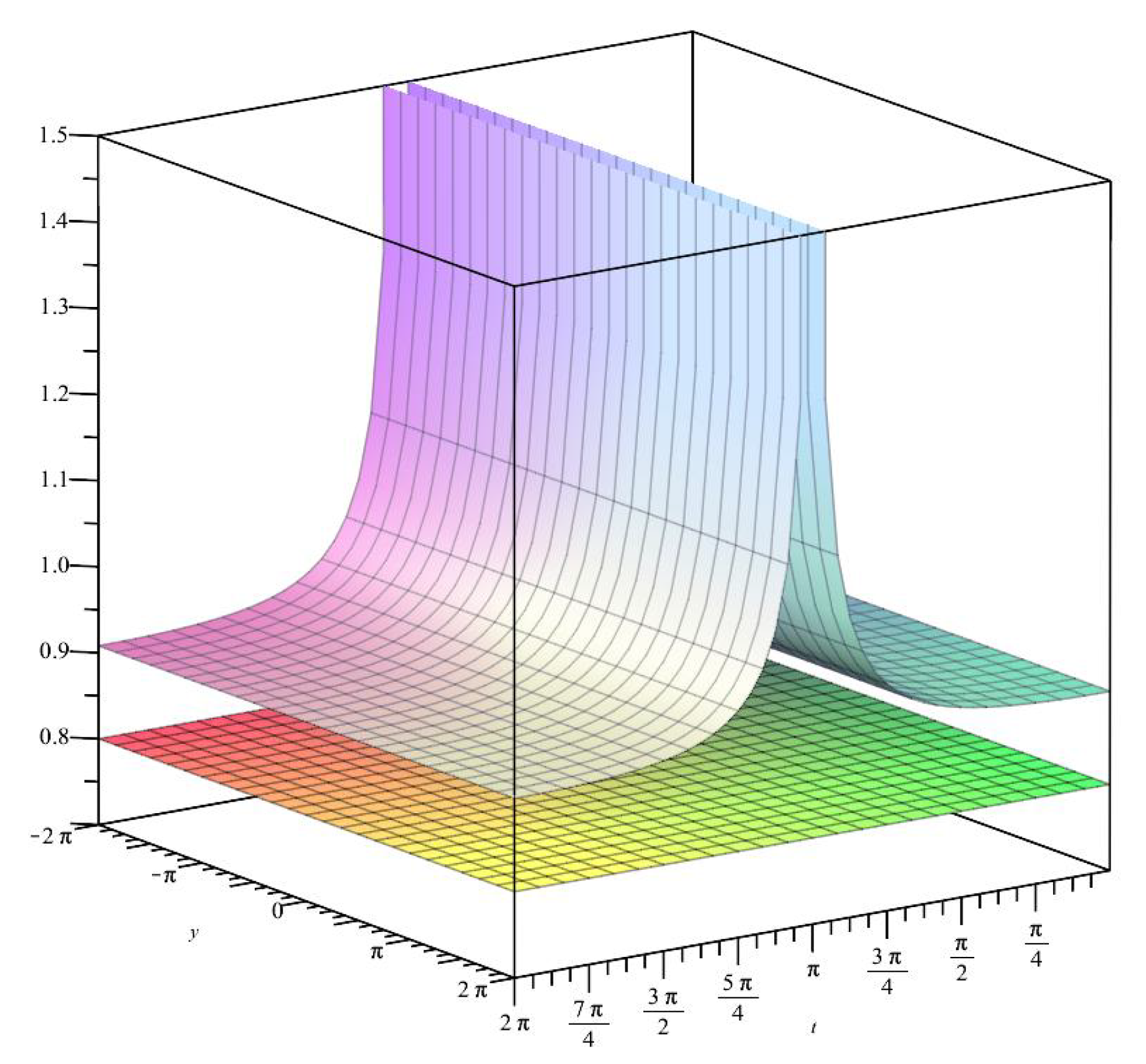
1. For the function $\mathfrak{G}$ we have $\mathfrak{G}\left(0\right)=1$, ${\mathfrak{G}}^{\prime }\left(0\right)\ne 0$, and using the 3D plot of the MAPLE™ computer software, we obtain that the image of the open unit disk $\mathbb{D}$ by the function

$$\mathrm{U}\left(z\right):=Re\frac{z{\mathfrak{G}}^{\prime }\left(z\right)}{\mathfrak{G}\left(z\right)-1},z\in \mathbb{D},$$

is positive, hence $\mathfrak{G}$ is a starlike (and also univalent) function with respect to the point 1 (see Figure 1).

2. We would like to emphasize that the class ${\mathfrak{HG}}_{\Sigma }$ is not empty. Thus, if we consider $f_{*}\left(z\right)={\displaystyle \frac{z}{1-az}}$, $\left|a\right|\le 1$, then it is easy to check that $f_{*}\in \mathcal{S}$, and moreover, $f_{*}\in \Sigma$ with $g_{*}\left(w\right)=f_{*}^{-1}\left(w\right)={\displaystyle \frac{w}{1+aw}}$.

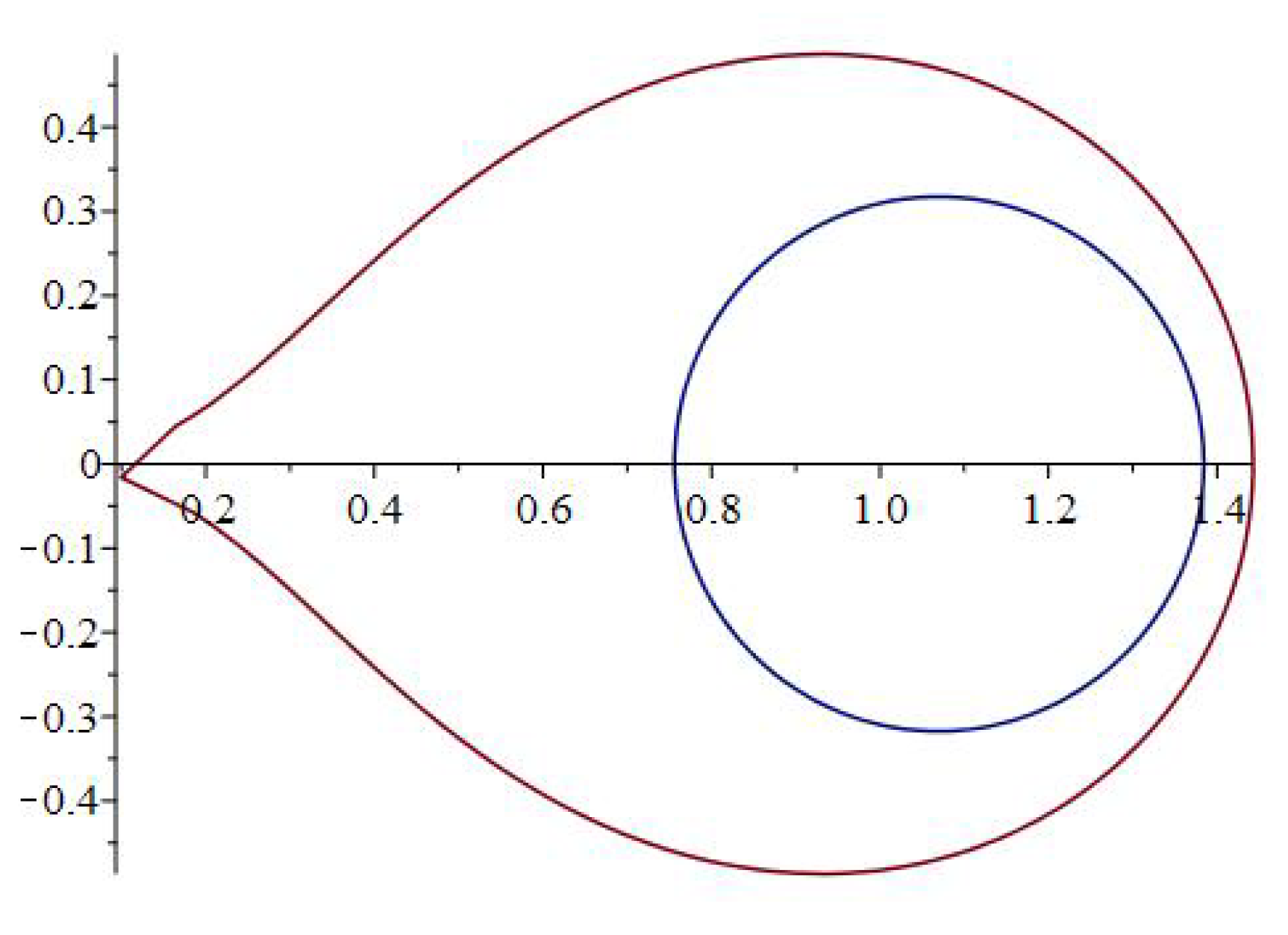
Using the fact that $f_{*}^{\prime }(-az)=g_{*}^{\prime }\left(az\right)$ for all $z\in \mathbb{D}$ it follows that $f_{*}^{\prime }\left(\mathbb{D}\right)=g_{*}^{\prime }\left(\mathbb{D}\right)$. For the particular case $a=0.15$, using the2D plotof the MAPLE™ computer software we obtain the image of the boundary $\partial \mathbb{D}$ by the functions $f_{*}^{\prime }$, $g_{*}^{\prime }$ and $\mathfrak{G}$ shown in the Figure 2. Since $\mathfrak{G}$ is univalent in $\mathbb{D}$, the previous reason yields that the subordinations $f_{*}^{\prime }\left(z\right)\prec \mathfrak{G}\left(z\right)$ and $g_{*}^{\prime }\left(w\right)\prec \mathfrak{G}\left(w\right)$ hold whenever $f_{*}^{\prime }\left(0\right)=g_{*}^{\prime }\left(0\right)=\mathfrak{G}\left(0\right)$ and $f_{*}^{\prime }\left(\mathbb{D}\right)=g_{*}^{\prime }\left(\mathbb{D}\right)\subset \mathfrak{G}\left(\mathbb{D}\right)$ (see Figure 2). Concluding, $f_{*}\in {\mathfrak{HG}}_{\Sigma }$, hence the class ${\mathfrak{HG}}_{\Sigma }$ is not empty and contains other functions than the identity.

In our first results we obtain the upper bounds for the modules of the first two coefficients for the functions that belong to the class ${\mathfrak{HG}}_{\Sigma }$ given in Definition 1. Further, we use the following lemmas, which were introduced by Zaprawa in [19,20] and we will discuss the Fekete-Szegő functional problems [15].

Let $\mathcal{P}\left(\beta \right)$, with $0\le \beta <1$, denotes the class of analytic functions p in $\mathbb{D}$ with $p\left(0\right)=1$ and $Rep\left(z\right)>\beta$, $z\in \mathbb{D}$. Especially, we will use the notation $\mathcal{P}$ instead of $\mathcal{P}\left(0\right)$ for the usual Carathéodory’s class of functions.

The next two lemmas will be used in our studies.

Lemma 1.

[21] If $p\in \mathcal{P}$ has the form $p\left(z\right)=1+c_{1}z+c_2{z}^2+\cdots$, $z\in \mathbb{D}$, then

$$|c_n|\le 2,n\ge 1,$$

(5)

and this inequality is sharp for each $n\in \mathbb{N}$.

We mention that this inequality is the well-known result for the Carathéodory Lemma [21] (see also [22, Corollary 2.3, p. 41], 23, Carathéodory’s Lemma, p. 41]).

The second lemma is a generalization of Lemma 6 from [20] that could be obtained for $l=1$:

Lemma 2.

[20, Lemma 7, p. 2] Let $k,l\in \mathbb{R}$ and $z_1,z_2\in \mathbb{C}$. If $|z_1|<R$ and $|z_2|<R$, then

$$|(k+l)z_1+(k-l)z_2|\le \left\{\begin{array}{ccc}2\left|k\right|R,\hfill & \mathrm{for}\hfill & \left|k\right|\ge \left|l\right|,\hfill \\ 2\left|l\right|R,\hfill & \mathrm{for}\hfill & \left|k\right|\le \left|l\right|.\hfill \end{array}\right.$$

The next result gives the upper bounds for the first two coefficients of the functions that belong to ${\mathfrak{HG}}_{\Sigma }$.

Theorem 1.

If $f\in {\mathfrak{HG}}_{\Sigma }$ is given by (1), then

$$\left|a_2\right|\le \sqrt{\frac{3}{74}}\simeq 0.0234\cdots ,\mathrm{and}\left|a_3\right|\le \frac{23}{111}\simeq 0.2072\cdots .$$

Proof. 

If $f\in {\mathfrak{HG}}_{\Sigma }$, from the Definition 1 the subordinations (3) and (4) hold. Then, there exists an analytic function u in $\mathbb{D}$ with $u\left(0\right)=0$ and $\left|u\right(z\left)\right|<1$, $z\in \mathbb{D}$, such that

$$f^{\prime }\left(z\right)=\mathfrak{G}\left(u\left(z\right)\right),z\in \mathbb{D},$$

(6)

and an analytic function v in $\mathbb{D}$ with $v\left(0\right)=0$ and $\left|v\right(w\left)\right|<1$, $w\in \mathbb{D}$, such that

$$g^{\prime }\left(w\right)=\mathfrak{G}\left(v\left(w\right)\right),w\in \mathbb{D}.$$

(7)

Therefore, the function

$$h\left(z\right)=\frac{1+u\left(z\right)}{1-u\left(z\right)}=1+c_{1}z+c_2{z}^2+\cdots ,z\in \mathbb{D},$$

belongs to the class $\mathcal{P}$, hence

$$u\left(z\right)=\frac{c_1}{2}z+\left(c_2-\frac{c_1^2}{2}\right)\frac{z^2}{2}+\left(c_3-c_1{c}_2+\frac{c_1^3}{4}\right)\frac{z^3}{2}+\cdots ,z\in \mathbb{D},$$

and

$$\begin{array}{c}\mathfrak{G}\left(u\left(z\right)\right)=1+\frac{c_1}{4}z+\frac{1}{48}\left(-7c_1^2+12c_2\right)z^2+\frac{1}{192}\left(17c_1^3-56c_1{c}_2+48c_3\right)z^3+\cdots ,\hfill \\ \hfill z\in \mathbb{D}.\end{array}$$

(8)

Similarly, the function

$$k\left(w\right)=\frac{1+v\left(w\right)}{1-v\left(w\right)}=1+d_{1}w+d_2{w}^2+\cdots ,w\in \mathbb{D},$$

belongs to the class $\mathcal{P}$, therefore

$$v\left(w\right)=\frac{d_1}{2}w+\left(d_2-\frac{d_1^2}{2}\right)\frac{w^2}{2}+\left(d_3-d_1{d}_2+\frac{d_1^3}{4}\right)\frac{w^3}{2}+\cdots ,w\in \mathbb{D},$$

and

$$\begin{array}{c}\mathfrak{G}\left(v\left(w\right)\right)=1+\frac{d_1}{4}w+\frac{1}{48}\left(-7d_1^2+12d_2\right)w^2+\frac{1}{192}\left(17d_1^3-56d_1{d}_2+48d_3\right)w^3+\cdots ,\hfill \\ \hfill w\in \mathbb{D}.\end{array}$$

(9)

From the equalities (6) and (7) we obtain that

$$f^{\prime }\left(z\right)=1+\frac{c_1}{4}z+\frac{1}{48}\left(-7c_1^2+12c_2\right)z^2+\cdots ,z\in \mathbb{D},$$

(10)

and

$$g^{\prime }\left(w\right)=1+\frac{d_1}{4}w+\frac{1}{48}\left(-7d_1^2+12d_2\right)w^2+\cdots ,w\in \mathbb{D}.$$

(11)

Since the function g has the form (2), upon comparing the corresponding coefficients in (10) and (11) we get

$$\begin{array}{ccc}& & 2a_2=\frac{c_1}{4},\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& & 3a_3=\frac{c_2}{4}-\frac{7}{48}{c}_1^2,\hfill \end{array}$$

(13)

$$\begin{array}{ccc}& & -2a_2=\frac{d_1}{4},\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & 3\left(2a_2^2-a_3\right)=\frac{d_2}{4}-\frac{7}{48}{d}_1^2.\hfill \end{array}$$

(15)

From (12) and (14) it follows that

$$c_1=-d_1$$

(16)

and

$$c_1^2+d_1^2=128a_2^2.$$

(17)

If we add the equalities (13) and (15) we get

$$6a_2^2=\frac{1}{4}\left(c_2+d_2\right)-\frac{7}{48}\left(c_1^2+d_1^2\right),$$

(18)

and substituting the value of $\left(c_1^2+d_1^2\right)$ from (17) in the right hand side of (18) we deduce that

$$a_2^2=\frac{3(c_2+d_2)}{296}.$$

(19)

Using (5) together with the triangle’s inequality in the relations (12) and (19) it follows

$$\left|a_2\right|\le \frac{1}{4}=0.25\mathrm{and}\left|a_2\right|\le \sqrt{\frac{3}{74}}\simeq 0.0234\cdots$$

that proves our first result.

Moreover, if we subtract (15) from (13) we obtain

$$6\left(a_3-a_2^2\right)=\frac{1}{4}(c_2-d_2)-\frac{7}{48}\left(c_1^2-d_1^2\right),$$

(20)

and in view of (16) the equality (20) becomes

$$a_3=a_2^2+\frac{1}{24}\left(c_2-d_2\right).$$

(21)

This relation combined with (12) leads to

$$a_3=\frac{c_1^2}{64}+\frac{1}{24}\left(c_2-d_2\right).$$

(22)

Using the triangle’s inequality and (5), from (22) we get

$$\left|a_3\right|\le \frac{1}{16}+\frac{1}{6}=\frac{11}{48}\simeq 0.2291\cdots$$

and using our first assertion together with (21) it follows

$$\left|a_3\right|\le \frac{3}{74}+\frac{1}{6}=\frac{23}{111}\simeq 0.2072\cdots ,$$

which completes the proof of our theorem. □

Using the above values for $a_2^2$ and $a_3$ we will prove the following Fekete–Szegő type inequality for the functions of the class ${\mathfrak{HG}}_{\Sigma }$.

Theorem 2.

If $f\in {\mathfrak{HG}}_{\Sigma }$ is given by (1), then for any $\mu \in \mathbb{R}$ the next inequality holds:

$$\left|a_3-\mu a_2^2\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{1}{6}},\hfill & \mathrm{for}\hfill & \mu \in \left[-{\displaystyle \frac{28}{9}},{\displaystyle \frac{46}{9}}\right],\hfill \\ {\displaystyle \frac{3|1-\mu |}{74}},\hfill & \mathrm{for}\hfill & \mu \in \left(-\infty ,-{\displaystyle \frac{28}{9}}\right]\cup \left[{\displaystyle \frac{46}{9}},+\infty \right).\hfill \end{array}\right.$$

Proof. 

If $f\in {\mathfrak{HG}}_{\Sigma }$ has the form (1), from (19) and (21) we get

$$a_3-\mu a_2^2=\left(1-\mu \right)\frac{3(c_2+d_2)}{296}+\frac{1}{24}\left(c_2-d_2\right)=\left(h\left(\mu \right)+\frac{1}{24}\right)c_2+\left(h\left(\mu \right)-\frac{1}{24}\right)d_2,$$

where

$$h\left(\mu \right)=\frac{3(1-\mu )}{296}.$$

According to Lemma 1 we have $\left|c_2\right|\le 2$ and we have $\left|d_2\right|\le 2$. Then, in view of Lemma 2 we obtain

$$\left|a_3-\mu a_2^2\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{1}{6}},\hfill & \mathrm{for}\hfill & \left|h\left(\mu \right)\right|\le {\displaystyle \frac{1}{24}},\hfill \\ 4\left|h\right(\mu \left)\right|,\hfill & \mathrm{for}\hfill & \left|h\left(\mu \right)\right|\ge {\displaystyle \frac{1}{24}},\hfill \end{array}\right.$$

which is equivalent to our result. □

3. Coefficient bounds for the class ${\mathfrak{GM}}_{\Sigma }\left(\mu \right)$

In the second results we will obtain the upper bounds for the modules of the first two coefficients for the functions that belong to the class ${\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ defined below, then we will study the Fekete-Szegő functional problems for this functions class.

Definition 2.

A function $f\in \Sigma$ given by (1) is said to be in the class ${\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ if the following subordinations hold:

$$\begin{array}{ccc}& & \Phi \left(z\right):=\left(1-\mu \right)\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}+\mu \left(1+\frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}\right)\prec \mathfrak{G}\left(z\right),\hfill \end{array}$$

(23)

$$\begin{array}{ccc}& & \Psi \left(w\right):=\left(1-\mu \right)\frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}+\mu \left(1+\frac{w{g}^{\prime \prime }\left(w\right)}{g^{\prime }\left(w\right)}\right)\prec \mathfrak{G}\left(w\right),\hfill \end{array}$$

(24)

where $0\le \mu \le 1$ and $g\left(w\right)=f^{-1}\left(w\right)$ is defined by (2).

By fixing $\mu =0$ or $\mu =1$, we have the following special subclasses:

Remark 2.

1. For $\mu =0$ let ${\mathfrak{GS}}_{\Sigma }:={\mathfrak{GM}}_{\Sigma }\left(0\right)$ the subclass of functions $f\in \Sigma$ satisfying

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}\prec \mathfrak{G}\left(z\right)\mathrm{and}\frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}\prec \mathfrak{G}\left(w\right),$$

with $g\left(w\right)=f^{-1}\left(w\right)$.

Fixing $\mu =1$ let ${\mathfrak{GV}}_{\Sigma }:={\mathfrak{GM}}_{\Sigma }\left(1\right)$ the subclass of functions $f\in \Sigma$ that satisfy

$$1+\frac{z{f}^{\prime \prime }\left(z\right)}{f^{\prime }\left(z\right)}\prec \mathfrak{G}\left(z\right)\mathrm{and}1+\frac{w{g}^{\prime \prime }\left(w\right)}{g^{\prime }\left(w\right)}\prec \mathfrak{G}\left(w\right),$$

where $g\left(w\right)=f^{-1}\left(w\right)$.

Remark 3.

We will prove that appropriate choice of the parameter μ the class ${\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ is not empty. Letting $f_{*}\left(z\right)={\displaystyle \frac{z}{1-az}}$, $\left|a\right|\le 1$, then it easily follows that $f_{*}\in \mathcal{S}$, and additionally, $f_{*}\in \Sigma$ with $g_{*}\left(w\right)=f_{*}^{-1}\left(w\right)={\displaystyle \frac{w}{1+aw}}$.

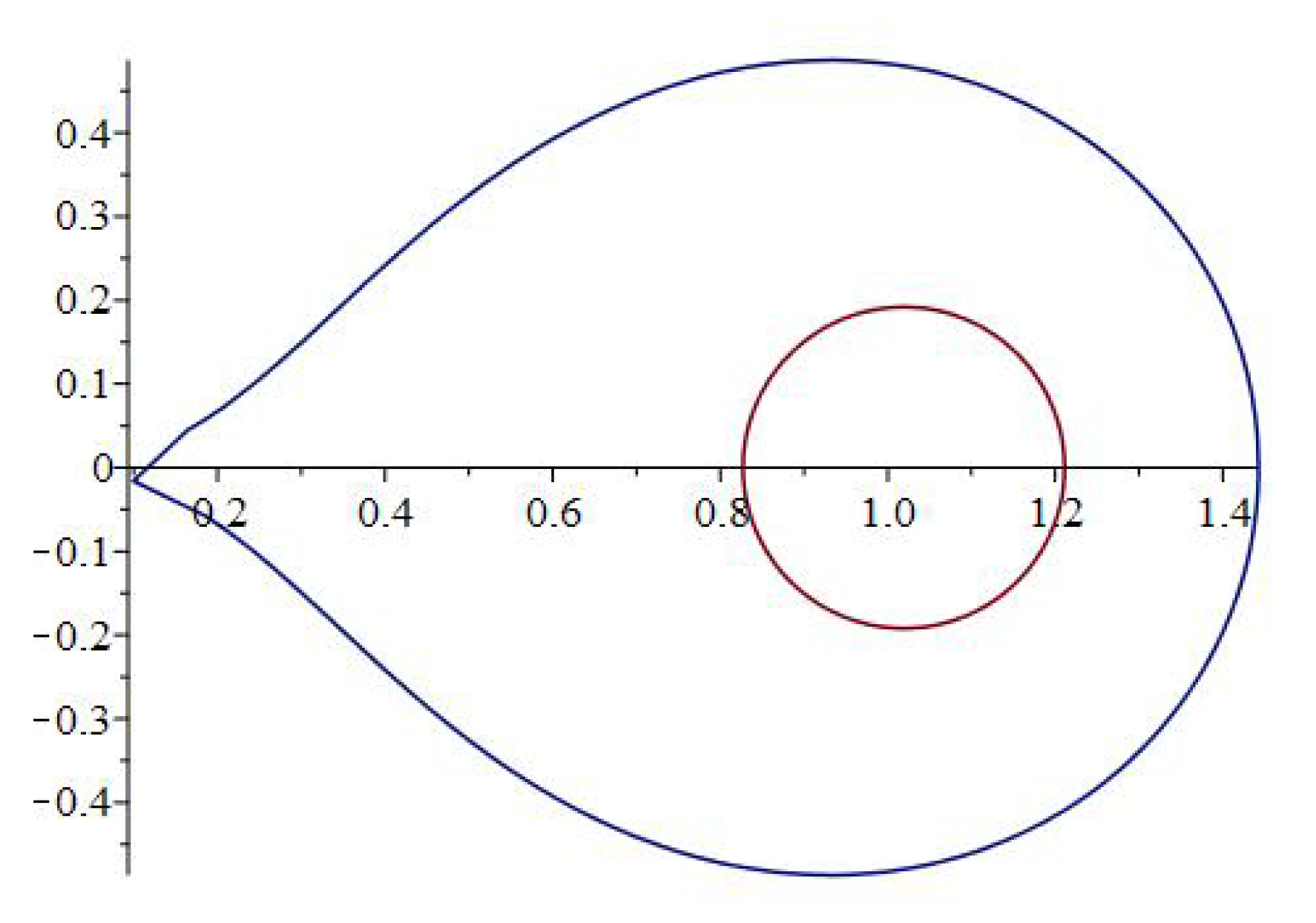
With the notations of (23) and (24) a simple computation shows that $\Phi (-az)=\Psi \left(az\right)$ for all $z\in \mathbb{D}$, which implies that $\Phi \left(\mathbb{D}\right)=\Psi \left(\mathbb{D}\right)$. Taking the particular case $a=0.15$ and $\mu =0.9$, by using the2D plotof the MAPLE™ computer software we obtain the image of the boundary $\partial \mathbb{D}$ by the functions Φ, Ψ and $\mathfrak{G}$ presented in the Figure 3. Using the fact that $\mathfrak{G}$ is univalent in $\mathbb{D}$, the above reasons show that the subordinations $\Phi \left(z\right)\prec \mathfrak{G}\left(z\right)$ and $\Psi \left(w\right)\prec \mathfrak{G}\left(w\right)$ hold whenever $\Phi \left(0\right)=\Psi \left(0\right)=\mathfrak{G}\left(0\right)$ and $\Phi \left(\mathbb{D}\right)=\Psi \left(\mathbb{D}\right)\subset \mathfrak{G}\left(\mathbb{D}\right)$ (see Figure 3). Therefore, $f_{*}\in {\mathfrak{GM}}_{\Sigma }\left(0.9\right)$, hence the class ${\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ is not empty and contains other functions than the identity.

Theorem 3.

If $f\in {\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ is given by (1), then

$$|a_2|\le \sqrt{\frac{3}{2(1+\mu )(10+7\mu )}}\mathrm{and}\left|a_3\right|\le \frac{7{\mu }^2+29\mu +16}{4(1+\mu )(10+7\mu )(1+2\mu )}.$$

Proof. 

If $f\in {\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ has the form (1), from the Definition 2, for some analytic functions in $\mathbb{D}$ namely u and v such that $u\left(0\right)=v\left(0\right)=0$ and $\left|u\right(z\left)\right|<1$, $\left|v\right(w\left)\right|<1$ for all $z,w\in \mathbb{D}$, we can write

$$\left(1-\mu \right)\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}+\mu \left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)=\mathfrak{G}\left(u\left(z\right)\right),z\in \mathbb{D},$$

(25)

and

$$\left(1-\mu \right)\frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}+\mu \left(1+\frac{w{g}^{″}\left(w\right)}{g^{\prime }\left(w\right)}\right)=\mathfrak{G}\left(v\left(w\right)\right),w\in \mathbb{D}.$$

(26)

From the equalities (25) and (26) combined with (8) and (9) we obtain

$$\left(1-\mu \right)\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}+\mu \left(1+\frac{z{f}^{″}\left(z\right)}{f^{\prime }\left(z\right)}\right)=1+\frac{c_1}{4}z+\frac{1}{48}\left(-7c_1^2+12c_2\right)z^2+\cdots ,z\in \mathbb{D},$$

(27)

and

$$\left(1-\mu \right)\frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}+\mu \left(1+\frac{w{g}^{″}\left(w\right)}{g^{\prime }\left(w\right)}\right)=1+\frac{d_1}{4}w+\frac{1}{48}\left(-7d_1^2+12d_2\right)w^2+\cdots ,w\in \mathbb{D}.$$

(28)

Thus, upon equating the first coefficients of (27) and (28) we have

$$\begin{array}{ccc}& & \left(1+\mu \right)a_2=\frac{c_1}{4},\hfill \end{array}$$

(29)

$$\begin{array}{ccc}& & 2\left(1+2\mu \right)a_3-\left(1+3\mu \right)a_2^2=\frac{1}{48}\left(-7c_1^2+12c_2\right),\hfill \end{array}$$

(30)

$$\begin{array}{ccc}& & -\left(1+\mu \right)a_2=\frac{d_1}{4},\hfill \end{array}$$

(31)

$$\begin{array}{ccc}& & \left(3+5\mu \right)a_2^2-2\left(1+2\mu \right)a_3=\frac{1}{48}\left(-7d_1^2+12d_2\right).\hfill \end{array}$$

(32)

From (29) and (31) it follows that

$$c_1=-d_1$$

(33)

and

$$2{\left(1+\mu \right)}^2{a}_2^2=\frac{c_1^2+d_1^2}{16},$$

(34)

that is

$$a_2^2=\frac{c_1^2+d_1^2}{32{\left(1+\mu \right)}^2}.$$

(35)

If we add (30) and (32) we get

$$2\left(1+\mu \right)a_2^2=\frac{1}{4}\left(c_2+d_2\right)-\frac{7}{48}\left(c_1^2+d_1^2\right),$$

(36)

and substituting the value of $\left(c_1^2+d_1^2\right)$ from (34) in the right hand side of (36) we deduce that

$$\frac{2}{3}\left[3\left(1+\mu \right)+7{(1+\mu )}^2\right]a_2^2=\frac{c_2+d_2}{4},$$

that is

$$a_2^2=\frac{3(c_2+d_2)}{8\left[3(1+\mu )+7{(1+\mu )}^2\right]}=\frac{3(c_2+d_2)}{8(1+\mu )(10+7\mu )}.$$

(37)

From the same reasons like in the proof of Theorem 1, using (5) in (29), (35) and (37) we find that

$$\left|a_2\right|\le \frac{1}{2(1+\mu )}=:A\left(\mu \right)\mathrm{and}\left|a_2\right|\le \sqrt{\frac{3}{2(1+\mu )(10+7\mu )}}=:B\left(\mu \right).$$

A simple computation shows that $A\left(\mu \right)>B\left(\mu \right)$ whenever $0\le \mu \le 1$, hence we obtain our first inequality.

Moreover, if we subtract (30) from (32) we obtain

$$4\left(1+2\mu \right)\left(a_3-a_2^2\right)=\frac{c_2-d_2}{4}-\frac{7}{48}\left(c_1^2-d_1^2\right).$$

(38)

In view of (33) and (35) the relation (38) becomes

$$a_3=\frac{c_1^2+d_1^2}{32{\left(1+\mu \right)}^2}+\frac{c_2-d_2}{16\left(1+2\mu \right)},$$

(39)

and using the triangle’s inequality together with (5) we conclude that

$$\left|a_3\right|\le \frac{1}{4{\left(1+\mu \right)}^2}+\frac{1}{4\left(1+2\mu \right)}=\frac{{\mu }^2+4\mu +2}{4{(1+\mu )}^2(1+2\mu )}=:C\left(\mu \right).$$

Also, taking into the account the relation (35) the formula (39) could be rewritten as

$$a_3=a_2^2+\frac{c_2-d_2}{16\left(1+2\mu \right)},$$

(40)

and from the triangle’s inequality together with (5) using the fact that $|a_2|\le B\left(\mu \right)$ it follows

$$\left|a_3\right|\le \frac{3}{2(1+\mu )(10+7\mu )}+\frac{1}{4\left(1+2\mu \right)}=\frac{7{\mu }^2+29\mu +16}{4(1+\mu )(10+7\mu )(1+2\mu )}=:D\left(\mu \right).$$

Since it’s easy to check that $C\left(\mu \right)>D\left(\mu \right)$ for $0\le \mu \le 1$, our second inequality is proved. □

The next result gives us an upper bound for the fekete–Szegő functional for the class ${\mathfrak{GM}}_{\Sigma }\left(\mu \right)$.

Theorem 4.

If $f\in {\mathfrak{GM}}_{\Sigma }\left(\mu \right)$ is given by (1), then

$$\left|a_3-k{a}_2^2\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{1}{4(1+2\mu )}},\hfill & \mathrm{for}\hfill & \left|{\rm Y}\left(k\right)\right|\le {\displaystyle \frac{1}{16\left(1+2\mu \right)}},\hfill \\ 4\left|{\rm Y}\left(k\right)\right|,\hfill & \mathrm{for}\hfill & \left|{\rm Y}\left(k\right)\right|\ge {\displaystyle \frac{1}{16\left(1+2\mu \right)}},\hfill \end{array}\right.$$

(41)

where

$${\rm Y}\left(k\right)=\frac{3(1-k)}{8(1+\mu )(10+7\mu )}.$$

(42)

Proof. 

If $f\in {\mathfrak{GM}}_{\Sigma }\left(\mu \right)$, using the same notations like in the proof of the previous theorem, from (37) and (40) we get

$$\begin{array}{cc}\hfill a_3-k{a}_2^2& =\left(1-k\right)\frac{3(c_2+d_2)}{8(1+\mu )(10+7\mu )}+\frac{c_2-d_2}{16\left(1+2\mu \right)}\hfill \\ \hfill & =\left[{\rm Y}\left(k\right)+\frac{1}{16\left(1+2\mu \right)}\right]c_2+\left[{\rm Y}\left(k\right)-\frac{1}{16\left(1+2\mu \right)}\right]d_2,\hfill \end{array}$$

where ${\rm Y}\left(k\right)$ is given by (42). According to Lemma 2, from the inequality (5) we obtain the conclusion (41). □

For $\mu =0$ and $\mu =1$ the above theorem reduces to the following two results, respectively:

Example 1.

1. If $f\in {\mathfrak{GS}}_{\Sigma }$ is given by (1), then

$$\left|a_2\right|\le \sqrt{\frac{3}{20}}\simeq 0.3872\cdots ,\left|a_3\right|\le \frac{2}{5}=0.4,$$

and

$$\left|a_3-k{a}_2^2\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{1}{4}},\hfill & \mathrm{for}\hfill & \left|1-k\right|\le {\displaystyle \frac{5}{3}},\hfill \\ {\displaystyle \frac{3}{20}}\left|1-k\right|,\hfill & \mathrm{for}\hfill & \left|1-k\right|\ge {\displaystyle \frac{5}{3}}.\hfill \end{array}\right.$$

2. If $f\in {\mathfrak{GV}}_{\Sigma }$ is given by (1), then

$$\left|a_2\right|\le \sqrt{\frac{3}{68}}\simeq 0.21004\cdots ,\left|a_3\right|\le \frac{13}{102}\simeq 0.1274\cdots ,$$

and

$$\left|a_3-k{a}_2^2\right|\le \left\{\begin{array}{ccc}{\displaystyle \frac{1}{12}},\hfill & \mathrm{for}\hfill & \left|1-k\right|\le {\displaystyle \frac{17}{9}},\hfill \\ {\displaystyle \frac{3}{68}}\left|1-k\right|,\hfill & \mathrm{for}\hfill & \left|1-k\right|\ge {\displaystyle \frac{17}{9}}.\hfill \end{array}\right.$$

4. Coefficient bounds of the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$

In this section we will obtain the upper bounds for the modules of the first two coefficients for the functions that belong to the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ that will be introduced, and we will find an upper bound for the Fekete-Szegő functional for this class.

Definition 3.

A function $f\in \Sigma$ given by (1) is said to be in the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ if the following subordinations are satisfied:

$$\begin{array}{ccc}& & \Theta \left(z\right):=\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}+\frac{1+e^{i\lambda }}{2}·\frac{z^2{f}^{″}\left(z\right)}{f\left(z\right)}\prec \mathfrak{G}\left(z\right),\hfill \\ & & \Lambda \left(z\right):=\frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}+\frac{1+e^{i\lambda }}{2}·\frac{w^2{g}^{″}\left(w\right)}{g\left(w\right)}\prec \mathfrak{G}\left(w\right),\hfill \end{array}$$

where $\lambda \in (-\pi ,\pi ]$ and $g\left(w\right)=f^{-1}\left(w\right)$ is defined by (2).

Remark 4.

Note that by fixing $\lambda =\pi$ we get ${\mathfrak{GS}}_{\Sigma }:={\mathfrak{G}}_{\Sigma }\left(\pi \right)$ as it was given in the Example 2. For $\lambda =0$ we obtain the class ${\mathfrak{QG}}_{\Sigma }:={\mathfrak{G}}_{\Sigma }\left(0\right)$.

Remark 5.

We will prove that for convenient choice of the parameter λ the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ is not empty. Taking $f_{*}\left(z\right)={\displaystyle \frac{z}{1-az}}$, $\left|a\right|\le 1$, it could be easily shown that $f_{*}\in \mathcal{S}$ and $f_{*}\in \Sigma$ with $g_{*}\left(w\right)=f_{*}^{-1}\left(w\right)={\displaystyle \frac{w}{1+aw}}$.

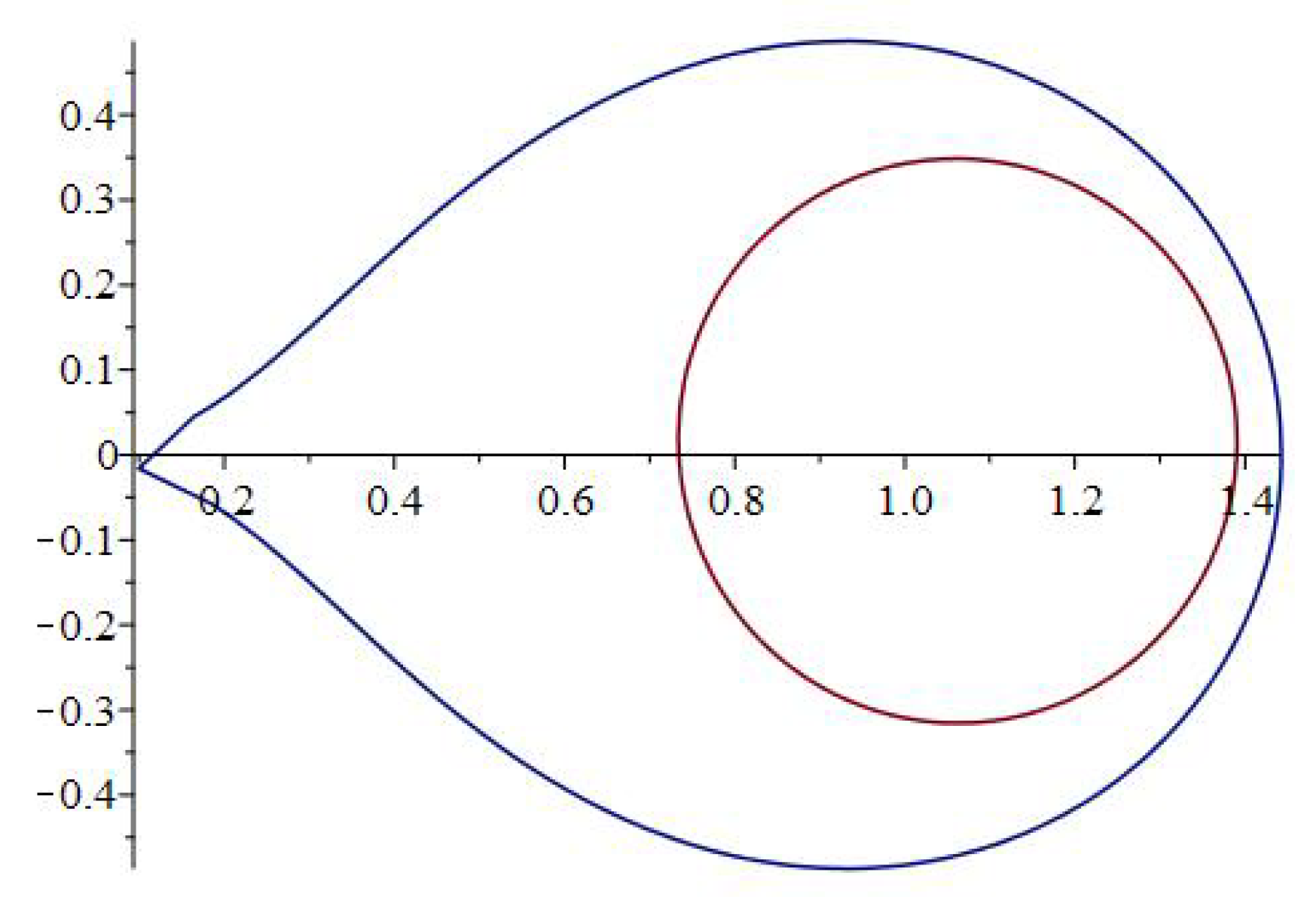
Using the notations of the Definition 3 it is easy to check that $\Theta (-az)=\Lambda \left(az\right)$ for all $z\in \mathbb{D}$, hence $\Phi \left(\mathbb{D}\right)=\Psi \left(\mathbb{D}\right)$. Taking the particular case $a=0.12$, $\lambda =\pi /3$, and using the 2D plot of the MAPLE™ computer software we obtain the image of the boundary $\partial \mathbb{D}$ by the functions Θ, Λ and $\mathfrak{G}$ presented in the Figure 4. Since the function $\mathfrak{G}$ is univalent in $\mathbb{D}$, hence the subordinations $\Theta \left(z\right)\prec \mathfrak{G}\left(z\right)$ and $\Lambda \left(w\right)\prec \mathfrak{G}\left(w\right)$ hold because $\Theta \left(0\right)=\Lambda \left(0\right)=\mathfrak{G}\left(0\right)$, $\Theta \left(\mathbb{D}\right)\subset \mathfrak{G}\left(\mathbb{D}\right)$ and $\Lambda \left(\mathbb{D}\right)\subset \mathfrak{G}\left(\mathbb{D}\right)$ (see Figure 4). Hence $f_{*}\in {\mathfrak{G}}_{\Sigma }(\pi /3)$, therefore the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ is not empty and contains other functions than the identity.

In the following theorem we will determine the results for the initial coefficients bounds of the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$.

Theorem 5.

If $f\in {\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ is given by (1), then

$$\left|a_2\right|\le min\left\{\frac{1}{2\left|2+e^{i\lambda }\right|};\sqrt{\frac{3}{2\left|37+20e^{i\lambda }+7e^{2i\lambda }\right|}}\right\},$$

and

$$\left|a_3\right|\le min\left\{\frac{1}{4{\left|2+e^{i\lambda }\right|}^2}+\frac{1}{2\left|5+3e^{i\lambda }\right|};\frac{3}{2\left|37+20e^{i\lambda }+7e^{2i\lambda }\right|}+\frac{1}{2\left|5+3e^{i\lambda }\right|}\right\}.$$

Proof. 

If $f\in {\mathfrak{G}}_{\Sigma }\left(\lambda \right)$, from the Definition 3 there exist two analytic functions in $\mathbb{D}$, namely u and v such that $u\left(0\right)=v\left(0\right)=0$ and $\left|u\right(z\left)\right|<1$, $\left|v\right(w\left)\right|<1$ for all $z,w\in \mathbb{D}$, with

$$\begin{array}{ccc}& & \frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}+\frac{1+e^{i\lambda }}{2}·\frac{z^2{f}^{″}\left(z\right)}{f\left(z\right)}=\mathfrak{G}\left(u\left(z\right)\right),z\in \mathbb{D},\hfill \end{array}$$

(43)

$$\begin{array}{ccc}& & \frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}+\frac{1+e^{i\lambda }}{2}·\frac{w^2{g}^{″}\left(w\right)}{g\left(w\right)}=\mathfrak{G}\left(v\left(w\right)\right),w\in \mathbb{D}.\hfill \end{array}$$

(44)

With the same notations like in the proof of the Theorem 3, from the equalities (43) and (44) we obtain that

$$\frac{z{f}^{\prime }\left(z\right)}{f\left(z\right)}+\frac{1+e^{i\lambda }}{2}·\frac{z^2{f}^{″}\left(z\right)}{f\left(z\right)}=1+\frac{c_1}{4}z+\frac{1}{48}\left(-7c_1^2+12c_2\right)z^2+\cdots ,z\in \mathbb{D},$$

(45)

and

$$\frac{w{g}^{\prime }\left(w\right)}{g\left(w\right)}+\frac{1+e^{i\lambda }}{2}·\frac{w^2{g}^{″}\left(w\right)}{g\left(w\right)}=1+\frac{d_1}{4}w+\frac{1}{48}\left(-7d_1^2+12d_2\right)w^2+\cdots ,w\in \mathbb{D}.$$

(46)

Equating the corresponding coefficients in (45) and (46) we have

$$\begin{array}{ccc}& & \left(2+e^{i\lambda }\right)a_2=\frac{c_1}{4},\hfill \end{array}$$

(47)

$$\begin{array}{ccc}& & \left(5+3e^{i\lambda }\right)a_3-\left(2+e^{i\lambda }\right)a_2^2=\frac{1}{48}\left(-7c_1^2+12c_2\right),\hfill \end{array}$$

(48)

and

$$\begin{array}{ccc}& & -\left(2+e^{i\lambda }\right)a_2=\frac{d_1}{4},\hfill \end{array}$$

(49)

$$\begin{array}{ccc}& & \left(8+5e^{i\lambda }\right)a_2^2-\left(5+3e^{i\lambda }\right)a_3=\frac{1}{48}\left(-7d_1^2+12d_2\right).\hfill \end{array}$$

(50)

The relations (47) and (49) lead to

$$c_1=-d_1$$

(51)

and

$$32{\left(2+e^{i\lambda }\right)}^2{a}_2^2=c_1^2+d_1^2,$$

that is

$$a_2^2=\frac{c_1^2+d_1^2}{32{\left(2+e^{i\lambda }\right)}^2}.$$

(52)

If we add (48) and (50) we get

$$2\left(3+2e^{i\lambda }\right)a_2^2=\frac{1}{4}\left(c_2+d_2\right)-\frac{7}{48}\left(c_1^2+d_1^2\right),$$

(53)

and substituting the value of $\left(c_1^2+d_1^2\right)$ from (52) in the right hand side of (53) we deduce that

$$\left[2\left(3+2e^{i\lambda }\right)+\frac{14}{3}{\left(2+e^{i\lambda }\right)}^2\right]a_2^2=\frac{1}{4}(c_2+d_2),$$

hence

$$a_2^2=\frac{3(c_2+d_2)}{4\left[6\left(3+2e^{i\lambda }\right)+14{\left(2+e^{i\lambda }\right)}^2\right]}.$$

(54)

Using (5) of Lemma 1 and the triangle’s inequality in (52) and (54) we obtain

$$\left|a_2\right|\le \frac{1}{2\left|2+e^{i\lambda }\right|}\mathrm{and}\left|a_2\right|\le \sqrt{\frac{3}{2\left|37+20e^{i\lambda }+7e^{2i\lambda }\right|}},$$

that proves our first inequality.

If we subtract (50) from (48) we obtain

$$2\left(5+3e^{i\lambda }\right)\left(a_3-a_2^2\right)=\frac{c_2-d_2}{4}-\frac{7}{48}\left(c_1^2-d_1^2\right),$$

and in view of (51) and (52) the above relation leads to

$$a_3=a_2^2+\frac{c_2-d_2}{8\left(5+3e^{i\lambda }\right)}=\frac{c_1^2+d_1^2}{32{\left(2+e^{i\lambda }\right)}^2}+\frac{c_2-d_2}{8\left(5+3e^{i\lambda }\right)}.$$

(55)

Using again Lemma 1 and the triangle’s inequality it follows that

$$\left|a_3\right|\le \frac{1}{4{\left|2+e^{i\lambda }\right|}^2}+\frac{1}{2\left|5+3e^{i\lambda }\right|}.$$

Similarly, in view of (54) and (51) the relation (55) could be written as

$$a_3=\frac{3(c_2+d_2)}{4\left[6\left(3+2e^{i\lambda }\right)+14{\left(2+e^{i\lambda }\right)}^2\right]}+\frac{c_2-d_2}{8\left(5+3e^{i\lambda }\right)},$$

and from Lemma 1 and the triangle’s inequality we conclude that

$$\left|a_3\right|\le \frac{3}{2\left|37+20e^{i\lambda }+7e^{2i\lambda }\right|}+\frac{1}{2\left|5+3e^{i\lambda }\right|},$$

and this proves the second result. □

To determine the upper bound of the Fekete–Szegő functional for the class ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ we will use the following lemma:

Lemma 3.

[24, (3.9), (3.10) p. 254] If $p\left(z\right)=1+c_{1}z+c_2{z}^2+\cdots$, $z\in \mathbb{D}$ with $p\in \mathcal{P}$, then there exist some x, ζ with $\left|x\right|\le 1$, $\left|\zeta \right|\le 1$, such that

$$\begin{array}{ccc}& & 2c_2=c_1^2+x\left(4-c_1^2\right),\hfill \\ & & 4c_3=c_1^3+2c_{1}x\left(4-c_1^2\right)-\left(4-c_1^2\right)c_1{x}^2+2\left(4-c_1^2\right)\left(1-{\left|x\right|}^2\right)\zeta .\hfill \end{array}$$

Theorem 6.

If $f\in {\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ is given by (1), then

$$\left|a_3-\rho a_2^2\right|\le \left\{\begin{array}{cc}{\displaystyle \frac{1}{2\left|5+3e^{i\lambda }\right|}},\hfill & \mathrm{for}|1-\rho |\le {\displaystyle \frac{4{\left|2+e^{i\lambda }\right|}^2}{3\left|5+3e^{i\lambda }\right|}},\hfill \\ {\displaystyle \frac{|1-\rho |}{4{\left|2+e^{i\lambda }\right|}^2}},\hfill & \mathrm{for}|1-\rho |\ge {\displaystyle \frac{4{\left|2+e^{i\lambda }\right|}^2}{3\left|5+3e^{i\lambda }\right|}}.\hfill \end{array}\right.$$

(56)

Proof. 

If $f\in {\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ has the form (1), using (51) and (52), we have $a_2^2={\displaystyle \frac{c_1^2}{16{\left(2+e^{i\lambda }\right)}^2}}$. Thus, from (54) and (55) we get

$$a_3-\rho a_2^2=(1-\rho )\frac{c_1^2}{16{\left(2+e^{i\lambda }\right)}^2}+\frac{c_2-d_2}{8(5+3e^{i\lambda })}.$$

With the same notations like in the proof of the Theorem 3, from Lemma 3 we have $2c_2=c_1^2+x\left(4-c_1^2\right)$ and $2d_2=d_1^2+y(4-d_1^2)$, $\left|x\right|\le 1$, $\left|y\right|\le 1$, and using (51) we get

$$c_2-d_2=\frac{4-c_1^2}{2}(x-y),$$

hence

$$a_3-\rho a_2^2=(1-\rho )\frac{c_1^2}{16{\left(2+e^{i\lambda }\right)}^2}+\frac{\left(4-c_1^2\right)(x-y)}{16(5+3e^{i\lambda })}.$$

Using the triangle’s inequality, taking $\left|x\right|=\delta$, $\left|y\right|=\kappa$, $\delta ,\kappa \in [0,1]$, and without losing of generality we can assume that $c_1\in \mathbb{R}$, $c_1=t\in [0,2]$, thus we obtain

$$|a_3-\rho a_2^2|\le |1-\rho |\frac{t^2}{16{\left|2+e^{i\lambda }\right|}^2}+\frac{1}{16\left|5+3e^{i\lambda }\right|}(4-t^2)(\delta +\kappa ).$$

Denoting $\mathcal{M}\left(t\right):={\displaystyle \frac{|1-\rho |t^2}{16{\left|2+e^{i\lambda }\right|}^2}}\ge 0$ and $\mathcal{N}\left(t\right):={\displaystyle \frac{4-t^2}{16\left|5+3e^{i\lambda }\right|}}\ge 0$ the above relation could be rewritten in the form

$$|a_3-\rho a_2^2|\le \mathcal{M}\left(t\right)+\mathcal{N}\left(t\right)(\delta +\kappa )=:\mathcal{Y}(\delta ,\kappa ),\delta ,\kappa \in [0,1].$$

Thus,

$$max\left\{\mathcal{Y}(\delta ,\kappa ):\delta ,\kappa \in [0,1]\right\}=\mathcal{Y}(1,1)=\mathcal{M}\left(t\right)+2\mathcal{N}\left(t\right)=:H\left(t\right),t\in [0,2].$$

and substituting the value $\mathcal{M}\left(t\right)$ and $\mathcal{N}\left(t\right)$ in the above last equality we obtain

$$H\left(t\right)=\frac{1}{16{\left|2+e^{i\lambda }\right|}^2}\left(|1-\rho |-\frac{2{\left|2+e^{i\lambda }\right|}^2}{\left|5+3e^{i\lambda }\right|}\right)t^2+\frac{1}{2\left|5+3e^{i\lambda }\right|}.$$

Now we will determine the maximum of H on $[0,2]$. Since

$$H^{\prime }\left(t\right)=\frac{1}{8{\left|2+e^{i\lambda }\right|}^2}\left(|1-\rho |-2\frac{{\left|2+e^{i\lambda }\right|}^2}{\left|5+3e^{i\lambda }\right|}\right)t,$$

it is clear that $H^{\prime }\left(t\right)\le 0$ if and only if $|1-\rho |\le {\displaystyle \frac{2{\left|2+e^{i\lambda }\right|}^2}{\left|5+3e^{i\lambda }\right|}}$. In this case function H is a decreasing function on $[0,2]$, therefore

$$max\left\{H\left(t\right):t\in [0,2]\right\}=H\left(0\right)=\frac{1}{2\left|5+3e^{i\lambda }\right|}.$$

Also, $H^{\prime }\left(t\right)\ge 0$ if and only if $|1-\rho |\ge {\displaystyle \frac{2{\left|2+e^{i\lambda }\right|}^2}{\left|5+3e^{i\lambda }\right|}}$, hence the function H is an increasing function on $[0,2]$, and consequently

$$max\left\{H\left(t\right):t\in [0,2]\right\}=H\left(2\right)=\frac{|1-\rho |}{4{\left|2+e^{i\lambda }\right|}^2},$$

and the estimation (56) is proved. □

5. Conclusions

In our present investigation we have introduced and studied the initial coefficient problems associated with each of the new subclasses ${\mathfrak{HG}}_{\Sigma }$, ${\mathfrak{M}}_{\Sigma }\left(\tau \right)$ and ${\mathfrak{G}}_{\Sigma }\left(\lambda \right)$ of the well-known bi-univalent class $\Sigma$. These bi-univalent function subclasses are given by Definitions 1 2, and 3 respectively. For the functions in each of these bi-univalent subclasses we have obtained the estimates of the Taylor–Maclaurin coefficients $\left|a_2\right|$ and $\left|a_3\right|$, and we gave solutions for the Fekete-Szegő functional problems. New results are shown to follow upon specializing the parameters involved in our main results as given in Remark 2 for the class of bi-starlike and bi-convex functions associated with Gregory coefficients which are new and not yet studied sofar. Further we can extend these type of studies based on generalized telephone numbers (see [25,26,27]).