Prerpints.org logo
Preprint
Review

Integration of GNSS Technology and Geometric Levelling for Accurate Height Determination in Uneven Terrains: A Case Study in Lebanon

Altmetrics

Downloads

122

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 February 2024

Posted:

22 February 2024

You are already at the latest version

Alerts
Abstract
The technology for determining the point’s coordinates on the earth’s surface using the global navigation satellite system (GNSS) is becoming the norm along with ground-based methods. In this case, determining coordinates does not cause any particular difficulties. However, to identify normal heights using this technology with a given accuracy, special research is required. The fact is that satellite determinations of geodetic heights (h) over an ellipsoid surface differ from ground-based measurements of normal height (HN) over a quasi-geoid surface by a certain value called quasi-geoid height or height anomaly (ζ). In relation to determining heights of a certain territory, the concept of geoid height (N) is usually operated when dealing with a geoid model. In this work, geodetic and normal heights are determined for 5 control points in three different regions in Lebanon, where measurements are carried out using GNSS technology and geometric levelling. The obtained quasi-geoid heights are compared with geoid heights derived from the global Earth model EGM2008. The results obtained showed that, in the absence of gravimetric data, the combination of global Earth model data, geometric levelling for selected areas and satellite determinations allows the creation of a high accurate altitude network for mountainous areas.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Geometric leveling still remains the most reliable method of high-precision determination of heights. This method involves direct measurements of elevations, from which normal heights are determined. Normal height system relates heights to a hypothetical surface called the quasi-geoid that closely approximates mean sea level, while geodetic height system is based on the reference ellipsoid which approximates the Earth's shape (Figure 1).
The active introduction of satellite determinations into geodetic practice was not only an alternative to geometric leveling, but also in many ways became its replacement. The main disadvantage of satellite leveling is the indirect determination of values from geodetic heights. In this case, a geoid/quasi-geoid model should be used, which includes a set of geoid/quasi-geoid heights above the ellipsoid on a regular grid that makes it possible to determine the difference between geodetic and normal heights (or orthometric heights in case of using a geoid model) anywhere on the planet.
The different magnitudes of gravity on Earth are mainly due to the uneven distribution of mass (rocks), resulting in different gravitational forces that ultimately create the current shape of the geoid. The task arises of identifying the degree of this heterogeneity (height anomalies, differences in the shape of the quasi-geoid from the ellipsoid), which, in particular, can be achieved for a certain area of the earth's surface by constructing local models of the quasi-geoid [1].
Currently, through GNSS technology, the geodetic coordinates (φ, λ, h) of a point of interest on Earth are effectively determined. However, the exact values of the normal heights (HN) of these points should still be determined on the basis of geometric leveling [2,3]. The object of the study is the territory of Lebanon, where there is neither official national geoid model, nor gravimetric data, and accordingly, there is no state altitude network. In this regard, the relevance of developing a method for determining normal heights is extremely high. Local quasi-geoid models can be determined by gravimetric, astro-geodetic or geometric methods. Publications [4,5,6] propose various methods for constructing local quasi-geoid models and assessing their accuracy. In the present study, normal heights are determined by geometric leveling method using 3-route levelling technique.
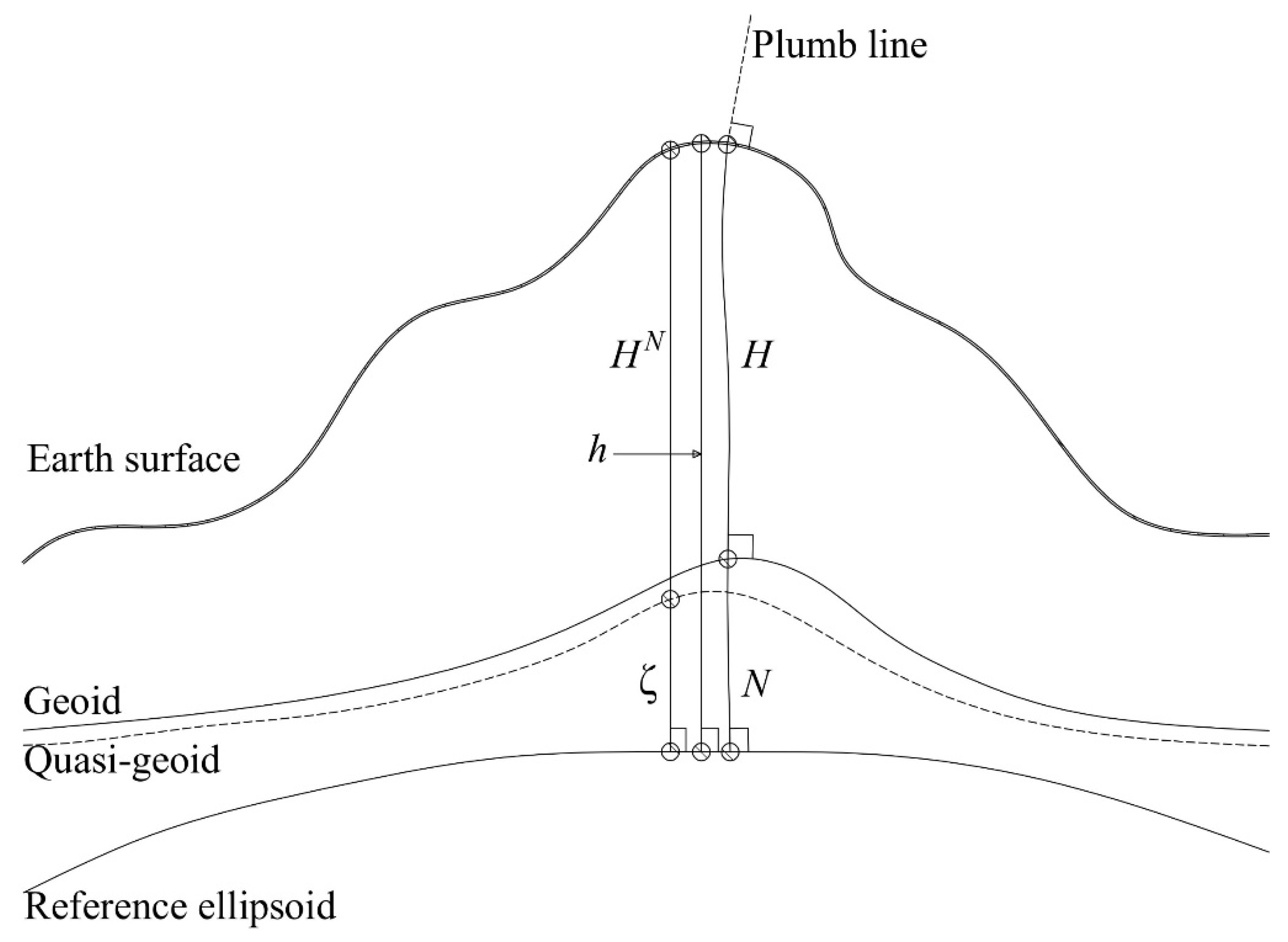
Preprints 99617 g001
Figure 1. Comparison of different height systems and their base surface.
Figure 1. Comparison of different height systems and their base surface.
Preprints 99617 g001
By default, GNSS is integrated with global models such as EGM2008. The specific choice of EGM2008 was mainly due to its wide application and high resolution [7,8,9]. Although the latest models of the global gravitational field, such as: EIGEN 6C4, EIGEN-6C2, EIGEN-6C3stat are considered more accurate, the practical results of their use (K.I. Markovich, D.Sh. Fazilova, etc.) show identical results when comparing models, or a difference within few millimeters when determining height anomalies. In this regard, the use of EGM2008, due to its extensive global validation in various settings, seems appropriate [10,11,12].
This study presents the determination of quasi-geoid height using geometric levelling and satellite measurements in three zones having different topographic characteristic in Lebanon. GNSS measurements in the Static mode provide accuracy in the calculation of geodetic heights (within a few millimeters), which allows for an assessment of geoid waviness and, therefore, more accurate calculations of normal heights [13,14,15]. It should be noted that in practical activities, for example, in construction, GNSS measurement technologies are widely used today, which significantly implies its high accuracy in determining coordinates [16,17,18].

2. Materials and Methods

The geometric method was utilized in three distinct zones in Lebanon to determine height anomalies. Zone A (Bekaa governorate), Zone B (Mount Lebanon governorate) and Zone C (North governorate). These sites were selected based on their contrasting topography. In each site, a total of five points were identified. Four of these points were arranged to form a quadrant, while the fifth point was allocated as a central point. These points were strategically positioned to encompass the surrounding area and capture any potential variations in the deviation of the plumb line.
Four satellite receivers were used in static mode, and carried out for 1 hour/session. Figure 2 shows the distribution of points in each zone. All GNSS measurements started based on a chosen control point from classes II or III in each study area. In (A), the control point 8F3Z from class-III was allocated. A1-A4 are the ancillary points that formed a quadrant with a central point CP. The created baselines between these points were measured starting from 8F3Z. The same procedure was followed in zone (B), where three available control points in the region were allocated, and measurements were based on them. The control points are 7MR5, 7JLB, and 7PRP are from class-III. However, in zone (C), the chosen control point was QDF7 from class-II.
The Raw data obtained in the three zones have been processed and adjusted to obtain the geodetic coordinates, and variances of the stations. The processing interval was set as automatic to determine the best interval setting to use based on the length of the baseline and the duration period. This option balances the highest processing efficiency with the highest results quality.
After processing the baselines in the three zones, the control points were used to perform the fully constrained adjustment. Fixing the control points shifts the observations to the correct location within the chosen datum. Then the adjusted coordinates for all other points in the network can be determined with respect to the project datum. The adjusted geodetic coordinates are shown in Table 1.
Normal heights are usually determined by the geometric levelling method, which is verified by taking measurements in two directions: forward and backward. However, the uneven distribution of the Earth's mass leads to an uneven gravitational field, which affects the waviness of the geoid [19,20,21]. This may appear in different values during the geometric levelling measurements along different routes. If the values turn out to be the same, then the gravitational field in the area of study can be considered negligible. To determine whether there are noticeable changes due to gravitational forces, measurements are taken between the baselines along three different routes, then the elevation differences are compared. The process of measuring heights through the three different routes (1 straight route and 2 curvilinear routes) occurs between 2 main points, passing through an intermediate point in each followed curvilinear route (Figure 3). For example, the points A1 and CP are measured three times, where back sight and fore sight readings are taken along the 1st route (straight: baseline-B), then along the 2nd route (curvilinear: baselines 2 and 5) passing through the intermediate point IP1, then along the 3rd route (curvilinear: baselines 21 and 24) passing through IP4. The same process is followed for other points. This process helps in estimating the gravitational influence in the area by comparing the values of the measured heights in each route.
Systematic errors such as collimation error, non-standard temperature error, earth curvature and atmospheric refraction, and disclosure error are eliminated [22,23,24]. The corrections of these errors are applied to the raw observations in each zone to indicate the adjusted elevation difference between the central point and the surrounding control points.
  • Collimation error:
e = B S 2 – F S 2 − ( B S 1 – F S 1 ) 2 ,
where e is the total vertical error in a horizontal sight, BS is the backsight reading, and FS is the foresight reading.
  • Non-standard temperature error:
C t = t m − t s × D × C E ,
where C t is the rod temperature correction, t m is the mean observed temperature of the rod, t s is the standardization temperature of the rod, D is the observed difference of elevation between the benchmarks,   C E is the mean coefficient of thermal expansion per unit length per degree temperature of the rod.
  • Earth curvature and atmospheric refraction:
C C & R = 0.0673 × D 2 ,
where D is the distance from the instrument to the staff station in kilometers.
  • Disclosure error:
e D = ∑ B S − ∑ F S ,
Assuming that the height of the starting point in each zone is 100 m, the elevation differences are calculated between all points, and adjusted based on the errors’ corrections (see Table 2). After determining the adjusted height difference, the least squares method (LSM) was applied in order to minimize the errors as much as possible. The LSM is expressed in the equations (5-11).
The weight matrix for an equivalent observation is:
W e = [ A . Q . A T ] − 1 ,
The unknown parameters are calculated by:
∆ = [ B T . W e . B ] − 1 [ B T . W e . f ] ,
Since this is a nonlinear equation system, the corrections in matrix ( ∆ ) are applied to the initial approximations, and the method is repeated until the system converges.
The equivalent residuals V e are:
V e = B ∆ − f ,
The observational residuals are:
V = Q A T W e V e ,
The reference variance for the adjustment can be computed using the equivalent residuals and weight matrix employing the equation:
σ 0 2 = V e T . W e . V e r ,
where r is the number of redundancies in the system and defined as: r = n − m .
The covariance matrix:
Σ ∆ ∆ = σ 0 2 . [ B T . W e . B ] − 1 ,
The standard deviation of the individual adjusted parameters is obtained from:
σ = σ 0 . a 1,1 ,
where a 1,1 is the diagonal element of the covariance matrix.
The results of the adjusted elevation differences (ΔHN) and the applied LSM for zone B are shown in Table 2. The same procedure was followed for both zones A and C.
Table 2. Correction of systematic errors, and applying LSM in Zone (B).
Table 2. Correction of systematic errors, and applying LSM in Zone (B).
Section Route Correction of Systematic errors (mm) Disclosure (m) ΔHN LSM
Collimation Earth curvature and atmospheric refraction Non-standard temperature
CP-A1 1 -0.268 0.312 -0.010 -0.001 -48.557 -48.549
2 0.175 1.137 -0.009 -0.001
3 -0.238 1.170 -0.007 0.000
CP-A2 1 -0.280 0.358 -0.004 -0.001 -28.732 -28.737
2 0.243 1.190 -0.005 -0.001
3 0.331 1.575 -0.007 0.000
CP-A3 1 0.050 0.315 -0.025 -0.002 -71.820 -71.816
2 0.231 1.349 -0.019 0.005
3 0.140 1.049 0.009 0.005
CP-A4 1 -0.686 0.517 0.000 0.001 0.576 0.573
2 0.173 1.148 0.001 -0.004
3 0.289 1.385 0.001 0.001
In order to evaluate the achieved accuracy using the proposed method (3-route levelling), the same adjustment process took place for the levelling measurements taken at the first route only (direct route between two points), excluding the two curvilinear routes, which is exactly the known classic levelling method. After correcting all the systematic errors, the LSM was applied. The obtained standard deviation in both methods are compared (classic levelling vs. 3-route levelling) as shown in Figure 4. The 3-route levelling technique shows consistent standard deviation values in the three zones, unlike the classic method. A consistent standard deviation implies the reliability of the model's performance, and thus, reliable measurements are less likely to contain systematic errors or biases.
Adjusted normal heights derived by the 3-route levelling method, and geodetic heights derived from GNSS measurements were used in order to calculate the quasi-geoid height (ζ) for each zone using equation 8 [25,26,27].
ζ = h − H N
The values of quasi-geoid heights are compared with the geoid heights derived from EGM2008 in order to estimate its accuracy in the Lebanese territory. By comparing these values, it can be noticed that the EGM2008 can be used in flat areas (zone A) as it shows high similarity in the values. However, in uneven terrains (zones B and C), the EGM2008 shows high discrepancies, which ensures the actual gravitational influence on the height accuracy in those areas (Figure 5). In fact, these discrepancies are due to the absence of gravimetric data in the country, and thus the proposed geometric method is recommended for use in engineering applications that require high accuracy in the vertical positioning [28,29,30]. The model’s accuracy can be achieved in other areas having similar topographic characteristics in the country.

3. Results

According on the varied topography in Lebanon, it is classified into zones based on elevation ranges starting from sea level and ending with the highest elevation of 3088 m above the sea level. This classification enables us to find a convenient coefficient for each zone that can be used independently for converting geodetic heights into normal heights based on the developed method for determining normal heights “the 3-route levelling technique”.
In general, coefficients serve to scale, adjust, or modify the magnitude, direction, or behaviour of the associated variable or term within the context of the equation or model in which they appear. A coefficient in the context of quasi-geoid height analysis represents a numerical value that adjusts the relationship between the observed quasi-geoid heights and the underlying geophysical or topographic factors influencing them. It acts as a multiplier or a scaling factor that modifies the magnitude or shape of the anomaly distribution curve, thereby enhancing the accuracy of the model. Through careful calibration and optimization, coefficients enable researchers to develop robust models that capture the underlying dynamics of the Earth's surface with greater accuracy.
The results of the determined quasi-geoid heights in the three selected zones in Lebanon are generalized to cover the surroundings of each zone taking into consideration the proximity of elevation ranges in these surroundings. A coefficient was calculated by averaging the difference between quasi-geoid heights and geoid heights. Considering this coefficient in each zone, an enhancement of the derived normal heights from geodetic heights will occur.
Geoid heights derived from EGM2008 at each point in the three zones, and the calculated quasi-geoid heights from normal and geodetic heights are shown in Table 3.
The average difference was determined in each zone and considered as an additive coefficient for the surrounding area to be used by GNSS user community (Table 4).
To verify the improved accuracy of the geoid heights using the obtained coefficients, a total of 12 check points with known normal and geodetic heights are selected within the surrounding areas of the three zones. These check points are carefully chosen to represent a range of elevations and terrain characteristics in each site. The measured geodetic coordinates of the check points (ϕ, λ, h) are used to extract the corresponding geoid height (N) value from EGM2008 model for each point. The coefficient is then added to the (N) value, by which the normal heights can be determined (equation 12). Table 5 shows the measured geodetic and normal heights, the derived geoid height (N) from EGM2008 model and its corresponding orthometric height.
After applying the corresponding coefficients to the geoid heights for each check point, the resulting (N) values are subtracted from geodetic heights in order to calculate new orthometric heights. Figure 6 shows the comparison between the check points’ known normal heights and the orthometric heights before and after adding the coefficient. D1 corresponds to the differences between heights before adding the coefficients, while D2 corresponds to the differences after adding the coefficients. It is noted that the obtained orthometric heights by the help of the coefficients serve a higher accuracy being closer to the 0 level when compared to the actual normal heights which ensures the validity of the proposed method.

5. Conclusions

This study highlights the importance of considering the gravitational influences when determining precise heights for engineering applications and many other disciplines. The presence of a local geoid/quasi-geoid model is crucial in accurately accounting for the irregularities in the Earth's gravitational field, which can significantly impact height calculations. The study findings revealed that the uneven distribution of mass within the Earth is affecting the determination of normal heights in Lebanon. This necessitates the creation of a local quasi-geoid model in the country to establish a reliable reference surface for height measurements. By calculating height anomaly using the GNSS and 3-route levelling measurements, and developing coefficients for each zone, a more refined quasi-geoid model can be created, enhancing the accuracy of height determinations, as well as the accuracy of geoid heights derived from EGM2008, which was found unsuitable to be used independently for all the regions of the country, particularly for areas with uneven terrain. For applications requiring high accuracy in height determination, it is absolutely recommended to use gravimetric data, otherwise the proposed combined geometric approach of GNSS and 3-route levelling technique can be used to enhance the accuracy and reliability of height determinations in Lebanon and similar countries, ultimately improving construction, infrastructure development, mine surveys, and urban planning in the country in the absence of a local geoid model.

Funding

This research was funded by St. Petersburg Mining University, Russia.

Acknowledgments

This study was carried out under the auspices of the Lebanese International University in Lebanon, and coordinated by the department of Engineering Geodesy in St. Petersburg Mining University, Russia. The authors would like to express their gratitude to the diligent editors and reviewers of the journal for their hard work.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Sjöberg, L.E. On the geoid and orthometric height vs. quasigeoid and normal height. J. Géod. Sci. 2018, 8, 115–120. [Google Scholar] [CrossRef]
  2. Novak, P.; Fernando, S. On correct definition and use of normal heights in geodesy. Stud. Geophys. Geod. 2024, 1–24. [Google Scholar] [CrossRef]
  3. Szelachowska, M.; Godah, W.; Krynski, J. Contribution of GRACE Satellite Mission to the Determination of Orthometric/Normal Heights Corrected for Their Dynamics—A Case Study of Poland. Remote. Sens. 2022, 14, 4271. [Google Scholar] [CrossRef]
  4. Li, J.; Shen, W.; Zhou, X. Direct regional quasi-geoid determination using EGM2008 and DEM: A case study for Mainland China and its vicinity areas. Geodesy Geodyn. 2015, 6, 437–443. [Google Scholar] [CrossRef]
  5. Morozova, K.; Jäger, R.; Zarins, A.; Balodis, J.; Varna, I.; Silabriedis, G. Evaluation of quasi-geoid model based on astrogeodetic measurements: case of Latvia. J. Appl. Geodesy 2021, 15, 319–327. [Google Scholar] [CrossRef]
  6. Foroughi, I.; Tenzer, R. Comparison of different methods for estimating the geoid-to-quasi-geoid separation. Geophys. J. Int. 2017, 210, 1001–1020. [Google Scholar] [CrossRef]
  7. Odera, P.A. Evaluation of the recent high-degree combined global gravity-field models for geoid modelling over Kenya. Geodesy Cartogr. 2020, 46, 48–54. [Google Scholar] [CrossRef]
  8. Pavlov, N.S.; Sannikova, A.P. Prerequisites of geodetic surveying of technical status of trunk gas pipeline's underwater crossings. Marksheyderiya i Nedropol'zovaniye 2016, 2, 61–63. (In Russian) [Google Scholar]
  9. Abeho, D.R.; Hipkin, R.; Tulu, B.B. Evaluation of EGM2008 by means of GPS Levelling Uganda. South Afr. J. Geomatics 2014, 3, 272–284. [Google Scholar] [CrossRef]
  10. Yahaya, S.I.; El Azzab, D. Assessment of recent GOCE-based global geopotential models and EGM2008 in Niger Republic. Geodesy Cartogr. 2019, 45, 116–125. [Google Scholar] [CrossRef]
  11. Izvoltova, J.; Dasa, B.; Jakub, C.; Stanislav, H. Preprocessing of Gravity Data. Computation 2022, 10, 82. [Google Scholar] [CrossRef]
  12. Isik, M.S.; Çevikalp, M.R.; Erol, B.; Erol, S. Improvement of GOCE-Based Global Geopotential Models for Gravimetric Geoid Modeling in Turkey. Geosciences 2022, 12, 432. [Google Scholar] [CrossRef]
  13. Menegbo, E. Determination of orthometric elevations using GNSS-derived height with the EGM2008 geoid height model. Int. J. Adv. Geosci. 2017, 5, 13–18. [Google Scholar] [CrossRef]
  14. Khudyakov, G.I. Development of methods of analytical geometry of a sphere for solving geodesy and navigation tasks. J. Min. Inst. 2017, 223, 70–81. [Google Scholar] [CrossRef]
  15. Liang, W.; Pail, R.; Xu, X.; Li, J. A new method of improving global geopotential models regionally using GNSS/levelling data. Geophys. J. Int. 2020, 221, 542–549. [Google Scholar] [CrossRef]
  16. Erol, S.; Erol, B.; Ayan, T. A general review of the deformation monitoring techniques and a case study: analyzing deformations using GPS/levelling. In XXth ISPRS congress, vol. 7, no. 5, p. 12. 2004.
  17. Gusev, N.; Blishchenko, A.A.; Sannikova, A.P. Study of a set of factors influencing the error of surveying mine facilities using a geodesic quadcopter. J. Min. Inst. 2022, 254, 173–179. [Google Scholar] [CrossRef]
  18. Albayrak, M.; Özlüdemir, M.T.; Aref, M.M.; Halicioglu, K. Determination of Istanbul geoid using GNSS/levelling and valley cross levelling data. Geodesy Geodyn. 2020, 11, 163–173. [Google Scholar] [CrossRef]
  19. Svitlana, N.; Roman, M.; Grygoriy, S.; Vira, S. Use of Different Geodesic Methods for Determining Heights. In International Conference Building Innovations; Springer International Publishing: Cham, Switzerland, 2022; pp. 473–487. [Google Scholar]
  20. Vystrchil, M.G.; Gusev, V.N.; Sukhov, A.K. A method of determining the errors of segmented grid models of open-pit mines constructed with the results of unmanned aerial photogrammetric survey. J. Min. Inst. 2023, 262, 562–570. (In Russian) [Google Scholar]
  21. Petrov, S. Compatible processing of results of high precision geometric levelling and inclination measurements. Mod. Achiev. Geod. Sci. Ind. 2015, 1, 29. [Google Scholar]
  22. Eliseeva, N.N.; Zubov, A.V.; Gusev, V.N. The application of search optimization methods in solving geodetic problems. Geodesy Aerophotosurveying 2020, 64, 491–498. [Google Scholar] [CrossRef]
  23. Soycan, M. Improving EGM2008 by GPS and leveling data at local scale. Boletim de Ciências geodésicas 2014, 20, 3–18. (In Portuguese) [Google Scholar] [CrossRef]
  24. Herbert, T.; Olatunji, R.I. Comparative Analysis of Change between Ellipsoidal Height Differences and Equivalent Orthometric Height Difference. Ghana J. Geogr. 2020, 12, 132–144. [Google Scholar] [CrossRef]
  25. Yilmaz, N. Assessment of latest global gravity field models by GNSS/Levelling Geoid. Int. J. Eng. Geosci. 2023, 8, 111–118. [Google Scholar] [CrossRef]
  26. Ziggah, Y.Y.; Yakubu, I.; Kumi-Boateng, B. Analysis of methods for ellipsoidal height estimation–the case of a local geodetic reference network. Ghana Min. J. 2016, 16, 1–9. [Google Scholar] [CrossRef]
  27. Kuzin, A.A.; Palkin, P.O. Coordinate method for determining position in geodetic monitoring of cracks. J. Physics 2021, 1728, 012010. [Google Scholar] [CrossRef]
  28. Eshagh, M.; Zoghi, S. Local error calibration of EGM08 geoid using GNSS/levelling data. J. Appl. Geophys. 2016, 130, 209–217. [Google Scholar] [CrossRef]
  29. Filmer, M.S.; Featherstone, W.E.; Kuhn, M. The effect of EGM2008-based normal, normal-orthometric and Helmert orthometric height systems on the Australian levelling network. J. Geodesy 2010, 84, 501–513. [Google Scholar] [CrossRef]
  30. Koks, D. A study of the EGM2008 model of Earth's gravitational field. J. Navig. 2022, 75, 1017–1034. [Google Scholar] [CrossRef]
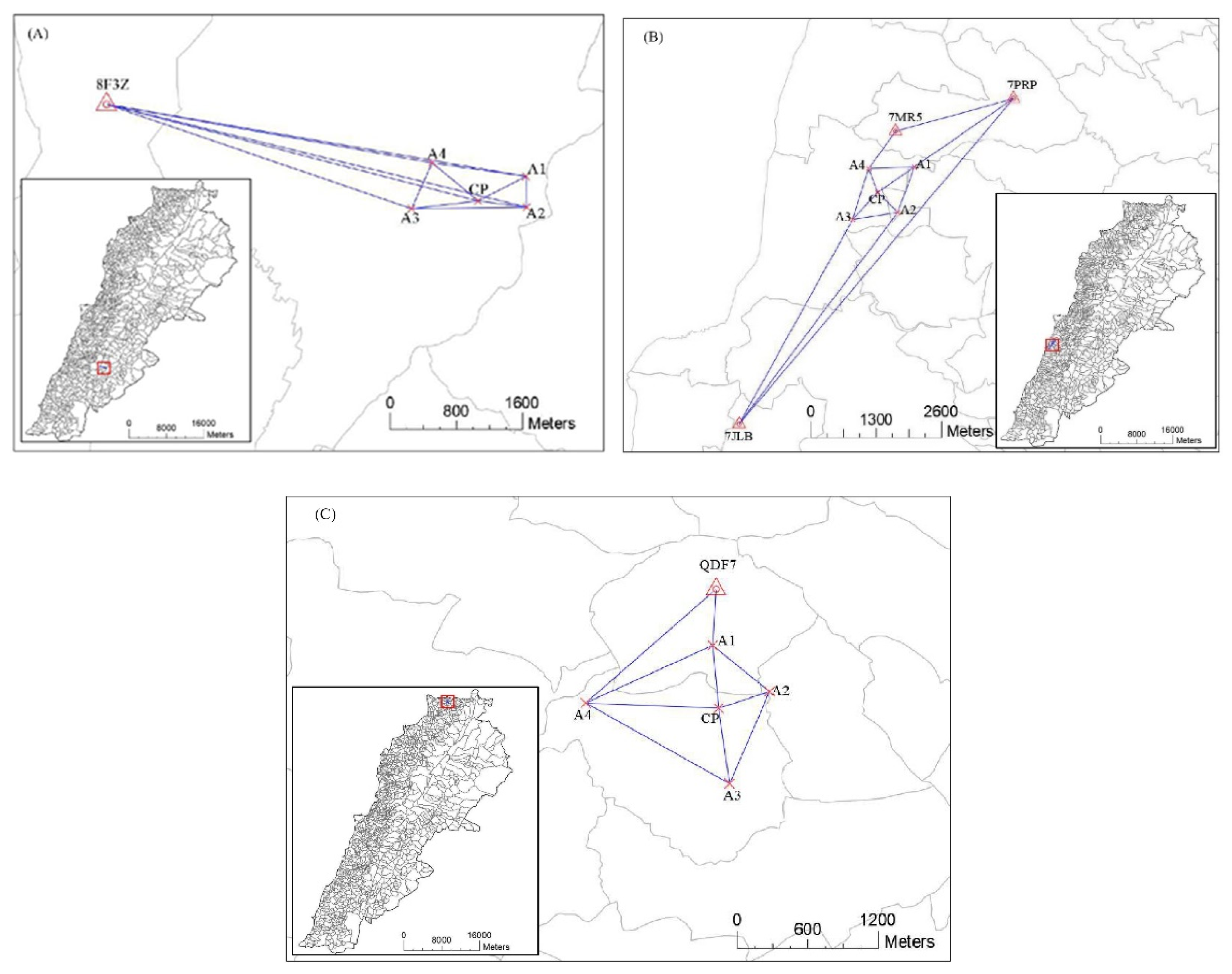
Preprints 99617 g002
Figure 2. Location of the three study areas in Lebanon.
Figure 2. Location of the three study areas in Lebanon.
Preprints 99617 g002
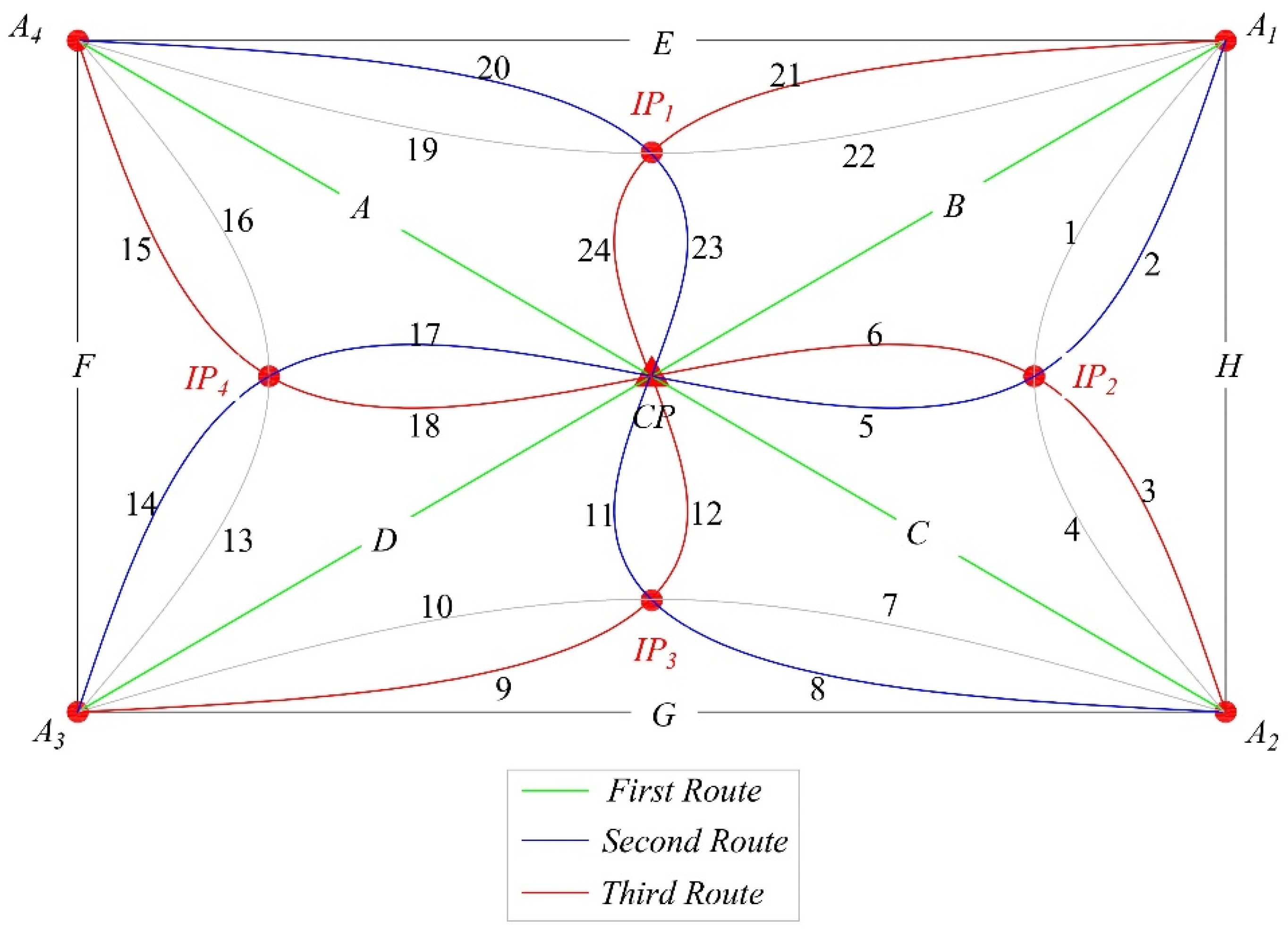
Preprints 99617 g003
Figure 3. Scheme of the levelling network: A1-4 corner points of the polygon; A, B, C, D, E, F, G, H – straight routes; 1-24 – curvilinear routes, and CP – central point.
Figure 3. Scheme of the levelling network: A1-4 corner points of the polygon; A, B, C, D, E, F, G, H – straight routes; 1-24 – curvilinear routes, and CP – central point.
Preprints 99617 g003
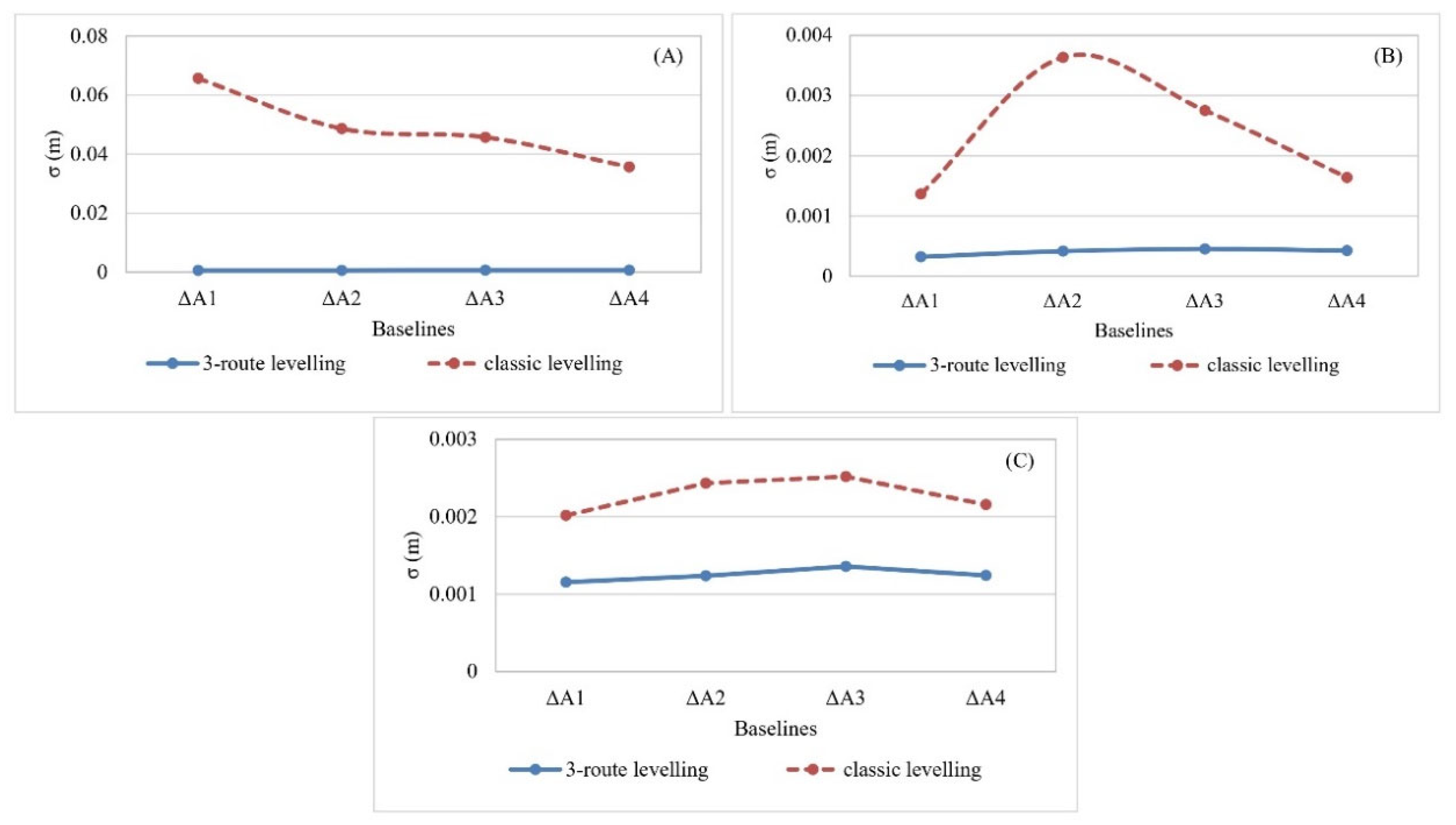
Preprints 99617 g004
Figure 4. Comparison of the standard deviation of heights calculated using both the classical and 3-route levelling methods.
Figure 4. Comparison of the standard deviation of heights calculated using both the classical and 3-route levelling methods.
Preprints 99617 g004
Preprints 99617 g005
Figure 5. Comparison between quasi-geoid heights (ζ) derived from Normal-Geodetic heights and geoid heights (N) derived from EGM2008 model in the three zones (A, B and C).
Figure 5. Comparison between quasi-geoid heights (ζ) derived from Normal-Geodetic heights and geoid heights (N) derived from EGM2008 model in the three zones (A, B and C).
Preprints 99617 g005
Preprints 99617 g006
Figure 6. Differences between normal heights and obtained orthometric heights before and after adding the coefficients to the geoid heights.
Figure 6. Differences between normal heights and obtained orthometric heights before and after adding the coefficients to the geoid heights.
Preprints 99617 g006
Table 1. Geodetic coordinates determined by GNSS static measurements.
Table 1. Geodetic coordinates determined by GNSS static measurements.
Point ϕ λ h(m)
Zone (A)
A1 N33°31'04.23088" E35°40'19.02209" 879.954
A2 N33°31'01.24131" E35°40'19.23139" 881.054
A3 N33°31'00.71578" E35°40'05.80162" 885.348
A4 N33°31'05.25177" E35°40'08.02764" 885.476
CP N33°31'01.69385" E35°40'13.54181" 882.446
Zone (B)
A1 N33°43'39.48678" E35°28'28.34842" 276.318
A2 N33°43'10.03531" E35°28'17.11964" 242.384
A3 N33°43'04.36187" E35°27'42.56322" 152.402
A4 N33°43'37.40257" E35°27'53.33982" 193.289
CP N33°43'22.26857" E35°28'00.94609" 192.591
Zone (C)
A1 N34°36'52.51739" E36°07'53.08944" 212.957
A2 N34°36'39.53158" E36°08'13.63695" 193.228
A3 N34°36'12.38280" E36°08'00.49453" 236.286
A4 N34°36'34.61689" E36°07'08.98025" 163.769
CP N34°36'34.27561" E36°07'55.86680" 164.500
Table 3. Differences between quasi-geoid heights and geoid heights in each zone.
Table 3. Differences between quasi-geoid heights and geoid heights in each zone.
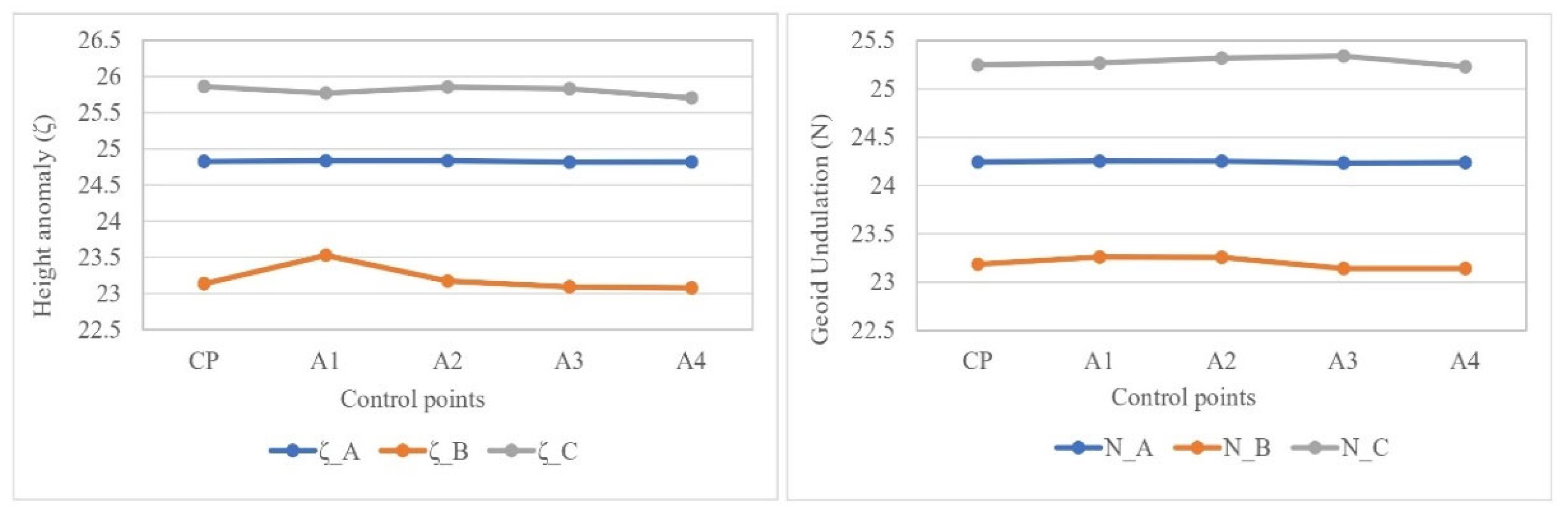
Point ζ (h - HN) N (EGM2008)
Zone A Zone B Zone C Zone A Zone B Zone C
CP 24.827 23.136 25.861 25.245 23.189 25.248
A1 24.836 23.529 25.769 25.254 23.260 25.271
A2 24.836 23.174 25.852 25.253 23.256 25.319
A3 24.816 23.092 25.831 25.234 23.142 25.341
A4 24.819 23.079 25.703 25.239 23.140 25.231
Table 4. Determined coefficient for each zone.
Table 4. Determined coefficient for each zone.
Zone (A) Zone (B) Zone (C)
Coefficient -0.4182 -0.1021 0.5212
Table 5. The measured geodetic and normal heights of the check points, and their derived geoid heights and orthometric heights from EGM2008.
Table 5. The measured geodetic and normal heights of the check points, and their derived geoid heights and orthometric heights from EGM2008.
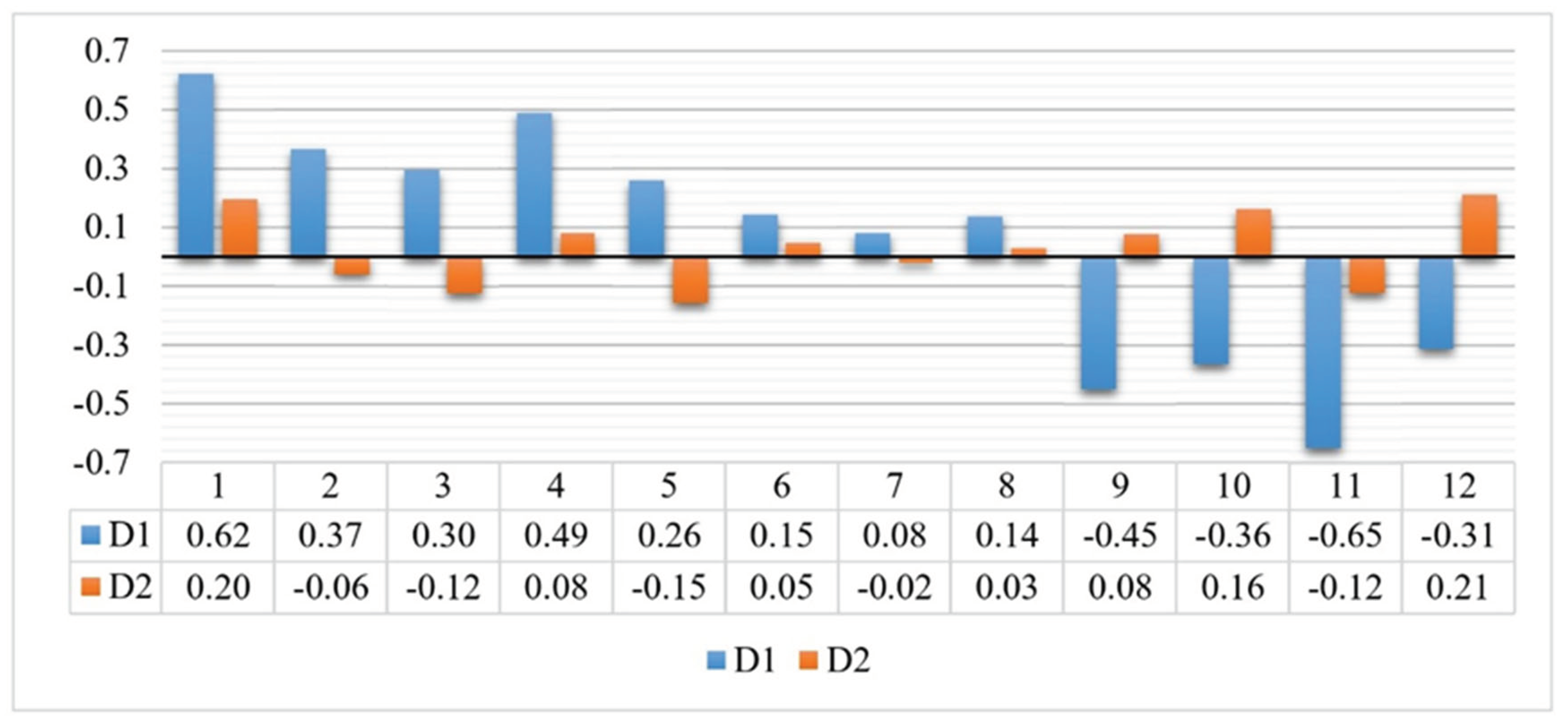
Check point ϕ λ h HN Geoid height (N) Orthometric height
1 35.66919 33.51608 883.009 857.965 25.66 857.34
2 35.66930 33.51757 884.935 859.637 25.66 859.27
3 35.67127 33.51815 879.181 853.828 25.65 853.53
4 35.67133 33.51651 879.411 854.252 25.66 853.76
5 35.47342 33.72284 265.147 238.731 26.68 238.47
6 35.46775 33.71645 201.866 175.286 26.73 175.14
7 35.45836 33.72328 80.887 54.162 26.81 54.08
8 35.47109 33.72965 222.225 195.670 26.69 195.53
9 36.13131 34.6029 236.914 213.032 23.44 213.48
10 36.12046 34.607 141.587 117.808 23.42 118.17
11 36.12918 34.61443 208.496 184.433 23.42 185.08
12 36.14072 34.61285 206.589 182.840 23.44 183.15
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated