Prerpints.org logo
Preprint
Article

Hearables: In-ear Multimodal Data Fusion for Robust Heart Rate Estimation

This version is not peer-reviewed.

Submitted:

22 February 2024

Posted:

22 February 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Ambulatory heart rate (HR) monitors that acquire electrocardiogram (ECG) or/and photoplethysmographm (PPG) signals from the torso, wrists, or ears are notably less accurate in tasks associated with high levels of movement compared to clinical measurements. However, reliable estimation of HR can be obtained through data fusion from different sensors. These methods are especially suitable for multimodal hearable devices, where heart rate can be tracked from different modalities, including electrical ECG, optical PPG, and sounds (heart tones). Combined information from different modalities can compensate for single source limitations. In this paper, we evaluate the possible application of data fusion methods in hearables. We assess data fusion for heart rate estimation from simultaneous in-ear ECG and in-ear PPG, recorded on eight subjects while performing 5-minute sitting and walking tasks. Our findings show that data fusion methods provide a similar level of mean absolute error as the best single-source heart rate estimation but with much lower intra-subject variability, especially during walking activities. We conclude that data fusion methods provide more robust HR estimation than a single cardiovascular signal. These methods can enhance the performance of wearable devices, especially multimodal hearables, in heart rate tracking during physical activity.
Keywords: 
Data fusion method
;  
Heart rate tracing
;  
Hearables
;  
Wearables
Subject: 
Engineering  -   Bioengineering

1. Introduction

Ambulatory wearable heart rate trackers provide physiological measurements during dynamic everyday real-world activities. However, they have been characterized as being less accurate in tasks associated with high levels of movement compared to data acquired in clinic. The accuracy of wearable devices is related to their placement; for example, a device on the wrist is more likely to catch movement artefacts than one on the chest [1]. Nonetheless, even when placed on the chest, the relative error of a heart rate monitor increases with the level of exercise intensity [2].
In addition, the performance of automatic heartbeat detection algorithms depends on signal-to-noise ratio [3]; for example, for signal-to-noise ratios below 5 dB, the R peak detection in electrocardiogram (ECG) is considered unreliable [4]. Generally, a detector sensitivity and positive predictive value decrease for ambulatory data compared to the standard system in a clinic [5]. Even when poor-quality data or data corrupted by motion artefacts are excluded from analysis, the accuracy of detectors applied to ambulatory data is typically worse than that for data acquired in clinics [6]. Georgiou et al. [7] pointed out that so far, wearable devices can only be used as a surrogate for heart rate variability at resting or mild exercise conditions, as their accuracy fades out with increasing exercise load.
Hearables are a very convenient wearables modality, owning the privileged position of the head and ear canal on the human body and the fixed distance to vital organs. However, the in-ear ECG [8] signal, measured between electrodes placed inside the ear canal, has a smaller amplitude that standard ECG acquired from torso and a lower signal-to-noise ratio, making it difficult to automatically detect R peaks with standard algorithms [9]. On the other hand, earpieces provide a good fit and benefit from collocated position of multiple sensors (electrodes, accelerometer, microphone, and photoplethysmography (PPG) sensor) on an earplug [10].
The multimodalities of hearables has already been employed in mental stress detection [11], showing that classification performance can be improved by utilizing heart rate variability features extracted from ear-ECG, with breathing and oxygen saturation features extracted from ear-PPG signals. Multimodality also has a crucial role in artefacts removal [12], where signals from microphones and accelerometer were used to model artefacts and remove them from ear-EEG recordings. Regarding the estimation of heart rate, it can be monitored using various in-ear signal modalities [13]:
  • Electrical (ECG) [11],
  • Optical (PPG) [14,15],
  • Sounds (heart tones) [16].
The multimodality of hearables provides an opportunity for more robust HR estimation by combining heart rate data from various sources using data fusion methods.
Data fusion techniques have the potential to improve estimation accuracy by sensor redundancy (e.g. multiple PPG signals), or by estimating HR from different sensor modalities (PPG and ECG). For example, data fusion can be achieved with weighted average, where weights are automatically adjusted based on signal quality indexes (SQI). This approach ensures that data from high SQI signals, i.e. likely to be more accurate, are used for HR estimation.
In this paper, we evaluate two methods of data fusion: the method described by Li et al. [17] and the method proposed by Rankawat and Dubey [18] for heart rate estimation from simultaneous in-ear ECG and in-ear PPG, recorded on eight subjects while performing 5-minute sitting and walking tasks.

2. Method

2.1. Data fusion methods

Rankawat and Dubey’s [18] method
Rankawat and Dubey [18] proposed a data fusion method whereby HR is estimated from n different sources and fused as a weighted average
H R = 1 ∑ i = 1 n w i ∑ i = 1 n w i H R i
The weight w i for the i-th source is estimated based on the Signal Quality Index (SQI) and the source type. Rankawat and Dubey [18] identified two categories of signals: cardiovascular, directly related to heart activity, such as ECG, PPG, and arterial blood pressure (ABP); and non-cardiovascular signals where the heart related component is an artefact, such as electroencephalogram, electrooculogram and electromyogram. For the latter, the Teager-Kaiser energy operator [19] was used to perform beat detection.
The weights for signals were taken according to Table 1.
Rankawat and Dubey [18] assessed SQI as a product of a “beat rhythm factor” and a “beat deviation factor”, calculated using eight previous beats. The beat rhythm factor ( C i ) was calculated as 1 minus the ratio of standard deviation ( σ i ) and the median of RR intervals ( μ i ) as
C i = 1 − σ i μ i
The beat deviation factor ( D i ) was assessed based on the deviation of the current RR interval ( x i ) from a mean value ( μ i ) as
D i = x i − μ i
  • Liet al.[17] method
Li et al. [17] data fusion method is performed in two steps: 1) HR estimation from each source is filtered using a Kalman filter; 2) HR fusion estimation is calculated for n signals as
H R = ∑ i = 1 n ( ∏ i = 1 , k ≠ i n σ i 2 ∑ i = 1 n ( ∏ j = 1 , j ≠ i n σ j 2 ) H R k ) k = 1 , 2 , . . . , n
where σ indicates the weight associated with each signal, and is calculated as
σ k = H R k − X k − S Q I k
where H R k is heart rate, X k − is Kalman filter state prediction and S Q I k is the signal quality index for the current beat.
The goal of the Kalman filter is to produce evolving optimal estimates of a modelled process from noisy measurements of the process. The Kalman filter is a set of mathematical equations that provide a computationally efficient way (recursive) to estimate the state of a process, by minimizing the mean squared error of estimations [20].
In the context of HR tracking, the state process of the filter can be modelled as a random walk, where a single state value (HR) in each step changes to a random value. Then, the previous HR value can be used to estimate HR at the next step. Therefore, in the initial step of the recursive filtering algorithm, the next state value ( X k + 1 − ) is predicted as:
X k + 1 − = X k
Then, the system state error covariance of the next step ( P k + 1 ) is calculated as
P k + 1 − = P k + + Q
Where Q is process covariance, which is set during filter design. Li et al. [17] empirically found Q = 0.1 as the optimal value. For higher Q, the filter starts to follow the HR observation too closely, while for lower values, the filter firmly trusts its own estimation and does not adapt to observations. The initial P 0 + is defined during the design of the filter.
Next, the Kalman gain ( K k ) is calculated as
K k = P k − ( P k − + R k )
where R k is the measurement covariance. Li et al. [17] adjusted R k based on the S Q I as
R k = R ∗ e ( 1 S Q I k 2 − 1 )
with R as the base covariance value set during filter design, and R k and Q indicate filter behaviour. As mentioned before, higher Q values result in the filter strongly following its own model prediction. Similarly, a higher R k causes the filter to follow measured values. An adjustable R k ensures that the filter will firmly follow its own prediction for low SQI, while it will prefer HR estimation for higher SQI. The last step of the Kalman filter algorithm is the correction of process state estimation and filter covariance:
X k + = X k − + K k ( Z k − X k − )
P k + = ( 1 − K k ) P k −
where Z k is the measured HR estimated from the signal. The corrected estimations X k + are the filter output used for data fusion.
As SQI, Li et al. [17] used values combined from four different SQI estimation: 1) based on comparison of different QRS detectors on a single lead ECG; 2) based on comparison of QRS detection using different leads; 3) based on signal kurtosis, similarity to Gaussian distribution; and 4) based on spectral distribution of ECG, the ratio of power spectral density of QRS complex (range from 5 to 14Hz) and power spectral density between 5 and 50 Hz.

2.2. Validation of methods on in-ear measurements

We recorded 10 healthy subjects (4 females and 6 males, aged 24-34) during 5 minutes of resting sitting and 5 minutes of walking on a treadmill at a speed of 4 km/h. We acquired a one-channel cross-head ECG by positioning one viscoelastic foam sensor [10] in each ear, where the biopotential was measured between electrodes placed in both ears and one standard torso ECG (modified Lead I configuration). Simultaneously, we measured signals from two PPG sensors MAX30101 (Maxim Integrated), placed in both ears’ conchae mounted on a flexible shell developed in our lab. PPG signals for green, red, and infrared light were recorded.
The study was conducted under the approval of the Imperial College ethics committee (JRCO 20IC6414), and all subjects provided full informed consent.
To detect onsets in PPG signals, we first performed inversion of acquired signal polarization and lowpass filtration (cut-off frequency = 12 Hz). Next, to detect the onsets of the PPG signals, we used the qppg function from the PhysioNet Cardiovascular Signal Toolbox [21]. Detections were performed for all six PPG signals (Red, Infrared and Green wavelengths for each of the 2 sensors) independently.
To detect R-peaks in Ear-ECG, we used a deep matched filter detector introduced by Davies et al. [22]. The detector consists of an encoder stage (trained as part of an encoder-decoder module to reproduce ground truth ECG), which operates as a Matched Filter. The encoder section searches for matches with an ECG template pattern in the input signal, prior to refining and filtering the matches with the subsequent convolutional layers and an R-peak classifier stage. This classifier consists of a single-layer 1D convolution, followed by a Sigmoid activation function, flattening, and a linear output layer. The proposed method has been shown to provide higher median R-peak recall and precision than standard matched filters[22]. The detector was previously trained using a separate dataset; we did not modify model weights for this study.
For the estimation of SQI in heart signals, the calculate_ppgsqi function from PhysioNet Cardiovascular Signal Toolbox was used. This function employs multiple-template matching stages, and was described by Li et al. [23]. Firstly, a signal beat dynamic template was built by averaging beats in a 30-second signal window. Then fiducial points were chosen as the detected onsets and the R peaks for the PPG and ECG signals respectively. Each beat starts from the fiducial point and ends at the fiducial point of the next beat. The mean SQI was obtained from four SQIs estimation methods. Three SQIs were based on the correlation of the template with: a beat, a linear interpolation of the beat, and the beat after dynamic time warping to match the template. The fourth SQI was the percentage of samples that were saturated (to the maximum or minimum values). We applied this method to all acquired signals: in-ear PPGs and in-ear ECG.
To detect the R peaks in torso ECG, we used the Two Moving Average detector [24], implemented from https://github.com/berndporr/py-ecg-detectors.git.
We averaged the estimated HR and SQI values from each of 7 sources and data fusion methods over 10-second windows without overlapping. We calculate mean absolute errors for each HR estimation method with respect to the HR values obtained from torso ECG, used as a ground truth.

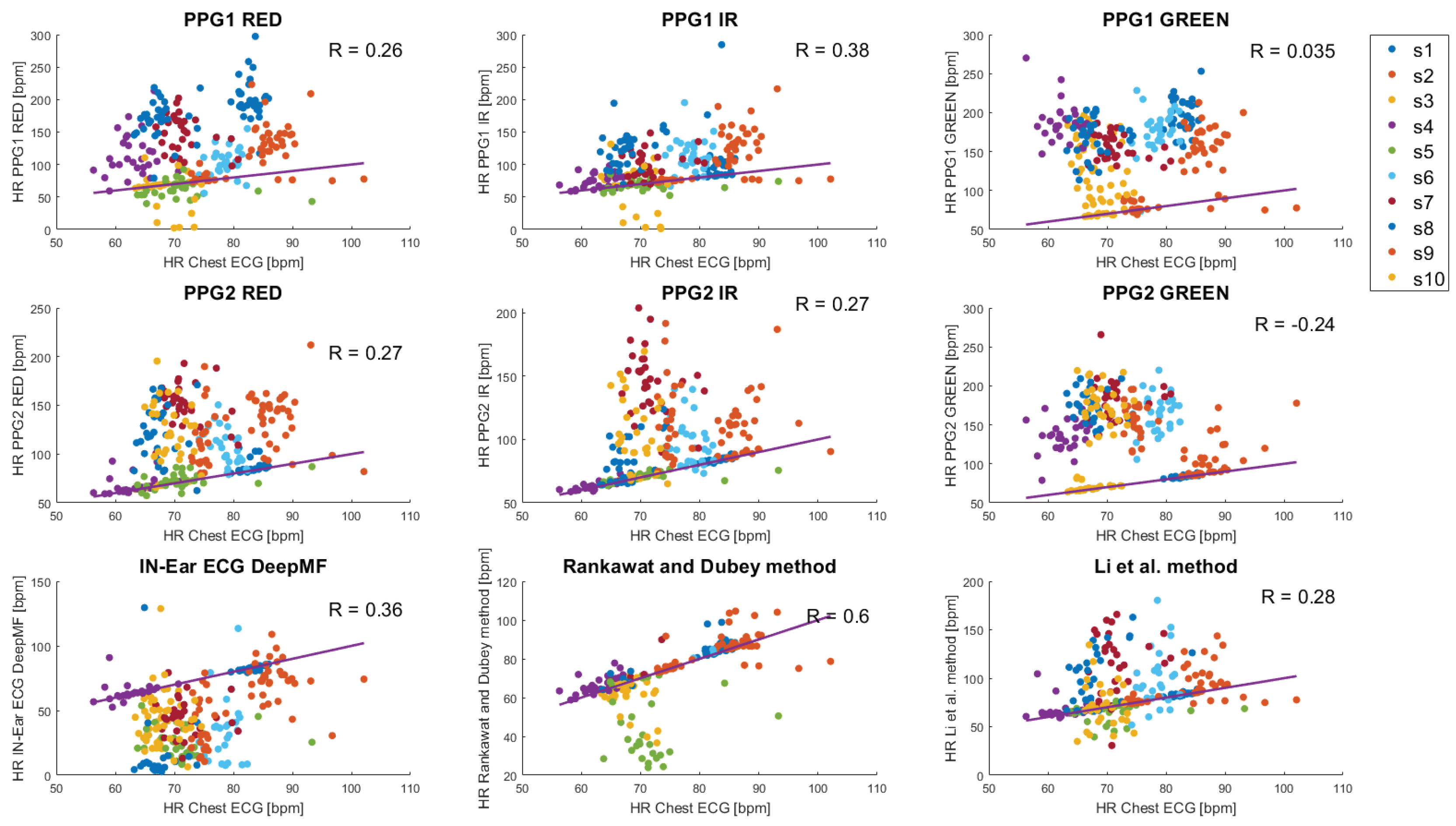
3. Results

Figure 1 shows scatter plots that illustrate the relationship between the HR estimates obtained from source in-ear signals and the HR values derived from data fusion methods to ground true the HR estimation from torso ECG. The highest correlation to the reference for a single source was R=0.38 for PPG1 IR signal, while the highest correlation R=0.60 was obtained when using the Rankawat and Dubey’s method [18].
Notably, the HR estimates derived from PPG signals tend to be overestimated (frequently above the perfect correlation y=x orange line). On the other hand, HR estimates obtained from in-ear signals using the DeepMF method are more likely to underestimate the true HR values.
It is important to note that the Rankawat and Dubey’s method has the capability to reject outliers and may not provide results in cases where the signal does not have an adequate SQI value. For example, in subject 7 the method gave results only in two segments from thirty.
Table 2 summarized MAE obtained during sitting from in-ear source signals and data fusion methods. The corresponding MAEs values during the walking activity are summarized in Table 3.
The Rankawat and Dubey’s method consistently demonstrated the lowest mean MAE across subjects for both activities, with values of 8.0 bpm during sitting and 15 bpm during walking. Notably, the Li et al. method outperformed the best single source HR estimation method, specifically during sitting based on the PPG2 IR signal (17 bpm compared to 23 bpm) and during walking (18 bpm compared to 23 bpm for Green PPG2).
Rankawat and Dubey’s method had high MAE values in subjects 2, 5, 10 (Table 2). However in subject 2 and 10 the method had the lowest MAE value among all. In subject 5, the method follows too closely the results obtained from the DeepMF, while better outcomes are observed when using the Red and IR PPG signals. (Figure 1).
During walking, Rankawat and Dubey’s method maintained an acceptable MAE (below 5 bpm) in 3 subjects (1, 4 and 8). Otherwise, low acceptable MAE values were only obtained in subject 1 when using PPG2 IR and Green signals.
Figure 2 shows the relationship between MAE of HR estimation and mean SQI values, with each data point representing values for different subjects. For PPG signals, when the SQI values are high, the MAE was consistently below 20 bpm. With SQI values below 50, the MAE tend to rise. In contrast, for in-ear ECG signals, the relationship between MAE and SQI was not as clear. The MAE was low for subjects 1 and 4, even though their SQI is below 50, and higher SQI like subjects 3 and 5 had larger MAE.

4. Discussion

We have shown that data fusion methods have lower MAE than single source HR estimations (Table 2). Furthermore, data fusion methods reduced the variation of MAE and provided more robust HR estimation, especially during the walking activity (Table 3) when signals are affected by motion artefacts.
The major concept of data fusion methods is to select the best available sources for HR estimation. The main advantage of Rankawat and Dubey’s method is its ability to reject measurements when there is no valid source (every signal has SQI lower than 0.7). In this case, the method does not provide HR estimation. On the other hand, the Li et al. [17] weighting algorithm uses information from all sources, even from low quality ones. When all of them are poor and have very low SQI, the resulting HR estimation will include information from all of them and provide an unreasonable estimation.
In this study, for in-ear recordings during sitting, the HR estimated from five subjects (subjects: 2, 6, 7, 8 and 10), based on individual signals, had MAE greater than 5 bpm. In these situations, Rankawat and Dubey’s method [25] correctly rejected invalid measurements and kept MAE values at a reasonable level, lower than single source estimation. On the other hand, Li et al. [17] algorithm resulted in MAE slightly higher than the best single source method.
For correct data fusion, it is critical to correctly estimate SQIs and to prevent the usage of invalid data when estimating HR. Rahman et al. [25] evaluated the performance of different SQIs on synthetic data (ECG recordings with artificially added noises). They found that the performance of SQI considerably fluctuated against varying datasets and concluded that fixed threshold-based SQIs cannot be used as a robust noise detection system. They suggested using adaptive thresholds and machine learning mechanisms to improve signal quality assessment.
In our study, quality SQI estimation was especially challenging in subject 5 (Figure 1), where SQI for in-ear ECG were overestimated and led to incorrect estimations of HR provided by Rankawat and Dubey’s method.
This was also observed for SQI estimation in an in-ear ECG recording (Figure 2). SQIs did not seem to be related to MAE, while in a standard scenario, higher SQI should lead to lower MAEs, as in the case of PPG signals. The method used in this study for estimating SQI is based on the correlation of an individual beat with a template built on the average of 30 previous beats. This method seems reasonable for PPG signals where repeatable pulsation has a much larger amplitude than noise. However, it does not seem to be working properly in the case of in-ear ECG signals where signal to noise ratio is likely to be lower (noise level is similar to ECG amplitude).
The in-ear ECG signal requires a more dedicated method for SQI estimation. Improvements in signal quality assessment, for example with deep neural networks [26] or cascade of classifiers [27], may further improve the performance of data fusion methods.
Notably, the HR estimates derived from PPG and ECG show opposite trends. When employing the DeepMF method, ECG signals tend to underestimate HR (i.e. miss a few peaks), while PPG signals tend to overestimate it (i.e. identify more peaks than the real ones), as depicted in Figure 1. This contrasting behaviour makes this problem well-suited for data fusion methods, where the combination of different estimates compensates for distinct and opposite biases, resulting in a more reliable estimation.
Beat detectors for PPG performed well on high-quality PPG signals, but their performance decreases for noisy or low-amplitude signals such as those from in-ears. The reliability of PPG towards HR estimation has been questioned recently. Weiler et al. [28] compared averaged HR readings from PPG and ECG signals, and they did not find a statistically significant difference, but when the HR reached a value around 155-160 bpm, a difference of ± 5 bpm was observed. Charlton et al. [29] evaluated 8 different beat detectors for PPG and found that detectors performed well on hospital data and at rest, but performed worse during movement, stress, atrial fibrillation, and in neonates. In the study, detectors denoted MSPTD [30] and qppg [21] (used in this study) performed best, with complementary performance characteristics. MSPTD looks for peaks in PPG signals without using a priori knowledge of the characteristics of the signal, while qppg searches for systolic up-slopes based on their expected characteristics.
The performance of detectors may be improved; for example Galli et al. [31] proposed an algorithm that combines three sequential signal processing stages of signal denoising by joint principal component analysis of PPG and accelerometer signals, Fourier-based heart rate measurement, and smoothing HR estimation via Kalman filtering. Galli et al. [31] showed that the average deviation from reference values was 1.66 bpm during running and 2.92 bpm during boxing activity. The development of a dedicated onset detector for in-ear PPG signals, such as DeepMF for in-ear ECG, is an interesting route for further study.
Moreover, PPG quality is affected by different skin colours, interfering reflection of light used for measurement, and disturbing optical measurements. Racial bias for blood oxygen saturation measurement using PPG were observed [32]. Different measurement sites can have thinner epidermis compared with the finger and lower exposure to sunlight and may be less prone to the influence of melanin and pigmentation [33]. Hartman et al. [34] discussed that PPG acquired from different locations vary in amplitude and shape, and in some cases may be unsuitable for analysis. In the Hartman et al. [34] study, 95% of recordings from the finger were suitable for analysis, followed by 86% of recordings on the wrist, and 81% on the earlobe.
Data fusion methods seem to be a necessity for PPG in the earlobe location, where the signal amplitudes are smaller and likely to be corrupted by motion artefacts. Data fusion methods and Kalman filter used by Li et al. [17] provide ways to reject outlier results. Further improvement of data fusion can be made by modifying the weighting equation. Our observations suggest that better result should come from the fusion operation in a winner-take-all fashion. We hypothesize that data fusion should mostly use the best available signal, and weights should be associated with the best signal and drop rapidly with a relative drop of SQI.
Data fusion methods provide more robust HR estimation than a single cardiovascular signal. In particular, data fusion methods are useful for data recorded during movement, where signals may be affected by motion artefacts. Data fusion methods through integration of multimodal signals available from in-ear location, can enhance the performance of a wearable device in HR tracking.
Future work will include:
1.
Enhancement of data fusion methods by refining the assessment of weights.
2.
Development of PPG beat detector optimized for low-amplitude in-ear PPG signals.
3.
Improvement of SQI estimation methods towards more reliable HR estimation.

Author Contributions

Conceptualization, M.Z. and E.O.; methodology, M.Z. and E.O.; software, M.Z.; validation, E.O. and M.Z.; formal analysis, M.Z. and E.O.; investigation, M.Z.; resources, M.B., A.N, A.M., and H.D.; data curation, M.Z.; writing—original draft preparation, M.Z.; writing—review and editing, E.O. and A.N.; visualization, M.Z. and E.O.; supervision, D.M.; project administration, D.M.; funding acquisition, D.M. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported in part by USSOCOM MARVELS grant EESB P85655.

Institutional Review Board Statement

The study was conducted under the approval of the Imperial College ethics committee (JRCO 20IC6414).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

Dataset available on request from the authors.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
HR heart rate
ECG electrocardiogram
PPG photoplethysmographm
SQI signal quality index

References

  1. Ruiz-Alias, S.A.; García-Pinillos, F.; Soto-Hermoso, V.M.; Ruiz-Malagón, E.J. Heart rate monitoring of the endurance runner during high intensity interval training: Influence of device used on training functions. Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology 2021, p. 17543371211037035. [Google Scholar] [CrossRef]
  2. Hernando, D.; Garatachea, N.; Almeida, R.; Casajus, J.A.; Bailón, R. Validation of heart rate monitor Polar RS800 for heart rate variability analysis during exercise. The Journal of Strength & Conditioning Research 2018, 32, 716–725. [Google Scholar]
  3. Fariha, M.; Ikeura, R.; Hayakawa, S.; Tsutsumi, S. Analysis of Pan-Tompkins algorithm performance with noisy ECG signals. Journal of Physics: Conference Series. IOP Publishing, 2020, Vol. 1532, p. 012022.
  4. Smital, L.; Haider, C.R.; Vitek, M.; Leinveber, P.; Jurak, P.; Nemcova, A.; Smisek, R.; Marsanova, L.; Provaznik, I.; Felton, C.L.; others. Real-time quality assessment of long-term ECG signals recorded by wearables in free-living conditions. IEEE Transactions on Biomedical Engineering 2020, 67, 2721–2734. [Google Scholar] [CrossRef] [PubMed]
  5. Khamis, H.; Weiss, R.; Xie, Y.; Chang, C.W.; Lovell, N.H.; Redmond, S.J. QRS detection algorithm for telehealth electrocardiogram recordings. IEEE Transactions on Biomedical Engineering 2016, 63, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
  6. Liu, F.; Liu, C.; Jiang, X.; Zhang, Z.; Zhang, Y.; Li, J.; Wei, S. Performance analysis of ten common QRS detectors on different ECG application cases. Journal of Healthcare Engineering 2018, 2018. [Google Scholar] [CrossRef] [PubMed]
  7. Georgiou, K.; Larentzakis, A.V.; Khamis, N.N.; Alsuhaibani, G.I.; Alaska, Y.A.; Giallafos, E.J. Can wearable devices accurately measure heart rate variability? A systematic review. Folia Medica 2018, 60, 7–20. [Google Scholar] [CrossRef]
  8. von Rosenberg, W.; Chanwimalueang, T.; Goverdovsky, V.; Peters, N.S.; Papavassiliou, C.; Mandic, D.P. Hearables: Feasibility of recording cardiac rhythms from head and in-ear locations. Royal Society Open Science 2017, 4, 171214. [Google Scholar] [CrossRef]
  9. Yarici, M.; Von Rosenberg, W.; Hammour, G.; Davies, H.; Amadori, P.; Ling, N.; Demiris, Y.; Mandic, D.P. Hearables: feasibility of recording cardiac rhythms from single in-ear locations. Royal Society Open Science 2024, 11, 221620. [Google Scholar] [CrossRef]
  10. Goverdovsky, V.; Von Rosenberg, W.; Nakamura, T.; Looney, D.; Sharp, D.J.; Papavassiliou, C.; Morrell, M.J.; Mandic, D.P. Hearables: Multimodal physiological in-ear sensing. Scientific Reports 2017, 7, 6948. [Google Scholar] [CrossRef]
  11. Tian, H.; Occhipinti, E.; Nassibi, A.; Mandic, D.P. Hearables: Heart Rate Variability from Ear Electrocardiogram and Ear Photoplethysmogram (Ear-ECG and Ear-PPG). 45th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2023.
  12. Occhipinti, E.; Davies, H.J.; Hammour, G.; Mandic, D.P. Hearables: Artefact removal in Ear-EEG for continuous 24/7 monitoring. IEEE International Joint Conference on Neural Networks (IJCNN), 2022, pp. 1–6.
  13. Hammour, G.; Yarici, M.; von Rosenberg, W.; Mandic, D.P. Hearables: Feasibility and validation of in-ear electrocardiogram. 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE, 2019, pp. 5777–5780.
  14. Passler, S.; Müller, N.; Senner, V. In-ear pulse rate measurement: A valid alternative to heart rate derived from electrocardiography? Sensors 2019, 19, 3641. [Google Scholar] [CrossRef] [PubMed]
  15. Ferlini, A.; Montanari, A.; Min, C.; Li, H.; Sassi, U.; Kawsar, F. In-ear PPG for vital signs. IEEE Pervasive Computing 2021, 21, 65–74. [Google Scholar] [CrossRef]
  16. Butkow, K.J.; Dang, T.; Ferlini, A.; Ma, D.; Mascolo, C. hEARt: Motion-resilient Heart Rate Monitoring with In-ear Microphones. the 2023 IEEE International Conference on Pervasive Computing and Communications (PerCom). IEEE, 2023, pp. 200–209.
  17. Li, Q.; Mark, R.G.; Clifford, G.D. Robust heart rate estimation from multiple asynchronous noisy sources using signal quality indices and a Kalman filter. Physiological Measurement 2007, 29, 15. [Google Scholar] [CrossRef]
  18. Rankawat, S.A.; Dubey, R. Robust heart rate estimation from multimodal physiological signals using beat signal quality index based majority voting fusion method. Biomedical Signal Processing and Control 2017, 33, 201–212. [Google Scholar] [CrossRef]
  19. Rankawat, S.A.; Rankawat, M.; Dubey, R. ECG artifacts detection in noncardiovascular signals using Slope Sum Function and Teager Kaiser Energy. 2015 International Conference on BioSignal Analysis, Processing and Systems (ICBAPS). IEEE, 2015, pp. 6–10.
  20. Welch, G.F. Kalman filter. Computer Vision: A Reference Guide 2020, pp. 1–3.
  21. Vest, A.N.; Da Poian, G.; Li, Q.; Liu, C.; Nemati, S.; Shah, A.J.; Clifford, G.D. An open source benchmarked toolbox for cardiovascular waveform and interval analysis. Physiological Measurement 2018, 39, 105004. [Google Scholar] [CrossRef]
  22. Davies, H.J.; Hammour, G.; Zylinski, M.; Nassibi, A.; Mandic, D.P. A Deep Matched Filter For R-Peak Detection in Ear-ECG. arXiv preprint arXiv:2305.14102 2023.
  23. Li, Q.; Clifford, G.D. Signal quality and data fusion for false alarm reduction in the intensive care unit. Journal of Electrocardiology 2012, 45, 596–603. [Google Scholar] [CrossRef] [PubMed]
  24. Elgendi, M.; Jonkman, M.; De Boer, F. Frequency Bands Effects on QRS Detection. Biosignals 2010, 2003, 2002. [Google Scholar]
  25. Rahman, S.; Karmakar, C.; Natgunanathan, I.; Yearwood, J.; Palaniswami, M. Robustness of electrocardiogram signal quality indices. Journal of the Royal Society Interface 2022, 19, 20220012. [Google Scholar] [CrossRef] [PubMed]
  26. Jin, Y.; Li, Z.; Qin, C.; Liu, J.; Liu, Y.; Zhao, L.; Liu, C. A novel attentional deep neural network-based assessment method for ECG quality. Biomedical Signal Processing and Control 2023, 79, 104064. [Google Scholar] [CrossRef]
  27. Liu, S.; Zhong, G.; He, J.; Yang, C. Multi-task cascaded assessment of signal quality for long-term single-lead ECG monitoring. Biomedical Signal Processing and Control 2023, 83, 104674. [Google Scholar] [CrossRef]
  28. Weiler, D.T.; Villajuan, S.O.; Edkins, L.; Cleary, S.; Saleem, J.J. Wearable heart rate monitor technology accuracy in research: A comparative study between PPG and ECG technology. Human Factors and Ergonomics Society Annual Meeting. SAGE Publications Sage CA: Los Angeles, CA, 2017, Vol. 61, pp. 1292–1296.
  29. Charlton, P.H.; Kotzen, K.; Mejía-Mejía, E.; Aston, P.J.; Budidha, K.; Mant, J.; Pettit, C.; Behar, J.A.; Kyriacou, P.A. Detecting beats in the photoplethysmogram: Benchmarking open-source algorithms. Physiological Measurement 2022, 43, 085007. [Google Scholar] [CrossRef] [PubMed]
  30. Bishop, S.M.; Ercole, A. Multi-scale peak and trough detection optimised for periodic and quasi-periodic neuroscience data. Intracranial Pressure & Neuromonitoring XVI. Springer, 2018, pp. 189–195.
  31. Galli, A.; Frigo, G.; Narduzzi, C.; Giorgi, G. Robust estimation and tracking of heart rate by PPG signal analysis. IEEE International Instrumentation and Measurement Technology Conference (I2MTC). IEEE, 2017, pp. 1–6.
  32. Sjoding, M.W.; Dickson, R.P.; Iwashyna, T.J.; Gay, S.E.; Valley, T.S. Racial bias in pulse oximetry measurement. New England Journal of Medicine 2020, 383, 2477–2478. [Google Scholar] [CrossRef] [PubMed]
  33. Bermond, M.; Davies, H.J.; Occhipinti, E.; Nassibi, A.; Mandic, D.P. Reducing racial bias in SpO2 estimation: The effects of skin pigmentation. 45th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), 2023.
  34. Hartmann, V.; Liu, H.; Chen, F.; Qiu, Q.; Hughes, S.; Zheng, D. Quantitative comparison of photoplethysmographic waveform characteristics: Effect of measurement site. Frontiers in Physiology 2019, 10, 198. [Google Scholar] [CrossRef] [PubMed]
Preprints 99629 g001
Figure 1. Scatter plots of HR estimated during sitting, from in-ear source signals and with data fusion methods, relative to the ground truth HR estimated from torso ECG. Different colors are associated with different subjects.
Figure 1. Scatter plots of HR estimated during sitting, from in-ear source signals and with data fusion methods, relative to the ground truth HR estimated from torso ECG. Different colors are associated with different subjects.
Preprints 99629 g001
Preprints 99629 g002
Figure 2. Relationship between the MAE value and SQI for different sources.
Figure 2. Relationship between the MAE value and SQI for different sources.
Preprints 99629 g002
Table 1. Values of weights associated by Rankawat and Dubey [18] based on SQI and source type.
Table 1. Values of weights associated by Rankawat and Dubey [18] based on SQI and source type.
Source type SQI ≥ 0.9 0.9>SQI ≥ 0.8 0.8>SQI ≥ 0.7
Cardiovascular signals 5 3 1
Non-cardiovascular signals 3 2 0
Table 2. MAE values for single source HR estimation and data fusion methods during the sitting activity. The smallest value in each row is designated in bold.
Table 2. MAE values for single source HR estimation and data fusion methods during the sitting activity. The smallest value in each row is designated in bold.
PPG1 PPG2 In-Ear ECG Data fusion
Subject RED IR GREEN RED IR GREEN DeepMF Rankawat and Dubey Li et al.
1 119 19 113 3.6 0.9 0.9 0.5 3.0 2.2
2 107 39 124 16 46 65 17 14 35
3 1.6 9.0 94 0.7 0.6 2.3 26 3.5 1.3
4 53 12 124 4.4 1.5 73 2.5 3.7 4.4
5 13 7.3 - 5.6 2.4 - 45 27 7.6
6 26 36 98 28 19 85 48 1.6 25
7 74 29 84 80 73 108 28 6.6 44
8 101 55 101 55 15 107 57 2.7 32
9 6.1 3.3 5.9 38 35 78 37 3.6 3.6
10 45 49 16 56 37 106 30 16 17
Mean 54 26 84 29 23 69 29 8.0 17
std 40 19 50 28 24 42 17 8.4 16
Table 3. MAE values for single source HR estimation and data fusion methods during the walking activity. The smallest value in each row is designated in bold.
Table 3. MAE values for single source HR estimation and data fusion methods during the walking activity. The smallest value in each row is designated in bold.
PPG1 PPG2 In-Ear ECG Data fusion
Subject RED IR GREEN RED IR GREEN DeepMF Rankawat and Dubey Li et al.
1 50 51 73 30 4.6 2.8 32 2.2 5.8
2 71 63 82 71 71 8.8 31 14 12
3 18 28 101 65 29 12 58 31 15
4 56 51 76 56 22 9.5 13 4.1 14
5 43 36 - 28 24 - 77 16 34
6 34 33 44 51 53 44 71 28 23
7 20 18 31 15 13 25 72 24 18
8 20 22 41 55 60 51 79 3.6 34
9 22 17 21 18 22 35 63 11 14
10 20 16 13 12 31 15 26 15 14
Mean 35 33 54 40 33 23 52 15 18
std 19 17 33 22 21 18 24 10 9
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

208

Views

103

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated