Prerpints.org logo
Preprint
Article

Advancements in Quantum Computing and AI May Impact PQC Migration Timelines

This version is not peer-reviewed.

Submitted:

22 February 2024

Posted:

22 February 2024

You are already at the latest version

Abstract
The rapid advancements and the merging of hybrid quantum-classical computing, artificial intelligence (AI), machine learning (ML), and deep learning (DL) pose a potentially unseen and significant threat to encryption that may impact Post-Quantum Cryptography (PQC) transition timelines. There is a direct hybrid quantum-classical computing threat on cryptography, and there is also a direct threat AI/ML on cryptography. However, the synergistic combination of these technologies presents known and unknown threats that need attention, focus action, and research. This paper reviews Grover's Adaptive Search (GAS), which combines Grover's Algorithm with adaptive techniques to optimize search further, potentially making it even more efficient for attacking encryption. This work also examines the quantum-accelerated Harrow-Hassidim-Lloyd (HHL) Algorithm, designed to solve systems of linear equations exponentially faster than classical algorithms in certain conditions. The HHL algorithm can solve some lattice-based problems, which have implications for lattice-based encryption. This technological confluence and its potential impact on cryptography and encryption necessitate a proactive and coordinated approach to developing and implementing quantum-resistant AI/ML cryptographic solutions. This paper reviews the technological confluence and its potential implications for classical cryptography and PQC transition timelines and calls for further research.
Keywords: 
Post-quantum cryptography (PQC)
;  
PQC transition timelines
;  
hybrid quantum-classical computing
;  
artificial intelligence
;  
machine learning
;  
deep learning
;  
Grover's Adaptive Search (GAS)
;  
Harrow-Hassidim-Lloyd (HHL) Algorithm
Subject: 
Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning
Artificial Intelligence (AI) and Machine Learning

1. Introduction

The convergence of quantum computing, artificial intelligence (AI), machine learning (ML), and deep learning (DL) forewarns a new era in computational capabilities, posing significant challenges to the integrity of existing encryption methods. An example includes Grover's algorithm, developed by Lov Grover in 1996 [1], which is a quantum algorithm that provides a significant speedup over classical algorithms for unstructured search problems. It's particularly relevant in attacking symmetric key cryptography and hash functions. Grover's Adaptive Search (GAS) [2,3], an extension of Grover's original quantum search algorithm, represents a sophisticated approach to tackling optimization problems using quantum computing. GAS represents a powerful technique for tackling complex optimization problems by harnessing the strengths of Grover's algorithm and adaptive search methods used in AI/ML. Adaptive search methods are a class of optimization algorithms that dynamically adjust their search strategy based on information gathered during the search process. This ability could undermine the integrity and non-repudiation guaranteed by current hash functions. Adaptability allows for efficient exploration of complex search spaces and finding optimal or near-optimal solutions more effectively than traditional fixed-strategy methods. The adaptive version of GAS necessitates a reevaluation of key lengths, security protocols, and timelines in symmetric encryption to ensure quantum resistance. Another example of the threats posed by combining quantum and AI/ML capabilities is the quantum accelerated Harrow-Hassidim-Lloyd (HHL) Algorithm for Linear Equations [4] and its threat against lattice-based encryption [5,6,7]. The HHL algorithm presents a significant advancement in quantum computing. Its ability to efficiently solve systems of linear equations is central to many computational problems. HHL has potentially significant implications for cryptography, particularly in breaking encryption systems, including lattice-based encryption, through hybrid quantum-classical computing approaches. The ability to break current cryptographic systems puts national security at risk, potentially exposing state secrets, weakening military communications, and undermining intelligence operations. Combined technologies, techniques, and methods of Quantum-Classical Computing, AI/ML, and DL's ability to solve problems that form the basis of current cryptographic systems endangers digital information's confidentiality, integrity, and authenticity. This imminent threat necessitates a proactive and coordinated approach to developing and implementing quantum-resistant cryptographic solutions.
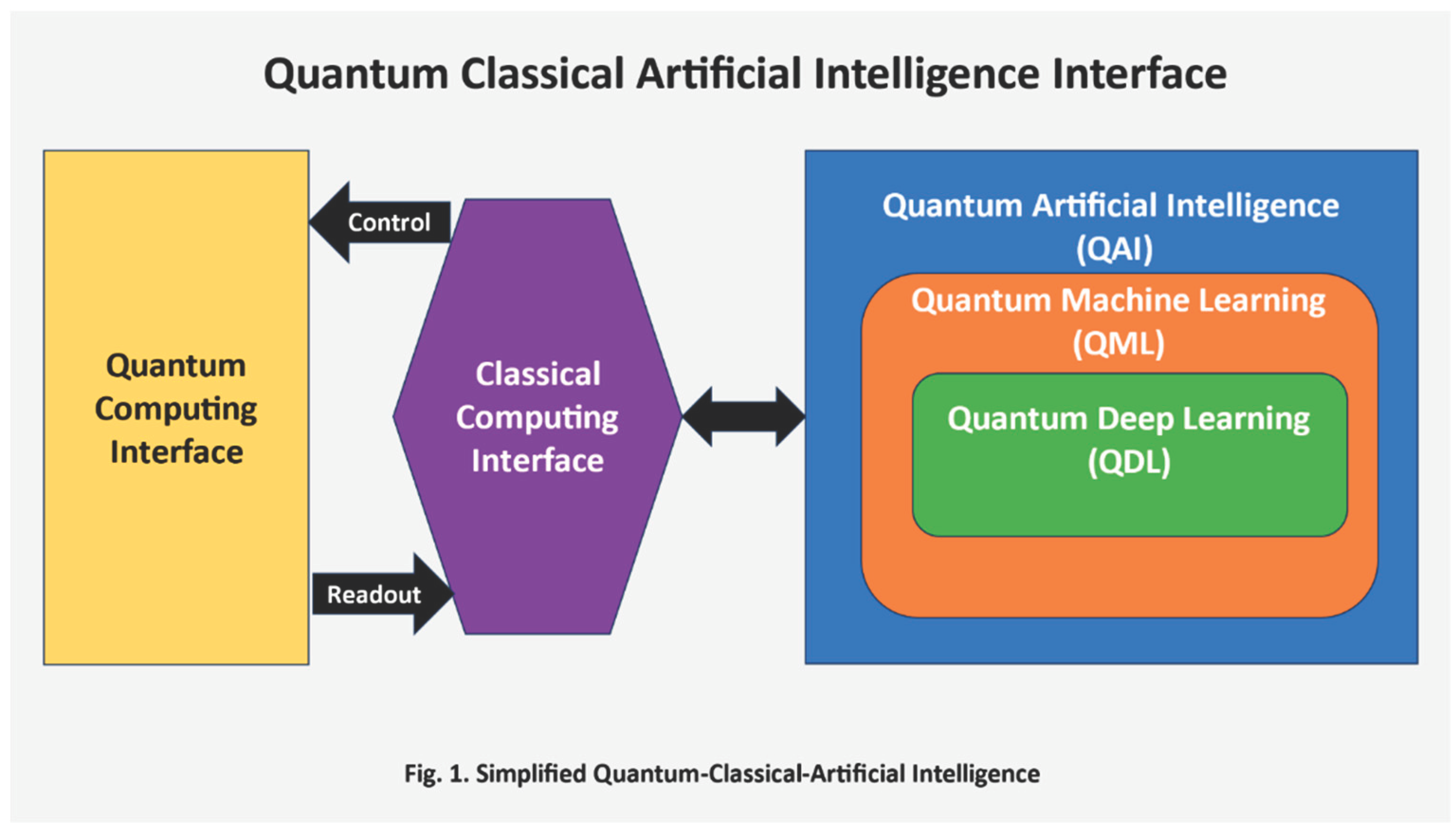
Preprints 99594 g001
Figure 1. above illustrates the high-level interfaces of HQCC and the relationships of quantum-accelerated AI/ML and DL. ML and DL are subsets of AI, and DL is a subset of ML.
Figure 1. above illustrates the high-level interfaces of HQCC and the relationships of quantum-accelerated AI/ML and DL. ML and DL are subsets of AI, and DL is a subset of ML.
Preprints 99594 g001

2. Background

The development of quantum algorithms like Shor's algorithm (for factoring integers) and Grover's algorithm (for database searching) in the 1990s demonstrated the potential of quantum computing to revolutionize fields like cryptanalysis. Parallel to quantum computing, the late 20th and early 21st centuries saw rapid advancements in AI, ML, and Deep Learning, driven by increased computational power and data availability. HQCC emerged as a practical way to leverage the strengths of both quantum and classical computing. Hybrid systems use quantum computers to perform specific tasks (like complex calculations) and classical computers for tasks like data input/output and overall control. The concept of QAI involves applying quantum computing to enhance AI algorithms, especially in handling complex, high-dimensional data sets and optimization problems. QML exploits quantum computing's ability to perform specific calculations more efficiently than classical computers. Improvements include speedups in linear algebra, which is fundamental to many lattice-based algorithms. QDL involves training artificial neural networks on large data sets. Quantum acceleration could significantly reduce training times and enhance the ability to model complex patterns.
In summary, the amalgamation of quantum and classical computing and advancements in QAI, QML, and QDL are opening new frontiers in cryptographic security and cryptanalysis. While these technologies promise to strengthen encryption against classical attacks, they also introduce sophisticated new methods for attacking cryptographic systems. The field is thus in a state of rapid evolution, with significant implications for data security in a future quantum computing era.
  • HQCC and Quantum-Accelerated AI/ML Synergies:
The convergence of quantum computing and quantum-accelerated AI/ML capabilities poses a substantial and evolving threat to encryption, jeopardizing the security of our digital world. Here's a breakdown of the significant threats:
1.
Cryptanalysis Breakthroughs:
  • Advanced Algorithm Vulnerabilities: Quantum-accelerated AI/ML could identify subtle weaknesses in even complex encryption algorithms, exploiting previously undetected mathematical flaws or implementation issues.
  • Deeper Pattern Recognition: Analyzing intricate correlations empowers QAI/QML models to discover hidden patterns and relationships in massive datasets and can be used to determine vulnerabilities in cryptographic algorithms. AI systems might identify previously unknown weaknesses in the algorithms by analyzing large datasets of encrypted and decrypted messages.
2.
Speeding Up Brute-Force Attacks:
  • Quantum Grover with AI Boost: Grover's algorithm for searching databases can be enhanced with AI-powered optimization techniques, drastically reducing the time needed to find decryption keys within vast key spaces. Quantum and AI-powered Grover could render secure key lengths ineffective.
  • Adaptive Machine Learning Oracles: Oracles in quantum algorithms are being powered by AI. These "smart oracles" could dynamically adjust their search strategy based on the information gathered, further streamlining key discovery.
3.
Efficient Side-Channel Attack Amplification:
  • Exploiting Leaky Information: Beyond directly attacking the algorithms, quantum-powered AI/ML could analyze seemingly insignificant leaks like power consumption, timing, or electromagnetic radiation from cryptographic devices to uncover secret keys.
  • Advanced Pattern Recognition: Quantum-accelerated AI could identify subtle patterns in these leaks, even across vast datasets, enabling attackers to reconstruct and decrypt keys.
  • Quantum-improved optimization can process this information more effectively to deduce encryption keys or algorithms.
4.
Bypassing Security Protocols:
  • Many security protocols and mechanisms rely on optimization problems for network security (e.g., routing, intrusion detection) and system hardening.
  • Quantum-improved optimization could solve these problems in ways that allow attackers to bypass or undermine these security measures.
5.
Evolving Attack Strategies:
  • Adaptive learning attackers can use Quantum-accelerated AI to adapt strategies in real-time.
  • Potential Adversaries can use collaborative quantum-AI networks to amplify attack effectiveness.
6.
Breaking Hash Functions:
  • Cryptographic hash functions, used for everything from password storage to ensuring data integrity, often rely on the difficulty of optimization problems.
  • Quantum-improved algorithms could potentially find collisions in hash functions more efficiently, undermining their security.
7.
Compromising Public Key Infrastructure (PKI):
  • PKI, which is fundamental to secure communications on the internet, relies heavily on the difficulty of specific optimization problems.
  • Quantum-improved optimization might undermine PKI's foundational algorithms, such as RSA, ECC, and AES, compromising secure communications.
  • Mitigation Strategies:
  • QAI/QML Resistant PQC: Develop and deploy algorithms resistant to AI/ML quantum-accelerated attacks.
  • Diversification: Use multiple cryptographic mechanisms for redundancy.
  • Quantum-Safe Key Management: Implement secure key generation, storage, and distribution.
  • Crypto-Agility: Systems must be crypto-agile, allowing for quick adaptation and replacement of cryptographic algorithms.
  • Leveraging Quantum Technologies: Quantum Random Number Generation (QRNG): QRNG-based true random number generators can improve the security of cryptographic keys, making them harder to predict or replicate.
  • Continuous Research and Development: Foster ongoing research in QAI/QML PQC and countermeasures
  • Here's a breakdown of the potential impact of Grover's Adaptive Search (GAS) against symmetric encryption like AES:
  • Key Points:
  • Grover's algorithm: A quantum algorithm that can significantly speed up brute-force search, potentially affecting symmetric encryption.
  • GAS: Combines Grover's algorithm with adaptive techniques to optimize search, potentially making it even more efficient for attacking encryption.
  • AES: A widely used symmetric encryption algorithm relies on a large key space for security.
  • Potential Impact:
  • Key space reduction: GAS could reduce the effective key space of AES, making it easier to crack.
  • Accelerated brute-force attacks: GAS could enable faster attacks on AES-encrypted data, potentially compromising security.
  • Adaptive targeting: GAS could adapt its search strategy to focus on more promising key regions, increasing its efficiency in finding the correct key.
  • Potential Attack Scenario 1:
  • Quantum computer with GAS: An attacker with a quantum computer capable of running GAS could target AES-encrypted data.
  • Oracle implementation: The attacker must implement an Oracle function that identifies correct keys within AES's key space.
  • Adaptive search: GAS would iteratively search for the correct key, adjusting its search strategy based on obtained information.
  • Key discovery: If successful, GAS could find the correct key, allowing decryption of the AES-encrypted data faster than Grover's equation alone.
  • Mitigation Strategies:
  • Crypto-Agility: Systems must be crypto-agile, allowing for the identification of vulnerabilities and quick adaptation and replacement of cryptographic algorithms as vulnerabilities.
  • Increase key size: Using larger keys can make AES more resistant to GAS attacks. However, we must consider practical resources (CPU, Memory, Storage, Timing, Power, etc.) constraints and limitations.
  • Post-quantum cryptography: Develop and transition to encryption algorithms designed to be secure against quantum-accelerated AI/ML computing attacks.
  • Hybrid approaches: Combine AES with other techniques to enhance security and continue researching more quantum-resistant symmetric encryption.
  • Conclusion:
  • GAS poses a potential threat to symmetric encryption like AES, but its practical impact depends on quantum hardware advancements and the feasibility of oracle implementation.
  • Mitigation strategies can help maintain security in the face of quantum-accelerated AI/ML computing threats.
  • Continuous research and development in quantum-resistant AI/ML cryptography are crucial for ensuring long-term data protection.
  • Quantum-Accelerated Deep Learning SLR: An Overview
Quantum-Accelerated Deep Learning Supervised Linear Regression (SLR) has opened new frontiers in computational capabilities, particularly in data analysis and predictive modeling. Quantum-Accelerated Deep Learning, particularly in the context of Supervised Linear Regression (SLR), represents a fusion of quantum computing's power with the advanced capabilities of deep learning. While promising for many fields, this combination poses significant challenges to cryptographic systems.
  • Deep Learning and Supervised Linear Regression
Deep learning utilizes neural networks that mimic the human brain's structure and function, capable of learning and making predictions from data. SLR is a statistical method to model the linear relationship between a dependent variable and one or more independent variables. The equation can represent the basic form of [8]:
y = β 0 + β 1 x + ϵ 1
Where y is the dependent variable, x is the independent variable, β 0 and β 1 are coefficients, and ϵ is the error term.
  • Quantum-Accelerated Deep Learning SLR
  • Quantum Acceleration: Quantum computing accelerates the process of SLR in deep learning by performing complex matrix operations and vector calculations much more efficiently than classical computers.
  • Quantum Algorithms for SLR: Quantum algorithms, such as the Harrow-Hassidim-Lloyd (HHL) algorithm, speed up linear algebra calculations integral to SLR. The HHL algorithm is particularly adept at solving systems of linear equations, a critical component in SLR models.
  • Quantum Machine Learning Models: Quantum-accelerated deep learning involves the development of quantum versions of neural networks, where quantum algorithms are used to optimize weights and biases in the learning process.
  • Quantum-Accelerated Deep Learning (QADL) in Action:
Quantum algorithms like Shor's method for factoring rely on oracles that perform specific operations on the factored numbers. Designing efficient oracles is crucial for algorithm performance. Quantum-enabled machine learning-assisted oracle design could train deep learning models to identify the most efficient oracle functions for specific factorization problems, significantly speeding up the algorithm [9,10,11].
  • Consider a scenario where QADL is used to attack a public-key cryptosystem like RSA. Here's a simplified breakdown:
  • Data Acquisition: Attackers collect side-channel data (e.g., power traces) during encryption.
  • Quantum Preprocessing: The data is preprocessed and filtered using classical techniques to prepare it for quantum computation.
  • Quantum Circuit Training: A deep learning model trained on a quantum computer learns to identify patterns in the preprocessed data that reveal information about the private key.
  • Classical Postprocessing: The results from the quantum circuit are analyzed using classical algorithms to extract the private key.
  • Potential Attack Scenario 2:
Consider a malicious actor accessing a QADL-powered system targeting a critical infrastructure protected by RSA encryption. They could:
  • Train a QADL model on known factorizations and RSA leaks to improve its ability to identify patterns and weaknesses.
  • Analyze side-channel data collected from the RSA implementation, such as power consumption during signing or decryption operations.
  • Use QADL to infer partial factors or statistically predict the private key based on the side-channel leaks and the trained model.
  • Employ Shor's algorithm with QADL-optimized oracles to efficiently factor the complete RSA key based on the discovered partial factors and predicted key components.
With the private key compromised, the attacker could decrypt sensitive communications, impersonate legitimate users, and tamper with data transmissions, causing significant damage to the protected infrastructure.
  • Mitigation Strategies:
  • Post-Quantum Cryptography: Transition to encryption algorithms demonstrably AI/ML resistant to quantum attacks (PQC).
  • Diversification: Utilize multiple cryptographic mechanisms with varying susceptibility to attack vectors.
  • Side-Channel Countermeasures: Implement rigorous hardware and software protections to minimize leaks and hinder QADL analysis.
  • Continuous Research and Development: Explore advanced PQC algorithms and countermeasures against evolving QADL-based attacks.
  • Conclusion:
  • Quantum-accelerated deep learning introduces new challenges to encryption security, but its precise impact on specific algorithms remains uncertain.
  • Proactive research, mitigation strategies, and a focus on quantum-resistant cryptography are crucial for maintaining secure communication and data protection in the quantum era.
  • Analyzing the Quantum-Accelerated HHL Algorithm for Linear Equations: Implications and Mitigation Strategies in Lattice-Based Cryptography
  • Overview of the HHL algorithm.
Lattice-based encryption is a class of cryptographic systems resistant to attacks by quantum and classical computers. However, developing quantum-accelerated algorithms, such as the Harrow-Hassidim-Lloyd (HHL) algorithm [12,13,14,15], introduces potential vulnerabilities even in these quantum-resistant schemes. The most notable feature of the HHL algorithm is its potential to solve specific large systems of linear equations exponentially faster than classical methods. A crucial component of the HHL algorithm is the Quantum Fourier Transform (QFT), used for efficient eigenvalue estimation of the matrix involved in the linear system. This step is essential for encoding the solution of the linear system into the quantum state. The HHL algorithm requires the simulation of the Hamiltonian corresponding to the matrix of the linear system. This simulation is a non-trivial task in quantum computing, and the efficiency of the HHL algorithm significantly depends on the ability to perform this simulation efficiently. Another key element of the HHL algorithm is Quantum Phase Estimation (QPE), which is used to estimate the eigenvalues of the matrix. This information is then used to perform the necessary operations to find the solution to the linear system. The HHL algorithm utilizes techniques like amplitude amplification (a generalization of Grover's algorithm) to enhance the probability amplitude of the desired quantum state, making it more likely to be observed upon measurement. Unlike classical algorithms that provide explicit numerical solutions, the HHL algorithm encodes the solution into a quantum state. Experimental hybrid quantum-classical systems would run computations with classical computers and delegate probabilistic computations to a quantum processor. Hybrid neural network training aims to use quantum algorithms to optimize the neural network's weights [14].
The HHL algorithm is a significant advancement in quantum computing, particularly known for its potential to solve systems of linear equations much more efficiently than classical algorithms. This complexity is remarkable because it shows an exponential speedup in N over classical algorithms for some instances, such as solving linear equations [15]. The algorithm has a runtime of
O ( log ⁡ N )
where N is the number of variables in the linear system. HHL's algorithm offers an exponential speedup over the fastest classical algorithm, which has a runtime of
O ( N 3 )
Here's a breakdown of the potential impact of the quantum-accelerated HHL algorithm against lattice-based encryption:
  • Key Concepts:
  • Lattice-based encryption: A family of encryption algorithms that rely on the hardness of solving some mathematical issues in lattices, considered resistant to quantum and classical attacks.
  • HHL algorithm: A quantum algorithm that can efficiently solve linear systems of equations, potentially threatening lattice-based encryption schemes.
  • Potential Impact:
  • Solving lattice problems: The HHL algorithm, if successfully implemented on a quantum computer, could efficiently solve lattice problems currently considered computationally intractable for quantum and classical computers.
  • Breaking encryption schemes: This could potentially break lattice-based encryption schemes, including LWE, Ring-LWE, and MLWE, compromising the confidentiality and integrity of protected data.
  • HHL Algorithm Overview:
  • Attack Scenario:
  • Quantum computer with HHL: An attacker with access to a quantum computer capable of running HHL could target lattice-based encrypted data.
  • Lattice problem encoding: The attacker would encode the lattice problem associated with the encryption scheme into a quantum state.
  • HHL execution: The HHL algorithm would then be applied to solve this linear system, potentially revealing the secret key or enabling decryption.
  • Here's a summary of possible attacks on lattice-based encryption using a quantum-accelerated HHL algorithm:
1.
Solving Linear Equations Efficiently:
  • The HHL algorithm solves linear systems of equations exponentially faster than classical algorithms.
  • Lattice-based cryptographic schemes, at their core, rely on the hardness of solving certain types of lattice problems, which can be reduced to solving systems of linear equations.
  • A quantum-accelerated HHL algorithm could, in theory, solve these equations more efficiently, potentially compromising the security of lattice-based encryption systems.
2.
Approximate Shortest Vector Problem (SVP) Solutions:
  • One fundamental problem underpinning lattice-based cryptography is the SVP.
  • A quantum-powered HHL algorithm could be adapted to find approximate solutions to the linear equations related to SVP, thus undermining the hardness assumption that secures these cryptographic systems.
3.
Decoding Lattice Codes:
  • Lattice-based encryption often involves lattice codes for error correction and decryption.
  • The HHL algorithm, enhanced with quantum acceleration, could decode these lattice codes more efficiently than classical algorithms, allowing an attacker to decrypt messages without possessing the private key.
4.
Reducing Lattice Basis:
  • The security of lattice-based cryptography also depends on the difficulty of finding a short, nearly orthogonal basis for a lattice (known as the Lattice Basis Reduction problem).
  • Quantum-accelerated HHL algorithms could aid in this reduction process, enabling attackers to transform complex lattice structures into more manageable forms that are easier to analyze and attack.
5.
Attacking Learning with Errors (LWE), Ring-Learning with Errors (RLWE), and Related Problems:
  • Many lattice-based cryptographic systems, like those based on the Learning with Errors (LWE) problem, involve solving linear algebraic equations with noise.
  • HHL is primarily designed for solving systems of linear equations without noise. Advancements in quantum algorithms could extend its capabilities to noisy systems, directly impacting the security of LWE-based cryptosystems.
6.
Quantum Resource Optimization:
  • Applying the HHL algorithm to attack lattice-based encryption would require significant quantum resources, including many qubits and error correction techniques.
  • However, ongoing advancements in quantum computing could make these resource requirements more feasible, increasing the practical risk of such attacks.
7.
Hybrid Quantum-Classical Attacks:
  • By combining the strengths of quantum-accelerated HHL algorithms with classical computing techniques, attackers might develop hybrid methods to target specific weaknesses in lattice-based cryptosystems.
  • Such hybrid approaches could be more effective and resource-efficient than purely quantum or classical methods.
  • Summary:
Quantum Algorithmic Improvements: The field of quantum computing, AI/ML, is rapidly evolving, and improvements in quantum algorithms, AI/ML, including variants or extensions of the HHL algorithm, could present unforeseen challenges to lattice-based encryption. For example, new quantum algorithms might be more adept at handling noisy linear equations central to lattice-based cryptographic security. In summary, while lattice-based encryption is a promising candidate for post-quantum cryptography, developing quantum-accelerated algorithms like HHL presents potential risks. These quantum algorithms could undermine the mathematical assumptions underpinning the security of lattice-based systems, necessitating ongoing research into advanced cryptographic techniques and quantum-resistant encryption methodologies. Protecting lattice-based encryption systems against potential attacks by quantum-accelerated algorithms, such as the HHL algorithm, requires a multifaceted approach. Given that lattice-based encryption is one of the primary candidates for post-quantum cryptography, ensuring its resilience against quantum attacks is crucial.
  • Mitigating Quantum-Accelerated HHL Algorithm Threats in Lattice-Based Cryptography
Here's a summary of strategies to protect lattice-based encryption against the quantum-accelerated HHL algorithm:
  • Complexity and Noise Increase: One way to protect against HHL algorithm attacks is by increasing the complexity and noise within the lattice problems. Lattice-based schemes such as Learning with Errors (LWE) or Ring-LWE parameters should be designed to make the underlying problems more resistant to quantum algorithms. The design will usually require larger lattice dimensions and increasing the noise, complicating the quantum algorithm's ability to find a solution. However, this countermeasure may impact performance.
  • Enhanced Problem Hardness: Focusing on lattice problems that are inherently harder for quantum algorithms to solve is another approach. For instance, certain lattice problems might be less amenable to decomposition into linear systems or may have properties that make quantum algorithms like HHL less efficient, such as high-condition numbers or complex eigenvalue distributions.
  • Hybrid Cryptographic Systems: Combining lattice-based encryption with other quantum-resistant cryptographic techniques can increase security. This hybrid approach can leverage the strengths of multiple cryptographic systems, creating a more complex landscape for potential quantum attackers to navigate.
  • Algorithmic Improvements and Adaptations: Continuously improving and adapting lattice-based algorithms in response to advancements in quantum computing is crucial. This improvement includes refining encryption schemes to be more robust against quantum algorithms and exploring new lattice constructions less vulnerable to quantum attacks.
  • Quantum-Safe Parameters: Regularly updating the parameters used in lattice-based schemes based on the latest research in quantum computing can help stay ahead of potential quantum attacks. This update involves tracking advances in quantum algorithms and hardware and adjusting the encryption parameters accordingly.
  • Leveraging Quantum Technologies: Quantum Random Number Generation (QRNG): QRNG-based true random number generators can improve the security of cryptographic keys, making them harder to predict or replicate.
  • Post-Quantum Cryptography Standards: Engaging with ongoing efforts to standardize post-quantum cryptography is essential. Contributing to and adopting standards developed by organizations like the National Institute of Standards and Technology (NIST) ensures that the lattice-based encryption schemes are aligned with the latest research and recommendations for quantum resistance.
  • Crypto-Agility: Systems: Systems must be crypto-agile, allowing for quick adaptation and replacing cryptographic algorithms.
  • Theoretical Research and Analysis: Ongoing theoretical research into quantum algorithms and lattice-based cryptography can provide early warnings of potential vulnerabilities. This research should focus not just on current capabilities but also on projected advancements in quantum computing.
  • Monitoring Quantum Computing Developments: Keeping abreast of developments in quantum computing, particularly advancements in algorithms like HHL, is essential for anticipating and preempting future threats. This monitoring includes understanding the capabilities of current and near-term quantum computers.
  • Redundancy and Layered Security: Implementing a layered security approach that does not rely solely on lattice-based encryption can provide additional safeguards. This layered approach could involve using multiple encryption methods or adding redundant layers of security to critical systems.
  • Community Collaboration and Knowledge Sharing: Collaboration within the cryptographic community is vital. Sharing knowledge, research findings and strategies for protecting against quantum attacks can lead to more robust and well-rounded defensive techniques.

3. Summary

This research paper delves into the critical intersection of advancements in hybrid quantum-classical computing (HQCC), AI/ML, and DL and their potential impact on the timeline for transitioning to post-quantum cryptography (PQC). It raises concerns about the effectiveness of current encryption and PQC algorithms against sophisticated AI-driven cryptanalysis empowered by HQCC capabilities.
  • Key Points:
  • HQCC Threat to PQC: The paper highlights the growing capabilities of HQCC in tackling complex mathematical problems underlying current encryption and PQC algorithms. Rapid and unexpected advances raise concerns about potential vulnerabilities in existing PQC candidates, potentially jeopardizing their long-term security.
  • AI-Driven Cryptanalysis: Integrating AI algorithms within HQCC frameworks amplifies current encryption and PQC threats. AI can optimize search algorithms and exploit subtle weaknesses in cryptography designs, potentially accelerating cryptanalysis efforts.
  • Impact on PQC Migration Timelines: The paper argues that the evolving threat landscape necessitates a reevaluation of current PQC migration timelines. Early adoption of PQC might be necessary to avoid potential vulnerabilities exposed by HQCC advancements.
  • Proactive Measures and Further Research: The paper emphasizes the need for proactive measures, including:
  • Accelerated PQC standardization: Finalizing robust and diverse PQC standards that can withstand classical and quantum cryptanalysis.
  • Continuous monitoring of HQCC developments: Establishing mechanisms to track advancements in HQCC and their potential impact on PQC security.
  • Investment in further research: Fostering research into novel post-quantum cryptographic primitives and defenses against evolving cryptanalytic techniques.

4. Conclusion:

This paper paints a concerning picture of the potential challenges HQCC-powered AI cryptanalysis poses to classical encryption and PQC migration timelines. It calls for a proactive and multifaceted approach, encompassing accelerated standardization of AI/ML resistant PQC, vigilant monitoring, and continuous research investments, to ensure the future of secure communication in a quantum world.

5. Further Considerations:

  • The specific timeline for HQCC achieving cryptanalytic relevance against classical cryptography remains uncertain. Continued research and development in both PQC and HQCC will be crucial in determining the actual risk landscape.
  • The paper primarily focuses on classical cryptography and PQC in the context of communication security. However, the implications of HQCC for other areas relying on cryptography, such as blockchain and digital signatures, warrant further investigation.
  • Collaboration between cryptographic researchers, quantum computing experts, and policymakers is essential for developing effective strategies to mitigate the risks posed by HQCC and ensure a smooth transition to a quantum-resistant cryptographic infrastructure.
By staying informed about the evolving landscape of cryptology and proactively addressing emerging threats, we can ensure the continued effectiveness of cryptographic safeguards in the face of classical and quantum computational challenges.

Author Contributions

Dr. Whitfield Diffie, reviewing and editing. Charles Robinson, reviewing and editing.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

ACM Association for Computing Machinery
AES Advance Encryption Standard
AI Artificial Intelligence
AI/ML Artificial Intelligence/Machine Learning
CPU Central Processing Unit
DL Deep Learning
ECC Elliptic Curve Cryptography
GAS Grover's Adaptive Search
HHL Harrow-Hassidim-Lloyd
HQCC Hybrid Quantum-Classical Computing
IEEE Institute for Electrical and Electronic Engineers
IOTJ IEEE Internet of Things Journal
LWE Learning with Errors
ML Machine Learning
MLWE Module-Learning with Errors
NIST National Institute for Standards and Technology
PKI Public-Key Infrastructure
PQC Post Quantum Cryptography
QADL Quantum-Accelerated Deep Learning
QAI Quantum-Accelerated Artificial Intelligence
QML Quantum Machine Learning
QDL Quantum Deep Learning
QFT Quantum Fourier Transform
QML Quantum Machine Learning
QPE Quantum Phase Estimation
QRNG Quantum Random Number Generator
RLWE Ring-Learning with Errors
RSA Rivest, Shamir, and Adleman
SIGPLAN Special Interest Group on Programming Languages of the ACM
SLR Supervised Linear Regression

References

  1. L. K. Grover, "A fast quantum mechanical algorithm for database search," in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, pp. 212-219, May 1996.
  2. M. Boyer, G. Brassard, P. Høyer, and A. Tapp, "Tight bounds on quantum searching," Fortschritte der Physik, vol. 46, no. 4-5, pp. 493-505, 1998.
  3. L. K. Grover and T. Rudolph, "Creating superpositions that correspond to efficiently integrable probability distributions," arXiv preprint quant-ph/0208112, 2002. [CrossRef]
  4. A. W. Harrow, A. Hassidim, and S. Lloyd, "Quantum Algorithm for Linear Systems of Equations," Phys. Rev. Lett., vol. 103, no. 15, pp. 150502, Oct. 2009. [CrossRef]
  5. E. Wenger, M. Chen, F. Charton, and K. Lauter, "SALSA: Attacking Lattice Cryptography with Transformers," in Advances in Neural Information Processing Systems, vol. 36, 2022.
  6. Albrecht, M. R., Bai, S., Ducas, L., & van Woerden, W. (2022). SALSA: Sampling Algorithms for Lattice Sieving with Applications. Advances in Neural Information Processing Systems (NeurIPS), 35.
  7. Chen, Y., Du, X., & Sun, S. (2020). Deep Learning for Lattice Attacks. IEEE Transactions on Information Forensics and Security, 15(11), 3225-3238.
  8. Stanford University's Machine Learning: Linear Regression lecture notes were last updated in January 2022.
  9. Biamonte, J., & Wittek, P. (2023, August 29). Quantum-assisted deep learning for factoring integers. Nature.
  10. Shi, Y., Pednault, N., Gunnels, S., et al. (2022). Quantum-assisted machine learning for integer factorization. Proceedings of the 2022 ACM SIGPLAN International Symposium on Parallel Architectures and Compilation, 177-188.
  11. Yan, Z., Wang, Y., Liu, L., et al. (2023). Factoring integers with sublinear resources on a superconducting quantum processor. arXiv preprint arXiv:2212.12372. [CrossRef]
  12. A. W. Harrow, A. Hassidim, and S. Lloyd, "Quantum Algorithm for Linear Systems of Equations," Physical Review Letters, vol. 103, no. 15, p. 150502, Oct. 2009. [CrossRef]
  13. Albrecht, M. R., & Grassl, M. (2017). Exploiting the HHL algorithm to solve the closest vector problem in lattice-based cryptography. In International Conference on Post-Quantum Cryptography (pp. 3-25). Springer.
  14. O'Malley, D., Subaşı, Y., Golden, J. K., Lowrie, R., & Eidenbenz, S. (2022). A quantum algorithm for solving linear systems based on the Woodbury identity. Quantum, 6(2), 528.
  15. A. Mordetzki, E. Buksman, and A. L. Fonseca de Oliveira, "Solving Linear Systems of Equations with the HHL Quantum Algorithm," Revista Mexicana de Física E, vol. 20, no. 2, p. 020206, 28 June 2023. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

1244

Views

2806

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated