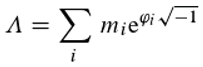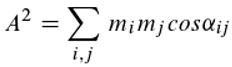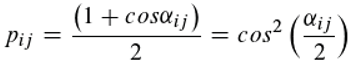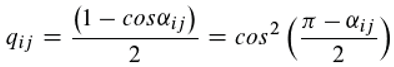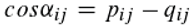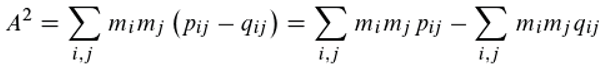Prerpints.org logo
Preprint
Article

The Interference of Light as Photon Pair Interaction Mediated by Matter under the Assumption of Alternative („classical”) Photon Paths in Multi-path Experiments

This version is not peer-reviewed.

Submitted:

21 February 2024

Posted:

22 February 2024

You are already at the latest version

Abstract
Light can interfere like a wave in a multi-path experiment, but it also has particle properties when interacting with matter. In a closer look, the interference pattern is created by many individual detections ("clicks"), which do not all occur simultaneously. An established assumption is therefore that a single light particle is capable of interfering with itself by superimposing all possibilities to get from the source to the detector. This is in stark contrast to our experience with macroscopic objects, which always "decide" in favour of only one of the alternative paths.In 2010, Jin et al. (Ref. 15) described an event-based model which allowed the authors to show that an interference pattern consisting of clicks can arise in a multi-path experiment even if photons, like macroscopic objects, only follow one path. To do this, photons must be able to transmit the information about their travelling duration to the detector and the detector must have a basic memory. A threshold function uses the message of several light quanta to decide whether a single detection is initiated, which is not the evidence for a single photon. In this "proof of principle", the authors do not claim that the detector function is a realistic one.In the present paper, this detector is replaced by a material consisting of ionizable molecules whose interaction with light takes place according to a modified version of Einstein's radiation laws. Based on this, a photon pair interaction mediated by matter takes place, which in a multi-path experiment generates an interference pattern of clicks at the detector, even if an arbitrary amount of time elapses between the individual detections. In the present model an interference pattern with minima that have less than half the intensity of the maxima is the result of a peculiar behaviour of the detector: In this case, the entirety of its electrons must be described as a unit (a “field”) with many equidistant energy levels. The results of a simulation are presented which enable the model to be tested in experiments.
Keywords: 
double-slit experiment
;  
multi-path experiment
;  
Einstein's radiation laws
;  
photon
;  
light interference
;  
Copenhagen interpretation
Subject: 
Physical Sciences  -   Quantum Science and Technology

supplementary.docx (124.36KB )

Introduction

In 1802, the English ophthalmologist T. Young carried out an experiment [24] to clarify whether light consists of particles or is a wave. The experimental set-up was very simple in principle: light travelled from a source onto a plate with two very narrow, parallel slits. Behind the plate (viewed from the source), there was an observation screen at some distance, on which light and dark stripes were recognisable, which Young interpreted as interference pattern. Light was thus a wave, contrary to I. Newton's theory. This view remained unchallenged for more than a hundred years. But then A. Einstein's explanation of the photoelectric effect in 1905 [3] brought the realisation that not all phenomena involving light could be understood in terms of its wave nature, which ultimately led to the development of the concept of “wave-particle duality” or "light quanta". G. I. Taylor repeated the experiment in 1909 with a very weak light source and a very long exposure time [20]. In this case, too, an interference pattern emerged, which was interpreted to mean that individual light quanta that cannot interact with others are also capable of superposition. The view developed that each particle interferes with itself, whereby the detector should play a passive role in the formation of the pattern.
For R. Feynman, the observation that an interference pattern can be composed of spatially and temporally separated, individual detection events was "impossible, absolutely impossible to explain in any classical way and has in it the heart of quantum mechanics" [11]. In his (and G. Wentzel's) path integral method [10,24], a possible formulation of quantum mechanics, the probability of a particle being detected is calculated as the superposition of all possible paths that the particle can take from the source to the detector (Equation (1)). However, such a view is difficult to reconcile with "common sense", as we are used to having to choose between several available paths and not being able to take them all at the same time. Ultimately, many of the most influential physicists came to the conclusion that, at the quantum level, individual events cannot be explained according to the cause-and-effect principle, and even worse, that individual events cannot be described at all.
Some scientists disagreed with this interpretation, which was originally formulated by W. Heisenberg and N. Bohr (Copenhagen interpretation), especially A. Einstein. For him, quantum theory, as formulated by W. Heisenberg and E. Schrödinger, was merely an ensemble theory with no significance for individual events [9]. He had wanted to establish a theory based on an understanding of the basal interactions between electromagnetic radiation and matter and made significant contributions to this in 1905, 1914, 1916, 1917, 1919 and 1924 [3–8]. With the discovery of induced emission, he laid the foundation for the development of the laser [5]. He was also able to show, among other things, that photons are not emitted as waves, as they cause a molecule to bounce in a certain direction during emission [6], which is difficult to reconcile with the assumption that a light quantum should not take a defined path. He was also able to predict the diffraction of matter at a lattice [8] and to show the conditions under which this is possible (the interference of a hot gas of C60 and C70 at a lattice is an interesting phenomenon, but does not follow from quantum theory).
There are still scientists who insist on a causal view of the world and thus move beyond the mainstream. Particularly noteworthy are H. de Raedt and K. Michielsen, who, together with others, have shown in numerous computer simulations since 2005 that the experimental results and observed phenomena can also be explained without self-interference or entanglement. Among other things, they also investigated the double-slit experiment or "two-path interference" under the assumption that each photon behaves like a classical particle in that it only passes through one of the slits on its way from the light source to the detector, i.e. it “decides” in favour of one of the available paths, as we must do [15]. In order for an interference pattern to appear despite of this, the light quanta must have some properties that are not usually attributed to them. The author of the present paper adopts them completely from the cited publication for his model. The detector is modelled in [1,15–17] by a threshold function, which is explicitly mentioned as having no claim to reality. The detector is a unitary object about which nothing else is known, whereas in this publication it consists of countless molecules that can be ionised by light. As will be shown, this difference is crucial.
The interaction between detector molecules and light is modelled here according to a modification of Einstein's radiation laws [23], which was originally developed to describe the formation of coherent light in the laser as density-dependent selection and from which it follows that a photon pair interaction mediated by matter takes place. In this case, it can be seen that Born's rule is not an ad hoc postulate as in quantum theory, but arises as a matter of course.

The Light Source

Now that the experimental set-up has been roughly described, we will choose a suitable light source. For the sake of simplicity, we will assume that it produces monochromatic, coherent light.

Properties of the Photon

For our model, we adopt the features that were already attributed to the light quantum in [15]:
  • In the model, photons do not interact directly, but do interact with matter (the detector) and only indirectly with each other in this way (the fact that electromagnetic waves do not interact with each other in a vacuum follows from Maxwell's theory. However, the phenomenon of Halpern Scattering [Light-by-Light Scattering] is attributed to the direct interaction of photons, but is not relevant in this context).
  • During the journey of the photons from the source to the detector, no communication takes place between them (this also follows from point 1). They are independent of each other and therefore not part of a wave.
  • There is no superposition of different photon paths in the model and hence no self-interference. In the double slit experiment, for example, each light quantum follows exactly one path from the source, passes through only one of the two slits and thus reaches the detector in the shortest possible time allowed by this path. In this respect, it behaves like a macroscopic object.
  • Photons are particles that oscillate at a frequency μ=E/h (they are "de Broglie oscillators"; E: energy; h: Plank's quantum of action). In the model, they are neither waves, nor wave and particle or sometimes this, sometimes that.
  • In our model, each photon carries a message. This consists of information about the travelling time Δt modulo the period 1/μ. One might imagine that the light quantum carries a periodic rotator, a clock with only one hand, which moves throughout the journey. The position of the hand on arrival is the message that is transmitted to the detector molecule and ultimately causes the interference pattern to form. We call it the phase of the photon. More about time and the phenomenon of duration can be found in Supplement 1, more about information in Supplement 2.

Properties of the Detector

In our model (in contrast to quantum theory), the detector plays a very active role in the creation of the interference pattern. We imagine it to be relatively small and it must therefore be moved perpendicular to the slits so that the entire interference pattern can be "scanned". Nevertheless, it consists of countless molecules that can be ionised by light. The number of electrons released by irradiation (or the number of "clicks") is the signal of the detector. In [1,15–17] the detector has a memory. The same applies to the molecules of our detector. In the excited state, they memorise the message of the absorbed photon, i.e. its phase at the time of absorption.
As in [15], a detection event (a "click") does not simply correspond to the absorption of a photon. Therefore, the number of clicks cannot easily be used to infer the number of photons emitted by the source (which is important in view of the Taylor experiment mentioned in the introduction). In any case, there is no one-to-one correspondence between emission at the source and absorption at the detector, because the probability of the release of an electron results from the difference between the two messages transmitted by two photons to the same molecule.

Modification of Einstein's Laws of Radiation for the Interaction of Light with Matter

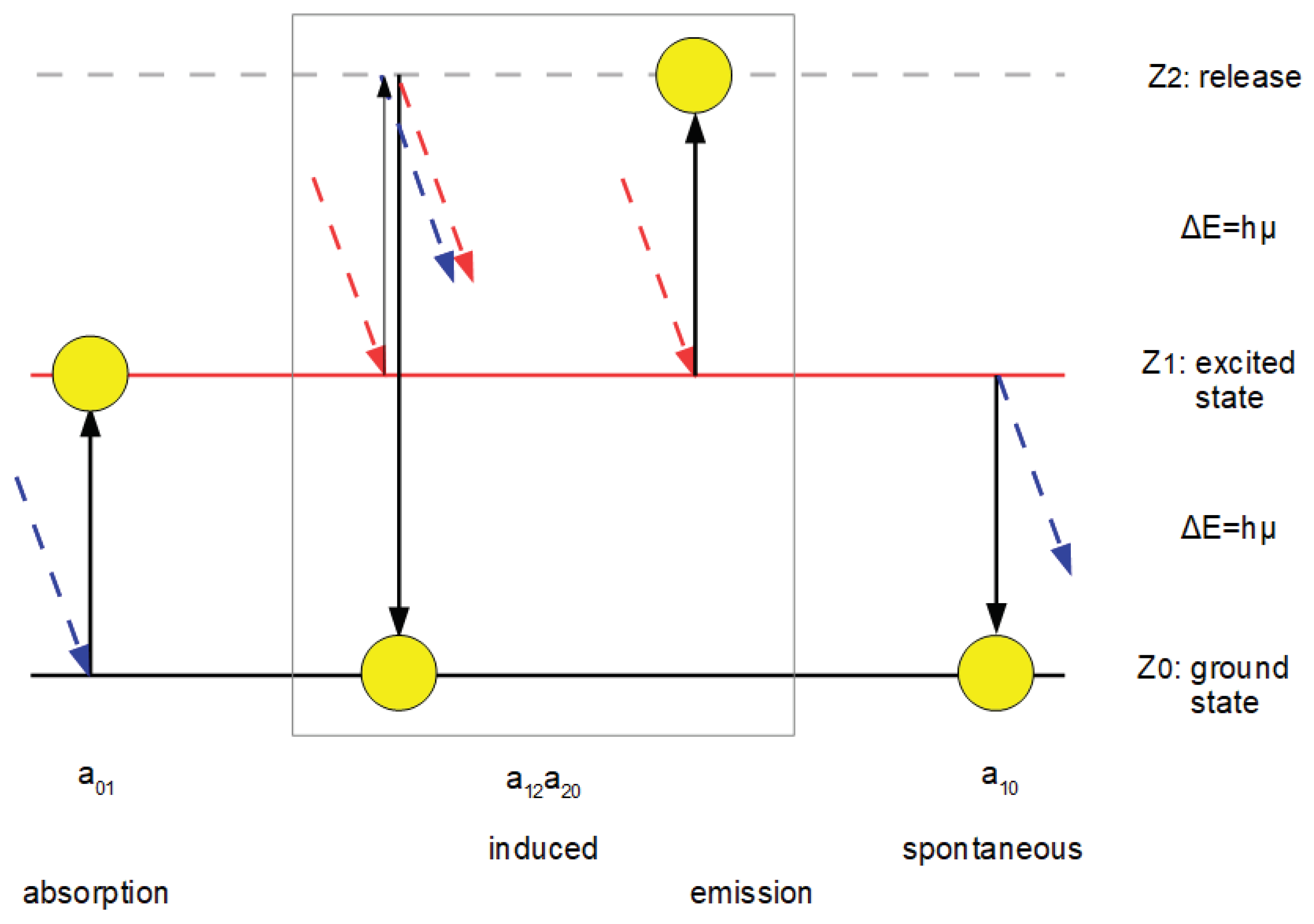
In 1916, A. Einstein [5] developed a theory on the emission and absorption of electromagnetic radiation (subsequently often referred to simply as "light") by matter, based on his explanation of the photoelectric effect in 1905 [3] and the law of blackbody radiation established by M. Planck in 1900 [18]. Einstein found that, in addition to absorption, there must be two types of emission, namely spontaneous emission, which finds its analogue in radioactive decay, and induced (stimulated) emission. The latter is triggered by irradiating a molecule or atom with light of the same frequency as the absorbed photon has (the actual interaction takes place between the photon and the shell electron). This transition between two (of in general many possible) energy levels is schematised in the following figure:
By absorbing a photon (symbolised by a blue arrow), the atom moves from the ground state Z0 to the excited state Z1, and an electron (symbolised by a yellow circle) is raised to a higher energy level. The emission is a reversal of this event. The corresponding transition probabilities for the period Δt are given by a01 for the absorption, a10 for the spontaneous and b10 for the induced (stimulated) emission. The states Z0 and Z1 differ by the amount of energy ΔE=hμ, where, as already mentioned, h stands for Plank's quantum of action, a constant, and μ for the frequency of the photon.
By considering the equilibrium between absorption and emission and using the Boltzmann distribution and Planck's radiation equation, which he assumed to be correct, Einstein also discovered that a01=b10, an interesting result that should be made plausible in an event-based model.
The wave picture is often used to illustrate induced emission. Viewed as a wave, a photon is able to shake the atom, whereupon it passes from the excited to the ground state and emits a photon. The photon pair has the phase of the inducing one, symbolised in Figure 1 by the colour identity (it also takes on other properties such as polarisation and axis of flight, but here it is the phase identity that is of interest). Obviously there is no precise idea of how this should happen (according to the Copenhagen interpretation it would be nonsensical to devise one). As mentioned, however, in the model we want to develop here, the photon is not a wave but just a particle, a de Broglie oscillator, which is one of the reasons why the author has proposed some changes in a previous publication under this premise, which make the wave picture superfluous [23].
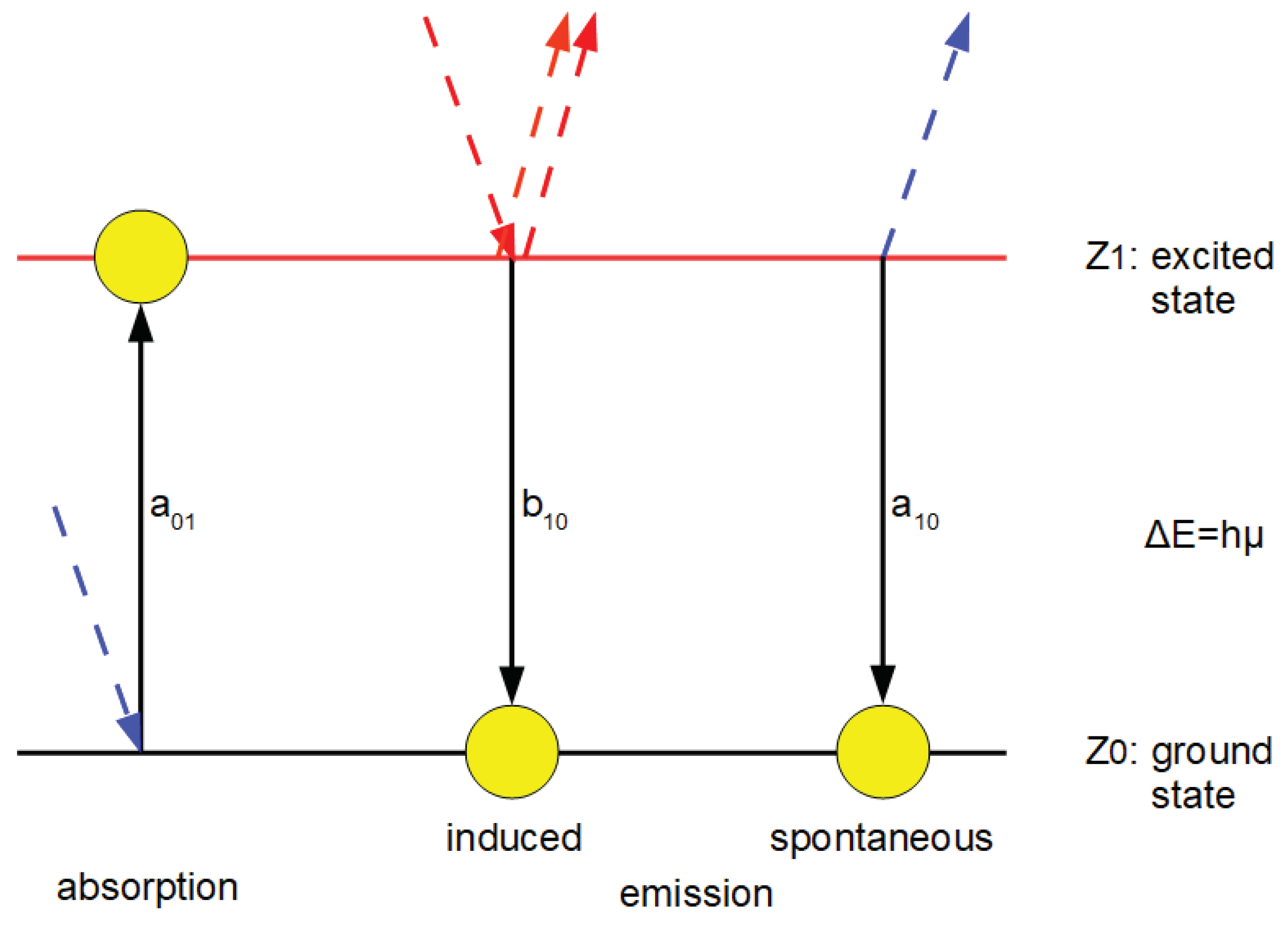
Accordingly, the induced emission would actually be a combination of the absorption of another photon with the same frequency or momentum, which causes the atom to change from a single to a double excited state (Figure 2). The transition probability for this event is a12. This is followed by the immediate transition to the ground state with the release of a photon pair. The transition probability for this is a20 and for the entire process a12a20. Since the first event is an absorption, it is not implausible to assume that a01=a12. If the decay of the doubly excited state really occurs immediately, a20=1 and therefore b10=a12a20=a01, which must be the case, as A. Einstein discovered.
An essential difference for the model, however, is that the decay of the doubly excited state can result in either a photon pair with identical phases (with probability p), or two photons whose phases are arbitrary to each other (with counter-probability q). The postulate of the existence of two different decay possibilities - identical or random phases in the released photon pair - may seem arbitrary here, but it is a compelling conclusion from the fact that the formation of coherent light in lasers, in which induced emission plays a special role, can be described by the selection equation of replicator dynamics. More on this in Supplement 2.
In Figure 2, the photons considered to be of the same frequency are represented by arrows of different colours, with the colour symbolising the phase. It does not have to be the same for the two absorbed photons, but if the phases of the two photons released during the decay of the doubly excited state are identical, they coincide with that of the photon absorbed later, in accordance with A. Einstein's model. We regard the phase as the message that a photon passes on, overwrites or copies, and it is the present that overwrites the past, as we know from experience. The author's assumption presented earlier [23] that both photons are the same from the moment of absorption is certainly wrong, i.e. it contradicts reality. Equally wrong is the idea that the "trapped" photon continues to oscillate, because in this case two photons coherently emitted from one source would always be in phase when they meet in the doubly excited state, regardless of the time delay with which the second arrives (e.g. because it travels a longer distance). However, we need the possibility of a phase difference for our model. In any case, the phase of the photon at the time of absorption is stored by the atom. This is the message that is passed on. The photon itself no longer exists.

A Detector Based on the Photoelectric Effect

If the energy of a photon pair is sufficient to "lift" an electron out of an atom or molecule, we may obtain a free electron and an ion as products of the interaction between two photons and a molecule (or between an excited molecule and a photon). It is also possible that only one photon is relevant for the energy budget of the reaction, the second acts as a kind of catalyst and a photon is released in addition to the electron when the doubly excited state decays. In our model, however, this does not happen, only the electron is released. The number of free electrons is the signal of the detector.
As Figure 3 shows, the detector model is essentially a modification of the concept shown in Figure 2 of how the interaction of light and matter takes place. The induced emission can either result in an electron being released (with probability p) or the molecule returning to the ground state (with counter probability q) by releasing two non-coherent photons. The ionisation in Figure 3 replaces the release of the coherent photon pair in Figure 2.
If an interference pattern is to appear at the detector, p and q must somehow depend on the messages of the two photons, i.e. their phases at the time of their absorption.

The Multi-Slit Experiment

A source should emit monochromatic and coherent light of one of the frequencies that the detector molecules can absorb. It reaches an opaque plate with a series of k parallel slits. Only through these can photons reach a detector behind it, which works on the basis of the photoelectric effect, as described above. The detector should be small and can move perpendicular to the slits. The length of the path from source to detector across different slits will usually be different, causing a difference in the duration of the flight and thus a phase difference between the incoming photons at the time of absorption. As the detector position changes, the phase difference also changes. At the time of absorption, we therefore have photons that have k different phases φi (i=1,...,k) and whose relative frequencies are mi (Σmi=1). The number of photons released by the source and reaching the detector in the time interval Δt is M.
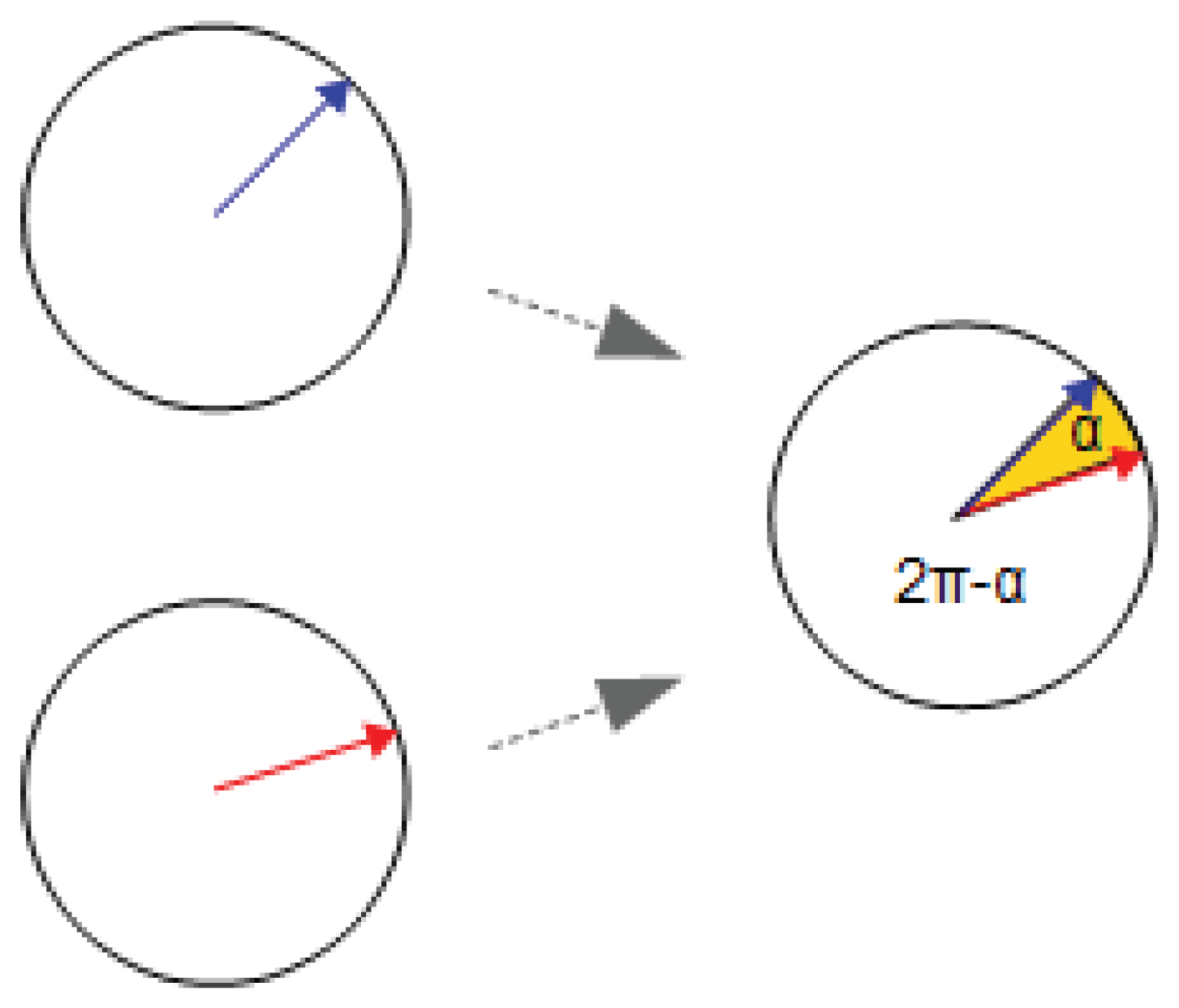
In the following, we postulate a relationship between the phase difference αij=φi-φj (i,j=1,...,k) of the two photons involved in the ionisation of a molecule (the angle between the hand position on the clock face in the illustrative Figure 4) and the probability p that the detector molecule is ionised, i.e. that an electron is released. If this relationship is known, it would no longer be difficult to construct the resulting interference pattern for a given distance between source and plate, between plate and detector and with a known slit distance. But our ambition does not go that far. Knowing the detector signal as a function of the phase difference is enough for us. We develop the model for k slits, but use k=2 for our simulation, i.e. the situation that occurs in the double-slit experiment.

Interference of Photons

The term interference originally refers to partial waves that emanate from the slits in a slit experiment, for example, and meet at some point and interact there. No part of a wave is independent of its other parts, but particles are. In the context of quantum theory, we are dealing with particles, quanta, but it is often assumed that a single photon can interfere with itself by - simply put - a superposition of all paths that are possible from the source to the detector through all slits (this is, of course, an interpretation that does not necessarily follow from the mathematical formulation of the path integral; see [10,24]. In the context of the model, however, the paths are alternatives, of which the individual photon chooses only one. So whatever makes the interference pattern appear happens at the detector.
The probability d of a detection for the given experimental set-up according to Born's rule isd=|Λ|2=Λ*Λ, where Λ is the probability amplitude calculated for the multi-slit-experiment as the sum of complex numbers, each one associated to a possible path from source to detector (Λ* is the complex number conjugated to Λ, which results from Λ by reversing the sign of the imaginary part). Using our notation, the amplitude is given by:
Preprints 99490 i001
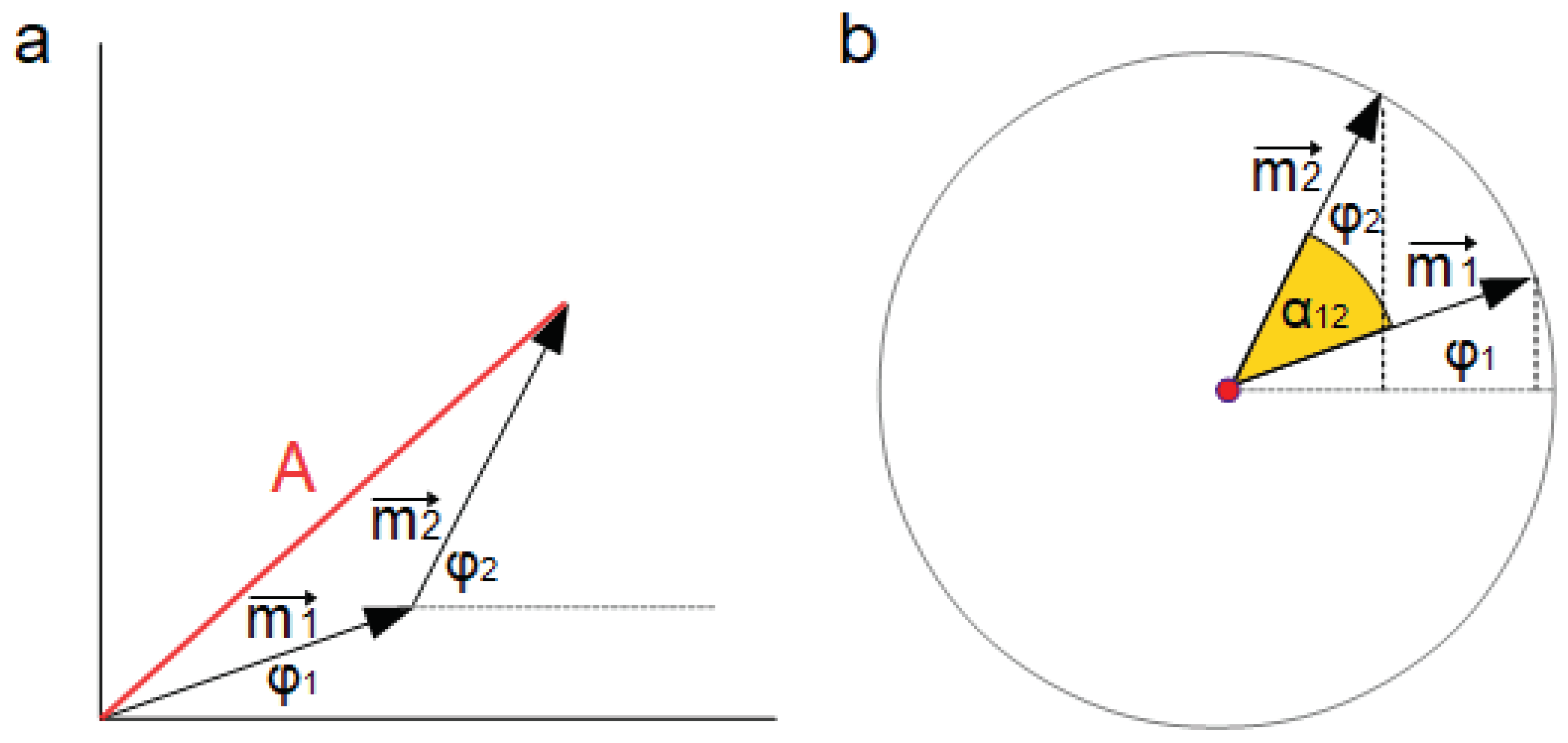
This can be visualised as a series of arrows, where the distance between the origin of the first arrow and the tip of the last is the absolute value of the amplitude (Figure 5a for two slits and therefore two paths from the source to the detector).
To arrive at this result, one does not need any conception of how the detector works and what happens during the interaction of photons and molecules (this is a basic property of quantum theory, that one can apply it without having to know too much about the events involved. Conversely, it also says nothing about the individual events).
An alternative way of calculating the detection probability d=A2, which has nothing to do with the summation of complex numbers or vectors, is (for notation see Figure 5b):
Preprints 99490 i002
where αij=φi-φj. Equations (1) and (2) correspond to each other, as shown in Supplement 3, insofar as they give the same result: |Λ|2 = A2. According to Equation (2), A2 is the mean value of all pairwise photon phase comparisons cos αij. There are always pairs, even if the number of slits k is greater than two. This representation (Equation (2)) is interesting for us because it is in harmony with the idea of an interaction of photon pairs, as it follows from our interpretation of Einstein's radiation laws. Moreover, Born's rule emerges here as a self-evident consequence of pairwise comparison, whereas its validity in quantum theory remains an unexplained postulate (for experimental verification of Born's rule, see [19]).
We must now return to our concept of the interaction of light and matter in the detector (Figure 3). There we developed the idea that the induced emission can occur in two different ways, namely on the one hand with probability p leading to ionisation of the excited molecule, but on the other hand the excited molecule will return to the ground state with the opposite probability q by emitting two non-coherent photons. We now postulate that p depends on the angle (αij or 2π-αij) that the phases of the two photons had at the time of their absorption (i.e. on their message). Since pij (we now add the indices) is a probability, it must also be 0≤pij≤1. Because the cosine has a value range from -1 to 1, one can obtain a value range between zero and two by adding one and one from zero to one (as desired) by dividing by two. Therefore, the very simple Equation (3) fulfils the requirements, whereby it does not matter for the result whether αij is replaced by 2π-αij (because cosα = cos (2π-α)):
Preprints 99490 i003
Because pij and qij are counter probabilities, i.e. pij+qij=1, the following results using -cosα = cos(π-α):
Preprints 99490 i004
One quickly realises that the following must apply:
Preprints 99490 i005
From this it follows using Equation (2):
Preprints 99490 i006
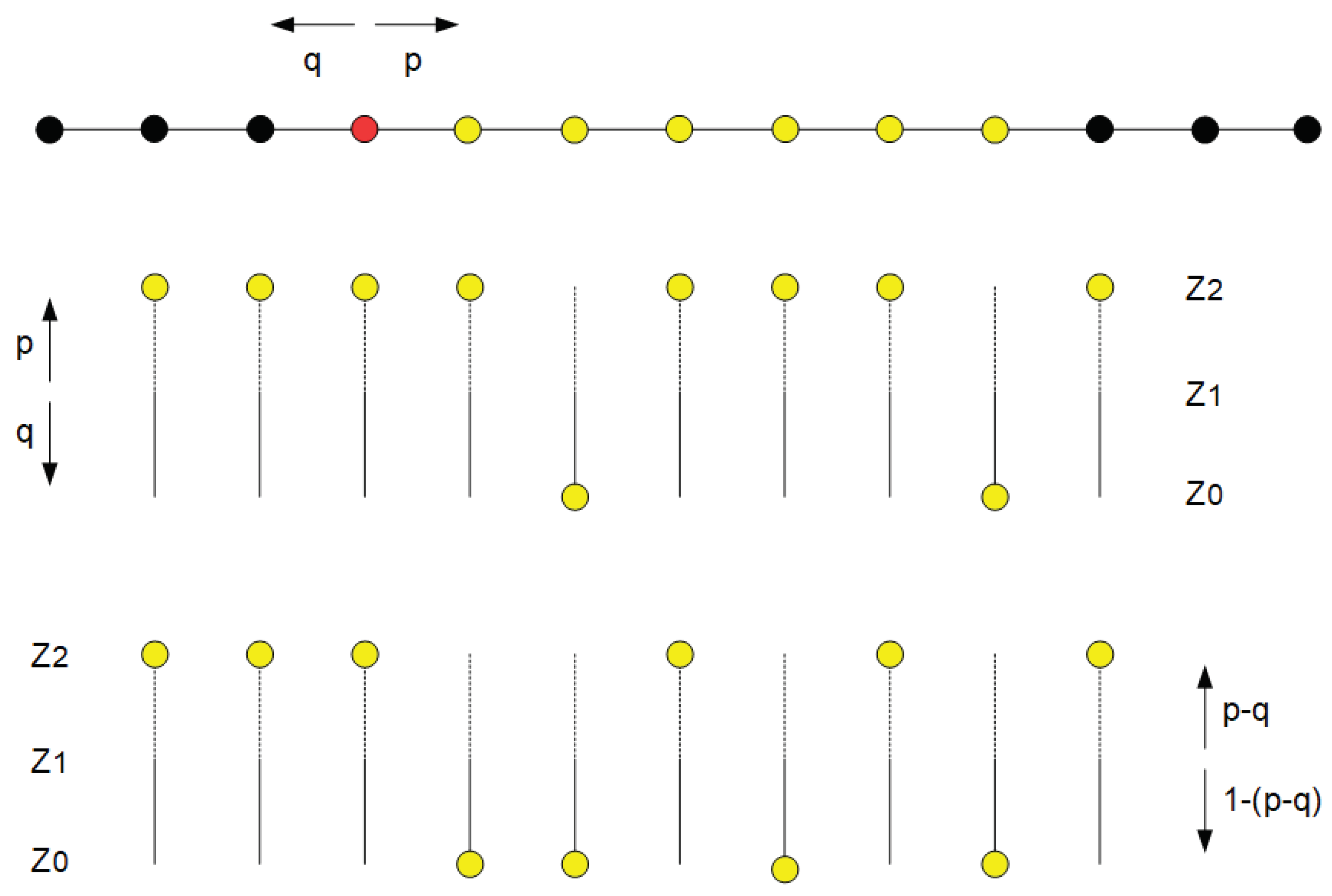
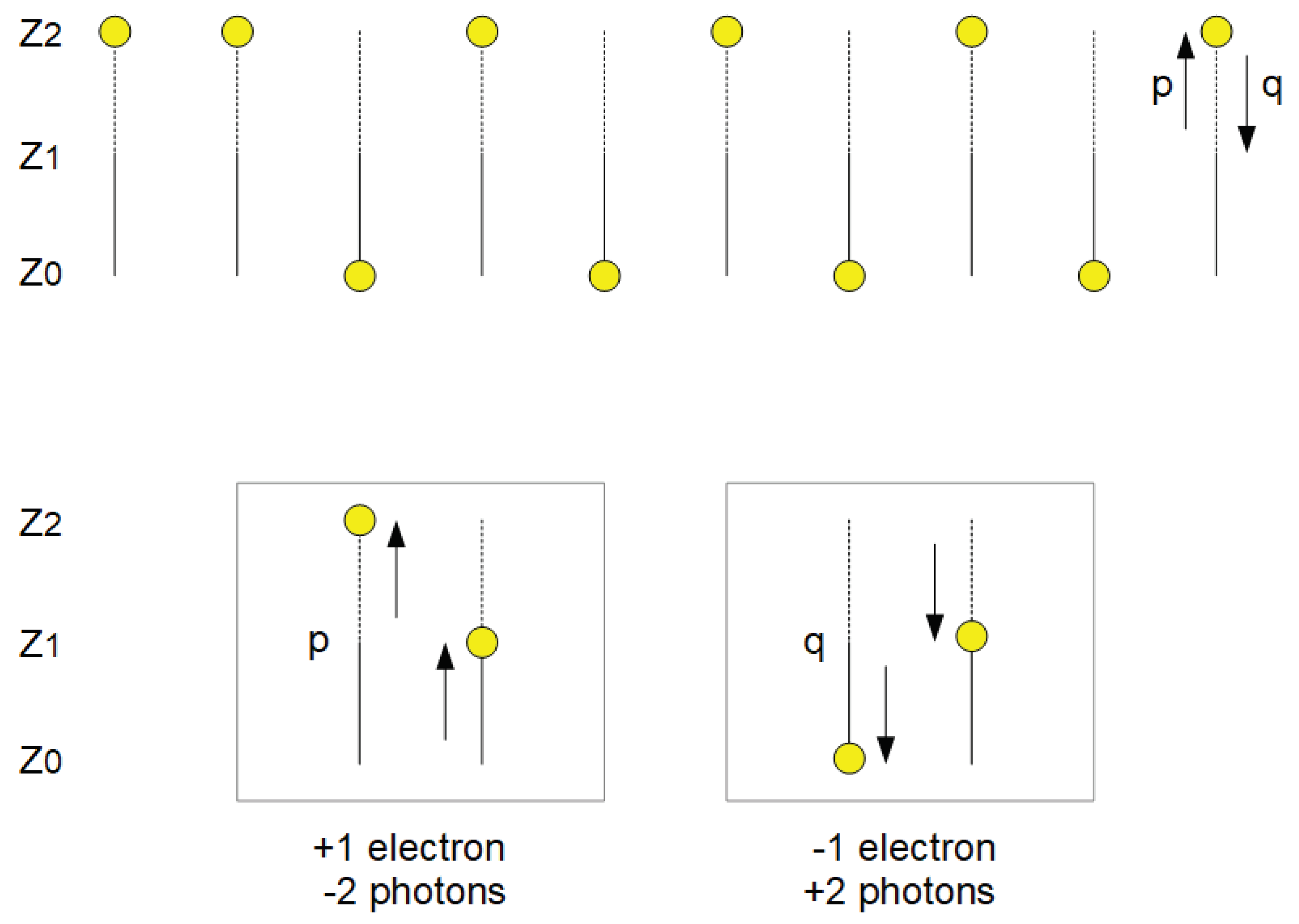
Equation 6 tells us that we need to look for a procedure whose result is determined by the difference between probability and counter-probability. We can find this in a one-dimensional random walk, for example, where one step to the right is carried out with probability p and one to the left with counter-probability q (Figure 6 above). Stagnating is not an option. An equivalent result is provided by a counter that increments with probability p (adds one) and decrements with probability q (subtracts one).
Figure 6 above shows a random walk with p=0.8 and q=0.2. After 10 repeats, the position "six, right" has been reached (eight times to the right, two times to the left). In a random process, the result could of course also be different, but this is the most probable outcome. The individual events occur independently of each other and the order in which they occur is irrelevant to the result. However, the detector must be considered here as a whole, not as consisting of independent parts (molecules); as if the detector were a single "electron entity" (an “electron field”) with many possible equidistant energy levels, which are arranged like the steps of a ladder (depending on the model, the distance between neighbouring steps is hμ or 2hμ). If all molecules are in state Z1, the actual level is at zero. Positive values correspond to released electrons, negative values to incoherent photon pairs. Each of the two release events is capable of cancelling out the other. Before we accept this, let us look at a few examples of what happens if we assume the independence of the molecules.
Figure 6, centre, shows the most obvious interpretation from a classical point of view. There are ten independent molecules, all of which are initially in the singly excited state Z1, but which move to Z2 with probability p and to Z0 with q. The most probable final result is that eight molecules are ionised and two are in the ground state. This outcome does not correspond to the expectation according to Equation (6) and is therefore incorrect. The reason is that Z1→Z0 and Z1→Z2 are events that occur alternatively from an initial situation. However, they would have to be inversions of each other, which is impossible as they start from the same state.
In Figure 6 below, a kind of "superposition" of the two possible outcomes of the induced emission is assumed, so that ionisation is achieved with probability p-q, while the ground state is achieved with 1-(p-q). Then the most probable final outcome is that six molecules are ionised, as expected. But the result is still wrong according to Equation (6). To understand this, we assume that photons of the two different phase classes are present with the same abundance and that destructive interference is present, i.e. that αij=π for i≠j. We know that in this case no electrons are released and for αij=π we get pij=qij and therefore pij-qij=0. This seems to correspond to the expected result. However, the matrix over which Equation (6) sums always also contains the diagonal i=j, for which αij=0 and therefore pij=1 and qij=0. This matches the situation when two in-phase-photons are absorbed by the molecule. In this case, the molecule is ionised and an electron is released, which is not observed in this type of interference. The result is therefore also incorrect for a superposition of the type p-q.
In an earlier publication [23], the author developed the idea that ionisation takes place with probability p, but that the electron is not yet free and only becomes either free with the interaction of another photon or is bound to the molecule again with probability q (Figure 7 above). This is equivalent to the situation of two separate events (because only one event that has already taken place can be cancelled) Z1→Z2 and Z2→Z1, which are each reversals of the alternative. However, since p and q are counter-probabilities to each other, they certainly belong to one event and not to two. In addition, the result would also be simply wrong here because of the "i=j diagonal dilemma".
Figure 7, below, shows a method that provides the correct result according to Equation (6), but requires the cooperation of two molecules in each case (the requirement that they are independent is therefore abandoned). Whenever one molecule leaves the Z1 state, the other must enter it in such a way that, in the case of ionisation of the first (Z1→Z2), the second passes from the ground state to the singly excited one (Z0→Z1). The outcome consists of the release of an electron into the environment and the absorption of two photons. In the other case, an induced emission with transition Z1→Z0, the other molecule must move from Z2 to Z1, i.e. absorb an electron. A total of two photons are released. It is clear that such a process cannot always work, e.g. if all molecules are initially in the Z1 state, and the active absorption of electrons and photons from the environment due to another molecule undergoing a certain change is also an unrealistic scenario.
It is therefore not easy to devise an uncomplicated and plausible process in which electrons that have already been released are bound again to the correct extent (and usually at a different location). In the author's opinion, a result consistent with observation can only be obtained if the molecules of the detector, or at least their electrons, are not regarded as independent of each other but as a unit in which independent events take place in any order (the "field" must be limited in space and time, however, otherwise it would not be possible to recognise the diffraction pattern on an observation screen). Apparently, the assumption that photons follow only one path in the multi-path experiment, like macroscopic objects, comes at the price of having to give up the assumption of the independence of the electrons in the detector. At least the author recognises no easy way to escape this conclusion if the fundamentals of the model are correct. However, this must be checked (and will so in the next section).
It is clear that the "counter" approach can only work if there is no individuality in the events. If the electron releases or photon pair emissions were individually distinguishable from each other, it would no longer make no difference to the result in which order the events take place and which are cancelled when decrementing (or in the minus range when incrementing). E. T. Jaynes made the following remark criticising quantum theory [14]: "You and I cannot distinguish between the particles; therefore the particles behave differently than if we could. ... A standard of logic that would be considered a psychiatric disorder in other fields, is the accepted norm in quantum theory." As illogical as it may be, we seem to be facing exactly this situation here (although we are not postulating causality).
Does it make sense to ask in the "quantum realm" how the individual events take place and to ask about cause and effect in the description of these events (this is denied in the Copenhagen interpretation)? In the author's opinion, this is the case. If the detector is replaced after each click, the situation shown in Figure 6, centre (or by the light blue dots in Figure 8) follows in the model, which can in principle be described in a "classical" (i.e. imaginable) way: We can assume that the number of photons hitting the detector is the same at the interference minimum as at the maximum, and the difference in the detector signal arises only from the different probabilities p with which electrons are released during the induced emission. In the selected scenario, it is therefore irrelevant whether the photons are considered as independent units or whether the electromagnetic field is said to reach a lower energy level due to absorption. Both considerations lead to the same result. There is therefore no reason not to ask about the nature of the individual events.
If the detector is not replaced between the clicks and the individual detections follow each other quickly and are not too far apart, the individuality of the single events is obviously lost and paradoxes occur: Since in the model the electromagnetic field and the "electron field" are not independent of each other, each time an electron is released (or the next energy level of the "electron field" is reached), two (or, depending on the submodel, only one) photon(s) are also removed from the electromagnetic field (which thus reaches a lower energy level). If we consider the case of destructive interference this time not for the electrons but for the photons, we find that, due to the "i=j diagonal dilemma", the observed situation (= no clicks) only occurs if zero (ideally) photons induce an emission at the molecules of the detector (which would usually be interpreted as meaning that no light quantum arrives at the detector). However, it is only during the induced emission that it is decided on the basis of the comparison of the messages received from the photons whether a click is triggered, i.e. the event "causes" in the selected scenario (destructive interference) that it cannot take place at all because no photons reach the detector!
Does the phase comparison take place or not? Of course it does, because Equation (6) does not say that nothing happens, but that there is compensation. In any case, what occurs is not at all complicated in reality, because the underlying mathematics is very simple, as is the rule that determines the transition from "classical" to apparently weird. Of course, these considerations are only relevant if the model is at all suitable for describing reality.

The Falsifiability of the Model

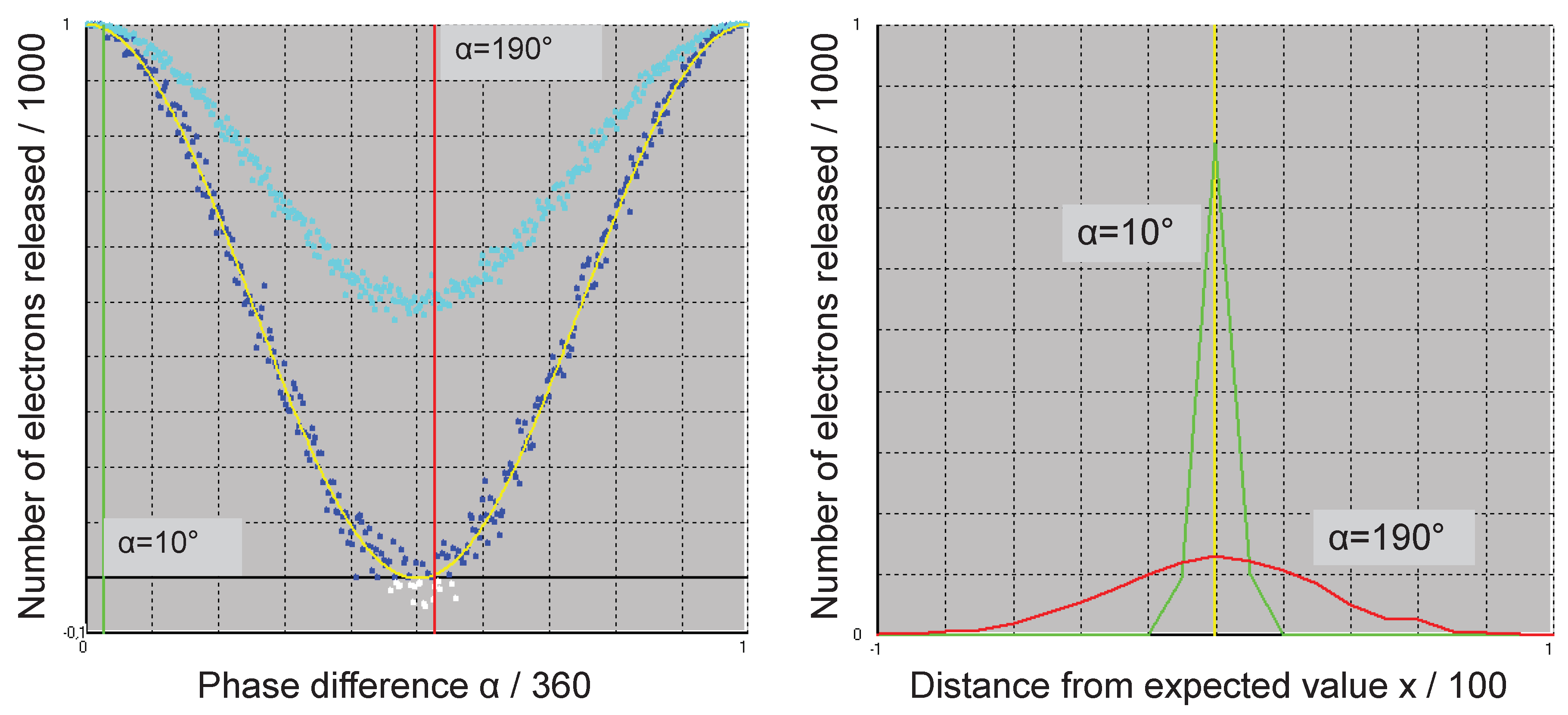
In order to make the model testable, predictions are needed that are confirmed in the experiment or, if not, lead to its falsification. For this purpose, a very simple simulation was carried out based on the double-slit experiment in that it is assumed that photons can follow two different paths from a source emitting monochromatic and coherent light to the detector. The photons are therefore characterised by two often different phases when they reach the detector (k=2). A molecule can absorb a pair of in-phase or out-of-phase photons. What actually happens is determined by the random number generator, which selects one or the other photon (or one or the other phase) with equal probability and does so twice in succession. After the photon pair has been determined, the phase difference and thus pij is calculated according to Equation (3). The random number generator determines whether the event, whose probability is pij, actually occurs. If this is the case, a counter increments, if not, it decrements. This procedure is repeated 1000 times and the value of the counter is plotted against the phase difference of the photons involved (dark blue or, in the case of negative values, white dots in Figure 8, left).
A positive value of the counter is interpreted as the number of electrons released, the absolute value of a negative one as the number of non-coherent photon pairs released. In Figure 8, left, the expected value resulting from Equation (1) is also shown as a yellow line. As can be seen, the simulation values scatter around the expected value, whereby the extent of this scatter depends on the photon phase difference. As the right-hand sub-figure of Figure 8 shows, it is lower for a small difference than for a high one, reaching a maximum at a difference of π (or 180°). However, negative values occur at a phase angle of π, i.e. the model predicts that in this case non-coherent photon pairs are released instead of electrons.
These are already two predictions that can be falsified, as other models suggest different results. If a superposition of both photon paths takes place, in the case of a phase difference of zero there is always, in the case of a phase difference of π (modulo of the period), there is never a detection. As the experimenter does not have complete control over the experimental set-up, the observed values will in reality be scattered, e.g. because not always the same number of photons reach the detector in the period Δt. However, with a phase difference of zero, this should lead to a large scattering, with a phase difference of π to a very small one (actually to none at all); a situation contrary to the predictions of the model discussed here.
The occurrence of non-coherent light in the case of destructive interference (a phase difference of π) is also not predicted by other models to the author's knowledge. However, the faint glimmer of this "counter-interference pattern" is certainly very difficult to detect, as the detector is "bathed" in light during the experiment.
If the time between the individual detections becomes large compared to the mean undisturbed lifetime of the single excited state, the interference pattern should change and the relationship between released electrons and photon phase difference should become closer to the result shown by the light blue dots on the left in Figure 8. If, as suggested in [15], the detector is exchanged between the individual detections and the interference pattern is subsequently reconstructed, it should turn out that half as many electrons are detected in the minima as in the maxima and not none at all. In this case, the event shown in Figure 6, centre, should replace the one presented in the figure above. In terms of the simulation, this means that the counter increments, but it does not decrement.
It is interesting to note that of the two possible events, ionisation and the release of a photon pair (Figure 3), we can only observe one, namely ionisation, in the vast majority of cases.
We assumed that in the multi-path experiment, photons, like macroscopic objects, only follow one of the alternative paths from the source to the detector. In order for an interference pattern to appear at the detector, we had to attribute to the photon the ability to transfer information about its travelling duration to the detector and the detector must have a memory. Einstein's modified radiation laws served as a model for the interaction between light and matter, whereby the modification concerns the induced emission. The interference ultimately results from a photon pair interaction in which ionizable molecules are involved. Released electrons form the detector signal. It follows from the model that the entirety of the detector electrons can be described as a unit (“field”) with equidistant energy levels, whereas the attempt to consider the detector molecules as completely independent of each other does not succeed.
In the context of the model, Born's rule proves to be superfluous. We have carried out a very simple simulation that allows us to predict some effects that can be observed in principle and that make it possible to falsify the model by experiment, since these effects would not occur if the interference pattern were the result of superimposing all possibilities to get from the source to the detector.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

I would like to thank Hans De Raedt for his commentary and Dagmar, Gernot and Martin Tiefenbrunner for further valuable suggestions.

References

  1. De Raedt, H., Michielsen, K., Event-by-event simulation of quantum phenomena, Ann. Phys. 524, 8, 393–410 (2012). [CrossRef]
  2. Eigen, M., Selforganisation of matter and the evolution of biological macromolecules. Die Naturwissenschaften 58, 465-523 (1971). [CrossRef]
  3. Einstein, A., Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt, Ann. Phys. 322(6), 132-148,1905.
  4. Einstein, A., Beiträge zur Quantentheorie, Deutsche Physikalische Gesellschaft, Verhandlungen 16, 820-828, 1914.
  5. Einstein, A., Strahlungs-Emission und -Absortion nach der Quantentheorie, Deutsche Physikalische Gesellschaft, Verhandlungen 18, 318-323, 1916.
  6. Einstein, A., Zur Quantentheorie der Strahlung, Physikalische Zeitschrift, 18, 121-128, 1917.
  7. Einstein, A., Zum Quantensatz von Sommerfeld und Epstein, Deutsche Physikalische Gesellschaft, Verhandlungen 19, 82-92, 1919.
  8. Einstein, A., Quantentheorie des einatomigen idealen Gases, erste und zweite Abhandlung, Zeitschrift für Physik 25, 37–41, 1924.
  9. Einstein, A., Physik und Realität, Journal of The Franklin Institute, 221, 313-347, 1936.
  10. Feynman, R. P., Space-time approach to non-relativistic quantum mechanics, Rev. Mod. Phys. 20, 367–387, 1948. [CrossRef]
  11. Feynman, R. P., Leighton, R. B., Sands, M., Vorlesungen über Physik, Band III, Quantenmechanik, R. Oldenbourg Verlag München Wien, 1988. The Feynman Lectures on Physics, Volume III, 1963-1965. https://www.feynmanlectures.caltech.edu/.
  12. Haken, H., Theory of coherence of laser light, Physical review letters, 13 (11), 329-331, 1964. [CrossRef]
  13. Haken, H., Erfolgsgeheimnisse der Natur, Deutsche Verlagsanstalt, 1981.
  14. Jaynes, E., T., Clearing up mysteries - the original goal. In: Maximum Entropy and Bayesian Methods , J. Skilling, Editor, Kluwer Academic Publishers, 1-27, 1989.
  15. Jin, F., Yuan, S., De Raedt, H., Michielsen, K., Miyashita, S., Corpuscular Model of Two-Beam Interference and Double-Slit Experiments with Single Photons, Journal of the Physical Society of Japan, 79, 074401-1-13, 2010. [CrossRef]
  16. Michielsen, K., , Jin, F., De Raedt, H., Nonclassical effects in two-photon interference experiments: event-by-event simulations, arXiv, 1-11, 2013. [CrossRef]
  17. Michielsen, K., Mohanty, S., Arnold, L., De Raedt, H., Event-based simulation of interference with alternatingly blocked particle sources, AIP Conf. Proc., 1424, 246-250, 2012. [CrossRef]
  18. Planck, M., Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum, Verhandlungen der Deutschen physikalischen Gesellschaft 2(17), 237–245, 1900.
  19. Sinha, U., Couteau, C., Jennewein, T., Laflamme, R., Weihs, G., Ruling out Multi-Order Interference in Quantum Mechanics, Science, 329, 418-421, 2010. [CrossRef]
  20. Taylor, G. I., Interference fringes with feeble light, Proceedings of the Cambridge Philosophical Society, 15, 114-115, 1909.
  21. Schuster, P., Sigmund K., Replicator Dynamics, J. theor. Biology, 100, 533-538, 1983. [CrossRef]
  22. Tiefenbrunner, W., Change of information by positive frequency-dependent selection in two very different models (laser-like and chirality of shell-coiling in the snail Partula suturalis), bioRχiv. [CrossRef]
  23. Tiefenbrunner, W., The Light Quantum as Replicator: Phase Copying by Photon-pair Interaction Mediated by Matter, MDPI-Preprints, 1-23, 2023. [CrossRef]
  24. Wentzel, G., Zur Quantenoptik, Zeitschrift für Physik, 193-199, 1924. [CrossRef]
  25. Young, T., On the theory of light and colours (The 1801 Bakerian Lecture), Philosophical Transactions of the Royal Society of London, 92,12-48, 1802. [CrossRef]
Preprints 99490 g001
Figure 1. Energy budget of the interaction between light and electromagnetic radiation according to Einstein 1916.
Figure 1. Energy budget of the interaction between light and electromagnetic radiation according to Einstein 1916.
Preprints 99490 g001
Preprints 99490 g002
Figure 2. Modified model for the interaction of light and matter. Induced emission is a sequence of absorption followed immediately by spontaneous emission, which may or may not result in a coherent photon pair. The axx are the transition probabilities from one state to another. The dotted arrows symbolise photons.
Figure 2. Modified model for the interaction of light and matter. Induced emission is a sequence of absorption followed immediately by spontaneous emission, which may or may not result in a coherent photon pair. The axx are the transition probabilities from one state to another. The dotted arrows symbolise photons.
Preprints 99490 g002
Preprints 99490 g003
Figure 3. Modified model for the interaction of light and matter in the detector. Compared to Figure 2, the ionisation of the molecule "replaces" the generation of a coherent photon pair as a possible outcome of induced emission.
Figure 3. Modified model for the interaction of light and matter in the detector. Compared to Figure 2, the ionisation of the molecule "replaces" the generation of a coherent photon pair as a possible outcome of induced emission.
Preprints 99490 g003
Preprints 99490 g004
Figure 4. α or 2π-α are the angles that correspond to the difference between the phases of the two photons at the time of absorption. Photons as a clock face with a hand.
Figure 4. α or 2π-α are the angles that correspond to the difference between the phases of the two photons at the time of absorption. Photons as a clock face with a hand.
Preprints 99490 g004
Preprints 99490 g005
Figure 5. (a) Geometric representation for calculating the absolute value of the amplitude (see Equation (1)). (b) The relationship between the notation of Equations (1) and (2).
Figure 5. (a) Geometric representation for calculating the absolute value of the amplitude (see Equation (1)). (b) The relationship between the notation of Equations (1) and (2).
Preprints 99490 g005
Preprints 99490 g006
Figure 6. Possible (top) and impossible (centre,bottom) interpretations of Equation (6).
Figure 6. Possible (top) and impossible (centre,bottom) interpretations of Equation (6).
Preprints 99490 g006
Preprints 99490 g007
Figure 7. Further postulated molecular transformations whose compatibility with Equation (6) is discussed.
Figure 7. Further postulated molecular transformations whose compatibility with Equation (6) is discussed.
Preprints 99490 g007
Preprints 99490 g008
Figure 8. Result of a simulation of the detector as a function of the photon phase difference. The left-hand side shows how many electrons (dark blue dots) or non-coherent photon pairs (white dots) are released at the detector as a function of the photon phase difference. Yellow line: expected value according to Equation (1). Light blue dots show the result in the case that the counter only increments but does not decrement. On the right, the scattering of the simulation values around the expected value is shown for a photon phase difference of αij=10° or αij=190° (k=2).
Figure 8. Result of a simulation of the detector as a function of the photon phase difference. The left-hand side shows how many electrons (dark blue dots) or non-coherent photon pairs (white dots) are released at the detector as a function of the photon phase difference. Yellow line: expected value according to Equation (1). Light blue dots show the result in the case that the counter only increments but does not decrement. On the right, the scattering of the simulation values around the expected value is shown for a photon phase difference of αij=10° or αij=190° (k=2).
Preprints 99490 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

88

Views

24

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated