Submitted:
02 February 2024
Posted:
19 February 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Background
Equivalent SIF models
Crack growth models
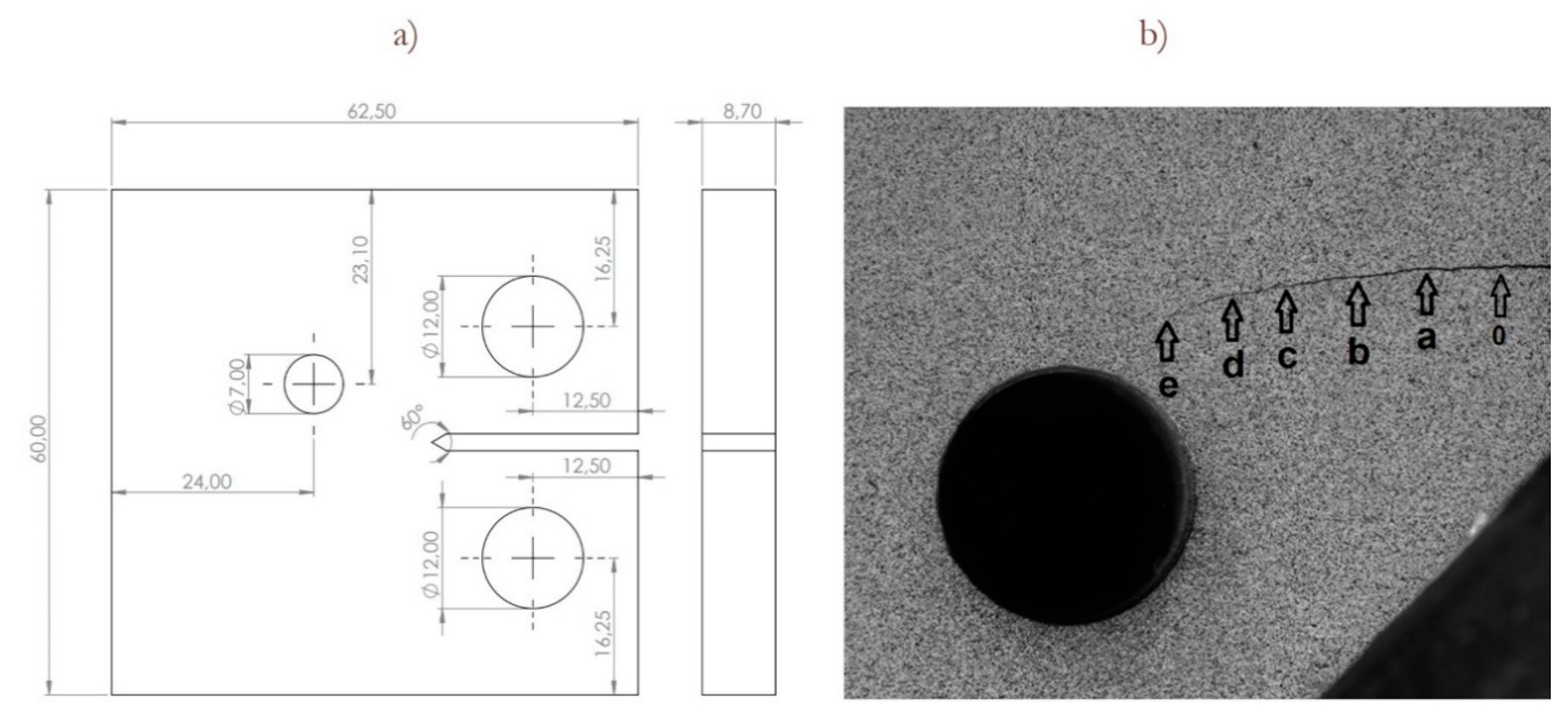
3. Materials and Methods
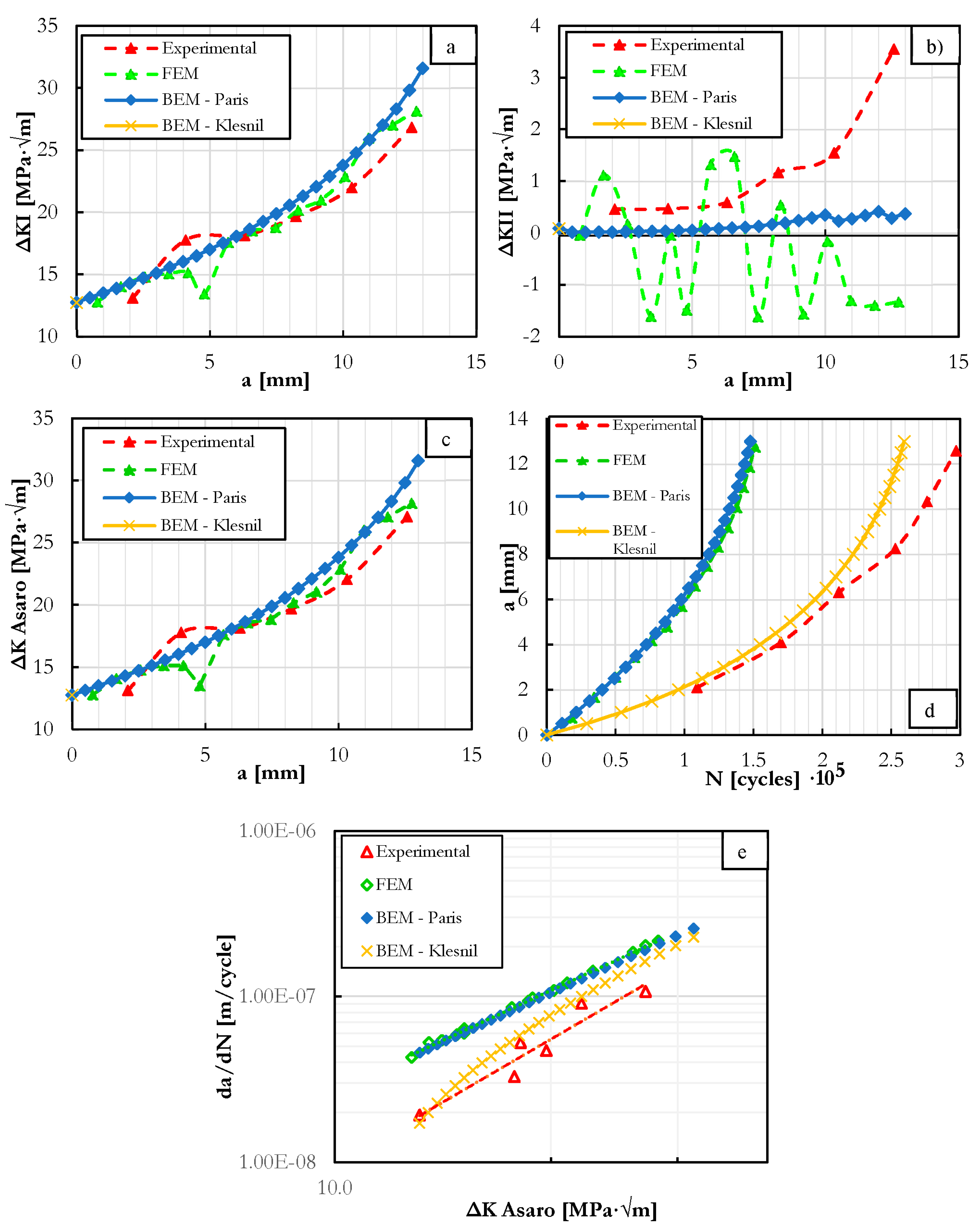
4. Results
Parametric models
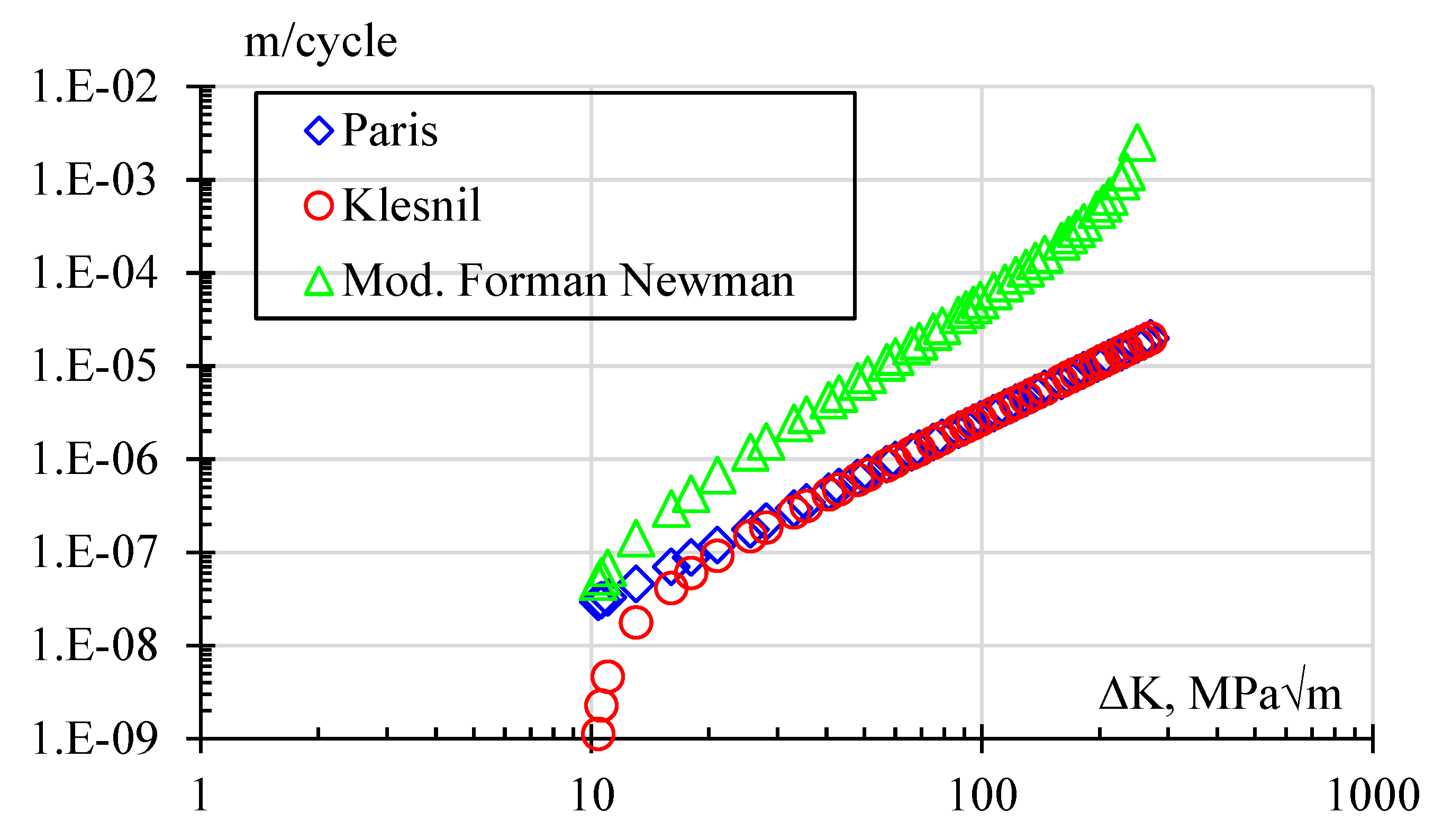
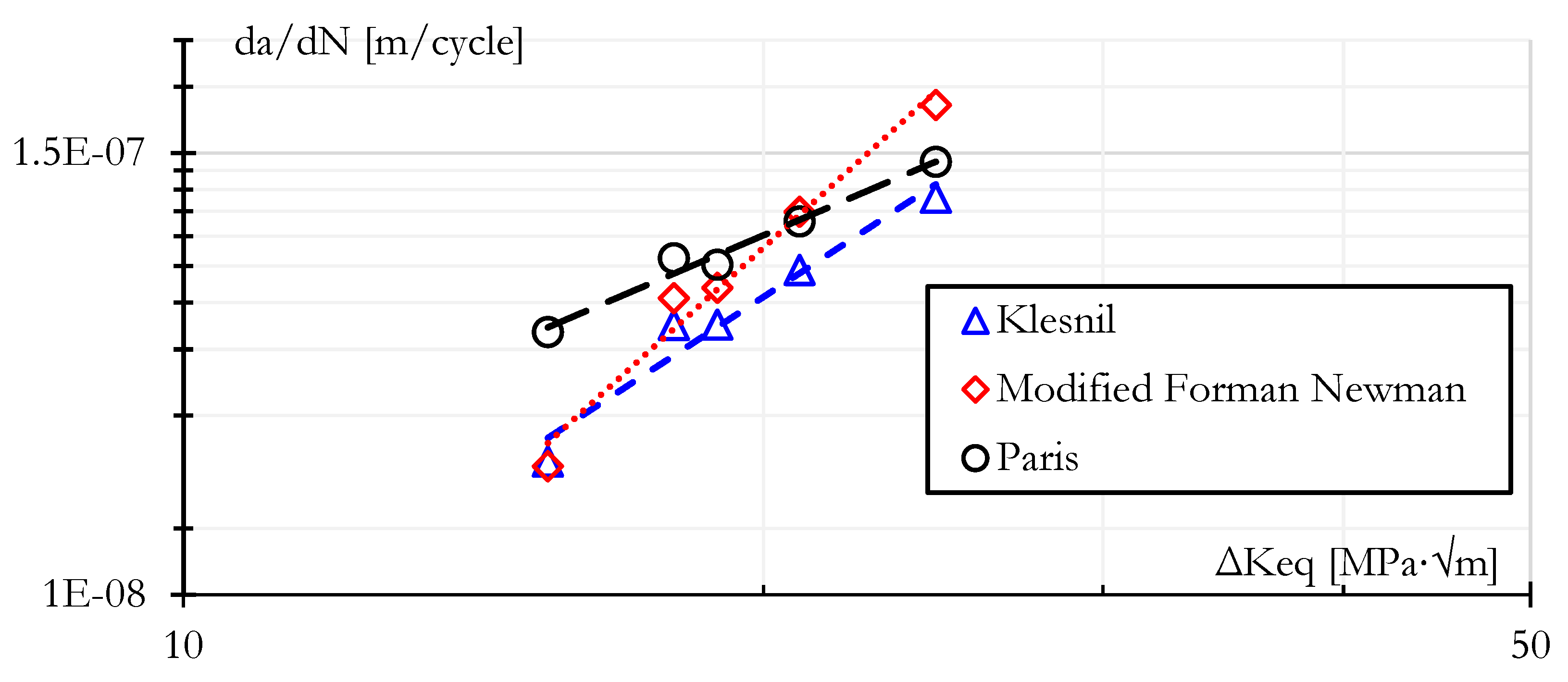
Paris rule
Modified Forman Newman
Klesnil
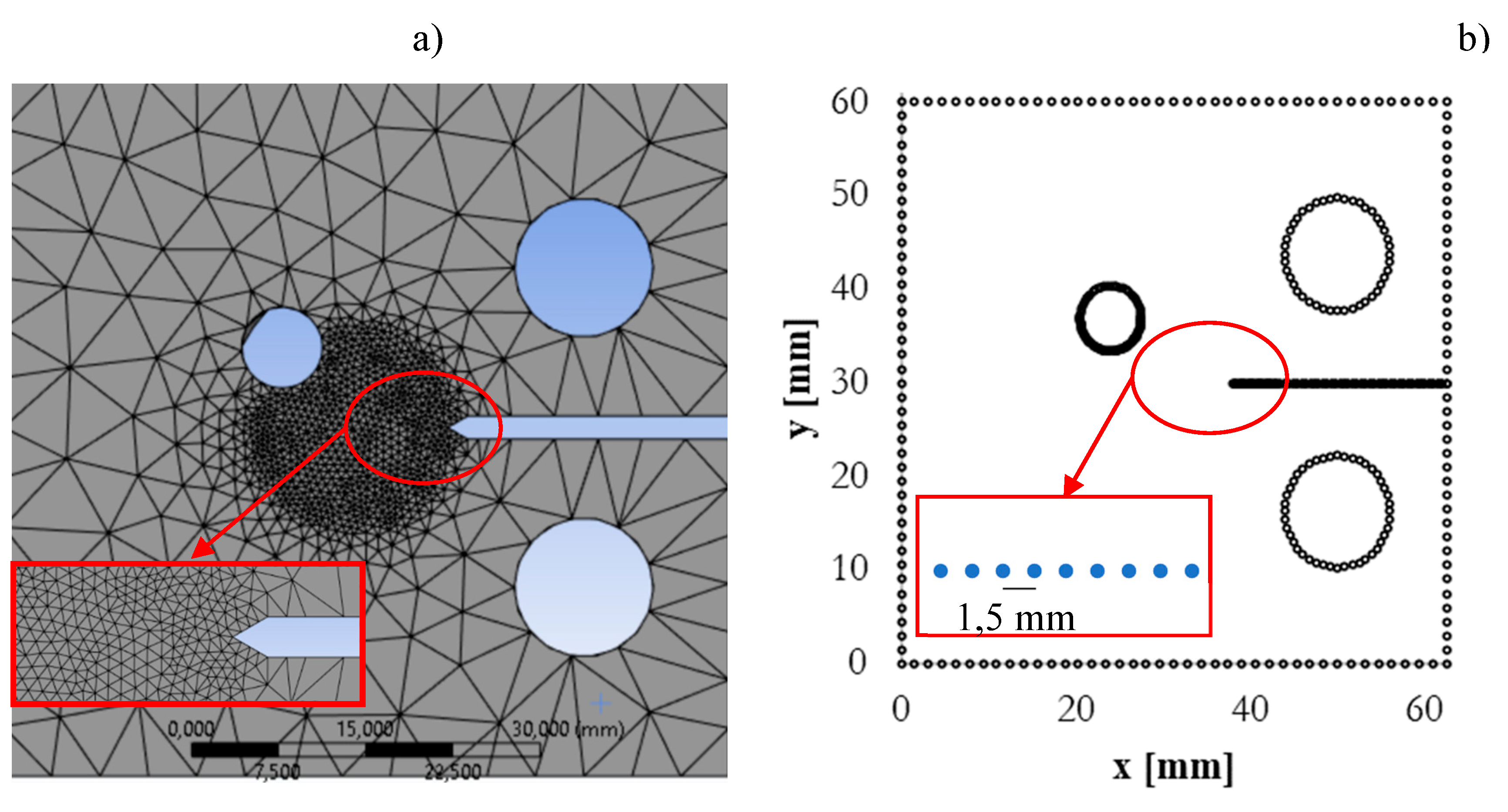
Numerical FEM
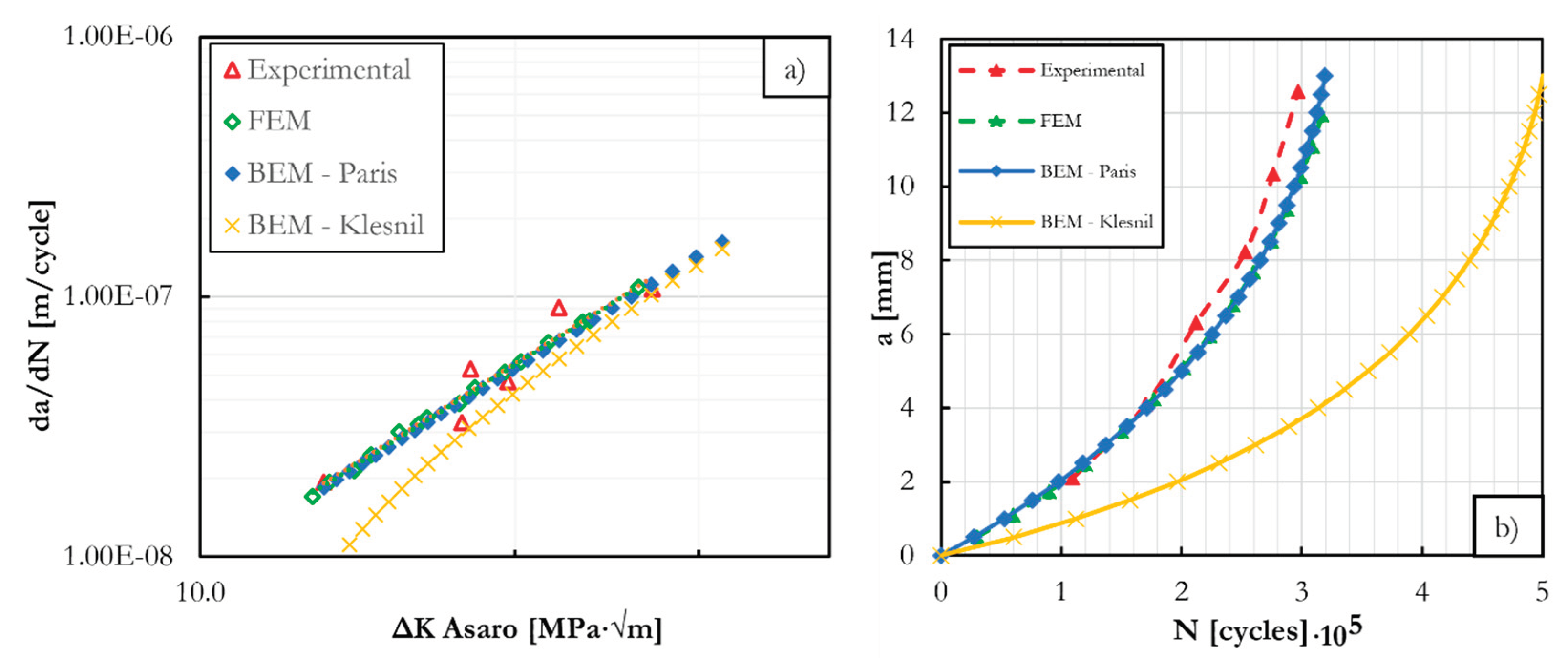
Numerical BEM
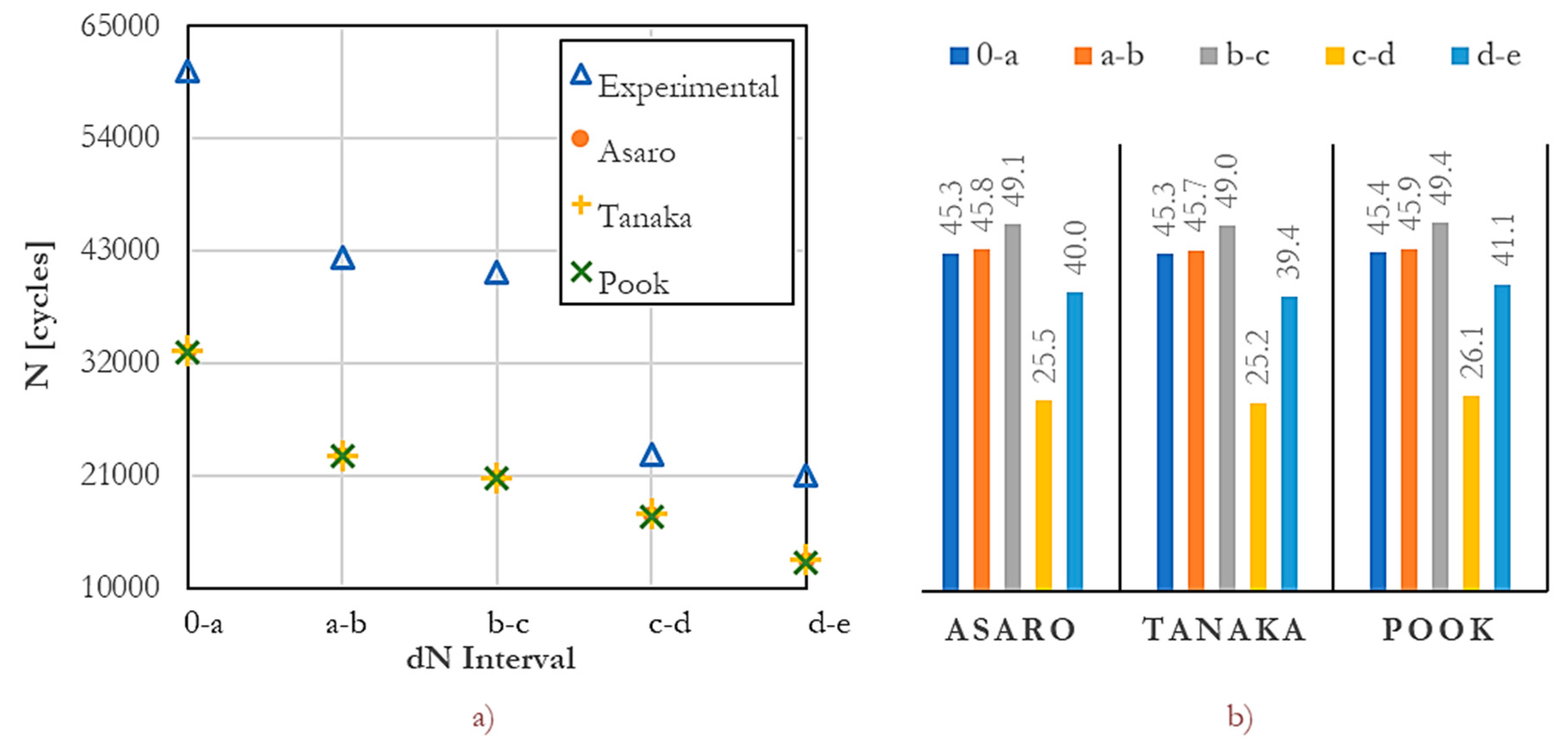
5. Discussion
6. Conclusion
References
- K. P. Mróz and Z. Mróz, “On crack path evolution rules,” Eng Fract Mech, vol. 77, no. 11, pp. 1781–1807, 2010. [CrossRef]
- J. G. Díaz and J. L. de F. Freire, “LEFM crack path models evaluation under proportional and non-proportional load in low carbon steels using digital image correlation data,” Int J Fatigue, vol. 156, p. 106687, Mar. 2022. [CrossRef]
- P. O. Bouchard, F. Bay, and Y. Chastel, “Numerical modelling of crack propagation: automatic remeshing and comparison of different criteria,” Comput Methods Appl Mech Eng, vol. 192, no. 35–36, pp. 3887–3908, Aug. 2003. [CrossRef]
- H. A. Richard and M. Sander, Fatigue Crack Growth: Detect—Assess—Avoid, vol. 227. 2016.
- Dieter. Radaj and M. Vormwald, Advanced Methods of Fatigue Assessment, 1st ed. 20. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013. [CrossRef]
- Sajith, K. S. R. K. Murthy, and P. S. Robi, “Fatigue crack growth and life prediction under mixed-mode loading,” AIP Conf Proc, vol. 1943, no. April 2018, pp. 1–8, 2018. [CrossRef]
- S. Floros, K. I. Tserpes, and T. Löbel, “Mode-I, mode-II and mixed-mode I+II fracture behavior of composite bonded joints: Experimental characterization and numerical simulation,” Compos B Eng, vol. 78, pp. 459–468, Sep. 2015. [CrossRef]
- M. Srinivas and S. V. Kamat, “Effect of strain rate on fracture toughness of mild steel,” Materials Science and Technology, vol. 17, no. 5, pp. 529–535, 01. [CrossRef]
- M. Alshoaibi and Y. A. Fageehi, “Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory,” Materials, vol. 15, no. 1, p. 363, Jan. 2022. [CrossRef]
- S. A. Kanth, G. A. Harmain, and A. Jameel, “Modeling of Nonlinear Crack Growth in Steel and Aluminum Alloys by the Element Free Galerkin Method,” Mater Today Proc, vol. 5, no. 9, pp. 18805–18814, 2018. [CrossRef]
- R. R. Yarullin, M. M. Yakovlev, N. V. Boychenko, and N. M. Lyadov, “Effect of mixed-mode loading on surface crack propagation in steels,” Eng Fract Mech, vol. 295, p. 109717, Jan. 2024. [CrossRef]
- D. R. Berrios-Barcena, R. Franco-Rodríguez, and F. A. Rumiche-Zapata, “Calibration of nasgro equation for mixed-mode loading using experimental and numerical data,” Revista Facultad de Ingeniería Universidad de Antioquia, Apr. 2019. [CrossRef]
- H. Dirik and T. Yalçinkaya, “Crack path and life prediction under mixed mode cyclic variable amplitude loading through XFEM,” Int J Fatigue, vol. 114, pp. 34–50, Sep. 2018. [CrossRef]
- J. M. Vasco-Olmo, F. A. Díaz, F. V. Antunes, and M. N. James, “Characterisation of fatigue crack growth using digital image correlation measurements of plastic CTOD,” Theoretical and Applied Fracture Mechanics, vol. 101, no. 18, pp. 332–341, 2019. [CrossRef]
- S. Sajith, K. S. R. Krishna Murthy, and P. S. Robi, “Prediction of Accurate Mixed Mode Fatigue Crack Growth Curves using the Paris’ Law,” Journal of The Institution of Engineers (India): Series C, vol. 100, no. 1, pp. 165–174, 2019. [CrossRef]
- W. Zhan, N. Lu, and C. Zhang, “A new approximate model for the R-ratio effect on fatigue crack growth rate,” Eng Fract Mech, vol. 119, pp. 85–96, Mar. 2014. [CrossRef]
- L. L. Silva, A. M. P. de Jesus, J. Xavier, J. A. F. O. Correia, and A. A. Fernandes, “Combined analytical-numerical methodologies for the evaluation of mixed-mode (I + II) fatigue crack growth rates in structural steels,” Eng Fract Mech, vol. 185, pp. 124–138, 2017. [CrossRef]
- Khazal, and A. K. F. Hassan, “Experimental study on repair of cracked pipe under internal pressure,” Periodicals of Engineering and Natural Sciences (PEN), vol. 10, no. 6, p. 67, Dec. 2022. [CrossRef]
- X.-K. Zhu and J. A. Joyce, “Review of fracture toughness (G, K, J, CTOD, CTOA) testing and standardization,” Eng Fract Mech, vol. 85, pp. 1–46, 12. 20 May. [CrossRef]
- Y. Wang, W. Wang, B. Zhang, and C.-Q. Li, “A review on mixed mode fracture of metals,” Eng Fract Mech, vol. 235, p. 107126, Aug. 2020. [CrossRef]
- Xie, J. Song, B. Zhao, C. Li, and Z. Zhao, “Curved fatigue crack growth prediction under variable amplitude loading by artificial neural network,” Int J Fatigue, vol. 142, no. 20, p. 105886, 2021. [CrossRef]
- M. Surendran, S. Natarajan, G. S. Palani, and S. P. A. Bordas, “Linear smoothed extended finite element method for fatigue crack growth simulations,” Eng Fract Mech, vol. 206, pp. 551–564, Feb. 2019. [CrossRef]
- J. A. Mantilla Villalobos, D. E. Poveda Díaz, and M. del J. Martínez, “Estimación del factor de intensidad de esfuerzo en una probeta wedge splitting bajo carga estática mediante el método de elementos finitos,” Respuestas, vol. 26, no. 1, pp. 53–61, Mar. 2021. [CrossRef]
- K. Tanaka, “Fatigue crack propagation from a crack inclined to the cyclic tensile axis,” Eng Fract Mech, vol. 6, no. 3, 1974. [CrossRef]
- H. Wang, S. Tanaka, S. Oterkus, and E. Oterkus, “Study on two-dimensional mixed-mode fatigue crack growth employing ordinary state-based peridynamics,” Theoretical and Applied Fracture Mechanics, vol. 124, p. 103761, Apr. 2023. [CrossRef]
- S. Sajith, S. S. Shukla, K. S. R. K. Murthy, and P. S. Robi, “Mixed mode fatigue crack growth studies in AISI 316 stainless steel,” European Journal of Mechanics, A/Solids, vol. 80, no. 19, p. 103898, 2020. [CrossRef]
- J. Newman and I. S. Raju, “Stress intensity factor equations for cracks in three-Dimensional finite bodies,” ASTM Special Technical Publication, vol. 791, pp. 238–265, 1983.
- L. P. Pook, “The Significance Of Mode I Branch Cracks For Combined Mode Failure,” in Fracture and Fatigue, Elsevier, 1980, pp. 143–153. [CrossRef]
- J.-H. Kim and G. H. Paulino, “T-stress, mixed-mode stress intensity factors, and crack initiation angles in functionally graded materials: a unified approach using the interaction integral method,” Comput Methods Appl Mech Eng, vol. 192, no. 11–12, pp. 1463–1494, Mar. 2003. [CrossRef]
- P. Paris and F. Erdogan, “A critical analysis of crack propagation laws,” Journal of Fluids Engineering, Transactions of the ASME, vol. 85, no. 4, pp. 528–533, 1963. [CrossRef]
- R. Branco, F. V. Antunes, J. A. Martins Ferreira, and J. M. Silva, “Determination of Paris law constants with a reverse engineering technique,” Eng Fail Anal, vol. 16, no. 2, pp. 631–638, Mar. 2009. [CrossRef]
- M. Klesnil and P. Lukáš, “Influence of strength and stress history on growth and stabilisation of fatigue cracks,” Eng Fract Mech, vol. 4, no. 1, pp. 77–92, Mar. 1972. [CrossRef]
- J. G. Díaz Rodríguez, G. Gonzales, J. A. Ortiz Gonzalez, and J. Freire, “Analysis of Mixed-mode Stress Intensity Factors using Digital Image Correlation Displacement Fields,” in Procceedings of the 24th ABCM International Congress of Mechanicl Engineering, ABCM, 2017. [CrossRef]
- S. E. Ferreira, J. T. P. Castro, and M. A. Meggiolaro, “Fatigue crack growth predictions based on damage accumulation ahead of the crack tip calculated by strip-yield procedures,” Int J Fatigue, vol. 115, pp. 89–106, Oct. 2018. [CrossRef]
- Aliabadi, and D. P. Rooke, “The dual boundary element method: Effective implementation for crack problems,” Int J Numer Methods Eng, vol. 33, no. 6, pp. 1269–1287, Apr. 1992. [CrossRef]
- Y. A. Fageehi and A. M. Alshoaibi, “Investigating the Influence of Holes as Crack Arrestors in Simulating Crack Growth Behavior Using Finite Element Method,” Applied Sciences, vol. 14, no. 2, p. 897, Jan. 2024. [CrossRef]
- Y. Wang, W. Wang, B. Zhang, Y. Bian, and C. Q. Li, “Fracture resistance characteristics of mild steel under mixed mode I-II loading,” Eng Fract Mech, vol. 258, no. August, p. 108044, 2021. [CrossRef]
- S. Cruces, M. Mokhtarishirazabad, B. Moreno, M. Zanganeh, and P. Lopez-Crespo, “Study of the biaxial fatigue behaviour and overloads on S355 low carbon steel,” Int J Fatigue, vol. 134, p. 105466, 20. [CrossRef]
- L. M. Palacios-Pineda et al., “Study of the Evolution of the Plastic Zone and Residual Stress in a Notched T-6061 Aluminum Sample,” Materials, vol. 15, no. 4, p. 1546, Feb. 2022. [CrossRef]
- M. Sabsabi, E. Giner, and F. J. Fuenmayor, “Experimental fatigue testing of a fretting complete contact and numerical life correlation using X-FEM,” Int J Fatigue, vol. 33, no. 6, pp. 811–822, 2011. [CrossRef]
- H. Proudhon and S. Basseville, “Finite element analysis of fretting crack propagation,” Eng Fract Mech, vol. 78, no. 4, pp. 685–694, Mar. 2011. [CrossRef]
- G. L. G. Gonzáles, J. G. Diaz, J. A. O. González, J. T. P. Castro, and J. L. F. Freire, “Determining SIFs Using DIC Considering Crack Closure and Blunting,” in Conference Proceedings of the Society for Experimental Mechanics Series, vol. 4, 2017, pp. 25–36. [CrossRef]
- Meite, F. Dubois, and J. Absi, “Identification algorithm for fracture parameters by combining DIC and FEM approaches,” Int J Fract, vol. 170, no. 2, pp. 101–114, Aug. 2011. [CrossRef]
- V. Farahani, P. J. Tavares, P. M. G. P. Moreira, and J. Belinha, “Stress intensity factor calculation through thermoelastic stress analysis, finite element and RPIM meshless method,” Eng Fract Mech, vol. 183, pp. 66–78, Oct. 2017. [CrossRef]
- J. Vázquez, C. Navarro, and J. Domínguez, “Two dimensional versus three dimensional modelling in fretting fatigue life prediction,” Journal of Strain Analysis for Engineering Design, vol. 51, no. 2, pp. 109–117, 2016. [CrossRef]
- Martínez, J. González, and M. González, “Análisis numérico del crecimiento de grieta por fatiga del CPVC: efecto de la temperatura y frecuencia de carga,” Revista UIS Ingenierías, vol. 18, no. 1, pp. 177–186, Feb. 2019. [CrossRef]
- S. Kibey, H. Sehitoglu, and D. A. Pecknold, “Modeling of fatigue crack closure in inclined and deflected cracks,” Int J Fract, vol. 129, no. 3, pp. 279–308, Oct. 2004. [CrossRef]
- J. Nicholls, “the Relation Between Crack Blunting and Fatigue Crack Growth Rates,” Fatigue Fract Eng Mater Struct, vol. 17, no. 4, pp. 459–467, 1994. [CrossRef]
- H. Heirani and K. Farhangdoost, “Mixed mode I/II fatigue crack growth under tensile or compressive far-field loading,” Mater Res Express, vol. 4, no. 11, p. 116505, Nov. 2017. [CrossRef]
- S. S. Shukla and K. S. R. K. Murthy, “A study on the effect of different Paris constants in mixed mode (I/II) fatigue life prediction in Al 7075-T6 alloy,” Int J Fatigue, vol. 176, no. August, p. 107895, 2023. [CrossRef]
| Element | Fe | C | Si | Mn | P | S | Other |
|---|---|---|---|---|---|---|---|
| % | 98.9 | 0.268 | 0.046 | 0.68 | 0.0042 | 0.025 | 0.0768 |
| Point | a [mm] | Load [kN] | N *1 10^5 [cycles] | MPa√m | MPa√m | |
|---|---|---|---|---|---|---|
| 0 | 2.1 | 0 | 7 | 1.09 | 13.12 | 0.46 |
| a | 4.1 | 0 | 6.2 | 1.70 | 17.78 | 0.47 |
| b | 6.31 | -5 | 5.6 | 2.12 | 18.14 | 0.59 |
| c | 8.24 | -5 | 5 | 2.53 | 19.67 | 1.17 |
| d | 10.33 | -7 | 4.6 | 2.76 | 22 | 1.55 |
| e | 12.58 | -24 | 4.1 | 2.97 | 26.85 | 3.55 |
| Model | m | p | q | ||||
|---|---|---|---|---|---|---|---|
| Paris – Klesnil | 2.73E^-10 | 2 | 10.2 | - | - | - | - |
| Modified Forman Newman | 4.56E^-13 | 3.1 | 10.2 | 285 | 0.5 | 0.5 | 2.1 |
| Point | N [cycles] | |||||
|---|---|---|---|---|---|---|
| 0 | 1.09E5 | 13.12 | 0.46 | 13.13 | 13.12 | 13.14 |
| a | 1.70E5 | 17.78 | 0.47 | 17.79 | 17.78 | 17.80 |
| b | 2.12E5 | 18.14 | 0.59 | 18.15 | 18.14 | 18.17 |
| c | 2.53E5 | 19.67 | 1.17 | 19.70 | 19.67 | 19.77 |
| d | 2.76E5 | 22 | 1.55 | 22.05 | 22.00 | 22.16 |
| e | 2.97E5 | 26.85 | 3.55 | 27.08 | 26.86 | 27.53 |
| Mixed-mode model | m | ||
|---|---|---|---|
| Experimental | 9.07E^-9 | 0.9312 | 0.9147 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





