Watermarking Method Based on Neural Network with JPEG Quantization Represented by Quantized Activation Function

1. Introduction

People are now easily able to upload photos and illustrations to the Internet, owing to smartphones and personal computers. To protect content creators, we need to prevent unauthorized copying and other abuses because digital content is not degraded by copying or transmissions. Digital watermarking is effective against such unauthorized use.

In digital watermarking, secret information is embedded in digital content by making slight changes to the content. In the case of an image, the image in which the information is embedded is called a stego-image, and the embedded information is called a digital watermark. There are two types of digital watermarking: blind and non-blind. The blind method does not require the original image to extract the watermark from the stego-image. However, the non-blind method requires the original image when extracting a watermark from a stego-image. Therefore, the blind method is more practical. In addition, because stego-images may be attacked by various kinds of image processing, watermarking methods must have the ability to extract watermarks from degraded stego-images. Two types of attacks on stego images can occur: geometric attacks such as rotation, scaling, and cropping and non-geometric attacks such as noise addition and JPEG compression.

Neural-network-based methods have been proposed, ones that learn from embedding to extraction processes in an end-to-end manner [1,2,3,4]. Zhu et al.’s [1] method has an attack layer that simulates attacks such as Gaussian blurring, per-pixel dropout, cropping, and JPEG compression on images during training. Here, the implementation of JPEG compression is approximated by JPEG-Mask, which sets the high-frequency components of the discrete cosine transform (DCT) coefficients to zero, and JPEG-Drop, which uses progressive dropout to eliminate the high-frequency components of the DCT coefficients. Therefore, this implementation does not meet the standard for quantization in the JPEG compression process. Hamamoto and Kawamura’s method [3] also introduces a layer of additive white Gaussian noise as an attack layer to improve robustness against JPEG compression. Moreover, Ahmadi et al. [4] proposed attack layers implementing salt-and-pepper noise, Gaussian noise, JPEG compression, and mean smoothing filters. The quantization of the JPEG compression is approximated by adding uniform noise. As described, the quantization process has been replaced by the process of adding noise, and the quantization process as per the JPEG standard has not been introduced.

In this paper, we propose a quantized activation function that can simulate quantization of JPEG compression according to a standard. We apply this function to the attack layer of the method of Ahmadi et al. [4]. The robustness against the JPEG compression is expected to be improved using a standard-based function. The effectiveness of our method was evaluated by comparing JPEG compressed images with images in which the quantized activation function was applied. The image quality of the stego-image was also evaluated.

This paper is organized as follows. In Section 2, we present the details of the quantization process of JPEG compression and related research. In Section 3, we define the quantized activation function and describe the structure of the proposed network. In Section 4, we show the effectiveness of the function and demonstrate the performance of our network in computer simulations. We conclude in Section 5.

2. Related works

2.1. Quantization of JPEG compression

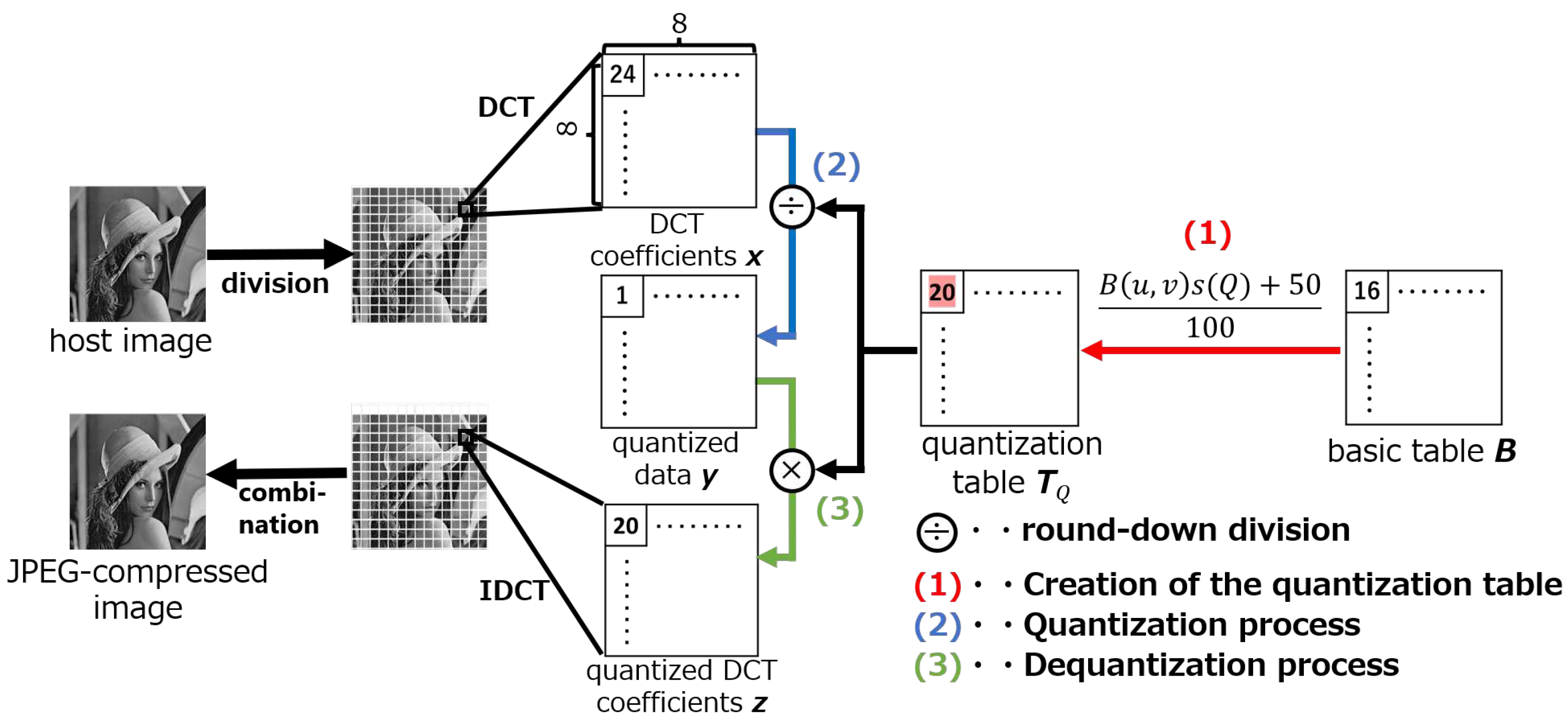
JPEG compression is a lossy compression that reduces the amount of information in an image to reduce the file size. In this kind of compression, an image is divided into $8\times 8$-pixel blocks. Then, in each block, the processes of the DCT, quantization, and entropy coding are sequentially performed. In JPEG compression, the process of reducing the amount of information is the quantization process of the DCT coefficients. We focus on the quantization of the DCT coefficients of the luminance component in an image because the watermark is embedded in these coefficients of the image.

Figure 1 shows the quantization process in JPEG compression for DCT coefficients. The process consists of three steps: 1) creation of the quantization table ${\mathit{T}}_Q$, 2) the quantization process, and 3) the dequantization process.

2.1.1. Creation of the quantization table $T_Q$

During the quantization process, the DCT coefficients are quantized based on a default basic table or a self-defined basic table. The default basic table $\mathit{B}$ is defined as

$$\mathit{B}=\left[\begin{array}{cccccccc}16& 11& 10& 16& 24& 40& 51& 61\\ 12& 12& 14& 19& 26& 58& 60& 55\\ 14& 13& 16& 24& 40& 57& 69& 56\\ 14& 17& 22& 29& 51& 87& 80& 62\\ 18& 22& 37& 56& 68& 109& 103& 77\\ 24& 35& 55& 64& 81& 104& 113& 92\\ 49& 64& 78& 87& 103& 121& 120& 101\\ 72& 92& 95& 98& 112& 100& 103& 99\end{array}\right].$$

(1)

The quantization table is then determined using the quality factor (Q) and the basic table $\mathit{B}$. The quantization table $T_Q(u,v)$ for the quantization level Q at coordinates $(u,v),u=0,1\cdots ,7,v=0,1\cdots ,7$ is defined as

$$T_Q(u,v)=⌊\frac{B(u,v)s\left(Q\right)+50}{100}⌋,$$

(2)

where $\lfloor ·\rfloor$ is the floor function and where $B(u,v)$ is the $(u,v)$ component of the basic table $\mathit{B}$. Also, the scaling factor $s\left(Q\right)$ is given by

$$s\left(Q\right)=\left\{\begin{array}{cc}\frac{5000}{Q}\hfill & (Q<50)\hfill \\ 200-2Q\hfill & (Q\ge 50)\hfill \end{array}\right..$$

(3)

2.1.2. Quantization process

The quantization process is performed using the quantization table ${\mathit{T}}_Q$. Let $y(u,v)$ be the quantized data, and let $x(u,v)$ be the DCT coefficients in an $8\times 8$-pixel block. The quantization process is performed as

$$y(u,v)=\mathrm{round}\left(\frac{x(u,v)}{T_Q(u,v)}\right),$$

(4)

where $\mathrm{round}\left(a\right)$ is given by

$$\mathrm{round}\left(a\right)=\left\{\begin{array}{cc}\lfloor a+0.5\rfloor \hfill & (a\ge 0)\hfill \\ -\lfloor -a+0.5\rfloor \hfill & (a<0)\hfill \end{array}\right..$$

(5)

2.1.3. Dequantization process

Let $z(u,v)$ be the quantized DCT coefficients; then, the dequantization process is performed as

$$z(u,v)=y(u,v)T_Q(u,v).$$

(6)

2.2. Implementation of quantization in related works

As mentioned in 1 introduction, the quantization process in existing methods is implemented by adding noise at the attack layer. In Ahmadi et al. [4], the quantization process is approximated using the quantization table $T_Q(u,v)$ and uniform noise $ϵ$. Let $x(u,v)$ represent the DCT coefficients of an $8\times 8$-pixel block of a stego image, and the quantized DCT coefficients $z(u,v)$ are given as

$$\begin{array}{}\mathrm{(7)}& \hfill z(u,v)& =\left(\frac{x(u,v)}{T_Q(u,v)}+ϵ\right)T_Q(u,v)\hfill \mathrm{(8)}& & =x(u,v)+T_Q(u,v)ϵ.\hfill \end{array}$$

In their method, the quantization process is equivalent to adding a uniform noise $ϵ$ proportional to the quantization table $T_Q(u,v)$.

3. Proposed method

We propose an attack layer that implements JPEG quantization using a quantized activation function (QAF). To demonstrate the effectiveness of the QAF, we compared it with the method of Ahmadi et al. (ReDMark) [4] using the same model as that in ReDMark for the watermark embedding and extraction networks.

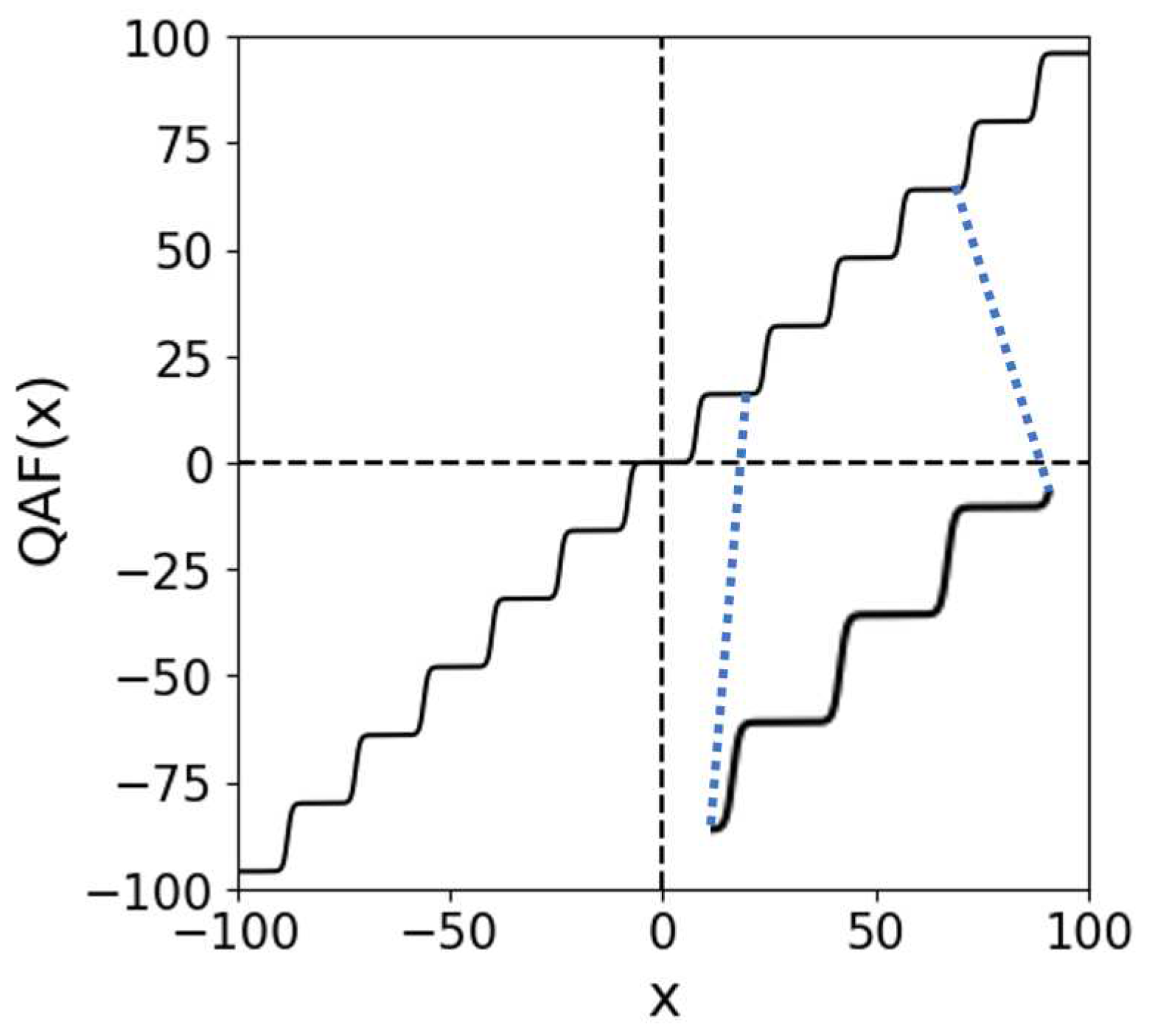
3.1. Quantized activation function

We propose a quantized activation function for neural networks to implement the quantization process of the JPEG compression according to the standard. The QAF consists of n hyperbolic tangent functions tanh and is defined as

$$\mathrm{QAF}\left(x|t_Q\right)=\sum _{i=0}^n\frac{t_Q}{2}tanh\left\{\beta \left(x\pm \frac{t_Q}{2}\pm i·t_Q\right)\right\},$$

(9)

where $t_Q$ is the value of the quantization table $T_Q(u,v)$ when the quantization level is Q. Also, $\beta$ is the slope of the hyperbolic tangent function. Figure 2 shows $\mathrm{QAF}\left(x\right|16)$ when the slope $\beta$ is 1 and when the value of the quantization table $T_Q(u,v)$ is 16.

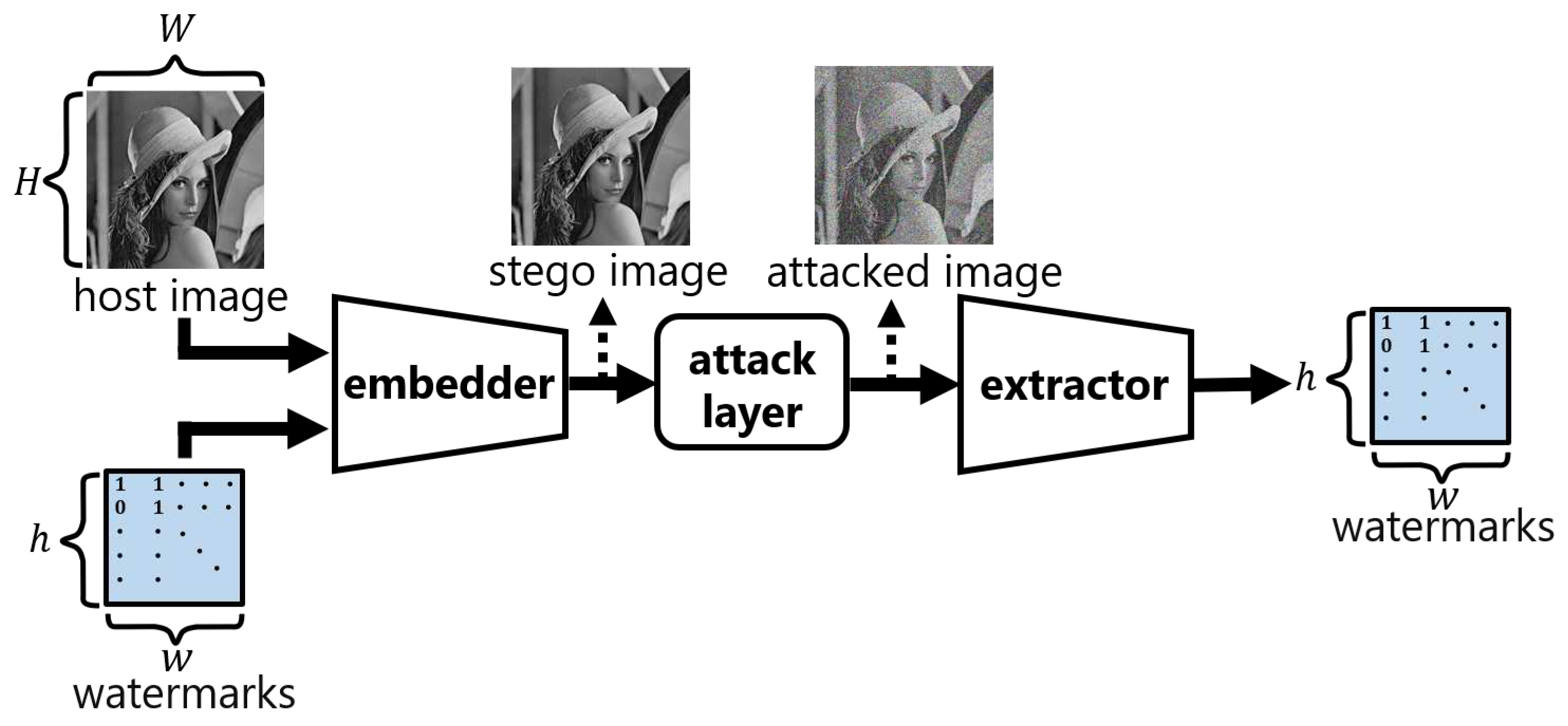
3.2. ReDMark

Figure 3 shows the overall structure of ReDMark [4], which consists of an embedding layer, an extraction layer, and an attack layer. The h and w are the height and width of the 2D watermark, and H and W are the height and width of the original and stego images. The images are divided into $M\times N$-pixel blocks, where $M=N=8$ as it is in ReDMark.

In ReDMark [4], normalization and reshaping are performed on the input image in preprocessing. For the input image $I_{\mathrm{in}}(i,j),i=0,1,\cdots ,H-1,j=0,1,\cdots ,W-1$, the normalized image is given by

$$I(i,j)=\frac{I_{\mathrm{in}}(i,j)-128}{255}.$$

(10)

Reshape is an operation that divides an image into $M\times N$-pixel blocks and transforms them into a 3D tensor representation. The image size $H\times W$ is assumed to satisfy $H=hM,W=wN$. The reshaped image is represented by a 3-dimensional tensor of $h\times w\times MN$. This image is called the image tensor of size $(h,w,MN)$. If necessary, the tensor is inverse transformed back to its original dimension.

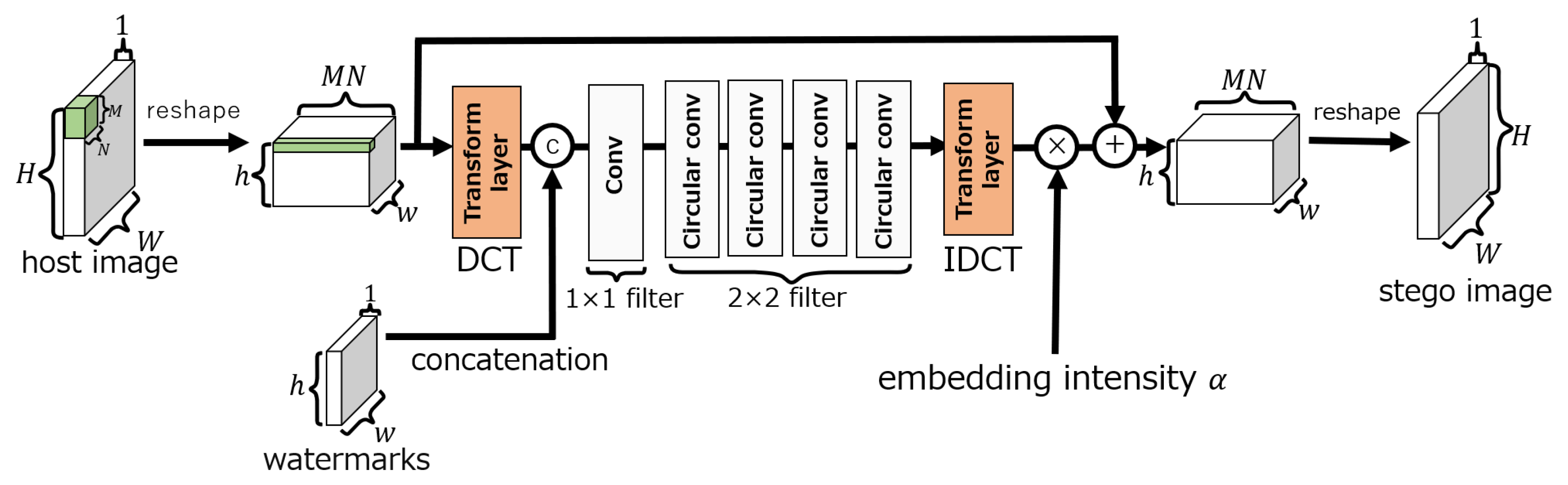
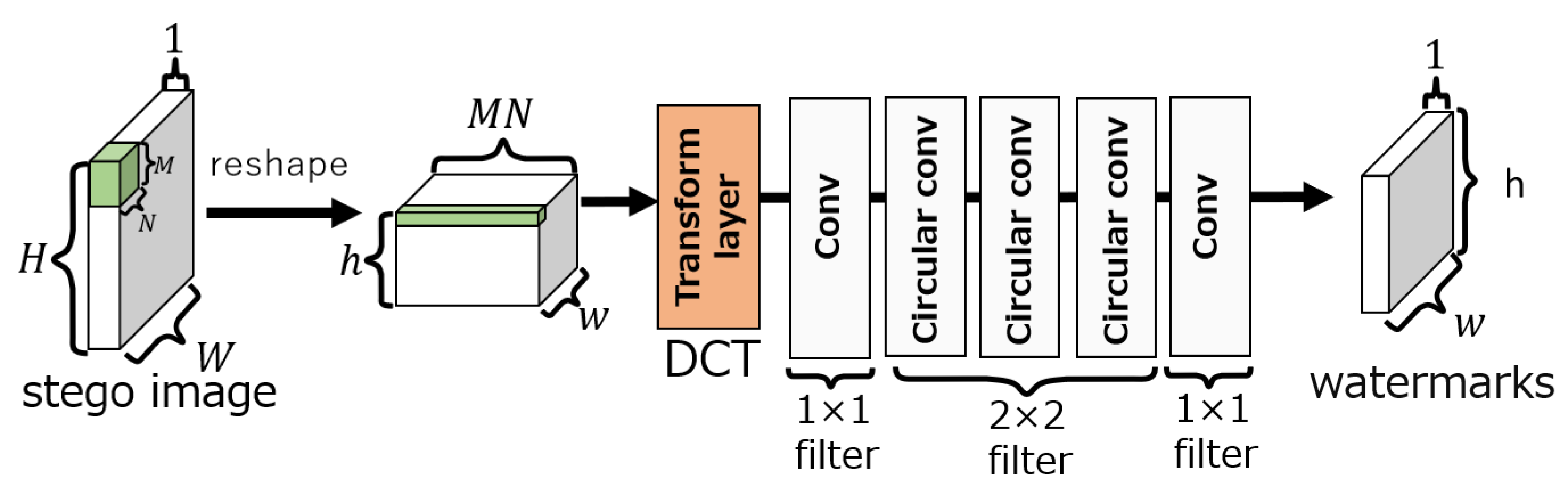
3.3. Embedding network

The embedding network, as shown in Figure 4, consists of three layers: convolution, circular convolution, and transform. The transform layer can perform lossless linear transforms using $1\times 1$ convolutional layers, e.g., the DCT, wavelet transform, and Hadamard transform. In our method, the DCT is selected as the transform layer as it is in ReDMark. The circular convolution layer extends the input to make it cyclic before the convolution is performed. 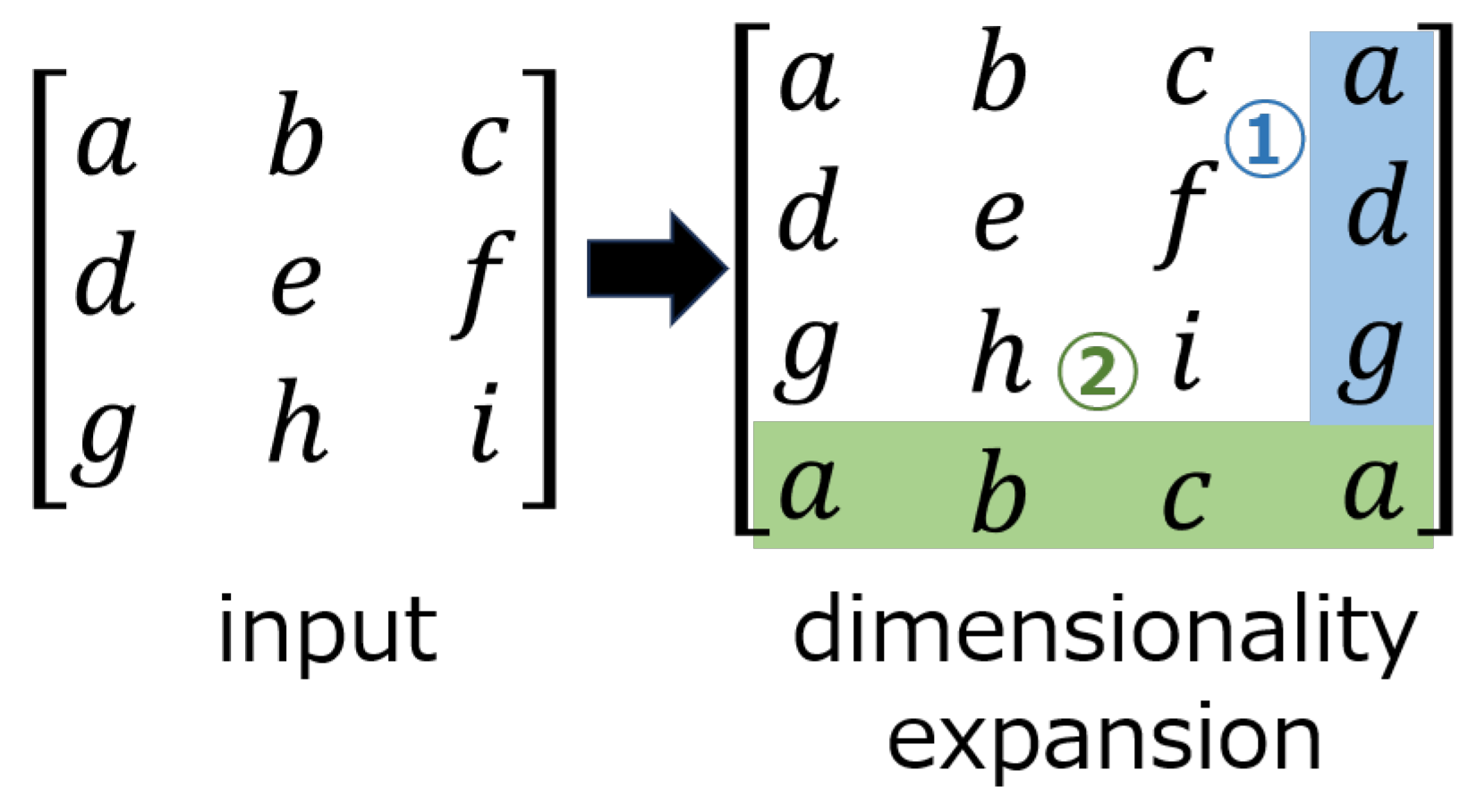Figure 5 shows an example of applying a circular convolution layer with a $2\times 2$ filter when the input is $3\times 3$ pixels. When a circular convolution layer is used, the dimension of the output after convolution is the same as the dimension of the input.

In the embedding network, the convolution and circular convolution layers use $1\times 1$ and $2\times 2$ filters, respectively, and both have 64 filters. In each layer, an exponential linear unit (ELU) activation function is used. The output of the embedding layer is obtained by summing the output of the transform layer performing the inverse DCT (IDCT) (for the IDCT layer) with the input image tensor of size $(h,w,MN)$ and then by performing the inverse process of reshaping. Here, the output of the IDCT layer can be adjusted by the embedding intensity $\alpha$. The intensity is fixed as $\alpha =1$ during training and can be changed during an evaluation.

3.4. Extraction network

The extraction network consists of a convolution layer, a circular convolution layer, and a transform layer, as shown in Figure 6. The transform layer of the extraction network also performs the DCT. The filter sizes of the convolutional and circular convolutional layers are $1\times 1$ and $2\times 2$, respectively. The number of filters is 64 for the fourth layer and 1 for the fifth layer. The activation function up to the fourth layer is ELU [14], and a sigmoid function is used in the fifth layer. Let $p_o(i,j)$ be the output of the extraction network, and the estimated watermark $p_e(i,j)$ is given by

$$p_e(i,j)=\left\{\begin{array}{cc}1,\hfill & p_o(i,j)>0.5\hfill \\ 0,\hfill & p_o(i,j)\le 0.5\hfill \end{array}\right..$$

(11)

3.5. Attack layer

Various attacks can be simulated in the attack layer. In the attack layer of ReDMark, three attack layers are used depending on the type of attack: a GT-Net (a Gaussian-trained network), a JT-Net (a JPEG-trained network), and a MT-Net (a multi-attack-trained network). Because the JT-Net was trained to simulate the JPEG compression, it is compared with our network. The proposed attack layer consists of three sub-layers: a DCT layer, a layer introducing QAF (a QAF layer), and an IDCT layer. Note that in our network, the DCT coefficients are quantized as in the JPEG compression. Figure 7 shows the structure of the network. The embedding and extraction layers have the same structure as that of ReDMark [4]. The output $O(i,j,k),i=0,1,\cdots ,h-1,j=0,1,\cdots ,w-1,k=0,1,\cdots ,MN-1$ of the DCT layer is processed by the QAF (9) at the QAF layer. The output $z(i,j,k)$ of this layer is calculated by

$$z(i,j,k)=\mathrm{QAF}\left(O(i,j,k)\left|\frac{T_Q(u,v)}{255}\right.\right).$$

(12)

Note that the quantization table $T_Q(u,v)$ is divided by 255 because it is normalized by (10). The quantization table values in (12) are determined according to $T_Q(u,v)$ because the quantization table values are different for each of the coordinates $(u,v)$ of the DCT coefficients. The coordinates $(u,v)$ are defined by

$$u=⌊\frac{k}{8}⌋,v=k-8⌊\frac{k}{8}⌋$$

(13)

The attack layer [4] in ReDMark performs noise addition to the coefficients, while the one in our network performs the quantization with the QAF.

3.6. Training method

The embedding and extraction networks are trained in the same way as they were in ReDMark [4], respectively. The loss function $L_1$ of the embedding network is defined as

$$\begin{array}{cc}\hfill L_1& =1-\mathrm{SSIM}(\mathit{I},{\mathit{I}}_o)\hfill \\ \hfill \mathrm{SSIM}(\mathit{I},{\mathit{I}}_o)& =\frac{\left(2\mu {\mu }_o+c_1\right)\left(2\mathrm{Cov}(\mathit{I},{\mathit{I}}_o)+c_2\right)}{\left({\mu }^2{\mu }_o^2+c_1\right)\left({\sigma }^2{\sigma }_o^2+c_2\right)},\hfill \end{array}$$

(14)

where $\mathit{I}$ is the original image given as a teacher and where ${\mathit{I}}_o$ is the output of the embedding network. $\mu$ and ${\mu }_o$ are the mean of $\mathit{I}$ and ${\mathit{I}}_o$, respectively. $\sigma$ and ${\sigma }_o$ are the variances of each image, and $\mathrm{Cov}(\mathit{I},{\mathit{I}}_o)$ is the covariance between the two images. Let $c_1$ and $c_2$ be constants, and let $c_1={10}^{-4},c_2=9\times {10}^{-4}$. Because the output of the embedding network takes a real number, the stego-image ${\mathit{I}}_{\mathrm{st}}$ is obtained by converting it back to 256 levels of the pixel value. That is, it is given by

$$I_{\mathrm{st}}(i,j)=\left\{\begin{array}{cc}255,\hfill & I_{\mathrm{o}}(i,j)>0.5\hfill \\ ⌊255I_o(i,j)+128⌋.\hfill & -0.5\le I_{\mathrm{o}}(i,j)\le 0.5\hfill \\ 0,\hfill & I_{\mathrm{o}}(i,j)<-0.5\hfill \end{array}\right.$$

(15)

The loss function $L_2$ of the extraction network is defined as

$$\begin{array}{ccc}\hfill L_2& =& -\sum _{i=0}^{h-1}\sum _{j=0}^{w-1}\left\{p(i,j)log\left(p_o(i,j)\right)\right.\hfill \\ & & \left.+(1-p(i,j))log\left(1-p_o(i,j)\right)\right\},\hfill \end{array}$$

(16)

where $\mathit{p}$ is the watermark used as a teacher for the extraction network. ${\mathit{p}}_o$ is the output of the sigmoid function of the extraction network. That is, it takes a value between 0 and 1. The total loss function L of our network is defined as

$$L=\gamma L_1+(1-\gamma )L_2,$$

(17)

where the parameter $\gamma$ determines the balance between the two loss functions. The embedding and extraction network are trained by the back propagation [7] using stochastic gradient descent (SGD) as the optimization method.

4. Computer Simulation

4.1. Evaluation of the QAF

First, we tested our method using a computer simulation in which the QAF could approximate the quantization process of JPEG compression. Because the DCT and quantization were applied to $8\times 8$-pixel blocks in the JPEG compression, the QAF was also applied to $8\times 8$-pixel blocks. Three images of $512\times 512$ pixels as shown in Figure 8 were selected from the dataset provided by the University of Granada [11]. Each image was normalized by (10) and was divided into $8\times 8$-pixel blocks. The DCT was performed on each block. Let $I_b^{\mu },\mu =1,2,\cdots ,4096$ be the DCT coefficients of the $\mu$-th block. The QAF was applied to the $\mu$-th block as

$$I_{\mathrm{QAF}}^{\mu }(i,j)=\mathrm{QAF}\left(I_b^{\mu }(i,j)\left|\frac{T_{70}(i,j)}{255}\right.\right),$$

(18)

where the quantization level of the JPEG compression was set to $Q=70$. The parameters of the QAF in (9) were set as gradient $\beta =1000$ and the number of the hyperbolic tangent functions $n=500$. For all the QAF-applied blocks, an IDCT was performed, and the luminance values were inversely normalized using (15). Next, all blocks were combined. The combined image was converted back to the original image size. Then, the QAF-applied image was given by

$${\mathit{I}}_{\mathrm{QAF}}=\left({\mathit{I}}_{\mathrm{QAF}}^1,{\mathit{I}}_{\mathrm{QAF}}^2,\cdots ,{\mathit{I}}_{\mathrm{QAF}}^{4096}\right).$$

(19)

In general, the peak signal to noise ratio (PSNR) of an evaluated image ${\mathit{I}}^{\prime }$ against a reference image $\mathit{I}$ is defined by

$$\mathrm{PSNR}\left({\mathit{I}}^{\prime }|\mathit{I}\right)=10{log}_{10}\left(\frac{{255}^2}{\mathrm{MSE}\left({\mathit{I}}^{\prime },\mathit{I}\right)}\right)\left[\mathrm{dB}\right],$$

(20)

where

$$\mathrm{MSE}\left({\mathit{I}}^{\prime },\mathit{I}\right)=\frac{1}{HW}\sum _{i=0}^{H-1}\sum _{j=0}^{W-1}{\left\{I^{\prime }(i,j)-I(i,j)\right\}}^2.$$

(21)

The accuracy of the QAF can be measured by the PSNR of a QAF-applied image against a JPEG-compressed image, that is, $\mathrm{PSNR}\left({\mathit{I}}_{\mathrm{QAF}}|{\mathit{I}}_{\mathrm{jpeg}}\right)$, where ${\mathit{I}}_{\mathrm{jpeg}}$ is the JPEG-compressed image. Note that the PSNR was measured in the JPEG-compressed image, not the original image, to see the difference with the JPEG-compressed image. Figure 9 shows the three QAF-applied images and their PSNRs. The PSNRs were (a) $51.52$, (b) $53.12$, and (c) $49.55$, all of which were sufficiently high. Thus, we found that the QAF adequately represents the quantization of the JPEG compression.

4.2. Evaluation of the proposed attack layer

We compared the JT-Net in the ReDMark and the proposed attack layer based on the image quality of stego-images and the BER of watermarks extracted from stego-images after the JPEG compression.

4.2.1. Experimental conditions

The training and test images were selected as they were in ReDMark [4]. The training images were 50,000 $32\times 32$-pixel images from CIFAR10 ($H=32,W=32$). An $h\times w$-bit watermark was embedded, where $h=4,w=4$. The watermark was randomly generated. In the parameters used for training, the block height and width sizes were set to $M=8$ and $N=8$, respectively. The parameter of the loss function (17) was set to $\gamma =0.75$, the number of learning epochs was set to 100, and the mini-batch size was set to 32. For the parameters of SGD, the training rate was set to ${10}^{-4}$, and the moment was set to $0.98$. The quantization level for the JPEG compression was set to $Q=70$, and the quantization table ${\mathit{T}}_{70}$ was used. For training the proposed attack layer, the gradient of the QAF (9) was set to $\beta =1000$, and the number of the hyperbolic tangent functions was set to $n=500$. The embedding, attack, and extraction layers were all connected, and the network was trained using the training images and watermarks. Here, the embedding intensity and quantization level were fixed at $\alpha =1$ and $Q=70$, respectively.

For testing, 49 images of $512\times 512$ pixels from the University of Granada were used. These images were divided into $32\times 32$ pixel subimages, and the embedding process was performed on each of them. The 256 subimages were given to the network as test images. Meanwhile, a $32\times 32$ bit watermark was randomly generated. One watermark was embedded four times in one image. That is, the watermark was divided into $4\times 4$-bit subwatermarks, and finally each subwatermark was embedded in one subimage. An estimated watermark was determined by bit-by-bit majority voting because the same watermark was embedded four times in one image.

The attack layer was not used during testing. The test images and the watermarks were used to output stego-images in the embedding network. Here, the embedding intensity was set to values from $\alpha =0.5$ to $1.0$. The stego-images were JPEG compressed at quantization levels $Q=10,20,\cdots ,90$. The compressed stego-images were input to the extraction network, and the estimated watermarks were output. These networks were trained 10 times with different initial values for the comparison of our network with the JT-Net on image quality and BER. The mean and standard deviation of structural similarity index measures (SSIMs), PSNRs, and BERs were calculated.

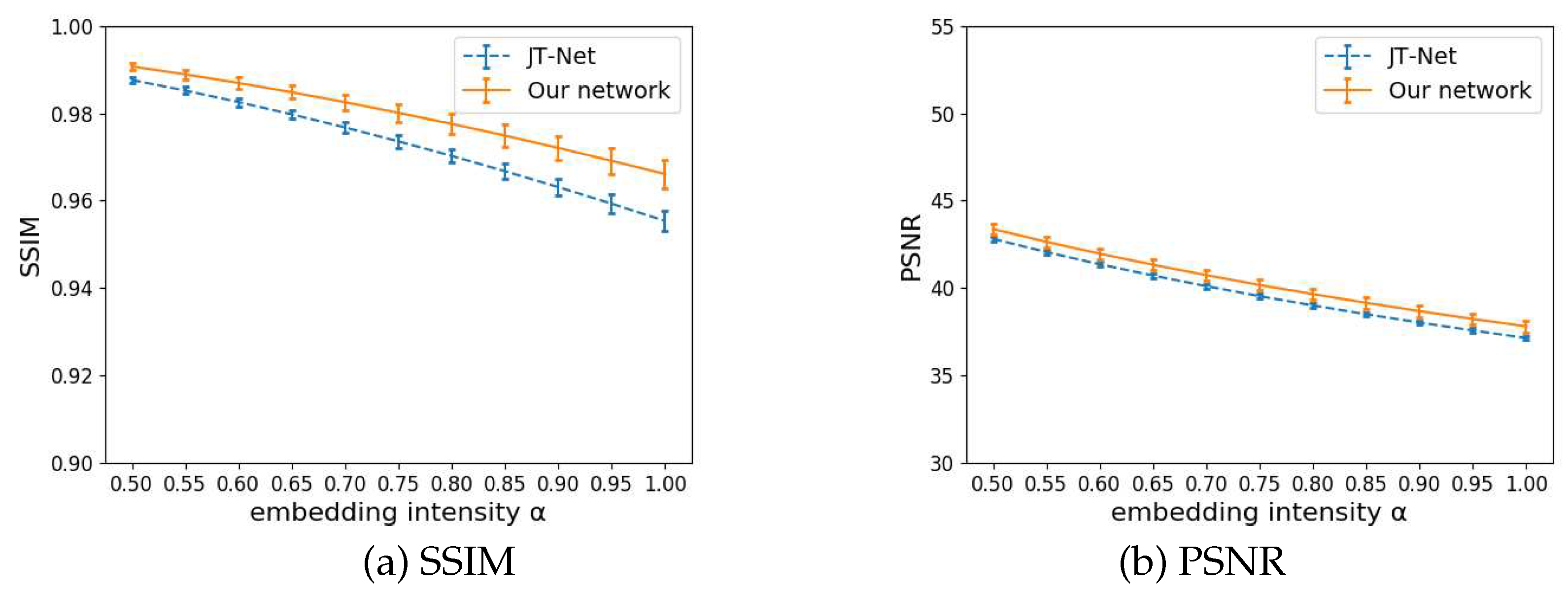
4.2.2. Evaluation of the image quality

The image quality of the stego-images obtained from the JT-Net and our network was evaluated using the SSIMs and PSNRs. The image quality of the stego-image ${\mathit{I}}_{st}$ against the original image $\mathit{I}$ can be expressed as $\mathrm{SSIM}\left({\mathit{I}}_{st},\mathit{I}\right)$ and $\mathrm{PSNR}\left({\mathit{I}}_{st}|\mathit{I}\right)$ by (14) and (20). Figure 10 shows the SSIM and PSNR. The horizontal and vertical axes represent the embedding intensity $\alpha$ and SSIM or PSNR, respectively. The error bars represent the standard deviation of the SSIMs and PSNRs. Embedding the watermark strongly causes degradation in the image quality. Therefore, the SSIM and PSNR decreased as the intensity $\alpha$ increased. The image quality of our network was higher than that of the JT-Net. In other words, our network can reduce the degradation of image quality even with the same embedding intensity.

4.2.3. Evaluation of the BER

The robustness of our network against the JPEG compression was evaluated. The estimated watermark obtained by (11) was evaluated by using the BER. The BER of the estimated watermark ${\mathit{p}}_e$ can be defined by

$$\mathrm{BER}=\frac{1}{hw}\sum _{i=0}^{h-1}\sum _{j=0}^{w-1}p(i,j)\oplus p_e(i,j),$$

(22)

where $\mathit{p}$ is the original watermark, and ⊕ represents the exclusive OR.

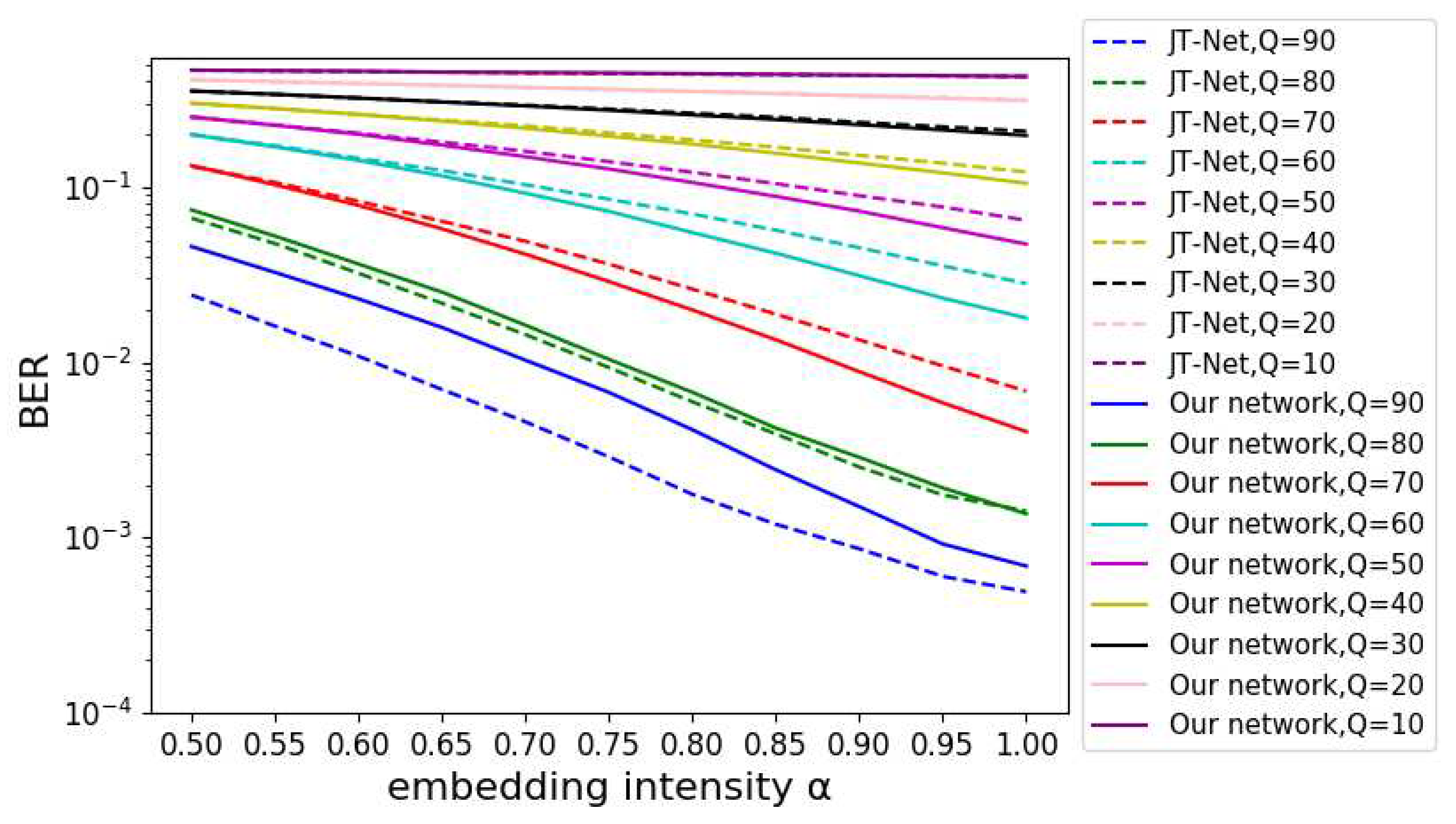
First, we compared the robustness of our network with that of the JT-Net using the same embedding intensity $\alpha$. Figure 11 shows the BER of the estimated watermark for the embedding intensity $\alpha$. The horizontal and vertical axes represent the intensity $\alpha$ and BER, respectively. The solid and dashed lines were the results of our network and the JT-Net for various compression levels Q, respectively. When the watermark was strongly embedded, it was extracted correctly. Therefore, the BER decreased as the intensity $\alpha$ increased. The lowest BER was obtained when $\alpha =1.0$. At compression level $Q\le 70$, the BER of the proposed network was lower than that of the JT-Net. Also, at $Q=80$, they had almost the same BER. Furthermore, at $Q=90$, the BER of our network was higher than that of the JT-Net. In practical use, $50\le Q\le 70$ is normally used, so our network was demonstrated to be effective.

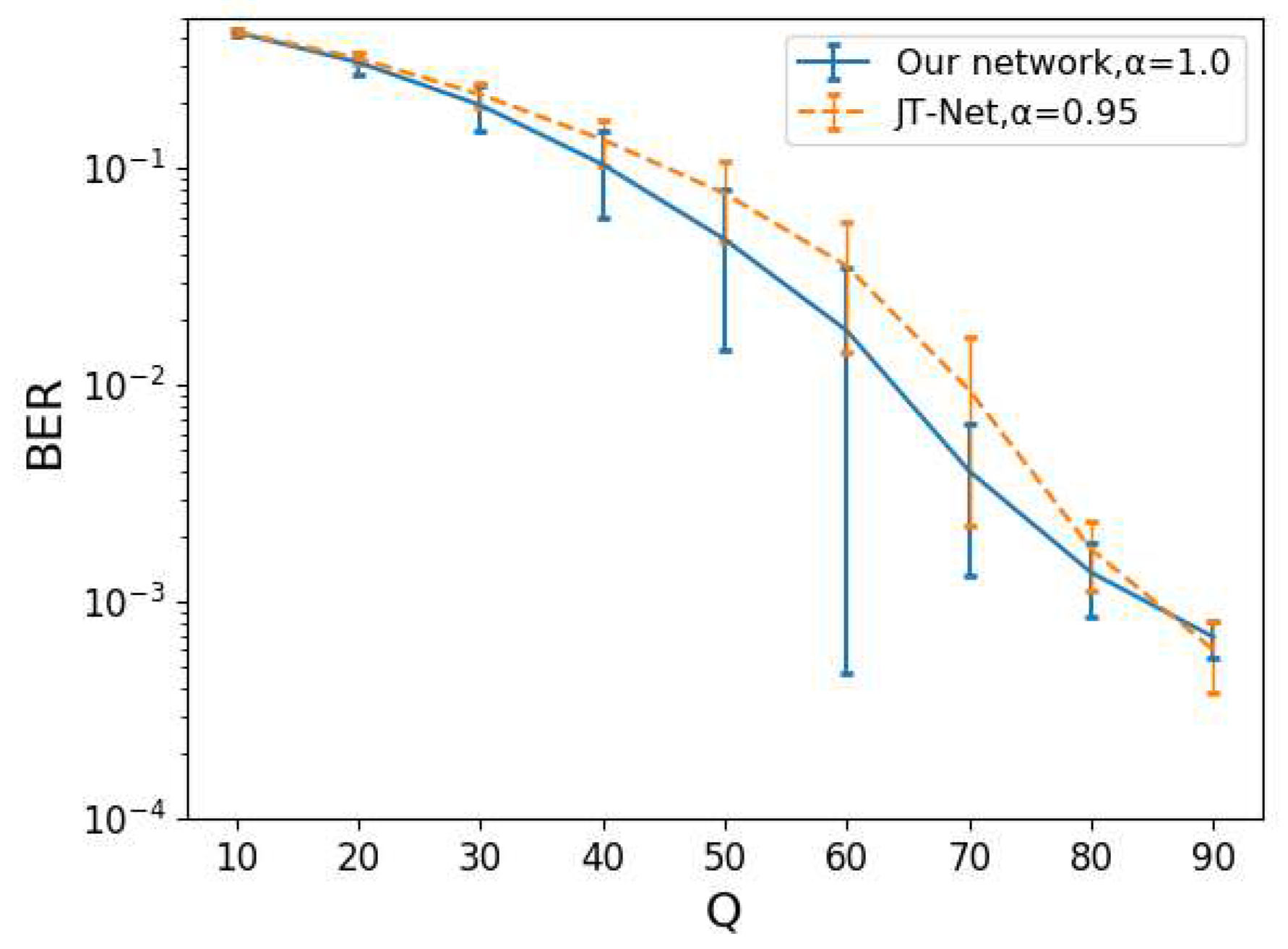
Even with the same embedding intensity, the image quality of our network differs from that of the JT-Net. Therefore, we next adjusted the embedding intensity so that the PSNR of both networks was almost the same, and we compared the BERs of both networks under this condition. Figure 12 is the BER for the compression level Q. The error bars are the standard deviation of the BERs. The intensity $\alpha$ was chosen as part of our evaluation of the robustness against the JPEG compression so that the PSNR obtained from both networks was almost the same. The intensity for the JT-Net and for our network was set to $\alpha =0.95$ (PSNR=$37.58$) and $\alpha =1.0$ (PSNR=$37.81$), respectively. The BER of the estimated watermark for our network was lower than that for the JT-Net. Thus, we can say that our network can generate watermarks with fewer errors under the given PSNR.

5. Conclusion

The JT-Net in ReDMark [4] is a network that simulates JPEG compression. This network substituted the quantization process with a process that adds noise proportional to the value of the quantization table. In this paper, we proposed the quantized activation function (QAF), which can approximate the quantization process of the JPEG compression according to the standard. By approximating the quantization of the JPEG compression using the QAF, we expected to improve the robustness against the JPEG compression. The results of computer simulations showed that the QAF represented quantization with sufficient accuracy. Also, we found that the network trained with the QAF was more robust against the JPEG compression than those trained with the JT-Net. Because the embedding and extraction networks were more robust against the JPEG compression when trained with the QAF, we conclude that our method is more suitable for simulating JPEG compression than conventional methods applying additive noise.