Submitted:
08 February 2024
Posted:
09 February 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Methods
2.1. Estimating the parameters of the Gumbel distribution
- -
- Probability density function (pdf):
- -
- The cumulative distribution function (cdf):
- -
- The quantile function:where, is the scale parameter, and is the position parameter; .
- -
- MOM:
- -
- L-moments:
- -
- LH-moments:where is the arithmetic mean (expected value), represents the variation, and is Euler’s constant; and represent the first two linear moments; and represent the first two high order linear moments.
2.1.1. Method of Ordinary Moments (MOM)
2.1.2. The method of linear moments (L-moments)
2.1.3. The method of high-order linear moments (LH-moments)
2.1.4. The probability weighted moment method (PWM)
2.1.5. The method of maximum likelihood estimation(MLE)
2.1.6. The least squares method (LSM)
2.1.7. The weighted least squares method (WLSM)
2.1.8. The entropy weight method (ENT)
2.1.9. The method of mixed moments (MIX)
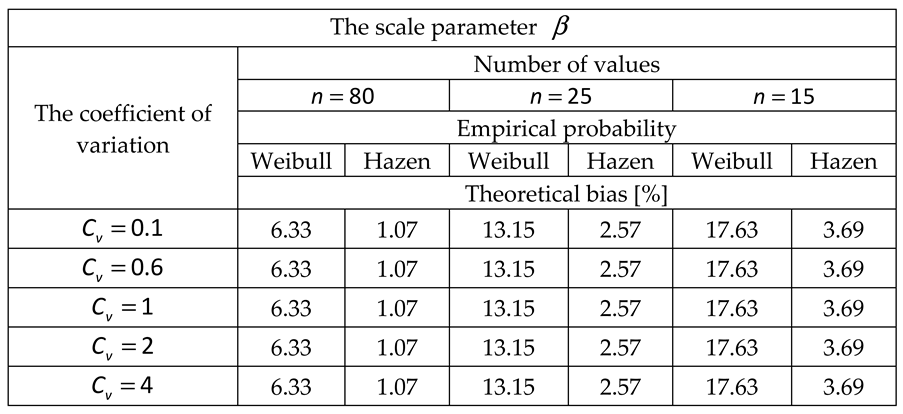
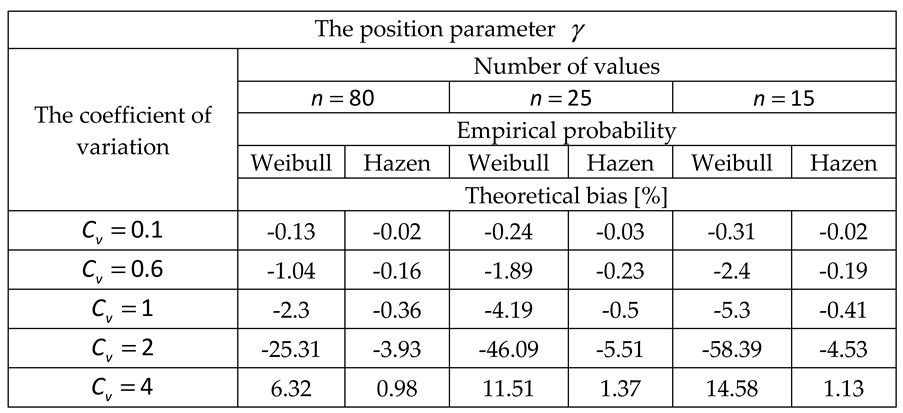
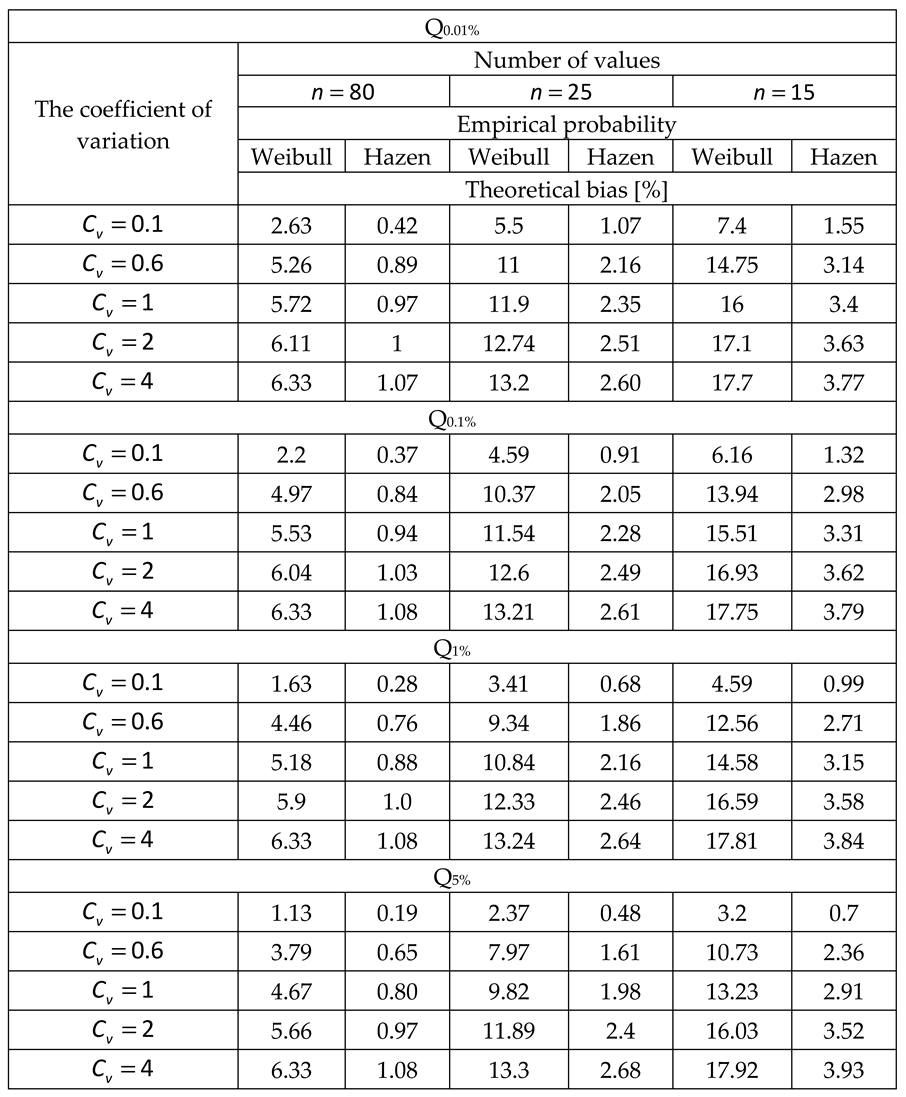
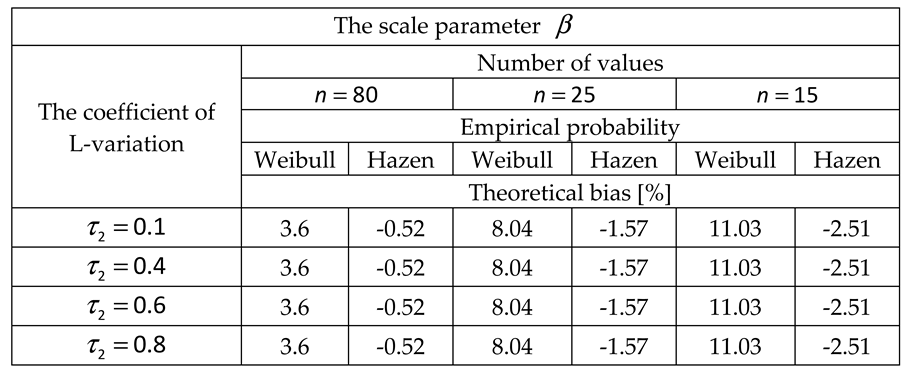
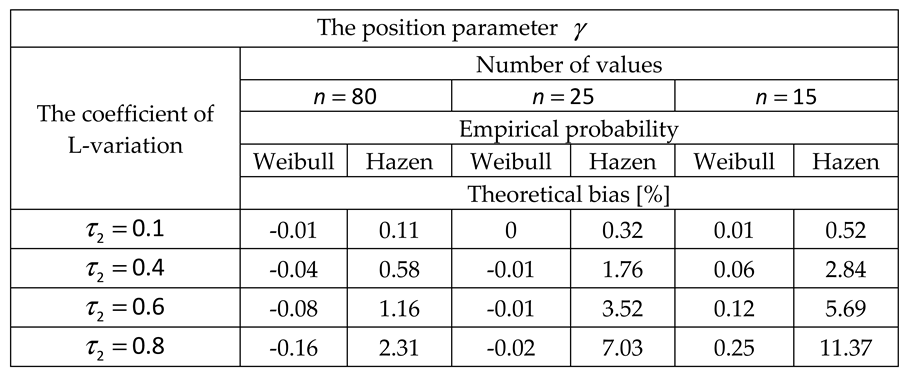
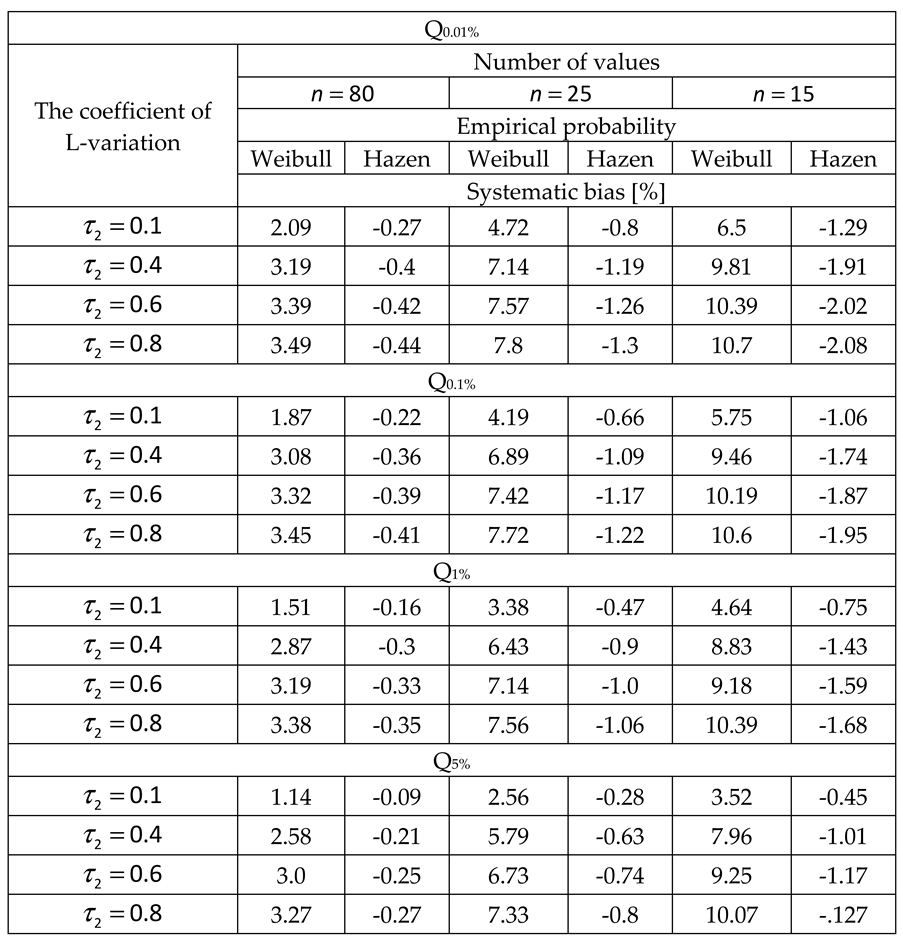
2.2. Systematic biases due to the variability of data lengths
2.2.1. Method of ordinary moments
2.2.2. The method of linear moments
2.3. Choosing the best model
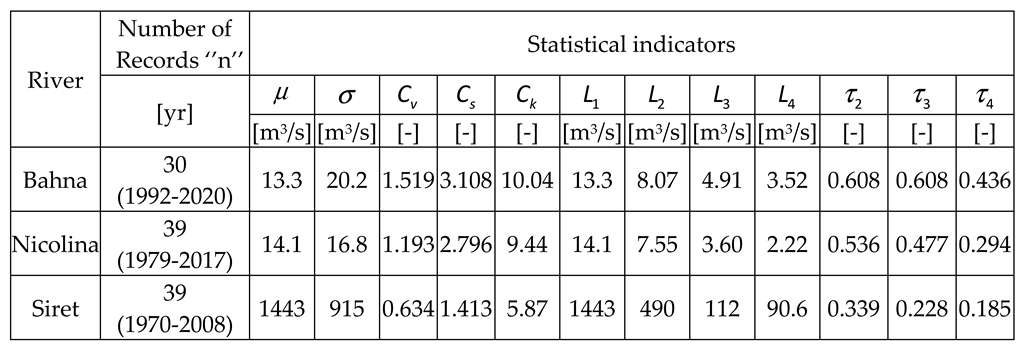
3. Case Studies and Data
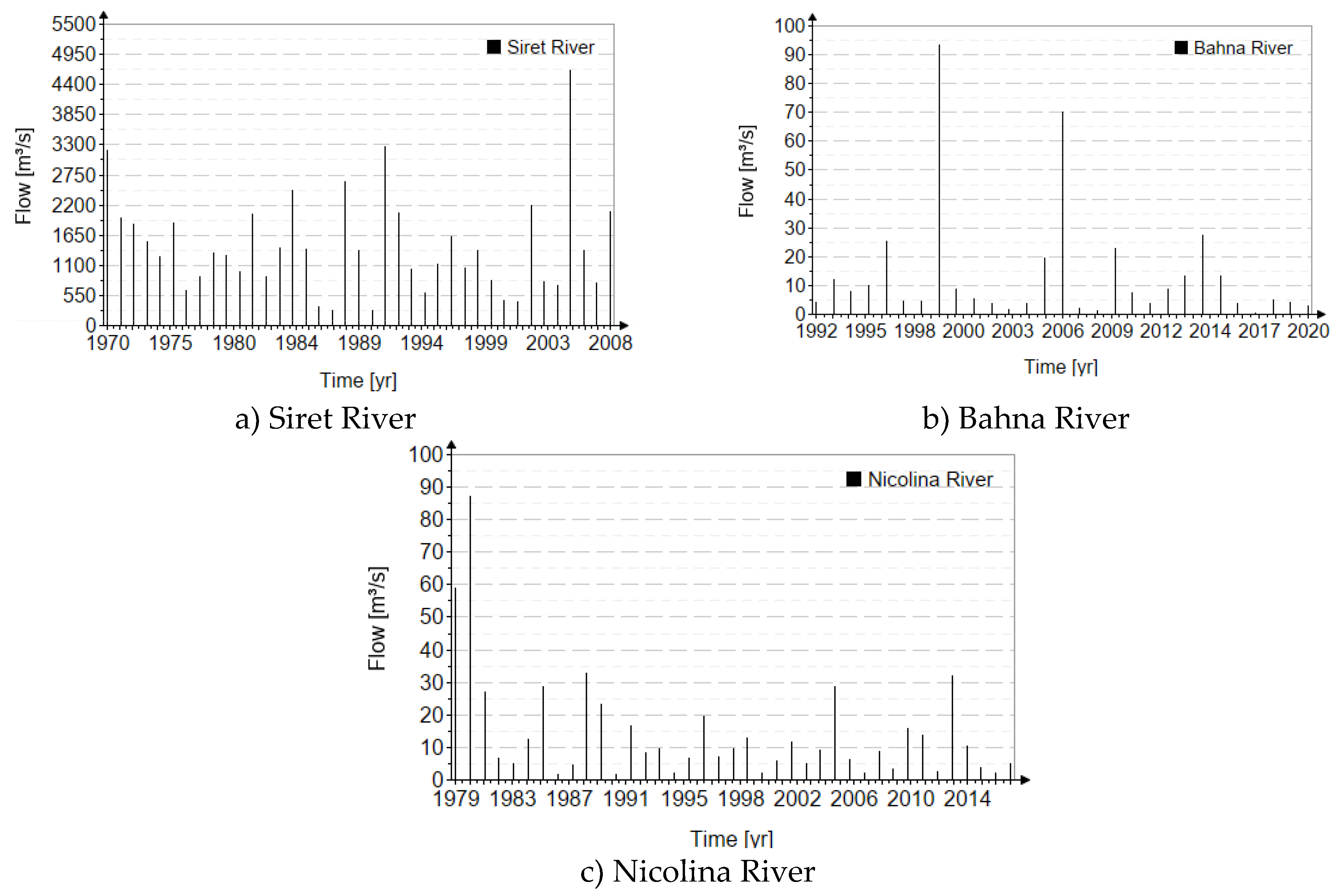
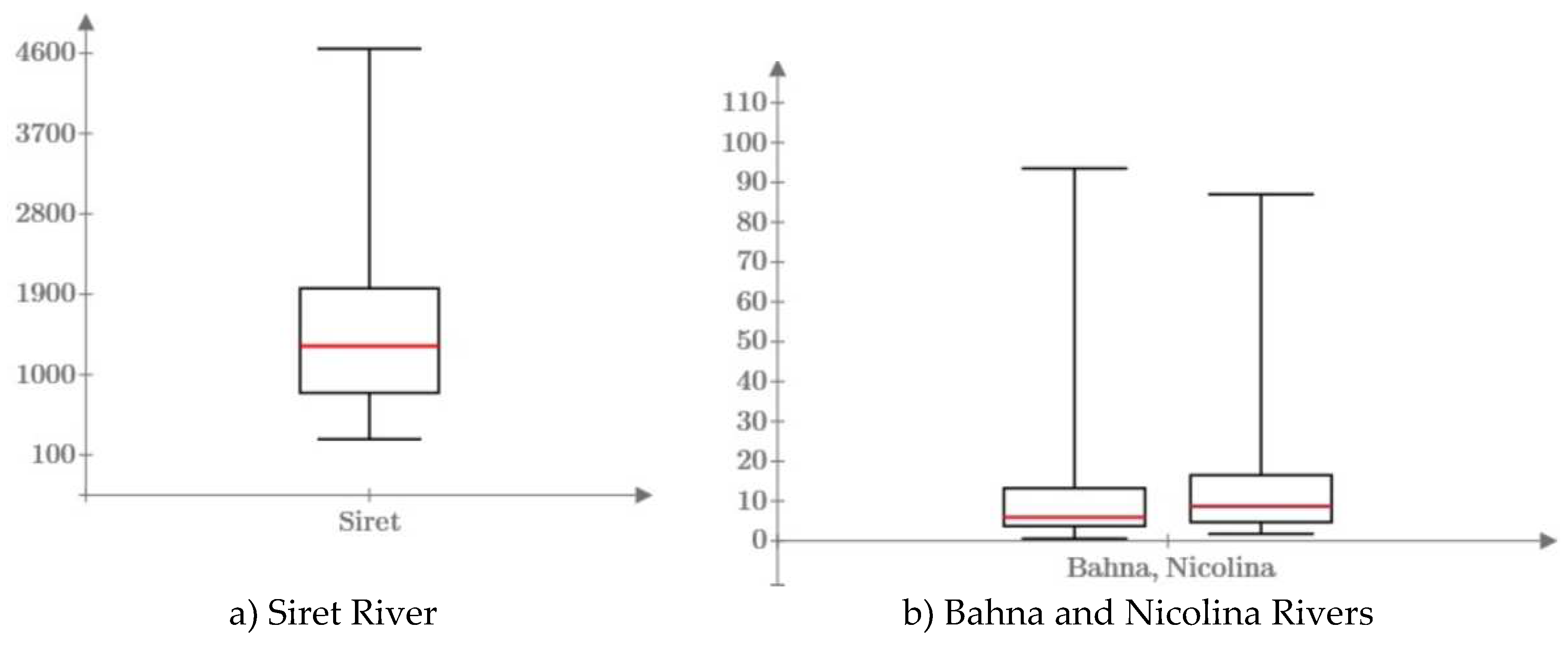
3.1. Flood Frequency Analysis
3.2. Annual Maximum Daily Rainfall
4. Results and Discussions
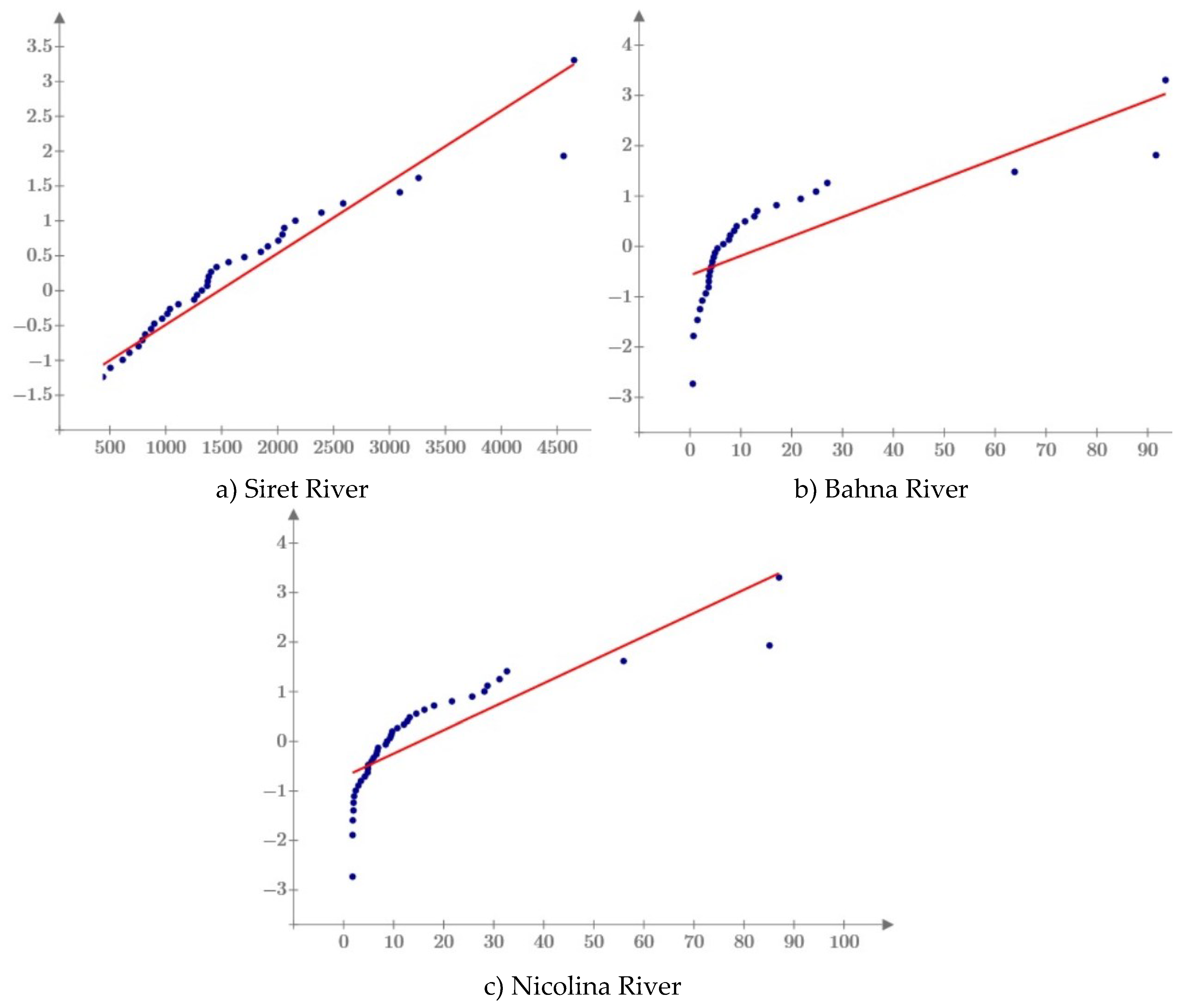
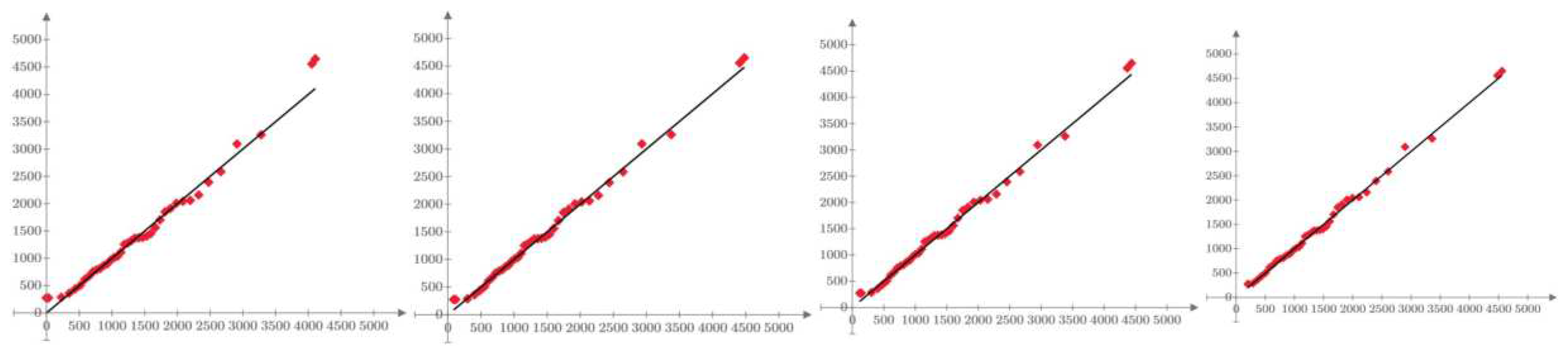
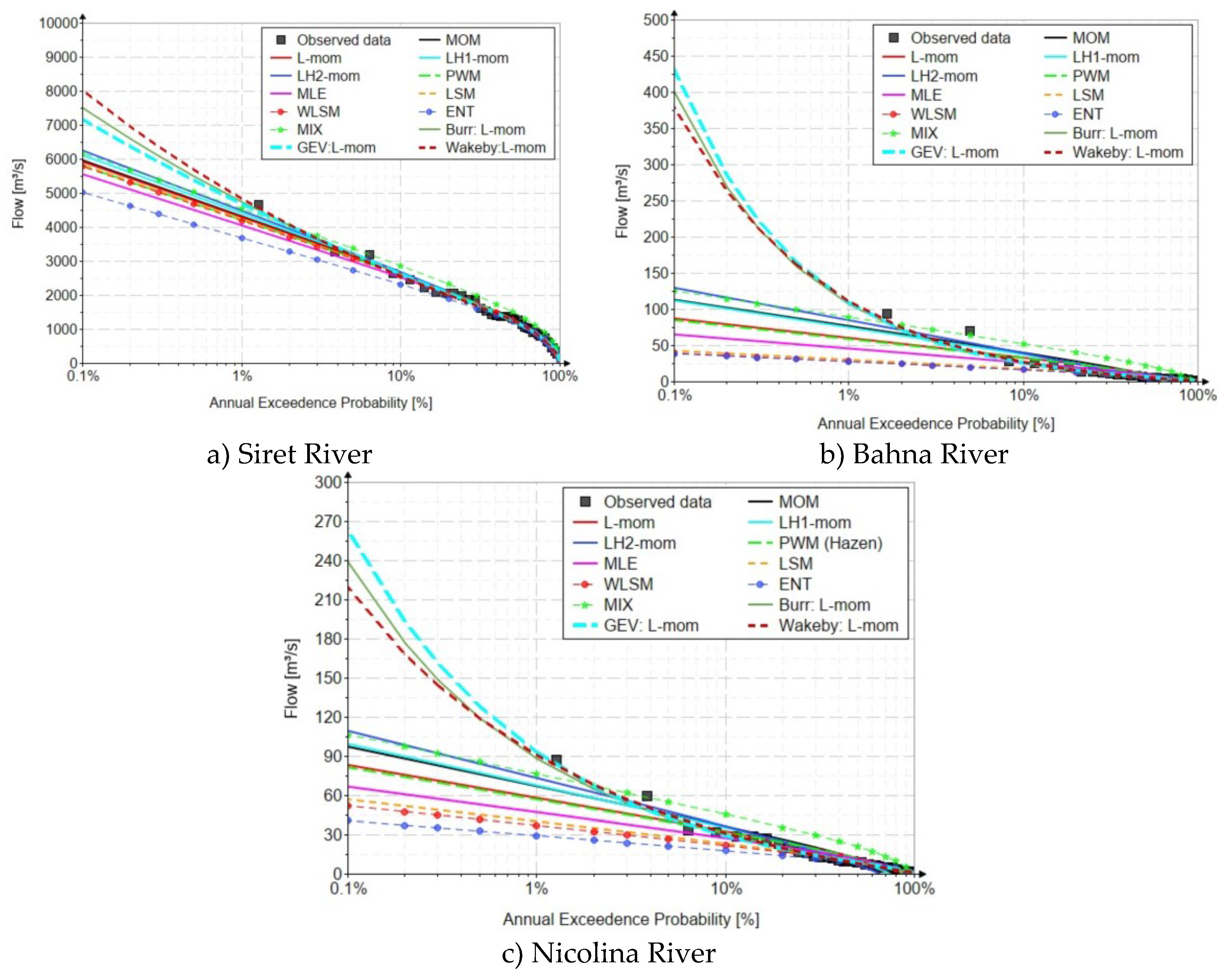
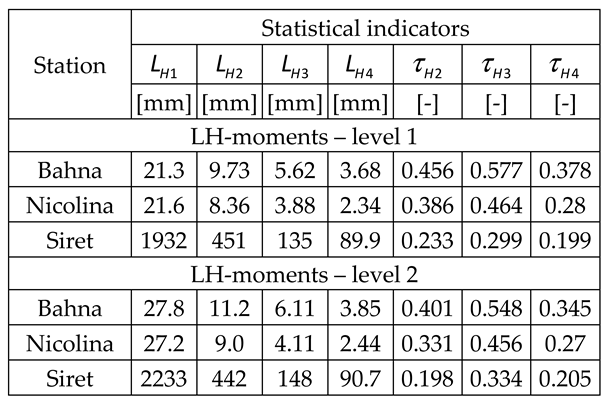
4.1. Flood Frequency Analysis
4.1.1. Verification of normality
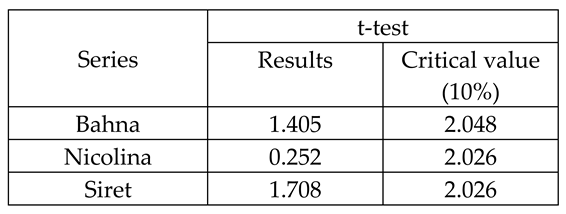
4.1.2. The verification of stationarity and outliers
4.1.3. Statistical analysis on the field of recorded data
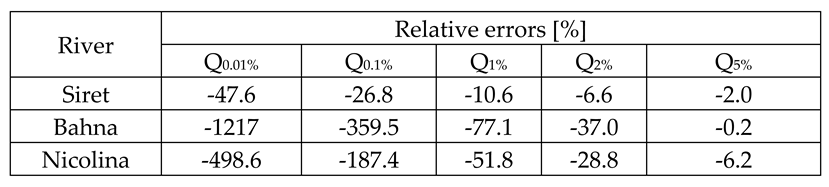
4.1.4. Statistical analysis on the field of low annual exceedance probabilities.
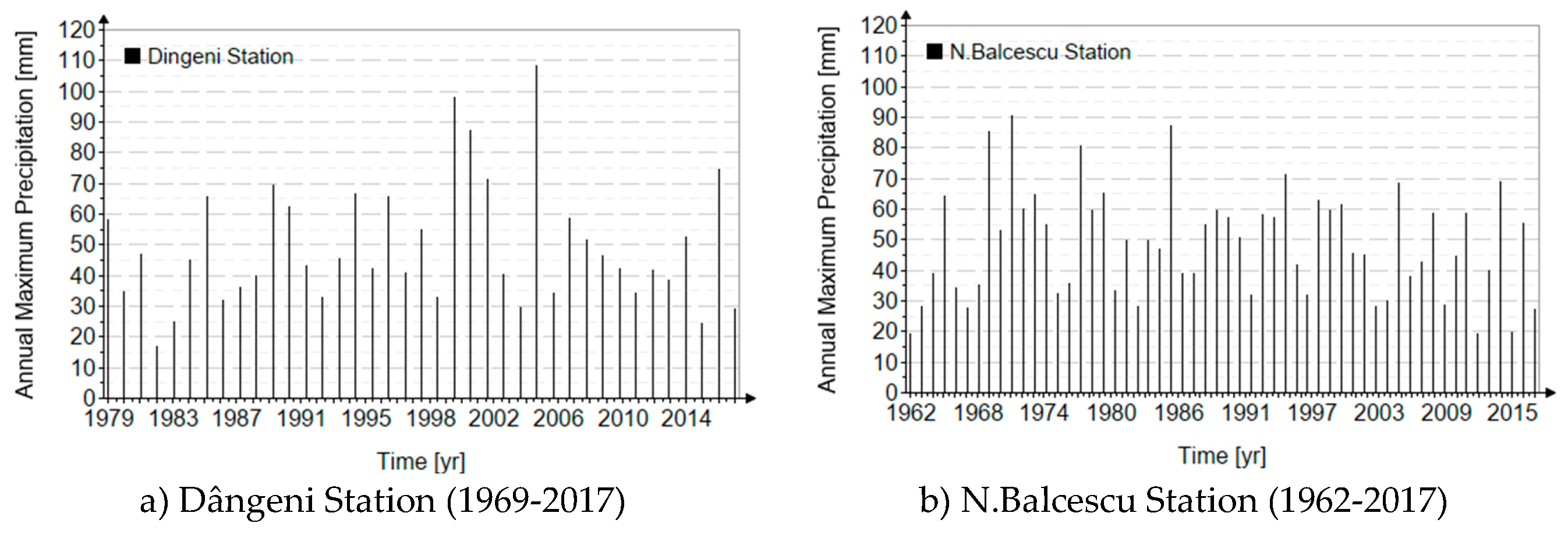
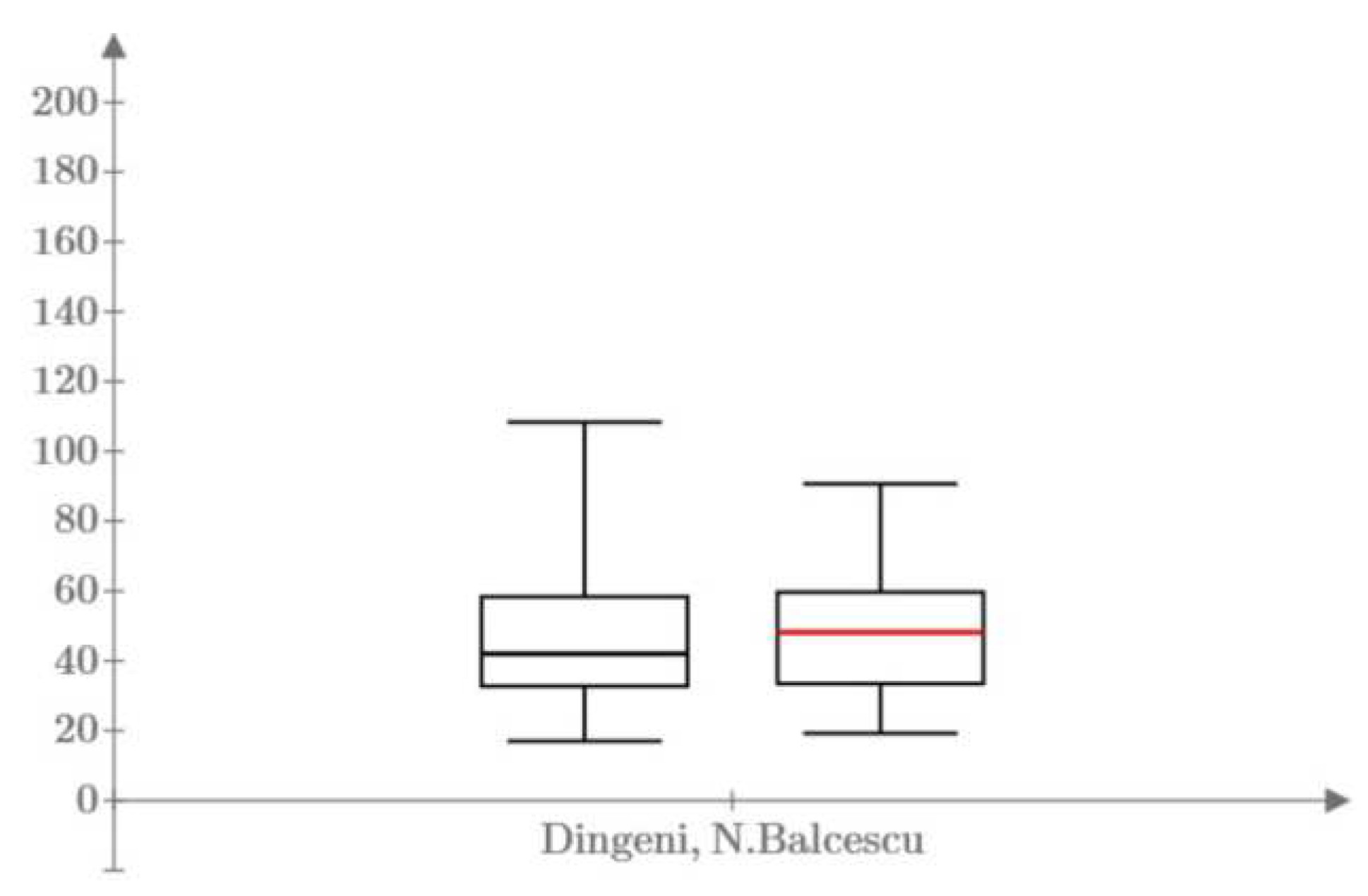
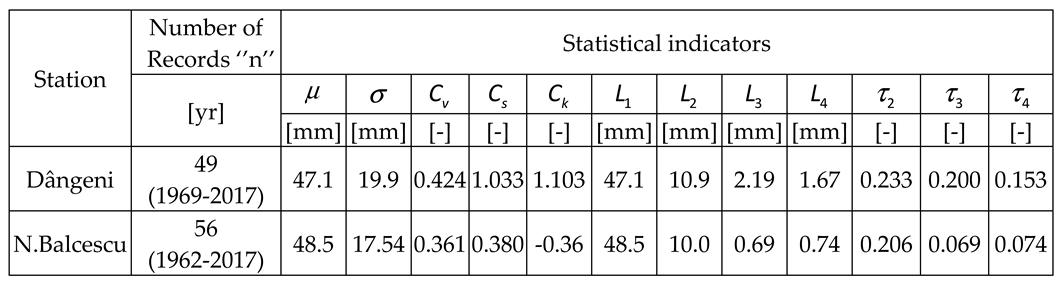
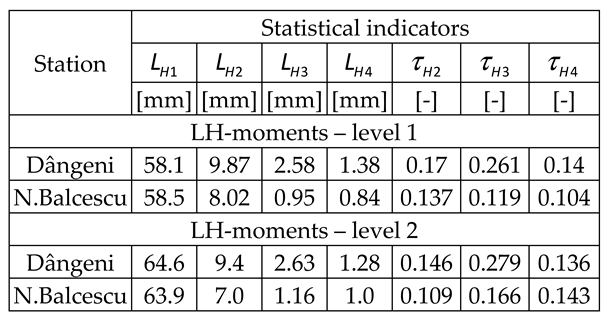
4.2. Annual Maximum Daily Rainfall (24h)
4.2.1. Verification of normality
4.2.2. The verification of stationarity and outliers
4.2.3. Analysis of forecasted values
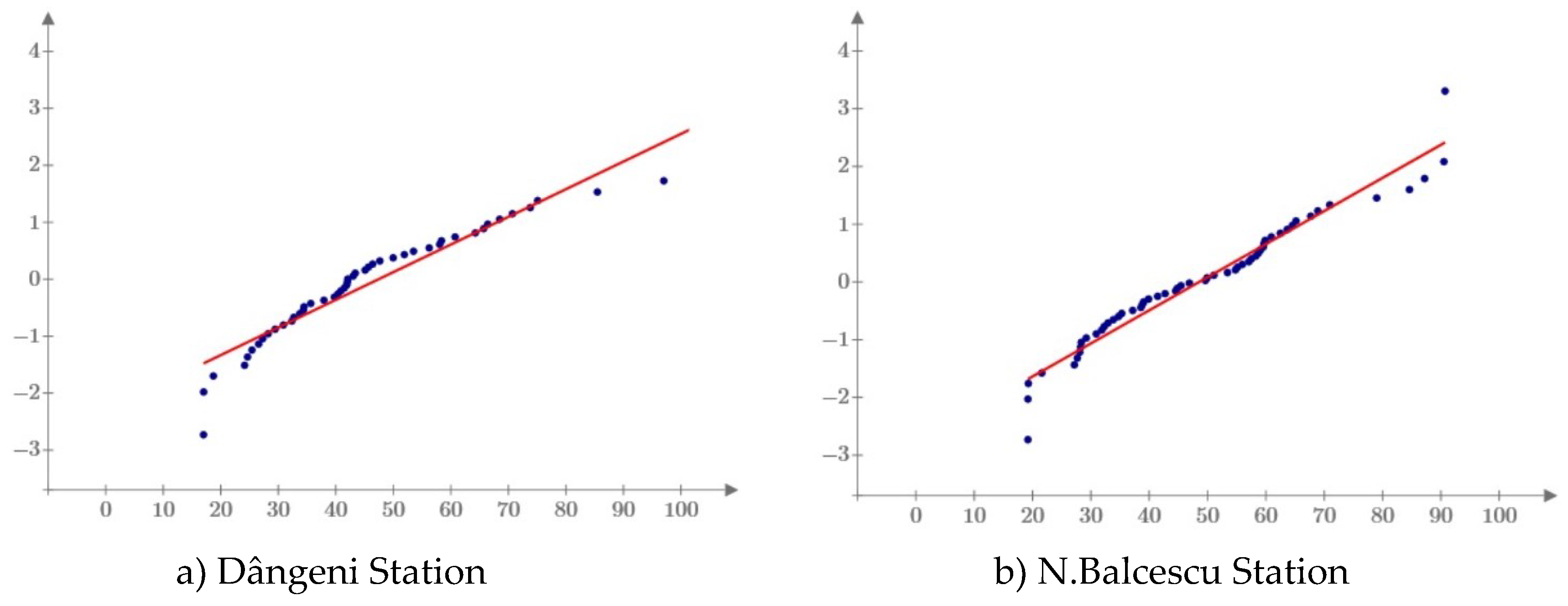
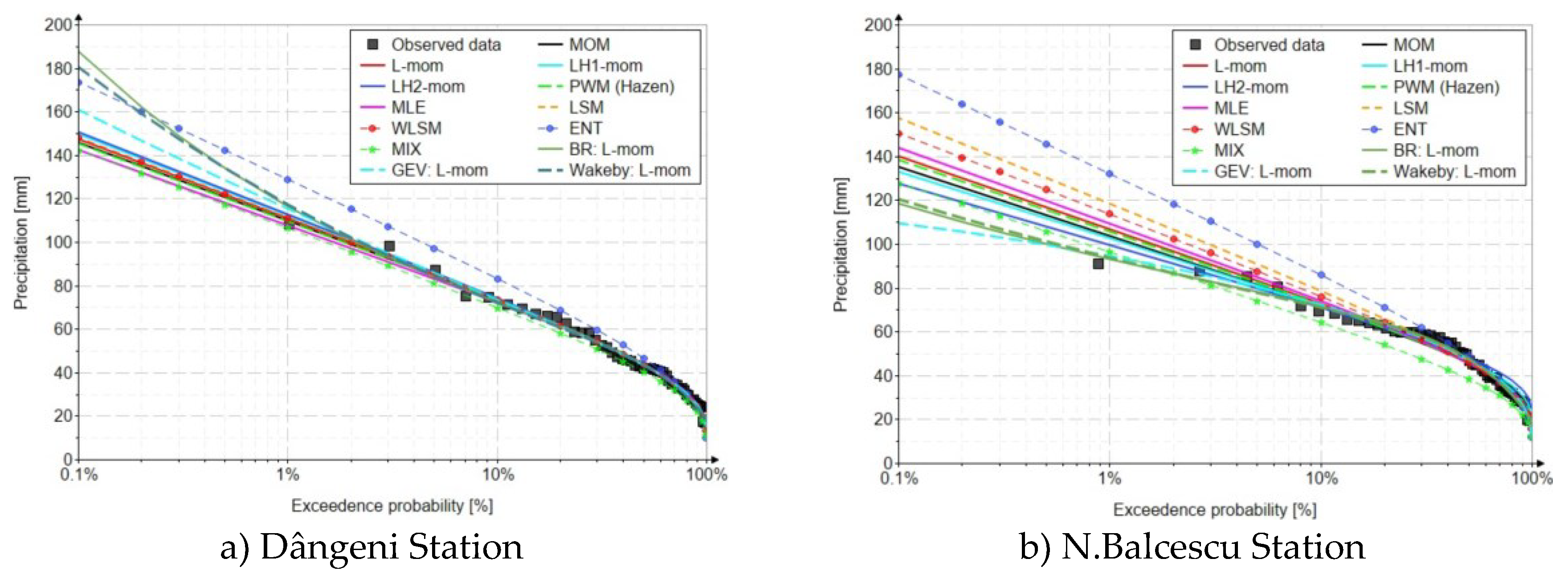
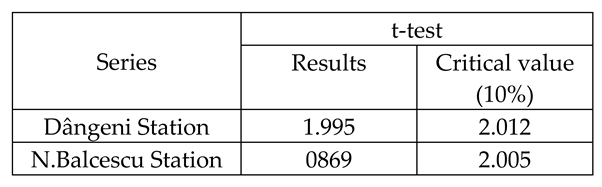
Dângeni station results
N.Balcescu station
| Distribution | Parameter estimation method | Statistical measures | |
|---|---|---|---|
| RME | RAE | ||
| Gumbel | MOM | 0.0102 | 0.0575 |
| L-mom | 0.0089 | 0.0512 | |
| LH1-mom | 0.0131 | 0.0716 | |
| LH2-mom | 0.0196 | 0.104 | |
| PWM | 0.0093 | 0.0528 | |
| MLE | 0.0088 | 0.051 | |
| LSM | 0.0133 | 0.0585 | |
| WLSM | 0.0096 | 0.0533 | |
| ENT | 0.0186 | 0.0947 | |
| MIX | 0.0227 | 0.1608 | |
| GEV | L-mom | 0.0091 | 0.0477 |
| Burr | L-mom | 0.0060 | 0.0340 |
| Wakeby | L-mom | 0.0061 | 0.0346 |

5. Conclusions
References
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press: Boca Raton, FL, USA, 2000; ISBN 9780849300837.
- Bulletin 17B Guidelines for Determining Flood Flow Frequency; Hydrology Subcommittee; Interagency Advisory Committee on Water Data; U.S. Department of the Interior; U.S. Geological Survey; Office of Water Data Coordination: Reston, VA, USA, 1981.
- Bulletin 17C Guidelines for Determining Flood Flow Frequency; U.S. Department of the Interior; U.S. Geological Survey: Reston, VA, USA, 2017.
- Dutta, P., & Deka, S. (2023). Reckoning flood frequency and susceptibility area in the lower Brahmaputra floodplain using geospatial and hydrological approach. River, 2, 384–401. [CrossRef]
- Stefanyshyn, D. V. "On the use of the type I Gumbel distribution to assess risks given floods." Математичне мoделювання в екoнoміці (2018).
- Pawar, U.V., Hire, P.S., Gunjal, R.P. et al. Modeling of magnitude and frequency of floods on the Narmada River: India. Model. Earth Syst. Environ. 6, 2505–2516 (2020). [CrossRef]
- Sandeep Samantaray, Abinash Sahoo; Estimation of flood frequency using statistical method: Mahanadi River basin, India. H2Open Journal 1 January 2020; 3 (1): 189–207. [CrossRef]
- Oyatayo, Kehinde & Ndabula, Christopher & Jidauna, Godwill & Abaje, I.B. (2023). ANALYSIS OF GUMBEL EXTREME VALUE DISTRIBUTION FOR PREDICTION OF EXTREME FLOOD EVENTS OF RIVER BENUE ALONG IBI, TARABA STATE, NIGERIA. 8. 85-090.
- Oyatayo, Kehinde & Christopher, Ndabula & Kushi, Zumunta & Jidauna, Godwill. (2017). GUMBEL’S FLOOD FREQUENCY PROBABILITY ANALYSIS OF RIVER DONGA, TARABA STATE. Journal of Geography and Development. 7. 766-782.
- Bochare, Rewa & farkya, mitika. (2020). Regional Flood Frequency Analysis of River Chambal – A Case Study. 3. 56.
- Oyatayo, Kehinde & Ndabula, Christopher & Adamu, G & Jidauna, Godwill. (2021). INTEGRATING DIGITAL ELEVATION MODEL, LANDUSE/LANDCOVER AND FLOOD FREQUENCY ANALYSIS: A DETERMINISTIC APPROACH TO FLOOD INUNDATION AND RISK MODELING OF MAKURDI ALONG ITS RIVER BENUE REACH. FUDMA Journal of Sciences. 5. 477-489. [CrossRef]
- Bhagat, Nirman. (2017). Flood Frequency Analysis Using Gumbel’s Distribution Method: A Case Study of Lower Mahi Basin, India. Ocean Development and International Law. 6. 51-54. [CrossRef]
- Ibeje, Andy. (2020). Flood Frequency Analysis of River Niger, Shintaku Gauging Station, Kogi State, Nigeria. FUOYE Journal of Engineering and Technology. 5. 194-199. [CrossRef]
- Önen, Fevzi & Bagatur, Tamer. (2017). Prediction of Flood Frequency Factor for Gumbel Distribution Using Regression and GEP Model. Arabian Journal for Science and Engineering. 42. [CrossRef]
- Win, Ni & Win, Khin. (2014). Comparative Study of Flood Frequency Analysis on Selected Rivers in Myanmar. [CrossRef]
- Ahad, Ummar & Ali, Umair & Inayatullah, Meer & Shah, Abdul. (2022). Flood Frequency Analysis: A Case Study of Pohru River Catchment, Kashmir Himalayas, India. Journal of the Geological Society of India. 98. 1754-1760. [CrossRef]
- Griffis, V.W.; Stedinger, J.R. Evolution of flood frequency analysis with Bulletin 17. J. Hydrol. Eng. 2007, 12, 283–297. [CrossRef]
- Rao, P. & Ramana, M. & Reddy, K Madhusudhana & Kumar, A.. (2022). Flood Frequency Analysis of Araniar Medium Irrigation Project in Chittoor District by using Gumbel’s Distribution. International Journal of Environment and Climate Change. 538-544. [CrossRef]
- Vivekanandan, N. (2012). Assessing Adequacy of a Probability Distribution for Estimation of Design Flood. Bonfring International Journal of Industrial Engineering and Management Science. 2. 22-27. [CrossRef]
- Sharma, Priyank & Patel, Prem Lal & Jothiprakash, Vinayakam. (2016). AT-SITE FLOOD FREQUENCY ANALYSIS FOR UPPER TAPI BASIN, INDIA.
- Saeed, Saeb & Mustafa, Ayad & Al Aukidy, Mustafa. (2021). Assessment of Flood Frequency Using Maximum Flow Records for the Euphrates River, Iraq. IOP Conference Series: Materials Science and Engineering. 1076. 012111. [CrossRef]
- Sinam, Rebati. (2019). At Site Flood Frequency Analysis of Baitarani River at Champua Watershed, Odisha. International Journal of Scientific Research in Science and Technology. 54-64. [CrossRef]
- Pal, Jnan. (2023). Estimation of Probable Maximum Flood by Flood Frequency Analysis at Tiuni Barrage Site on River Tons. Journal of The Institution of Engineers (India): Series A. 104. [CrossRef]
- Sonowal, Gulap & Thakuriah, Gitika. (2019). FLOOD FREQUENCY ANALYSIS USING GUMBEL’S DISTRIBUTION METHOD: A LOWER DOWNSTREAM OF LOHIT RIVER (DANGORI RIVER), ASSAM (INDIA). International Journal of Civil Engineering and Technology. 10. 229-234.
- Malakar, Kousik. (2020). Flood Frequency Analysis Using Gumbel’s Method: A Case Study of Lower Godavari River Division, India.
- Mandal, Kajal & Dharanirajan, Kesavan & Sarkar, Sabyasachi. (2021). Application of Gumbel’s Distribution Method for Flood Frequency Analysis of Lower Ganga Basin (Farakka Barrage Station), West Bengal, India. Disaster Advances. 14. 51-58. [CrossRef]
- Ganamala, Kalpalatha & Pitta, Sundara. (2017). A case study on flood frequency analysis. International Journal of Civil Engineering and Technology. 8. 1762-1767.
- St, Syafalni & Setyandito, Oki & Lubis, F.R. & Wijayanti, Yureana. (2015). Frequency analysis of design-flood discharge using Gumbel distribution at Katulampa weir, Ciliwung River. International Journal of Applied Engineering Research. 10. 9935-9946.
- Baliboyina, Prasad & Brahmaji, Rao & Ramamohanarao, P. & Sarathkumar,. (2022). Flood Frequency Analysis of Lower Krishna Basin using Gumbel Method at Prakasam Barrage, Vijayawada, Andhra Pradesh. Disaster Advances. 16. 30-35. [CrossRef]
- Muça, Orland. (2019). Flood Frequency Analysis Using Gumbel’s Distribution: A Case Study Of Komani Basin.
- Ramasamy, M. & Nagan, S. & Kumar, P.. (2022). A case study of flood frequency analysis by intercomparison of graphical linear log-regression method and Gumbel’s analytical method in the Vaigai river basin of Tamil Nadu, India. Chemosphere. 286. 131571. [CrossRef]
- Prasanchum, Haris & Sirisook, Panuthat & Lohpaisankrit, Worapong. (2020). Flood risk areas simulation using SWAT and Gumbel distribution method in Yang Catchment, Northeast Thailand. Geographia Technica. 15. 29-39. [CrossRef]
- Nyikadzino, Ben & Chitakira, Munyaradzi & Muchuru, Shepherd. (2022). Flood risk analysis in the Limpopo River basin using the Gumbel distribution method: Case of the Limpopo River.
- Chakraborty, Shiulee & Issac, R.K & M.Imtiyaz,. (2012). Probability Analysis for prediction of rainfall of Raipur region (Chhattisgarh).
- Madhusudhan, MS & Surendra, HJ & Harshitha, J & Lekhana, PS & Kusumanjali, TS. (2022). Estimation of Flood Discharges for Various Return Periods at Kabini Dam Using Statistical Approach. [CrossRef]
- Okonofua, Ehizonomhen & OGBEIFUN, Prince. (2013). Flood Frequency Analysis of Osse River Using Gumbel’s Distribution. Civil Engineering and Environmental Systems. 3. 55.
- Pandey, H. & Dwivedi, Shivam & Kumar, Kamlesh. (2018). Flood Frequency Analysis of Betwa River, Madhya Pradesh India. Journal of the Geological Society of India. 92. 286-290. [CrossRef]
- Kumar, Rajesh. (2019). Flood Frequency Analysis of the Rapti River Basin using Log Pearson Type-III and Gumbel Extreme Value-1 Methods. Journal of the Geological Society of India. 94. 480–484. [CrossRef]
- Hart, Lawrence & Stanley, Eke. (2020). FLOOD FREQUENCY ANALYSIS USING GUMBEL DISTRIBUTION EQUATION IN PART OF PORT HARCOURT METROPOLIS. 11.
- Strupczewski, W. G. et al. (2014). On Return Periodof the Largest Historical Flood. Journal of Geoscience and Environment Protection, 2, 144-152. [CrossRef]
- Payrastre, O., Gaume, E., and Andrieu, H.: Use of historical data to assess the occurrence of floods in small watersheds in the French Mediterranean area, Adv. Geosci., 2, 313–320. [CrossRef]
- Izinyon, Chris & Agbonaye, Engr Augustine. (2017). Best-Fit Probability Distribution Model for Rainfall Frequency Analysis of Three Cities in South Eastern Nigeria. Nigerian Journal of Environmental Sciences and Technology (NIJEST). 1. 34-42. [CrossRef]
- Pawar, Nikunj & Dhamge, Dr & Kharkar, Om & Yeole, Vedanti & Siddham, Utkarsh & Meshram, Nikhil. (2023). Frequency Analysis of Rainfall Data. International Journal for Research in Applied Science and Engineering Technology. 11. 2181-2186. [CrossRef]
- Shamkhi, Mohammed & Azeez, Marwaa & Obeid, Zahraa. H. (2022). Deriving rainfall intensity–duration–frequency (IDF) curves and testing the best distribution using EasyFit software 5.5 for Kut city, Iraq. Open Engineering. 12. 834-843. [CrossRef]
- Markiewicz, I. Depth–Duration–Frequency Relationship Model of Extreme Precipitation in Flood Risk Assessment in the Upper Vistula Basin. Water 2021, 13, 3439. [CrossRef]
- Ratnasingam, Suthakaran & Perera, Kanthi & Wikramanayake, Nalin. (2014). RAINFALL INTENSITY-DURATION-FREQUENCY RELATIONSHIP FOR COLOMBO REGION IN SRI LANKA.
- Prerana Chitrakar, Ahmad Sana, Sheikha Hamood Nasser Almalki, Regional distribution of intensity– uration–frequency (IDF) relationships in Sultanate of Oman, Journal of King Saud University - Science, Volume 35, Issue 7, 2023, ISSN 1018-3647. [CrossRef]
- Danielle M. Barna, Kolbjørn Engeland, Thordis L. Thorarinsdottir, Chong-Yu Xu, Flexible and consistent Flood–Duration–Frequency modeling: A Bayesian approach, Journal of Hydrology, Volume 620, Part B, 2023, ISSN 0022-1694. [CrossRef]
- Demarée, G. R. and Van de Vyver, H.: Construction of intensity-duration-frequency (IDF) curves for precipitation with annual maxima data in Rwanda, Central Africa, Adv. Geosci., 35, 1–5. [CrossRef]
- Młyński, D.; Wałęga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating Maximum Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2019, 10, 43. [CrossRef]
- Aminu Saad Said, Isma’il Mahmud Umar, Ponselvi Jeevaragagam, Sobri Harun (2023). Frequency Analysis Of Rainfall In Johor State Using Probability Distribution. Journal Of Business Leadership And Management, 1(2), 104 - 113. [CrossRef]
- Mayasari, Devita, & Pratiwi Setyaning Putri. "Regional Frequency Analysis of Rainfall, using L-Moment Method, as A Design Rainfall Prediction." Journal of the Civil Engineering Forum [Online], 7.2 (2021): 165-176. Web. 11 Jan. 2024.
- Aysar Tuama Al-Awadi, Riyadh Jasim Mohammed Al-Saadi & Abdul Khider Aziz Mutasher (2023) Frequency analysis of rainfall events in Karbala city, Iraq, by creating a proposed formula with eight probability distribution theories, Smart Science, 11:3, 639-648. [CrossRef]
- Tasir Khan, Yejuan Wang, Mohammad Anwar et al. Analysis of Annual Maximum Rainfall for Frequency Distribution to Determine the Best-fitted Probability Distribution for Different Sites in Pakistan., 17 August 2021. [CrossRef]
- Singh, Bhim & Rajpurohit, Deepak & Vasishth, Amol & Singh, Jitendra. (2012). Probability Analysis for Estimation of Annual One Day Maximum Rainfall of Jhalarapatan Area of Rajasthan. Plant Archives. 12. 1093-1100.
- Ashok Kumar, K., Sudheer, K.V.S., Pavani, K. et al. Extreme Rainfall Analysis for Development of Rainfall Intensity Duration Frequency Curves for Semiarid Region of Andhra Pradesh in India. Natl. Acad. Sci. Lett. (2023). [CrossRef]
- N. Vivekanandan (2013) Comparison of estimators of the Gumbel distribution for modelling annual maximum rainfall, International Journal of Management Science and Engineering Management, 8:3, 166-172. [CrossRef]
- Matalas, N.C. Probability Distribution of Low Flows. In Statistical Studies in Hydrology; Geological Survey; United States Covernment Printing Office: Washington, DC, USA, 1963.
- World Meteorological Organization. (WMO-No.1029) 2008 Manual on Low-Flow Estimation and Prediction; Operational Hydrology Report no. 50; WHO: Geneva, Switzerland, 2008.
- Institute of Hydrology. (IH) 1992 Low Flow Estimation in the United Kingdom; Report no. 108; Institute of Hydrology: Lancaster, UK, 1992.
- UNESCO. Methods of Computation of Low Streamflow, Studies and Reports in Hydrology; UNESCO: Paris, France, 1982; ISBN 92-102013-7.
- Loganathan, G.V.; Kuo, C.Y.; McCormick, T.C. Frequency Analysis of Low Flow. Nord. Hydrol. 1985, 16, 105–128.
- EM 1110-2-1415 Hydrologic Frequency Analysis, Engineering and Design; Department of the Army U.S. Army Corps of Engineers: Washington, DC, USA, 1993.
- Hosking, J.R.M. L-moments: Analysis and Estimation of Distributions using Linear, Combinations of Order Statistics. J. R. Statist. Soc. 1990, 52, 105–124. [CrossRef]
- Gubareva, T.S.; Gartsman, B.I. Estimating Distribution Parameters of Extreme Hydrometeorological Characteristics by L-Moment Method. Water Resour. 2010, 37, 437–445. [CrossRef]
- Grimaldi, S.; Kao, S.-C.; Castellarin, A.; Papalexiou, S.-M.; Viglione, A.; Laio, F.; Aksoy, H.; Gedikli, A. Statistical Hydrology. In Treatise on Water Science; Elsevier: Oxford, UK, 2011; Volume 2, pp. 479–517.
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis, An Approach Based on L-Moments; Cambridge University Press, the Edinburgh Building: Cambridge, UK, 1997; ISBN 13 978-0-521-43045-6.
- Wang, Q.J. LH moments for statistical analysis of extreme events. Water Resour. Res. 1997, 33, 2841–2848. [CrossRef]
- Md Sharwar, M.; Park, B.-J.; Jeong, B.-Y.; Park, J.-S. LH-Moments of Some Distributions Useful in Hydrology. Commun. Stat. Appl. Methods 2009, 16, 647–658. [CrossRef]
- Anghel, C.G.; Stanca, S.C.; Ilinca, C. Extreme Events Analysis Using LH-Moments Method and Quantile Function Family. Hydrology 2023, 10, 159. [CrossRef]
- Anghel, C.G.; Ilinca, C. Predicting Flood Frequency with the LH-Moments Method: A Case Study of Prigor River, Romania. Water 2023, 15, 2077. [CrossRef]
- Ilinca, C.; Stanca, S.C.; Anghel, C.G. Assessing Flood Risk: LH-Moments Method and Univariate Probability Distributions in Flood Frequency Analysis. Water 2023, 15, 3510. [CrossRef]
- Singh, V.P. Entropy-Based Parameter Estimation in Hydrology; Springer: Dordrecht, The Netherlands, 1998; ISBN1 978-90-481-5089-2. ISBN2 978-94-017-1431-0.
- 7Seçkin, Neslihan et al. Comparison of probability weighted moments and maximum likelihood methods used in flood frequency analysis for Ceyhan River basin. The Arabian Journal for Science and Engineering.
- K.Arora, V.P.Singh - AN EVALUATION OF SEVEN METHODS FOR ESTIMATING PARAMETERS OF EVl DISTRIBUTION Hydrologic Frequency Modeling, Proceedings of the International Symposium on Flood Frequency and Risk Analyses, 1986.
- Domma, F.; Condino, F. Use of the Beta-Dagum and Beta-Singh-Maddala distributions for modeling hydrologic data. Stoch. Environ. Res. Risk Assess. 2017, 31, 799–813. [CrossRef]
- Helu, A. The principle of maximum entropy and the probability-weighted moments for estimating the parameters of the Kumaraswamy distribution. PLoS ONE 2022, 17, e0268602. [CrossRef]
- Gaume, E. Flood frequency analysis: The Bayesian choice. WIREs Water. 2018, 5, e1290. [CrossRef]
- Huang, Hening. (2022). Practitioner’s perspective on the GUM revision, part I: two key problems and solutions. [CrossRef]
- Yan, H., Moradkhani, H. A regional Bayesian hierarchical model for flood frequency analysis. Stoch Environ Res Risk Assess 29, 1019–1036 (2015). [CrossRef]
- Shasha Han, Paulin Coulibaly, Bayesian flood forecasting methods: A review, Journal of Hydrology, Volume 551, 2017, Pages 340-351, ISSN 0022-1694. [CrossRef]
- Kochanek, K.; Markiewicz, I. Statistical Approach to Hydrological Analysis. Water 2022, 14, 1094. [CrossRef]
- Shin, Y.; Park, J.-S. Modeling climate extremes using the four-parameter kappa distribution for r-largest order statistics. Weather. Clim. Extrem. 2023, 39, 100533. [CrossRef]
- Çitakoğlu, H.; Demir, V.; Haktanir, T. L−Momentler yöntemiyle karadeniz’e dökülen akarsulara ait yillik anlik maksimum akim değerlerinin bölgesel frekans analizi. Ömer Halisdemir. Üniversitesi. Mühendislik Bilim. Derg. 2017, 6, 571–580. [CrossRef]
- Papukdee, N.; Park, J.-S.; Busababodhin, P. Penalized likelihood approach for the four-parameter kappa distribution. J. Appl. Stat. 2021, 49, 1559–1573. [CrossRef]
- Anghel, C.G.; Ilinca, C. Parameter Estimation for Some Probability Distributions Used in Hydrology. Appl. Sci. 2022, 12, 12588. [CrossRef]
- Ilinca, C.; Anghel, C.G. Flood Frequency Analysis Using the Gamma Family Probability Distributions. Water 2023, 15, 1389. [CrossRef]
- Ilinca, C.; Anghel, C.G. Frequency Analysis of Extreme Events Using the Univariate Beta Family Probability Distributions. Appl. Sci. 2023, 13, 4640. [CrossRef]
- Anghel, C.G.; Ilinca, C. Evaluation of Various Generalized Pareto Probability Distributions for Flood Frequency Analysis. Water 2023, 15, 1557. [CrossRef]
- Anghel, C.G.; Stanca, S.C.; Ilinca, C. Two-Parameter Probability Distributions: Methods, Techniques and Comparative Analysis. Water 2023, 15, 3435. [CrossRef]
- Anghel, C.G.; Ilinca, C. Predicting Future Flood Risks in the Face of Climate Change: A Frequency Analysis Perspective. Water 2023, 15, 3883. [CrossRef]
- Ilinca, C.; Anghel, C.G. Flood-Frequency Analysis for Dams in Romania. Water 2022, 14, 2884. [CrossRef]
- Anghel, C.G.; Ilinca, C. Hydrological Drought Frequency Analysis in Water Management Using Univariate Distributions. Appl. Sci. 2023, 13, 3055. [CrossRef]
- Crooks, G.E. Field Guide to Continuous Probability Distributions; Berkeley Institute for Theoretical Science: Berkeley, CA, USA, 2019.
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill, Inc.: New York, NY, USA, 1988; ISBN 007-010810-2.
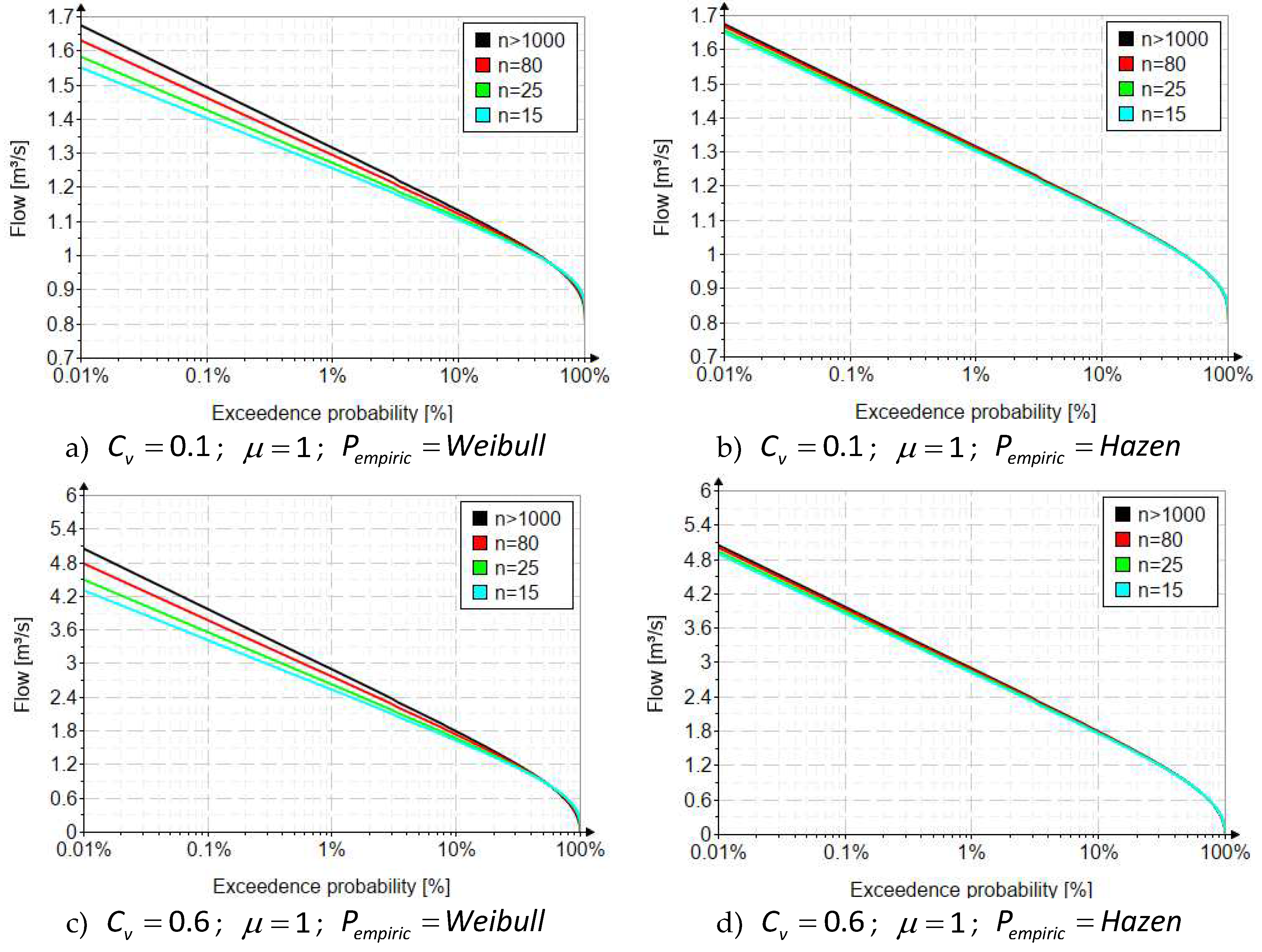
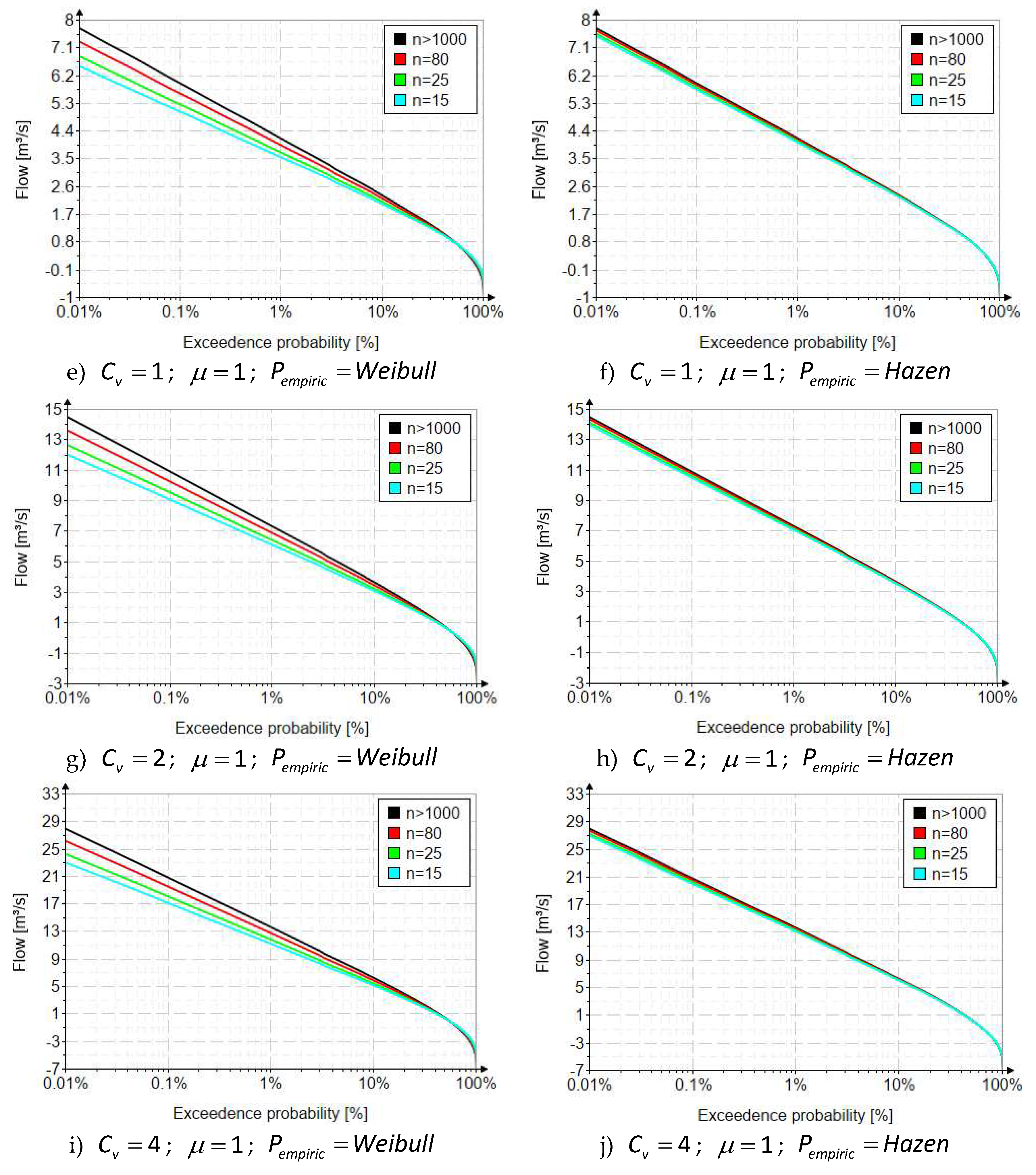
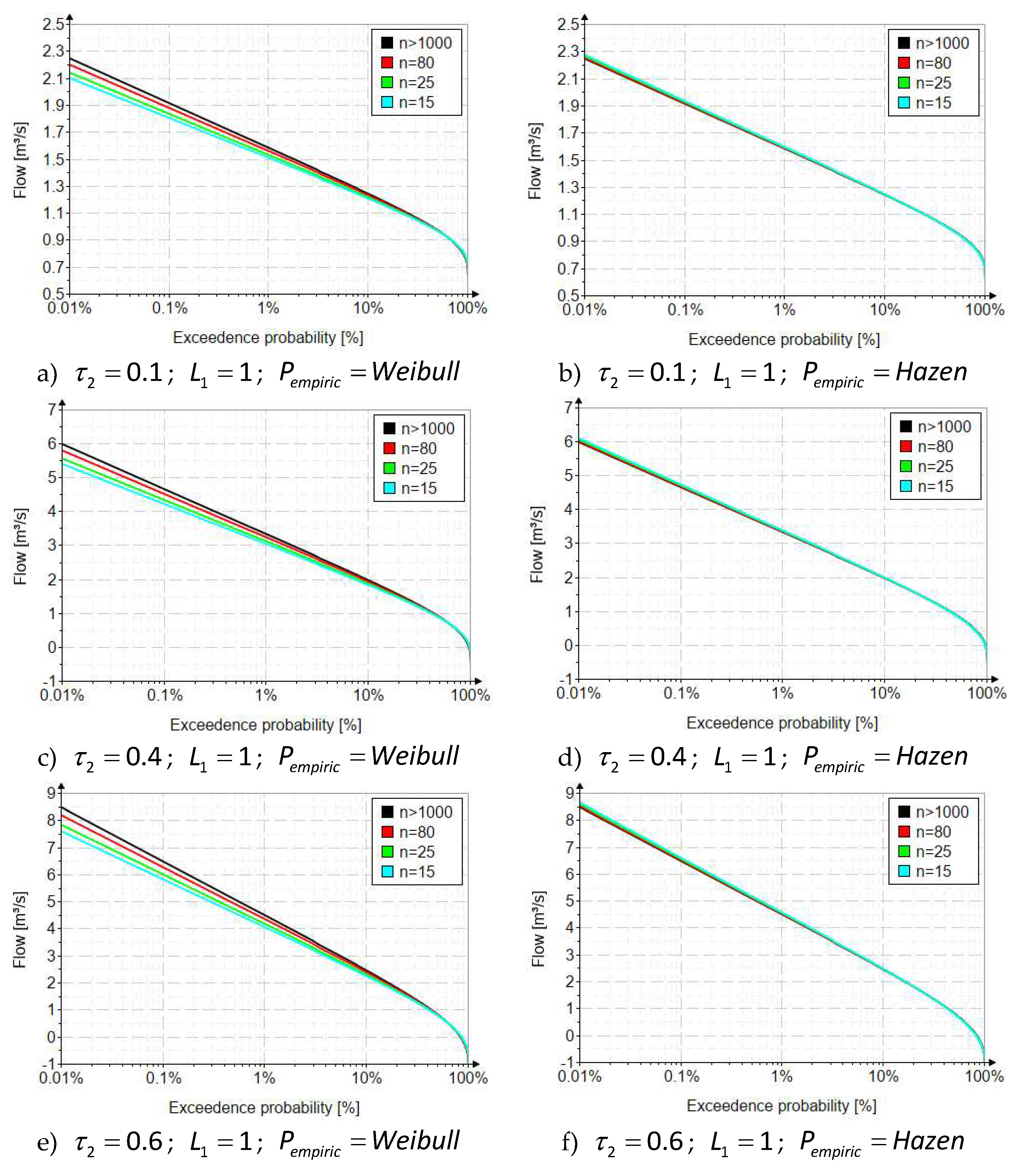
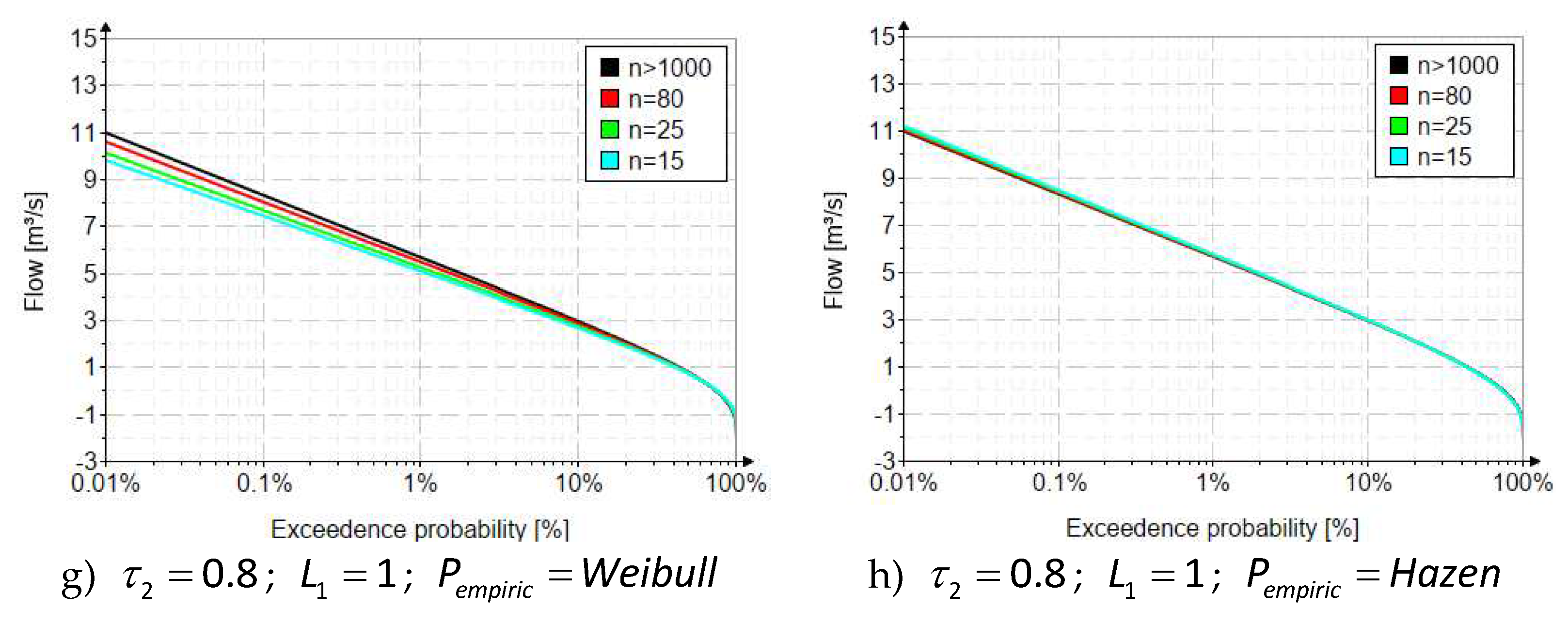
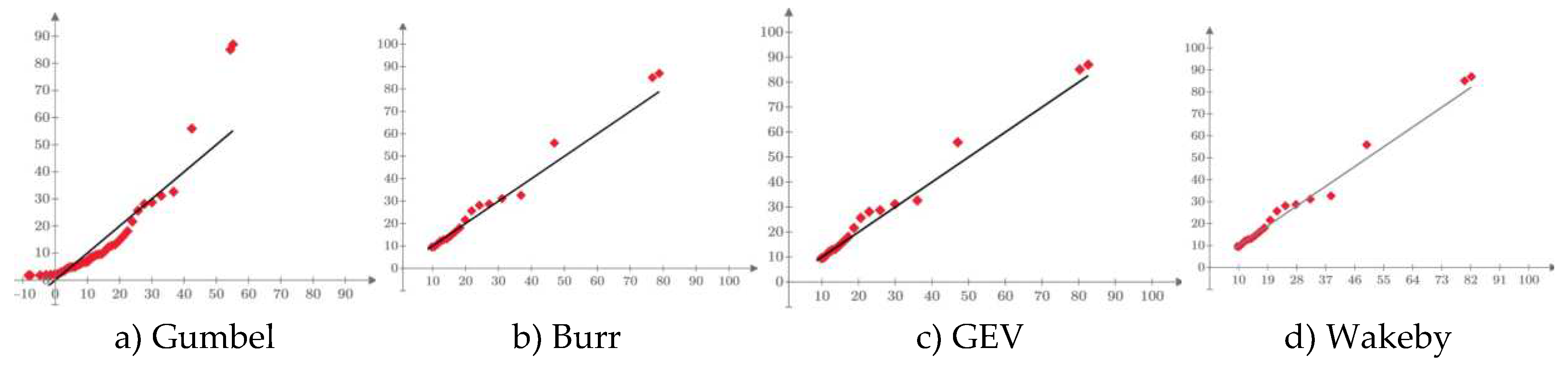
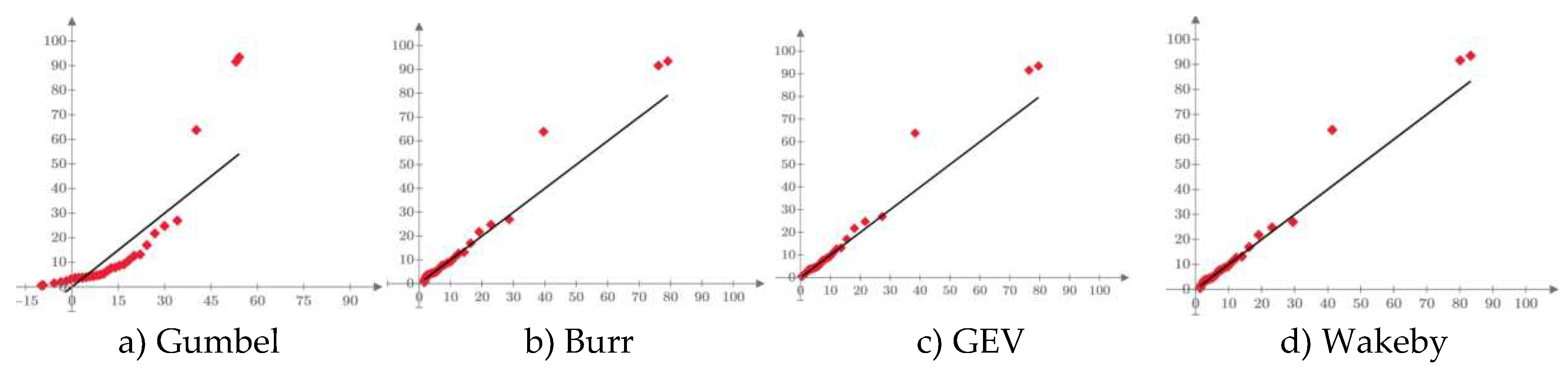
| Distribution | Parameter estimation method | Statistical measures | |
|---|---|---|---|
| RME | RAE | ||
| Gumbel | MOM | 0.0061 | 0.0311 |
| L-mom | 0.0065 | 0.0323 | |
| LH1-mom | 0.0081 | 0.0366 | |
| LH2-mom | 0.0092 | 0.0417 | |
| PWM | 0.0061 | 0.031 | |
| MLE | 0.006 | 0.0321 | |
| LSM | 0.0072 | 0.0337 | |
| WLSM | 0.0069 | 0.0331 | |
| ENT | 0.0167 | 0.0935 | |
| MIX | 0.0145 | 0.0823 | |
| GEV | L-mom | 0.0056 | 0.0294 |
| Burr | L-mom | 0.0069 | 0.0373 |
| Wakeby | L-mom | 0.0075 | 0.0399 |

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





