Prerpints.org logo
Preprint
Article

Research on Active Repetitive Control for Tracking Lissajous Scan Trajectories with Voice Coil Motors Actuated Fast Steering Mirror

Altmetrics

Downloads

89

Views

26

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 January 2024

Posted:

01 February 2024

You are already at the latest version

Alerts
Abstract
The performance of laser beams in tracking Lissajous scan trajectories is severely limited by beam jitter. To enhance the performance of fast steering mirror (FSM) control in tracking Lissajous scan trajectories, this paper proposed a fractional order active disturbance rejection controller (FOADRC) and verified its effectiveness in improving system scanning tracking accuracy. A dynamic mathematical model of fast steering mirror was studied and the design of parameters for the control mode of the closed-loop system was determined. A reduced order linear active disturbance rejection controller suitable for FSM systems was designed and the corresponding fractional order proportional differentiation (FOPD) controller were determined according to the mathematical model. The use of the designed controller enabled high-performance tracking of high-frequency Lissajous scanning curves (X-axis 500 Hz, Y-axis 350 Hz) and met the need for high-frequency repetitive scanning. The controller has the characteristics of simple implementation and low computational complexity and is suitable for closed-loop control applications in engineering.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

The Fast Steering Mirror (FSM) plays a crucial role in the adjustment and stabilization of the visual axis or beam pointing in optical systems [1,2]. It offers several advantages, including its compact size, precise construction, wide bandwidth, and rapid speed. Consequently, it has found extensive applications in significant domains such as space laser communication, astronomical telescopes, optical stability, high-precision laser processing equipment, and carrier laser systems [3,4,5].
With the development of optoelectronic detection technology, the requirements for detection range and accuracy, along with the design of scanning FSMs, are becoming increasingly strict. To meet the need for large field-of-view scanning and detection, the travel requirements of scanning FSMs are also becoming more stringent, which increases the difficulty of assembling and debugging components. In addition, as a scanning FSM follows the phases of acceleration (start), uniform swing, deceleration (stop), and acceleration (return) during operation, it needs to move according to a predetermined curve. Optical scanning trajectories are widely used in FSM applications. Lissajous scan trajectories, which follow a self-repeating pattern in which both the X-axis and the Y-axis are driven by sinusoids with a suitable frequency ratio, can be regarded as a promising alternative to raster scan trajectories, with their extremely simple spectrum for both axes and easy implementation for sequential scanning [6,7]. Although repetitive control schemes have been successfully utilised to improve the tracking performance of Lissajous trajectories, most existing application research has focused on piezoelectric driven scanners, which are limited by the small travel characteristics of piezoelectric ceramics themselves, resulting in limited scanning travel. The main driving mechanisms for FSMs are voice coil motors and piezoelectric ceramics [8,9,10]. The voice coil motor is a direct drive motor with the advantages of a large stroke, small size, and low drive voltage [11]. Piezoelectric ceramic actuators have the advantages of small size, light weight, high accuracy and resolution, high frequency response, large bearing capacity, and no noise [12,13]. Compared with piezoelectric ceramics, voice coil motors have a lower driving voltage and larger stroke. Therefore, voice coil motor drivers are better suited to applications with large strokes.
Position control is the basic working mode of FSMs and requires not only precise positioning but also a high response speed and minimal overshoot in the position transition process [14]. FSM control is a typical position control strategy, as only the position sensor is used as the feedback component [15]. Existing FSM control systems are based on feedback control, namely a post-correction step: when an output error is detected, the controller adjusts the output. Therefore, when the tracking error is large, the use of large gains to adjust the control output may lead to overshoot [16,17]. A controller based on the traditional proportional–integral–derivative (PID) method typically produces a large control output under the joint action of the gain and the integration link [18]. Differential control and velocity measurement feedback are employed in classical control strategies to increase system damping and reduce overshoot, but they afford only limited reductions in overshoot [19]. Consequently, many researchers have developed novel control strategies, such as plug-in module acceleration feedback control [20], model reference adaptive control [21], and feedforward control, based on the results of error and disturbance observations [22,23,24].
Control strategies for FSMs have been reported in the literature. G. Wang et al. [25] proposed a comprehensive model of a two-axis FSM system through synthetical consideration of each physical component. V. Hassani et al. [26] represented various mathematical models of hysteresis and different methods of system identification. J. Ling et al. [27] proposed a new online neural network based sliding mode control scheme to obtain robust adaptive precision motions. The nonlinearity of piezoelectric actuator has been identified online and compensated for using singularity-free neural networks. A. K. Babarinde et al. [28] proposed the design, analysis, and experimental validation of the simultaneous method for a positive acceleration, velocity, and position feedback control-based combined damping and tracking scheme. C. Chang [29] proposed a 4-degree-of-freedom (DOF) actuator for FSM compensation systems to compensate for 4-DOF laser errors. Nastaran Nikooienejad et al. [30] presented a control scheme for video-rate atomic force microscopy with a rosette pattern. They designed an iterative learning controller to improve the tracking performance of the feedback-controlled scanner by rejecting the repetitive disturbances arising from system nonlinearities. C. Li et al. [31] proposed a modified repetitive control based approach for high-speed tracking of nano-positioning stages. Based on the above research, an effective control strategy requires accurate modelling of the system, early data collection, and the addition of sensors. The methods reported in the studies above rely heavily on early data or prior information, and they may even increase system costs. Therefore, practical engineering applications using these methods are not feasible or achievable. Active disturbance rejection controllers are widely used in engineering practice due to their simple structure, strong anti-interference ability, convenience of adjustment, and lack of model dependence. Active disturbance rejection controllers, which do not rely on the model information of the controlled object, provide a unique solution for the control of Lissajous scanning objects [32]. However, many problems with this approach, such as complex parameter tuning, high control bandwidth, short sampling intervals, and large observation errors, remain to be solved [33]. The FOPD controller is an extension of the traditional PD controller [34,35]. By adding an adjustable fractional order, the FOPD design can be more flexible, and attain better performance [36]. The FOPD controller can perform better than classical PD. Nevertheless, for high-control performance requirements, the capacity of the FOPD is still limited.
Aiming to overcome the above limitations on the use of FSMs for Lissajous scanning tracking, we designed a fractional order active disturbance rejection controller (FOADRC) for precisely tracking Lissajous scan trajectories with voice coil motors driven FSM. A forward tracking differentiator (TD) was applied to process the position command and a second TD was introduced into the feedback channel to obtain the differential of the output value. By fully exploiting known information, such as the model and sensor output, we designed a reduced-order ESO with fractional order proportional differentiation (FOPD) controller to enhance the dynamic performance of the position step response. To evaluate the performance of the FOADRC in tracking Lissajous scan trajectories, comparative experiments with a PID controller and ADRC were conducted. The experimental results verified the advantages of the proposed FOADRC for FSMs in Lissajous scanning.
For Lissajous scanning applications, a detailed model was produced and a controller was designed for voice coil motors driven FSM. The main contributions of this study are: (a) By tracking the transition process of the differentiator to obtain the set value and obtaining its non-integer order differential signal, the system can quickly and smoothly achieve zero overshoot, meeting the requirements of Lissajous scanning without overshoot. (b) Based on the model characteristics of the controlled object and combined with external sensor information, the extended state observer was redesigned. The improved reduced order extended state observer was found to achieve accurate observation of the extended state. (c) We combined the FOPD controller replaced the PD controller, by adding an adjustable fractional order, the FOPD design can be more flexible, and attain better performance in term of improved steady-state error, good disturbance rejection, and superior behavior with nonlinearities.

2. Lissajous Scan Trajectory

The tracking Lissajous scanning experimental platform was implemented as shown in Figure 1. The experimental platform contained a light source, a collimator to transform the beam into collimated parallel light, a detector, and the FSM. These devices were installed on an optical floating platform to isolate the components from external vibrations. A small lamp was used to illuminate the target, which was placed in the front section of the collimator to simulate a target at infinity. The parallel beam was transmitted to the optical system through the collimator, and after being reflected by the FSM, the detector formed an image. The combined Lissajous spot image was obtained.
By inputting two sets of sine curves in the orthogonal X-Y direction, the Lissajous scanning trajectory can be formed, and the signals of the two axes can be represented as
x ( t ) = A x sin ( 2 π f 1 t ) sin ( 2 π f 2 t + ϕ x )
y ( t ) = A y sin ( 2 π f 1 t ) sin ( 2 π f 2 t )
A x and f x are the amplitude and frequency along the X-axis. A y and f y are the amplitude and frequency along the Y-axis. This paper mainly focuses on high-frequency scanning, therefore the frequency ratio is
f 1 f 2 = 10 7

3. Dynamic Model and Parameter Design of Control System

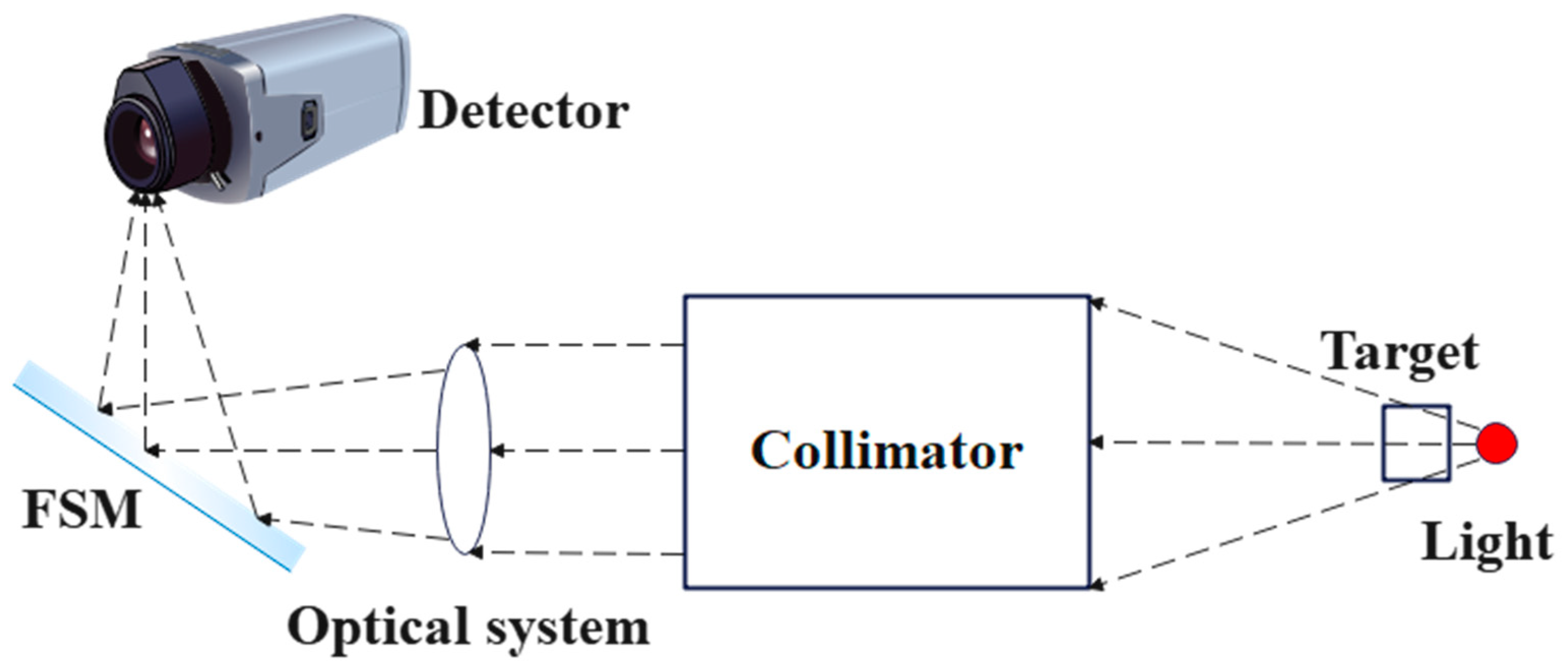
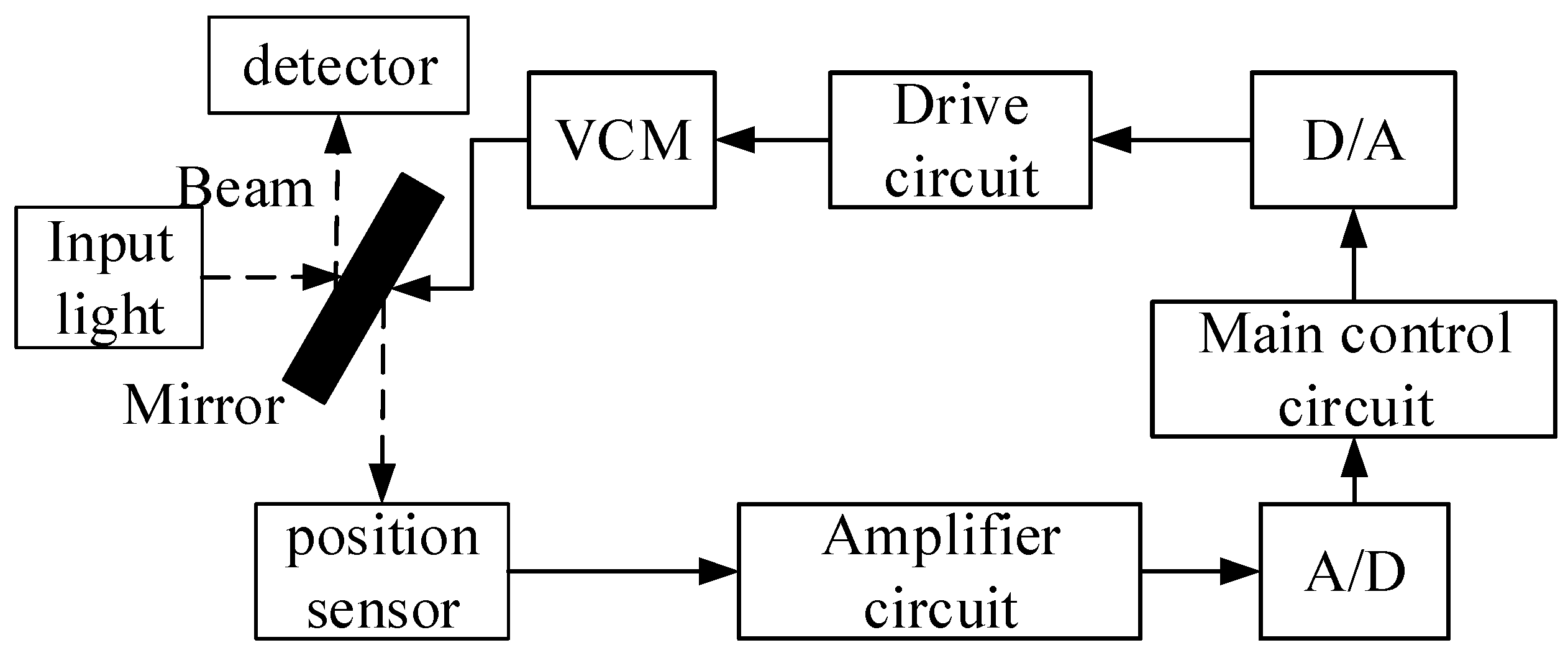
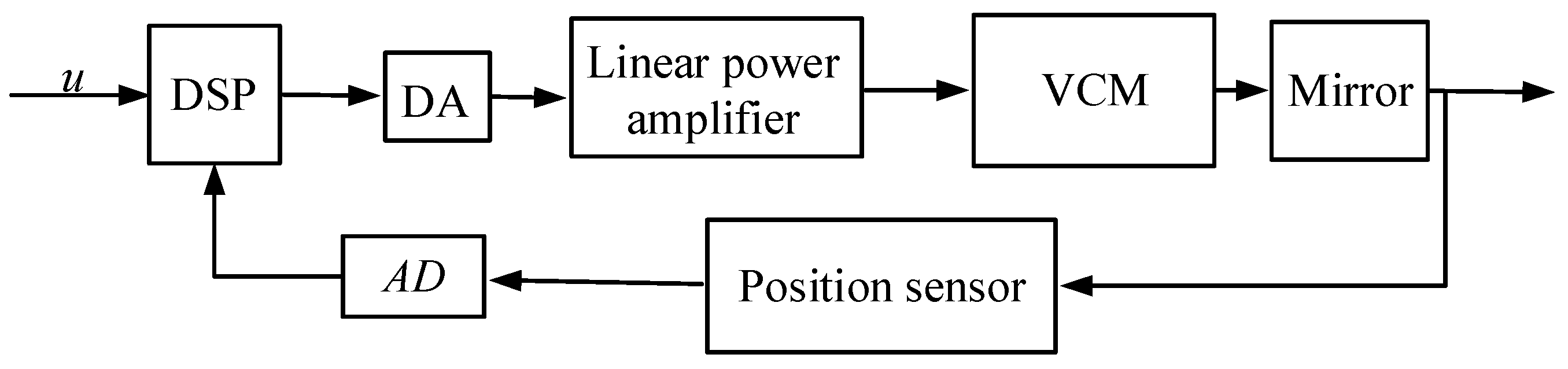
The design of FSM system is a typical nonlinear control problem. FSM is susceptible to external interference factors such as base disturbances. Therefore, in order to achieve better control effects and higher performance indicators, it is necessary to propose corresponding control methods for applications. The voice coil motors drive FSM mainly consists of the following parts: the control circuit, the drive circuit, a mirror, and the position sensor [37,38]. Figure 2 shows a block diagram of the position control loop.
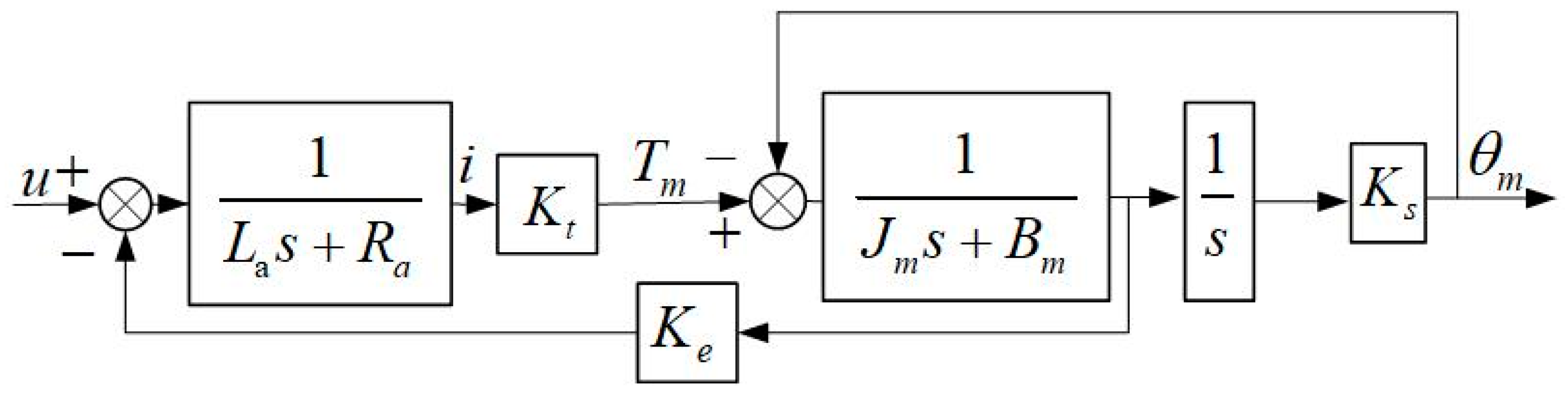
According to the dynamic characteristics, the block diagram of FSM is established as shown in Figure 3.
In Figure 3, La is armature inductance, Ra is armature resistance, i is armature current, Kt is electromagnetic torque constant, Ke is back EMF coefficient, Tm is motor output torque, Jm is motor inertia, Bm is viscous damping coefficient of the motor end, θm is motor angle, Ks is mechanical stiffness of the shaft.
According to Figure 3, the transfer function of the controlled object is obtained as
θ m u = K t [ ( L a s + R a ) ( J m s + B m ) + K t K e ] s + K s ( L a s + R a )
In actual systems, the inductance of the motor is very small and can be ignored, so the above equation can be simplified as
θ m u = K t R a J m s 2 + ( R a B m + K t K e ) s + K s R a
The second-order oscillation system is used to fit the model of the fast steering mirror. K represents the gain, ω n is the natural frequency and ζ is the damping coefficient.
G ( s ) = K ω n s 2 + 2 ζ ω n s + ω n 2
Although some advanced control algorithms for FSM systems can achieve good closed-loop control effects through theoretical analysis and proof, some algorithms have complex structures, high computational complexity, and unclear physical meanings of parameters, which hinders their application in practical engineering. This paper focuses on the research of FSM control for imaging scanning, emphasizing not only the in-depth study of control theory and methods, but also the rationality of theoretical research oriented towards applications.
An extended state observer (ESO) employs a new state variable to reflect all of the disturbances affecting a control output. In most engineering applications, the output values of the front and back sampling periods are differentiated. Because sampling periods are small, large differential noise may easily be introduced during this process. Therefore, in this paper, a TD was incorporated into the feedback channel to obtain the differential of the output value as the input of the ESO. The ESO was used to realise the observation and estimation of the system states and external disturbances, and incorporated into the closed-loop control. The traditional nonlinear ESO is difficult to implement in engineering, due to its large number of tuning parameters and complex calculations. 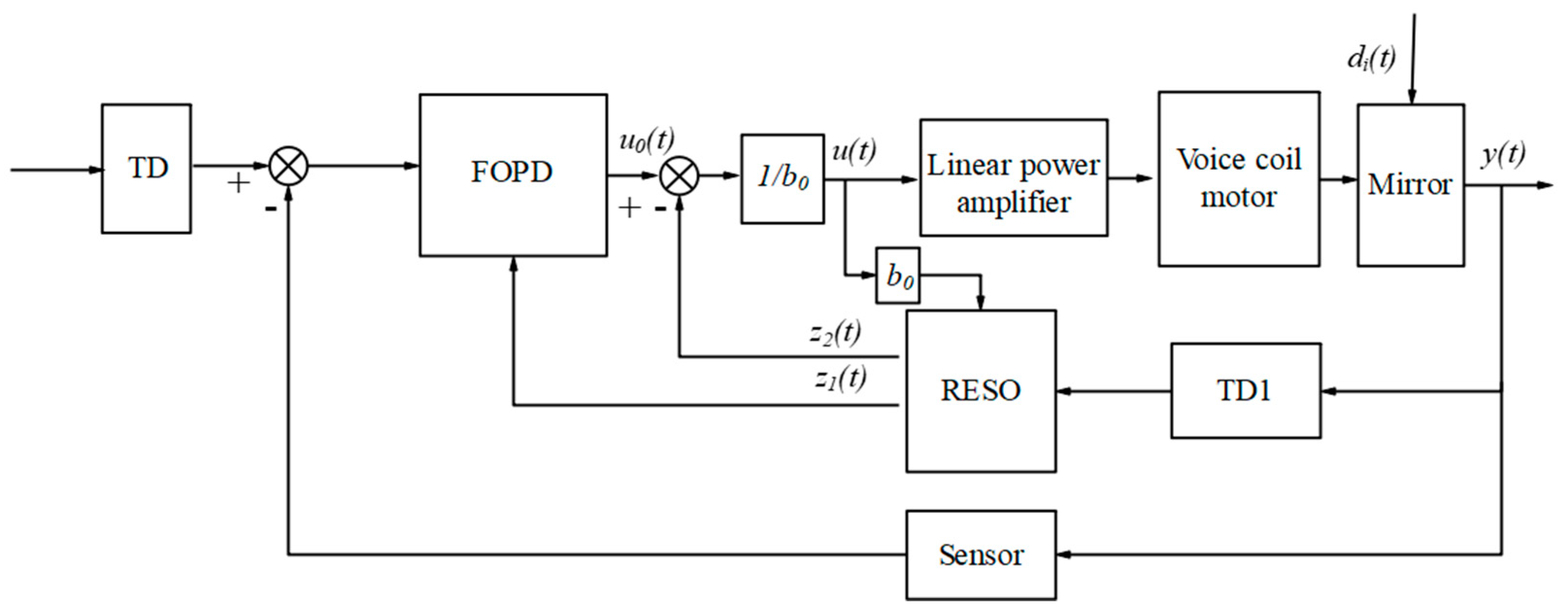Therefore, in this study, a linear ESO (LESO) was used to enhance the observational accuracy of the system state and the ADRC performance [39,40,41]. An FOADRC was designed by adding a TD to the forward channel and an ESO to the feedback channel, with the FOPD control rate designed according to the system characteristics. Figure 4 depicts the structural block diagram.
Figure 4 shows that the TD was used to track the input and could thus arrange the transition process. TD1 was used to track the output and extract the differential signal of the output.
The state-space matrix form is
{ x ˙ = A x + B u + E f ˙ y = C x
where, A = [ 0 1 0 − ω n 2 − 2 ζ ω n 1 0 0 0 ] , B = [ 0 b 0 0 ] , C = [ 1 0 0 ] , E = [ 0 0 1 ] , f is the total disturbance.
The state observer after being expanded from the second order to the third order is
{ z ˙ = A z + B u + L ( y − y ∧ ) y ∧ = C z
where L is the observer gain vector.
As the position sensor signal is known, z 1 is the estimate of position sensor y, z 2 is the estimate of the differential of the output signal y ⋅ , and z 3 is the estimate of the total disturbance f .
[ z ˙ 1 z ˙ 2 z ˙ 3 ] = ( A − L C ) [ z 1 z 2 z 3 ] + B u + L y
The position of the FSM could be directly measured by the sensor. The full-order ESO is transformed into a reduced-order ESO. The reduced-order state observer model becomes
{ x ˙ 1 = x 2 − ω n 2 y − 2 ζ ω n x 1 + b 0 u x ˙ 2 = f ˙ y ˙ = x 1
where x1 is the differential of the position sensor output, and x2 is the total disturbance.
{ x ˙ = A R x + B R u + H R y + E R f ˙ y ˙ = C R x
where, A R = [ − 2 ζ ω n 1 0 0 ] , B R = [ b 0 0 ] , C R = [ 1 0 ] , E R = [ 0 1 ] , H R = [ − ω n 2 0 ] .
The reduced-order ESO is
{ z ˙ = A R z + B R u + H R y + L ( y ˙ − y ∧ ) y ∧ = C R x
According to the bandwidth design method, the observer bandwidth was set to ω o , and the expected characteristic formula is obtained
λ ( s ) = ( s + ω o ) 2 = s 2 + 2 ω o s + ω o 2
Then, the observer gain vector is obtained
L R = [ β 1 β 2 ] = [ 2 ω o − 2 ζ ω n ω o 2 ]
Subsequently, we obtain
[ z ˙ 1 z ˙ 2 ] = ( A R − L R C R ) [ z 1 z 2 ] + L R y ˙
As the actual control model could be transformed into a unit second-order underdamped system,
G ( s ) = K ( s ω n ) 2 + 2 ζ s ω n + 1
The FSM model was simplified as a second-order integral series, and the control design was completed by using the design theory of bandwidth parameters and fractional order proportional differentiation (FOPD) controller. Compared with traditional integer order proportional differential controllers, Fractional Order Proportional Derivative Controller (FOPD) increases the adjustable differential order,
u = K P + K d s μ
where K P = ω c 2 / K , K P = 2 ε ω c / K ω n , and ε represents differential adjustment factors. s is the Laplace operator, μ is the adjustable differential order factor and the value range between 0 and 1.

4. Simulation Analysis

Model identification is used to identify the theoretical model. The actual model is obtained by the sweep frequency method.
G ( s ) = 2045 s 2 + 22 s + 18424
The sampling frequency selected for the system was 40 kHz. The operation step and filter factor were designed as h = T = T s . The controller bandwidth, observer bandwidth, differential adjustment factor, and disturbance compensation factor of the controller needed to be set according to the aforementioned controller design results. The fast factor of the TD for processing position-related instructions was set to 4,000,000; and the fast factor of TD1, which was used to extract output differential signals in FOADRC, was set to 10,000,000. The parameters of the FOPD controller are set as : the proportional factor is 2.5, the differential factor is 0.05, and the adjustable differential order factor is 0.7.The signal with an amplitude of 1,000 µrad and a cycle of 500 Hz was mixed with a random signal, and the resulting mixed noise signal was used as the position input command. 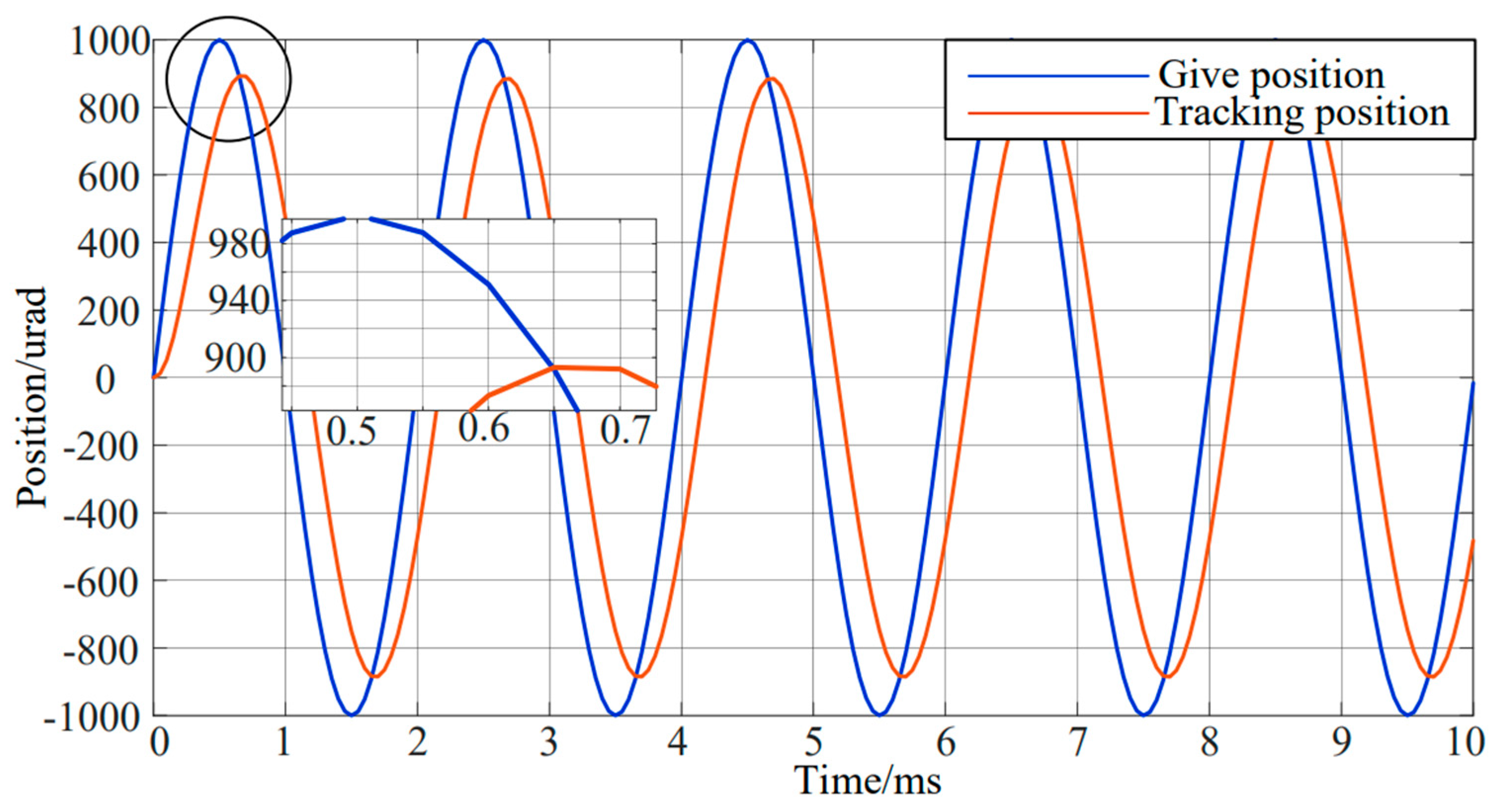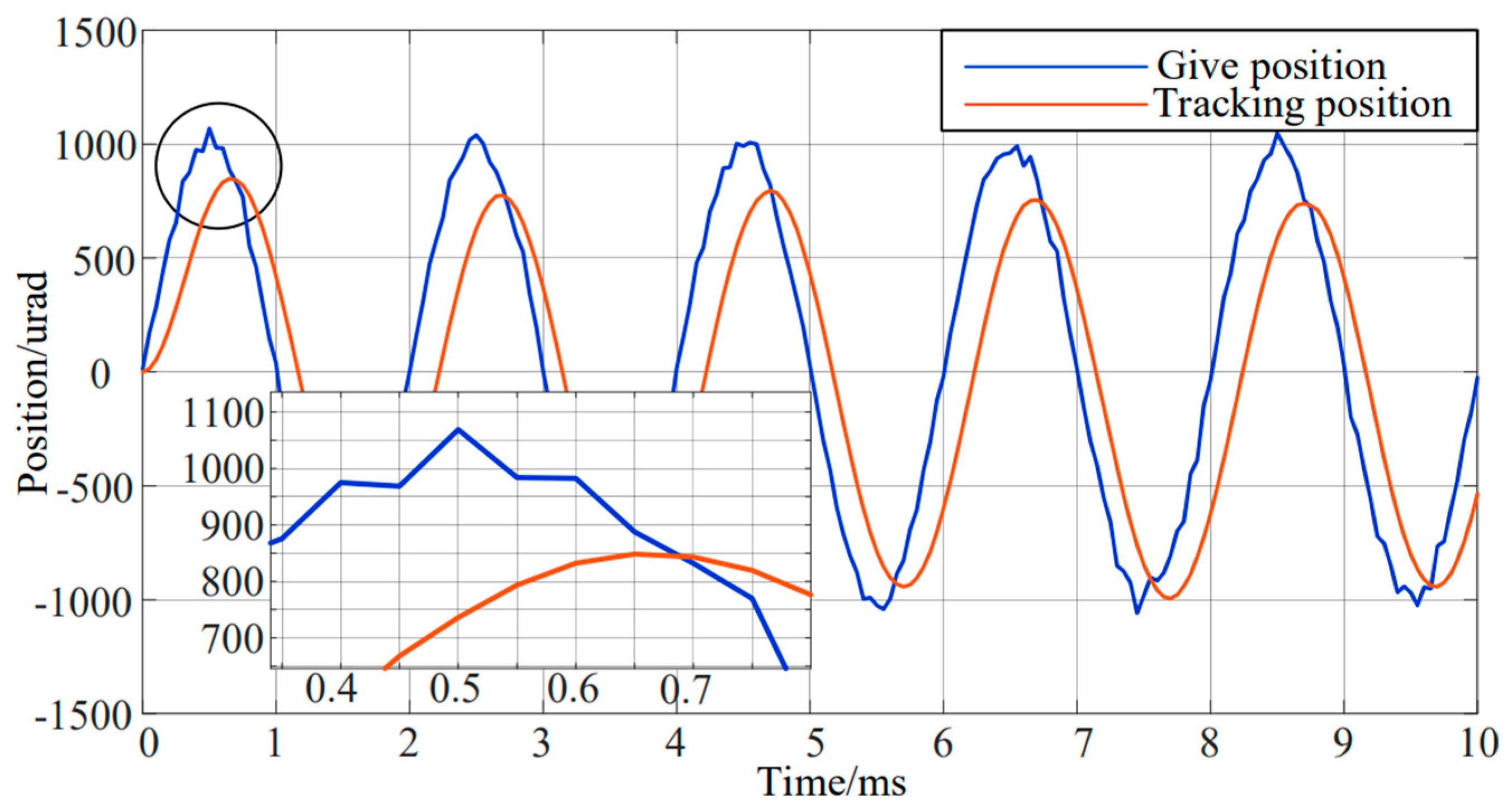Figure 5 presents the tracking position response curve of the FOADRC algorithm without random signal, and Figure 6 illustrates the tracking position response curve of the FOADRC algorithm with random signal.
As presented in Figure 5, devised algorithm could excellent tracking of high-frequency sine signal, which may have a phase lag of −27°. As shown in Figure 6, the system effectively tracks the input signal and has a good suppression effect on random noise. The response signal almost coincided with the command signal, and the phase lag was −27°. The lag could be reduced by adjusting the size of the fast factor. An increase in the value of the fast factor resulted in a decrease in the phase lag. The selection of the fast factor depends on the bearing capacity and available control capacity of the controlled object. Specifically, the greater the bearing capacity and available control capacity of an object, the higher the value of the fast factor, resulting in a closer match to the reference step input form. However, the bearing and control capacities of an actual system are limited. Thus, the fast factor can only be increased by a certain extent.

5. Experimental Verification

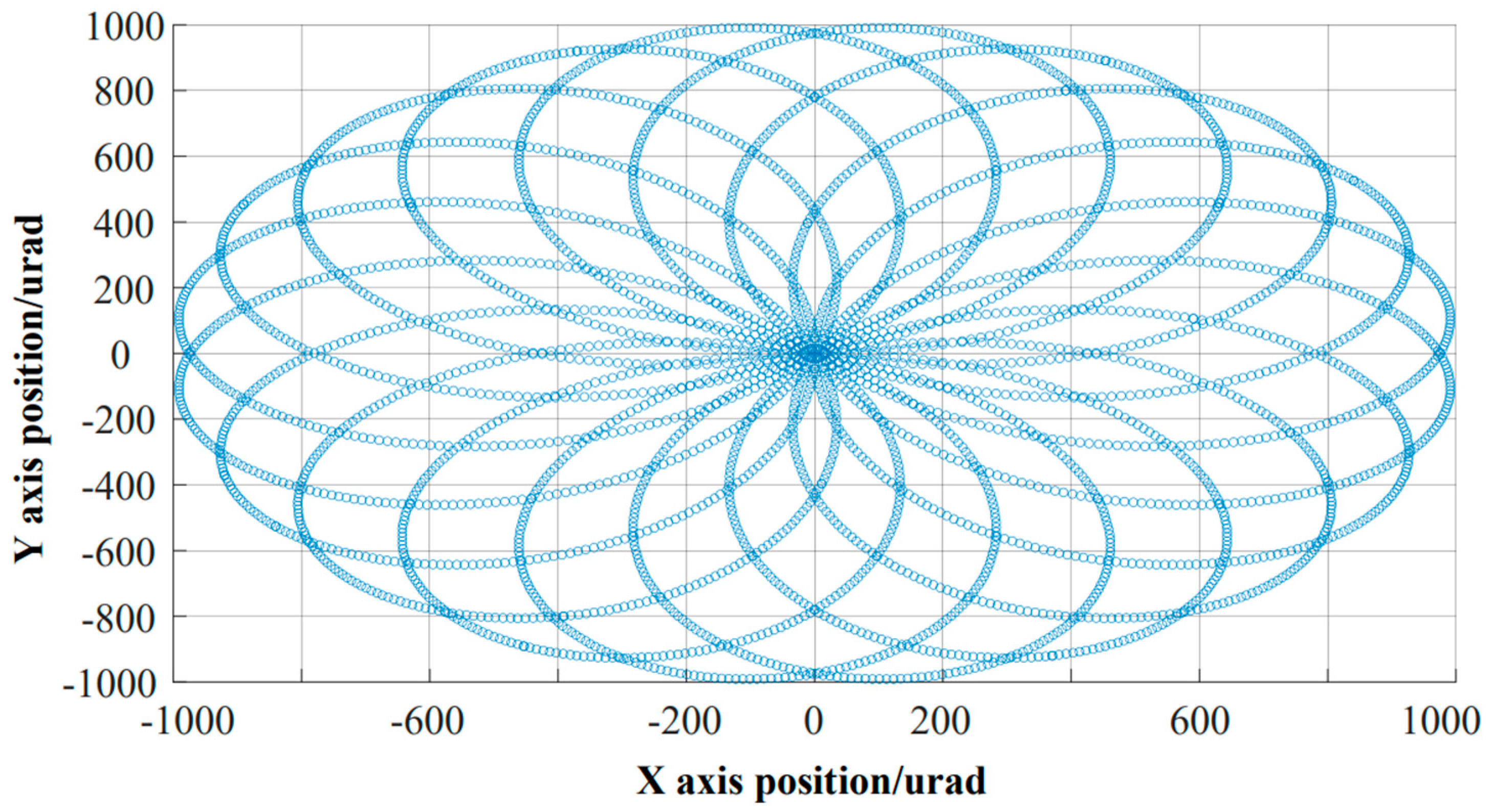
To meet the practical requirements of large field of scanning detection, through the study of FSM design and scanning methods, the transformation from Orthogonal coordinate system to Cartesian coordinate system is designed to achieve large stroke and high bandwidth scanning curves. After designing a scanning scheme to synthesize the scanning curve from the X and Y orthogonal coordinate system to the Cartesian coordinate system, the petal scanning curve was achieved. Figure 7 shows the scan curve after synthesizing the X and Y orthogonal coordinate systems into the Cartesian coordinate system. The scanning frequency of the X-axis in Figure 7 is 500Hz, and the scanning frequency of the Y-axis is 350Hz. With the increase of scanning frequency, the frequency requirements for FSM are becoming higher and higher.
x ( t ) = 1000 sin ( 1000 π t ) sin ( 700 π t + π 2 )
y ( t ) = 1000 sin ( 1000 π t ) sin ( 700 π t )
As shown in Figure 7, the high-frequency undistorted repetitive scanning curve can provide a good prerequisite for scanning imaging. To verify the tracking characteristics and control algorithm, two axis FSM designed in this paper was tested using TMS320F28335 DSP as the processor. The control schematic diagram is shown in Figure 8. The DSP collects sensor data through an A/D converter and outputs the control signal of the voice coil motors to the linear driving circuit through the D/A converter. The control voltage of the voice coil motors is equal and opposite in direction to achieve a differential push and pull effect. To improve FSM performance, a higher sampling frequency should be used as much as possible. This system adopts a sampling frequency of 200 kHz and a sampling period of 0.000005 seconds. During each sampling cycle, it is necessary to complete sensor data collection and control algorithm calculations.
As the scanning frequency increased, the frequency requirements became increasingly high. The actual dual axis input was converted to a Cartesian coordinate system with different scanning frequencies, and the synthesized motion trajectory is shown in Figure 8. As shown in the Figure 8, through a reasonable closed-loop control strategy, it was possible to achieve trajectory planning for large stroke and high frequency scanning.
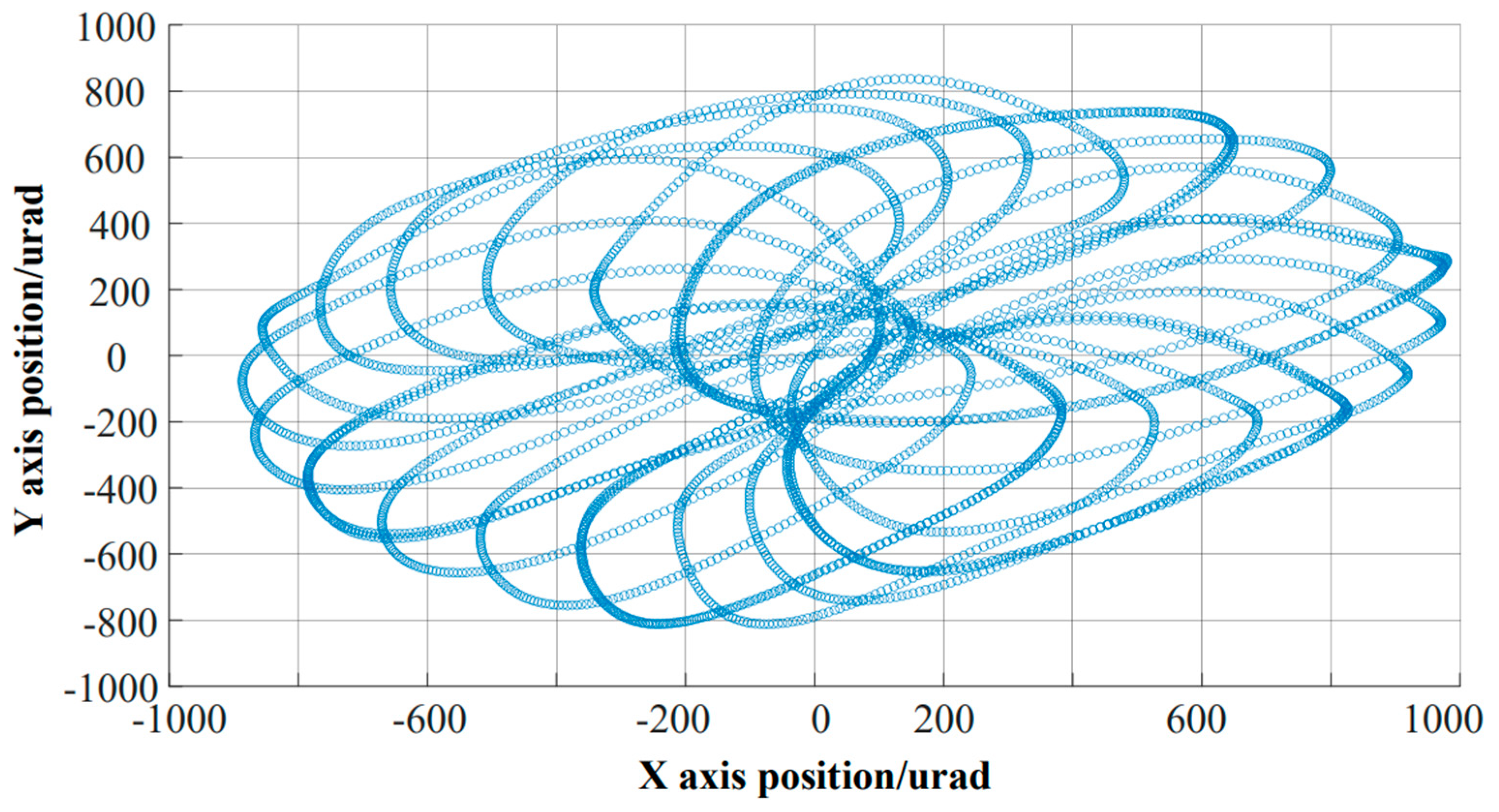
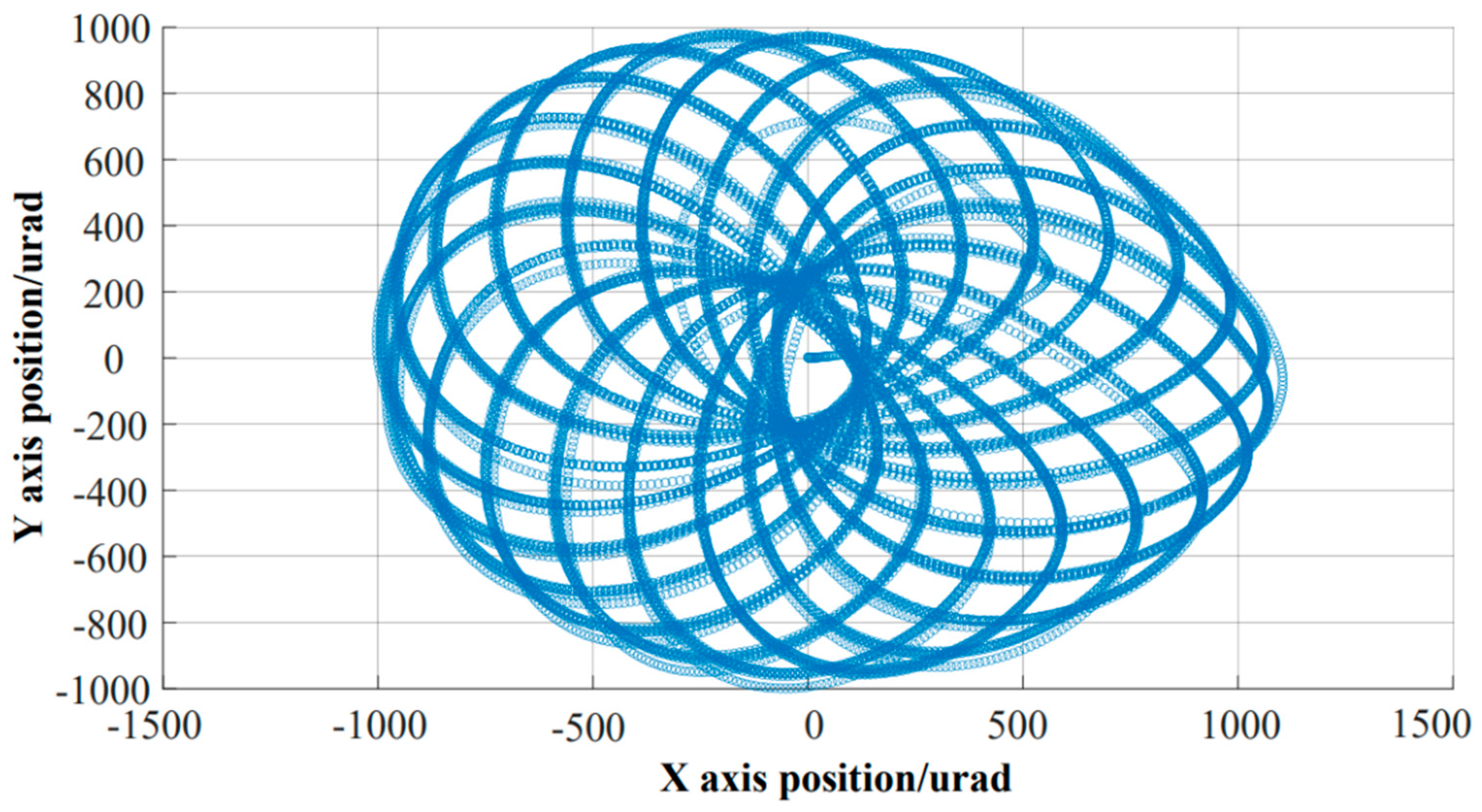
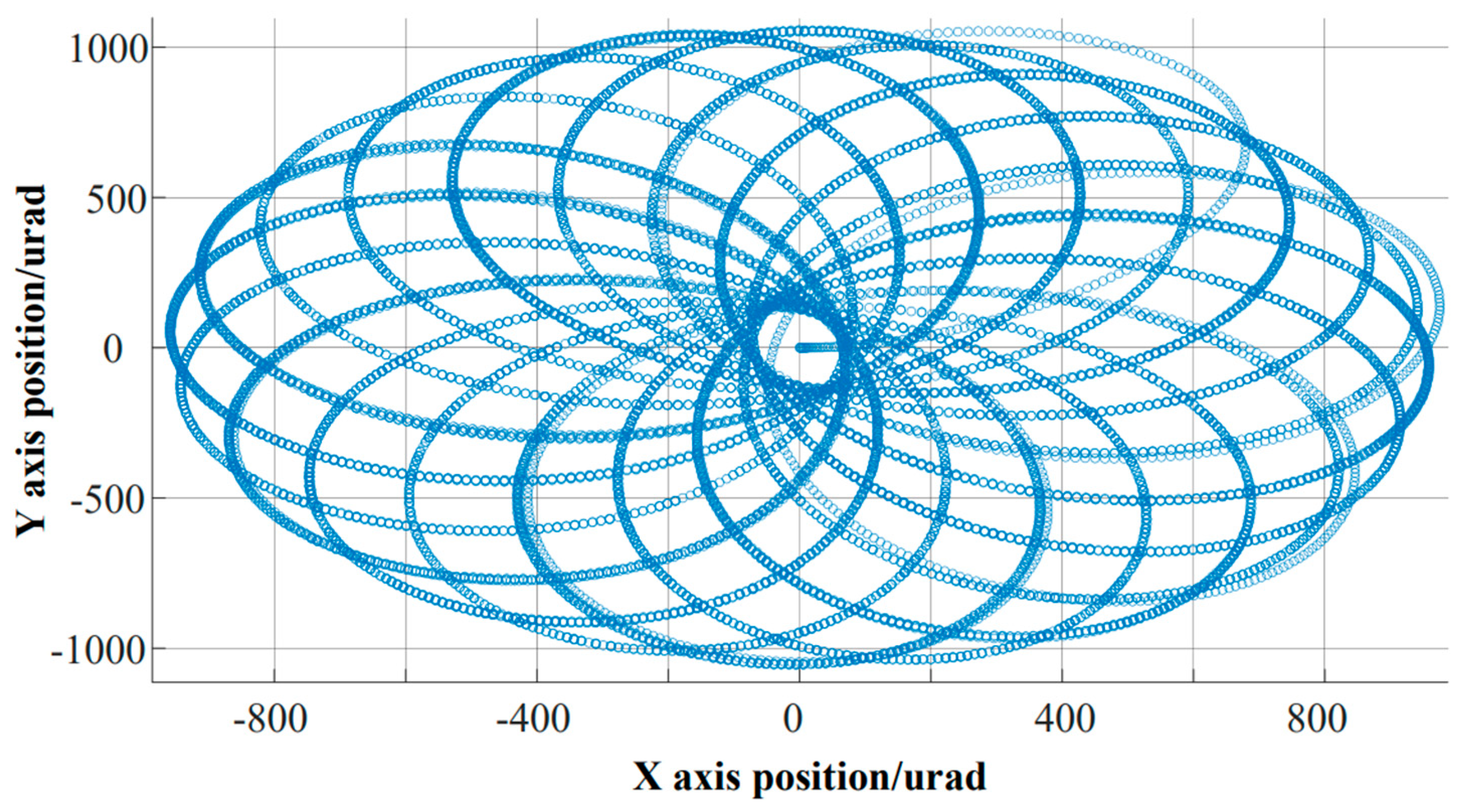
The scanning experimental platform is shown in Figure 9. FSM is fixed on the air flotation platform, and the light source is placed parallel to the zero position of the FSM. When the FSM scans at high frequency according to the input command, the actual scanned petal image is projected onto the wall. By observing the effect of the petals and collecting feedback data from the two axes of the system, the closed-loop scanning effects of PID, ADRC, and the proposed control strategy are compared, as shown in Figure 10, Figure 11 and Figure 12.
Figure 9 shows the scanning pattern obtained by using FSM to scan Figure 7. Scanning experiments were conducted on the above scanning curves in the laboratory. Due to insufficient exposure time of the camera, it was not possible to fully capture the dynamics of the curves. Therefore, during recording, some dynamic curves may be recorded incompletely. However, we can still analyze and compare the scanning curves from the recorded curves, Analyze the advantages and disadvantages of the scanning curves corresponding to the three different methods proposed in this experiment based on the requirements of the experiment.
By adopting three control strategies, the Lissajous curve tracking function of the same system was achieved. Comparing the three actual tracking effects, it is evident that the traditional PID closed-loop control strategy led to distortion in high-frequency scanning, causing the scanning function to fail. The ADRC strategy had the problem of local distortion, making it impossible to ensure repeatability. In contrast, the FOADRC strategy ensured a repetitive tracking curve. Although there were some point distortions, the input scanning curve was reproduced, so changing the distortion did not cause the scanning function to fail. These results verify the advantages of the FOADRC in repetitive Lissajous scanning tracking.

6. Conclusions

Focusing on the problem of scanning distortion suppression in tracking Lissajous trajectories, this study developed an experimental platform for research on tracking Lissajous control schemes and proposed an FOADRC with excellent control performance and anti-interference ability for future study and implementation. A mathematical model of the control system was established based on the structure of the designed FSM. The control method was verified using the beam jitter control platform built in this study. The experimental results showed that the novel control scheme showed greatly improved performance in suppressing beam jitter compared with the traditional control method. To fairly evaluate the advantages of the FOADRC, comparative experiments with an ADRC and PID controller were conducted on the FSM. The experimental results are illustrated here in terms of tracking Lissajous scan trajectories. At the scanning rates of 500 Hz and 350 Hz, the FOADRC strategy could completely track the input curve, while the PID and ADRC strategies had distortion problems. This verified the advantages of the proposed FOADRC in Lissajous scanning. The FSM design controller offers simple implementation and low computational complexity, thereby improving the dynamic performance of the FSM. The design serves as a reference for engineering applications.

Funding

National Key R&D Program of China [Grant No. 2022YFC3803700], Jilin Provincial Key R&D Projects [Grant No. 20230201007GX] and Shanxi Province Postdoctoral Research Project [Grant No. 2023BSHEDZZ316].

Acknowledgments

This paper is funded by National Key R&D Program of China and Jilin Provincial Key R&D Projects.

Data Availability Statement

Data underlying the results presented in this paper are not publicly available at this time but maybe obtained from the authors upon reasonable request.

Disclosures

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. E. Csencsics; G. Schitter. System Design and Control of a Resonant Fast Steering Mirror for Lissajous-Based Scanning. IEEE/ASME Trans. Mech. 2017, 22, 1963–1972. [CrossRef]
  2. J. Zhong; R. Nishida; T. Shinshi. Design and precision tracking control of a high-bandwidth fast steering mirror for laser beam machining. Precis. Eng. 2022, 73, 128–139. [CrossRef]
  3. B. Ran; P. Yang; L. Wen; R. Du; B. Xu. Design and analysis of a reactionless large-aperture fast steering mirror with piezoelectric actuators. Appl. Opt. 2020, 59, 1169–1179. [CrossRef]
  4. Y. Fan; Y. He; U.X. Tan. Real-Time Compensation System via Gyroscope and Fast Steering Mirror for Wide-Bandwidth Multiple-Frequency Vehicle Disturbance. IEEE/ASME Trans. Mech. 2020, 25, 650–660. [CrossRef]
  5. Z.Y. Zhou; Z. Y. Feng; H. Xian; L. H. Huang. Single Preloaded Piezoelectric Ceramic Stack Actuator Based Fast Steering Mirror with Ultrahigh Natural Frequency. Appl. Opt. 2020, 59, 3871–3877. [CrossRef]
  6. L. Li; W. W. Huang; X. Wang; L. Zhu. Dual-Notch-Based Repetitive Control for Tracking Lissajous Scan Trajectories With Piezo-Actuated Nanoscanners. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [CrossRef]
  7. J. Schlarp; E. Csencsics; G. Schitter. Optical Scanning of a Laser Triangulation Sensor for 3-D Imaging. IEEE Trans. Instrum. Meas. 2020, 69, 3606–3613. [CrossRef]
  8. J. Zhong; L. Li; R. Nishida; T. Shinshi. Design and evaluation of a PEA-driven fast steering mirror with a permanent magnet preload force mechanism. Precis. Eng. 2020, 62, 95–105. [CrossRef]
  9. Xu, Y.; Luo, Y.; Luo, X.; Chen, Y.; Liu, W. Fractional-Order Modeling of Piezoelectric Actuators with Coupled Hysteresis and Creep Effects. Fractal Fract. 2024, 8, 3. [Google Scholar] [CrossRef]
  10. Q. Chang; W. Chen; J. Liu; H. Yu; J. Deng; Y. Liu. Development of a novel two-DOF piezo-driven fast steering mirror with high stiffness and good decoupling characteristic. Mechan. Syst. Signal Process. 2021, 159, 107851. [CrossRef]
  11. Shinshi T; Shimizu D; Kodeki K; K Fukushima. A Fast Steering Mirror Using a Compact Magnetic Suspension and Voice Coil Motors for Observation Satellites. Electronics 2020, 9, 1997. [CrossRef]
  12. R. Xiao;M. Xu;S. Shao; Z. Tian. Design and wide-bandwidth control of large aperture fast steering mirror with integrated-sensing unit. Mechan. Syst. Signal Process. 2019, 126, 211–226. [CrossRef]
  13. Z.Y. Zhou; Z. Y. Feng;H. Xian; L. H. Huang. Single Preloaded Piezoelectric Ceramic Stack Actuator Based Fast Steering Mirror with Ultrahigh Natural Frequency. Appl. Opt. 2020, 59, 3871–3877. [CrossRef] [PubMed]
  14. Csencsics E; Schlarp J; Schopf T; Schitter G. Compact high performance hybrid reluctance actuated fast steering mirror system. Mechatronics. 2019, 62, 102251. [CrossRef]
  15. W. Han; S. Shao; S. Zhang; Z. Tian; M. Xu. Design and modeling of decoupled miniature fast steering mirror with ultrahigh precision. Mechan. Syst. Signal Process. 2022, 167, 108521. [CrossRef]
  16. Dong F; Lei X ; Chou W. A Dynamic Model and Control Method for a Two-Axis Inertially Stabilized Platform. IEEE Trans. Ind. Electron. 2016, 64, 432–439. [CrossRef]
  17. Wang G; Wang B; Zhao J. Robust tracking for nanopositioning stages using sliding mode control with active disturbance rejection: Design and implementation. J. Vib. Control. 2023, 29, 3809–3822. [CrossRef]
  18. Tang T; Ma J; Ge R. PID-I controller of charge coupled device-based tracking loop for fast-steering mirror. Opt. Eng. 2011, 50, 283. [CrossRef]
  19. W. Liu; K. Yao; D. Huang; X.D. Lin; L. Wang; Y.W. Lv. Performance evaluation of coherent free space optical communications with a double-stage fast-steering-mirror adaptive optics system depending on the Greenwood frequency. Opt. Express 2016, 24, 13288–13302. [CrossRef] [PubMed]
  20. C. Deng; W. Ren; Y. Mao; G. Ren. Plug-in module acceleration feedback control for fast steering mirror-based beam stabilization systems. Opt. Eng. 2017, 56, 084105. [CrossRef]
  21. Sanfedino F; Preda V;Pommier-Budinger V; Alazard D; Bennani, S. Robust Active Mirror Control Based on Hybrid Sensing for Spacecraft Line-of-Sight Stabilization. IEEE Trans. Contr. Syst. T. 2021, 29, 220–235. [CrossRef]
  22. Y. Luo; W. Ren; Y. Huang; Q. He; Q. Wu; X. Zhou; Y. Mao. Feedforward Control Based on Error and Disturbance Observation for the CCD and Fiber-Optic Gyroscope-Based Mobile Optoelectronic Tracking System. Electronics 2018, 7, 223. [CrossRef]
  23. H.S. Kim; D.H. Lee; D.J. Hur; D.C. Lee. Development of two-dimensional piezoelectric laser scanner with large steering angle and fast response characteristics. Rev. Sci. Instrum. 2019, 90, 065004. [CrossRef] [PubMed]
  24. W.C. Xue; W.Y. Bai; S. Yang S; K. Song; Y. Huang; H. Xie. ADRC with adaptive extended state observer and its application to air–fuel ratio control in gasoline engines. IEEE Trans. Ind. Electron. 2015, 62, 5847–5857. [CrossRef]
  25. G. Wang; Y. Wang; H. Zhou; F. Bai; G. Chen; J. Ma. Comprehensive approach to modeling and identification of a two-axis piezoelectric fast steering mirror system based on multi-component analysis and synthesis. Mechan. Syst. Signal Process. 2019, 127, 50–67. [CrossRef]
  26. V. Hassani; T. Tjahjowidodo; T. N. Do. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [CrossRef]
  27. J. Ling; F. Zhao; D. D. Zheng; J. Yang;H. Y. Yu; X.H. Xiao. Robust adaptive motion tracking of piezoelectric actuated stages using online neural-network-based sliding mode control. Mechan. Syst. Signal Process. 2021, 150, 107235. [CrossRef]
  28. K. Babarinde; L. Li; L. Zhu; S. S. Aphale, Experimental validation of the simultaneous damping and tracking controller design strategy for high-bandwidth nanopositioning - a PAVPF approach. IET Control Theory & Applications 2020, 14, 3506–3514. [CrossRef]
  29. Chang. Design and characterisation of a compact 4-degree-of-freedom fast steering mirror system based on double Porro prisms for laser beam stabilization. Sensors Actuat. A-Phys. 2021, 322, 112639. [CrossRef]
  30. Nikooienejad; M. Maroufi; S. O. R. Moheimani. Iterative Learning Control for Video-Rate Atomic Force Microscopy. IEEE/ASMETrans. Mechatron. 2021, 26, 2127–2138. [CrossRef]
  31. C.X. Li; G.Y. Gu; M.J. Yang; L.M. Zhu. High-Speed Tracking of a Nanopositioning Stage Using Modified Repetitive Control. IEEE Trans. Autom. Sci. Eng. 2017, 14, 1467–1477. [CrossRef]
  32. Z.Q. Gao. Scaling and bandwidth-parameterization based controller tuning. Proceedings of the 2003 American Control Conference 2003, 6, 4989–4996. [CrossRef]
  33. Du, Y.; Cao, W.; She, J. Analysis and Design of Active Disturbance Rejection Control With an Improved Extended State Observer for Systems With Measurement Noise. IEEE Trans. Ind. Electron. 2023, 70, 855–865. [Google Scholar] [CrossRef]
  34. Chen, P.; Luo, Y. A two-degree-of-freedom controller design satisfying separation principle with fractional-order PD and generalized ESO. IEEE/ASME Trans. Mechatron. 2021, 27, 137–148. [Google Scholar] [CrossRef]
  35. Wang, S.; Gan, H.; Luo, Y.; Luo, X.; Chen, Y. A Fractional-Order ADRC Architecture for a PMSM Position Servo System with Improved Disturbance Rejection. Fractal Fract. 2024, 8, 54. [Google Scholar] [CrossRef]
  36. Xu, K.; Cheng, T.; Lopes, A.M.; Chen, L.; Zhu, X.; Wang, M. Fuzzy Fractional-Order PD Vibration Control of Uncertain Building Structures. Fractal Fract. 2022, 6, 473. [Google Scholar] [CrossRef]
  37. C.L. Hsieh; C.S. Liu; C.C. Cheng. Design of a 5 degree of freedom–voice coil motor actuator for smartphone camera modules. Sens. Actuators A Phys. 2020, 309, 112014. [CrossRef]
  38. C.S. Liu; Y.C. Wu; Y.J. Lan. Design of 4-DOF Voice Coil Motor with Function of Reducing Laser Geometrical Fluctuations. Actuators 2021, 10, 320. [CrossRef]
  39. H. Zhang; Y. Xie; Xiao G. A Simple Discrete-Time Tracking Differentiator and Its Application to Speed and Position Detection System for a Maglev Train. IEEE Trans. Contr. Syst. Tech. 2018, 27, 1728–1734. [CrossRef]
  40. C.W. Wang; L. Quan; S.J. Zhang; H.J. Meng; Y. Lan. Reduced-order model based active disturbance rejection control of hydraulic servo system with singular value perturbation theory. ISA Trans. 2017, 67, 455–465. [CrossRef]
  41. J.Q. Han. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [CrossRef]
Preprints 97766 g001
Figure 1. Schematic diagram of imaging system.
Figure 1. Schematic diagram of imaging system.
Preprints 97766 g001
Preprints 97766 g002
Figure 2. Block diagram of the position control loop of the FSM.
Figure 2. Block diagram of the position control loop of the FSM.
Preprints 97766 g002
Preprints 97766 g003
Figure 3. Block diagram of fast steering mirror.
Figure 3. Block diagram of fast steering mirror.
Preprints 97766 g003
Preprints 97766 g004
Figure 4. Principal block diagram of controller.
Figure 4. Principal block diagram of controller.
Preprints 97766 g004
Preprints 97766 g005
Figure 5. The tracking position response curve of the FOADRC without random signal.
Figure 5. The tracking position response curve of the FOADRC without random signal.
Preprints 97766 g005
Preprints 97766 g006
Figure 6. The tracking position response curve of the FOADRC algorithm with random signal.
Figure 6. The tracking position response curve of the FOADRC algorithm with random signal.
Preprints 97766 g006
Preprints 97766 g007
Figure 7. The scan curve after synthesizing the X and Y orthogonal coordinate systems into the Cartesian coordinate system.
Figure 7. The scan curve after synthesizing the X and Y orthogonal coordinate systems into the Cartesian coordinate system.
Preprints 97766 g007
Preprints 97766 g008
Figure 8. FSM control schematic diagram.
Figure 8. FSM control schematic diagram.
Preprints 97766 g008
Preprints 97766 g009
Figure 9. Optical scanning experimental platform.
Figure 9. Optical scanning experimental platform.
Preprints 97766 g009
Preprints 97766 g010
Figure 10. Experimental image of petal biaxial scanning based on PID strategy.
Figure 10. Experimental image of petal biaxial scanning based on PID strategy.
Preprints 97766 g010
Preprints 97766 g011
Figure 11. Experimental image of petal biaxial scanning based on ADRC strategy.
Figure 11. Experimental image of petal biaxial scanning based on ADRC strategy.
Preprints 97766 g011
Preprints 97766 g012
Figure 12. Experimental image of petal biaxial scanning based on FOADRC strategy.
Figure 12. Experimental image of petal biaxial scanning based on FOADRC strategy.
Preprints 97766 g012
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated