On the Kullback-Leibler Divergence Formalism (Kldf) of the Stable Mg1 Queue Manifold, Its Information Geometric Structure and Its Matrix Exponential

1. Introduction

1.1. Early Dawn of Minimum Relative Entropy(MRE)

In the context of probabilistic inverse approaches[1], it has become conventional to treat both measurable data and unknown parameters for the model being uncertain. This method provides deeper understanding of the uncertainty associated with the measured data and model parameters. [2,3,4,5,6,7,8,9,10]. KLD [11,12,13,14,15,16] is a method used to compare two probability distributions. In Probability and Statistics, when we need to simplify complex distributions or approximate observed data, KL Divergence helps us quantify the amount of information lost in the process of choosing an approximation. KLD  measures the difference between the two distributions and assists us with comprehending the trade-off between accuracy and simplicity in statistical modelling.

Shannonian entropic measure[9,17] ,namely  $H\left(p\right)$ reads as

With KL divergence we can calculate exactly how much information is lost when we approximate one distribution with another.

1.2. Information geometry(IG)

Many domains, including statistical inference, system control, and neural networks, have made extensive use of information geometry. In other words, IG seeks to apply differential geometry techniques to statistics.

A manifold [18，19,20,21] is a topological finite-dimensional Cartesian space, ${\mathbb{R}}^n$, where an infinite-dimensional manifold exists. In Figure 1, model parameter inference from data is depicted as a decision-making problem. Information geometry offers a differential-geometric manifold structure M that may be used to create decision rules.

The matrix exponential is a concept that holds significance in the study of Lie groups[22], which are mathematical structures used to analyze continuous symmetries. In the context of the given text, there is a research paperthat explores the geometry of M/D/1 queues, a type of queuing system, by introducing a geometric structure based on the characteristics of queue length routes. This innovative approach aims to provide a new perspective on analysing and understanding these queues. In the context of the study, a geometric approach is used in analogy to Information Theory because it allows for the examination of figure invariance and equivariancewithout relying on specific coordinates. This means that geometric methods provide a coordinate-free manner to analyze and understand the properties of figures, which is beneficial in certain applications. Ricci curvature measures how the Riemannian metric deviates from the standard Euclidean metric, while scalar curvature quantifies the difference in volume between a geometric ball and a Euclidean ball of the same radius, as illustrated by Figure 2(c,f., [23]).

This revolutionary paper contributes to:

i)The provision of both FIM and IFIM for KLDF manifold.

ii)First-time calculation of $\alpha$-connection[26]. iii) KLD and JD are calculated for the underlying queue iv) The compressibility (non-solenoidality) of KLDF manifold [27]. v)First time unification between queueing and matrix theories.

vi) The Rényi divergence (RD), $D_R^{\gamma }\left(p\right|\left|q\right)$ and the  S, AB-divergence, $D_{s,AB}^{\gamma ,\eta }\left(p\right|\left|q\right)$ for KLDF  are devised. Notably,  computed divergence measure in this paper set the foundation towards the information theory of Queue Learning(QL)

vi)Numerical Experiments on The Rényi divergence (RD) , $D_R^{\gamma }\left(p\right|\left|q\right)$ and the  S, AB-divergence, $D_{s,AB}^{\gamma ,\eta }\left(p\right|\left|q\right)$ of the KLDF manifold to illustrate how  both analytic and numerical experiments agree.

vii) A giant step towards the unification of KLDF of stable M/G/1 QM and its Information geometric structure is devised. viii) Introducing novel well-defined statistical queueing functionals, SQFs and investigate their algebraic structures.

This paper provides a roadmap of its contents, starting with early definitions in section 2 and an overview of consistency axioms in section 3. In the remaining sections, it introduces the KL formalism of the stable M/G/1 queue and devises service time distribution and cumulative functions. The paper also obtains the threshold theorem of KLDF, introduces the Fisher's information matrix and metric, explores the 𝛼-connection of the queue manifold, and reveals the compressibility and developability of the manifold. Additionally, it discusses the Scalar Curvature, Einstein Tensor, and stress-energy tensor in relation to information theory, queuing theory, and General Relativity. The paper concludes with the introduction of Rényi divergence and S, AB-divergence, numerical experiments, unification of KLDF and its information geometric structure, and the introduction of statistical queueing functionals.

2. Main Definitions in Information Geometry

The authors have presented  a novel (dis)similarity measure, namely ${\mathit{D}}_{\mathit{s},\mathit{A}\mathit{B}}^{\mathit{\gamma },\mathit{\eta }}\left(\mathit{p}\right|\left|\mathit{q}\right)$ (c.f., (2.10). Moreover, it  has been illustrated that $D_{s,AB}^{\gamma ,\eta }\left(p\right|\left|q\right)$ is potentially robust.

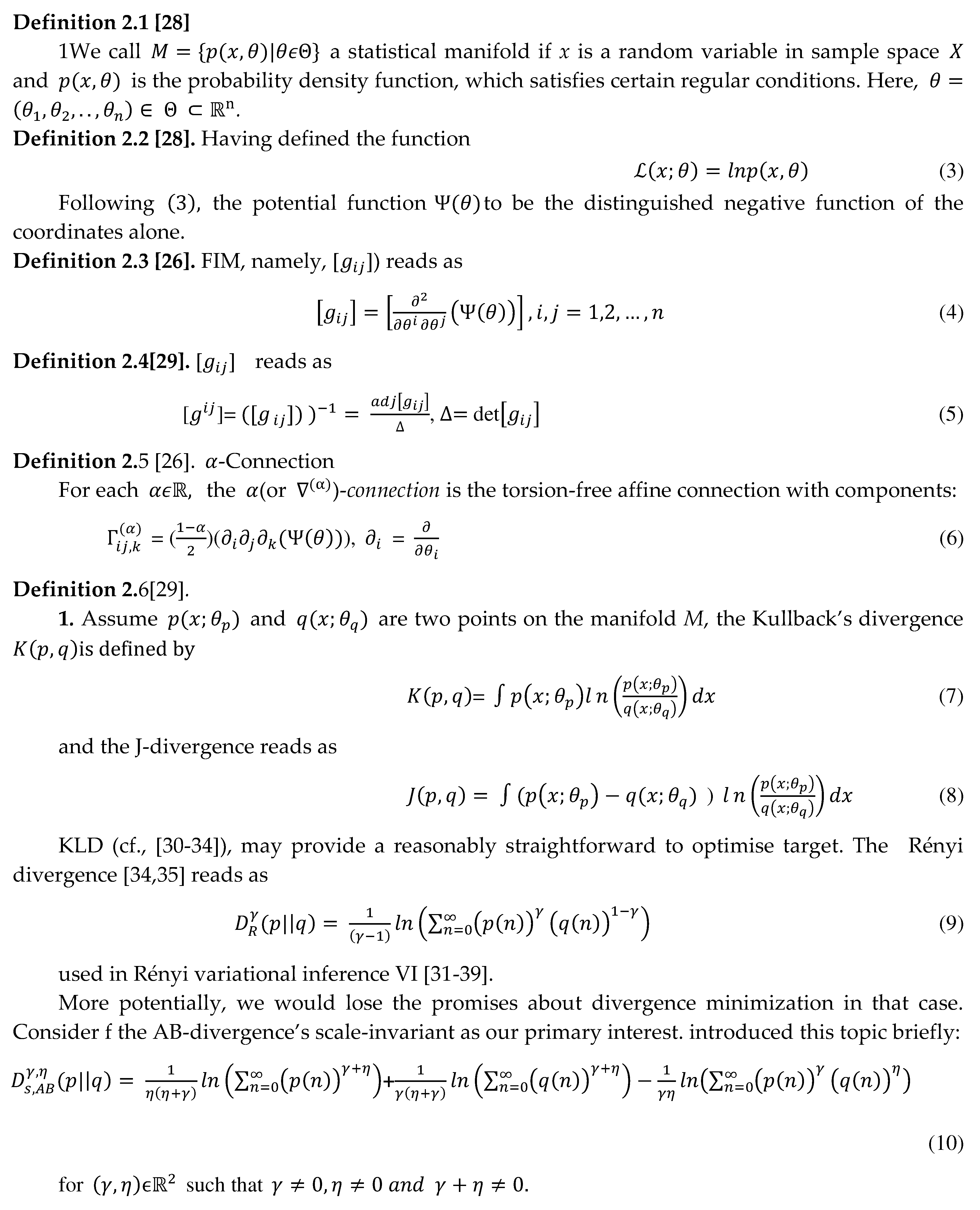
2.7. Well Defined Functions and Bijective Functions

Figure 4. Depiction of how conical sections in the manifold differ in volume from corresponding conical locations in Euclidean space (c.f., [47]).

Figure 4. Depiction of how conical sections in the manifold differ in volume from corresponding conical locations in Euclidean space (c.f., [47]).

Figure 5. The three kinds of developable surfaces: a, left) tangential; b, centre) conical; c, right) cylindrical. Curves in bold are directrix or base curves; straight lines in bold are directors or generating lines (curves) (c.f., [49]).

Figure 5. The three kinds of developable surfaces: a, left) tangential; b, centre) conical; c, right) cylindrical. Curves in bold are directrix or base curves; straight lines in bold are directors or generating lines (curves) (c.f., [49]).

According to Kouvatsos [50], the maximum entropy state probability of the generalized geometric solution of a stable M/G/1 queue, subject to normalisation, mean queue length (MQL), L and server utilisation, $\rho$(<1) is given by

Figure 6. A Stable M/G/1 queue.

Figure 6. A Stable M/G/1 queue.

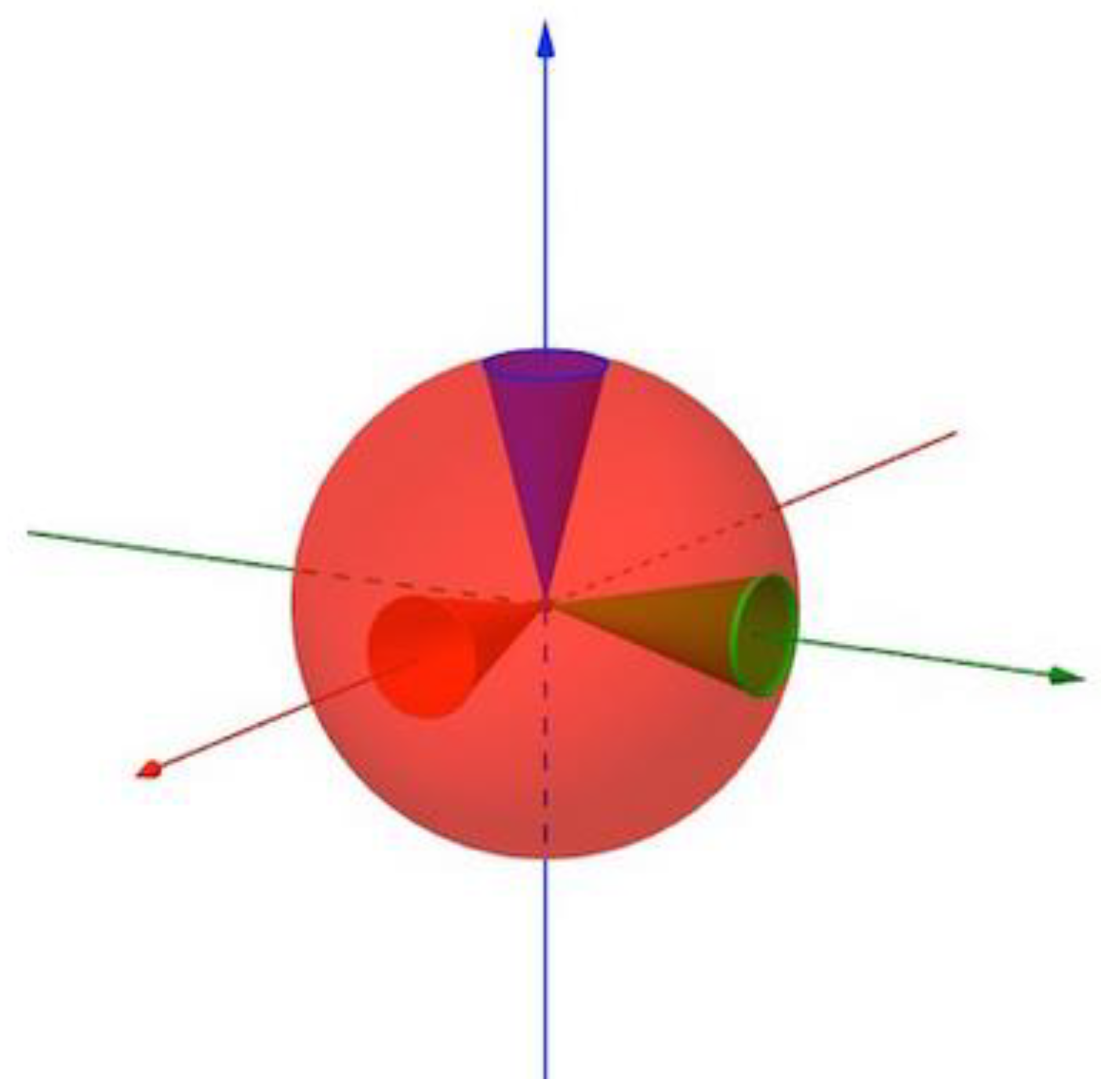
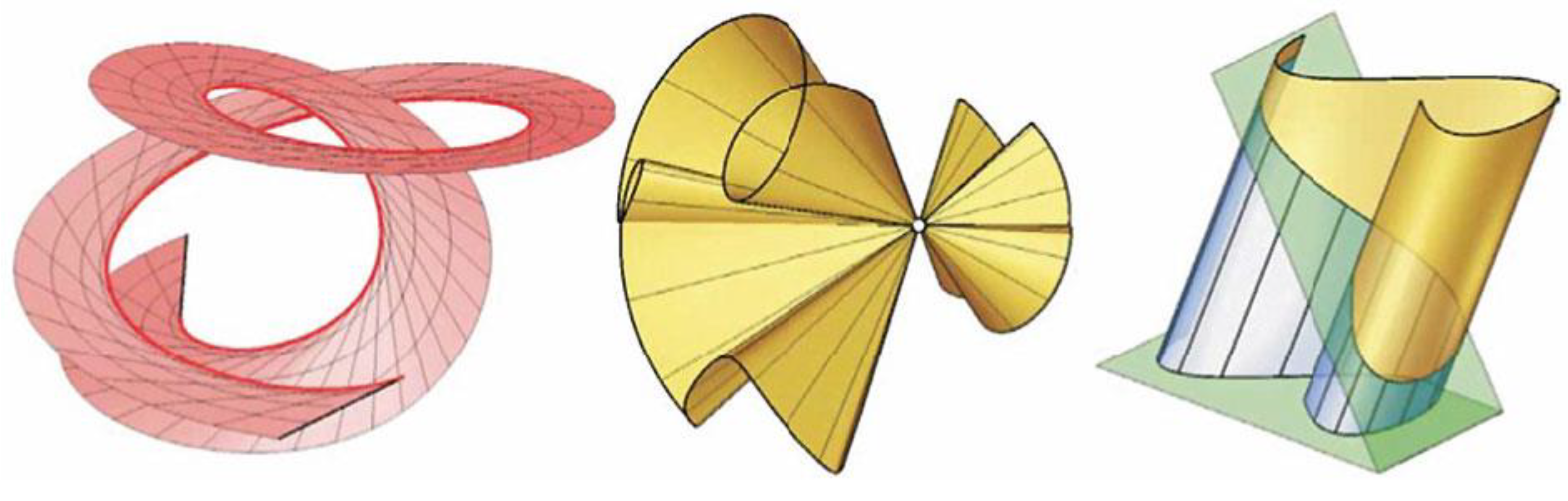
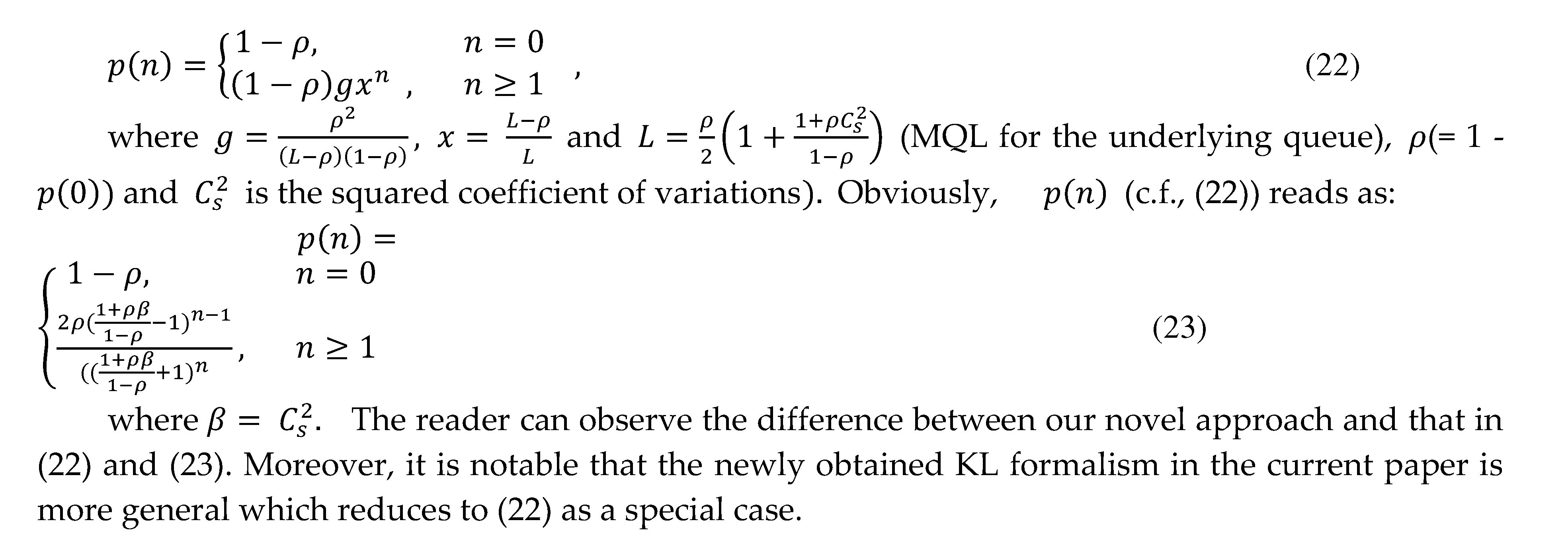
2.11. Scalar Curvature(Ricci Scalar), $\mathcal{R}$ and Einestein Tensor, $\wp$

3.1. NME Formalisms and EME Consistency Axioms

evaluated the credibility of Tsallis' NME formalism in terms of the four consistency axioms for large systems. Tsallis' formalism, although satisfying the consistency axioms of uniqueness, invariance, and subset independence, defied the axiom of system independence, as it should, due to the existence of 'long-range' interactions.

The credibility of Rényi's NME formalism as a method of inductive reasoning is also investigated in this context in terms of the four EME consistency axioms in Appendix A. Because of the presence of long-range interactions, the joint NME state probability distribution of two independent non-extensive systems Q and V challenges the assumption of system independence (cf., [6]). As a result, these NME formalisms are obviously adequate for quantitative analyses of non-extensive dynamic systems with long queue tails and asymptotic power law behaviour.

The devised analytic proof on the credibility of RxE9;nyi’s NME formalism follows a similar methodology to the one employed for Tsallis’s NME formalism by Kouvatsos and Assi and it can be seen in Appendix A.

3.2. A Stable M/G/1 Queue with Long-Range Interactions

Throughout this paper we shall use QM as an acronym for queueing manifold, IG for Information Geometry  and QT for queueing theory.

3.3. Background:Shannon’s EME State Probability of a Stable M/G/1 Queue

3.4. KLDF

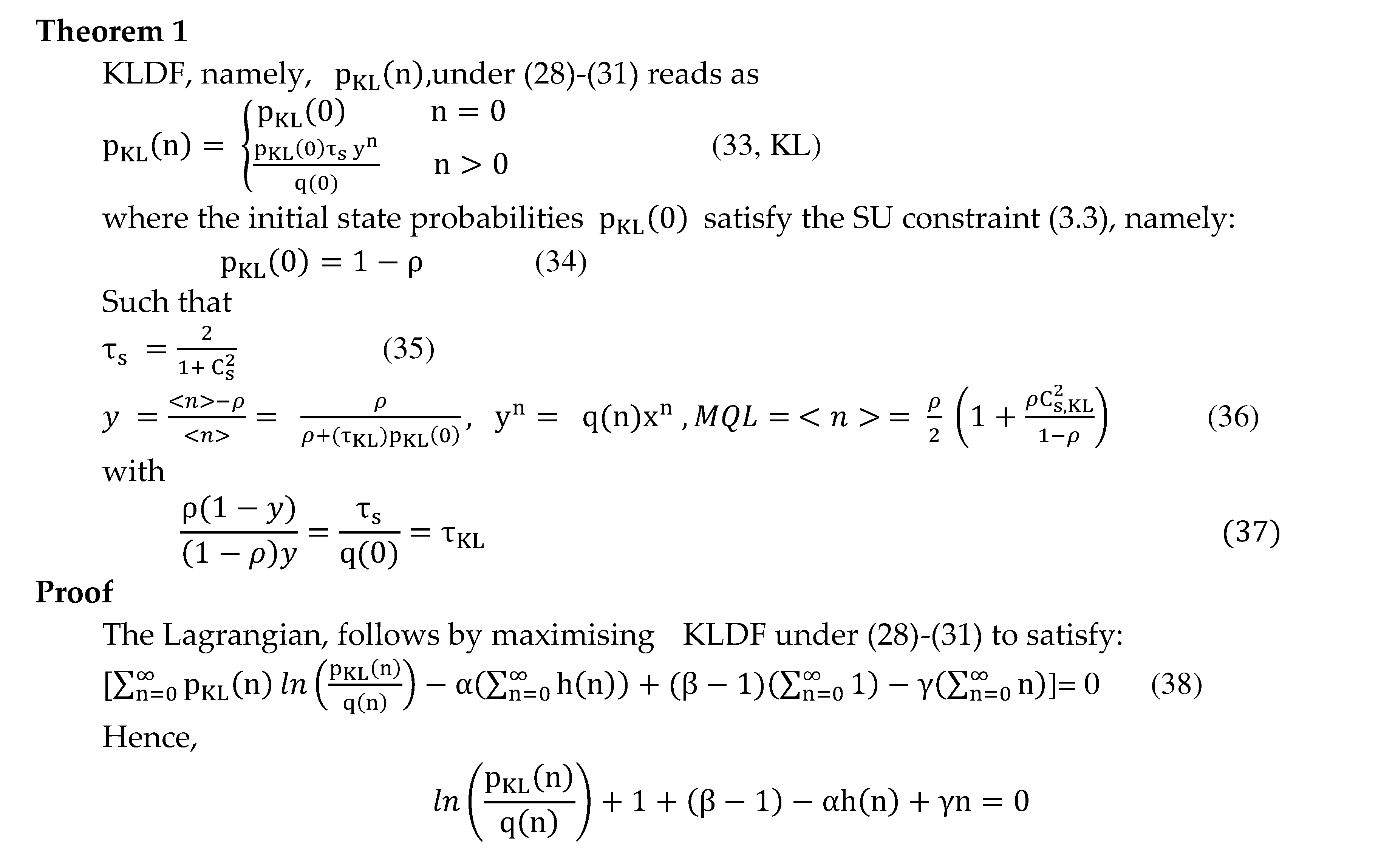
3.5. Exact KL NME State Probabilities with Distinct GE_KL-type Service Time Distributions

4. THE THRESHOLD THEOREMS OF KL FORMALISM, ${\mathit{F}}_{\mathit{s},\mathit{K}\mathit{l}}\left(\mathit{t}\right)$ and ${\mathit{C}}_{\mathit{s},\mathit{K}\mathit{L}}^2\mathit{}$FOR THE UNDERLYING MANIFOLD

If $f^{\text{'}}\left(x\right)>0$ ($<0)$for all $x\in (c,d)$ ,then f is increasing(decreasing) on $\left(c,d\right).$                                                        (61)                                                              

4.1. The Threshold Theorem of KL Formalism of The Stable MG1 Queueing System

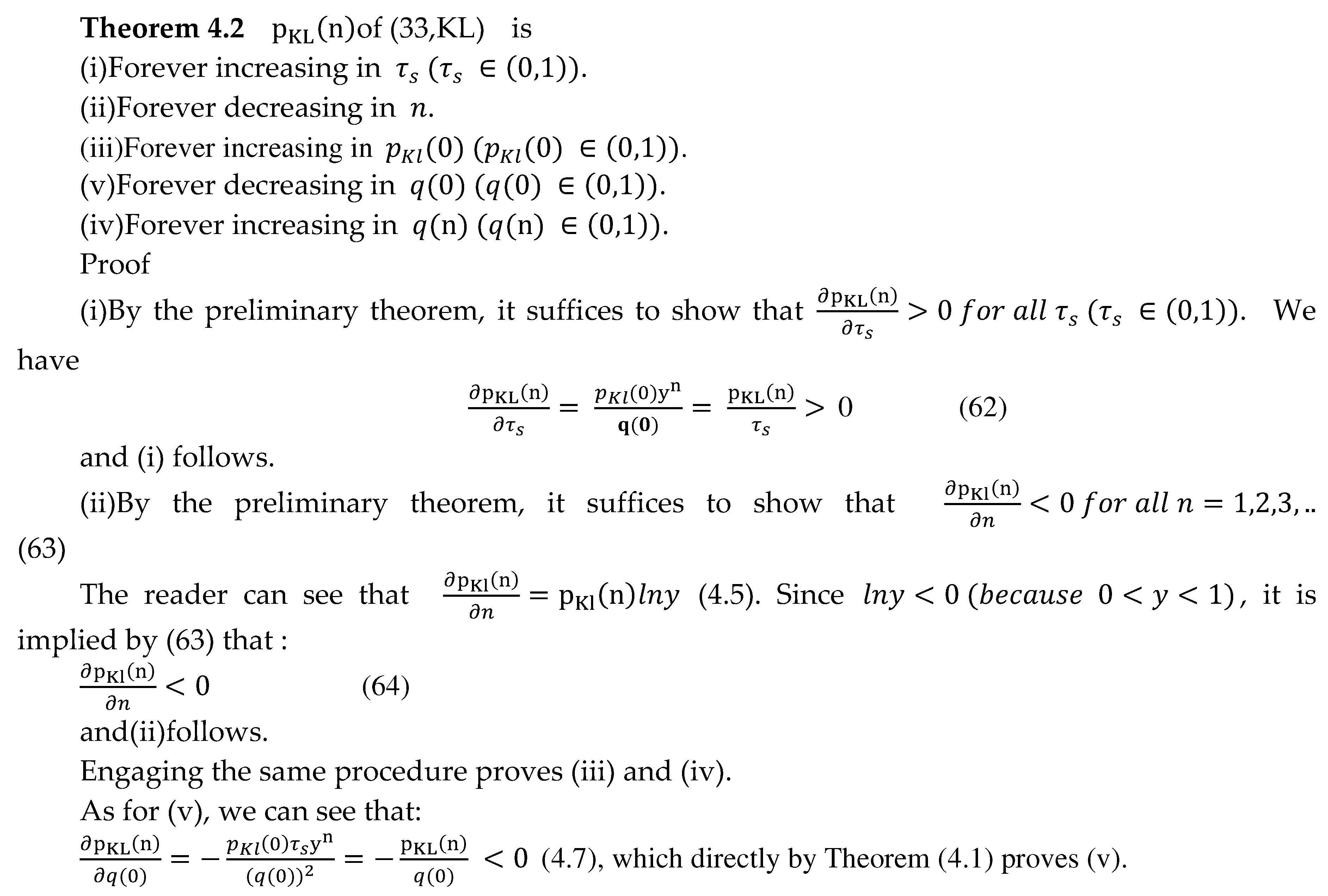
4.2. The Threshold Theorem of ${\mathit{F}}_{\mathit{s},\mathit{K}\mathit{l}}\left(\mathit{t}\right)$ of The Stable MG1 Queueing System

which by the preliminary theorem (4.1), the proof follows.

Engaging the same procedure, the remaining proof is immediate.

It is observed that Theorem (4.3), part (ii) presents a novel temporal threshold for ${\mathrm{F}}_{\mathrm{s},\mathrm{K}\mathrm{L}}\left(\mathrm{t}\right)$. This temporal threshold is significantly dependent on μ and ${\tau }_{KL},$ which is, ${\mathsf{\tau }}_{\mathrm{s}}=\frac{2}{1+{\mathrm{C}}_{\mathrm{s}}^2}$ impcated , the initial boundary steady state probaility of the comparable distribution q(0).

Also, it is clearly obvious that this novel temploral thrshold is influenced by the newly devised $C_{s,KL}^2,{\mathsf{\tau }}_{\mathrm{K}\mathrm{L}}=\frac{2}{1+{\mathrm{C}}_{\mathrm{s},\mathrm{K}\mathrm{L}}^2}$

In the following section, it is obtained that $C_{s,KL}^2$ of (60)  is forever decreasing in ${\tau }_{KL}$.

4.2. The Threshold Theorem of ${\mathit{C}}_{\mathit{s},\mathit{K}\mathit{L}}^2$ of The Stable MG1 Queueing System

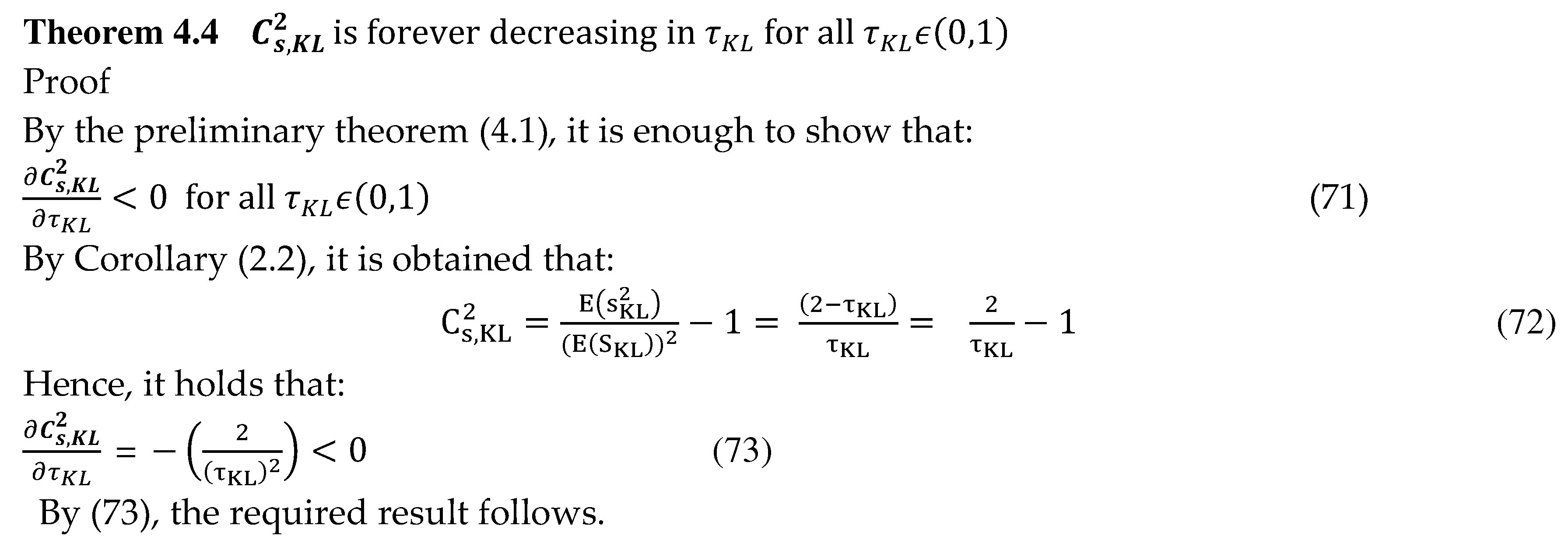
5. FIM and IFIM for KLDF manifold

According to Kouv [53], the maximum entropy state probability of the generalized geometric solution of a stable M/G/1 queue, subject to normalisation, mean queue length (MQL), L and server utilisation, $\rho$(<1) is given by:

This proves (iii).

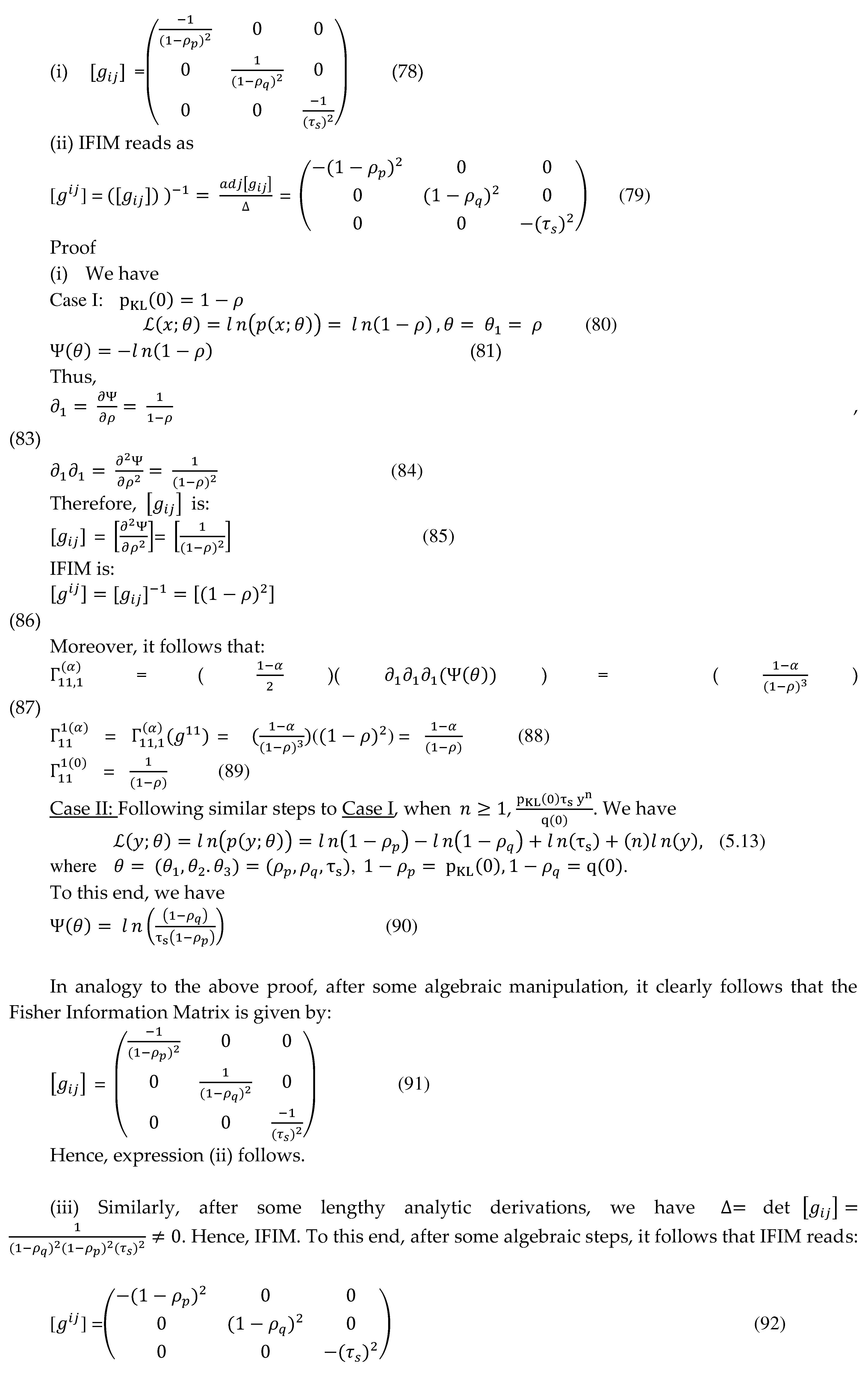
6. The α-connection of the KLDF manifold

7. The Compressibility ( Non-Solonoidability ) of KL Formalism of the Stable M/G/1 QM

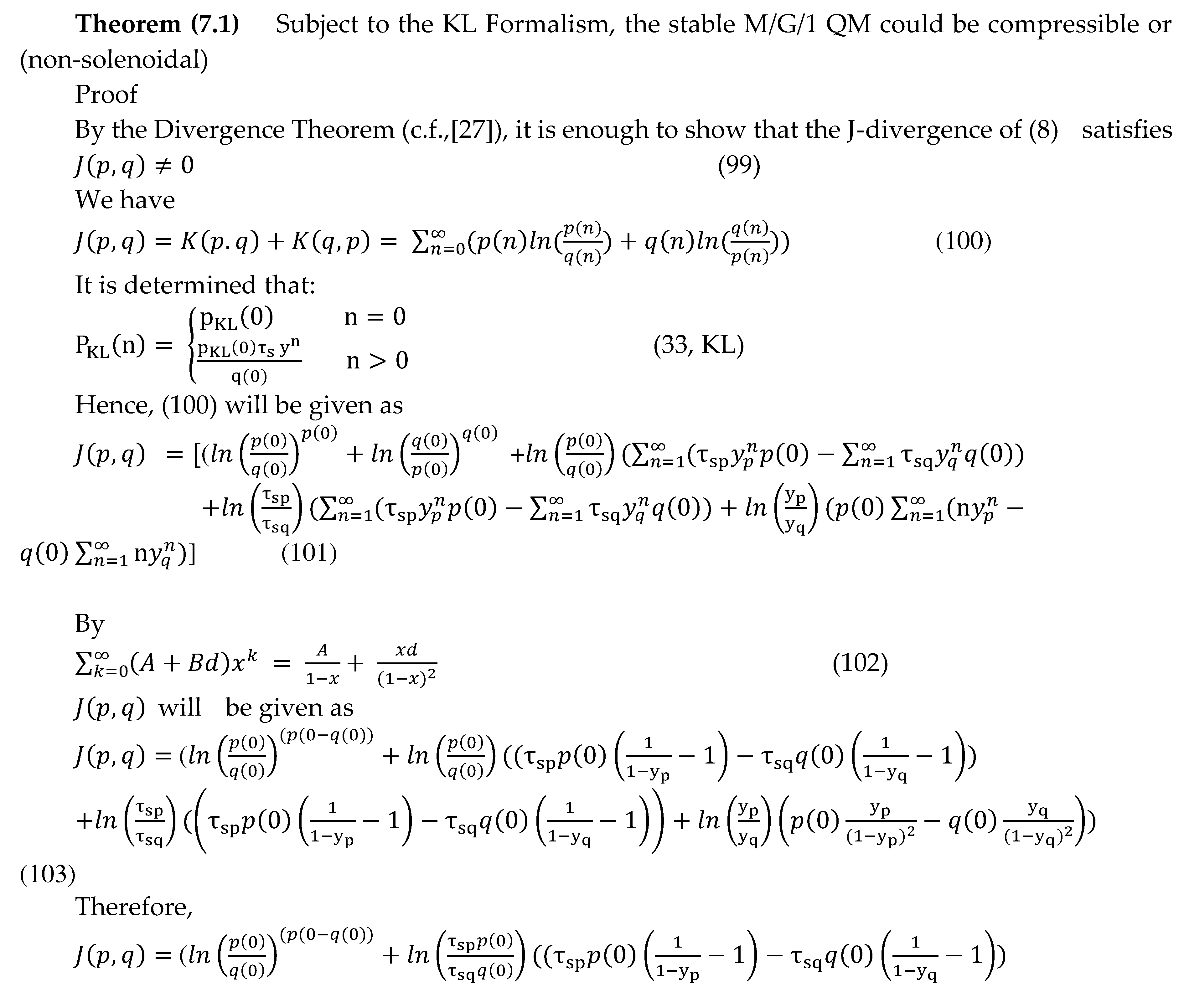
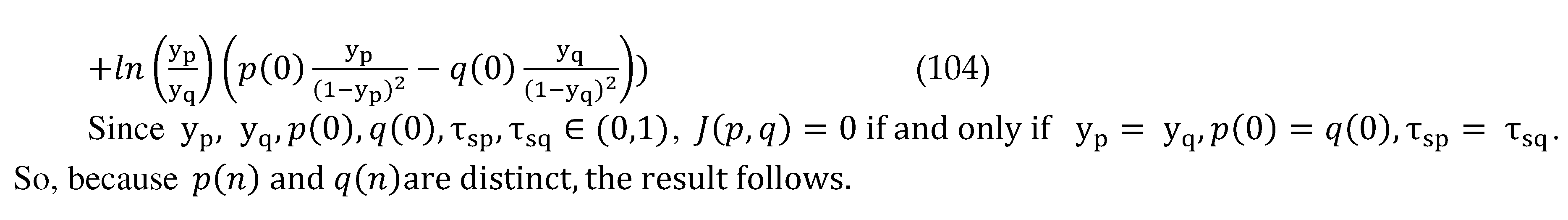
8. The Developability of the Stable M/G/1 QM, the Positivity of Its Ricci Curvature Tensor and The Threshold Theorem of Ricci Curvature Tensor

Figure 7.

Figure 7.

ii)Forever  increasing in the curvature parameter α, α > 0

$\alpha >1,{\rho }_p=0.5$

Figure 8.

Figure 8.

(iii)Forever  decreasing in the curvature parameter α, α < 0

$\alpha <1,{\rho }_p=0.5$

Figure 9.

Figure 9.

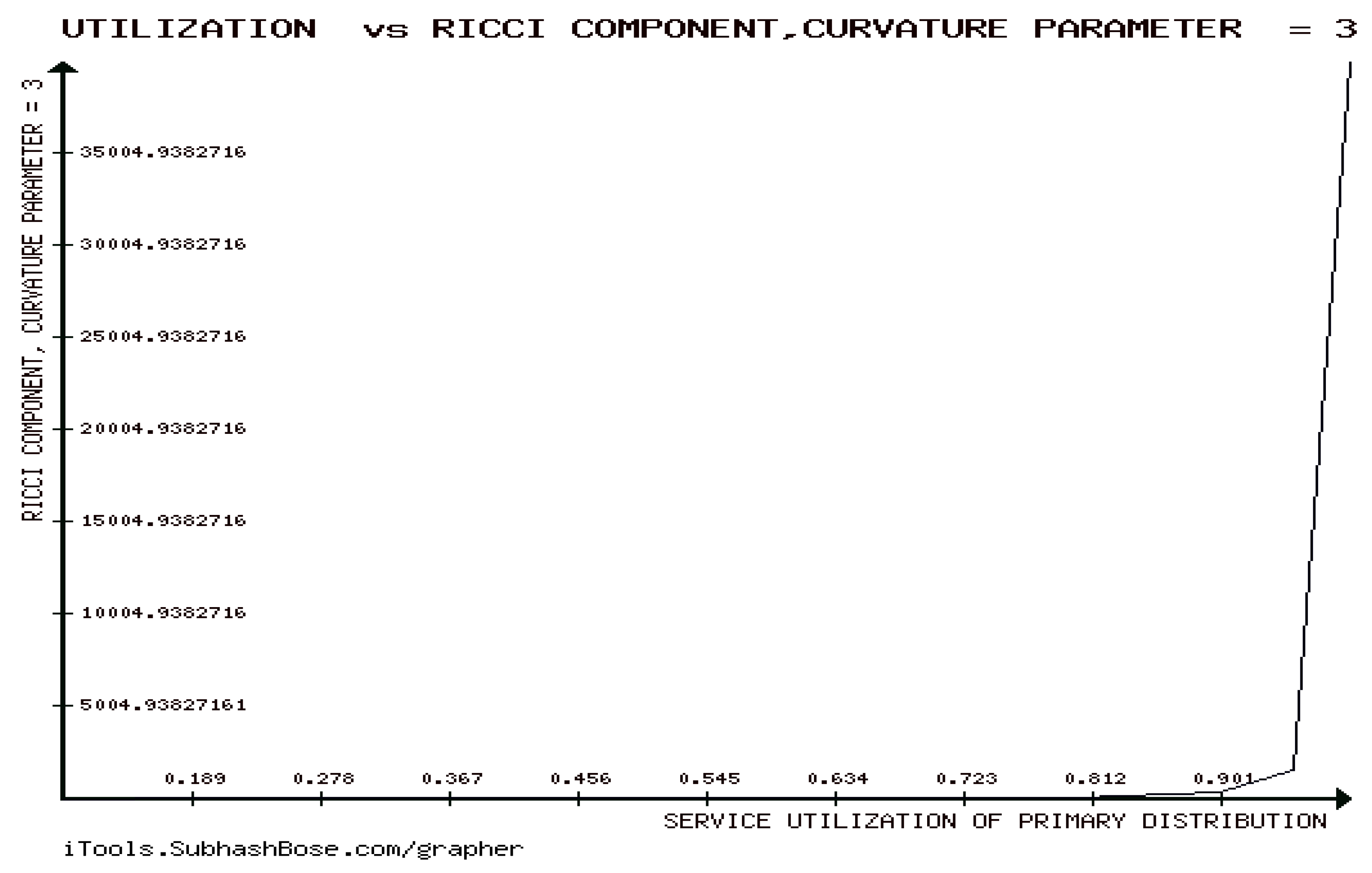
9. e^A of the underlying manifold

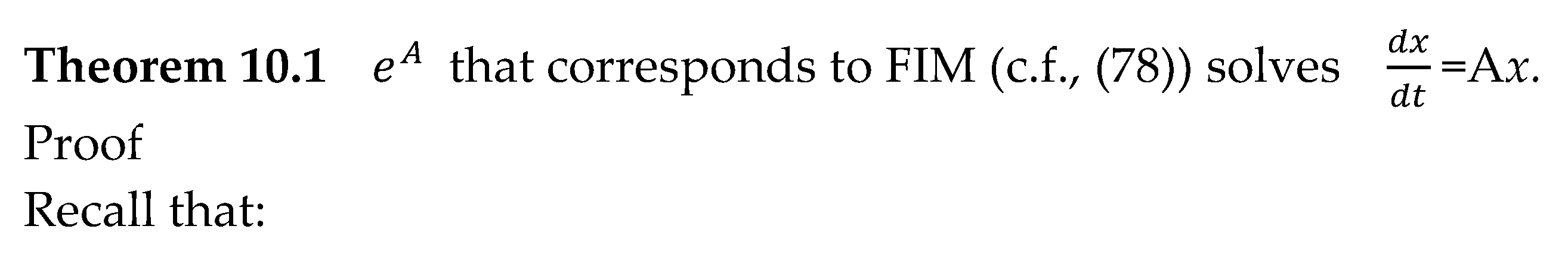
10. Scalar Curvature(Ricci Scalar), $\mathcal{R}$ and Einestein Tensor, $\mathit{\wp }$ and the stress-energy tensor, $\mathit{\varpi }$ of the KLF manifold

This section reports a new discovery of the missing link between information theory, queuing theory and General Relativity, namely the Scalar Curvature(Ricci Scalar), $\mathcal{R}$ and Einestein Tensor, $\wp$ and the stress-energy tensor,$\varpi$ of the underlying Kull-Leibler formalism, KLF for the investigated manifold.

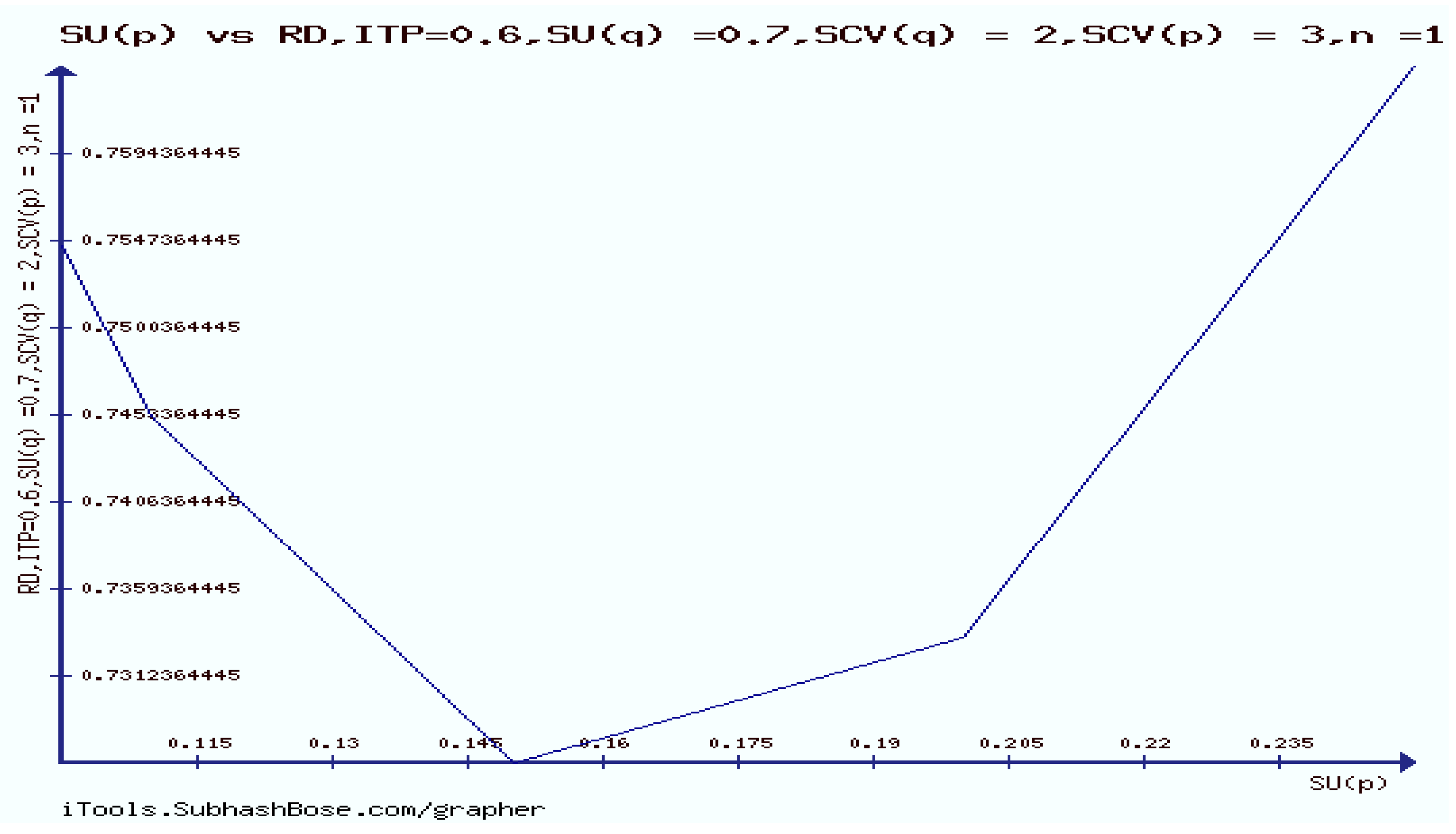
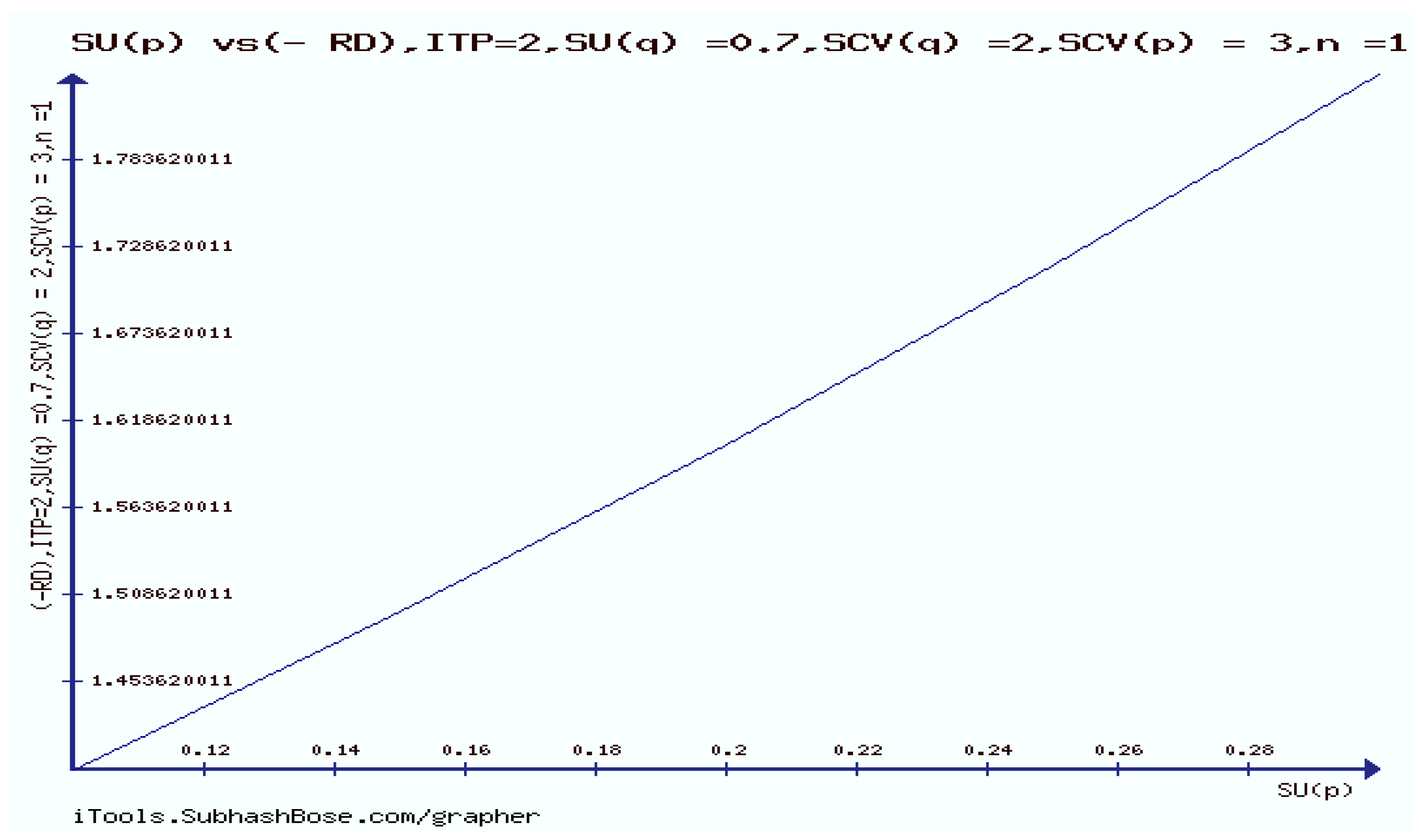
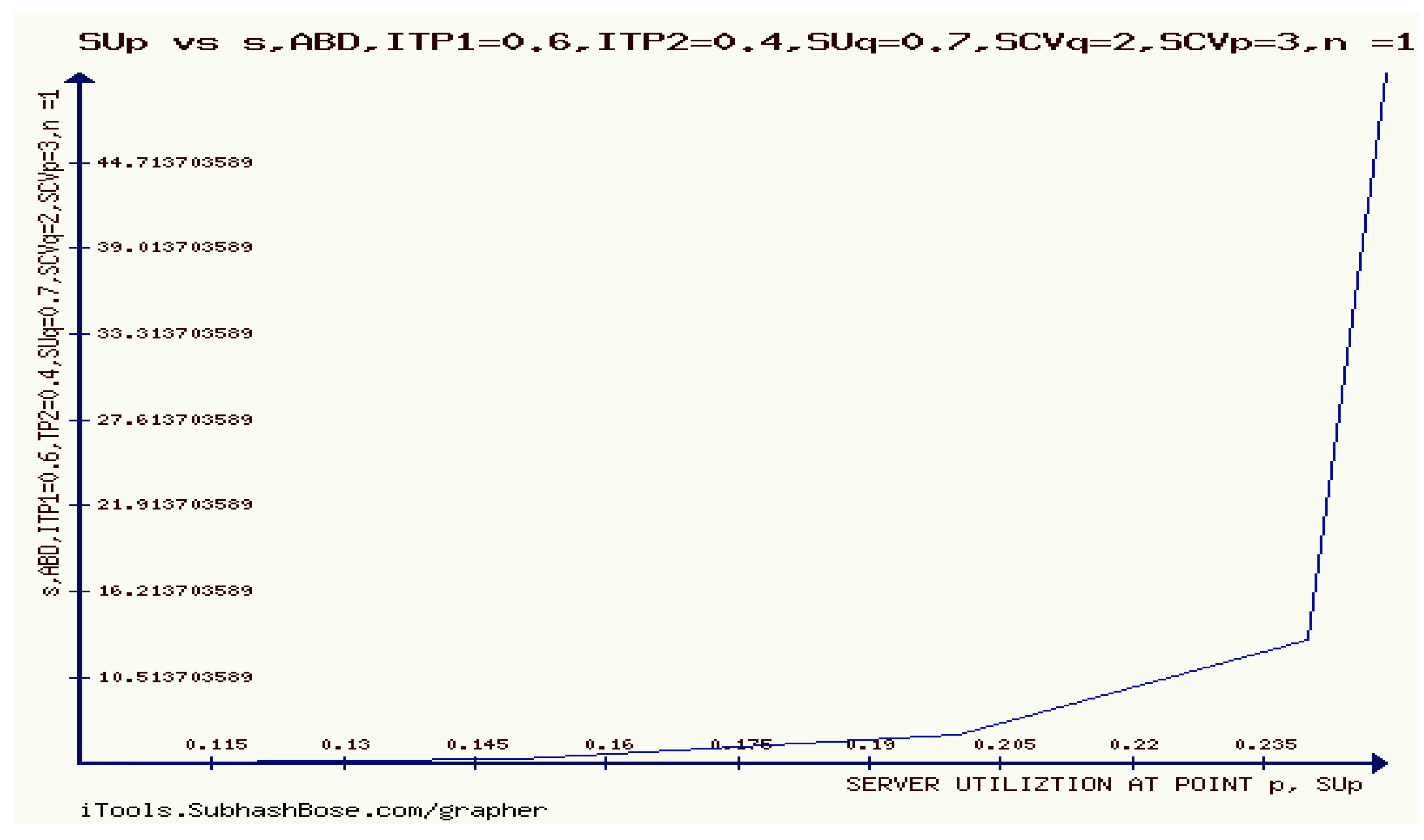
11. The Rényi divergence (RD), ${\mathit{D}}_{\mathit{R}}^{\mathit{\gamma }}\left(\mathit{p}\right|\left|\mathit{q}\right)$ and the S, AB-divergence, ${\mathit{D}}_{\mathit{s},\mathit{A}\mathit{B}}^{\mathit{\gamma },\mathit{\eta }}\left(\mathit{p}\right|\left|\mathit{q}\right)$of the KLF manifold

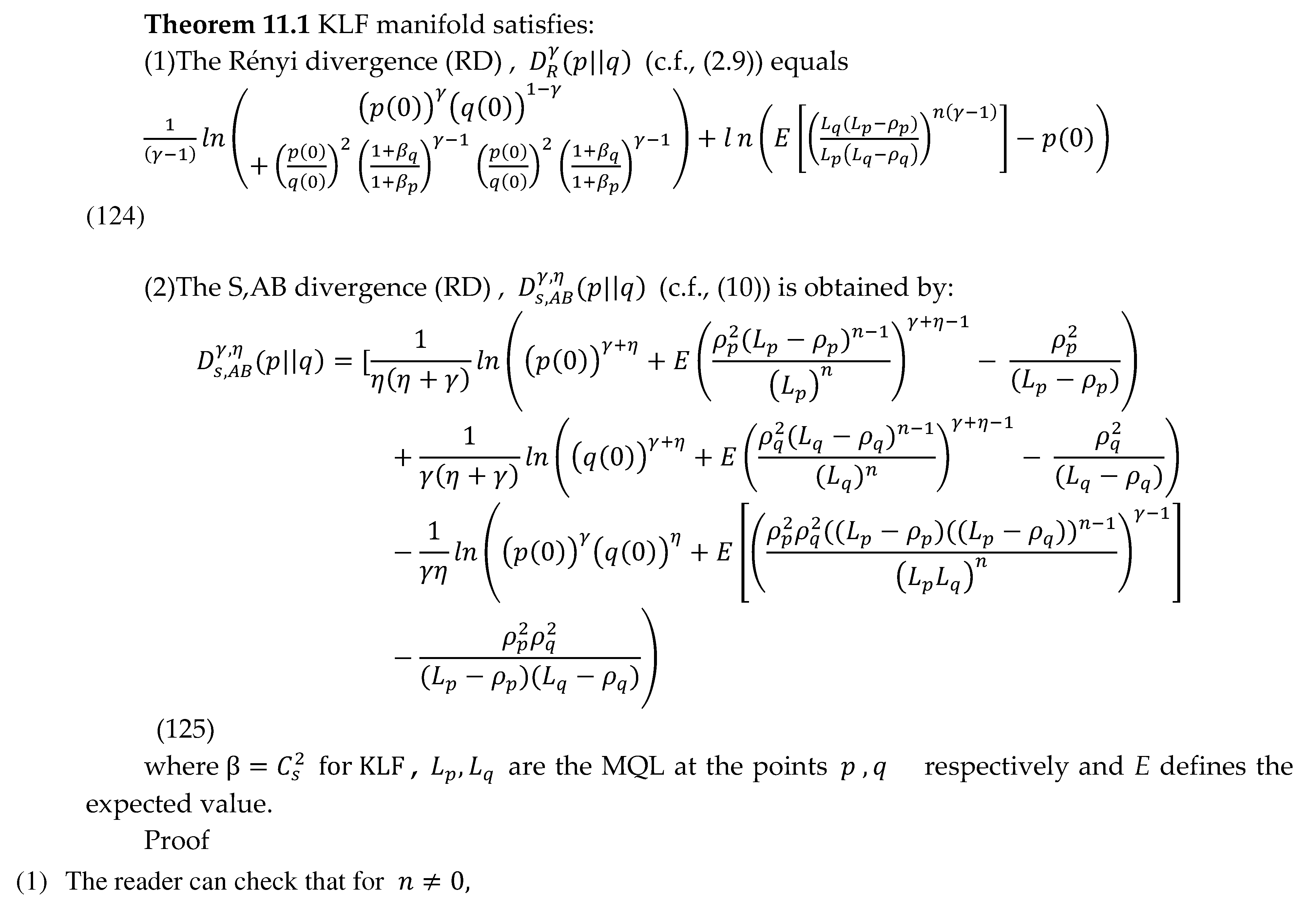
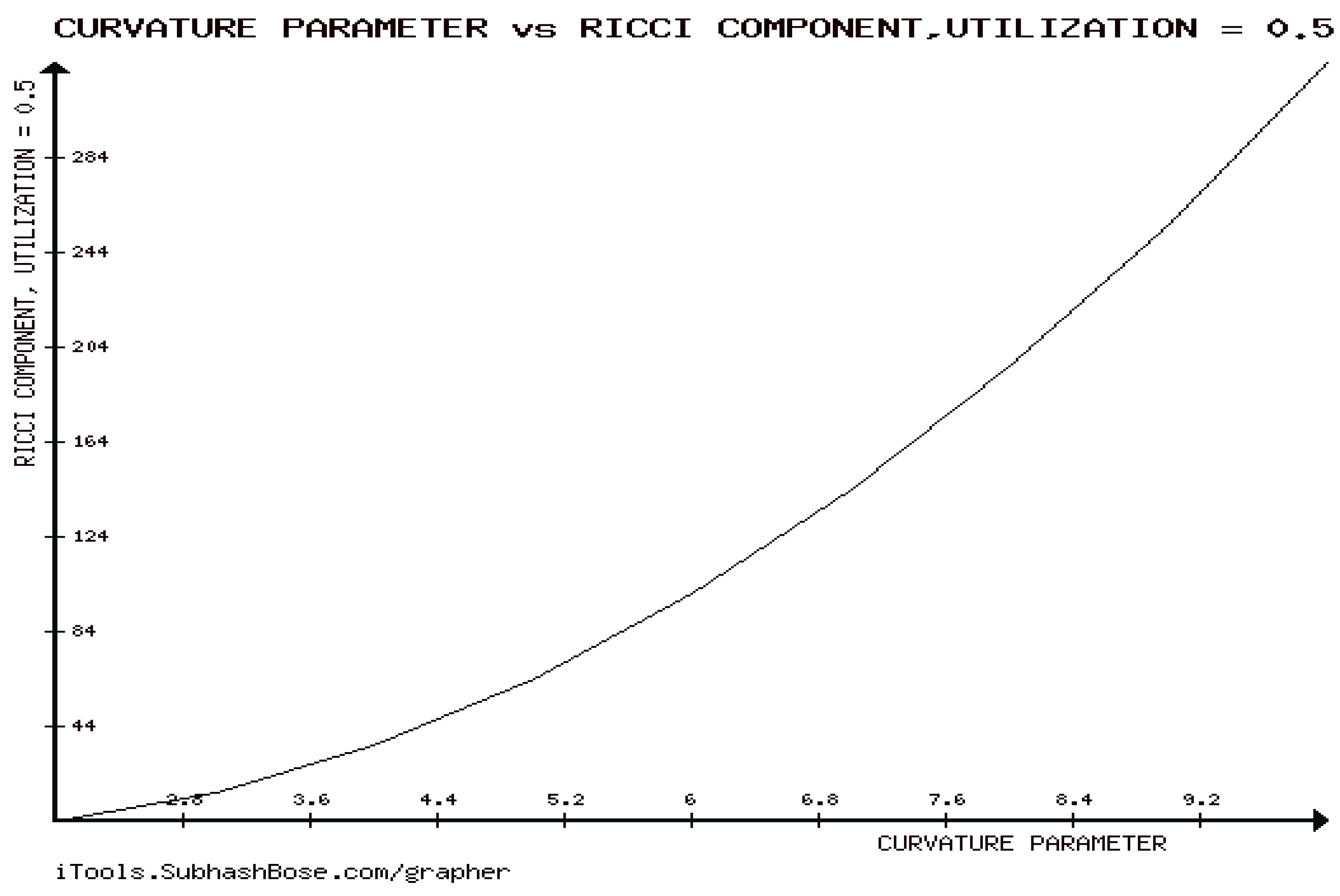
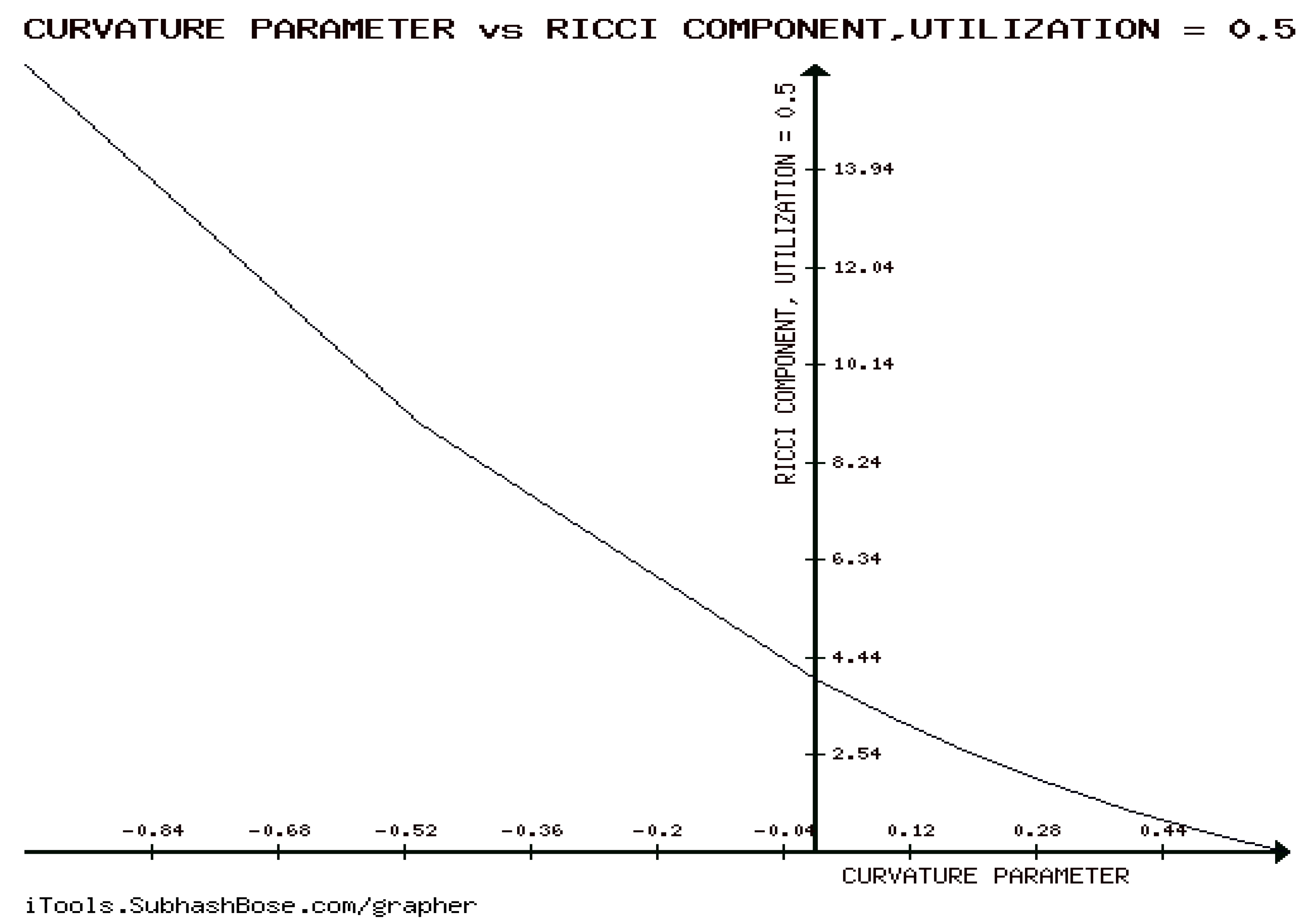
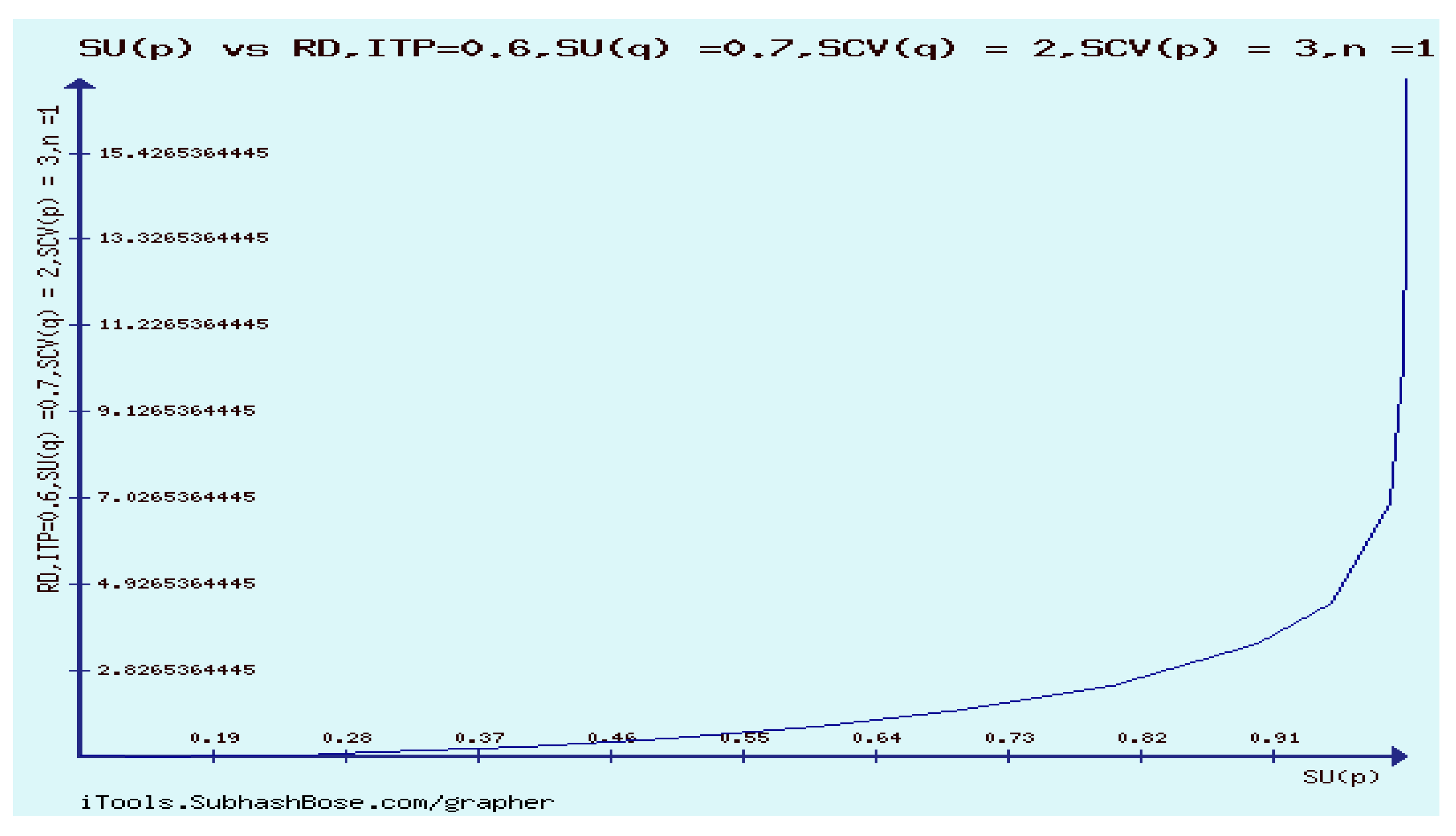
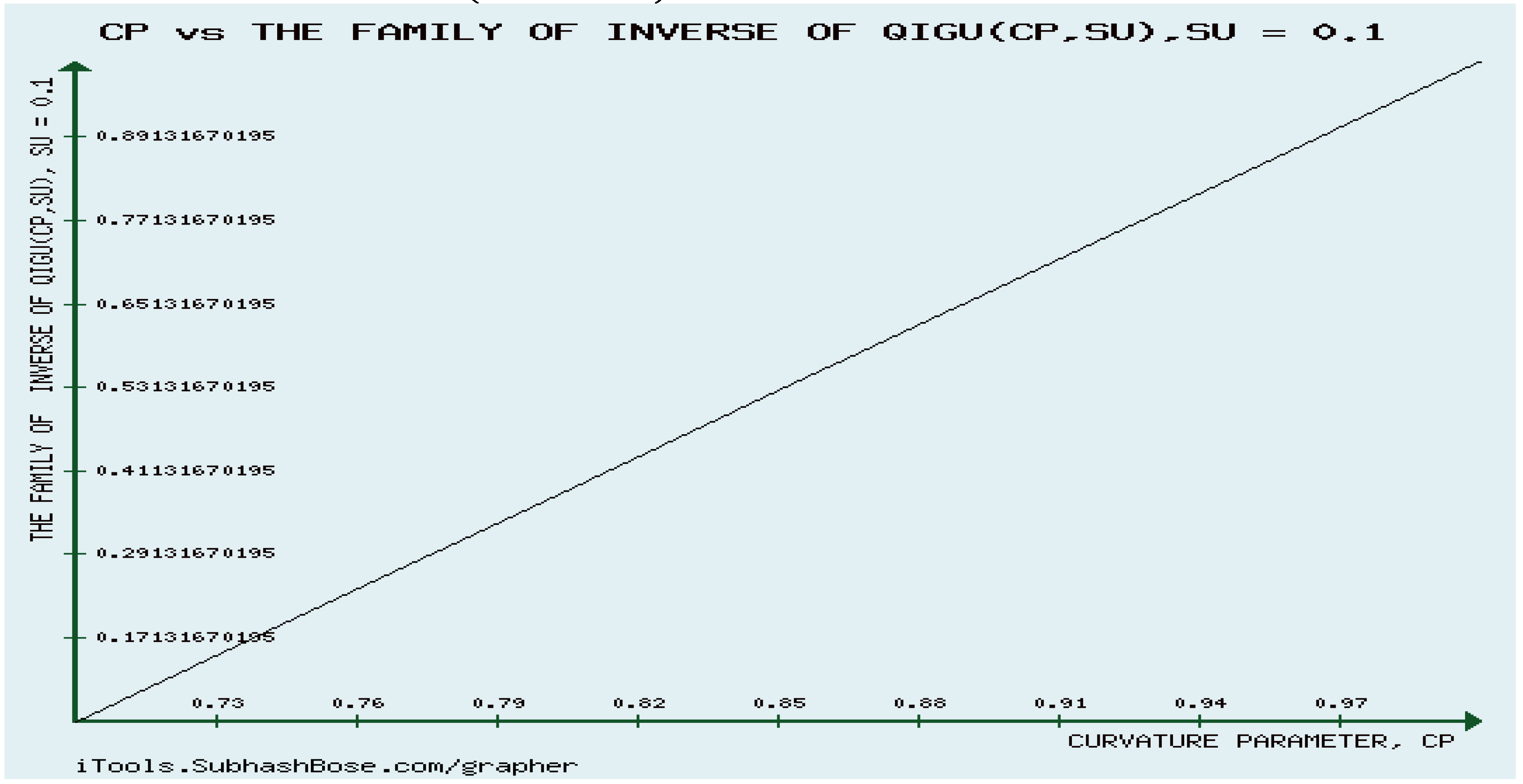
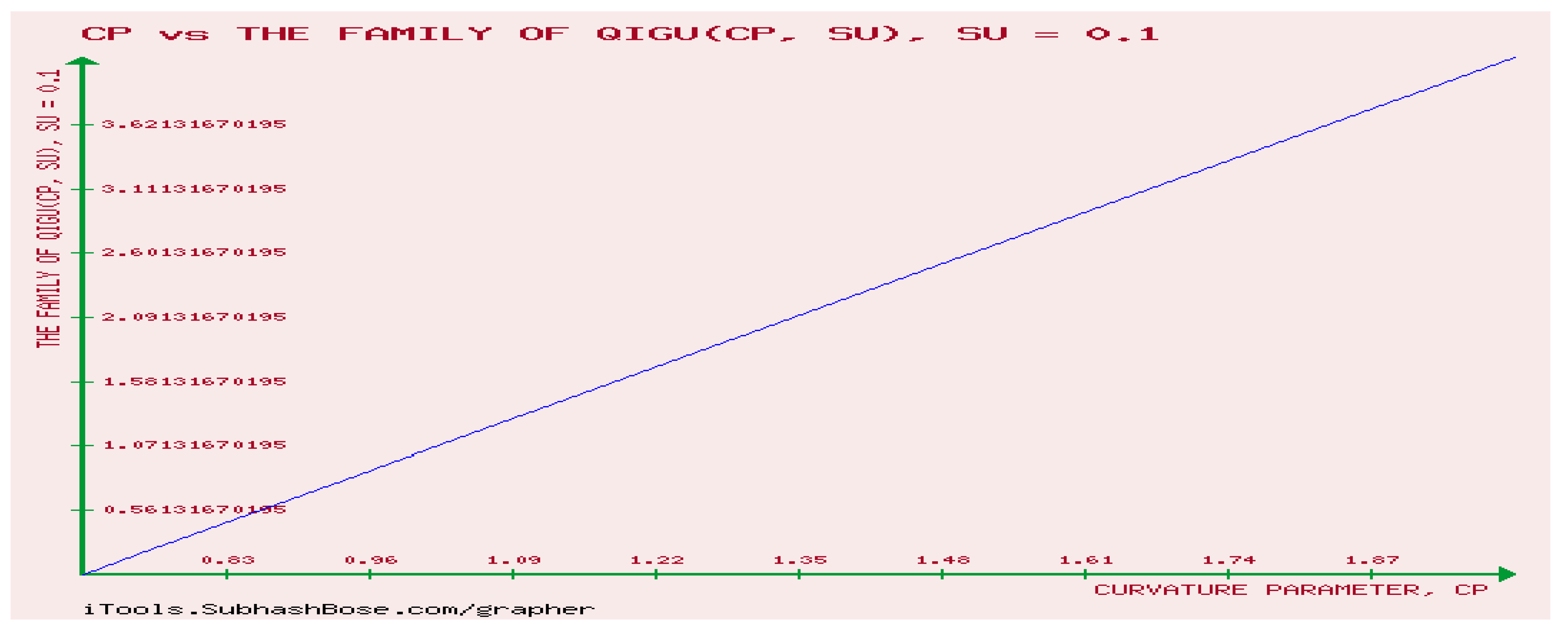
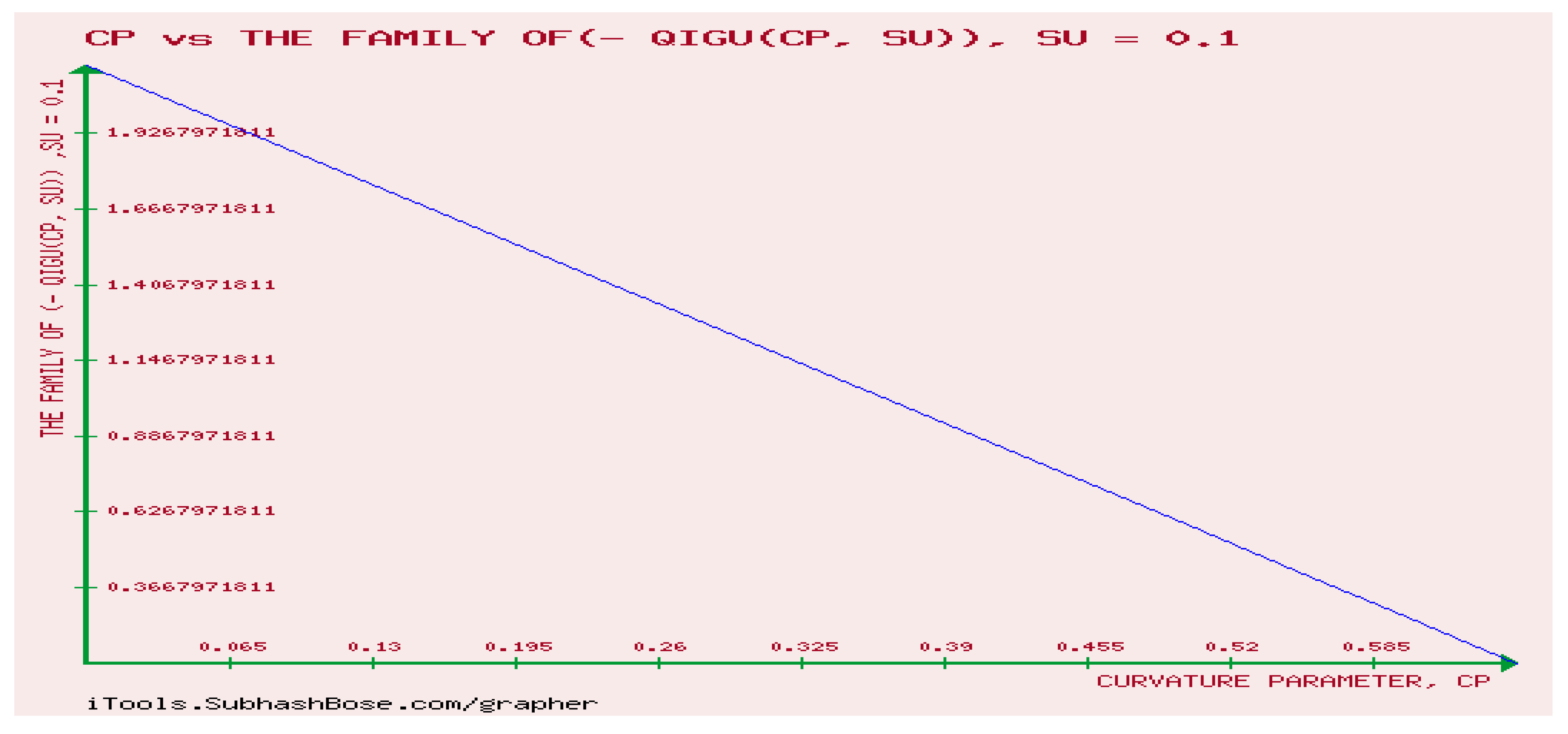
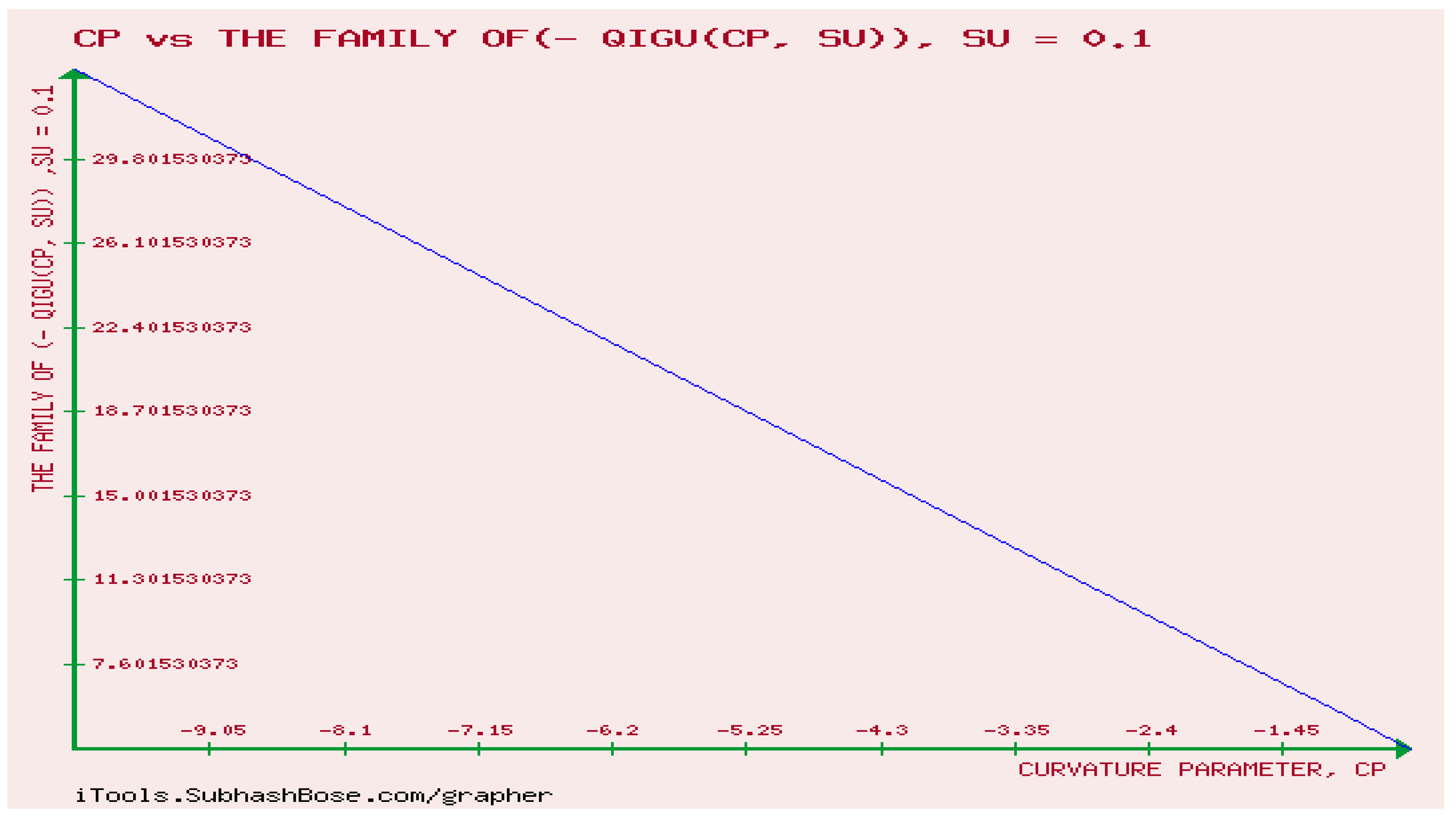
12. Numerical Experiments on The Rényi divergence (RD), ${\mathit{D}}_{\mathit{R}}^{\mathit{\gamma }}\left(\mathit{p}\right|\left|\mathit{q}\right)$ and the S, AB-divergence, ${\mathit{D}}_{\mathit{s},\mathit{A}\mathit{B}}^{\mathit{\gamma },\mathit{\eta }}\left(\mathit{p}\right|\left|\mathit{q}\right)$ of the KLF of stable M/G/ 1 QM

For non-extensive information theoretic parameter, ITP = $\gamma$, figure 10 records the physical phenomenon of increasability of RD by the increase of server utilization and progressively RD approaches infinity as server utilization approaches unity, which drifts the underlying M/G/1 into instability phase. It is slightly observable that at the lower values of server utilization, RD decreases. This is quite clear by observing figure 11. This clearly shows the queueing impact represented by server utilization   on RD.

It is observed by figure 12, that for extensive ITP, the dual information theoretic and queueing theoretic significant impact on RD is clear as RD decreases immensely by the increase of server utilization until it approaches $-\infty$ as server utilization approaches unity(instability phase). Combining all the numerical findings, RD is significantly influenced by both $\rho \mathrm{a}\mathrm{n}\mathrm{d}\gamma$.

The increasability of  $D_{s,AB}^{\mathrm{0.6,0.4}}\left(p\right|\left|q\right)$ is shown by figure 13 as in below. As  $\rho$ progresses to increase beyond 0.25, $D_{s,AB}^{\mathrm{0.6,0.4}}\left(p\right|\left|q\right)$ attains complex values.

13. Unification of Queueing Systems and KLF of stable M/G/ 1 QM

The following theorem is a groundbreaking functional approach which unifies queueing theory with IG.

Let $\rho =0.1,\alpha \in \left(1-\sqrt{0.1},1\right)=\left(\mathrm{0.683772234,1}\right)$. So, we have

Figure 14 supports the analytic findings as it shows the significant impact of the curvature parameter on the performance of the family of inverse of the functionals QIGU, queueing-information geometric unifiers.

Let $\rho =0.1\alpha \notin \left(1-\sqrt{0.1},1\right)=\left(\mathrm{0.683772234,1}\right)$. So, we have

Figure 15 shows the immense increase of ${\phi }_{\alpha }^{-1}\left(0.1\right)$  as $\alpha$ increases, until it approaches infinity for sufficiently large $\alpha ,$whereas in figure 16, $\alpha \notin \left(1-\sqrt{0.1},1\right)$, it is observed that ${\phi }_{\alpha }^{-1}\left(0.1\right)$ is negative and increasing . This is seen from figure 16.

Let $\rho =0.1\alpha \notin \left(1-\sqrt{0.1},1\right)=\left(\mathrm{0.683772234,1}\right)$. So, we have

More to the extreme, for negative values of $\alpha$, ${\phi }_{\alpha }^{-1}\left(0.1\right)$ increases by the increase of α, until it approaches $-\infty$ for sufficiently large α. this is recorded by figure 17

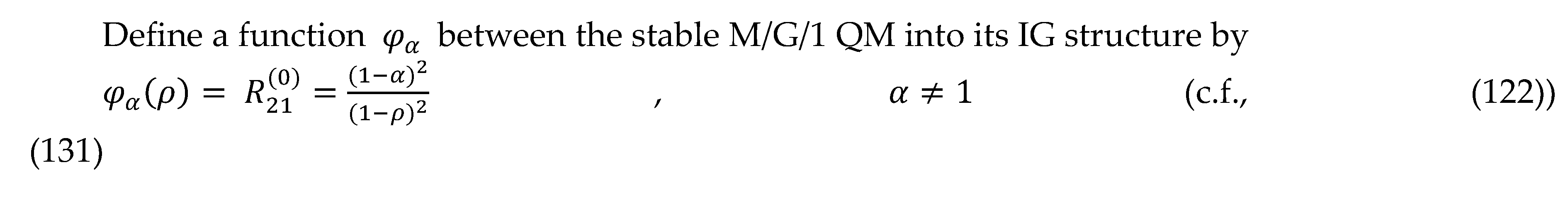
14. Statistical Queueing functionals (SQFs)of KLF of stable M/G/ 1 QM

There are several SQFs representations. In what follows, we introduce some novel well-defined SQFs and investigate their algebraic structures.

14.1. The first representation

14.2. The second representation

viii)Let $f_2\left(\rho \right)=\frac{1}{2}\left(1+\frac{\rho \zeta }{1-\rho }\right)=z$, $\rho \in (0,1)$.This implies $\rho =\frac{2z-1}{\left(2z-1+\zeta \right)}$.Consequently, $f_{2,\zeta }^{-1\mathrm{}}\left(\rho \right)=\frac{2\rho -1}{\left(2\rho -1+\zeta \right)}$ (c.f., (141))

14.3. The third representation

14.4. The fourth representation

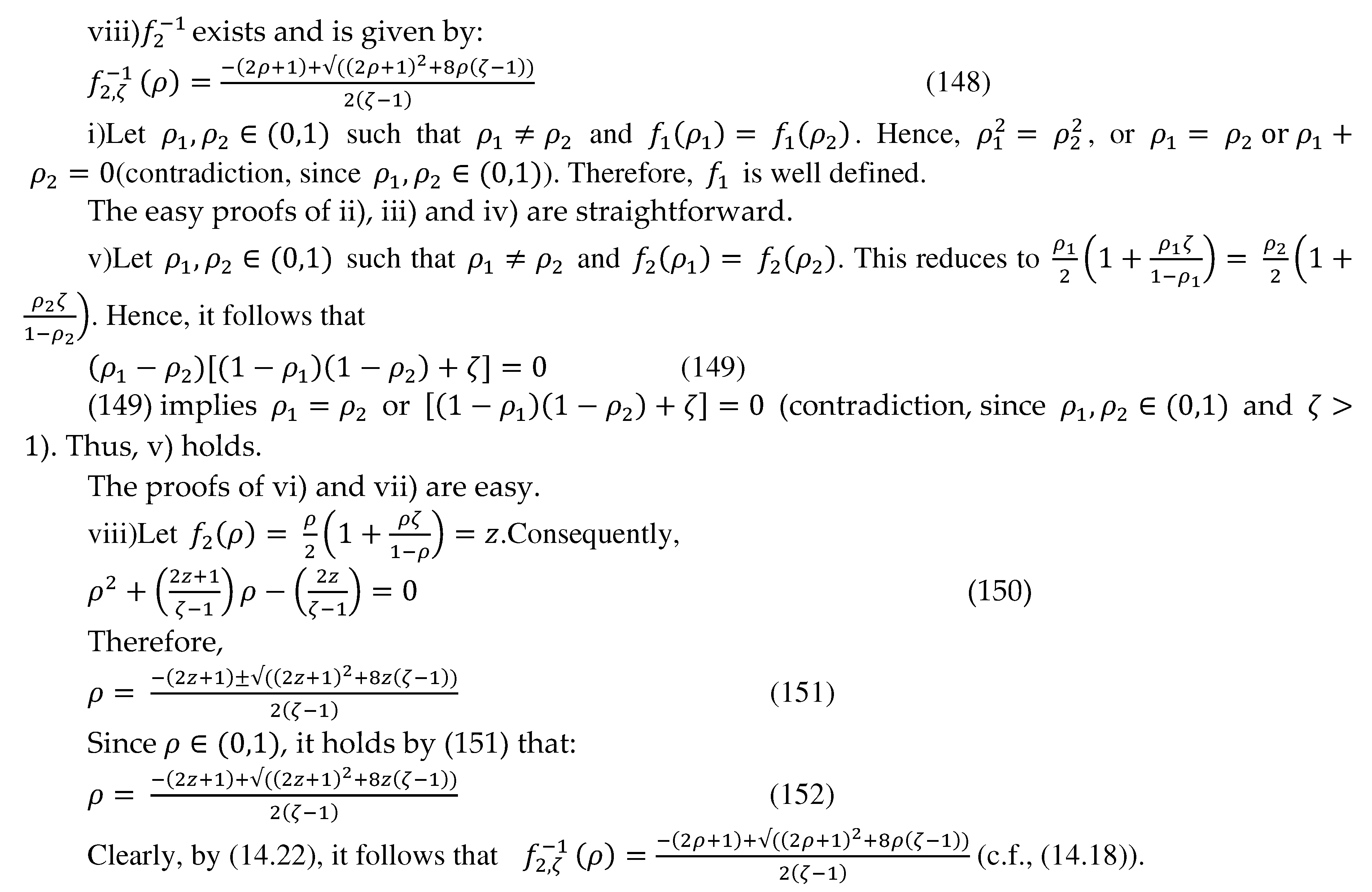
14.5. The fifth representation

15. Closing remarks and next phase of research

FIM, and $\alpha$-connection for KLDF manifold is presented. Geodesic equations, Kullback divergence, and J-divergence are also developed for this KLDF manifold. According to the findings, the  compressibility for the KLDF manifold is proven. Additionally, the underlying manifold  possesses a non-zero RCT. Furthermore, the exponential of the FIM is demonstrated to be a differential equation solution, and the work develops information geometric ties to provide queueing-theoretic unification with other mathematical disciplines.

1. Uniqueness

It is implied that  $\frac{\left({\mathrm{}\mathrm{h}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\right)}{q\left(N\right)}=1$, ln( $\frac{\left({\mathrm{}\mathrm{h}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\right)}{q\left(N\right)})=0$. This implies by (A.6), $\gamma >1,$ that  $\gamma \left(ln\gamma \right)=0$ (Contradiction)

$q\left(N\right)>$ ${\mathrm{}\mathrm{h}}_{\mathrm{K}\mathrm{L},\mathrm{N}}$

It is implied that  $\frac{\left({\mathrm{}\mathrm{h}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\right)}{q\left(N\right)}<1$, ln( $\frac{\left({\mathrm{h}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\right)}{q\left(N\right)})<0$.  Hence, KL divergence is negative , which contradicts that fact that KL divergence is non-negative(c.f.[57]).

Therefore., “there cannot be two distinct probability distributions ${\mathrm{f}}_{\mathrm{k}\mathrm{L},\mathrm{N}},\mathrm{}{\mathrm{h}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\mathsf{ϵ}\mathsf{\Omega }$having the same KL divergence measure in $\mathsf{\Omega }$.Thus, KL formalism satisfies the axiom of uniqueness (c.f., [6]).

2. Invariance

The invariance axiom states that “The same solution should be obtained if the same inference problem is solved twice in two different coordinate systems” (c.f., [58]).Following the analytic methodology proposed in and adopting the notation of Subsection 1, let $\mathsf{\Xi }$be a coordinate transformation from state $\{{\mathrm{S}}_{\mathrm{n}},\mathrm{}\mathrm{n}=\mathrm{1,2},\dots ,\mathrm{N}\}$ to state $\{{\mathrm{M}}_{\mathrm{n}},\mathrm{}\mathrm{n}=\mathrm{1,2},\dots ,\mathrm{N}\}$, where Mbe a transformed set of N possible discrete states, namely $\mathrm{M}=\left\{{\mathrm{M}}_{\mathrm{n}},\mathrm{}\mathrm{n}=\mathrm{1,2},\dots ,\mathrm{N}\right\}$with$\Gamma ({\mathrm{p}}_{\mathrm{K}\mathrm{l},\mathrm{N}}\left({\mathrm{M}}_{\mathrm{n}}\right)$= ${\mathsf{\Xi }}^{-1}({\mathrm{p}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\left({\mathrm{S}}_{\mathrm{n}}\right)$, where J is the Jacobian$\mathrm{J}=\frac{\partial \left({\mathrm{M}}_{\mathrm{n}}\right)}{\partial \left({\mathrm{S}}_{\mathrm{n}}\right)}$. Moreover, let $\mathsf{\Gamma }\mathsf{\Omega }$be the closed convex set of all probability distributions $\mathsf{\Gamma }$ defined on M such that $\mathsf{\Xi }\left({\mathrm{p}}_{\mathrm{K}\mathrm{l},\mathrm{N}}\left({\mathrm{M}}_{\mathrm{n}}\right)\right)$> 0 for all ${\mathrm{M}}_{\mathrm{n}}\mathrm{}\mathsf{ϵ}\mathrm{}\mathrm{M}$, n = 1, 2, ...,Nand$\sum _{\mathrm{n}=1}^{\mathrm{N}}\mathsf{\Xi }\left({\mathrm{p}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\left({\mathrm{M}}_{\mathrm{n}}\right)\right)=1.\mathrm{}\mathrm{}$It can be clearly seen that, transforming variables from ${\mathrm{S}}_{\mathrm{n}}$∈ S into${\mathrm{}\mathrm{R}}_{\mathrm{n}}$∈ R, the extended  KL divergence (c.f., (2.1)) is transformation invariant namely

${\mathrm{H}}_{\mathrm{K}\mathrm{L}}^{\mathrm{*}}\left({\mathrm{}\mathrm{p}}_{\mathrm{K}\mathrm{L},\mathrm{N}}\right)=\mathrm{}{\mathrm{H}}_{\mathrm{K}\mathrm{L}}^{\mathrm{*}}\left(\mathsf{\Xi }\left({\mathrm{p}}_{\mathrm{K}\mathrm{L},,\mathrm{N}}\right)\right)$(A.7)

Thus, the EME formalism satisfies the axiom of invariance since the minimum in$\mathsf{\Xi }\mathsf{\Omega }$ corresponds to the minimum in $\mathsf{\Omega }$” (c.f., [57]).

3. System Independence

4. Subset Independence(SI)

SI in a physical interpretation reads as “It does not matter whether one treats an independent subset of system states in terms of a separate conditional density or in terms of the full system density” (c.f., [59]).

In the given context, the notation and concepts related to an aggregate state of a system, denoted as x, and its associated probability distribution ${\mathrm{f}}_{\mathrm{K}\mathrm{l}}\left(\mathrm{x}\right)$. The probability distribution represents the likelihood of the random variable X taking the value x. The text also mentions that the aggregate states ${\mathsf{\xi }}_{\mathrm{i}}$, where$i$ ranges from 1 to L, can be expressed using this notation.