Prerpints.org logo
Preprint
Article

Numerical Simulation of Cavitation Control around a Circular Cylinder Using Porous Surface by Volume Penalized Method

Altmetrics

Downloads

87

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 January 2024

Posted:

25 January 2024

You are already at the latest version

Alerts
Abstract
In this work, we conducted a numerical study on the cavitation flow around a circular cylinder through the implementation of a porous coating. The primary objective addressed the effectiveness of utilizing a porous surface to control cavitation. We analyzed the cavitation dynamics around the cylinder and the hydrodynamic performance at different permeability levels of the porous surfaces. The flow was governed by the density based homogeneous mixture model and the volume penalization method was used to deal with the porous layer. A high-order accurate numerical method was adopted for the simulation of the cavitating flow through solving the preconditioned multiphase equations. The results revealed that the application of porous layer led to effective suppression of the cavitation vortex shedding. In addition, a reduction of the shedding frequency was obtained which accompanied by thinner and elongated vortices in the wake region of the cylinder. With the proper porous layer, the inception of the cavitation on the cylinder was suppressed and the amplitude of pressure pulsations due to the cavitation shedding mechanism was mitigated.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

The formation and subsequent collapse of vapor bubbles in a fluid can have detrimental effects on various engineering systems, including propellers, rudders, pumps, impeller and hydraulic turbines. Over the years, multiple numerical and experimental investigations have been conducted to unveil the mechanisms of cavitation around the cylinders, including the previous works by [1,2,3,4,5]. The phenomenon of cavitation can lead to significant damage and erosion on the solid boundaries, hydrodynamic efficiency reduction, and increasing of the noise and vibration on the immersible bodies [6,7]. To mitigate these undesirable effects, engineers have been exploring various methods to control and suppress the cavitation and its destructive effects. There have been several proposed methods for controlling the cavitation dynamics on the immersible bodies, which can be classified as either active or passive control method. Active control methods involve introducing additional force or momentum to the low-energy boundary layer, such as through the use of air injection or synthetic jets [8,9]. They employed synthetic jet actuators to effectively mitigate cavitation occurring on hydrofoils. Their results showed that the active control method can reduce the adverse effects of the cavitation during the operation of the hydrofoils.
By generation of controlled air or fluid jets through synthetic jet actuators, the cavitation dynamics and pressure pulsations around the hydrofoil can be manipulated at the cavitating regimes. Timoshevskiy et al. [10] found that tangential injection of liquid from the middle of a hydrofoil surface can effectively suppress cavitation. They presented that their technique is a promising way to suppress the partial unsteady cavity and cavitation cloud. In addition, the pressure fluctuations in the cloud cavitation regime was mitigated using the fluid injection. Despite the considerable advantages that active flow control methods, active methods need external energy sources and the implementation of air/water injection systems, adding complexity to the manufacturing process and limiting their applicability in long-distance navigation scenarios. It is worth noting that passive control methods for cavitation manipulation have attracted more attention due to their practicality and effectiveness compared to active approaches [11,12,13,14,15,16]. Kadivar et al. [17,18] studied the control of unsteady cloud and cavitation surge using different types of the vortex generators mounted on the surface of hydrofoils. They used wedge-type and hemispherical-type vortex generators to control the pressure pulsations due to the cavitation on the hydrofoils.
Modifying the surface properties, such as applying porous coatings to the body’s surface, has proven to be an effective and promising strategy for control of the cavitation. This approach involves altering the physical characteristics of the surface, introducing porous structures that can disrupt the formation and collapse of vapor bubbles in the cavitating flow [13]. The porous layer allows the fluid to penetrate into its structure, effectively reducing the pressure fluctuations and preventing the formation of the large-scale cavity structures. By introducing a porous layer, the cavitating flow is forced to pass through the interconnected pores, dissipating the energy of the flow and suppressing cavitation. Yu et al. [13] experimentally and numerically studied the dynamics of an unsteady cavitation around a hemisphere cylinder with and without porous layer. They concluded that the porous layer can suppress the cavitation inception and vortex structures around the cylinder. They indicated that different factors of the porous layer such as material properties, pore size, pore distribution, and porosity can influence the effectiveness of porous layers for control of the cavitation. Additionally, the thickness and surface roughness of the porous layer play a crucial role in determining the flow characteristics [14]. The ability to handle complexities in the geometry of porous layers, accurately and efficiently are the main issues in the computational fluid dynamics. To address these complexities, the Immersed Boundary Method (IBM) has emerged as an effective approach [19,20,21,22,23].
Within this methodological framework, the volume penalization technique, which is categorized as an immersed boundary method, plays a main role to simulate flow around complex geometries [21]. The volume penalization technique is particularly useful when dealing with flow problems that involve solid obstacles or porous media, where the grid generation or meshing can be challenging. In this technique, the flow domain is divided into two regions: the fluid region and the obstacle region. The flow equations, typically the Navier-Stokes equations, are solved over the entire domain, however a penalization term is introduced in the governing equations within the obstacle region [21]. This penalization term enforces the no-slip boundary condition and simulates the presence of the solid obstacle or porous medium. It essentially acts as a forcing term to account for the presence of the solid structure, ensuring that the flow behaves as if the porous medium is present [22].
Although numerous studies were performed to control cavitation on hydrofoils using passive flow control methods, numerical simulation of the porous layer potential as a cavitation control mechanism in a typical test case such as a circular cylinder has not received extensive attention in previous researches. Consequently, there is a significant gap in the existing literature regarding a comprehensive numerical investigation of this particular cavitation control strategy. For this research topic, fluid dynamics, materials science, and computational modeling are integrated to simulate and quantify the effect of porous surfaces on the cavitation control around blunt bodies. In the scope of our present research, one of the primary objective was to conduct a comprehensive investigation of the influence of the permeability of a porous layer with a certain thickness on control of the cavitation around a circular cylinder. To achieve this aim, we employed numerical simulation techniques, allowing us to explore and understand the dynamics of cavitation phenomenon around the circular cylinder with and without porous layers. The rest of the present work is organized as follows: the solution methodology based on the penalized Navier–Stokes equations with the homogeneous mixture model and numerical procedure are presented in the Section 2. Validation and results are discussed in the Section 3. Finally, the conclusions are given in the Section 4.

2. Methodology

In this research, the penalized Navier–Stokes equations for porous media was utilized, as proposed by [23], to simulate two-phase flow in the presence of the porosity. Furthermore, our study incorporates the homogeneous mixture model [24], which assumes that the phase mixture behaves as a single compressible fluid. Within this model, a linear combination of liquid and vapor densities was considered while assuming isothermal conditions and local kinematic equilibrium between the phases:
∂ ρ ∂ t + ∂ ∂ x j ρ u j = − 1 ∅ − 1 χ ∂ ∂ x j ρ u j
∂ ρ u i ∂ t + ∂ ∂ x j ρ u i u j = ∂ p ∂ x i + ∂ τ i j ∂ x j − χ μ K u i − u i 1 ∅ − 1 χ ∂ ∂ x j ρ u j
∂ ρ Y ∂ t + ∂ ∂ x j Y u j = 0
the last term in the right side of the continuity equation (equation 1) and last two terms in the right side of the momentum equations (equation 2) are a volume penalization of the flow inside the body. Here, ∅ is the porosity and μ is the mixture viscosity. The permeability denoted as K , is determined by the structural of porous materials. The permeability signifies the material’s capacity to allow the flow of fluids or gases through its porous structure. Following the homogenous equilibrium model for compressible two-phase gas-liquid systems [24], the mixture density ρ is expressed as a linear combination of gas density ρ g and liquid density ρ l   in the following manner:
ρ = 1 − α ρ l + α ρ g
The relationship between the void fraction α and the gas mass fraction Y can be described as follows:
1 − Y = 1 − α ρ l / ρ
Y = α ρ g / ρ
In the case of a pure liquid phase, the equation of state is described as follows [25]:
p + p c = ρ l k T + T c
For the vapor phase, the ideal gas equation of state is assumed:
p = ρ g R T
where p c = 1944.61 M P a , T c = 3837 K , k = 472.27 J / k g K and R = 462 J / k g K are the pressure, temperature, liquid and gas constants, respectively. The mixture viscosity is expressed by [25]:
μ = 1 − α 1 + 2.5 α μ l + α μ g
In the penalization technique, the mask function χ is defined as follows:
χ = 1   i n s i d e   t h e   r i g i d   b o d y 0                                           o t h e r w i s e s
When χ = 0 , the ordinary Navier–Stokes equations are regenerated. For the spatial derivatives, the fourth-order compact finite-difference method [26] is applied and to avoid the oscillatory solutions, the high-order low-pass spatial filter [27] has been applied to the solution.
Two-phase flows, marked by significant sound speed variations due to the varying compressibility of the liquid and the two-phase mixture, pose a challenge in simulation. Demonstrating a solution, a preconditioned technique is established. The governing equations (1)-(3) with preconditioning are rewritten in the vector form as:
Γ ∂ W ∂ τ + ∂ Q ∂ t + ∂ F j ∂ x j = S
where, t is the physical time, τ is a pseudo-time, W and Γ are the primitive variable vector and Jacobian matrix, respectively. Q is the conservative vector, F is the flux vector and S is the penalized term. For the two-dimensional flows, the vectors and matrix are defined as:
W = P u v Y Q = ρ ρ u ρ v ρ Y
F = ρ u j ρ u u j + p δ i j + τ 1 j ρ v u j + p δ 2 j + τ 2 j ρ u j Y , S = − 1 ∅ − 1 χ ∂ ∂ x j ρ u j − χ μ K u − u 1 ∅ − 1 χ ∂ ∂ x j ρ u j − χ μ K v − v 1 ∅ − 1 χ ∂ ∂ x j ρ u j 0
Γ = ρ p ρ 0 ρ Y u ρ p ρ 0 u ρ Y v ρ p ρ 0 v ρ Y Y ρ p ρ 0 Y ρ Y + ρ
Here, ρ p = ∂ ρ ∂ p | T , which represents inverse of the square of the isothermal speed of sound. Also ρ Y = ∂ ρ ∂ Y | T = ρ 2 1 ρ l − 1 ρ g . To ensure reliable accuracy, ρ p in Γ is replaced by ρ ´ p = 1 u ∞ 2 and preconditioning matrix Γ P is introduced as follows [28]:
Γ P = ρ ´ p ρ 0 ρ Y u ρ ´ p ρ 0 u ρ Y v ρ ´ p ρ 0 v ρ Y Y ρ ´ p ρ 0 Y ρ Y + ρ
The second-order backward differencing for the physical-time derivative and explicit Euler for the pseudo-time derivative [29] is applied.
Γ P W m + 1 − W m ∆ τ + 3 Q n + 1 − 4 Q n + Q n − 1 2 ∆ t = R H S m
R H S m = S ( Q m ) − ∂ F j ( Q m ) ∂ x j
In this paper, n denotes the index for physical time, while m represents the index for pseudo-time (see [29] for more details).

3. Results and Discussion

In this section, the flow field over an isolated circular cylinder at Re=200 and cavitation numbers σ = 1 was governed with porous layer thickness h = 0.3 D and porosity φ=0.98. The cavitation number σ and Reynolds number Re was given by σ = p 0 − p v / 0.5 ρ 0 u 0 2 and R e = ρ 0 u 0 D / μ 0 . A small void fraction of α o = 0.01 was used to start the cavitation. Considering that the cell diameter of the porous material was in the micrometer orders, the permeability K typically spans from 10 − 12 to 10 − 9 m 2 [30]. Indeed, as K decreases, the fluid permeability to the porous layer diminishes, and it assumes a more solid-like behavior. A rectangular grid system with non-uniform spacing was applied for the mesh type. 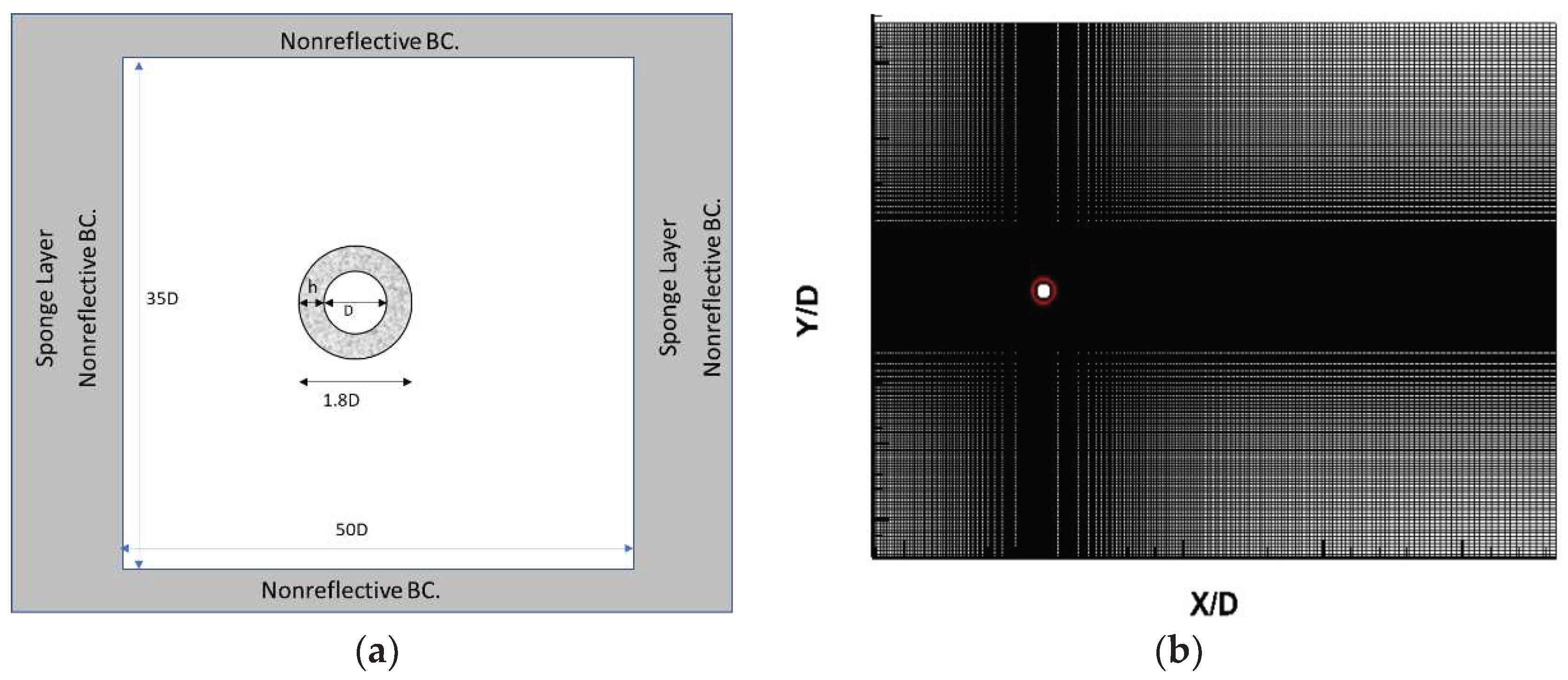The non-reflective boundary conditions presented by Tam and Dong [31] are imposed for all the free boundaries. To remove the possible reflections from the boundaries, the sponge layer with the grid stretching was utilized. The computational domain is presented schematically in Figure 1.

3.1. Validation

In order to examine the accuracy and efficiency of the methodology, we firstly considered single phase flow around the circular cylinder with Re=150. The Mach number of uniform flow was set to 0.2. The cylinder was wrapped by a porous layer with a thickness   h = 0.4 D . In order to compare the results with the available data, we assumed 1 / η = μ K in Eq. (2) is constant. 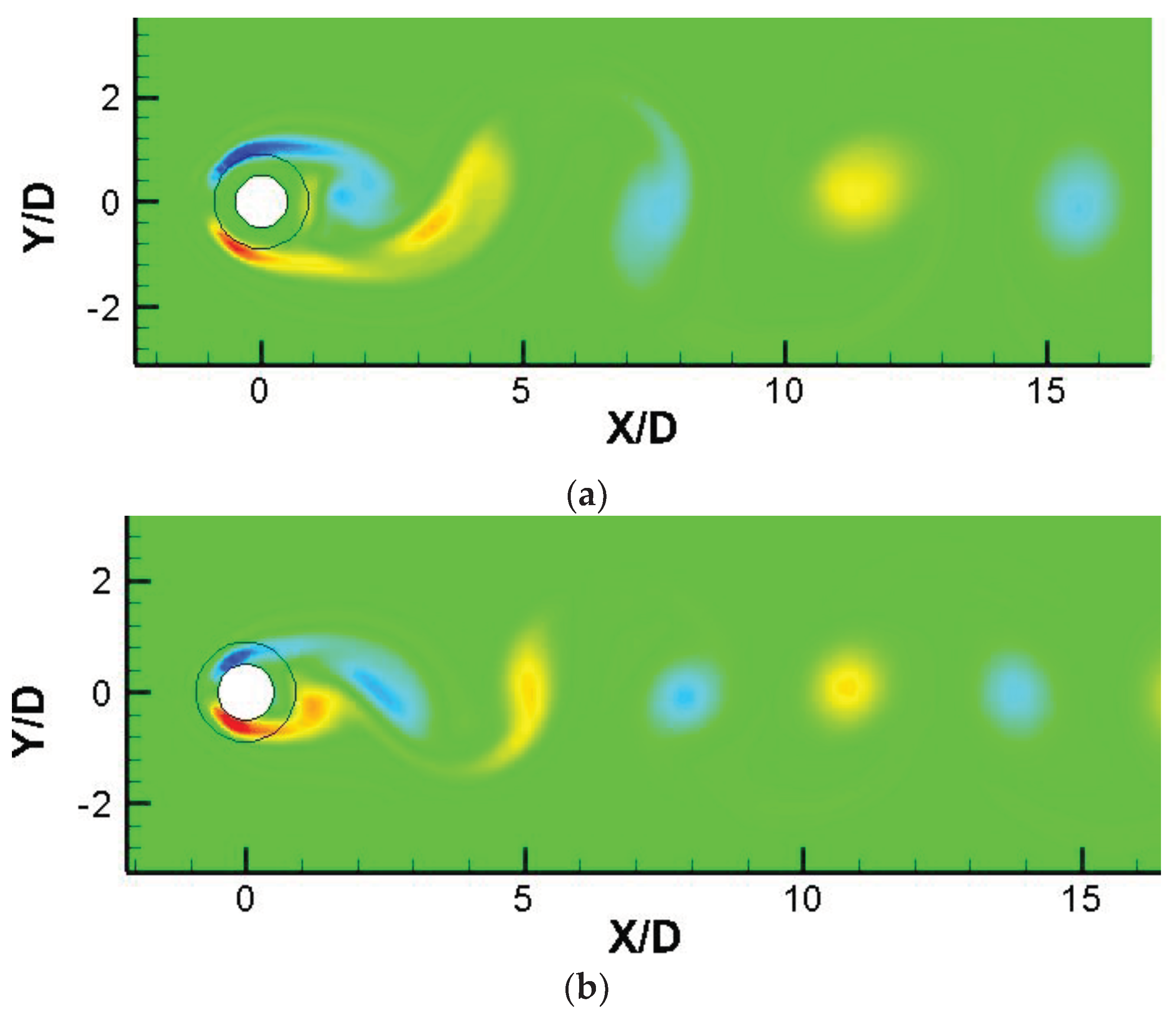Three values of η = 10 − 3 , 10 and η = 10 3 , with porosity φ=0.98 are studied for the corresponding simulation. For better understanding the effect of permeability on the aerodynamic results, the instantaneous spanwise vorticity fields of cylinders covered by the porous layer of different η are shown in Figure 2. The outer solid line represents the porous layer. It can be observed, when the permeability is very low ( η = 10 − 3 ), the porous materials act like solid, and the vortex shedding happens from the surface of the porous coating. In contrast, when the permeability is quite high η = 10 3 , the porous materials act like pure fluid and the vortex shedding occurs around the inner solid cylinder. At η = 10 , shear flow around the body is slightly deviated towards the outer layer, resulting in an attenuation of the vortex strength.
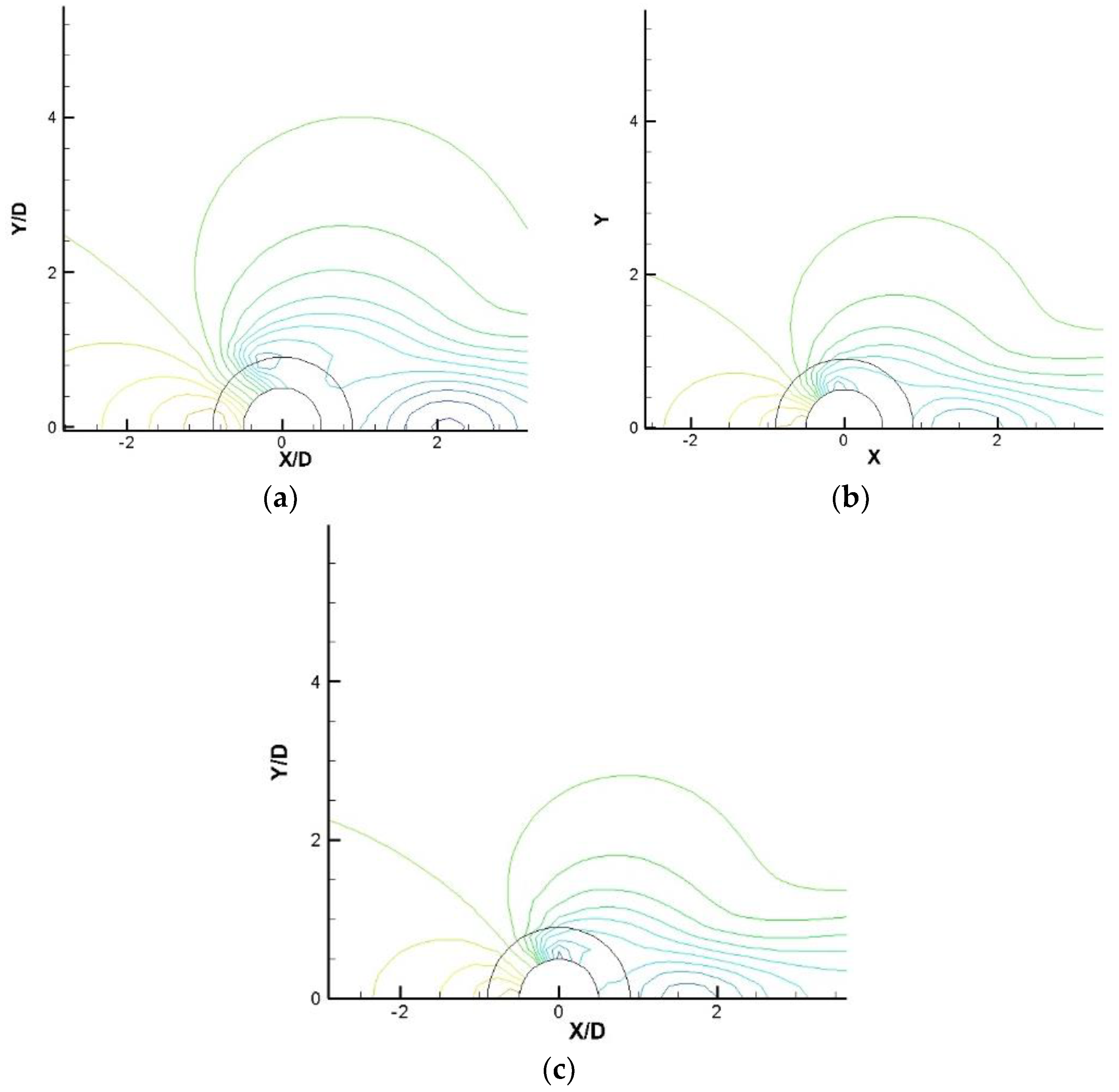
In Figure 3, the time-averaged pressure contours for the smooth cylinder ( η = 10 3 ), the porous cylinder ( η = 10 ), and the larger cylinder ( η = 10 − 3 ) are displayed. It is evident that the presence of the porous layer results in a weakening of the low-pressure zones. In the cylinder with extremely low permeability, the low-pressure zone shifts towards the outer layer of the porous material. 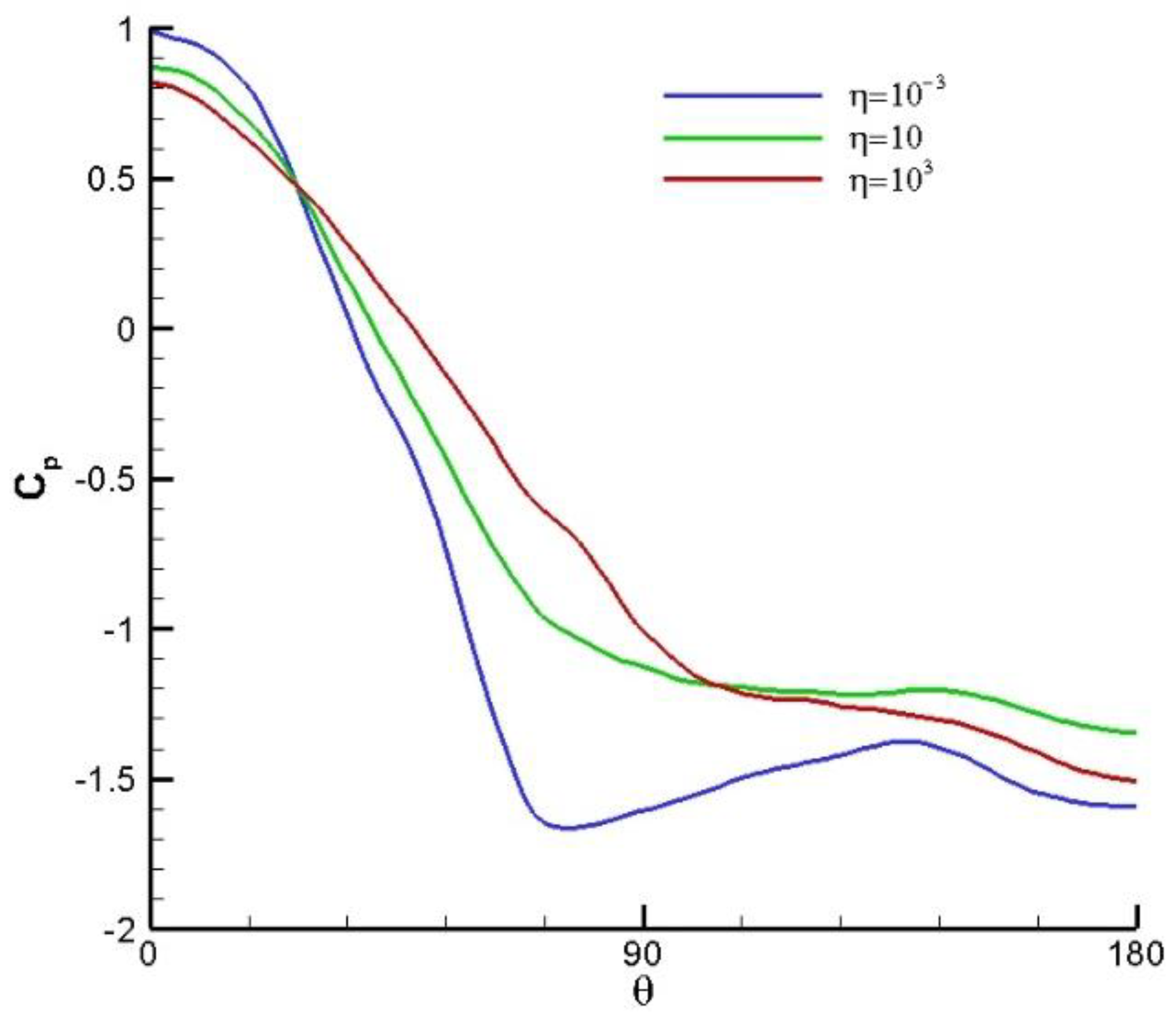Figure 4 displays the mean pressure coefficient C p around the cylinder at the porous layer. Despite the increased windward pressure at η=10 when compared to the smooth cylinder, the presence of porosity leads to a recovery in the pressure coefficient on the leeward side of the cylinder. Table 1 shows the drag coefficient C d , which is match well with the previous works [32] at the single-phase flow around the circular cylinder.

3.2. Grid-Independence Study

To ensure the grid independence, three different mesh types were created with varying grid resolutions: coarse, medium, and fine meshes. These meshes were designed for the comparison purposes. The grid numbers for each mesh type in the context of a smooth cylinder case are outlined in Table 2. The grid size dependency is represented by the drag coefficient ( C d ) and the Strouhal number (St), reflecting the sensitivity of the hydrodynamic characteristics to variations of the grid resolution. The comparison between the results obtained from the medium mesh and the fine mesh indicated only a minor discrepancy. Therefore, the medium mesh was selected for subsequent numerical simulations proved to be adequate. This decision was made to optimize computational resources and reduce costs while still maintaining an acceptable level of accuracy in capturing the essential flow dynamics.

3.3. Results

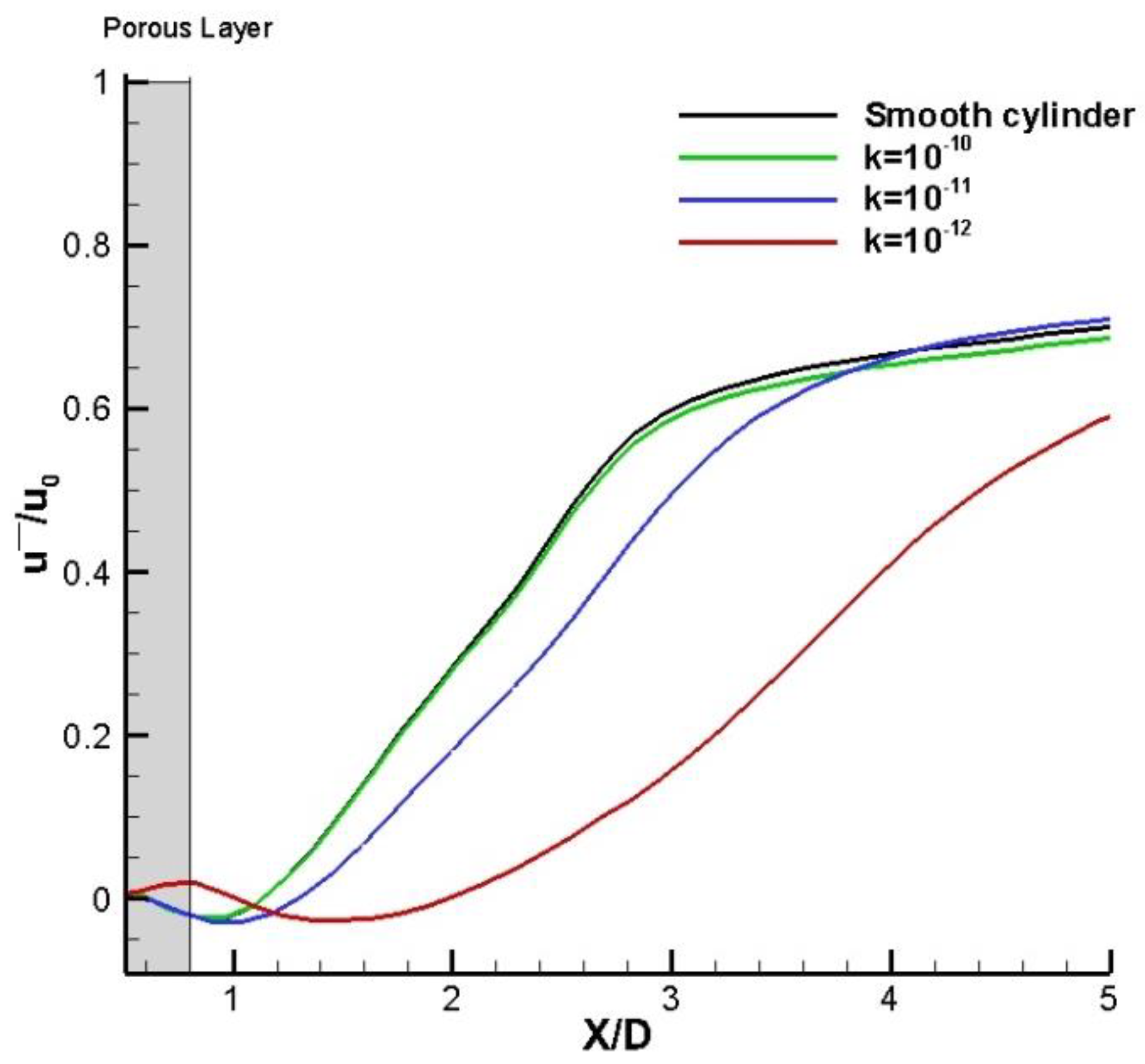
In this section, the hydrodynamics and the results of the cavitating flow over an isolated circular cylinder are presented. Unlike the previous section, μ K is not constant here because the viscosity of the mixture varies within the field. Therefore, the permeability changes are considered for values of K = 10 − 12 , 10 − 11 , 10 − 10 . Figure 5 displays the time-averaged streamwise velocity along the centerline. There is a negative velocity region downstream of the cylinder, which is actually a distinct recirculation zone. For the smooth cylinder, the velocity reaches its minimum value around X / D = 0.9 . Beyond this point, the flow velocity gradually begins to recover and increase along the downstream range at X / D = 0.9 . As observed in streamwise velocity profile, the porous covering with low permeability exhibits a shift in the minimum flow velocity from the cylinder surface compared to the smooth cylinder. At K = 10 − 11 , the minimum velocity shifts to X / D = 1.03 , while at K = 10 − 12 , it shifts to X / D = 1.5 . Figure 6 shows the streamwise velocity profiles along the vertical centerline at different X / D locations. Due to the blockage of the porous matrix, the streamwise velocity decreases. Once the porous media is applied around the cylinder, the wake region surrounding the cylinder widens. Specifically, the velocity within the wake, particularly near the central area (at Y / D = 0 ), initially experiences a reduction followed by an enhancement compared to the velocity observed around a smooth cylinder. Based on the results presented in the Figure 5 and Figure 6, the porous layer with a permeability of K = 10 − 10 does not significantly affect the mean velocity profiles. Therefore, two other cases are further investigated in the following.
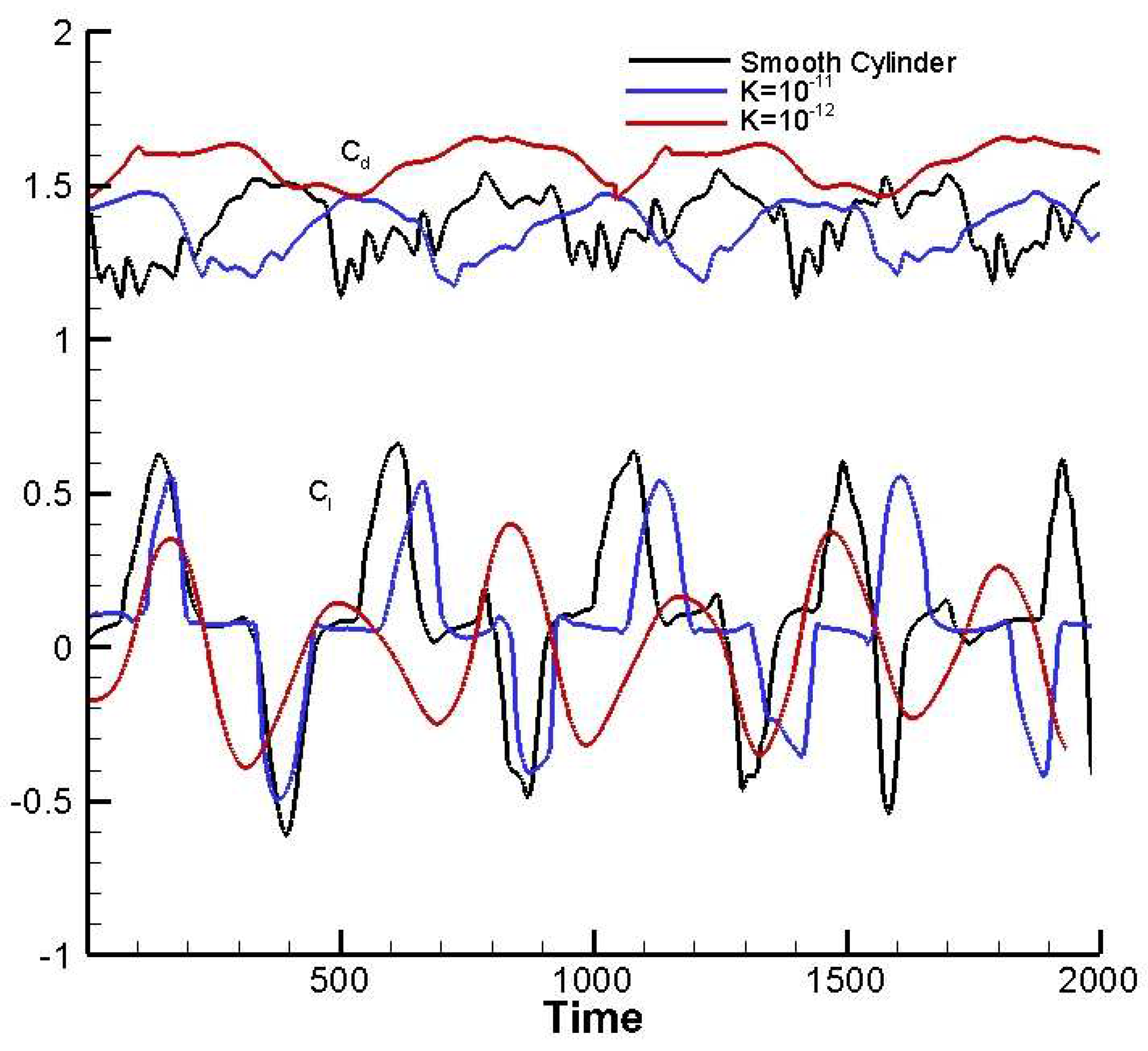
The time histories of the lift and drag coefficients are shown in Figure 7 for the cylinder coated with different permeability of K = 10 − 12 , 10 − 11 and with the thickness of the porous layer. Here, a reduction around 15% for K = 10 − 11 and 39% for K = 10 − 12 in the amplitudes of the lift fluctuation are evident across the cylinder coated with porous materials compared to the uncoated smooth cylinder. The drag coefficient is also depicted in Figure 7. In the figure, it can be deduced that the drag coefficient decreased around 2% with applying the porous layer at K = 10 − 11 . However, as permeability diminishes further, the drag coefficient begins to increase more than 13%. The reason for this behavior is the formation of blockage against the flow due to the reduction in the permeability. As the permeability of the porous layer decreases excessively, it behaves like a solid body, resulting in significant less flow passing through the porous layer. In addition, Table 3 shows the comparison of the lift coefficient and Strouhal number with various permeability. The results reveals that the porous layer leads to a reduction in the frequency of the dominant vortex behind the cylinders.
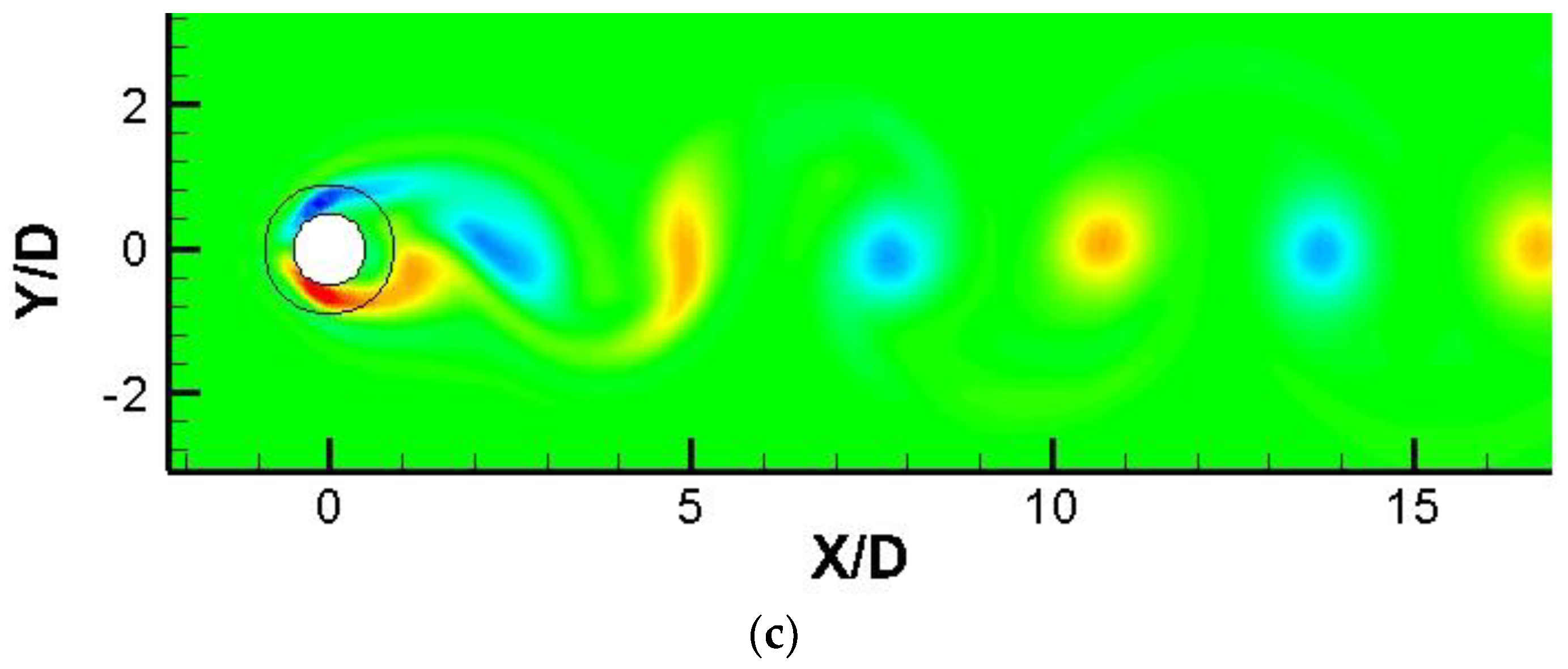
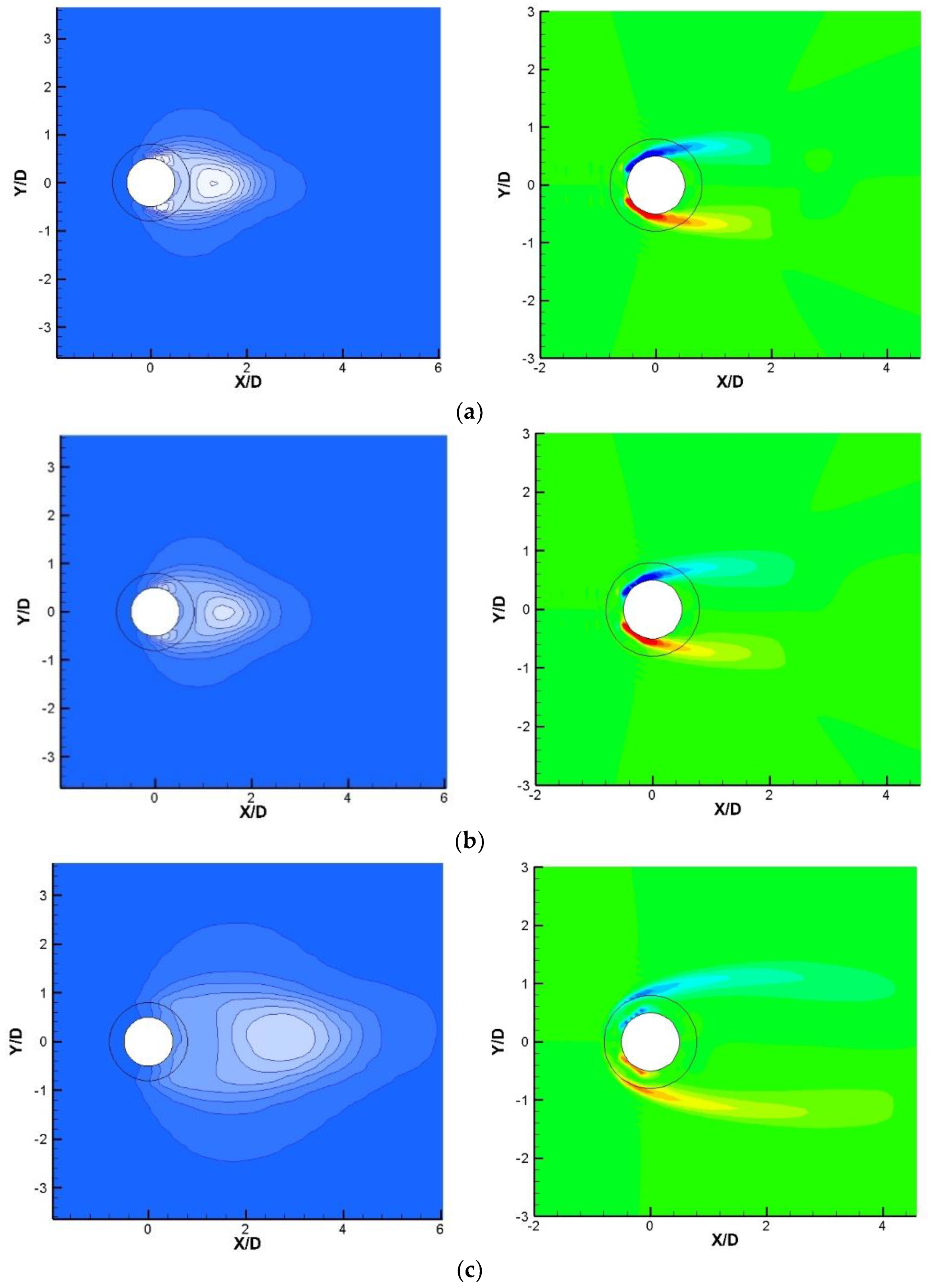
With the addition of a porous layer on the cylinder surface, the strength of the separated shear layers tends to decrease. In the smooth cylinder, vorticity primarily spreads from the surface into the surrounding external flow.
However, with the porous layer, vorticity diffusion occurs not only into the external flow field but also penetrates into the internal flow field within the porous layer itself. The right column of Figure 8 shows the mean vorticity contours around the smooth cylinder and porous-coated cylinders. The solid line encircling the cylinder represents the boundary between the porous material and the fluid. By applying the porous layer, the results reveal that the vortex range within the wake region of the cylinder becomes weaker and more elongated. A secondary shedding vortex develops along the solid wall of the cylinder at K = 10 − 12 , but it was swiftly dissipated by the effects of the porous layer on the leeward side.
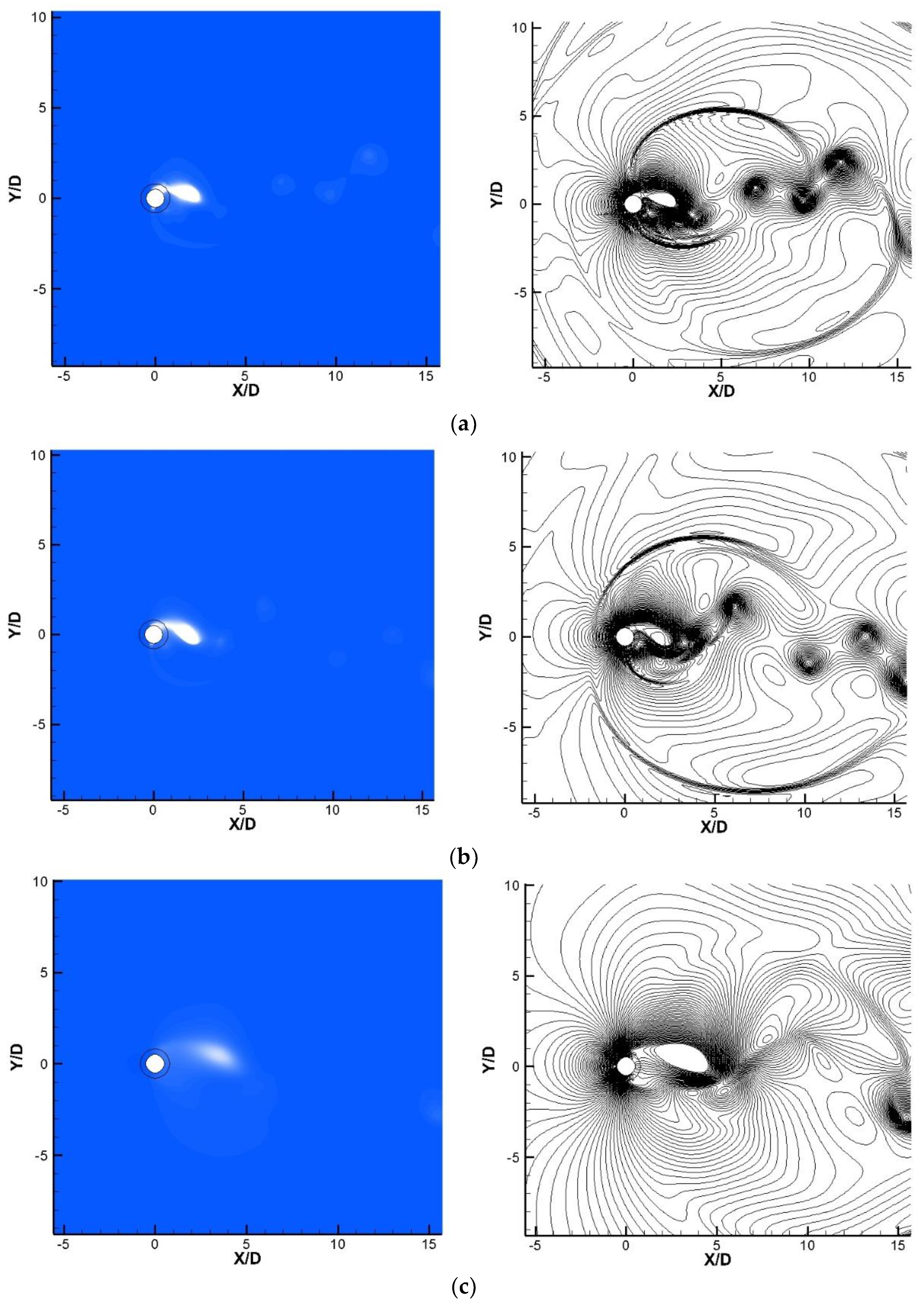
Figure 9 provides evidence that the existence of the porous layer leads to a noticeable reduction in the strength of cavitation regions. The presence of the porous layer weakens and the attached cavitation zones on the cylinder’s wall, particularly with the low permeability K = 10 − 12 . The porous materials altered the local pressure distribution around the surface of the cylinder. They act as pressure manipulators, smoothing out the pressure gradients that might otherwise lead to the cavitation inception. This pressure redistribution is often linked to the ability of porous media to diffuse and absorb gas or vapor, reducing the low-pressure zones. Particular for the case K = 10 − 12 , no strong shock waves due to the collapse of cavitation structures behind the cylinder was observed. It can be deduced that the application of the porous layer plays an important role in the weakening or mitigating of the destructive effects of the unsteady cavitation such as strong pressure waves behind the circular cylinder. Therefore, the porous layer can be suggested as a passive control method to control the unsteady cavitation in different applications.

5. Conclusions

This study presents a passive approach to control cavitation around a circular cylinder by employing a porous layer. The investigation focused on the study of different permeabilities of this porous layer to understand their effects on controlling cavitation. Initially, we validated our numerical approach by the simulation of a single-phase flow around the cylinder without and with the porous layers, utilizing the Navier–Stokes equation through the volume penalized method. Our findings showed that the appropriate thickness and permeability for the porous layer can have a notable reduction in the high-pressure amplitudes on the cylinder’s wall surface and in the associated vortex structures.
The results revealed that the appropriate porous coating on the cylinder can elongate the wake region, suppress vortex shedding, and stabilize the flow behind the cylinder. Furthermore, our results demonstrated a potential disappearance of the attached cavities on the cylinder and a weakening of the cavitation zone in the wake region of the cylinder using the porous layer. In addition, the shedding frequency was observed to be lower in the presence of the porous layer compared to the smooth cylinder. The mean value of the lift and drag fluctuations was decreased for the cylinder with the optimal porous layer. In general, use of a porous layer is effective in stabilizing the flow and controlling the cavitation behind the cylinders. However, the key lies in selecting the optimal permeability parameter. Selecting a material with a high permeability may diminish its effectiveness, as evident at K = 10 − 10 . Conversely, a very low permeability, as seen at K = 10 − 12 , can lead to an undesirable increase in drag.

References

  1. Saito, Y.; Sato, K. Cavitation bubble collapse and impact in the wake of a circular cylinder. Fifth Int. Symp. Cavitation 2003, 3–8. [Google Scholar]
  2. Brandao, F.L.; Bhatt, M.; Mahesh, K. Numerical study of cavitation regimes in flow over a circular cylinder. J. Fluid Mech. 2019, 885, A19. [Google Scholar] [CrossRef]
  3. Sadri, M.; Kadivar, E. Numerical investigation of the cavitating flow and the cavitation-induced noise around one and two circular cylinders. Ocean. Eng. 2023, 277, 114178. [Google Scholar] [CrossRef]
  4. Lin, Y.; Kadivar, E.; el Moctar, O. Experimental Study of the Cavitation Effects on Hydrodynamic Behavior of a Circular Cylinder at Different Cavitation Regimes. Fluids 2023, 8, 162. [Google Scholar] [CrossRef]
  5. Wu, J.; Deijlen, L.; Bhatt, A.; Ganesh, H.; Ceccio, S.L. Cavitation dynamics and vortex shedding in the wake of a bluff body. J. Fluid Mech. 2021, 917, A26. [Google Scholar] [CrossRef]
  6. Kadivar, E. Experimental and Numerical Investigations of Cavitation Control using Cavitating-Bubble Generators. Ph.D. Thesis, University of Duisburg–Essen, Duisburg, Germany, 2020. [Google Scholar]
  7. Dular, M.; Požar, T.; Zevnik, J.; Petkovšek, R. High-speed observation of damage created by a collapse of a single cavitation bubble. Wear 2019, 418–419, 13–23. [Google Scholar] [CrossRef]
  8. Giorgi, M.G.D.; Ficarella, A.; Fontanarosa, D. Active Control of Unsteady cavitating flows in turbomachinery. ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 2019.
  9. Gu, Y.; Yin, Z.; Yu, S.; He, C.; Wang, W.; Zhang, J.; Wu, D.; Mou, J.; Ren, Y. Suppression of unsteady partial cavitation by a bionic jet. Int. J. Multiph. Flow 2023, 164, 104466. [Google Scholar] [CrossRef]
  10. Timoshevskiy, M.V.; Zapryagaev, I.I.; Pervunin, K.S.; Markovich, D.M. Cavitation control on a 2D hydrofoil through a continuous tangential injection of liquid: experimental study. In Proceedings of the 18th International Conference on the Methods of Aerophysical Research, Perm, Russia, 27 June–3 July 2016. [Google Scholar]
  11. Kawanami, Y. Mechanism and control of cloud cavitation. J. Fluid Eng. 1997, 236, 788–794. [Google Scholar] [CrossRef]
  12. Kadivar, E.; Lin, Y.; el Moctar, O. Experimental Investigation of the Effects of Cavitation Control on the Dynamics of Cavitating Flows Around a Circular Cylinder. Ocean. Eng. 2023, 286, 115634. [Google Scholar] [CrossRef]
  13. Yu, F.; Zhang, Y.; Liu, H.; Zhou, Q. Experimental and numerical investigation of cavitation control with porous material on the hemisphere cylinder. Ocean. Eng. 2022, 266, 112984. [Google Scholar] [CrossRef]
  14. Churkin, S.A.; Pervunin, K.S.; Kravtsova, A.Y. Cavitation on NACA0015 hydrofoils with different wall roughness: high-speed visualization of the surface texture effects. J. Vis. 2016, 19, 587–590. [Google Scholar] [CrossRef]
  15. Kadivar, E.; el Moctar, O.; Javadi, K. Investigation of the effect of cavitation passive control on the dynamics of unsteady cloud cavitation. Appl. Math. Model. 2018, 64, 333–356. [Google Scholar] [CrossRef]
  16. Zaresharif, M.; Ravelet, F.; Kinahan, D.J.; Delaure, Y.M.C. Cavitation control using passive flow control techniques. Phys. Fluids 2021, 33, 121301. [Google Scholar] [CrossRef]
  17. Kadivar, E.; el Moctar, O. Investigation of cloud cavitation passive control method for hydrofoils using cavitating-bubble generators (CGs). In Proceedings of the 10th International Symposium on Cavitation, Baltimore, MA, USA, 14–16 May 2018. [Google Scholar]
  18. Kadivar, E.; Ochiai, T.; Iga, Y.; el Moctar, O. An experimental investigation of transient cavitation control on a hydrofoil using hemispherical vortex generators. J. Hydrodyn. 2020, 33, 1139–1147. [Google Scholar] [CrossRef]
  19. Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 479–517. [Google Scholar] [CrossRef]
  20. Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
  21. Coupez, *!!! REPLACE !!!*; et al. A penalization method to take into account obstacles and holes in unstructured mesh-based flows. J. Comput. Phys. 2015, 284, 122–146. [Google Scholar]
  22. Colella, P.; et al. A Cartesian grid embedded boundary method for solving the Poisson equation on irregular domains. J. Comput. Phys. 2008, 227, 706–727. [Google Scholar]
  23. Komatsu, R.; Iwakami, W.; Hattori, Y. Direct numerical simulation of aeroacoustic sound by volume penalization method. Comput. Fluids 2016, 130, 24–36. [Google Scholar] [CrossRef]
  24. Shin, B.R.; Iwata, Y.; Ikohagi, T. Numerical simulation of unsteady cavitating flows using a homogeneous equilibrium model. Comput. Mech. 1999, 30, 388–395. [Google Scholar] [CrossRef]
  25. Seo, H.; Moon, Y.J.; Rog, B. Prediction of cavitating flow noise by direct numerical simulation. J. Comput. Phys. 2008, 227, 6511–6531. [Google Scholar] [CrossRef]
  26. Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
  27. Visbal, M.R.; Gaitonde, D.V. On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 2002, 181, 155–185. [Google Scholar] [CrossRef]
  28. Development of a fully-compressible multi-phase Reynolds-averaged Navier-Stokes model. 15AIAA Computational Fluid Dynamics Conference, 2001, 2648.
  29. Bhatt, M.; Mahesh, K. A numerical approach to address the acoustic stiffness in cavitating flows. Int. J. Multiph. Flow 2021, 141, 103568. [Google Scholar] [CrossRef]
  30. Yu, P.; Zeng, Y.; Lee, T.S.; Bai, H.X.; Low, H.T. Wake structure for flow past and through a porous square cylinder. Int. J. Heat Fluid Flow 2010, 31, 141–153. [Google Scholar] [CrossRef]
  31. Tam, C.K.W.; Don, Z. Radiation and outflow boundary conditions for direct computation of acoustic and flow disturbances in a nonuniform mean flow. J. Comput. Acoust. 1996, 4, 175–187. [Google Scholar] [CrossRef]
  32. Sato, Y.; Hattori, Y. Mechanism of reduction of aeroacoustic sound by porous material: Comparative study of microscopic and macroscopic models. J. Fluid Mech. 2021, 929, A34. [Google Scholar] [CrossRef]
Preprints 97063 g001
Figure 1. (a) Computational domain, and (b) computations grid.
Figure 1. (a) Computational domain, and (b) computations grid.
Preprints 97063 g001
Preprints 97063 g002aPreprints 97063 g002b
Figure 2. Instantaneous vorticity contours for a) η = 10 − 3 , b) η = 10 ,and c) η = 10 3 .
Figure 2. Instantaneous vorticity contours for a) η = 10 − 3 , b) η = 10 ,and c) η = 10 3 .
Preprints 97063 g002aPreprints 97063 g002b
Preprints 97063 g003
Figure 3. Comparison of the average pressure fields for the cases a) η = 10 − 3 , b) η = 10 ,and c) η = 10 3 .
Figure 3. Comparison of the average pressure fields for the cases a) η = 10 − 3 , b) η = 10 ,and c) η = 10 3 .
Preprints 97063 g003
Preprints 97063 g004
Figure 4. Pressure coefficient on the outer boundary of porous material.
Figure 4. Pressure coefficient on the outer boundary of porous material.
Preprints 97063 g004
Preprints 97063 g005
Figure 5. A comparison of time-averaged streamwise velocities along the centerline.
Figure 5. A comparison of time-averaged streamwise velocities along the centerline.
Preprints 97063 g005
Preprints 97063 g006
Figure 6. Time averaged velocity profiles at different locations.
Figure 6. Time averaged velocity profiles at different locations.
Preprints 97063 g006
Preprints 97063 g007
Figure 7. The time history of the drag and lift coefficients.
Figure 7. The time history of the drag and lift coefficients.
Preprints 97063 g007
Preprints 97063 g008
Figure 8. Contours of mean void fraction (left column) and mean vorticity (right column) for a) smooth cylinder, b) K = 10 − 11 , and c) K = 10 − 12 .
Figure 8. Contours of mean void fraction (left column) and mean vorticity (right column) for a) smooth cylinder, b) K = 10 − 11 , and c) K = 10 − 12 .
Preprints 97063 g008
Preprints 97063 g009
Figure 9. Instantaneous void fraction contours (left column) and Instantaneous pressure contours (right column) for a) smooth cylinder b) K = 10 − 11 , and c) K = 10 − 12 .
Figure 9. Instantaneous void fraction contours (left column) and Instantaneous pressure contours (right column) for a) smooth cylinder b) K = 10 − 11 , and c) K = 10 − 12 .
Preprints 97063 g009
Table 1. Comparison of the drag coefficient for single-phase flow around the circular cylinder at R = 150 .
Table 1. Comparison of the drag coefficient for single-phase flow around the circular cylinder at R = 150 .
Ref. η = 10 − 3 η = 10 η = 10 3
Sato, Y. and Hattori, Y. [32] 2.5 1.955 1.4
Present 2.21 1.72 1.42
Table 2. Comparison of drag coefficient and Strouhal number for various grid resolutions.
Table 2. Comparison of drag coefficient and Strouhal number for various grid resolutions.
smooth cylinder coarse medium fine
C d 1.32 1.41 1.40
St 0.146 0.159 0.159
Table 3. Comparison of the lift coefficient and Strouhal number with various permeability.
Table 3. Comparison of the lift coefficient and Strouhal number with various permeability.
St
Smooth cylinder 0.159
K = 10 − 11 0.145
K = 10 − 12 0.110
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated