A Hardware Implementation of the PID Algorithm Using Floating-Point Arithmetic

Preprint

Article

A Hardware Implementation of the PID Algorithm Using Floating-Point Arithmetic

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

23 January 2024

Posted:

24 January 2024

You are already at the latest version

Alerts

Abstract

The paper proposes a new implementation of the PID algorithm in digital hardware. The proposed circuit implements an advanced PID formula, containing a non ideal derivative component, and weighting coefficients, which enable reducing influence of setpoint changes in the proportional and derivative components. The implementation operates on standard single precision (32 bit) floating-point numbers. The proposed circuit structure is optimized for cost. It uses just one arithmetic block, performing the multiply-and-add operation. The calculations are carried out in a sequential manner. The circuit was implemented in a Cyclone V FPGA device from Intel, using the Quartus Prime software. Proper operation of the circuit was verified by simulation. The proposed solution is comparable in terms of speed with other hardware implementations of the PID algorithm operating on standard single precision floating-point numbers, while being significantly cheaper. However, it outperforms by several orders of magnitude the speed of any software-based implementation, including solutions using PLCs, and CPU/MCUs. The proposed circuit structure, together with the overall regulator device concept, suit well the SoC (System on Chip), or SoPC (System on Programmable Chip) idea, i. e. a device, that contains a CPU core immersed in “FPGA fabric” - logic resources characteristic for FPGA devices.

Keywords:

Subject: Computer Science and Mathematics - Hardware and Architecture

1. Introduction

For several decades the PID (Proportional–Integral–Derivative) algorithm has been accepted as a standard way to control continuous processes in industrial plants. Its popularity is driven by its versatility, relatively simple principle of operation, and simplicity of application, i. e. usually only some basic information concerning the controlled object parameters is required, to achieve acceptable quality of the control process.

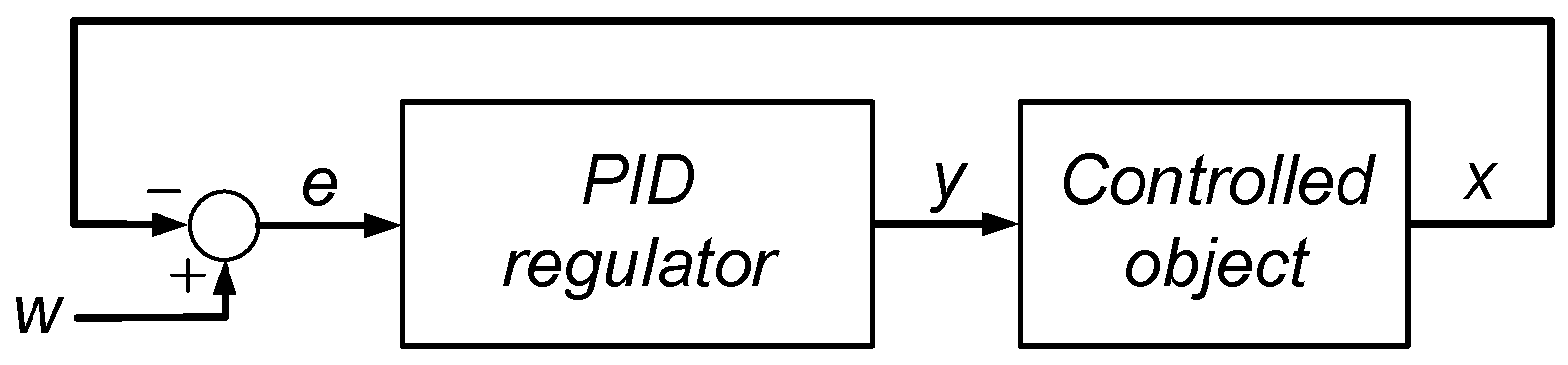
A typical application of the PID algorithm assumes that the PID regulator is included in a feedback loop (Figure 1).

The PID regulator is expected to tune the process variable x, which is not directly accessible, as close to the setpoint w, as possible. This is accomplished by appropriate driving the manipulated variable y. The regulator evaluates the required value of the manipulated variable basing on the error signal e = w – x, which is formed in the summing node.

In the classical form, the algorithm executed by the regulator is described by the mathematical formula presented in Equation 1 [1].

Y (S) = K_{P} (E (S) + \frac{1}{T_{I} S} \cdot E (S) + T_{D} S \cdot E (S))

(1)

where

E (S) = W (S) - X (S)

(2)

The result generated by the regulator consists of three components: proportional, , integral, and derivative.

However, in practical applications the ideal formula, described by Equation 1, is often replaced by more complex relationships. A popular extension of the ideal PID formula is described by equation 3:

Y (S) = K_{P} ((b \cdot W (S) - X (S)) + \frac{1}{T_{I} S} (W (S) - X (S)) + \frac{T_{D} S}{a \cdot T_{D} S + 1} (c \cdot W (S) - X (S)))

(3)

The first problem is that an ideal derivative function is not feasible in practical circuits. It is thus substituted by a high-pass filter function characterized by the delay coefficient a. Anoter problem is that the output y, described by Equations 1 and 2, depends on the error signal

e = w - x

, and thus it reacts the same strong to changes of both the process variable x, and the setpoint w. In practical applications we can expect, that the setpoint value is changed quite rarely, but it is usually a step change. This causes overreaction of the regulator, which is a result of contribution of the proportional, and derivative components. Introducing and appropriate tuning the b and c weighting coefficients enables obtaining a smoother, and more “bumpless” operation of the regulator in the case of a step change of the setpoint. This prevents unnecessary wear-out of the actuators.

First PID regulators were implemented as mechanical, and electromechanical devices, operating in the continuous time domain. In contemporary technologies PID regulators are implemented as digital electronic circuits, operating in discrete time. If the PID algorithm is calculated by a digital device, e. g. a microprocessor, one of the most important parameters to be considered is sampling period T_S. The minimum sampling period achievable for a particular digital regulator limits the speed of the process the regulator is capable to control. A practical rule of thumb says that the sampling period T_S should be at least an order of magnitude shorter than the equivalent delay (which includes the dominant time constant) characterizing the controlled object [2].

The most popular way of implementing the PID algorithm in contemporary control systems consists in writing an appropriate program for a PLC (Programmable Logic Controller). Modern PLCs contain special instructions, or library functions, that calculate the PID algorithm, and provide some supplementary functions, like number format conversion, value scaling, and error detection [2,3,4]. The PID formula is in such a case calculated by the main CPU (Central Processing Unit) of the PLC, while executing the control program. The PID instruction should be invoked inside a cyclic interrupt handling procedure. We can expect that the minimum period available for a cyclic interrupt in a PLC is 1 ms. However, this is quite a theoretical limit. Executing the PID instruction can be quite time consuming, as it involves performing a number of operations on floating-point numbers. Sample experiments show, that the PID instruction executes in 190 – 230 µs in the popular Simatic S7-1200 PLC [5]. A short review of the PID instruction execution times achievable in some other PLCs can be found in [6].

The CPU is required to process the overall control program at a sufficient speed, and servicing interrupt routines must not consume too much CPU time. In practical applications, if the PID algorithm is implemented in a PLC, we can expect the sampling periods to be no less than several milliseconds, and most often the value of 100 ms is recommended.

Another option to implement the PID calculations in a dedicated/standalone CPU/MCU (Microcontroller Unit). There are works reporting, that it is possible to obtain sampling periods below 1 ms using general purpose MCU-s (e. g. 300 µs in [7]). This approach can be especially efficient, if a DSP (Digital Signal Processor) is applied, as such devices can contain hardware accelerators, supporting evaluation of a digital filter response [8].

Further increase of the regulator speed is possible, if the calculations are implemented in hardware. Flexibility and logic capacity of modern FPGA (Field Programmable Gate Array) devices make them a convenient platform for implementing various kinds of functions, including arithmetic operations. This approach was applied in a number of works [6,7,10,11,12,13,14,15]. The sampling periods achieved vary from 13 ns [10] to 600 ns [13]. In most of the cases the PID regulator is used for controlling operation of a DC-DC converter [9,10], or for motion control [12,14]. The PWM method is used to convert the result generated by the regulator to the analog domain.

Apart from the speed, two other factors need to be considered, when we analyze and compare hardware implementation of arithmetic functions: number format, and cost of the implementation. The analog PID formulas presented by equations 1 or 3 describe relationships between real numbers. The real numbers need to be somehow approximated, and represented in a digital system. The way this is accomplished influences, apart from accuracy of the result, the system complexity, and speed. For representation of a real number in a digital system, fixed-point, and floating-point formats can be considered. Implementation of arithmetic functions operating on fixed-point numbers is much simpler, and cheaper in terms of logic resources consumed. In most of the works mentioned above a fixed-point representation is used, with the length of the binary number ranging from 8 [10] to 16 bits [14]. Due to a more complex structure of floating-point formats, implementation of floating-point arithmetic is much more demanding in terms of logic resources.

However, using fixed-point arithmetic for complex calculations is always bound with the risk of too low accuracy, and too narrow range. For a recursive algorithm, in which the n-th sample depends on previous samples, the errors can build-up, and it is difficult to determine the bit width of the number that assures a required accuracy. This problem is highly avoided when using floating-point formats. For this reason using single precision (32-bit) floating-point numbers became a standard de facto at least for PID blocks/functions implemented in modern PLCs.

Concerning the works reported in the reference materials, standard single precision floating-point numbers were applied in [15]. A kind of floating-point representation, but with lower precision (20 bits) was used in [13]. In both cases this is achieved at the expense of with much greater consumption of logic resources of the programmable chip.

The purpose of this paper is to propose an alternative solution, which uses standard single precision floating-point numbers, is comparable in terms of speed with the solutions presented in [13], and [15], but is significantly cheaper in terms of logic resources. What’s more, the proposed solution implements the more complex PID formula described by Equation 3, while the works reported in [13], and [15] use the simplified form shown in Equation 1.

The proposed structure benefits on register-rich architecture of FPGA devices. The calculations are carried out in a serially-cyclic manner, using just one arithmetic block.

2. Discretization of the PID Formula

As it was mentioned above, the more complex form of the PID algorithm, described by Equation 3, will be the starting point.

Before a relationship described in continuous time domain is implemented in a digital system, it needs to be discretized, i. e. converted to discrete time domain. To accomplish this, three methods can be considered: the forward-difference method, the backward difference method, and the bilinear transform. Using the forward difference method involves a risk of facing stability problems. On the other hand, applying the bilinear transform method leads to significantly more complex relationships in the discrete time domain, and, as a consequence, more expensive, and slower implementations in hardware. The decision was made to use the backwards difference method, which is in fact the most popular approach.

Discretization of a continuous-time formula using the backwards difference method is most conveniently carried out in the operator domain, and consists in substituting

\frac{1}{T_{S}} (1 - z^{- 1})

for

S

The most obvious, and popular approach to the PID formula discretization consists in discretizing the three components contributing to the result, i. e. the proportional, integral, and derivative functions, separately. This approach was used in [11], and [15]. If applied to the formula described by Equation 3, we obtain

Y_{P} (z) = K_{P} (b \cdot W (z) - X (z))

(4)

Y_{I} (z) = K_{P} \frac{T_{S}}{T_{I} (1 - z^{- 1})} (W (z) - X (z))

(5)

Y_{D} (z) = K_{P} \frac{T_{D} (1 - z^{- 1})}{a \cdot T_{D} (1 - z^{- 1}) + T_{S}} (c \cdot W (z) - X (z))

(6)

and

Y (z) = Y_{P} (z) + Y_{I} (z) + Y_{D} (z)

(7)

Converting to time domain yields

y_{P} (n) = K_{P} (b \cdot w (n) - x (n))

(8)

y_{I} (n) = K_{P} \frac{T_{S}}{T_{I}} (w (n) - x (n)) + y_{I} (n - 1)

(9)

y_{D} (n) = K_{P} \frac{c \cdot (w (n) - w (n - 1)) - (x (n) - x (n - 1))}{(a + \frac{T_{S}}{T_{D}})} + \frac{a}{(a + \frac{T_{S}}{T_{D}})} y_{D} (n - 1)

(10)

and

y (n) = y_{P} (n) + y_{I} (n) + y_{D} (n)

(11)

Apart from the integral component

y_{I} (n)

, also the derivative component

y_{D} (n)

depends on its previous samples. This means, that the

y_{I} (n - 1)

, and

y_{D} (n - 1)

values need to be stored somewhere in the system, and the

y_{P} (n)

y_{I} (n)

, and

y_{D} (n)

components have to be calculated separately. This is not a problem, if the formulas are implemented in software. However, in hardware implementations this leads to an irregular, and less optimal structure.

In this paper we want to propose another approach – discretization of the PID formula as a whole. By substituting

\frac{1}{T_{S}} (1 - z^{- 1})

for

S

in equation 3 we obtain

Y (z) = K_{P} ((b \cdot W (z) - X (z)) + \frac{T_{S}}{T_{I} (1 - z^{- 1})} (W (z) - X (z)) + \frac{T_{D} (1 - z^{- 1})}{a \cdot T_{D} (1 - z^{- 1}) + T_{S}} (c \cdot W (z) - X (z)))

(12)

The formula needs to be ordered with respect to negative powers of z, the Y, X and W signals, and then converted to time domain. After performing appropriate transformations we obtain

y (n) = c_{0} y (n - 1) + c_{1} y (n - 2) + c_{2} w (n) + c_{3} w (n - 1) + c_{4} w (n - 2) + c_{5} x (n) + c_{6} x (n - 1) + c_{7} x (n - 2)

(13)

The

c_{0}

–

c_{7}

coefficients depend on the regulator parameters K_P, T_I, T_D, a, b, c and the sampling period T_S as follows:

c_{0} = \frac{2 a T_{D} + T_{S}}{a T_{D} + T_{s}}

(14)

c_{1} = - \frac{a T_{D}}{a T_{D} + T_{s}}

(15)

c_{2} = K_{P} \frac{b (a T_{D} + T_{S}) + \frac{T_{S}}{T_{I}} (a T_{D} + T_{S}) + c T_{D}}{a T_{D} + T_{s}}

(16)

c_{3} = - K_{P} \frac{b (2 a T_{D} + T_{S}) + a \frac{T_{S}}{T_{I}} T_{D} + 2 c T_{D}}{a T_{D} + T_{s}}

(17)

c_{4} = K_{P} T_{D} \frac{a b + c}{a T_{D} + T_{s}}

(18)

c_{5} = - K_{P} \frac{(a T_{D} + T_{S}) + \frac{T_{S}}{T_{I}} (a T_{D} + T_{S}) + T_{D}}{a T_{D} + T_{s}}

(19)

c_{6} = K_{P} \frac{(2 a T_{D} + T_{S}) + a \frac{T_{S}}{T_{I}} T_{D} + 2 T_{D}}{a T_{D} + T_{s}}

(20)

c_{7} = - K_{P} T_{D} \frac{a + 1}{a T_{D} + T_{s}}

(21)

According to Equation 13, the current sample of the regulator output signal y(n) can be calculated using two previous samples of y, and current values, and two previous samples of the process variable x, and the setpoint w.

If the same method is applied to the simplified PID formula shown in Equation 1, the regulator is reduced to a second order IIR (Infinite Impulse Response) filter. This approach was used in [7,8,9,10,12].

The PID formula described by Equation 13 is very regular. It gives a hardware designer many options to arrange hardware components, performing the relevant arithmetic operations. This includes parallel, serial, and mixed structures.

Two previous samples of the regulator output y, the process variable x, and the setpoint w need to be stored in the system. However, this is more convenient, than storing samples of the integral, and derivative components. The y, x and w signals are directly available either at regulator inputs, or outputs, so they do not need to be calculated separately by dedicated hardware.

3. The proposed Circuit Structure

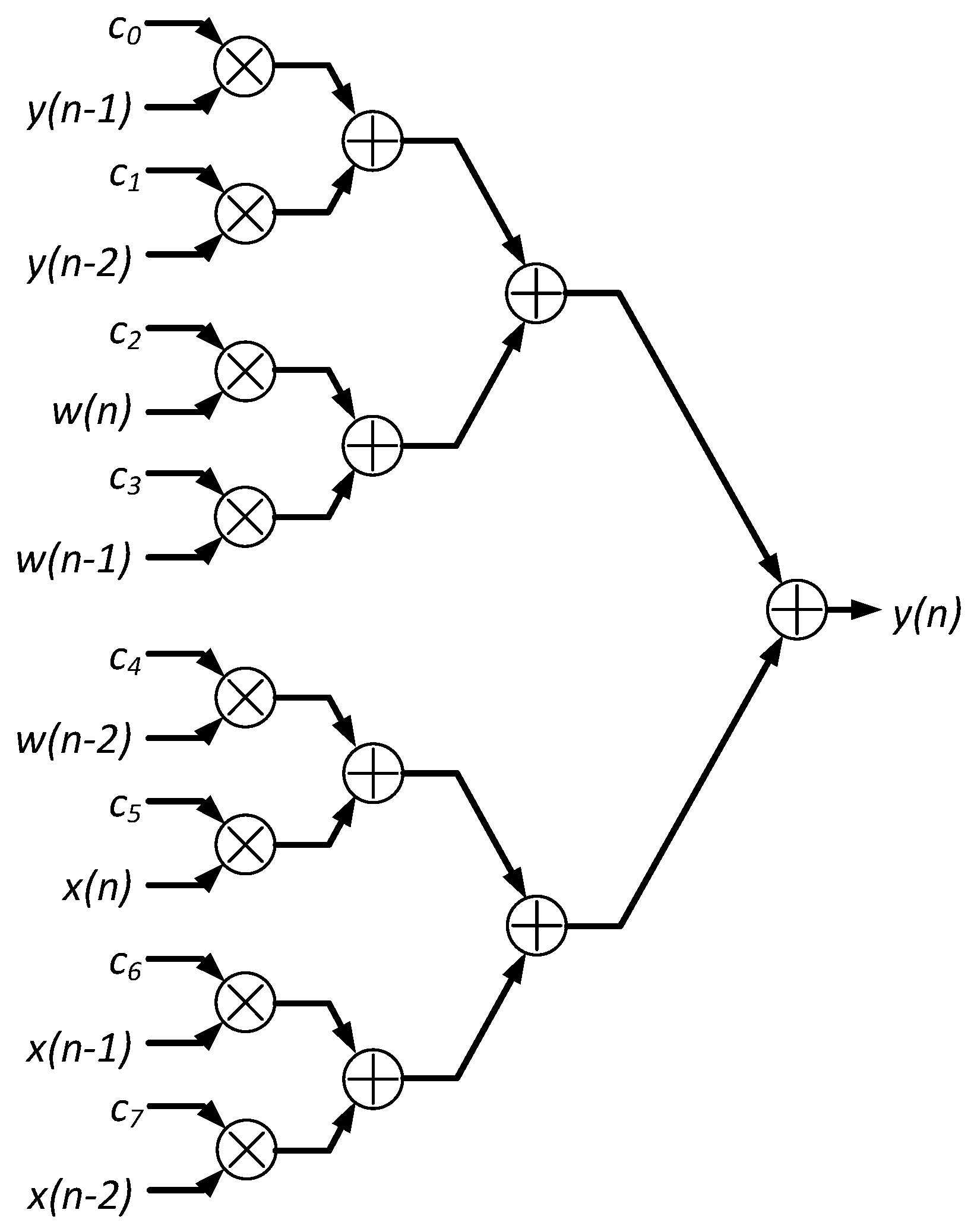
As it was mentioned above, the regular form of Equation 13 gives to the hardware designer much freedom in designing the structure of the circuit calculating the PID formula. One of the solutions, that can be considered, is the parallel, tree-shaped structure presented in Figure 2. Typically, parallel structures are supposed to provide the fastest operation of a system.

Implementation of the structure presented in Figure 2 requires 8 multipliers, and 7 adders. As the calculations need to be performed on floating-point numbers, it is expected that the implementation will consume a significant amount of logic resources.

Further on in this paper we will assume that the floating-point operations will be handled by “ready-made” IP cores shipped together with synthesis software, which will be used to design the whole system. IP cores of various kinds, in particular IP cores performing arithmetic operations on floating-point numbers, became a standard utility available in CAD software supporting FPGA design, delivered by all main FPGA vendors. IP cores developed by FPGA vendors are carefully optimized, basing on knowledge of device architecture details. It is possible to design one’s own IP core, but it is quite unlikely to obtain a solution which is more efficient in terms of performance, and cost.

Sample experiments were carried out to estimate parameters of the possible parallel structure. The tests were accomplished using the Quartus Prime software from Intel (version 22.1, Lite edition), and a Cyclone V (5CGTFD9E5F35C7 [17]) device. For a given frequency of 100 MHz, implementation of a floating-point multiplier IP core (the “FP Functions Intel FPGA” core [16]) requires 2 onboard fixed-point multipliers, and 242 LUT (Look-up Table) blocks. The latency estimated by the IP Core generator is 4 clock cycles. Implementation of a floating-point adder (again the “FP Functions Intel FPGA” core) requires 873 LUTs, and the latency is 5 clock cycles. This means, that implementation of the parallel structure presented in Figure 2 would consume at least 6303 LUTs, and the expected latency would be at least 19 clock cycles, i. e. 190 ns. Latency, divided by the maximum clock frequency, constitutes the low limit on the sampling period, and, as a consequence, on possible regulator speed.

Further on in this paper we will propose another approach, which is much more efficient in terms of logic resources usage, while not much slower comparing to the possible parallel solution.

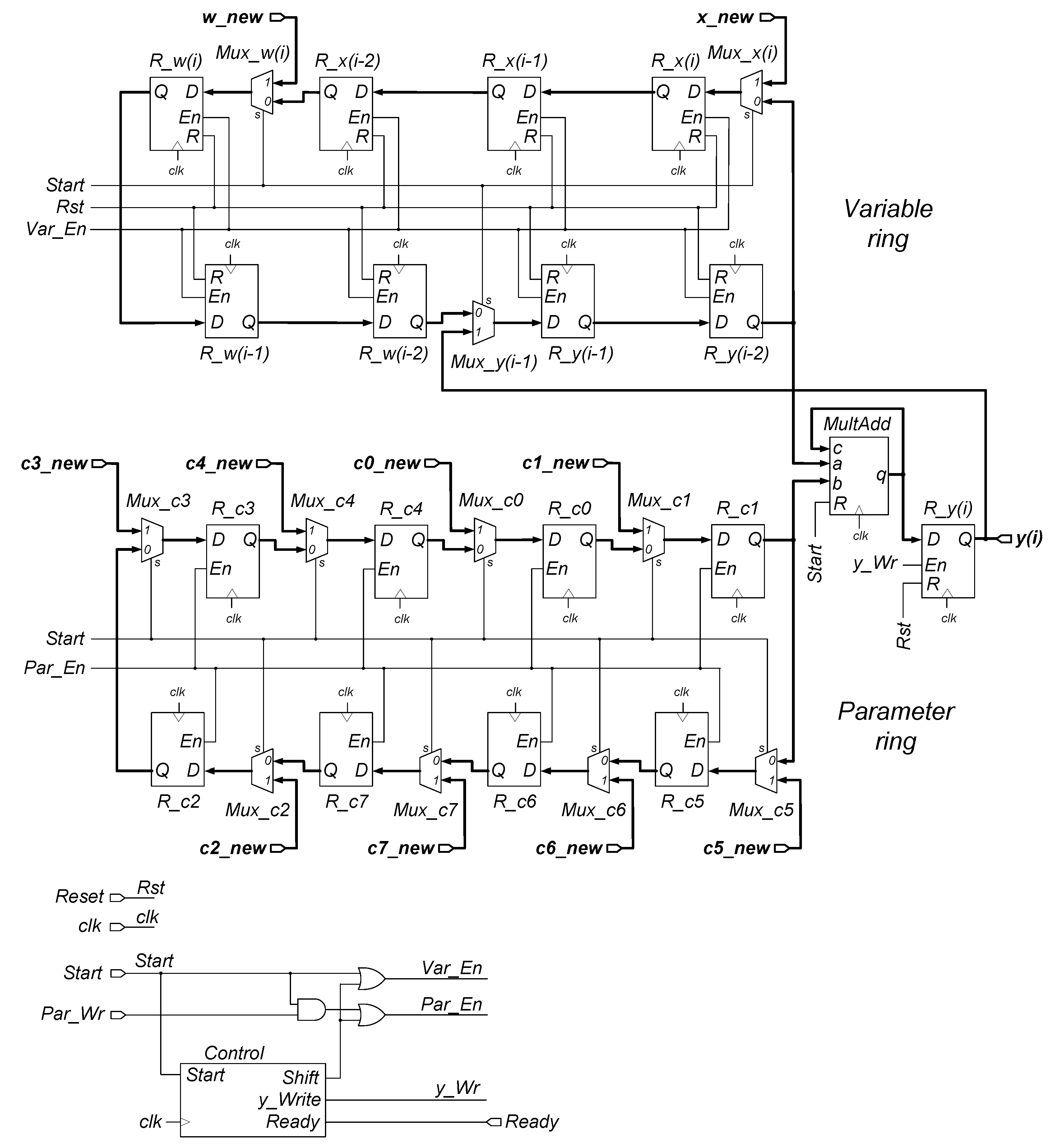
The proposed structure is presented in Figure 3. The circuit is fully synchronous, i. e. all the parallel registers, and the MultAdd block are synchronized by a common clock signal.

The heart of the circuit is the MultAdd block, which should be implemented as an IP Core capable of performing simultaneously multiplication and addition on floating-point numbers (see Equation 22).

q = a \cdot b + c

(22)

Another crucial elements are parallel registers, which are arranged in two rings, 8 registers in each. The registers in the upper ring (the “variable ring”) store current and delayed samples of the process variable x(n), x(n-1), x(n-2), the setpoint w(n), w(n-1), w(n-2), and the regulator output y(n-1), and y(n-2). The registers in the lower ring (the “parameter ring”) store values of the

c_{0}

–

c_{7}

coefficients.

The output q of the MultAdd block is routed back to the block input c. This way a structure capable of storing temporary results for further processing is obtained, i. e. a kind of a cumulative adder.

The calculations described by Equation 13 are performed sequentially, i. e. the

c_{1} \cdot y (n - 2)

product is calculated first, then the data in the rings are shifted right, the product

c_{0} \cdot y (n - 1)

is calculated, and added to

c_{1} \cdot y (n - 2)

, which is available at the MultAdd block output q, after the first product is calculated. After this is completed, the data are shifted again, and the

c_{4} \cdot w (n - 2)

product is calculated, and added to the result of previous operations. Subsequently, the

c_{3} \cdot w (n - 1)

c_{2} \cdot w (n)

c_{7} \cdot x (n - 2)

c_{6} \cdot x (n - 1)

, and

c_{5} \cdot x (n)

products are calculated, and added to the temporary sum. After eight shift and calculate operations, the new sample of the manipulated variable y(n) is available at the MultAdd block output. The value is stored in a parallel register to be available for reading by external circuitry, and the circuit is ready for calculating the next sample of y.

Before a new calculation cycle is started, samples of the process variable x, the setpoint w, and the regulator output y must be updated. This is accomplished by inserting 2 to 1 multiplexers at appropriate positions into the “variable” register ring. The “Select” inputs of the multiplexers are controlled by the external Start signal. The Start signal should be activated for one clock cycle before the actual calculations begin. Activating the Start signal lets new data to be written to the registers storing x(n), w(n), and y(n-1). The remaining data are shifted right, following the ring. This way the old value of the x(n) sample is transferred to the register storing x(n-1), x(n-1) is transferred to x(n-2), w(n) to w(n-1), and so on.

Updating the

c_{0}

–

c_{7}

coefficients is accomplished in a similar manner. The registers in the “parameter ring” are interlaced with 2 to 1 multiplexers, and the “Select” inputs of the multiplexers are controlled by the Start input. However, it is assumed, that the values of the coefficients do not need to be updated every time, a new calculation cycle is initiated.

When a set of new values for the

c_{0}

–

c_{7}

coefficients is ready, they can be simultaneously transferred to the R_c0 – R_c7 registers. The transfer should be triggered at the beginning of a new calculation cycle. This is accomplished by appropriate driving the En (Enable) inputs of the R_c0 – R_c7 registers. Apart from the Shift signal, which will be explained further, writing new data to the R_c0 – R_c7 registers is enabled, when the condition

P a r_W r a n d S t a r t

is active. Start and Par_Wr are circuit inputs (see Figure 3). The Start signal has to be activated to initiate a new calculation cycle. The Par_Wr signal should be activated every time a modification of the regulator parameters is required, and a set of new, consistent data is available at the

c 0_n e w

–

c 7_n e w

inputs. Updating the

c_{0}

–

c_{7}

coefficients will be commented to a more detail in section 6.

Operation of the whole circuit is governed by the Control block. The Control bock contains two counter-like circuits in its internal structure. The first of them is responsible for generating the Shift signal, which triggers the shift operation in both rings, i. e. transferring data from R_x(n) to R_x(n-1) from R_x(n-1) to R_x(n-2), etc. in the “variable ring”, and from R_c5 to R_c6, from R_c6 to R_c7, etc. in the “parameter ring”.

Performing the multiply-and-add operation on floating-point numbers is a complex task, for which a number of clock cycles is required. Assuming that the MultAdd block generates a valid result after l clock cycles, the first counter-like circuit activates the Shift signal every l-th clock cycle.

The second counter-like circuit is responsible for counting the subsequent multiply-and-add operations. After the eight multiply-and-add, and shift operations are completed, the counter triggers writing the result to the R_y(i) register, activates the Ready output, and blocks operation of the whole circuit, until a new calculation cycle is initiated by activating the Start input.

4. Implementation of the Proposed Circuit

The circuit presented in Figure 3 was implemented in the Quartus Prime, v. 22.1, Lite Edition software from Intel. The register blocks, the control unit, and the whole circuit structure were described in the Verilog language. The MultAdd block was implemented using the “FP Functions Intel FPGA” IP core [16] configured for the multiply-and-add operation. The single precision floating-point (32 bits) number format was selected for calculations.

The IP core generates a valid result after a number of clock cycles (i. e. latency), which can be selected within a certain range during the core configuration. Setting the latency parameter influences the maximum clock frequency, at which the core is able to run, and its cost, i. e. amount of logic resources required to synthesize it. In general, setting a low latency (e. g. l = 2) generates solutions requiring less logic resources, but running at lower frequencies. On the other hand, setting high latencies generates more expensive solutions, but running at higher frequencies. So, setting the right parameters for the IP core is a kind of trade-off between speed and cost.

For the solution presented in this paper the latency l was set to 10. The IP core generator estimated the maximum clock frequency at 102 MHz, and the cost at 2 multiplier blocks plus 1192 LUTs.

Evaluation of the formula presented in Equation 13 requires eight multiply-and-add operations. Assuming this we can find, that the actual calculations take 8 x l = 80 clock cycles. One additional clock cycle is necessary for transferring the result to the output register, after the result is ready. So the whole calculation cycle for generating one sample of the output signal takes 81 clock cycles.

The circuit was synthesized for a Cyclone V device (5CGTFD9E5F35C7 [17]), which is classified as a cost-efficient option for an FPGA designer. After the design was actually synthesized, it turned out that the estimation of the maximum clock frequency delivered by the IP core generator was too pessimistic. The static timing analyzer module of the Quartus Prime system estimated the maximum clock frequency at 157.1 MHz. We can thus estimate the execution time T_E, i. e. the time delay, which is required, before a valid result is available at the circuit output, at 81 x 1/157.1 = 516 ns.

A comparison of parameters obtained for the proposed approach against some other solutions presented in the reference materials is shown in Table 1. The terms “simplified” and “complex”, in the column of the table labelled “PID formula”, refer to the “simplified” and “complex” PID formulas described by Equations 1 and 3, respectively.

Most of the structures presented in the table require a number of clock cycles to calculate a valid result. To enable realistic assessment of speed of the proposed solutions, the T_E (i. e. “Execution time”) parameter was introduced. The “Execution time” is equal to the number of clock cycles N required to complete the calculations, divided by the maximum clock frequency estimation f_Max delivered by static timing analysis tools.

t_{E} = \frac{N}{f_{M a x}}

(23)

The T_E parameter constitutes the low limit on the sampling period, which is achievable for a particular case.

While analyzing the results presented in the table, one should keep in mind, that the comparison is somewhat blurred by the fact, that the designs use different FPGA devices, that can differ with respect to logic resources available onboard (e. g. availability of multiplier/DSP blocks), and their properties. In particular, the Spartan 6, and Cyclone V FPGAs contain LUT blocks featuring 6 inputs, and thus offering bigger logic capacity, than 4-input LUTs contained in all the other devices.

The shortest execution times T_E, along with the least resources usage, were reported by Sreenivasappa and Udaykumar [10]. However, an open question is whether accuracy and dynamic range provided by the 8-bit fixed-point number format is sufficient for a wider class of applications, than the one described in the paper.

Yuen Fong Chan and Moallem [11] experimented with two regulator structures operating on 16-bit fixed-point numbers. The first structure utilizes parallel multipliers. It is capable of generating the result in one clock cycle. The second implementation uses serial multipliers, for which a number of clock cycles is required to obtain a valid result.

Using a floating-point format for number representation makes the circuit much more complex, and thus the implementations are slower, and more demanding in terms of resources usage.

Table 1. A comparison of parameters obtained for various implementations of a PID regulator in FPGA devices.

Work	PID formula	Number format	FPGA device	T_E [ns]	Logic resources
Sreenivasappa, B. V.; Udaykumar, R. Y [10]	simplified	Fixed-point, 8 bits	Spartan 3E	13	122 LUTs, 2 multipliers, 59 registers
Sreenivasappa, B. V.; Udaykumar, R. Y [10]	simplified	Fixed-point, 8 bits	Cyclone I	13	224 LUTs, 32 registers
Yuen Fong Chan; Moallem, M. [11] (parallel structure)	complex	Fixed-point, 16 bits	Spartan 2E	67	1142 slices (2284 LUTs), 327 registers
Yuen Fong Chan; Moallem, M. [11] (serial structure)	complex	Fixed-point, 16 bits	Spartan 2E	361	437 slices (874 LUTs), 406 registers
Milik, A., Hrynkiewicz, E. [18]	complex	Fixed-point, 32 bits	Spartan 6	78	271 LUTs, 442 registers, 2 multiplier blocks
Yankai Xu; et al. [13]	complex	Floating-point (mantissa – 15 bits, exponent – 5 bits)	Cyclone I	600	1377 LEs (1377 LUTs, 1377 registers)
Zębiński, A., et al. [15]	simplified	Floating-point, 32 bits	Virtex 4	215	4457 registers, 83695 equivalent logic gates
Zębiński, A., et al. [15]	simplified	Floating-point, 32 bits	Spartan 2E	539	4482 registers, 83799 equivalent logic gates
This work	complex	Floating-point, 32 bits	Cyclone V	516	1173 LUTs (339 with more than 4 inputs), 1026 registers, 1 DSP block

Flexibility of FPGA devices allows to easily manipulate the lengths of the mantissa and the exponent components in the floating-point representation. An open question is, how this influences quality of regulation, and what sizes are required to assure a stable and reliable process. Using the standard single precision 32-bit wide floating-point number format, with 8 bits reserved for the exponent, and 23 bits for the mantissa, is commonly accepted, at least in PLCs. It is believed to provide sufficient accuracy for great majority of regulation tasks.

Yankai Xu et al. [13] implemented a number format resembling the classical floating-point concept, and using a 5-bit wide exponent, and 15-bit wide mantissa.

The standard single precision floating-point number format was used by Ziębiński et al. [15], and in this work. Unfortunately exact data concerning logic resources usage expressed in LUT blocks, are not reported in [15]. Nevertheless we can expect numbers which are comparable to the register counts, i. e. thousands. However, to be honest, the solution implemented by Ziębiński et, al., apart from the actual arithmetic unit calculating samples of the y(n) signal, contains some additional circuitry responsible for regulator parameter update.

I the authors’ opinion, an interesting case, giving a more general view of what is ever possible, and feasible, is comparison with the results reported by Milik and Hrynkiewicz [18]. Research works carried out by Milik are focused on developing algorithms that enable direct implementation of functions described by a PLC program, in hardware resources available in FPGA devices. The solution reported in [18] was one of the benchmarks used by the authors to verify efficiency of their algorithms. So the regulator structure was not designed by a human designer, but it was automatically generated by software algorithms from a program in the IL (Instruction List) language. Some more examples following this approach can be found in [19].

The comparison presented in Table 1 indicates, that the proposed structure is comparable in terms of speed with the other implementations operating on floating-point numbers, while being significantly cheaper. It also needs to be noted, that the regulator described by Ziębiński et al. implements the simplified PID formula (Equation 1), while the circuit proposed in this paper uses the complex form (Equation 3).

5. Testing and Verification

To verify correctness of the proposed circuit structure and its proper operation, a number of tests were carried out. The testes were accomplished using the Questa Intel Starter FPGA Edition-64 2021.2 simulator from Siemens/Mentor Graphics.

A simple Verilog testbench was prepared for providing appropriate samples of the x(n), and w(n) signals to the circuit inputs, and for capturing samples of the output signal y(n). The open loop configuration was tested, i. e. the regulator as a standalone block, without the manipulated object, and not surrounded by the negative feedback loop (see Figure 1).

Operation of the circuit was simulated for unit-step excitations applied to the circuit inputs x, and w. A unit-step response in time domain contains full information concerning dynamic properties of an analyzed object, while being much easier to generate using common simulation tools, than any response in the frequency domain.

1000 samples of the output signal, following the unit step at the input, were recorded for various sets of regulator parameters K_P, T_I, T_D, a, b, c, and T_S.

To provide the relevant reference data, a simple program in the C++ language was written. The program implements the “obvious” approach, i. e. the PID formula with the proportional, integral, and derivative components discretized separately (Equations 8 to 11). The program operates on double-precision (64-bit) floating-point numbers.

Samples of the y(n) signal, obtained from simulation in the Questa software, were compared against the reference data provided by the C++ program. The greatest value of relative error, which was recorded for parameter sets containing only the P, and PD components, is 1.2 x 10^-6. This is a result of limited accuracy of single-precision floating-point number representation, which is estimated at c. a. 6 - 7 significant digits.

Errors greater by an order of magnitude were, in general, recorded for parameter sets containing the integral component. The greatest value of the relative error, which was recorded, is 7.6 x 10^-5. The errors resulting from limited precision of the number format tend to build-up in the integral component.

Nevertheless, we can expect similar effects in the analog counterparts, which suffer from limited precision of analog components, e. g. offset voltage. These effects are highly reduced in the closed-loop configuration containing the negative feedback (see Figure 1).

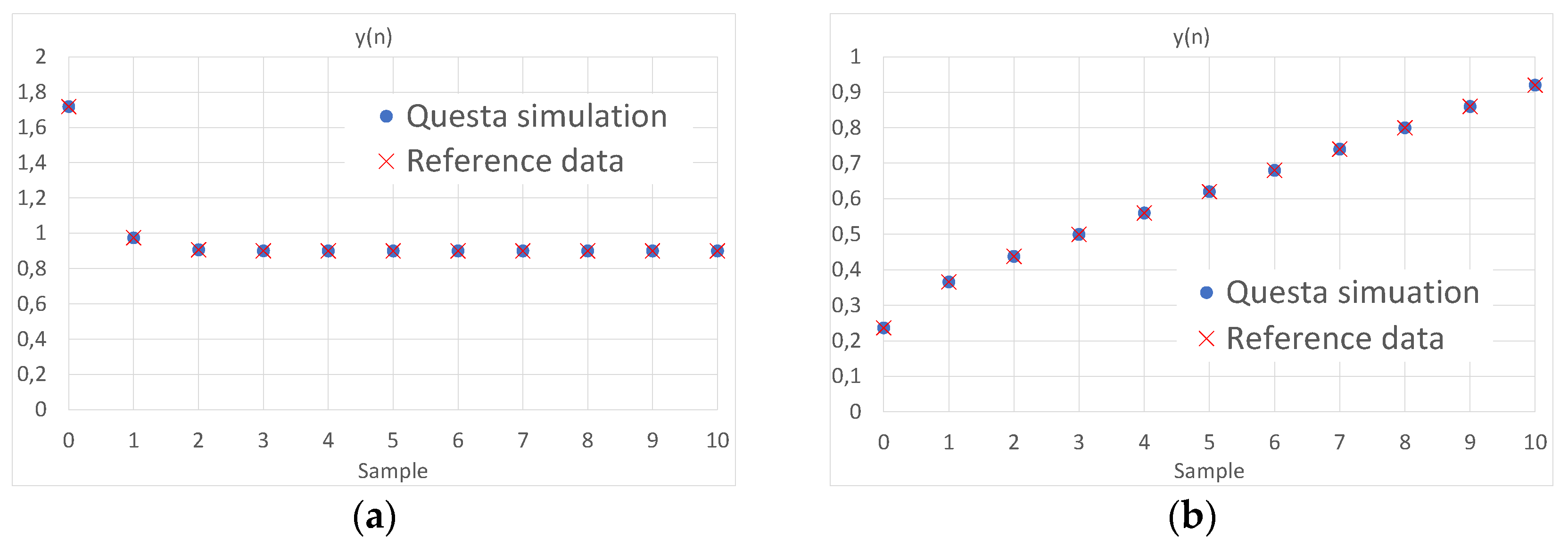
Sample plots, showing a comparison of the data obtained from the simulation, against the reference data generated by the C++ program, are presented in Figure 4. Figure 4a shows data obtained for a PD regulator with the following parameters: K_P = 1, T_I = ∞, T_D = 1, a = 0.1, b = 1, c = 1, and T_S = 1. Figure 4b presents data obtained for a PID regulator with K_P = 0.5, T_I = 0.75, T_D = 0.2, a = 0.1, b = 0.62, c = 0, and T_S = 0.1. The latter set of parameters was generated by the autotuner included in the TIA Portal software from Siemens, for a popular S7-1200 PLC controlling a small DC drive. In both cases the simulated circuit was excited by unit step signals with the magnitudes of 0.1, and 1 applied to the x and w inputs, respectively.

Analysis of the data obtained during the verification process described above indicates, that the proposed circuit properly implements the digitalized version of the “complex” PID formula described by Equation 3.

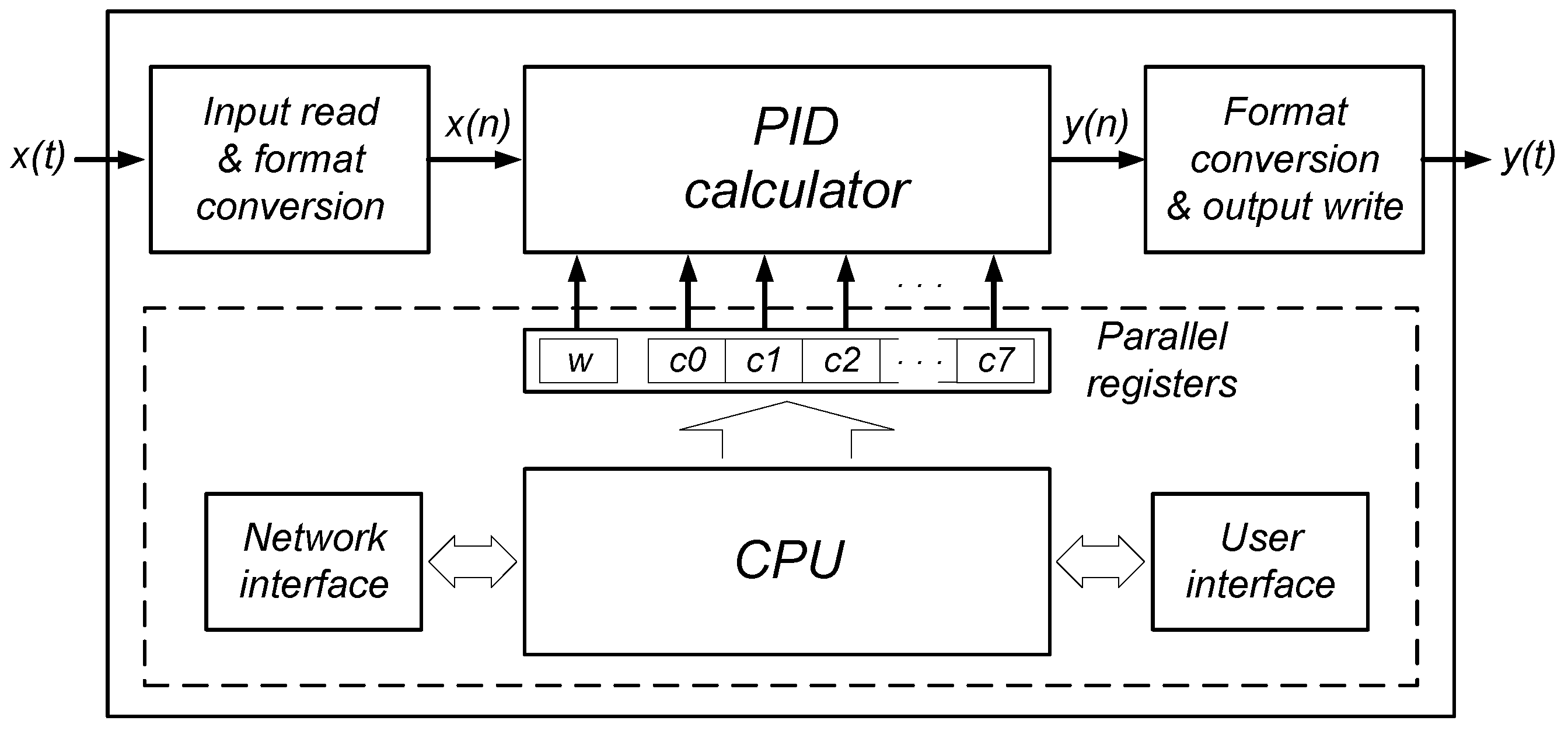
6. A general Concept of the entire Regulator Device

The circuit described in section 3 can serve as the “execution unit”, i. e. the main part of an actual regulator. However, it must be accompanied by some additional circuitry to form a fully functional device. The proposed concept of the entire regulator is presented in Figure 5.

The “PID calculator” described in section 3 operates on floating-point numbers. Samples of the process variable x need to be delivered to it in the appropriate format. Similarly, samples of the manipulated variable y, calculated by the “PID calculator”, need to be converted and transferred to the regulator output. These operations should be accomplished by the “Input read & format conversion” and “Format conversion & output write” blocks.

We expect that the process variable x is an analog signal. Thus the “Input read & format conversion” block should contain in particular an A/D converter, and circuitry that converts a fixed-point number, delivered by the A/D converter, to the floating-point format processed by the execution unit. Similarly the “Format conversion & output write” block should contain a kind of D/A converter (e. g. a circuitry generating a PWM signal), and a circuit that converts the floating point number evaluated by the execution unit to a fixed-point representation, which is appropriate for D/A conversion.

If modifying the regulator parameters is a required functionality of the device, the circuit should contain a CPU/MCU core, responsible in particular for converting the regulator parameters K_P, T_I, T_D, a, b, c, and T_S to the

c_{0}

–

c_{7}

coefficients used by the execution unit. During normal operation of a PID regulator, the K_P, T_I, T_D, a, b, c, and T_S parameters are accessed and manipulated, rather than

c_{0}

–

c_{7}

. This concerns both a human operator, and a high level application software, e. g. an autotuner, which is capable of finding the best values of the regulator parameters for a particular object.

The

c_{0}

–

c_{7}

coefficients are complex functions of K_P, T_I, T_D, a, b, c, and T_S, containing in particular the division operation (see Equations 14 to 21). Implementing the conversion functions in hardware would be very expensive in terms of logic resources consumed. On the other hand, a change of the PID regulator parameters is quite a rare condition, if compared to cyclic and permanent calculation of new samples of the regulator output. Calculating new values of the

c_{0}

–

c_{7}

coefficients is not a time-critical task and it can be conveniently handled by software running on the CPU. Moreover, introducing a CPU core to the device structure facilitates implementation of many additional useful functionalities, like handling user interface, network communication, self diagnostic, or, in particular, autotuning algorithms.

After analysis of Equations 14 to 21, we draw a conclusion, that modifying even one of the regulator parameters will usually cause a change in most of the

c_{0}

–

c_{7}

coefficients. A possible update of the coefficients should thus always include all of them. A need for modifying a coefficient separately is very unlikely.

To enable smooth operation of the regulator, without the need to stop the regulation every time a parameter is modified, a set of eight parallel registers should be planned to provide the source of new data for the

c 0_n e w

–

c 7_n e w

inputs (see Figure 3). The registers should be integrated with the CPU system, e. g. as parallel I/O ports. This way the CPU core will be able to access them freely, at moments convenient with respect to the program the CPU is executing. When a consistent set of new values of the coefficients is ready to be accessed by the execution unit, the CPU can trigger parameter update by activating the Par_Wr input together with the Start input (see Figure 3). ). It is important to change all the coefficients at once in order to prevent unpredictable behavior of the regulator.

The second possible application of the circuit presented in Figure 3 is using it in a regulator, which is dedicated for a particular object (e. g. a DC-DC converter). In such a case it is quite possible, that the regulator parameters will not change during whole lifecycle of the device. The set of regulator parameters can thus be calculated once, before the circuit is actually synthesized, and the new values for the

c_{0}

–

c_{7}

coefficients can be implemented as constants. In such a case the CPU/MCU core is not required, and the components of the circuit presented in Figure 3, responsible for controlling the coefficient update, i. e. the

P a r_W r

input, together with the corresponding And functor, can be deleted.

Furthermore, in certain technologies, e. g. in modern SRAM-based FPGA devices, it is possible to freely set initial values of all memory elements. If a regulator is implemented in such a device, the

c_{0}

–

c_{7}

coefficients can be downloaded to the Reg_c0 – Reg_c7 registers after reset, together with the device configuration, and the Mux_c0 – Mux_c7 multiplexers can be avoided, too.

7. Conclusions

The paper proposes a new implementation of the PID algorithm in digital hardware. The proposed circuit implements a more advanced PID formula (Equation 3), containing a non ideal derivative component, and weighting coefficients in the proportional and derivative components, which enables reducing influence of rapid changes of the setpoint to the regulator output.

The PID formula is discretized and converted to a form, in which samples of the output signal y depend on current values of the process variable x, the setpoint w, and two previous samples of y, x and w (Equation 13). Eight multiplication, and seven addition operations are required to evaluate the result. The final formula is very regular. This gives a hardware designer many options to arrange hardware components performing the relevant arithmetic operations.

The implementation presented in the paper operates on standard single precision (32 bit) floating-point numbers. The proposed circuit structure is optimized for cost, i. e. the amount of logic resources required for implementation. It contains just one arithmetic block. The structure consists of three main parts: the Mult_Add block, responsible for performing the actual calculations, and two sets of parallel registers arranged in two rings: the “variable ring”, and the “parameter ring” (see Figure 3). The “variable ring” stores current and previous samples of the y, x, and w variables, while the “parameter ring” contains a set of eight parameters, which depend on the actual regulator parameters K_P, T_I, T_D, a, b, c, and T_S.

The calculations are accomplished in a sequential manner: the data in the both rings are shifted and subsequently applied to the Mult_Add block inputs, in which the partial and final results are actually evaluated.

The circuit was implemented in a Cyclone V FPGA device from Intel, using the Quartus Prime software. The Mult_Add block was implemented as an IP-core available in the tool. Validation of the circuit was carried out as simulation in the Questa Sim simulator.

For the particular implementation, which is described in the paper, 81 clock cycles are required to evaluate one sample of the output signal. As the maximum clock frequency was estimated by the static timing analysis tools at c. a. 150 MHz, we can estimate the delay, which is required, before a valid result is available at the circuit output, at c. a. 550 ns.

It is important to note that if the controller would be physically implemented as part of an ASIC SoC design, rather than synthetized within programmable logic of an FPGA, even faster operation would be achievable.

The implementation presented in the paper is comparable in terms of speed with other hardware implementations of the PID algorithm operating on standard single precision floating-point numbers, while being significantly cheaper. However, it outperforms by several orders of magnitude the speed of any software-based implementation, including solutions using PLCs, and dedicated CPU/MCUs.

If modifying the regulator parameters is a required functionality of the device, the circuit described in the paper should be included as the “execution unit” in a bigger system governed by a CPU/MCU core. Such a system can be conveniently implemented in a SoC (System on Chip), or SoPC (System on Programmable Chip) device, i. e. a device, that, apart from the “FPGA fabric”, contains also a CPU core. Devices of this kind are delivered by all main PLD vendors, and gain increasing popularity.

Author Contributions

Conceptualization, J.K. and F.J.; methodology, J.K.; implementation, J.K.; software, F.J.; validation, J.K. and F.J.; formal analysis, F.J.; resources, J.K. and F.J.; writing—original draft preparation, J.K.; writing—review and editing, F.J.; supervision, J.K. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by funding from the Ministry of Science and Higher Education for Statutory Activities of Digital Systems Division of the Silesian University of Technology in Gliwice (BK237/RAU12/2023).

Conflicts of Interest

The authors declare no conflict of interest.

References

Visioli, A. Practical PID control, Springer-Verlag: London, 2006;
Siemens, AG. SIMATIC. Standard PID control manual, Documentation No. A5E00204510-02, Edition 03/2003, Siemens AG, 2003.
Rockwell Automation. Logix 5000 Advanced Process Control and Drives Instructions. Reference Manual. Publication 1756-RM006O-EN-P - November 2023, Rockwell Automation, 2023.
OMRON Corporation. Function block reference manual. Cat. No. W407-E1-10, OMRON Corporation, August 2022.
Siemens, AG. S7-1200 Programmable controller. System Manual. Documentation No. A5E02486680-AO, Edition 04/2021, Siemens AG, 2021.
Dhanabalan, G.; Tamil Selvi, S.; Mahdal, M. Scan Time Reduction of PLCs by Dedicated Parallel-Execution Multiple PID Controllers Using an FPGA. Sensors 2022, 22, 4584. [Google Scholar] [CrossRef] [PubMed]
Kyungnam Lee; Youngmin Kim. Design and Analysis of Digital PID Controller in MCU and FPGA. In Proceedings of the International SoC Design Conference ISOCC 2018, Daegu, Korea, 2018.
Chu Zhou; Qiongying Zhang; Ezechias, D.D.; Yu Gao; Hongtao Deng; Shaocheng Qu. A General Digital PID Controller Based on PWM for Buck Converter. In Proceedings of the 11-th World Congress on Intelligent Control and Automation, Shenyang, China, 2014.
Kartik Sharma; Dheeraj Kumar Palwalia. Design of Digital PID Controller for Voltage Mode Control of DC-DC Converters. In Proceedings of the International conference on Microelectronic Devices, Circuits and Systems ICMDCS’2017, Vellore, India, 2017.
Sreenivasappa, B. V.; Udaykumar, R. Y. Design and Implementation of FPGA Based Low Power Digital PID Controllers. In Proceedings of the Fourth International Conference on Industrial and Information Systems, ICIIS 2009, Sri Lanka, 2009.
Yuen Fong Chan; Moallem, M.; Wei Wang. Design and Implementation of Modular FPGA-Based PID Controllers. IEEE Transactions on Industrial Electronics 2007, Vol. 54, No. 4.
Kocur, M.; Kozak, S.; Dvorscak, B. Design and Implementation of FPGA - Digital Based PID Controller. In Proceedings of the 15th International Carpathian Control Conference ICCC’2014, 2014.
Yankai Xu; Kai Shuang; Shan Jiang; Xiaoliang Wu. FPGA Implementation of a Best-precision Fixed-point Digital PID Controller. In Proceedings of the International Conference on Measuring Technology and Mechatronics Automation ICMTMA’2009, 2009.
Wang, J.; Li, M.; Jiang, W.; Huang, Y.; Lin, R. A Design of FPGA-Based Neural Network PID Controller for Motion Control System. Sensors 2022, 22, 889. [CrossRef]
Zębiński, A.; Glinianowicz, M.; Lachowski, G. Implementacja regulatora PID w strukturze FPGA. Pomiary, Automatyka, Kontrola, PAK 2008, vol. 54, nr 8. (in Polish).
Intel Corporation. Floating-Point IP Cores User Guide, Documentation No. UG-01058, 2023.05.05, Intel Corporation, 2023.
Intel Corporation. Cyclone^® V Device Handbook, Documentation No. CV-5V2, 2023.10.18, Intel Corporation, 2023.
Milik, A.; Hrynkiewicz, E. Hardware Mapping Strategies of PLC Programs in FPGAs. In Proceedings of the 15th IFAC Conference on Programmable Devices and Embedded Systems PDeS 2018: Ostrava, Czech Republic, 23—25 May 2018. [CrossRef]
Milik, A. On hardware synthesis and implementation of PLC programs in FPGAs. Microprocessors and Microsystems 2016, Vol. 44, pp. 2-16. [CrossRef]

Figure 1. A structure of a typical control system containing a PID regulator in the feedback loop.

Figure 2. A parallel implementation of the PID formula.

Figure 3. The proposed structure of the circuit calculating the PID algorithm.

Figure 4. Sample plots showing a response to a unit step of: (a) a PD regulator; (b) a PID regulator.

Figure 5. A general structure of the proposed PID regulator device.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Hardware Implementation of the PID Algorithm Using Floating-Point Arithmetic

Abstract

1. Introduction

2. Discretization of the PID Formula

3. The proposed Circuit Structure

4. Implementation of the Proposed Circuit

5. Testing and Verification

6. A general Concept of the entire Regulator Device

7. Conclusions

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe