1. Introduction
The health status of plastic water conveyance pipelines exerts a substantial influence on economic development, transportation, and societal well-being[
1,
2]. Vigilant monitoring of plastic water pipelines is imperative, particularly in the context of strain surveillance within the pipeline framework. Cutting-edge, expansive distributed intelligent sensing components, exemplified by Fiber Bragg Grating (FBG) sensors, lay the groundwork for the evolution of health monitoring systems for pipeline structures[
3,
4]. FBG strain sensors, characterized by robust immunity to electromagnetic interference, elevated precision, commendable longevity, and the capacity for distributed measurement, are instrumental in this regard. During the health monitoring of pipelines, optical fiber strain sensors are typically operated within dynamic scenarios[
5]. Any inaccuracies in the measurement data of these sensors may introduce adverse effects on subsequent control, monitoring, and fault diagnostic systems, potentially resulting in detrimental occurrences such as misdiagnoses and false alarms, with significant repercussions. Therefore, it becomes imperative to subject FBG strain sensors utilized in practical scenarios to calibration processes to ensure the precision of measurement outcomes.
The main challenge faced by many researchers is the accuracy of FBG compared with the traditional sensing technology such strain gauges. Recently investigators have examined the effects of strain transfer on the optical fiber sensors. Fiber optic sensors are composed of a fiber core and a sheath, which can be affixed to the structure's surface by adhesive, buried within the structure, or secured to the structure by mechanical devices. Regardless of the method chosen, the actual strain of the structure to be measured is inevitably subjected to losses as it passes through the adhesive, sheath, and other intermediate media to reach the core part of the fiber optic sensor. Consequently, a certain gap exists between the strain measured by the fiber optic core and the actual deformation of the structure, giving rise to what is known as the strain transfer loss phenomenon. The strain loss resulting from this transfer is termed the rate of strain transfer, and the strain transfer loss constitutes one of the primary sources of measurement error in optical fiber.
The utilization of the strain transfer theory to calculate the optical fiber strain transfer rate has been proposed by researchers[
6] to eliminate the measurement error of optical fibers. The strain transfer theory, originally introduced by Cox[
7], focuses on investigating the collaborative deformation of adjacent materials under external forces and was initially applied to analyze thread breakage and drawing behavior in textiles. Subsequently, enhancements to the strain transfer theory were made by Eshelby[
8], who adapted the theory to meet the specific requirements of physics and engineering. They employed the dissection-deformation-combination analytical method to scrutinize the forces acting on composites wrapped with different geometries of built-ups, exploring the impact of material inhomogeneity in wrapped bodies and elliptical built-ups on their overall deformation field. Furthermore, Rosen[
9], CHOON[
10], and others utilized the strain transfer theory to analyze the shear hysteresis phenomenon occurring at the material contact surface due to the unilateral stressing of composites. As a result, strain transfer theory is also recognized as shear lag theory.
One major theoretical issue that has dominated the field for many years concerns is the parameter sensitive of strain loss. The effect of paster method on strain transfer loss is studies by Nanni[
11], Duck[
12], Dasgupta[
13], contains external and embedded layout. The influence of layers on strain transfer loss is examined by Yuan[
14], Ansari[
15], Lau[
16], LeBlanc[
17], Her[
18,
19], involving two, three, four layers, respectively. The design of fiber armed is investigated by Torres[
20], Li[
21,
22], Billon[
23], Luyckx[
24], addressing its impact on strain transfer loss and encompassing naked fiber, PVC armed, mini pipe, mental armed. Strain transfer loss is analyzed concerning the service circumstance, with contributions from Wang[
25,
26,
27], Liu[
28,
29,
30], Ansari[
31] who highlighting in uneven matrix, fatigue load, distribution of external forces.
Such approaches, however, have failed to address the strain transfer loss of FBG subjected by dynamic loads. Firstly, much of the research up to now has been descriptive and theoretical, which is lack validation by experimental data. Secondly, researchers have not treated dynamic loading in much detail, which is not treated as a background in the analysis. Thirdly, although extensive research has been carried out on strain transfer loss, no single study exists which paste methods is suitable for pipe deformation measurement. Lastly, previous analysis does not take account of the difference of FBG attached on various pipe materials, nor does the examination of strain sensing technology such as FBG, OFTR and BOTDA. With such shortage, it is not clear whether the measured result of FBG attached on ABR pipe and other water support pipe is believable or not.
In conclusion, the foregoing discussion has underscored the significance of strain transfer ratio of FBG. The identified gaps in the current understanding of strain transfer loss highlight the need for further investigation. The primary objective of this study is to study the strain transfer of FBG attached on a novel pipe material (ABR) under static and dynamic load with calibration test, shedding light on the strain loss relate to the dynamic force. A three-layer dynamic strain transfer theory for the calculation of STR and ASTR of FBG subjected by dynamic loading is deduced, and the parameter sensitive is analyzed. The calibration test for ABR-measurement FBG is designed, and the test results of ASTR is compared with the theoretical outcome. The experimental and theoretical work presented here provides one of the first investigations into how to analysis the strain transfer loss of FBG attached on ABR pipe, which will be used on a large scale in the project.
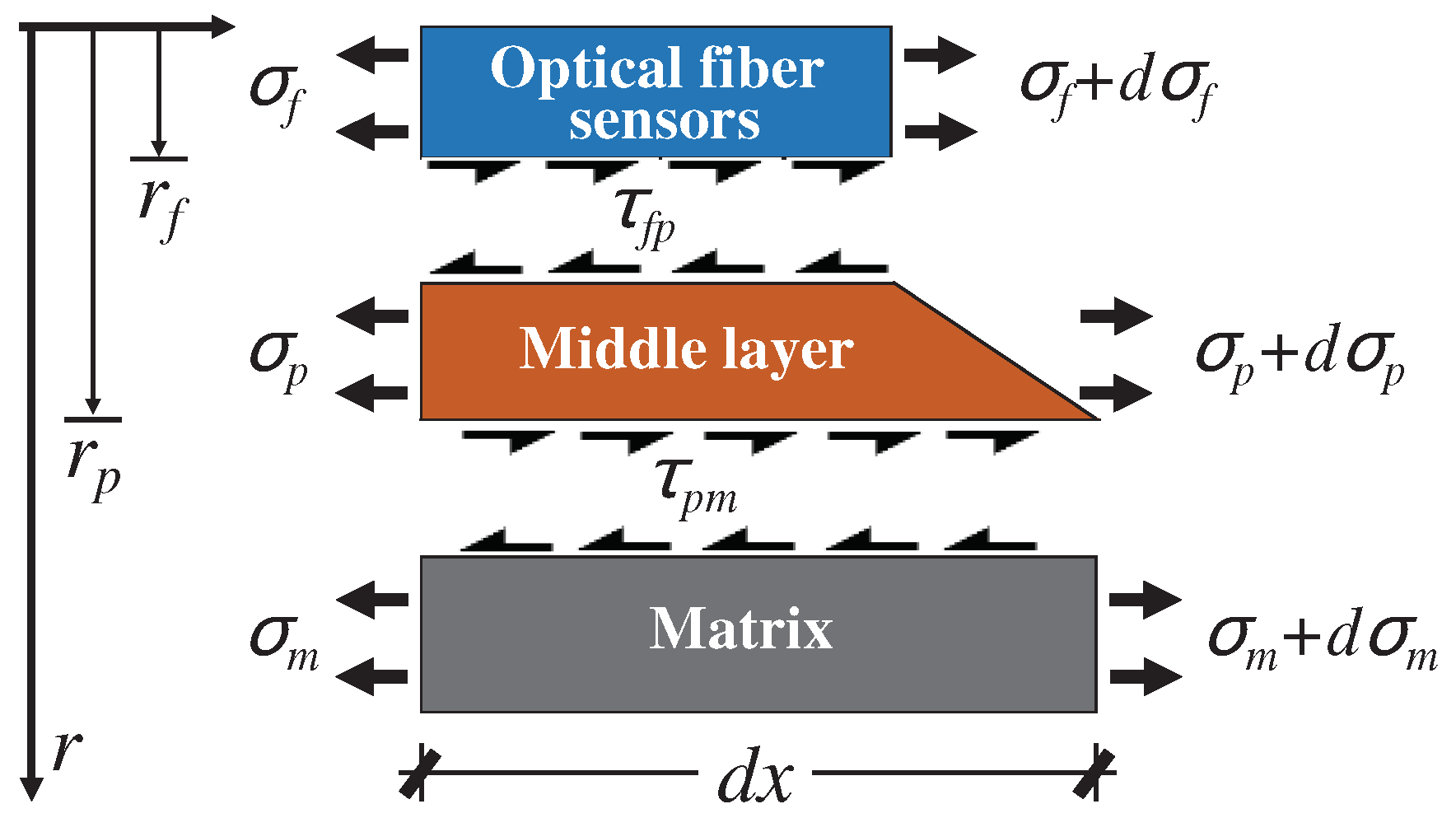
Figure 1.
Performance analysis model for fiber optic monitoring.
Figure 1.
Performance analysis model for fiber optic monitoring.
Figure 2.
Force on fiber optic sensor.
Figure 2.
Force on fiber optic sensor.
Figure 3.
Force on middle layer.
Figure 3.
Force on middle layer.
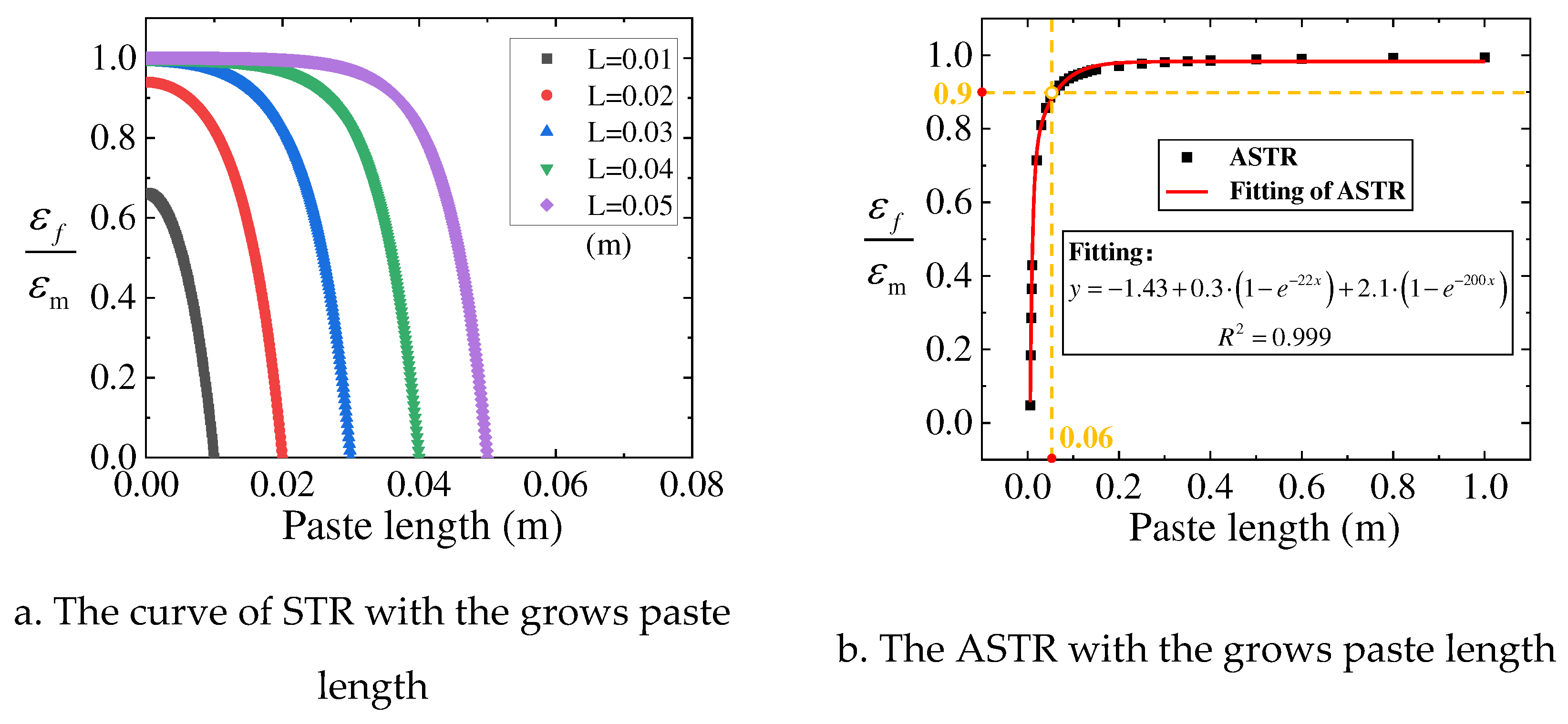
Figure 4.
The trend of STR and ASTR with the grows of paste length.
Figure 4.
The trend of STR and ASTR with the grows of paste length.
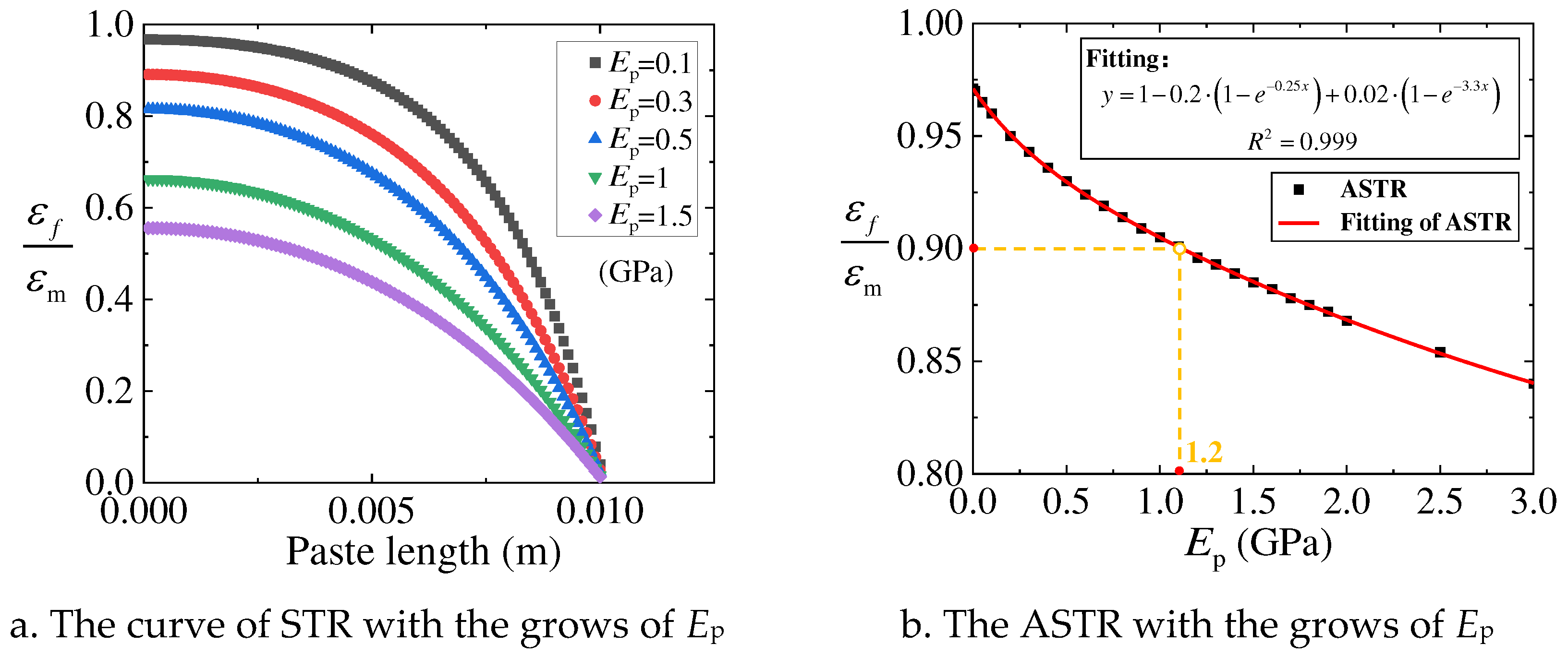
Figure 5.
The trend of STR and ASTR with the grows of Ep.
Figure 5.
The trend of STR and ASTR with the grows of Ep.
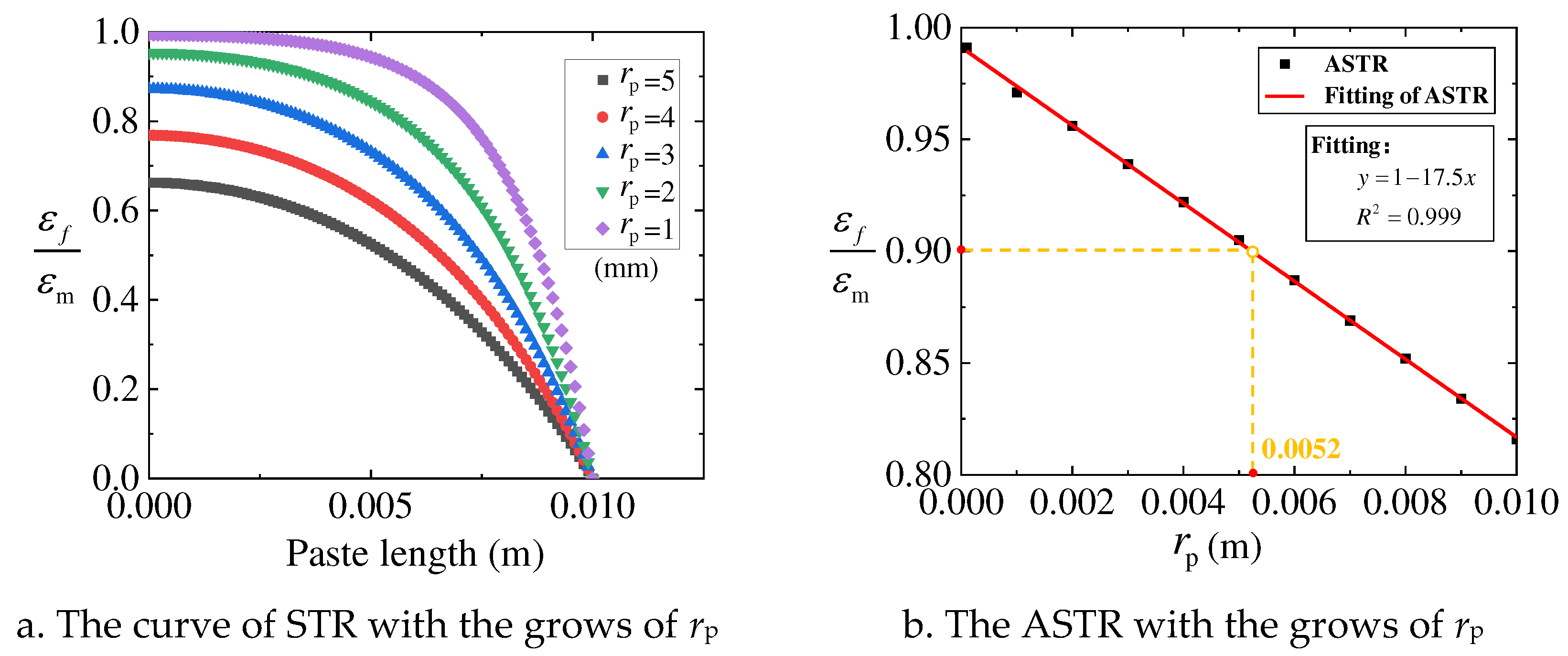
Figure 6.
The trend of STR and ASTR with the grows of rp.
Figure 6.
The trend of STR and ASTR with the grows of rp.
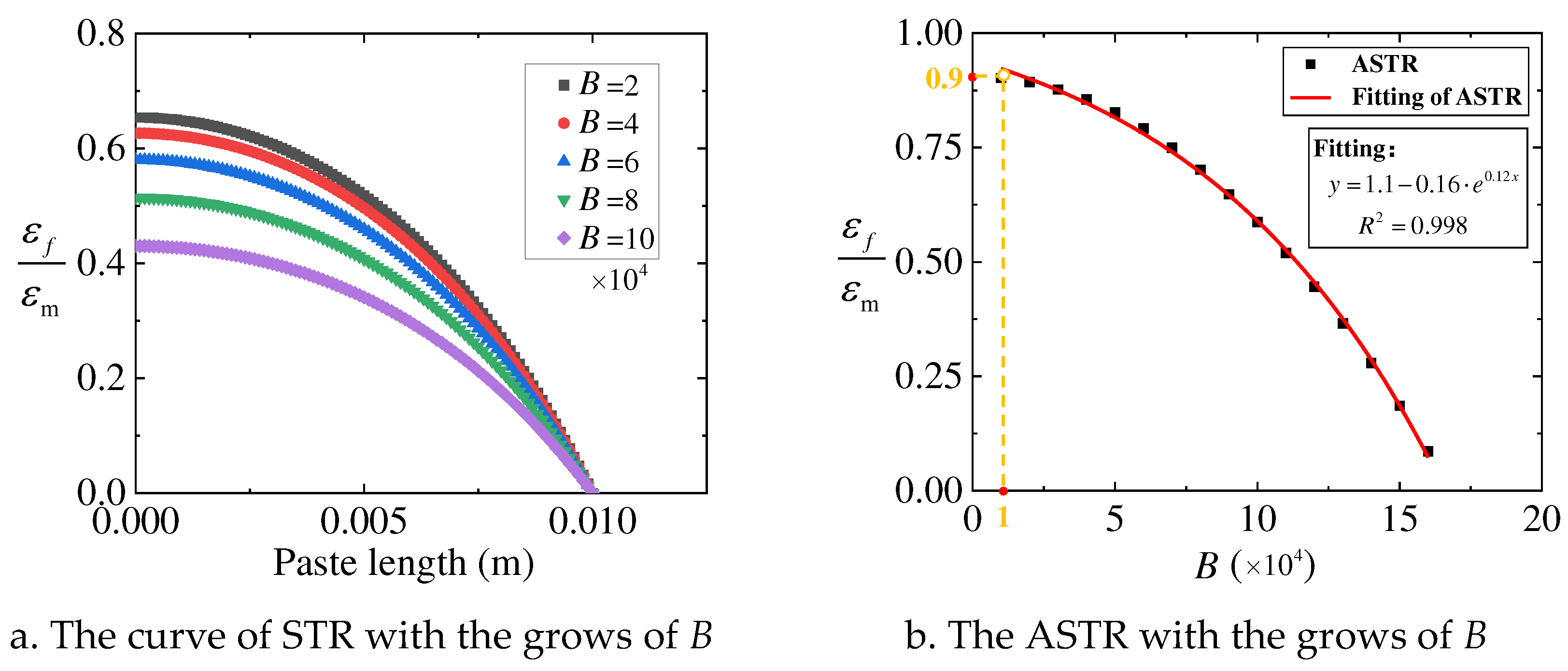
Figure 7.
The trend of STR and ASTR with the grows of B.
Figure 7.
The trend of STR and ASTR with the grows of B.
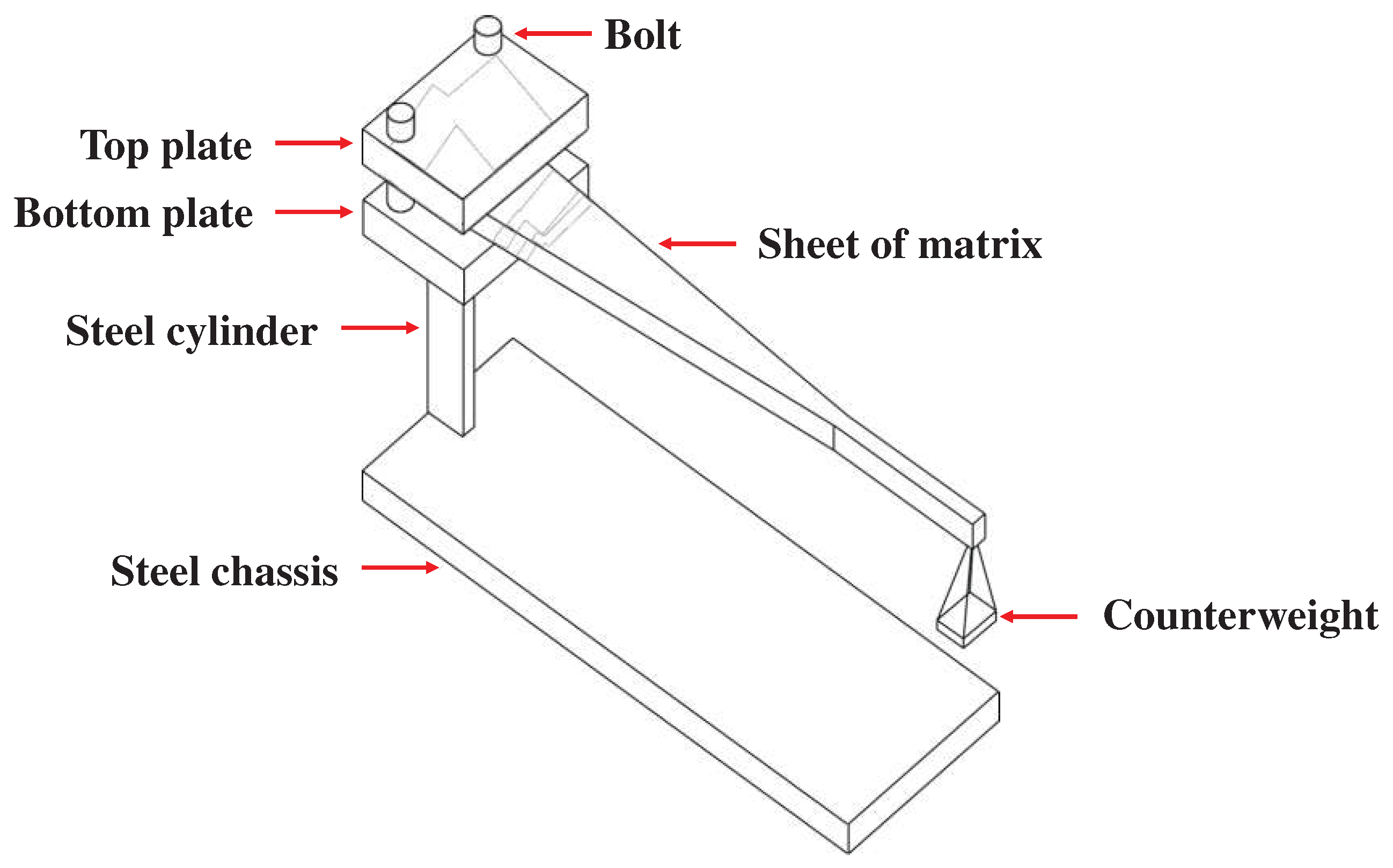
Figure 8.
Structure of the calibration device.
Figure 8.
Structure of the calibration device.
Figure 9.
Details of the static calibration test.
Figure 9.
Details of the static calibration test.
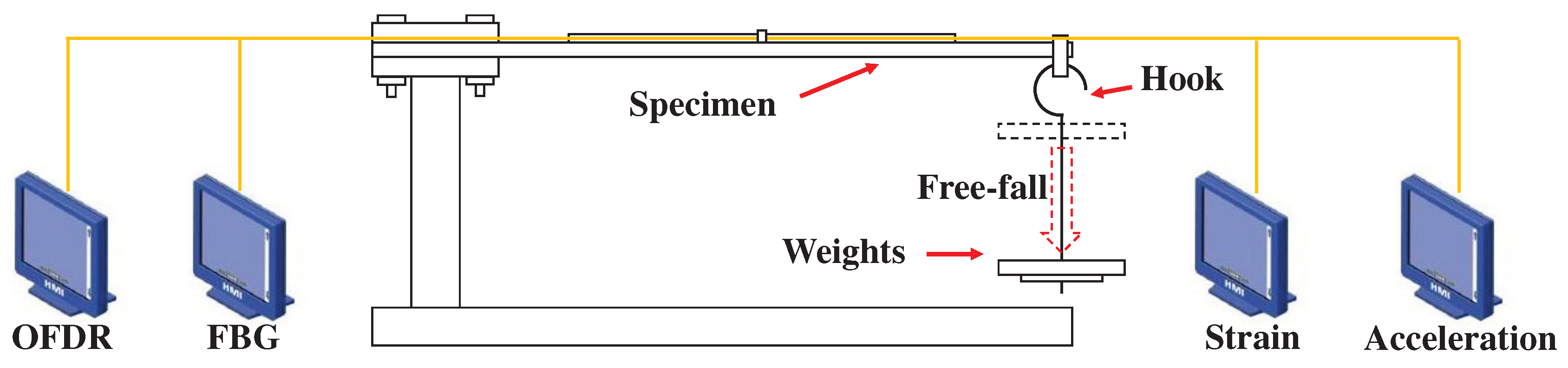
Figure 10.
Details of the dynamic calibration test.
Figure 10.
Details of the dynamic calibration test.
Figure 11.
Details of the calibration test.
Figure 11.
Details of the calibration test.
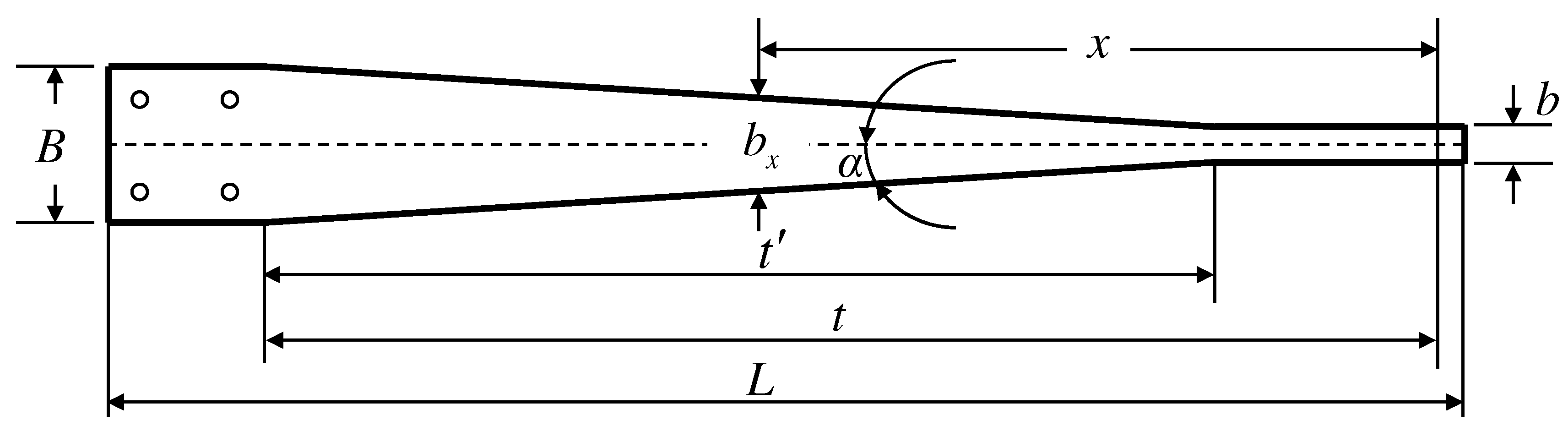
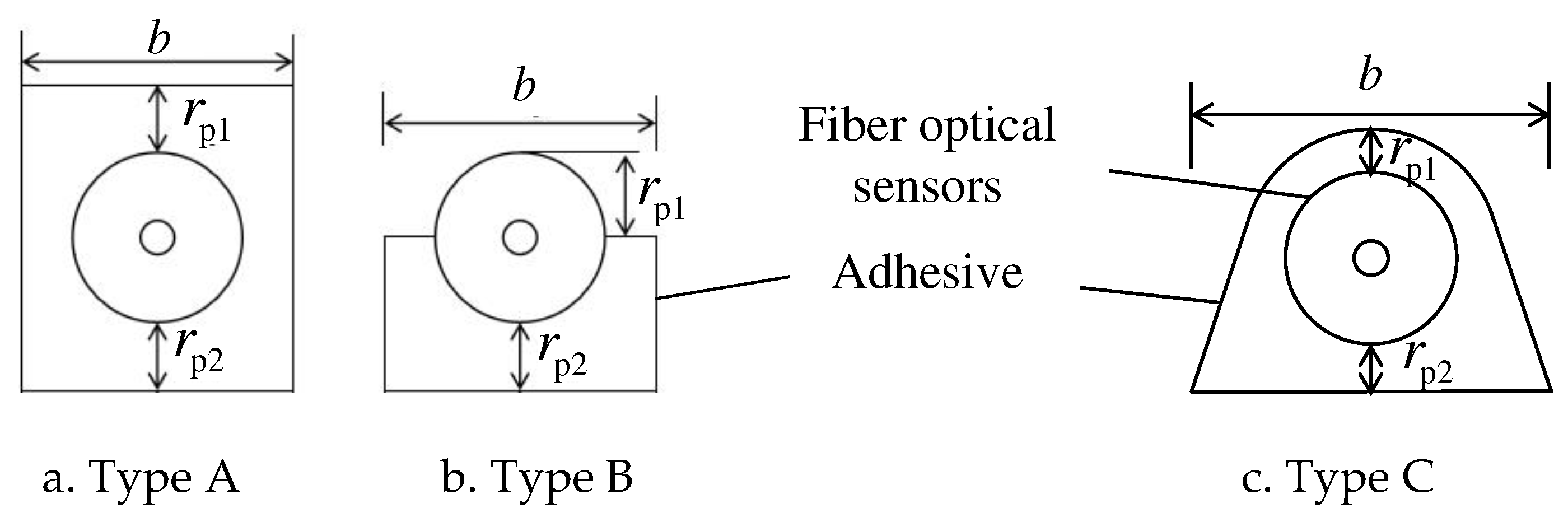
Figure 12.
Geometry of the sheet.
Figure 12.
Geometry of the sheet.
Figure 13.
optical fiber sensors in this test.
Figure 13.
optical fiber sensors in this test.
Figure 14.
Type of paste method.
Figure 14.
Type of paste method.
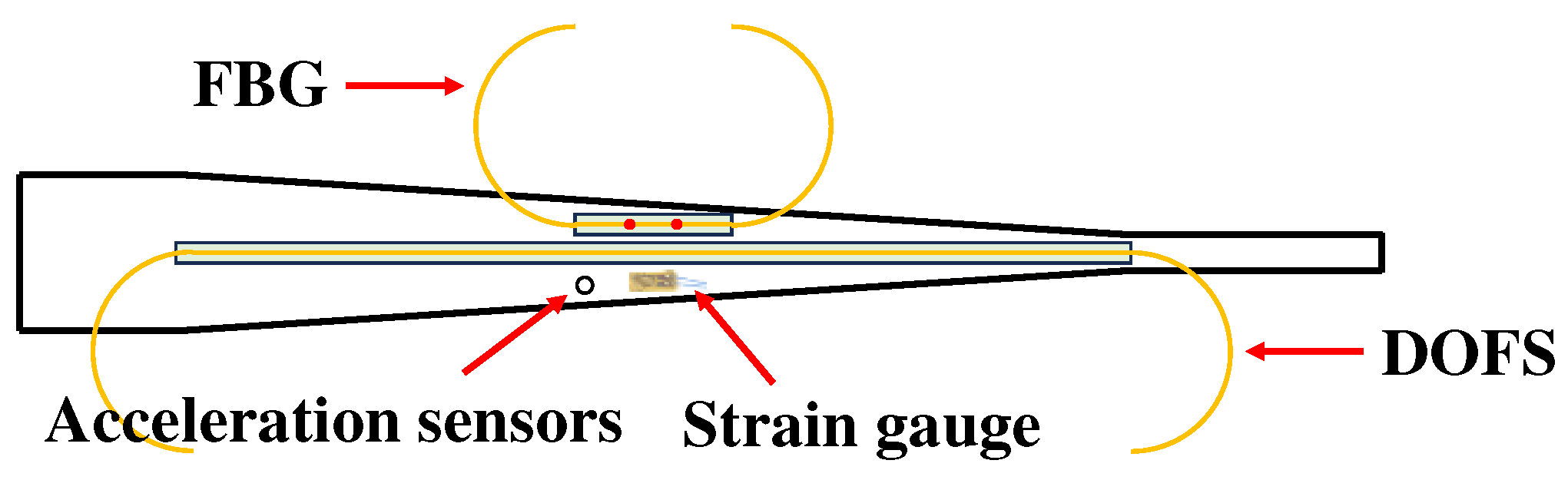
Figure 15.
The layout of the optical fiber sensors.
Figure 15.
The layout of the optical fiber sensors.
Figure 16.
The layout of the optical fiber sensors.
Figure 16.
The layout of the optical fiber sensors.
Figure 17.
Fiber grating demodulator(Type Zx-fg-c04-1).
Figure 17.
Fiber grating demodulator(Type Zx-fg-c04-1).
Figure 18.
Distributed fiber optic demodulator(Type DITEST STA-R Series).
Figure 18.
Distributed fiber optic demodulator(Type DITEST STA-R Series).
Figure 19.
Dynamic distributed fiber optic demodulator(Type OSI-D).
Figure 19.
Dynamic distributed fiber optic demodulator(Type OSI-D).
Figure 20.
Dynamic distributed fiber optic demodulator(Type OSI-D).
Figure 20.
Dynamic distributed fiber optic demodulator(Type OSI-D).
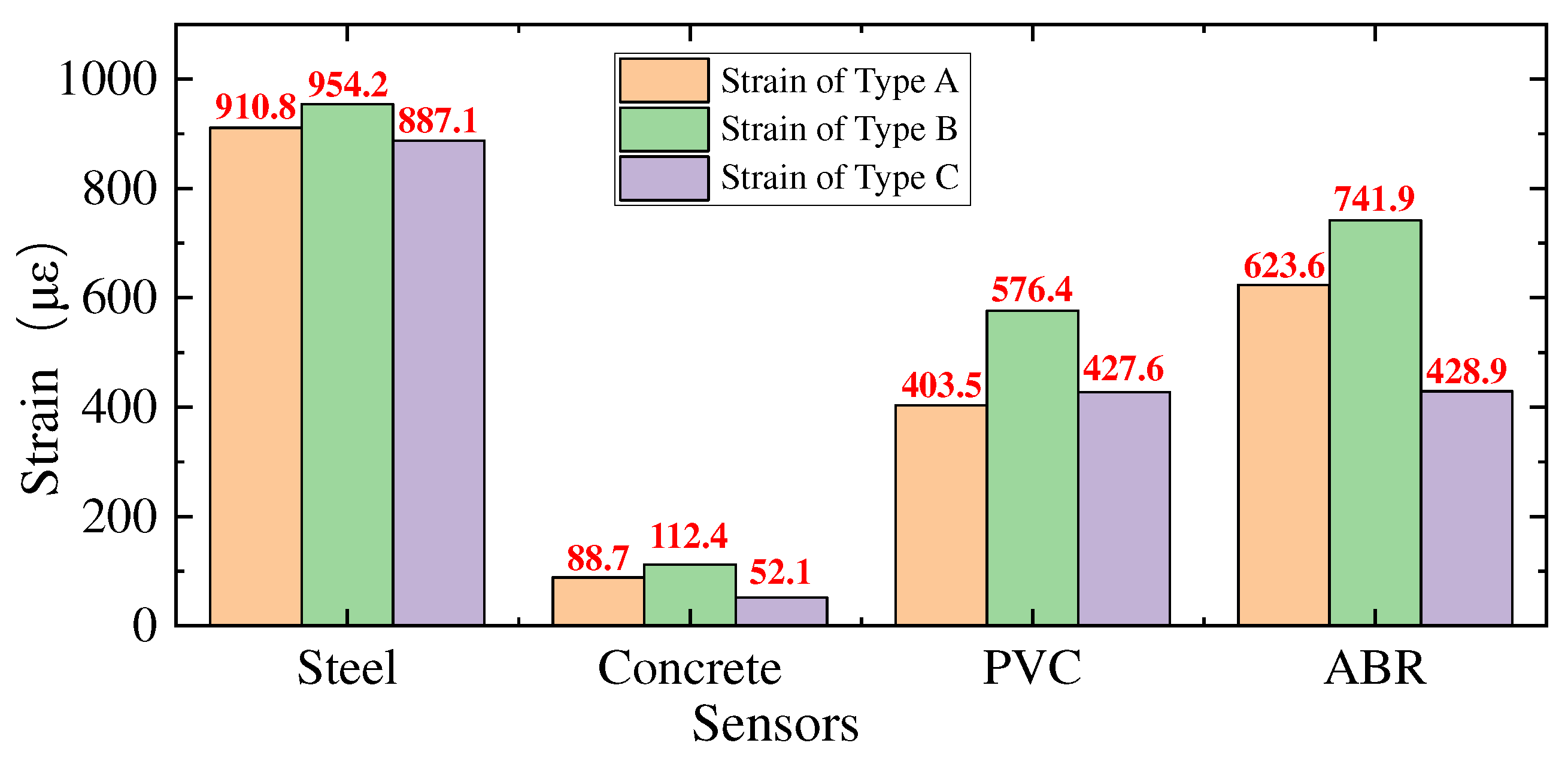
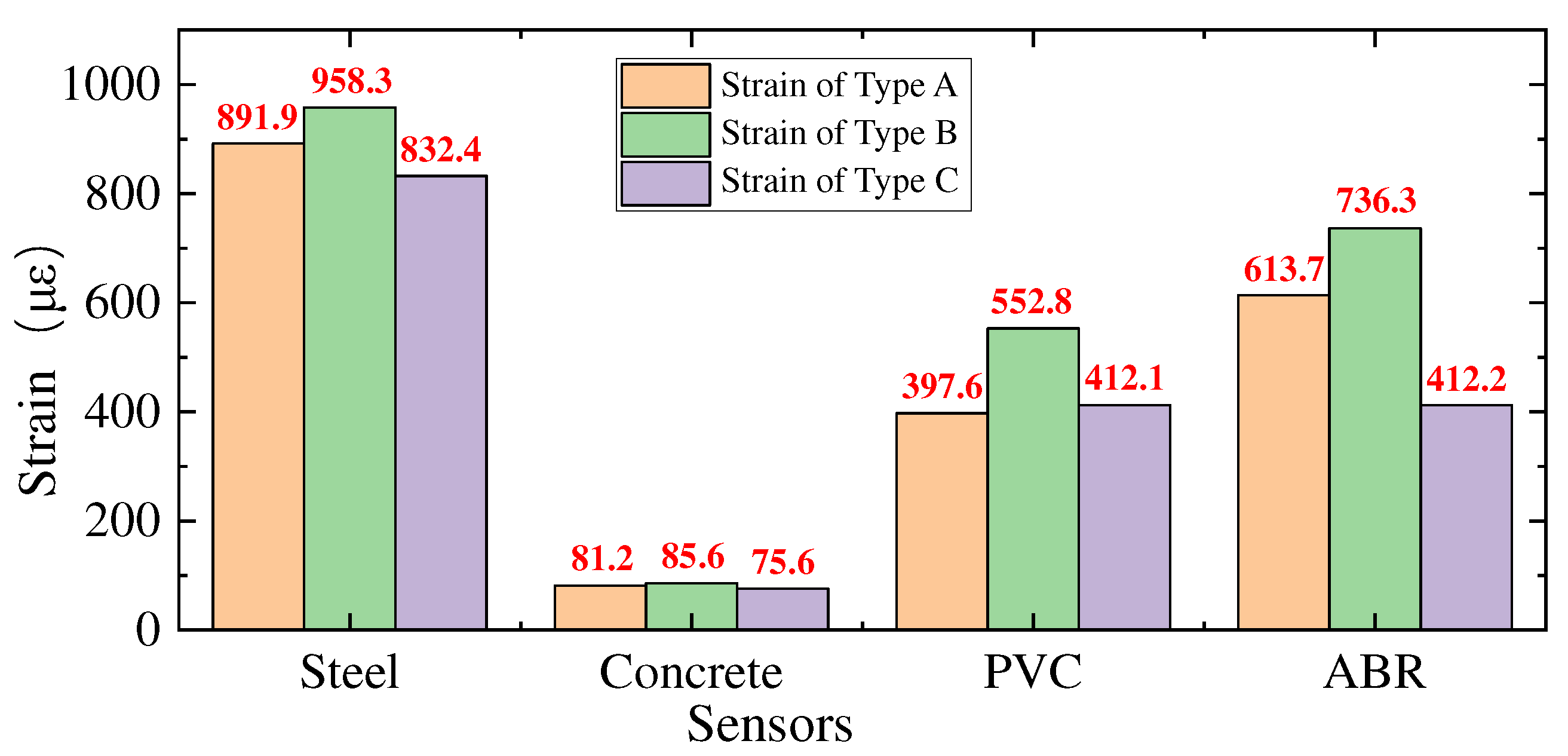
Figure 21.
Strain comparison of FBG attached on each sheet.
Figure 21.
Strain comparison of FBG attached on each sheet.
Figure 22.
Strain comparison of DOFS attached on each sheet.
Figure 22.
Strain comparison of DOFS attached on each sheet.
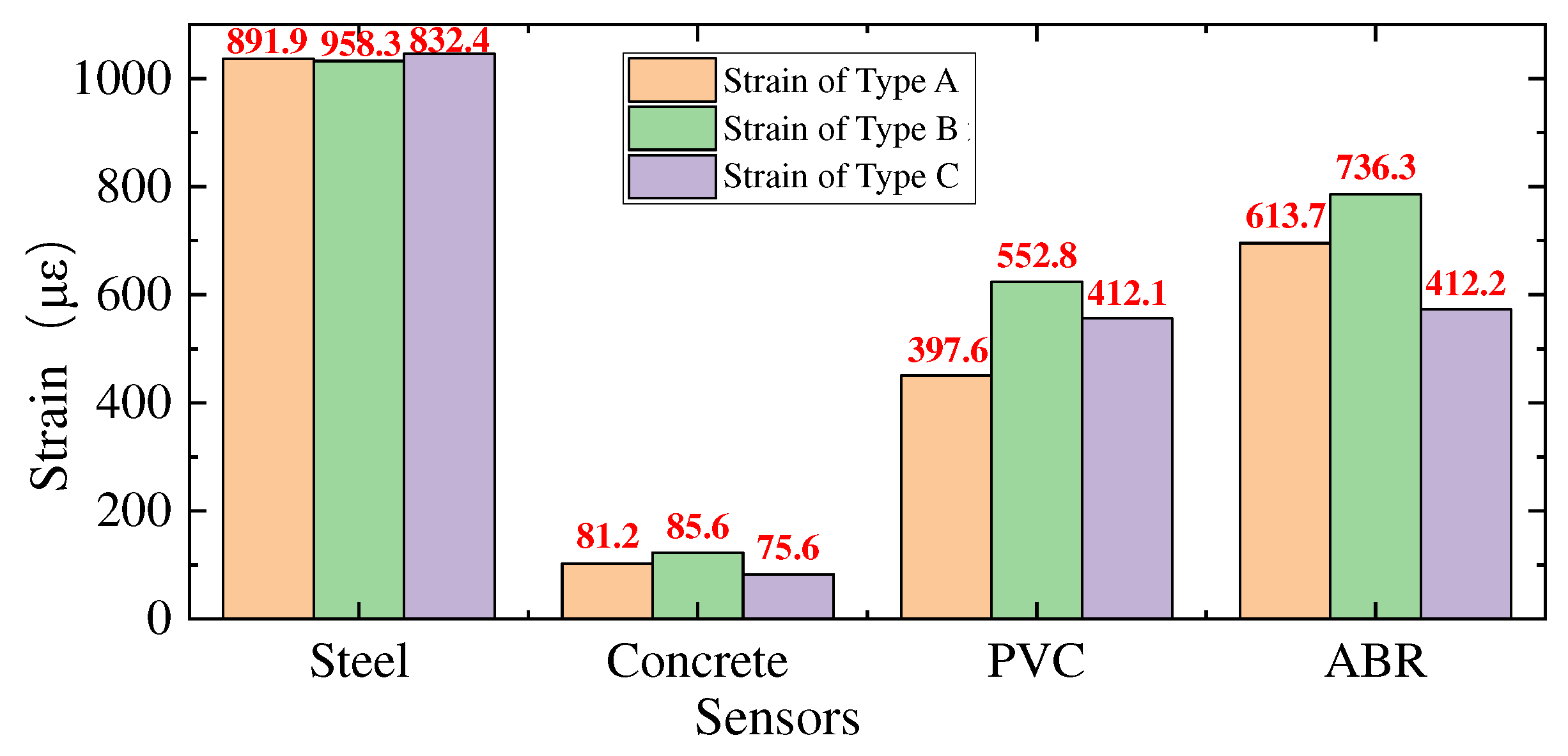
Figure 23.
Strain comparison of Strain gauge attached on each sheet.
Figure 23.
Strain comparison of Strain gauge attached on each sheet.
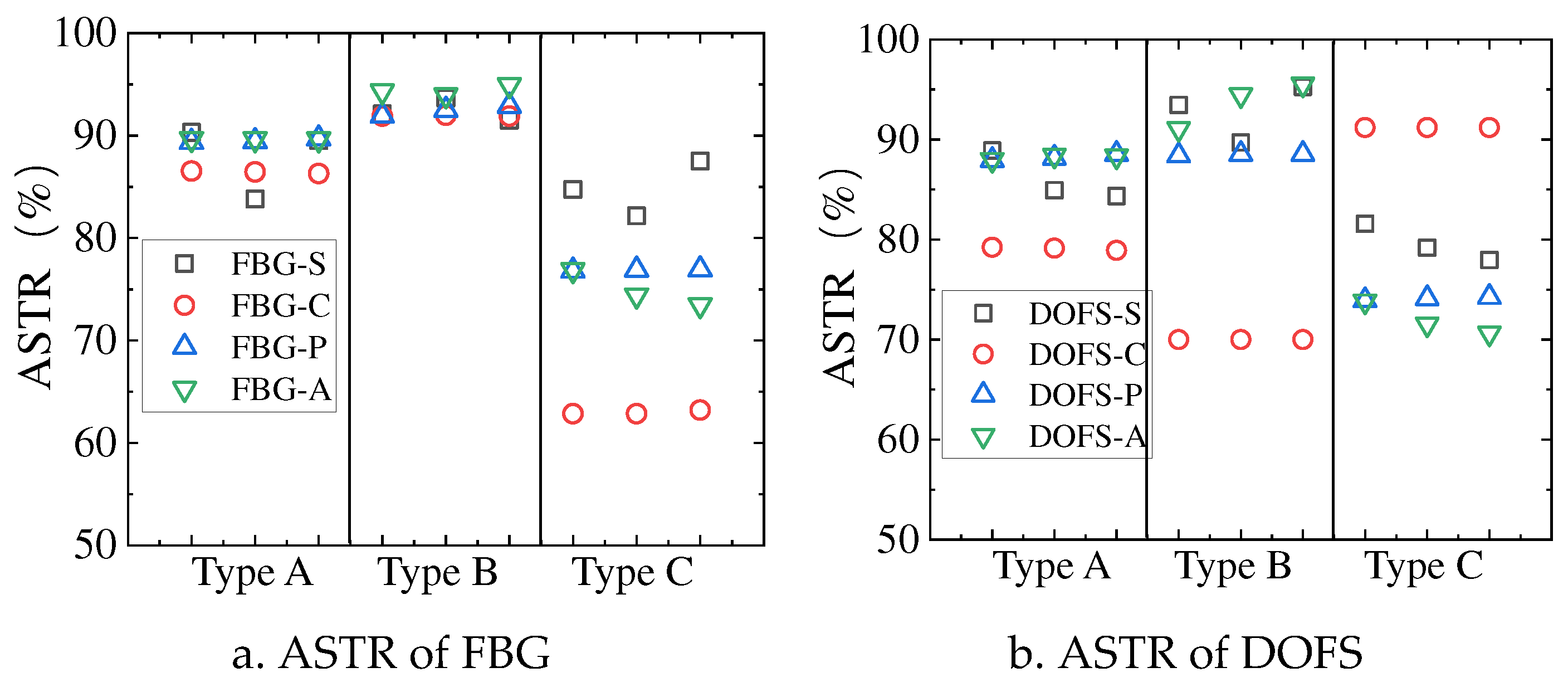
Figure 24.
ASTR comparison of sensors attached on each sheet.
Figure 24.
ASTR comparison of sensors attached on each sheet.
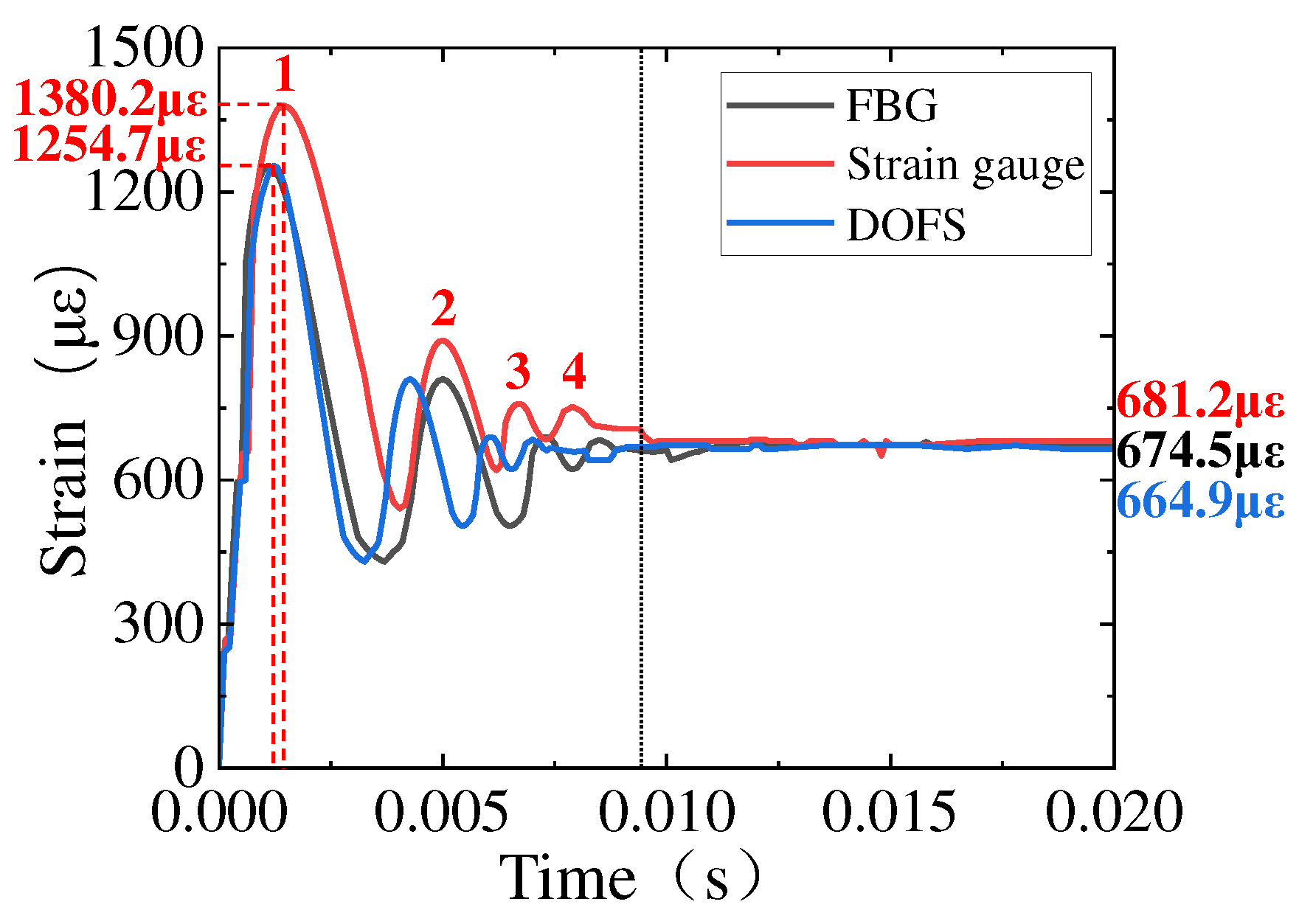
Figure 25.
ASTR comparison of sensors attached on the sheet S-1.
Figure 25.
ASTR comparison of sensors attached on the sheet S-1.
Table 1.
Material parameters for theoretical calculation.
Table 1.
Material parameters for theoretical calculation.
| Parameters |
Fiber core
(f) |
Protective layer
(p) |
Adhesive
(a) |
ABR
(m) |
|
E (GPa) |
72 |
0.00255 |
1 |
3 |
|
r (m) |
0.0000625 |
0.0009 |
0.005 |
0.05 |
| v |
0.17 |
0.48 |
0.38 |
0.3 |
|
ρ (kg/m3) |
2200 |
1200 |
1200 |
1200 |
|
G (GPa) |
30.8 |
0.00085 |
0.21 |
1.154 |
Table 2.
Dynamic parameters for theoretical calculation.
Table 2.
Dynamic parameters for theoretical calculation.
| Amplification |
Attenuation coefficient |
Frequency |
Cross-section area |
|
A (kN) |
B |
f (Hz) |
Sm(m2) |
| 100 |
800 |
80 |
0.01 |
Table 6.
Performance of dynamic distributed fiber optic demodulator(Type OSI-D).
Table 6.
Performance of dynamic distributed fiber optic demodulator(Type OSI-D).
| Parameter |
Units |
Details |
| Distance |
m |
20 |
| Spatial resolution |
mm |
0.64~10.24 |
| Sample rate |
Hz |
100 |
| Resolution of Temperature |
℃ |
0.4 |
| Resolution of Strain |
με |
4 |
| Range of Temperature |
℃ |
-200~1200 |
| Temperature of operation |
℃ |
10~40 |
Table 7.
The strain of FBG, DOFS and Strain gauge (Specimen S and C).
Table 7.
The strain of FBG, DOFS and Strain gauge (Specimen S and C).
| Sensors |
S-1 |
S-2 |
S-3 |
C-1 |
C-2 |
C-3 |
| FBG |
903.5 |
942.5 |
885.2 |
88.7 |
112.4 |
52.1 |
| 887.5 |
963.7 |
863.7 |
88.7 |
112.5 |
52.1 |
| 941.5 |
956.4 |
912.4 |
88.8 |
112.4 |
52.4 |
| DOFS |
889.2 |
956.2 |
852.1 |
81.2 |
85.6 |
75.6 |
| 899.3 |
923.1 |
832.4 |
81.2 |
85.6 |
75.6 |
| 887.2 |
995.6 |
812.6 |
81.2 |
85.6 |
75.6 |
| Strain gauge |
1000.3 |
1023.2 |
1044.5 |
102.5 |
122.3 |
82.9 |
| 1058.9 |
1029.1 |
1051.2 |
102.6 |
122.3 |
82.9 |
| 1051.8 |
1045.3 |
1042.5 |
102.9 |
122.3 |
82.9 |
Table 8.
The strain of FBG, DOFS and Strain gauge (Specimen P and A).
Table 8.
The strain of FBG, DOFS and Strain gauge (Specimen P and A).
| Sensors |
P-1 |
P-2 |
P-3 |
A-1 |
A-2 |
A-3 |
| FBG |
402.9 |
573.2 |
427.2 |
623.5 |
741.1 |
427.8 |
| 403.2 |
576.8 |
427.7 |
623.5 |
741.7 |
429.5 |
| 404.4 |
579.3 |
427.9 |
623.9 |
743.1 |
429.5 |
| DOFS |
396.4 |
551.1 |
411.1 |
611.7 |
715.6 |
410.8 |
| 397.4 |
552.1 |
412.2 |
614.7 |
745.6 |
412.9 |
| 399.1 |
552.1 |
412.9 |
614.7 |
747.6 |
412.9 |
| Strain gauge |
450.8 |
623.5 |
556.2 |
695.2 |
785.6 |
556.4 |
| 450.8 |
623.6 |
556.2 |
695.3 |
789.4 |
577.2 |
| 450.8 |
623.6 |
556.2 |
695.9 |
782.6 |
584.6 |
Table 9.
The strain of FBG, DOFS and Strain gauge attached on the sheet S-1.
Table 9.
The strain of FBG, DOFS and Strain gauge attached on the sheet S-1.
| Sensors |
1 |
2 |
3 |
4 |
Average |
| FBG |
1253.2 |
842.5 |
702.8 |
674.5 |
|
| FBG/ Strain gauge |
90.8% |
93.5% |
93.7% |
99.1% |
94.3% |
| DOFS |
1254.7 |
833.6 |
693.1 |
664.9 |
|
| DOFS/ Strain gauge |
90.9% |
92.6% |
92.4% |
97.6% |
93.4% |
| Strain gauge |
1380.2 |
900.7 |
750.4 |
681.2 |
|
| FBG/ DOFS |
99.9% |
101.1% |
101.4% |
101.4% |
101.1% |
Table 11.
The ASTR of the FBG attached on each sheet.
Table 11.
The ASTR of the FBG attached on each sheet.
| Specimen |
S-1 |
S-2 |
S-3 |
C-1 |
C-2 |
C-3 |
| Theoretical results |
96.7% |
90.8% |
87.4% |
96.7% |
90.8% |
60.1% |
| Test results |
88.1% |
92.4% |
85.2% |
87.1% |
92.4% |
63.1% |
| Specimen |
P-1 |
P-2 |
P-3 |
A-1 |
A-2 |
A-3 |
| Theoretical results |
96.7% |
90.5% |
77.8% |
96.7% |
90.5% |
77.8% |
| Test results |
90.5% |
92.4% |
78.9% |
91.1% |
93.9% |
75.1% |
Table 12.
The ASTR of the DOFS attached on each sheet.
Table 12.
The ASTR of the DOFS attached on each sheet.
| Specimen |
P-1 |
P-2 |
P-3 |
A-1 |
A-2 |
A-3 |
| Theoretical results |
99.3% |
98.2% |
97.3% |
99.3% |
98.1% |
90.5% |
| Test results |
86.5% |
93.7% |
80.1% |
79.1% |
70.4% |
91.4% |
| Specimen |
P-1 |
P-2 |
P-3 |
A-1 |
A-2 |
A-3 |
| Theoretical results |
99.3% |
97.9% |
95.8% |
99.3% |
97.9% |
83.3% |
| Test results |
89.8% |
88.8% |
75.5% |
89.2% |
95.7% |
71.4% |
Table 13.
The ASTR of the FBG attached on each sheet (Specimen S and C).
Table 13.
The ASTR of the FBG attached on each sheet (Specimen S and C).
| Specimen |
S-1 |
S-2 |
S-3 |
C-1 |
C-2 |
C-3 |
| Theoretical results |
90.5% |
93.5% |
92.1% |
90.5% |
93.5% |
92.1% |
| Test results |
90.1% |
92.4% |
89.1% |
87.8% |
96.5% |
88.5% |
| 85.6% |
94.2% |
88.4% |
88.5% |
91.2% |
89.5% |
| 88.6% |
92.7% |
89.6% |
93.4% |
90.5% |
91.5% |
Table 14.
The ASTR of the FBG attached on each sheet (Specimen P and A).
Table 14.
The ASTR of the FBG attached on each sheet (Specimen P and A).
| Specimen |
P-1 |
P-2 |
P-3 |
A-1 |
A-2 |
A-3 |
| Theoretical results |
90.5% |
93.5% |
92.1% |
90.5% |
93.5% |
92.1% |
| Test results |
91.5% |
92.5% |
90.5% |
93.9% |
90.2% |
91.6% |
| 90.1% |
92.4% |
87.7% |
84.1% |
90.1% |
92.6% |
| 88.2% |
92.1% |
94.7% |
88.4% |
90.1% |
91.6% |
Table 15.
The ASTR of the DOFS attached on each sheet (Specimen S and C).
Table 15.
The ASTR of the DOFS attached on each sheet (Specimen S and C).
| Specimen |
S-1 |
S-2 |
S-3 |
C-1 |
C-2 |
C-3 |
| Theoretical results |
98.1% |
99.5% |
99.1% |
98.1% |
99.5% |
99.1% |
| Test results |
91.2% |
93.5% |
87.5% |
77.2% |
56.2% |
88.1% |
| 92.4% |
94.2% |
89.5% |
65.2% |
92.5% |
79.5% |
| 89.9% |
96.5% |
74.5% |
81.3% |
56.9% |
85.4% |
Table 16.
The ASTR of the DOFS attached on each sheet (Specimen P and A).
Table 16.
The ASTR of the DOFS attached on each sheet (Specimen P and A).
| Specimen |
P-1 |
P-2 |
P-3 |
A-1 |
A-2 |
A-3 |
| Theoretical results |
98.1% |
99.5% |
99.1% |
98.1% |
99.5% |
99.1% |
| Test results |
77.5% |
81.6% |
78.4% |
65.8% |
80.5% |
76.8% |
| 82.9% |
96.2% |
82.5% |
77.5% |
92.4% |
75.7% |
| 66.2% |
83.3% |
87.5% |
73.1% |
83.7% |
88.4% |