Analysis of the Methodology for Experimental Measuring of the Performance Criteria of the Laser-Using Collaborative Robot’s Path Accuracy

This paper describes design of experimental methodology developed to measure the working properties of accuracy of the path traversed by a collaborative robot. The methodology proposed here uses a collaborative robot and a laser measuring system Gepard from Raytec. The main parts of the measuring chain and the ISO 9283 standard are described. The proposed experimental methodology should examine working properties of industrial robots, such as the properties of position and path. The focus of this paper lies on the path accuracy of robots. Currently, the interest in this topic is on the rise and the measuring systems capable of recording this parameter are too costly. This paper focuses on experimental measuring of the path properties, describing them in more detail. The measuring and results were processed in the software tool developed for Gepard.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

The most important factors in choosing the right robot are its accuracy and repeatability. Selecting a robot suitable for performing the envisioned task requires giving a thought to all working properties of the robot, covering the entire range of its deployment. A further issue is the economic aspect of the robot used. Small firms lack the capital to procure a new, fully functioning robot to be safely deployed in a robotic application. That is why it is often the case that small enterprises are indirectly forced to purchase an already deployed robot, which necessitates its prior complete restructuring [1].

The overall condition of the robot can be determined from measuring its working properties, which should then be evaluated in view of the suitability of the robot’s redeployment. The results of such evaluation should facilitate the decision on fitness of the robot to be redeployed, whether it has any speed constraints or whether such constraints should be introduced, or whether the operating load of the end-effector of the robot should be reduced [2]. These measurements are subject to standardization, such as that of the international ISO 9283 standard. A standard represents individual working properties of industrial robots and the procedures for their proper measurement. These standards were developed in the wake of requirements of the robotic systems manufacturers that must satisfy the applicable directives.

Standards addressing the robotic systems and general properties are the following:

ISO 10218 – Robots and robotics devices – Safety requirements for industrial robots,

ISO 13482 – Robots and robotics devices – Safety requirements for personal care robots,

ISO 9283 – Manipulating industrial robots – Performance criteria and related test methods.

This paper will take a closer look at the ISO 9283 standard, which sets out the path accuracy measurements. High-performance industrial or collaborative robots are a commodity indispensable for successful delivery of orders in technological process. At present, many robotic systems‘ manufacturers provide little or limited information on working properties of their robots. In many aspects, we encounter only basic accuracy or repeatability information. Evaluating all working properties is taxing not only for the control unit of the robot itself but also in terms of data processing using metrological apparatus, which is very expensive [3].

Many metrological devices ensuring precise measurements of the end effector, thus harvesting the data needed, already exist. The principles on which these devices work vary. Nevertheless, they yield high-precision data. Working properties of industrial robots are practically measured most frequently with devices based on laser interferometry [X], coordinate measuring devices [X] or the so-called telescopic ballbars [X]. The most available universal machine for measuring the mentioned properties is the so-called coordinate measuring machine (CMM). This machine suffers from many disadvantages. For example, it can only make static measurements or calibration. That is why it is not very suitable for measuring working properties of robots. The group of devices based on laser interferometry includes one from Renishaw XL-80 [X], used for high-performance measuring and calibration of moving systems. Despite this calibration of the laser speed and precision, it is not used in industrial robots. If it is used, then rather as an exception [4]. Another measuring technology is known as a telescopic ballbar, first introduced in 1982, used in robotics ever since. Verification by telescopic ballbar offers a relatively easy and fast check of CNC machining machines positioning according to globally recognized ISO, ANSI standards. The ISO 230-1 standard mentions the ballbar as the regular tool, which made it to be most frequently used for verifying properties of not only industrial robots. It offers troubleshooting, enables problem detection, thus making it possible to identify the source of error. Furthermore, many cheaper methods and tools can be found, such as positioning with a reference object in space (measuring cube or sphere) [5].

An interesting contribution to this topic is also contribution [6]. The main objective of the present paper was to verify the repeatability of the Panasonic TM-2000 welding robot at a manufacturing company. The paper describes the workflow of the robot control program in the simulation software RoboDK, which created a complete welding station. The measurement, as well as the simulation, were possible thanks to designing the measuring device, the imaginary ISO cube, the measuring plane, the measuring points, and last but not least, the cycle that determined in which order the points were measured. The analytical part of the paper resulted in a direct measurement of the position repeatability of the welding robot.

The most frequently used method is a spotlight mounted on the robot’s end flange. Using laser tracker, the position of the spotlight is measured each millisecond, thus enabling verification of both dynamic and static parameters of the robot. A drawback of this method lies in the price of the laser tracker system. The method described in this paper focuses on the robot’s linear path, located in the ISO cube, prescribed by the ISO 9283 standard. Thanks to this method, it can be established whether the path traveled by the robot shows excess deviations which might prove crucial in the case of, e.g., high-precision welding. High-precision welding requires a path without significant deviations, so the procedure outlined above is capable of detecting an emerging device error, resulting in prevention of costly repairs [7].

2. Measuring system Gepard by Raytec

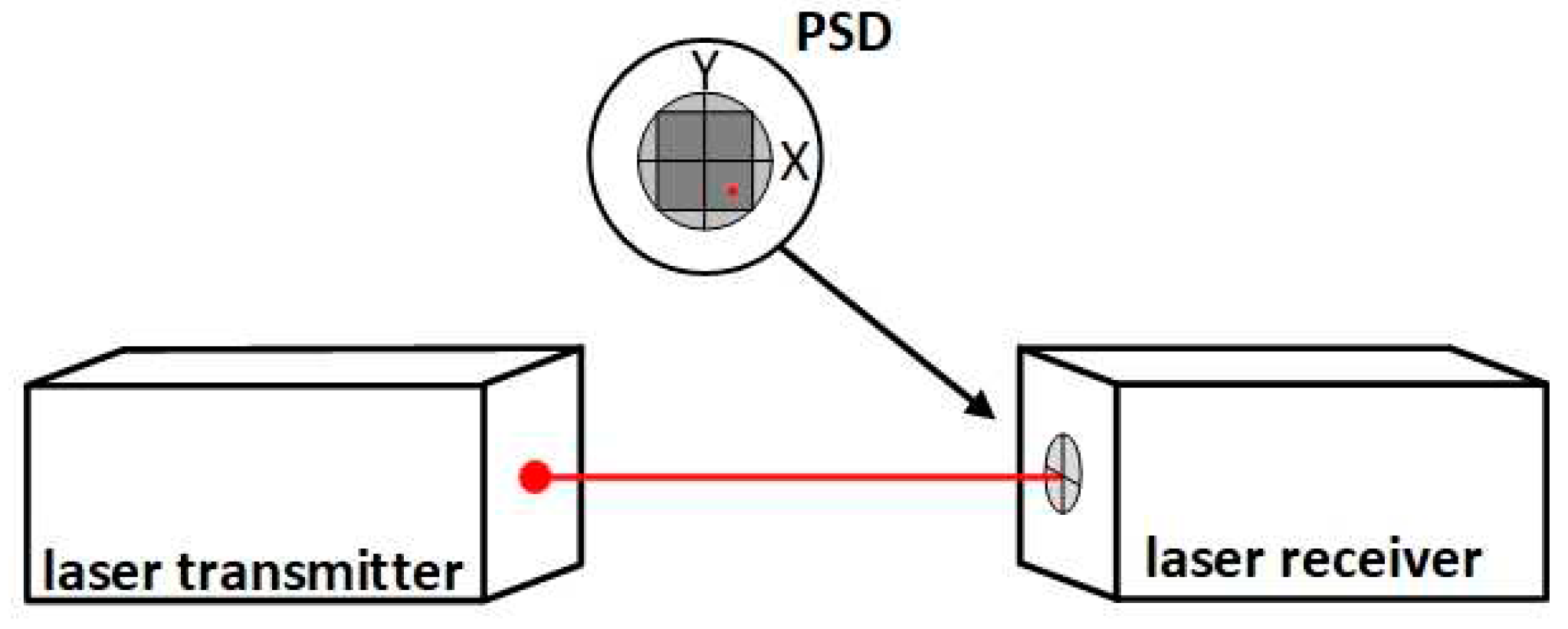
The GEPARD device is primarily used for measuring linearity, parallelism, perpendicularity of linear guides, but also for measuring position deviations and coaxiality. It works with a laser beam as a reference standard for linearity. The device consists of a laser transmitter and a laser receiver. The laser beam is simply aimed parallel to the linear guide, targeting the laser receiver. The latter can detect subtle changes in the position of the incident beam on the receiving sensor in a very simple way. The linearity of the path is measured by moving the receiver along the linear trajectory and continuously measuring the beam deflections [8].

In comparison to conventional solutions, a huge advantage of the device is that it enables measuring deviations in both directions perpendicular to each other at the same time, even in dynamic mode. This mode enables the user, for example, to align the guiding, with final curves being evaluated in real time. Significant advantage is wireless interconnection of all components. The laser receiver communicates with the computer through Bluetooth technology. Both the laser transmitter and the receiver are powered by batteries [9]. The main part of the receiver is a sensitive position detection matrix (PSD) and the amplifying and evaluating electronics. The Gepard (type 5) matrix is 10 x 10 mm in size. The laser beam hits the matrix through a ground opening, so the transverse range of measurement in the X, Y axes is 5 x 5 mm [10].

Figure 1. Laser receiver – transmitter with PSD.

To measure linearity, place the laser transmitter at the beginning of the measured guiding and guide the transmitter beam to target the laser receiver position sensor. To set the beam, use micrometric screws. In the software, select the position measuring mode. In this mode, the area of the beam position sensor will appear on the personal computer screen, indicating the place where the beam falls. Using micrometric screws, we make the place of the beam incidence more precise, as close to the geometric center of the sensor as possible, in the range of the measured length. [11].

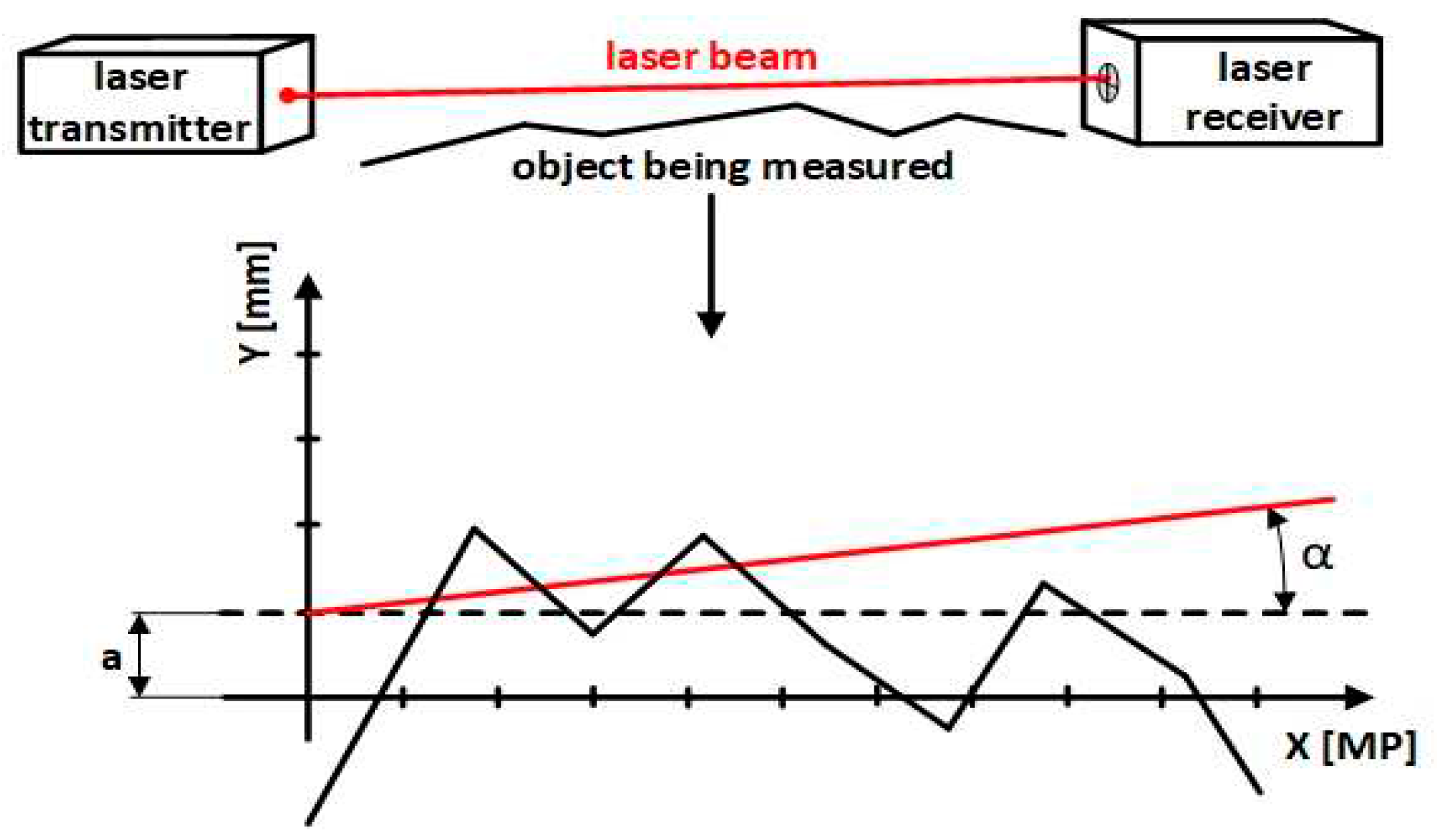
Laser receiver gradually moves along the measured path to selected points and at each point, the position of the incident laser beam is measured in the x and y axes. The measured data appear on the computer screen and are plotted in two ready-made charts [12], with the axis x showing the receiver distances from the first measured point and the axis y showing the measured deviations. The values measured on axis x are plotted in the first graph and those measured on axis y in the second, Figure 2 [13].

Using the least squares method, the software lays a straight line, which is called the regression line, over the measured points. The least squares method is a mathematical and statistical method of approximating pairs of measured data [x;y]. Approximation means the closest representation of the real value. The simplest case of using the least squares method is approximation of the measured data by using the straight line ŷ = kx + q. The resulting sum of areas of all the squares must be the smallest possible:

S = \sum_{i = 1}^{n} {(Δ y_{i})}^{2}

(1)

Upon inserting the dependence function for the straight line, we get the following:

S = \sum_{i = 1}^{n} {[y_{i} - (k x_{i} + q)]}^{2}

(2)

We are looking for the k and q factors, so that all the Δyi deviations are the smallest possible. A criterion is that the sum of the second power of all deviations must have the least value. We use the second power to get a positive value. Thus, in terms of geometry, we deal with the square [14].

For the user to see an exact deviation of lengthwise measurements from zero or the reference line, the individual measured values must be mathematically processed to compensate for deflection (a) and the tilt angle (α). In this way, the regression line becomes the “zero line“ of the graph.

Figure 3. Representation of measure taken via the ISO line.

An overview of the receiver and transmitter parameters of the measuring system Gepard is shown in Table 1.

3. Standardization ISO 9283 – path accuracy

Conditions for conducting measurements must comply with recommendations of the manufacturer, especially where it comes to installation. The robot should be functioning and installed correctly from the manufacturer’s point of view, and all its balancing should be appropriate. If a start-up phase is indicated, it should be done. The standard sets the ambient temperature at 20 ± 2˚C or ranging between 5 to 40 °C. The measurements were done at the ambient temperature of 20 °C on the collaborative robot Fanuc CRX-10iA with a suitable control cabinet and a pendant. Verification was done using a mechanical flange interface connected to the measuring device, with the maximum load of 10 kg. The measured path was set on a measuring plane as prescribed by the standard [15].

Definitions of the path accuracy and repeatability do not depend on the shape of the programmed path. Two examples of the programmed paths‘ different shapes are shown in Figure 4 and Figure 5 [16].

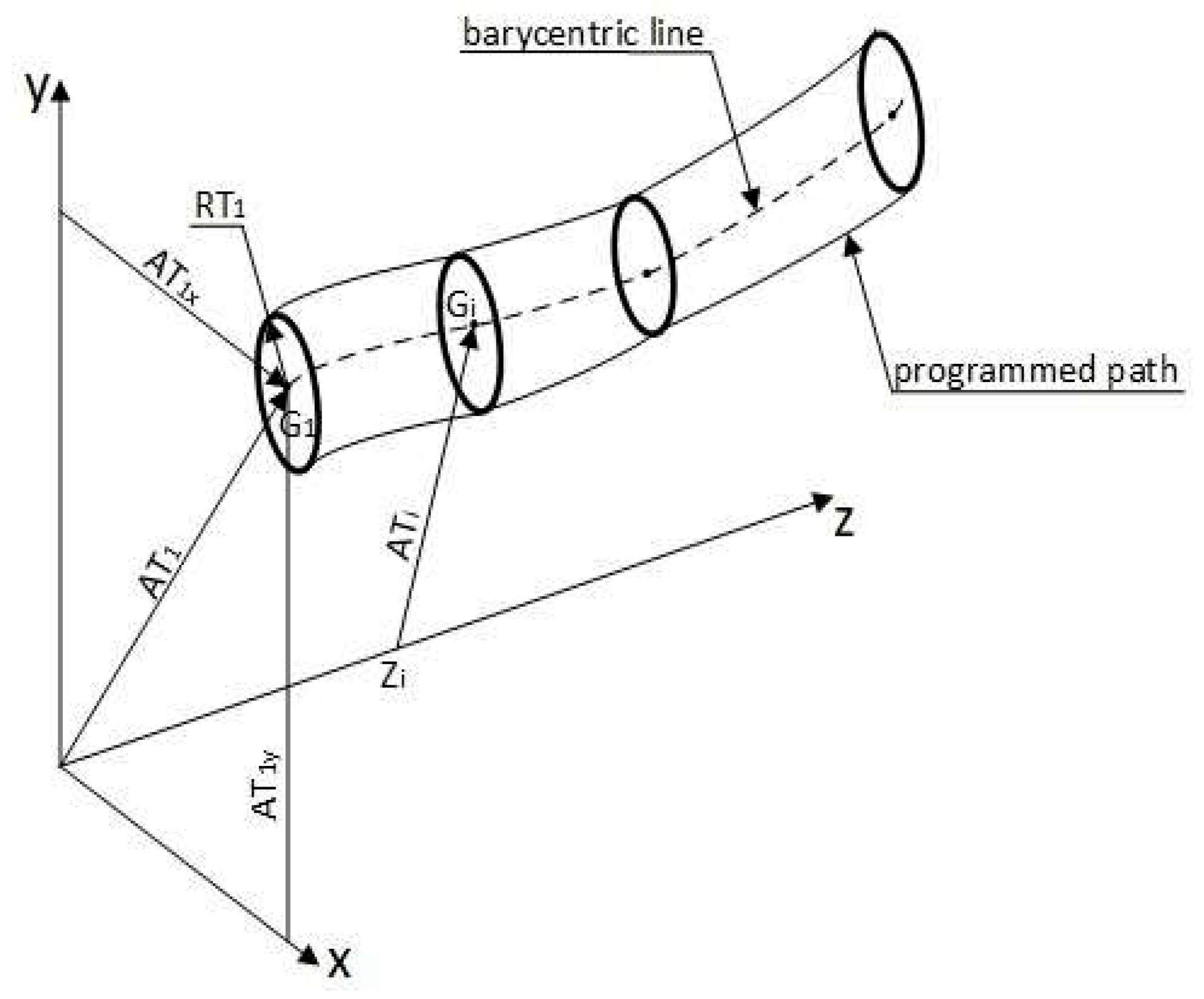
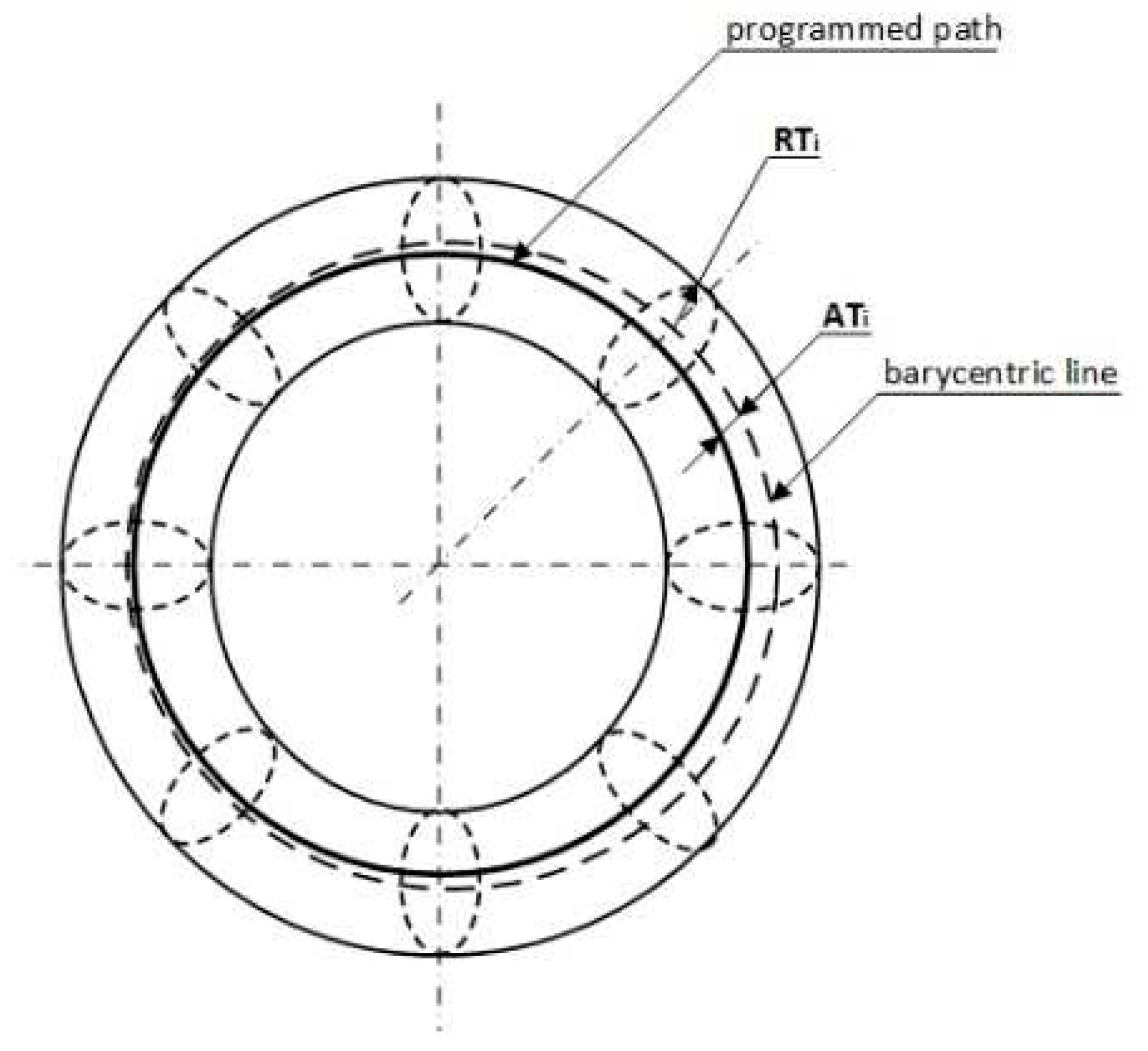
Path accuracy describes the robot’s ability to move through its interface along the programmed path n-times in one direction and n-times in the opposite direction. Path accuracy is determined by two factors:

a difference between the programmed path and the barycentric line of the set of the paths taken, Figure 4,
a difference between the programmed angular orientation and the mean value of the angular orientation achieved (accuracy of the path orientation).

Thus, the path accuracy is the utmost path deviation obtained during positioning and orientation. Accuracy of the path positioning, AT, is defined as the utmost distance between the programmed path and the barycenters Gi n in measurements of each of the number of measuring points (m) along the path [17]. If the programmed path is defined as the axis Z, then the path positioning accuracy will be calculated from the following equation:

A T = \binom{m}{\binom{m a x}{i = 1}} \sqrt{{(x_{c i} - \bar{x_{i}})}^{2} + {(y_{c i} - \bar{y_{i}})}^{2}}

(3)

{A T}_{x} = \binom{m}{\binom{m a x}{i = 1}} |(x_{c i} - \bar{x_{i}})|

(4)

{A T}_{y} = \binom{m}{\binom{m a x}{i = 1}} |(y_{c i} - \bar{y_{i}})|

(5)

, whereas:

\bar{x_{i}} = \frac{1}{n} \sum_{j = 1}^{n} x_{i j}

(6)

\bar{y_{i}} = \frac{1}{n} \sum_{j = 1}^{n} y_{i j}

(7)

, where:

x_{c i}, y_{c i}

—point coordinates on the programmed path corresponding to the measuring point

z_{i}

x_{i j}, y_{i j}

—point coordinates of the achieved path corresponding to the measuring point

z_{i}

for j^th repetition.

Accuracies of the ATa, ATb, ATc path orientation are defined as the utmost deviation from the programmed angles along the path. However, this experimental method does not allow for their exact determination [18].

While the path accuracy definition defines the path accuracy as a distance-dependent value, measuring of the achieved path may be done either as the function of distance or of time. Where significant speed fluctuations along the path are present, repeated measurements must be done as the function of time. Repeated measurements must relate to the same points in space along the programmed path. 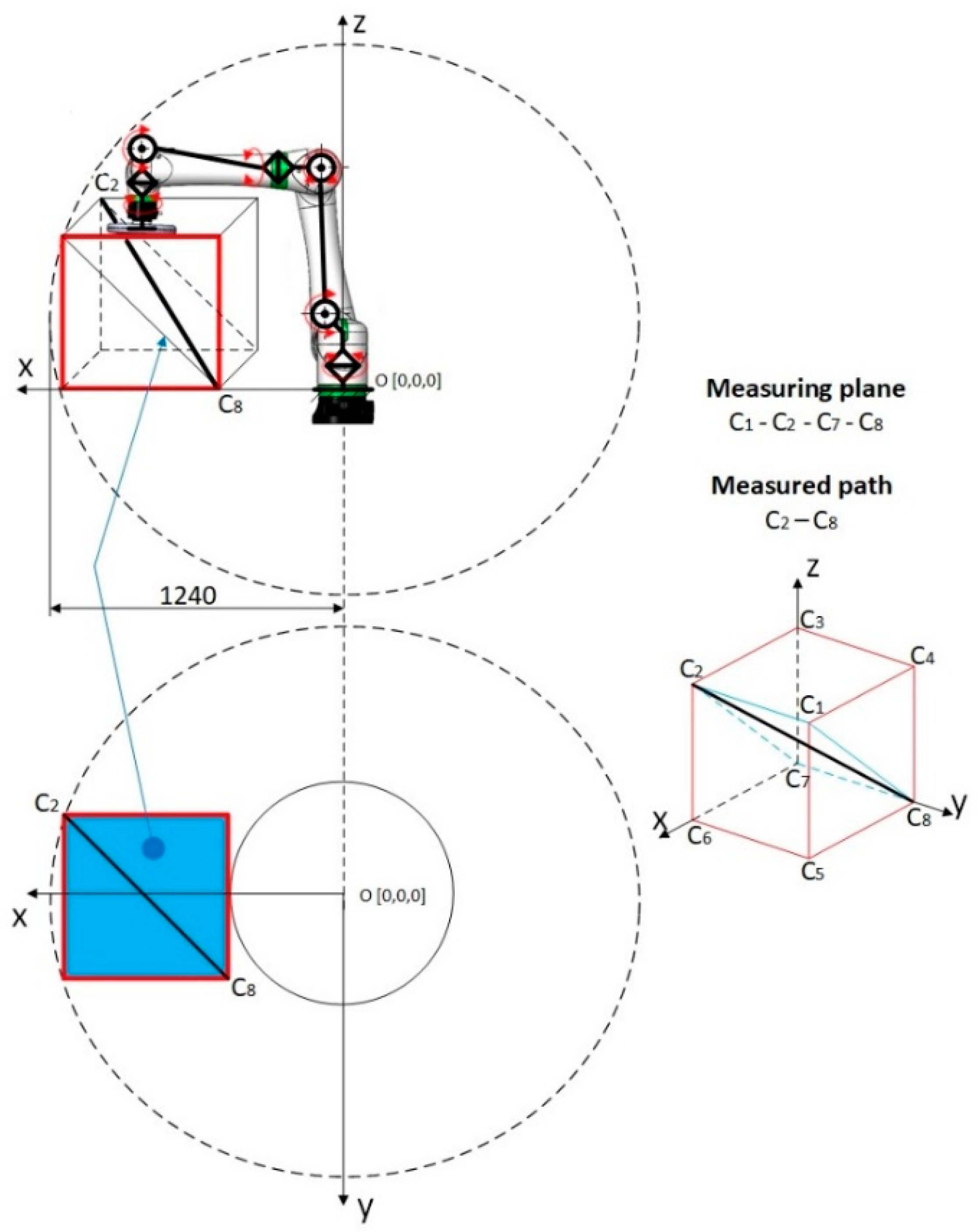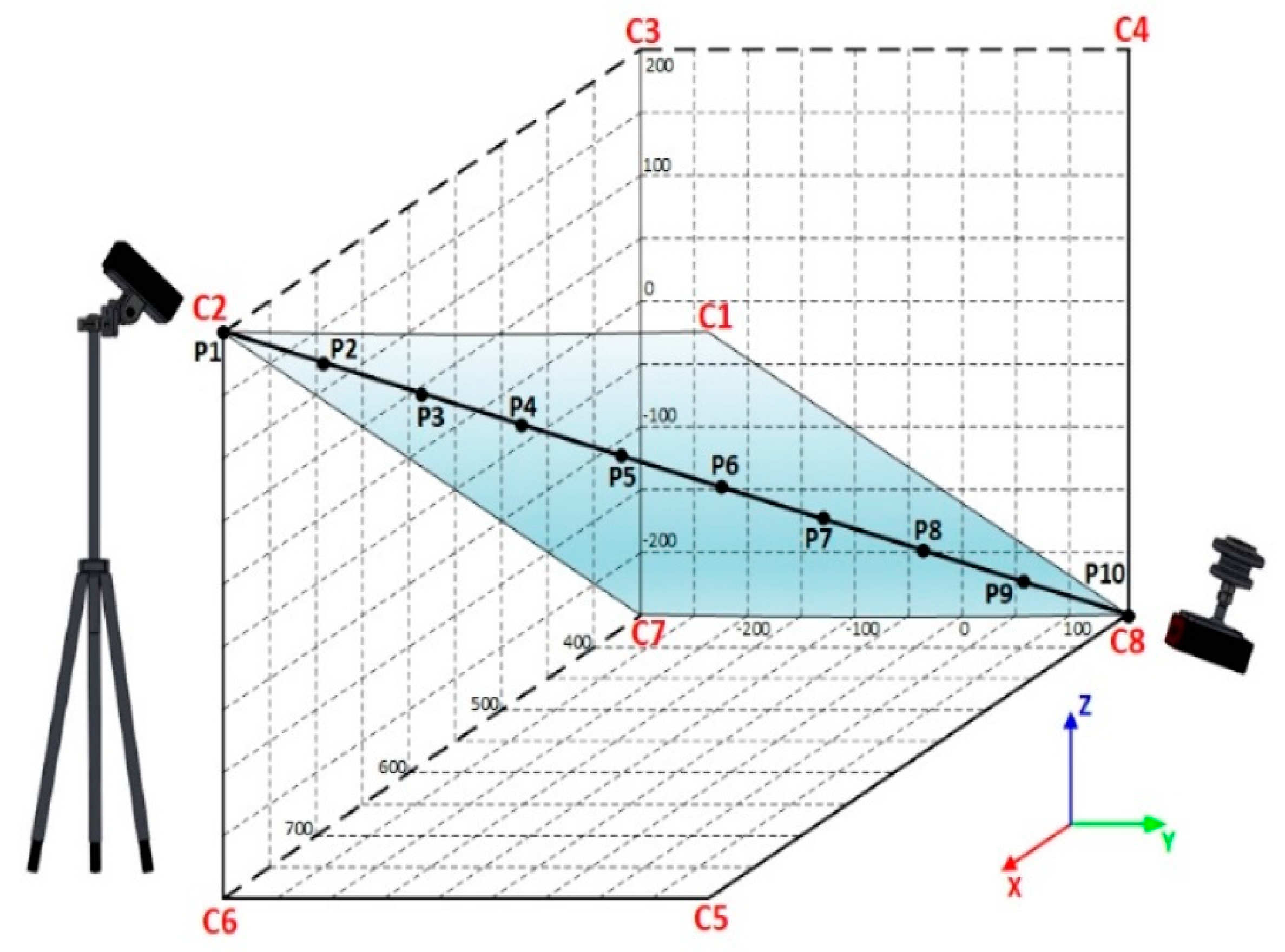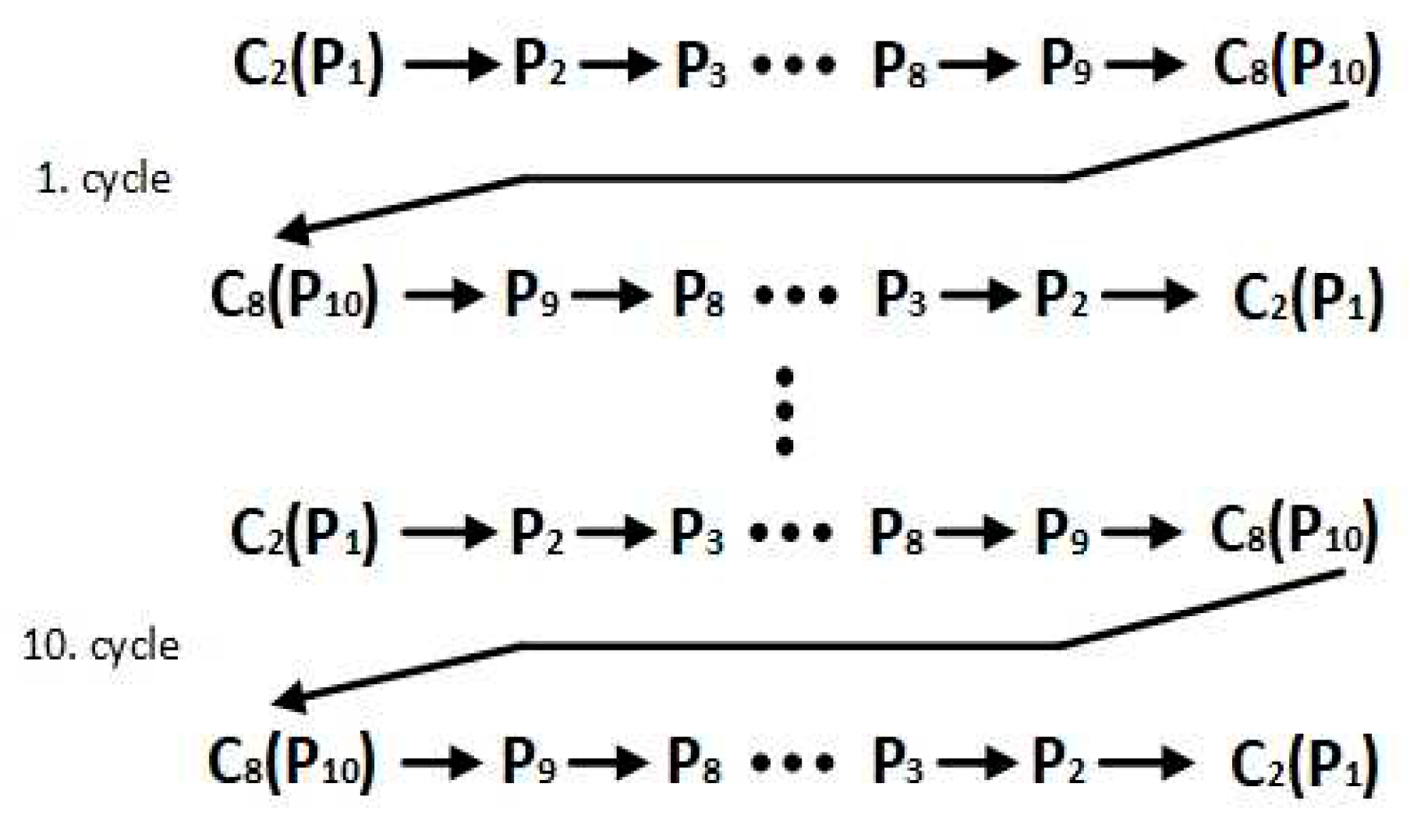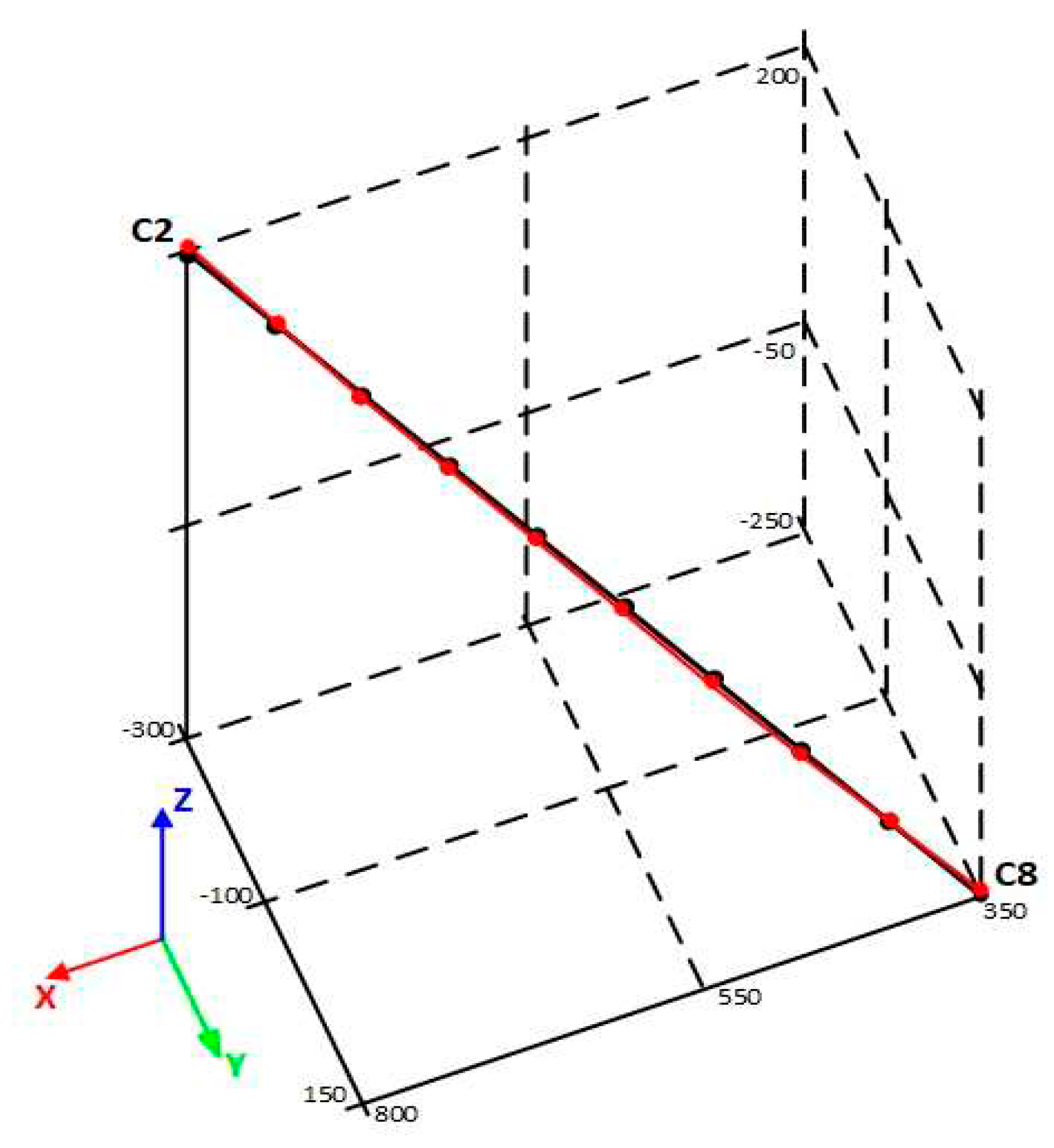The initial measuring point must lie outside the testing plane and the checks must be bidirectional [19]. Testing cycles complied with the standard. C1 to C8 denote apexes of a simple cube, lying in a section of the workspace where the use of robot is expected to be most frequent. Testing plane and testing path are shown in Figure 6.

3.1. Robot Fanuc CRX-10iA

The collaborative robot CRX-10iA is heavily guarded against dust or oil leaks in the industrial setting and it fully complies with the ISO 10218-1 safety standards. Thanks to it being lightweight, CRX can be easily installed in a wide range of applications, for example, in one using automatically guided vehicles (AGV) [20].

Typical for CRX are the same reliable functions as are common in other collaborative robots. Its sensors are sensitive and they immediately actuate the emergency stop upon contact with a human body. Figure 7 shows the robot, the payload, and also the transmitter and the receiver of the measuring system Gepard.

Table 2 gives an overview of the basic parameters of the Fanuc CRX-10iA robot.

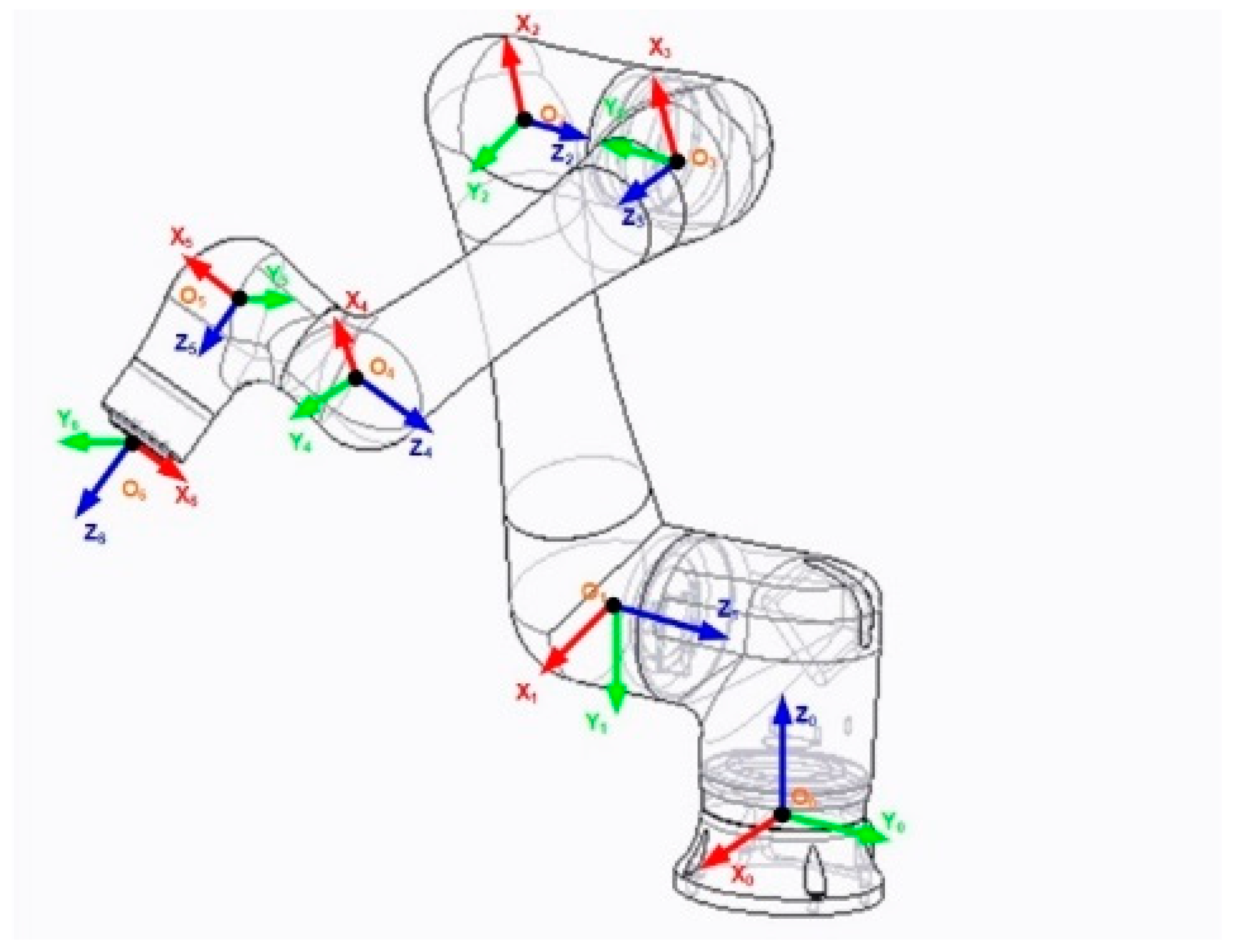
3.2. Mathematical background of CRX-10iA

An important part of the robot analysis is a complete kinematic model of the mechanical system. It is a description of the position and orientation of the working end point in time and the corresponding course of position-taking by individual parts of the mechanism. The Fanuc CRX-10IA robot’s structure is a serial kinematic RRR. That is why the kinematics was described using Denavit-Hartenberg convention, enabling to describe the robot’s kinematics using DH parameters. Kinematic model, Figure 8, makes it possible to study the processes of the robot’s movement in time-space [21].

The kinematic description using Denavit-Hartenberg parameters is given in Table 3.

Inverse transformation yielded the courses of position-taking by tilting drives that enabled measurement. The last part of the robot will move at a constant speed with linear approximation. We will obtain the individual drives values of speed and acceleration through derivation.

\dot{q} (t), \ddot{q} (t)

(8)

The speed of each material point of the part, as well as that of its local coordinate system, can be calculated from the following equation:

ω_{i} (t) = ω_{i - 1} (t) + ω_{i - 1}^{i}

(9)

where ωi is the angular speed of the i^th coordinate system, ωi-1 is the angular speed of the previous coordinate system and ω_(i-1)^i is a relative angular speed of two adjacent coordinate systems, which can be expressed as follows:

ω_{i - 1}^{i} \{\begin{matrix} k_{i - 1} \dot{q} R \\ 0 T \end{matrix}

(10)

Angular speed of the naught coordinate system is zero. In this way, velocities of all 6 local coordinate systems can be expressed, and thus those of the robot parts from its base to its end point. Derivation of translational speed necessitates derivation of the positional vector between two coordinate systems.

\frac{d p_{i}}{d t} = \frac{d p_{i - 1}}{d t} + \frac{d p_{i - 1}^{i}}{d t}

(11)

A robotic system enables setting the trajectory by setting individual points and then setting the type of movement. In our case, a linear movement at constant speed is selected between the extreme points of the measuring cube.

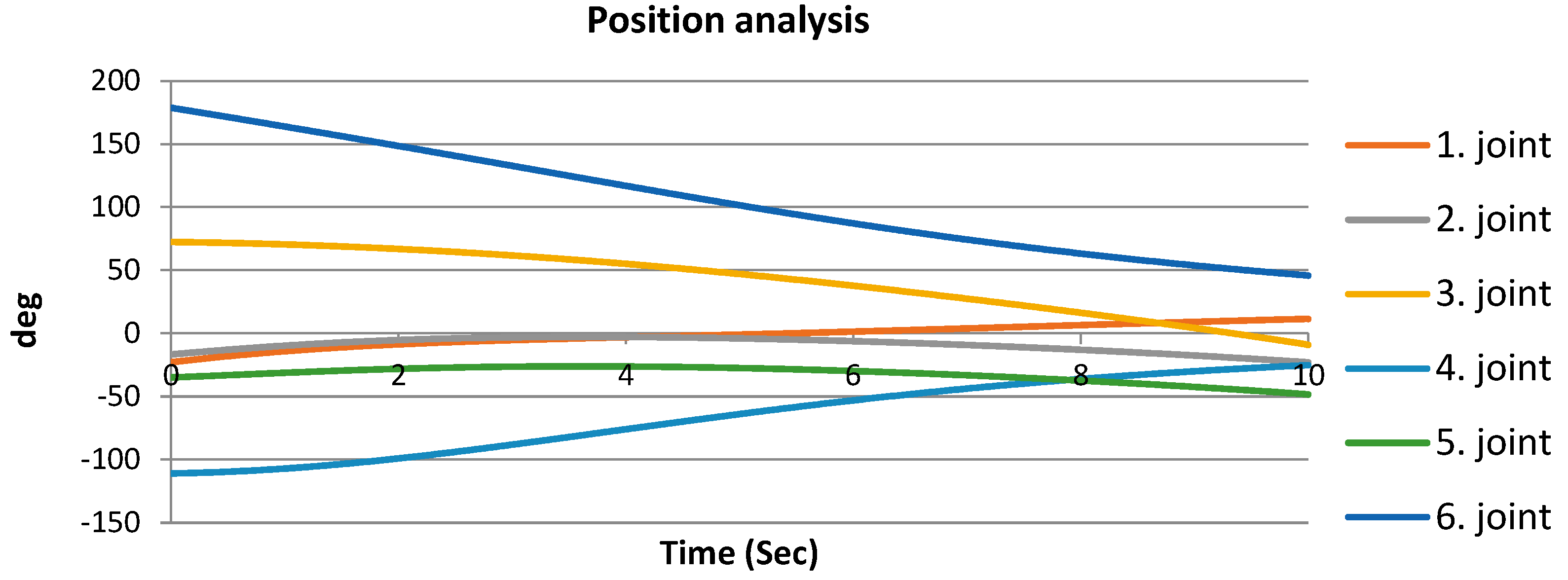
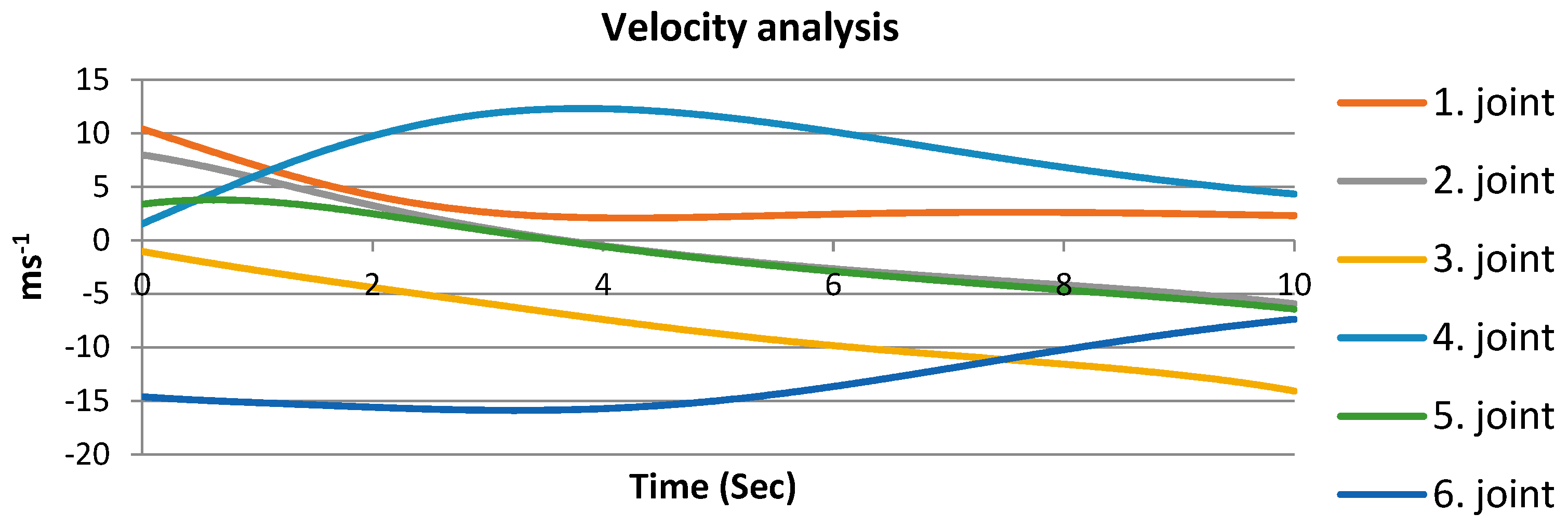
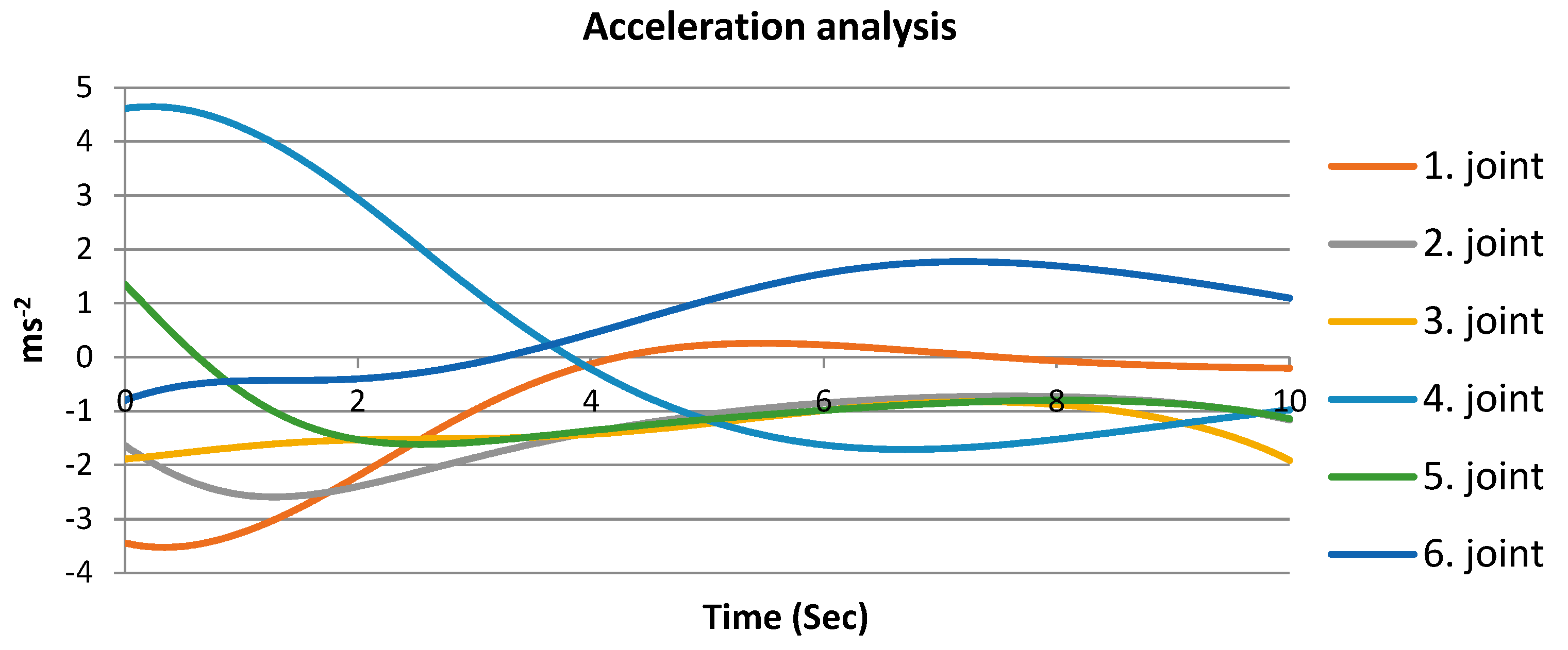
Dynamic parameters were simulated in Creo. The courses of position-taking, speed and acceleration describing the movement of individual drives during linearity measurement are shown in Figure 9, Figure 10 and Figure 11. For the given collaborative robot model, a continuous linear path containing measuring points was simulated. The results of position analysis of the course movement of individual joints are shown in Figure 9. The individual trend lines justify a belief that all robot joints participated in the movement defined. The greatest change was noted in the sixth joint.

In planning the path, its calculation is sampled with a period defined by the speed of the inverse kinematic task calculation. In addition, path planning also accounts for sudden changes in movement so that permissible velocities and accelerations of individual drives are not exceeded. A path calculated in this way differs from the ideal one. Inaccuracy is influenced by several other factors, such as individual drives‘ positioning precision, robot rigidity etc., which have an effect on the resulting accuracy. Measurement can identify real deviation from the ideal path [22].

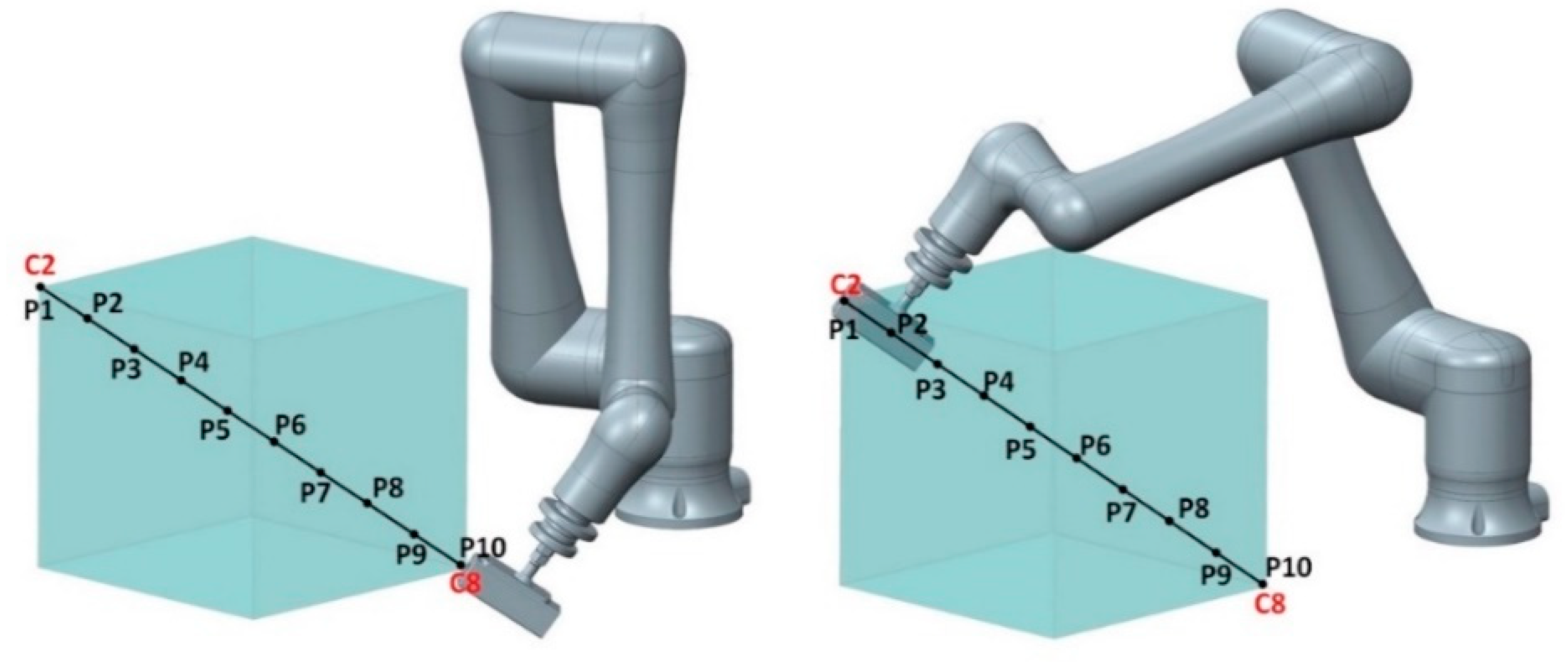
Of basic importance to the entire line of matrix methods of kinematic and dynamic analysis and synthesis are homogenous transformations which we use for describing the position and orientation of parts. Suiting the needs of visual systems, homogenous transformations put global position of parts into the context. The left-hand side of Figure 12 shows the first point in the measuring cycle C8 and the right-hand side shows the last measuring point C2.

The resulting transformation matrix between adjacent coordinate systems is obtained through multiplying individual partial transformation matrices in the order in which the movements were made. The result of multiplication, describing the position of the first measuring point, is as follows:

A_{i - 1}^{i} = [\begin{matrix} 0.577 & - 0.707 & 0.408 & 323.758 \\ - 0.577 & - 0.707 & - 0.408 & 102.47 \\ 0.577 & 0 & - 0.816 & 7.295 \\ 0 & 0 & 0 & 1 \end{matrix}]

(12)

Homogenous transformation matrix for the last point measured:

A_{i - 1}^{i} = [\begin{matrix} 0.577 & - 0.707 & 0.408 & 773.758 \\ - 0.577 & - 0.707 & - 0.408 & - 347.530 \\ 0.577 & 0 & - 0.816 & 457.295 \\ 0 & 0 & 0 & 1 \end{matrix}]

(13)

3.3. Implementation and evaluation of experimental measuring

The object of path accuracy measurement was the robotic arm of a collaborative robot by Fanuc designated as CRX-10iA. Overall, 6 types of measurements were done. These were the measurements prescribed by the standard under a 100 % nominal load and at 100, 50 and 10 % speed. Furthermore, measurements under 50 % and 10 % load, respectively, and the velocities of 100, 50% and 10 % were done. The number of cycles for each measurement was 10. Figure 12 shows the measuring plane, along which measurements that took place from points C2 to C8. A total of 10 points, subject to deviations detection, lay on this programmed path [23].

Figure 13. Location of the measuring cube, plane, and the path measured.

The measurements were done according to the relevant standard. The measurement involved a weight installed on the robot’s end flange, with the attached Gepard device.

Figure 14 shows the measuring setup used in the measuring cycle. The testing cycle was bidirectional, i.e., the measuring started at point C2, from which the robot passed over to C8 and then returned back to point C2. This cycle was repeated 10 times under 100 % load at three velocities of 100, 50 and 10 %, respectively. The initial point was outside the measuring cube, as prescribed by the standard. Figure 14 represents the cycles of measurements. Each measurement involved every joint of the robot.

4. Results

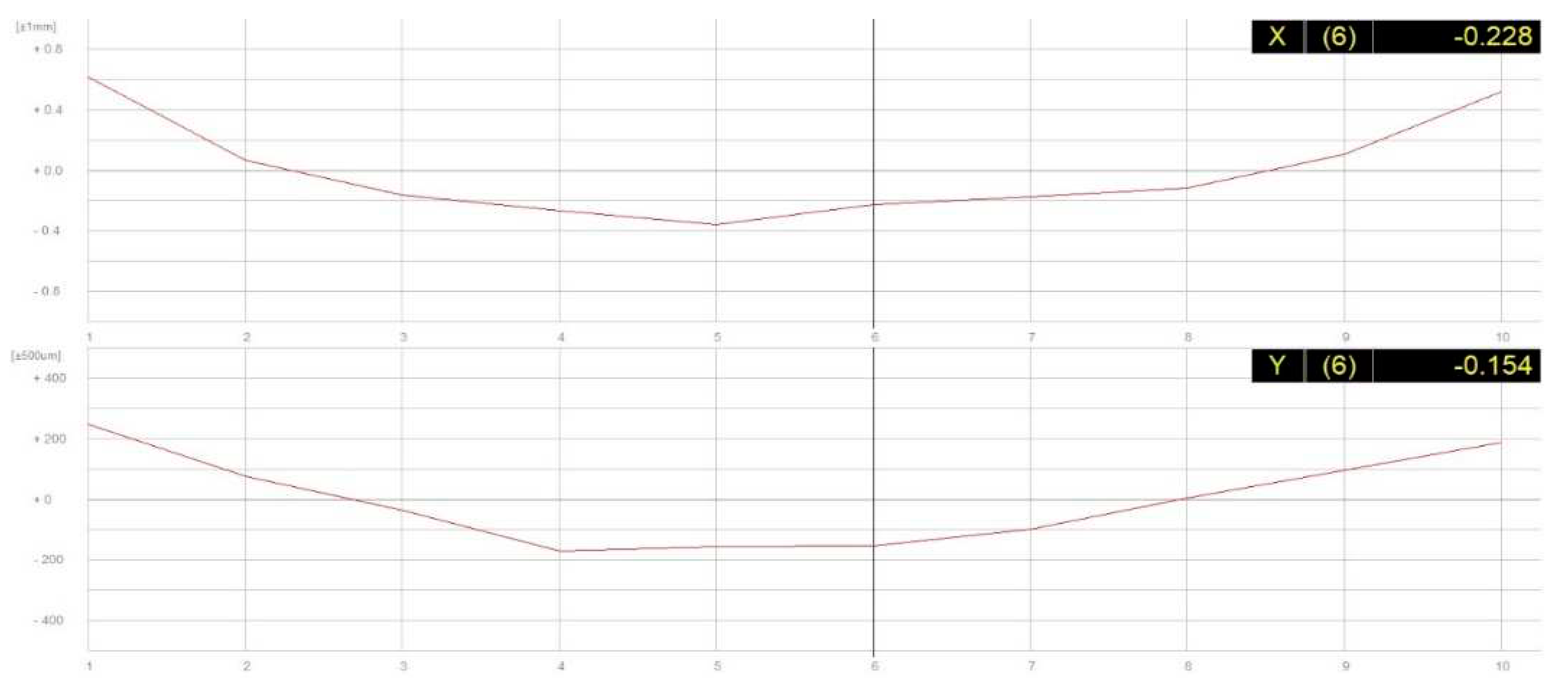
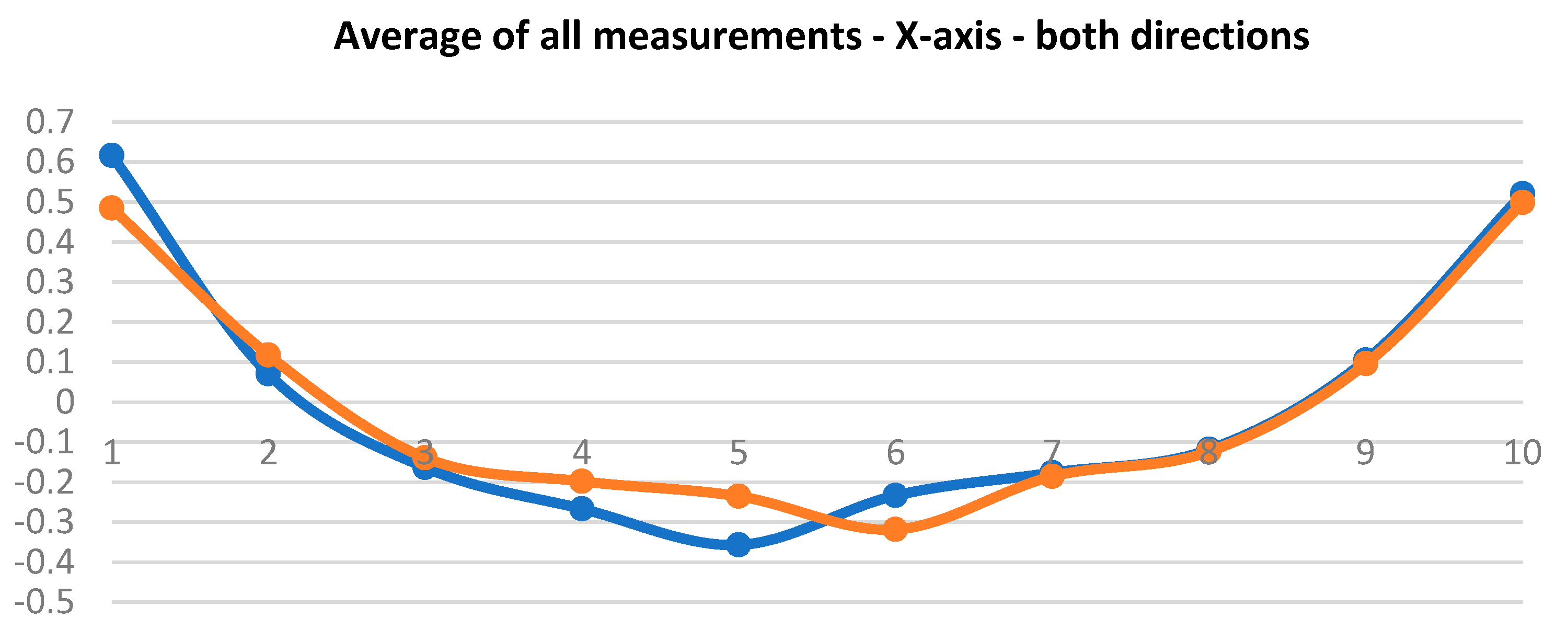
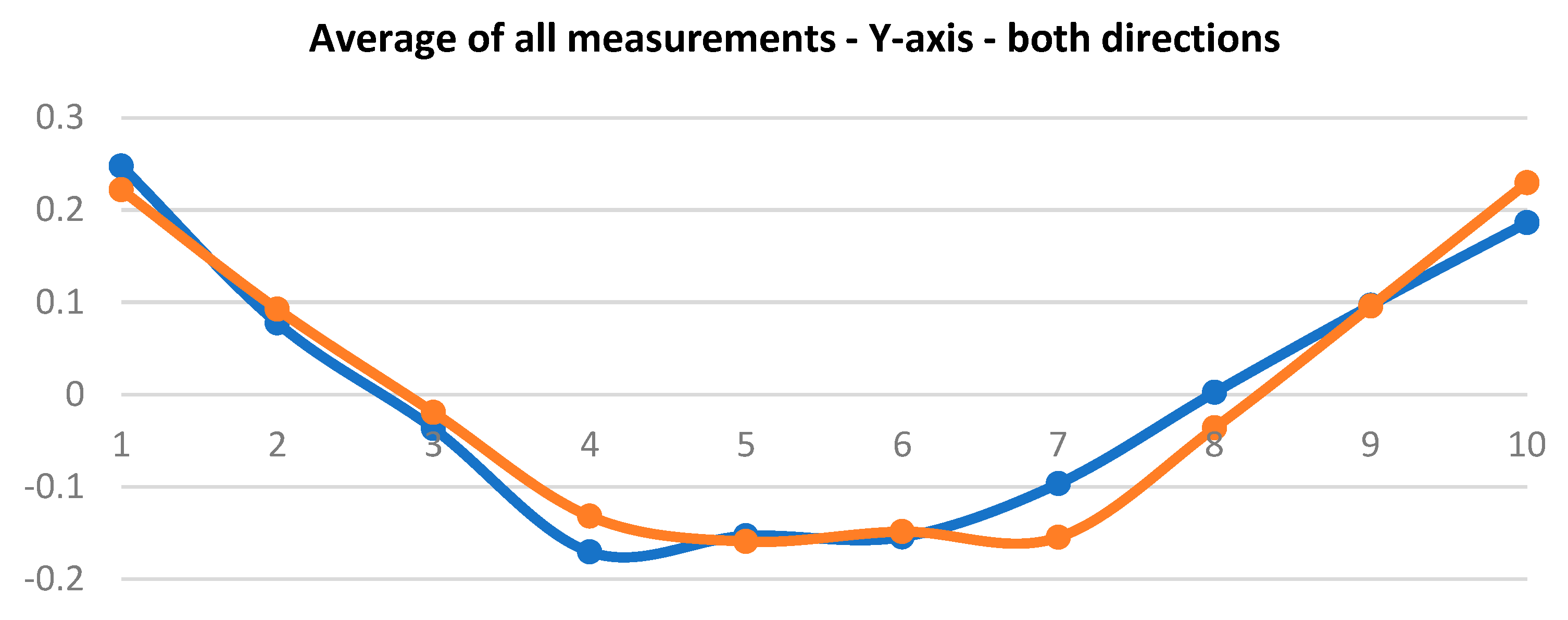
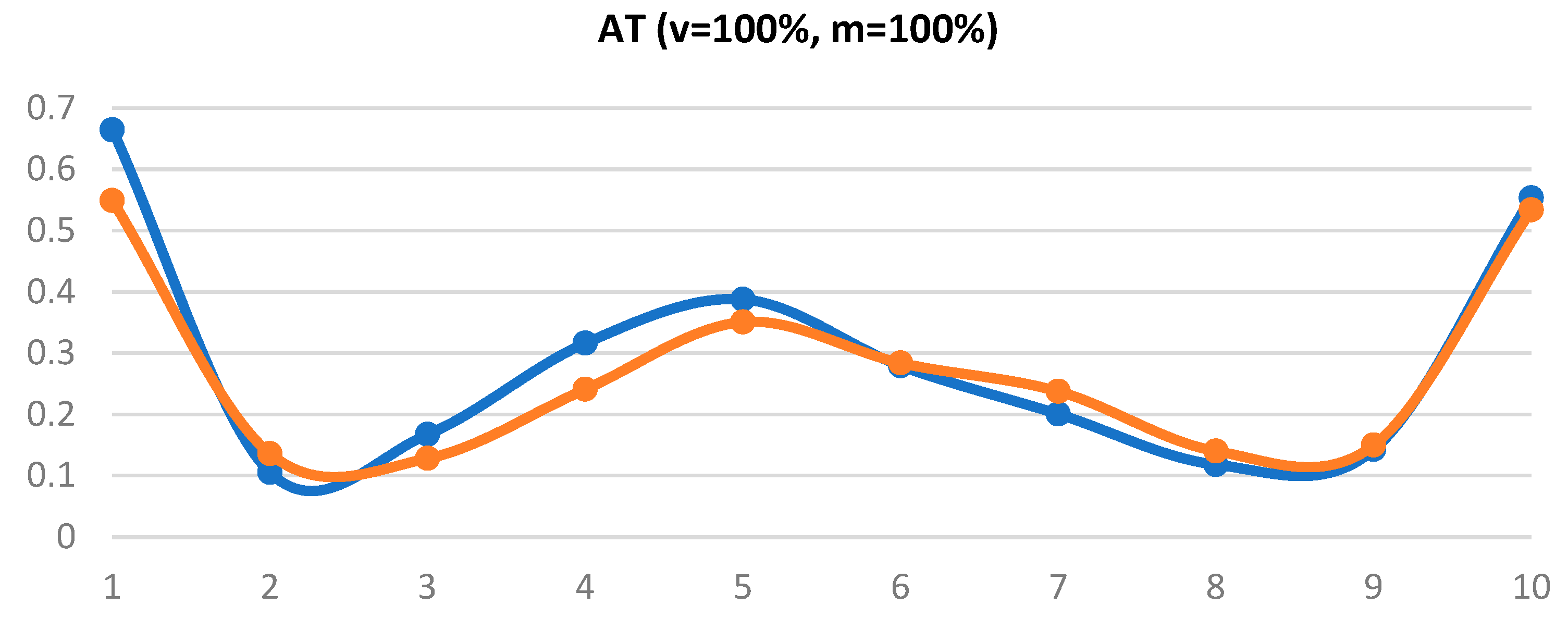
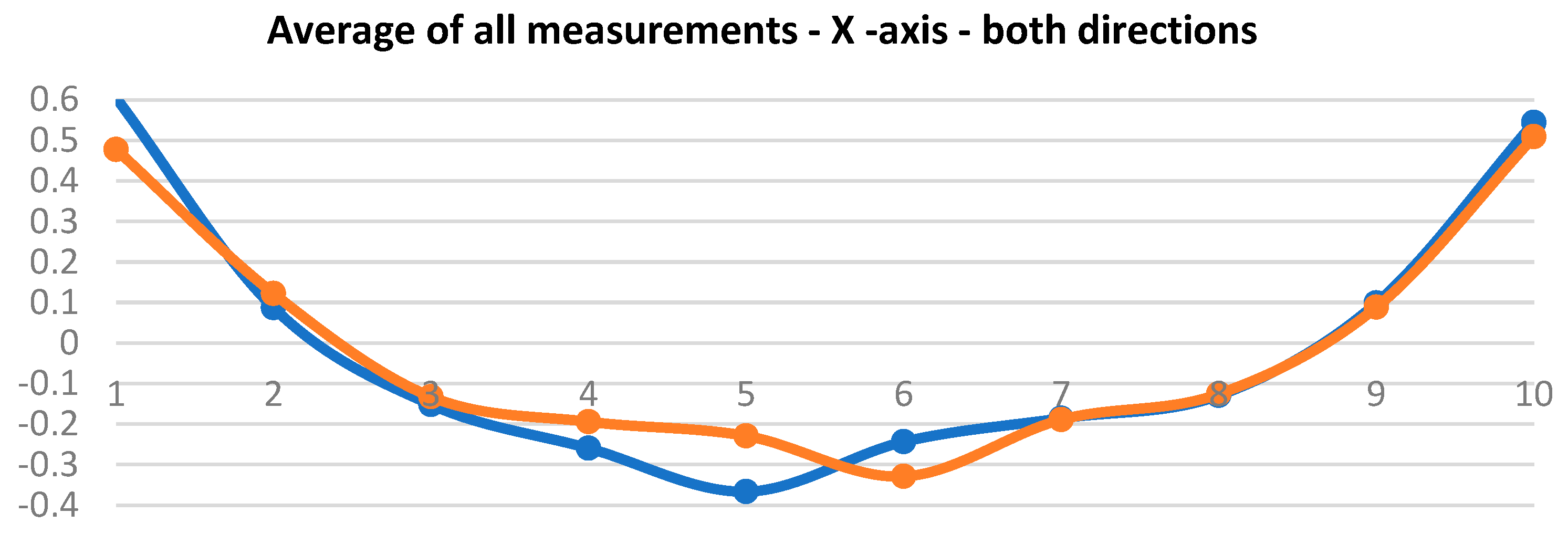
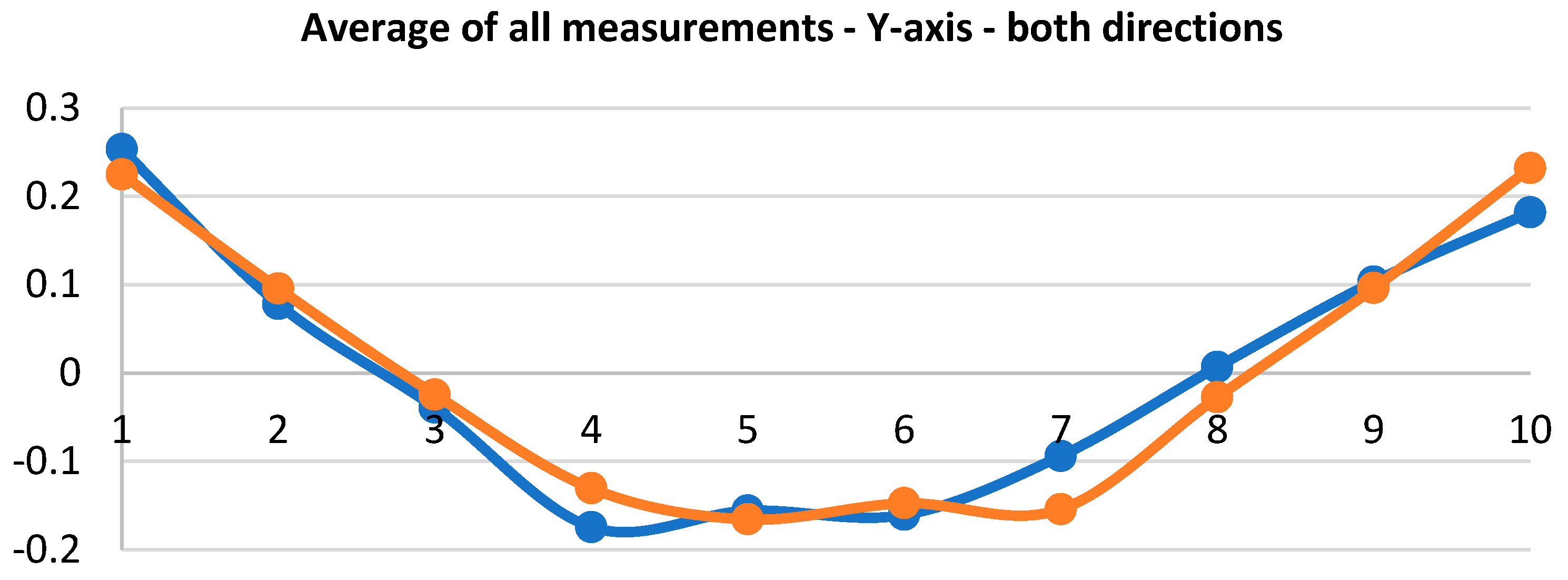
Table 4 lists averages of 10 measurements at 100 % speed and under 100 % load. The table contains values recorded by Gepard at measuring points P1 to P10, namely in both directions.

These obtained values were used for calculating path deviation values resulting from positioning. Positioning accuracy was then calculated as the utmost distance between the programmed path and the barycenters Gi for n measurements at each of the number of measuring points along the path.

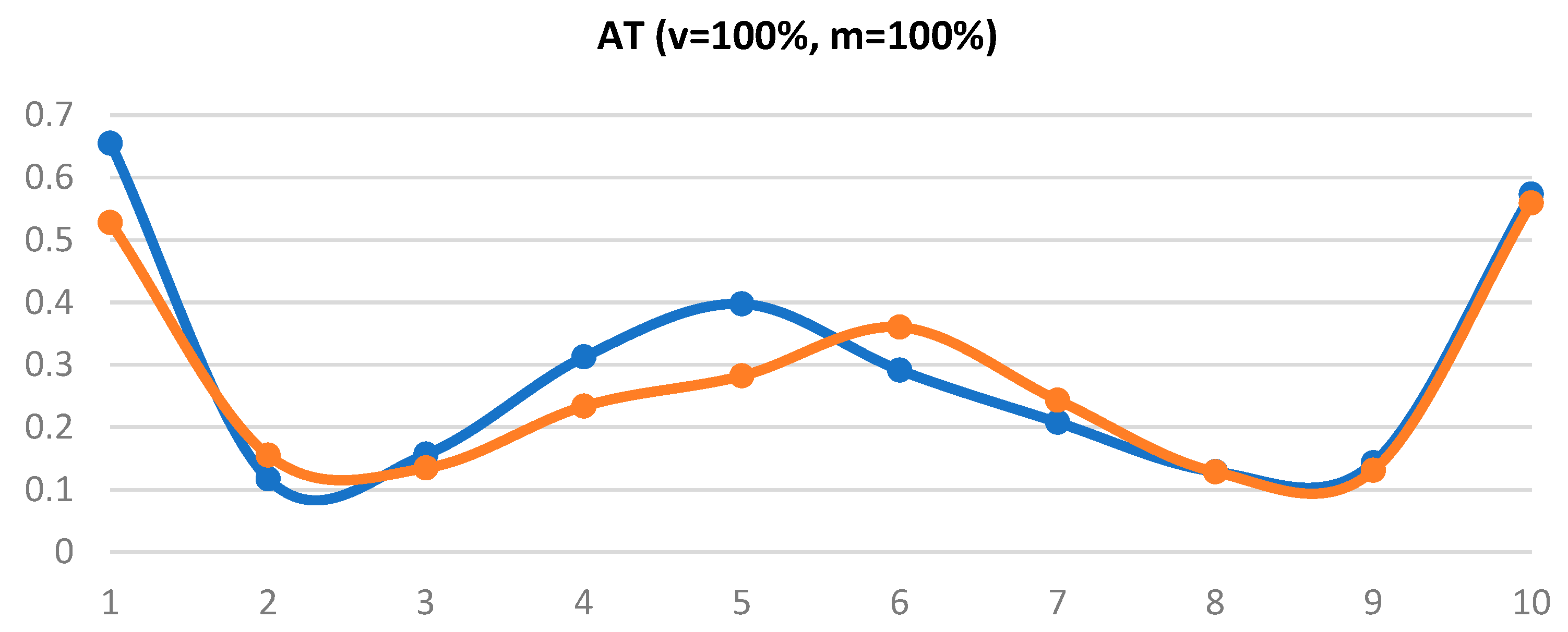
Figure 16 and Figure 17 show the measured averages of all measurements. It can be said that the measurements were almost identical and the robot did not manifest any abrupt deviations. These values served for subsequent calculation of the path accuracy values and those are shown in Figure 18. The manufacturer does not state path accuracy values for this robot type, so the purpose of these charts is only to gain better orientation in the topic.

Table 5 lists averages of 10 measurements at 50% speed and under 100 % load. The table shows values recorded by Gepard at the measuring points P1 to P10, namely in both directions.

Figure 19 and Figure 20 shows measurements plotted at half the speed and maximum load for axes x and y. These measurements did not manifest any abrupt changes compared to previous measurements at maximum speed. The obtained values served as a basis for calculating the path accuracy values and those are shown in Figure 21.

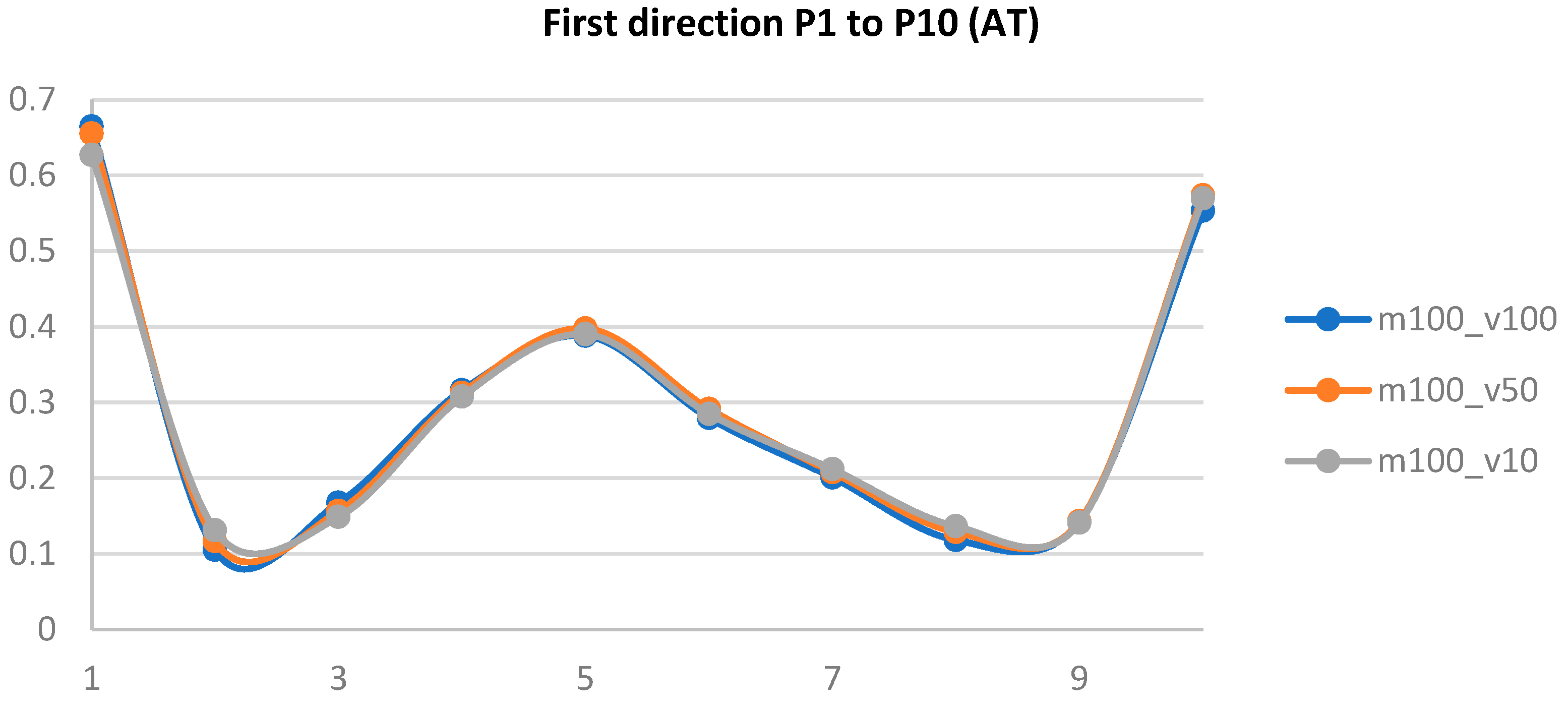
Overall measurements involving all three speed options and the overall path accuracy are plotted in Figure 22 and Figure 23. For better clarity, each direction is shown separately.

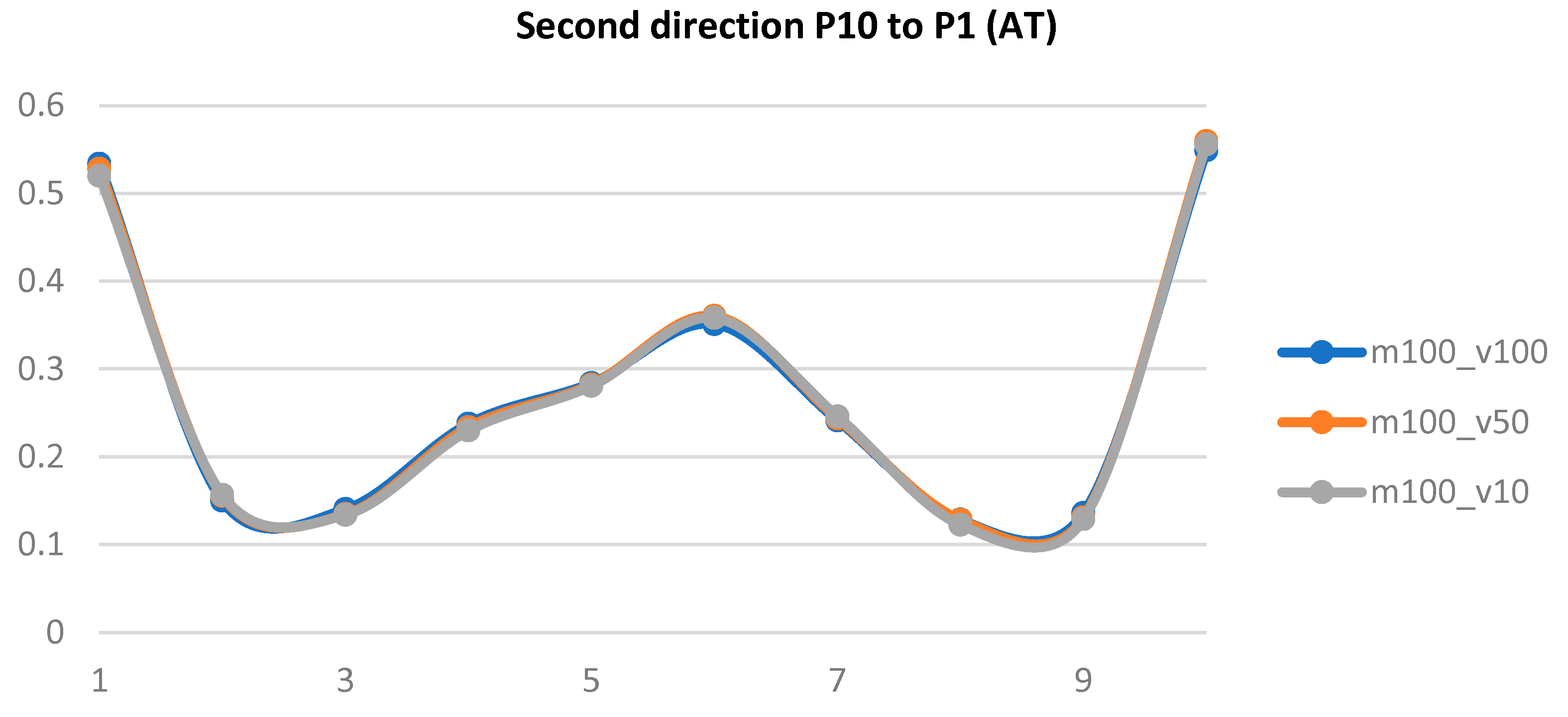
Figure 22 and Figure 23 present the total measurements done and the path accuracy results achieved at measuring points P1 to P10. In the ISO cube, these points are also referred to as points C2 to C8. Figure 24 shows this ISO cube, with the outlined overall path measured in P1 to P10 direction.

5. Discussion

The overall analysis of all the data measured and calculated has shown that a change in the nominal speed, namely from 10% to 50% or 100%, does not affect the overall path accuracy of the collaborative Fanuc robot. The ISO standard prescribes these measurements be done under full nominal load, which in our case meant 10 kg. The path accuracy values remained at the same levels at changed speed, or deviations were very small. Repeated measurements have manifested no abrupt deviations in the robot. As has been shown in the plotted overall path accuracy, it is clear that throughout its travel, the robot maintained a very stable path and neither an increase nor a decrease in speed resulted in any errors.

The main advantage of the proposed experimental method is that the measuring system it has used, i.e., Gepard, is highly precise. Uncertainty of measurement can be assessed from several points of view. The certainty of measurement is influenced by the measuring device, especially the PSD sensor, and the repeatability of aiming the center of the laser rays‘ beam at the PSD sensor. The manufacturer states the repeatability of measurement of the device itself is ±1 µm. Another effect influencing accuracy may be the situation of the receiver in direction of the z axis and the effect of the angle of the incident laser beam on the PSD sensor. This inaccuracy may be in the order of microns, yet precise positioning and aiming is capable of mostly eliminating it. The most important effect is the environment traversed by the laser beam. This impacts all measurements where the beam passes through inhomogeneous environment, even those where measurement is done by autocollimator.

In addition, another advantage of this device compared to laser tracker technology is that it is several times cheaper. This experimental method is of a specific type the main benefit of which is lower price of the measuring chain, starting with the measuring system all the way up to making a flange with the weight. Further modification might yield automated data harvesting and rendering of the required charts that could serve the purpose of error detection, i.e., searching for significant deviations in the robot’s operation. The predictive power of these data should lead to prevention of costly maintenance.

6. Conclusions

This paper describes results of measurements and a detailed analysis of path accuracy of the Fanuc Crx- 10iA robot. All measurements were done using an imaginary cube defined by the ISO standard 9283, placed in the most-frequently used workspace of the robot. The procedure for all measurements was created using this standard. Path accuracy was measured with a measuring device Gepard 5bt with a suitable measuring setup. The results were then processed in its respective software. Measurements were done under 100 % load on the robot‘s interface at three speed levels prescribed by the standard, namely at 10, 50 and 100 % speed. The measurements were done bidirectionally, from point P1 to point P10 and back. That is, a total of 20 data for axes x and y was processed with respect to each measurement. The paper describes experimental methodology of measuring path accuracy, which enabled measuring of data and using the ISO standard 9283, necessary data were further calculated and plotted in charts. Since the manufacturer does not provide the path accuracy value for this robot type, the results are to inform further research.

Author Contributions

Conceptualization, J.S. and R.J.; methodology, P.T and P. M..; software, M.S.; validation, S.O..; data curation, P.M.; writing—review and editing, P.M.; visualization, J.S.; supervision, J.Sv.

Acknowledgments

This research was supported by project KEGA: 020TUKE-4/2022 Development and implementation of new approaches in teaching industrial and collaborative robotics, KEGA: 043TUKE-4/2024 Creation of prospective educational tools for the field of additive manufacturing with the implementation of progressive elements of virtual reality and VEGA: 1/0215/23 Research and development of robotic workplaces equipped with industrial and collaborative robots.

Conflicts of Interest

The authors declare no conflict of interest.

References

Semjon, J.; Sukop, M.; Vagaš, M.; Jánoš, R.; Tuleja, P.; Koukolova, L.; Marcinko, P.; Juruš, O.; Varga, J. Comparison of the delta robot ABB IRB 360 properties after collisions. Commun. Sci. Lett. Univ. Zilina, 2018, 20, p. 42 – 46. [CrossRef]
Svetlík, J., Demeč, P. Methods of Identifying the Workspace of Modular Serial Kinematic Structures. 2013. Applied Mechanics and Materials, vol. 309, p. 75-79. [CrossRef]
Nubiola, A.; Bonev, I. Absolute calibration of an ABB IRB 1600robot using a laser tracker. 2013. Robotics and Computer-Integrated Manufacturing, Vol. 29, p. 236 – 245. [CrossRef]
Slamani, M.; Joubair, A.; Bonev, I. A comparative evaluation of three industrial robots using three reference measuring techniques 2015. Industrial Robot: An International Journal, Vol. 42, p. 572 – 585. [CrossRef]
Chachane, K.; Ohol, S.; Chiwande, S. Industrial robot performance analysis using low cost set-up. 2021-01, IOP Conference Series; Materials Science and Engineering, Vol. 1012, p. 012010. [CrossRef]
Pollák, M; Goryl, K. Simulation Design and Measurement of Welding Robot Repeatability Utilizing the Contact Measurement Method, 2023-07, Machines, Vol. 11, p. 1-15. [CrossRef]
Szybicki, D.; Obal, P.; Kurc, K.; Gierlak, P. Programming of Industrial Robots Using a Laser Tracker, 2022-08, Sensors, Vol. 22, P. 6464. [CrossRef]
Raytec Systems. Available online: https://www.raytec.ch/en/products/gepard-system.html (accessed on 20 August 2023).
Ondočko, Š.; Svetlík, J.; Šašala, M.; Bobovský, Z.; Stejskal, T.; Dobránsky, J.; Demeč, P.; Hrivniak, L. Inverse Kinematics Data Adaptation to Non-Standard Modular Robotic Arm Consisting of Unique Rotational Modules. Appl. Sci. 2021, 11, 1203. [CrossRef]
Semjon, J.; Janos, R.; Sukop, M.; Tuleja, P.; Hajduk, M.; Jurus, O.; Marcinko, P.; Virgala, I.; Vagas, M. Verification of the UR5 Robot´s Properties after a Crash Caused by a Fall of a Transfered Load from a Crane. International Journal of Advanced Robotics Systems 2020, Vol. 17, p. 1 – 9. [CrossRef]
Hoffmann, Ch. Accuracy-Tests for Industrial Robots. 1988. IFAC Proceedings Volumes, Vol. 21, No. 16, p. 103 – 108. [CrossRef]
Simiński P., Kończak J., Przybysz K., Analysis and Testing of Reliability Information Systems in Analysis of the Operation-Related Process in the Army. Journal of Konbin Volume & Issue: Volume 47 (2018) - Issue 1 (December 2018), Page range: 105 – 122. [CrossRef]
Shu, T.; Gharaaty, S.; Xie, W.-F.; Joubair, A.; Bonev, I. Dynamic Path Tracking of Industrial Robots With High Accuracy Using Photogrammetry Sensor, 2018-03, IEEE/ASME Transactions on Mechatronics, Vol. PP, p. 1-1. [CrossRef]
Fan, K.-Ch.; Wang, H.-Y.; Yang, h.-w.; Chen, L.-M. Techniques of multi-degree-of-freedom measurement on the linear motion errors of precision machines, 2014-08, Advanced Optical Technologies, Vol.3, p. 376 – 387. [CrossRef]
ISO. Available online: https://emanual.robotis.com/docs/en/dxl/mx/mx-28/ (accessed on 25 August 2022).
Kuric, I.; Tlach, V.; Sagova, Z.; Císar, M.; Gritsuk, I. Measurement of industrial robot pose repeatability. 2018-01. MATEC Web of Conferences, Vol. 244, P. 01015. [CrossRef]
Lin, Z.; Dai., H.; Wu, Z.; Zeng, Y.; Su., S.; Xia, X.; Lin, M.; Yu, P. Analysis of a Six-Axis Industrial Robot´s Dynamic Path Accuracy Based on an Optical Tracker, 2017-09, p. 178 – 184. [CrossRef]
Morozov, M.; Riise, J.; Summan, R.; Pierce, S.; Mineo, C.; MacLeod, Ch.; Brown, R. Assesing the Accuracy of Industrial Robots through Metrology for the Enhancement of Automated Non-Destructive Testing, 2016-09. [CrossRef]
Breedon, P.; Sivayoganathan, L.; Balendran, V.; Al-Dabass, D. Multi-axis fuzzy control and performance analysis for an industrial robot, 2002-02, Vol. 1, p. 500-505. [CrossRef]
Fanuc CRX-10iA. Available online: https://www.fanuc.eu/sk/sk/robots/robot-filter-page/spolupracuj%C3%BAce-roboty/crx-10ia (accessed on 5 September 2022).
Slamani, M.; Nubiola, A.; Bonev, I. Assessment of the positioning performance of an industrial robot, 2012-01, Industrial Robot: An International Journal, Vol. 39, p. 57-68. [CrossRef]
Kuric, I.; Tlach, V.; Císar, M.; Sagova, Z.; Zajacko, I. Examination of industrial robot performance parameters utilizing machine tool diagnostic methods, 2020-02, International Journal of Advanced Robotic Systems, Vol. 17, p. 172988142090572. [CrossRef]
Liu, Y.; Li, Y.; Zhuang, Z.; Song, T. Improvement of Robot Accuracy with an Optical Tracking System, Sensors 2020, 20(21), 6341. [CrossRef]

Figure 2. Software Gepard.

Figure 4. Path accuracy for linear path.

Figure 5. Path accuracy for circular path.

Figure 6. Measuring cube with measuring plane (C1 – C2 – C7 – C8).

Figure 7. Measuring with Gepard (receiver – transmitter).

Figure 8. Kinematic model of CRX-10iA.

Figure 9. The course of position measurement as plotted on the graph.

Figure 10. The course of velocity measurement as plotted on the graph.

Figure 11. The course of acceleration analysis as plotted on the graph.

Figure 12. First and last measuring point in the ISO cube.

Figure 14. Measuring setup.

Figure 15. Cycles of measurements.

Figure 16. Plot of values for axis X with maximum speed 1000 mm/s.

Figure 17. Plot of values for axis Y with maximum speed 1000 mm/s.

Figure 18. Path accuracy under 100 % load and at 100 % speed.

Figure 19. Plot of values for axis X at maximum speed of 500 mm/s.

Figure 20. Plot of values for axis Y at maximum speed of 500 mm/s.

Figure 21. Path accuracy at 50% speed and under 100% load.

Figure 22. Overall path accuracy plotted under 100 % load and at 100 %, 50%, 10% speed, respectively, for points P1 to P10.

Figure 23. Overall path accuracy plotted under 100 % load and at 100 %, 50 %, 10 % speed, respectively, for points P10 to P1.

Figure 24. Overall path accuracy in measuring points C2 to C8.

Table 1. Table of parameters Gepard 5 bt system.

Laser transmitter	Gepard 5bt	Laser receiver	Gepard 5bt
Laser power	< 1 mW	Measuring range	15 x 15 mm
Laser class	2	Measurement resolution	0,5 μm
Wavelength	650 nm	Linearity	0,04 %
Beam cross section	circle	Repeatability	± 0,25 μm
Power supply	Li-on 7,2 V	Power supply	Li-on 7,2 V
Dimensions	142x50x50 mm	Dimensions	142x50x50 mm
Weight	730 g	Temperature range	10 – 45 °C
Beam adjustment	Yes	Measuring distance	0 – 15 m

Table 2. Parameters of robot Fanuc CRX-10iA.

Model	CRX-10iA
Type	6 axes (J1, J2, J3, J4, J5, J6)
Reach	1249 mm
Axis	Motion range (maximum speed)
Axis J1	380° (120°/s) 6.63 rad (2.09 rad/s)
Axis J2	360°(120°/s) 6.28 rad (2.09 rad/s)
Axis J3	570°(180°/s) 9.95 rad (3.14 rad/s)
Axis J4	380°(180°/s) 6.63 rad (3.14 rad/s)
Axis J5	360°(180°/s) 6.28 rad (3.14 rad/s)
Axis J6	450°(180°/s) 7.85 rad (3.14 rad/s)
Mode of speed	Maximum speed
Collaborative speed	1000 m/s
High speed mode	2000 m/s
Repeatability	± 0.04 mm

Table 3. D-H parameters.

Link	α_i	a_i	Φ_i	d_i
1	-π/2	0.218	q₁	0.159
2	0	0.54	q₂	0
3	-π/2	0	q₃	0.218
4	π/2	0	q₄	0.54
5	-π/2	0	q₅	0.15
6	0	0	q₆	0.16

Table 4. Measured averages for the x and y axes and the calculated AT values (m = 100% and v = 100%).

P	X	Y	AT
1	0.61656	0.24771	0.66445954
2	0.07099	0.07766	0.10521718
3	-0.16345	-0.03696	0.16757668
4	-0.2664	-0.17036	0.31621431
5	-0.35648	-0.15309	0.38796203
6	-0.23309	-0.15427	0.27951777
7	-0.17611	-0.09639	0.20076296
8	-0.11829	0.00238	0.11831394
9	0.10513	0.09689	0.14296849
10	0.52112	0.18639	0.55345035
10	0.49866	0.22946	0.54892047
9	0.09615	0.0959	0.13579997
8	-0.12323	-0.03595	0.1283668
7	-0.18524	-0.15453	0.24123304
6	-0.31795	-0.14858	0.3509533
5	-0.23497	-0.15929	0.28387357
4	-0.19777	-0.13178	0.23765299
3	-0.13899	-0.01929	0.14032222
2	0.118	0.09257	0.14997735
1	0.48535	0.22178	0.53362064

Table 5. contains measurements at 50 % speed and under full load (mm).

P	X	Y	AT
1	0.60428	0.25339	0.655256294
2	0.08724	0.07807	0.117071527
3	-0.15178	-0.03909	0.156732883
4	-0.2594	-0.1744	0.312575943
5	-0.36602	-0.15575	0.397779717
6	-0.24323	-0.16048	0.291401207
7	-0.18541	-0.09385	0.207809265
8	-0.12881	0.00687	0.128993074
9	0.09918	0.10342	0.143291203
10	0.54393	0.18183	0.573517213
10	0.50901	0.23198	0.559379925
9	0.08881	0.09629	0.130992291
8	-0.12534	-0.02731	0.128280753
7	-0.18845	-0.15421	0.243503853
6	-0.3289	-0.14737	0.360406891
5	-0.22857	-0.16561	0.282260371
4	-0.19401	-0.13044	0.233782963
3	-0.13236	-0.02441	0.134592042
2	0.12231	0.09572	0.155312764
1	0.47754	0.22489	0.52784464

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer