1. Introduction
Muscle coactivation is one of the strategies used by the central nervous system (CNS) to simplify movements and ensure adequate joint stiffness by regulating the time and amplitude of simultaneous activity of a pair or group of muscles [
1,
2,
3,
4]. Muscle coactivation is thought to maintain effector-level control (low dimensional), removing the need for individual muscle coordination control (high dimensional) [
2].
Although muscle coactivation has been extensively studied during gait in both healthy and patients with a variety of motor disorders (for a review, see [
2], only a few studies have looked at muscle coactivation during running [
5,
6,
7,
8,
9]. Walking to running represents a critical transition time that corresponds to a change in CNS activation [
10], leg geometry [
11,
12], joint compliance [
13], and a robust mechanical energy transformation [
14,
15,
16,
17].
Most humans will voluntarily switch from walking to running at 6.8 and 7.5 Km/h [
18,
19,
20,
21]. At these higher speeds, running becomes less expensive than walking by utilizing a mass-spring mechanism that exchanges kinetic and potential energy in very different ways [
15,
17]. Most studies on muscle activation during running have concentrated on the activity of single muscles [
22,
23,
24]. Running has been linked to increased activation of all lower limb muscles in general [
5,
25,
26,
27], despite the fact that some muscles (e.g., gluteus maximus) appear to play a larger role in running than in walking [
28]. Only a few studies have looked at the activation of muscle pairs while running [
9,
29]. When compared to a single-joint muscle solution, these studies discovered that a longer duration of muscle coactivation between the rectus femoris and gastrocnemius during stance provided a better metabolic solution to multiple joint stability, implying that biarticular muscles redistribute mechanical power from proximal joints to distal joints, and ultimately to the ground. Moore et colleagues [
9] discovered that coactivation in the distal and leg flexor muscles decreases with speed while running, implying that when both legs are off the ground, muscle coactivation must be reduced to allow for more leg propulsion both upwards and forwards.
A critical missing piece is whether the descending motor commands for running are set up to coactivate the lower limb muscles as a whole entity within a gross motor strategy. Taking previous evidence into account [
9,
29], it is possible to hypothesize that descending commands for running cause an increase in whole limb stiffness to stabilize the limb during ground contact on the one hand, and a decrease in limb stiffness to facilitate forward progression of the leg during air stepping on the other. This basic descending motor control would imply that flexor muscles are activated during air stepping, when whole-limb stiffness is reduced, and that muscle coactivation occurs via top-down (rostro-caudal) recruitment (from L3 to S2). This strategy would greatly simplify motor control at the low-dimensional effector level during shock absorption, allowing for motor control decentralization while relying on peripheral feedback via muscle-reflex to generate the required muscle coactivations and regulate each muscle's gain.
We recently proposed a novel approach to studying time-varying multi-muscle coactivation function (TMCf) [
30,
31] which is a good indicator of the CNS's overall strategy for modulating the simultaneous activation of many lower limb muscles during locomotion. This approach provides a new perspective on the spatiotemporal motor control of the lower limbs, emphasizing how all muscles of the lower limb are synchronously coactivated in an attempt to increase whole-limb stiffness, regardless of single-joint antagonist muscles or modular activation of a group of muscles [
32].
The objectives of this study were to observe the differences in lower limb muscles coactivation strategies during locomotion across speeds from walking to running. We hypothesized that the behavior of lower limb muscles in terms of coactivation parameters, may differ across the speeds, particularly between walking and running, and that the coactivation parameters may vary based on the muscular functions (flexion or extensor functions), and across the rostro-caudal recruitment map.
2. Materials and Methods
2.1. Subjects
Nineteen healthy runners were recruited (9 men, 10 women; mean age, 40.95±7.96 years; mean weight, 66.47±14.60 kg). Each runner has declared of running for at least 5 years and that runs at least 3 times per week for at least 5 kilometers per training session.
None of the runners had any known diseases that might affect their regular gait or running pattern. The study was authorized by the local ethics committee (N. 0078009/2021) after all participants gave written informed consent and the study's design met with the Declaration of Helsinki.
2.2. Experimental procedure
Each runner was asked to walk at thirteen various speeds, ranging from 0.8 km/h to 6.8 km/h, and run at five different speeds, ranging from 7.3 km/h to 9.3 km/h, with increase steps of 0.5 km/h, on a treadmill. We chose 7.3 km/h as the transition speed because it is consistent with earlier researches [
18,
20,
21] in which this transition was determined considering metabolic energy cost of locomotion, as well as the human capacity for purposeful gait modulation and the importance of physiologic and metabolic demands.
Before the recording session, the participants practiced for a few minutes to become acclimated to the task. To avoid fatigue, the trials were separated by 1-minute rest periods. Each trial was performed for 30 seconds before moving on to the next speed that was chosen at random.
2.3. Data acquisition
A bipolar 16-channel wireless acquisition device (Mini Wave System; Cometa, Italy) was used to record all the surface myoelectric activity at a sampling rate of 2 kHz. After skin preparation, twelve Ag/AgCl pre-gelled electrodes (Kendall ARBO, inter-electrode distance: 2 cm) were placed over each participant's right side lower limb muscles over the following muscles:
gluteus medius (GM),
rectus femoris (RF),
vastus lateralis (VL),
vastus medialis (VM),
tensor fascia latae (TFL),
semitendinosus (ST),
biceps femoris (BF),
tibialis anterior (TA),
gastrocnemius medialis (GasM),
gastrocnemius lateralis (GasL),
soleus (S), and
peroneus longus (P) (Merletti and Cerone, 2020; Merletti and Muceli, 2019), following the European Recommendations for Surface Electromyography (Hermens et al., 2000), the Atlas of Muscle Innervation Zones [
33], and best practices [
34,
35,
36].
A stereo-photogrammetric motion analysis system with optoelectronic technology (SMART-DX 6000 system: BTS, Italy) and with a sampling rate of 340Hz was employed to collect the kinematics data. Eight infrared cameras were used to record five passive spherical markers, covered with aluminum powder, positioned above the sacrum and bilaterally on the anterior superior iliac spines, heel, metatarsal head, and lateral malleoli (Davis et al., 1991).
A video camera (BTS Vixta; BTS, Italy) was used to record each task at a frame rate of 25-30 frames per second and a video resolution of 640x480 pixels.
All the data collected were synchronized.
2.4. Data analysis
3D reconstruction software (SMART Tracker and SMART Analyzer: BTS, Italy) and MATLAB (R2019b 9.7; MathWorks, USA) were used to process the sEMG and kinematics data.
2.4.1. Cycle definition and temporal normalization
The heel strike (HS) and toe-off (TO) events were determined in this study along the antero-posterior trajectories through the maximum point of the heel and the minimum point of the metatarsal, respectively. The gait and run cycle, were defined as the time between two consecutive HS of the same leg.
Ten cycles for each gait speed level for each runner were analysed and a polynomial approach was used to time-normalize the electromyographic and kinematic data on 201 samples [
31,
37,
38,
39].
2.4.2. Global, flexor, extensor and rostro-caudal coactivation of lower limb muscles
The raw sEMG signals were visually reviewed to remove any artifact-containing cycles. They were then band-pass filtered with a zero-lag fifth-order Butterworth (20–450Hz) [
40,
41] to keep only the signal of interest and then full wave rectified and low-pass filtered with a zero-lag fifth-order Butterworth (10 Hz) [
42]. The elaborated sEMG signals of each muscle were amplitude-normalized (0-100%) for each runner in relation to the mean of their individual three largest peaks values detected throughout all cycles (Burden, 2010; Fiori et al., 2020).
The TMCf was used to calculate the simultaneous activation of the lower-limb muscles based on the processed sEMG signals [
3,
30,
31,
37,
38,
39,
43]. The full-wave-rectified, low-pass-filtered, and 0–100% amplitude normalized sEMG signals were used as inputs to this sigmoid-weighted time-dependent function for the inclusion of multiple muscles during walking and running. This function's values ranged from 0 to 100%, and they were calculated as follows:
where
M is the number of muscles considered,
is the sEMG sample value of the
muscle at instant
,
and
are constants equal to 12 and 0.5 respectively (Ranavolo et al., 2015), and
is the mean of the differences between each pair among the 12
values at instant
:
is the total number of possible differences between each pair of .
has the following properties: inverse relationship with the mean of the differences d(i), i.e., values close to the mean activation of the muscle sample values considered when is close to 0, and values close to 0 when is close to 1. The smaller the differences in muscle activations are, and the closer the values are to 0, the closer the sigmoid-coefficient values are to 1, the closer the value close is to its mean value. In contrast, the greater the differences in muscle activations and the higher and the lower the sigmoid coefficient, lowering the values. Data over individual strides was calculated for each runner and speed, and then averaged across cycles.
All the acquired muscles were inserted in the calculation of the TMCf to assess global coactivation (TMCf
glob). The coactivation of extensor (TMCf
ext), flexor (TMCf
flex) muscles separately, and according to the rostro-caudal organization (TMCf
L3; TMCf
L4; TMCf
L5; TMCf
S1; TMCf
S2) [
44,
45,
46,
47] was assessed using subgroups of muscles (see
Table 1). Muscles were considered as flexors or extensors based on their concentric function in the sagittal plane [
47]. The biarticular muscles were considered as flexors or extensors based on their proximal function [
48,
49].
2.4.3. Coactivation Parameters
Within the gait cycle, the following parameters were calculated for each map, runner and speed:
i) the synthetic coactivation index (CIglob; CIext; CIflex; CIL3; CIL4; CIL5; CIS1; CIS2), which is calculated as the mean value of the TMCf and represents the average of the coactivation level [% coactivation]; ii) the maximum value of the TMCf (Maxglob; Maxext; Maxflex; MaxL3; MaxL4; MaxL5; MaxS1; MaxS2) [% coactivation].
iii) the full width at half maximum (FWHMglob; FWHMext; FWHMflex; FWHML3; FWHML4; FWHML5; FWHMS1; FWHMS2) of the coactivation, which reflects the sum of the time durations, within the gait cycle, during which the TMCf curve is higher than its half maximum value [% gait cycle].
iv) the center of activity (CoA
glob; CoA
ext; CoA
flex; CoA
L3; CoA
L4; CoA
L5; CoA
S1; CoA
S2), which is calculated with circular statistics and plotted in polar coordinates to show where the most coactivation is concentrated within the walk and run cycles and, in this study, also to show the instant of coactivation onset on the rostro-caudal maps [% gait cycle] [
31,
50]:
v) the coefficient of multiple correlation (CMC), which measures the overall waveform similarity of a group of curves (the closer to 1 the CMC is, the more similar the curves are) [
51,
52,
53]. CMC was calculated according to the following formula:
(number of points within the curve), is the number of curves, is the value at the point in the curve, is the average of the two curves at point , and is the grand mean of all .
Data over individual strides was calculated for each runner and speed, and then averaged across cycles. Within (CMC_Wtglob, CMC_Wtext, CMC_Wtflex, CMC_WtL3, CMC_WtL4, CMC_WtL5, CMC_WtS1, CMC_WtS2) and between (CMC_Btglob, CMC_Btext, CMC_Btflex, CMC_BtL3, CMC_BtL4, CMC_BtL5, CMC_BtS1, CMC_BtS2) runners, the CMC was calculated.
2.4.4. Cross-correlation
The shape similarity overall the coactivation maps was evaluated using bidimensional normalized cross-correlation [
31,
37,
54]. In detail, the central value of cross-correlation function
, with an amplitude ranging from 0 to 1, was used to measured shape similarity between the global coactivation map and the extensor (R
G-E) and flexor (R
G-F) coactivation maps, as well as the shape similarity between the global coactivation map and the rostro-caudal coactivation maps (R
G-L3, R
G-L4, R
G-L5, R
G-S1, R
G-S2).
2.4.5. Center of Mass Displacement and Spatiotemporal parameters
The whole-body CoM for each speed and runner was calculated using the “reconstructed pelvis method” [
55,
56,
57], i.e., the geometric center of the triangle formed by the markers over the two anterior superior iliac spines and the sacrum, which is the pelvic center. The displacement in vertical (CoM
y) and medio-lateral (CoM
z) directions was then calculated from the COM as the difference between the maximum and minimum values in their respective directions.
The following spatiotemporal parameters were determined for each speed and runner:
i)
Toe-off event (TO
e) [% gait cycle];
ii)
stride length [cm];
iii)
stride frequency [Hz];
iv)
foot lift [cm] [
37,
56,
58,
59]; with the latter calculated as the maximum elevation along the vertical direction (y coordinate) of the centroid formed by the heel, metatarsal head, and lateral malleoli.
2.4.6. Statistical analysis
Repeated measurement ANOVA was used to determine the significance of differences in coactivation parameters computed from global, flexor, extensor, and rostro-caudal maps, as well as CoM and spatiotemporal parameters, with gait speed as a between-group factor (18 levels: from 0.8 to 9.3 Km/h), followed by a Bonferroni's pot-hoc analysis to determine whether there were significant differences between speeds.
An unpaired two-sample t test was used to compare the shape similarity of the global vs extensor coactivation maps and the global vs flexor coactivation maps. A univariate ANOVA was performed with coactivation map shape similarity as a between-group factor (5 levels: global vs each rostro-caudal coactivation map) and Bonferroni's post-hoc analysis was performed to assess the significant differences between each shape similarity.
The Watson-Williams test for circular data was applied to CoAs calculated from global, flexor, and extensor coactivation maps, with gait speed as the between-group factor, followed by a Bonferroni's pot-hoc analysis to see if there were any significant differences between the speeds [
37,
39,
50,
60]. Whereas the Harrison-Kanji test for circular data was applied to CoAs calculated from rostro-caudal maps, with gait speed and spinal level as between and within-group factors, a Bonferroni's pot-hoc analysis was used to determine whether there were significant differences between spinal levels and speeds [
61].
A partial correlation analysis was performed, excluding the effects of gait speed, between each calculated global, flexor-extensor, rostro-caudal coactivation map, and each CoM and spatiotemporal parameter. Strong correlations were defined as significant correlation coefficients > 0.69 [
62].
The significance level was set to 0.05, and all analyses were carried out in MATLAB (8.3.0.532, MathWorks, USA).
3. Results
3.1. Global, flexor, extensor and rostro-caudal coactivation maps and parameters
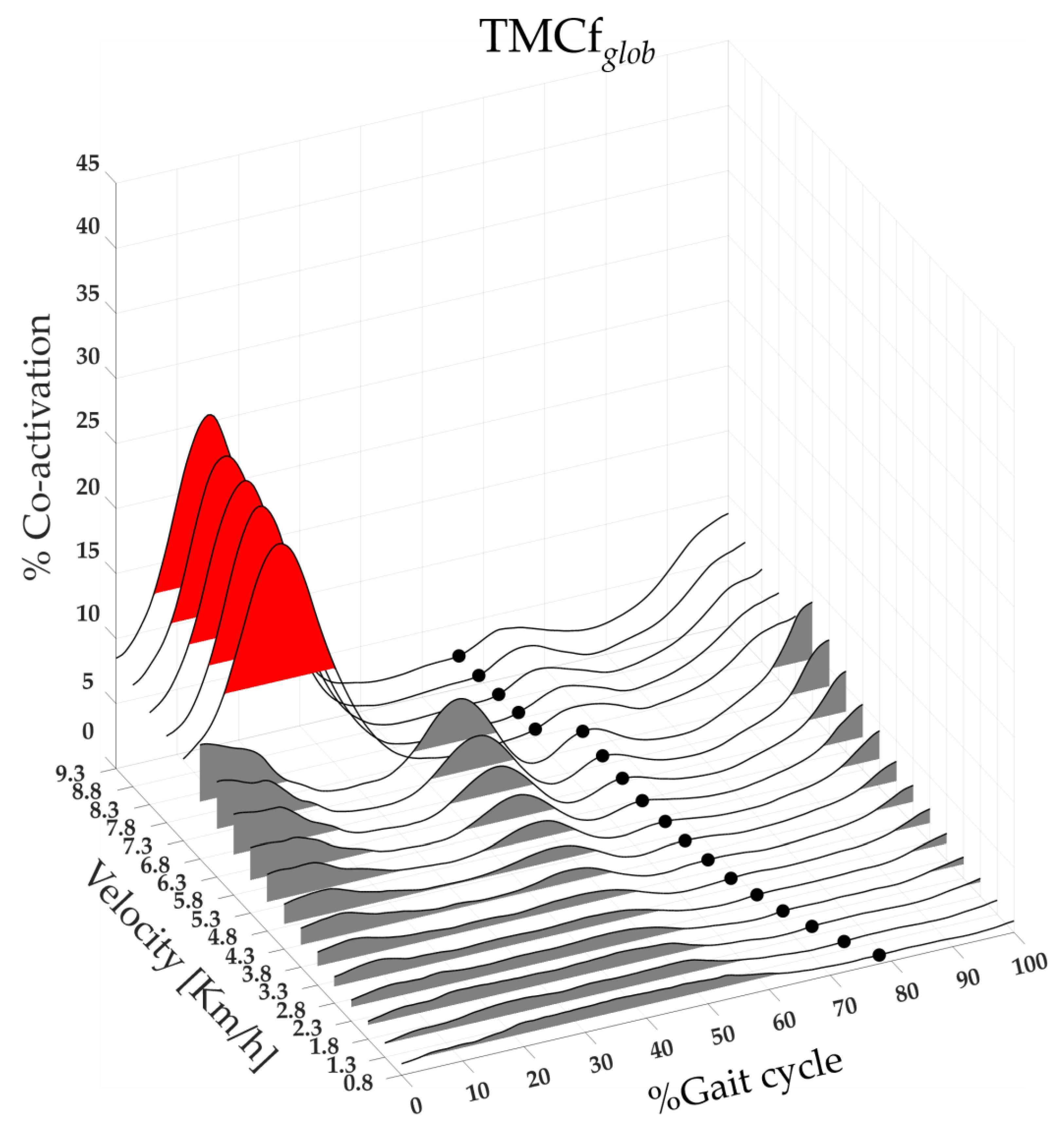
Figure 1 shows the three-dimensional global map of lower limb muscle coactivation from slow walking to running.
The map was created using the average TMCfglob curves (black line) of 19 runners calculated on whole gait cycle, from 0% to 100% (x-axis), for each speed of walking and running performed, from 0.8 to 9.3 km/h (y-axis), and with amplitudes ranging from 0% to 100% of coactivation (z-axis). The TOe (black dots) and FWHMglob (the area underlying the TMCfglob, red and grey for run and walk respectively) for each speed as a mean between all runners are also shown on the map.
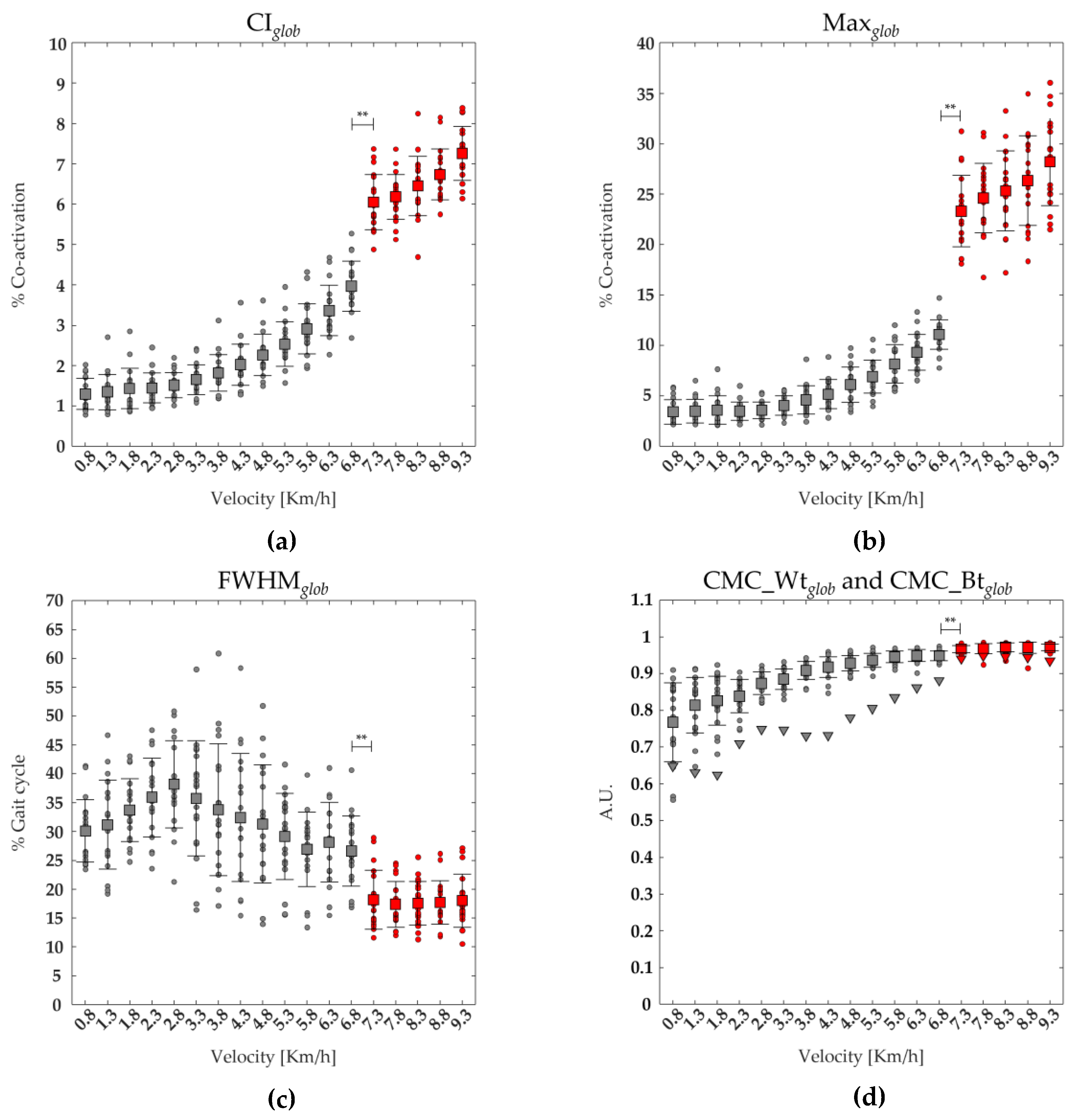
Figure 2 shows the average and standard deviation of 19 runners' coactivation parameters (CI
glob, Max
glob, FWHM
glob, CMC_Wt
glob and CMC_Bt
glob) from slow walking to running. A significant main effect of gait speed was found on CI
glob, on the Max
glob, FWHM
glob, CMC_Wt
glob (see
Table 2). The post-hoc analysis revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values of CIglob, Max
glob, CMC_Wt
glob and CMC_Bt
glob were significantly higher, whereas the value of FWHM
glob was significantly lower (see
Figure 2 and
Table 2).
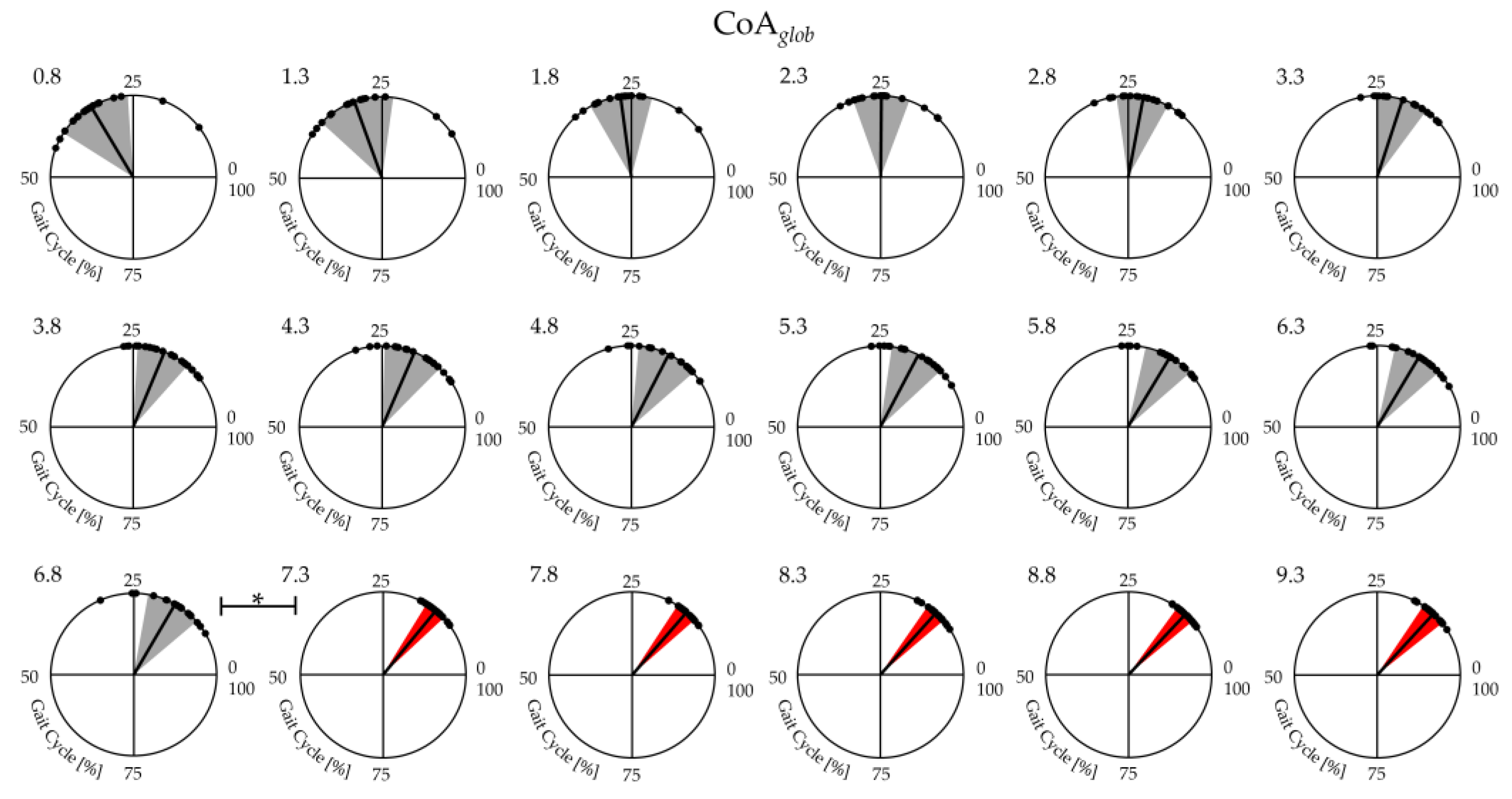
Figure 3 shows the average and the standard deviation of 19 runners' CoA
glob from slow walking to running. A significant effect of gait speed was found on CoA
glob (See
Table 2). The post-hoc analysis revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values of CoA
glob was significantly lower (see
Figure 2, and
Table 2).
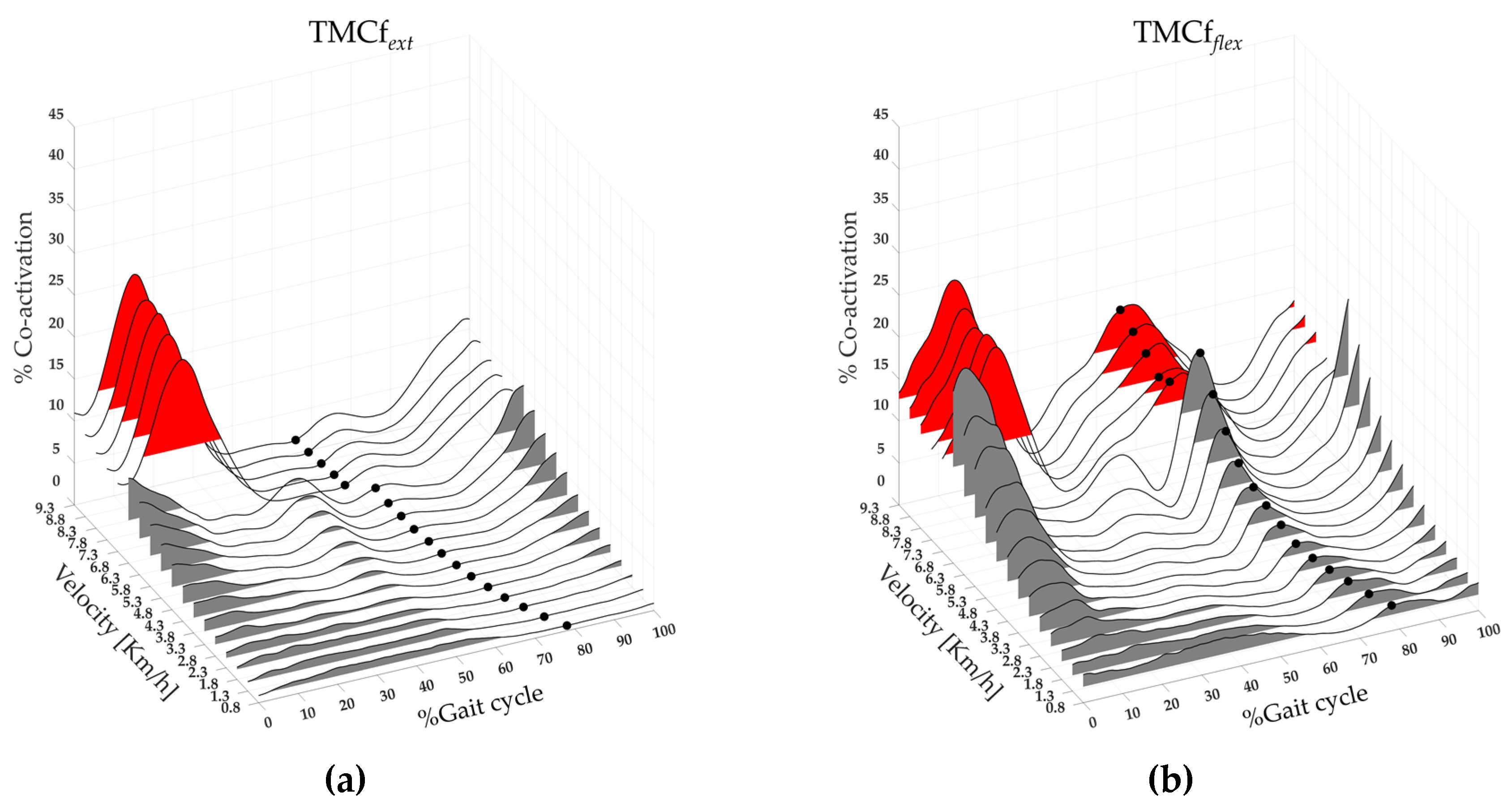
Figure 4 shows the extensor (left side) and flexor (right side) maps of lower limb muscle coactivation from slow walking to running, with the averages TMCf
ext and TMCf
flex curves (black lines), TO
e (black dots), and FWHM
ext and FWHM
flex (the area underlying the TMCf
ext and TMCf
flex red and grey for run and walk respectively) of all 19 runners. A significant effect of speed was found on extensor and flexor parameters: CI
ext and CI
flex, on the Max
ext and Max
flex, FWHM
ext and FWHM
flex, CMC_Wt
ext, and CMC_Wt
flex (see
Table 2). The post-hoc analysis revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values of CI
ext, Max
ext, CMC_Bt
ext were significantly higher, whereas the value of CMC_Bt
flex was significantly lower (see
Table 2).
A significant effect of gait speed was found on CoA
ext and CoA
flex (see
Table 2). The post-hoc analysis revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values CoA
ext was significantly higher, whereas the value of CoA
flex was significantly lower (see
Table 2).
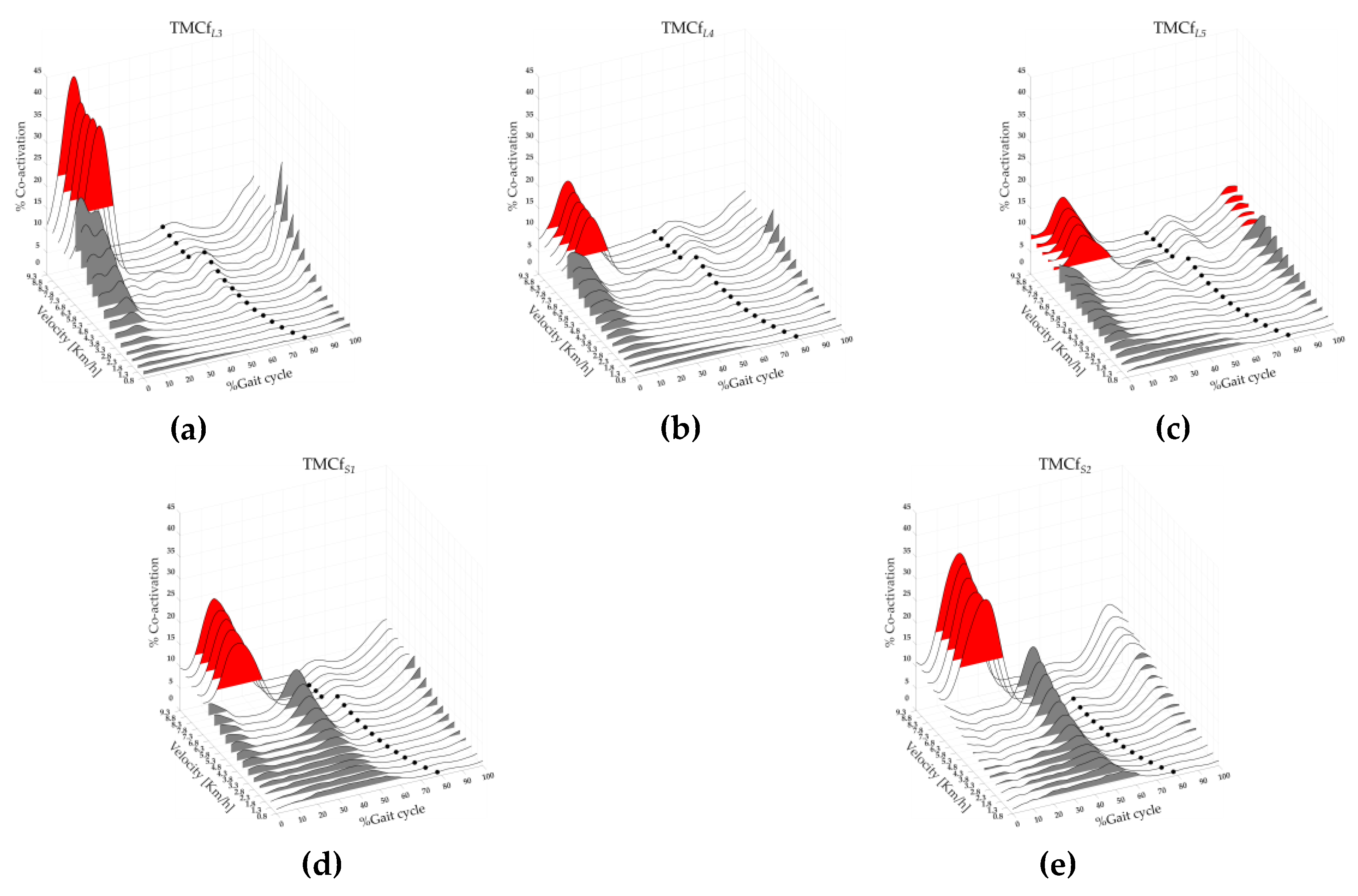
Figure 5 shows the rostro-caudal (from L3 to S2 spinal level) maps of lower limb muscle coactivation from slow walking to running with the averages TMCf
L3, TMCf
L4, TMCf
L5, TMCf
S1, TMCf
S2 (black lines), TO
e (black dots), and FWHM
L3, FWHM
L4, FWHM
L5, FWHM
S1, FWHM
S2 (the area underlying the curves, red and grey for run and walk respectively) of all 19 runners.
A significant effect of gait speed was found on CI
L3, CI
L4, CI
L5, CI
S1, CI
S2, on the Max
L3, Max
L4, Max
L5, Max
S1, Max
S2, on the FWHM
L3, FWHM
L4, FWHM
L5, FWHM
S1, FWHM
S2, CMC_Wt
L3, CMC_Wt
L4, CMC_Wt
L5, CMC_Wt
S1, CMC_Wt
S2 (see Tab 2). The post-hoc analysis revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values of CI
L4, CI
L5, CI
S1, CI
S2, Max
S1, Max
S2, CMC_Wt
S1, CMC_Bt
L3, CMC_Bt
L4, CMC_Bt
S1 and CMC_Bt
S2 were significantly higher, whereas the value of CMC_Bt
L5 were significantly lower (see
Table 2).
A significant effect of gait speed and level were found on CoA
L3, CoA
L4, CoA
L5, CoA
S1, CoA
S2 (see
Table 2 and
Table 3). The post-hoc analysis on speed revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values CoA
L3, CoA
L4 and CoA
L5 were significantly higher, whereas the value of CoA
S1 and CoA
S2 were significantly lower (see
Table 2). The post-hoc analysis on spine levels revealed that at the transition between walking (6.8 Km/h) and running (7.3 Km/h) the values CoA
S1 were significantly higher than CoA
L3, CoA
L4, CoA
L5, as well as the values CoA
S2 were significantly higher than CoA
L3, CoA
L4, CoA
L5 (see
Table 3).
3.2. Cross-Correlation
A significantly higher shape similarity between the global and the extensor coactivation map then global and flexor coactivation map was found (see
Table 4).
A significant effect of shape similarity was found between the global and rostro-caudal coactivation maps (see
Table 4). The post-hoc analysis revealed that the value of shape similarity between global and S1 coactivation map was significantly higher than global and L3, L5 and S2 coactivation maps, as well as the shape similarity between global and L4 coactivation map was significantly higher than global and L3, S2 coactivation maps (see
Table 4).
3.3. Center of Mass Displacement and Spatiotemporal parameters
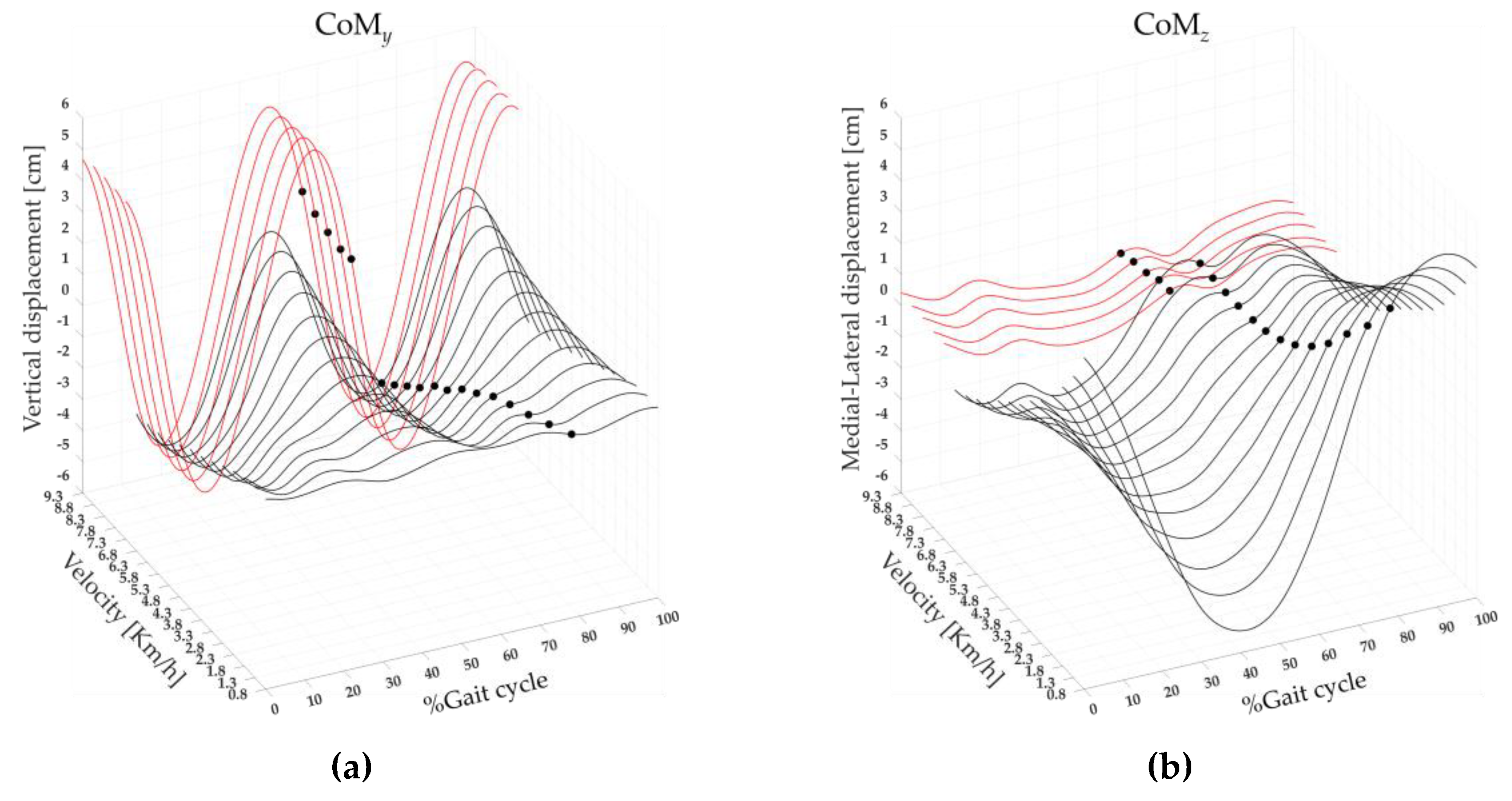
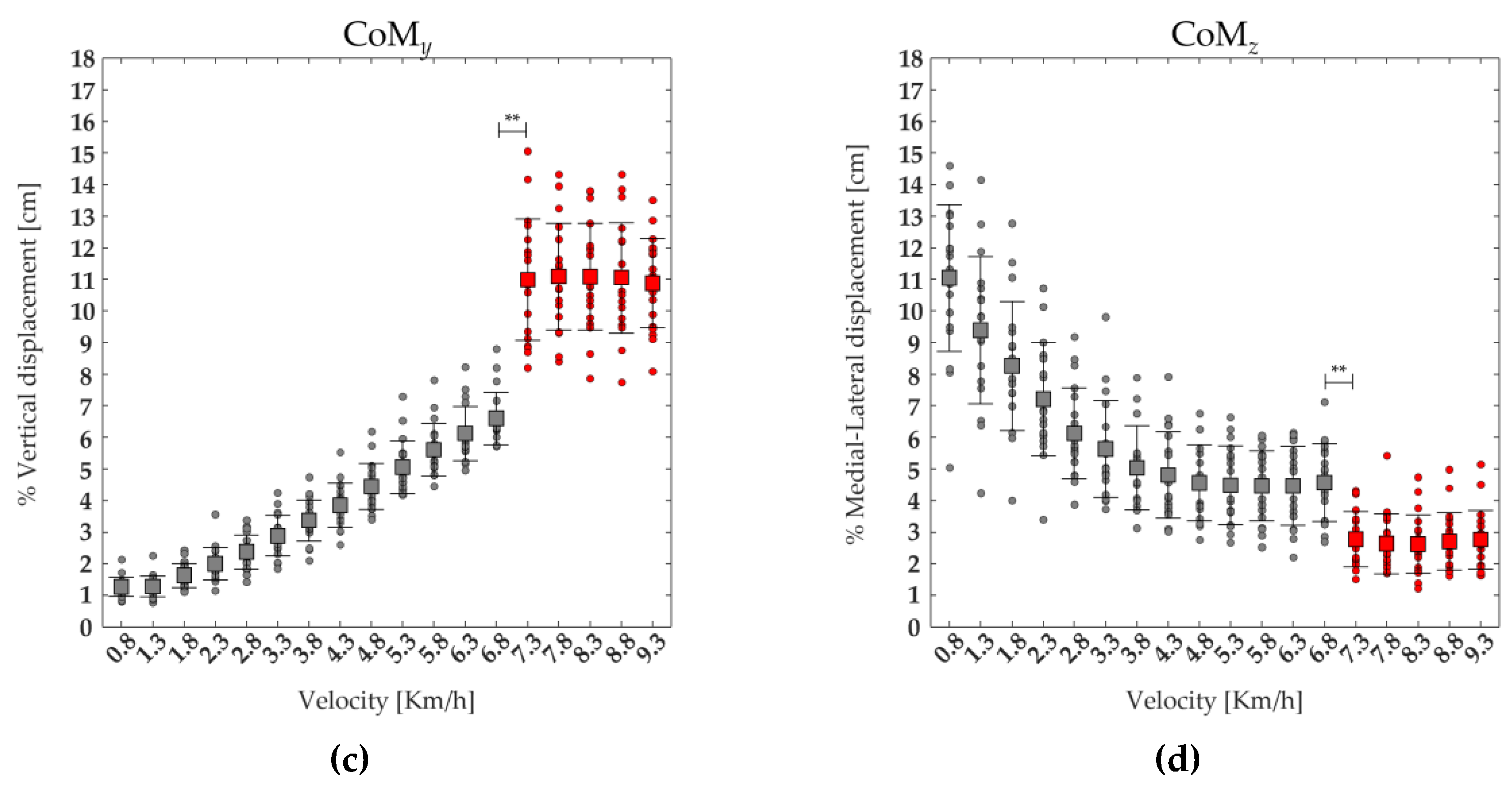
Figure 6 shows three-dimensional CoM maps in the vertical (CoM
y) and medio-lateral (CoM
z) directions. The maps were created using the CoM
y and CoM
z displacement average curves of 19 runners calculated on the gait cycle, from 0% to 100% (x-axis), for each speed of walking and running performed, from 0.8 to 9.3 km/h (y-axis) and with a variable amplitude (z-axis). A significant effect of the speed was found on CoM
y and on the CoM
z. The post-hoc analysis revealed that at the transition between walking (6.8 km/h) and running (7.3 km/h) the values of CoM
y displacement was significantly higher, whereas the value of CoM
z displacement was significantly lower (see
Figure 6, and
Table 2).
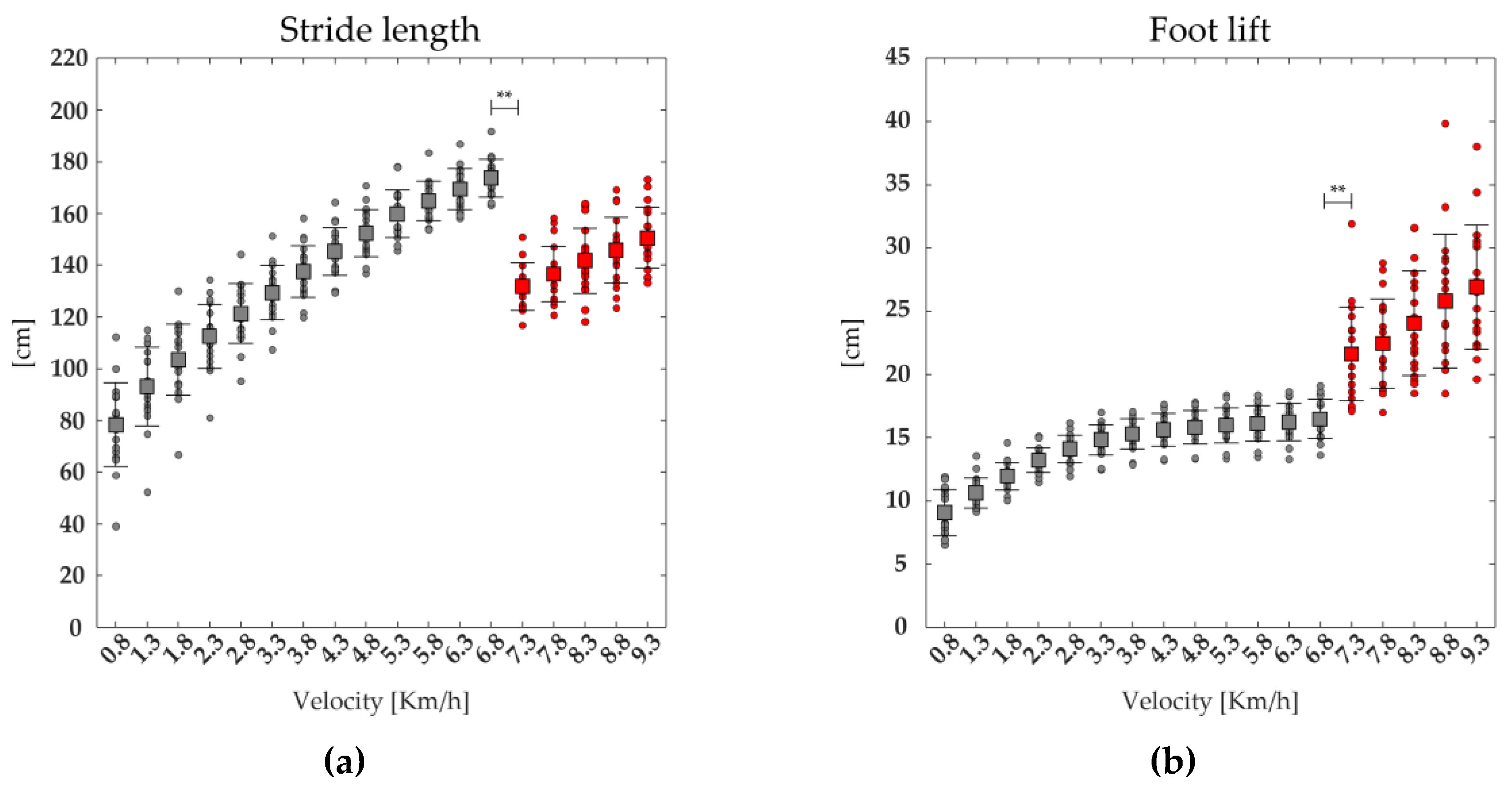
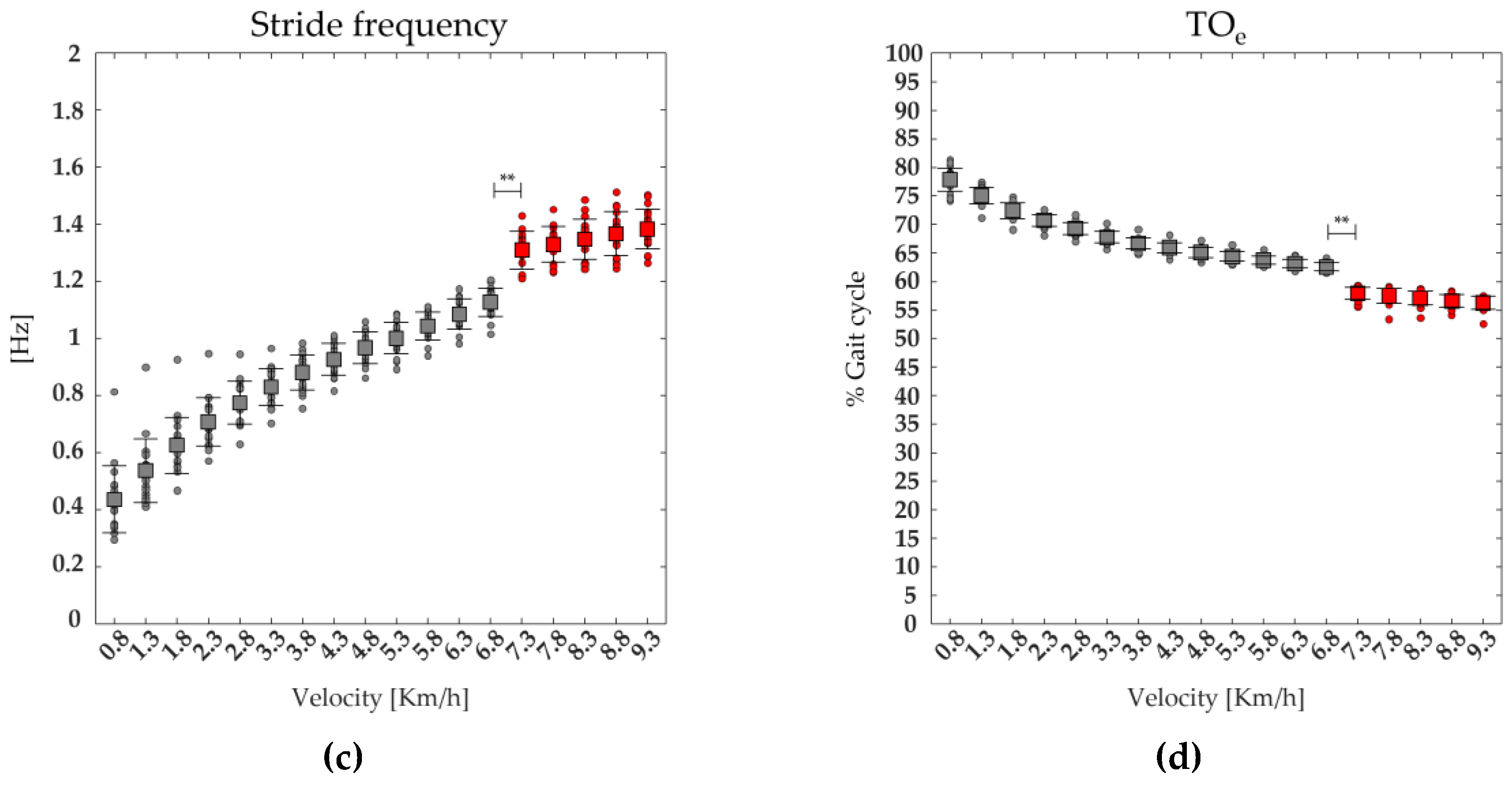
A significant effect of the speed was found on TO
e,
stride length,
stride frequency,
foot lift. The post-hoc analysis revealed that the value of
stride length,
foot lift and
stride frequency were significantly higher, whereas the values of TO
e, was significantly lower at the transition between walking (6.8 km/h) and running (7.3 km/h) (see
Figure 7, and
Table 2).
3.4. Correlations
Regardless of gait speed, CoMy was positively correlated with higher CIglob (r = 0.88, p < 0.001) and Maxglob (r = 0.89, p < 0.001), and negatively correlated with FWHMglob (r = -0.83, p < 0.001) values, whereas CoMz was positively correlated with CoAglob values (r = 0.97, p < 0.001). Stride length values were negatively correlated with CIglob, (r = - 0.98, p < 0.001) and Maxglob (r = -0.99, p < 0.001) values, and positively correlated with FWHMglob (r = 0.80, p < 0.001). Foot lift values were positively correlated with Maxglob values (r = 0.72, p = 0.001), cadence values were negatively correlated with CoAglob values (r = - 0.72, p < 0.001), whereas TOe values were positively correlated with CoAglob values (r = 0.79, p < 0.001).
4. Discussion
The objective of this study was to explore the behavior of the lower limb muscles' coactivation across several speeds, ranging from walking to running, as an expression of the CNS's global strategy for controlling the simultaneous activation of several lower limb muscles during locomotion.
We found that at higher speeds, the global coactivation index rises with increasing coactivation function values, and that coactivation occurs earlier and for a shorter period than at slower speeds. This is especially evident while transitioning from walking to running, as indicated by higher CI
glob and Max
glob values when walking and lower CoA
glob and FWHM
glob values while running (see
Figure 2 and
Figure 3). We also found that running resulted in increased vertical displacement, foot lift, stride frequency, and decreased lateral displacement and stride length, compared to walking (see
Figure 7,
Figure 6), which is consistent with earlier research on the biomechanics of running [
18,
19,
20,
21]. Interestingly, regardless of gait speed, global coactivation co-activation occurring earlier and in a confined portion of the gait cycle was positively correlated with higher vertical displacement, stride frequency, foot lift, and negatively correlated with lower lateral displacement and stride length.
From slow walking to running, we found a different set of curve shapes in lower limb muscle coactivation (see
Figure 1). The time-varying multi-muscle coactivation function revealed a one-hump configuration during slow walking, a four-hump configuration during fast walking, and a three-hump configuration during running. The lonely hump we found during slow walking, as well as the first hump we discovered during running, paralleled the entire duration of the stance contact phase, whereas the first two humps of fast walking distinctly corresponded to the loading (in the range of 10-20% of the gait cycle) and push-off (in the range of 40-60% of the gait cycle) subphases, respectively.
Overall, these humps reflected an increase in whole-limb stiffness in response to ground impact for weight acceptance and pushing on the ground for propulsive purposes, which was consistent with previous findings that the spatiotemporal profile of global coactivation matches that of ground reaction force (GRF) [
31,
37]. Both gait variability and CoM oscillation are known to increase during slow walking, resulting in less stable walking compared to faster gait [
9,
63,
64]. The longer duration, lower magnitude (see
Figure 1), and higher within and between subject variability of lower limb global coactivation observed at slow walking, as expressed by CMC values (See
Figure 2), suggest that the increase in whole-limb stiffness is exerted within a long-lasting and variable "safety strategy," primarily designed to maintain dynamic balance during body progression [
63,
64].
Conversely, the shorter duration, higher magnitude (see
Figure 1), and lower within and between-subject variability of lower limb global coactivation (see
Figure 2) observed in running suggest that whole-limb stiffness is exerted in a more synchronized and stable muscle activation. It also implies that when transitioning from walking to running, the increased whole-limb muscle coactivation during the foot contact phase is intended to absorb ground impact and generate propulsive forces in a single motor act, most likely within a unique motor strategy. As a result, the CI could be a useful index for reflecting and assessing the efficiency of the "leg-spring" stiffness mechanism, which is correlated with a more economical running [
65,
66].
The findings of the partial correlation analysis support the observed mechanisms of global coactivation. Regardless of gait speed, earlier and shorter values of global coactivation during the gait cycle reduce stride length while increasing vertical and decreasing lateral CoM displacements. As a result, rather than being the result of changes in gait speed, it is possible to hypothesise that the observed differences in spatiotemporal and kinematic variables between walking and running could be the result of global coactivation, which is a sensory-control integration process used by the CNS to deal with a more demanding and potentially unstable task like running [
67,
68,
69]. This explains why similar results in terms of coactivation indexes and kinematic characteristics were found in subjects with abnormal gait stability control, such as cerebellar ataxia, who attempt to compensate for gait instability by using global coactivation [
37,
56,
58].
When we analysed the coactivation of either flexor or extensor muscles separately, we found that the function curve of the extensor muscles matched that of the whole limb, whereas that of the flexor muscles clearly differed from it (see
Figure 4). These findings suggest that the main contribution to the whole limb stiffening during walking and running is mainly given by the coactivation of the extensor muscles according to their role in weight acceptance and propulsive function [
70]. Such an extensors activation clearly corresponds to the first hump of the global coactivation of both running and walking (both slow and fast) curves, as well as to the second hump of fast walking. Conversely, the coactivation curve of the flexor muscles increased during the early step air phase in line with the role the flexor muscles in limb lifting [
70]. The coactivation of the flexor muscles, although small, was clearly present in running as second hump of the global coactivation curve and in fast walking as third hump (see
Figure 4). This last result is of particularly interest because it suggests that the flexor muscles is a key factor in transitioning from fast walking to running. It also fits well with the observation of a propagation delay in muscle coactivation from L3 to S2 (see
Figure 5). These findings are in line with previous findings on walking [
46,
71,
72] and reinforce the hypothesis that the coactivation of the flexor muscles (e.g., rectus femoris, iliopsoas), whose motoneurons are located more rostrally within the spinal cord, may play a crucial role in the switch from walking to running. Interestingly, although there was a clear progressive increase in the amount of coactivation of either global extensors or flexors from slow to fast walking, we found an increase in flexor coactivation just before the running speed threshold in the late fast walking trials, followed by a mild reduction in coactivation in the early running trials (see
Figure 4 and
Table 2). One of the key features in the passage from fast walking to running is the optimal exploitation of the mass-spring mechanism to generate kinetic energy in running [
15,
17]. We might infer that such an advantage, which occurs during ground contact, is related to the global coactivation, and reduces the need to coactivate the flexor muscles during the step air phase in early running compared to late fast walking. It is important to note that the coactivation of the flexor muscles corresponded to a small peak (second hump) in the “hollow” of the global coactivation curve, possibly suggesting that the flexor muscles need to be coactivated when the limb stiffness is reduced to facilitate the forward progression.
This study has several limitations. First, due to the experimental setup, antero-posterior CoM displacements could not be assessed, and thus kinetic energy parameters could not be calculated. We also did not account for oxygenation parameters, so our data cannot provide a complete characterization of global coactivation on running economy. However, because greater neuromuscular activation, vertical stiffness, and the ability to rapidly produce force throughout the lower limb during ground contact have been shown to correlate with more economical running [
66,
73,
74], it is expected that CI values may correlate with the energetic running profile in future studies evaluating running performances. Another limitation is related to the superimposition of gait speeds through the use of treadmill, which might have affected some gait parameters [
75]. Therefore, further studies examining global coactivation indices during overground running are needed.
Author Contributions
Conceptualization, L.F., G.C., M.S., A.T., T.V. and A.R.; methodology, L.F., G.C., F.D., A.T., T.V. and A.R.; software, L.F.; validation, L.F., G.C., M.S., A.T., T.V. and A.R.; formal analysis, L.F., A.T. and T.V.; investigation, L.F., S.F.C., G.C., F.D., F.S., M.S., A.T., T.V. and A.R.; resources, L.F., S.F.C., G.C., F.D., F.S., M.S., A.T., T.V. and A.R.; data curation, , L.F., A.T. and T.V.; writing—original draft preparation, L.F., S.F.C., G.C., M.S., A.T., T.V. and A.R.; writing—review and editing, L.F., S.F.C., G.C., F.D., F.S., M.S., A.T., T.V. and A.R.; visualization, L.F., S.F.C., G.C., F.D., F.S., M.S., A.T., T.V. and A.R.; supervision, F.D., M.S. and A.R..; project administration, F.D., M.S. and A.R..; funding acquisition, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented in this article was carried out as part of the SOPHIA project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 871237 and as part of “Bando Ricerche in Collaborazione” 2022 ID 57 funded by INAIL.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki and approved by the local Ethics Committee (N. 0078009/2021).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hasan, Z. Biological Cybernetics Optimized Movement Trajectories and Joint Stiffness in Unperturbed, Inertially Loaded Movements; 1986; Vol. 53; [CrossRef]
- Latash, M.L. Muscle Coactivation: Definitions, Mechanisms, and Functions. J Neurophysiol 2018, 120, 88–104. [Google Scholar] [CrossRef] [PubMed]
- Le, P.; Best, T.M.; Khan, S.N.; Mendel, E.; Marras, W.S. A Review of Methods to Assess Coactivation in the Spine. Journal of Electromyography and Kinesiology 2017, 32, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Rosa, M.C.N.; Marques, A.; Demain, S.; Metcalf, C.D.; Rodrigues, J. Methodologies to Assess Muscle Co-Contraction during Gait in People with Neurological Impairment – A Systematic Literature Review. Journal of Electromyography and Kinesiology 2014, 24, 179–191. [Google Scholar] [CrossRef] [PubMed]
- Cappellini, G.; Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Motor Patterns in Human Walking and Running. J Neurophysiol 2006, 95, 3426–3437. [Google Scholar] [CrossRef] [PubMed]
- Heise, G.D.; Morgan, D.W.; Hough, H.; Craib, M. Relationships between Running Economy and Temporal EMG Characteristics of Bi-Articular Leg Muscles. Int J Sports Med 1996, 17, 128–133. [Google Scholar] [CrossRef] [PubMed]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five Basic Muscle Activation Patterns Account for Muscle Activity during Human Locomotion. J Physiol 2004, 556, 267–282. [Google Scholar] [CrossRef] [PubMed]
- Kellis, E.; Zafeiridis, A.; Amiridis, L.G. Muscle Coactivation Before and After the Impact Phase of Running Following Isokinetic Fatigue. J Athl Train 2011, 46, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Moore, I.S.; Jones, A.M.; Dixon, S.J. Relationship between Metabolic Cost and Muscular Coactivation across Running Speeds. J Sci Med Sport 2014, 17, 671–676. [Google Scholar] [CrossRef]
- Shik, M.L.; Severin, F. V.; Orlovsky, G.N. Control of Walking and Running by Means of Electrical Stimulation of the Mesencephalon. Electroencephalogr Clin Neurophysiol 1969, 26, 549. [Google Scholar] [PubMed]
- Blickhan, R. The Spring-Mass Model for Running and Hopping. J Biomech 1989, 22, 1217–1227. [Google Scholar] [CrossRef]
- McMahon, T.A.; Cheng, G.C. The Mechanics of Running: How Does Stiffness Couple with Speed? J Biomech 1990, 23, 65–78. [Google Scholar] [CrossRef]
- Sharbafi, M.A.; Seyfarth, A. FMCH: A New Model for Human-like Postural Control in Walking. 2015. [Google Scholar] [CrossRef]
- Alexander, R.M. Energy-Saving Mechanisms in Walking and Running. Journal of Experimental Biology 1991, 160, 55–69. [Google Scholar] [CrossRef] [PubMed]
- Cavagna, G.A.; Thys, H.; Zamboni, A. The Sources of External Work in Level Walking and Running. J Physiol 1976, 262, 639–657. [Google Scholar] [CrossRef] [PubMed]
- Farley, C.T.; Glasheen, J.; McMahon, T.A. Running Springs: Speed and Animal Size. Journal of Experimental Biology 1993, 185, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Ker, R.F. The Design of Soft Collagenous Load-Bearing Tissues. Journal of Experimental Biology 1999, 202, 3315–3324. [Google Scholar] [CrossRef] [PubMed]
- Hreljac, A.; Imamura, R.T.; Escamilla, R.F.; Edwards, W.B. When Does A Gait Transition Occur During Human Locomotion? J Sports Sci Med 2007, 6, 36. [Google Scholar]
- Rotstein, A.; Berginsky, T.; Meckel, Y. Preferred Transition Speed between Walking and Running: Effects of Training Status. Med. Sci. Sports Exerc 2005, 37, 1864–1870. [Google Scholar] [CrossRef] [PubMed]
- Segers, V.; Aerts, P.; Lenoir, M.; De Clercq, D. Spatiotemporal Characteristics of the Walk-to-Run and Run-to-Walk Transition When Gradually Changing Speed. Gait Posture 2006, 24, 247–254. [Google Scholar] [CrossRef]
- Segers, V.; Aerts, P.; Lenoir, M.; De Clerq, D. Dynamics of the Body Centre of Mass during Actual Acceleration across Transition Speed. Journal of Experimental Biology 2007, 210, 578–585. [Google Scholar] [CrossRef]
- Hof, A.; Gazendam, M. Averaged EMG Profiles in Running Compared to Walking. Gait Posture 2006, 24, S77–S78. [Google Scholar] [CrossRef]
- Howard, R.; Conway, R.; Biomechanics, A.H.-S. ; 2018, undefined Muscle Activity in Sprinting: A Review. 2018; 17. [Google Scholar] [CrossRef]
- Zavorsky, G.S.; Montgomery, D.L.; Pearsall, D.J. Effect of Intense Interval Workouts on Running Economy Using Three Recovery Durations. Eur J Appl Physiol Occup Physiol 1998, 77, 224–230. [Google Scholar] [CrossRef] [PubMed]
- Peterson, D.S.; Martin, P.E. Effects of Age and Walking Speed on Coactivation and Cost of Walking in Healthy Adults. Gait Posture 2010, 31, 355–359. [Google Scholar] [CrossRef]
- Prilutsky, B.I.; Gregor, R.J. Swing- and Support-Related Muscle Actions Differentially Trigger Human Walk–Run and Run–Walk Transitions. Journal of Experimental Biology 2001, 204, 2277–2287. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A.; Yack, H.J. EMG Profiles during Normal Human Walking: Stride-to-Stride and Inter-Subject Variability. Electroencephalogr Clin Neurophysiol 1987, 67, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, D.E.; Raichlen, D.A.; Pontzer, H.; Bramble, D.M.; Cutright-Smith, E. The Human Gluteus Maximus and Its Role in Running. Journal of Experimental Biology 2006, 209, 2143–2155. [Google Scholar] [CrossRef] [PubMed]
- Heise, G.; Shinohara, M.; Binks, L. Biarticular Leg Muscles and Links to Running Economy. Int J Sports Med 2008, 29, 688–691. [Google Scholar] [CrossRef]
- Ranavolo, A.; Mari, S.; Conte, C.; Serrao, M.; Silvetti, A.; Iavicoli, S.; Draicchio, F. A New Muscle Co-Activation Index for Biomechanical Load Evaluation in Work Activities. 2015, 58, 966-979. [CrossRef]
- Varrecchia, T.; Rinaldi, M.; Serrao, M.; Draicchio, F.; Conte, C.; Conforto, S.; Schmid, M.; Ranavolo, A. Global Lower Limb Muscle Coactivation during Walking at Different Speeds: Relationship between Spatio-Temporal, Kinematic, Kinetic, and Energetic Parameters. Journal of Electromyography and Kinesiology 2018, 43, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Ivanenko, Y.P.; Cappellini, G.; Dominici, N.; Poppele, R.E.; Lacquaniti, F. Modular Control of Limb Movements during Human Locomotion. Journal of Neuroscience 2007, 27, 11149–11161. [Google Scholar] [CrossRef]
- Barbero, M.; Merletti, R.; Rainoldi, A. Atlas of Muscle Innervation Zones: Understanding Surface Electromyography and Its Applications. 2012. [CrossRef]
- Benedetti, M.G.; Beghi, E.; De Tanti, A.; Cappozzo, A.; Basaglia, N.; Cutti, A.G.; Cereatti, A.; Stagni, R.; Verdini, F.; Manca, M.; et al. SIAMOC Position Paper on Gait Analysis in Clinical Practice: General Requirements, Methods and Appropriateness. Results of an Italian Consensus Conference. Gait Posture 2017, 58, 252–260. [Google Scholar] [CrossRef] [PubMed]
- Merletti, R.; Cerone, G.L. Tutorial. Surface EMG Detection, Conditioning and Pre-Processing: Best Practices. 2020; 54. [Google Scholar] [CrossRef]
- Merletti, R.; Muceli, S. Tutorial. Surface EMG Detection in Space and Time: Best Practices. 2019; 49. [Google Scholar] [CrossRef]
- Fiori, L.; Ranavolo, A.; Varrecchia, T.; Tatarelli, A.; Conte, C.; Draicchio, F.; Castiglia, S.F.; Coppola, G.; Casali, C.; Pierelli, F.; et al. Impairment of Global Lower Limb Muscle Coactivation During Walking in Cerebellar Ataxias. Cerebellum 2020, 19, 583–596. [Google Scholar] [CrossRef]
- Serrao, M.; Rinaldi, M.; Ranavolo, A.; Lacquaniti, F.; Martino, G.; Leonardi, L.; Conte, C.; Varrecchia, T.; Draicchio, F.; Coppola, G.; et al. Gait Patterns in Patients with Hereditary Spastic Paraparesis. PLoS One 2016, 11, e0164623. [Google Scholar] [CrossRef]
- Tatarelli, A.; Serrao, M.; Varrecchia, T.; Fiori, L.; Draicchio, F.; Silvetti, A.; Conforto, S.; Marchis De, C.; Ranavolo, A. Global Muscle Coactivation of the Sound Limb in Gait of People with Transfemoral and Transtibial Amputation. Sensors 2020, Vol. 20, Page 2543 2020, 20, 2543. [Google Scholar] [CrossRef] [PubMed]
- Butler, H.L.; Newell, R.; Hubley-Kozey, C.L.; Kozey, J.W. The Interpretation of Abdominal Wall Muscle Recruitment Strategies Change When the Electrocardiogram (ECG) Is Removed from the Electromyogram (EMG). Journal of Electromyography and Kinesiology 2009, 19, e102–e113. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.D.M.; Callaghan, J.P. Elimination of Electrocardiogram Contamination from Electromyogram Signals: An Evaluation of Currently Used Removal Techniques. Journal of Electromyography and Kinesiology 2006, 16, 175–187. [Google Scholar] [CrossRef]
- Winter, D. Biomechanics and Motor Control of Human Movement. 2009.
- Rinaldi, M.; D’Anna, C.; Schmid, M.; Conforto, S. Assessing the Influence of SNR and Pre-Processing Filter Bandwidth on the Extraction of Different Muscle Co-Activation Indexes from Surface EMG Data. Journal of Electromyography and Kinesiology 2018, 43, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Dewolf, A.H.; Sylos-Labini, F.; Cappellini, G.; Zhvansky, D.; Willems, P.A.; Ivanenko, Y.; Lacquaniti, F. Neuromuscular Age-Related Adjustment of Gait When Moving Upwards and Downwards. Front Hum Neurosci 2021, 15, 621. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Dominici, N.; Lacquaniti, F. Development of Independent Walking in Toddlers. Exerc Sport Sci Rev 2007, 35, 67–73. [Google Scholar] [CrossRef] [PubMed]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Spinal Cord Maps of Spatiotemporal Alpha-Motoneuron Activation in Humans Walking at Different Speeds. J Neurophysiol 2006, 95, 602–618. [Google Scholar] [CrossRef] [PubMed]
- Kendall, F.; McCreary, E.; Provance, P.; Rodgers, M. Muscles: Testing and Function with Posture and Pain. 2005.
- NILSSON, J.; THORSTENSSON, A.; HALBERTSMA, J. Changes in Leg Movements and Muscle Activity with Speed of Locomotion and Mode of Progression in Humans. Acta Physiol Scand 1985, 123, 457–475. [Google Scholar] [CrossRef] [PubMed]
- Prilutsky, B.I. Coordination of Two- and One-Joint Muscles: Functional Consequences and Implications for Motor Control. Motor Control 2000, 4, 1–44. [Google Scholar] [CrossRef]
- Martino, G.; Ivanenko, Y.P.; Serrao, M.; Ranavolo, A.; d’Avella, A.; Draicchio, F.; Conte, C.; Casali, C.; Lacquaniti, F. Locomotor Patterns in Cerebellar Ataxia. J Neurophysiol 2014, 112, 2810–2821. [Google Scholar] [CrossRef] [PubMed]
- Kadaba, M.P.; Ramakrishnan, H.K.; Wootten, M.E.; Gainey, J.; Gorton, G.; Cochran, G.V.B. Repeatability of Kinematic, Kinetic, and Electromyographic Data in Normal Adult Gait. Journal of Orthopaedic Research 1989, 7, 849–860. [Google Scholar] [CrossRef]
- Ranavolo, A.; Don, R.; Draicchio, F.; Bartolo, M.; Serrao, M.; Padua, L.; Cipolla, G.; Pierelli, F.; Iavicoli, S.; Sandrini, G. Modelling the Spine as a Deformable Body: Feasibility of Reconstruction Using an Optoelectronic System. Appl Ergon 2013, 44, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Varrecchia, T.; Serrao, M.; Rinaldi, M.; Ranavolo, A.; Conforto, S.; De Marchis, C.; Simonetti, A.; Poni, I.; Castellano, S.; Silvetti, A.; et al. Common and Specific Gait Patterns in People with Varying Anatomical Levels of Lower Limb Amputation and Different Prosthetic Components. Hum Mov Sci 2019, 66, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Wren, T.A.L.; Patrick Do, K.; Rethlefsen, S.A.; Healy, B. Cross-Correlation as a Method for Comparing Dynamic Electromyography Signals during Gait. J Biomech 2006, 39, 2714–2718. [Google Scholar] [CrossRef] [PubMed]
- Ranavolo, A.; Conte, C.; Iavicoli, S.; Serrao, M.; Silvetti, A.; Sandrini, G.; Pierelli, F.; Draicchio, F. Walking Strategies of Visually Impaired People on Trapezoidal- and Sinusoidal-Section Tactile Groundsurface Indicators, 2011, 54, 246-256. [CrossRef]
- Rinaldi, M.; Ranavolo, A.; Conforto, S.; Martino, G.; Draicchio, F.; Conte, C.; Varrecchia, T.; Bini, F.; Casali, C.; Pierelli, F.; et al. Increased Lower Limb Muscle Coactivation Reduces Gait Performance and Increases Metabolic Cost in Patients with Hereditary Spastic Paraparesis. Clinical Biomechanics 2017, 48, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Whittle, M.W. Three-Dimensional Motion of the Center of Gravity of the Body during Walking. Hum Mov Sci 1997, 16, 347–355. [Google Scholar] [CrossRef]
- Serrao, M.; Ranavolo, A.; Casali, C. Neurophysiology of Gait. Handb Clin Neurol 2018, 154, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Varrecchia, T.; Rinaldi, M.; Serrao, M.; Draicchio, F.; Conte, C.; Conforto, S.; Schmid, M.; Ranavolo, A. Global Lower Limb Muscle Coactivation during Walking at Different Speeds: Relationship between Spatio-Temporal, Kinematic, Kinetic, and Energetic Parameters. Journal of Electromyography and Kinesiology 2018, 43, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Watson, G.S.; Williams, E.J. On the Construction of Significance Tests on the Circle and the Sphere. Biometrika 1956, 43, 344. [Google Scholar] [CrossRef]
- Harrison, D.; Kanji, G.K. The Development of Analysis of Variance for Circular Data 2006, 15, 197-223. [CrossRef]
- Schober, P.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth Analg 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. Effects of Walking Speed on Gait Biomechanics in Healthy Participants: A Systematic Review and Meta-Analysis. Syst Rev 2019, 8, 1–11. [Google Scholar] [CrossRef]
- Tesio, L.; Rota, V. The Motion of Body Center of Mass During Walking: A Review Oriented to Clinical Applications. Front Neurol 2019, 10, 999. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Wang, D.; Zhang, Q.; Shi, Y.; Ding, H.; Li, F. Relationship Between Isokinetic Lower-Limb Joint Strength, Isometric Time Force Characteristics, and Leg-Spring Stiffness in Recreational Runners. Front Physiol 2022, 12, 2421. [Google Scholar] [CrossRef]
- Struzik, A.; Karamanidis, K.; Lorimer, A.; Keogh, J.W.L.; Gajewski, J. Application of Leg, Vertical, and Joint Stiffness in Running Performance: A Literature Overview. Appl Bionics Biomech 2021. [Google Scholar] [CrossRef] [PubMed]
- Dzeladini, F.; van den Kieboom, J.; Ijspeert, A. The Contribution of a Central Pattern Generator in a Reflex-Based Neuromuscular Model. Front Hum Neurosci 2014, 8, 371. [Google Scholar] [CrossRef]
- Feldman, A.G.; Levin, M.F.; Garofolini, A.; Piscitelli, D.; Zhang, L. Central Pattern Generator and Human Locomotion in the Context of Referent Control of Motor Actions. Clinical Neurophysiology 2021, 132, 2870–2889. [Google Scholar] [CrossRef] [PubMed]
- Minassian, K.; Hofstoetter, U.S.; Dzeladini, F.; Guertin, P.A.; Ijspeert, A. The Human Central Pattern Generator for Locomotion: Does It Exist and Contribute to Walking? Neuroscientist 2017, 23, 649–663. [Google Scholar] [CrossRef]
- Møller, M.; Sinkjaer, T.; Duysens, J. Contributions to the Understanding of Gait Control. 2014.
- Dewolf, A.H.; Ivanenko, Y.P.; Zelik, K.E.; Lacquaniti, F.; Willems, P.A. Differential Activation of Lumbar and Sacral Motor Pools during Walking at Different Speeds and Slopes. J Neurophysiol 2019, 122, 872–887. [Google Scholar] [CrossRef] [PubMed]
- Martino, G.; Ivanenko, Y.P.; d’Avella, A.; Serrao, M.; Ranavolo, A.; Draicchio, F.; Cappellini, G.; Casali, C.; Lacquaniti, F. Neuromuscular Adjustments of Gait Associated with Unstable Conditions. J Neurophysiol 2015, 114, 2867–2882. [Google Scholar] [CrossRef] [PubMed]
- Tam, N.; Tucker, R.; Santos-Concejero, J.; Prins, D.; Lamberts, R.P. Running Economy: Neuromuscular and Joint-Stiffness Contributions in Trained Runners. Int J Sports Physiol Perform 2019, 14, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Nassis, G.P.; Chen, S.; Shi, Y.; Li, F. Not Lower-Limb Joint Strength and Stiffness but Vertical Stiffness and Isometric Force-Time Characteristics Correlate With Running Economy in Recreational Male Runners. Front Physiol 2022, 13, 1321. [Google Scholar] [CrossRef]
- Fallahtafti, F.; Gonabadi, A.M.; Samson, K.; Yentes, J.M. Margin of Stability May Be Larger and Less Variable during Treadmill Walking Versus Overground. Biomechanics 2021, Vol. 2021; 1. [Google Scholar] [CrossRef]
Figure 1.
Three-dimensional global map of lower limb muscle coactivation from slow walking to running. Each curve represented the average TMCfglob curves (black line) of 19 runners. The TOe (black dots) and FWHMglob (grey and red area for walk and run velocity respectively).
Figure 1.
Three-dimensional global map of lower limb muscle coactivation from slow walking to running. Each curve represented the average TMCfglob curves (black line) of 19 runners. The TOe (black dots) and FWHMglob (grey and red area for walk and run velocity respectively).
Figure 2.
The average (squares) and standard deviation (black bars) of 19 runners' (dot) global coactivation parameters ranging from slow walking (gray) to running (red) are reported: (a) average of the global coactivation level [% coactivation] (CIglob,), (b) maximum value of the global coactivation (Maxglob), (c) the full width at half maximum of global coactivation (FWHMglob), (d) coefficient of multiple correlation within runners of global coactivation (CMC Wtglob). Triangles turned (d) represent the coefficient of multiple correlation of global coactivation between runners (CMC Btglob).
Figure 2.
The average (squares) and standard deviation (black bars) of 19 runners' (dot) global coactivation parameters ranging from slow walking (gray) to running (red) are reported: (a) average of the global coactivation level [% coactivation] (CIglob,), (b) maximum value of the global coactivation (Maxglob), (c) the full width at half maximum of global coactivation (FWHMglob), (d) coefficient of multiple correlation within runners of global coactivation (CMC Wtglob). Triangles turned (d) represent the coefficient of multiple correlation of global coactivation between runners (CMC Btglob).
Figure 3.
Center of activity (CoA) of the lower limb muscle coactivation curves from slow walking to running: each dot in the circumference represents a single subject’s mean CoA value, whereas the mean value and SD of the CoA of all subjects are represented by the solid line and the width of the circular sector, respectively.
Figure 3.
Center of activity (CoA) of the lower limb muscle coactivation curves from slow walking to running: each dot in the circumference represents a single subject’s mean CoA value, whereas the mean value and SD of the CoA of all subjects are represented by the solid line and the width of the circular sector, respectively.
Figure 4.
Three-dimensional extensor (a) and flexor (b) maps of the lower limb muscle coactivation from slow walking to running. Each curve (black line) represents the average coactivation of extensor (TMCfext (a)) and flexor (TMCfflex (b)) muscles of 19 runners, black dots ((a) and (b)) represent the Toe-off event, grey and red area represent the full width at half maximum of extensor (a) and flexor (b) muscle coactivation for walk and run velocity, respectively.
Figure 4.
Three-dimensional extensor (a) and flexor (b) maps of the lower limb muscle coactivation from slow walking to running. Each curve (black line) represents the average coactivation of extensor (TMCfext (a)) and flexor (TMCfflex (b)) muscles of 19 runners, black dots ((a) and (b)) represent the Toe-off event, grey and red area represent the full width at half maximum of extensor (a) and flexor (b) muscle coactivation for walk and run velocity, respectively.
Figure 5.
Three-dimensional rostro-caudal (from L3 to S2 spinal level) maps of the lower limb muscle coactivation from slow walking to running: (a) L3 coactivation (TMCfL3), (b) L4 coactivation (TMCfL4), (c) L5 coactivation (TMCfL5), (d) S1 coactivation (TMCfS1), (e) S2 coactivation (TMCfS2). Each curve represented the average TMCfL3 (a), TMCfL4 (b), TMCfL5 (c), TMCfS1 (d), TMCfS2 (e) curves (black line) of 19 runners. The black dots represent the Toe-off event, and grey and red area represent the full width at half maximum of L3 (a), L4 (b), L5 (c), S1 (d) and S2 (2) coactivations for walk and run velocity respectively.
Figure 5.
Three-dimensional rostro-caudal (from L3 to S2 spinal level) maps of the lower limb muscle coactivation from slow walking to running: (a) L3 coactivation (TMCfL3), (b) L4 coactivation (TMCfL4), (c) L5 coactivation (TMCfL5), (d) S1 coactivation (TMCfS1), (e) S2 coactivation (TMCfS2). Each curve represented the average TMCfL3 (a), TMCfL4 (b), TMCfL5 (c), TMCfS1 (d), TMCfS2 (e) curves (black line) of 19 runners. The black dots represent the Toe-off event, and grey and red area represent the full width at half maximum of L3 (a), L4 (b), L5 (c), S1 (d) and S2 (2) coactivations for walk and run velocity respectively.
Figure 6.
The three-dimensional CoM maps from slow walking to running in the vertical (CoMy, (a)) and medio-lateral (CoMz, (b)) directions. Each curve represented the average CoMy and CoMz (black line) curves of 19 runners, as well as the Toe-off event (black dots). The average (squares) and standard deviation (black bars) of 19 runners' (dot) CoMy (c) and CoMz (d) displacements, ranging from slow walking (gray) to running (red).
Figure 6.
The three-dimensional CoM maps from slow walking to running in the vertical (CoMy, (a)) and medio-lateral (CoMz, (b)) directions. Each curve represented the average CoMy and CoMz (black line) curves of 19 runners, as well as the Toe-off event (black dots). The average (squares) and standard deviation (black bars) of 19 runners' (dot) CoMy (c) and CoMz (d) displacements, ranging from slow walking (gray) to running (red).
Figure 7.
The average (squares) and standard deviation (black bars) of 19 runners' (dot) spatiotemporal parameters: stride length (a), foot lift (b), stride frequency (c), Toe-off event (TOe, (d)), ranging from slow walking (gray) to running (red).
Figure 7.
The average (squares) and standard deviation (black bars) of 19 runners' (dot) spatiotemporal parameters: stride length (a), foot lift (b), stride frequency (c), Toe-off event (TOe, (d)), ranging from slow walking (gray) to running (red).
Table 1.
Each dot in the table indicates muscles included in the time-varying coactivation (TMCf) function for each muscle coactivation investigated: global, extensor, flexor, and rostro-caudal organization. Smallest dots indicate a halved weight (amplitude of muscle activity multiplied by 0.5) for that specific muscle in the TMCf function.
Table 1.
Each dot in the table indicates muscles included in the time-varying coactivation (TMCf) function for each muscle coactivation investigated: global, extensor, flexor, and rostro-caudal organization. Smallest dots indicate a halved weight (amplitude of muscle activity multiplied by 0.5) for that specific muscle in the TMCf function.
| |
|
Maps |
| |
Global |
Extensor |
Flexor |
L3 |
L4 |
L5 |
S1 |
S2 |
| Muscles |
GM |
● |
● |
|
|
● |
● |
● |
|
| RF |
● |
|
● |
● |
● |
|
|
|
| VL |
● |
● |
|
|
● |
|
|
|
| VM |
● |
● |
|
● |
● |
|
|
|
| TFL |
● |
|
● |
● |
● |
● |
● |
|
| ST |
● |
● |
|
|
● |
● |
● |
● |
| BF |
● |
● |
|
|
|
● |
● |
● |
| TA |
● |
|
● |
|
● |
● |
● |
|
| GasM |
● |
● |
|
|
|
|
● |
● |
| GasL |
● |
● |
|
|
|
|
● |
● |
| S |
● |
|
|
|
|
● |
● |
● |
| P |
● |
|
|
|
● |
● |
● |
|
Table 2.
Main effect and post-hoc comparisons at the transition between walking (6.8 km/h) and running (7.3 km/h), with corresponding values, for each muscle coactivation studied: global, extensor, flexor, and rostro-caudal organization, as well as each parameter.
Table 2.
Main effect and post-hoc comparisons at the transition between walking (6.8 km/h) and running (7.3 km/h), with corresponding values, for each muscle coactivation studied: global, extensor, flexor, and rostro-caudal organization, as well as each parameter.
| Parameters |
Main effect Velocity |
Post-hoc velocity transition |
| |
F(df) |
p |
Value at 6.8 Km/h
(mean ± std) |
Value at 7.3 Km/h
(mean ± std) |
p value |
|
CIglob
|
F(1,17) = 641.04 |
<0.001 |
3.97±0.62 |
6.05±0.69 |
<0.001 |
|
CIext
|
F(1,17) =388.04 |
<0.001 |
3.82±0.83 |
6.53±0.99 |
<0.001 |
|
CIflex
|
F(1,17) =240.06 |
<0.001 |
9.03±1.72 |
10.3±2.4 |
/ |
|
CIL3
|
F(1,17) =137.28 |
<0.001 |
6.21±2.06 |
8.09±2.28 |
/ |
|
CIL4
|
F(1,17) =409.77 |
<0.001 |
3.85±0.71 |
5.22±0.72 |
<0.001 |
|
CIL5
|
F(1,17) = 351.04 |
<0.001 |
4.22±0.72 |
5.87±0.78 |
<0.001 |
|
CIS1
|
F(1,17) =461.13 |
<0.001 |
5.14±0.70 |
6.88±0.91 |
<0.001 |
|
CIS2
|
F(1,17) =464.98 |
<0.001 |
5.83±1.26 |
9.24±1.5 |
<0.001 |
|
Maxglob
|
F(1,17) =321.71 |
<0.001 |
11.08±1.48 |
23.30±3.54 |
<0.001 |
|
Maxext
|
F(1,17) =152.36 |
<0.001 |
12.32±2.77 |
24.42±5.48 |
<0.001 |
|
Maxflex
|
F(1,17) =104.01 |
<0.001 |
30.16±8.91 |
26.51±7.28 |
/ |
|
MaxL3
|
F(1,17) =76.83 |
<0.001 |
31.5±14.27 |
40.2±14.41 |
/ |
|
MaxL4
|
F(1,17) =156.75 |
<0.001 |
11.93±3.75 |
14.47±4.13 |
/ |
|
MaxL5
|
F(1,17) =93.91 |
<0.001 |
11.7±2.33 |
15.18±3.5 |
/ |
|
MaxS1
|
F(1,17) =192.85 |
<0.001 |
16±3.07 |
24.64±4.39 |
<0.001 |
|
MaxS2
|
F(1,17) =189.34 |
<0.001 |
18.91±4.04 |
34.19±6.3 |
<0.001 |
|
FWHMglob
|
F(1,17) =29,31 |
<0.001 |
26.62±6.08 |
18.17±5.14 |
0.01 |
|
FWHMext
|
F(1,17) =9.31 |
<0.001 |
21.15±6.3 |
20.07±6.7 |
/ |
|
FWHMflex
|
F(1,17) =11.13 |
<0.001 |
20.74±6.66 |
31.14±8.65 |
/ |
|
FWHML3
|
F(1,17) =11.37 |
<0.001 |
14.45±3.81 |
15.69±3.39 |
/ |
|
FWHML4
|
F(1,17) =20.28 |
<0.001 |
16.86±4.58 |
18.32±4.6 |
/ |
|
FWHML5
|
F(1,17) =8.22 |
<0.001 |
25.45±7 |
29.33±7.67 |
/ |
|
FWHMS1
|
F(1,17) =13.48 |
<0.001 |
20.68±6.17 |
20.53±5.81 |
/ |
|
FWHMS2
|
F(1,17) =4.06 |
<0.001 |
20.34±7.9 |
20.08±5.65 |
/ |
|
CoAglob
|
F(1,17) =24.96 |
<0.001 |
16.74±5.38 |
14.05±2.12 |
<0.01 |
|
CoAext
|
F(1,17) =22.95 |
<0.001 |
9.1±4.09 |
12.76±2.88 |
<0.001 |
|
CoAflex
|
F(1,17) =8.74 |
<0.001 |
97.18±11.8 |
15.63±13.91 |
<0.001 |
|
CoAL3
|
F(4,17) = 58.01 |
<0.001 |
7.31±2.58 |
13.2±2.28 |
<0.001 |
|
CoAL4
|
5.96±2.93 |
11.63±2.31 |
<0.001 |
|
CoAL5
|
5.72±5.31 |
8.89±3.82 |
<0.01 |
|
CoAS1
|
30.35±4.3 |
15.2±2.17 |
<0.001 |
|
CoAS2
|
28.01±5.1 |
15.88±2.98 |
<0.001 |
CMC_Wtglob
(CMC_Btglob)
|
F(1,17) =54.38 |
<0.001 |
0.95±0.01
(0.86) |
0.97±0.01
(0.88) |
0.02 |
CMC_Wtext
(CMC_Btext)
|
F(1,17) =44.98 |
<0.001 |
0.95±0.02
(0.86) |
0.96±0.01
(0.89) |
/ |
CMC_Wtflex
(CMC_Btflex)
|
F(1,17) = 55.77 |
<0.001 |
0.93±0.04
(0.79) |
0.92±0.03
(0.75) |
/ |
CMC_WtL3
(CMC_BtL3)
|
F(1,17) =24.31 |
<0.001 |
0.97±0.02
(0.81) |
0.96±0.02
(0.90) |
/ |
CMC_WtL4
(CMC_BtL4)
|
F(1,17) =42.25 |
<0.001 |
0.96±0.01
(0.87) |
0.96±0.01
(0.92) |
/ |
CMC_WtL5
(CMC_Btglob)
|
F(1,17) =38.82 |
<0.001 |
0.93±0.02
(0.84) |
0.92±0.03
(0.83) |
/ |
CMC_WtS1
(CMC_BtS1)
|
F(1,17) =49.56 |
<0.001 |
0.94±0.01
(0.86) |
0.96±0.01
(0.91) |
0.04 |
CMC_WtS2
(CMC_BtS2)
|
F(1,17) =48.76 |
<0.001 |
0.94±0.02
(0.85) |
0.95±0.02
(0.89) |
0.02 |
|
CoMy
|
F(1,17) = 426.2 |
<0.001 |
6.60±0.83 |
10.99±1.92 |
<0.001 |
|
CoMz
|
F(1,17) =120.29 |
<0.001 |
4.57±1.23 |
2.78±0.88 |
<0.001 |
|
TOe
|
F(1,17) =940.64 |
<0.001 |
62.57±0.70 |
57.91±1.06 |
<0.001 |
|
stride length
|
F(1,17) =253.03 |
<0.001 |
173.78±7.25 |
131±9.24 |
<0.001 |
|
stride frequency
|
F(1,17) =714.22 |
<0.001 |
1.13±0.05 |
1.31±0.07 |
<0.001 |
|
foot lift
|
F(1,17) = 108.03 |
<0.001 |
16.47±1.57 |
21.63±3.69 |
<0.01 |
Table 3.
Main effect and post-hoc comparisons of each spinal level (from L3 to S2) at walking (6.8 km/h) and running (7.3 km/h), with corresponding values for the lower limb muscle coactivation maps.
Table 3.
Main effect and post-hoc comparisons of each spinal level (from L3 to S2) at walking (6.8 km/h) and running (7.3 km/h), with corresponding values for the lower limb muscle coactivation maps.
| Main effect Level |
Velocity |
Post-hoc Level |
| F(df) |
p |
|
|
CoAL3
|
CoAL4
|
CoAL5
|
CoAS1
|
CoAS2
|
|
F(4,17) = 511.50
|
< 0.001 |
6.8 Km/h |
CoAL3
|
/ |
|
|
|
|
| CoAL4
|
<0.01 |
/ |
|
|
|
| CoAL5
|
0.01 |
0.04 |
/ |
|
|
| CoAS1
|
< 0.001 |
< 0.001 |
< 0.001 |
/ |
|
| CoAS2
|
< 0.001 |
< 0.001 |
< 0.001 |
<0.01 |
/ |
| 7.3 Km/h |
CoAL3
|
/ |
|
|
|
|
| CoAL4
|
<0.01 |
/ |
|
|
|
| CoAL5
|
< 0.001 |
< 0.001 |
/ |
|
|
| CoAS1
|
<0.01 |
< 0.001 |
< 0.001 |
/ |
|
| CoAS2
|
< 0.001 |
< 0.001 |
< 0.001 |
< 0.001 |
/ |
Table 4.
Statistical significance (and corresponding mean and standard deviation values) shape similarity between the global and the extensor coactivation map as well as global and flexor coactivation map. Main effect and post-hoc comparisons (and corresponding mean and standard deviation values) of shape similarity between the global and rostro-caudal (from L3 to S2 spinal level) coactivation maps.
Table 4.
Statistical significance (and corresponding mean and standard deviation values) shape similarity between the global and the extensor coactivation map as well as global and flexor coactivation map. Main effect and post-hoc comparisons (and corresponding mean and standard deviation values) of shape similarity between the global and rostro-caudal (from L3 to S2 spinal level) coactivation maps.
| |
Shape similarity
(mean ± std)
|
t-test p |
| RG-E |
0.97±0.02 |
< 0.001 |
| RG-F |
0.70±0.12 |
| |
|
Main effect shape similarity |
Post-hoc shape similarity |
| |
|
F(df) |
p |
|
RG-L3 |
RG-L4 |
RG-L5 |
RG-S1 |
RG-S2 |
| RG-L3 |
0.88±0.08 |
F(1,4) = 11.23 |
< 0.001 |
RG-L3 |
/ |
|
|
|
|
| RG-L4 |
0.93±0.03 |
RG-L4 |
0.02 |
/ |
|
|
|
| RG-L5 |
0.89±0.04 |
RG-L5 |
/ |
/ |
/ |
|
|
| RG-S1 |
0.96±0.02 |
RG-S1 |
< 0.001 |
/ |
< 0.01 |
/ |
|
| RG-S2 |
0.87±0.06 |
RG-S2 |
/ |
< 0.01 |
/ |
< 0.001 |
/ |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).