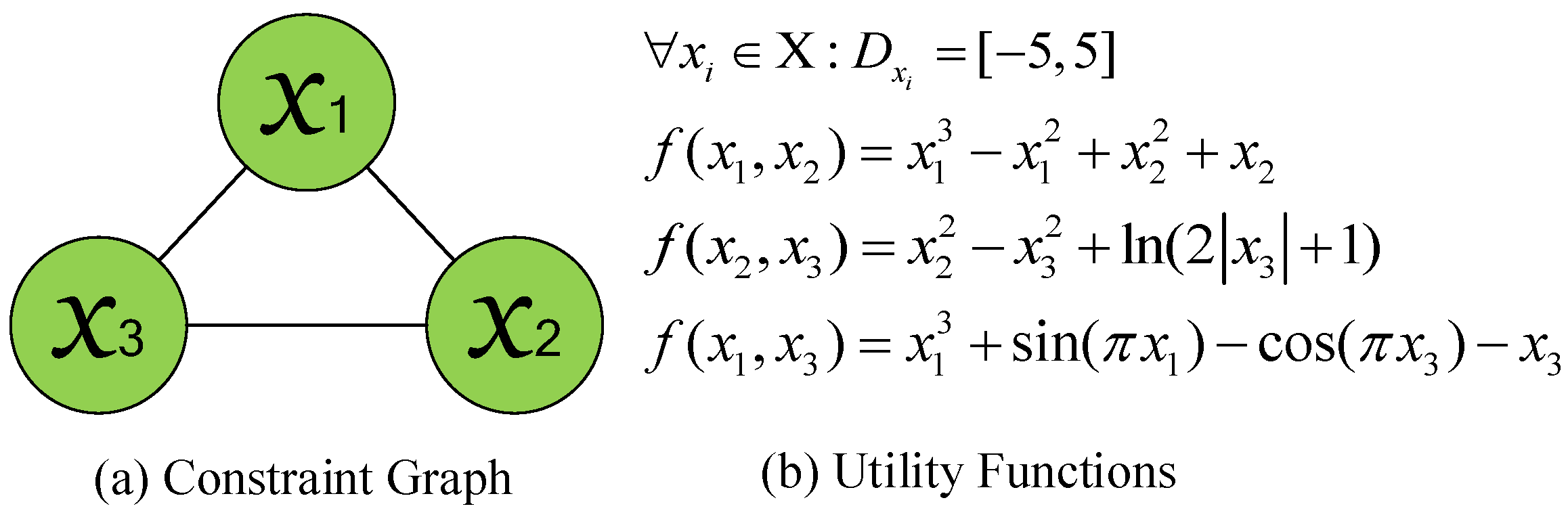A Class of Local Search Based Anytime Algorithms for Continuous Distributed Constraint Optimization Problems

Preprint

Article

A Class of Local Search Based Anytime Algorithms for Continuous Distributed Constraint Optimization Problems

Altmetrics

Downloads

109

Views

Comments

Xin Liao^*,

Khoi Hoang

Xin Liao^*,

Khoi Hoang

This version is not peer-reviewed

Submitted:

15 January 2024

Posted:

16 January 2024

You are already at the latest version

Alerts

Abstract

Continuous Distributed Constraint Optimization Problem (C-DCOPs) are a powerful framework to model problems with continuous variables in multi-agent systems. Previous works about C-DCOP algorithms mainly use pseudo-trees to guarantee the anytime property or are without anytime property guarantees. However, there is a risk of privacy leakage in the pseudo-tree due to utility passing between agents. Therefore, based on the basic constraint graph instead of the pseudo-tree, we (i) extend the Maximum Gain Message (MGM) algorithm by combining the local search strategy to solve C-DCOPs, named Continuous MGM (C-MGM), and it’s able to guarantee the monotonicity of the solution quality; (ii) propose a Parallel C-MGM (C-PMGM) algorithm to improve the solution quality through parallel random search; and (iii) introduce the differential search into C-PMGM to design a Parallel Differential Search C-MGM (C-PDSM) algorithm, which constructs a heuristic method to speed up convergence and improve solution quality. Compared to other anytime C-DCOP algorithms using pseudo-trees, the proposed three algorithms can exhibit better performance in avoiding privacy violations. We theoretically prove that the proposed algorithms are the anytime algorithms and empirically demonstrate that our algorithms outperform the state-of-the-art C-DCOP algorithms.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

The Distributed Constraint Optimization Problems (DCOPs) [1,2,3,4] are an efficient framework to solve the cooperative problems of multi-agent systems. In DCOPs, agents communicate directly or indirectly to coordinate their value assignments of variables to optimize the aggregate constraint utilities, where the variables are discrete and the constraint utilities are presented in tabular form. DCOPs have been successfully applied to model the problems in the real world like distributed meeting scheduling [5,6], sensor networks [7], multi-robot coordination [8,9], smart grid [10,11], and smart home [12,13]. Some improved methods such as [14,15,16,17] and some improvements of key metrics like privacy [18,19,20] have been proposed. In addition, there are some extensions of DCOPs like Asymmetric DCOPs [21,22,23,24] and Dynamic DCOPs [25,26,27].

Over the years, researchers have proposed several different types of algorithms to solve DCOPs, including exact search-based algorithms [28,29], exact inference-based algorithms [2,30], approximate search-based algorithms [31], approximate inference-based algorithms [7], and approximate sampling-based algorithms [32,33]. Although the DCOP algorithms have excellent performance for discrete problems, it is not satisfactory for solving continuous problems, such as target tracking sensor orientation. Therefore, Continuous DCOPs (C-DCOPs) [34] were proposed to model problems with continuous variables, and the constraint utilities are functional forms. Correspondingly, researchers proposed new C-DCOP algorithms to deal with the modification of the C-DCOP formulation, including Continuous Max-Sum (CMS) [34], Hybrid CMS (HCMS) [35], Bayesian Distributed Pseudo-tree Optimization Procedure (B-DPOP) [36], Particle Swarm Based Continuous DCOP (PCD) [37], Exact Continuous DPOP (EC-DPOP) [38] and extensions (Approximate Continuous DPOP (AC-DPOP), Clustered AC-DPOP (CAC-DPOP), and Continuous DSA (C-DSA)), Continuous Cooperative Constraint Approximation (C-CoCoA) [39], and Particle Swarm with Local Decision Based Continuous DCOP (PCD-LD) [40].

The CMS algorithm is a continuous extension of discrete Max-Sum (MS) algorithm, which approximates the utility functions as piece-wise linear functions to solve C-DCOPs. Similarly, HCMS improves the solution quality according to the non-linear optimization method based on the MS algorithm. Later, B-DPOP combines the Bayesian Optimization framework with DPOP to solve C-DCOPs. After that, Hoang et al. propose three extensions of the inference-based DPOP algorithm and one extension of search-based Distributed Stochastic Algorithm (DSA): EC-DPOP, AC-DPOP, CAC-DPOP, and C-DSA, where the first algorithm provides an exact approach to solve general C-DCOPs, and the second and third provide approximate methods. In addition, C-DSA extends DSA to the continuous domain. C-CoCoA is a semi-greedy non-iterative algorithm that can get a high-quality solution with less execution time and overhead.

Unfortunately, none of the above C-DCOP algorithms is an anytime algorithm. An anytime algorithm should have two characteristics:

(i)

The algorithm can be stopped at any time to output a solution, which means it is iterative;

(i i)

The algorithm guarantees the monotonicity of the solution quality over time. PCD introduces the Particle Swarm Optimization (PSO) algorithm to solve C-DCOPs, and PCD-LD combines local decisions with PCD to improve the solution quality. They are two iterative algorithms and collect all utilities by constructing a Breadth First Search (BFS) pseudo-tree to guarantee the monotonicity of the solution quality. Although PCD and PCD-LD are anytime algorithms, the utility passing in the pseudo-tree causes privacy violations [41].

In the wake of the above analysis, we extend Maximum Gain Message (MGM) [31] algorithm so that it’s able to solve C-DCOPs. Three main reasons prompt us to customize MGM for C-DCOPs as follows:

We consider that anytime property is an important problem concerned for the C-DCOP algorithm. Since communication may be halted arbitrarily, an algorithm without the anytime property risk being terminated at an unsatisfactory assignment combination. Therefore, an anytime algorithm guarantees lower bounds on performance in anytime environments when given acceptable starting conditions.
The MGM algorithm is an iterative, search-based algorithm that performs a distributed local search, and it can guarantee the monotonicity of the solution quality through local interactions. In other words, the MGM algorithm is an anytime algorithm.
Compared with the anytime algorithms using the BFS pseudo-tree, the MGM algorithm solves problems without any restriction on the graph structure. Specifically, MGM uses a basic constraint graph and local interactions to maintain the privacy of agents.

Therefore, we provide three MGM-based C-DCOP algorithms, namely Continuous MGM (C-MGM), Parallel C-MGM (C-PMGM), and Parallel Differential Search C-MGM (C-PDSM). Firstly, C-MGM is an approximation C-DCOP algorithm that is similar to MGM. In C-MGM, each agent compares the gain of its local utility with neighbors to strictly increase the aggregate utility. Then, C-PMGM extends C-MGM and generates a competing solution for each solution to solve C-DCOPs in parallel. Finally, C-PDSM is an improvement based on C-PMGM that uses differential search to update competing solutions. We empirically evaluate the performance of proposed algorithms on benchmark problems, and the results show that our algorithms outperform the state-of-the-art C-DCOP algorithms.

The remainder of this paper is organized as follows. The next section introduces the necessary background, including the DCOP and C-DCOP frameworks, and the standard MGM algorithm. The details of our algorithms are described in Section 3. Then, we present theoretical analysis in Section 4. Afterward, Section 5 reports the empirical evaluation of our algorithms against the state-of-the-art algorithms. Finally, we provide conclusions and future work in Section 6.

2. Background

In this section, we provide the definition of the DCOP framework. Then, we introduce the C-DCOP framework and provide an example of a C-DCOP. Finally, we describe the MGM algorithm, which is the basis of our proposed algorithms.

2.1. Distributed Constraint Optimization Problems

A Distributed Constraint Optimization Problem (DCOP) is a tuple

〈 A, X, D, F, α 〉

, where

$A = {a_{i}}_{i = 1}^{n}$ is a set of agents, an agent can control one or more variables.
$X = {x_{i}}_{i = 1}^{m}$ is a set of discrete variables, each variable is controlled by one of the agents.
$D = {D_{x}}_{x \in X}$ is a set of discrete domains and each variable $x \in X$ takes value from the set $D_{x}$ .
$F = {f_{i}}_{i = 1}^{l}$ is a set of utility functions and each utility function is defined over a set of variables: $f_{i} \in F : \prod_{x \in x^{f_{i}}} D_{x} \to R$ , where the $x^{f_{i}} \subseteq X$ is the scope of $f_{i}$ .
$α :$ is a mapping function that associates each variable to one agent. In this paper, we assume one agent controls only one variable.

In this paper, we assume that one agent only controls one variable, thus

n = m

and the terms "agent" and "variable" could be used interchangeably. In addition, we assume that all utility functions are binary functions between two variables, thus

f_{i j} \in F : D_{x_{i}} \times D_{x_{j}} \to R

and the

x^{f_{i j}} = {x_{i}, x_{j}}

A solution of a DCOP is an assignment combination

X^{*}

to all variables that are consistent with their respective domains. The goal of the solution is to minimize1 the aggregate utility as shown in Equation (1), where the aggregate utility is the sum of utilities across all the applicable utility functions.

\begin{matrix} X^{*} = \underset{d_{i} \in D_{x_{i}}, d_{j} \in D_{x_{j}}}{\arg \min} \sum_{f_{i j} \in F} f_{i j} (x_{i} = d_{i}, x_{j} = d_{j}) \end{matrix}

(1)

2.2. Continuous Distributed Constraint Optimization Problems

The Continuous DCOP (C-DCOP) framework extends the DCOP framework by modeling the variables as continuous variables. It is defined by a tuple

〈 A, X, D, F, α 〉

, where

A

F

, and

α

are the same as DCOP. The set of variables

X

and the set of domains

D

are defined as follows:

$X = {x_{i}}_{i = 1}^{m}$ is the set of continuous variables.
$D = {D_{x}}_{x \in X}$ is the set of continuous domains and each continuous variable takes any value from the domain $D_{x} = [L B_{x}, U B_{x}]$ , where $L B$ and $U B$ represent the lower and upper bounds of the domain, respectively.

The goal of a C-DCOP is the same as Equation (1), where the variables x and domain

D_{x}

are continuous. Figure 1 provides an example of a C-DCOP, where Figure 1(a) is a constraint graph with three variables controlled by the agents and three constraints. Figure 1(b) defines the utility functions corresponding to the constraints and gives the domain of variables.

2.3. Maximum Gain Message

The MGM algorithm is an anytime, local search algorithm for solving DCOPs. Its main idea is to guarantee the agent with maximum gain changes its variable through competition between neighboring agents. In this decision method, only one agent can change its value in each local, which can completely avoid the uncertainty of the result caused by the simultaneous assignment of neighboring agents. Therefore, the solution quality improves steadily with iterations.

The framework of MGM is presented in Algorithm 1. Firstly, each agent randomly selects a value and sends it to neighbors (Algorithm 1: Lines 2-3). After receiving these values from neighbors, the agent assumes that the neighbors’ values remain unchanged and chooses a new value that maximizes the local gain. Then, the agent sends the local gain to neighbors and simultaneously receives gains from neighbors. If the agent with the maximum gain in the current local, it’s assigned the new value, otherwise it remains the chosen random value. Finally, the agent sends the updated value to neighbors and executes the loop (Algorithm 1: Lines 5-12) until the condition is met.

Algorithm 1: Maximum Gain Message Algorithm (MGM)

3. Our Algorithms

In this section, we introduce the three proposed algorithms in detail. Let us define a solution set

S = {S_{k}}_{k = 1}^{K}

containing K solutions, where

S_{k} = {S_{k} . x_{i}}_{i = 1}^{n}

represents an assignment combination (i.e. a solution) of n variables controlled by agents. Therefore, an agent

x_{i}

holds the value assignments of K solutions on the

i^{t h}

dimension, denoted as

S . x_{i} = {S_{k} . x_{i}}_{k = 1}^{K}

. In addition, we use

S_{k} . x_{i}

to represent the variable of the

k^{t h}

solution held by agent

x_{i}

, and its local utility is

L_{i} (S_{k}, S_{k}) = \sum_{j \in N_{i}} f_{i j} (S_{k} . x_{i}, S_{k} . x_{j})

, where

(k, k)

represents two variables on the

k^{t h}

solution and

N_{i}

represents the neighbors of agent

x_{i}

. For example, we construct a solution set with two solutions for Figure 1 as

S = {S_{1}, S_{2}}

, where

S_{1} = {S_{1} . x_{1}, S_{1} . x_{2}, S_{1} . x_{3}}

and

S_{2} = {S_{2} . x_{1}, S_{2} . x_{2}, S_{2} . x_{3}}

. For agent

x_{1}

, its value assignments are

S . x_{1} = {S_{1} . x_{1}, S_{2} . x_{1}}

and the local utility of

S_{1} . x_{1}

L_{i} (S_{1}, S_{1})

. It is worth noting that since we consider minimizing the aggregate utility, we use absolute gain to represent the local utility reduced, which is a negative value.

3.1. Continuous Maximum Gain Message

Algorithm 2 shows the process of the Continuous Maximum Gain Message (C-MGM) algorithm, including three phases: Initialization, Calculation, and Comparison.

Algorithm 2: Continuous MGM (C-MGM)

Initialization: Firstly, C-MGM constructs a solution set for K solutions. Then, each agent assigns a random value from its domain to each solution on the current dimension and generates a variable

G_{i}

to record the gain value of agent

x_{i}

. Finally, the agent

x_{i}

sends ValueMessage(

{i, S_{r} . x_{i}}

) to all neighbors (Algorithm 2: Lines 1-7), where

S_{r} . x_{i}

is a random value in

S . x_{i}

Calculation: After receiving ValueMessage(

{j, S_{r} . x_{j}}

) from neighbors, the agent

x_{i}

calculates the local utility for each solution according to its value assignments

S . x_{i}

, respectively (Algorithm 2: Lines 12-14). We define

L_{i} (S_{r}, S_{r})

to represent the basic local utility of agent

x_{i}

, which is the local utility assuming that the values of agent

x_{i}

and its neighboring agents are not changed, calculated by

\sum_{j \in N_{i}} f_{i j} (S_{r} . x_{i}, S_{r} . x_{j})

. Then, the

G_{i}

is assigned a difference value between the minimum and basic local utility (Algorithm 2: Lines 15-16). Finally, the agent

x_{i}

sends GainMessage(

{i, G_{i}}

) to neighbors.

Comparison: Similarly, the agent

x_{i}

enters the comparison phase after receiving GainMessage(

{j, G_{j}}

) from each neighbor

N_{i_{j}} \in N_{i}

. If the current agent with the minimum gain value among all gain values of neighbors and the gain is less than 0, the agent

x_{i}

assigns the value that minimizes local utility to

S_{r} . x_{i}

(Algorithm 2: Lines 18-20). In general, after the size of the domain is determined, the variable of the standard MGM algorithm can take a finite number of values from its domain, but there is an infinite number of values to be selected in the variable of C-MGM. We consider updating the value assignments for each agent to search its domain and avoid falling in the local optimum by adding randomness. Therefore, the agent

x_{i}

updates each value

S_{k} . x_{i}

to a random value from its domain

D_{x_{i}}

(Algorithm 2: Line 22).

3.2. Parallel C-MGM

We consider solving K solutions in parallel based on C-MGM. Therefore, we propose the Parallel C-MGM (C-PMGM) algorithm as shown in Algorithm 3, which also consists of three phases: Initialization, Calculation, and Comparison.

Algorithm 3: Parallel C-MGM (C-PMGM)

Initialization: Except for the similar initialization as C-MGM, C-PMGM additionally generates a competing solution set

C

, which is the same as the solution set

S

. In addition, each agent uses a gain set

G

to record the gain values of K solutions (Algorithm 3: Lines 7-9). It is worth noting that the ValueMessage(

{i, S . x_{i}}

) sent by agent

x_{i}

in C-PMGM to neighbors is the value assignments instead of a random value in

S . x_{i}

(Algorithm 3: Line 10).

Calculation: Since the computational overhead of solving K solutions according to the way of C-MGM is expensive, we consider using the values from the corresponding competing solution set to calculate the gains for K solutions (Algorithm 3: Lines 11-16), which means that the indexes of the two solution sets (

S

and

C

) are consistent. Later, the agent

x_{i}

sends GainMessage(

{i, G_{i}}

) to neighbors.

Comparison: Similar to C-MGM, the agent

x_{i}

in C-PMGM compares K gains with all neighbors. For each gain

G_{k, i}

in the gain set of agent

x_{i}

, if the gain value is the smallest in the current local and less than 0, the value

S_{k} . x_{i}

is assigned to its competing value

C_{k} . x_{i}

(Algorithm 3: Lines 18-21). Since an agent only calculates one local utility for a solution instead of K local utilities (such as Algorithm 2: Lines 13-14), the idea is to search as many competing values as possible. Therefore, the agent

x_{i}

resets each competing value

C_{k} . x_{i}

to a value from its domain, whether or not the value

S_{k} . x_{i}

is changed.

3.3. Parallel Differential Search C-MGM

Based on C-PMGM, we construct a heuristic method to guide the exploitation of the competing solution set. Specifically, we extend the update of value assignments in C-PMGM by combining a differential search, named Parallel Differential Search C-MGM (C-PDSM). The details of C-PDSM can be found in Algorithm 4.

Algorithm 4: Parallel Differential Search C-MGM (C-PDSM)

The difference between C-PDSM and C-PMGM is the update of value assignments (Algorithm 4: Line 22). For a gain set in one agent, the agent filters each absolute gain and adds it to an absolute gain set

Ω

(Algorithm 4: Lines 26-29). Since the differential search method we used requires at least two absolute gains, we provide two ways to update value assignments (Algorithm 4: Lines 30-34):

(i)

If the number of absolute gains is less than two, the agent update the value assignments of the competing solution set through random search.

(i i)

Otherwise, the agent updates value assignments by differential search, as shown in Equation (2). Our motivation is that the current value learns the exploitation ability from other values with absolute gain, which can improve the convergence speed of the algorithm.

\begin{matrix} \begin{matrix} C_{k} . x_{i} = C_{k} . x_{i} & + ω * (C_{{\arg \min}_{k} {Ω}} . x_{i} - C_{k} . x_{i}) \\ + ω * (C_{{\arg \max}_{k} {Ω}} . x_{i} - C_{k} . x_{i}) \end{matrix} \end{matrix}

(2)

where

ω

is a scaling factor

\in [0, 2]

, which controls the amplification of the differential variation [42]. The "

{\arg \min}_{k} {Ω}

" and "

{\arg \max}_{k} {Ω}

" represent the indexes of competing solution set with the minimum and maximum absolute gain values, respectively.

3.4. An Example of Algorithms

We take Figure 1 as an example to realize the three phases of C-MGN, C-PMGM, and C-PDSM.

In the Initialization phase, we assume that the size of the solution set is

K = 2

and the solution sets of the three algorithms are all

S = {S_{1} = {3, 1, 5}, S_{2} = {- 2, 2, 4}}

. Therefore, the value assignments held by agent

x_{1}

are

S . x_{1} = {S_{1} . x_{1} = 3, S_{2} . x_{1} = - 2}

, the value assignments of agent

x_{2}

are

S . x_{2} = {1, 2}

, and the value assignments of agent

x_{3}

are

S . x_{3} = {5, 4}

For C-MGM, the values randomly selected by each agent are $S_{r} . x_{1} = 3$ , $S_{r} . x_{2} = 2$ , and $S_{r} . x_{3} = 4$ .
For C-PMGM and C-PDSM, we assume the competing solution sets both are $C = {C_{1} = {- 4, - 1, 0}, C_{2} = {- 3, 3, - 5}}$ and the scaling factor $ω$ in C-PDSM is 1.4.

In the Calculation phase, the agent

x_{i}

calculates the local utility and gain after receiving the random value

S_{r} . x_{j}

or value assignments

S . x_{j}

from neighbors

N_{i_{j}} \in N_{i}

. Let’s take the agent

x_{1}

as an example for calculation.

For C-MGM:

$L_{1} (S_{1}, S_{r}) = f (3, 2) + f (3, 4) = 46$

$L_{1} (S_{2}, S_{r}) = f (- 2, 2) + f (- 2, 4) = - 19$

$L_{1} (S_{r}, S_{r}) = f (3, 2) + f (3, 4) = 46$

$G_{1} = - 19 - 46 = - 65$ ;
For C-PMGM and C-PDSM:

$L_{1} (S_{1}, S_{1}) = f (3, 1) + f (3, 5) = 43$

$L_{1} (C_{1}, S_{1}) = f (- 4, 1) + f (- 4, 5) = - 146$

$G_{1, 1} = - 146 - 43 = - 189$ ;

$L_{1} (S_{2}, S_{2}) = f (- 2, 2) + f (- 2, 4) = - 19$

$L_{1} (C_{2}, S_{2}) = f (- 3, 2) + f (- 3, 4) = - 62$

$G_{2, 1} = - 62 - (- 19) = - 43$ ;

In the Comparison phase, each agent compares the gains to action. Simultaneously, there are different way to update value assignments in C-MGM, C-PMGM, and C-PDSM. We assume that the agent

x_{1}

with maximum gain among its neighbors, and its actions and updates are as follows:

For C-MGM:

$S_{r} . x_{1} = {\arg \min}_{S_{k}} {46, - 19} = S_{2} . x_{1} = - 2$ ;

$S . x_{1} = {1, - 1}$ (assumed random values);
For C-PMGM:

$S_{1} . x_{1} = C_{1} . x_{1} = - 4$ , $S_{2} . x_{1} = C_{2} . x_{1} = - 3$ ;

$C . x_{1} = {2, - 2}$ (assumed random values);
For C-PDSM:

$S_{1} . x_{1} = C_{1} . x_{1} = - 4$ , $S_{2} . x_{1} = C_{2} . x_{1} = - 3$ ;

Since both gain values (-189 and -43) are less than 0, $| Ω | = 2$ .

$C_{1} . x 1 = - 4 + 1.4 * [- 4 - (- 4)] + 1.4 * [- 3 - (- 4)] = - 2.6$

$C_{2} . x 1 = - 3 + 1.4 * [- 4 - (- 3)] + 1.4 * [- 3 - (- 3)] = - 4.4$ ;

Finally, C-MGM outputs a solution as

X^{*} = {- 2, 2, 4}

. The two solutions output by C-PMGM and C-PDSM are

X_{1}^{*} = {- 4, 1, 5}

and

X_{2}^{*} = {- 3, 2, 4}

, the difference between C-PMGM and C-PDSM is that the value assignments of agent

x_{1}

in the competing solution set are

C . x_{1} = {2, - 2}

and

C . x_{1} = {- 2.6, - 4.4}

, respectively.

4. Theoretical Analysis

In this section, we prove that C-MGM, C-PMGM, and C-PDSM are three anytime algorithms, and we provide some theoretical properties of our algorithms in terms of communication, computation, and memory. We assume that the graph structure is a binary constraint graph

G = (N, E)

, the number of nodes is

| A |

, and the number of edges in the constraint graph is

| F |

. In addition, we define one iteration as the complete process of the algorithm completing Calculation and Comparison phase.

Theorem 1.

C-MGM, C-PMGM, and C-PSDM are three anytime algorithms.

Proof.

On the one hand, the three algorithms are iterative, which means they can be terminated at any time and output solutions. On the other hand, we assume that the aggregate utility (U) of C-MGM at t iteration is

U_{t} = \sum_{f_{i j} \in F} f_{i j}

, which represents the sum of utility on all constraints. When an agent calculates local utility, the same constraint is calculated twice by two neighboring agents, the aggregate utility can be modified as

U_{t} = \frac{1}{2} \sum_{x_{i} \in X} L_{i}

. Therefore, the aggregate utility of the

t + 1

iteration in C-MGM can represent

U_{t + 1} = \frac{1}{2} \sum_{x_{i} \in X} L_{i} + \sum_{x_{i} \in X} G_{i}

, where

X \subseteq X

represents a set of variables that change their values. In each local, since only one variable with local utility reduced changes its value, we can get that

\sum_{x_{i} \in X} G_{i} < 0

. Therefore,

U_{t + 1} < U_{t}

, which means the aggregate utility strictly decreases with increasing iterations. Similarly, C-PMGM and C-PDSM solve K solutions in parallel, the aggregate utilities’ change of one solution in them is the same as that of C-MGM. Hence, C-MGM, C-PMGM, and C-PSDM are three anytime algorithms. □

Theorem 2.

The total number of messages of C-MGM, C-PMGM, and C-PDSM with t iterations all are

4 t | F |

Proof.

For each constraint

f_{i j} (x_{i}, x_{j})

in one iteration, the agents of the three algorithms need to send value assignments to neighbors in the Calculation phase and vice versa, there are two messages per edge. Therefore, the number of messages is

2 | F |

in this phase, where

| F |

is the number of constraints (edges). In the Comparison phase, the agents of the three algorithms share gain or gain sets with neighbors to compare their values, thus the number of messages is also

2 | F |

. Finally, the total number of messages of C-MGM, C-PMGM, and C-PDSM with t iterations all are

t * (2 | F | + 2 | F |) = 4 t | F |

. □

Theorem 3.

In one iteration, the message size of C-MGM, C-PMGM, and C-PDSM are respectively 1, K, and K, where K is the number of solutions.

Proof.

In the Calculation phase, the agent in C-MGM sends a random value to its neighbors to calculate the local utility, the message size of the random value is 1. However, the agents in C-PMGM and C-PDSM send value assignments to neighbors. The size of value assignments is K, where K is the number of solutions. In the Comparison phase, the size of the gain message in C-MGM is 1, but the size of gain sets in the other two algorithms is K. Hence, since

m a x {1, 1} = 1

m a x {K, K} = K

, and

m a x {K, K} = K

, the message size of C-MGM, C-PMGM, and C-PDSM are respectively 1, K, and K in one iteration. □

Theorem 4.

In one iteration, the computational overhead of one agent in C-MGM, C-PMGM, and C-PSAM are respectively

K | N | + 1

K (2 | N | + 1)

, and

2 K (| N | + 1)

, where K is the number of solutions and

| N |

is the number of neighbors. Further, the overall computational overhead of C-MGM, C-PMGM, and C-PSAM in one iteration are

2 K | F | + | A |

K (4 | F | + | A |)

, and

K (4 | F | + 2 | A |)

, respectively.

Proof.

We define the number of neighbors of one agent as

| N |

. For C-MGM, the agent

x_{i}

needs to calculate the local utility for K solutions in one iteration, including the basic local utility. In addition, the agent calculates the gain once. Therefore, in one iteration, the computational overhead of one agent in C-MGM is

K | N | + 1

. Since

\sum_{x_{i} \in X} | N_{i} | = 2 | F |

, and the overall computational overhead of C-MGM is

\sum_{x_{i} \in X} K | N_{i} | + 1 = 2 K | F | + | A |

For C-PMGM, the agent calculates the basic local utility and competing local utility (Algorithm 3: Line 15) for K solutions with neighbors, and the agent calculates the gain set, including K gains. Hence, the computational overhead of one agent in C-PMGM is

2 K | N | + K = K (2 | N | + 1)

, the overall computational overhead is

K (4 | F | + | A |)

Compared to C-PMGM, an agent of C-PDSM additionally updates the value of K solutions based on C-PMGM. Therefore, the computational overhead of one agent in C-PDSM in one iteration is

2 K | N | + K + K = 2 K (| N | + 1)

, and the overall computational overhead is

K (4 | F | + 2 | A |)

. □

5. Experimental Results

In this section, we empirically evaluate the solution quality of our three algorithms and the state-of-the-art algorithms, PCD, C-CoCoA, and PCD-LD. Firstly, we set initialization parameters for each algorithm. Specially, we evaluate the performance of C-PDSM with different scaling factors to find the most suitable scaling factor for comparison experiments. Then, we compare the solution quality of the six algorithms when the algorithm runs completely. Finally, we use the runtime to evaluate the performance of all algorithms.

Although C-MGM, C-PMGM, and C-PDSM can use any form of the utility function, we use the utility function in the form of

a x^{2} + b x + c x y + d y + e y^{2} + f

to fairly show the results for consistency with researchers’ work [38,40], where

a, b, c, d, e

, and f are random numbers in the range

[- 5, 5]

. Furthermore, we set the domain of each variable to

[- 50, 50]

and the number of iterations to 500. It is worth mentioning that we choose the best solutions in C-PMGM and C-PDSM to present comparisons. For each benchmark problem, we independently run each algorithm on 30 different sets of function coefficients (

a, b, c, d, e

, and f) and take the average solution quality as the experimental result. The experiments are carried out on a computer equipped with Intel(R) Core(TM) i5-10500 CPU, 3.10GHz processor, and 8GB RAM.

We choose three benchmark problems and set their parameters:

(i)

Random Graphs: we use the Erdös-Rényi model [43] to generate random graphs with two different settings: D1: Sparse random graphs (

p = 0.1

) and D2: dense random graphs (

p = 0.6

), where p represents the probability of connection between two nodes in a graph;

(i i)

D3: Scale-free Networks: we refer to the Barabási-Albert (BA) [44] model to generate scale-free networks with an initial set of

m_{1} = 10

connected agents, and at each iteration, a new agent that connected to

m_{2} = 3

other agents is added to the current network; and

(i i i)

D4: Small-world Networks: we use the Newman-Watts model [45] to provide small-world networks. The number of nearest nodes is set to 8 and the probability of connection adding is set to 0.1.

5.1. Parameter Configuration

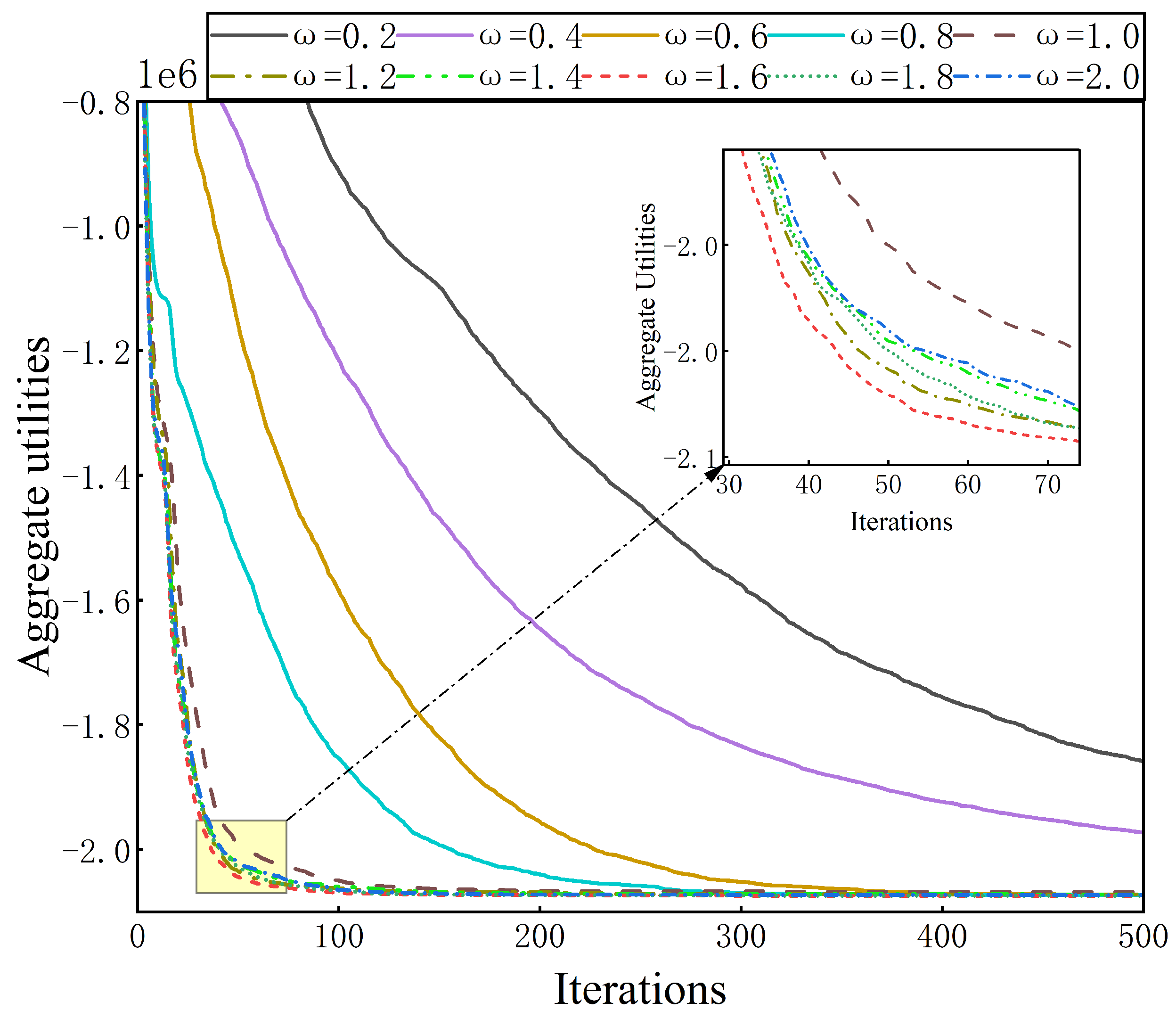
In C-MGM, C-PMGM, and C-PDSM, K represents the size of the solution set, which is also the number of solutions that need to be optimized. Considering the previous work of some researchers using the solution set [37,40], we uniformly set K to 1000. For the scaling factor in C-PDSM, we use different scaling factors to compare the solution quality of C-PDSM on sparse random graphs with 100 agents. Figure 2 shows the convergence curves of C-PDSM with different scaling factors, where an obvious parameter setting is

ω = 1.0

. When

ω < 1.0

, the convergence speed of C-PDSM becomes slower as

ω

decreases. Conversely, the solution quality of C-PDSM with different parameters is similar when

ω > 1.0

. However, we can observe that there is a slight superiority in terms of convergence when

ω = 1.6

. Therefore, we set

ω

to 1.6 for C-PDSM. In addition, we set the parameters for competing algorithms according to the references [37,39,40].

5.2. Comparison of Solution Quality

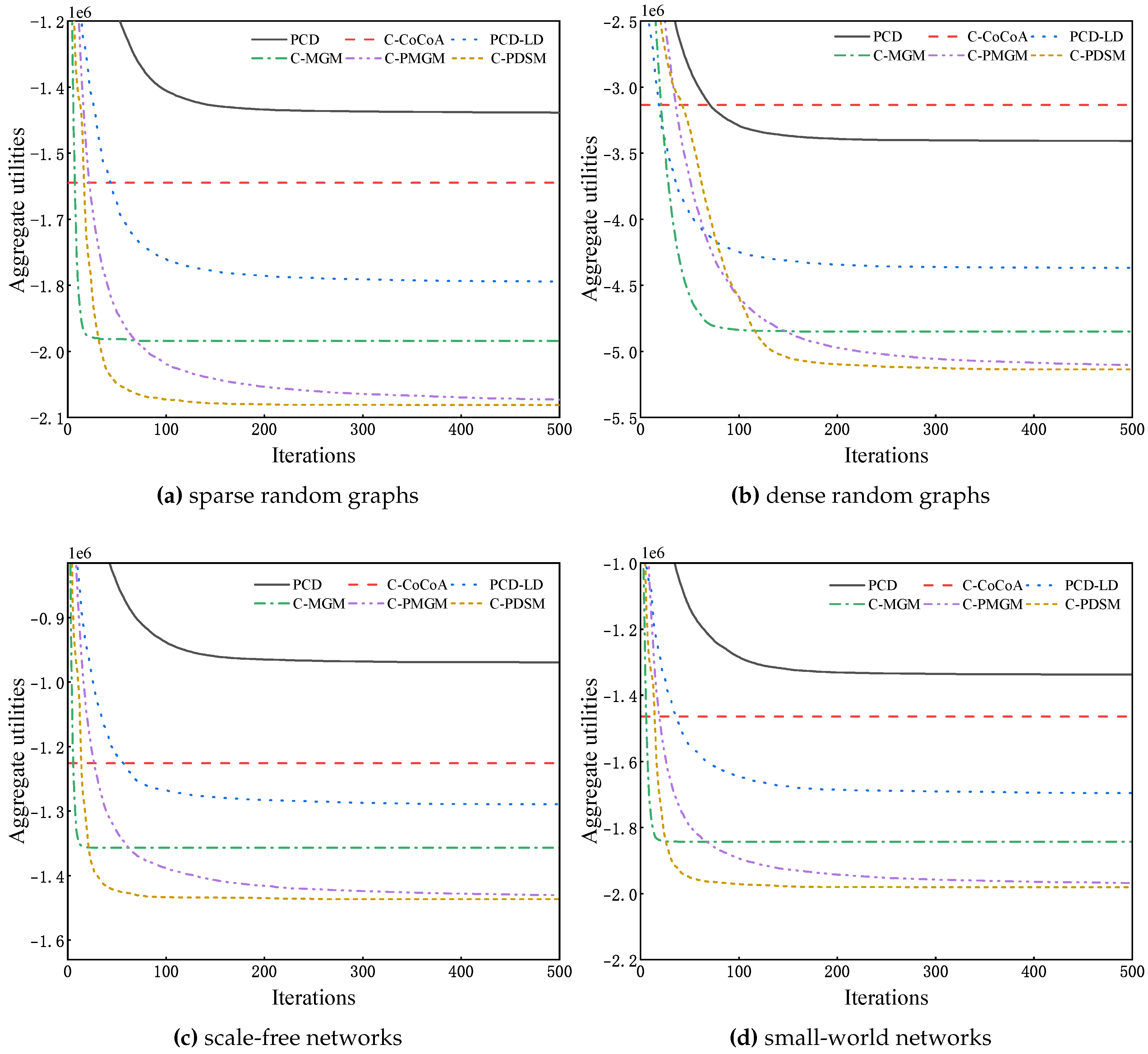
We show convergence curves of our algorithms and competing algorithms on three benchmark problems with 100 agents. Since C-CoCoA is a non-iterative algorithm, we use a straight line to represent its solution quality.

Figure 3a and Figure 3b show the solution quality of the six algorithms on sparse and dense random graphs, respectively. It can be seen that the solution quality of our three algorithms is significantly better than that of competing algorithms. Compared to performance on sparse random graphs, our three algorithms require more iterations to improve the solution quality. The most critical reason is that each agent has more neighbors in the dense configuration. Since only one of the two neighboring agents is allowed to change its value in our algorithms, there are fewer agents to improve their local utilities in one iteration. Therefore, our algorithms converge slower. Nevertheless, the solution quality of the three algorithms is superior to competing algorithms at about 100 iterations.

The convergence curves of the six algorithms on scale-free and small-world networks are presented in Figure 3c and Figure 3d, respectively. The performance of our algorithms is similar to that on sparse random graphs. C-MGM can obtain a high-quality solution and converge after a few iterations, and C-PMGM can improve the solution quality as the number of iterations increases. Compared to C-MGM, C-PDSM can converge faster since it uses heuristics to enhance the exploitation of solutions.

Further, we evaluate the solution quality of the six algorithms on each benchmark problem with 80 and 90 agents, respectively. The detailed results are shown in Table 1. We can observe clearly that the solution quality of C-MGM, C-PMGM, and C-PDSM significantly outperforms that of competing algorithms on different benchmark problems with varying numbers of agents, and C-PDSM has the best solution quality among all algorithms.

5.3. Comparison of Algorithms Using Runtime

We compare the best solution quality reached by C-MGM, C-PMGM, C-PDSM, and competing algorithms on each benchmark problem after runtime in 1000 milliseconds (ms).

Table 2 lists the solution quality of algorithms on benchmark problems with different numbers of agents. Since C-MGM uses multiple local utilities to find the maximum gain compared to C-PMGM and C-PDSM, it can quickly find a high-quality solution. In addition, the solution quality of C-MGM outperforms competing algorithms on each benchmark problem except for the comparison with C-CoCoA on dense random graphs, the reason is that C-MGM converges slower due to the increase of neighbors.

6. Conclusion and Future Work

Researchers propose C-DCOPs to model distributed problems with continuous variables as an extension of DCOPs. In this paper, we design three algorithms C-MGM, C-PMGM, and C-PDSM for solving C-DCOPs and prove that they are three anytime algorithms. Since the C-MGM algorithm resets value assignments to expend the search space and chooses the maximum gain, it can obtain high-quality solutions with few iterations. The C-PMGM algorithm extends C-MGM by searching multiple solutions in parallel, which can significantly improve the solution quality. Based on C-PMGM, C-PDSM combines differential search to strengthen the exploitation of solutions, which can effectively improve the convergence speed and the solution quality. Extensive experiments on three benchmark problems show that C-MGM, C-PMGM, and C-PDSM outperform the state-of-the-art C-DCOP algorithms. In future work, we plan to improve the convergence speed of the three algorithms on some dense graphs.

Author Contributions

Conceptualization, Xin Liao and Khoi Hoang; methodology, Xin Liao; software, Xin Liao; validation, Xin Liao; formal analysis, Xin Liao; investigation, Xin Liao; resources, Khoi Hoang; data curation, Xin Liao; writing—original draft preparation, Xin Liao; writing—review and editing, Xin Liao; visualization, Khoi Hoang; supervision, Khoi Hoang; project administration, Khoi Hoang; funding acquisition, Khoi Hoang. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The code and benchmark problems for this paper can be found at https://github.com/chattedlx/MGM-extensions.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Modi, P.; Shen, W.M.; Tambe, M.; Yokoo, M. ADOPT: Asynchronous Distributed Constraint Optimization with Quality Guarantees. Artificial Intelligence 2005, 161, 149–180. [CrossRef]
Petcu, A.; Faltings, B. A Scalable Method for Multiagent Constraint Optimization. In Proceedings of the Proceedings of the 19th International Joint Conference on Artificial Intelligence, 2005, IJCAI, pp. 266–271.
Yeoh, W.; Yokoo, M. Distributed Problem Solving. AI Magazine 2012, 33, 53–65.
Fioretto, F.; Pontelli, E.; Yeoh, W. Distributed Constraint Optimization Problems and Applications: A Survey. Journal of Artificial Intelligence Research 2018, 61, 623–698. [CrossRef]
Maheswaran, R.T.; Tambe, M.; Bowring, E.; Pearce, J.P.; Varakantham, P. Taking DCOP to the Real World: Efficient Complete Solutions for Distributed Multi-Event Scheduling. In Proceedings of the Proceedings of the 3rd International Conference on Autonomous Agents and Multiagent Systems, 2004, AAMAS, pp. 310–317.
Di, B.; Jennings, N.R. A Contract-based Incentive Mechanism for Distributed Meeting Scheduling: Can Agents Who Value Privacy Tell the Truth? Autonomous Agents and Multiagent Systems 2021, 35, 35.
Farinelli, A.; Rogers, A.; Jennings, N.R. Agent-Based Decentralised Coordination for Sensor Networks Using the Max-sum Algorithms. Autonomous Agents and Multiagent Systems 2014, 28, 337–380. [CrossRef]
Zivan, R.; Yedidsion, H.; Okamoto, S.; Glinton, R.; Sycara, K.P. Distributed Constraint Optimization for Teams of Mobile Sensing Agents. Autonomous Agents and Multiagent Systems 2015, 29, 495–536. [CrossRef]
Harel, Y.; Roie, Z. Applying DCOP_MST to a Team of Mobile Robots with Directional Sensing Abilities. In Proceedings of the Proceedings of the 15th International Conference on Autonomous Agents and Multiagent Systems, 2016, AAMAS, pp. 1357–1358.
Fioretto, F.; Yeoh, W.; Pontelli, E.; Ma, Y.; Ranade, S.J. A Distributed Constraint Optimization (DCOP) Approach to the Economic Dispatch with Demand Response. In Proceedings of the Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, 2017, AAMAS, pp. 999–1007.
Miller, S.; Ramchurn, S.D.; Rogers, A. Optimal Decentralised Dispatch of Embedded Generation in the Smart Grid. In Proceedings of the Proceedings of the 11st International Conference on Autonomous Agents and Multiagent Systems, 2012, AAMAS, pp. 281–288.
Rust, P.; Picard, G.; Ramparany, F. Using Message-Passing DCOP Algorithms to Solve Energy-Efficient Smart Environment Configuration Problems. In Proceedings of the Proceedings of the 25th International Joint Conference on Artificial Intelligence, 2016, IJCAI, pp. 468–474.
Fioretto, F.; Yeoh, W.; Pontelli, E. A Multiagent System Approach to Scheduling Devices in Smart Homes. In Proceedings of the Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, 2017, AAMAS, pp. 981–989.
Chen, Z.; Deng, Y.; Wu, T. An Iterative Refined Max-sum_AD Algorithm via Single-side Value Propagation and Local Search. In Proceedings of the Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, 2017, AAMAS, pp. 195–202.
Chen, Z.; Wu, T.; Deng, Y.; Zhang, C. An Ant-based Algorithm to Solve Distributed Constraint Optimization Problems. In Proceedings of the Proceedings of the 32nd AAAI Conference on Artificial Intelligence, 2018, AAAI, pp. 4654–4661.
Hoang, K.D.; Fioretto, F.; Yeoh, W.; Pontelli, E.; Zivan, R. A Large Neighboring Search Schema for Multi-agent Optimization. In Proceedings of the Proceedings of the 24th International Conference on Principles and Practice of Constraint Programming, 2018, CP, pp. 688–706.
Khan, M.M.; Tran-Thanh, L.; Jennings, N.R. A Generic Domain Pruning Technique for GDL-Based DCOP Algorithms in Cooperative Multi-Agent Systems. In Proceedings of the Proceedings of the 17th International Conference on Autonomous Agents and Multiagent Systems, 2018, AAMAS, pp. 1595–1603.
Grinshpoun, T.; Tassa, A.; Levit, V.; Zivan, R. Privacy Preserving Region Optimal Algorithms for Symmetric and Asymmetric DCOPs. Artificial Intelligence 2019, 266, 27–50. [CrossRef]
Tassa, T.; Grinshpoun, T.; Yanai, A. A Privacy Preserving Collusion Secure DCOP Algorithm. In Proceedings of the Proceedings of the 28th International Joint Conference on Artificial Intelligence, 2019, IJCAI, pp. 4774–4780.
Tassa, T.; Grinshpoun, T.; Yanai, A. PC-SyncBB: A Privacy Preserving Collusion Secure DCOP Algorithm. Artificial Intelligence 2021, 297, 103501.
Deng, Y.; Chen, Z.; Chen, D.; Zhang, W.; Jiang, X. AsymDPOP: Complete Inference for Asymmetric Distributed Constraint Optimization Problems. In Proceedings of the Proceedings of the 28th International Joint Conference on Artificial Intelligence, 2019, IJCAI, pp. 223–230.
van Leeuwen, C.J.; Pawelczak, P. CoCoA: A Non-Iterative Approach to a Local Search (A)DCOP Solver. In Proceedings of the Proceedings of the 35th AAAI Conference on Artificial Intelligence, 2017, AAAI, pp. 3944–3950.
Zivan, R.; Parash, T.; Cohen-Lavi, L.; Naveh, Y. Applying Max-sum to Asymmetric Distributed Constraint Optimization Problems. Autonomous Agents and Multiagent Systems 2020, 34, 1–29. [CrossRef]
Deng, Y.; Chen, Z.; Chen, D.; Jiang, X.; Li, Q. PT-ISABB: A Hybrid Tree-based Complete Algorithm to Solve Asymmetric Distributed Constraint Optimization Problems. In Proceedings of the Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, 2019, AAMAS, pp. 1506–1514.
Hoang, K.D.; Hou, P.; Fioretto, F.; Yeoh, W.; Zivan, R.; Yokoo, M. Infinite-Horizon Proactive Dynamic DCOPs. In Proceedings of the Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems, 2017, AAMAS, pp. 212–220.
Hoang, K.D.; Fioretto, F.; Hou, P.; Yokoo, M.; Yeoh, W.; Zivan, R. Proactive Dynamic Distributed Constraint Optimization. In Proceedings of the Proceedings of the 15th International Conference on Autonomous Agents and Multiagent Systems, 2016, AAMAS, pp. 597–605.
Hoang, K.D.; Fioretto, F.; Hou, P.; Yeoh, W.; Yokoo, M.; Zivan, R. Proactive Dynamic Distributed Constraint Optimization Problems. Journal Of Artificial Intelligence Research 2022, 74, 179–225. [CrossRef]
Gutierrez, P.; Meseguer, P.; Yeoh, W. Generalizing ADOPT and BnB-ADOPT. In Proceedings of the Proceedings of the 22th International Joint Conference on Artificial Intelligence, 2011, IJCAI, pp. 554–559.
Yeoh, W.; Felner, A.; Koenig, S. BnB-ADOPT: An Asynchronous Branch-and-Bound DCOP Algorithm. Journal of Artificial Intelligence Research 2010, 38, 85–133.
Vinyals, M.; Rodríguez-Aguilar, J.A.; Cerquides, J. Constructing A Unifying Theory of Dynamic Programming DCOP Algorithms via the Generalized Distributive Law. Autonomous Agents and Multiagent Systems 2011, 22, 439–464. [CrossRef]
Maheswaran, R.T.; Pearce, J.P.; Tambe, M. Distributed Algorithms for DCOP: A Graphical-Game-Based Approach. In Proceedings of the Proceedings of the 17th International Conference on Parallel and Distributed Computing Systems, 2004, PDCS, pp. 432–439.
Ottens, B.; Dimitrakakis, C.; Faltings, B. DUCT: An Upper Confidence Bound Approach to Distributed Constraint Optimization Problems. ACM Transactions on Intelligent Systems and Technology 2017, 8, 69:1–69:27.
Nguyen, D.T.; Yeoh, W.; Lau, H.C.; Zivan, R. Distributed Gibbs: A Linear-Space Sampling-Based DCOP Algorithm. Journal of Artificial Intelligence Research 2019, 64, 705–748. [CrossRef]
Stranders, R.; Farinelli, A.; Rogers, A.; Jennings, N.R. Decentralised Coordination of Continuously Valued Control Parameters Using the Max-sum Algorithm. In Proceedings of the Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems, 2009, AAMAS, pp. 601–608.
Voice, T.; Stranders, R.; Rogers, A.; Jennings, N.R. A Hybrid Continuous Max-Sum Algorithm for Decentralised Coordination. In Proceedings of the Proceedings of the 19th European Conference on Artificial Intelligence, 2010, ECAI, pp. 61–66.
Fransman, J.; Sijs, J.; Dol, H.; Theunissen, E.; Schutter, B.D. Bayesian-DPOP for Continuous Distributed Constraint Optimization Problems. In Proceedings of the Proceedings of the 18th International Conference on Autonomous Agents and Multiagent Systems, 2019, AAMAS, pp. 1961–1963.
Choudhury, M.; Mahmud, S.; Khan, M.M. A Particle Swarm Based Algorithm for Functional Distributed Constraint Optimization Problems. In Proceedings of the Proceedings of the 34th AAAI Conference on Artificial Intelligence, 2020, AAAI, pp. 7111–7118.
Hoang, K.D.; Yeoh, W.; Yokoo, M.; Rabinovich, Z. New Algorithms for Continuous Distributed Constraint Optimization Problems. In Proceedings of the Proceedings of the 19th International Conference on Autonomous Agents and Multiagent Systems, 2020, AAMAS, pp. 502–510.
Sarker, A.; Choudhury, M.; Khan, M.M. A Local Search Based Approach to Solve Continuous DCOPs. In Proceedings of the Proceedings of the 20th International Conference on Autonomous Agents and Multiagent Systems, 2021, AAMAS, pp. 1127–1135.
Shi, M.; Liao, X.; Chen, Y. A Particle Swarm with Local Decision Algorithm for Functional Distributed Constraint Optimization Problems. International Journal of Pattern Recognition and Artificial Intelligence 2022, 36, 2259025. [CrossRef]
Zivan, R.; Okamoto, S.; Peled, H. Explorative Anytime Local Search for Distributed Constraint Optimization. Artificial Intelligence 2014, 212, 1–26. [CrossRef]
Storn, R.; Price, K.V. Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization 1997, 11, 341–359. [CrossRef]
Paul, E.; Rényi, A. On the Evolution of Random Graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences 1960, 5, 17–60.
Albert-László, B.; Réka, A. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512.
Newman, M.; Watts, D. Renormalization Group Analysis of the Small-World Network Model. Physics Letters A 1999, 263, 341–346. [CrossRef]

1	We are going to consider the minimization in this paper.

Figure 1. An example of a C-DCOP, where (a) is a constraint graph with four variables, and (b) represents four utility functions.

Figure 2. The convergence curves of different scaling factors for C-PDSM.

Figure 3. The solution quality of the proposed algorithms and competing algorithms on different benchmark problems.

Table 1. The solution quality of the proposed algorithms and competing algorithms on benchmark problems with different numbers of agents.

Number	Type	PCD	C-CcCoA	PCD-LD	C-MGM	C-PMGM	C-PDSM
$\| A \| = 80$	D1	-1042798	-1101989	-1304624	-1366430	-1465110	-1473604
	D2	-2585639	-2393154	-3241010	-3529010	-3725781	-3749835
	D3	-883870	-979241	-1074588	-1127033	-1213038	-1220117
	D4	-1191145	-1273078	-1465341	-1547525	-1650405	-1660851
$\| A \| = 90$	D1	-1259013	-1387131	-1576550	-1657470	-1798312	-1810145
	D2	-3102676	-2821139	-3769051	-4128793	-4364131	-4393997
	D3	-990772	-1120876	-1221272	-1285462	-1379148	-1386262
	D4	-1231794	-1332859	-1527462	-1634378	-1748604	-1761438
$\| A \| = 100$	D1	-1407602	-1567222	-1791288	-1926485	-2059722	-2071917
	D2	-3407684	-3135087	-4367475	-4849739	-5103759	-5137080
	D3	-1000479	-1203417	-1286422	-1373971	-1469692	-1477799
	D4	-1337766	-1463976	-1695295	-1842810	-1967855	-1980617

Table 2. The solution quality and runtime of the proposed algorithms and competing algorithms on benchmark problems with different numbers of agents, where time represents the runtime (ms) when the algorithm reaches its best solution quality.

Number	Type	PCD (time)	C-CcCoA (time)	PCD-LD (time)	C-MGM (time)	C-PMGM (time)	C-PDSM (time)
$\| A \| = 80$	D1	-555861 (960)	-1111394 (136)	-896276 (952)	-1355370 (978)	-1004208 (956)	1150880 (948)
	D2	-1197702 (931)	-2332978 (407)	-2157473 (986)	-2200719 (954)	-1280861 (953)	-1706260 (985)
	D3	-467112 (949)	-1024342 (141)	-774797 (959)	-1127708 (952)	-880713 (927)	-1065422 (941)
	D4	-608475 (956)	-1254330 (157)	-916351 (946)	-1552279 (976)	-1157349 (940)	-1327593 (944)
$\| A \| = 90$	D1	-619407 (968)	-1380270 (157)	-1073774 (961)	-1658509 (998)	-1234988 (983)	-1370201 (995)
	D2	-1237887 (907)	-2829167 (486)	-2339043 (883)	-2339654 (988)	-1345707 (944)	-1728215 (938)
	D3	-513043 (987)	-1103239 (126)	-828157 (949)	-1274467 (997)	-988866 (949)	-1171402 (985)
	D4	-610568 (980)	-1340294 (157)	-993353 (966)	-1647306 (972)	-1200160 (965)	-1299064 (950)
$\| A \| = 100$	D1	-684657 (988)	-1533802 (188)	-1138453 (923)	-1888946 (992)	-1314583 (942)	-1462948 (979)
	D2	-1197062 (935)	-3176851 (578)	-2445525 (929)	-2501213 (982)	-1346609 (891)	-1764955 (969)
	D3	-531285 (971)	-1204229 (141)	-868545 (987)	-1366420 (981)	-1009219 (950)	-1298292 (973)
	D4	-637169 (956)	-1504482 (159)	-1135444 (932)	-1830023 (954)	-1361162 (989)	-1497704 (942)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Class of Local Search Based Anytime Algorithms for Continuous Distributed Constraint Optimization Problems

Abstract

1. Introduction

2. Background

2.1. Distributed Constraint Optimization Problems

2.2. Continuous Distributed Constraint Optimization Problems

2.3. Maximum Gain Message

3. Our Algorithms

3.1. Continuous Maximum Gain Message

3.2. Parallel C-MGM

3.3. Parallel Differential Search C-MGM

3.4. An Example of Algorithms

4. Theoretical Analysis

5. Experimental Results

5.1. Parameter Configuration

5.2. Comparison of Solution Quality

5.3. Comparison of Algorithms Using Runtime

6. Conclusion and Future Work

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe