1. Introduction
The paradigm of power production in the electrical industry is undergoing a transformative shift from traditional fossil fuel-based sources to renewable energy sources (RES) [
1]. Notably, many RES function as distributed generators (DGs) in power networks, interconnected through power electronics converters to enhance network reliability and security [
2]. When a low-voltage distribution network operates within a defined area with an amalgamation of DGs, energy storage systems (ESSs), controllers, and loads, it qualifies as a microgrid [
3]. The distinctive characteristics of converter-based microgrids set them apart from conventional centralized electrical power generators. Notably, the presence of intermittent energy resources and sources poses a unique challenge, necessitating tailored control strategies. Converter-based DGs inherently exhibit traits such as fast response and reduced inertia, demanding meticulous consideration in the design of controllers aimed at regulating voltage and enhancing power quality for local services [
2].
Microgrids operate in two primary modes: (i) grid-connected and (ii) isolated or islanded [
4]. In the grid-connected mode, power flow occurs bidirectionally between the microgrid and the main grid to address any disparities between generated power and load demand. Synchronous generators, linked to the primary grid, play a pivotal role in balancing power through the stored energy in rotating inertia, consequently influencing frequency dynamics [
5]. In this scenario, Distributed Generators (DGs) within the microgrid function akin to current sources, aligning their voltage frequency with that of the microgrid or grid utility. This synchronization facilitates seamless power exchange between the microgrid and the larger grid utility [
6].
Conversely, islanded microgrids operate in isolation from external power grids, rendering power transfer unfeasible during imbalances between supply and demand. In both operational modes, stringent frequency regulation becomes imperative to uphold power balance within the microgrid. This dual-mode operation underscores the versatility and adaptability of microgrids in catering to diverse energy scenarios and requirements.
Household PV systems, when integrated into the microgrid, offer flexibility, allowing installation either with or without battery storage. In certain configurations, these systems can even be leveraged for trading, enabling users to obtain rebates. On the other hand, Commercial DER (CDER) units adhere to established grid codes, emphasizing proper power-sharing mechanisms for ensuring stable operation [
7]. Achieving effective power-sharing among CDER units poses challenges, especially in the absence of synchronous generators that traditionally incorporate speed governors to regulate power output in response to demand fluctuations [
8]. Given the economic constraints and practical limitations associated with connecting synchronous generators, devising automatic power-sharing strategies becomes imperative for CDER units [
9].
Several control approaches have been proposed, with or without the integration of communication lines [
10,
11,
12,
13,
14], aiming to facilitate proper power-sharing within microgrids [
15]. Communication-enabled centralized control has been explored in research such as [
16,
17], where secondary control sends calculated corrective commands to inverter control units, compensating for frequency deviations. However, studies highlight potential performance degradation in microgrids employing centralized control, attributed to issues like message delays and dropouts [
3,
18,
19,
20]. This underscores the significance of robust and distributed control strategies to overcome these challenges and enhance microgrid performance.
In the pursuit of efficient power-sharing within microgrids, various control strategies have been proposed, each offering distinct advantages and addressing specific challenges. However, it’s crucial to critically examine these approaches to ensure their suitability for different operational scenarios. Monshizadeh et al. [
6] proposed a communication-free master-slave microgrid, employing a voltage source inverter (VSI) that emulates the behavior of a synchronous generator. Despite its innovative approach, this strategy faces limitations in achieving rapid frequency restoration, potentially jeopardizing network stability. Additionally, the absence of consideration for Phase-Locked Loop (PLL) dynamics in their model poses further challenges. Pota et al. [
21] introduced a droop-based controller for power-sharing, assuming an ideal voltage source behind inverters. While this assumption is valid in scenarios involving parallel-connected inverters [
22], understanding the true response of renewable energy sources behind ideal voltage sources is essential. Recent literature [
23,
24] has explored the deloading technique to simulate the inertial response of PV systems for frequency regulation in grid-connected microgrids. Barik et al. [
25] proposed a robust controller for a microgrid comprising a PV system, doubly-fed induction generator (DFIG) connected wind generator, and Battery Energy Storage System (BESS) to enhance network stability under islanded operation. However, this approach did not guarantee proper power-sharing among distributed generators. Hossain et al. [
10] introduced a novel power control technique employing a voltage band in the DC-link voltage to maintain voltage stability and power quality during temporary disturbances. This approach offers a unique strategy for addressing network challenges. Parvizimosaed et al. [
26] presented an intelligent power-sharing (IPS) approach that dispatches active and reactive power among Distributed Generators (DGs) based on droop control gains and operating power capabilities. While promising, this approach relies on communication, adding complexity and cost to the system. In the pursuit of optimal power-sharing, there is a compelling need for an accurate and communication-independent strategy applicable to diverse DG units connected in parallel. This ensures proportional power-sharing, stability, and robust performance in microgrid operations. In [
27], a novel grid-forming inverter based on photovoltaic (PV) sources, equipped with modified virtual synchronous machine control, and a battery-supported inverter employing enhanced droop control are introduced. These solutions aim to operate effectively under non-ideal grid voltage conditions and in isolated mode scenarios. However, certain limitations exist, particularly concerning the power-sharing capabilities of the PV inverter during significant demand changes. The assumption of the PV system as an ideal voltage source may hinder its performance in practical implementations. Additionally, both grid-forming and grid-following inverters in [
27] contribute to frequency changes during power-sharing, potentially resulting in substantial network frequency variations, especially under dynamic demand conditions.
Despite the contributions of the aforementioned literature, certain drawbacks remain prevalent. These include the assumption of an ideal voltage source for the inverter input, which may not align seamlessly with practical implementations. Moreover, a limited number of papers consider the utilization of the deloading technique to emulate inertial response, and there is a notable absence of model validation using industry-standard software.
To address these gaps, this paper proposes a systematic design of a proportional control strategy for converter-interfaced generators. The developed control algorithm is validated using the PowerFactory-DigSILENT software in a medium-voltage network. The key innovation lies in the application of droop-based control for both grid-forming and grid-following Distributed Energy Resource (DER) units, ensuring proportional power sharing within an islanded microgrid lacking a synchronous generator. Specifically, the Battery Energy Storage System (BESS) with a Pulse Width Modulation (PWM) inverter is designated as grid-forming, while PV systems and Doubly Fed Induction Generators (DFIG) serve as grid-following components.
In order to assess the stability of the proposed controller, a dynamic model is developed for a multiple-Distributed Generation (DG) microgrid, focusing on small-signal dynamics. Sensitivity analysis is conducted after linearizing the model and selecting operating point parameters. Given the potential challenges in large inverter-based microgrids, the Ziegler-Nichols (ZN) and particle swarm optimization (PSO) methods are employed. These methods aid in accurately determining the suitable range for the designed droop parameters. Through the analysis, it is evident that the proposed technique adeptly achieves precise and swift power sharing among Energy Internet-Connected DG (EI-DG) units. This approach facilitates optimal power allocation in accordance with the units’ power ratings and eliminates the need for individual Battery Energy Storage Systems (BESS) for each DER unit.
The main contributions of this study are shown as follows.
Equitable Load Distribution Controllers: Development of specialized controllers designed to facilitate fair distribution of load changes among Distributed Generation (DG) units, taking into account the ratings of Distributed Energy Resources (DER) units within the microgrid. Two distinct controller types are formulated for this purpose: (1) a grid-forming controller, intricately connected to the Battery Energy Storage System (BESS); (2) a grid-following controller, specifically designed for DER units.
Optimal Coefficient Determination for Droop Controllers: Identification and optimization of the key coefficients for droop controllers, a critical aspect ensuring the stability of the system. The aim is to achieve: (1) system stability under varying conditions; (2) swift restoration of the frequency to its nominal value following disturbances; and (3) proportional power sharing among DER units, aligning with their individual power ratings.
Small-Signal Analysis for Stability: Implementation of small-signal analysis to finely tune the control parameters, offering a deeper understanding of the system’s stability margin. This analysis contributes to the robust design of controllers, improving the microgrid’s responsiveness.
Thorough Performance Validation: Rigorous testing and validation of the proposed power-sharing technique on a benchmark medium voltage network using industry-standard commercial software. The results demonstrate the accuracy, speed, and effectiveness of the proposed technique in sharing power among DGs.
This novel approach seeks to overcome the limitations observed in previous literature, offering a more practical and validated solution for microgrid control in real-world applications.
The rest of this paper is arranged as follows. Section II briefly describes the generic system model where the cases are studied. The proposed control for power-sharing has been described in section III. Sections IV deals with general small-signal analysis after linearization of the model and a method to determine the co-efficient of the proposed controllers. Section V shows the simulation results after implementing the proposed algorithm for 4 and 9 bus systems. Moreover, Section VI concludes the results obtained from the analysis of the study system.
2. System overview
A microgrid consisting of several Power-electronics elements can operate in parallel, grid-connected, or islanded mode.
Figure 1 shows a general structure of the microgrid, which consists of one-off BESS and
n DER units. The microgrid is connected to the utility system through a static transfer switch (STS) at the point of common coupling (PCC). As depicted in
Figure 1, each DER unit comprises a renewable energy source (RES).
Moreover, a power electronic interface is comprised of a dc-ac inverter. Each DER can be directly connected to a predefined load or to the ac common bus to supply power. Now, for the network shown in
Figure 1, the complex power can be written as:
Also,
Where,
is the complex power at i-th bus
is the active power at i-th bus
is the reactive power at i-th bus
is the voltage at i-th bus
is the current at i-th bus
is the current angle at i-th bus
is the current angle at i-th bus
The currents and voltages of the micro-grid buses shown in
Figure 1 are related to:
where,
The equation for the active power at i-th bus can be written as follows:
where
is the angle of the impedance
.
2.1. BESS Model
The dc/ac inverter connected to the BESS is classified as grid forming voltage source inverters (VSIs). The control mode of the PWM converter connected to the BESS is Vac-phi where the terminal voltage magnitude and phase are specified. The main purpose of BESS is to provide a fast frequency regulation response and share the load burden of conventional power generation units.
With Vac-phi control mode, the existing BESS does not have the specified active power set point. The BESS is connected to the slack bus (bus no. 1), and if there is any load change event that happens, the active power changes as per the load flow Eq. (1)-(6).
The selection of BESS over other energy storage devices is based on several factors that make BESS well-suited for the proposed research. BESS offers advantages such as fast response times, high efficiency, and the ability to provide both active power support and energy storage. Additionally, BESS technology has been widely adopted in various power systems and microgrid applications, making it a practical and established choice for addressing power-sharing, stability, and frequency control challenges in the context of this research. The decision to focus on BESS is rooted in its proven performance, versatility, and relevance to contemporary power system applications.
2.2. DER Model
Due to the high prevalence of RESs, frequency stability challenges are significant [
28], as RESs tend to have low or no inertial responses [
29]. For example, solar photovoltaic plants do not provide an inertia response to the power grid. On the other hand, variable-speed wind turbines are usually connected to the grid via power electronic converters, freeing them from power system transients. As a result, replacing traditional sources with renewable energy sources will reduce the inertia of the entire power system. For this reason, the frequency deviation will increase, as reported in [
30]. This section describes the use of deloading technique for solar PV and wind turbines from literature to overcome the frequency stability challenges. In this paper, deloading technique has been used for proportional power-sharing.
2.2.1. PV System
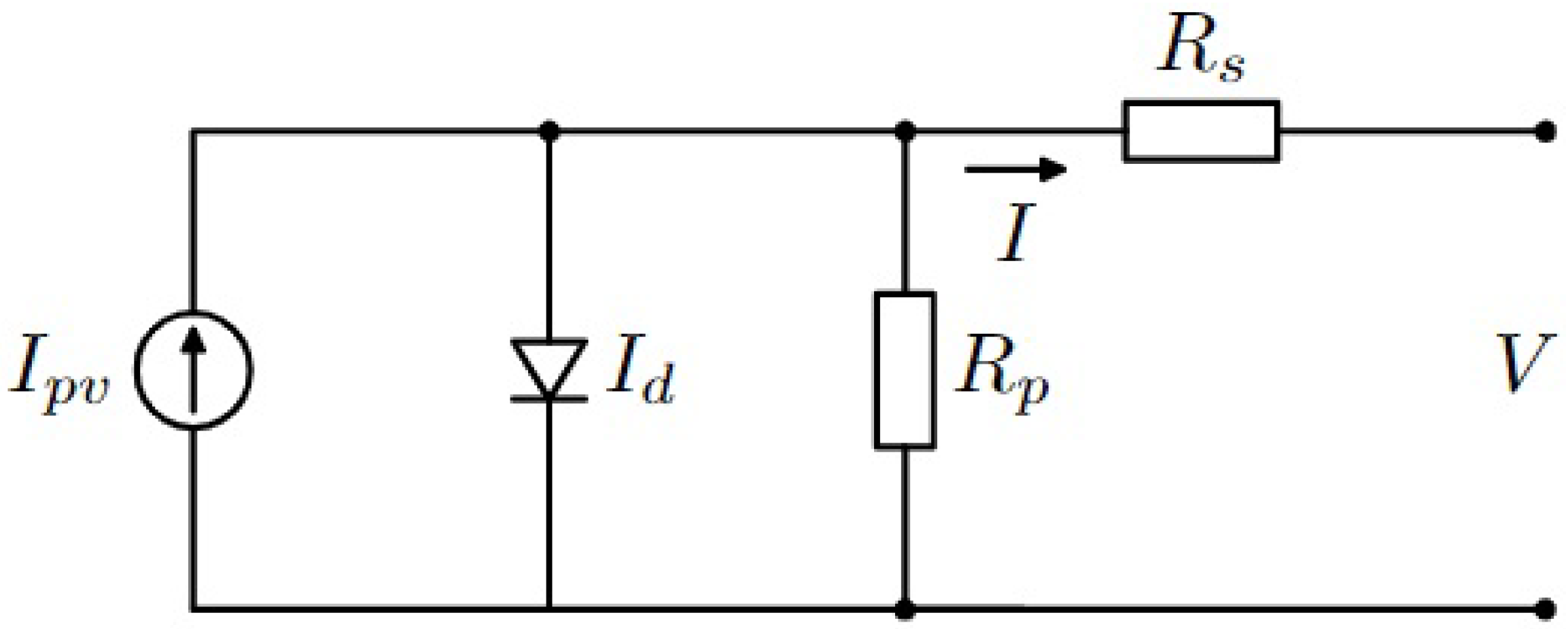
In PV systems, there are two parts[
31]: solar conversion and electronic conversion.
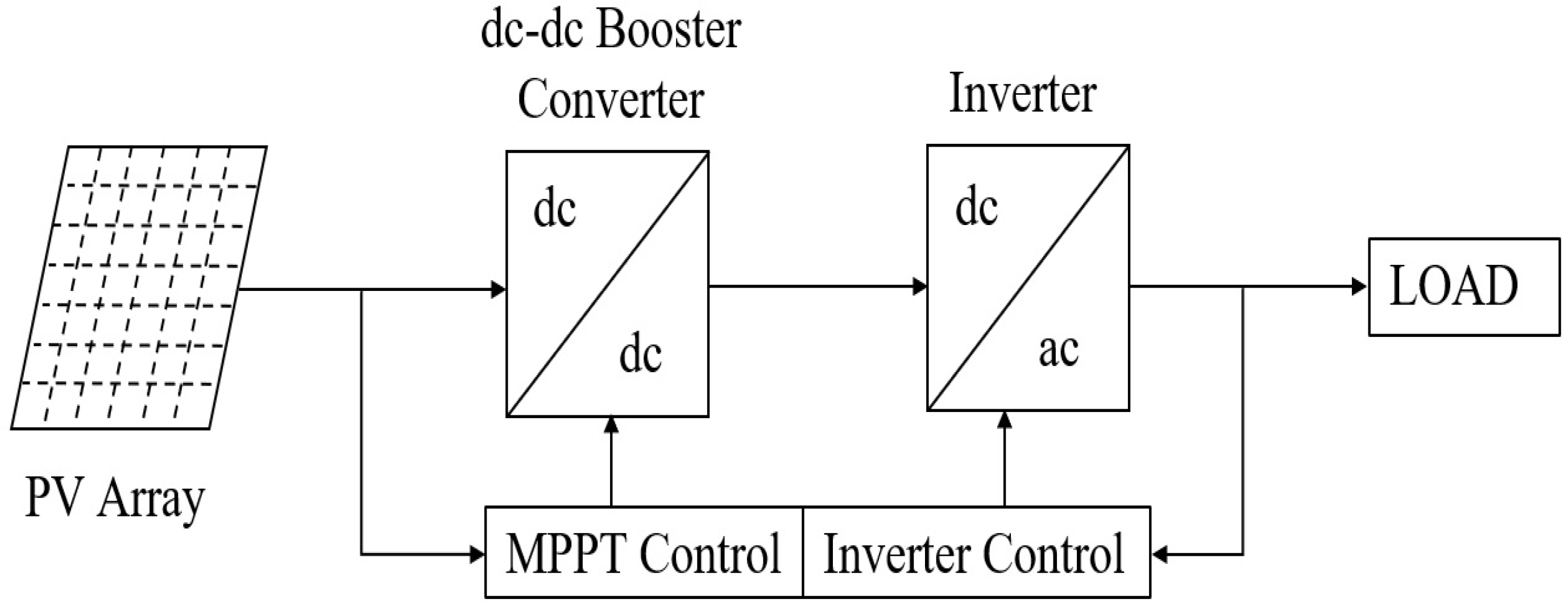
Figure 2 shows the inverter (dc-ac converter) connects PV arrays to loads via a dc-dc converter (boost converter). A dc-dc boost converter achieves the maximum output power conversion from the PV array to the inverter, and an inverter converts that power into ac to supply the ac load.
Most of the PV systems operate in the maximum power operation region to obtain an energy benefit. The system proposed in [
23,
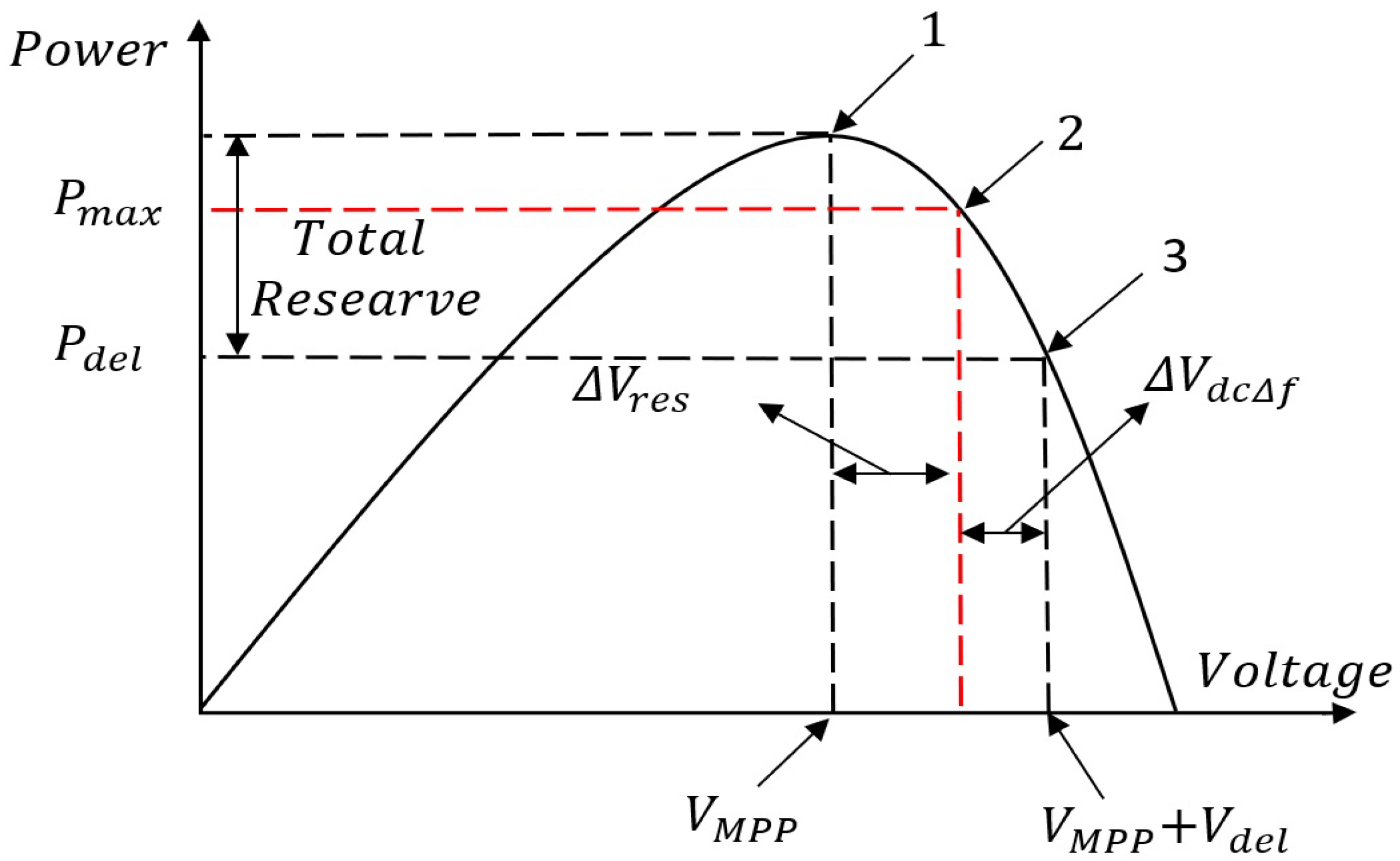
32] is one in which a few systems work away from the MPPT point to provide for a margin of available reserve power. In
Figure 4, how de-loading provides a cushion for active power-sharing is represented. PV arrays can maintain some reserve power by increasing
by voltage
.
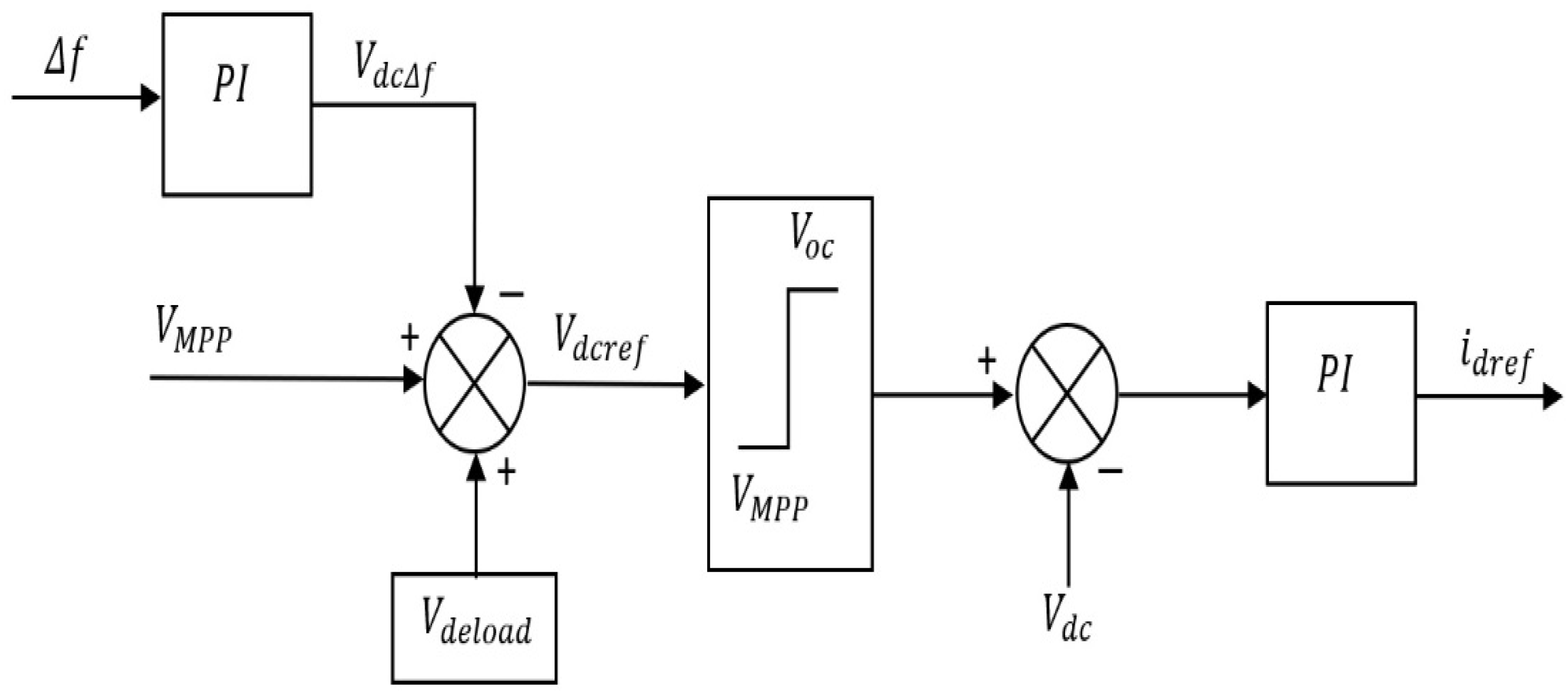
Until the system’s frequency deviates from its nominal value, this reserve power will not be released. A control signal proportional to the frequency deviation
is added to the DC reference voltage under these conditions. In
Figure 5, it is clear that the change in the direct current
, i.e., output power of a PV depends on the
value and the frequency deviation, as demonstrated by Eq. (7).
Figure 4 also shows how the PV voltage is maintained at point 3 to keep some reserve power. When the system frequency decreases, a control signal related to the frequency deviation reduces the PV voltage and makes it operate at point 2. The PV voltage is then forced to operate at a point away from the MPPT one by using the deloading technique so that a
is available in the system. This reserve is used to attribute the inertial response to the PV generator to share the active power when an active power change occurs in the network. How much active power can be shared depends on the reserve available in the system. In de-loaded condition, if
is the available reserve:
where
is the power output at the MPPT point and
the power injected into the grid. The change in the active power load triggers the BESS controller to change the frequency of the network. This can be compensated by making use of the reserve as:
2.2.2. DFIG-connected Wind Power Generator
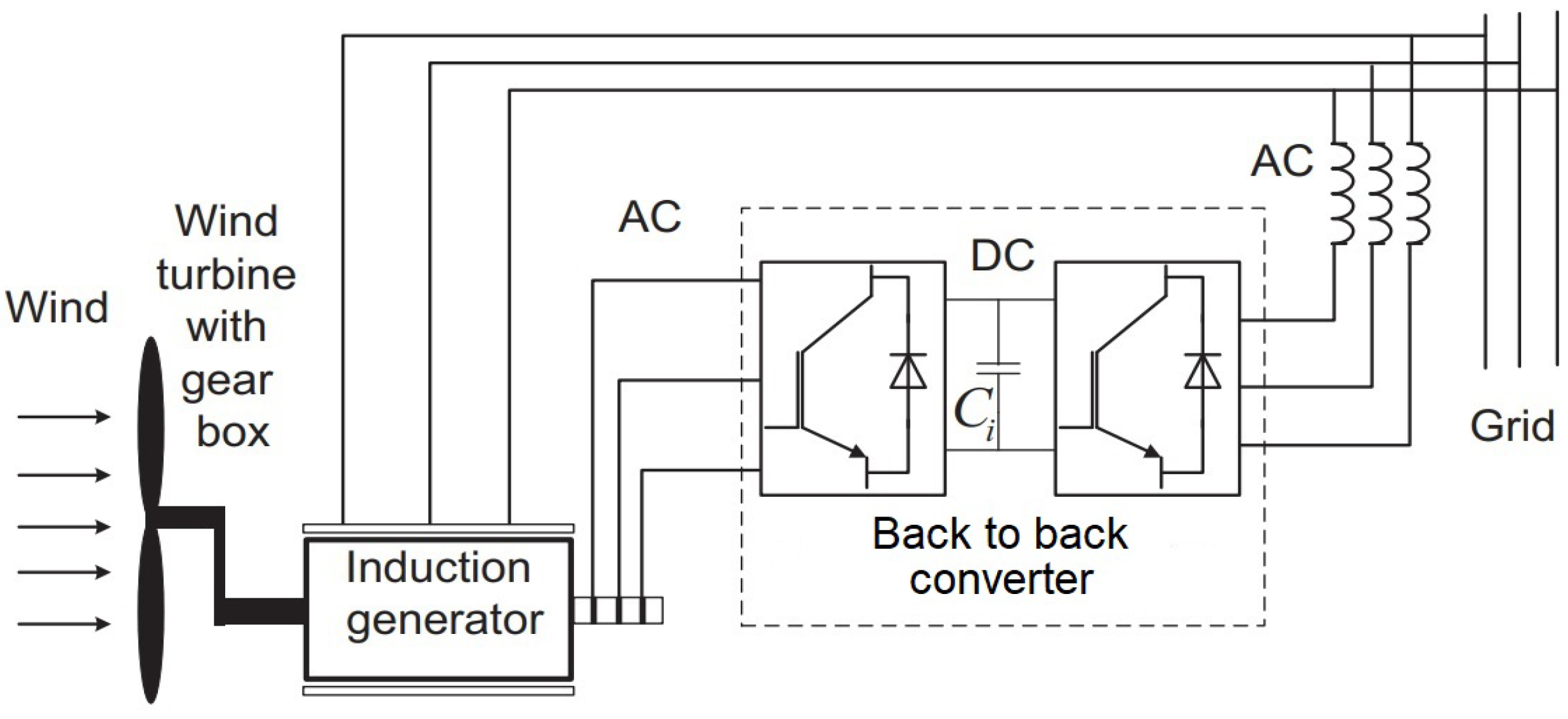
Figure 6 shows how wind turbines are typically coupled with a DFIG to transform wind energy into electrical power. Firstly, its wind blades create a mechanical torque in the rotor shaft of the induction generator. Then, a set of Back to Back converters is fed from the grid to the induction generator to, control the generator’s real and reactive power outputs. [
25].
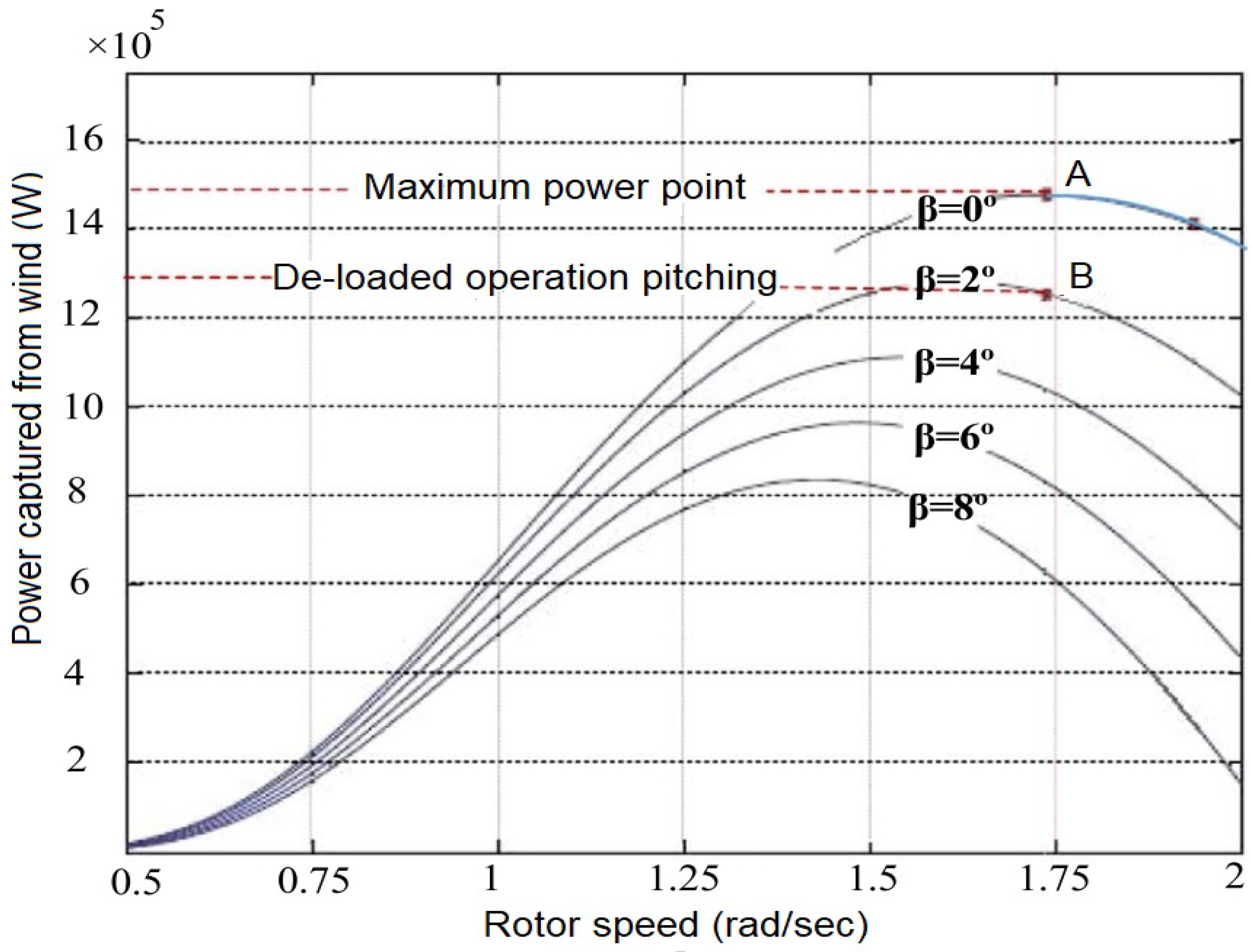
Optimal power extraction curves are used to design wind turbines from an economic standpoint. As a result, it does not participate in power-sharing or frequency regulation. Therefore, the system must have adequate reserve capacity to handle any frequency variations. De-loading is a new technique for ensuring a reserve margin by altering the wind turbine’s operating point from its optimal power extraction curve to a lower power level. De-loading can be achieved by increasing the blade’s angle. In
Figure 7, the power-rotor speed curves of a DFIG wind turbine running at point A under different pitch angles are shown. The pitch angle controller increases the angle of the wind turbine’s blades and moves the operating point from A to B despite any variation in the rotor’s speed.
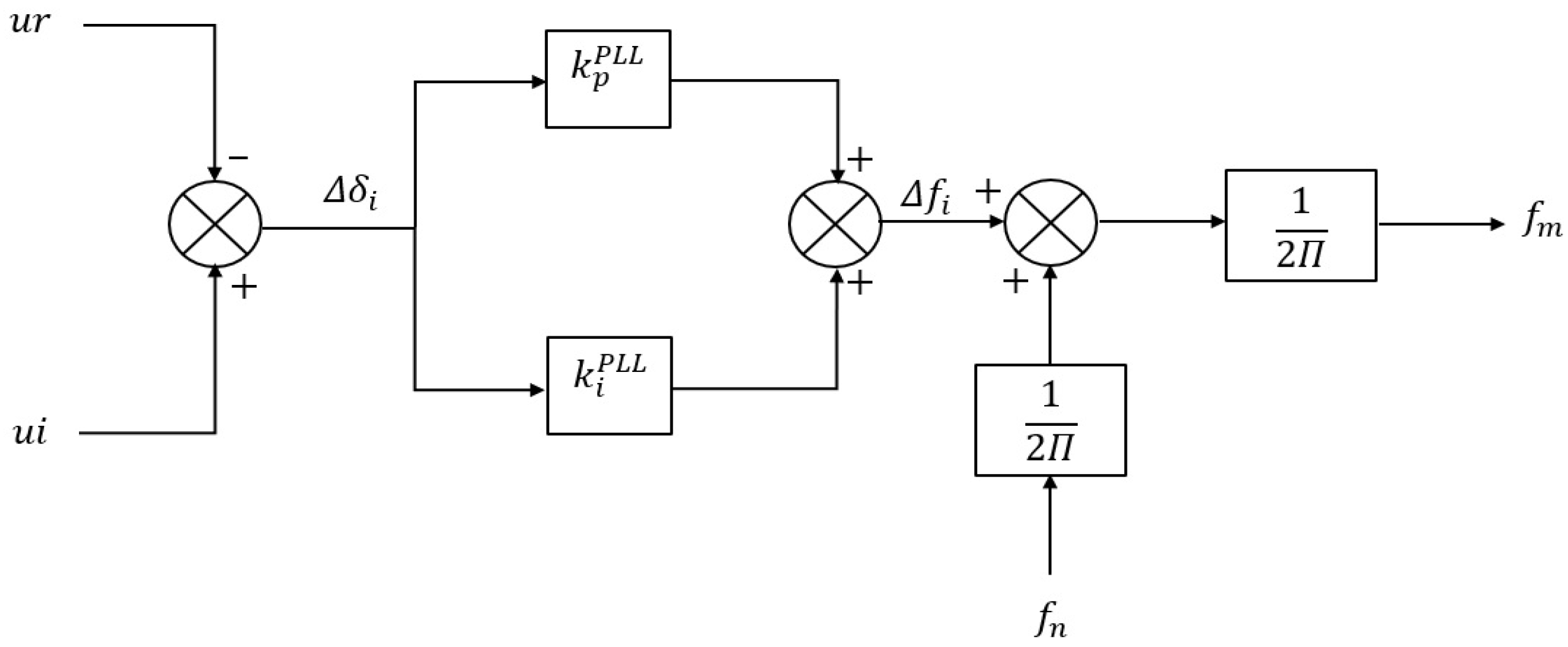
2.3. PLL
PLLs are frequently used for synchronization and controller functions. They can also be used for frequency-modulated signals[
34]. The phase-locked loop element measures the frequency and phase of a voltage in the system.
Figure 8 shows the PLL block diagram used in the DigSILENT Power Factory software[
35].
DIgSILENT PowerFactory is a program designed to analyze transmission, distribution, and industrial electrical power systems. The main objective of the software is to plan and optimize operations. It is designed as an advanced integrated and interactive software package for the electrical power system and control analysis. The accuracy and validity of Power Factory’s results have been confirmed by many organizations involved in the planning and operation of power systems worldwide[
35].
From
Figure 8 we can see the block diagram of the PLL to measure the frequency of the network.
It can be seen that the dynamics of the PLL for measuring the frequency of the network is:
where
and
are the proportional and integral coefficients of the PLL, respectively,
denotes frequency change while
changes the angle at the i-th bus. In this paper. as the value of
is chosen as almost zero, Eq. (10) can be written as:
2.4. Observations
All the DER units are connected to the PV bus. So, there is an initial active power set-point for all DER units. However, all the DER units are capable of changing the active power set-point if there is any frequency deviation in the network to restore the system frequency to nominal value.
The synchronous generator connected to the main grid balances the power from the power stored in the rotating inertia, resulting in a change in frequency in the network. As there are no synchronous generators connected to the network as per
Figure 1, so there is no change in frequency in the network. The BESS is connected at slack bus no 1 through a grid-forming inverter. So, any active power demand change in the network will be balanced by BESS. All other connected DER units will not participate in the power sharing and there is a necessity to implement a new controller to make sure all other DER units are participating proportionally.
3. Proposed power sharing
The load-sharing method proposed in this paper is designed to operate in the absence of a synchronous generator, where changes in inertia directly impact frequency. In such a scenario, the absence of a synchronous generator means that changes in load demand won’t lead to frequency variations in the network. To address this, the grid-forming DER unit is assigned the responsibility of inducing frequency changes in response to variations in power demand. All other grid-following inverters then utilize the frequency changes initiated by the grid-forming DER unit as feedback to ensure proportional power sharing.
There is no frequency change in the network as there is no synchronous generator connected to it. In this proposed controller, the system utilizes the deviation of the frequency as a control variable. This essentially conveys information to the local controller regarding the consumption/generation balance of the grid. However, the frequency change in the network is facilitated by the grid-forming inverter connected to the BESS, depending on the demand load changes in the network. The alteration in active power demand is measured by the active power measurement device connected to the slack bus (bus-1). The new frequency is then set by the converter connected to the BESS, following the equations (
12) and (
13) presented in sub-section 3.1. The connected DER units function as grid followers, responding to frequency changes in the network to ensure power sharing among the DER units. Phase-Locked Loops are connected to all DER units to measure the new frequency and frequency deviation, serving as control variables for the new active power set point of the DER units. The subsequent sections provide detailed information on the proposed controllers.
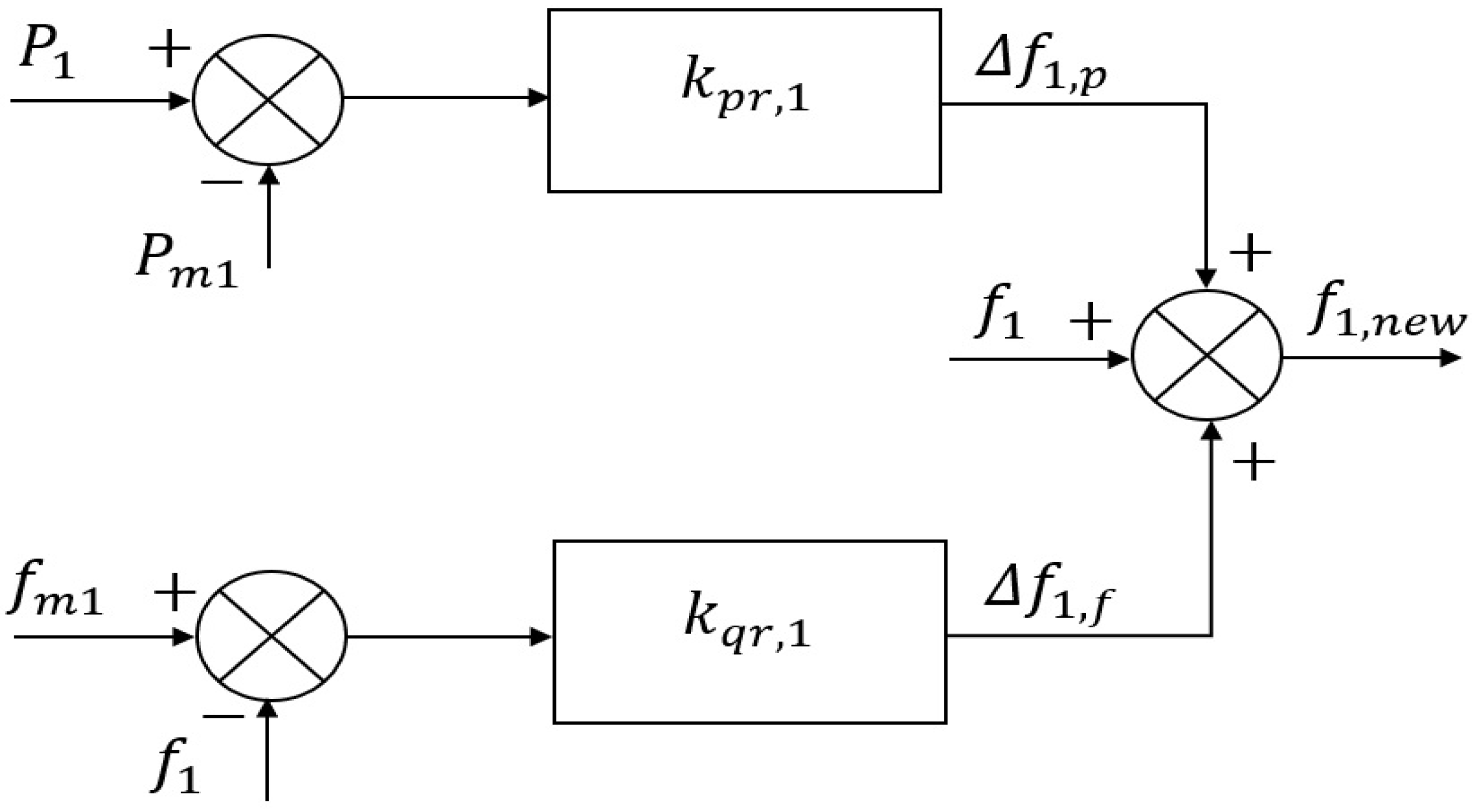
3.1. BESS
The main purpose of a BESS is to provide a fast frequency regulation response and share the load burden of conventional power generation units.
Figure 9 shows the proposed control structure of the grid-forming inverter connected to the BESS.
As per this figure, the new frequency is defined by:
where
is the new reference frequency of the BESS,
reference frequency,
the measured frequency,
proportional droop co-efficient of BESS for a frequency change,
proportional droop co-efficient for its power sharing,
measured output power and
reference output
As, in Eq. (12) there are two droop co-efficient
and
, with a change in load the frequency can be changed and, at the same time, power can be shared. In a normal mode of operation, when all the connected DER units are capable of sharing the active power, the BESS doesn’t share and
. Nevertheless, when the DER units are capable of sharing the power with a change in load, the BESS changes the value of
. In this paper, the non-active power-sharing mode of a BESS is emphasized and a small-signal analysis is performed based on it. Therefore, Eq. (12) can be simplified to:
Furthermore, the VSI connected to the slack bus acts as a synchronous generator and changes its voltage frequency according to changes in loads. This is almost the same as the inertial response of the synchronous generator which can ensure proper sharing of the active power among the DER units. All the connected DER units respond to frequency changes in the network; for example, the frequency will decrease if the DGs supply more than the load demand of the network and vice-versa. Later, the grid-following inverters respond to frequency deviations and ensure power-sharing at the same time. The new frequency generated by the VSI of the BESS is measured by the PLLs of all the grid-following DER units connected to the network. As the frequency changed by the BESS will be the same in all the buses and no other DER units change the frequency of the network, .
Please note that we assume that the BESS has the capability to adjust its State of Charge (SOC) based on changes in power demand. We acknowledge the importance of considering the dynamic behavior of SOC in the power management strategy, especially when reaching lower or upper limits, which will be explored in future work.
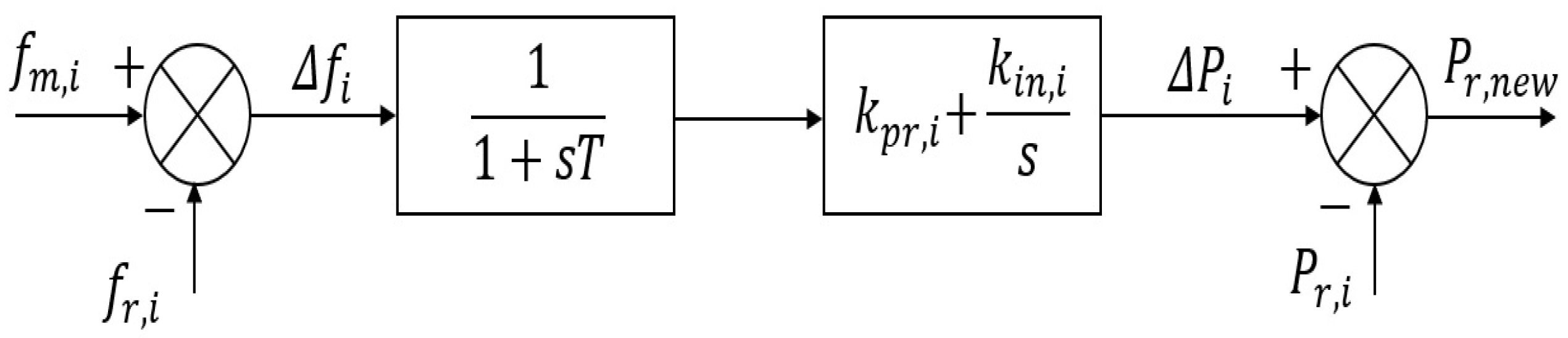
3.2. DER units
All the connected DER units are considered dispatchable and grid following. Therefore, they have their own local controllers to share the active and reactive powers. The control structure of all these units is shown in
Figure 10.
Then, the equation for active power sharing is:
where,
is a change in the active power set-point,
represents the measured change of frequency at the i-th bus,
is the proportional droop coefficient of the DER unit at the i-th bus,
is a different coefficient related to the DER unit at the i-th bus, and
T is the time coefficient.
Therefore, the active power set points of the DER units change as per Eq. (14). To ensure proper power sharing according to the power ratings of DER units, the droop coefficients can be selected as [
7]:
where
and
are the rated power of the DER units connected to m-th and n-th buses, respectively.
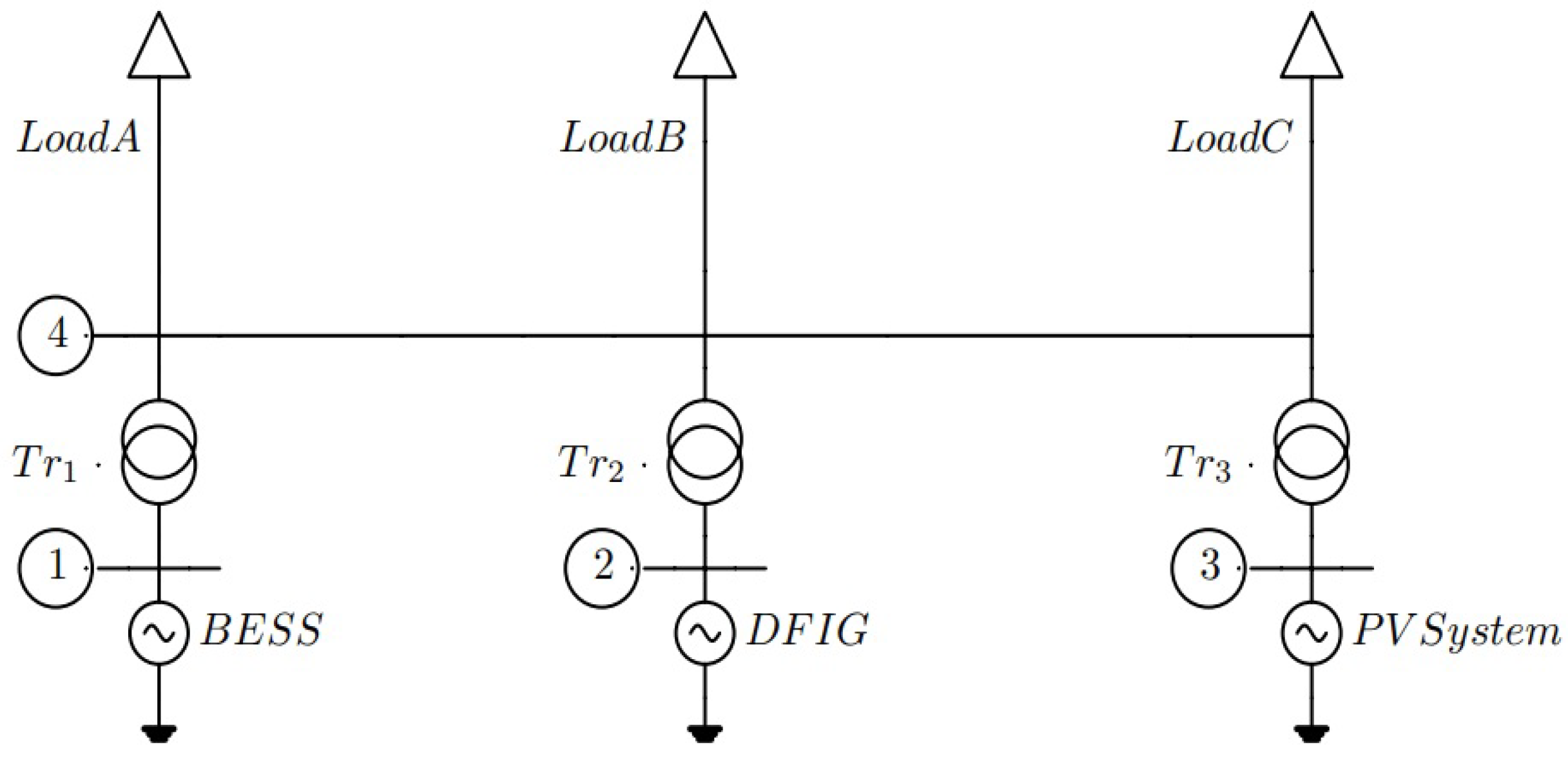
In this paper, the proposed algorithms are implemented in a 9-bus network in which there are a BESS and 2 off DER units (DFIG -connected wind power generator and PV system). Their inverters connected to the BESS are grid -forming whereas the inverters connected to DER units are grid-following. All the controller’s coefficients are evaluated in section 3.
5. Simulation results
In this section, a new droop-based controller for an islanded microgrid that can share power proportionally during load changes is implemented and evaluated. Different case studies are conducted on L-type 4-bus and RL-type 9-bus systems to verify the effectiveness of the designed controller for an islanded microgrid described in the below subsections.
5.1. L-type 4-bus system
The L-type 4-bus microgrid test system used in this research is shown in
Figure 23.
A BESS of 4.0 MVA is connected to node 1, a wind generator of 1.0 MVA to node 2, and a solar panel of 0.5 MVA to node 3, with the common resistive Load A, B, and C sharing node 4. This microgrid is connected to the main grid via a 69/20 kV substation at node 4. In this simulation, it is operated in a standalone mode, with both the solar system and wind power generator operated in a deloading mode. Also, the solar radiation, temperature of the PV system and wind speed of the wind generator remain unchanged. The line data and Initial values of the DFIG, PV system, BESS and loads are shown in
Table 5 and
Table 6, respectively.
The initial calculated values of the known and unknown variables after a load flow analysis are shown in
Table 7.
Node 1, the BESS is connected, is the slack bus of the network with it initial voltage and angle and , respectively. Nodes 2 and 3 are PV buses with initial voltages . The DFIG is connected to node 2 and the PV system to node 3 with initial active powers of and , respectively. The Loads-A, B and C are connected to PQ bus-4 with their initial active and reactive powers , , , and , , respectively.
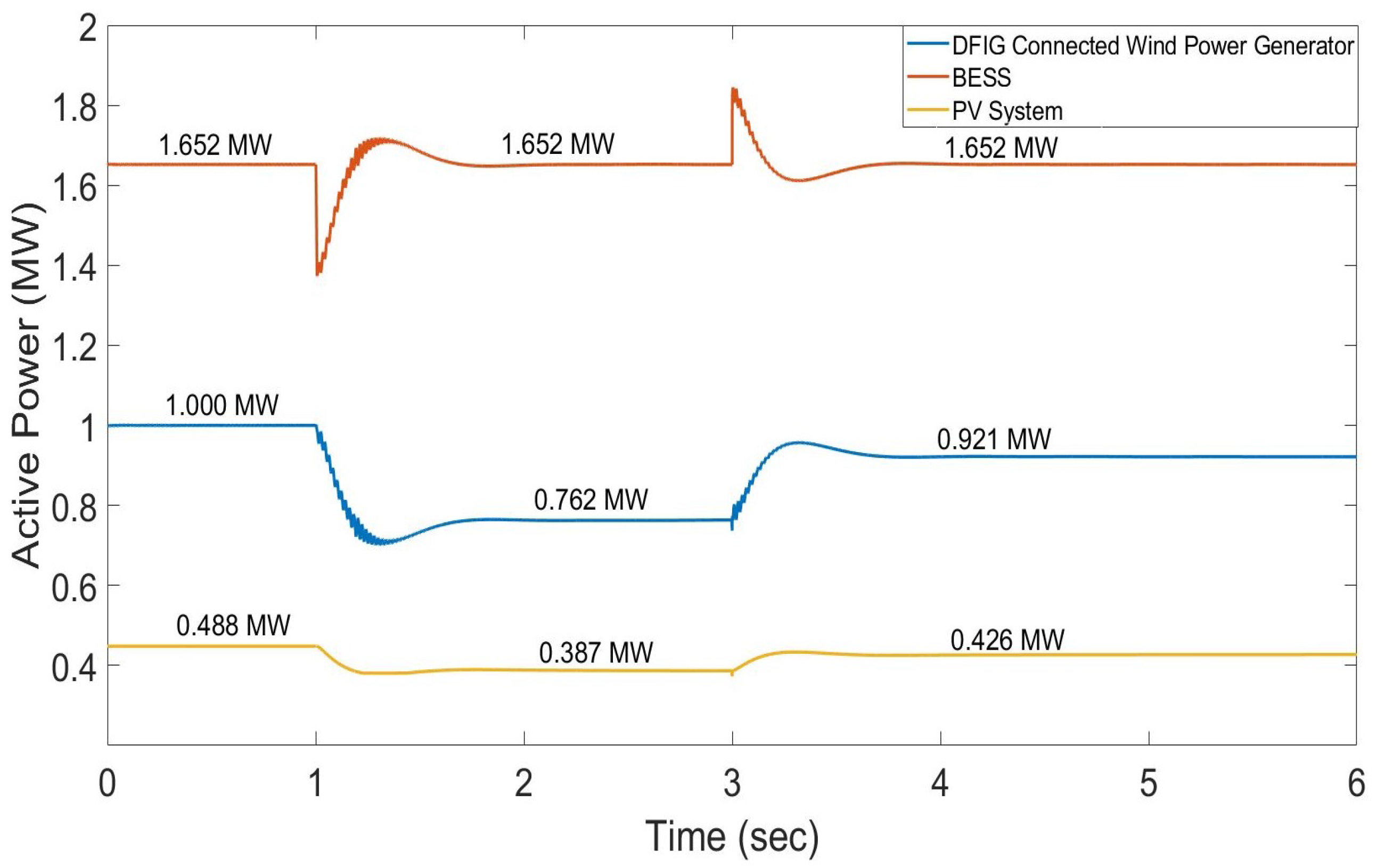
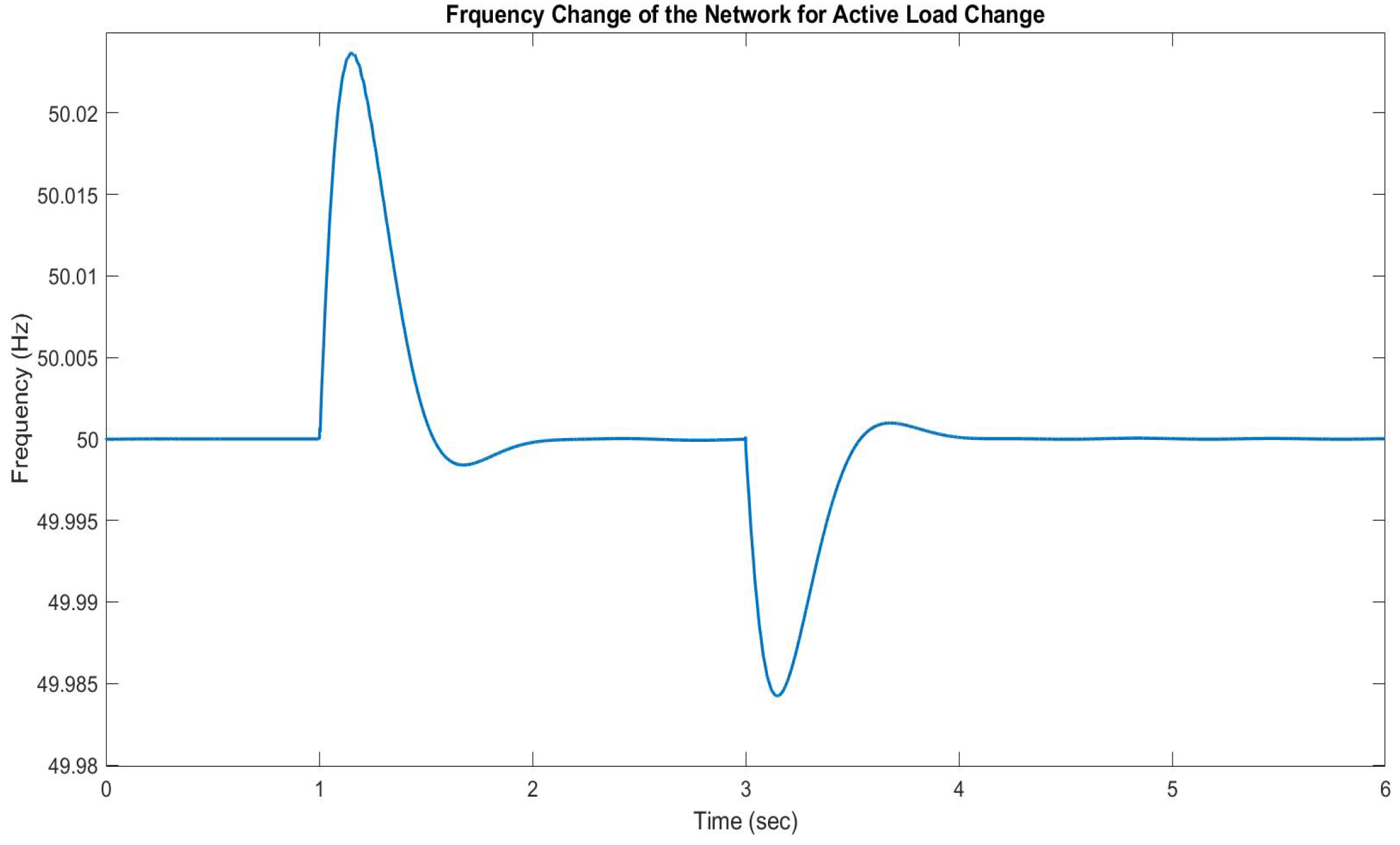
Load B is disconnected from node 4 at 1 sec to check the performance of the controllers implemented in the DER units and BESS. Before that event, load C was disconnected from node 4. In
Figure 24, how the DER units share the active power is shown.
It can be seen that the BESS initially shares the unbalanced active power as it is connected to the slack bus. Its implemented controller then changes the frequency of the network as per the control algorithm. This change is measured immediately by the PLLs connected to the DER units and used as feedback to share the power. The PV system and wind generator use the deloading technique to change the active power set point.
It is clear that the wind generator and PV system run with MPPT and, maintain maximum active powers of 1.0 MW and 0.448 MW, respectively. The BESS supplies the remaining active power of 1.652 MW to keep the total supply and load unchanged. When, at
, resistive load B (0.3 MW) is disconnected from node 4, the BESS immediately reduces its active power set-point to keep the network stable and, at the same time, it increases the network’s voltage frequency, as shown in
Figure 25. The PLLs connected to the DER units measure this change and sends control feedback to the DER controllers. In
Figure 24, it can be seen that the wind generators and PV systems change their active power set points which, within less than
, are 0.762 MW and 0.387 MW, respectfully. The BESS returns to its original one of 1.652 MW and the network’s voltage frequency returns to its nominal value of
within
and keeps the network stable.
At
, load C (0.2 MW) is connected to node 4 to determine how the controllers respond to the addition of an active load. As shown in
Figure 24, the BESS initially increases its active power set point by 0.2 MW and decreases its voltage frequency. Both the wind generators and PV systems operate away from MPPT as they have reserve power and can increase their active power set points according to a change in the network’s voltage frequency. In
Figure 24, it can be seen that both the new active power set points of the wind generator and PV system are 0.921 MW and 0.426 MW, respectively.
The control parameters used for the controllers of BESS, wind generator and PV system are shown in
Table 8.
5.2. RL-type 9-bus system
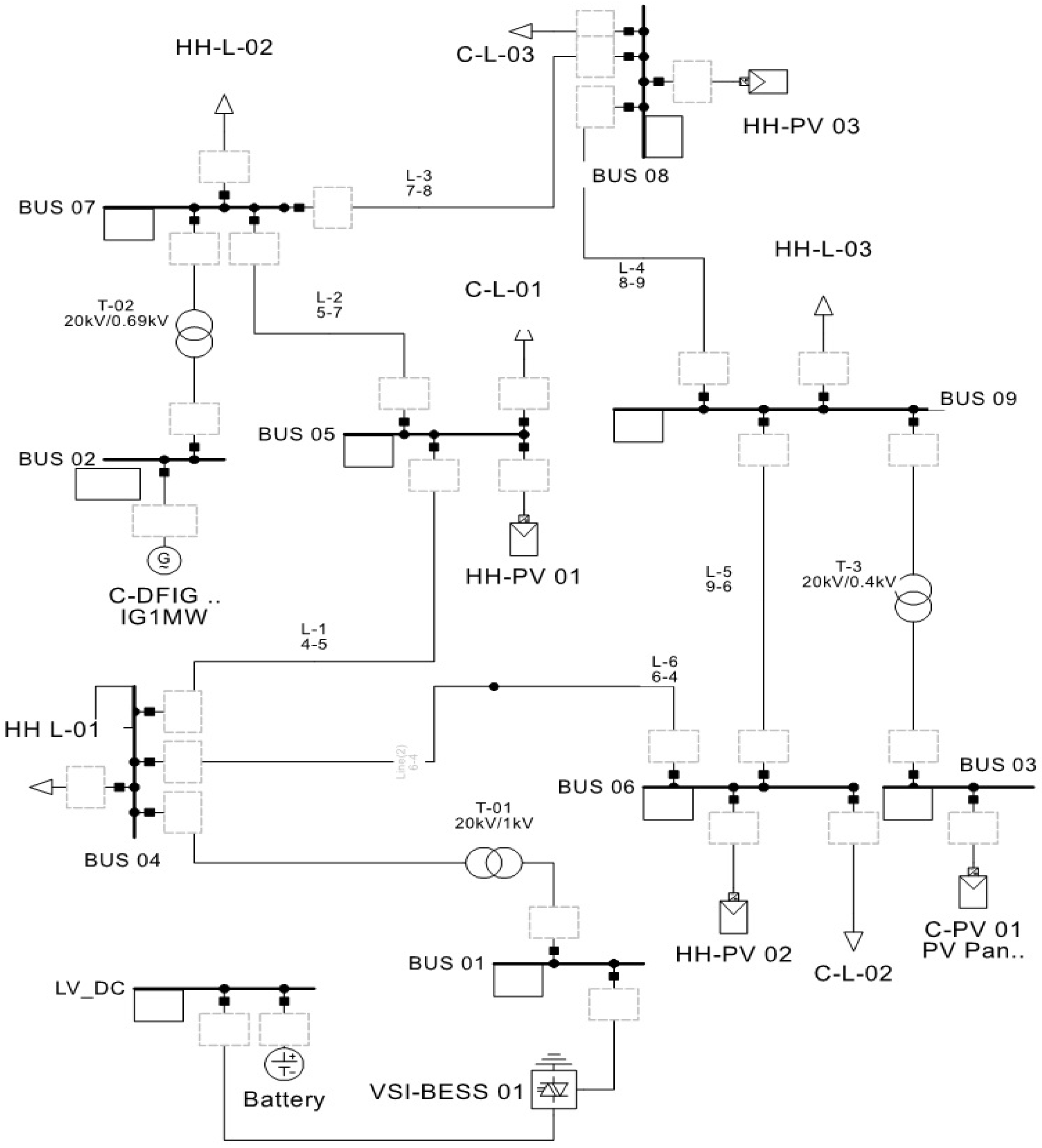
To check the performance of the proposed controller in a medium voltage network, the modified RL-type benchmark microgrid test system shown in
Figure 26 is used. The system consists of a BESS, two commercial DER units, three household DER units, three commercial loads, and three household loads. The nominal capacities of BESS, commercial wind generator and commercial PV system are 4.0 MVA, 1.0 MVA and 0.5 MVA, respectively. This microgrid is connected to the main grid via a 69/20 kV substation at node 8. All the initial values of DFIG, PV system, BESS, and loads are given in
Table 9.
In this simulation, the microgrid is operated in a stand-alone mode, and both the PV system and wind power generators are operated in a de-loading mode. It is also considered that the level of solar radiation and temperature of the PV system as well as the wind speeds of the generators remain unchanged.
The line parameters of the network are shown in
Table 10. The bus voltages and their angles, as well as real and reactive powers obtained from the load flow analysis, are shown in
Table 11.
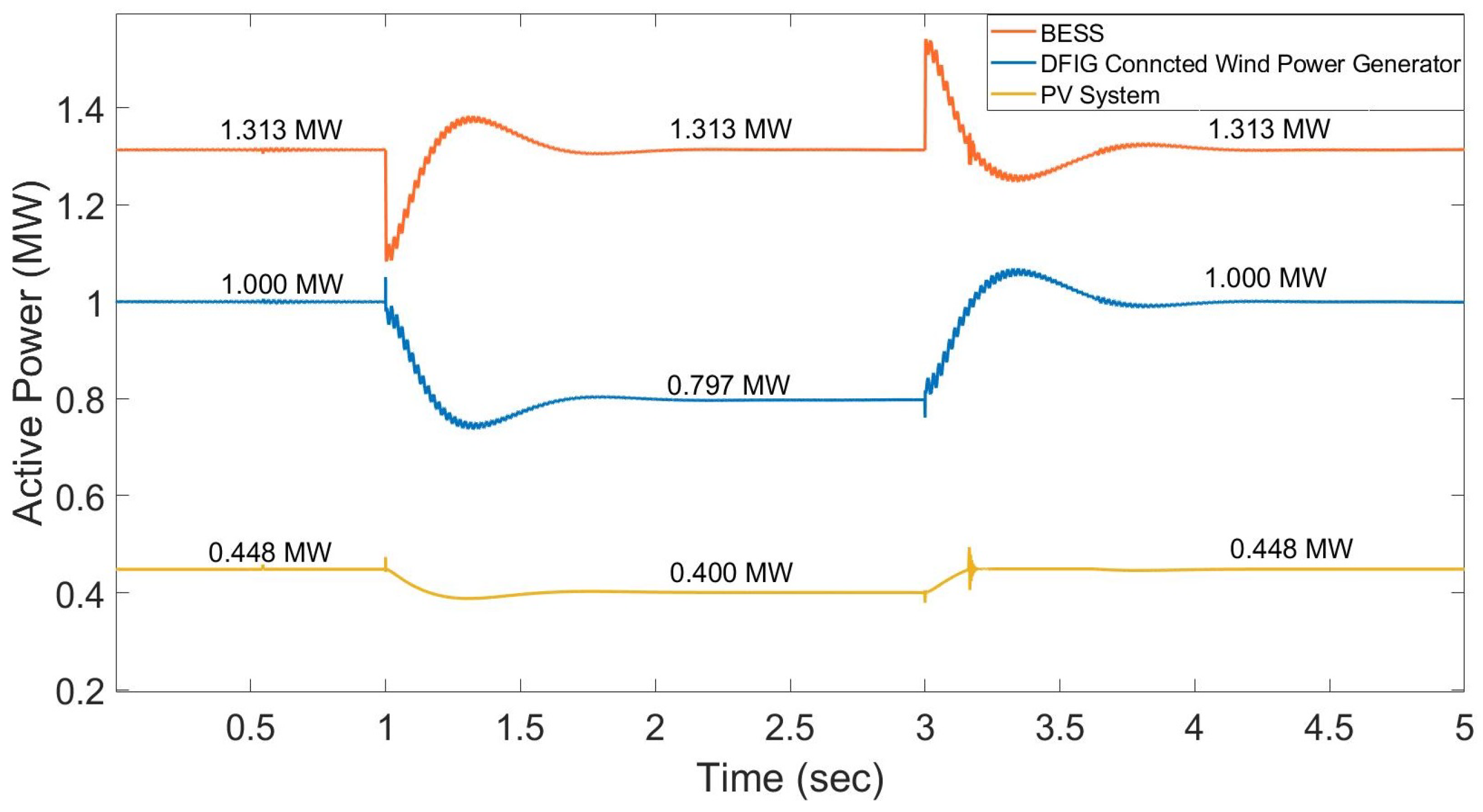
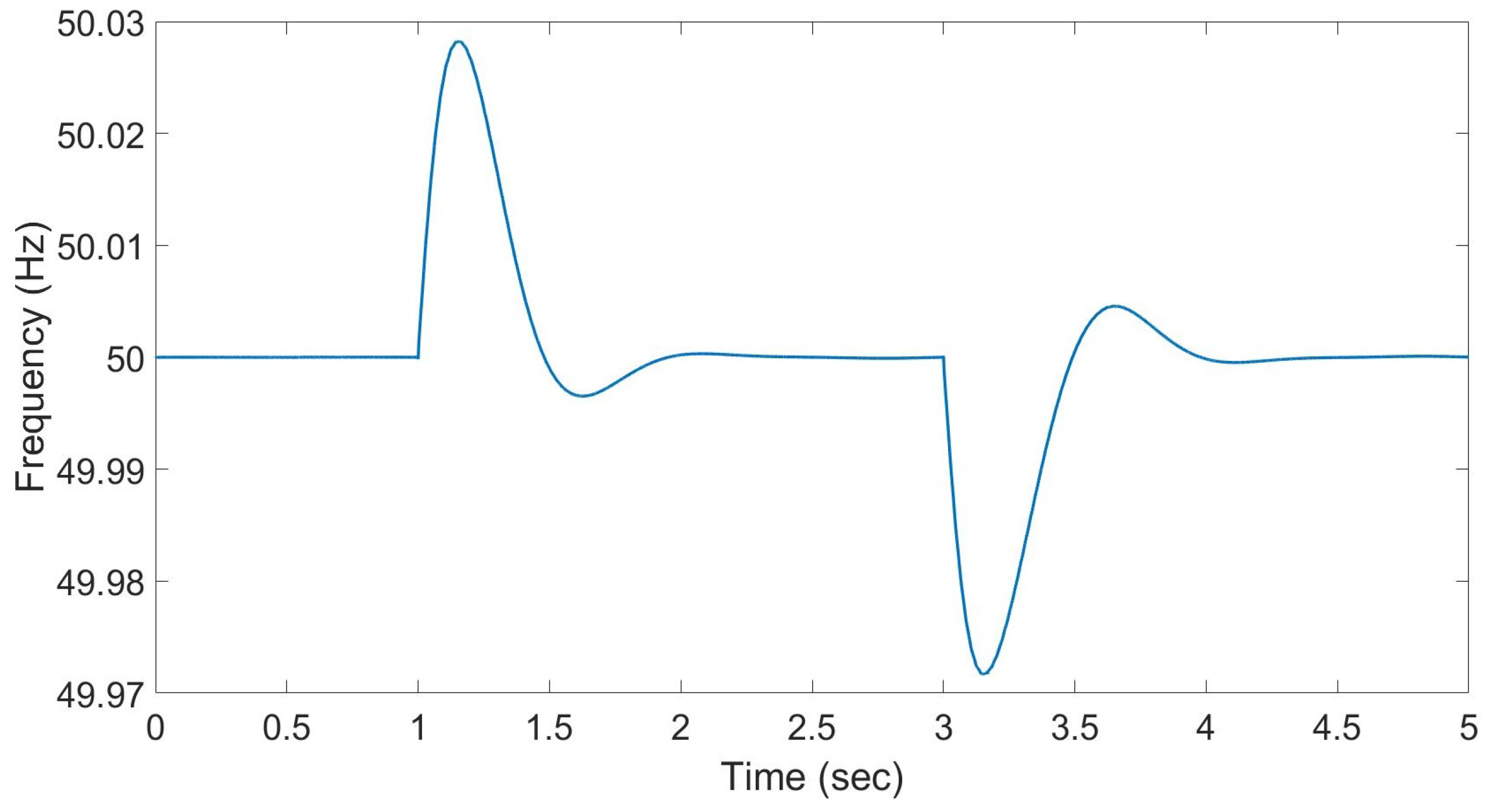
In
Figure 27, it is evident that the wind generators and the PV systems run with MPPT, which maintains their maximum active powers of 1.0 MW and 0.448 MW respectively. The BESS supplies the remaining active power of 1.33 MW to maintain the total amount of supply and load. When, at
, the resistive load C-L-02 (0.25 MW) is disconnected from node 6, the BESS immediately reduces its active power set point to keep the network stable while simultaneously increasing the network voltage frequency as shown in
Figure 28.
The PLLs connected to the DER units measure this change in frequency and send control feedback to the DER controllers. The wind generators and PV systems adjust their active power set points, as shown in
Figure 27. Within less than
, they reach new set points of
and
, respectively, while the BESS returns to its original set point of
. The network voltage frequency returns to its nominal value of
within
and keeps the network stable, as illustrated in
Figure 28.
The load C-L-02 (0.25 MW) is connected again to node 6 at
. The BESS initially increases its active power set-point by 0.25 MW and decreases its voltage frequency. Both the wind generators and the PV systems operate away from MPPT; as shown in
Figure 27. They have reserve power and can increase their active power set-points according to changes in the network’s voltage frequency. Both these new active power set points return to their maximum active powers of 1.0 MW and 0.448 MWrespectively.
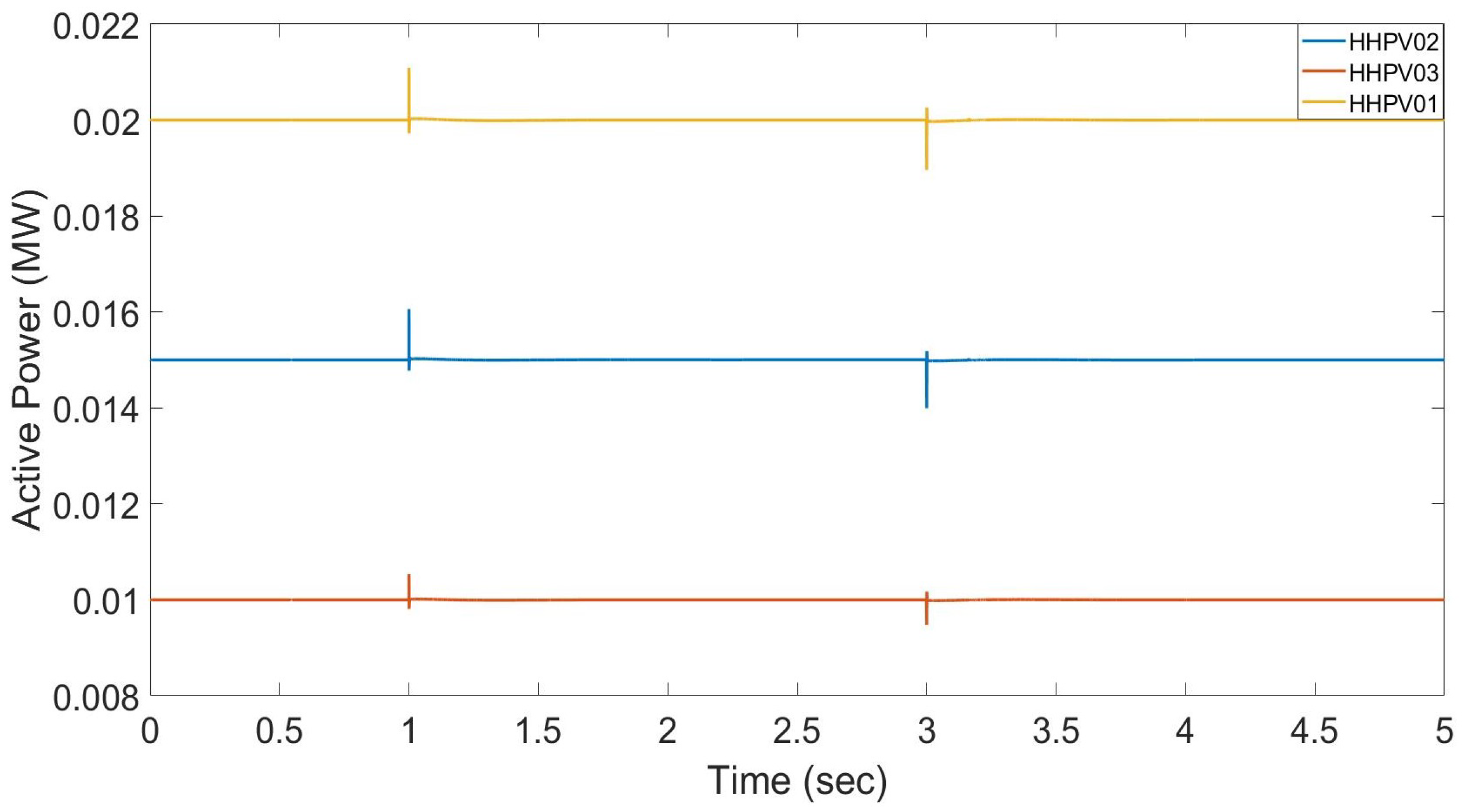
With a change in the voltage frequency, there is no impact on the household PV systems running with MPPT which maintains their maximum active power because no controllers are implemented for active power-sharing (
Figure 29).
The control parameters used for the controllers of the BESS, wind generators and PV systems are shown in
Table 12.
5.3. Power-sharing mode of BESS controller
The BESS’s proposed controller can also switch its operational mode to ’sharing’. The BESS is capable of sharing the active power if any change in it occurs. To test the performance of the proposed controller in the ’sharing’ mode, the L-type 4-bus microgrid test system shown in
Figure 23 is used.
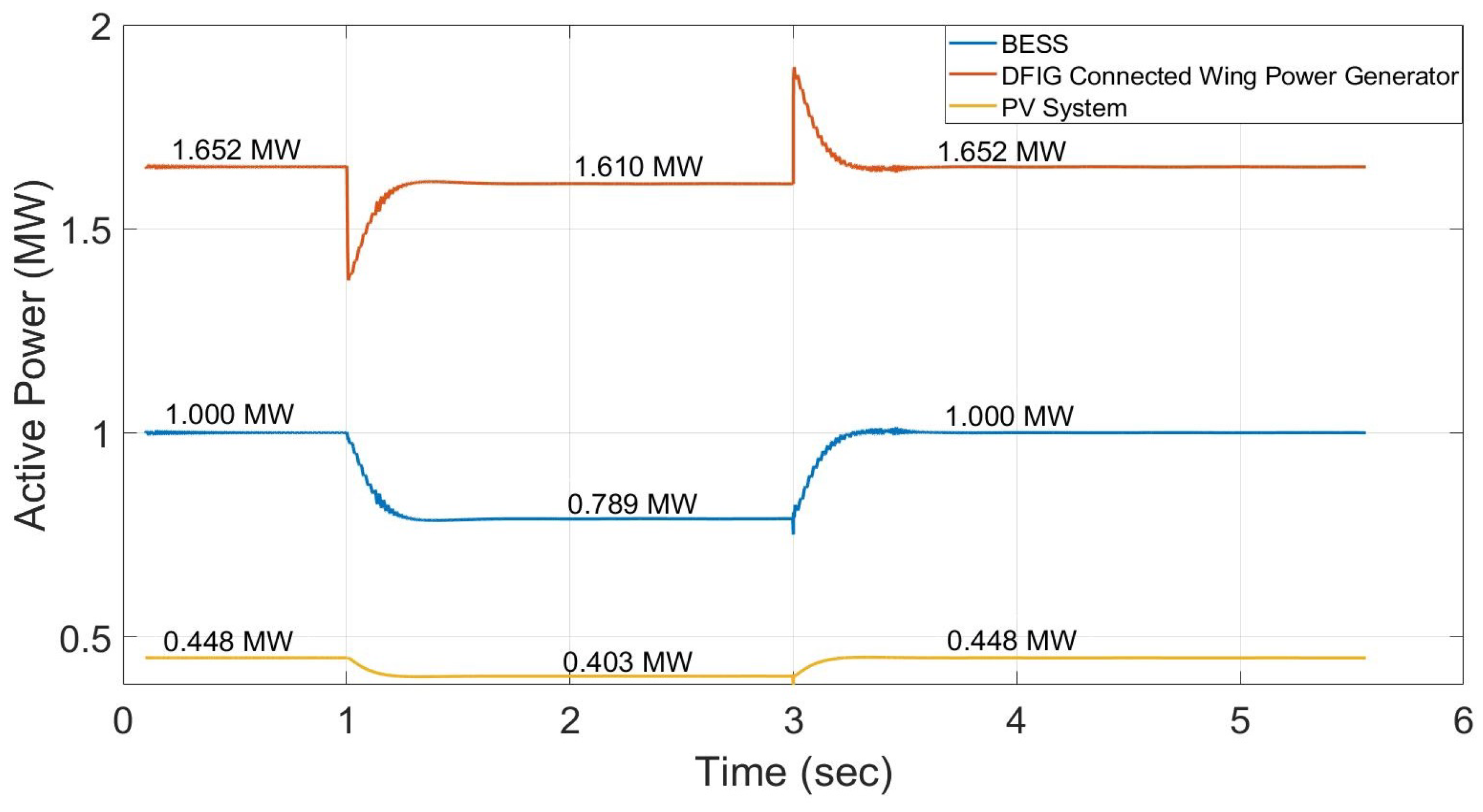
Load B is disconnected from node 4 at 1 sec to check the performance of the controllers. How the DER units and BESS share is shown in Figure 30.
In which it can be seen that the BESS initially shares the unbalanced active power as it is connected to the slack bus. The controller implemented at the BESS then changes the frequency of the network according to the control algorithm. A change in the network’s frequency is measured immediately by the PLLs connected to the DER units and BESS. The controllers use this frequency deviation as feedback to share the power. Both PV systems and wind generators use the deloading technique to change their active power set-points while the BESS uses a battery bank to change its own
The wind generators and PV systems are run with MPPT which maintains their maximum active powers of 1.0 MW and 0.448 MW, respectively. The BESS supplies the remaining active power of 1.652 MW to keep the total amount of supply and load unchanged. When resistive load B (0.3 MW) is disconnected from node 4 at , the BESS immediately reduces its active power set-point to keep the network stable and, at the same time, increases the network’s voltage frequency. The PLLs connected to the DER units measure the frequency changes and send control feedback to the controllers of DER units and BESS. The BESS, wind generators, and PV systems change their active power set-points, as shown in Figure 30. Then, within less than they find their new active power set-points 1.610 MW, 0.789 MW and 0.403 MW respectfully.
At , load B (0.3 MW) is connected again to node 4 to determine how the controllers respond with the addition of an active load. The BESS initially increases its active power set-point by 0.3 MW and decreases its voltage frequency (Figure 30). This is because both the wind generators and PV systems operate away from MPPT. They have reserve power and can increase their active power set-points according to changes in the network’s voltage frequency. Both their new active power set-points return to their maximum active powers 1.0 MW and 0.448 MW, respectively, and BESS to its original set-point of 1.652 MW. The control parameters used for the controllers of the BESS, wind generators and PV systems are shown in Table XIII.
6. Conclusion
While most power-sharing methods in the literature are designed for voltage source converters that cannot be considered true models of ideal sources for renewable power generation in practice, this paper demonstrates power-sharing techniques for solar and wind power generation without assuming them to be ideal voltage sources. The entire PV system model, along with its dynamic equations and DFIG wind turbine in the network, is adopted from existing literature and utilized for designing an appropriate power-sharing technique. The technique is designed to respond to changes in loads and power generation without relying on a conventional synchronous generator. An energy storage system maintains a balanced power supply and demand across the network. PLLs at each generation bus are used to calculate the local deviation from the reference voltage and frequency due to disturbances.
The stability of the system is confirmed through the developed linearized model, which determines the system’s stability margin and selects the desired gain for the proposed controller. Control parameters were initially chosen using the ZN method and further optimized to ensure proportional power sharing among DER units and the restoration of voltage frequency within a second.
Finally, the proposed control scheme is applied to a PV and wind-based microgrid test system. The results demonstrate that the proposed controller effectively shares power among renewable energy sources, restores the system frequency to a nominal value within the shortest period, and ensures network stability. Subsequently, the BESS’s "power-sharing mode" confirms that the BESS compels DER units to participate in power-sharing and can also participate if necessary.
The proposed controllers are designed and tested for medium-voltage (MV) networks with a low R/X ratio. Therefore, in future work, this algorithm will be tested on a system with a high R/X ratio, such as a low-voltage (LV) system. Additionally, a comparison with other available optimization methods will be carried out.
Figure 1.
General model of the network.
Figure 1.
General model of the network.
Figure 2.
Schematic block diagram of a PV system.
Figure 2.
Schematic block diagram of a PV system.
Figure 3.
Schematic block diagram of a PV system.
Figure 3.
Schematic block diagram of a PV system.
Figure 4.
Reserve power in de-loaded PV system.
Figure 4.
Reserve power in de-loaded PV system.
Figure 5.
Controller for de-loaded solar PV[
32].
Figure 5.
Controller for de-loaded solar PV[
32].
Figure 6.
Schematic diagram of a wind generation system with the DFIG[
25].
Figure 6.
Schematic diagram of a wind generation system with the DFIG[
25].
Figure 7.
Power rotor-speed curves for different values of pitch angle for a 1.5 MW wind turbine (wind speed: 10 m/s)[
33].
Figure 7.
Power rotor-speed curves for different values of pitch angle for a 1.5 MW wind turbine (wind speed: 10 m/s)[
33].
Figure 8.
PLL block diagram.
Figure 8.
PLL block diagram.
Figure 9.
Control structure of grid forming VSI for active power sharing.
Figure 9.
Control structure of grid forming VSI for active power sharing.
Figure 10.
Control structure for grid following inverters for active power sharing.
Figure 10.
Control structure for grid following inverters for active power sharing.
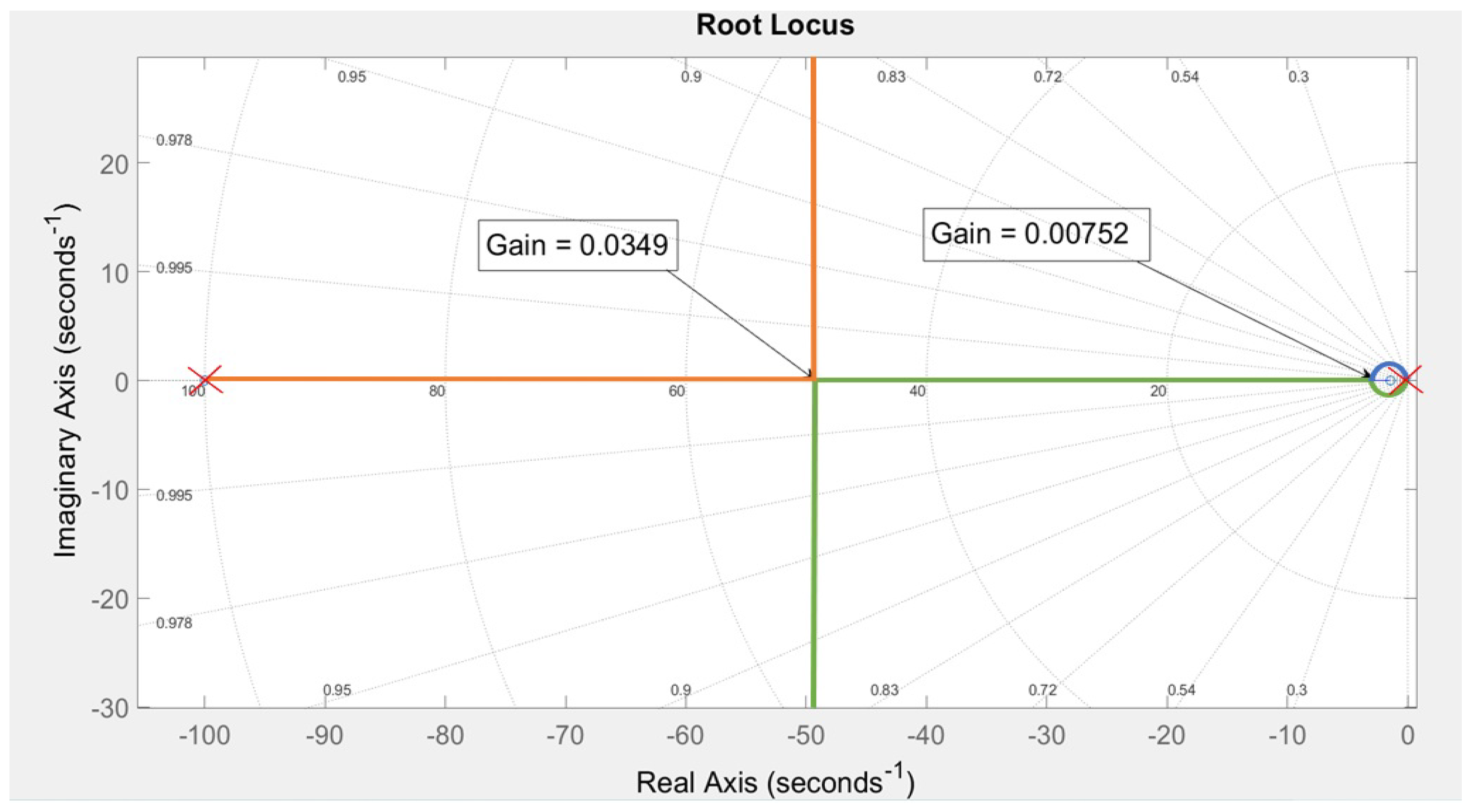
Figure 11.
Poles and zeroes map.
Figure 11.
Poles and zeroes map.
Figure 12.
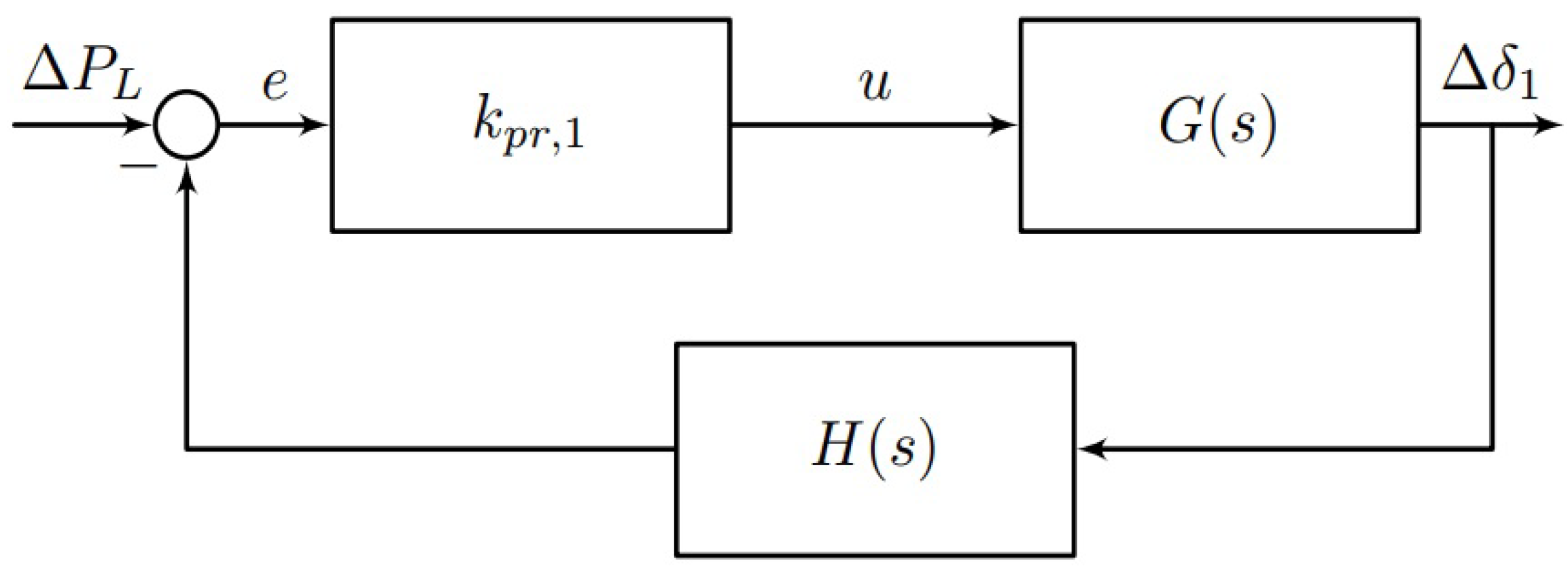
Block diagram of transfer function.
Figure 12.
Block diagram of transfer function.
Figure 14.
Frequency change with load change events.
Figure 14.
Frequency change with load change events.
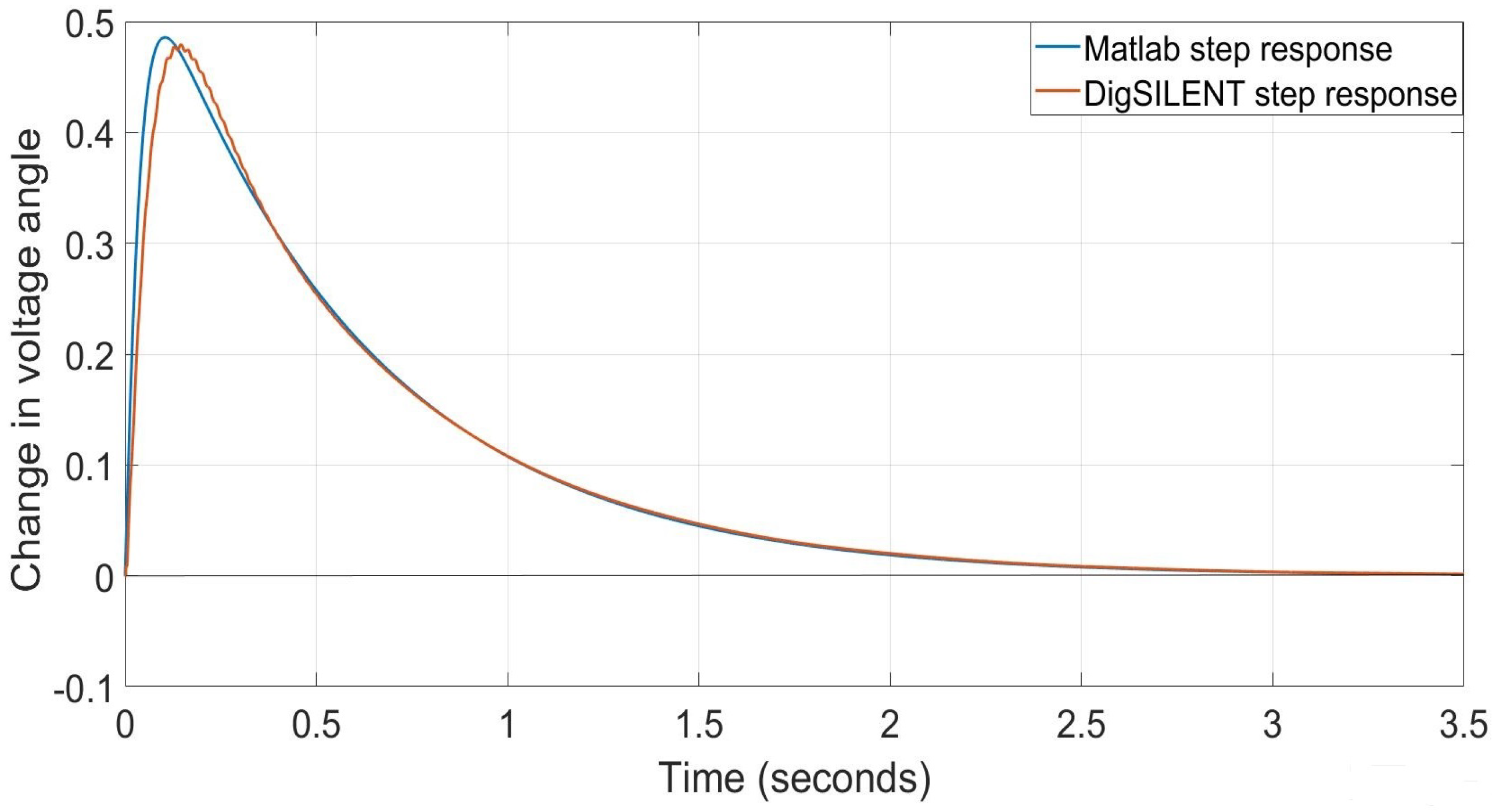
Figure 15.
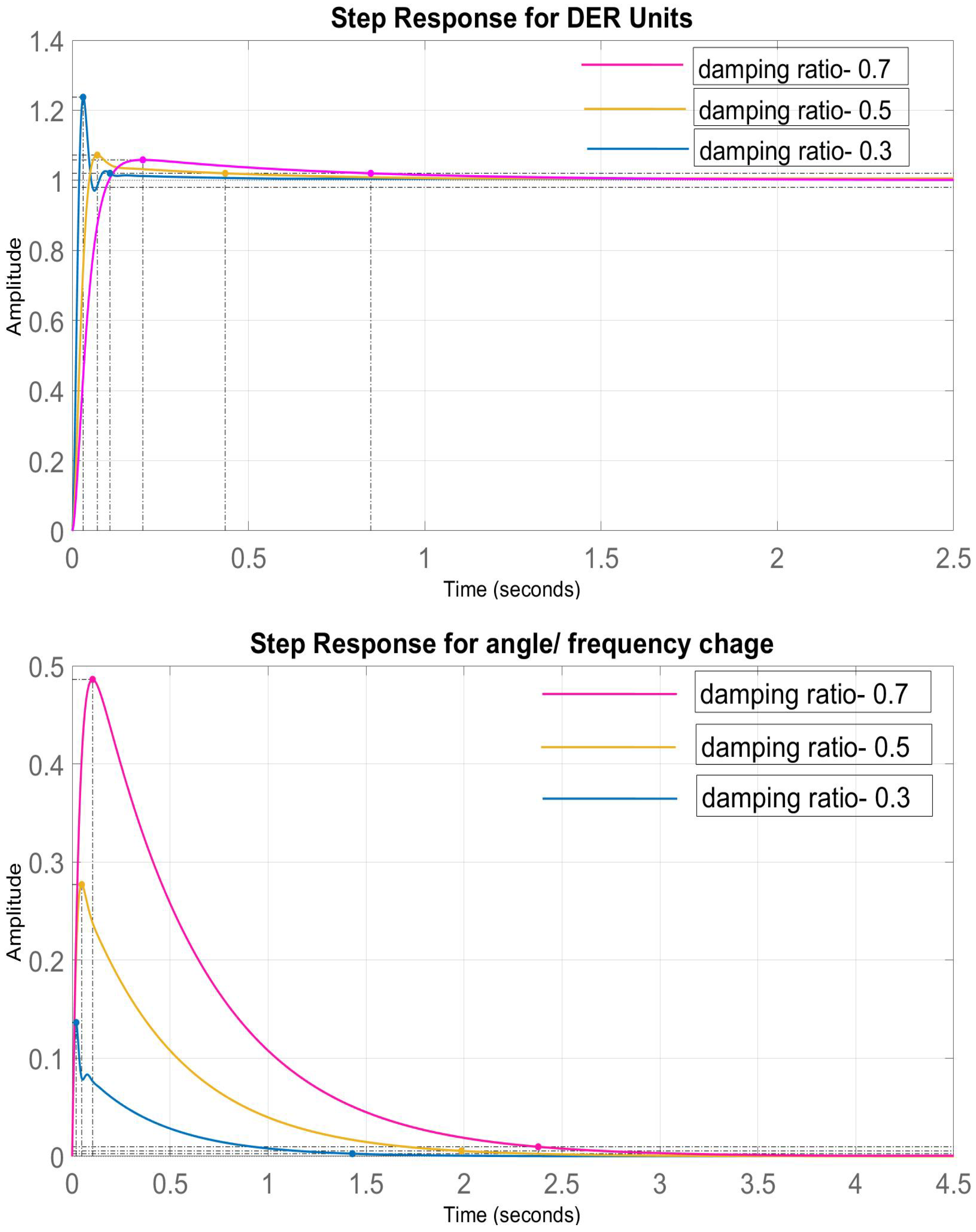
Step response for total changes in active power and power angle/ frequency by DER units.
Figure 15.
Step response for total changes in active power and power angle/ frequency by DER units.
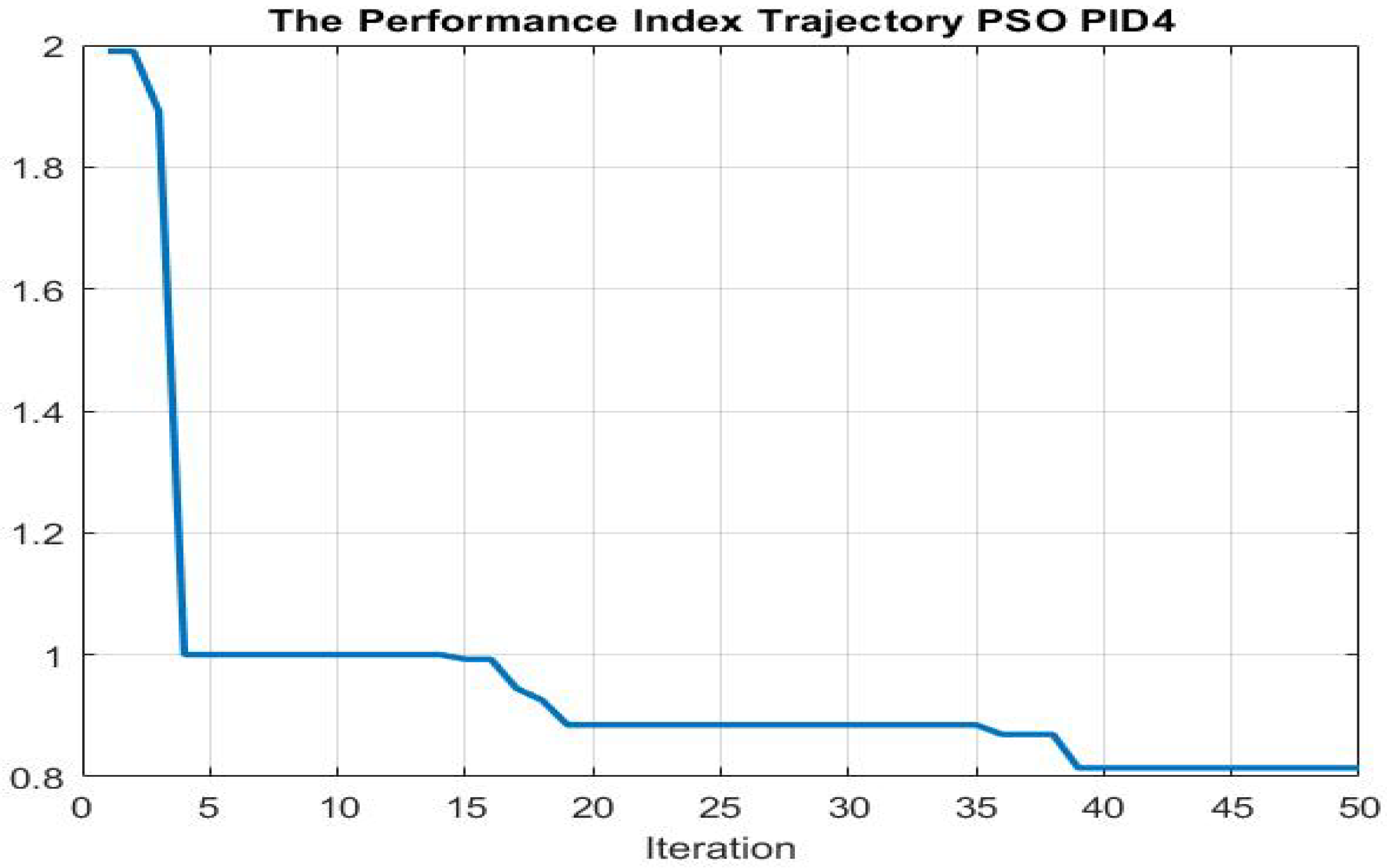
Figure 16.
Trajectory of performance index (PSO-PID4).
Figure 16.
Trajectory of performance index (PSO-PID4).
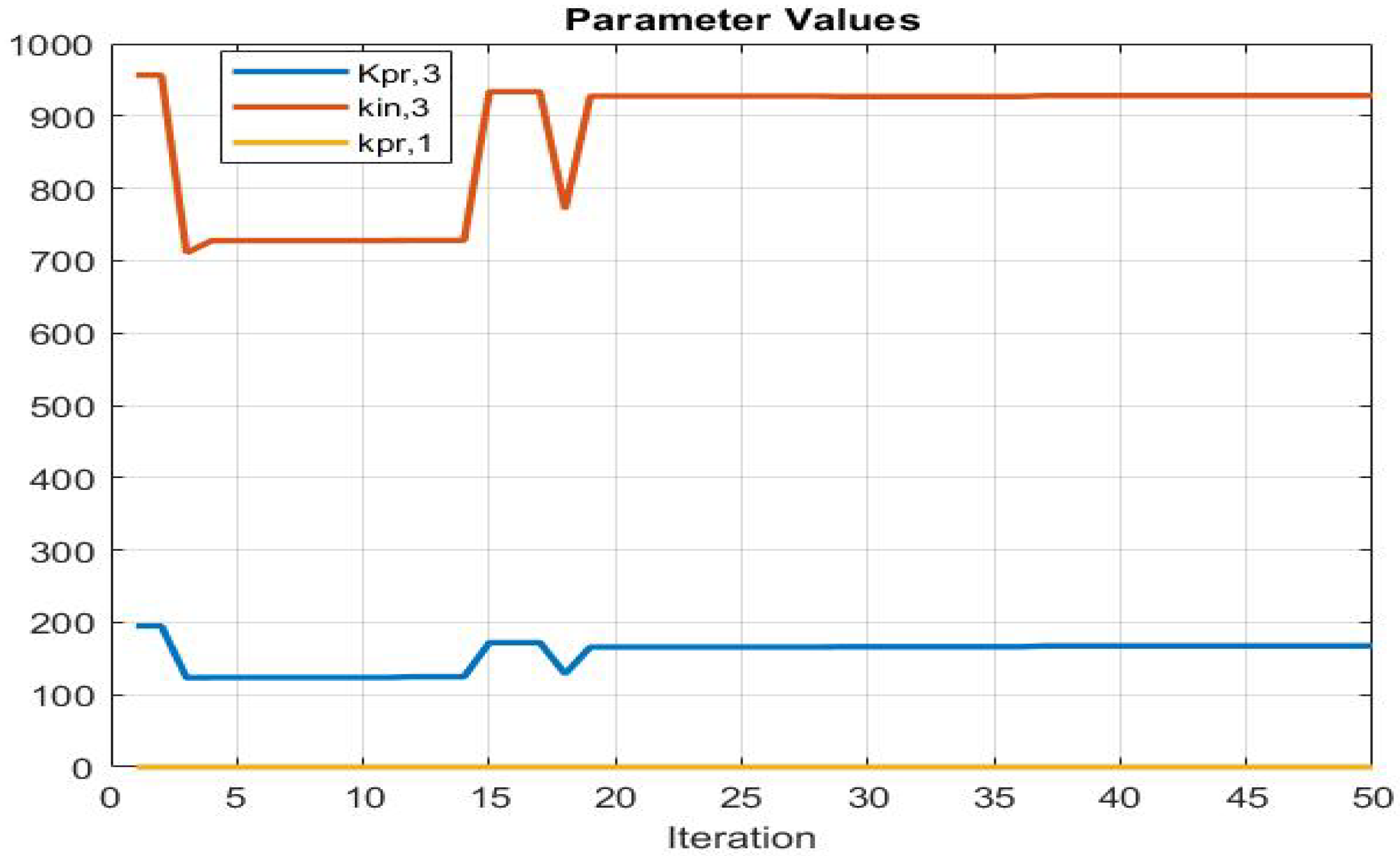
Figure 17.
Parameter values.
Figure 17.
Parameter values.
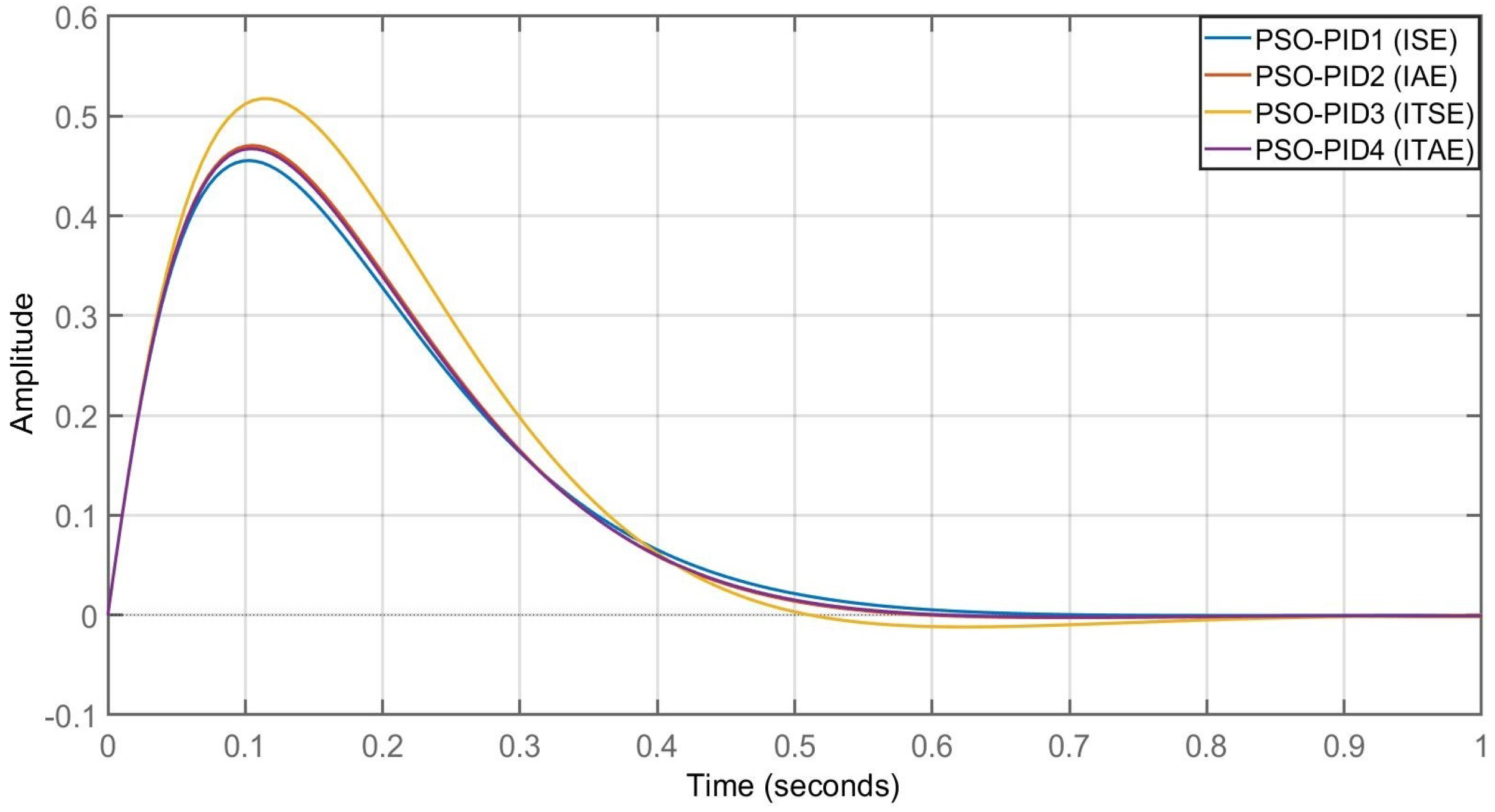
Figure 18.
Comparison of step responses of PI controllers for active power changes.
Figure 18.
Comparison of step responses of PI controllers for active power changes.
Figure 19.
Comparison of step responses of PI controllers for frequency changes.
Figure 19.
Comparison of step responses of PI controllers for frequency changes.
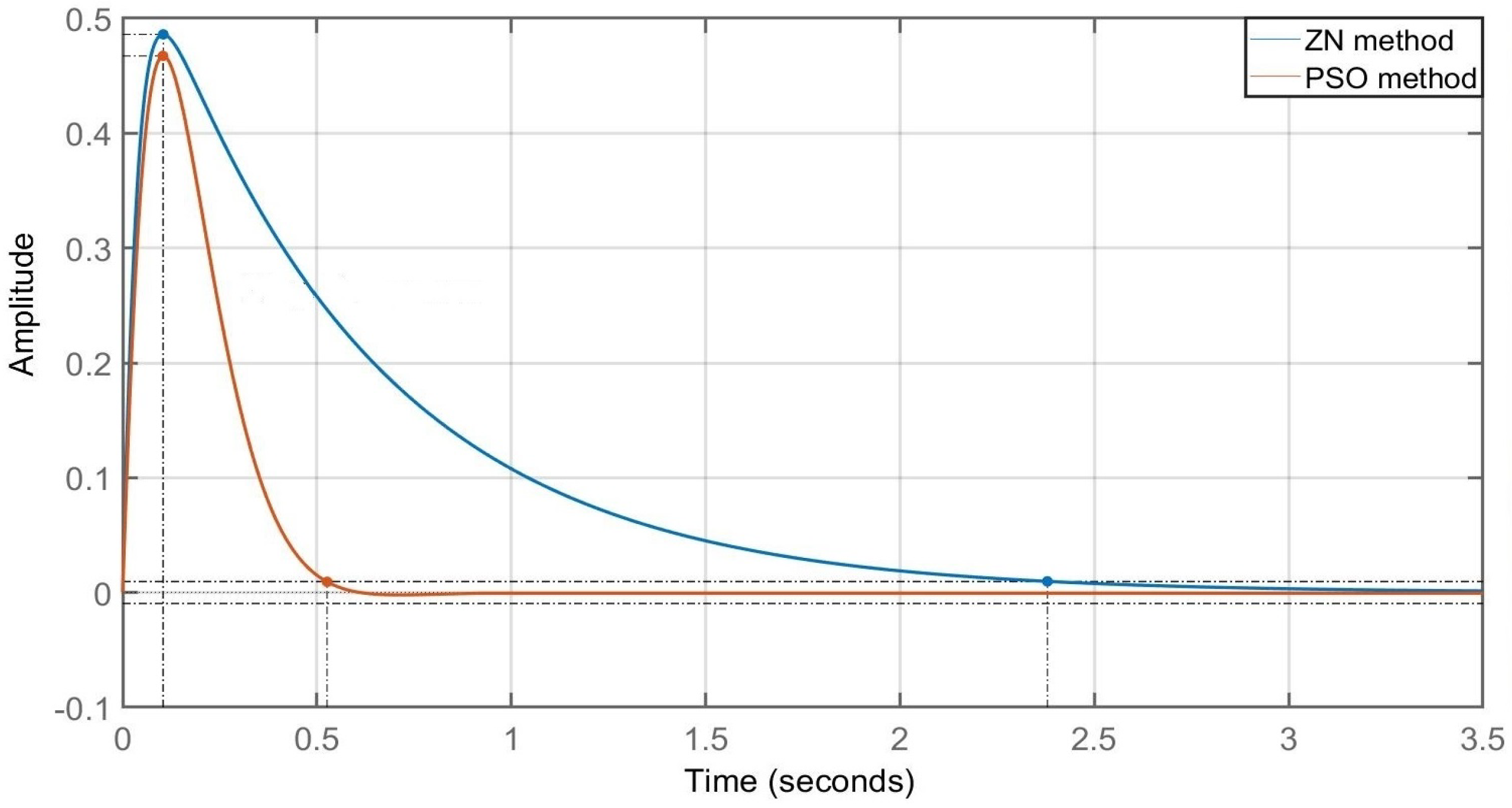
Figure 20.
Comparison of step responses of of frequency changes using Ziegler-Nichols and PSO methods.
Figure 20.
Comparison of step responses of of frequency changes using Ziegler-Nichols and PSO methods.
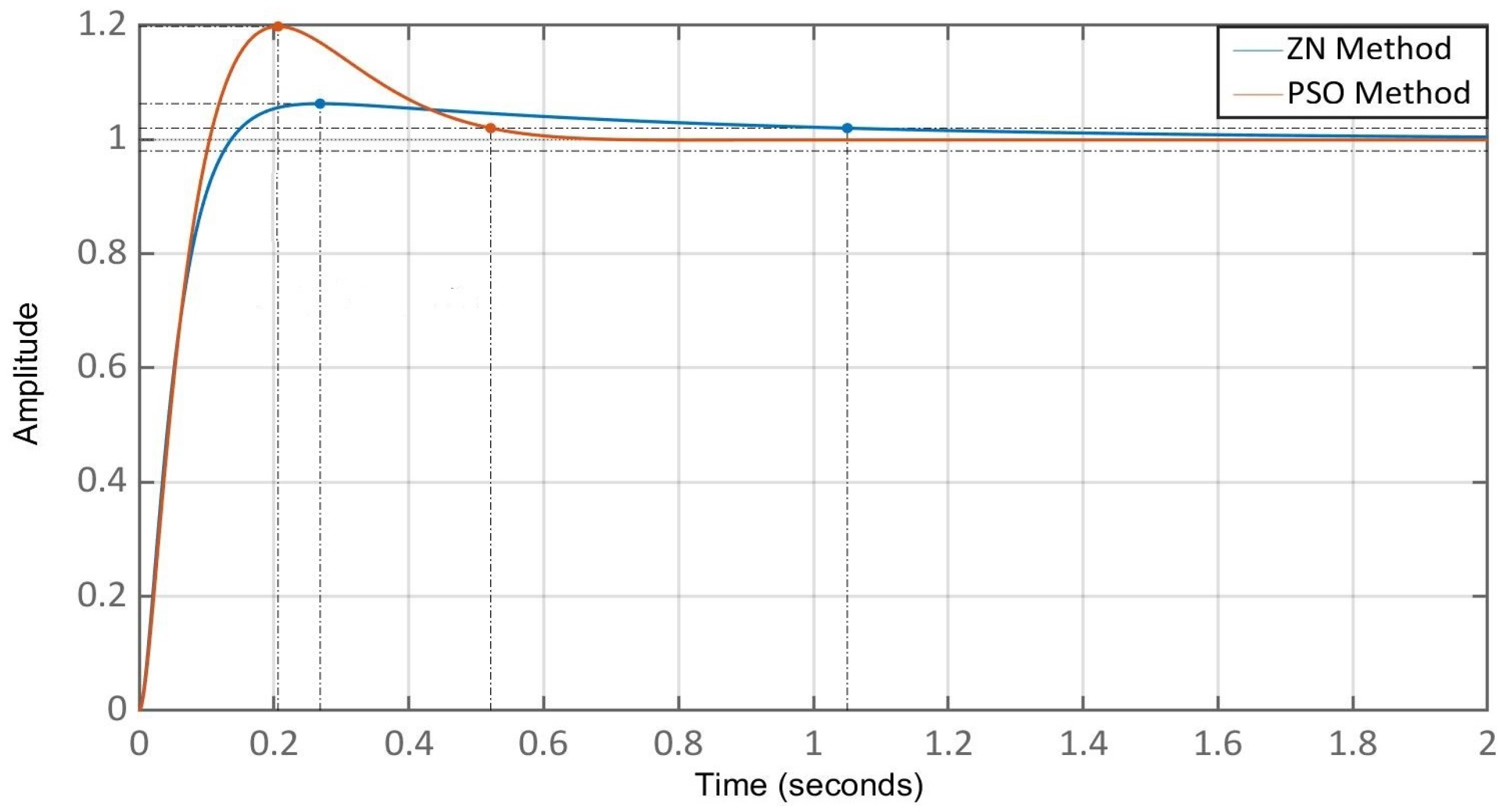
Figure 21.
Comparison of step responses of active power changes using Ziegler-Nichols and PSO methods.
Figure 21.
Comparison of step responses of active power changes using Ziegler-Nichols and PSO methods.
Figure 22.
General model of the network.
Figure 22.
General model of the network.
Figure 23.
Active power-sharing by DER units (wind generator, BESS and PV system) for L-type 4-bus network.
Figure 23.
Active power-sharing by DER units (wind generator, BESS and PV system) for L-type 4-bus network.
Figure 24.
Frequency changes in network for active load change.
Figure 24.
Frequency changes in network for active load change.
Figure 26.
Active power-sharing by DER units (wind generator, BESS and PV system) for RL-type 9-bus network.
Figure 26.
Active power-sharing by DER units (wind generator, BESS and PV system) for RL-type 9-bus network.
Figure 27.
Frequency of network while sharing active power- RL-type 9 bus.
Figure 27.
Frequency of network while sharing active power- RL-type 9 bus.
Figure 28.
Active power-sharing by household DER units (wind generator, BESS and PV system) for RL-type 9-bus network.
Figure 28.
Active power-sharing by household DER units (wind generator, BESS and PV system) for RL-type 9-bus network.
Figure 29.
Active power-sharing by DER units (wind generator, BESS (in ‘sharing’ mode) and PV system) for L-type 4-bus network.
Figure 29.
Active power-sharing by DER units (wind generator, BESS (in ‘sharing’ mode) and PV system) for L-type 4-bus network.
Table 1.
Ziegler-Nichols closed-loop tuning parameter.
Table 1.
Ziegler-Nichols closed-loop tuning parameter.
| Control Type |
|
|
| PI |
0.45
|
0.45
|
Table 2.
Calculated control tuning parameters as per Ziegler-Nichols method.
Table 2.
Calculated control tuning parameters as per Ziegler-Nichols method.
| Value of
|
|
|
|
|
|
|
| 0.3 |
2369.7 |
0.4867 |
2132.7 |
5258.4 |
1066.4 |
2629.2 |
| 0.5 |
853.08 |
0.6283 |
767.78 |
1466.3 |
383.89 |
733.17 |
| 0.7 |
435.25 |
0.7434 |
391.72 |
632.29 |
195.86 |
316.14 |
Table 3.
Optimized PI parameters for 4-bus L type network.
Table 3.
Optimized PI parameters for 4-bus L type network.
| Tuning method |
|
|
|
|
|
| ZN method |
0.0243 |
571 |
952 |
285 |
475 |
| PSO-PID1 (ISE) |
0.0312 |
355 |
1860 |
167 |
930 |
| PSO-PID2 (IAE) |
0.0312 |
331 |
1848 |
165 |
924 |
| PSO-PID3 (ITSE) |
0.0312 |
289 |
1690 |
144 |
845 |
| PSO-PID4 (ITAE) |
0.0312 |
334 |
1856 |
167 |
928 |
Table 4.
Optimized PI parameters for 9-bus L type network.
Table 4.
Optimized PI parameters for 9-bus L type network.
| Tuning method |
|
|
|
|
|
| ZN method |
0.0243 |
571 |
952 |
285 |
475 |
| PSO-PID1 (ISE) |
0.01 |
485 |
1536 |
242 |
768 |
| PSO-PID2 (IAE) |
0.0539 |
277 |
1553 |
138 |
776 |
| PSO-PID3 (ITSE) |
0.0539 |
458 |
1536 |
229 |
768 |
| PSO-PID4 (ITAE) |
0.0539 |
222 |
1465 |
111 |
732 |
Table 5.
Line parameters of L-type 4 bus network.
Table 5.
Line parameters of L-type 4 bus network.
| Node From |
Node To |
Resistance, (p.u.) |
Reactance, (p.u.) |
| 1 |
4 |
0 |
4.0 |
| 2 |
4 |
0 |
4.0 |
| 3 |
4 |
0 |
1.5 |
Table 6.
Initial values of DFIG, PV system, BESS and loads L-type 4 bus system.
Table 6.
Initial values of DFIG, PV system, BESS and loads L-type 4 bus system.
| Element Name |
Bus Type |
Real Power () MW |
Reactive Power () MVar |
Voltage () kV |
Voltage Angle() |
| VSI-BESS 01 |
Slack |
- |
- |
1.0 |
0
|
| DFIG-Wind Gen. |
PV |
1.00 |
- |
0.69 |
- |
| PV System |
PV |
0.448 |
- |
0.4 |
- |
| Load A |
PQ |
2.8 |
0.0 |
20.0 |
- |
| Load B |
PQ |
0.3 |
0.0 |
20.0 |
- |
| Load C |
PQ |
0.2 |
0.0 |
20.0 |
- |
Table 7.
Initial values of known and unknown variables after load flow analysis- L-type 4 bus system.
Table 7.
Initial values of known and unknown variables after load flow analysis- L-type 4 bus system.
| Bus no |
Voltage (p.u). |
Voltage Angle
|
Real Injected Power (MW) |
Reactive Injected Power (MVAR) |
| 1 |
1.0000 |
0.0 |
1.652 |
0.046 |
| 2 |
1.0000 |
0.8728 |
1.000 |
0.030 |
| 3 |
1.0000 |
-0.3933 |
0.448 |
0.006 |
| 4 |
0.9996 |
-1.4205 |
-3.1 |
0.0 |
Table 8.
RL-type 9-bus system.
Table 8.
RL-type 9-bus system.
| System name |
Co-efficient |
Value |
| BESS |
|
0.0312 |
| Wind generator |
|
334.88 |
| Wind generator |
|
1856.54 |
| PV System |
|
167.44 |
| PV System |
|
928.27 |
Table 9.
Initial values of DFIG, PV system, BESS and loads.
Table 9.
Initial values of DFIG, PV system, BESS and loads.
| Element Name |
Bus Type |
Real Power () MW |
Reactive Power () MVar |
Voltage () kV |
Voltage Angle() |
| C-DFIG 01 |
PV |
1.00 |
- |
0.69 |
- |
| C-PV 01 |
PV |
0.448 |
- |
0.4 |
- |
| VSI-BESS 01 |
Slack |
- |
- |
1.0 |
0
|
| HH-PV 01 |
PQ |
0.02 |
0.0 |
20.0 |
- |
| HH-PV 02 |
PQ |
0.015 |
0.0 |
20.0 |
- |
| HH-PV 03 |
PQ |
0.01 |
0.0 |
20.0 |
- |
| HH-L-01 |
PQ |
0.01 |
0.0 |
20.0 |
- |
| HH-L-02 |
PQ |
0.018 |
0.0 |
20.0 |
- |
| HH-L-03 |
PQ |
0.025 |
0.0 |
20.0 |
- |
| C-L-01 |
PQ |
1.7 |
0.0 |
20.0 |
- |
| C-L-02 |
PQ |
0.25 |
0.0 |
20.0 |
- |
| C-L-03 |
PQ |
0.8 |
0.0 |
20.0 |
- |
Table 10.
Parameters of the 9 bus network.
Table 10.
Parameters of the 9 bus network.
| Node From |
Node From |
Resistance,
|
Reactance,
|
| 1 |
4 |
0 |
2.0 |
| 2 |
7 |
0 |
1.5 |
| 3 |
9 |
0 |
3.0 |
| 4 |
5 |
0.14475 |
0.09175 |
| 4 |
6 |
0.072375 |
0.045875 |
| 5 |
7 |
0.217125 |
0.137625 |
| 6 |
9 |
0.188175 |
0.119275 |
| 7 |
8 |
0.2316 |
0.1468 |
| 8 |
9 |
0.26055 |
0.16515 |
Table 11.
All the initial values of known and unknown variables after load flow analysis.
Table 11.
All the initial values of known and unknown variables after load flow analysis.
| Bus no |
Voltage (p.u). |
Voltage Angle
|
Real Injected Power (MW) |
Reactive Injected Power (MVAR) |
| 1 |
1.0000 |
0.0 |
1.313 |
0.015 |
| 2 |
1.0000 |
-0.3678 |
1.000 |
0.027 |
| 3 |
1.0000 |
–3623 |
0.448 |
0.012 |
| 4 |
0.9998 |
-1.2224 |
-0.01 |
0.0 |
| 5 |
0.9946 |
-1.4122 |
-1.68 |
0.0 |
| 6 |
0.9997 |
-1.2267 |
-0.235 |
0.0 |
| 7 |
0.9998 |
-1.2275 |
-0.018 |
0.0 |
| 8 |
0.9988 |
-1.2601 |
-0.79 |
0.0 |
| 9 |
0.9999 |
-1.2219 |
-0.025 |
0.0 |
Table 12.
Values of controller co-coefficients-RL-type 9 bus.
Table 12.
Values of controller co-coefficients-RL-type 9 bus.
| System name |
Co-efficient name |
Value |
| BESS |
|
0.0243 |
| Wind generator |
|
222.68 |
| Wind generator |
|
1465.13 |
| PV System |
|
111.34 |
| PV System |
|
732.56 |