Prerpints.org logo
Preprint
Article

Alternative Approach of Firefly Algorithm and Hybrid Method Based on the Artificial Bees Colony and Cultural Algorithm for Reservoir Operation

Altmetrics

Downloads

93

Views

70

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

10 January 2024

Posted:

10 January 2024

You are already at the latest version

Alerts
Abstract
In reservoir operations rule curves, it is necessary to apply rule curves to guide long-term reservoir management. This paper proposes an approach to optimize the reservoir operation rule curves (RORC) using intelligent optimization techniques from the Firefly Algorithm (FA) and a unique combination method utilizing the Artificial Bees Colony and Cultural Algorithm (ABC-CA). The aim is to establish a connection with the simulation model to determine the optimal RORC for flood control. The proposed model was used to determine the Nam-Oon Reservoir (NOR) is optimal flood control RORC in Northeastern Thailand. The minimum frequency and a minimum average of ex-cess water were given as an objective function for assessing the efficiency of the search process. The evaluation of the effectiveness of flood control RORC involved expressing water scarcity and excess water situations in terms of frequency, magnitude, and duration using historical inflow data syn-thesized from 1000 events. The results demonstrate that when using the obtained RORC to simulate the NOR system for reducing flooding in long-term operations, situations of excess water were smaller than those using the current RORC. The results indicated that situations of excess water using the obtained RORC from the proposed model were smaller than those using the current RORC situations. In decreasing flood situations, the newly acquired RORC from the suggested FA and ABC-CA models performed better than the current RORC.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Numerous nations now face enormous difficulties in managing their natural resources, especially when it comes to water resources, which are essential for improving human welfare and quality of life. The issue of water resources remains a serious and substantial concern, and its complexity makes it even more hazardous, owing to the influence of climate change and alterations in land use [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Adequate water management necessitates two essential components: proper water organization and the suitable tools for managing the water resources. Hardware, such as water control structures, and software, such as organizational structures and non-construction tools, are needed to manage water resources [2,3,15,16,17,18,19,20,21,22,23,24,25,26].
Frequently, enhancing the operation of reservoirs is a fevered technique because it can be swiftly implemented and does not involve construction. RORC is a complicated issue that involves optimizing multiple objectives with numerous competing constraints [27,28,29]. RORC, which provide the monthly required water levels or planned storage amounts for each reservoir, are essential recommendations for RORC. These RORC are comprised of upper and lower curves for long-term management of the monthly stored water. Nevertheless, their effectiveness can decrease over time or if there are any changes to the data [12], necessitating the search for optimal values and improvements [19,20,21,22,23,24,25,26].
Various optimization methods have been employed to find optimal RORC, including dynamic programming [31,32], genetic algorithm [15,16,17,33,34,35], simulated annealing algorithm [36], particle swarm optimization [4], ant colony optimization [37], harmony search algorithm [38,39], and cuckoo search [40], among others. Although the above-mentioned techniques can solve the RORC problem, they also have several disadvantages, such as convergence to the optimal solution often depends on the initial value. There is also the possibility of getting localized solutions rather than the most appropriate solutions. Therefore, researchers have developed artificial intelligence (AI) techniques, or intelligent techniques and the science of swarm intelligence. It is advisable to investigate an alternative optimization approach if it is user-friendly and suitable for the task at hand. Over the past decade, a novel method called the firefly algorithm (FA) has gained popularity. FA is a swarm-based metaheuristic algorithm that is based on the flashing behavior of fireflies. It is a simple and efficient algorithm that can be readily implemented [41,42,43,44,45,46,54]. Cultural Algorithm (CA) is one of the computational sciences of evolution that was developed by R. Reynolds in 1994 [47] to enhance the efficiency of the Artificial Bee Colony Algorithm (ABC), which is a form of evolutionary computation. By simulating social evolution and utilizing the information and experience that accumulates over time, it integrates with the Agent-Based Modelling (ABM) learning process [48,49]. Cultural processes are very helpful in reducing the difficulty of determining the right response and increasing the efficiency of finding the best solution in a search space. The belief and population spaces are the two primary parts of the cultural process. The population space refers to all potential solutions within the search space. In contrast, the belief space represents the knowledge or information that solutions gather while striving for the best possible answers. The information gathered in this belief space is shared throughout the population space and can be applied to all population-based optimization techniques [47].
This article presents a solution to the most suitable reservoir management problem by using cultural processes, which is one of the evolutionary computational sciences, to help improve the efficiency of finding solutions in the bee colony process. The artificial bee colony process is used as the population space for cultural processes. By using Normative knowledge, which is knowledge or information about samples or important events, and Situational knowledge, which is a group of solutions or a population whose values are within the desired range and are acceptable in the process of finding the most appropriate value. To increase the efficiency of finding the solution of the bee swarm process to use in finding the solution in the search space and applying it to solve the most suitable reservoir management problem. By calculating the minimum frequency value and the minimum average value of excess water are determined as the objective function to evaluate the efficiency of the search process. By testing with RORC and comparing the results and efficiency in finding answers with the firefly algorithm technique, which has previously been used to solve the RORC problem in Nam-Oon Reservoir. Consequently, it is feasible to employ alternative techniques such as utilizing FA and ABC-CA in combination with a reservoir simulation model (RSM) to identify the most favorable RORC.
This article suggests employing an alternative method that utilizes FA and ABC-CA in combination with a RSM to find optimal flood RORC in flood control areas. The study employed the proposed models to identify the optimal flood RORC for the NOR, situated in the Northeastern Thailand. Two objective functions—minimizing the average excess water and minimizing the frequency of excess water—directed the search methods.

2. Methodology

2.1. Research Area

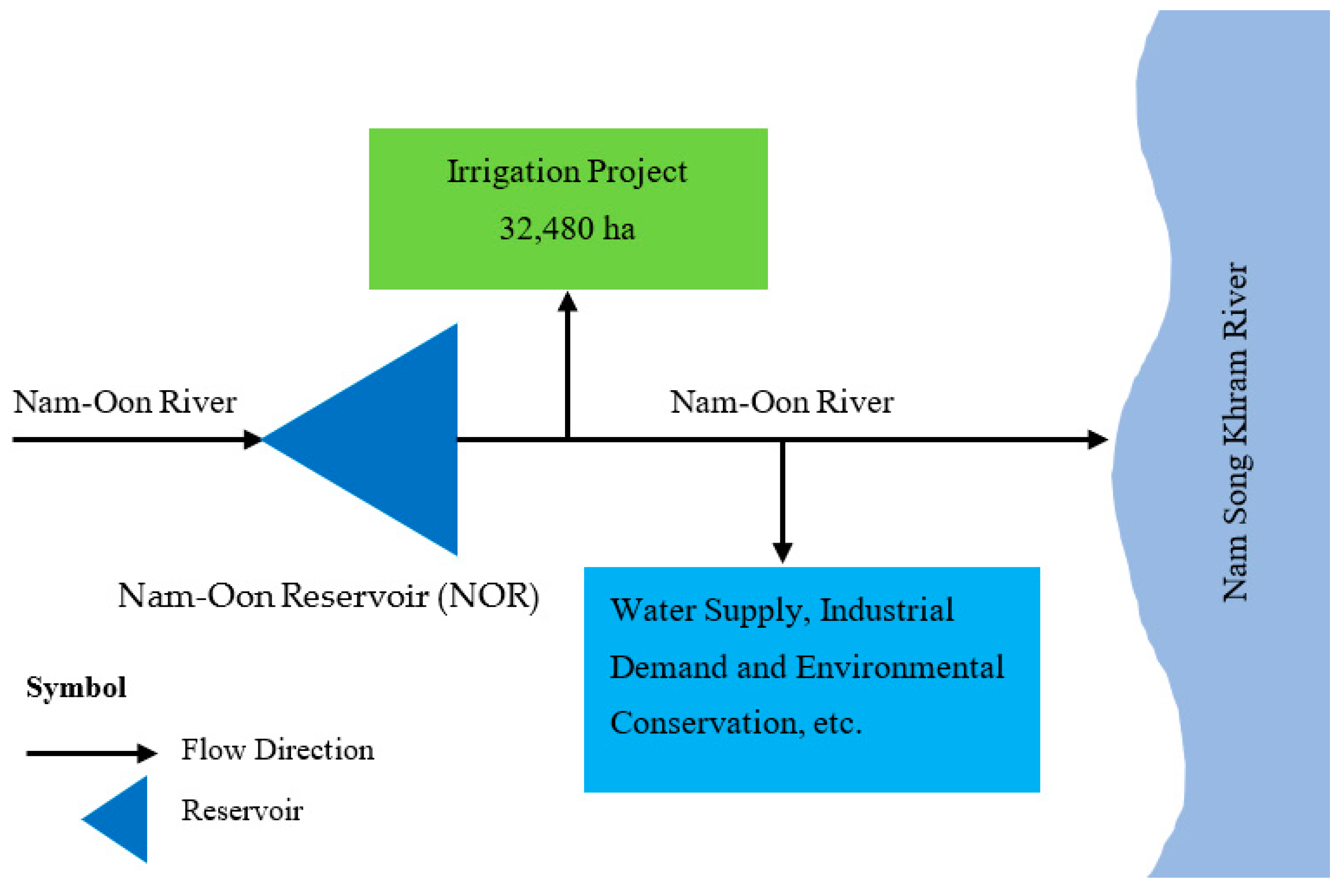
The research area, as shown in Figure 1, is situated in Sakolnakorn province, Thailand, and the research was conducted between 2021 and 2022. The NOR has an irrigation area of 32,480 hectares and is located in the Songkham Basin in northeastern Thailand. The storage capacity of the reservoir is 520.000 million cubic meters (MCM), while the average annual inflow is 404.835 MCM. Data on the inflow were collected over a period of 28 years, from 1994 to 2021. Schematic diagrams of the NOR system, which provides domestic water supply, irrigation, industry demand, and conservation of the environment, are shown in Figure 2.

2.2. Model for Simulating the Operation of a Reservoir

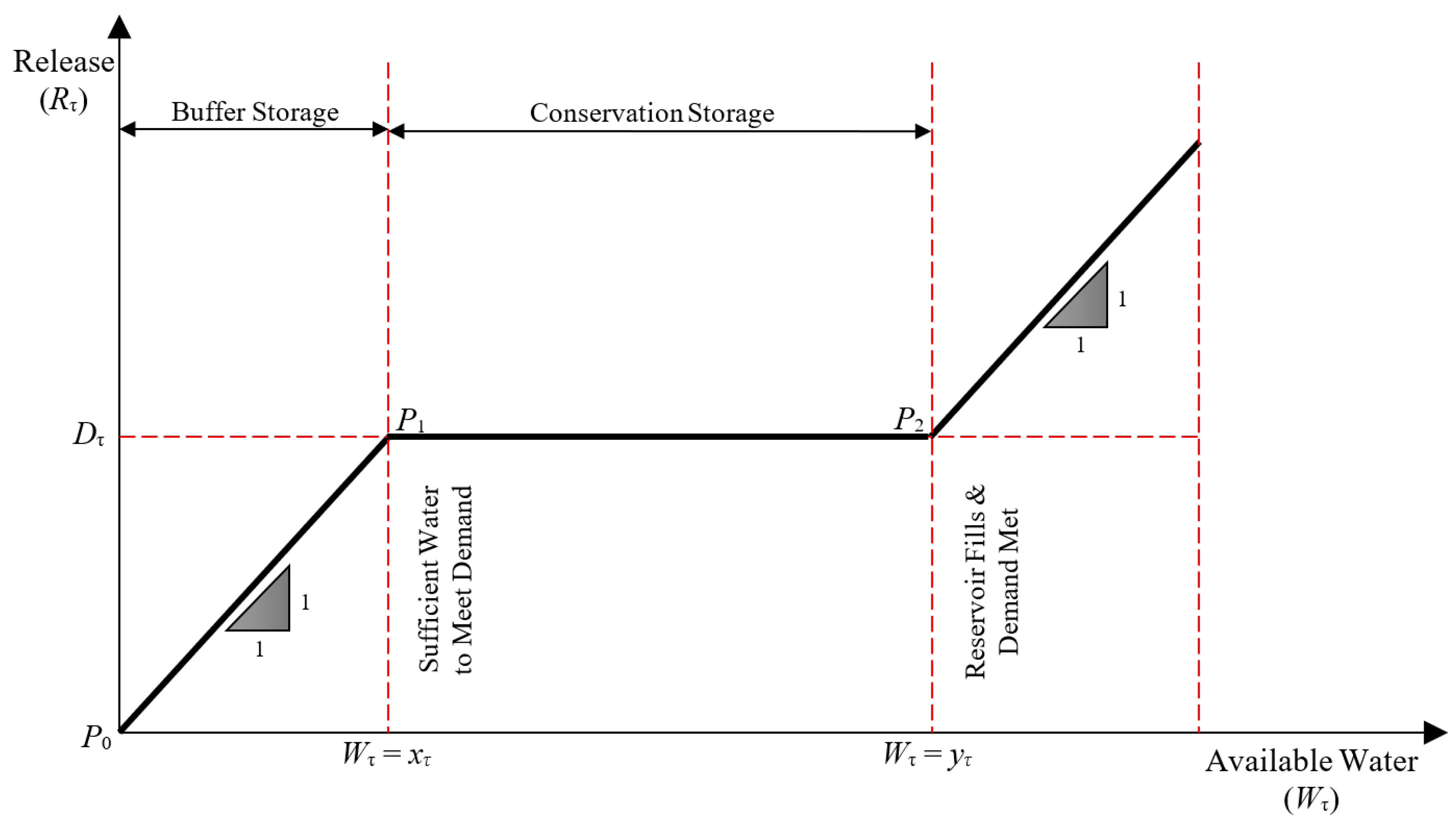
The reservoir system was simulated by applying the water balancing concept, which necessitated hydrologic data, physical reservoir data, water demand data from the reservoir, and other relevant data. The available water was computed using Equation 1, based on this concept. The estimation of the monthly water release considered the available water resources, the specified release requirements, standard operating procedures, and the represented RORC displayed in Figure 3.
W τ = S τ − 1 + I τ + P τ − E τ
The equation represents the calculation of available water during month τ, taking into account different parameters. Wτ refers to water availability during month τ, Sτ-1 denotes the amount of water that is stored at the conclusion of the month τ - 1, which is initially set to full reservoir capacity. The calculation is derived from the inflow to the reservoir (Iτ), the amount of precipitation during the month (Pτ), and the average evaporation loss during the month (Eτ).
Subsequently, the monthly water release rate (Rτ) was determined to calculate water scarcity and excess water levels. These levels are represented by the average yearly excess water amount (the initial objective function in the search procedure) and the yearly frequency of excess water (the second objective function utilized during the search procedure), as shown in Equations 2 and 4, respectively. In these equations, xτ refers to the lower RORC during month τ while yτ denotes the upper RORC during month τ.
M i n   A v r i = 1 n ∑ v = 1 n S p v
if   R τ > D τ ; Then   S p v = ∑ v = 1 n ( R τ − D τ )
M i n F r e i = 1 n ∑ v = 1 n S f ν
In this equation, Avri represents the average amount of excess water per year during iteration i, Spv denotes the excess water during year v, where releases exceed the target demand, Frei is the frequency of excess water, Sfv indicates the number of annual floods, which is the year when releases exceed the target demand, Dτ represents the monthly goal demand from the reservoir, which is determined by utilizing data from previous studies and calculating the water demand in the downstream area [50]. The variable i represents the iteration number.

2.3. Firefly Algorithm (FA)

The firefly algorithm was first proposed by Xin-She Yang in 2008 [51]. It was inspired by the flashing behavior of fireflies, where the intensity of the light emitted is proportional to the attractiveness of the firefly. This leads to fireflies that are closer together being more likely to fly towards each other. The algorithm is based on the following ideas: 1) no separation of sexes, where each firefly can attract others regardless of gender, 2) attraction of a firefly is proportional to its brightness, and fireflies with lower brightness move towards those with higher brightness, and 3) brightness is determined by an objective function. The algorithm is described in the following steps.
Step 1: Define objectives, constraints, and boundaries for the function.
Step 2: Specify the attractiveness of the light source, the number of fireflies, the filter efficiency of the medium, and the variables for movement distance, number of movements, or stopping conditions of the fireflies.
Step 3: Create an initial population of fireflies using non-chance-based random sampling where each firefly represents the answer to the considered problem and store the locations of all fireflies.
Step 4: Check if the fireflies randomly generated are within the constraint function or not. If not, generate a new set of fireflies until all of them meet the constraint function.
Step 5: Move the firefly with the least brightness towards the firefly with the greatest brightness among all fireflies.
Step 6: Check if the variables are within the defined boundaries. If not, adjust them to be within the boundaries.
Step 7: Check if all fireflies are within the constraint function. If not, adjust them to be within the constraint function.
Step 8: Compare the values of all fireflies to find the most suitable value for this movement.
Step 9: Check the stopping conditions. If met, proceed to Step 10. If not, repeat from Step 5.
Step 10: Use the value obtained from Step 9 as the optimal solution, and the calculation is completed.

2.4. Artificial Bees Colony and Cultural Algorithm (ABC-CA)

2.4.1. Cultural Algorithm (CA)

Cultural evolution is one of the computational sciences of evolution that was developed by R. Reynolds in 1994 [47,48]. It is a simulation of the social evolution model that is integrated with various Agent-Based learning techniques. It utilizes experience and knowledge gained over time. Cultural evolution is highly beneficial in developing the effectiveness of finding appropriate answers in searching spaces, making global answers more easily accessible. Generally, cultural evolution can be divided into two main components: belief space and population space. Population space is the space of possible solutions in the search space, while belief space is the space of knowledge or information that is accumulated during the search process for the most appropriate solution. The information accumulated in the belief space is shared with the population space and can be used to simulate and apply to all techniques of finding the most appropriate solution in a population-based manner.

2.4.2. Artificial Bees Colony (ABC)

The ABC algorithm is a smart and intelligent group-based technique developed by D.T. Pham in 2005 [34] to simulate the process of bees searching for food sources. The efficiency of the bee colony optimization algorithm is comparable to other intelligent group-based techniques, but it requires the configuration of various parameters, such as the number of bees (n) that explore the environment, the number of food sources (m) that bees investigate, the number of best food sources (e), the number of bees selected to the best food sources (nep), the number of bees selected to other food sources (nsp), the initial size of the flower petals (ngh), and the criteria for stopping all processes. The bee colony optimization algorithm starts by randomly placing n bees in the search space, and then finding the fitness values of the number of food sources investigated by the bee colony. Although the bee colony optimization algorithm has been used to solve various optimization problems, including the control and planning of power systems, and is one of the interesting intelligent group-based techniques, it still has some limitations, especially the problem of converging to the global optimum, which may occur when the search space is large, leading to slower computation time. Therefore, various techniques, such as cultural algorithm, have been used to overcome these limitations and improve efficiency.
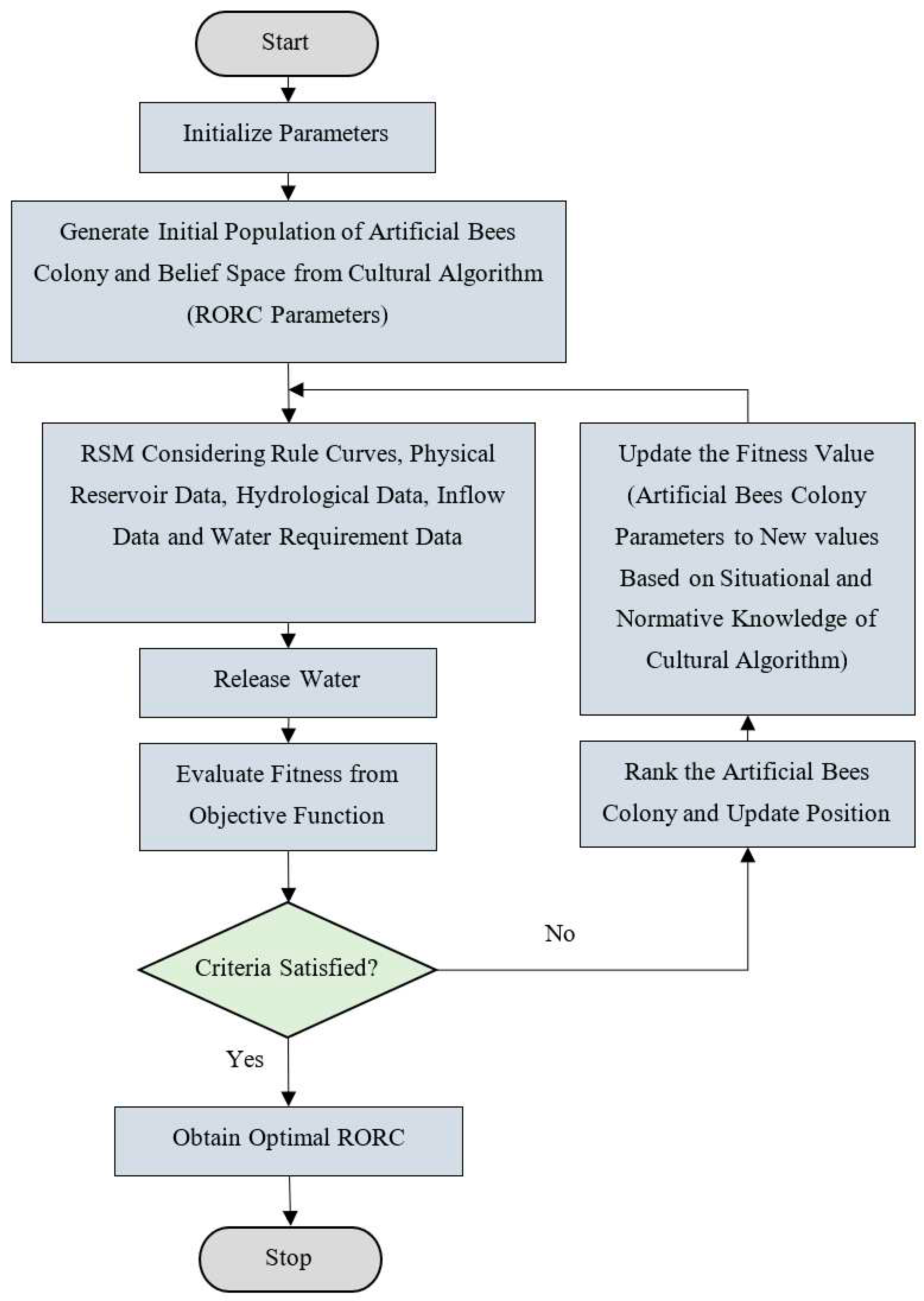
In this article, the artificial bee colony process has been used as a population model for cultural processes, and normative knowledge, which is knowledge or information about various important examples or events, and situational knowledge, which is a group of solutions or populations that are valuable in the desired range and are acceptable in the process of finding the most appropriate value, have been used to help improve the efficiency of bees. It explores finding solutions in the search space and applies them to solve the problem of reservoir operation by calculating the appropriate control curve of the reservoir using the bee colony process as a cultural model. The most appropriate solution for solving the problem of RORC is shown in Figure 5.

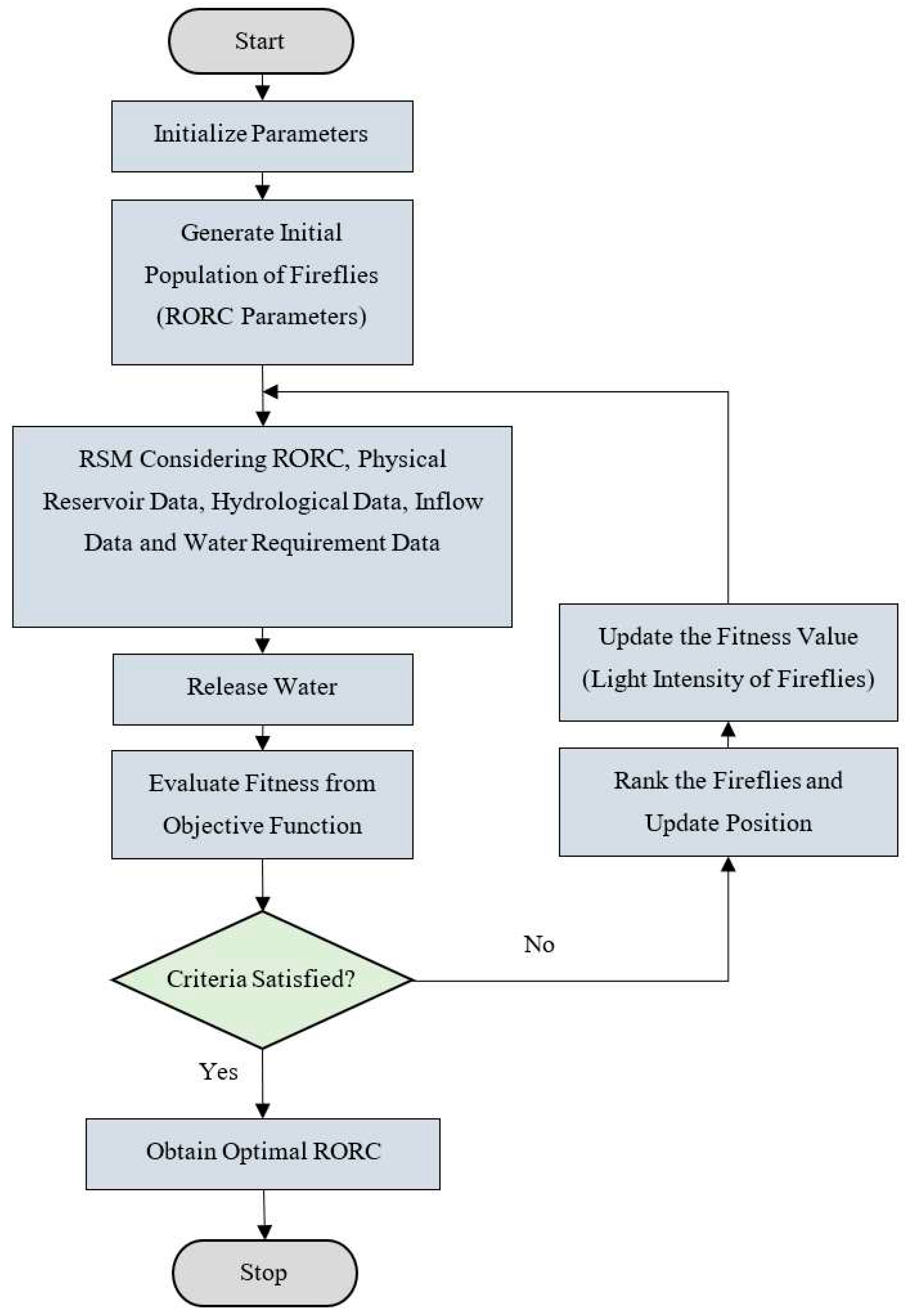
2.5. Firefly Algorithm Incorporating Reservoir Simulation Model (RSM)

The FA and RSM are linked by starting with initializing the essential data, including the full capacity level, normal high-water level, dead storage level, and monthly water demands. Subsequently, a starting population of fireflies is generated by the model where each firefly symbolizes the monthly RORC of the reservoirs which defines the upper and lower RORC. The first set of fireflies in the initial population consisting of 24 decision variables (To find the optimal value for RORC, there are 24 decision variables, namely 12 upper RORC and 12 lower RORC, depending on the number of months in a year) is then used in the RSM to obtain the monthly release of water considering those RORC and standard operating rule. The water that has been discharged is employed to calculate the objective functions that were previously described. Subsequently, the fitness evaluations and the updating of fitness values were performed for the objective function. Subsequently, the fireflies were assigned rankings, their locations were updated, and the stop criterion was checked. This process is iterated until the criteria are satisfied and the most optimal RORC values are achieved. Figure 4 depicts the FA and RSM utilized for searching the RORC.

2.6. Artificial Bees Colony and Cultural Algorithm Incorporating RSM

The ABC-CA and reservoir simulation model are linked by starting with initializing the essential data includes the full capacity level, normal high-water level, dead storage level, and monthly water demands. Next, the initial population of ABC and Belief Space from CA is generated by the model where each ABC denotes the monthly RORC of the reservoirs that define the upper and lower RORC. The initial population of the ABC consists of 24 decision variables (To find the optimal value for RORC, there are 24 decision variables, namely 12 upper RORC and 12 lower RORC, depending on the number of months in a year) is then used in the RSM to obtain the monthly release of water considering those RORC and standard operating rule. The water that has been discharged is employed to calculate the objective functions that were previously described. Subsequently, the fitness evaluations and the updating of fitness values were performed for the objective function. The ABC parameters were reassigned to new values using situational and normative knowledge of CA. Subsequently, their ranking and position were revised, and the stopping criterion was evaluated. This process is iterated until the criteria are satisfied and the most optimal RORC values are achieved. Figure 5 depicts the ABC-CA and RSM utilized for searching the RORC.

2.7. Assessment of the obtained RORC

The RORC obtained through the FA and ABC-CA and RSM were tested by applying them to the reservoir system for each inflow scenario. Initially, the historic inflow data of 28 years were used in the RSM, followed by the evaluation of 1,000 synthetic inflow events generated from the same historic inflow data in the same conditions in the RSM by using the HEC-4 model. Finally, the evaluation results were presented, considering the occurrence, magnitude, and duration of water scarcity and excess water situations.

2.8. Analysis of data using statistical methods.

The frequency was determined by dividing the number of annual floods or droughts by the total number of years considered. The magnitude of water scarcity or excess water was determined by dividing the total water scarcity or excess water by the total number of years considered. The maximum magnitude of water scarcity or excess water was determined by selecting the yearly water scarcity or excess water with the highest value for all years considered. The duration of water scarcity or excess water was determined by dividing the number of consecutive years with floods or droughts by the total number of groups of successive years with floods or droughts. The maximum duration of water scarcity or excess water was determined by selecting the maximum number of consecutive years with floods or droughts for all years considered. The results were presented as the mean ± standard deviation for synthetic inflow cases.

3. Results

3.1. Optimal RORC

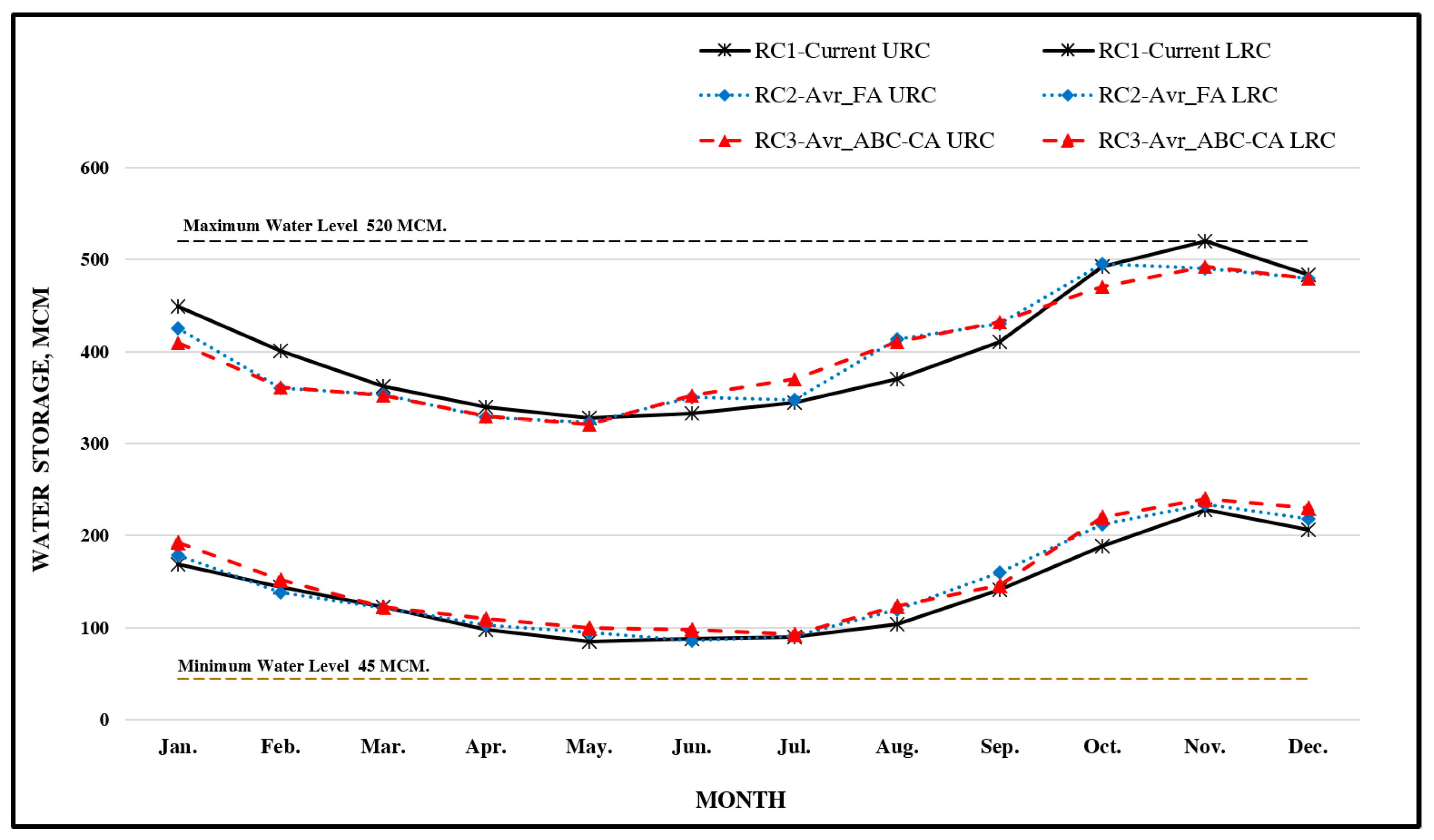
The FA model introduced in this research produced optimal RORC, as depicted in Figure 6. The search process employed the objective of minimizing yearly excess water, considering historical and projected inflow data. The RORC labeled as RC2-Avr_FA, RC3-Avr_ABC-CA, and the existing ones (RC1-Current) display a similar trend. The lower RORC derived from both historical and projected inflow data surpass the current RORC from March to July. However, the upper RORC of the newly optimized rules exceed the current ones from June to September. It's important to highlight that the obtained upper RORC (RC3-Avr_ABC-CA) are below the current upper RORC for October - November.
The optimal RORC generated by the FA and ABC-CA models introduced in this study are illustrated in Figure 6. The search procedure involves utilizing the objective function to minimize annual excess water, using historical inflow data as a basis. The RORC obtained from the FA model (RC2-Avr_FA), the RORC derived from the ABC-CA model (RC3-Avr_ABC-CA), and the current RORC (RC1-Current) all exhibit similar trends. Nonetheless, the RORC resulting from the FA and ABC-CA models surpasses the current RORC between March and July. On the other hand, the novel optimal RORC will surpass the current RORC from June - September. It's important to highlight that the upper RORC derived from the ABC-CA model (RC3-Avr_ABC-CA) is lower than the current upper RORC throughout the October–November period.
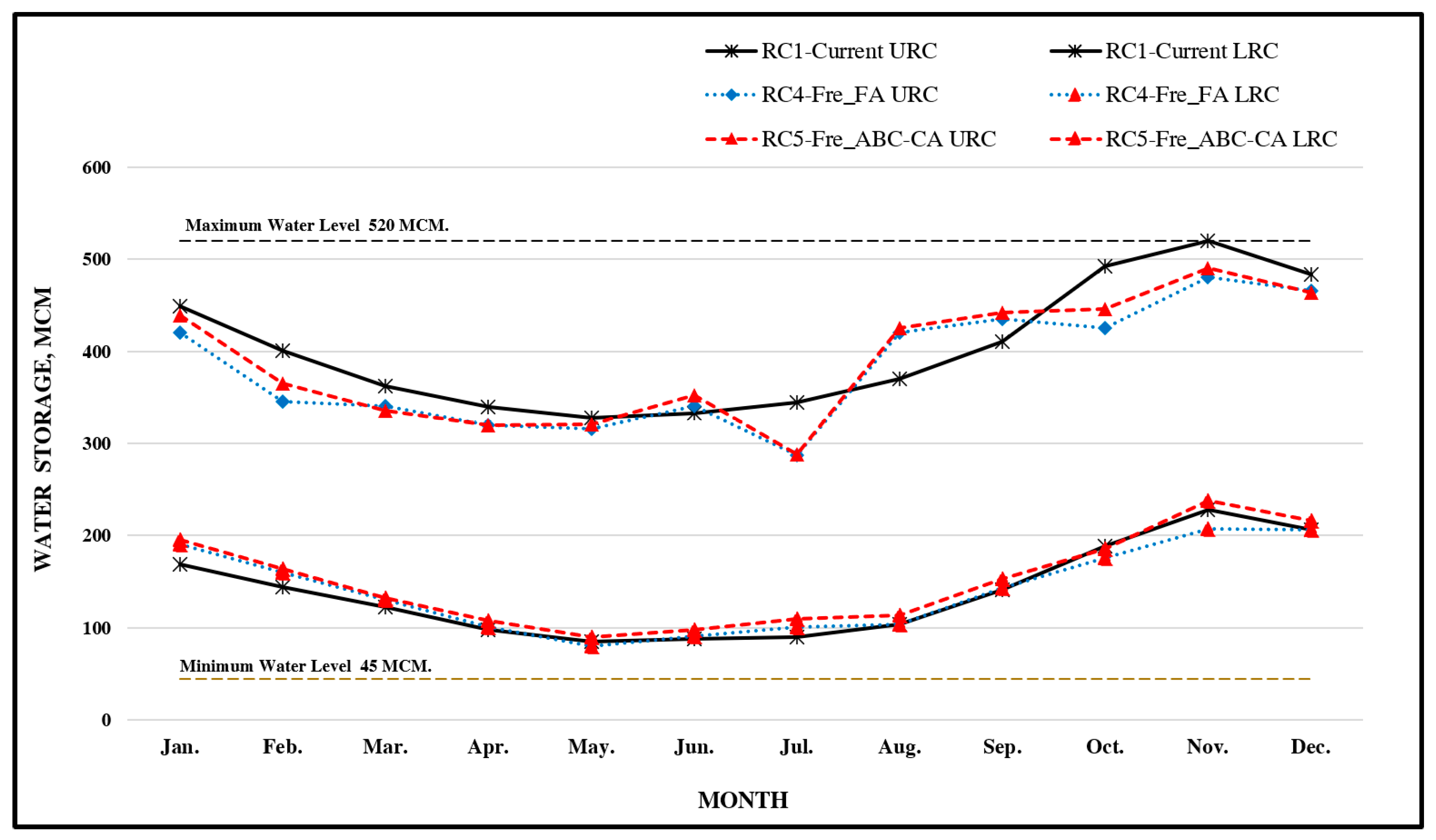
Figure 7 Illustrates the optimized RORC for the NOR. These curves were obtained by minimizing the frequency of excess water through a search process that considered historical data as the optimization objective. The patterns observed in RC4-Fre_FA, RC5-ABC-CA, and the current RORC are resemblant. They also demonstrate that the lower RORC resulting from the utilization of historical and future inflow data (RC4-Fre_FA and RC5-ABC-CA) are greater than the current RORC from January - June. Conversely, the upper RORC of the newly derived optimal RORC are lower than the current RORC in July.

3.2. Efficiency of the obtained RORC

The effectiveness of the recently derived RORC from all search scenarios was assessed through RSM that considered historical inflow data for the NOR, spanning 28 years on a monthly basis. The assessment considered instances of water scarcity and excessive water within RORC, and the results are outlined in Table 1. These findings highlighted that the RORC based on ABC-CA (RC5-Avr_ABC-CA), generated by minimizing average excess water as the optimization goal, yielded the lowest occurrences of water scarcity (0.464 times per year, 19.926 MCM per year, and 1.684 years for frequency, magnitude, and duration respectively) as well as excessive water release (0.627 times per year, 85.641 MCM per year, and 2.00 years for frequency, magnitude, and duration respectively) in comparison to other RORC. Moreover, the analysis demonstrated that the newly developed RORC were more effective in mitigating both water scarcity and excessive release situations than the existing RORC within the historic scenario.
Additionally, the 1,000 sets of simulated inflow data were generated for each reservoir based on their historical inflow records. Table 2 presents the frequency of excessive water and water scarcity in the NOR region. This analysis is based on synthetic inflow data of one thousand instances in the RORC simulation. The findings revealed that the instances of water scarcity (16.271±7.224 MCM/year) and excessive water (66.221±17.001 MCM/year) using the ABC-CA RORC, obtained by minimizing average excess water as the optimization objective (RC3-Avr_ABC-CA), were the lowest in comparison to other RORC. Conversely, when the current RORC were employed for assessment, the outcomes indicated the highest values.

4. Discussion

The patterns of the newly derived RORC from all search scenarios and the current RORC (as depicted in Figure 6-7) exhibit similarities due to the impact of seasonal inflow patterns and consistent conditional effects, which align with findings from other studies [2,33,34,53,54,55]. The updated lower RORC surpass the current lower RORC during dry seasons. This setup helps regulate the amount of released water by reducing water discharge to conserve more water during periods of low rainfall, a strategy observed in similar studies. In contrast, the newly established upper RORC for the months of June to September exceed the corresponding current upper RORC. These arrangements enable greater water conservation by mitigating excessive water release and maintaining elevated water levels. On the other hand, the newly obtained upper RORC are lower than the existing upper RORC for the months of October to November. As a result, these updated RORC have the potential to better manage flood scenarios compared to the current RORC, as they involve increased water release to create additional reserve volume.
The outcomes from assessing the newly acquired RORC (presented in Table 1 and Table 2) revealed that the occurrences of water scarcity and excessive water using ABC-CA RORC, which were developed by incorporating historical inflow data in the search process, were the lowest compared to other RORC. This similarity arises from their creation involving the utilization of historical inflow data, a strategy akin to other studies [34,53,54,56,57]. It is crucial to conduct a comparative analysis between the results of the proposed FA and ABC-CA techniques and the outcomes of alternative methods.

5. Conclusions

In this research, the Firefly Algorithm (FA) and the Artificial Bees Colony combined with Cultural Algorithm (ABC-CA) were employed alongside a RSM to search for optimal RORC. The findings highlighted that the proposed approach, utilizing two distinct objective functions, yielded novel RORC. The similarities in patterns of these RORC are attributed to seasonal inflow dynamics and consistent search conditions. Nonetheless, there exist variations, particularly notable during the rainy season. Additionally, the results demonstrated that RORC generated by minimizing average excess water and incorporating historical inflow data into the search process are more effective in mitigating excessive water scenarios compared to other RORC, in both historical and synthetic inflow scenarios.
This research revealed the utilization of the Firefly Algorithm (FA) and the combination of the Artificial Bees Colony and Cultural Algorithm (ABC-CA) in conjunction with a simulation model to explore flood control RORC that offer potential benefits in terms of optimization. The RORC derived from the newly proposed FA and ABC-CA models outperform the current RORC in mitigating flood scenarios. This study serves as a valuable resource for researchers engaged in the pursuit of optimal flood control RORC for reservoirs situated in flood-prone regions.

Author Contributions

Conceptualization, A.P.; methodology, A.P. and A.K.; software, A.P.; validation, A.P., O.S. and S.K.; formal analysis, A.P. and R.H.; investigation, A.P. and A.K.; resources, S.K.; data curation, A.P. and S.K.; writing—original draft preparation, A.P. and A.K.; writing—review and editing, A.P., O.S., S.K., R.H. and A.K.; visualization, A.P. and S.K.; supervision, A.P. and A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was financially supported by University of Phayao and Mahasarakham University.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The author would like to appreciate the University of Phayao, Mahasarakham University and Water Management and maintenance division, Regional Irrigation Office 5 for supporting information, tools, and research units.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Chaiyason, T.; Yamoat, N.; Sivanpheng, O.; Kangrang, A. Application of Harmony Search Algorithm for Improvement of Reservoir Rule Curves Under Dynamic Data of Water Requirements. International Review of Civil Engineering (IRECE) 2023, 14 (3), pp. 247-258. [CrossRef]
  2. Techarungruengsakul, R.; Kangrang, A. Application of Harris Hawks Optimization with Reservoir Simulation Model Considering Hedging Rule for Network Reservoir System. Sustainability 2022, 14(9), 4913. [Google Scholar] [CrossRef]
  3. Phumiphan, A.; Kangrang, A. Development of Decision-Making Support Tools for Future Reservoir Management Under Climate and Land Cover Variability: A Case Study. International Review of Civil Engineering (IRECE) 2021, 12 (4), pp. 271-283. [CrossRef]
  4. Bozorg-Haddad, O.; Azad, M.; Fallah-Mehdipour, E.; Delpasand, M.; Chu, X. Verification of FPA and PSO algorithms for rule curve extraction and optimization of single- and multi-reservoir systems' operations considering their specific purposes. Water Supply 2021, 21(1), 166–188. [Google Scholar] [CrossRef]
  5. Barati, A.; Zhoolideh,M.; Azadi, H.; Lee, J.; Scheffran, J. Interactions of land-use cover and climate change at global level: How to mitigate the environmental risks and warming effects, Ecological Indicators 2023, 146, 10982. [CrossRef]
  6. Zhou, Y.; Guo, S. Incorporating ecological requirement into multipurpose reservoir operating rule curves for adaptation to climate change. Journal of Hydrology 2013, 498, 153–164. [Google Scholar] [CrossRef]
  7. Zhang, Y.; Tang, C.; Ye, A.; Zheng, T.; Nie, X.; Tu, A.; Zhu, H.; Zhang, S. Impacts of Climate and Land-Use Change on Blue and Green Water: A Case Study of the Upper Ganjiang River Basin, China. Water 2020, 12, 2661. [Google Scholar] [CrossRef]
  8. Duan, W.; Chen, Y.; Zou, S.; Nover, D. Managing the water-climate- food nexus for sustainable development in Turkmenistan. J. Clean Prod. 2019, 220, 212–224. [Google Scholar] [CrossRef]
  9. Zhang, X.; Chen, X.; Zhang, W.; Peng, H.; Xu, G.; Zhao, Y.; Shen, Z. Impact of Land Use Changes on the Surface Runoff and Nutrient Load in the Three Gorges Reservoir Area, China. Sustainability 2022, 14, 2023. [Google Scholar] [CrossRef]
  10. Tanachaichoksirikun, P.; Seeboonruang, U. Distributions of Groundwater Age under Climate Change of Thailand’s Lower Chao Phraya Basin. Water 2020, 12, 3474. [CrossRef]
  11. Tanachaichoksirikun, P.; Seeboonruang, U. Effect of Climate Change on Groundwater Age of Thailand’s Lower Chao Phraya Basin. In Proceedings of the 5th International Conference on Engineering, Applied Sciences and Technology, Luang Prabang, Laos, 2–5 July 2019; p. 639. [Google Scholar] [CrossRef]
  12. Pholkern, K.; Saraphirom, P.; Srisuk, K. Potential impact of climate change on groundwater resources in the Central Huai Luang Basin, Northeast Thailand. Sci. Total Environ, 2018, 633, 1518–1535. [CrossRef]
  13. IPCC. Climate Change 2014. Synthesis Report. Versión Inglés; IPCC: Geneva, Switzerland, 2014; ISBN 9789291691432. [Google Scholar]
  14. Sieler, K.P.; Gu, W.Z.; Stichler, W. Transient response of groundwater systems to climate changes. Geol. Soc. Spec. Publ, 2008, 288, 111–119. [CrossRef]
  15. SeethaRam, K. V. Three level rule curves for optimum operation of a multipurpose reservoir using genetic algorithms. Water Resources Management 2021, 35(1), 353–368. [Google Scholar] [CrossRef]
  16. Visweswararao, M.; Viswanadh, G.K. Operation of a Upstream Reservoir Using Rule Curve to Improve the Performance of the Downstream Reservoirs. International Journal of Civil Engineering and Technology 2019, 10(7), pp. 14-21.
  17. Lei, X.; Zhang, J.; Wang, H.; Wang, M.; Khu, S.-T.; Li, Z.; Tan, Q. Deriving mixed reservoir operating rules for flood control based on weighted non-dominated sorting genetic algorithm II. J. Hydrol, 2018, 564, 967–983. [CrossRef]
  18. Wang, Q.; Ding, W.; Wang, Y. Optimization of Multi-Reservoir Operating Rules for a Water Supply System. Water Resour. Manag. 2018, 32, 4543–4559. 4543. [Google Scholar] [CrossRef]
  19. Ashrafi, S.M.; Dariane, A.B. Coupled Operating Rules for Optimal Operation of Multi-Reservoir Systems. Water Resour. Manag, 2017, 31, 4505–4520. 4505; 31. [Google Scholar] [CrossRef]
  20. Tan, Q.; Wang, X.; Wang, H.; Wang, C.; Xiong, Y.; Zhang, W. Derivation of optimal joint operating rules for multi-purpose multi-reservoir water-supply system. J. Hydrol, 2017, 551, 253–264. [CrossRef]
  21. Zhong, X.; Duan, M.; Zhang, X.; Cheng, P. A hybrid differential evolution based on gaining-sharing knowledge algorithm and harris hawks optimization. PLoS ONE, 2021, 16, e0250951. 0250. [Google Scholar] [CrossRef]
  22. Donyaii, A.; Sarraf, A.; Ahmadi, H. Water Reservoir Multiobjective Optimal Operation Using Grey Wolf Optimizer. Shock Vib, 2020, 2020, 10. 2020. [Google Scholar] [CrossRef]
  23. Pagano, A.; Giordano, R.; Vurro, M. A Decision Support System Based on AHP for Ranking Strategies to Manage Emergencies on Drinking Water Supply Systems. Water Resour. Manag, 2021, 35, 613–628. doi. 35. [CrossRef]
  24. Bozorg-Haddad, O.; Azad, M.; Fallah-Mehdipour, E.; Delpasand, M.; Chu, X. Verification of FPA and PSO Algorithms for Rule Curve Extraction and Optimization of Single- and Multi-Reservoir Systems’ Operations Considering Their Specific Purposes. Water Sci. Technol. Water Supply, 2021, 21, 166–188. doi. [CrossRef]
  25. Moeini, R.; Nasiri, K. Hybridizing ANN-NSGA-II Model with Genetic Programming Method for Reservoir Operation Rule Curve Determination (Case Study Zayandehroud Dam Reservoir). Soft Comput, 2021, 25, 14081–14108. doi. 1408; 25. [Google Scholar] [CrossRef]
  26. Ngoc, T.A.; Hiramatsu, K.; Harada, M. Optimizing the Rule Curves of Multi-Use Reservoir Operation Using a Genetic Algorithm with a Penalty Strategy. Paddy Water Environ, 2014, 12, 125–137. [CrossRef]
  27. Bahrami, N.; Afshar, A.; Afshar, M. H. An agent-based framework for simulating interactions between reservoir operators and farmers for reservoir management with dynamic demands. Agricultural Water Management 2022, 259, 107237. [Google Scholar] [CrossRef]
  28. Beshavard, M.; Adib, A.; Ashrafi, S. M.; Kisi, O. Establishing effective warning storage to derive optimal reservoir operation policy based on the drought condition. Agricultural Water Management 2022, 274, 107948. [Google Scholar] [CrossRef]
  29. Moeini, R.; Hadiyan, P. P. Hybrid methods for reservoir operation rule curve determination considering uncertain future condition. Sustainable Computing: Informatics and Systems, 2022, 35, 100727. [CrossRef]
  30. Luo, P.; Sun, Y.; Wang, S.; Wang, S.; Lyu, J.; Zhou, M.; Nakagami, K.; Takara, K.; Nover, D. Historical assessment and future sustainability challenges of Egyptian water resources management. Journal of Cleaner Production 2020, 263, 121154. [Google Scholar] [CrossRef]
  31. Ji, C.; Jiang, Z.; Sun, P.; Zhang, Y.; Wang, L. Research and application of multidimensional dynamic programming in cascade reservoirs based on multilayer nested structure. Journal of Water Resources Planning and Management 2015, 141(7), 1–13. [Google Scholar] [CrossRef]
  32. To, T.N.; Vu, H.C.; Le, H. An optimisation approach for the operating rule curves of the A Vuong reservoir, Vietnam. Water Supply, 7750. [Google Scholar] [CrossRef]
  33. Thongwan, T.; Kangrang, A.; Prasanchum, H. Multi-objective future rule curves using conditional tabu search algorithm and conditional genetic algorithm for reservoir operation. Heliyon 2019, 5(9), e02401. [Google Scholar] [CrossRef] [PubMed]
  34. Kangrang, A.; Prasanchum, H.; Hormwichian, R. Development of future rule curves for multipurpose reservoir operation using conditional genetic and tabu search algorithms. Advances in Civil Engineering 2018, 6474870. [Google Scholar] [CrossRef]
  35. Zhangrong, Q.; Zhang, L.; Xuan, Z.; Binghai, W.; Chaoying, Z. Hybrid algorithm of gene clustering based on GPU. Journal of Software Engineering 2017, 11, 183–193. [Google Scholar] [CrossRef]
  36. Rouzegari, N.; Hassanzadeh, Y.; Sattari, M. T. Using the hybrid simulated annealing-M5 tree algorithms to extract the if-then operation rules in a single reservoir. Water Resources Management 2019, 33(10), 3655–3672. [Google Scholar] [CrossRef]
  37. Afshar, M.H. A parameter free Continuous Ant Colony Optimization Algorithm for the optimal design of storm sewer networks: Constrained and unconstrained approach. Advances in Engineering Software, 2010, 41(2), pp. 188-195. doi. [CrossRef]
  38. Ashrafi, S. M.; Mahmoudi, M. Developing a semi-distributed decision support system for great Karun water resources system. Journal of Applied Research in Water and Wastewater 2019, 6(1), 16–24. [Google Scholar] [CrossRef]
  39. Bashiri-Atrabi, H.; Qaderi, K.; Rheinheimer, D. E.; Sharifi, E. Application of harmony search algorithm to reservoir operation optimization. Water Resources Management 2015, 29(15), 5729–5748. [Google Scholar] [CrossRef]
  40. Ming, B.; Chang, J.X.; Huang, Q.; Wang, Y.M.; Huang, S.Z. Optimal operation of multi-reservoir system based on cuckoo search algorithm. Water Resources Management 2015, 29(15), 5671–5687. [Google Scholar] [CrossRef]
  41. Yelghi, A.; Köse, C. A modified firefly algorithm for global minimum optimization. Applied Soft Computing 2018, 62, 29–44. [Google Scholar] [CrossRef]
  42. Jing, Y.; Shoulin, Y.; Hang, L. An improved particle filter based on firefly algorithm used for indoor localization. Journal of Software Engineering 2017, 11, 224–229. [Google Scholar] [CrossRef]
  43. Udaiyakumar, K.C.; Chandrasekaran, M. Application of firefly algorithm in job shop scheduling problem for minimization of make span. Procedia Engineering 2014, 97, 1798–1807. [Google Scholar] [CrossRef]
  44. Bharathi Raja, S.; Sathiya Narayanan, N.; Srinivas Pramod, C.V.; Ragunathan, A.; Raju Vinesh, S.; Vamshee Krishna, K. Optimization of constrained machining parameters in turning operation using firefly algorithm. Journal of Applied Sciences, 2012, 12: 1038-1042. [CrossRef]
  45. Yang, XS. Firefly Algorithm, Lévy Flights and Global Optimization. In: Bramer, M., Ellis, R., Petridis, M. (eds) Research and Development in Intelligent Systems XXVI. Springer, London, 2010. [Google Scholar] [CrossRef]
  46. Yang, XS. Firefly Algorithms for Multimodal Optimization. In: Watanabe, O., Zeugmann, T. (eds) Stochastic Algorithms: Foundations and Applications. SAGA, 2009. Lecture Notes in Computer Science, vol 5792. Springer, Berlin, Heidelberg. 5792. [Google Scholar] [CrossRef]
  47. Reynolds, R.G. An Introduction to Cultural Algorithms, Proceedings of the 3rd Annual Conference on Evolutionary Programming 1994, World Scientific Publishing, pp 131–139.
  48. Reynolds, R.G.; Ali, M. Z. Exploring Knowledge and Population Swarms via an Agent-Based Cultural Algorithms Simulation Toolkit (CAT). Proceedings of IEEE Congress on Computational Intelligence 2007. [Google Scholar] [CrossRef]
  49. Reynolds, R.G.; Peng, B. Knowledge Learning and Social Swarms in Cultural Systems. Journal of Mathematical Sociology, 2005, vol. 29, pp. 1–18. [CrossRef]
  50. Li, X.; Guo, S.; Liu, P.; Chen, G. Dynamic control of flood limited water level for reservoir operation by considering inflow uncertainty. Journal of hydrology, 2010, 391(1-2), 124-132. [CrossRef]
  51. Yang, X. S. Nature-Inspired Metaheuristic Algorithms. Luniver Press, 2008, ISBN 978-1-905986-10-1.
  52. Pham, D. T.; Ghanbarzadeh, A.; Koc, E.; Otri, S.; Rahim, S.; Zaidi, M. The bees algorithm. Technical report, Manufacturing Engineering Centre, Cardiff University, UK, 2005.
  53. SeethaRam, K.V. Three Level Rule Curve for Optimum Operation of a Multipurpose Reservoir using Genetic Algorithms. Water Resources Management, 2021, 35, pp. 353-368. [CrossRef]
  54. Kangrang, A.; Srikamol, N.; Hormwichian, R.; Prasanchum, H.; Sriwanpheng, O. Alternative Approach of Firefly Algorithm for Flood Control Rule Curves. Asian Journal of Scientific Research, 2019, 12, 431–439. [CrossRef]
  55. Kangrang, A.; Prasanchum, H.; Hormwichian, R. Active future rule curves for multi-purpose reservoir operation on the impact of climate and land use changes. Journal of Hydro-environment Research, 2019, 24, 1–13. [CrossRef]
  56. Turgeon, A. Stochastic optimization of multi-reservoir operation: the optimal reservoir trajectory approach. Water Resources Research, 2017, 43(5), pp. 1–10. [CrossRef]
  57. Sriworamas, K.; Kangrang, A.; Thongwan, T.; Prasanchum, H. Optimal Reservoir of Small Reservoirs by Optimization Techniques on Reservoir Simulation Model. Advances in Civil Engineering 2021, 6625743. [Google Scholar] [CrossRef]
Preprints 95979 g001
Figure 1. The whereabouts of the Nam-Oon Reservoir (NOR).
Figure 1. The whereabouts of the Nam-Oon Reservoir (NOR).
Preprints 95979 g001
Preprints 95979 g002
Figure 2. Illustration depicting the schematic diagram of the Nam-Oon Reservoir (NOR) system.
Figure 2. Illustration depicting the schematic diagram of the Nam-Oon Reservoir (NOR) system.
Preprints 95979 g002
Preprints 95979 g003
Figure 3. Standard Operating Reservoir Rules.
Figure 3. Standard Operating Reservoir Rules.
Preprints 95979 g003
Preprints 95979 g004
Figure 4. Firefly Algorithm incorporating RSM to search for optimal RORC.
Figure 4. Firefly Algorithm incorporating RSM to search for optimal RORC.
Preprints 95979 g004
Preprints 95979 g005
Figure 5. ABC-CA incorporating RSM to search for optimal RORC.
Figure 5. ABC-CA incorporating RSM to search for optimal RORC.
Preprints 95979 g005
Preprints 95979 g006
Figure 6. Optimal RORC of the NOR using the objective function of minimizing the average excess water in the search procedure.
Figure 6. Optimal RORC of the NOR using the objective function of minimizing the average excess water in the search procedure.
Preprints 95979 g006
Preprints 95979 g007
Figure 7. Optimal RORC of the NOR using the objective function of minimizing the frequency excess water in the search procedure.
Figure 7. Optimal RORC of the NOR using the objective function of minimizing the frequency excess water in the search procedure.
Preprints 95979 g007
Table 1. There are situations of excess water and water scarcity in the NOR, considering the historical inflow during the past 28 years.
Table 1. There are situations of excess water and water scarcity in the NOR, considering the historical inflow during the past 28 years.
Situations RORC Frequency
(times/year)		 Volume Time period
Average Maximum Average Maximum
Water scarcity RC1-Current 0.962 45.884 154.000 13.500 14.000
RC2-Avr_FA 0.584 21.378 130.000 2.500 3.000
RC3-Avr_ABC- 0.464 19.926 126.000 1.684 3.000
RC4-Fre_FA 0.782 38.411 142.000 6.000 8.000
RC5-Fre_ABC-CA 0.994 38.407 140.000 10.500 12.000
Excess water RC1-current 0.754 113.402 476.959 4.000 6.000
RC2-Avr_FA 0.794 89.226 479.080 3.000 5.000
RC3-Avr_ABC- 0.797 86.844 465.867 3.000 4.000
RC4-Fre_FA 0.704 89.381 465.083 2.000 4.000
RC5-Fre_ABC-CA 0.627 85.641 436.372 2.000 3.000
Table 2. There are situations of excess water and water scarcity of the NOR region, considering 1,000 synthetic inflow samples.
Table 2. There are situations of excess water and water scarcity of the NOR region, considering 1,000 synthetic inflow samples.
Situations RORC Frequency (times/year) Volume (MCM) Time period (year)
Average Maximum Average Maximum
Water scarcity RC1-Current μ 0.971 42.445 131.774 17.442 22.637
σ 0.032 6.831 36.226 6.804 4.937
RC2-Avr_FA μ 0.673 18.014 110.824 2.653 5.292
σ 0.109 8.224 29.344 0.968 2.447
RC3-Avr_ABC-CA μ 0.473 16.271 108.097 2.307 4.065
σ 0.106 7.224 27.744 0.747 2.044
RC4-Fre_FA μ 0.811 33.227 120.224 6.242 10.388
σ 0.108 7.723 34.220 3.584 4.335
RC5-Fre_ABC-CA μ 0.989 33.407 119.379 15.124 18.066
σ 0.051 6.837 30.055 7.225 5.097
Excess water RC1-Current μ 0.699 91.994 358.622 3.009 7.717
σ 0.107 20.931 77.022 1.554 2.249
RC2-Avr_FA μ 0.638 68.734 328.771 2.557 5.334
σ 0.155 18.984 81.229 0.899 2.227
RC3-Avr_ABC-CA μ 0.557 66.221 324.073 2.458 5.365
σ 0.104 17.001 80.177 0.975 2.005
RC4-Fre_FA μ 0.687 80.812 350.401 2.844 6.113
σ 0.110 19.003 79.773 1.098 2.502
RC5-Fre_ABC-CA μ 0.644 79.991 345.374 3.009 6.302
σ 0.105 20.224 77.780 1.224 2.708
μ : Mean, σ : Standard deviation.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated