A Simple Quantum Picture of the Relativistic Doppler Effect

1. Introduction

When a moving car beeps its horn, the driver and a bystander on the pavement hear the sound at different frequencies. The frequency shift resulting from the relative motion of the driver and the bystander is known as the Doppler effect [1,2] and is well understood in classical physics. For example, the frequency heard by the resting observer depends on the speed of the car relative to the pavement and the original frequency of the signal. Due to its simplicity, the Doppler effect has already found a wide range of applications, including the policing of speed limit violations by irresponsible drivers. The relativistic Doppler effect [3,4,5,6,7,8,9] also accounts for differences in how observers experience space and time. Observers in different inertial reference frames which move at a relative speed close to the speed of light receive signals which differ not only in frequency and wavelength but also in amplitude.

According to Einstein’s principle of relativity [10,11,12,13,14,15,16], there is no privileged frame of reference. The same physical laws apply in all reference frames if these move with respect to each other at constant velocity. For example, wave packets of light with a well-defined direction of propagation move at the speed of light, c, in any reference frame. Some authors might still debate whether this assumption is true or not [17] but many experiments already verified the constancy of the speed of light with high accuracy [18,19]. Moreover, any physical theory that involves space and time requires a way of measuring both using clocks and meters. In the following, we assume that all clocks and meters are calibrated such that light travels at the same speed in all reference frames. We then have a fresh look at the relativistic Doppler effect [5] with only a minimum of assumptions.

Instead of considering frequency space, in this paper we study the relativistic Doppler effect [3,5,6,7,8] in position space [20,21,22,23]. As we shall see below, this space can accommodate spatial and time translational symmetries in a straightforward way. Although our results are consistent with the existing literature [24,25,26,27,28,29,30,31,32], our approach paves the way for systematic studies of more complex scenarios, like the Unruh effect [33,34] and quantum electrodynamics in reference frames with time-varying accelerations without the need for approximations, such as the usual assumption of a flat spacetime [35]. Moreover, the insights obtained here might have applications in relativistic quantum information [36,37,38,39,40,41]. In the following, we review the relativistic Doppler effect before studying its implications for the quantised electromagnetic (EM) field in different inertial reference frames.

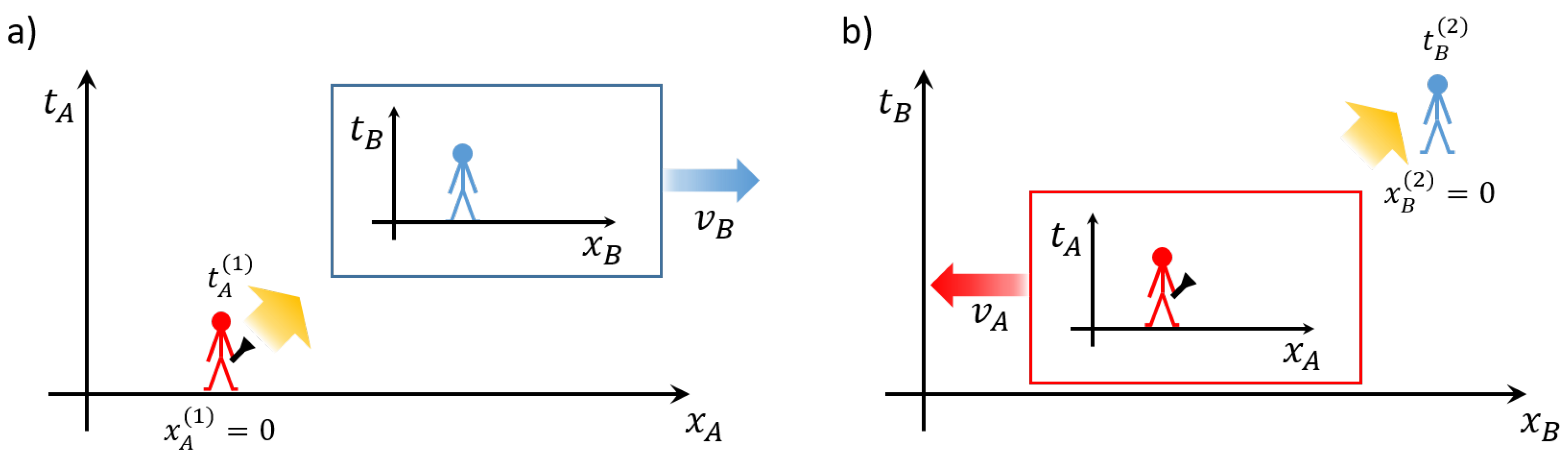
Suppose an observer—let us call her Alice (A)—is watching a wave packet of light with a well-defined direction of propagation s and a well-defined polarisation $\lambda$ traveling along the x axis. Then the electric field amplitudes $E_{\mathrm{A}}(x_{\mathrm{A}},t_{\mathrm{A}})$ seen by Alice at positions $x_{\mathrm{A}}$ at times $t_{\mathrm{A}}$ equal

$$\begin{array}{ccc}\hfill E_{\mathrm{A}}(x_{\mathrm{A}},t_{\mathrm{A}})& =& E_{\mathrm{A}}(x_{\mathrm{A}}-sc{t}_{\mathrm{A}},0)\hfill \end{array}$$

(1)

if the initial electric field amplitudes of the wave packet are given by $E_{\mathrm{A}}(x_{\mathrm{A}},0)$. Here $s=-1$ and $s=1$ correspond to wave packets propagating in the direction of decreasing and increasing $x_{\mathrm{A}}$ respectively. Hence, if the physical properties of a wave packet seen by Alice are known at one instant in time, they are known at all times. The same applies to the electric field amplitudes $E_{\mathrm{B}}(x_{\mathrm{B}},t_{\mathrm{B}})$ seen at $(x_{\mathrm{B}},t_{\mathrm{B}})$ by a second observer—who we call Bob (B)—and

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}(x_{\mathrm{B}},t_{\mathrm{B}})& =& E_{\mathrm{B}}(x_{\mathrm{B}}-sc{t}_{\mathrm{B}},0),\hfill \end{array}$$

(2)

in analogy to Equation (1). The electric field observables perceived by both Alice and Bob at any position and time are only characterised by the value of the parameters ${\alpha }_i=x_i-sc{t}_i$ with $i=\mathrm{A},\mathrm{B}$. In the remainder of this paper, we shall use a shorthand notation and replace $E_i(x_i,t_i)$ by $E_i\left({\alpha }_i\right)$.

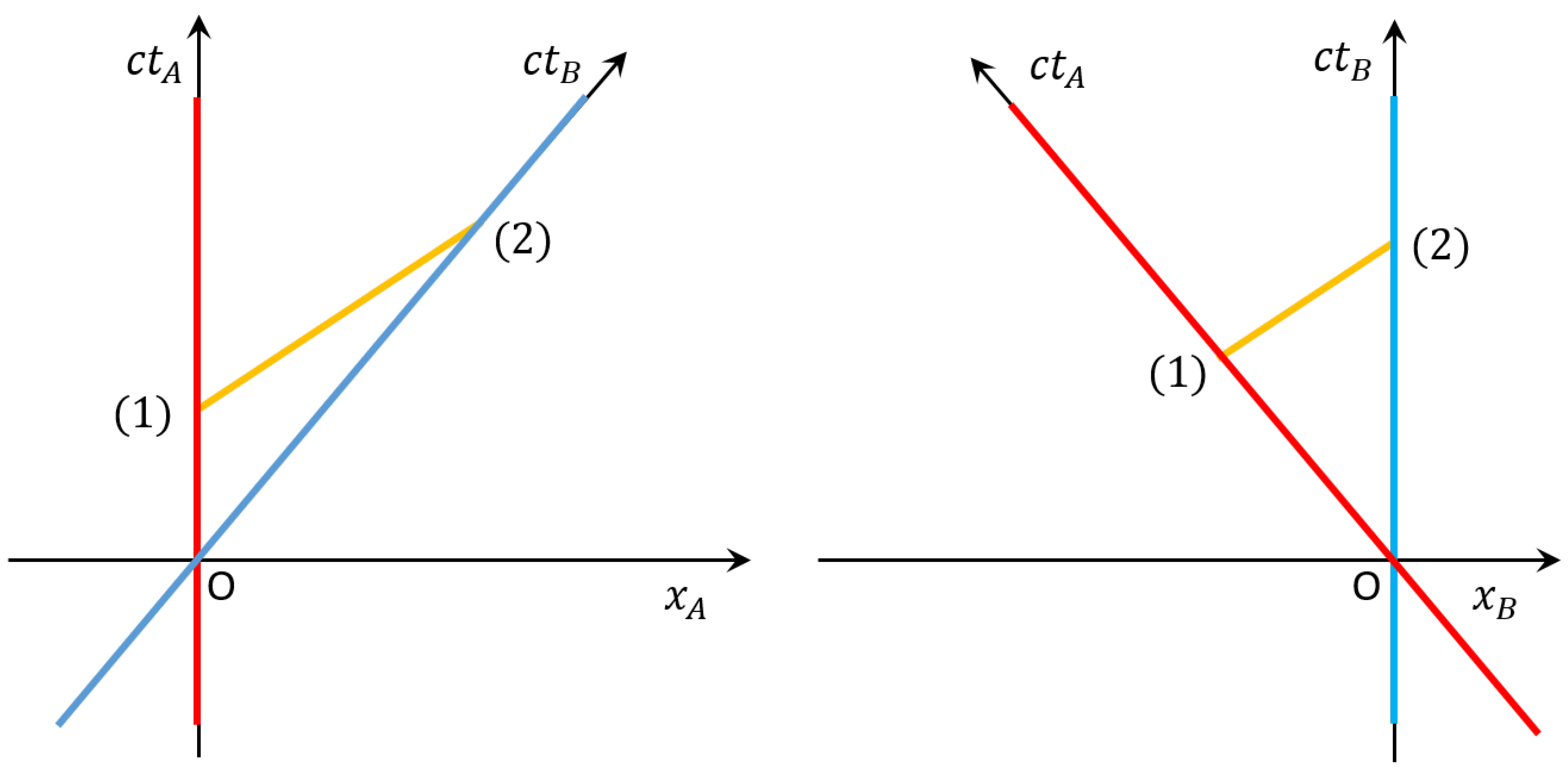
The principle of relativity also suggests that the electric and magnetic field transformations from observer A to observer B and vice versa need to be formally the same. The only difference is that the relative speed of their reference frames changes from $v_{\mathrm{B}}$ to $v_{\mathrm{A}}=-v_{\mathrm{B}}$. This suggests a linear dependence between electric field amplitudes $E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)$ and $E_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)$ at the same point in the spacetime diagram since this transformation is the only transformation which remains formally the same when reversed. We therefore assume in the following that

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)& =& {\xi }_{\mathrm{BA}}{E}_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)\hfill \end{array}$$

(3)

where the coordinates ${\alpha }_{\mathrm{A}}$ and ${\alpha }_{\mathrm{B}}$ specify the same spacetime trajectory and ${\xi }_{\mathrm{BA}}$ denotes a transformation constant. Analogously, we also know that

$$\begin{array}{ccc}\hfill E_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)& =& {\xi }_{\mathrm{AB}}{E}_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right).\hfill \end{array}$$

(4)

The principle of relativity also tells us that the transformation constants ${\xi }_{\mathrm{AB}}$ and ${\xi }_{\mathrm{BA}}$ relate to each other such that

$$\begin{array}{ccc}\hfill {\xi }_{\mathrm{AB}}(s,v_{\mathrm{B}})& =& {\xi }_{\mathrm{BA}}(s,-v_{\mathrm{B}}),\hfill \end{array}$$

(5)

since the direction of propagation s of the wave packet is the same in both reference frames, but the relative speed of the frames changes sign. When combining Equations (3)–(5) we therefore find that

$$\begin{array}{c}\hfill {\xi }_{\mathrm{BA}}(s,v_{\mathrm{B}})=1/{\xi }_{\mathrm{BA}}(s,-v_{\mathrm{B}}).\end{array}$$

(6)

In the following, this is taken into account when we determine ${\xi }_{\mathrm{AB}}$ and ${\xi }_{\mathrm{BA}}$.

Next we notice that the spatial and time translational symmetries of the EM field tell us that the above relations must hold for all spacetime coordinates. Hence the transformation factors ${\xi }_{\mathrm{BA}}$ and ${\xi }_{\mathrm{AB}}$ can only depend on the direction of propagation s of the wave packet and on the relative speed $v_{\mathrm{B}}$ of Bob’s reference frame with respect to Alice’s reference frame and not on where and when electric and magnetic field amplitudes are measured. The above arguments thus reduce the question, how do local electric and magnetic field observables transform from one inertial frame to another, to the simpler question, namely, how do the field observables transform at a single point in the spacetime diagram? Unfortunately, the above equations are not enough to determine the transformation factor ${\xi }_{\mathrm{BA}}$ in Equation (3). An additional assumption is needed.

Our final assumption in the derivation of the relativistic Doppler effect is based on energy conservation. To implement this we consider a “box” that moves at the speed of light along the x axis in the reference frame of observer B. By integrating over the volume inside the “box” at a fixed time we can calculate the amount of energy it contains. As the “box” propagates at the speed of light, any light initially caught inside or outside of that “box” will remain here for all time, and the total energy that it encloses will be conserved. Nevertheless, as Alice and Bob experience space and time differently, the “box” observed by Bob will appear deformed to Alice and the energy of the field will be measured differently. For example, parts of the wave packet that occur simultaneously in the frame of observer A appear at different times $t_{\mathrm{B}}$ in the reference frame of observer B. Taking this into account, we can finally identify the dependence of ${\xi }_{\mathrm{AB}}$ and ${\xi }_{\mathrm{BA}}$ on s and on $v_{\mathrm{B}}$. When applying Fourier transforms to local electric field amplitudes, we obtain the usual momentum changes of the relativistic Doppler effect.

As mentioned already above, the main purpose of this paper is to obtain a simple quantum picture of the relativistic Doppler effect. In the following we use a local photon approach and proceed as described in Refs. [20,21,22] to quantise the EM field in different inertial reference frames. Given the principle of relativity, neither observer A nor observer B should be able to perform measurements on photonic wave packets which tell them about their relative speed. Taking this into account, we find that the local photon annihilation operators of Alice and Bob are the same when they refer to the same location in the spacetime diagram. However, the transformation of the annihilation operators of monochromatic photons is more complex. As we will see below, both observers Alice and Bob need to assign different quantum states $|{\psi }_{\mathrm{A}}\left(t_{\mathrm{A}}\right)\rangle$ and $|{\psi }_{\mathrm{B}}\left(t_{\mathrm{B}}\right)\rangle$ to wave packets of light, even when describing the same wave packet.

This paper is structured as follows. Section 2 reviews the relativistic Doppler effect in classical physics. We first study how the coordinates ${\alpha }_{\mathrm{A}}$ and ${\alpha }_{\mathrm{B}}$ of two inertial observers A and B relate to each other when they correspond to the same point in the spacetime diagram. Afterwards, we derive the electric field transformation rates ${\xi }_{\mathrm{AB}}$ and ${\xi }_{\mathrm{BA}}$ in Equations (1) and (2) by imposing the above described conditions. Section 3 reviews a local description of the quantised EM field [21,22] for light propagation in one dimension. Section 4 combines this description with the results of Section 2 to obtain a quantum picture of the relativistic Doppler effect and to identify the relationship between the quantum states $|{\psi }_{\mathrm{A}}\left(t_{\mathrm{A}}\right)\rangle$ and $|{\psi }_{\mathrm{B}}\left(t_{\mathrm{B}}\right)\rangle$ of a wave packet of light seen by observers A and B in different inertial frames. Finally, we summarise our findings in Section 5.

2. The Relativistic Doppler Effect

The motion of an observer affects both the time and distance separating two events in spacetime, as well as their electric and magnetic field observables. The change in duration and separation between events can be expressed as a transformation between the natural coordinates of the two observers involved; one taken as a reference observer. In this section, we provide a derivation of the coordinate transformations between an observer at rest and an observer moving with constant velocity. Afterwards, we use these coordinate transformations to determine the transformation constant ${\xi }_{\mathrm{BA}}$ in Equation (3).

2.1. Coordinate Transformations

In this paper we consider two observers, Alice and Bob, in a flat 1+1 dimensional spacetime (Minkowski space). In the following, we assume our first observer, Alice, who will provide a point of reference, to be at rest. Our second observer, Bob, is travelling at a constant velocity $v_{\mathrm{B}}$ relative to Alice along the $x_{\mathrm{A}}$ axis, as illustrated in Figure 1. The position and time at which an event takes place from Alice’s point of view are denoted $x_{\mathrm{A}}$ and $t_{\mathrm{A}}$ respectively. Analogously, from Bob’s point of view, events take place at a position $x_{\mathrm{B}}$ at a time $t_{\mathrm{B}}$. For simplicity, we assume that both observers, who are stationary with respect to their own position coordinates, are located at the origin of these coordinates. This means that we choose Alice’s position to be $x_{\mathrm{A}}=0$ for all times $t_{\mathrm{A}}$, while Bob’s position equals $x_{\mathrm{B}}=0$ for all $t_{\mathrm{B}}$. Moreover, we assume in the following that Alice’s and Bob’s spacetime diagrams overlap at the origin. Hence Bob meets Alice only once at the initial time $t_{\mathrm{A}}=t_{\mathrm{B}}=0$.

As mentioned already in the Introduction, in a stationary reference frame, Maxwell’s equations tell us that light propagates along the $x_{\mathrm{A}}$ axis at the speed of light c. Therefore, if Alice sends a localised pulse of light to Bob, she will observe that its position $x_{\mathrm{A}}$ at any time $t_{\mathrm{A}}$ satisfies the relation

$$\begin{array}{ccc}\hfill {\alpha }_{\mathrm{A}}& =& \mathrm{const}.\hfill \end{array}$$

(7)

with ${\alpha }_{\mathrm{A}}=x_{\mathrm{A}}-sc{t}_{\mathrm{A}}$. Physically, ${\alpha }_{\mathrm{A}}$ is the position of the light pulse at $t_{\mathrm{A}}=0$. The speed of light measured relative to the rest frame of an inertial observer is always constant and independent of the motion of the source. Hence, from Bob’s point of view, the position $x_{\mathrm{B}}$ of the light pulse at any time $t_{\mathrm{B}}$ satisfies the relation

$$\begin{array}{ccc}\hfill {\alpha }_{\mathrm{B}}& =& \mathrm{const}.\hfill \end{array}$$

(8)

with ${\alpha }_{\mathrm{B}}=x_{\mathrm{B}}-sc{t}_{\mathrm{B}}$. Here ${\alpha }_{\mathrm{B}}$ may not be equal to ${\alpha }_{\mathrm{A}}$, but the direction of propagation s of the light pulse must be the same in both reference frames. As both Equations (7) and (8) must be satisfied simultaneously for a single light pulse, it can be shown that

$$\begin{array}{ccc}\hfill \frac{{\alpha }_{\mathrm{B}}}{{\alpha }_{\mathrm{A}}}& =& \kappa .\hfill \end{array}$$

(9)

The relating constant $\kappa$ may depend on s and provides a connection between the coordinates adopted by Alice and the ones adopted by Bob. The difference in the way position and time are perceived by Alice and Bob has a crucial influence on the way electric and magnetic fields are measured. The aim of this subsection, therefore, is to determine the factor $\kappa$ in Equation (9).

Suppose Alice sends a short light pulse from her own position at $x_{\mathrm{A}}^{\left(1\right)}=0$ at a time $t_{\mathrm{A}}^{\left(1\right)}$ to Bob, as illustrated in Figure 1. From Bob’s point of view, the light is emitted from a position $x_{\mathrm{B}}^{\left(1\right)}<0$ at a time $t_{\mathrm{B}}^{\left(1\right)}$ and arrives at Bob’s position $x_{\mathrm{B}}^{\left(2\right)}=0$ when his watch reads a time $t_{\mathrm{B}}^{\left(2\right)}$. As Alice’s and Bob’s positions are always zero in their respective reference frames, Equation (9) tells us that

$$\begin{array}{ccc}\hfill t_{\mathrm{B}}^{\left(2\right)}& =& \kappa t_{\mathrm{A}}^{\left(1\right)}.\hfill \end{array}$$

(10)

This relation takes into account both the time it takes the light to propagate from Alice to Bob and any difference in the rate at which their clocks are running. To determine the relation between $t_{\mathrm{B}}^{\left(2\right)}$ and $t_{\mathrm{B}}^{\left(1\right)}$ and between $t_{\mathrm{A}}^{\left(2\right)}$ and $t_{\mathrm{A}}^{\left(1\right)}$, respectively, we consider the spacetime diagrams for the experiment from both Alice’s and Bob’s points of view. As illustrated in Figure 2, according to Alice’s measurements, Bob receives the light pulse at a position $x_{\mathrm{A}}^{\left(2\right)}>0$ at a time $t_{\mathrm{A}}^{\left(2\right)}$ with $t_{\mathrm{A}}^{\left(2\right)}=t_{\mathrm{A}}^{\left(1\right)}+x_{\mathrm{A}}^{\left(2\right)}/c$. As Bob travels at a constant speed $v_{\mathrm{B}}$ with respect to Alice, the position of Bob when the signal is received is $x_{\mathrm{A}}^{\left(2\right)}=v_{\mathrm{B}}{t}_{\mathrm{A}}^{\left(2\right)}$. Putting these two relations together, we find that

$$\begin{array}{ccc}\hfill t_{\mathrm{A}}^{\left(1\right)}& =& (1-\beta )t_{\mathrm{A}}^{\left(2\right)}\hfill \end{array}$$

(11)

with $\beta =v_{\mathrm{B}}/c$. Moreover, from Bob’s point of view, Alice travels to the left with a velocity $v_{\mathrm{A}}=-v_{\mathrm{B}}$. Hence $t_{\mathrm{B}}^{\left(1\right)}=t_{\mathrm{B}}^{\left(2\right)}-v_{\mathrm{B}}{t}_{\mathrm{B}}^{\left(1\right)}/c$, which leads to

$$\begin{array}{ccc}\hfill t_{\mathrm{B}}^{\left(2\right)}& =& (1+\beta )t_{\mathrm{B}}^{\left(1\right)}.\hfill \end{array}$$

(12)

Equations (11) and (12) specify the relationship between the times at which the light is emitted and received from the points of view of both observers.

In Bob’s reference frame, the time elapsed between two events may not be the same as the time elapsed between the same events in Alice’s frame [11,12,13,14]. In general, a moving clock will tick at a different rate than a stationary clock, and we must consider this. According to Alice, the position at which the signal is received varies with time, whereas for Bob it does not. If a moving clock ticks more slowly than a stationary one by a rate of $\gamma$, then it follows that [15,16]

$$\begin{array}{c}\hfill t_{\mathrm{A}}^{\left(2\right)}=\gamma t_{\mathrm{B}}^{\left(2\right)}.\end{array}$$

(13)

As the position of the emitter is stationary with respect to Alice but moving at a constant velocity with respect to Bob, it must also be that

$$\begin{array}{c}\hfill t_{\mathrm{B}}^{\left(1\right)}=\gamma t_{\mathrm{A}}^{\left(1\right)}.\end{array}$$

(14)

By combining Equations (13) and (14) with Equations (11) and (12) it can be shown that

$$\begin{array}{c}\hfill \gamma =\frac{1}{\sqrt{1-{\beta }^2}}.\end{array}$$

(15)

Since $\gamma$ is always larger than 1, clocks run slower in a moving frame.

By putting together Equations (12) and (14) the factor $\kappa$ can be determined. We find that for light propagating to the right $\kappa =\gamma (1+\beta )$ where $\gamma$ is defined in Equation (15). By carrying out a similar set of calculations for left-propagating light that is transmitted by Alice at some time $t_{\mathrm{A}}<0$ we can determine the complete relation

$$\begin{array}{ccc}\hfill {\alpha }_{\mathrm{B}}& =& \gamma (1+s\beta ){\alpha }_{\mathrm{A}}.\hfill \end{array}$$

(16)

The two equations (one for each value of s) given in Equation (16) relate the trajectory of a light pulse in Bob’s reference frame to a light pulse in Alice’s reference frame. What is more, by solving these equations we can derive the point-like coordinate transformations for $x_{\mathrm{B}}$ and $t_{\mathrm{B}}$. The equations

$$\begin{array}{ccc}\hfill x_{\mathrm{B}}& =& \gamma (x_{\mathrm{A}}-\beta c{t}_{\mathrm{A}}),\hfill \\ \hfill c{t}_{\mathrm{B}}& =& \gamma (c{t}_{\mathrm{A}}-\beta x_{\mathrm{A}})\hfill \end{array}$$

(17)

establish a connection between spacetime coordinates $(x_{\mathrm{A}},t_{\mathrm{A}})$ and $(x_{\mathrm{B}},t_{\mathrm{B}})$ which refer to the same point in the spacetime diagram.

2.2. Field Amplitude Transformations

Since Alice and Bob perceive space and time differently (cf. Equation (17)), wave packets of light appear to have different shapes in each reference frame. What is more, the electric and magnetic field amplitudes of wave packets differ for Alice and Bob even at points which correspond to the same location in the spacetime diagram. This means that the same wave packet carries a different amount of energy from the point of view of Alice than it does from the point of view of Bob. Despite these changes, we know that light carries a conserved and invariant energy flux $\mathit{v}$. Here $\mathit{v}$ is a vector which points along the trajectory of light in the spacetime diagram and whose amplitude quantifies the total amount of energy that is moving in this direction. Since the speed of light is the same in all reference frames, a component of this energy flux will always intersect the $x_{\mathrm{A}}$ and $x_{\mathrm{B}}$ position axes. It is these components that correspond to the energy of the EM field as measured by Alice and Bob and relate closely to their field amplitudes. Hence in this subsection, we use energy flux conservation to identify the field amplitude transformations between inertial frames, i.e., the factor ${\xi }_{\mathrm{BA}}$ in Equation (3).

Suppose that a short light pulse propagating through spacetime is confined to a “box” that propagates along the x-axis at the speed of light in the same direction as the wave packet. The light pulse remains confined to this “box” in all reference frames. Suppose that the edge of the “box” is parallel to the $x_{\mathrm{B}}$ axis in Bob’s reference frame and that it has the length $\Delta x_{\mathrm{B}}$ as illustrated in Figure 3(a). Figure 3(b) shows the same “box” from the point of view of Alice. Here the “box” also travels at the speed of light, but is deformed. Most importantly, any light initially in the “box” cannot exit and any light outside cannot enter. Hence the energy flux $\mathit{v}$ within the “box” must be the same in both reference frames.

To take advantage of the invariance of $\mathit{v}$, we notice that the EM field energy seen by Alice and by Bob respectively can be written as

$$\begin{array}{ccc}\hfill H_{\mathrm{energy}}^{\left(i\right)}& =& \mathit{v}·{\widehat{\mathit{t}}}_i\hfill \end{array}$$

(18)

with $i=\mathrm{A},\mathrm{B}$. In the above equation, ${\widehat{\mathit{t}}}_{\mathrm{A}}$ and ${\widehat{\mathit{t}}}_{\mathrm{B}}$ are unit vectors oriented in the future directions of Alice and Bob, as illustrated in Figure 3. Using the coordinate transformations in Equation (17), it can be shown that

$$\begin{array}{ccc}\hfill {\widehat{\mathit{t}}}_{\mathrm{B}}& =& \gamma {\widehat{\mathit{t}}}_{\mathrm{A}}-\gamma \beta {\widehat{\mathit{x}}}_{\mathrm{A}}.\hfill \end{array}$$

(19)

The vector ${\widehat{\mathit{t}}}_{\mathrm{B}}$ is normalized under the Lorentzian inner product. Taking into account that, for a given direction of propagation,

$$\begin{array}{ccc}\hfill \mathit{v}·{\widehat{\mathit{x}}}_{\mathrm{A}}& =& s{H}_{\mathrm{energy}}^{\left(\mathrm{A}\right)}\hfill \end{array}$$

(20)

where ${\widehat{\mathit{x}}}_{\mathrm{A}}$ is a unit vector oriented in the direction of increasing $x_{\mathrm{A}}$ and using Equation (19), we find that

$$\begin{array}{ccc}\hfill H_{\mathrm{energy}}^{\left(\mathrm{B}\right)}& =& \gamma \left(1-s\beta \right)H_{\mathrm{energy}}^{\left(\mathrm{A}\right)}\hfill \end{array}$$

(21)

where $H_{\mathrm{energy}}^{\left(\mathrm{A}\right)}$ is the energy of the light with energy flux $\mathit{v}$ measured by Alice.

In Alice’s and Bob’s reference frames, the total energy of the EM field is obtained after integrating the energy density $h_{\mathrm{energy}}^{\left(i\right)}\left(x_i\right)$ over the entire $x_i$ axes with $i=\mathrm{A},\mathrm{B}$ respectively. These energy densities are given by [42]

$$\begin{array}{ccc}\hfill h_{\mathrm{energy}}^{\left(i\right)}\left({\alpha }_i\right)& =& \frac{A\epsilon }{2}\left[E_{\mathrm{i}}{\left({\alpha }_i\right)}^2+c^2{B}_{\mathrm{i}}{\left({\alpha }_i\right)}^2\right]\hfill \end{array}$$

(22)

where A denotes the area that the light occupies in the $y-z$ plane and $\epsilon$ denotes the free space permittivity. As we already know, however, we cannot yet compare the field densities in the two reference frames. To proceed we first take advantage of the fact that the s-propagating electric and magnetic fields are constant along the $x_i-sc{t}_i$ light cones. Consequently, the total energy at times $t_{\mathrm{A}}=t_{\mathrm{B}}=0$ can be expressed as an integral over the ${\alpha }_i=x_i-sc{t}_i$ rather than the $x_i$ axes. Hence, the total energy of the fields experienced by Alice and Bob equals

$$\begin{array}{ccc}\hfill H_{\mathrm{energy}}^{\left(i\right)}& =& {\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_i{h}_{\mathrm{energy}}^{\left(i\right)}\left({\alpha }_i\right)\hfill \end{array}$$

(23)

at any time due to energy conservation. Now the coordinate transformation in Equation (16) can be used to transform the integration measures. Referring also to Equation (21), we determine the following transformation for the energy densities:

$$\begin{array}{ccc}\hfill h_{\mathrm{energy}}^{\left(\mathrm{B}\right)}\left({\alpha }_{\mathrm{B}}\right)& =& {\left[\gamma (1+s\beta )\right]}^{-2}{h}_{\mathrm{energy}}^{\left(\mathrm{A}\right)}\left({\alpha }_{\mathrm{A}}\right).\hfill \end{array}$$

(24)

Here the coordinates $x_{\mathrm{B}}$ and $t_{\mathrm{B}}$ are related to $x_{\mathrm{A}}$ and $t_{\mathrm{A}}$ by the coordinate transformation in Equation (17). If we now reconsider Equation (3), we can show that

$$\begin{array}{ccc}\hfill {\xi }_{\mathrm{BA}}(s,v_{\mathrm{B}})& =& \frac{1}{\gamma (1+s\beta )}=\gamma (1-s\beta )\hfill \end{array}$$

(25)

where $\beta =v_{\mathrm{B}}/c$. This expression for the transformation constant ${\xi }_{\mathrm{BA}}$ satisfies Equation (6).

2.3. Frequency and Wavelength Transformations

Normally the Doppler effect is associated with frequency and wavelength shifts of monochromatic waves seen by two different inertial observers [43]. For completeness, we therefore now also have a look at the electric field amplitude transformations in momentum space. Since the electric field amplitudes ${\tilde{E}}_i(k_i,t_i)$ and $E_i(x_i,t_i)$ in momentum and in position space relate to each other via a Fourier transform, we have [22]

$$\begin{array}{ccc}\hfill E_i(x_i,t_i)& =& \frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mathrm{d}{k}_i{\mathrm{e}}^{\mathrm{i}s{k}_i{x}_i}{\tilde{E}}_i(k_i,t_i)\hfill \\ & =& \frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mathrm{d}{k}_i{\mathrm{e}}^{\mathrm{i}s{k}_i(x_i-sc{t}_i)}{\tilde{E}}_i(k_i,0)\hfill \end{array}$$

(26)

for $i=\mathrm{A},\mathrm{B}$. Here $c{k}_{\mathrm{A}}$ and $c{k}_{\mathrm{B}}$ are the frequencies of a monochromatic wave observed by Alice and Bob respectively. Whilst the previous subsection deals only with changes in the magnitude of the local energy, we now show that the above discussion of the relativistic Doppler effect automatically implies an accompanying change in the frequency and wavelength of monochromatic waves. This is not surprising, since the frequency of a monochromatic wave seen by Alice and by Bob is the number of complete wavelengths that pass their position per unit time. Frequency and wavelength are therefore strongly connected with the clock or meter being used as a measuring device [44].

Next we employ the above Fourier transform and the coordinate transformation in Equation (16). When combining Equations (3) and (25), we see that

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)& =& \gamma (1-s\beta )E_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right).\hfill \end{array}$$

(27)

Substituting Equation (28) into this relation yields

$$\begin{array}{ccc}\hfill & & \frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mathrm{d}{k}_{\mathrm{B}}{\mathrm{e}}^{\mathrm{i}s{k}_{\mathrm{B}}{\alpha }_{\mathrm{B}}}{\tilde{E}}_{\mathrm{B}}(k_{\mathrm{B}},0)\hfill \\ & =& \frac{1}{\sqrt{2\pi }}\gamma (1-s\beta ){\int }_{-\infty }^{\infty }\mathrm{d}{k}_{\mathrm{A}}{\mathrm{e}}^{\mathrm{i}s{k}_{\mathrm{A}}{\alpha }_{\mathrm{A}}}{\tilde{E}}_{\mathrm{A}}(k_{\mathrm{A}},0).\hfill \end{array}$$

(28)

By taking the inverse transformation with respect to the coordinate ${\alpha }_{\mathrm{B}}$, it can now be shown that

$$\begin{array}{ccc}\hfill {\tilde{E}}_{\mathrm{B}}(k_{\mathrm{B}},0)& =& \frac{1}{2\pi }\gamma (1-s\beta ){\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{B}}{\int }_{-\infty }^{\infty }\mathrm{d}{k}_{\mathrm{A}}\hfill \\ & & \times {\mathrm{e}}^{\mathrm{i}s(k_{\mathrm{A}}{\alpha }_{\mathrm{A}}-k_{\mathrm{B}}{\alpha }_{\mathrm{B}})}{\tilde{E}}_{\mathrm{A}}(k_{\mathrm{A}},0).\hfill \end{array}$$

(29)

After substituting Equation (16) into this equation, the ${\alpha }_{\mathrm{B}}$ integration can be solved which yields a delta function in $\gamma (1-s\beta )k_{\mathrm{A}}-k_{\mathrm{B}}$. One therefore finds that

$$\begin{array}{ccc}\hfill {\tilde{E}}_{\mathrm{B}}(k_{\mathrm{B}},0)& =& {\tilde{E}}_{\mathrm{A}}(\gamma (1+s\beta )k_{\mathrm{B}},0).\hfill \end{array}$$

(30)

This equality specifies the relationship between the Fourier components ${\tilde{E}}_{\mathrm{A}}(k_{\mathrm{A}},0)$ and ${\tilde{E}}_{\mathrm{B}}(k_{\mathrm{B}},0)$ of the electric field amplitudes measured by Alice and by Bob. If, for instance, ${\tilde{E}}_{\mathrm{A}}(k_{\mathrm{A}},0)$ is non-zero for a single frequency $k_{\mathrm{A}}c$ only, then Bob observes a monochromatic wave with frequency

$$\begin{array}{ccc}\hfill c{k}_{\mathrm{B}}& =& \frac{c{k}_{\mathrm{A}}}{\gamma (1+s\beta )}=\gamma (1-s\beta )c{k}_{\mathrm{A}}.\hfill \end{array}$$

(31)

This shift in frequency is consistent with previous derivations of the relativistic Doppler shift for light propagating in the s direction.

3. The Quantised EM Field in the Stationary Frame

For a long time, it has been believed that photons do not have a wave function and that light cannot be localised [45,46,47]. However, quantum physics should apply to all particles and photons should not be an exception. When a single-photon detector clicks, it measures the position of the arriving photon at that instant in time [48,49]. The origin of the problem was that many authors like to identify the wave function of the photon with its electric field amplitudes, but electric field amplitudes at different positions do not commute. The eigenstates of the electric field observable are therefore not local, although they can be made to appear local by altering the scalar product that is used to calculate the overlap of quantum state vectors [20,50].

An alternative way of establishing the wave function of a single photon is to separate its field from its carriers [21,22,23]. The carriers of the quantised EM field in momentum space are non-local monochromatic waves. However, their Fourier transforms, so-called blips (which stands for bosons localised in position) provide a complete orthonormal set of basis states for the quantised EM field in position space. Like a point mass is a carrier for a gravitational field, blips are carriers of non-local electric and magnetic field amplitudes. Using the blip annihilation operators, it is for example possible to design locally-acting mirror Hamiltonians [21] and to gain more insight into the Casimir effect [51]. In this section we express the free, quantised, and 1-dimensional electric and magnetic field observables in terms of blips. As we shall see below, the EM field observables usually depend on contributions from blips at all points along the position axis. By applying a constraint to the blip dynamics, a relativistically form-invariant representation is derived. Later these expressions are used to derive a transformation between blips in Alice’s and Bob’s reference frames.

3.1. Local Photons

Let us first have a closer look at the modeling of the quantised EM field in Alice’s resting reference frame. Here blips are characterised by their position $x_{\mathrm{A}}\in (-\infty ,\infty )$ at a given time $t_{\mathrm{A}}\in (-\infty ,\infty )$ as well as their direction of propagation s and their polarisation $\lambda$. For boosts and translations along the $x_{\mathrm{A}}$ and $t_{\mathrm{A}}$ axes, s and $\lambda$ are invariant. The parameter $s=\pm 1$ denotes propagation in the direction of increasing and decreasing $x_{\mathrm{A}}$ respectively. We shall assume that $\lambda =\mathsf{H},\mathsf{V}$ are two linear polarisations orthogonal to the $x_{\mathrm{A}}$ axis [21,22]. The creation operator $a_{s\lambda }^{†}\left(x_{\mathrm{A}}\right)$ adds to the system a single blip located at a position $x_{\mathrm{A}}$ at a time $t_{\mathrm{A}}=0$ with direction of propagation s and polarisation $\lambda$. In the above † denotes complex conjugation and distinguishes $a_{s\lambda }^{†}\left(x_{\mathrm{A}}\right)$ from the corresponding annihilation operator $a_{s\lambda }\left(x_{\mathrm{A}}\right)$ which removes the same blip from the system.

For consistency with Maxwell’s equations, all blips must propagate at the speed of light. This constraint imposes the following condition on the blip operators: at some other time $t_{\mathrm{A}}$, the time-evolved operator $U_{\mathrm{A}}(t_{\mathrm{A}},0)a_{s\lambda }^{†}\left(x_{\mathrm{A}}\right)U_{\mathrm{A}}^{†}(t_{\mathrm{A}},0)$ must be equivalent to the blip creation operator at a position $x_{\mathrm{A}}-sc{t}_{\mathrm{A}}$. Hence

$$\begin{array}{ccc}\hfill U_{\mathrm{A}}(t_{\mathrm{A}},0)a_{s\lambda }^{†}\left(x_{\mathrm{A}}\right)U_{\mathrm{A}}^{†}(t_{\mathrm{A}},0)& =& a_{s\lambda }^{†}(x_{\mathrm{A}}-sc{t}_{\mathrm{A}})\hfill \end{array}$$

(32)

where $U_{\mathrm{A}}(t_{\mathrm{A}},0)$ is the time evolution operator of the quantised EM field in Alice’s reference frame. As a consequence of this constraint, blips characterised by a single value of ${\alpha }_{\mathrm{A}}=x_{\mathrm{A}}-sc{t}_{\mathrm{A}}$ are identical. From this point onwards we shall therefore denote blip creation and annihilation operators in Alice’s frame $a_{s\lambda }^{†}\left({\alpha }_{\mathrm{A}}\right)$ and $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ respectively. Blips that are characterised by non-identical values of ${\alpha }_{\mathrm{A}}$, s or $\lambda$ are distinguishable from one another, and therefore pairwise orthogonal. Hence, we can determine that

$$\begin{array}{c}\hfill \left[a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right),a_{s^{\prime }{\lambda }^{\prime }}^{†}\left({\alpha }_{\mathrm{A}}^{\prime }\right)\right]={\delta }_{s{s}^{\prime }}{\delta }_{\lambda {\lambda }^{\prime }}\delta ({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime }).\end{array}$$

(33)

All creation operators commute with one another, as do the annihilation operators.

3.2. Field Observables in Position Representation

As shown in Refs. [21,22], an analogous description applies to vertically and to horizontally polarised photons. As in Section 2 and for simplicity, we therefore restrict ourselves in the following to only one polarisation $\lambda$. Let us say $\lambda =\mathsf{H}$. In this case, we do not need to consider the direction of Alice’s electric and magnetic field vectors. In the following, $E_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)$ and $B_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)$ represent the observables of the electric and magnetic field amplitudes respectively at position $x_{\mathrm{A}}={\alpha }_{\mathrm{A}}$ at the initial time $t_{\mathrm{A}}=0$ and everywhere along the ${\alpha }_{\mathrm{A}}$ trajectory. In the position representation, the field observables are expressed as an Hermitian, linear superposition of the blip creation and annihilation operators over Alice’s entire position axis and

$$\begin{array}{ccc}\hfill E_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)& =& \sum _{s=\pm 1}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}^{\prime }c\mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })a_{s\mathsf{H}}\left({\alpha }_{\mathrm{A}}^{\prime }\right)+\mathrm{H}.\mathrm{c}.,\hfill \\ \hfill B_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)& =& \sum _{s=\pm 1}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}^{\prime }s\mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })a_{s\mathsf{H}}\left({\alpha }_{\mathrm{A}}^{\prime }\right)+\mathrm{H}.\mathrm{c}.\hfill \\ \hfill \end{array}$$

(34)

In the expressions above, the contribution of each blip to Alice’s field observables are weighted by a non-local distribution $\mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })$, which we shall refer to as the regularisation function. By taking into account that a single monochromatic photon has the positive energy $\hslash c|k_{\mathrm{A}}|$, the function $\mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })$ can be determined explicitly and can be shown to be equal to [20,22,23]

$$\begin{array}{ccc}\hfill \mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })& =& -\sqrt{\frac{\hslash }{4\pi \epsilon cA}}·\frac{1}{|{\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime }{|}^{3/2}}.\hfill \end{array}$$

(35)

As $\mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })$ is non-zero for all values of ${\alpha }_{\mathrm{A}}\ne {\alpha }_{\mathrm{A}}^{\prime }$, we view each blip as carrying non-local electric and magnetic fields. The energy observable in Alice’s frame is defined analogously to the classical energy. In particular, by substituting the real field observables into the energy density in Equation (22), Alice’s energy observable becomes

$$\begin{array}{ccc}\hfill H_{\mathrm{energy}}^{\left(\mathrm{A}\right)}& =& \frac{A\epsilon }{2}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}\left[E_{\mathrm{A}}{\left({\alpha }_{\mathrm{A}}\right)}^2+c^2{B}_{\mathrm{A}}{\left({\alpha }_{\mathrm{A}}\right)}^2\right].\hfill \end{array}$$

(36)

As is usual in the Schrödinger picture, this observable describes the energy of the EM field seen by Alice at a fixed time $t_{\mathrm{A}}$, e.g., $t_{\mathrm{A}}=0$, and is conserved.

3.3. Non-Local Contributions to a Relativistic Observer

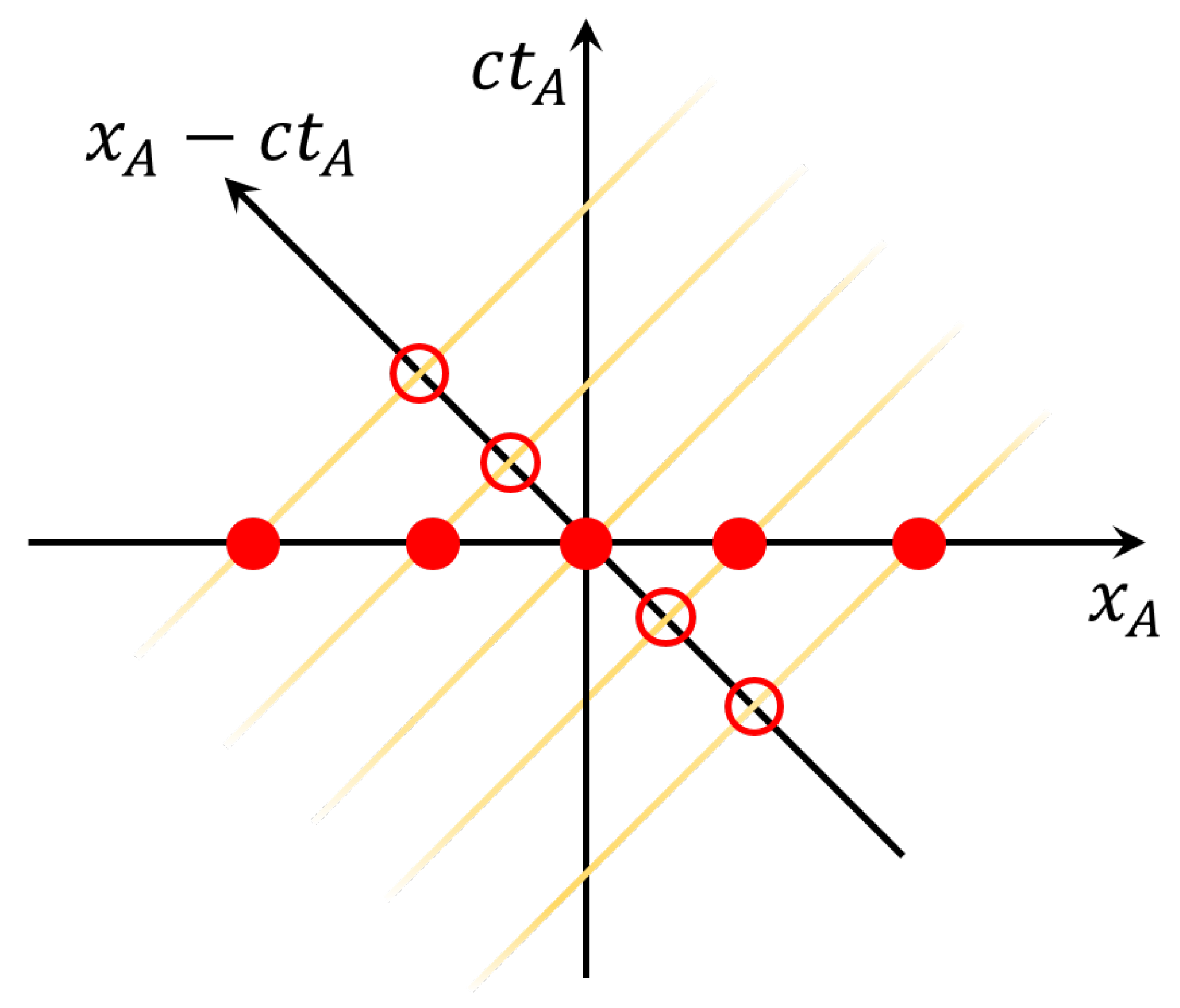
For Alice, who is at rest, the above non-locality of the electric and magnetic field observables—even when generated by a local source—can be viewed as the simultaneous contribution of blips from all points along her position axis, as discussed in Ref. [22]. For a moving observer like Bob, however, events that take place along the $x_{\mathrm{A}}$ axis at a fixed time $t_{\mathrm{A}}$ are no longer simultaneous and do not occur at a single time $t_{\mathrm{B}}$. For this reason, the superposition of blips over the position axis is not a relativistically reliable means of defining the field observables. Fortunately, the above representation of the field observables which characterises them by their world-line coordinate ${\alpha }_{\mathrm{A}}$ and not by a single position $x_{\mathrm{A}}$ avoids this problem. Above we defined the field observables at a point $(x_{\mathrm{A}},t_{\mathrm{A}})$ as non-local superpositions of blips along the $x_{\mathrm{A}}-sc{t}_{\mathrm{A}}$ axis. 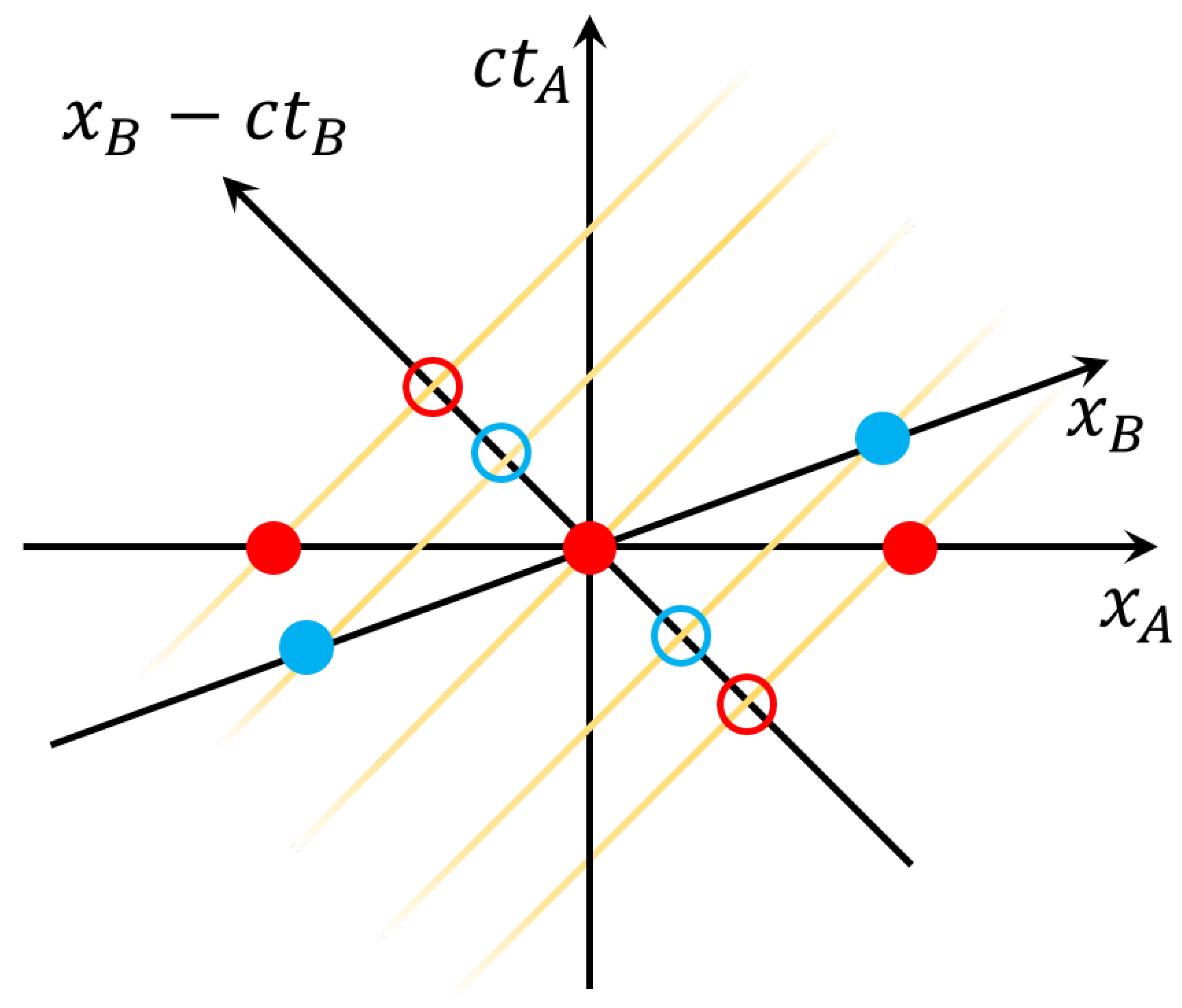This change in representation is illustrated in Figure 4 for a field propagating to the right. In this diagram the field observable at the origin can be determined as a non-local superposition of blips along the $x_{\mathrm{A}}$ axis at a fixed $t_{\mathrm{A}}$ (marked in red). Alternatively they can be identically determined as a superposition of blips dispersed along the $x_{\mathrm{A}}-c{t}_{\mathrm{A}}$ axis. The advantage of this representation is that points along Alice’s light cones are also points along the light cones for any other observer, including those who, like Bob, are not at rest in Alice’s reference frame. Consequently, the same blips that contribute to Alice’s field observables also contribute to Bob’s field observables. In the next section we will show that this description of the field allows a comparison between blips in Bob’s frame and those in Alice’s frame.

4. A Quantum Picture of the Relativistic Doppler Effect

Next we have a closer look at how Bob experiences the quantised EM field in his moving reference frame. Afterwards, we determine a relation between Alice’s and Bob’s field observables by using the classical field amplitude transformations derived in Section 2.2. By first taking into account that Bob can also express his field observables as a superposition of blips along the ${\alpha }_{\mathrm{B}}=x_{\mathrm{B}}-sc{t}_{\mathrm{B}}$ axis, a local transformation is determined between blips in Bob’s and those in Alice’s reference frame.

4.1. The Doppler Effect in Position Space

In the following, we denote the annihilation and creation operators for a blip at a position $x_{\mathrm{B}}$ at an initial time $t_{\mathrm{B}}=0$ in Bob’s frame $b_{s\lambda }\left(x_{\mathrm{B}}\right)$ and $b_{s\lambda }^{†}\left(x_{\mathrm{B}}\right)$ respectively with s and $\lambda$ indicating again its direction of propagation and its polarisation. According to Bob, blips travel at the speed c along the relevant boundary of the light cone and

$$\begin{array}{ccc}\hfill U_{\mathrm{B}}(t_{\mathrm{B}},0)b_{s\lambda }^{†}\left(x_{\mathrm{B}}\right)U_{\mathrm{B}}^{†}(t_{\mathrm{B}},0)& =& b_{s\lambda }^{†}(x_{\mathrm{B}}-sc{t}_{\mathrm{B}}),\hfill \end{array}$$

(37)

in analogy to Equation (32). Here $U_{\mathrm{B}}(t_{\mathrm{B}},0)$ denotes the time evolution operator of the EM field in Bob’s reference frame. As in the previous subsection, constraining the blips in this way allows us to introduce annihilation operators $b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)$ for blips at $x_{\mathrm{B}}$ and $t_{\mathrm{B}}$ where ${\alpha }_{\mathrm{B}}=x_{\mathrm{B}}-sc{t}_{\mathrm{B}}$ and with

$$\begin{array}{c}\hfill \left[b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right),b_{s^{\prime }{\lambda }^{\prime }}^{†}\left({\alpha }_{\mathrm{B}}^{\prime }\right)\right]={\delta }_{s{s}^{\prime }}{\delta }_{\lambda {\lambda }^{\prime }}\delta ({\alpha }_{\mathrm{B}}-{\alpha }_{\mathrm{B}}^{\prime })\end{array}$$

(38)

in analogy to Equation (33). The blip operators in Bob’s reference frame satisfy an identical set of commutation relations to Alice’s operators, as one would expect from the principle of relativity.

Entirely analogous to the generalisation of Alice’s field observables, any non-local contributions of blips to Bob’s field observables can be expressed in terms of their separation from Bob along the ${\alpha }_{\mathrm{B}}$ axis. Hence, we define Bob’s field observables

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)& =& \sum _{s=\pm 1}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{B}}^{\prime }c\mathcal{R}({\alpha }_{\mathrm{B}}-{\alpha }_{\mathrm{B}}^{\prime })b_{s\mathsf{H}}\left({\alpha }_{\mathrm{B}}^{\prime }\right)+\mathrm{H}.\mathrm{c}.\hfill \\ \hfill B_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)& =& \sum _{s=\pm 1}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{B}}^{\prime }s\mathcal{R}({\alpha }_{\mathrm{B}}-{\alpha }_{\mathrm{B}}^{\prime })b_{s\mathsf{H}}\left({\alpha }_{\mathrm{B}}^{\prime }\right)+\mathrm{H}.\mathrm{c}.\hfill \\ \hfill \end{array}$$

(39)

with ${\alpha }_{\mathrm{B}}=x_{\mathrm{B}}-sc{t}_{\mathrm{B}}$. Here $x_{\mathrm{B}}$ and $t_{\mathrm{B}}$ are the spacetime coordinates of the point where the field amplitude measurement is made. The distribution $\mathcal{R}({\alpha }_{\mathrm{B}}-{\alpha }_{\mathrm{B}}^{\prime })$ in the above equation is the same as in Equation (35) but with ${\alpha }_{\mathrm{A}}$ and ${\alpha }_{\mathrm{A}}^{\prime }$ replaced by ${\alpha }_{\mathrm{B}}$ and ${\alpha }_{\mathrm{B}}^{\prime }$ respectively.

Although the same regularisation function is used by both Alice and Bob, as Alice measures the separation of blips along the ${\alpha }_{\mathrm{A}}$ axis and Bob along the ${\alpha }_{\mathrm{B}}$ axis, the contribution of blips to their field observables is different. This is illustrated in Figure 5. In the diagram, Alice’s blips (solid red) are distributed at regular intervals along the $x_{\mathrm{A}}$ axis. Bob’s blips (solid blue) are distributed at identical intervals along the $x_{\mathrm{B}}$ axis. Since $\mathcal{R}(x-x^{\prime })$ is used for both observers, the two outermost red blips have the same contribution to Alice’s field observables as the two outermost blue blips do to Bob’s field observables. By identifying the blips with their counterparts along the $x_{\mathrm{B}}-c{t}_{\mathrm{B}}$ as in Figure 5, however, we can see that the blips defined by Bob appear closer to Alice than her own. As a result, the regularisation function used by Bob appears squeezed from Alice’s point of view. Conversely, for light propagating to the left the regularisation function appears stretched. As mentioned already above, events that occur simultaneously in Alice’s reference frame are not simultaneous in Bob’s and vice versa.

Now that the operators $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ and $b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)$ have been defined by constructing field observables for the two observers (cf. Equations (34) and (39)), a relationship between these operators can be found by imposing the field relation in Equation (3). In order to compare the electric field observables $E_{\mathrm{A}}\left({\alpha }_{\mathrm{A}}\right)$ and $E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)$, we now express $E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)$ in terms of Alice’s coordinates ${\alpha }_{\mathrm{A}}$. Combining Equations (3), (16) and (34), we see that

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)& =& \sum _{s=\pm 1}{\xi }_{\mathrm{BA}}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}^{\prime }c\mathcal{R}({\alpha }_{\mathrm{A}}-{\alpha }_{\mathrm{A}}^{\prime })a_{s\mathsf{H}}\left({\alpha }_{\mathrm{A}}^{\prime }\right)\hfill \\ & & +\mathrm{H}.\mathrm{c}.\hfill \end{array}$$

(40)

with ${\alpha }_{\mathrm{B}}=\gamma (1+s\beta ){\alpha }_{\mathrm{A}}$. Substituting ${\alpha }_{\mathrm{B}}^{\prime }=\gamma (1+s\beta ){\alpha }_{\mathrm{A}}^{\prime }$ into this equation, using Equation (25) and taking into account the explicit form of the regularisation function in Equation (35) we find that

$$\begin{array}{ccc}\hfill E_{\mathrm{B}}\left({\alpha }_{\mathrm{B}}\right)& =& \sum _{s=\pm 1}{\left|\gamma (1-s\beta )\right|}^{1/2}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{B}}^{\prime }c\mathcal{R}({\alpha }_{\mathrm{B}}-{\alpha }_{\mathrm{B}}^{\prime })\hfill \\ & & \times a_{s\mathsf{H}}\left(\gamma (1-s\beta ){\alpha }_{\mathrm{B}}^{\prime }\right)+\mathrm{H}.\mathrm{c}.\hfill \end{array}$$

(41)

By comparing this equation with Equation (39), we see that both expressions are only the same if

$$\begin{array}{ccc}\hfill b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)& =& {\left[\gamma (1-s\beta )\right]}^{1/2}{a}_{s\lambda }\left(\gamma (1-s\beta ){\alpha }_{\mathrm{B}}\right)\hfill \\ & =& {\left[\gamma (1-s\beta )\right]}^{1/2}{a}_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)\hfill \end{array}$$

(42)

where the coordinates ${\alpha }_{\mathrm{A}}$ and ${\alpha }_{\mathrm{B}}$ define the same light-like trajectory in Alice’s and Bob’s coordinate systems respectively.

The above transformation shows that a single blip in Alice’s reference frame is observed by Bob as a single blip at exactly the same position in the spacetime diagram. The additional factor ${\left[\gamma (1-s\beta )\right]}^{1/2}$ in Equation (42) is the result of Alice and Bob using different coordinates to describe the same point. One can easily check that the annihilation operators on both sides of Equation (42) obey bosonic commutation relations. Hence, the annihilation operators $b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)$ and $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ are identical and completely interchangeable. Consequently, the relativistic Doppler effect is simply an immediate consequence of the fact that Alice and Bob experience time and space differently. A single local photon in Alice’s reference frame also appears a single local photon in Bob’s. For example, if both perform a linear optics experiment, like the Hong-Ou Mandel effect [52,53] in which two identical photons approach a beam splitter from opposite sides, both see both photons leaving the setup through the same output port. The dynamics of the quantised EM field is essentially the same in all inertial reference frames, as stated by Einstein’s principle of relativity [10].

4.2. The Doppler Effect in the Momentum Representation

For completeness and since the relativistic Doppler effect is usually studied in momentum space [9], we finally have a closer look at the implications of the above equations on the momentum representation of the quantised EM field. In this representation, the electric and magnetic field observables are expressed in a basis of bosonic excitations with a definite frequency, polarisation and direction of propagation. These excitations are an alternative representation and are introduced by Fourier transforming the blip annihilation operators that have been used so far [21,22]. In Alice’s and Bob’s reference frames, we define

$$\begin{array}{ccc}\hfill {\tilde{a}}_{s\lambda }\left(k_{\mathrm{A}}\right)& =& \frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}{\mathrm{e}}^{-\mathrm{i}s{k}_{\mathrm{A}}{\alpha }_{\mathrm{A}}}{a}_{s\lambda }\left({\alpha }_{\mathrm{A}}\right),\hfill \\ \hfill {\tilde{b}}_{s\lambda }\left(k_{\mathrm{B}}\right)& =& \frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{B}}{\mathrm{e}}^{-\mathrm{i}s{k}_{\mathrm{B}}{\alpha }_{\mathrm{B}}}{b}_{s\lambda }\left({\alpha }_{\mathrm{B}}\right).\hfill \end{array}$$

(43)

These operators satisfy the bosonic commutation relations

$$\begin{array}{ccc}\hfill \left[{\tilde{a}}_{s\lambda }\left(k_{\mathrm{A}}\right),{\tilde{a}}_{s^{\prime }{\lambda }^{\prime }}^{†}\left(k_{\mathrm{A}}^{\prime }\right)\right]& =& {\delta }_{s{s}^{\prime }}{\delta }_{\lambda {\lambda }^{\prime }}\delta (k_{\mathrm{A}}-k_{\mathrm{A}}^{\prime }),\hfill \\ \hfill \left[{\tilde{b}}_{s\lambda }\left(k_{\mathrm{B}}\right),{\tilde{b}}_{s^{\prime }{\lambda }^{\prime }}^{†}\left(k_{\mathrm{B}}^{\prime }\right)\right]& =& {\delta }_{s{s}^{\prime }}{\delta }_{\lambda {\lambda }^{\prime }}\delta (k_{\mathrm{B}}-k_{\mathrm{B}}^{\prime })\hfill \end{array}$$

(44)

where $k_{\mathrm{A}}$ and $k_{\mathrm{B}}$ are wave numbers seen by Alice and Bob with respect to $t_{\mathrm{A}}$ and $t_{\mathrm{B}}$ respectively.

In the position representation, the blip operators $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ and $b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)$ defined in Alice’s and Bob’s frames respectively satisfy the transformation (42) which is consistent with the classical field transformations for the field observables. Substituting Equation (42) into (43), we can now determine an analogous relationship between the momentum space annihilation operators. Taking into account that ${\alpha }_{\mathrm{B}}=\gamma (1+s\beta ){\alpha }_{\mathrm{A}}$ (cf. Equation (16)), we find that

$$\begin{array}{ccc}\hfill {\tilde{b}}_{s\lambda }\left(k_{\mathrm{B}}\right)& =& \frac{1}{\sqrt{2\pi }}{\left[\gamma (1+s\beta )\right]}^{1/2}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}\hfill \\ & & \times {\mathrm{e}}^{-\mathrm{i}s\gamma (1+s\beta )k_{\mathrm{B}}{\alpha }_{\mathrm{A}}}{a}_{s\lambda }\left({\alpha }_{\mathrm{A}}\right).\hfill \end{array}$$

(45)

Substituting for $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ the inverse of Equation (43) yields

$$\begin{array}{ccc}\hfill {\tilde{b}}_{s\lambda }\left(k_{\mathrm{B}}\right)& =& \frac{1}{2\pi }{\left[\gamma (1+s\beta )\right]}^{1/2}{\int }_{-\infty }^{\infty }\mathrm{d}{\alpha }_{\mathrm{A}}{\int }_{-\infty }^{\infty }\mathrm{d}{k}_{\mathrm{A}}\hfill \\ & & \times {\mathrm{e}}^{\mathrm{i}s(k_{\mathrm{A}}-\gamma (1+s\beta )k_{\mathrm{B}}){\alpha }_{\mathrm{A}}}{\tilde{a}}_{s\lambda }\left(k_{\mathrm{A}}\right).\hfill \end{array}$$

(46)

After performing first the ${\alpha }_{\mathrm{A}}$ and then the $k_{\mathrm{A}}$ integrations, we therefore see that

$$\begin{array}{ccc}\hfill {\tilde{b}}_{s\lambda }\left(k_{\mathrm{B}}\right)& =& {\left[\gamma (1+s\beta )\right]}^{1/2}{\tilde{a}}_{s\lambda }\left(\gamma (1+s\beta )k_{\mathrm{B}}\right)\hfill \\ & =& {\left[\gamma (1+s\beta )\right]}^{1/2}{\tilde{a}}_{s\lambda }\left(k_{\mathrm{A}}\right)\hfill \end{array}$$

(47)

with $k_{\mathrm{A}}=\gamma (1+s\beta )k_{\mathrm{B}}$. Hence a single monochromatic photon of frequency $c{k}_{\mathrm{B}}$ observed by Bob corresponds to a single monochromatic photon of frequency $c{k}_{\mathrm{A}}=\gamma (1+s\beta )c{k}_{\mathrm{B}}$ observed by Alice. This transformation is in complete agreement with the classical Doppler shift derived in Section 2.3 and found in the literature. Whilst this transformation is very simple, a change in the frequency of the excitation is not the same in all reference frames. Whilst working in the position representation, however, a local photon is viewed as a local photon by all inertial observers at the same point in the spacetime diagram. The only difference is that different observers use different coordinates to characterise this point.

5. Conclusions

This paper offers an alternative perspective on the relativistic Doppler effect which is usually referred to only in momentum space and discussed in terms of frequency, wavelength and amplitude changes of wave packets of light when measured in different inertial reference frames. In this paper, we study the relativistic Doppler effect in position space using the spacetime coordinates ${\alpha }_{\mathrm{A}}=x_{\mathrm{A}}-sc{t}_{\mathrm{A}}$ and ${\alpha }_{\mathrm{B}}=x_{\mathrm{B}}-sc{t}_{\mathrm{B}}$ of two inertial observers: Alice in the stationary frame and Bob in the frame moving with constant velocity $v_{\mathrm{B}}$ with respect to Alice. This alternative approach allows us to accommodate time and spatial translational symmetries in a relatively straightforward way. In addition, we identify an invariant energy flux and take advantage of the principle of relativity.

For example, symmetry arguments and the principle of relativity are used to show that local electric field amplitudes seen by Alice and Bob only differ by a constant factor which we denote ${\xi }_{\mathrm{AB}}$ and ${\xi }_{\mathrm{BA}}$ respectively. Energy flux conservation can be used to calculate these factors as a function of the propagation direction s and the velocity of Bob’s reference frame $v_{\mathrm{B}}$ with respect to Alice’s frame. For simplicity, we assume here that both observers are stationary in their respective coordinate systems and place them at the origin. When transforming our local description of the relativistic Doppler effect into momentum space, we recover the usual predictions which shows that our approach is consistent with the findings of other Authors.

In Section 3 and Section 4, we concentrate on the local description of the quantized EM field for light propagation in one dimension of Minkowski spacetime to obtain a quantum picture of the relativistic Doppler effect. Our aim here is to identify the relationship between the quantum states of a wave packet of light seen by Alice and Bob in different inertial frames. Our main result is the straightforward relationship between the annihilation operators $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ and $b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)$ used by Alice and Bob for the description of local excitations—so-called blips—of the quantised EM field. When considering the same point in the spacetime diagram, i.e., when ${\alpha }_{\mathrm{A}}$ and ${\alpha }_{\mathrm{B}}$ depend on each other as stated in Equation (16), both observers measure the same number of field excitations and the operators $a_{s\lambda }\left({\alpha }_{\mathrm{A}}\right)$ and $b_{s\lambda }\left({\alpha }_{\mathrm{B}}\right)$. The relativistic Doppler effect is simply the result of Alice and Bob using different spacetime coordinates and experiencing space and time differently, while the speed of light is the same in all inertial reference frames [4]. For example, electric field amplitudes which are simultaneous in Alice’s reference frame appear at different times $t_{\mathrm{B}}$ in Bob’s reference frame and vice versa.

The results of this paper might have applications in different areas of physics, including quantum communication [36] and relativistic quantum information [37,38,39,40,41]. In the current study, the concentration was on a well-expected result as a transformation between the stationary frame and moving with constant velocity frame in a classical and relativistic representation in order to explore it for blips as well. In the future, our approach can be used to study more complicated situations and systems like an accelerating frame.