Prerpints.org logo
Preprint
Article

Experimental and Numerical Investigation on Flexural Strengthening of Precast Concrete Corbel Connections with Fiber-reinforced Plastic Sheet

Altmetrics

Downloads

88

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 January 2024

Posted:

04 January 2024

You are already at the latest version

Alerts
Abstract
This paper presents the results of experimental and numerical investigations aimed at enhancing the flexural capacity of Precast Concrete Corbel Beam-Column Connections (PC-CBCC) using Fiber-Reinforced Plastic (FRP) sheets. The experimental study primarily focused on assessing the flexural capacity of pinned PC-CBCCs reinforced with FRP layers, comparing them to a moment-resisting connection. A series of half-scale specimens, including three PC-CBCCs with varying FRP configurations, were tested alongside one in-situ concrete fixed connection. The objective was to quantify the ultimate flexural capacity of PC-CBCCs reinforced by FRP sheets. The effects of FRP layer thickness, locations, and potential debonding were examined under unidirectional static tests while applying a constant axial compressive load to the columns and subjecting the beams to lateral loads until fracture. Additionally, a precise finite element model of the PC-CBCCs and a fixed joint was developed and verified to simulate nonlinear static analyses of the connections in ANSYS software. A comprehensive comparison was conducted to determine their responses by employing various FRP configurations and properties. The tests and numerical results demonstrate that wrapping PC-CBCCs with anchored FRPs can transform pin connections into moment-resistant joints. Moreover, critical design parameters such as bond length, thickness, and placement of FRP sheets, along with appropriate mechanical anchorage, are identified to prevent debonding and delamination.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Precast reinforced concrete structures have gained widespread popularity due to their numerous advantages, including superior quality control, rapid construction speed, reduced labor requirements, and lower construction costs. Many types of precast concrete components can be used in different structural systems and applications. These include beam-column connections [1,2,3], precast beams and girders with double-tee, inverted-tee, L-shaped, I-shaped, and box-shaped [4], which are horizontal members that span between columns or walls and support floor or roof slabs. Precast concrete columns and walls [5,6] with rectangular, circular, octagonal, H-shaped, and C-shaped are vertical members that support beams, girders, or slabs, and provide stability and lateral resistance to the structure. Precast concrete floors [7] are horizontal members that form a structure with common hollow-core, solid, ribbed, waffle, and coffered slabs. Each of these components can be either prestressed or reinforced with cast-in-place concrete, steel plates, or Fiber-Reinforced Plastic (FRP) sheets [8,9].
In precast concrete structures, the connections between elements are pivotal during severe wind and seismic loadings. These connections are broadly categorized into two types: wet and dry connections [10,11]. Wet connections involve the use of protruding reinforcement bars from the precast concrete components and the application of cast-in-place concrete [12]. These connections exhibit seismic performance akin to monolithic joints, demonstrating good energy dissipation and bearing capacity [13]. The dry connections either are pinned connections or rely on high-strength bolts and steel plates [14]. Dry connections offer time-efficient assembly and ease of construction, making them commonly used in precast structures. However, these connections, particularly those with pinned types, can have low flexural capacity and ductility, which allows beams to rotate freely without effectively transferring lateral forces to columns [15,16]. This deficiency in rotational capacity to dissipate seismic energy absorption can lead to significant damage during seismic events in precast structures [17]. Hence, researchers are investigating methods to transform these pinned connections into flexural joints, aiming to enhance the structures' performance against both gravitational and lateral loads.
There are several techniques to increase the resilience of the pinned precast connections, by employing replaceable energy dissipation connectors [18], Fiber Reinforced Polymers (FRP) [19], end plate and bolted connections [20,21], dowel bars [22], steel billet [23], steel box section [24], etc. These connectors can improve the seismic performance of the precast structure and make post-earthquake repair more convenient. This paper aims to enhance the seismic performance of a Precast Concrete Corbel Beam-Column Connection (PC-CBCC) with FRP sheets and appropriate mechanical anchorage. The FRP materials are known for their high strength-to-weight ratio and excellent corrosion resistance, making them suitable for use in seismic retrofitting of existing structures [25]. Through the confinement of concrete members, the flexural, shear, and axial capacities of reinforced concrete elements can be increased, thereby enhancing energy absorption [26]. Furthermore, the FRP sheets and bars exhibit significantly greater strength and resistance against corrosion, along with enhanced remoldability, when compared to steel materials [27,28].
Over the past decades, extensive research has focused on reinforcing cast in-situ beam-column connections using FRP and other techniques [29,30,31]. However, several aspects concerning the identification and mitigation of weaknesses in precast connection details when exposed to lateral loads remain unexplored [32]. The primary drawbacks associated with precast connections involve shear-moment failure due to inadequate bond length and a lack of diagonal shear strength within the connection core. Gergely et al. [33] and Parvin and Granata [34] conducted studies focusing on reinforcing the shear-moment capacity of T-joints and corbel connections using CFRP composites. Additionally, investigations into CFRP separation reinforcing beam-column connections have been conducted in various studies [35,36] to explore shear stress distribution during separation from the concrete surface of beams. However, the existing knowledge regarding enhancing the flexural capacity of pinned precast connections is limited to specific cases, highlighting the need for further analysis and investigation. To address this, this study encompasses comprehensive experimental and numerical investigations to explore the application of FRP sheets. Its primary aim is to enhance the understanding of transforming pinned precast concrete connections into moment-resistant ones. The feasibility of this transformation involves employing various bonding methods, such as wrapping corbels and focusing on critical zones of beams and columns. The study seeks to increase knowledge regarding the feasibility of using FRP sheets to alter the structural behavior from pinned to moment-resistant connections.
The subsequent sections introduce the experimental testing program, encompassing descriptions of the specimens, preparation of test archetypes, material properties, and test setup, along with instrumentation details. Following this, the experimental results are presented to demonstrate the effectiveness of the FRP layers in enhancing the flexural capacity of the PC-CBCC. Subsequently, the numerical modeling of both fixed and pinned connections employing various wrapping methods is simulated, and the obtained results are compared across a comprehensive set of illustrative examples.

2. Experimental testing program

2.1. Description of test specimens

In this study, four ½-scaled specimens, serving as representative examples of exterior beam-column connections in a building, were designed and tested. The prototypes included a moment-resisting (fixed) connection with cast in-situ concrete, referred to as 'FC,' and PC-CBCC, designated as 'PC.' Figure 1 illustrates the details of the FC and PC specimens. Both FC and PC prototypes were designed per the weak beam-strong column theory as per ACI 318 [37]. The maximum longitudinal reinforcement ratio for beams was set at 0.3 of their cross-sectional area (ρmax=0.3), while the longitudinal bars for columns were established at 3.5%. Their transverse bars and bond lengths were also designed to comply with ACI 318 requirements for earthquake-prone regions. As depicted in Figure 1, unlike the FC specimen, the PC archetypes featured pinned joints, wherein the beam rested on the corbel of the column, and the space between them was filled with cement grout.
Figure 2 depicts three methods, namely PC-1, PC-2, and PC-3, aimed at improving the flexural capacity of the pinned PC archetypes. In PC-1, L-shape and full-wrap FRPs were employed, while in PC-2 and PC-3, both U-shaped and full-wrap layers were utilized to reinforce the corbel connection. Moreover, the external anchorage was incorporated in the PC-3 specimen to examine its impact on delaying the debonding of the FRP layers during lateral loading.

2.2. Preparation of test archetypes

The concrete mix design for the beam-column connections followed the specifications outlined in ACI 211 [38]. Accordingly, the Portland cement Type II with a slump ranging from 78 to 100 mm and a water-to-cement ratio of 0.56 (equivalent to 216 kg/m³ of water) was used in the mixture. The standard gradation curve was adhered to, restricting the maximum grain size to 12.5 mm.
The construction process involved assembling a metal framework and placing concrete on a horizontal surface of ground level. During the curing process, the samples were consistently watered thrice daily for a week and subsequently maintained at laboratory temperature for 30 days. Following concrete curing, the precast beam and column specimens were strategically placed adjacent to each other, with 30-mm free contraction joints filled using grout. A 25 mm chamfer was integrated into all concrete members to mitigate stress concentration in the spiraled FRP sheets enveloping the beams and columns. Additionally, the surface was rubbed using a soft sander to reach a roughness of 0.5 mm. The first layer of FRP underwent saturation with Sikadur-330 resin [39] and was affixed to the surface. Compression was meticulously applied using a rubber roller to extrude excess adhesive, repeating the process for subsequent layers until reaching the desired thickness.

2.3. Material properties

Table 1 presents a summary of the 28-day cylinder strength, ultimate failure load, and other characteristics of the specimens, including the percentage of longitudinal FRP and the ratio of corbel and beam spirals. The test specimens used to measure the 28-day compressive strength (f’c) comprised three cylindrical samples, each with a diameter of 150 mm. To ensure the accuracy of concrete properties, two of these cylindrical specimens underwent an identical curing process to that of the main specimen, ensuring consistent conditions for result comparison. In contrast, the third specimen was subjected to saturated curing conditions, offering insight into the material's behavior under varying curing environments. As observed, the 28-day compressive strength ranged from 21.1 to 23.2 MPa, reflecting a variation of approximately 1.0655 MPa in terms of variance calculated across the dataset. The tensile reinforcement comprised AIII-type steel with a yield strength of fy = 420 MPa. Additionally, AII-type steel bars, also with a fy=300 MPa, were used in the stirrups and bottom longitudinal bars of beams. The technical specifications for the FRP sheet used in this study, specifically the SikaWrap-200C, are detailed in Table 2. This type of FRP is known for its high strength-to-weight ratio and excellent corrosion resistance. The longitudinal FRP ratio of the beam (ρfb) and transverse FRP ratio wrapped around both the beam and corbel (ρfw) were determined with FRP area (Af) to the beam sectional area (Ab=bh). According to Table 1, the percentage values of ρfb for the PC-1 to PC-3 specimens were considered almost identical, while the ρfw value for the PC-1 specimen was designed as half of those for the PC-2 and PC-3 archetypes.

2.4. Test setup and instrumentation

Figure 3 illustrates the experimental setup and the specifications of the specimens. These tests aimed to evaluate the structural behavior of the PC-CBCC specimens under specific loading conditions. The experiments were conducted with precision and care in the structural engineering laboratory of Isfahan University of Technology (IUT). Considering the available capacity and dimensions of the apparatuses, the specimens were intentionally crafted at a 1/2 scale of the actual beam-column connection. To correspond with the assumed inflection points situated at the midpoint of the beam and column, the pinned connections were designed and positioned at the extremities of the specimens. Consequently, specimens with a column height of 1500 mm and a beam length of 1000 mm were precisely fabricated and situated within the reaction frame, as depicted in Figure 3. A variable vertical load was incrementally applied to the end of the beam, 1000 mm away from the connection, utilizing a computer-controlled hydraulic jack with a capacity of 2500 kN. Simultaneously, a constant uniaxial load, equal to P= 0.2 f’cAg, was applied to the column head by a portable hydraulic jack. Furthermore, the typical instrumentation, as illustrated in Figure 3, was employed to measure the beam-to-column rotations, displacements, and applied forces. These include a 500 kN load cell with 250 N precision, an actuator for load-displacement control, and five LVDTs with 0.001 mm precision used to record displacement distributions along the beam and column faces.

3. Experimental results

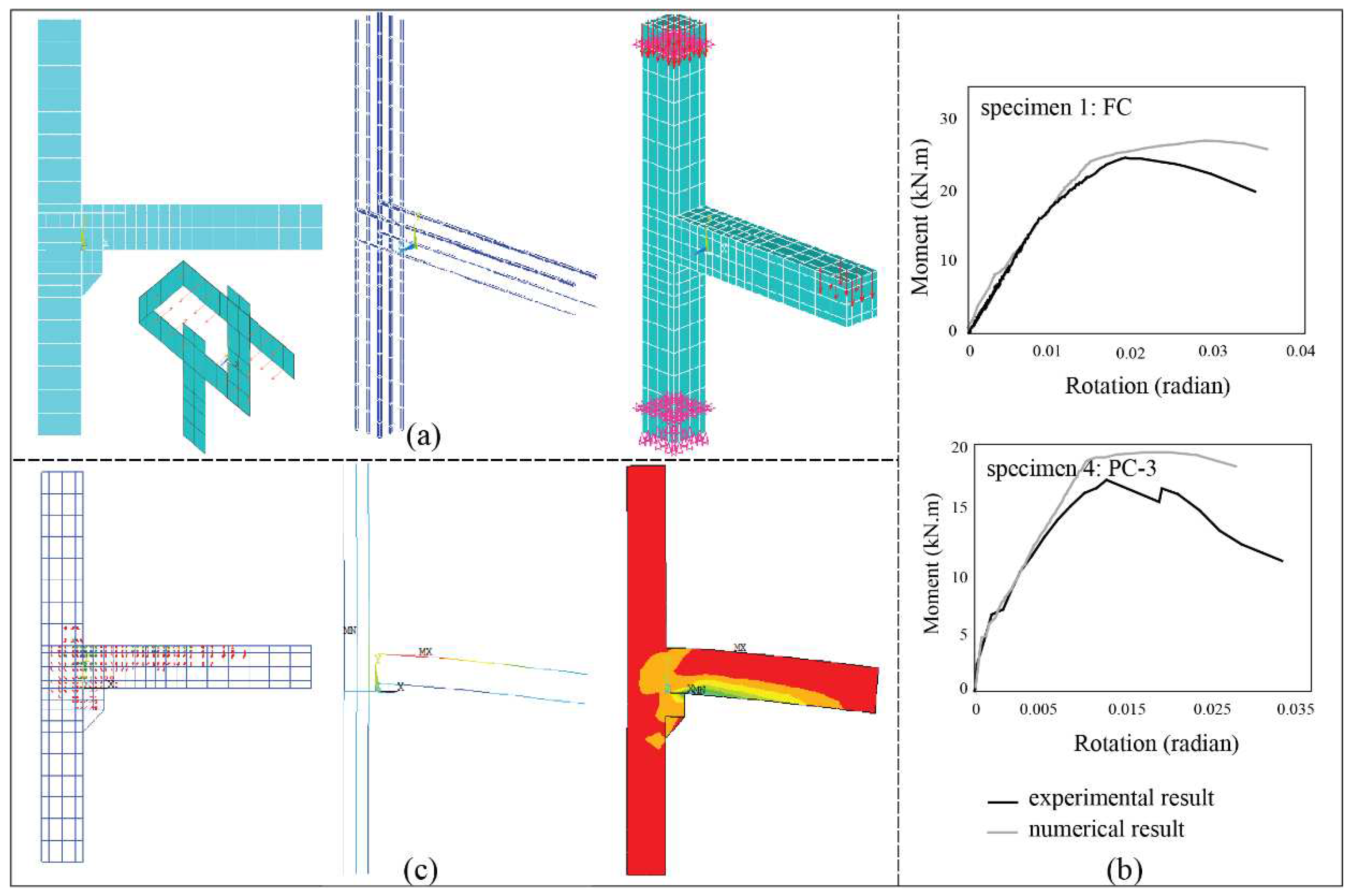
3.1. Specimen 1: FC archetype

Figure 4 indicates the deformed shape and moment-rotation capacity curve of the initial specimen (FC) beyond 0.03 radians. Laboratory tests conducted on the FC archetype revealed that the longitudinal reinforcement of the beam yielded near the bearing, closely matching the anticipated theoretical yield in a cantilever beam with the fixed-base condition. The presence of diagonal micro-fractures within the panel zone of the connection was observed, stemming from inadequate transverse reinforcement. Furthermore, the tensile reinforcement slid despite compliance with seismic-resistant design provisions for the longitudinal reinforcement and bond length. The failure observed was brittle, indicating a lack of proper ductility in the connection.

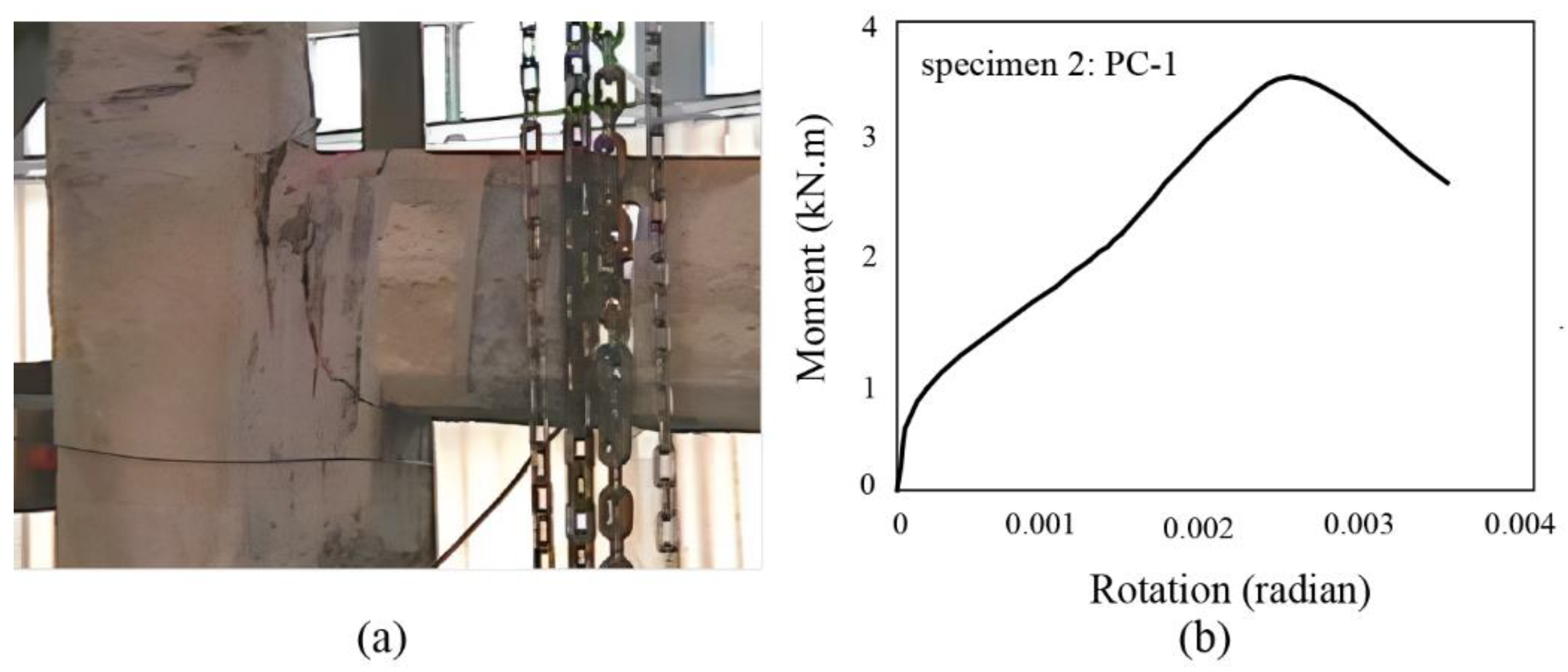
3.2. Specimen 2: PC-1 archetype

Figure 5 illustrates the failure mechanism of the second specimen (PC-1) alongside its corresponding moment-rotation curve. The connection's fracture initiation occurred as the spiral FRP wrapped around the beam and the corbel tore at its ultimate tensile capacity, i.e., ɛu =0.0155. Concurrently, 25% of the L-shaped FRP sheets, positioned at the connection's bottom, also tore. Consequently, the connection experienced a 30% reduction in its ultimate moment capacity, primarily carried by the L-shaped sheets. Consequently, the impact of the top and bottom FRPs on enhancing the flexural reinforcement of the PC-CBCC was found to be insignificant. This lack of significant contribution can be attributed to the high concentration of shear stress in the L-shaped FRP sheets while transferring the beam's tensile force to the spiral FRPs around the column. The tearing of these L-shaped sheets occurred at the folding point when they reached their maximum tensile strain.

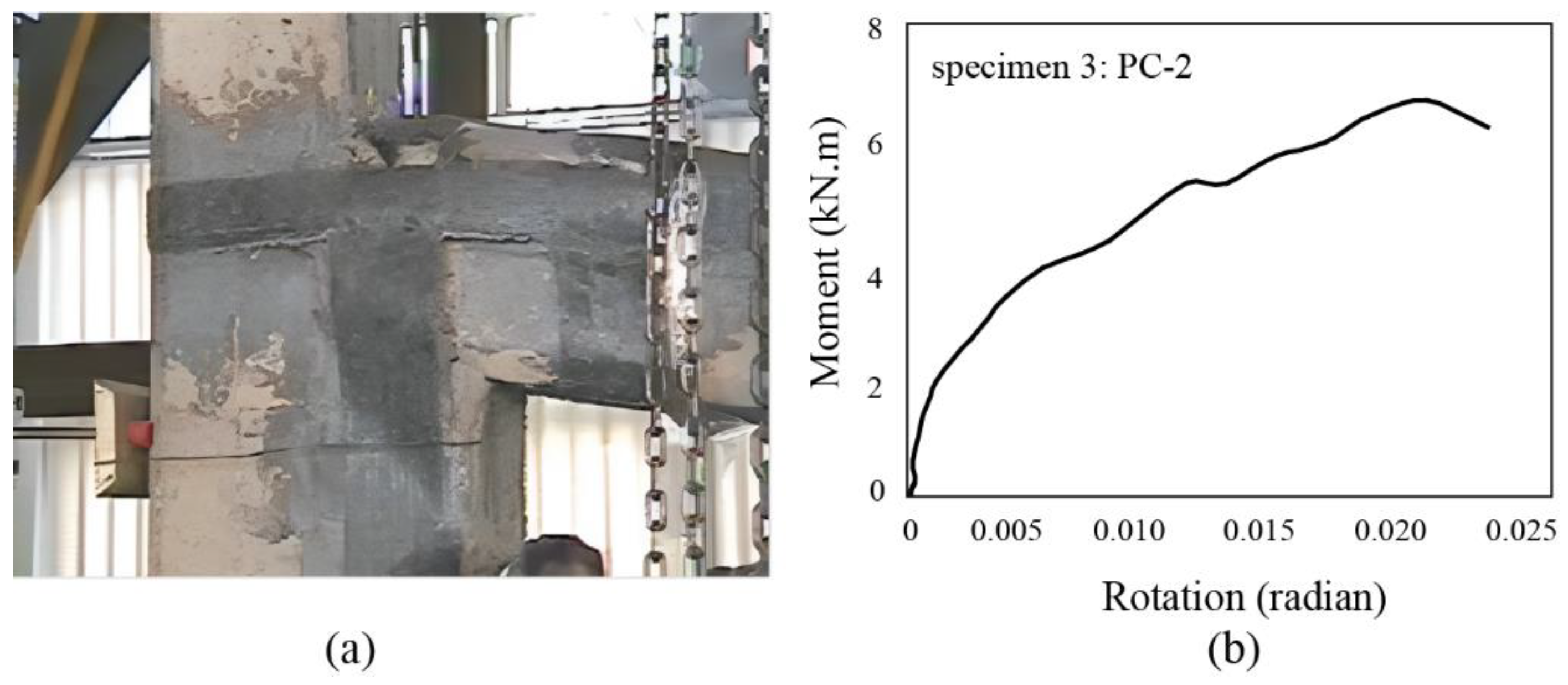
3.3. Specimen 3: PC-2 archetype

In the case of the third specimen (PC-2 archetype), the debonding of the U-shaped FRP sheet from the column was observed during the initial loading stages, specifically at a lateral force of 4000 N, as depicted in Figure 6. This separation of the FRP from the concrete surface resulted from concentrated shear stress at the location of flexural-crack initiation and propagation across the width of the column. Consequently, the tearing of the beam and corbel FRP-spiral commenced at their connection to the U-shaped sheet upon reaching a loading of 5500 N. The tensile fracture of the FRP-spiral sheets, caused by the portion of the moment in the corbel at the connection, transpired at the ultimate FRP capacity of ɛu = 0.0155, aligning closely with 95% conformity to the equilibrium and compatibility equations. Despite the debonding of the U-shaped sheet occurring at ɛ = 0.001, the adherence of the FRP-spiral sheets to the beam could postpone the connection failure up to ɛu = 0.002. Consequently, at ɛu = 0.002, the U-shaped sheet abruptly separated as the connection reached only 1/7 of the ultimate capacity of the FRP. To validate the observed debonding load, the debonding stress of the U-shaped sheet, calculated from equilibrium and compatibility equations, was compared to the modified Holzenkampfer formula [40], Eq. (1), resulting in an agreement of up to 98%.
f f ,   deb = f f ,   max = c 1 E f f ctm n f t f     for     l b ≥ l b ,   max ;     f f ,     deb = f f ,   max l b l b ,   max ( 2 - l b l b ,   max )     for     l b < l b ,   max   ;   l b ,   max = E f n f t f c 2 f ctm
where fctm represents the tensile strength of concrete, and Ef denotes the module of elasticity of the fibers. lb, lb,max, tf, and nf refer to the bond length, effective bond length, thickness, and the number of FRP layers, respectively. c1 and c2 are equal to 0.64 and 2, respectively [32].

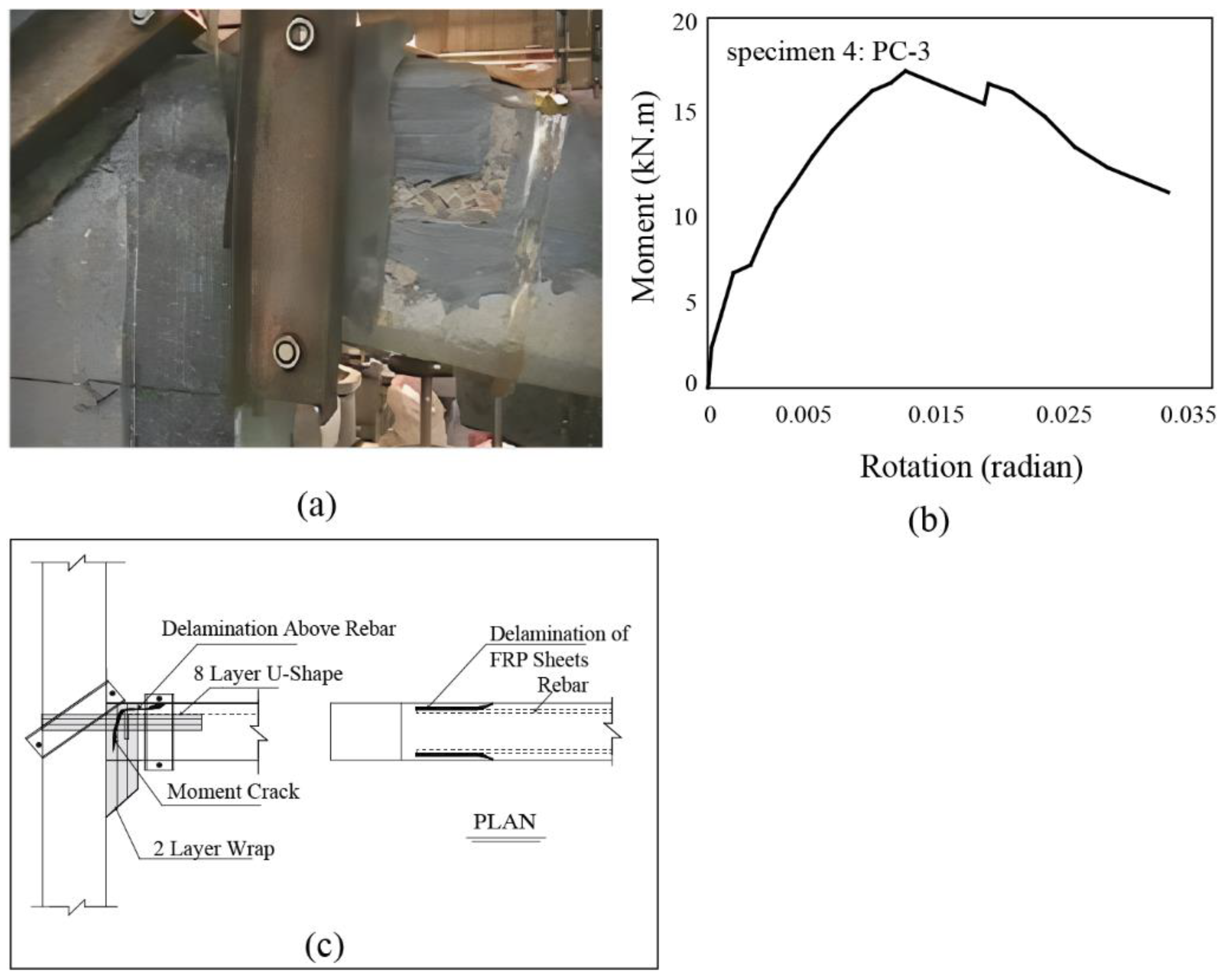
3.4. Specimen 4: PC-3 archetype

To prevent the debonding of the layers affixed to the concrete surface during loading, a highly efficient mechanical anchor was applied to secure the U-shaped FRP sheets onto the column. This anchoring mechanism played a crucial role in enhancing the adhesion and preventing separation during the testing of the PC-3 specimen (Figure 7). This was facilitated by the generation of compressive stress on the sheet's surface, augmenting the shear-friction resistance of the boundary layer across the column's width. Unlike the PC-2 sample, where the beam and corbel spiral experienced tearing, the PC-3 sample did not undergo significant tensile force on the beam and corbel spiral. This absence of force was attributed to the U-shaped sheet's adhesion to the column and its adequate rigidity, allowing for moment transferring. Ultimately, the rupture of the concrete near the U-shaped sheet, the longitudinal reinforcement, and the upper cover of the beam led to the connection's failure under a 19500 N load. For a visual representation of the failure mechanism in PC-3 in comparison to other archetypes, refer to Figure 8.
In this case, the separation of the U-shaped sheet occurred at ɛu=0.0053, where 34% of the FRP's ultimate capacity. The delay in the separation of the U-shaped sheet attached to the column, owing to appropriate mechanical anchorage, extended from ɛu = 0.001 to beyond ɛu = 0.0053. This extension corresponds to a range from ɛu = 0.002 to ɛu = 0.0053 for the U-shaped sheet affixed to the beam. The observed debonding strain of the U-shaped sheet aligns closely with the ultimate strain suggested by Sharif [41] (ɛu =0.005) and Arya and Farmer [42] (ɛu =0.006), corresponding to 95% and 84% of their strain, respectively. Additionally, the ultimate strain of the FRP sheet was aligned with up to 72% agreement with the values obtained from the ACI 440 [43] for beams, as follows:

4. Numerical modeling and analysis

4.1. Simulation of archetypes

The ANSYS software was employed for the three-dimensional modeling and analysis of reinforced concrete connections, as shown in Figure 9(a). Concrete materials were simulated using Octahedral elements, specifically Solid65 elements. These elements implemented the Wiliam-Warnek five-parameter failure criterion, considering compression failure and tension cracking. To prevent concrete failure modes in compression and tension, significantly impacting connection strength, the following assumptions were made: A 25% of shear resistance was assumed for concrete cracks opening under tension, whereas 99% of shear capacity for closed cracks occurring in concrete under compression. Steel elements were modeled using the Link element, while the FRP sheets were simulated by the Solid46 element. Considering previous investigations and the observed negligible effects of the reinforcement sliding in the connection, identical deformation was considered for both concrete and steel bars. However, the opening in the precast connection filled with both grout and adhesive was integrated and modeled as a unified entity.
Loadings were applied to multiple joints near the ends of the beam and column head to conduct nonlinear analyses. Precise boundary conditions were established within the finite element model to incorporate the interaction of all involved components during loading effectively. Accordingly, degrees of freedom along the x and z directions were constrained on the upper end of the column, while all three degrees of freedom for displacement at the lower end were restricted. As illustrated in Figure 9(b), the experimental results obtained from the tested specimen were utilized to validate the modeling. Once the accuracy of these basic models was confirmed, subsequent archetypes, in addition to the ones tested in the laboratory, including … archetypes, were modeled and analyzed using the software. Various parameters were measured during the analysis and comparison among different archetypes, including the rotation-moment curve, stress in concrete at specific steps, strain in tensile longitudinal reinforcements and FRP sheets, crack distribution, ultimate capacity, etc. (Figure 9(c)).

4.2. Analysis of illustrative examples

Based on failure theory and the experimental findings, the most effective solution for flexural reinforcement is utilizing U-shaped FRP sheets. Therefore, a set of precast connections, resembling the PC-3 configuration, were modeled employing U-shaped sheets with varying lengths and widths. These archetypes were denoted as PC-4 to PC-93, as listed in Table 3, consisting of 8 layers of U-shaped FRP sheets, arranged, and fastened around both the beam and column. As shown in Figure 10(a), three bond lengths (Lx) were considered: (1) 400 mm, covering the entire connection length; (2) 300 mm, similar to the PC-3 specimen; and (3) 200 mm, representing half of the connection length in the beam (the maximum required bond length for the sheet). Furthermore, to evaluate the influence of the U-shaped sheet's width (Wx) on the connection's capacity, the effects of three widths including 50 mm, 130 mm, and 200 mm were examined. Given that the entire width of the U-shaped sheet is under tension, a width of 50 mm (above the neutral axis), matching the laboratory specimen, was chosen to maximize its tensile capacity. With a width of 130 mm, the FRP reinforcement was extended below the neutral axis to accommodate positive moments induced by actual reciprocal earthquake loading. To cover the entire width of the beam a width of 200 mm was selected. This decision was based on the absence of chamfers at the corner of the beam, allowing for the entire beam width to be utilized for reinforcement.
Across PC-4 to PC-12 archetypes (Figure 10(b) and (c)), wider U-shaped sheets resulted in reduced tensile stress and strain. Tearing did not occur in any sample. In these samples, the widening of U-shaped sheets resulted in reduced tensile stress and strain, with no tearing observed. For instance, in the PC-4 connection, the FRP strain reached approximately 60% of its ultimate strain at 0.0091 during the yield tensile of beam rebars. Additionally, increasing the sheet width from 50 mm in PC-4 to 130 mm in PC-5 and 200 mm in PC-6 enhanced the moment capacity corresponding to the yield stress of rebars from 25 kN.m to 25.65 kN.m and 28.5 kN.m, respectively. Therefore, widening the FRP sheets covered the neutral axis of the cross-section of the beam, and enhanced the moment strength of the connection by increasing their contribution to both the concrete's compressive capacity and the beam's tensile rebar.
Connections PC-13 to PC-21 were similar to PC-4 to PC-12 archetypes in geometry and U-shaped sheet reinforcement. However, two layers were surrounded at the U-shaped sheet's end (Figure 11(a)). This full-wrap FRP was added to potentially improve crack development and stress distribution. Results revealed a 10% strain reduction in the U-shaped sheet due to the full-warp sheets. For instance, PC-19 exhibited approximately 10% less strain under the same loading in its U-shaped sheet than PC-10 (Figure 11(a)). As the U-shaped sheet width increased, the effectiveness of the added FRPs in reducing strain and stress weakened. This effect became less prominent in wider sheets, such as PC-15, PC-18, and PC-21, where the width reached 200 mm. The increased U-shaped sheet width resulted in reduced shear stress transmission by the full-wrap sheets, as illustrated in Figure 11(a). For cases with 200 mm wide U-shaped sheets, such as PC-21 and PC-12, which exhibited similar strains of 0.0104, there was minimal strain reduction. Moreover, wider U-shaped sheets displayed lower tensile stress in the end spiral. At the same load, PC-21 with a 200 mm wide U-shaped sheet experienced a 49% reduction in tensile stress compared to PC-19 with a 50 mm wide U-shaped sheet, decreasing from 271.33 MPa to 138.69 MPa. This reduction in the effect of the end wrap in shear stress transfer is responsible for the decline, as most shear stress is transferred by the U-shaped sheet surface rather than the full wrap. Additionally, analysis results from PC-13 to PC-21 indicated that these sheets could not significantly delay or increase the load transfer of the tensile reinforcement, affect the final anchor amount, or diminish crack propagation on the reinforcement's side. The curves obtained from these archetypes closely resembled those without the end full-wrap sheet.
Connections PC-22 to PC-30 mirror connections PC-13 to PC-21 but include additional side sheets to reinforce the U-shaped sheet (as depicted in Figure 11(b)). These side sheets are typically incorporated at the beam's end of the U-shaped sheet to prevent FRP separation and the crack's propagation. However, the analysis results of these connections revealed that the side sheets did not reduce the tensile stress in the U-shaped sheet (Table 3). Instead, they caused an increase in tensile stress in the beam's side plates compared to the full spiral configuration. For instance, the tensile stress in the side sheets of PC-28 was 30% higher than PC-19 (Figure 11(a)). This heightened stress concentration at the end of the beam's side sheets led to FRP debonding, which requires proper mechanical restraint to prevent. Moreover, with increased U-shaped sheet width, the tensile stress in the side sheets decreased. At the same load, the side sheet's tensile stress in sample PC-30 with a 200 mm wide U-shaped sheet showed a 68% reduction compared to sample PC-28 with a 50 mm wide U-shaped sheet (Figure 11(b)). This reduction resulted from the diminished effectiveness of the side sheets in shear stress distribution. The analysis results further demonstrated that the side sheets did not impact increasing or delaying the yield load of the tensile reinforcement, enhancing the final anchor, or reducing crack propagation on the reinforcement's yield side. The behavior of these samples closely matched those without the side sheets at the end of the U-shaped sheet.
The two layers of U-shaped sheets are positioned below the beam of the PC-31 to PC-39 connections (Figure 11(b)). However, analysis revealed that these sheets did not reduce the tensile stress in the U-shaped sheet compared to the samples with a full wrap at the end (Table 3). The main difference was the heightened tensile stress in the final U-shaped sheet compared to the full spiral state. For instance, the tensile stress in the side plates of sample PC-36 was 30% higher than that of PC-19. Similarly, widening the U-shaped sheet led to decreased tensile stress in the final U-shaped sheet. The tensile stress of the sheet adjacent to the beam in sample PC-39 with a 200 mm wide U-shaped sheet showed a 53% reduction compared to sample PC-36 with a 50 mm wide U-shaped sheet.
The analysis of connections PC-40 to PC-57 was developed to assess the impact of wrapping the beam and corbel with U-shaped and side sheets. Notably, the strain in the U-shaped sheet of PC-46 and PC-55 were reduced to 0.0092 and 0.0115, compared to PC-10 with 0.013, marking 44% and 12% reduction, respectively (Figure 11(c)). However, widening the U-shaped sheet decreased the effectiveness of the beam and corbel’s FRPs in reducing tensile stress. For example, the tensile stress of the side sheets in PC-57 with a 200 mm U-shaped sheet reached 352.27 MPa, while the stress was 1427.0 MPa for PC-55 with a 50 mm wide U-shaped sheet. Furthermore, the analysis demonstrated that the surrounded beam and corbel with FRPs did not significantly increase the ultimate capacity, delay the yielding load of tensile reinforcement, or reduce crack propagation. The curves obtained from these archetypes closely resembled those without beam and corbel wrapping (Table 3), albeit with slightly increased connection stiffness. For instance, Figure 11(c) compares the moment rotation curves of PC-46 and PC-55 connections with those of PC-10.
As illustrated in Figure 12, PC-58 to PC-66 connections were simulated to incorporate the effects of the two layers with 1000 mm length on both sides of the column. Meanwhile, PC-67 to PC-75 employed dual corbel spirals to reinforce the corbel's bending, and PC-76 to PC-84 featured a full-wrap beam and column with two layers at specific locations. Lastly, through PC-85 to PC-93 archetypes, the interaction effect of the corbel and column FRP wraps was investigated along with side longitudinal sheets, employing U-shaped sheets with varied dimensions. The analysis results revealed that the employed side sheets to the column did not alter the tensile stress within the U-shaped sheet. For instance, in comparison to PC-19, the strain within the U-shaped sheet for PC-73, PC-82, and PC-93 were 0.0131, 0.0129, 0.0113 respectively, with corresponding tensile stresses of 0.0117 (10% increase), 0.0117 (10% increase), and 0.0104 (8% increase). Additionally, wrapping the column did not influence the bending behavior of the connection, serving as a reinforcement only in specific cases of structural vulnerability. Moreover, to prevent the buckling of the FRP wrap of the corbel, it is advisable to employ any suitable external restraint.
To explore the influence of longitudinal reinforcement ratio (ρ), as well as the type of layers of FRPs and concrete strength, three additional samples were examined. Results indicated that increased ρ in the beam amplified connection capacity, whereas reduced reinforcement lessened their strengths. Notably, the initial and secondary branches of the moment-rotation curve remained unaltered. For instance, the PC-4 was analyzed with equivalent beam reinforcement, and its moment-rotation curve was plotted in Figure 13(a). Elevated concrete strength (Figure 13(b)) augmented connection stiffness across the initial and secondary stiffness of the push curve, albeit without substantial capacity increments. This rise in concrete strength effectively bolstered shear strength, delaying micro-cracks and debonding. Moreover, increased stiffness in FRP fibers (Figure 13(c)) corresponded to stiffer connections, while reduced fiber stiffness resulted in decreased stiffness. None of the samples exceeded the ultimate sheet strain at load, avoiding any tearing. Hence, reducing the number of layers was feasible in all archetypes, as long as separation or sheet buckling didn't occur until the ultimate strain. Furthermore, thinning the sheet lessened stress linearly concerning the resistant cross-sectional area (i.e., sheet thickness, as width remains constant).

5. Results:

This paper delves into experimental and numerical investigations concerning precast concrete corbel beam-column connections strengthened by FRP sheets and external mechanical anchorage plates. Comparative analyses are made between these connections and in-situ concrete fixed joints. The findings and key outcomes of this research are as follows:
  • Strengthening the PC-1 specimen's connection with L-shaped FRP sheets at the top and bottom minimally impacted the flexural capacity due to high shear-stress concentration. Similarly, relying solely on the spiral U-shaped FRP sheets without a mechanical anchorage for reinforcing the PC-2 connection did not result in significant bending capacity due to occurring debonding. With the incorporation of spiral sheets in PC-2, the debonding capacity of fibers improved by up to 100%, thereby extending the ultimate strain of the sheets from εu=0.001 to εu=0.002.
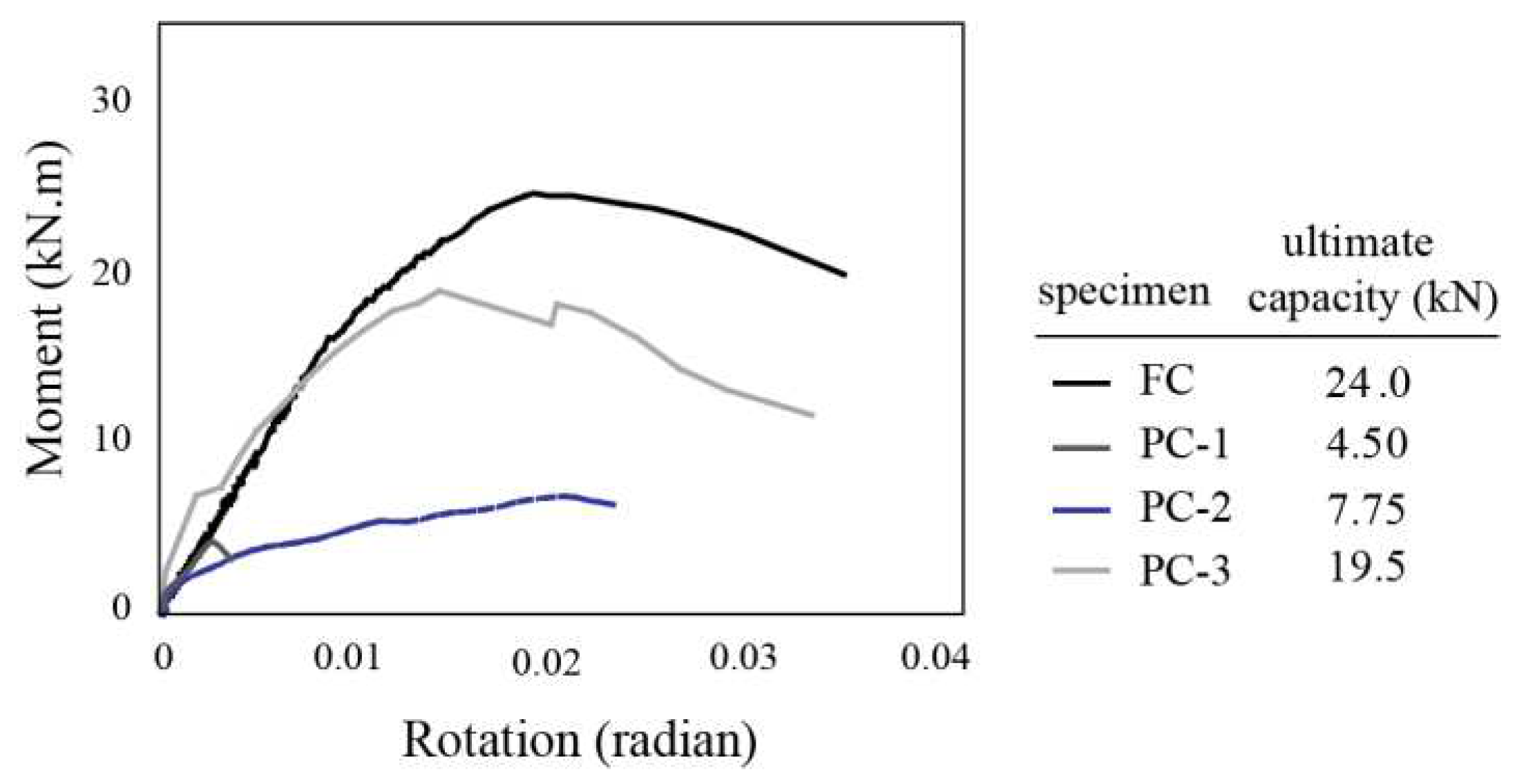
  • The PC-3 connection managed to enhance the moment capacity to 81% of a fixed connection's flexural capacity. In this specimen, the debonding phenomenon was effectively controlled by employing an anchoring system. The mechanical anchors notably amplified the ultimate separation capacity of FRP sheets by 530%. Consequently, the ultimate separation strain of the FRP sheets increased from 0.001 to over 0.0053, accounting for 34% of the ultimate tensile strain of FRP.
  • It was observed that the number and thickness of FRP layers influenced the ultimate debonding strain of FRP. Furthermore, the mechanical anchors over the U-shaped FRP sheet could postpone the reinforcement yielding.
  • The theoretical analysis based on experimental findings of the PC-3 archetype revealed the mobilization of 35% of the ultimate capacity of FRP, while simulation results demonstrated a 41% contribution. This showcases a 6% difference between the numerical modeling and theoretical outcomes, affirming the accuracy of the numerical predictions. Moreover, the ultimate strain acquired from simulating the PC-3 corresponds to an 86% agreement with the strain derived from ACI-440 for simple beams.
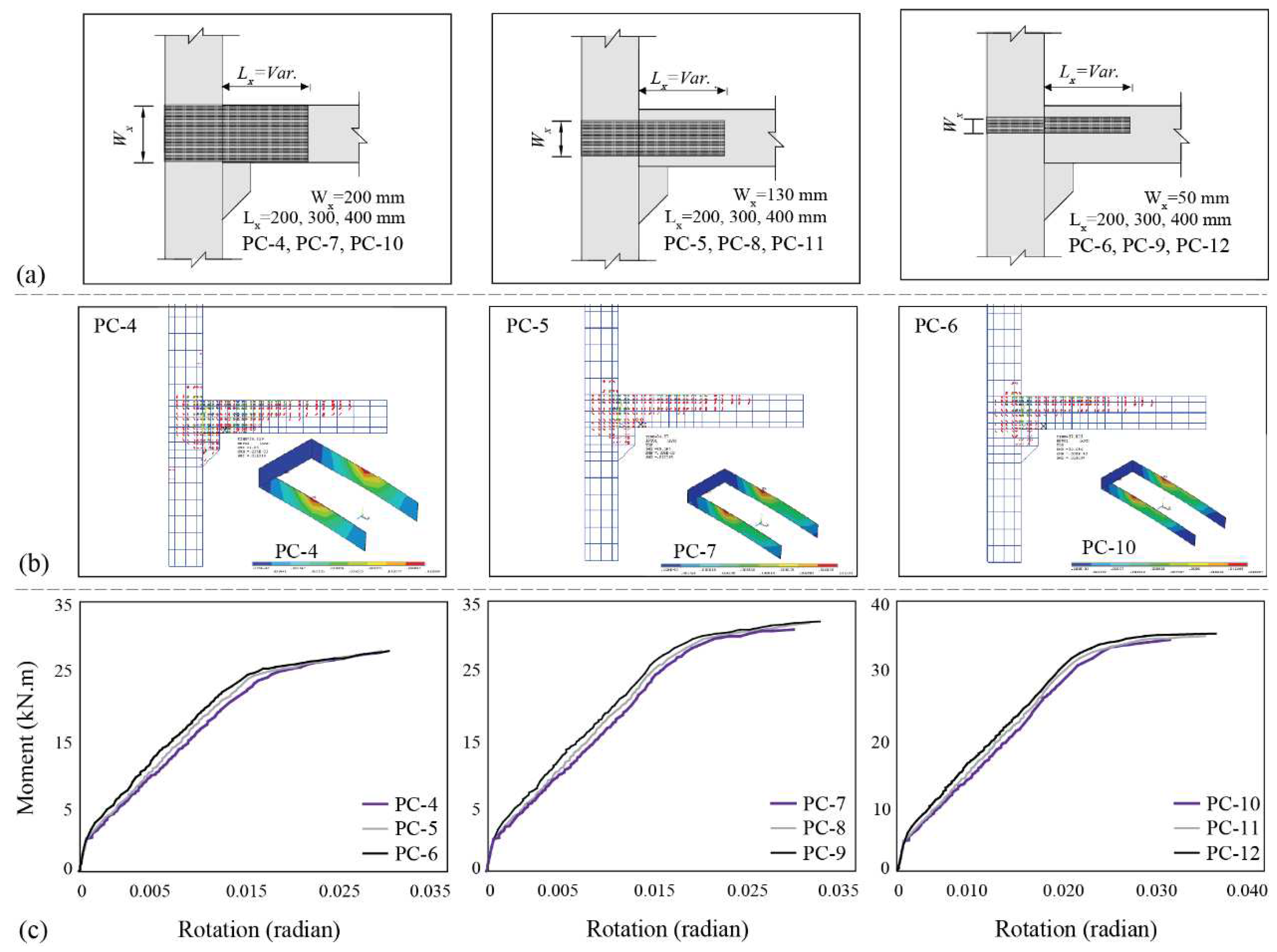
  • The implementation of U-shaped FRP sheets in the tensile region resulted in a shift of the critical cross-section, which was originally at the beam’s end. This modification has the potential to convert the pinned connection into a fully fixed one. As a result, the connection’s flexural strength is significantly enhanced, surpassing that of the cast-in-place FC specimen by approximately 1.19 to 1.5 times. This improvement underscores the potential of U-shaped FRP sheets in bolstering the structural integrity of precast concrete connections.
  • The ultimate moment capacity of the connection is enhanced by increasing the bond length of the U-shaped sheet. This increase in bond length also elevates the tensile strength of the U-shaped sheet at the edge of the connections, thereby boosting the bearing capacity of the connection. Similarly, expanding the width of the U-shaped sheet augments the resisting moment of the connection to a certain degree. This expansion in sheet width also escalates the tensile strength of the U-shaped sheet at the edge of the connections, resulting in an increased bearing capacity of the connection.
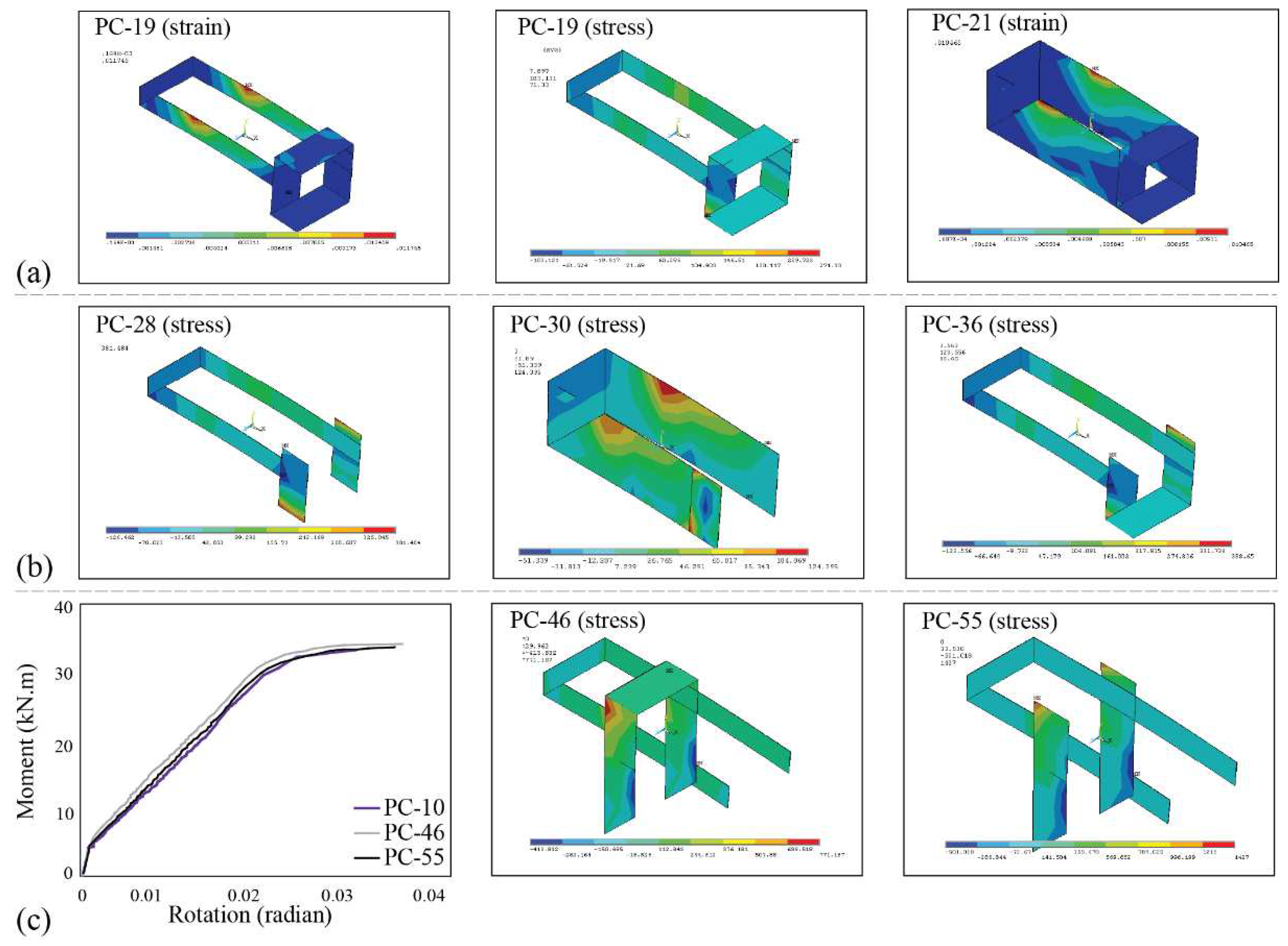
  • In neither of the archetypes did the FRP sheet strain reach beyond the ultimate strain at the peak load, thereby preventing any tearing. Consequently, there is potential to increase the number of sheet layers across all samples, if separation or buckling doesn't occur until the sheet's ultimate strain. Additionally, reducing the sheet thickness linearly decreased the stress within the sheet.
  • Full wrap or side sheets at the end of the U-shaped sheet showed minimal impact on reducing stress or enhancing the connection's load-bearing capacity. However, the spirals over the beam and corbel side sheets significantly reduced stress in the U-shaped sheet. In contrast, the effect of column-side FRP sheets and full wrap on the column or corbel displayed negligible impact on stress reduction or moment resistance in the connection.
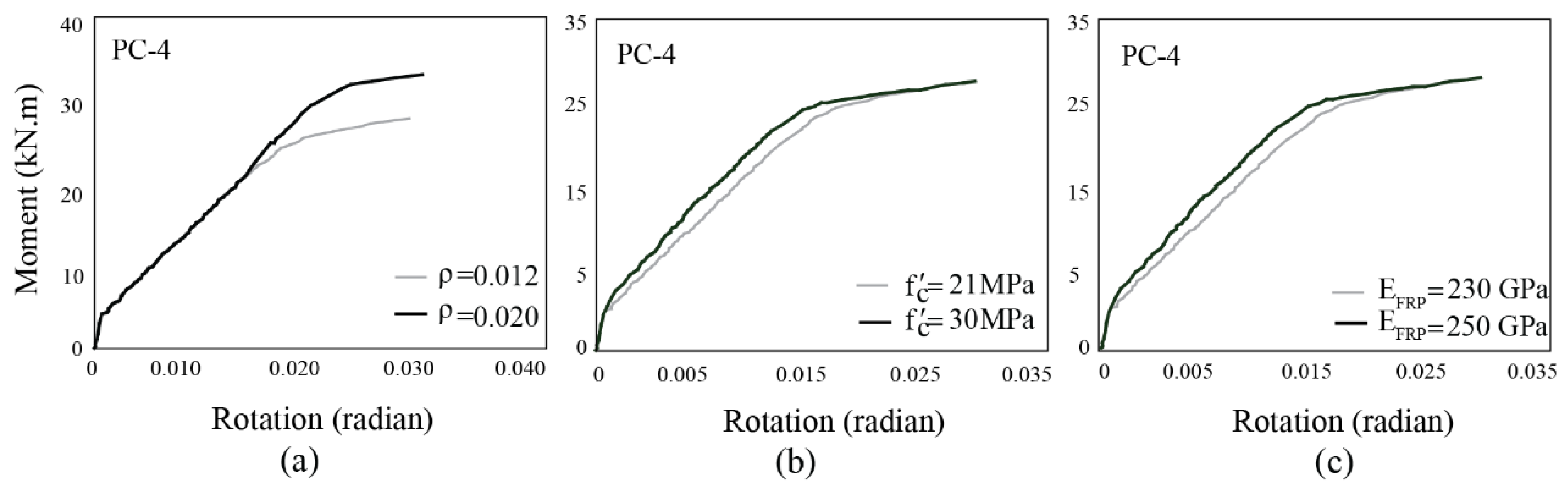
  • Variations in longitudinal beam reinforcement ratios directly affect the connection's load-bearing capacity, altering it upon increase or decrease. Concrete strength impacted stiffness more than rotational moment capacity, while increased FRP fiber elastic modulus enhanced connection stiffness.
The study was limited to a few experimental tests focusing on specific reinforcements and FRP sheets under static loads. Further investigation across a broader range of variables is necessary to comprehensively analyze the effectiveness of these reinforcements, particularly those related to anchored U-shaped reinforcement.

Author Contributions

Conceptualization, N.R., N.R.; methodology, N.R., N.R.; software, N.R., N.R.; validation, N.R., N.R.; formal analysis, N.R., N.R.; investigation, N.R., N.R.; writing—original draft preparation, N.R., N.R.; writing—review and editing, N.R., N.R.; visualization, N.R., N.R.; supervision, N.R., N.R.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data was created.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Neuberger, Y. M.; de Lima Araújo, D. An improved analytical model for two-step corbels in a precast concrete system. Eng. Struct. 2023, 284, 115947. [Google Scholar] [CrossRef]
  2. Ghayeb, H. H., Razak, H. A.; Sulong, N. R. Performance of dowel beam-to-column connections for precast concrete systems under seismic loads: A review. Constr. Build. Mater. 2020, 237, 117582. [Google Scholar] [CrossRef]
  3. Akguzel, U.; Pampanin, S. Assessment and design procedure for the seismic retrofit of reinforced concrete beam-column joints using FRP composite materials. J. of Comp. for Constr. 2012, 16, 21–34. [Google Scholar] [CrossRef]
  4. Huang, C., Song, J., Zhang, N.; Lee, G. C. Seismic performance of precast prestressed concrete bridge girders using field-cast ultrahigh-performance concrete connections. J. Bridge Eng. 2019, 24, 04019046. [Google Scholar] [CrossRef]
  5. Sritharan, S., Aaleti, S., Henry, R. S., Liu, K. Y.; Tsai, K. C. Precast concrete wall with end columns (PreWEC) for earthquake resistant design. Earthquake Eng. Struct. Dyn. 2015; 44, 2075–2092. [Google Scholar]
  6. Singhal, S., Chourasia, A., Chellappa, S.; Parashar, J. Precast reinforced concrete shear walls: State of the art review. Struct. Concr. 2019; 20, 886–898. [Google Scholar]
  7. Abaev, Z., Valiev, A.; Kodzaev, M. Modeling of the precast concrete hollow-core floor diaphragm with tie beams under seismic action. AIP Conf. Proc. 2023; 2833. [Google Scholar]
  8. Kurama, Y. C., Sritharan, S., Fleischman, R. B., Restrepo, J. I., Henry, R. S., Cleland, N. M., et al. Seismic-resistant precast concrete structures: State of the art. J. Struct. Eng. 2018; 144, 03118001. [Google Scholar]
  9. Del Vecchio, C.; Di Ludovico, M.; Balsamo, A.; Prota, A.; Manfredi, G.; Dolce, M. Experimental investigation of exterior RC beam-column joints retrofitted with FRP systems. J of Comp. for Const. 2014, 18(4), 04014002. [Google Scholar] [CrossRef]
  10. Aninthaneni, P. K., Dhakal, R. P., Marshall, J.; Bothara, J. Experimental investigation of “dry” jointed precast concrete frame sub-assemblies with steel angle and tube connections. Bull. Earthquake Eng. 2020, 18, 3659–3681. [Google Scholar] [CrossRef]
  11. Li, H., Chen, W.; Hao, H. Dynamic response of precast concrete beam with wet connection subjected to impact loads. Eng. Struct. 2019, 191, 247–263. [Google Scholar] [CrossRef]
  12. Martins, R., Carmo, R. D., Costa, H.; Júlio, E. A review on precast structural concrete walls and connections. Adv. Struct. Eng. 2023, 26(14), 2600–2620. [CrossRef]
  13. Zhang, J., Ding, C., Rong, X., Yang, H., Wang, K.; Zhang, B. Experimental seismic study of precast hybrid SFC/RC beam–column connections with different connection details. Eng. Struct. 2020; 208, 110295. [Google Scholar]
  14. Psycharis, I. N.; Mouzakis, H. P. Shear resistance of pinned connections of precast members to monotonic and cyclic loading. Eng. Struct. 2012, 41, 413–427. [Google Scholar] [CrossRef]
  15. Holly, I.; Abrahoim, I. Connections and joints in precast concrete structures. Slovak J. Civil Eng. 2020, 28(1), 49–56. [Google Scholar] [CrossRef]
  16. Iverson, J. K.; Hawkins, N. M. Performance of Precast/Prestressed Concrete Building Structures During the Northridge Earthquake. PCI J. 1994, 65–76. [Google Scholar] [CrossRef]
  17. Wu, G., Feng, D. C.; Wang, C. L. Ductile Precast Concrete Frame with Dry-Connections. In Novel Precast Concrete Structure Systems; Springer Nature Singapore. 2023; 33–86. [Google Scholar]
  18. Xie, L., Wu, J., Zhang, J.; Liu, C. Experimental study on mechanical behaviour of replaceable energy dissipation connectors for precast concrete frames. Struct. 2021, 33, 3147–3162. [Google Scholar] [CrossRef]
  19. Mostofinejad, D.; Arefian, B. Generic assessment of effective bond length of FRP-concrete joint based on the initiation of debonding: Experimental and analytical investigation. Compos. Struct. 2021, 277, 114625. [Google Scholar] [CrossRef]
  20. Aninthaneni, P. K., R. P. Dhakal, J. Marshall, and J. Bothara. Nonlinear cyclic behaviour of precast concrete frame sub-assemblies with “dry” end plate connection. Struct. 2018, 14, 124–136. [Google Scholar] [CrossRef]
  21. Li, Z. Y., Kang, S. B., He, H., Lu, W. Q., Liu, H. J.; Lu, C. J. Seismic behaviour of precast concrete beam-column connections with bolted end plates. Struct. 2023; 58, 105343. [Google Scholar]
  22. Rajeswari, M.; Jaya, K. P. Cyclic performance of emulative precast beam to column connection with corbel using dowel bar. Rev. de la construcción. 2022; 21, 354–367. [Google Scholar]
  23. Nimse, R. B., Joshi, D. D.; Patel, P. V. Experimental study on precast beam column connections constructed using RC corbel and steel billet under progressive collapse scenario. In Structures congress. 2015, 1101–1117. [Google Scholar]
  24. Bahrami, S., Madhkhan, M., Shirmohammadi, F.; Nazemi, N. Behavior of two new moment resisting precast beam to column connections subjected to lateral loading. Eng. Struct. 2017; 132, 808–821. [Google Scholar]
  25. Dasgupta, A. Retrofitting of concrete structure with fiber reinforced polymer. Int. J. 2018, 4(9), 42–49. [Google Scholar]
  26. Saadatmanesh, H.; Ehsani, M. Fiber composite plates can strengthen beams. Concrete Int. 1997, 12(3), 65–76. [Google Scholar]
  27. Granata, P.; Parvin, A. An Experimental Study on Kevlar Strengthening of Beam-Column Connections. Compos, 2001, 53, 163–171. [Google Scholar] [CrossRef]
  28. Huynh-Xuan, T., Do-Dai, T., Ngo-Huu, C., Pham, T. M.; Nguyen-Minh, L. Effect of corroded reinforcement on capacity of square reinforced concrete columns confined with FRP sheets under eccentric loads. Eng. Struct. 2023, 283, 115821. [Google Scholar] [CrossRef]
  29. Li, J., Bakoss, S. L., Samali, B.; Ye, L. Reinforcement of concrete beam–column connections with hybrid FRP sheet. Compos. Struct. 1999; 47, 805–812. [Google Scholar]
  30. Shrestha, R., Smith, S. T.; Samali, B. Strengthening RC beam–column connections with FRP strips. Proc. Instit. Civil Eng. Struct. Build. 2009; 162, 323–334. [Google Scholar]
  31. Allam, K., Mosallam, A. S.; Salama, M. A. Experimental evaluation of seismic performance of interior RC beam-column joints strengthened with FRP composites. Eng. Struct. 2019; 196, 109308. [Google Scholar]
  32. Antonopoluos, C. P.; Triantafillou, T. C. Analysis of FRP-Strengthened RC Beam-Column Joints. Compos. for Constr. 2002, 6(1), 41–51. [Google Scholar] [CrossRef]
  33. Gergely, I., Pantelides, C. P.; Reaveley, L. D. Shear Strengthening of RC T-joints Using CFRP Composites. Compos. for Constr. 2000; 4, 56–64. [Google Scholar]
  34. Parvin, A.; Granata, P. External Fiber Composite Reinforcement of Concrete Structural Members. Proc. of the Japan-U.S. Conference on Composite Materials, 1998; 942–948. [Google Scholar]
  35. Antonopoluos, C. P.; Triantafillou, T. C. Experimental Investigation of FRP-Strengthened RC Beam-Column Joints. Compos. for Constr. 2003, 6(1), 39–49. [Google Scholar] [CrossRef]
  36. Harmon, T. G., Kim, Y. J., Johnson, T.; Stark, A. Bond of Surface-Mounted Fiber-Reinforced Polymer Reinforcement for Concrete Structures. ACI Struct. J. 2003; 57, 557–564. [Google Scholar]
  37. ACI Committee. Building code requirements for structural concrete (ACI 318-08) and commentary. Am. Concrete Inst.
  38. Mass, G. R. Proportioning mass concrete incorporating Pozzolans using ACI 211.1. Concrete Int. 1982, 4(8), 48–55. [Google Scholar]
  39. Hernandez, D. A.; Orlandi, M. O. Mechanical properties of composites materials SIKACARBODURS512, SIKADUR 30 and SIKADUR 330. 22o CBECiMat–Congresso Brasileiro de Engenharia e Ciência dos Materiais, 2016.
  40. Holzenkampfer, O. Ingenieurmodelle des verbundes geklebter bewehrung fur betonbauteile. PHD Dissertation, TU Braunschweig (in German)., 1994.
  41. Sharif, A., Al-Sulaimani, G. J., Basunbul, I. A., Baluch, M. H., Ghaleb, B. N. Strengthening of Initially Loaded Reinforced Concrete Beams Using FRP Plates. ACI Struct. J. 1994; 91, 160–168. [Google Scholar]
  42. Arya, C., Farmer, N. Design guidelines for flexural strengthening of concrete members using FRP composites. FRPRCS-5: Fibre-reinforced plastics for reinforced concrete structures, 2001; 167–176. [Google Scholar]
  43. ACI Committee 440. Guide for the design and construction of externally bonded FRP systems for strengthened concrete structures, ACI 440.2R-02.
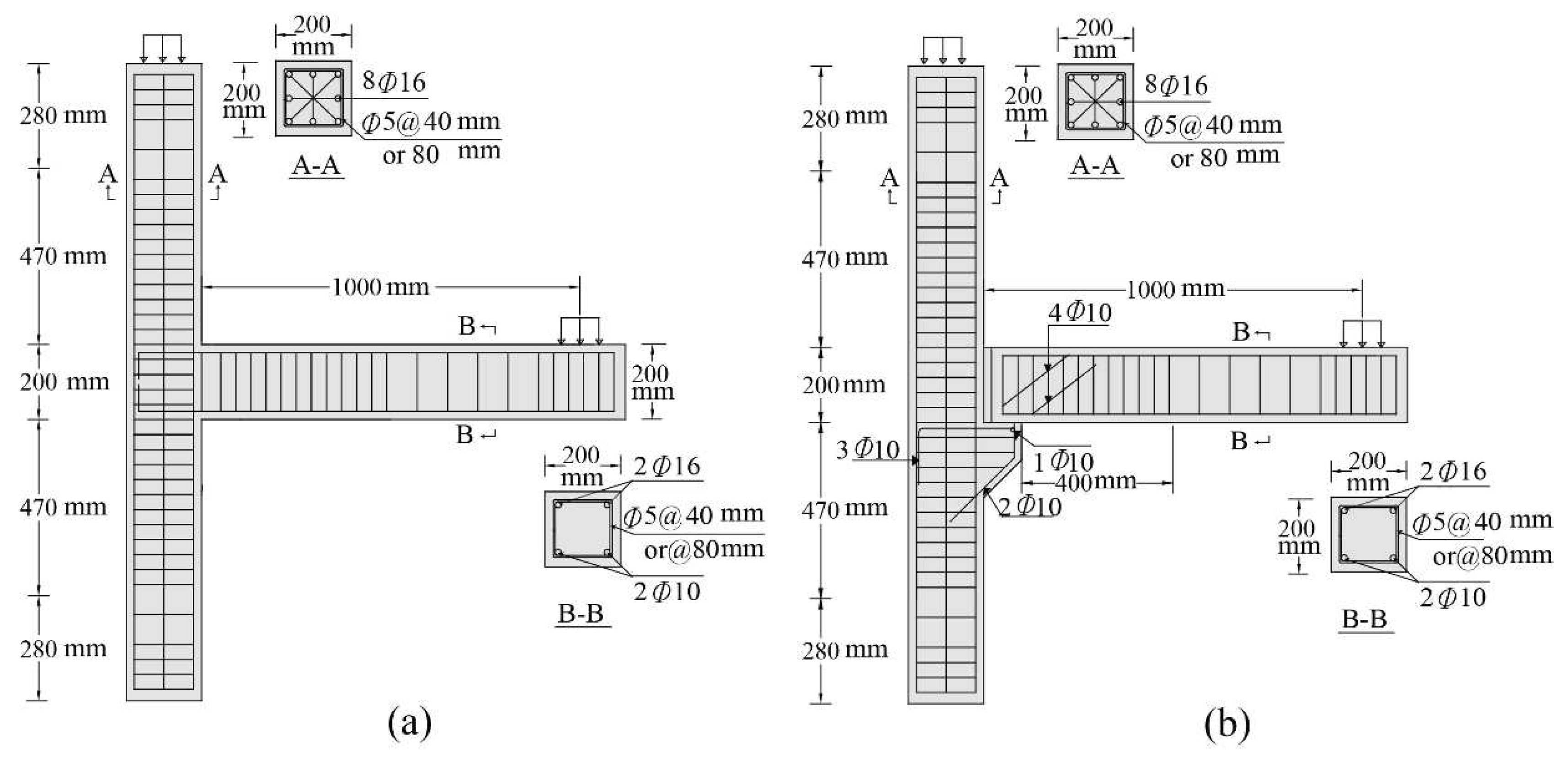
Preprints 95432 g001
Figure 1. Reinforcement details of test specimens: (a) fixed (FC) and (b) pinned (PC) connections.
Figure 1. Reinforcement details of test specimens: (a) fixed (FC) and (b) pinned (PC) connections.
Preprints 95432 g001
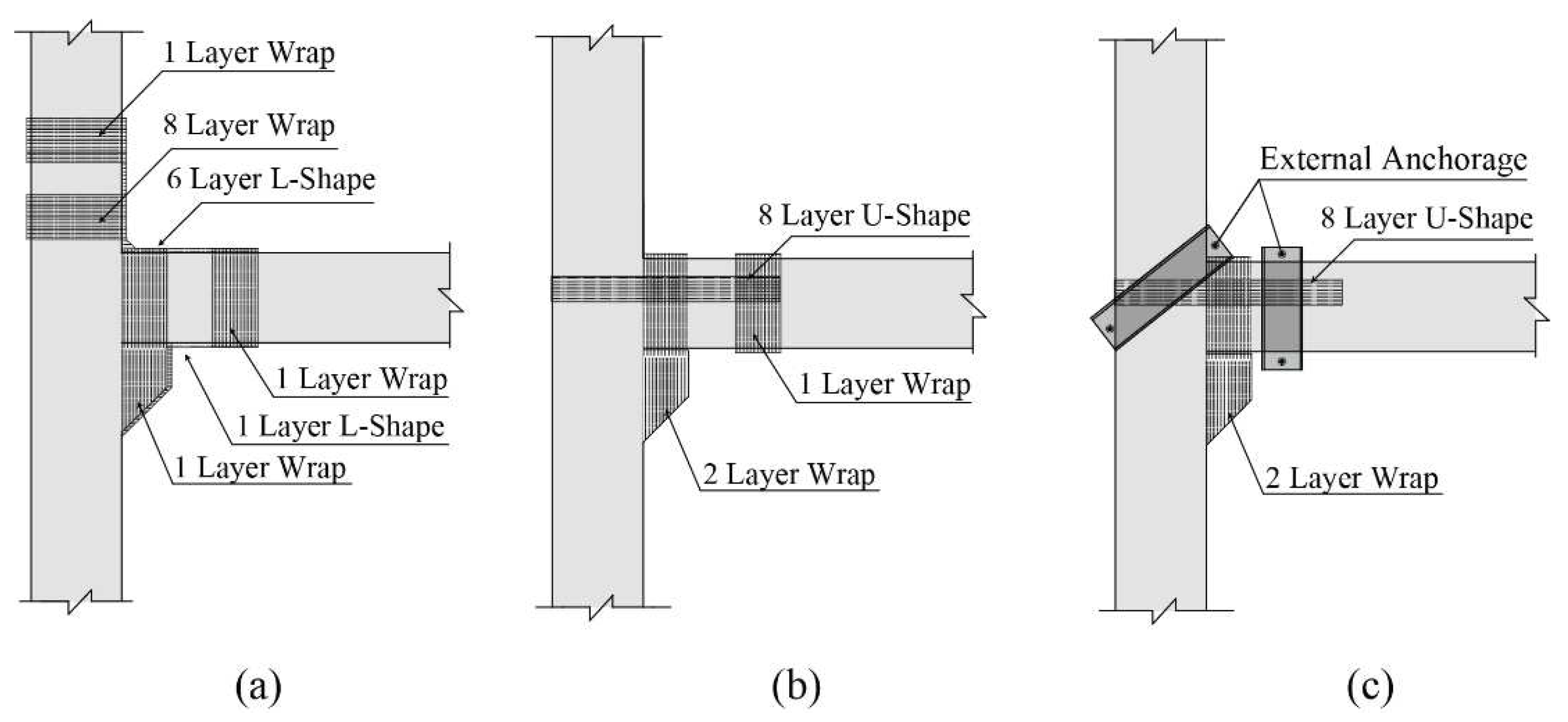
Preprints 95432 g002
Figure 2. Detailing of FRP wrap layout for (a) PC-1, (b) PC-2, and (c) PC-3 specimens.
Figure 2. Detailing of FRP wrap layout for (a) PC-1, (b) PC-2, and (c) PC-3 specimens.
Preprints 95432 g002
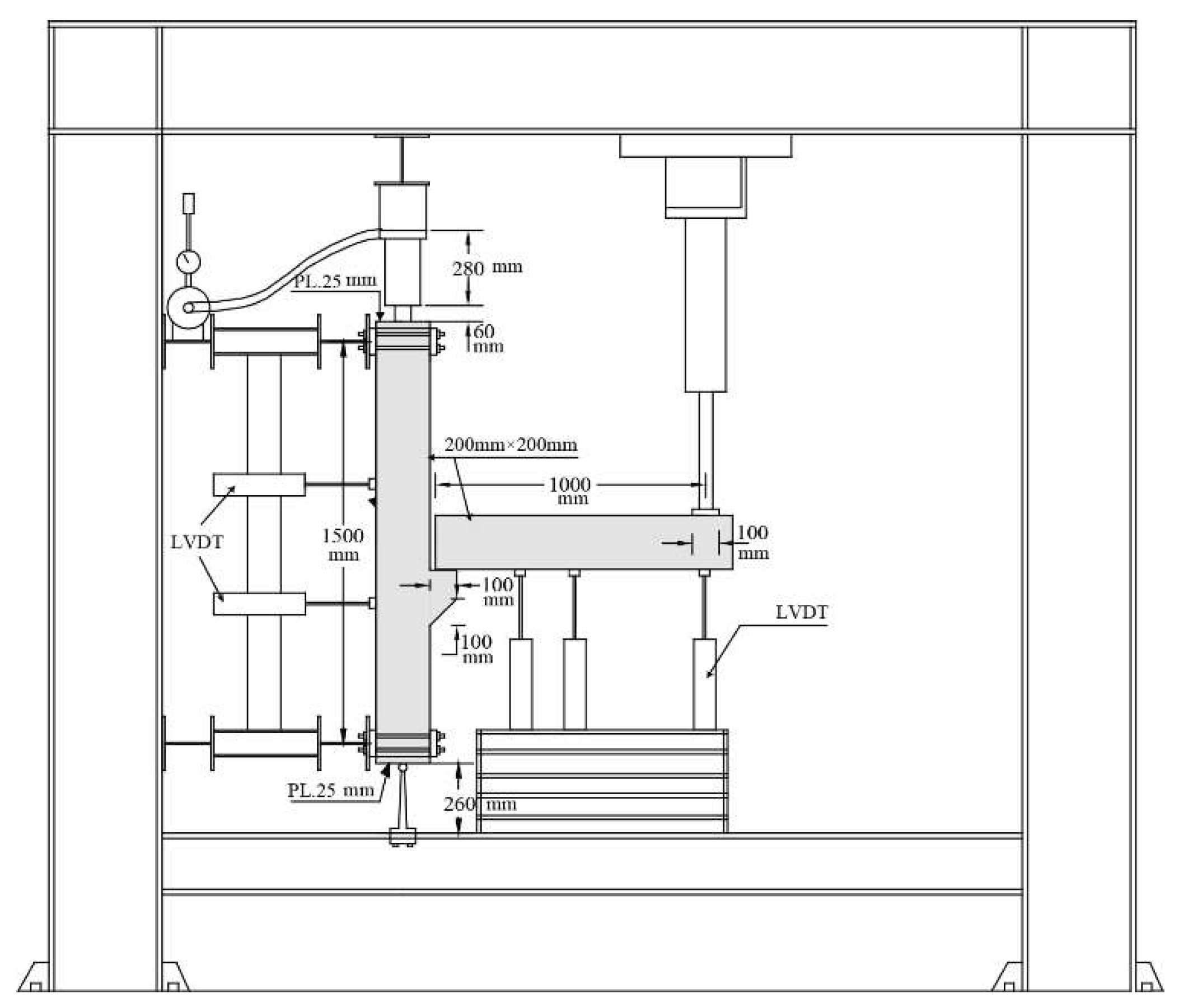
Preprints 95432 g003
Figure 3. A typical illustration and dimensions of test specimens and apparatuses.
Figure 3. A typical illustration and dimensions of test specimens and apparatuses.
Preprints 95432 g003
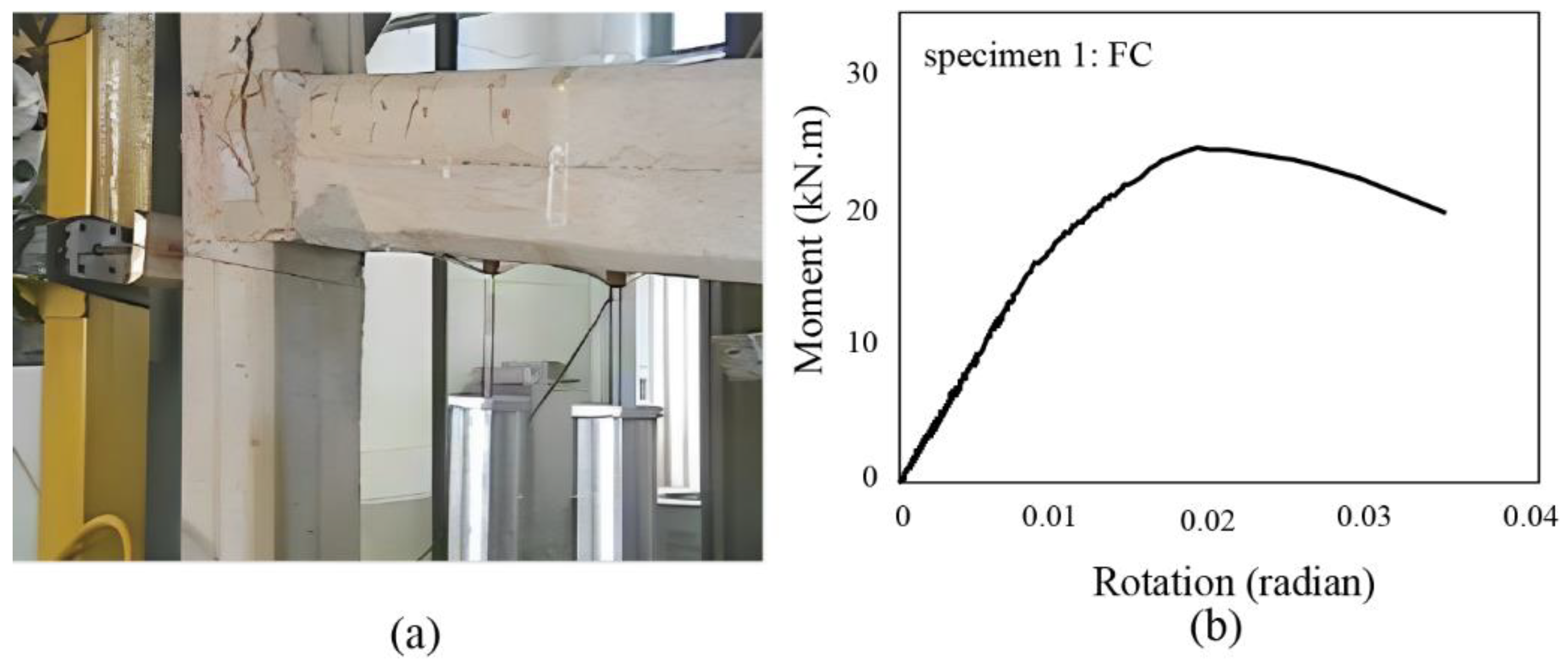
Preprints 95432 g004
Figure 4. FC specimen: (a) fractures occurred near and within the core, and (b) moment-rotation capacity curve.
Figure 4. FC specimen: (a) fractures occurred near and within the core, and (b) moment-rotation capacity curve.
Preprints 95432 g004
Preprints 95432 g005
Figure 5. PC-1 specimen: (a) tearing of spiral and L-shaped FRP sheets, and (b) moment-rotation capacity curve.
Figure 5. PC-1 specimen: (a) tearing of spiral and L-shaped FRP sheets, and (b) moment-rotation capacity curve.
Preprints 95432 g005
Preprints 95432 g006
Figure 6. PC-2 specimen: (a) separation of U-shaped FRP sheets around the column and tearing of spiral FRP of beam and corbel, and (b) moment-rotation capacity curve.
Figure 6. PC-2 specimen: (a) separation of U-shaped FRP sheets around the column and tearing of spiral FRP of beam and corbel, and (b) moment-rotation capacity curve.
Preprints 95432 g006
Preprints 95432 g007
Figure 7. PC-3 specimen: (a) FRP debonding at the end of the U-shaped sheet, (b) moment-rotation capacity curve, and (c) failure mechanism.
Figure 7. PC-3 specimen: (a) FRP debonding at the end of the U-shaped sheet, (b) moment-rotation capacity curve, and (c) failure mechanism.
Preprints 95432 g007
Preprints 95432 g008
Figure 8. Comparison of moment-rotation capacity curves among FC, PC-1, PC-2, and PC-3 archetypes.
Figure 8. Comparison of moment-rotation capacity curves among FC, PC-1, PC-2, and PC-3 archetypes.
Preprints 95432 g008
Preprints 95432 g009
Figure 9. Modeling and analysis of FC and PC archetypes: (a) three-dimensional simulation, (b) schematic of analysis results, and (c) verification of numerical modeling.
Figure 9. Modeling and analysis of FC and PC archetypes: (a) three-dimensional simulation, (b) schematic of analysis results, and (c) verification of numerical modeling.
Preprints 95432 g009
Preprints 95432 g010
Figure 10. Specifications of U-shaped FRP sheet with (a) different dimensions. (b) distribution of cracks in connections and stress in FRPs, (c) Moment rotation curves of the archetypes.
Figure 10. Specifications of U-shaped FRP sheet with (a) different dimensions. (b) distribution of cracks in connections and stress in FRPs, (c) Moment rotation curves of the archetypes.
Preprints 95432 g010
Preprints 95432 g011
Figure 11. Effects of (a) full-wrap and (b) 2- and 3-side wrap at the end of the U-shaped sheet and (c) wrapping on corbel location.
Figure 11. Effects of (a) full-wrap and (b) 2- and 3-side wrap at the end of the U-shaped sheet and (c) wrapping on corbel location.
Preprints 95432 g011
Preprints 95432 g012
Figure 12. Effects of confinement of the column along with wrapping (a) beam with U-shaped FRP, (b) corbel with 2-side sheets, (c) corbel with dual spirals, and (d) full-wrap beam and column.
Figure 12. Effects of confinement of the column along with wrapping (a) beam with U-shaped FRP, (b) corbel with 2-side sheets, (c) corbel with dual spirals, and (d) full-wrap beam and column.
Preprints 95432 g012
Preprints 95432 g013
Figure 13. Moment-rotation curves of the PC-4 connection considering differences in (a) reinforcement ratios, (b) concrete strengths, (c) and modulus of elasticity of FRPs.
Figure 13. Moment-rotation curves of the PC-4 connection considering differences in (a) reinforcement ratios, (b) concrete strengths, (c) and modulus of elasticity of FRPs.
Preprints 95432 g013
Table 1. Material and specifications properties of concrete and FRP sheets.
Table 1. Material and specifications properties of concrete and FRP sheets.
Archetype f’c (MPa) ρfb (%) ρfw (%)
FC 21.3 0.00 0.00
PC-1 23.2 0.25 0.11
PC-2 23.1 0.22 0.22
PC-3 21.1 0.22 0.22
Table 2. Material properties of FRP sheets.
Table 2. Material properties of FRP sheets.
Type E (GPa) W(g/m2) γ (g/m3) Fu (MPa) ɛu (%) t (mm)
SikaWrap-200C 230 200 ± 5% 1.80 3900 1.55 0.11
Table 3. Dimensions of the U-shaped FRP (Lx and Wx), ultimate and normalized moment strength of the connection (Mu) and strain in FRP.
Table 3. Dimensions of the U-shaped FRP (Lx and Wx), ultimate and normalized moment strength of the connection (Mu) and strain in FRP.
Archetype Lx
(mm)		 Wx
(mm)		 Mu
(kN.mm)		 Mu / Mu, FC ɛu(U-Shap) ɛ/ɛu
FC(1) - - 24 1.00 - -
PC-3(1) 300 50 19.5 0.81 - -
PC-4, PC-13, PC-22, PC-31 200 50 28.5 1.19 0.0111 0.72
PC-5, PC-14, PC-23, PC-32 200 130 2. 95 1.21 0.0105 0.68
PC-6, PC-15, PC-24, PC-33 200 200 29.2 1.22 0.0099 0.64
PC-7, PC-16, PC-25, PC-34 300 50 31.2 1.30 0.0122 0.79
PC-8, PC-17, PC-26, PC-35 300 130 32.3 1.35 0.0115 0.74
PC-9, PC-18, PC-27, PC-36 300 200 32.5 1.35 0.0108 0.7
PC-10, PC-19, PC-28, PC-37 400 50 34.1 1.42 0.0131 0.84
PC-11, PC-20, PC-29, PC-38 400 130 35.0 1.46 0.0115 0.74
PC-12, PC-21, PC-30, PC-39 400 200 35.4 1.47 0.0104 0.67
PC-40(2) 200 50 29.7 1.24 0.0074 0.48
PC-41(2) 200 130 29.4 1.23 0.0081 0.52
PC-42(2) 200 200 29.5 1.23 0.0089 0.57
PC-43(2) 300 50 32.2 1.34 0.0081 0.52
PC-44(2) 300 130 32.7 1.37 0.0092 0.59
PC-45(2) 300 200 32.8 1.37 0.0097 0.63
PC-46(2) 400 50 35.1 1.46 0.0087 0.56
PC-47(2) 400 130 35.7 1.49 0.0092 0.59
PC-48(2) 400 200 35.9 1.50 0.0093 0.6
PC-49(2) 200 50 29.6 1.23 0.0087 0.56
PC-50(2) 200 130 29.4 1.23 0.0088 0.57
PC-51(2) 200 200 29.3 1.22 0.0088 0.57
PC-52(2) 300 50 3.21 0.13 0.0097 0.62
PC-53(2) 300 130 32.7 1.36 0.0097 0.62
PC-54(2) 300 200 32.7 1.36 0.0097 0.62
PC-55(2) 400 50 35.0 0.15 0.0102 0.66
PC-56(2) 400 130 35.6 1.48 0.0104 0.67
PC-57(2) 400 200 35.8 1.49 0.0105 0.68
PC-58(3) 200 50 29.3 1.23 0.0111 0.72
PC-59(3) 200 130 29.8 1.25 0.0105 0.68
PC-60(3) 200 200 30.1 1.26 0.0099 0.64
PC-61(3) 300 50 32.1 1.34 0.0122 0.79
PC-62(3) 300 130 33.3 1.39 0.0115 0.74
PC-63(3) 300 200 33.4 1.39 0.0108 0.7
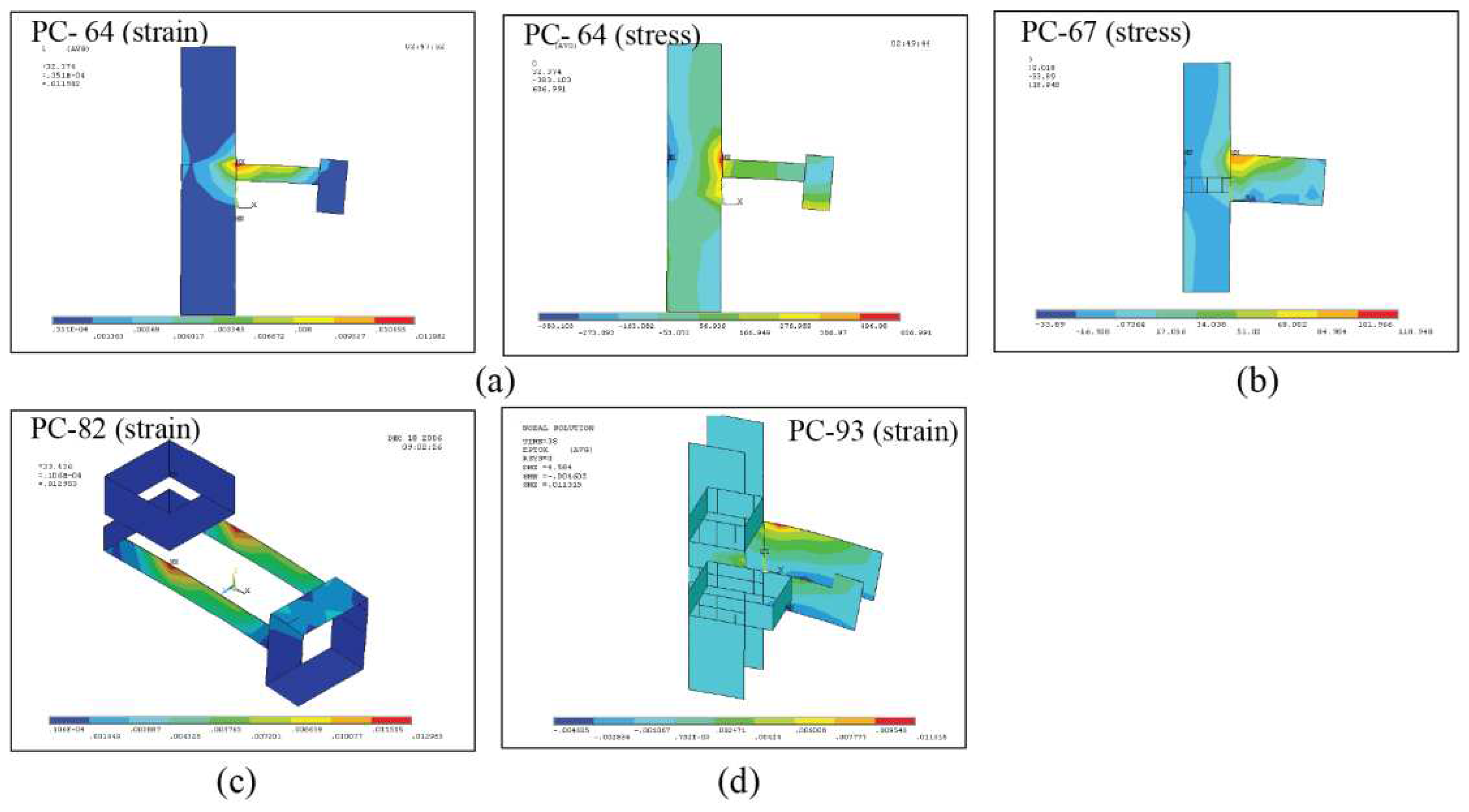
PC-64(3) 400 50 35.1 1.46 0.0131 0.84
PC-65(3) 400 130 36.0 1.50 0.0115 0.74
PC-66(3) 400 200 36.4 1.51 0.0104 0.67
PC-67(2,3), PC-76(2,3) 200 50 28.2 1.19 0.0107 0.69
PC-68(2,3), PC-77(2,3) 200 130 27.5 1.15 0.0097 0.62
PC-69(2,3), PC-78(2,3) 200 200 27.4 1.15 0.009 0.58
PC-70(2,3), PC-79(2,3) 300 50 32.1 1.34 0.0122 0.79
PC-71(2,3), PC-80(2,3) 300 130 31.3 1.31 0.0108 0.7
PC-72(2,3), PC-81(2,3) 300 200 30.9 1.29 0.01 0.64
PC-73(2,3), PC-82(2,3) 400 50 34.3 1.43 0.0128 0.82
PC-74(2,3), PC-83(2,3) 400 130 36.6 1.53 0.0117 0.75
PC-75(2,3), PC-84(2,3) 400 200 37.1 1.54 0.0106 0.68
PC-85(2,3) 200 50 32.2 1.36 0.0122 0.79
PC-86(2,3) 200 130 32.6 1.36 0.0115 0.74
PC-87(2,3) 200 200 32.9 1.38 0.0108 0.7
PC-88(2,3) 300 50 35.3 1.47 0.0134 0.93
PC-89(2,3) 300 130 36.5 1.53 0.0126 0.81
PC-90(2,3) 300 200 36.5 1.52 0.0118 0.76
PC-91(2,3) 400 50 38.6 1.61 0.0144 0.93
PC-92(2,3) 400 130 39.4 1.65 0.0126 0.81
PC-93(2,3) 400 200 39.9 1.66 0.0114 0.74
(1) Experimental models. (2) Connections with FRP-wrapped corbels. (3) Connections with FRP-wrapped columns.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated