Nomenclature (in order of appearance)
| Symbol |
Definition |
Unit |
|
Total height of the tank |
m |
|
Base height of the tank |
m |
|
Height of the liquid in the tank |
m |
|
External diameter of the tank |
m |
|
Inner diameter of the tank |
m |
|
Maximum penetration depth |
m |
|
Beating frequency |
s-1
|
|
Height of the beater |
m |
|
Bottom clearance of the beater |
m |
|
Mixing time number |
Dimensionless |
|
Viscosity |
Pa.s |
|
Density |
kg.m-3
|
|
Acceleration of gravity |
m.s-2
|
|
Mixing time |
s |
|
Reynolds number |
Dimensionless |
|
Penetration depth ratio |
Dimensionless |
|
Galilei number |
Dimensionless |
|
Characteristic velocity |
m.s-1
|
|
Characteristic length |
m |
1. Introduction
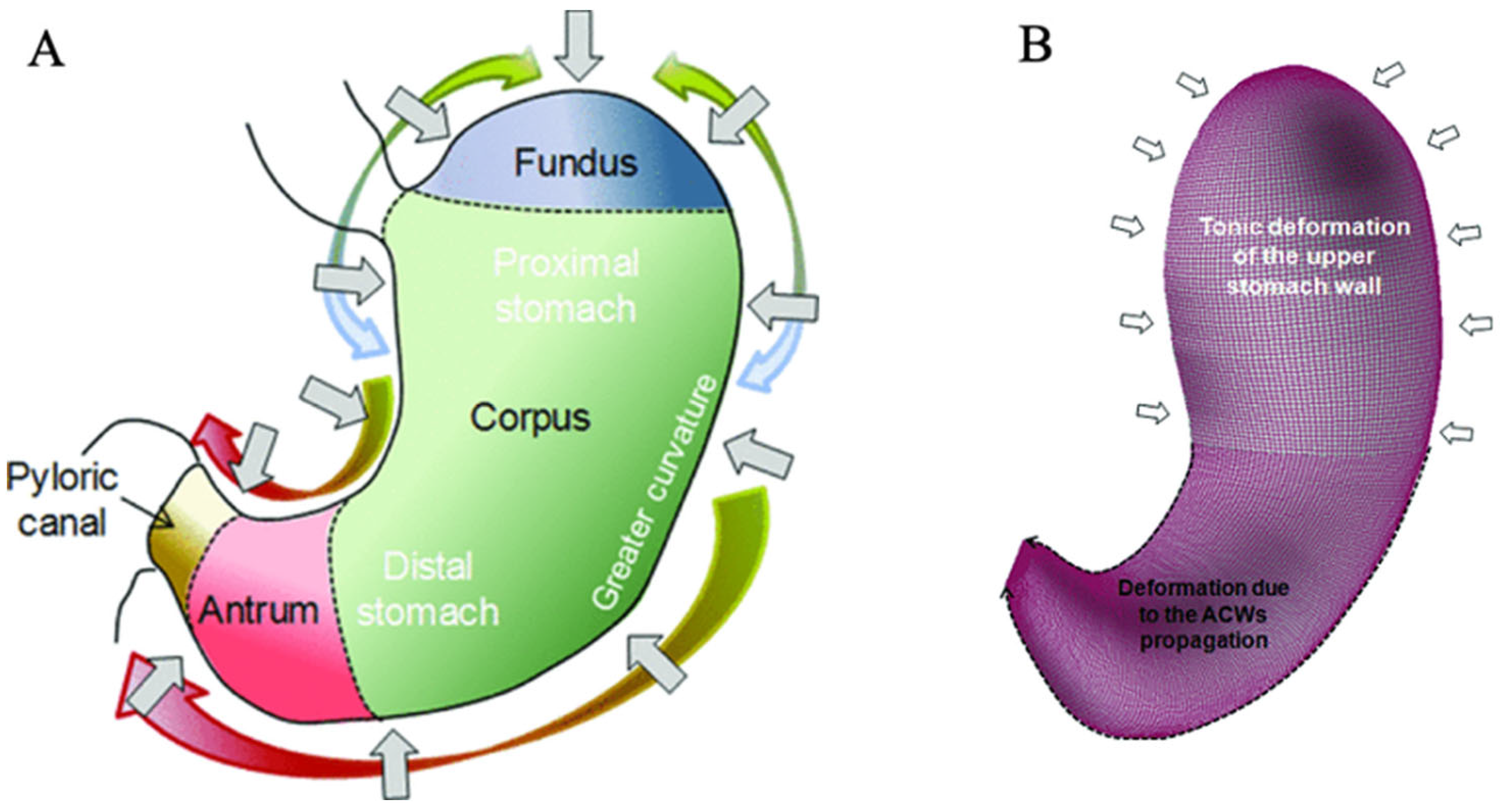
Human digestion has become a major concern in recent years due to the rapid development of nutrition-related chronic diseases such as obesity and diabetes, now affecting a growing population in both western and emerging countries. Digestion relies on combined effects of enzymatic reactions and homogenization of the gastro intestinal tract content by mechanical solicitations. The human stomach is an elastic organ, composed of different zones (antrum, corpus composed of proximal and distal regions, fundus) capable of dilating, acting as a holding and mixing chamber when receiving and storing ingested meals. The motility patterns in the stomach after consumption of a meal vary greatly, depending on the intragastric location (e.g., proximal or distal region). The proximal region undergoes tonic contractions or sustained muscle contractions of low frequency and amplitude (Bornhorst, 2017), resulting in lower and more ordered bulk motions. In contrast, the distal stomach undergoes antral contraction waves (ACWs, also named phasic, peristaltic muscular contractions), which move from the gastric pacemaker region to the pylorus, inducing faster and irregular fluid motions. ACWs periodically compress and stretch the distal stomach to achieve homogenization of gastric contents (Kwiatek et al. 2006; Treier et al. 2006; Imai et al., 2013; Ferrua et al., 2015; Bornhorst 2017).
Several computational fluid dynamic (CFD) models of the stomach with physiologically accurate geometry and motility have been developed, including both 2D and 3D approaches (Jeffrey et al., 2003; Pal et al., 2004; Ferrua and Singh, 2010; Kozu et al. 2010; Ferrua et al., 2014), in order to better simulate the flow patterns and mixing in the stomach. All these studies found that stomach mixing was largely confined to its distal region due to the ACWs, creating recirculating eddies and a retropulsive jet–type flow (Ferrua et al., 2014). Yet, the role of wall contraction on the advective and diffusion processes of gastric secretions with a liquid meal (i.e., liquid-liquid mixing of viscous media) is still not fully understood. Namely, the effects of gastric motility (frequency and amplitude of contraction) and viscosity of gastric content on the dynamics of gastric digesta and transport phenomena in the gastro intestinal tract require further clarification.
The dynamic of homogenization and mixing performance of a novel mixing device (Soft Elastic Reactor – SER) that induces mixing by tank wall vibration has been recently reported (Delaplace et al. 2018; Xiao et al. 2018; Li et al., 2018). Beyond a better characterization of liquid-liquid homogenization in such innovative reactors, these studies pave the road towards a better understanding of the mixing of intragastric fluid under stomach contraction. Fluid homogenization induced by vibrating walls has drawn a lot of attention in the fluid mechanics community, in order to explain and characterize the steady streaming generated by the vibration of solid boundaries (Stuart, 1966; Carlson et al., 2005; Vladimirov, 2008). Unfortunately, such theoretical approaches, involving fictitious devices with imposed wall deformations, were not supported by experimental mixing data. Indeed, the oscillatory displacement of the wall was most of the time considered as boundary conditions for the flow domain and therefore the whole tank wall delimiting the flow domain was concerned. In the case of the SER studied herein, the fluctuating external perturbation is restricted to the wall area in contact with the beater, whose periodic motion is induced by a real slider crank.
The objective of this paper is to discuss the influences of contraction amplitude, contraction extent and viscosity of the digesta on the human gastric homogenization process, based on the knowledge of the mixing curve of an innovative SER, that induces mixing by vibration of its wall in a similar way as antral contraction waves promoting stomach motility (Xiao et al., 2018; Delaplace et al., 2018). After recalling the SER mixing characteristics, the similarity between SER and stomach peristalsis is established to present the methodology to apply the SER process relationship to data taken from the literature. An overview of the influences of stomach peristalsis and meal viscosity on gastric fluid homogenization and the results of the application of the SER model are discussed.
2. Materials and Methods
2.1. Soft elastic reactor mixing curves
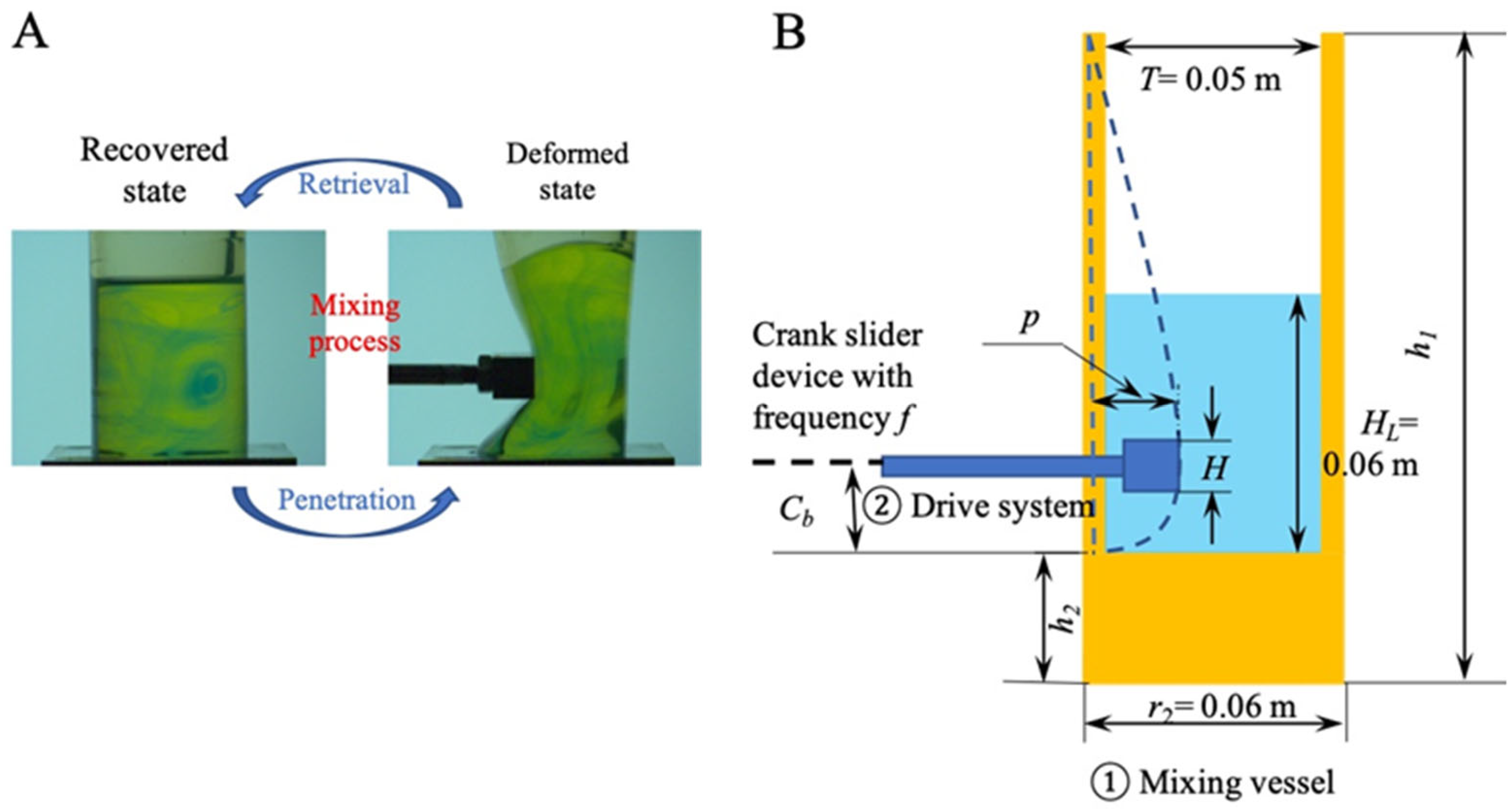
The SER developed by Chen and the co-workers (Chen and Liu, 2015, Chen, 2016, Liu et al., 2018) consists in promoting mixing through elastic wall movements (
Figure 1A), with no limitation regarding corrosive fluids compared to conventional stirred reactors as the agitator is not immerged in the agitated media. It consists of two key elements (
Figure 1B): i) a tank made of transparent silicone with soft and elastic properties and ii) a slider crank device constituting the excitatory system responsible for the local deformation of the wall.
In order to assess the mixing performance and improve the design of such reactors, Xiao et al. (2018) developed an effective and robust method based on colorimetric diagnosis. Using this approach, Delaplace et al. (2018) determined the mixing time
for highly viscous Newtonian fluids (viscosity
ranging from 0.0285 Pa.s to 1.187 Pa.s) and established a pertinent reduced configuration of mixing time number
as a function of operating conditions (Since
/
experimentally had a poor influence on mixing time, it was neglected, Equation (1)):
with as beating frequency (Hz), as mixing time (s), as number of beating required to achieve the desired degree of homogeneity, the Reynolds number as an internal measurement of viscosity, as density of the liquid (kg.m-3), as inner diameter of the tank (m), as viscosity of the liquid (Pa.s), as penetration depth ratio, the Galilei number as a dimensionless number considering the effect of gravity on free surface of liquid and as acceleration of gravity (m.s-2).
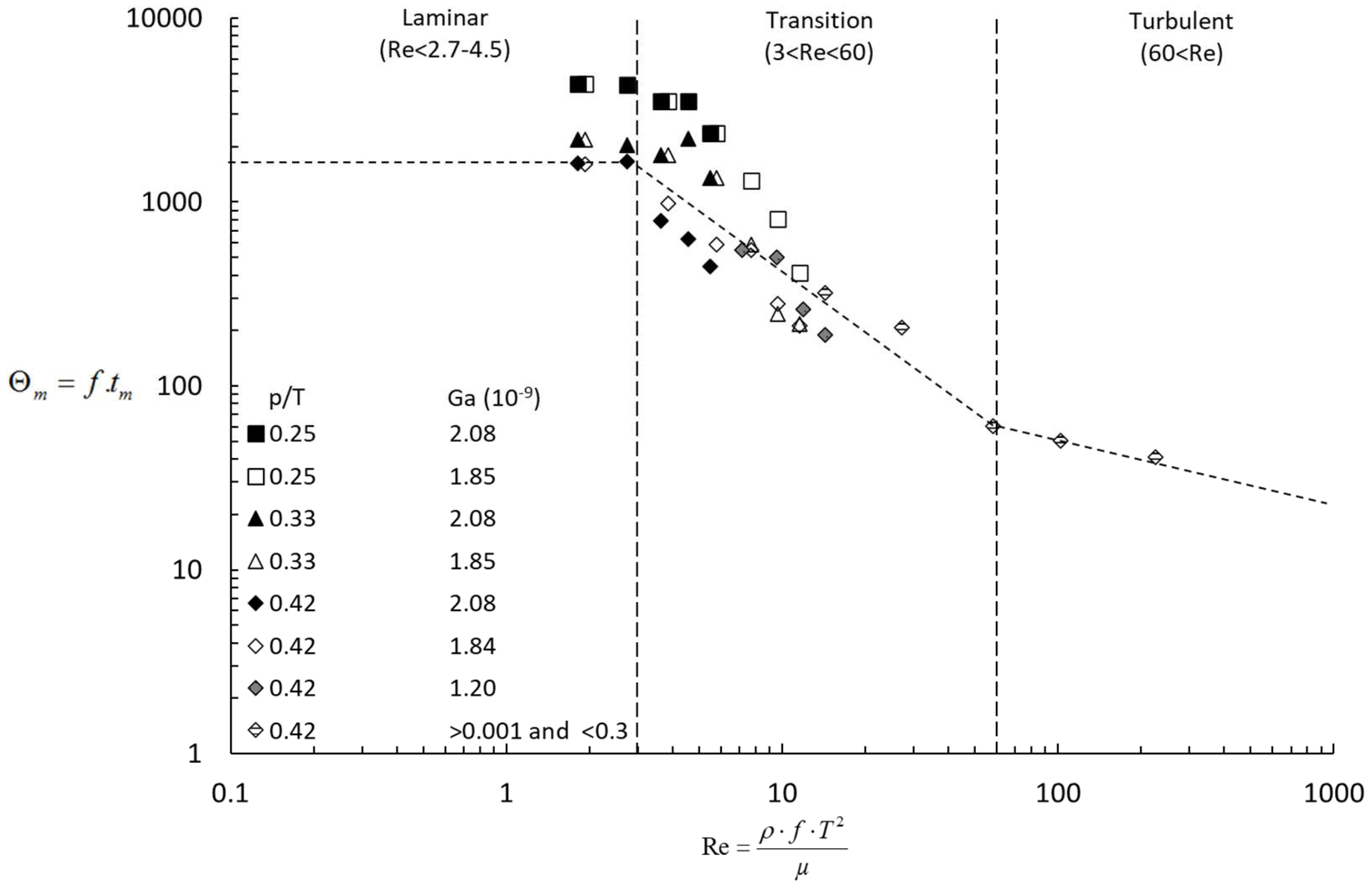
Mixing curve of dimensionless mixing time number
varying
and
ratios that was established is presented in
Figure 2. For the maximum
(= 0.42), it was showed that a constant
was needed to achieve the desired degree of homogeneity under the laminar regime, while a sharp decrease in
could be identified when the laminar regime is over.
required to achieve desired degree of homogeneity increased when decreases but the sigmoidal shape of the mixing curve remained similar, whatever the fixed values. required for meeting homogeneity with decreasing values seemed coherent with the theory. Indeed, it is expected that should have a more pronounced influence under a laminar regime when convection of fluid element is limited rather than in the transition and turbulent regimes. In this sense, the less pronounced influence of values in a transition and turbulent regime is logical. Moreover, the authors highlighted that had no influence on the evolution of , in coherence with the absence of free surface deformation for the range of perturbations and liquid viscosities considered.
Three zones in the sigmoidal mixing curve of the SER could be identified:
In laminar regime (Re<2.7-4.5), a constant value of ranging from 1500 (=0.42) to 4600 (=0.25) is observed, meaning that the number of strikes required to achieve the desired degree of homogeneity is independent on both viscosity and beating frequency, but still influenced by the penetration depth: the fact that decreasing the value of led to an increase of the number of strikes required to achieve homogeneity under laminar regime is in coherence with the expected physical meaning. Moreover, a large number of strikes is required to achieve homogeneity since the high level of viscosity is an obstacle for dissipating convection;
In the transition regime (3<Re<60), a decreasing value of meaning that a lower beating frequency is required to reach a desired degree of homogeneity for a given penetration depth;
For Re>60, reached an asymptotic value close to 40 (=0.42) and appeared to be here again independent of Re when getting closer to the turbulent regime. More data would be required to be more precise on this plateau value.
From a general point of view, the process relationship illustrated in
Figure 2 demonstrated the strong influence of the viscosity of the liquid contained in the SER, the beating frequency and maximum penetration depth on the overall homogenization performance of the SER in the range of operating conditions investigated (0.5<
<3 s
-1 and 0.03<
<1.25 Pa.s). Indeed, depending on the value of the Reynolds number and penetration extent, the number of strikes required to achieve homogenization could be largely different, ranging from 40 to 4600).
Figure 2.
Mixing time characteristics of the SER using the reduced configuration defined in Equation (1) obtained at varying Galilei number and penetration depth ratio () ratios. Each symbol represents a . Dotted line, plotted for mixing time experiments performed at constant value of 0.42, is a guide to the eye (from Delaplace et al., 2018).
Figure 2.
Mixing time characteristics of the SER using the reduced configuration defined in Equation (1) obtained at varying Galilei number and penetration depth ratio () ratios. Each symbol represents a . Dotted line, plotted for mixing time experiments performed at constant value of 0.42, is a guide to the eye (from Delaplace et al., 2018).
2.2. Hypotheses for considering the stomach as soft elastic reactor
The human stomach and the pattern of the ACWs during digestion are illustrated in
Figure 3. It is recognized that after a typical meal, an average-sized human stomach has a width of 0.10 m at its widest point and a capacity of about 0.94 L, with the greater curvature being around 0.30 m long. The pyloric ring diameter is 1.1 cm or less. The average diameter of the distal region under relaxed conditions was considered to be 0.052 m (Ferrua et al., 2014).
The motility pattern of the stomach wall is still not fully characterized, due to the experimental limitations and despite recent advances in medical imaging technologies that allowed a more accurate description of the ACWs (Pal et al., 2004; Kwiatek et al., 2006; Schwizer et al., 2006; Treier et al., 2006; Pal et al., 2007). From these studies, it can be retained that ACWs were initiated every 20 s (3 cycles per minute) at around 15 cm from the pylorus. Consequently, the ACWs frequency is
s
-1. The average amplitude of the initial antral contraction, that may be viewed as corresponding to the maximum penetration depth of the SER, was shown to be equal to 7.0 ±0.8 10
-3 m (Kwiatek et al., 2006;
Figure 4). The ACWs propagated down with an average horizontal speed velocity of 0.002 m·s
-1.
The fact that deformation location and liquid free surface deformation have few impacts on the mixing time for the soft reactor supports the comparison of the SER to the stomach. Although different exciting modes were used (crank slider for the soft reactor and ACW for the stomach), the resulting effect of deformation may be viewed as being similar, i.e., the propagation of a contraction wave along the stomach/soft reactor wall.
Figure 4.
Computed analysis of ACWs as seen by MRI. The average distance ( and , cm) between the bases (x) of the indentations in the antral wall, representative of ACWs, denoted the width of ACWs, . The average distance ( and , cm) between the tips (o) of these indentations and the line linking the bases (x) of the indentations corresponds to the amplitude of ACWs, . Extracted from Kwiatek et al. (2006).
Figure 4.
Computed analysis of ACWs as seen by MRI. The average distance ( and , cm) between the bases (x) of the indentations in the antral wall, representative of ACWs, denoted the width of ACWs, . The average distance ( and , cm) between the tips (o) of these indentations and the line linking the bases (x) of the indentations corresponds to the amplitude of ACWs, . Extracted from Kwiatek et al. (2006).
3. Results and discussions
3.1. Influence of meal viscosity on gastric fluid homogenization by stomach peristalsis
In this part, we review the current knowledge on the gastric mixing process by antral contraction based on 2D- and 3D-CFD simulations in order to present the framework of the work that we propose. The gastric mixing process is influenced by the viscosity as well as the rheological properties of the meal (Jeffrey et al., 2003; Pal et al., 2004; Kozu et al., 2010; Ferrua and Singh, 2010; Ferrua et al., 2014).
Using a simplified 2D-model of the distal region, Kozu et al. (2010) screened the flow behaviour of Newtonian fluids with viscosities ranging from 0.73×10-3 to 4.7×103 Pa⋅s. Their results illustrated the detrimental influence of fluid viscosity on the dynamics of retropulsive motions and vortical structures at the wake of the propagating ACWs.
In their 3D-model of the stomach, Ferrua and Singh (2010) and Ferrua et al. (2014) investigated the flow during gastric digestion and the spatial distribution and temporal history of stretching applied to an element of fluid via computation of Lyapunov exponent, a parameter characterizing the stretching abilities, evolution with time. They showed that the retropulsive jet and recirculating eddies that could be observed for low-viscosity fluids were greatly reduced for honey, whose viscosity ( Pa·s) is 1000-fold higher than that of water. They noticed that for a highly viscous liquid meal, the mixing performance of the stomach was greatly reduced, even if they pointed out that the suspension of the food particles was favored in this case, making their transfer to the small intestine easier compared to low viscosity fluids in which the particles were falling to the bottom of the antrum. From a general point of view, these studies demonstrated the limited influence of the large retropulsive and vortical structures commonly used to describe the dynamics of gastric digesta on the overall performance of gastric mixing. Precisely, they pointed out that an increase in gastric viscosity from 0.001 Pa·s (water) to 0.17 Pa·s (tomato juice) induced less recirculation between the proximal and distal stomach. When digesting fluids with viscosities higher than 0.17 Pa·s, the Lyapunov exponents decreased by one order of magnitude, transforming the proximal stomach into a segregated flow region unable to promote any stretching at all. These results led the authors to conclude that once fluid viscosity exceeded a given threshold (0.17 Pa·s), the role of fluid viscosity on the advective properties of flow became largely negligible. Note that in these studies, the tomato-juice is not really a Newtonian fluid but a shear thinning liquid. However, based on the shear rate field within the distal region, more than 93% of the flow showed an apparent viscosity equal to its maximum (0.17 Pa·s). The viscosity could hence be considered as independent of shear rate and the tomato juice as Newtonian within the distal region.
Furthermore, Marciani et al. (2001) used echoplanar magnetic resonance imaging techniques to measure in vivo gastric mixing. They showed that a high-viscosity meal was not uniformly mixed after 72 min of digestion, whereas a low viscosity meal was more evenly mixed. Assuming an average phasic contraction frequency of ∼3 cycles.min-1, this result means that 216 contractions were sufficient for the mixing of a low-viscosity meal but not for a high-viscosity one (Marciani et al., 2001).
To sum up, these works on gastric mixing suggest that the intragastric mixing performance of stomach (flow and mixing patterns) is greatly reduced when the fluid viscosity becomes too high. It is also suggested that when viscosity exceeds a critical threshold value (0.17 Pa·s according to Ferrua et al., 2014), even if further works are needed to confirm this value), the mixing performance becomes independent of the digesta viscosity. Finally, it was also shown that the number of antral contractions experienced by the meal during its residence time in the stomach is not always sufficient to achieve homogeneity.
3.2. Application of the soft elastic reactor model to data from litterature
In order to reinforcing the fundamental understanding of gastric fluid mixing by antral contraction in the stomach, we have evaluated how far the
values and the penetration depth ratios induced by ACWs when mixing digesta of various viscosity are to the range of experimental mixing runs on the SER. For that, we have used the experimental data from Ferrua et al. (2014) who studied the mixing of water (10
-3 Pa·s), tomato juice (0.17 Pa·s) and honey (1 Pa·s) in the stomach. These authors calculated the corresponding
values using
as repeated physical parameters (Equation (2)), where
is the average horizontal linear speed of ACW propagation considered as the characteristic velocity:
Considering the average diameter of the distal region under relaxed conditions m as characteristic length and an average horizontal linear speed of ACW propagation m.s-1, these authors obtained values of 116, 0.7 and 0.1 for water, tomato juice and honey, respectively.
For the SER, the characteristic speed of propagation
was not experimentally determined, as the beating frequency
was the only accessible parameter. Therefore, a
definition with
as physical repeated variables was adopted:
In order to compare stomach peristalsis and SER mixing, values encountered in the distal region were re-calculated using Equation (3) for water, tomato juice and honey, considering the corresponding density values given in Ferrua et al. (2014), an average antral contraction frequency s-1 and a characteristic length m. We obtained values equal to 150, 0.91 and 0.13 for water, tomato juice and honey respectively, in the range of those covered in SER.
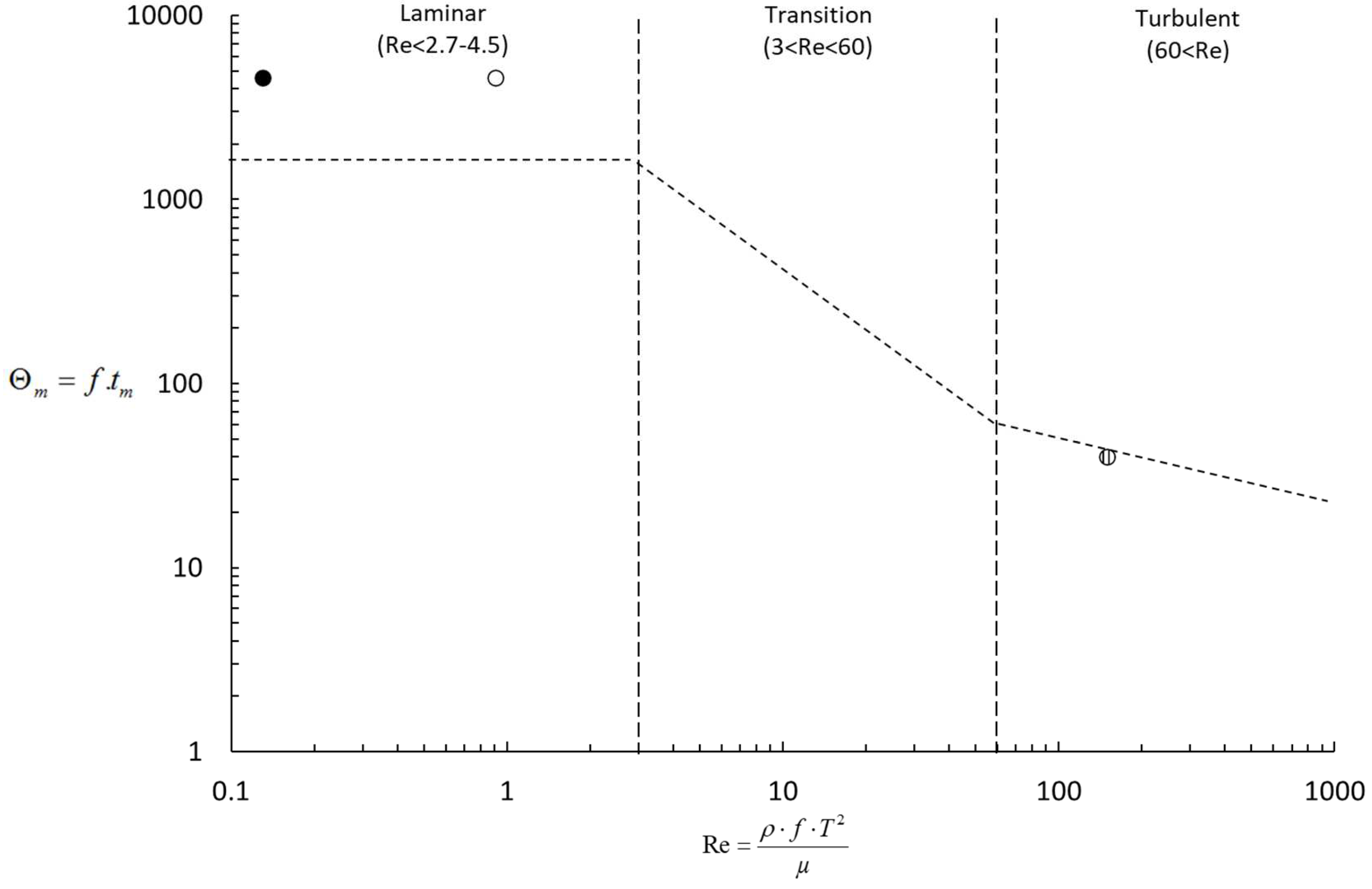
Penetration depth ratio of the distal region was found to be
and was thus lower although in the same order of magnitude as the range of contraction covered in the SER experiments (
i.e., 0.25-0.42;
Figure 2).
From these
and
, it is expected that the gastric mixing of both tomato juice and honey in the distal region was performed under laminar regime (
). Consequently, it is expected from the process relationship (
Figure 2) that a constant number of contractions should be performed for these two digesta, independently of their viscosity values. The expected number of contractions
is probably higher than
since
is lower than
, for which this plateau value was obtained in SER mixing time experiments (
Figure 5). Given an average frequency of 3 cycles.min
-1 (
s
-1), it could be expected that 1530 min is required to achieve complete homogeneity.
On the contrary, the number of contractions
required to achieve homogeneity should decrease for water, as the
value is higher in this case (
). Once again, this value could not be exactly determined since experimental study for the SER was not performed at this penetration depth
. However, at least 40 antral contractions should be necessary according to the mixing curve, which means more than 13 min at the same average frequency of 3 cycles.min
-1 (
Figure 5).
As the number of contractions was limited to 15 (corresponding to 5 min of residence time) in the study of Ferrua et al. (2014), these authors logically concluded to a poor ability of the stomach to advect gastric contents, regardless of the nature of the digesta. Indeed and as underlined above, homogeneity could not be achieved for water, tomato juice and honey after such residence time in human stomach.
Figure 5.
deduced for honey (⬤), tomato juice (⭘) and water (◍) using the mixing time characteristics of the SER from
Figure 2.
Figure 5.
deduced for honey (⬤), tomato juice (⭘) and water (◍) using the mixing time characteristics of the SER from
Figure 2.
3.3. Comparison between gastric fluid homogenization by stomach peristalsis and SER mixing
The previous observations are coherent with the mixing curve obtained for the SER, as the number of strikes required to achieve homogeneity in the SER largely depends on the liquid viscosity (
Figure 5). When the viscosity becomes so high that the fluid enters the laminar regime for a given frequency of contraction, a constant number of strikes (dependent on the penetration depth) is necessary to achieve the desired degree of homogeneity of the liquid media. In this case, the mixing performance is solely dependent on the mixing time in the soft elastic reactor. Thus, the desired degree of homogeneity will be only achieved if the time spent by the liquid in the reactor (human stomach or SER) is long enough.
At this stage, it is difficult to go further in the analysis since
There is not a strict superposition of the deformations induced in SER and in the distal region of the stomach. Namely, geometrical parameters defining the contraction are not strictly equivalent (penetration depth ratio versus , height ratio of initial deformation versus ) and the elastic properties of wall are not similar either;
The criteria adopted for assessing the degree of mixing in the SER and in the human stomach are not the same in the different studies;
Different mixing regions exist in the stomach and the characteristic dimension of the distal region is larger than that of the SER (diameter).
However, the fact that the scale of the soft reactor is smaller than that of human stomach and that it was the region of best mixing performance that was characterized for this latter allow us to ascertain that the mixing performance of human stomach provided by mechanical solicitations is less effective than that observed for the soft elastic reactor. This confirms the result of Ferrua et al. (2014) who noticed that value of Lyupanov exponents for human stomach was one order of magnitude lower than those associated with a laminar stirred tank of similar size.
5. Conclusions
Although recent CFD studies made it possible to get insight on the influence of the rheological properties of the gastric content on the efficiency of its mixing by antral contraction, this process is yet far from being fully understood. As for other mixing operations, a more global and generic approach, based on chemical engineering tools, is needed to identify the key mechanisms and limiting factors of this step. This paper is an attempt to tackle this issue by taking advantage of the similarity of gastric mixing with an innovative SER, whose mixing curve has been recently established. The fundamental understanding obtained by analyzing the mixing curve of the SER confirmed that the level of mechanical solicitation provided by human peristalsis was not as high as expected, and that the mixing performance of distal region, confined in laminar regime, was limited and not only due to mechanical solicitations. This approach based on a classic chemical engineering tool (dimensional analysis, which is commonly applied for investigating performance of reactors) allowed us to definitively assess that the level of solicitation induced by antral contraction is not high enough to achieve homogenization performance of distal region. It seems that antral contraction mainly ensures a role in transfer of gastric media. Help of gastric secretion is thus essential for achieving a good level of homogeneity. Further efforts are required to investigate the role of other physiological processes such as gastric secretions and gastric emptying in mixing performance of intragastric fluid homogenized by the antral contraction.
Author Contributions
Conceptualization, G.D., R.J., J.X. and XD.C.; methodology, G.D., R.J. and J.L.; formal analysis, G.D., R.J., J.L., M.L. and D.D.; writing—original draft preparation, G.D., R.J., J.L. and D.D.; writing—review and editing, G.D., R.J., J.L., J.X., D.D. and XD.C.; visualization, R.J. and J.L.; supervision, G.D., R.J. and XD.C.; project administration, G.D., R.J. and XD.C.; funding acquisition, G.D., R.J. and XD.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key Research and Development Program of China (International S&T Cooperation Program, ISTCP, 2016YFE0101200).
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: [link/accession number].
Acknowledgments
In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bornhorst, G.M. Gastric Mixing During Food Digestion: Mechanisms and Applications. Annu. Rev. Food Sci. Technol. 2017, 8, 523–542. [Google Scholar] [CrossRef]
- Carlsson, F.; Sen, M.; Löfdahl, L. Fluid mixing induced by vibrating walls. Eur. J. Mech. B Fluids 2005, 24, 366–378. [Google Scholar] [CrossRef]
- Chen, X.D.; Liu, M.H. Material preparation and procedures for making a soft elastic reactor and the methods for mixing in this reactor. Patent number: CN104841299A. 2015 August 19. 19 August.
- Chen, X.D. Scoping biology-inspired chemical engineering. Chin. J. Chem. Eng. 2016, 24, 1–8. [Google Scholar] [CrossRef]
- Delaplace, G.; Gu, Y.Y.; Liu, M.; Jeantet, R.; Xiao, J.; Chen, X.D. Homogenization of liquids inside a new soft elastic reactor: Revealing mixing behavior through dimensional analysis. Chem. Eng. Sci. 2018, 192, 1071–1080. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Singh, R.P. Modeling the fluid dynamics in a human stomach to gain insight of food digestion. J Food Sci. 2010, 75, 151–162. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Xue, Z.; Singh, R.P. On the kinematics and efficiency of advective mixing during gastric digestion—a numerical analysis. J. Biomech. 2014, 47, 3664–3673. [Google Scholar] [CrossRef]
- Ferrua, M.J.; Xue, Z.; Singh, R.P. Computational modelling of gastric digestion: current challenges and future directions. Curr. Opinion Food Sci. 2015, 4, 116–123. [Google Scholar] [CrossRef]
- Imai, Y.; Kobayashi, I.; Ishida, S.; Ishikawa, T.; Buist, M.; Yamaguchi, T. Antral recirculation in the stomach during gastric mixing. Am. J. Physiol. Gastrointest. Liver Physiol. 2013, 304, 536–542. [Google Scholar] [CrossRef]
- Jeffrey, B.; Udaykumar, H.S.; Schulze, K.S. Flow fields generated by peristaltic reflex in isolated guinea pig ileum: impact of contraction depth and shoulders. Am. J. Physiol. Gastrointest. Liver Physiol. 2003, 285, 907–918. [Google Scholar] [CrossRef]
- Kozu, H.; Kobayashi, I.; Nakajima, M.; Uemura, K.; Sato, S.; Ichikawa, S. Analysis of flow phenomena in gastric contents induced by human gastric peristalsis using CFD. Food Biophys. 2010, 5, 330–336. [Google Scholar] [CrossRef]
- Kwiatek, M.A.; Steingoetter, A.; Pal, A.; Menne, D.; Brasseur, J.G.; Hebbard, G.S.; Boesiger, P.; Thumshirn, M.; Fried, M.; Schwizer, W. Quantification of distal antral contractile motility in healthy human stomach with magnetic resonance imaging. J. Magn. Reson. Imaging 2006, 24, 1101–1109. [Google Scholar] [CrossRef]
- Li, C.Y.; Xiao, J.; Zhang, Y.; Chen, X.D. Mixing in a soft-elastic reactor (SER): A simulation study. Can. J. Chem. Eng. 2018, 9999, 1–11. [Google Scholar] [CrossRef]
- Liu, M.H.; Xiao, J.; Chen, X.D. A soft-elastic reactor inspired by the animal upper digestion tract. Chem. Eng. Technol. 2018, 41, 1051–1056. [Google Scholar] [CrossRef]
- Marciani, L.; Gowland, P.A.; Spiller, R.C.; Manoj, P.; Moore, R.J.; Young, P.; Fillery-Travis, A.J. Effect of meal viscosity and nutrients on satiety, intragastric dilution, and emptying assessed by MRI. Am. J. Physiol. Gastrointest. Liver Physiol. 2001, 280, G1227–G1233. [Google Scholar] [CrossRef]
- Pal, A.; Indireshkumar, K.; Schwizer, W.; Abrahamsson, B.; Fried, M.; Brasseur, J.G. Gastric flow and mixing studied using computer simulation. Proc. R. Soc. Lond.; B, Biol. Sci. 2004, 271, 2587–2594. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Brasseur, J.G.; Abrahamsson, B. A stomach road or “Magenstrasse” for gastric emptying. J Biomech. 2007, 40, 1202–1210. [Google Scholar] [CrossRef]
- Schwizer, W.; Steingoetter, A.; Fox, M. Magnetic resonance imaging for the assessment of gastrointestinal function. Scand. J. Gastroenterol. 2006, 41, 1245–1260. [Google Scholar] [CrossRef]
- Stuart, J.T. Double boundary layers in oscillatory viscous flow. J. Fluid Mech. 1966, 24, 673–687. [Google Scholar] [CrossRef]
- Treier, R.; Steingoetter, A.; Weishaupt, D.; Goetze, O.; Boesiger, P.; Fried, M.; Schwizer, W. Gastric motor function and emptying in the right decubitus and seated body position as assessed bymagnetic resonance imaging. J. Magn. Reson. Imaging 2006, 23, 331–338. [Google Scholar] [CrossRef]
- Vladimirov, V. Viscous flows in a half space caused by tangential vibrations on its boundary. Stud. Appl. Math. 2008, 121, 337–367. [Google Scholar] [CrossRef]
- Xiao, J.; Zou, C.; Liu, M.; Zhang, G.D.; Delaplace, G.; Jeantet, R.; Chen, X.D. Mixing in a soft-elastic reactor (SER) characterized using an RGB based image analysis method. Chem. Eng. Sci. 2018, 181, 272–285. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).