Performance Investigation of Force-Projecting Bilateral Control for Pneumatic Manipulator

Preprint

Article

Performance Investigation of Force-Projecting Bilateral Control for Pneumatic Manipulator

Altmetrics

Downloads

102

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

22 December 2023

Posted:

25 December 2023

You are already at the latest version

Alerts

Abstract

This paper proposes the application of force-projecting bilateral control to a master-follower teleoperation system with a pneumatic manipulator on the follower side, and evaluates its effectiveness. The proposed method directly projects the operating force on the master side to the driving force on the follower side, eliminating the need for both position control and external force detection on the follower side, thereby solving the problem of low rigidity and response delay of pneumatic manipulators and providing highly stable sensor-less force presentation against variable environments. In this study, dynamic response analyses of a 1-DOF master-follower system were performed by numerical simulation using a linear system model, followed by experimental verification by implementing an actual system with an external force estimator. The results showed that the proposed force-projecting bilateral control has significantly higher positioning rigidity and better force control stability than the conventional force-reflecting bilateral control. A theoretical consideration was also given using equivalent transformation of force transfer functions to provide evidence for the high stability.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

1.1. Research Background

Bilateral control is a teleoperation method that simultaneously controls the position and force of both the master and follower, and has been studied in the fields of surgical robotics [1], space robotics [2], and radioactive material manipulation [3]. These control methods are based on the assumption that they are applied to electric manipulators with high positioning rigidity and fast force response. On the other hand, pneumatic manipulators have high affinity with humans and environments due to their softness caused by the compressibility of air, light weight, high power, high shock and vibration resistance, electromagnetic noise free, and the ability to estimate external force without a force sensor. Taking advantage of these characteristics, pneumatic manipulators have been applied to surgical assist robots[4][5], humanoid robots[6], rehabilitation robots [7][8], construction machinery operating robots[9] and so on. For these systems, accurate and stable bilateral control is also desired for remote work and teaching operation. However, most existing bilateral control methods are systems that assume high rigidity and fast response of the follower robot. If these are applied to a low-rigidity manipulator such as a pneumatic manipulator, the positional deviation between the master and follower may reduce operability, and the system may become unstable due to delayed response. Furthermore, in environments where the robot cannot be equipped with a force sensor, the above problems are more likely to occur as uncertain values of external force estimation are fed back to the master. Therefore, it is necessary to develop a practical method of highly rigid and highly stable bilateral control method suitable for such a compliant manipulator with low rigidity and low response.

1.2. Related Works

Bilateral control begins with basic control methods such as a symmetrical bilateral control and a force-reflecting bilateral control (Force-Reflecting Type), and many methods have been developed to reproduce delicate tactile sensations and obtain high stability. Miyazaki et al. [10] proposed a parallel bilateral control with small phase delay and high stability by giving equal position commands to the master and follower. Tachi et al. [11][12][13] proposed an impedance-controlled bilateral control that can determine the virtual mass and viscosity of the master and follower to arbitrary values. In particular, Lawrence [14] defined "transparency" as a quantitative index of force sensation reproduction in bilateral control, and Yokokoji et al. [15][16][17] proposed a 4-channel bilateral control that achieves ideal transparency. However, these control methods assume a system with high control rigidity, so they are not suitable for flexible pneumatic manipulators. In addition, a force sensor is required to measure external force, which is difficult to use in harsh operating environments where sensors cannot be installed on the manipulator.

On the other hand, there are studies such as Iida et al. [18][19][20] that have applied an observer-based acceleration control theory [21] to bilateral control and achieved high transparency without using force sensors. This method uses a disturbance observer (DOB) and a reaction force observer (RFOB) to achieve high-speed force control without a force sensor. However, this acceleration-based bilateral control requires the actuator to have quick responsiveness to well perform acceleration control, and is not suitable for pneumatic actuators that have a significant response delay in driving force.

Related works on bilateral control systems for pneumatic manipulators include a control method using a passive controller for a force amplification system develped by Durbra et al.[22], and a sliding mode control method for controlling pneumatic pressures using an inexpensive solenoid valve proposed by Moreau et al.[23]. However, these do not solve the aforementioned problems of pneumatic manipulators such as low response and low rigidity. In addition, Tadano et al.[24][25] developed pneumatically-driven robotic surgical instruments capable of external force estimation without using force sensors, and constructed the Force-Reflecting Type bilateral control system. However, there remained problems such as large position deviation between the master and follower due to low control rigidity on the follower side, and errors in external force estimation due to modeling errors, resulting in system instability and an unnatural operational feel.

In contrast to the existing studies mentioned above, Kaneko et al.[26] have proposed a robust control method that does not require high-precision specifications for bilateral control systems. Kanaoka et al. [27][28] named this method “force-projecting bilateral control” and proposed a design method that can be practically applied. The force-projecting bilateral control (Force-Projecting Type) directly projects operating forces on the master side to the driving force on the follower side, and was applied to the control of force-amplifying manipulators [29] that require high rigidity and large output. The feature of this control method is that it does not require position control on the follower side, so the system performance does not depend on the control stiffness of the follower device. Another important point is that there is no need for external force feedback from the follower to the master, so there is no need for force sensors or external force estimation.

1.3. Research Objective

Therefore, in this study, we focus on the advantages of the force-projecting bilateral control mentioned above, and aim to solve the problems of positional deviation and system instability caused by the low rigidity and slow response characteristics of a pneumatic manipulator in a master-follower operation system.

This study deals with a one-degree-of-freedom(DOF) bilateral control system consisting of an electric drive master and a pneumatic drive follower with a single axis linear-motion, in order to facilitate an essential understanding of the system behavior. First, a theoretical model of the system is constructed, and its transient responses and frequency responses are investigated by numerical simulation. Next, an actual system is developed assuming a situation where the follower-side manipulator cannot be equipped with a force sensor. The transient responses and frequency responses are investigated experimentally in the same way as the simulation. In addition, an operation experiment by human is also performed to investigate the system behavior and its operability. Through the numerical analyses and experiments, we compare the control performance and stability of the proposed Force-Projecting Type with the conventional Force-Reflecting Type, and demonstrate the superiority of the Force-Projecting Type.

2. System Modeling and Control Architecture

2.1. One-DOF Master-Follower Dynamic Model

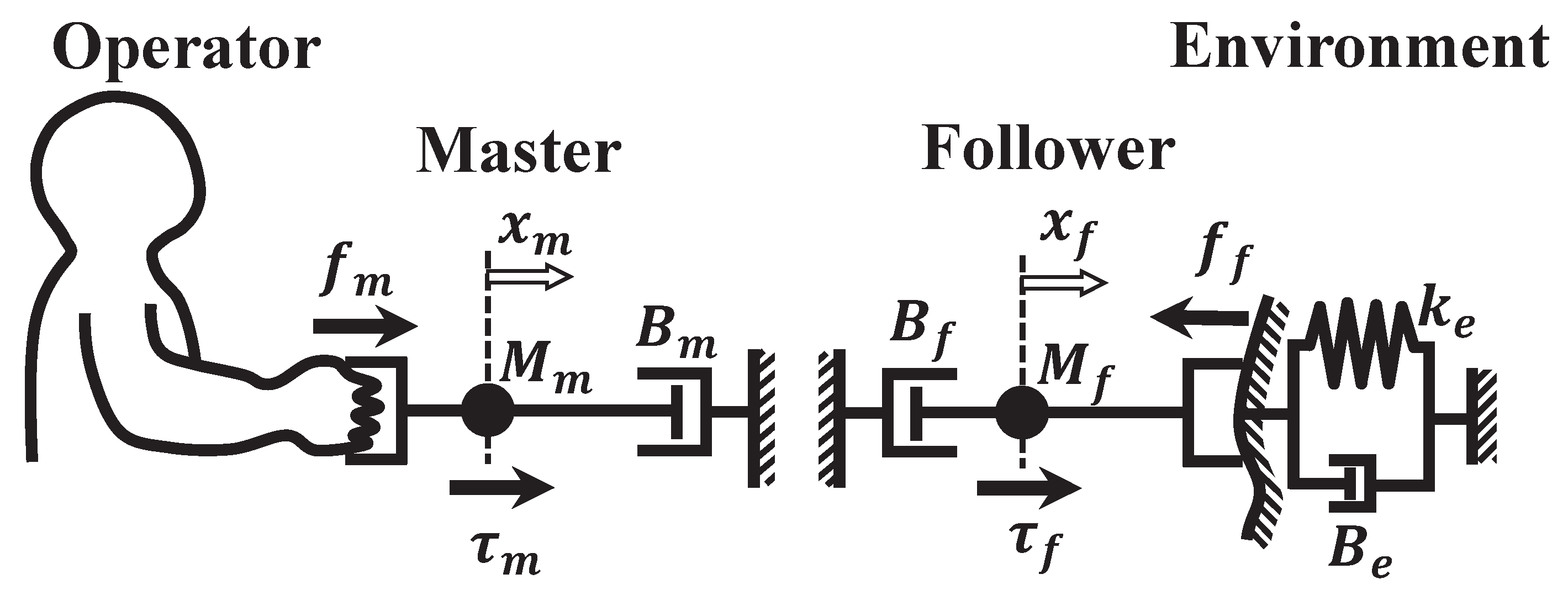
A master-follower system is a teleoperation technique in which an operator manipulates a master and a follower reproduces the movements of the master. To analyze such a system, we consider a model with one DOF as shown in Figure 1. The physical parameters and constants that each symbol and subscript signify are as shown in Table 1. In this model, on the master side, the operating force

f_{m}

applied by the operator, the master driving force

τ_{m}

, and the damping force

B_{m} {\dot{x}}_{m}

act on the master mass

M_{m}

, and acceleration

{\ddot{x}}_{f}

is generated. Similarly, on the follower side, the reaction force

f_{f}

received from the environment, the follower driving force

τ_{f}

, and the damping force

B_{f} {\dot{x}}_{m}

act on the follower mass

M_{f}

, generating an acceleration

{\ddot{x}}_{f}

. In such a model, the equation of motion of the master can be expressed as (1).

\begin{matrix} M_{m} {\ddot{x}}_{m} + B_{m} {\dot{x}}_{m} & = & f_{m} + τ_{m} \end{matrix}

(1)

Similarly, the equation of motion of the follower can be expressed as (2).

\begin{matrix} M_{f} {\ddot{x}}_{f} + B_{f} {\dot{x}}_{f} & = & - f_{f} + τ_{f} \end{matrix}

(2)

Next, the Laplace transform is performed on these equations of motion. Letting X, F, and T be the Laplace transforms of x, f, and

τ

, respectively, and the Laplace transforms of the equations (1) and (2) can be expressed as (3) and (4), respectively. In this paper, s denotes the Laplace operator.

M_{m} X_{m} s^{2} + B_{m} X_{m} s = F_{m} + T_{m}

(3)

M_{f} X_{f} s^{2} + B_{f} X_{f} s = - F_{f} + T_{f}

(4)

Here, these equations of motion are expressed as transfer functions. Transforming the equation of motion of the master (3) results in the following equation:

\begin{matrix} X_{m} s & = & \frac{1}{M_{m} s + B_{m}} (F_{m} + T_{m}) \end{matrix}

(5)

In equation (5), the relationship between the force acting on the master and the resulting velocity is described as an impedance

Z_{m}

, and the transfer function related to the dynamic characteristics of the master is obtained. That is,

\begin{matrix} X_{m} s & = & Z_{m} (F_{m} + T_{m}) \\ Z_{m} & = & \frac{1}{M_{m} s + B_{m}} \end{matrix}

(6)

Similarly for the follower, transforming the equation of motion of the follower (4) results in the following equation:

\begin{matrix} X_{f} s & = & \frac{1}{M_{f} s + B_{f}} (- F_{f} + T_{f}) \end{matrix}

(7)

In equation (7), the relationship between the force acting on the follower and the resulting velocity is described as an impedance

Z_{f}

, and the transfer function related to the dynamic characteristics of the follower is obtained. That is,

\begin{matrix} X_{f} s & = & Z_{f} (- F_{f} + T_{f}) \\ Z_{f} & = & \frac{1}{M_{f} s + B_{f}} \end{matrix}

(8)

In addition, we describe a model of the environment in which followers act. As shown in Figure 1, the environment is described as a wall with a spring constant

k_{e}

and a damping coefficient

B_{e}

. In this study, in order to make analyses and experiments convenient, it is assumed that the follower is connected to the environment and never leaves. Under this condition, the reaction force

F_{f}

that the follower receives can be expressed as follows:

\begin{matrix} F_{f} & = & k_{e} X_{f} + B_{e} X_{f} s \\ = & (\frac{k_{e} + B_{e} s}{s}) X_{f} s \end{matrix}

(9)

In equation (9), the relationship between the follower reaction force and the resulting velocity is described as the impedance

Z_{e}

, and the transfer function related to the dynamic characteristics of the environment is obtained. That is,

\begin{matrix} F_{f} & = & Z_{e} X_{f} s \\ Z_{e} & = & \frac{k_{e} + B_{e} s}{s} \end{matrix}

(10)

2.2. Design of Bilateral Control Systems

This research proposes the application of the force-projecting bilateral control to a master-follower system with a pneumatic manipulator, and evaluates its performance and stability by comparing them with the conventional force-reflecting bilateral control. These two control methods have completely opposite schemes for exchanging position information and force information between master and follower.

2.2.1. Force-Reflecting Type

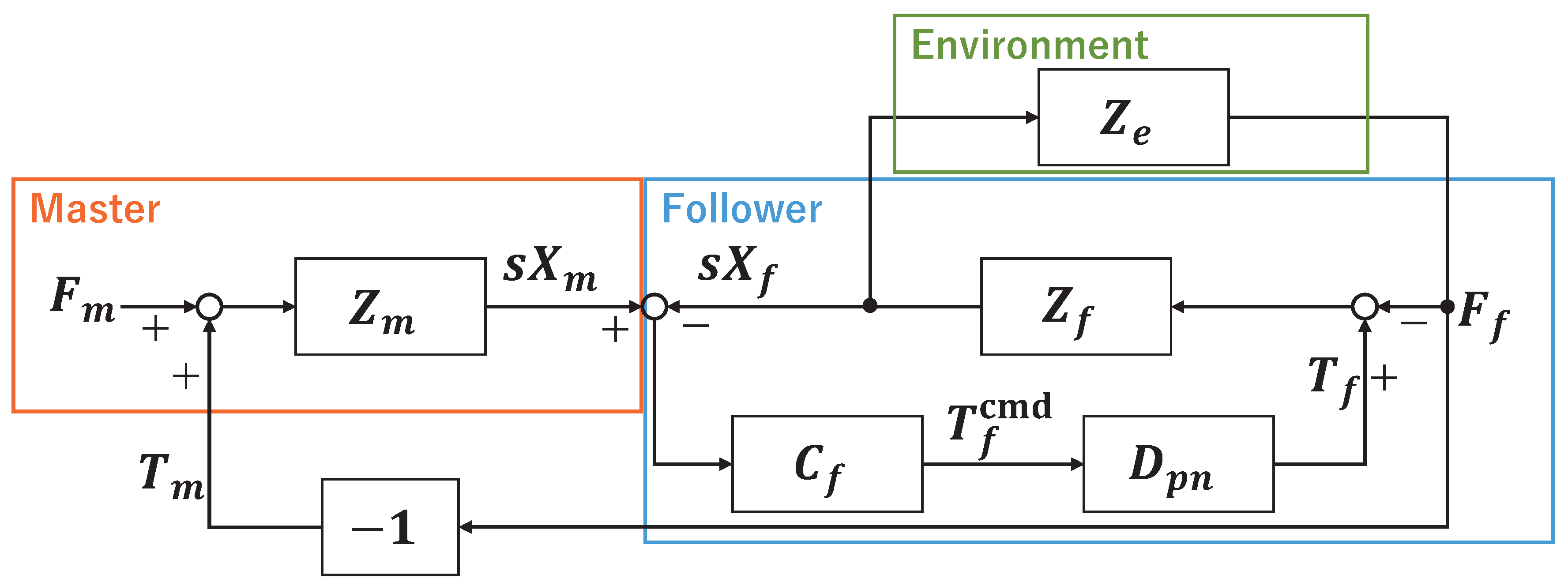
First, we describe the conventional force-reflecting bilateral control system. The block diagram of the Force-Reflecting Type used in this study is shown in Figure 2. The meanings of each block and transfer function are shown in Table 2.

In the Force-Reflecting Type, the master driving force

τ_{m}

projects the reaction force

f_{f}

from the environment received by the follower, and the follower driving force

τ_{f}

is controlled so that the positional deviation

X_{f} - X_{m}

of the master and follower becomes zero. This control scheme is given by the following equations:

\{\begin{matrix} T_{m} = - F_{f} \\ T_{f}^{cmd} = C_{f} (X_{m} s - X_{f} s) \end{matrix}

(11)

where

C_{f}

denotes a controller of the follower motion.

C_{f} = \frac{K_{p f} + K_{v f} s}{s}

(12)

In equation (12),

K_{p f}

and

K_{v f}

are feedback gains of the follower position and velocity, respectively.

Here we describe the response delay characteristics of the pneumatically driven follower manipulator, which is the subject of this study. In a typical pneumatic servo drive, a control signal is applied to a servo valve as a voltage to drive a mechanical spool that regulates the cross-sectional area of air flow. Then, air flows into the actuator through tubing, resulting in an actual driving force by changing the internal pressure. Therefore, the system has a non-negligible response delay of the pneumatic driving force. In this study, the pneumatic delay is modeled approximately by the second-order delay element

D_{p n}

[4]. The relationship between the driving force command and the actual driving force is expressed as follows:

T_{f} = D_{p n} T_{f}^{cmd}

(13)

Therefore, the equation (11) of the control system can be re-written including the pneumatic response delay of the follower side.

\{\begin{matrix} T_{m} = - F_{f} \\ T_{f} = D_{p n} T_{f}^{cmd} = D_{p n} C_{f} (X_{m} s - X_{f} s) \end{matrix}

(14)

2.2.2. Force-Projecting Type

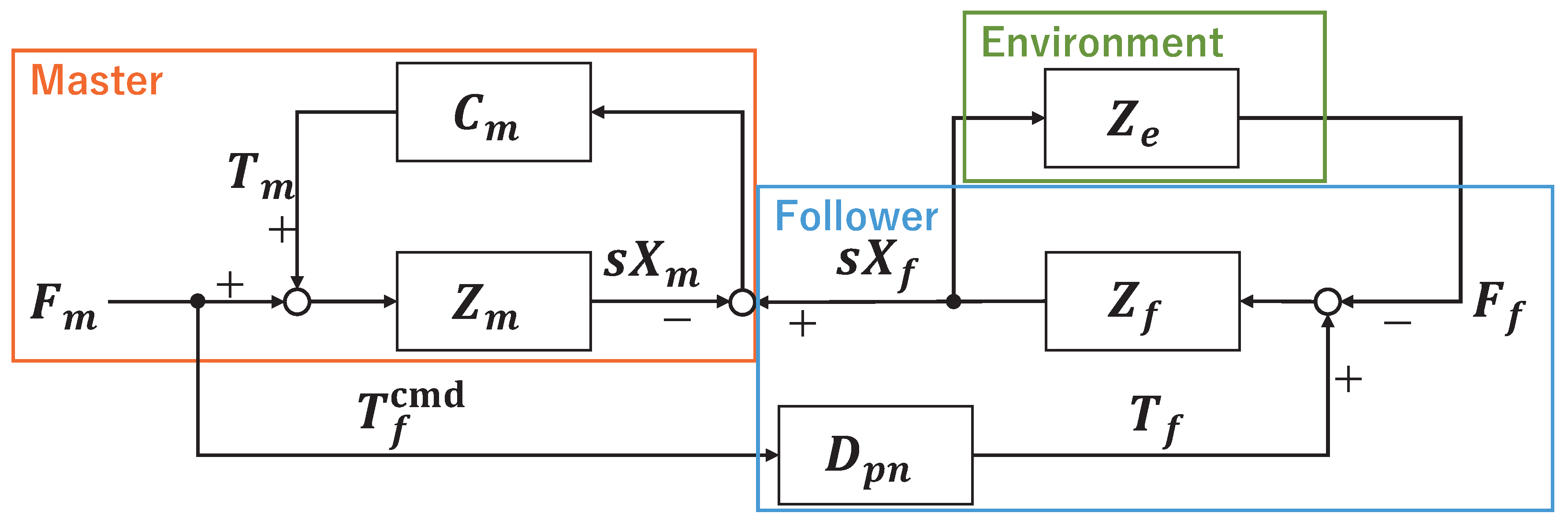
Next, we describe the proposed force-projecting bilateral control system. The block diagram of the Force-Projecting Type developed in this study is shown in Figure 3. The meanings of each block and transfer function are shown in Table 2.

In the Force-Projecting Type, the master driving force

τ_{m}

is controlled so that the position deviation

X_{f} - X_{m}

between the master and follower becomes zero, and the follower driving force

τ_{f}

is controlled by directly projecting the operational force

f_{m}

acting on the master. In the Force-Projecting Type, the control scheme of position and force is the exact opposite of the Force-Reflecting Type and can be expressed as follows:

\{\begin{matrix} T_{m} = C_{m} (X_{f} s - X_{m} s) \\ T_{f}^{cmd} = F_{m} \end{matrix}

(15)

where

C_{m}

is the master position controller. It constitutes a PD controller for the master position, and is given by the following equation using a position feedback gain

K_{p m}

and a velocity feedback gain

K_{v m}

\begin{matrix} C_{m} = \frac{K_{p m} + K_{v m} s}{s} \end{matrix}

(16)

Here the response delay of the pneumatic manipulator on the follower side is approximated by the equation (13). The equation (15) describing the control law of the Force-Projecting Type can be re-written as follows:

\{\begin{matrix} T_{m} = C_{m} (X_{f} s - X_{m} s) \\ T_{f} = D_{p n} T_{f}^{cmd} = D_{p n} F_{m} \end{matrix}

(17)

3. Numerical Simulation

In this section, numerical analyses are performed on the block diagrams of the two bilateral control systems shown in Figure 2 and Figure 3 to theoretically understand fundamental behavior of each system.

3.1. Conditions of Analysis

Parameters used in the analyses are shown in Table 3. Each parameter was set according to identified values of the experimental system described in Section 4.

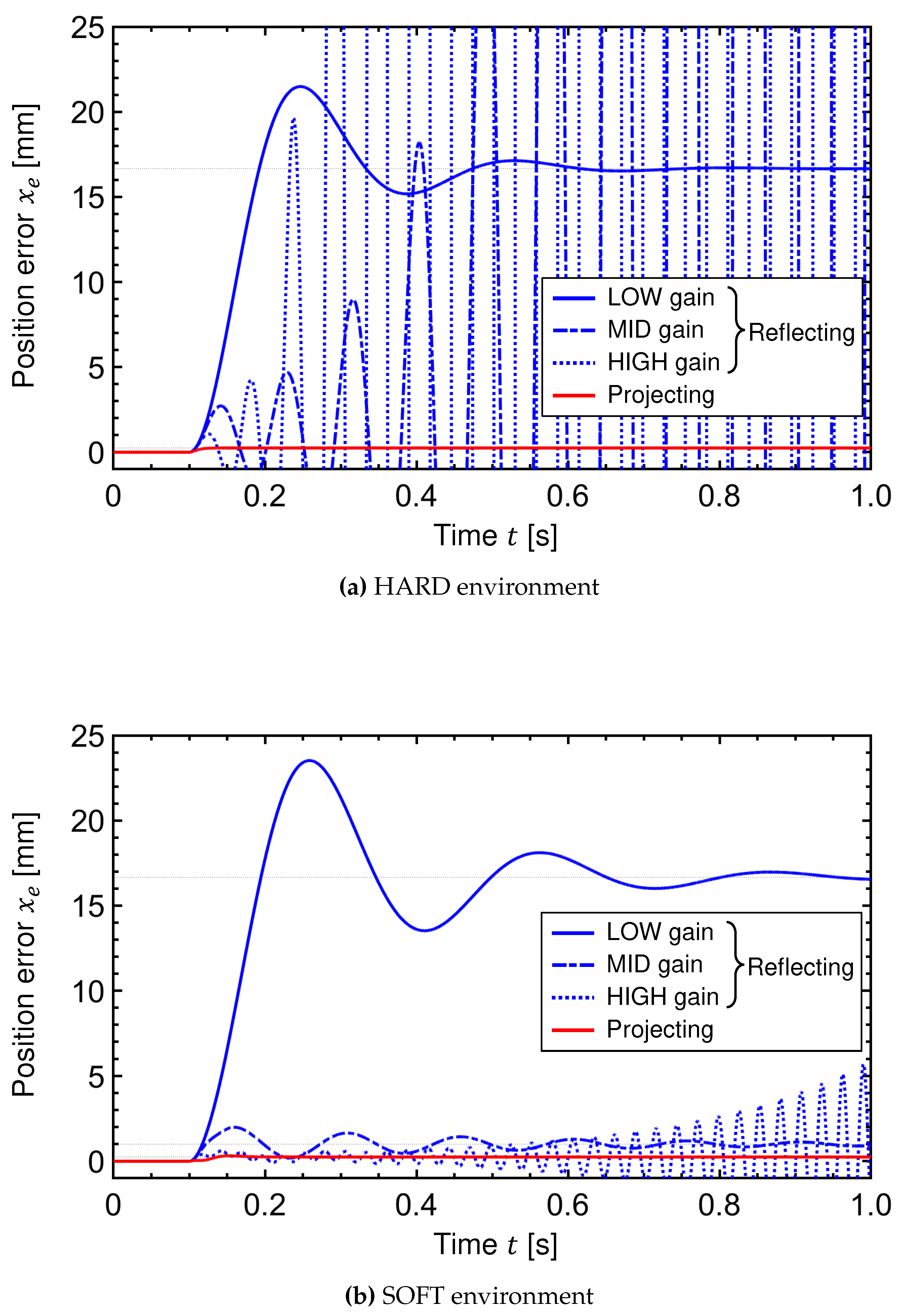
For the Force-Reflecting Type, we set three different position gains

K_{p f}

on the pneumatic follower manipulator: "LOW", "MID", and "HIGH". The value of HIGH gain is equal to the position gain

K_{p m}

of the electric master. While the actual experiment system operated stably only at LOW gain, we will show in this simulation that the system becomes unstable with the larger values of

K_{p f}

. The velocity gains

K_{v m}

and

K_{v f}

are set to be the critical damping factor of the mechanical vibration system.

For the environmental characteristics, two types of environments were prepared: a "HARD" environment with high spring constant and low damping ratio, and a "SOFT" environment with low spring constant and high damping ratio. Also, for simplicity, the mass of the environment is assumed to be negligible, and the follower shall always be in contact with the environment, moving in unison and never separating.

For numerical calculation, we used the Control System Toolbox software package in MATLAB^® R2022b.

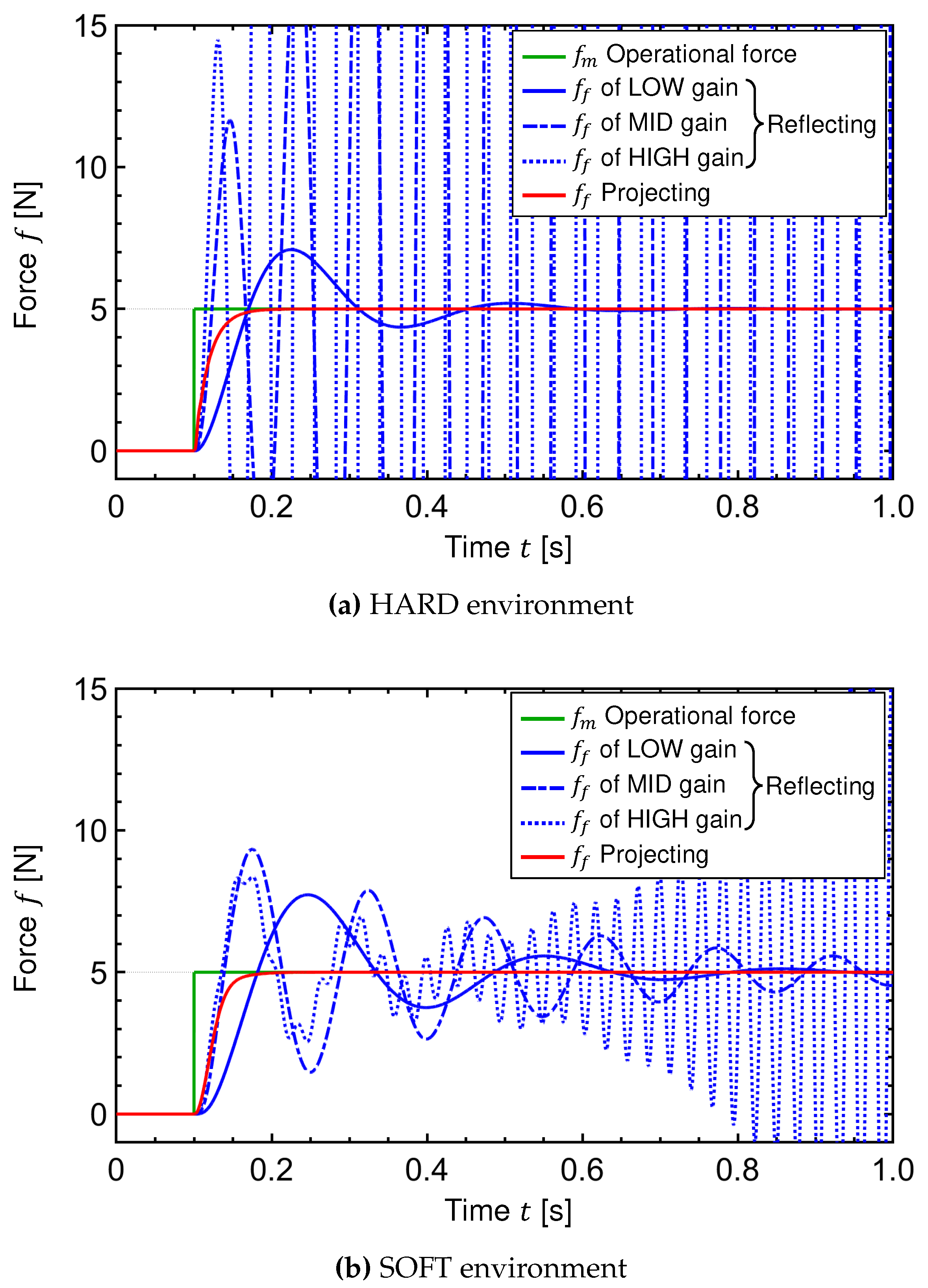
3.2. Step Response

Transient responses were analyzed for the two bilateral control systems and the two types of environments by applying a step input of 5 N to the master operating force

f_{m}

. The resulted time responses of the follower reaction force

f_{f}

and the position error between master and follower

x_{e} = x_{m} - x_{f}

are shown in Figure 4 and Figure 5, respectively. These results provide a clear theoretical evaluation about the behavior of the two types of bilateral control systems. In the Force-Projecting Type, the driving force response delay at the follower is coupled with the position control system, resulting in a quite oscillatory response. Only the LOW gain barely stabilized in both environments, but the positioning rigidity is very low, resulting in a large position error with the master. On the other hand, in the Force-Projecting Type, the follower reaction force stably and accurately follows the master operation force of 5N. Position control is not required on the follower side, but is performed by the master side with high positioning rigidity, thus maintaining high system stability and a very small position error even with a response delay of the pneumatic drive on the follower.

3.3. Frequency Response

To analyze the frequency response, objective transfer functions

G_{f}

and

G_{x}

are defined by the following equations (18) and (19), respectively.

\begin{matrix} G_{f} & = & \frac{F_{f}}{F_{m}} \end{matrix}

(18)

\begin{matrix} G_{x} & = & \frac{X_{m} - X_{f}}{F_{m}} \end{matrix}

(19)

G_{f}

represents the characteristics from the master operating force

F_{m}

to the follower reaction force

F_{f}

, and

G_{x}

represents the characteristics from the master operating force

F_{m}

to the position error

X_{m} - X_{f}

between the master and follower.

The results of frequency response analysis for

G_{f}

and

G_{x}

for the two bilateral control laws are shown in Figure 6 and Figure 7. Since Bode diagram is effective for stable systems, the analysis for the Force-Reflecting Type was performed only for the LOW gain

K_{p f} = 0.3

[N/mm], where the step response was stable in both environments.

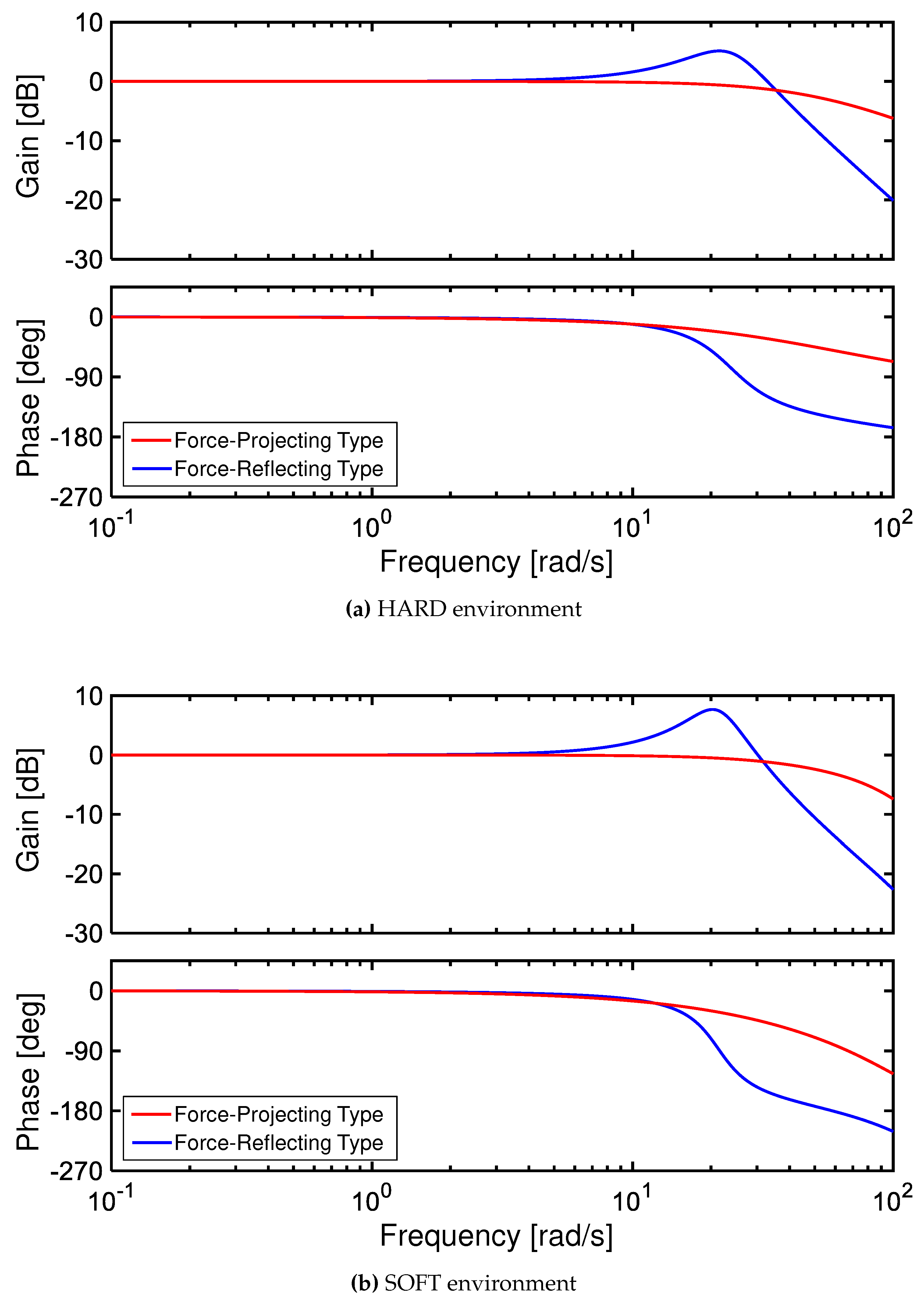
First, for the force transfer function

G_{f}

in Figure 6, the ideal bilateral control response is

F_{m} = F_{f}

, i.e.

G_{f} = 0

dB. In the Force-Reflecting Type, the follower reaction force

F_{f}

resonates around 20 rad/s in both environments. This resonance originates from the resonance frequency

\sqrt{K_{p} f / M_{m}} = 21.1

rad/s of the follower position gain

K_{p f}

and master mass

M_{m}

, which causes system instability within the main operating band due to low control stiffness. On the other hand, the Force-Projecting Type showed a desirable response for its gain close to 0 dB over a wider range than the Force-Reflecting Type. The slight drop in gain above 80 rad/s is thought to be due to the response delay

D_{p n}

of the pneumatic drive system.

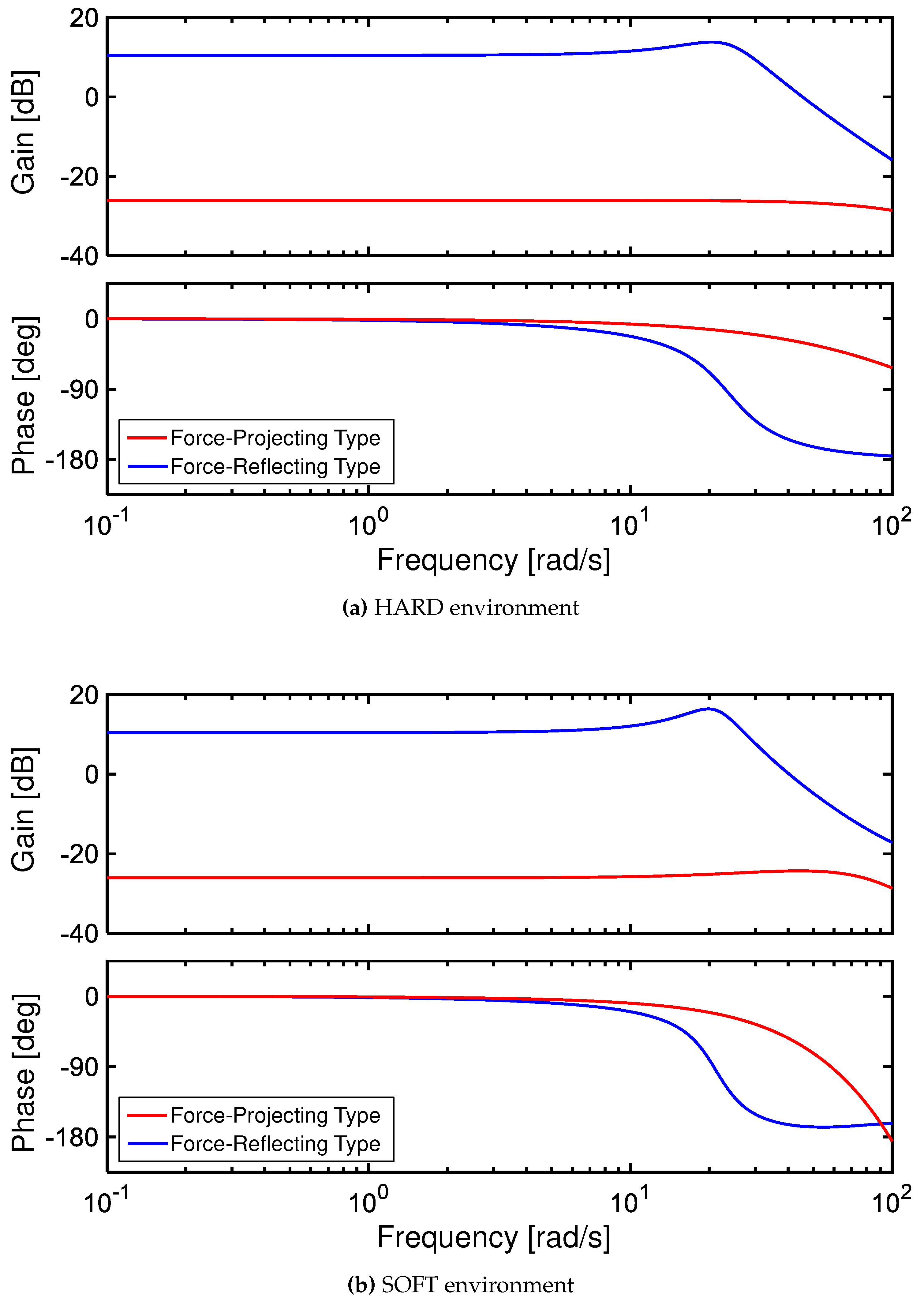
Second, for the position error transfer function

G_{x}

in Figure 7, the ideal bilateral control response is

X_{m} - X_{s} = 0

, i.e.

G_{x} = - \infty

dB. The smaller the gain, the more desirable the response. The Force-Reflecting Type showed a large gain of more than 10 dB and a harmful resonance in both environments, due to the low positioning stiffness of the follower. On the other hand, the Force-Projecting Type maintained a low value of -25 dB over a wide frequency range and showed no resonance. It can be seen that in the Force-Projecting Type, position control is performed on the master side with high positioning stiffness, which is not affected by the low stiffness of the pneumatic follower.

4. Experimental System Implementation

The numerical analyses in the previous section suggested that the Force-Projecting Type is effective for the basic model of a master-follower system with a pneumatic manipulator on the follower side. In the following sections, this will be verified through experiments on actual equipment.

4.1. Hardware Configuration

Figure 8 shows the configuration of a 1-DOF master-follower manipulator constructed for the experiment. This manipulator system consists of an electric linear motor on the master side and a pneumatic cylinder on the follower side. The linear motor can move smoothly along the linear bearing guides with almost no frictional resistance, and it is capable of highly responsive thrust control. On the other hand, the pneumatic cylinder is a low-friction type with a bore diameter of 16 mm, which also has high backdrivability. The end of the cylinder rod on the follower side can be connected to the environmental wall, and the follower reaction force is measured by a force sensor placed on the environmental wall. As shown in Figure 9, a resin plate is used for the "HARD" environment and a sponge is used for the "SOFT" environment. Their mechanical properties are shown in Table 3. A series of experiments is performed with the cylinder rod end of the follower connected to these environmental walls.

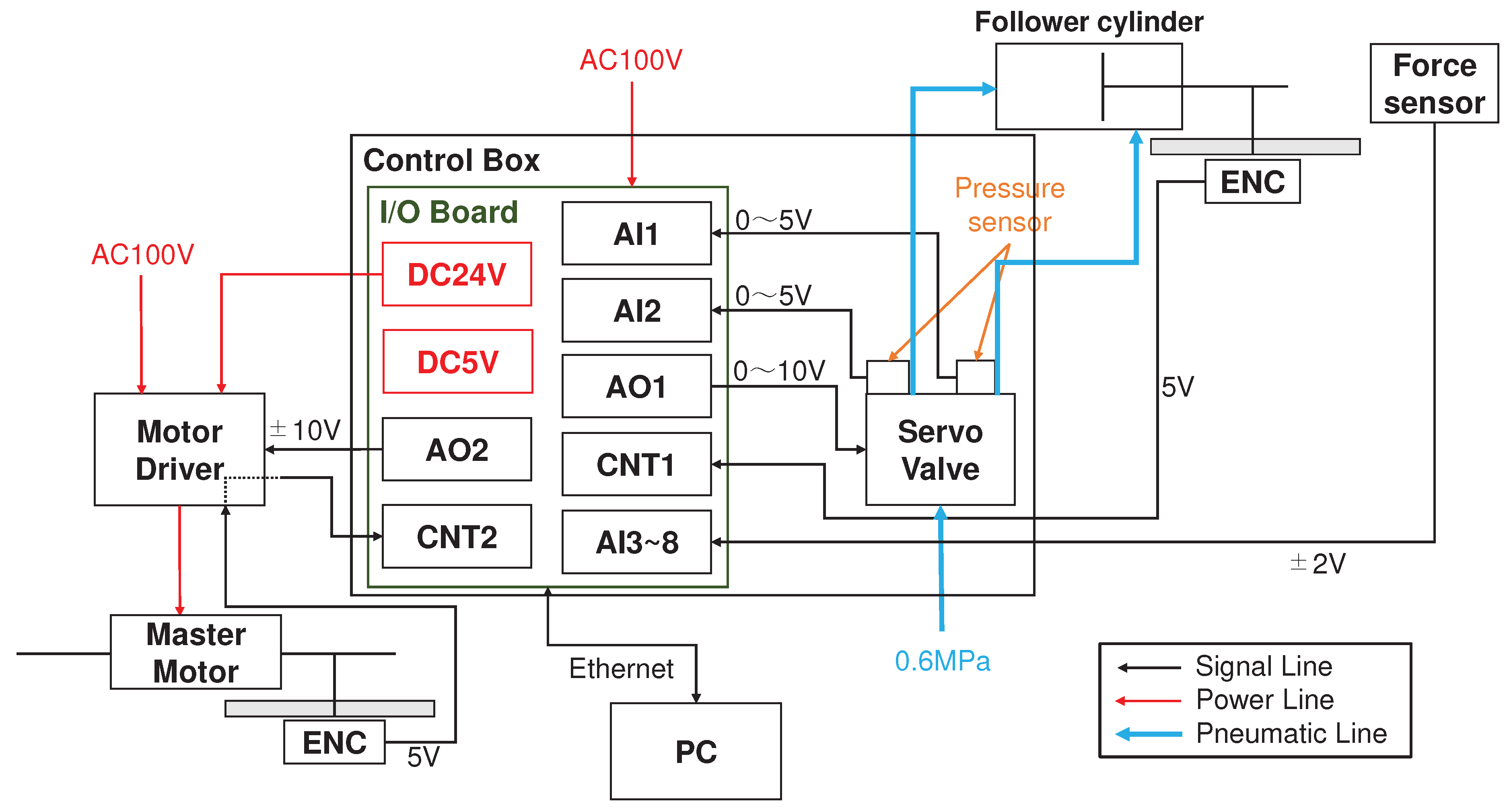
The overall configuration of the experimental apparatus and its system diagram are shown in Figure 10 and Figure 11, respectively. The measurement and control period for the entire system is 1 ms. The follower-side pneumatic cylinder is connected to a servo valve through air tubes approximately 1 m long and 4 mm in diameter. The pneumatic driving force and position control of the cylinder are realized by precisely controlling the differential pressure using measured values of the pressure sensors attached to the two output ports of the servo valve [4]. The response delay of the pneumatic drive force is mainly due to the slow control response of the servo valve. Note that the force sensor is used only for measurement of reaction force to validate, and never used as a control signal.

Models and specifications of main components in the experimental system are listed in Table 4.

4.2. Design and Characteristics of Pneumatic Servo Drive System

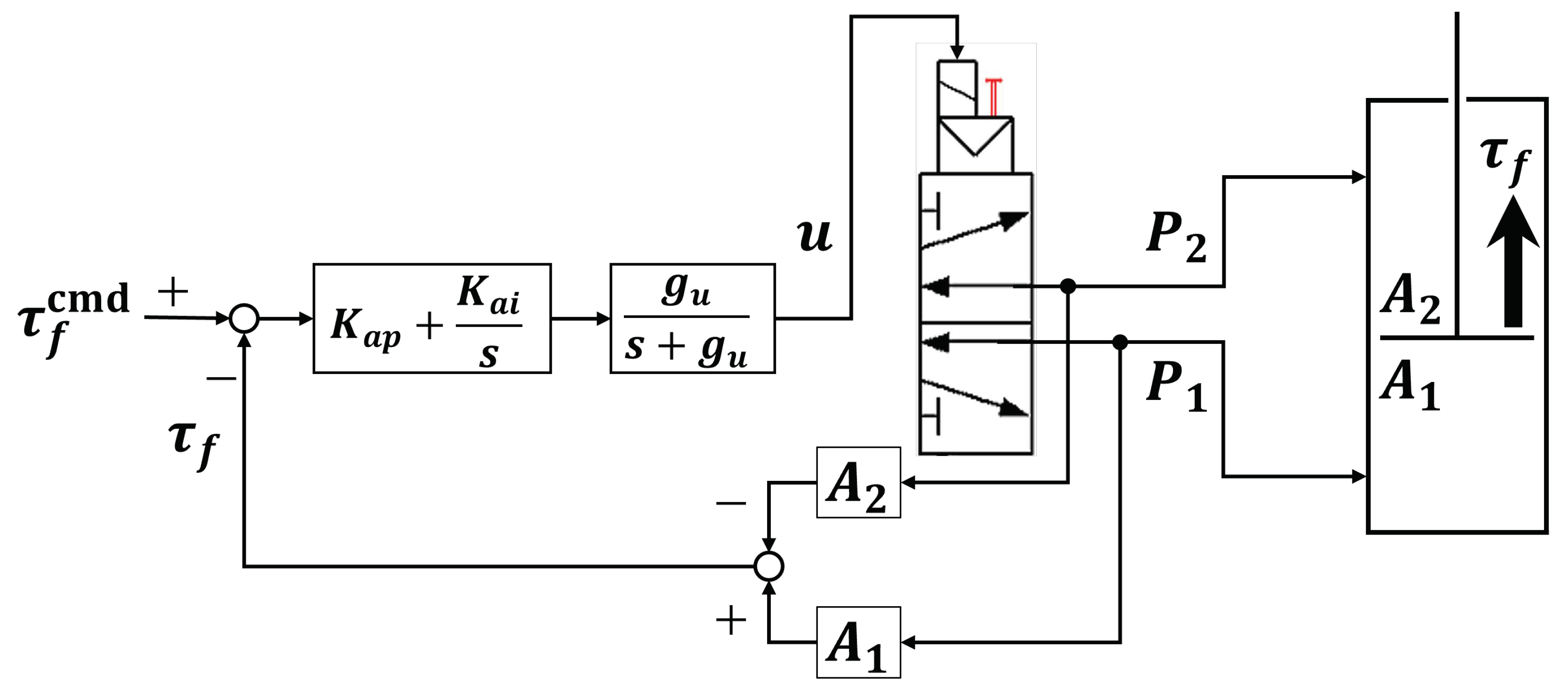
This subsection clarifies the response delay characteristics of the pneumatic driving force in the experimental system. Figure 12 shows the block diagram of the pneumatic force controller developed in this study. In this system, the driving force

τ_{f}

of the pneumatic cylinder is calculated from the pressure

P_{1}

and

P_{2}

measured on the servo valve and the pressure receiving area

A_{1}

and

A_{2}

of the cylinder rod. Then the voltage input u to the servo valve is determined by the PI controller with a low-pass filter for noise reduction. The applied feedback gains and the cut-off frequency are shown in Table 5.

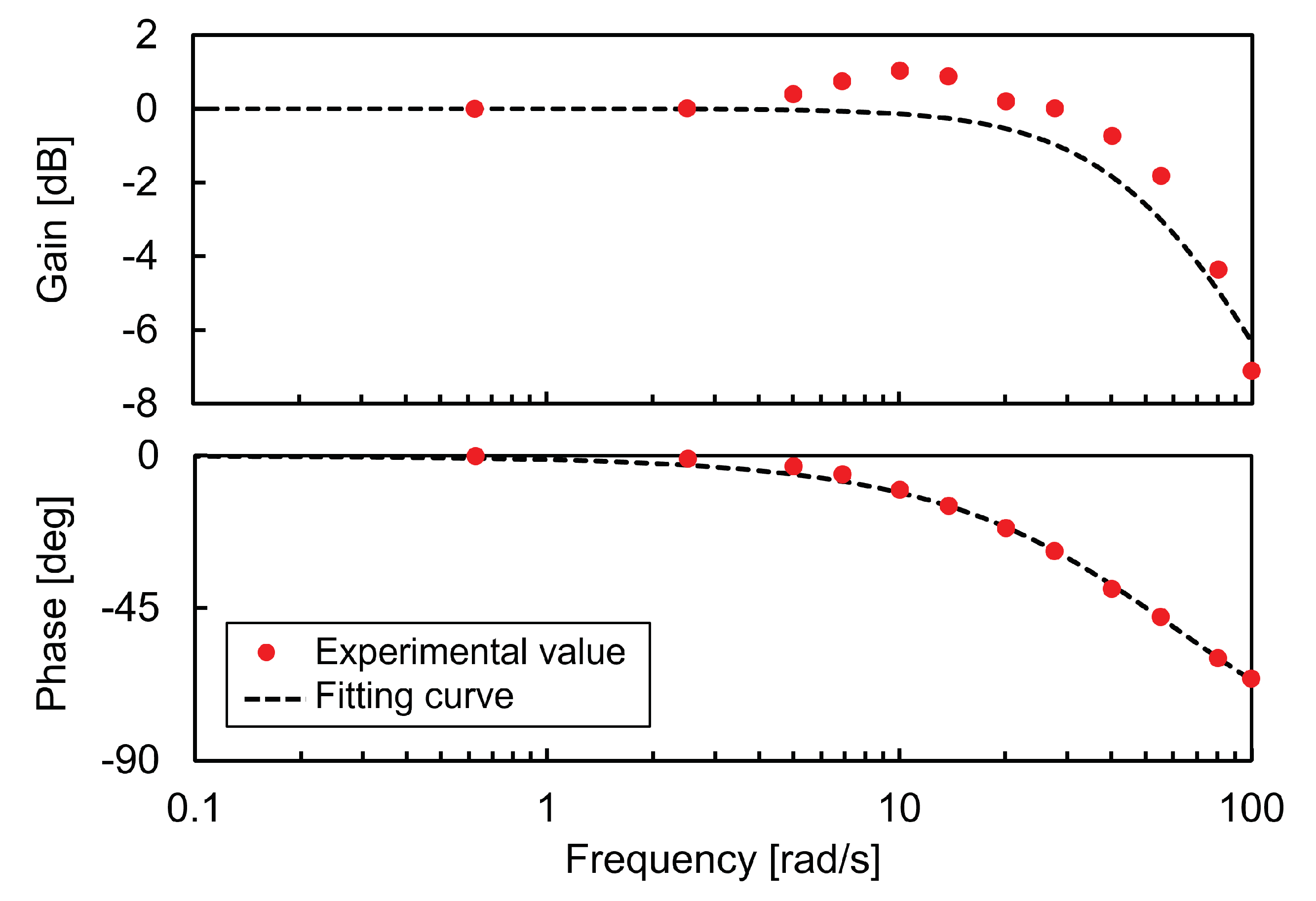
Using this control system, we investigated a frequency response of the pneumatic driving force control. The experiment was conducted by giving a driving force command

τ_{f}^{cmd}

as a sinusoidal input with the follower cylinder fixed in the center position, and recording the amplitude and phase of the output response

τ_{f}

. The experimental result is shown in Figure 13 as a Bode diagram. The control bandwidth is only about 65 rad/s because the control gains cannot be set high due to large noise on the servo valve control voltage. The slight resonance near 10 rad/s is considered to be caused by overshoot due to the integral control. The resulted frequency characteristics is identified as the second-order delay element

D_{p n}

(see Table 2) to obtain the natural angular frequency

ω_{p n}

and damping ratio

ζ_{p n}

values shown in Table 3. The fitting curve in Figure 13 is a least-squares approximation to a second-order delay system according to the phase characteristics to reproduce the response delay of the pneumatic force control. Note that in this experimental system, the dynamic effect of the air tubes (1 m long and 4 mm in diameter) is very small compared to the effect of the servo valve responsiveness.

4.3. Implementation of Bilateral Control Systems with External Force Estimator

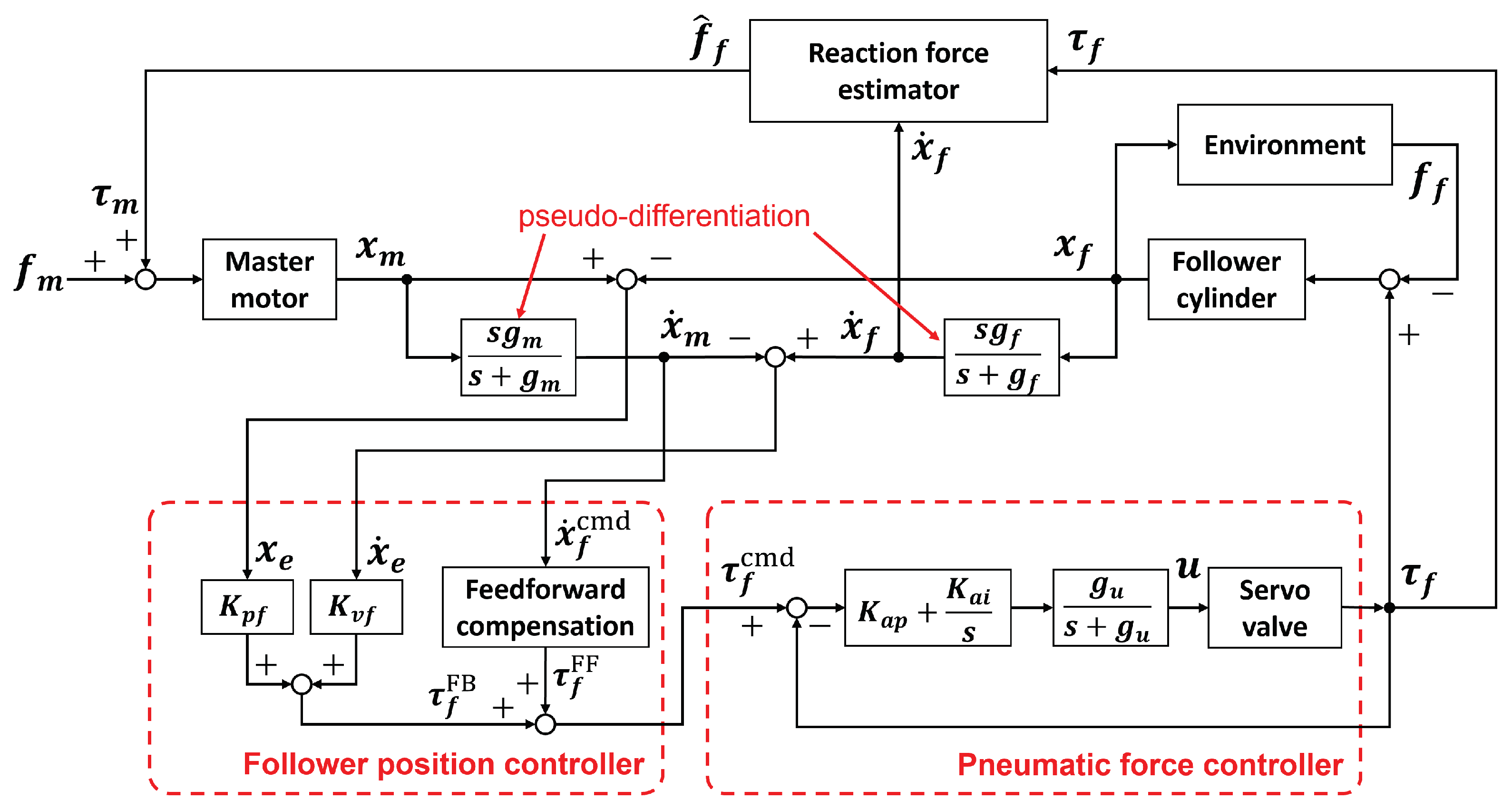
4.3.1. Force-Reflecting Type

Figure 14 shows the block diagram of the Force-Reflecting Type implemented in the experimental system. Regarding the follower, it is desirable to consider sliding friction of the pneumatic cylinder for the actual system implementation. Here the equation of motion on the follower manipulator is updated from Eq.(2) as follows:

\begin{matrix} y_{f} & = & M_{f} {\ddot{x}}_{f} + B_{f} {\dot{x}}_{f} + f_{f r i c} sgn ({\dot{x}}_{f}) \\ = & - f_{f} + τ_{f} \end{matrix}

(20)

where

y_{f}

denotes internal dynamics of the follower and

f_{f r i c}

denotes coulomb friction of the pneumatic cylinder. In the experiment system, since the mass of the pneumatic cylinder is small and required motion is not so fast, the inertial term

M_{f} {\ddot{x}}_{f}

in Eq.(20) is assumed to be negligible. Based on this dynamic model, a feedforward compensation was applied for the position controller.

τ_{f}^{FF} = B_{f} {\dot{x}}_{f}^{cmd} + f_{f r i c} sgn ({\dot{x}}_{f}^{cmd})

(21)

In addition, we implemented a reaction force estimator because this study assumes a situation where a force sensor cannot be mounted on the follower manipulator. The follower reaction force

f_{f}

can be estimated using the relation in Eq.(20).

{\hat{f}}_{f} = τ_{f} - y_{f}

(22)

The estimated reaction force

{\hat{f}}_{f}

is directly transferred to the master motor to output the driving force

τ_{m}

. However, the low control bandwidth of the pneumatic servo system causes chattering in the velocity signal, resulting in oscillatory reaction force estimation. Therefore, by using the command value of follower velocity

{\dot{x}}_{f}^{cmd}

in the dynamics calculation for the reaction force estimation, the oscillation of the estimated value can be reduced to enhance the system stability.

The values of each parameter applied to the control system of the Force-Reflecting Type are shown in Table 6.

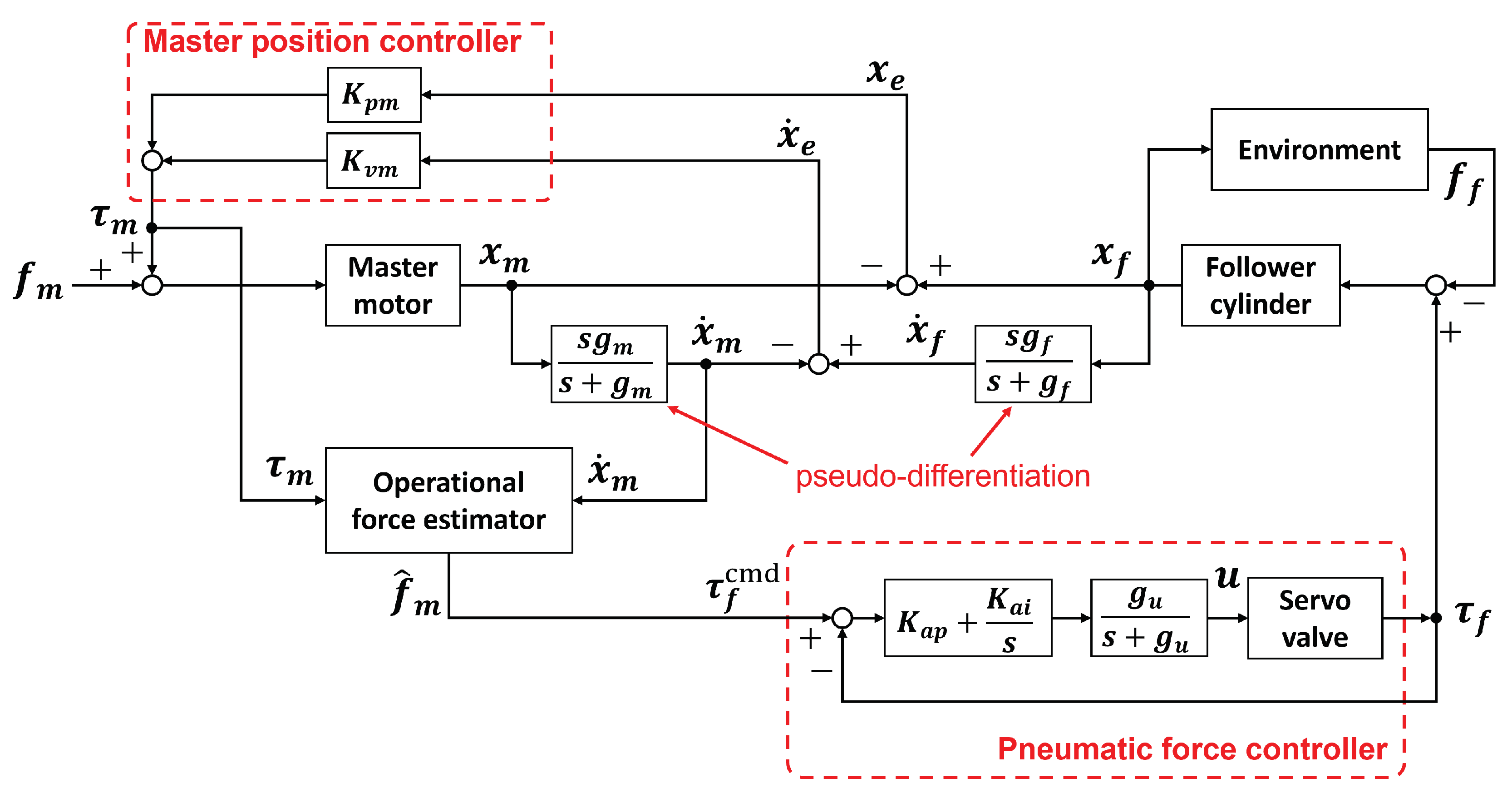
4.3.2. Force-Projecting Type

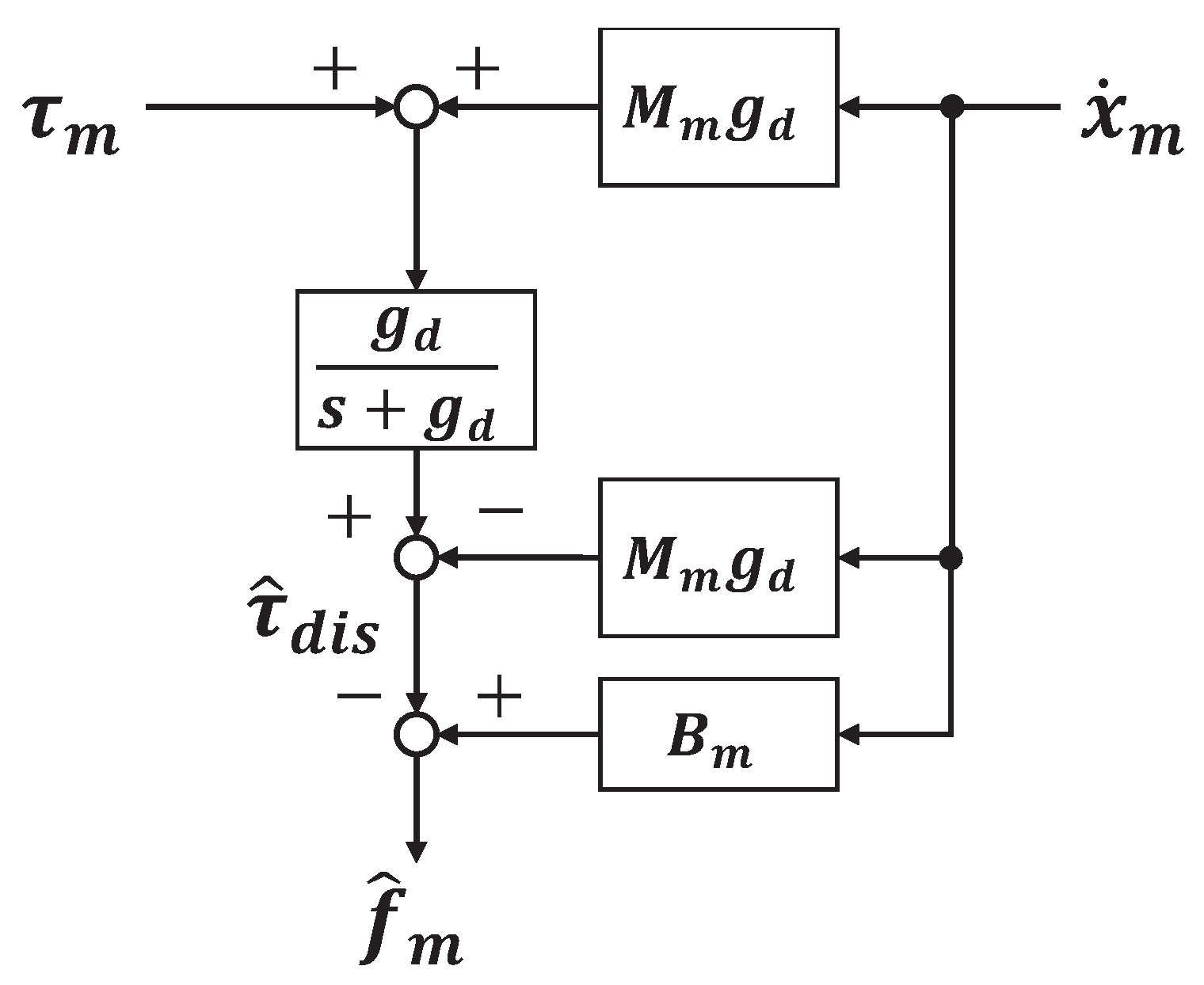
Figure 15 shows the block diagram of the Force-Projecting Type implemented in the experimental system. In the Force-Projecting Type, it is necessary to measure the operating force at the master side. On the master side, where design flexibility is high, it is not difficult to mount a force sensor to directly measure the operating force. However, especially in this experimental system, the operating force estimator is implemented without using a force sensor because the friction of the master arm is very small and its dynamics can be easily modeled. The equation of motion of the master is given by Eq.(1), of which the master operating force and the viscous damping force are collectively defined as the disturbance to the motor

τ_{d i s}

, yielding the following equation.

\begin{matrix} M_{m} {\ddot{x}}_{m} & = & τ_{m} - τ_{d i s} \end{matrix}

(23)

\begin{matrix} τ_{d i s} & = & B_{m} {\dot{x}}_{m} - f_{m} \end{matrix}

(24)

It is known that the disturbance observer [30] is effective in accurately estimating the motor disturbance

τ_{d i s}

from Eq. (23). Once the motor disturbance

τ_{d i s}

is obtained, the master operating force

f_{m}

can be estimated from the relation in Eq. (24).

{\hat{f}}_{m} = B_{m} {\dot{x}}_{m} - {\hat{τ}}_{d i s}

(25)

The implementation of operational force estimator is shown in Figure 16 as a block diagram.

The values of each parameter applied to the control system of the Force-Projecting Type are shown in Table 7.

5. Bilateral Control Experiment

Using the constructed 1-DOF master-follower manipulator system, a series of bilateral control experiments were conducted under the same conditions as in the numerical simulations conducted in the previous section.

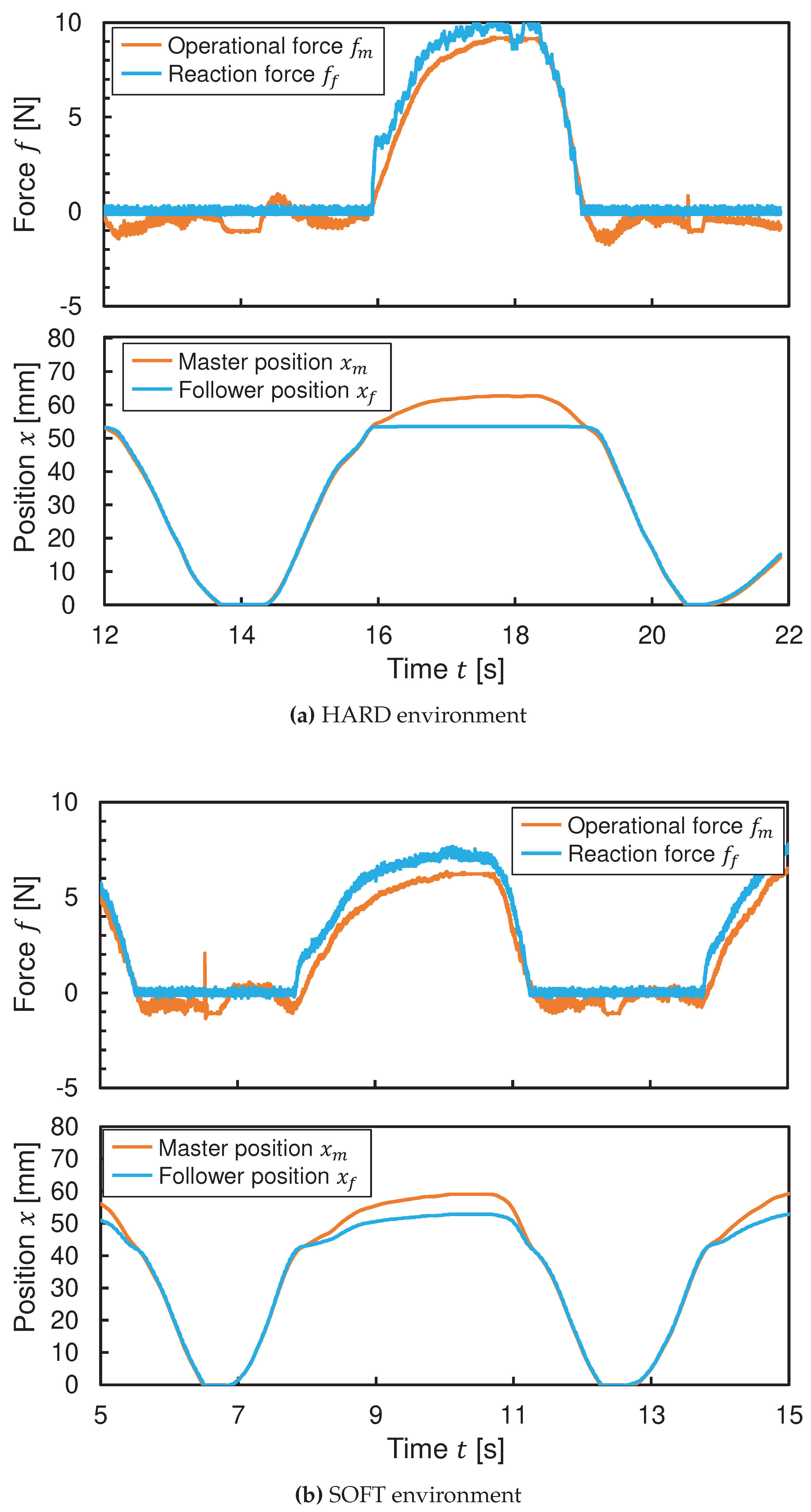
5.1. Step Response

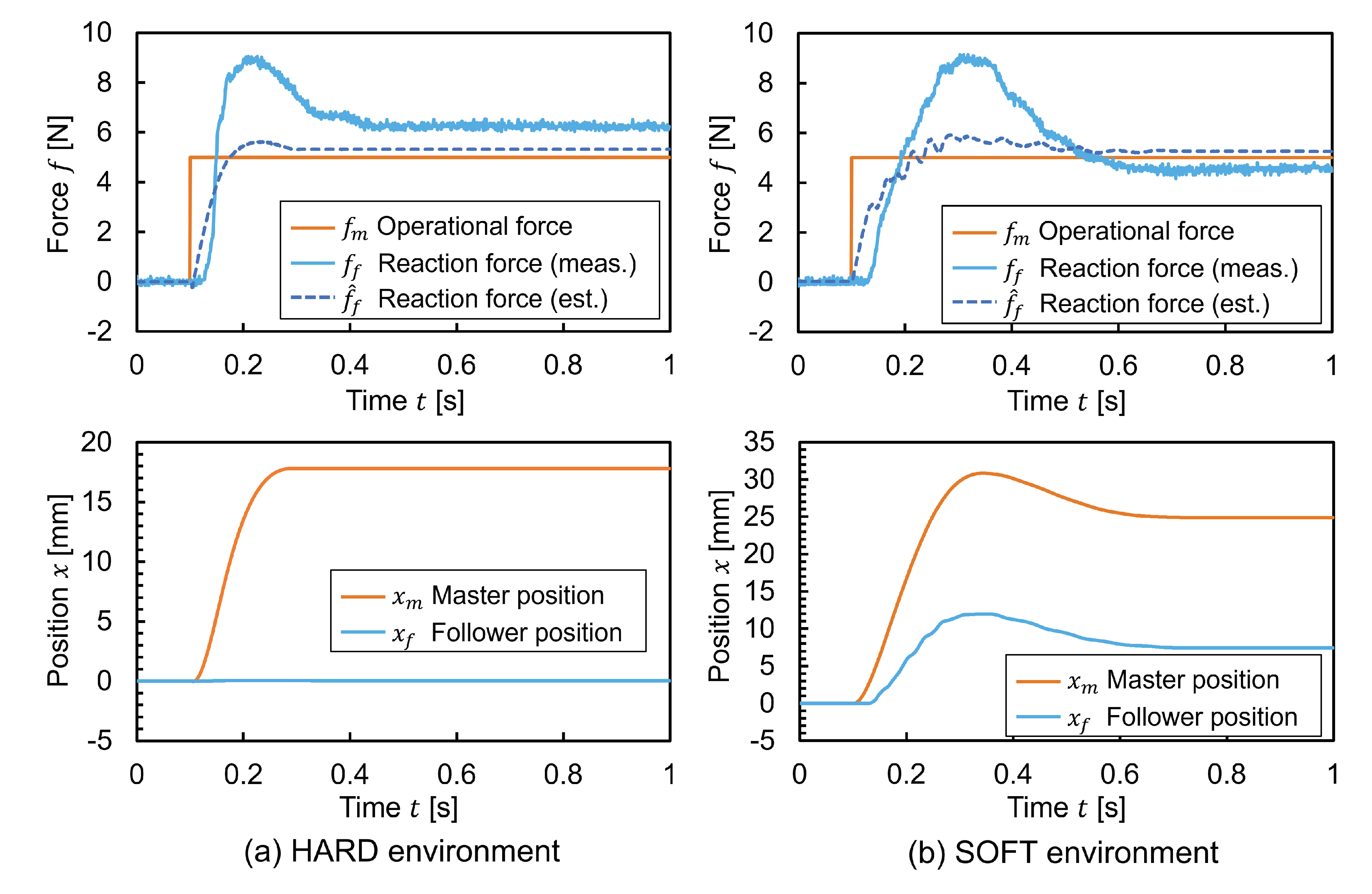
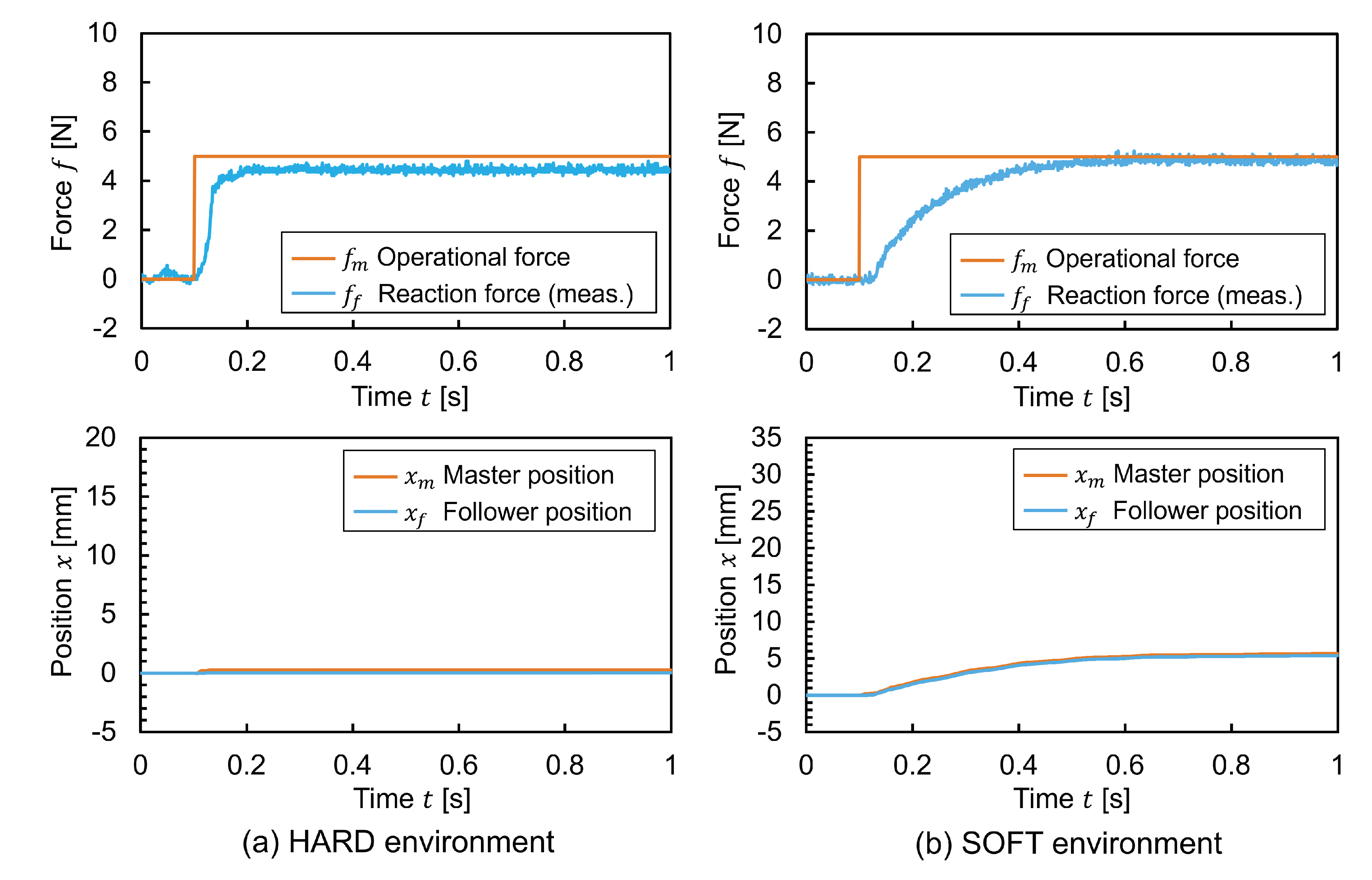
The master operational force

f_{m}

was controlled to be a step input of 5 N. The responses of the follower reaction force

f_{f}

and the manipulator positions

x_{m}

and

x_{f}

were investigated. The experimental results for the two types of environments and the two types of bilateral control methods are shown in Figure 17 and Figure 18, respectively. The ideal behavior in this experiment is for the forces and positions of the master and follower to be equal, respectively.

First, in the Force-Reflecting Type, the measured follower reaction forces had large overshoots unlike the estimated values. This was mainly due to low positioning rigidity of the follower as well as modeling uncertainties in the reaction force estimation, resulting in large errors with the actual motion state and inaccurate force feedback. The variation in the reaction force at equilibrium state may depend on the static friction conditions of the pneumatic cylinder. Needless to say, the position responses had large deviations between the master and follower due to low positioning rigidity of the pneumatic cylinder.

Next, in the Force-Projecting Type, the response of the reaction force was quite stable. However, the reaction force at equilibrium state is considered to depend on the static friction conditions of the pneumatic cylinder. The slow rise of the measured reaction force in the SOFT environment was due to the driving force consumed by sliding friction when the pneumatic cylinder was actuated by the input operating force. In addition, very good tracking performance was obtained for the position response due to the control rigidity of the master.

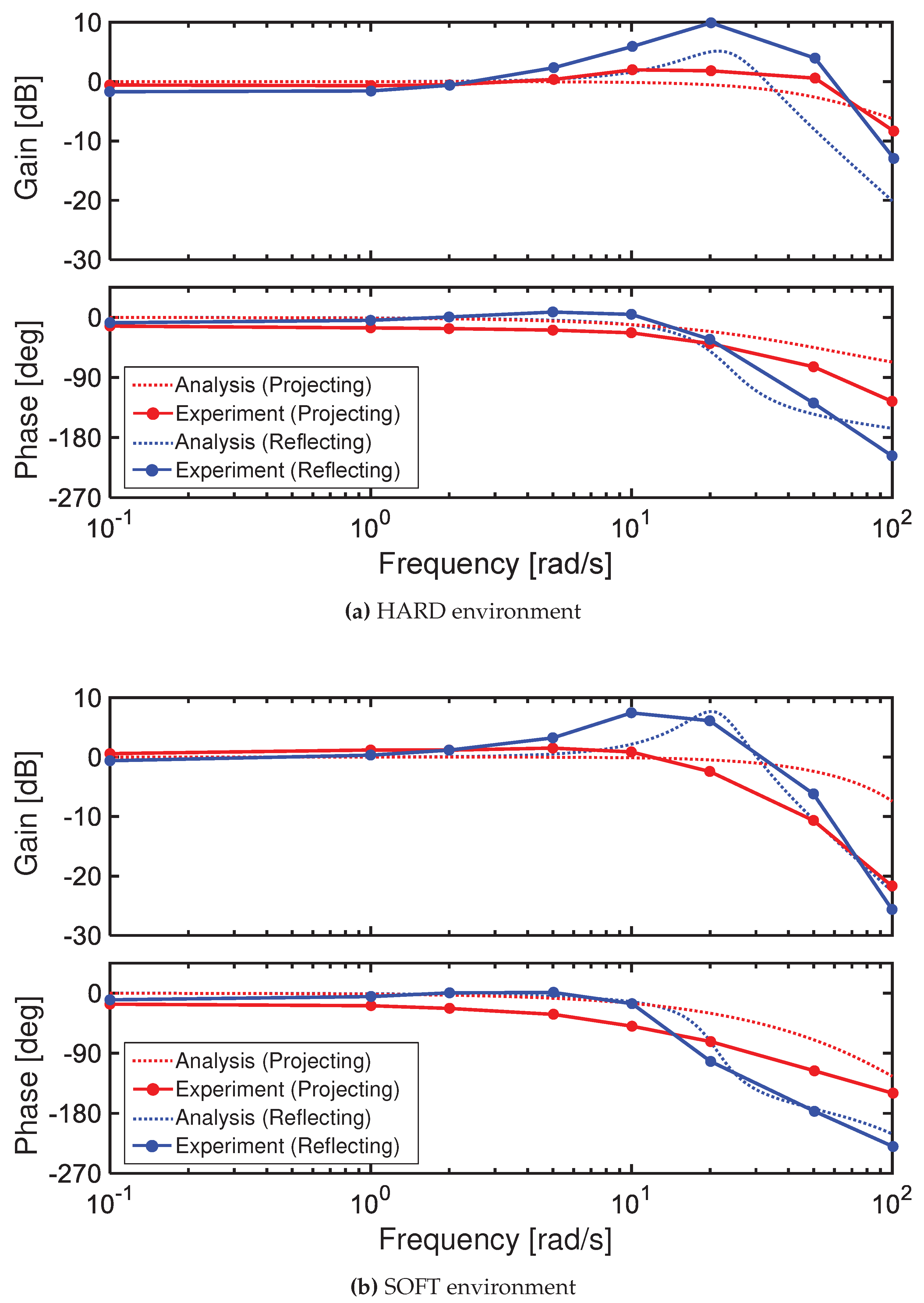
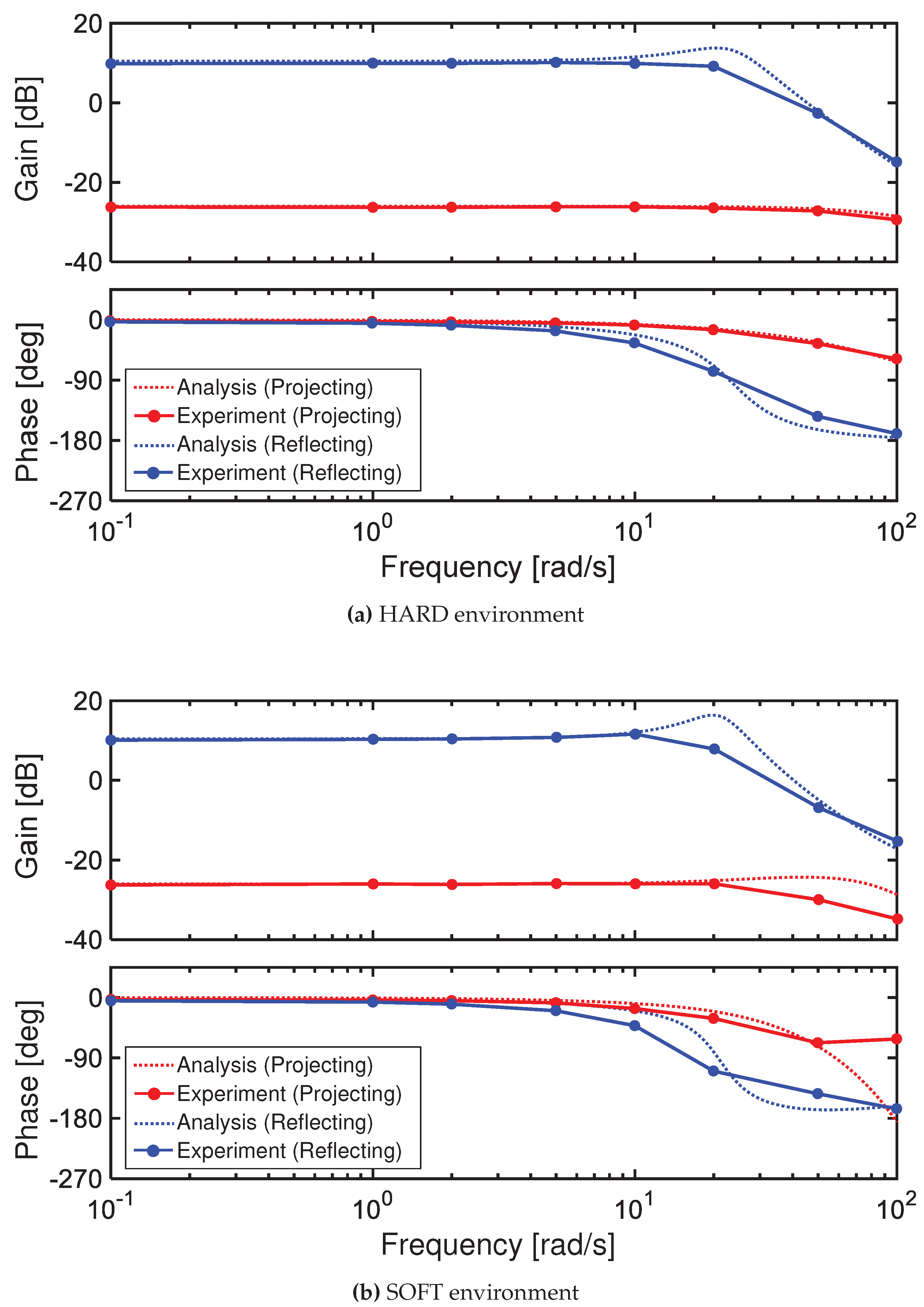
5.2. Frequency Response

Frequency response experiments of the bilateral control systems were conducted for the force transfer function

G_{f}

and the position error transfer function

G_{x}

defined by equations (18) and (19), respectively. The master driving force was controlled so that the master operating force was a sinusoidal input of

f_{m} = 5 sin (ω t)

, and the amplitude and phase difference of

G_{f}

and

G_{x}

were measured. The experimental results are shown in Figure 19 and Figure 20 as Bode diagrams. The results of the numerical simulation are plotted overlaid with dotted lines for comparison.

In Figure 19, the Force-Reflecting Type showed a significant resonance in both environments, consistent with the trend in the numerical analysis. Particular in the HARD environment, the resonant gain got larger due to errors in the external force estimation. On the other hand, the Force-Projecting Type had no significant resonance, and stability can be confirmed over the entire main bandwidth. Compared to the numerical analysis, the gain dropped significantly above about 20 rad/s. This is because sliding friction of the pneumatic cylinder caused the follower displacement to be smaller, resulting in a smaller force acting on the environment.

In Figure 20, naturally, the Force-Projecting Type with high control stiffness showed a excellent response close to the ideal. In the Force-Reflecting Type, a resonance was suppressed compared to the numerical analysis. This is because sliding friction of the pneumatic cylinder had a greater damping effect.

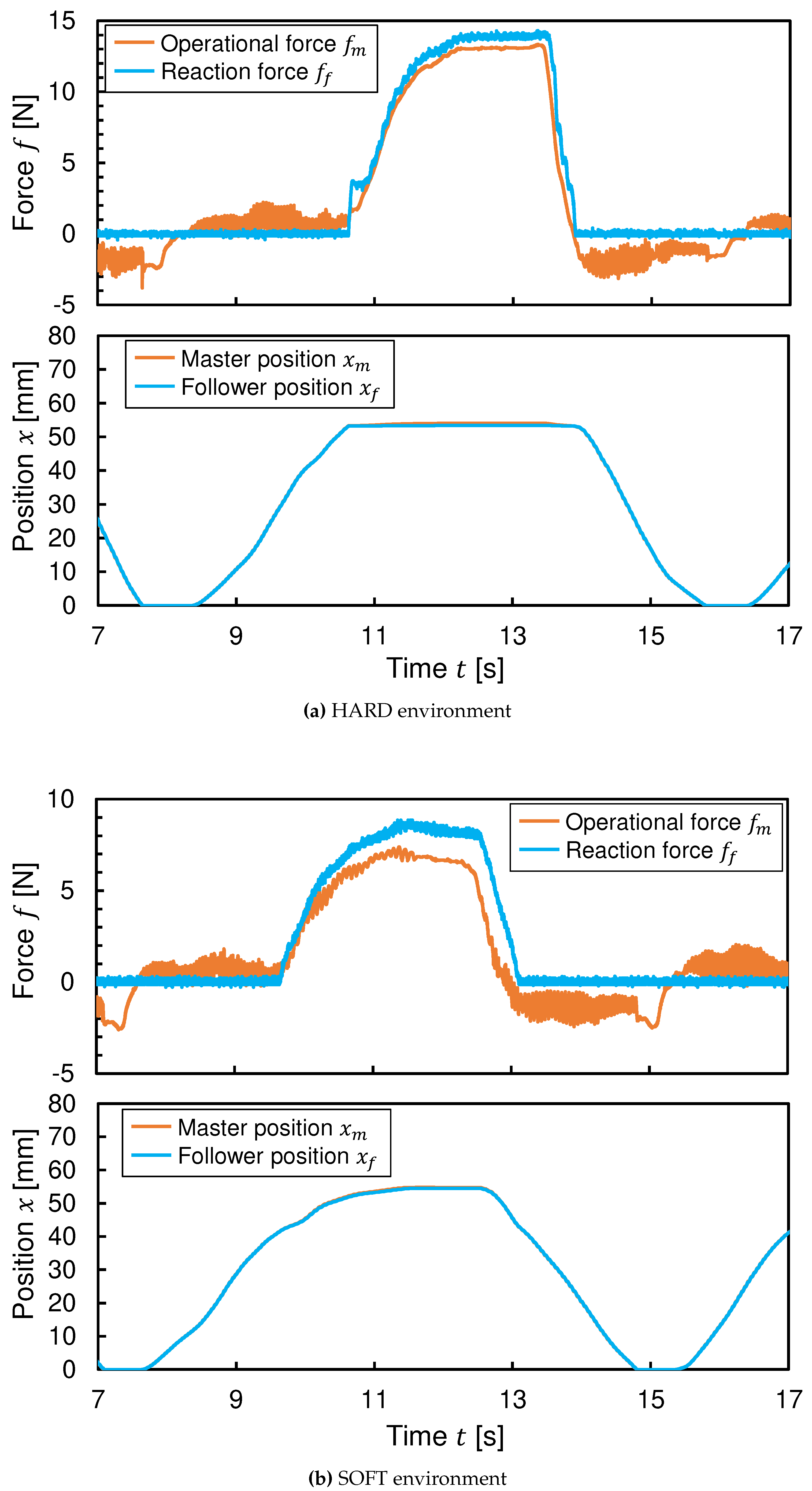
5.3. Response by a Human Operation

Finally, one of the authors operated the master by hand and tried to perform the task of pushing the two different environments with the follower. The force and position responses in this experiment are shown in Figure 21 and Figure 22.

According to the result of the Force-Reflecting Type in Figure 21, the force responses showed that the operating forces during free motion were generally less than 2N, indicating that the master arm could be operated with light force. The errors between the operating force and reaction force when in contact with the environment were mainly due to dynamic modeling uncertainties in the reaction force estimation. However, significant position errors had occurred when in contact with the environment. Under such condition, the stiffness of the environment may not be correctly identified as a force sensation.

The results of the Force-Projecting Type showed that the operational forces during free movement were about 3 N, resulting in a slightly heavier operational feel than the Force-Reflecting Type. This is because in the Force-Projecting Type, the follower dynamics (e.g., viscosity and friction of the pneumatic cylinder) need to be compensated by the master’s operational force. In addition, the error of the follower reaction force became larger when in contact with the SOFT environment. This may be due to the fact that when the follower was backdriven by a force from the environment, it was not only affected by the follower dynamics, but also by frictional force on the master that was not modeled in the operational force estimator. With respect to position response, the system exhibited very good tracking performance, enabling accurate operation.

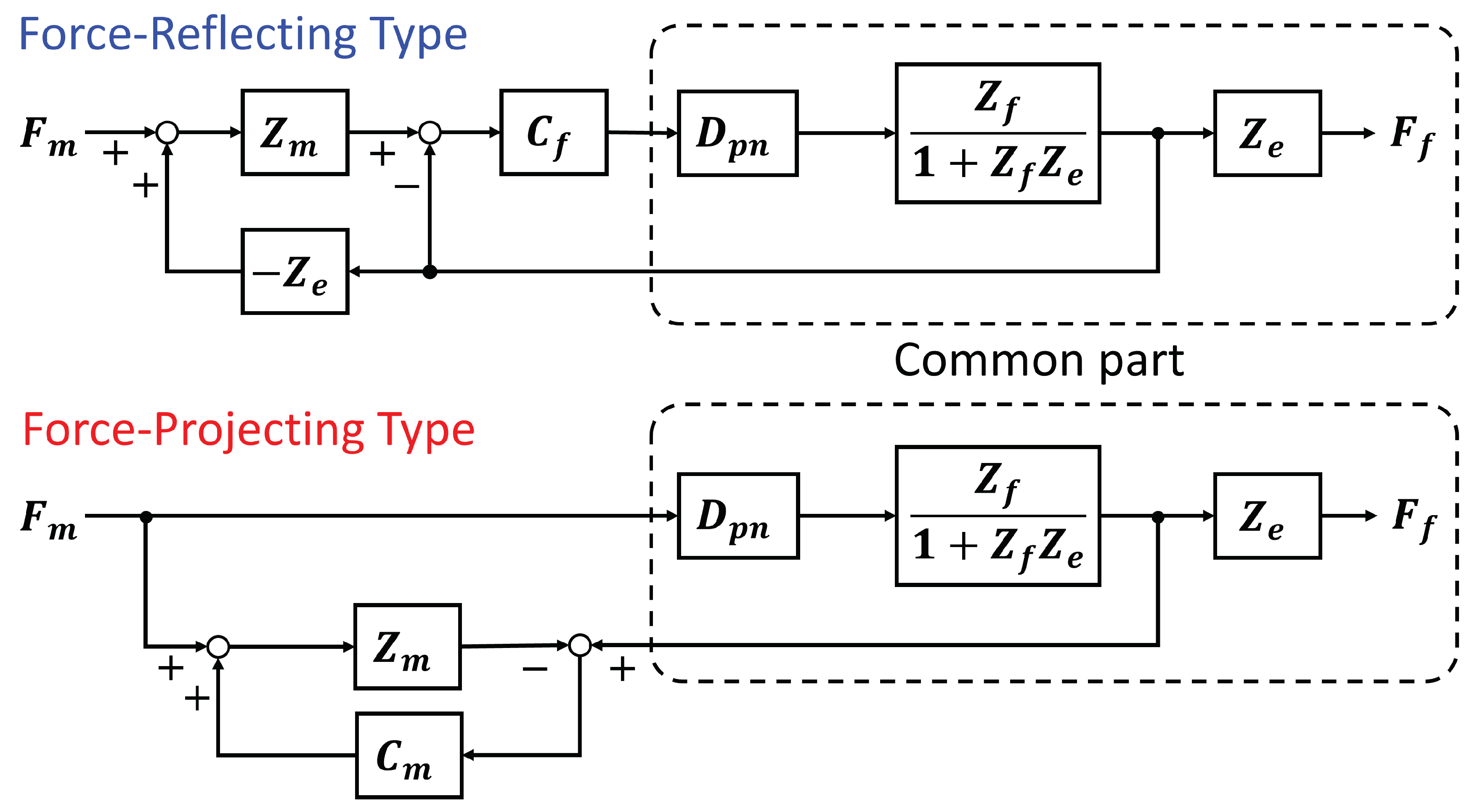
6. Discussion

The analyses and experiments so far showed that the Force-Projecting Type is more stable in force response and has high positioning rigidity than the Force-Reflecting Type. Here we can give a theoretical consideration about the force response stability by analyzing structures of the transfer function

G_{f}

. Figure 23 shows equivalent transformations of block diagrams of the force transfer function

G_{f}

in the two bilateral control system. Both control methods partly have structures in common, so we can focus the different parts other than that. In the Force-Reflecting Type, the master dynamics

Z_{m}

and follower position controller

C_{f}

exist between operational force

F_{m}

and the common part. Therefore, the force response is affected by these characteristics. Here is a major problem when a pneumatic manipulator with low control rigidity is used as a follower. Moreover, there is a feedback from the environmental impedance

Z_{e}

. Hence, the stability changes as the contact environment changes. In contrast, the Force-Projecting Type has a transfer function of "1” from

F_{m}

to the common part. Moreover, there is also an environmental impedance

Z_{e}

, but this does not affect the force response. Therefore, the Force-Projecting Type is also robust to changes in environmental characteristics.

In this study, we assumed severe situations where it is difficult to mount a force sensor directly on the follower-side manipulator, for example, in surgical assist robots and construction machine operating robots. In the Force-Reflecting Type, therefore, a reaction force estimator was implemented, but it is difficult to achieve accurate estimation due to uncertainty of the dynamics model and oscillatory slow response of the pneumatic follower. Considering implementation in multi-DOF manipulators with more complex dynamics, it is obvious that the accuracy of the reaction force estimator will deteriorate further. On the other hand, the Force-Projecting Type is highly applicable to multi-DOF manipulators from the viewpoint of the robust stability of force response as described above, as well as the advantage of accurate position control utilizing the high stiffness of the electric master.

For a future challenge, we plan to develop a control method to precisely match the master operating force with the follower reaction force, while taking advantage of the Force-Projecting Type that does not require force measurement at the follower side. This will also lead to improvement of the heaviness of the operational feel caused by follower dynamics in the Force-Projecting Type.

Author Contributions

Conceptualization, D.H.; methodology, D.H.; software, D.H. and R.M.; validation, D.H.; formal analysis, R.M.; investigation, R.M.; resources, D.H.; data curation, R.M.; writing—original draft preparation, D.H.; writing—review and editing, D.H.; visualization, D.H. and R.M.; supervision, D.H.; project administration, D.H.; funding acquisition, D.H. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by JSPS KAKENHI Grant Number 23K03783.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest

The authors declare no conflict of interest.

References

Diolaiti, N.; Melchiorri, C. Teleoperation of a mobile robot through haptic feedback. IEEE International Workshop HAVE Haptic Virtual Environments and Their, 2002, pp. 67–72.
Yoon, W.K.; Goshozono, T.; Kawabe, H.; Kinami, M.; Tsumaki, Y.; Uchiyama, M.; Oda, M.; Doi, T. Model-based space robot teleoperation of ETS-VII manipulator. IEEE Transactions on Robotics and Automation 2004, 20, 602–612. [Google Scholar] [CrossRef]
Wei, W.; Kui, Y. Teleoperated manipulator for leak detection of sealed radioactive sources. IEEE International Conference on Robotics and Automation, 2004. Proceedings. ICRA ’04. 2004, 2004, Vol. 2, pp. 1682–1687 Vol.2.
Tadano, K.; Kawashima, K. Development of a master–slave system with force-sensing abilities using pneumatic actuators for laparoscopic surgery. Advanced Robotics 2010, 24, 1763–1783. [Google Scholar] [CrossRef]
Zhou, D.; Tadano, K.; Haraguchi, D. Motion control and external force estimation of a pneumatically driven multi-DOF robotic forceps. Applied Sciences 2020, 10, 3679. [Google Scholar] [CrossRef]
Todorov, E.; Hu, C.; Simpkins, A.; Movellan, J. Identification and control of a pneumatic robot. 2010 3rd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics. IEEE, 2010, pp. 373–380.
Mat Dzahir, M.A.; Yamamoto, S.i. Recent trends in lower-limb robotic rehabilitation orthosis: Control scheme and strategy for pneumatic muscle actuated gait trainers. Robotics 2014, 3, 120–148. [Google Scholar] [CrossRef]
Liu, Q.; Zuo, J.; Zhu, C.; Xie, S.Q. Design and control of soft rehabilitation robots actuated by pneumatic muscles: State of the art. Future Generation Computer Systems 2020, 113, 620–634. [Google Scholar] [CrossRef]
Sasaki, T.; Kawashima, K. Remote control of backhoe at construction site with a pneumatic robot system. Automation in Construction 2008, 17, 907–914. [Google Scholar] [CrossRef]
Miyazaki, T.; Hagihara, S. Parallel control method for a bilateral master-slave manipulator. Journal of the Robotics Society of Japan 1989, 7, 446–452. [Google Scholar] [CrossRef]
Tachi, S.; Sakaki, T. Impedance controlled master-slave manipulation system. Part 1. Basic concept and application to the system with a time delay. Advanced Robotics 1991, 6, 483–503. [Google Scholar] [CrossRef]
Sakaki, T.; Tachi, S. Impedance-controlled master-slave manipulation system. Part II. Modification of force sensation and extension of operational capability. Advanced Robotics 1992, 7, 3–24. [Google Scholar] [CrossRef]
Sakaki, T.; Tachi, S. Impedance Controlled Master Slave Manipulation System Part III Ideal Bilateral Response of Generalized Impedance Controlled MSMS. Journal of the Robotics Society of Japan 1992, 10, 418–421. [Google Scholar] [CrossRef]
Lawrence, D.A. Stability and transparency in bilateral teleoperation. IEEE Transactions on Robotics and Automation 1993, 9, 624–637. [Google Scholar] [CrossRef]
Yokokohji, Y.; Yoshikawa, T. Bilateral control of master-slave manipulators for ideal kinesthetic coupling-formulation and experiment. IEEE Transactions on Robotics and Automation 1994, 10, 605–620. [Google Scholar] [CrossRef] [PubMed]
Yokokohji, Y.; Hosotani, N.; Yoshikawa, T. Analysis of maneuverability and stability of micro-teleoperation systems. Proceedings of the 1994 IEEE International Conference on Robotics and Automation. IEEE, 1994, pp. 237–243.
Yokokohji, Y.; Imaida, T.; Iida, Y.; Doi, T.; Oda, M.; Yoshikawa, T. Bilateral teleoperation: Towards fine manipulation with large time delay. Experimental Robotics VII. Springer, 2001, pp. 11–20.
Iida, W.; Ohnishi, K. Reproducibility and operationality in bilateral teleoperation. The 8th IEEE International Workshop on Advanced Motion Control, 2004. AMC’04. IEEE, 2004, pp. 217–222.
Matsumoto, Y.; Katsura, S.; Ohnishi, K. An analysis and design of bilateral control based on disturbance observer. IEEE International Conference on Industrial Technology, 2003. IEEE, 2003, Vol. 2, pp. 802–807.
Suzuki, A.; Ohnishi, K. Novel four-channel bilateral control design for haptic communication under time delay based on modal space analysis. IEEE Transactions on Control Systems Technology 2012, 21, 882–890. [Google Scholar] [CrossRef]
Komada, S.; Ohnishi, K. Control of robotic manipulators by joint acceleration controller. 15th Annual Conference of IEEE Industrial Electronics Society. IEEE, 1989, pp. 623–628.
Durbha, V.; Li, P.Y. Passive Bilateral Tele-Operation and Human Power Amplification With Pneumatic Actuators. ASME 2009 Dynamic Systems and Control Conference, Volume 2 2009, pp. 863–870.
Moreau, R.; Pham, M.; Tavakoli, M.; Le, M.; Redarce, T. Sliding-mode bilateral teleoperation control design for master–slave pneumatic servo systems. Control Engineering Practice 2012, 20, 584–597. [Google Scholar] [CrossRef]
Tadano, K.; Kawashima, K. Development of 4-DOFs forceps with force sensing using pneumatic servo system. Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006. IEEE, 2006, pp. 2250–2255.
Haraguchi, D.; Kanno, T.; Tadano, K.; Kawashima, K. A pneumatically driven surgical manipulator with a flexible distal joint capable of force sensing. IEEE/ASME Transactions on Mechatronics 2015, 20, 2950–2961. [Google Scholar] [CrossRef]
Kaneko, K.; Tokashiki, H.; Tanie, K.; Komoriya, K. Macro-micro bilateral teleoperation based on operational force feedforward-operational force feedforward bilateral teleoperation and its dexterity. Proceedings. 1998 IEEE/RSJ International Conference on Intelligent Robots and Systems. Innovations in Theory, Practice and Applications (Cat. No. 98CH36190). IEEE, 1998, Vol. 3, pp. 1761–1769.
Kanaoka, K.; Kikuuwe, R. Master-slave system, 2014. US9855653B2.
Kikuuwe, R.; Kanaoka, K.; Kumon, T.; Yamamoto, M. Phase-lead stabilization of force-projecting master-slave systems with a new sliding mode filter. IEEE Transactions on Control Systems Technology 2015, 23, 2182–2194. [Google Scholar] [CrossRef]
Kanaoka, K.; Shirogauchi, G.; Nakamura, H. Power pedal as a man-machine synergy effector—Bipedal walking with human skill and robot power—. 2008 IEEE International Conference on Robotics and Automation. IEEE, 2008, pp. 1779–1780.
Sariyildiz, E.; Oboe, R.; Ohnishi, K. Disturbance observer-based robust control and its applications: 35th anniversary overview. IEEE Transactions on Industrial Electronics 2019, 67, 2042–2053. [Google Scholar] [CrossRef]

Figure 1. 1-DOF model of master-follower system

Figure 2. Block diagram of the force-reflecting bilateral control.

Figure 3. Block diagram of the force-projecting bilateral control.

Figure 4. Step response analysis of the follower reaction force.

Figure 5. Step response analysis of the position error between master and follower.

Figure 6. Bode diagram of the force transfer function

G_{f}

in numerical simulation

Figure 6. Bode diagram of the force transfer function

G_{f}

in numerical simulation

Figure 7. Bode diagram of the position error transfer function

G_{x}

in numerical simulation

Figure 7. Bode diagram of the position error transfer function

G_{x}

in numerical simulation

Figure 8. One-DOF master-follower manipulator constructed for the experiment

Figure 9. Two types of environmental walls connected by the follower cylinder rod

Figure 10. Overall configuration of the experimental apparatus

Figure 11. System diagram of the master-follower manipulator

Figure 12. Model of pneumatic servo drive system

Figure 13. Frequency response of the pneumatic driving force control

Figure 14. Block diagram of the 1-DOF force-reflecting bilateral control implemented into experimental system

Figure 15. Block diagram of the 1-DOF force-projecting bilateral control implemented into experimental system

Figure 16. Block diagram of the operational force estimator

Figure 17. Experimental result of step responses about the forces and positions with two different environments (Force-Reflecting Type)

Figure 18. Experimental result of step responses about the forces and positions with two different environments (Force-projecting type)

Figure 19. Bode diagram of the force transfer function

G_{f}

in experiment

Figure 19. Bode diagram of the force transfer function

G_{f}

in experiment

Figure 20. Bode diagram of the position error transfer function

G_{x}

in experiment

Figure 20. Bode diagram of the position error transfer function

G_{x}

in experiment

Figure 21. Experimental result of master-follower operation by human (Force-Reflecting Type)

Figure 22. Experimental result of master-follower operation by human (Force-Projecting Type)

Figure 23. Comparison of equivalent block diagrams of the force transfer function

G_{f}

Figure 23. Comparison of equivalent block diagrams of the force transfer function

G_{f}

Table 1. Symbols and Indices

Description	Symbol and Index
Laplace operator	s
Position	$X (= L [x])$
Operational force at master	$F_{m} (= L [f_{m}])$
Reaction force at follower	$F_{f} (= L [f_{f}])$
Driving force	$T (= L [τ])$
Mass	M
Spring constant	k
Damping coefficient	B
Position gain	$K_{p}$
Velocity gain	$K_{v}$
Natural frequency	$ω$
Damping ratio	$ζ$
Index of master	$◯_{m}$
Index of follower	$◯_{f}$

Table 2. Transfer functions of block diagrams.

Meaning	Transfer function
Master impedance	$Z_{m} = \frac{1}{s M_{m} + B_{m}}$
Follower impedance	$Z_{f} = \frac{1}{s M_{f} + B_{f}}$
Master position controller	$C_{m} = \frac{K_{p m} + s K_{v m}}{s}$
Follower position controller	$C_{f} = \frac{K_{p f} + s K_{v f}}{s}$
Environment impedance	$Z_{e} = \frac{k_{e} + s B_{e}}{s}$
Pneumatic delay	$D_{p n} = \frac{ω_{p n}^{2}}{s^{2} + s 2 ζ_{p n} ω_{p n} + ω_{p n}^{2}}$

Table 3. Parameters used for numerical analyses

Side	Coefficient	Symbol	Value
Master	Mass	$M_{m}$	0.676	[kg]
	Damping	$B_{m}$	3.84	[Ns/m]
	Position gain	$K_{p m}$	20.0	[N/mm]
	Velocity gain	$K_{v m}$	$2 \sqrt{M_{m} K_{p m}}$	[Ns/mm]
Follower	Mass	$M_{f}$	0.125	[kg]
	Damping	$B_{f}$	11.5	[Ns/m]
	Position gain	$K_{p f}$	LOW Gain : 0.30	[N/mm]
			MID Gain : 5.0	[N/mm]
			HIGH Gain : 20.0	[N/mm]
	Velocity gain	$K_{v f}$	$2 \sqrt{M_{f} K_{p f}}$	[Ns/mm]
Environment	Spring constant	$k_{e}$	HARD : 97.4	[N/mm]
			SOFT : 1.48	[N/mm]
	Damping ratio	$ζ_{e}$	HARD : 0.174	[-]
			SOFT : 0.249	[-]
	Damping	$B_{e}$	$2 ζ_{e} \sqrt{M_{f} k_{e}}$	[Ns/m]
Pneumatic	Natural frequency	$ω_{p n}$	39.6	[Hz]
Pneumatic	Damping ratio	$ζ_{p n}$	2.36	[-]

Table 4. Main components of the master-follower manipulator system

Master	Linear motor	Maker	GMC Hillstone Co.,Ltd.
		Model	s160Q
		Stroke	100 mm
		Rated thrust	20 N
		Mass of moving part	0.676 kg
	Motor driver	Maker	Panasonic Corp.
		Model	MINAS-A6L
	Linear encoder	Maker	Technohands Co.,Ltd.
		Model	TAi-200
		Position resolution	1.0 $μ$ m
Follower	Air cylinder	Maker	SMC Corp.
		Model	CJ2XE16-100Z
		Bore	$ϕ$ 16 mm
		Stroke	100 mm
		Actuation type	Double acting
		Mass of moving part	0.125 kg
	Servo valve	Maker	Festo
		Model	MPYE-5-M5-010-B
	Pressure sensor	Maker	SMC corp.
		Model	PSE540A-R04
	Linear encoder	Maker	Technohands Co.,Ltd.
		Model	TAi-200
		Position resolution	1.0 $μ$ m

Table 5. Parameters for the pneumatic force controller

Parameter	Symbol	Value
Proportional gain	$K_{a p}$	0.12	[V/N]
Integral gain	$K_{a i}$	1.49	[V/Ns]
Cut-off frequency	$g_{u}$	50.0	[Hz]

Table 6. Parameters applied to experiment system (Force-reflecting type)

Feedback control gains:
Follower position gain	$K_{p f}$	0.30	[N/mm]
Follower velocity gain	$K_{v f}$	0.38	[Ns/mm]
Proportional gain of pneumatic drive force	$K_{a p}$	0.12	[V/N]
Integral gain of pneumatic drive force	$K_{a i}$	1.49	[V/Ns]
Follower inverse dynamics parameters:
Damping coefficient	$B_{f}$	11.5	[Ns/m]
Coulomb friction force	$f_{fric}$	1.0	[N]
Cut-off frequencies:
Master pseudo-differentiation	$g_{m}$	20	[Hz]
Follower pseudo-differentiation	$g_{f}$	20	[Hz]
Valve command voltage	$g_{u}$	50	[Hz]

Table 7. Parameters applied to experiment system (Force-projecting type)

Feedback control gains:
Master position gain	$K_{p m}$	20.0	[N/mm]
Master velocity gain	$K_{v m}$	7.35	[Ns/mm]
Proportional gain of pneumatic drive force	$K_{a p}$	0.12	[V/N]
Integral gain of pneumatic drive force	$K_{a i}$	1.49	[V/Ns]
Master inverse dynamics parameters:
Mass of the moving part	$M_{m}$	0.676	[kg]
Damping coefficient	$B_{m}$	3.84	[Ns/m]
Cut-off frequencies:
Master pseudo-differentiation	$g_{m}$	300	[Hz]
Follower pseudo-differentiation	$g_{f}$	20	[Hz]
Operational force estimator	$g_{d}$	100	[Hz]
Valve command voltage	$g_{u}$	50	[Hz]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Performance Investigation of Force-Projecting Bilateral Control for Pneumatic Manipulator

Abstract

1. Introduction

1.1. Research Background

1.2. Related Works

1.3. Research Objective

2. System Modeling and Control Architecture

2.1. One-DOF Master-Follower Dynamic Model

2.2. Design of Bilateral Control Systems

2.2.1. Force-Reflecting Type

2.2.2. Force-Projecting Type

3. Numerical Simulation

3.1. Conditions of Analysis

3.2. Step Response

3.3. Frequency Response

4. Experimental System Implementation

4.1. Hardware Configuration

4.2. Design and Characteristics of Pneumatic Servo Drive System

4.3. Implementation of Bilateral Control Systems with External Force Estimator

4.3.1. Force-Reflecting Type

4.3.2. Force-Projecting Type

5. Bilateral Control Experiment

5.1. Step Response

5.2. Frequency Response

5.3. Response by a Human Operation

6. Discussion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe