Adaptive Event-based Dynamic Output Feedback Control for Unmanned Marine Vehicle Systems Under DoS Attack

Preprint

Article

Adaptive Event-based Dynamic Output Feedback Control for Unmanned Marine Vehicle Systems Under DoS Attack

Altmetrics

Downloads

103

Views

Comments

A peer-reviewed article of this preprint also exists.

Chunping Wang^*,Wendong Xie,

Jinfeng Gao^*

Ping Wu,

Peter Xiaoping Liu

Chunping Wang^*,Wendong Xie,

Jinfeng Gao^*

Ping Wu,

Peter Xiaoping Liu

This version is not peer-reviewed

Submitted:

18 December 2023

Posted:

21 December 2023

You are already at the latest version

Alerts

Abstract

An event-based dynamic output feedback control (DOFC) strategy for unmanned marine vehicle (UMV) systems is concerned. The whole UMV systems are composed of an UMV closed-loop system, a land-based control unit and the communication network. To increase the effectiveness of data transmission in the network channel and better enable the control unit against attack, an adaptive event-triggered mechanism (AETM) is applied. Moreover, a quantizer is installed between the sampler and the control unit. The quantizer further reduces the communication burden. The occurrence of aperiodic denial-of-service (DoS) attack is considered in the channel from the control unit to the UMV system. Sufficient criterion for ensuring global exponential stability of system with an expected H∞ disturbance attenuation index is obtained. Co-design of the dynamic output feedback controller and the AETM is derived. The effectiveness of the proposed approach is verified in the given illustrative simulation. The simulation results indicate that the reduction percentages of yaw angle amplitudes and yaw velocity accumulative error of the UMV system with the control strategy proposed in this paper are 43.2%and 45.9%, respectively, which are 0.3% and 5.8% improvement in both metrics compared to the previously published work.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

In recent years, Artificial Intelligence, Cloud Computing, Big Data and other internet fields develop rapidly [1]. All these rapid developments are inextricably linked to wireless network technology. The networked control systems (NCSs) become a hot area of research due to its practical applications. It enables the remote control in a networked environment [2,3,4,5,6]. As the significant advantages of lower cost of design and easier maintenance, NCSs are widely used in unmanned marine vehicle (UMV). The networked UMV is often used for its practical applications in the fields of military or non-military missions, management of fishery resources, marine environmental monitoring or cleaning, the exploration of oil and gas [7]. With the exploitation of the oceans, the analysis of UMV systems is emerged as a hot subject of investigation. UMV systems are inevitably subject to the effects of climate, waves and other uncertainties when carrying out tasks. As a result, plentiful control methods are proposed to guarantee the performance of the UMV systems, such as, sliding mode control [8,9], formation control [10,11,12], trajectory tracking control [13,14,15], neural network control [16,17] and so on.

In reference [18], the coordinated path tracking problem for UMV systems with directional topologies based on distributed control is investigated. A guidance method based finite-time line-of-slight is introduced to track the desired path for independent UMV. In [19], a dynamic output feedback control (DOFC) strategy is designed for UMV tracking problems with delay and packet loss. To resist disturbances, in reference [20], a coordinated tracking control strategy of UMV systems with unknown dynamics and external disturbances is studied. A wavelet neural network-based distributed tracking controller is introduced to accurately estimate unknown dynamics and external disturbances. A dwell control method for UMV systems is presented in [21] to counteract the effects of unknown size and orientation disturbances. An adaptive law for slow changes to gently alter the navigation of the vehicle is proposed to minimise positioning errors. In addition to the above-mentioned interference from environmental factors, UMV systems are vulnerable to cyber attavk as the open nature of the wireless network. Generally, there exist two main categories of cyber attack on NCSs. One is the denial-of-service (DoS) attack that blocks data transmission and the other is the deception attack that injects false information into the transmitted data [22,23]. The network-based Takagi-Sugeno (T-S) fuzzy UMV systems under DoS attack are studied and a semi-Markovian jumping system description of the DoS attack phenomenon is presented in [24]. In reference [25], hybrid attack including DoS attack and deception attack is investigated. A model which based on the T-S fuzzy system with random switching is proposed to defend against the hybrid attack.

More critically, traditional time-triggered control completes the sampling task within a fixed sampling period where sampling method inevitably wastes the network resources. The network channel is congested in severe cases and further causes packet loss and transmission delay. The event-triggered mechanism (ETM) is first proposed in [26]. It gradually becomes a hot research topic in past few decades and a significant number of achievements are emerged [27,28,29]. In reference [30], the problem of event-triggered dynamic localisation of switched UMV systems is investigated . A novel weighted ETM that considers the switching characteristics is studied. The containment problem of networked under actuated UMV systems is investigated in [31]. To guide the UMV systems toward the corresponding points of reference, an event-triggered control scheme is designed for individual UMV based on the observational data. This method effectively reduces the communication burden. In reference [32], a novel robust adaptive fault-tolerant control strategy and an improved multiplied ETM for UMV systems are introduced. An estimation model with a parsimonious form is used to design the ETM. As can be seen from the above research results, saving network resources is particularly important. As the quantizer can moderately compress the signal before transmission, the network bandwidth occupied by the signal transmission is significantly reduced [33,34]. It improves the utilization rate of communication resources. However, to the best of our knowledge, rare work on the problem of adaptive event-triggered mechanism (AETM) and quantitative mechanism based DOFC for UMV systems in the presence of DoS attack is performed yet. Therefore, the main motivation of this paper to shorten such a gap by initiating a systematic study.

Based on the above discussions and considering that the state vectors of the UMV system may not be all measurable due to the various complex environmental factors, a DOFC strategy which based on the ETM and the quantitative mechanism is investigated in this paper. The measurement data from the sampler is processed by the event-triggered unit and the quantitative unit. The processed measurement data is then sent to the land-based control unit. The calculated control signal is eventually transmitted to the UMV closed-loop system through the communication channel. The occurrence of aperiodic DoS attack is considered in the transmission channel of the control signal. In addition, an AETM is adopted. The threshold parameter for trigger condition is adjusted online by AETM. Through the construction of the Lyapunov functional, the conditions of global exponential stability for the UMV systems are obtained. Finally, the effectiveness of the proposed methods is verified by simulation. The main contributions are summarized in the following points:

(i): A novel closed loop system model of networked UMV systems with an event-triggered unit and a quantizer is established. The impact of network induced delay, external disturbance and aperiodic DoS attack are involved.
(ii): A quantitative mechanism is installed on the basis of adaptive event-triggered unit which can further save the network resources. And an environment accompanied by more severe cyber attack is considered.

The paper is organized as follows. In section 2, the modeling of the closed UMV systems are obtained. And a dynamic output feedback controller based on AETM and quantitative mechanism under aperiodic DoS attack is designed. Section 3 gives the sufficient criterion for ensuring global exponential stability of system with an expected

H_{\infty}

disturbance attenuation index and the design method of controller. A numerical simulation to verify the effectiveness of the proposed control strategy is given in Section 4. In section 5, conclusions and future work are shown.

1.1. Notation

Throughout this paper, the notation as follows is used:

R^{n}

denotes the n-dimensional Euclidean space,

{∥\cdot∥}_{2}

denotes the Euclidean vector norm,

P > 0

means that the matrix

P

is real symmetric positive definite,

I

is the identity matrix with appropriate dimension, the symbol ∗ denotes the symmetric term in a matrix,

s y m (P)

denotes

P + P^{T}

λ_{\min} (A)

and

λ_{\max} (A)

denotes the minimum or maximum eigenvalue of the matrix

A

, respectively.

2. Preliminaries and problem formulation

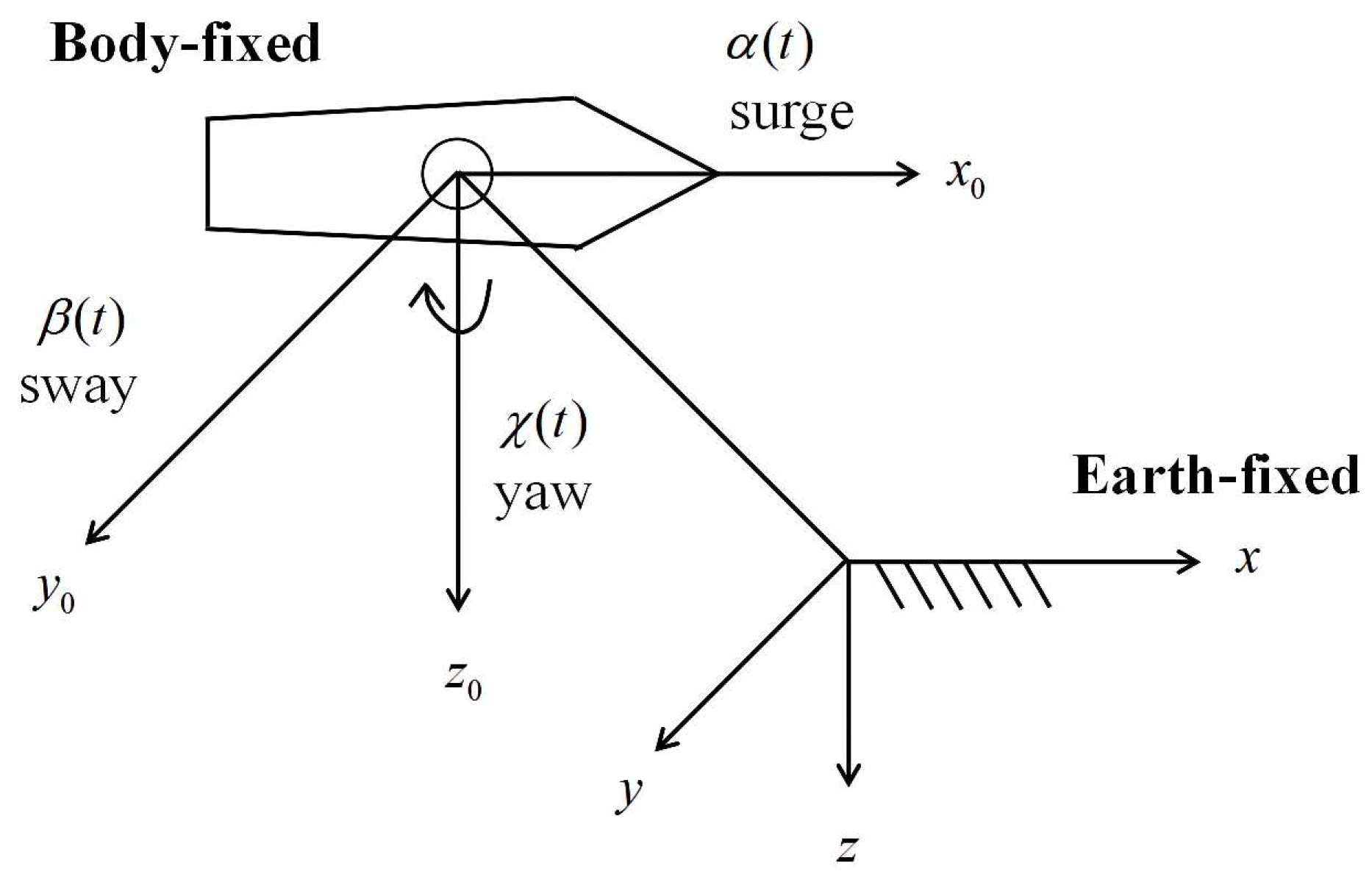
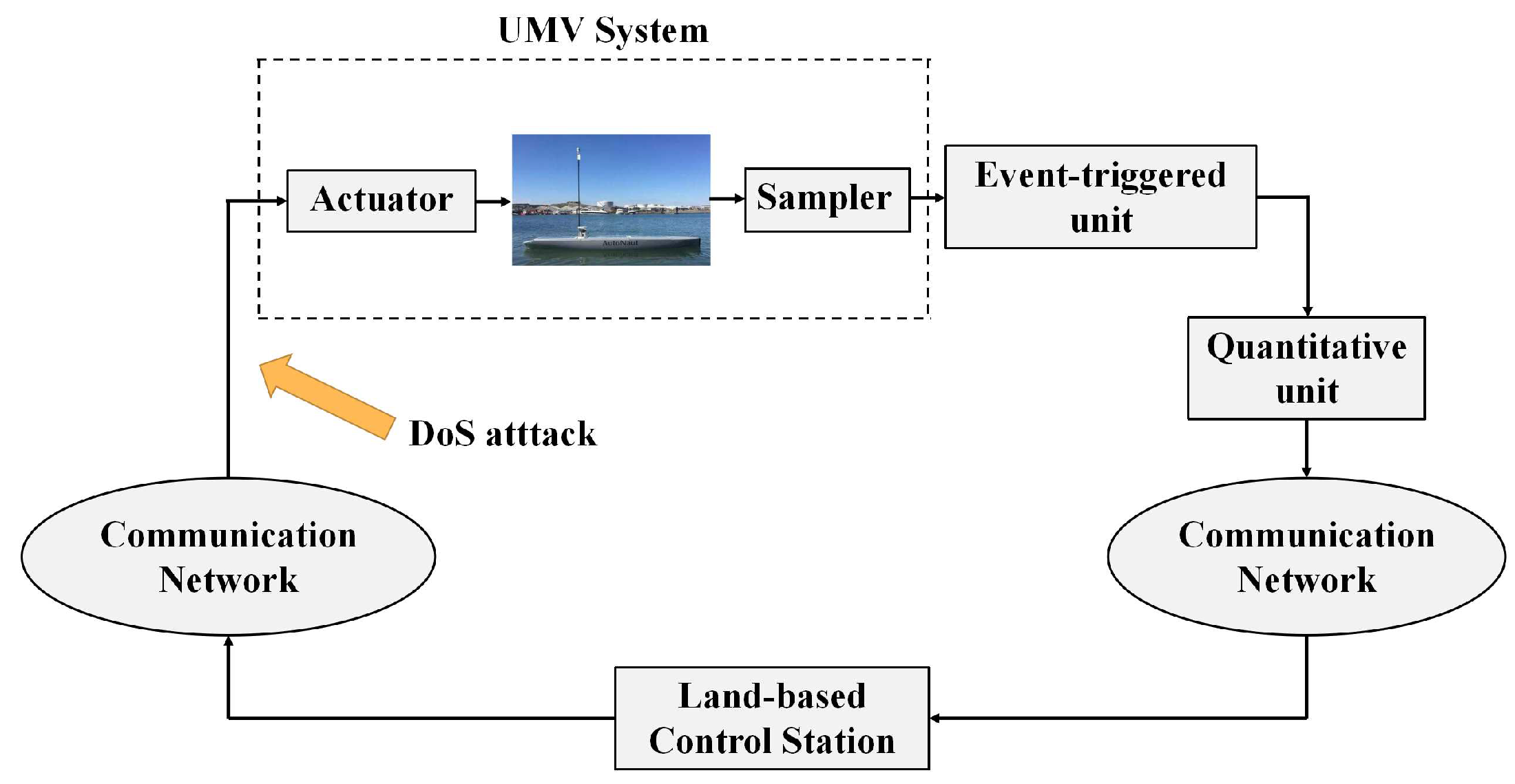
2.1. Networked modelling for the UMV system

The main work is done in this section to model the UMV. As the usual model for describing the marine vehicle dynamics is the first order Nomoto model. The model of a nominally higher order state space is comparable to it [35]. Consequently, a three degrees of freedom UMV which is supplied with thrusters is served as a reference model for the target plant. In Figure 1, a structural diagram of the considered UMV system is shown with the ground-mounted frame and the body-mounted frame. Where

x_{0}

y_{0}

and

z_{0}

indicate the vertical, horizontal and normal axes in the frame, respectively. The earth-fixed reference frames are represented as x , y and z.

The body-fixed equation for the UMV is described as the formula below:

\begin{matrix} M \dot{v} + N v (t) + G η (t) = u (t) \end{matrix}

(1)

where

v (t) = {[α (t) β (t) γ (t)]}^{T}

represents the velocity vector. The velocity of surge, sway and yaw is denoted as

α (t), β (t)

and

γ (t)

, respectively.

η (t) = {[x_{f} (t) y_{f} (t) φ_{f} (t)]}^{T}

denotes a vector containing position and angle, where

x_{f} (t)

and

y_{f} (t)

represent positions,

φ_{f}

represents the yaw angle. The control input vector is denoted as

u (t) = {[u_{1} (t) u_{2} (t) u_{3} (t)]}^{T}

. The forces of surge and sway are denoted as

u_{1} (t)

u_{2} (t)

and the moment in yaw is denoted as

u_{3} (t)

, respectively;

M

is the matrix of inertia and it satisfies

M = M^{T} > 0

. Matrix

N

indicates damping. And matrix

G

indicates mooring forces. The function

η (t)

is satisfied as

\begin{matrix} \dot{η} = K (ψ (t)) v (t) \end{matrix}

(2)

where

K (ψ (t)) = [\begin{matrix} cos (ψ (t)) & - sin (ψ (t)) & 0 \\ sin (ψ (t)) & cos (ψ (t)) & 0 \\ 0 & 0 & 1 \end{matrix}]

Due to UMV may stop or anchor when executing tasks. We assume the yaw angle

ψ (t)

is sufficiently small. As the result,

sin (ψ (t)) \approx 0

and

cos (ψ (t)) \approx 1

can be obtained. Then the matrix

K (ψ (t)) \approx I

is obtained. Give some definitions as

M^{- 1} G = A_{1}

- M^{- 1} N = A

B = M^{- 1}

and

v (t) = x (t)

. Such that the system (1) is expressed as:

\begin{matrix} \dot{x} (t) = A x (t) + B u (t) - A_{1} g (t, x (t)) \end{matrix}

(3)

where

g (t, x (t)) = η (t)

, and it represents a vector-valued function of state vector

x (t)

which is nonlinear. Inevitable disturbances such as wind and waves are denoted as

\tilde{ω} (t)

. The system (3) is then obtained as

\begin{matrix} \dot{x} (t) = A x (t) + B u (t) + \tilde{ω} (t) - A_{1} g (t, x (t)) \end{matrix}

(4)

As mentioned above, there is a high degree of uncertainty when marine vehicles operates on the ocean. The main objective is to mitigate the yaw velocity error amplitude. It is accomplished by keeping state

x (t)

track an anticipated reference as accurately as possible. Through a combination of items

\tilde{ω} (t)

and

A_{1} g (t, x (t))

. Equation (4) is rewritten to:

\begin{matrix} \dot{x} (t) = A x (t) + B u (t) + \hat{ω} (t) \end{matrix}

(5)

where

\hat{ω} (t) = \tilde{ω} - A_{1} g (t, x (t))

For the given reference state

x_{r} (t)

. The tracking error

e (t)

is then expressed as

e (t) = x (t) - x_{r} (t)

. Based on the definition of

e (t)

and Equation (5), we have:

\begin{matrix} \dot{e} (t) = A e (t) + B u (t) + ω (t) \end{matrix}

(6)

where

ω (t) = {[ω_{1} (t) ω_{2} (t) ω_{3} (t)]}^{T} = A x_{r} (t) + \hat{ω} (t)

The controlled output

z (t)

is described as:

\begin{matrix} z (t) = C_{z} e (t) \end{matrix}

(7)

where

C_{z}

is the output matrix with

C_{z} = [0 0 1]

From the above equations (6) and (7), one can get that:

\begin{matrix} \{\begin{matrix} \dot{e} (t) = A e (t) + B u (t) + ω (t) \\ z (t) = C_{z} e (t), e (t_{0}) = e_{0} \end{matrix} \end{matrix}

(8)

where

e (t) \in R^{n}

and

u (t) \in R^{u}

represent the error state and the control input, respectively.

ω (t) \in R^{w}

represents the uncertain disturbance and it belongs to

L_{2} [0, \infty)

e_{0} \in R^{n}

represents the initial vector of the error state. The constant matrices

A

B

of appropriate dimensions are known.

In this section, a dynamic error system for the UMV is established. The entire networked UMV systems are illustrated in Figure 2. It integrates an UMV system, a control unit and the communication network. The data packets are transmitted from the sampler to the control unit via the communication network. And the successful transmission of the sampling signal is determined by an ETM. In addition, a quantitative mechanism is also considered to further reduce communication resources. As the communication channel is vulnerable to cyber attack, the considered DOS attack is a common type that can severely jam communication channel. And the UMV closed-loop system cannot successfully receive control signal during the interval that the DoS attack signal occurs.

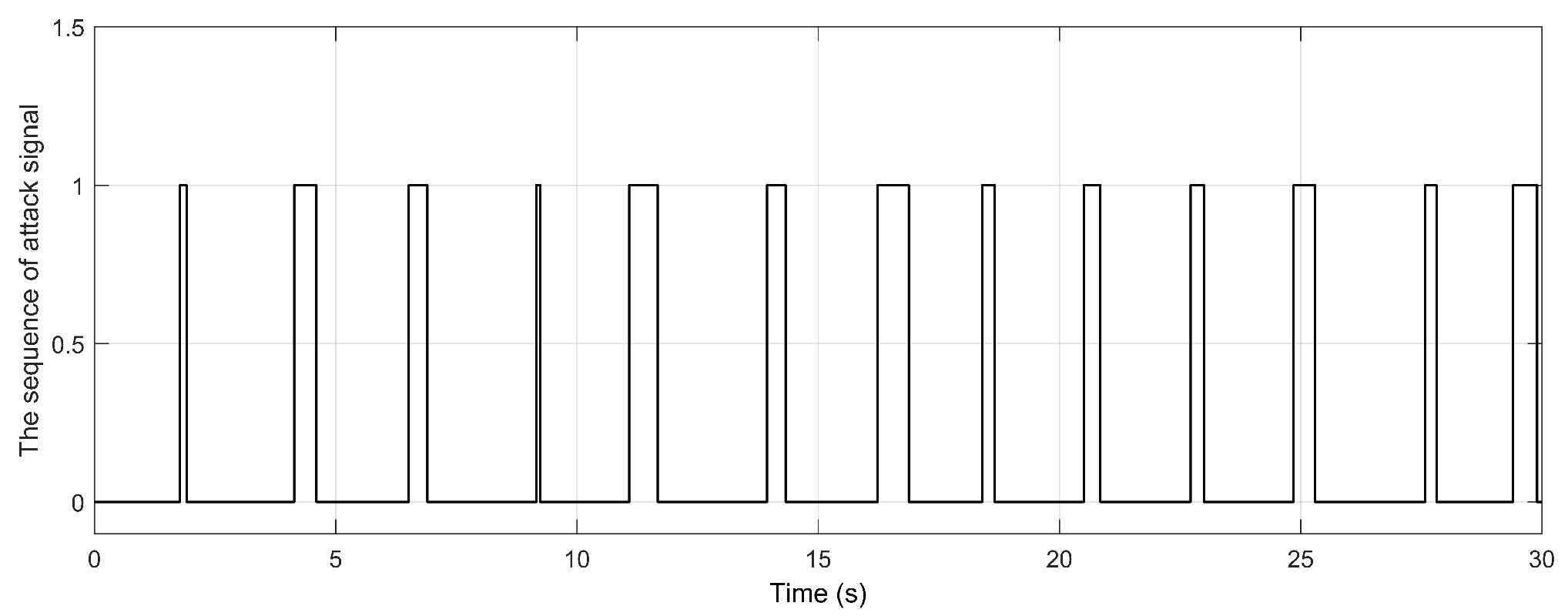
2.2. Aperiodic DoS attack

The occurrence of aperiodic DoS attack is integrated into the network channel between the land-based control unit and the UMV system. The

n^{t h}

DoS attack interval is represented as

S_{n} ≜ [l_{n}, l_{n} + δ_{n}), (n \in N, l_{n} \geq 0, l_{0} = 0)

. During this interval, the network channel allows the data packet transmission and the attack signal is inactive [36]. Similarly, define

T_{n} ≜ [l_{n} + δ_{n}, l_{n + 1})

as the

n^{t h}

DoS attack interval, the attack signal during this time interval is active. Released data packets from the control unit cannot be transmitted to the UMV system. It should be noted that

δ_{n} > 0

represents the sleeping length of the attack signal. We can get that the occurrence of the attack within a period appears at the time instant

l_{n} + δ_{n}

until the end of the time instant

l_{n + 1}

, which satisfies

l_{n + 1} > l_{n} + δ_{n}

. In addition, the DoS attack signal is aperiodic. It indicates there are variations in sleeping length

δ_{n}

. With the above discussions, the aperiodic attack signal is defined by a piecewise function as follows to represent whether the attack is active or not:

\begin{matrix} ℘_{D o S} = \{\begin{matrix} 0, t \in S_{n} \\ 1, t \in T_{n} \end{matrix} \end{matrix}

(9)

where the constant 0 in the piecewise function (9) indicates the DoS attack signal is inactive, the value of 1 indicates the DoS attack signal is active.

Note that if the DoS attack lasts long enough, the closed-loop system will be unstable and difficult to meet the desired performance indicators. To limit the dwell time and frequency of the attack signal, the assumptions are introduced to aid in the theoretical derivation.

Assumption 1

[36]: There are two positive scalars

δ_{\min}

ϑ_{\max}

, which satisfy

δ_{\min} \leq \inf_{n \in N} δ_{n}

for

S_{n}

ϑ_{\max} \geq \sup_{n \in N} \{l_{n + 1} - l_{n} - δ_{n}\}

for

T_{n}

, respectively.

Assumption 2

[36]: The frequency of the DoS attack signal transition from active to inactive is defined as

N_{t} (0, t)

during the time interval

[0, t)

. It is expressed as

N_{t} (0, t) = c a r d \{n \in N | t > l_{n} + δ_{n}\}

, the symbol

c a r d

indicates the number of items contained in the set. Given a parameter

τ_{D} \in R > 0

, arbitrary

\hat{k} \in R \geq 0

, the DoS frequency constraint is satisfied by the sequence of attack signal given by

T_{n}

for all

\forall t \in R \geq 0

, the following condition is guaranteed:

\begin{matrix} N_{t} (0, t) \leq \hat{k} + \frac{t}{τ_{D}} \end{matrix}

With the consideration of DoS attack, the error dynamic system is obtained as:

\begin{matrix} \{\begin{matrix} \{\begin{matrix} \dot{e} (t) = A e (t) + B u (t) + ω (t), t \in S_{n} \\ \dot{e} (t) = A e (t) + ω (t), t \in T_{n} \end{matrix} \\ z (t) = C_{z} e (t), e (t_{0}) = e_{0} \end{matrix} \end{matrix}

(10)

Remark 1.

According to the Assumptions 1 and 2, the lower sleep length boundary

δ_{\min}

, the upper attacking length boundary

ϑ_{\max}

and the DoS attack frequency

N_{t} (0, t)

are defined. The scalar

τ_{D}

in the constraint frequency condition is the average dwell-time. In addition, the upper sleeping length boundary is defined as

δ_{\max} ≜ \sup_{n \in N} \{δ_{n}\}

2.3. The adaptive event-triggered communication mechanism

Due to a large number of data packets are transmitted from the sampler to the land-based control unit. The network channel is inevitably blocked. The considered ETM in UMV systems can not only reduce the amount of data traffic in the channel, but also protect against DoS attack. The sampling period of sampler is defined as h. And it satisfies

0 < h < δ_{n}

. We define a sampled-packet

(k, y (k h))

which contains the released sampled signal

y (k h), k \in \{1, 2, . . .\}

and the corresponding marker k. The packets are transmitted from the event-triggered unit to the quantizer via channel after encapsulation. When the

k t h

data packet is transmitted successfully, we define this moment as

t_{k}

t \in N_{+}

and one can obtain that

t_{1} < t_{2} < \cdot \cdot \cdot < t_{k} < \cdot \cdot \cdot

It should be noted that an ETM with dynamic threshold is investigated in this paper. It compares the last successfully released packet

(t_{k}, y (t_{k} h)), t_{k} \in l

with the current packet

(t_{k} + d, y (t_{k} h + d h))

d \in \{1, 2, . . .\}

to make the decision whether to transmit the current packet. In reference [37], the current packet released from the event-triggered unit and update the trigger time instant if the condition (11) holds:

\begin{matrix} t_{k + 1} h = \inf \{t_{k} h + d h > t_{k} h | g (t_{k} + d) h > 0\} \end{matrix}

(11)

where

g ((t_{k} + d) h) = {[y ((t_{k} + d) h) - y (t_{k} h)]}^{T} Φ [y ((t_{k} + d) h) - y (t_{k} h)] - σ ((t_{k} + d) h) y {(t_{k} h)}^{T} Φ y (t_{k} h)

, the item

σ ((t_{k} + d) h)

represents the threshold parameter which is dynamic and variable, the weighting matrix

Φ

satisfies

Φ > 0

, which is determined in the next section. And the threshold parameter

σ

is satisfied with the condition (12):

\begin{matrix} σ ((k + 1) h) = (1 - κ σ ((k + 1) h) σ (k h) r (k h) \end{matrix}

(12)

where

r (k h) = {[(y (t_{k} + k) h) - y (t_{k} h)]}^{T} Φ [(y (t_{k} + k) h) - y (t_{k} h)]

(t_{k} + k) h \in [t_{k} h, t_{k + 1} h)

κ > 0

is a given constant.

Lemma 1.

[19] For the condition (12) of the dynamic threshold parameter, an initial threshold

σ_{0} \in [0, 1)

is given that satisfies the condition below

\begin{matrix} 0 \leq σ (k h) \leq σ_{0} \leq 1 \end{matrix}

(13)

for all

k \in N

. And

\{σ (k h)\}

represents a sequence consisting of threshold parameters at different moments. Remark 2. It should be mentioned that the event-triggered condition is only related to the current sample signal and the previous trigger signal. The current data packets are passed to the control unit when the trigger condition (11) is fulfilled. The control signal is updated once. In addition, the threshold parameter in (11) is not always fixed and its value is dynamically adjusted based on condition (12).

Nevertheless, the condition of ETM (11) has some limitations. When the DoS attack occurs, condition (11) cannot be used directly. With this situation, the time instant of the event trigger is redefined as:

\begin{matrix} t_{k, n} h = {t_{k} h satisfying (11) | t_{k} h \in S_{n}} \cup {l_{n}} \end{matrix}

(14)

The quantitative unit receives packets released by the event-triggered unit is defined as

\bar{y} (t) = y (t_{k, n} h)

2.4. The quantitative mechanism

A quantizer is considered to be installed in the communication channel between the sampler and the control unit. The measurement output signal

\bar{y} (t)

is quantized by quantizer

Q (\bar{y} (t))

before being transmitted. And it is redefined as

\tilde{y} (t)

. The static logarithmic and time-invariant quantizer [38] is investigated to process signal in this paper. The quantitative level is given as:

\begin{matrix} U = \{\pm u_{m}, u = ρ_{m} u_{0}, m = 0, \pm 1, \pm 2, . . .\} \cup \{\pm u_{0}\} \cup \{0\} \end{matrix}

(15)

where

0 < ρ < 1

represents the quantification density and

u_{0} > 0

. The quantification function

Q (\cdot)

is by the definition as (16):

\begin{matrix} Q (ν) = \{\begin{matrix} u_{m}, \frac{1}{1 + δ_{y}} u_{m} < υ < \frac{1}{1 - δ_{y}} u_{m} \\ 0, ν = 0 \\ - Q (- ν), ν < 0 \end{matrix} \end{matrix}

(16)

where

δ_{y} = \frac{1 - ρ}{1 + ρ}

The quantizer

Q (\bar{y} (t))

is denoted as the following form:

\begin{matrix} Q (\bar{y} (t)) = {[Q ({\bar{y}}_{1} (t)), Q ({\bar{y}}_{2} (t)), . . ., Q ({\bar{y}}_{n} (t))]}^{T} \end{matrix}

(17)

For the quantification effects, we deal with quantification errors with the help of the sector constraint method which introduced in [38], where the quantizer is remodelled as:

\begin{matrix} Q (\bar{y} (t)) - \bar{y} (t) = Δ_{y} \bar{y} (t) \end{matrix}

(18)

where

Δ_{y} = d i a g \{Δ_{y_{1}}, Δ_{y_{2}}, . . ., Δ_{y_{n}}\}, Δ_{y_{*}} \in [- δ_{y_{*}}, δ_{y_{*}}]

Based on the above discussions, the quantified data packets

\tilde{y} (t)

is expressed as (19):

\begin{matrix} \tilde{y} (t) = (I + Δ_{y}) \bar{y} (t) = (I + Δ_{y}) y (t_{k, n} h) \end{matrix}

(19)

Network induced delay in communication channel is inevitable. The networked delay is represented as

τ_{k, n}

which occurs at time instant

t_{k, n}

. It satisfies condition

0 \leq τ_{t_{k, n}} \leq \bar{τ}

. Such that, the controller successfully receives the released data packets at time

t_{k, n} h + τ_{t_{k, n}}

and held until time

t_{k + 1, n} h + τ_{t_{k + 1, n}}

. We make the following definition

K_{k, n} = [t_{k, n} h + τ_{t_{k, n}}, t_{k + 1, n} h + τ_{t_{k + 1, n}})

, from Equation (14), we have

t_{0, n} ≜ h_{0}

, and

k \in C (n) ≜ \{0, 1, . . ., k (n)\}

, where

k (n) = \sup \{k \in N | t_{k, n} \leq h_{n} + δ_{n}\}

, if

t_{k (n)} h \leq h_{n} + δ_{n}

, there must exist a time instant

t_{k (n) + 1}

satisfying

t_{k (n) + 1} h > h_{n} + δ_{n}

. In addition, the event interval

K_{k, n}

is divided into the forms as follows:

\begin{matrix} K_{k, n} = ⋃_{d = 0}^{d_{k}} ζ_{d} \end{matrix}

(20)

where

\begin{matrix} d_{k} & = t_{k + 1, n} - t_{k, n} - 1 \\ ζ_{0} & = [t_{k, n} h + τ_{t_{k, n}}, t_{k, n} h + h + τ_{t_{k, n}}) \\ ζ_{d} & = [t_{k, n} h + d h + τ_{t_{k, n}}, t_{k, n} h + (d + 1) h + τ_{t_{k, n}}) \\ ζ_{d_{k}} & = [t_{k, n} h + d_{k} h + τ_{t_{k, n}}, t_{k + 1, n} h + τ_{t_{k + 1, n}}) \end{matrix}

The delay of the time instant t and error function are defined as

τ_{k, n} (t)

and

η_{k, n} (t)

, respectively. And the following equations are obtained:

\begin{matrix} τ_{k, n} (t) = t - t_{k, n} h - d h \end{matrix}

(21)

\begin{matrix} η_{k, n} = y (t_{k, n} h) - y ((t_{k, n} + d) h) \end{matrix}

(22)

From equations (16), (17) and (18), we can obtain that the differentiable piecewise linear function

τ_{k, n} (t)

satisfies the condition as follows:

\begin{matrix} 0 \leq τ_{t_{k, n}} \leq τ_{t_{k, n}} (t) \leq \max \{τ_{t_{k, n}}, τ_{t_{k + 1, n}}\} + h \leq τ_{m} + h ≜ τ_{M} \end{matrix}

(23)

where

t_{m}

denotes the networked delay upper bound. And

τ_{M}

denotes the boundary parameter parameter. It is related to the sampling period h and the networked delay

τ_{k, n}

. Such that, one can obtain that:

\begin{matrix} \bar{y} (t) = y (t_{k, n} h) = y (t_{k, n} h + d h) + η_{k, n} (t) \end{matrix}

(24)

The signal received by the controller is described as:

\begin{matrix} \tilde{y} (t) = (I + Δ_{y}) \bar{y} (t) = (I + Δ_{y}) [y (t - τ_{k, n} (t)) + η_{k, n} (t)] \end{matrix}

(25)

2.5. The investigated dynamic output feedback control strategy

The dynamic output feedback controller is considered as follows:

\begin{matrix} \{\begin{matrix} {\dot{x}}_{c} (t) = A_{c} x_{c} (t) + B_{c} \tilde{y} (t) + D_{c} x_{c} (t - τ_{k, n} (t)) \\ u (t) = \{\begin{matrix} C_{c} x_{c} (t), t \in S_{n} \cap K_{k, n} \\ 0, t \in T_{n} \end{matrix} \end{matrix} \end{matrix}

(26)

where

x_{c} (t) \in R^{n}

represents the state vector of the controller. Matrices

A_{c}

B_{c}

C_{c}

and

D_{c}

are controller gains with appropriate dimensions. Defining

\tilde{x} (t) = c o l \{e (t), x_{c} (t)\}

. By combining error dynamic system (10), trigger time instant condition (11) and the system (27), an extended state space equation is obtained as:

\begin{matrix} \{\begin{matrix} \dot{\tilde{x}} (t) = \{\begin{matrix} {\tilde{A}}_{1} \tilde{x} (t) + {\tilde{B}}_{1} \tilde{x} (t - τ_{k, n} (t)) + {\tilde{B}}_{2} η_{k, n} (t) + {\tilde{B}}_{ω} ω (t), \\ t \in S_{n} \cap K_{K, N} \\ {\tilde{A}}_{2} \tilde{x} (t) + {\tilde{B}}_{1} \tilde{x} (t - τ_{k, n} (t)) + {\tilde{B}}_{2} η_{k, n} (t) + {\tilde{B}}_{ω} ω (t), \\ t \in T_{n} \end{matrix} \\ z (t) = \tilde{C} \tilde{x} (t) \end{matrix} \end{matrix}

(27)

where

{\tilde{A}}_{1} = [\begin{matrix} A & B C_{c} \\ 0 & A_{c} \end{matrix}]

{\tilde{B}}_{1} = [\begin{matrix} 0 & 0 \\ (I + Δ_{y}) B_{c} C & D_{c} \end{matrix}]

{\tilde{B}}_{2} = [\begin{matrix} 0 \\ (I + Δ_{y}) B_{c} \end{matrix}]

{\tilde{B}}_{ω} = [\begin{matrix} I \\ 0 \end{matrix}]

{\tilde{A}}_{2} = [\begin{matrix} A & 0 \\ 0 & A_{c} \end{matrix}]

\tilde{C} = [\begin{matrix} C_{z} & 0 \end{matrix}]

. From equations (11), (13), (14) above, for

t \in S_{n} \cap K_{k, n}

, the inequality as follows is obtained:

\begin{matrix} η_{k, n}^{T} (t) Φ η_{k, n} (t) \leq σ_{0} Θ^{T} Φ Θ \end{matrix}

(28)

where

Θ = η_{k, n} (t) + C H \tilde{x} (t - τ_{k, n} (t))

and matrix

H

is selected as

{[\begin{matrix} I & 0 \end{matrix}]}^{T}

The model of dynamic output feedback controller and an extended state space equation are given in this section. For analyzing the global exponentially stability of the system (27) in the next section, some preparations are given below.

Definition 1.

[36]: The global exponentially stability of system (27) with

ω (t) = 0

is guaranteed, if there exist positive scalars

μ > 0

and

ρ > 0

, which satisfy:

\begin{matrix} \tilde{x} (t) \leq μ^{- ρ t} {∥℘_{0}∥}_{τ} \end{matrix}

(29)

for

\forall t \geq 0

, where

{∥℘_{0}∥}_{τ} = \sup_{- τ \leq t \leq 0} \{∥\tilde{x} (t)∥, ∥\dot{\tilde{x}} (t)∥\}

ρ

denotes the decay rate.

Lemma 2.

[39]: Given a matrix

Y

which is positive define symmetric and it satisfies

Y > 0

, a scalar a, arbitrary vector

x

, the inequality as the following form:

\begin{matrix} - a \int_{t - a}^{t} {\dot{x}}^{T} (s) Y \dot{x} (s) d s \leq - Ξ_{1}^{T} Y Ξ_{1} + Ξ_{1}^{T} Z Ξ_{2} + Ξ_{1}^{T} Z^{T} Ξ_{2} - Ξ_{2}^{T} Y Ξ_{2} \end{matrix}

(30)

holds, where

Ξ_{1} = x (t - τ (t)) - x (t)

and

Ξ_{2} = x (t - a) - x (t - τ (t))

and

Z

denotes a real matrix which satisfies

\begin{matrix} [\begin{matrix} Y & Z \\ * & Y \end{matrix}] \geq 0 \end{matrix}

Lemma 3.

[40]: Given a matrix

U

which is positive define symmetric and it satisfies

U > 0

, the inequality as the following form:

\begin{matrix} P Q + {(P Q)}^{T} \leq P U P^{T} + Q^{T} U^{- 1} Q \end{matrix}

(31)

holds, where

P

and

Q

are real matrices with appropriate dimensions.

3. Main result

A lemma is first introduced to help with the subsequent theoretical analysis. The

H_{\infty}

performance and the exponential stability of the system (27) is analyzed, and the design of the controller (26) is given. Based on the previous descriptions, the construction of a piecewise Lyapunov functional is expressed as:

\begin{matrix} V (t) = \{\begin{matrix} V_{1} (t), t \in S_{n} \cap K_{k, n} \\ V_{2} (t), t \in T_{n} \end{matrix} \end{matrix}

(32)

where

V_{i} (t) = {\tilde{x}}^{T} (t) P_{i} \tilde{x} (t) + \int_{t - τ_{M}}^{t} {\tilde{x}}^{T} (s) ζ_{i} R_{i} \tilde{x} (s) d s + τ_{M} \int_{- τ_{M}}^{0} \int_{t + θ}^{t} {\tilde{x}}^{T} (s) ζ_{i} Z_{i} \tilde{x} (s) d s d θ

and

ζ_{i} = e^{2 {(- 1)}^{i} α_{i} (t - s)}

Lemma 4.

[28]: Given the parameters

δ_{m i n}

ϑ_{m a x}

τ_{D} \in R > 0

of the DoS attack, and the boundary parameter

τ_{M} > 0

, consider the system (27) without disturbance

ω (t)

under DoS attack (9) and the controller (26). If for the given constants

α_{i} \in (0, + \infty)

σ_{0} \in (0, 1)

, there are some symmetric positive define matrices

P_{i}

R_{i}

Z_{i}, (i = 1, 2)

and

Φ

with appropriate dimensions. Such that, along the trajectories of the system (27), the following inequalities are obtained:

\begin{matrix} V (t) = \{\begin{matrix} e^{- 2 α_{1} (t - l_{n})} V (l_{n}), t \in S_{n} \\ e^{2 α_{2} (t - l_{n} - δ_{n})} V (l_{n} + δ_{n}), t \in T_{n} \end{matrix} \end{matrix}

(33)

Based on the above lemmas and definition. The stability analysis of the system (27) is given below.

3.1. The analysis of stability

Theorem 1.

Given fixed parameters

δ_{m i n}

ϑ_{m a x}

τ_{D} \in R

of the DoS attack, and the boundary parameter

τ_{M} > 0

, consider the system (27) without disturbance

ω (t)

and the controller (26). If for the given scalars

σ_{0} \in (0, 1)

α_{i} \in (0, + \infty)

, there are some symmetric positive define matrices

P_{i}

R_{i}

Z_{i}

(i \in 1, 2)

and Φ of appropriate dimensions, the conditions as follows are satisfied.

\begin{matrix} P_{1} \leq μ_{2} P_{2}, P_{2} \leq μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} P_{1}, \\ R_{i} \leq μ_{3 - i} R_{3 - i}, Z_{i} \leq μ_{3 - i} Z_{3 - i}, \end{matrix}

(34)

\begin{matrix} 0 < ε ≜ \frac{2 α_{1} δ_{m i n} - 2 (α_{1} + α_{2}) τ_{M} - 2 α_{2} ϑ_{m a x} - \ln (μ_{1} μ_{2})}{τ_{D}} . \end{matrix}

(35)

such that, the system (27) under aperiodic DoS attack (9) is globally exponentially stable (GES) with decay rate

ρ ≜ ε / 2

Proof.

Based on the Lemma 4, for

t \geq 0

, the inequalities as follows:

\begin{matrix} \{\begin{matrix} V_{1} (t) \leq e^{- 2 α_{1} (t - l_{n})} V_{1} (l_{n}), t \in S_{n} \\ V_{2} (t) \leq e^{- 2 α_{2} (t - l_{n} - δ_{n})} V_{2} (l_{n} + δ_{n}), t \in T_{n} \end{matrix} \end{matrix}

(36)

hold. When

t \to l_{n}

, combining inequalities (34), we can obtain:

\begin{matrix} V ({(l_{n})}^{+}) & = {\tilde{x}}^{T} ({(l_{n})}^{+}) P_{1} \tilde{x} ({(l_{n})}^{+}) + \int_{l_{n} - τ_{M}}^{l_{n}} {\tilde{x}}^{T} (s) e^{- α_{1} (l_{n} - s)} R_{1} \tilde{x} (s) d s \\ + τ_{M} \int_{- τ_{M}}^{0} \int_{l_{n} + θ}^{l_{n}} {\dot{\tilde{x}}}^{T} (s) e^{- α_{1} (l_{n} - s)} Z_{1} \dot{\tilde{x}} (s) d s d θ \\ \leq μ_{2} [{\tilde{x}}^{T} ({l_{n}}^{-}) P_{2} \tilde{x} ({l_{n}}^{-}) + \int_{l_{n} - τ_{M}}^{l_{n}} {\tilde{x}}^{T} (s) e^{2 α_{2} (l_{n} - s)} R_{2} \tilde{x} (s) d s \\ + τ_{M} \int_{- τ_{M}}^{0} \int_{l_{n} + θ}^{l_{n}} {\dot{\tilde{x}}}^{T} (s) e^{α_{2} (l_{n} - s)} Z_{2} \dot{\tilde{x}} (s) d s d θ] \end{matrix}

Similarly, when

t \to l_{n} + d_{n}

, the inequality

e^{- 2 α_{1} (t - s)}

\geq e^{- 2 α_{1} τ_{M}}

\geq e^{2 α_{2} (t - s) - 2 (α_{1} + α_{2}) τ_{M}}

can be obtained for

\forall s \in [t - τ_{M}, t]

. The following inequality is obtained:

\begin{matrix} V_{2} ((l_{n} + δ_{n})^{+})) & \leq μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} {\tilde{x}}^{T} (l_{n} + δ_{n}) P_{1} \tilde{x} (l_{n} + δ_{n}) \\ + \int_{l_{n} + δ_{n} - τ_{M}}^{l_{n} + δ_{n}} μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} {\tilde{x}}^{T} (s) e^{- 2 α_{1} (l_{n} + δ_{n} - s)} R_{1} \tilde{x} (s) d s \\ + τ_{M} \int_{- τ_{M}}^{0} \int_{l_{n} + δ_{n} + θ}^{l_{n} + δ_{n}} μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} {\dot{\tilde{x}}}^{T} (s) e^{- 2 α_{1} (l_{n} + δ_{n} - s)} Z_{2} \dot{\tilde{x}} (s) d s d θ \\ = μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} V_{1} (l_{n} + δ_{n}) = μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} V_{1} {((l_{n} + δ_{n})}^{-}) \end{matrix}

From the inequalities above, one can obtain that:

\begin{matrix} \{\begin{matrix} V_{1} (l_{n}) \leq μ_{2} V_{2} (l_{n}^{-}) \\ V_{2} (l_{n} + δ_{n}) \leq μ_{1} e^{2 (α_{1} + α_{2}) τ_{M}} V_{1} ({(l_{n} + δ_{n})}^{-}) \end{matrix} \end{matrix}

(37)

1. For

t \in S_{n}

, it is well known from Assumption 1, Equations (36) and (37) that

\begin{matrix} V_{1} (t) & \leq e^{- 2 α_{1} (t - l_{n})} V_{1} (l_{n}) \leq μ_{2} e^{- 2 α_{1} (t - l_{n})} V_{2} (l_{n}^{-}) \leq \dots \leq e^{g_{1}} V_{1} (0) \leq e^{f_{1}} V_{1} (0) \end{matrix}

where

g_{1} = 2 n (α_{1} + α_{2}) τ_{M} + 2 α_{2} [(l_{n} - l_{n - 1} - δ_{n - 1}) + (l_{n - 1} - l_{n - 2} - δ_{n - 2}) + \dots + (l_{1} - l_{0} - δ_{0})] - 2 α_{1} (δ_{n - 1} + δ_{n - 2} + \dots + δ_{0}) + n \ln (μ_{1} μ_{2}), f_{1} = 2 n (α_{1} + α_{2}) τ_{M} + 2 α_{2} n ϑ_{\max} - 2 α_{1} n δ_{\min} + n \ln (μ_{1} μ_{2})

By combining Assumption 2 and Condition (35) , one can obtain that:

\begin{matrix} V_{1} (t) \leq V_{1} (0) e^{ϖ_{1}} e^{- 2 ρ t} \end{matrix}

(38)

where

ϖ_{1} = [2 (α_{1} + α_{2}) τ_{M} + 2 α_{2} ϑ_{\max} - 2 α_{1} δ_{\min} + \ln (μ_{1} μ_{2})] \hat{k}

2. For

t \in T_{n}

, the following conclusion is obtained as the same way

\begin{matrix} V_{2} (t) & \leq e^{2 α_{2} (t - l_{n} - δ_{n})} V_{2} (l_{n} + δ_{n}) \leq μ_{1} e^{2 α_{2} (t - l_{n} - δ_{n}) + 2 (α_{1} + α_{2}) τ_{M}} V_{1} ({(l_{n} + δ_{n})}^{-}) \\ \leq \dots \leq \frac{1}{μ_{2}} e^{g_{2}} V_{1} (0) \leq \frac{1}{μ_{2}} e^{f_{2}} V_{1} (0) \end{matrix}

where

g_{2} = 2 (n + 1) (α_{1} + α_{2}) τ_{M} + 2 α_{2} [(l_{n + 1} - l_{n} - δ_{n}) + (l_{n} - l_{n - 1} - δ_{n - 1}) + \dots + (l_{1} - l_{0} - δ_{0})] - 2 α_{1} (δ_{n} + δ_{n - 1} + \dots + δ_{0}) + (n + 1) \ln (μ_{1} μ_{2})

f_{2} = 2 (n + 1) (α_{1} + α_{2}) τ_{M} + 2 α_{2} (n + 1) ϑ_{\max} - 2 α_{1} (n + 1) δ_{\min} + (n + 1) \ln (μ_{1} μ_{2}) .

By combining Assumption 2 and Condition (35) , one can obtain that:

\begin{matrix} V_{2} (t) \leq \frac{1}{μ_{2}} V_{1} (0) e^{ϖ_{2}} e^{- 2 ρ t} \end{matrix}

(39)

where

ϖ_{2} = [2 (α_{1} + α_{2}) τ_{M} + 2 α_{2} ϑ_{\max} - 2 α_{1} δ_{\min} + \ln (μ_{1} μ_{2})] (\hat{k} + 1) .

Make the following definitions:

a ≜ \max \{e^{ϖ_{1}}, \frac{1}{μ_{2}} e^{ϖ_{2}}\}

b_{1} ≜ λ_{\min} (P_{i})

b_{2} ≜ λ_{\max} (P_{i})

b_{3} ≜ b_{2} + τ_{M} λ_{\max} (R_{1}) + \frac{τ_{M}^{2}}{2} λ_{\max} (Z_{1}) .

From inequalities (38) and (39), we have

\begin{matrix} V (t) \leq a e^{- 2 ρ t} V_{1} (0) \end{matrix}

(40)

Alternatively, since

\begin{matrix} V (t) \geq b_{1} {∥\tilde{x} (t)∥}^{2}, V_{1} (0) \leq b_{3} {∥℘_{0}∥}_{h}^{2} \end{matrix}

(41)

Finally, combining inequalities (40) and (41), we have

\begin{matrix} ∥\tilde{x} (t)∥ \leq \sqrt{\frac{a b_{3}}{b_{1}}} e^{- ρ t} {∥℘_{0}∥}_{h} \end{matrix}

(42)

which proves the system (27) is GES with decay rate

ρ

. □

Remark 3.

The value of n in the above proof is related to

N_{t} (0, t)

which is defined in Assumption 2. Furthermore, a large decay rate

ρ

is required to ensure the desirable system performance. From the condition (35), we know that the decay rate

ρ

is related to the DoS attack parameters

δ_{\min}

and

ϑ_{\max}

and the average dwell-time

τ_{D}

. Such that, the smaller the degree of DOS attack, the larger value of

ρ

obtained.

3.2. The analysis of $H_{\infty}$ performance

Theorem 2.

Given fixed parameters

δ_{m i n}

ϑ_{m a x}

τ_{D} \in R > 0

for the DoS attack, and the boundary parameter

τ_{M}

, the controller (26). If for the given scalars

γ \in (0, + \infty)

μ_{i} \in (0, + \infty)

α_{i} \in (0, + \infty)

and

σ_{0} \in (0, 1)

, there are some symmetric positive define matrices

P_{i}

R_{i}

Z_{i}

Φ > 0

and matrix

Y_{i}

(i \in 1, 2)

of appropriate dimensions, such that (34), the matrix inequalities as follows:

\begin{matrix} [\begin{matrix} Σ_{1} & Σ_{21} & Σ_{31} & Σ_{41} & Σ_{5} & Σ_{6} \\ * & - Φ & 0 & {\tilde{B}}_{2}^{T} & I & 0 \\ * & * & - γ^{2} I & {\tilde{B}}_{ω}^{T} & 0 & 0 \\ * & * & * & Σ_{71} & 0 & 0 \\ * & * & * & * & Σ_{8} & 0 \\ * & * & * & * & * & - I \end{matrix}] < 0 \end{matrix}

(43)

\begin{matrix} [\begin{matrix} Σ_{2} & Σ_{22} & Σ_{32} & Σ_{42} & Σ_{5} & Σ_{6} \\ * & - Φ & 0 & {\tilde{B}}_{2}^{T} & I & 0 \\ * & * & - γ^{2} I & {\tilde{B}}_{ω}^{T} & 0 & 0 \\ * & * & * & Σ_{72} & 0 & 0 \\ * & * & * & * & Σ_{8} & 0 \\ * & * & * & * & * & - I \end{matrix}] < 0 \end{matrix}

(44)

hold, where

\begin{matrix} Σ_{1} = & u_{1}^{T} [sym (P_{1} {\tilde{A}}_{1} + R_{1} + 2 α_{1} P_{1})] u_{1} + u_{1}^{T} sym (P_{1} {\tilde{B}}_{1}) u_{2} - u_{3}^{T} e^{- 2 α_{1} τ_{M}} R_{1} u_{3} \\ + e^{- 2 α_{1} τ_{M}} [- {(u_{2} - u_{1})}^{T} Z_{1} (u_{2} - u_{1}) - {(u_{3} - u_{2})}^{T} Z_{1} (u_{3} - u_{2}) \\ + {(u_{2} - u_{1})}^{T} Y_{1} (u_{3} - u_{2}) + {(u_{3} - u_{2})}^{T} Y_{1}^{T} (u_{2} - u_{1})], \\ Σ_{2} = & u_{1}^{T} [sym (P_{2} {\tilde{A}}_{2} + R_{2} + 2 α_{2} P_{2})] u_{1} + u_{1}^{T} sym (P_{2} {\tilde{B}}_{1}) u_{2} - u_{3}^{T} R_{1} u_{3} \\ + [- {(u_{2} - u_{1})}^{T} Z_{2} (u_{2} - u_{1}) - {(u_{3} - u_{2})}^{T} Z_{2} (u_{3} - u_{2}) \\ + {(u_{2} - u_{1})}^{T} Y_{2} (u_{3} - u_{2}) + {(u_{3} - u_{2})}^{T} Y_{2}^{T} (u_{2} - u_{1})], \end{matrix}

\begin{matrix} Σ_{21} = u_{1}^{T} P_{1} {\tilde{B}}_{2}, Σ_{31} = u_{1}^{T} P_{1} {\tilde{B}}_{ω}, Σ_{41} = u_{1}^{T} {\tilde{A}}_{1}^{T} + u_{2}^{T} {\tilde{B}}_{1}^{T}, Σ_{5} = u_{2}^{T} H^{T} C^{T}, \\ Σ_{6} = u_{1}^{T} H^{T} C_{z}^{T}, Σ_{71} = - {(τ_{M}^{2} Z_{1})}^{- 1}, Σ_{8} = - {(σ_{0} Φ)}^{- 1}, Σ_{22} = u_{1}^{T} P_{2} {\tilde{B}}_{2}, \\ Σ_{32} = u_{1}^{T} P_{2} {\tilde{B}}_{ω}, Σ_{42} = u_{1}^{T} {\tilde{A}}_{2}^{T} + u_{2}^{T} {\tilde{B}}_{1}^{T}, Σ_{72} = - {(τ_{M}^{2} Z_{2})}^{- 1}, \\ u_{1} = [\begin{matrix} I_{2 n} & 0_{2 n \times 4 n} \end{matrix}], u_{1} = [\begin{matrix} 0_{2 n \times 2 n} & I_{2 n} & 0_{2 n \times 2 n} \end{matrix}], u_{1} = [\begin{matrix} 0_{2 n \times 4 n} & I_{2 n} \end{matrix}] . \end{matrix}

The system (27) under the aperiodic DoS attack is GES with a prescribed

H_{\infty}

attenuation index

\tilde{γ} = \sqrt{\frac{F_{2}}{F_{1}}} γ

, where

F_{1} = \min \{μ_{2}^{- 1}, 1\}

F_{2} = \max \{μ_{2}^{- 1} e^{2 α_{1} δ_{\max}}, e^{2 α_{2} ϑ_{\max}}\}

, respectively.

Proof.

Based on the construction of the piecewise Lyapunov functional in (32). For analyzing the

H_{\infty}

performance of system (27) for any nonzero

ω (t)

, the inequalities as follows need to be guaranteed:

For

t \in S_{n} \cap K_{k, n}

\begin{matrix} {\dot{V}}_{1} (t) + 2 α_{1} V_{1} (t) + z^{T} (t) z (t) - γ^{2} ω^{T} (t) ω (t) \leq 0 \end{matrix}

(45)

For

t \in T_{n}

\begin{matrix} {\dot{V}}_{2} (t) - 2 α_{2} V_{2} (t) + z^{T} (t) z (t) - γ^{2} ω^{T} (t) ω (t) \leq 0 \end{matrix}

(46)

In accordance with the Lyapunov functional in (32), we have

\begin{matrix} {\dot{V}}_{1} (t) = & 2 {\tilde{x}}^{T} (t) P_{1} \dot{\tilde{x}} (t) + \tilde{x} {(t)}^{T} R_{1} \tilde{x} (t) - {\tilde{x}}^{T} (t - τ_{M}) e^{- 2 α_{1} τ_{M}} R_{1} \tilde{x} (t - τ_{M}) \\ - 2 α_{1} \int_{t - τ_{M}}^{t} {\tilde{x}}^{T} (s) e^{- 2 α_{1} (t - s)} R_{1} \tilde{x} (s) d s + τ_{M}^{2} {\dot{\tilde{x}}}^{T} (t) Z_{1} \dot{\tilde{x}} (t) \\ - τ_{M} \int_{t - τ_{M}}^{t} \dot{\tilde{x}} (s) e^{2 α_{1} (t - s)} Z_{1} \tilde{x} (s) d s \\ - 2 α_{1} τ_{M} \int_{- τ_{M}}^{0} \int_{t + θ}^{t} \dot{\tilde{x}} (s) e^{- 2 α_{1} (t - s)} Z_{1} \tilde{x} (s) d s d θ \\ \leq 2 {\tilde{x}}^{T} (t) P_{1} \dot{\tilde{x}} (t) + {\tilde{x}}^{T} (t) R_{1} \tilde{x} (t) - {\tilde{x}}^{T} (t - τ_{M}) e^{- 2 α_{1} τ_{M}} R_{1} \tilde{x} (t - τ_{M}) \\ - 2 α_{1} \int_{t - τ_{M}}^{t} {\tilde{x}}^{T} (s) e^{- 2 α_{1} (t - s)} R_{1} \tilde{x} (s) d s + τ_{M}^{2} {\dot{\tilde{x}}}^{T} (t) Z_{1} \dot{\tilde{x}} (t) \\ - τ_{M} e^{- 2 α_{1} τ_{M}} \int_{t - τ_{M}}^{t} \dot{\tilde{x}} (s) Z_{1} \tilde{x} (s) d s \\ - 2 α_{1} τ_{M} \int_{- τ_{M}}^{0} \int_{t + θ}^{t} \dot{\tilde{x}} (s) e^{- 2 α_{1} (t - s)} Z_{1} \tilde{x} (s) d s d θ \end{matrix}

(47)

Based on the Lemma 2 and inequality (47). Define

ℏ (t) = \{\tilde{x}, \tilde{x} (t - τ_{k, n} (t)), \tilde{x} (t - τ_{M})\}

. The inequality (45) is converted to the following form:

\begin{matrix} {\dot{V}}_{1} (t) + 2 α_{1} V_{1} (t) + z^{T} (t) z (t) - γ^{2} ω^{T} (t) ω (t) \\ \leq ℏ^{T} (t) \{u_{1}^{T} [sym (P_{1} {\tilde{A}}_{1}) + R_{1} + 2 α_{1} P_{1}] u_{1} + u_{1}^{T} sym (P_{1} {\tilde{B}}_{1}) u_{2} - u_{3}^{T} e^{- 2 α_{1} τ_{M}} R_{1} u_{3} \\ + e^{- 2 α_{1} τ_{M}} [- {(u_{2} - u_{1})}^{T} Z_{1} (u_{2} - u_{1}) - {(u_{3} - u_{2})}^{T} Z_{1} (u_{3} - u_{2}) \\ + {(u_{2} - u_{1})}^{T} Y_{1} (u_{3} - u_{2}) + {(u_{3} - u_{2})}^{T} Y_{1}^{T} (u_{2} - u_{1})]\} ℏ (t) + τ_{M}^{2} {\dot{\tilde{x}}}^{T} (t) Z_{1} \dot{\tilde{x}} (t) \\ + z^{T} (t) z (t) - γ^{2} ω^{T} (t) ω (t) + η_{k, n}^{T} (t) Φ η_{k, n} (t) - η_{k, n}^{T} (t) Φ η_{k, n} (t) \end{matrix}

By Schur complement and inequality (28), inequality (45) is converted to matrix inequality (43), and the establishment of condition (43) guarantees that inequality (45) holds. In the same way, if condition (44) is guaranteed, then condition (46) holds.

From condition (35), the following inequality is obtained:

\begin{matrix} μ_{2}^{- 1} e^{2 α_{1} δ_{\min}} - μ_{1} e^{2 (α_{1} + α_{2}) τ_{M} + 2 α_{2} ϑ_{\max}} \geq 0 \end{matrix}

(48)

Defining

{\hat{F}}_{1} (n) = μ_{2}^{- 1} e^{2 α_{1} (t - l_{n})}

and

{\hat{F}}_{2} (n) = e^{- 2 α_{2} (t - l_{n + 1})}

, for

t \in [0, l_{n + 1})

, the following inequality is derived:

\begin{matrix} \sum_{k = 0}^{n} \int_{l_{k}}^{l_{k} + δ_{k}} {\hat{F}}_{1} (k) [γ^{2} ω^{T} (t) ω (t) - z^{T} (t) z (t)] d t \\ + & \sum_{k = 0}^{n} \int_{l_{k} + δ_{k}}^{l_{k + 1}} {\hat{F}}_{2} (k) [γ^{2} ω^{T} (t) ω (t) - z^{T} (t) z (t)] d t > 0 \end{matrix}

For

t \in [l_{k}, l_{k} + d_{k})

, we have

\begin{matrix} 1 \leq e^{2 α_{1} (t - l_{k})} \leq e^{2 α_{1} δ_{k}} \leq e^{2 α_{1} δ_{\max}} \end{matrix}

(49)

For

t \in [l_{k} + d_{k}, l_{k + 1})

, we have

\begin{matrix} 1 \leq e^{2 α_{2} (l_{k + 1} - t)} \leq e^{2 α_{2} (l_{k + 1} - l_{k} - δ_{k})} \leq e^{2 α_{2} ϑ_{\max}} \end{matrix}

(50)

Defining

F_{1} = \min \{μ_{2}^{- 1}, 1\}

and

F_{2} = \max \{μ_{2}^{- 1} e^{2 α_{1} δ_{\max}}, e^{2 α_{2} ϑ_{\max}}\}

, for

\forall t \in [0, l_{n + 1})

and with the zero initial condition, the inequality as follows is obtained:

\begin{matrix} \sum_{k = 0}^{n} [\int_{l_{k}}^{l_{k + 1}} F_{1} z^{T} (t) z (t) d t] \leq \sum_{k = 0}^{n} [\int_{l_{k}}^{l_{k + 1}} F_{2} γ^{2} ω^{T} (t) ω (t) d t] \end{matrix}

which is equivalent to

\begin{matrix} \int_{0}^{l_{n + 1}} z^{T} (t) z (t) d t \leq {(\sqrt{\frac{F_{2}}{F_{1}}} γ)}^{2} \int_{0}^{l_{n + 1}} ω^{T} (t) ω (t) d t \end{matrix}

Based on the results of the above discussions, we know that when

l_{n + 1} \to \infty

, one can obtain that

\begin{matrix} \int_{0}^{\infty} z^{T} (t) z (t) d t \leq {(\sqrt{\frac{F_{2}}{F_{1}}} γ)}^{2} \int_{0}^{\infty} ω^{T} (t) ω (t) d t \end{matrix}

(51)

This means that

{∥z (t)∥}_{2} \leq \tilde{γ} {∥ω (t)∥}_{2}

for

ω (t) \in L_{2} [0, \infty)

, where

\tilde{γ} = \sqrt{\frac{F_{2}}{F_{1}}} γ

Consequently, the

H_{\infty}

performance and the exponential stability are guaranteed for the system (27) under aperiodic DoS attack. □

Remark 4.

The sufficient criterion for ensuring global exponential stability of system (27) with a desired

H_{\infty}

disturbance attenuation index is given in the above theorems. However, the matrix parameters of the controller (26) are unknown. These unknown matrices appear in the matrix inequality as a non-linear manner, these matrices can not be derived by solving matrix inequalities through the above theorems. To address such problem, a new theorem as follows is proposed to satisfy the gain matrix design requirements for the designed controller.

Theorem 3.

Given fixed parameters

δ_{m i n}

ϑ_{m a x}

τ_{D} \in R > 0

of the DoS attack, and the boundary parameter

τ_{M} > 0

, an appropriate scalar

δ_{y}

, matrices ϕ,

T_{n}

(n = 1, 2, 3)

, consider the controller (26). If for the given scalars

α_{i} \in (0, + \infty)

μ_{i} \in (0, + \infty)

γ \in (0, + \infty)

and

σ_{0} \in (0, 1)

, there are some symmetric positive define matrices

{\tilde{R}}_{i} > 0

{\tilde{Z}}_{i} > 0

{\tilde{U}}_{i} > 0

Φ > 0

X > 0

, matrices

{\tilde{Y}}_{i}

S_{i}

W_{i j}

(i = 1, 2; j = 1, 2, . . ., 5)

with appropriate dimensions and scalars

ε_{1} > 0

ε_{2} > 0

, such that (34), the matrix inequalities as follows:

\begin{matrix} Υ_{1} = [\begin{matrix} {\tilde{Υ}}_{1} & Ψ_{11}^{T} & Ψ_{21}^{T} \\ * & - ε_{1} I & 0 \\ * & * & - ε_{1} I \end{matrix}] < 0 \end{matrix}

(52)

\begin{matrix} Υ_{2} = [\begin{matrix} {\tilde{Υ}}_{2} & Ψ_{12}^{T} & Ψ_{21}^{T} \\ * & - ε_{2} I & 0 \\ * & * & - ε_{2} I \end{matrix}] < 0 \end{matrix}

(53)

hold, where

\begin{matrix} {\tilde{Υ}}_{1} = [\begin{matrix} {\tilde{Σ}}_{1} & u_{1}^{T} Π_{13} & u_{1}^{T} Π_{14} & Π_{11} & Π_{12} & u_{1}^{T} Π_{15} \\ * & - Φ & 0 & Π_{13}^{T} & I & 0 \\ * & * & - γ^{2} I & Π_{14}^{T} & 0 & 0 \\ * & * & * & {\tilde{Ω}}_{14} & 0 & 0 \\ * & * & * & * & {\tilde{Ω}}_{5} & 0 \\ * & * & * & * & * & - I \end{matrix}] < 0 \end{matrix}

(54)

\begin{matrix} {\tilde{Υ}}_{2} = [\begin{matrix} {\tilde{Σ}}_{2} & u_{1}^{T} Π_{23} & u_{1}^{T} Π_{24} & Π_{21} & Π_{12} & u_{1}^{T} Π_{15} \\ * & - Φ & 0 & Π_{23}^{T} & I & 0 \\ * & * & - γ^{2} I & Π_{24}^{T} & 0 & 0 \\ * & * & * & {\tilde{Ω}}_{24} & 0 & 0 \\ * & * & * & * & {\tilde{Ω}}_{5} & 0 \\ * & * & * & * & * & - I \end{matrix}] < 0 \end{matrix}

(55)

\begin{matrix} Ψ_{11} = [\begin{matrix} [\begin{matrix} 0 & δ_{y} S_{1}^{T} \end{matrix}] u_{1} & 0 & 0 & δ_{y} S_{1}^{T} & 0 & 0 \end{matrix}], \end{matrix}

\begin{matrix} Ψ_{21} = [\begin{matrix} B_{c} [\begin{matrix} C X & C \end{matrix}] u_{2} & B_{c} & 0 & 0 & 0 & 0 \end{matrix}], \end{matrix}

\begin{matrix} Ψ_{12} = [\begin{matrix} [\begin{matrix} 0 & δ_{y} S_{2}^{T} \end{matrix}] u_{1} & 0 & 0 & δ_{y} S_{2}^{T} & 0 & 0 \end{matrix}], \end{matrix}

\begin{matrix} {\tilde{Σ}}_{1} & = u_{1}^{T} [sym ([\begin{matrix} {X A}^{T} + W_{14} B^{T} & W_{11} \\ A^{T} & A^{T} U_{1} \end{matrix}]) + {\tilde{R}}_{1} + 2 α_{1} [\begin{matrix} X & I \\ I & U_{1} \end{matrix}]] u_{1} \\ + u_{1}^{T} sym ([\begin{matrix} 0 & 0 \\ W_{15}^{T} & W_{13} C \end{matrix}]) u_{2} - u_{3}^{T} e^{- 2 α_{1} τ_{M}} {\tilde{R}}_{1} u_{3} \\ + e^{- 2 α_{1} τ_{M}} [- {(u_{2} - u_{1})}^{T} {\tilde{Z}}_{1} (u_{2} - u_{1}) - {(u_{3} - u_{2})}^{T} {\tilde{Z}}_{1} (u_{3} - u_{2}) \\ + {(u_{2} - u_{1})}^{T} {\tilde{Y}}_{1} (u_{3} - u_{2}) + {(u_{3} - u_{2})}^{T} {\tilde{Y}}_{1}^{T} (u_{2} - u_{1})], \end{matrix}

\begin{matrix} {\tilde{Σ}}_{2} & = u_{1}^{T} [sym ([\begin{matrix} {X A}^{T} + W_{24} B^{T} & W_{21} \\ A^{T} & A^{T} U_{2} \end{matrix}]) + {\tilde{R}}_{2} - 2 α_{2} [\begin{matrix} X & I \\ I & U_{2} \end{matrix}]] u_{1} \\ + u_{1}^{T} sym ([\begin{matrix} 0 & 0 \\ W_{25}^{T} & W_{23} C \end{matrix}]) u_{2} - u_{3}^{T} {\tilde{R}}_{2} u_{3} \\ + [- {(u_{2} - u_{1})}^{T} {\tilde{Z}}_{2} (u_{2} - u_{1}) - {(u_{3} - u_{2})}^{T} {\tilde{Z}}_{2} (u_{3} - u_{2}) \\ + {(u_{2} - u_{1})}^{T} {\tilde{Y}}_{2} (u_{3} - u_{2}) + {(u_{3} - u_{2})}^{T} {\tilde{Y}}_{2}^{T} (u_{2} - u_{1})], \end{matrix}

\begin{matrix} Π_{11} = u_{1}^{T} [\begin{matrix} X A^{T} + W_{14} B^{T} & W_{11} \\ A^{T} & A^{T} U_{1} \end{matrix}] + u_{2}^{T} [\begin{matrix} 0 & W_{15} \\ 0 & C^{T} W_{13}^{T} \end{matrix}] Π_{12} = u_{2}^{T} [\begin{matrix} X C^{T} \\ C \end{matrix}], \\ Π_{13} = u_{2}^{T} [\begin{matrix} 0 \\ W_{13} \end{matrix}], Π_{14} = u_{2}^{T} [\begin{matrix} I & K \\ U_{1} & U_{1} K \end{matrix}], Π_{15} = u_{2}^{T} [\begin{matrix} X C_{z}^{T} \\ C_{z}^{T} \end{matrix}], \end{matrix}

\begin{matrix} {\tilde{Ω}}_{14} = \frac{1}{τ_{M}^{2}} (T_{1} {\tilde{Z}}_{1} T_{1}^{T} - T_{1} G_{1}^{T} - G_{1} T_{1}^{T}), {\tilde{Ω}}_{5} = T_{2} Φ T_{2}^{T} - σ_{0}^{- \frac{1}{2}} T_{2}^{T} - σ_{0}^{- \frac{1}{2}} T_{2}, \end{matrix}

\begin{matrix} Π_{21} = u_{1}^{T} [\begin{matrix} X A^{T} & W_{21} \\ A^{T} & A^{T} U_{2} \end{matrix}] + u_{2}^{T} [\begin{matrix} 0 & W_{25} \\ 0 & C^{T} W_{23}^{T} \end{matrix}], \\ Π_{23} = u_{2}^{T} [\begin{matrix} 0 \\ W_{23} \end{matrix}], Π_{24} = u_{2}^{T} [\begin{matrix} I & K \\ U_{2} & U_{2} K \end{matrix}], \end{matrix}

\begin{matrix} {\tilde{Ω}}_{24} = \frac{1}{τ_{M}^{2}} (T_{3} {\tilde{Z}}_{2} T_{3}^{T} - T_{3} G_{2}^{T} - G_{2} T_{3}^{T}), \end{matrix}

and

\begin{matrix} [\begin{matrix} {\tilde{Z}}_{i} & {\tilde{Y}}_{i} \\ * & {\tilde{Z}}_{i} \end{matrix}] \geq 0, \end{matrix}

(56)

\begin{matrix} G_{i} = [\begin{matrix} X & I \\ I & U_{i} \end{matrix}] \geq 0, \end{matrix}

(57)

the globally exponentially stability is guaranteed for the system (27) with the

H_{\infty}

attenuation level

\tilde{γ}

under aperiodic DoS attack. And the matrix parameters of the controller (26) are obtained as the following equations:

\begin{matrix} A_{c} = S_{1}^{- 1} {(W_{11} - W_{12} U_{1})}^{T} N^{- T} \\ B_{c} = S_{1}^{- 1} W_{13} \\ C_{c} = W_{14}^{T} N^{- T} \\ D_{c} = S_{1}^{- 1} {(W_{15} - S^{T} C^{T} W_{13}^{T})}^{T} N^{- T} \end{matrix}

Proof.

First, two matrices are defined as the following form:

\begin{matrix} Γ_{1} = [\begin{matrix} X & I \\ N^{T} & 0 \end{matrix}], Γ_{2 i} = [\begin{matrix} I & U_{i} \\ 0 & S_{i}^{T} \end{matrix}] \end{matrix}

one can obtain that

\begin{matrix} P_{i} = Γ_{2 i} Γ_{1}^{- 1} = [\begin{matrix} U_{i} & S_{i} \\ * & N^{- 1} X (U_{i} - X^{- 1}) X N^{- T} \end{matrix}] > 0 \end{matrix}

Define

{\tilde{Z}}_{i} = Γ_{1}^{T} Z_{i} Γ_{1}

{\tilde{R}}_{i} = Γ_{1}^{T} R_{i} Γ_{1}

{\tilde{Y}}_{i} = Γ_{1}^{T} Y_{i} Γ_{1}

, and

Z_{i} > 0

Φ > 0

, by Lemma 3, the following inequalities are obtained

\begin{matrix} {(- τ_{M}^{2} Z_{1})}^{- 1} \leq \frac{1}{τ_{M}^{2}} (T_{1} {\tilde{Z}}_{1} T_{1}^{T} - T_{1} G_{1}^{T} - G_{1} T_{1}^{T}) \\ - {(σ_{0} Φ)}^{- 1} \leq T_{2} Φ T_{2}^{T} - T_{2}^{T} σ_{0}^{- \frac{1}{2}} - T_{2} σ_{0}^{- \frac{1}{2}} \\ {(- τ_{M}^{2} Z_{2})}^{- 1} \leq \frac{1}{τ_{M}^{2}} (T_{3} {\tilde{Z}}_{2} T_{3}^{T} - T_{3} G_{2}^{T} - G_{2} T_{3}^{T}) \end{matrix}

Let

Q = d i a g \{Γ_{1}^{T}, I, I, Γ_{2 i}^{T}, I, I\}, (i = 1, 2)

, then left-multiplying inequality (43) by Q and right-multiplying by the transpose of Q, respectively. And convert the resulting matrix inequality into the following form

\begin{matrix} \tilde{Υ_{1}} + {\tilde{L}}_{1}^{T} Δ_{y} {\tilde{L}}_{2} + {\tilde{L}}_{2}^{T} Δ_{y}^{T} {\tilde{L}}_{1} < 0 \end{matrix}

(58)

where

{\tilde{Υ}}_{1} = [\begin{matrix} {\tilde{Σ}}_{1} & u_{1}^{T} Π_{13} & u_{1}^{T} Π_{14} & Π_{11} & Π_{12} & u_{1}^{T} Π_{15} \\ * & - Φ & 0 & Π_{13}^{T} & I & 0 \\ * & * & - γ^{2} I & Π_{14}^{T} & 0 & 0 \\ * & * & * & {\tilde{Ω}}_{14} & 0 & 0 \\ * & * & * & * & {\tilde{Ω}}_{5} & 0 \\ * & * & * & * & * & - I \end{matrix}]

\begin{matrix} {\tilde{L}}_{1} = [\begin{matrix} 0 & S_{1}^{T} u_{1} & 0 & 0 & 0 & 0 & S_{1}^{T} & 0 & 0 \end{matrix}], \\ {\tilde{L}}_{2} = [\begin{matrix} B_{c} C X u_{2} & B_{c} C u_{2} & B_{c} & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] . \end{matrix}

By the lemma in [41], there exist a scalar

ε_{1} > 0

such that

\begin{matrix} {\tilde{Υ}}_{1} + ε_{1} {\tilde{L}}_{1}^{T} Δ_{y}^{2} {\tilde{L}}_{1} + ε_{1}^{- 1} {\tilde{L}}_{2}^{T} {\tilde{L}}_{2} < 0 \end{matrix}

(59)

where

Δ_{y}^{2} < δ_{y}^{2}

By using Schur complement, condition (52) is obtained. Similarly, condition (53) can also be obtained. Which means conditions (54) and (55) are satisfied. It provides further evidence that conditions (43) and (44) are guaranteed and the system (27) is of a prescribed

H_{\infty}

performance level

\tilde{γ}

On the other hand, define some variables

W_{i j}, (i = 1, 2; j = 1, 2, . . ., 5)

so that the dynamic output feedback controller gain matrices are given by the equations as follows

\begin{matrix} A_{c} = S_{1}^{- 1} {(W_{11} - W_{12} U_{1})}^{T} N^{- T} \\ B_{c} = S_{1}^{- 1} W_{13} \\ C_{c} = W_{14}^{T} N^{- T} \\ D_{c} = S_{1}^{- 1} {(W_{15} - S^{T} C^{T} W_{13}^{T})}^{T} N^{- T} \end{matrix}

The proof is completed. □

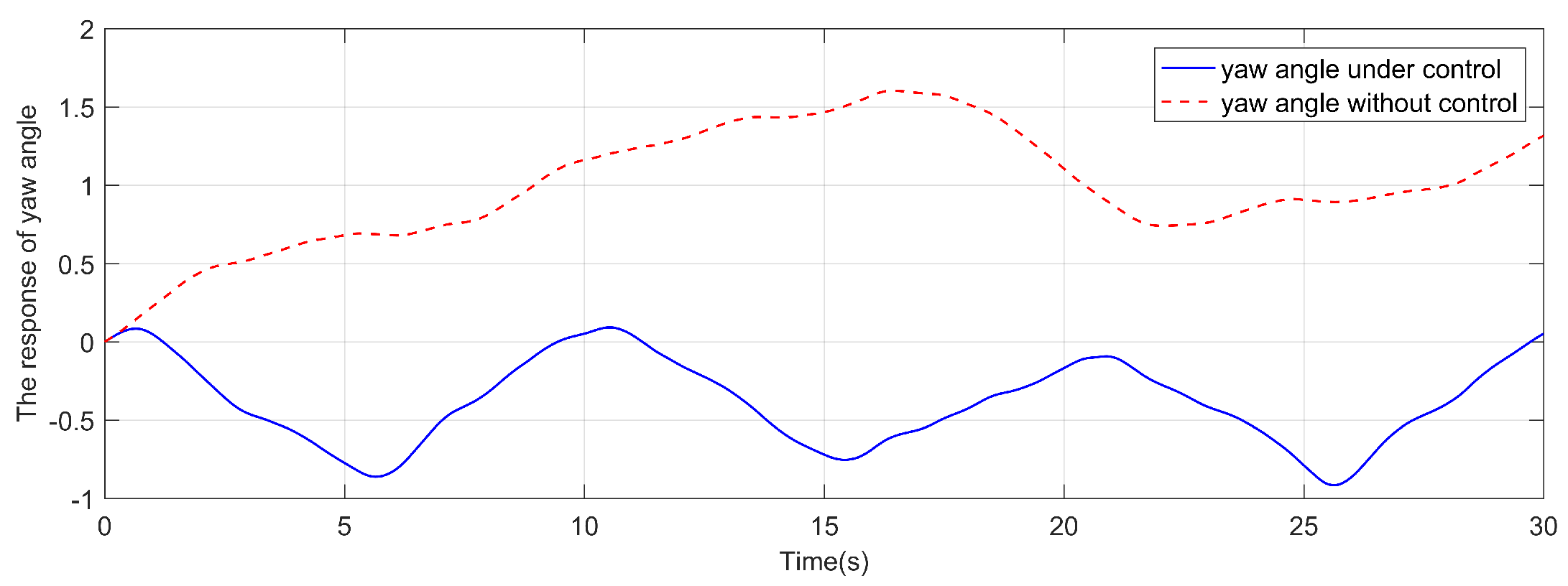
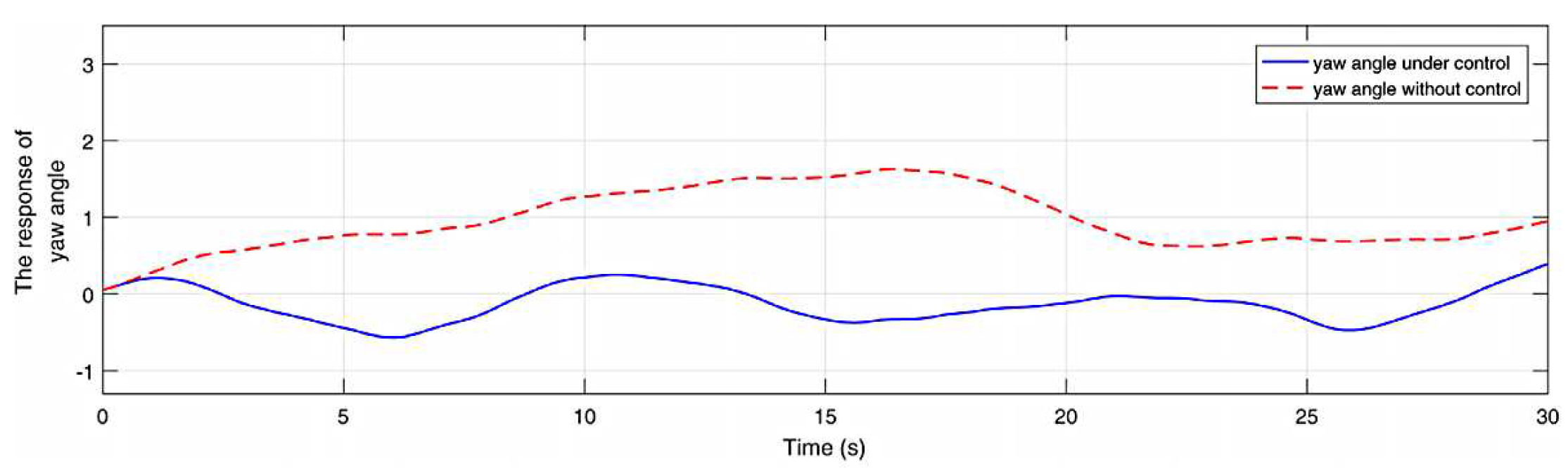
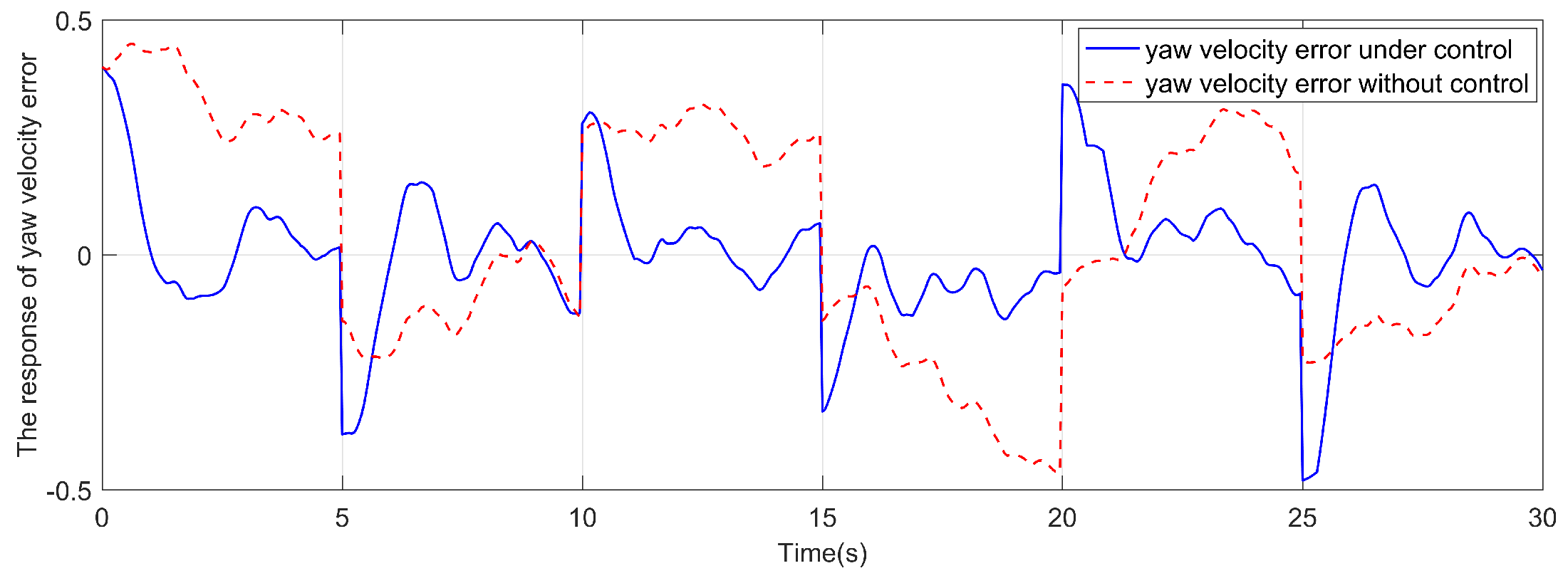
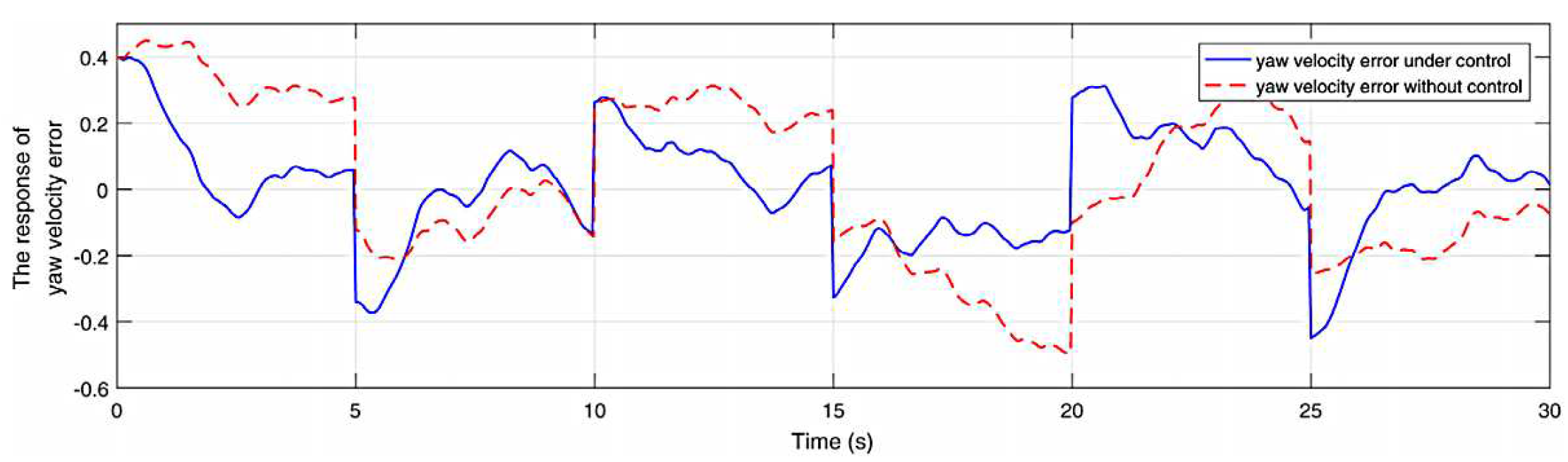
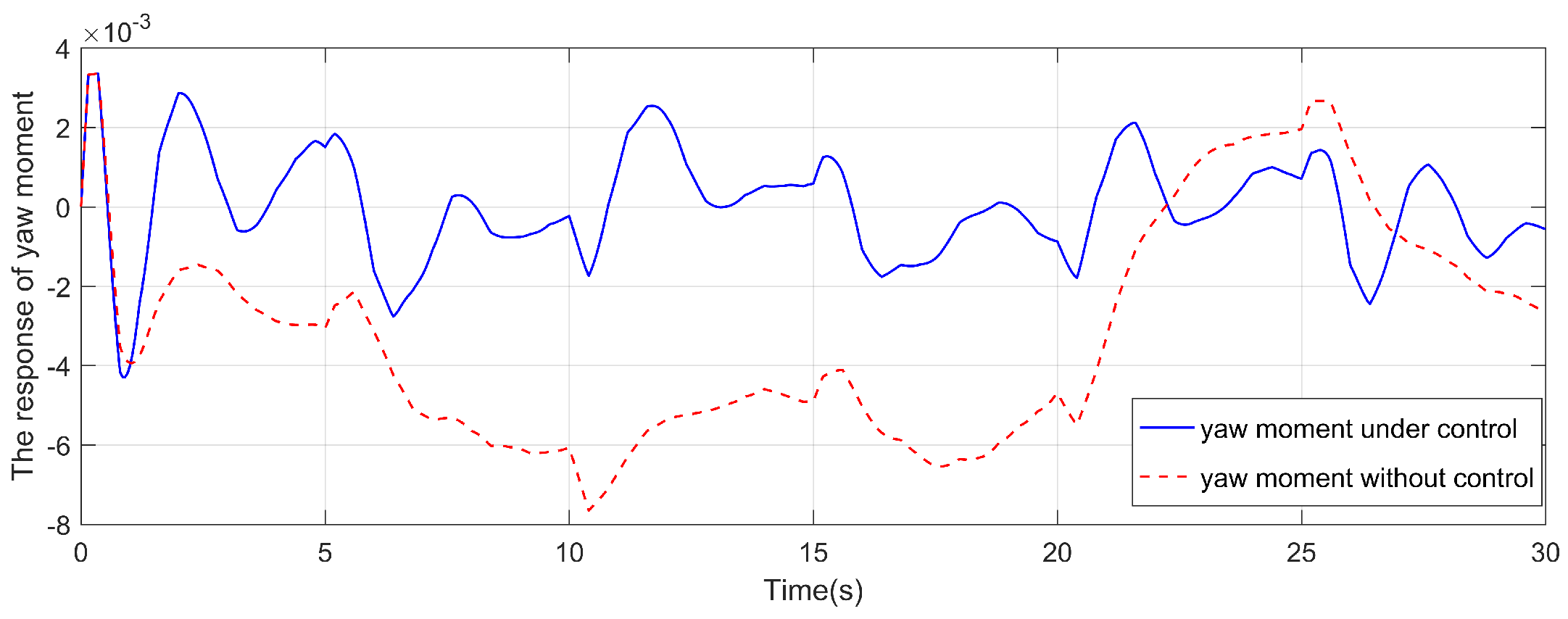
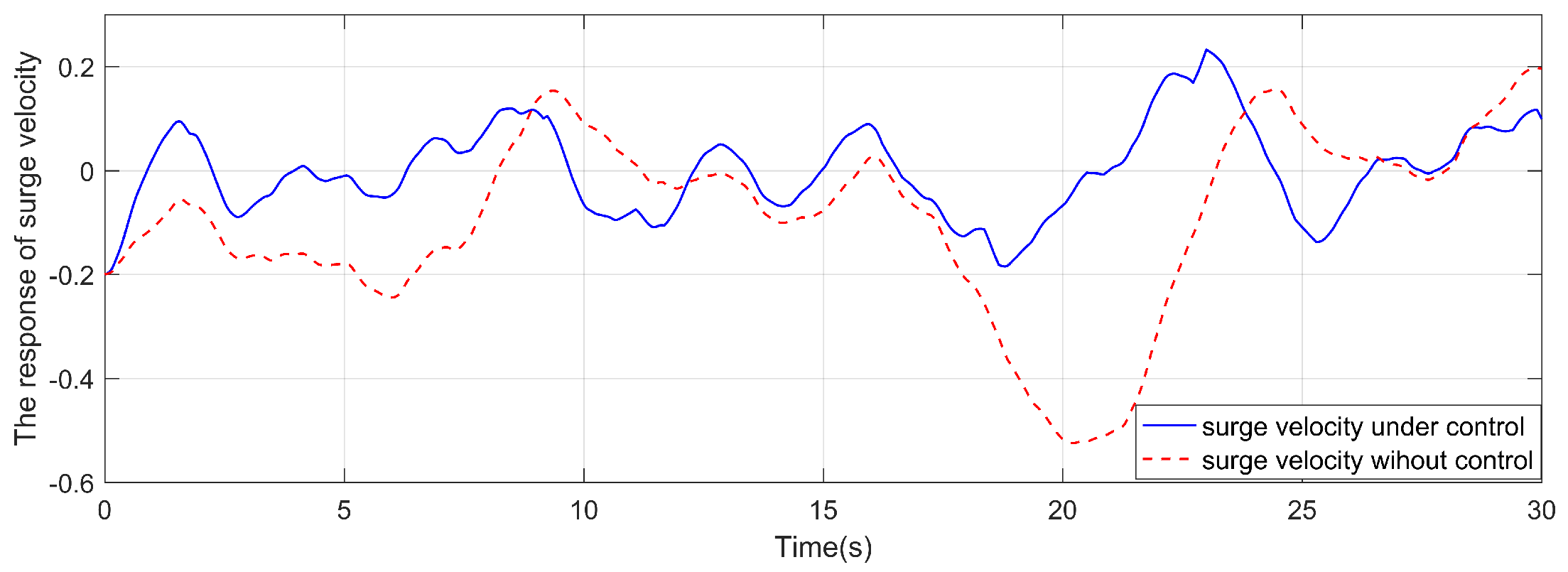
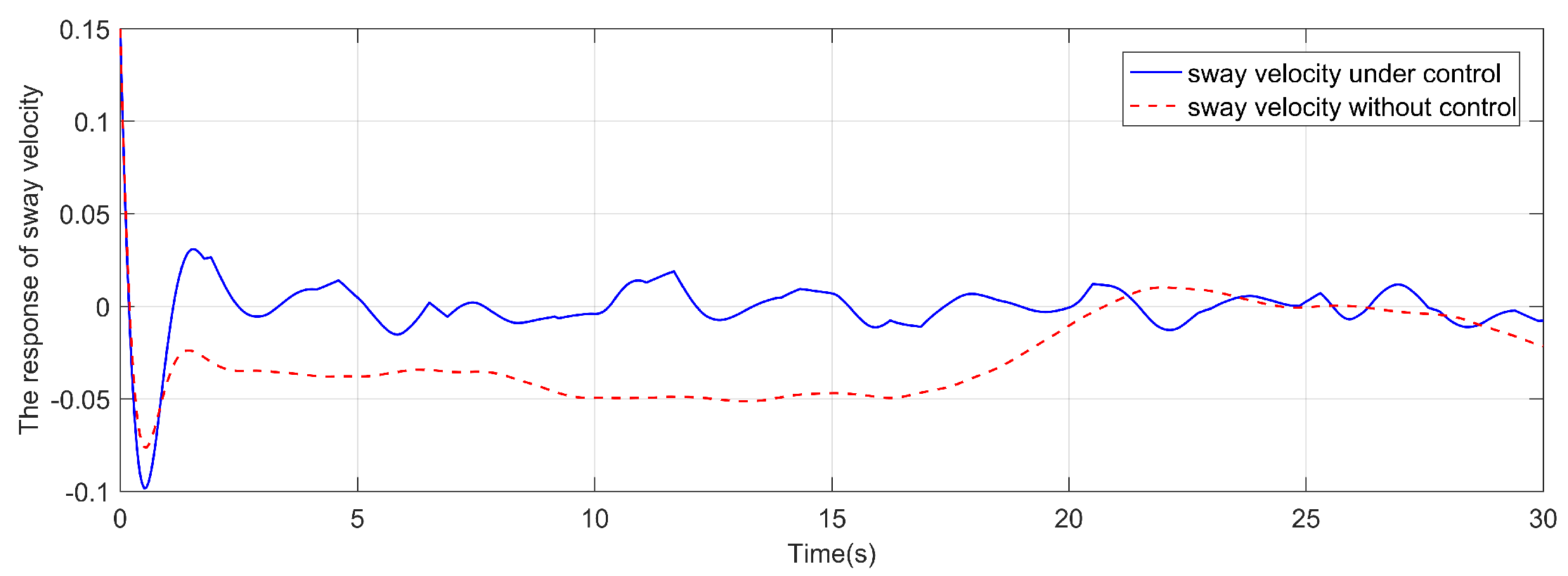
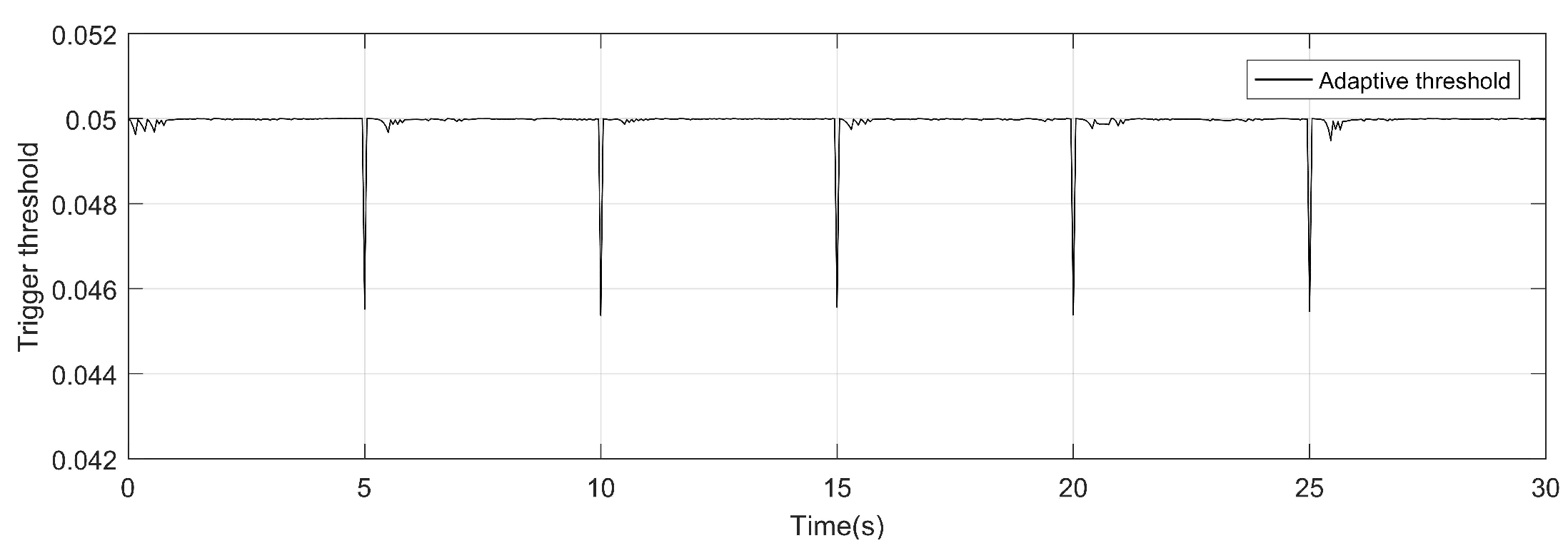
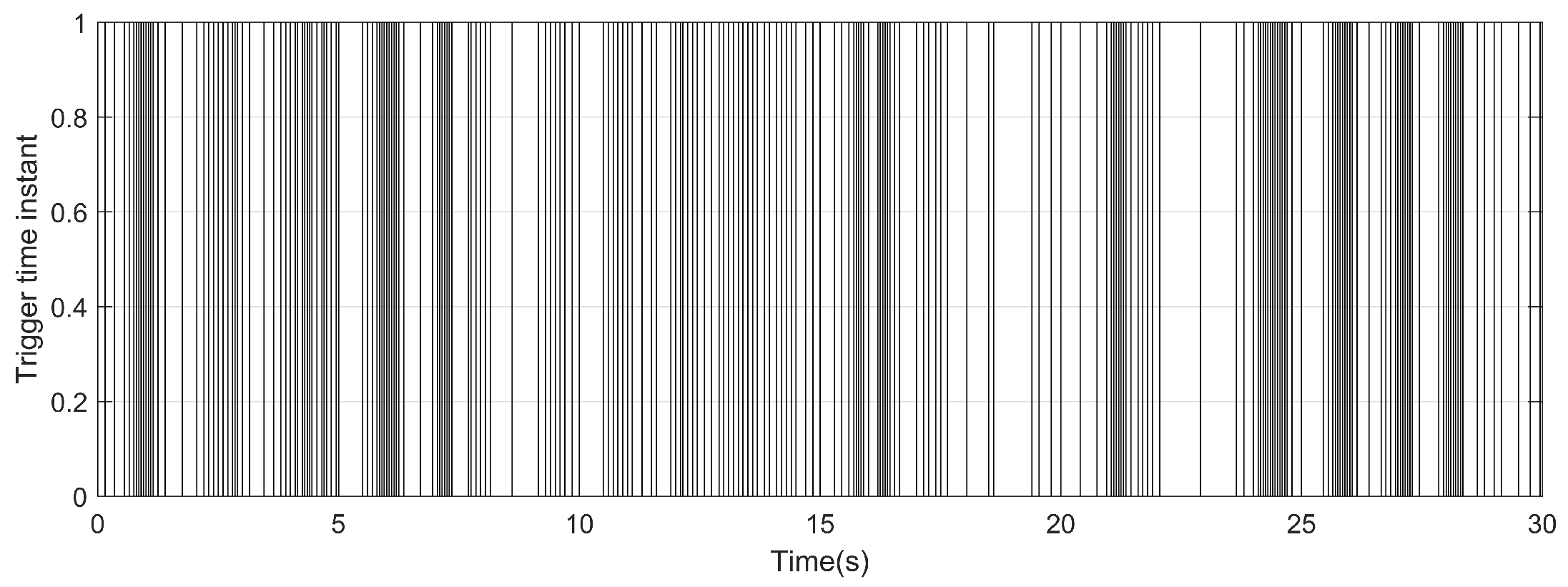
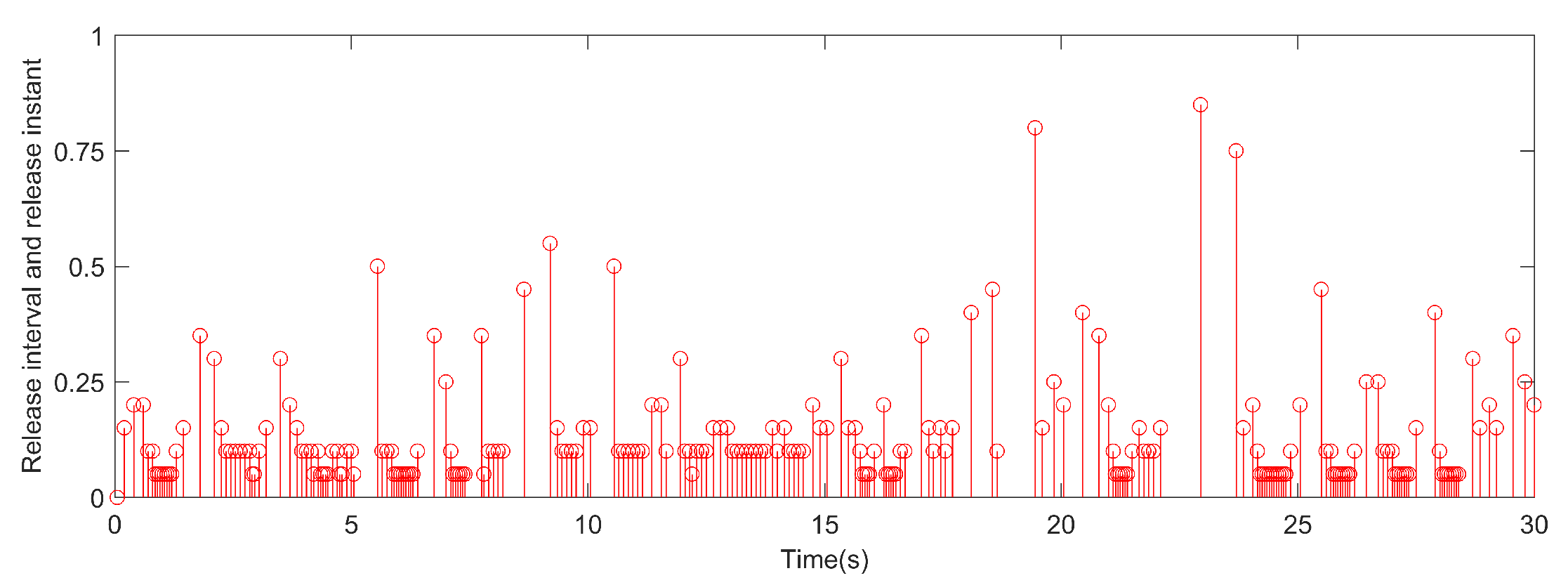
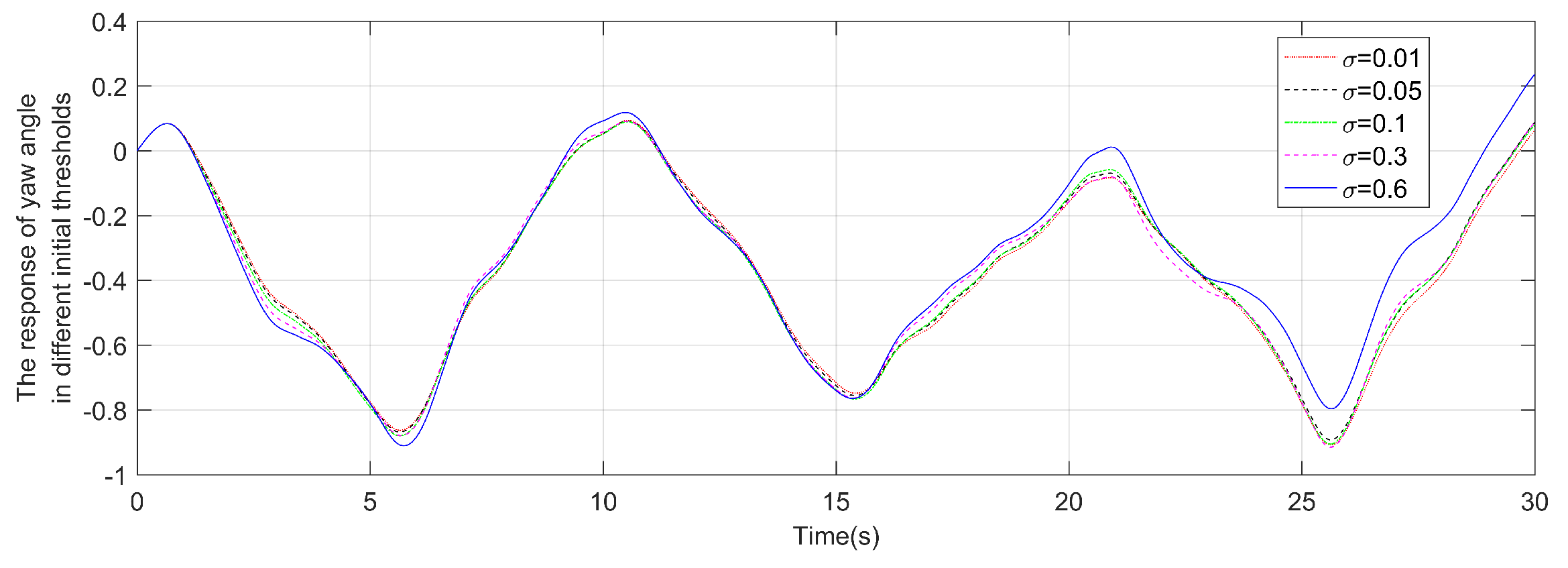
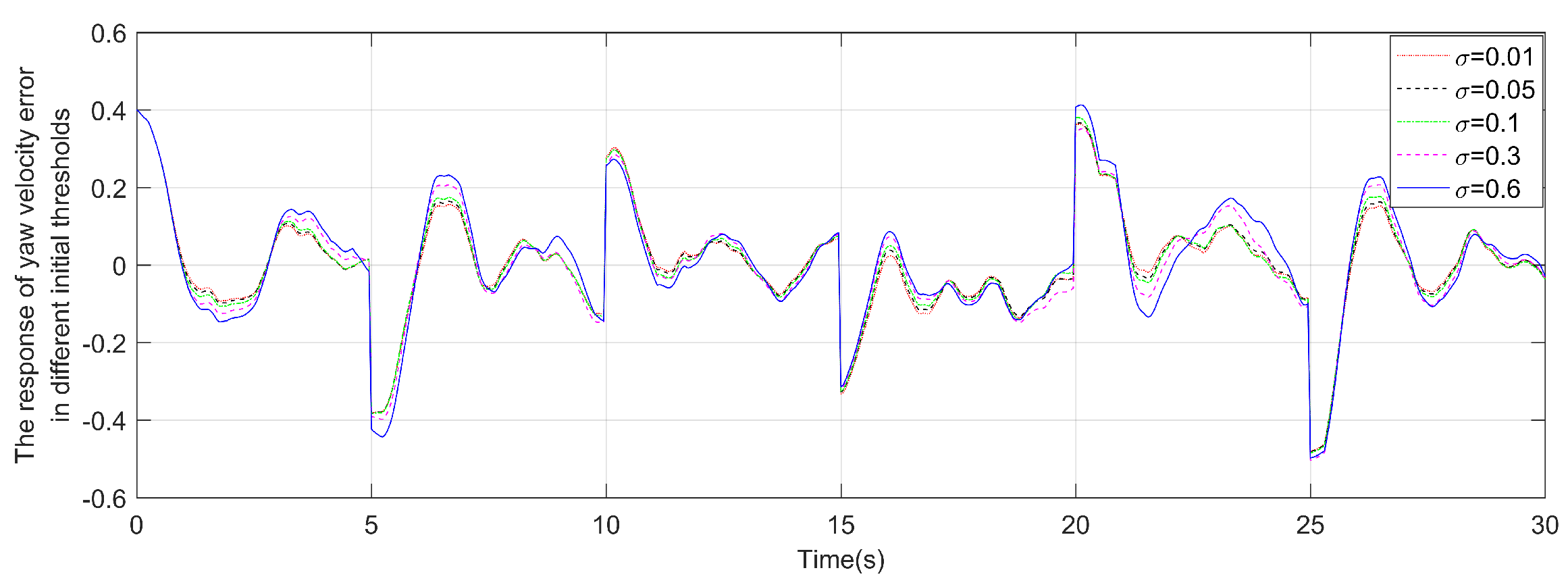
4. Simulation and analysis

The effectiveness of the designed controller (26) for the network-based UMV systems under the aperiodic DoS attack is demonstrated within this section. The network-based UMV systems matrix parameters [42] are given as:

\begin{matrix} M = [\begin{matrix} 1.0852 & 0 & 0 \\ 0 & 2.0575 & - 0.4087 \\ 0 & - 0.4087 & 0.2153 \end{matrix}], \\ N = [\begin{matrix} 0.0865 & 0 & 0 \\ 0 & 0.0762 & 0.0151 \\ 0 & 0.0151 & 0.031 \end{matrix}], \\ G = [\begin{matrix} 0.0389 & 0 & 0 \\ 0 & 0.0266 & 0 \\ 0 & 0 & 0 \end{matrix}] . \end{matrix}

For the formulas as

A = - M^{- 1} N

B = M^{- 1}

, such that the matrix parameters are obtained as:

\begin{matrix} A = [\begin{matrix} - 0.0797 & 0 & 0 \\ 0 & - 0.0818 & - 0.0577 \\ 0 & - 0.2254 & - 0.2535 \end{matrix}], \\ B = [\begin{matrix} 0.9215 & 0 & 0 \\ 0 & 0.7802 & 1.4811 \\ 0 & 1.4811 & 7.4562 \end{matrix}] . \end{matrix}

It is clear that matrix

C_{z}

in section 2 is selected as

C_{z} = [\begin{matrix} 0 & 0 & 1 \end{matrix}]

and

C

is selected as

C = I

. The matrices

T_{n}

Œ

in theorem 3 are selected as the identity matrices with appropriate dimensions. For the parameters of DoS attack, we assume that

ϑ_{\max} = 0.7 s

δ_{\min} = 1.8 s

τ_{D} = 1.15 s

. The whole operating time is set to

t = 30 s

. Select

μ_{1} = μ_{2} = 1.04

α_{1} = 0.018

α_{2} = 0.043

τ_{M} = 0.1 s

l = 0.05 s

γ = 2

κ = 2

ρ = 0.1

. And the initial threshold for the AETM is given as

σ_{0} = 0.05

The vector

e_{0} = {[\begin{matrix} - 0.2 & 0.15 & 0.2 \end{matrix}]}^{T}

is select as the initial value of system (10). The reference signals are given as

α (t) = β (t) = 0

, and the piecewise constant function

γ (t)

is described as:

\begin{matrix} γ (t) = \{\begin{matrix} - 0.2, t \in [0, 5) s \cup [10, 15) s \cup [20, 25) s \\ 0.2, t \in [5, 10) s \cup [15, 20) s \cup [25, 30) s \end{matrix} \end{matrix}

The disturbance

ω_{1} (t)

ω_{2} (t)

and

ω_{3} (t)

in surge, sway and yaw motions are

\begin{matrix} \{\begin{matrix} ω_{1} (t) = 0.51 F_{1} (s) N_{1} (t) + I_{1} A x_{r} \\ ω_{2} (t) = - cos (3 t) e^{- 2.4 t} + I_{2} A x_{r} \\ ω_{3} (t) = 0.45 F_{2} (s) N_{2} (t) + I_{3} A x_{r} \end{matrix} \end{matrix}

(60)

where

F_{1} (s)

and

F_{2} (s)

denote the shaping filters described by

F_{1} = \frac{K_{ω 1} s}{s^{2} + 2 ϱ_{1} ζ_{1} s + ζ_{1}^{2}}

and

F_{2} = \frac{K_{ω 2} s}{s^{2} + 2 ϱ_{2} ζ_{2} s + ζ_{2}^{2}}

, respectively; The wave strength coefficients are denoted as

K_{ω 1}

and

K_{ω 2}

which

K_{ω 1} = 0.2

and

K_{ω 2} = 0.6

. The damping coefficients ares selected as

ϱ_{1} = 0.5

and

ϱ_{2} = 1.6

, respectively. The encountering wave frequencies are defined as

ζ_{1}

and

ζ_{2}

where

ζ_{1} = 0.7

and

ζ_{2} = 0.1

; The band-limited white noise is denoted as

N_{1} (t)

and

N_{2} (t)

with the noise powers are 2 and 1.8; In addition,

I_{1} = [\begin{matrix} 1 & 0 & 0 \end{matrix}]

I_{2} = [\begin{matrix} 0 & 1 & 0 \end{matrix}]

I_{3} = [\begin{matrix} 0 & 0 & 1 \end{matrix}]

. Since the definition of yaw velocity error leads to the same amplitude of oscillation for yaw velocity and yaw velocity error, only yaw velocity error and yaw angle are investigated in the simulations of this paper.

The matrix parameters of the controller (26) are obtained by solving linear matrix inequalities (LMIs) (52) and (53) in Theorem 3 as follows:

\begin{matrix} A_{c} = [\begin{matrix} - 0.0275 & 0 & 0 \\ 0 & 0.0380 & - 0.2742 \\ 0 & 0.2098 & 1.4254 \end{matrix}], \\ B_{c} = [\begin{matrix} 0.1138 & 0 & 0 \\ 0 & 0.1098 & - 0.0248 \\ 0 & - 0.0215 & 0.1452 \end{matrix}], \\ C_{c} = [\begin{matrix} - 239.1 & 0 & 0 \\ 0 & - 229.69 & 137.3 \\ 0 & 441.3 & 150.5 \end{matrix}], \\ D_{c} = [\begin{matrix} - 0.823 & 0 & 0 \\ 0 & 0.6979 & 0.1483 \\ 0 & 0.0973 & - 0.9530 \end{matrix}] . \end{matrix}

To demonstrate the effectiveness of the DOFC strategy, the response results with and without controller are investigated separately in this section. The simulation results and the comparison with reference [19] are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.

As shown in Figure 3, the square wave with a value of 1 means that the aperiodic DoS attack signal is active and 0 means that the aperiodic DoS attack signal is inactive. Different from the DoS attack signal in reference [19], the lower bound

δ_{min}

is set to a smaller value of

1.5 s

and the upper bound

ϑ_{max}

is set to a larger value of

0.7 s

. The yaw angle response is shown in Figure 4 and the yaw velocity error response is shown in Figure 6. The comparison responses of the reference are shown in Figure 5 and Figure 7, respectively. It is clear that the yaw velocity error amplitude and the yaw angle amplitude are greatly mitigated by the action of the considered controller under the more severe cyber attack environment. The response of yaw moment is shown in Figure 8. The responses of sway velocity and surge velocity are shown in Figure 9 and Figure 10. The amplitude of the sway velocity is also significantly reduced compared to the reference.

To give a more visual indication of the effect of DOFC strategy on system (27), the percentage reduction in yaw angle and yaw velocity error is represented as:

\begin{matrix} R_{y a} & = (1 - \frac{A_{y a} (yaw angle under control)}{A_{y a} (yaw angle without control)}) \times 100 % \\ R_{y v e} & = (1 - \frac{A C_{y v e} (yaw velocity error under control)}{A C_{y v e} (yaw velocity error without control)}) \times 100 % \end{matrix}

where

A_{y a}

represents the oscillation amplitudes of yaw angle,

A C_{y v e}

represents the accumulative error of yaw velocity error. The percentage reduction in the yaw angle amplitudes and the yaw velocity accumulative error is denoted as

R P_{y a}

and

R P_{y v e}

, respectively. As can be seen from Table 1, the proposed DOFC strategy based the ETM and the quantitative mechanism has tangible effectiveness in reducing the value of yaw velocity accumulative error. The amplitude of yaw angle oscillations is also reduced. And significant improvement in effectiveness compared to the reference.

Table 1. The comparison of the system performance under two strategies.

	$A_{y a}$	$R P_{y a}$	$A C_{y v e}$	$R P_{y v e}$
No control(Reference [19])	1.6805	-	6.3338	-
No control	1.6808	-	6.3868	-
With control(Reference [19])	0.9602	42.9%	3.7957	40.1%
With control	0.9554	43.2%	3.4580	45.9%

The variation of threshold

σ

is shown in Figure 11. The trigger time instant and the release time interval of AETM are illustrated in Figure 12 and Figure 13.

Only 232 times are triggered during the whole simulation process. It saves

61.3 %

of communication resources.

To demonstrate the strengths of the AETM in this work, two different transmission schemes are presented for comparison, i.e., fixed threshold ETM in [43] and AETM in [44] is given. The relevant quantitative comparison results of the data are given in Tables 2–4, respectively.

The comparison of the number of triggers under different mechanisms is shown in Table 2. The comparison results of the yaw angle oscillation amplitude and the yaw velocity error accumulative error under different initial thresholds are given in Tables 3 and 4. It can be seen from the results that compared with reference [43], the system performance is better when we have fewer trigger times. And we greatly reduce the number of triggers under the similar system performance compared with reference [44].

Table 2. Comparison of the number of triggers under different event-triggered mechanisms.

Threshold parameter $σ_{0}$	0.05	0.1	0.6	0.8
Reference [43]	232	174	65	60
Reference [44]	302	236	96	86
This work	232	174	64	58

Table 3. Comparison of the yaw angle oscillation amplitudes under different event-triggered mechanisms.

Threshold parameter $σ_{0}$	0.05	0.1	0.6	0.8
Reference [43]	0.9795	0.9848	1.2082	1.2317
Reference [44]	0.9712	0.9776	1.1970	1.2073
This work	0.9795	0.9848	1.2054	1.2119

Table 4. Comparison of the yaw velocity error accumulative error under different event-triggered mechanisms.

Threshold parameter $σ_{0}$	0.05	0.1	0.6	0.8
Reference [43]	3.4709	3.5263	4.2739	4.4751
Reference [44]	3.4574	3.4992	3.8627	4.0627
This work	3.4680	3.5213	4.0428	4.4620

The performance of the system is significantly influenced by the threshold parameter

σ

. Such that, different cases of initial threshold

σ_{0}

are provided in Table 5. The selection rule of parameter

σ_{0}

is followed by condition (13), where

A_{y a}

R P_{y a}

A C_{y v e}

and

R P_{y v e}

represent the same meanings as in Table 1.

Table 5. System performance indexes at five specific initial thresholds

σ_{0}

Table 5. System performance indexes at five specific initial thresholds

σ_{0}

	$A_{y a}$	$R P_{y a}$	$A C_{y v e}$	$R P_{y v e}$	Trigger times
No control	1.6808	-	6.3868	-	600
$σ_{0} = 0.01$	0.9249	45.0%	3.4296	46.3%	395
$σ_{0} = 0.05$	0.9544	43.2%	3.4680	45.9%	232
$σ_{0} = 0.1$	0.9595	42.9%	3.5213	44.9%	175
$σ_{0} = 0.3$	0.9658	42.5%	3.7041	42.0%	99
$σ_{0} = 0.6$	1.1420	32.1%	4.0428	36.7%	69

As shown in Table 5 and Figure 14 and Figure 15, when the parameter

σ_{0}

increases, the performance of the system will decrease, but at the same time less data is transmitted. It should be noted that if

σ_{0}

is too large, the stability of system (27) is hard to be guaranteed. For this reason, the advantages and disadvantages associated with its variation should be considered when selecting the triggering threshold parameter.

5. Conclusion

To guarantee the desired performance of the UMV systems under aperiodic DoS attack, a DOFC strategy which based on the ETM and the quantitative mechanism is investigated in this paper. Some uncertainties such as external interference and network-induced delay are considered in the UMV systems. For the purpose of reducing the communication burden and optimizing data transmission, an AETM and a quantizer are incorporated into the communication channel between the sampler and the control unit. And sufficient conditions for global exponential stability of system with

H_{\infty}

disturbance attenuation are given, the matrix parameters of the controller are obtained in terms of the LMIs. The simulation results and the performance analysis are demonstrated that the designed scheme has the tangible effectiveness on reducing the amplitude and deviation of the UMV systems.

Since this paper uses a conventional switching system to model acyclic DoS attacks, the attack signal is subject to conditional restrictions (35). Markovian jump systems, semi-Markovian systems and other methods provide a new perspective for modeling DoS attack signal. Within the proposed generic framework, the research directions can be expanded to hybrid attacks, network attack detection and so on, which are reserved for our future work.

Author Contributions

Methodology, writing-original draft, C.W.; Simulation, validation, W.X.; Writing-review editing, conceptualization, J.G.; Formal analysis, P.W.; Investigation, X.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China under Grant 62073296 and the Zhejiang Province Natural Science Foundation of China under Grant LZ23F030010.

Conflicts of Interest

The authors declare no conflict of interest.

References

Nieto-Hidalgo, M.; Gallego, A.J.; Gil, P.; Pertusa, A. Two-Stage Convolutional Neural Network for Ship and Spill Detection Using SLAR Images. IEEE Transactions on Geoscience & Remote Sensing 2018, 56, 5217–5230. [Google Scholar]
Zhang, D.; Liu, G. Predictive control for networked high-order fully actuated systems subject to communication delays and external disturbances. ISA Transactions 2023. [Google Scholar] [CrossRef] [PubMed]
Wang, W.; Wang, Y.; Liu, X.; Zhiwei, L. Quantized control for networked switched systems under denial-of-service attacks via a barrier event-triggered mechanism. Nonlinear Analysis: Hybrid Systems 2023, 49. [Google Scholar] [CrossRef]
Chen, P.; Wu, J.; Tian, E. Stochastic Event-Triggered H_∞ Control for Networked Systems Under Denial of Service Attacks. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2022, 52, 4200–4210. [Google Scholar] [CrossRef]
Zhang, L.; Nguang, S.; Yan, S. Event-triggered H∞ control for networked control systems under denial-of-service attacks. Transactions of the Institute of Measurement and Control 2021, 43(5), 1077–1087. [Google Scholar] [CrossRef]
Wang, H.; Dong, Z.; Qi, S.; Zhang, Z.; Zhang, H. Trajectory-tracking control of an underactuated unmanned surface vehicle based on quasi-infinite horizon model predictive control algorithm. Transactions of the Institute of Measurement and Control 2022. [Google Scholar] [CrossRef]
Wang, N.; Qian, C.; Sun, J.; Liu, Y. Adaptive Robust Finite-Time Trajectory Tracking Control of Fully Actuated Marine Surface Vehicles. IEEE Transactions on Control Systems Technology 2016, 24(4), 1454–1462. [Google Scholar] [CrossRef]
Hao, L.; Yu, y.; Li, T.; Li, H. Quantized Output-Feedback Control for Unmanned Marine Vehicles With Thruster Faults via Sliding-Mode Technique. IEEE Transactions on Cybernetics 2022, 52, 9363–9376. [Google Scholar] [CrossRef] [PubMed]
Li, X.; Pan, H.; Deng, Y.; Han, S.; Yu, H. Finite-time event-triggered sliding mode predictive control of unmanned underwater vehicles without velocity measurements. Ocean Engineering 2023, 276. [Google Scholar] [CrossRef]
Huang, C.; Xu, H.; Batista, P.; Zhang, X.; Guedes Soares, C. Fixed-time leader-follower formation control of underactuated unmanned surface vehicles with unknown dynamics and ocean disturbances. European Journal of Control 2023, 70. [Google Scholar] [CrossRef]
Tang, C.; Zhang, H.T.; Wang, J. Flexible Formation Tracking Control of Multiple Unmanned Surface Vessels for Navigating Through Narrow Channels with Unknown Curvatures. IEEE Transactions on Industrial Electronics 2023, 70, 2927–2938. [Google Scholar] [CrossRef]
Ma, Y.; Zhu, P.; Zhu, G.; Yan, X. Cooperative towing for double unmanned surface vehicles connected with a floating rope via vertical formation and adaptive moment control. Ocean Engineering 2023, 279. [Google Scholar] [CrossRef]
Qin, H.; Chen, X.; Sun, Y. Adaptive state-constrained trajectory tracking control of unmanned surface vessel with actuator saturation based on RBFNN and tan-type barrier Lyapunov function. Ocean Engineering 2022, 253. [Google Scholar] [CrossRef]
Wan, L.; Cao, Y.; Sun, Y.; Hongde, Q. Fault-tolerant trajectory tracking control for unmanned surface vehicle with actuator faults based on a fast fixed-time system. ISA Transactions 2022, p. [Google Scholar] [CrossRef] [PubMed]
Wang, Y.; Jiang, B.; Wu, Z.; Xie, S.; Peng, Y. Adaptive Sliding Mode Fault-Tolerant Fuzzy Tracking Control With Application to Unmanned Marine Vehicles. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2021, 51, 6691–6700. [Google Scholar] [CrossRef]
Tang, F. Coverage path planning of unmanned surface vehicle based on improved biological inspired neural network. Ocean Engineering 2023, 278. [Google Scholar] [CrossRef]
Zhang, G.; Dong, X.; Liu, J.; Zhang, X. Nussbaum-type function based robust neural event-triggered control of unmanned surface vehicle subject to cyber and physical attacks. Ocean Engineering 2023, 270. [Google Scholar] [CrossRef]
Li, M.; Guo, C.; Yu, H. Global finite-time control for coordinated path following of multiple underactuated unmanned surface vehicles along one curve under directed topologies. Ocean Engineering 2021, 237. [Google Scholar] [CrossRef]
Ye, Z.; Zhang, D.; Wu, Z. Adaptive event-based tracking control of unmanned marine vehicle systems with DoS attack. Journal of the Franklin Institute 2021, 358(3), 1915–1939. [Google Scholar] [CrossRef]
Liang, X.; Qu, X.; Hou, Y.; Li, Y.; Zhang, R. Distributed coordinated tracking control of multiple unmanned surface vehicles under complex marine environments. Ocean Engineering 2020, 205. [Google Scholar] [CrossRef]
Qu, Y.; Cai, L. Nonlinear station keeping control for underactuated unmanned surface vehicles to resist environmental disturbances. Ocean Engineering 2022, 246. [Google Scholar] [CrossRef]
Deng, Y.; Yin, X.; Hu, S. Event-triggered predictive control for networked control systems with DoS attacks. Information Sciences 2021, 542, 71–91. [Google Scholar] [CrossRef]
Lian, J.; Han, Y. Switching-Like Event-Triggered Control for Networked Markovian Jump Systems Under Deception Attack. IEEE Transactions on Circuits and Systems II: Express Briefs 2021, 68, 3271–3275. [Google Scholar] [CrossRef]
Ye, Z.; Zhang, D.; Yan, H.; Wu, Z. A semi-Markovian jumping system approach to secure DPC of nonlinear networked unmanned marine vehicle systems with DoS attack. Journal of the Franklin Institute 2021. [Google Scholar] [CrossRef]
Ye, Z.; Zhang, D.; Wu, Z.; Yan, H. A3C-Based Intelligent Event-Triggering Control of Networked Nonlinear Unmanned Marine Vehicles Subject to Hybrid Attacks. IEEE Transactions on Intelligent Transportation Systems 2021. [Google Scholar] [CrossRef]
Arzen, K.E. A simple event-based PID controller. Proceedings of IFAC World Congress 1999, 32(2), 8687–8692. [Google Scholar]
Han, X.; Zhao, X.; Sun, T.; Xu, N.; Zong, G. Event-Triggered Optimal Control for Discrete-Time Switched Nonlinear Systems With Constrained Control Input. IEEE Transactions on Systems Man Cybernetics-Systems 2021, 51, 7850–7859. [Google Scholar] [CrossRef]
Li, Y.; Yang, G. Adaptive Neural Control of Pure-Feedback Nonlinear Systems With Event-Triggered Communications. IEEE Transactions on Neural Networks and Learning Systems 2018, 29(12), 6242–6251. [Google Scholar] [CrossRef] [PubMed]
Hu, S.; Yue, D.; Xie, Y.; Ma, Y.; Yin, Y. Stabilization of Neural-Network-Based Control Systems via Event-Triggered Control With Nonperiodic Sampled Data. IEEE Transactions on Neural Networks and Learning Systems 2018, 29(3), 573–585. [Google Scholar] [CrossRef]
Ma, L.; Wang, Y.; Han, Q. Event-Triggered Dynamic Positioning for Mass-Switched Unmanned Marine Vehicles in Network Environments. IEEE Transactions on Cybernetics 2022, 52, 3159–3171. [Google Scholar] [CrossRef]
Li, M.; Guo, C.; Yu, H.; Yuan, Y. Event-triggered containment control of networked underactuated unmanned surface vehicles with finite-time convergence. Ocean Engineering 2022, 246. [Google Scholar] [CrossRef]
Zhang, G.; Chu, S.; Huang, J.; Zhang, W. Robust adaptive fault-tolerant control for unmanned surface vehicle via the multiplied event-triggered mechanism. Ocean Engineering 2022, 249. [Google Scholar] [CrossRef]
Li, Z.; Xiong, J. Event-triggered fuzzy filtering for nonlinear networked systems with dynamic quantization and stochastic cyber attacks. ISA Transactions 2022, 121, 53–62. [Google Scholar] [CrossRef] [PubMed]
Zhao, Z.; Yi, X.; Ma, L.; Bai, X. Quantized recursive filtering for networked systems with stochastic transmission delays. ISA Transactions 2022, 127, 99–107. [Google Scholar] [CrossRef] [PubMed]
Kahveci, N.; Ioannou, P. Adaptive steering control for uncertain ship dynamics and stability analysis. Automatica 2013, 49, 685–697. [Google Scholar] [CrossRef]
Ma, Y.; Nie, Z.; Hu, S.; Li, Z.; Malekian, R.; Sotelo, M. Fault Detection Filter and Controller Co-Design for Unmanned Surface Vehicles Under DoS Attacks. IEEE Transactions on Intelligent Transportation Systems 2021, 22(3), 1422–1434. [Google Scholar] [CrossRef]
Ge, X.; Han, Q. Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism. IEEE Transactions on Industrial Electronics 2017, 64(10), 8118–8127. [Google Scholar] [CrossRef]
Fu, M.; Xie, L. The sector bound approach to quantized feedbackcontrol. IEEE Transactions on Automatic Control 2005, 50(11), 1698–1711. [Google Scholar]
Ge, X.; Han, Q. Distributed event-triggered H_∞ filtering over sensor networks with communication delays. Information Sciences 2015, 291, 128–142. [Google Scholar] [CrossRef]
Zhang, X.; Han, Q. Event-triggered dynamic output feedback control for networked control systems. IET Control Theory and Applications 2014, 8(4), 226–234. [Google Scholar] [CrossRef]
Xu, S.; Dooren, P.V.; Stefan, R.; J., L. Robust stability and stabilization for singular systems with state delay and parameter uncertainty. IEEE Transactions on Automatic Control 2002, 47, 1122–1128. [CrossRef]
Wang, Y.; Han, Q. Network-based modelling and dynamic output feedback control for unmanned marine vehicles in network environments. Automatica 2018, 91, 43–53. [Google Scholar] [CrossRef]
Ma, Y.; Nie, Z.; Hu, S.; Li, Z.; Malekian, R.; Sotelo, M. Fault Detection Filter and Controller Co-Design for Unmanned Surface Vehicles Under DoS Attacks. IEEE Transactions on Intelligent Transportation Systems 2021, 22, 1422–1434. [Google Scholar] [CrossRef]
Wang, H.; Xue, A. Adaptive event-triggered H∞ filtering for discrete-time delayed neural networks with randomly occurring missing measurements. Signal Processing 2018, 153, 221–230. [Google Scholar] [CrossRef]

Figure 1. The reference frames of Earth-fixed and body-fixed.

Figure 2. Networked structure for the UMV systems.

Figure 3. The signal of DoS attack

(δ_{min} = 1.5 s, ϑ_{max} = 0.7 s)

Figure 3. The signal of DoS attack

(δ_{min} = 1.5 s, ϑ_{max} = 0.7 s)

Figure 4. The yaw angle response.

Figure 5. The yaw angle response in reference.

Figure 6. The yaw velocity error response.

Figure 7. The yaw velocity error response in reference.

Figure 8. The yaw moment response.

Figure 9. The surge velocity response.

Figure 10. The sway velocity response.

Figure 11. The adaptive threshold of event-triggered mechanism.

Figure 12. The trigger time instant of adaptive event-triggered mechanism.

Figure 13. The release time interval of adaptive event-triggered mechanism.

Figure 14. The response of yaw angle in different initial thresholds.

Figure 15. The response of yaw velocity error in different initial thresholds.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Adaptive Event-based Dynamic Output Feedback Control for Unmanned Marine Vehicle Systems Under DoS Attack

Abstract

1. Introduction

1.1. Notation

2. Preliminaries and problem formulation

2.1. Networked modelling for the UMV system

2.2. Aperiodic DoS attack

2.3. The adaptive event-triggered communication mechanism

2.4. The quantitative mechanism

2.5. The investigated dynamic output feedback control strategy

3. Main result

3.1. The analysis of stability

3.2. The analysis of H ∞ performance

4. Simulation and analysis

5. Conclusion

Author Contributions

Funding

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.2. The analysis of $H_{\infty}$ performance