Submitted:
20 December 2023
Posted:
21 December 2023
You are already at the latest version
Abstract
Keywords:
PART 1: The Riemann Zeta function ζ() [RZF]
- 1.
-
As defined in literature (Sondow et al, Weisstein, Edwards, Jekel)
- 1.1.
-
- 1.2.
- Euler Product Formula that links with the distribution of prime numbers
Example for k=2- 1.3.
- Integral definition of :
Where , is the Gamma function- 1.4.
- Analytical continuation of for :
Re(s)>0: [Dirichlet]0<Re(s)<1:-k<Re(s) [Kopp, Konrad. 1945]:- 1.5.
- Laurent series of :where are the Stieltjes constants.
- 1.6.
- Hurwitz function :
- 1.7.
- Generalized Harmonic Function :
- 1.8.
- 1.9.
- An approximation for the values of for s>1 in R
One can calculate that:And:Based on this expression, for s sufficiently large, one can represent as a multiple of :with a very good approximation given by:The error between the calculated and actual is very small for s>4.Some calculated values of calculated and actual:Table 2. Values of calculated and actual.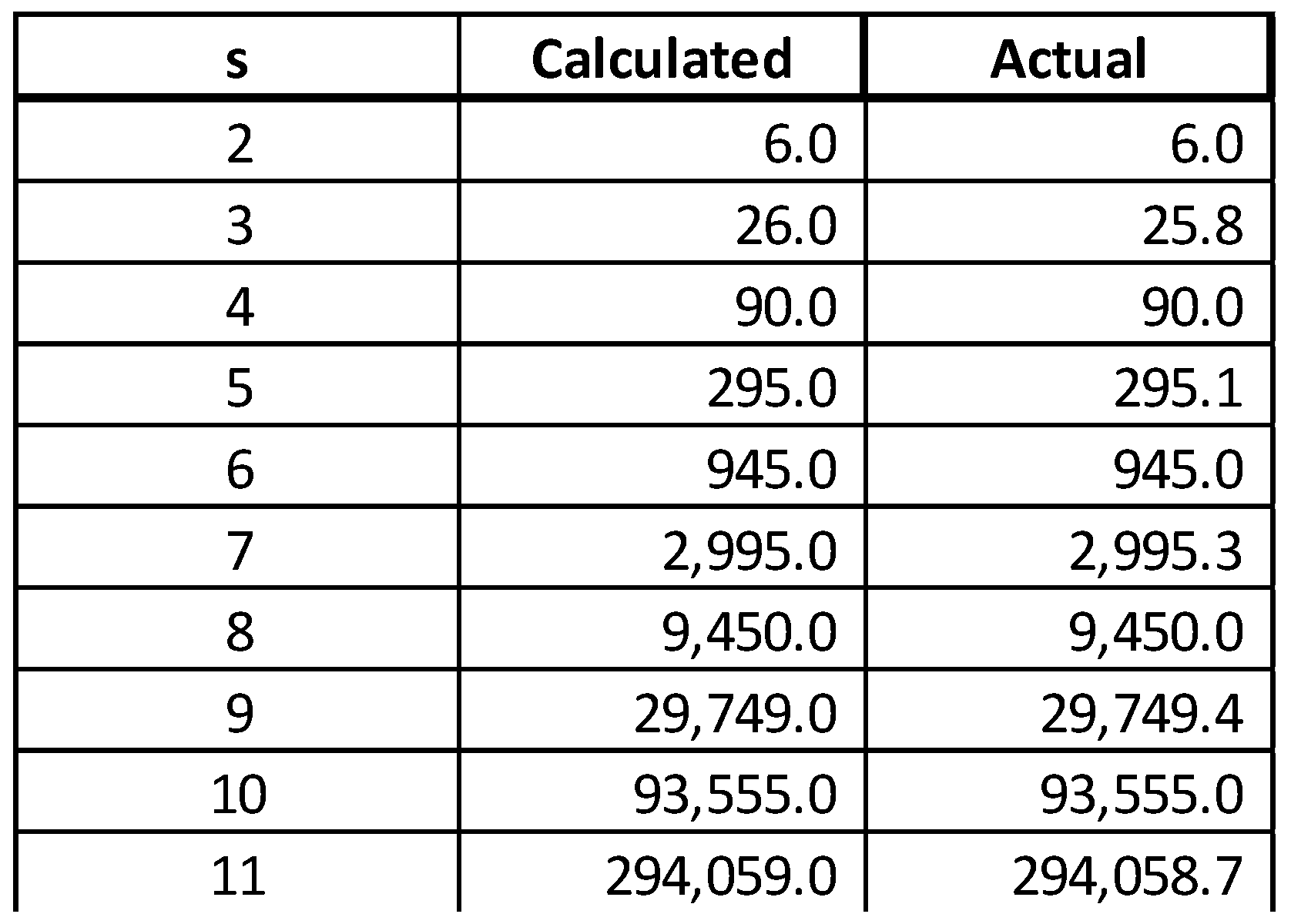 One can use [2] to propose the following approximation for :Table 3. Comparing and CZ(s).
One can use [2] to propose the following approximation for :Table 3. Comparing and CZ(s).s=3 s=4 s=10 s=14 1.20206 1.0823 1.000994 1.0000612 1.18659 1.0784 1.000988 1.0000611 Graphically:
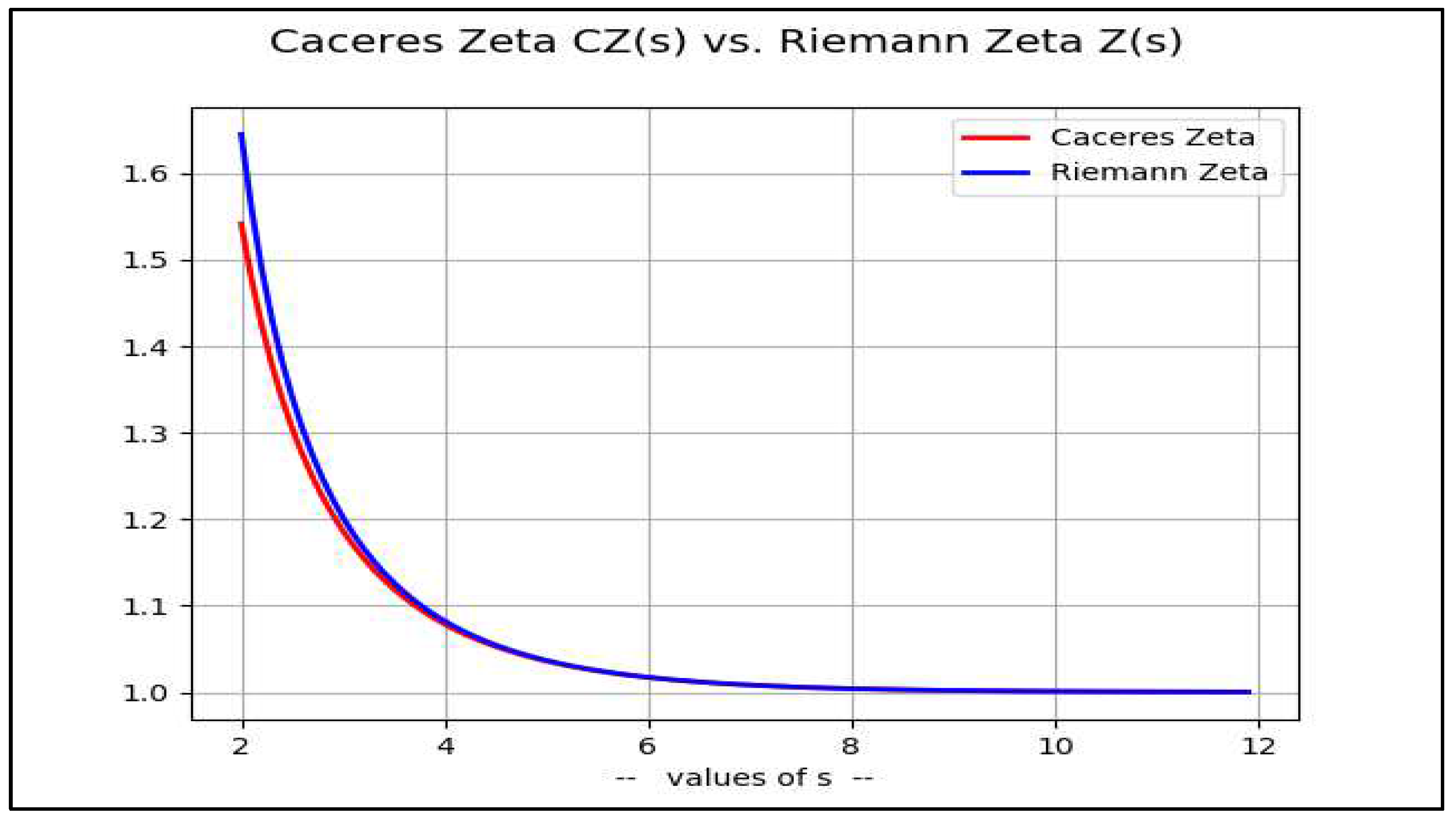
-
- 1.10.
-
Zeros of (Weisstein)
- 1.10.1.
There are no zeros of . converges for s>1.- 1.10.2.
is the Harmonic function and diverges, and:(the Euler-Mascheroni constant)- 1.10.3.
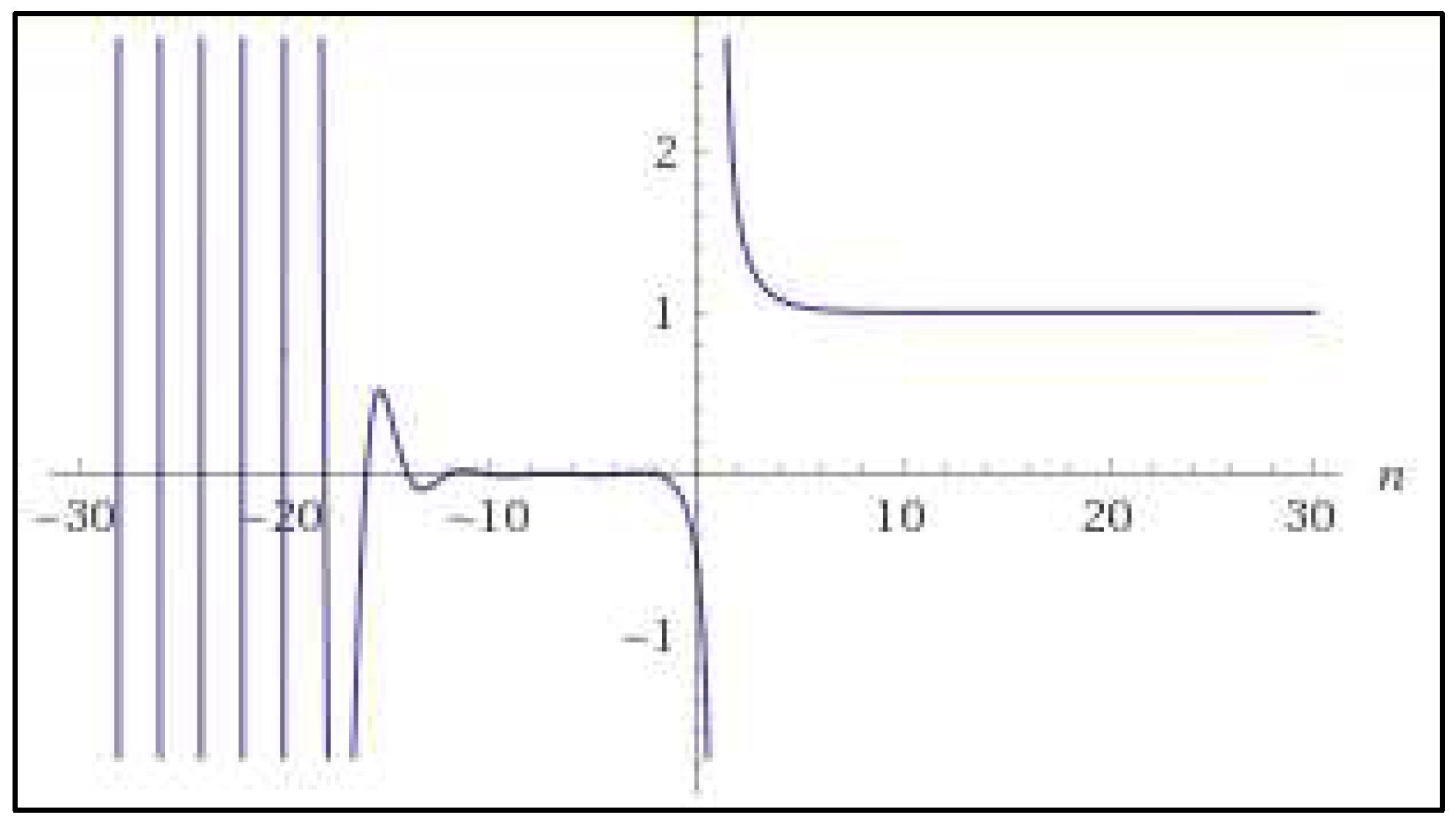
has trivial zeros at , with natural numbershas nontrivial zeros at at the critical line (Brentt)The Riemann Hypothesis [RH] establishes that all nontrivial zeros of zeta have List of imaginary part of the first nontrivial zeros of zeta (Odlyzko):- ß(1) = 14.134725142
- ß(3) = 25.010857580
- ß(4) = 30.424876126
- ß(6) = 37.586178159
- ß(7) = 40.918719012
- ß(9) = 48.005150881
- ß(10) = 49.773832478
Representation of |:
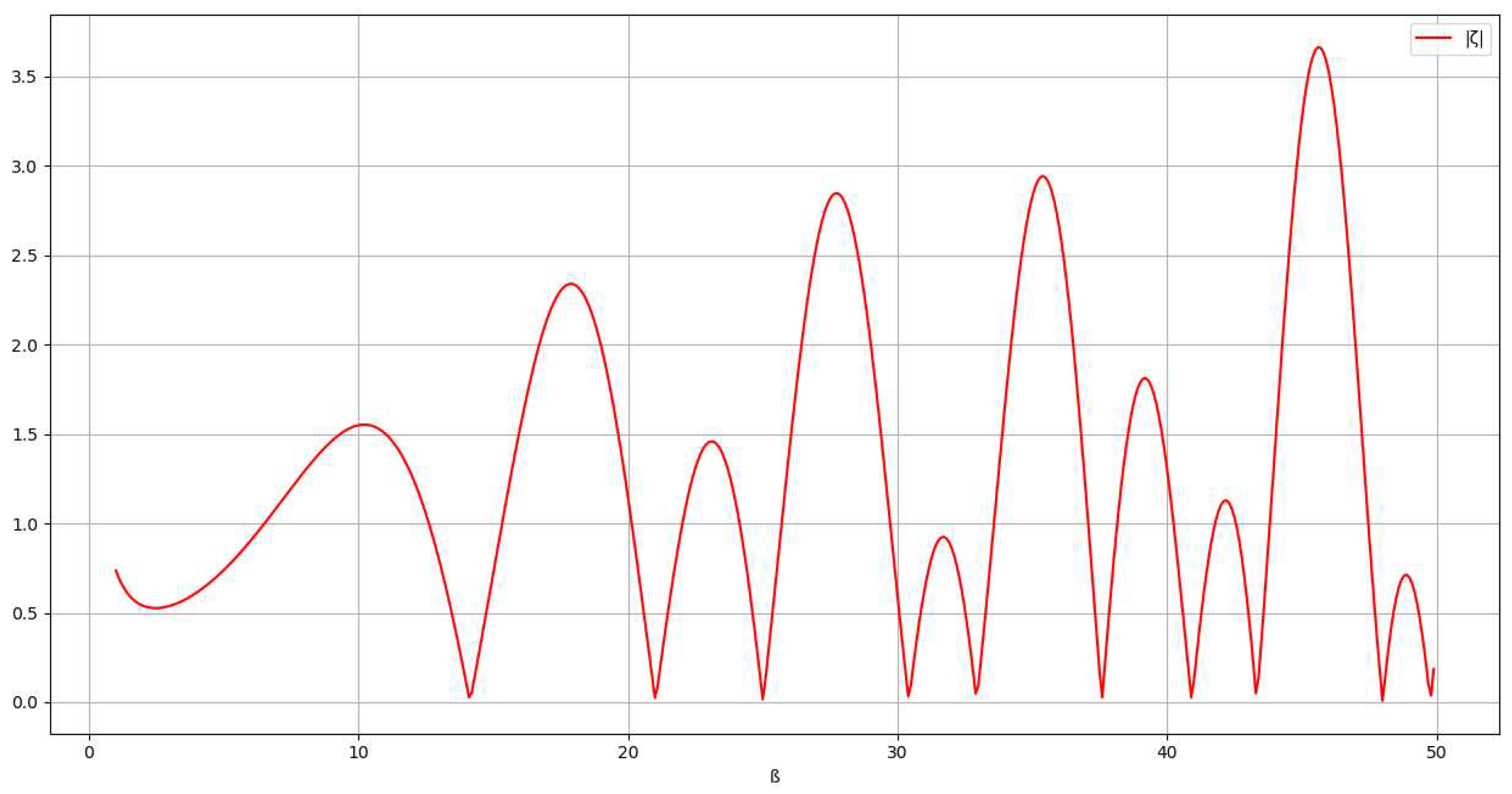
PART 2: The C-Transformation
- 1.
-
C-Transformation of f(x)Let’s define the C-transformation of an integrable function f(x) by:And the C-values is the limit, if it exists, of the C-transformation when :1.1. C-Transformation of for :And the C-Value of is (Euler-Mascheroni constant)1.2. C-Transformation of for :And the C-Value of are the Stieltjes constants that occur in the Laurent series expansion of the Riemann zeta function:
 1.3. C-Transformation of , for constant:and the C-values of f(x) =m constant is:1.4. C-Transformation of for :And the C-values of are in the interval:One can also calculate that:1.5. C-Transformation of for :And the C-values of are:1.6. C-Transformation of for , s>1:and the C-value of is the Riemann Zeta function for s>1:1.7. C-Transformation of forOne can use Euler’s identity:To calculate for z=α+ßi:And:One can now express the real and imaginary components of as:One can calculate that, for α=Re(z)>1, and for any arbitrarily small, there is a value of n=N such that for n>N, - ζ()< , as the following table shows:Table 4. Values of for α=Re(z)>1 for N=500.
1.3. C-Transformation of , for constant:and the C-values of f(x) =m constant is:1.4. C-Transformation of for :And the C-values of are in the interval:One can also calculate that:1.5. C-Transformation of for :And the C-values of are:1.6. C-Transformation of for , s>1:and the C-value of is the Riemann Zeta function for s>1:1.7. C-Transformation of forOne can use Euler’s identity:To calculate for z=α+ßi:And:One can now express the real and imaginary components of as:One can calculate that, for α=Re(z)>1, and for any arbitrarily small, there is a value of n=N such that for n>N, - ζ()< , as the following table shows:Table 4. Values of for α=Re(z)>1 for N=500.α ß for N=500 ζ ( ) ζ ( )| 2 0 1.644934068 1.654934067 2 1 1.150355702 + 0.437530865 i 1.150355703+0.437530866 i 3 3 0 1.202056903 1.202056903 That shows that the C-values of for Re(z)>1 is
PART 3: A decomposition of ζ(z) based on the C-transformation of . for
- C-Transformation of for
| A | ß | ζ ( ) | ζ ( )| | |
| 0.0 | 0 | CN{f} for N=500 | -0.5 | 0.5 |
| 0.2 | 2 | 0.399824505+0.322650799 i | 0.360103 + 0.266246 i | |
| 0.7 | 0 | -2.777900606 | -2.7783884455 |
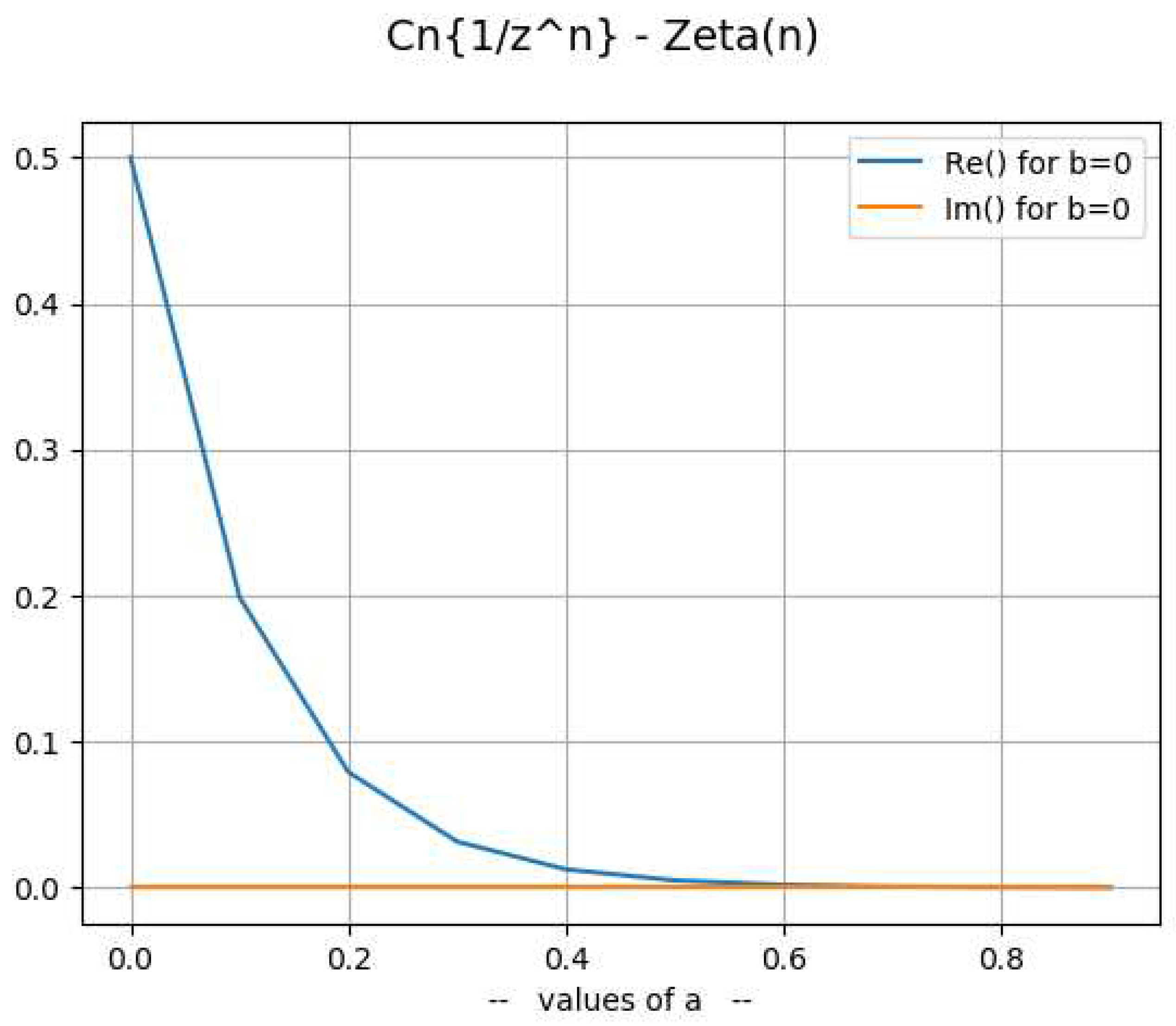
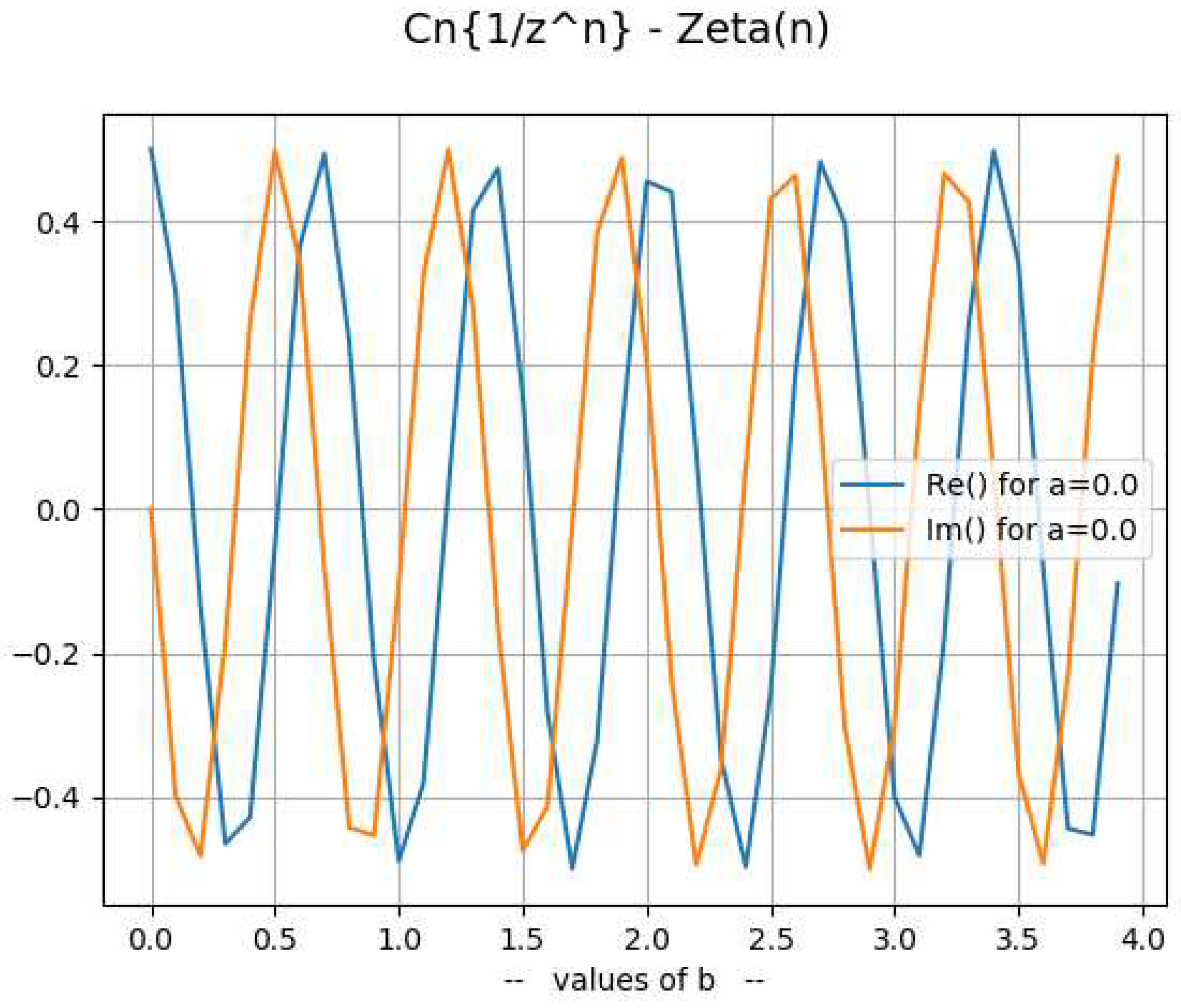
- 2.
-
Decomposition ofOne can rewrite [8] and [9] creating the and functions:where:and define:to write:The following table compared the values of and :Table 6. ζ(z) compared to X(z) - Y(z).
z= 0 +j* 0 and n=500 Zeta(z) = -0.5 + i* 0.0
X(z)-Y(z) = -0.5 +i* 0.0
---> Error = 0.0 +i* 0.0z= 0.2 +j* 2 and n=500 Zeta(z) = 0.360102590022591 + i* -0.266246199765574
X(z)-Y(z) = 0.360102741838091 +i* -0.266246128959438
---> Error= -1.5181550 e-7 +i* -7.080613 e-8z= 0.4 +j* 0 and n=500 Zeta(z) = -1.13479778386698 + i* 0.0
X(z)-Y(z) = -1.1347977871726 +i* 0.0
---> Error= 3.305619 e-9 +i* 0.0The highest error for αn=1000 is . - 3.
- Representation of the function for Re(z)=1/2
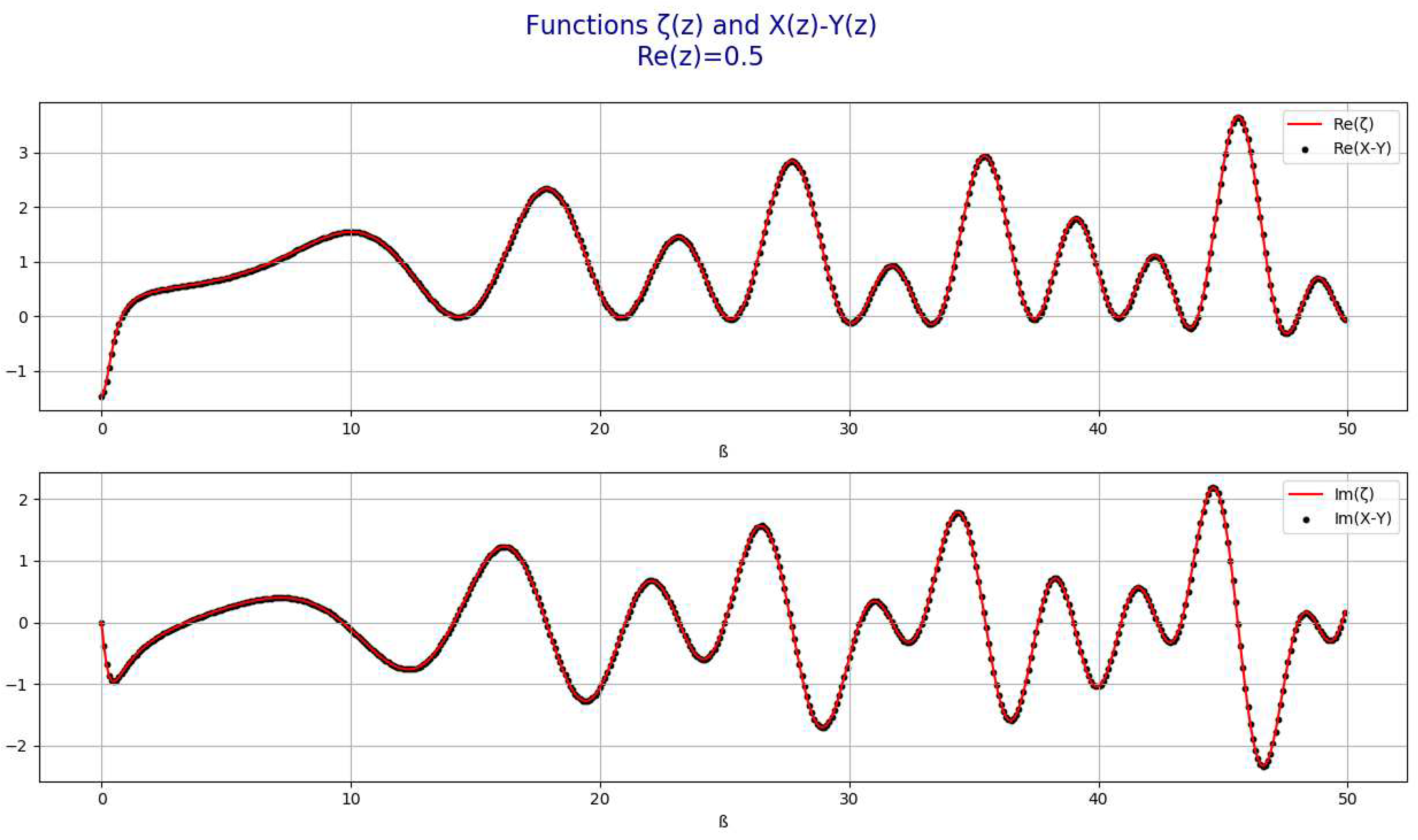
- 4.
- Representation of the function for Re(z)=1/2
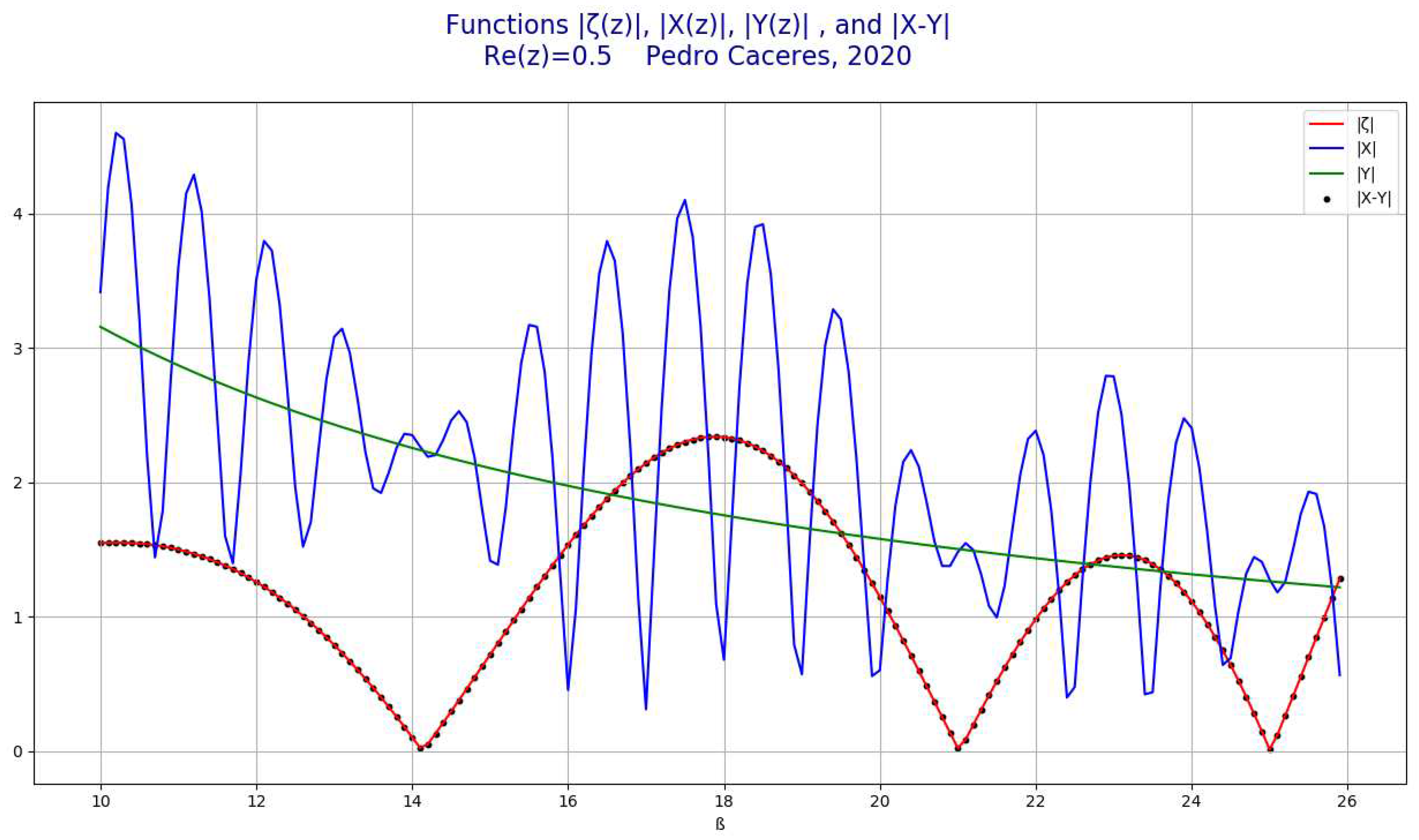
- 5.
-
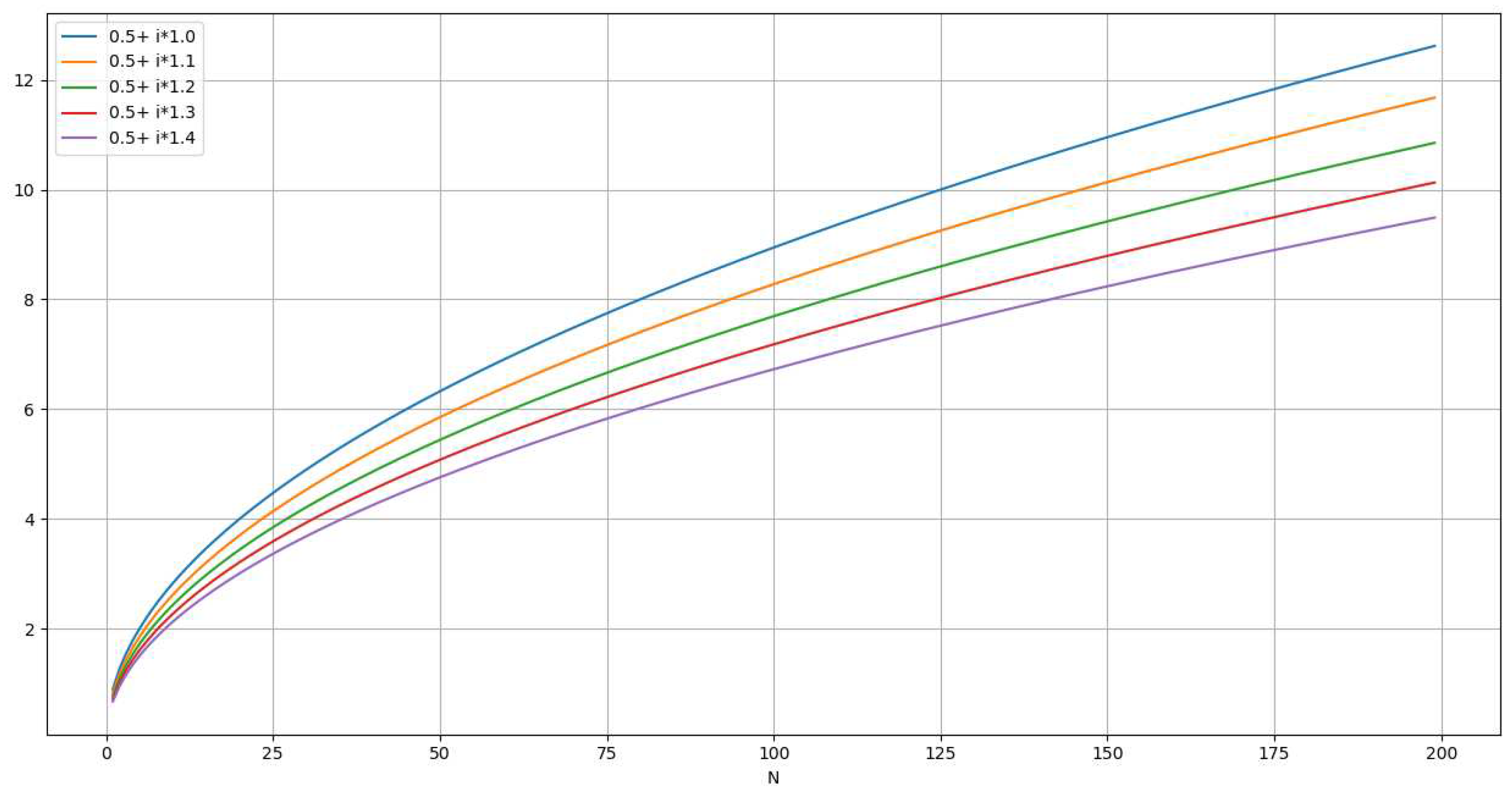
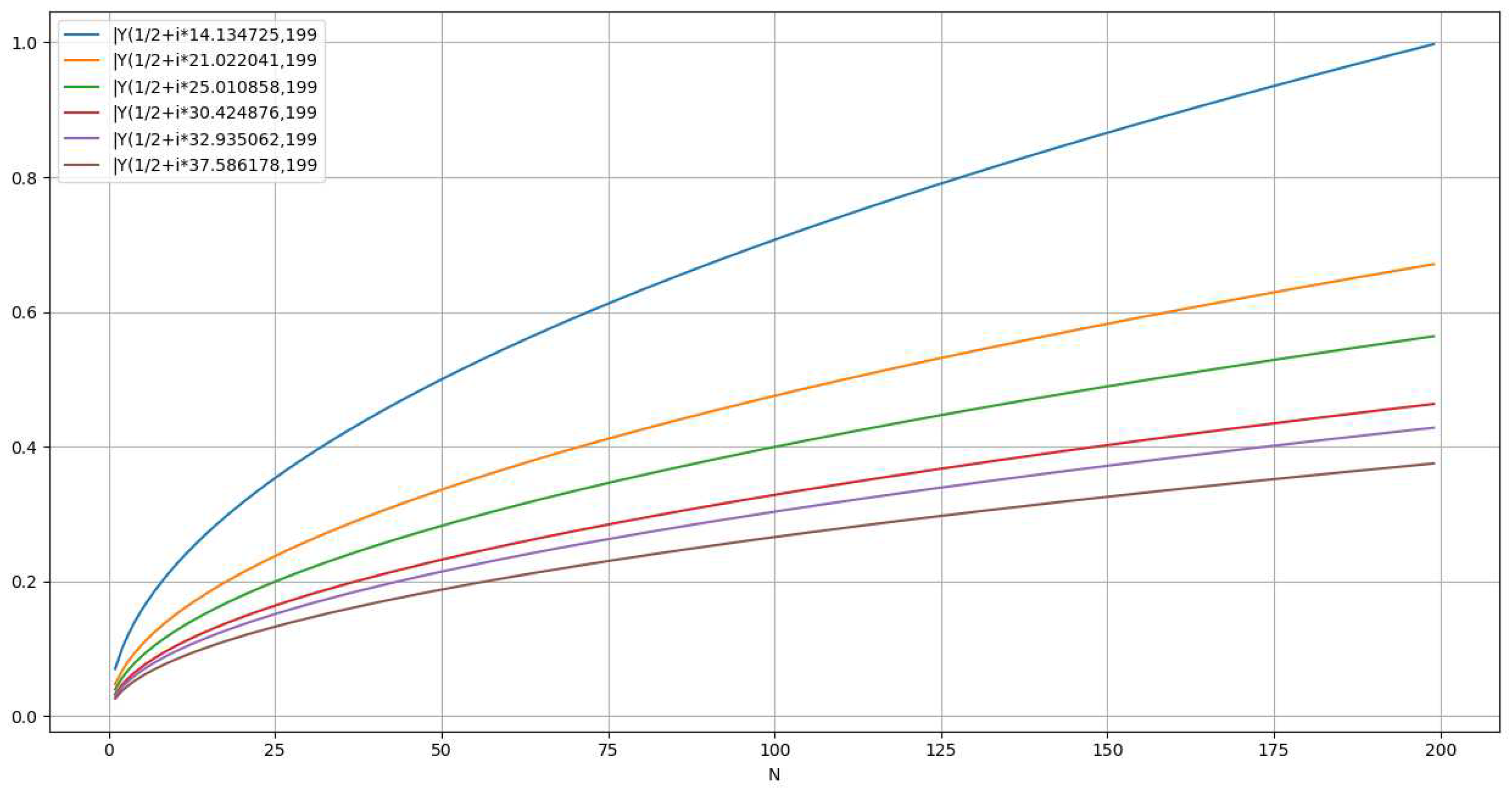
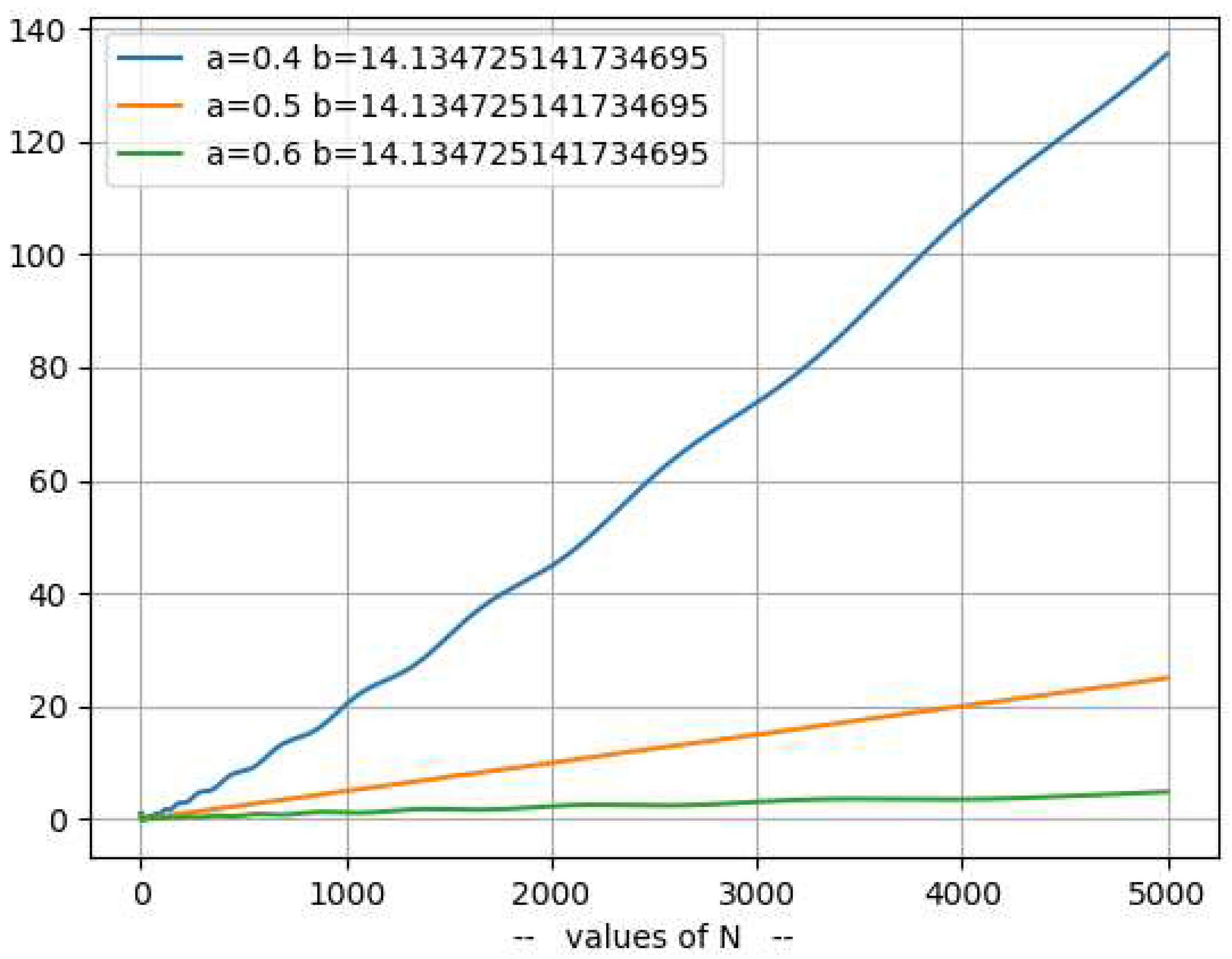
Representation of the function )The following chart represents for and and .
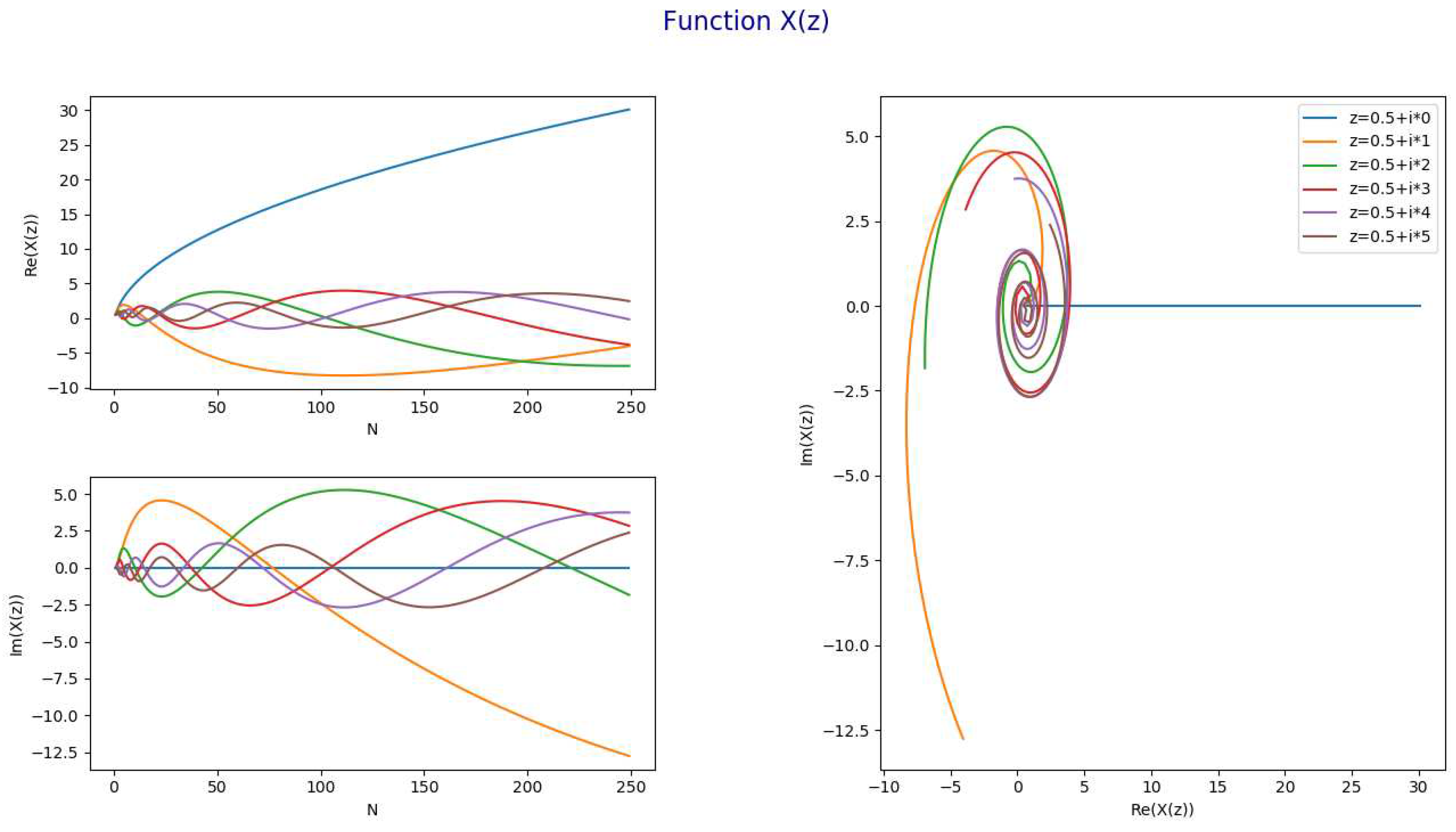
- The following chart represents for and and .
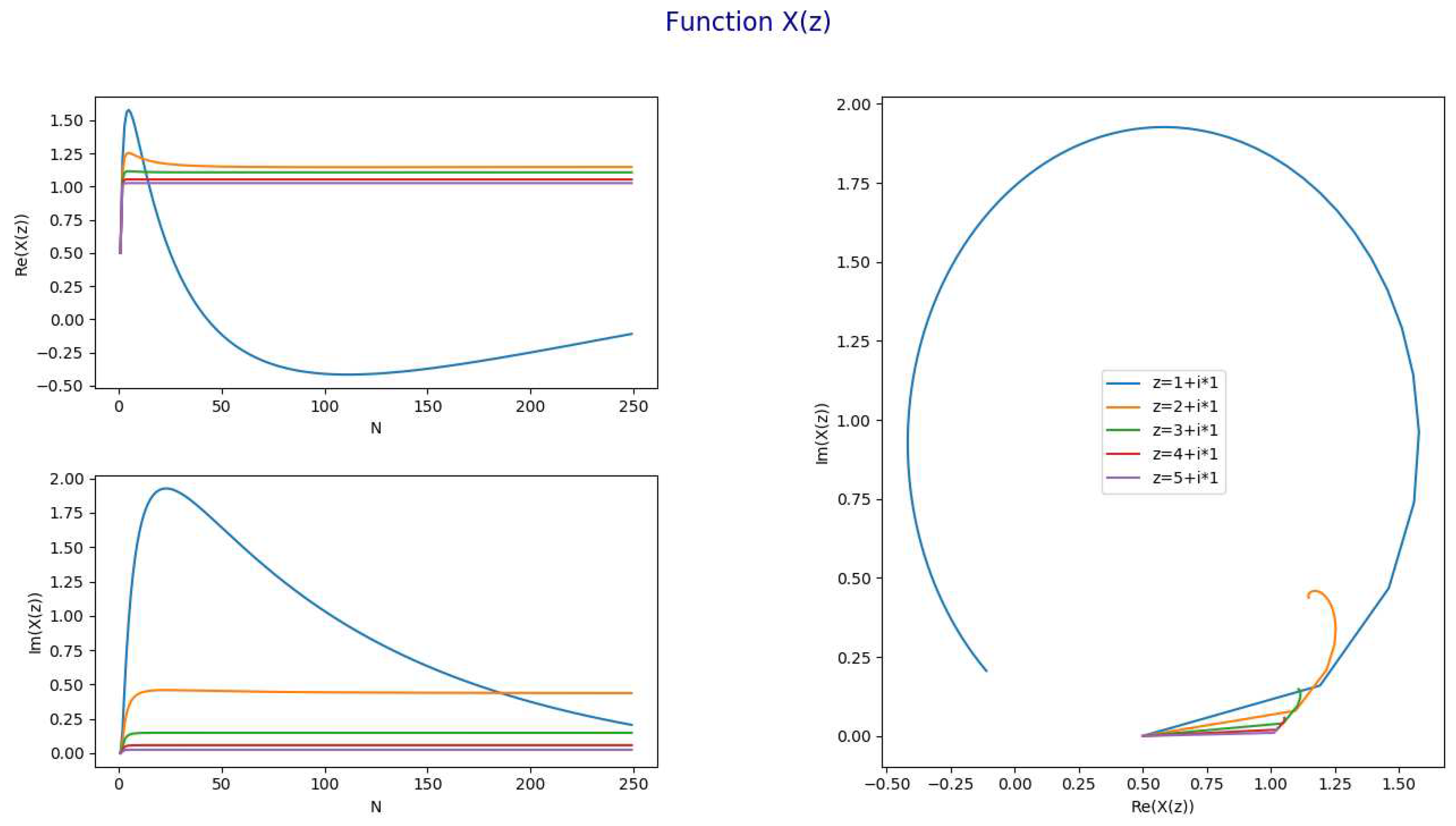
- 6.
-
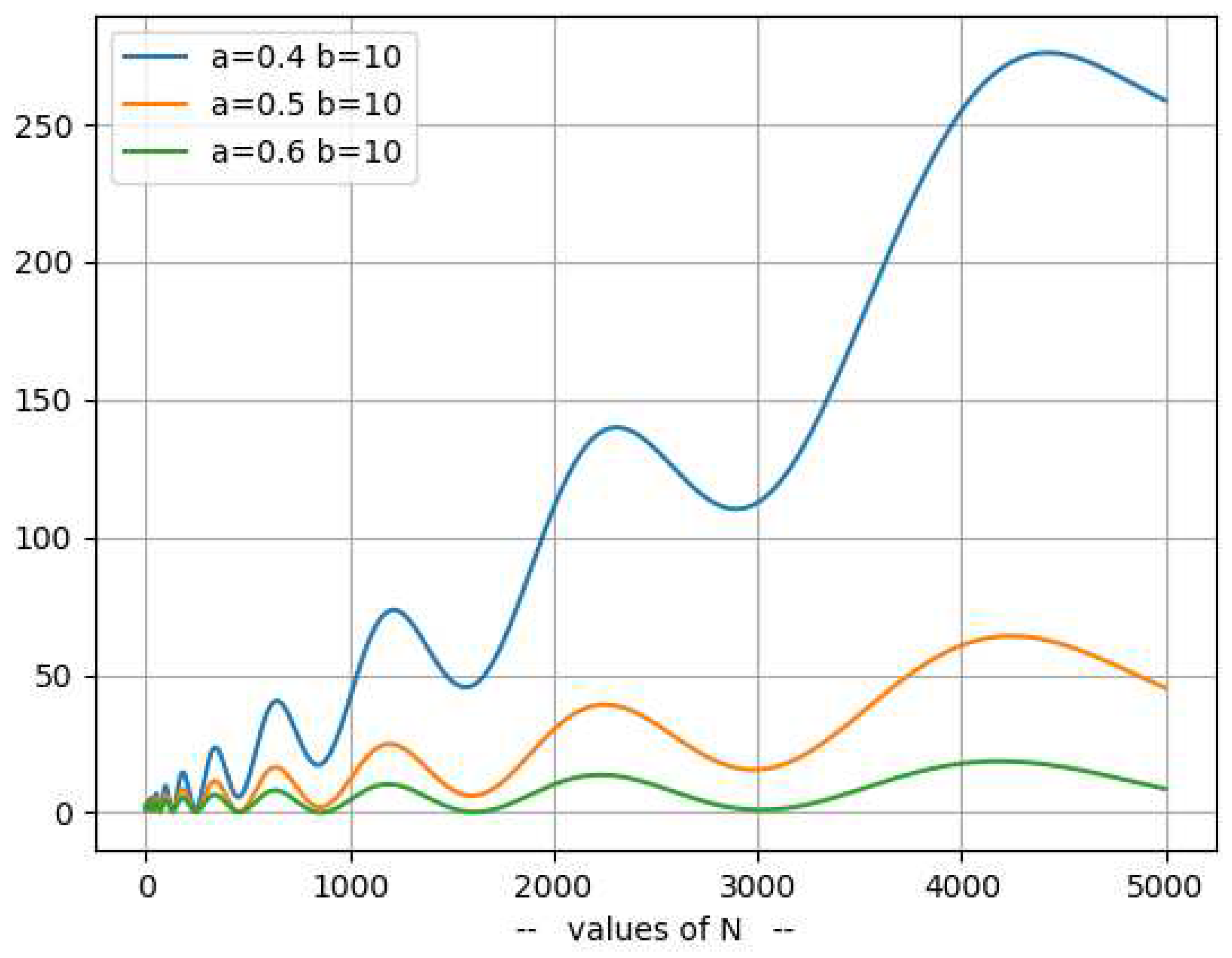
Representation of the functionThe following chart represents for and and
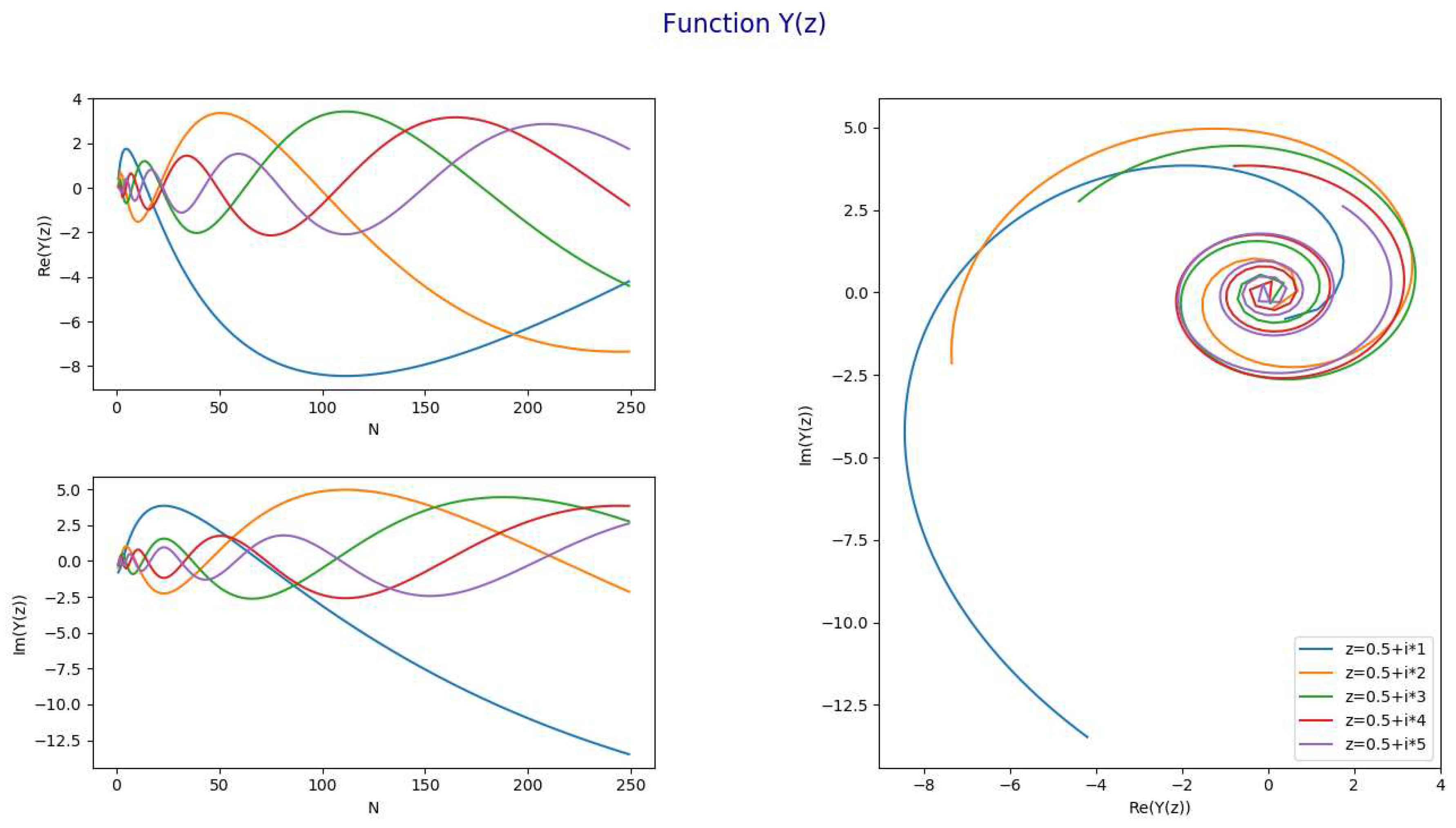
- The following chart represents for and and
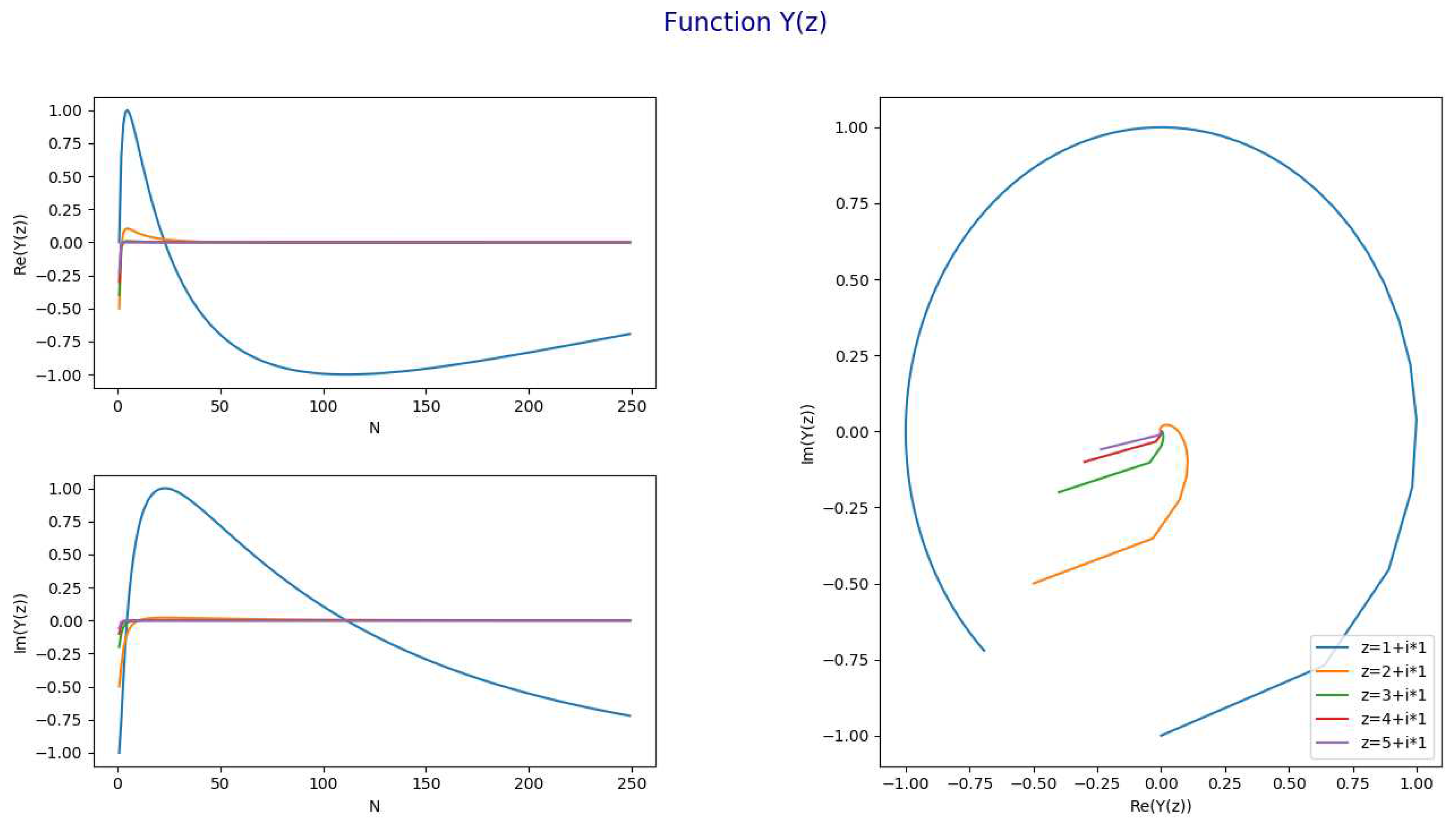
- 7.
-
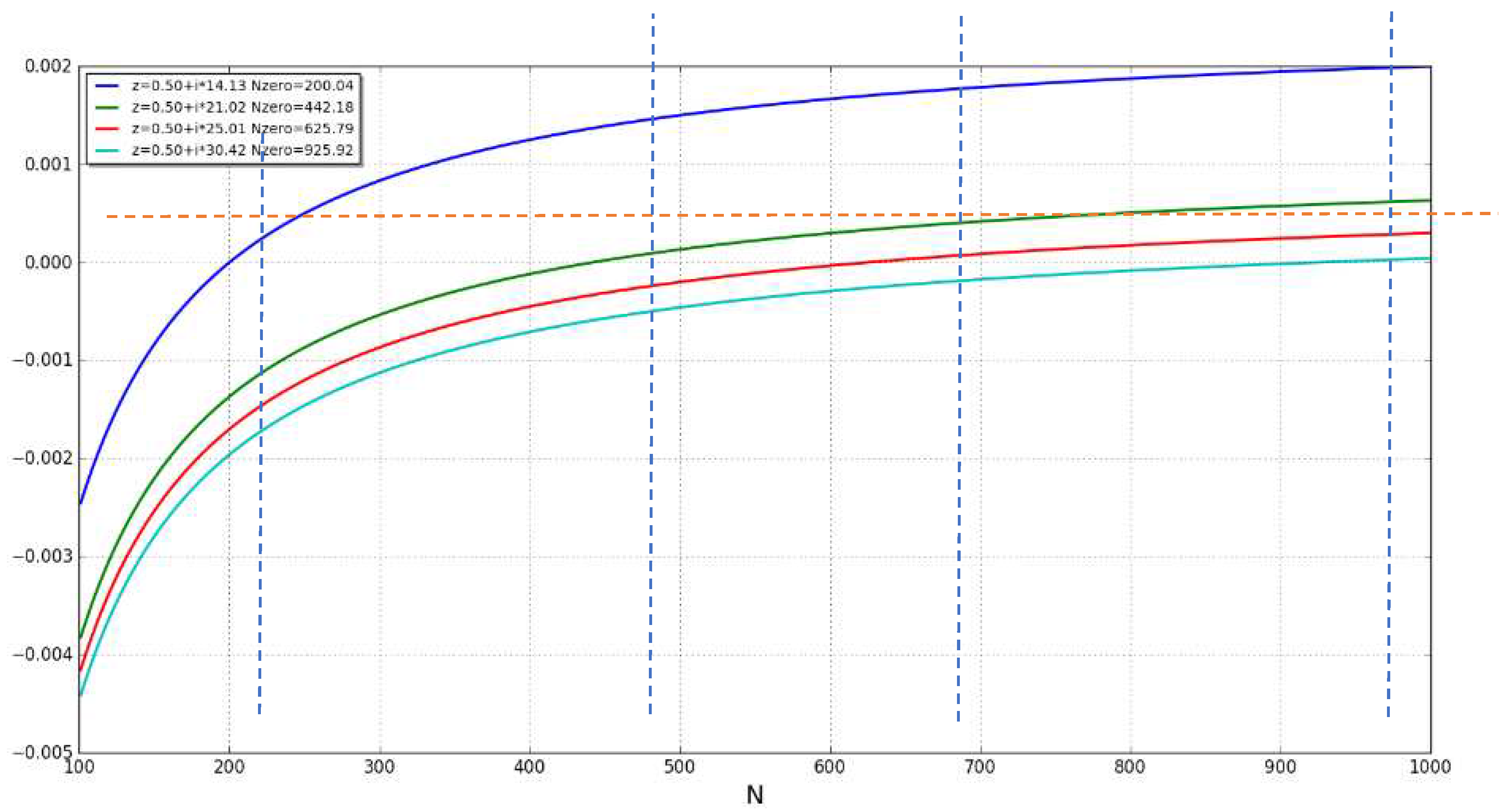
Representation of |Wave representation for . [Figure. 11]
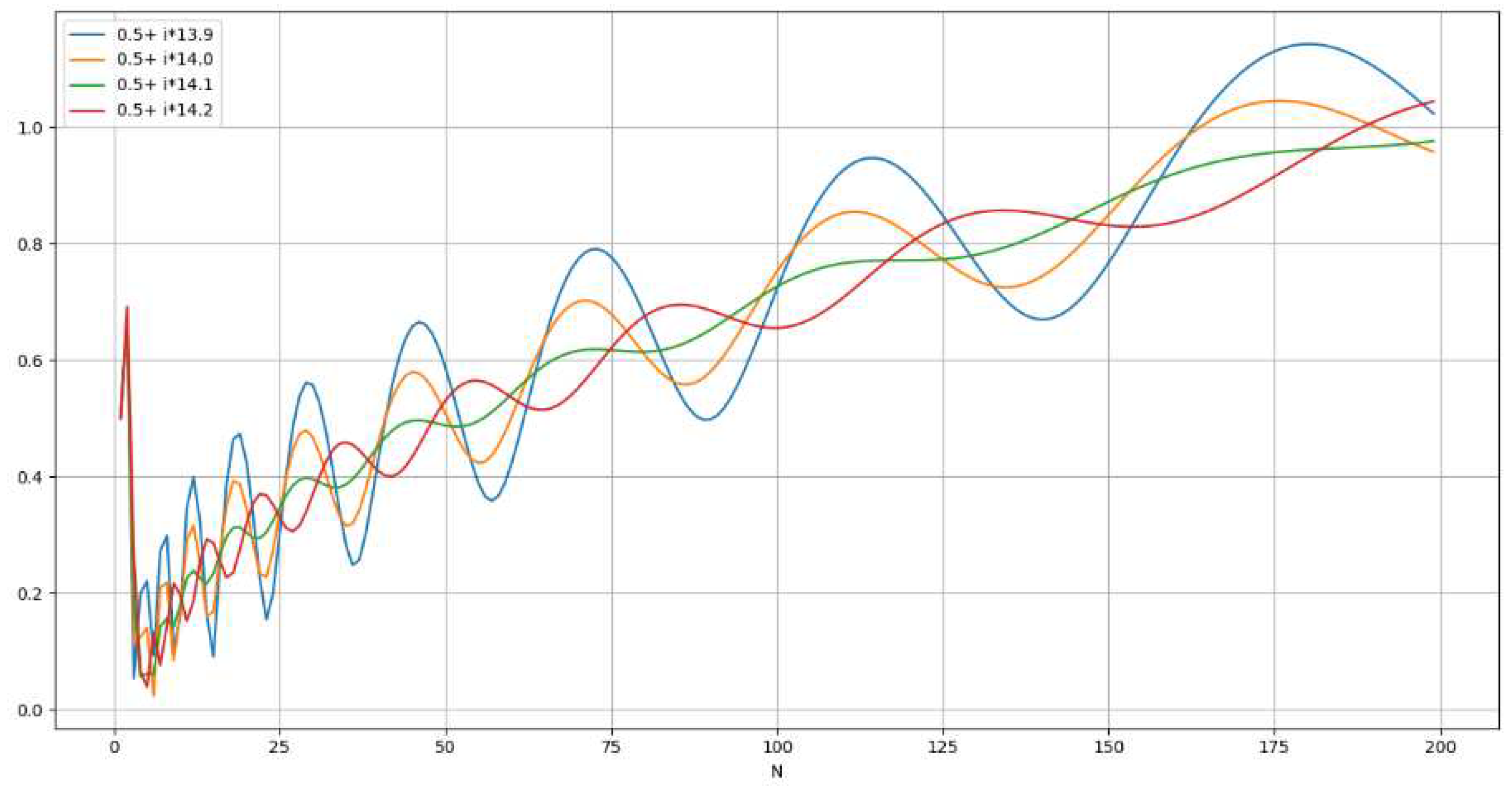
- Parabolic representation for | [Figure. 12]
- Linear representation for | [Figure. 13]
- 8.
-
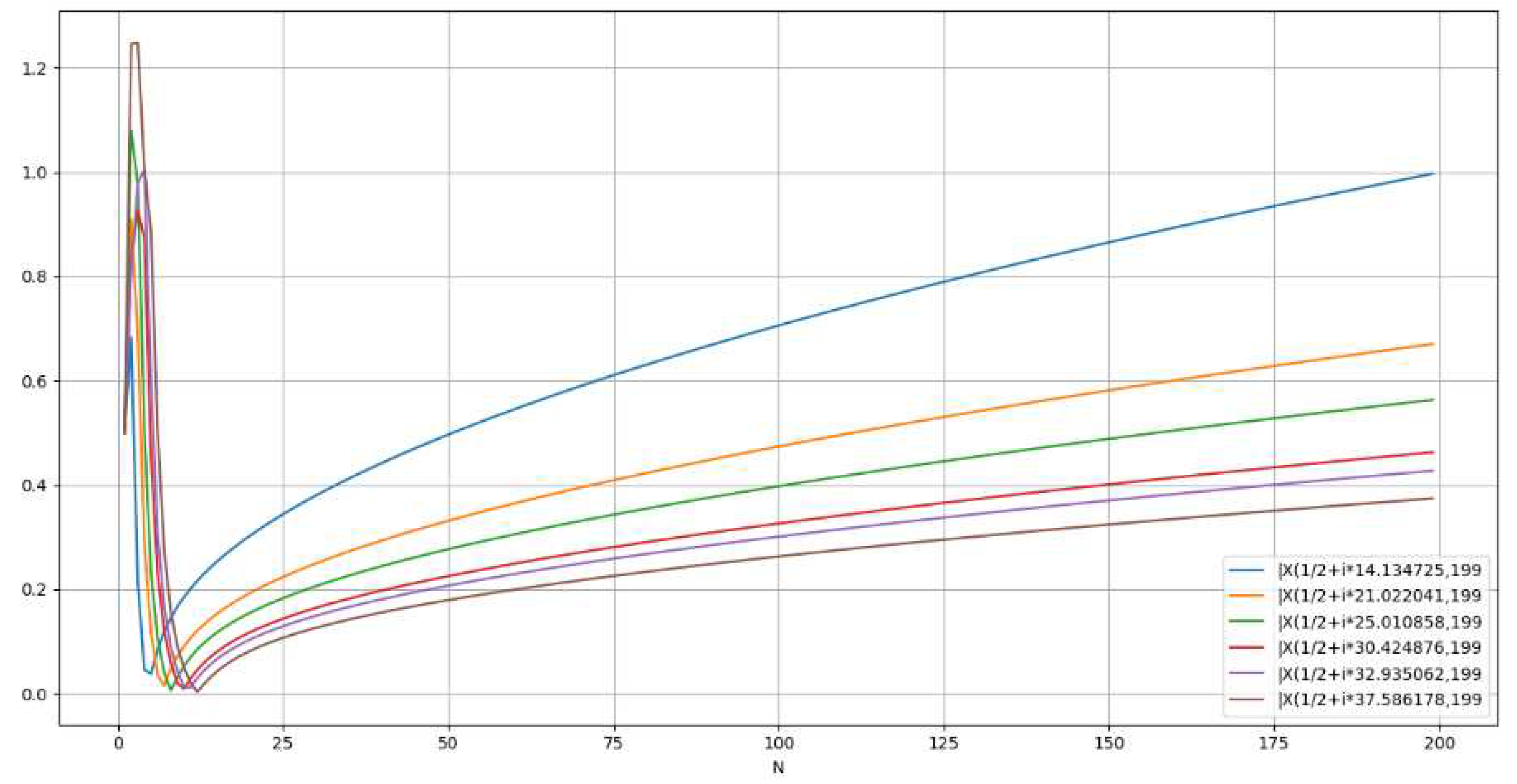
Representation of |Polynomial representation for . [Figure. 14]
- Parabolic representation for . [Figure. 15]
- Linear representation for . [Figure. 16]
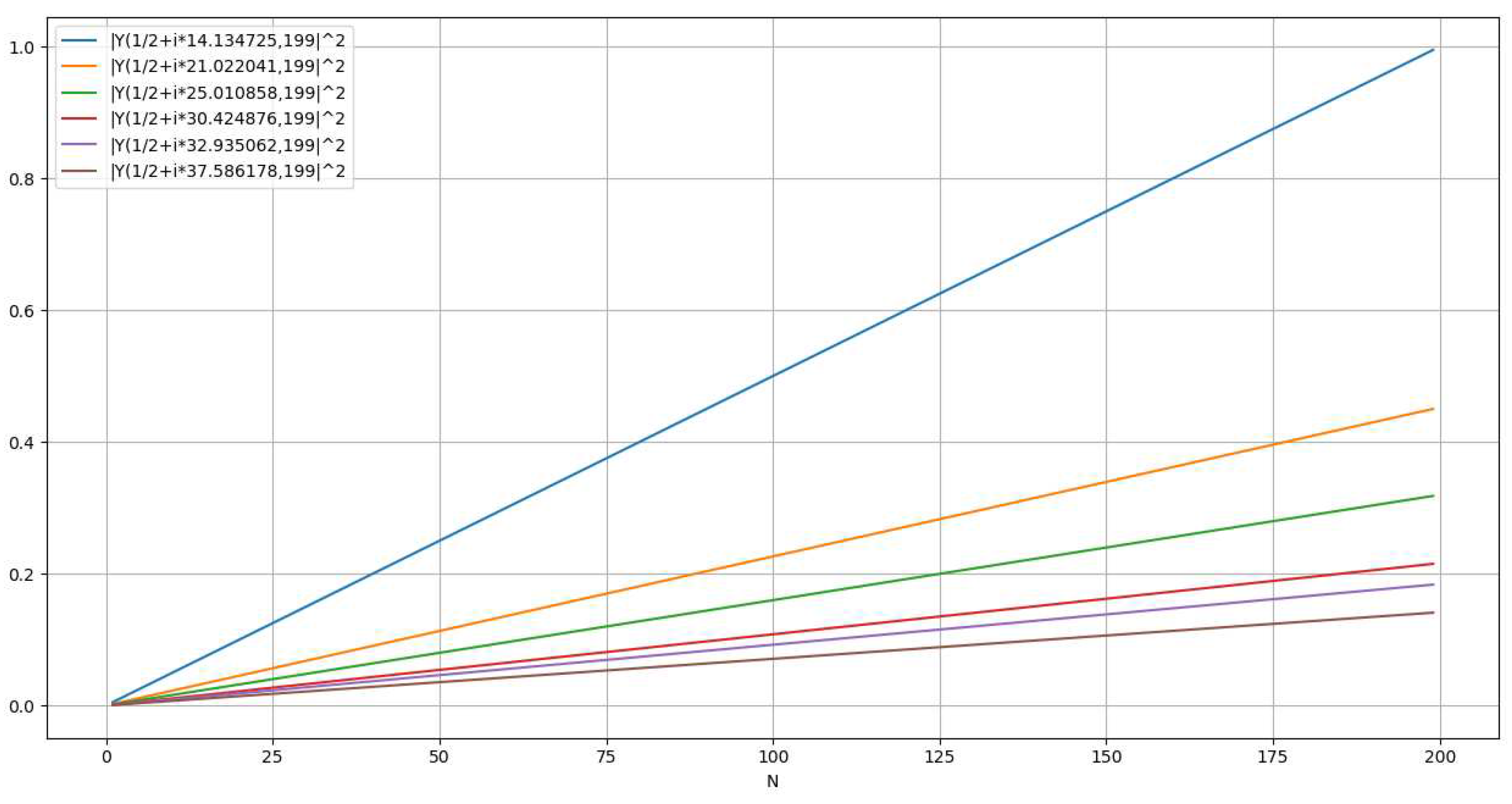
- 9.
- Conclusion PART 3
- has a wave representation
- becomes a parable when z is a nontrivial zero of Riemann Zeta
- becomes a line when z is a nontrivial zero of RZF with slope equal
- has a polynomial representation
- becomes a parable when z is a nontrivial zero of Riemann Zeta
- becomes a line when Re(z)=1/2 with slope equal
PART 4: Proof of the Riemann Hypothesis using the decomposition.
- 1.
-
Analysis of Absolute SquareThis could be observed in Figure. 14, 15, 16.1.1. is a straight line if and only ifThe slope of with respect to n is given by:Which equals to:can only be a line when the slope is constant, which can only happen if and only if:therefore:1.2. Summary for for :
- ⇨
- the slope is constant if and only if
- ⇨
- When α=1/2, =
- ⇨
- The slope for is for
- 2.
-
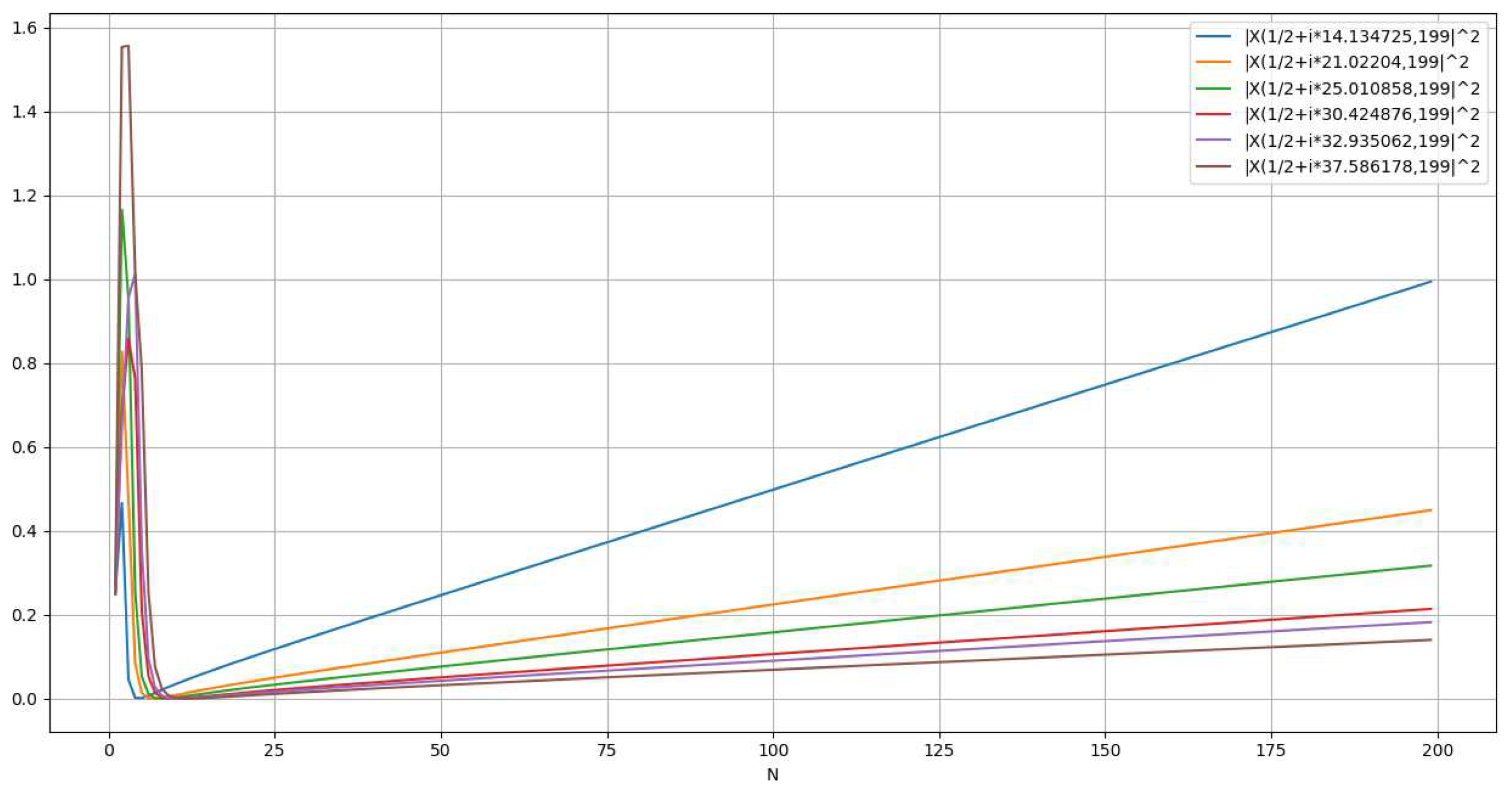
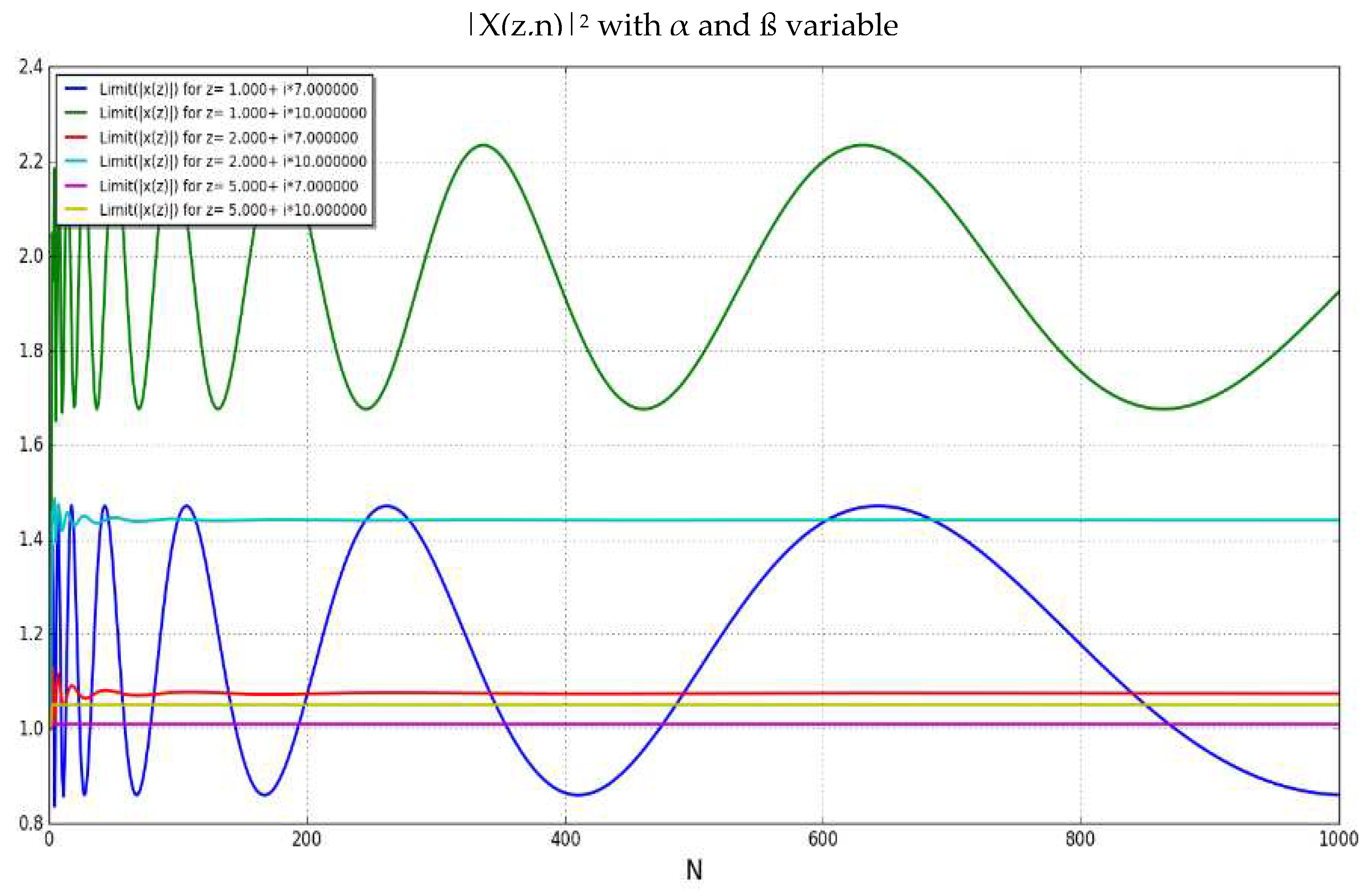
Analysis of Absolute SquareApplying properties of infinite series (Kopp):One can express the previous expression replacing:With:When is represented graphically, one can observe that:
- -
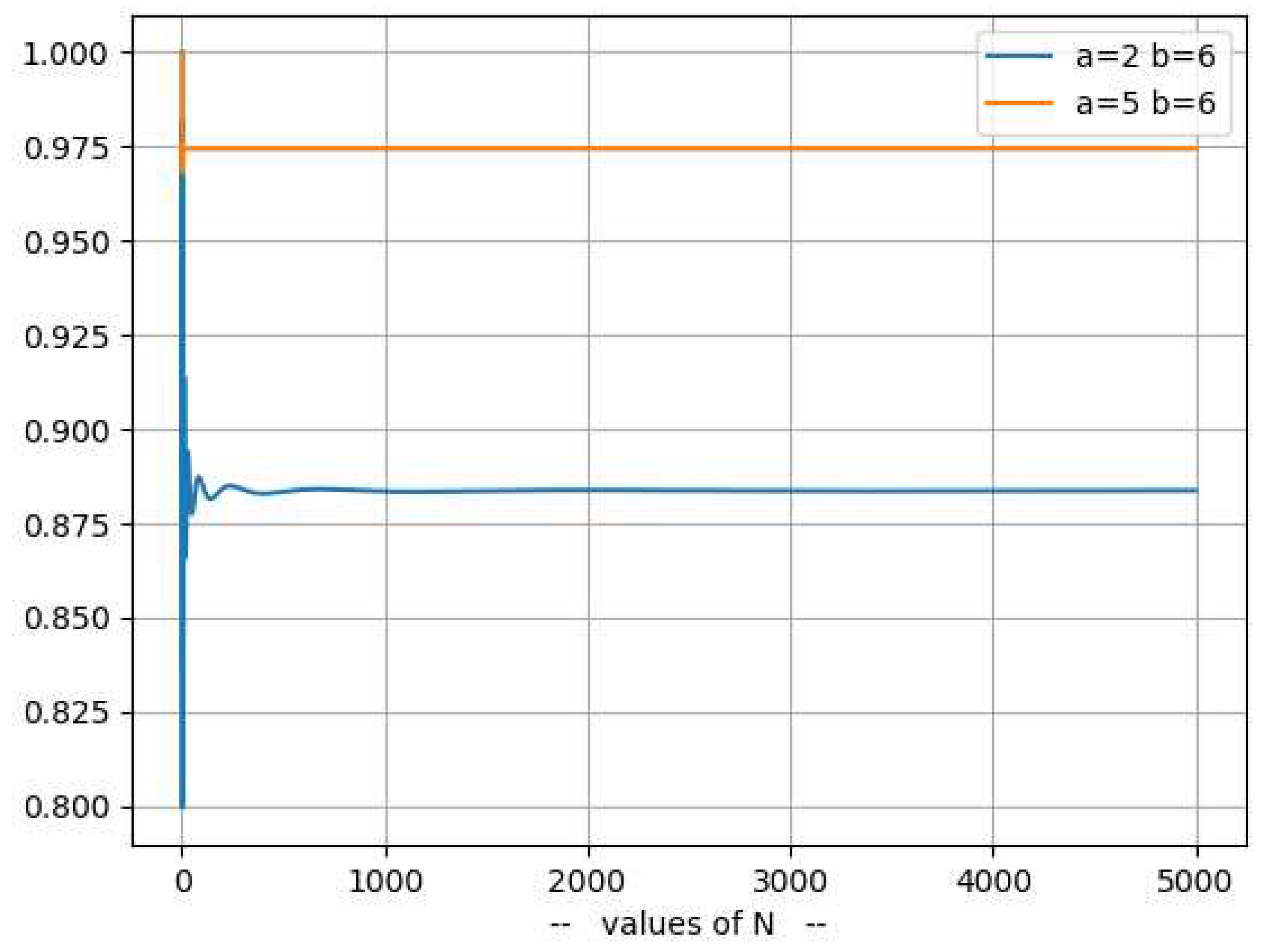
- is a wave that converges when and α>1 (Figure 17)
- -
- is a wave that does not converge when and α<1 (Figure 18)
- -
- is a wave that collapses to a line when and α=1/2 and ß=Im( ) (Figure 19) where z* is a nontrivial zero of RZF.
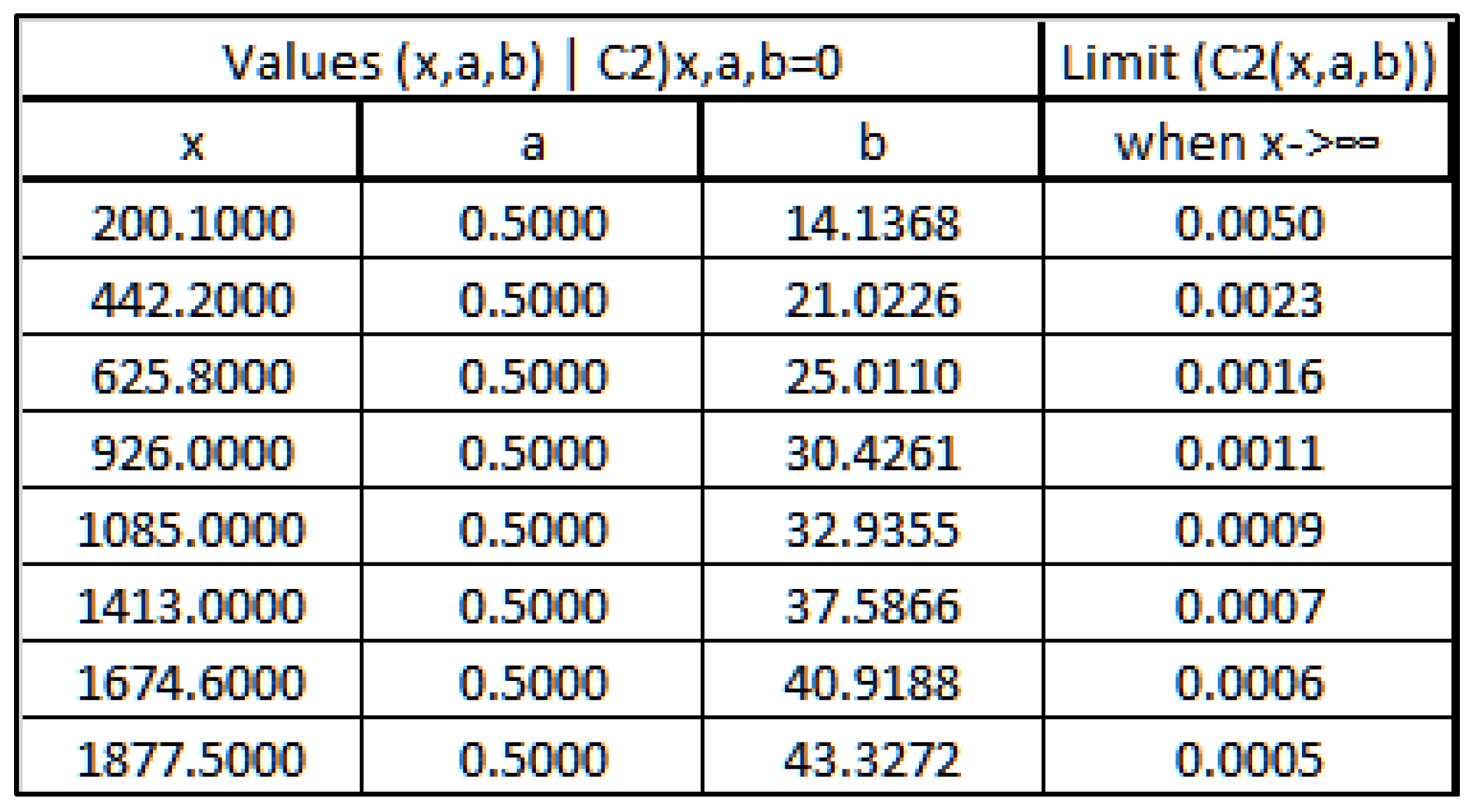
2.1. converges when and α>1 toThe limit of outside the critical strip [0,1] can be calculated using [16]:As one can see in some examples in the following table where z=α+iß:Table 7.α ß 1.0 7 1.074711506185445 1.074756 1.0 10 1.4413521753699579 1.441430 2.5 7 1.0093487944300192 1.009349 2.5 10 1.0507402208589398 1.050740 And also, in the following Figure 20:One can observe that the graphs for α=1 do not converge while graphs for α>1 they all converge.This observation can be used to prove that there are no zero values of ζ(z) for z with Re(z)>1.2.2. diverges when for α1diverges when for α<1 because of [16] and [17]:And:Therefore:2.3. does not collapse to any polynomial functionOne can prove it with a reduction to absurd.Let’s assume that where C and t integers C>0 and t>0But:And:So, must be 0 which is an absurd.2.4. collapses to a straight-lineThe proposition says that the following limit exists only for Re(z) = 1/2;Using the expression:2.4.1. For α>1/2, one can see that /= 0:= 0 because 2α>1 and the series is convergentSo:2.4.2. For α<1/2, one can see that/=as:And:Where the summations are replaced by the number of elements in the matrix (n x n) times the smallest value in each row (1/n) then 1>(2-1-2α)>0 when α<1/22.4.3. Limit for α=1/2.When α=1/2, one can express (/n) as:Using the integral approximation of the infinite seriesSo, if exists will be equal to:if z=1/2+ißAnd this limit can only exist when is monotonous which means that the curve will cross the x-axis only once.
- 3.
-
Calculating the zeros ofLet’s define the function in R (where z=a+bi) such that:With the following wave representation for :
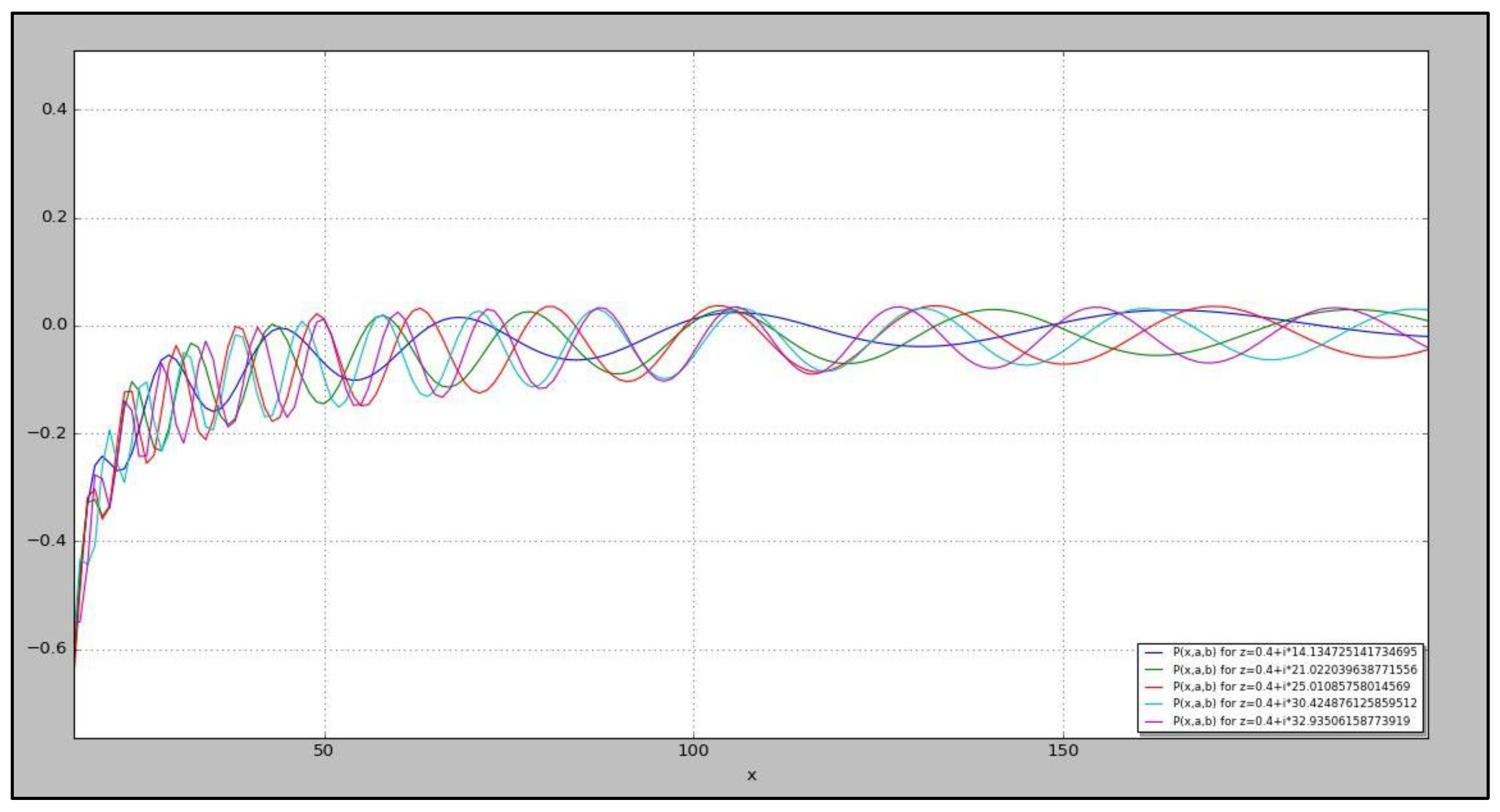
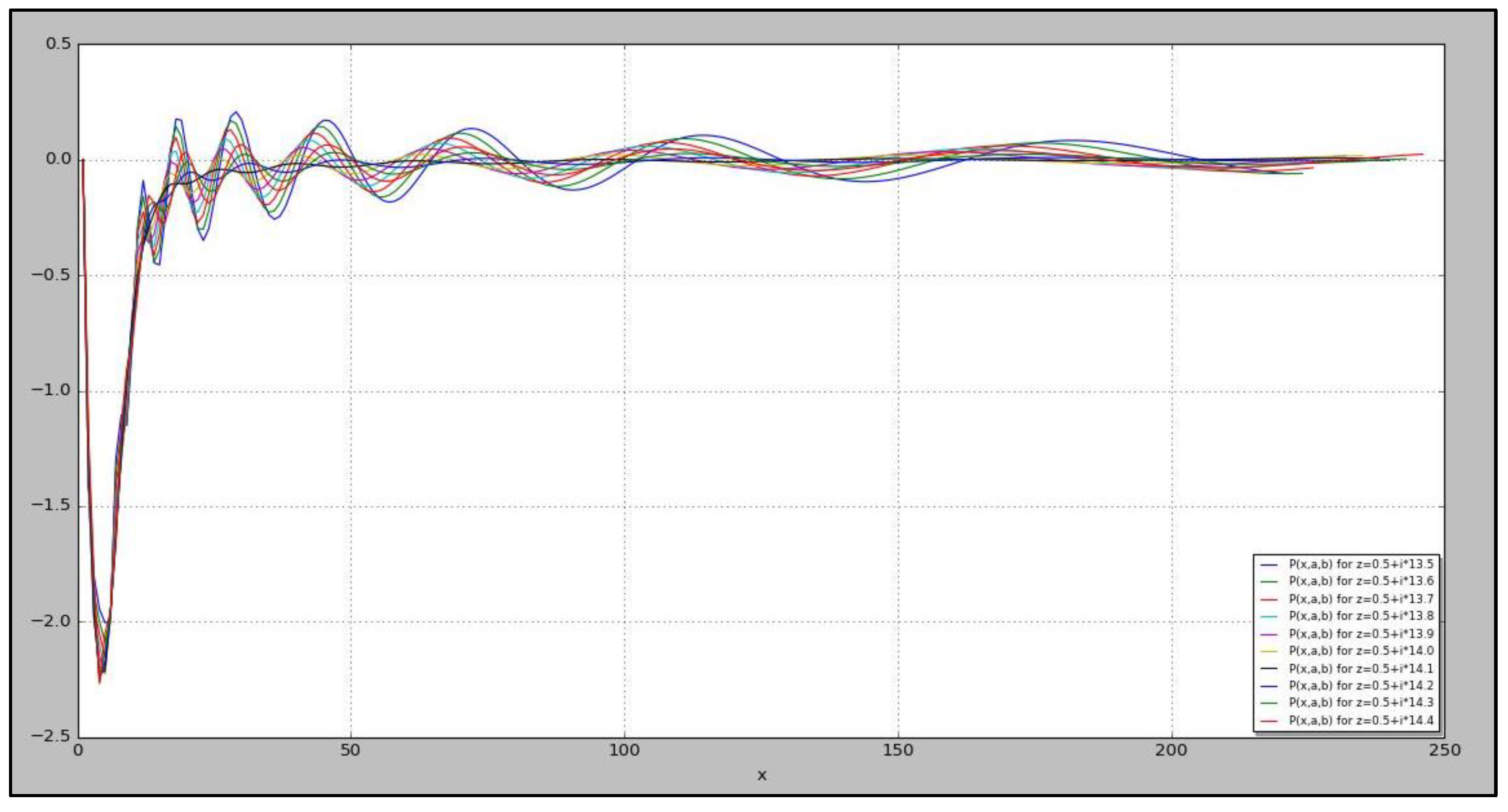
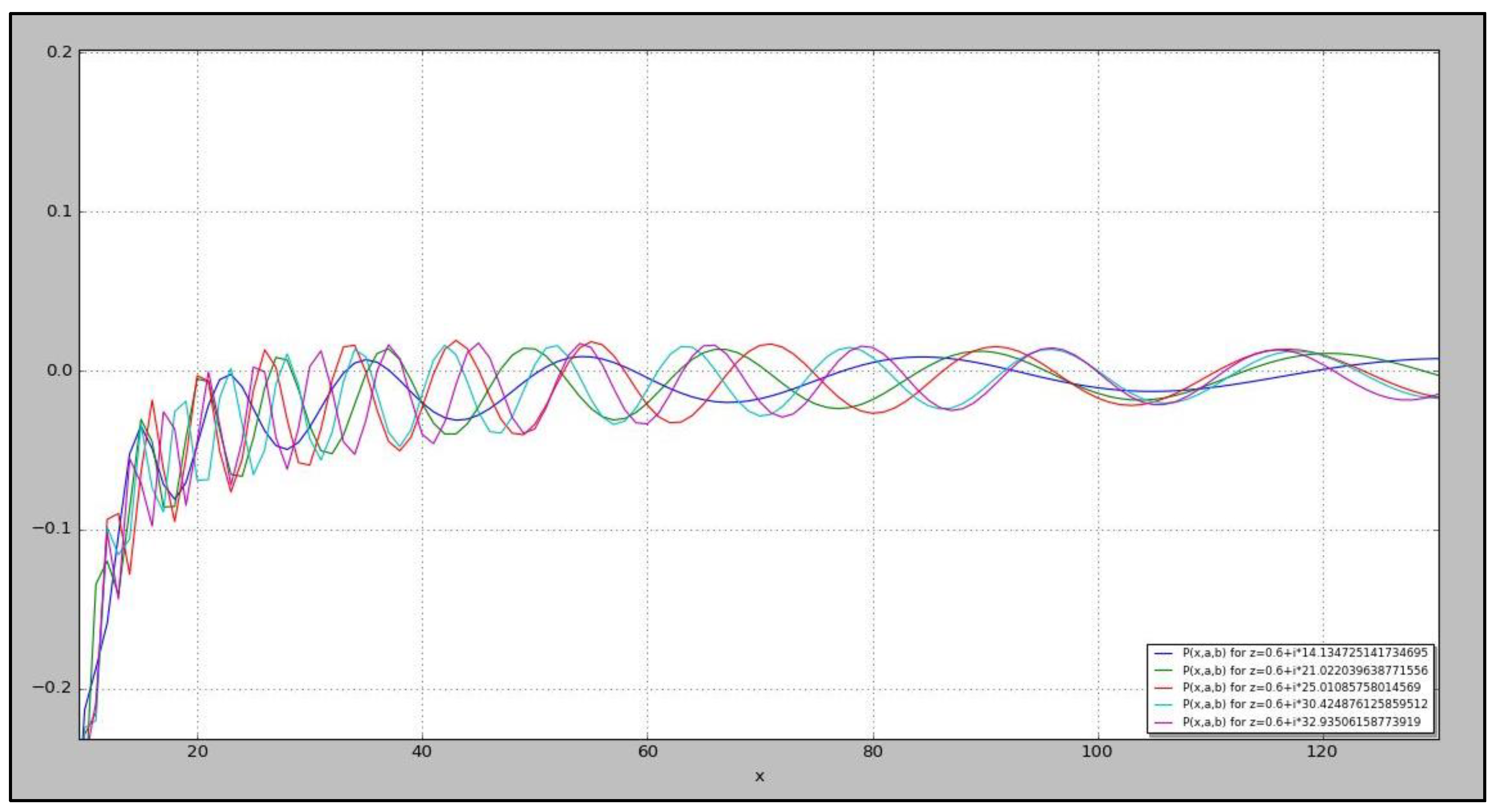
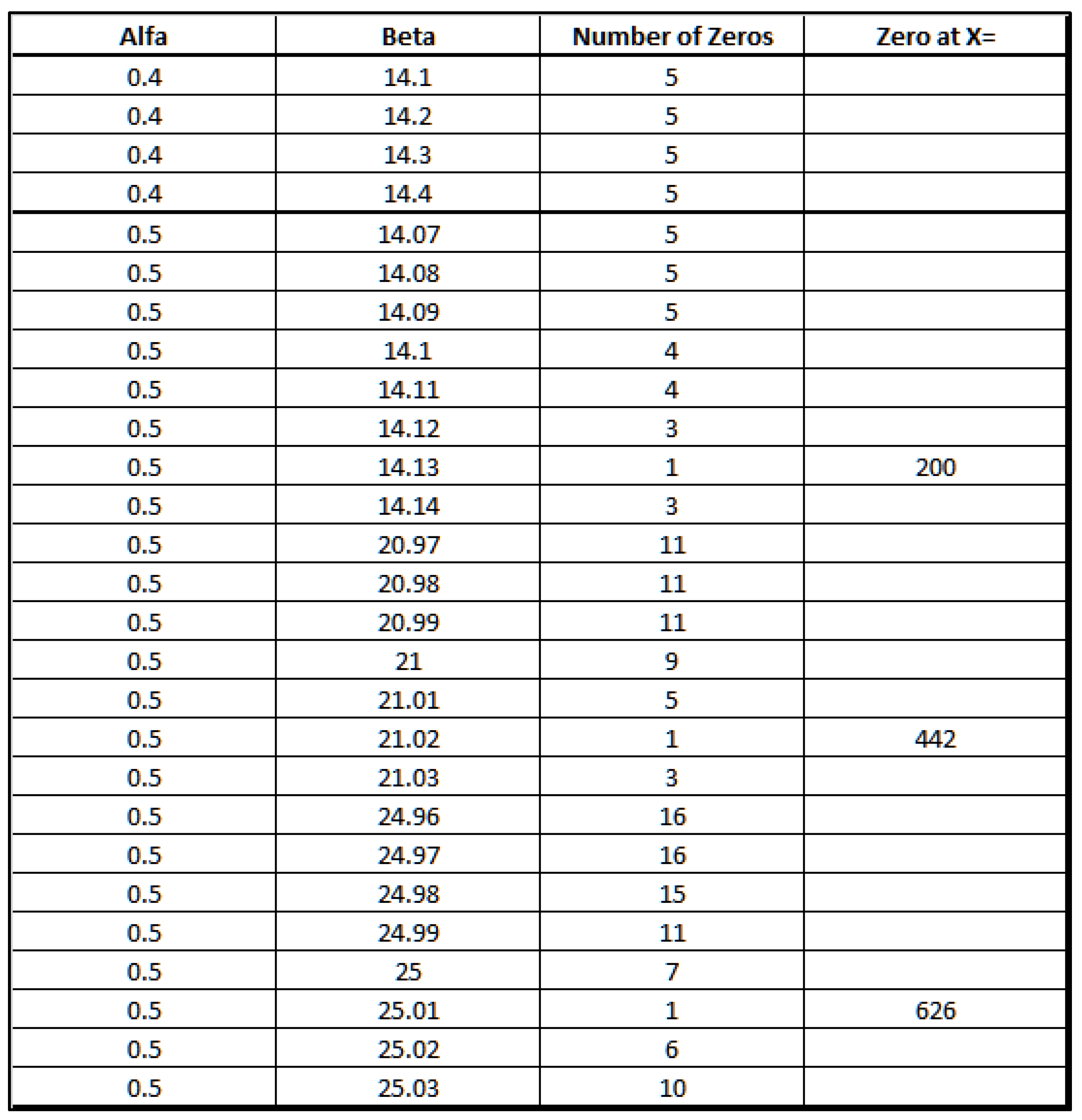
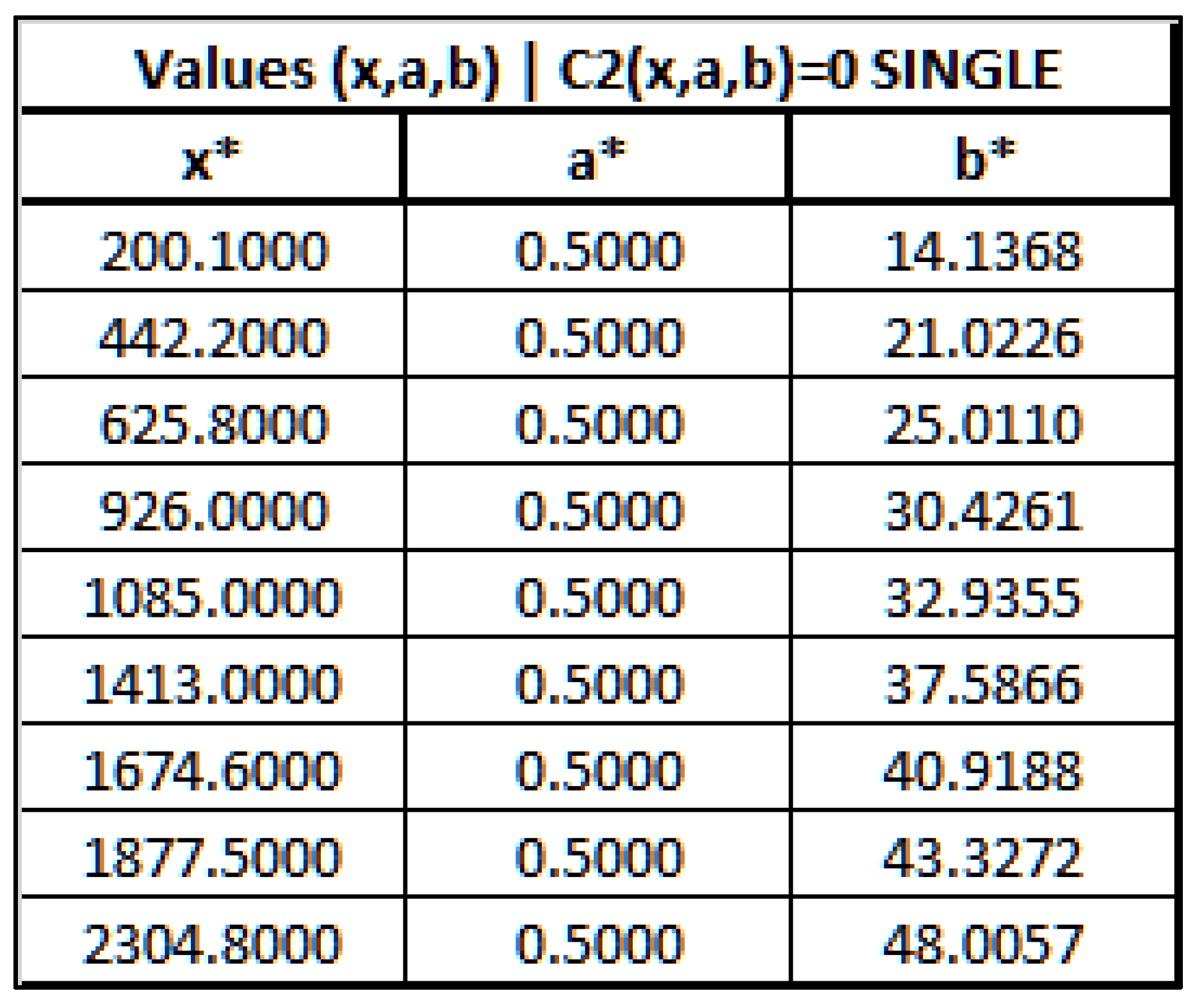
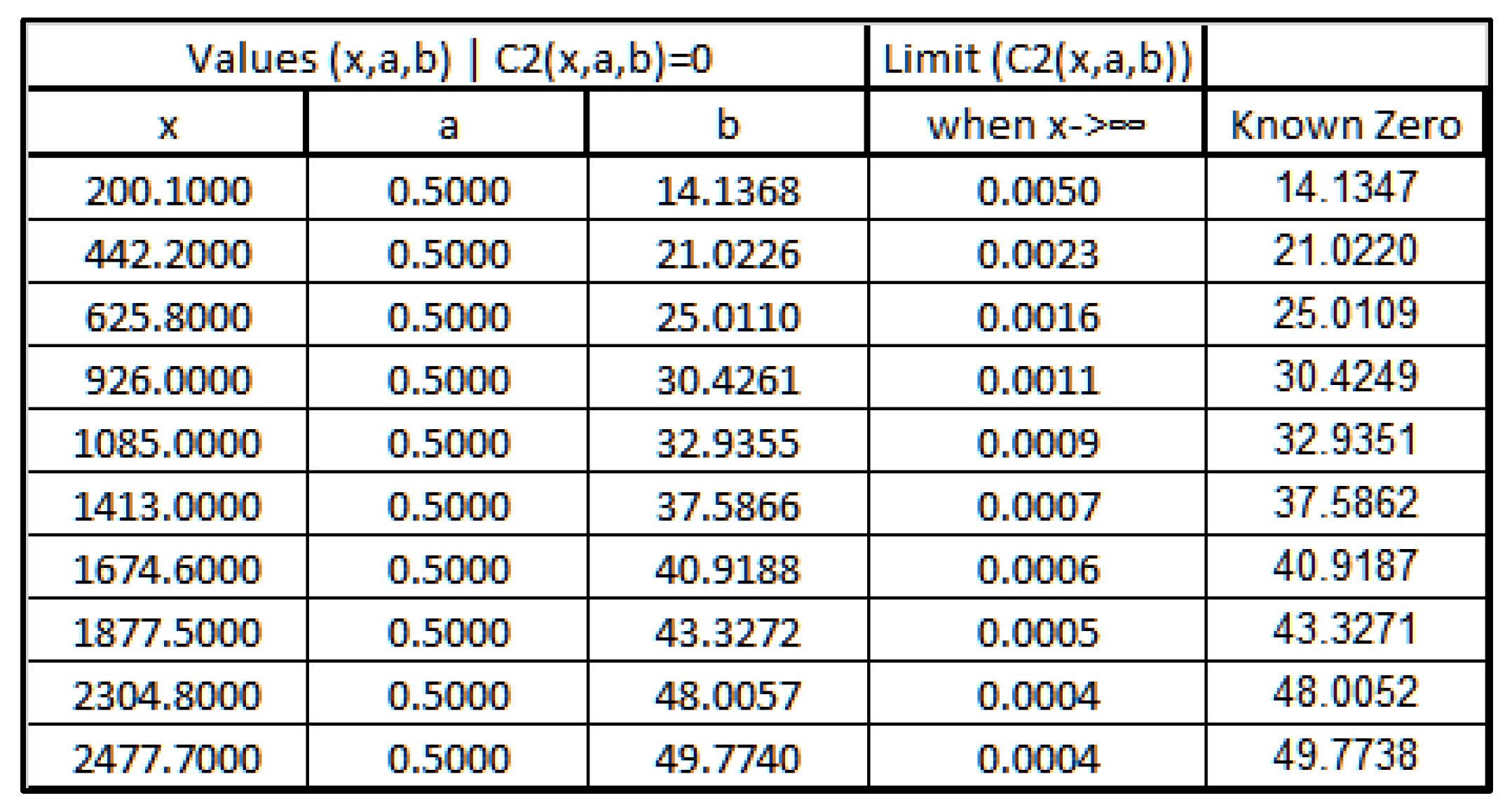
- 4.
-
Theorem: For Re(z)≥0, if z* is a nontrivial zero of ζ(z), then Re(z*)=1/2Proof:
- ⮚
- From [10], [11], [12]: ζ(z) = X(z) − Y(z) for Re(z)>0, z≠1
- ⮚
- From [13]: |Y(z, n)|2 is always a polynomial line.
- ⮚
- From [14]: |Y(z, n)|2 is only straight line if and only if Re(z)= ½
= tends to a straight line with slope- ⮚
- From [15]: |X(z, n)|2 is a wave function that has only one polynomial representation in the form of a straight line if and only if Re(z)= ½ [18] and for certain values of Im(z)=ß* calculated using [19]. These values of ß* coincide with the imaginary parts of the nontrivial zeros of Riemann Zeta z*, so:
= tends to a straight line with slopewhen Re(z)=1/2 and ß=NTZ of RZF- ⮚
- Therefore and only occur when Re(z*) = ½
- ⮚
- As ζ(z)=X(z)-Y(z), therefore all zeros of ζ(z) for z>=0, z≠1 have Re(z)=1/2. [QED]
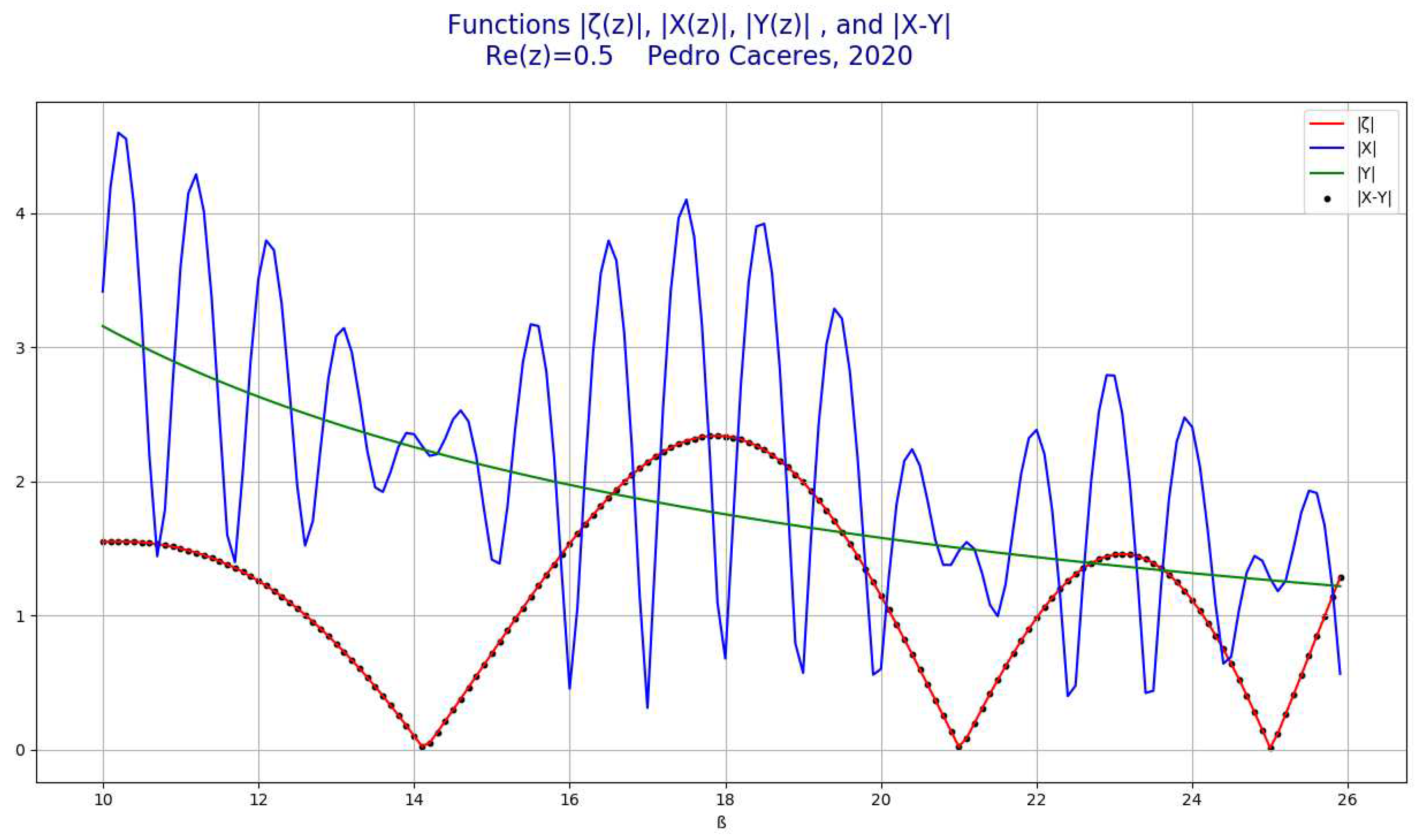
PART 5: On the distribution of the zeroes of the RZF in the critical line
- 1.
-
From [17] one can write:therefore, the limit ofFrom [18], if exists will be equal to:
- 2.
- Calculating the nontrivial zeros of ζ(z) using the Harmonic function
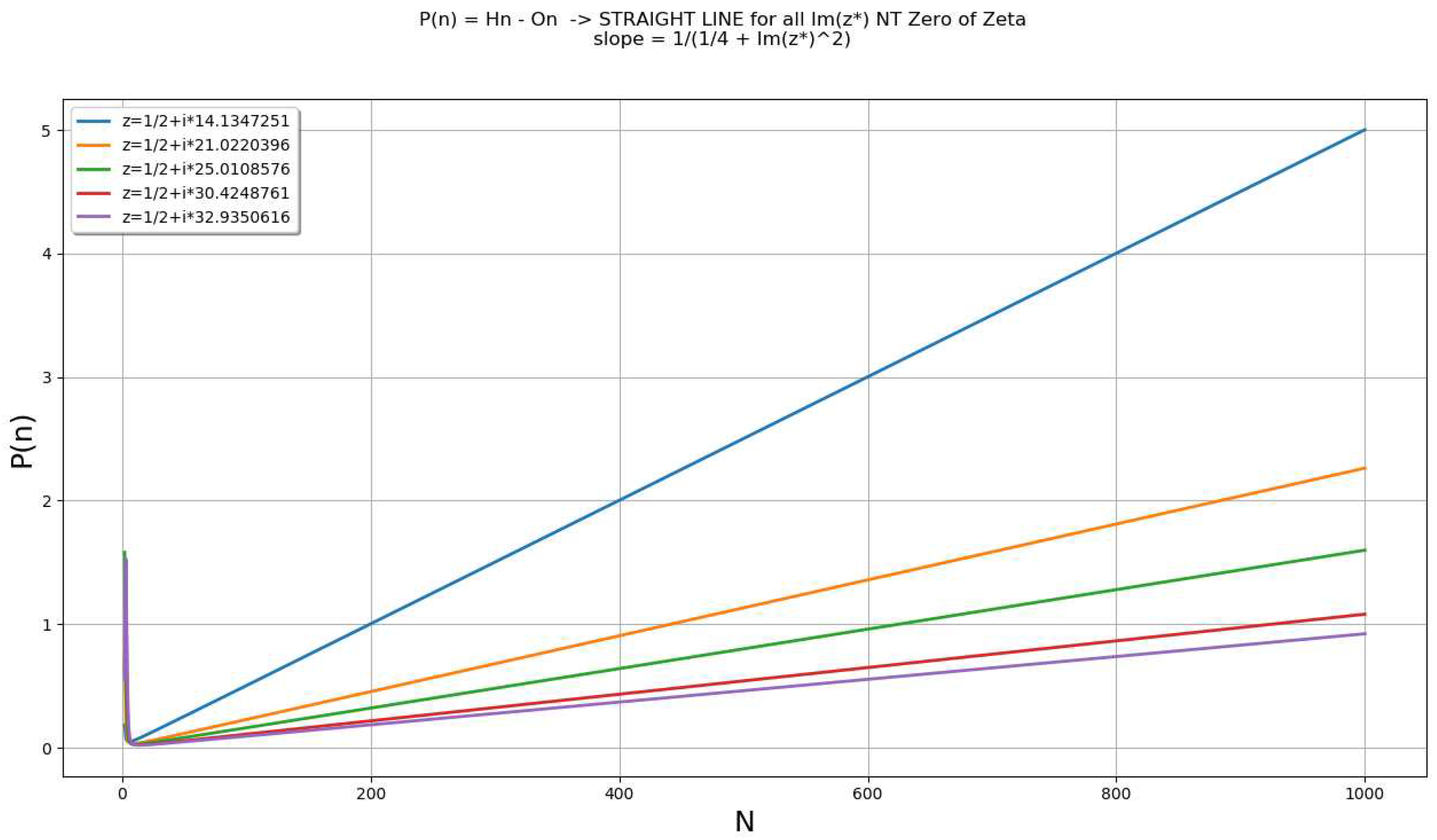
- ß(1) = 14.134725142
- ß(3) = 25.010857580
- ß(4) = 30.424876126
- ß(6) = 37.586178159
- ß(7) = 40.918719012
- ß(9) = 48.005150881
- ß(10) = 49.773832478
- ß(3) = 25.010857580
- ß(4) = 30.424876126
- 3.
- Conclusion
Nomenclature and conventions
- –
- ζ(z)= is the Riemann Zeta Function (RZF).
- –
- z* is any nontrivial zero (NTZ) of the RZF verifying that ζ(z*) = 0.
- –
- ß*(n) is the nth zero of the Riemann function in the critical line Re(z)=1/2 in C
- –
- α=Re(z) is the real part of z
- –
- ß=Im(z) is the imaginary part of z
- –
- If z=α+iß, Modulus(z)= and SquareAbsolute(z)
References
- B. Riemann, “Ueber die Anzahl der Primzahlen unter einer gegebenen Grӧsse”, Monat. der Kӧnigl. Preuss. Akad. der Wissen. zu Berlin aus der Jahre 1859 (1860), 671–680; also, Gesammelte math. Werke und wissensch. Nachlass, 2. Aufl. 1892, 145–155.
- Brent, R. P. ``On the Zeros of the Riemann Zeta Function in the Critical Strip.'' Math. Comput. 33, 1361-1372, 1979. [CrossRef]
- Edwards , Harold M. Riemann’s Zeta Function. 1974. Dover Publications.
- Encyclopedia Britannica, Editors, 2008, https://www.britannica.com/science/Riemann-zeta-function, accessed March 2018.
- Jekel, David. The Riemann Zeta Function. 1963. University of Washington. https://sites.math.washington.edu/~morrow/336_13/papers/david.pdf.
- Kopp, Konrad. “Theory and Application of Infinite Series.” Blackie & Son Limited, London, 1928.
- Odlyzko, A. “The 10^20 th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors.”.
- Python Software Foundation. Python Language Reference, version 3.7. Available at http://www.python.org.
- Sloane, N. J. A. Sequence A002432. An On-Line Version of the Encyclopedia of Integer Sequences. http://oeis.org/search?q=A002432&language=english&go=Search.
- Sondow, Jonathan and Weisstein, Eric W. "Riemann Zeta Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RiemannZetaFunction.html.
- Weisstein, Eric W. "Riemann Zeta Function Zeros." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/RiemannZetaFunctionZeros.html.
- Weisstein, Eric, 1999. “Riemann Zeta Function”, https://archive.lib.msu.edu/crcmath/math/math/r/r316.htm.
- Weisstein, Eric, 1999. “Riemann Hypothesis”, https://archive.lib.msu.edu/crcmath/math/math/r/r294.htm.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





